Экспоненциальный рост: определение, примеры, формула расчета
Что такое экспоненциальный рост?
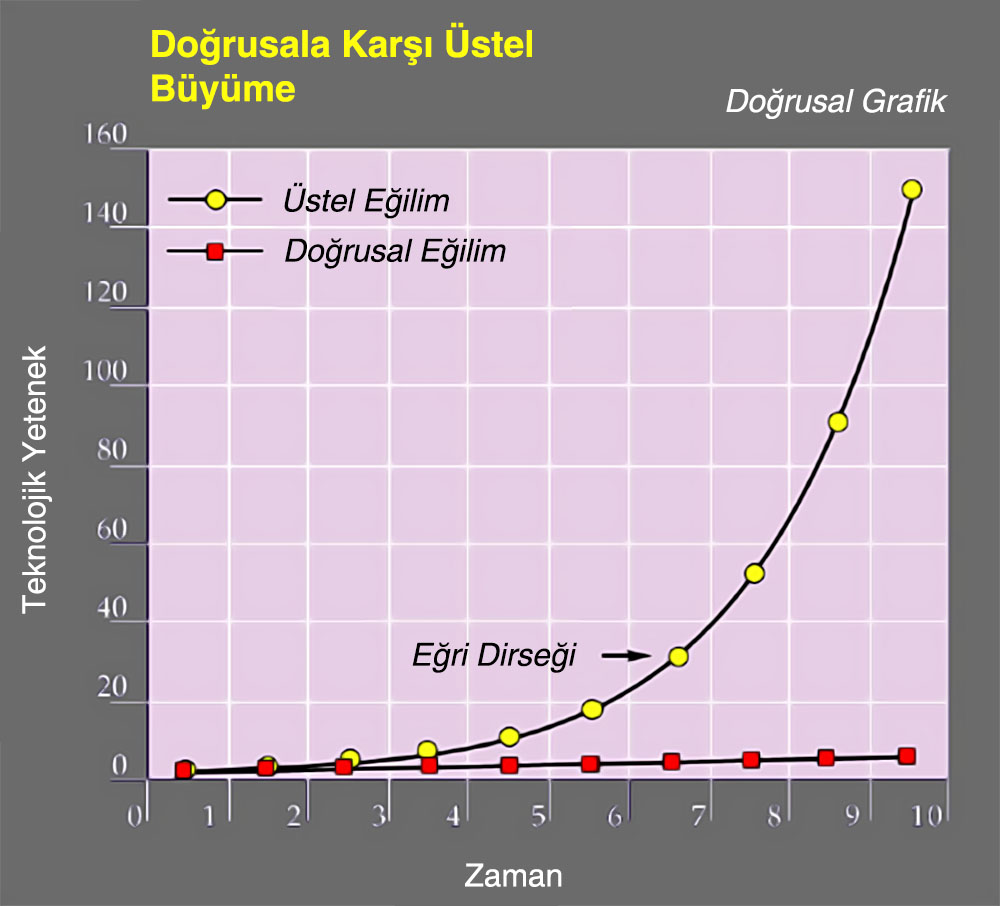
Экспоненциальный рост — это модель изменения данных, при которой величина растет с ускорением, то есть скорость роста увеличивается с течением времени. График экспоненциального роста имеет характерную форму кривой, круто уходящей вверх.
Ключевые особенности экспоненциального роста:
- Величина растет не на постоянную величину, а умножается на некоторый коэффициент на каждом шаге
- Скорость роста постоянно увеличивается
- За равные промежутки времени величина увеличивается в одно и то же число раз
- На графике видна характерная экспоненциальная кривая
Формула экспоненциального роста
Экспоненциальный рост описывается формулой:
y = a * b^x
Где:
- y — конечное значение величины
- a — начальное значение
- b — основание (коэффициент роста)
- x — количество периодов
Примеры экспоненциального роста
Экспоненциальный рост встречается во многих природных и экономических процессах:

- Рост популяции бактерий при делении клеток
- Распространение вирусных заболеваний
- Рост капитала при реинвестировании прибыли
- Инфляция при избыточной эмиссии денег
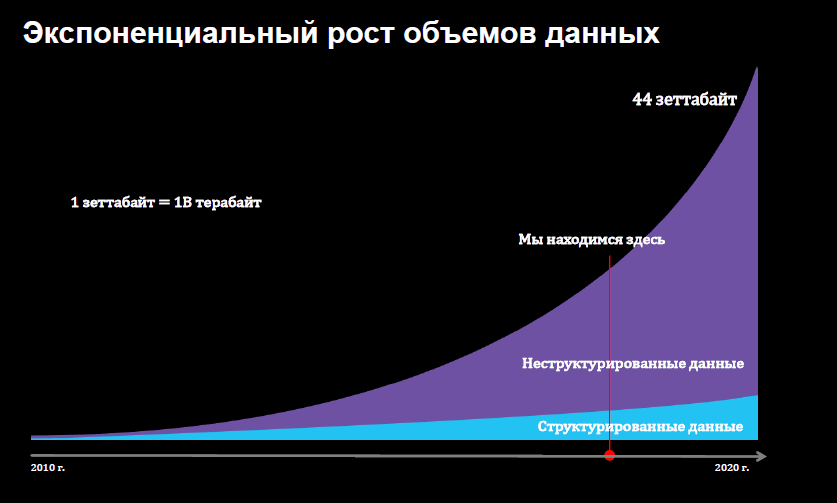
- Рост пользователей социальных сетей на начальном этапе
Отличия от других моделей роста
Чем экспоненциальный рост отличается от других моделей:
- Линейный рост — величина растет на постоянную величину
- Геометрический рост — величина умножается на постоянный коэффициент
- Экспоненциальный рост — коэффициент роста постоянно увеличивается
Применение экспоненциального роста в финансах
В финансовой сфере экспоненциальный рост проявляется в следующих процессах:
- Сложные проценты по вкладам и кредитам
- Рост капитала при реинвестировании дивидендов
- Увеличение стоимости активов в долгосрочной перспективе
- Рост доходов успешных компаний
Как рассчитать экспоненциальный рост?
Чтобы рассчитать экспоненциальный рост, нужно выполнить следующие шаги:
- Определить начальное значение величины
- Задать коэффициент роста (во сколько раз будет увеличиваться величина на каждом шаге)
- Выбрать количество периодов
- Подставить значения в формулу y = a * b^x
- Вычислить результат
Преимущества и недостатки экспоненциального роста
Экспоненциальный рост имеет свои плюсы и минусы:
Преимущества:
- Позволяет быстро достичь больших значений
- Дает существенное преимущество в долгосрочной перспективе
- Характерен для многих успешных бизнес-моделей
Недостатки:
- Неустойчив — небольшие изменения могут привести к резким колебаниям
- Может приводить к перегреву экономики и образованию пузырей
- Часто нереалистичен в долгосрочной перспективе из-за ограниченности ресурсов
Где применяется экспоненциальный рост?
Модель экспоненциального роста используется в различных областях:
- Биология — для описания роста популяций
- Экономика — при анализе инфляции, сложных процентов
- Физика — для описания цепных реакций
- Информатика — при оценке сложности алгоритмов
- Социология — для моделирования распространения информации
Экспоненциальный рост в природе
В природе экспоненциальный рост наблюдается во многих процессах:
- Размножение бактерий и одноклеточных организмов
- Рост популяций животных при благоприятных условиях
- Распространение инфекционных заболеваний
- Увеличение количества листьев на растениях
- Рост кристаллов при определенных условиях
Ограничения экспоненциального роста
Экспоненциальный рост не может продолжаться бесконечно. Основные ограничивающие факторы:
- Исчерпание доступных ресурсов
- Достижение предельной емкости среды
- Включение механизмов саморегуляции
- Внешние ограничивающие воздействия
Экспоненциальный рост в экономике
В экономике экспоненциальный рост проявляется в следующих процессах:
- Рост ВВП быстроразвивающихся стран
- Увеличение капитализации успешных компаний
- Рост числа пользователей новых технологий
- Гиперинфляция при кризисных явлениях
- Увеличение государственного долга некоторых стран
Заключение
Экспоненциальный рост — это мощная модель, позволяющая описать процессы быстрого увеличения различных величин. Понимание принципов экспоненциального роста важно для анализа многих явлений в природе, обществе и экономике. При этом нужно учитывать ограничения данной модели и не экстраполировать ее на длительные периоды без учета сдерживающих факторов.


