Изоморфны: ИЗОМОРФИЗМ — это… Что такое ИЗОМОРФИЗМ?
изоморфный — Викисловарь
Морфологические и синтаксические свойства[править]
| падеж | ед. ч. | мн. ч. | |||
|---|---|---|---|---|---|
| муж. р. | ср. р. | жен. р. | |||
| Им. | изомо́рфный | изомо́рфное | изомо́рфная | изомо́рфные | |
| Рд. | изомо́рфного | изомо́рфного | изомо́рфной | изомо́рфных | |
| Дт. | изомо́рфному | изомо́рфному | изомо́рфной | изомо́рфным | |
| одуш. | изомо́рфного | изомо́рфное | изомо́рфную | изомо́рфных | |
| неод. | изомо́рфный | изомо́рфные | |||
| Тв. | изомо́рфным | изомо́рфным | изомо́рфной изомо́рфною | изомо́рфными | |
| Пр. | изомо́рфном | изомо́рфном | изомо́рфной | изомо́рфных | |
| Кратк. форма | изомо́рфен | изомо́рфно | изомо́рфна | изомо́рфны | |
и·зо-мо́рф-ный
Прилагательное, относительное, тип склонения по классификации А. Зализняка — 1*a.
Корень: -изо-; корень: -морф-; суффикс: -н; окончание: -ый [Тихонов, 1996].
Произношение[править]
Семантические свойства[править]
Значение[править]
- сходный по форме и свойствам структуры ◆ Цикл развития изоморфный (более древний) или гетероморфный. Лукьянов В.А., Стифеев А.И., «Прикладные аспекты применения микроводорослей в агроценозе», 2014 г.
Синонимы[править]
Антонимы[править]
- антиизоморфный
Гиперонимы[править]
Гипонимы[править]
Родственные слова[править]
Этимология[править]
Происходит от ἴσος «равный, одинаковый, подобный», далее, предположительно, из праиндоевр. *aikʷ- «ровный» + μορφή «вид, наружность, форма», далее из неустановленной формы.
Фразеологизмы и устойчивые сочетания[править]
Перевод[править]
Библиография[править]
Изоморфизм — Википедия
|
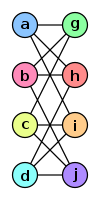
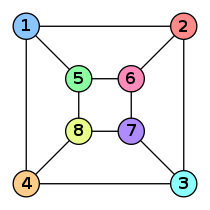
| Пример двух изоморфных графов. Изоморфизм ставит в соответствие вершинам одного графа вершины другого графа того же цвета: две вершины соединены ребром в одном графе тогда и только тогда, когда вершины тех же цветов соединены ребром в другом графе. |
Изоморфи́зм (от др.-греч. ἴσος — «равный, одинаковый, подобный» и μορφή — «форма») — это очень общее понятие, которое определяется по-разному в различных разделах математики. Изоморфизм определяется для множеств, наделённых некоторой структурой (например, для групп, колец, линейных пространств и т. п.). В общих чертах его можно описать так: обратимое отображение (биекция) между двумя множествами, наделёнными структурой, называется изоморфизмом, если оно сохраняет эту структуру. Если между такими структурами существует изоморфизм, то они называются изоморфными. Изоморфизм всегда задаёт отношение эквивалентности на классе таких структур.
Так, например, два графа называются изоморфными, если между ними существует изоморфизм: то есть вершинам одного графа можно сопоставить вершины другого графа, так чтобы соединённым вершинам первого графа соответствовали соединённые вершины второго графа и наоборот. Иными словами, два графа изоморфны, если они «одинаковы» (с точностью до переименования вершин).
В общем случае, объекты, между которыми существует изоморфизм, являются «одинаково устроенными» в смысле этой структуры.
Другим классическим примером изоморфных систем могут служить множество R {\displaystyle \mathbb {R} } всех вещественных чисел с определённой на нём операцией сложения и множество R + {\displaystyle \mathbb {R} _{+}} положительных вещественных чисел с заданной на нём операцией умножения. Отображение x ↦ exp ( x ) {\displaystyle x\mapsto \exp(x)} в этом случае является изоморфизмом.
Общая алгебра
В общей алгебре изоморфизмом называется обратимое отображение, которое является гомоморфизмом. Ниже приводятся несколько примеров.
Группы
Пусть G {\displaystyle G} и H {\displaystyle H} — две группы. Биекция f : G → H {\displaystyle f\colon G\to H} называется изоморфизмом, если для любых a , b ∈ G {\displaystyle a,\;b\in G}
- f ( a ) f ( b ) = f ( a b ) {\displaystyle f(a)f(b)=f(ab)} .
Если группа является топологической, добавляется условие гомеоморфности соответствующих топологических пространств.[1]
Поля
Пусть F 1 {\displaystyle F_{1}} и F 2 {\displaystyle F_{2}} — поля. Биекция f : F 1 → F 2 {\displaystyle f\colon F_{1}\to F_{2}} называется изоморфизмом, если она сохраняет обе операции поля, то есть для любых a , b ∈ F 1 {\displaystyle a,b\in F_{1}} выполняется
- f ( a ) + f ( b ) = f ( a + b ) {\displaystyle f(a)+f(b)=f(a+b)} ,
- f ( a ) ⋅ f ( b ) = f ( a ⋅ b ) {\displaystyle f(a)\cdot f(b)=f(a\cdot b)} .
Пример. Фактор-кольцо для кольца многочленов с вещественными коэффициентами R [ x ] {\displaystyle \mathbb {R} [x]} по модулю многочлена x 2 + 1 {\displaystyle x^{2}+1} является полем, изоморфным[2] полю комплексных чисел C : {\displaystyle \mathbb {C} :}
- R [ x ] / ( x 2 + 1 ) ⟶ ≅ C {\displaystyle \mathbb {R} [x]/(x^{2}+1)\ {\stackrel {\cong }{\longrightarrow }}\ \mathbb {C} }
Для полей с дополнительной структурой (упорядоченные, топологические поля и т. д.) может добавляться условие, что биекция сохраняет также эти дополнительные структуры.
Теория множеств
В теории множеств любая биекция является изоморфизмом.
К примеру, два частично упорядоченных множества изоморфны, если между ними есть биекция, сохраняющая порядок[3].
Изоморфизм в теории категорий
В теории категорий изоморфизм есть обратимый морфизм, то есть морфизм φ {\displaystyle \varphi } , для которого существует такой морфизм φ − 1 {\displaystyle \varphi ^{-1}} , что композиции φ − 1 ∘ φ {\displaystyle \varphi ^{-1}\circ \varphi } и φ ∘ φ − 1 {\displaystyle \varphi \circ \varphi ^{-1}} — тождественные морфизмы. Определения категории групп, категории колец, категории векторных пространств и других структур строятся таким образом, что классические определения изоморфизма групп, колец, векторных пространств совпадают с общим определением изоморфизма в категории.
Нормированные пространства
Для нормированных пространств отображение одного из них в другое называется изоморфизмом нормированных пространств, если оно линейно, непрерывно и биективно, и обратное отображение тоже непрерывно. В этом смысле изоморфизм сохраняет структуру линейного пространства и топологию, но не обязательно сохраняет норму. Если изоморфизм еще и сохраняет норму, то он называется изометрическим изоморфизмом или изометрией[4].
Граф G {\displaystyle G} называется изоморфным графу H {\displaystyle H} , если существует биекция f {\displaystyle f} из множества вершин графа G {\displaystyle G} в множество вершин графа H {\displaystyle H} , обладающая следующим свойством: если в графе G {\displaystyle G} есть ребро из вершины A {\displaystyle A} в вершину B {\displaystyle B} , то в графе H {\displaystyle H} должно быть ребро из вершины f ( A ) {\displaystyle f(A)} в вершину f ( B ) {\displaystyle f(B)} и наоборот — если в графе H {\displaystyle H} есть ребро из вершины A {\displaystyle A} в вершину B {\displaystyle B} , то в графе G {\displaystyle G} должно быть ребро из вершины f − 1 ( A ) {\displaystyle f^{-1}(A)} в вершину f − 1 ( B ) {\displaystyle f^{-1}(B)} . В случае ориентированного графа эта биекция также должна сохранять ориентацию ребра. В случае взвешенного графа биекция также должна сохранять вес ребра.
В теории вычислительной сложности до сих пор является открытым вопрос о сложности задачи изоморфности графов. На данный момент не доказана ни её принадлежность классу P {\displaystyle P} , ни её N P {\displaystyle NP} -полнота.
Связанные определения
Изоморфизм алгебраической системы на себя называется автоморфизмом.
История
Понятие изоморфизма возникло в математике применительно к группам и было естественным образом распространено на более широкий класс математических структур.
Вариации и обобщения
- Некоторая общая теория, уточняющая понятия изоморфизма (и других близких понятий) была предложена группой Бурбаки в их книге «Теория множеств» (Глава 4. Структуры).
См. также
Примечания
- ↑ Л. С. Понтрягин Непрерывные группы стр. 392
- ↑ Фаддеев Д. К. Лекции по алгебре. — М.: Наука, 1984. — С. 200—201. — 416 с.
- ↑ Верещагин Н. К., Шень А. Лекции по математической логике и теории алгоритмов. Часть 1. Начала теории множеств. стр. 48
- ↑ Петр Бородин, А. Савчук, И. Шейпак. Задачи по функциональному анализу. — МЦНМО, 2017. — С. 28. — 337 с. — ISBN 9785040485147.
Литература
Ссылки
Изоморфизм — Википедия с видео // WIKI 2
 
|
| Пример двух изоморфных графов. Изоморфизм ставит в соответствие вершинам одного графа вершины другого графа того же цвета: две вершины соединены ребром в одном графе тогда и только тогда, когда вершины тех же цветов соединены ребром в другом графе. |
Изоморфи́зм (от др.-греч. ἴσος — «равный, одинаковый, подобный» и μορφή — «форма») — это очень общее понятие, которое определяется по-разному в различных разделах математики. Изоморфизм определяется для множеств, наделённых некоторой структурой (например, для групп, колец, линейных пространств и т. п.). В общих чертах его можно описать так: обратимое отображение (биекция) между двумя множествами, наделёнными структурой, называется изоморфизмом, если оно сохраняет эту структуру. Если между такими структурами существует изоморфизм, то они называются изоморфными. Изоморфизм всегда задаёт отношение эквивалентности на классе таких структур.
Так, например, два графа называются изоморфными, если между ними существует изоморфизм: то есть вершинам одного графа можно сопоставить вершины другого графа, так чтобы соединённым вершинам первого графа соответствовали соединённые вершины второго графа и наоборот. Иными словами, два графа изоморфны, если они «одинаковы» (с точностью до переименования вершин).
В общем случае, объекты, между которыми существует изоморфизм, являются «одинаково устроенными» в смысле этой структуры.
Другим классическим примером изоморфных систем могут служить множество R {\displaystyle \mathbb {R} } всех вещественных чисел с определённой на нём операцией сложения и множество R + {\displaystyle \mathbb {R} _{+}} положительных вещественных чисел с заданной на нём операцией умножения. Отображение x ↦ exp ( x ) {\displaystyle x\mapsto \exp(x)} в этом случае является изоморфизмом.
Энциклопедичный YouTube
-
1/5
Просмотров:769
3 816
4 045
526
2 238
-
✪ Лекция 1 | Проблема изоморфизма графов | Илья Пономаренко | Лекториум
-
✪ С чего начать новую жизнь, или как выбрать правильное окружение || Лариса Парфентьева
-
✪ Теория сетей: 3. Основы теории графов
-
✪ Базис линейного пространства (01)
Содержание
Общая алгебра
В общей алгебре изоморфизмом называется обратимое отображение, которое является гомоморфизмом. Ниже приводятся несколько примеров.
Группы
Пусть G {\displaystyle G} и H {\displaystyle H} — две группы. Биекция f : G → H {\displaystyle f\colon G\to H} называется изоморфизмом, если для любых a , b ∈ G {\displaystyle a,\;b\in G}
- f ( a ) f ( b ) = f ( a b ) {\displaystyle f(a)f(b)=f(ab)} .
Если группа является топологической, добавляется условие гомеоморфности соответствующих топологических пространств.[1]
Поля
Пусть F 1 {\displaystyle F_{1}} и F 2 {\displaystyle F_{2}} — поля. Биекция f : F 1 → F 2 {\displaystyle f\colon F_{1}\to F_{2}} называется изоморфизмом, если она сохраняет обе операции поля, то есть для любых a , b ∈ F 1 {\displaystyle a,b\in F_{1}} выполняется
- f ( a ) + f ( b ) = f ( a + b ) {\displaystyle f(a)+f(b)=f(a+b)} ,
- f ( a ) ⋅ f ( b ) = f ( a ⋅ b ) {\displaystyle f(a)\cdot f(b)=f(a\cdot b)} .
Пример. Факторкольцо для кольца многочленов с вещественными коэффициентами R [ x ] {\displaystyle \mathbb {R} [x]} по модулю многочлена x 2 + 1 {\displaystyle x^{2}+1} является полем, изоморфным[2] полю комплексных чисел C : {\displaystyle \mathbb {C} :}
- R [ x ] / ( x 2 + 1 ) ⟶ ≅ C {\displaystyle \mathbb {R} [x]/(x^{2}+1)\ {\stackrel {\cong }{\longrightarrow }}\ \mathbb {C} }
Для полей с дополнительной структурой (упорядоченные, топологические поля и т. д.) может добавляться условие, что биекция сохраняет также эти дополнительные структуры.
Теория множеств
В теории множеств любая биекция является изоморфизмом.
К примеру, два частично упорядоченных множества изоморфны, если между ними есть биекция, сохраняющая порядок[3].
Изоморфизм в теории категорий
В теории категорий изоморфизм есть обратимый морфизм, то есть морфизм φ {\displaystyle \varphi } , для которого существует такой морфизм φ − 1 {\displaystyle \varphi ^{-1}} , что композиции φ − 1 ∘ φ {\displaystyle \varphi ^{-1}\circ \varphi } и φ ∘ φ − 1 {\displaystyle \varphi \circ \varphi ^{-1}} — тождественные морфизмы. Определения категории групп, категории колец, категории векторных пространств и других структур строятся таким образом, что классические определения изоморфизма групп, колец, векторных пространств совпадают с общим определением изоморфизма в категории.
Нормированные пространства
Для нормированных пространств отображение одного из них в другое называется изоморфизмом нормированных пространств, если оно линейно, непрерывно и биективно, и обратное отображение тоже непрерывно. В этом смысле изоморфизм сохраняет структуру линейного пространства и топологию, но не обязательно сохраняет норму. Если изоморфизм ещё и сохраняет норму, то он называется изометрическим изоморфизмом или изометрией[4].
Граф G {\displaystyle G} называется изоморфным графу H {\displaystyle H} , если существует биекция f {\displaystyle f} из множества вершин графа G {\displaystyle G} в множество вершин графа H {\displaystyle H} , обладающая следующим свойством: если в графе G {\displaystyle G} есть ребро из вершины A {\displaystyle A} в вершину B {\displaystyle B} , то в графе H {\displaystyle H} должно быть ребро из вершины f ( A ) {\displaystyle f(A)} в вершину f ( B ) {\displaystyle f(B)} и наоборот — если в графе H {\displaystyle H} есть ребро из вершины A {\displaystyle A} в вершину B {\displaystyle B} , то в графе G {\displaystyle G} должно быть ребро из вершины f − 1 ( A ) {\displaystyle f^{-1}(A)} в вершину f − 1 ( B ) {\displaystyle f^{-1}(B)} . В случае ориентированного графа эта биекция также должна сохранять ориентацию ребра. В случае взвешенного графа биекция также должна сохранять вес ребра.
В теории вычислительной сложности до сих пор является открытым вопрос о сложности задачи изоморфности графов. На данный момент не доказана ни её принадлежность классу P {\displaystyle P} , ни её N P {\displaystyle NP} -полнота.
Связанные определения
Изоморфизм алгебраической системы на себя называется автоморфизмом. Совокупность всех автоморфизмов некоторой алгебраической системы с операцией композиции и тождественным отображением в качестве нейтрального элемента образует группу. Группа автоморфизмов алгебраической системы K {\displaystyle K} обозначается Aut K {\displaystyle \operatorname {Aut} K} . Наиболее простой пример автоморфизма — это автоморфизм множества, то есть перестановка элементов этого множества.
Любой элемент g {\displaystyle g} группы определяет следующий автоморфизм, который называют внутренним автоморфизмом: каждому элементу группы x {\displaystyle x} ставится в соответствие сопряжённый ему элемент g x g − 1 {\displaystyle gxg^{-1}} :
- f ( x ) = g x g − 1 {\displaystyle f(x)=gxg^{-1}} .
История
Понятие изоморфизма возникло в математике применительно к группам и было естественным образом распространено на более широкий класс математических структур.
Вариации и обобщения
- Некоторая общая теория, уточняющая понятия изоморфизма (и других близких понятий) была предложена группой Бурбаки в их книге «Теория множеств» (Глава 4. Структуры).
Первая теорема об изоморфизме
Теоремы об изоморфизме
Теоремы об изоморфизме в алгебре — ряд теорем, связывающих понятия фактора, гомоморфизма и вложенного объекта. Утверждением теорем является изоморфизм некоторой пары групп, колец, модулей, линейных пространств, алгебр Ли или прочих алгебраических структур (в зависимости от области применения). Обычно насчитывают три теоремы об изоморфизме, называемые Первой (также основная теорема о гомоморфизме), Второй и Третьей. Хотя подобные теоремы достаточно легко следуют из определения фактора и честь их открытия никому особо не приписывается, считается, что наиболее общие формулировки дала Эмми Нётер.
См. также
Примечания
- ↑ Л. С. Понтрягин Непрерывные группы стр. 392
- ↑ Фаддеев Д. К. Лекции по алгебре. — М.: Наука, 1984. — С. 200—201. — 416 с.
- ↑ Верещагин Н. К., Шень А. Лекции по математической логике и теории алгоритмов. Часть 1. Начала теории множеств. стр. 48
- ↑ Петр Бородин, А. Савчук, И. Шейпак. Задачи по функциональному анализу. — МЦНМО, 2017. — С. 28. — 337 с. — ISBN 9785040485147.
Литература
Ссылки
 Эта страница в последний раз была отредактирована 15 февраля 2020 в 05:21.
Эта страница в последний раз была отредактирована 15 февраля 2020 в 05:21.
Изоморфизм — Википедия
 
|
| Пример двух изоморфных графов. Изоморфизм ставит в соответствие вершинам одного графа вершины другого графа того же цвета: две вершины соединены ребром в одном графе тогда и только тогда, когда вершины тех же цветов соединены ребром в другом графе. |
Изоморфи́зм (от др.-греч. ἴσος — «равный, одинаковый, подобный» и μορφή — «форма») — это очень общее понятие, которое определяется по-разному в различных разделах математики. Изоморфизм определяется для множеств, наделённых некоторой структурой (например, для групп, колец, линейных пространств и т. п.). В общих чертах его можно описать так: обратимое отображение (биекция) между двумя множествами, наделёнными структурой, называется изоморфизмом, если оно сохраняет эту структуру. Если между такими структурами существует изоморфизм, то они называются изоморфными. Изоморфизм всегда задаёт отношение эквивалентности на классе таких структур.
Так, например, два графа называются изоморфными, если между ними существует изоморфизм: то есть вершинам одного графа можно сопоставить вершины другого графа, так чтобы соединённым вершинам первого графа соответствовали соединённые вершины второго графа и наоборот. Иными словами, два графа изоморфны, если они «одинаковы» (с точностью до переименования вершин).
В общем случае, объекты, между которыми существует изоморфизм, являются «одинаково устроенными» в смысле этой структуры.
Другим классическим примером изоморфных систем могут служить множество R {\displaystyle \mathbb {R} } всех вещественных чисел с определённой на нём операцией сложения и множество R + {\displaystyle \mathbb {R} _{+}} положительных вещественных чисел с заданной на нём операцией умножения. Отображение x ↦ exp ( x ) {\displaystyle x\mapsto \exp(x)} в этом случае является изоморфизмом.
Общая алгебра
В общей алгебре изоморфизмом называется обратимое отображение, которое является гомоморфизмом. Ниже приводятся несколько примеров.
Группы
Пусть G {\displaystyle G} и H {\displaystyle H} — две группы. Биекция f : G → H {\displaystyle f\colon G\to H} называется изоморфизмом, если для любых a , b ∈ G {\displaystyle a,\;b\in G}
- f ( a ) f ( b ) = f ( a b ) {\displaystyle f(a)f(b)=f(ab)} .
Если группа является топологической, добавляется условие гомеоморфности соответствующих топологических пространств.[1]
Поля
Пусть F 1 {\displaystyle F_{1}} и F 2 {\displaystyle F_{2}} — поля. Биекция f : F 1 → F 2 {\displaystyle f\colon F_{1}\to F_{2}} называется изоморфизмом, если она сохраняет обе операции поля, то есть для любых a , b ∈ F 1 {\displaystyle a,b\in F_{1}} выполняется
- f ( a ) + f ( b ) = f ( a + b ) {\displaystyle f(a)+f(b)=f(a+b)} ,
- f ( a ) ⋅ f ( b ) = f ( a ⋅ b ) {\displaystyle f(a)\cdot f(b)=f(a\cdot b)} .
Пример. Фактор-кольцо для кольца многочленов с вещественными коэффициентами R [ x ] {\displaystyle \mathbb {R} [x]} по модулю многочлена x 2 + 1 {\displaystyle x^{2}+1} является полем, изоморфным[2] полю комплексных чисел C : {\displaystyle \mathbb {C} :}
- R [ x ] / ( x 2 + 1 ) ⟶ ≅ C {\displaystyle \mathbb {R} [x]/(x^{2}+1)\ {\stackrel {\cong }{\longrightarrow }}\ \mathbb {C} }
Для полей с дополнительной структурой (упорядоченные, топологические поля и т. д.) может добавляться условие, что биекция сохраняет также эти дополнительные структуры.
Теория множеств
В теории множеств любая биекция является изоморфизмом.
К примеру, два частично упорядоченных множества изоморфны, если между ними есть биекция, сохраняющая порядок[3].
Изоморфизм в теории категорий
В теории категорий изоморфизм есть обратимый морфизм, то есть морфизм φ {\displaystyle \varphi } , для которого существует такой морфизм φ − 1 {\displaystyle \varphi ^{-1}} , что композиции φ − 1 ∘ φ {\displaystyle \varphi ^{-1}\circ \varphi } и φ ∘ φ − 1 {\displaystyle \varphi \circ \varphi ^{-1}} — тождественные морфизмы. Определения категории групп, категории колец, категории векторных пространств и других структур строятся таким образом, что классические определения изоморфизма групп, колец, векторных пространств совпадают с общим определением изоморфизма в категории.
Нормированные пространства
Для нормированных пространств отображение одного из них в другое называется изоморфизмом нормированных пространств, если оно линейно, непрерывно и биективно, и обратное отображение тоже непрерывно. В этом смысле изоморфизм сохраняет структуру линейного пространства и топологию, но не обязательно сохраняет норму. Если изоморфизм еще и сохраняет норму, то он называется изометрическим изоморфизмом или изометрией[4].
Граф G {\displaystyle G} называется изоморфным графу H {\displaystyle H} , если существует биекция f {\displaystyle f} из множества вершин графа G {\displaystyle G} в множество вершин графа H {\displaystyle H} , обладающая следующим свойством: если в графе G {\displaystyle G} есть ребро из вершины A {\displaystyle A} в вершину B {\displaystyle B} , то в графе H {\displaystyle H} должно быть ребро из вершины f ( A ) {\displaystyle f(A)} в вершину f ( B ) {\displaystyle f(B)} и наоборот — если в графе H {\displaystyle H} есть ребро из вершины A {\displaystyle A} в вершину B {\displaystyle B} , то в графе G {\displaystyle G} должно быть ребро из вершины f − 1 ( A ) {\displaystyle f^{-1}(A)} в вершину f − 1 ( B ) {\displaystyle f^{-1}(B)} . В случае ориентированного графа эта биекция также должна сохранять ориентацию ребра. В случае взвешенного графа биекция также должна сохранять вес ребра.
В теории вычислительной сложности до сих пор является открытым вопрос о сложности задачи изоморфности графов. На данный момент не доказана ни её принадлежность классу P {\displaystyle P} , ни её N P {\displaystyle NP} -полнота.
Связанные определения
Изоморфизм алгебраической системы на себя называется автоморфизмом.
История
Понятие изоморфизма возникло в математике применительно к группам и было естественным образом распространено на более широкий класс математических структур.
Вариации и обобщения
- Некоторая общая теория, уточняющая понятия изоморфизма (и других близких понятий) была предложена группой Бурбаки в их книге «Теория множеств» (Глава 4. Структуры).
См. также
Примечания
- ↑ Л. С. Понтрягин Непрерывные группы стр. 392
- ↑ Фаддеев Д. К. Лекции по алгебре. — М.: Наука, 1984. — С. 200—201. — 416 с.
- ↑ Верещагин Н. К., Шень А. Лекции по математической логике и теории алгоритмов. Часть 1. Начала теории множеств. стр. 48
- ↑ Петр Бородин, А. Савчук, И. Шейпак. Задачи по функциональному анализу. — МЦНМО, 2017. — С. 28. — 337 с. — ISBN 9785040485147.
Литература
Ссылки
В психологии термин «И.» неразрывно связывается с классической берлинской школой гештальт-психологии. Теоретики гештальта использовали его для характеристики своего особого подхода к вопросу об отношении разума и мозга: они утверждали, что объективные мозговые процессы, к-рые лежат в основе конкретного феноменологического опыта и коррелируют с ним, изоморфны субъективному опыту (т. е. имеют функционально ту же форму и структуру).
Этимология слова И. делает его подходящим термином для такой теории. Греческий корень «изо-» означает «равный, одинаковый, подобный», а «морф-» значит «форма, конфигурация, организация или структура». Прибегнув к понятию И., гештальт-психологи хотели выразить идею, что гештальт-качества — форма, конфигурация, организация и структура — биофизических электрохимических процессов мозга, лежащих в основе субъективного когнитивного опыта, идентичны гештальт-качествам — форме, конфигурации, организации и структуре — самого опыта. Эта концепция резко контрастирует с относительно пассивными коннекционистскими теориями отношений между разумом и мозгом, преобладавшими в психологии 1-й половины XX в. и рассматривавшими мозг скорее как гигантский коммутатор с изолированными цепями из проводов и переключателей, чем как динамическую систему взаимозависимых электрохимических биолог. процессов, составляющих сложное поле взаимодействий.
Поскольку такая динамическая, интерактивно-полевая концепция функции и активности мозга радикально отличалась от значительно более статической и механистичной концепции мозга, безоговорочно принимавшейся на веру большинством живших и работавших в то время психологов, гештальтистская идея И. осталась практически непонятой. Теоретик гештальт-психологии Мэри Хенли писала: «Я не знаю второго такого понятия в психологии, к-рое было бы более превратно понято и более искажено, чем понятие И.».
Одна из причин подобного непонимания и искажения заключается в том, что этот термин, задолго до заимствования его гештальт-психологами, использовался в таких областях, как химия, кристаллография и математика, в значении, к-рое подразумевало ориентацию на части, совершенно чуждую концепции гештальта. В мат. теории множеств, напр., две группы элементов изоморфны, если существует взаимно однозначное соответствие между этими двумя множествами, т. е., если каждому элементу первого множества можно подобрать в пару один и только один элемент второго множества, и наоборот.
Такое взаимно однозначное соответствие между двумя изоморфными процессами или феноменами противоречит гештальтистскому подходу. Напр., две окружности, одна из к-рых образована 20 точками, а вторая — 22, с т. зр. гештальтистов изоморфны, ибо их функциональные формы идентичны: если точек достаточно для того, чтобы форма объекта была недвусмысленно обозначена и очевидна, то их абсолютное количество не имеет значения. Принципиальное значение имеет сама форма, конфигурация или структура, а не количество элементов, к-рым случилось образовать ее «части». Думать об абсолютном совпадении количества точек на окружностях двух кругов — значит думать не о целом, а о частях, и игнорировать динамические характеристики непрерывности траектории окружности круга, равную удаленности каждой части окружности от ее центра и т. д., к-рые и образуют эссенциальный гештальт или конфигурацию круга. Два круга — независимо от количества составляющих их «элементов», их цвета или размера — изоморфны просто потому, что оба являются кругами (т. е. оба имеют одинаковую, круглую форму). Точно так же изоморфны и два квадрата, даже если они образованы разными «элементами», по-разному окрашены или освещены или отличаются своей площадью. Более того, хотя при переходе из одной тональности в другую состав нот, характерный для данной мелодии, изменяется, их порядок в одной тональности изоморфен их порядку в др. тональности, и мы слышим ту же, прежнюю мелодию; вариации на эту музыкальную тему остаются изоморфными до тех пор, пока сама мелодия остается узнаваемой (несмотря на то, что число нот в одной вариации может значительно превышать их число в другой).
Первое упоминание о мозговых процессах, изоморфных — в гештальтистском смысле — перцептивным процессам, появляется в опубликованной в 1912 г. статье Макса Вертгеймера о кажущемся движении, к-рая, как принято считать, положила начало школе гештальта. Это упоминание касается процессов в головном мозге, предположительно соответствующих одной из разновидностей фи-феномена, или восприятию движения при фактическом отсутствии движения физ. раздражителя. Представим себе, к примеру, две короткие вертикальные линии, x и у, длиной примерно по дюйму, расстояние между к-рыми равно тоже примерно 1 дюйму. Если испытуемому предъявить на неск. секунд линию x, затем убрать ее и букв. через долю секунды предъявить линию у, ему может показаться, что он видел не две разные линии, предъявленные последовательно, а одну линию, к-рая переместилась с одного места на другое (с места х на место y). Продолжив эту процедуру т. о., что спустя очень короткий промежуток времени после исчезновения линии х вновь предъявить линию у, а затем быстро снова заменить ее линией х и т. д., поддерживая на приемлемом уровне соотношение между расстоянием, разделяющим две линии, и межстимульным интервалом, испытуемому будет казаться, что он видит одну линию, непрерывно перемещающуюся взад-вперед. Если межстимульный интервал слишком велик, испытуемый воспринимает две стационарные линии, расположенные на расстоянии друг от друга и предъявляемые ему поочередно; если межстимульный интервал слишком короток (или если в какой-то момент предъявляются сразу две линии), испытуемый воспринимает две стационарные линии, предъявляемые в двух разных местах.
Что происходит в головном мозге при условии (как в выше описанном эксперименте), что испытуемый видит единственную перемещающуюся линию? Как утверждал Вертгеймер, фактически любая теория отношения между разумом и мозгом признает, что при этом должно иметь место возбуждение определенных участков зрительной коры: один очаг возбуждения соответствует линии х, а другой, по соседству, — линии у. Однако дальнейшие рассуждения Вертгеймера расходятся со всеми др. теориями отношения разума и мозга: при восприятии движения линий между участком мозга, соответствующим линии x, и прилегающим к нему участком мозга, соответствующим линии у, должно происходить что-то вроде короткого замыкания; это короткое замыкание является мозговым процессом, изоморфным субъективному опыту (experience) одной перемещающейся линии. Гештальт-качества процесса, протекающего в мозге, должны каким-то образом соответствовать гештальт-качествам видения одной перемещающейся линии, а не двух отдельных, неподвижно закрепленных линий.
Вертгеймер лишь заложил теорет. основы концепции, к-рая впоследствии была детально разработана его коллегами — гештальт-психологами Куртом Коффкой и Вольфгангом Кёлером (в ходе широких исслед. поведения животных и экспериментов в области восприятия). Исходя из данной теории, Кёлер и его коллеги сделали неск. довольно неожиданных предсказаний и сумели экспериментально их подтвердить. Целая монография была посвящена тому, что Кёлер и Ганс Валлах называли фигуративными послеэффектами, т. е. совокупности воспринимаемых искажений фигур, порождаемых предшествующим длительным рассматриванием других фигур.
Предположим, к примеру, что воспринимаемое расстояние между двумя точками в зрительном поле, x и у, изоморфно электрическому сопротивлению между их соотв. локализациями в зрительной коре — X и Y. Если это сопротивление повышается, то мозговые процессы X и Y функционально удаляются друг от друга, и воспринимаемое расстояние между соотв. точками в зрительном поле, х и у, должно увеличиться. Если функциональное расстояние (т. е. электрическое сопротивление) между двумя мозговыми процессами X и Y становится меньше, то воспринимаемое расстояние между их данными в опыте (experienced) изоморфными эквивалентами — точками х и у — должно тж уменьшиться.
Теперь представим себе, что мы нашли способ изменять электрическое сопротивление между двумя точками зрительной коры. Результатом такого изменения должно стать и соотв. изменение изоморфного зрительного опыта. Известно, что любой процесс возбуждения, продолжающийся какое-то время в нервной ткани, обычно порождает процесс, к-рый тормозит продолжение этого процесса возбуждения; любое продолжительное возбуждение порождает свое собственное торможение. Согласно теории И., это торможение представляет собой насыщение (сатиацию), или повышение электрического сопротивления. Следовательно, одним из способов увеличения электрического сопротивления между двумя точками зрительной коры является ее возбуждение с помощью подходящего визуального раздражителя. Если участок мозга, соотв. пространству между двумя точками в зрительном поле, стимулируется какое-то время визуально предъявленной фигурой, находящейся в этом пространстве, должно возрасти насыщение, или сопротивление, этого участка, и — как следствие этого — две точки зрительного тюля будут восприниматься как более удаленные друг от друга. Кёлер и Валлах провели множество экспериментов для проверки этого предсказания, и такие перцептивные искажения действительно получили в них подтверждение.
Теория И. породила огромное количество экспериментов, к-рые стали предметом широкого обсуждения в середине XX в. В начале 50-х гг. два выдающихся представителя нейронауки, Карл Лешли и Роджер Сперри, пытаясь развенчать эту теорию, поставили ряд радикальных экспериментов на животных. Они изменяли электрические свойства зрительной коры кошек и обезьян, надрезая мозг и вводя изолирующий материал в разрезы или помещая золотую фольгу либо танталовую проволоку (обладающие повышенной электропроводимостью) непосредственно на поверхность зрительной коры животного или в нее. Ученые считали, что если теория И. Кёлера верна, то подобное вторжение в электрохимию и биофизику мозга должно сильнейшим образом повлиять на способность животных к зрительному различению объектов, приобретенную ими ранее в результате соотв. научения. Однако ничего подобного не произошло: какими бы глубокими ни были изменения зрительной коры животных, последние различали зрительные раздражители точно так же, как делали это до хирургического вмешательства.
Отвечая на критику Лешли и Сперри и отмечая нек-рые технические недостатки их экспериментов, Кёлер утверждал, что локальные изменения электрических характеристик прооперированного мозга должны почти мгновенно перераспределять и реорганизовывать его полевые свойства, так что никаких нарушений в исполнении, направляемом зрительной системой, быть не должно. Ни Лешли, ни Сперри не смогли опровергнуть подобную аргументацию, однако Карл Прибрам, еще один выдающийся нейропсихолог, провел в конце 50-х цикл исслед., к-рые можно назвать продолжением экспериментов Лешли и Сперри. Он изменял электрическую активность зрительной коры низших обезьян, раздражая ее пастой гидроокиси алюминия. Как и в опытах Лешли — Сперри, это воздействие на мозг обезьян не сказалось отрицательно на сохранении ранее приобретенных ими навыков зрительной дискриминации; к тому же, целью экспериментов Прибрама было не опровержение утверждения Кёлера о том, что естественные физические полевые процессы мгновенно перераспределяют изменение нервной ткани, вызванное локальным раздражением.
В 60-е и в 70-е гг. интерес к гештальтистской гипотезе И. пошел на спад, а в 80-е она уже редко упоминалась в книгах, посвященных восприятию и проблемам физиолог. психологии. На рубеже 80-х и 90-х гг. представления о функциях мозга, разделявшиеся большинством нейроанатомов, нейрофизиологов и нейропсихологов, уже не оставляли места для процессов, к-рые были бы динамичными и взаимодействующими, носили бы полевой и системно-ориентированный характер, как это предполагала гештальтистская теория И.
См. также Головной мозг, Черепные нервы, Восприятие формы/очертаний, Гештальт-психология, Иллюзии, Представления, Вопрос об отношении души и тела, Молярные/молекулярные конструкты, Перцептивная организация, Исследование расщепленного мозга, Зрительные представления
М. Вертгеймер
.
изоморфизм — Викисловарь
Морфологические и синтаксические свойства[править]
| падеж | ед. ч. | мн. ч. |
|---|---|---|
| Им. | изоморфи́зм | изоморфи́змы |
| Р. | изоморфи́зма | изоморфи́змов |
| Д. | изоморфи́зму | изоморфи́змам |
| В. | изоморфи́зм | изоморфи́змы |
| Тв. | изоморфи́змом | изоморфи́змами |
| Пр. | изоморфи́зме | изоморфи́змах |
и·зо-мор-фи́зм
Существительное, неодушевлённое, мужской род, 2-е склонение (тип склонения 1a по классификации А. А. Зализняка).
Корень: -изо-; корень: -морф-; суффикс: -изм [Тихонов, 1996].
Произношение[править]
- МФА: [ɪzəmɐrˈfʲizm]
Семантические свойства[править]
Значение[править]
- матем. соответствие (отношение) между объектами, выражающее тождество их структуры (строения) ◆ Отсутствует пример употребления (см. рекомендации).
- хим. свойство веществ, аналогичных по химическому составу, кристаллизоваться в одинаковых формах ◆ Отсутствует пример употребления (см. рекомендации).
- лингв. параллелизм в организации звуковой и смысловой сторон языка ◆ Отсутствует пример употребления (см. рекомендации).
Синонимы[править]
- изоморфия
Антонимы[править]
- алломорфизм
Гиперонимы[править]
Гипонимы[править]
- автоморфизм
Родственные слова[править]
Этимология[править]
Происходит от ἴσος «равный, одинаковый, подобный», далее, предположительно, из праиндоевр. *aikʷ- «ровный» + μορφή «вид, наружность, форма», далее из неустановленной формы.
Фразеологизмы и устойчивые сочетания[править]
Перевод[править]
Библиография[править]
Морфологические и синтаксические свойства[править]
изоморфизм
Существительное.
Корень: —.
Произношение[править]
Семантические свойства[править]
Значение[править]
- хим. изоморфизм ◆ Отсутствует пример употребления (см. рекомендации).
Синонимы[править]
Антонимы[править]
Гиперонимы[править]
Гипонимы[править]
Родственные слова[править]
| Ближайшее родство | |
Этимология[править]
От ??
Фразеологизмы и устойчивые сочетания[править]
Библиография[править]
Морфологические и синтаксические свойства[править]
изоморфизм
Существительное.
Корень: —.
Произношение[править]
Семантические свойства[править]
Значение[править]
- хим. изоморфизм ◆ Отсутствует пример употребления (см. рекомендации).
Синонимы[править]
Антонимы[править]
Гиперонимы[править]
Гипонимы[править]
Родственные слова[править]
| Ближайшее родство | |
Этимология[править]
От ??
Фразеологизмы и устойчивые сочетания[править]
Библиография[править]
Морфологические и синтаксические свойства[править]
изоморфизм
Существительное.
Корень: —.
Произношение[править]
Семантические свойства[править]
Значение[править]
- хим. изоморфизм ◆ Отсутствует пример употребления (см. рекомендации).
Синонимы[править]
Антонимы[править]
Гиперонимы[править]
Гипонимы[править]
Родственные слова[править]
| Ближайшее родство | |
Этимология[править]
От ??
Фразеологизмы и устойчивые сочетания[править]
Библиография[править]
Морфологические и синтаксические свойства[править]
изоморфизм
Существительное.
Корень: —.
Произношение[править]
Семантические свойства[править]
Значение[править]
- хим. изоморфизм ◆ Отсутствует пример употребления (см. рекомендации).
Синонимы[править]
Антонимы[править]
Гиперонимы[править]
Гипонимы[править]
Родственные слова[править]
| Ближайшее родство | |
Этимология[править]
От ??
Фразеологизмы и устойчивые сочетания[править]
Библиография[править]
изоморфный — Толковый словарь Ефремовой
изоморфный
I прил.
1. Соотносящийся по знач. с сущ. изоморфизм I, связанный с ним.
2. Свойственный изоморфизму изоморфизм I, характерный для него.
II прил.
1. Соотносящийся по знач. с сущ. изоморфизм II, связанный с ним.
2. Сходный по форме и свойствам кристаллов.
Источник: Современный толковый словарь русского языка на Gufo.me
Значения в других словарях
- изоморфный — ИЗОМ’ОРФНЫЙ, изоморфная, изоморфное (минер.). Сходный по форме и свойствам кристаллов, обладающий изоморфизмом. Известковый шпат и доломит являются изоморфными телами. Толковый словарь Ушакова
- изоморфный — орф. изоморфный; кр. ф. -фен, -фна Орфографический словарь Лопатина
- изоморфный — изоморфный кр. ф. -фен, -фна, -фно Орфографический словарь. Одно Н или два?
- изоморфный — -ая, -ое. хим. Отличающийся сходным строением кристаллов, обладающий изоморфизмом. Малый академический словарь
- изоморфный — Изоморфный, изоморфная, изоморфное, изоморфные, изоморфного, изоморфной, изоморфного, изоморфных, изоморфному, изоморфной, изоморфному, изоморфным, изоморфный, изоморфную, изоморфное, изоморфные, изоморфного, изоморфную, изоморфное, изоморфных… Грамматический словарь Зализняка
- изоморфный — ИЗОМОРФНЫЙ -ая, -ое. Хим. Сходный по форме и свойствам кристаллов. Известковый шпат и доломит изоморфны. И-ые вещества. Толковый словарь Кузнецова
- изоморфный — [изо… + гр. форма] – сходный по форме Большой словарь иностранных слов
- изоморфный — Изо/мо́рф/н/ый. Морфемно-орфографический словарь
- изоморфный — прил., кол-во синонимов: 2 изоструктурный 1 сходный 32 Словарь синонимов русского языка

изоморфно — это … Что такое изоморфно?
изоморфный — Великобритания США / ˈaɪsəmɔːfɪk / прилагательное [перед существительным] ► то же или похожее по структуре или форме: изоморфное расположение / давление / сила »Аутсорсинг может создать изоморфное давление на другие фирмы, которые могут захотеть, чтобы их воспринимали как подкованных и конкурентоспособные… Финансовые и деловые условия
Изоморфный — я так * морфический, а. 1. Изоморфный. [1913 Webster] 2. (Biol.) Похожий по форме; проявляющий изоморфизм.[Webster 1913 Suppl.] 3. Из или относящихся к множествам, связанным изоморфизмом. [PJC]… Совместный международный словарь английского языка
изоморфный — 1862, из ISO (ср. Iso) + Gk. morphe (см. MORPHEUS (ср. Morpheus))… Этимологический словарь
изоморфный — ► ПРИЛОЖЕНИЕ ▪ соответствующий по форме и отношениям. ПРОИЗВОДНЫЕ изоморфизм существительное изоморфное прилагательное… словарь английских терминов
изоморфный — [΄΄sō môr’fəs, ī΄sə môr’fəsī΄sō môr’fik, İ΄səmôr’fik] прил.1. имеющие сходную или идентичную структуру или форму 2. Биол. Химреагент показывающий изоморфизм: также изоморфный [ī΄sō môr′fəs, ī΄sə môr′fəs]… Английский словарь мира
изоморфный — прилагательное Дата: 1862 1. a. быть идентичной или похожей по форме, форме или структуре b. имеющие спорофитные и гаметофитные поколения, одинаковые по размеру и форме 2. связанные изоморфизмом •… Новый университетский словарь
изоморфный — Одна система изоморфна другой, если существует одно-одно представление или отображение ее свойств, связывающее их со свойствами другой системы.Сказать, что между двумя системами существует изоморфизм, значит сказать, что они…… философский словарь
изоморфный — прил. [Gr. изос, равный; морф, форма] похожий или идентичный по внешности; изоморфными; см. анизоморфный… Словарь зоологии беспозвоночных
изоморфный — / uy seuh mawr fik /, прил. 1. Биол. отличается по происхождению, но имеет одинаковую форму или внешний вид. 2. Хим., Кристалл. изоморфными. 3. Математика относится к двум множествам, связанным изоморфизмом.[1860 65; ISO + MORPHIC] * * *… Universalium
изоморфный — прилагательное / ˌaɪsəˈmɔɹfɪk / a) имеющее структуру, подобную чему-то, что не связано генетически b) связано изоморфизмом… Викисловарь
изоморфный — SYN: изоморфный. * * * iso · mor · phic .ī sə mȯr fik adj, идентичной или похожей по форме или форме или структуре * * * iso · mor · phic (i ″ so morґfik) изоморфный… Медицинский словарь
изоморфный — Викисловарь
Английский [править]
Этимология [править]
Из изо- + -морфический .
Произношение [редактировать]
Прилагательное [править]
изоморфный ( не сопоставим )
- (математика), связанные изоморфизмом; имея однозначное соответствие, сохраняющее структуру.
- 2003 , Бернд Зигфрид Вальтер Шредер, стр. 254
- Пусть A, B — упорядоченные множества на рисунке 10.3. Пусть C — прямое произведение бесконечного числа копий двухэлементной цепочки 2 . Тогда A C является изоморфным для B C , но A не изоморфно B .
- 2003 , Бернд Зигфрид Вальтер Шредер, стр. 254
- (биология) Имея структуру или функцию, аналогичную чему-то, что не связано генетически или посредством эволюции.
- 1993 , Маркус Якобсон, Основы нейронауки , стр. 106
- Тот факт, что различные структуры могут быть показаны функционально изоморфными , подразумевает, что они аналогичны, а не гомологичны.
- 1993 , Маркус Якобсон, Основы нейронауки , стр. 106
- Имеет идентичную соответствующую структуру; сохраняя структуру, подвергаясь определенным обратимым преобразованиям.
- 1981 , Джон Лайонс, Язык и лингвистика: Введение , стр. 60
- Например, поскольку письменный и разговорный английский являются изоморфными (то есть имеют одинаковую структуру), они являются одним и тем же языком: нет ничего, кроме их структуры, которая у них общая.
- 1981 , Джон Лайонс, Язык и лингвистика: Введение , стр. 60
Примечания по использованию [править]
- В математике это прилагательное может использоваться в таких выражениях, как «A и B изоморфны», «A изоморфна B» и, реже, «A изоморфна B».
Антонимов [править]
Координатные термины [править]
Производные термины [править]
Связанные термины [править]
Переводы [править]
(, биология ), имеющая сходную структуру или функцию без генетического родства
с идентичной соответствующей структурой


