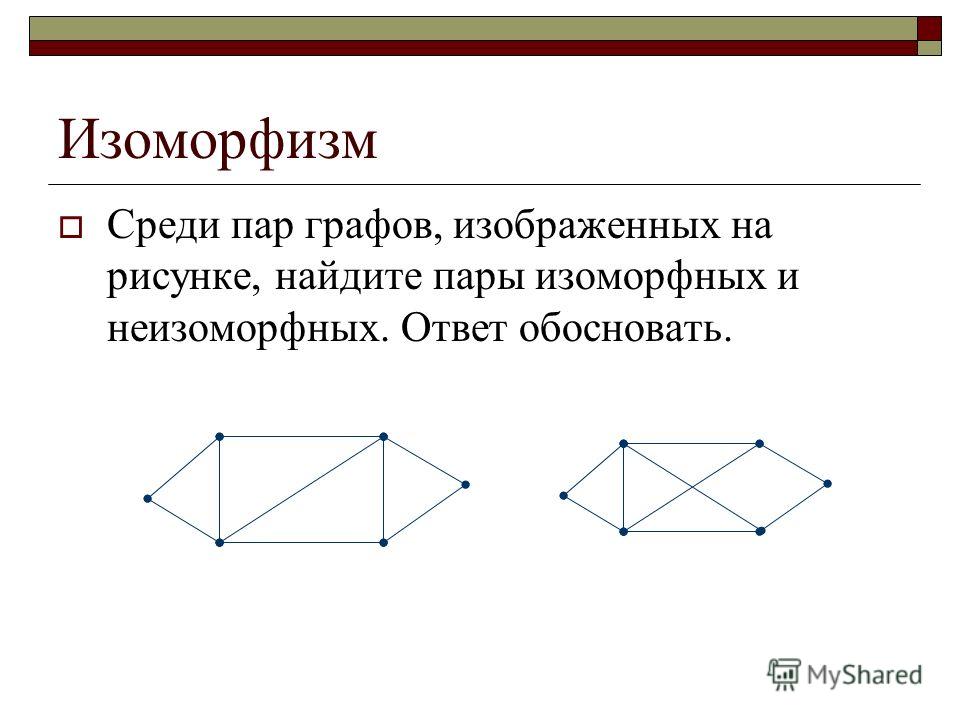
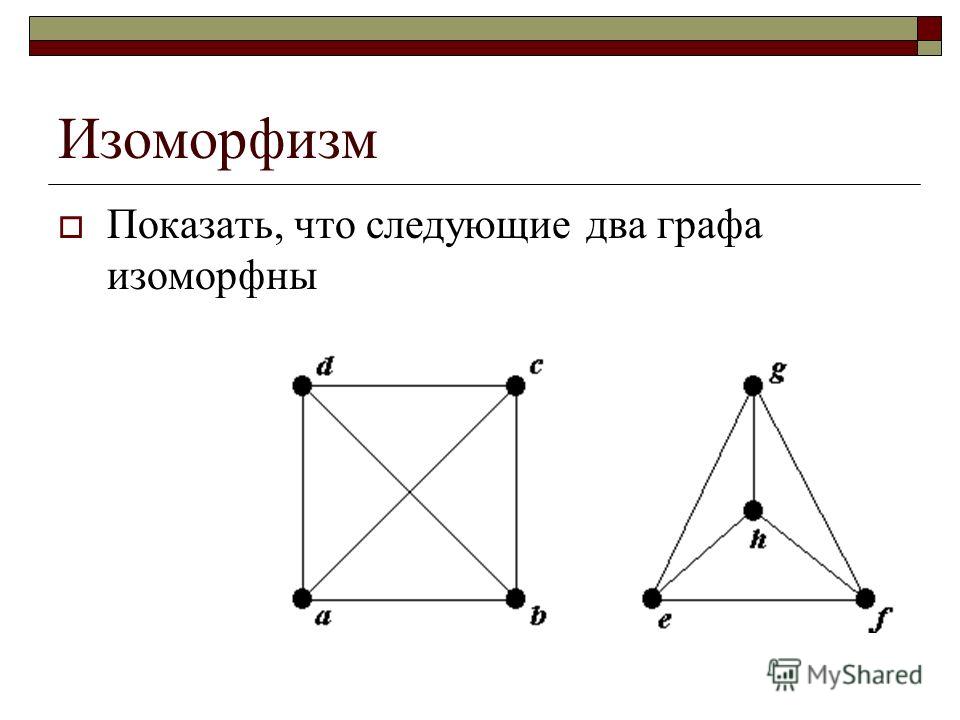
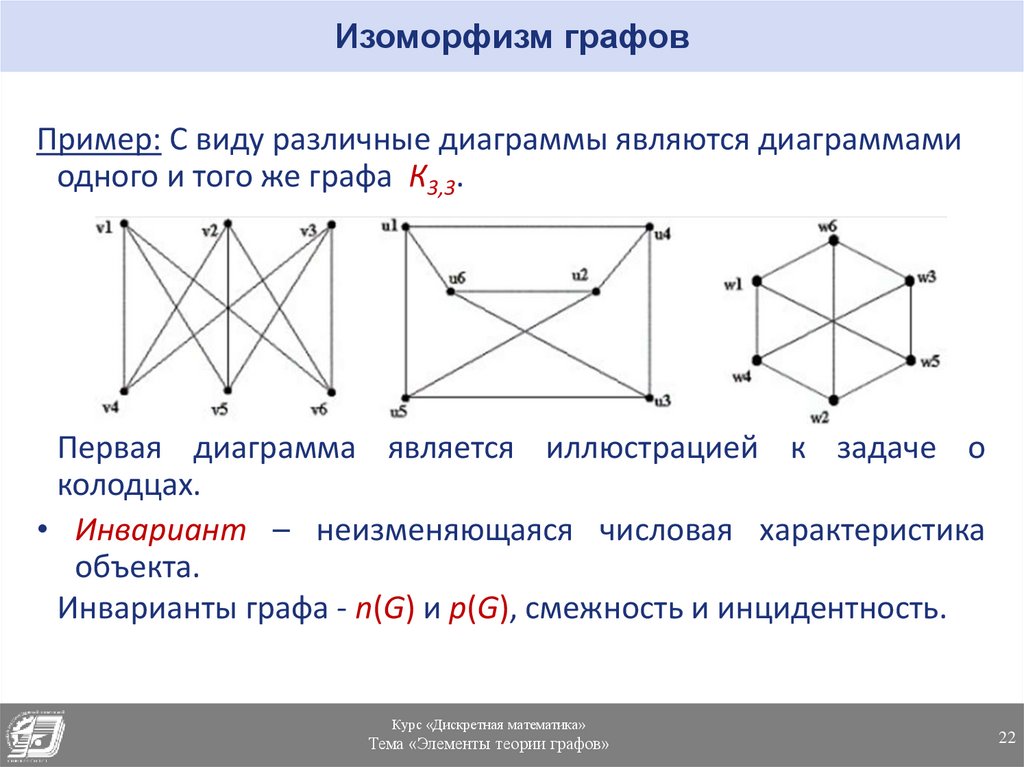
Изоморфный это: Изоморфный | это… Что такое Изоморфный?
Что значит изоморфный — Значения слов
Словарь медицинских терминов
Толковый словарь русского языка. Д.Н. Ушаков
изоморфный
изоморфная, изоморфное (мин.). Сходный по форме и свойствам кристаллов, обладающий изоморфизмом. Известковый шпат и доломит являются изоморфными телами.
Новый толково-словообразовательный словарь русского языка, Т. Ф. Ефремова.
изоморфный
прил. Сходный в организации звуковой и смысловой сторон языка.
прил. Сходный по форме и свойствам кристаллов.

Энциклопедический словарь, 1998 г.
Примеры употребления слова изоморфный в литературе.
И все утро говорил, только не замечал этого — смотри-ка, до изоморфного СП добрался!
Это созвездие субмодальностей, будучи прослежено во времени, приведет к изоморфным опытам с похожими эмоциональноповеденческими последовательностями, и в конечном счете этот процесс вызывает более законченную репрезентацию первоначального опыта.
Заметьте, что для извлечения первоначального опыта требуются репрезентации и последовательности только значимых событий в изоморфном опыте.
Полный набор трансформаций может представлять нечто, подобное следующему: Поскольку изоморфная трансформация в нашем примере касалась только взаимоотношений, а не контекста, то относительно природы контекста или идентичности персонажей не может быть никаких ограничений.
Подобное требование означает: что является значимым для метафоры, то и является изоморфной репрезентацией отношений и процессов, обнаруженных в проблеме.
НГ — оказывались вместе О — они Н — извлекали выгоду Н — времени НГ — радовать Данная метафора является адекватной изоморфной репрезентацией проблемы Сэмюэля, а также содержит способы ее разрешения.
Большая часть данной киши посвящена тому, чтобы обеспечить вас необходимыми навыками для гарантированной изоморфной репрезентации ваших метафор на уровнях их оперирования.
А вспомните, что весь дух современной науки запрещает нам постулировать СП, изоморфное с Землей, Николай.
Мы уже отмечали в начале брошюры, что простран-ство в кинематографе, как и во всяком искусстве, — пространство отграниченное, заключенное в опреде-ленные рамки и, одновременно, изоморфное безгра-ничному пространству мира.
Исходя из предъявленных ранее примеров, когда субмодальные различения способны уводить нас в прошлое сквозь изоморфные опыты, мы можем теперь показать, что субмодальные эквивалентности и наложения описывают пары классов опыта, которые перцептуально эквивалентны.
Поэтому мы можем считать, что два варианта фильма в целом имеют изоморфные темпоритмические структуры, и общий их принцип более отчетливо просматривается в международном варианте.
Повторение этих изоморфных опытов обусловлено идентичностью субмодальных созвездий.
Поскольку эти опыты организованы таким образом, что каждый из них генерирует своего преемника и регенерирует своего предшественника, изменение в любом из этих изоморфных опытов будет распространяться на все остальные.
Дебора отправила Стива в более далекое прошлое, к множеству других изоморфных опытов.
Другое ограничение, налагаемое на использование скрытых метафор, связано с приобретенным мастерством терапевта в применении как изоморфных контекстов, так и паттернов опыта, описанных в частях 3, 4, 5.
Источник: библиотека Максима Мошкова
Изоморфный JavaScript — будущее веб-приложений / Хабр
В компании Airbnb мы многому научились за последние несколько лет, создавая мощные веб-приложния. Мы погрузились в мир одностраничных приложений в 2011 г., делая мобильную версию нашего сайта, с тех пор, кроме прочего, мы запустили Wish Lists и новый поиск. Все это — большие JavaScript приложения, что означает то, что тонны кода запускаются в браузере, чтобы обеспечить современный интерактивный пользовательский опыт.
Мы погрузились в мир одностраничных приложений в 2011 г., делая мобильную версию нашего сайта, с тех пор, кроме прочего, мы запустили Wish Lists и новый поиск. Все это — большие JavaScript приложения, что означает то, что тонны кода запускаются в браузере, чтобы обеспечить современный интерактивный пользовательский опыт.
Это обычный подход сегодня, когда такие библиотеки, как backbone.js, ember.js и angular.js помогают разработчикам создавать мощные JavaScript приложения. Мы поняли, однако, что такие приложения имеют несколько критических ограничений. Чтобы стало понятно, давайте предпримем небольшой тур по истории веб-приложений.
Картинка из статьи для привлечения внимания
JavaScript взрослеет
На заре Веб взаимодействие с браузерами было таким: веб-браузер запрашивал каждую страницу (например, www.geocities.com) заставляя сервер, находящийся где-то в Интернете генерировать HTML, и отсылать обратно. Этот был хороший подход, так как браузеры в то время были еще не особенно мощными, да и HTML-страницы, в основном, были статичными и автономными. JavaScript, созданный чтобы позволить веб-страницам быть более динамичными, не позволял сделать что-либо более сложное чем слайд-шоу или виджет подбора даты.
JavaScript, созданный чтобы позволить веб-страницам быть более динамичными, не позволял сделать что-либо более сложное чем слайд-шоу или виджет подбора даты.
После нескольких лет развития компьютерных технологий, энтузиасты-разработчики вытолкнули веб за его ограничения, заставив эволюционировать. Сейчас веб развит настолько, что превратился в полноценную платформу для приложений — и быстрый JavaScript и html5-стандарт позволяет разработчикам создавать мощные приложения, такие которые раньше можно было сделать только под определенную платформу.
Одностраничные приложения
Через некоторое время разработчики начали создавать целые приложения в браузере, используя JavaScript и новые возможности. Приложения, подобные Gmail, (классический пример одностраничного приложения) могут мгновенно реагировать на действия пользователей, больше не нужно бегать по полному кругу на сервер, только лишь для того чтобы отобразить новую страницу.
О библиотеках типа backbone. js, ember.js и angular.js часто говорят как о клиентских MVC или MVVM библиотеках. Классическая клиентская MVC архитектура выглядит примерно так:
js, ember.js и angular.js часто говорят как о клиентских MVC или MVVM библиотеках. Классическая клиентская MVC архитектура выглядит примерно так:
Большое количество логики приложения (представления, шаблоны, контроллеры, модели, интернационализация и т.д.) живет на клиенте, для данных используется специальное API. Сервер может быть написан на любом языке, таком как Ruby, Python или Java. В большинстве случаев их роль заключается в отдаче каркасной страницы. Как только JavaScript файлы загружаются браузером, они выполняться, клиентское приложение инициализируется, подгружаются данные через соответствующее API и отрисовывается оставшаяся часть HTML.
Это хорошо для пользователей, потому что, один раз загрузившись, приложение может быстро переключаться между страницами без перезагрузки, и, если все сделано правильно, даже работать в оффлайне.
Это хорошо и для разработчиков, так как у идеального одностраничного приложения есть четкое разделение задач на клиентские и серверные, что обеспечивает прекрасный процесс разработки и предотвращает необходимость дублировать слишком много логики между двумя средами, которые к тому же часто написаны на разных языках.
Неприятности в Раю
На практике, однако, у этого подхода есть несколько фатальных недостатков, которые не позволяют его использовать во многих случаях.
Поисковая оптимизация
Приложение, которое работает только на клиенте не может нормально взаимодействовать с поисковыми роботами, то есть плохо приспособлено для SEO по умолчанию. Поисковые роботы работают, создавая запросы к веб-серверу и интерпретируя полученные результаты, но если сервер возвращает лишь пустую страницу — от этого мало пользы. Существуют конечно и обходные пути, но не без пляски с бубном.
Производительность
По той же самой причине, если сервер не генерирует страницу целиком, а вместо этого приходится ждать загрузки JavaScript на клиент, пользователи несколько критических секунд видят пустую страницу или значок загрузки. Проводилось множество исследований изучающих то, какой эффект оказывают медленные сайты на пользователей, и, соответственно, на прибыль.
Поддержка
Это в идеале должен получиться милый, четко разделенный код, в жизни ;t неизбежно часть логики приложения или логики отображения оказывается продублированной между клиентом и сервером, зачастую написанных на разных языках. Стандартный пример — форматирование даты или валюты, валидация форм и логика маршрутизации. Все это превращает поддержку в кошмар, особенно в случае сложных приложений.
Некоторые разработчики, включая меня, набивают здесь шишки — часто только после того как ты потратил кучу времени и усилий на создание одностраничного приложения — эти недостатки всплывают наружу.
Гибридный подход
В итоге, нам нужен гибрид нового и старого подходов: мы хотим получать полностью сформированный HTML с сервера по причинам производительности и SEO, но нам нужны так же скорость и гибкость приложений клиентской стороны.
Чтобы добиться этого, мы, в Airbnb, экспериментируем с «изоморфными JavaScript приложениями», JavaScript приложениями, которые могут работать как на клиенте так и на сервере.
Изоморфное приложение выглядит примерно так. Озаглавлено “Клиент-серверное MVC”:
Здесь часть логики приложения или отображения может выполняться как на сервере так и на клиенте. Это дает много возможностей: оптимизация выполнения, лучшая поддержка, СЕО по умолчанию, и более контролируемые веб-приложения.
C node.js — быстрой, стабильной серверной JavaScript частью, мы наконец можем претворить эту мечту в реальность. Создав необходимые абстракции, мы можем написать логику нашего приложения такой, чтобы она исполнялась и на сервере и на клиенте — это и есть изоморфный JavaScript.
Изоморфный JavaScript в дикой среде
Идея не нова — Nodejitsu сделал хорошее описание архитектуры изоморфного JavaScript еще в 2011 г. — но она была трудно адаптируемой. С тех пор появились еще несколько изоморфных фреймворков.
С тех пор появились еще несколько изоморфных фреймворков.
Mojito был первым известным изоморфным фремворком с открытыми исходными кодами. Это продвинутый, фулстек-фреймворк, основанный на node.js, но он зависел от yui, да и причуды yahoo не способствовали его особой популярности в JavaScript сообществе с момента, как он стал открытым в апреле 2012 г.
Meteor — вероятно самый широко-известный изоморфный проект сегодня. Метеор создан с нуля для поддержки приложений реального времени, и его команда создала целую экосистему вокруг своей пакетной системы и инструментов развертывания. Как и Mojito, это большой, чрезмерно самоуверенный node.js-фреймворк. Однако многое было сделано для привлечения JavaScript-сообщества, и их наиболее ожидаемый релиз 1.0 уже не за горами (прим. пер. в начале 2014 г.). Метеор — это проект за которым нужно следить — звездная команда, $11.2 млн. финансирование от Andreessen Horowitz — неслыханно для компании, полностью сфокусированной на выпуске продукта с открытыми исходными кодами.
Asana, приложение по управлению задачами основанное Facebook с со-основателем Дастином Московицем, имеет интересную изоморфную историю. Не испытывая проблем с финансированием, учитывая статус Московица, как самого молодого миллиардера в мире, Асана провела годы исследований, разрабатывая свой фреймворк Luna с закрытыми исходными кодами — один из самых продвинутых примеров изоморфного JavaScript. Luna, изначально созданная на v8cgi (в дни предшествующие node.js) позволяла запускать копию приложения на сервере для каждой пользовательской сессии. Для каждого пользователя запускался отдельный серверный процесс, выполняя тот же JavaScript-код который запущен на клиенте. Это давало все преимущества продвинутой оптимизации, такие как устойчивость к оффлайну и быструю реакцию.
Мы тоже создали свою изоморфную библиотеку в этом году. Называется она Rendr. Она позволяет создавать backbone.js + handlebars.js одностраничные приложения, которые так же могут полностью формировать страницы на сервере. Rendr — это результат нашего опыта переделки мобильной версии Airbnb для улучшения скорости загрузки, что особо важно для мобильных пользователей которым свойственны высокие задержки при передаче данных. Rendr — скорее библиотека, чем фреймворк, решающий несколько задач (если вы будете сравнивать с Mojito или Meteor), но он легок для изменения и расширения.
Rendr — это результат нашего опыта переделки мобильной версии Airbnb для улучшения скорости загрузки, что особо важно для мобильных пользователей которым свойственны высокие задержки при передаче данных. Rendr — скорее библиотека, чем фреймворк, решающий несколько задач (если вы будете сравнивать с Mojito или Meteor), но он легок для изменения и расширения.
Абстракции, абстракции, абстракции
Все эти проекты довольно большие — что говорит о том, что фулстек фреймворки сталкиваются с довольно сложными проблемами. Клиент и сервер — довольно различные окружения, поэтому необходимо создать определенный набор абстракций, которые отделят логику приложения от базовых реализаций, так чтобы можно было сформировать единый API для разработчиков приложений…
Маршрутизация
Нам нужен единый набор маршрутов, которые сопоставляют определенные URI-шаблоны соответствующим обработчикам. Этим обработчикам должны быть доступны: HTTP заголовки, куки, информация из URI и возможность перенаправления без прямого доступа к windows. location (в браузере) и req и res (в node.js).
location (в браузере) и req и res (в node.js).
Загрузка и сохранение данных
Необходимо как-то описать ресурсы, нужные для отрисовки конкретных страниц или компонент, не зависимо от механизмов подгрузки. Описание ресурсов должно быть простым URI, указывающим на конкретный JSON, либо, для больших приложений, может быть полезно инкапсулировать ресурсы в модели и коллекции и определить класс модели и первичный ключ, которые, каким-либо образом, транслировались бы в URI.
Генерация страницы
Собираемся ли мы менять DOM вручную, или, используя HTML-шаблонизаторы, или же используя какую-либо библиотеку компонент, абстрагирующую от DOM, в любом случае, нужно иметь возможность генерировать разметку изоморфно. Должна быть возможность генерировать любое представление как на сервере, так и на клиенте, в зависимости от потребностей приложения.
Сборка и упаковка
Оказывается написание изоморфного кода приложений — это только половина дела. Инструменты, такие как grunt и browserify — неотъемлемая часть процесса создания и запуска приложений. Для сборки обычно нужно выполнить несколько шагов: компиляция шаблонов, включение клиентских зависимостей, применение трансформаций, минификация и т.д. В простейшем случае нужно собрать весь код приложения, представление и шаблоны в единый пакет, но для больших приложений, это может обернуться необходимостью передавать сотни килобайт клиенту. Более продвинутый подход — это создать динамическую связку и предоставить возможность отложенной загрузки, однако в этом случае сложность быстро возрастает. Инструменты статистического анализа кода, такие как Esprima позволяют честолюбивым разработчикам провести продвинутую оптимизацию и метапрограммирование, чтобы уменьшить количество шаблонного кода.
Инструменты, такие как grunt и browserify — неотъемлемая часть процесса создания и запуска приложений. Для сборки обычно нужно выполнить несколько шагов: компиляция шаблонов, включение клиентских зависимостей, применение трансформаций, минификация и т.д. В простейшем случае нужно собрать весь код приложения, представление и шаблоны в единый пакет, но для больших приложений, это может обернуться необходимостью передавать сотни килобайт клиенту. Более продвинутый подход — это создать динамическую связку и предоставить возможность отложенной загрузки, однако в этом случае сложность быстро возрастает. Инструменты статистического анализа кода, такие как Esprima позволяют честолюбивым разработчикам провести продвинутую оптимизацию и метапрограммирование, чтобы уменьшить количество шаблонного кода.
Собираем из маленьких модулей
Выйти на рынок с первым изоморфным фреймворком означает, что вам удалось решить все эти проблемы. Но в результате может получиться огромный, неповоротливый фреймворк, который будет трудно адаптировать и интегрировать в уже существующие приложения.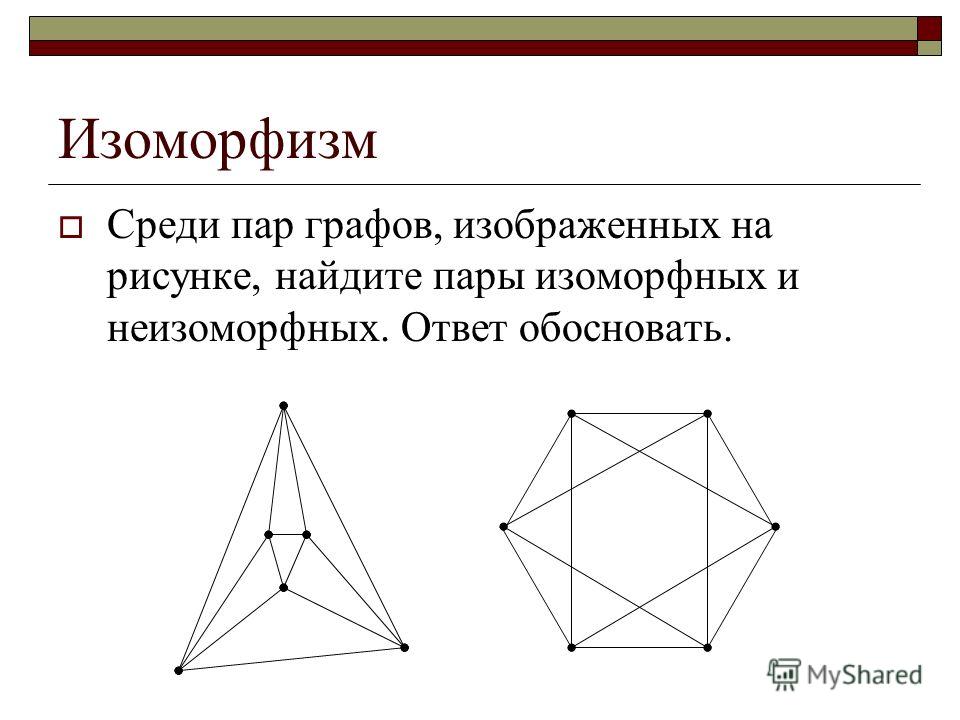 Так как все больше больше разработчиков подключаются к решению этих проблем, мы скоро столкнемся с появлением большого количества небольших, приспособленных для повторного использования модулей, которые можно будет соединять вместе для создания изоморфных приложений.
Так как все больше больше разработчиков подключаются к решению этих проблем, мы скоро столкнемся с появлением большого количества небольших, приспособленных для повторного использования модулей, которые можно будет соединять вместе для создания изоморфных приложений.
Очевидно, что большинство JavaScript-модулей могут уже быть использованы изоморфно либо без, либо с небольшими модификациями. Например, такие популярные библиотеки, как undrscore, backbone, handlebars, moment и даже jquery уже можно использовать на сервере.
Чтобы продемонстрировать все это, я создал небольшое приложение, названное изоморфный туториал которое вы можете взять с GitHub. Комбинируя вместе несколько модулей, каждое из которых может быть использовано изоморфно, довольно просто создать небольшое изоморфное приложения в сотню строк кода. Здесь используются: Director для серверной и браузерной маршрутизации, Superagent для HTTP запросов и handlebars для шаблонизации, все это собрано поверх обычного express. js приложения. Конечно с ростом сложности приложения, нужно будет добавлять дополнительные слои абстракции, но я надеюсь на то, что чем больше разработчиков будут экспериментировать с этим подходом, тем больше новых библиотек и стандартов будет появляться.
js приложения. Конечно с ростом сложности приложения, нужно будет добавлять дополнительные слои абстракции, но я надеюсь на то, что чем больше разработчиков будут экспериментировать с этим подходом, тем больше новых библиотек и стандартов будет появляться.
Оглядимся
Чем больше организаций будут запускать node.js в продакшен, тем неумолимей это будет приводить к тому, что все больше и больше кода будут разделяться между клиентом и сервером. Важно помнить, что изоморфный JavaScript можно использоваться и локально для узких и для широких задач — можно начать с разделения шаблонов, продвигаясь дальше до разделения всей подсистемы отображения, и завершая полным разделением бизнес логики приложения. Конкретный способ разделения JavaScript между средами целиком зависит от того как приложение создается и от его особенностей.
Nicholas C. Zakas отлично описал то, как по его мнению в приложениях произойдет переход UI-слоя с клиента на сервер, давая выигрыш в производительности и лучшую поддержку. Чтобы использовать изоморфный JavaScript, не нужно будет отказываться от существующего бэкэнда и заменять его node.js, выплескивая ребенка вместе с водой. Вместо этого, создавая правильный API и используя RESTful-подход, традиционный бэкенд может спокойно жить рядом с node.js.
Чтобы использовать изоморфный JavaScript, не нужно будет отказываться от существующего бэкэнда и заменять его node.js, выплескивая ребенка вместе с водой. Вместо этого, создавая правильный API и используя RESTful-подход, традиционный бэкенд может спокойно жить рядом с node.js.
В Airbnb мы уже начали переделывать процесс создания клиентской стороны, используя базирующиеся на node инструменты, такие как grunt и browserify. Наше основное rails-приложение может быть никогда и не будет полностью вытеснено node.js, но, используя их вместе, становится даже проще разделять определенные части JavaScript между окружениями.
5.6: Изоморфизмы — Математика LibreTexts
-
- Последнее обновление
- Сохранить как PDF
- Идентификатор страницы
- 14529
- Кен Каттлер
- Университет Бригама Янга via Lyryx 9{м}\) соответственно.
 Отображение \(T:V\rightarrow W\) называется линейным преобразованием или линейным отображением , если оно сохраняет алгебраические операции сложения и скалярного умножения. В частности, если \(a,b\) являются скалярами и \(\vec{x},\vec{y}\) являются векторами,
Отображение \(T:V\rightarrow W\) называется линейным преобразованием или линейным отображением , если оно сохраняет алгебраические операции сложения и скалярного умножения. В частности, если \(a,b\) являются скалярами и \(\vec{x},\vec{y}\) являются векторами,
\[T\left( a\vec{x}+b\vec{y}\right) =aT(\vec{x})+bT(\vec{y})\nonumber \]
Рассмотрим следующее важное определение.
Определение \(\PageIndex{1}\): изоморфизм
Линейная карта \(T\) называется изоморфизм , если выполняются следующие два условия.
- \(T\) один к одному. То есть, если \(T(\vec{x})=T(\vec{y}),\), то \(\vec{x}=\vec{y}.\)
- \(T\) включен. То есть, если \(\vec{w}\in W,\) существует \(\vec{v}\in V\) такое, что \(T(\vec{v})=\vec{w}\ ).
Два таких подпространства, которые имеют описанный выше изоморфизм, называются -изоморфными.
Рассмотрим следующий пример изоморфизма.
92\) определяется как \[T \left [ \begin{array}{c} x \\ y \end{array} \right ] = \left [ \begin{array}{c} x + y \\ x — y \end{array} \right ] \nonumber\] Покажите, что \(T\) является изоморфизмом.
Решение
Чтобы доказать, что \(T\) — изоморфизм, мы должны показать
- \(T\) — линейное преобразование;
- \(T\) один к одному;
- \(T\) включен.
Действуем следующим образом.
- \(T\) является линейным преобразованием:
Пусть \(k, p\) — скаляры. \[\begin{align} T \left( k \left [ \begin{array}{c} x_1 \\ y_1 \end{array} \right ] + p \left [ \begin{array}{c} x_2 \ \ y_2 \end{массив} \right ] \right) &= T \left( \left [ \begin{array}{c} kx_1 \\ ky_1 \end{массив} \right ] + \left [ \begin{массив }{c} px_2 \\ py_2 \end{массив} \right ] \right) \\ &= T \left( \left [ \begin{массив}{c} kx_1 + px_2 \\ ky_1 + py_2 \end{массив } \right ] \right) \\ &= \left [ \begin{array}{c} (kx_1 + px_2) + (ky_1 + py_2) \\ (kx_1 + px_2) — (ky_1 + py_2) \end{array } \right ] \\ &= \left [ \begin{array}{c} (kx_1 + ky_1) + (px_2 + py_2) \\ (kx_1 — ky_1) + (px_2 — py_2) \end{array} \right ] \\ &= \left [ \begin{array}{c} kx_1 + ky_1 \\ kx_1 — ky_1 \end{array} \right ] + \left [ \begin{array}{c} px_2 + py_2 \\ px_2 — py_2 \end{массив} \right ] \\ &= k \left [ \begin{array}{c} x_1 + y_1 \\ x_1 — y_1 \end{массив} \right ] + p \left [ \begin{ array}{c} x_2 + y_2 \\ x_2 — y_2 \end{array} \right ] \\ &= k T \left( \left [ \begin{array}{c} x_1 \\ y_1 \end{array} \right ] \right) + p T \left( \left [ \begin{array}{c} x_2 \\ y_2 \end{array} \right ] \right)\end{aligned}\] 92\), то следует, что \(\vec{x} = \vec{0}\).
 Пусть \(\vec{x} = \left [ \begin{array}{c} x \\ y \end{array} \right ]\).
Пусть \(\vec{x} = \left [ \begin{array}{c} x \\ y \end{array} \right ]\). \[T \left( \left [ \begin{array}{c} x \\ y \end{array} \right ] \right) = \left [ \begin{array}{c} x + y\\ x — y \end{array} \right ] = \left [ \begin{array}{c} 0 \\ 0 \end{array} \right ]\nonumber \] Это дает систему уравнений, заданную \[\ begin{aligned} x + y &= 0\\ x — y &= 0\end{aligned}\] Вы можете убедиться, что решение этой системы, если \(x = y =0\). Поэтому \[\vec{x} = \left [ \begin{array}{c} x \\ y \end{array} \right ] = \left [ \begin{array}{c} 0 \\ 0 \end {массив} \right ]\nonumber \] и \(T\) один к одному.
- \(T\) находится на:
Пусть \(a,b\) — скаляры. Мы хотим проверить, всегда ли существует решение \[T \left( \left [ \begin{array}{c} x \\ y \end{array} \right ] \right) = \left [ \begin{ array}{c} x + y\\ x — y \end{array} \right ] = \left [ \begin{array}{c} a \\ b \end{array} \right ]\nonumber\]
Это можно представить в виде системы уравнений \[\begin{aligned} x + y &= a\\ x — y &= b\end{aligned}\]
Настройка расширенной матрицы и сокращения строк дает \[\left [ \begin{array}{cc|c} 1 & 1 & a \\ 1 & -1 & b \end{array} \right ] \rightarrow \cdots \rightarrow \left [ \begin{array}{cc|c} 1 & 0 & \frac{a+b}{2} \\ 0 & 1 & \frac{a-b}{2} \end{array} \right ]\nonumber\] Это имеет решение для всех \(a,b\) и, следовательно, \(T\) находится на.
 9н\). Тогда \(S\circ T\), определяемый как \(\left( S\circ T\right) \left( \vec{v} \right) = S\left( T\left( \vec{v} \right ) \right)\) также является изоморфизмом.
9н\). Тогда \(S\circ T\), определяемый как \(\left( S\circ T\right) \left( \vec{v} \right) = S\left( T\left( \vec{v} \right ) \right)\) также является изоморфизмом. - Доказательство
-
Предположим, что \(T:V\rightarrow W\) и \(S:W\rightarrow Z\) являются изоморфизмами. Почему \(S\circ T\) является линейной картой? Для \(a,b\) скаляров
\[\begin{align} S\circ T\left( a\vec{v}_{1}+b(\vec{v}_{2})\right) &= S\left( T\left (a\vec{v}_{1}+b\vec{v}_{2}\right) \right) =S\left( aT\vec{v}_{1}+bT\vec{v} _{2}\right) \\ &=aS\left( T\vec{v}_{1}\right) +bS\left( T\vec{v}_{2}\right) = a\left ( S\circ T\right) \left( \vec{v}_{1}\right) +b\left( S\circ T\right) \left( \vec{v}_{2}\right) \end{выровнено}\nonumber\]
Следовательно, \(S\circ T\) — линейное отображение. Если \(\left( S\circ T\right) \left( \vec{v} \right) =0,\), то \(S\left( T\left( \vec{v} \right) \right ) =0\) и отсюда следует, что \(T(\vec{v})=\vec{0}\) и, следовательно, снова по этой лемме \(\vec{v}=\vec{0}\).
 Таким образом, \(S\circ T\) один к одному. Осталось убедиться, что он включен. Пусть \(\vec{z} \in Z\). Тогда, поскольку \(S\) находится на, существует \(\vec{w} \in W\) такое, что \(S(\vec{w})=\vec{z}.\) Кроме того, поскольку \( T\) на, существует \(\vec{v}\in V\) такое, что \(T(\vec{v})=\vec{w}.\) Отсюда следует, что \(S\left( T\left( \vec{v}\right) \right) =\vec{z}\) и, таким образом, \(S\circ T\) тоже на.
Таким образом, \(S\circ T\) один к одному. Осталось убедиться, что он включен. Пусть \(\vec{z} \in Z\). Тогда, поскольку \(S\) находится на, существует \(\vec{w} \in W\) такое, что \(S(\vec{w})=\vec{z}.\) Кроме того, поскольку \( T\) на, существует \(\vec{v}\in V\) такое, что \(T(\vec{v})=\vec{w}.\) Отсюда следует, что \(S\left( T\left( \vec{v}\right) \right) =\vec{z}\) и, таким образом, \(S\circ T\) тоже на.
Рассмотрим два подпространства \(V\) и \(W\) и предположим, что существует изоморфизм, отображающий одно в другое. Таким образом, два подпространства связаны, что мы можем записать как \(V \sim W\). Тогда два предыдущих утверждения вместе утверждают, что \(\sim\) является отношением эквивалентности. То есть: \(\sim\) удовлетворяет следующим условиям:
- \(В\сим В\)
- Если \(V\sim W,\), то \(W\sim V\)
- Если \(V\sim W\) и \(W\sim Z,\), то \(V\sim Z\) 9н\). Если \(T\) один к одному, то оно обладает тем свойством, что если \(\left\{ \vec{u}_{1},\cdots ,\vec{u}_{k}\right\} \) линейно независим, так что \(\left\{T(\vec{u}_{1}),\cdots ,T(\vec{u}_{k})\right\}\).

В более общем случае \(T\) является изоморфизмом тогда и только тогда, когда \(\left\{ \vec{v}_{1},\cdots ,\vec{v}_{n}\right\} \) является базисом для \(V,\), то \(\left\{ T (\vec{v}_{1}),\cdots ,T(\vec{v}_{n})\ right\}\) является основой для \(W\).
- Доказательство 9{n}c_{i}\vec{u}_{i}=0\nonumber\] Теперь тот факт, что \(\left\{ \vec{u}_{1},\cdots ,\vec{u} _{n}\right\}\) линейно независима, следует, что каждый \(c_{i}=0\). Следовательно, \(\left\{ T(\vec{u} _{1}),\cdots ,T(\vec{u}_{n})\right\}\) линейно независим.
- Наверх
-
- Была ли эта статья полезной?
-
- Тип изделия
- Раздел или Страница
- Автор
- Кен Каттлер
- Лицензия
- СС BY
- Версия лицензии
- 4,0
- Показать страницу TOC
- нет
-
- Теги
-
- изоморфизм
- линейная карта
- линейное преобразование
- источник@https://lyryx.
 com/first-course-linear-алгебра
com/first-course-linear-алгебра
- Развлечения и поп-культура
- География и путешествия
- Здоровье и медицина
- Образ жизни и социальные вопросы
- Литература
- Философия и религия
- Политика, право и правительство
- Наука
- Спорт и отдых
- Технология
- Изобразительное искусство
- Всемирная история
- В этот день в истории
- Викторины
- Подкасты
- Словарь
- Биографии
- Резюме
- Популярные вопросы
- Обзор недели
- Инфографика
- Демистификация
- Списки
- #WTFact
- Компаньоны
- Галереи изображений
- Прожектор
- Форум
- Один хороший факт
- Развлечения и поп-культура
- География и путешествия
- Здоровье и медицина
- Образ жизни и социальные вопросы
- Литература
- Философия и религия
- Политика, право и правительство
- Наука
- Спорт и отдых
- Технология
- Изобразительное искусство
- Всемирная история
- Britannica объясняет
В этих видеороликах Britannica объясняет различные темы и отвечает на часто задаваемые вопросы.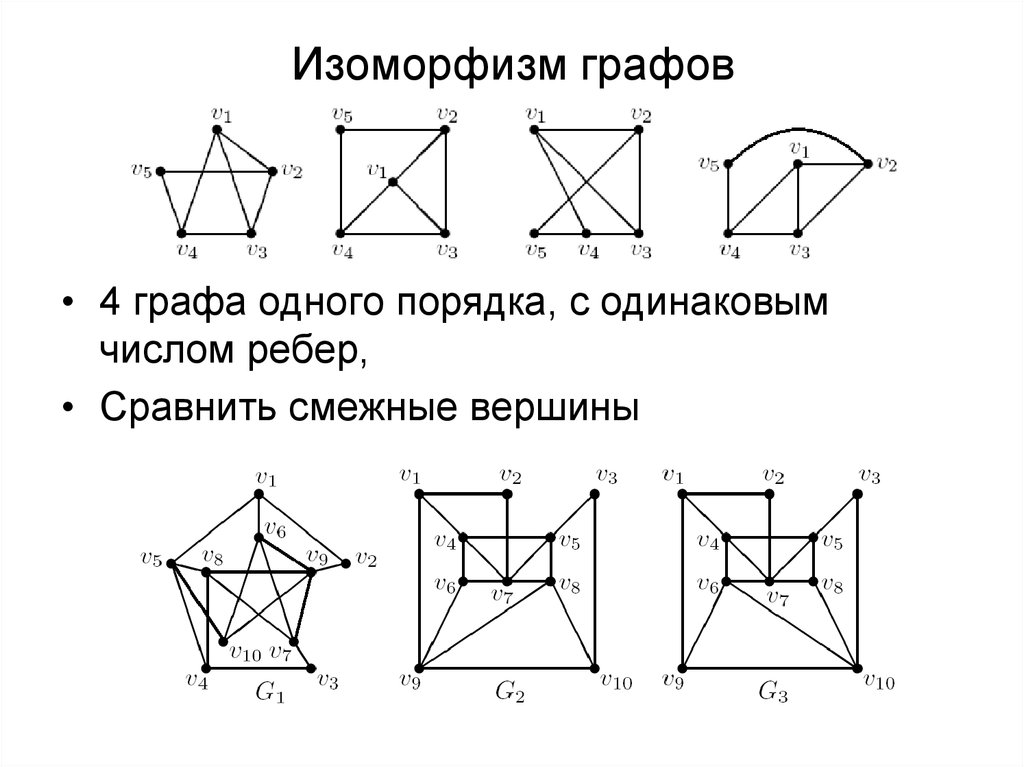
- Britannica Classics
Посмотрите эти ретро-видео из архивов Encyclopedia Britannica. - Демистифицированные видео 904:35 В «Демистификации» у «Британники» есть все ответы на ваши животрепещущие вопросы.
- #WTFact Видео
В #WTFact Britannica делится некоторыми из самых странных фактов, которые мы можем найти. - На этот раз в истории
В этих видеороликах узнайте, что произошло в этом месяце (или любом другом месяце!) в истории. - Студенческий портал
Britannica — лучший ресурс для учащихся по ключевым школьным предметам, таким как история, государственное управление, литература и т. д. - Портал COVID-19
Хотя этот глобальный кризис в области здравоохранения продолжает развиваться, может быть полезно обратиться к прошлым пандемиям, чтобы лучше понять, как реагировать сегодня. - 100 женщин
Britannica празднует столетие Девятнадцатой поправки, выделяя суфражисток и политиков, творящих историю.
Теперь предположим, что \(T\) является изоморфизмом и \(\left\{ \vec{v}_{1},\cdots ,\vec{ v}_{n}\right\}\) является базисом для \(V\). Только что было показано, что \(\left\{ T(\vec{v} _{1}),\cdots ,T(\vec{v}_{n})\right\}\) линейно независим. Осталось проверить, что span\(\left\{ T(\vec{v}_{1}),\cdots ,T(\vec{v}_{n})\right\}=W\). Если \(\vec{w}\in W,\), то поскольку \(T\) находится на, существует \(\vec{v}\in V\) такое, что \(T(\vec{v})= \vec{ш}\).
 {n} \hat{c}_{i}\vec{v}_ {i}\right)\end{aligned}\] Таким образом, \(T\) является линейным преобразованием. 9{n}c_{i}\vec{v}_{i}\right)\nonumber \], показывающий, что \(T\) также включен. Следовательно, \(T\) — изоморфизм, а значит, \(V\) и \(W\) изоморфны.
{n} \hat{c}_{i}\vec{v}_ {i}\right)\end{aligned}\] Таким образом, \(T\) является линейным преобразованием. 9{n}c_{i}\vec{v}_{i}\right)\nonumber \], показывающий, что \(T\) также включен. Следовательно, \(T\) — изоморфизм, а значит, \(V\) и \(W\) изоморфны. Далее предположим, что \(T:V \mapsto W\) является изоморфизмом, поэтому эти два подпространства изоморфны. Тогда для \(\left\{ \vec{v}_{1},\cdots ,\vec{v}_{n}\right\}\) базиса для \(V\) следует, что базис для \(W\) является \(\left\{ T(\vec{v}_{1}),\cdots ,T(\vec{v}_{n})\right\}\), показывающим, что два подпространства имеют одинаковую размерность.
Теперь предположим, что два подпространства имеют одинаковую размерность. Рассмотрим три заявленные эквивалентности.
Сначала рассмотрим утверждение, что \(1.)\Rightarrow 2.).\) Если \(T\) взаимно однозначно и если \(\left\{ \vec{v}_{1},\cdots , \vec{v} _{n}\right\}\) является базисом для \(V,\), тогда \(\left\{ T(\vec{v}_{1}),\cdots ,T( \vec{v }_{n})\right\}\) линейно независим.
 {n}c_{i}\vec{v} _{i}=\vec{0}\). Таким образом, \(T\) взаимно однозначно, так же как и на, и, следовательно, является изоморфизмом. 9{3}\) и пусть \(W\) обозначает \[\mathrm{span}\left\{ \left [ \begin{array}{r} 1 \\ 2 \\ 1 \\ 1 \end{array} \right ] ,\left [ \begin{array}{r} 0 \\ 1 \\ 0 \\ 1 \end{array} \right ] ,\left [ \begin{array}{r} 1 \\ 1 \ \ 2 \\ 0 \end{массив} \right ] \right\}\nonumber \] Покажите, что \(V\) и \(W\) изоморфны.
{n}c_{i}\vec{v} _{i}=\vec{0}\). Таким образом, \(T\) взаимно однозначно, так же как и на, и, следовательно, является изоморфизмом. 9{3}\) и пусть \(W\) обозначает \[\mathrm{span}\left\{ \left [ \begin{array}{r} 1 \\ 2 \\ 1 \\ 1 \end{array} \right ] ,\left [ \begin{array}{r} 0 \\ 1 \\ 0 \\ 1 \end{array} \right ] ,\left [ \begin{array}{r} 1 \\ 1 \ \ 2 \\ 0 \end{массив} \right ] \right\}\nonumber \] Покажите, что \(V\) и \(W\) изоморфны. Решение
Сначала заметим, что оба этих подпространства имеют размерность 3 и поэтому они изоморфны по теореме \(\PageIndex{1}\). Легко увидеть, что три вектора, которые охватывают \(W\), являются линейно независимыми, если сделать их столбцами матрицы и строки, сводящимися к редуцированной форме строки-эшелона.
Вы можете продемонстрировать изоморфизм этих двух пространств следующим образом. \[T(\vec{e}_{1})=\left [ \begin{array}{c} 1 \\ 2 \\ 1 \\ 1 \end{array} \right ], T(\vec{ e}_{2})=\left [ \begin{array}{c} 0 \\ 1 \\ 0 \\ 1 \end{array} \right ], T(\vec{e}_{3}) =\left [ \begin{array}{c} 1 \\ 1 \\ 2 \\ 0 \end{array} \right ]\nonumber \] и продолжить линейно.
 Напомним, что матрица этого линейного преобразования — это просто матрица, столбцами которой являются эти векторы. Таким образом, матрица этого изоморфизма равна \[\left [ \begin{array}{rrr} 1 & 0 & 1 \\ 2 & 1 & 1 \\ 1 & 0 & 2 \\ 1 & 1 & 0 \end{array } \right ]\nonumber \] Вы должны проверить, что умножение слева на эту матрицу действительно воспроизводит заявленный эффект, полученный в результате применения \(T\). 9{3}\) и пусть \(W\) обозначает
Напомним, что матрица этого линейного преобразования — это просто матрица, столбцами которой являются эти векторы. Таким образом, матрица этого изоморфизма равна \[\left [ \begin{array}{rrr} 1 & 0 & 1 \\ 2 & 1 & 1 \\ 1 & 0 & 2 \\ 1 & 1 & 0 \end{array } \right ]\nonumber \] Вы должны проверить, что умножение слева на эту матрицу действительно воспроизводит заявленный эффект, полученный в результате применения \(T\). 9{3}\) и пусть \(W\) обозначает \[\mathrm{span}\left\{ \left [ \begin{array}{c} 1 \\ 2 \\ 1 \\ 1 \end{ array} \right ] ,\left [ \begin{array}{c} 0 \\ 1 \\ 0 \\ 1 \end{array} \right ] ,\left [ \begin{array}{c} 1 \\ 1 \\ 2 \\ 0 \end{массив} \right ] \right\}\nonumber \]
Пусть \(T: V \mapsto W\) определяется следующим образом. \[T\left [ \begin{array}{c} 1 \\ 1 \\ 0 \end{array} \right ] =\left [ \begin{array}{c} 1 \\ 2 \\ 1 \\ 1 \end{array} \right ] ,T\left [ \begin{array}{c} 0 \\ 1 \\ 1 \end{array} \right ] =\left [ \begin{array}{c} 0 \\ 1 \\ 0 \\ 1 \end{массив} \right ] ,T\left [ \begin{array}{c} 1 \\ 1 \\ 1 \end{массив} \right ] =\left [ \ begin{array}{c} 1 \\ 1 \\ 2 \\ 0 \end{array} \right ]\nonumber \] Найдите матрицу этого изоморфизма \(T\).
 {-1}=\left [ \begin{array}{rrr} 1 & 0 & 0 \\ 0 & 2 & -1 \\ 2 & -1 & 1 \\ -1 & 2 & -1 \end{массив} \right ]\nonumber \] 9{3}\) и пусть \(W\) обозначает \[\mathrm{span}\left\{ \left [ \begin{array}{c} 1 \\ 0 \\ 1 \\ 1 \end{array} \right ] ,\left [ \begin{array}{c} 0 \\ 1 \\ 0 \\ 1 \end{array} \right ] ,\left [ \begin{array}{c} 1 \\ 1 \ \ 1 \\ 2 \end{array} \right ] \right\}\nonumber \] Пусть \(T: V \mapsto W\) определяется следующим образом. \[T\left [ \begin{array}{c} 1 \\ 1 \\ 0 \end{array} \right ] = \left [ \begin{array}{c} 1 \\ 0 \\ 1 \\ 1 \end{array} \right ] ,T\left [ \begin{array}{c} 0 \\ 1 \\ 1 \end{array} \right ] =\left [ \begin{array}{c} 0 \\ 1 \\ 0 \\ 1 \end{массив} \right ] ,T\left [ \begin{array}{c} 1 \\ 1 \\ 1 \end{массив} \right ] =\left [ \ begin{array}{c} 1 \\ 1 \\ 1 \\ 2 \end{array} \right ]\nonumber \] Найдите матрицу этого линейного преобразования.
{-1}=\left [ \begin{array}{rrr} 1 & 0 & 0 \\ 0 & 2 & -1 \\ 2 & -1 & 1 \\ -1 & 2 & -1 \end{массив} \right ]\nonumber \] 9{3}\) и пусть \(W\) обозначает \[\mathrm{span}\left\{ \left [ \begin{array}{c} 1 \\ 0 \\ 1 \\ 1 \end{array} \right ] ,\left [ \begin{array}{c} 0 \\ 1 \\ 0 \\ 1 \end{array} \right ] ,\left [ \begin{array}{c} 1 \\ 1 \ \ 1 \\ 2 \end{array} \right ] \right\}\nonumber \] Пусть \(T: V \mapsto W\) определяется следующим образом. \[T\left [ \begin{array}{c} 1 \\ 1 \\ 0 \end{array} \right ] = \left [ \begin{array}{c} 1 \\ 0 \\ 1 \\ 1 \end{array} \right ] ,T\left [ \begin{array}{c} 0 \\ 1 \\ 1 \end{array} \right ] =\left [ \begin{array}{c} 0 \\ 1 \\ 0 \\ 1 \end{массив} \right ] ,T\left [ \begin{array}{c} 1 \\ 1 \\ 1 \end{массив} \right ] =\left [ \ begin{array}{c} 1 \\ 1 \\ 1 \\ 2 \end{array} \right ]\nonumber \] Найдите матрицу этого линейного преобразования. Решение
Обратите внимание, что в этом случае три вектора, которые охватывают \(W\), не являются линейно независимыми.
 {-1}=\left [ \begin{array}{rrr} 1 & 0 & 0 \\ 0 & 0 & 1 \\ 1 & 0 & 0 \\ 1 & 0 & 1 \end{array} \right ]\nonumber \]
{-1}=\left [ \begin{array}{rrr} 1 & 0 & 0 \\ 0 & 0 & 1 \\ 1 & 0 & 0 \\ 1 & 0 & 1 \end{array} \right ]\nonumber \] Очевидно, что столбцы этой последней матрицы не являются линейно независимыми.
Эта страница под названием 5.6: Isomorphisms распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована Кеном Каттлером (Lyryx) с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.
Изоморфизм | математика | Британика



