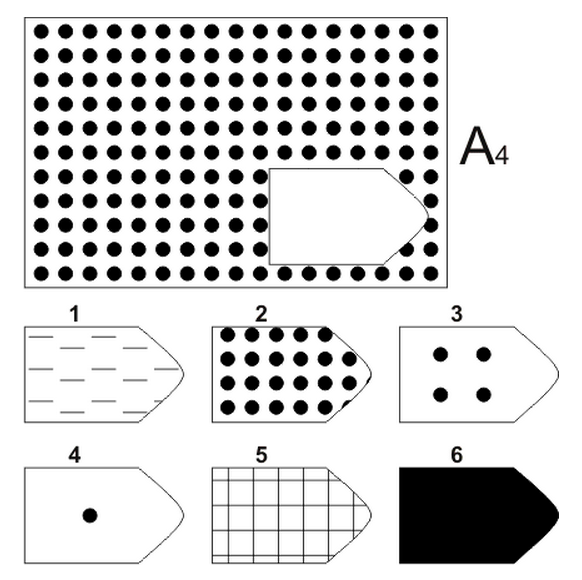
Матрицы равена: Прогрессивные матрицы Равена || Пройти тест онлайн
Применение Теста Стандартные Прогрессивные Матрицы Равена в Режиме Ограничения Времени (Administered of the Raven’s Standard Progressive Matrices with a time limit ) by Denis Davydov, Ekaterina Chmykhova :: SSRN
Voprosy Psikhologii, (2016)
18 Pages Posted: 15 Nov 2017
See all articles by Denis Davydov
Open University for the Humanities and Economics; Modern University for the Humanities, Research and Innovation Department; Russian Academy of National Economy and Public Administration under the President of the Russian Federation (RANEPA)
Open University for the Humanities and Economics; Modern University for the Humanities
Date Written: September 2016
Abstract
Russian Abstract: В статье представлены результаты исследования интеллекта с помощью Стандартных прогрессивных матриц Равена (SPM) на российской выборке (n=7894 чел. ). Показано, что тест SPM, применяемый с 20-минутным ограничением времени, является валидной, достоверной и дискриминативной методикой, удобной для практического использования. Полученные данные могут быть использованы как тестовые нормы для применения SPM в режиме 20 мин. ограничения. Результаты исследования уточняют возрастную динамику интеллекта: наиболее высокие значения показателей теста SPM наблюдаются в возрасте от 16 до 48 лет, а снижение показателей можно заметить лишь в возрастных группах старше 50 лет. Гендерных различий в показателях SPM у испытуемых старше 12 лет не выявлено. С опорой на полученные данные в статье рассмотрены вопросы природы интеллекта.
). Показано, что тест SPM, применяемый с 20-минутным ограничением времени, является валидной, достоверной и дискриминативной методикой, удобной для практического использования. Полученные данные могут быть использованы как тестовые нормы для применения SPM в режиме 20 мин. ограничения. Результаты исследования уточняют возрастную динамику интеллекта: наиболее высокие значения показателей теста SPM наблюдаются в возрасте от 16 до 48 лет, а снижение показателей можно заметить лишь в возрастных группах старше 50 лет. Гендерных различий в показателях SPM у испытуемых старше 12 лет не выявлено. С опорой на полученные данные в статье рассмотрены вопросы природы интеллекта.
English Abstract: The paper presents the study of intelligence assessed by the Raven’s Standard Progressive Matrices (SPM) in the Russian sampling aged 11-65 years (n = 7,894). It is shown SPM administered with a time limit of 20 minutes is valid and discriminative test, suitable for practical application.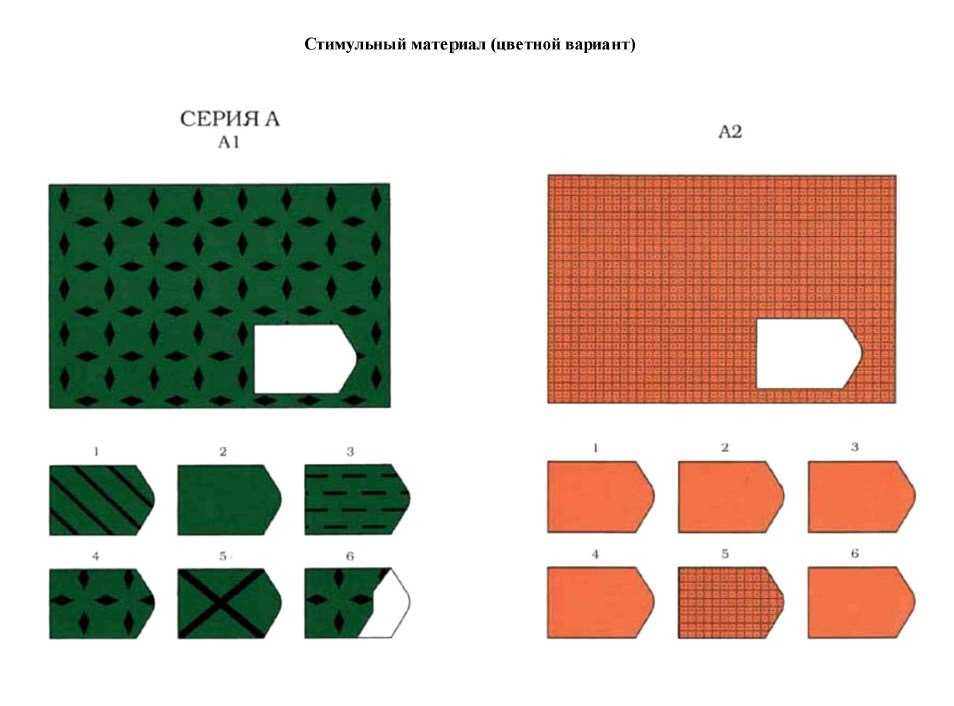 Obtained data can be used as norms for 20-minute timed version SPM. Moreover the age dynamics of intelligence was clarified: the highest SPM test scores have been observed in the age from 16 to 48 years, and the scores decline can be seen since 50 years old. Gender differences were not identified, since the age of 12 years. The results of this study are discussed with respect to nature of intelligence and its measurement.
Obtained data can be used as norms for 20-minute timed version SPM. Moreover the age dynamics of intelligence was clarified: the highest SPM test scores have been observed in the age from 16 to 48 years, and the scores decline can be seen since 50 years old. Gender differences were not identified, since the age of 12 years. The results of this study are discussed with respect to nature of intelligence and its measurement.
Note: Downloadable document is available in Russian.
Keywords: интеллект, стандартные прогрессивные матрицы Равена, тестовые нормы, психометрика
Suggested Citation: Suggested Citation
Davydov, Denis and Chmykhova, Ekaterina, Применение Теста Стандартные Прогрессивные Матрицы Равена в Режиме Ограничения Времени (Administered of the Raven’s Standard Progressive Matrices with a time limit ) (September 2016).
Как решить равенство матриц?
Равенство матриц — это математическое понятие, при котором две или более матриц равны при сравнении. Прежде чем изучать концепцию равенства матриц, нам нужно знать, что такое матрица. Массив чисел или символов прямоугольной или квадратной формы, организованный в строки и столбцы для представления математического объекта или одного из его атрибутов, в математике называется матрицей. Горизонтальные линии называются строками, а вертикальные — столбцами. Например, это матрица с 3 строками и 3 столбцами. Ее можно назвать матрицей «3 на 3», и она является квадратной матрицей. С другой стороны, это матрица 2 на 3 и прямоугольная матрица.
Что такое равенство матриц?
Когда две или более матриц равны, это называется равенством матриц. Матрицы считаются равными, если они имеют одинаковое количество строк и столбцов, а также одинаковое количество элементов. Равенство матриц не выполняется ни для одного из ранее упомянутых условий. Две матрицы называются неравными, если порядок матриц не равен или хотя бы одна пара соответствующих элементов не равна. Это понятие актуально как для прямоугольных, так и для квадратных матриц.
Равенство матриц не выполняется ни для одного из ранее упомянутых условий. Две матрицы называются неравными, если порядок матриц не равен или хотя бы одна пара соответствующих элементов не равна. Это понятие актуально как для прямоугольных, так и для квадратных матриц.
Условия для матриц равенства
Равенство матриц — это концепция матриц, которые определяются путем сравнения двух или более матриц, имеющих одинаковые размеры и все одинаковые соответствующие элементы. Если «A = [a ij ] m×n » и «B = [b ij ] p×q » являются двумя матрицами, то следующие три требования к матричному равенству для матриц:
- Число строк в матрицах A и B одинаково, т. е. m = p.
- Количество столбцов в матрицах A и B одинаково, т. е. n = q.
- Для любых i и j соответствующие элементы A и B равны, т. е. a ij = b ij .
Пример:
Скажи . Найдите значения a и z.
Поскольку порядок двух матриц одинаков, матрицы равны тогда и только тогда, когда их соответствующие элементы также равны.
Таким образом, сравнивая a и c с соответствующими элементами другой матрицы, мы имеем a = 69и z = 420.
Решение равенства матриц
Мы узнали, что подразумевается под равенством матриц, а также условия, необходимые для равенства матриц. Теперь решим равенство матриц. Например, рассмотрим две матрицы: A = [aij] и B = [bij]. Теперь две матрицы A и B называются равными тогда и только тогда, когда порядок обеих матриц одинаков, а также равны их соответствующие элементы, т. е. a ij = b ij для всех i и j.
Сначала рассмотрим две одинаковые матрицы A и B.
Так как данные матрицы равны, то A = B. матриц выполняется тогда и только тогда, когда соответствующие элементы также равны.
Итак, 2a + 3b = 5 ⇢ (1)
a + b = 1 ⇢ (2)
a = 1 − b ⇢ (3)
Теперь подставим значение a = 1 − b в уравнение (1)
⇒ 2 (1 − b) + 3b = 5
⇒ 2 − 2b + 3b = 5
⇒ 2 + b = 5
⇒ b = 5 − 2 = 3
Теперь подставим значение б =3 в уравнении (3)
⇒ a = 1 − 3 = −2
Таким образом, данные матрицы называются равными, если a = −2 и b = 3.
Примеры задач
Задача 1. Равны ли матрицы и ?
Решение:
Данные матрицы имеют одинаковый порядок, а значит, имеют одинаковое количество строк и столбцов. В результате выполнен первый критерий равенства матриц. Первое условие равенства матриц выполнено. Теперь необходимо рассмотреть второе условие, т. е. равенство соответствующих элементов. Как видно, элемент в первой строке и первом столбце первой матрицы равен 2 в первой матрице и -1 во второй матрице, что указывает на то, что не все элементы равны.
Следовательно, две матрицы не равны.
Задача 2. Найдите значения a, b, x, если A = [a+b 6 8 2x 3b] и B = [3 6 8 14 9] равны.
Решение:
Так как матрицы A и B равны, то их соответствующие элементы также равны. Имеем
a + b = 3, 2x = 14, 3b = 9
⇒ x = 24/2 = 12, b = 9/3 = 3
⇒ a + 3 = 3 [Из b = 3]
⇒ а = 0,
⇒ a = 0, b = 3, x = 7
Задача 3. Если , найдите значения a, b, x и y.
Если , найдите значения a, b, x и y.
Решение:
3x + 4y = 2, ⇢ (1)
x – 2y = 4, ⇢ (2)
a + b = 5, ⇢ ( 3)
2а – б = -5 ⇢ (4)
Решая уравнения (1) и (2),
x = 2y + 4 [Из (2)]
Подставляя вышеизложенное в (1),
3(2y + 4) + 4г = 2
⇒ 6г + 12 + 4г = 2
⇒ 10y = 2 – 12
⇒ 10y = -10
⇒ y = -1
⇒ x = 2(-1) + 4
= -2 + 4
= 2
Аналогично, решая уравнения (3) и (4), мы имеем a = 0 и b = 5.
Задача 4: Из определения равенства матриц определите, равны ли приведенные ниже матрицы или нет.
Решение:
Порядок данных матриц M и N равен «3 × 2», т. е. они имеют 3 строки и 2 столбца. Таким образом, обе матрицы имеют одинаковое количество строк и столбцов. Итак, первые два условия равенства матриц выполнены.
Теперь давайте проверим соответствующие элементы данных двух матриц.
Мы видим, что элемент во второй строке и втором столбце матрицы M равен 5, тогда как матрица N равна 7. Так как 3 ≠ 7, данные матрицы не удовлетворяют третьему условию, т. е. соответствующие элементы заданного матрицы должны быть одинаковыми.
Следовательно, заданные матрицы M и N не равны.
Задача 5. Если матрицы A и B равны и A = [6 -12 18 24], то что такое матрица B?
Решение:
Учитывая, что матрицы A и B равны.
Порядок матрицы A — «1 × 4».
Значит, порядок матрицы B должен быть таким же, т. е. «1 × 4».
Мы знаем, что равенство матриц выполняется для тех, которые имеют одинаковые размерности и все одинаковые соответствующие элементы.
Теперь искомая матрица B = [6 -12 18 24].
Задача 6. Если , найдите значения x и y.
Так как матрицы A и B заданы равными, то их соответствующие элементы также равны.
У нас есть
x + y = -7
x – y = 2
Складывая два уравнения, мы имеем:
2x = -5
x = -5/2
Итак -5/2 -2 = 7
y = 9/2
Задача 7. Равны ли матрицы и ?
Решение:
Данные матрицы имеют одинаковый порядок, а значит, имеют одинаковое количество строк и столбцов. В результате выполнен первый критерий равенства матриц. Первое условие равенства матриц выполнено. Теперь необходимо рассмотреть второе условие, т. е. равенство соответствующих элементов. Как видно, элемент во второй строке и втором столбце первой матрицы равен 4 в первой матрице и 5 во второй матрице, что указывает на то, что не все элементы равны.
Следовательно, две матрицы не равны.
Часто задаваемые вопросы о равенстве матриц
Вопрос 1: Что такое равенство матриц?
Ответ:
Равенство матриц — это понятие матриц, которое определяется путем сравнения двух или более матриц, имеющих одинаковые размеры и все одинаковые соответствующие элементы.
Вопрос 2: Каковы условия равенства матриц?
Ответ:
Ниже приведены необходимые условия равенства матриц A = [a ij ] m×n и B = [b ij ] 9 0011 п×к чтобы быть правдой:
Матрицы A и B должны иметь одинаковое количество строк, т. е. m = p.
Матрицы A и B должны иметь одинаковое количество столбцов, т. е. n = q.
Соответствующие элементы матриц A и B должны быть равны, т. е. a ij = b ij для всех i и j.
Вопрос 3: Как доказать, что две матрицы равны?
Ответ:
Чтобы доказать равенство двух матриц, нужно доказать, что порядок данных матриц равен, т. е. одинаковое количество строк и столбцов, а также равны и соответствующие элементы .
Вопрос 4: Как решить равенство матриц?
Ответ:
Две равные матрицы можно решить, сравнив их соответствующие элементы.
Если есть какие-то неизвестные переменные, то решить их, приравняв их соответствующим элементам в другой матрице.
Объяснение урока: Равные матрицы | Nagwa
В этом объяснителе мы узнаем, как определить условия равенства двух матриц.
Учитывая, что линейная алгебра отличается от обычной алгебры, неудивительно, что существует речь идет о принципиально разных понятиях. Такие идеи, как порядок, тип и транспонирование просто не появляются в обычной алгебре. В традиционной алгебре две величины равны, если они имеют одинаковое значение. Например, если у нас есть 𝑥=5 и 𝑦=5, то мы можем сказать, что эти две величины равны, и, следовательно, написать 𝑥=𝑦.
В качестве альтернативы, если у нас есть 𝑎=5 и 𝑏=−10, то, очевидно,
эти величины не равны, и мы будем писать 𝑎≠𝑏. Однако эти
количества связаны, и один из таких примеров состоит в том, чтобы сказать, что 𝑎=−12𝑏
или, что то же самое, 𝑏=−2𝑎.
Чтобы линейная алгебра была корректно определена, нам нужно иметь определение равенства, что позволит нам описать отношения между матрицами. Понятие равенства в обычная алгебра такова, как мы описали выше, но для линейной алгебры нам нужно рассмотреть что матрицы имеют несколько элементов, и поэтому наше определение равенства должно учитывать этот.
Определение: равенство двух матриц
Рассмотрим две матрицы, 𝐴 с порядком 𝑚×𝑛 и 𝐵 с порядком 𝑝×𝑞, описываемые их записями следующим образом: 𝐴=𝑎,𝐵=𝑏.
Тогда мы говорим, что две матрицы равны, т. е.
𝐴=𝐵, если их размерности равны и
соответствующие записи идентичны.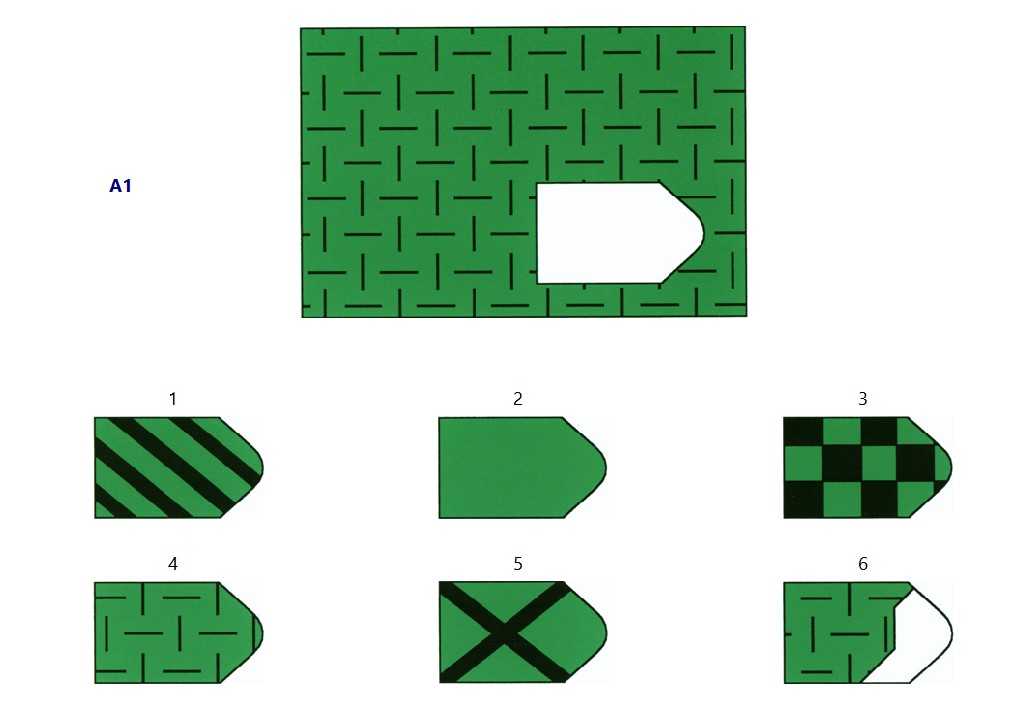 Другими словами, следующие два
должны быть выполнены условия:
𝑚=𝑝,𝑛=𝑞,𝑎=𝑏,𝑖,𝑗.для всех
Другими словами, следующие два
должны быть выполнены условия:
𝑚=𝑝,𝑛=𝑞,𝑎=𝑏,𝑖,𝑗.для всех
И наоборот, если 𝑚≠𝑝 или 𝑛≠𝑞, или есть какие-то 𝑖 и 𝑗 такой, что 𝑎≠𝑏, тогда две матрицы не равны; то есть 𝐴≠𝐵.
Заметим, что это определение равенства явно более строгое, чем регулярное равенство вида 𝑎=𝑏, так как нам нужно проверить оба размеры матриц и все элементы в каждой матрице для равенство. В частности, даже если все возможные пары записей равны, если размерности также не равны, то матрицы не могут быть равными. Мы продемонстрируем это на следующем примере.
Пример 1: Условия равенства матриц
Учитывая, что 𝐴=333333,𝐵=3333, верно ли, что 𝐴=𝐵?
Ответ
Матрицы 𝐴 и 𝐵 можно записать в виде 𝐴=𝑎,𝐵=𝑏.
Напомним, что для того, чтобы две матрицы были равны, обе их размерности
и их записи должны быть равны. При этом мы замечаем, что некоторые
пары записей равны. Например, у нас есть
𝑎=𝑏=3,𝑎=𝑏=3,𝑎=𝑏=3,𝑎=𝑏=3.0003
Например, у нас есть
𝑎=𝑏=3,𝑎=𝑏=3,𝑎=𝑏=3,𝑎=𝑏=3.0003
Однако порядки матриц не равны. Матрица 𝐴 состоит из двух строк. и три столбца, так что это матрица 2 × 3, а матрица 𝐵 имеет две строки и два столбца, что делает ее Матрица 2×2. Мы обводим этот дополнительный столбец ниже:
Поскольку порядки этих матриц не эквивалентны, неверно, что 𝐴=𝐵.
Обратите внимание, что наличие двух матриц одного порядка является необходимым условием равенства, но не достаточное условие. Тот факт, что две матрицы имеют один и тот же порядок, не означает, что что они автоматически равны. Это очень просто продемонстрировать с помощью двух матрицы ниже:
Обе эти матрицы имеют 3 строки и 4 столбца, поэтому обе имеют порядок 3×4. Это также очень простые матрицы, в которых каждая запись равна нулю.
кроме 𝑎, которые мы выделили. Однако, учитывая, что
𝑎≠𝑏, эти матрицы не равны, поэтому мы пишем
𝐴≠𝐵.
Пример 2. Определение равенства матриц
Если 𝐴=−53−7−3,𝐵=−5−3−73, верно ли, что 𝐴=𝐵?
Ответ
Напомним, что для проверки равенства двух матриц необходимо подтвердить что они имеют одинаковый порядок и что 𝑎=𝑏 для все 𝑖 и 𝑗.
Эти две матрицы имеют порядок 2×2, поэтому для проверки на равенство нам придется проверять каждую запись. В приведенных ниже матрицах мы выделили каждую запись другим цветом для удобства сравнения: 𝐴=−53−7−3,𝐵=−5−3−73.
Сравнивая верхние левые записи, мы находим, что
𝑎=𝑏=−5 и сравнивая нижний левый
записей, мы получаем 𝑎=𝑏=−7. Однако,
изучив записи в правом верхнем углу, мы находим, что
𝑎=3, а 𝑏=−3; следовательно
𝑎≠𝑏. Точно так же в правом нижнем углу
мы можем видеть, что 𝑎=−3, а
𝑏=3, поэтому
𝑎≠𝑏. Поскольку эти матрицы не удовлетворяют
условие 𝑎=𝑏 для всех
𝑖,𝑗, они не равны.
При работе с большими матрицами тот же принцип действует точно так же, только с большим количеством сравнений. На практике вместо того, чтобы записывать каждый одно сравнение, мы просматривали бы две матрицы, чтобы найти любую разницу между парами записи. Например, рассмотрим две матрицы порядка 3×3: 𝐴=−214320−152,𝐵=−214310−1−52.
Учитывая, что эти матрицы имеют одинаковый порядок, мы затем ищем пары элементов, которые различаются: 𝐴=−214320−152,𝐵=−214310−1−52.
У нас есть это 𝑎≠𝑏 и это 𝑎≠𝑏, что дает две причины, почему 𝐴≠𝐵.
Пример 3. Решение уравнений с помощью матричного равенства
Учитывая, что 3𝑥−3−3−10𝑦−1=0−3−105𝑦−5, найдите значения 𝑥 и 𝑦.
Ответ
Напомним, что для равенства двух матриц при условии, что они имеют тот же порядок, мы должны иметь это 𝑎=𝑏 для всех 𝑖 и 𝑗.
Начнем с выделения всех записей, которые мы должны сравнить:
3𝑥−3−3−10𝑦−1=0−3−105𝑦−5.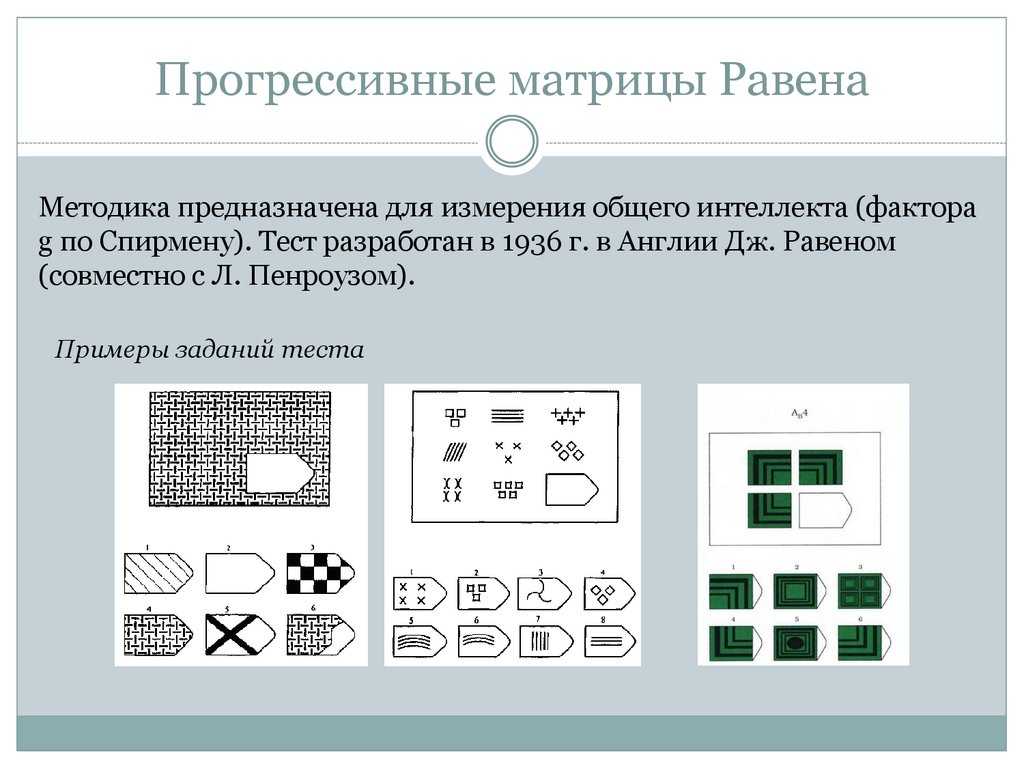
Имеются две пары элементов, явно равных в обеих матрицах, а именно, что 𝑎=𝑏=−3 и что 𝑎=𝑏=−10.
Чтобы убедиться, что эти матрицы равны, мы устанавливаем 𝑎=𝑏, что подразумевает, что 3𝑥−3=0, что дает 𝑥=1. Теперь мы устанавливаем 𝑎=𝑏, что дает 𝑦−1=5𝑦−5 и следовательно, 𝑦=1. Таким образом, окончательная матрица 0−3−100, и 𝑥=1, 𝑦=1.
Приведенный выше вопрос показывает, насколько сильно условие равенства матриц является ограничительным. обе матрицы в предыдущем вопросе были порядка 2 × 2 и, следовательно, имели по 4 записи в каждой. Сразу же мы могли заметить, что две пары записей были идентичны во всех обе матрицы. Несмотря на то, что мы нашли два случая равенства, нам все равно нужно было проверить два оставшиеся пары записей. Если бы любая из этих пар элементов была неравной, матрицы не были бы равными по определению.
Следующие два примера демонстрируют, как равенство между матрицами может основываться на
правильное вычисление нескольких переменных.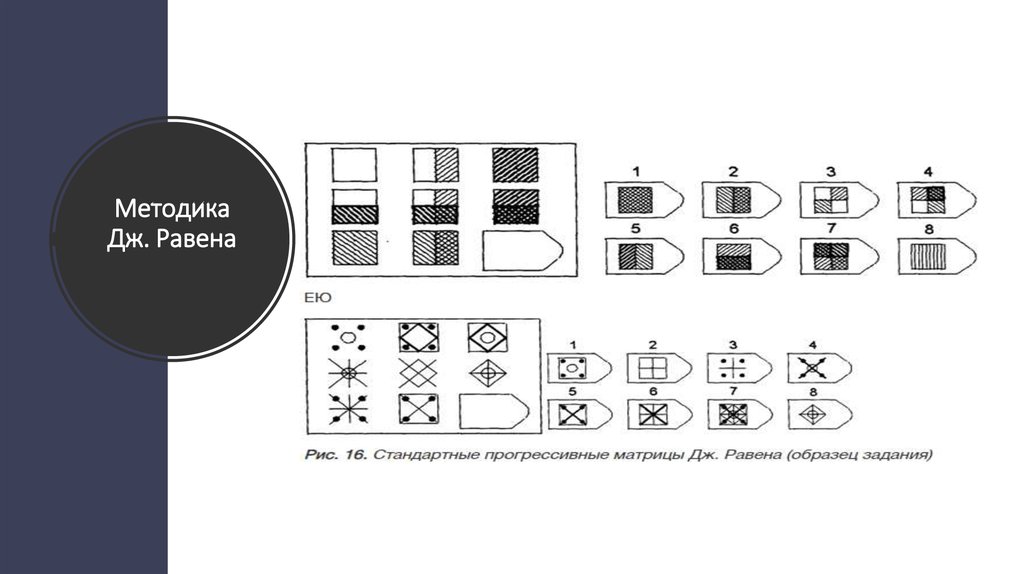
Пример 4. Решение уравнений с использованием матричного равенства
Найдите значения 𝑥 и 𝑦, учитывая следующее: 10𝑥+102−39=2022𝑦+99.
Ответ
Мы выделяем каждую пару записей, как показано: 𝑎=𝑏=9, поэтому для этих записи.
Полагая 𝑎=𝑏, получаем уравнение 10𝑥+10=20. Решая это для 𝑥, мы получаем 10𝑥=10𝑥=1𝑥=±1.
Установив 𝑎=𝑏, имеем −3=2𝑦+9, что означает что 𝑦=−6. Таким образом, 𝑥=±1 и 𝑦=−6.
Пример 5. Решение уравнений с помощью матричного равенства
Учитывая, что 𝑐, и 𝑑.
Ответ
Напомним, что для двух матриц одного порядка они равны только если все их соответствующие записи равны. Таким образом, мы можем сделать сравнение для каждой записи: 𝑎+𝑏𝑎−𝑏𝑎+𝑏+𝑐𝑎−7𝑏−𝑑=−3−17−5−64, что дает систему линейные уравнения
Заметим, что первые два уравнения, 𝑎+𝑏=−3 и
𝑎−𝑏=−17, можно сложить вместе, чтобы исключить член 𝑏. Это дает нам
2𝑎=−20𝑎=−10.
Это дает нам
2𝑎=−20𝑎=−10.
Подставив это значение 𝑎 в первое уравнение (хотя второе тоже можно использовать), получаем −10+𝑏=−3𝑏=7.
Теперь, когда мы нашли 𝑎 и 𝑏, мы замечаем, что можем решить 𝑎+𝑏+𝑐=−5 для 𝑐. Это дает нам −10+7+𝑐=−5𝑐=−2.
Наконец, мы можем найти 𝑑 из последнего уравнения, 𝑎−7𝑏−𝑑=−64: −10−7×7−𝑑=−64−𝑑=−5𝑑=5.
Таким образом, мы получаем 𝑎=−10, 𝑏=7, 𝑐=−2 и 𝑑=5.
В поверхностном смысле проверка на равенство матриц есть не что иное, как проверка на
несколько отдельных экземпляров равенства для всех элементов матрицы. В конечном счете, это
Мягкая оценка абсолютно точна, как и определение матричного равенства.
требуют сравнения всех элементов двух задействованных матриц. Однако ситуация меняется
когда мы работаем с матрицами, у которых есть записи, которые в некоторой степени заполнены
переменные, а также числа. Эта гибкость в сочетании с другими операциями из
линейная алгебра (например, умножение матриц, возведение матриц в степень и обращение матриц),
позволяет строить более сложные математические задачи, как мы видели выше.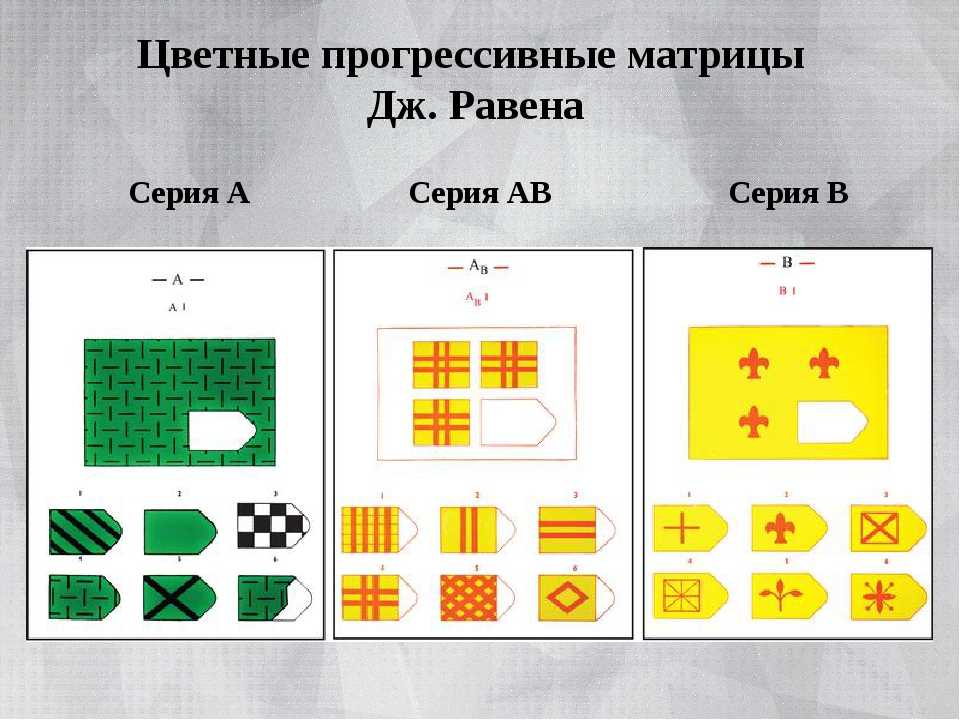 Для
Например, когда матричное умножение определено, можно закодировать все
системы линейных уравнений в терминах простых матричных уравнений, обеспечивающих мощный и
краткий язык для работы с такими сложными понятиями. Хотя определение матричного равенства
может показаться ненужным или тривиальным, это имеет решающее значение для понимания линейной
алгебра и многие незаменимые математические инструменты, которые предоставляет эта область.
Для
Например, когда матричное умножение определено, можно закодировать все
системы линейных уравнений в терминах простых матричных уравнений, обеспечивающих мощный и
краткий язык для работы с такими сложными понятиями. Хотя определение матричного равенства
может показаться ненужным или тривиальным, это имеет решающее значение для понимания линейной
алгебра и многие незаменимые математические инструменты, которые предоставляет эта область.
Ключевые точки
- Рассмотрим две матрицы, 𝐴 с порядком 𝑚×𝑛 и 𝐵 с порядком 𝑝×𝑞, описываемые своими записями следующим образом: 𝐴=𝑎,𝐵=𝑏. Тогда 𝐴=𝐵 тогда и только тогда, когда 𝑚=𝑝,𝑛=𝑞,𝑎=𝑏,𝑖,𝑗.для всех
- Равенство матриц является строгим условием. Если есть 𝑖 и 𝑗 такие, что 𝑎≠𝑏, тогда 𝐴≠𝐵.
- Кроме того, если 𝐴 и 𝐵 имеют разные порядки, тогда 𝐴≠𝐵.
- Мы можем найти пропущенные значения, которые делают две матрицы равными, на
составление и решение уравнений.




 Мы видим, что элемент во второй строке и втором столбце матрицы M равен 5, тогда как матрица N равна 7. Так как 3 ≠ 7, данные матрицы не удовлетворяют третьему условию, т. е. соответствующие элементы заданного матрицы должны быть одинаковыми.
Мы видим, что элемент во второй строке и втором столбце матрицы M равен 5, тогда как матрица N равна 7. Так как 3 ≠ 7, данные матрицы не удовлетворяют третьему условию, т. е. соответствующие элементы заданного матрицы должны быть одинаковыми. У нас есть
У нас есть
 Если есть какие-то неизвестные переменные, то решить их, приравняв их соответствующим элементам в другой матрице.
Если есть какие-то неизвестные переменные, то решить их, приравняв их соответствующим элементам в другой матрице.