Таблицы равена для детей: Недопустимое название — Psylab.info
НОРМЫ МАТРИЦЫ РАВЕНА
НОРМЫ ПО ТЕСТУ «МАТРИЦЫ РАВЕНА»
% | 5.03-5.08 | 5.09-6.03 | 6.04-6.08 | 6.09-7.02 | 7.03-7.08 | 7.09-8.02 | 8.03-8.08 | 8.09-9.02 | 9.03-9.08 | 9.09-10.02 | 10.03-10.08 | 10.09-11.02 | 11. |
95 | 22 | 24 | 26 | 28 | 31 | 32 | 33 | 34 | 35 | 35 | 35 | 35 | 35 |
90 | 20 | 21 | 23 | 25 | 28 | 30 | 32 | 33 | 33 | 33 | 34 | 35 | 35 |
75 | 18 | 19 | 20 | 21 | 23 | 25 | 27 | 29 | 31 | 32 | 33 | 33 | 34 |
50 | 15 | 16 | 17 | 18 | 20 | 22 | 24 | 26 | 28 | 30 | 31 | 31 | 32 |
25 | 12 | 13 | 14 | 16 | 17 | 18 | 20 | 22 | 24 | 25 | 26 | 28 | 30 |
10 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 19 | 21 | 22 | 23 | 25 |
5 | 8 | 9 | 11 | 12 | 13 | 14 | 14 | 15 | 16 | 17 | 18 | 20 | 22 |
КАК РАБОТАТЬ С ЭТОЙ ТАБЛИЦЕЙ?
1.
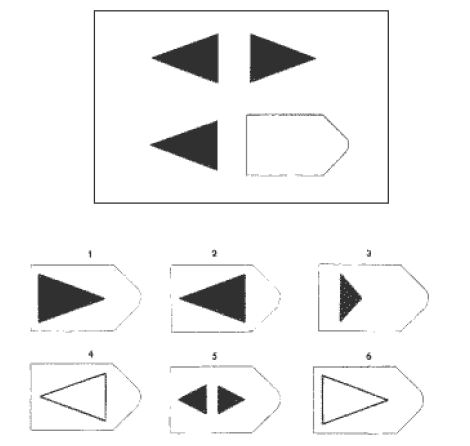Чётко зафиксируйте возраст ребёнка (сколько лет, сколько месяцев на момент
обследования). Найдите его возрастную
категорию в самой верхней строке таблицы.
Каждый столбец таблицы включает группу
детей с разницей в полгода между самым
младшим и самым старшим в этой группе,
например: 8.03-8.08 (столбец 8). Это значит,
что в данном столбце представлены данные
по детям от 8 лет 3 месяцев до 8 лет 8
месяцев.
2. Когда ребёнок выполняет тест, фиксируйте количество верно решённых заданий (удобно ставить палочку в протоколе за каждое верно решённое задание).
Если Вы проводите тест в классическом варианте, Вы присваиваете верно решённой задаче 1 балл, всем нерешённым – 0 баллов.
Если же Вы даёте и модифицированный вариант, то Вы помогаете ребёнку с теми заданиями, с которыми он не справился, задавая наводящие вопросы. Тогда баллы начисляются так:
1 балл – за самостоятельное верное решение
½ балла – за решение, когда сначала ребёнок ошибся, но Вы сказали: «Посмотри, что ещё тут подойдёт? Какой ещё вариант может быть?» — и он дал верный ответ
¼ балла – за решение, когда Вы помогали
его найти (видишь, тут квадратики, а тут
ромбики, значит у нас будет что?.
3. Подсчитайте сумму баллов. В классическом варианте вы считаете просто количество верных ответов. В модифицированном варианте Вы считаете отдельно сумму единиц (самостоятельно решённых заданий) и отдельно сумму всех решённых заданий (единицы + половинки баллов + четвертинки баллов). Когда Вы будете анализировать результаты ребёнка, Вы сравните, насколько велико улучшение в модифицированном варианте. Эта информация позволяет седлать вывод об уровне обучаемости ребёнка.
4. Вам нужно найти, на какой процентиль
работал ваш испытуемый, то есть, соотнести
его результат с нормой. В самом первом
столбце таблицы указаны процентили.
Процентиль – это то, какой процент детей
данного возраста выполнил задания на
такой же балл и хуже, чем Ваш испытуемый.
Серым цветом выделена середина (50
процентиль). Нормой считается 50
— вернитесь к тому столбцу, где указан
возраст испытуемого.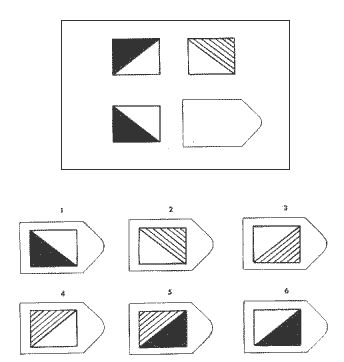
— найдите в столбце число, указывающее его сумму баллов. Например, ребёнок верно выполнил 27 заданий – смотрим – это 75 процентиль (он выполнил задание лучше и также, как 75% его ровесников. Высокий уровень невербального интеллекта). Если ребёнок выполнил верно 24 задания, это 50 процентиль (норма).
— Если Вашей суммы нет в таблице, Вам надо самостоятельно подсчитать, какому процентилю примерно соответствует его результат. Например, ребёнок верно выполнил 25 заданий. Мы работаем так:
— ближайшее к нашему значение в таблице – 24 балла (50 процентиль). Между 24 и 27 баллами (ближайшие к нашему значения в таблице) находится 3 балла (27 – 24 = 3) и 25 процентилей (75 – 50 = 25). Ваш испытуемый сделал на 1 балл лучше, то есть, на треть. Посмотрим на процентили. Треть от 25 – это около 8. Значит, ваш испытуемый получает 50 + 8 проценить = 58 процентиль – уровень высокой возрастной нормы.
Приведём ещё пример.
Испытуемому 6 лет
9 месяцев, и он верно выполнил 15 заданий.
Алгоритм работы:
— находим его столбец (это пятый столбец: 6.09-7.02).
— 15 баллов (наш результат) там не встречается. Ближайшее к 15 значение – 16, соответствует 25 процентилю. Между этим значением и более низким (16 и 13) 3 балла разницы и 15 процентилей (25-10=15). Наш испытуемый сделал на 1 балл, на треть хуже, чем 25 процентиль. Треть от 15 – это 5.
— находим его процентиль: 15 баллов = 25-5=20 – 20 процентиль – это уровень ниже возрастной нормы. Невербальное развитие отстаёт от возрастной нормы.
5. Аккуратно оформляем запись в своих протоколах и в заключении. Записываем балл, процентиль, особенности выполнения теста (может быть, ребёнок утомлялся? Не хотел делать? Уже делал тест? Слишком поспешно находил ответ, а потом видел верное решение? – и т.п.). Это может очень сильно сказываться на результатах обследования.
Если Ваш испытуемый продемонстрировал
низкий уровень интеллекта, а также если
он показал высокие результаты, а учителя
/ родители / другие специалисты считают
его неразвитым, ОБЯЗАТЕЛЬНО сочетайте
этот тест с другими методиками оценки
интеллекта.
Лучше всего – с «Четвёртый
лишний» — Вы увидите вербальный интеллект.
Вообще, к оценке интеллекта надо подходить
очень осторожно; очень корректно
преподносить результаты; всегда
расшифровывать, какие именно
интеллектуальные способности стоят за
заданиями методики.
1 2 3
1 2 3 База данных защищена авторским правом ©dogmon. | Главная страница Автореферат Анализ Анкета Биография Глава Диплом Дипломная работа Диссертация Доклад Задача Закон | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
, переработанное — 68 с., приложения 
М. Акимова М.К Борисова Е.М. Козлова В.Т. Логинова Г.П.
.. 
Буком в 1948 г. Н-Т-Р (английская абривиатура теста Дом-дерево-человек)
П. Андрющенко Д.В.
П. Борисова Е.М.
.. 
Л.
org 2022Исследования уровня и динамики интеллектуального развития детей дошкольного и младшего школьного возраста
Библиографическое описание:Щербакова, Т. А. Исследования уровня и динамики интеллектуального развития детей дошкольного и младшего школьного возраста / Т. А. Щербакова. — Текст : непосредственный // Молодой ученый. — 2009. — № 2 (2). — С. 324-327. — URL: https://moluch.ru/archive/2/78/ (дата обращения: 18.10.2022).
Рассмотрим, что такое интеллект – это общая способность к познанию и решению проблем, определяющая успешность любой деятельности и лежащая в основе других способностей; это система всех познавательных способностей человека: ощущения, восприятия, памяти, представления, мышления, воображения; это способность к решению проблем «в уме», без проб и ошибок.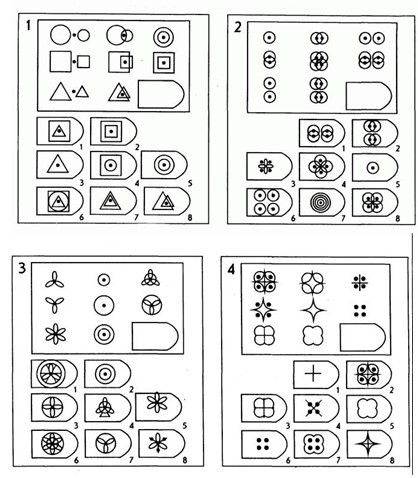
Следовательно, в понятие интеллекта можно включить и формирование речи, и формирование привычных навыков самообслуживания, так или иначе, влияет на умственную деятельность ребенка [4].
Л.С. Выготский ввел понятие о двух уровнях умственного развития ребенка: первый уровень – зона активного развития; второй уровень – зона ближайшего развития.
Первый уровень характеризует собой уже доступный ребенком уровень развития. Это уровень интеллектуальных задач, которое он способен решать полностью самостоятельно, без помощи взрослого.
Второй уровень обнаруживается не в самостоятельном, а в совместном с взрослыми решении задач ребенком. Второй уровень выше первого, т.к. ребенок еще не в состоянии справиться с заданием самостоятельно, поэтому решает поставленную задачу при помощи взрослого более сложные задачи.
В детском саду и в школе учат чему-то новому, продвигая ребенка в его развитии, давая возможность постараться, сделать немножко больше, чем-то, что ему и так легко дается.
Ребенок еще не в состоянии справиться с заданием самостоятельно, поэтому решает поставленную задачу при помощи взрослых.
Л.С. Выготский сделал следующие выводы:
— обучение создает зону ближайшего развития, которая затем переходит в сферу актуального развития;
— обучение двигает вперед развитие, опираясь не только на созревание функции, но и на те, которые еще созревают. Обучение должно идти вперед развития.
— педагогика должна ориентироваться не на вчерашний, а на завтрашний день развития (зона ближайшего развития ребенка) [2].
Институтом гигиены детей и подростков разработаны и отобраны критерии, при котором можно косвенно судить об умственном развитии и степени функциональной готовности детей к обучению в школе. Если уровень развития соответствует стандарту, то ребенок может быть признан готовым к школе.
При помощи тестов можно изучить эффективность разных программ и выяснить, насколько они способствуют умственному развитию детей. Во многих зарубежных странах результаты тестовых обследований служат основанием для распределения детей по разным типам классов и школ.
Тесты могут оказать большую помощь при выявлении детей с задержками развития, которые могут быть вызваны слабым состоянием здоровья, снижением слуха, недостатками воспитания. Поэтому, вслед за тестами должны применяться другие методы исследования детей.
Наибольшее значение имеют тесты, направленные на определение уровня общего умственного развития детей, так называемые интеллектуальные тесты. Они всегда состоят из незнакомых детям заданий, выполнение которых требует применения различных умственных действий, следовательно, дают возможность обнаружить, в какой-то мере ребенок этими действиями владеет.
Качество интеллектуального теста зависит от того, насколько научно обоснован подбор входящих в него заданий. Умственное развитие ребенка очень сложный процесс, включающий много сторон и проявлений. Тестовые задания должны выявлять уровень развития главных из этих сторон, определяющих все остальные, чтобы по ним действительно можно было сделать вывод об умственном развитии в целом [7].
Несмотря на то, что тесты Керна, М. Ирасека Г. Вицлака, А.З. Зака являются распространенным способом диагностики уровня умственного развития, объемность (громоздкость) диагностирования по данным тестам привели к необходимости поиски показателей, позволяющих исследовать детей в протяжении многих лет, не требуя специальных условий, не занимая много времени, не утомляя детей, найти более динамичную форму проведения исследования. Диагностика умственного развития должна вскрывать не мифический, интеллектуальный потенциал, а реальные достижения ребенка, сложившиеся в ходе воспитания и обучения [3].
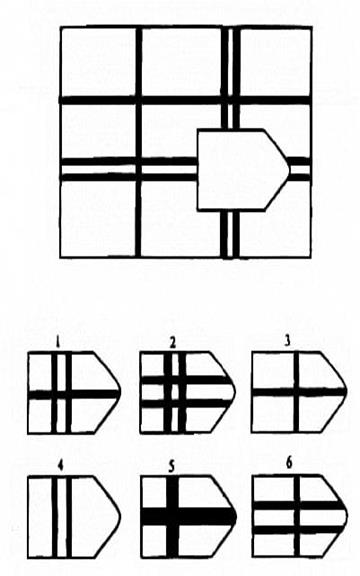
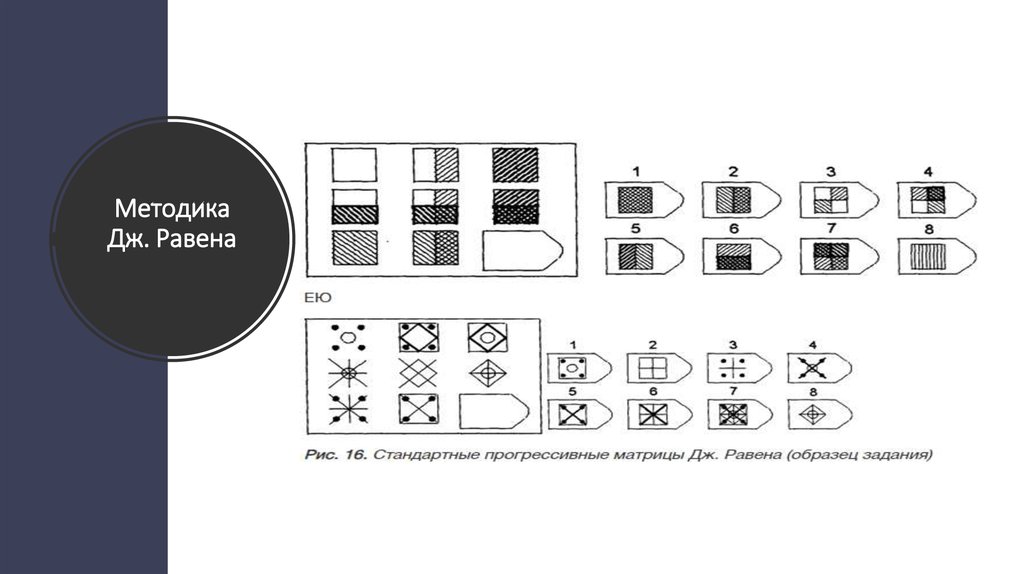
Более приемлемой формой исследования нам подошла методика Равена – одна из наиболее прогностических методик для исследования невербального интеллекта. Может использоваться как в комплексе с другими психодиагностическими методиками, так и отдельно. Обследование вызывает позитивную реакцию испытуемых. Может применяться как индивидуально, так и в группе. Матрицы Равена предназначены для определения уровня интеллектуального развития.
Серия карточек (матриц) с заданиями возрастающей сложности может применяться при обследовании лиц с любым языковым и социокультурным фоном, с любым уровнем речевого развития, что создает преимущества их использования при обследовании детей с речевыми нарушениями первичного характера.
При исследовании по этому методу можно выявить способности систематизации в мышлении, способности логически мыслить и раскрывать существенные связи между предметами и явлениями.
Цветной вариант матриц, предназначен для обследования детей от 5 до 11 лет. В процессе выполнения составляющих тест заданий проявляются три основных психических процесса: внимание, восприятие и мышление. В результате анализа ответов можно судить об уровне развития наглядных форм мышления.
Кроме уровня интеллектуального развития детей методика Равена дает возможность проанализировать и процесс решения задачи. Скорость ответа ребенка (время реакции) позволяет выделить импульсивных детей, которые отвечают не подумав, практически сразу после того, как они услышали инструкцию.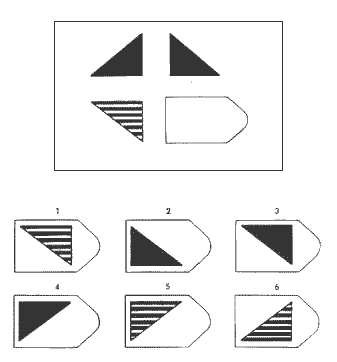
Время реакции у таких детей – 15-20 секунд. Большое количество неправильных ответов (до 50%) у них связано не с интеллектуальными трудностями, а с нарушением внимания, его низкой концентрацией, а также с неумением спланировать свою деятельность. Эти дефекты, не будучи собственно дефектами мышления, могут существенно снизить успеваемость ребенка в школе, а потому очень важно во время их выявить и, по возможности, скорректировать. Уменьшение поля обзора помогает снизить разброс внимания, а поэтому количество правильных ответов возрастает, когда мы закрываем три из шести предлагаемых для анализа вариантов. При занятиях с такими детьми необходимо специально выделять основные этапы ориентировки и последовательность операций, необходимых для правильного решения задачи. Возможно, прилагать специально вычерченные схемы деятельности, которые также помогут ребенку ее организовать.
Анализ процесса решения заданий в тесте Равена помогает также выявить обучаемость детей, которая часто соответствует их способностям.
Так, детям, которым трудно выполнять первые, достаточно легкие задания, необходимо объяснить путь их решения. В том случае, если дети моментально схватывают объяснения взрослого, быстро обучаются решать задачи этого типа, они могут перенести усвоенный прием и на более трудные, последние задания. Поэтому общий невысокий уровень работы этих детей, связан не с интеллектуальным дефектом, а с низким уровнем знаний, что может быть легко скорректировано при обучении. Иногда дети легко справляются с первыми заданиями, а более трудные не решают, не смотря на помощь взрослого. В этом случае можно говорить низкой обучаемости и необходимости большего внимания со стороны взрослых, более полных и длительных объяснений нового материала. Таким образом, в тесте Равена важно не только высчитать общее количество правильных ответов, но и выяснить, какие именно задания решил ребенок – только первые или и последние тоже [6].
Организация опытно-экспериментальной работы проходила в соответствии с традиционной схемой организации исследования, деления и определения экспериментальных и контрольных групп.
Для проведения исследования были выбраны экспериментальная группа (ЭГ), контрольная группа – (КГ-1) и контрольная группа – 2 (КГ-2). Всего 60 человек (10 мальчиков и 10 девочек в каждой группе). В ДОУ в ЭГ с 3 летнего возраста до 7 лет занятия проводились по Типовой программе и программе «Радуга», разработанная коллективом Института общего образования при Министерстве образования России под руководством Т.Н. Дороновой. Целью программы «Радуга» является обеспечение здорового образа жизни, полноценного физического и психического воспитания дошкольников (от 2 до 7 лет). В КГ-1 занятия проводились по Типовой программе и по развитию познавательных процессов (экологическое воспитание). В КГ-2 занятия проводились по Типовой программе с дополнением элементов ТРИЗ. После выпуска из детского сада дети пошли в разные школы с 3-ех и 4-ех летним начальным обучением, поэтому мы охватили 5-ые классы с учетом одного возраста. В СОШ в ЭГ и КГ-1 учителя начальных классов работали по образовательной программе.
Школа-гимназия (КГ-2) работала по концепции (системе) Л.В. Занкова, основанная на приоритетности развитие познавательных возможностей учеников (обучение на высоком уровне трудности).
Для проверки различия результатов контрольной и экспериментальной групп интеллектуального развития использовали методы математической статистики (методику расчета связных рангов, коэффициент корреляции Спирмена r при наличии связных рангов) [1, 5].
Для проверки существенности различий средних показателей интеллектуального развития (по тесту Равена) нами было проранжированы средние значения по группам. Расчеты подтверждают и по диаграмме видно [таблица 1], что средние показатели интеллектуального развития девочек в ЭГ и КГ-2 выше, чем в КГ-1. Проведенные по аналогичной методике расчеты в группе мальчиков подтверждают, что средние показатели интеллектуального развития [таблица 2] в ЭГ оказались ниже, чем в КГ-2, но выше, чем в КГ-1. Это можно объяснить тем, что в школу-гимназию были выбраны способные дети, которые прошли отбор.
Таблица 1
Таблица 2
Таким образом, результаты исследований интеллектуального развития детей дошкольного и младшего школьного возраста позволяют нам утверждать, что дошкольные учреждения в данных исследуемых группах работали на завтрашний день развития (зона ближайшего развития ребенка), а учителя начальных классов в данных исследуемых группах работали на зону активного развития ребенка [таблицы 1 и 2]. Полного использования резервов познавательных возможностей дошкольников достигнуто не было, следовательно, интеллектуальный потенциал дошкольников не был полностью востребован.
В результате исследования нами были сделаны следующие выводы:
1. Неполное использование резервов зоны ближайшего развития ребенка.
2. Поиск новых форм, методов, содержания и определения путей дальнейшего развития системы начального образования.
3. Для эффективного осуществления интеллектуального развития детей начального звена в общеобразовательной школе учитывать критический этап возрастного развития.
4. Создать необходимые условия и среду обучения.
Поиск новых путей активизации интеллектуального развития дошкольников и младшего школьного возраста детей является одной из неотложных задач современной психологии и педагогики.
Литература
1. Айвазян С.А. Теория вероятностей и прикладная статистика: учеб. для .
вузов /С.А. Айвазян, В.С. Мхитарян. М.: Юнити — Дана, 2001.- 656 с.
1. Выгодский Л.С. Избранные психологические исследования /Л.С. Выгодский. М.: Педагогика, 1982. – 125 с.
2. Диагностика умственного развития дошкольников. /Научно исследовательский институт дошкольного воспитания. Академия наук СССР. М.: Педагогика, 1978. — 132 с.
4. Дружинин А., Дружинина О. Ваш ребенок от 0 до 7 лет. Как развить интеллект вашего малыша. /Дружинин А., Дружинина О. М.: ЗАО Центрполиграф, 2008. — 191 с.
5. Железняк Ю.Д. Основы – научно методической деятельности в физической культуре и спорте: учеб. пособие для студ. высш. учеб.
заведений /Ю.Д. Железняк, П.К. Петров. — 3-е изд., испр. М.: Издательский центр «Академия», 2007. — 272 с.
6. Марценковская Т.Д. Диагностика психического развития детей. Пособие по практической психологии. /Т.Д. Марценковская. М.: Линка-Пресс, 2008. — 176 с.
7. Мухина В.С. Возрастная психология: учеб. для студ. вузов. /В.С. Мухина. М.: Издат. центр Академия, 1997. — 432 с.
Авторская справка
Щербакова Тамара Аркадьевна – старший преподаватель кафедры физического воспитания ФГОУ ВПО «Чувашская государственная сельскохозяйственная академия».
Контактный телефон: раб.т. – 8352- 62-20-14; дом.т. – 8352-53-36-28;
Электронная почта: tomrika.60@ mail.ru.
Хотели бы получить журнал, кол. 1 экз.
42800 Чувашская Республика г. Чебоксары ул. К. Маркса д. 29
Основные термины (генерируются автоматически): ребенок, умственное развитие, уровень, ближайшее развитие ребенка, задание, интеллектуальное развитие, интеллектуальное развитие детей, помощь взрослого, Типовая программа, уровень развития.
Факты об умножении: как учить таблицу умножения — Кейт Сноу
Изучите простой и эффективный метод обучения вашего ребенка таблице умножения. Кроме того, это ошибка № 1, которую допускают родители, обучая своих детей правилам умножения.
Как НЕ учить таблице умножения
В этой статье вы узнаете пошаговый план обучения ваших детей фактам умножения.
Но сначала давайте разберемся, чего НЕЛЬЗЯ делать.
Для многих людей запоминание фактов умножения равно механическому обучению . Итак, эти замечательные, благонамеренные родители считают, что есть только один способ помочь своим детям освоить факты умножения: сделать большую стопку карточек и начать сверлить.
Эти родители хотят для своих детей самого лучшего, но пропускают несколько шагов… и делают весь процесс намного более болезненным и утомительным, чем он должен быть.
Практика и упражнение действительно помогают детям запомнить факты умножения. Но они приходят в конец процесса, а не начало .
Пссс… хотите универсальный, открытый и доступный ресурс для обучения фактам умножения? Я собрал все эти шаги в одну книгу, чтобы помочь вашим детям освоить факты умножения.
Какие факты умножения (или таблицы умножения)? Почему они так важны?
Факты умножения (также известные как таблицы умножения) — это все задачи на умножение от 1 × 1 = 1 до 10 × 10 = 100.
- Связанный: Бесплатная печатная таблица умножения (пустая и заполненная)
Можете ли вы представить себе попытку найти общие знаменатели или эквивалентные дроби, не зная 5 × 6? Или пытаетесь выполнить деление в длинное, когда не совсем уверены, что такое 7 × 7? И даже не заставляйте меня разлагать полиномы на множители…
Помните это из Алгебры 1? Без полного овладения фактами умножения дети с трудом начинают решать деление, дроби и задачи с большими числами.
Они используют так много своей рабочей памяти для простых вычислений, что у них остается мало места в мозгу для понимания новых концепций.
В каком классе мои дети должны изучать факты умножения?
Третий класс . Таким образом, они хорошо подготовлены к решению математических тем третьего и четвертого классов, таких как многозначное умножение, эквивалентные дроби и деление. Но независимо от того, сколько лет вашему ребенку, изучение фактов умножения сделает его более уверенным и успешным в математике. Если ваш старший ребенок не усвоил факты умножения, еще не поздно.
Что мои дети должны знать, прежде чем запоминать факты умножения?
Прежде чем запоминать факты умножения, ваш ребенок должен сначала выучить факты сложения и факты вычитания. Каждый набор фактов логически строится на предыдущем наборе, поэтому важно, чтобы ваш ребенок изучал их именно в этом порядке.
Прежде чем ваш ребенок начнет запоминать факты умножения, вы должны сначала убедиться, что он понимает, что означает умножение.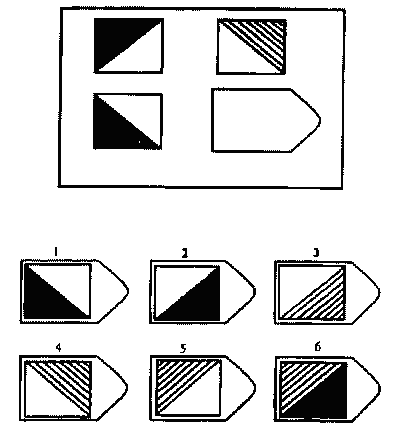
(Например, 3 × 8 означает «3 группы по 8».) Также помогает, если она умеет мысленно складывать однозначные числа с двузначными. (Вы узнаете больше о том, почему в шаге 3 ниже.)
Как быстро мои дети должны знать факты умножения?
Не более 3 секунды на каждый факт и быстрее, если возможно. Но многое зависит от вашего ребенка. Дети, которые очень быстро обрабатывают информацию, вполне способны усвоить каждый факт менее чем за 1 секунду, но детям с более медленным процессором всегда может потребоваться несколько секунд. Вы родитель и знаете своего ребенка лучше всех, поэтому подстраивайте свои ожидания под каждого конкретного ребенка.
Независимо от того, сколько лет вашему ребенку, старайтесь, чтобы время занятий было расслабленным и позитивным. Тесты на умножение и упражнения на время не нужны, если только ваш ребенок не чувствует цейтнота и не находит удовлетворение в том, чтобы бить часы.
Как научить ребенка фактам умножения
Обучение предшествует практике
Чтобы освоить факты умножения, нужно выполнить 5 шагов:
- Шаг 1.
Разбейте факты на удобные фрагменты. - Шаг 2. Конкретизируйте факты с помощью простого наглядного изображения.
- Шаг 3. Научите ребенка использовать простые факты в качестве трамплина к более сложным фактам.
- Шаг 4: Практикуйте каждую таблицу умножения отдельно, пока не освоите ее.
- Шаг 5. Попрактикуйтесь в сочетании фактов умножения.
Разбейте факты на удобные фрагменты.Обратите внимание, что практика не приходит до шага 4? Практика важна, но это не то, с чего вы начинаете! Обучение предшествует практике .
Шаг 1: Разбейте его.
Это короткий и простой шаг, но важный. Не перегружайте ребенка всеми 100 фактами умножения сразу. Вместо этого сосредоточьтесь только на одной таблице умножения за раз. (Таблица умножения — это всего лишь один набор фактов умножения. Например, таблица × 6 — это 1 × 6, 2 × 6, 3 × 6 и так далее до 10 × 6.)
Разбивка фактов умножения делает освоение таблиц намного более выполнимым (для детей и родителей ).
Кроме того, ваш ребенок может затем использовать более простые факты в качестве трамплина к более сложным фактам.
Шаг 2: Конкретизируйте факты с помощью массива умножения.
Для каждой таблицы умножения сначала убедитесь, что ваш ребенок точно понимает, что означают задачи на умножение. В противном случае числа — это просто последовательности абстрактных символов, и их намного сложнее запомнить.
В общем, я большой поклонник практических манипуляций, помогающих детям понять математику. Но с умножением манипуляции могут стать довольно громоздкими. У вас может уйти весь урок математики только на то, чтобы сосчитать 6 групп из 8 предметов, и ваш ребенок, вероятно, не будет намного ближе к тому, чтобы запомнить, что 6 × 8 равно 48.
Вместо этого я предпочитаю использовать простую сетку кругов, называемую точечный массив. С точечным массивом вы можете надеть L-образную крышку на верхнюю часть массива и показать любой факт умножения, который вы хотите, от 1 × 1 до 10 × 10.
Вот как выглядит массив точек и L-покрытие.
Вот как их использовать. Например, допустим, мы хотели помочь вашему ребенку понять, как выглядит 6 × 8. 6 × 8 означает «6 групп по 8», поэтому сдвиньте L-образную крышку, чтобы массив точек выглядел так.
В каждом из 6 рядов по 8 точек, поэтому имеется 6 групп по 8 точек. Таким образом, общее количество точек в массиве является ответом на 6 × 8.
- Связано: Загрузите свой собственный печатный массив умножения и L-обложку.
Как визуализация фактов умножения помогает детям запомнить ответы? Вот где начинается Шаг 3.
Шаг 3: Научите ребенка использовать более простые факты в качестве трамплина к более сложным фактам.
Умножение немного похоже на восхождение на огромную кучу камней. Когда вы пытаетесь достичь вершины, гораздо проще взобраться на несколько небольших камней, чем пытаться взобраться на отвесную скалу.
Вам определенно не стоит пытаться разобраться в этом! С фактами умножения гораздо проще использовать факты, которые вы уже выучили, в качестве «трамплина» к более сложным фактам, чем запоминать их наизусть.
Массив точек поможет вашему ребенку сделать это!
Например, давайте вернемся к 6 × 8. Это один из самых сложных фактов для запоминания детьми, но большинству детей это довольно легко, когда они используют 5 × 8 в качестве трамплина.
Вот как вы научите своего ребенка использовать простые факты в качестве трамплина к 6 × 8:
- 5 × 8 равно 40. арифметика обычно упрощает изучение фактов ×5.)
- 6 × 8 — это всего лишь еще одна группа из 8, чем 5 × 8.
- Итак, вы можете просто сложить 40 + 8, чтобы найти ответ: 6 × 8 = 48.
Эта стратегия работает для всех фактов ×6. И хорошая новость заключается в том, что для всех фактов умножения есть похожие стратегии!
- Связанный: Стратегии умножения, которые помогут вашему ребенку освоить таблицу умножения
Чтобы использовать ступени, полезно, если ваш ребенок умеет мысленно прибавлять однозначное число к двузначному. Если вашему ребенку не помешало бы еще немного попрактиковаться в умственном сложении, я подготовил небольшой урок и игру, которые помогут ему освежить этот навык.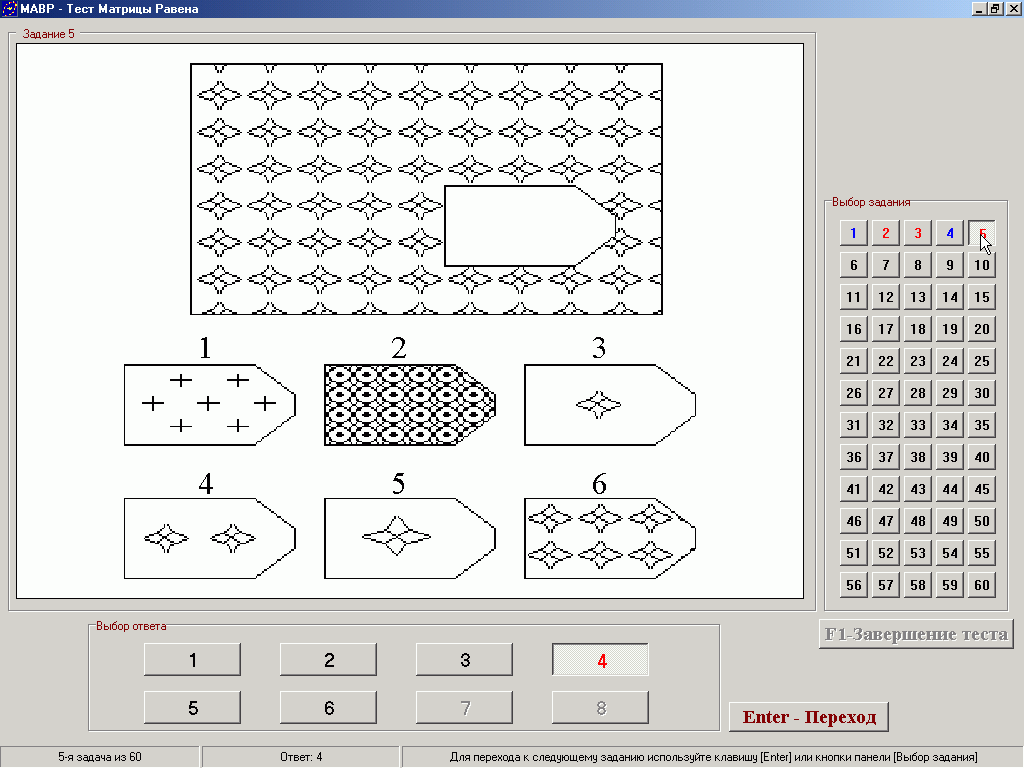
- Связанный: Умственная игра на сложение, которая на самом деле является игрой на умножение
С помощью этой комбинации массива точек и ступенчатых фактов у вашего ребенка есть план игры, чтобы навсегда освоить все факты умножения. (Без необходимости запоминать каждый факт по отдельности.) Теперь все, что вам нужно, это несколько эффективных практических приемов, которые помогут вашему ребенку полностью автоматизировать все факты умножения.
Шаг 4: Практикуйте каждую таблицу умножения отдельно, пока не освоите ее.
Как только ваш ребенок научится использовать начальные факты для таблицы умножения, сосредоточьтесь на этой конкретной таблице умножения в течение нескольких дней. Используйте сочетание практических методов, чтобы дать вашему ребенку разнообразие и сделать обучение умножению увлекательным. Мне нравится сочетать декламацию, игры и рабочие листы, чтобы дети говорили, видели и записывали факты.
Чтение
Я знаю, чтение таблицы умножения может показаться старомодным.
Но произнесение информации вслух помогает закрепить ее в памяти вашего ребенка. Кроме того, чтение каждой таблицы по порядку помогает вашему ребенку понять, как связаны факты в таблице. Например, повторение «1 × 7 равно 7. 2 × 7 равно 14. 3 × 7 равно 21…» напомнит вашему ребенку, что каждый новый факт в таблице × 7 на 7 больше, чем предыдущий факт. Таким образом, он может добавить 7 к каждому предыдущему факту, чтобы помочь ему запомнить следующий, потому что факты в таблице каждый раз добавляют новую группу из 7.
Игры
Люблю математические игры! Они делают математику веселой и общительной, но они также имеют огромное обучающее преимущество: когда вы играете с ребенком в игру на умножение, вы можете следить за тем, насколько хорошо ваш ребенок использует стратегии, и исправлять любые ошибки до того, как они укоренятся.
Рабочие листы
Рабочие листы не самые интересные, но они являются важным компонентом практики, так как ваш ребенок будет часто использовать умножение в своих письменных работах.
Рабочие листы должны быть короткими и понятными, чтобы ваш ребенок оставался бдительным и сосредоточенным.
Шаг 5: Смешайте эти факты умножения с другими таблицами умножения.
После того, как ваш ребенок освоил новую таблицу умножения, пришло время смешать эти факты умножения с фактами, которые он уже освоил. Смешивание их вместе обеспечивает кумулятивный обзор, так что факты закрепляются в ее долговременной памяти. Продолжайте использовать декламацию, игры и рабочие листы (и даже карточки, если хотите), пока ваш ребенок не выучит наизусть все 100 фактов.
- Связанный: 3 Веселые (и бесплатные!) Игры с фактами на умножение для печати для отработки фактов смешанного умножения
Обучение фактам умножения, которые НАПИСЫВАЮТСЯ
Итак, это все 5 шагов! Теперь у вас есть все необходимое для того, чтобы научить вашего ребенка фактам умножения (а не просто разучивать стопки карточек).
. (И эй, если вам нравится делать такие вещи, дерзайте!) Но если у вас есть другие дела, я уже сделал всю работу за вас.
Умножение фактов, которые запоминаются Он дает вам подробные планы уроков, веселые игры и простые рабочие листы для каждого шага процесса, так что вы можете научить своего ребенка фактам умножения, которые действительно склеивают .
Таблицы времени обучения с примерами из реальной жизни
Начальная математика
Несмотря на установленную законом проверку таблиц умножения, таблицы умножения важнее, чем просто запоминание сумм — они могут стать запоминающейся основой для более глубокого понимания детьми математики
- по Карен Уайлдинг
ПРОЧИТАЙТЕ, ЧТОБЫ УЗНАТЬ…
- «Почему» и «как», а не просто «что» о том, как учить таблицу умножения
- Как учить умножению помимо простого теста на таблицу умножения
- Как облегчить детям изучение более сложной таблицы умножения
- Примеры из жизни для использования при обучении таблице умножения
Прочтите за 6-8 минут…
» Многим детям умножение кажется всего лишь тем, что вы делаете с числами на уроках математики в школе: оно не имеет никакого отношения к реальному миру.
Понимание математики для детей младшего возраста 5-9 лет , Дерек Хейлок
» Что касается изучения математики, возможно, одна из немногих вещей, с которыми все согласны, это важность знания фактов умножения.
Тем не менее, зачем они нам нужны и как лучше их изучать остаются горячими темами, обсуждаемыми на протяжении веков.
Знание фактов умножения и таблиц умножения в качестве ключевой части нашего внутреннего «математического инструментария» чрезвычайно важно, потому что мы постоянно используем их в повседневной жизни.
Ключевые этапы 1 и 2 национальной учебной программы по математике
К сожалению, для большинства детей (и для поколений до них) основная цель изучения этих «таблиц умножения» не сосредоточена на этом осмысленном и мотивационном приложении, а вместо этого заучивает каждый факт наизусть, чтобы пройти классный тест, и часто на скорости. Что не весело.
Неспособность запомнить и быстро вспомнить эти факты приводится многими взрослыми в качестве доказательства их неудач в математике, что приводит к мышлению, которое полностью отвращает их от изучения этого замечательного предмета.
Итак, давайте согласимся, что факты умножения являются жизненно важными навыками для успешного математика.
Однако вместо традиционных подходов, использующих механическое заучивание, которые заставляют детей работать на значительно более низком уровне, чем те, кого учат с упором на «общую картину и связи» (Boaler, Mathematical Mindsets ), давайте посмотрим, как мы можем все они вовлекают детей со смыслом и применением, создавая прочные умственные связи и гибкость, работая с тем, как мы знаем, что мозг учится лучше всего.
Умножение как понятие – знание «Почему?» и «Как?», а не только «Что?»
Наличие «концептуального понимания» означает, что мы знаем, почему и как что-то работает, а не просто «как это сделать».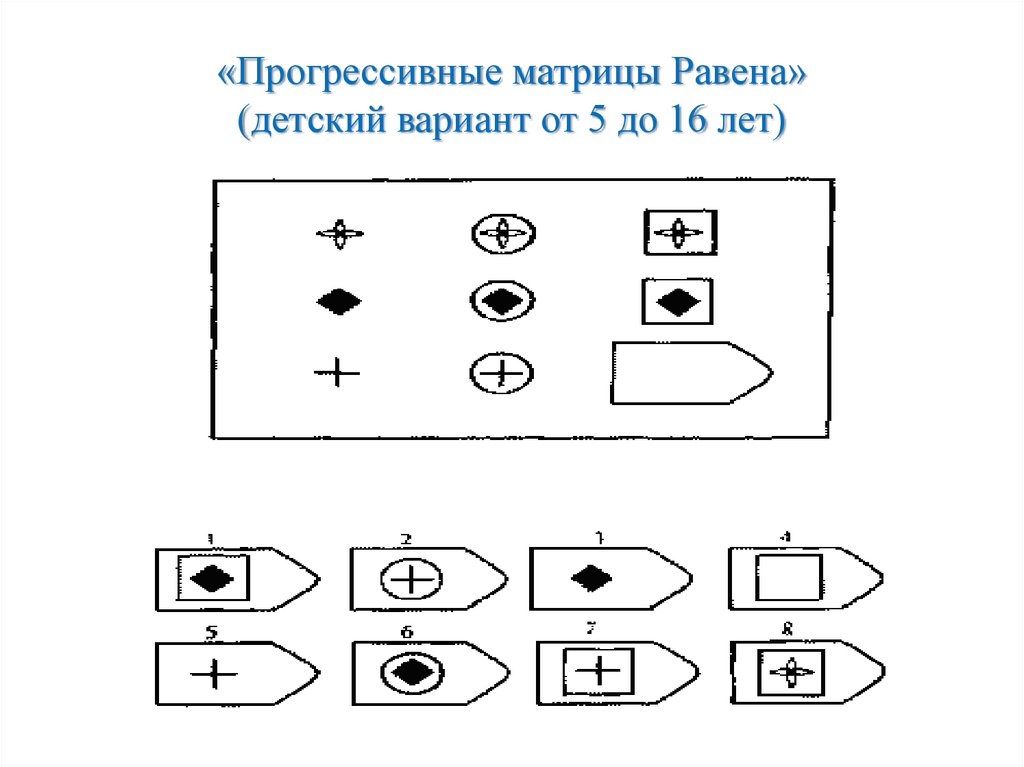
Традиционно математика в Великобритании сосредоточена на процедурах и запоминании, что означает, что дети не могут участвовать в происходящих жизненно важных процессах, что приводит как к плохой успеваемости, так и к отсутствию понимания фактической математики.
Итак, что мы подразумеваем под умножением? Ответ не так прост, как мы могли бы подумать. Здесь работают две основные структуры:
Умножение повторным сложением
Группы одинакового размера добавляются неоднократно, например, 3 + 3 + 3 = 3 x 3 (кстати, многие дети скажут вам, что 3 x 3 = 6, когда увидят это в записи, демонстрирующее отсутствие концептуального понимания)
Умножение путем масштабирования
Значение масштабируется по определенному коэффициенту, например, «Гигант был в 4 раза выше меня», что означает «Если мой рост составляет 1 метр, то 1 м x 4 = 4 м, поэтому великан должен быть 4 м в высоту»
Изучение таблицы умножения — это первая из этих двух структур — «повторяющееся сложение», — но, как мы видим, это также знания, на которые мы опираемся при решении задач, связанных с масштабированием.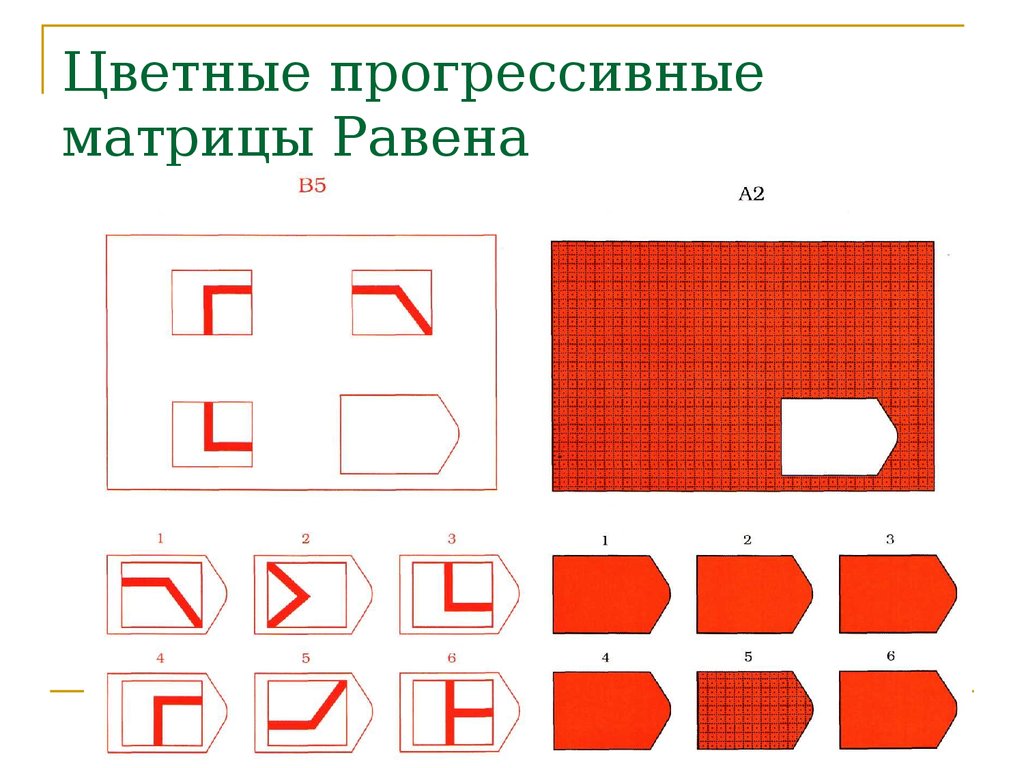
Идеи и подходы к обучению умножению с уместностью и пониманием
Следующие задания призваны помочь учителям и родителям представить изучение таблицы умножения как значимое и увлекательное занятие для всех детей. Человеческий мозг наиболее успешно усваивает математические факты через связь и осмысленное применение.
Счет и умножение – замечание и создание равных групп
Умножение как группировка является формой «быстрого» счета. Когда у нас есть три группы по три человека, мы можем сосчитать объекты единицами — 1, 2, 3, 4 и т. д. — но зная, что в первой группе 3, что к концу второй группы у нас будет 6, и что конце третьей группы у нас будет 9, означает, что нам нужно назвать только три цифры (вместо девяти).
Этот «быстрый счет» имеет смысл только тогда, когда дети могут видеть и связывать происходящие процессы.
Всем детям нужен большой опыт счета единицами, и если сравнить это с тем, что происходит, когда мы говорим только сумму групп, которые мы складываем (так, три группы по три в этом примере), чтобы они видели, что такое таблица умножения и как они ускоряют нашу способность считать и вычислять.
Остерегайтесь фразы «У Мэри был ягненок…» подходы к изучению таблицы умножения
Обучение детей перечислению чисел может звучать так, как будто у них есть знания по умножению: «Давайте посчитаем по 2 — 2, 4, 6, 8, 10…».
Но если мы рассмотрим это более внимательно, они часто начинают каждый раз с одного и того же места и, по сути, только что научились декламировать эквивалент детской песенки. Гибкое использование и применение этих знаний становится практически невозможным.
Таблица умножения – «учил» или «выучил»?
Взрослый: «Какая столица Франции?» Ребенок: «Париж!» Взрослый: «Вау, да. Удивительно, что ты был таким быстрым. Расскажите мне о Париже и Франции. Ребенок: Что такое «Париж и Франция»?
Изучение таблицы умножения с помощью человеческого тела
Ваше тело — отличная отправная точка для понимания и применения нашей таблицы умножения!
Подход «замечать и удивляться» к обучению
Начните это упражнение, попросив группу детей подойти и встать так, чтобы все могли их видеть.
Что мы замечаем в равных группах частей тела? Что мы можем увидеть и описать? Есть несколько вещей.
Что приходит за 2 секунды? Руки, ноги, ноги, глаза, уши?
Можем ли мы увидеть другие равные группы?
«Пальцы идут группами по 10 и 5», или нет? Что с большими пальцами? Означает ли это, что пальцы делятся на группы по 8 и 4? Сколько ушей у 2 детей? Или 5 детей?
Успешное изучение математики — это гораздо больше, чем процесс, а не цель. Чтобы гарантировать, что мы хвалим способность детей объяснять и доказывать свое понимание (вместо того, чтобы быстро выявлять факты, которые они могут знать, но не понимать).
«Конкретно-графический-абстрактный» подход к таблице умножения
Используйте взаимосвязанные кубики, чтобы изобразить равные группы «человеческого тела», которые замечают дети.
Ноги идут группами по две, так что здесь три группы ног — 2, 4, 6!
Поскольку наша система счета работает с основанием 10, используйте группы взаимосвязанных кубиков чередующихся цветов, чтобы создать числовую линию и объяснить, что происходит с суммами, когда мы добавляем более равные группы.
Здесь у нас есть три группы по два (представляющие нашу «историю о ногах»), и мы сравниваем их с группами по 10. Мы видим, что три группы по два на четыре меньше, чем 10. Нам нужно еще две группы, чтобы получить 10.
Задача умножения абстрактных символов
Теперь мы можем говорить о том, что мы построили, и зафиксировать это сначала как язык, а затем как символы, чтобы представить наше понимание.
Итак, я вижу 2 + 2 + 2 = 6
Таблицы времени ног животных
Думали ли мы когда-нибудь о том, чтобы использовать животных для изучения таблицы умножения? Только подумайте, сколько разного количества ног у животных — 2, 4, 6, 8, 10 — и у некоторых их так много, что их очень трудно сосчитать (а они не часто стоят на месте с таким количеством ног!).
Попросите детей провести исследование, чтобы выяснить, какие животные имеют определенное количество ног, и отсортировать их соответствующим образом.
Теперь создайте конкретные представления.
У собак четыре ноги, так что это может быть четыре собаки! Или львы, или жирафы, или муравьеды! 4, 8, 12, 16…
Теперь я могу сравнить четыре группы по четыре на моей числовой прямой, состоящей из десятков. Я вижу, что четыре группы по четыре больше 10 и меньше 20. Есть место для еще одной группы, равной 20, поэтому пять четверок должны быть 20.
Свободное владение математикой – Работа в группах по 9 человек
Научиться считать в группах по 9 значительно сложнее, чем считать в группах по 10. Итак, как мы можем использовать наше понимание счета в группах по 10, чтобы найти шаблон для счета девятками?
Как насчет 9 х 5?
Итак, 10 x 5 = 50. Но каждая группа состоит только из 9, а не из 10. Девять на 1 меньше 10, поэтому в каждой группе из 10 должно быть 1 недостающее. Это пять единиц, или 5 x 1, что равно 5. Там ответ должен быть на 5 меньше 50, то есть 45!
Попробуйте этот трюк для работы с восьмерками.
Мы знаем, что 8 на 2 меньше 10, поэтому постройте модель 8 x 5 и посмотрите, что вы заметите, когда соберете 10 из разноцветных кубиков, точно так же, как мы сделали с 9.
Как насчет других способов умножения на 9? 8 х 9.
Ну, я знаю, что 8 x 10 = 80, и если у меня всего 9 групп по 8, то это на 8 меньше, чем 80, что равно 72!
Посмотрите, работает ли это с 14 x 9.
Возможно, начните с того, что вы знаете о 14 x 10, создайте модель и заставьте модель рассказывать историю, например: «У меня есть 9пакеты по 14 штук в каждом. Сколько предметов всего? История помогает нам визуализировать проблему и увидеть, как представление о том, что у нас есть 10 сумок вместо 9, поможет нам в вычислениях.
Другие способы упростить более сложную таблицу умножения, используя то, что мы уже знаем
Подсчет группами по 7
Представьте, мне интересно, сколько дней в 6 неделях. Это будет 7 дней x 6, поэтому мне понадобится моя таблица умножения на 7 или 6 (потому что 7 x 6 = 6 x 7).
Давайте построим его из кубиков. Мы будем использовать массив:
Вот 6 групп по 7. Я пока не умею считать по 7.
Используйте «Уведомление и удивление»: что я могу увидеть в массивах? Могу ли я увидеть какие-либо факты, которые мне уже известны или которые легче вычислить?
А, теперь я вижу 5 и 2 внутри 7.
Так что я мог вычислить 5 х 5, а затем 2 х 5.
Массив охотится
Равное группирование фактов умножения легче всего увидеть и понять, когда мы создаем массивы.
Мы уже использовали массивы в этой статье, создавая равные строки и столбцы кубов.
Массивы позволяют нам легко видеть факты умножения и разбивать факты на части, чтобы мы могли видеть, что 6 x 4 можно вычислить как «удвоить 6 плюс удвоить 6» или «5 x 9» как «(5 x 10) – 5».
Массивы в реальной жизни
Массивы существуют повсюду в реальной жизни, когда мы начинаем смотреть вокруг себя. Они являются фантастической отправной точкой для наблюдения и описания фактов умножения (и, следовательно, деления).
Они также могут вызвать некоторые более сложные вопросы, такие как: «Если мы знаем площадь одной из этих потолочных плит, как мы можем использовать это для расчета площади всего потолка, и нужно ли нам считать каждую отдельную плитку?»
Примеры массивов
- Блок ящиков
- Яичные коробки
- Старые окна
- Потолочные плитки
- Полные плитки
- Wire Fencing
- Фотографии, отображаемые на стене
- Стояние в Спинках на 4037 Harhtiers Arthiers4040404040404040404040404040404040404040404040404040404040404040404040404040404040403 гг.
- Мультипакеты с водой, йогуртом, пирожными и т. д.
- Кусочки шоколада в баре
- Люди, сидящие в театре, на стадионе и т. д.
- Выкройки на ткани и оберточной бумаге
большая компанияЧтобы узнать больше о Karen Wilding Education и ее услугах, посетите сайт karenwildingeducation.co.uk.
Почему все дети должны учить таблицу умножения — и интересные способы научить их
Недавно один родитель спросил меня, в каком возрасте дети должны научиться умножать числа. Он был потрясен, когда я сказал, что дети в детском саду могут быть экспертами в умножении.
Маленькие дети нередко произносят вслух предварительную «таблицу умножения», когда они «пропускают счет». «Два, четыре, шесть, восемь, 10» и «три, шесть, девять, 12» — одни из первых шагов в изучении кратных чисел.
На самом деле, взрослые могут помочь в подсчете пропусков, используя два инструмента, которые есть в каждом доме: калькулятор и часы.
Ваш ребенок может «научить» калькулятор пропускать счет до четырех, например, просто введя «4» на калькуляторе, затем нажав «+» и «4», а затем несколько раз нажав знак равенства.
Вы можете следить за тем, как дисплей меняется с четырех на восемь, затем на 12, затем на 16, затем на 20, что представляет собой число, кратное четырем в таблице умножения на четыре. Чтобы сосчитать до шести (или любого другого числа), просто измените начальное число и первое добавленное число.
В качестве альтернативы вы и ваш ребенок можете открыть таблицу пятикратного умножения на циферблате аналоговых часов. Это просто, потому что часы имеют пятиминутный интервал и пронумерованы от 1 до 12. Количество минут соответствует факту умножения, поэтому, например, 5 х 5 = 25 . Это также помогает детям научиться читать время.
Создание мышечной памяти в мозгу
Эти семейные математические занятия «за кухонным столом» являются примерами стратегий, которые предлагают повторную практику, делая задачу изучения таблицы умножения более увлекательной и увлекательной.
Что еще более важно, эти и другие игры с фактами «Поиграем в математику» служат для создания «мышечной памяти» в мозгу, одновременно позволяя учащимся запоминать числовые факты и закладывая основу для более сложных вычислений и приложений в будущем.
Знакомство и умение пользоваться таблицами умножения являются важным строительным блоком в математике.
Он открывает двери для многозначного умножения и демистифицирует такие процессы, как деление в длинную и упрощение дробей. Он закладывает основу для алгебры.
Подход «Математика имеет смысл»
На семинарах я часто прошу учителей и родителей посмотреть на следующие примеры работ учащихся от ученого-педагога Деборы Болл. Я прошу их определить, кто из этих студентов, по их мнению, использует метод, который можно использовать для умножения ЛЮБЫХ двух чисел, и объяснить, почему.
В первом случае Студент А умножает сверху вниз, справа налево:
5 X 25 = 125 и 3(0) X 25 = 75(0) .
К счастью, ученица получает правильный ответ, частично благодаря простому умножению (учащиеся связывают умножение 25 с использованием 25-центовых монет) и потому, что она правильно расположила 75 .
Студент B умножает справа налево:
5 X 35 (мысленно посчитав 2 X 35 = 70 , таким образом, 4 X 35 = 140 , таким образом 5 X 35 = 140 + 35 или 175 ) и 90 0 70 4 (получив 90 0 0 0 4 ) затем складывает частичные суммы вместе, чтобы получить конечный продукт.
Стратегия дает «правильный ответ», но «работа» ученика непрозрачна.
Учащийся C использует пошаговый процесс разряда, который будет работать ВСЕГДА:
Учащийся умножает 5 X 5 , затем 5 X 30 , затем 20 X 5 и 20 X 30 , чтобы получить 25 + 150 + 100 + 600 , что в сумме равно 045 90.
Этот «математический подход» к умножению многозначных чисел (также называемый «методом частичных произведений») нравится учащимся, потому что он ценит их предшествующее обучение, логически и эффективно используя факты об основных числах.
Он не требует никаких ненужных построчных правил «перенеси единицу и сдвинься влево, добавляя нули в качестве заполнителей», и он универсален.
Он работает для чисел любой величины благодаря своей математической простоте, элегантности и, что наиболее важно, обобщаемости.
Взгляд в будущее
Стол. Сетка. Алгебра. Математики и исследователи в области образования, которые помогли классным учителям внедрить эту простую вычислительную процедуру, стремятся подчеркнуть, что их энтузиазм отчасти объясняется их «взглядом в будущее», сосредоточенным на средней и высшей математике.
Модель «значения разряда» для многоразрядного умножения (работающего слева направо или справа налево) может быть представлена визуально с помощью модели умножения «площадь».
По мере того, как учащиеся продвигаются по классам, «площадная» модель умножения становится все более важной.
Переход от …
Таблица [ (100 + 40 + 3) X (20 + 7) ] к
Сетка [ (40 + 8) X (20 + 6) ] до
Алгебра [ (х + 3) Х (х + 2) ]
… следует за естественным развитием математической сложности.
Преодоление математического барьера
В последнее время мы стали свидетелями многих движений «за» математику по всему континенту и по всему миру: например, «С математикой, которую я могу» и «Глобальный математический проект».
В них мы увидели новый акцент на усилиях, направленных на поддержку ВСЕХ детей в успешном изучении математики и, таким образом, преодоление математического барьера, который, как было доказано, ограничивает успехи в школе, карьере и жизни.