Векторы характера: 8 векторов | Психологические тренинги и курсы он-лайн. Системно-векторная психология

Опубликовано автором

Мирный характер векторов Вектор для бесплатного скачивания

аннотация искусство художественные

Vector Abstract Background 3

аннотация искусство фон

Abstract Blue Background Vector Art

аннотация искусство художественные

Abstract Colorful Waves Vector Background Graphic

аннотация абстракция искусство

Abstract Background for Design

луки свечи пламя

Beautiful Christmas Ornaments

красивая голубой яркий

Blue Glow Green

abstract adobe art artistic artwork backdrop background beautiful beauty botanical botany clip-art clipart concepts coreldraw creative curl curves decor decoration design

Beautiful Floral Pattern

аннотация искусство фон

Neon Glowing Light Frame

взрослый алкоголь только

Beauty Girl

искусство справочная информация мяч

Blue Christmas vector banners background

аннотация фон справочная информация

Beautiful dynamic

красота в природе букет бутон.

Free Vector Spring Lily Flower Background

аннотация искусство красивая

Swirl Floral Graphics Vector Set

животное черный справочная информация

Бабочка на цветах

аннотация искусство фон

Абстрактный фон с листьями

beautiful logo логотипы логотип

004-Set of Simplistic Logos

красивая собака

Красивая собака вектор 1

20.

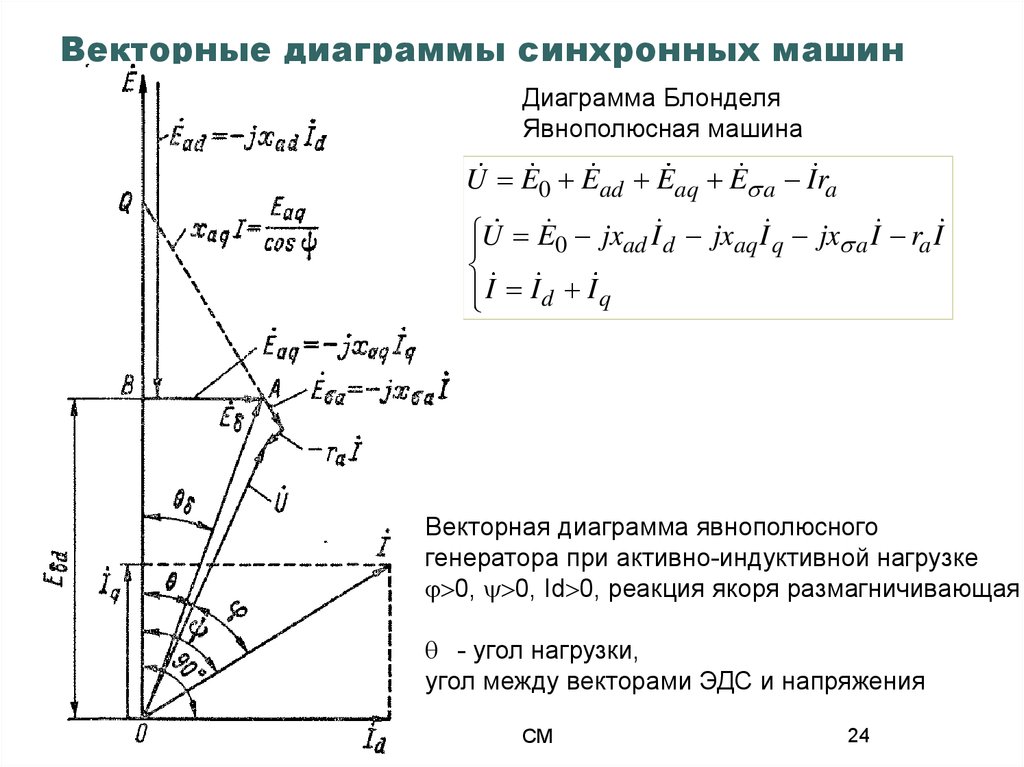Векторы: определение, линейные операции, характер.

Вектор-отрезок который хар-ся длинной, напр-ем, расположением (на пл-ти или в пр-ве). Длина вектора-число, обознач длину отрезка изображ вектор. Ноль вектор-вектор у которого начало и конец совпадает. единичный вектор-вектор длина которого равна единице. Противопол вектор: вектор противоп вектору а назыв вектор обознач –а и меющ с вектором а одинаковую длину и противопол направление. Векторы по величине не сравниваются(понятие >< не существ). Существ понятие равенство векторов. а=в, если |a|=|b|, направления совпадают, они коллинеарны(т.е распол на одой прямой либо на паралл прямых).

ЛИНЕЙНЫЕ ОПЕРАЦИИ. Сложение. Правило параллелогр, треугольника(нарисовать). Св-ва операций сложения векторов: а+в=в+а(переместит),а+(в+с)=(а+в)+с(сочитат), а+(-а)=0. Разность векторов а и в. Под разностью векторов а и в (а-в) понимают такой вектор с, который с вектором в дает вектор а.(рис) Умножение вектора на число. Н*а. н=const, н>0, а сонаправлен с вектором н*а. |н*а|>|а| в н раз больше длины вектора а. Говорят при этом что н*а составлен из вектора а растяжением в н раз без изменения напревления. Св-ва. н*а=а*н, (н+м)*а=н*а+м*а, (нм)*а=н(м*а), с*а=а*а*а*…*а(с слагаемых), 0*а=0, а/н=(1/н)*а

21.Нелинейные операции над векторами: скалярное произведение векторов. Применение скалярного произведения (определение, свойство)

Скалярное произведение векторов равно произведению их длин на косинус угла между ними. А*в=|a||b|cos α. Другая форма скалярного произвед векторов а и в через проекцию одного вектора через другой. Пр в на а=|b|cos α пр а на в= |a|cos α, ab=пр

a b |a|= прb a |b|. cos α= ab/|a||b|. Cв-ва скалярно произведения векторов. ав=ва, а(в+с)=ав+ас, аа=|a|2, a0=0a=0. Условие перпендикулярности векторов.а┴в значит cos α=0, α=П/2, ав=0. Выражение скалярн произвед векторов в координатн форме. а{x1,y1,z1}, b{x2,y2,z1}. тройка векторов I,j,k назыв коорлин базисам, если эти вектора удовлетв условия: i на Оx, j на Oy, k на Оz, их направл-ие соответств с положительным направлением сист координат, их длины =1 |i|=|j|=|k|=1-базисные орты. Если i,j,k координ базис прямых системы координат, Oxyz, то каким бы ни был вектор а его можно представить в виде разложения по базису I,j,k которая имеет вид: а=xi+yj+zk, : а1=x1i+y1j+z1k, : а2=x2i+y2j+z
2k. Ab= (xi+yj+zk)( x1i+y1j+z1k)( x2i+y2j+z2k)=…..=x1x2+y1y2+z1z2, cos α= (x1x2+y1y2+z1z2)/ корень(x12+y12+z12)корень(x22+y22+z22). Ab=0, x1x2+y1y2+z1z2=0, a||b, x1/x2=y1/y1=z1/z2. Применение скалярного произведения. А=FS

22.Нелинейные операции над векторами: векторное произведение векторов, применение (определение, свойства). Векторное произведение векторов а и в назыв вектор, удовлетв следующим условиям: длина этого вектора является произвед длины этого вектора на sin угла между ними (|a||b|sin α) , расположен этот вектор ┴пл-ти векторов а и в, направление этого вектора находится по правилу правой руки. |а×b|=|a||b|sin α, [a×b] ┴a, [a×b] ┴b.

Св-ва векторн произвед векторов. [a×b] = -[b×а], a×[b+c]=a×b+a×c, a×a=0. координаты векторного произвед векторов. a{x1, y1,z1} b{x2,y2,z2}. (формула) Условие коллинеарн-ти векторов в координ-ой форме. a||b следоват a×b=0. Применение векторного произвед векторов: в геометрии. Длина векторного произв векторов а и в численно равна пл-ди параллелогр постр на векторах а и в. В физике момент силы на вектор плеча M=F×OM.

24.Уравнение прямой на плоскости: все виды перечислить и уметь выводить уравнение прямой на плоскости (в векторной+координатной форме)

дано: M0€l, N┴l, 1) M€l 2) M0M€l M0M{x-x0,y-y0} 3) N┴M0M (рассмотр располож векторов) т.

к N┴l, M0M€l (условие ┴векторов M и M0M) 4) N*M0M=0-уравнение прямой, прох через заданную точку. Это усл записыв в координ форме A(x-x0)+b(y-y0)=0, M(x0,y0) €l, M(x,y)-текущая точка на прямой. Уравнение прямой с угловым коэффициентом, прох через задан точку. A(x-x0)+B(y-y0)=0, y-y0=-(A/B)(x-x0), K=-A/B-угловой коэфициент, y-y0=K(x-x0), K=tg α-угол наклона прямой l к оси Ox. Уравнение прямой в общем виде. A(x-x0)+B(y-y0)=0, Ax+By+(-Ax0-By0)=0, (-Ax0-By0)=const=C, Ax+By+C=0
-уравнение прямой в общем виде. N{A,B}┴l, M(x,y)-текущая точка на прямой. Уравнение прямой с угловым коэффициентом. Ax+By+C=0, y=-A/b x –C/b; k=-A/B; b=-C/B, y=Kx+B, k-угловой коэффициент прямой, k=tgα. Уравнение прямой в нормальном виде.M{x,y} €l, m ┴l, M1=m×l, OM{x,y}, OM1=p=прmOM. направление вект m можно определить по напр вект р0 – единичный вектор этого направл. p=прр0ОМ= (ро OM)/|p0|, p= (ро OM)/|p0|, |po|=1, p0{cos α,cos β}, cos β=cos(90- α), cos β=sin α, po{cos α,sin α}, cos2 α+sin2 α=1, p= (ро OM)/|p0|, p=p0 OM
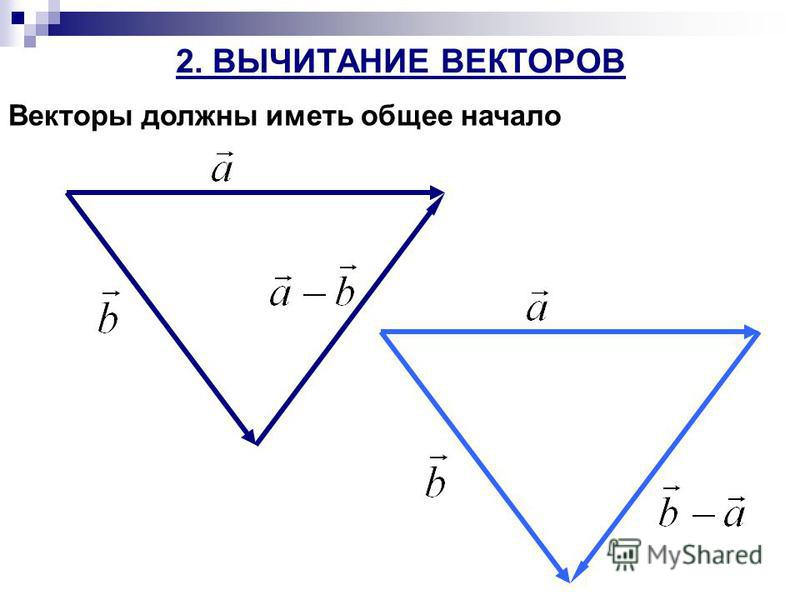—нормальное уравнение прямой в векторной форме, p=xcos α+ysin α, -p+xcos α+ysin α=0-уравнение прямой в нормальном виде, р-свободный член. Уравнение прямой прох через 2 заданные точки М1М2 ×М1М=0 – уравнение прямой в векторной форме прох через 2 заданн точки. (x-x1)/(x2-x1)=(y-y1)/(y2-y1). Уравнение прямой в каноническом виде. (x—x0)/m=(y—y0)/n, S{m,n}-направляющий вектор прямой, M(x,y)-текущая точка на прямой. Параметрич уравнение прямой x=mt+x0 и y=nt+y0-параметрич уравнение прямой, n,m-координаты направл вектора прямой.

25.Уравнение прямой на плоскости в полярном виде. Полярное уравнение прямой.

M(ρ,φ)-текущая точка на прямой l, m┴l, M1=m×l, OM1=прмOM=p, p=ρcos(α-φ)-уравнение прямой в полярных координатах.

28.Расположение прямой на плоскости.

l1||l2, A1x+B1y+C1=0

A2x+B2y+C2=0, N1||N2 (если они паралл или совпадают) A1/A2=B1/B2 или A1/A2=B1/B2=C1/C2 – если прямые совпадают

2) пересечение прямых

l1┴l2 и N1┴N2, N1N2=0, A1A2+B1B2=0-условие ┴ прямых.

как углы с взаисно перпендик сторонами. cos α=N1N2/|N1||N2|, cosα=(A1A2+B1B2)/корень(A12+B12)корень(A22+B22)—

нахожление угла между пересек прямыми. Другая формула нахождения угла.

α1-угол между l1 и Ox, α2-угол между l2 и Oy, tg α1=K1, tg α2=K2, φ= α2 – α1,tgφ=tg(α2-α1), tg φ=(tg α2-tg α1)/(1+tg α2tg α1), tg φ=(K2-K1)/(1-K2K1), если φ=180, то l1||l2, tg φ=0 K1=K2 если φ=90, l1 ┴l2 tg φ→∞. 1+K1+K2=0 → K1K2=-1

текста в строковых и символьных массивах — MATLAB & Simulink

Open Live Script

Существует два способа представления текста в MATLAB®. Вы можете хранить текст в строковых массивах . И в любой версии MATLAB вы можете хранить текст в массивах символов. Обычно массивы символов используются для хранения фрагментов текста в виде векторов символов . MATLAB отображает строки с двойными кавычками и векторами символов с одинарными кавычками.

Представление текста массивами строк

Вы можете сохранить любую последовательность символов размером от 1 до n в виде строки, используя тип данных строка . Заключите текст в двойные кавычки, чтобы создать строку.

 ул = "Привет, мир" 
 ул =
"Привет, мир"

Хотя текст "Hello, world" состоит из 12 символов, str сама по себе является строкой 1 на 1, или строковым скаляром . Вы можете использовать строковый скаляр, чтобы указать имя файла, метку графика или любую другую текстовую информацию.

Чтобы найти количество символов в строке, используйте функцию strlength .

 n = длина длины(str) 
 n = 12

Если текст содержит двойные кавычки, используйте в определении две двойные кавычки.

 str = "Они сказали "Добро пожаловать!"" и помахали." 
 стр =
«Они сказали: «Добро пожаловать!» и помахали».

Чтобы добавить текст в конец строки, используйте оператор «плюс» + . Если переменную можно преобразовать в строку, то плюс преобразует его и добавляет.

 градусов по Фаренгейту = 71;
по Цельсию = (32 по Фаренгейту)/1,8;
tempText = "температура " + по Цельсию + "C" 
 tempText =
"температура 21,6667С"

Вы также можете объединить текст, используя функцию append .

 tempText2 = добавить ("Сегодня", tempText) 
 tempText2 =
"Сегодняшняя температура 21,6667С"

Функция string может преобразовывать различные типы входных данных, например числовые значения, дату и время, продолжительность и категориальные значения. Например, преобразуйте вывод pi в строку.

 пс = строка (пи) 
 пс =
"3,1416"

Вы можете хранить несколько фрагментов текста в массиве строк. Каждый элемент массива может содержать строку с разным количеством символов без заполнения.

 ул = ["Меркурий","Близнецы","Аполлон";...
       "Skylab", "Skylab B", "ISS"] 
 str =  2x3 string 
    «Меркурий», «Близнецы», «Аполлон».
    "Скайлэб" "Скайлэб Б" "МКС"

str представляет собой массив строк 2 на 3. Вы можете найти длины строк с длина строки функция.

 N = длина длины(str) 
 N =  2×3 
     7 6 6
     6 8 3

Массивы строк поддерживаются во всех продуктах MATLAB и MathWorks®. Функции, которые принимают массивы символов (и массивы ячеек из символьных векторов) в качестве входных параметров, также принимают массивы строк.

Представление текста с векторами символов

Чтобы сохранить последовательность символов 1 на n в виде вектора символов, используя char , заключите его в одинарные кавычки.

 chr = «Привет, мир» 
 chr =
'Привет, мир'

Текст 'Hello, world' имеет длину 12 символов, и chr хранит его как вектор символов 1 на 12.

 whos chr 
 Имя Размер Байты Класс Атрибуты
  чр 1x12 24 символа

Если текст содержит одинарные кавычки, используйте в определении две одинарные кавычки.

 chr = 'Они сказали "Добро пожаловать!" и помахали рукой.' 
 хр =
«Они сказали: «Добро пожаловать!» и помахал.

Векторы символов имеют два основных применения:

  • Для указания отдельных фрагментов текста, таких как имена файлов и метки графиков.

  • Для представления данных, закодированных с использованием символов. В таких случаях вам может понадобиться легкий доступ к отдельным символам.

Например, вы можете сохранить последовательность ДНК как вектор символов.

 seq = 'GCTAGAATCC';

Вы можете получить доступ к отдельным символам или подмножествам символов с помощью индексации, как если бы вы индексировали числовой массив.

 сл(4:6) 
 анс =
'АГА'

Объедините вектор символов с помощью квадратных скобок, как вы объединяете другие типы массивов.

 последовательность 2 = [последовательность 'ATTAGAAACC'] 
 последовательность 2 =
'GCTAGAATCCATTAGAAACC'

Начиная с R2019a, вы также можете объединять текст, используя , добавляя . добавить 9Функция 0014 рекомендуется, потому что она последовательно обрабатывает массивы строк, символьные векторы и массивы ячеек из символьных векторов.

 последовательность 2 = добавить (последовательность, 'ATTAGAAACC') 
 последовательность 2 =
'GCTAGAATCCATTAGAAACC'

Функции MATLAB, которые принимают массивы строк в качестве входных данных, также принимают вектора символов и массивы ячеек из векторов символов.

См. также

строка | символ | сотовая улица | длина длины | плюс | Хорзкат | добавить

Связанные темы

  • Создание массивов строк
  • Анализ текстовых данных с помощью массивов строк
  • Часто задаваемые вопросы о массивах строк
  • Обновление кода для приема строк Числовой, Символ, и Logical

    В последней главе вы получили общее представление об объектах R и о том, как выполнять присваивание объектов. В этом разделе мы начнем знакомить с первым и, возможно, самым фундаментальным типом объектов R, называемым 9.0197 вектор . Вектор — простейший объектный тип в R, который содержит одно или несколько значений того же типа . В этом разделе мы представим числовой вектор, вектор символов и логический вектор. Начнем с числового вектора.

    2.1.1 Числовой вектор

    а. Создание числовых векторов

    Числовой вектор — это тип вектора, который содержит только значения числового типа. Например, 6 — это числовой вектор с одним элементом со значением 6. Для векторов количество элементов соответствует длине вектора, поэтому 6 — числовой вектор длины 1.

    После присвоения значения 6 имени x1 вы создали новый вектор x1 с тем же значением, что и 6 , поэтому x1 также является числовым вектором. . И вы можете ссылаться на x1 в последующих расчетах.

     6 #числовой вектор длины 1
x1 <- 6 #x1 также является числовым вектором длины 1
x1 #проверить значение x1

    Но может ли числовой вектор содержать более одного значения? Ответ - большое ДА! В R вы можете использовать функцию c() ( c — сокращение от «объединить») для объединения элементов в числовой вектор.

     c(1, 3, 3, 5, 5) #используйте c() для объединения элементов в числовой вектор длины 5
y1 <- c(1, 3, 3, 5, 5) #y1 также является числовым вектором длины 5
y1 #проверить значение y1
length(y1) #длина вектора

    В этом примере вы создали объект длины 5, используя c() функция с аргументами, содержащими пять элементов, разделенных запятой. Поскольку значение каждого элемента является числом, объект представляет собой числовой вектор.

    Если вы присвоите значения имени y1, вы получите новый числовой вектор y1 с 5 значениями. Обратите внимание, что второй и третий элементы имеют одинаковое значение 3 в y1 . Вы можете проверить содержимое y1 и проверить его длину с помощью функции length() .

    Если вы включаете несколько числовых векторов в c() , вы также создадите числовой вектор как комбинацию входных числовых векторов. Например, вы можете создать числовой вектор со значениями из двух числовых векторов. Конечно, вы можете создать новый числовой вектор z1 , используя присваивание объекта.

     c(c(1,2), c(3,4)) #используйте c() для объединения нескольких числовых векторов в один числовой вектор
z1 <- с(с(1,2), с(3,4))
z1
length(z1)

    После создания векторов вы можете использовать функцию class() для проверки их класс .

     класс(x1)
#> [1] "числовой"
класс (y1)
#> [1] "числовой"
класс (z1)
#> [1] "numeric"

    Из результатов вы узнаете, что x1 , y1 и z1 являются числовыми, поэтому они называются числовыми векторами .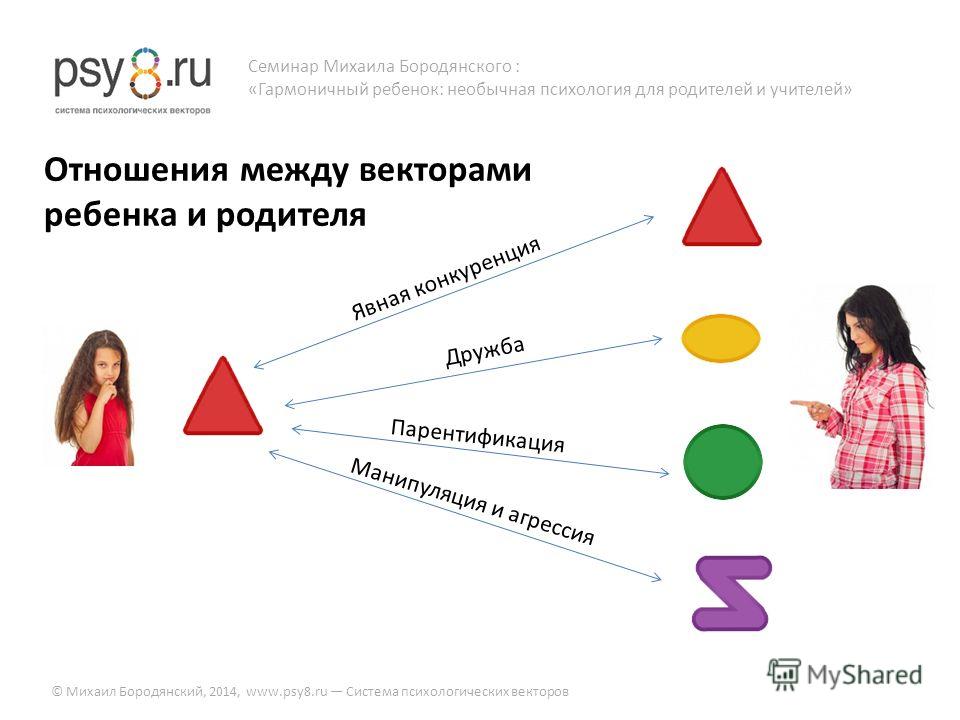

    б. Извлечь векторный элемент и обновить его значение Чтобы извлечь элемент из вектора, вы можете использовать индекс элемента с парой [ и ] , окружающих его, после имени вектора.

     y1[2] # извлечь второй элемент `y1`
#> [1] 3
y2[3] # извлечь третий элемент `y2`
#> [1] 5

    Вы также можете обновить определенный элемент вектора, используя оператор присваивания с выражением извлечения слева и новым значением справа.

     у1
#> [1] 1 3 3 5 5
y1[2] <- 100 # обновить второй элемент `y1` до 100
у1
#> [1] 1 100 3 5 5

    Как вы можете видеть здесь, второй элемент y1 изменен на 100, что отражается проверкой значения y1 .

    в. Операции между двумя числовыми векторами

    Поскольку числовые векторы состоят из чисел, вы можете выполнять арифметических операций между ними, точно так же, как причудливый калькулятор в разделе 1. 2. Если два вектора имеют одинаковую длину , вычисление выполняется поэлементно . Другими словами, R будет выполнять операцию отдельно для каждого элемента. Во-первых, давайте создадим еще один вектор x2 длины 1 и выполним сложение с x1 .

     x2 <- 3
х1 + х2
#> [1] 9

    Тогда, очевидно, вы получите 9!

    Точно так же вы можете создать еще один вектор y2 той же длины, что и вектор y1 . Затем вы можете выполнять операции между y1 и y2 .

     у2 <- с(2, 4, 1, 3, 2)
у1 + у2
#> [1] 3 104 4 8 7

    Результатом является еще один вектор длины 5. Чтобы убедиться, что вычисление действительно было выполнено поэлементно, вы можете проверить, что значение первого элемента равно \(1 + 2 = 3\), а значение второго элемента равно \(3 + 4 = 7\) и т. д.

    Поскольку вычисления выполняются поэлементно, люди обычно хотят, чтобы два вектора имели одинаковую длину. Однако в R есть правило повторного использования , которое иногда оказывается весьма полезным и позволяет нам писать более простой код. В частности, если один вектор короче другого, R будет перерабатывать (повторять) более короткий вектор, пока его длина не совпадет с более длинным. Эта переработка особенно полезна для оператора между длина>1 вектор и длина-1 вектор. Давайте посмотрим пример.

     у1 + х1
#> [1] 7 106 9 11 11

    Из результата видно, что к каждому элементу в y1 добавляется 6.

    Ниже приведены несколько дополнительных примеров, которые вы можете попробовать.

     у1 * х2
у1/5
y2 - x1

    2.1.2 Вектор символов

    а. Создайте векторы символов

    Теперь давайте перейдем к векторам символов. В вектор символов , значение каждого элемента имеет символьный тип, что означает, что каждое значение является строкой . Строка — это последовательность символов (включая буквы, цифры или символы), заключенная в двойные ( "" ) или одинарные ( '' ) кавычки. Чтобы быть последовательными, в этой книге мы будем использовать двойные кавычки.

    Давайте сначала создадим вектор символов овечьей студии , который имеет только один элемент. Затем вы можете проверить значение этого вектора, введя его имя, и проверить тип вектора, используя класс() .

     овечья студия <- "овца@007"
овечья студия
class(sheepstudio)

    Подобно числовому вектору, вы можете использовать функцию c() для объединения нескольких строк для создания вектора символов. Вы можете проверить количество строк в векторе символов, используя length() , а nchar() поможет вам получить количество символов в каждой строке.

     животных <- c("овца@29", "свинья$29", "обезьяна")
животные
длина (животные)
нчар (животные)

    Обратите внимание, что если у вас есть вектор, состоящий из чисел, заключенных в двойные кавычки, он также является вектором символов. («4» и «29» — строки)

     num_vec <- c(4, 29)
char_vec <- с ("4", "29")
класс (num_vec)
#> [1] "числовой"
класс (char_vec)
#> [1] "символ"

    b. Объединение нескольких строк в одну строку

    Далее мы покажем, как объединить несколько строк в одну строку. Для этого можно использовать вставить() функция. Во-первых, давайте создадим вектор символов с четырьмя элементами,

     four_strings <- c("This", "is", "Sheep@29", "$Studio")
length(four_strings) #проверьте количество строк

    Затем используйте paste() вместо c() ,

     one_long_string <- paste("This", "is", "Sheep@29", "$ Студия")
one_long_string
#> [1] "Это Sheep@29 $Studio" 
     class(one_long_string)
length(one_long_string) # проверить количество строк

    Из результатов видно, что one_long_string — это вектор символов с длиной 1, а значение one_long_string — это одна строка с пробелом между отдельными строками.

    Вы могли заметить, что в paste() разделителем по умолчанию между отдельными строками является пробел. На самом деле вы можете изменить разделитель, установив аргумент sep в paste() . Например, вы можете разделить отдельные строки запятой,

     запятая <- вставить("Это", "есть", "Овца@29", "$Studio", sep = ",")
запятая
#> [1] "This,is,Sheep@29,$Studio"

    Если вы не хотите использовать разделитель, вы можете использовать функцию paste0() .

     Nosep <- paste0("Это", "есть", "Овца@29", "$Studio")
носовой упор
#> [1] "ThisisSheep@29$Studio"

    Если вы хотите объединить строки вектора в более длинную строку, вам нужно указать в качестве разделителя аргумент свернуть вместо сен в функции paste() .

     вставить (четыре строки, свернуть = "")
#> [1] "ThisisSheep@29$Studio"
вставить (четыре_строки, свернуть = ",")
#> [1] "Это,это,Овца@29,$Studio"
paste(four_strings) ##не работает без аргумента сворачивания
#> [1] "This" "is" "Sheep@29" "$Studio"

    Помимо вставки нескольких строк в одну длинную строку, вы также можете использовать функцию paste() для вставки двух векторов символов, где пара строк будет вставлена ​​поэлементно.

     paste(c("Июль", "Август"), c("2007", "2008"))
#> [1] «Июль 2007 г.» «Август 2008 г.»

    c. Изменить регистр

    В символьных векторах каждая строка может содержать как прописные, так и строчные буквы. Вы можете унифицировать регистры всех букв внутри вектора. Давайте сначала рассмотрим вектор символов four_strings ,

     four_strings <- c("This", "is", "Sheep@29", "$Studio")
четыре_строки
#> [1] "Это" "это" "Овца@29""$Studio"

    Затем используйте функцию tolower() для преобразования всех букв в нижний регистр,

     tolower(four_strings)
#> [1] "this" "is" "sheep@29" "$studio"

    Противоположной функцией tolower() является toupper() , которая преобразует все буквы в верхний регистр,

     toupper( четыре_строки)
#> [1] "THIS" "IS" "SHEEP@29" "$STUDIO"

    2.1.3 Логический вектор

    До сих пор мы создали несколько числовых векторов и векторов символов. Некоторые векторы имеют имена, а некоторые нет. Вы можете увидеть все именованных объектов с помощью функции ls() .

     лс()
#> [1] "животные" "char_vec" "запятая" "четыре_строки"
#> [5] "nosep" "num_vec" "one_long_string" "sheepstudio"
#> [9] "x1" "x2" "y1" "y2"
#> [13] "y3" "z1"

    Как было показано в Разделе 1.3, еще один способ проверить именованные объекты — через панель среды, как показано на рисунке 2.2.

    Рисунок 2.2: Окружающая среда

    Мы видим, что панель среды имеет два столбца, первый столбец показывает список имен объектов, а второй столбец показывает соответствующую информацию для каждого объекта. Информация включает тип вектора ( chr — сокращение от символа и num — сокращение от числа), длину вектора и первые несколько значений вектора. Обратите внимание, что если длина вектора равна 1 (например, x1 ), среда не покажет ни тип, ни длину.

    К настоящему времени вы создали несколько объектов, и вы обнаружите, что объекты не будут сохранены в R, если вы не присвоите их значения именам, например, результаты x1 + x2 и y1 + y2 не отображаются в среде.

    Прежде чем представить логический вектор , давайте сначала изучим функцию is.numeric() , которая проверяет, имеет ли вектор числовой тип,

     is.numeric(y1) #Is y1 числового типа?
#> [1] ИСТИНА

    Подобно is.numeric() , вы также можете использовать функцию is.character() , чтобы проверить, является ли заданный вектор символьным типом.

     is.character(y1) # Является ли y1 символьным типом?
#> [1] FALSE

    Вы можете заметить, что результаты TRUE или FALSE из приведенных выше кодов. На самом деле логических векторов — это векторы, которые используют только ИСТИНА или ЛОЖЬ в качестве значений. Обратите внимание, что ИСТИНА и ЛОЖЬ — это логические константы в R. Точно так же вы можете использовать is.logical() , чтобы проверить, имеет ли вектор логический тип, или вы можете использовать class() , чтобы узнать точный тип.

     logic1 <- c(TRUE, FALSE, TRUE) #вы также можете использовать функцию c() для создания логического вектора
is.logical(logic1)
class(logic1)

    Вы также можете использовать T для представления TRUE и F для представления FALSE в логических векторах.

     логика2 <- с(Т, Ф, Ф)
is.logical(logic2)
класс (логика2)

    Стоит отметить, что вы не хотите помещать пару двойных кавычек вокруг TRUE или FALSE , когда вы используете их в качестве логических значений. Если вы это сделаете, вместо этого будет сгенерирован вектор символов.

     char <- c("ИСТИНА", "ЛОЖЬ", "ИСТИНА")
is.logical(char)

    Обратите внимание, что ключевые слова TRUE и FALSE чувствительны к регистру, и все буквы внутри них должны быть в верхнем регистре . Если вы измените любую букву на строчную, вы получите ошибку, потому что True не является ни логической константой, ни определенным объектом.