Дерево интерпретация: Page not found : Психолог

Опубликовано автором

Содержание

Страничка психолога Зуевой Юлии: Тест «Дерево»

ТЕСТ «ДЕРЕВО» (АВТОР Д. ЛАМПЕН, В АДАПТАЦИИ Л.П. ПОНОМАРЕНКО)
Рисунок с нумерацией
Рисунок без нумерации
 Методика «Дерево» Л.П. Пономаренко может использоваться для оценки успешности адаптации ребенка в начале школьного обучения и при переходе в среднее звено. Методика позволяет достаточно быстро определить особенности протекания адаптационного процесса, выявить возможные проблемы ребенка. Дети, погружаясь в рисуночную деятельность, с удовольствием выполняют предложенные задания, легко отождествляют себя с тем или иным человечком.
Содержание методики: Ученикам предлагаются листы с готовым изображением сюжета: дерево и располагающиеся на нем и под ним человечки. Каждый учащийся получает лист с изображением дерева и расположенных на нем человечков 
(но без нумерации фигурок). Не рекомендуется предлагать учащимся сразу подписывать на листе свою фамилию, так как это может повлиять на их выбор. (когда берешь у ребёнка лист с выполненным заданием, скажи ему: «подпиши»).
«Рассмотрите это дерево. Вы видите на нем и рядом с ним множество человечков. У каждого из них разное настроение, и они занимают различное положение. Возьмите красный фломастер и разукрасьте того человечка, который напоминает вам себя, похож на вас, ваше настроение в школе и ваше положение. Возможно, чем выше на дереве находится человечек, тем выше его достижения, тем более он успешен в школе. Теперь возьмите зеленый фломастер и разукрасьте того человечка, которым вы хотели бы быть и на чьем месте вы хотели бы находиться». Бывает так, что некоторые дети просят разрешения обозначить позиции двух человечков. В этом случае не следует ограничивать их выбор, но необходимо зафиксировать, какой человечек был отмечен в первую очередь, какой во вторую, так как соотношение этих выборов может быть достаточно информативным.
 Интерпретация результатов: Интерпретация результатов выполнения проективной методики «Дерево» проводится исходя из того, какие позиции выбирает данный ученик, с положением какого человечка отождествляет свое реальное и идеальное положение, есть ли между ними различия. Интерпретация разработана с учетом опыта практического применения методики и сравнения ее результатов с наблюдениями за поведением учеников, данных, полученных от учителей и родителей, из беседы с ребенком. Для удобства объяснения каждой фигурке присвоен свой номер. Следует заметить, что позицию № 16 учащиеся не всегда понимают как позицию «человечка, который несет на себе человечка № 17», а склонны видеть в ней человека, поддерживаемого и обнимаемого другим.
Источник: Л.П. Пономаренко. Психологическая профилактика дезадаптации учащихся в начале обучения в средней школе. Методические рекомендации для школьных психологов. — Одесса: Астра-Принт, 1999.

Методика может использоваться и с более младшими детьми:

Благодаря тесту можно понять уровень самооценки ребенка, выявить причины проблем в общении и понять, насколько адекватно малыш воспринимает себя в обществе.

Предложите ребенку рассмотреть картинку. На ней 21 человечек и дерево. У каждого свое занятие, все находятся в разных местах, у них определенное настроение.

Затем попросите раскрасить картинку. Коричневым карандашом — ствол и ветки. За это время ребенок успеет рассмотреть всех человечков получше.

Затем пусть красным карандашом ребенок раскрасит человечка, который напоминает ему самого себя, собственное настроение и положение в школе или среди друзей. А зеленым — того человечка, которым хотелось бы быть и на чьем месте хочется оказаться.

Оцените, с положением какого человечка ребенок отождествляет свое реальное и идеальное положение, есть ли между ними различия.

Ключ к тесту

№ 1, 3, 6, 7 — установка на преодоление препятствий

№ 2, 11, 12, 18, 19 — настрой на общительность, дружескую поддержку

№ 4 — устойчивость положения (желание добиваться успехов, не преодолевая трудностей)

№ 5 — утомляемость, общая слабость, небольшой запас сил, застенчивость

№ 8 — отстраненность от учебного процесса, уход в себя

№ 9 — мотивация на развлечения

№ 10, 15 — комфортное состояние, нормальная адаптация

№ 13, 21 — отстраненность, замкнутость, тревожность

№ 14 — кризисное состояние, «падение в пропасть»

№ 16 — дети не всегда понимают как позицию человечка, который несет на себе человечка № 17 — они склонны видеть в ней человека, поддерживаемого и обнимаемого другим

№ 17 — неспособность самостоятельно справиться с возникающими проблемами

№ 20 — завышенная самооценка и установка на лидерство

Интерпретация дерева, двоичного дерева и двоичного дерева поиска

1.

Введение

Во-вторых, дерево и двоичное дерево

1. Значок древовидной структуры

2. Некоторые основные понятия деревьев

1. Узлы. Элементы данных в дереве называются узлами.
2. Корень. Верхний узел называется корнем. Дерево имеет только один корень и развивается из корня. С другой стороны, каждый узел Считается корнем его поддерева
3. Отец: верхний узел узла
4. Братья: узлы с одним и тем же отцом называются братьями
5. Степень узла: количество поддеревьев, принадлежащих узлу, называется степенью узла
6. Лист: узел со степенью 0, также называемый терминальным узлом
7. Узел ветвления: узел, степень которого не равна 0, также называемый нетерминальным узлом или внутренним узлом
8. Уровень узла: дерево веток на пути от корневого узла к узлу в дереве называется уровнем узла, уровень корневого узла определяется как 1, остальные Уровень узла равен уровню его родительского узла +1

9. Глубина дерева: максимальное количество слоев узлов в дереве

3.

Бинарное дерево


Концепция:Каждый узел не может иметь более двух дочерних узлов.
Одним из свойств двоичного дерева являетсяСредняя глубина двоичного дерева меньше, чем количество узловЭто свойство очень важно, особенно для бинарного дерева особого типа, а именно бинарного дерева поиска, средняя глубина которого составляет O (logN), что значительно уменьшит временную сложность поиска.
Конечно, двоичное дерево имеет серьезные проблемы, когда оно не используется должным образом, а именно:

вырождается в структуру, похожую на связанный список. Это дерево называетсяНесбалансированное бинарное деревоКонечно, существуют также сбалансированные бинарные деревья: AVL, красно-черные деревья и т. Д., Которые будут представлены позже.

Три, двоичное дерево поиска

Требуются следующие условия:

  • Двоичное дерево поиска — это двоичное дерево
  • Значение каждого узла двоичного дерева поиска: больше, чем значение всех узлов в его левом поддереве, меньше, чем значение всех узлов в его правом поддереве
  • Каждое из его поддеревьев также является двоичным деревом поиска.
    выглядит следующим образом:

    Получите природу дерева двоичного поиска:
  • Сохраненные узлы должны быть сопоставимы.

4. Другое (последующее дополнение)

  • AVL дерево (последующее добавление)
  • Red Black Tree (последующее дополнение)
    http://www.cnblogs.com/xrq730/p/5187032.html
    Связанное содержание «Введение в алгоритм»

Народные сказки в современной интерпретации – жителям и гостям Казани представили спектакль «О чем поют деревья» — Новости

Фото: Марат Мугинов

(Город Казань KZN.RU, 12 августа, Камиля Губайдуллина). Несколько сотен казанцев и гостей города стали первыми зрителями уникальной постановки «О чем поют деревья», премьера которой состоялась накануне в парке им.Горького. Специально для спектакля в эти дни там организована импровизированная сцена под открытым небом.

Гостям уличного показа предстояло увидеть творческую работу, объединившую 4 сказки – удмуртскую «Красавица береза», чувашскую «Юман-батыр», мордовскую «Дуболго Пичай» и марийскую «Волшебный меч».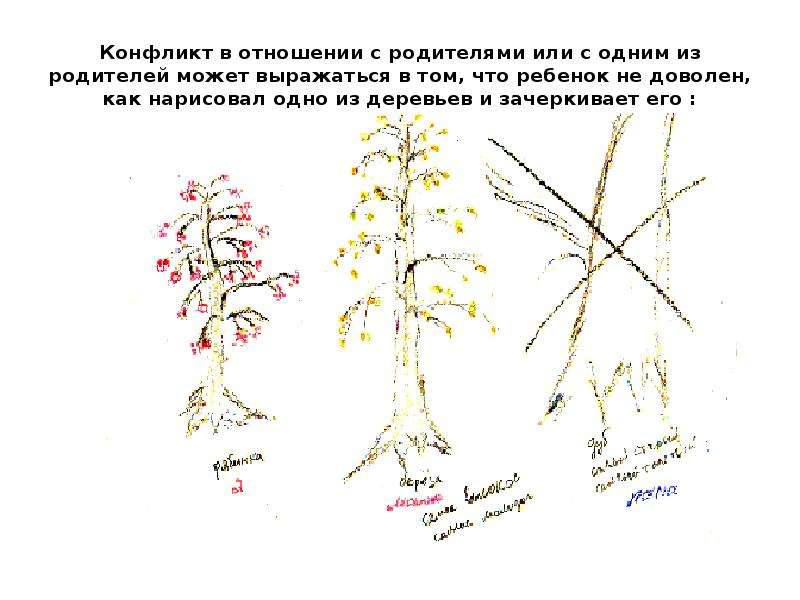 Каждое из этих произведений показывает самобытность, традиции и дух народов, населяющих Поволжье.

Желающих оценить старания творческой группы в премьерный день оказалось очень много. «Специально спешила в парк после работы, чтобы ничего не пропустить. Эти народные сказки я не знаю, поэтому будет вдвойне интересно посмотреть постановку», – рассказала студентка Анна Трофимова.

А вот Александр Еремин оказался знаком с одной из сказок. Уроженец Мордовии, уже несколько лет проживающий в Казани, рассказал, что «Дуболго Пичай» – одна из самых известных мордовских сказок, которую особенно любят дети. «Пришел сегодня, потому что очень хотелось увидеть сказку в новом прочтении, и вот такая отличная возможность появилась, еще и на свежем воздухе. Надеюсь, главный смысл произведения будет передан правильно», – отметил молодой человек перед началом спектакля.

Интерес к постановке проявили как молодые казанцы, так и представители старшего поколения. Наталья Васильева призналась, что питает особую любовь к театру, поэтому от этой постановки ждет самые неожиданные решения. «Объединить сразу несколько народных сказок в одну постановку, должно быть, очень нелегко, поэтому безумно хочется увидеть результат. Решение показать спектакль в парке мне кажется очень удачным, на такой площадке все задумки авторов будет легче уловить. Я пришла заранее и уже успела разглядеть декорации – они минималистичны, но так красивы», – отметила она.

Так, посреди большого зеленого поля появилась «зеркальная река», на берегу которой расположились четыре дома. К началу постановки в импровизированном театре под открытым небом наступила тишина, которую нарушали лишь народные песни. Зрителям сюжеты известных произведений раскрыли через танцы, музыку и обычаи. В постановке были представлены особенности уклада жизни людей разных национальностей, но в то же время показаны их общие ценности. Все четыре сказки объединила тема природы и любви к ней, ведь с древнейших времен у народов Поволжья существовало понятие о мировом древе. Например, марийцы и удмурты почитали священные рощи, мордва, жившая в лесной зоне, поэтизировала деревья, а у чувашей существовали многовековые традиции бережного отношения к лесу.

Сделать спектакль еще более ярким и насыщенным помог многонациональный творческий коллектив. Над постановкой работала бурятский режиссер Сойжин Жамбалова, московский художник-постановщик Ольга Богатищева, хореограф-постановщик из Осетии Мария Сиукаева и композитор Дахалэ Жамбалов из Бурятии. Роли исполнили 15 актеров из Казани, Москвы и Нижнего Новгорода. Среди них студенты театральных вузов и действующие актеры. Некоторые из них также являются представителями народов, чьи сказки послужили основой постановки. Творческая команда подошла к проекту с особым вниманием, тщательно изучала традиции, образы, мифы и легенды народов. 

Важная особенность постановки заключается в том, что это не фольклорная реконструкция, а современная интерпретация произведений на театральном языке. Такой необычный формат многие казанцы и гости города встретили с восторгом. Наталья Пралькова, приехавшая из Чебоксар на несколько дней, осталась под впечатлением от увиденного. «Я приехала в Казань на несколько дней отдохнуть и случайно увидела анонс этого мероприятия. А когда прочитала, что там будет наша чувашская сказка, поняла, что не могу это пропустить. Мне очень понравилось. Свет, звук, костюмы, атрибутика – все на высшем уровне. Такие нестандартные подходы использовались. Наверное, некоторые моменты были понятны не всем, а что-то каждый интерпретировал по-своему. Сходить на постановку стоит определенно, никого равнодушным не оставит», – поделилась впечатлениями зрительница.

Посмотреть уникальную постановку жители города смогут на протяжении еще двух дней – 12 и 13 августа. Показы начнутся в 18:30. Продолжительность постановки составляет 2 часа. Спектакль идет на русском языке, к просмотру допускаются зрители старше 16 лет.

Напомним, проект инициирован Мэрией Казани в Год родных языков и народного единства.

Методика «Дерево для 1-4 классов»

 

ТЕСТ «ДЕРЕВО» (АВТОР Д. ЛАМПЕН, В АДАПТАЦИИ Л.П. ПОНОМАРЕНКО)

Методика «Дерево» Л.П. Пономаренко может использоваться для оценки успешности адаптации ребенка в начале школьного обучения и при переходе в среднее звено. Методика позволяет достаточно быстро определить особенности протекания адаптационного процесса, выявить возможные проблемы ребенка. Дети, погружаясь в рисуночную деятельность, с удовольствием выполняют предложенные задания, легко отождествляют себя с тем или иным человечком.

Содержание методики:

Ученикам предлагаются листы с готовым изображением сюжета: дерево и располагающиеся на нем и под ним человечки. Каждый учащийся получает лист с изображением дерева и расположенных на нем человечков (ЭТО ВАЖНО! ФИУГРЫ ДОЛЖНЫ БЫТЬ БЕЗ НУМЕРАЦИИ).

Не рекомендуется предлагать учащимся сразу подписывать на листе свою фамилию, так как это может повлиять на их выбор (когда берешь у ребёнка лист с выполненным заданием, скажи ему: «подпиши»). По этой же причине (может повлиять на выбор ребенка) не рекомендуется давать стимульный материал (лист с изображением дерева и расположенных на нем человечков) с подписанными номерами фигур.

Инструкция дается в следующей форме:

«Рассмотрите это дерево. Вы видите на нем и рядом с ним множество человечков. У каждого из них разное настроение, и они занимают различное положение. Возьмите красный фломастер и разукрасьте того человечка, который напоминает вам себя, похож на вас, ваше настроение в школе и ваше положение. Возможно, чем выше на дереве находится человечек, тем выше его достижения, тем более он успешен в школе. Теперь возьмите зеленый фломастер и разукрасьте того человечка, которым вы хотели бы быть и на чьем месте вы хотели бы находиться».

Бывает так, что некоторые дети просят разрешения обозначить позиции двух человечков или самостоятельно обозначают одним цветом две позиции.

В этом случае не следует ограничивать их выбор.

Если вы заметили такое во время проведения методики (или когда ребёнок сдавал вам свой лист с деревом), попросите ответить кого первого, а кого второго из двух/трех (и такое бывает!) человечков ребенок закрасил.

Соотношение этих выборов может быть достаточно информативным.

Интерпретация результатов:

Интерпретация результатов выполнения проективной методики «Дерево» проводится исходя из того, какие позиции выбирает данный ученик, с положением какого человечка отождествляет свое реальное и идеальное положение, есть ли между ними различия.

Интерпретация разработана с учетом опыта практического применения методики и сравнения ее результатов с наблюдениями за поведением учеников, данных, полученных от учителей и родителей, из беседы с ребенком.

Для удобства объяснения каждой фигурке присвоен свой номер.

Следует заметить, что позицию № 16 учащиеся не всегда понимают как позицию «человечка, который несет на себе человечка № 17», а склонны видеть в ней человека, поддерживаемого и обнимаемого другим.

Человечки с подписями

№ позиции фигурки

Характеристика

1, 3, 6, 7

характеризует установку на преодоление препятствий

2, 11, 12, 18, 19

общительность, дружескую поддержку

4

устойчивость положения (желание добиваться успехов, не преодолевая трудности)

5

утомляемость, общая слабость, небольшой запас сил, застенчивость

9

мотивация на развлечения

13, 21

отстраненность, замкнутость, тревожность

8

отстраненность от учебного процесса, уход в себя

10, 15

комфортное состояние, нормальная адаптация

14

кризисное состояние, «падение в пропасть»

20

часто выбирают как перспективу учащиеся с завышенной самооценкой и установкой на лидерство.

 

Здесь можете взять диагностический бланк с человечками без подписей. (http://www.stotestov.ru/product/дерево-тест-лампен)
Или скачать компьютерную версию теста «Дерево с человечками». (http://www.stotestov.ru/product/komp-test-derevo/)

Источник методики в печати: Л.П. Пономаренко. Психологическая профилактика дезадаптации учащихся в начале обучения в средней школе. Методические рекомендации для школьных психологов. — Одесса: Астра-Принт, 1999.


 

Скачано с www.znanio.ru

Дерево, Интерпретация, Vacoa, Остров воссоединения, Остров, Встреча, сад, Тело, рука, диаграмма

Дерево, Интерпретация, Vacoa, Остров воссоединения, Остров, Встреча, сад, Тело, рука, диаграммаPublic Domain

Free for commercial use, DMCA Связаться с нами

Ключевые слова фото

  • Дерево
  • Интерпретация
  • Vacoa
  • Остров воссоединения
  • Остров
  • Встреча
  • сад
  • Тело
  • рука
  • диаграмма
  • Ствол дерева
  • Крупным планом
  • день
  • нет людей
  • на открытом воздухе
  • ствол дерева
  • хобот
  • дерево
  • растение
  • Фокус на переднем плане
  • природа
  • Текстурированный
  • рост
  • Древесина — материал
  • шаблон
  • грубый
  • Коричневый
  • Естественный узор
  • лес
  • Спокойствие
  • Земля
  • кора
  • естественное состояние
Выберите разрешение и скачайте это фото

PC(720P, 1080P, 2K, 4K):

  • 1366×768
  • 1920×1080
  • 1440×900
  • 1600×900
  • 1280×800
  • 1024×768
  • 1280×1024
  • 1536×864
  • 1680×1050
  • 1280×720
  • 1360×768
  • 2560×1440
  • 2560×1080
  • 1920×1200
  • 1280×768
  • 800×600
  • 3840×2160
  • 4096×2304
  • 5120×2880
  • 2880×1800
  • 2560×1600

Mobile(iPhone, Android):

  • 320×480
  • 640×960
  • 640×1136
  • 750×1334
  • 1242×2208
  • 1125×2436
  • 1242×2688
  • 828×1792
  • 720×1280
  • 1080×1920
  • 480×854
  • 480×800
  • 540×960
  • 600×1024
  • 800×1280
  • 1440×2560
  • 320×480

Tablet(iPad, Android):

  • 1024×768
  • 2048×1536
  • 2224×1668
  • 2388×1668
  • 2732×2048
  • 2736×1824
  • 2048×1536
  • 1024×600
  • 1600×1200
  • 2160×1440

5.

4 Дерево решений | Интерпретируемое машинное обучение

Дерево решений

Модели линейной регрессии и логистической регрессии не работают в ситуациях, когда взаимосвязь между функциями и результатом является нелинейной или когда функции взаимодействуют друг с другом. Время блеснуть деревом решений! Модели на основе дерева разделяют данные несколько раз в соответствии с определенными значениями отсечения в элементах. Посредством разделения создаются разные подмножества набора данных, каждый экземпляр принадлежит одному подмножеству.Конечные подмножества называются конечными или листовыми узлами, а промежуточные подмножества называются внутренними узлами или разделенными узлами. Чтобы предсказать результат в каждом листовом узле, используется средний результат обучающих данных в этом узле. Деревья можно использовать для классификации и регрессии.

Существуют различные алгоритмы, с помощью которых можно вырастить дерево. Они различаются возможной структурой дерева (например, количеством разбиений на узел), критериями того, как находить разбиения, когда прекращать разбиение и как оценивать простые модели внутри конечных узлов. Алгоритм деревьев классификации и регрессии (CART), вероятно, является самым популярным алгоритмом индукции деревьев. Мы сосредоточимся на CART, но интерпретация аналогична для большинства других типов деревьев. Я рекомендую книгу «Элементы статистического обучения» (Фридман, Хасти и Тибширани, 2009) для более подробного введения в CART.

РИСУНОК 5.16: Дерево решений с искусственными данными. Экземпляры со значением свойства x1 больше 3 попадают в узел 5. Все остальные экземпляры назначаются узлу 3 или 4, в зависимости от того, превышают ли значения свойства x2 1.Mc_m {} I \ {x \ in {} R_m \} \]

Каждый экземпляр попадает ровно в один листовой узел (= подмножество \ (R_m \)). \ (I _ {\ {x \ in {} R_m \}} \) — функция идентичности, которая возвращает 1, если \ (x \) находится в подмножестве \ (R_m \), и 0 в противном случае. Если экземпляр попадает в листовой узел \ (R_l \), прогнозируемый результат будет \ (\ hat {y} = c_l \), где \ (c_l \) — среднее значение всех обучающих экземпляров в листовом узле \ (R_l \ ).

Но откуда берутся подмножества? Это довольно просто: CART использует функцию и определяет, какая точка отсечения минимизирует дисперсию y для задачи регрессии или индекс Джини распределения классов y для задач классификации.Дисперсия говорит нам, насколько значения y в узле разбросаны вокруг своего среднего значения. Индекс Джини показывает, насколько «нечистым» является узел, например если все классы имеют одинаковую частоту, узел нечист, если присутствует только один класс, он максимально чистый. Дисперсия и индекс Джини минимизируются, когда точки данных в узлах имеют очень похожие значения для y. Как следствие, лучшая точка отсечения делает два результирующих подмножества максимально разными по отношению к целевому результату. Для категориальных функций алгоритм пытается создать подмножества, пробуя различные группировки категорий.После определения наилучшего отсечения для каждого признака алгоритм выбирает объект для разделения, который приведет к лучшему разбиению с точки зрения дисперсии или индекса Джини, и добавляет это разбиение в дерево. Алгоритм рекурсивно продолжает этот поиск и разделение в обоих новых узлах, пока не будет достигнут критерий остановки. Возможные критерии: Минимальное количество экземпляров, которые должны быть в узле перед разделением, или минимальное количество экземпляров, которые должны быть в конечном узле.

Интерпретация

Расшифровка проста: Начиная с корневого узла, вы переходите к следующим узлам, и ребра сообщают вам, на какие подмножества вы смотрите.Как только вы достигнете конечного узла, он сообщит вам прогнозируемый результат. Все края соединяются «И».

Шаблон: если объект x [меньше / больше], чем порог c И…, то прогнозируемый результат — это среднее значение y экземпляров в этом узле.

Важность характеристики

Общую важность функции в дереве решений можно вычислить следующим образом: Просмотрите все разбиения, для которых использовалась функция, и измерьте, насколько она уменьшила дисперсию или индекс Джини по сравнению с родительским узлом. Сумма всех значений масштабируется до 100. Это означает, что каждую важность можно интерпретировать как долю от общей важности модели.

Древовидная декомпозиция

Индивидуальные прогнозы дерева решений можно объяснить, разложив путь решения на один компонент для каждой функции. Мы можем отслеживать решение по дереву и объяснять предсказание вкладом, добавленным в каждом узле решения.

Корневой узел в дереве решений — наша отправная точка.п \ text {feat.contrib (j, x)} \]

Прогноз для отдельного экземпляра — это среднее значение целевого результата плюс сумма всех вкладов D-разбиений, которые происходят между корневым узлом и конечным узлом, в котором экземпляр заканчивается. Однако нас интересуют не отдельные вклады, а особенности. Функция может использоваться более чем для одного разделения или не использоваться вообще. Мы можем добавить вклады для каждой из функций p и получить интерпретацию того, сколько каждая функция внесла в прогноз.

Пример

Давайте еще раз посмотрим на данные по аренде велосипедов. Мы хотим спрогнозировать количество арендованных велосипедов в определенный день с помощью дерева решений. Выученное дерево выглядит так:

РИСУНОК 5.17: Дерево регрессии, построенное на данных проката велосипедов. Максимально допустимая глубина для дерева была установлена ​​равной 2. Для разбиения были выбраны функция тренда (дни с 2011 г.) и температура (темп). Коробчатые диаграммы показывают распределение количества велосипедов в конечном узле.

Первое разбиение и одно из вторых разбиений были выполнены с помощью функции тренда, которая считает дни с начала сбора данных и отражает тенденцию к тому, что услуги по аренде велосипедов становятся все более популярными с течением времени. Для дней до 105-го дня прогнозируемое количество велосипедов составляет около 1800, между 106-м и 430-м днем ​​- около 3900. Для дней после 430-го дня прогноз будет либо 4600 (если температура ниже 12 градусов), либо 6600 (если температура выше 12 градусов).

Важность функции говорит нам, насколько функция помогла улучшить чистоту всех узлов. Здесь использовалась дисперсия, поскольку прогнозирование аренды велосипедов — это задача регрессии.

Визуализированное дерево показывает, что для разбиения использовались и температурный, и временной тренд, но не дает количественной оценки, какая функция была более важной. Мера важности функции показывает, что временной тренд гораздо важнее температуры.

РИСУНОК 5.18: Важность характеристик, измеренная по тому, насколько в среднем улучшается чистота узла.

Преимущества

Древовидная структура идеальна для захвата взаимодействий между функциями в данных.

Данные попадают в отдельных групп , которые часто легче понять, чем точки на многомерной гиперплоскости, как при линейной регрессии. Интерпретация, возможно, довольно проста.

Древовидная структура также имеет естественную визуализацию с узлами и краями.

Деревья создают хорошие объяснения , как определено в главе «Дружественные человеку объяснения».Древовидная структура автоматически предлагает рассматривать предсказанные значения для отдельных экземпляров как противоречащие фактам: «Если бы объект был больше / меньше точки разделения, прогноз был бы y1 вместо y2». Объяснения дерева контрастны, так как вы всегда можете сравнить предсказание экземпляра с соответствующими сценариями «что, если» (как определено деревом), которые являются просто другими листовыми узлами дерева. Если дерево короткое, например, от одного до трех разломов, получаемые объяснения будут выборочными.Дерево с глубиной три требует максимум трех функций и точек разделения, чтобы создать объяснение для прогноза отдельного экземпляра. Правдивость прогноза зависит от прогнозирующей способности дерева. Объяснения коротких деревьев очень простые и общие, потому что для каждого разбиения экземпляр попадает либо в один, либо в другой лист, и бинарные решения легко понять.

Нет необходимости преобразовывать объекты. В линейных моделях иногда необходимо логарифмировать признак.Дерево решений одинаково хорошо работает с любым монотонным преобразованием объекта.

Недостатки

Деревья не поддерживают линейные отношения . Любая линейная связь между входным объектом и результатом должна быть аппроксимирована разбиениями, создавая ступенчатую функцию. Это неэффективно.

Это идет рука об руку с недостаточной плавностью . Незначительные изменения входных данных могут иметь большое влияние на прогнозируемый результат, что обычно нежелательно.Представьте себе дерево, которое предсказывает стоимость дома, и дерево использует размер дома в качестве одного из элементов разделения. Раскол происходит на 100,5 квадратных метрах. Представьте себе пользователя оценщика цен на жилье, использующего вашу модель дерева решений: Они измеряют свой дом, приходят к выводу, что в доме 99 квадратных метров, вводят его в калькулятор цен и получают прогноз в 200 000 евро. Пользователи замечают, что забыли обмерять небольшую кладовку в 2 квадратных метра. У кладовки наклонная стена, поэтому они не уверены, смогут ли они посчитать всю площадь или только ее половину.Поэтому они решили попробовать и 100,0, и 101,0 квадратных метра. Результаты: Калькулятор цен выводит 200 000 евро и 205 000 евро, что довольно не интуитивно, потому что не было изменений с 99 квадратных метров на 100.

Деревья тоже довольно нестабильны . Несколько изменений в наборе обучающих данных могут создать совершенно другое дерево. Это потому, что каждое разбиение зависит от родительского разбиения. И если в качестве первого разбиенного объекта выбран другой объект, изменяется вся древовидная структура.Если структура так легко меняется, это не создает уверенности в модели.

Деревья решений очень интерпретируемы — пока они короткие. Количество конечных узлов быстро увеличивается с глубиной. Чем больше конечных узлов и чем глубже дерево, тем труднее понять правила принятия решений в дереве. Глубина 1 означает 2 конечных узла. Глубина 2 означает макс. 4 узла. Глубина 3 означает макс. 8 узлов. Максимальное количество конечных узлов в дереве — 2 в степени глубины.

Программное обеспечение

Для примеров в этой главе я использовал пакет rpart R, который реализует CART (деревья классификации и регрессии). CART реализован на многих языках программирования, включая Python. Возможно, CART — довольно старый и несколько устаревший алгоритм, и есть несколько интересных новых алгоритмов для подгонки деревьев. Вы можете найти обзор некоторых пакетов R для деревьев решений в представлении задач CRAN машинного обучения и статистического обучения под ключевым словом «Рекурсивное разбиение».

Что такое древовидная диаграмма? Системный или иерархический анализ

Глоссарий качества Определение: древовидная диаграмма

Также называется: систематическая диаграмма, анализ дерева, аналитическое дерево, диаграмма иерархии

Древовидная диаграмма — это новый инструмент планирования управления, который отображает иерархию задач и подзадач, которые необходимо выполнить и достичь цели. Древовидная диаграмма начинается с одного элемента, который разветвляется на два или более, каждый из которых разветвляется на два или более, и так далее. Готовая схема напоминает дерево со стволом и множеством ветвей.

Используется для разбивки широких категорий на все более мелкие уровни детализации. Разработка древовидной диаграммы поможет вам шаг за шагом перейти от общих к конкретным.

Когда использовать древовидную диаграмму

  • Когда проблема известна или решается в общих чертах, и вы должны перейти к конкретным деталям, например, при разработке логических шагов для достижения цели
  • При разработке действий по реализации решения или другого плана
  • При подробном анализе процессов
  • При поиске основной причины проблемы
  • При оценке проблем реализации для нескольких потенциальных решений
  • После того, как диаграмма родства или диаграмма взаимосвязей выявили ключевые проблемы
  • Как средство коммуникации, чтобы объяснять детали другим

Древовидная диаграмма Процедура

  1. Разработайте формулировку цели, проекта, плана, проблемы или того, что изучается.Напишите его вверху (для вертикального дерева) или далеко слева (для горизонтального дерева) вашей рабочей поверхности.
  2. Задайте вопрос, который приведет вас к следующему уровню детализации. Например:
    • Чтобы получить цель, план действий или иерархическую структуру работ, спросите: «Какие задачи должны быть выполнены для этого?» или «Как это можно сделать?»
    • Для анализа первопричин спросите: «Что вызывает это?» или «Почему это происходит?»
    • Для диаграммы Гозинто спросите: «Какие компоненты?» («Гозинто» буквально происходит от фразы «Что в нем входит?»)
  3. Проведите мозговой штурм по всем возможным ответам.Если диаграмма родства или диаграмма взаимосвязи была сделана ранее, идеи могут быть взяты оттуда. Запишите каждую идею в строке ниже (для вертикального дерева) или справа от (для горизонтального дерева) первого утверждения. Показывать связи между уровнями стрелками.
  4. Проведите проверку на «необходимое и достаточное». Все ли предметы этого уровня необходимы для того, что находится на уровне выше? Если бы все предметы на этом уровне присутствовали или были выполнены, было бы их достаточно для того, что на уровне выше?
  5. Каждое новое изложение идеи теперь становится предметом: целью, задачей или постановкой проблемы.Для каждого из них задайте вопрос еще раз, чтобы раскрыть следующий уровень детализации. Создайте еще один уровень утверждений и покажите связи с предыдущим уровнем идей с помощью стрелок. Проведите проверку на «необходимое и достаточное» для каждого набора предметов.
  6. Продолжайте превращать каждую новую идею в предметное изложение и задавайте вопросы. Не останавливайтесь, пока не дойдете до фундаментальных элементов: конкретных действий, которые можно выполнить, компонентов, которые нельзя разделить, основных причин.
  7. Проведите «необходимую и достаточную» проверку всей схемы.Все ли предметы необходимы для достижения цели? Если бы все пункты присутствовали или были выполнены, было бы их достаточно для достижения цели?

Пример древовидной диаграммы

Pearl River, Школьный округ Нью-Йорка, получивший в 2001 году Национальную премию качества Малкольма Болдриджа, использует древовидную диаграмму, чтобы показать, как цели округа переводятся в подцели и отдельные проекты. Они называют этот связанный подход «Золотой нитью».

Округ преследует три основные цели.Первый, предназначенный для повышения успеваемости, частично показан на рисунке ниже. Руководители округа определили две стратегические цели, выполнение которых приведет к повышению успеваемости: академическая успеваемость и прием в колледж.

Пример древовидной диаграммы

Лаг-индикаторы рассчитаны на долгосрочную перспективу и ориентированы на результат. Показателем отставания в академической успеваемости является процент дипломов Риджентс: процент студентов, получивших государственный диплом, сдав восемь экзаменов Риджентс.

Лид-индикаторы краткосрочны и ориентированы на процесс. Начиная с 2000 года, основным показателем аттестата регентов были результаты новых государственных тестов четвертого и восьмого классов.

Наконец, на основе причинно-следственного анализа определяются годовые проекты, которые улучшают производительность. В 2000-2001 гг. Было реализовано четыре проекта по повышению успеваемости. Таким образом, эта древовидная диаграмма представляет собой взаимосвязанный ряд целей и показателей, отслеживающих причины общесистемной успеваемости сначала через количество дипломов средней школы, затем через более низкие оценки и обратно к конкретным проектам улучшения.

Адаптировано из The Quality Toolbox, Second Edition , ASQ Quality Press.

Анализ дерева решений — Навыки принятия решений от MindTools.com

© iStockphoto
Nikada

Деревья решений помогут вам оценить ваши варианты.

Деревья решений

— отличный инструмент, который поможет вам выбрать один из нескольких вариантов действий.

Они обеспечивают высокоэффективную структуру, в которой вы можете разложить варианты и исследовать возможные результаты выбора этих вариантов.Они также помогают вам составить сбалансированную картину рисков и выгод, связанных с каждым возможным курсом действий.

Рисование дерева решений

Вы начинаете дерево решений с решения, которое вам нужно принять. Нарисуйте небольшой квадрат слева от большого листа бумаги.

Из этого поля нарисуйте линии вправо для каждого возможного решения и напишите это решение вдоль линии. Держите строки как можно дальше друг от друга, чтобы вы могли расширить свои мысли.

В конце каждой строки рассмотрите результаты. Если результат принятия этого решения неясен, нарисуйте маленький кружок. Если в результате вам нужно принять другое решение, нарисуйте еще один квадрат. Квадраты представляют решения, а круги — неопределенные результаты. Напишите решение или множитель над квадратом или кружком. Если вы завершили решение в конце строки, просто оставьте его пустым.

Начиная с новых квадратов решений на диаграмме, нарисуйте линии, представляющие варианты, которые вы могли выбрать.Из кругов нарисуйте линии, представляющие возможные результаты. Снова сделайте краткую пометку в строке, говоря, что она означает. Продолжайте делать это до тех пор, пока не извлечете как можно больше возможных результатов и решений, которые, как вы можете видеть, вытекают из исходных решений.

Пример того, что у вас получится, показан на рисунке 1:

.

После этого просмотрите свою древовидную диаграмму. Бросьте вызов каждому квадрату и кружку, чтобы увидеть, есть ли какие-либо решения или результаты, которые вы не рассматривали.Если есть, втяните их. При необходимости перекрасьте дерево, если его части слишком перегружены или неопрятны. Теперь вы должны хорошо понимать диапазон возможных результатов ваших решений.

Оценка дерева решений

Теперь вы готовы оценить дерево решений. Здесь вы можете решить, какой вариант является для вас наиболее ценным. Начните с присвоения денежной оценки или оценки каждому возможному исходу. Оцените, сколько, по вашему мнению, это будет стоить для вас, если такой результат наступит.

Подпишитесь на нашу рассылку новостей

Получайте новые карьерные навыки каждую неделю, а также наши последние предложения и бесплатное загружаемое учебное пособие по личному развитию.

Прочтите нашу Политику конфиденциальности

Затем посмотрите на каждый кружок (представляющий точку неопределенности) и оцените вероятность каждого результата.Если вы используете проценты, общая сумма должна составлять 100 процентов в каждом кружке. Если вы используете дроби, они должны составлять в сумме 1. Если у вас есть данные о прошлых событиях, вы можете сделать точные оценки вероятностей. В противном случае запишите свое лучшее предположение.

Это даст вам дерево, подобное изображенному на рисунке 2:

Расчет значений дерева

После того, как вы определили ценность результатов и оценили вероятность результатов неопределенности, пора приступить к вычислению значений, которые помогут вам принять решение.

Начните с правой стороны дерева решений и вернитесь влево. Когда вы завершите набор вычислений на узле (квадрате решения или круге неопределенности), все, что вам нужно сделать, это записать результат. С этого момента вы можете игнорировать все вычисления, которые приводят к такому результату.

Расчет стоимости узлов неопределенного результата

Если вы рассчитываете ценность неопределенных результатов (кружки на диаграмме), делайте это, умножая ценность результатов на их вероятность.Итог для этого узла дерева — это сумма этих значений.

В примере на рисунке 2 значение «новый продукт, тщательная разработка» составляет:

0,4 ​​(вероятность хорошего исхода) x 1000000 долларов (стоимость) =

 400 000 долл. США
0,4 (исход со средней вероятностью) x 50 000 долл. США (значение) = 20 000 долл. США
0,2 (вероятность неблагоприятного исхода) x 2000 долларов (стоимость) = 400 долл. США
ИТОГО 420 400 долл. США

На рисунке 3 показан расчет узлов с неопределенным исходом:

Обратите внимание, что значения, рассчитанные для каждого узла, показаны в полях.

Расчет значения узлов принятия решения

Когда вы оцениваете узел решения, запишите стоимость каждого варианта по каждой строке решения. Затем вычтите стоимость из уже рассчитанного значения результата. Это даст вам ценность, отражающую пользу от этого решения.

Обратите внимание, что уже потраченные суммы не учитываются в данном анализе — это «невозвратные затраты» и (несмотря на эмоциональные контраргументы) не должны учитываться при принятии решения.

Когда вы подсчитали эти преимущества решения, выберите вариант, который дает наибольшую выгоду, и примите это как принятое решение. Это значение этого узла решения.

На рисунке 4 показан этот расчет узлов принятия решений в нашем примере:

В этом примере выгода, которую мы ранее рассчитали для «нового продукта, тщательная разработка», составила 420 400 долларов. Мы оцениваем будущую стоимость этого подхода в 150 000 долларов. Это дает чистую прибыль в размере 270 400 долларов США.

Чистая выгода от «нового продукта, быстрое развитие» составила 31 400 долларов.Поэтому в этой ветви мы выбираем наиболее ценный вариант «новый продукт, тщательная разработка» и присваиваем это значение узлу принятия решения.

Результат

Применяя эту технику, мы видим, что лучший вариант — это разработка нового продукта. Для нас гораздо важнее не торопиться и получить правильный продукт, чем спешить с выпуском продукта на рынок. Лучше просто улучшить наши существующие продукты, чем испортить новый продукт, даже если это будет обходиться нам дешевле.

Ключевые моменты

Деревья решений обеспечивают эффективный метод принятия решений, потому что они:

  • Четко изложите проблему, чтобы можно было оспорить все варианты.
  • Позвольте нам полностью проанализировать возможные последствия решения.
  • Обеспечьте основу для количественной оценки ценности результатов и вероятностей их достижения.
  • Помогите нам принимать оптимальные решения на основе имеющейся информации и предположений.

Как и все методы принятия решений, анализ дерева решений следует использовать в сочетании со здравым смыслом — деревья решений являются лишь одной из важных частей вашего набора инструментов принятия решений.

Анализ дерева классификации

Classification Tree Analysis (CTA) — это тип алгоритма машинного обучения, используемый для классификации данных дистанционного зондирования и вспомогательных данных в поддержку картографирования и анализа земного покрова. Дерево классификации — это структурное отображение бинарных решений, которые приводят к решению о классе (интерпретации) объекта (например, пикселя). Хотя иногда его называют деревом решений, более правильно это тип дерева решений, которое приводит к категориальным решениям.Дерево регрессии, другая форма дерева решений, приводит к количественным решениям.

Дерево классификации состоит из ветвей, которые представляют атрибуты, а листья представляют решения. При использовании процесс принятия решения начинается со ствола и следует по ветвям, пока не будет достигнут лист. На рисунке выше показано простое дерево решений, основанное на учете коэффициента отражения пикселя в красном и инфракрасном диапазоне.

Classification Tree Analysis (CTA) — это аналитическая процедура, в которой используются примеры известных классов (т.д., обучающие данные) и строит дерево решений на основе измеренных атрибутов, таких как отражательная способность. В TerrSet модуль CTA основан на алгоритме C4.5. По сути, алгоритм итеративно выбирает атрибут (например, полосу отражательной способности) и значение, которые могут разделить набор образцов на две группы, минимизируя вариабельность внутри каждой подгруппы, одновременно увеличивая контраст между группами.

В комплект входит набор инструментов для обучения и сокращения дерева классификации. График
мониторинга показывает постепенное включение обучающих пикселей для каждого класса во время анализа.После завершения анализа
доля неправильно классифицированных пикселей тренировочного сайта будет отображаться, а также
в виде дерева, показывающего разбиения для соответствующих входных изображений и пороговое значение разделения. Детали листа
включают количество пикселей в листе, процент этих пикселей, которые принадлежат к общему количеству
пикселей в этом классе, и индекс чистоты, который представляет собой процент правильных пикселей, принадлежащих указанному классу
в этом листе для общее количество пикселей в листе.

Поскольку он может взять набор обучающих данных и построить дерево решений, анализ дерева классификации представляет собой форму машинного обучения, подобную нейронной сети. Однако, в отличие от нейронной сети, такой как Multi-Layer Perceptron (MLP) в TerrSet, CTA создает решение «белого ящика», а не «черного ящика», потому что природа выученного процесса принятия решения явно выводится. Это одна из главных достопримечательностей CTA. Структура дерева дает нам информацию о процессе принятия решения.

Другая привлекательность состоит в том, что он прост для понимания и непараметрический — он не требует, чтобы данные, связанные с определенным классом по определенному атрибуту, следовали какому-либо определенному распределению (например, нормальному распределению). Таким образом, например, он способен работать с классом с необычными характеристиками, такими как непроницаемые поверхности, которые содержат как низкие (асфальт), так и высокие (бетон) отражатели.

Как и в случае со всеми классификаторами, при использовании CTA следует учитывать некоторые предостережения.База двоичных правил CTA устанавливает логику классификации, по существу идентичную классификатору параллелепипеда. Таким образом, наличие корреляции между независимыми переменными (что является нормой для дистанционного зондирования) приводит к очень сложным деревьям. Этого можно избежать, предварительно преобразовав основные компоненты (PCA в TerrSet) или, что еще лучше, канонические компоненты (CCA в TerrSet). Однако дерево, хотя и проще, теперь труднее интерпретировать.

Второе предостережение заключается в том, что, как и нейронные сети, CTA прекрасно может изучать даже недиагностические характеристики класса.Например, если бы мы использовали CTA, чтобы научиться различать широколиственные и хвойные леса, и если бы наша обучающая выборка для широколиственных пород включала некоторые пробелы с подлеском травы, то все участки травы были бы классифицированы как широколиственные. Таким образом, CTA включает процедуры обрезки бессмысленных листьев. Правильно обрезанное дерево восстановит общность процесса классификации.

Модуль CTA предоставляет жесткие и / или мягкие классифицированные выходные карты. Для каждого класса есть один программный выход. Каждый пиксель в мягком выходном изображении связан со степенью принадлежности к классу на том конкретном листе, из которого он был классифицирован.Если пиксель не связан с этим классом, ему будет присвоен ноль.

Обучение

Пользователь должен сначала использовать обучающие образцы, чтобы вырастить дерево классификации. Это называется этапом обучения. Затем все изображение классифицируется с помощью этого дерева.

Для начала все обучающие пиксели из всех классов назначаются корню. Поскольку корень содержит все обучающие пиксели из всех классов, начинается итерационный процесс роста дерева и отделения классов друг от друга.В Terrset CTA использует бинарную древовидную структуру, а это означает, что из корня, а также из всех последующих ветвей может вырасти не более двух новых междоузлий, прежде чем он должен снова разделиться или превратиться в лист. Правило двоичного разделения идентифицируется как порог в одном из нескольких входных изображений, который изолирует наибольшее однородное подмножество обучающих пикселей от оставшейся части обучающих данных.

Дерево растет путем рекурсивного разделения данных в каждом междоузлии на новые междоузлия, содержащие постепенно более однородные наборы обучающих пикселей.Вновь выросшее междоузлие может стать листом, если оно содержит обучающие пиксели только из одного класса, или пиксели из одного класса доминируют над совокупностью пикселей в этом междоузлии, и это преобладание находится на приемлемом уровне, заданном пользователем. Когда больше нет междоузлий для разделения, формируются окончательные правила дерева классификации.

Классификация

Второй шаг метода CTA — классификация изображений. На этом этапе каждый пиксель помечается классом, использующим решающие правила ранее обученного дерева классификации.Сначала пиксель вводится в корень дерева, значение в пикселе сравнивается с тем, что уже есть в дереве, и пиксель отправляется в междоузлия в зависимости от того, где он попадает по отношению к точке разделения. Процесс продолжается до тех пор, пока пиксель не достигнет листа, а затем помечается классом.

Благодаря интуитивно понятному графическому дисплею в интерфейсе правила классификации от корня до листа просты для понимания и интерпретации. Входные изображения могут быть числовыми, например значениями отражательной способности данных дистанционного зондирования, категориальными изображениями, такими как слой землепользования, или их комбинацией.

Если известно, что набор данных подчиняется определенному шаблону распределения, вы можете использовать соответствующий параметрический классификатор, отличный от подхода дерева классификации. Например, если известно, что данные изображения подчиняются распределению Гаусса, может быть предпочтительным параметрический классификатор, такой как MAXLIKE в TerrSet.

Как интерпретировать филогенетические деревья — документация Nextstrain

Передаточные деревья против филогенетических деревьев

Патогены распространяются путем быстрой репликации в одном хозяине с последующей передачей другому хозяину.Эпидемия может начаться только тогда, когда одна инфекция приводит к более чем одной последующей инфекции.

По мере того, как патоген реплицируется и распространяется, его геном необходимо многократно реплицировать, и в геноме будут накапливаться случайные мутации (ошибки копирования). Такие случайные мутации могут помочь отследить распространение патогена и узнать о путях и динамике его передачи.

На иллюстрации выше показан эскиз дерева передачи с подмножеством случаев, которые были отобраны (синий).На практике дерево передачи неизвестно, и обычно доступны только приблизительные оценки количества случаев. Последовательности генома позволяют нам делать выводы о частях дерева передачи. В этом примере на дереве обозначены три мутации (маленькие ромбики). Последовательности с одинаковыми мутациями более тесно связаны, поэтому эти мутации позволяют сгруппировать образцы в кластеры близкородственных вирусов, принадлежащих к одним и тем же цепям передачи.

Чтение филогенетического дерева

Ниже мы видим иллюстрацию с филогенетическим деревом слева, где мутации показаны в виде цветных кружков.Справа соответствующие последовательности, также с мутациями, показанными цветными кружками. Мы видим, что последовательности, имеющие одни и те же мутации, группируются вместе. Когда последовательности кажутся связанными плоской вертикальной линией, например A и B, это означает, что между ними нет различий — их последовательности идентичны.

Когда последовательность находится в длинной строке сама по себе, например, C или E, это означает, что у нее есть уникальные мутации, которых нет в других последовательностях. Чем длиннее линия, тем больше мутаций. A и B также имеют уникальные мутации (зеленый кружок), не общие для других последовательностей, но они идентичны друг другу.

На данный момент филогения нового коронавируса (COVID-19) может не сильно походить на «дерево». Многие последовательности идентичны — они расположены вместе на вертикальных линиях, таких как A и B (некоторые находятся в самой левой части дерева). У других есть уникальные или общие мутации, поэтому они располагаются на линиях или «ветвях», идущих вправо. Вы можете увидеть, сколько мутаций имеет ветка, наведя на нее указатель мыши.

Чтение типизированного филогенетического древа

Филогенетические деревья часто содержат дополнительную информацию, например, откуда были изолированы географически отдельные последовательности.Кроме того, возможные местоположения внутренних узлов также могут быть выведены с помощью математических моделей. Однако интерпретировать их следует с осторожностью, поскольку отбор проб и секвенирование или их отсутствие могут существенно повлиять на интерпретацию,

В следующем примере мы сначала показываем полностью отобранное филогенетическое дерево с образцами из двух разных мест, обозначенных оранжевым и синим. В полностью отобранном случае справа наша интерпретация произошедшего заключалась в том, что было три разных введения от оранжевого до синего.При удалении одной оранжевой последовательности в середине, наша интерпретация теперь такова, что было одно введение в синий цвет, которое произошло намного раньше. В последнем примере у нас есть только одна последовательность из оранжевого, что может наводить нас на мысль, что было одно введение из оранжевого в синий.

В целом, предполагаемые местоположения того, где родословная была в прошлом, следует рассматривать как весьма неопределенные.

Анализ и интерпретация рисунков деревьев — это метод подсознательной коммуникации, который может помочь в терапии и понимании.

Анализ чертежа дерева

Альтернативное подсознательное общение с арт-терапией

Рисование дерева с помощью цвета — отличный способ развить понимание внутреннего разума, потому что подсознание автоматически создает символы и значения, которые понимает внутренний разум, и показывает их в форме дерева.

Этот метод поможет понять подсознание, изучив этот язык и интерпретируя его для общения с этим внутренним разумом.

ИНТЕРПРЕТАЦИЯ ЧЕРТЕЖА ДЕРЕВА Шерил Мартин

Я увлекся интерпретацией рисунков деревьев в аспирантуре и сразу увидел положительные последствия. Позже, когда я был ведущим терапевтом шести психиатров в стационаре, мой клинический директор доктор Стюарт Фелпс разрешил мне работать с арт-терапевтом одно утро в неделю. За это время я усовершенствовал интерпретацию рисунков деревьев.

Она подарила мне книгу, которая с тех пор стала ключом к пониманию тех, кто хотел бы принять мои наставления, разбавить их и использовать неправильно.Арт-терапевт дал мне книгу, чтобы показать простую технику ее включения, но также сказал: «Надеюсь, вы понимаете, что она отваживается далеко от проверенных формул». «Всегда придерживайтесь терапевтически проверенных формул, и рисование дерева никогда вас не подведет».

Я два года писала учебник, а мой муж еще год занимался графикой, форматированием и сборкой всего этого. В книге правдивые истории и рассказывается о жизни людей. Рисунок дерева является планом для их подсознания и проходит через многие сеансы собеседований, чтобы извлечь правду из подсознания.

Я читал курс о королеве Марии на национальном съезде. Я попросил участников признать, что это было частью моего обучения миру, и использовать его, но не пытаться преподавать его, потому что это был всего лишь четырехчасовой семинар. Я также упомянул название книги и рассказал историю арт-терапевта, который дал мне ее в этом классе. Я упустил часть о арт-терапевте, в котором говорилось, что причина, по которой книга не вышла в свет в долгосрочной перспективе, заключалась в том, что автор добавила свои собственные интерпретации, не подтвержденные тестами на надежность, и книга не имела печати традиционного психологического одобрения. из-за этого.

Вы угадали! На этот семинар из Техаса приехал человек, который выдавал себя за дипломированного психолога из Техаса. Он посетил мой семинар и получил учебное пособие. Позже он начал обучать женщину, которая проводила семинары по выходным в Техасе, все еще называя себя лицензированным психологом в Техасе.

Он появляется в Национальной гильдии гипноза с торговым столом, и ЕГО КНИГА продается за его столом. Я купил ее, и в большинстве своем это МОЯ КНИГА прямо с машины XEROX.На копирование трехлетней работы у него, должно быть, ушло два часа.

Конечный результат: Мы наняли адвоката, который проверил этого человека. Нет лицензии по психологии ни в Техасе, ни где-либо еще. Мы с ним договорились, и он перестал продавать книгу. Между прочим, он добавил то, что могло быть только СВОИМИ ДИКИЕ ТОЛКОВАНИЯ в той небольшой части, которую добавил.

Другие предлагают книгу, о которой я упоминал в своем первом выступлении (та, которую арт-терапевт сказал мне, была хорошей идеей, но не вышла, потому что женщина использовала неверную информацию).Они также ссылаются на то, что пошли к человеку, который выдавал себя за лицензированного психолога, но никогда не имел лицензии ни на что.

Итак, на этом сайте я поделюсь настоящими рисунками деревьев людьми, их историями и интерпретациями. Я сделаю это проверяемым, достоверным и надежным способом. Это покажет действенность и терапевтические преимущества этой техники.

У вас также будет возможность интерпретировать ваш собственный рисунок дерева вместе с судебно-графологической интерпретацией вашего собственного анализа почерка.

Оба этих анализа вместе взятые дадут вам важную информацию о вас самих, ваших целях и личности.

Помните, что интерпретация должна быть сделана в правильной форме с использованием этих достоверных методов, чтобы информация была правдивой.

Просмотрите следующие древовидные рисунки и их интерпретацию.

Не такая уж и праздничная елка Рисунок истолкованный

Рисунки в интерпретации детей одной семьи

Старшие — 10 лет Рисунки деревьев

Средний ребенок — 7 лет Рисунки деревьев

Младший — 2 года Рисунки деревьев

Заказать самостоятельно: Интерпретация / анализ личного чертежа дерева
от Cheryl W.Мартин

Позвоните Шерил, чтобы узнать подробности. звоните 205 322 7284

Шерил В. Мартин, автор

Alabama Hypnosis Clinic

of The Path Foundation
1715 11th Avenue South
Birmingham, Alabama (AL) 35205
in Alabama call (205) 322 PATH (7284)
Техасский институт гипноза (Хьюстон)

2400 Augusta Drive, Suite 372
Houston, Texas 77057
в Техасе звоните (281) 359 PATH (7284)
Anywhere Позвоните нам по номеру 1-205-322-PATH (7284)

Электронная почта: адрес электронной почты @ найденный путь.com

Интерпретация хронологий древовидных колец (Интерпретация от Jahrringchronologien) в JSTOR

Абстрактный

Die Interpretation publizierter Jahrringchronologien und deren Verwendung in geographischen Studien setzt ein Verständnis wesentlicher Aspekte der Chronologiebildung voraus. Zahlreiche Chronologien rekonstruieren beispielsweise klimatische Variationen mit Wellenlängen von Jahren bis zu Dekaden. Längerfristige, etwa säkulare Trends sind generell schwieriger zu betonen und fehlen häufig in den Chronologien.Diese Sachverhalte zu erklären und ein grundlegendes Verständnis für die aktuellen Techniken der Dendrochronologie zu wecken, ist das Ziel des vorliegenden Beitrages. Damit soll die Interpretation von Jahrringchronologien erleichtert und das Potential dieser Methode verdeutlicht werden /// Для интерпретации опубликованных хронологий годичных колец и использования этих результатов для географических исследований необходимы знания об основных аспектах построения хронологии. Например, большинство хронологий отображают климатические колебания в диапазоне от лет до десятилетий.Тенденции в более длительных временных масштабах, такие как колебания в масштабе столетия, как правило, труднее выделить и часто отсутствуют в хронологиях годичных колец. Здесь мы стремимся объяснить такие факты и сформировать базовое понимание современных дендрохронологических методов, что позволит понять успешную интерпретацию хронологий годичных колец и силу этого метода.

Информация о журнале

С момента основания Карлом Троллем в 1947 году Erdkunde — Archive of Scientific Geography зарекомендовал себя как успешный международный географический журнал.Эрдкунде публикует научные статьи, охватывающие весь спектр физической и человеческой географии. Журнал предлагает современные отчеты о последних тенденциях и событиях в конкретных областях географии, а также всесторонние и критические обзоры новых географических публикаций. Все рукописи перед публикацией проходят процедуру рецензирования. Известными отличительными чертами Erdkunde являются всемирно известная картография и регулярные крупноформатные приложения, а также стандартные цветные рисунки и фигурки.

Информация об издателе

Компания Erdkunde была основана в 1947 году немецким географом Карлом Троллем в Боннском университете. На протяжении всех лет Эрдкунде руководил Департаментом географии в Бонне, но производственные процессы, а также продажи и маркетинг оставались на стороне. Все время Эрдкунде носила разная от природы группа редакторов. Текущий состав редакции состоит из ведущих немецких профессоров географии.В 2008 году редакция решила реструктурировать и переконцентрировать все производственные процессы в Департаменте географии в Бонне.