Изоморфизм примеры: Изоморфизм спешит на помощь / Хабр

ИЗОМОРФИЗМ — Что такое ИЗОМОРФИЗМ?

Слово состоит из 10 букв: первая и, вторая з, третья о, четвёртая м, пятая о, шестая р, седьмая ф, восьмая и, девятая з, последняя м,

Слово изоморфизм английскими буквами(транслитом) — izomorfizm

• Буква и встречается 2 раза. Слова с 2 буквами и
• Буква з встречается 2 раза. Слова с 2 буквами з
• Буква о встречается 2 раза. Слова с 2 буквами о
• Буква м встречается 2 раза. Слова с 2 буквами м
• Буква р встречается 1 раз. Слова с 1 буквой р
• Буква ф встречается 1 раз. Слова с 1 буквой ф

Изоморфизм

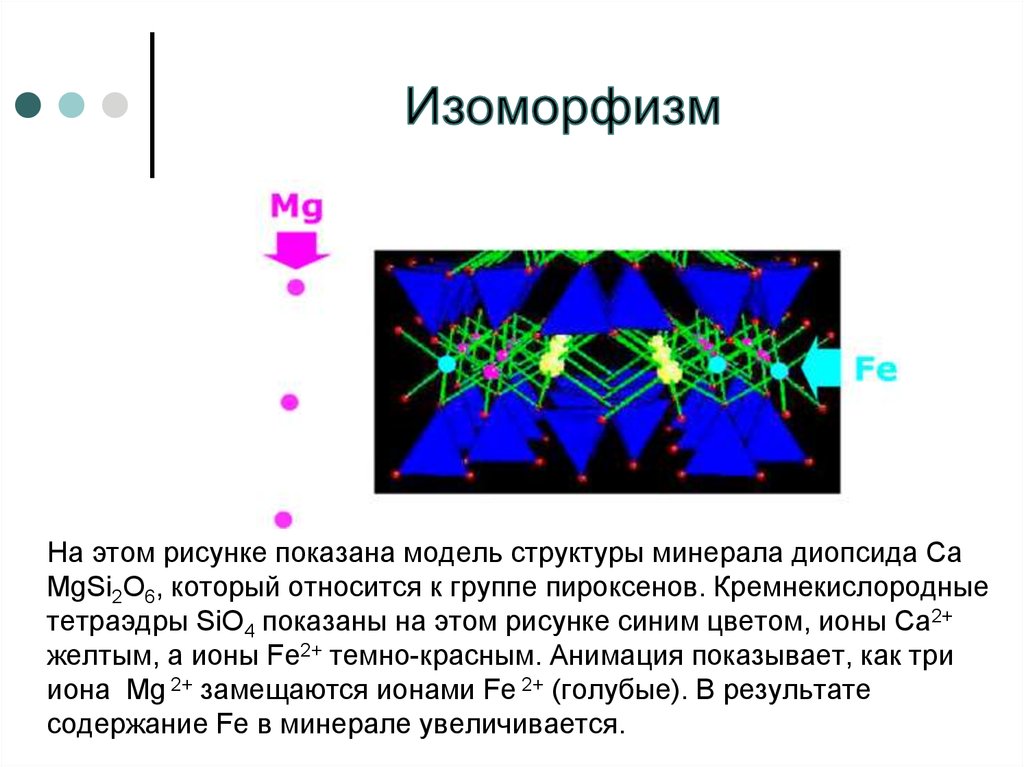
ИЗОМОРФИЗМ (от изо и греч. morphe — форма, вид), способность атомов, ионов или молекул замещать друг друга в кристаллич.

структурах. В результате изоморфизма образуются твердые р-ры замещения.

Химическая энциклопедия

Изоморфи́зм (от др.-греч. ἴσος — «равный, одинаковый, подобный» и μορφή — «форма») — это очень общее понятие, которое употребляется в различных разделах математики.

ru.wikipedia.org

Изоморфизм [isomorphism] — понятие математики и логики, означающее соотношение между двумя любыми объектами тождественной структуры. Между элементами изоморфных объектов существует взаимно однозначное отношение…

slovar-lopatnikov.ru

ИЗОМОРФИЗМ (от греч. isos – равный, однозначный и morphe – форма) понятие, выражающее тождественность, идентичность форм. В психологии идентичность (теоретическая) между гештальтами в переживании непосредственно созерцаемого и в процессах…

Философская энциклопедия

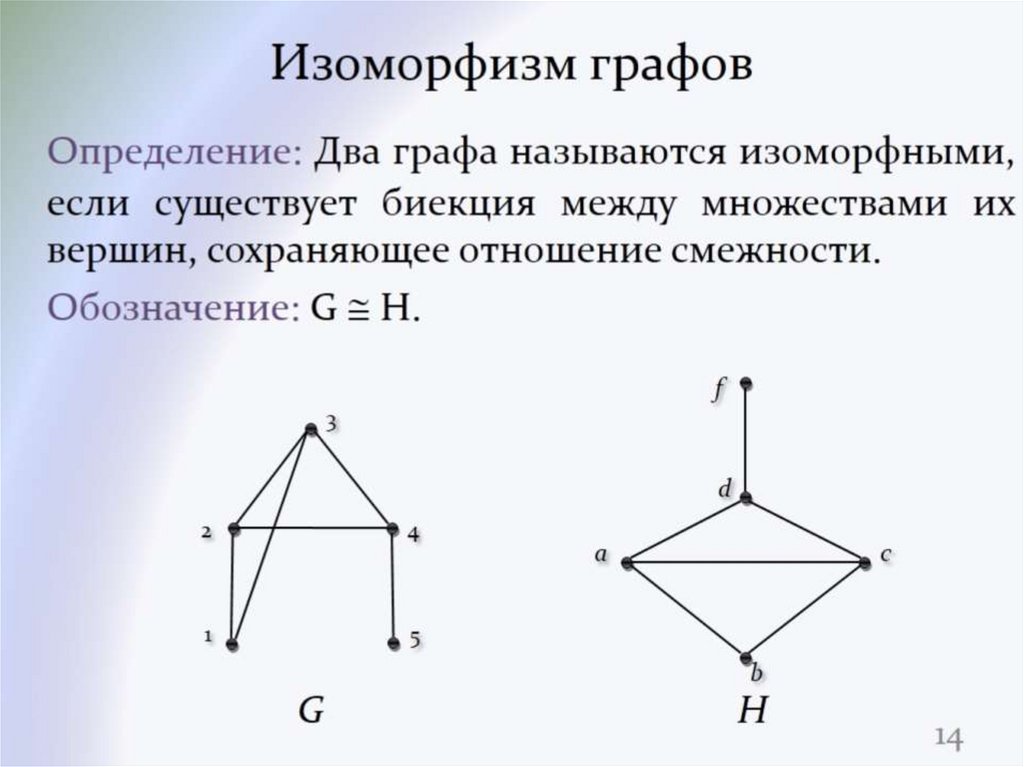
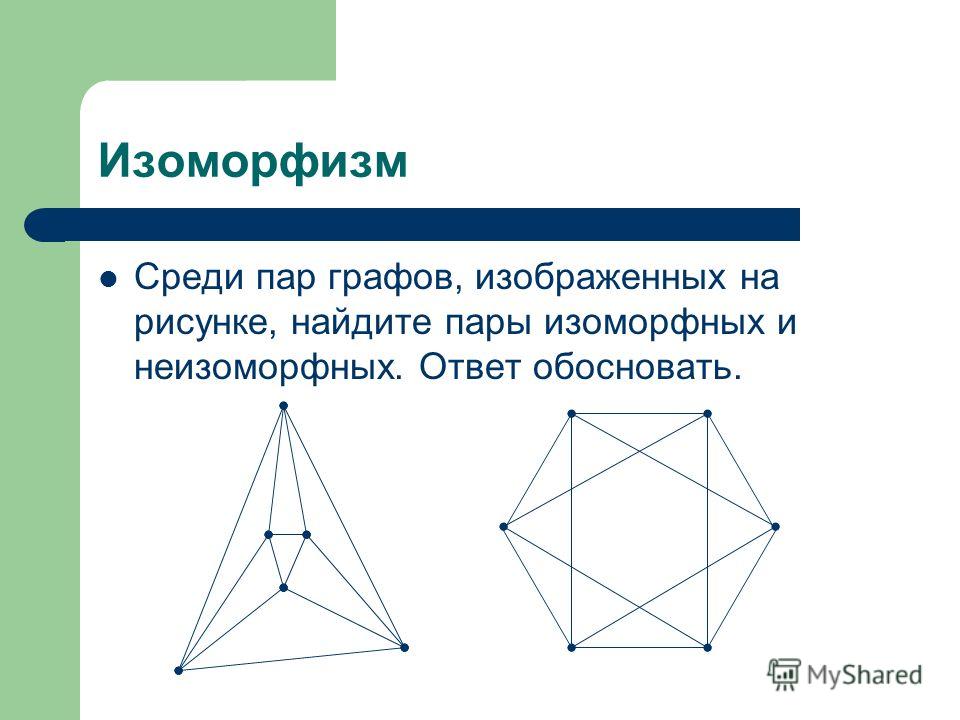
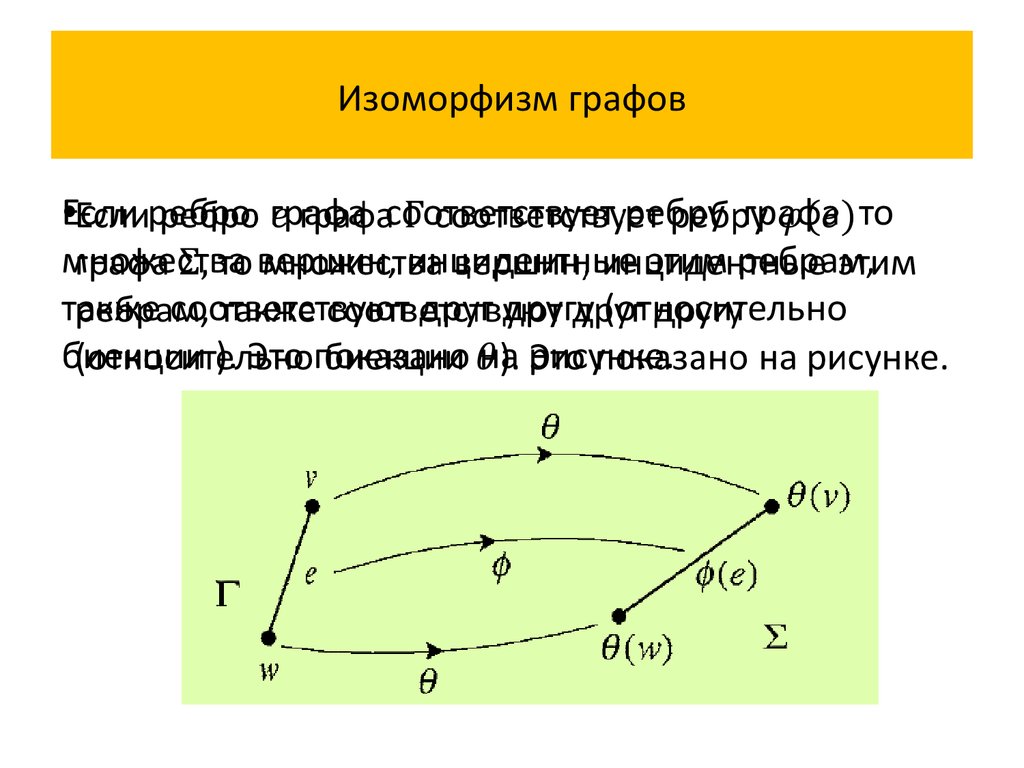
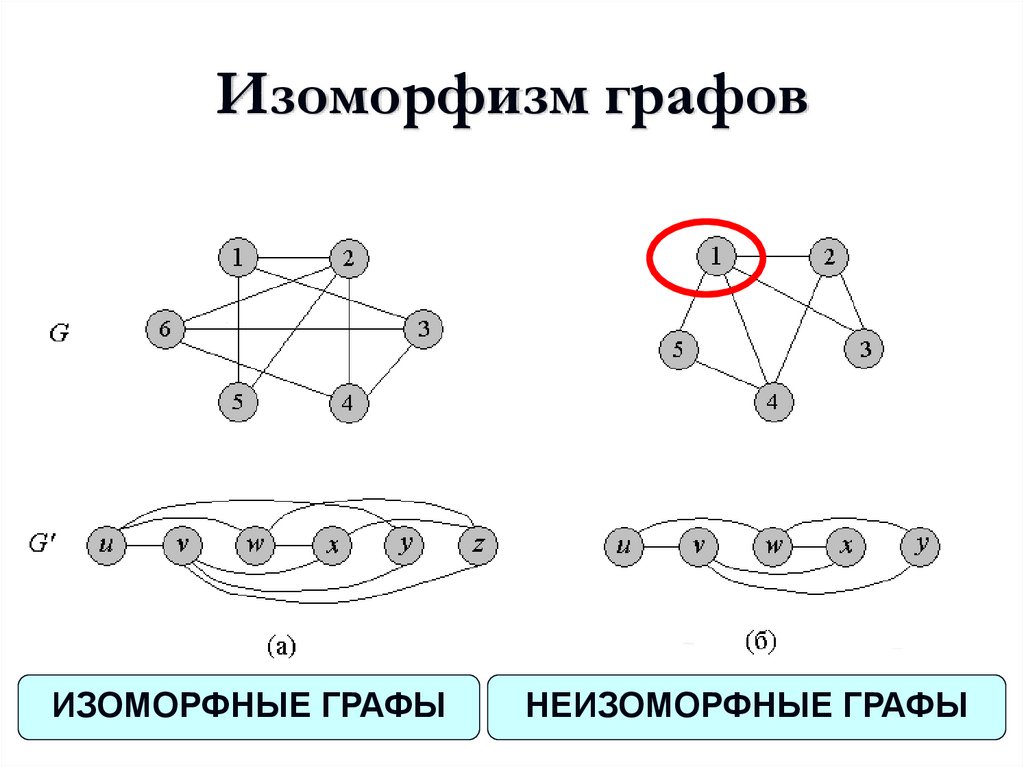
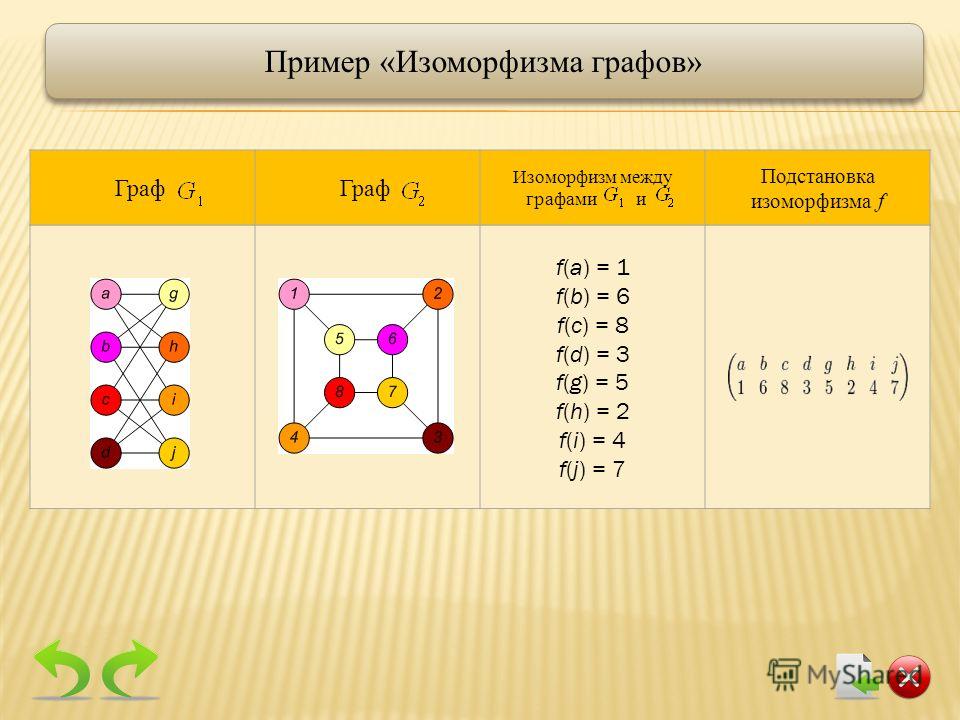
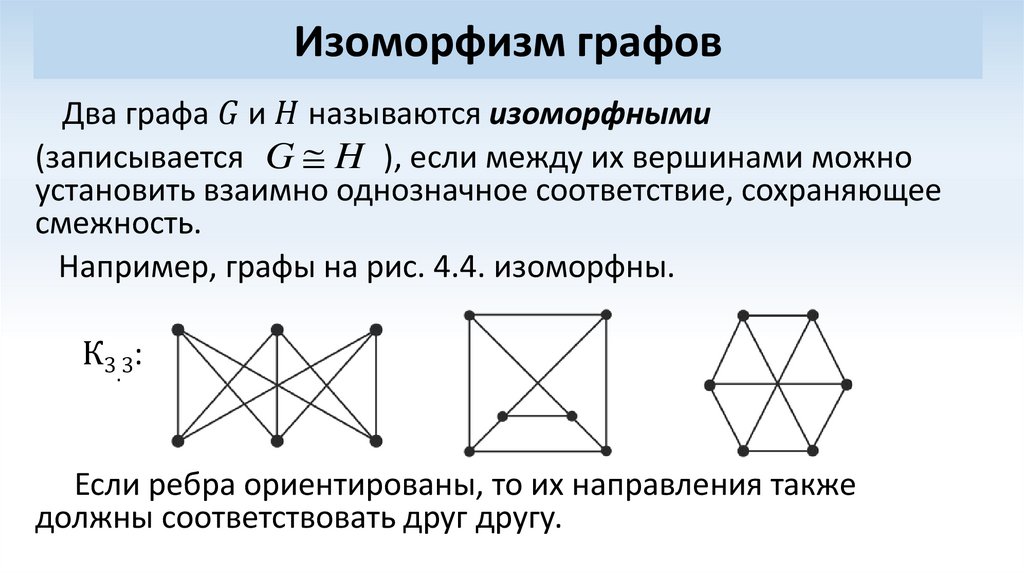
Изоморфизм графов

Если изоморфизм графов установлен, они называются изоморфными и обозначаются как. Иногда биекция записывается в виде подстановки изоморфизма.

ru.wikipedia.org

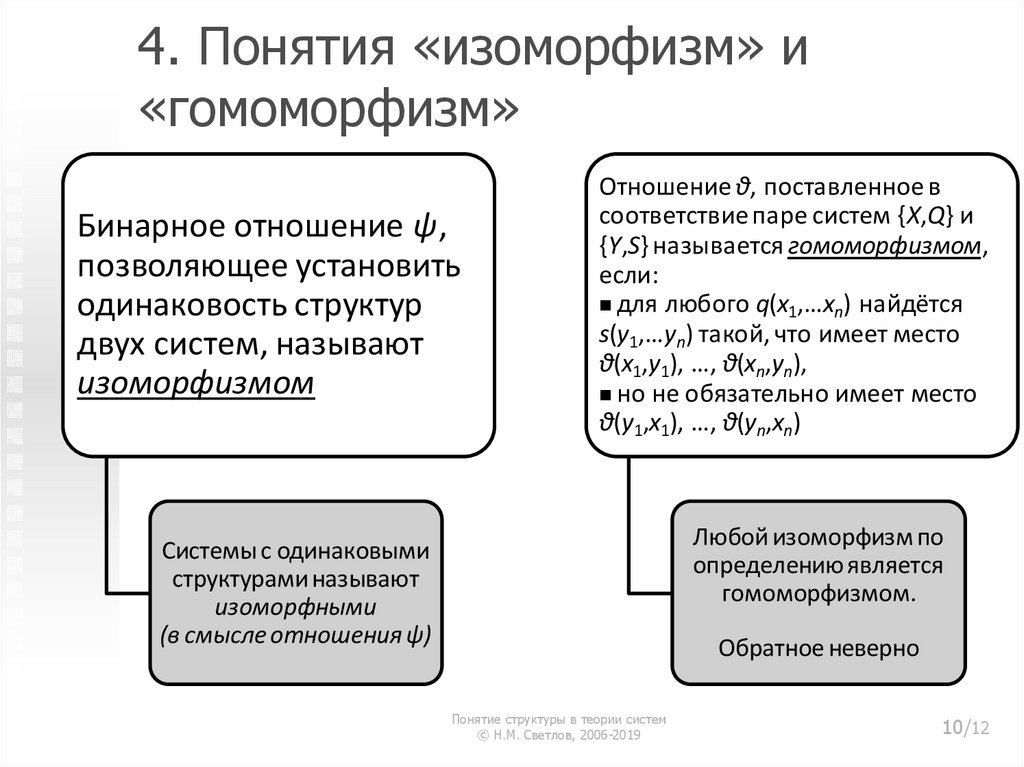
Изоморфизм и гомоморфизм

ИЗОМОРФИЗМ И ГОМОМОРФИЗМ — понятия, выражающие одинаковость (изоморфизм; от греч. isos — одинаковый и morphe — форма) либо подобие (гомоморфизм; от греч. homoios— подобный) строения (структуры) систем (множеств, процессов, конструкций).

Философская энциклопедия

ИЗОМОРФИЗМ И ГОМОМОРФИЗМ — логико-математич. понятия, выражающие одинаковость (изоморфизм; от греч. — одинаковый и — форма) либо уподобление (гомоморфизм; от греч. — один и тот же, равный) строения (структуры) систем…

Философская энциклопедия

ИЗОМОРФИЗМ И ГОМОМОРФИЗМ — логико-математич. понятия, выражающие одинаковость либо уподобление строения (структуры) систем (множеств, процессов, конструкций).

Советский философский словарь. — 1974

ТОМА ИЗОМОРФИЗМ

ТОМА ИЗОМОРФИЗМ — изоморфизм между (обобщенными) (ко)гомологиями базы векторного (сферического) расслоения и (ко)гомологиями его Тома пространства Пусть n-мерное векторное расслоение над конечным клеточным пространством X ориентируемо в некоторой…

Математическая энциклопедия. — 1977-1985

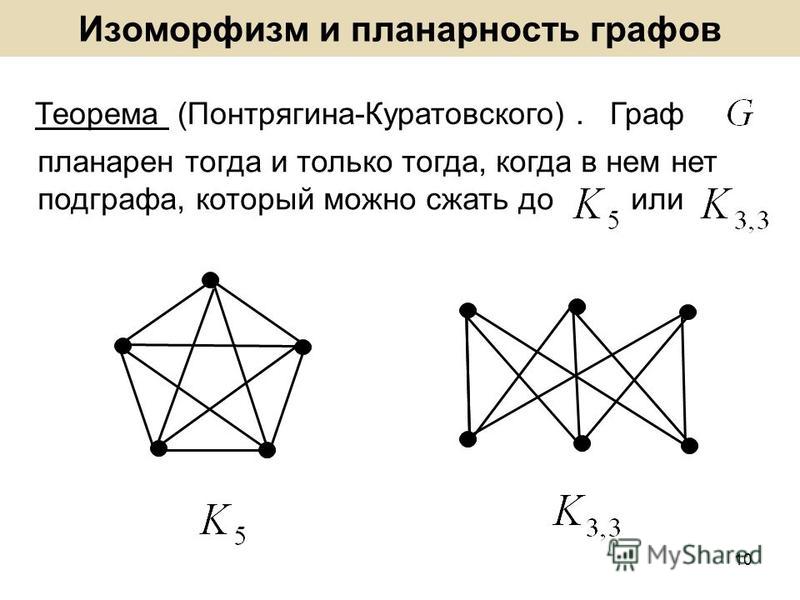
ГРАФОВ ИЗОМОРФИЗМ

ГРАФОВ ИЗОМОРФИЗМ — отношение эквивалентности на множестве графов. Изоморфным отображением одного неориентированного графа на другой наз. взаимно однозначное отображение вершин и ребер одного графа соответственно на вершиныи ребра другого графа…

Математическая энциклопедия. — 1977-1985

Теоремы об изоморфизме

Теоремы об изоморфизме в алгебре — ряд теорем, связывающих понятия фактора, гомоморфизма и вложенного объекта. Утверждением теорем является изоморфизм некоторой пары групп, колец, модулей, линейных пространств…

ru.wikipedia.org

Гомоморфизм Изоморфизм

Гомоморфизм Изоморфизм — аЧ логико-математические понятия, выражающие уподобление (гомоморфизм) либо одинанковость (изоморфизм) строения систем. Две системы А и В назынваются изоморфными, если между их элементами, а также функнциями…

Словарь по логике. — 1997

МЕТРИЧЕСКИЙ ИЗОМОРФИЗМ

МЕТРИЧЕСКИЙ ИЗОМОРФИЗМ — пространств с мерой и — биективное отображение при к-ром образы и прообразы измеримых множеств измеримы и имеют ту же меру (здесь — нек-рая булева -алгебра или -кольцо подмножеств пространства, называемых измеримыми…

Математическая энциклопедия. — 1977-1985

Гомоморфизм, изоморфизм

Гомоморфизм, изоморфизм — логико-математические понятия, выражающие уподобление (гомоморфизм) либо одинаковость (изоморфизм) строения систем.

Две системы А и В называются изоморфными, если между их элементами, а также функциями…

Словарь по логике. — 1997

Русский язык

Изо/морф/и́зм/.

Морфемно-орфографический словарь. — 2002

Изоморфи́зм, -а.

Орфографический словарь. — 2004

---

• Слова из слова «изоморфизм»
• Слова на букву «и»
• Слова, начинающиеся на «из»
• Слова c буквой «м» на конце
• Слова c «зм» на конце
• Слова, начинающиеся на «изо»
• Слова, начинающиеся на «изом»
• Слова, оканчивающиеся на «изм»
• Слова, заканчивающиеся на «физм»

1. изомнутся
2. изомнут
3. изомну
4. изоморфизм
5. изоморфный
6. изонефа
7. изонеф

ХиМиК.

ru — ИЗОМОРФИЗМ — Химическая энциклопедия

А Б В Г Д Е Ж З И К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Э Ю Я

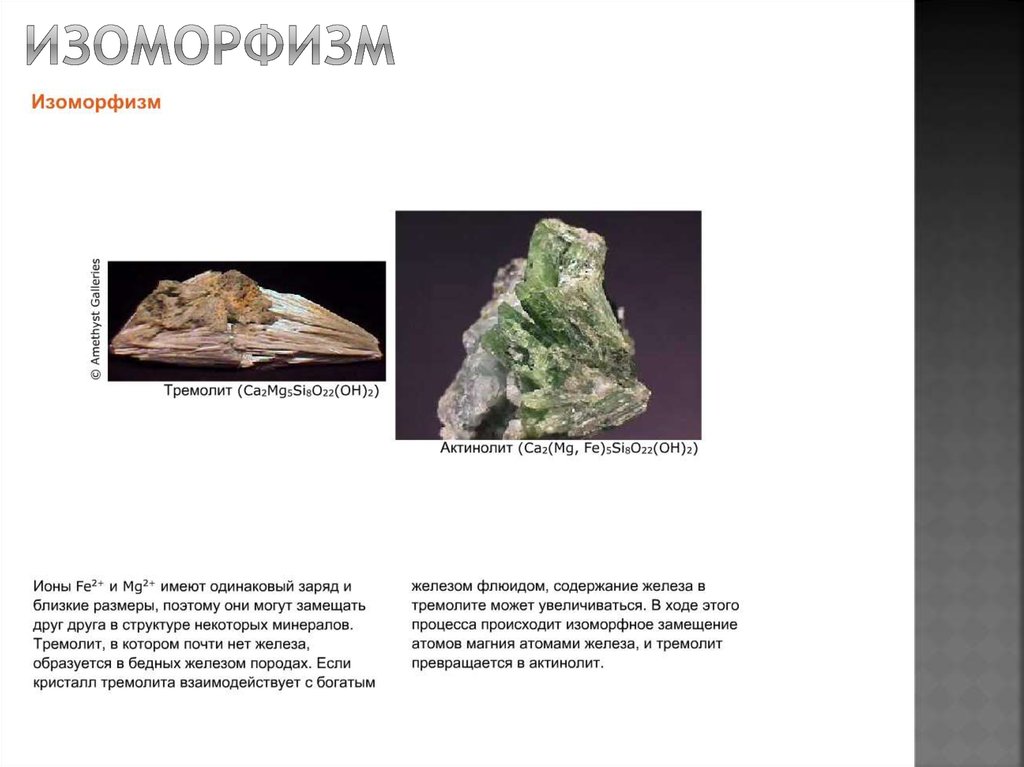
ИЗОМОРФИЗМ (от изо… и греч. morphe — форма, вид), способность атомов, ионов или молекул замещать друг друга в кристаллич. структурах. В результате изоморфизма образуются твердые р-ры замещения. В-ва, к-рым присущ изоморфизм, наз. изоморфными. Изоморфные в-ва могут кристаллизоваться совместно, давая смешанные кристаллы — изоморфные смеси. Эти смеси образуются лишь тогда, когда замещающие друг друга частицы (атомы, ионы, молекулы) близки по своим эффективным размерам. Согласно правилу Гольдшмидта, образование изоморфных смесей с широким диапазоном концентраций возможно при тождестве знака заряда и близкой поляризуемости замещающих друг друга атомов (или ионов), если их ионные радиусы различаются не более чем на 15%.

Если два в-ва дают изоморфные смеси любых концентраций (непрерывный ряд твердых р-ров), изоморфизм наз. совершенным. В противном случае говорят о несовершенном (ограниченном) изоморфизме. Совершенный изоморфизм характерен только для изоструктурных в-в, имеющих сходное пространств. расположение атомов или ионов и поэтому сходные по внеш. форме кристаллы. Для ограниченного изоморфизма условие изоструктурности необязательно. Пример совершенного изоморфизма — кристаллы квасцов KAl(SO₄)₂.12H₂O, в к-рых ионы К⁺ м. б. частично или полностью замещены ионами Rb ⁺ или NH₄⁺, а ионы Аl³⁺ионами Сr³⁺ или Fe³⁺ . Пример несовершенного изоморфизма для изоструктурных в-в, образующих смешанные кристаллы в огранич. пределах, Mg₂SiO₄ и Ca₂SiO₄, для неизоструктурных — минерал сфалерит ZnS, в к-ром до 20% атомов Zn м. б. замещены атомами Fe, причем ZnS и FeS имеют разл. кристаллич. структуры.

Если замещающие друг друга атомы имеют одинаковую степень окисления, такой изоморфизм наз. изовалентным (напр., KH₂PO₄-KH₂AsO₄), если разную — гетеровалентным. Так, при образовании смешанных кристаллов FeCO₃-ScBO₃ происходит замещение Fe²⁺ на Sc³⁺ и одновременно — С

4+ на В³⁺ , в результате чего формальные валентности оказываются скомпенсированными. Гетеровалентный изоморфизм, при к-ром Si⁴⁺ замещается на Аl³⁺ и в то же время однозарядный катион (напр., Na⁺) замещается на двухзарядный (напр., Са²⁺ ), характерен для алюмосиликатов(напр., непрерывный ряд твердых р-ров NaAlSi₃O₈-CaAl₂Si₂O₈). Гетеровалентный изоморфизм может осуществляться как без изменения числа атомов в элементарной ячейке, так и с изменением, т.е. как с заполнением пространства кристаллич. структуры, так и с вычитанием. Пример изоморфизма с заполнением пространства — смешанные кристаллы CaF₂-YF₃. Структуру CaF₂ можно описать как простую кубич. кладку ионов F^—, где ионы Са²⁺ занимают половину кубич. пустот (см. Плотная упаковка). По мере растворения YF ₃ в CaF₂ионы Са²⁺ замещаются ионами Y³⁺ , а избыточные ионы F^— внедряются в своб. кубич. пустоты. При образовании твердых р-ров изоморфных орг. в-в происходит замена молекулы на молекулу, при этом осн. роль играет геом. форма молекул.Наряду с изоморфизмом, при к-ром замещаются атомы, ионы или молекулы, возможен «аномальный» (блочный) изоморфизм, когда замещаются цепи, слои или объемные блоки. Напр., смешанослойные кристаллы встречаются среди слоистых силикатов.Изоморфные замещения имеют статистич. характер и приводят к образованию частично неупорядоченной структуры, поэтому смешанные кристаллы часто рассматривают как дефектные системы (с точечными, одномерными, двухмерными или объемными дефектами). Развивается энергетич. концепция изоморфизма, к-рая позволяет в сравнительно простых случаях на основе расчета энергии атомизации изоморфных смесей предсказать пределы изоморфных замещений в зависимости от т-ры.Изоморфизм широко распространен в природе. Б. ч. минералов представляет собой изоморфные смеси сложного переменного состава. С изоморфизмом связано геохим. поведение редких и рассеянных элементов, их распространение в горных породах и рудах, где они содержатся в виде изоморфных примесей. Изоморфное замещение определяет мн. полезные св-ва искусств. материалов совр. техники — полупроводников, ферромагнетиков, пьезо- и сегнетоэлектриков, люминофоров, лазерных материалов и др. (см., напр., Гранаты синтетические).Термин «изоморфизм» предложен Э. Мичерлихом в 1819.
===
Исп. литература для статьи «ИЗОМОРФИЗМ»: Франк-Каменецкий В. А., Природа структурных примесей и включений в минералах, Л., 1964; Макаров Е. С., Изоморфизм атомов в кристаллах, М., 1973; Урусов В. С., Энергетическая кристаллохимия, М., 1975.П. М. Зоркий.

Страница «ИЗОМОРФИЗМ» подготовлена по материалам химической энциклопедии.

А Б В Г Д Е Ж З И К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Э Ю Я

Изоморфизм линейных пространств — ПриМат

Пусть заданы два линейных пространства над полем [latex]\mathbb{P}[/latex]: [latex]A[/latex] и [latex]B[/latex]. Тогда изоморфизмом f (обозначается как [latex]A \cong B[/latex]) называется биекция из [latex]A[/latex] в [latex]B[/latex], удовлетворяющая следующим условиям:
1) [latex]f(a+b) = f(a) + f(b)[/latex]
2) [latex]f(\lambda\cdot a) = \lambda\cdot f(a) [/latex]

Изоморфными пространствами называются такие линейные пространства, между которыми можно установить изоморфизм.

Свойства изоморфизма:
1) [latex]f(0) = 0[/latex]
2)[latex]f(-a) = -f(a)[/latex]
3) [latex]f(\sum_{j=1}^{k}a_j a_j) = \sum_{j=1}^{k}a_j f(a_j)[/latex]
4) При изоморфном отображении линейно независимая система не может стать линейно зависимой. Обратное также верно.
5) Базис [latex]A[/latex] отображается в базис [latex]B[/latex].
6) Прямая сумма подпространств в [latex]A[/latex] отображается в прямую сумму образов этих подпространств в [latex]B[/latex].

 

 

Теорема. Любые два конечномерные линейные пространства, имеющие одинаковую размерность и заданные над одним и тем же полем, изоморфны.

Зададим два линейных пространства [latex]X[/latex] и [latex]Y[/latex] над полем P, [latex]\textrm{dim} X = \textrm{dim} Y[/latex]. Пусть базис [latex]X[/latex] — [latex]e_1,e_2,\dots ,e_n [/latex]; Y — [latex]e’_1,e’_2,\dots , e’_n[/latex]. Возьмём в пространстве [latex]X[/latex] векторы $$x_{1} = \alpha_1 e_1+\alpha_2 e_2+\dots+\alpha_n e_n$$ и $$x_2 = \beta_1 e_1+\beta e_2+\dots+\beta e_n $$Тогда при изоморфизме [latex]X \cong Y[/latex]
$$
f(x_1+x_2)=f((\alpha_1 + \beta_1)e_1 + (\alpha_2 + \beta_2)e_2 + \dots + (\alpha_n + \beta_n)e_n) = \\
= (\alpha_1 + \beta_1)e’_1 + (\alpha_2 + \beta_2)e’_2 + \dots + (\alpha_n + \beta_n)e’_n = \\
=(\alpha_1 e’_1 + \alpha_2 e’_2 + \dots + \alpha_n e’_n ) + (\beta_1 e’_1 + \beta_2 e’_2 + \dots + \beta_n e’_n) = f(x_1) + f(x_2). n[/latex] над полем [latex]\mathbb{P}[/latex].

Примеры

1. Привести пример отображения из [latex]\mathbb{R}[/latex] в [latex]\mathbb{\mathbb{N}_0}[/latex], которое является изоморфизмом.

Решение

Пусть [latex]x’ = 2x[/latex]. Тогда [latex]f(a + b) = 2(a + b) = 2a + 2b = f(a) + f(b)[/latex] и [latex]f(\lambda a) = 2(\lambda a) = \lambda 2a = \lambda \cdot f(a)[/latex]. Значит, это отображение является изоморфизмом.

[свернуть]

2. Доказать первое свойство ([latex]f(0) = 0[/latex]).

Решение

[latex]f(a) = f(a + 0) = f(a) + f(0)[/latex], значит [latex]f(0) = 0[/latex].

[свернуть]

 

• В.В.Воеводин Линейная алгебра. М.: Наука, 1980. -С.63-65.
• А.Г. Курош. Курс высшей алгебры. М.: Наука, 1968. -С.187-188.
• Конспект лекций Белозёрова Г.С.

Изоморфизм линейных пространств

Тест на знание изоморфизма линейных пространств.

Автор Даниил КадочниковОпубликовано 06/06/202010/06/2020Рубрики Алгебра, Курсовая работаМетки абстрактные линейные пространства, Биекция, изоморфизм, Линейное пространство, линейные операторы, отображение, Отображения

© 2012-2016: Нохум-Даниэль Блиндер (11), Анастасия Лозинская (10), Юлия Стерлянко (8), Денис Стехун (8), Валентин Малявко (8), Елизавета Савицкая (8), Игорь Любинский (8), Олег Шпинарев (7), Александр Базан (7), Анна Чалапчий (7), Константин Берков (7), Татьяна Корнилова (6), Влад Радзивил (6), Максим Швандт (6), Людмила Рыбальченко (6), Кирилл Волков (6), Марина Чайковская (5), Екатерина Шибаева (5), Мария Корень (5), Анна Семененко (5), Мария Илларионова (5), Сергей Черкес (5), Алиса Ворохта (5), Валерия Заверюха (5), Елизавета Снежинская (5), Вадим Покровский (5), Даниил Радковский (5), Влад Недомовный (5), Александр Онищенко (5), Андрей Метасов (5), Денис Базанов (5), Александр Ковальский (5), Александр Земсков (5), Святослав Волков (4), Иван Мясоедов (4), Владислав Стасюк (4), Алёна Гирняк (4), Николай Царев (4), Валентин Цушко (4), Павел Жуков (4), Роман Бронфен-Бова (4), Артём Романча (4), Анна Шохина (4), Иван Киреев (4), Никита Савко (4), Кондрат Воронов (4), Алина Зозуля (4), Иван Чеповский (4), Артем Рогулин (4), Игорь Чернега (4), Даниил Кубаренко (4), Ольга Денисова (4), Татьяна Осипенко (4), Яков Юсипенко (4), Ольга Слободянюк (4), Руслан Авсенин (4), Екатерина Фесенко (4), Дмитрий Заславский (4), Алина Малыхина (4), Андрей Лисовой (4), Полина Сорокина (4), Кирилл Демиденко (4), Дмитрий Стеценко (4), Александр Рапчинский (4), Таисия Ткачева (3), Владислав Бебик (3), Илья Бровко (3), Максим Носов (3), Филип Марченко (3), Катя Романцова (3), Илья Черноморец (3), Евгений Фищук (3), Анна Цивинская (3), Михаил Бутник (3), Станислав Чмиленко (3), Катя Писова (3), Дмитрий Дудник (3), Дарья Кваша (3), Игорь Стеблинский (3), Артем Чернобровкин (3), Виктор Булгаков (3), Дмитрий Мороз (3), Богдан Павлов (3), Игорь Вустянюк (3), Андрей Яроцкий (3), Лаура Казарян (3), Екатерина Мальчик (3), Анатолий Осецимский (3), Иван Дуков (3), Дмитрий Робакидзе (3), Вячеслав Зелинский (3), Данила Савчак (3), Дмитрий Воротов (3), Стефания Амамджян (3), Валерия Сиренко (3), Георгий Мартынюк (3), Виктор Иванов (3), Вячеслав Иванов (3), Валерия Ларикова (3), Евгений Радчин (3), Андрей Бойко (3), Милан Карагяур (3), Александр Димитриев (3), Иван Василевский (3), Руслан Масальский (3), Даниил Кулык (3), Стас Коциевский (3), Елизавета Севастьянова (3), Павел Бакалин (3), Антон Локтев (3), Андрей-Святозар Чернецкий (3), Николь Метри (3), Евелина Алексютенко (3), Константин Грешилов (3), Марина Кривошеева (3), Денис Куленюк (3), Константин Мысов (3), Мария Карьева (3), Константин Григорян (3), Колаев Демьян (3), Станислав Бондаренко (3), Ильдар Сабиров (3), Владимир Дроздин (3), Кирилл Сплошнов (3), Карина Миловская (3), Дмитрий Козачков (3), Мария Жаркая (3), Алёна Янишевская (3), Александра Рябова (3), Дмитрий Байков (3), Павел Загинайло (3), Томас Пасенченко (3), Виктория Крачилова (3), Надежда Кибакова (2), Майк Евгеньев (2), Евгений Колодин (2), Денис Карташов (2), Александр Довгань (2), Нина Хоробрых (2), Роман Гайдей (2), Антон Джашимов (2), Никита Репнин (2), Инна Литвиненко (2), Яна Юрковская (2), Гасан Мурадов (2), Богдан Подгорный (2), Алексей Никифоров (2), Настя Филипчук (2), Гук Алина (2), Михаил Абабин (2), Дмитрий Калинин (2), Бриткариу Ирина (2), Никита Шпилевский (2), Алексей Белоченко (2), Юлиана Боурош (2), Никита Семерня (2), Владимир Захаренко (2), Дмитрий Лозинский (2), Яна Колчинская (2), Юрий Олейник (2), Кирилл Бондаренко (2), Елена Шихова (2), Татьяна Таран (2), Наталья Федина (2), Настя Кондратюк (2), Никита Гербали (2), Сергей Запорожченко (2), Николай Козиний (2), Георгий Луценко (2), Владислав Гринькив (2), Александр Дяченко (2), Анна Неделева (2), Никита Строгуш (2), Настя Панько (2), Кирилл Веремьев (2), Даниил Мозгунов (2), Андрей Зиновьев (2), Андрей Данилов (2), Даниил Крутоголов (2), Наталия Писаревская (2), Дэвид Ли (2), Александр Коломеец (2), Александра Филистович (2), Евгений Рудницкий (2), Олег Сторожев (2), Евгения Максимова (2), Алексей Пожиленков (2), Юрий Молоканов (2), Даниил Кадочников (2), Александр Колаев (2), Александр Гутовский (2), Павел Мацалышенко (2), Таня Спичак (2), Радомир Сиденко (2), Владислав Шиманский (2), Илья Балицкий (2), Алина Гончарова (2), Владислав Шеванов (2), Андрей Сидоренко (2), Александр Мога (2),

5.

6: Изоморфизмы — Математика LibreTexts

1. Последнее обновление

2. Сохранить как PDF

Идентификатор страницы

14529

• Кен Каттлер
• Университет Бригама Янга via Lyryx 9{м}\) соответственно. Отображение \(T:V\rightarrow W\) называется линейным преобразованием или линейным отображением , если оно сохраняет алгебраические операции сложения и скалярного умножения. В частности, если \(a,b\) являются скалярами и \(\vec{x},\vec{y}\) являются векторами,

  \[T\left( a\vec{x}+b\vec{y}\right) =aT(\vec{x})+bT(\vec{y})\nonumber \]

  Рассмотрим следующее важное определение.

  Определение \(\PageIndex{1}\): изоморфизм

  Линейная карта \(T\) называется изоморфизм , если выполняются следующие два условия.

  • \(T\) один к одному. То есть, если \(T(\vec{x})=T(\vec{y}),\), то \(\vec{x}=\vec{y}.\)
  • \(T\) включен. То есть, если \(\vec{w}\in W,\) существует \(\vec{v}\in V\) такое, что \(T(\vec{v})=\vec{w}\ ).

  Два таких подпространства, которые имеют описанный выше изоморфизм, называются -изоморфными.

  Рассмотрим следующий пример изоморфизма.

  92\) определяется как \[T \left [ \begin{array}{c} x \\ y \end{array} \right ] = \left [ \begin{array}{c} x + y \\ x — y \end{array} \right ] \nonumber\] Покажите, что \(T\) является изоморфизмом.

  Решение

  Чтобы доказать, что \(T\) — изоморфизм, мы должны показать

  1. \(T\) — линейное преобразование;
  2. \(T\) один к одному;
  3. \(T\) включен.

  Действуем следующим образом.

  1. \(T\) является линейным преобразованием:

     Пусть \(k, p\) — скаляры. \[\begin{align} T \left( k \left [ \begin{array}{c} x_1 \\ y_1 \end{array} \right ] + p \left [ \begin{array}{c} x_2 \ \ y_2 \end{массив} \right ] \right) &= T \left( \left [ \begin{array}{c} kx_1 \\ ky_1 \end{массив} \right ] + \left [ \begin{массив }{c} px_2 \\ py_2 \end{массив} \right ] \right) \\ &= T \left( \left [ \begin{массив}{c} kx_1 + px_2 \\ ky_1 + py_2 \end{массив } \right ] \right) \\ &= \left [ \begin{array}{c} (kx_1 + px_2) + (ky_1 + py_2) \\ (kx_1 + px_2) — (ky_1 + py_2) \end{array } \right ] \\ &= \left [ \begin{array}{c} (kx_1 + ky_1) + (px_2 + py_2) \\ (kx_1 — ky_1) + (px_2 — py_2) \end{array} \right ] \\ &= \left [ \begin{array}{c} kx_1 + ky_1 \\ kx_1 — ky_1 \end{array} \right ] + \left [ \begin{array}{c} px_2 + py_2 \\ px_2 — py_2 \end{массив} \right ] \\ &= k \left [ \begin{array}{c} x_1 + y_1 \\ x_1 — y_1 \end{массив} \right ] + p \left [ \begin{ array}{c} x_2 + y_2 \\ x_2 — y_2 \end{array} \right ] \\ &= k T \left( \left [ \begin{array}{c} x_1 \\ y_1 \end{array} \Правильно ] \ right) + p T \left( \left [\begin{array}{c} x_2 \\ y_2 \end{array} \right ] \right)\end{aligned}\] 92\), то следует, что \(\vec{x} = \vec{0}\). Пусть \(\vec{x} = \left [ \begin{array}{c} x \\ y \end{array} \right ]\).

     \[T \left( \left [ \begin{array}{c} x \\ y \end{array} \right ] \right) = \left [ \begin{array}{c} x + y\\ x — y \end{array} \right ] = \left [ \begin{array}{c} 0 \\ 0 \end{array} \right ]\nonumber \] Это дает систему уравнений, заданную \[\ begin{aligned} x + y &= 0\\ x — y &= 0\end{aligned}\] Вы можете убедиться, что решение этой системы, если \(x = y =0\). Поэтому \[\vec{x} = \left [ \begin{array}{c} x \\ y \end{array} \right ] = \left [ \begin{array}{c} 0 \\ 0 \end {массив} \right ]\nonumber \] и \(T\) один к одному.

  2. \(T\) находится на:

     Пусть \(a,b\) — скаляры. Мы хотим проверить, всегда ли существует решение \[T \left( \left [ \begin{array}{c} x \\ y \end{array} \right ] \right) = \left [ \begin{ array}{c} x + y\\ x — y \end{array} \right ] = \left [ \begin{array}{c} a \\ b \end{array} \right ]\nonumber\]

     Это можно представить в виде системы уравнений \[\begin{aligned} x + y &= a\\ x — y &= b\end{aligned}\]

     Настройка расширенной матрицы и сокращения строк дает \[\left [ \begin{array}{cc|c} 1 & 1 & a \\ 1 & -1 & b \end{array} \right ] \rightarrow \cdots \rightarrow \left [ \begin{array}{cc|c} 1 & 0 & \frac{a+b}{2} \\ 0 & 1 & \frac{a-b}{2} \end{array} \right ]\nonumber\] Это имеет решение для всех \(a,b\) и, следовательно, \(T\) находится на. 9н\). Тогда \(S\circ T\), определяемый как \(\left( S\circ T\right) \left( \vec{v} \right) = S\left( T\left( \vec{v} \right ) \right)\) также является изоморфизмом.

     Доказательство

     Предположим, что \(T:V\rightarrow W\) и \(S:W\rightarrow Z\) являются изоморфизмами. Почему \(S\circ T\) является линейной картой? Для \(a,b\) скаляров

     \[\begin{align} S\circ T\left( a\vec{v}_{1}+b(\vec{v}_{2})\right) &= S\left( T\left (a\vec{v}_{1}+b\vec{v}_{2}\right) \right) =S\left( aT\vec{v}_{1}+bT\vec{v} _{2}\right) \\ &=aS\left( T\vec{v}_{1}\right) +bS\left( T\vec{v}_{2}\right) = a\left ( S\circ T\right) \left( \vec{v}_{1}\right) +b\left( S\circ T\right) \left( \vec{v}_{2}\right) \end{выровнено}\nonumber\]

     Следовательно, \(S\circ T\) — линейное отображение. Если \(\left( S\circ T\right) \left( \vec{v} \right) =0,\), то \(S\left( T\left( \vec{v} \right) \right ) =0\) и отсюда следует, что \(T(\vec{v})=\vec{0}\) и, следовательно, снова по этой лемме \(\vec{v}=\vec{0}\). Таким образом, \(S\circ T\) один к одному. Осталось убедиться, что он включен. Пусть \(\vec{z} \in Z\). Тогда, поскольку \(S\) находится на, существует \(\vec{w} \in W\) такое, что \(S(\vec{w})=\vec{z}.\) Кроме того, поскольку \( T\) на, существует \(\vec{v}\in V\) такое, что \(T(\vec{v})=\vec{w}.\) Отсюда следует, что \(S\left( T\left( \vec{v}\right) \right) =\vec{z}\) и, таким образом, \(S\circ T\) тоже на.

     Рассмотрим два подпространства \(V\) и \(W\) и предположим, что существует изоморфизм, отображающий одно в другое. Таким образом, два подпространства связаны, что мы можем записать как \(V \sim W\). Тогда два предыдущих утверждения вместе утверждают, что \(\sim\) является отношением эквивалентности. То есть: \(\sim\) удовлетворяет следующим условиям:

     • \(В\сим В\)
     • Если \(V\sim W,\), то \(W\sim V\)
     • Если \(V\sim W\) и \(W\sim Z,\), то \(V\sim Z\) 9н\). Если \(T\) один к одному, то оно обладает тем свойством, что если \(\left\{ \vec{u}_{1},\cdots ,\vec{u}_{k}\right\} \) линейно независим, так что \(\left\{T(\vec{u}_{1}),\cdots ,T(\vec{u}_{k})\right\}\).

       В более общем случае \(T\) является изоморфизмом тогда и только тогда, когда \(\left\{ \vec{v}_{1},\cdots ,\vec{v}_{n}\right\} \) является базисом для \(V,\), то \(\left\{ T (\vec{v}_{1}),\cdots ,T(\vec{v}_{n})\ right\}\) является основой для \(W\).

       Доказательство

       9{n}c_{i}\vec{u}_{i}=0\nonumber\] Теперь тот факт, что \(\left\{ \vec{u}_{1},\cdots ,\vec{u} _{n}\right\}\) линейно независима, следует, что каждый \(c_{i}=0\). Следовательно, \(\left\{ T(\vec{u} _{1}),\cdots ,T(\vec{u}_{n})\right\}\) линейно независим.

       Теперь предположим, что \(T\) является изоморфизмом и \(\left\{ \vec{v}_{1},\cdots ,\vec{ v}_{n}\right\}\) является базисом для \(V\). Только что было показано, что \(\left\{ T(\vec{v} _{1}),\cdots ,T(\vec{v}_{n})\right\}\) линейно независим. Осталось проверить, что span\(\left\{ T(\vec{v}_{1}),\cdots ,T(\vec{v}_{n})\right\}=W\). Если \(\vec{w}\in W,\), то поскольку \(T\) находится на, существует \(\vec{v}\in V\) такое, что \(T(\vec{v})= \vec{ш}\). {n} \hat{c}_{i}\vec{v}_ {i}\right)\end{aligned}\] Таким образом, \(T\) является линейным преобразованием. 9{n}c_{i}\vec{v}_{i}\right)\nonumber \], показывающий, что \(T\) также включен. Следовательно, \(T\) — изоморфизм, а значит, \(V\) и \(W\) изоморфны.

       Далее предположим, что \(T:V \mapsto W\) является изоморфизмом, поэтому эти два подпространства изоморфны. Тогда для \(\left\{ \vec{v}_{1},\cdots ,\vec{v}_{n}\right\}\) базиса для \(V\) следует, что базис для \(W\) является \(\left\{ T(\vec{v}_{1}),\cdots ,T(\vec{v}_{n})\right\}\), показывающим, что два подпространства имеют одинаковую размерность.

       Теперь предположим, что два подпространства имеют одинаковую размерность. Рассмотрим три заявленные эквивалентности.

       Сначала рассмотрим утверждение, что \(1.)\Rightarrow 2.).\) Если \(T\) взаимно однозначно и если \(\left\{ \vec{v}_{1},\cdots , \vec{v} _{n}\right\}\) является базисом для \(V,\), тогда \(\left\{ T(\vec{v}_{1}),\cdots ,T( \vec{v }_{n})\right\}\) линейно независим. {n}c_{i}\vec{v} _{i}=\vec{0}\). Таким образом, \(T\) взаимно однозначно, так же как и на, и, следовательно, является изоморфизмом. 9{3}\) и пусть \(W\) обозначает \[\mathrm{span}\left\{ \left [ \begin{array}{r} 1 \\ 2 \\ 1 \\ 1 \end{array} \right ] ,\left [ \begin{array}{r} 0 \\ 1 \\ 0 \\ 1 \end{array} \right ] ,\left [ \begin{array}{r} 1 \\ 1 \ \ 2 \\ 0 \end{массив} \right ] \right\}\nonumber \] Покажите, что \(V\) и \(W\) изоморфны.

       Решение

       Сначала заметим, что оба этих подпространства имеют размерность 3 и поэтому они изоморфны по теореме \(\PageIndex{1}\). Легко увидеть, что три вектора, которые охватывают \(W\), являются линейно независимыми, если сделать их столбцами матрицы и строки, сводящимися к редуцированной форме строки-эшелона.

       Вы можете продемонстрировать изоморфизм этих двух пространств следующим образом. \[T(\vec{e}_{1})=\left [ \begin{array}{c} 1 \\ 2 \\ 1 \\ 1 \end{array} \right ], T(\vec{ e}_{2})=\left [ \begin{array}{c} 0 \\ 1 \\ 0 \\ 1 \end{array} \right ], T(\vec{e}_{3}) =\left [ \begin{array}{c} 1 \\ 1 \\ 2 \\ 0 \end{array} \right ]\nonumber \] и продолжить линейно. Напомним, что матрица этого линейного преобразования — это просто матрица, столбцами которой являются эти векторы. Таким образом, матрица этого изоморфизма равна \[\left [ \begin{array}{rrr} 1 & 0 & 1 \\ 2 & 1 & 1 \\ 1 & 0 & 2 \\ 1 & 1 & 0 \end{array } \right ]\nonumber \] Вы должны проверить, что умножение слева на эту матрицу действительно воспроизводит заявленный эффект, полученный в результате применения \(T\). 9{3}\) и пусть \(W\) обозначает

       \[\mathrm{span}\left\{ \left [ \begin{array}{c} 1 \\ 2 \\ 1 \\ 1 \end{ array} \right ] ,\left [ \begin{array}{c} 0 \\ 1 \\ 0 \\ 1 \end{array} \right ] ,\left [ \begin{array}{c} 1 \\ 1 \\ 2 \\ 0 \end{массив} \right ] \right\}\nonumber \]

       Пусть \(T: V \mapsto W\) определяется следующим образом. \[T\left [ \begin{array}{c} 1 \\ 1 \\ 0 \end{array} \right ] =\left [ \begin{array}{c} 1 \\ 2 \\ 1 \\ 1 \end{array} \right ] ,T\left [ \begin{array}{c} 0 \\ 1 \\ 1 \end{array} \right ] =\left [ \begin{array}{c} 0 \\ 1 \\ 0 \\ 1 \end{массив} \right ] ,T\left [ \begin{array}{c} 1 \\ 1 \\ 1 \end{массив} \right ] =\left [ \ begin{array}{c} 1 \\ 1 \\ 2 \\ 0 \end{array} \right ]\nonumber \] Найдите матрицу этого изоморфизма \(T\). {-1}=\left [ \begin{array}{rrr} 1 & 0 & 0 \\ 0 & 2 & -1 \\ 2 & -1 & 1 \\ -1 & 2 & -1 \end{массив} \right ]\nonumber \] 9{3}\) и пусть \(W\) обозначает \[\mathrm{span}\left\{ \left [ \begin{array}{c} 1 \\ 0 \\ 1 \\ 1 \end{array} \right ] ,\left [ \begin{array}{c} 0 \\ 1 \\ 0 \\ 1 \end{array} \right ] ,\left [ \begin{array}{c} 1 \\ 1 \ \ 1 \\ 2 \end{array} \right ] \right\}\nonumber \] Пусть \(T: V \mapsto W\) определяется следующим образом. \[T\left [ \begin{array}{c} 1 \\ 1 \\ 0 \end{array} \right ] = \left [ \begin{array}{c} 1 \\ 0 \\ 1 \\ 1 \end{array} \right ] ,T\left [ \begin{array}{c} 0 \\ 1 \\ 1 \end{array} \right ] =\left [ \begin{array}{c} 0 \\ 1 \\ 0 \\ 1 \end{массив} \right ] ,T\left [ \begin{array}{c} 1 \\ 1 \\ 1 \end{массив} \right ] =\left [ \ begin{array}{c} 1 \\ 1 \\ 1 \\ 2 \end{array} \right ]\nonumber \] Найдите матрицу этого линейного преобразования.

       Решение

       Обратите внимание, что в этом случае три вектора, которые охватывают \(W\), не являются линейно независимыми. {-1}=\left [ \begin{array}{rrr} 1 & 0 & 0 \\ 0 & 0 & 1 \\ 1 & 0 & 0 \\ 1 & 0 & 1 \end{array} \right ]\nonumber \]

       Очевидно, что столбцы этой последней матрицы не являются линейно независимыми.

       ---

       Эта страница под названием 5.6: Isomorphisms распространяется под лицензией CC BY 4.0 и была создана, изменена и/или курирована Кеном Каттлером (Lyryx) с использованием исходного контента, который был отредактирован в соответствии со стилем и стандартами платформы LibreTexts; подробная история редактирования доступна по запросу.

       1. Наверх

       • Была ли эта статья полезной?

       1. Тип изделия

          Раздел или Страница

          Автор

          Кен Каттлер

          Лицензия

          СС BY

          Версия лицензии

          4,0

          Показать страницу TOC

          нет

       2. Теги

          1. изоморфизм
          2. линейная карта
          3. линейное преобразование
          4. источник@https://lyryx. com/first-course-linear-алгебра

       Первая теорема об изоморфизме

       Первая теорема об изоморфизме

       Теорема 9 о первом изоморфизме 0347 помогает определить частные группы как «известные» или «знакомые» группы.

       Я начну с доказательства полезной леммы.

       Предложение. Позвольте быть групповой картой. инъективен тогда и только тогда, когда .

       Доказательство. ( ) Предположим, инъективен. С , . Обратно, пусть , так что . Тогда, значит, по инъективности. Поэтому , так .

       ( ) Предполагать . Я хочу показать, что это инъективно. Предполагать . Я хочу показать это.

       Отсюда , так , и . Следовательно, инъективен.

       ---

       Пример. ( Доказательство того, что карта группы является инъективной ) Определить по

       Докажите, что f инъективно.

       Как обычно, это группа при сложении векторов. Я могу написать f в форме

       Поскольку f было представлено как умножение на постоянную матрицу, это линейное преобразование, поэтому это групповая карта.

       Чтобы показать, что f инъективно, я покажу, что ядро ​​f состоит из только тождество: . Предполагать . затем

       Так как я знаю из линейной алгебры, что матрица уравнение имеет только тривиальное решение: . Это доказывает, что если , то так . Поскольку , следует, что .

       Следовательно, f инъективен.

       ---

       Теорема. ( Первый Теорема изоморфизма ) Позвольте быть картой группы, и пусть быть фактором карты. Там является изоморфизмом таким, что следующая диаграмма коммутирует:

       Доказательство. Поскольку отображает G на и , универсальное свойство частное дает карту, такую ​​​​что приведенная выше диаграмма коммутирует. С сюръективен, так что ; в самом деле, если , по коммутативности

       Осталось показать, что оно инъективно.

       По предыдущей лемме достаточно показать, что . Так как карты из , «1» здесь тождество элемент группы, который является подгруппа . Так что мне нужно показать это.

       Однако это сразу следует из коммутативности диаграммы. Ибо тогда и только тогда . Это эквивалентно к , или , или — т.е.

       ---

       Пример. ( Использование первого Теорема изоморфизма, показывающая, что две группы изоморфны ) Используйте Первая теорема об изоморфизме, доказывающая, что

       это группа ненулевых действительных чисел под умножение. это группа положительные действительные числа при умножении. это группа, состоящая из 1 и -1 под умножение (изоморфно ).

       Я определяю карту группы, ядром которой является .

       Определить по

       это групповая карта:

       Если — положительное действительное число, то

       Следовательно, сюръективно: .

       Наконец, явно отправляет 1 и -1 в идентичность, и это единственные два элемента которых отображаются в 1. Следовательно, .

       По первой теореме об изоморфизме

       Обратите внимание, что я не создавал карту явно; Первая теорема об изоморфизме строит изоморфизм для меня.

       ---

       Пример. — группа по компонентному сложению и является группой при добавлении. Позволять

       Докажи это .

       Определить по

       Обратите внимание, что

       Поскольку f можно выразить как умножение на постоянную матрицу, линейное преобразование и, следовательно, групповое отображение.

       Позволять . затем

       Следовательно, , и, следовательно .

       Позволять . затем

       Следовательно,

       Следовательно, . Следовательно, .

       Позволять . Обратите внимание, что

       Следовательно, .

       Таким образом,

       ---

       Пример. — это группа под покомпонентное сложение и представляет собой группу при сложении. Докажи это

       Определить по

       f может быть представлен матричным умножением:

       Следовательно, это групповая карта.

       Позволять . затем

       Таким образом, .

       Позволять . затем

       Теперь но. По лемме Евклида . Сказать . затем

       Следовательно,

       Таким образом, .

       Следовательно, .

       Позволять . Обратите внимание, что

       Умножая на z, я получаю

       затем

       Это доказывает, что .

       Следовательно,

       ---

       Пример. — это группа под покомпонентное сложение. Рассмотрим подгруппу

       Докажи это .

       (группа под покомпонентное сложение.)

       Определить по

       Обратите внимание, что

       Поскольку f определяется умножением матриц, это линейная трансформация. Следовательно, это групповая карта.

       Позволять . затем

       Следовательно, и .

       Позволять . затем

       Приравнивая первые компоненты, у меня , значит . Приравнивая вторые компоненты, имеем , так . Таким образом,

       Поэтому , и так .

       Позволять . затем

       Следовательно, .

       Таким образом,

       Первое равенство следует из . Изоморфизм следует из первого Теорема изоморфизма. Второе равенство следует из .

       ---

       Предложение. Если карта сюръективной группы и , то .

       Доказательство. , значит , и .

       Пусть так. затем

       Следовательно, является подгруппой.

       (Обратите внимание, что это не использует тот факт, что K является нормальным. Следовательно, я фактически доказал, что образ подгруппы является подгруппой.)

       Теперь пусть , , так . Я хочу показать это. Поскольку является сюръективным, для некоторых . затем

       А потому что К нормальный. Следовательно, . Это следует, что это нормально подгруппа H.

       Теорема. ( Второй Теорема об изоморфизме) Пусть , . затем

       Доказательство. Я воспользуюсь первой теоремой об изоморфизме. Для этого мне нужно определить карту группы.

       Чтобы определить эту карту группы, я буду использовать универсальное свойство Коэффициент.

       Частная карта групповая карта. По лемме, предшествующей универсальному свойству Коэффициент, . Поскольку , следует, что .

       Поскольку это групповая карта и , универсальное свойство Фактор подразумевает, что существует групповое отображение данный

       Если , то . Следовательно, сюръективен.

       Я утверждаю, что.

       Во-первых, если (так), то . Поскольку H тождество в , это следует из того .

       Обратно, предположим, так

       Из последнего уравнения следует, что , поэтому .

       Таким образом, .

       По первой теореме об изоморфизме

       Существует также Третья теорема об изоморфизме (иногда называемый модульным изоморфизмом или изоморфизм Нётер ). Утверждается, что если а потом

       Вы можете доказать это, используя первую теорему об изоморфизме, таким образом подобно тому, что использовалось при доказательстве второй теоремы об изоморфизме.

       ---

       Контактная информация

       Домашняя страница Брюса Икенаги

       Copyright 2018 Брюс Икенага

       ct.category theory — Пример неестественного изоморфизма

       Asked 9 лет, 2 месяца назад

       Изменено 3 года, 8 месяцев назад

       Просмотрено 7 тысяч раз

       $\begingroup$

       Кто-нибудь может привести пример неестественного изоморфизма? Или, может быть, кто-нибудь может объяснить, почему противоестественных изоморфизмов не существует. 9\ast$ для конечномерных векторных пространств не пустяк: один функтор ковариантен, другой контравариантен, так что они даже не функторы между одними и теми же категориями. Под функтором здесь следует понимать ковариантный функтор.

       • ct.категория-теория

       $\endgroup$

       3

       $\begingroup$

       В качестве более простого, но, возможно, более искусственного примера, чем пример Марка, возьмем $\mathcal{C}$ в качестве категории с одним объектом и двумя морфизмами. Тогда тождественный функтор $\mathcal{C}\to\mathcal{C}$ «неестественно изоморфен» функтору, переводящему оба морфизма в тождественное отображение.

       $\endgroup$

       3

       $\begingroup$

       Если функторы $F,G : C \to D$ такие, что $F(x) \cong G(x)$ для каждого $x \in C$, я бы назвал $F,G$ «поточечно изоморфными» . Вы просите привести примеры неизоморфных функторов, которые поточечно изоморфны. Примеров из природы предостаточно.

       1. Рассмотрим категорию интервалов $I=\{0 \to 1\}$. Категория функторов $I \to C$ изоморфна категории морфизмов в $C$. Конечно, для большинства $C$ существуют неизоморфные морфизмы в $C$, область определения и область значений которых изоморфны или даже равны. Например, возьмите тождество и постоянную карту на нетривиальном множестве или пространстве.

       2. Пусть $C$ — категория конечных множеств с биекциями как морфизмами. Тогда у нас есть функтор $\mathrm{Sym} : C \to C$, который отображает каждое множество в его множество перестановок, и функтор $\mathrm{Ord} : C \to C$, который отображает каждое множество в его множество полных порядков; действие на морфизмах является «сопряжением». Эти функторы поточечно изоморфны, но не изоморфны (ведь между этими функторами вообще нет естественного преобразования). На самом деле этот пример (при ограничении множествами заданного размера) можно рассматривать как частный случай следующего.

       3. Пусть $G$ — группа (или моноид), рассматриваемая как категория с одним объектом $\star$. Тогда функтор $G \to \mathsf{Set}$ совпадает с $G$-множеством. На самом деле категория $G$-множеств изоморфна категории функторов $G \to \mathsf{Set}$. Значение в $\star$ является базовым набором. Конечно, для $G \neq 1$ существуют неизоморфные $G$-множества, базовые множества которых изоморфны (например, базовое множество $G$ с регулярным действием и с тривиальным действием $G$). 9n(X;G),\qquad X\mapsto \mathrm{Ext}(H_{n-1}(X),G)\oplus\mathrm{Hom}(H_n(X),G)$$ изоморфны, но не естественно так. См. «Алгебраическую топологию» Хэтчера, глава 3.1 (в частности, упражнение 11 в конце этого раздела).

          $\endgroup$

          2

          $\begingroup$

          Ваш не-пример векторных пространств и их двойников можно превратить в реальный пример.

          Пусть $C$ — группоид конечномерных векторных пространств и линейных изоморфизмов. {op}$, который имеет место для любого группоида. Эти функторы неестественно изоморфны. 91$. Карты индуцируются $1,2,3\maps в 1,1,2$ и $1,2,3\maps в 1,2,2$).

          $\endgroup$

          2

          $\begingroup$

          Возьмем $C = BG$ для некоторой группы $G$ и возьмем $D = \text{Set}$. Функтор $BG \to \text{Set}$ является $G$-множеством. Два $G$-множества неестественно изоморфны тогда и только тогда, когда они имеют одинаковую мощность, и легко найти два $G$-множества одинаковой мощности, которые не изоморфны $G$-множествам, например найти группу с двумя несопряженными подгруппами одного индекса.

          $\endgroup$

          1

          $\begingroup$

          Вот хороший пример, который недавно возник в вопросе MSE. Пусть $k$ — поле, $Vect$ — категория $k$-векторных пространств, $Aff$ — категория $k$-аффинных пространств. Каждое векторное пространство является аффинным пространством, дающим забывающий функтор $F:Vect\to Aff$. С другой стороны, каждому аффинному пространству соответствует векторное пространство той же размерности (векторное пространство формальных разностей), дающее функтор $G:Aff\to Vect$. Композиция $GF:Vect\to Vect$ естественным образом изоморфна тождеству. С другой стороны, композиция $FG:Aff\to Aff$ только неестественно изоморфна тождеству: она переводит каждое аффинное пространство в другое аффинное пространство той же размерности, но это нельзя сделать совместимым с морфизмами.

          $\endgroup$

          $\begingroup$

          Структурная теорема для конечно порожденных абелевых групп дает для каждого $A$ изоморфизм $A\cong T(A)\oplus \frac{A}{T(A)}$, где $T$ — кручение. Это семейство поточечных изоморфизмов между $1_{\mathsf{Ab}_\text{f.g}}$ и функтором $T\oplus \frac 1T$.

          Претензия. Эти функторы естественно не изоморфны. В частности, изоморфизмы структурной теоремы не являются естественными.

          Доказательство. Моноид эндоморфизма единичного функтора есть мультипликативный моноид $\mathbb Z$. В этом можно убедиться, посмотрев на отображение квадратов естественности из $\mathbb Z$ и используя его универсальное свойство как свободную абелеву группу на одном генераторе. С другой стороны, функтор $T\oplus \frac 1T$ допускает нильпотентных эндоморфизмов $$T\oplus \frac 1T\overset{ \begin{pmatrix} 0 & \альфа\\ 0 & 0 \end{pmatrix} }{\longrightarrow}T\oplus \frac 1T$$, где $\alpha:\frac 1T\Rightarrow T$ задается покомпонентно $\frac{A}{T(A)}\ в T(A)\oplus \frac{A}{T(A)}\to T(A)$. Таким образом, $1,T\oplus \frac 1T$ имеют неизоморфные моноиды эндоморфизмов, поэтому они сами являются неизоморфными функторами.

          $\endgroup$

          1

          $\begingroup$

          Я привел более сложный пример неестественности расщепления универсальных коэффициентов в своей статье «Когомологии с цепями в качестве коэффициентов», Proc. Лондонская математика. Соц . (3) 14 (1964), 545-565, доступно здесь. Там доказано, что для цепных комплексов $K,L$, свободных и равных нулю ниже размерности $0$, существует изоморфизм для любой абелевой группы $G$

          9Y$, где $k$ — когомологическая операция (см. статью «О надстройках Куннета», Proc. Camb. Phil. Соц . 60 (1964) 713-720, доступно здесь.

          $\endgroup$

          $\begingroup$

          Кажется, что функтор на бесконечном множестве категорий, который добавляет одну непересекающуюся точку * к любому множеству, не является естественно изоморфным функтору единицы.

          $\endgroup$

          2

          $\begingroup$

          9n \mid \eta_0 (x)$ для всех $n$, откуда следует, что $\eta_0(x) = 0$ и, следовательно, $\eta = 0$.

          $\endgroup$

          2

          $\begingroup$

          Я почти уверен, что можно также классифицировать тот факт, что для обычных комплексных представлений конечных групп количество неприводимых представлений = количеству классов сопряженности. Как и в этом тесно связанном вопросе, существует биекция (которая приводит к поточечному изоморфизму), но не естественная.

          (Два функтора, о которых я здесь думаю, являются контравариантными функторами из категории конечных групп в категорию $k$-линейных категорий. Первый — это $F_1(G) = \mathrm{rep}_{\mathbb {C}}(G)$. Второй, $F_2$, переводит конечную группу $G$ в $k$-линейную категорию, свободно порожденную классами сопряженности $G$. Мне нужно подумать о том, как определить $F_2$ на морфизмах, но я не думаю, что существует какой-либо выбор определения $F_2$ на определениях $F_2$ на морфизмах, который сделал бы $F_1$ и $F_2$ естественно изоморфными, несмотря на то, что они поточечно изоморфны.)

          $\endgroup$

          3

          $\begingroup$

          Хотя ответов уже слишком много, позвольте мне добавить наблюдение, что одним из реальных мотивов создания «Общей теории естественных эквивалентностей» было понимание различия между тем фактом, что конечномерное векторное пространство изоморфно своему двойственному пространству , но естественно изоморфный своему второму двойственному.