Изоморфизм примеры: Мегаэнциклопедия Кирилла и Мефодия

Опубликовано автором

ИЗОМОРФИЗМ — Что такое ИЗОМОРФИЗМ?

Слово состоит из 10 букв: первая и, вторая з, третья о, четвёртая м, пятая о, шестая р, седьмая ф, восьмая и, девятая з, последняя м,

Слово изоморфизм английскими буквами(транслитом) — izomorfizm

  • Буква и встречается 2 раза. Слова с 2 буквами и
  • Буква з встречается 2 раза. Слова с 2 буквами з
  • Буква о встречается 2 раза. Слова с 2 буквами о
  • Буква м встречается 2 раза. Слова с 2 буквами м
  • Буква р встречается 1 раз. Слова с 1 буквой р
  • Буква ф встречается 1 раз. Слова с 1 буквой ф

Изоморфизм

ИЗОМОРФИЗМ (от изо и греч. morphe — форма, вид), способность атомов, ионов или молекул замещать друг друга в кристаллич.

структурах. В результате изоморфизма образуются твердые р-ры замещения.

Химическая энциклопедия

Изоморфи́зм (от др.-греч. ἴσος — «равный, одинаковый, подобный» и μορφή — «форма») — это очень общее понятие, которое употребляется в различных разделах математики.

ru.wikipedia.org

Изоморфизм [isomorphism] — понятие математики и логики, означающее соотношение между двумя любыми объектами тождественной структуры. Между элементами изоморфных объектов существует взаимно однозначное отношение…

slovar-lopatnikov.ru

ИЗОМОРФИЗМ (от греч. isos – равный, однозначный и morphe – форма) понятие, выражающее тождественность, идентичность форм. В психологии идентичность (теоретическая) между гештальтами в переживании непосредственно созерцаемого и в процессах…

Философская энциклопедия

Изоморфизм графов

Если изоморфизм графов установлен, они называются изоморфными и обозначаются как. Иногда биекция записывается в виде подстановки изоморфизма.

ru.wikipedia.org

Изоморфизм и гомоморфизм

ИЗОМОРФИЗМ И ГОМОМОРФИЗМ — понятия, выражающие одинаковость (изоморфизм; от греч. isos — одинаковый и morphe — форма) либо подобие (гомоморфизм; от греч. homoios— подобный) строения (структуры) систем (множеств, процессов, конструкций).

Философская энциклопедия

ИЗОМОРФИЗМ И ГОМОМОРФИЗМ — логико-математич. понятия, выражающие одинаковость (изоморфизм; от греч. — одинаковый и — форма) либо уподобление (гомоморфизм; от греч. — один и тот же, равный) строения (структуры) систем…

Философская энциклопедия

ИЗОМОРФИЗМ И ГОМОМОРФИЗМ — логико-математич. понятия, выражающие одинаковость либо уподобление строения (структуры) систем (множеств, процессов, конструкций).

Советский философский словарь. — 1974

ТОМА ИЗОМОРФИЗМ

ТОМА ИЗОМОРФИЗМ — изоморфизм между (обобщенными) (ко)гомологиями базы векторного (сферического) расслоения и (ко)гомологиями его Тома пространства Пусть n-мерное векторное расслоение над конечным клеточным пространством X ориентируемо в некоторой…

Математическая энциклопедия. — 1977-1985

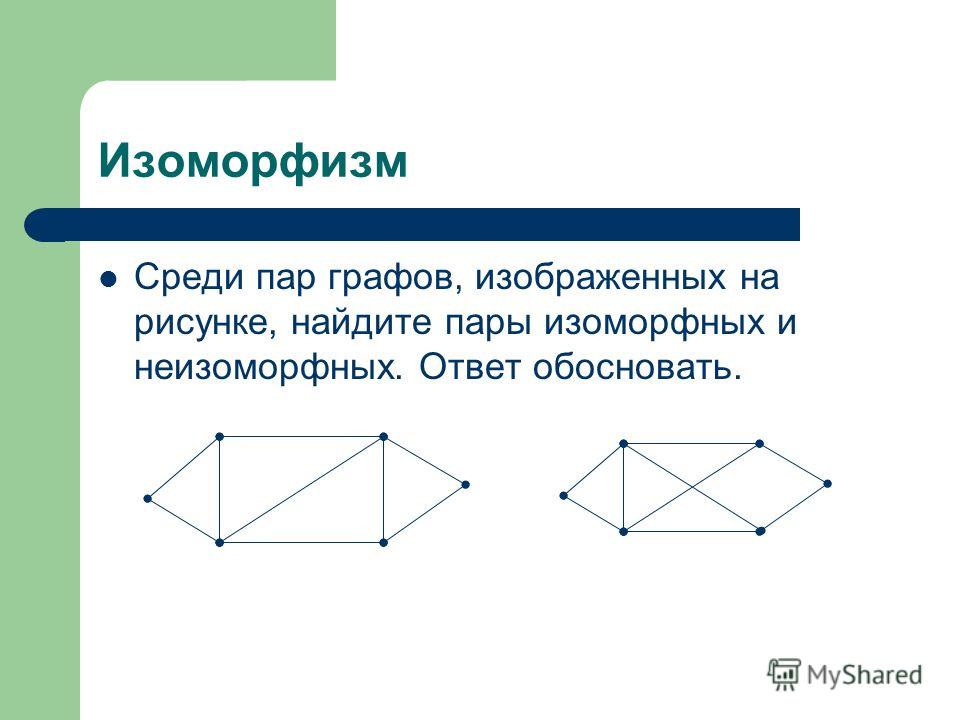
ГРАФОВ ИЗОМОРФИЗМ

ГРАФОВ ИЗОМОРФИЗМ — отношение эквивалентности на множестве графов. Изоморфным отображением одного неориентированного графа на другой наз. взаимно однозначное отображение вершин и ребер одного графа соответственно на вершиныи ребра другого графа…

Математическая энциклопедия. — 1977-1985

Теоремы об изоморфизме

Теоремы об изоморфизме в алгебре — ряд теорем, связывающих понятия фактора, гомоморфизма и вложенного объекта. Утверждением теорем является изоморфизм некоторой пары групп, колец, модулей, линейных пространств…

ru.wikipedia.org

Гомоморфизм Изоморфизм

Гомоморфизм Изоморфизм — аЧ логико-математические понятия, выражающие уподобление (гомоморфизм) либо одинанковость (изоморфизм) строения систем. Две системы А и В назынваются изоморфными, если между их элементами, а также функнциями…

Словарь по логике. — 1997

МЕТРИЧЕСКИЙ ИЗОМОРФИЗМ

МЕТРИЧЕСКИЙ ИЗОМОРФИЗМ — пространств с мерой и — биективное отображение при к-ром образы и прообразы измеримых множеств измеримы и имеют ту же меру (здесь — нек-рая булева -алгебра или -кольцо подмножеств пространства, называемых измеримыми…

Математическая энциклопедия. — 1977-1985

Гомоморфизм, изоморфизм

Гомоморфизм, изоморфизм — логико-математические понятия, выражающие уподобление (гомоморфизм) либо одинаковость (изоморфизм) строения систем.

Две системы А и В называются изоморфными, если между их элементами, а также функциями…

Словарь по логике. — 1997

Русский язык

Изо/морф/и́зм/.

Морфемно-орфографический словарь. — 2002

Изоморфи́зм, -а.

Орфографический словарь. — 2004
  • Слова из слова «изоморфизм»
  • Слова на букву «и»
  • Слова, начинающиеся на «из»
  • Слова c буквой «м» на конце
  • Слова c «зм» на конце
  • Слова, начинающиеся на «изо»
  • Слова, начинающиеся на «изом»
  • Слова, оканчивающиеся на «изм»
  • Слова, заканчивающиеся на «физм»
  1. изомнутся
  2. изомнут
  3. изомну
  4. изоморфизм
  5. изоморфный
  6. изонефа
  7. изонеф

ХиМиК.

ru — ИЗОМОРФИЗМ — Химическая энциклопедия

А Б В Г Д Е Ж З И К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Э Ю Я

ИЗОМОРФИЗМ (от изо… и греч. morphe — форма, вид), способность атомов, ионов или молекул замещать друг друга в кристаллич. структурах. В результате изоморфизма образуются твердые р-ры замещения. В-ва, к-рым присущ изоморфизм, наз. изоморфными. Изоморфные в-ва могут кристаллизоваться совместно, давая смешанные кристаллы — изоморфные смеси. Эти смеси образуются лишь тогда, когда замещающие друг друга частицы (атомы, ионы, молекулы) близки по своим эффективным размерам. Согласно правилу Гольдшмидта, образование изоморфных смесей с широким диапазоном концентраций возможно при тождестве знака заряда и близкой поляризуемости замещающих друг друга атомов (или ионов), если их ионные радиусы различаются не более чем на 15%.

Если два в-ва дают изоморфные смеси любых концентраций (непрерывный ряд твердых р-ров), изоморфизм наз. совершенным. В противном случае говорят о несовершенном (ограниченном) изоморфизме. Совершенный изоморфизм характерен только для изоструктурных в-в, имеющих сходное пространств. расположение атомов или ионов и поэтому сходные по внеш. форме кристаллы. Для ограниченного изоморфизма условие изоструктурности необязательно. Пример совершенного изоморфизма — кристаллы квасцов KAl(SO4)2.12H2O, в к-рых ионы К+ м. б. частично или полностью замещены ионами Rb
+ или NH4+, а ионы Аl3+ионами Сr3+ или Fe3+ . Пример несовершенного изоморфизма для изоструктурных в-в, образующих смешанные кристаллы в огранич. пределах, Mg2SiO4 и Ca2SiO4, для неизоструктурных — минерал сфалерит ZnS, в к-ром до 20% атомов Zn м. б. замещены атомами Fe, причем ZnS и FeS имеют разл. кристаллич. структуры.

Если замещающие друг друга атомы имеют одинаковую степень окисления, такой изоморфизм наз. изовалентным (напр., KH2PO4-KH2AsO4), если разную — гетеровалентным. Так, при образовании смешанных кристаллов FeCO3-ScBO3 происходит замещение Fe2+ на Sc3+ и одновременно — С4+ на В3+ , в результате чего формальные валентности оказываются скомпенсированными. Гетеровалентный изоморфизм, при к-ром Si

4+ замещается на Аl3+ и в то же время однозарядный катион (напр., Na+) замещается на двухзарядный (напр., Са2+ ), характерен для алюмосиликатов(напр., непрерывный ряд твердых р-ров NaAlSi3O8-CaAl2Si2O8). Гетеровалентный изоморфизм может осуществляться как без изменения числа атомов в элементарной ячейке, так и с изменением, т.е. как с заполнением пространства кристаллич.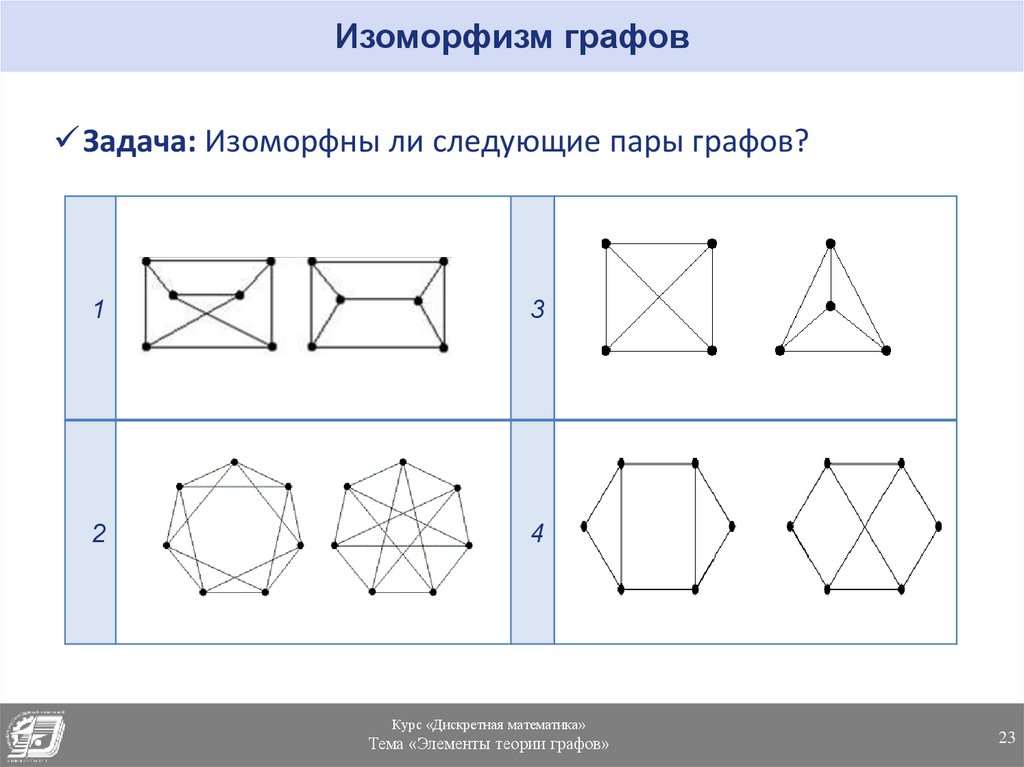 структуры, так и с вычитанием. Пример изоморфизма с заполнением пространства — смешанные кристаллы CaF2-YF3. Структуру CaF2 можно описать как простую кубич. кладку ионов F—, где ионы Са2+ занимают половину кубич. пустот (см. Плотная упаковка). По мере растворения YF3 в CaF
2ионы Са2+ замещаются ионами Y3+ , а избыточные ионы F— внедряются в своб. кубич. пустоты. При образовании твердых р-ров изоморфных орг. в-в происходит замена молекулы на молекулу, при этом осн. роль играет геом. форма молекул.Наряду с изоморфизмом, при к-ром замещаются атомы, ионы или молекулы, возможен «аномальный» (блочный) изоморфизм, когда замещаются цепи, слои или объемные блоки. Напр., смешанослойные кристаллы встречаются среди слоистых силикатов.Изоморфные замещения имеют статистич. характер и приводят к образованию частично неупорядоченной структуры, поэтому смешанные кристаллы часто рассматривают как дефектные системы (с точечными, одномерными, двухмерными или объемными дефектами). Развивается энергетич. концепция изоморфизма, к-рая позволяет в сравнительно простых случаях на основе расчета энергии атомизации изоморфных смесей предсказать пределы изоморфных замещений в зависимости от т-ры.Изоморфизм широко распространен в природе. Б. ч. минералов представляет собой изоморфные смеси сложного переменного состава. С изоморфизмом связано геохим. поведение редких и рассеянных элементов, их распространение в горных породах и рудах, где они содержатся в виде изоморфных примесей. Изоморфное замещение определяет мн. полезные св-ва искусств. материалов совр. техники — полупроводников, ферромагнетиков, пьезо- и сегнетоэлектриков, люминофоров, лазерных материалов и др. (см., напр., Гранаты синтетические).Термин «изоморфизм» предложен Э. Мичерлихом в 1819.
===
Исп. литература для статьи «ИЗОМОРФИЗМ»: Франк-Каменецкий В. А., Природа структурных примесей и включений в минералах, Л., 1964; Макаров Е. С., Изоморфизм атомов в кристаллах, М., 1973; Урусов В.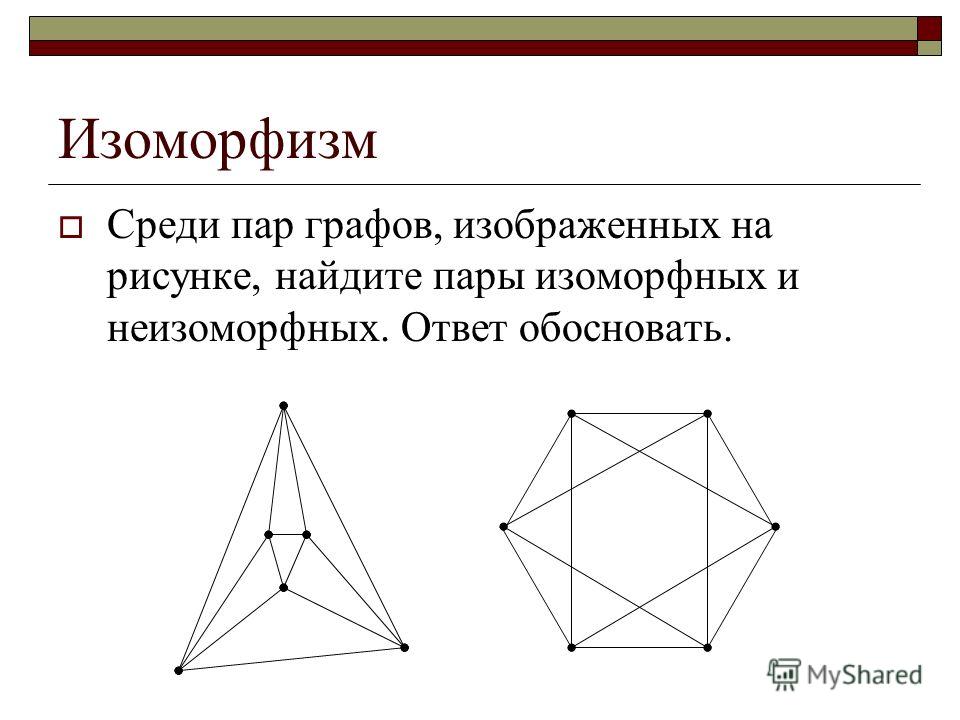 С., Энергетическая кристаллохимия, М., 1975.П. М. Зоркий.

Страница «ИЗОМОРФИЗМ» подготовлена по материалам химической энциклопедии.

А Б В Г Д Е Ж З И К Л М Н О П Р С Т У Ф Х Ц Ч Ш Щ Э Ю Я

2}$$

$$1$$

$$\омега $$

 

$$ + \left( {\bmod 3} \right)$$

$$\влево\{ 0 \вправо\}$$

$$\влево\{ 1 \вправо\}$$

$$\влево\{ 2 \вправо\}$$

$$\влево\{ 0 \вправо\}$$

$$\влево\{ 0 \вправо\}$$

$$\влево\{ 1 \вправо\}$$

$$\влево\{ 2 \вправо\}$$

$$\влево\{ 1 \вправо\}$$

$$\влево\{ 1 \вправо\}$$

$$\влево\{ 2 \вправо\}$$

$$\влево\{ 0 \вправо\}$$

$$\влево\{ 2 \вправо\}$$

$$\влево\{ 2 \вправо\}$$

$$\влево\{ 0 \вправо\}$$

$$\влево\{ 1 \вправо\}$$ 92}} \right) \\ \end{gathered} \]

Пример 2 : Показать, что аддитивная группа $$G = \left\{ { \ldots , – 2, – 1,0 ,1,2, \ldots } \right\}$$ изоморфна аддитивной группе $$G’ = \left\{ { \ldots , – 2m, – m,0,m,2m, \ldots } \ right\}$$ для любого заданного целого числа $$m$$.

Решение :
Определим отображение $$f$$ как $$f:G \to G’:f\left( a \right) = ma$$, где $$a \in G,\,\,ma \in G’$$ и показать, что $$f$$ является изоморфизмом $$G$$ на $$G’$$.

Мы видим, что $$f$$ является единицей, так как два разных элемента $$G$$ имеют два разных образа $$f – $$ в $$G’$$ – это образ $$f – $$ элемента из $$G$$.

Еще раз:
\[\begin{gathered} f\left( {a + b} \right) = m\left( {a + b} \right) = ma + mb \\ \Rightarrow f\left( { a + b} \right) = f\left( a \right) + f\left( b \right) \\ \end{gathered} \]

Таким образом, $$f$$ также сохраняет композицию. Следовательно, $$f$$ является изоморфным отображением $$G$$ на $$G’$$.

⇐ Теорема Кэли ⇒ Необходимое и достаточное условие для подгруппы ⇒

4.8 Гомоморфизмы и изоморфизмы | MATH0007: Алгебра для совместных студентов с отличием

Пусть \(G,*\) и \(H,\треугольник\) — группы. Функция \(f:G\to H\) не обязательно расскажите что-нибудь о соотношении G и H как группы , если только мы не настаиваем на том, чтобы они взаимодействовали каким-то особым образом. с групповыми операциями \(*\) и \(\triangle\). Мы определяем группа гомоморфизм \(G \to H\) в функцию, которая уважает группу структуру на G и H в следующем смысле:

Определение 4.14 Пусть \(G,*\) и \(H,\треугольник\) — группы.

  • групповой гомоморфизм \(f:G \to H\) есть такая функция, что для всех \(x,y \in G\) имеем \[ f(x*y)= f(x) \треугольник f(y).\]
  • Изоморфизм группы является гомоморфизмом группы, который является биекцией.

Обычно мы говорим просто гомоморфизм и изоморфизм вместо группы гомоморфизм и изоморфизм групп.

Пример 4.10

  • Тождественное отображение \(G \to G\) является изоморфизмом.
  • . Пусть \(G,*\) и \(H,\треугольник\) — произвольные группы. Отображение \(f: G \в H\), заданное формулой \(f(g)=e_H\) для всех \(g \in G\), является групповым гомоморфизмом.
  • Отображение \(f: \zz \to \zz_n\), заданное выражением \(f(z)=[z]_n\), является групповым гомоморфизмом. Чтобы убедиться в этом, мы должны проверить, что \(f(z+w) = f(z)+f(w)\). Это верно, потому что \(f(z+w)=[z+w]_n\) и по определению \([z]_n+[w]_n=[z+w]_n\). 9{-1}) \end{уравнение*}\]

Определение 4.15 Пусть \(f:G \to H\) — гомоморфизм групп.

  • \(\ker f\), ядро ​​ f , определяется как \(\{ g \in G: f(g) = e_H\}\).
  • \(\im f\), образ f определяется как \(\{ f(g): g \in G\}\).

Последнее не является новым определением — это просто образ функции f в том виде, в каком мы ее уже определили.

Предложение 4.8 9{-1} \in \ker f\), который, следовательно, замкнут относительно инверсий, и если \(g,h \in \ker f\), затем \[\begin{align*} f(g*h) & =f(g)\triangle f(h) & \text{as } f \text{ является гомоморфизмом} \\ &= e_H \треугольник e_H & \text{as } g,h \in \ker f \\ &= e_H \end{align*}\] так \(g*h \in \ker f\).

Добавить комментарий

Ваш адрес email не будет опубликован. Обязательные поля помечены *