Изоморфны – Изоморфизм — Википедия
Изоморфизм — Википедия
|
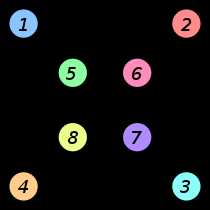
| Пример двух изоморфных графов. Изоморфизм ставит в соответствие вершинам одного графа вершины другого графа того же цвета: две вершины соединены ребром в одном графе тогда и только тогда, когда вершины тех же цветов соединены ребром в другом графе. |
Изоморфи́зм (от др.-греч. ἴσος — «равный, одинаковый, подобный» и μορφή — «форма») — это очень общее понятие, которое определяется по-разному в различных разделах математики. Изоморфизм определяется для множеств, наделённых некоторой структурой (например, для групп, колец, линейных пространств и т. п.). В общих чертах его можно описать так: обратимое отображение (биекция) между двумя множествами, наделёнными структурой, называется изоморфизмом, если оно сохраняет эту структуру. Если между такими структурами существует изоморфизм, то они называются изоморфными. Изоморфизм всегда задаёт отношение эквивалентности на классе таких структур.
Так, например, два графа называются изоморфными, если между ними существует изоморфизм: то есть вершинам одного графа можно сопоставить вершины другого графа, так чтобы соединённым вершинам первого графа соответствовали соединённые вершины второго графа и наоборот. Иными словами, два графа изоморфны, если они «одинаковы» (с точностью до переименования вершин).
В общем случае, объекты, между которыми существует изоморфизм, являются «одинаково устроенными» в смысле этой структуры.
Другим классическим примером изоморфных систем могут служить множество R{\displaystyle \mathbb {R} } всех вещественных чисел с определённой на нём операцией сложения и множество R+{\displaystyle \mathbb {R} _{+}} положительных вещественных чисел с заданной на нём операцией умножения. Отображение x↦exp(x){\displaystyle x\mapsto \exp(x)} в этом случае является изоморфизмом.
В общей алгебре изоморфизмом называется обратимое отображение, которое является гомоморфизмом. Ниже приводятся несколько примеров.
Группы[править | править код]
Пусть G{\displaystyle G} и H{\displaystyle H} — две группы. Биекция f:G→H{\displaystyle f\colon G\to H} называется изоморфизмом, если для любых a,b∈G{\displaystyle a,\;b\in G}
- f(a)f(b)=f(ab){\displaystyle f(a)f(b)=f(ab)}.
Если группа является топологической, добавляется условие гомеоморфности соответствующих топологических пространств.[1]
Поля[править | править код]
Пусть F1{\displaystyle F_{1}} и F2{\displaystyle F_{2}} — поля. Биекция f:F1→F2{\displaystyle f\colon F_{1}\to F_{2}} называется изоморфизмом, если она сохраняет обе операции поля, то есть для любых a,b∈F1{\displaystyle a,b\in F_{1}} выполняется
- f(a)+f(b)=f(a+b){\displaystyle f(a)+f(b)=f(a+b)},
- f(a)⋅f(b)=f(a⋅b){\displaystyle f(a)\cdot f(b)=f(a\cdot b)}.
Пример. Факторкольцо для кольца многочленов с вещественными коэффициентами R[x]{\displaystyle \mathbb {R} [x]} по модулю многочлена x2+1{\displaystyle x^{2}+1} является полем, изоморфным
- R[x]/(x2+1) ⟶≅ C{\displaystyle \mathbb {R} [x]/(x^{2}+1)\ {\stackrel {\cong }{\longrightarrow }}\ \mathbb {C} }
Для полей с дополнительной структурой (упорядоченные, топологические поля и т. д.) может добавляться условие, что биекция сохраняет также эти дополнительные структуры.
В теории множеств любая биекция является изоморфизмом.
К примеру, два частично упорядоченных множества изоморфны, если между ними есть биекция, сохраняющая порядок[3].
В теории категорий изоморфизм есть обратимый морфизм, то есть морфизм φ{\displaystyle \varphi }, для которого существует такой морфизм φ−1{\displaystyle \varphi ^{-1}}, что композиции φ−1∘φ{\displaystyle \varphi ^{-1}\circ \varphi } и φ∘φ−1{\displaystyle \varphi \circ \varphi ^{-1}} — тождественные морфизмы. Определения категории групп, категории колец, категории векторных пространств и других структур строятся таким образом, что классические определения изоморфизма групп, колец, векторных пространств совпадают с общим определением изоморфизма в категории.
Для нормированных пространств отображение одного из них в другое называется изоморфизмом нормированных пространств, если оно линейно, непрерывно и биективно, и обратное отображение тоже непрерывно. В этом смысле изоморфизм сохраняет структуру линейного пространства и топологию, но не обязательно сохраняет норму. Если изоморфизм еще и сохраняет норму, то он называется изометрическим изоморфизмом или изометрией[4].
Граф G{\displaystyle G} называется изоморфным графу H{\displaystyle H}, если существует биекция f{\displaystyle f} из множества вершин графа G{\displaystyle G} в множество вершин графа H{\displaystyle H}, обладающая следующим свойством: если в графе G{\displaystyle G} есть ребро из вершины A{\displaystyle A} в вершину B{\displaystyle B}, то в графе H{\displaystyle H} должно быть ребро из вершины f(A){\displaystyle f(A)} в вершину f(B){\displaystyle f(B)} и наоборот — если в графе H{\displaystyle H} есть ребро из вершины A{\displaystyle A} в вершину B{\displaystyle B}, то в графе G{\displaystyle G} должно быть ребро из вершины f−1(A){\displaystyle f^{-1}(A)} в вершину f−1(B){\displaystyle f^{-1}(B)}. В случае ориентированного графа эта биекция также должна сохранять ориентацию ребра. В случае взвешенного графа биекция также должна сохранять вес ребра.
В теории вычислительной сложности до сих пор является открытым вопрос о сложности задачи изоморфности графов. На данный момент не доказана ни её принадлежность классу P{\displaystyle P}, ни её NP{\displaystyle NP}-полнота.
Изоморфизм алгебраической системы на себя называется автоморфизмом.
Понятие изоморфизма возникло в математике применительно к группам и было естественным образом распространено на более широкий класс математических структур.
- Некоторая общая теория, уточняющая понятия изоморфизма (и других близких понятий) была предложена группой Бурбаки в их книге «Теория множеств» (Глава 4. Структуры).
- ↑ Л. С. Понтрягин Непрерывные группы стр. 392
- ↑ Фаддеев Д. К. Лекции по алгебре. — М.: Наука, 1984. — С. 200—201. — 416 с.
- ↑ Верещагин Н. К., Шень А. Лекции по математической логике и теории алгоритмов. Часть 1. Начала теории множеств. стр. 48
- ↑ Петр Бородин, А. Савчук, И. Шейпак. Задачи по функциональному анализу. — МЦНМО, 2017. — С. 28. — 337 с. — ISBN 9785040485147.
ru.wikipedia.org
Изоморфизм групп — Википедия
Изоморфизм групп — взаимно-однозначное соответствие между элементами двух групп, сохраняющее групповые операции. Если существует изоморфизм между двумя группами, группы называются изоморфными. С точки зрения теории групп изоморфные группы имеют одни и те же свойства и их можно не различать.
Если заданы две группы (G, ∗) и (H, ∘{\displaystyle \circ }). Изоморфизм групп из (G, ∗) в (H, ∘{\displaystyle \circ }) — это биективный гомоморфизм групп из G в H.
Другими словами, изоморфизм групп — это биекция f:G→H{\displaystyle f:G\rightarrow H}, такая, что для любых u и v из G выполняется
- f(u∗v)=f(u)∘f(v){\displaystyle f(u*v)=f(u)\circ f(v)}.
- Две группы (G, ∗) и (H, ∘{\displaystyle \circ }) изоморфны, если существует изоморфизм из одной в другую. Это записывается следующим образом:
- (G,∗)≅(H,∘){\displaystyle (G,*)\cong (H,\circ )}
- Часто используется более короткая и простая запись. Если групповые операции не приводят к двусмысленности, их опускают:
- G≅H{\displaystyle G\cong H}
- (Иногда даже пишут просто G = H. Не приведёт ли такая запись к путанице и двусмысленности, зависит от контекста. Например, употребление знака равно не очень подходит в случае, когда две группы являются подгруппами одной и той же группы.)
- Группа всех вещественных чисел по сложению, (R,+){\displaystyle (\mathbb {R} ,+)}, изоморфна группе всех положительных вещественных чисел по умножению (R+,⋅){\displaystyle (\mathbb {R} ^{+},\cdot )}:
- (R,+)≅(R+,⋅){\displaystyle (\mathbb {R} ,+)\cong (\mathbb {R} ^{+},\cdot )}
- посредством изоморфизма
- f(x)=ex{\displaystyle f(x)=e^{x}}
- (смотрите экспонента).
- (R/Z,+)≅(S1,⋅){\displaystyle (\mathbb {R} /\mathbb {Z} ,+)\cong (S^{1},\cdot )}
- Изоморфизм задаётся выражением
- f(x+Z)=e2πxi{\displaystyle f(x+\mathbb {Z} )=e^{2\pi xi}}
- для любого x из R{\displaystyle \mathbb {R} }.
Для некоторых групп можно доказать изоморфизм, исходя из аксиомы выбора, но такое доказательство не показывает, каким образом сконструировать конкретный изоморфизм. Примеры:
- Группа (R{\displaystyle \mathbb {R} }, +) изоморфна группе (C{\displaystyle \mathbb {C} }, +) всех комплексных чисел по сложению.[1]
- Группа (C∗,⋅){\displaystyle (\mathbb {C} ^{*},\cdot )} ненулевых комплексных чисел по умножению изоморфна группе S1, упомянутой выше.
Циклические группы[править | править код]
Если (G, ∗) является бесконечной циклической группой, то (G, ∗) изоморфна целым числам (по сложению). С алгебраической точки зрения это означает, что множество всех целых чисел (по сложению) является единственной бесконечной циклической группой.
Все конечные циклические группы заданного порядка изоморфны (Zn,+){\displaystyle (\mathbb {Z} _{n},+)}.
Пусть G — циклическая группа и n — порядок группы G. G является группой, порождённой элементом <x>={e,x,…,xn−1}{\displaystyle <x>=\{e,x,…,x^{n-1}\}}. Мы покажем, что
- G≅(Zn,+){\displaystyle G\cong (\mathbb {Z} _{n},+)}
Определим
- φ:G→Zn={0,1,…,n−1}{\displaystyle \varphi :G\rightarrow \mathbb {Z} _{n}=\{0,1,…,n-1\}}, так что φ(xa)=a{\displaystyle \varphi (x^{a})=a}. Ясно, что φ{\displaystyle \varphi } биективно.
Таким образом,
- φ(xa⋅xb)=φ(xa+b)=a+b=φ(xa)+φ(xb){\displaystyle \varphi (x^{a}\cdot x^{b})=\varphi (x^{a+b})=a+b=\varphi (x^{a})+\varphi (x^{b})}, что доказывает, что G≅(Zn,+){\displaystyle G\cong (\mathbb {Z} _{n},+)}.
- Ядро изоморфизма из (G, ∗) в (H, ∘{\displaystyle \circ }) всегда равно {eG}, где eG — нейтральный элемент группы (G, ∗)
- Если (G, ∗) изоморфна (H,∘{\displaystyle \circ }) и если G абелева, то H тоже абелева.
- Если f — изоморфизм между (G, *) и (H, ∘{\displaystyle \circ }), тогда, если a принадлежит G и имеет порядок n, то такой же порядок имеет f(a).
Из определения следует, что любой изоморфизм f:G→H{\displaystyle f:G\rightarrow H} отображает нейтральный элемент G в нейтральный элемент H,
- f(eG)=eH{\displaystyle f(e_{G})=e_{H}},
откуда следует, что обратные отображаются в обратные,
- f(u−1)=[f(u)]−1{\displaystyle f(u^{-1})=\left[f(u)\right]^{-1}}
и n-е степени в n-е степени,
- f(un)=[f(u)]n{\displaystyle f(u^{n})=\left[f(u)\right]^{n}}
для всех u из G, а также что обратное отображение f−1:H→G{\displaystyle f^{-1}:H\rightarrow G} тоже является изоморфизмом.
Отношение «изоморфно» удовлетворяет всем аксиомам отношения эквивалентности. Если f является изоморфизмом двух групп G и H, то все утверждения, верные для G, связанные со структурой группы, можно перенести посредством f на такие же утверждения в H, и наоборот.
Изоморфизм из группы (G, ∗) в себя называется автоморфизмом этой группы. Так как изомофизм f:G→G{\displaystyle f:G\rightarrow G} биективен,
- f(u)∗f(v)=f(u∗v){\displaystyle f(u)*f(v)=f(u*v)}.
Автоморфизм всегда отображает нейтральный элемент в себя. Образ класса сопряжённости всегда является классом сопряжённости (тем же самым или другим). Образ элемента имеет тот же порядок, что и сам элемент.
Композиция двух автоморфизмов снова является автоморфизмом, и эта операция с множеством всех автоморфизмов группы G, обозначаемая Aut(G), образует группу, группу автоморфизмов G.
Для всех абелевых групп имеется, по меньшей мере, автоморфизм, переводящий элементы группы в их обратные. Однако в группах, где все элементы равны своим обратным, этот автоморфизм является тривиальным, например, в четверной группе Клейна (для этой группы все перестановки трёх, не являющихся нейтральными, элементов группы являются автоморфизмами, так что группа изоморфизмов изоморфна S3 и Dih3).
В Zp для простого числа p, один, не являющийся нейтральным, элемент может быть заменён другим, с соответствующими изменениями в других элементах. Группа автоморфизмов изоморфна Zp − 1. Например, для n = 7, умножение всех элементов Z7 на 3 (по модулю 7), является автоморфизмом порядка 6 в группе автоморфизмов, поскольку 36 ≡ 1 (по модулю 7), а меньшие степени 1 не дают. Таким образом, этот автоморфизм порождает Z6. Имеется ещё один автоморфизм с этим свойством — умножение всех элементов Z7 на 5 (по модулю 7). Таким образом, эти два автоморфизма соответствуют элементам 1 и 5 Z6, в этом порядке или обратном.
Группа автоморфизмов Z6 изоморфна Z2, поскольку только эти два элемента 1 и 5 порождают Z6.
Группа автоморфизмов Z2 × Z2 × Z2 = Dih2 × Z2 имеет порядок 168, что можно показать следующим образом. Все 7 элементов, не являющихся нейтральными, играют одну и ту же роль, так что мы можем выбрать, который играет роль (1,0,0). Любой из оставшихся шести может быть выбран для роли (0,1,0). Эти два определяют, что соответствует (1,1,0). (0,0,1) мы можем выбрать из четырёх, и этот выбор определяет оставшиеся элементы. Таким образом, получим 7 × 6 × 4 = 168 автоморфизмов. Они соответствуют автоморфизмам плоскости Фано, 7 точек которой соответствуют 7 элементам, не являющихся нейтральными. Прямые, соединяющие три точки, соответствуют операции группы: a, b, и c на прямой означают a + b = c, a + c = b, и b + c = a. См. также Полная линейная группа над конечным полем.
Для абелевых групп все автоморфизмы, за исключением тривиального, называются внешними автоморфизмами[en].
Неабелевы группы имеют нетривиальные внутренние автоморфизмы, и, возможно, внешние автоморфизмы.
- ↑ Ash. A Consequence of the Axiom of Choice // Journal of the Australian Mathematical Society. — 1973. — Т. 19. — С. 306—308.
Herstein, I. N. Topics in Algebra. — 2 edition. — Wiley, 1975. — ISBN 0-471-01090-1..
ru.wikipedia.org
изоморфный — Викисловарь
Морфологические и синтаксические свойства[править]
| падеж | ед. ч. | мн. ч. | |||
|---|---|---|---|---|---|
| муж. р. | ср. р. | жен. р. | |||
| Им. | изомо́рфный | изомо́рфное | изомо́рфная | изомо́рфные | |
| Рд. | изомо́рфного | изомо́рфного | изомо́рфной | изомо́рфных | |
| Дт. | изомо́рфному | изомо́рфному | изомо́рфной | изомо́рфным | |
| Вн. | одуш. | изомо́рфное | изомо́рфную | изомо́рфных | |
| неод. | изомо́рфный | изомо́рфные | |||
| Тв. | изомо́рфным | изомо́рфным | изомо́рфной изомо́рфною | изомо́рфными | |
| Пр. | изомо́рфном | изомо́рфном | изомо́рфной | изомо́рфных | |
| Кратк. форма | изомо́рфен | изомо́рфно | изомо́рфна | изомо́рфны | |
и·зо-мо́рф-ный
Прилагательное, относительное, тип склонения по классификации А. Зализняка — 1*a.
Корень: -изо-; корень: -морф-; суффикс: -н; окончание: -ый [Тихонов, 1996].
Произношение[править]
Семантические свойства[править]
Значение[править]
- сходный по форме и свойствам структуры ◆ Цикл развития изоморфный (более древний) или гетероморфный. Лукьянов В.А., Стифеев А.И., «Прикладные аспекты применения микроводорослей в агроценозе», 2014 г.
Синонимы[править]
Антонимы[править]
- антиизоморфный
Гиперонимы[править]
Гипонимы[править]
Родственные слова[править]
Этимология[править]
Происходит от ἴσος «равный, одинаковый, подобный», далее, предположительно, из праиндоевр. *aikʷ- «ровный» + μορφή «вид, наружность, форма».
Фразеологизмы и устойчивые сочетания[править]
Перевод[править]
Библиография[править]
ru.wiktionary.org
Изоморфизм — это… Что такое Изоморфизм?
Изоморфи́зм (от др.-греч. ἴσος — «равный, одинаковый, подобный» и μορφή — «форма») — это очень общее понятие, которое употребляется в различных разделах математики. В общих чертах его можно описать так: пусть даны два множества с определённой структурой (группы, кольца, линейные пространства и т. п.). Биекция между ними называется изоморфизмом, если она сохраняет эту структуру. Если между такими множествами существует изоморфизм, то они называются
Объекты, между которыми существует изоморфизм, являются в определённом смысле «одинаково устроенными», они называются изоморфными. Классическим примером изоморфных систем могут служить множество всех вещественных чисел с определённой на нём операцией сложения и множество положительных вещественных чисел с заданной на нём операцией умножения. Отображение в этом случае является изоморфизмом.
Абстрактная алгебра
В абстрактной алгебре изоморфизмом называется биекция, которая является гомоморфизмом. Ниже приводятся несколько примеров.
Группы
Пусть и — две группы. Биекция называется изоморфизмом, если для любых
- .
Если группа является топологической, добавляется условие гомеоморфности соответствующих топологических пространств.[1]
Поля
Пусть и — поля. Биекция называется изоморфизмом, если для любых выполняется
- ,
- .
В теории категорий изоморфизм есть обратимый морфизм, то есть морфизм , для которого существует такой морфизм , что произведения и — тождественные морфизмы.
Ограниченный линейный оператор между нормированными пространствами называется изоморфизмом, если существует положительное вещественное число такое, что для всех векторов . Любой изоморфизм является взаимно-однозначным. Легко видеть, что является изоморфизмом тогда и только тогда, когда обратим на своем образе, и обратный оператор ограничен. Говорят, что два нормированных пространства являются изоморфными, если найдется сюръективный изоморфизм из одного из них на другое.
Граф называется изоморфным графу , если существует биекция из множества вершин графа в множество вершин графа , обладающая следующим свойством: если в графе есть ребро из вершины в вершину , то в графе должно быть ребро из вершины в вершину и наоборот — если в графе есть ребро из вершины в вершину , то в графе должно быть ребро из вершины в вершину . В случае ориентированного графа эта биекция также должна сохранять ориентацию ребра. В случае взвешенного графа биекция также должна сохранять вес ребра.
В теории вычислительной сложности до сих пор является открытым вопрос о сложности задачи изоморфности графов. На данный момент не доказана ни её принадлежность классу , ни её -полнота.
Связанные определения
Изоморфизм алгебраической системы на себя называется автоморфизмом.
История
Понятие изоморфизма возникло в математике применительно к группам и было естественным образом распространено на более широкий класс математических структур.
Вариации и обобщения
- Некоторая общая теория, уточняющая понятия изоморфизма (и других близких понятий) была предложена группой Бурбаки в их книге «Теория множеств» ( Глава 4. Структуры).
См. также
Примечания
- ↑ Л.С. Понтрягин Непрерывные группы стр. 392
Литература
dic.academic.ru
Изоморфизм (кристаллохимия) — Википедия
Изоморфизм (от др.-греч. ἴσος — «равный, одинаковый, подобный» и др.-греч. μορφή — «форма») — свойство элементов замещать друг друга в структуре кристалла. Изоморфизм возможен при одинаковых координационных числах атомов, а в ковалентных соединениях при тождественной конфигурации связей. Степень совершенства (при данных температуре и давлении) изоморфизма определяется близостью межатомных расстояний, состоянием химической связи и строением электронной оболочки атомов.
Термин предложен Эйльхардом Мичерлихом в 1819 году для обозначения внешнего сходства кристаллической формы у веществ, родственных по химическому составу.
При изоморфизме ионы (атомы) одного элемента замещают в кристаллической постройке минерала ионы (атомы) другого элемента.
В более сложных случаях замещение происходит не между отдельными ионами (атомами), а между группами, комплексами ионов. Изоморфные замещения могут происходить как между ионами с одинаковой валентностью, так и между разновалентными ионами. В соответствии с этим выделяют изовалентный и гетеровалентный изоморфизм. При изовалентном изоморфизме в структуре минерала замещаются ионы равной валентности. При гетеровалентном изоморфизме в кристаллической решётке замещаются ионы разной валентности. При этом важным условием является выравнивание электростатического баланса соединения, которое может происходить следующими путями:
- Помимо гетеровалентного замещения двух элементов происходит ещё дополнительное изоморфное замещение других двух элементов. Оба эти замещения дают суммарный эффект, при котором баланс электрических зарядов не меняется.
- Выравнивание электрического баланса изоморфной смеси может осуществляться также за счёт замещения неодинакового числа ионов, как это происходит в слюдах.
- В том случае, когда решётка кристалла обладает вакантными местами, компенсация зарядов при гетеровалентном изоморфизме осуществляется дополнительными ионами. В итоге один ион большей валентности замещается двумя ионами, сумма валентностей которых равна валентности первого иона. Этот вид гетеровалентного изоморфизма широко распространён в роговых обманках.
Помимо изовалентного и гетеровалентного изоморфизма некоторые авторы выделяют ещё особый вид изоморфизма, при котором в кристаллическую решётку одного вещества оказываются включенными слои или блоки другого вещества субмикроскопических размеров. Однако следует подчеркнуть, что если первые два вида изоморфизма дают продукты в виде твёрдых растворов, принципиально сопоставимых с обычными жидкими растворами по степени их гомогенности, то предлагаемый особый вид изоморфизма, строго говоря, должен быть сопоставлен скорее с коллоидными системами, чем с обычными растворами. Комплекс причин, от которых зависит характер изоморфизма, его направленность и интенсивность можно разделить на две группы: причины внешние и внутренние. К внешним причинам относятся температура, давление и концентрация вещества в определённой среде, к внутренним свойства самих элементов, участвующих в изоморфизме, особенности строения и размеров их атомов (ионов) и состояния кристаллической постройки, в которой происходит замещение. К внутренним факторам изоморфизма относятся ионные (атомные) радиусы, поляризационные свойства ионов, удельные заряды ионов, потенциалы ионизации и функция электрического поля, энергия кристаллической решётки, электроотрицательность элементов.
Изоморфизмом в кристаллохимии называют два несколько разных явления:
Изоструктурными называются вещества с одинаковой кристаллической структурой. Изоморфными — те изоструктурные вещества, которые состоят из химически схожих компонентов. Это близость структуры и формы кристаллов различного (но родственного) химического состава. В этом смысле изоструктурными можно назвать NaCl, MgO и FeN, а изоморфными MgO и FeO. Изоморфизм структур вместе с другими важнейшими категориями кристаллохимии: полиморфизмом, морфотропией и структурной гомологией является важнейшим свойством кристаллических решёток.
С другой стороны, термином «изоморфизм» обозначается явление взаимозамещения атомов и иных структурных единиц в кристаллических фазах переменного состава. Такие вещества также называют изоморфными смесями или твердыми растворами. В этом смысле понятие изоморфизма употребляется гораздо чаще.[источник не указан 923 дня][1]
Растворы замещения — один из наиболее распространённых типов соединений переменного состава.
Изоморфизм с заполнением пространства происходит, когда кроме замещающегося атома в позицию входят дополнительные атомы, располагающиеся в дополнительных позициях решётки.
Растворы внедрения (твёрдые растворы второго рода) это растворы, в которых атомы примеси не замещают атомы минерала хозяина, а располагаются в промежутках между ними. Растворяющиеся атомы входят в промежутки между атомами матрицы, статистически заселяя новую не занятую ранее позицию. Иногда атомы матрицы называют узлами и тогда говорят, что примесь входит в междоузлия. Растворимость по типу внедрения обычно невелика — порядка нескольких процентов и лишь в редких случаях достигает 10 %. В растворах замещения необходимое условие — схожий характер связи с различных компонентах. В растворах внедрения тип связи может быть совершенно иным.
Встречается в тех случаях, когда размеры атомов обоих компонентов значительно различаются. Он особенно характерен для систем металл — неметалл, причём размер атома неметалла значительно меньше, чем размер атома металла. Наименьшие атомы будут у следующих элементов: H (0,46), N (0,71), C (0,77). Они часто образуют с металлами твёрдые растворы второго рода, носящие названия гидридов, нитридов и карбидов. Многие из них являются тугоплавкими твердыми сплавами и широко применяются в промышленности.
Классический пример раствора внедрения — аустенит. Это раствор углерода в γ-модификации железа. В качестве растворов внедрения можно рассматривать силикаты с полостями и каналами, в которые входит переменное количество различных ионов. Например в берилле в каналы могут входить ионы и вода.
Другой замечательный пример раствора включения: образование гидридов некоторых металлов, в особенности палладия. Палладий может растворять огромное количество водорода, в несколько раз превышающее его объём. Водород отдает свой электрон металлу и он обобществляется. Лишённый электрона водород превращается в исключительно мелкий ион, который распределяется по междоузлиям палладиевой решётки, не искажая её.
Растворы вычитания — фазы переменного состава, в которых при наличии устойчивой решётки одного из компонентов, содержание другого компонента варьирует, так как он замещается вакансиями. Такие структуры называют дефектными или дефицитными.
В качестве примера фазы вычитания можно привести пирротин, в котором наблюдается нестехиометричное соотношение железа и серы.
Закон Гольдшмидта. Правило диагонального изоморфизма, ограничение по электроотрицательности[править | править код]
Для того чтобы элементы замещали друг друга должно выполняться несколько условий. В первую очередь должно выполняться так называемое правило Гольдшмидта, которое постулирует, что изоморфизм возможен только между ионами, размер которых различается не больше чем на 10-15 %. Однако этого недостаточно для изоморфного замещения атомов. Натрий и медь имеют очень близкие по размеру ионы, но почти никогда не образуют значительных изоморфных замещений. Причина этого в большой разнице электроотрицательностей этих элементов. Поэтому второе условие изоморфизма формулируется следующим образом: твёрдые растворы возможны, если разница электроотрицательностей меньше 0,4
Впрочем, известны примеры, когда близкие по размеру ионы не замещают друг друга. Так, классические ионные радиусы Na и Cu практически одинаковы, около 1 Å, и нет геометрических препятствий для взаимных замещений между этими ионами. В таких случаях причиной несмесимости, то есть невозможности образовать твёрдый раствор, является разный характер химической связи в соединениях Na и Cu, так как разность их электроотрицательностей составляет 0,9. И если в первом случае образуются чисто ионные связи, то во втором частично ковалентный характер связи становится весьма существенным. Подобны же причины несмесимости в твёрдом состоянии близких по размеру атомов Ca и Hg, Sr и Pb, K и Ag и др.
Диагональный изоморфизм[править | править код]
В таблице Менделеева с движением вниз по столбцам и вправо по строкам размер ионов увеличивается. соответственно на элементы, которые расположены по диагонали к друг другу действует два противоположно направленных фактора: увеличивается заряд и уменьшается радиус иона. В результате радиус иона изменяется на 6 — 10 %. Такие параметры идеально подходят для гетеровалентного изоморфизма. Первым эту закономерность заметил Ферсман, и и сформулировал правило диагонального изоморфизма.
Элементы, расположенные в клетках, расположенных по диагонали, ниже и правее, часто гетеровалентно замещают ионы. Исключением являются элементы 6-го ряда, радиус которых благодаря лантаноидному сжатию сокращается до величин, наиболее подходящих для изоморфизма.
Свойства кристаллов с изоморфными рядами постепенно меняются от одного компонента к другому. Закон Вегарда утверждает, что размер элементарной ячейки пропорционален содержанию компонентов. Аналогично правило Ретгерса утверждает, что плотность изоморфной смеси пропорциональна составу.
Возможно четыре варианта упорядоченности замещающих атомов:
- Распределение атомов совершенно произвольно, вероятность встретить «белый» и «чёрный» атомы в любой точке кристаллической структуры пропорциональна относительному количеству тех и других атомов. Этот случай соответствует полной неупорядоченности.
- Имеется упорядоченность в ближайших координационных сферах — упорядоченность ближнего порядка. Не найдется ни одной пары «чёрных» атомов, располагающихся на кратчайшем друг к другу расстоянии a{\displaystyle a} или же на расстоянии a2{\displaystyle a{\sqrt {2}}}. Все имеющиеся сведения о тонком строении твёрдых растворов указывают на то, что именно такое расположение характеризует подавляющее большинство твёрдых растворов.
- Кроме ближнего порядка наблюдается и дальний порядок. Однако он не достигает 100 %. Большинство интерметаллических соединений характеризуется именно такой степенью упорядоченности, причём её часто выражают определённым процентом от идеальной упорядоченности.
- Взаимное расположение разносортных атомов в пространстве полностью упорядочено. Практически при таком распределении образуется новое соединение промежуточного состава. Примером можно назвать доломит — промежуточное соединение между магнезитом и кальцитом. Таковы структуры многих неорганических соединений.
Можно отметить, что резких границ между твёрдым раствором и соединением не существует. Упорядоченные твёрдые растворы и не полностью упорядоченные соединения являются теми самыми случаями, которые обычно реализуются в природе и в лаборатории.
- ↑ Г. Реми. Курс неорганической химии..
- Гольдшмидт В. М. Кристаллохимия. Перевод И. Д. Борнеман-Старынкевич. Л.: Химтеорет. 1937. — 62 с.
- Макаров Е. С. Изоморфизм атомов в кристаллах. М.: Атомиздат, 1973. — 288 с.
- Урусов В. С. Теория изоморфной смесимости. М.: Наука, 1977. — 251 с.
ru.wikipedia.org
Изоморфизм — Википедия
|
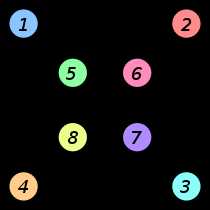
| Пример двух изоморфных графов. Изоморфизм ставит в соответствие вершинам одного графа вершины другого графа того же цвета: две вершины соединены ребром в одном графе тогда и только тогда, когда вершины тех же цветов соединены ребром в другом графе. |
Изоморфи́зм (от др.-греч. ἴσος — «равный, одинаковый, подобный» и μορφή — «форма») — это очень общее понятие, которое определяется по-разному в различных разделах математики. Изоморфизм определяется для множеств, наделённых некоторой структурой (например, для групп, колец, линейных пространств и т. п.). В общих чертах его можно описать так: обратимое отображение (биекция) между двумя множествами, наделёнными структурой, называется изоморфизмом, если оно сохраняет эту структуру. Если между такими структурами существует изоморфизм, то они называются изоморфными. Изоморфизм всегда задаёт отношение эквивалентности на классе таких структур.
Так, например, два графа называются изоморфными, если между ними существует изоморфизм: то есть вершинам одного графа можно сопоставить вершины другого графа, так чтобы соединённым вершинам первого графа соответствовали соединённые вершины второго графа и наоборот. Иными словами, два графа изоморфны, если они «одинаковы» (с точностью до переименования вершин).
В общем случае, объекты, между которыми существует изоморфизм, являются «одинаково устроенными» в смысле этой структуры.
Другим классическим примером изоморфных систем могут служить множество R{\displaystyle \mathbb {R} } всех вещественных чисел с определённой на нём операцией сложения и множество R+{\displaystyle \mathbb {R} _{+}} положительных вещественных чисел с заданной на нём операцией умножения. Отображение x↦exp(x){\displaystyle x\mapsto \exp(x)} в этом случае является изоморфизмом.
Общая алгебра
В общей алгебре изоморфизмом называется обратимое отображение, которое является гомоморфизмом. Ниже приводятся несколько примеров.
Группы
Пусть G{\displaystyle G} и H{\displaystyle H} — две группы. Биекция f:G→H{\displaystyle f\colon G\to H} называется изоморфизмом, если для любых a,b∈G{\displaystyle a,\;b\in G}
- f(a)f(b)=f(ab){\displaystyle f(a)f(b)=f(ab)}.
Если группа является топологической, добавляется условие гомеоморфности соответствующих топологических пространств.[1]
Поля
Пусть F1{\displaystyle F_{1}} и F2{\displaystyle F_{2}} — поля. Биекция f:F1→F2{\displaystyle f\colon F_{1}\to F_{2}} называется изоморфизмом, если она сохраняет обе операции поля, то есть для любых a,b∈F1{\displaystyle a,b\in F_{1}} выполняется
- f(a)+f(b)=f(a+b){\displaystyle f(a)+f(b)=f(a+b)},
- f(a)⋅f(b)=f(a⋅b){\displaystyle f(a)\cdot f(b)=f(a\cdot b)}.
Пример. Фактор-кольцо для кольца многочленов с вещественными коэффициентами R[x]{\displaystyle \mathbb {R} [x]} по модулю многочлена x2+1{\displaystyle x^{2}+1} является полем, изоморфным[2] полю комплексных чисел C:{\displaystyle \mathbb {C} :}
- R[x]/(x2+1) ⟶≅ C{\displaystyle \mathbb {R} [x]/(x^{2}+1)\ {\stackrel {\cong }{\longrightarrow }}\ \mathbb {C} }
Для полей с дополнительной структурой (упорядоченные, топологические поля и т. д.) может добавляться условие, что биекция сохраняет также эти дополнительные структуры.
Теория множеств
В теории множеств любая биекция является изоморфизмом.
К примеру, два частично упорядоченных множества изоморфны, если между ними есть биекция, сохраняющая порядок[3].
Изоморфизм в теории категорий
В теории категорий изоморфизм есть обратимый морфизм, то есть морфизм φ{\displaystyle \varphi }, для которого существует такой морфизм φ−1{\displaystyle \varphi ^{-1}}, что композиции φ−1∘φ{\displaystyle \varphi ^{-1}\circ \varphi } и φ∘φ−1{\displaystyle \varphi \circ \varphi ^{-1}} — тождественные морфизмы. Определения категории групп, категории колец, категории векторных пространств и других структур строятся таким образом, что классические определения изоморфизма групп, колец, векторных пространств совпадают с общим определением изоморфизма в категории.
Нормированные пространства
Для нормированных пространств отображение одного из них в другое называется изоморфизмом нормированных пространств, если оно линейно, непрерывно и биективно, и обратное отображение тоже непрерывно. В этом смысле изоморфизм сохраняет структуру линейного пространства и топологию, но не обязательно сохраняет норму. Если изоморфизм еще и сохраняет норму, то он называется изометрическим изоморфизмом или изометрией[4].
Граф G{\displaystyle G} называется изоморфным графу H{\displaystyle H}, если существует биекция f{\displaystyle f} из множества вершин графа G{\displaystyle G} в множество вершин графа H{\displaystyle H}, обладающая следующим свойством: если в графе G{\displaystyle G} есть ребро из вершины A{\displaystyle A} в вершину B{\displaystyle B}, то в графе H{\displaystyle H} должно быть ребро из вершины f(A){\displaystyle f(A)} в вершину f(B){\displaystyle f(B)} и наоборот — если в графе H{\displaystyle H} есть ребро из вершины A{\displaystyle A} в вершину B{\displaystyle B}, то в графе G{\displaystyle G} должно быть ребро из вершины f−1(A){\displaystyle f^{-1}(A)} в вершину f−1(B){\displaystyle f^{-1}(B)}. В случае ориентированного графа эта биекция также должна сохранять ориентацию ребра. В случае взвешенного графа биекция также должна сохранять вес ребра.
В теории вычислительной сложности до сих пор является открытым вопрос о сложности задачи изоморфности графов. На данный момент не доказана ни её принадлежность классу P{\displaystyle P}, ни её NP{\displaystyle NP}-полнота.
Связанные определения
Изоморфизм алгебраической системы на себя называется автоморфизмом.
История
Понятие изоморфизма возникло в математике применительно к группам и было естественным образом распространено на более широкий класс математических структур.
Вариации и обобщения
- Некоторая общая теория, уточняющая понятия изоморфизма (и других близких понятий) была предложена группой Бурбаки в их книге «Теория множеств» (Глава 4. Структуры).
См. также
Примечания
- ↑ Л. С. Понтрягин Непрерывные группы стр. 392
- ↑ Фаддеев Д. К. Лекции по алгебре. — М.: Наука, 1984. — С. 200—201. — 416 с.
- ↑ Верещагин Н. К., Шень А. Лекции по математической логике и теории алгоритмов. Часть 1. Начала теории множеств. стр. 48
- ↑ Петр Бородин, А. Савчук, И. Шейпак. Задачи по функциональному анализу. — МЦНМО, 2017. — С. 28. — 337 с. — ISBN 9785040485147.
Литература
Ссылки
wikipedia.green
Изоморфизм (математика) — это… Что такое Изоморфизм (математика)?
Изоморфи́зм — это очень общее понятие, которое употребляется в различных разделах математики. В общих чертах его можно описать так: Пусть даны два множества с определённой структурой (группы, кольца, линейные пространства и т. п.). Биекция между ними называется изоморфизмом, если она сохраняет эту структуру. Такие множества со структурой называются изоморфными. Изоморфизм всегда задаёт отношение эквивалентности на классе таких множеств со структурой.
Объекты, между которыми существует изоморфизм, являются в определённом смысле «одинаково устроенными», они называются изоморфными. Классическим примером изоморфных систем могут служить множество всех вещественных чисел с определённой на нём операцией сложения и множество положительных вещественных чисел с заданной на нём операцией умножения. Отображение в этом случае является изоморфизмом.
Абстрактная алгебра
В абстрактной алгебре изоморфизмом называется биекция, которая является гомоморфизмом.
Пусть и суть две группы. Биекция называется изоморфизмом, если для любых
Если группа является топологической, добавляется условие гомеоморфности соответствующих топологических пространств.[1]
В теории категорий изоморфизм есть обратимый морфизм, то есть морфизм , для которого существует такой морфизм , что произведения и — тождественные морфизмы.
Ограниченный линейный оператор T между нормированными пространствами называется изоморфизмом, если существует положительное вещественное число c такое, что для всех векторов x. Любой изоморфизм является взаимно-однозначным. Легко видеть, что T является изоморфизмом тогда и только тогда, когда T обратим на своем образе, и обратный оператор ограничен. Говорят, что два нормированных пространства являются изоморфными, если найдется сюръективный изоморфизм из одного из них на другое.
Граф G называется изоморфным графу H, если существует биекция f из множества вершин графа G в множество вершин графа H, обладающая следующим свойством: если в графе G есть ребро из вершины A в вершину B, то в графе H должно быть ребро из вершины f(A) в вершину f(B) и наоборот — если в графе H есть ребро из вершины A в вершину B, то в графе G должно быть ребро из вершины f − 1(A) в вершину f − 1(B). В случае ориентированного графа эта биекция также должна сохранять ориентацию ребра. В случае взвешенного графа биекция также должна сохранять вес ребра.
В теории вычислительной сложности до сих пор является открытым вопрос о сложности задачи изоморфности графов. На данный момент не доказана ни её принадлежность классу P, ни её NP-полнота.
Связанные определения
Изоморфизм алгебраической системы на себя называется автоморфизмом.
История
Понятие изоморфизма возникло в математике применительно к конкретным алгебраическим системам (прежде всего к группам) и было естественным образом распространено на более широкий класс математических структур.
См. также
Примечания
- ↑ Л.С. Понтрягин Непрерывные группы стр. 392
Литература
Wikimedia Foundation. 2010.
dic.academic.ru


