Матрица равена тест: Тест Равена — Онлайн тест

Опубликовано автором

Прогрессивные матрицы Равена: краткое описание

 

Тест применяется для диагностики уровня интеллектуального развития испытуемых в возрасте от 8 до 14 лет и от 20 до 65 лет. Тест Равена относится к культурно-инвариантным тестам, так как в минимальной степени показатели по этому тесту зависят от наличия знаний, обусловленных жизнью и определенной культурой.

Материал теста в черно-белом варианте состоит из 60 матриц или композиций с пропущенным элементом. Задания разделены на пять заданий (А, В, С, Д и Е) по 12 однотипных по возрастающей сложности заданий в каждой серии. Трудность задания возрастает при переходе от серии к серии. Обследуемый должен выбрать недостающий элемент матрицы среди 6-8 предложенных вариантов ответов.

Серия А — диагностируется способность к дифференциации основных элементов структуры и раскрытию связей между ними, идентификации недостающих частей фигуры и сличению ее с представленными образцами (обследуемому необходимо дополнить недостающую часть изображения).

Серия В — оценивается способность к аналогии.

Серия С — диагностируется способность выявлять сложные изменения закономерностей непрерывного развития, обогащения по вертикали и горизонтали.

Серия Д — оценивает способность к пространственной перестановке фигур в матрице по горизонтальному и вертикальному направлениям.

Серия Е — выявляется способность к аналитико-синтетической мыслительной деятельности (задания этой серии включают анализ фигур основного изображения и последующую «сборку» недостающей фигуры по частям).

Обработка полученных результатов заключается в подсчете общего количества баллов, как в отдельной серии, так и в целом по всему тесту.

 

Тесты для детей

  • Анкета «Мотивы выбора друга»
  • Анкета по Г. Хорну
  • Вопросник-характеристика неуспевающего ученика
  • Диагностика периферических нарушений речи у детей
  • Диагностическая методика В. М. Когана
  • Интервью «Волшебный мир»
  • Исследование памяти с помощью методики заучивания десяти слов
  • Методика «Аналогии»
  • Методика «Аналогии» (версия 2)
  • Методика «Вербальная фантазия»
  •     . .. и другое

Тесты способностей

  • Диагностика периферических нарушений речи у детей
  • Диагностика структуры интеллекта тестом Амтхауэра
  • Диагностическая методика «Проблема Эверье»
  • Исследование памяти с помощью методики заучивания десяти слов
  • КОСКОМ 2
  • Корректурная таблица Бентона
  • Корректурные пробы
  • Культурно-свободный тест на интеллект Р. Кеттелла: краткое описание
  • Метод определения яркости и контролируемости представлений путем самооценки (опросник Р. Гордона)
  • Метод оценки устойчивости представлений
  •     … и другое

 

   RSS     [email protected] 

Тест Равена. Шкала прогрессивных матриц

Нажмите для полного просмотра!

Содержание ▲

  • Тест Равена. Шкала прогрессивных матриц …
  • История тесты Методика «Шкала…
  • Применение теста Тест прогрессивные…
  • Описание методики Тест состоит из 60…
  • Описание серий теста …
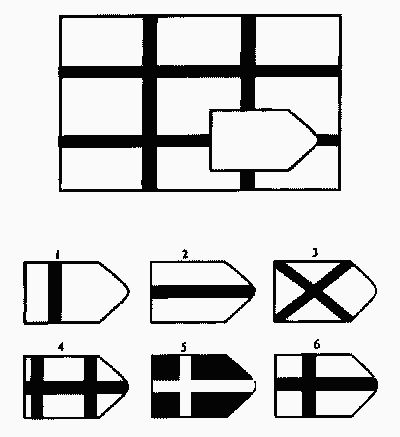
  • Пример тестового вопроса …

Вы можете ознакомиться и скачать презентацию на тему Тест Равена.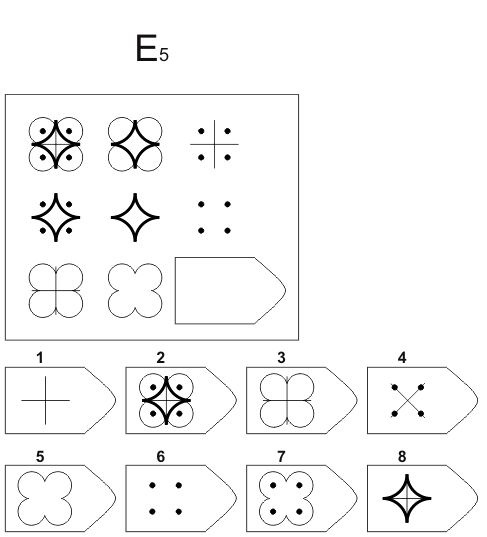 Шкала прогрессивных матриц. Доклад-сообщение содержит 6 слайдов. Презентации для любого класса можно скачать бесплатно. Если материал и наш сайт презентаций Mypresentation Вам понравились – поделитесь им с друзьями с помощью социальных кнопок и добавьте в закладки в своем браузере.


Слайд 1


Описание слайда:

Тест Равена. Шкала прогрессивных матриц

Слайд 2


Описание слайда:

История тесты Методика «Шкала прогрессивных матриц» была разработана в 1936 году Джоном Равеном (совместно с Л. Пенроузом).  Автору методики удалось создать тест, который был бы теоретически обоснован, однозначно интерпретируем, и оценка которого минимально зависела бы от различий в образовании, происхождении и в жизненном опыте людей. 

Слайд 3


Описание слайда:

Применение теста Тест прогрессивные матрицы Равена (ПМР) предназначен для диагностики уровня интеллектуального развития и оценивает способность к систематизированной, планомерной, методичной интеллектуальной деятельности (логичность мышления).

Слайд 4


Описание слайда:

Описание методики Тест состоит из 60 таблиц (5 серий). В каждой серии таблиц содержатся задания нарастающей трудности.

В то же время характерно и усложнение типа заданий от серии к серии. Время прохождения теста ограничено и составляет 20 мин.

Слайд 5


Описание слайда:

Описание серий теста

Слайд 6


Описание слайда:

Пример тестового вопроса


Теги Тест Равена. Шкала прогрессивных матриц

Похожие презентации

{1/2}. \end{aligned}$$

По определению распределения \(\mathcal {MN}\) имеем \(vec(X_1),vec(X_2)\sim N_{dm}(vec(M_1), { \ varSigma }_1\otimes \varPsi _1).\) Тогда имеем \(vec(X_1)-vec(X_2)\sim N_{dm}(0, 2{ \varSigma }_1 \otimes \varPsi _1 )\).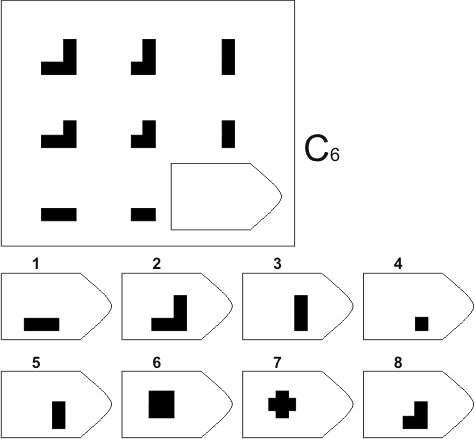

Предположим, что \(\{\lambda _i\},i=1,\ldots ,d\) являются собственными значениями для \({\varSigma}_1\) и \(\{\theta _j\},j=1, \ldots ,m\) являются собственными значениями для \(\varPsi _1\), можно показать, что \(\{2\lambda _i\theta _j\},i=1,\ldots ,d,j=1,\ ldots ,m\) являются собственными значениями для \(2{\varSigma}_1\otimes \varPsi _1\). Следовательно, у нас есть 9{dm-1}\),

$$\begin{aligned} 2E|a'({\varvec{u}}_1-{\varvec{v}}_1)|-E|a'({\varvec {u}}_1-{\varvec{v}}_2)|-E|a'({\varvec{v}}_1-{\varvec{v}}_2)|\ge 0. \end{выровнено} $$

(24)

Равенство выполняется тогда и только тогда, когда распределения \(a'{\varvec{u}}_1\) и \(a'{\varvec{v}}_1\) совпадают. Интегрируя по \(\mu \) в обе части неравенства (24), имеем

$$\begin{aligned} 2E||{\varvec{u}}_1-{\varvec{v}}_1 ||_{Eu}-E||{\varvec{u}}_1-{\varvec{u}}_2||_{Eu}-E||{\varvec{v}}_1-{\varvec{ v}}_2||_{Eu}\ge 0. \end{aligned}$$ 9{ita’ v_1}) \) непрерывны, равенство в (25) имеет место тогда и только тогда, когда \({\varvec{u}}_1\) и \({\varvec{v}}_1\) имеют одинаковые Фурье преобразование, которое подразумевает \(F=G\).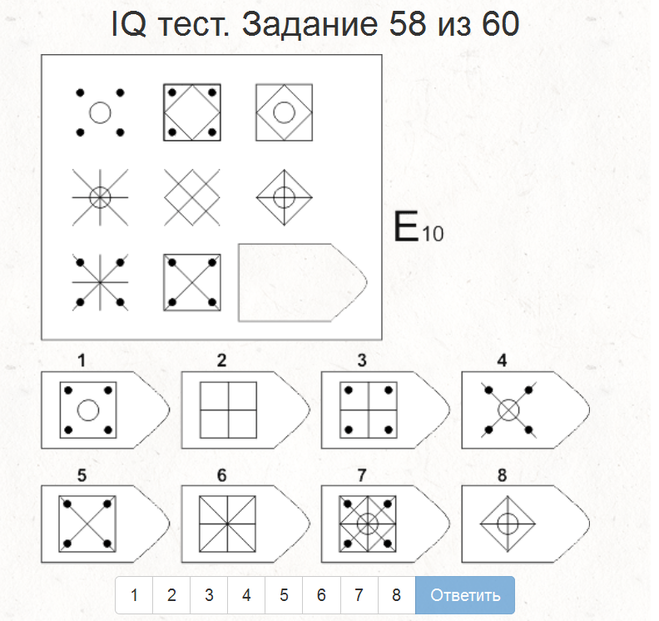 По определению норм Фробениуса и Евклида имеем \(\mu _{FF}=E||X_1-X_2||_{Fr}=E||{\varvec{u}}_1-{\varvec{ u}}_2||_{Eu}\), \(\mu _{GG}=E||Y_1-Y_2||_{Fr}=E||{\varvec{v}}_1-{\varvec {v}}_2||_{Eu}\), \(\mu _{FG}=E||X_1-Y_1||_{Fr}=E||{\varvec{u}}_1-{\ varvec{v}}_1||_{Eu}\). Следовательно, имеем \(2\mu _{FG}-\mu _{FF}-\mu _{GG}\ge 0\), и равенство имеет место тогда и только тогда, когда \(F=G\). \(\квадрат \)

Доказательство теоремы 2

Пусть \(h(X_i,X_j;Y_p,Y_q)\) — вещественнозначная функция такая, что

$$\begin{aligned} h(X_i,X_j;Y_p,Y_q) =||X_i-Y_p||_{Fr}+||X_j-Y_q||_{Fr}+||X_i-X_j||_{Fr}+||Y_p-Y_q||_{Fr}. \end{aligned}$$

(26)

Ясно, что h симметрично в пределах каждого аргумента \((X_i,X_j)\) и \((Y_p,Y_q)\). Можно показать, что EN является U -статистикой, соответствующей функции ядра h . то есть 9{n_2}h(X_i,X_j;Y_p,Y_q). \end{aligned}$$

(27)

Если распределения F и G идентичны, по теореме 1 имеем \(E(h(X_1,X_2;Y_1,\)\(Y_2 )) =0\). Кроме того, поскольку \(E[X_1,X_2;Y_1,Y_2|X_1={\mathbb {X}}_1,Y_1={\mathbb {Y}}_1]=0\) почти для всех матричных реализаций \(( {\mathbb {X}}_1,{\mathbb {Y}}_1)\), EN является U-статистикой с вырожденным ядром. Асимптотическое распределение EN можно вывести из работы Хёффдинга и Роббинса (19).2_1\) случайные величины. \(\square \)

Доказательство теоремы 3

Если \(\mu _{FF}= \mu _{GG}= \mu _{FG}\), то \(2\mu _{FG }-\mu _{FF}-\mu _{GG}= 0\), откуда по теореме 1 следует \(F=G\). Предположим, что \(F=G\) распределения \(\mathbf{ X}_1, \mathbf{X}_2,\mathbf{Y}_1\) и \(\mathbf{Y}_2\) равны. Следовательно, распределения \( ||\mathbf{X}_1-\mathbf{X}_2||_{Fr}, ||\mathbf{Y}_1-\mathbf{Y}_2||_{Fr} \) и \(||\mathbf{X}_1-\mathbf{Y}_1||_{Fr}\) также равны, из чего следует, что \(\mu _{FF}= \mu _{GG }= \mu_{FG}\). \(\квадрат \) 92), \end{align}$$

, где \({\hat{\mu}}_{FF} \) и \({\hat{\mu}}_{GG} \) даны в уравнениях . (8)–(10). Из теоремы 2 имеем \({n}\cdot EN(\mathscr {A},\mathscr {B})=O_p(1)\), и, следовательно, \(\sqrt{n}\cdot EN(\mathscr {A},\mathscr {B}) \overset{p}{\стрелка вправо }0\), как \(n\стрелка вправо \infty \).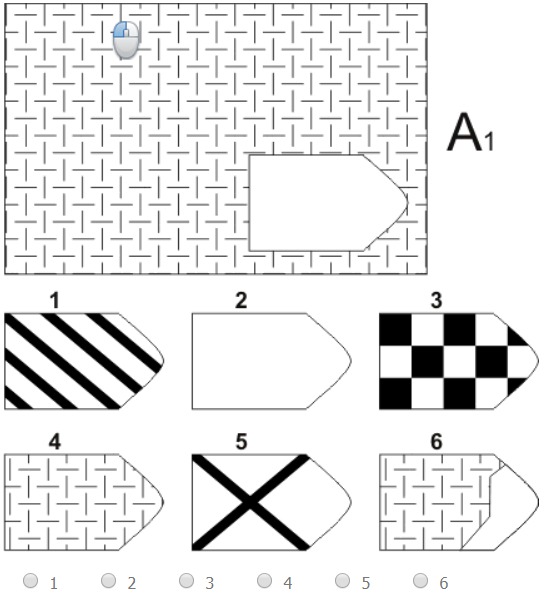

Пусть \(\mu _{FF}=E||\mathbf{X}_1-\mathbf{X}_2 ||_{Fr}\) и \(\mu _{GG}=E||\ mathbf{Y}_{1}-\mathbf{Y}_{2} ||_{Fr}\). При нулевой гипотезе мы имеем \(\mu _{FF}=\mu _{GG}\), и, следовательно, \(\sqrt{n}({\hat{\mu}}_{FF} -{\hat {\ mu}} _ {GG}) = \ sqrt {n} [({\ hat {\ mu}} _ {FF} — \ mu _ {FF}) — ({\ hat {\ mu}} _ { GG} -\mu _{GG})].\) Обратите внимание, что 9{n_1}(||\mathbf{X}_i-\mathbf{X}_j||_{Fr}-\mu _{FF}) \end{aligned}$$

— U-статистика с симметричным ядром функция \(h(\mathbf{X}_i,\mathbf{X}_j)=||\mathbf{X}_i-\mathbf{X}_j||_{Fr}-\mu _{FF}\) . Следовательно, мы имеем \(R_1=\sqrt{n_1}({\hat{\mu}}_{FF} -\mu _{FF})\overset{d}{\rightarrow}N(0,4{\ сигма}_0)\), где \({\sigma}_0=Var[E(||\mathbf{X}_1-\mathbf{X}_2||_{Fr}|\mathbf{X}_1)] \). Точно так же мы имеем \(R_2=\sqrt{n_2}({\hat{\mu}}_{GG} -\mu _{GG})\overset{d}{\rightarrow}N(0,4{\ сигма }_0)\). Поскольку \({\hat{\mu}}_{FF} \) и \({\hat{\mu}}_{GG} \) независимы, можно показать 92. \end{aligned}$$

\(\square \)

Проверка равенства двух положительно определенных матриц с применением к проверке информационных матриц ☆ Глоссарий обозначений и программных кодов, написанных в GAUSS для наших симуляций, доступен по адресу: http://web.

yonsei.ac.kr/jinseocho/research.htm

Чтобы прочитать этот контент, выберите один из вариантов ниже:

Джин Со Чо и

Халберт Уайт б

Очерки в честь Питера CB Phillips

ISBN : 978-1-78441-183-1

Дата публикации: 21 ноября 2014 г.

Аннотация

Мы даем новую характеристику равенства двух положительно определенных матриц A и B , и мы используем ее, чтобы предложить несколько новых удобных в вычислительном отношении статистических тестов на равенство двух неизвестных положительно определенных матриц. Наше основное внимание сосредоточено на проверке равенства информационных матриц (например, белые, 1982, 1994).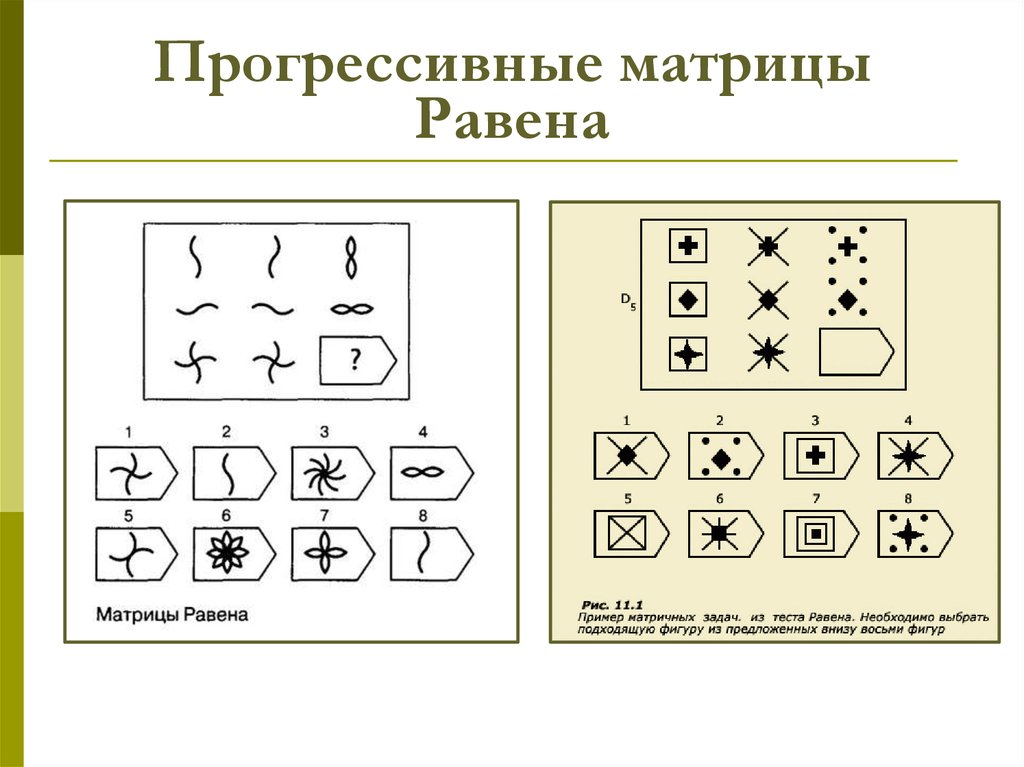 Мы характеризуем асимптотическое поведение нашей новой тестовой статистики информационной матрицы с детерминантом трассы при нулевом и альтернативном значениях и исследуем их производительность с конечной выборкой для различных моделей: линейной регрессии, экспоненциальной продолжительности, пробит и тобит. Параметрический бутстрап, предложенный Горовицем (1994), дает критические значения, обеспечивающие замечательное поведение уровня, даже в таких небольших выборках, как n  =   50. Наши новые тесты часто обладают большей мощностью, чем версия традиционного IMT с параметрическим бутстрапом; когда они этого не делают, они, тем не менее, работают достойно.

Ключевые слова

  • Равенство матриц
  • Тест информационной матрицы
  • Собственные значения
  • След
  • Определитель
  • С01
  • С12
  • С52

Благодарности

Второй автор (Галберт Уайт) скончался до того, как была завершена окончательная версия. Первый автор хотел бы отметить его вклад в эту статью. Он сформировал наброски текущей статьи. Кроме того, авторы очень благодарны соредакторам Yoosoon Chang, Tom Fomby и Joon Y. Park, а также одному анонимному рецензенту. Мы также признательны Анилу Бера, Стефану Бономму, Ричарду Голдену, Стивену Хенли, Ацуши Иноуэ, Джинуку Чону, Кихо Чону, Майклу Кашнеру, Хаку Бэ Ли, Джин Ли, Ки Ён Паку, Сан Су Паку, Питеру Си Би Филлипсу, Роберту Строудерман, Юн Джэ Ван, Бёнсам Ю, Виктория Зинде-Уолш и другие участники 14-й конференции «Достижения в области эконометрики» в честь Питера К. Б. Филлипса (Южный методистский университет, 2013 г.), Совместной конференции по экономике 2012 г. и 17-го совместного семинара Университет Йонсей, Университет Хоккайдо (Университет Хоккайдо, 2012 г.) и Международная конференция KEA (Корейский университет, 2012 г.). Кроме того, Taeyoun Kim и Myungkoo Song оказали прекрасную помощь в проведении наших экспериментов методом Монте-Карло.

Цитата

Чо, Дж.