Матрицы равена детский вариант: Цветные прогрессивные матрицы Равена. Блог Лого-Эксперт
Матрицы Дж. Равена (цветной вариант). Стимульный материал, бланки для ответов испытуемых. | Учебно-методический материал на тему:
Опубликовано 07.06.2015 — 19:44 — Синдеева Татьяна Сергеевна
Матрицы Дж. Равена. Материалы подготовлены для двустороннего распечатывания и складывания в книжечку (стимульный материал). Также прилагаются бланки для ответов испытуемых.
Скачать:
Предварительный просмотр:
Предварительный просмотр:
ФИ_____________________________
Возраст__________ Класс__________
№ задания | Серия A | Серия AB | Серия B |
1 | |||
2 | |||
3 | |||
4 | |||
5 | |||
6 | |||
7 | |||
8 | |||
9 | |||
10 | |||
11 | |||
12 | |||
Сумма правильн. ответов |
Общее время выполнения теста ____ мин.
Общая сумма баллов _______________
ФИ_____________________________
Возраст__________ Класс__________
№ задания | Серия A | Серия AB | Серия B |
1 | |||
2 | |||
3 | |||
4 | |||
5 | |||
6 | |||
7 | |||
8 | |||
9 | |||
10 | |||
11 | |||
12 | |||
Сумма правильн. ответов |
Общее время выполнения теста ____ мин.
Общая сумма баллов _______________
ФИ_____________________________
Возраст__________ Класс__________
№ задания | Серия A | Серия AB | Серия B |
1 | |||
2 | |||
3 | |||
4 | |||
5 | |||
6 | |||
7 | |||
8 | |||
9 | |||
10 | |||
11 | |||
12 | |||
Сумма правильн. ответов |
Общее время выполнения теста ____ мин.
Общая сумма баллов _______________
ФИ_____________________________
Возраст__________ Класс__________
№ задания | Серия A | Серия AB | Серия B |
1 | |||
2 | |||
3 | |||
4 | |||
5 | |||
6 | |||
7 | |||
8 | |||
9 | |||
10 | |||
11 | |||
12 | |||
Сумма правильн. ответов |
Общее время выполнения теста ____ мин.
Общая сумма баллов _______________
По теме: методические разработки, презентации и конспекты
Портфель читателя в цветном варианте ( к проекту «Успешное чтение»)
Портфель читателя в цветном варианте ( к проекту «Успешное чтение»)…
Литературный бук в цветном варианте ( к проекту «Успешное чтение»)
Литературный бук в цветном варианте ( к проекту «Успешное чтение»)…
Диагностика, направленная на определение сформированности познавательных универсальных учебных действий. Прогрессивные матрицы Равена.
Как продиагностировать познавательные УУД у младших школьников? Хорошим подспорьем для этого являются прогрессивные матрицы Равена….
Бланки для ответов демоверсии » Успешность чтения» для выпускников начальной школы.
Представленные бланки дают возможность учащимся отработать алгоритм фиксирования ответов демоверсии » Успешность чтения» для выпускников начальной школы, 2015-2016 учебный год.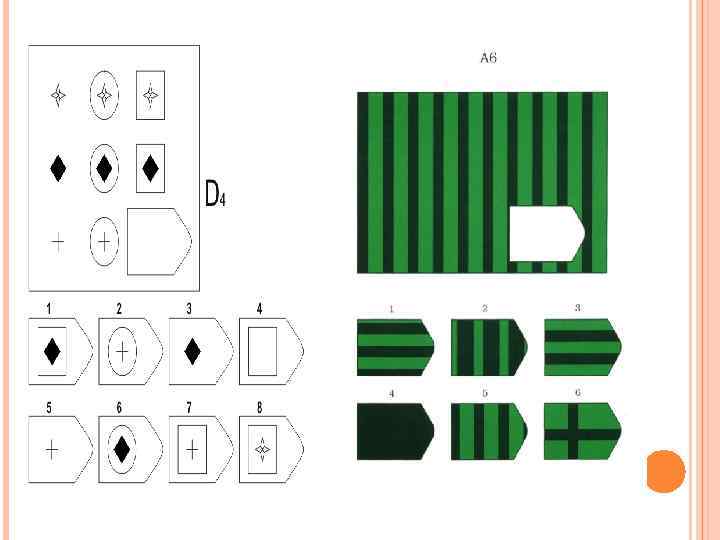 …
…
Стимульный материал для диагностики УУД в 1 классе
для 1 класса…
Стимульный материал для диагностики УУД во 2 классе
2 класс…
Матрицы Равена
Матрицы Равена…
Поделиться:
|
Навигация: Главная Случайная страница Обратная связь ТОП Интересно знать Избранные Топ: Когда производится ограждение поезда, остановившегося на перегоне: Во всех случаях немедленно должно быть ограждено место препятствия для движения поездов на смежном пути двухпутного… Определение места расположения распределительного центра: Фирма реализует продукцию на рынках сбыта и имеет постоянных поставщиков в разных регионах. Увеличение объема продаж… Динамика и детерминанты показателей газоанализа юных спортсменов в восстановительном периоде после лабораторных нагрузок до отказа. Интересное: Финансовый рынок и его значение в управлении денежными потоками на современном этапе: любому предприятию для расширения производства и увеличения прибыли нужны… Отражение на счетах бухгалтерского учета процесса приобретения: Процесс заготовления представляет систему экономических событий, включающих приобретение организацией у поставщиков сырья… Инженерная защита территорий, зданий и сооружений от опасных геологических процессов: Изучение оползневых явлений, оценка устойчивости склонов и проектирование противооползневых сооружений — актуальнейшие задачи, стоящие перед отечественными… Дисциплины: Автоматизация Антропология Археология Архитектура Аудит Биология Бухгалтерия Военная наука Генетика География Геология Демография Журналистика Зоология Иностранные языки Информатика Искусство История Кинематография Компьютеризация Кораблестроение Кулинария Культура Лексикология Лингвистика Литература Логика Маркетинг Математика Машиностроение Медицина Менеджмент Металлургия Метрология Механика Музыкология Науковедение Образование Охрана Труда Педагогика Политология Правоотношение Предпринимательство Приборостроение Программирование Производство Промышленность Психология Радиосвязь Религия Риторика Социология Спорт Стандартизация Статистика Строительство Теология Технологии Торговля Транспорт Фармакология Физика Физиология Философия Финансы Химия Хозяйство Черчение Экология Экономика Электроника Энергетика Юриспруденция |
⇐ ПредыдущаяСтр 4 из 7Следующая ⇒ Тест предназначен для оценки уровня развития невербальной составляющей интеллекта. 3. Методика «Классификация предметов» (детский вариант) Методика позволяет исследовать характеристики обобщения и абстрагирования, сформированность основных понятий, цветовых и абстрактных аспектов объекта, их возрастную соотнесенность. 4. Методика исследования способности формирования понятий (методика Выготского — Сахарова, модификация для детей дошкольного возраста) Модификация широко известной методики позволяет проводить исследование уровня развития абстрактных обобщений и их классификацию, выявить возможности объединения наглядно представленных абстрактных объектов на основе объединения одного или нескольких ведущих признаков. Кроме того, анализируется возможность переключения и распределения внимания, гностическая деятельность. 5. Методика «Классификация объектов по двум признакам» (лото В.М. Когана) Методика направлена на исследование возможности распределения и переключения внимания в сенсибилизированных условиях, а также сужения объема активного внимания. При этом возможны варианты использования с учетом времени выполнения и качественный анализ выполнения. Методика позволяет, оценить характеристики работоспособности, утомляемость, пресыщаемость, а также отметить инертность деятельности. Данные, получаемые в ходе исследования, дают возможность провести оценку качества процессов сериации и классификации объектов на основе вычленения наглядно представленных признаков. Для детей дошкольного возраста используется вариант методики с таблицей 5×5. Методика «Разрезные фигуры» Методика направлена на исследование возможности перцептивного моделирования, оценку способности смыслового и пространственного соотнесения частей и целого и их пространственной координации, т.е. исследование возможностей синтеза на предметном уровне. С помощью этой методики выявляется уровень развития способов построения симультанно расчлененного образа объекта. Выполнение этого задания возможно лишь при определеннойсформированности наглядно-образного мышления. Результаты выполнения заданий разного уровня сложности позволяют оценить особенности внимания; конструктивного анализа и синтеза, сформированность представления о пространственных отношениях, гностические характеристики. Данные по результатам выполнения методики отражаются в соответствующих разделах заключения.
Общие условия выбора системы дренажа: Система дренажа выбирается в зависимости от характера защищаемого. Индивидуальные и групповые автопоилки: для животных. Схемы и конструкции… Опора деревянной одностоечной и способы укрепление угловых опор: Опоры ВЛ — конструкции, предназначенные для поддерживания проводов на необходимой высоте над землей, водой… Кормораздатчик мобильный электрифицированный: схема и процесс работы устройства… |
Алгебра матриц — сложение, умножение, правила и примеры
Алгебра матриц — раздел математики, изучающий векторные пространства между различными измерениями. Инновация матричной алгебры возникла благодаря n-мерным плоскостям, присутствующим в нашем координатном пространстве.
Матрица (множественное число: матрицы ) представляет собой расположение чисел, выражений или символов в прямоугольном массиве. Это расположение выполняется в горизонтальных рядах и вертикальных столбцах, имеющих порядок количество строк x количество столбцов. Каждая пара точек в трехмерном пространстве представляет собой уникальное уравнение с одним или несколькими решениями.
Основная идея или центральная идея прикладной математики вращается вокруг линейной алгебры. Например, заново переживая правила и предписания или, вернее, аксиомы, мы приходим к обобщению векторного пространства, которое с помощью исчисления приводит к решению дифференциальных уравнений.
Алгебра матриц
Алгебра матриц включает операции с матрицами, такие как сложение, вычитание, умножение и т. д.
Давайте лучше поймем работу матрицы-
Сложение/вычитание матриц
Две матрицы можно складывать/вычитать тогда и только тогда, когда количество строк и столбцов обеих матриц одинаково или порядок матриц одинаков.
При сложении/вычитании каждый элемент первой матрицы прибавляется/вычитается к элементам, присутствующим во второй матрице.
\(\begin{array}{l}\begin{bmatrix} A_{11}& A_{12} &… & A_{1n} \\ A_{21}& A_{22} &… & A_{2n} \\ …& … & … & … \\ A_{m1}& A_{m2} & … & A_{mn} \\\end{bmatrix}+\begin{bmatrix} B_{11}& B_{12} & … & B_{1n} \\ B_{21}& B_{22} & … & B_{2n} \\ …& … & … & … \\ B_{m1}& B_{m2} & … & B_{mn } \\\end{bmatrix}=\begin{bmatrix} A_{11}+B_{11}& A_{12}+B_{12} & … & A_{1n}+B_{1n} \\ A_{21 }+B_{21}& A_{22}+B_{22} & … & A_{2n}+B_{2n} \\ …& … & … & … \\ A_{m1}+B_{m1}& A_ {m2}+B_{m2} & … & A_{mn}+B_{mn} \\\end{bmatrix}\end{массив} \)
Пример:
\(\begin{array}{l}\begin{bmatrix} 2 & 0 & 5\\ 3 & 2 & 9 \end{bmatrix} + \begin{bmatrix} 7 & 4 & 1 \\ 8 & 13 & 0 \end{bmatrix} = \begin{bmatrix} 9 & 4 & 6 \\ 11 & 15 & 9 \end{bmatrix}\end{array} \)
Также читайте:
Умножение матриц
Подобную матрицу можно умножить двумя способами,
(i) Скалярное умножение
(ii) Умножение на другую матрицу
- Скалярное умножение – Умножение скалярной величины на матрицу.

Например-
\(\begin{array}{l}5 \times \begin{bmatrix} 5 & 7\\ 12 & 3 \\ 6 & 2 \end{bmatrix} = \begin{bmatrix} 25 & 35\\ 60 & 15 \\ 30 & 10 \end{bmatrix}\end{массив} \)
- Умножение матрицы на другую матрицу: Две матрицы можно перемножить тогда и только тогда, когда количество столбцов первой матрицы равно количеству строк второй матрицы.
Рассмотрим две матрицы M1 и M2, , имеющие порядок m 1 × n 1 и m 2 × n 2 .
Перемножение матриц возможно тогда и только тогда, когда n 1 = m 2 .
\(\begin{array}{l}\begin{bmatrix}1 & 2 & 3 \\\end{bmatrix}_{1\times 3}.\begin{bmatrix}2 & 1 & 3 \\3 & 3 & 2 \\ 4 & 1 & 2 \\\end{bmatrix}_{3 \times 3}=\begin{bmatrix}1.2+2.3+3.4 & 1.1+2.3+3.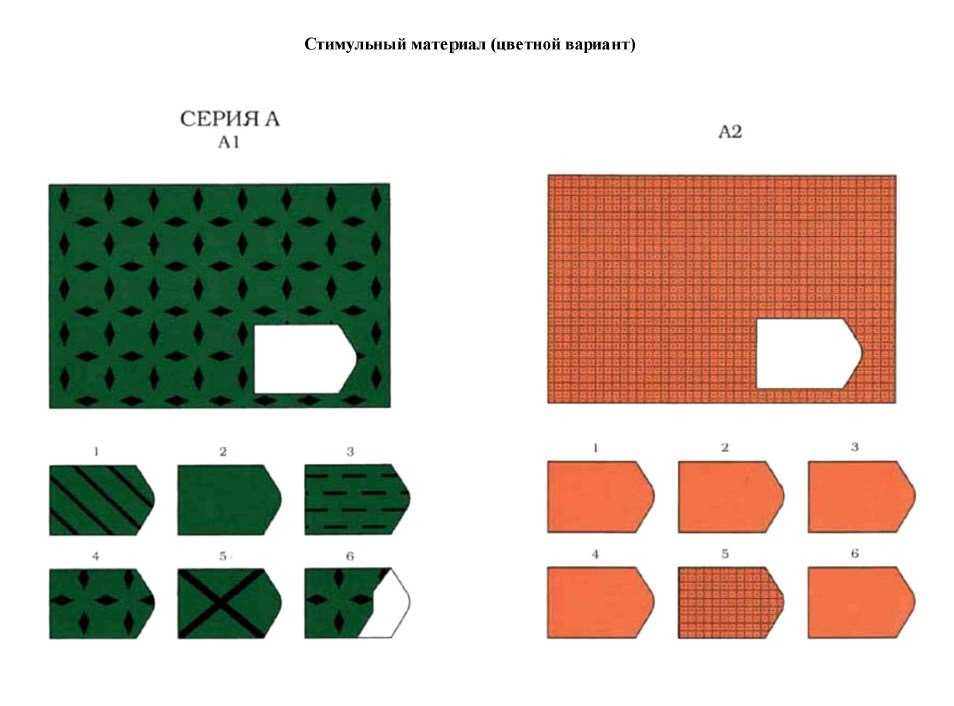 1 & 1.3+2.2+3.2 \\\ конец{bматрица}\конец{массив} \)
1 & 1.3+2.2+3.2 \\\ конец{bматрица}\конец{массив} \)
\(\begin{array}{l}\begin{bmatrix}1 & 2 & 3 \\\end{bmatrix}_{1\times 3}.\begin{bmatrix}2 & 1 & 3 \\3 & 3 & 2 \\4 & 1 & 2 \\\end{bmatrix}_{3 \times 3}= \begin{bmatrix}20 & 10 & 13 \\\end{bmatrix}_{1 \times 3}\ конец {массив} \)
Матрицы, приведенные выше, удовлетворяют условию умножения матриц, следовательно, эти матрицы можно умножать.
Результирующая матрица, полученная умножением двух матриц, имеет порядок m 1 , n 2 , где m 1 — количество строк в 1-й матрице, а n 2 — номер столбца во 2-й матрице.
Правило матричной алгебры
Алгебра матриц следует некоторым правилам сложения и умножения. Рассмотрим три различные квадратные матрицы A, B и C. A’ — транспонирование, а A -1 — инверсия A. I — единичная матрица, а R — действительное число.
Теперь по правилам законов матриц:
- A+B = B+A → переместительный закон сложения
- A+B+C = A +(B+C) = (A+B)+C →Ассоциативный закон сложения
- ABC = A(BC) = (AB)C →Ассоциативный закон умножения
- A(B+C) = AB + AC → Распределительный закон матричной алгебры
- Р(А+В) = РА + РБ
Также смотрите здесь правила перестановки матриц:
- (А’)’ = А
- (А+В)’ = А’+В’
- (АВ)’ = Б’А’
- (ABC) = C’B’A’
Обратные правила матриц следующие:
- АИ = ИА = А
- АА -1 = А -1 А = I
- (А -1 ) -1 = А
- (АВ) -1 = В -1 А -1
- (ABC) -1 = С -1 В -1 А -1
- (А’) -1 = (А -1 )’
Решенные проблемы
Пример 1:
\(\begin{array}{l}Дано\ A= \begin{bmatrix} 3 &-5 \\ -1 &7 \end{bmatrix} и B= \begin{bmatrix} 1 &4 \\ 8 &3 \end {bmatrix}.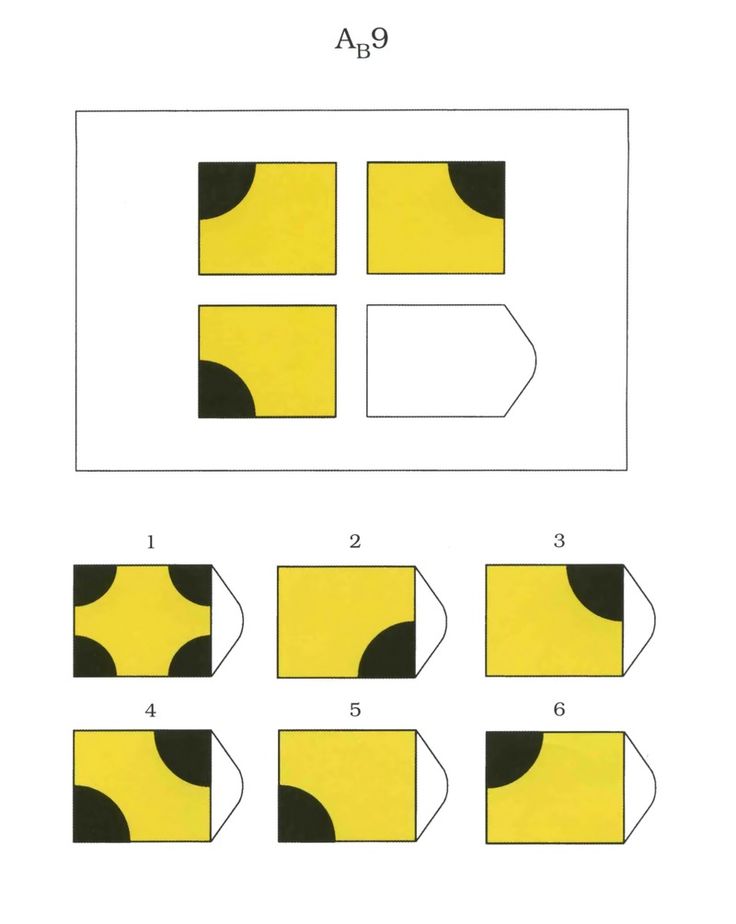 \ Найти A + B.\end{массив} \)
\ Найти A + B.\end{массив} \)
Решение:
Дано,
\(\begin{array}{l}A= \begin{bmatrix} 3 &-5 \\ -1 &7 \end{bmatrix} \ and\ B= \begin{ bmatrix} 1 &4 \\ 8 &3 \end{bmatrix}\end{массив} \)
Сложение A и B:\(\begin{array}{l}A+B= \begin{bmatrix} 3 &-5 \\ -1 &7 \end{bmatrix}+ \begin{bmatrix} 1 &4 \ \ 8 &3 \end{bmatrix}\\ =\begin{bmatrix} 3+1 &-5+4 \\ -1+8 &7+3 \end{bmatrix}\\=\begin{bmatrix} 4 &-1 \\ 7 &10 \end{bmatrix}\end{массив} \)
Пример 2:
\(\begin{array}{l}If\ P= \begin{bmatrix} 5 &4 \\ 2 &9 \end{bmatrix}\ и\ Q = \begin{bmatrix} 1 &5 \\ 0&2 \end{bmatrix },\ затем\ найти\ P – Q.\end{массив} \)
Решение:
Дано,
\(\begin{array}{l}P= \begin{bmatrix} 5 &4 \\ 2 &9 \end{bmatrix} \ and\ Q= \begin{bmatrix} 1 &5 \\ 0&2 \end{bmatrix}\end{массив} \)
Вычитание матриц P и Q:\(\begin{array}{l}P-Q= \begin{bmatrix} 5 &4 \\ 2 &9\end{bmatrix}- \begin{bmatrix} 1 &5 \\ 0 &2 \end{bmatrix}\\ =\begin{bmatrix} 5-1 &4-5 \\ 2-0 &9-2 \end{bmatrix}\ \=\begin{bmatrix} 4 &-1 \\ 2 &7 \end{bmatrix}\end{массив} \)
Пример 3:
\(\begin{array}{l}If\ A= \begin{bmatrix} 4 &-2 \\ 7 &0 \end{bmatrix} \ and\ B= \begin{bmatrix} 3 &5 \\ 2 &- 3 \end{bматрица},\ затем\ найти\ произведение\ А\ и\ В. \end{массив} \)
\end{массив} \)
Решение:
Дано
\(\begin{array}{l}A= \begin{bmatrix} 4 &-2 \\ 7 &0 \end{bmatrix} \ and\ B= \begin{bmatrix} 3 &5 \\ 2 &-3 \end{bmatrix}\end{массив} \)
Произведение/умножение A и B равно:\(\begin{array}{l}A\times B= \begin{bmatrix} 4 &-2 \\ 7 &0 \end{bmatrix}\times \begin{bmatrix} 3 &5 \\ 2 &-3 \end{bmatrix} \\=\begin{bmatrix} 4(3)+(-2)2 & 4(5)+(-2)(-3)\\ 7(3 )+0(2) &7(5)+0(-3) \end{bmatrix}\\ =\begin{bmatrix} 12-4 &20+6 \\ 21& 35 \end{bmatrix}\\=\begin{ bmatrix} 8 и 26\\ 21& 35 \end{bmatrix}\end{массив} \)
Это было все об алгебре матриц, чтобы понять больше таких понятий, как обратная матрица, работа с матрицей, определители и т. д., посетите наш сайт BYJU’S.
Умножение матриц | Как умножать матрицы
В линейной алгебре матрицы играют важную роль при работе с различными понятиями. Матрица представляет собой прямоугольный массив или таблицу чисел, символов или выражений, расположенных в строках и столбцах по математике.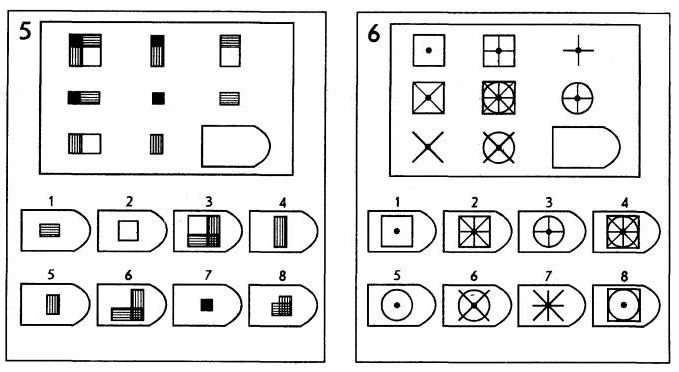 Мы можем выполнять различные операции с матрицами, такие как сложение, вычитание, умножение и так далее. В этой статье вы узнаете, как умножить матрицу на другую матрицу, его алгоритм, формулу, умножение матриц 2×2 и 3×3 с подробными примерами.
Мы можем выполнять различные операции с матрицами, такие как сложение, вычитание, умножение и так далее. В этой статье вы узнаете, как умножить матрицу на другую матрицу, его алгоритм, формулу, умножение матриц 2×2 и 3×3 с подробными примерами.
Содержание:
|
Определение умножения матриц
Умножение матриц, , также известное как произведение матриц и умножение двух матриц, дает одну матрицу. Это тип бинарной операции.
Если две матрицы A и B, то произведение двух матриц A и B обозначается:
Х = АВ
Следовательно, произведение двух матриц является скалярным произведением двух матриц.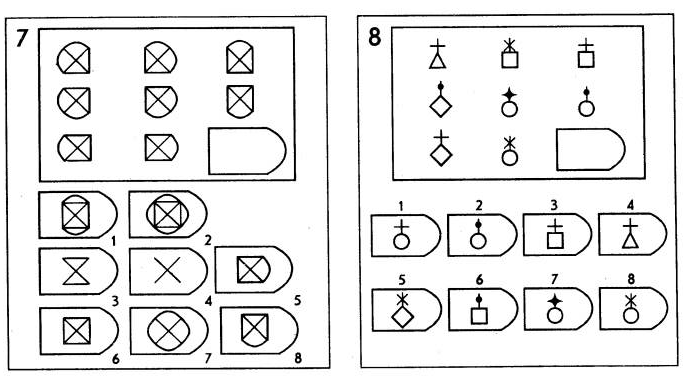
Умножение матрицы на скаляр
Умножение целого числа на матрицу — это просто скалярное умножение.
Мы знаем, что матрица — это массив чисел. Он состоит из строк и столбцов. Если вы умножаете матрицу на скалярное значение, то это называется скалярным умножением. Другой случай состоит в том, что можно умножить матрицу на другую матрицу. Давайте посмотрим на пример, приведенный ниже для того же самого.
Мы можем определить умножение матрицы на скаляр математически как:
Если A = [a ij ] m × n — матрица, а k — скаляр, то kA — другая матрица, полученная путем умножения каждого элемента A на скаляр k.
Другими словами, kA = k [a ij ] m × n = [k (a ij )] m × n , то есть (i, j)-й элемент kA равен ka ij для всех возможных значений i и j.
Пример:
\(\begin{array}{l} Умножить\ the\ matrix\ A=\begin{bmatrix} 3 &4 &-1 \\ 0 &9 & 5 \end{bmatrix} на\ 4.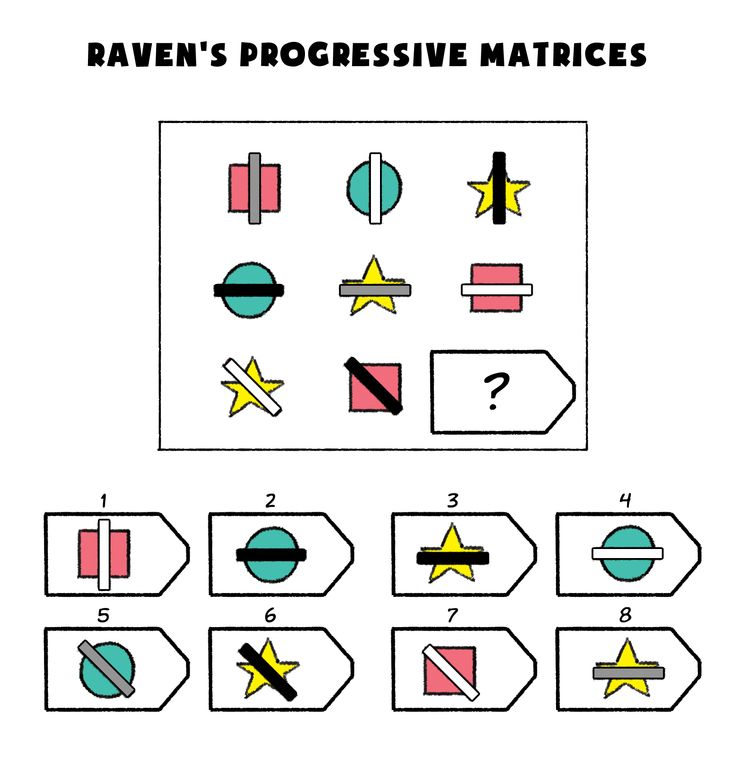 \end{array } \)
\end{array } \)
Решение:
Дано,
\(\begin{array}{l}A=\begin{bmatrix} 3 &4 &-1 \\ 0 &9 & 5 \end{bmatrix}\end{array} \)
\(\begin{array}{l}4 \times A = 4\times \begin{bmatrix} 3 &4 &-1 \\ 0 &9 & 5 \end{bmatrix}\end{массив} \)
Теперь нам нужно умножить каждый элемент матрицы A на 4.
\(\begin{array}{l}=\begin{bmatrix} 12 &16 &-4 \\ 0 &36 & 20 \end{bmatrix}\end{array} \)
Это искомая матрица после умножения данной матрицы на константное или скалярное значение, т.е. 4.
Умножение матриц Условие
Чтобы выполнить умножение двух матриц , мы должны убедиться, что количество столбцов в 1-й матрице равно количеству строк во 2-й матрице. Следовательно, результирующее матричное произведение будет иметь количество строк 1-й матрицы и количество столбцов 2-й матрицы. Порядок полученной матрицы равен 9.0236 порядок умножения матрицы .
Также читайте:
Теперь давайте разберемся, как выполнять умножение матриц с разными порядками или разными типами матриц.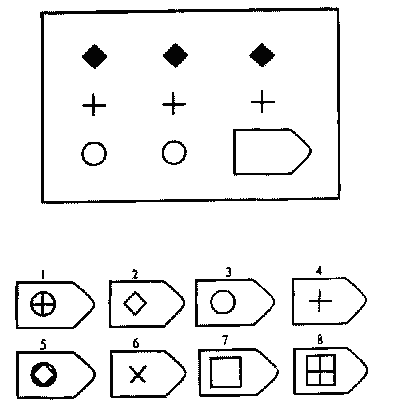
Как умножать матрицы?
Давайте научимся умножать матрицы.
Рассмотрим матрицу A, представляющую собой матрицу размера b × b, и матрицу B, представляющую собой матрицу размера b × c.
Тогда матрица C = AB определяется как матрица A × B.
Элемент в матрице C, C 9{b} A_{xk}B_{ky}\end{массив} \)
Для x = 1…… a и y = 1…….c
Это одна из самых важных тем в 12 классе. Матрицы для 12 класса подробно объясняет типы матриц.
Обозначение
Если A — матрица размера m×n, а B — матрица размера p×q, то матричное произведение A и B представлено следующим образом:
Х = АВ
Где X — результирующая матрица размера m×q.
Формула умножения матриц
Давайте рассмотрим пример, чтобы понять эту формулу.
Предположим, что A и B — две матрицы, такие, что
\(\begin{array}{l}A =\begin{bmatrix} A_{11} &A_{12} & \cdots & A_{1n}\\ A_{21} & A_{22} &\cdots & A_ {2n} \\ &………….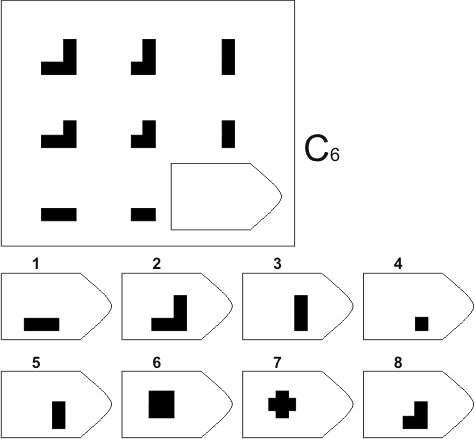 &\\ A_{m1} & A_{m2} &\cdots & A_{mn} \end{bmatrix}, B= \begin{bmatrix} B_{11} &B_{ 12} & \cdots & B_{1n}\\ B_{21} &B_{22} &\cdots & B_{2n} \\ &………….& \\ B_{m1} & B_{m2} &\ cdots & B_{mn} \end{bmatrix}\end{массив} \)
&\\ A_{m1} & A_{m2} &\cdots & A_{mn} \end{bmatrix}, B= \begin{bmatrix} B_{11} &B_{ 12} & \cdots & B_{1n}\\ B_{21} &B_{22} &\cdots & B_{2n} \\ &………….& \\ B_{m1} & B_{m2} &\ cdots & B_{mn} \end{bmatrix}\end{массив} \)
Тогда матрица C = AB обозначается цифрой 9{b} A_{xk}B_{ky}\end{массив} \)
Для x = 1……a и y= 1…….c
Алгоритм умножения матриц
В последние годы было проведено значительное количество работ в области алгоритмов умножения матриц, поскольку они нашли свое применение во многих областях. Существует четыре типа алгоритмов:
- Итеративный алгоритм
- Алгоритм «разделяй и властвуй»
- Субкубические алгоритмы
- Параллельные и распределенные алгоритмы
В основном используется в различных языках программирования, таких как C, Java и т. д., для онлайн-умножения. Наиболее распространены 2×2, 3×3 и 4×4, умножение матриц.
Операция является двоичной с записями в наборе, на котором определены операции сложения, вычитания, умножения и деления. Эти операции аналогичны соответствующим операциям над действительными и рациональными числами.
Эти операции аналогичны соответствующим операциям над действительными и рациональными числами.
Несмотря на то, что существует множество применений матриц, умножение матриц, по сути, является операцией в линейной алгебре. Линейное отображение, которое включает скалярное сложение и умножение, представлено умножением матриц.
Также можно найти широкий спектр алгоритмов на сетках. Этот тип алгоритма разработан, чтобы свести к минимуму неэффективность, присущую стандартным алгоритмам массива, где может быть задержка в поступлении данных из 2 разных матриц.
Правила умножения матриц
Из определенной выше формулы и процедуры мы можем записать следующие правила и свойства для умножения матриц.
- Произведение двух матриц A и B определяется, если количество столбцов матрицы A равно количеству строк матрицы B.
- Если AB определен, то BA не нужно определять
- Если и A, и B являются квадратными матрицами одного порядка, то и AB, и BA определены.
- Если определены и AB, и BA, нет необходимости, чтобы AB = BA.
- Если произведение двух матриц является нулевой матрицей, то необязательно, чтобы одна из матриц была нулевой матрицей.
Умножение матриц 2×2
Рассмотрим простое умножение матриц 2 × 2
\(\begin{array}{l}A = \begin{bmatrix} 3 и 7\\ 4 и 9\end{bmatrix} \ и\ B = \begin{bmatrix} 6 и 2\\ 5 и 8 \end{bmatrix}\end{массив} \)
Теперь каждый из элементов матрицы произведения AB можно рассчитать следующим образом:
- AB 11 = 3 × 6 + 7 × 5 = 53
- AB 12 = 3 × 2 + 7 × 8 = 62
- AB 21 = 4 × 6 + 9 × 5 = 69
- AB 22 = 4 × 2 + 9 × 8 = 80
Следовательно,
\(\begin{array}{l}AB = \begin{bmatrix} 53&62 \\ 69& 80 \end{bmatrix}\end{массив} \)
Умножение матриц 3×3
Чтобы понять произведение двух матриц 3 × 3, рассмотрим две матрицы 3 × 3 A и B.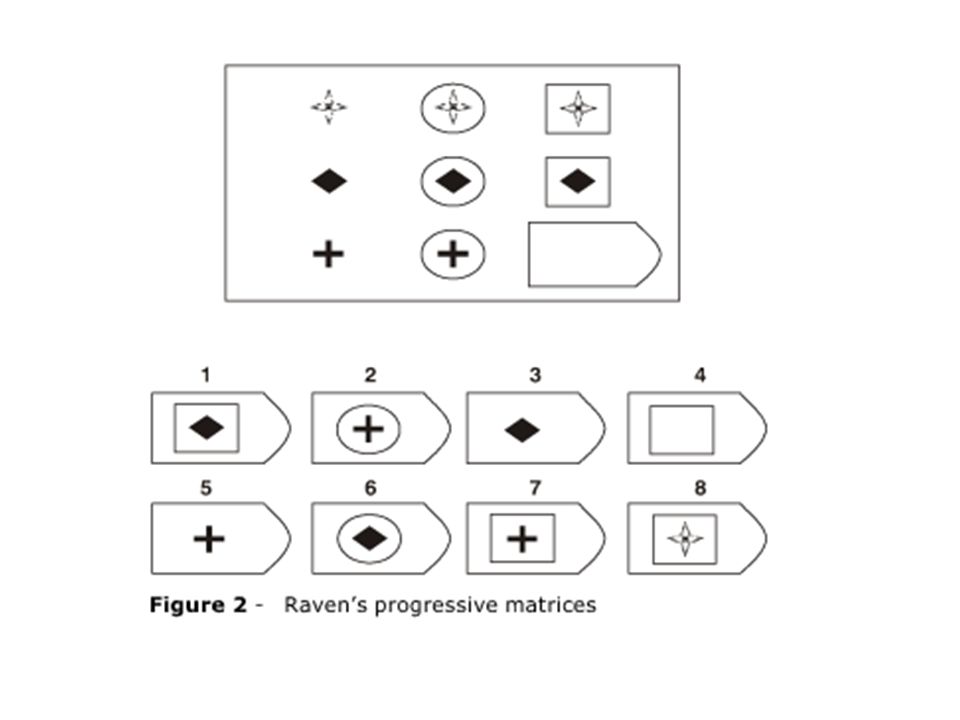
\(\begin{array}{l} A = \begin{bmatrix} 12 &8 &4 \\ 3&17 &14 \\ 9 & 8& 10 \end{bmatrix} ,\ B = \begin{bmatrix} 5 & 19 &3 \ \ 6 &15 &9 \\ 7& 8 & 16 \end{bmatrix}\end{массив} \)
Каждый элемент матрицы продукта AB можно рассчитать следующим образом:
- AB 11 = 12×5 + 8×6 + 4×7 = 136
- AB 12 = 12×19 + 8×15 + 4×8 = 380
- AB 13 = 12×3 + 8×9+4×16 = 172
- АВ 21 = 3×5 + 17×6 + 14×7 = 215
- AB 22 = 3×19 + 17×15 + 14×8 = 424
- AB 23 = 3×3 + 17×9 + 14×16 = 386
- AB 31 = 9×5 + 8×6 + 10×7 = 163
- АВ 32 = 9 × 19 + 8 × 15 + 10 × 8 = 371
- АБ 33 = 9×3 + 8×9 + 10×16 = 259
Следовательно,
\(\begin{array}{l}AB =\begin{bmatrix} 136 & 380 &172 \\ 215 &424 &386 \\ 163& 371 & 259 \end{bmatrix}\end{массив} \)
Попробуйте : Калькулятор умножения матриц
Свойства умножения матриц
Ниже приведены свойства умножения матриц:
Коммутативная собственность
Умножение матриц не является коммутативным.
Предположим, что если A и B являются двумя матрицами 2×2,
АВ ≠ ВА
При умножении матриц порядок имеет большое значение.
Например,
\(\begin{array}{l}If\ A = \begin{bmatrix} 1 & 2\\ 3 & 4 \end{bmatrix} \ and\ B = \begin{bmatrix} 3 & 2\\ 1 & 4 \end{bmatrix} \ являются\ двумя\ матрицами,\ then\end{массивом} \)
\(\begin{array}{l}A\times B = \begin{bmatrix} 1 & 2\\ 3 & 4 \end{bmatrix}\times \begin{bmatrix} 3 & 2\\ 1 & 4 \ конец{bматрица}\конец{массив} \)
\(\begin{array}{l}A\times B = \begin{bmatrix} 5 и 10\\ 13 и 22 \end{bmatrix}\end{массив} \)
Но,
\(\begin{array}{l}B\times A = \begin{bmatrix} 3 & 2\\ 1 & 4 \end{bmatrix}\times \begin{bmatrix} 1 & 2\\ 3 & 4 \ конец{bmatrix}\конец{массив} \)
\(\begin{array}{l}B\times A = \begin{bmatrix} 9 и 14\\ 13 и 18 \end{bmatrix}\end{массив} \)
Это показывает, что матрица AB ≠BA.
Следовательно, умножение двух матриц некоммутативно.
Ассоциативное свойство
Если A, B и C являются тремя матрицами, ассоциативное свойство матричного умножения утверждает, что
(АВ) С = А(ВС)
\(\begin{array}{l} Пусть\ A =\begin{bmatrix} 1 и 2\\ 1& 1 \end{bmatrix}\end{массив} \)
\(\begin{array}{l}B =\begin{bmatrix} 3 & 2\\ 1& 2 \end{bmatrix}\end{array} \)
\(\begin{array}{l}C =\begin{bmatrix} 0 & 1\\ 2& 3 \end{bmatrix}\end{array} \)
LHS = (AB) C
\(\begin{array}{l}A\times B = \begin{bmatrix} 1 & 2\\ 1 & 1 \end{bmatrix} \times \begin{bmatrix} 3 & 2 \\ 1 & 2 \ конец{bmatrix}\конец{массив} \)
\(\begin{array}{l}A\times B = \begin{bmatrix} 5 и 6\\ 4 и 4 \end{bmatrix}\end{массив} \)
\(\begin{array}{l}(AB)C = \begin{bmatrix} 5 & 6\\ 4 & 4 \end{bmatrix} \times \begin{bmatrix} 0 & 1\\ 2 & 3 \ конец{bmatrix}\конец{массив} \)
\(\begin{array}{l}(AB)C = \begin{bmatrix} 12 и 23\\ 8 & 16 \end{bmatrix}\end{array} \)
RHS = A(BC)
\(\begin{array}{l}BC = \begin{bmatrix} 3 & 2\\ 1 & 2 \end{bmatrix}\times \begin{bmatrix} 0 & 1\\ 2 & 3 \end{bmatrix }\конец{массив} \)
\(\begin{array}{l}BC = \begin{bmatrix} 4 & 9\\ 4 & 7 \end{bmatrix}\end{array} \)
\(\begin{array}{l}A(BC)= \begin{bmatrix} 1 & 2\\ 1 & 1 \end{bmatrix}\times \begin{bmatrix} 4 & 9\\ 4 & 7 \ конец{bmatrix}\конец{массив} \)
\(\begin{array}{l}A(BC)= \begin{bmatrix} 12 и 23\\ 8 & 16 \end{bmatrix}\end{array} \)
Таким образом, ассоциативность матричного умножения доказана.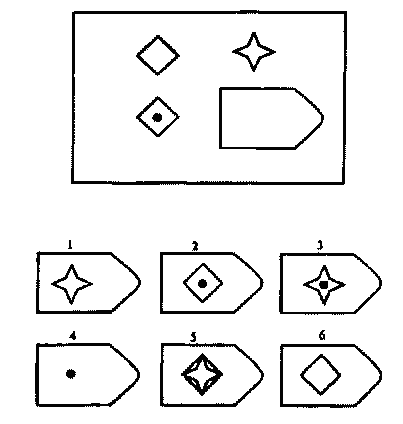
Распределительная собственность
Если A, B и C являются тремя матрицами, дистрибутивное свойство матричного умножения утверждает, что
- (В+С)А = БА +КА
- А(В+С) = АВ + АС
Свойство мультипликативной идентичности
Свойство идентичности матричного умножения утверждает, что
- I = I. А = А
Где A — матрица размера n × n, а «I» — единичная матрица порядка n.
\(\begin{array}{l} Пусть\ A = \begin{bmatrix} 2 и 3\\ 1 и 6 \end{bmatrix} \ и\ I = \begin{bmatrix} 1 & 0\\ 0 и 1 \end{bmatrix}\end{массив} \)
\(\begin{array}{l}A . I = \begin{bmatrix} 2 & 3\\ 1 & 6 \end{bmatrix}\times \begin{bmatrix} 1 & 0\\ 0 & 1 \end {bmatrix}\конец{массив} \)
\(\begin{array}{l}A . I = \begin{bmatrix} 2 & 3\\ 1 & 6 \end{bmatrix} = A\end{массив} \)
Свойство измерения
При умножении матриц произведение матрицы m × n и матрицы n × a представляет собой матрицу m × a.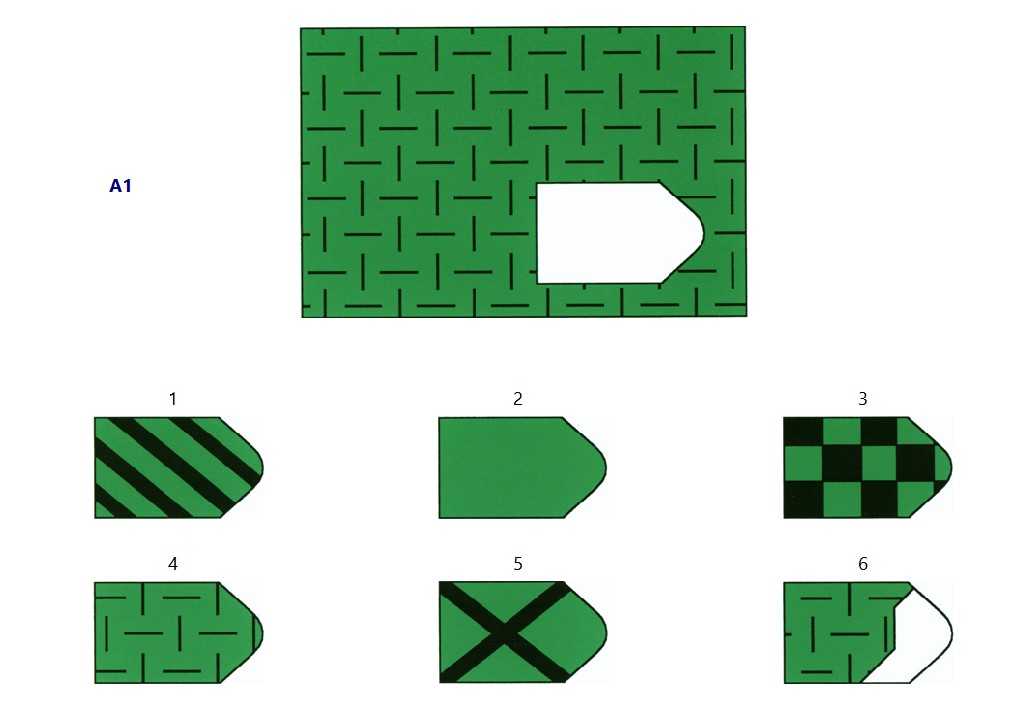
Например, матрица A — это матрица 2 × 3, а матрица B — это матрица 3 × 4, тогда AB — это матрица 2 × 4.
Мультипликативное свойство Зеро
Если матрица умножается на нулевую матрицу, результирующая матрица является нулевой матрицей.
\(\begin{array}{l}If\ A = \begin{bmatrix} 2 & 1\\ 1 & 2 \end{bmatrix} \ is\ умножается\ на\ ноль\ матрица\end{массив} \)
\(\begin{array}{l}т.е.,\ \begin{bmatrix} 0 & 0\\ 0 & 0 \end{bmatrix},\end{array} \)
\(\begin{array}{l}Продукт\ становится\ \begin{bmatrix} 0 & 0\\ 0 & 0 \end{bmatrix}\end{array} \)
Решенный пример
Умножение матриц 4×4 объясняется ниже для двух матриц 4×4 A и B.
\(\begin{array}{l}A =\begin{bmatrix} 7 & 14 & 15 & 6 \\ 4 & 8 & 12 & 3 \\ 14 & 21 & 6 & 9 \\ 13 & 7 & 6 & 4 \end{ bmatrix},\ B = \begin{bmatrix} 5& 7 & 14 & 2\\ 8& 16 & 4 & 9\\ 13 & 6& 8 & 4\\ 6& 3 & 2 & 4 \end{bmatrix}\end{array } \)
Следуя тем же шагам, что и в предыдущих двух примерах, мы можем построить матрицу AB.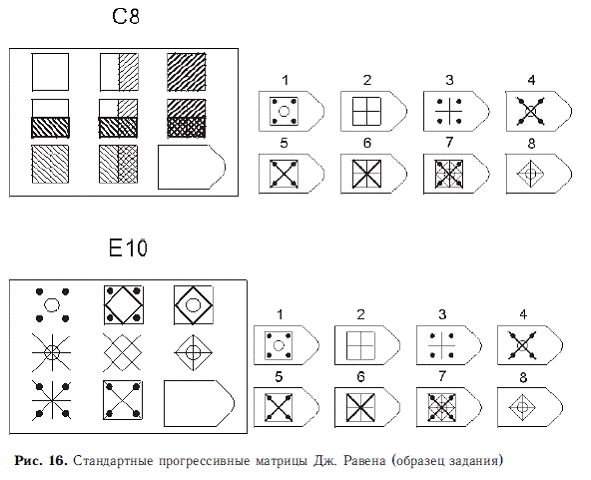
\(\begin{array}{l}AB = \begin{bmatrix} 378 &381 & 286 &224 \\ 258 & 237 & 190 & 140\\ 370 & 497& 346 & 277\\ 223& 251& 266 & 129 \end{ bmatrix}\end{массив} \)
Практические задачи на умножение матриц
Решите следующие проблемы:
-
\(\begin{array}{l}Найти\ произведение:\ 3\begin{bmatrix} 7 и 5\\ 2 & 1 \end{bmatrix}\end{array} \)
-
\(\begin{array}{l}Упростить\ следующие\ 3×3 \ матрицу:\ \begin{bmatrix} 1 & 6 & 2 \\ 2 & 3 & 1\\ 1 & 1 & 5 \ end{bmatrix}\times \begin{bmatrix} 1 & 8 & 7 \\ 4 & 2 & 3 \\ 2 & 6 & 1 \end{bmatrix}\end{массив} \)
-
\(\begin{array}{l}Найти\ произведение\ AB,\ если\ A =\begin{bmatrix} 5 & 3\\ 9 & 1 \end{bmatrix} \ and\ B = \begin{bmatrix} 1 и 0\\ 6 и 12 \end{bmatrix}\end{массив} \)
-
\(\begin{array}{l}Найти\ произведение\ матрицы\,\ если\ A = \begin{bmatrix} 4\\ 2\\ 1 \end{bmatrix} \ и\ \ begin{bmatrix} 2 & 4 & 6 \end{bmatrix}\end{массив} \)
-
\(\begin{array}{l}Вычислить:\ \frac{-4}{7}\begin{bmatrix} -22\\ 49\\ 35 \end{bmatrix}\end{array} \)
Узнайте больше о матрицах и других связанных темах в увлекательной и увлекательной форме.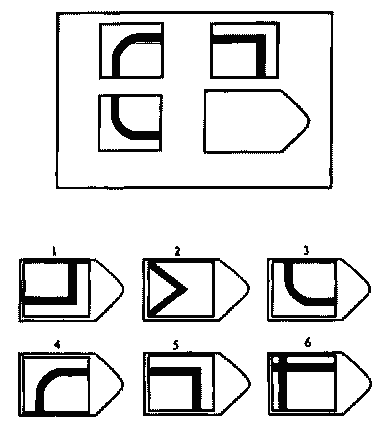 Загрузите BYJU’S — обучающее приложение сегодня.
Загрузите BYJU’S — обучающее приложение сегодня.
Часто задаваемые вопросы – Часто задаваемые вопросы
Что такое умножение матриц?
Умножение матриц — это метод нахождения произведения двух матриц для получения результата в виде одной матрицы. Это тип бинарной операции.
Как умножить две заданные матрицы?
Чтобы умножить одну матрицу на другую, нужно сначала проверить, равно ли количество столбцов первой матрицы количеству строк второй матрицы. Теперь умножьте каждый элемент столбца первой матрицы на каждый элемент строк второй матрицы и сложите их все. Нам нужно сделать скалярное произведение столбцов и строк здесь.
Какой результат умножения матрицы (2×3) на матрицу (3×3)?
Результатом умножения матрицы (2×3) и матрицы (3×3) будет только матрица 2×3.
Как умножить матрицу 3×3?
Умножьте каждую строку первой матрицы на каждый столбец второй матрицы и сложите все, чтобы получить первый элемент.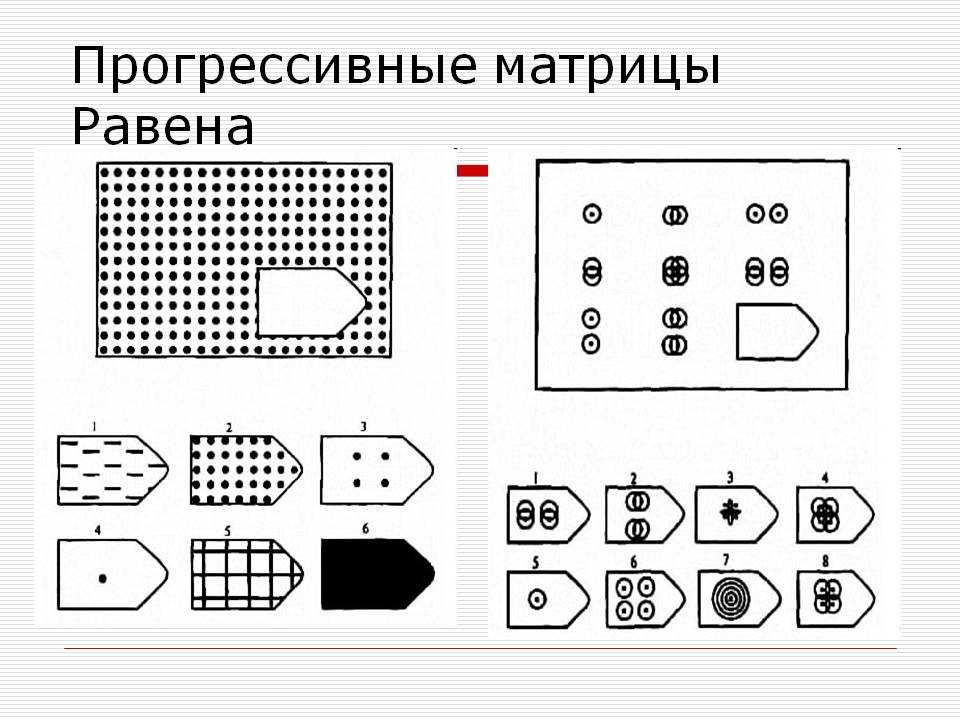




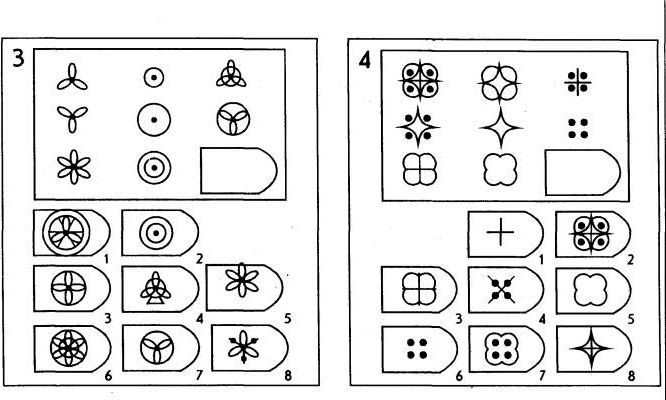
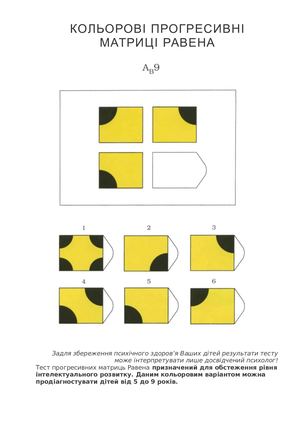

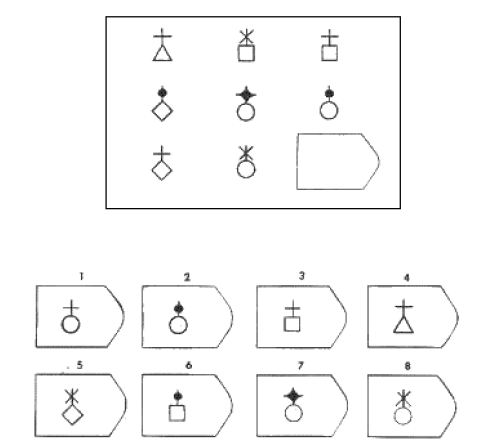
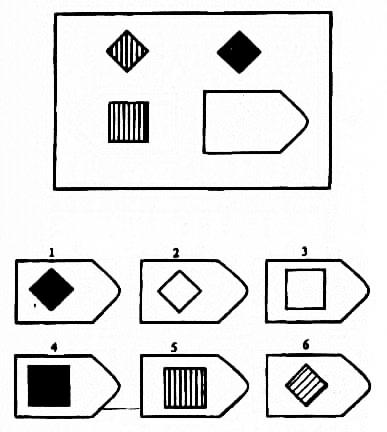
 Принцип прогрессивности, реализованный в данном тесте, позволяет определить возможность анализа навыков обучения. В работе с тестом выявляется сформированность таких психических процессов, как внимание, перцепция и мышление в их наглядно-образной составляющей. Из 36 заданий цветного варианта прогрессивных матриц 28 направлены на выявление сформированности операций дополнения до целого, установления тождества, выявление принципа центральной и осевой симметрии. 8 заданий способствуют установлению сформированности мыслительных операций (установление отношений по принципу решения простых и сложных аналогий). Данные теста используются вразделах «
Принцип прогрессивности, реализованный в данном тесте, позволяет определить возможность анализа навыков обучения. В работе с тестом выявляется сформированность таких психических процессов, как внимание, перцепция и мышление в их наглядно-образной составляющей. Из 36 заданий цветного варианта прогрессивных матриц 28 направлены на выявление сформированности операций дополнения до целого, установления тождества, выявление принципа центральной и осевой симметрии. 8 заданий способствуют установлению сформированности мыслительных операций (установление отношений по принципу решения простых и сложных аналогий). Данные теста используются вразделах «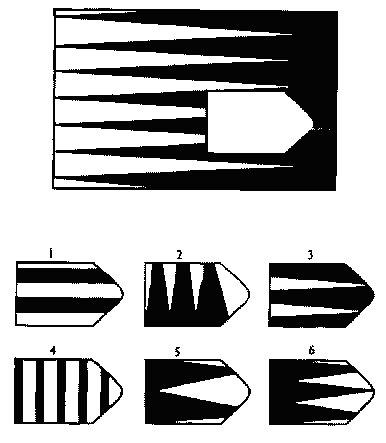 С помощью этой методики можно также выявлять возможности логики последовательности умозаключений, критичности и обдуманности действий, особенностей объема и устойчивости активного внимания, объема поля зрения, специфики цветоразличения и зрительного восприятия в целом, а также особенностей специфических личностных реакций и характеристик работоспособности. Данные, получаемые с помощью методики, описываются в разделах «
Работоспособность», «Интеллектуальное развитие», «Особенности внимания», «Гнозис», «Исследование эмоционально-личностных особенностей».
С помощью этой методики можно также выявлять возможности логики последовательности умозаключений, критичности и обдуманности действий, особенностей объема и устойчивости активного внимания, объема поля зрения, специфики цветоразличения и зрительного восприятия в целом, а также особенностей специфических личностных реакций и характеристик работоспособности. Данные, получаемые с помощью методики, описываются в разделах «
Работоспособность», «Интеллектуальное развитие», «Особенности внимания», «Гнозис», «Исследование эмоционально-личностных особенностей».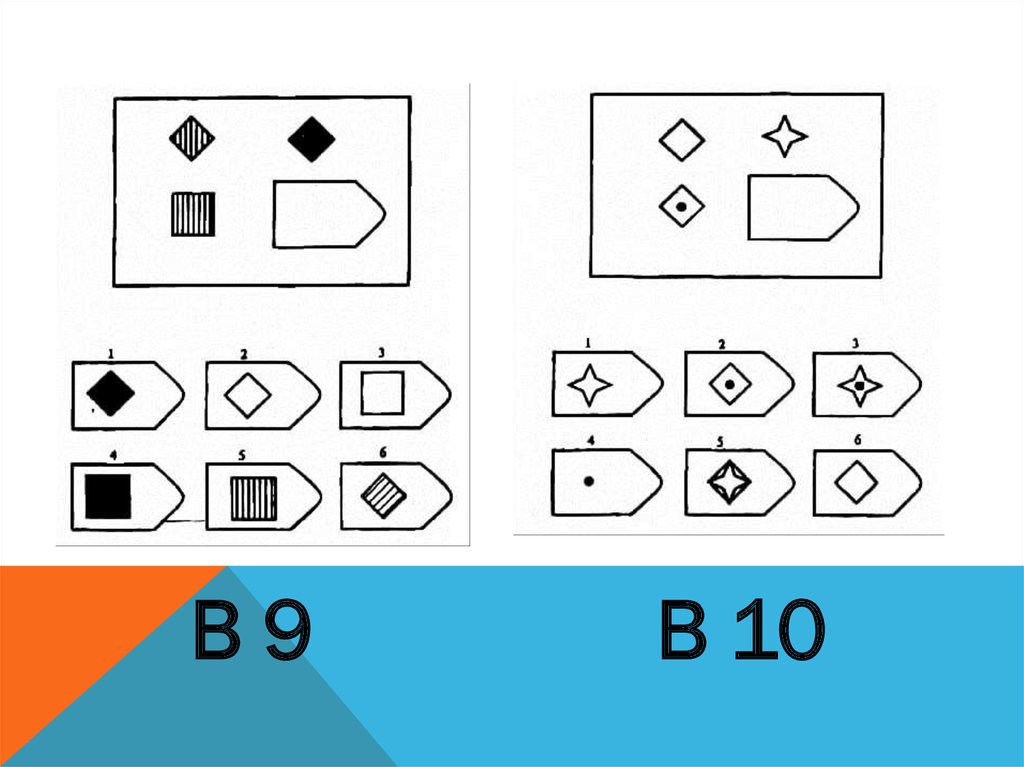
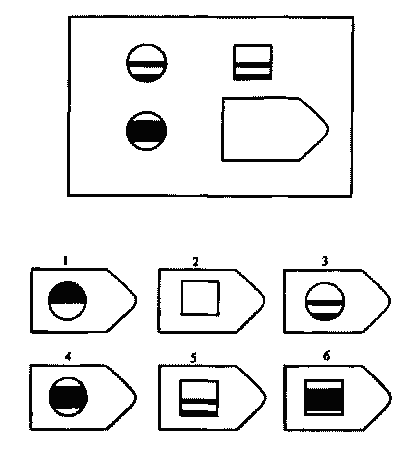
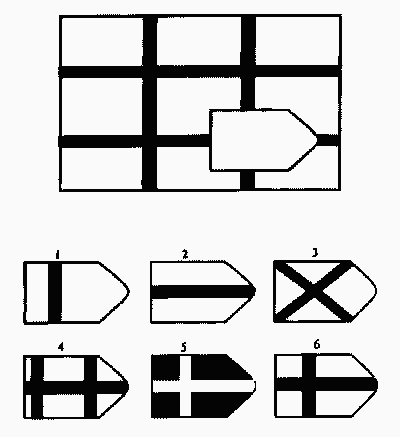 ..
..