Методика равена для младших школьников: Тест прогрессивных матриц Равена для младших школьников
11.Прогрессивные матрицы Равена
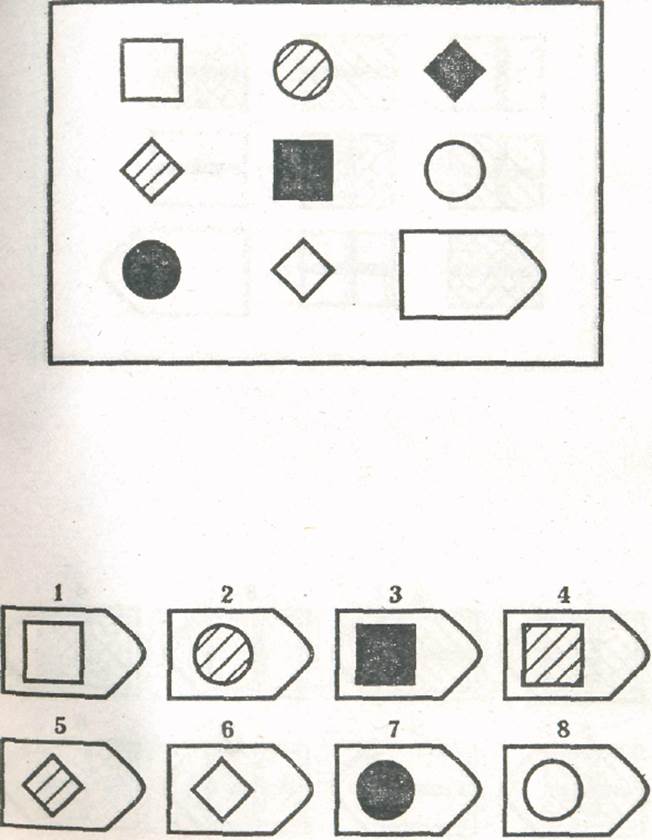
Батарея тестов на наглядное мышление по аналогии, разработанная английским психологом Дж. Равеном (1938). Каждая задача состоит из двух частей: основного рисунка (какого-либо геометрического узора) с пробелом в правом нижнем углу и набора из 6 или 8 фрагментов, находящихся под основным рисунком. Из этих фрагментов требуется выбрать один, который, будучи поставленным на место пробела, точно подходил бы к рисунку в целом. Прогрессивные матрицы Равена разделяются на 5 серий, по 12 матриц в каждом. Прогрессивные матрицы Равена широко используется во многих странах как невербальные тесты умственной одаренности.
Эта
методика предназначается для оценивания
наглядно-образного мышления у младшего
школьника. Здесь под наглядно-образным
мышлением понимается такое, которое
связано с оперированием различными
образами и наглядными представлениями
при решении задач.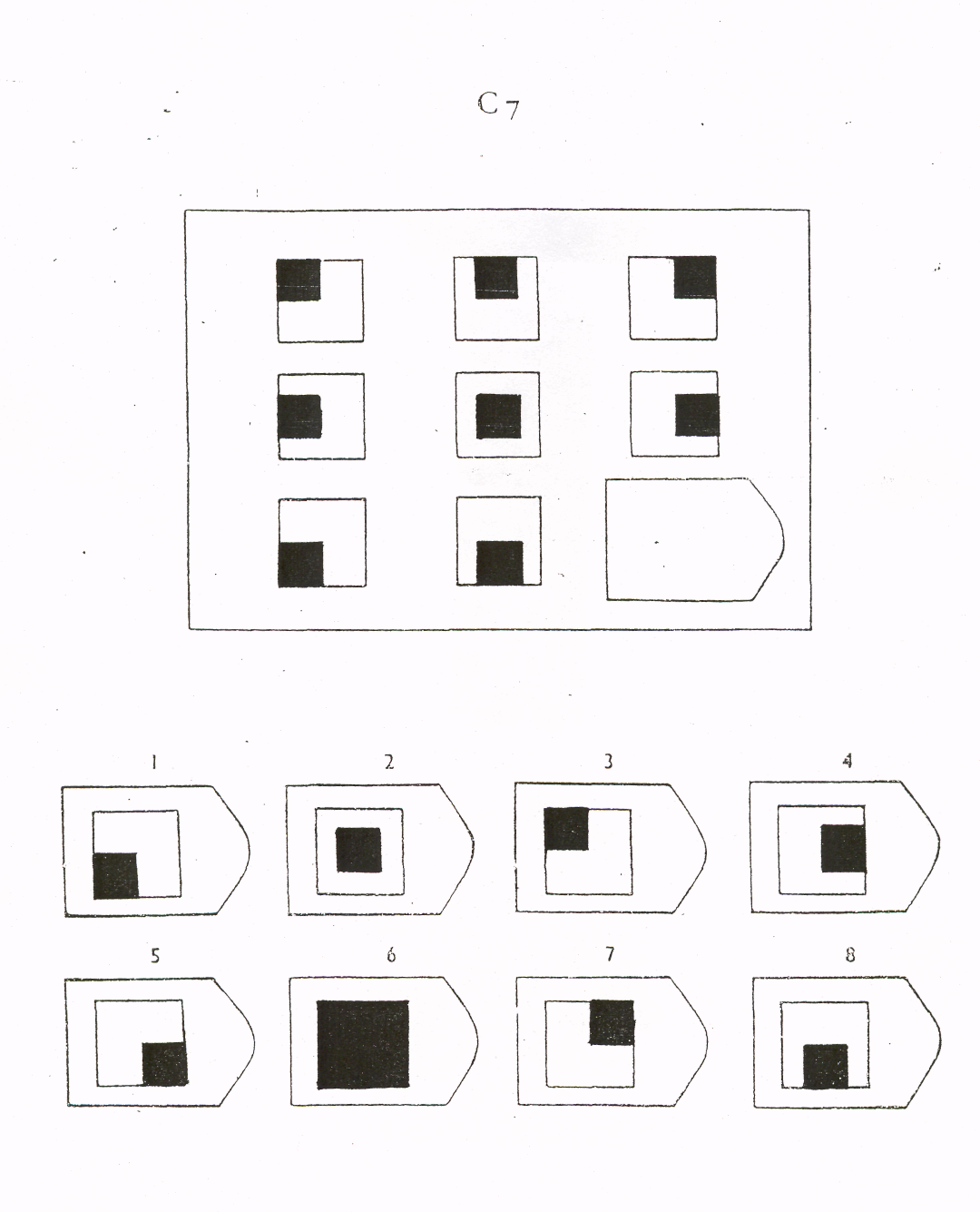
На
выполнение всех десяти заданий ребенку
отводится 10 минут.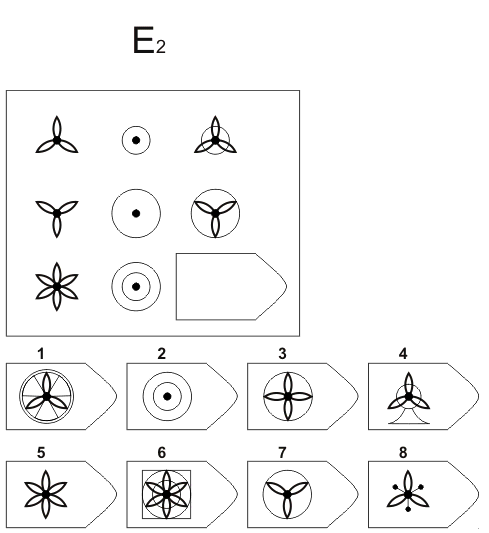
По истечении этого
времени эксперимент прекращается и
определяется количество правильно
решенных матриц, а также общая сумма
баллов, набранных ребенком за их решения.
Каждая правильно, решенная матрица
оценивается в 1 балл. Правильные, решения
всех десяти матриц следующие (первая
из приводимых ниже пар цифр указывает
на номер матрицы, а вторая — на правильный
ответ: 1—7,2—6,3—6,4—1,5—2,6—5,7—6,
8-1,9-3,10-5.)
Выводы об уровне развития
10 баллов — очень высокий 8-9 баллов — высокий. 4-7 баллов — средний. 2-3 балла — низкий. 0-1 балл — очень низкий. |
12.
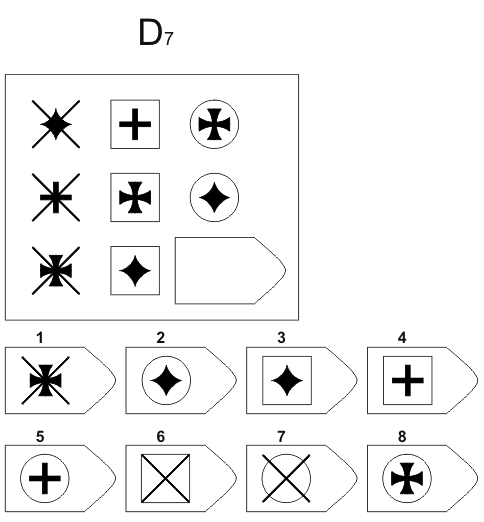Тест Гилфорда (модифицированный)Данный тест направлен на изучение креативности, творческого мышления. Исследуемые факторы:
1) Беглость (легкость, продуктивность) — этот фактор характеризует беглость творческого мышления и определяется общим числом ответов.
2) Гибкость — фактор характеризует гибкость творческого мышления, способность к быстрому переключению и определяется числом классов (групп) данных ответов.
3) Оригинальность — фактор характеризует оригинальность, своеобразие творческого мышления, необычность подхода к проблеме и определяется числом редко приводимых ответов, необычным употреблением элементов, оригинальностью структуры ответа.
4)
Точность — фактор, характеризующий
стройность, логичность творческого
мышления, выбор адекватного решения,
соответствующего поставленной цели.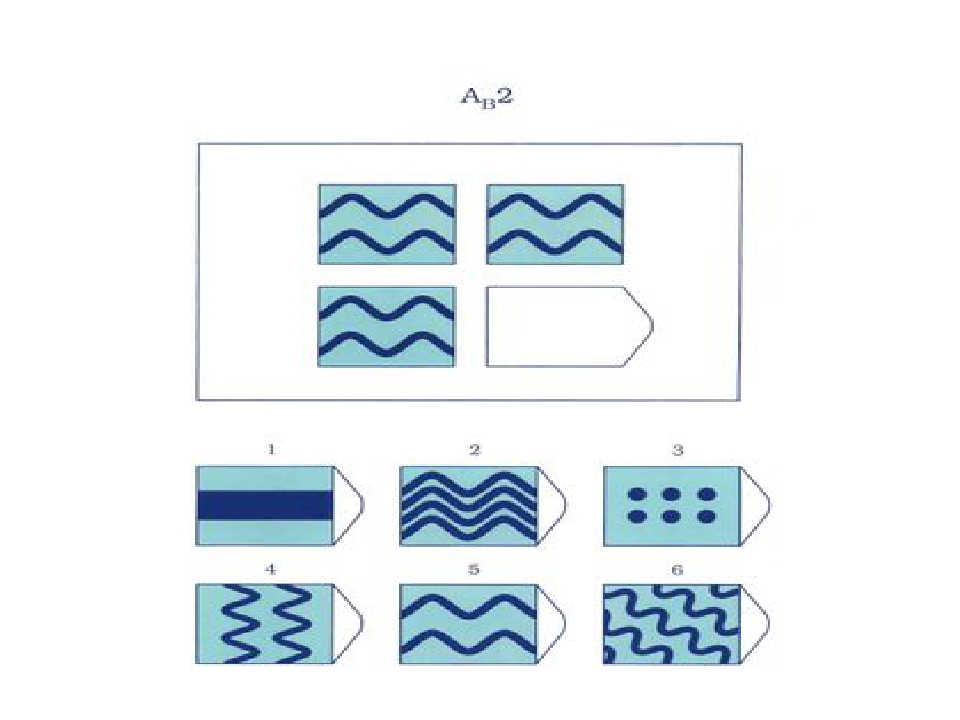
Данная батарея тестов была предложена Е. Туник. Большинство тестов являются модификацией тестов Гилфорда или Торренса. Время проведения процедуры — около 40 минут. Тесты предназначены для возрастной группы от 5 до 15 лет. С детьми от 5 до 8 лет процедура проводится в индивидуальной форме. С возрастной группой от 9 до 15 лет работа с тестами проводится в групповой форме (возможно проведение и в индивидуальной форме). Следует отметить, что субтест 3 (слова или выражение) имеет две модификации, одна модификация — слова — предназначена для детей от 5 до 8 лет, вторая модификация — выражение — предназначена для детей 9—15 лет.
Субтест 1. Использование предметов (варианты употребления)
Задача:
перечислить как можно больше необычных
способов использования предмета.
Инструкция для испытуемого: газета
используется для чтения. Ты же можешь
придумать другие способы ее использования.
Что из нее можно сделать? Как ее можно
еще использовать? Инструкция зачитывается
устно.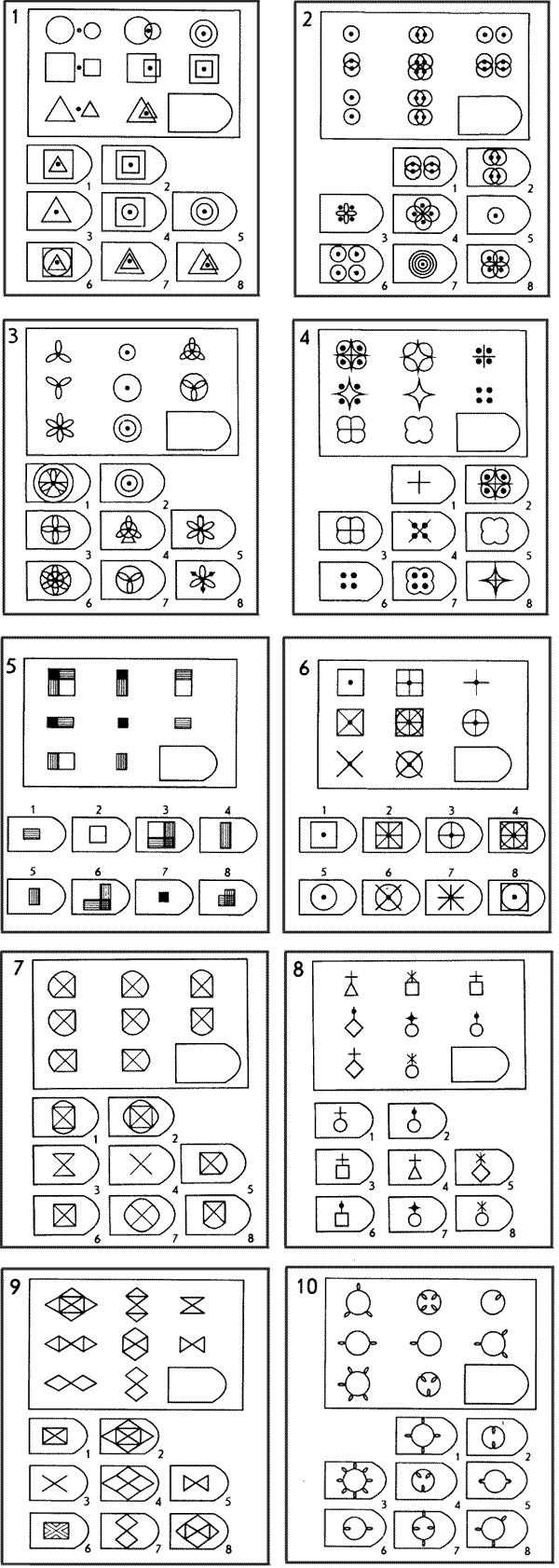
Время выполнения субтеста — 3
мин. При индивидуальной форме проведения
все ответы дословно записываются
психологом. При групповой форме проведения
ответы записывают сами испытуемые.
Время засекается после прочтения
инструкции.
Оценивание.Результаты выполнения теста оцениваются в баллах. Имеются три показателя.
Динамика когнитивных параметров у младших школьников в результате прохождения медитативного тренинга
Автор: А.М. Демильханова, А.Ф. Желонкина
Программа детского медитативного тренинга разработана на основании реабилитационно- восстановительного психотерапевтического комплекса при лечении аддиктивного поведения в Медицинском Центре доктора Назаралиева.
В настоящей работе мы анализируем результаты изменения когнитивной сферы на группе младших школьников.
Выборку составили 20 человек младшего школьного возраста (7-11 лет), 8 девочек и 12 мальчиков.
Используемые методики: Прогрессивные матрицы Равена для диагностики уровня интеллекта и процессов мышления; Таблицы Шульте — для исследования переключения и объема внимания, а также темпа работы, тест креативности П. Торренса.
В результате медитативного тренинга мы ожидали изменение когнитивной сферы в сторону увеличения креативности. Как основную методику мы взяли тест Торренса , автор теста утверждает, что творческие возможности далеко не всегда отражаются в интеллектуальных тестах, творчество может стимулироваться не столько многообразием имеющихся знаний, сколько восприимчивостью к новым идеям, ломающим устоявшиеся стереотипы. Творческие решения часто приходят в момент релаксации, рассеянного, а не напряженного внимания (П. Торренс, 1995).
В результате проведенного обследования до и после прохождения тренинга, мы получили следующие данные: после прохождения тренинга по методике Равена повышение уровня интеллекта составляет 7 баллов (41 до и 48 после)(Р<0.05).
Такой рост свидетельствует о росте возможности выявлять связи и соотношения, приходить к выводам, непосредственно не представленным в заданной ситуации, и способности использовать прошлый опыт и усвоенную информацию. Увеличение показателей так же говорит о нарастании возможностей дифференцировок по нескольким признакам и улучшении процессов абстрагирования.
В нашей работе мы использовали фигурный тест П. Торренса «Нарисуй картинку».
Полученные результаты представлены ниже:
Как видно на графике все качественные показатели увеличились.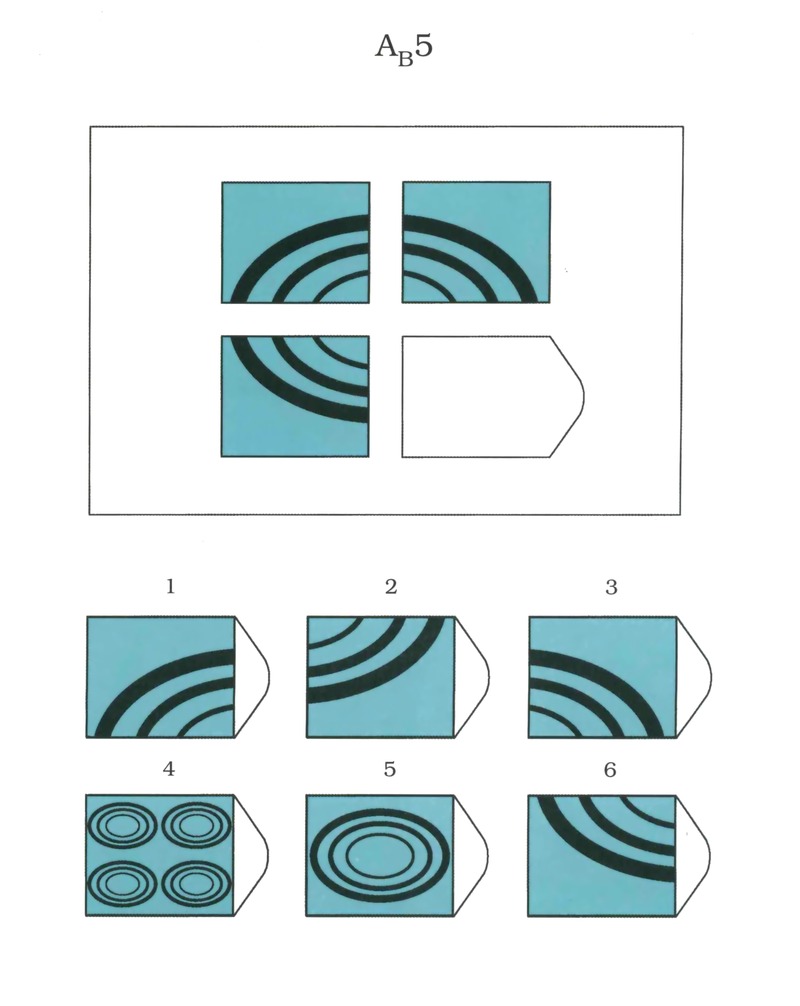
Показатель беглости 8,8 до прохождения тренинга соответствует средненормативному показателю для учащихся начальной школы, а после прохождения программы увеличился до 9,7.
Показатель гибкости варьирует в пределах средней нормы, хотя и дает незначительное увеличение после прохождения тренинга.
Особенно убедительно увеличение наиболее значимой для показателя креативности характеристики — оригинальности. Показатель оригинальности характеризует способность выдавать идеи, отличающиеся от очевидных, общеизвестных и общепринятых изменился от 7 до 11,8 (Р<0.01), что показывает значительное увеличение креативности у наших испытуемых.
Показатель разработанности до и после прохождения медитативного тренинга остается в пределах средней нормы и не дает значительных изменений. Учитывая, что увеличение показателя разработанности может нести как позитивные, так и негативные психологические характеристики, незначительное изменение этого показателя оценивается как психологическая стабильность испытуемых.
Исходя из того, что креативность – естественный процесс, который порождается сильной потребностью человека в снятии напряжения, возникающего в ситуации неопределенности, незавершенности, мы можем говорить о том, что медитативные техники значительно влияют на креативные когнитивные процессы в сторону их улучшения.
Щукин А.В., Елецкая О.В. Особенности интеллекта у младших школьников с дисграфией
Щукин А.В., Елецкая О.В.
Библиографическая ссылка на статью:
Щукин А.В., Елецкая О.В. Особенности интеллекта у младших школьников с дисграфией // Современные научные исследования и инновации. 2012. № 2 [Электронный ресурс]. URL: https://web.snauka.ru/issues/2012/02/7130 (дата обращения: 26.08.2021).
Проблема интеллектуального развития детей, обучающихся в массовой школе, является важнейшей в управлении потенциалами общественного развития. Регулирующая и формирующая роль речи в становлении человека как личности и субъекта деятельности общеизвестна.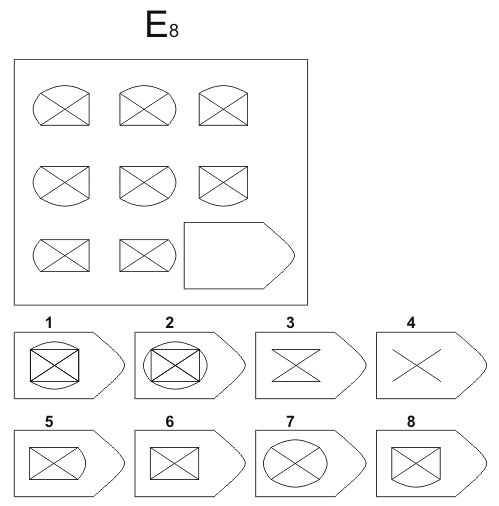
В последнее время увеличивается число учащихся, испытывающих трудности в усвоении письма и чтения. По данным зарубежной литературы таких детей 15 – 20 % в американских школах, до 10 % – в европейских (Корнев А.Н., 1997). В отечественных исследованиях до недавнего времени приводился меньший показатель – 8,7 % (Певзнер М.С., Явкин В.М., 1977). Однако М.М. Безруких и С.П. Ефимова приводят сведения о том, что у 20 – 30 % учеников начальной школы формирование письма проходит со значительными сложностями, а это уже не несколько учеников в каждой параллели, а 7-9 учеников в каждом классе (Безруких М.М., Ефимова С.П., 1991).
Овладение грамотой – это сложная умственная деятельность, которая требует определенной степени зрелости многих психических функций ребенка: слуховой дифференциации звуков, правильного их произношения, языкового анализа и синтеза, сформированности лексико-грамматической стороны речи, зрительного анализа и синтеза, пространственных представлений.
Несформированность какой-либо из указанных функций может вызывать нарушение процесса овладения письмом, дисграфию.
Учитывая тот факт, что активность интеллектуальных процессов, имеет большое значение в формировании навыка письма у школьников, нами было предпринято исследование, позволяющее определить структурно-уровневые характеристики интеллекта у детей с дисграфией, отражающих особенности формирования базовых составляющих правильного письма.
При изучении протекания интеллектуальных процессов детей с дисграфическими нарушениями, для получения более достоверной и полной информации, был использован комплексный подход к исследованию, предложенный Б.Г. Ананьевым. Для реализации поставленных задач использовался комплекс психодиагностических методик для исследования интеллектуального детей младшего школьного возраста: методика Д. Векслера (WISC) и методика Дж. Равена (RavenProgressiveMatrices).
В исследовании принимали участие учащиеся вторых и третьих классов 9 – 10 лет средних общеобразовательных школ № 77, № 337, № 574 г.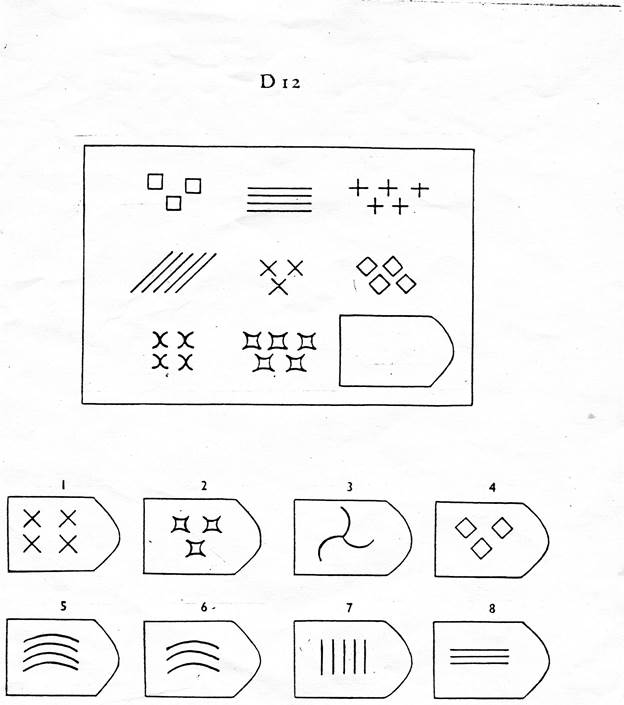
Санкт-Петербурга. Нами было обследовано 150 школьников (88 мальчиков и 62 девочки), все обследуемые были разделены на две группы.
В первую группу вошло 75 младших школьников (47 мальчиков и 28 девочек) с дисграфическими нарушениями. У детей данной группы отмечается наличие специфических (не связанных с применением орфографических правил) ошибок при письме. Эти ошибки носят стойкий и повторяющийся характер. Наиболее типичными являются пропуски и перестановки букв и слогов, замены и смешения букв, обозначающих звуки, близкие по акустико-артикуляторным признакам, смешение букв сходных по начертанию. У всех детей данной группы была диагнозцирована смешанная форма дисграфии с преобладанием одной из следующих: нарушения фонемного распознавания, нарушения языкового анализа и синтеза, оптическая дисграфия. Во вторую группу вошли 75 младших школьников (41 мальчик и 34 девочки), которые не имели трудностей в формировании навыков письменной речи и учатся в тех же классах, что и дети с дисграфией.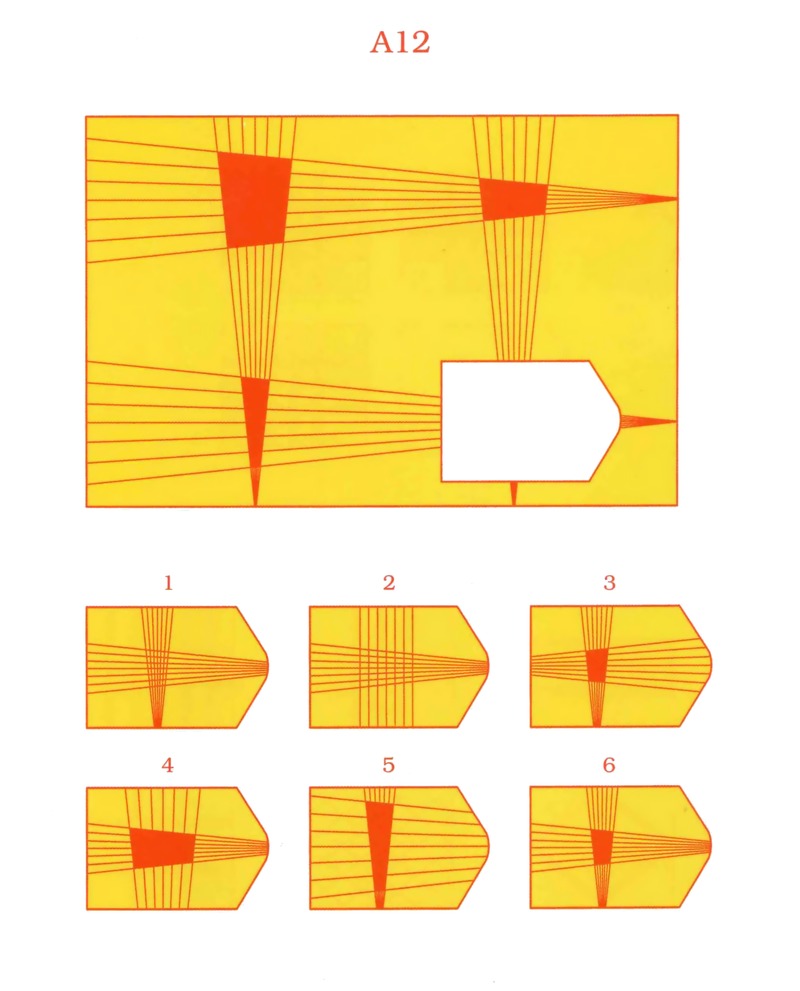
Все учащиеся данной группы показывают высокую успеваемость по основным учебным предметам (математика, чтение, письмо).
Проведенное исследование по методике Д. Векслера показало, что по уровню интеллектуального развития учащиеся с дисграфией находятся в диапазоне средней нормы. Средние значения общего интеллектуального показателя составляют 107,64 единиц IQ. Учащиеся контрольной группы находятся в диапазоне выше средней нормы (средние значения общего интеллектуального показателя составляют 120,62 единиц IQ). Различия в уровнях интеллектуального развития между двумя группами оказалось достоверно значимым (p<0.01).
Различия в показателях вербального и невербального интеллекта между двумя группами учащихся значимы на уровне (p<0.01). У детей с дисграфией отмечается преобладание уровня невербального интеллекта (107,65) над вербальным (106,19). Аналогичная картина наблюдается и в контрольной группе (119,01 и 118,60 соответственно).
В структуре вербального интеллекта в группе учащихся с дисграфией наименьшие результаты были получены по субтесту 6 «Повторение цифр» (9,30).
Наибольшие значения получены по субтесту 4 «Сходство» (13,06)
Рис. SEQ Рисунок * ARABIC 2. Средние показатели по субтестам методики Векслера у младших школьников с дисграфией и детей контрольной группы.
Учащиеся контрольной группы показали низкие результаты по субтесту 6 «Повторение цифр» (10,57), а высокие – по субтесту 2 «Понятливость» (14,64). Статистически достоверными в структуре вербального интеллекта оказались различия между двумя группами по субтестам «Осведомленность», «Понятливость», «Повторение цифр» (p<0.01). Дети с дисграфией продемонстрировали более низкий уровень запаса общих знаний и сведений об окружающем, отмечалось снижение способности к принятию самостоятельных решений. При выполнении субтеста «Повторение цифр» наибольшую трудность представляли задания повторения ряда цифр в обратном порядке. В структуре невербального интеллекта дети с дисграфией наименьшие результаты показали по субтесту 11 «Шифровка» (9,87), а наибольшие – при выполнении заданий субтеста 7 «Недостающие детали» и субтеста 9 «Кубики Косса» (12,11).
В контрольной группе наименьшие результаты были продемонстрированы по субтесту 10 «Складывание фигур» (11,24), а наибольшие по субтесту 9 «Кубики Косса» (14,85). Статистически достоверными оказались различия между двумя группами по субтестам «Кубики Косса», «Складывание фигур» и «Шифровка»(p<0.01).
Качественный анализ показал, что при выполнении заданий направленных на способность к аналитико-синтетической деятельности на предметном уровне у детей с дисграфией отмечался замедленный темп работы, затруднения при расположении деталей в пространстве соответственно заданному образцу. Часть детей затруднялась в планомерном исследовании образца, они использовали непродуктивные способы работы (метод «проб и ошибок»). Хаотичные манипуляции с деталями снижали эффективность выполнения заданий, и детям не хватало времени. Однако, ошибок персеверативного типа, обратного воспроизведения, ошибок соположения у детей с дисграфией не наблюдалось. На наш взгляд в основе затруднений в аналитико-синтетической деятельности у детей с дисграфией лежит недостаточная сформированность зрительно-пространственных отношений.
При выполнении задания субтеста «Шифровка» учащиеся с дисграфией получили более низкие оценки, чем их сверстники из контрольной группы за счет медленного включения в работу и более медленной общей скорости зрительно-двигательной координации.
Корреляционный анализ показал взаимосвязь вербальных и невербальных интеллектуальных характеристик со степенью выраженности дисграфии.
Чем более выражена степень дисграфических нарушений, тем более низкие результаты младшие школьники с дисграфией показывают по 4 вербальным субтестам «Осведомленность» (r = -0.38, p<0.01), «Понятливость» (r = -0.44, p<0.01), «Сходство» (r = -0.28, p<0.05), «Повторение цифр» (r = -0.50, p<0.01) и по двум невербальным субтестам «Недостающие детали» (r = -0.24, p<0.05), «Шифровка» (r = -0.49, p<0.01). Показатели аналитико-синтетической деятельности на предметном уровне (субтесты «Кубики Косса» и «Складывание фигур») положительно связаны с показателями перцептивных способностей, включенных в зрительное узнавание знакомых объектов (субтест «Недостающие детали», r =+0.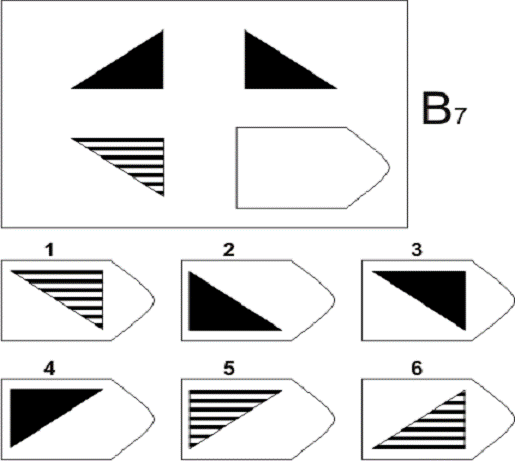
35, p<0.01).
Анализ взаимосвязей интеллектуальных показателей у детей контрольной группы показал наличие тесной интеркорреляционной структуры интеллекта и кратковременной слуховой памяти. Обнаружены положительные взаимосвязи между уровнем объема перцептивного внимания, наблюдательности, умения выделять существенные признаки и показателями кратковременной слуховой памяти, распределения внимания, способности к вербализации обобщений. В свою очередь показатели уровня развития свойств внимания, восприятия, зрительно-моторной координации, скорости формирования новых навыков, способности к интеграции зрительно-двигательных стимулов (субтест «Шифровка») положительно связаны с аналитико-синтетической деятельностью на предметном уровне и уровнем общей образованности (субтесты «Кубики Косса» (r =+0.56, p<0.01), «Складывание фигур» (r =+0.59, p<0.01), «Осведомленность» (r =+0.50, p<0.01)) (3 связи при p<0.01).
Таким образом, можно сказать, что уровень общего интеллекта у детей с дисграфией в целом соответствует возрастной норме, отмечается незначительное преобладание невербального интеллекта над вербальным.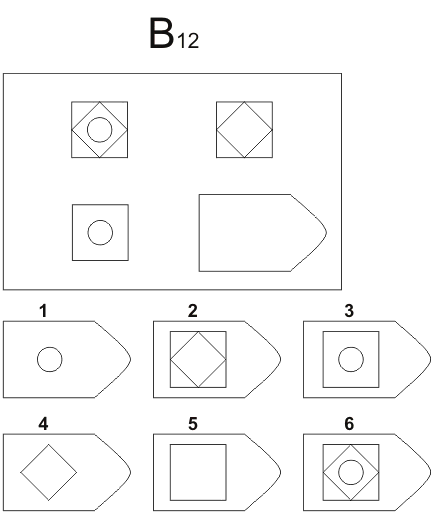
У мальчиков и девочек с дисграфией, по сравнению с детьми контрольной группы, выявлено снижение запаса общих знаний и сведений об окружающем, в сложных ситуациях они затрудняются в принятии самостоятельных решений. При выполнении заданий, связанных с воспроизведением ряда цифр, наибольшие затруднения вызывает воспроизведение цифр в обратном порядке. Отмечается замедленный темп работы, недостаточная сформированность различения зрительно-пространственных отношений.
В структуре невербальных характеристик интеллекта мы дополнительно рассматривали данные, полученные по методике Д. Равена.
Анализ полученных данных показал, что учащиеся с дисграфией в основном правильно дифференцировали структуру целого, сравнивали достающие структуры с недостающими, находили аналогии между двумя парами фигур (серии А и В). Статистически достоверных различий в оценках, полученных за выполнение этих серий у детей данной группы в сравнении с контрольной группой, не выявлено. Различия в оценках по сериями С, D и Е оказались статистически достоверными (p<0.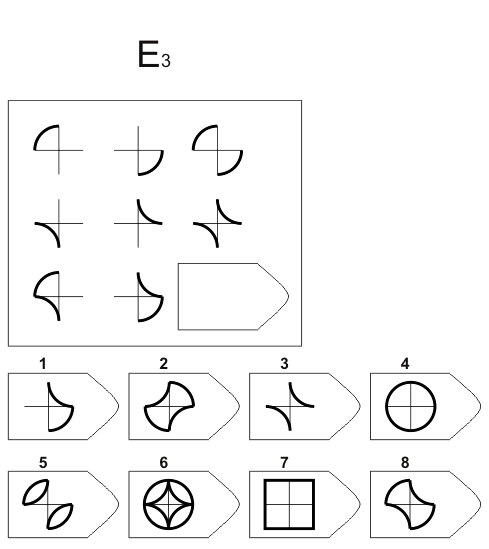
01). Качественный анализ показал, что наибольшую трудность у детей с дисграфией вызывали задания серии С (среднее значение 3,0 балла), которые основаны на усложняющихся изменениях фигур в матрицах в соответствии с определеным логическим принципом непрерывного развития положения фигур в пространстве. В целом дети правильно находили нужную фигуру, но путали ее пространственное расположение. Это может говорить о том, что при дисграфии у детей недостаточно развита способность к прослеживанию непрерывных изменений, происходящих с фигурами матриц.
Также дети испытывали трудности при решении заданий D и Е, где требовался целенаправленный анализ основного изображения и синтез недостающей фигуры по частям. Выполнение этих заданий требовало тщательного сосредоточения на задании, устойчивости и распределения внимания. Следует отметить, что и для учащихся с дисграфией и для детей контрольной группы серии D и Е представляли одинаковые трудности при решении. Однако у детей с дисграфией наблюдались более выраженные признаки утомления, они чаще пытались произвольно угадать недостающую фигуру (серия Е), чем дети контрольной группы.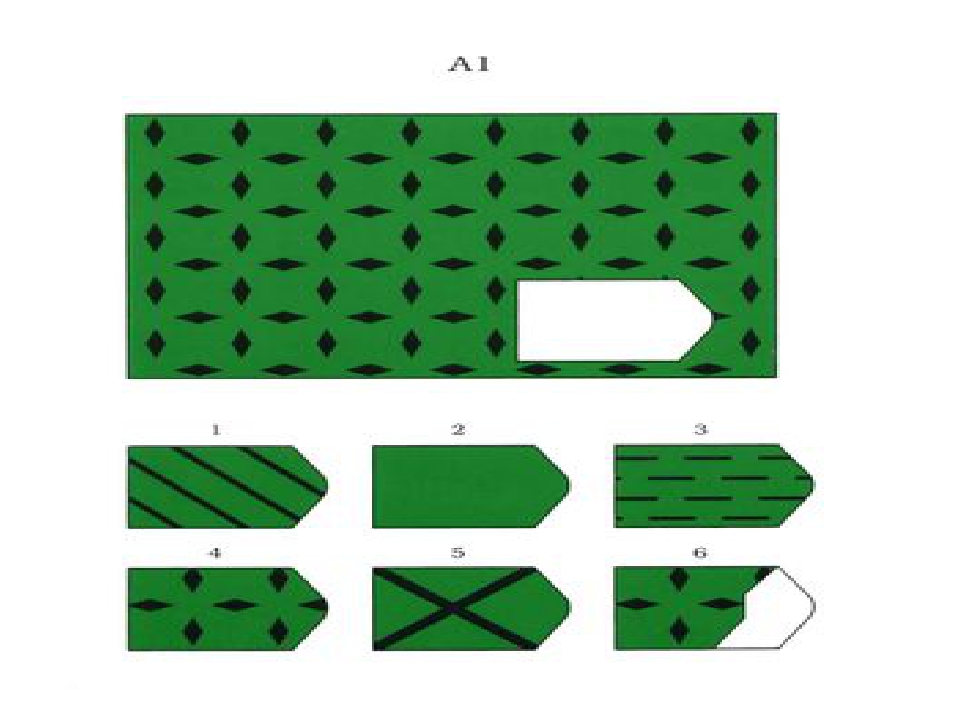
Различия между мальчиками с дисграфией и мальчиками контрольной группы, а также между девочками с дисграфией и девочками контрольной группы, были аналогичны общей картине выполнения заданий методики Д. Равена. Достоверных различий между мальчиками и девочками с дисграфией выявлено не было.
В целом, можно отметить, что учащиеся с дисграфией выполняют более легкие задания методики Д. Равена также как и их сверстники из контрольной группы. По мере усложнения заданий дети начинают путать пространственное расположение фигур, затрудняются в анализе основного изображения и синтезе составляющих его частей, отмечаются выраженные признаки утомления.
Обращает на себя внимание положительная взаимосвязь успешности выполнения серии В методики Д. Равена с сериями А(r =+0.80, p<0.01), С(r =+0.80,p<0.01), D(r =+0.81, p<0.01), Е(r =+0.59, p<0.01) (4 связи при p<0.01). По-видимому, задачи, связанные с нахождением аналогий между зрительными образами, являются для учащихся с дисграфией своего рода «зоной актуального развития», которая оказывает влияние на успешность выполнения более сложных заданий.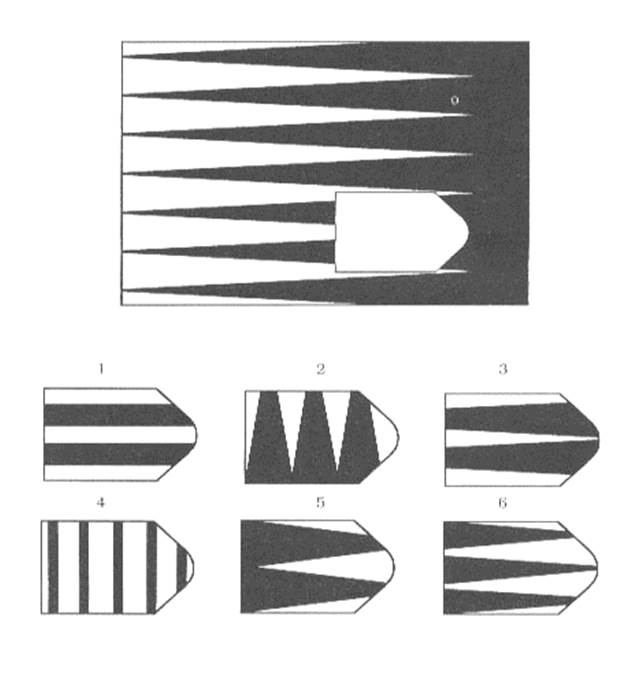
Следует отметить, что если у младших школьников с дисграфией ведущим является умение находить аналогии между зрительными образами, то у их сверстников из контрольной группы на первый план выходят более сложные умения, а именно умение отслеживать прогрессивные изменения в зрительных образах, что демонстрирует положительная взаимосвязь успешности выполнения серии С методики Д. Равена, с сериями А (r =+0.76, p<0.01), В (r =+0.82,p<0.01), D (r =+0.76, p<0.01) и Е (r =+0.82, p<0.01) (4 связи при p<0.01).
Обобщая вышесказанное, можно сказать, что у детей с дисграфией формирование и развитие интеллектуальных составляющих, определяющих успешность овладения навыком письма по правилам графики, требуют специальных методов комплексного психолого-педагогического воздействия.
Количество просмотров публикации: Please wait
Все статьи автора «[email protected]»
ИНДИВИДУАЛЬНЫЕ ОСОБЕННОСТИ НЕВЕРБАЛЬНОГО ИНТЕЛЛЕКТА У МЛАДШИХ ШКОЛЬНИКОВ
Журнал «Вестник КРСУ», 2013 год, Том 13, № 3, Стр.
94-98. УДК 159.922.72-057.87
Давыдова Юлия Александровна – ст. преподаватель кафедры психологии КРСУ, тел.: (996-543) 129590, e-mail: [email protected]
Птуха Мария Владимировна – ст. преподаватель кафедры психологии КРСУ, тел.: (996-543) 945532, e-mail: [email protected]
ИНДИВИДУАЛЬНЫЕ ОСОБЕННОСТИ НЕВЕРБАЛЬНОГО ИНТЕЛЛЕКТА У МЛАДШИХ ШКОЛЬНИКОВ
Давыдова Ю.А., Птуха М.В. Аннотация на русском языке:Описываются индивидуальные особенности невербального интеллекта у младших школьников с использованием методики “Прогрессивные матрицы Равена”.
Ключевые слова на русском языке:интеллект; невербальный интеллект; младший школьник; прогрессивные матрицы Равена
ИНДИВИДУАЛЬНЫЕ ОСОБЕННОСТИ НЕВЕРБАЛЬНОГО ИНТЕЛЛЕКТА У МЛАДШИХ ШКОЛЬНИКОВ
Давыдова Ю.
А., Птуха М.В.
Аннотация на кыргызском языке:Описываются индивидуальные особенности невербального интеллекта у младших школьников с использованием методики “Прогрессивные матрицы Равена”.
Ключевые слова на кыргызском языке:интеллект; невербальный интеллект; младший школьник; прогрессивные матрицы Равена
ИНДИВИДУАЛЬНЫЕ ОСОБЕННОСТИ НЕВЕРБАЛЬНОГО ИНТЕЛЛЕКТА У МЛАДШИХ ШКОЛЬНИКОВ
Давыдова Ю.А., Птуха М.В. Аннотация на английском языке:Описываются индивидуальные особенности невербального интеллекта у младших школьников с использованием методики “Прогрессивные матрицы Равена”.
Ключевые слова на английском языке:интеллект; невербальный интеллект; младший школьник; прогрессивные матрицы Равена
Давыдова Ю.
А. ИНДИВИДУАЛЬНЫЕ ОСОБЕННОСТИ НЕВЕРБАЛЬНОГО ИНТЕЛЛЕКТА У МЛАДШИХ ШКОЛЬНИКОВ / Ю.А. Давыдова, М.В. Птуха // Вестник КРСУ. 2013. Т. 13. № 3. С. 94-98.
Прогрессивные матрицы Равенна
Батарея тестов на наглядное мышление по аналогии, разработанная английским психологом Дж. Равеном (1938). Каждая задача состоит из двух частей: основного рисунка (какого-либо геометрического узора) с пробелом в правом нижнем углу и набора из б или 8 фрагментов, находящихся под основным рисунком. Из этих фрагментов требуется выбрать один, который, будучи поставленным на место пробела, точно подходил бы к рисунку в целом. П.м.Р. разделяются на 5 серий, по 12 матриц в каждом.
П.м.Р широко используется во многих странах как невербальные тесты умственной одаренности. По мнению сторонников концепции независимости мышления от речи, П.м.Р (как и другие невербальные тесты) позволяют изучать интеллект в «чистом виде», исключающая влияние языка и знаний. Однако подобный вывод не подтверждается современными психологическими и электрофизическими исследованиями, свидетельствующими от участии внутренней речи в решении сложных матричных задач.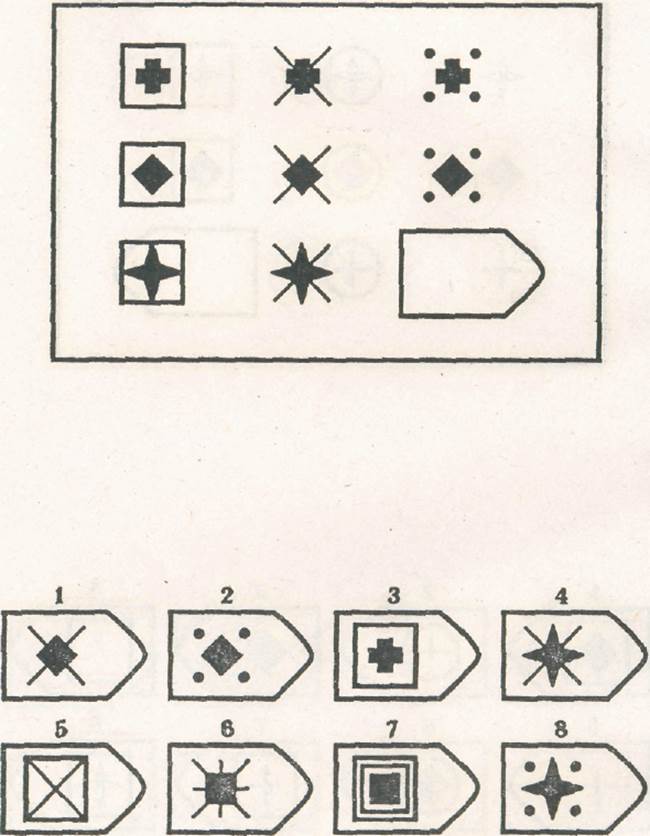
Эта методика предназначается для оценивания наглядно-образного мышления у младшего школьника. Здесь под наглядно-образным мышлением понимается такое, которое связано с оперированием различными образами и наглядными представлениями при решении задач.
Конкретные задания, используемые для проверки уровня развития наглядно-образного мышления, в данной методике взяты из известного теста Равена. Они представляют собой специальным образом подобранную выборку из 10 постепенно усложняющихся матриц Равена
Ребенку предлагается серия из десяти постепенно усложняющихся задач одинакового типа: на поиск закономерностей в расположении деталей на матрице (представлена в верхней части указанных рисунков в виде большого четырехугольника) и подбор одного из восьми данных ниже рисунков в качестве недостающей вставки к этой матрице, соответствующей ее рисунку (данная часть матрицы представлена внизу в виде флажков с разными рисунками на них). Изучив структуру большой матрицы, ребенок должен указать ту из деталей (тот из восьми имеющихся внизу флажков), которая лучше всего подходит к этой матрице, т.
е. соответствует ее рисунку или логике расположения его деталей по вертикали и по горизонтали.
На выполнение всех десяти заданий ребенку отводится 10 минут. По истечении этого времени эксперимент прекращается и определяется количество правильно решенных матриц, а также общая сумма баллов, набранных ребенком за их решения. Каждая правильно, решенная матрица оценивается в 1 балл.
Правильные, решения всех десяти матриц следующие (первая из приводимых ниже пар цифр указывает на номер матрицы, а вторая — на правильный ответ: 1—7,2—6,3—6,4—1,5—2,6—5,7—6, 8-1,9-3,10-5.
Выводы об уровне развития
10 баллов — очень высокий
8-9 баллов — высокий.
4-7 баллов — средний.
2-3 балла — низкий.
0-1 балл — очень низкий.
Приложение 4
Результаты диагностики мышления младших школьников на констатирующем и контрольном этапах эксперимента, в баллах
| № | Исключение лишнего | Сравнение понятий | Аналогии (тест Равена) | |||
| 1 срез | 2 срез | 1 срез | 2 срез | 1 срез | 2 срез | |
Хср.
| 3,83 | 4,47 | 18,1333 | 23,77 | 5,87 | 7,4 |
Приложение 5
Конспекты уроков по предмету «Окружающий мир»
Урок «Мы и окружающий мир. Кто поет в зимнем лесу»
Тема:Кто поет в зимнем лесу.
Цели:
1) Уточнить знания учащихся о многообразии зимующих птиц и их значении для природы.
2) Уточнение знаний учащихся о значении природных условий для жизни птиц. Развивать умение находить взаимосвязи в природе.
3) Совершенствовать умение учащихся узнавать птиц по их устному описанию.
4) Уточнить знания о видах кормушек и о кормах, используемых для подкормки зимующих птиц.
5) Развивать внимание, память, логическое мышление, речь учащихся.
6) Воспитывать любовь к природе, доброе и бережное отношение ко всему живому.
Оборудование: Иллюстрации зимующих птиц; таблица «Зимующие птицы»; различные книги о зимующих птицах; иллюстрации различных видов кормушек; аудиозаписи — «Голоса птиц», стихотворение «Пороша» С. Есенина, «Времена года» — Чайковский; портрет С.Есенина.
Ход урока
I. Организационный момент
Особенности познавательных процессов у детей, больных сахарным диабетом | Чуваков
В настоящее время в поддержании состояния компенсации у больных сахарным диабетом большое значение придают обучению их самоконтролю заболевания [1, 2, 4, 12]. Вместе с тем метаболический контроль нельзя считать удовлетворительным, и эффективность обучения самоконтролю заболевания остается еще низкой [1, 13, 14]. Следовательно, на сегодня проблема обучения больных сахарным диабетом самоконтролю заболевания является актуальной в диабетологии.
В ’’Школе больного сахарным диабетом’’ много внимания уделяют содержательному аспекту обучения и упускают из вида возможность к обучению больного диабетом, его обучаемость. Обучаемость включает многие показатели, параметры личности человека. К ним относятся прежде всего познавательные возможности человека (особенности памяти, внимания, мышления и др.), особенности личности — мотивации; характера, эмоциональных проявлений; отношение к усваиваемому учебному материалу, учебной группе и преподавателю [6]. По данным зарубежных исследований, качество обучения на 50% зависит от так называемых когнитивных факторов, т. е. от относительно устойчивых индивидуальных особенностей личности, определяющих успех в познавательной деятельности (интеллект, память, внимание и др.), на 25% — от аффективных факторов (преимущественно от мотивов обучения, эмоционального отношения к преподавателю, предмету, членам группы) и только на 25% — от качества обучения [11]. Изучения познавательных возможностей детей и подростков, больных сахарным диабетом, в известной нам литературе мы не встретили.
Целью настоящего исследования явилось изучение особенностей функционирования познавательных психических процессов памяти, внимания и мышления у детей с инсулинзависимым сахарным диабетом (ИЗСД).
Материалы и методы
Для решения поставленной задачи обследовано 133 ребенка дошкольного и школьного возраста, больных ИЗСД, и 90 их практически здоровых сверстников. Познавательные процессы исследовали с помощью следующих методик: память у больных ИЗСД и здоровых детей изучали с помощью методик А. А. Смирнова [8]; оценку внимания у дошкольников проводили по методике А. В. Запорожца и Д. Б. Эльконина [7], а у школьников — по методике «Переключение внимания» с использованием таблицы Горбова—Шульте [5]; мышление изучали с помощью методики Равена [9]. Содержание гликированного гемоглобина НЬ А1с исследовали на анализаторе IMX фирмы «Abbot» (США) стандартизованными наборами для НЬ А1с. Уровень гликированного гемоглобина у здоровых детей составил 5,95 ± 0,17%. У детей с ИЗСД уровень гликированного гемоглобина до 9% оценивали как компенсацию, а более 10% — как декомпенсацию диабета.
Результаты и их обсуждение
С целью оценки степени компенсации заболевания на момент обследования у всех детей определяли уровень гликированного гемоглобина. Как показали результаты обследования, большинство (76%) детей находились в суби декомпенсированном состоянии, и уровень гликированного гемоглобина у них был более 9%. Аналогичные результаты при оценке степени компенсации заболевания у детей с ИЗСД получены и другими исследователями [2, 3, 10].
Результаты наших исследований показали, что объем различных видов памяти у 75,9% детей с ИЗСД был ниже предела возрастной нормы. Данные исследования непроизвольной и произвольной памяти у детей дошкольного возраста, больных сахарным диабетом, представлены в табл. 1.
Как видно из табл. 1, объем непроизвольной и произвольной памяти и объем произвольной па-
Таблица 1
Сравнительные результаты исследования непроизвольной и произвольной памяти у детей с ИЗСД и здоровых детей дошкольного возраста
Группа обследованных | Число обследованных | Возраст, годы | Объем непроизвольной памяти, ед. информации | Объем произвольной памяти, ед. информации | Объем произвольной памяти с использованием приемов классификации, ед. информации |
Здоровые | 30 | 5,5 ± 0,4 | 8,8 ± 0,8 | 10,3 ± 0,6 | 14,0 ± 0,6 |
Больные ИЗСД К | 6 | 6,2 ± 0,2 | 8,0 ± 0,58 | 9,7 ± 0,29 | 13,3 ± 0,3 |
Р\ | > 0,05 | > 0,05 | > 0,05 | > 0,05 | |
Больные изсдд | 23 | 5,7 ± 0,5 | 5,1 ± 0,5 | 6,8 ± 0,5 | 11,0 ± 0,8 |
Р2 | > 0,05 | < 0,01 | < 0,01 | < 0,01 |
Примечание. Здесь и в табл. 2, 3: ИЗСД К — больные ИЗСД в состоянии компенсации, ИЗСД Д — больные ИЗСД в состоянии декомпенсации. р{ — достоверность различий показателей больных диабетом в состоянии компенсации с нормой; Р2 — достоверность различий показателей больных диабетом в состоянии декомпенсации с нормой.
мяти с использованием приемов классификации у больных детей дошкольного возраста в декомпенсированном состоянии значительно ниже, чем у здоровых сверстников и больных, состояние которых расценено нами как компенсированное.
В табл. 2 представлены сравнительные результаты изучения логической и механической памяти у детей школьного возраста, страдающих сахарным диабетом.
Из представленных в табл. 2 данных видно, что у детей младшего школьного возраста, как и у подростков, больных сахарным диабетом, находящихся в состоянии декомпенсации, результаты исследования памяти по сравнению с группой здоровых детей и детей с диабетом в состоянии компенсации того же возраста достоверно ниже.
Сравнительный анализ результатов исследования памяти детей с ИЗСД в зависимости от давности заболевания показал следующее. Так, у детей, страдающих ИЗСД в течение 3,0 ± 0,8 года, объем смысловой и механической памяти составил соответственно 19,3 ±1,25 и 16,0 ± 2,0 ед. информации. Объем данных видов памяти оказался значительно выше (р < 0,05), чем у детей, стаж болезни которых был больше (р > 0,05) и составил 6,3 ± 0,25 года. У больных ИЗСД с давностью заболевания 6,3 ± 0,25 года объем смысловой памяти составил 14,3 ± 1,76 ед. информации, а механической памяти — 10,5 ± 1,49 ед. информации.
Изучение мнемической деятельности у больных диабетом детей с одинаковым стажем болезни в зависимости от состояния углеводного обмена выявило следующее. Среди детей, болеющих ИЗСД в течение 5,7 ± 0,86 года, у которых уровень гликированного гемоглобина в среднем составил 8,6 ± 0,3%, показатели смысловой памяти равнялись 17,3 ± 1,7 ед. информации, механической памяти — 12,7 ± 1,0 ед. информации. У детей с давностью заболевания 6,6 ± 0,89 года, статистически не отличающихся от предшествующей группы (р > 0,05), но с достоверно большим уровнем гликированного гемоглобина, составившим в среднем 12,1 ± 0,66% (р < 0,05), объем смысловой и механической памяти равнялся соответственно 11,0 ± 2,4 и 7,8 ± 1,56 ед. информации. Показатели исследуемых видов памяти у данных детей были достоверно ниже (р < 0,05). Следовательно, объем механической и смысловой памяти у детей с ИЗСД ниже по сравнению со здоровыми сверстниками. Показатели различных видов памяти у детей с ИЗСД ниже у тех больных, которые находятся в состоянии хронической декомпенсации заболевания. Ухудшение памяти, с одной стороны, может быть причиной затруднений в обучении их самоконтролю заболевания, а с другой — плохо контролируемое заболевание способствует и ухудшению памяти.
В обучении большое значение имеет не только память, но и внимание, так как нарушение концентрации внимания даже при хорошей памяти может привести к трудностям в обучении.
Диагностическое исследование внимания показало, что у 24,1% детей, больных сахарным диабетом, объем внимания равен нижнему пределу возрастной нормы. Так, исследование произвольного внимания у детей дошкольного возраста (5,7 ± 0,5 года) с ИЗСД в состоянии компенсации (уровень гликированного гемоглобина не превышал 9%) при стаже болезни 1,0 ± 0,4 года не выявило различий со здоровыми сверстниками в возрасте 5,5 ± 0,4 года. Показатель произвольного внимания у этих больных составил 5,5 ± 0,8 ед. информации, а у здоровых — 6,6 ± 0,5 ед. информации (р > 0,05). У детей дошкольного возраста (5,6 ± 0,4 года) с диабетом в состоянии декомпенсации (уровень гликированного гемоглобина более 10%) со стажем болезни 2,6 ± 0,3 года показатель произвольного внимания был существенно (/? < 0,05) ниже, чем у здоровых детей дошкольного возраста и больных в состоянии компенсации, — 4,0 ± 0,86 ед. информации. Результаты исследования переключения внимания у больных ИЗСД младшего школьного возраста и подростков представлены в табл. 3.
Табл и ца 2
Сравнительные результаты исследования логической и механической памяти у здоровых и больных ИЗСД детей младшего школьного и подросткового возраста (в ед. информации)
Группа обследованных | Число обследованных | Возраст, годы | Объем смысловой памяти | Объем механической памяти | ||||
количество слов 1-го ряда (а) | количество запомнившихся слов (Ь) | коэффициент смысловой памяти (с) | количество слов 2-го ряда (al) | количество запомнившихся слов (Ы) | коэффициент механической памяти (cl) | |||
Младший школьный возраст: | ||||||||
здоровые | 30 | 9,0 ± 0,4 | 30 | 23,6 ± 1,9 | 0,78 ± 0,06 | 30 | 19,2 ± 1,6 | 0,46 ± 0,05 |
больные ИЗСД К | 11 | 10,5 ± 0,25 | 30 | 19,3 ± 2,0 | 0,64 ± 0,07 | 30 | 16,4 ± 1,7 | 0,55 ± 0,06 |
Pi | > 0,05 | > 0,05 | > 0,05 | > 0,05 | > 0,05 | |||
больные ИЗСД Д | 31 | 9,4 ± 0,5 | 30 | 10,5 ± 0,95 | 0,34 ± 0,03 | 30 | 6,5 ± 0,5 | 0,21 ± 0,02 |
Р1 | > 0,05 | < 0,01 | < 0,01 | < 0,01 | < 0,01 | |||
Подростки: | ||||||||
здоровые | 30 | 15,0 ± 0,14 | 30 | 27,5 ± 0,7 | 0,91 ± 0,02 | 30 | 23,6 ± 0,95 | 0,79 ± 0,03 |
больные ИЗСД К | 15 | 15,8 ± 0,4 | 30 | 25,3 ± 1,5 | 0,84 ± 0,05 | 30 | 21,5 ± 1,4 | 0,72 ± 0,046 |
Р\ | > 0,05 | > 0,05 | > 0,05 | > 0,05 | > 0,05 | |||
больные ИЗСД Д | 47 | 15,0 ± 0,4 | 30 | 14,6 ± 1,9 | 0,48 ± 0,06 | 30 | 11,6 ± 1,6 | 0,38 ± 0,05 |
Р2 | > 0,05 | < 0,01 | < 0,01 | < 0,01 | < 0,01 | |||
Как видно из представленных в табл. 3 данных, младшие школьники, больные ИЗСД, находящиеся в декомпенсированном состоянии (уровень гликированного гемоглобина у них превышал 10%), затратили существенно меньше времени на переключение внимания при выполнении всех трех заданий по сравнению со здоровыми сверстниками и больными диабетом в состоянии компенсации. Однако в отличие от своих здоровых сверстников и больных, находящихся в состоянии компенсации, при выполнении задания они допускали значительно больше ошибок. Причем в самом сложном задании «в» ими допущено большее количество ошибок (р < 0,05), чем здоровыми детьми и детьми с компенсированным диабетом. Превышение времени на переключение внимания у здоровых детей и больных с компенсированным диабетом при выполнении трех заданий (”а”, «б”, «в»), очевидно, связано с тем, что они выполняли их под большим самоконтролем, чем дети с декомпенсированным диабетом. Последних интересовали, скорее, конечный результат, быстрое выполнение задания на время. При выполнении задания они допускали ошибки, неточности. Их невнимательность, по нашему мнению, свядетельствует о несформированности у них действий контроля.
Показатели переключения внимания у подростков с ИЗСД (см. табл. 3) существенно хуже таковых у здоровых подростков и подростков с компенсированным диабетом. При выполнении всех трех заданий подросток с декомпенсированным диабетом затрачивает больше времени, чем здоровый ребенок и его сверстник с компенсированным диабетом. При выполнении самого сложного задания «в” они тратят в 9,8 раза больше времени, чем здоровые дети, тогда как в группе здоровых детей наблюдается незначительная тенденция к снижению затрат времени на выполнение задания от более простого ”а” к самому сложному «в”. Это, очевидно, связано с тем, что в группе здоровых сверстников от первого задания к последующим наблюдается более высокая обучаемость детей по сравнению с подростками, страдающими ИЗСД. У подростков с ИЗСД в декомпенсированном состоянии отмечается обратная тенденция к замедлению переключения внимания и увеличению числа ошибок в трех заданиях. Следует отметить, что здоровые подростки все 3 задания выполнили без ошибок. Итак, среди обследованных нами подростков только у больных ИЗСД в декомпенсированном состоянии внимание и самоконтроль за ходом выполнения своей деятельности значительно снижены. Они торопятся выполнять задания, проявляя мотивацию достижения, которая не всегда коррелирует с результативностью и качеством выполнения данных заданий.
Изучение переключения внимания больных ИЗСД в зависимости от длительности болезни и метаболического контроля выявило, что среди больных со стажем болезни 6,4 ± 0,5 года и уровнем гликированного гемоглобина 12,1 ± 0,7% время переключения вимания при выполнении трех заданий «а», «б”, «в» составило соответственно
- ± 3,2, 78,8 ± 3,3, 250,8 ± 10,1 с, а у больных ИЗСД с длительностью болезни 1,52 ± 0,13 года, уровнем гликированного гемоглобина 8,9 ± 0,5% показатели переключения внимания при выполнении этих заданий были равны 17,0 ± 0,9,
- ± 1,2, 97,0 ± 4,0 с соответственно. У детей, длительно болеющих диабетом, с неудовлетворительной компенсацией заболевания переключение внимания существенно замедлено по сравнению с детьми с ИЗСД с небольшим стажем болезни и удовлетворительной компенсацией заболевания (р < 0,05). Дети, давно болеющие ИЗСД, допустили существенно большее количество ошибок при выполнении трех заданий, чем их здоровые сверстники. Следовательно, выявленное нами снижение результативности показателей различных видов памяти у детей с ИЗСД усугубляется и обнаруженным нарушением внимания.
Мы исследовали логичность мышления как у младших школьников и подростков с ИЗСД, так и у их здоровых сверстников с помощью теста возрастающей трудности (методика Равена). Средний возраст обследованных нами детей составил
Таблица 3
Сравнительные результаты исследования переключения внимания у здоровых детей и больных ИЗСД младшего школьного возраста и подростков
Группа обследованных | Число обследованных | Возраст, годы | Время переключения внимания в трех заданиях, с | Количество ошибок, % | ||||
а | б | в | а | б | в | |||
Младший школьный возраст: | ||||||||
здоровые | 30 | 9,1 ± 0,4 | 85,0 ± 19,0 | 180,0 ± 32,0 | 330 ± 49,0 | — | — | 19 |
больные ИЗСД К | 11 | 9,0 ± 0,6 | 83,0 ± 16,0 | 132,0 ± 18,0 | 251,0 ± 21,0 | — | — | 5 |
Р1 | > 0,05 | > 0,05 | > 0,05 | > 0,05 | ||||
больные ИЗСД Д | 31 | 9,8 ± 0,4 | 40,6 ± 14,3 | 39,7 ± 15,0 | 142,5 ± 10,9 | 8 | 29 | 50 |
Р2 | > 0,05 | < 0,05 | < 0,05 | < 0,05 | ||||
Подростки: | ||||||||
здоровые | 30 | 14,8 ± 1,3 | 20,1 ± 2,7 | 20,0 ± 2,2 | 18,0 ± 1,18 | — | — | — |
больные ИЗСД К | 15 | 15,8 ± 0,4 | 19,4 ± 2,2 | 23,4 ± 2,1 | 21,3 ± 1,5 | — | — | — |
Р\ | > 0,05 | > 0,05 | > 0,05 | > 0,05 | ||||
больные ИЗСД Д | 47 | 15,3 ± 0,4 | 37,6 ± 8,4 | 48,1 ± 11,8 | 177,0 ± 44,5 | 19 | 21 | 26 |
Р2 | > 0,05 | < 0,05 | < 0,05 | < 0,05 | ||||
- ± 0,4 года. Уровень интеллектуального развития здоровых детей составил 76,3 ±1,1 балла, у 23% детей с ИЗСД этот показатель равнялся
- ± 0,7 балла, что не отличается от контрольной группы детей (р > 0,05).
У 77% больных диабетом показатель мышления по методике Равена был достоверно ниже, чем в группе здоровых детей, и составил
- ± 1,7 балла (р < 0,01).
Сравнение результатов, полученных по тесту Равена, у детей с ИЗСД в зависимости от длительности болезни и степени компенсации показало, что у детей со стажем болезни 3,0 ± 0,8 года, поддерживающих удовлетворительный метаболический контроль, уровень гликированного гемоглобина составил 8,9 ± 0,62%, уровень невербального интеллекта не отличался от детей контрольной группы и составлял 69,4 ± 0,7 балла. У детей с большим стажем болезни (6,4 ± 0,2 года) и недостаточным контролем обмена веществ уровень гликированного гемоглобина составил 12,1 ± 0,7%, уровень интеллектуального развития — 37,5 ± 0,8 балла (р < 0,05).
Таким образом, познавательные возможности у детей, длительно болеющих сахарным диабетом с плохим метаболическим контролем, снижены. Выявленные особенности функционирования познавательных процессов у этих детей, по-видимому, необходимо учитывать при организации их обучения вопросам терапии заболевания.
Выводы
- У 76% обследованных нами детей с ИЗСД выявлена неудовлетворительная компенсация заболевания.
- У подавляющего большинства детей с ИЗСД (77%) выявлена недостаточная эффективность познавательных процессов.
- Эффективность познавательных процессов памяти, внимания и мышления детей с ИЗСД ухудшается по мере увеличения длительности заболевания и при отсутствии метаболического контроля заболевания.
Диагностика мышления и интелекта младших школьников
Диагностика мышления и интеллекта младших школьников.
Актуальность обусловлена тем, что в период младшего школьного возраста происходят существенные изменения в психике ребёнка усвоение новых знаний, новых представлений об окружающем мире перестраивает сложившиеся ранее у детей житейские понятия, а школьное мышление способствует развитию теоретического мышления в доступных учащимся этого возраста формах.
Благодаря развитию нового уровня мышления, происходит перестройка всех остальных психических процессов, т. е. по словам Д. Б. Эльконина «Память становится мыслящей, а восприятие – думающим». Поэтому именно перестройка всей познавательной сферы в связи с развитием теоретического мышления составляет основное содержание умственного развития в младшем школьном возрасте.
Как показывают многочисленные исследования учёных, в том числе Л. С. Выготского, развитие теоретического мышления, т.е. мышления в понятиях, способствует возникновению к концу младшего школьного возраста важнейших новообразований:
рефлексии, которая преображает не только познавательную деятельность учащихся, но и характер их отношения к окружающим людям и самим себе, произвольности и способности к саморегуляции.
Уровень сформированности мышления служит показателем умственного развития ребёнка. По мнению Л. В. Занкова такими показателями служат:
-доказательность мышления;
-критичность;
-гибкость мышления.
З. И. Колмыкова добавляет к ним:
-экономичность;
-самостоятельность мышления.
Диагностика (изучение мышления и интеллекта)
Были проведены диагностика способности к смысловой обработке запоминаемого материала и диагностика уровня развития логического мышления. В эксперименте участвовал 3 класс, 19 человек.
Были проведены тесты:
1. «Группировка».
Цель. Определение способностей к смысловой обработке запоминаемого материала.
Для запоминания предъявляется ряд из 20 группирующихся по смыслу слов (всего 5 групп по 4 слова в каждой). Запоминание осуществляется по методу неполного заучивания (материал предъявляется и воспроизводится трижды).
Инструкция. Для первого воспроизведения: Я сейчас прочитаю ряд слов. Ты внимательно послушай, а потом повтори в удобном для тебя порядке. Внимание!
Для второго воспроизведения: Сейчас я еще раз прочитаю все слова. Ты послушай, а затем скажи все слова, которые запомнил. Назови слова, что ты первый раз говорил и вновь запомненные. Все понятно? Внимание!
Для третьего воспроизведения: Сейчас я еще раз прочитаю все слова. Ты послушай, а затем скажи все слова, которые запомнил. Назови слова, что ты говорил первый и второй раз и вновь запомненные. Все понятно? Внимание!
Солнце | Шапка | Липа | Небо |
Тополь | Медведь | Блюдце | Елка |
Чашка | Сосна | Звезда | Белка |
Заяц | Ложка | Лиса | Кружка |
Луна | Юбка | Платье | Кофта |
Обработка. Фиксируются и подсчитываются воспроизведенные слова, определяется их объединенность в группы.
Нормативы. Ограничение объема кратковременного запоминания сказывается обычно при первом и втором воспроизведении. Первое воспроизведение характеризуется нижним пределом нормального распределения, т. е. 3 слова для 6-7 лет и 5 слов для 14 лет. При втором воспроизведении появляются 1-2 частично сформированные группы и при третьем – 3-4 группы по 2-3 слова. В младшем школьном возрасте бывает не больше трех смысловых групп. В старшем –четыре группы.
Данные по исследованию приведены в таблице № 1.
2. Таблица Равена
Назначение методики. С помощью теста Равена исследователи судят о способности систематизированной, планомерной, методической, интеллектуальной деятельности. Методика состоит из невербальных заданий, следовательно, можно считать, что она меньше учитывает приобретенные обследуемые в жизненном опыте умения. Методика помогает определить уровень интеллекта, интеллектуальную инициативу, уровень обучаемости школьников. Учащимся были предложены 30 таблиц (четные номера) из 5-й серии: А, В, С, Д, Е. Проверяли уровень интеллекта младших школьников. Данные по исследованию приведены в таблице № 2.
3. Для определения уровня развития логического мышления учащихся начальной школы использовалась методика «Четвёртый лишний».
Ребёнку зачитываются четыре слова, три из которых связаны между собой по смыслу, а одно слово не подходит к остальным. Ребёнку предлагается найти «лишнее» слово и объяснить, почему оно «лишнее».
Cтимульный материал: 11 карточек с четырьмя словами (или четырьмя изображениями), одно из которых лишнее:
стол, кровать, пол, шкаф;
молоко, сливки, сало, сметана;
ботинки, сапоги, шнурки, валенки;
молоток, топор, пила, гвоздь;
трамвай, автобус, трактор, троллейбус;
берёза, сосна, дерево, дуб;
самолёт, телега, человек, корабль;
Василий, Фёдор, Семён, Иванов;
сантиметр, метр, килограмм, километр;
токарь, учитель, врач, книга;
дедушка, учитель, папа, мама.
Инструкция: «Прочитай эти слова (или «Посмотри на эти картинки»). Одно из них здесь лишнее, оно не связано с остальными словами. Подумай, какое это слово и назови его. Объясни почему?»
Ход проведения. В первом задании нужно добиться от ребёнка правильного ответа. Оно не оценивается. В процессе тестирования ребёнку последовательно предъявляются все двенадцать карточек. Помощь взрослого заключается только в дополнительных вопросах типа: «Хорошо ли ты подумал?», «Ты уверен, что выбрал правильное слово?», но не в прямых подсказках. Если ребёнок после такого вопроса исправляет свою ошибку, ответ считается правильным. За каждый правильный ответ начисляется 1 балл, за неправильный — 0 баллов.
10-8 баллов – высокий уровень развития логического мышления;
7-5 баллов – средний уровень развития логического мышления;
4 и менее баллов – логическое мышление развито слабо.
Полученные результаты приведены в таблице 3.
Таблица № 1 Диагностика способности к смысловой обработке запоминаемого материала.
№ | Смысловая обработка запоминаемого материала | |||||
I Восп | Группы Слов | II восп | Группы Слов | III Восп | Группы Слов | |
1 | 7 | 1 группа | 14 | 3 группа | 15 | 4 группа |
1 | 15 | 16 | 6 | 4 группа | ||
3 | 7 | 10 | 2 группа | 6 | 4 группа | |
4 | 11 | 12 | 2 группа | 3 | 3 группа | |
5 | 9 | 7 | 1 группа | 5 | 3 группа | |
6 | 9 | 2 группа | 13 | 3 группа | 5 | 4 группа |
7 | 11 | 1 группа | 13 | 2 группа | 6 | 4 группа |
8 | 10 | 11 | 1 группа | 6 | 4 группа | |
9 | 7 | 11 | 4 группа | 4 | 5 группа | |
10 | 9 | 7 | 1 группа | 5 | 3 группа | |
11 | 9 | 12 | 3 группа | 7 | 5 группа | |
12 | 10 | 1 группа | 12 | 3 группа | 6 | 3 группа |
13 | 10 | 2 группа | 15 | 3 группа | 6 | 5 группа |
14 | 8 | 1 группа | 8 | 8 | 2 группа | |
15 | 9 | 14 | 4 группа | 6 | 3 группа | |
16 | 10 | 1 группа | 12 | 3 группа | 6 | 5 группа |
17 | 9 | 2 группа | 14 | 4 группа | 3 | 5 группа |
18 | 8 | 11 | 2 группа | 5 | 4 группа | |
19 | 6 | 1 группа | 8 | 1 группа | 4 | 3 группа |
5 чел – по 5 групп
7 чел – по 4 группы
6 чел – по 3 группы
1 чел – по 2 группы
№ | Методика Равена | ||||||
А | В | С | Д | Е | Кол. балл. | В % | |
1 | 4-12-67% | 6-26-100% | 3-13-42% | 3-20-50% | 1-4-10% | 75 | 48% |
2 | 4-12-67% | 4-17-65% | 4-19-61% | 3-20-50% | 1-7-18% | 75 | 48% |
3 | 18-100% | 21-81% | 17-55% | 33-83% | 0 | 89 | 57% |
4 | 5-13-72% | 5-20-77% | 4-20-65% | 2-12-30% | 1-7-18% | 72 | 47% |
5 | 5-17-94% | 4-17-65% | 2-10-32% | 4-27-68% | 0 | 71 | 46% |
6 | 6-18-100% | 5-20-77% | 2-11-36% | 4-26-65% | 0 | 75 | 48% |
7 | 6-18-100% | 5-20-77% | 3-13-42% | 2-12-30% | 0 | 63 | 41% |
8 | 15-83% | 14-54% | 13-42% | 27-60% | 0 | 69 | 45% |
9 | 6-18-100% | 18-100% | 4-20-65% | 33-83% | 1-8-20% | 91 | 63% |
10 | 18-100% | 20-77% | 17-55% | 13-33% | 0 | 68 | 44% |
11 | 17-94% | 21-81% | 14-46% | 26-65% | 0 | 78 | 50% |
12 | 13-72% | 20-77% | 3-13-42% | 13-33% | 0 | 59 | 38% |
13 | 18-100% | 18-100% | 17-55% | 33-83% | 0 | 86 | 56% |
14 | 6-18-100% | 5-20-77% | 2-7-23% | 2-13-33% | 0-8% | 58 | 37% |
15 | 5-13-72% | 4-14-54% | 2-11-36% | 2-13-33% | 1-8-20% | 59 | 38% |
16 | 13-72% | 20-77% | 11-36% | 33-83% | 0 | 77 | 50% |
17 | 6-18-100% | 18-10% | 19-61% | 33-83% | 1-7-18% | 95 | 61% |
18 | 7-39% | 23-89% | 0% | 33-83% | 0 | 63 | 41% |
19 | 6-18-100% | 5-20-77% | 2-10-32% | 2-13-33% | 0 | 61 | 39% |
Таблица №3. Уровень развития логического мышления младших школьников.
кол-во баллов | уровень развития мышления | |
1 | 7 | средний |
2 | 10 | высокий |
3 | 9 | высокий |
4 | 9 | высокий |
5 | 5 | средний |
6 | 7 | средний |
7 | 10 | высокий |
8 | 4 | низкий |
9 | 4 | низкий |
10 | 10 | высокий |
11 | 9 | высокий |
12 | 6 | средний |
13 | 9 | высокий |
14 | 10 | высокий |
15 | 8 | высокий |
16 | 8 | высокий |
18 | 9 | высокий |
17 | 8 | высокий |
19 | 7 | средний |
Анализ результатов исследования
Для диагностики возможностей обработки материала использовали методику «Группировка». После первого запоминания слов ребята разделились на 2 группы, половина ребят воспроизвела слова, выделяя по одной группе (2 чел. – по 2 группы), а половина запоминала слова в той последовательности, в которой их произносили. Особых приемов запоминания учащиеся не использовали. После второго прослушивания слов 17 человек догадались, что для полного воспроизведения слов их следует разбить на группы по признакам. При третьем воспроизведении появилось от 3 до 5 групп (кроме 1 ребенка). За счет группировки слов увеличилось количество запоминаемых слов.
При предъявлении методики Равена дети продемонстрировали средние интеллектуальные способности. У них есть возможность для дальнейшего развития логического мышления. Нужно обратить внимание на тех, у кого показатели ниже, чем у других ребят. С ними нужно проводить и дальше индивидуальную работу по развитию интеллектуальных способностей. У группы ребят есть показатели, которые ближе к интеллекту выше среднего.
Проанализируем уровень развития логического мышления. Для большинства детей характерен высокий уровень развития логического мышления (64%), 26% детей имеют средний уровень развития интеллекта, а у 10 % учеников логическое мышление развито слабо. Из данных результатов можно сделать следующий вывод. Во данном классе имеются большие перспективы для работы по развитию логического мышления как у детей со слабым и средним уровнем, так и у детей с высоким уровнем. Эта работа будет направлена на развитие и совершенствование логических операций мышления.
Справедливое — это не равно: семь советов в классе
Если вы спросите учащихся, какие качества учителя им нравятся больше всего, одно из самых важных качеств, о которых упоминается во всем мире, — это справедливость. Учителя и школы стремятся быть справедливыми и строят программы и политику, основанные на этой ценности.
Но что справедливо? Многие определяют это как отношение ко всем одинаково, но я бы сказал, что это самый несправедливый способ обращения со студентами. Студенты не такие. У них разные мотивы своего выбора, разные потребности, разные причины плохого поведения и разные цели.Думаю, это хорошо, ведь разве мир не был бы очень скучным, если бы мы все были одинаковыми?
Самый яркий пример недопонимания между справедливым и равным — организация прогрессивных последствий. Первое нарушение приводит к одинаковым последствиям для всех; второе нарушение, более серьезное, остается неизменным для всех. Это продолжается на протяжении всей последовательности. Подавляющее большинство школ и классов используют эту модель. Есть большая опасность в использовании схем прогрессивных последствий.Никто не пойдет к врачу, который лечит все головные боли одинаково, поскольку причиной одного может быть аллергия, а другого — опухоль. Идентичное лечение двух учеников, которые не выполняют домашнее задание по разным причинам — одного, который должен помогать в семейном бизнесе после школы, а другого, который слишком много смотрит телевизор, — ничем не отличается от этого сумасшедшего доктора с единым лекарством для всех. головные боли.
Требуется ли больше времени для справедливого обращения со студентами? Не так много, как неудачные решения проблем с поведением, которые в течение года продолжают отнимать учебное время отрезками от пяти до пятнадцати минут.
Вот как реализовать эту концепцию.
1. Правила у всех одинаковые.
Могут быть исключения для необычных обстоятельств, но позитивное социальное взаимодействие практически одинаково для всех.
2. Последствия гибкие.
Когда правило нарушается, учитель может выбрать из большого набора возможных последствий. Эти последствия работают лучше всего, когда их заранее разъясняют учащимся, администраторам и родителям. Нет определенного порядка или прогресса.Выберите тот, который работает лучше всего или тот, который, по вашему мнению, будет эффективным, исходя из ваших знаний об ученике. Часто очень эффективно дать студенту возможность выбора из списка вместе с обещанием улучшить его или возможностью потерять право выбора.
3. Равное не всегда справедливо.
Помните, что использование прогрессивных последствий не означает, что вы относитесь к студентам одинаково. Сколько раз ученик будет проходить через прогресс, зависит от того, кого поймают и как будут доставлены последствия.Следующий пример — сильно преувеличенный, но даже когда учитель гораздо тоньше, ученики улавливают его.
«Джонни, перестань перебивать. Это твое предупреждение. Спасибо».
В отличие от:
«Бесси, маленькая ласка. Сколько раз я должен говорить тебе, чтобы ты не перебивал? Я действительно устал от этого. Ты получаешь еще одно предупреждение, прежде чем я сделаю что-то гораздо более серьезное. . »
С обоими учениками обращались одинаково, потому что они оба получили предупреждение, но было ли это справедливо?
4.Обучите свой класс концепции справедливого и равного, прежде чем реализовывать ее.
Выполняя домашнее задание, обсуждая в классе или занимаясь в классе, попросите учащихся привести примеры из дома, школы или общества, где очень справедливо и хорошо относиться к людям по-разному. Затем приведите несколько примеров того, как вы собираетесь быть справедливым, но не равным. Учащиеся K-12 могут понять и принять это, если объяснение будет соответствовать их способностям.
5. Следуйте основным принципам высокой дисциплины.
Сохраняйте конфиденциальность общения между вами и учеником, нарушившим правило, за исключением случаев, когда это невозможно.
6. Будьте готовы обсудить свою стратегию со студентами.
Когда ученики жалуются, что «это несправедливо», если их последствия отличаются от последствий другого ученика, напомните им, что:
- Справедливые не равны.
- Говорить о других — это сплетня, и ты не будешь этого делать. Добавьте, что вы не будете рассказывать о них другим.
- Спросите их, что было бы справедливо. Когда они ответят, сопровождайте их словами вроде: «Хорошо, если вы можете гарантировать, что, когда я последую вашему совету, вы остановитесь (или начнете делать».. .). Если ваша идея сработает, это будет здорово, но если нет, то мы сделаем это по-своему ». Это дает студентам ответственность меняться, понимая, что поставлено на карту.
7. Будьте готовы обсудить ваша стратегия с родителями
Если родитель жалуется на несправедливость, расизм или на то, что вы не любите его ребенка, попробуйте разговор, включающий следующие моменты:
- «Я очень рад, что вы здесь. Приятно работать с заботливыми родителями, у которых такая же цель, как и у меня: помочь Хуану стать лучше.»
- » Я хотел бы услышать ваше мнение по поводу этой ситуации. Вы знаете Хуана лучше, чем я, поэтому скажите мне, что работает дома ». (Это отличный вопрос для выравнивания.)
- « Я понимаю, почему вы можете быть обеспокоены, но вместе мы можем улучшить положение Хуана ».
- «Я готов изменить свое решение на то, которое, по вашему мнению, будет работать лучше, но если оно не удастся, тогда давайте попробуем мою первоначальную идею».
- Вот лучший способ завершить обсуждение: «Я действительно забочусь о Хуан, и я готов сделать все возможное, чтобы помочь ему улучшить свое поведение.Но есть одна вещь, которую я никогда не сделаю, несмотря ни на что. Я никогда не буду относиться к нему как к остальным. Ваш ребенок заслуживает большего ».
Быть по-настоящему справедливым труднее и требует больше работы в краткосрочной перспективе, чем просто отношение ко всем одинаково. В долгосрочной перспективе это экономит время и более эффективно. чтобы относиться ко всем одинаково, каждый ребенок заслуживает большего.
Группа способностей | Когда учащихся с аналогичными способностями или уровнем достижений помещают в класс или группу на основании наблюдаемого поведения или успеваемости.Группировка способностей — это не то же самое, что отслеживание. Прочтите позицию NAGC по группировке способностей. |
Разгон | Стратегия обучения более быстрыми темпами или старше нормы. Это может произойти из-за пропусков класса или ускорения по предмету (например, ученик пятого класса изучает математику в шестом классе). Просмотрите отчет Обманутая нация Института исследований и политики в области ускорения. Ознакомьтесь с рекомендациями по созданию политики ускорения. |
Подотчетность | Обязанность учащихся, учителей, администраторов и другого школьного персонала за результаты обучения. Прочтите заявление NAGC об ответственности за обучение одаренных студентов. |
Тесты достижений | Тесты, предназначенные для измерения того, что учащиеся уже изучили, в основном в определенных областях содержания. Примером теста достижений являются Тесты базовых навыков штата Айова (ITBS). |
Advanced Placement (AP) | Программа, разработанная Советом колледжей, где средние школы предлагают курсы, соответствующие критериям, установленным высшими учебными заведениями. Во многих случаях кредит колледжа может быть получен после успешного завершения экзамена AP в определенных областях содержания (поскольку этот кредит варьируется в зависимости от колледжа и университета, рекомендуется направлять вопросы об этом процессе в колледж или университет по выбору студента. ).Программа Pre-AP предлагается младшим школьникам в качестве подготовки к курсам высшего уровня. Предложение курсов AP не эквивалентно предложению программы для одаренных. |
Эффективная учебная программа | Учебная программа, которая фокусируется на осознании личности / общества и адаптации и включает изучение ценностей, отношений и себя. Иногда называется социально-эмоциональной учебной программой. Посетите раздел «Поддержка эмоциональных потребностей одаренных». |
Aptitude | Склонность преуспеть в выполнении определенного навыка. |
Тест на способности | Тест, прогнозирующий будущую успеваемость студента в определенной области. Одним из таких тестов является SAT Test. См. Дополнительную информацию о тестировании. |
Асинхронность | Термин, используемый для описания несопоставимых темпов интеллектуального, эмоционального и физического роста или развития, которые часто демонстрируют одаренные дети. Более подробную информацию можно найти здесь. |
Под угрозой | Термин, используемый для описания учащихся, чьи экономические, физические, эмоциональные или академические потребности остаются неудовлетворенными или служат препятствием для признания или развития талантов, тем самым подвергая их опасности неуспеваемости или исключения из учебы. Прочтите больше информации. |
Аутентичная оценка | Оценка обучения студентов с помощью портфолио студентов, успеваемости или наблюдений вместо или в сочетании с более традиционными показателями успеваемости, такими как тесты и письменные задания.Этот процесс позволяет оценивать учащихся с помощью оценок, которые больше напоминают реальные задачи. Прочтите заявление о позиции NAGC по оценке. Посетите эти ссылки для получения дополнительной информации об аутентичных оценках и оценках, основанных на результатах. |
Таксономия Блума | Разработанная в 1956 году Бенджамином Блумом, систематика часто используется для разработки учебных программ для одаренных детей. В таксономии есть шесть уровней, которые переходят от базового к высокому уровню мышления.Первоначальные уровни включали знания, понимание, применение, анализ, синтез и оценку. Позднее таксономия была обновлена, чтобы отразить навыки 21-го века, при этом уровни изменились на запоминание, понимание, применение, анализ, оценку и творчество. |
Мозговой штурм | Мозговой штурм — это деятельность, используемая для генерирования множества творческих идей, на которые нет правильных или неправильных ответов и которые принимаются без критики.Эффективный мозговой штурм характеризуется беглостью и гибкостью мысли. |
Группировка кластеров | Групповое задание для одаренных учеников в обычном гетерогенном классе. Как правило, пять или шесть одаренных учеников со схожими потребностями, способностями или интересами «сгруппированы» в одном классе, что позволяет учителю более эффективно различать задания для группы продвинутых учеников, а не для одного или двух учеников.Посмотреть дополнительную информацию. |
Общие основные государственные стандарты (CCSS) | Набор академических стандартов по математике и искусству / грамотности английского языка (ELA), предложенный в 2013 году, в которых излагается, что ученик должен знать и уметь делать в конце каждого класса. В стандартах делается акцент на том, чтобы помочь студентам получить навыки и знания, необходимые для преуспевания в колледже и карьеры. Ознакомьтесь с заявлением о позиции NAGC по CCSS. Просмотрите список часто задаваемых вопросов об общих основных государственных стандартах и образовании для одаренных людей. |
Одновременная или двойная регистрация | Чаще всего относится к учащимся старших классов, посещающим курсы колледжа, часто для получения кредита в колледже. Двойное зачисление рассматривается как обеспечение преимуществ для старшеклассников, таких как более широкий доступ к более широкому спектру строгих академических и технических курсов, экономия времени и денег на получение степени в колледже, повышение эффективности обучения и улучшение приема и удержания в колледже. Эти термины также могут использоваться для обозначения учащихся среднего класса, посещающих курсы средней школы и получающих кредит по окончании учебы. |
Творчество | Процесс разработки новых, необычных или уникальных идей. Федеральное определение одаренности определяет творчество как особый компонент одаренности. |
Тестирование по критериям | Оценка, которая сравнивает результаты теста учащегося с его или ее владением совокупностью знаний или конкретными навыками, а не связывает баллы с успеваемостью других учащихся. |
Учащиеся с разнообразным культурным и языковым разнообразием (CLD) | Студенты из разных слоев общества, включая чернокожих, испаноязычных и азиатских национальностей, тех, кто изучает английский как второй язык, и тех, кто из малообеспеченных слоев общества. Часто считается, что эти студенты недостаточно представлены в одаренных программистах. Иногда их можно отнести к разным в культурном, лингвистическом и экономическом отношении студентам (CLED). Ознакомьтесь с позиционным документом NAGC по выявлению и обслуживанию этих студентов. |
Сжатие учебных программ | Методика обучения, которая позволяет учителям корректировать учебную программу для учащихся, определяя, какие учащиеся уже усвоили большую часть или все результаты обучения, и предлагая заменяющие инструкции или действия, которые позволяют более активно и продуктивно использовать время учащегося. Дополнительную информацию можно найти в Центре образования для одаренных детей им. Нэга при Университете Коннектикута. |
Дифференциация | Изменение учебной программы и инструкций в соответствии с содержанием, темпами и / или продуктом для удовлетворения уникальных потребностей учащихся в классе. |
Дистанционное обучение | Когда учащийся проходит курс удаленно (чаще всего через Интернет) в школе или учителе, отличном от его или ее местного / домашнего округа. Это могут быть онлайн-школы, массовые открытые онлайн-курсы (МООК), курсы с двойным зачетом в университетах или курсы, предлагаемые программами поиска талантов. Посетите Институт Дэвидсона для получения дополнительной информации. |
Изучающие английский язык | Студенты, изучающие английский как дополнительный язык.Особое внимание следует уделить тому, чтобы правильно идентифицировать этих студентов для одаренного программирования. Ознакомьтесь с руководством по выявлению и обслуживанию этой группы населения из Центра Белина Бланка. |
Обогащение | Мероприятия, которые дополняют существующую учебную программу или выходят за ее рамки. Они могут происходить в классе или в отдельной обстановке, например, в программе выездного обучения. |
Гибкое группирование | Учебная стратегия, при которой учащиеся объединяются в группы для получения соответствующих сложных инструкций.Настоящая гибкая группировка позволяет студентам входить и выходить из различных шаблонов группировки в зависимости от содержания курса. Группировка может быть определена по способностям, размеру и / или интересам. Прочтите позицию NAGC по группировке. |
одаренных и талантливых студентов | Федеральный закон о начальном и среднем образовании определяет одаренных и талантливых студентов как «студентов, детей или молодежь, которые демонстрируют высокие достижения в таких областях, как интеллектуальные, творческие, артистические или лидерские способности, или в определенных академических областях, и которые нуждаются в услугах и мероприятиях, которые обычно не предоставляются школой, для полного развития этих способностей.[Название IX, Часть A, Определение 22. (2002)] Многие штаты и округа следуют федеральному определению. Узнайте больше о том, как была определена одаренность, в исследовании | .
Гетерогенная группировка | Группировка студентов по смешанным способностям или уровням готовности. Разнородный класс — это класс, в котором от учителя ожидается удовлетворение широкого спектра потребностей или уровней готовности учащихся. Также называется инклюзивным или инклюзивным классом. Ознакомьтесь с изложением позиции NAGC по группировке способностей. |
Однородная группировка | Группировка студентов по потребностям, способностям или интересам. Хотя в однородном классе существуют различия между учениками, цель этого шаблона группирования — ограничить диапазон готовности учеников или потребностей, которые должен учитывать учитель. |
Идентификационный номер | Процесс определения студентов, подходящих для одаренных или продвинутых навыков программирования, идентификация чаще всего происходит с помощью интеллектуального или другого тестирования.Многие исследователи делают акцент на использовании нескольких способов идентификации, добавлении кандидатур учителей, родителей или сверстников или аутентичных оценок, таких как портфолио студенческих работ, в процесс. Более подробную информацию можно найти здесь. |
Инклюзивный класс | В инклюзивном классе учатся учащиеся разного уровня подготовки. Для получения дополнительной информации см. Гетерогенное группирование (выше). |
Независимое исследование | Стратегия самостоятельного обучения, при которой учитель выступает в роли наставника или фасилитатора, а ученик играет более активную роль в разработке и управлении своим собственным обучением, часто по теме, представляющей особый интерес для ученика. |
Индивидуальный план обучения (IEP) | IEP — это документ, определяющий услуги специального образования для учащихся с особыми потребностями. IEP включает в себя любые изменения, которые требуются в обычном классе, а также любые дополнительные специальные программы или услуги. Федеральный закон и большинство штатов не требуют IEP для одаренных учащихся. |
Интеллект | Способность учиться, рассуждать и решать проблемы.Споры вращаются вокруг природы интеллекта относительно того, является ли он врожденным качеством или чем-то, что развивается в результате взаимодействия с окружающей средой. Многие исследователи считают, что это комбинация этих двух факторов. |
Коэффициент интеллекта (IQ) | Числовое представление интеллекта. IQ получается путем деления умственного возраста (результат теста интеллекта) на хронологический возраст, умноженный на 100. Традиционно средний IQ считается равным 100. |
Программа международного бакалавриата (IB) | Сложная предуниверситетская программа, которую студенты могут пройти, чтобы заработать кредит колледжа. IB делает упор на критическое мышление и понимание других культур или точек зрения. По завершении программы IB выдается диплом, который позволяет выпускникам поступать в университеты по всему миру. Программа IB теперь включает программы среднего и начального классов. См. Статью из Центра обучения одаренных детей и развития талантов им. Ника |
Стили обучения / предпочтения обучения | Предпочтительный (ые) способ (ы), с помощью которых люди взаимодействуют или обрабатывают новую информацию в трех областях обучения, определенных в таксономии целей образования: когнитивный (знания), психомоторный (навыки) и аффективный (отношение).Предпочтения / стиль обучения человека — это то, как он или она учится лучше всего. |
Магнитные школы | Программа государственной школы, ориентированная на конкретную область обучения, такую как математика, естественные науки, технологии или исполнительское искусство. Магнитные школы были созданы для удовлетворения особых образовательных потребностей одаренных людей. |
Наставник | Член сообщества, который делится своим опытом со студентом, имеющим аналогичную карьеру или область обучения. |
Научные стандарты нового поколения (NGSS) | Набор академических стандартов в области естественных наук, предложенный в 2013 году, в котором излагается, что ученик должен знать и уметь делать в конце каждого класса. Стандарты делают упор на том, чтобы помочь студентам получить навыки и знания, необходимые для успешной учебы в колледже и карьеры. Щелкните здесь, чтобы ознакомиться с изложением позиции NAGC по NGSS. Просмотрите список часто задаваемых вопросов о стандартах и образовании для одаренных людей. |
Испытания на соответствие нормам | Оценка, которая сравнивает результаты отдельного человека с большой группой людей, которые прошли такую же оценку (которые называются «нормирующей группой»).Примеры включают в себя тесты SAT и Iowa по базовым навыкам. |
Повышенная возбудимость | Теория, предложенная Казимежем Домбровски, польским психологом, психиатром и врачом, которая предполагает, что некоторые люди имеют повышенную чувствительность, осведомленность и интенсивность в одной или нескольких из пяти областей: психомоторной, чувственной, интеллектуальной, образной и эмоциональной. |
Портфели | Являясь альтернативой или дополнением к традиционным методам измерения одаренности, портфолио предлагает набор студенческих работ с течением времени, которые могут помочь определить достижения и прогресс.Многие элементы портфолио не могут быть зафиксированы стандартным тестом. Больше информации здесь. |
Проблемно-ориентированное обучение (PBL) | Учебная программа и модель обучения, в которой учащимся предлагается решать реальные, сложные или открытые проблемы, используя исследования, принятие решений, творческое и критическое мышление и другие навыки 21 века. Узнайте больше в этой статье в информационном бюллетене Центра развития талантов. |
Программа вытягивания | Программа, которая выводит учащегося из обычного класса в течение учебного дня для специального программирования. |
Ответ на вмешательство (RtI) | RtI — это общеобразовательный метод выявления и обслуживания учащихся с различными образовательными потребностями, особенно детей с ограниченными возможностями. Прочтите описание RtI и того, как его можно использовать, Ассоциация одаренных / Совета по делам исключительных детей. |
Рубрика | Рубрика — это таблица, состоящая из критериев оценки и уровней выполнения этих критериев. Рубрика позволяет проводить стандартизированную оценку в соответствии с заданными критериями, делая ее более простой и прозрачной. |
Социально-эмоциональные потребности | Одаренные и талантливые ученики могут иметь аффективные потребности, которые включают повышенную или необычную чувствительность к самосознанию, эмоциям и ожиданиям от самих себя или других, а также чувство справедливости, морального суждения или альтруизма.Консультанты, работающие в этой области, могут решать такие проблемы, как перфекционизм, депрессия, заниженная самооценка, издевательства или низкая успеваемость. Ознакомьтесь с позиционным документом NAGC по социально-эмоциональным потребностям одаренных детей. |
ШТОК | Акроним для областей науки, технологий, инженерии и математики, обеспечивающий учебную программу STEM, поощряется как способ развития интересов и потенциала учащихся в этих областях. Некоторые исследователи относят искусство (STEAM) к этой категории обучения.Более подробную информацию можно найти здесь. |
Развитие талантов | Программы, учебные планы и услуги для одаренных и талантливых учащихся, которые могут наилучшим образом удовлетворить их потребности, способствовать их достижениям в жизни и способствовать развитию нашего общества, когда школы выявляют сильные стороны талантов учащихся и ориентируют образовательные услуги на эти таланты. Узнайте больше о развитии талантов от Пола Ольшевски-Кубилюса, директора Центра развития талантов Северо-Западного университета. |
Поиск талантов | Специальная программа, в которой используется внеклассное тестирование (обычно SAT или ACT) для выявления учащихся с высоким потенциалом и предоставления им возможности участвовать в различных внешкольных мероприятиях. Это могут быть субботние или летние курсы или программы дистанционного обучения. В США ведется четыре основных поиска талантов: Программа идентификации талантов Университета Дьюка (TIP), Центр развития талантов Северо-Западного университета (CTD), Центр талантливой молодежи Университета Джона Хопкинса (CTY) и Центр ярких детей (ранее Rocky Mountain Talent Search) в Денвере, штат Колорадо. |
Телескоп | Чтобы покрыть тот же объем материалов или заданий за меньшее время, тем самым предоставив больше времени для дополнительных заданий и проектов, которые лучше соответствуют интересам, потребностям и уровням готовности одаренных учащихся. |
Двойное исключение | Термин, используемый для описания одаренного ученика и инвалида. Эти студенты могут также упоминаться как имеющие двойную исключительность или как одаренные неспособностью к обучению (GT / LD).Это также относится к учащимся с одаренным СДВГ или аутизмом. Ознакомьтесь с позиционным документом NAGC. |
Неуспеваемость /Неуспеваемость | Термин, используемый для описания несоответствия между успеваемостью учащегося и его или ее потенциалом или способностью действовать на гораздо более высоком уровне. |
4 проверенных стратегии инклюзивного образования для преподавателей + 6 ресурсов
Учителя общего образования и учителя специального образования одинаково признают преимущества инклюзивного образования.Такой подход к обучению направлен на создание равноправной и благоприятной для каждого ученика среды обучения.
Что такое инклюзивное образование?
Инклюзивное обучение предоставляет всем учащимся доступ к гибким возможностям обучения и эффективным путям для достижения образовательных целей в местах, где они испытывают чувство принадлежности. В среде инклюзивного образования все дети, независимо от способностей или инвалидности, учатся вместе в одном классе, соответствующем их возрасту.Он основан на понимании того, что все дети и семьи ценятся одинаково и заслуживают доступа к одинаковым возможностям.
Инклюзивное обучение идет рука об руку с Универсальным дизайном для обучения (UDL), набором принципов разработки учебных программ, который дает всем учащимся равные возможности для обучения. По данным Национального центра универсального дизайна обучения, «UDL предоставляет план для создания учебных целей, методов, материалов и оценок, которые работают для всех, — не единого универсального решения, а достаточно гибких подходов, которые могут быть настроенным и приспособленным к индивидуальным потребностям.UDL имеет много общего с теорией множественного интеллекта, выдвинутой профессором Гарварда Говардом Гарднером, чья работа задокументировала «степень, в которой студенты обладают разным умом и, следовательно, учатся, запоминают, действуют и понимают по-разному».
ЗАРАБОТАЙТЕ ВАШЕГО МАСТЕРА! Видео исследует азбуку онлайн-медицины M.Ed. >>
Преимущества инклюзивного образования
Исследования показали преимущества инклюзивных классов для детей с ограниченными возможностями и их сверстников.Вместо того, чтобы вытаскивать детей из класса, чтобы предложить им специализированное обучение, в инклюзивном классе учителя специального образования входят в класс. Это позволяет учителям общего образования и специалистам работать вместе в одной учебной среде, принося пользу всем учащимся, которым предлагаются дополнительные ресурсы и поддержка. Такая поддержка часто приводит к большей академической успеваемости учащихся с ограниченными возможностями, а также учащихся без инвалидности.
[СВЯЗАННЫЕ] Как сделать карьеру: руководство для преподавателей >>
Think Inclusive сообщил об исследовании 2001 года, в котором изучалась «успеваемость учащихся с ограниченными возможностями в общеобразовательных и автономных классах за два года.47,1% учащихся с ограниченными возможностями в общеобразовательных школах добились успехов в математике по сравнению с 34% в автономных классах. Прогресс чтения был сопоставим в обеих настройках. Интересно, что исследование показало, что типичные сверстники лучше успевают по математике, когда присутствуют ученики с ограниченными возможностями. Исследователи предположили, что дополнительная помощь и поддержка в этих классах принесла пользу всем учащимся ».
Дополнительные преимущества включают улучшение коммуникативных и социальных навыков учащихся с ограниченными возможностями, а также меньшее количество случаев деструктивного поведения и пропусков занятий.
Стратегии инклюзивного образования
Готовы ли вы ввести в свой класс среду инклюзивного образования? Сделать это означает бросить вызов существующему положению вещей, устранить препятствия в учебной программе и интересно представить образовательные цели, чтобы вовлечь всех учащихся и на равноправной основе служить всем учащимся. Ниже приведены четыре важные стратегии, которые следует учитывать при разработке инклюзивного класса и учебной программы.
- Используйте универсальные принципы дизайна для создания доступных классных комнат
UDL — это набор принципов, рожденных из желания предоставить каждому ученику равные возможности для обучения, основанных на идее, что у каждого человека есть свои уникальные и индивидуальные особенности. стиль обучения.Согласно UDL, существуют три основные сети мозга, которые отвечают за то, как человек учится: сеть распознавания, стратегическая сеть и аффективная сеть. Три основных принципа UDL — представление (что изучается), действие и выражение ( как учиться), Вовлеченность (зачем учиться) — были сформированы на основе этих трех мозговых сетей. Понимание основы UDL — принципов и сетей мозга — необходимо учителям, которые хотят внедрить UDL в классе.Национальный центр универсального дизайна для обучения имеет множество ресурсов и информации для преподавателей, интересующихся универсальным дизайном. Вы найдете видео с полезными советами и идеями по внедрению в разделе «Принципы и методы UDL» на их канале YouTube.
Луис Перес, автор книги Mobile Learning for All, предлагает начать с малого. В статье в The Journal он сказал: «Вы не собираетесь применять все (рекомендации) к каждому уроку. Это зависит от того, какие из них соответствуют вашим целям обучения.Начните с одного урока или упражнения, а затем добивайтесь успеха, а затем начните изучать другие части своей учебной программы ». - Используйте различные форматы обучения
Первый принцип универсальной теории дизайна — это «что» обучения. В нем говорится об использовании «множественных средств представления». В то время как некоторые ученики обучаются визуально, другие могут лучше усваивать информацию, когда она представлена в виде текста, или когда она произносится устно или преподается посредством кинестетического обучения.Некоторым ученикам лучше всего удается сочетать вышеперечисленное. Хотя эти дифференцированные методы обучения могут удовлетворить потребности учащихся с ограниченными возможностями, они также предлагают разнообразное обучение всему классу, давая каждому учащемуся возможность учиться так, как он умеет. Точно так же использование различных средств для представления информации и вовлечения учащихся важно в инклюзивных классах. Помните, что второй принцип универсальной теории дизайна призывает к использованию «множественных средств действия и выражения.«Некоторые студенты могут обнаружить, что их лучший выход и средства выражения — это письмо, в то время как другие могут предпочесть сделать устную презентацию, разыграть пьесу или создать произведение искусства. Каждый студент индивидуален, и им следует дать возможность выразить свое мнение. их знания с помощью методов, которые лучше всего подходят для них. Кроме того, учителя могут использовать различные материалы и средства для привлечения учащихся. Примеры средств массовой информации могут включать театр, искусство, видео и компьютерное программное обеспечение в дополнение к традиционным средствам лекций и текстов.Используя различные методы и средства обучения, учителя могут повысить вовлеченность всего класса, а не только учащихся, которые реагируют на определенный стиль обучения и выражения. - Знайте IEP / 504 ваших студентов
Чтобы создать равную среду обучения для всех, важно ознакомиться с IEP или планами 504 студентов. Если у вас есть ученик с планом 504 или IEP, вы по закону обязаны сделать все необходимые приспособления, как указано в планах 504 или IEP.Вы можете работать со школьным консультантом или специалистами по обучению, чтобы лучше понять конкретные потребности учащегося. Подобно концепции инклюзивного обучения, модели 504 были разработаны для обеспечения того, чтобы учащимся с ограниченными возможностями было разрешено учиться в обычной классной среде, но при этом они были обеспечены услуги, учебные пособия или приспособления, которые могут им потребоваться. IEP лишь немного отличается от 504; разница в том, что учащимся с IEP могут потребоваться дополнительные образовательные услуги вне обычного класса.Эти услуги обычно предоставляются и контролируются дополнительным вспомогательным персоналом. - Разработайте план управления поведением
Деструктивное поведение в классе может повлиять не только на учителя, но и на других учеников в классе. Разработка плана управления поведением может помочь вам подготовиться к неизбежному моменту, когда ученик или ученики проявят деструктивное поведение — с пониманием того, что одни виды поведения имеют гораздо меньшие последствия, чем другие (вне очереди против разговоров.План поведения должен быть представлен родителям и учащимся, чтобы все знали об ожиданиях и последствиях, если эти ожидания не оправдаются. Наиболее эффективные планы обычно включают в себя множество положительных подкреплений и четкое понимание ожиданий. Существует несколько различных типов планов управления поведением, которые вы можете реализовать в зависимости от потребностей вашего класса, в том числе план для всей группы, план для небольшой группы, индивидуальный план или индивидуальный план, разработанный для особо сложных учеников.
Инклюзивные учебные ресурсы для учителей
- Сеть инклюзивных школ — ISN — это цифровой ресурс для семей, школ и сообществ, желающих разработать и внедрить эффективные инклюзивные школы. Они предлагают широкий спектр ресурсов, включая инструменты оценки, стратегии сотрудничества, советы по технологиям и многое другое.
- Национальный центр по проблемам обучаемости — NCLD защищает людей с ограниченными возможностями, предлагая программы и ресурсы для родителей, молодых людей, специалистов и преподавателей.Они также публикуют отчеты и исследования по ряду тем, связанных с инвалидностью, и предлагают информацию о стипендиях для студентов с проблемами обучения и внимания.
- Wrightslaw– Wrightslaw — отличный ресурс для тех, кто хочет узнать больше или оставаться в курсе последних новостей о специальном образовании, законодательстве об образовании и защите интересов детей с ограниченными возможностями.
- TASH — TASH работает над продвижением инклюзивных сообществ посредством защиты интересов, исследований, профессионального развития, политики и информации, а также ресурсов для родителей, семей и самозащитников.Они предлагают несколько различных публикаций, включая блог, годовые отчеты, подкаст и многое другое.
- ASCD — Ассоциация по надзору и разработке учебных программ (ASCD) охватывает ряд образовательных тем, не ограничиваясь инклюзивным обучением. Это отличный ресурс для преподавателей по всем дисциплинам и уровням обучения, независимо от того, хотят ли они создать инклюзивную школу или просто найти новые стратегии для повышения своей эффективности в классе.
В Университете Сан-Диего мы верим в силу инклюзивного обучения.Мы также понимаем важность образованных преподавателей, когда речь идет о инклюзивном и специальном образовании. Вот почему мы предлагаем 100% онлайн-степень магистра образования со специализацией в инклюзивном обучении, специальном образовании и универсальном дизайне. Чтобы узнать больше и просмотреть учебную программу, посетите страницу программы USD Master of Education.
Педагогика: все, что вам нужно знать о практике обучения
«Обычно в жизни знания приобретаются для использования.Но школьное обучение чаще соответствует метафоре Фрейре: со знаниями обращаются как с деньгами, которые нужно отложить в банк на будущее ». Сеймур Пейперт, Детская машина: переосмысление школы в век компьютеров
Принципы и практика преподавания — это одновременно искусство и наука. Образование влияет на наши самые молодые поколения, оно вдохновляет детей мыслить иначе и развивает критическое мышление в молодых, влиятельных умах.
В школе дети приобретают языковые, естественные и математические навыки, которые они могут использовать в дальнейшей жизни.Образование оказывает повторяющееся воздействие спустя долгое время после того, как дети становятся взрослыми.
Принципы обучения постоянно развиваются; совместное обучение, перевернутое обучение и глубокое обучение — все это основа современного обучения.
Что такое педагогика?
Если обучение — это акт поощрения учебной деятельности посредством открытий и приобретенных знаний, то педагогика — это метод обучения, как академический предмет, так и теоретическая концепция.
В педагогике существует четыре основных профиля обучения:
- Слушатели извлекают пользу из информации, представленной им в классе. Они учатся устно, слушая инструкции учителя и аудиозаписи.
- Тактильные / кинестетические учащихся усваивают знания посредством прикосновений и движений. Они предпочитают работать с практическими устройствами и учебными пособиями.
- Зрительные ученики предпочитают видеть информацию, чтобы визуализировать взаимосвязь между идеями и концепциями, чтобы понять их.
- Учащиеся, обучающиеся чтению и письму предпочитают воспринимать информацию, читая тексты. Эти учащиеся могут дополнительно усваивать информацию, уплотняя и перефразируя ее.
Сегодня учителя имеют преимущество в использовании традиционных методов обучения при одновременном использовании новых образовательных технологий для создания разнообразной, дифференцированной классной комнаты, готовой для учеников со смешанными способностями.
Хотите узнать, как учителя могут создать более дифференцированную среду? Ознакомьтесь с нашей инфографикой — переосмыслением современного класса.
Почему обучение должно быть совместным?
Совместное обучение — это метод активного обучения, основанный на принципе совместной работы двух или более студентов для достижения общей цели. Эти виды деятельности сильно различаются, но большинство из них сосредоточено на изучении учащимся или применении учебной программы, а не просто на точке зрения учителя.
Совместное обучение дает ученикам уверенность в том, что они могут учить и учиться у своих сверстников и учителей.Особенно в начальных школах совместное обучение поможет развить межличностные навыки в более раннем возрасте, помогая детям стать более эффективными коммуникаторами.
Различия между совместным обучением и совместным обучением могут быть взаимозаменяемыми для педагогов, однако совместное обучение побуждает учащихся добиваться индивидуального прогресса в тандеме с другими. Между тем совместное обучение способствует взаимозависимости подотчетности. Узнайте больше о преимуществах совместного обучения.
Узнайте, как совместный подход помогает развивать у учащихся навыки межличностного общения и как преодолевать препятствия на пути к совместному обучению, из нашего бесплатного руководства.
Что более эффективно — современное или традиционное обучение?
Сегодня в школьном образовании часто используются технологии и различные стили обучения. Однако многие из современных методов обучения представляют собой эволюцию более традиционных методов обучения.
Ключ к расширенному и целостному обучению заключается в том, чтобы взять принципы как традиционного, так и современного обучения и объединить их для создания полностью иммерсивной учебной среды.
Наша инфографика показывает, как современные технологии помогают учителям придать своим традиционным методам обучения новый современный вид.
Как учителя могут повысить вовлеченность учеников
Удержание внимания учеников — постоянная битва для учителей.Однако при использовании правильных инструментов и методов вовлечение учеников становится гораздо более достижимым.
Вовлеченность студентов можно измерить на трех уровнях:
- Поведенческие участие с демонстрацией хорошего поведения в классе
- Эмоциональная вовлеченность путем оценки того, что они изучают
- Когнитивное взаимодействие посредством демонстрации максимальных усилий для понимания предмета
Чем больше воодушевлены и увлечены ученики, тем внимательнее они будут относиться к предмету, что способствует более эффективному обучению.
Молодое поколение окружено технологиями, поэтому образовательные технологии могут быть сильным отличием в классе, чтобы поддерживать их вовлеченность, но при этом должны поддерживать потребности учеников и результаты обучения.
В конце концов, обучение должно доставлять удовольствие. Он должен побуждать к активности и стимулировать дискуссии среди учеников. Например, викторины могут способствовать активному участию учеников.
Загрузите наше бесплатное руководство, чтобы получить практические советы и рекомендации по повышению вовлеченности в вашей школе.
Руководство по обучению персонала и поддержке образовательных технологий, чтобы ваши вложения в ИТ принесли пользу всей школе.
Получите свой фреймворкПоколение Z учится иначе, чем миллениалы и старшее поколение?
Те, кто родился после 1995 года, считаются нео-миллениалами, или поколением Z. Это поколение наиболее технически подкованное и цифровое. Итак, нужно ли учителям адаптировать свои методы обучения с учетом своих предпочтений? Или младшим школьникам просто нужно учиться так же, как и всем предшествующим поколениям?
Ученики младшего возраста могут предпочесть цифровой подход к обучению, но стоит отметить, что недостаточно использовать больше технологий ради этого.Между тем обучение неомилленариев — это особый метод, который предполагает более широкое использование технологий и мультимедиа для обеспечения возможности обучения на 360 градусов.
Это связано с тем, что у поколения Z или нео-миллениалов разные предпочтения, цели и ценности по сравнению с предыдущими поколениями, даже миллениалами. Таким образом, некоторые эксперты по педагогике предложили адаптировать методы обучения к предпочтениям этой группы.
В отличие от старшего поколения, поколение Z лучше учится благодаря:
- Интерактивные занятия
- Совместные проекты
- Практические задачи
Тем не менее, роль учителя по-прежнему является наиболее важным аспектом обучения; интерактивные инструменты не могут заменить традиционную педагогику.
Прочтите, как новые подходы к современному обучению улучшают успеваемость учащихся и успеваемость в школе.
Как и почему учителя должны использовать социальные сети в обучении?
В мире цифровых технологий ученики окружены платформами социальных сетей. Могут ли быть социальные сети в образовании, которые в значительной степени отвлекают учителей или создают угрозу электронной безопасности?
«Технологии, используемые в образовании, могут иметь положительный эффект.Однако социальные сети сегодня являются одной из самых больших проблем, влияющих на поведение и вовлеченность в школе ». Заместитель директора, Хартлпул, Отчет о состоянии технологий в образовании, 2016/17
Однако в некоторых сценариях может быть полезно адаптировать платформы социальных сетей, такие как Twitter, Facebook и даже Snapchat, для современного класса.
- Помогите ученикам исследовать темы и выявлять фейковые новости в Twitter
- Развивайте совместное обучение и развивайте творческое мышление с Pinterest
- Предложите ученикам рассказать о школьных мероприятиях с помощью Snapchat
Полное руководство по использованию Pinterest для поиска и обмена ресурсами для учителей и вдохновляющих учеников можно найти в нашем блоге.
Почему перевернутое обучение эффективно?
Перевернутое обучение — это метод, который дает учащимся время дома, чтобы заняться предметом или темой, прежде чем приступить к выполнению соответствующих задач и практических занятий в школьные часы.
«Формальное обучение похоже на поездку в автобусе: водитель решает, куда едет автобус; пассажиры едут вместе. Неформальное обучение похоже на езду на велосипеде: гонщик выбирает пункт назначения, скорость и маршрут.Джей Кросс, «Неформальное обучение: новое открытие естественных путей, которые вдохновляют на инновации и производительность»
Три четверти опрошенных учителей сообщают о более высоком уровне вовлеченности в классе после внедрения перевернутого обучения. Так. почему обратное обучение так эффективно в современном классе?
Может быть, это гибкий подход?
Перевернутое обучение позволяет учащимся получать доступ к материалам в удобное для них время.
Снижено ли бремя домашней работы?
Перевернутое обучение позволяет ученикам усваивать основную информацию дома и сохранять более общие вопросы и предложения для часов занятий.
Существуют некоторые препятствия для реализации перевернутого обучения, такие как самодисциплина у учеников и нехватка ресурсов, но в целом такой подход позволяет более активно проводить время в классе.
Чтобы изучить влияние совместной работы как в классе, так и за его пределами, загрузите наше бесплатное руководство.
Откройте для себя специальные технологии, разработанные учителями для максимальной учебной ценности
Запросить демоЧто такое глубокое обучение?
Глубокое обучение позволяет студенту взять принципы из одной ситуации и применить их к другой.
Подготовка учеников к будущему может быть невероятно сложной задачей для учителей.
Тем более во все более управляемом данными, автоматизированном мире; сегодняшние ученики растут по сценарию, при котором половина завтрашних рабочих мест еще не существует. Итак, овладение передаваемыми, реальными навыками даже более важно для сегодняшних учеников, чем вчерашние.
«Навыки, которым проще всего обучить, проверить метод и вспомнить, также легче всего автоматизировать». Отчет о непрерывном обучении, Институт директоров
Ученикам необходимо шесть основных навыков для глубокого обучения:
- Сотрудничество
- Творчество
- Критическое мышление
- Гражданство
- Персонаж
- Связь
Прочтите в нашем блоге, почему глубокое обучение следует применять в современной учебной среде.
Как в школах должны преподаваться классы для детей с разными уровнями подготовки?
Способность ученика к обучению не является синонимом его готовности или мотивации. Есть три основных условия обучения, которые влияют на подход ученика к обучению.
- Готовность к обучению
- Обучение Способность
- Обучение интерес
Преподавание в классе смешанного профиля проблематично; может потребоваться дифференцированное обучение, чтобы вовлечь весь класс.Учителя со смешанными классами полагаются на творческие методы обучения и интерактивные ресурсы. Важно, что учителя должны:
- Индивидуализировать содержание обучения
- Плюрализируйте своих методов обучения
Сначала важно определить различия между профилями обучения в классе. К ним относятся:
- невидимый ребенок
- отстающий
- правильное место, неправильное время учащийся
- Обучаемый с потенциальной специализацией
- немотивированных учеников
- отлично подготовлен ученик
- нуждающийся ученик
Существуют методы дифференциации, которые можно использовать для вовлечения всех профилей учащихся.В конечном итоге участие является ключом к развитию мотивации и уверенности в классе.
Стандартов для математической практики | Инициатива Common Core State Standards
Стандарты математической практики описывают различные виды знаний, которые преподаватели математики на всех уровнях должны стремиться развивать у своих учеников. Эти практики опираются на важные «процессы и навыки», имеющие давнюю важность в математическом образовании.Первыми из них являются стандарты процесса NCTM для решения проблем, обоснования и доказательства, коммуникации, представления и связей. Вторые — это направления математической подготовки, указанные в отчете Национального исследовательского совета Adding It Up : адаптивное мышление, стратегическая компетентность, концептуальное понимание (понимание математических концепций, операций и отношений), беглость процедур (умение гибко выполнять процедуры, точно, эффективно и уместно) и продуктивному расположению (привычная склонность считать математику разумной, полезной и стоящей, в сочетании с верой в усердие и собственную эффективность).
Стандарты в этой области:
CCSS.Math.Practice.MP1 Осознавайте проблемы и упорно продолжайте их решать.
Студенты со знанием математики начинают с объяснения себе значения проблемы и поиска точек входа для ее решения. Они анализируют данные, ограничения, отношения и цели. Они строят предположения о форме и значении решения и планируют путь решения, а не просто предпринимают попытки решения. Они рассматривают аналогичные проблемы и пробуют частные случаи и более простые формы исходной проблемы, чтобы получить представление о ее решении.Они отслеживают и оценивают свой прогресс и при необходимости меняют курс. Старшие ученики могут, в зависимости от контекста задачи, преобразовывать алгебраические выражения или изменять окно просмотра на своем графическом калькуляторе, чтобы получить необходимую информацию. Математически опытные студенты могут объяснять соответствия между уравнениями, словесными описаниями, таблицами и графиками или рисовать диаграммы важных функций и отношений, графических данных и искать закономерности или тенденции. Младшие ученики могут полагаться на использование конкретных предметов или изображений, чтобы помочь осмыслить и решить проблему.Математически опытные ученики проверяют свои ответы на задачи, используя другой метод, и они постоянно спрашивают себя: «Имеет ли это смысл?» Они могут понимать подходы других к решению сложных проблем и определять соответствия между разными подходами.
CCSS.Math.Practice.MP2 Размышляйте абстрактно и количественно.
Учащиеся со знанием математики понимают величины и их отношения в проблемных ситуациях. Они привносят две взаимодополняющие способности для решения проблем, связанных с количественными отношениями: способность деконтекстуализировать — абстрагироваться от данной ситуации и представлять ее символически и манипулировать символами представления, как если бы они жили своей собственной жизнью, не обязательно обращая внимание на своих референтов. — и возможность контекстуализировать , останавливаться по мере необходимости во время процесса манипуляции, чтобы исследовать референты для задействованных символов.Количественные рассуждения влекут за собой привычку создавать связное представление о рассматриваемой проблеме; с учетом задействованных единиц; внимание к значению количеств, а не только к тому, как их вычислить; знание и гибкое использование различных свойств операций и объектов.
CCSS.Math.Practice.MP3 Создавайте жизнеспособные аргументы и критикуйте рассуждения других.
Студенты со знанием математики понимают и используют заявленные предположения, определения и ранее установленные результаты при построении аргументов.Они делают предположения и выстраивают логическую последовательность утверждений, чтобы исследовать истинность своих предположений. Они могут анализировать ситуации, разбивая их на случаи, распознавать и использовать контрпримеры. Они обосновывают свои выводы, сообщают их другим и отвечают на аргументы других. Они индуктивно рассуждают о данных, приводя правдоподобные аргументы, учитывающие контекст, из которого эти данные возникли. Математически опытные учащиеся также могут сравнивать эффективность двух правдоподобных аргументов, отличать правильную логику или рассуждения от ошибочных и — если в аргументе есть изъян — объяснять, что это такое.Учащиеся начальной школы могут строить аргументы, используя конкретные референты, такие как объекты, рисунки, диаграммы и действия. Такие аргументы могут иметь смысл и быть правильными, даже если они не обобщаются и не принимаются формально до более поздних оценок. Позже студенты учатся определять области, к которым применим аргумент. Учащиеся всех классов могут слушать или читать аргументы других, решать, имеют ли они смысл, и задавать полезные вопросы, чтобы прояснить или улучшить аргументы.
CCSS. Математика. Практика.Модель MP4 с математикой.
Студенты со знанием математики могут применять полученные знания для решения задач, возникающих в повседневной жизни, в обществе и на рабочем месте. В младших классах это может быть так же просто, как написать дополнительное уравнение для описания ситуации. В средних классах ученик может применять пропорциональное рассуждение для планирования школьного мероприятия или анализа проблемы в сообществе. В старшей школе ученик может использовать геометрию для решения проектной задачи или использовать функцию, чтобы описать, как одна интересующая величина зависит от другой.Математически опытные студенты, которые могут применять то, что они знают, комфортно делают предположения и приближения, чтобы упростить сложную ситуацию, понимая, что они могут потребовать пересмотра позже. Они могут определять важные величины в практической ситуации и отображать свои отношения с помощью таких инструментов, как диаграммы, двусторонние таблицы, графики, блок-схемы и формулы. Они могут математически проанализировать эти отношения, чтобы сделать выводы. Они обычно интерпретируют свои математические результаты в контексте ситуации и размышляют о том, имеют ли результаты смысл, возможно, улучшая модель, если она не служит своей цели.
CCSS.Math.Practice.MP5 Стратегически используйте соответствующие инструменты.
Студенты, разбирающиеся в математике, рассматривают доступные инструменты при решении математической задачи. Эти инструменты могут включать карандаш и бумагу, конкретные модели, линейку, транспортир, калькулятор, электронную таблицу, систему компьютерной алгебры, статистический пакет или программное обеспечение для динамической геометрии. Опытные студенты в достаточной мере знакомы с инструментами, соответствующими их классу или курсу, чтобы принимать обоснованные решения о том, когда каждый из этих инструментов может быть полезен, признавая как понимание, которое необходимо получить, так и их ограничения.Например, старшеклассники со знанием математики анализируют графики функций и решений, сгенерированные с помощью графического калькулятора. Они обнаруживают возможные ошибки, стратегически используя оценки и другие математические знания. Создавая математические модели, они знают, что технологии могут позволить им визуализировать результаты различных предположений, исследовать последствия и сравнивать прогнозы с данными. Учащиеся с математическими знаниями в различных классах могут определять соответствующие внешние математические ресурсы, такие как цифровой контент, размещенный на веб-сайте, и использовать их для постановки или решения задач.Они могут использовать технологические инструменты для изучения и углубления понимания концепций.
CCSS.Math.Practice.MP6 Внимание к точности.
Учащиеся со знанием математики стараются общаться с другими именно так. Они пытаются использовать четкие определения в обсуждениях с другими и в своих собственных рассуждениях. Они заявляют значение выбранных символов, в том числе используют знак равенства последовательно и надлежащим образом. Они осторожны при указании единиц измерения и маркировке осей, чтобы уточнить соответствие количеству в проблеме.Они производят точные и эффективные вычисления, выражают числовые ответы со степенью точности, соответствующей контексту проблемы. В начальных классах ученики дают друг другу тщательно сформулированные объяснения. К моменту поступления в среднюю школу они научились проверять утверждения и четко использовать определения.
CCSS.Math.Practice.MP7 Ищите и используйте структуру.
Студенты, разбирающиеся в математике, внимательно приглядываются, чтобы различить образец или структуру. Например, молодые студенты могут заметить, что три и семь больше равны семи и еще трем, или они могут отсортировать набор фигур в зависимости от того, сколько сторон у них.Позже студенты увидят, что 7 × 8 равно хорошо запоминающимся 7 × 5 + 7 × 3, при подготовке к изучению свойства распределения. В выражении x 2 + 9 x + 14 старшие школьники могут видеть 14 как 2 × 7 и 9 как 2 + 7. Они осознают значение существующей линии в геометрической фигуре и могут использовать стратегия рисования вспомогательной линии для решения задач. Они также могут сделать шаг назад для обзора и изменения перспективы. Они могут видеть сложные вещи, такие как некоторые алгебраические выражения, как отдельные объекты или состоящие из нескольких объектов.Например, они могут видеть 5-3 ( x — y ) 2 как 5 минус положительное число, умноженное на квадрат, и использовать это, чтобы понять, что его значение не может быть больше 5 для любых действительных чисел x и y .
CCSS.Math.Practice.MP8 Ищите и выражайте закономерность в повторяющихся рассуждениях.
Студенты, разбирающиеся в математике, замечают, если вычисления повторяются, и ищут как общие методы, так и ярлыки. При делении 25 на 11 ученики старших классов могут заметить, что они повторяют одни и те же вычисления снова и снова, и прийти к выводу, что у них есть повторяющаяся десятичная дробь.Уделяя внимание вычислению наклона, поскольку они неоднократно проверяют, находятся ли точки на прямой, проходящей через (1, 2) с наклоном 3, ученики средней школы могут абстрагироваться от уравнения ( y — 2) / ( x — 1) = 3. Обратите внимание на регулярность отмены терминов при раскрытии ( x — 1) ( x + 1), ( x — 1) ( x 2 + x + 1), и ( x — 1) ( x 3 + x 2 + x + 1) может привести их к общей формуле для суммы геометрического ряда.Работая над решением задачи, ученики с математическими навыками следят за процессом, уделяя внимание деталям. Они постоянно оценивают обоснованность своих промежуточных результатов.
Соединение стандартов математической практики со стандартами математического содержания
Стандарты математической практики описывают способы, с помощью которых развивающиеся студенты, практикующие математическую дисциплину, должны все больше вовлекаться в предмет по мере того, как они растут в математической зрелости и опыте на протяжении младших, средних и старших классов школы.Разработчики учебных программ, оценивания и повышения квалификации должны уделять внимание необходимости увязать математические практики с математическим содержанием в обучении по математике.
Стандарты математического содержания представляют собой сбалансированное сочетание процедуры и понимания. Ожидания, начинающиеся со слова «понять», часто являются особенно хорошей возможностью связать практики с содержанием. Студенты, которым не хватает понимания темы, могут слишком сильно полагаться на процедуры.Без гибкой основы для работы они с меньшей вероятностью будут рассматривать аналогичные проблемы, связно представлять проблемы, обосновывать выводы, применять математику к практическим ситуациям, осознанно использовать технологии для работы с математикой, точно объяснять математику другим ученикам, сделайте шаг назад, чтобы получить обзор, или отклонитесь от известной процедуры, чтобы найти ярлык. Короче говоря, непонимание фактически мешает студенту заниматься математической практикой.
В этом отношении те стандарты содержания, которые устанавливают ожидания понимания, являются потенциальными «точками пересечения» между Стандартами математического содержания и Стандартами математической практики.Эти точки пересечения предназначены для взвешивания по отношению к центральным и генеративным концепциям школьной программы математики, которые в наибольшей степени заслуживают времени, ресурсов, инновационной энергии и внимания, необходимых для качественного улучшения учебной программы, обучения, оценивания, профессионального развития и успеваемости учащихся в школе. математика.
Как мне помочь моим ученикам преодолеть их альтернативные концепции (заблуждения) относительно обучения
Александр, П. А. (2006).Психология в обучении и обучении. Верхняя Сэдл-Ривер, Нью-Джерси: Pearson Education, Inc.
Arnaudin, M., & Mintzes, J. (1985). Альтернативные представления студентов о системе кровообращения человека: исследование разных возрастов. Научное образование, 69 (5), 721-733.
Arnaudin, M., & Mintzes, J. (1986). Сердечно-сосудистая система: детские представления и заблуждения. Наука и дети, 23 (5), 48-51.
Этвуд, Р. К., и Этвуд, В.А. (1996). Представления учителей начальной школы о причинах времен года. Журнал исследований в области преподавания естественных наук , 33 (5), 553-563.
Айылдз, Ю., и Тархан, Л. (2013). Примеры использования на уроке химии: газы, жидкости и твердые тела. Исследования и практика химического образования, 14 (4), 408-420.
Бакстер, Дж. (1995). Детское понимание астрономии и наук о Земле. В S.M. Glynn & R.Дуит (ред.), Изучение науки в школах (стр. 155-178). Махва, Нью-Джерси: Эрлбаум.
Бит, М. Э. (1998). Преподавание естественных наук в 5-м классе: учебные цели, поддерживающие концептуальные изменения. Журнал исследований в области преподавания естественных наук, 35 (10), 1091-1101.
Beeth, M. E., & Hewson, P. W. (1999). Цели обучения в образцовой практике учителя естественных наук: когнитивные и социальные факторы в обучении для концептуальных изменений. Естественное образование , 83 (6), 738-760.
Брансфорд, Дж. Д., Браун, А. Л., и Кокинг, Р. Р. (ред.). (2000). Как люди учатся: мозг, разум, опыт и школа. Вашингтон, округ Колумбия: Национальная академия прессы.
Брюэр, В. Ф. и Чинн, К. А. (1991). Меняются укоренившиеся убеждения, противоречивая информация и знания. В Л. Бирнбауме (ред.), Международная конференция обучающихся наук: Материалы конференции 1991 г. (стр. 67-73). Шарлоттсвилль, Вирджиния: Ассоциация развития вычислительной техники в образовании.
Браун, Д. Э. (1992). Использование примеров и аналогий для исправления неправильных представлений в физике: факторы, влияющие на концептуальные изменения. Журнал исследований в области преподавания естественных наук, 29 (1), 17-34.
Браун Д. Э. и Клемент Дж. (1989). Преодоление заблуждений с помощью рассуждений по аналогии: абстрактный перенос против построения объяснительной модели. Международная наука, 18, 237-261.
Браун, Дж. С., и Бертон, Р. Р. (1978). Диагностические модели для процедурных ошибок в основных математических навыках. Когнитивная наука , 2, 155–192.
Бургун, Джейкоб Н., Хеддл, Мэнди Л., и Дюран, Эмилио. (2010). Пересмотр сходства между представлениями учителя и ученика о физических науках. Journal of Science Teacher Education, (7), 859-872.
Кэри, С. (1985). Концептуальные изменения в детстве. Кембридж, Массачусетс: MIT Press.
Кэри, С. (1986). Когнитивная наука и естественнонаучное образование. Американский психолог, 41, 1123-1130.
Картер, Пруденс Л. (2006). Трансграничные границы: идентичность, культура и школа. Социология образования, 79 (4), Том 79 (4), с.304.
Кейс, Р. (1997). Разработка концептуальных конструкций. В книге Д. Куна и Р. С. Сиглера (ред.), Справочник по детской психологии (том 2): восприятие, познание и язык (стр. 745-800). Нью-Йорк: Вили.
Шампанское, А. Б., Ганстон, Р. Ф., и Клопфер, Л. Е. (1985).Влияние изменений когнитивных структур у студентов-физиков. В Х. Т. Уэст и А. Л. Пайнс (ред.), Когнитивная структура и концептуальные изменения (стр. 61-90). Орландо, Флорида: Academic Press.
Чи, М. Т. Х. (1992). Концептуальные изменения внутри и между онтологическими категориями: последствия для обучения и открытий в науке. В Р. Гиере (ред.), Миннесотские исследования в философии науки (Том XV): Когнитивные модели науки (стр. 129-186). Миннеаполис, Миннесота: Университет Миннесоты Press.
Чи, М. Т. Х. (2000). Самообъясняющий: двойной процесс создания вывода и исправления ментальных моделей. В Р. Глейзере (ред.), Достижения в педагогической психологии (Том 5): Образовательный дизайн и когнитивная наука (стр. 161-238). Махва, Нью-Джерси: Эрлбаум.
Чи, М. Т. Х. (2005). Здравые представления о возникающих процессах: почему некоторые заблуждения устойчивы. The Journal of Learning Sciences, 14, 161–199.
Чинн, К.А., И Брюэр, У. Ф. (1993). Роль аномальных данных в приобретении знаний: теоретическая основа и значение для научного обучения. Обзор исследований в области образования, 63, 1-49.
Чинн, К. А., и Брюер, В. Ф. (1998). Эмпирический тест таксономии ответов на аномальные данные в науке. Журнал исследований в области преподавания естественных наук, 35 (6), 623-654.
Чинн, К. А., и Малхотра, Б. А. (2002). Реакция детей на аномальные научные данные: как препятствуют концептуальным изменениям? Журнал педагогической психологии, 94 (2), 327-343.
Чиу М. Х. и Лин Дж. У. (2005). Содействие концептуальному изменению представления четвероклассниками об электрическом токе с помощью множества аналогий. Журнал исследований в области преподавания естественных наук , 42 (4), 429-464.
Клемент, Дж. (1982). Предвзятые мнения студентов по вводной механике. Американский журнал физики , 50 (1), 66-71.
Комитет по естественным наукам, от детского сада до восьмого класса (2007). Использование естественных наук в школе: изучение и преподавание естественных наук в классах K-8.Вашингтон, округ Колумбия: Национальная академия прессы.
Диакидой, И. А., Кендеу, П., и Иоаннидес, К. (2003). Чтение об энергии: влияние структуры текста на научное обучение и концептуальные изменения. Современная психология образования , 28 (3), 335-356.
Duschl, R., & Osborne, J. (2002). Поддержка и продвижение дискурса аргументации. Исследования в области естественнонаучного образования, 38, 39-72.
Эрыылмаз, А. (2002). Влияние концептуальных заданий и обсуждений концептуальных изменений на неправильные представления и достижения учащихся в отношении силы и движения.Журнал исследований в области преподавания естественных наук, 39 (10), 1001-1015.
Фолкнер, К. П., Леви, Л., и Карпентер, Т. П. (1999). Детское понимание равенства: основа алгебры. Обучение детей математике , 6 (4), 232-236.
Фишбейн, Э., Дери, М., Нелло, М., и Марино, М. (1985). Роль неявных моделей в решении вербальных задач умножения и деления. Журнал исследований в области математического образования, 16, 3-17.
Гельман Р., И Лукариелло, Дж. (2002). Роль обучения в когнитивном развитии. В справочнике Стивенса по экспериментальной психологии: H. Pashler (Series Ed.) И C.R. Gallistel (Vol. Ed.). 3. Обучение, мотивация и эмоции (3-е изд., Стр. 395-443). Нью-Йорк: Вили.
Гулдинг М., Роуленд Т. и Барбер П. (2002). Это имеет значение? Предметные знания учащихся начальных классов по математике. Британский журнал исследований в области образования, 28 (5), 689-704.
Ганстон, Р.Ф., Робин Грей К. М. и Сирл П. (1992). Некоторые долгосрочные последствия неосведомленных концептуальных изменений. Научное образование, 76 (2), 175–197.
Гуццетти, Б. Дж. (2000). Изучение противоречивых научных концепций: что мы узнали из более чем десятилетних исследований? Чтение и письмо Ежеквартально , 16 (2), 89-98.
Гуццетти, Б. Дж., Снайдер, Т. Е., Гласс, Г. В., и Гамас, В. С. (1993). Содействие концептуальным изменениям в науке: сравнительный мета-анализ учебных вмешательств от обучения чтению и обучения естествознанию.Reading Research Quarterly, 28, 116-159.
Хартнетт П. и Гельман Р. (1998). Раннее понимание чисел: пути или препятствия на пути к построению нового понимания? Обучение и обучение , 8 (4), 341-374.
Хатано Г., Сиглер Р. С., Ричардс Д. Д., Инагаки К., Стави Р. и Вакс Н. (1997). Развитие биологических знаний: многонациональное исследование. Когнитивное развитие , 8, 47-62.
Хейс, Б.К., Гудхью А., Хейт Э. и Гиллан Дж. (2003). Роль разнообразного обучения в концептуальном изменении. Журнал экспериментальной детской психологии , 86, 253-276.
Хайнд, К. Р. (2001). Опровергающие тексты и процесс изменения. Международный журнал исследований в области образования , 35 (7), 699-714.
Инагаки, К., и Хатано, Г. (2002). Наивное мышление маленьких детей о биологическом мире. Нью-Йорк: Психология Пресс.
Кейл, Ф.С. (1979). Семантическое и концептуальное развитие: онтологическая перспектива. Кембридж, Массачусетс: Издательство Гарвардского университета.
Киран, К. (1981). Понятия, связанные с символом равенства. Образовательные исследования по математике , 12, 317-326.
Киран, К. (1992). Изучение и преподавание школьной алгебры. В D. A. Grouws (Ed.), Справочник исследований по преподаванию и обучению математике (стр. 390-419). Нью-Йорк: Макмиллан.
Кикас, Э.(1998). Влияние обучения на определения и объяснения астрономических явлений учащимися. Обучение и обучение , 8 (5), 439-454.
Кикас, Э. (2003). Представления студентов вузов о различных физических явлениях. Журнал развития взрослых , 10 (3), 139-150.
Кикас, Э. (2004). Представления и заблуждения учителей относительно трех природных явлений. Журнал исследований в области преподавания естественных наук , 41, 432-448.
Клар Д. и Нигам М. (2004). Эквивалентность траекторий обучения в раннем научном обучении: эффекты прямого обучения и обучения открытию. Психологическая наука, 15, 661-667.
Кнут, Э. Дж., Алибали, М. В., Макнейл, Н. М., Вайнберг, А., и Стивенс, А. С. (2005). Понимание учащимися средней школы основных алгебраических понятий: эквивалентность и переменная. Международный журнал математического образования, 37, 1-9.
Kuchemann.(1978). Детское понимание числовых переменных. Математика в школе, 7 (4), 23-26.
Кун, Д. (2006). По-разному ли учатся дети и взрослые? Журнал познания и развития , 7, 279-293.
Ларкин, Дуглас. (2012). Заблуждения о «заблуждениях»: Preservice взгляды учителей средних естественных наук на ценность и роль студенческих идей. Естественное образование, (5), 927-959.
Ли О., Эйхингер Д.К., Андерсон, К. В., Беркхаймер, Г. Д., и Блейксли, Т. Д. (1993). Изменение представлений учащихся средней школы о веществе и молекулах. Журнал исследований в области преподавания естественных наук, 30 (3), 249-270.
Ломбарди, Дуг и Синатра, Гейл М. (2012). Представления студентов колледжей о вероятности изменения климата, вызванного деятельностью человека. Исследования в области естественнонаучного образования, (2), 201-217.
МакГрегор, М., и Стейси, К. (1997). Понимание студентами алгебраических обозначений: 11-15.Образовательные исследования по математике, 33, 1-19.
Мария К. и Макджинити В. (1987). Изучение текстов, опровергающих предыдущие знания читателя. Чтение исследований и инструкций, 26, 222-238.
Мейсон, Л. (2002). Развитие эпистемологического мышления для стимулирования концептуальных изменений в различных областях. В М. Лимон и Л. Мейсон (ред.), Пересмотр концептуальных изменений: проблемы теории и практики (стр. 301-335). Нидерланды: Kluwer Academic Publishers.
Мейсон К. и Раддок Г. (1986). Десятичные дроби. Виндзор, Онтарио, Канада: APU / NFER-Nelson.
Майер Р. Э. (1993). Иллюстрации, которые наставляют. В Р. Глейзер (ред.), Достижения в педагогической психологии (том 4, стр. 253-284). Хиллсдейл, Нью-Джерси: Эрлбаум.
Майер Р. Э. (2008). Обучение и обучение (2-е изд.). Верхняя Сэдл-Ривер, Нью-Джерси: Pearson Education, Inc.
Майер Р. Э. и Галлини Дж. К. (1990). Когда иллюстрация стоит десять тысяч слов? Журнал педагогической психологии, 82 (4), 715-726.
Макклоски, М. (1983). Интуитивная физика. Scientific American, 248 (4), 122–130.
Макклоски М., Карамазза А. и Грин Б. (1980). Криволинейное движение при отсутствии внешних сил: наивные представления о движении объектов. Science, 210, 1139-1141.
Макнил, Н. М., и Алибали, М. В. (2005). Почему ты не передумаешь? Знание операционных схем затрудняет обучение и выполнение уравнений. Развитие ребенка , 76, 883-899.
Минстрелл Дж. (1982). Объяснение состояния «покоя» объекта. Учитель физики , 20, 10-14.
Минстрелл Дж. (1984). Обучение развитию понимания идей: Силы на движущиеся объекты. В К. В. Андерсоне (ред.), Наблюдение за классами: перспективы исследований и практики (стр. 67-85). Колумбус, Огайо: Государственный университет Огайо.
Минстрелл, Дж. (1989). Обучение науке для понимания. В Л. Б.Резник и Л. Э. Клопфер (ред.), На пути к учебной программе мышления: текущие когнитивные исследования (стр. 129-149). Александрия, Вирджиния: Ассоциация по надзору и разработке учебных программ.
Нуньес, Т., и Брайант, П. (ред.). (1996). Дети занимаются математикой. Оксфорд: Блэквелл.
Охала, Дж. (1997). Потерянный в космосе? Представления о планетных явлениях придерживаются учащиеся учителей начальных классов. Международные исследования в области географического и экологического образования, 6, 183-203.
Пелаес, Н. Дж., Бойд, Д. Д., Рохас, Дж. Б., и Гувер, М. А. (2005). Распространенность неправильных представлений о кровообращении среди будущих учителей начальных классов. Достижения в области физиологического образования , 29, 172-181.
Пиаже Дж. И Инелдер Б. (1969). Психология ребенка. Нью-Йорк: Основные книги ,.
Познер, Г. Дж., Страйк, К. А., Хьюсон, П. В., и Герцог, В. А. (1982). Приспособление научной концепции: к теории концептуальных изменений.Научное образование, 66 (2), 211-227.
Рэй А. и Бердсли П. (2008). Преодоление заблуждений студентов о фотосинтезе: подход на основе модели и исследования с использованием водных растений. Научная деятельность: школьные проекты и идеи учебных программ, 45 (1), 13-22.
Резник, Л. Б. (1983). Математика и естествознание: новая концепция. Наука, 220, 477-478.
Резник, Л. Б., Нешер, П., Леонард, Ф., Магоне, М., Омансон, С., и Пелед, И. (1989). Концептуальные основы арифметических ошибок: случай десятичных дробей. Журнал исследований в области математического образования, 20 (1), 8-27.
Росник, П. (1981). Некоторые заблуждения относительно концепции переменной. Учитель математики , 74, 418-420.
Рот, К. Дж. (1990). Естественнонаучное образование: недостаточно «делать» или «относиться». Американский педагог, 13 (4), 16-22, 46-48.
Райан, Дж., & МакКрэй, Б. (2005). Знание предмета: ошибки и заблуждения начинающих преподавателей. В: П. Кларксон, А. Даунтаун, Д. Гронн, М. Хорн, А. Макдонаф, Р. Пирс и А. Рош (редакторы), Построение связей: исследования, теория и практика: материалы 28-й ежегодной конференции Исследовательская группа математического образования Австралазии, (том 2, стр. 641-648). Мельбурн, Австралия: Университет Дикина.
Sackur-Grisvard, C., & Leonard, F. (1985).Промежуточная когнитивная организация в процессе усвоения математического понятия: порядок положительных десятичных чисел. Познание и обучение, 2, 157-174.
Самарапунгаван, А. (1992). Детские суждения в задачах выбора теории: научная рациональность в детстве. Познание , 45, 1-32.
Савинайнен А. и Скотт П. (2002). The Force Concept Inventory: инструмент для мониторинга обучения студентов. Физическое образование, 37 (1), 45-52.
Савинайнен А., Скотт П. и Виири Дж. (2005). Использование связующего представления и социальных взаимодействий для стимулирования концептуальных изменений: разработка и оценка последовательности обучения для третьего закона Ньютона. Научное образование , 89 (2), 175-195.
Зиглер Р. С. (2003). Значение исследований когнитивных наук для математического образования. В Дж. Килпатрик, В. Б. Мартин и Д. Э. Шифтер (ред.), Исследовательский компаньон по принципам и стандартам школьной математики (стр.219-233). Рестон, Вирджиния: Национальный совет учителей математики.
Смит К. Л., Маклин Д., Гросслайт Л. и Дэвис Х. (1997). Обучение для понимания: изучение теорий материи до обучения студентов и сравнение эффективности двух подходов к обучению материи и плотности. Познание и обучение , 15 (3), 317-393.
Смит, К. Л., Маклин, Д., Хоугтон, К., и Хеннесси, М. Г. (2000). Эпистемология науки учащихся шестого класса: влияние школьного опыта науки на эпистемологическое развитие. Познание и обучение , 18 (3), 349-422.
Стейнберг, Р. М., Слиман, Д. Х., и Кторза, Д. (1990). Знание студентов алгебры об эквивалентности уравнений. Журнал исследований в области математического образования, 22 (2), 112-121.
Стовалл, Г., & Несбит, К. Р. (2003). Попробуем исследование действий! Наука и дети, 40, 44-48.
Страйк, К. А., и Познер, Г. Дж. (1985). Концептуальное изменение взгляда на обучение и понимание.В Л. Х. Т. Уэст и А. Л. Пайнс (ред.), Когнитивная структура и концептуальные изменения. Нью-Йорк: Academic Press.
Страйк, К. А., и Познер, Г. Дж. (1992). Ревизионистская теория концептуальных изменений. В книге Р. А. Душля и Р. Дж. Гамильтона (редакторы), «Философия науки, когнитивная психология, а также теория и практика образования» (стр. 147-176). Олбани, штат Нью-Йорк: Статуя Университета Нью-Йорк Пресс.
Тирош Д. (2000). Повышение уровня знаний будущих учителей о детских представлениях: случай деления на фракции.Журнал исследований в области математического образования, 31 (1), 5-25.
Восняду С. (1994). Захват и моделирование процесса концептуальных изменений. Обучение и инструктаж , 4 (1), 45-69.
Vosniadou, S., & Brewer, W. F. (1992). Ментальные модели земли: исследование концептуальных изменений в детстве. Когнитивная психология , 24, 535-585.
Vosniadou, S., & Brewer, W. F. (1994). Ментальные модели дневного / ночного цикла. Когнитивная наука , 18, 123-183.
Vosniadou, S., Ioannides, C., Dimitrakopoulou, A., & Papademetriou. Э. (2001). Разработка учебных сред для содействия концептуальным изменениям в науке. Обучение и инструктаж , 11 (4), 381-419.
Сварщик, Рэйчел М. (2012). Улучшение подготовки к алгебре: последствия исследования заблуждений и трудностей студентов. Школа естественных наук и математики, (4), 255-264.
Белая, Б.Ю. (1993). Инструменты мыслителя: причинные модели, концептуальные изменения и научное образование. Познание и обучение , 10 (1), 1-100.
Уайт, Б. Ю., и Фредериксен, Дж. Р. (1998). Исследование, моделирование и метапознание: сделать науку доступной для всех учащихся. Познание и обучение , 16 (1), 3-118.
Уильямс Дж. И Райан Дж. (2000). Национальное тестирование и улучшение преподавания в классе: могут ли они сосуществовать? Британский журнал исследований в области образования, 26 (1), 49-73.
Победитель, Э. (1997). Смысл слов: детское понимание метафоры и иронии. Кембридж, Массачусетс: Издательство Гарвардского университета.
Йылмаз, С., Эрилмаз, А., и Гебан, О. (2006). Оценка влияния мостовых аналогий в механике. Школьные науки и математика, 106 (6), 220-230.
Ип, Д. (1998). Заблуждения учителей о системе кровообращения. Журнал биологического образования, 32 (3), 207-216.
Что такое взаимное обучение и почему оно важно?
Люди:
В сообщении ниже рассматривается все еще недостаточно используемый ресурс, студенты учатся у других студентов.Это из главы 1 «Введение: переход к взаимному обучению» в книге «взаимное обучение в высшем образовании: обучение друг с другом и друг с другом» под редакцией Дэвида Буда, Рут Коэн и Джейн Сэмпсон. Издано Kogan Page Limited 120 Pentonville Road, London N1 9JN, UK и Stylus Publishing Inc. 22883 Quicksilver Drive Sterling, VA 20166-2012, США. http://www.styluspub.com/ Авторские права? Дэвид Боуд, Рут Коэн, Джейн Сэмпсон и отдельные участники, 2002 г. Перепечатано с разрешения.
С уважением,
Рик Рейс
reis @ stanford.edu
UP NEXT: Успех в Башне из слоновой кости
Преподавание и обучение завтрашнего дня
——————————- 1049 слов —————- ————-
ЧТО ТАКОЕ ОБУЧЕНИЕ И ПОЧЕМУ ЭТО ВАЖНО?
Дэвид Бауд
Обучение сверстников — это не единая недифференцированная образовательная стратегия. Он включает в себя широкий спектр мероприятий. Например, исследователи из Ольстерского университета выделили 10 различных моделей взаимного обучения (Griffiths, Housten and Lazenbatt, 1995).Они варьировались от традиционной модели проктора, в которой старшие студенты обучают младших, до более инновационных учебных ячеек, в которых учащиеся одного года формируют партнерские отношения, чтобы помогать друг другу как по содержанию курса, так и по личным вопросам. Другие модели включали дискуссионные семинары, частные учебные группы, parrainage (система друзей) или консультирование, схемы взаимной оценки, совместный проект или лабораторные работы, проекты в группах разного размера (каскадные), наставничество на рабочем месте и деятельность сообщества.
Однако термин «взаимное обучение» остается абстрактным. Смысл, в котором мы его здесь используем, предполагает двустороннюю взаимную учебную деятельность. Совместное обучение должно быть взаимовыгодным и предполагать обмен знаниями, идеями и опытом между участниками. Его можно описать как способ перехода от независимого к взаимозависимому или взаимному обучению (Boud, 1988).
Студенты многому учатся, объясняя свои идеи другим и участвуя в мероприятиях, в которых они могут учиться у своих сверстников.Они развивают навыки организации и планирования учебной деятельности, совместной работы с другими, предоставления и получения обратной связи и оценки собственного обучения. Совместное обучение становится все более важной частью многих курсов и используется в различных контекстах и дисциплинах во многих странах.
Потенциал взаимного обучения начинает реализовываться, но изучение способов, которыми оно используется в существующих курсах, предполагает, что практики часто вводятся произвольно, без учета их последствий.Когда такие практики используются бессистемно, учащиеся, незнакомые с этим подходом, не понимают, что они должны делать, они вообще упускают возможности для обучения и не могут развить ожидаемые от них навыки. В большинстве случаев взаимное обучение происходит неформально, без участия персонала, и студенты, которые уже являются эффективными учениками, как правило, извлекают непропорционально большую пользу, когда это предоставляется случаю.
Формализованное взаимное обучение может помочь учащимся эффективно учиться. В то время, когда ресурсы университета ограничены, а требования к персоналу растут, он предлагает студентам возможность учиться друг у друга.Это дает им значительно больше практики, чем традиционные методы преподавания и обучения, в принятии на себя ответственности за собственное обучение и, в более общем плане, в обучении тому, как учиться. Это не замена преподаванию и деятельности, разработанной и проводимой сотрудниками, а важное дополнение к репертуару преподавательской и учебной деятельности, которое может повысить качество образования.
Важно учитывать, кто является «сверстниками» при взаимном обучении. Как правило, сверстники — это люди, находящиеся в схожей ситуации друг с другом, которые не играют в этой ситуации роли учителя или практикующего специалиста.Они могут иметь значительный опыт и знания или относительно немного. Они разделяют статус однокурсников, и их принимают как таковые. Что наиболее важно, они не имеют власти друг над другом в силу своего положения или обязанностей. На протяжении всей книги мы будем обсуждать роль учеников, которые учатся в тех же классах, что и те, у кого они учатся.
Обучение со стороны сверстников или наставничество со сверстниками — это гораздо более инструментальная стратегия, в которой продвинутые ученики или ученики старшего возраста берут на себя ограниченную обучающую роль.Часто требуется кредит или оплата в той или иной форме для преподавателя. Обучение сверстников — это устоявшаяся практика во многих университетах, в то время как взаимное обучение часто рассматривается как случайный компонент других более привычных стратегий, таких как дискуссионные группы (см., Например, Brookfield and Preskill, 1999). Как следствие, до недавнего времени взаимное обучение не считалось самостоятельным явлением, которое можно было бы использовать в интересах студентов.
Взаимное взаимное обучение обычно вовлекает учащихся определенного класса или когорты. Это упрощает организацию взаимного обучения, поскольку возникает меньше проблем с расписанием. Также нет необходимости платить или вознаграждать в кредит более опытных студентов, ответственных за взаимное обучение. Учащиеся во взаимном взаимном обучении по определению являются сверстниками, поэтому меньше путаницы в ролях по сравнению с ситуациями, когда один из «сверстников» является старшим учеником, или находится в продвинутом классе, или имеет особый опыт.
Взаимное взаимное обучение подчеркивает, что студенты одновременно учатся и вносят свой вклад в обучение других студентов. Такое общение основано на взаимном опыте, поэтому они лучше могут вносить равный вклад. Это более близко соответствует понятию Хабермаса об «идеальном речевом акте», в котором вопросы власти и господства менее заметны, чем когда одна партия играет назначенную «обучающую» роль и, таким образом, берет на себя определенный вид власти на время деятельность.
Таким образом, мы определяем взаимное обучение в самом широком смысле, как «учащиеся учатся друг у друга как формальным, так и неформальным образом». Акцент делается на процессе обучения, включая эмоциональную поддержку, которую учащиеся предлагают друг другу, а также на самой учебной задаче. При взаимном обучении роли учителя и ученика фиксированы, тогда как при взаимном обучении они либо не определены, либо могут меняться в процессе обучения. Персонал может активно участвовать в качестве фасилитатора группы или просто инициировать мероприятия под руководством студентов, такие как семинары или учебные партнерства.
Согласно обзору литературы Топпинга, было проведено на удивление мало исследований либо диадического взаимного обучения сверстников, либо группового обучения одного года (Topping, 1996). Он выделил только 10 исследований, все с очень узкой эмпирической направленностью. Это говорит о том, что модель обучения, а не модель обучения, по-прежнему является наиболее распространенным способом понимания того, как учащиеся помогают друг другу. Хотя модель обучения имеет ценность, мы также должны учитывать сам процесс обучения, если мы хотим наилучшим образом использовать сверстников в качестве ресурсов для обучения.