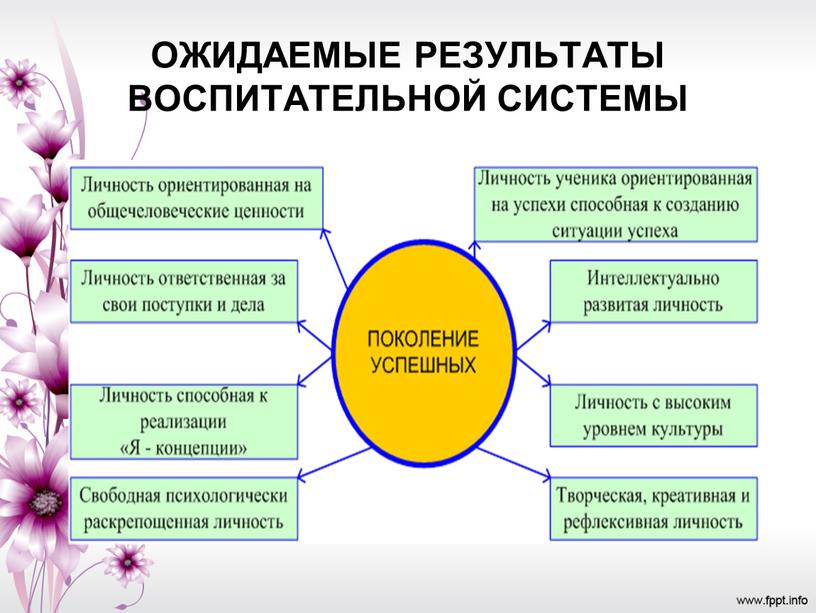
Наличие сформированности у обучающегося внутренней позиции называется: Система оценки достижения планируемых результатов
21.12.2021 Городской семинар «ОЦЕНИВАНИЕ ОБРАЗОВАТЕЛЬНЫХ РЕЗУЛЬТАТОВ В УСЛОВИЯХ ФГОС СОО»
+7 (812) 628-78-28, +7 (812) 956-67-42, +7 (921) 856-03-61, +7 (921) 856-03-62 [email protected]
- Подробности
- Просмотров: 2372
Для педагогов начального образования, среднего образования, дополнительного образования
Городской семинар
Дата проведения: 21.12.2021
Время проведения: 10:00 — 11:30
Ведущая: Владимирская Ольга Дмитриевна, директор АНОО «Центр ДПО «АНЭКС», к.п.н.
Цель: формирование современных подходов к организации целостного интегрированного оценивания образовательных результатов в контексте ФГОС СОО
План работы
- Подходы к оцениванию образовательных результатов: проблемы, пути решения
- Опыт решения проблем оценивания в условиях ФГОС СОО (СПб КВК).
- Разработка и использование дидактического инструментария по оцениванию деятельности обущающихся на уроке и внеурочной деятельности.
Спикеры
Царёв Иван Николаевич, начальник Санкт-Петербургского кадетского военного корпуса, к.п.н., заслуженный военный специалист.
Фирсова Наталия Владиславовна, заведующий сектором оценочных механизмов и региональных мониторингов центра мониторинга и оценки качества образования ГАОУ ДПО «Ленинградский областной институт развития образования», к. ист. наук.
Лузанова Нина Николаевна, исполнительный директор Центра ДПО АНЕКС, к.п.н.
Матюк Сергей Борисович, заместитель начальника по учебной работе, эксперт КО СПб по государственному контролю и надзору в сфере образования.
Новоселова Лариса Сергеевна, методист учебного отдела, заслуженный учитель РФ СПб КВК
Сергеева Татьяна Алексеевна, методист учебного отдела СПб КВК, заслуженный учитель РФ
Беликова Татьяна Ивановна, методист учебного отдела СПб КВК
Список секций:
Секция 1.
«КОМПЛЕКСНЫЙ ПОДХОД К ОЦЕНКЕ ОБРАЗОВАТЕЛЬНЫХ РЕЗУЛЬТАТОВ ОБУЧАЮЩИХСЯ»
Секция 2. «ОЦЕНИВАНИЕ РЕЗУЛЬТАТОВ – ЭЛЕМЕНТ ОБЕСПЕЧЕНИЯ КАЧЕСТВА ОБУЧЕНИЯ ИНОСТРАННОМУ ЯЗЫКУ»
Секция 3. «СИСТЕМА ОЦЕНИВАНИЯ РЕЗУЛЬТАТОВ ОБУЧЕНИЯ ПРИ РЕАЛИЗАЦИИ ПРОГРАММ ДОПОЛНИТЕЛЬНОГО ОБРАЗОВАНИЯ»
Записаться на мероприятие и оставить свои тезисы
- Назад
- Вперёд
Учебное пособие по физике: узлы и промежуточные узлы
Как упоминалось ранее в уроке 4, стоячая волна представляет собой явление интерференции. Он образуется в результате идеально синхронизированной интерференции двух волн, проходящих через одну и ту же среду. Паттерн стоячей волны на самом деле не является волной; скорее это картина, возникающая в результате присутствия двух волн одной частоты с разными направлениями движения в одной и той же среде.
Что такое узлы и пучности?
Одной из характеристик каждой модели стоячей волны является наличие точек вдоль среды, которые кажутся неподвижными.
Эти точки, иногда описываемые как точки отсутствия смещения, обозначаются как узлов . Вдоль среды есть и другие точки, которые испытывают колебания между большим положительным и большим отрицательным смещением. Это точки, которые претерпевают максимальное смещение в течение каждого колебательного цикла стоячей волны. В некотором смысле эти точки противоположны узлам, поэтому их называют пучности . Паттерн стоячей волны всегда состоит из чередующихся узлов и пучностей. Анимация, показанная ниже, изображает веревку, вибрирующую в виде стоячей волны. Узлы и пучности отмечены на диаграмме. Когда в среде устанавливается картина стоячей волны, узлы и пучности всегда располагаются в одном и том же месте вдоль среды; они стоят на месте . Именно за эту характеристику модель получила название , стоящая волна 9.0016 е.
Flickr Physics Photo
Стоячая волна создается на вибрирующей струне с помощью гармонического генератора и генератора частоты.
Строб используется для освещения струны несколько раз в течение каждого цикла. Палец указывает на узловое положение.
Расположение узлов и пучностей в модели стоячей волны можно объяснить, сосредоточив внимание на интерференции двух волн. Узлы производятся в местах, где возникают деструктивные помехи. Например, узлы образуются в местах, где гребень одной волны встречается с впадиной второй волны; или 
Пучности всегда колеблются между этими точками большого положительного и большого отрицательного смещения; это потому, что во время полного цикла вибрации гребень встречается с гребнем; а затем через полцикла впадина встретится с впадиной. Поскольку пучности колеблются взад и вперед между большим положительным и большим отрицательным смещением, диаграмму стоячей волны иногда изображают, рисуя форму среды в определенный момент времени и в момент времени на полцикла позже. Это сделано на схеме ниже.
Узлы и пучности не следует путать с гребнями и впадинами. Когда обсуждается движение бегущей волны, принято называть точку большого максимального смещения гребнем, а точку большого отрицательного смещения — впадиной. Они представляют собой точки возмущения , которые перемещаются из одного места в другое через среду. С другой стороны, пучностью является точка на среде , которая остается в том же месте. Кроме того, пучность колеблется взад и вперед между большим смещением вверх и большим смещением вниз.
И, наконец, узлы и пучности на самом деле не являются частью волны. Напомним, что стоячая волна на самом деле не является волной, а представляет собой узор, возникающий в результате интерференции двух или более волн. Поскольку стоячая волна технически не является волной, пучность технически не является точкой на волне. Узлы и пучности — это просто уникальные точки на среде, составляющие волновую картину.
Мы хотели бы предложить …
Зачем просто читать об этом и когда вы могли бы взаимодействовать с ним? Взаимодействие — это именно то, что вы делаете, когда используете один из интерактивов The Physics Classroom.
Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего интерактивного шаблона стоячих волн. Вы можете найти его в разделе Physics Interactives на нашем сайте. Интерактивные модели стоячих волн предоставляют учащимся среду для изучения формирования стоячих волн, моделей стоячих волн и математических взаимосвязей для моделей стоячих волн.
Посетите: Интерактивные модели стоячих волн
Проверьте свое понимание
1. Предположим, что имеется аттракцион в парке развлечений под названием Стоячая волна . Какое место — узел или пучок — в поездке доставило бы наибольшее удовольствие?
2. Стоячая волна образуется при ____.
а. волна преломляется из-за изменения свойств среды.
б. волна отражается от стены каньона и слышна вскоре после ее образования.
в. красные, оранжевые и желтые волны огибают взвешенные атмосферные частицы.
д. две одинаковые волны, движущиеся в разных направлениях вдоль одной и той же среды, интерферируют.
3. Количество узлов в стоячей волне, показанной на диаграмме справа, равно ____.
|
4. Количество пучностей в стоячей волне, показанной на диаграмме вверху справа, равно ____.
а. 6
б. 7
в. 8
д. 14
При ответе на следующие два вопроса рассмотрите модель стоячей волны справа.
5. Количество узлов во всем узоре ___.
|
6. Из всех отмеченных точек разрушающая интерференция возникает в точке(ах) ____.
а. Б, В и Г
б. А, Е и F
в. Всего
д. C только
эл. все точки
Учебник по физике: образование стоячих волн
Паттерн стоячей волны — это вибрационный паттерн, создаваемый в среде, когда частота колебаний источника вызывает интерференцию волн, отраженных от одного конца среды, с падающими волнами от источника.
Это вмешательство происходит таким образом, что определенные точки среды кажутся неподвижными. Поскольку наблюдаемая волновая картина характеризуется точками, которые кажутся неподвижными, ее часто называют моделью стоячих волн 9.0016 . Такие узоры создаются в среде только на определенных частотах вибрации. Эти частоты известны как частоты гармоник или просто гармоник . На любой частоте, кроме частоты гармоники, интерференция отраженных и падающих волн приводит к результирующему возмущению среды, которое является нерегулярным и неповторяющимся.
Как формируется стоячая волна?
Но как формируются стоячие волны? И почему они образуются только при вибрации среды на определенных частотах? И что делает эти так называемые гармонические частоты такими особенными и магический ? Чтобы ответить на эти вопросы, давайте рассмотрим змейку, растянувшуюся по комнате примерно на 4 метра из конца в конец. («Змея» — это устройство, похожее на змейку, состоящее из большого количества металлических катушек малого диаметра.
) Если на левый конец змейки подать смещенный вверх импульс, он будет перемещаться по змейке вправо, пока не достигнет фиксированный конец на правой стороне змейки. Достигнув фиксированного конца, одиночный импульс отразится и подвергнется инверсии. То есть импульс, смещенный вверх, станет импульсом, смещенным вниз. Теперь предположим, что второй импульс, смещенный вверх, поступает в змейку точно в тот момент, когда первый гребень претерпевает фиксированное конечное отражение. Если это сделать точно по времени, пульс, движущийся вправо и смещенный вверх, встретится с пульсом, движущимся влево и смещенным вниз точно в середине змейки. Когда два импульса проходят друг через друга, они будут подвергаться деструктивной интерференции. Таким образом, будет создана точка отсутствия смещения точно посередине змейки. Анимация ниже показывает несколько моментальных снимков встречи двух импульсов на разных стадиях их интерференции. Отдельные импульсы нарисованы синим и красным цветом; результирующая форма среды (найденная по принципу суперпозиции) показана зеленым цветом.
Обратите внимание, что на диаграмме есть точка точно посередине среды, которая никогда не испытывает никакого смещения от положения равновесия.
Смещенный вверх импульс, введенный с одного конца, будет деструктивно интерферировать точно в середине змейки со вторым смещенным вверх импульсом, введенным с того же конца, если введение второго импульса выполняется точно по времени. То же самое можно было бы применить к двум смещенным вниз импульсам, введенным с одного и того же конца. Если второй импульс ввести точно в тот момент, когда первый импульс отражается от неподвижного конца, то деструктивная интерференция произойдет точно в середине змейки.
Приведенное выше обсуждение только объясняет, почему два импульса могут деструктивно интерферировать, создавая точку отсутствия смещения в середине змейки. Волна, безусловно, отличается от импульса. Что, если в среде распространяются две волны? Понимание того, почему две волны, введенные в среду в идеальное время, могут привести к смещению точки в середине среды, является простым продолжением вышеизложенного.
В то время как импульс — это одиночное возмущение, которое движется через среду, волна — это повторяющийся узор из гребней и впадин. Таким образом, волну можно представить себе как импульс, смещенный вверх (гребень), за которым следует импульс, смещенный вниз (впадина), за которым следует импульс, смещенный вверх (гребень), за которым следует импульс, смещенный вниз (впадина), за которым следует… . Поскольку за введением гребня следует введение впадины, каждый гребень и впадина будут деструктивно интерферировать таким образом, что середина среды станет точкой отсутствия смещения.
Конечно, все это требует идеального выбора времени. В приведенном выше обсуждении идеальное время было достигнуто, если каждый гребень волны вводился в змейку в точное время, когда предыдущий гребень волны начинал свое отражение на фиксированном конце. В этой ситуации внутри змеи, движущейся вправо в каждый момент времени, будет одна полная длина волны; эта падающая волна будет встречаться с одной полной длиной волны, движущейся влево в каждый момент времени.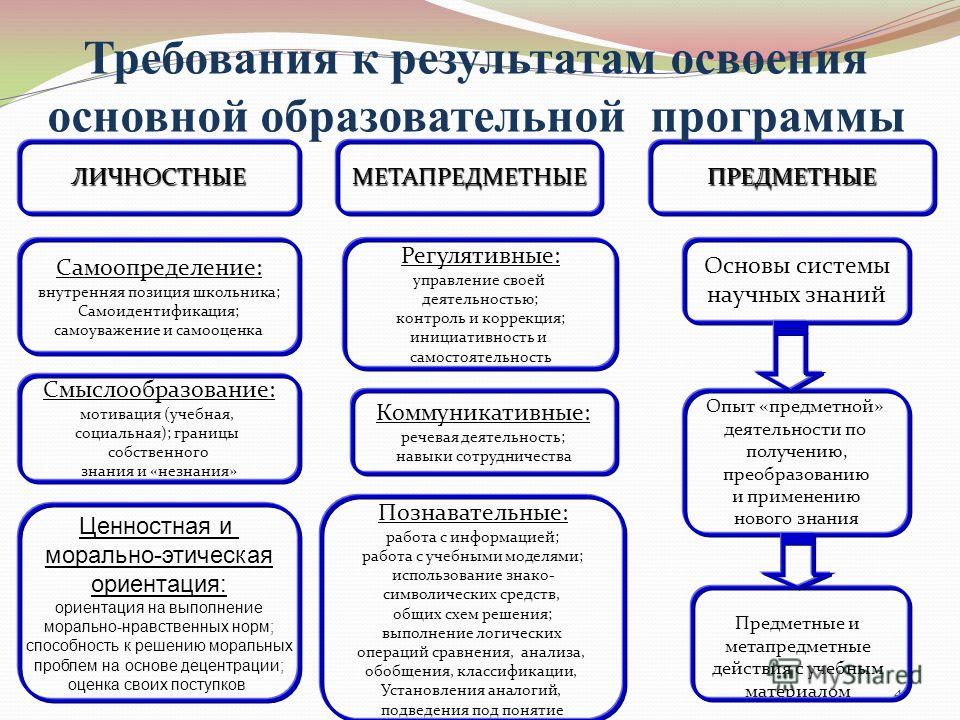
В этих условиях деструктивная интерференция всегда возникает в середине змейки. Либо полный гребень встречается с полной впадиной, либо полугребень встречается с полугребнем или четвертьгребень встречается с четвертью желоба в этой точке. Анимация ниже представляет собой несколько снимков двух волн, движущихся в противоположных направлениях по одной и той же среде. Волны интерферируют таким образом, что в одних и тех же местах вдоль среды возникают точки отсутствия смещения. Эти точки вдоль среды известны как узлов и помечены N . Вдоль среды также есть точки, которые колеблются между точками большого положительного смещения и точками большого отрицательного смещения. Эти точки известны как пучностей и помечены AN . Две отдельные волны нарисованы синим и зеленым цветом, а результирующая форма среды — черным.
Есть и другие способы добиться этого идеального момента.
Основная идея синхронизации заключается в том, чтобы ввести гребень в тот момент, когда другой гребень находится либо на полпути через среду, либо в конце среды. Независимо от количества гребней и впадин, находящихся между ними, если гребень вводится в тот момент, когда другой гребень подвергается отражению от фиксированного конца, в середине среды будет формироваться узел (точка отсутствия смещения). Количество других узлов, которые будут присутствовать вдоль среды, зависит от количества гребней, которые присутствовали между двумя 9 точками.0015 время гребни . Если гребень ввести в тот момент, когда другой гребень находится на середине среды, то в середине среды за счет конструктивной интерференции образуется пучность (точка максимального смещения). В таком случае также могут быть узлы и пучности, расположенные в другом месте среды.
Стоячая волна представляет собой явление интерференции. Он образуется в результате идеально синхронизированной интерференции двух волн, проходящих через одну и ту же среду.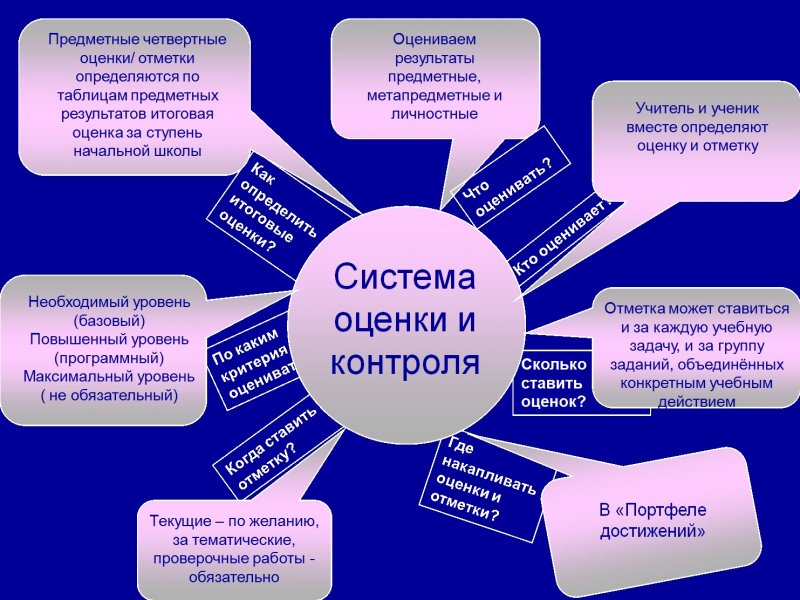
Паттерн стоячей волны на самом деле не является волной; скорее это картина, возникающая в результате присутствия двух волн (иногда больше) одной и той же частоты с разными направлениями движения в одной и той же среде. Физика музыкальных инструментов основана на концептуальных и математических аспектах стоячих волн. По этой причине эта тема будет повторно рассмотрена в разделе «Звук и музыка» учебного пособия по физике.
Мы хотели бы предложить …
Зачем просто читать об этом и когда вы могли бы взаимодействовать с ним? Взаимодействие — это именно то, что вы делаете, когда используете один из интерактивов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего интерактивного шаблона стоячих волн. Вы можете найти его в разделе Physics Interactives на нашем сайте. Интерактивные модели стоячих волн предоставляют учащимся среду для изучения формирования стоячих волн, моделей стоячих волн и математических взаимосвязей для моделей стоячих волн.