Примерный рассчет тревожности по крускаллу: [Видео] Интерпретация результатов расчета критерия Н Крускалла Уоллеса в SPSS

H-тест Крускала-Уоллиса в SPSS Statistics

Введение

H-критерий Крускала-Уоллиса (иногда также называемый «однофакторным ANOVA по рангам») представляет собой ранговый непараметрический критерий, который можно использовать для определения наличия статистически значимых различий между двумя или более группами независимой переменной по непрерывная или порядковая зависимая переменная. Он считается непараметрической альтернативой однофакторному дисперсионному анализу и расширением U-критерия Манна-Уитни, позволяющим сравнивать более двух независимых групп.

Например, вы можете использовать H-критерий Крускала-Уоллиса, чтобы понять, отличаются ли результаты экзамена, измеряемые по непрерывной шкале от 0 до 100, в зависимости от уровня тревожности (т. е. вашей зависимой переменной будет «успеваемость на экзамене», а переменной будет «уровень тестовой тревожности», который имеет три независимые группы: студенты с «низким», «средним» и «высоким» уровнем тестовой тревожности). В качестве альтернативы вы можете использовать H-критерий Крускала-Уоллиса, чтобы понять, различается ли отношение к дискриминации в оплате труда, где отношение измеряется по порядковой шкале, в зависимости от занимаемой должности (т. е. вашей зависимой переменной будет «отношение к дискриминации в оплате труда», измеряемое по по 5-балльной шкале от «полностью согласен» до «полностью не согласен», а вашей независимой переменной будет «описание работы», которое состоит из трех независимых групп: «цех», «менеджеры среднего звена» и «зал заседаний»).

Примечание. Если вы хотите принять во внимание порядковый характер независимой переменной и иметь упорядоченную альтернативную гипотезу, вы можете запустить критерий Джонкхира-Терпстры вместо Н-критерия Крускала-Уоллиса.

Важно понимать, что H-критерий Крускала-Уоллиса является статистическим показателем омнибуса и не может сказать вам, какие конкретные группы вашей независимой переменной статистически значимо отличаются друг от друга; это только говорит вам, что по крайней мере две группы были разными.

Поскольку в вашем проекте исследования может быть три, четыре, пять или более групп, важно определить, какие из этих групп отличаются друг от друга. Вы можете сделать это с помощью апостериорного теста (обратите внимание, мы обсуждаем апостериорные тесты позже в этом руководстве).

В этом кратком руководстве показано, как выполнить H-критерий Крускала-Уоллиса с помощью SPSS Statistics, а также интерпретировать и представить результаты этого теста. Однако, прежде чем мы познакомим вас с этой процедурой, вам необходимо понять различные предположения, которым должны соответствовать ваши данные, чтобы H-критерий Крускала-Уоллиса дал вам достоверный результат. Далее мы обсудим эти предположения.

Статистика SPSS

Предположения

Когда вы решите анализировать данные с помощью H-критерия Крускала-Уоллиса, часть процесса включает в себя проверку того, что данные, которые вы хотите проанализировать, действительно можно проанализировать с помощью H-критерия Крускала-Уоллиса.

Вы должны сделать это, потому что использовать H-критерий Крускала-Уоллиса уместно только в том случае, если ваши данные «проходят» четыре предположения, которые требуются для того, чтобы H-критерий Крускала-Уоллиса дал вам достоверный результат. На практике проверка этих четырех допущений просто увеличивает время анализа, требуя от вас нажатия еще нескольких кнопок в SPSS Statistics при выполнении анализа, а также еще немного обдумывания ваших данных, но это не сложная задача.

Прежде чем мы познакомим вас с этими четырьмя допущениями, не удивляйтесь, если при анализе ваших собственных данных с помощью SPSS Statistics одно или несколько из этих допущений будут нарушены (т. е. не выполнены). Это не редкость при работе с реальными данными, а не с примерами из учебников, которые часто только показывают вам, как выполнять H-тест Крускала-Уоллиса, когда все идет хорошо! Однако не волнуйтесь. Даже если ваши данные не соответствуют определенным предположениям, часто есть решение, позволяющее обойти это.

Во-первых, давайте взглянем на эти четыре предположения:

• Предположение №1: Ваша зависимая переменная должна быть измерена на порядковом или непрерывном уровне (т. е. интервал или отношение ). Примеры порядковых переменных включают шкалу Лайкерта (например, 7-балльную шкалу от «полностью согласен» до «полностью не согласен»), а также другие способы ранжирования категорий (например, 3-балльную шкалу, объясняющую, насколько покупателю понравилось продукт в диапазоне от «Не очень много» до «Все в порядке» до «Да, много»). Примеры непрерывные переменные включают время пересмотра (измеряется в часах), интеллект (измеряется с помощью показателя IQ), успеваемость на экзамене (измеряется от 0 до 100), вес (измеряется в кг) и так далее. Вы можете узнать больше о порядковых и непрерывных переменных в нашей статье: Типы переменных.
• Допущение #2: Ваша независимая переменная должна состоять из двух или более категориальных , независимых групп . Как правило, тест Крускала-Уоллиса H используется, когда у вас три или более категориальных, независимых групп, но его можно использовать только для двух групп (т. е. U-критерий Манна-Уитни чаще используется для двух групп). Примеры независимых переменных, отвечающих этому критерию, включают этническую принадлежность (например, три группы: европеоиды, афроамериканцы и латиноамериканцы), уровень физической активности (например, четыре группы: малоподвижный образ жизни, низкий, средний и высокий), профессию (например, пять групп: хирург, врач, медсестра, стоматолог, терапевт) и так далее.
• Предположение №3: У вас должна быть независимость наблюдений , что означает отсутствие связи между наблюдениями в каждой группе или между самими группами. Например, в каждой группе должны быть разные участники, при этом ни один участник не может входить более чем в одну группу. Это скорее проблема дизайна исследования, чем то, что вы можете проверить, но это важное предположение H-теста Крускала-Уоллиса. Если ваше исследование не соответствует этому предположению, вам нужно будет использовать другой статистический тест вместо H-критерия Крускала-Уоллиса (например, критерий Фридмана). Если вы не уверены, соответствует ли ваше исследование этому допущению, вы можете воспользоваться нашим селектором статистических тестов, который является частью нашего расширенного контента.

Поскольку H-критерий Крускала-Уоллиса не предполагает нормальность данных и гораздо менее чувствителен к выбросам, его можно использовать, когда эти предположения были нарушены и использование однофакторного дисперсионного анализа нецелесообразно. Кроме того, если ваши данные порядковые, однофакторный дисперсионный анализ не подходит, а H-критерий Крускала-Уоллиса — нет. Тем не менее, H-критерий Крускала-Уоллиса включает в себя дополнительное рассмотрение данных, Предположение № 4 , которое обсуждается ниже:

• Предположение № 4: Чтобы знать, как интерпретировать результаты H-критерия Крускала-Уоллиса, вы должны определить, соответствуют ли распределений в каждой группе (т. е. распределение оценок для каждой группы независимых переменная) имеют ту же форму (что также означает ту же изменчивость ). Чтобы понять, что это означает, взгляните на диаграмму ниже:

  Copyright 2014. Laerd Statistics

  
  На схеме слева вверху распределение баллов для групп «кавказцев», «афроамериканцев» и «латиноамериканцев» имеет одинаковую форму . С другой стороны, на диаграмме справа выше распределение баллов для каждой группы не совпадает с (т. е. они имеют различных форм и вариаций).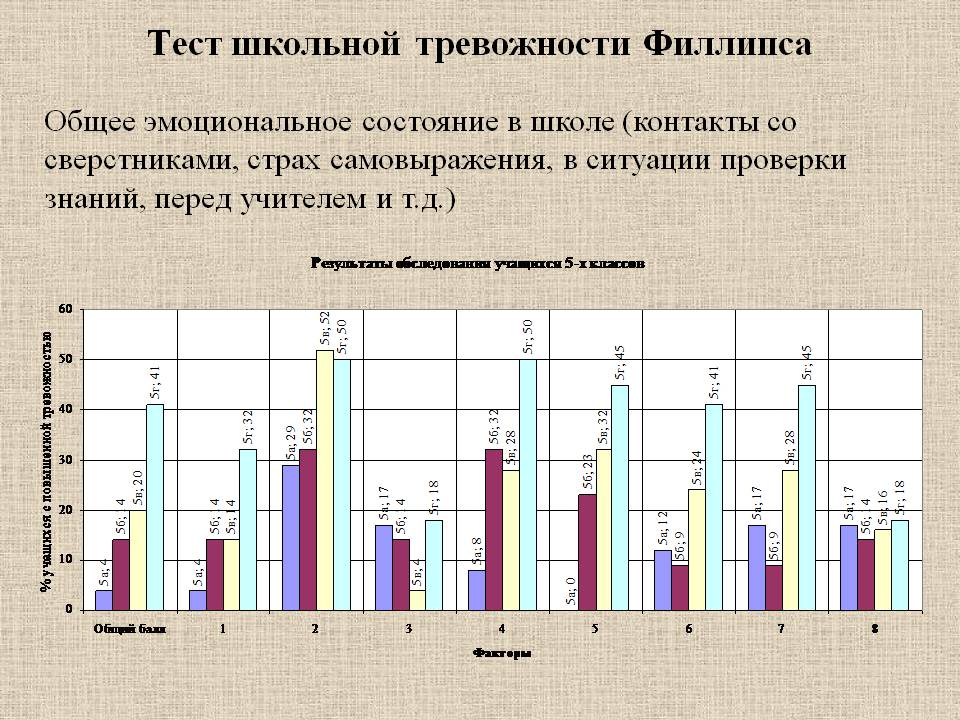

  Если ваши распределения имеют одинаковую форму, вы можете использовать SPSS Statistics для проведения H-критерия Крускала-Уоллиса для сравнения

  медиан вашей зависимой переменной (например, «показатель вовлеченности») для различных групп независимой переменной, которую вы интересуют (например, группы европеоидов, афроамериканцев и латиноамериканцев для независимой переменной «этническая принадлежность»). Однако, если ваши дистрибутивы имеют различной формы , вы можете использовать H-критерий Крускала-Уоллиса только для сравнения средних рангов . Имея подобные распределения, вы просто можете использовать 90 026 медиан 90 027, чтобы представить сдвиг в расположении между группами (как показано на диаграмме слева выше). Таким образом, очень важно проверить это предположение, иначе вы можете неправильно интерпретировать свои результаты.

Вы можете проверить предположение №4 с помощью SPSS Statistics.

Вам также следует проверить, соответствуют ли ваши данные предположениям № 1, № 2 и № 3, что можно сделать без использования SPSS Statistics. Просто помните, что если вы не проверите предположение № 4, вы не будете знать, можете ли вы сравнивать медианы или просто средние ранги, а это означает, что вы можете неправильно интерпретировать и сообщить результат H-критерия Крускала-Уоллиса. Вот почему мы посвящаем ряд разделов нашего расширенного руководства по тестированию Kruskal-Wallis H, чтобы помочь вам сделать это правильно. Вы можете узнать больше о допущении № 4 и о том, что вам нужно будет интерпретировать, в разделе 9.0026 Предположения нашего расширенного руководства по тестированию Краскела-Уоллиса H, доступ к которому вы можете получить, подписавшись на Laerd Statistics.

В разделе «Процедура тестирования в SPSS Statistics» этого «краткого руководства» мы иллюстрируем процедуру SPSS Statistics для выполнения H-критерия Крускала-Уоллиса, предполагая, что ваши распределения не имеют одинаковой формы и вам нужно интерпретировать средние ранги, а не медианы.

. Во-первых, мы приводим пример, который мы используем для объяснения процедуры H-теста Крускала-Уоллиса в SPSS Statistics.

Статистика SPSS

Пример

Медицинский исследователь слышал неофициальные данные о том, что некоторые антидепрессивные препараты могут иметь положительный побочный эффект в виде уменьшения неврологической боли у людей с хронической неврологической болью в спине, если их вводить в дозах ниже тех, которые назначают при депрессии. Исследователь-медик хотел бы исследовать это неподтвержденное свидетельство с помощью исследования. Исследователь выделяет 3 хорошо известных антидепрессивных препарата, которые могут иметь этот положительный побочный эффект, и маркирует их как Препарат А, Препарат В и Препарат С. Затем исследователь набирает группу из 60 человек с одинаковым уровнем болей в спине и случайным образом относит их к одной из трех групп — группам лечения препаратом А, препаратом В или препаратом С — и прописывает соответствующий препарат на 4-недельный период. В конце 4-недельного периода исследователь просит участников оценить свою боль в спине по шкале от 1 до 10, где 10 указывает на самый сильный уровень боли. Исследователь хочет сравнить уровни боли, испытываемой различными группами в конце периода лечения наркотиками. Исследователь проводит H-критерий Крускала-Уоллиса, чтобы сравнить этот порядковый зависимый показатель (Pain_Score) между тремя лекарственными препаратами (т. е. независимая переменная, Drug_Treatment_Group, представляет собой тип препарата с более чем двумя группами).

SPSS Statistics

Процедура тестирования в SPSS Statistics

Восемь приведенных ниже шагов показывают, как анализировать данные с помощью H-критерия Крускала-Уоллиса в SPSS Statistics. В конце этих восьми шагов мы покажем вам, как интерпретировать результаты H-критерия Крускала-Уоллиса. Если вы хотите выяснить, в чем заключаются различия между вашими группами (т. е. H-критерий Крускала-Уоллиса только говорит вам, была ли статистически значимая разница между вашими группами), вам нужно будет продолжить H-критерий Крускала-Уоллиса с помощью апостериорный тест. Мы также покажем вам, как выполнять эти апостериорные тесты с использованием SPSS Statistics в нашем расширенном руководстве по H-тестам Краскела-Уоллиса, доступ к которому вы можете получить, подписавшись на Laerd Statistics.

Примечание 1. В SPSS Statistics есть две разные процедуры, которые можно использовать для запуска H-критерия Крускала-Уоллиса: процедура Устаревшие диалоги > K независимых выборок и процедура Непараметрические тесты > Независимые выборки . Процедура, которую мы изложили ниже, представляет собой процедуру Legacy Dialogs > K Independent Samples . Мы показываем вам эту процедуру, потому что ее можно использовать с широким спектром версий SPSS Statistics. Однако у него есть недостаток из , а не автоматически запускает апостериорные тесты. Поэтому мы покажем вам, как выполнить процедуру Непараметрические тесты > K независимых выборок в нашем расширенном руководстве по H-тесту Крускала-Уоллиса, потому что оно имеет преимущество из автоматически запуска апостериорных тестов, что значительно ускоряет процедуру анализа. и проще.

Примечание 2. Нижеследующая процедура идентична для SPSS Statistics версий с 17 по 28 , а также для подписка версии SPSS Statistics, версия 28 и подписка версии являются последними версиями SPSS Statistics. Однако в версии 27 и подписной версии SPSS Statistics представила новый вид своего интерфейса под названием « SPSS Light », заменив предыдущий вид для версий 26 и более ранних версий , который назывался « Стандарт SPSS «. Поэтому, если у вас есть SPSS Statistics версий 27 или 28 (или подписной версии SPSS Statistics), следующие изображения будут светло-серыми, а не синими. Однако процедура идентична .

1. Нажмите A nalyze > N onparametric Tests > L egacy Dialogs > K Independent Samples. .. в верхнем меню, как показано ниже:

   Опубликовано с письменного разрешения SPSS Statistics, IBM Corporation.

   
   Вам будет представлено диалоговое окно « Tests for Multiple Independent Samples », как показано ниже:

   Опубликовано с письменного разрешения SPSS Statistics, IBM Corporation.

   Примечание. Флажок K Ruskal-Wallis H в области «Тип теста» должен быть установлен по умолчанию, но если это не так, обязательно установите этот флажок. Этот параметр указывает SPSS Statistics запустить H-критерий Крускала-Уоллиса для переменных, которые вы собираетесь передать на следующем шаге этой процедуры.

2. Перенесите зависимую переменную Pain_Score в поле T est Variable List: и независимую переменную Drug_Treatment_Group в поле G rouping Variable:. Вы можете передать эти переменные, либо перетащив каждую переменную в соответствующие поля, либо выделив (т. е. щелкнув) каждую переменную и нажав соответствующую кнопку. В итоге вы получите экран, аналогичный приведенному ниже:

   Опубликовано с письменного разрешения SPSS Statistics, IBM Corporation.

3. Нажмите на кнопку. Вам будет представлено диалоговое окно « Несколько независимых выборок: определить диапазон », как показано ниже:

   Примечание. Если кнопка неактивна (т. е. выглядит блеклой, как показано на рисунке ), убедитесь, что переменная Drug_Treatment_Group выделена желтым цветом (как показано выше на шаге 2), щелкнув ее. Это активирует кнопку.

   Опубликовано с письменного разрешения SPSS Statistics, IBM Corporation.

4. Введите « 1 » в поле Mi n imum: и « 3 » в поле Ma x imum. Эти значения представляют собой диапазон кодов, которые вы дали группам независимой переменной Drug_Treatment_Group (т. е. от препарата А до кода С от «1» до препарата С, который был закодирован как «3»). Вы получите экран, подобный показанному ниже:

   Опубликовано с письменного разрешения SPSS Statistics, IBM Corporation.

   Примечание. Если у вас есть четыре группы (например, от препарата А до препарата D) и вы хотите проанализировать только препарат В и препарат D, вы можете ввести «2» и «4» в Mi 9.0172 n imum: и Ma x imum, соответственно (при условии, что вы упорядочили группы по номерам).

5. Нажмите кнопку, и вы вернетесь в диалоговое окно « Тесты для нескольких независимых выборок », но теперь с заполненным полем G Переменная группировки:, как показано ниже:

   Опубликовано с письменного разрешения SPSS Statistics, IBM Corporation.

6. Нажмите на кнопку. Вам будет представлена ​​» Несколько независимых выборок: Опции «диалоговое окно, как показано ниже:

   Опубликовано с письменного разрешения SPSS Statistics, IBM Corporation.

7. Установите флажок D описательный, если вам нужны описательные данные, и/или флажок Q uartiles, если вам нужны медианы и квартили. Если вы выбрали опцию «Описания», вам будет представлен следующий экран:

   Опубликовано с письменного разрешения SPSS Statistics, IBM Corporation.

8. Нажмите на кнопку. Вы вернетесь в диалоговое окно « тестов для нескольких независимых выборок ».
9. Нажмите на кнопку. Это приведет к результатам.

SPSS Statistics

SPSS Statistics Выходные данные для H-критерия Крускала-Уоллиса

Вам будут представлены следующие выходные данные (при условии, что вы не установили описательный флажок D в » Несколько независимых выборок: варианты » диалоговое окно):

Опубликовано с письменного разрешения SPSS Statistics, IBM Corporation. можно использовать для сравнения эффекта различных лекарственных препаратов.Различные показатели боли в этих группах медикаментозного лечения можно оценить с помощью таблицы Test Statistics , в которой представлены результаты Н-критерия Крускала-Уоллиса.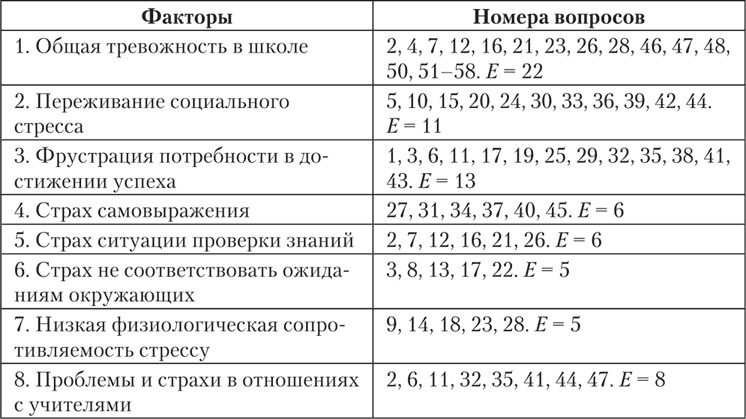 квадрат статистики (» Chi-Square «), степени свободы (строка » df «) теста и статистическая значимость теста (строка » Asymp. Sig. «).

SPSS Statistics

Отчет о результатах H-теста Крускала-Уоллиса

Используя данные из двух вышеприведенных таблиц, вы можете представить результат как:

В нашем расширенном руководстве по H-тесту Краскела-Уоллиса мы покажем вам, как запустить H-критерий с использованием непараметрических тестов > K независимых выборок 9Процедура 0027 в SPSS Statistics, которая включает постфактум-тест, чтобы вы могли определить, в чем заключаются различия между вашими группами. Например, вы можете использовать апостериорный тест, чтобы определить, статистически значимо различается показатель боли между препаратом А и препаратом Б. Мы также покажем вам, как записывать свои результаты, если вам нужно сообщить о них в диссертации, задании или исследовательский отчет. Мы делаем это, используя стили Гарварда и APA.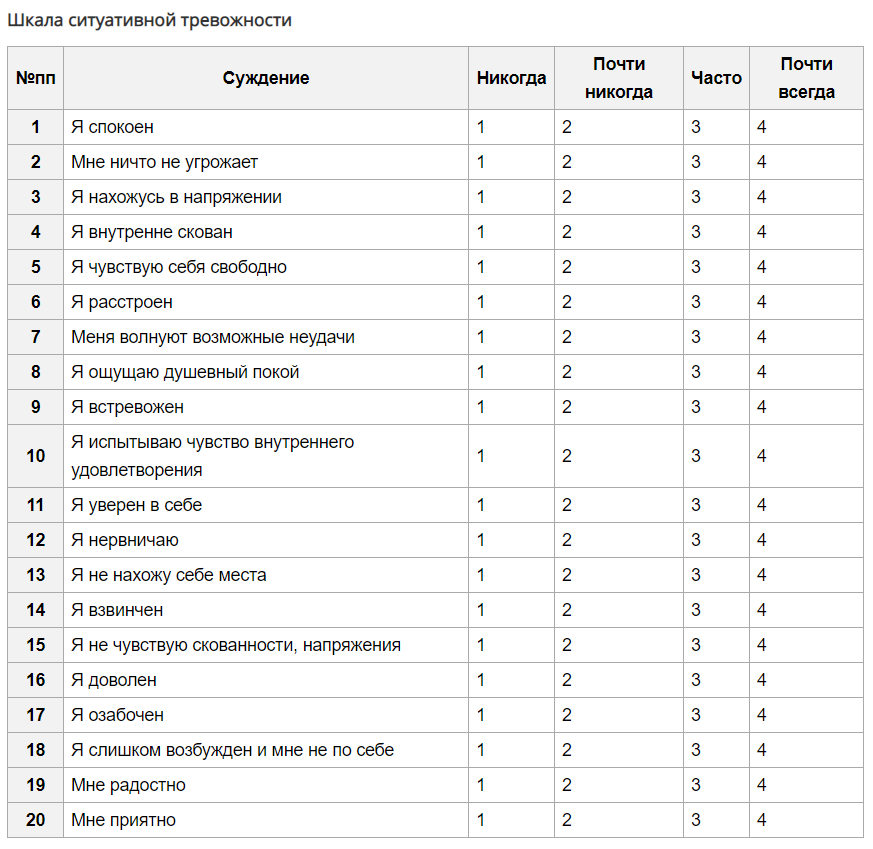 Помните, что распределение ваших данных будет определять, сможете ли вы сообщать о различиях в медианах. В нашем расширенном руководстве мы не только объясняем, как проверить это предположение, но также показываем, как интерпретировать и сообщать о результатах независимо от того, соответствуете ли вы этому предположению или нет. Вы можете узнать больше о нашем расширенном контенте в наших возможностях: Обзор стр.

Критерий Крускала-Уоллиса в программировании на R

Критерий Крускала-Уоллиса в языке программирования R представляет собой ранговый тест, аналогичный U-критерию Манна-Уитни, но может применяться к односторонним данным с более чем две группы. Это непараметрическая альтернатива однофакторному тесту ANOVA, который расширяет тест Уилкоксона для двух выборок. Группа выборок данных является независимой, если они получены из несвязанных совокупностей и выборки не влияют друг на друга. Используя тест Крускала-Уоллиса, можно решить, являются ли распределения населения похожими, не предполагая, что они следуют нормальному распределению. Выполнить тест Крускала-Уоллиса на языке R очень просто.

Примечание. Результат теста Крускала-Уоллиса говорит о наличии различий между группами, но не говорит о том, какие группы отличаются от других групп.

Примеры:

1. Пусть кто-то хочет выяснить, как социально-экономический статус влияет на отношение к повышению налога с продаж. Здесь независимой переменной является « социально-экономический статус » с тремя уровнями: рабочий класс, средний класс и богатый. Зависимая переменная измеряется по 5-балльной шкале Лайкерта от «полностью согласен» до «полностью не согласен».
2. Если кто-то хочет узнать, как страх перед экзаменом влияет на фактические результаты теста. Независимая переменная «тестовая тревожность» имеет три уровня: отсутствие тревожности, низкая-средняя тревожность и высокая тревожность. Зависимой переменной является экзаменационный балл, который оценивается от 0 до 100%.

Допущения для теста Крускала-Уоллиса в R

Переменные должны иметь:

• Одна независимая переменная с двумя или более уровнями. Тест чаще используется при наличии трех и более уровней. Для двух уровней вместо теста Крускала-Уоллиса рассмотрите возможность использования U-тест Манна-Уитни.
• Зависимой переменной должна быть порядковая шкала, шкала отношений или шкала интервалов.
• Наблюдения должны быть независимыми. Другими словами, не должно быть корреляции между членами каждой группы или внутри групп.
• Все группы должны иметь одинаковое распределение формы.

Реализация в R

R предоставляет метод kruskal.test() , доступный в пакете stats для выполнения теста суммы рангов Крускала-Уоллиса.

Синтаксис: kruskal.test(x, g, формула, данные, подмножество, na.action, …)

Параметры:

• x: числовой вектор значений данных или список числовых векторы данных.
• g: объект вектора или фактора, задающий группу для соответствующих элементов x
• формула: формула формы ответ ~ группа, где ответ дает значения данных и группирует вектор или фактор соответствующих групп.
• данные: необязательная матрица или фрейм данных, содержащий переменные в формуле.
• подмножество: необязательный вектор, указывающий используемое подмножество наблюдений.
• na.action: функция, которая указывает, что должно произойти, когда данные содержат NA

…: дополнительные аргументы, которые должны быть переданы в методы или из них.

Пример:

Давайте воспользуемся встроенным набором данных R с именем PlantGrowth. Он содержит массу растений, полученных при контроле и двух различных условиях обработки.

Р

myData = PlantGrowth print (myData)   print ( levels (myData$group))

  Output:

 весовая группа
1 4. 17 Ctrl
2 5,58 Ctrl
3 5.18 Ctrl
4 6.11 Ctrl
5 4,50 Ctrl
6 4,61 Ctrl
7 5.17 Ctrl
8 4,53 Ctrl
9 5.33 Ctrl
10 5.14 Ctrl
11 4,81 тр1
12 4.17 тр1
13 4,41 тр1
14 3,59тр1
15 5,87 тр1
16 3,83 тр1
17 6.03 тр1
18 4,89 тр1
19 4,32 тр1
20 4,69 тр1
21 6.31 тр2
22 5.12 тр2
23 5,54 тр2
24 5,50 тр2
25 5,37 тр2
26 5,29 тр2
27 4,92 тр2
28 6.15 тр2
29 5,80 тр2
30 5,26 тр2
[1] "ctrl" "trt1" "trt2" 

Здесь столбец «группа» называется фактором, а различные категории («ctr», «trt1», «trt2») называются уровнями факторов. Уровни расположены в алфавитном порядке. Постановка задачи заключается в том, что мы хотим знать, есть ли существенная разница между средним весом растений в трех экспериментальных условиях. А тест можно выполнить с помощью функции kruskal.test() , как указано ниже.

R

myData = PlantGrowth   result = kruskal. Добавить комментарий Отменить ответ Ваш адрес email не будет опубликован. Обязательные поля помечены * Комментарий * Имя * Email * Сайт