Проективные матрицы равена онлайн: Прогрессивные матрицы Равена || Пройти тест онлайн

Матрицы Равена: уникальный тест на определение уровня интеллекта

Д. Равен вместе с Л. Пенроузом создали в 1936 году уникальные матрицы Равена. Прогрессивная методика была разработана для определения умственного уровня и оценки способностей к систематизации, методологии, логическому мышлению. Джон Равен придумал универсальный тест, результат которого почти не зависит от знаний, уровня жизни и опыта испытуемых. Стандартные матрицы предназначены как для тестирования взрослых людей, так и для детей.

Как проводится тестирование?

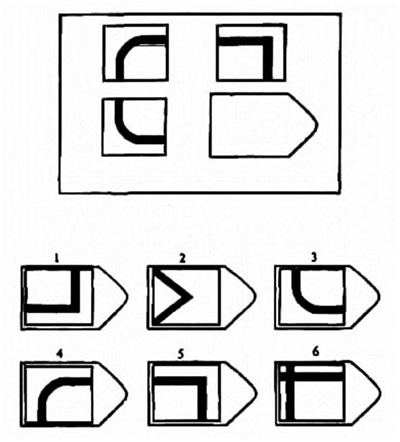
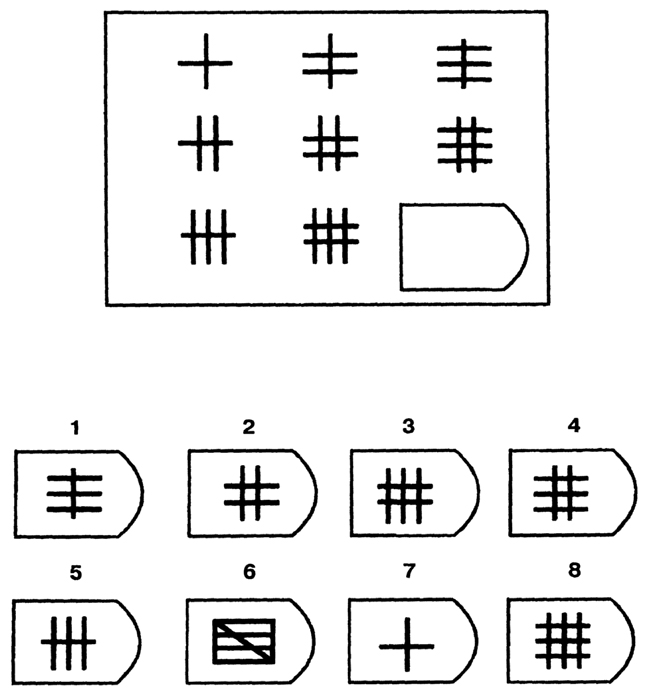
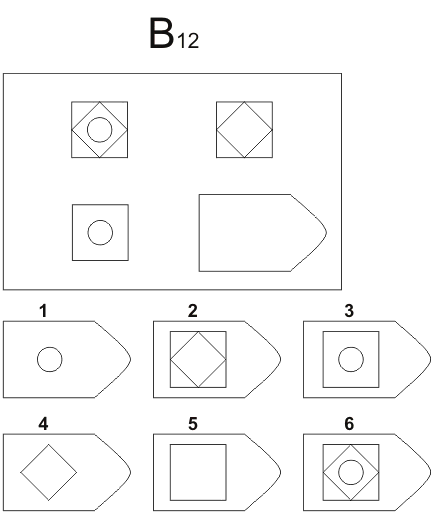
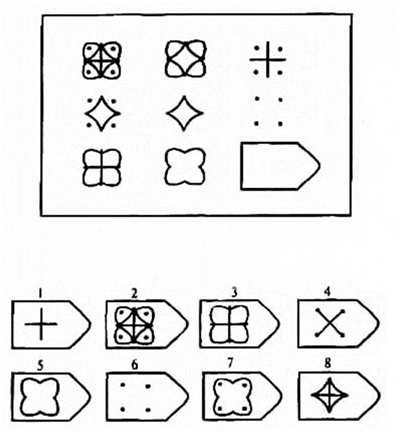
В матрицы входят 60 графических рисунков. В рисунке недостает простой фигуры, например, прямоугольника. Под рисунком размещены 6 или 8 фрагментов, которые почти подходят по размеру к недостающей фигуре. Основной задачей является обработка и поиск фрагментов той фигуры, которая точно подходила бы в пустое место. Суть проективного метода заключается в том, чтобы логически определить по какому принципу составлен графический рисунок, к которому необходимо подобрать недостающую фигуру.

Матрицы Равена поделены на 5 групп, в каждой из которой 15 рисунков. Серии рисунков разделены по определенным принципам и типам сложности. В каждой группе содержатся задания разного уровня:

Первая серия А разработана по принципу определения структуры рисунка и ее взаимосвязи. Необходимо найти одну из частей рисунка, которая точно подойдет к недостающей части основного рисунка. Задание направлено на детальную оценку составляющих изображения и поиск таких же деталей в одном из предложенных фрагментов.

Серия В содержит принцип поиска аналогии между несколькими фигурами. Человеку необходимо понять закономерность, по которой создана каждая фигура и, ориентируясь на это, определить отсутствующую часть рисунка. Нужно отыскать осевую симметрию, размещенную в фигуре.

Серия С разработана по принципу усовершенствования и усложнения фигур. С каждой серией фигуры видоизменяются, то есть происходит постепенное непрерывное развитие. Фигуры заполняются новыми частями по определенному принципу, по которому можно найти в последующих рисунках отсутствующие фигуры.

Серия D содержит принцип перестановки основных фигур. Человеку необходимо определить в разных плоскостях (горизонтальном и вертикальном) перегруппировку.

Серия Е составлена по принципу разделения основных фигур на части. Подходящие фигуры нужно собрать, определив закономерность составления фигур.

Где используются продвинутые матрицы Равена?

1. В научной сфере для изучения умственных способностей людей из других этнических и культурных групп, исследования генетических и образовательных различий интеллектуальных процессов.
2. В профессиональной сфере, где необходимо определить сильные стороны работников, например, эффективных администраторов или менеджеров, кураторов или маркетологов.
3. В образование деятельности, где есть потребность в прогнозе будущих результатов учащихся, независимо от уровня их жизни и опыта .
4. В медицинской сфере для определения нейропсихологических проблем, для подтверждения результатов, которые были получены другими методами при измерение интеллектуальной способности.

Тестирование людей на определение уровня интеллекта является востребованным почти в любой сфере деятельности. Важно постоянно прокачивать свой мозг, продвигать себя, как специалиста, развивать компетенции и узнавать что-то новое. На платформе «Россия — страна возможностей» размещены бесплатные онлайн-курсы по маркетингу, личностному росту, финансам, менеджменту и другие. Пройдите курс «Личная ответственность за результат: результат-ориентированное мышление» и повысьте свой уровень интеллекта в моменте. Результат-ориентированное мышление помогает быстрее добиваться целей, осознанно принимать решения и грамотно использовать имеющиеся ресурсы. После обучения вы сможете самостоятельно разработать карту точек вашего роста и научитесь концентрироваться на достижении результата, сможете быстрее и качественнее выполнять задачи.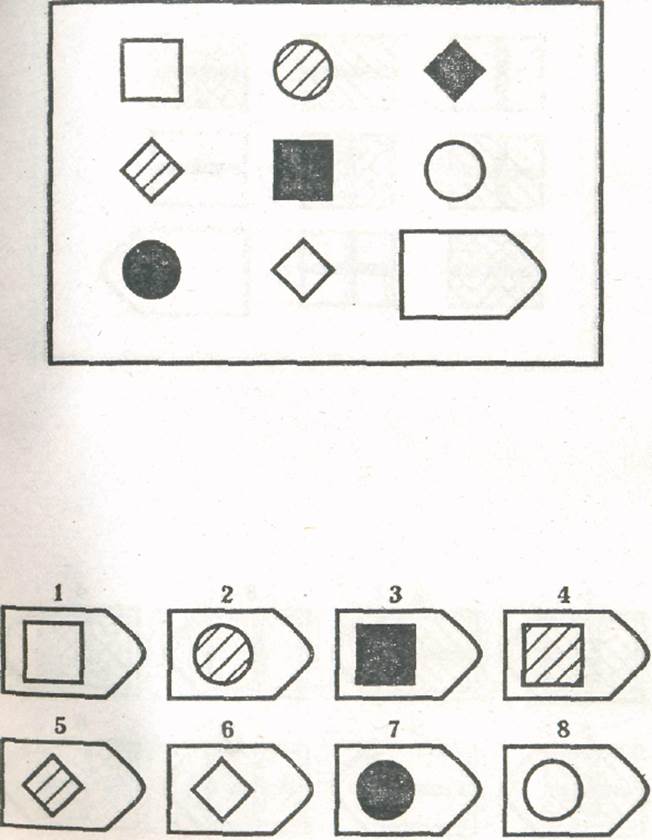

Когнитивная психология — Психология — Библиотека

Тренинг «HR-диагностика: надежные тестовые методики для оценки персонала»

В результате участники получают:

1. Инструкции, описания и интерпретации результатов тестовых методик в печатном и электронном виде.
2. Возможность научиться корректно проводить изучение и обрабатывать результаты психодиагностических методик.

Структура знакомства с каждой методикой:

1. Краткая информация о методике (методик) и области ее (их) применения.
2. Знакомство с методикой, выполнение, обработка и интерпретация своих результатов.
3. Закрепление навыка обработки и интерпретации на дополнительном примере.

Программа тренинга по методикам оценки персонала

1. «Тесты способностей: внимание, память, интеллект»

Вниманию участников будут представлены следующие методики:

1. «Переплетенные линии»,
2. «Расстановка чисел»,
3. «Методика 10 слов»,
4. «Воспроизведение рассказов»,
5. «Интеллектуальная лабильность»,
6. «Гибкость мышления»,
7. «Лабиринт»,
8. «Краткий Ориентировочный Тест»,
9. «Матрицы Равена»,
10. «Оперативность мышления».

2. «Организационный тест (Оргтест)»

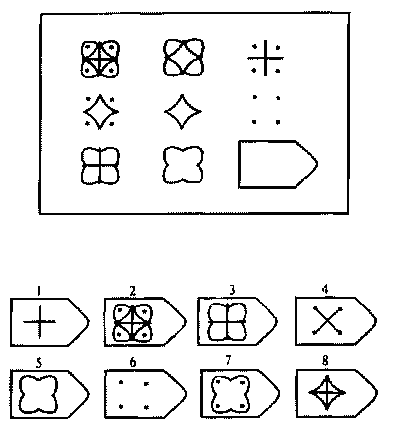
3. «Папка руководителя»

4. «Проективные методики»

Город: Новосибирск

Звоните: +7 (383) 248-78-16

Пишите: [email protected]

WhatsApp: +7 962-828-78-16

Skype: bulgakova-siyanie

Подписаться на рассылку

Решение и ответы на тесты онлайн ММУ

Примеры вопросов по предмету

Психодиагностика

o Психодиагностика 1-1 o Для какой валидности важен критерий внутренней согласованности теста? o Тесты способностей показывают: o Когда психологическая диагностика выделилась в самостоятельную дисциплину? o Каково исходное назначение опросника Т. Лири: o Понятие «самонаблюдение» является синонимом термина: o Методологической основой психодиагностики является: o Содержательная валидность теста – это: o Фактор социальной желательности оказывает наибольшее влияние в: o Для чего нужны профильные оценки? o Способ исследования структуры и характера межличностных отношений людей на основе измерения межличностного выбора называется: o Какая валидность теста обеспечивается за счет соответствия пунктов измеряемому фактору? o Что одно из перечисленного является существенным элементом предложенного А.Ф. Лазурским «естественного эксперимента» в отличие от лабораторного: o Надежность теста показывает: o С какими теоретическими принципами связаны тестовые методики? o Получение субъектом данных о собственных психических процессах и состояниях в момент их протекания или вслед за ним – это: o В каком году в России был наложен запрет на применение тестов? o Какой из тестов позволяет сопоставить вербальные и невербальные способности: o Возможность исследователя вызвать какой-то психический процесс или свойство является главным достоинством: o На что ориентирован идеографический подход в психодиагностике? o Кто впервые использовал психодиагностические опросники? o Что такое выборка стандартизации? o Какой из перечисленных факторов может приводить к снижению показателей по вербальному тесту Векслера: o Что отражает трудность заданий теста? o Сколько периодов выделяют в развитии отечественной психодиагностики? o Как можно установить надежность частей теста? o Краткое, стандартизированное психологическое испытание, в результате которого делается попытка оценить тот или иной психологический процесс или личность в целом, – это: o На что ориентирован номотетический подход в психодиагностике? o Когда завершилось формирование психологической диагностики в самостоятельную область исследований? o Активное вмешательство исследователя в деятельность испытуемого с целью создания условий для установления психологического факта называется: o Целевые установки пробы Бурдона и матриц Равена соотносятся как: o Как устанавливается эмпирическая валидность теста? o Что является родоначальником проективных техник? o Работы, каких двух исследователей стояли у истоков метода тестирования: o С какой областью преимущественно связана общая психодиагностика? o Какой из перечисленных тестов НЕ является проективным: o Тест фрустрации Розенцвейга относится к одной из названных групп: o Когда появились первые тесты для определения индивидуальных психологических различий? o Оценка коэффициента интеллекта опирается на сопоставление: o Опросник Спилберга-Ханина позволяет: o Проективные тесты и методики отличаются от объективных тестов и стандартизированных самоотчетов тем, что: o Какой из цветов в тесте Люшера НЕ относится к основным: o Оценка согласованности показателей, получаемых при повторном тестировании тех же испытуемых и тем же самым тестом или эквивалентной его формой, характеризует тест с точки зрения его: o Идея стандартизации методик и тестов принадлежит: o Что отсутствует среди психодиагностических подходов? o 16-факторный личностный опросник разработал … o Какая шкала используется для классификации объектов? o С какой областью преимущественно связана частная психодиагностика? o Когда психотехника сформировалась как особая отрасль отечественной психологии? o В чем состоит психометрический парадокс? o Какой из тестов содержит 3 шкалы валидности и 10 клинических шкал: o Что явилось первым диагностическим методом? o Какой из перечисленных тестов НЕ предназначен для оценки интеллектуальных способностей: o В чем заключается надежность методики? o Какое из утверждений верно описывает назначение теста Розенцвейга: o Нелинейное преобразование стандартных показателей необходимо для того, чтобы: o Во взрослом и детском вариантах теста Векслера наиболее культурально-зависимы результаты по тесту: o Социально-психологический норматив – это: o Если выборка репрезентативна срезу популяции, то: o Сколько выделяют уровней диагностических заключений? o Какие тесты поставляют наиболее точные и объективные результаты? o Какое шкалирование составляет основу психометрических измерений? o Стандартизация – это: o Кто является автором тематического апперцептивного теста? o Ананьев Б. Г. относит лонгитюдный метод исследования: o Что представляет собой график нормального распределения переменных? o Что относится к малоформализованным методикам? o Какие тесты проводятся только в индивидуальной форме? o Кто создал научную характерологию как направление дифференциальной психологии? o В каких методиках от испытуемого требуется получить правильный ответ? o Метод активного воздействия исследователя на изменения психики ребенка – это: o Тип результатов, регистрируемых с помощью опросников и других методов самооценок, называется: o Какая тестовая задача относится к задачам закрытого типа? o На чем основан контент-анализ? o Какой тест называется гомогенным? o Первые интеллектуальные тесты для детей были разработаны: o Какие диалогические техники могут иметь невербальный характер? o Какая из контрольных шкал может использоваться отдельно от основной методики? o Таблицы Шульте предназначены для исследования объема внимания, а таблицы Шульте-Горбова для исследования: o Какие тесты первыми стали применяться в психодиагностике? o Когда в психодиагностике начали применять контент-анализ? o В чем состоит особенность практических тестов? o Какое из приведенных утверждений НЕ отражает основных правил оценки профиля MMPI: o Какой тест не является бланковым? o Какой тип шкалирования используется при исследовании самооценки по типу семантического дифференциала? o Что объединяет проективные техники с формализованными методиками? o Сколько параметров достаточно для анализа кривой нормального распределения? o Что такое параллельная форма теста? o Длительное и систематическое наблюдение, изучение одних и тех же людей, позволяющее анализировать психологическое развитие на различных этапах жизненного пути и на основе этого делать определённые выводы, принято называть исследованием: o Минимальный возраст, начиная с которого может использоваться цветовой тест отношений А. М. Эткинда: o Целенаправленное, планомерно осуществляемое восприятие объектов, в познании которых заинтересована личность, является: o В каком пункте указаны методики, лучше всего позволяющие выявить разноплановость мышления: o В каких психодиагностических методиках ответы испытуемого всегда оцениваются как правильные или не правильные? o К формализованным методикам относятся: o Валидность – это: o Тест «чернильных пятен» создан Г. Роршахом: o Метод познания, который ограничивается регистрацией выявленных фактов при исследовании возрастных особенностей, называется: o Включенное наблюдение – это: o Прием, используемый для повторного обследования испытуемых с помощью одной и той же методики для проверки стабильности диагностируемого признака, называется: o На какие методики меньше всего влияет личность психодиагноста? o Какая из контрольных шкал направлена на анализ тенденции к ухудшению результатов обследования? o Какой вид стандартизированных самоотчетов предполагает последующий контент-анализ? o Какая шкала не является в строгом смысле измерительной? o Каков минимальный объем выборки, необходимый для получения достоверных результатов при проверке методик? o Что представляе6т собой вербальная шкала? o Что такое гетерогенный тест? o Какая измерительная шкала имеет фиксированное начало отсчета? o На результат каких техник больше всего влияет личность психодиагноста? o Данные о реальном поведении человека, полученные в ходе внешнего поведения, называются: o Синонимом формирующего эксперимента является: o Какая шкала используется для оценивания результатов психометрических тестов? o К малоформализованным методикам НЕ относят: o Каково максимально допустимое количество лиц при групповом тестировании? o Какая тестовая задача относится к задачам открытого типа? o Что относится к формализованным психодиагностическим методикам? o В чем состоит принципиальное достоинство проективных методик? o Методика Дембо-Рубинштейн представляет собой: o Как называется пригодность методики для измерения того, для чего она была создана? o Что такое пилотажное исследование? o Надежность – это:

Проверка профессиональных и личностных качеств кандидата

Проверка профессиональных и личностных качеств – это определение соответствия профессиональных знаний, навыков и качеств кандидата предъявляемым требованиям.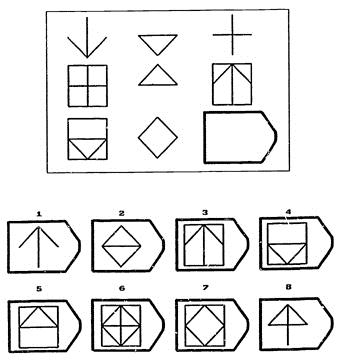 Целью данного этапа является получение информации для объективной стандартизированной оценки кандидатов на должность.

С целью определения профессиональных и личностных качеств кандидата применяются анкетирование, тестирование, выполнение пробных заданий и т. д.

При отборе кандидатов на должность применяется четыре группы тестов: личностные опросники, тесты способностей, тесты достижений, проективные тесты.

Личностные опросники – группа психодиагностических методик, предназначенных для определения степени выраженности у человека определенных личностных особенностей. Личностные опросники представляют собой списки вопросов, ответы на которые испытуемого представлены количественно (16 факторный личностный опросник Кэттела, опросник MBTI, тест «Уровень субъективного контроля», Миннесотский многофакторный личностный опросник MMPI и т. п.).

Пример: 16-факторный тест Р. Кэттелла («Sixteen Personality Factor Questionnaire») позволяет провести диагностику таких существенных характеристик личности, как:

• степень эмоциональной вовлеченности;
• способность к логическому анализу;
• эффективность интеграции поведения;
• доминантность или зависимость;
• свобода действий или скованность;
• уровень энергетического потенциала;
• уровень реалистичности и практичности;
• способность подчинять свое поведение системе правил;
• уровень удовлетворенности ситуацией и своей ролью в ней;
• потребность в переживаниях и склонность к риску;
• зависимость от поддержки группы или самодостаточность;
• способность к самоконтролю;
• степень напряженности неудовлетворенных потребностей.

Тесты способностей – это группа методик, которые содержат специально подобранные стандартизованные наборы заданий, служащие для оценки потенциальной способности человека решать различные задачи. Например: Тест структуры интеллекта Амтхауэра; Тест определения интеллектуальной лабильности; Прогрессивные Матрицы Равена; Тест Векслера и др.

Тесты на общий уровень интеллекта содержат наборы заданий, которые включают математические, логические, лингвистические и прочие подобные задачи, на решение которых отводится ограниченное время.

Пример: В компании Procter & Gamble тест на определение способности к логическому мышлению содержит 40 заданий на русском языке. Кандидат должен в течение 65 минут выбрать правильный вариант ответа из нескольких представленных. Основу составляют тесты из математических задач, психометрические и SHL тесты, задания на понимание текста и анализ изображений.

Тесты достижений – методики диагностики, позволяющие выявить степень владения кандидатом конкретными знаниями, умениями, навыками (тесты профессиональных знаний).

Не нашли что искали?

Преподаватели спешат на помощь

Пример: Для банковских структур разработаны компьютерные профессиональные тесты оценки знаний персонала по таким тематическим разделам, как Кассовые операции, Операционная работа, Межбанковские расчеты, Кредитные операции, Валютные операции, Ценные бумаги, Внутрибанковский учет и отчетность и т. д.

Пример: При отборе персонала в международных компаниях осуществляется проверка знания иностранного языка.

Другим способом проверки профессиональной пригодности кандидата является выполнение им пробных заданий. Как правило, пробные задания применяются при отборе на должности, требующие определенных знаний и навыков. Например, кандидату на позицию программиста может быть предложено задание разработать алгоритм решения какой-либо задачи; на должность пресс-секретаря – написать краткий пресс-релиз; на должность маркетолога – подготовить отчет по имеющимся данным.

Проективные методики предполагают создание для обследуемого достаточно неопределенной ситуации, оставляющей ему свободу действий (в рамках инструкций), что допускает выбор ответа в очень широких пределах.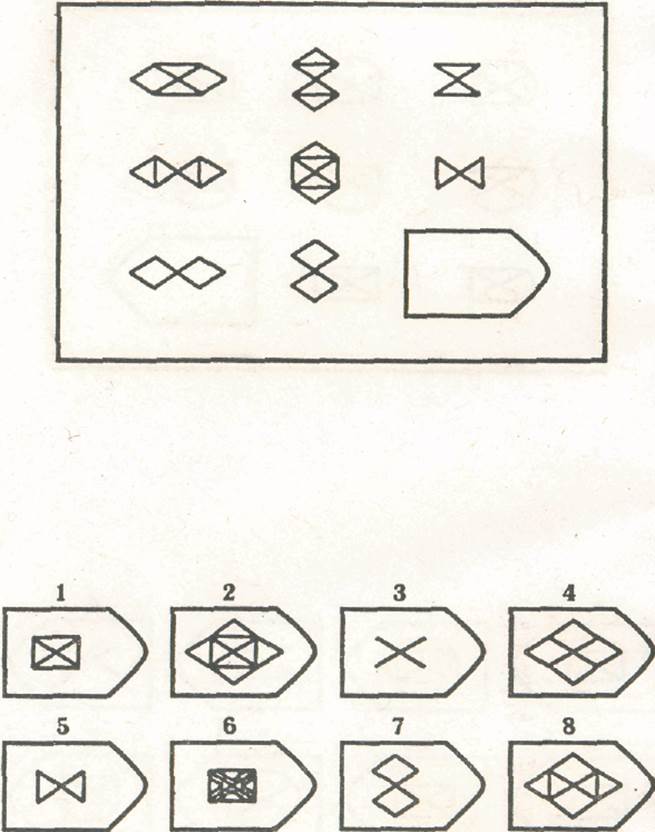 Например, тест «Несуществующее животное», тест фрустрационных реакций Розенцвейга, цветовой тест Люшера и т. д.

Пример: Тест Люшера основан на предположении о том, что предпочтения одних цветов другим определенным образом связаны с устойчивыми личностными характеристиками человека и особенностями его переживания актуальной ситуации.

Перечень тестов для проверки кандидатов при отборе персонала зависит от категории должности, на которую они претендуют, и содержания будущей работы.

Изучение особенностей личности кандидата предполагает оценку актуального психоэмоционального состояния, диагностику межличностных отношений и комплексную оценку личностного портрета.

На основании психологического тестирования психолог составляет прогноз психологической адаптации работника и выдает руководству соответствующие рекомендации.

Типичные психодиагностические процедуры. Анкеты, личностные опросники, тесты интеллекта, проективные методики, репертуарные методики, тесты достижений и экспертные оценки

Феноменологическая типология диагностических процедур включает: 1) анкеты; 2) личностные опросники; 3) тесты интеллек­та; 4) проективные методики; 5) репертуарные методики; 6) тесты достижений; 7) экспертное оценивание.

Анкетирование –это опрос с помощью анкеты. Анкета – это специально оформленный список вопросов, обращенных к определенной категории респондентов. Анкета представляет собой совокупность вопросов о предпочтениях, мотивах, мнениях, оценках. Она, как правило, состоит из трех частей: вводной, основной и демографической

Личностные опросники.Каждый из таких опросников опирается на какие-либо тео­ретические положения о личности и ее проявлениях, исходя из кото­рых строится предполагаемая модель исследуемого феномена, от­бирается ряд диагностических признаков, формируется набор вопросов, о поведении или предпочтениях обследуемого, позволяющих оценить степень выраженности указанных признаков. Обычно в вопросниках для подсчета количества баллов используется такой критерий, как частота проявления того или иного признака.

Классическими методиками подобного типа принято считать MMPI (Миннесотский многопрофильный личностный опросник), 16PF (16 личностных факторов – Р.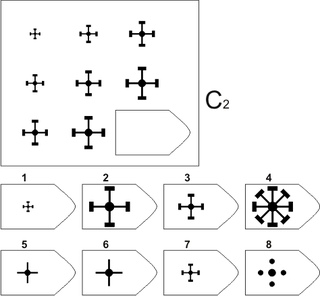 Кэттелл) и ПДО (психодиаг­ностический опросник на выявление акцентуаций). Эти перечни вопросов (или утверждений) могут применяться как для самооце­нок, так и для получения экспертных оценок.

Тесты интеллекта представляют совокупность заданий, выполнение которых не требует специальных знаний, умений, на­выков (как правило) и позволяет оценить общий уровень интел­лекта. Каждый из таких тестов основыва­ется на какой-либо модели интеллекта.

Наиболее часто используемые тесты подобного типа:

1) прогрессивные матрицы Равена;

2) структуры интеллекта Амтхауэра;

3) шкалы измерения интеллекта Векслера;

4) школьный тест умственного развития (ШТУР).

Проективные методики.В основе проективных методов лежит принцип психоло­гической проекции,согласно которому испытуемый проектирует, т.е. отражает (или выражает), на достаточно неструктурирован­ный (неупорядоченный) стимульный материал (цвета, сказочные персонажи, пятна неопределенной формы и т. п.) свои неосознава­емые или скрываемые потребности, комплексы, вытеснения, пере­живания, мотивы.

Различают несколько групп проективных методик:

1. Конститутивные.

2. Конструктивные.

3. Интерпретативные.

4. Катарсические.

5. Экспрессивные.

6. Импрессивные.

7. Аддитивные.

Наиболее типичными из них являются: тест Роршаха, тест цветовых выборов Люшера, тест базовых влечений Сонди, тест на фрустрацию Розенцвейга, тематической апперцепции тест (ТАТ).

Исследователи выделяют ряд признаков проективных ме­тодик:

— относительную свободу в выборе ответа и тактики поведе­ния испытуемого;

— отсутствие внешних показателей оценочного отношения к испытуемому со стороны экспериментатора;

— обобщенное оценивание взаимоотношения личности с ее социальным окружением или интегральную диагностику ряда личностных свойств, а не измерение какой-либо отдельной пси­хической функции

Репертуарные методы – сравнительно недавно возникшее направление диагностики, дают возмож­ность прогнозировать ряд ситуативных методов проявлений личности или группы, служить основой для коррекции и развития.

Исходными этих методов являются набор (репертуар), объ­ектов оценивания и совокупность (или система) конструктов (заданных или выявленных). Конструкты имеют форму бипо­лярных понятий (например, белый – черный, хороший – плохой, эгоист – альтруист). Конструкт– это «личностное изобретение», это истолкование, которое накладывается на реальность (Дж. Келли). В функционировании конструкта обобщение и различение имеют место одновременно. Словом, конструкт – это элемен­тарная единица нашего восприятия, мышления, отношения и т.п., в которой соединены объективные сведения и их субъективная интерпретация.

После выявления объектов производится оценивание их по сооьвеьсьвующим онструктам. В итоге получается матрица оценок, которая подвергается обработке с целью получения ряда показателей, характеризующих диагностируемый феномен.

Тесты достижений.Еще одной группой типичных диагностических процедур являются тесты достижений,позволяющие оценить уровень овла­дения каким-либо видом деятельности. Частным случаем таких тестов являются тесты педагогиче­ские, предназначенные для диагностики успешности овладения учащимися различными компонентами учебной деятельности.

Экспертные оценки.В основе экспертного оценивания лежит опрос экспертов, который отличается от других видов опросов в первую очередь уровнем компетентности опрашиваемых в интересующей психо­лога проблеме и процедурными моментами, связанными с отбором экспертов и анализом получаемой от них информации.

Экспертный опрос приобретает в диагностике особую значимость как один из способов проверки валидности используе­мых методик и диагностирования конкретных социально-психо­логических явлений, для которых адекватные методики еще не разработаны или недостаточно надежны. Незаменимую услугу экспертные опросы могут оказать в прогнозировании социально-психологических явлений, особенно массовых. Сюда можно отнести, хотя и несколько условно, метод мозгового штурма.

Тренинг «HR-диагностика: надежные тестовые методики для оценки персонала» | Новосибирск

Цель тренинга: овладеть надежными и эффективными инструментами оценки, используемых при подборе персонала и формировании кадрового резерва, а также при построении профиля должности и модели компетенций.

В результате участники получают:

1. Инструкции, описания и интерпретации результатов тестовых методик в печатном и электронном виде.
2. Возможность научиться корректно проводить изучение и обрабатывать результаты психодиагностических методик.

Структура знакомства с каждой методикой:

1. Краткая информация о методике (методик) и области ее (их) применения.
2. Знакомство с методикой, выполнение, обработка и интерпретация своих результатов.
3. Закрепление навыка обработки и интерпретации на дополнительном примере.

Программа тренинга по методикам оценки персонала

1. «Тесты способностей: внимание, память, интеллект»

Простые и проверенные инструменты с высокой валидностью дают информацию о том, насколько качественно и быстро кандидаты способны обрабатывать и делать верные выводы из комплексной информации. Они необходимы для прогноза по компетенциям: внимание к деталям, аналитичность, обучаемость, готовность к изменениям, принятие решений.

Вниманию участников будут представлены следующие методики:

1. «Переплетенные линии»,
2. «Расстановка чисел»,
3. «Методика 10 слов»,
4. «Воспроизведение рассказов»,
5. «Интеллектуальная лабильность»,
6. «Гибкость мышления»,
7. «Лабиринт»,
8. «Краткий Ориентировочный Тест»,
9. «Матрицы Равена»,
10. «Оперативность мышления».

2. «Организационный тест (Оргтест)»

Письменное задание, моделирующее процесс работы управленца. Он позволяет оценить: системность мышления; способность к анализу, систематизации и обобщению разрозненной информации; способность к планированию собственных действий; гибкость и нестандартность мышления; ориентацию на конкретный результат; рациональность и самостоятельность в принятии решений; умение работать в условиях дефицита времени и недостатка информации; навыки делегировании, постановки задачи.

3. «Папка руководителя»

В данном письменном упражнении каждый участник принимает на себя роль руководителя и планирует решение ряда задач. Данная методика дает представление об уровне развития управленческих компетенций (постановка целей и задач, планирование, мотивирование и развитие персонала), системности мышления, ориентации на результат, клиентоориентированности, умение работать в условиях дефицита времени и недостатка информации.

4. «Проективные методики»

Позволяют выявить интересы и установки личности, мотивация, ценностные ориентации, страхи и тревоги, неосознаваемые потребности и побуждения: методика цветовых метафор (И.Л.Соломина) и методика «Агрессивность» (Модификация теста Розенцвейга).

БИЗНЕС-ТРЕНЕР — 

• Практический опыт управления персоналом (оценка и развитие персонала, тренерская деятельность) с 2001 года.
• Реализованы проекты подбора, оценки и развития потенциала в регионах Сибири для более, чем 30 организаций и компаний.
• Проведено более 3000 интервью, более 50-ти центров оценки и развития по всей Сибири.
• Опубликовано около 10 статей в научных региональных и федеральных изданиях.

Приобретая готовый видеокурс вы получаете скидку 10%

По окончании тренинга выдается именной сертификат!

Необходима предварительная регистрация!

Лекция 16: Матрицы проекции и наименьшие квадраты | Видео-лекции | Линейная алгебра | Математика

ОК. Вот шестнадцатая лекция, и, если вы помните, я закончил последнюю лекцию этой формулой для того, что я назвал матрицей проекции.

И, может быть, я смогу на минутку вспомнить, что делает эта волшебная формула?

Например, он должен быть — он должен создавать проекцию, если я умножу на b, поэтому я беру P умножить на b, я должен проецировать этот вектор b на ближайшую точку в пространстве столбца.

ОК. Могу я просто … один из способов резюмировать — это взять два крайних случая.

Предположим, что вектор b находится в пространстве столбцов?

Тогда что я получу, применив проекцию P? Итак, я проецирую в пространство столбца, но в этом случае я начинаю с вектора, который уже находится в пространстве столбца, поэтому, конечно, когда я проецирую его, я снова получаю B, верно.

И я хочу показать вам, как это получается из этой формулы.

Позвольте мне сделать другую крайность.

Предположим, что вектор перпендикулярен пространству столбцов.

Итак, представьте пространство колонн как плоскость и представьте, что b торчит прямо перпендикулярно ей.

Какая точка в пространстве столбца находится ближе всего к b в этом случае?

Итак, какова проекция на плоскость, ближайшая точка на плоскости, если вектор b, на который я смотрю, — не имеет компонента в пространстве столбцов, он полностью прилипает к нему — девяносто градусов, тогда Pb должно быть равно нулю, верно.

Итак, это два крайних случая.

Средний вектор имеет компонент P в пространстве столбцов и компонент, перпендикулярный ему, и что делает проекция, так это то, что она убивает эту часть и сохраняет эту часть.ОК. Можем ли мы просто понять, почему это правда?

Просто — эта формула должна работать.

Итак, позвольте мне начать с этого. Какие векторы в — перпендикулярны столбцу

пробела? Как мне увидеть, что я действительно получаю ноль?

Я должен подумать, что значит для вектора b быть перпендикулярным пространству столбца?

Итак, если он перпендикулярен всем столбцам, значит, он находится в каком-то другом пространстве.

У нас есть четыре пробела, поэтому я делаю это по той причине, что идеально использую то, что мы знаем о наших четырех пробелах.Какие векторы перпендикулярны пространству столбцов?

Это ребята в нулевом пространстве транспонирования А,

, верно? Это первый раздел этой главы, это ключевая геометрия этих пространств.

Если я перпендикулярен пространству столбца, я нахожусь в нулевом пространстве транспонирования A. ОК. Итак, если я нахожусь в нулевом пространстве транспонирования A и умножаю эту большую формулу на b, так что теперь я получаю Pb, теперь это проекция Pb, вы видите, что я получаю ноль?

Конечно, я получаю ноль.

Прямо в конце, транспонирование b сразу даст мне ноль.

Так вот почему этот ноль здесь.

Потому что, если я перпендикулярен пространству столбца, тогда я нахожусь в нулевом пространстве транспонирования A и транспонирования b в порядке, как насчет другой возможности. пшик. Как я могу увидеть, что эта формула дает мне правильный ответ, если b находится в пространстве столбца?

Так какой же типичный вектор в пространстве столбцов?

Это комбинация столбцов.

Как мне написать комбинацию столбцов? Итак, скажите мне, как мне написать, знаете ли, ваш повседневный вектор, который находится в пространстве столбцов?

Это будет иметь вид A, умноженный на несколько x, верно?

Это то, что находится в пространстве столбцов, умноженное на что-то.

Это комбинация столбцов.

Значит, эти b были в нулевом пространстве транспонирования A.

Эти парни в пространстве столбцов, эти b — Ax-s. Верно?

Если b находится в пространстве столбца, то он имеет вид Ax.

Я обязательно добавлю это в викторину или в финал.

Это вы должны осознать — потому что мы уже тысячу раз говорили, что объекты в пространстве столбцов являются векторами A, умноженными на x. ОК. А вы видите, что теперь произойдет, если мы воспользуемся нашей формулой?

Есть транспонирование A A.

Отменяется своей инверсией.

У нас остается А, умноженное на х.

Итак, результатом был Axe.

Который был б.

Вы видите, что это работает?

Вот и весь бизнес.

Отмена, отмена, выход из Ax.

И топор был б.

Так что в данном случае оказалось b. Итак, геометрически мы видим, что мы берем вектор — у нас есть пространство столбцов, и перпендикулярно ему является нулевое пространство транспонирования A.

И наш типичный вектор b здесь.

Там ноль, так что это наш типичный вектор b, и мы проецируем его на P. И — и, конечно же, в то же время мы находим другую его часть, которая является e. .

Таким образом, две части, выступ и ошибка, складываются в исходный b. ОК. Это похоже на то, что делает наша матрица.

Итак, это P — P — это P — Ab, извините — это Pb, это проекция, примененная к b, и эта — хорошо, это тоже проекция.

Это проекция на то пространство.

Какая для этого хорошая формула?

Предположим, я прошу вас о проекции матрицы проекции на — это пространство, это перпендикулярное пространство?

Итак, если эта проекция была P, какая проекция дает мне e?

Я хочу получить остальную часть вектора, так что это будет просто I минус P, умноженное на b, это тоже проекция.

Это проекция на перпендикулярное пространство.

ОК. Итак, если P — проекция, I минус P — это проекция.

Если P симметрично, I минус P симметрично.

Если P в квадрате равно P, тогда I минус P в квадрате равно I минус P. Это просто — алгебра — делает только то, что ваша — картинка полностью говорит вам. Но алгебра приводит к этому выражению.

Это выражение для P дано — дано основание для подпространства, дано матрица A, столбцы которой являются базой для нашего пространства столбцов. Хорошо, это резюме, потому что вам — вам нужно увидеть эту формулу более одного раза.

А теперь я могу разобраться в использовании?

Итак, теперь — и это — это как, позвольте мне сделать это еще раз, я сразу рассмотрю задачу, которую я начал в конце, а именно найти лучшую прямую линию.

Вы помните ту задачу, я — я выбрал определенный набор точек, они не были особенно блестящими, t равнялись единице, двум, трем, высота была одна, две, а затем снова две.

Итак, они были — высота была той точкой, этой точкой, из-за чего это выглядело так, как будто у меня есть хорошая линия в сорок пять градусов, — но тогда третья точка не лежала на этой линии.

И я хотел найти лучшую прямую.

Итак, я ищу — эту строку, y = C + Dt. И он не пройдет через все три точки, потому что ни одна линия не проходит через все три точки.

Итак, я собираюсь выбрать лучшую линию, лучшую — это та, которая делает общую ошибку настолько маленькой, насколько я могу ее сделать.

Теперь я должен сказать вам, что это за общая ошибка?

И — потому что это определяет выигрышную линию.

Если мы не знаем — я имею в виду, мы должны решить, что мы подразумеваем под ошибкой — а затем мы минимизируем и находим правильный — лучшие C и D.Итак, если я прошел через это — если я прошел через это,

ОК. Я бы решил уравнение C + D = 1. Потому что при t, равном единице, у меня было бы C плюс D, и все получилось бы правильно. Если бы он прошел через эту точку, у меня было бы C плюс два D, равное

двум. Потому что при t, равном двум, я хотел бы получить ответ

два. В третьей точке у меня C плюс три D, потому что t равно трем, но — ответ, к которому я стремлюсь, — это

снова два. Итак, это мои три уравнения.

И у них нет решения.

Но у них есть лучшее решение.

Что я подразумеваю под лучшим решением?

Итак, позвольте мне выделить время, чтобы вспомнить, о чем я говорю, для лучшего решения.

Итак, это мое уравнение Ax = b. A — это матрица, один, один, один, один, два, три. x мой — только два неизвестных, C и D, а b — моя правая часть, один, два, три. ОК. Нет решения.

Три уравнения — у меня есть матрица три на два, у меня есть два независимых столбца — так что у меня есть основа для пространства столбцов, эти два столбца независимы, они являются основой для пространства столбцов, но пространство столбца не включает этот вектор.

Итак, самое лучшее в этом — что означает наилучшее из возможных? К линейным уравнениям можно прийти следующим образом: я — я хочу свести их к минимуму — я собираюсь сделать здесь ошибку.

Я здесь сделаю ошибку.

Я здесь сделаю ошибку.

И я собираюсь просуммировать, возвести в квадрат и сложить эти ошибки.

Итак, это сумма квадратов.

Я ищу решение методом наименьших квадратов.

Итак, если I — эти ошибки и есть разница между Ax и b.

Вот что я хочу сделать маленьким.

А то, как я это измеряю — это вектор,

верно? Это e1, e2, e3. Axe-b, это е.

Вектор ошибок.

А маленький значит его длина.

Длина этого вектора.

Это то, что я постараюсь минимизировать.

И это удобно на квадрат.

Если я делаю что-то маленькое, я делаю — это никогда не отрицательное количество, верно?

Длина этого вектора.

Длина будет равна нулю, когда — когда у меня здесь нулевой вектор.

Это именно тот случай, когда я могу точно решить, b находится в пространстве столбцов, все отлично.

Но я сейчас не в том случае.

У меня будет вектор ошибок, например.

Что это за вектор ошибки на моем изображении?

Думаю, я пытаюсь сказать, что есть две фотографии того, что происходит.

Есть две фотографии того, что происходит.

Одно изображение — это три точки и линия.

И какие три ошибки на этой картинке?

Три ошибки — вот что я упустил в этом уравнении.

Так вот, вот этот кусочек.

Это расстояние по вертикали до линии.

Есть один — извините, есть один, и есть C плюс D.

И в этом разница.

Вот два, а вот C + 2D. Итак, это расстояние по вертикали — эта маленькая ошибка — е1. Вот эта маленькая ошибка — е2. Появляется небольшая ошибка e3.e3. И какова моя общая ошибка?

Квадрат е1 плюс квадрат е2 плюс квадрат е3.

Вот что я пытаюсь сделать маленьким.

I — некоторые статистики — это большая часть статистики, подгонка прямых линий — большая часть науки, и особенно статистики, где правильным словом будет регрессия.

Я здесь регрессирую.

Линейная регрессия. И я использую эту сумму квадратов как меру ошибки.

Опять же, некоторые статистики скажут: «Хорошо, я решу эту проблему, потому что это чистая проблема».

Это приводит к красивой линейной системе.

Но они будут немного осторожнее с этими квадратами, потому что — в этом случае.

Если одна из этих точек была далеко.

Предположим, у меня было измерение при t, равном нулю, которое было очень далеким.

Хорошо, была бы прямая линия, лучшая линия была бы такой же, если бы у меня была эта четвертая точка?

Предположим, у меня есть четвертая точка данных.

Нет, конечно, линия будет — это не будет — это не лучшая линия.

Потому что эта линия будет иметь гигантскую ошибку — и когда я возведу ее в квадрат, она окажется вне поля зрения по сравнению с другими.

Таким образом, статистики будут называть это выбросом, и они не будут рады, если бы вся проблема перевернулась из-за этого выброса, который, в конце концов, может быть ошибкой.

Так что они не … поэтому они не хотели бы возводить в квадрат, если бы были выбросы, они бы захотели их идентифицировать. ОК. Я не собираюсь — я не хочу предлагать, чтобы метод наименьших квадратов не использовался, он используется чаще всего, но он используется не исключительно, потому что он немного … чрезмерно компенсирует выбросы.Из-за этого квадрата. ОК. Предположим, у нас нет этого парня, у нас есть только три уравнения.

А я хочу сделать — минимизировать эту ошибку. ОК. Я сказал, что есть две картинки, на которые стоит посмотреть.

Вот одна фотография.

Три точки, лучшая линия.

И ошибки. Итак, на этой картинке, что это за точки на линии, точки, которые действительно находятся на линии?

Итак, они — точки, позвольте мне называть их P1, P2 и P3, это три числа, так что это — эта высота — P1, эта высота — P2, эта высота — P3, и что это за парни ?

Предположим, что это были три значения вместо — там b1, все это все видели — извините, мое искусство, как обычно, не самое лучшее, но есть данное b1, данное b2 и данное b3.Обещаю, что больше не буду писать на этой картинке ни одной буквы. ОК. Там b1, P1 — это один на линии, а e1 — это расстояние

между ними. То же самое в точках два и то же в точках три. Хорошо, так в чем дело?

Что там с псами? P1, P2, P3, что это такое?

Это компоненты, они лежат на линии,

верно? Это точки, которые, если бы вместо одного, двух, двух, которые были буквами b, предположим, что я поставил сюда P1, P2, P3.

Я выясню через минуту, что это за числа.

Но я просто хочу получить представление о том, что я делаю.

Если я добавлю P1, P2, P3 в эти три уравнения, что будет хорошего в трех уравнениях?

Я мог их решить. Линия проходит через Пс.

Итак, вектор P1, P2, P3 находится в пространстве столбца

. Это комбинация этих столбцов.

Это наиболее близкая комбинация.

Это фотография.

Видите, у меня есть две картинки, вот картинка, которая показывает точки, это картинка на плоскости доски, вот картинка, которая показывает векторы.

Вектор b, который в данном случае является вектором один, два, два.

Пространство столбца в данном случае занято — ну, вы видите там A.

Пространство столбцов матрицы один, один, один, один, два, три.

А это изображение показывает ближайшую точку.

Вот… эта точка P1, P2, P3, которую я собираюсь вычислить до конца этого часа, является ближайшей точкой в ​​пространстве столбцов. ОК. Позвольте мне — я больше не смею оставлять это — могу я просто вычислить это сейчас.

Итак, я хочу посчитать — найти P. Хорошо.

Найдите P. Найдите x, то есть CD, найдите P и P. ОК. И мне действительно стоит надеть эти маленькие шляпки, чтобы напомнить себе, что они оцениваются как лучшая линия, а не идеальная линия. ОК. ОК. Как мне продолжить?

Давайте просто пробежимся по механике.

Какое уравнение для x?

Шляпа — или x.

Уравнение для этого: A транспонировать A x шляпа равно A транспонировать x — A транспонировать b.

Самое важное — я — рискну называть это уравнение самым важным в статистике.

И в прикидке.

И чем бы вы ни были — везде, где у вас есть ошибки и помехи, это оценка, которую вы используете в первую очередь. ОК. Когда вы подбираете объекты по нескольким параметрам, используйте это уравнение. Хорошо, давайте решим это.

Что такое транспонирование А?

Итак, я должен выяснить, что это за матрицы.

Один, один, один, один, два, три и один, один, один, один, два, три, который дает мне некоторую матрицу, которая дает мне матрицу, что я получаю из этого, три, шесть, шесть, и один, и четыре, и девять, четырнадцать.

ОК. И что я ожидаю увидеть в этой матрице, и что я вижу, непосредственно перед тем, как продолжить вычисления?

Я ожидаю, что эта матрица будет симметричной.

Я ожидаю, что он обратимый.

И ближе к концу курса я собираюсь сказать, что я ожидаю, что это будет положительно определенным, но это будущий факт об этой важной матрице, транспонировании A.

Хорошо. А теперь позвольте мне переставить фигуру A b.

Итак, позвольте мне — я могу добавить b как дополнительный столбец здесь, один, два, два?

И закрепка на дополнительном транспонировании A b выглядит как пять и один и четыре и шесть, одиннадцать.

Я думаю, что в моих уравнениях три C плюс шесть D равно пяти, а шесть D плюс четыре-шесть C плюс четырнадцать D равно одиннадцати.

Могу я из соображений безопасности посмотреть, правильно ли я все сделал?

Один, один, один раз один, два, два равно пять.

Один, два, три, это один, четыре и шесть, одиннадцать.

Выглядит хорошо.

Это мои уравнения.

Это мое — они называются нормальными уравнениями.

Я просто запишу это слово, потому что оно… поэтому я решаю их.

Я решаю это для C и D. Я хотел бы — прежде чем я их решу, могу ли я сделать одну вещь, которая находится на — это чуть выше здесь?

Я хотел бы — я хотел бы найти эти уравнения из исчисления.

Я бы хотел найти их из этой минимизирующей штуки.

Так в чем же первая ошибка?

Первая ошибка — это то, что я пропустил в первом уравнении.

C плюс D минус один квадрат.

И вторая ошибка — это то, что мне не хватает во втором уравнении.

C плюс два D минус два в квадрате.

И третий квадрат ошибки равен C плюс три D минус два в квадрате.

Это моя общая квадратичная ошибка, которую я пытаюсь минимизировать. ОК. Так как бы вы это минимизировали? Хорошо, линейная алгебра дала нам уравнения для минимума.

Но мы тоже можем использовать исчисление.

Это функция двух переменных, C и D, и мы ищем минимум.

Так как же его найти?

Непосредственно из исчисления мы берем частные производные, верно, у нас есть две переменные, C и D, поэтому возьмите частную производную по C и установите ее равной нулю, и вы получите это уравнение.

Возьмите частную производную с уважением — я не собираюсь все это выписывать, просто — вы будете.

Частная производная по D, это — вы знаете, она будет линейной, в этом прелесть этих квадратов, что если у меня есть квадрат чего-то, и я беру его производную, я получаю кое-что. получать. линейный.

Итак, это производная ошибки по отношению к нулю, и производная ошибки по отношению к нулю.

Куда ни глянь, эти уравнения продолжают появляться.

Итак, теперь я думаю, я собираюсь решить эту проблему, что я буду делать, я вычту, я сделаю устранение, конечно, потому что это единственное, что я знаю, как это сделать.

Два из них вдали от этого дадут мне — давайте посмотрим, шесть, так будет ли это два Ds равняться одному?

га. Так что это не так — я боялся, что эти цифры будут ужасными.

Но если я уберу два из них, у меня останется уравнение: два D равно единице, поэтому я думаю, что D равно половине, а C — это то, что дает обратная подстановка, шесть D равно трем, поэтому три C плюс три пять, я делаю обратную замену сейчас, верно, три, могу я сделать это светлыми буквами, три C плюс шесть D равно трем равным пяти, поэтому три C равно двум, поэтому я думаю, что C составляет две трети.Половина и две трети. Итак, лучшая линия, лучшая линия — это постоянные две трети плюс половина t.

А я — моя картинка более-менее правильная?

Позвольте мне написать, позвольте мне снова скопировать эту лучшую строчку, две трети с половиной.

Позвольте мне — я вставлю две трети с половиной.

ОК. Итак, что это за P1, это значение при t, равное единице.

При t, равном единице, у меня две трети плюс половина, то есть — что это, четыре шестых и три шестых, так что P1, о, я обещал не писать об этом еще — я ‘ Сотру P1 и поставлю семь шестых.ОК. И да, он больше единицы, а e1 — одна шестая, верно. Вы все это видите.

Верно? Что такое P2? ОК. В точке t, равной двум, где моя линия?

При t, равном двум, это две трети плюс один, верно?

Это пять третей. Две трети и t равно двум, так что две трети и одна составляют пять третей. И это — конечно же, это меньше двух точных цифр.

А затем последний P3, когда t равно трем, ох, сколько две трети плюс три половины? Это то же самое, что и три половины плюс две трети.Это — может быть, четыре шестых и девять шестых, может быть, тринадцать шестых. Хорошо, и еще раз, посмотри, о, посмотри на это, хорошо. Вы должны восхищаться красотой этого ответа. Что это за первая ошибка?

Итак, вот ошибки. e1, e2 и e3. Хорошо, что это была за первая ошибка, e1? Что ж, если считать ошибки подсчетом, то одна шестая. И последняя ошибка, тринадцать шестых минус две правильные, снова одна шестая.

А что это за ошибка посередине?

Посмотрим, правильный ответ был два, два.

И у нас есть пять третей, и это другое направление, минус одна треть, минус две шестых. Это наш вектор ошибок.

Вот он, на нашей картинке, на другой картинке.

Мы только что нашли P и e. e — это вектор, одна шестая, минус две шестых, одна шестая, а P — этот парень.

Ну, может быть, у меня есть признаки ошибки, я думаю, что у меня есть, позвольте мне исправить.

Потому что я хотел бы эту одну шестую — я хотел бы, чтобы это плюс P давало исходное b.

Я хочу, чтобы P плюс e соответствовал b.

Итак, я хочу, чтобы минус шестая плюс семь шестых давала правильное b, равное единице.

ОК. Теперь — я собираюсь сделать здесь глубокий вдох и спросить, что мы знаем об этом векторе ошибки e?

Теперь вы видели, что вся эта проблема решена полностью, и я даже думаю, что цифры верные.

Итак, есть P, так что позвольте мне — я напишу — если я могу это записать здесь, B — это P плюс e.

б По-моему, раз, два, два.

В ближайшей точке было семь шестых, каковы были остальные? Пять третей и тринадцать шестых.И вектор е был минус шестая, две шестых, одна треть, другими словами, и минус шестая. ОК. Расскажите мне кое-что об этих двух векторах.

Расскажите мне что-нибудь об этих двух векторах, ну, они складываются с b, верно, отлично.

ОК. Что еще?

Что еще насчет этих двух векторов, P, вектора проекции P и вектора ошибки e.

Что еще вы о них знаете?

Они перпендикулярны, вправо.

Осмелимся ли мы это проверить?

Можете ли вы взять скалярное произведение этих векторов?

У меня вроде минус семь на тридцать шесть, могу я изменить это на десять шестых? О, Боже, выходи прямо сюда.

Минус семь из тридцати шести, плюс двадцать из тридцати шести, минус тринадцать из тридцати шести. Спасибо тебе, Господи.

ОК. А что еще мы должны знать об этом векторе?

На самом деле мы знаем — я должен сказать, что мы знаем даже немного больше.

Этот вектор, e, перпендикулярен P, но он также перпендикулярен другим объектам.

Это перпендикулярно не только этому парню в пространстве столбца, это точно находится в пространстве столбца.

Это перпендикулярно пространству столбца.

Так что дайте мне другой вектор, перпендикулярный ему.

Другой, потому что он перпендикулярен всему пространству столбца, а не только этому — этой конкретной проекции, которая — находится в пространстве столбца, но перпендикулярна другим вещам, независимо от того, что находится в пространстве столбца, так что скажите мне другой вектор в пространстве — о, ну, я записал матрицу, так что скажите мне другой вектор в пространстве столбцов.

Выберите хороший.

Один, один, один.

Так думают все.Хорошо, один, один, один находится в пространстве столбца.

И этот парень должен быть перпендикулярен одному,

один, один. Это?

Конечно. Если я возьму скалярное произведение с единицей, единицей и единицей, я получу минус шестую, плюс две шестых, минус шестую, ноль.

И это перпендикулярно одному, двум, трем.

Потому что, если я возьму скалярное произведение с единицей, двумя, тремя, я получу минус один, плюс четыре, минус три, снова ноль. Хорошо, вы видите — я надеюсь, вы видите две картинки.

Изображение здесь для векторов и, изображение здесь для лучшей линии, и это то же самое изображение, только — это в плоскости, и оно показывает линию, это никогда не показывало линию, это — в этом фотография, C и D никогда не появлялись.

На этом снимке C и D были — вы знаете, они определили эту линию.

Но эти два совершенно одинаковые.

C и D — комбинация двух столбцов, которая дает P. OK. Вот эти квадраты.

И особый, но самый важный пример подгонки по прямой линии, так что домашнее задание, которое приходит в среду, требует от вас подгонки по прямым линиям.

Итак, вы просто собираетесь решить ключевое уравнение.

Вы собираетесь решить это ключевое уравнение, и тогда P будет Axe hat.

Вот и все. ОК. Теперь, могу ли я добавить небольшой кусочек линейной алгебры, о котором я упоминал ранее, снова упоминал, но я никогда не писал?

И я — я должен делать это правильно. Речь идет об этой матрице А транспонировать А. Там.

Я был уверен, что эта матрица будет обратимой.

И, конечно, я хотел быть уверенным, что он обратимый, потому что я планировал решить эту систему с этой матрицей.

Итак, я объявил, как и раньше — поскольку глава только начиналась, я объявил, что она будет обратимой.

Но теперь я — могу я вернуться к этому? ОК. Итак, я сказал, что если A имеет независимые столбцы, то транспонирование A обратимо. И я хотел бы — прежде всего повторить тот важный факт, что это требование, которое заставляет все здесь идти. Именно эти независимые столбцы A гарантируют, что все пройдет.

И подумайте почему. Почему эта матрица A транспонирует A, почему она обратима, если столбцы A независимы? Хорошо, есть — так что, если это не было обратимым, я — вот я хочу это доказать.

Если он не обратимый, что тогда?

Я хочу достичь — я хочу следовать этому — следовать этой линии — мышления и видеть, к чему я пришел.

Допустим, так доказательство.

Предположим, что транспонированная Ax равна нулю.

Я пытаюсь это доказать.

Теперь это нужно доказать.

Я не люблю вдаваться в слишком много доказательств в этом курсе.

Но это как центральный факт, и он включает в себя все, что мы знаем.

ОК. Итак, я начну доказательство.

Предположим, что транспонированная Ax равна нулю. Что — и я стремлюсь доказать, что транспонирование A обратимо.

Итак, что я хочу сейчас доказать?

Итак, я хочу доказать этот факт.

Я использую это, и я стремлюсь доказать, что эта матрица обратима, хорошо, поэтому, если я предполагаю, что транспонированная Ax равна нулю, то к какому выводу я хочу прийти? Я хотел бы знать, что x должен быть равен нулю.

Я хочу показать, что x должен быть равен нулю.

Чтобы показать сейчас — чтобы доказать, x должен быть нулевым вектором.

Верно, это то, над чем мы работали в предыдущей главе, чтобы понять, что матрица обратима, когда ее нулевое пространство является только нулевым вектором.

Вот что я хочу показать.

Почему, если транспонированная ось A равна нулю, почему x должен быть равен нулю?

В чем будет причина? На самом деле у меня есть два способа сделать это.

Позвольте мне показать вам один путь.

Это — вот, уловка.

Возьмите скалярное произведение обеих сторон на x.

Итак, я умножу обе стороны на транспонирование x.

x транспонировать A транспонировать Ax равно нулю.

Я не должен был писать фокус.

Это звучит как глупая идея.

Замечательная идея, надо было поставить.

ОК. Я просто поставлю идею.

ОК. Итак, я подошел к этому уравнению, x транспонировать A транспонировать Ax = 0, и я надеюсь, что вы видите правильный способ — взглянуть на это уравнение. Что я могу сделать из этого уравнения, что если у меня есть x транспонировать A — ну, что такое x транспонировать A транспонировать Ax?

Это — что это дает вам? Это снова будет заключено в круглые скобки, я смотрю на Axe, и что я здесь вижу?

Его транспонировать.

Итак, я вижу вот это Axe transpose Axe.

Равняется нулю.

Теперь, если Ax транспонирует Ax, так что давайте назовем его y или что-то в этом роде, если y transpose y равно нулю, что это мне говорит?

Что вектор должен быть нулевым, верно?

Это длина в квадрате, это длина вектора Ax в квадрате, это Ax, умноженное на Ax.

Итак, я прихожу к выводу, что Ax должен быть равен нулю.

Ну, я кое-что получу.

Теперь, когда я знаю, что Ax равен нулю, я собираюсь использовать свою маленькую гипотезу.

Где-то каждый математик должен использовать гипотезу.

Верно?

Теперь, если у A есть независимые столбцы и мы — мы находимся в точке, где Ax равен нулю, о чем это нам говорит?

Могу — я имею в виду, что это может быть как вопрос для заполнения на выпускном экзамене.

Если A имеет независимые столбцы и если Ax равен нулю, то что?

Скажите, пожалуйста. x равен нулю, верно.

Именно это мы и хотели доказать.

Это — вы понимаете, почему это так?

Если Ax eq- равен нулю, теперь мы используем — здесь мы использовали это был квадрат чего-то, поэтому я заключу в маленькие скобки то наблюдение, которое мы сделали, это был квадрат, который равен нулю, так что вещь должно быть равно нулю.

Теперь мы используем гипотезу о независимых столбцах в точке A имеет независимые столбцы.

Если A имеет независимые столбцы, это говорит мне, что x находится в своем нулевом пространстве, и единственное, что находится в нулевом пространстве такой матрицы, — это нулевой вектор.

ОК. Итак, это аргумент, и вы видите, как он на самом деле использовал наше понимание нулевого пространства.

ОК. Замечательно.

Хорошо.

Так где же мы тогда? Эта плата похожа на теорию резервного копирования, которая говорит мне, что эта матрица должна быть обратимой, потому что эти столбцы были независимыми.ОК. есть один случай независимого — есть один случай, когда геометрия становится еще лучше.

Когда — есть один случай, когда столбцы обязательно будут независимыми.

И позвольте мне это сказать — позвольте мне записать это, и это будет предметом обсуждения в следующий раз.

Колонны уверены — безусловно, независимы, определенно независимы, если они перпендикулярны.

О, я должен исключить нулевой столбец, позвольте мне дать им длину единицу, поэтому они не могут быть нулевыми, если они являются перпендикулярными единичными векторами.

Как векторы один, ноль, ноль, ноль, один, ноль и ноль, ноль, один.

Эти векторы являются единичными векторами, они перпендикулярны и, безусловно, независимы.

И более того, предположим, они … о, это так мило, я имею в виду, что такое транспонирование A для этой матрицы?

Для матрицы с этими тремя столбцами?

Это личность.

Итак, вот ключ к предстоящей лекции.

Если мы имеем дело с перпендикулярными единичными векторами, и слово для этого будет — видите, я мог бы сказать ортогональный, но я сказал перпендикулярный — и эти единичные векторы вводятся как слово «нормальный».

Ортонормированные векторы.

Это лучшие колонки, о которых вы могли бы мечтать.

Матрицы с — чьи столбцы ортонормированы, они перпендикулярны друг другу и являются единичными векторами, ну, они не обязательно должны быть этими тремя, позвольте мне сделать последний пример здесь, как насчет одного при таком угле и девяноста градусах этот вектор будет cos theta, sine theta, единичным вектором, и этот вектор будет минус sine theta cos theta.

Это наша любимая пара ортонормированных векторов.

Они оба являются единичными векторами и перпендикулярны.

Этот угол составляет девяносто градусов.

Итак, наша задача в следующий раз — сначала понять, почему ортонормированные векторы хороши, а затем сделать векторы ортонормированными, выбрав правильный базис. Ладно, увидимся.

Спасибо.

Ортогональная проекция

Начнем с исправления некоторых обозначений.

Обозначение

Пусть W — подпространство в Rn, а x — вектор в Rn. Обозначим ближайший к x вектор на W через xW.

Сказать, что xW — ближайший вектор к x на W, означает, что разность x − xW на ортогональна векторам в W:

Другими словами, если xW⊥ = x − xW, то мы имеем x = xW + xW⊥, где xW находится в W, а xW⊥ находится в W⊥. Первым делом нужно доказать, что ближайший вектор всегда существует.

Теорема (ортогональное разложение)

Пусть W — подпространство в Rn, а x — вектор в Rn. Тогда мы можем записать x однозначно как

x = xW + xW⊥

, где xW — ближайший к x вектор на W, а xW⊥ находится в W⊥.

Доказательство

Пусть m = dim (W), поэтому n − m = dim (W⊥) по этому факту в разделе 6.2. Пусть v1, v2, …, vm — базис W, а vm + 1, vm + 2, …, vn — базис W⊥. При доказательстве этого факта в разделе 6.2 мы показали, что {v1, v2, …, vm, vm + 1, vm + 2, …, vn} линейно независима, поэтому она составляет основу Rn. Следовательно, мы можем написать

x = (c1v1 + ··· + cmvm) + (cm + 1vm + 1 + ··· + cnvn) = xW + xW⊥,

, где xW = c1v1 + ··· + cmvm и xW⊥ = cm + 1vm + 1 + ··· + cnvn. Поскольку xW⊥ ортогонален W, вектор xW является ближайшим к x вектором на W, поэтому это доказывает, что такое разложение существует.

Что касается уникальности, предположим, что

x = xW + xW⊥ = yW + yW⊥

для xW, yW в W и xW⊥, yW⊥ в W⊥. Перестановка дает

xW − yW = yW⊥ − xW⊥.

Поскольку W и W⊥ являются подпространствами, левая часть уравнения находится в W, а правая часть — в W⊥. Следовательно, xW − yW находится в W и в W⊥, поэтому он ортогонален самому себе, что влечет xW − yW = 0. Следовательно, xW = yW и xW⊥ = yW⊥, что доказывает единственность.

Определение

Пусть W — подпространство в Rn, а x — вектор в Rn.Выражение

x = xW + xW⊥

для xW в W и xW⊥ в W⊥, называется ортогональным разложением x относительно W, а ближайший вектор xW — это ортогональная проекция x на W.

Поскольку xW — ближайший вектор на W до x расстояние от x до подпространства W — это длина вектора от xW до x, то есть длина xW⊥. Чтобы пересчитать:

Ближайший вектор и расстояние

Пусть W — подпространство в Rn, а x — вектор в Rn.

• Ортогональная проекция xW — это ближайший к x вектор в W.
• Расстояние от x до W равно BxW⊥B.

Теперь перейдем к проблеме вычисления xW и xW⊥. Конечно, поскольку xW⊥ = x − xW, на самом деле все, что нам нужно, это вычислить xW. Следующая теорема дает метод вычисления ортогональной проекции на пространство столбцов. Чтобы вычислить ортогональную проекцию на общее подпространство, обычно лучше переписать подпространство как пространство столбцов матрицы, как в этом важном примечании в разделе 2.6.

Теорема

Пусть A — матрица размера m × n, пусть W = Col (A), и пусть x — вектор в Rm. Тогда матричное уравнение

ATAc = ATx

в неизвестном векторе c согласовано, а xW равно Ac для любого решения c.

Проба

Пусть x = xW + xW⊥ — ортогональное разложение относительно W. По определению xW лежит в W = Col (A), поэтому существует вектор c в Rn с Ac = xW. Выберите любой такой вектор c. Мы знаем, что x − xW = x − Ac лежит в W⊥, что равно Nul (AT) в соответствии с этим важным замечанием из раздела 6.2. Таким образом, мы имеем

0 = AT (x-Ac) = ATx-ATAc

и так

ATAc = ATx.

Это в точности означает, что ATAc = ATx согласован. Если c — любое решение для ATAc = ATx, то, обращая вышеуказанную логику, мы заключаем, что xW = Ac.

Пример (Ортогональная проекция на линию)

Пусть L = Span {u} — прямая в Rn, а x — вектор в Rn. По теореме, чтобы найти xL, мы должны решить матричное уравнение uTuc = uTx, где мы рассматриваем u как матрицу размера n × 1 (пространство столбцов этой матрицы в точности равно L!).Но uTu = u · u и uTx = u · x, поэтому c = (u · x) / (u · u) является решением uTuc = uTx, и, следовательно, xL = uc = (u · x) / (u · u) u.

повторить:

Рецепт: Ортогональная проекция на линию

Если L = Span {u} — линия, то

для любого вектора x.

Когда A — матрица с более чем одним столбцом, вычисление ортогональной проекции x на W = Col (A) означает решение матричного уравнения ATAc = ATx. Другими словами, мы можем вычислить ближайший вектор, решив систему линейных уравнений .Чтобы быть явным, сформулируем теорему в виде рецепта:

Рецепт: вычислить ортогональное разложение

Пусть W — подпространство в Rm. Вот метод вычисления ортогонального разложения вектора x относительно W:

0. Перепишите W как пространство столбцов матрицы A. Другими словами, найдите остовное множество для W, и пусть A будет матрицей с этими столбцами.
1. Вычислить матрицу ATA и вектор ATx.
2. Сформируйте расширенную матрицу для матричного уравнения ATAc = ATx в неизвестном векторе c и уменьшите строку.
3. Это уравнение всегда непротиворечиво; выбрать одно решение c. потом

   xW = AcxW⊥ = x − xW.

В контексте вышеприведенного рецепта, если мы начнем с базиса W, то окажется, что квадратная матрица ATA автоматически обратима! (Всегда бывает, что ATA имеет квадратную форму, и уравнение ATAc = ATx согласовано, но ATA в целом не обязательно должна быть обратимой.)

Следствие

Пусть A — матрица размера m × n с линейно независимыми столбцами, и пусть W = Col (A).Тогда матрица ATA размера n × n обратима, и для всех векторов x из Rm имеем

xW = A (ATA) −1ATx.

Проба

Мы покажем, что Nul (ATA) = {0}, что влечет обратимость по теореме об обратимой матрице из раздела 5.1. Предположим, что ATAc = 0. Тогда ATAc = AT0, поэтому по теореме 0W = Ac. Но 0W = 0 (ортогональное разложение нулевого вектора равно 0 = 0 + 0), поэтому Ac = 0, и, следовательно, c находится в Nul (A). Поскольку столбцы A линейно независимы, мы имеем c = 0, поэтому Nul (ATA) = 0, что и нужно.

Пусть x будет вектором в Rn и пусть c будет решением ATAc = ATx. Тогда c = (ATA) −1ATx, поэтому xW = Ac = A (ATA) −1ATx.

Следствие применимо, в частности, к случаю, когда у нас есть подпространство W в Rm и базис v1, v2, …, vn для W. Чтобы применить следствие, возьмем A как матрицу размера m × n со столбцами v1, v2, …, вн.

В этом подразделе мы меняем перспективу и рассматриваем ортогональную проекцию xW как функцию от x. Эта функция оказывается линейным преобразованием со многими хорошими свойствами и является хорошим примером линейного преобразования, которое изначально не определялось как матричное преобразование.

Свойства ортогональных проекций

Пусть W — подпространство в Rn, и определим T: Rn → Rn как T (x) = xW. Тогда:

1. T — линейное преобразование.
2. T (x) = x тогда и только тогда, когда x находится в W.
3. T (x) = 0 тогда и только тогда, когда x принадлежит W⊥.
4. T◦T = T.
5. Диапазон T равен W.

1. Мы должны проверить определяющие свойства линейности в разделе 3.3. Пусть x, y — векторы в Rn, и пусть x = xW + xW⊥ и y = yW + yW⊥ — их ортогональные разложения.Поскольку W и W⊥ подпространства, суммы xW + yW и xW⊥ + yW⊥ лежат в W и W⊥ соответственно. Следовательно, ортогональное разложение x + y есть (xW + yW) + (xW⊥ + yW⊥), поэтому

   Т (х + у) = (х + у) W = xW + yW = Т (х) + Т (у).

   Пусть теперь c — скаляр. Тогда cxW находится в W, а cxW⊥ находится в W so, поэтому ортогональное разложение cx есть cxW + cxW⊥, и, следовательно,

   T (cx) = (cx) W = cxW = cT (x).

   Поскольку T удовлетворяет двум определяющим свойствам из раздела 3.3, это линейное преобразование.
2. См. Этот пример.
3. См. Этот пример.
4. Для любого x из Rn вектор T (x) принадлежит W, поэтому T◦T (x) = T (T (x)) = T (x) по 2.
5. Любой вектор x в W находится в диапазоне T, потому что T (x) = x для таких векторов. С другой стороны, для любого вектора x в Rn выход T (x) = xW находится в W, поэтому W — это диапазон T.

Мы вычисляем стандартную матрицу ортогональной проекции так же, как и для любого другого преобразования: вычисляя стандартные векторы координат. В данном случае это означает проецирование стандартных координатных векторов на подпространство.

В предыдущем примере мы могли использовать тот факт, что

EC10−1D, C110DF

образует основу для W, так что

T (x) = xW = AA (ATA) −1ATBxforA = C1101−10D

по следствию. В этом случае мы уже выразили T как матричное преобразование с матрицей A (ATA) −1AT. См. Этот пример.

Пусть W — подпространство в Rn с базой v1, v2, …, vm, и пусть A — матрица со столбцами v1, v2, …, vm. Тогда стандартная матрица для T (x) = xW равна

А (АТА) -1АТ.

Мы можем перевести указанные выше свойства ортогональных проекций в свойства соответствующей стандартной матрицы.

Свойства матриц проекций

Пусть W — подпространство в Rn, определим T: Rn → Rn как T (x) = xW, и пусть B — стандартная матрица для T. Тогда:

1. Столбец (B) = W.
2. Нул (B) = W⊥.
3. B2 = В.
4. Если WA = {0}, то 1 является собственным значением B и 1-собственным подпространством для B является W.
5. Если WA = Rn, то 0 — собственное значение B и 0-собственное подпространство для B — это W⊥.
6. B аналогична диагональной матрице с m единицами и n − m нулями на диагонали, где m = dim (W).

Первые четыре утверждения представляют собой перевод свойств 5, 3, 4 и 2, соответственно, с использованием этого важного примечания в разделе 3.1 и этой теоремы в разделе 3.4. Пятое утверждение равносильно второму тем, что изложено в п. 5.1.

В качестве последнего утверждения при доказательстве этой теоремы мы показали, что существует базис в Rn вида {v1, …, vm, vm + 1, …, vn}, где {v1, …, vm} — базис для W, а {vm + 1, …, vn} — базис для W⊥. Каждый vi является собственным вектором B: действительно, для i≤m мы имеем

Bvi = T (vi) = vi = 1 · vi

, потому что vi находится в W, а для i> m имеем

Bvi = T (vi) = 0 = 0 · vi

, потому что vi находится в W⊥. Таким образом, мы нашли базис из собственных векторов с соответствующими собственными значениями 1, …, 1,0, …, 0 (m единиц и n − m нулей). Теперь воспользуемся теоремой о диагонализации из раздела 5.4.

Подчеркнем, что свойства матриц проекций будет очень трудно доказать в терминах матриц.Перевод всех утверждений в утверждения о линейных преобразованиях делает их намного более прозрачными. Например, рассмотрим матрицу проекции, которую мы нашли в этом примере. Просто глядя на матрицу, совсем не очевидно, что, возведя матрицу в квадрат, вы получите ту же матрицу.

  function WebGLBox () {
  
  this.canvas = документ.getElementById ('холст');
  this.canvas.width = window.innerWidth;
  this.canvas.height = window.innerHeight;
  this.gl = MDN.createContext (холст);

  var gl = this.gl;

  
  this.webglProgram = MDN.createWebGLProgramFromIds (gl, 'вершинный шейдер', 'фрагмент-шейдер');
  gl.useProgram (this.webglProgram);

  
  this.positionLocation = gl.getAttribLocation (this.webglProgram, 'позиция');
  this.colorLocation = gl.getUniformLocation (this.webglProgram, 'цвет');

  
  
  gl.enable (gl.DEPTH_TEST);

}
  

  WebGLBox.prototype.draw = function (settings) {
  
  

  var data = new Float32Array ([

    
    settings.left, settings.bottom, settings.depth,
    settings.right, settings.bottom, settings.depth,
    settings.left, settings.top, settings.depth,

    
    settings.left, settings.top, settings.depth,
    settings.right, settings.bottom, settings.depth,
    settings.right, settings.top, settings.depth
  ]);

  

  
  

  var gl = this.gl;

  
  var buffer = gl.createBuffer ();
  gl.bindBuffer (gl.ARRAY_BUFFER, буфер);
  gl.bufferData (gl.ARRAY_BUFFER, данные, gl.STATIC_DRAW);

  
  gl.enableVertexAttribArray (this.positionLocation);
  gl.vertexAttribPointer (this.positionLocation, 3, gl.FLOAT, false, 0, 0);

  
  gl.uniform4fv (this.colorLocation, settings.color);

  
  gl.drawArrays (gl.TRIANGLES, 0, 6);
}