Смешанный тип реагирования это: В. шапарь практическая психология. Проективные методики
|
Серия «Психологический факультет»
Ростов-на-Дону «Феникс» 2006
УДК 159.9 ББК 88.3 КТК 016 Ш 23 Рецензенты: Д-р психол. наук A.B. Тимченко Д-р психол. наук Л. Т. Балабанова Шапарь В. Б., Шапарь О. В. Ш 23 Практическая психология. Проективные методики. / В. Б. Шапарь, О. В. Шапарь. — Ростов н/Д: Феникс, 2006. — 480 с. (Психологический факультет). Книга посвящена проективным методикам исследования личности, теория и практика которых образуют самостоятельный раздел современной психодиагностики. Важнейшей отличительной особенностью проективных методик является то, что в них используются неопределенные или слабоструктурированные стимулы, создающие наиболее оптимальные условия для проявления внутреннего мира человека.  В настоящее время подобной литературы, изданной на территории стран СНГ, нет. Книга предназначена для студентов и аспирантов, изучающих психологию, психологов-практиков и всех интересующихся проблемами психологического исследования личности.
9785222085059 УДК 159.9 ББК 88.3
© Шапарь В. Б., Шапарь О. В., 2006 © Оформление: изд-во «Феникс», 2006
ВМЕСТО ВВЕДЕНИЯ (из истории проективного метода) Проективные методики представляют собой специфическую, довольно неоднородную группу психодиагностических приемов клинической ориентации/Последнее означает не столько направленность проективных методик на выявление тех или иных аномалий личности, сколько способность методик прогнозировать индивидуальный стиль поведения, переживания и аффективного реагирования в значимых или конфликтных ситуациях, выявлять неосознаваемые аспекты личности. История проективных методик — это и хронология, отмечающая особо важные вехи развития проективной техники, и история развития проективного метода как целостного подхода к пониманию природы личности и способов ее экспериментального изучения. др.), для отграничения нормы от патологии (Г. Кент и А. Розанов). Тесты незаконченных предложений и рассказов также нередко считают ведущими свое происхождение от ассоциативного теста Юнга (Анастази Б. Подлинный триумф проективной диагностики связан с появлением в 1921 г. «Психодиагностики» Г. Роршаха, опубликованной в Берне на немецком языке. Личная биография Германа Роршаха, его профессиональный путь, по-видимому, немало способствовали направлению его исследований и созданию оригинального метода, ставшего одним из самых известных в мировой психологии. Отказавшись от профессии художника, Роршах, тем не менее, много интересовался историей искусств, и живописи в частности. Ему было известно, что великий Леонардо да Винчи тренировал свое воображение путем длительного рассматривания и интерпретаций причудливых конфигураций облаков на небе, влажных подтеков и неровностей на стене, лунных отблесков на застывшей воде. Заметим, что способность человека одушевлять («чувствовать», по выражению Т. Липпса) окружающий предметный мир присуща всем людям, детям и художникам в особенности. Вспомним излюбленный прием Г. Так, И. Сельвинский (1972) писал: Отчего, когда глядим на волны, Видим вечность и судьбу людей? Отчего пургу зовем «седою», «Шепот» слышим там, где камыши? Оттого, что втайне красотою Мы зовем полет своей души. Диссертация Г. Роршаха по медицине была посвящена изучению механизмов галлюцинаций, где он, между прочим, ссылается на однажды пережитое им состояние: во время первой в его медицинской практике аутопсии он явственно «видел», как ему пласт за пластом разрезают «мозг» и эти пласты падают перед ним один за другим (Anzieu D., 1967). Переживание было очень ясным, живым и не только зрительным, но и сопровождалось явственными тактильными и моторными ощущениями. Г. Роршах предположил, что в наших мечтах и фантазиях наряду со зрительными образами присутствует память и о пережитых движениях — кинетические образы, которые слагаются в особый способ, модус мышления. Известно, что до и независимо от Г. Роршаха с чернильными пятнами экспериментировали и другие психологи (например, Ц. Е. Рыбаков в России, А. Бине и В. Анри — во Франции), однако именно Роршах был первым, кто доказал связь образов фантазии с основополагающими чертами и свойствами личности. «Роршахиана» как дальнейшее развитие исследований и идей Г. Роршаха в настоящее время представлена двумя ведущими направлениями — американским (Beck S., 1944; Klopfer В., Davidson H., 1962; Rapaport D. et al., 1945-1946) и европейским (Bцhm Е., 1978; Loosli — Usteri M., 1965). Американских психологов отличает тенденция к теоретическому обоснованию теста в русле идей «нового взгляда» и психологии «эго», а также стремление к более строгому формализованному представлению и анализу эмпирических результатов. Европейские психологи в значительной мере сохраняют верность оригинальной версии Роршаха, развивая и дополняя ее в духе ортодоксального психоанализа. За время, прошедшее после выхода в свет «Психодиагностики», появились методики, родственные тесту Роршаха. Наиболее известны среди них Бен-Роршах («Вего») тест, тест Цулли-гера и тест Хольцмана. «Вего-тест» создавался Г Роршахом и его непосредственным сотрудником как параллельная серия оригинальному набору таблиц. Работа над тестом была закончена Г. Цуллигером, также работавшим вместе с Роршахом. Цул-лигеру удалось доказать, что по основным показателям теста (общему количеству ответов, количеству целостных ответов, ответов на белое пространство, ответов с участием цвета и движения) «Вего-тест» эквивалентен оригинальному набору таблиц. Г. Цуллигером в 1948 г. был предложен и собственный вариант теста — Z-тест, который состоит из трех таблиц — черно-белой, полихромной и черно-красной; обработка включает ряд отсутствующих в финальной версии показателей; главное отличие теста — краткость, формализованность анализа результатов. Методика чернильных пятен Хольцмана (H.I. В отечественной психологии первые, крайне немногочисленные попытки применения теста Роршаха относятся к 20-30-м годам и имеют выраженную направленность на выявление аномалий личности в связи с конституционными типами для диагностики неврозов и психопатий, а также при исследовании больных эпилепсией (цит. по: Бурлачук Л. Ф., 1979). С 60-х годов тест Роршаха все шире внедряется в исследовательскую и клинико-диагностическую работу психологов, выходят первые методические руководства (Белая И. И., 1978; Белый Б. И., 1981 ; Бурлачук Л. Ф., 1979; Соколова Е. Т., 1980; Беспалько И. Г., 1978; Беспалько И. Интересной и многообещающей выглядит попытка А. М. Эт-кинда трактовать природу связи перцепции и личности в терминах «образа мира» как изоформизм двух структур — чувственной ткани перцептивного образа и аффективно-когнитивного единства личности (ЭткиндА. М,, 1981). Продолжая хронологический обзор истории развития проективных методов, мы, естественно, не можем не отметить 1935 год, когда впервые в журнальном варианте под двойным авторством появилось сообщение о Тематическом апперцептивном тесте (TAT) как методике экспериментального изучения фантазии (Morgan С, Murray Н. Появление Тематического апперцептивного теста остро поставило ряд проблем, дискутируемых и по сей день. Одна из них касается прогностичности TAT. Исследования 30—50-х годов, проведенные в русле идей «нового взгляда», в целом подтвердили положение Мюррея об отражении в рассказах TAT фрустрируемых или отвергаемых «Я»-потребностей. Лишение сна, пищевая, сексуальная депривация, предшествующие успехи или неудачи существенно сказываются на ответах по TAT. Однако в этих же экспериментах обнаружилось, что «сила» потребности и ее отражение в TAT связаны не линейной, а U-образной зависимостью: наиболее непосредственно в рассказах проявляются потребности умеренной интенсивности; очень сильная депривация приводит к вытеснению или искажению соответствующих образов фантазии (Sanford R., 1936). Тот же компенсаторный принцип действует и применительно к так называемым латентным или социально неодобряемым потребностям, например агрессии или гомосексуальности. В итоге действия защитных механизмов в рассказах TAT может искажаться реальная картина личностных особенностей. Так, Эриксон и Лазарус показали, что лица, страдающие скрытым гомосексуализмом, на провоцирующие таблицы TAT дают нейтральные рассказы (Eriksen С. W., 1951, 1968). Еще более сложным является вопрос о соотношении рассказов и реального поведения. Согласно Г. Мюррею, латентные потребности не осознаются и невыводимы из открыто наблюдаемого поведения, а проявляются только в фантазиях и фантазиоподобной активности типа TAT. Между тем, лица, уже совершившие особо тяжкие преступления, могут продуцировать нейтральные или подчеркнуто просоциальные темы (Станишевская M. М., Гульдан В. В., Владимирская M. Т., 1974). Существенной детерминантой ответа оказывается и сама ситуация обследования. Если она воспринимается как экспертная, проявления агрессии строго контролируются. Из сказанного следует, что прогноз реального поведения на основе прямого отождествления «героя» и обследуемого осуществим только для ограниченного круга личностных черт и тенденций. Так, например, вариант TAT Д. Мак-Клелланда и Дж. Аткинсона оказался высоко валидным в отношении мотивации достижения (Atkinson J., 1958). Возвращаясь к хронологии, следует остановиться на работах Лоуренса Фрэнка 1939-1948 гг. Наиболее существенной чертой проективных мет щик Л. Фрэнк считал неопределенность стимульных условий, позволяющих испытуемому проецировать свой способ видения жизни, свои мысли и чувства. Чем более неструктурированным является «стимульное поле», тем в большей степени его струк-турация индивидом будет изоморфична структуре его реального жизненного пространства (Frank L., 1939). Концепция Л. Фрэнка, испытавшая сильное влияние «холистических» теорий личности, в том числе и К. Левина, акцентирует ряд моментов, чрезвычайно важных, на наш взгляд, для понимания назначения и диагностических границ проективных методик. Проективные методики направлены на раскрытие внутреннего мира личности, мира субъективных переживаний, чувств, мыслей, ожиданий, а вовсе не на экспресс-диагностику реального поведения. Исследования Л. Франка, теоретико-методологические по своей сути, породили множество экспериментальных исследований, среди которых особо следует выделить два направления — изучение роли стимула в проекции личностнозначимого материала и изучение феномена проекции как психологического механизма, лежащего в основе действенности этой группы методов. Неопределенность стимульных условий неоднократно указывалась в качестве признака, дифференцирующего
проективные методики от других, например психометрических, процедур.  Тест Роршаха и TAT дают примеры двух типов сти-мульной неопределенности — структурного и содержательно-смыслового. Неопределенной является для испытуемого и сама ситуация обследования, не ограничивающая его действия какими-либо стандартами и нормативными оценками, но предоставляющая максимально широкий выбор способов поведения (Lindzey D., 1959; Бурлачук Л. Ф., 1979; Соколова Е. Т., 1980; Анастази Б., 1982). Дж. Брунер также предполагал, что неопределенность, неоднозначность или «зашумленность» — необходимые стимульные условия для предоставления приоритета личностным субъективным факторам в детерминации восприятия и других видов познавательной активности (Брунер Дж., 1977; Abt L., Bellak L., 1950). Тест Роршаха и TAT дают примеры двух типов сти-мульной неопределенности — структурного и содержательно-смыслового. Неопределенной является для испытуемого и сама ситуация обследования, не ограничивающая его действия какими-либо стандартами и нормативными оценками, но предоставляющая максимально широкий выбор способов поведения (Lindzey D., 1959; Бурлачук Л. Ф., 1979; Соколова Е. Т., 1980; Анастази Б., 1982). Дж. Брунер также предполагал, что неопределенность, неоднозначность или «зашумленность» — необходимые стимульные условия для предоставления приоритета личностным субъективным факторам в детерминации восприятия и других видов познавательной активности (Брунер Дж., 1977; Abt L., Bellak L., 1950).
В духе экспериментов «нового взгляда» в 40—50-е годы складывались теоретические обоснования теста Роршаха (DragunsJ., 1967) и TAT (Bellak L., 1950). Акцентирование неопределенности стимульных условий позволило, кроме всего прочего, согласовать проективные методы с психоаналитическим стилем клинического мышления. Не все исследователи склонны были следовать традиции ортодоксального психоанализа. Набиравшая силу «психология Эго», как и конкретные экспериментальные клинические исследования, формировали новую теоретическую парадигму для обоснования проективного подхода. Значительный вклад был внесен американскими клиническими психологами во главе с Давидом Рапапортом (Rapoport D., 1944-1945; 1968). В частности, проанализировав исследования «нового взгляда», особен- но той его ветви, которая занималась изучением когнитивного стиля, Рапапорт по-новому определяет специфику процессов, детерминирующих проективный ответ. Вслед за работами Д. Рапапорта и его коллег началось интенсивное изучение роли стимульных факторов в характеристике проективных ответов. Применительно К TAT, в частности, было продемонстрировано наличие таблиц, стойко провоцирующих стандартные темы, например депрессию и суицид (TAT, табл. 3, 14, 15), сексуальные перверзии (TAT, табл. 13, 18) (Bellak L., 1978; RapoportD., 1968). Интересны в этой связи результаты, полученные при исследовании сопутствующего значения стимульных характеристик таблиц Роршаха методом семантического дифференциала (Kenny О., 1964). Так, оказалось, что каждая таблица обладает определенным эмоциональным значением:
Д.  Кении приходит к выводу, что высокоструктурированные изображения, «насыщенные» тем или иным побуждением, максимально выявляют индивидуальные различия по степени выраженности этого побуждения. Другие авторы полагают, что проекция того или иного побуждения на слабо структурированные стимулы зависит от интенсивности данного побуждения, а также от готовности субъекта к самораскрытию. Кении приходит к выводу, что высокоструктурированные изображения, «насыщенные» тем или иным побуждением, максимально выявляют индивидуальные различия по степени выраженности этого побуждения. Другие авторы полагают, что проекция того или иного побуждения на слабо структурированные стимулы зависит от интенсивности данного побуждения, а также от готовности субъекта к самораскрытию.
С учетом проведенных исследований в настоящее время имеется достаточно обширный выбор вариантов и модификаций TAT с таблицами, «значения» которых подобраны заранее с учетом диагностических задач. Среди них наиболее известны серии Д. Мак-Клелланда и Дж. Аткинсона для диагностики мотивации достижения (McCleland D., Atkinson J., 1953), TAT для детей и пожилых людей (Bellak L., 1978), TAT для подростков (Symonds D., 1949), TAT для исследования семейных установок (Jackson L., 1950), TAT для национальных меньшинств. Установлено, что оптимальное условие для проекции глубинных слоев личности — умеренный уровень неоднозначности стимульного материала. Тест Роршаха и TAT представляют две группы наиболее распространенных проективных методик по критерию ответной реакции испытуемого, относимых соответственно к тестам на структурирование («конституирование» — по Фрэнку) и интерпретацию. Предполагается также, что эти методики наиболее удачно дополняют друг друга, выявляя соответственно формальный аспект личности — индивидуальный когнитивный стиль, способы аффективного реагирования и контроля и содержательный аспект — структуру потребностей, содержание конфликтных переживаний, апперцепцию «Я» и своего социального окружения. Не ставя перед собой задачу обзорного анализа существующих проективных приемов, хотелось бы кратко обрисовать относительно новые и малоизвестные по отечественной литературе направления в проективной психологии. Это, прежде всего, тенденция рассматривать в качестве проективных или квазипроективных методики, традиционно направленные на диагностику интеллекта и познавательных процессов в целом. Впервые эта точка зрения наиболее четко была сформулирована Д. Рапапортом в уже упоминавшихся исследованиях 1946 г. и затем в более поздних работах его сотрудников по Меннингерской клинике (например, Klein G., 1970), атакже Г. Виткином (Witkin H., 1954, 1974). Можно сказать, что авторы имеют в виду качественней анализ выполнения испытуемым интеллектуальных проб, однако на самом деле речь идет о феноменах, в которых находит выражение влияние личностных и аффективно-мотивационных факторов на познавательные процессы. Для иллюстрации приведем пример анализа процесса мышления на основе известной нам методики Выготского-Сахарова (цит. по: Semeonoff В., 1976). Д. Рапапорт, использовавший эту методику в целях дифференциальной диагностики при исследовании психически больных разных нозологии, выделяет пять категорий «личностных форм мышления», по существу представляющих собой феномены, описанные Б. Давая оценку этому направлению, следует подчеркнуть, что расширительное толкование интеллектуальных тестов как проективных имеет своей целью привлечение внимания клинических психологов к процессу выполнения интеллектуальных задач, его качественному анализу, что, несомненно, более точно отвечает специфике клинической диагностики. Другое направление в развитии проективных методов связано с активной разработкой проблем межличностного восприятия и взаимодействия и исследования «Я-образа». В определенном смысле все проективные методы направлены на изучение того, как субъект воспринимает других людей и самого себя. Наиболее распространено мнение, что проективные методики выявляют неосознаваемый компонент социальной перцепции и «Я-образа» (Wylie R., 1974). Неспецифическими методиками указанной ориентации являются TAT и тест Роршаха. Предполагается, что в рассказах TAT находит отражение не столько реальный характер межличностных отношений обследуемого, сколько их апперцепция, т. е. эмоциональное отношение и пристрастное видение этих отношений. Изображенные на картинках фигуры кроме буквальных значений имеют и символический смысл. С 60-х годов начал разрабатываться и получил широкое распространение тест Роршаха для исследования общения — Совместный тест Роршаха (СТР), используемый более всего для диагностики внутрисемейных отношений. Развитие семейного консультирования и семейной психотерапии послужило толчком к созданию ряда методик, нацеленных на диагностику семейных отношений. К ним прежде всего следует отнести тест семейных установок Л. Джексона (Jackson L. К относительно новому направлению, инициировавшему создание новых методик, относится исследование «Я-образа». Среди традиционных проективных методик следует отметить тест Роршаха, выявляющий формальные характеристики «Я-образа» — самоконтроль, самооценку, самореализацию, а также специальную модификацию теста для диагностики физического «Я-образа», «границ образа физического Я» (Fisher S., ClevelendS., 1958). Общая недостаточная валидность и надежность проективных методик заставляют исследователей искать новые диагностические парадигмы. К ним относится включение в проективные процедуры психометрических принципов — так построены вариант TAT Столина В. В. и Кальвиньо М. (1982), методика косвенного исследования системы самооценок Соколовой Е. Т. и Федотовой Е. О. (1982). Продуктивным оказывается также создание процедур так называемой управляемой проекции (Столин В. Общая оценка проективных методик как психодиагностических процедур исторически связана с обсуждением так называемой проблемы проекции. В отечественной литературе дискуссия по этому поводу также достаточно освещена, однако сама проблема, на наш взгляд, далека от своего разрешения. Как известно, Л. Фрэнк ввел термин «проекция», не определив его конкретного психологического содержания. Подразумевалось, что благодаря неопределенности стимульного материала личность «проецируется» на него, как на экран (Frank L., 1939). Образное выражение Фрэнка породило представление о проективных методиках как о своего рода «рентгеновских
лучах», высвечивающих глубины личности. Ясно, что подобное истолкование механизма проекции не удовлетворяло исследователей. Первые содержательные интерпретации проекции как феномена, возникающего в ситуации проективного исследования, связывались в теоретическом отношении с концепцией 3.  Фрейда; для подтверждения психоаналитической концепции привлекались также эксперименты Г. Мюррея, Р. Сэнфорда и других по изучению мотивации через продукты воображения (Bellak L., 1944). Однако фрейдовское понятие «проекции» не отличалось однозначностью, что сразу же породило ряд трудностей при попытках интерпретировать проективные методики с позиций психоанализа, что отмечалось и отечественными исследователями (Бурлачук Л. Ф., 1979; Реньге В. Э., 1979). Фрейда; для подтверждения психоаналитической концепции привлекались также эксперименты Г. Мюррея, Р. Сэнфорда и других по изучению мотивации через продукты воображения (Bellak L., 1944). Однако фрейдовское понятие «проекции» не отличалось однозначностью, что сразу же породило ряд трудностей при попытках интерпретировать проективные методики с позиций психоанализа, что отмечалось и отечественными исследователями (Бурлачук Л. Ф., 1979; Реньге В. Э., 1979).
Главные из этих трудностей могут быть сформулированы в трех пунктах: 1 ) недостаточная разработанность, многозначность термина «проекция» в психоанализе, многообразие описываемых явлений; 2) лишь частичное сходство феноменов, обозначаемых в психоанализе этим термином, с процессами, имеющими место в проективном исследовании; 3) различие типов проекции в разных проективных тестах. Остановимся на анализе каждого из перечисленных пунктов. Впервые термин «проекция» в его психологическом значении был использован 3. Таким образом, проекцией Фрейд называет два существенно отличающихся друг от друга явления, в основе которых лежат процесс самозащиты и процесс «самоуподобления». Их объединяет неосознаваемость трансформаций, которым подвергаются исходные влечения, — в сознании выступает лишь продукт этих преобразований. Со временем проекция стала столь расхожим термином, что дифференцировать ее от явлений идентификации, перенесения и некоторых других психоаналитических феноменов стало чрезвычайно трудно (Lapiance J., Pontalis J., 1963). Например, говорят о проекции в психотерапевтической ситуации, когда на врача переносятся чувства, предназначенные другому лицу; называют проекцией своеобразное отождествление художника со своим творением (Г. Флобер говорил: «Эмма — это я»), а также «сопереживание» при восприятии художественных произведений; проекцией объясняют существование расовых и этнических предрассудков. Б. Мюрштайн и Р. Прайер (Murstein В., Prier R., 1959), критикуя многозначность и, следовательно, недостаточную разработанность понятия проекции, предлагают различать несколько видов проекции. Классическая защитная проекция Фрейда находит подтверждение во многих клинических наблюдениях. Атрибутивная проекция — приписывание собственных мотивов, чувств и поступков другим людям (по смыслу близка к фрейдовскому «уподоблению»). Артистическая проекция — детерминированность восприятия потребностями воспринимающего; для иллюстрации этого вида проекции авторы ссылаются на эксперименты New Look. Рациональная проекция отличается от классической «рациональной» мотивировкой: например, по данным одного из экспериментов, когда студентам предложили высказать свои замечания по структуре учебного процесса, оказалось, что на отсутствие дисциплины жаловались отпетые прогульщики, а недостаточной квалификацией преподавателей были недовольны двоечники. Здесь, как в случае обычной рационализации, вместо признания собственных недостатков испытуемые склонны были приписывать ответственность за собственные неудачи внешним обстоятельствам или другим людям. 
Д. Холмс, подводя итоги многолетних исследований, считает необходимым выделить два «измерения» проекции (Holmes D., 1968) (см. табл.). Первое из них относится к тому, что проецируется: субъект воспринимает в другом свои собственные черты или черты, ему самому не присущие. Второе измерение — осознает ли субъект обладание той чертой, которая проецируется, или нет. Комбинация этих измерений позволяет классифицировать все известные виды проекции. Поделитесь с Вашими друзьями: |
|
Продолжение ТАБЛИЦЫ ИНТЕРПРЕТАЦИЙ +8+3. Смешанный тип реагирования, создающий внутреннее напряжение и конфликт разнонаправленных тенденций. Мотивация избегания неуспеха и осторожность противодействуют спонтанной активности, стремлению к самореализации, высокой поисковой активности, мотивации достижения. Эгоцентричность установок при внешней сдержанности их проявлений. +1 (СИНИЙ) +1. Потребность в прочной и глубокой привязанности, эмоциональном комфорте и защите от внешних воздействий. Дружелюбие, конформность установок. Аффилиативная потребность является ведущей и поэтому — наиболее травмируемой мишенью. Интровертированность, избирательность в контактах, аналитический склад ума, вдумчивый подход к решению проблем, инертность в принятии решений. Пассивная позиция. Тормозные черты, преобладание трофотропных тенденций, всплески активности быстро сменяются усилением парасимпатического тонуса. Таблица II: «х«-функции =1=6. Застенчивость и пассивность, затрудняющие чувственную раскованность. =5 (ФИОЛЕТОВЫЙ) =7(ЧЕРНЫЙ) Таблица IV: «—»-функции -8 (СЕРЫЙ)
-2 (ЗЕЛЕНЫЙ) +1 (СИНИЙ) +5 (ФИОЛЕТОВЫЙ) +7 (ЧЕРНЫЙ) [1] [2] |
Стандартизированный многофакторный методисследования личности СМИЛ (модифицированный тест MMPI)Интерпретация
Зная личностные особенности и характеристики состояний, которые определяются отдельными шкалами, а также учитывая их влияние друг на друга можно перейти к целостной оценке профиля. В первую очередь профиль должен рассматриваться через призму установки обследуемого на процедуру тестирования которая выявляется соотношением шкал достоверности и высотой их показателей.
Должны настораживать сглаженные профили, в которых контрастирующие по их содержательной стороне шкалы оказываются почти на одинаковом уровне, а показатели шкалы К или L достаточно высоки. При высоком F высота профиля может быть связана с разными причинами, приведенными ранее однако в любом случае профиль будет заострен и завышен, что необходимо принимать во внимание при интерпретации.
При повышении в пределах нормативного разброса 1-й и 3-й шкал с относительно низкой 2-й и без значимого повышения профиля по другим шкалам следует обратить внимание на показатели L и К. Если они повышены (выше 60 Т. или более чем на 7 Т выше шкалы F), то скорее всего речь идет о тенденции испытуемого “показать себя в лучшем свете”, о стремлении к отрицанию каких-либо трудностей и проблем, об установке на улучшение результатов, о попытке дать “сверхнормальные” ответы и подчеркнуть свое дружелюбие, конформность, альтруизм, в то время как на самом деле это может быть лишь фасадом, за которым скрываются различные проблемы и иной характер У таких испытуемых иногда и по шкале “?” может оказаться достаточно высокий показатель. Интерпретация такого профиля сводиться к констатации наличия установки на соответствие нормативности, профиль (особенно если он по четырем – пяти шкалам утоплен) расценивается как “гипернормальный”. Обследование стоит повторить.
В достоверном профиле интерпретация проводится согласно общим правилам, при этом характеристика 3-й шкалы поглощает свойства 1-й. так как эмоциональная яркость ее признаков нивелирует сдержанность, отражаемую 1-й шкалой. Лишь преобладание 1-й над 3-й на 5 Т и более дает основание ориентироваться на интерпретацию 1-й шкалы.
Сочетание 1-й с повышенными (или высокими) 2-й, 6-й. 7-й, 8-й и 0-й при низкой 9-й отражает проблему подавленной враждебности и характерно для так называемого “язвенного типа личности” отличающегося педантизмом, догматическим стилем мышления, повышенной раздражительностью, дистантностью, требовательностью как к себе, так и к другим в вопросах морали, долга, ответственности. При высокой исполнительности, принципиальности и честности в работе, они проявляют мелочный деспотизм в контактах узкого круга, скрытны, неловки и скованы в общении, тон высказываний назидательный, внешняя жесткость сочетается с внутренне ощущаемым напряжением и ранимостью по отношению к средовым воздействиям.
Высокие показатели 2-й шкалы, сочетающиеся со значительным повышением 1-й и 3-й, которые находятся в соподчиненной по отношению к 2-й шкале позиции, а также повышенными 7-й и 8-й при пониженной 9-й, свидетельствуют о выраженном эмоциональном дискомфорте, трудностях адаптации хронического характера и чаще всего бывают связаны с невротическим развитием. Внешне поведение таких людей не бросается в глаза как отклоняющееся от нормы, но внутренняя дисгармония сказывается в постоянно ощущаемом индивидом напряжении, сниженном настроении с неуверенностью в себе, чувством несчастливости, заниженной самооценкой, преобладанием мотивации избегания неуспеха, низкой мотивацией достижения. 5-я шкала по-разному влияет на тип реагирования в мужских и женских профилях, а 8-я приобретает разные значения в зависимости от остальных показателей профиля.
Успешность социальной адаптации – это хорошо сбалансированное соотношение между эгоцентрическими потребностями человека и требованиями социальной среды. Абсолютно уравновешенная, гармоничная личность отличается полной сбалансированностью умеренно выраженной тенденции к самореализации с хорошим самоконтролем, обеспечивающим полное соблюдение нормативных требований среды. Чем больше выражен характер и индивидуальность человека, тем большая нагрузка выпадает на функцию контролирующих систем, сохраняющих баланс. Это – основное отличие между конкордантной и дискордантной личностью: у последней внешние атрибуты нормативного поведения скрывают внутреннюю напряженность.
Цена, которую “платит” личность за соответствие требованиям социума, может быть достаточно высокой.
Если “Я” индивида разрушается давлением социума и не происходит самореализация личности (не удовлетворяются потребности, не реализуются способности), то происходит невротизация, отражающаяся в профиле преобладанием гипотимных, тормозимых черт. Если же баланс нарушается в связи с ослабленным самоконтролем в сторону спонтанной самореализации, то столкновение интересов самоутверждающейся личности с требованиями социума находит свое отражение в поведенческих реакциях, проявляющихся в профиле преобладанием гипертимных признаков. Цена этого дисбаланса в основном оплачивается трудностями социума. Если и тот и другой механизмы удержания баланса задействованы одновременно, то мы наблюдаем реализацию психосоматического механизма, проявляющегося физическими расстройствами разного рода.
Для удобства целостной интерпретации профиля шкалы методики следует сгруппировать таким образом, чтобы по ведущим пикам можно было определить сперва обобщенно основной тип реагирования, а затем уже на основании значений шкал выявлять индивидуально-личностные особенности и уровень адаптированности обследуемого. 2-я, 7-я и 0-я шкалы отражают свойства гипостенического типа реагирования и свидетельствуют о преобладании тормозимых черт характера. Если в профиле эти шкалы значимо превалируют над другими, то выявляется конформность, социальная податливость, нормативность личности, отказ от самореализации. В любом профиле, отражающем реакцию личности на психотравмирующую ситуацию, конфигурация с ведущими шкалами гипостенического регистра выявляет невротический вариант дезадаптации или декомпенсацию личности в сторону усиления тормозимых реакций. 4-я, 6-я и 9-я шкалы формируют стенический тип реагирования и позволяют описывать личность в характеристиках активности, силы, преобладания возбудимых черт. Умеренное повышение этих шкал в профиле свидетельствует о выраженной тенденции к самореализации и о противодействии средовому влиянию. Если высота профиля говорит о нарушении адаптации, то вариант дезадаптации, соответствующий данному типу реагирования, проявляется поведенческими реакциями асоциальной или антисоциальной направленности. Это может быть конфликтное поведение, неконформность, авторитарность и стремление к доминированию, повышенное чувство независимости и отталкивание от навязываемых авторитетов (в том числе проблемы пубертатного периода). Высокие показатели гиперстенического профиля могут также отражать проблему алкоголизации, наркомании, делинквентного поведения.
Сочетание разнонаправленных тенденций, т.е. показателей как гипотак и гиперстенических свойств, выявляет смешанный тип реагирования, при котором высокая потребность самореализации сочетается со столь же высоким самоконтролем и тенденцией к оттормаживанию, сдерживанию поведенческих реакций. В этом случае оказываются перекрытыми каналы как невротического, так и поведенческого отреагирования, что сказывается на общем перенапряжении и проявляется соматизацией внутреннего конфликта, т.е. психосоматическим вариантом дезадаптации, мишенью которого окажется наиболее слабое звено той или иной функциональной системы организма человека.
Показатели 1-й и 3-й шкал уже несут в себе характеристики смешанного типа реагирования, независимо от остальной структуры профиля, так как отражают проблему подавленной враждебности. Их присутствие в профиле как правило выявляет смешанный тип реагирования, а другие показатели профиля – лишь дополнительная информация. Определив надежность полученных данных и тот ракурс, который позволяет через призму выявленных у испытуемого установок рассматривать сам профиль, после того, как выявлен общий тип реагирования, следует обратить внимание на степень адаптированности личности. Утопленный профиль может быть результатом неискренности ответов (об этом скажут шкалы достоверности), но может также свидетельствовать об определенной гипоэмотивности испытуемого, о вялости его реакций, о сниженном уровне мотивации достижения, о суженном диапазоне интересов.
Нормальная, гармоничная личность может проявляться показателями линейного профиля, в котором все свойства уравновешены и ни одно из них не выражено более ярко, чем остальные. Но уравновешенность может проявляться и сбалансированностью разнонаправленных тенденций при повышенных показателях, что создает почву для определенной напряженности внутренне противоречивого личностного паттерна; однако внешне усилия, ценою которых личность достигает самокомпенсации, могут быть незаметны или проявляться крайне редко Поэтому в профиле который находится на верхней границе нормы или слегка его превышает, выявляется пограничное между нормой и патологией состояние – будь это повседневные трудности акцентуированной личности или заострение личностных особенностей в объективно сложной ситуации.
Понимание стоящих за этими показателями проблем должно опираться на соотношение шкал, выявляющих гипостенический, стенический или смешанный тип реагирования, на характеристики разных шкал и их взаимное влияние друг на друга, усиливающее или ослабляющее стоящие за ними тенденции. В высоко расположенном профиле при интерпретации нас интересуют в первую очередь пики, выносящие контур профиля за пределы нормы. Они определяют состояние испытуемого и показывают уровень личностной дезинтеграции, выявляя структуру ведущего синдрома, степень выраженности эмоционального напряжения, аффективной насыщенности переживаний обследуемого Чем более выражены пики и чем меньше сопутствующие подъемы шкал, отражающих противоположные данному пику тенденции, тем больше оснований говорить об устоявшейся структуре отношения испытуемого к сложившейся ситуации, о хронически протекающей психической дезадаптации, а также о дефиците компенсаторных ресурсов личности. Напротив плавающий профиль, в котором большинство шкал расположено выше верхней границы нормы, свидетельствует о состоянии общего стресса в котором задействованы различные защитные механизмы и напряжены множественные компенсаторные функции психической деятельности. направленные на нивелировку дезадаптации И хотя при этом психическая напряженность увеличивается, прогностически такой профиль более перспективен в плане нормализации состояния, особенно если речь идет о психогенных пограничных расстройствах.
В то же время умеренно повышенные профили (65-75 Т), сочетающие в себе разнообразие шкал. отражающих выраженность разнонаправленных тенденций, могут быть результатом невротического (если преобладают шкалы гипостенического регистра) или патохарактерологического (если превалируют стенические признаки) развития. При этом сопутствующие ведущим пикам повышения являются отражением компенсаторной напряженности вторичных защитных механизмов. Все эти нюансы становятся интересными для тех специалистов, которые уже имеют опыт работы с данной методикой.
Интерпретация полученных данных в известной степени подлежит обсуждению с испытуемым или теми лицами, от которых зависит судьба обследованных При этом необходимо помнить, что любая на первый взгляд лестная характеристика, также как иные излишне суровые эпитеты, представляют собой достаточно одностороннюю интерпретацию того или иного феномена Каждое личностное свойство диалектично и имеет как “лицевую” так и “обратную сторону медали”. Характеристики, выявляемые той или иной шкалой, несут в себе разную смысловую нагрузку и по-разному могут рассматриваться в контексте личностных и общественных отношений, в сфере профессиональной деятельности. Упрямство и педантизм одновременно несут в себе такие позитивные качества, как устойчивость интересов и соревновательность: повышенная тревожность наряду с робостью в принятии решений проявляется совестливостью и эмпатийностью в отношениях с окружающими, и т д.
В связи с этим при интерпретации следует обратить особое внимание на то. чтобы описание профиля не носило характера отзыва о плохих и хороших качествах индивида и не повредило человеку в глазах окружающих, а также не снизило его самооценку, поскольку позитивная самооценка является одним из непременных условий нормального существования личности: тем более это условие должно соблюдаться в контактах психолога с обследуемым, какую бы форму эти контакты ни принимали.
Человек никогда не бывает плох или хорош в зависимости лишь от того, какой у него тип нервной деятельности – сильный или слабый, или от того, какой у него стиль когнитивной или поведенческой активности – холистический. коммуникабельный, или формально-логический, интровертный. Люди просто – разные, а плох человек или хорош – это категория ситуативной оценки его действий окружающими и целиком зависит от морально-нравственных установок социума, сложившихся культурно-исторических ценностей конкретной группы населения Вне этих условий человек такой, какой есть и у него (за исключением грубой патологии) нет намерений творить зло другим людям Если он это делает, то, чаще всего, защищая свои интересы, чем и оправдывает свои “плохие” поступки и высказывания, болезненно и негативно воспринимая критику в свой адрес. Чем эгоистичнее поступает человек, тем чаще и сильнее он рискует ущемить интересы других людей.
Невольно вспоминаются строки из дневника юной Анны Франк, трагичность жизни которой трудно преувеличить: “Несмотря ни на что, я все-таки верю что люди в глубине души действительно добры”. Нередко стеничность перерастающая в агрессию и проявляющаяся в жестких поступках или высказываниях, является проявлением гиперкомпенсаторных реакций по-своему несчастливого человека. При этом люди редко задумываются над тем, что их жесткость зачастую может проявляться в отношении ни в чем не повинных людей как неотреагированная защитная реакция на обиду, исходящую из совсем другого источника. Следует всегда иметь в виду, что у каждого “плохого” человека внутренняя картина собственного “Я” – позитивная, а своим плохим поступкам он всегда находит оправдание. Если же картина “Я” сводится к образу “плохого” или никчемного человека, то такие переживания могут привести к аутоагрессии. то есть, к суицидальным тенденциям. Для плодотворного сотрудничества с обследуемыми (а именно это необходимо психологу, для того, чтобы его работа приносила позитивные результаты и профессиональное удовлетворение) в процессе обсуждения полученных результатов нужно соблюдать следующее непреложное правило: необходимо сохранять достаточно высокую самооценку человека, так как это непременное условие его нормального существования. Так утверждал известный всему миру гуманнейший психотерапевт Карл Роджерс. Это подтверждается и накопленным в отечественной психологии опытом. При этом следует помнить, что завышенная, но неустойчивая самооценка импульсивных, возбудимых акцентуантов или психопатических личностей также подчиняется этому правилу, так как за этим часто скрывается неуверенность в себе и неумелая попытка скрыть собственные комплексы, а агрессивность носит гиперкомпенсаторный характер.
Этика психологического исследования предусматривает, что полученные данные должны служить интересам обследуемого человека и не приносить ему вреда. В противном случае, доверие, проявленное обследованным лицом по отношению к психологу, будет неоправданно или полностью подорвано, а сама психология в глазах людей дискредитирована.
Психодиагностика – тонкое и обоюдоострое оружие, она многое может – потому и необходима, но потому же и опасна. Только тот, кто ответственно относится к непрерывному повышению своего профессионального мастерства, строг и требователен к себе и другим при выборе не только инструмента тестирования, но и средств реализации его эффекта, способен понастоящему помочь людям и удостоиться чести носить имя “инженера человеческих душ” от науки.
При самой искусной интерпретации следует помнить, что, помимо сопутствующих любому исследованию 10% недостоверных профилей, в которых мотивационные искажения определяются шкалами достоверности, как правило, встречаются не менее 2% формально достоверных, но, благодаря хитроумию обследованных, недостаточно искренних или надуманных профилей, звучащих в известном смысле диссонансом по отношению к данным других психологических методик и наблюдаемой объективной реальности. Такие профили могут встречаться при обследовании лиц с достаточно высоким интеллектом в ситуации, когда результаты тестирования могут иметь особую значимость для их дальнейшей судьбы.
Сочетание объективно имеющихся проблем с симулятивными тенденциями (сюрсимуляция, т.е. тенденция к симуляции у настоящего больного, который при этом себя таковым не считает) проявляется такими контурами профиля, в которых можно усмотреть нарушение закономерностей декларируемой патологии. Так, реально переживаемое состояние психогенного стресса, отраженное в профиле в виде признаков, соответствующих по остроте характеристикам эмоционально сохранной личности, при попытке симулировать шизофрению может переплетаться с искусственно вкрапленными показателями эмоциональной холодности, аутичности.
Учитывая характер требования вербальных методик, следует всегда помнить о том, что они могут спровоцировать у испытуемого достаточно изощренную защитную реакцию на процедуру обследования. Поэтому, опираясь на данные только методики СМИЛ (или другого варианта ММРI) не следует рассчитывать более чем на 75% достоверность. Надежность психологического тестирования повышается, если используется батарея тестовых методик. Особенно эффективно использование вербальных методик в сочетании с невербальными.
Прекрасным дополнением к ММРI является метод цветовых выборов (адаптированный вариант цветового теста Люшера), миокинетическая психодиагностика Мира-и-Лопеса, метод портретных выборов Сонди, рисованный апперцептивный тест РАТ, Роршах-тест. Не все из них являются методами достаточно формализованными и стандартизированными, но психологическое исследование всегда было и останется в известной степени искусством, а методика – всего лишь инструмент, который только в умелых руках способствует ваянию образа личности. Строгая стандартизация, увеличивая надежность метода, одновременно уменьшает зону исследовательского поиска, оставляя за рамками эксперимента значительное количество вариаций личностных паттернов, не вошедших в структуру математической модели методики.
Наименее устойчивы индивидуально-личностные характеристики детей и подростков. Недостаточно контролируемы и устойчивы эти характеристики у 16 – 20-летней молодежи. Поэтому данные методики СМИЛ, обрисовывающие достаточно объективную картину субъективного “Я” человека, необходимо сопоставлять с тем, что обнаружат невербальные тесты, направленные на выявление неосознаваемых тенденций. Прекрасным дополнением к тесту СМИЛ, в основном раскрывающим внутреннюю картину индивидуального “Я”, являются: метод портретных выборов МПВ, основанный на модификации теста восьми влечений Сонди, метод цветовых выборов МЦВ (адаптированный восьмицветовой тест Люшера), а также рисованный апперцептивный тематический тест РАТ (модификация Тематического апперцептивного теста Мюррея).
Однако, получив такой многосторонний портрет индивидуально-личностных свойств, вправе ли мы считать полностью изученной сложную структуру того, что в целом мы называем словом личность? В этот момент становится как никогда актуальным тот аспект психической индивидуальности, который напрямую связан с усвоенным социально-историческим опытом своего этноса, своего социального окружения и тех морально-нравственных критериев, которые являются основой конкретного сообщества. При индивидуально обусловленном тропизме к тем или иным видам деятельности, к определенным ценностям и к кругу общения, человек реально может обратиться лишь к тем из них, которые ему доступны, о которых ему что-либо известно, которые его окружают. С учетом интериоризированных социальных установок и культурно-исторического опыта, почерпнутых индивидом в его окружении, мы формируем целостную картину личности. Имея в виду тот факт, что формализованные данные психодиагностического исследования образуют лишь базисный паттерн, канву психологической сущности человека.
Л. Н. Собчик
Тем, кто хочет меня знать, как облупленную 🙂 — Девяносто два дня
Результаты моего вчерашнего тестирования.1. Достоверность тестирования.
Данные достоверны. Стремление уйти от илишней откровенности. Показатель Уэлша -18.
2. Характеристика основного профиля.
3. Общая оценка типа реагирования.
Смешанный тип реагирования с преобладанием гиперстенических тенденций.
4. Позиция.
Оборонительная. Достаточно уверенная позиция. Позиция изменчивая и находится в сильной зависимости от установок референтной группы.
5. Мотивационная направленность.
В благоприятной обстановке проявляется мотив самоутверждения. Мотивация прагматично-ориентированная. Неустойчивая мотивация, гибко меняющаяся в зависимости от ситуации. Поведение мотивировано собственной убежденностью и своим видением проблемы.
6. Эмоциональный фон.
Легко возникает чувство обиды. Эмоциональное своеобразие. Сосредоточенность на самой себе. Эмоциональная лабильность. Артистичность. Некоторое своеобразие эмоций.
7. Индивидуальный тип реагирования.
Умеренно выраженный упорно-стеничный. Лабильный. Индивидуализм.
8. Стиль общения.
Стремление укрепить свои позиции в коллективе. Избыточная общительность, широкий круг знакомств без глубокой привязанности. Гибкость в построении отношений с людьми. Умение менять стиль поведения в зависимости от круга общения. Обособленность.
9. Реакция на стресс.
Внешенобвиняющая. Чувствительность к стрессу. Иррациональная.
10. Защитные механизмы.
Рационализация. Стремление снизить ценность того, что кажется недостижимым. Сублимация нереализованных потребностей в социальную или профессиональную активность. Подсознательное отторжение информации, травмирующей личность, несовместимое с образом «Я». Стремление дать ситуации свое собственное объяснение, не всегда совпадающее с общепринятым.
11. Тип восприятия.
Системный. Наглядно-образный. Абстрактный тип мышления.
12. Ведущие потребности.
Потребность в удержании своих позиций и сохранении авторитета. Поиски признания своих лучших качеств окружающими. Потребность в сохранении собственной индивидуальности.
13. Коррекционный подход.
Коррекцию затрудняет ригидность установок испытуемой и защита по типу проекции. Социо-тренинг. Школа женского обаяния. Рычагом корригирующего воздействия может быть повышенная внушаемость, которая, однако, проявляется лишь в отношении лиц, пользующихся особым авторитетом у обследуемой. На мнение обследуемой воздействовать трудно без предварительного изучения ее убеждений.
14. Черты характера.
Умеренно выражены такие черты, как обидчивость, упрямство, соревновательность, недоверчивость. При этом не отмечается замкнутость, отгороженность. Артистичность, умение нравится окружающим. Самобытность.
15. Условия оптимальной эффективности.
Гибкость со стороны непосредственного руководства, отсутствие конфронтации со стороны окружающих. Возможность проявить определенную самостоятельность в деловой сфере. Эмоциональная вовлеченность. Повышенное внимание со стороны окружающих. Необходимо терпение окружающих к индивидуальным особенностям личности.
16. Возможный тип дезадаптации.
Раздражительность и застревание на обидах. Затруднения в сфере межличностных контактов. При перенапряжении — эмоциональная неустойчивость. Некоторые затруднения в социальной адаптации.
17. Рекомендации по выбору профессии.
Работа, позволяющая проявить выдумку и изобретательность. Работа, связанная с человеком и его проблемами. Работа, позволяющая реализовать творческий потенциал в своеобразной сфере интересов. Рекомендуется следующий список профессий: предприниматель, дилер, деловая женщина.
Метод цветовых выборов
МЕТОД ЦВЕТОВЫХ ВЫБОРОВ
Метод цветовых выборов представляет собой адаптированный вариант цветового теста Люшера1. Разработчик оригинального варианта теста — Макс Люшер, врач и социолог, доцент кафедры психотерапии швейцарского антропологического института в Базеле. Его восьмицветовой тест — методика чрезвычайно интересная, отличающаяся от большинства психодиагностических методик стимульным материалом, который воздействует как мощный аккорд одновременно на разные стороны человеческой психики.
Разработка теста базируется на чисто эмпирическом подходе и изначально связана с установкой на изучение эмоционального и физиологического состояния человека. В основе весьма эклектичной интерпретационной схемы автора лежит социально-историческая символика цветов, элементы психоаналитического и психосоматического подхода. Издано немало книжек на эту тему, в которых отечественные авторы ограничивались переводом зарубежного издания теста Люшера, Исключение составляют серьезные публикации, в которых авторы (Г.Е. Бреслав, А.М. Эткинд, Е.Ф. Бажин, П.В. Яньшин, О.В. Сафуанова, Л. Сивик и др.) отражают свои взгляды на цветовосприятие.
Так как первые попытки применения теста на практике обнаружили весьма выраженную его эффективность, это вызвало серьезное желание понять феноменологию теста, соотнести результаты обследования с концептуальным подходом к пониманию термина «личность» в теории ведущих тенденций, а также приспособить тест для изучения психологических особенностей и актуального состояния детей. Для этого было предпринято изучение данных восьмицветового теста Люшера параллельно с системным психодиагностическим исследованием репрезентативной группы лиц, разных по возрасту, по уровню полученного образования и по профессиональной ориентации. Подробно результаты апробации и адаптации методики приведены в практическом руководстве2. В этой книге помимо подробного описания метода приводятся результаты многолетнего изучения восьмицветового теста в сравнительном анализе с теоретически обоснованной моделью психодиагностического исследования целостного конструкта личности.
Опыт изучения восьмицветового теста Люшера в отечественных условиях не только подтвердил его эффективность, но и позволил осмыслить феноменологию этого метода в контексте современного научного мировоззрения. Преимущество теста Люшера перед многими другими личностными тестами заключается в том, что он лишен культурно-этнических основ и не провоцирует (в отличие от большинства других, особенно вербальных тестов) реакций защитного характера. Методику можно применять при обследовании лиц любого возраста, в том числе и для изучения особенностей детской психики, начиная чуть ли не со дня рождения ребенка. Методика выявляет не столько осознанное, субъективное отношение испытуемого к цветовым эталонам, сколько его неосознанные реакции, что позволяет считать метод глубинным, проективным.
МЕХАНИЗМ ВОЗДЕЙСТВИЯ РАЗНЫХ ЦВЕТОВ НА ЧЕЛОВЕЧЕСКУЮ ПСИХИКУ
Г.Е. Бреслав3 считает, что мы ошибаемся, когда рассматриваем цвет как свойство материала. Он утверждает, что в природе цвета нет, что цвет — «одна из особенностей восприятия человека: наш глаз по-разному ощущает потоки света с разными физическими характеристиками. Большинство наблюдаемых нами предметов сами не испускают световые лучи, а видны потому, что падающий на них свет рассеивается и попадает в наши глаза. Цвет — это ощущение, возникающее в мозгу человека как реакция на свет определенной длины волны, попавший в сетчатку его глаза».
П.В. Яньшин4 утверждает, что цвета взаимодействуют не только со зрением, но и со всем организмом человека, что «цвет несет в себе нечто, ставящее его в совершенно особенные отношения с человеческой душевной организацией». Понять это «нечто» невероятно трудно, с чем нельзя не согласиться.
В работах, направленных на исследование семантического поля цветовых предпочтений (Ч.Е. Осгуд, Л. Сивик, О.В. Сафуанова), изучался в основном вербальный аспект цветовых ассоциаций и транскультуральные особенности цветовосприятия.
Мы же понимаем цветовое виденье как процесс восприятия каждого конкретного цвета и через призму опосредующего субъективного опыта, и через неосознаваемые, чисто физиологические реакции «старого мозга», то есть диэнцефальной области, которая является дирижером в сложном оркестре автономных систем организма и имеет индивидуальные различия в зависимости от генетически заложенных индивидных особенностей (темперамента человека).
Основной вывод, который можно сделать из проведенного исследования, — это то, что выбор цветового ряда зависит как от набора устойчивых (базисных) личностных характеристик, так и от актуального состояния, обусловленного конкретной ситуацией. Данные тестирования с помощью теста Люшера оказались сопоставимыми с индивидуально-типологическим подходом, который согласуется с концепцией целостного многоуровневого понимания личности в рамках теории ведущих тенденций5.
ОБЩАЯ ХАРАКТЕРИСТИКА МЕТОДИКИ
Изучение восьмицветового теста с этих методологических позиций значительно расширило рамки применения методики и позволило приблизить методику к нуждам и интересам школьного психолога. Методика подкупает лаконичностью и простотой в предъявлении, способностью выявлять наиболее непосредственные, неподвластные сознанию индивидуально-личностные свойства. Естественно, в сочетании с другими методиками (например, с индивидуально-типологическим детским опросником ИТДО6) надежность полученных данных повышается, хотя такого рода комплексное обследование занимает всего 10—15 минут. Компьютерный вариант, предусматривающий как прямой диалог с компьютером, так и ввод полученных при обследовании данных вручную, еще в большей мере облегчает работу школьного психолога, выдавая на выходе готовую интерпретацию и рекомендации по выбору профессии и мер психологической коррекции.
ПРОЦЕДУРА ОБСЛЕДОВАНИЯ
Ребенку предлагается выбрать из разложенных перед ним цветовых таблиц самый приятный цвет, сообразуясь с тем, насколько этот цвет предпочитаем в сравнении с другими при данном выборе и в данный момент.
Раскладывая перед обследуемым цветовые эталоны, следует использовать индифферентный фон.
Освещение должно быть равномерным, достаточно ярким (лучше проводить исследование при дневном освещении).
Расстояние между цветовыми таблицами должно быть не менее 2 см.
Выбранный эталон убирается со стола или переворачивается лицом вниз.
При этом психолог записывает номер каждого выбранного цветового эталона. Запись идет слева направо. Номера, присвоенные цветовым эталонам, таковы:
темно-синий — 1,
сине-зеленый — 2,
оранжево-красный — 3,
желтый — 4,
фиолетовый — 5,
коричневый — 6,
черный — 7,
серый — 0.
Каждый раз испытуемому следует предложить выбрать наиболее приятный цвет из оставшихся, пока все цвета не будут отобраны.
Через 2—5 минут, предварительно перемешав цветовые таблицы, нужно снова разложить их перед испытуемым в другом порядке и полностью повторить процедуру выбора, сказав при этом, что исследование не направлено на изучение памяти и что он волен выбирать заново нравящиеся ему цвета так, как ему это будет угодно.
М. Люшер допускает интерпретацию данных тестирования и на основании однократного выбора. Но когда речь идет о детях, то нельзя не учитывать, что психика ребенка еще крайне неустойчива, эмоциональная сфера чрезвычайно лабильна. В обследовании они видят игровой компонент, интуитивно хотят понять, чего от них ожидают. Их реакции могут носить подражательный характер. Вместо того выбора, который шел бы «от сердца», они могут придумать такую игру, в которой отражается не отношение к цветам, а выдуманные правила игры. Так, один мальчик, проследив работу бригады психологов, подошел и сказал: «Я знаю, как надо выбирать цвета», и разложил их по порядку: 1, 2, 3, 4, 5, 6, 7, 0. Поэтому процедура обследования должна быть весьма продуманной.
Если ребенок делает каждый раз другой выбор, ничем не похожий на предыдущий, то, скорее всего, это — уход от раскрытия, желание поморочить психологу голову. В таких ситуациях ребенку следует дать понять серьезность обследования, создать мотивацию на искренность (допустим, пообещать рекомендации по выбору профессии). После повторных выборов, записав последний, перепутать карточки и разложить их в том порядке, как ребенок выбрал их в последний раз. Затем спросить, хочет ли он что-либо изменить или готов остановиться на этом выборе.
Цвета разделяются на основные (1 — темно-синий, 2 — сине-зеленый, 3 — оранжево-красный и 4 — светло-желтый) и дополнительные, среди которых 7 (черный) и 0 (серый) — ахроматические, а 5 (фиолетовый) и 6 (коричневый) — смешанные.
В норме и при полной уравновешенности, яркие цветовые эталоны должны находиться на первых позициях. Дополнительным цветам отводится роль как бы разделяющих или разбавляющих. Подробная обработка цветовых выборов с выделением функциональных пар и подсказки по их интерпретации приводятся в практическом руководстве, упомянутом ранее.
ОБЩИЕ ОРИЕНТИРЫ
Однако есть весьма важные общие ориентиры, на которых можно строить изучение ведущих индивидуально-типологических тенденций и выявлять степень адаптированности (или дезадаптации) обследуемого ребенка. При этом следует учитывать тот факт, что мы имеем дело с еще не сложившейся, слабо интегрированной структурой, незрелой личностью. Поэтому для выявления более или менее устойчивых индивидуально-типологических черт следует проводить повторные, лонгитюдные исследования. При этом нужно обязательно иметь в виду конкретную ситуацию, которая в значительной степени сказывается на цветовых выборах ребенка.
Изучение разных по индивидуально-личностным особенностям детей, относимых к психической норме, убедительно показало значимость цвета в определении ведущей, корневой индивидуально-психологической тенденции. Причем эта значимость тем выше, чем левее оказывается позиция того или иного основного цвета.
Таким образом, первые 4 выбора (позиции) цвета определяют личностные особенности как сочетание первоочередных (I позиция), вторичных (II позиция) и второстепенных (III и IV позиции) индивидуально-типологических свойств, однако с оговоркой: если этот выбор не носит сугубо случайного характера, если это — устойчивый, свойственный ребенку на протяжении длительного периода выбор.
Для повышения надежности результатов сама процедура обследования детей несколько трансформирована: если первый и второй выборы заметно отличаются, испытуемому предлагается уточнить свое отношение к изменившим позицию цветам в процессе их парного сравнения. Например, при двух выборах
1 2 4 3 5 6 0 7
2 4 1 3 5 6 0 7
дополнительная инструкция должна звучать так: «Какой из этих двух цветов ты предпочитаешь: синий или желтый? Зеленый или желтый? Желтый или красный? Зеленый или синий?» При этом пара 2 4 в данном выборе может оказаться случайной, если конечным выбором будут 2 1 4 3 или 1 2 3 4 на первых позициях, что встречается нередко.
ИНТЕРПРЕТАЦИЯ ЦВЕТОВЫХ ПРЕДПОЧТЕНИЙ С ПОЗИЦИЙ ИНДИВИДУАЛЬНО-ТИПОЛОГИЧЕСКОГО ПОДХОДА
1-й цветовой эталон, устойчиво занимающий в цветовом ряду первую позицию, свидетельствует о том, что ребенок соответствует сензитивно-интровертному типу личности. Черты пассивности сочетаются с повышенной тревожностью, проявляется склонность к пессимистичности. Неуверенные в себе дети этого типа постоянно нуждаются в надежной опоре и спокойствии, вследствие чего формируются черты зависимости, крайней чувствительности к средовым воздействиям, тенденция к укреплению своей позиции за счет привязанности и защиты со стороны других лиц, а потребность в теплых отношениях является ведущей. Среди девочек этот тип реагирования встречается значимо чаще, чем среди мальчиков.
В поведенческом плане у детей этого типа обнаруживается конформность установок, избегание конфликта, стремление к устойчивому стереотипу жизни, страх перед трудностями, нерешительность в принятии решений, вдумчивость, способность к сопереживанию, пассивность в отношении актуальных проблем, повышенная склонность к рефлексии (самоанализу).
Эти качества усугубляются и проявляются тревожно-мнительными чертами при сочетании 1-го с 0-м эталоном на первых позициях. В этой ситуации интровертированность уже звучит как проблема трудности общения и проявляется избыточной нерешительностью, застенчивостью, ощущением непонятости, неприятия значимыми другими, эгоцентричной невротической сосредоточенностью на своих проблемах. Сочетание предпочитаемого 1-го эталона с 7-м свидетельствует об эмоциональной (одновременно с вегетативной) неустойчивости, контрастных проявлениях ранимости с агрессивностью, обидчивости и раздражительности. Здесь выявляется проблема подавленной агрессии, что в целом свойственно детям с психосоматической предиспозицией и вегетососудистым дисбалансом.
Сочетание предпочитаемого 1-го эталона с другими яркими цветами придает эмоциональному паттерну определенные оттенки, усложняющие его меланхолическую основу.
Сочетание 1 2 выявляет несколько «смягченные» благодаря синему цвету атрибуты зеленого цвета. Умеренно выраженный (неакцентуированный) характер этого типа содержит в себе наряду со сдержанностью, постоянством в привязанностях и глубиной переживаний оборонительные черты, стремление к точности, повышенное чувство аккуратности, практичность, склонность к систематизации опыта и накоплению негативных эмоциональных переживаний.
Сочетание 1 2 отражает потребность в самоуважении и уважении окружающих, сензитивность в отношении критических замечаний, стремление к упорному отстаиванию своих позиций социально поощряемыми или неагрессивными способами. Это же сочетание, смещенное с первых позиций ахроматическими таблицами и смешанными цветами, соответствует актуальности проблемы самоутверждения, задетого самолюбия и стремления к отстаиванию личностной позиции с оттенком уязвленности.
Если же 1 2 находятся на III—IV позициях, а первые позиции заняты яркими цветами, то такой вариант может трактоваться как сочетание стенических и гипостенических тенденций у гармонично сбалансированной личности.
Присутствие 2-го цветового эталона на первых позициях отражает смешанный тип реагирования с преобладанием пассивно-оборонительных тенденций, если он сочетается с 0-м или 1-м эталоном, и проявляется большей агрессивностью в сочетании с яркими цветами, придавая оборонительный характер позиции, при которой собственная агрессия оправдывается идущей извне угрозой и переживается личностью как вторичная, ситуативно обусловленная защитная реакция на агрессию окружающих.
Дети, постоянно выбирающие 2-й эталон на первые позиции, отличаются ригидностью установок, упорством и настойчивостью, склонностью к систематизации, способностями к точным наукам, тенденцией к опоре на накопленный опыт, повышенной чувствительностью к социальным критериям внешней оценки своей личности, отсюда — амбициозность, проблема собственного престижа, устойчивость привязанностей и интересов, чувство соперничества, соревновательность, аккуратность или даже педантизм. Подчинение для них неприятно, отсюда стремление к лидированию или, по крайней мере, к самостоятельности и социальному признанию. Этот тип реагирования значимо чаще встречается среди мальчиков.
Если 2-й эталон сочетается с 0-м, то можно говорить об усилении черт обособленности, о межличностном конфликте, трудностях общения, ощущении непонятости, неприятии окружающими, преувеличенной чувствительности к критике, субъективной уверенности в своей правоте.
Иррациональный, дезадаптирующий аспект 5-го эталона усугубляет подозрительность 2-го, и они в сочетании 5 2 или 2 5 на первых позициях выявляют тенденцию к систематизации субъективных, надуманных оценок по отношению к окружающим лицам и сложившейся ситуации.
Расположение 2-го эталона на последних позициях цветового ряда свидетельствует о фрустрированной потребности в социальном самоутверждении, ущемленном самолюбии, нереализованных притязаниях. Сочетание 2 3 или 3 2 на первых позициях усиливает характеристики 2-го эталона, тип реагирования характеризуется как более стеничный, позиция — как активно-оборонительная (2 3) или агрессивно-оборонительная (3 2) и отражает сплав свойств, присущих каждому из цветов в отдельности. Это сочетание представляется как столкновение сильных тенденций, создающих предиспозицию к взрывным реакциям.
Сочетание на первых позициях цветового выбора 2-го и 4-го эталонов является еще более конфликтным: характеристики ригидности противопоставлены эмоциональной неустойчивости; склонность к накоплению отрицательных эмоций сочетается с высокой спонтанностью, безудержностью эмоциональных реакций; тенденция к самоконтролю — с плохой контролируемостью; подозрительность — с демонстративностью; недоверчивость — с открытостью; аккуратность — с безалаберностью; оборонительная враждебность — с неразборчивой общительностью; осторожность — с беззаботностью. Если эти качества выражены умеренно, то это дает в сумме нормальную сбалансированность гармоничной личности, в которой противоречиво направленные тенденции уравновешены и разумно дозируются соответственно конкретной ситуации. Но при избыточной выраженности каждой из этих тенденций характер приобретает черты заметной неустойчивости с резкими изменениями поведенческого паттерна, вспышками чрезмерных эмоциональных переживаний, склонностью к взрывным реакциям в ситуации задетого самолюбия.
Если выбор 1-го эталона на первые позиции характерен для лиц с сензитивной акцентуацией, то выбор 2-го в аналогичной позиции свойствен ригидным в нашей классификации личностям с эпилептоидными чертами характера, особенно если 2-й эталон сочетается с 5-м или 7-м, а у ригидных интровертов — с 0-м.
3-й эталон в качестве предпочитаемого характерен для детей, у которых отмечается сильный, стенический тип реагирования, и выявляет напряженность потребности в активности, направленной на достижение цели, на овладение всем тем, что доставляет радость и наслаждение; в том числе это и высокая сексуально-эротическая вовлеченность у подростков. Выбор этого эталона на первые позиции свойствен детям с выраженной самостоятельностью, независимым, авторитарным, быстро принимающим решения. Им свойственны высокая поисковая активность, любознательность, преобладание эмоций интереса, любопытства. Высказывания и поступки могут опережать их продуманность в силу спонтанности поведения, раскованности чувств. Это — стремление к самореализации, проявляющееся напряжением аффекта, если реализация потребностей в данный момент невозможна. У дисгармоничной личности это качество выливается в импульсивность, сниженный самоконтроль, агрессивные высказывания и поступки.
Возможность безудержного поведения с компульсивной агрессией возрастает, если 3-й эталон находится на одной из последних позиций (фрустрированность насущных, жизненно важных потребностей, невозможность самореализации), а 7-й эталон при этом находится на одной из первых позиций (иррациональные и безудержные протестные реакции).
Если сочетание со 2-м и 4-м предпочитаемыми цветами по-своему дополняет характеристики 3-го цвета, выявляя смешанные варианты реагирования по ригидно-импульсивному и неустойчиво-импульсивному типу, то при сочетании 3 1 «сильные», возбудимые черты, свойственные 3-му эталону, входят в противоречивое взаимодействие с характеристиками слабого, тормозимого типа — пассивностью, сензитивностью, пессимистичностью, мягкостью, вдумчивостью, зависимостью, женственностью. Люшер выделяет этот вариант как идеально-гармоничный. Однако наш опыт показывает, что этот тип личности, хотя и выглядит внешне достаточно уравновешенным в силу выраженного самоконтроля, отличается выраженной внутренней напряженностью.
Выбор, в котором на первых позициях находятся 3-й и 0-й эталоны, свойствен нарциссическому варианту личности; при этом эгоцентризм и жажда жизни сочетаются с холодно-дистантным отношением к окружающим. Сочетание 3 7 как на первых, так и на последних позициях говорит о способности к импульсивным агрессивным поступкам. При низком интеллекте такие дети отличаются своевольным и непокладистым характером, повышенным чувством независимости, иррациональными поведенческими реакциями, стремлением выделиться, не быть подвластными общепринятым нормам, что в определенных неблагоприятных условиях может выражаться в антисоциальных тенденциях (особенно при сочетании 3 5 7, 3 7 5, 7 5 3 на первых позициях).
Выбор 4-го эталона на первую позицию свойствен детям эмотивного склада. Переживания и процесс общения сами по себе им насущно необходимы; ведущая потребность — быть вовлеченными в процесс эмоционально насыщенного межличностного взаимодействия. Активность ради активности, общение ради общения, жизнь ради жизни — таковы потребности данного типа личности. В отличие от 3-го эталона, характерного для тех, кто зажигает других своей целеустремленностью и жаждой жизни, выбор 4-го эталона на первые позиции присущ детям, которые загораются от общения с другими как спичка от прикосновения к ребру спичечного коробка.
У лиц, предпочитающих 4-й цвет, выбор профессии больше ориентирован на сам процесс деятельности, приносящий удовлетворение, чем на достигаемые этой деятельностью цели. При выраженной дезадаптации эти черты перерастают в истероидные, фобические и неврастенические проявления, то есть в те невротические расстройства, которые свойственны эмоционально неустойчивым личностям. Для детей с акцентуированным характером по данному типу характерна склонность к страхам, экзальтация чувств, неустойчивость интересов, избыточный оптимизм, непостоянство, нетерпеливость, демонстративность.
Черты демонстративности усиливаются при сочетании 5 4. Здесь они сопровождаются признаками избыточной эмотивности, сниженным самоконтролем, защитным механизмом вытеснения, иррациональным способом достижения целей в основном путем перекладывания трудностей на плечи других.
Сочетание 4 1 выявляет выраженную чувствительность к средовым воздействиям в связи с тем, что каждый цвет в отдельности по-своему связан с высокой чувствительностью к факторам внешнего влияния. В сочетании же они выявляют циклотимный тип личности со склонностью к перепадам настроения, легко провоцируемым внешними поводами, с быстрыми переходами от грусти к экзальтированной веселости, личности, тяжело переживающей одиночество, испытывающей повышенную потребность в общении, что делает ее зависимой от авторитетного для нее лица и мнения референтной группы. В сочетаниях, где 4-й эталон оказывается на одной из последних позиций, этот признак является предвестником дезадаптации.
Смешанные и ахроматические цветовые эталоны, выбираемые на первые позиции, определяют степень и индивидуальный тип дезадаптации.
5-й эталон на первой позиции статистически чаще встречается у детей и подростков с эмоциональной незрелостью, с недифференцированной полоролевой и социальной позицией. Так же он отражает богатую фантазию, творческий, нешаблонный подход к решению заданий, своеобразие интересов, высказываний и поступков. Детский период характеризуется тем, что личность еще не сформирована, отсюда слабая интеграция «Я». Трудности подросткового возраста связаны с тем, что ребенок переживает промежуточный период между детством и взрослостью. Непосредственный способ восприятия, когда каждая ситуация воспринимается как впервые переживаемая, а способность использовать накопленный опыт и готовые штампы еще не стала привычкой, отражает свойственное детям богатое воображение, которое чаще всего угасает с повзрослением. Как показывает опыт, сохранным оно остается у творческих, оригинально мыслящих личностей.
Один из часто встречающихся выборов среди акцентуированных личностей — предпочитаемый 5-й и 4-й эталоны. В этом выборе 5-й эталон отражает неустойчивость адаптации и сниженный контроль над эмоциональной сферой, что усиливает непосредственность, неустойчивость эмоций, повышенную чувствительность к средовым воздействиям, подверженность сиюминутным настроениям, нетерпеливость, склонность к вытеснению проблем, свойственные характеристикам 4-го эталона, обогащая их иррациональными тенденциями, необузданной фантазией, трудностями идентификации, усиливающими подражательные тенденции, богатым воображением, художественным складом мышления, иногда — выраженными истероидными чертами.
Предпочитаемый 6-й эталон отражает проблему тревожности с витальной (соматической) окраской, переживание чувства неуверенности и приниженности; при сочетании 6-го эталона с 3-м можно говорить о напряженности физиологических потребностей, в ряде случаев об ипохондрической фиксированности, дискомфорте общесоматического плана или неудовлетворенности гедонической личности. 6-й эталон на третьей и четвертой позиции часто означает ситуативно обусловленный дискомфорт, отражая тем самым адаптивную реакцию на изменение привычного стереотипа.
7-й эталон на первой позиции выявляет не только протест против сложившейся ситуации и негативное отношение к ней, но и агрессивность, крайний субъективизм, чувство обособленности и непокорность, активное противодействие среде. Агрессивность увеличивается и принимает компульсивный (неуправляемый) характер при сочетании 7-го эталона с 3-м на первых позициях и проявляется как затаенная агрессия, контролируемая (хотя и с трудом) при сочетании этих же эталонов на последних позициях.
Сочетание 7-го эталона с 4-м характерно для состояний, связанных с переживанием навязчивых страхов, а с 5-м выявляет иррациональную, субъективную позицию ребенка-индивидуалиста.
0-й эталон в качестве предпочитаемого может означать: временную усталость; ситуативные трудности в межличностных контактах; интровертированность как константное свойство личности, если такого рода выбор постоянно повторяется.
Часто 0-й или 7-й эталон «выскакивают» на первое место в тех случаях, когда ребенка проводимое обследование настораживает или вызывает протестную реакцию. Спокойный и доброжелательный тон психолога снимает настороженность, и тогда ахроматические цвета сразу уходят на последнюю или одну из последних позиций в цветовом ряду.
ОЦЕНКА ТРЕВОЖНОСТИ
Выбор 6 0 7 выявляет состояние выраженного стресса независимо от того, чем и у кого этот стресс вызван. Это может быть объективно сверхсложная ситуация или невротическая реакция у неустойчивой личности на жизненные трудности.
При нарушенной или затрудненной социально-психологической адаптации интенсивность показателя тревожной напряженности измеряется количеством знаков «!».
Их следует вычислять следующим образом.
Наличие в цветовом ряду 1-го, 2-го, 3-го или 4-го эталонов на VI позиции оценивается как один знак «!» (1 балл тревожности), на VII позиции — как два «!!» (2 балла), на VIII — как три «!!!» (3 балла).
К этим баллам тревожности, выраженным суммой знаков «!», вычисленных в связи с нахождением ярких цветовых эталонов на последних позициях цветового выбора, добавляются те, которые обозначают присутствие ахроматических цветовых эталонов на первых позициях: это значит, что присутствие 6-го, 7-го или 0-го эталона на III позиции оценивается как «!» (1 балл тревожности), на II позиции — «!!» (2 балла), на I позиции — «!!!» (3 балла).
Все баллы тревожности суммируются (5-й цвет не обозначается «!» ни на какой позиции). Таким образом, тревога в целом может быть оценена максимально 12 баллами. Сравнение количества знаков «!» в первом и втором выборе является прогностически важным признаком и показывает тенденцию к нарастанию тревоги, если во втором выборе знаков «!» больше, чем в первом, и, наоборот, свидетельствует о тенденции к снижению тревоги в перспективе, если количество «!» больше в первом выборе.
Чем ближе к началу ряда предпочитаемый цвет, тем больше значимость выявляемой им ведущей индивидуально-личностной тенденции, а сочетание основных цветов между собой образует мозаику характера, которая определяется их пропорциональными соотношениями, в зависимости от близости к первой позиции цветового выбора. Сочетание неразрозненных ахроматическими цветами ярких цветовых эталонов отражает хорошую работоспособность и называется собранной «рабочей группой». Это позитивный фактор, отражающий устойчивость к стрессам и преходящий характер признаков дезадаптации, если таковые обнаружены.
ПРОФОРИЕНТАЦИОННЫЕ АСПЕКТЫ ЦВЕТОВЫХ ПРЕДПОЧТЕНИЙ
Исследование с помощью цветового теста репрезентативных групп лиц, объединенных профессиональной принадлежностью, показало, что предпочтение 1-го эталона свойственно довольно широкому кругу представителей профессий, в которых требуются такие качества, как вдумчивость, сосредоточенность на содержательной, смысловой структуре информации, гуманистический характер деятельности, тяга к кабинетному стилю работы без вовлеченности в широкий круг контактов. Это, как правило, лица с преобладанием вербального стиля познавательной деятельности. При высоком интеллекте это могут быть научные деятели, теоретики, искусствоведы, словесники, литераторы. При невысоком интеллекте лица этого круга в силу ответственности и старательности успешно справляются с канцелярской работой, с выполнением деятельности, четко регламентированной определенными правилами и инструкциями, с теми видами работы, где нет необходимости принимать самостоятельные решения. Типологически эти личности отличаются сензитивностью, тревожностью, интровертированностью.
Предпочтение 2-го эталона чаще встречается у лиц с формально-логическим мышлением, опирающимся на цифровую знаковую систему, тяготеющих к точным сферам знаний. В сочетании с 1-м эталоном он формирует пару, которая отражает способности к математике, технике или физике, стремление системно оценивать информацию, опираясь при этом на конкретный опыт. Отсюда и сфера их интересов нередко лежит в области экономики, инженерно-конструкторской деятельности, связана с бухгалтерским делом, а также выявляет способности к преподаванию точных наук и к военной кадровой службе. Если специальность не насыщает ведущую потребность в кропотливой, точной работе, то люди, оказывающие стойкое предпочтение 2-му цвету, в свободное время занимаются выпиливанием, рисованием, вязанием, шитьем, конструированием и др. Разные виды ремесел, связанных с ручным, требующим точности трудом, также нередко представляют вид деятельности, к которому тянутся люди данного типа, отличающиеся чертами педантизма, интровертированности, ригидности.
3-й эталон на первых позициях встречается весьма часто в разных профессиональных группах как признак лидерства, предприимчивости, целеустремленности, склонности к риску. Большинство руководителей, администраторов, общественных активистов отличаются предпочтением 3-го цвета. Кроме того, такой выбор часто встречается среди летчиков, шоферов, танцоров, артистов. В сочетании с 5-м цветом он особенно подчеркивает наступательную позицию и творческую независимость личности, высокую поисковую активность, спонтанность и неконформность поступков и суждений, импульсивность и повышенную интуицию, нередко подменяющую опору на опыт.
Предпочтение 4-го эталона встречается у людей, профессия которых так или иначе связана с широкими контактами, вовлеченностью в разные сферы общения. В любом деле сам процесс деятельности, субъективно нравящийся, значит для индивида гораздо больше, чем та цель, к которой эта деятельность ведет. К тому же явное предпочтение оказывается тем видам работы, в которых меньше формальностей и больше простора для свободного выбора действий. Это — люди с преобладанием художественного склада ума и образного восприятия. Сочетание 4-го эталона с 5-м часто встречается среди артистов, учителей и лиц, увлекающихся общественно-благотворительной деятельностью; типологически эти личности относятся к эмоционально-лабильным, впечатлительным, тревожным и в то же время оптимистичным, с чертами демонстративности.
5-й эталон, за исключением детей и подростков, предпочитаем лицами с оригинальным, нестандартным мышлением и своеобразием интересов. Дети и подростки, выбирая 5-й цвет, демонстрируют тем самым и эмоциональную незрелость, и отсутствие стереотипов мышления, что создает определенные предпосылки для дальнейшего развития творческого, самобытного начала в структуре личности, реализация которого в значительной степени зависит от процесса воспитания и бережного подхода к индивидуальности ребенка. Выбор профессии у лиц, предпочитающих 5-й цвет, нередко связан с сублимацией нереализованных потребностей (педагогика, искусство) и со своеобразием иерархии ценностей (психология, философия, психиатрия, нетрадиционные методы врачевания, астрология).
Предпочтение ахроматических и смешанных цветов свидетельствует о затрудненной адаптации.
Что же касается когнитивного стиля, то он определяется предпочтением ярких эталонов.
Предпочтение 1-го эталона выявляет преобладание вербального типа мышления, аналитического стиля познавательной деятельности; предпочтение 2-го эталона означает наличие системного, формально-логического, конкретного, опирающегося на язык цифр и других символов склада ума; предпочтение 3-го говорит об интуитивном, целостном, опережающем опыт эвристическом когнитивном стиле; предпочтение 4-го — о наглядно-образном, художественном типе восприятия.
В норме наличие всех ярких цветовых эталонов свидетельствует о сочетании разных типов мышления, но цвет, находящийся на первой позиции, как правило, выявляет преобладающий когнитивный стиль.
Это означает, что следует развивать все варианты познавательной деятельности, но при выборе любимого предмета и будущей профессии ребенок тянется (не всегда осознанно) к тому виду активности, который органично связан с его ведущей индивидуально-типологической тенденцией и с производным от нее преобладающим стилем когнитивной деятельности. Это должен учитывать и педагог для выработки дифференцированных мер обучения, и школьный психолог, принимающий участие как в формировании индивидуализированного образовательного процесса, так и в оказании помощи ученикам при выборе будущей профессии.
Стандартизированный многофакторный метод
Стандартизированный многофакторный метод исследования личности СМИЛ (модифицированный тест MMPI)
Вводные замечания
Методику СМИЛ по ее значимости и эффективности по праву можно назвать «тяжелой артиллерией» психодиагностики. И не потому, что некоторые специалисты, мало знакомые с методикой, считают ее громоздкой и трудоемкой: на самом деле это — около часа работы самого обследуемого (при этом психолог может даже не присутствовать) и 10 минут на обсчет данных. Главное, что после этого психолог получает многосторонний портрет человека, включающий помимо количественных и качественных характеристик устойчивых профессионально важных свойств богатый спектр таких структурных компонентов личности как мотивационная направленность, самооценка, стиль межличностного поведения, полоролевой статус, черты характера, тип реагирования на стресс, защитные механизмы, когнитивный стиль, ведущие потребности, фон настроения, сексуальная ориентация, степень адаптированности индивида и возможный тип дезадаптации, наличие психических отклонений, выраженность лидерских черт, склонность к суициду, предрасположенность к алкоголизму и пр. При этом большим преимуществом данной методики является наличие в ее структуре шкал достоверности, позволяющих определить не только надежность результатов, но и установку испытуемого на саму процедуру обследования. Это дает возможность интерпретации полученных данных через призму выявленных с помощью шкал достоверности тенденций к преувеличиванию имеющихся проблем или к их сглаживанию.
Стандартизированный многофакторный метод исследования личности СМИЛ представляет собой модификацию теста MMPI, созданного в 1942-49 гг. в целях профессионального отбора летчиков во время Второй мировой войны. Авторы — американские психологи И.Маккинли и С.Хатэуэй. Это — квантифицированный (количественный) метод оценки личности, который, благодаря автоматизированному способу обработки результатов обследования, исключает зависимость получаемых результатов от субъективности и опыта экспериментатора. Высокая надежность методики, наличие шкал достоверности и полифакторный характер интерпретации создали базу для широкой популярности этой методики в разных странах мира.
В основу создания опросника теста было положено количественное сопоставление ответов, полученных в психологическом интервью с представителями нормативной группы, с типичными ответами больных, у которых в картине клинических расстройств четко преобладал тот или иной синдром: ипохондрия, депрессия, истерия, психопатия, психастения, паранойя, шизофрения, гипомания. Эти названия и были приданы соответствующим шкалам, измеряемым методикой. Такой принцип построения психологических методик применялся многими психологами, которые представляли себе личностные особенности нормы как «разбавленную» патологию. Известный отечественный психолог Б.В.Зейгарник оправдывала такой подход, утверждая, что патологическое состояние суть заостренная модель нормы. Все то, что у психически здорового человека уравновешено и сглажено, у больного проявляется в виде гротеска — резко и обнаженно. Разработанный американскими психологами тест MMPI в Америке до сих пор в основном применяется как дифференциально-диагностический метод. Усовершенствованный вариант MMPI — тест СМИЛ , в первую очередь нацелен на изучение личности, так как многолетний опыт применения методики показал, что она в большей мере раскрывает канву психологически понятных переживаний и свойства личности, чем диагностирует психопатологию.
Многолетний опыт изучения личностных свойств в разных профессиональных группах показал, что данные методики СМИЛ могут оказать значительную помощь при выявлении устойчивых профессионально важных личностных свойств. Кроме того, методика уже получила большое распространение среди социологов, врачей и психологов, занимающихся семейным консультированием, суицидологией, психотерапией, алкоголизмом, психосоматикой, изучением кадровых резервов, проблемой менеджмента, а также в спортивной психологии, в судебной экспертизе, в юриспруденции, в Армии, в военной и гражданской авиации, в системе МВД, в центрах занятости населения, в школах, гимназиях, колледжах и в области высшего образования.
В работе практического психолога данные СМИЛ позволяют понять причины некоторых поворотов в судьбе конкретного человека , напрямую связанных с его индивидуально-личностными особенностями, характером, стилем общения с окружающими, с его способностью к самореализации.
В связи с реадаптацией методики и расширением сферы ее применения, автором модифицированного варианта большинству базисных шкал метрдики приданы новые названия, соответствующие их психологической сущности, соответственно: 1-я шкала — шкала «невротического сверхконтроля», 2-я -«пессимистичности», 3-я -«эмоциональной лабильности», 4-я -«импульсивности», 6-я -«ригидности», 7-я — «тревожности», 8-я — «индивидуа-листичности», 9-я — «оптимизма и активности». Не изменились названия двух шкал: 5-й -«шкала женственности-мужественности» и 0-й -«шкала социальной интроверсии’. Что касается почти двухсот дополнительных шкал, не входящих в построение личностного профиля, то после рестандартизации названия их не менялись. Эти шкалы по сравнению с профилем базисных шкал намного проще интерпретируются, в основном их суть отражает само название каждой шкалы. Они разрабатывались разными авторами в связи с разными прикладными проблемами и могут использоваться в дополнение к шкалам основного профиля. Что касается базисных шкал, то они формируют целостный личностный профиль, отражающий портрет личности во всей его сложности и разнообразии. Каждая же дополнительная шкала лишь добавляет к этому портрету какое-либо определенное качество, которое, преломляясь через личностный образ, может приобретать то или иное звучание.
Профиль СМИЛ — это та ломаная линия, которая соединяет между собой количественные показатели 10-ти базисных шкал К нему примыкает маленький профиль шкал достоверности: шкала»?» показывает, сколько утверждений опросника попали в категорию ответов «не знаю». Шкала «L» — шкала «Лжи» — показывает, насколько искренним был обследуемый в процессе тестирования. Шкала «F» — шкала «достоверности» — показывает уровень надежности полученных данных в зависимости от его откровенности и готовности к сотрудничеству. Шкала «К» — шкала «коррекции» выявляет степень искажения профиля под влиянием закрытости испытуемого. В зависимости от показателей этих шкал профиль признается как достоверный или недостоверный, а его особенности рассматриваются через призму установок испытуемого по отношению к процедуре обследования.
Методика предъявляется испытуемому в виде книжечки-буклета, содержащей 566 утверждений (сокращенный вариант, позволяющий получить личностный профиль, но уже без дополнительных шкал, содержит 360 утверждений). Почему в опроснике приводятся не вопросы, а утверждения? Потому, что человек более искренно отвечает на интересующие психолога вопросы, если они звучат в форме утверждения. В такой ситуации человек чувствует себя анализирующим свое «Я» как бы наедине с самим собой и это способствует большей откровенности, нежели вопросительная форма, звучащая как допрос
Утверждения носят разный характер, в зависимости от того, какая сфера человеческих проблем ими освещается. Большинство из них направлено на выявление черт характера, на стиль общения с окружающими, и отражает субъективные пристрастия и вкусы обследуемого человека, его взгляды на разные жизненные ценности, особенности эмоциональных реакций, оценку собственного самочувствия и ряда физиологических функций, фон настроения и пр. Важна не сама сентенция утверждения. Это — всего лишь стандартный набор моделируемых экспериментом ситуаций, на которые разные люди по-разному реагируют. Важна сама избирательность ответов, обрисовывающая в конечном итоге индивидуально-личностные свойства конкретного человека. Анализ результатов основан не на изучении смысла ответов испытуемого, а на статистической процедуре обсчета данных, в процессе которой выявляется количественная дисперсия разных вариантов ответов по отношению, с одной стороны, к средненормативной усредненности, а с другой, к патологической заостренности психологического фактора, содержащего в себе по сути дела ту или иную индивидуально-личностную тенденцию. Большинство утверждений звучит так, что испытуемый, отвечая, далеко не всегда представляет, каким образом это его охарактеризует, что значительно затрудняет стремление «улучшить» или «ухудшить» результаты обследования. На первый взгляд, методика позволяет обрисовать субъективную внутреннюю картину «Я» обследуемого лица. Реально же, благодаря отчасти проективному звучанию многих утверждений, в эксперименте выявляются и те психологические аспекты, которые не осознаются человеком или лишь частично поддаются контролю сознания. Поэтому лишь при статистически недостоверных данных профиль личности искажается настолько, что его нет смысла интерпретировать. В рамках же достоверных данных даже при наличии тенденций, влияющих на усиление или сглаживание рисунка профиля, интерпретация отражает истинную картину личности. При этом возможна весьма дифференцированная градация степени выраженности разных личностных свойств в их сложном сочетании, когда принимаются во внимание не только высокие показатели, но и их соотношение с низкими показателями. В то же время отклонение от средненормативных показателей, более чем вдвое превышающее среднеквадратичную ошибку, выявляет избыточную степень выраженности той или иной личностной черты, выводя ее за пределы достаточно широкого (от 30 до 70 стандартных баллов Т) коридора нормативного разброса. Такие данные не обязательно свидетельствуют о патологии. Состояние стресса, объективно сложная ситуация, физическое недомогание — все это может вызвать состояние временной дезадаптации. Поэтому интерпретация полученных данных должна вестись в соответствии со всей имеющейся об испытуемом информации, не говоря уже о том, что для адекватного представления об испытуемом не мешает взглянуть на него самого. «Слепая» интерпретация может использоваться лишь в исследовательских целях, когда проверяется надежность методики, а также при крупномасштабных обследованиях, когда интерпретируется не личность отдельного человека, а некоторые обобщенные тенденции больших по численности групп.
В модифицированном варианте из опросника выделены 26 утверждений, которые оказались балластными: они не только вводили в заблуждение и шокировали обследуемых, но и провоцировали неадекватные ответы В основном — это утверждения, «работающие» на шкалу достоверности «F» и 8-ю — шкалу «шизофрении». Так, утверждение «Я часто вижу людей, животных и другие предметы, которых не видят другие окружающие меня люди» провоцировало ответ «верно» у тех, кто по роду деятельности (например, спортсмены) много ездят по разным странам, в то время как утверждение нацелено на выявление нарушений восприятия.
Опросники в модифицированном виде делятся на мужской, женский и подростковый варианты, отличие которых отражается лишь в форме изложения некоторых утверждений. Ключи, с помощью которых подсчитываются сырые баллы по каждой шкале, коррекция сырых показателей для формирования профиля личности в стандартных показателях Т, а также интерпретационная схема абсолютно идентичны для всех форм опросника, кроме некоторой разницы в обработке данных по 5-ой шкале в мужском и женском профиле . Имеются также полный (566) и сокращенный (360) опросники, разница между которыми помимо объема лишь в том, что сокращенный вариант не позволяет получить показатели по дополнительным шкалам теста.
Профильные листы взрослой и подростковой версии имеют различия лишь в зависимости от пола испытуемого в стандартах по ряду базисных и по большинству дополнительных шкал. Поэтому очень важно, чтобы перед началом работы специалист убедился в том. что у него и сам опросник, и ключи, и профильные листы, и, наконец, интерпретационный подход, принадлежат одному автору. Отличаются как от оригинала (MMPI), так и от СМИЛ разработанный в ВНИИ неврологии и психиатрии им. Бехтерева Стандартизованный клинический опросник СКЛО и адаптированный Ф.Б.Березиным и М.П.Мирошниковым ММИЛ. Несравним по всем параметрам с методикой СМИЛ опросник на 71 утверждение, клинически ориентированный Мини-мульт, разработанный шведской психологессой Кинканнон и адаптированный в русском варианте В.П.Зайцевым и В.Н.Козюлей.
Как показывает опыт, методика в основном рассчитана на обследование контингента взрослых лиц (от 16 до 80 лет) с законченным начальным образованием (7-8 классов средней школы) с сохранным интеллектом. В связи с тем, что автором книги совместно с педагогами Б.Н.Кодесс и Т.В.Кодесс в 1984 г. был разработан и адаптирован подростковый вариант СМИЛ, границы применения методики несколько расширились Если обычный взрослый вариант широко и эффективно уже много лет используется в практике профконсультирования при обследовании старшеклассников в возрасте 16-17 лет, то подростковый вариант последние годы успешно применяется при изучении детей несколько более младшего возраста, начиная с 12 лет (при условии хорошего общего развития). Отмечено, что недостоверные результаты часто находятся в прямой зависимости не столько от искаженной установки испытуемого на обследование, сколько от плохого понимания содержания утверждений, что может быть связано, во-первых, с недостаточно развитым вербальным интеллектом, во-вторых, с плохим знанием русского языка Поэтому в регионах, где люди говорят на другом языке, методика должна быть переведена на родной язык, но при этом необходимо также провести рестандартизацию количественной базы методики, так как нормативные стандарты могут иметь свои региональные отличия
Процедура обследования требует соблюдения следующих условий: испытуемый не должен испытывать настороженности в отношении целей исследования; он может претендовать на определенную информацию о результатах тестирования; психолог-экспериментатор или консультант обязан в первую очередь соблюдать интересы обследуемого человека и никогда не интерпретировать данные обследования ему во вред, так как роль психолога в обществе в основном сводится к защите человека во всех смыслах этого слова. Если это правило будет нарушено, люди потеряют доверие к психологу и дальнейшие психологические исследования станут невозможными. Отсюда вытекает и остальное: интерпретация полученных данных должна вестись с позиций психотерапевтического, щадящего подхода. Каждое индивидуально-личностное свойство как правило несет в себе и положительную, и отрицательную информацию. Поэтому, всегда есть возможность начать собеседование с освещения позитивных характеристик, а затем на этом фоне выделить те особенности и свойства личности, которые создают определенные сложности и негативно влияют на судьбу человека. Но делать это следует осторожно и именно в том стиле, который является для данного индивида оптимальным (см. коррекционный подход по каждой из повышенных в профиле шкал).
Л. Н. Собчик
Кодирование профиля
Помимо графического изображения профиля в повседневной практической работе и при изложении материала в публикациях профили удобно описывать в закодированном виде, что требует знания правил кодирования. Наиболее точно отражающим особенности профиля является метод кодирования по Уэлшу. При этом все базисные шкалы записываются соответственно их порядковому номеру в такой последовательности, чтобы на первом месте находилась наиболее высокая шкала, затем — остальные по мере их снижения. Чтобы показать их место на графике в соответствии со шкалой Т-баллов, необходимо поставить следующие знаки:
отделить номера шкал, находящихся на уровне 120 Т и выше знаком » !! «,
-шкалы, идущие вслед за ними, но расположенные выше 110 Т отделить от остальных знаком » ! «,
-шкалы, расположенные в профиле выше 100 Т — знаком » ** «,
-выше 90 Т — » * «,
-выше 80 Т — » » «,
-выше 70 Т — » ‘ «,
-выше 60 Т — » — «,
-выше 50 Т — » / «,
-выше 40 Т — » : «,
-выше 30 Т — знаком » # «.
Тот же принцип обозначений для шкал достоверности. К примеру, закодированный таким образом профиль 2*34″ 187’0 — 6/5:9 FК/1 — означает, что ведущий пик по 2-й шкале расположен выше 90 T, 3-я и 4-я шкалы расположены выше 80 Т и находятся на одном уровне (об этом говорит черта под обозначениями этих шкал в коде), 1-я, 8-я и 7-я шкалы расположены выше 70 Т, из них 1-я — наиболее высоко расположенная, затем соответственно по степени снижения идут 8-я и 7-я; 0-я шкала — выше 60 Т, 6-я выше 50 Т, 5-я — выше 40 Т, 9-я — выше 30 Т, F выше К и L и расположена выше 60 Т /но до 70 Т/, К выше 50 Т, а I — ниже 50 Т, но выше 40 Т.
Намного лаконичнее и проще способ кодирования по Хатэуэю. Шкалы, находящиеся в зоне 46-54Т не записываются вовсе; шкалы, расположенные выше 70 Т отделяются апострофом «‘», за ними приводятся шкалы, находящиеся на 55 Т и выше; вместо шкал, находящихся в зоне 46 — 54 ставится прочерк, затем после знака «/» записываются шкалы, расположенные ниже 46; показатели шкал достоверности приводятся в сырых баллах последовательно, соответственно L:F:К через двоеточие, при этом ставится знак «X» перед рядом шкал достоверности, если хотя бы по одной из них профиль недостоверен. Описанный выше профиль при кодировании по Хатэуэю выглядит следующим образом:
234187’0-/59 Х5:17:13
Кодирование удобно для более краткого описания профиля, а также для более четкого и быстрого разбиения материала на типологически или клинически сходные группы. Кодирование способствует выявлению в изучаемой группе наиболее общих характеристик и закономерностей.
Интерпретация
Целостная оценка профиля
Зная личностные особенности и характеристики состояний, которые определяются отдельными шкалами, а также учитывая их влияние друг на друга можно перейти к целостной оценке профиля. В первую очередь профиль должен рассматриваться через призму установки обследуемого на процедуру тестирования которая выявляется соотношением шкал достоверности и высотой их показателей.
Должны настораживать сглаженные профили, в которых контрастирующие по их содержательной стороне шкалы оказываются почти на одинаковом уровне, а показатели шкалы К или L достаточно высоки. При высоком F высота профиля может быть связана с разными причинами, приведенными ранее однако в любом случае профиль будет заострен и завышен, что необходимо принимать во внимание при интерпретации.
При повышении в пределах нормативного разброса 1-й и 3-й шкал с относительно низкой 2-й и без значимого повышения профиля по другим шкалам следует обратить внимание на показатели L и К. Если они повышены (выше 60 Т. или более чем на 7 Т выше шкалы F), то скорее всего речь идет о тенденции испытуемого «показать себя в лучшем свете», о стремлении к отрицанию каких-либо трудностей и проблем, об установке на улучшение результатов, о попытке дать «сверхнормальные» ответы и подчеркнуть свое дружелюбие, конформность, альтруизм, в то время как на самом деле это может быть лишь фасадом, за которым скрываются различные проблемы и иной характер У таких испытуемых иногда и по шкале «?» может оказаться достаточно высокий показатель. Интерпретация такого профиля сводиться к констатации наличия установки на соответствие нормативности, профиль (особенно если он по четырем — пяти шкалам утоплен) расценивается как «гипернормальный». Обследование стоит повторить.
В достоверном профиле интерпретация проводится согласно общим правилам, при этом характеристика 3-й шкалы поглощает свойства 1-й. так как эмоциональная яркость ее признаков нивелирует сдержанность, отражаемую 1-й шкалой. Лишь преобладание 1-й над 3-й на 5 Т и более дает основание ориентироваться на интерпретацию 1-й шкалы.
Сочетание 1-й с повышенными (или высокими) 2-й, 6-й. 7-й, 8-й и 0-й при низкой 9-й отражает проблему подавленной враждебности и характерно для так называемого «язвенного типа личности» отличающегося педантизмом, догматическим стилем мышления, повышенной раздражительностью, дистантностью, требовательностью как к себе, так и к другим в вопросах морали, долга, ответственности. При высокой исполнительности, принципиальности и честности в работе, они проявляют мелочный деспотизм в контактах узкого круга, скрытны, неловки и скованы в общении, тон высказываний назидательный, внешняя жесткость сочетается с внутренне ощущаемым напряжением и ранимостью по отношению к средовым воздействиям.
Высокие показатели 2-й шкалы, сочетающиеся со значительным повышением 1-й и 3-й, которые находятся в соподчиненной по отношению к 2-й шкале позиции, а также повышенными 7-й и 8-й при пониженной 9-й, свидетельствуют о выраженном эмоциональном дискомфорте, трудностях адаптации хронического характера и чаще всего бывают связаны с невротическим развитием. Внешне поведение таких людей не бросается в глаза как отклоняющееся от нормы, но внутренняя дисгармония сказывается в постоянно ощущаемом индивидом напряжении, сниженном настроении с неуверенностью в себе, чувством несчастливости, заниженной самооценкой, преобладанием мотивации избегания неуспеха, низкой мотивацией достижения. 5-я шкала по-разному влияет на тип реагирования в мужских и женских профилях, а 8-я приобретает разные значения в зависимости от остальных показателей профиля.
Успешность социальной адаптации — это хорошо сбалансированное соотношение между эгоцентрическими потребностями человека и требованиями социальной среды. Абсолютно уравновешенная, гармоничная личность отличается полной сбалансированностью умеренно выраженной тенденции к самореализации с хорошим самоконтролем, обеспечивающим полное соблюдение нормативных требований среды. Чем больше выражен характер и индивидуальность человека, тем большая нагрузка выпадает на функцию контролирующих систем, сохраняющих баланс. Это — основное отличие между конкордантной и дискордантной личностью: у последней внешние атрибуты нормативного поведения скрывают внутреннюю напряженность.
Цена, которую «платит» личность за соответствие требованиям социума, может быть достаточно высокой.
Если «Я» индивида разрушается давлением социума и не происходит самореализация личности (не удовлетворяются потребности, не реализуются способности), то происходит невротизация, отражающаяся в профиле преобладанием гипотимных, тормозимых черт. Если же баланс нарушается в связи с ослабленным самоконтролем в сторону спонтанной самореализации, то столкновение интересов самоутверждающейся личности с требованиями социума находит свое отражение в поведенческих реакциях, проявляющихся в профиле преобладанием гипертимных признаков. Цена этого дисбаланса в основном оплачивается трудностями социума. Если и тот и другой механизмы удержания баланса задействованы одновременно, то мы наблюдаем реализацию психосоматического механизма, проявляющегося физическими расстройствами разного рода.
Для удобства целостной интерпретации профиля шкалы методики следует сгруппировать таким образом, чтобы по ведущим пикам можно было определить сперва обобщенно основной тип реагирования, а затем уже на основании значений шкал выявлять индивидуально-личностные особенности и уровень адаптированности обследуемого. 2-я, 7-я и 0-я шкалы отражают свойства гипостенического типа реагирования и свидетельствуют о преобладании тормозимых черт характера. Если в профиле эти шкалы значимо превалируют над другими, то выявляется конформность, социальная податливость, нормативность личности, отказ от самореализации. В любом профиле, отражающем реакцию личности на психотравмирующую ситуацию, конфигурация с ведущими шкалами гипостенического регистра выявляет невротический вариант дезадаптации или декомпенсацию личности в сторону усиления тормозимых реакций. 4-я, 6-я и 9-я шкалы формируют стенический тип реагирования и позволяют описывать личность в характеристиках активности, силы, преобладания возбудимых черт. Умеренное повышение этих шкал в профиле свидетельствует о выраженной тенденции к самореализации и о противодействии средовому влиянию. Если высота профиля говорит о нарушении адаптации, то вариант дезадаптации, соответствующий данному типу реагирования, проявляется поведенческими реакциями асоциальной или антисоциальной направленности. Это может быть конфликтное поведение, неконформность, авторитарность и стремление к доминированию, повышенное чувство независимости и отталкивание от навязываемых авторитетов (в том числе проблемы пубертатного периода). Высокие показатели гиперстенического профиля могут также отражать проблему алкоголизации, наркомании, делинквентного поведения.
Сочетание разнонаправленных тенденций, т.е. показателей как гипотак и гиперстенических свойств, выявляет смешанный тип реагирования, при котором высокая потребность самореализации сочетается со столь же высоким самоконтролем и тенденцией к оттормаживанию, сдерживанию поведенческих реакций. В этом случае оказываются перекрытыми каналы как невротического, так и поведенческого отреагирования, что сказывается на общем перенапряжении и проявляется соматизацией внутреннего конфликта, т.е. психосоматическим вариантом дезадаптации, мишенью которого окажется наиболее слабое звено той или иной функциональной системы организма человека.
Показатели 1-й и 3-й шкал уже несут в себе характеристики смешанного типа реагирования, независимо от остальной структуры профиля, так как отражают проблему подавленной враждебности. Их присутствие в профиле как правило выявляет смешанный тип реагирования, а другие показатели профиля — лишь дополнительная информация. Определив надежность полученных данных и тот ракурс, который позволяет через призму выявленных у испытуемого установок рассматривать сам профиль, после того, как выявлен общий тип реагирования, следует обратить внимание на степень адаптированности личности. Утопленный профиль может быть результатом неискренности ответов (об этом скажут шкалы достоверности), но может также свидетельствовать об определенной гипоэмотивности испытуемого, о вялости его реакций, о сниженном уровне мотивации достижения, о суженном диапазоне интересов.
Нормальная, гармоничная личность может проявляться показателями линейного профиля, в котором все свойства уравновешены и ни одно из них не выражено более ярко, чем остальные. Но уравновешенность может проявляться и сбалансированностью разнонаправленных тенденций при повышенных показателях, что создает почву для определенной напряженности внутренне противоречивого личностного паттерна; однако внешне усилия, ценою которых личность достигает самокомпенсации, могут быть незаметны или проявляться крайне редко Поэтому в профиле который находится на верхней границе нормы или слегка его превышает, выявляется пограничное между нормой и патологией состояние — будь это повседневные трудности акцентуированной личности или заострение личностных особенностей в объективно сложной ситуации.
Понимание стоящих за этими показателями проблем должно опираться на соотношение шкал, выявляющих гипостенический, стенический или смешанный тип реагирования, на характеристики разных шкал и их взаимное влияние друг на друга, усиливающее или ослабляющее стоящие за ними тенденции. В высоко расположенном профиле при интерпретации нас интересуют в первую очередь пики, выносящие контур профиля за пределы нормы. Они определяют состояние испытуемого и показывают уровень личностной дезинтеграции, выявляя структуру ведущего синдрома, степень выраженности эмоционального напряжения, аффективной насыщенности переживаний обследуемого Чем более выражены пики и чем меньше сопутствующие подъемы шкал, отражающих противоположные данному пику тенденции, тем больше оснований говорить об устоявшейся структуре отношения испытуемого к сложившейся ситуации, о хронически протекающей психической дезадаптации, а также о дефиците компенсаторных ресурсов личности. Напротив плавающий профиль, в котором большинство шкал расположено выше верхней границы нормы, свидетельствует о состоянии общего стресса в котором задействованы различные защитные механизмы и напряжены множественные компенсаторные функции психической деятельности. направленные на нивелировку дезадаптации И хотя при этом психическая напряженность увеличивается, прогностически такой профиль более перспективен в плане нормализации состояния, особенно если речь идет о психогенных пограничных расстройствах.
Немножко разнообразия, я описана не таким сахарным ангелком, как раньше. — @дневники: асоциальная сеть
psytests.org/result?v=szn1FpOMCypnEy8p8u5Интерпретация даётся в двух формах: психоаналитической (краткие значения векторов влечений по учебнику Сонди) и индивидуально-личностной (сводные характеристики личности на основе ярко выраженных факторов по методу портретных выборов). Надо помнить, что полноценная интерпретация результатов теста Сонди во всей их взаимосвязи и в сопоставлении с результатами других методик и наблюдений – задача для опытного психолога-психоаналитика. Онлайн-тестирование даёт поверхностный результат и является скорее демонстрацией возможностей методики, чем диагностическим инструментом.
Психоаналитическая интерпретация
Вектор S: сексуальное влечение
Любовь к конкретному человеку с пассивной готовностью ему отдаться. У мужчин – инверсия цели. Доминирование мазохизма.
Вектор P: пароксизмальное / этико-моральное влечение
Грубые аффекты подавлены моральным скептиком.
Вектор Sch: «Я»-влечение (характерологические черты)
Экстраверсия. Позитивизм, рационализм, сухость. Холодность, жестокость, строгость. Стремление к знаниям ради увеличения способности обладать. Излишнее стремление к формализму, логике, аккуратности и порядку. Бесчувственность, холодность чувств. Эгоизм. Корыстолюбие, жадность. Своенравие и упрямство. Самоизоляция, стремление к уединению.
Вектор C: влечение к контакту
Бесконтактность в отношениях с миром. Избалованное дитя. Дезинтеграция влечения к контактам.
Индивидуально-личностная интерпретация
Не следует ни удивляться, ни пугаться, если в целостном портрете личности обнаруживаются кажущиеся противоречия: человек соткан из противоречий. Сбалансированная, гармоничная личность уравновешивается именно за счет этого противопоставления умеренно выраженных разнонаправленных свойств, в то время как акцентуация характера проявляется перевесом какой-либо заостренной черты.
1. Биологические предпосылки
(s− Слабый тип высшей нервной деятельности.
(e− Ригидный тип высшей нервной деятельности.
(k+) Смешанный, ригидный, левополушарный тип высшей нервной деятельности.
2. Конституциональный тип
(s− Лептосомная (астеническая) конституция, гипостенический, гипотимный тип реагирования.
(e− Атлетический, агрессивный, смешанный тип реагирования, эксплозивный.
(k+) Лептосомный (астенический), шизоидный ригидный тип реагирования.
3. Характерологические особенности
(s− Нерешительность, мягкость, зависимость, склонность к идеализации объекта привязанности, конформность, сочувствие к людям, тенденция к самоограничению ради близких, склонность к глубокой привязанности при слабо выраженной сексуальной озабоченности, миротворческие тенденции. Приоритет культурных ценностей.
(e− Тенденция к накоплению негативных эмоций с последующей разрядкой в виде приступов ярости, злопамятность, мстительность, завистливость, ревность, представление об окружающем мире как враждебно настроенном, чем оправдывается собственная жестокость.
(k+) Рассудочность, эмоциональная холодность, эгоистическая сосредоточенность на внутреннем мире собственных переживаний, оторванность от практических забот, склонность к широким обобщениям, оригинальность и независимость суждений, своеобразие поступков, формальность и избирательность в общении, педантичность, недоверчивость, скрытность, замкнутость.
4. Личностные свойства
(s− Высокий уровень мотивации избегания неуспеха. Стиль межличностного поведения зависимый, пассивный. Тип восприятия вербально-аналитический. В стрессе – ограничительное поведение, повышение контроля сознания. Защитный механизм – отказ от самореализации.
(e− Устойчивость мотивации достижения, упорство в преследовании своих целей, внешнеобвиняющий тип реагирования, конфликтность в межличностных отношениях, стиль мышления конкретно-логический, тип реакции на стресс – агрессивный, взрывной; защитный механизм – враждебные поведенческие реакции или рациональная переработка.
(k+) Созерцательная позиция, субъективная мотивация, раздвоенное «Я», интеллект довлеет над эмоциями, стиль межличностного поведения – интровертный, стиль мышления – формально-логический. В стрессе блокировка или непредсказуемые действия, защитная реакция – бегство в мир фантазии.
5. Выбор профессии
(s− Медицинский работник, врач, медсестра, парикмахер, маникюрша, воспитатель, библиотекарь, канцелярский или архивный работник, делопроизводитель, научный работник, филолог, искусствовед.
(e− Моряк, шофер, летчик, машинист, пожарник, артиллерист, кузнец, кочегар, пиротехник, спортсмен (боксер, штангист, вольная борьба, карате, самбо), администратор, начальник домоуправления, ЖЭКа или РЭО, заведующий гаражом.
(k+) Математик, бухгалтер, солдат, печатник, фермер, инженер, механик, лаборант, экономист, счетовод, прикладное творчество, поделка по дереву, скульптор, плотник, физик-теоретик, литературный критик.
6. Социальная активность
(s− В сфере культуры и гуманистической деятельности.
(e− Противопоставление своих установок этико-моральным устоям.
(k+) Деятельность носит оторванный от повседневных нужд характер и связана с экономикой, математикой, физикой.
7. Болезненная деформация влечения
(s− Мазохизм, фетишизм, самоуничижение, суицидальные тенденции.
(e− Эпилептоидный педантизм и эксплозивность.
(k+) Болезненно заостренные черты трансформируются в шизоидные проявления, кататонические симптомы, аутичность, а отклоняющееся поведение – в бродяжничество, социальную дезадаптацию.
Статистика | Бесплатный полнотекстовый | Многомерная модель смешанного отклика с попарным методом составного правдоподобия
1. Введение
Клинические исследования, такие как исследования токсичности и лабораторные исследования, могут предоставить важную информацию для измерения воздействия различных методов лечения или экспериментов на пациентов. Этот тип исследования требует совместного анализа различных экспериментальных результатов, в то время как результаты исследований, собранные во время лечения, коррелируют и смешивают как с категориальными, так и с непрерывными переменными.Например, мы изучаем эффективность лечения наряду с токсичностью и побочными реакциями на лекарства одновременно. В этом случае степень тяжести может быть измерена как дискретные или порядковые данные, в то время как результаты клинического обследования, такие как измерения крови, являются непрерывными. При традиционном подходе эти множественные исходы анализируются с помощью различных линейных моделей для оценки эффектов лечения вместе с соответствующей клинической и демографической информацией. Однако этот подход игнорирует корреляцию между результатами и дает лишь маргинальные выводы.Таким образом, желательно разработать многомерный подход, который может совместно моделировать множественные реакции смешанного типа с лечебными и клиническими ковариатами.
В недавней литературе есть два основных подхода к построению совместной модели для переменных со смешанным ответом. Модель условного гауссова распределения (CGDM) может разложить совместное распределение переменных смешанного отклика на комбинацию условного распределения и маржинального распределения. В двумерном смешанном случае модель условного гауссовского распределения может производить условное распределение категориальных переменных с учетом непрерывных переменных и маргинального распределения для непрерывных переменных.В частности, Кокс [1] представил логистическое условное распределение для бинарных переменных, а Кокс и Вермут [2] расширили модель с помощью функции пробит-типа и показали потенциальную связь с моделью скрытых переменных. Другая модель условного гауссовского распределения, называемая общей моделью расположения (GLOM), была предложена Олкиным и Тейтом [3]. Они приняли противоположную факторизацию, которая состоит из условного нормального распределения с учетом категориальных переменных и маргинального полиномиального распределения.Teixeira-Pinto и Normand [4] сравнили этот подход с моделями, предложенными Sammel et al. [5,6] во всестороннем обзоре. Ян и др. [7] расширили модель до смешанных переменных Пуассона и непрерывного отклика с помощью подхода, основанного на правдоподобии. Сгруппированная непрерывная модель (GCM), предложенная Андерсоном и Пембертоном [8] и де Леоном [9], обеспечивает другое решение этой проблемы. Фундаментальный метод позволяет рассматривать категориальные переменные как разделенные непрерывные скрытые переменные с различными неперекрывающимися интервалами (Пун и Ли [10]; Скрондал и Рабе-Хескет [11]).Этот тип преобразования позволяет скрытым переменным следовать многомерному распределению Гаусса. Пун и Ли [10] продемонстрировали оценку максимального правдоподобия для скрытых переменных с полихорическими корреляциями. В качестве расширения сгруппированной непрерывной модели де Леон [9] предложил условную сгруппированную непрерывную модель (CGCM) для построения совместной модели для переменных, смешанных с категориальными и непрерывными результатами. Каталано и Райан [12], Каталано [13] и Наджита и др. [14] применили условную сгруппированную непрерывную модель к исследованиям токсичности плода для получения продольных данных.Георгиева и Агрести [15] предложили, что оценка коррелированных переменных смешанного отклика может быть получена с помощью алгоритма ожидания-максимизации (EM). Zhang et al. [16] распространил это на расширенный по параметрам алгоритм EM в рамках подхода полного правдоподобия. де Леон и Каррьер [17,18] разработали общую модель смешанных данных, которая объединяет CGDM и CGCM для совместного анализа коррелированных номинальных, порядковых и непрерывных данных. По-прежнему сложно оценить совместное распределение многомерных смешанных данных с вычислительной точки зрения.Метод составного правдоподобия основан на составных распределениях меньшей размерности, которые предлагают альтернативное решение проблемы оценивания (Линдсей [19], Кокс и Рид [20], Варин [21], Варин и др. [22] и Рейд и др. [23]). Faes et al. [24] применили этот метод к лонгитюдным данным со смешанными результатами. В их модели корреляционная структура вызвана случайным эффектом, который не имеет выражения в замкнутой форме. Мы стремимся следовать подходу CGCM и использовать метод составного правдоподобия для анализа совместного распределения многомерных переменных ответа смешанного типа, где переменные категориального ответа моделируются непрерывными скрытыми переменными.Параметры средней структуры, а также корреляция между различными исходами могут быть оценены одновременно с помощью численного алгоритма. Предлагаемый метод составного правдоподобия состоит из трех типов двумерных плотностей суставов: двух непрерывных результатов; два дискретных исхода, моделируемые двумя непрерывными скрытыми переменными; и два смешанных результата с одной непрерывной и одной категориальной переменной.Мы предлагаем численный алгоритм для оценки составного правдоподобия и обсуждаем асимптотические свойства оценок составного правдоподобия.Кроме того, мы выводим три статистических критерия совокупного правдоподобия для совместного вывода на основе многомерной модели смешанного ответа. Имитационные исследования были проведены для проверки эмпирических характеристик предлагаемого метода по сравнению с традиционными подходами. Алгоритм был применен к клиническим данным исследования колоректального рака. Мы анализируем влияние лечения и других клинических факторов на множественные коррелированные ответы пациентов.
2. Методология
2.1. Настройка модели
Предположим, что имеется n наблюдений z1, z2, ⋯, zi, ⋯, zn в наборе клинических данных, и каждое наблюдение содержит q нескольких результатов zi = (zi1, zi2, ⋯, zij, ⋯, ziq) T, которые коррелированы и смешаны с непрерывными и двоичными переменными. Предположим, мы хотим смоделировать эффекты набора ковариат, и обобщенная линейная модель может быть построена для каждого результата как в котором ковариата xij с i = 1,2, ⋯, n и j = 1,2, ⋯, q для разных ответов может быть одинаковой или разной, а gj обозначает функцию связи, используемую для j-го ответа.Если мы хотим анализировать эти многомерные результаты смешанного типа одновременно с соответствующими ковариатами, традиционный подход, основанный на правдоподобии, должен определять многомерные совместные плотности всех ответов. В качестве альтернативы мы можем настроить попарную функцию правдоподобия для ответов zij и zik какLjk (θjk) = ∏i = 1nf (zij, zik),
(1)
где θjk обозначает параметры, связанные с попарным правдоподобием. Функция логарифма правдоподобия задается выражением ljk (θjk) = logLjk (θjk), а функция оценки задается выражениемUjk (θjk) = ∑i = 1nf (zij, zik) −1∂∂θjkf (zij, zik).
(2)
Согласно Линдсею [19] и Коксу и Рейду [20], попарная составная функция правдоподобия этих q переменных отклика является произведением парных q2 функций правдоподобия:CL (θ) = ∏j = 1q − 1∏k = j + 1qLjk (θjk),
а функция оценки строится путем определения составной функции логарифмического правдоподобия:U (θ) = ∂∂θlogCL (θ).
(3)
Наша многомерная модель со смешанным откликом оценивает интересующие параметры θ путем численного решения сложной функции оценки (3), равной 0, с помощью метода Ньютона – Рафсона [25].Поскольку результаты смешаны с непрерывными и категориальными переменными, функция оценки (2) может быть получена с использованием трех различных двумерных структур: результаты с обеими переменными непрерывного ответа, результаты с обеими переменными бинарного ответа и результаты, смешанные с одним непрерывным и одним бинарным ответом. Переменная.2.1.1. Случай 1: Непрерывные результаты
Сначала мы обсудим случай, когда оба ответа zij и zik являются непрерывными, и предположим, что они подчиняются двумерному нормальному распределению:zijzik∼N2μijμik, σj2, ρjkσjσkρjkσjσk, σk2,
где средняя структура zij и zik связана с обобщенными линейными моделями как μij = xijTβj и μik = xikTβk.Таким образом, попарная плотность zij и zik такая же, как двумерная нормальная плотность, основанная на Джонсоне и Уичерне [26]:f (zij, zik) = 12πσjσk1 − ρjk2exp [−12 (1 − ρjk2) × (zij − μij) 2σj2−2ρ (zij − μij) (zik − μik) σjσk + (zik − μik) 2σk2].
Попарная функция сложного правдоподобия может быть построена следующим образом:Ljk (θjk) = ∏i = 1nf (zij, zik),
с интересующими параметрами θjk = {βj, βk, σj, σk, ρjk} и функцией логарифма правдоподобия ljk (θjk) = ∑i = 1nlogf (zij, zik), которая дает функцию оценки обоих используемых непрерывных ответов в уравнении (2):Ujk (θjk) = ∂ljk (θjk) ∂θjk.
(4)
2.1.2. Случай 2: двоичные результаты
Для двоичных результатов преобразование может быть получено с использованием порогового значения t, так что если скрытая переменная zij * ≥t, то ответ zij = 1, в противном случае zij = 0. Без ограничения общности, значение t устанавливается равным 0, и мы имеем μij = P (zij = 1) = P (zij * ≥0). Мы следуем настройкам сгруппированной непрерывной модели с предположениями распределения zij∼Bernoulli (μij) и zij * ∼N (μij *, σj2). Таким образом, модель может быть построена с ковариатами xij как Поскольку среднее значение μij * и дисперсия σj2 невозможно идентифицировать одновременно, мы следуем методу изменения масштаба, основанному на Дансоне [27], устанавливая σj2 = 1.Следовательно, среднее значение скрытой переменной можно упростить как μij * = xijTβj. Поскольку мы совместно анализируем двоичные переменные zij и zik, парные скрытые переменные zij * и zik * генерируются из модели с полихорической корреляцией. Таким образом, совместная функция (zij, zik) может быть получена с помощью функций сложного правдоподобия в четырех случаяхP (zij = 1, zik = 1) = P (zij * ≥0, zik * ≥0) = Φ2 (μij *, μik *, ρjk), P (zij = 1, zik = 0) = P (zij * ≥0, zik * <0) = Φ2 (μij *, - μik *, - ρjk), P (zij = 0, zik = 1) = P (zij * <0, zik * ≥0) = Φ2 (−μij *, μik *, - ρjk), P (zij = 0, zik = 0) = P (zij * <0, zik * <0) = Φ2 (−μij *, - μik *, ρjk),
где ± ρjk представляет полихорическую корреляцию при различных сценариях, а Φ2 обозначает двумерную нормальную кумулятивную функцию плотности.Приведенные выше уравнения можно переписать какP (zij, zik) = Φ2 ((2zij − 1) μij *, (2zik − 1) μik *, (2zij − 1) (2zik − 1) ρjk) = Φ2 (sijμij *, sikμik *, sijsikρjk),
с sij = (2zij − 1) и sik = (2zik − 1). Функция логарифмического правдоподобия парных двоичных ответов имеет видljk (θjk) = ∑i = 1nlogΦ2 (sijμij *, sikμik *, sijsikρjk).
Функция оценки может быть получена какUjk (θjk) = ∑i = 1nP (zij, zik) −1∂∂θjklogP (zij, zik).
(5)
2.1.3. Случай 3: Смешанные результаты
Когда одна переменная отклика zij является бинарной, а другая переменная отклика zik является непрерывной, мы можем смоделировать смешанные результаты вместе, приняв скрытую нормальную переменную zij * в качестве условной сгруппированной непрерывной модели.Таким образом, они следуют двумерному нормальному распределению с учетом полисериальной корреляции ρjk:zij * zik∼N2μij * μik, σj2, ρjkσjσkρjkσjσk, σk2.
Метод факторизации может применяться для совместного двумерного нормального распределения с предельной плотностью для непрерывного отклика P (zik) и условной плотностью для скрытой переменной P (zij * | zik) при непрерывном отклике.
- zik — это непрерывный отклик
- zij * — скрытая переменная для двоичного ответа zij:
zij * | zik∼Nμij | k = μij * + ρjkσjσk (zik − μik), σj | k2 = σj2 (1 − ρjk2).
P (zij * | zik) = Φ (dij), если zij = 0, Φ (−dij), если zij = 1.
Функция попарного правдоподобия и функция логарифма правдоподобия задаются следующим образом:Ljk = ∏i = 1nP (zij * | zik) p (zik), ljk = ∑i = 1nlogP (zik) + log1 (zij = 0) Φ (dij) + log1 (zij = 1) Φ (−dij).
Функция оценки может быть получена какUjk = ∑i = 1n1P (zik) ∂P (zik) ∂θjk + 1 (zij = 0) Φ (dij) −1 (zij = 1) 1 − Φ (dij) ∂Φ (dij) ∂θjk.
(6)
Аналогичная формулировка была распространена на продольные параметры Najita et al.(MCLE) для параметров θ путем численного решения функции оценки. Наш численный алгоритм представлен ниже (алгоритм 1):| Алгоритм 1: Алгоритм многомерной модели смешанного отклика. |
|
2.2. Статистический вывод с использованием метода составного правдоподобия
Кокс и Хинкли [28] и Кент [29] представили различные процедуры проверки гипотез с использованием функции полного правдоподобия. Функция составного правдоподобия может рассматриваться как неверно заданная функция правдоподобия.Его асимптотические свойства были рассмотрены и обсуждены Варином и др. [22], Reid et al. [23], Цзинь [30], Гао и Сун [31]. Следуя этой схеме, попарная функция составного правдоподобия, реализованная в предлагаемой нами модели, дает оценки, которые являются согласованными и асимптотически нормально распределенными. Информация Годамбе [32] G параметров θ для логарифмической функции составного правдоподобия включает матрицу чувствительности H и матрица изменчивости J:G (θ) = H (θ) J − 1 (θ) H (θ),
где матрица чувствительности и матрица изменчивости определены какH (θ) = Eθ {−∇θU (θ; zi)} и J (θ) = Varθ {U (θ; zi)},
где U (θ; zi) обозначает функцию оценки i-го наблюдения, а функция общей оценки U (θ) = ∑i = 1nU (θ; zi). −ψ0), имеющее асимптотическое распределение χq2.}. Однако асимптотическое распределение отношения сложного правдоподобия при H0 определяется выражением ∑j = 1qλjχ1 (j) 2, где χ1 (j) 2 — независимые переменные χ12, а λ1, λ2 ⋯, λq — собственные значения матрицы Hψψ, λGψψ с Hψψ, λ = Hψψ − HψλHλλ − 1Hλψ. Существуют различные корректировки этого нестандартного взвешенного распределения хи-квадрат (Ротницки и Джуэлл [33], Гейс и др. [34] и Пейс и др. [35]). Например, мы можем применить корректировку, введя коэффициент масштабирования λ¯ = ∑j = 1qλj / q, тогда скорректированное отношение совокупного правдоподобия будет иметь такое же асимптотическое распределение, что и We (ψ0) и Wu (ψ0):Следовательно, Метод составного правдоподобия может упростить моделирование коррелированных ответов с помощью нескольких обобщенных линейных моделей и позволить пользователям делать статистические выводы по интересующим параметрам из различных обобщенных линейных моделей.Кроме того, мы можем выбрать подмножество параметров и провести дальнейшую логическую оценку при наличии мешающих параметров.
3. Моделирование
Были реализованы различные имитационные исследования, чтобы показать валидность многомерной модели смешанного отклика. Результаты оценки предложенной модели сравниваются с подходами полного правдоподобия и маржинальностью соответственно.
3.1. Сравнение с оценкой максимального правдоподобия
В многомерной регрессии с коррелированными непрерывными результатами оценка полного правдоподобия может проводиться без численного интегрирования.Таким образом, мы можем сравнить оценки максимального совокупного правдоподобия с подходом полного правдоподобия посредством моделирования. Смоделированные выборки содержат четыре переменных непрерывного отклика zic1, zic2, zic3 и zic4, которые генерируются из уравнения (8):zic1 = αc1 + βc1xic1 + γc1yic1 + εic1, zic2 = αc2 + βc2xic2 + γc2yic2 + εic2, zic3 = αc1 + βc1xic1 + γc1yic1 + εic1, zic4 = αc2 + βc2xic2 + γc2yic2.
(8)
Ковариаты {xic1, xic2, xic1, xic2} ∼N (0,1) и {yic1, yic2, yic1, yic2} ∼N (0,0.5) моделируются независимо.Ошибки коррелируются и генерируются из многомерного нормального распределения N4 (0, Σ), а матрица дисперсии-ковариации Σ задается следующим образом:σc12σc1σc2ρc1c2σc1σc3ρc1c3σc1σc4ρc1c4σc1σc2ρc1c2σc22σc2σc3ρc2c4σc2σc4ρc2c4σc1σc3ρc1c3σc2σc3ρc2c3σc32σc3σc4ρc3c4σc1σc4ρc1c4σc2σc4ρc2c4σc3σc4ρc3c4σc42.
При моделировании дисперсии рассчитываются как σc12 = 1, σc22 = 1, σc32 = 2,25 и σc32 = 4, и между ошибками в процессе генерации данных применяется идентичная корреляция ρ = 0,3.
Результаты моделирования (рис. 1) были получены с помощью 1000 независимых повторов.Оценщики максимального совокупного правдоподобия демонстрируют схожую производительность по сравнению с подходом полного правдоподобия. Результаты моделирования также показывают, что оценки близки друг к другу, а оценки максимального правдоподобия имеют немного более высокую относительную эффективность.3.2. Сравнение с маржинальным подходом
Для регрессии со смешанным исходом подход полного правдоподобия сложен с вычислительной точки зрения, и для проведения анализа часто прибегают к маргинальной регрессии.Мы реализовали имитационные исследования, чтобы оценить эффективность предлагаемого нами метода по сравнению с маргинальной регрессией. Сначала мы проверили общую эффективность точечных оценок, когда результаты имели разные уровни зависимости и ковариаты. Далее мы сосредоточились на тестировании составной статистики. Модель многомерного смешанного отклика может обеспечить статистический вывод с помощью мешающих параметров и достигает более высокой статистической мощности с точки зрения работы с совместным выводом.
3.2.1. Параметры моделирования
Мы сгенерировали данные выборки, состоящие из двух двоичных ответов zib1 и zib2 и двух непрерывных ответов zic1 и zic2. Бинарные переменные были получены на основе соответствующих скрытых нормальных переменных zib1 * и zib2 * с помощью функции пробит-ссылки:пробит (μib1) = μib1 *, пробит (μib2) = μib2 *.
Моделирование откликов основано на уравнении (9), связанном с ковариатами xi = {xib1, xib2, xic1, xic2} и yi = {yib1, yib2, yic1, yic2} соответственно:zib1 * = αb1 + βb1xib1 + γb1yib1 + εib1, zib2 * = αb2 + βb2xib2 + γb2yib2 + εib2, zic1 = αc1 + βc1xic1 + γc1yic1 + εic1, zic2 = αc2 + βc2xic2 + γcic2.
(9)
Мы предоставили различные сценарии моделирования значений ковариат и три уровня корреляции для анализа переменных отклика с помощью предлагаемой модели. Параметры регрессии были выбраны произвольно и установлены на фиксированные значения в каждом исследовании моделирования. Ошибки в уравнении (9) следуют многомерному нормальному распределению N4 (0, Σ), а матрица ковариации дисперсии Σ задается формулойσb12σb1σb2ρb1b2σb1σc1ρb1c1σb1σc2ρb1c2σb1σb2ρb1b2σb22σb2σc1ρb2c1σb2σc2ρb2c2σb1σc1ρb1c1σb2σc1ρb2c1σc12σc1σc2ρc1c2σb1σc2ρb1c2σb2σc2ρb2c2σc1σc2ρc1c2σc22.
В следующих процессах генерации данных значения параметров ковариации и дисперсии устанавливаются как σb12 = 1, σb22 = 1, σc12 = 16 и σc22 = 25, а корреляция рассчитывается на низких уровнях (все ρ = 0,3), средний (все ρ = 0,5) и высокий (все ρ = 0,7), соответственно, для оценки базовой модели. Поскольку нет ограничений на знак корреляции, отрицательную корреляцию можно оценить с помощью нашего алгоритма без дополнительных предположений. Наши симуляционные исследования сосредоточены на общей производительности многомерной модели смешанного ответа посредством независимых повторений.
3.2.2. Точечные оценки
Были разработаны различные сценарии моделирования для оценки эффективности базовой модели по точечным оценкам с помощью 1000 независимых повторений. Существует два разных набора моделирования процесса генерации данных, и в каждой настройке мы анализируем три уровня корреляции соответственно. Как показано в таблице 1, значения параметров регрессии и стандартное отклонение переменных непрерывного отклика даны во всех исследованиях моделирования.В первой настройке моделирования мы предоставляем 300 выборок, и переменные смешанного ответа связаны с ковариатами различных значений. Наборы ковариаций xi и yi идентично и независимо моделируются из нормального распределения N (0,1), соответственно, в каждой линейной модели. Во второй настройке моделирования мы представляем многомерную модель смешанного отклика, имеющую дело с общей ковариатой. Что касается процесса генерации данных с 1000 выборок, все ответы имеют одну общую ковариату, которая была сгенерирована из нормального распределения N (0,1), например xib1 = xib2 = xic1 = xic2 в уравнении (9).Вторые ковариаты yi взяты из уравнения Бернулли (0,5), и они различны для каждого ответа. Этот параметр представляет собой сценарий на практике, когда общий фактор включен во все модели отклика. В таблице 1 мы приводим отношение среднеквадратичной ошибки (MSE) предлагаемого метода к предельным подходам. Это соотношение представляет собой относительную эффективность предлагаемого метода по сравнению с маржинальным методом при различных условиях. В большинстве настроек моделирования коэффициенты отношения MSE значительно ниже 1.Когда ответы сильно коррелированы и имеют разные наборы ковариат, наш метод может снизить MSE на 50%, что указывает на большой выигрыш в эффективности.3.2.3. Статистический тест
Тест составной статистики правдоподобия может совместно оценивать интересующие параметры в различных обобщенных линейных моделях, в то время как традиционные методы не могут этого достичь. Имитационные исследования были проведены для измерения частоты ошибок типа I и мощности по сравнению с маржинальными подходами.
Это моделирование было проведено для проверки гипотезы. Коррелированные ответы были получены на основе уравнения (9) со всей корреляцией ρ = 0,3. Представляющими интерес параметрами являются коэффициенты регрессии {βb1, βb2, βc1, βc2} первых ковариат в четырех обобщенных линейных моделях, а первые ковариаты xi независимо моделируются из N (0,1). Коэффициенты регрессии вторых ковариат yi и других параметров являются мешающими параметрами с yi∼N (0, .5). В исследовании моделирования для оценки частоты ошибок типа 1 параметры регрессии {βb1, βb2, βc1, βc2} равны нулю во всех обобщенных линейных моделях, в то время как другие параметры имеют те же значения, что и в предыдущем моделировании в таблице 1.Для оценки мощности мы зафиксировали значения параметров регрессии как βb1 = βb2 = 0,1 для бинарных ответов и βc1 = βc2 = 0,3 для непрерывных ответов. Для сравнения, мы объединили результаты маржинальных подходов, применив поправку Бонферрони. Таблица 2 иллюстрирует результаты более 2000 независимых повторений. Предлагаемая модель анализирует все ответы одновременно, и смоделированные коэффициенты ошибок типа I действительны и близки к 0,05. Благодаря тесту совместного воздействия интересующей ковариаты на все ответы, смоделированная мощность улучшается с помощью предлагаемой нами модели по сравнению с результатами теста Бонферрони.По мере увеличения размера выборки с 500 до 1000 статистика совокупного правдоподобия увеличивает статистическую мощность примерно с 0,800 до 0,989. Общая производительность показывает, что составная статистика более эффективна, чем традиционный подход.4. Анализ данных
В этом разделе многомерная модель смешанного ответа применяется к клиническим данным исследования колоректального рака. Данные состоят из клинических наблюдений и демографической информации о 743 пациентах, которые смешаны как с категориальными, так и с непрерывными данными.Наш исследовательский интерес состоял в том, чтобы оценить влияние лечения и других клинических факторов на исходы токсичности. Мы сосредоточились на четырех типичных случаях токсичности, связанных с лечением колоректального рака. Во-первых, мы выбрали тошноту и диарею в качестве двух категориальных ответов. Они состоят из порядковых данных, измеряющих тяжесть токсичности от 1 до 4. В нашей модели мы учитывали только тошноту и диарею для каждого пациента. Таким образом, эти два ответа были разработаны как бинарные переменные, которые кодируются как 1, если они произошли, и 0, если во время лечения нет записей.Непрерывные ответы включают два показателя анализа крови, а именно количество гемоглобина (HGB) и количество лейкоцитов (WBC). У каждого пациента во время лечения было несколько анализов крови, и мы взяли наивысшее значение для анализа. Объясняющие переменные содержат эффект лечения, демографическую информацию, статус опухоли и генетические маркеры для каждого пациента. В этом исследовании колоректального рака используются два разных метода лечения. Демографические и клинические данные пациента, такие как возраст, рост и вес, собирались как непрерывные переменные.Опухоль, идентифицированная либо в толстой, либо в прямой кишке, регистрировалась как бинарная переменная. В исследование также включены генетические маркеры, такие как PERF1, PERF2 и KRAS, которые представляют собой бинарные переменные, показывающие наличие мутации. Всего нам потребовалось совместно оценить 68 параметров для коэффициентов четырех линейных моделей и корреляцию между каждым результатом.
Таблица 3 показывает основной результат воздействия лечения, а полный результат представлен в Приложении B. Мы можем заметить, что статистические выводы об эффекте лечения с помощью двух моделей совпадают.Вторая лечебная терапия привела к более низким показателям гемоглобина и указывает на отрицательную связь с возникновением тошноты и диареи, в то время как разница в влиянии на показатели лейкоцитов незначительна. Мы можем использовать совокупную статистику для совместной оценки общего эффекта этой терапии на четыре ответа. В таблице 4 представлены стандартное отклонение и корреляция четырех клинических исходов, оцененных на основе предложенной модели.Используя традиционный подход, мы не можем сделать статистический вывод по разным линейным моделям.Предлагаемая модель может проверить гипотезу H0: βb1 = βb2 = βc1 = βc2 = 0 на основе асимптотических свойств сложной функции правдоподобия. Тестовая статистика составной статистики Вальда под H0 составляет приблизительно 138,5890, статистика составной оценки составляет 476,975, а скорректированное отношение совокупного правдоподобия составляет 264,3069, что все больше, чем критическое значение χ42. Таким образом, мы можем отвергнуть нулевую гипотезу и сделать вывод, что два разных лечения имеют статистически значимое различие с точки зрения реакции пациента на токсичность.Более конкретно, в наших результатах оценки мы делаем вывод, что существует значительная разница с точки зрения возникновения тошноты и диареи, а также значительная разница в HGB между двумя видами лечения.
5. Обсуждение
Проблема смешанных результатов широко обсуждается в исследованиях, связанных со здоровьем. В результате вычислительной сложности большинство существующих методов в основном сосредоточены на случае двух исходов, смешанных с одной непрерывной переменной и одной категориальной переменной.В качестве расширения условной сгруппированной непрерывной модели мы представляем многомерную модель смешанного ответа для решения многомерных смешанных многомерных регрессий. Наша модель построена с использованием метода попарного составного правдоподобия, так что несколько результатов анализируются с помощью разных двумерных моделей одновременно. Что касается данных, смешанных с непрерывными и бинарными ответами, наш метод упрощает проблему множественных результатов до трех типов сценариев, которые являются гибкими с методологической точки зрения и привлекательными с аналитической точки зрения.По результатам моделирования, оценки предложенной модели демонстрируют более низкую MSE, чем маржинальные подходы. Комбинированная статистика также обеспечивает повышенную статистическую мощность для совместной проверки гипотез по различным обобщенным линейным моделям, что может сделать этот подход подходящим для анализа клинических данных с множественными ответами смешанного типа.
Кроме того, модель может быть обобщена для одновременной работы с порядковыми и непрерывными данными. При той же настройке скрытая переменная zij * нормально распределена со средним значением μij * = xijTβj и дисперсией σj2 = 1.Если скрытая нормальная переменная zij * ∈ [tl − 1, tl) с пороговыми значениями −∞ = t0Функцию оценки можно получить, взяв производные от ∑i = 1n∑j = 1q − 1∑k = j + 1qlogP (zij = l, zik = l ′), и пороги tl должны быть оценены с помощью монотонной ограничение.Оценка максимального совокупного правдоподобия для смешанных исходов может быть проведена с помощью тех же подходов, которые предложены в этой статье. Будут рассмотрены дальнейшие исследования для анализа многомерных результатов с различными распределениями.
Вклад авторов
Концептуализация, H.B. и X.G .; Методология, H.B., Y.Z. и X.G .; Программное обеспечение, H.B. и Y.Z .; Проверка, Y.Z., X.G. и W.X .; Формальный анализ, H.B., Y.Z., X.G. и W.X .; Investigation, Y.Z., X.G. и W.X .; Ресурсы, W.ИКС.; Data Curation, W.X .; Письмо — подготовка оригинального черновика, H.B. и Y.Z .; Написание — просмотр и редактирование, X.G. и W.X .; Надзор, X.G. и W.X .; Администрация проекта, X.G. и W.X .; Финансирование Приобретение, X.G. Все авторы прочитали и согласились с опубликованной версией рукописи.
Финансирование
Исследования Чжун и Гао поддерживаются Канадским советом по естественным и инженерным исследованиям (NSERC).
Конфликт интересов
Авторы заявляют об отсутствии конфликта интересов.
Приложение A. Производные для переменных смешанного ответа
Функция оценки (6) содержит производную логарифма предельной нормальной плотности и логарифм условной вероятности:Ujk = ∂∂θjklogP (zk) +1 (zj = 0) Φ (dj) −1 (zj = 1) 1 − Φ (dj) ∂Φ (dj) ∂θjk.
Чтобы проиллюстрировать вывод, пусть zj и zk представляют переменные ответа вектора n × 1 с матрицами проекта Xj и Xk, соответственно. Позволятьck = (zk − μk) σk и dj = μj * + ρjkσjσk (zk − μk) σj1 − ρjk2.
Нормальный CDF имеет следующие свойства:Φ ′ (dj) = ϕ (dj), ϕ ′ (ck) = — ckϕ (ck), ϕ ″ (ck) = (ck2−1) ϕ (ck).
Первый компонент в функции оценки можно упростить как∂∂θjklogP (zk) = ∂∂θjklog (1σkϕ (ck)) = 1ϕ (ck) ∂ϕ (ck) ∂θjk − 1σk∂σk∂θjk = −ck∂ck∂θjk − 1σk∂σk∂θjk, ∂2logP (zk) ∂θjk∂θjkT = 1σk2∂σk∂θjk∂σk∂θjkT − 1σk∂2σk∂θjk∂θjkT − ∂ck∂θjk∂ck∂θjkT − ck∂2ck∂θjk∂θjkT.
Производные второго компонента имеют простой формат относительно dj:∂Φ (dj) ∂θjk = ϕ (dj) ∂dj∂θjk, ∂2Φ (dj) ∂θjk∂θjkT = −djϕ (dj) ∂dj∂θjk∂dj∂θjkT + ϕ (dj) ∂2dj∂θjkT∂ θjkT.
Путем сложения результатов, приведенных выше, функция оценки и ее производная могут быть заданы следующим образом:∂ljk∂θjk = −1σk∂σk∂θjk − ck∂ck∂θjk + 1 (zj = 0) Φ (dj) −1 (zj = 1) 1 − Φ (dj) ϕ (dj) ∂dj∂θjk∂ 2ljk∂θjk∂θjkT = 1σk2∂σk∂θjk∂σk∂θT − 1σk∂2σk∂θjk∂θjkT − ∂ck∂θjk∂ck∂θjkT − ck∂2ck∂θjk∂θjkT − 1 (zj = 0) (Φ ( dj)) 2 + 1 (zj = 1) 1 − Φ (dj) 2ϕ (dj) 2∂dj∂θjk∂dj∂θjkT + 1 (zj = 0) Φ (dj) −1 (zj = 1) 1− Φ (dj) × −djϕ (dj) ∂dj∂θjk∂dj∂θjkT + ϕ (dj) ∂2dj∂θjk∂θjkT.
Более того,∂ck∂βk = −1σkXk, ∂ck∂σk = −1σkck, ∂2ck∂σk2 = 2σk2ck, ∂2ck∂βk∂σk = 1σk2Xk.
Для члена dj здесь приводится больше выводов:∂dj∂βk = ρjkXkσk1 − ρjk2, ∂dj∂βj = −Xjσj1 − ρjk2, ∂dj∂σk = ρjkckσk1 − ρjk2, ∂dj∂σj = Xjβjσj21 − ρjk2, ∂dj∂ρjk − 1 −ρjk2) 32 − ρjk2ck (1 − ρjk2) 32, ∂2dj∂σk2 = −2ρjkckσk21 − ρjk2,
∂2dj∂σj2 = −2XjTβjσj31 − ρjk2, ∂2dj∂ρjk2 = −ckρjk (1 − ρjk2) 32 − XjTβjσj1 (1 − ρjk2) 32 + 3ρjk2 (1 − ρjk2) 52 − ck2ρjk (1 − ρjk2) 52 − ck2ρjk2 (1 − ρjk2) 52 − ck2ρjk (1 − ρjk2) 1 − ρjk2) 52, ∂2dj∂ρjk∂σk = ckσk11 − ρjk2 + ρjk2 (1 − ρjk2) 32, ∂2dj∂βj∂σj = Xjσj21 − ρjk2, ∂2dj∂βj∂ρjk = −Xjρjkσj (1 − ρjk2) 32, ∂2dj∂βk∂ρjk = Xkσk11 − ρjk2 + ρjk2 (1 − ρjk2) 32, ∂2dj∂σk∂βk = −ρjkXkσk21 − ρjk2.
В заключение, функция оценки Ujk (θjk) по каждому параметру определяется выражением∂ljk∂βk = ckσkXk + 1 (zj = 0) Φ (dj) −1 (zj = 1) 1 − Φ (dj) ϕ (dj) ρjkXkσk1 − ρjk2, ∂ljk∂βj = 1 (zj = 0) Φ (dj) −1 (zj = 1) 1 − Φ (dj) −ϕ (dj) Xjσj1 − ρjk2, ∂ljk∂σk = −1σk + ck2σk + 1 (zj = 0) Φ (dj) −1 (zj = 1) 1 − Φ (dj) ϕ (dj) ρjkckσk1 − ρjk2, ∂ljk∂σj = 1 (zj = 0) Φ (dj) −1 (zj = 1) 1 − Φ (dj) ϕ (dj) Xjβjσj21− ρjk2, ∂ljk∂ρjk = 1 (zj = 0) Φ (dj) −1 (zj = 1) 1 − Φ (dj) ϕ (dj) × −ck1 − ρjk2 − Xjβjρjkσj (1 − ρjk2) 32 − ρjk2ck ( 1 − ρjk2) 32.
Приложение B. Результаты оценки клинических данных исследования колоректального рака
Таблица A1. Расчетные коэффициенты регрессии β и стандартное отклонение (sd). GLM: оценка с помощью обобщенной линейной модели; MRM: оценка с помощью предложенной многомерной модели смешанного ответа; в столбце * перечислены важные ковариаты.
Таблица A1. Расчетные коэффициенты регрессии β и стандартное отклонение (sd). GLM: оценка с помощью обобщенной линейной модели; MRM: оценка с помощью предложенной многомерной модели смешанного ответа; в столбце * перечислены важные ковариаты.
| 1. Тошнота | 2. Диарея | 3. HBG | 4. WBC | |||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Параметры | GLM | MMR | GLM | 57 MMR 5 MMR 900 MMRGLM | MMR | * | ||||
| Перехват | −0,2685 (1,277) | −0,2793 (1,317) | 0,6631 (1,304) | 0,6741 (1,329) | 160.3759 (16,831) | 160,3775 (16,829) | 12,2949 (4,761) | 12,2946 (4,855) | 3, 4 | |
| Обработка | -0,2644 (0,097) | -0,2724 (0,099) | 23(0,098) | −0,6422 (0,101) | −12,4921 (1,274) | −12,4957 (1,252) | −0,1591 (0,360) | −0,1597 (0,358) | 1, 2, 3 | |
| OS | -0,0037 (0,009) | -0,0039 (0,009) | 0.0219 (0,009) | 0,0228 (0,009) | 0,5674 (0,115) | 0,5675 (0,117) | -0,1764 (0,032) | -0,1764 (0,029) | 2, 3, 4 | |
| OS событие | 0,0650 (0,195) | 0,0702 (0,194) | 0,1173 (0,200) | 0,1208 (0,194) | 1,5154 (2,592) | 1,5159 (2,614) | 0,1290 (0,733) | 0,1295 (0,5362) | ||
| ПФС | 0,0305 (0.020) | 0,0315 (0,020) | 0,0066 (0,021) | 0,0062 (0,022) | -0,1628 (0,259) | -0,1627 (0,258) | 0,1242 (0,073) | 0,1243 (0,062) | ||
| IN | −0,0204 (0,188) | −0,0200 (0,190) | −0,8622 (0,203) | −0,8907 (0,212) | −11,1599 (2,486) | −11,1621 (2,932) | 80 (−0257) 0,703)−0,0803 (0,810) | 2, 3 | ||
| PD | 0.1263 (0,136) | 0,1319 (0,139) | -0,1375 (0,136) | -0,1432 (0,142) | -7,1013 (1,782) | -7,1005 (1,667) | -0,3695 (0,504) | -0,3689 0,528) | 3 | |
| PR | -0,0213 (0,169) | -0,0207 (0,171) | 0,0691 (0,176) | 0,0707 (0,174) | 3,6782 (2,234) | 3,6781 (2,2710) | 3,6781 (2,2710) | 3,6781 (2,2710) | 0,4003 (0,632)0,4005 (0,5277) | |
| Возраст | −0.0142 (0,008) | -0,0091 (0,005) | 0,0029 (0,008) | 0,0018 (0,005) | -0,1463 (0,061) | -0,1464 (0,061) | -0,0382 (0,017) | -0,0382 (0,018) ) | 3, 4 | |
| Пол | -0,0086 (0,005) | -0,0091 (0,005) | 0,0016 (0,005) | 0,0018 (0,005) | 9,0894 (1,798) | 9,0836 (1,825) | -0,1079 (0,509) | -0,1096 (0,534) | 1, 3 | |
| Двоеточие | 0.2313 (0,165) | 0,2378 (0,169) | 0,1017 (0,170) | 0,1059 (0,177) | -1,1366 (2,189) | -1,1338 (2,105) | 0,5706 (0,619) | 0,5713 (0,6376) | 0,5713 (0,6376) | |
| Прямая кишка | -0,0075 (0,154) | -0,0111 (0,157) | 0,1760 (0,158) | 0,1844 (0,166) | -1,6947 (2,032) | -1,6940 (1,913) | (0,575757) )0,9094 (0,649) | |||
| Высота | 0.0048 (0,007) | 0,0050 (0,008) | -0,0050 (0,007) | -0,0051 (0,008) | -0,0820 (0,097) | -0,0820 (0,097) | 0,0237 (0,028) | 0,0237 (0,028) | ||
| Вес | 0,0023 (0,003) | 0,0024 (0,003) | 0,0012 (0,003) | 0,0012 (0,003) | 0,0906 (0,044) | 0,0907 (0,042) | -0,0189 (0,012) | −0,0189 (0,012) | 3 | |
| PERF1 | 0.2046 (0,107) | 0,2132 (0,110) | 0,0898 (0,109) | 0,0933 (0,110) | -4,8490 (1,414) | -4,8469 (1,352) | 0,6028 (0,400) | 0,607836 (0,380) 3 | ||
| PERF2 | 0,5041 (0,187) | 0,5244 (0,187) | 0,2637 (0,189) | 0,2692 (0,193) | −7,1494 (3,814) | −7,1455 (2,628) | (0,688)) 1,8 | 1,8176 (0,685) | 1, 3, 4 | |
| KRAS | −0.0407 (0,292) | -0,0387 (0,295) | 0,0080 (0,293) | 0,0150 (0,294) | 1,3456 (3,814) | 1,3455 (3,285) | -0,7323 (1,079) | -0,7325 (0,936) | ||
Ссылки
- Cox, D.R. Анализ многомерных двоичных данных. J. R. Stat. Soc. Сер. C Прил. Стат. 1972 , 21, 113–120. [Google Scholar] [CrossRef]
- Cox, D.R .; Вермут, Н. Модели отклика для смешанных бинарных и количественных переменных.Биометрика 1992 , 79, 441–461. [Google Scholar] [CrossRef]
- Olkin, L .; Тейт, Р.Ф. Многомерные корреляционные модели со смешанными дискретными и непрерывными переменными. Анна. Математика. Стат. 1961 , 32, 448–456. [Google Scholar] [CrossRef]
- Teixeira-Pinto, A .; Норманд, С. Коррелированные двумерные непрерывные и двоичные результаты: проблемы и приложения. Стат. Med. 2009 , 28, 1753–1773. [Google Scholar] [CrossRef] [PubMed]
- Sammel, M.D .; Райан, Л.М .; Леглер, Дж. М. Модели со скрытыми переменными для смешанных дискретных и непрерывных исходов. J. R. Stat. Soc. Сер. B Methodol. 1997 , 59, 667–678. [Google Scholar] [CrossRef]
- Sammel, M.D .; Lin, X .; Райан, Л.М.Многовариантные линейные смешанные модели для множественных результатов. Стат. Med. 1999 , 18, 2479–2492. [Google Scholar] [CrossRef]
- Yang, Y .; Kang, J .; Mao, K .; Чжан, Дж. Регрессионные модели для смешанных пуассоновских и непрерывных продольных данных. Стат. Med. 1961 , 26, 3782–3800.[Google Scholar] [CrossRef]
- Anderson, J.A .; Пембертон, Дж. Д. Сгруппированная непрерывная модель для многомерных упорядоченных категориальных переменных и ковариантной корректировки. Биометрия 1985 , 41, 875–885. [Google Scholar] [CrossRef]
- Де Леон, А. Подход попарного правдоподобия к сгруппированной непрерывной модели и ее расширению. Стат. Вероятно. Lett. 2005 , 75, 49–57. [Google Scholar] [CrossRef]
- Poon, W.Y .; Ли, С.Ю. Оценка максимального правдоподобия многомерных полисериальных и полихорических коэффициентов корреляции.Психометрика 1987 , 52, 409–430. [Google Scholar] [CrossRef]
- Skrondal, A .; Рабе-Хескет, С. Моделирование скрытых переменных: обзор; Блэквелл: Оксфорд, Великобритания, 2007; Том 34. [Google Scholar]
- Catalano, P .; Райан, Л. Двумерные модели скрытых переменных для кластерных дискретных и непрерывных результатов. Варенье. Стат. Доц. 1992 , 50, 1078–1095. [Google Scholar] [CrossRef]
- Каталано, П.Дж. Двумерное моделирование сгруппированных непрерывных и упорядоченных категориальных результатов.Стат. Med. 1997 , 16, 883–900. [Google Scholar] [CrossRef]
- Najita, J.S .; Li, Y .; Каталано, П.Дж. Новое применение модели двумерной регрессии для бинарных и непрерывных результатов исследования токсичности плода. J. R. Stat. Soc. Сер. C Прил. Стат. 2009 , 58, 555–573. [Google Scholar] [CrossRef] [PubMed]
- Георгиева, Р.В .; Агрести, А. Коррелированная пробит-модель для совместного моделирования сгруппированных бинарных и непрерывных ответов. Варенье. Стат. Доц. 2001 , 96, 1102–1112.[Google Scholar] [CrossRef]
- Zhang, H .; Liu, D .; Zhao, J .; Би, X. Моделирование гибридных черт для сопутствующих заболеваний и генетических исследований совместной зависимости от алкоголя и никотина. Анна. Прил. Стат. 2018 , 12, 2359–2378. [Google Scholar] [CrossRef]
- De Leon, A.R .; Carriégre, K.C. Общая модель смешанных данных: расширение общих локационных и сгруппированных непрерывных моделей. Жестяная банка. J. Stat. 2007 , 35, 533–548. [Google Scholar] [CrossRef]
- De Leon, A.R .; Каррьегр, К.C. Анализ смешанных данных; Чепмен и Холл / CRC: Нью-Йорк, Нью-Йорк, США, 2013. [Google Scholar]
- Линдси Б. Методы составного правдоподобия. Contemp. Математика. 1988 , 80, 220–239. [Google Scholar]
- Cox, D.R .; Рид Н. Заметка о псевдодостоверности, построенной на основе предельных плотностей. Биометрика 2004 , 91, 729–737. [Google Scholar] [CrossRef]
- Варин, К. О составных предельных вероятностях. Adv. Стат. Анальный. 2008 , 92, 1–28. [Google Scholar] [CrossRef]
- Varin, C.; Reid, N .; Ферт, Д. Обзор методов составного правдоподобия. Стат. Грех. 2011 , 21, 5–42. [Google Scholar]
- Reid, N .; Линдси, Б.; Лян, К. Введение в методы составного правдоподобия. Стат. Грех. 2011 , 21, 1–3. [Google Scholar]
- Faes, C .; Aerts, M .; Molenberghs, G .; Гейс, H .; Teuns, G .; Бийненс, Л. Многомерная совместная модель для продольных результатов различной природы. Стат. Med. 2008 , 27, 4408–4427. [Google Scholar] [CrossRef] [PubMed]
- Аткинсон, К.E. Введение в численный анализ; John Wiley and Sons Inc .: Нью-Йорк, Нью-Йорк, США, 1989. [Google Scholar]
- Johnson, R.A .; Wichern, D.W. Прикладной многомерный статистический анализ; Prentice Hall: Upper Saddle River, NJ, USA, 1998. [Google Scholar]
- Dunson, D.B. Байесовские модели латентных переменных для кластерных смешанных результатов. J. R. Stat. Soc. 2000 , 62, 355–366. [Google Scholar] [CrossRef]
- Cox, D.R .; Хинкли, Д.В. Теоретическая статистика; Чепмен и Холл: Лондон, Великобритания, 1974.[Google Scholar]
- Kent, J.T. Устойчивые свойства тестов отношения правдоподобия. Биометрика 1982 , 69, 19–27. [Google Scholar]
- Джин, З. Аспекты составного вывода правдоподобия. Кандидат наук. Диссертация, Университет Торонто, Торонто, Онтарио, Канада, 2010. [Google Scholar]
- Gao, X .; Песня, P.X.K. Байесовские информационные критерии составного правдоподобия для выбора модели в данных большой размерности. Варенье. Стат. Доц. 2010 , 105, 1531–1540. [Google Scholar] [CrossRef]
- Годамбе, В.Оптимальное свойство регулярной оценки максимального правдоподобия. Анна. Математика. Стат. 1960 , 31, 1208–1211. [Google Scholar] [CrossRef]
- Rotnitzky, A .; Джуэлл, Н. Проверка гипотез о параметрах регрессии в полупараметрических обобщенных линейных моделях для кластерных коррелированных данных. Биометрика 1990 , 77, 485–497. [Google Scholar] [CrossRef]
- Geys, H .; Molenberghs, G .; Райан, Л.М.Моделирование псевдодостаточности многомерных исходов в токсикологии развития.Варенье. Стат. Доц. 1999 , 94, 734–745. [Google Scholar] [CrossRef]
- Pace, L .; Salvan, A .; Сартори, Н. Регулировка статистики составного отношения правдоподобия. Стат. Грех. 2011 , 21, 129–148. [Google Scholar]
Рисунок 1. Сравнение между оценкой максимального полного правдоподобия и оценкой максимального совокупного правдоподобия для коэффициентов регрессии для многомерных непрерывных результатов. Отношение среднеквадратичной ошибки (MSE) вычислялось с использованием MSE оценки максимального совокупного правдоподобия (MCLE) к MSE оценки максимального правдоподобия (MLE)..
Рисунок 1. Сравнение между оценкой максимального полного правдоподобия и оценкой максимального совокупного правдоподобия для коэффициентов регрессии для многомерных непрерывных результатов. Отношение среднеквадратичной ошибки (MSE) вычислялось с использованием MSE оценки максимального совокупного правдоподобия (MCLE) к MSE оценки максимального правдоподобия (MLE). .
Таблица 1. Отношение среднеквадратичной ошибки (MSE) многомерной модели смешанного ответа (MMR) к маргинальной модели (GLM).Результаты основаны на 1000 независимых симуляциях при двух разных сценариях и трех разных уровнях корреляции.
Таблица 1. Отношение среднеквадратичной ошибки (MSE) многомерной модели смешанного ответа (MMR) к маргинальной модели (GLM). Результаты основаны на 1000 независимых симуляциях при двух разных сценариях и трех разных уровнях корреляции.
| Моделирование I * | Моделирование II † | ||||||
|---|---|---|---|---|---|---|---|
| Низкое | Среднее | Высокое | Низкое | Среднее | Высокое | ||
| .2 | 1,00 | 0,99 | 0,98 | 0,97 | 0,92 | 0,85 | |
| βb1 = 0,3 | 0,93 | 0,81 | 0,66 | 1,00 | 0,99 | 0,97 | |
| γb1 0,3 | 0,93 | 0,81 | 0,66 | 0,95 | 0,85 | 0,71 | |
| αb2 = 0,2 | 1,00 | 0,98 | 0,97 | 0,97 | 0.92 | 0,86 | |
| βb2 = 0,3 | 0,94 | 0,84 | 0,69 | 1,00 | 0,98 | 0,95 | |
| γb2 = 0,5 | 0,94 | 0,83 | 0,70 | 0,95 | 0,86 | 0,71 | |
| αc1 = 0,5 | 1,00 | 1,00 | 1,00 | 0,96 | 0,89 | 0,79 | |
| βc1 = 8 | 0,89 | 0.73 | 0,50 | 1,00 | 1,00 | 1,00 | |
| γc1 = 10 | 0,90 | 0,74 | 0,51 | 0,93 | 0,80 | 0,59 | |
| σc1 = 4 | 1,01 | 1,01 | 1,01 | 1,01 | 1,01 | 1,01 | |
| αc2 = 0,4 | 1,00 | 1,00 | 1,00 | 0,97 | 0,90 | 0,79 | |
| βc2 = 5 | 0.92 | 0,77 | 0,53 | 1,00 | 1,00 | 1,00 | |
| γc2 = 8 | 0,92 | 0,75 | 0,50 | 0,94 | 0,80 | 0,57 | |
| σc75 = 5 | 1.011.01 | 1.01 | 1.01 | 1.01 | 1.01 | ||
Таблица 2. Частота ошибок типа 1 и мощность при разных размерах выборки (N = 500 и N = 1000).
Таблица 2. Частота ошибок типа 1 и мощность при разных размерах выборки (N = 500 и N = 1000).
| Ошибка типа I | Power | |||
|---|---|---|---|---|
| N = 500 | N = 1000 | N = 500 | N = 1000 | |
| Составной метод Likel | ||||
| H0: βb1 = βb2 = βc1 = βc2 = 0 | ||||
| Отношение правдоподобия | 0.054 | 0,043 | 0,804 | 0,988 |
| Статистика Вальда | 0,058 | 0,043 | 0,800 | 0,989 |
| Статистика скоринга | 0,058 | 0,042 | 0,798 900 | Множественный тест |
| Тест Бонферрони | 0,051 | 0,040 | 0,569 | 0,902 |
Таблица 3. Разница в эффекте лечения между двумя лечебными терапиями. GLM: обобщенная линейная модель; MMR: многомерная модель смешанного ответа.
Таблица 3. Разница в эффекте лечения между двумя лечебными терапиями. GLM: обобщенная линейная модель; MMR: многомерная модель смешанного ответа.
| Параметр регрессии | Модели | ||||
|---|---|---|---|---|---|
| GLM | MMR | ||||
| zb1: появление тошноты | |||||
| Intercept αb1 | −0.2685 ± 2,502 | −0,2793 ± 2,582 | |||
| (значение p) | (0,833) | (0,832) | |||
| Эффект лечения βb1 | −0,2644 ± 0,190 | −0,2724 ± 0,193 | |||
| (значение p) | (0,006) | (0,006) | |||
| zb2: возникновение диареи | |||||
| Intercept αb2 | 0,6631 ± 2,557 | 0,6741 ± 2,605 | |||
| (значение p ) | (0.611) | (0,612) | |||
| Эффект лечения βb2 | −0,6231 ± 0,192 | −0,6422 ± 0,198 | |||
| (значение p) | (<0,001) | (<0,001) | |||
| zc1: измерение гемоглобина | |||||
| Intercept αc1 | 160,3758 ± 32,989 | 160,3775 ± 32,984 | |||
| (значение p) | (<0,001) | (<0,001) | −12.492 ± 2,498 | −12,496 ± 2,454 | |
| (значение p) | (<0,001) | (<0,001) | |||
| zc2: измерение лейкоцитов | |||||
| Перехват αc2 | 12,295 ± 9,331 | 12,2946 ± 9,515 | |||
| (значение p) | (0,010) | (0,011) | |||
| Эффект лечения βc2 | -0,1591 ± 0,706 | -0,1597 ± 0,7074 | (значение p) | (0.659) | (0,656) |
Таблица 4. Результаты оценки II: оцениваемые параметры содержат вторые моменты каждого исхода.
Таблица 4. Результаты оценки II: оцениваемые параметры содержат вторые моменты каждого исхода.
| Расчетная корреляция | Расчетное стандартное отклонение | ||||
|---|---|---|---|---|---|
| Тошнота | Диарея | HGB | WBC | ||
| Тошнота | 1.0000 | 0,3954 | 0,0736 | 0,0899 | — |
| Диарея | 1,0000 | 0,0351 | −0,0126 | — | |
| HGB | 25 00 | 00 16.796 | |||
| WBC | 1.0000 | 4.7507 | |||
© 2020 Авторы. Лицензиат MDPI, Базель, Швейцария.Эта статья представляет собой статью в открытом доступе, распространяемую в соответствии с условиями лицензии Creative Commons Attribution (CC BY) (http://creativecommons.org/licenses/by/4.0/).
Совместное моделирование и метод оценки многомерных продольных данных со смешанными типами ответов для анализа данных о физической активности, генерируемых акселерометрами
. 2017 10 ноября; 36 (25): 4028-4040. DOI: 10.1002 / sim.7401. Epub 2017 7 августа.Принадлежности Расширять
Принадлежности
- 1 Отделение онкологии и общественных наук о здоровье, Университет Калгари, Калгари, Канада.
- 2 Отделение онкологии, Университет Калгари, Калгари, Канада.
- 3 Департамент статистики Техасского университета A&M, Колледж-Стейшен, США.
- 4 Школа математических и физических наук, Технологический университет Сиднея, Бродвей, Австралия.
- 5 Кафедра кинезиологии, Калифорнийский политехнический государственный университет, Сан-Луис-Обиспо, США.
- 6 Национальный институт рака, Бетесда, США.
Элемент в буфере обмена
Haocheng Li et al. Stat Med. .
Бесплатная статья PMC Показать детали Показать вариантыПоказать варианты
Формат АннотацияPubMedPMID
.2017 10 ноября; 36 (25): 4028-4040. DOI: 10.1002 / sim.7401. Epub 2017 7 августа.Принадлежности
- 1 Отделение онкологии и общественных наук о здоровье, Университет Калгари, Калгари, Канада.
- 2 Отделение онкологии, Университет Калгари, Калгари, Канада.
- 3 Департамент статистики Техасского университета A&M, Колледж-Стейшен, США.
- 4 Школа математических и физических наук, Технологический университет Сиднея, Бродвей, Австралия.
- 5 Кафедра кинезиологии, Калифорнийский политехнический государственный университет, Сан-Луис-Обиспо, США.
- 6 Национальный институт рака, Бетесда, США.
Элемент в буфере обмена
Полнотекстовые ссылки Опции CiteDisplayПоказать варианты
Формат АннотацияPubMedPMID
Абстрактный
Предлагается модель смешанного эффекта для совместного анализа многомерных продольных данных с непрерывными, пропорциональными, счетными и бинарными ответами.Связь переменных моделируется посредством корреляции случайных эффектов. Мы используем приближение типа квази-правдоподобия для нелинейных переменных и преобразовываем предложенную модель в многомерную линейную смешанную модель для оценки и вывода. За счет расширения подхода EM разработан эффективный алгоритм, соответствующий модели. Этот метод применяется к данным о физической активности, в которых используется носимый акселерометр для измерения ежедневных перемещений и информации о расходах энергии.Наш подход также оценивается с помощью моделирования.
Ключевые слова: акселерометры; продольные данные; модель смешанных эффектов; многомерные продольные данные; оштрафованная квазивероятность.
Авторские права © 2017 John Wiley & Sons, Ltd.
Цифры
Рисунок 1
Примеры данных от двух субъектов…
Рисунок 1
Пример данных от двух субъектов на неделях 0, 3, 6, 9 и 12.…
Рисунок 1Выборочные данные от двух субъектов на неделях 0, 3, 6, 9 и 12. Сплошные линии и метки «X» отображают наблюдения пациента с ID 4. Пунктирные линии и метки «O» представляют результаты для человека с ID 5. (a) Y (1) : непрерывная переменная для ежедневных часов малоподвижного образа жизни; (b) Y (2) : непрерывная переменная для расхода энергии; (c) Y (3) : доля времени, проведенного в сидячем положении более 20 минут, (d) Y (4) : доля активного времени более 5 минут; (e) Y (5) : подсчитать количество ежедневных вставок; (f) Y (6) : подсчет количества ежедневных шагов; (g) Y (7) : двоичная переменная для определения того, превышает ли время ежедневной умеренной или высокой физической активности (MVPA) один час; (h) Y (8) : двоичная переменная, определяющая, превышает ли максимальное значение расхода энергии, измеренное метаболическими эквивалентами (MET) за 10 минут, 3.
Рисунок 2
Результаты моделирования для условного…
Рисунок 2
Результаты моделирования для условных ожиданий для ℓ = 1, 2, определенных в…
фигура 2Результаты моделирования для условных ожиданий для ℓ = 1, 2, определенных в разделе 4.(a) (b) сценарий среднего размера выборки с n = 200 и J i = 5, (c) (d) сценарий большого размера выборки с n = 400 и J i = 9. Пунктирные линии обозначают истинные значения условного ожидания. Сплошные линии представляют собой усредненные значения оценок из нашего метода JOINT-PQL2. Затененные области отображают квантили от 10% до 90% расчетных значений за 500 прогонов моделирования. Толстые и тонкие пунктирные линии представляют собой усредненные оценки, полученные методами NAIVE1 и NAIVE2 соответственно.
Рисунок 3
Оценки условных ожиданий…
Рисунок 3
Оценки условных ожиданий в течение пяти недель для ежедневных часов сидячего образа жизни (…
Рисунок 3Оценка условных ожиданий в течение пяти недель для ежедневного сидячего образа жизни. (Yij (1)) и уровни расхода энергии (Yij (2)), определенный в разделе 5.Лицо, которое соответствует критериям Раздела 5 на неделе 0, определяется как активный участник, в то время как те, кто не соответствует ни одному условию на неделе 0, определяется как неактивный участник. Толстые и тонкие линии представляют оценки активных и неактивных участников соответственно. Сплошные и пунктирные линии отображают группу упражнений и контрольную группу соответственно.
Похожие статьи
-
Методы трехкомпонентного совместного моделирования сложных функциональных данных, смешанных с раздутыми пропорциями с нулевым и единичным завышением, и непрерывными результатами с нулевым завышением и асимметрией.
Ли Х, Штауденмайер Дж, Ван Т., Кидл С.К., Кэрролл Р.Дж. Ли Х и др. Stat Med. 2018 20 февраля; 37 (4): 611-626. DOI: 10.1002 / sim.7534. Epub 2017 19 октября. Stat Med. 2018. PMID: 239 Бесплатная статья PMC.
-
Иерархические функциональные данные со смешанными непрерывными и двоичными измерениями.
Ли Х., Штауденмайер Дж., Кэрролл Р.Дж. Ли Х и др.Биометрия. 2014 декабрь; 70 (4): 802-11. DOI: 10.1111 / biom.12211. Epub 2014 18 августа. Биометрия. 2014 г. PMID: 25134936
-
Многомерные t нелинейные модели со смешанными эффектами для продольных данных с несколькими исходами с пропущенными значениями.
Ван В.Л., Лин Т.И. Ван В.Л. и др. Stat Med. 2014 30 июля; 33 (17): 3029-46. DOI: 10.1002 / sim.6144. Epub 2014 17 марта. Stat Med.2014 г. PMID: 24634345
-
Методы выбора модели для ковариационной матрицы для неполных продольных данных.
Грейди Дж. Дж., Хелмс Р. У. Грэди Дж. Дж. И др. Stat Med. 1995 г., 15 июля; 14 (13): 1397-416. DOI: 10.1002 / sim.4780141302. Stat Med. 1995 г. PMID: 7481180 Рассмотрение.
-
Анализ многомерных продольных данных: обзор.
Verbeke G, Fieuws S, Molenberghs G, Davidian M. Verbeke G, et al. Stat Methods Med Res. 2014 Февраль; 23 (1): 42-59. DOI: 10.1177 / 0962280212445834. Epub 2012 20 апреля. Stat Methods Med Res. 2014 г. PMID: 22523185 Бесплатная статья PMC. Рассмотрение.
Процитировано
1 артикул-
Обзор статистического анализа данных о физической активности, полученных с акселерометров.
Чжан Ю., Ли Х, Кидл С.К., Мэтьюз К.Э., Кэрролл Р.Дж. Zhang Y, et al. Stat Biosci. 2019; 11 (2): 465-476. DOI: 10.1007 / s12561-019-09250-6. Epub 2019 28 июня. Stat Biosci. 2019. PMID: 32863980 Бесплатная статья PMC.
LinkOut — дополнительные ресурсы
-
Источники полных текстов
-
Другие источники литературы
цитировать
КопироватьФормат: AMA APA ГНД NLM
Модель GLMM на основе копул для многомерных продольных данных со смешанными типами ответов
Aas, K., Czado, C., Frigessi, A. и Bakken, H. (2009). Парно-связочные конструкции множественной зависимости. Страхование: математика и экономика 44 , 2, 182–198.
MathSciNet МАТЕМАТИКА Google ученый
Айткин М. (1999). Общий анализ максимального правдоподобия компонентов дисперсии в обобщенных линейных моделях. Биометрия 55 , 1, 117–128.
MathSciNet МАТЕМАТИКА Статья Google ученый
Bandyopadhyay, S., Гангули Б. и Чаттерджи А. (2011). Обзор многомерного лонгитюдного анализа данных. Статистические методы в медицинских исследованиях 20 , 4, 299–330.
MathSciNet МАТЕМАТИКА Статья Google ученый
Бедфорд, Т. и Кук, Р. М. (2002). Vines: новая графическая модель для зависимых случайных величин. Анналы статистики 30 , 4, 1031–1068.
MathSciNet МАТЕМАТИКА Статья Google ученый
Батлер, С.М. и Луи Т. А. (1992). Модели случайных эффектов с непараметрическими априорными значениями. Статистика в медицине 11 , 14-15, 1981–2000.
Артикул Google ученый
Чен, Ю., Фей, Ю. и Пан, Дж. (2015). Квази-Монте-Карло оценка в обобщенной линейной смешанной модели с коррелированными случайными эффектами. Журнал библиотеки открытого доступа 2 , 10, 1.
Google ученый
Чо, Х.(2016). Анализ многомерных продольных данных с использованием многомерных маржинальных моделей. Журнал многомерного анализа 143 , 481–491.
MathSciNet МАТЕМАТИКА Статья Google ученый
Диссманн, Дж., Брехманн, Э. К., Чадо, К. и Куровицка, Д. С. (2013). Выбор и оценка регулярных связок виноградной лозы и их применение для получения финансовой прибыли. Вычислительная статистика и анализ данных 59 , 52–69.
MathSciNet МАТЕМАТИКА Статья Google ученый
Феддаг, М. Л., Грама, И. и Месбах, М. (2003). Обобщенные оценочные уравнения (GEE) для смешанных логистических моделей. Коммуникации в статистике, теории и методах 32 , 4, 851–874.
MathSciNet МАТЕМАТИКА Статья Google ученый
Fieuws, S., Verbeke, G., Maes, B.и Ванрентергхем Ю. (2007). Прогнозирование почечной недостаточности трансплантата с использованием многомерных продольных профилей. Биостатистика 9 , 3, 419–431.
MATH Статья Google ученый
Флеминг Т. Р. и Харрингтон Д. П. (1991). Процессы подсчета и анализ выживаемости . Вили, Нью-Йорк.
MATH Google ученый
Галлант, А.Р. и Нычка, Д. В. (1987). Полупараметрическая оценка максимального правдоподобия. Econometrica: Journal of the Econometric Society , 363–390.
Хе Дж., Ли Х., Эдмондсон А. К., Рейдер Д. Дж. И Ли М. (2012). Подход гауссовой связки для анализа вторичных фенотипов в исследованиях генетических ассоциаций случай-контроль. Биостатистика 13 , 3, 497–508.
MATH Статья Google ученый
Яффо, М.А., Гебрегзиабер М., Латтрелл Д. К., Латтрелл Л. М. и Яффа А. А. (2016). Многомерные обобщенные линейные смешанные модели со случайными перехватами для анализа маркеров сердечно-сосудистого риска у пациентов с диабетом 1 типа. Журнал прикладной статистики 43 , 8, 1447–1464.
MathSciNet Статья Google ученый
Джо, Х. (1996). Семейства m-переменных распределений с заданными границами и параметрами двумерной зависимости m (m-1) / 2. Конспект лекций — серия монографий , 120–141.
Джо, Х. (1997). Многомерные модели и концепции многомерной зависимости . Чепмен и Холл, Лондон.
MATH Книга Google ученый
Килличес, М. и Чадо, К. (2017). Модель на основе копулы D-Vine для повторных измерений, расширяющая линейные смешанные модели с однородной корреляционной структурой. arXiv: 1705.06261.
Ким, Д., Ким, Дж. М., Ляо, С. М. и Юнг, Ю. С. (2013). Смесь связок D-Vine для моделирования зависимости. Вычислительная статистика и анализ данных 64 , 1–19.
MathSciNet МАТЕМАТИКА Статья Google ученый
Лэрд, Н. М. и Уэр, Дж. Х. (1982). Модели со случайными эффектами для продольных данных. Биометрия , 963–974.
Ламберт, П.и Vandenhende, F. (2002). Модель на основе связок для многомерных ненормальных продольных данных: анализ исследования безопасности титрования дозы нового антидепрессанта. Статистика в медицине 21 , 21, 3197–3217.
Артикул Google ученый
Лян, К. Ю. и Зегер, С. Л. (1986). Продольный анализ данных с использованием обобщенных линейных моделей. Биометрика 73 , 1, 13–22.
MathSciNet МАТЕМАТИКА Статья Google ученый
Луис, Т.А. (1982). Нахождение наблюдаемой информационной матрицы при использовании алгоритма EM. Журнал Королевского статистического общества. Серия B (Методологическая) , 226–233.
Мин, Ю. и Агрести, А. (2005). Модели со случайным эффектом для повторных измерений нулевых данных подсчета. Статистическое моделирование 5 , 1, 1–19.
MathSciNet МАТЕМАТИКА Статья Google ученый
Нельсен Р.(2006). Введение в связки , 2-е изд. Спрингер, Нью-Йорк.
MATH Google ученый
Панагиотелис А., Чадо К. и Джо Х. (2012). Конструкции парных копул для многомерных дискретных данных. Журнал Американской статистической ассоциации 107 , 499, 1063–1072.
MathSciNet МАТЕМАТИКА Статья Google ученый
Пиньейру, Дж.К. и Бейтс, Д. М. (1995). Аппроксимация логарифмической функции правдоподобия в нелинейной модели смешанных эффектов. Журнал вычислительной и графической статистики 4 , 1, 12–35.
Google ученый
Рочон, Дж. (1996). Анализ двумерных повторяющихся измерений для дискретных и непрерывных переменных результата. Биометрия 52 , 740–750.
MATH Статья Google ученый
Скляр, А.(1959). Функции перераспределения по размерам и границам. Публикации Статистического института Парижского университета , 8 , 229–231.
Смит, М., Мин, А., Алмейда, К. и Чадо, К. (2010). Моделирование продольных данных с использованием парно-связочного разложения серийной зависимости. Журнал Американской статистической ассоциации 105 , 492, 1467–1479.
MathSciNet МАТЕМАТИКА Статья Google ученый
Сонг, П.X. К., Ли, М. и Юань, Ю. (2009). Совместный регрессионный анализ коррелированных данных с использованием гауссовых копул. Биометрия 65 , 1, 60–68.
MathSciNet МАТЕМАТИКА Статья Google ученый
Сан, Дж., Фрис, Э. В. и Розенберг, М. А. (2008). Продольное моделирование данных с тяжелыми хвостами с использованием связок. Страхование: математика и экономика 42 , 2, 817–830.
MATH Google ученый
Вербеке, Г.и Lesaffre, E. (1997). Эффект неправильного определения распределения случайных эффектов в линейных смешанных моделях для продольных данных. Вычислительная статистика и анализ данных 23 , 4, 541–556.
MathSciNet МАТЕМАТИКА Статья Google ученый
Verbeke, G., Fieuws, S., Molenberghs, G. и Davidian, M. (2014). Анализ многомерных продольных данных: обзор. Статистические методы в медицинских исследованиях 23 , 1, 42–59.
MathSciNet Статья Google ученый
Ван, Ю. Г. и Кэри, В. (2003). Неправильная спецификация, оценка и ковариативный дизайн рабочей корреляционной структуры: последствия для работы обобщенных оценочных уравнений. Биометрика 90 , 1, 29–41.
MathSciNet МАТЕМАТИКА Статья Google ученый
Зегер, С. Л. и Лян, К.Ю. (1991). Модели обратной связи для дискретных и непрерывных временных рядов. Statistica Sinica , 51–64.
Чжан Д. и Давидян М. (2001). Линейные смешанные модели с гибкими распределениями случайных эффектов для продольных данных. Биометрия 57 , 3, 795–802.
MathSciNet МАТЕМАТИКА Статья Google ученый
Зилко А.А., Куровицка Д. (2016). Копула в многомерной смешанной дискретно-непрерывной модели. Вычислительная статистика и анализ данных 103 , 28–55.
MathSciNet МАТЕМАТИКА Статья Google ученый
MissForest — непараметрическое вменение пропущенных значений для данных смешанного типа | Биоинформатика
Аннотация
Мотивация: Современный сбор данных на основе высокопроизводительной технологии часто сталкивается с проблемой отсутствия данных. Алгоритмы, обычно используемые при анализе таких крупномасштабных данных, часто зависят от полного набора.Вменение пропущенных значений предлагает решение этой проблемы. Однако большинство доступных методов вменения ограничены только одним типом переменных: непрерывными или категориальными. Для данных смешанного типа разные типы обычно обрабатываются отдельно. Следовательно, эти методы игнорируют возможные отношения между типами переменных. Мы предлагаем непараметрический метод, который может работать с разными типами переменных одновременно.
Результатов: Мы сравниваем несколько современных методов вменения пропущенных значений.Мы предлагаем и оцениваем метод итеративного вменения (missForest) на основе случайного леса. Посредством усреднения по множеству необрезанных деревьев классификации или регрессии случайный лес по сути представляет собой схему множественного вменения. Используя встроенные оценки ошибок случайного леса, мы можем оценить ошибку вменения без использования тестового набора. Оценка выполняется на нескольких наборах данных, полученных из разнообразного набора биологических полей с искусственно введенными пропущенными значениями в диапазоне от 10% до 30%.Мы показываем, что missForest может успешно обрабатывать отсутствующие значения, особенно в наборах данных, включающих различные типы переменных. В нашем сравнительном исследовании missForest превосходит другие методы вменения, особенно в настройках данных, где предполагается наличие сложных взаимодействий и нелинейных отношений. Оценки ошибок условного исчисления для missForest оказываются адекватными во всех условиях. Кроме того, missForest демонстрирует привлекательную вычислительную эффективность и может работать с данными большого размера.
Доступность: Пакет ℝ missForest находится в свободном доступе по адресу http://stat.ethz.ch/CRAN/.
Контактное лицо: [email protected]; [email protected]
1 ВВЕДЕНИЕ
Вменение пропущенных значений часто является решающим шагом в анализе данных. Многие устоявшиеся методы анализа требуют полностью наблюдаемых наборов данных без каких-либо пропущенных значений. Однако сегодня в медицинских и биологических исследованиях такое бывает редко.Постоянная разработка новых и усовершенствованных методов измерения в этих областях ставит перед аналитиками данных задачи, вызванные не только многомерными многомерными данными, в которых количество переменных может значительно превышать количество наблюдений, но также и смешанными типами данных, где непрерывные и категориальные переменные присутствуют. В нашем контексте категориальные переменные могут возникать в любом виде, начиная от технических настроек масс-спектрометра и заканчивая диагностическим экспертным заключением о состоянии болезни.Кроме того, такие наборы данных часто содержат сложные взаимодействия и структуры нелинейных отношений, которые, как известно, трудно уловить с помощью параметрических процедур.
Наиболее распространенные методы вменения, например k ближайших соседей [KNNimpute, Troyanskaya et al. (2001)] для непрерывных данных, насыщенная полиномиальная модель (Schafer, 1997) для категориальных данных и многомерное вменение посредством связанных уравнений [MICE, Van Buuren and Oudshoorn (1999)] для смешанных типов данных зависят от параметров настройки или спецификации параметрического модель.Выбор таких параметров настройки или моделей без предварительных знаний затруднен и может существенно повлиять на производительность метода. За исключением MICE, вышеуказанные методы и большинство других методов вменения ограничены одним типом переменных. Кроме того, все эти методы делают предположения о распределении данных или подмножеств переменных, что приводит к сомнительным ситуациям, например в предположении нормального распределения.
Литература по вменению данных смешанного типа довольно скудна.Его первое появление было в развивающейся области множественного вменения, о которой говорил Рубин (1978). Литтл и Шлухтер (1985) представили подход, основанный на оценке максимального правдоподобия, сочетающий многомерную нормальную модель для непрерывных и пуассоновскую / полиномиальную модель для категориальных данных. Позднее эта идея была развита в книге Литтла и Рубина (1987). См. Также Ли (1988), Рубин и Шафер (1990) и Шафер (1997). Ван Бюрен и Оудшорн (1999) предложили более совершенный метод объединения различных регрессионных моделей для данных смешанного типа с использованием связанных уравнений.Условная модель в MICE может быть указана для недостающих данных в каждой неполной переменной. Следовательно, не требуется указывать многомерную модель, охватывающую весь набор данных. Однако предполагается, что такое полное многомерное распределение существует и пропущенные значения отбираются из условных распределений на основе этого полного распределения (подробнее см. Раздел 3). Другой аналогичный метод с использованием условных распределений с переменными значениями был предложен Raghunathan et al. (2001) называется многомерным вменением последовательной регрессии.В отличие от MICE, предикторы не должны быть неполными. Метод ориентирован на данные опроса и, следовательно, включает стратегии для включения ограничений на подвыборки лиц и логических границ, основанных на знании предметной области о переменных, например только женщины могут иметь зарегистрированное количество беременностей.
Наша мотивация состоит в том, чтобы ввести метод вменения, который может обрабатывать любые типы входных данных и делает как можно меньше предположений о структурных аспектах данных. Случайный лес [RF, Breiman (2001)] может работать с данными смешанного типа, и в качестве непараметрического метода он допускает интерактивные и нелинейные (регрессионные) эффекты.Мы решаем проблему отсутствующих данных, используя итеративную схему вменения, обучая RF на наблюдаемых значениях на первом этапе, с последующим прогнозированием отсутствующих значений и последующим итеративным действием. Mazumder et al. (2010) используют аналогичный подход для задачи завершения матрицы, используя SVD с мягким пороговым значением, итеративно заменяя пропущенные значения. Мы выбрали RF, потому что он может обрабатывать данные смешанного типа и, как известно, очень хорошо работает в бесплодных условиях, таких как большие размеры, сложные взаимодействия и нелинейные структуры данных.Благодаря своей точности и надежности, RF хорошо подходит для использования в прикладных исследованиях, часто имеющих такие условия. Кроме того, алгоритм RF позволяет оценивать частоту ошибок вне сумки (OOB) без необходимости в тестовом наборе. Для получения дополнительной информации см. Breiman (2001).
Здесь мы сравниваем наш метод с вменением ближайшего соседа k [KNNimpute, Troyanskaya et al. (2001)] и алгоритм чередующегося лассо с образцом отсутствия (MissPALasso) Стедлера и Бюльмана (2010) для наборов данных, содержащих только непрерывные переменные.Для случаев категориального и смешанного типа переменных мы сравниваем наш метод с алгоритмом MICE Ван Бюреном и Оудшорном (1999) и фиктивной переменной, закодированной KNNimpute. Сравнение выполняется на нескольких наборах данных из разных областей наук о жизни с использованием различных пропорций пропущенных значений.
Мы показываем, что наш подход конкурентоспособен или превосходит сравниваемые методы на используемых наборах данных, независимо от состава типов переменных, размерности данных, источника данных или количества пропущенных значений.В некоторых случаях уменьшение ошибки вменения составляет до 50%. Такая производительность обычно достигается всего за несколько итераций, что делает наш метод привлекательным с точки зрения вычислений. Оценки ошибки вменения OOB дают очень хорошее приближение к истинной ошибке вменения, имеющей в среднем пропорциональное отклонение не более 10–15%. Кроме того, наш подход не требует параметра настройки, поэтому прост в использовании и не требует предварительных знаний о данных.
2 ПОДХОД
Мы предполагаем, что X = ( X 1 , X 2 ,…, X p ) как n × p -мерная матрица данных.Мы предлагаем использовать RF для вменения недостающих значений из-за его ранее упомянутых преимуществ в качестве метода регрессии. В RF-алгоритм есть встроенная процедура для обработки пропущенных значений путем взвешивания частоты наблюдаемых значений в переменной с RF-близостями после обучения на первоначально рассчитанном наборе данных среднего значения (Breiman, 2001). Однако этот подход требует полной переменной отклика для обучения леса.
Вместо этого мы напрямую прогнозируем недостающие значения, используя RF, обученный на наблюдаемых частях набора данных.Для произвольной переменной X s , включая пропущенные значения в записях i ( s ) mis ⊆ {1,…, n }, мы можем разделить набор данных на четыре части: Обратите внимание, что x ( s ) obs обычно не наблюдается полностью, поскольку индекс i ( s ) obs соответствует наблюдаемым значениям переменной X s .Аналогично, x ( s ) mis обычно не полностью отсутствует.
-
Наблюдаемые значения переменной X s , обозначенные как y ( s ) obs ;
-
пропущенные значения переменной X s , обозначенные y ( s ) mis ;
-
переменные, отличные от X s с наблюдениями i ( s ) obs = {1,…, n } ∖ i s ( s ) mis обозначается x ( s ) obs ; и
-
переменные, отличные от X s с наблюдениями i ( s ) mis , обозначенное x ( s )
92 .1591 mis
Для начала сделайте первоначальное предположение для отсутствующих значений в X , используя вменение среднего или другой метод вменения. Затем отсортируйте переменные X s , s = 1,…, p в соответствии с количеством пропущенных значений, начиная с наименьшего значения. Для каждой переменной X s недостающие значения рассчитываются путем первой подгонки RF с ответом y ( s ) obs и предикторов x ( s ) obs ; затем прогнозирование отсутствующих значений y ( s ) mis путем применения обученного RF к x ( s ) mis .Процедура вменения повторяется до тех пор, пока не будет выполнен критерий остановки. Псевдоалгоритм 1 дает представление о методе missForest.
Критерий остановки γ выполняется, как только разница между новой вмененной матрицей данных и предыдущей увеличивается в первый раз по обоим типам переменных, если они есть. Здесь разница для набора непрерывных переменных N определяется как и для набора категориальных переменных F , где #NA — количество пропущенных значений в категориальных переменных.После подстановки пропущенных значений производительность оценивается с использованием нормализованной среднеквадратичной ошибки [NRMSE, Oba et al. (2003)] для непрерывных переменных, которая определяется как где X истинно, — это полная матрица данных, а X имп — матрица вмененных данных. Мы используем mean и var в качестве кратких обозначений для эмпирического среднего и дисперсии, вычисленных только по непрерывным пропущенным значениям. Для категориальных переменных мы используем долю ошибочно классифицированных записей (PFC) по сравнению с категориальными пропущенными значениями, Δ F .В обоих случаях хорошая производительность приводит к значению, близкому к 0, а плохая — к значению около 1.Когда RF соответствует наблюдаемой части переменной, мы также получаем оценку ошибки OOB для этой переменной. После того, как критерий остановки γ был соблюден, мы усредняем набор переменных одного и того же типа, чтобы аппроксимировать истинные ошибки вменения. Мы оцениваем эффективность этой оценки, сравнивая абсолютную разницу между истинной ошибкой вменения и оценкой ошибки вменения внепланового взноса во всех прогонах моделирования.
3 МЕТОДА
Мы сравниваем missForest с четырьмя методами на 10 различных наборах данных, где мы различаем ситуации только с непрерывными переменными, только категориальными переменными и смешанными типами переменных.
Наиболее известным методом вменения непрерывных наборов данных, особенно в области анализа экспрессии генов, является алгоритм KNNimpute Троянской и др. (2001). Переменная с отсутствующим значением X j рассчитывается путем нахождения ее ближайших наблюдаемых переменных k и взятия средневзвешенного значения этих k переменных для вменения.Таким образом, веса зависят от расстояния переменной X j . Само расстояние обычно выбирается равным евклидову расстоянию.
При использовании KNNimpute выбор параметра настройки k может иметь большое влияние на производительность вменения. Однако заранее этот параметр не известен. Поскольку наш метод не содержит такого параметра, мы реализуем перекрестную проверку (алгоритм 2) для получения подходящего значения k .
В оригинальной статье Троянской и др. (2001) данные не были стандартизированы до применения алгоритма KNNimpute. Это не составляет проблемы в случае данных об экспрессии генов, потому что такие данные обычно состоят из переменных схожих масштабов. Однако мы применяем алгоритм KNNimpute к наборам данных с различными масштабами переменных. Чтобы избежать взвешивания переменных на основе дисперсии, мы масштабируем их до единицы SD. Мы также центрируем переменные в нуле. После вменения данные повторно преобразуются, так что ошибка вычисляется по исходным шкалам.Этот последний шаг выполняется, потому что missForest не нуждается в преобразовании данных, и мы хотим сравнить производительность методов на исходных масштабах данных.
Другой подход к непрерывным данным, особенно в случае многомерных нормальных матриц данных, представлен Städler и Bühlmann (2010) с использованием алгоритма типа EM. В их алгоритме чередования паттернов отсутствия и l 1 штрафов (MissPALasso) пропущенные переменные регрессируют по наблюдаемым переменным с использованием штрафа лассо Тибширани (1996).На следующем этапе E полученные коэффициенты регрессии используются для частичного обновления скрытого распределения. MissPALasso также имеет параметр настройки λ для штрафа. Как и в случае с KNNimpute, мы используем перекрестную проверку для настройки λ (см. Алгоритм 2). При применении MissPALasso данные стандартизируются, поскольку регуляризация с одним λ требует, чтобы разные регрессии были в одном масштабе.
В сравнительных экспериментах с категориальными переменными или переменными смешанного типа мы используем алгоритм MICE Ван Бюрена и Оудшорна (1999), основанный на многомерной схеме множественного вменения Шафера (1997).В отличие от последнего, условное распределение для недостающих данных в каждой неполной переменной задается в MICE, функция, названная Ван Бюреном (2007) полностью условной спецификацией. Однако предполагается существование многомерного распределения, из которого можно легко получить условное распределение. Кроме того, итеративная выборка Гиббса из условных распределений может генерировать результаты из многомерного распределения. Мы хотим отметить, что MICE в своей настройке по умолчанию в основном не предназначен для простого вменения пропущенных значений.Используя схему множественного вменения, MICE позволяет оценить неопределенность вмененных значений. Он включает в себя функции для объединения нескольких вменений, выбора индивидуальных процедур выборки и позволяет пассивное вменение, контролирующее синхронизацию преобразованных переменных. В наших экспериментах мы использовали MICE либо с линейной регрессией с нормальными ошибками, либо с вменением среднего для непрерывных переменных, логистической регрессией для двоичных переменных и политомической логистической регрессией для категориальных переменных с более чем двумя категориями.
Для сравнения различных типов переменных мы применяем алгоритм KNNimpute с фиктивным кодированием категориальных переменных. Это делается путем кодирования категориальной переменной X j в m дихотомических переменных . Применение алгоритма KNNimpute для категориальных данных можно резюмировать следующим образом:
-
Кодировать все категориальные переменные в {-1,1} -думанные переменные;
-
стандартизировать все переменные до значений 0 и SD 1;
-
применить перекрестно проверенный метод KNNimpute из алгоритма 2;
-
повторно преобразует матрицу вмененных данных в исходные масштабы;
-
кодировать фиктивные переменные обратно в категориальные переменные; и
-
вычислили ошибку вменения.
Для каждого эксперимента мы выполняем 50 независимых симуляций, в которых 10, 20 или 30% значений удаляются полностью случайным образом. Затем применяется каждый метод и вычисляются NRMSE, PFC или и то, и другое (Раздел 2). Мы проводим парный тест Вилкоксона для оценки частоты ошибок сравниваемых методов по сравнению с частотой ошибок missForest. Кроме того, оценки ошибок OOB для missForest записываются при каждом моделировании.
4 РЕЗУЛЬТАТЫ
4.1 Только непрерывные переменные
Во-первых, мы сосредотачиваемся на непрерывных данных. Мы исследуем следующие четыре общедоступных набора данных:
-
Сеть изопреноидных генов в Arabidopsis thaliana : эта сеть генов включает P = 39 генов, каждый с n = 118 профилями экспрессии генов, соответствующими различным экспериментальным условиям. Для получения дополнительных сведений об этом наборе данных см. Wille et al. (2004).
-
Голосовые измерения у пациентов с болезнью Паркинсона: данные, описанные Little et al. (2008) содержит ряд биомедицинских измерений голоса 31 человека, 23 из которых страдали болезнью Паркинсона (БП). Есть P = 22 отдельных измерения голоса и n = 195 записей голоса от этих людей. Набор данных также содержит переменную ответа, дающую статус работоспособности. Имея дело только с непрерывными переменными, ответ был удален из данных. Мы вернемся к этому позже.
-
Формы молекул мускуса: этот набор данных описывает 92 молекулы, из которых 47 являются мускусами, а 45 — немускусами.Для каждой молекулы P = 166 признаков описывают ее конформацию, но поскольку молекула может иметь много конформаций из-за вращающихся связей, в наборе имеется n = 476 различных низкоэнергетических конформаций. Разделение на мускусные и немускусные молекулы удалено.
-
Экспрессия гена инсулина: этот большой набор данных основан на анализе Wu et al. (2007) из обширных мышц бедра и биопсий мышц трех разных типов пациентов после лечения инсулином.Эти три типа — это инсулино-чувствительные, инсулинорезистентные и диабетические пациенты. Анализ включает P = 12’626 генов, уровни экспрессии которых были измерены из n = 110 биопсий мышц. Из-за времени вычислений мы выполняем только 10 симуляций вместо 50.
Результаты представлены на рисунке 1. Мы видим, что missForest работает хорошо, иногда снижая средний NRMSE до 25% по сравнению с KNNimpute. В случае данных о молекулах мускуса снижение составляет даже> 50%.MissPALasso работает немного лучше, чем missForest, по данным экспрессии генов. Однако для набора данных инсулина результатов для MissPALasso нет, потому что высокая размерность делает вычисления невозможными.
Рис. 1.
Непрерывные данные. Среднее значение NRMSE для KNNimpute (серый), MissPALasso (белый) и missForest (черный) для четырех разных наборов данных и трех разных количеств пропущенных значений, то есть 10, 20 и 30%. Стандартные ошибки имеют порядок величины 10 908 · 10 −4 .Уровни значимости парных тестов Вилкоксона в пользу missForest кодируются как «*» <0,05, «**» <0,01 и «***» <0,001. Если средняя ошибка сравниваемого метода меньше, чем у missForest, уровень значимости кодируется хешем (#) вместо звездочки. В самом нижнем наборе данных результаты для MissPALasso отсутствуют из-за ограниченных возможностей реализации в отношении больших измерений.
Рис. 1.
Непрерывные данные. Среднее значение NRMSE для KNNimpute (серый), MissPALasso (белый) и missForest (черный) для четырех разных наборов данных и трех разных количеств пропущенных значений, т.е.е. 10, 20 и 30%. Стандартные ошибки имеют порядок величины 10 908 · 10 −4 . Уровни значимости парных тестов Вилкоксона в пользу missForest кодируются как «*» <0,05, «**» <0,01 и «***» <0,001. Если средняя ошибка сравниваемого метода меньше, чем у missForest, уровень значимости кодируется хешем (#) вместо звездочки. В самом нижнем наборе данных результаты для MissPALasso отсутствуют из-за ограниченных возможностей реализации в отношении больших измерений.
Для непрерывных данных алгоритм missForest обычно достигает критерия остановки довольно быстро, требуется около пяти итераций. Вменение занимает в ~ 10 раз больше времени, чем выполнение перекрестной проверки KNNimpute, где {1,…, 15} — это набор возможных чисел соседей. Для набора данных инсулина вменение занимает в среднем 2 часа на обычном доступном настольном компьютере.
4.2 Только категориальные переменные
Мы также рассматриваем наборы данных только с категориальными переменными.Здесь мы используем алгоритм MICE, описанный в разделе 3, вместо MissPALasso. Мы используем фиктивную реализацию алгоритма KNNimpute для работы с категориальными переменными (раздел 3). Мы применяем эти методы к следующим наборам данных:
-
Изображения кардиальной однофотонной эмиссионной компьютерной томографии (ОФЭКТ): Курган et al. (2001) обсуждают этот обработанный набор данных, обобщающий более 3000 изображений 2D SPECT от n = 267 пациентов в P = 22 образцах двоичных признаков.
-
Последовательности промоторного гена в Escherichia coli : набор данных содержит последовательности, найденные Harley and Reynolds (1987) для промоторов, и последовательности, найденные Towell et al. (1990) для непромоторов всего n = 106. Для каждого кандидата была записана последовательность из 57 п.н. Каждая переменная может принимать один из четырех нуклеотидов ДНК, то есть аденин, тимин, гуанин или цитозин. Другая переменная различает промоторные и непромоторные экземпляры.
-
Данные области лимфографии: наблюдения были получены на пациентах, страдающих раком лимфатической системы иммунной системы.Для каждой из n = 148 лимфом было зарегистрировано P = 19 различных свойств в основном номинальным образом. Есть девять двоичных переменных. Остальные переменные имеют три и более уровней.
На рисунке 2 мы видим, что missForest всегда вычисляет пропущенные значения лучше, чем сравниваемые методы. В некоторых случаях, а именно для данных SPECT, снижение PFC по сравнению с MICE составляет до 60%. Однако для других наборов данных снижение менее выражено и составляет около 10–20%, но все же снижение есть.С другой стороны, количество пропущенных значений, похоже, лишь незначительно влияет на производительность всех методов. За исключением MICE по данным SPECT, частота ошибок остается почти постоянной, увеличиваясь только на 1-2%. Ранее мы указывали, что MICE не предназначен в первую очередь для выполнения вменения, но предлагает дополнительные возможности оценки неопределенности вмененных значений из-за схемы множественного вменения. Как бы то ни было, результаты с использованием перекрестной проверки KNNimpute (алгоритм 2) для категориальных переменных с фиктивным кодом вызывают удивление.Для вменения missForest требуется в среднем в пять раз больше времени, чем для вменения с перекрестной проверкой с использованием KNNimpute.
Рис. 2.
Категориальные данные. Среднее значение PFC для перекрестно проверенных KNNimpute (серый), MICE (белый) и missForest (черный) для трех разных наборов данных и трех разных количеств пропущенных значений, то есть 10, 20 и 30%. Стандартные ошибки имеют порядок величины 10 908 · 10 −4 . Уровни значимости парных тестов Вилкоксона в пользу missForest кодируются как «*» <0.05, «**» <0,01 и «***» <0,001.
Рис. 2.
Категориальные данные. Среднее значение PFC для перекрестно проверенных KNNimpute (серый), MICE (белый) и missForest (черный) для трех разных наборов данных и трех разных количеств пропущенных значений, то есть 10, 20 и 30%. Стандартные ошибки имеют порядок величины 10 908 · 10 −4 . Уровни значимости парных тестов Вилкоксона в пользу missForest кодируются как «*» <0,05, «**» <0,01 и «***» <0,001.
4.3 Переменные смешанного типа
Далее мы исследуем четыре набора данных, в которых первый уже был введен, т.е. молекулы мускуса данных, включая категориальный ответ, дающий классификацию. Другие наборы данных следующие:
-
Протеомические биомаркеры болезни Гоше: Болезнь Гоше — это редкая наследственная недостаточность ферментов. В этом наборе данных Smit et al. (2007) представляют наборы белков для биомаркеров ( P = 590) из образцов сыворотки крови ( n = 40).Бинарный ответ различает статус болезни.
-
Поиск генов сверх предсказания (GFOP) пептидный поиск: этот набор данных включает масс-спектрометрические измерения n = 595 пептидов из двух экспериментов по протеомике дробовика на нематоде Caenorhabditis elegans . Набор из P = 18 биологических, технических и аналитических переменных имел целью обнаружение новых пептидов при поиске в расширенной базе данных с использованием известных методов прогнозирования генов.
-
Данные детской больницы: этот набор данных является продуктом систематического долгосрочного обзора детей с врожденными пороками сердца после операций на открытом сердце. Наряду с переменными, связанными с дефектом и хирургическим вмешательством, также оценивались долгосрочная психологическая адаптация и качество жизни, связанное со здоровьем. После удаления наблюдений с пропущенными значениями набор данных состоит из n = 55 пациентов и P = 124 переменных, из которых 48 являются непрерывными, а 76 — категориальными.Для получения дополнительной информации см. Latal et al. (2009).
Результаты этого сравнения приведены на рисунке 3. Мы видим, что missForest работает лучше, чем два других метода, что снова снижает ошибку условного исчисления во многих случаях на> 50%. Для данных GFOP KNNimpute имеет немного меньшее значение NRMSE, чем missForest, но допускает вдвое больше ошибок для категориальных переменных. Как правило, в отношении количества пропущенных значений NRMSE имеет тенденцию иметь большую изменчивость, чем PFC, который остается в основном таким же.
К результатам условного исчисления MICE по данным Детской больницы следует относиться осторожно. Поскольку этот набор данных содержит плохо распределенные и почти зависимые переменные, например Для двоичных переменных с очень небольшим количеством наблюдений в одной категории шаблон отсутствия имеет прямое влияние на работоспособность реализации MICE в статистическом программном обеспечении R. Ошибка вменения, показанная на рисунке 3, была вычислена на основе 50 успешных симуляций путем случайной генерации шаблонов отсутствия, которые не включали только полные случаи или вообще не включали полные случаи в категории переменных.Следовательно, фактическое количество имитаций было> 50 для всех трех сумм пропущенных значений. Кроме того, почти зависимые переменные удалялись после каждого введения пропущенных значений. Это приводит к в среднем семи удаленным переменным в каждой моделировании. Из-за этой специальной манипуляции для обеспечения работоспособности реализации MICE мы не сообщаем заявления о значимости для ошибки вменения.
Рис. 3.
Данные смешанного типа. Среднее значение NRMSE (левая полоса) и PFC (правая полоса, заштриховано) для KNNimpute (серый), MICE (белый) и missForest (черный) в четырех разных наборах данных и трех разных количествах пропущенных значений, т.е.е. 10, 20 и 30%. Стандартные ошибки имеют порядок величины 10 908 · 10 −3 . Уровни значимости парных тестов Вилкоксона в пользу missForest кодируются как «*» <0,05, «**» <0,01 и «***» <0,001. Если средняя ошибка сравниваемого метода меньше, чем у missForest, уровень значимости кодируется хешем (#) вместо звездочки. Обратите внимание, что из-за плохого распределения и близкой зависимости данных Детской больницы к результатам MICE следует относиться с осторожностью (Раздел 4.3).
Рис. 3.
Данные смешанного типа. Среднее значение NRMSE (левая полоса) и PFC (правая полоса, заштриховано) для KNNimpute (серый), MICE (белый) и missForest (черный) в четырех разных наборах данных и трех разных количествах пропущенных значений, то есть 10, 20 и 30%. Стандартные ошибки имеют порядок величины 10 908 · 10 −3 . Уровни значимости парных тестов Вилкоксона в пользу missForest кодируются как «*» <0,05, «**» <0,01 и «***» <0,001. Если средняя ошибка сравниваемого метода меньше, чем у missForest, уровень значимости кодируется хешем (#) вместо звездочки.Обратите внимание, что из-за плохого распределения и близкой зависимости данных Детской больницы к результатам MICE следует относиться с осторожностью (раздел 4.3).
4.4 Ошибка вменения
В каждом эксперименте мы получаем для каждого прогона моделирования внеплановую оценку ошибки вменения. На рисунке 4 показаны различия истинной ошибки вменения, err , истинной , и оценок ошибки OOB, для непрерывных и категориальных наборов данных.Также отображается среднее значение истинной ошибки вменения и оценки ошибки OOB по всем моделям.
Рис. 4.
Разница истинной ошибки вменения err true и оценка ошибки вменения внепланового исчисления для непрерывных наборов данных ( A ) и наборов категориальных данных ( B ) и трех различных количеств пропущенных значений, т.е. 0,1, 0,2 и 0,3. В каждом случае приводится среднее значение ошибки , истинное значение (кружок) и среднее значение (плюс) по всем симуляциям.
Рис. 4.
Разница между истинной ошибкой вменения err true и оценкой ошибки вменения внебольничного исчисления для непрерывных наборов данных ( A ) и категориальных наборов данных ( B ) и трех различных количеств пропущенных значений, т. Е. 0,1 , 0,2 и 0,3. В каждом случае приводится среднее значение ошибки , истинное значение (кружок) и среднее значение (плюс) по всем симуляциям.
Мы видим, что для наборов данных Isoprenoid и Musk оценки OOB очень точны и отличаются от истинной ошибки вменения только на несколько процентов.В случае набора данных Паркинсона оценки OOB демонстрируют гораздо большую изменчивость, чем во всех других наборах данных. Однако в среднем оценка сравнительно хорошая. Для категориальных наборов данных точность оценки одинакова для всех сценариев. Оценки OOB обычно занижают ошибку вменения с увеличением количества пропущенных значений. По-видимому, абсолютный размер ошибки вменения, кажется, играет второстепенную роль в точности оценок OOB, что хорошо видно при сравнении данных SPECT и данных Promoter.
4.5 Вычислительная эффективность
Мы оцениваем вычислительные затраты missForest, сравнивая время выполнения вменения в предыдущих наборах данных. В таблице 1 показано время выполнения в секундах всех методов в проанализированных наборах данных. Мы видим, что KNNimpute — безусловно, самый быстрый метод. Однако missForest работает значительно быстрее, чем MICE и MissPALasso. Кроме того, применение missForest не требовало предшествующей стандартизации данных, трудоемкого фиктивного кодирования категориальных переменных или реализации выбора CV для настройки параметров.
Таблица 1.Среднее время выполнения (в секундах) для импортирования проанализированных наборов данных
| Набор данных . | n . | -п. . | КНН . | MissPALasso . | МЫШИ . | миссФорест . |
|---|---|---|---|---|---|---|
| Изопреноид | 118 | 39 | 0.8 | 170 | — | 5,8 |
| Паркинсона | 195 | 22 | 0,7 | 120 | — | 6,1 |
| Мускус (продолжение) | 476 | 1614 13 | 1400 | — | 250 | |
| Инсулин | 110 | 12 626 | 1800 | NA | — | 6200 |
| | ||||||
| 2614 SPECT7 | 926SPECT | 1.3 | — | 37 | 5.5 | |
| Промотор | 106 | 57 | 14 | — | 4400 | 38 |
| Лимфография | 148 | — 19 | 14 — | 900 | 93 | 7,0 |
| | ||||||
| Мускус (смешанный) | 476 | 167 | 27 | — | 2800 | 500 |
| Gaucher’s | 1.3 | — | 130 | 29 | ||
| GFOP | 595 | 18 | 2,7 | — | 1400 | 40 |
| Дети | 55 | 124 | 4000 | 110 | ||
| Набор данных . | n . | -п. . | КНН . | MissPALasso . | МЫШИ . | миссФорест . | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Изопреноид | 118 | 39 | 0,8 | 170 | — | 5,8 | ||||||
| Болезнь Паркинсона | 195 | 22 | 0,7 | 14— 12078 | 146,112078 | |||||||
| Маск (продолж.) | 476 | 166 | 13 | 1400 | — | 250 | ||||||
| Инсулин | 110 | 12 626 | 1800 | NA | — | 6200 8 | ||||||
| SPECT | 267 | 22 | 1,3 | — | 37 | 5,5 | ||||||
| Промотор | 106 | 57 | 14 | — | 926mp14 44003878 | 148 | 19 | 1.1 | — | 93 | 7.0 | |
| | ||||||||||||
| Мускус (смешанный) | 476 | 167 | 27 | — | 2800 | 500 | ||||||
| 590 | 1,3 | — | 130 | 29 | ||||||||
| GFOP | 595 | 18 | 2,7 | — | 1400 | 40 | ||||||
| Детский | 124— | 4000 | 110 | |||||||||
Среднее время выполнения (в секундах) для импортирования проанализированных наборов данных
| Набор данных . | n . | -п. . | КНН . | MissPALasso . | МЫШИ . | миссФорест . |
|---|---|---|---|---|---|---|
| Изопреноид | 118 | 39 | 0.8 | 170 | — | 5,8 |
| Паркинсона | 195 | 22 | 0,7 | 120 | — | 6,1 |
| Мускус (продолжение) | 476 | 1614 13 | 1400 | — | 250 | |
| Инсулин | 110 | 12 626 | 1800 | NA | — | 6200 |
| | ||||||
| 2614 SPECT7 | 926SPECT | 1.3 | — | 37 | 5.5 | |
| Промотор | 106 | 57 | 14 | — | 4400 | 38 |
| Лимфография | 148 | — 19 | 14 — | 900 | 93 | 7,0 |
| | ||||||
| Мускус (смешанный) | 476 | 167 | 27 | — | 2800 | 500 |
| Gaucher’s | 1.3 | — | 130 | 29 | ||
| GFOP | 595 | 18 | 2,7 | — | 1400 | 40 |
| Дети | 55 | 124 | 4000 | 110 | ||
| Набор данных . | n . | -п. . | КНН . | MissPALasso . | МЫШИ . | миссФорест . | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Изопреноид | 118 | 39 | 0,8 | 170 | — | 5,8 | ||||||
| Болезнь Паркинсона | 195 | 22 | 0,7 | 14— 12078 | 146,112078 | |||||||
| Маск (продолж.) | 476 | 166 | 13 | 1400 | — | 250 | ||||||
| Инсулин | 110 | 12 626 | 1800 | NA | — | 6200 8 | ||||||
| SPECT | 267 | 22 | 1,3 | — | 37 | 5,5 | ||||||
| Промотор | 106 | 57 | 14 | — | 926mp14 44003878 | 148 | 19 | 1.1 | — | 93 | 7.0 | |
| | ||||||||||||
| Мускус (смешанный) | 476 | 167 | 27 | — | 2800 | 500 | ||||||
| 590 | 1,3 | — | 130 | 29 | ||||||||
| GFOP | 595 | 18 | 2,7 | — | 1400 | 40 | ||||||
| Детский | 124— | 4000 | 110 | |||||||||
Есть два возможных способа ускорить вычисления. Первый — уменьшить количество деревьев, выращиваемых в каждом лесу. Во всех сравнительных исследованиях количество деревьев было установлено равным 100, что обеспечивает высокую точность, но увеличивает время выполнения. В таблице 2 мы видим, что изменение количества деревьев в лесу оказывает постоянное влияние на ошибку вменения, но сильно влияет на время вычислений, которое приблизительно линейно по количеству деревьев.
Таблица 2.Средняя ошибка вменения (NRMSE / PFC в процентах) и время выполнения (в секундах) с различным количеством деревьев ( n дерево ), выращенных в каждом лесу, и опробованными переменными ( m попытка ) в каждом узел деревьев
| м попробовать . | n дерево . | ||||
|---|---|---|---|---|---|
| . | 10 . | 50 . | 100 . | 250 . | 500 . |
| 1 | 36,8 / 35,5 | 27,4 / 32,3 | 20,4 / 31,3 | 17,2 / 30,0 | 16,0 / 30,8 |
| 2,5 с | 3,2 с | 3,8 с | 9269,2 с | ||
| 2 | 34,9 / 31,8 | 24,8 / 29.2 | 18,3 / 28,8 | 16,0 / 28,6 | 15,5 / 29,1 |
| 6,9 с | 11,8 с | 15,0 с | 25,2 с | 39,3 с | |
| 4 | 34,9 / 31,3 24,4 / 28,9 | 17,9 / 28,2 | 15,4 / 28,2 | 15,8 / 28,7 | |
| 16,5 с | 25,1 с | 35,0 с | 49,0 с | 83,3 с | |
| 8 | 34.7 / 31,4 | 24,3 / 28,9 | 18,1 / 27,8 | 15,2 / 27,8 | 15,7 / 28,6 |
| 39,2 с | 57,4 с | 84,4 с | 130,2 с | 190,8 с | |
| 34,6 / 30,9 | 24,3 / 28,7 | 18,1 / 28,0 | 15,4 / 27,8 | 15,6 / 28,5 | |
| 68,7 с | 99,7 с | 172,2 с | 237,6 с | 9782614 400,7 с237,6 с | 9782614 400,7 с|
| м попробовать . | n дерево . | |||||
|---|---|---|---|---|---|---|
| . | 10 . | 50 . | 100 . | 250 . | 500 . | |
| 1 | 36,8 / 35,5 | 27,4 / 32,3 | 20,4 / 31,3 | 17,2 / 30,0 | 16,0 / 30,8 | |
| 2,5 с | 3.2 с | 3,9 с | 5,8 с | 9,2 с | ||
| 2 | 34,9 / 31,8 | 24,8 / 29,2 | 18,3 / 28,8 | 16,0 / 28,6 | 15,5 / 29,1 | |
| 6,9 с | 11,8 с | 15,0 с | 25,2 с | 39,3 с | ||
| 4 | 34,9 / 31,3 | 24,4 / 28,9 | 17,9 / 28,2 | 15,4 / 28,2 | 15,8 / 28,774 | 25,1 с | 35,0 с | 49,0 с | 83,3 с |
| 8 | 34,7 / 31,4 | 24,3 / 28,9 | 18,1 / 27,8 | 15,2 / 27,8 | 7 / 28,6 | |
| 39,2 с | 57,4 с | 84,4 с | 130,2 с | 190,8 с | ||
| 16 | 34,6 / 30,9 | 24,3 / 28,7 | 18,1 / 28,0 | 15,4 / 27,8 | 15.6 / 28,5 | |
| 68,7 с | 99,7 с | 172,2 с | 237,6 с | 400,7 с | ||
Средняя ошибка вменения (NRMSE / PFC в процентах) и время выполнения (в секундах) с различное количество деревьев ( n дерево ), выращенных в каждом лесу, и проверенные переменные ( m try ) в каждом узле деревьев
| m try . | n дерево . | |||||
|---|---|---|---|---|---|---|
| . | 10 . | 50 . | 100 . | 250 . | 500 . | |
| 1 | 36,8 / 35,5 | 27,4 / 32,3 | 20,4 / 31,3 | 17,2 / 30,0 | 16,0 / 30,8 | |
| 2,5 с | 3.2 с | 3,9 с | 5,8 с | 9,2 с | ||
| 2 | 34,9 / 31,8 | 24,8 / 29,2 | 18,3 / 28,8 | 16,0 / 28,6 | 15,5 / 29,1 | |
| 6,9 с | 11,8 с | 15,0 с | 25,2 с | 39,3 с | ||
| 4 | 34,9 / 31,3 | 24,4 / 28,9 | 17,9 / 28,2 | 15,4 / 28,2 | 15,8 / 28,774 | 25,1 с | 35,0 с | 49,0 с | 83,3 с |
| 8 | 34,7 / 31,4 | 24,3 / 28,9 | 18,1 / 27,8 | 15,2 / 27,8 | 7 / 28,6 | |
| 39,2 с | 57,4 с | 84,4 с | 130,2 с | 190,8 с | ||
| 16 | 34,6 / 30,9 | 24,3 / 28,7 | 18,1 / 28,0 | 15,4 / 27,8 | 15.6 / 28,5 | |
| 68,7 с | 99,7 с | 172,2 с | 237,6 с | 400,7 с | ||
| м попробовать . | n дерево . | |||||
|---|---|---|---|---|---|---|
| . | 10 . | 50 . | 100 . | 250 . | 500 . | |
| 1 | 36,8 / 35,5 | 27,4 / 32,3 | 20,4 / 31,3 | 17,2 / 30,0 | 16,0 / 30,8 | |
| 2,5 с | 3,2 с | 3,8 с | 9269,2 с | |||
| 2 | 34,9 / 31,8 | 24,8 / 29,2 | 18,3 / 28,8 | 16,0 / 28,6 | 15,5 / 29,1 | |
| 6,9 с | 11.8 с | 15,0 с | 25,2 с | 39,3 с | ||
| 4 | 34,9 / 31,3 | 24,4 / 28,9 | 17,9 / 28,2 | 15,4 / 28,2 | 15,8 / 28,7 | |
| 16,8 / 28,7 | ||||||
| 25,1 с | 35,0 с | 49,0 с | 83,3 с | |||
| 8 | 34,7 / 31,4 | 24,3 / 28,9 | 18,1 / 27,8 | 15,2 / 27,8 | | 57,4 с | 84,4 с | 130,2 с | 190,8 с |
| 16 | 34,6 / 30,9 | 24,3 / 28,7 | 18,1 / 28,0 | 15,4 / 27,8 | 15,6 / 28,5 | |
| 68,7 с | 99,7 с | 172,2 с | 237,6 с | 400,7 с | ||
Второй — уменьшить количество переменных, случайно выбранных на каждом узле ( м попробуйте ), чтобы установить вверх по расколу.Таблица 2 показывает, что увеличение m try имеет ограниченное влияние на ошибку вменения, но время вычисления сильно увеличивается. Обратите внимание, что для м попробуйте = 1, у нас больше нет RF, поскольку больше нет выбора между переменными для разделения. Это приводит к гораздо более высокой ошибке вменения, особенно для случаев с небольшим количеством бутстрэп-деревьев. Мы используем для всех экспериментов значение по умолчанию, например в данных GFOP это равно 4.
5 ЗАКЛЮЧЕНИЕ
Наш новый алгоритм, missForest, позволяет вменять отсутствующие значения практически для любых данных.В частности, он может обрабатывать многомерные данные, состоящие из непрерывных и категориальных переменных одновременно. MissForest не нуждается ни в настройке параметров, ни в предположениях относительно распределительных аспектов данных. Мы показываем на нескольких реальных наборах данных, поступающих из различных биологических и медицинских областей, которые misForest превосходит установленные методы вменения, такие как вменение k -ближайших соседей или многомерное вменение с использованием связанных уравнений. Используя наши оценки ошибок вменения OOB, missForest предлагает способ оценить качество вменения без необходимости откладывать тестовые данные или выполнять трудоемкие перекрестные проверки.Для последующего анализа эти оценки ошибок представляют собой среднее значение неформальной проверки надежности для каждой переменной. Полный потенциал missForest раскрывается, когда данные включают сложные взаимодействия или нелинейные отношения между переменными разного масштаба и разных типов. Кроме того, missForest можно применять к многомерным наборам данных, где количество переменных может значительно превышать количество наблюдений, но при этом дает отличные результаты условного исчисления.
БЛАГОДАРНОСТИ
За исключением данных изопреноида, лимфографии, детской больницы и GFOP, все остальные наборы данных были получены из репозитория машинного обучения UCI (Frank and Asuncion, 2010).Набор данных GFOP был получен из Института молекулярной системной биологии, Цюрих, Швейцария. Спасибо L. Reiter за предоставленные данные. Набор данных лимфографии был получен из Университетского медицинского центра, Института онкологии, Любляна, Словения. Спасибо М. Цвиттеру и М. Сокличу за предоставленные данные. Набор данных детской больницы был получен из Центра развития ребенка при Университетской детской больнице, Цюрих, Швейцария. Спасибо Б. Латалу и И. Беку за предоставленные данные.Наконец, мы благодарим двух анонимных рецензентов за их конструктивные комментарии.
Финансирование: Работа частично финансировалась за счет гранта Swiss SystemsX.ch Initiative в рамках проекта LiverX Центра компетенции по системной физиологии и метаболическим заболеваниям. Проект LiverX получил оценку Швейцарского национального научного фонда.
Конфликт интересов : не заявлен.
ССЫЛКИ
.Случайные леса
,Мах.Учиться.
,2001
, т.45
(стр.5
—32
),. ,Репозиторий машинного обучения UCI.
,2010
,.
Анализ e. coli промоторные последовательности
,Nucleic Acids Res.
,1987
, т.15
(стр.2343
—2361
) и др.Подход к открытию знаний для автоматизированной диагностики сердца для ОФЭКТ
,Artif. Intell. Med.
,2001
, т.23
(стр.149
—169
) и др.Психологическая корректировка и качество жизни у детей и подростков после операции на открытом сердце по поводу врожденного порока сердца: систематический обзор
,BMC Pediatr.
,2009
, т.9
стр.6
.Расчет с использованием цепей Маркова
,J. Stat. Comput. Simul.
,1988
, т.30
(стр.57
—79
) и др.Пригодность измерений дисфонии для дистанционного мониторинга болезни Паркинсона
,Nature Precedings.
,2008
,. ,Статистический анализ с отсутствующими данными.
,1987
Нью-Йорк
Wiley
,.Оценка максимального правдоподобия для смешанных непрерывных и категориальных данных с пропущенными значениями
,Biometrika
,1985
, vol.72
(стр.497
—512
) и др.Алгоритмы спектральной регуляризации для обучения больших неполных матриц
,Дж. Мах. Учиться. Res.
,2010
, т.11
(стр.2287
—2322
) и др.Байесовский метод оценки пропущенных значений для данных профиля экспрессии генов
,Bioinformatics
,2003
, vol.19
(стр.2088
—2096
) и др.Многомерный метод для умножения вменения пропущенных значений с использованием последовательности регрессионных моделей
,Surv. Методол.
,2001
, т.27
(стр.85
—96
).Множественное вменение в выборочных обследованиях — феноменологический байесовский подход к неполучению ответов
,Труды Секции методов исследования опросов, Американская статистическая ассоциация
,1978
Американская статистическая ассоциация
(стр.20
—34
),.Эффективное создание множественных вменений для неполных многомерных нормальных данных
,Труды Секции статистических вычислений Американской статистической ассоциации
,1990
Американская статистическая ассоциация
(стр.83
—88
). ,Анализ неполных многомерных данных.
,1997
UK
Chapman & Hall
, et al.Оценка статистической достоверности биомаркеров на основе протеомики
,Anal. Чим. Acta
,2007
, т.592
(стр.210
—217
),. ,Алгоритм попеременной максимизации шаблонов для пропущенных данных большой размерности.
,2010
.
Регрессионное сжатие и отбор с помощью лассо
,J. R. Stat. Soc. Сер. В
,1996
, т.58
(стр.267
—288
) и др.Уточнение приближенных теорий предметной области с помощью нейронных сетей, основанных на знаниях
,Труды восьмой национальной конференции по искусственному интеллекту
,1990
AAAI press
(стр.861
—866
) и др.Методы оценки недостающих значений для ДНК-микрочипов
,Bioinformatics
,2001
, vol.17
(стр.520
—525
).Множественное вменение дискретных и непрерывных данных по полностью условной спецификации
,Stat. Методы Мед. Res.
,2007
, т.16
(стр.219
—242
),. ,Гибкий многомерный расчет с помощью MICE.
,1999
Лейден, Нидерланды
Центр профилактики TNO
, et al.Гауссово разреженное графическое моделирование сети изопреноидных генов у Arabidopsis thaliana
,Genome Biol.
,2004
, т.5
стр.R92
и др.Влияние инсулина на экспрессию генов и биохимические пути в скелетных мышцах человека
,Эндокринные
,2007
, vol.31
(стр.5
—17
)Заметки автора
© Автор 2011. Опубликовано Oxford University Press. Все права защищены. Для получения разрешений обращайтесь по электронной почте: [email protected]
Представляем DenseClus, пакет кластеризации с открытым исходным кодом для данных смешанного типа
Сегодня мы объявляем об альфа-версии DenseClus, пакета с открытым исходным кодом для кластеризации многомерных данных смешанного типа. DenseClus использует алгоритмы аппроксимации и проекции однородного многообразия (UMAP) и кластеризации на основе иерархической плотности (HDBSCAN), чтобы прийти к решению кластеризации как для категориальных, так и для числовых данных. Используя DenseClus, вы предоставляете фрейм данных, который затем будет генерировать однородные кластеры без необходимости в обширной предварительной обработке или беспокойстве о том, как обрабатывать категориальные функции.Эта возможность открывает широкий спектр вариантов использования, от сегментации клиентов в маркетинге до картирования клеток в биомедицине.
Все программное обеспечение в проекте DenseClus выпущено под лицензией MIT. Мы приглашаем вас ознакомиться с кодом DenseClus на GitHub и присоединиться к сообществу.
Что такое DenseClus?
Кластеризация — сложная проблема, потому что никогда не бывает по-настоящему «правильного» ответа, когда метки неизвестны. Что еще больше усложняет ситуацию, нет бесплатного обеда для алгоритмов кластеризации.Даже если один алгоритм может хорошо соответствовать определенному набору данных, нет никаких гарантий, что он будет работать с другим набором данных точно так же. Аналогичным образом отмечается, что кластеризация «сильно зависит от контекста, целей и решений исследователя», что усиливает аргумент о том, что не существует такой вещи, как «универсально оптимальный метод, который будет просто создавать естественные кластеры» (см. « Что такое истинные кластеры? »Кристиан Хенниг).
Более того, хорошо обобщающие методы кластеризации, такие как KMeans, предполагают, что данные являются числовыми и сферическими.Наличие данных смешанных типов с высокой размерностью также создает проблемы для последующей задачи кластеризации, поскольку классические методы, такие как анализ главных компонентов (PCA) для уменьшения размерности, не работают, когда включены категориальные значения. Эта ситуация приводит к головоломке для практикующего специалиста, когда необходимо формализовать конкретные схемы определения характеристик — например, включение только числовых значений или преобразование всех в категориальные с последующим использованием вместо них анализа множественных соответствий (MCA).
DenseClus стремится решить как проблему поиска алгоритма кластеризации по умолчанию, так и обойти трудности, возникающие, когда данные находятся в форме смешанного типа. DenseClus использует комбинацию UMAP и HDBSCAN для отображения данных смешанного типа в плотное пространство с более низкой размерностью. Из этого плотного пространства он затем иерархически выстраивает группы в кластеры на основе плотности точек. Такой подход делает DenseClus простым в использовании решением, которое можно применять к широкому спектру данных для поиска значимых кластеров.
Начало работы с DenseClus
DenseClus зарегистрирован на PyPi, а код доступен на GitHub. Самый простой способ установить его напрямую — из pip для Python 3.7 или 3.8:
python3.8 -m pip install Amazon-DenseClus
DenseClus требует ввода данных Panda с числовыми и категориальными столбцами. Вся предварительная обработка и извлечение выполняются под капотом; вызвать функцию fit , а затем получить кластеры.
из плотного кластера импортного DenseClus
clf = DenseClus (
umap_combine_method = "correction_union_mapper",
)
clf.fit (df)
печать (clf.score ())
Попробовать
Мы очень рады запуску альфа-версии DenseClus. Вы можете найти более подробное пошаговое руководство в записной книжке DenseClus Example NB.ipynb в репозитории GitHub. Мы приглашаем вас опробовать его, сообщить о проблемах, отправить запросы на вытягивание и сообщить нам, что вы думаете.
Чарльз Френцель
Чарльз — старший научный сотрудник отдела профессиональных услуг в Токио, Япония. Он напрямую работает с клиентами AWS над созданием моделей машинного обучения для производства. В свободное время он с детьми ездит на велосипеде, тренируется с гирями и пьет чай матча.
Байчуань Сунь
Д-р Байчуань Сунь — старший научный сотрудник AWS AI / ML.Он увлечен предоставлением клиентам стратегических бизнес-решений с использованием методологии, основанной на данных в облаке, и возглавлял проекты в сложных областях, включая робототехнику, компьютерное зрение, прогнозирование временных рядов, оптимизацию цен, профилактическое обслуживание, фармацевтическую разработку, систему рекомендаций по продуктам и т. Д. В свободное время он любит путешествовать и гулять с семьей и друзьями.
Иден Дати
AWS Professional Service Machine Learning, лидер в регионе APJC.
Инь Сун
Инь Сун (Yin Song) — специалист по обработке данных из группы AWS ProServe ML APJC с мая 2019 года. Он очень тесно сотрудничает с несколькими предприятиями и отраслями (например, телекоммуникациями, горнодобывающей промышленностью, FSI и т. Д.) Над разработкой и применением решений машинного обучения и искусственного интеллекта, а также создавать ценность для клиентов. До прихода в AWS Инь работал в Telstra, крупнейшей телекоммуникационной компании Австралии, и выполнил несколько проектов по оптимизации работы с клиентами и сети.Ранее он работал специалистом по обработке данных в области интернет-рекламы и руководил оптимизацией рекламы на основе машинного обучения. Я получил докторскую степень еще в 2014 году, и моя диссертация была посвящена вероятностному машинному обучению и приложениям.
Дробное вменение для порядковых и смешанных ответов с отсутствующими наблюдениями
Абстрактные
В этой диссертации рассматриваются два существенных аспекта крупномасштабных файлов данных общего пользования, включающих порядковые и смешанные ответы с пропущенными наблюдениями: (i) создание единых полных наборов данных с вменением для пропущенных значений; и (ii) статистический анализ вмененных наборов данных пользователями общедоступных данных с различными целями.Сборы крупномасштабных данных обычно собираются статистическими агентствами, исследовательскими институтами или коммерческими организациями, и отсутствующие наблюдения являются обычным явлением. Наше исследование сосредоточено на сценариях, в которых один порядковый ответ или несколько ответов смешанного типа являются частью наборов данных и могут отсутствовать. Мы разрабатываем процедуру последовательного регрессионного дробного вменения для создания единых полных наборов данных, которые обеспечивают достоверный и эффективный статистический анализ для часто встречающихся проблем с выводами пользователей общедоступных данных.Порядковые переменные широко собираются и анализируются во многих областях науки. У них есть некоторые общие инструменты с анализом дискретных данных, но они имеют гораздо более богатую структуру для изучения по сравнению с общими категориальными переменными. Что еще более важно, статистические методы, разработанные для порядковых переменных, могут быть легко расширены для охвата категориальных данных. В этой диссертации мы представляем последовательную регрессионную стратегию дробного вменения в рамках трех основных исследовательских проектов, начиная с порядковых переменных и заканчивая ответами смешанного типа.Предлагаемый метод учитывает уникальные особенности порядковых ответов и является теоретически обоснованным и практически привлекательным. Первый проект рассматривает простой сценарий, в котором есть только один порядковый ответ с пропущенными значениями. Мы предоставляем подробные шаги для предлагаемой процедуры вменения и развиваем асимптотические свойства последующих оценок, полученных в общих условиях. Мы подробно обсуждаем три задачи вывода, имеющие практическое значение: (1) оценка вероятностей категорий; (2) регрессионный анализ с использованием всех доступных ковариат; и (3) регрессионный анализ, включающий подмножество всех ковариат.Для каждой проблемы предлагаемая процедура сравнивается с существующими альтернативными методами с точки зрения достоверности и эффективности анализа. Характеристики конечных образцов демонстрируются с помощью моделирования. Второй исследовательский проект расширяет предложенную процедуру на более сложные сценарии, в которых несколько переменных смешанных типов, включая непрерывные, упорядоченные и неупорядоченные категориальные переменные, содержат недостающие наблюдения. Мы очерчиваем ключевые этапы процедуры последовательной регрессии дробного вменения в общих условиях и представляем асимптотические результаты статистического анализа с помощью двух конкретных задач вывода: (1) проверка независимости двух порядковых ответов с помощью ассоциативных мер; и (2) регрессия порядкового отклика по непрерывным ковариатам, где и отклик, и ковариаты могут быть пропущены.Имитационные исследования показывают, что предлагаемая нами процедура обеспечивает лучшие результаты по сравнению с существующими методами. В третьем исследовательском проекте мы изучаем надежность оценок маргинальных количеств населения путем включения механизмов недостающих данных в предлагаемую процедуру. Рассмотрены два случая: один из одномерных порядковых ответов с пропущенными значениями, а другой — продольных порядковых ответов с монотонными пропущенными значениями. Мы показываем силу предложенной процедуры через приложение к проблеме причинного вывода в исследовании точечного лечения.Свойство двойной устойчивости оценщиков для маргинальных количеств населения, использующих наборы данных с дробным исчислением, в отношении неправильной спецификации моделей вменения, а также моделей вероятности отклика подтверждается результатами имитационных исследований.
Кластеризация выборок и переменных со смешанными данными
Abstract
Анализ данных, измеренных в различных масштабах, является актуальной задачей. Биомедицинские исследования часто сосредотачиваются на наборах данных с высокой пропускной способностью, например:г., количественные измерения. Однако необходимость интеграции других функций, возможно, измеряемых в разных масштабах, например клинические или цитогенетические факторы становятся все более важными. Затем визуализируются результаты анализа (например, выбор соответствующих генов) с добавлением дополнительной информации, такой как клинические факторы, вверху. Однако желателен более комплексный подход, при котором все доступные данные анализируются совместно, а также при визуализации различные источники данных объединяются более естественным образом.Здесь мы специально нацелены на интегральную визуализацию и представляем графический дисплей в стиле тепловой карты. С этой целью мы разрабатываем и исследуем методы кластеризации данных смешанного типа, уделяя особое внимание переменным кластеризации. Кластеризации переменных не уделяется столько внимания в литературе, как кластеризации выборок. Мы расширили методологию кластеризации переменных двумя новыми подходами, один из которых основан на сочетании различных мер ассоциации, а другой — на корреляции расстояний. С помощью моделирования мы оцениваем и сравниваем различные стратегии кластеризации.Применение конкретных методов для данных смешанного типа оказывается сопоставимым и во многих случаях выгодным по сравнению со стандартными подходами, применяемыми к соответствующим количественным или бинаризованным данным. Наши два новых подхода к переменным смешанного типа показывают схожую или лучшую производительность, чем существующие методы ClustOfVar и взаимная информация с поправкой на смещение. Кроме того, в отличие от ClustOfVar, наши методы предоставляют матрицы несходства, что является преимуществом, особенно для целей визуализации.Примеры реальных данных призваны дать представление о различных видах потенциальных приложений для интегральной тепловой карты и других графических дисплеев, основанных на матрицах несходства. Мы демонстрируем, что представленная интегральная тепловая карта предоставляет больше информации, чем обычные данные о взаимосвязи между переменными и выборками. Описанные методы кластеризации и визуализации реализованы в нашем пакете R CluMix , доступном по адресу https://cran.r-project.org/web/packages/CluMix.
Образец цитирования: Hummel M, Edelmann D, Kopp-Schneider A (2017) Кластеризация выборок и переменных с данными смешанного типа. PLoS ONE 12 (11): e0188274. https://doi.org/10.1371/journal.pone.0188274
Редактор: Чжаохун Дэн, Университет Цзяннань, КИТАЙ
Поступила: 07.05.2017; Принято к печати: 3 ноября 2017 г .; Опубликовано: 28 ноября 2017 г.
Авторские права: © 2017 Hummel et al.Это статья в открытом доступе, распространяемая в соответствии с условиями лицензии Creative Commons Attribution License, которая разрешает неограниченное использование, распространение и воспроизведение на любом носителе при условии указания автора и источника.
Доступность данных: Представленные методы реализованы в общедоступном R-пакете CluMix (https://cran.r-project.org/web/packages/CluMix). Пример набора данных, проанализированный в рукописи, доступен как R пакет ‘ВСЕ’ (https: // bioconductor.org / packages / release / data / эксперимент / html / ALL.html).
Финансирование: Работа MH была поддержана грантом 01ZX1609B Федерального министерства образования и исследований Германии (Bundesministerium für Bildung und Forschung, BMBF, https://www.bmbf.de/).
Конкурирующие интересы: Авторы заявили, что никаких конкурирующих интересов не существует.
Введение
В реальных ситуациях с данными различные интересующие факторы измеряются в разных масштабах, например.грамм. количественные значения экспрессии генов и категориальные клинические характеристики, такие как пол, стадия заболевания и т. д. Во многих случаях в первую очередь анализируются многомерные данные, а дополнительные характеристики пациента лишь «информативно» добавляются к представленным результатам. Однако это неудовлетворительно с точки зрения системной биологии. Растет число интегративных подходов, которые объединяют различные источники данных с самого начала анализа вместо апостериорного объединения результатов, полученных на отдельных этапах, например.грамм. интегративная кластеризация [1], многофакторный анализ со смешанными данными [2] или байесовские подходы [3, 4]. В этой работе мы следуем аналогичному направлению, однако наше внимание больше сосредоточено на визуализации, движимой идеей показать «полную картину» в виде презентации в стиле тепловой карты. Бикластеризация — это распространенный подход к обнаружению структур среди выборок и переменных одновременно, что означает, по сути, поиск «блоков» на тепловых картах. Однако, насколько известно автору, методы бикластеризации применимы либо к количественным [5], либо, в области анализа паттернов, к категориальным данным [6], но не к смеси данных разных типов.Пакет R caOmicsV [7] обеспечивает отображение тепловой карты для нескольких «омиков» и фенотипических данных. Однако различные наборы данных должны быть предоставлены на уровне гена, например, метилирование ДНК, мутации или вариации числа копий ДНК должны быть указаны для каждого гена, что непросто. Кроме того, к образцам или функциям, которые позволили бы обнаруживать структуры в данных, не применяется кластеризация. Подход интегративной кластеризации [1] также предоставляет тепловые карты, в то время как цель состоит в том, чтобы найти группы среди выборок, используя информацию из разных типов многомерных наборов данных одновременно.Структуры среди переменных отображаются только в разных наборах данных. Напротив, мы также хотим исследовать сходства между всеми переменными в одной унифицированной презентации и дополнительно включать низкоразмерные характеристики, которые можно использовать для исследовательского анализа и генерации гипотез. Например, можно найти подгруппы пациентов на основе всех соответствующих параметров и одновременно исследовать взаимосвязи между этими параметрами. Другой пример — проверка связей между переменными в процессе статистического моделирования до принятия решения об их включении или исключении из регрессионной модели.Наконец, интегральная иллюстрация играет важную роль в представлении результатов, показывая, например, прогностические факторы разных типов и их взаимосвязь между собой и с интересующим результатом.
Чтобы создать тепловую карту для переменных, измеряемых в разных масштабах, необходимы специальные меры сходства, определяющие i) расстояния между выборками (например, пациентов) на основе характеристик разных типов и ii) расстояния между различными переменными. Для кластеризации выборок с использованием переменных смешанного типа мы решили использовать коэффициент подобия Гауэра [8].Для кластеризации переменных разных типов мы предлагаем две новые стратегии: 1) Метод CluMix-ama ( a ssociation m easures a pproach) состоит из комбинации различных мер сходства. Предлагается новая стратегия, основанная на переупорядочивании категорий, для измерения связи между мультикатегориальной переменной и любым другим типом переменной. 2) Подход CluMix-dcor (соотношение d istance cor ) основан на новой мере сходства, которая выводится с использованием концепции обобщенных корреляций расстояний [9].Вместо того, чтобы всегда использовать евклидово расстояние, как в исходном определении корреляции расстояний [10, 11], мы применяем расстояния, соответствующие соответствующему типу переменной. В частности, мы будем использовать евклидово расстояние для упорядоченных и количественных переменных и дискретное расстояние для номинальных переменных.
Оба метода сравниваются с подходом ClustOfVar [12] и кластеризацией на основе взаимной информации с поправкой на смещение ( BCMI ) [13] путем моделирования.Используя иерархическую кластеризацию для смешанных данных, можно построить стандартные тепловые карты для непрерывных значений, с той разницей, что отдельные цветовые схемы иллюстрируют разные источники информации. На основе матриц подобия смешанных данных могут быть построены дополнительные простые графики, показывающие взаимосвязи между переменными. Полезность методов визуализации проиллюстрирована на примере реальных данных. Инструменты кластеризации и визуализации смешанных данных реализованы в нашем R-пакете CluMix .На рис. 1 представлен обзор функций пакета.
Рис. 1. Функциональные возможности пакета CluMix R.
Матрицы расстояний выводятся отдельно для выборок и переменных. Они создают основу для иерархической кластеризации и интегративной визуализации смешанных данных.
https://doi.org/10.1371/journal.pone.0188274.g001
Методы
В таблице 1 приведены наиболее важные символы, используемые в разделе «Методы» для облегчения чтения.
Кластеризация выборок
Мы хотим сгруппировать образцы (например, пациентов) на основе свойств, которые можно измерить в разных шкалах, то есть количественных, порядковых, категориальных или бинарных переменных. Существует множество литературы по кластеризации выборок, даже для смешанных числовых и категориальных данных, см. Таблицу 2 для обзора рассмотренных методов.
Таблица 2. Методы кластеризации или определения расстояний между выборками со смешанными данными.
Столбцы указывали, подходит ли иерархическая кластеризация (в отличие от разделения), можно ли получить матрицы расстояний, доступна ли функциональность в R (насколько известно авторам) и обрабатываются ли порядковые переменные особым образом.Во всей рукописи применяется только кластеризация на основе коэффициента сходства Гауэра.
https://doi.org/10.1371/journal.pone.0188274.t002
Большинство методов, таких как кластеризация скрытых классов [14], кластеризация k-прототипов [15], нечеткая кластеризация [16] и другие [19], стремятся при разделении данных на фиксированное количество кластеров, что, особенно для больших наборов данных, в вычислительном отношении более эффективно, чем иерархическая кластеризация, где требуется полная матрица несходства.Однако, имея в виду тепловую карту смешанных данных, мы предпочитаем схемы иерархической кластеризации, основанные на матрицах несходства, где не нужно заранее выбирать фиксированное количество кластеров. В области машинного обучения существует несколько подходов для оценки расстояний между выборками с использованием смешанных данных [17, 18]. Однако эти подходы довольно сложны и не предназначены для порядковых переменных. Вместо этого мы выбираем общий коэффициент подобия, предложенный Гауэром [8] для определения расстояний между образцами.Сходство между образцами i и j со значениями x i и x j , i , j = 1,…, n , на основе p переменных, определяется как где δ k ( x ik , x jk ) указывает, возможно ли сравнение i и j по переменной k k k = 1,…, p , т.е.е. δ k ( x ik , x jk ) = 0, если i и / или j имеют недостающее значение для k 916 δ k ( x ik , x jk ) = 1 в противном случае. Дополнительные веса w k могут быть указаны для повышения важности определенных переменных, которые априори считаются более важными.Если таких предпочтений нет, w k устанавливается равным 1 для всех k = 1,…, p . Оценка s k ( x ik , x jk ) отражает сходство между образцами i и j w.r.t. переменная к . Короче говоря, оценка определена за
.- качественные переменные:
- количественные переменные: s k ( x ik , x jk ) = 1 — | x ik — x jk | / R k ,
где R k 1642 — наблюдаемый диапазон переменной k.
С расширением Podani [20] можно также включать информацию для заказа переменных в порядковой шкале
- порядковые переменные:, где r k ( x mk ) — ранг значения x mk из выборки m для переменной в пределах всех наблюдений к .
Метод реализован в пакете R FD [21].
По значениям подобия s ( x i , x j ) рассчитываем расстояния d ( x i 1643 x ) = 1 — s ( x i , x j ). Как только подходящая матрица расстояний получена, все стандартные алгоритмы кластеризации, начиная с попарных различий, могут быть применены для исследования структур в данных.Для целей визуализации мы считаем наиболее подходящей иерархическую кластеризацию. В нашем анализе мы используем метод Уорда [22] для расчета расстояний между кластерами, но возможен и любой другой метод связи. Также могут применяться подходы секционированной кластеризации, например Partitioning Around Medoids (PAM), более надежная и гибкая версия классического алгоритма k-средних, где матрица несходства может быть выбрана пользователем [23].
Переменные кластеризации
Помимо кластеризации выборок, мы в основном нацелены на определение сходства между самими переменными, чтобы иметь возможность одновременно визуализировать отношения между выборками и переменными, как это обычно бывает в стандартных тепловых картах.Подходы, использующие взаимную информацию [24] или факторный анализ смешанных данных [2], могут быть использованы для оценки связей между функциями. Но эти методы, с одной стороны, довольно сложны, а с другой стороны, неясно, отражают ли сходства производных переменных ассоциации в духе корреляции, которая нас больше всего интересует. Тем не менее, мы считаем, что недавняя корректировка смещения взаимная информация ( BCMI ) [13], которая реализована в пакете R mpmi , для кластеризации переменных путем определения расстояний как 1 — BCMI .Далее мы оцениваем подход, основанный на несходстве ClustOfVar [12]. Здесь мы предлагаем две альтернативы, первая из которых представляет собой комбинацию отдельных мер ассоциации для разных пар типов данных. Мы называем эту стратегию подходом CluMix-ama . Второй подход использует корреляцию расстояний для вычисления расстояний между переменными и далее называется подходом CluMix-dcor . См. Таблицу 3 для обзора рассмотренных методов.
Подход CluMix-ama.
Начнем с выбора подходящих мер ассоциации для сравнения различных типов данных. Выбранные коэффициенты подобия должны использовать как можно больше информации (например, следует избегать категоризации количественных переменных), но быть как можно более надежными (например, в отношении выбросов и нелинейности). Наши решения о конкретных мерах были основаны на литературных исследованиях [25, 26] и небольшом моделировании. В некоторых случаях, когда коэффициент подобия недоступен, например.грамм. для измерения взаимосвязи между непрерывным и категориальным признаком с более чем двумя категориями предлагаются расширения существующих показателей. Следующие коэффициенты используются для измерения сходства между переменными k и l с соответствующими шкалами
- количественный и количественный / порядковый : абсолютный коэффициент корреляции Спирмена (т. Е. Корреляция Пирсона для рангов r k и r l значений x 42 k и k x l переменных k и l )
s kl = | ρ Копейщик ( x k , x l ) | = | ρ Pearson ( r k , r l ) | - порядковый номер в сравнении с порядковым и количественный / порядковый в сравнении с двоичным : абсолютный коэффициент Гудмана и Крускала γ [27]
s kl = | ( n 1642 c 915 d ) / ( n c + n d ) |
, где n c и n d — числа совпадающих и несогласованных пар наблюдений w.r.t. к и к . - количественное / порядковое в сравнении с номинальным : В литературе не было найдено подходящего коэффициента связи между переменной порядка ранжирования и номинальным фактором с более чем двумя категориями без какой-либо естественной упорядоченности. Чтобы оценить связь между этими типами переменных, мы применяем идею о том, что номинальная переменная могла бы считаться порядковой, если бы мы знали только «правильный» порядок. В качестве примера рассмотрим номинальный коэффициент X с категориями A , B и C , а также количественную переменную Y , которая связана с X таким образом, что она показывает аналогичные значения в выборках с уровни A и C , но повышенные значения в выборках с уровнем B .Следовательно, мы могли бы измерить эту связь, вычислив коэффициент корреляции Спирмена (если Y является количественным) или γ Гудмана и Крускала (если Y является порядковым) для X ′ и Y , где X ‘ X преобразовано в упорядоченный фактор с уровнями A < C < B . Чтобы определить «правильный» порядок категорий X по отношению к переменной Y , мы рассматриваем средние ранги значений Y внутри соответствующих категорий X .Поскольку в случае отсутствия реальной связи между X и Y эта стратегия дала бы слишком оптимистичные оценки связи, мы сначала выполняем тест Краскела-Уоллиса, чтобы выявить любые различия в средних Y в категориях Х . Только если результат теста значительный ( p <0,05), мы продолжаем переупорядочивание, как описано. В противном случае мы вычисляем корреляцию Спирмена или соответственно γ Гудмана и Крускала, используя исходные X , что будет представлять «случайное» упорядочение категорий и должно привести к коэффициенту, близкому к 0.
- номинальный / двоичный по сравнению с номинальным / двоичным : существуют меры связи данных кросс-таблицы, например, Коэффициент непредвиденных обстоятельств Пирсона или коэффициент V Крамера. Однако при моделировании мы нашли более подходящей стратегию, аналогичную описанной выше, где упорядочение «накладывается» на категориальные переменные. Эта идея уже описывалась, например, в [28] и [29], а также используется в анализе соответствий [30]. «Правильный» порядок категорий достигается путем «диагонализации» кросс-таблицы между двумя факторами с целью получения диагональных больших частот.Затем для переупорядоченной кросс-таблицы вычисляется коэффициент γ Гудмана и Краскала. Поскольку опять же, в случае отсутствия ассоциации эта стратегия приведет к чрезмерно оптимистичным результатам, предварительный тест ассоциации по хи-квадрат выполняется перед оптимизацией кросс-таблицы. В случае несущественного результата теста ( p > 0,05) для исходной таблицы непредвиденных обстоятельств рассчитывается коэффициент γ .
Несмотря на то, что кластеризация не является абсолютно необходимой, было бы полезно, чтобы выбранные расстояния имели метрические свойства, что, в частности, подразумевает, что неравенство треугольника выполняется для каждой тройки расстояний.Гауэр [31] показывает, что если матрица подобия S = ( s kl ) является положительно полуопределенной (p.s.d.), то матрица расстояний евклидова, что, конечно, подразумевает, что она метрическая. Комбинируя предложенные меры ассоциации с матрицей сходства S , легко найти пример, где S не является p.s.d. Для того чтобы по-прежнему выполнять неравенство треугольника и, следовательно, все расстояния были сопоставимы, мы вычислительным способом находим матрицу подобия S ‘, которая равна p.s.d. и является «ближайшим» к исходной матрице S в том смысле, что взвешенная норма Фробениуса разности двух матриц минимизирована [32]. Этот метод реализован в функции nearPD в R-пакете Matrix [33]. Из теоремы Гауэра следует, что матрица расстояний D , составленная из межпеременных расстояний, является евклидовой. На основе матрицы D расстояний группирование переменных может быть снова выполнено с помощью стандартной иерархической или разделенной кластеризации.
Подход CluMix-dcor.
Ковариация расстояний и корреляция расстояний — это новые меры зависимости, которые были первоначально предложены для одномерной постановки Фейервергером [34], а затем распространены на многомерные наблюдения Секели [10, 11]. С момента появления [10, 11] возник значительный интерес к статистическим приложениям коэффициента дистанционной корреляции. Примечательно, что дистанционная корреляция использовалась для вывода регуляторных сетей генов [35], тестирования ассоциаций между вариациями числа копий различных генов [36] и оценки ассоциаций семейных отношений, факторов образа жизни и смертности [37].
Коэффициент корреляции расстояния является мерой зависимости между p -мерным случайным вектором X и q -мерным случайным вектором Y , где p и q являются произвольными. Корреляция расстояния всегда положительна и равна 0 тогда и только тогда, когда векторы X и Y независимы. Это свойство означает, что корреляция расстояний может обнаруживать любую зависимость между X и Y .Недавно Лайонс [9] обобщил это понятие на метрические пространства. Для любых двух метрических пространств (т. Е. Подходящих наборов, на которых определены правильные расстояния) можно вывести обобщенную корреляцию расстояний между случайными величинами на этих двух разных наборах. Когда метрические пространства удовлетворяют дополнительному свойству, называемому строго отрицательным типом, мы даже сохраняем то свойство, что эта обобщенная корреляция расстояний равна 0 тогда и только тогда, когда две случайные величины независимы. Уменьшая значения этих случайных величин до расстояний, этот подход позволяет измерить зависимость между двумя случайными величинами на совершенно разных наборах.В этой статье мы ограничимся измерением зависимости между двумя переменными, где любая из этих двух переменных может быть количественной, порядковой или номинальной. В частности, аналогично тому, что использовалось для определения расстояний между выборками, для k ∈ {1,…, p } мы положим
- если k -я переменная — номинальная ,
- d k ( x ik , x jk ) = | x ik — x jk | если k -я переменная — это количественная ,
- d k ( x ik , x jk ) = | r k ( x ik ) — r k ( x jk ) | если k -я переменная — это порядковый номер , где r k ( x ik ) и r k (16 k 16 ) — это ряды значений x ik и x ik во всех наблюдениях для переменной k .
Мы определяем матрицы центрированных расстояний для k -й и l -й переменной, соответственно, как
Теперь, умножая эти матрицы, содержащие расстояния между выборками , мы получаем меру сходства между переменными . В частности, примерная версия обобщенной ковариации расстояния [9, стр. 3287] между переменной k и переменной l определяется как неотрицательный квадратный корень
Известно, что эта выборочная мера сильно смещена [38].Для лучшей производительности мы будем использовать версию с исправлением смещения, как описано в [38]: (1) где модифицированная матрица расстояний и определяется аналогично. В отличие от, может принимать отрицательные значения. Путем нормализации мы получаем обобщенную корреляцию расстояний: (2)
Здесь и относится к квадрату обобщенной дисперсии расстояния для k -ой и l -й переменной, соответственно (они вычисляются путем вставки расстояний от одной и той же переменной в уравнение (1)).Пока используются только количественные переменные, сводится к версии стандартной дистанционной корреляции с поправкой на смещение, как это определено Секели [10, 11, 38].
Используя тот факт, что и евклидово расстояние, и дискретное расстояние на счетном множестве имеют сильно отрицательный тип, мы можем вывести, что [9, теорема 3.11] почти наверняка сходится к 0 тогда и только тогда, когда k -е и l -я переменная независимы. Следовательно, мера несходства является значимой мерой для кластеризации смешанных переменных.
Из уравнения (2) можно вывести, что корреляция расстояний не зависит от масштаба. Следовательно, для расчета коэффициента корреляции расстояния нет разницы, если мы заменим метрику, используемую для количественных переменных, на d k ( x ik , x jk ) = | x ik — x jk | / R k и метрика, используемая для порядковых переменных, где R k — это диапазон 915 k -я переменная и r k ( x ik ) и r k ( x jk 92 значения) 915 915 x ik и x jk для переменной k .Эти расстояния в точности соответствуют слагаемым, отображаемым в расстоянии Гауэра, которое мы используем для кластеризации выборок. Эта аналогия может привести к экономии времени вычислений при одновременной кластеризации выборок и переменных.
Кластеризация на основе отсутствия подобия.
Метод ClustOfVar [12], реализованный в одноименном пакете R, основан на анализе главных компонентов и был специально разработан для кластеризации переменных. Авторы предлагают алгоритм разделения, основанный на сходстве между переменными.Для этого они используют квадратную каноническую корреляцию. Однако в базовом исследовании с использованием моделирования мы заметили, что, если сходство должно быть измерено в духе корреляции, эти сходства часто недооценивают действительно лежащие в основе сильные отношения. Сами авторы заявляют, что их альтернативный метод иерархической кластеризации обычно работает лучше. Этот метод не работает с заранее заданной полной матрицей расстояний, подключенной к обычному алгоритму иерархической кластеризации, а скорее решает агломерацию субкластеров в кластеры на основе соответствия между переменными внутри кластера и синтетической количественной переменной, которая является «репрезентативной». »Для кластера.Синтетические переменные вычисляются с помощью анализа главных компонентов для смешанных данных (PCAMIX), а мерой упомянутой адекватности является соответствующее первое собственное значение разложения PCAMIX.
Результаты: моделирование
Подтверждение мер сходства между переменными
Чтобы оценить сходство между переменными, рассчитанное для подхода CluMix-ama, наборы данных с различными типами переменных были смоделированы следующим образом.Сначала были сгенерированы случайные нормально распределенные переменные с заданной корреляцией Пирсона между собой. Затем были созданы категориальные факторы в «полном соответствии» с количественными переменными. Например, чтобы создать двоичную переменную из непрерывной переменной X , которая должна иметь такую же степень связи, что и сама X , с другой непрерывной переменной Y , X было классифицировано по среднему сечению. Точно так же, чтобы получить коэффициент с четырьмя уровнями, X было сокращено по его квартилям и так далее.Таким образом были созданы наборы данных с известными отношениями между различными переменными. Для выбора подходящих коэффициентов подобия для подхода CluMix-ama для каждой пары различных типов переменных было протестировано несколько показателей ассоциации, см. S1 Рис. Коэффициенты, предложенные в разделе «Методы» (выделены жирным шрифтом на S1 Fig), показывают наименьшее « чрезмерный оптимизм »в случае отсутствия отношений и лучше всего фиксировать крепкие отношения.
Затем мы более подробно исследовали, насколько хорошо навязанные (Пирсоновские) корреляции были зафиксированы мерами ассоциации, применяемыми к различным комбинациям типов данных.Мы смоделировали 1000 наборов данных для каждой комбинации нескольких наложенных корреляций между переменными ( ρ = 0, 0,25, 0,5, 0,75, 0,95) и размерами выборки ( n = 40, 96, 200, 400) — мы выбрали размеры выборки, кратные 8, так что категоризация переменных в K = 8 классов была идеально сбалансирована). Результаты показаны на рис. 2, в качестве примера для значений корреляции ρ = 0 и ρ = 0,75. Чем больше размер выборки, тем ближе мы подходим к наложенным значениям корреляции.Для небольших размеров выборки мы наблюдаем некоторую переоценку действительно несуществующей взаимосвязи ( ρ = 0, верхняя панель) для недавно предложенной стратегии переупорядочения категорий для оценки взаимосвязей между номинальными факторами и переменными любого другого типа. Но благодаря предварительному тесту ассоциации результаты все еще кажутся приемлемыми (например, переоценка не намного серьезнее, чем, например, для корреляции Спирмена при связывании двух количественных переменных). Стандартные меры для сравнения номинальных переменных (например,грамм. Крамера V) на самом деле был бы более оптимистичным в случае отсутствия реальной связи. Кроме того, для больших значений ρ эти меры иногда сильно занижают связь (см. S1 Рис.). Сильные ассоциации (нижняя панель) в целом хорошо улавливаются предлагаемыми мерами. Результаты для порядковых и номинальных переменных с K = 8 вместо четырех категорий очень похожи (данные не показаны). Для подхода CluMix-dcor мы не предоставляем аналогичный график. Это по той причине, что даже для двух количественных переменных корреляция Пирсона и корреляция расстояния между двумя переменными измеряют две разные величины и, как правило, не могут быть преобразованы друг в друга.Отметим, что для двумерной нормали корреляция расстояний всегда меньше или равна корреляции Пирсона [10, теорема 7], то же самое верно и для многих других параметрических распределений [39].
Рис. 2. Коробчатые диаграммы сходства переменных для 1000 смоделированных наборов данных в различных настройках.
Переменные моделировались с помощью базовой корреляции (Пирсона) ρ = 0 (синие прямоугольники) и ρ = 0,75 (оранжевые прямоугольники), обозначенных горизонтальными линиями. Количественные переменные были категоризированы в полном соответствии, так что связь между соответствующими переменными должна быть одинаковой.На разных панелях показаны значения сходства, рассчитанные для различных комбинаций типов данных, как указано сверху и слева от каждого столбца / строки графиков. На каждой панели показаны результаты для разных размеров выборки ( n = 40, 96, 200, 400; прямоугольные диаграммы слева направо).
https://doi.org/10.1371/journal.pone.0188274.g002
Проверка кластеризации переменных
В другом исследовании с использованием моделирования мы выяснили, дает ли кластеризация переменных предложенными методами ожидаемые результаты, если известны истинные классификации.Были смоделированы наборы данных с различными размерами выборки ( n = 25, 50, 100) и количеством переменных ( p = 50, 100, 200). Две группы переменных одинакового размера были определены путем отдельного извлечения из многомерных нормальных распределений с заданной внутригрупповой ковариационной структурой. Переменные внутри группы имели парные корреляции, уменьшающиеся от переменной максимальной корреляции ( ρ = 0,25, 0,5, 0,75) до 0. Необязательно, был внесен некоторый шум путем установки 0%, 20%, 40% межгрупповых корреляций на значение 0.5 вместо 0.
Полученные непрерывные наборы данных были сгруппированы с использованием стандартного евклидова расстояния в качестве ориентира. В качестве второй ссылки полностью бинаризованные данные (значения вырезания на медиане для каждой переменной) были сгруппированы с использованием простого расстояния коэффициентов соответствия. Впоследствии определенная часть переменных (10%, 25%, 50%, 75%, 100%) была отнесена к категориям таким же образом, как и в предыдущих исследованиях с использованием моделирования, тем самым сохранив те же исходные истинные классификации выборки и переменных.Для категоризации было случайным образом решено, сколько категорий ( K = 2,…, 8) должна иметь новая переменная и должна ли она быть порядковой или номинальной. Исключительно количественные данные и их частично или полностью категоризированные варианты были сгруппированы с использованием представленных подходов для кластеризации данных смешанного типа, а именно подходов CluMix-ama, CluMix-dcor, ClustOfVar и BCMI. Была применена иерархическая кластеризация с методом агломерации Уорда, и полученные дендрограммы были вырезаны для выявления двух классов переменных.Для каждой настройки моделирование повторялось 100 раз. Коэффициенты ошибочной классификации ( MCR = ( a 12 + a 21 ) / ( a 11 + a 12 + a 21
91 a 21 91 ) с записями a ij в классификационных таблицах) были рассчитаны для оценки и сравнения различных стратегий кластеризации и настроек моделирования.Коэффициенты ошибочной классификации для всех настроек моделирования показаны на S2 и S3 рис.На рис. 3 приведен пример настройки с 50 выборками, 100 переменными, внутригрупповой корреляцией 0,5 и 20% межгрупповой корреляции 0,5 вместо 0. Наши два новых подхода для данных смешанного типа и ClustOfVar дают очень похожие результаты с точки зрения восстановления истинной основной группировки переменных. Для полностью количественных данных эти методы кластеризации смешанных данных работают почти так же хорошо, как евклидова кластеризация. Однако цель и сила этих методов — это, конечно, кластеризация данных, включая также категориальные переменные.Для таких наборов данных более полезно сравнение с кластеризацией полностью бинаризованных данных стандартными методами. Из рис. 3 видно, что первые три подхода к смешанным данным обычно превосходят двоичную кластеризацию. Только для наборов данных с исключительно категориальными переменными дихотомия кажется более подходящей. Кластеризация на основе взаимной информации, скорректированной на смещение, в этой ситуации работает хуже, чем другие подходы к смешанным данным, и, за исключением наборов данных с небольшим количеством категориальных переменных, также хуже, чем кластеризация двоичных данных.Фигуры S2 и S3 предполагают, что взаимная информация лучше работает при больших размерах выборки и довольно сильных корреляциях между переменными. Для лучшего сравнения методов по всем параметрам моделирования мы вычислили медианные различия MCR между каждым методом и кластеризацией бинаризованных данных, см. Рис. 4. Медианные различия ниже нулевой линии указывают на лучшую производительность для соответствующего подхода смешанных данных по сравнению с бинарным. кластеризация. Мы снова видим, что первые три изученных метода работают очень похоже, в то время как BCMI работает хуже, за исключением больших размеров выборки и сильной корреляции.Для больших размеров выборки (левая панель) все четыре подхода к смешанным данным превосходят бинарную кластеризацию. Для малых и средних размеров выборки мы наблюдаем это преимущество только в том случае, если доля неколичественных переменных не превышает примерно 75%. В этих ситуациях подходы CluMix-ama и CluMix-dcor обычно дают несколько лучшие результаты, чем ClustOfVar. Также для низкой корреляции внутри кластера и отсутствия корреляции между кластерами (правая панель) есть небольшое преимущество двух новых подходов к кластеризации в случае большей доли категориальных переменных в данных.Однако и в этой ситуации дихотомия снова кажется лучшим вариантом. Если существует некоторая степень корреляции между кластерами («шум»), все методы работают одинаково плохо (сравните S3 Fig). Это неудивительно, поскольку для 20% или 40% переменных была выбрана межкластерная корреляция 0,5, что, следовательно, больше, чем внутрикластерная корреляция. Однако для умеренной внутрикластерной корреляции подходы со смешанными данными превосходят двоичную кластеризацию при наличии шума. Когда корреляция внутри кластера велика, все методы работают отлично.
Рис. 3. Частота ошибочной классификации переменных кластеризации по 100 смоделированных наборов данных каждый с использованием подходов CluMix-ama, CluMix-dcor, ClustOfVar и BCMI.
Наборы данных моделировались, как описано в разделе «Методы» для оценки кластеризации переменных. На этом графике показаны результаты настройки моделирования с 50 выборками, 100 переменными, внутригрупповой корреляцией 0,5 и 20% межгрупповых корреляций 0,5 вместо 0. MCR (ось Y) были рассчитаны на основе кластеризации с евклидовыми расстояниями. для чисто количественных наборов данных (белый), с тремя подходами для смешанных данных (фиолетовый: CluMix-ama, желтый: mCluMix-dcor, зеленый: ClustOfVar, оранжевый: BCMI) для наборов данных с различным количеством категориальных переменных (0%, 25 %, 75%, 100% слева направо) и с простым коэффициентом соответствия для полностью бинаризованных данных (серый цвет).
https://doi.org/10.1371/journal.pone.0188274.g003
Рис. 4. Медианная разница в частоте ошибок между каждым методом смешанных данных и двоичной кластеризацией.
Для всех настроек моделирования коэффициенты ошибочной классификации из кластеризации бинаризованных наборов данных с помощью простого сопоставимого помощника в качестве эталона вычитались из соответствующих MCR при использовании каждого из трех подходов к кластеризации переменных смешанных данных. Показаны медианы этих различий (фиолетовый квадрат: CluMix-ama, желтый треугольник: CluMix-dcor, зеленый кружок: ClustOfVar, оранжевая звезда: BCMI).На левой панели учитывались различные размеры выборки ( n = 25, 50, 100; столбцы панели) и количество переменных ( p = 50, 100, 200; строки панели), при сохранении фиксированной внутригрупповой корреляции. при 0,5 и доля ненулевых межгрупповых корреляций (со значением 0,5) на 20%. На правой панели настройки менялись по сравнению с внутригрупповые корреляции (corr = 0,25, 0,5, 0,75; столбцы панели) и доля корреляций между группами со значением 0,5 вместо 0 (шум = 0%, 20%, 40%; строки панели), при сохранении количества образцов и переменные с фиксированным значением 100 соответственно.Наборы данных были смоделированы с различным количеством категориальных переменных (0% –100%; слева направо в пределах каждой части рисунка).
https://doi.org/10.1371/journal.pone.0188274.g004
Результаты: Примеры реальных данных
Смешанные данные в сравнении со стандартными подходами к реальным данным
Мы хотели дополнительно изучить потенциальные преимущества применения конкретных методов кластеризации смешанных данных в реальных ситуациях по сравнению со стандартными подходами. Для этой общей цели мы изучили кластеризацию выборок, поскольку существуют реальные примеры с заданной принадлежностью к классам для выборок, тогда как «истинная» группировка переменных почти никогда не известна.В трех наборах данных с переменными разных типов мы сначала предварительно выбрали количественные переменные, которые связаны с соответствующим интересующим двоичным результатом. Затем мы сгруппировали образцы, чтобы восстановить два класса по i) евклидовым расстояниям, используя только количественные переменные в наборе данных, ii) простому расстоянию сопоставления после дихотомизации данных, iii) латентному классу, подходящему для смешанных данных, k-прототипу и Гауэр. Производительность методов сравнивается по сбалансированному коэффициенту ошибок ( BER = 0.5 ⋅ ( a 12 / ( a 11 + a 12 ) + a 21 / ( a 21 + a ), 22 ), 22 где a ij — элементы матрицы путаницы классификации), что более подходит, чем коэффициент ошибочной классификации в случае неравных размеров классов. Три набора данных в качестве примера:
- Ответ на лечение рака груди : Этот набор данных по раку груди [40], включающий 133 пациента, был использован для разработки классификатора на основе экспрессии генов для предоперационного ответа на лечение.Для нашего анализа мы выбираем 10 генов с наиболее дифференцированной экспрессией между «патологическим полным ответом» (34 пациента) и «остаточным заболеванием» (99 пациентов), а также категориальными переменными статусом рецептора эстрогена, статусом рецептора прогестерона, степенью опухоли и молекулярным подклассом.
- Выживаемость рака молочной железы : Из набора данных Нидерландского института рака для прогнозирования выживаемости без метастазов у 144 больных раком молочной железы с положительным лимфоузлом [41] мы используем ориентир 6-летней выживаемости в качестве бинарного результата для нашего анализа (89 пациенты выжили и 35 не выжили 6 лет; 20 пациентов, прошедших цензуру до достижения 6 лет, были исключены из анализа).Из опубликованной сигнатуры 70 генов мы выбираем 10 генов с наиболее дифференцированной экспрессией и категориальные переменные, статус рецептора эстрогена, степень опухоли и возрастной класс.
- Химический производственный процесс : Этот набор данных из 58 измерений на 176 образцах доступен в пакете R AppliedPredictiveModeling [42] и содержит информацию о химическом производственном процессе, цель которого — понять взаимосвязь между процессом и выход конечного продукта.Из измеренных количественных характеристик мы выбираем 10, которые наиболее связаны с хорошим / плохим урожаем (44 хороших, 132 плохих урожая), и далее пять бинарных переменных в наборе данных.
Таблица 4 показывает сбалансированные коэффициенты ошибок для описанных данных и методов кластеризации. В этих примерах использование подходов к кластеризации смешанных данных в большинстве случаев давало несколько лучшие результаты, чем более распространенные стратегии, где либо категориальные переменные опускаются, либо данные приводятся в одном масштабе.Кластеризация на основе коэффициента сходства Гауэра, который используется в этой статье, работает лучше, чем два алгоритма разделения смешанных данных.
Исследование ВСЕГО набора данных
Чтобы дать несколько примеров использования кластеризации данных смешанного типа и продемонстрировать методы визуализации, реализованные в нашем пакете R CluMix , мы проанализировали общедоступный набор данных из 128 пациентов с острым лимфобластным лейкозом (ОЛЛ) [43], который также доступен как пакет данных R ALL .Набор данных включает в себя клиническую информацию (возраст, пол, рецидив, ремиссия, непрерывная полная ремиссия в течение всего периода наблюдения (CCR), статус трансплантата, тип ALL (B-ALL / T-ALL)), а также молекулярные параметры (транслокации t (9; 22) и t (4; 11), молекулярная классификация ALL), а также меры экспрессии генов на микрочипах. Сначала была построена матрица сходства для доступных клинических и цитогенетических параметров с использованием подхода CluMix-ama. Матрица сходства была визуализирована с помощью тепловой карты, чтобы дать общее представление о взаимосвязях между различными функциями, см. Рис. 5.Интенсивность цвета указывает на силу ассоциации для каждой пары переменных. Кроме того, связанные переменные группируются иерархической кластеризацией. Этот дисплей в целом полезен, например, в регрессионном анализе, когда должны быть идентифицированы сильно связанные предикторы, чтобы избежать избыточной информации или коллинеарности в модели. Наиболее сильные ассоциации наблюдаются между молекулярной биологией ОЛЛ и двумя хромосомными транслокациями t (9; 22) и t (4; 11). Наличие транслокации t (9; 22) (Филадельфийская хромосома) является самым сильным индикатором подтипа BCR / ABL при ОЛЛ.Точно так же транслокация t (4; 11) определяет молекулярный подтип ALL-1 / AF4. Трансплантация костного мозга очень показана пациентам с транслокацией t (4; 11), что также можно увидеть по соответствующей сильной ассоциации на тепловой карте. Кроме того, тип ОЛЛ (В-ОЛЛ или Т-ОЛЛ) связан с молекулярной биологией, чего и следовало ожидать, поскольку большинство молекулярных подтипов ОЛЛ более заметны при В-ОЛЛ по сравнению с Т-ОЛЛ. Индикатор того, является ли пациент цитогенетически нормальным, также естественно связан с основными хромосомными транслокациями при ОЛЛ.Другой блок с большим сходством включает показатели ремиссии после лечения, CCR и рецидива. Обычно можно ожидать, что эти последующие индикаторы взаимосвязаны.
Рис. 5. Тепловая карта сходства между клиническими параметрами при ОЛЛ.
Сходства между переменными, доступными во ВСЕМ наборе данных, были рассчитаны с помощью подхода CluMix-ama. Более сильные связи между переменными обозначены более короткими расстояниями на дендрограммах и более темным синим цветом на тепловой карте.
https://doi.org/10.1371/journal.pone.0188274.g005
Используя ту же матрицу сходства для переменных, мы предлагаем новый тип иллюстраций, которые могут быть полезны в регрессионном анализе. Мы предполагаем достижение ремиссии после лечения в качестве переменной результата, а молекулярные подтипы — в качестве потенциального предиктора, представляющего наибольший интерес. Из полной матрицы подобия переменных извлекаются соответствующие строки для этих двух переменных. Затем значения подобия отображаются на диаграмме рассеяния, так что каждая точка на графике иллюстрирует сходство соответствующей третьей ковариаты как с результатом, так и с предсказателем, см. Рис. 6.Сами переменные результата и предиктора также включены в график и, очевидно, принимают значения 1 на оси y и x соответственно. Координата x результата и координата y предсказателя соответствуют связи между ними и, следовательно, дают представление о том, может ли связь быть значительной. Положение всех других переменных позволяет сделать выводы об их отношении как к результату, так и к предиктору: положение точек в направлении y дает первое представление о том, какие ковариаты могут повлиять на результат.Переменные, расположенные очень близко к положению переменной результата, потенциально могут рассматриваться как суррогатный результат. Как видно из рис. 5, снова становится очевидной сильная связь между ремиссией, рецидивом и CCR. Функции в правой нижней части рисунка тесно связаны с выбранной переменной-предиктором, но не связаны с результатом. Это, вероятно, не добавит существенной ценности регрессионной модели. Если есть переменные, очень близкие к положению переменной-предиктора, это может указывать на коллинеарность.В примере это, по-видимому, относится к ВСЕМ типам и цитогенетическим признакам. Это имеет смысл, поскольку конкретные транслокации определяют определенные молекулярные подтипы, и почти все пациенты с Т-клеточным ОЛЛ имеют подтип NEG. И, наконец, что не менее важно, эта цифра может помочь идентифицировать смешивающие переменные, поскольку сходства как для предиктора, так и для результата доступны с первого взгляда. Возможные факторы, влияющие на ситуацию, будут расположены в правом верхнем углу. В этом случае кажется, что трансплантации проводились только пациентам с определенными молекулярными подтипами, так что обе ковариаты смешаны.Обратите внимание, что расстояния между точками на графике не соответствуют напрямую переменным сходствам.
Рис. 6. Сходство каждой переменной с индикатором ремиссии, построенное против соответствующего сходства с молекулярным подтипом ALL.
Из полной матрицы сходства переменных (полученной с помощью подхода CluMix-ama) значения двух представляющих интерес переменных, а именно ремиссии и молекулярного подтипа, извлекаются и отображаются на диаграмме рассеяния, так что каждая точка на графике показывает сходство третьей ковариаты с обеими интересующими переменными.Символы на графике заменяются соответствующими именами переменных. Цвет указывает числовые (черный) и категориальные (фиолетовый) переменные. Такая иллюстрация может помочь идентифицировать суррогатные, коллинеарные и смешивающие переменные.
https://doi.org/10.1371/journal.pone.0188274.g006
Затем мы использовали тот же набор данных, чтобы показать пример неконтролируемого способа исследования глобальных структур среди пациентов и переменных, сочетая как клинические параметры, так и высокие показатели. данные размерной экспрессии генов.Данные микроматрицы сначала сокращали путем неспецифической фильтрации до набора из 100 самых разных генов. Чтобы упростить визуальный осмотр, информация в этом списке генов была дополнительно суммирована с помощью кластеризации k-средних до восьми кластеров генов, а затем центры кластеров были добавлены к клиническим параметрам. Пациенты были сгруппированы с использованием метода Гауэра. Для кластеризации переменных мы рассмотрели три подхода, описанные в разделе «Методы». Самой распространенной задачей визуализации полученных матриц расстояний для смешанных данных является создание тепловой карты, отображающей структуры между переменными и пациентами одновременно.На нашей тепловой карте со смешанными данными (см. Правую панель рис. 7) используются разные цветовые схемы для выделения различных типов переменных. Для числовых характеристик мы предлагаем синюю шкалу, а для порядковых множителей — зеленую цветовую шкалу. Структуры в данных должны стать видимыми как участки светлого или темного цвета соответственно. Для неупорядоченных категориальных данных мы берем цвета из красной цветовой палитры. Хотя для качественных данных обычно выбираются цвета, которые визуально не предполагают какого-либо упорядочения между категориями, можно также поспорить об использовании порядка категорий, найденного в подходе CluMix-ama, при вычислении сходства между упорядоченными по рангу и качественными переменными.Таким образом, категории, отображаемые светло / темно-красным цветом, могут совпадать со светлым / темным цветами в переменных, наиболее близких к категориальной переменной. Следовательно, структуры данных становятся более очевидными. На рис. 7 показано, что пациенты группируются в основном на B-ALL и T-ALL. Внутри пациентов с В-ОЛЛ видны дополнительные подгруппы, отражающие различные молекулярные подтипы ОЛЛ. На следующем уровне иерархии дендрограмм пациентов преобладает пол. Разделение на B-ALL и T-ALL поддерживается пятью из восьми кластеров генов.Некоторые из этих кластеров, по-видимому, связаны с молекулярными подтипами. Например, кластер 8, по-видимому, содержит гены, которые в основном активируются в подтипе ALL-1 / AF4. В кластере генов 7, по-видимому, преобладают гены, связанные с полом. Остальные два кластера генов не показывают очевидной связи с какими-либо другими исследуемыми факторами. Отношения между переменными, уже обсуждавшиеся выше, можно более подробно рассмотреть на этой тепловой карте. Например, связь между постоянной полной ремиссией и рецидивом явно отрицательная, а хромосомные транслокации t (9; 22) и t (4; 11) являются индикаторами для молекулярных подтипов ALL BCR / ABL и ALL-1 / AF4, соответственно.Чтобы подчеркнуть преимущества новой тепловой карты со смешанными данными, на левой панели рис. 7 показана «стандартная» тепловая карта, основанная только на данных экспрессии генов (здесь мы снова используем 100 самых разных генов вместо центров кластеров генов). Клинические и цитогенетические параметры не используются для кластеризации, а просто добавляются поверх изображения. Группировка пациентов на B-ALL и T-ALL все еще очевидна, что, по-видимому, является основной информацией, которую можно извлечь из паттернов экспрессии генов. Дальнейшее структурирование пациентов по молекулярным подгруппам или полу, как на тепловой карте со смешанными данными, здесь не очевидно.В общем, проверка дополнительных параметров довольно обременительна, если их больше, может быть, двух или трех. Напротив, на тепловой карте со смешанными данными они отображаются как группы связанных функций, что облегчает получение глобального обзора набора данных.
Рис. 7. Тепловые карты экспрессии генов и клинические данные пациентов при ОЛЛ.
Левая панель является результатом стандартного подхода, при котором для кластеризации используются только данные об экспрессии генов (100 самых разных генов). Клиническая и цитогенетическая информация добавляется сверху в виде цветных полос.На правой панели показана соответствующая новая тепловая карта со смешанными данными. Центры восьми кластеров генов k-средних вместе с другими клиническими параметрами были сгруппированы с использованием подхода CluMix-ama. Пациенты были сгруппированы с использованием расстояния Гауэра. Недостающие значения обозначаются белыми точками.
https://doi.org/10.1371/journal.pone.0188274.g007
При использовании подхода CluMix-dcor или ClustOfVar для тепловой карты смешанных данных вместо подхода CluMix-ama мы получаем аналогичные результаты, см. S4 и S5 Рис.Однако можно увидеть некоторые различия, например, при использовании групп кластера 5 генов CluMix-dcor вместе с транслокацией t (4; 11), тогда как при подходе CluMix-ama он находится в группе вместе с возрастом и кластером генов 4. С ClustOfVar только четыре кластера генов непосредственно связаны с B / T-ALL, тогда как кластер генов 8, как видно, более связан с транслокацией t (4; 11) и молекулярной классификацией ALL. Обычно трудно сказать, какие результаты кластеризации «имеют больше смысла», поскольку «истинная» группировка переменных неизвестна.Можно только попытаться объяснить, какие группы переменных правдоподобны, исходя из биологического фона. Здесь действительно носители транслокации t (4; 11), по-видимому, обладают специфически высокой экспрессией генов в кластере 8 генов. С другой стороны, например, прямая связь между транслокацией t (9; 22) и молекулярным подтипом BCR / ABL становится более очевиден при кластеризации с подходами CluMix-ama и CluMix-dcor по сравнению с ClustOfVar.
Мы также составили тепловую карту, используя непосредственно выбранные 100 наиболее вариабельных генов вместо кластеров генов (см. S6 рис.).Затем в кластеризации пациентов преобладает разделение на B- и T-ALL, тогда как дальнейшие подгруппы, т. Е. Отражающие молекулярную классификацию или пол, больше не видны. Вероятно, это связано с тем, что подавляющее большинство генов связано с B- или T-ALL. Введение переменных весов — это вариант, чтобы придать большее значение меньшинству клинических и цитогенетических параметров, см. S7 Рис. В качестве примера. Кластеризация переменных показывает аналогичные группировки, как и раньше, с использованием кластеров генов.Здесь мы можем напрямую идентифицировать гены, связанные с некоторыми другими параметрами, без необходимости возвращаться от кластеров к их соответствующим отдельным членам, например В-клеточные гены CD19 , CD79B или гены из семейства HLA (присутствуют в кластере генов 1 на фиг.7 и S4 фиг.), Гены, связанные с Т-клетками CD3D , LCK и MAL (в кластере генов 6) или гены DDX3Y и RPS4Y1 , расположенные на хромосоме Y и, таким образом, связанные с полом (кластер генов 7).
Обсуждение
Мы описали способы использования наборов данных, включающих параметры, измеренные в разных масштабах, в кластерном анализе — как отдельных выборок, так и измеряемых переменных — при этом данные не обязательно должны быть приведены в одном масштабе, что обычно означает потерю информации. Основное внимание в этой работе уделяется i) разработке и оценке новых стратегий для кластеризации переменных, которые, по нашему мнению, все еще недостаточно хорошо освещены в литературе, и ii) интегративной визуализации самих предварительно обработанных данных или результатов их обработки. Статистический анализ.Последнее все еще может быть сложным в случае многомерных данных из, возможно, разных источников.
Для кластеризации выборок мы использовали матрицы сходства, основанные на коэффициенте ассоциации Гауэра. С точки зрения восстановления истинных базовых классов образцов в смоделированных данных (не показаны) и в примерах реальных данных он работает так же хорошо или лучше, чем алгоритмы разделения, такие как кластеризация k-прототипов.
Для переменных кластеризации i) новый метод, основанный на матрицах сходства, созданных комбинацией мер ассоциации (CluMix-ama), ii) новый метод, основанный на матрицах различий, определенных корреляцией расстояний (CluMix-dcor), iii) подход иерархической кластеризации на основе PCA для данных смешанного типа (ClustOfVar) и iv) оценивалась кластеризация на основе взаимной информации с поправкой на смещение (BCMI).Для подхода i) была введена новая мера ассоциации для сравнения ранжированных и качественных переменных на основе переупорядочения категорий. Различные меры ассоциации комбинируются таким образом, что результирующая матрица расстояний имеет евклидовы свойства. Для подхода ii) мы вывели новую меру ассоциации для сравнения смешанных переменных, основанную на концепции обобщенных дистанционных корреляций. В отличие от конкурирующих мер, этот коэффициент равен 0 тогда и только тогда, когда лежащие в основе случайные величины независимы.
Имитационные исследования для нового подхода CluMix-ama показали, что с предложенными мерами связи между переменными истинные лежащие в основе корреляции переменных с. их сходство можно хорошо запечатлеть. Дальнейшие исследования моделирования были проведены для сравнения различных стратегий кластеризации смешанных данных в их способности восстанавливать истинные базовые структуры в данных. В случае исключительно количественных данных стандартные меры расстояния, такие как евклидово расстояние, по-прежнему будут лучшим выбором.Но для данных смешанного типа такие методы неприменимы без преобразования данных. Моделирование показало, что в целом использование конкретных методов для переменных смешанного типа может быть лучше, чем применение стандартных подходов к категоризированным версиям данных — по крайней мере, для примерно 50% категориальных переменных в наборе данных и для большого количества выборок и / или переменные. Подходы i) -iii) для кластеризации переменных смешанного типа показали очень похожую производительность. Наши два новых метода CluMix-ama и CluMix-dcor работают сравнимо или, особенно в случае больших фракций неколичественных переменных, лучше, чем существующий подход ClustOfVar, и в целом они работают лучше, чем BCMI.
Два новых подхода CluMix-ama и CluMix-dcor предоставляют матрицы расстояний. В отличие от подхода ClustOfVar, это дает пользователю полную гибкость с точки зрения того, какой тип алгоритма кластеризации применять. Кроме того, матрицы подобия полезны для целей визуализации. Также BCMI предоставляет матрицу подобия. Однако взаимная информация может быть больше 1, и, следовательно, соответствие значений корреляции менее четкое, чем для CluMix-ama и CluMix-dcor. Если в наборе данных линейные ассоциации ожидаются или представляют наибольший интерес, подход CluMix-ama может быть методом выбора, поскольку он был разработан для определения взаимосвязей, подобных корреляции.Для нелинейных или даже немонотонных отношений подход CluMix-dcor может быть лучшим вариантом, поскольку он улавливает все, что отличается от независимости между переменными. Если и в какой степени такие «нестандартные» отношения должны быть отражены в итоговой матрице расстояний и как различные методы работают в этом смысле, является предметом дальнейших исследований. Еще одной привлекательной особенностью подхода CluMix-dcor является тот факт, что мы вычисляем корреляции расстояний на основе сходств, эквивалентных тем, которые используются также для кластеризации образцов.Таким образом, мы получаем единый подход для одновременной кластеризации выборок и переменных. Предлагаемые методы обеспечивают расстояния, на которых выполняется неравенство треугольника. Тем не менее, неясно, могут ли определенные комбинации типов данных, например, две количественные переменные по сравнению с одной количественной и одной бинарной переменной систематически дают большее или меньшее расстояние. Этот вопрос требует дальнейшего изучения и разработки возможных исправлений.
Приложение реальных данных показало неконтролируемую иллюстрацию данных.Предлагаемый подход интегративной визуализации можно также использовать для контролируемых настроек, например, комбинированной визуализации результатов выбора контролируемых функций вместе с дополнительными ковариатами и интересующим результатом (см. S8 Рис. Для примера). Что касается времени вычислений, то подход CluMix-dcor является самым быстрым для наборов данных размеров, аналогичных нашим исследованиям моделирования, а также для больших наборов переменных. С другой стороны, при увеличении размера выборки ClustOfVar более эффективен. В нашей текущей реализации тепловая карта ограничена максимум 200 переменными, хотя матрицы сходства могут быть рассчитаны для большего количества переменных.Следовательно, уменьшение размеров по-прежнему необходимо при работе с наборами данных большой размерности. В любом случае, в большинстве случаев выбор или обобщение признаков необходимы, чтобы иметь возможность визуально различать структуры в данных.
Использование представленных мер подобия можно расширить несколькими способами. Для кластеризации выборок существует также взвешенная версия расстояния Гауэра, которая позволяет расставлять приоритеты для переменных. Веса могут быть получены, например, из предыдущего регрессионного анализа усадки.Помимо исследовательского анализа, лежащая в основе кластеризация на основе данных смешанного типа может найти другие потенциальные приложения в рамках статистического вывода. Сходства между выборками, оцениваемые с использованием признаков по разным шкалам, могут, например, использоваться для задач классификации. Кластеризация переменных обеспечивает иерархию связанных функций, которая может служить отправной точкой для иерархических подходов к тестированию.
Заключение
Способность определять сходства и кластеризовать наблюдения и переменные смешанных типов данных ценна для анализа и иллюстрации сложных наборов данных.Эта работа вносит свой вклад в методологию кластеризации переменных смешанного типа и уделяет особое внимание стратегиям интегративной визуализации.
Вспомогательная информация
S1 Рис. Сравнение показателей ассоциации для различных комбинаций типов данных.
Для каждого сравнения 1000 пар переменных были смоделированы следующим образом: две количественные переменные для 200 образцов были смоделированы, чтобы иметь корреляцию Пирсона (слева направо) 0, 0,3, 0,6 или 0,9, как показано красными линиями. .Порядковые, номинальные и бинарные коэффициенты были созданы путем категоризации непрерывных переменных в «полном соответствии», например медианным сокращением для двоичных факторов и сокращением квартилей для номинальных и порядковых факторов (в результате получается 4 категории). Для каждой комбинации типов переменных, как указано в соответствующих заголовках, было применено от трех до четырех различных общих или новых показателей ассоциации, где соответствующий коэффициент, выбранный для CluMix-ama в каждом случае, выделен жирным шрифтом (Пирсон = корреляция Пирсона, Спирмен = Корреляция Спирмена, Кендалл = тау Кендалла, GKgamma = гамма Гумана и Крускала, ClustOfVar = мера сходства, основанная на квадрате канонической корреляции, как используется в подходе ClustOfVar, SomersD = Somers ‘D, ContCoef = коэффициент контингентности Пирсона, V / ReorderCramersV reorderSp = гамма-корреляция Гудмана и Крускала / Спирмена, применяемая к «оптимальному» порядку категорий, см. основной текст).Очень похожие результаты наблюдались при использовании настроек моделирования с i) большим количеством категорий для номинальных переменных, ii) некоторой долей отсутствующих значений, iii) меньшими размерами выборки, iv) несбалансированными размерами категорий для номинальных переменных (данные не показаны).
https://doi.org/10.1371/journal.pone.0188274.s001
(TIFF)
S2 Рис. Частота ошибочной классификации из-за кластеризации переменных по 100 смоделированных наборов данных каждый, при разном размере выборки и количестве переменных.
Наборы данных были смоделированы, как описано в основной статье, с использованием внутригрупповой корреляции 0.5 и 20% межгрупповых корреляций 0,5 вместо 0. Были применены три подхода для кластеризации переменных: CluMix-ama (верхняя левая панель), CluMix-dcor (верхняя правая панель), ClustOfVar (нижняя левая панель) и BCMI ( нижняя правая панель). Настройки моделирования варьировались по-разному. размер выборки ( n = 25, 50, 100; столбцы панели) и количество переменных ( p = 50, 100, 200; строки панели). Коэффициенты ошибочной классификации (MCR) (ось Y) были рассчитаны на основе кластеризации с евклидовыми расстояниями для чисто количественных наборов данных (оранжевый) с подходами для смешанных данных для наборов данных с различным количеством категориальных переменных (0% -100%; от белого до темного синий) и с простым коэффициентом согласования для полностью бинаризованных данных (зеленый).
https://doi.org/10.1371/journal.pone.0188274.s002
(TIFF)
S3 Рис. Степень ошибочной классификации из-за кластеризации переменных по 100 смоделированных наборов данных каждая, с различной корреляцией и шумом.
Как S2 Fig, но с фиксированным числом выборок и 100 переменных соответственно. Настройки моделирования варьировались по-разному. внутригрупповые корреляции (corr = 0,25, 0,5, 0,75; столбцы панели) и доля межгрупповых корреляций со значением 0,5 вместо 0 (шум = 0%, 20%, 40%; строки панели).
https://doi.org/10.1371/journal.pone.0188274.s003
(TIFF)
S4 Рис. Тепловая карта кластеров генов и другие данные о пациентах для ALL с использованием CluMix-dcor для кластеризации переменных.
100 самых разных генов были сгруппированы методом k-средних в восемь кластеров. Соответствующие кластерные центры вместе с другими клиническими и цитогенетическими параметрами были сгруппированы с использованием подхода CluMix-dcor. Пациенты были сгруппированы с использованием расстояния Гауэра. Цветовые коды поясняются в легенде ниже.Недостающие значения обозначаются белыми точками.
https://doi.org/10.1371/journal.pone.0188274.s004
(JPEG)
S6 Рис. Тепловая карта 100 наиболее вариабельных генов и другие данные о пациентах при ОЛЛ.
100 самых разных генов были сгруппированы вместе с другими клиническими и цитогенетическими параметрами с использованием подхода ClustOfVar. Пациенты были сгруппированы с использованием расстояния Гауэра. Цветовые коды такие же, как на рис. S4 и S5.
https://doi.org/10.1371/journal.pone.0188274.s006
(JPEG)
S8 Рис. Тепловая карта переменных, выбранных для прогнозирования рецидива у ВСЕХ.
В качестве примера визуализации результатов контролируемого анализа была построена модель для прогнозирования рецидива у ВСЕХ пациентов. Во-первых, были предварительно отобраны гены, связанные с рецидивом. Во-вторых, модель штрафной регрессии была построена с 42 ранее отобранными генами с нескорректированным значением p <0,01, а также с клиническими и цитогенетическими параметрами. Модель привела к окончательному выбору возраста пациента, достижения полной непрерывной ремиссии (CCR) и экспрессии 14 генов.Эти выбранные функции показаны на тепловой карте, где для кластеризации переменных использовался подход CluMix-ama. Цветная полоса столбца показывает состояние рецидива переменной ответа.
https://doi.org/10.1371/journal.pone.0188274.s008
(TIF)
Благодарности
Мы благодарим Мартина Силла за предоставление утилит для построения пользовательских тепловых карт, Наталью Беккер за советы по исследованиям моделирования и Кристиана Хеннига за обсуждение этой темы.
Список литературы
- 1.Шен Р., Ольшен А.Б., Ладаньи М. Интегративная кластеризация нескольких типов геномных данных с использованием совместной модели скрытых переменных с применением к анализу подтипов рака груди и легких. Биоинформатика. 2009. 25 (22): 2906–12. pmid: 19759197
- 2. Бек-Берто М., Пейдж Дж. Многофакторный анализ и кластеризация смеси количественных, категориальных и частотных данных. Вычислительная статистика и анализ данных. 2008. 52 (6): 3255–3268.
- 3. Геваерт О., Де Смет Ф., Тиммерман Д., Моро Й., Де Моор Б.Прогнозирование прогноза рака груди путем интеграции клинических данных и микрочипов с байесовскими сетями. Биоинформатика. 2006; 22 (14): e184–90. pmid: 16873470
- 4. Tamayo P, Cho YJ, Cheriak A, Greulich H, Ambrogio L, Schouten-van Meeteren N, et al. Прогнозирование рецидива у пациентов с медуллобластомой путем интеграции данных клинических и геномных особенностей. J Clin Oncol. 2011. 29 (11): 1415–23. pmid: 21357789
- 5. Мадейра SC, Oliveira AL. Алгоритмы бикластеризации для анализа биологических данных: обзор.Протоколы IEEE по вычислительной биологии и биоинформатике. 2004. 1 (1): 24–45. pmid: 17048406
- 6. Хан Дж., Ченг Х., Синь Д., Ян Х. Частый анализ паттернов: текущее состояние и будущие направления. Data Min Knowl Disc. 2007; 15: 55–86.
- 7. Чжан Х. caOmicsV: Визуализация многомерных данных геномики рака. 2015; Пакет R версии 1.0.0.
- 8. Гауэр Дж. Общий коэффициент подобия и некоторые его свойства. Биометрия.1971; 27: 857–871.
- 9. Лайонс Р. Ковариация расстояний в метрических пространствах. Летопись вероятности. 2013. 41 (5): 3284–3305.
- 10. Секели Г.Дж., Риццо М.Л., Бакиров Н.К. Измерение и проверка независимости путем корреляции расстояний. Летопись статистики. 2007. 35 (6): 2769–2794.
- 11. Секели Г.Дж., Риццо М. Ковариация броуновского расстояния. Летопись прикладной статистики. 2009. 3 (4): 1236–1265.
- 12. Чавент М., Кюнц-Симоне В., Лике Б., Саракко Дж.ClustOfVar: пакет R для кластеризации переменных. Журнал статистического программного обеспечения. 2012; 50 (13): 1–16.
- 13. Парди С., Гэлбрейт С., Уилсон С.Р. Интегрированное исследование больших наборов данных большой размерности. Появиться в Анналах прикладной статистики.
- 14. Хенниг С., Ляо Т.Ф. Сравнение скрытых классов и кластеризации на основе различий для переменных смешанного типа с применением к социальной стратификации. Appl Statist. 2013. 62 (3): 309–369.
- 15.Хуанг З. Расширения алгоритма k-средних для кластеризации больших наборов данных с категориальными значениями. Интеллектуальный анализ данных и обнаружение знаний. 1998. 2 (3): 283–304.
- 16. Ян M-S, Hwang P-Y, Chen D-H. Алгоритмы нечеткой кластеризации для переменных со смешанными признаками. Нечеткие множества и системы. 2004. 141: 301–317.
- 17. Маккейн Б., Альберт М. Функции расстояния для категориальных и смешанных переменных. Письма о распознавании образов. 2008. 29 (7): 986–993.
- 18.Уилсон ДР, Мартинес ТР. Улучшенные функции разнородного расстояния. Журнал исследований искусственного интеллекта. 1997; 6 (1): 1–34.
- 19. Deng Z, Choi K-S, Jiang Y, Wang J, Wang S. Обзор мягкой кластеризации подпространств. Информационные науки. 2016; 348: 84–106.
- 20. Подани Дж. Расширение общего коэффициента сходства Гауэра на порядковые символы. Таксон. 1999. 48 (2): 331–340.
- 21. Лалиберте Э., Лежандр П., Шипли Б.FD: измерение функционального разнообразия по множеству признаков и другие инструменты функциональной экологии. 2014; Пакет R версии 1.0-12.
- 22. Ward JH. Иерархическая группировка для оптимизации целевой функции, Журнал Американской статистической ассоциации. 1963. 58: 236–244.
- 23. Kaufman L, Rousseeuw PJ. Поиск групп в данных: введение в кластерный анализ. Нью-Йорк: John Wiley & Sons; 1990.
- 24. Красков А, Грассбергер П.MIC: Иерархическая кластеризация на основе взаимной информации. В: Emmert-Streib F, Dehmer M, editors. Теория информации и статистическое обучение. США: Springer; 2009. С. 101–123.
- 25. Гонсалес Р., Нельсон К. Измерение порядковой связи в ситуациях, в которых есть равные баллы. Psychol Bull. 1996. 119 (1): 159–165. pmid: 8559859
- 26. Гоктас А., Иски О. Сравнение наиболее часто используемых показателей ассоциации для дважды упорядоченных квадратных таблиц непредвиденных расходов с помощью моделирования.Достижения в методологии и статистике. 2011; 8 (1): с. 17.
- 27. Гудман Л.А., Крускал WH. Меры ассоциации для перекрестных классификаций. Журнал Американской статистической ассоциации. 1954. 49: 732–764.
- 28. Гудман Л.А. Простые модели для анализа ассоциации в кросс-классификациях с упорядоченными категориями. Журнал Американской статистической ассоциации. 1979. 74 (367): 537–552.
- 29. Сирсма В., Крейнер С. Коэффициент связи между категориальными переменными с частичным или предварительным упорядочением категорий.Социологические методы исследования. 2009. 38 (2): 265–286.
- 30. Grenacre MJ. Теория и приложения анализа соответствий. Лондон: Academic Press; 1984.
- 31. Гауэр Дж. Некоторые дистанционные свойства скрытых корневых и векторных методов, используемых в многомерном анализе. Биометрика. 1966; 53: 325–338.
- 32. Хайэм Н. Вычисление ближайшей корреляционной матрицы — задача из финансов. Журнал численного анализа IMA. 2002; 22: 329–343.
- 33.Бейтс Д., Махлер М. Матрица: классы и методы разреженных и плотных матриц. 2015; Пакет R версии 1.2-2.
- 34. Feuerverger A. Последовательный тест на двумерную зависимость. Международное статистическое обозрение. 1993. 61 (3): 419–433.
- 35. Guo X, Zhang Y, Hu W, Tan H, Wang X. Вывод нелинейных сетей регуляции генов из данных экспрессии генов на основе корреляции расстояния. ПлоС один. 2014; 9 (2): e87446. pmid: 24551058
- 36. Горфин М., Гольдштейн Б., Фишман А., Хеллер Р., Хеллер Ю., Ламм А. Т..Функция генов, ассоциированных с раком, выявленная с помощью современных одномерных и многомерных ассоциативных тестов. ПлоС один. 2015; 10 (5): e0126544. pmid: 25965968
- 37. Kong J, Klein BE, Klein R, Lee KE, Wahba G. Использование корреляции расстояний и SS-ANOVA для оценки ассоциаций семейных отношений, факторов образа жизни, болезней и смертности. Труды Национальной академии наук. 2012. 109 (50): 20352–20357.
- 38. Секели Г.Дж., Риццо М.Л. T-критерий корреляции расстояний на независимость в высоком измерении.Журнал многомерного анализа 2013; 117: 193–213.
- 39. Дьюк Дж., Эдельманн Д., Ричардс Д. Коэффициенты дистанционной корреляции для распределений Ланкастера. Журнал многомерного анализа. 2017; 154: 19–39.
- 40. Hess KR, Anderson K, Fraser Symmans W., Valero V, Ibrahim N, Mejia JA и др. Фармакогеномный предиктор чувствительности к предоперационной химиотерапии паклитакселом и фторурацилом, доксорубицином и циклофосфамидом при раке молочной железы. Журнал клинической онкологии.2006. 24 (26): 4236–4244. pmid: 16896004
- 41. ван де Виджвер MJ, He YD, van’t Veer LJ, Dai H, Hart AAM, Voskuil DW и др. Сигнатура экспрессии гена как показатель выживаемости при раке груди. Медицинский журнал Новой Англии. 2002; 347 (25): 1999–2009. pmid: 124
- 42. Кун М., Джонсон К. AppliedPredictiveModeling: функции и наборы данных для прикладного прогнозного моделирования. 2014; Пакет R версии 1.1-6.
- 43. Кьяретти С., Ли Х, Джентльмен Р.



 Стало традиционным вести счет проективным методикам с теста словесных ассоциаций К. Юнга, созданного им в 1904-1905 гг. Метод вызова ответных ассоциаций в психологии известен со времен В. Вундта и Ф. Гальтона, однако именно К. Юнгу принадлежит открытие и доказательство феномена, лежащего в основе всех проективных методик, а именно возможности посредством косвенного воздействия на значимые области переживания и поведения человека («комплексы») вызывать пертурбации в экспериментальной деятельности. Юнг показал таким образом, что бессознательные переживания личности доступны объективной диагностике. Впоследствии разнообразные варианты ассоциативного теста применялись для выявления чувства вины (детекторы лжи М. Вертгаймера и А. Лурия), асоциальных вытесненных влечений (Дж. Бруйер, Р. Лазарус, Л. Постмен, Ч. Эриксен и
Стало традиционным вести счет проективным методикам с теста словесных ассоциаций К. Юнга, созданного им в 1904-1905 гг. Метод вызова ответных ассоциаций в психологии известен со времен В. Вундта и Ф. Гальтона, однако именно К. Юнгу принадлежит открытие и доказательство феномена, лежащего в основе всех проективных методик, а именно возможности посредством косвенного воздействия на значимые области переживания и поведения человека («комплексы») вызывать пертурбации в экспериментальной деятельности. Юнг показал таким образом, что бессознательные переживания личности доступны объективной диагностике. Впоследствии разнообразные варианты ассоциативного теста применялись для выявления чувства вины (детекторы лжи М. Вертгаймера и А. Лурия), асоциальных вытесненных влечений (Дж. Бруйер, Р. Лазарус, Л. Постмен, Ч. Эриксен и , 1982; Abt L., Bellak L., 1950; Semeonoff В., 1976;Anzieu D., 1967).
, 1982; Abt L., Bellak L., 1950; Semeonoff В., 1976;Anzieu D., 1967).

 Впоследствии Г. Роршах предположил, что чернильные пятна, адресованные зрительному воображению, растормаживают, оживляют моторные фантазии.
Впоследствии Г. Роршах предположил, что чернильные пятна, адресованные зрительному воображению, растормаживают, оживляют моторные фантазии.

 T.) отличается еще большей стандартизованностью и схематизацией. Она состоит из двух параллельных серий таблиц по 45 карточек в каждой; на каждую карточку испытуемый должен дать только один ответ. Достоинством H.I.T., сделавшим его наиболее валидным и надежным тестом среди дериватов методики Роршаха, является наличие нормативов и процентных показателей по основным категориям шифровки ответов.
T.) отличается еще большей стандартизованностью и схематизацией. Она состоит из двух параллельных серий таблиц по 45 карточек в каждой; на каждую карточку испытуемый должен дать только один ответ. Достоинством H.I.T., сделавшим его наиболее валидным и надежным тестом среди дериватов методики Роршаха, является наличие нормативов и процентных показателей по основным категориям шифровки ответов.

 , 1935). В то время тест не был обеспечен ни общей теоретической концепцией — в качестве метода исследования личности он стал рассматриваться в более поздних публикациях Г. Мюррея (Murray H., 1938, 1943), ни стандартизованным руководством по применению. У этого метода, как и у теста Роршаха, имелись свои предшественники и своя предыстория (см., напр., Abt L., Bellak L., 1950; Rapaport D., 1968). Психологам и психиатрам давно было известно, что рассказы по сюжетным картинкам, специально подобранным для исследуемого контингента, позволяют судить о склонностях, интересах и нередко выявляют болезненные состояния психики. На первый взгляд замысел TAT казался более простым и очевидным, чем идея Г. Роршаха. Действительно, разве Чарльзу Диккенсу, заканчивающему свой любимый роман о Дэвиде Копперфильде, не чудилось, как он сам писал, «будто он отпускает в сумеречный мир частицу самого себя» (ДиккенсЧ., 1984, т. 6)? Мы также различаем за нравственными страданиями героев Ф. М. Достоевского искания его собственной мятущейся души.
, 1935). В то время тест не был обеспечен ни общей теоретической концепцией — в качестве метода исследования личности он стал рассматриваться в более поздних публикациях Г. Мюррея (Murray H., 1938, 1943), ни стандартизованным руководством по применению. У этого метода, как и у теста Роршаха, имелись свои предшественники и своя предыстория (см., напр., Abt L., Bellak L., 1950; Rapaport D., 1968). Психологам и психиатрам давно было известно, что рассказы по сюжетным картинкам, специально подобранным для исследуемого контингента, позволяют судить о склонностях, интересах и нередко выявляют болезненные состояния психики. На первый взгляд замысел TAT казался более простым и очевидным, чем идея Г. Роршаха. Действительно, разве Чарльзу Диккенсу, заканчивающему свой любимый роман о Дэвиде Копперфильде, не чудилось, как он сам писал, «будто он отпускает в сумеречный мир частицу самого себя» (ДиккенсЧ., 1984, т. 6)? Мы также различаем за нравственными страданиями героев Ф. М. Достоевского искания его собственной мятущейся души.

 Эксперименты уточнили эту гипотезу: если потребность — явная или латентная — не имеет «моторной разрядки», фрустрируется в открытом социальном поведении, она находит компенсаторное удовлетворение в рассказах TAT (Lazarus R. S., 1961).
Эксперименты уточнили эту гипотезу: если потребность — явная или латентная — не имеет «моторной разрядки», фрустрируется в открытом социальном поведении, она находит компенсаторное удовлетворение в рассказах TAT (Lazarus R. S., 1961). , в которых автором были впервые сформулированы основные принципы проективной психологии. Ему же принадлежит приоритет в использовании термина «проекция» для обозначения особой группы методов исследования личности.
, в которых автором были впервые сформулированы основные принципы проективной психологии. Ему же принадлежит приоритет в использовании термина «проекция» для обозначения особой группы методов исследования личности. Узко прагматическая ориентация многих исследований часто игнорировала это ограничение, составляющее суть проективного метода как особого подхода, способа понимания человека. Важно не то, как человек действует, а то, что он чувствует и как управляет своими чувствами. Ясно, что совпадение поведенческого уровня и плана переживаний есть частный случай, поэтому возможность прогноза поведения по проективным методам ограничена, зато открывается перспектива проникновения в уникальный мир человеческих чувств и внутреннюю логику его построения.
Узко прагматическая ориентация многих исследований часто игнорировала это ограничение, составляющее суть проективного метода как особого подхода, способа понимания человека. Важно не то, как человек действует, а то, что он чувствует и как управляет своими чувствами. Ясно, что совпадение поведенческого уровня и плана переживаний есть частный случай, поэтому возможность прогноза поведения по проективным методам ограничена, зато открывается перспектива проникновения в уникальный мир человеческих чувств и внутреннюю логику его построения. Чем более неопределенны условия (т. е. чем меньше давление реальности), тем в большей степени психическая активность приближается по своей природе к «первичным» психическим процессам (воображению, галлюцинациям), движимым принципом удовольствия. Проективные методы на первый взгляд давали основание для подобного осмысления (см., напр., экспериментальные исследования аутистического восприятия), однако в этом случае необходимо было признать тождество «первичных процессов» и психической активности в ситуации проективного исследования.
Чем более неопределенны условия (т. е. чем меньше давление реальности), тем в большей степени психическая активность приближается по своей природе к «первичным» психическим процессам (воображению, галлюцинациям), движимым принципом удовольствия. Проективные методы на первый взгляд давали основание для подобного осмысления (см., напр., экспериментальные исследования аутистического восприятия), однако в этом случае необходимо было признать тождество «первичных процессов» и психической активности в ситуации проективного исследования.
 Проективная продукция рассматривается как результат сложной познавательной деятельности, в которой слиты воедино и собственно когнитивные моменты (отвечающие «реальности» — ситуации эксперимента, задаче инструкции, определенным характеристикам стимуль-ного материала), и аффективно-личностные факторы — «периферические» мотивы, индивидуальные способы контроля и защиты.
Проективная продукция рассматривается как результат сложной познавательной деятельности, в которой слиты воедино и собственно когнитивные моменты (отвечающие «реальности» — ситуации эксперимента, задаче инструкции, определенным характеристикам стимуль-ного материала), и аффективно-личностные факторы — «периферические» мотивы, индивидуальные способы контроля и защиты.
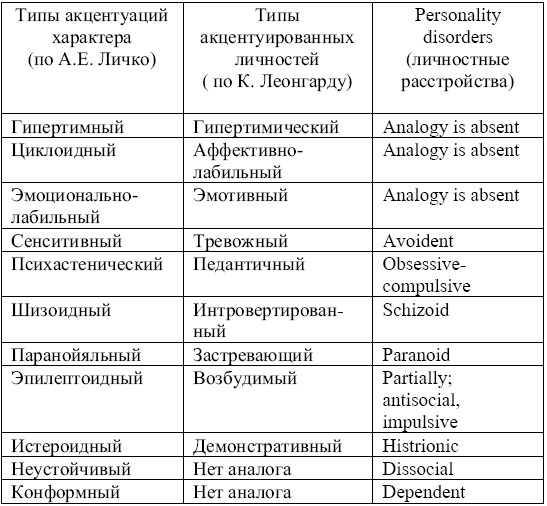 Индивидуальные вариации ответов на стандартные значения стимулов в этом случае оказываются более диагностически значимыми и выявляют не столько аффективные состояния и актуальную силу потребности, сколько устойчивые личностные характеристики, в том числе аномалии (Murstein В., 1963).
Индивидуальные вариации ответов на стандартные значения стимулов в этом случае оказываются более диагностически значимыми и выявляют не столько аффективные состояния и актуальную силу потребности, сколько устойчивые личностные характеристики, в том числе аномалии (Murstein В., 1963).
 В. Зейгарник как нарушения моти-вационного компонента мышления (Зейгарник Б. В., 1962). Например, депрессивные тенденции проявляются при выполнении методики в общей инертности, нежелании манипулировать фигурками, неспособности отказаться от ранее сформулированной ошибочной гипотезы. Реакция на фрустрацию, неудачу, затруднения выражается в аутоагрессии, дискредитации задания, нарушении планирования или настаивании на необычных идеях. Один и тот же «симптом», как мы видим, может по-разному проявляться у разных людей, что и позволяет говорить об индивидуальном стиле познавательной активности. Аналогичным образом различные индивидуальные стратегии выполнения какого-либо перцептивного теста (например теста вставленных фигур — EFT) позволяют делать вывод о соответствующих индивидуально-типологических особенностях личности — полезависимости-поленезависимости (Witkin H., 1954, 1974).
В. Зейгарник как нарушения моти-вационного компонента мышления (Зейгарник Б. В., 1962). Например, депрессивные тенденции проявляются при выполнении методики в общей инертности, нежелании манипулировать фигурками, неспособности отказаться от ранее сформулированной ошибочной гипотезы. Реакция на фрустрацию, неудачу, затруднения выражается в аутоагрессии, дискредитации задания, нарушении планирования или настаивании на необычных идеях. Один и тот же «симптом», как мы видим, может по-разному проявляться у разных людей, что и позволяет говорить об индивидуальном стиле познавательной активности. Аналогичным образом различные индивидуальные стратегии выполнения какого-либо перцептивного теста (например теста вставленных фигур — EFT) позволяют делать вывод о соответствующих индивидуально-типологических особенностях личности — полезависимости-поленезависимости (Witkin H., 1954, 1974). Снимается также противопоставление интеллектуальных и личностных тестов как относящихся к разным «областям» личности — иными словами, реализуется, правда несколько упрощенно ..целостный подход к личности как сплаву аффекта и интеллекта.
Снимается также противопоставление интеллектуальных и личностных тестов как относящихся к разным «областям» личности — иными словами, реализуется, правда несколько упрощенно ..целостный подход к личности как сплаву аффекта и интеллекта.
 Так, фигура немолодого мужчины — олицетворение отца, начальника, вообще власти и мужского начала. В этом случае интерпретация темы рассказа в зависимости от общего контекста сужается до анализа внутрисемейных отношений либо расширяется и рассматривается как отражение взаимоотношений обследуемого с широким социальным окружением, отношение к нормативам общества и его ценностям. Тест Роршаха также дает некоторую информацию об общей благоприятной или неблагоприятной аффективной установке обследуемого к другим людям — враждебно-защитной или аффилятивно-открытой.
Так, фигура немолодого мужчины — олицетворение отца, начальника, вообще власти и мужского начала. В этом случае интерпретация темы рассказа в зависимости от общего контекста сужается до анализа внутрисемейных отношений либо расширяется и рассматривается как отражение взаимоотношений обследуемого с широким социальным окружением, отношение к нормативам общества и его ценностям. Тест Роршаха также дает некоторую информацию об общей благоприятной или неблагоприятной аффективной установке обследуемого к другим людям — враждебно-защитной или аффилятивно-открытой.
 , 1950), тест семейных отношений Л. Бене и С. Антони (Bene R., Antony S., 1957), кинетический тест рисования семьи (Burns R., Kaufman S., 1972) и его варианты.
, 1950), тест семейных отношений Л. Бене и С. Антони (Bene R., Antony S., 1957), кинетический тест рисования семьи (Burns R., Kaufman S., 1972) и его варианты. В., 1981), позволяющей исследовать микроструктуру самоотношения в структуре самосознания.
В., 1981), позволяющей исследовать микроструктуру самоотношения в структуре самосознания.
 Фрейдом для объяснения патологических симптомов паранойи в 1896 г., а затем при разборе «случая Шре-бера» в 1911 г. В этих работах проекция понималась как приписывание другим людям социально неприемлемых желаний, в которых человек как бы отказывает сам себе. В этом случае проекция рассматривалась Фрейдом как механизм защиты против неосознаваемых асоциальных влечений, в частности гомосексуальности, которая лежит в основе бредообразования при паранойе. Впоследствии была описана так называемая фоби-ческая защитная проекция — вынесение вовне, экстериориза-ция страха, тревоги, в действительности имеющих эндогенную природу (Фрейд 3., 1924). В работах последующих лет наряду с концепцией защитной проекции, входящей в состав различных патологических состояний, Фрейд вводит понятие проекции как нормального психологического процесса, участвующего в формировании нашего восприятия внешнего мира. Проекция интерпретируется им как первичный процесс «уподобления» окружающей реальности собственному внутреннему миру (Фрейд 3.
Фрейдом для объяснения патологических симптомов паранойи в 1896 г., а затем при разборе «случая Шре-бера» в 1911 г. В этих работах проекция понималась как приписывание другим людям социально неприемлемых желаний, в которых человек как бы отказывает сам себе. В этом случае проекция рассматривалась Фрейдом как механизм защиты против неосознаваемых асоциальных влечений, в частности гомосексуальности, которая лежит в основе бредообразования при паранойе. Впоследствии была описана так называемая фоби-ческая защитная проекция — вынесение вовне, экстериориза-ция страха, тревоги, в действительности имеющих эндогенную природу (Фрейд 3., 1924). В работах последующих лет наряду с концепцией защитной проекции, входящей в состав различных патологических состояний, Фрейд вводит понятие проекции как нормального психологического процесса, участвующего в формировании нашего восприятия внешнего мира. Проекция интерпретируется им как первичный процесс «уподобления» окружающей реальности собственному внутреннему миру (Фрейд 3. , 1925). Таков, например, механизм детского или религиозно-мифологического мировосприятия.
, 1925). Таков, например, механизм детского или религиозно-мифологического мировосприятия.
 Избирательность в контактах. Интровертированность. Инертность, склонность к раздумью.
Избирательность в контактах. Интровертированность. Инертность, склонность к раздумью.  Стремление к избеганию ответственности.
Стремление к избеганию ответственности.  Потребность в освобождении от гнетущих обстоятельств, несправедливости. Наряду со сниженным фоном настроения и активности — эмоции гнева.
Потребность в освобождении от гнетущих обстоятельств, несправедливости. Наряду со сниженным фоном настроения и активности — эмоции гнева. Потребность в оберегании своей социальной позиции от посягательств, повышенное чувство собственного достоинства, потребность как в самоуважении, так и сохранении личностного реноме в глазах значимых окружающих. Склонность к системному мышлению, тяга к сферам точных знаний. Деликатность в сфере межличностных контактов сочетается с упрямством в отстаивании своей позиции. Мотивация избегания неуспеха при достаточно ригидных установках и упорстве в своих начинаниях. Черты повышенной аккуратности и внимания к деталям.
Потребность в оберегании своей социальной позиции от посягательств, повышенное чувство собственного достоинства, потребность как в самоуважении, так и сохранении личностного реноме в глазах значимых окружающих. Склонность к системному мышлению, тяга к сферам точных знаний. Деликатность в сфере межличностных контактов сочетается с упрямством в отстаивании своей позиции. Мотивация избегания неуспеха при достаточно ригидных установках и упорстве в своих начинаниях. Черты повышенной аккуратности и внимания к деталям.  Эротичность в сфере влечения к противоположному полу сочетается с эмпатийностью (умение сопереживать), что может служить основой для гармоничных отношений.
Эротичность в сфере влечения к противоположному полу сочетается с эмпатийностью (умение сопереживать), что может служить основой для гармоничных отношений. 