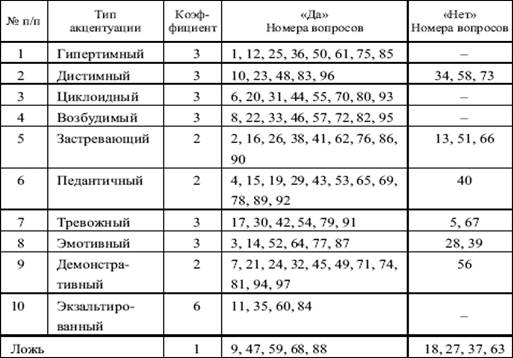
Тест леонгарда интерпретация результатов: Тест-опросник Шмишека и Леонгарда. Методика акцентуации характера и темперамента личности

Опубликовано автором

Содержание

Психолингвистические корреляты успеваемости по английскому языку // Экспериментальная психология — 2013. Том 6. № 1

Аннотация

Настоящая работа посвящена изучению психолингвистических коррелятов успеваемости по английскому языку. Результаты корреляционного анализа данных (индивидуальных отметок успеваемости и показателей ряда психологических и психолингвистических тестов) эмпирического исследования, проведенного на базе одного из учреждений начального профессионального образования, свидетельствуют о наличии связи успеваемости с такими психическими особенностями, как речедвигательная быстрота, высокая скорость выполнения операций при осуществлении предметной деятельности, потребность в освоении предметного мира, высокий уровень общительности и т. д.

Ключевые слова: психолингвистика, корреляционный анализ, успеваемость, английский язык

Рубрика издания:

Психолингвистика

Тип материала: научная статья

Для цитаты: Нуриахметов А. К. Психолингвистические корреляты успеваемости по английскому языку // Экспериментальная психология. 2013. Том 6. № 1. С. 137–141.

Фрагмент статьи

Успешная преподавательская деятельность невозможна без учета индивидуальных психологических особенностей обучающихся. Цель настоящей работы – выявление психолингвистических коррелятов академической успеваемости по английскому языку. Автором предпринята попытка эмпирического изучения психических особенностей и психологических свойств учащихся и их связи с уровнем академической успеваемости по английскому языку. Тема академической успеваемости обладает особой актуальностью для психологии и педагогики. В профессиональной среде часто высказываются обоснованные мнения о несовершенстве существующей системы педагогического контроля (Тимаева, 2012). Тем не менее, академическая успеваемость является единственным общепризнанным, документально фиксируемым показателем уровня усвоения знаний, умений и навыков, который используется в системе начального, среднего и высшего образования в России и большинстве зарубежных стран.

Правомерность подобного подхода подтверждается исследованиями ученых, занимающихся выявлением взаимосвязей академической успеваемости и индивидуальных особенностей обучающихся: нейропсихологических (Соболева, Потанина, 2004), личностных (Слободская и др., 2008), интеллектуальных (Корнилова, Новикова, 2012).

Полный текст

Успешная преподавательская деятельность невозможна без учета индивидуальных психологических особенностей обучающихся. Цель настоящей работы – выявление психолингвистических коррелятов академической успеваемости по английскому языку. Автором предпринята попытка эмпирического изучения психических особенностей и психологических свойств учащихся и их связи с уровнем академической успеваемости по английскому языку. Тема академической успеваемости обладает особой актуальностью для психологии и педагогики. В профессиональной среде часто высказываются обоснованные мнения о несовершенстве существующей системы педагогического контроля (Тимаева, 2012). Тем не менее, академическая успеваемость является единственным общепризнанным, документально фиксируемым показателем уровня усвоения знаний, умений и навыков, который используется в системе начального, среднего и высшего образования в России и большинстве зарубежных стран. Правомерность подобного подхода подтверждается исследованиями ученых, занимающихся выявлением взаимосвязей академической успеваемости и индивидуальных особенностей обучающихся: нейропсихологических (Соболева, Потанина, 2004), личностных (Слободская и др., 2008), интеллектуальных (Корнилова, Новикова, 2012).

Настоящая работа основывается на анализе и обобщении результатов комплексного психолингвистического исследования, проведенного на базе одного из учреждений начального профессионального образования города Стерлитамака Республики Башкортостан. В исследовании приняли участие 100 обучающихся мужского пола в возрасте от 15 до 19 лет, получающих образование по специальностям «Автомеханик» и «Мастер сельскохозяйственного производства».

В качестве показателя успеваемости использованы оценки по английскому языку за первое полугодие 2010/11 учебного года.

Для диагностики личностных, психодинамических, социально-психологических особенностей испытуемых были использованы такие методики, как тест Р. Кеттелла, тест Леонгарда-Шмишека, опросник В. М. Русалова, вопросник КОС), а также ряд психолингвистических методик: ассоциативный эксперимент, тест Г. Эббингауза. Для выявления взаимосвязей между оценками и показателями тестов проведен корреляционный анализ по методике Кендалла (Шишлянникова, 2009).

Личностный опросник Р. Кеттелла (Cattell, Mead, 2008) позволяет оценить индивидуально-психологические особенности по 16 параметрам. В ходе анализа данных обнаружена корреляция между успеваемостью по английскому языку и шкалой «общительность – замкнутость» (r = 0,293; p < 0,01). Лучшую успеваемость по предмету демонстрируют более общительные и менее замкнутые обучающиеся.

Также выявлена отрицательная корреляция между успеваемостью и уровнем подозрительности, догматичности, внутреннего напряжения (r = -0,172; p < 0,05), более высокий уровень выраженности данных личностных черт связан с более низкой успеваемостью.

Тест Леонгарда-Шмишека выявляет тип акцентуации характера (Аминев и др., 1987). В ходе исследования обнаружены корреляции успеваемости с двумя типами акцентуации: гипертимическим (r = 0,202; p < 0,05) и возбудимым (r = -0,181; p < 0,05). Высокая успеваемость по английскому языку характерна для обучающихся с повышенным фоном настроения, жаждой деятельности и высокой активностью, в то время как импульсивные, слабо контролирующие себя индивиды показывают плохую успеваемость.

В ходе исследования также выявлены корреляты успеваемости среди показателей темперамента, полученных на основе диагностики структуры темперамента по опроснику В. М. Русалова (Русалов, 1990).

Высоким уровнем успеваемости отличаются учащиеся, обладающие высоким уровнем эргичности (r = 0,166; p < 0,05), социальной эргичности (r = 0,193; p < 0,05), темпа (r = 0,212; p < 0,05) и социального темпа (r = 0,164; p < 0,05). Высокий уровень эргичности характеризуется потребностью в освоении предметного мира, жаждой деятельности, стремлением к напряженному труду, легкостью умственного пробуждения; высокие показатели социальной эргичности говорят о потребности в социальном контакте, жажде освоения социальных форм деятельности, стремлении к лидерству, общительности, освоении мира через коммуникацию. Кроме того, учащиеся лучшей по успеваемости группы отличаются высокими показателями темпа поведения, т.е. для них характерны высокая скорость выполнения операций при осуществлении предметной деятельности, моторно-двигательная быстрота, высокая психическая скорость, а высокий уровень социального темпа свидетельствует о речедвигательной быстроте, высокой скорости и возможностях речедвигательного аппарата.

Испытуемым также был предложен вопросник КОС (Профконсультационная работа…, 1980), результаты диагностики по которому в сопоставлении с показателями успеваемости выявили, что для обучающихся с высокой успеваемостью по английскому языку характерно преобладание организаторских склонностей (r = 0,221; p < 0,01).

В ходе проведения ассоциативного эксперимента (Белянин, 2004) испытуемым предъявлялись слова-стимулы, к которым они должны были подобрать ассоциации. Для эксперимента были выбраны стимулы: солнце, зима, мама, Россия, дружба, лето, яблоко, курить, осень, черный, весна, машина, животное, каникулы, работать, студент, белый, собака, учеба, будущее.

При интерпретации результатов особое внимание было нами обращено на среднюю длину ассоциативного ряда, а также на качественные характеристики ассоциаций, на то, какие именно ассоциации –синтагматические или парадигматические – преобладают в ответах испытуемых. Грамматический класс синтагматических ассоциаций не совпадает с грамматическим классом слова-стимула (стимул – медведь, ассоциация – бурый). Парадигматические ассоциации относятся к тому же грамматическому классу, что и слово-стимул (стимул – медведь, ассоциация – волк). Корреляционный анализ показал следующие результаты: успеваемость по английскому языку коррелирует со средней длиной ассоциативного ряда (r = 0,248; p < 0,01). Чем длиннее ассоциативный ряд обучающегося, тем большие успехи он показывает в освоении английского языка. Процентное соотношение парадигматических и синтагматических ассоциаций также взаимосвязано с успеваемостью. Чем больший процент парадигматических ассоциаций обнаруживается в ответах обучающегося, тем выше его оценка по английскому языку (
r = 0,168; p < 0,05).

В ходе проведения теста Г. Эббингауза (Ebbinghaus, Hermann, 2006) испытуемым предлагалось заполнить пропуски в тексте и восстановить исходное речевое сообщение (Сборник психологических тестов, 2006). Опыт проведения теста Эббингауза описан в нашей статье «Применение теста Г. Эббингауза для выявления индивидуальных особенностей речи обучающихся профессиональных училищ» (Нуриахметов, 2011). Такой параметр, как количество правильно заполненных в смысловом и грамматическом плане пропусков, послужил основой корреляционного анализа, который показал, что способность правильно заполнять пропуски в тексте и восстанавливать речевое сообщение также имеет прямую взаимосвязь с успеваемостью по английскому языку (

r = 0,291; p < 0,01).

Проведенное исследование выявило, что высокий уровень успеваемости по английскому языку имеет следующие психолингвистические корреляты:

-высокий уровень общительности;

-низкий уровень подозрительности;

-повышенный фон настроения, жажда деятельности, высокая активность;

-низкий уровень возбудимости;

-потребность в освоении предметного мира, стремление к напряженному труду;

-легкость умственного пробуждения;

-потребность в социальных контактах, жажда освоения социальных форм деятельности, общительность, стремление к лидерству и освоению мира через коммуникацию;

-высокая скорость выполнения операций при осуществлении предметной деятельности, моторно-двигательная быстрота, высокая психическая скорость;

-речедвигательная быстрота, высокая скорость и возможности речедвигательного аппарата;

-преобладание организаторских способностей над коммуникативными;

-большая длина ассоциативного ряда, преобладание парадигматических ассоциаций;

-способность правильно восстанавливать исходное речевое сообщение.

Литература

  1. Аминев Г. А., Ростовский В. П., Сафронов В. П. Опросник Леонгарда // Психология контрпропаганды: проблемы, методы, перспективы. Т. 2. Уфа: БашГУ, 1987.
  2. Белянин В. П. Психолингвистика: Учебник. М.: Флинта: Московский психолого-социальный институт, 2004.
  3. Корнилова Т. В., Новикова М. А. Самооценка интеллекта в структурных связях с психометрическим интеллектом, личностными свойствами и академической успеваемостью // Психологические исследования. 2012. Т. 5. № 23. С. 2.
  4. Нуриахметов А. К. Применение теста Г. Эббингауза для выявления индивидуальных особенностей речи обучающихся профессиональных училищ // Казанская наука. 2011. №11. С. 400–404.
  5. Профконсультационная работа со старшеклассниками / Под ред. Б.А. Федоришина. Киев: Радянська школа, 1980.
  6. Русалов В. М. Опросник структуры темперамента: Методическое пособие. М.: ИП РАН, 1990. 
  7. Сборник психологических тестов. Ч. II: Пособие / Сост. Е.Е. Миронова. Минск: Женский институт ЭНВИЛА, 2006.
  8. Слободская Е. Р., Сафронова М. В., Ахметова О. А. Личностные особенности и стиль жизни как факторы школьной успеваемости подростков // Психологическая наука и образование. 2008. №2. C. 70–79.
  9. Соболева А. Е., Потанина А. Ю. Специфические особенности зависимости успеваемости по основным школьным дисциплинам от состояния ВПФ у детей // Психологическая наука и образование. 2004. №2. С. 76–81.
  10. Тимаева В. С. Тестирование как метод контроля качества усвоения учебного материала учащимися [Электронный ресурс] // Фестиваль педагогических идей «Открытый урок». URL: http://festival.1september.ru/articles/500954/ (дата обращения: 25.09.2012).
  11. Шишлянникова Л. М. Применение корреляционного анализа в психологии // Психологическая наука и образование. 2009. №1. C. 98–107.
  12. Cattell H. E. P., Mead A. D. The Sixteen Personality Factor Questionnaire (16PF) / Eds. G. J. Boyle, G. Matthews, D. H. Saklofske // The SAGE handbook of personality theory and assessment. London: SAGE Publications Ltd, 2008. P. 135–178.
  13. Ebbinghaus, Hermann // Encyclopedia of Cognitive Science /Eds. K. R. Hoffman. M. Bamberg. N. Y.: John Wiley & Sons, 2006. P. 57–75.

Нуриахметов Айдар Канифович, аспирант кафедры психологии Стерлитамакского филиала Башкирского государсвенного университета, преподаватель английского языка Стерлитамакского многопрофильного профессионального колледжа, Россия, e-mail: [email protected]

Метрики

Просмотров

Всего: 3045
В прошлом месяце: 6
В текущем месяце: 0

Скачиваний

Всего: 840
В прошлом месяце: 2
В текущем месяце: 0

Номограмма для значений P | BMC Medical Research Methodology

  • Исследовательская статья
  • Открытый доступ
  • Опубликовано:
  • Леонард Хелд 1  

Методология медицинских исследований BMC том 10 , Номер статьи: 21 (2010) Процитировать эту статью

  • 12 тыс. обращений

  • 24 Цитаты

  • 22 Альтметрический

  • Сведения о показателях

Абстрактный

Фон

Значения P являются наиболее часто используемым инструментом для измерения доказательств против гипотезы. Было предпринято несколько попыток преобразовать значений P в минимальные байесовские факторы и минимальные апостериорные вероятности рассматриваемой гипотезы. Однако применение таких калибровок в клинических областях невелико из-за отсутствия опыта в интерпретации байесовских факторов и необходимости указывать априорную вероятность для получения нижней границы апостериорной вероятности.

Методы

Я предлагаю графический подход, который легко преобразует любую априорную вероятность и значение P в минимальные апостериорные вероятности. Подход позволяет визуально проверить зависимость минимальной апостериорной вероятности от априорной вероятности нулевой гипотезы. Аналогичным образом инструмент можно использовать для считывания для фиксированной апостериорной вероятности максимальной априорной вероятности, совместимой с заданным значением P . Также доступно максимальное значение P , совместимое с заданной априорной и апостериорной вероятностью.

Результаты

Использование номограммы проиллюстрировано на основе результатов рандомизированного исследования пациентов с раком легкого, сравнивающих новый метод лучевой терапии с традиционной лучевой терапией.

Заключение

Графическое устройство, предложенное в этой статье, улучшит понимание значений P как меры доказательства среди неспециалистов.

Отчеты экспертной оценки

Фон

Значения P являются наиболее часто используемым инструментом для измерения доказательств против гипотезы [1]. Значение P определяется как вероятность при допущении отсутствия эффекта (нулевая гипотеза H 0 ), получения результата, равного или более экстремального, чем тот, который фактически наблюдался. Сложность этого определения привела к широко распространенному неправильному толкованию и критике [2–5]. Действительно, значения P часто неправильно интерпретируются (а) как вероятность получения наблюдаемых данных при допущении отсутствия реального эффекта, (б) как «наблюдаемая» частота ошибок первого рода, (в) как частота ложных открытий , то есть вероятность того, что значимый вывод является «ложноположительным», и (d) как (апостериорная) вероятность нулевой гипотезы [6].

Последняя неверная интерпретация породила интересную работу о связи между значениями P и (апостериорными) вероятностями нулевой гипотезы. В рамках байесовской концепции апостериорная вероятность является функцией априорной вероятности и так называемого байесовского фактора, который суммирует доказательства против нулевой гипотезы.

Было предпринято несколько попыток преобразовать значений P в нижние границы байесовского фактора и результирующей апостериорной вероятности нулевой гипотезы [7–11]. В этом контексте байесовские факторы обычно ориентируются как P таким образом, чтобы меньшие значения давали более убедительные доказательства против нулевой гипотезы. Эти методы калибруют значения P таким образом, чтобы была оправдана интерпретация как минимального байесовского фактора или минимальной апостериорной вероятности. Хотя различные подходы не приводят к идентичным шкалам калибровки, всеобщий вывод заключается в том, что доказательства против простой нулевой гипотезы далеко не так сильны, как можно было бы предположить, исходя из значения P .

Однако приемка калиброванной P значения в клинических полях низкие. Преимущество минимальных байесовских факторов состоит в том, что они не зависят от априорной вероятности нулевой гипотезы [9], но их интерпретация требует интуитивного понимания шансов, аналогично отношениям правдоподобия в диагностических исследованиях [12]. Клиницисты, однако, предпочитают думать с точки зрения вероятностей. С другой стороны, расчет минимальной апостериорной вероятности требует принятия решения об априорной вероятности нулевой гипотезы. Фиксация априорной вероятности может быть трудной для клинициста, который, возможно, предпочел бы исследовать — для данного Значение P — зависимость (минимальной) апостериорной вероятности нулевой гипотезы от априорной вероятности.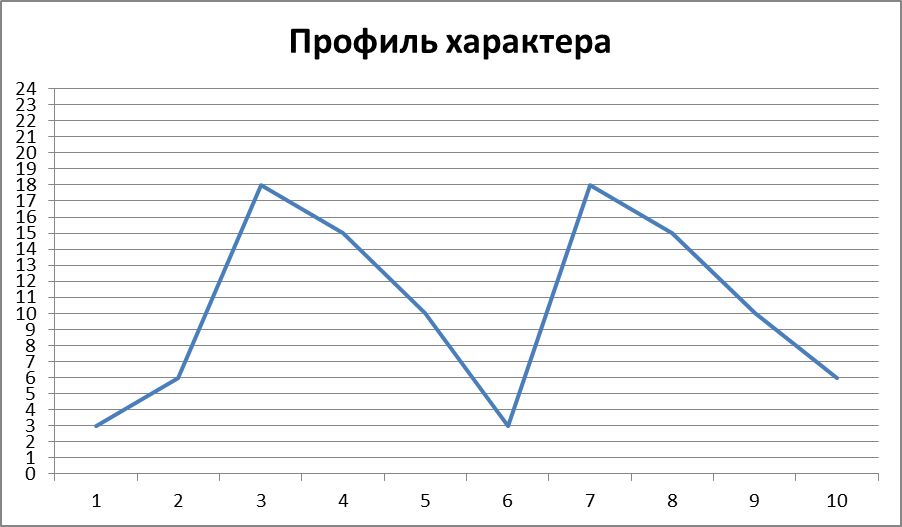

В этой статье я предлагаю графический подход, который легко переводит любую априорную вероятность и значение P в минимальные апостериорные вероятности. Аналогичным образом инструмент можно использовать для получения для фиксированной апостериорной вероятности максимальной априорной вероятности, совместимой с заданным значением P . Также может быть считано максимальное значение P в соответствии с заданной априорной и апостериорной вероятностью. Подход вдохновлен номограммой Фагана [13], используемой для получения посттестовой вероятности в диагностических тестах [12]. Это улучшит понимание и облегчит интерпретацию P значения как меры доказательства против нулевой гипотезы среди неспециалистов.

Методы

Калибровка

значений P

В основополагающей статье Эдвардс, Линдман и Сэвидж [7] (ELS) изучали взаимосвязь между значениями P и минимальными коэффициентами Байеса в нескольких условиях. Особый интерес представляет случай, когда тестовая статистика имеет нормальное распределение с неизвестным средним значением μ . Простая нулевая гипотеза H 0 соответствует определенному среднему значению μ = μ 0 . Расчет коэффициента Байеса требует фиксирования априорной плотности для μ при альтернативной гипотезе H 1 : мкм ≠ мкм 0 .

Этот сценарий хотя бы приблизительно отражает многие статистические процедуры, используемые в медицинских журналах.

Минимальный коэффициент Байеса получается

здесь z — это значение z , т. е. тестовая статистика, которая привела к наблюдаемому значению P . Эта нижняя граница может быть получена с использованием того факта, что фактор Байеса минимален, если альтернативная гипотеза имеет всю свою априорную плотность при одном конкретном значении μ , которое больше всего подтверждается данными (оценка максимального правдоподобия). Поскольку эта точка всегда находится по одну сторону от нулевой гипотезы, ELS предложил использовать значение z на основе одностороннего, а не двустороннего критерия значимости. Двусторонний тест, который приводит к несколько большим значениям z и до несколько меньших значений BF также предлагалось [9].

Для фиксированной априорной вероятности q , скажем, нулевой гипотезы, минимальный байесовский фактор BF может быть легко преобразован в нижнюю границу апостериорной вероятности нулевой гипотезы на основе теоремы Байеса:

( 1)

В первой строке таблицы 1 указана нижняя граница для q = 50% и P значений 0,05, 0,01 и 0,001, соответственно, с использованием подхода ELS. Поразительной особенностью является то, что нижняя граница апостериорной вероятности значительно больше, чем соответствующие Значение P .

Таблица 1 Нижние границы апостериорной вероятности нулевой гипотезы для различных значений P и равных априорных вероятностей нулевой и альтернативной гипотезы ( q = 50%).

Полноразмерная таблица

Подход ELS был усовершенствован Бергером и Селлке [8] (BS). Они получили нижние границы для фактора Байеса при более реалистичных семействах априорных распределений для μ в соответствии с альтернативной гипотезой. В частности, они рассмотрели (1) симметричные априорные распределения, (2) одномодальные и симметричные априорные распределения и (3) нормальные априорные распределения, все с центром в мк 0 . Как и следовало ожидать, соответствующие нижние границы апостериорной вероятности H 0 увеличиваются с увеличением ограничений на предшествующее семейство для μ , как видно из таблицы 1.

Возможно, самая простая и наиболее интуитивная калибровка была предложена Селлке, Баярри и Бергером [10] (SBB). Они используют тот факт, что значение P (при подходящих условиях регулярности) равномерно распределено, если H 0 верно. При альтернативной гипотезе меньшие значения P более вероятны, чем большие значения P , т. е. плотность значения P монотонно убывает. Гибкий класс убывающих плотностей на единичном интервале обеспечивают конкретные бета-плотности с одним неизвестным параметром. Тогда минимальный коэффициент Байеса равен

Здесь p — наблюдаемое значение P , а e = exp(1) ≈ 2,718 — постоянная Эйлера. Полученные нижние границы апостериорной вероятности нулевой гипотезы очень похожи на оценки, полученные с использованием подхода BS с унимодальной априорной плотностью для μ , как видно из таблицы 1. Обратите внимание, что границы SBB сохраняются в более общих условиях без предположения о бета-распределенном значении P при альтернативной гипотезе [10]. Совсем недавно минимальные байесовские коэффициенты для х 2 -распределенные тестовые статистики были изучены [11]. Такая тестовая статистика имеет дополнительный параметр, степени свободы ν , который зависит от конкретного типа применяемого теста. Была получена следующая нижняя граница коэффициента Байеса:

Здесь х — это значение х 2 — тестовая статистика, которая привела к наблюдаемому значению P . Легко показать, что BF уменьшается с увеличением степени свободы. Возможно, более интересно, что BF равно нижней границе BS для нормальных априорных значений для ν = 1, равно нижней границе SBB для ν = 2 и равно нижней границе ELS для ν → ∞ . Это показывает, что диапазон нижних границ апостериорной вероятности, приведенный в таблице 1, отражает большое разнообразие различных тестов и сценариев.

Номограмма для

значений P

Очевидная сложность формул, представленных в предыдущем разделе, может быть одной из причин, по которой предлагаемая калибровка значений P не вошла в рутинные научные исследования. Поэтому я предлагаю адаптировать графическое устройство, первоначально разработанное для диагностических тестов [13], к описанной выше настройке. Оригинальная номограмма Фагана позволяет визуально определить посттестовую вероятность для заданной дотестовой вероятности и отношения правдоподобия в рамках диагностического теста [12]. Отношение правдоподобия является функцией чувствительности, специфичности и фактического результата рассматриваемого диагностического теста. Отношение правдоподобия — это особая форма байесовского фактора, в которой обе рассматриваемые гипотезы (независимо от того, есть ли у пациента заболевание или нет) являются простыми, и не требуется никаких дополнительных предварительных предположений.

Предлагаемое графическое устройство показано на рисунке 1. Априорная вероятность для нулевой гипотезы расположена на первой оси и соединена с наблюдаемым значением P на второй оси. Минимальная апостериорная вероятность затем считывается с третьей оси. Масштабирование значения P по второй оси основано на калибровке SBB. Конечно, можно было бы использовать любую другую калибровку, обсуждавшуюся в предыдущем разделе, но подход SBB кажется особенно подходящим, поскольку он не предназначен для конкретной тестовой статистики (нормальной или 9-кратной).0047 х 2 ), но выводится в более общем виде.

Рисунок 1

Номограмма для P значений . Априорная вероятность нулевой гипотезы расположена на первой оси, наблюдаемое значение P — на второй оси, а минимальная апостериорная вероятность — на третьей оси.

Изображение в натуральную величину

Обратите внимание на некоторые заметные отличия от исходной номограммы Фагана. Во-первых, отношение правдоподобия заменяется на Значение P . Во-вторых, рассматриваются только значения P , меньшие 1/ e ≈ 0,37, поскольку BF является единицей для больших значений P , где нет доказательств против нулевой гипотезы. Следовательно, шкала априорной вероятности в левой части графика не идентична шкале апостериорной вероятности в правой части графика. Это отражает тот факт, что значения P являются асимметричными мерами доказательств, они количественно определяют доказательства против нулевой гипотезы, но не дают количественную оценку доказательств в пользу нулевой гипотезы. Это отличается от номограммы Фагана, где отношения правдоподобия могут быть как больше, так и меньше единицы. Наконец, третья ось дает не точное значение апостериорной вероятности нулевой гипотезы, а только минимальную апостериорную вероятность.

Результаты

Предложенную номограмму можно использовать тремя различными способами, как будет показано на следующем примере. В 1986 году был представлен новый метод лучевой терапии под названием CHART. Многообещающие пилотные исследования побудили Совет медицинских исследований Великобритании инициировать большое рандомизированное исследование пациентов с раком легких. Цель исследования состояла в том, чтобы оценить изменение выживаемости при применении CHART по сравнению с обычной лучевой терапией.

Перед испытанием у 11 клиницистов был получен q = 10% априорный шанс того, что CHART вообще не принесет пользы для выживания [5]. В конце исследования была обнаружена клинически важная и статистически значимая разница в выживаемости (9% улучшение 2-летней выживаемости, 95% ДИ: 3-15%, двустороннее значение P = 0,3%, т. е. 0,003) [14]. Теперь мы можем легко считать нижнюю границу около 0,5% для апостериорной вероятности нулевой гипотезы (зеленая линия на рисунке 2).

Рисунок 2

Применение в исследовании рака легких CHART . Для P значения 0,3% (0,003) нижнюю границу апостериорной вероятности можно считать по третьей оси для q = 10 % (зеленая линия), q = 50% (красная линия) и q = 90% (синяя линия) априорная вероятность.

Полноразмерное изображение

Из-за относительно небольшой априорной вероятности минимальная апостериорная вероятность нулевой гипотезы в этом примере численно довольно близка к значению P . Это будет отличаться для больших априорных вероятностей. Например, для q = 50% мы получаем минимальную апостериорную вероятность отсутствия выигрыша в выживании около 4,5% (красная линия). Для q = 90% минимальная апостериорная вероятность составляет 29,9% (синяя линия).

Есть два других способа использования номограммы: вычисление либо априорной вероятности, либо значения P . Например, чтобы получить апостериорную вероятность 0,3 % при значении P 0,3 %, априорная вероятность должна быть 6 % или меньше, что видно из красной линии на рис. 3. В качестве альтернативы может быть интересно в максимальном значении P , совместимом с уменьшением вероятности нулевой гипотезы с 50% априори до 0,3% апостериорно , скажем. Рисунок 3 показывает (зеленая линия), что для достижения этого нам нужно значение P 0,014% (0,00014) или меньше, что более чем на один порядок меньше целевой апостериорной вероятности 0,3%.

Рисунок 3

Применение в исследовании рака легких CHART . Априорная вероятность должна быть 6% или меньше, чтобы получить нижнюю границу 0,3% апостериорной вероятности (красная линия). Зеленая линия указывает, что нам нужно P значение 0,014% (0,00014) или меньше, чтобы уменьшить вероятность нулевой гипотезы с q = 50% априорно до 0,3% апостериорно .

Увеличенное изображение

Обсуждение

Номограмма Фагана [12] широко используется в контексте диагностических тестов, и я надеюсь, что предложенная номограмма для значений P достигнет такой же популярности. Он визуально преобразует значений P в минимальные апостериорные вероятности нулевой гипотезы и, таким образом, позволяет избежать сложных вычислений. Чувствительность по отношению к априорным предположениям можно изучить графически. Кроме того, для фиксированной апостериорной вероятности максимальная априорная вероятность, совместимая с данным Значение P можно считать. Также доступно максимальное значение P , совместимое с заданной априорной и апостериорной вероятностью.

Как подчеркивается в Spiegelhalter et al. [[5], с. 130-133], фактическая апостериорная вероятность нулевой гипотезы также будет зависеть от мощности (, т.е. размера выборки) исследования. Однако Hooper [15] недавно показал, что доказательство против нулевой гипотезы, обеспечиваемое точным значением P , не сильно зависит от мощности в диапазоне размеров исследований, которые обычно встречаются в клинических и эпидемиологических исследованиях. Для иллюстрации мы воспроизводим на нашем рисунке 4 верхнюю часть рисунка 3 из работы Хупера [15], на которой показана апостериорная вероятность нулевой гипотезы в зависимости от мощности (до исследования) при уровне значимости 5% для P = 0,05, 0,01 и 0,001. Расчет основан на нормальном априоре со средним значением μ . 0 и стандартное отклонение τ = 1 (левый график) и τ = 2 (правый график) при альтернативе (при условии, что одна единица соответствует минимальному клинически значимому различию). Это соответствует сценарию 3 от Berger & Sellke [8]. Мы добавили соответствующую нижнюю границу BS (короткий пунктир) апостериорной вероятности на рисунке 4. Фактическая апостериорная вероятность довольно близка к этому минимуму для всех мощностей, обычно встречающихся в клинических исследованиях, скажем, между 40% и 95%. Это верно как для τ = 1 (левый график на рис. 4), так и для τ = 2 (правый график). Только для очень маленьких или очень больших исследований апостериорная вероятность значительно больше, чем нижняя граница BS. Граница SBB, показанная длинной пунктирной линией, является более консервативной и, следовательно, немного ниже, чем нижняя граница BS.

Рисунок 4

Зависимость апостериорной вероятности от мощности исследования . Апостериорная вероятность нулевой гипотезы, построенная в зависимости от мощности (до исследования) при уровне значимости 5% для P = 0,05, 0,01 и 0,001 и априорная вероятность q = 90%. Расчет основан на нормальном априоре со стандартным отклонением τ = 1 (левый график) и τ = 2 (правый график) при альтернативе, предполагая, что одна единица соответствует минимальному клинически значимому различию. Пунктирные линии показывают минимальную апостериорную вероятность, полученную с помощью подходов BS (короткие пунктиры) и SBB (длинные пунктиры) соответственно.

Полноразмерное изображение

В этой статье я применил байесовский подход для расчета нижней границы апостериорной вероятности нулевой гипотезы, полученной из априорной вероятности и точного значения P . Даже Кокс [[16], с. 83] соглашается с тем, что «выводы, выраженные в терминах вероятности, на первый взгляд более убедительны, чем выводы, выраженные косвенно через доверительные интервалы и значения P . ] информация.» Однако Кокс считает, что «выводы, полученные с помощью частотного подхода, более надежны, чем выводы, полученные из большинства байесовских анализов», потому что [предыдущая] «информация обычно более ненадежна или даже туманна по сравнению с той, которая обычно получается более непосредственно из анализируемых данных. «. С другой стороны, Гудман [1, 3, 6, 9] утверждает, что неправильное понимание и неправильное использование значений P настолько широко распространено, что необходимы новые инструменты для правильной передачи убедительности доказательств, представленных данными исследований. Номограмма, предложенная в этой статье, является таким инструментом и особенно полезна для изучения чувствительности к априорной вероятности нулевой гипотезы, как показано на рисунке 2. В сочетании с точным значением P мы получаем диапазон правдоподобных значений для апостериорной вероятность нулевой гипотезы, которую гораздо легче интерпретировать, чем P Само значение.

Выводы

Графическое устройство, предложенное в этой статье, улучшает понимание и облегчает интерпретацию значений P как доказательств против нулевой гипотезы среди неспециалистов. Для размеров исследований, обычно встречающихся в клинических и эпидемиологических исследованиях, апостериорная вероятность нулевой гипотезы будет довольно близка к нижней границе, представленной номограммой. В настоящее время мы готовим апплет JAVA по адресу http://www.biostat.uzh.ch/static/pnomogram, который позволяет интерактивно использовать предложенную номограмму в Интернете.

Ссылки

  1. Серийный номер Goodman: P Значение. Энциклопедия биостатистики. 2005, Чичестер: Wiley, 3921-3925. 2

    Google Scholar

  2. Коэн Дж. Земля круглая (p < 0,05). Я психол. 1994, 49: 997-1003. 10.1037/0003-066Х.49.12.997.

    Артикул Google Scholar

  3. Гудман С.Н.: На пути к доказательной медицинской статистике. 1: P Ошибка ценности. Энн Инт Мед. 1999, 130: 995-1004.

    Артикул КАС пабмед Google Scholar

  4. Хаббард Р., Баярри М.Дж.: Путаница в отношении мер доказательства ( p ) по сравнению с ошибками ( α ) в классическом статистическом тестировании (с обсуждением). Ам Стат. 2003, 57: 171-182. 10.1198/0003130031856.

    Артикул Google Scholar

  5. Spiegelhalter DJ, Abrams KR, Myles JP: Байесовские подходы к клиническим испытаниям и оценке медицинского обслуживания. 2004, Нью-Йорк: Wiley

    Google Scholar

  6. Гудман С.Н.: Введение в байесовские методы I: измерение силы доказательств. Клинские испытания. 2005, 2: 282-290. 10.1191/1740774505cn098oa.

    Артикул пабмед Google Scholar

  7. Эдвардс В., Линдман Х., Сэвидж Л.Дж.: Байесовский статистический вывод в психологических исследованиях. Психическое Откр. 1963, 70: 193-242. 10.1037/h0044139.

    Артикул Google Scholar

  8. Berger JO, Sellke T: Проверка точечной нулевой гипотезы: несовместимость значений P и доказательств (с обсуждением). J Am Stat Assoc. 1987, 82: 112-139. 10.2307/2289131.

    Google Scholar

  9. Гудман С.Н.: На пути к доказательной медицинской статистике. 2: Фактор Байеса. Энн Инт Мед. 1999, 130: 1005-1013.

    Артикул КАС пабмед Google Scholar

  10. Селлке Т., Баярри М.Дж., Бергер Д.О. Калибровка значений p для проверки точных нулевых гипотез. Ам Стат. 2001, 55: 62-71. 10.1198/000313001300339950.

    Артикул Google Scholar

  11. Джонсон В.Е.: Факторы Байеса на основе тестовой статистики. J Roy Stat Soc B. 2005, 67: 689-701. 10.1111/j.1467-9868.2005.00521.х.

    Артикул Google Scholar

  12. Дикс Дж.Дж., Альтман Д.Г.: Диагностические тесты 4: отношения правдоподобия. Brit Med J. 2004, 329: 168-169. 10.1136/bmj.329.7458.168.

    Артикул пабмед ПабМед Центральный Google Scholar

  13. Фэган Т.Дж.: Письмо: Номограмма для теоремы Байеса. N Engl J Med. 1975, 293: 257-

    КАС пабмед Google Scholar

  14. Spiegelhalter DJ, Myles JP, Jones DR, Abrams KR: Байесовские методы оценки медицинских технологий: обзор. Оценка медицинских технологий. 2000, 4 (38):

  15. Хупер Р. Байесовская интерпретация P -значения слабо зависит от статистической мощности в реальных ситуациях. Дж. Клин Эпидемиол. 2009, 62: 1242-1247. 10.1016/j.jclinepi.2009.02.004.

    Артикул пабмед Google Scholar

  16. Cox DR: Принципы статистического вывода. 2005, Кембридж: Издательство Кембриджского университета

    Google Scholar

История до публикации

  • С историей до публикации этой статьи можно ознакомиться здесь: http://www.biomedcentral.com/1471-2288/10/21/prepub

Ссылки на скачивание

Благодарности

Я благодарен Каспару Руфибаху и двум рецензентам за полезные комментарии к более ранним версиям этой рукописи.

Информация об авторе

Авторы и организации

  1. Отдел биостатистики, Институт социальной и профилактической медицины, Цюрихский университет, Hirschengraben 84, 8001, Цюрих, Швейцария

    Leonhard Held

    90 004

Авторы

  1. Леонхард Хелд

    Просмотр публикаций автора

    Вы также можете искать этого автора в PubMed Google Scholar

Автор, ответственный за переписку

Связь с Леонард Хелд.

Дополнительная информация

Заявление о конкурирующих интересах

Я заявляю, что у меня нет конкурирующих интересов.

Оригинальные файлы изображений, представленные авторами

Ниже приведены ссылки на оригинальные файлы изображений, представленные авторами.

Авторский файл рисунка 1

Авторский файл рисунка 2

Авторский файл рисунка 3

Исходный файл авторов для рисунка 4

Права и разрешения

Эта статья опубликована по лицензии компании BioMed Central Ltd. Это статья с открытым доступом, распространяемая в соответствии с условиями лицензии Creative Commons Attribution License (http:/ /creativecommons.org/licenses/by/2.0), что разрешает неограниченное использование, распространение и воспроизведение на любом носителе при условии надлежащего цитирования оригинальной работы.

Перепечатка и разрешения

Об этой статье

Язык для сообщения частотных результатов об эффектах лечения — № 181 по Йохену — интерпретация исследования

R_cubed 176

f2harrell:

Обратите внимание на частое ограничение необходимости концентрироваться на доказательствах против против доказательств для .

Что вы думаете об ограничении использования термина «доказательство» исключительно обсуждением относительной подгонки двух моделей к данным (как это делается с помощью отношения правдоподобия) и упоминать информацию, содержащуюся в p-значении, как «неожиданную ” как рекомендует @sander? Я начинаю думать, что это прояснит большую путаницу. Если бы мне пришлось описывать результаты с большими неожиданностями, я бы использовал язык « достаточно удивительно , если предполагаемая модель верна.

AFAICT, неожиданность обратно связана с отношением правдоподобия в простом случае утвержденной тестовой гипотезы H_a и ее дополнения H_\neg{a} в том смысле, что высокая неожиданность (низкий p) указывает на то, что (вероятно) существует лучшая модель (модель с более высокой вероятностью) для текущих данных.

Термин «неожиданность» работает, когда p-значения масштабируются в единицах информации относительно предполагаемой модели, но мне трудно подобрать термин при преобразовании их в единицы, предполагающие альтернативу (т. е. \Phi(p) ).

1 Нравится

Сандер 177

Мне будет интересен ответ Фрэнка. Мой:

  1. Я бы никогда не стал ограничивать такой расплывчатый термин, как «доказательство», сравнением моделей, особенно когда большая часть фишеровской литературы (включая Фишера) ссылается на малое p как на свидетельство против его порождающей модели — и это свидетельство любой обычной языковое значение «доказательства», без единого компаратора.
  2. Я бы также изменил вашу фразу, сказав «удивительно, если предполагаемая модель сгенерировала данные», чтобы подчеркнуть гипотетическую природу модели — в моделировании «soft-science» мы редко имеем «истинные» модели в обычном значении « правда», и поэтому навешивание на них таких ярлыков приводит к путанице; но мы по-прежнему можем проводить мысленные эксперименты с моделями, чтобы оценить, насколько данные отличаются от них, что является источником P-значений и аргументов о частоте.
  3. Если p<1, всегда есть «лучшие модели», такие как насыщенные модели, которые идеально соответствуют данным, имея p = 1 и вероятность = максимально возможной при фоновых ограничениях. Я думаю, это иллюстрирует, как P-значения и вероятности недостаточны для выбора модели (по крайней мере, нам нужны штрафы за сложность, как в AIC, и за неправдоподобность, как с информативными априорными данными).
  1. Наконец, вопрос, требующий разъяснения: почему вы хотите преобразовать P-значение указанным вами способом? Если у вас есть альтернатива, сравнимая с вашей тестовой моделью, возьмите P-значение и S-значение для альтернативы, чтобы получить информацию об этой альтернативе. И если вы хотите сравнить модели, используйте для этой цели меру (которая опять же не является P-значением; сравнение моделей должно учитывать сложность и правдоподобие).

3 нравится

R_cubed 178

Блок-цитата
Я бы никогда не стал ограничивать такой расплывчатый термин, как «доказательство», сравнением моделей, особенно когда большая часть фишеровской литературы (включая Фишера) ссылается на малое p как на свидетельство против его генеративной модели — и это свидетельство в любом значении обычного языка «доказательств», без единого компаратора.

Хотя я нахожу аргументы Ричарда Ройалла в пользу правдоподобия довольно убедительными, различие между «неожиданностью» и «доказательством» проводят те, кто работает с методами Фишера.

Термин «доказательства» кажется перегруженным, когда он относится к p-значениям и вероятностям. Это приводит к непродуктивным дискуссиям о том, как p-значения «завышают» доказательства. Если провести различие между неожиданностью и прямыми измерениями свидетельства с помощью правдоподобия или коэффициентов Байеса, мы можем предотвратить обвинение p-значения в простой ошибке в интерпретации.

Цитата
Наконец, вопрос, требующий разъяснения: почему вы хотите преобразовать P-значение указанным вами способом?

Кулинская, Моргенталер и Стаудте написали текст по метаанализу, в котором подчеркивается преобразование p-значения или t-статистики в пробит-шкалу через отношение \Phi(p), где \Phi — стандартное нормальное кумулятивное распределение функция. Также в традициях Фишера они проводят различие между p-значениями как мерами неожиданности и «доказательствами», которые они измеряют в пробитах, связывая Фишера и школу мысли Неймана-Пирсона.

В другой теме вы разместили ссылку на видео, в котором вы, Джим Бергер и Роберт Мэтьюз обсуждали p-значения. Я обнаружил, что все предложения — граница -e \times p \times ln(p), байесовский коэффициент отклонения, S-значение и метод обратного Байеса — ценны.

Я много думал о том, как использовать эти методы, когда читал не только первичные исследования, но и метаанализы, в которых наивно вычисляются величины совокупного эффекта. Я разместил повторное исследование недавнего мета-анализа прогнозирования спортсменов с более высоким риском травмы передней крестообразной связки в этой теме:

Коллега привлек мое внимание к следующему рецензируемому мета-анализу 12 прогностических исследований, в которых пытались предсказать будущий риск повреждения передней крестообразной связки по кинематике коленного сустава. Название: Предсказывают ли кинематика и кинетика отведения колена будущий риск повреждения передней крестообразной связки? Систематический обзор и метаанализ проспективных исследований Авторы нашли 9 исследований с использованием 3 различных оценок, в которых делается попытка обнаружить избыточное угловое движение как предиктор будущей травмы передней крестообразной связки. Они сообщили…

f2harrell 179

Мне нравится все, что говорят. И мне нравится различие Сандера модели от модели . Мне нравится удивление или относительное свидетельство в качестве терминов. С точки зрения того, как p-значения завышают (относительные) доказательства, мы должны отметить p-значения следующим образом: P-значения — это вероятности крайних значений данных в рамках предполагаемой генеративной модели, а не эффектов.

3 отметок «Нравится»

180

Я тоже недавно думал об этом, и поэтому рад видеть вашу независимую — и ранее — поддержку использования термина «заметный»! Вот мое личное мнение: «Значительно? Вы действительно имеете в виду различимый | Две распространенные неправильные фразы о статистической значимости» https://towardsdatascience.com/significant-you-really-mean-detectable-b3e8819e3491?sk=e521f9c6fb98e7a953876581c58f10e5

Йохен 181

Я не думаю, что автор ссылки, на которую вы ссылаетесь, работает намного лучше. В своих «правильных интерпретациях» он все еще путает статистическую значимость с эффектом. Это не. Речь идет о данных в рамках предполагаемой модели (с конкретным ограничением этого «эффекта» [которое может быть просто нулем или любым другим значением]). Он мог бы написать, что наблюдаемые данные (или тестовая статистика) являются статистически значимыми в ограниченной модели. Это первый шаг в ловушку — перепутать наблюдаемые данные или наблюдаемую тестовую статистику (будь то разница, отношение шансов или наклон) с параметром модели. Это не является и не может быть значением параметра, которое является статистически значимым.

Это заблуждение, по-видимому, приводит автора к неправильному (ну, по крайней мере, проблематичному) утверждению, что статистически значимый результат будет означать, что статистика, «рассчитанная по выборке, является хорошей оценкой истинного, неизвестного [эффекта]» (выделено мной). Это не. Качество оценки не определяется тестом или касается только того минимального требования, чтобы оценка была отличима от значения, которым был ограничен параметр модели. Это не показатель «хорошей» или «плохой» оценки. Это достаточно просто, чтобы решить, можем ли мы утверждать, что значение параметра выше или ниже ограниченного значения (хотя это может быть «достаточно хорошим» для этой цели). Фактическая точечная оценка все еще может быть далека от истины (что лучше оценить с помощью доверительного интервала [или совместимости]).0023

Тут я вижу еще одну проблему в части «Подробное рассуждение». Здесь автор более корректно утверждает, что p-значение вычисляется статистически из данных под ограничением (хотя он не очень в этом разбирается), но затем он пишет, что p-значение является всего лишь приближением. К чему? Поскольку данные можно рассматривать как реализацию случайной величины, значение p, вычисленное из таких данных, можно рассматривать как реализацию случайной величины, назовем эту переменную P. Если тест задан правильно, мы знаем, что распределение P является однородным в модели с ограничениями и что он преимущественно смещен вправо при желаемом нарушении этой модели. Это все, что мы можем сказать. Любое наблюдаемое значение p является просто реализацией (не приближением) P, но мы не знаем распределения P. Значение p, близкое к нулю, принимается как свидетельство того, что распределение P скошено вправо и что ограниченная модель нарушается/не подходит для описания данных. В частности, при правильно заданной модели ожидается, что значения p будут резко прыгать по всему домену P (между 0 и 1), независимо от того, насколько велик размер выборки. Нет ничего, что оно «приближает». Только в том случае, если модель нарушается желаемым образом, мы можем увидеть значение p как приближение — нулевого значения (это предельное значение, к которому можно было бы приблизиться для размера выборки, стремящегося к бесконечности).

3 нравится

182

Кажется, в этой теме еще никто не упомянул GRADE (может ошибаться — не дочитал до конца). Я неоднозначно отношусь к этому. Лично я не нахожу языковые статусы особенно полезными — я предпочитаю смотреть на цифры, — но другие люди не разделяют эту точку зрения. Мне интересно, что люди думают об их рекомендуемых утверждениях, которые были в значительной степени приняты Кокраном, поэтому их видят многие люди.

Описано в этой статье:

sciencedirect.com

Рекомендации GRADE 26: информативные заявления для сообщения результатов…

Четкое изложение результатов систематических обзоров поможет читателям и лицам, принимающим решения. Мы опирались на предыдущую работу, чтобы разработать подход, улучшающий…

Я нахожу некоторые из них немного проблематичными. Например, я не люблю использовать слово «вероятно», когда мы не говорим о вероятностях. Самая большая проблема, которую я обнаружил, заключается в том, как они привыкают; Я вижу много результатов метаанализа с широкими 95% доверительные интервалы (в основном совместимые с большим вредом и большой пользой), описываемые (с использованием системы GRADE) как «вероятно, имеют небольшое значение или не имеют никакого значения», что кажется мне полностью вводящим в заблуждение.

В любом случае интересно узнать о GRADE.

2 лайка

183

Я все еще читаю это в первый раз, но не похоже, чтобы какие-либо соображения теории принятия решений повлияли на рекомендации. Это всего лишь более неформальная работа на гранях распространенных статистических ошибок, которую ни сторонник частот, ни байесовец не одобрят.

Пример: я бы заменил «точность» на «определенность», так как кажется, что они смешивают субъективные вероятности для предложений с частотами, основанными на данных, но не помещают их в надлежащий байесовский контекст.

Я тоже не фанат этих дискретных уровней. Разные вопросы требуют разного количества информации, поэтому единого ответа на вопрос быть не может.

2 лайков

184

Я нашел формулировку этого твита BMJ интересной (выделено мной):

Это рандомизированное контролируемое исследование предоставляет убедительные доказательства отсутствия статистически значимой разницы между традиционной гипсовой иммобилизацией и съемными корсетами при переломах лодыжки у взрослых

Судя по беглому чтению самой статьи, это ограничивается твитом — анализ выявил доверительные интервалы, которые находились внутри предварительно определенного клинически значимого поля в обоих направлениях, и сделал вывод «Не было обнаружено, что традиционная гипсовая повязка превосходит функциональную фиксацию у взрослых с переломом лодыжки».

3 лайков

185

Формулировка в твите настолько неправильная и запутанная, насколько это возможно, в дополнение к тому, что она клинически бессмысленна. Ух ты.

R_cubed 186

Те, кто интересуется оригинальной статьей, могут найти ее здесь:

The BMJ — 6 июля 21

Использование гипсовой иммобилизации в сравнении со съемным бандажом у взрослых с голеностопным суставом…

Цели Оценить функцию, качество жизни, использование ресурсов и осложнения у взрослых, получавших иммобилизацию гипсовой повязкой по сравнению со съемным корсетом по поводу перелома лодыжки. Дизайн Многоцентровое рандомизированное контролируемое исследование. Установка 20 травмпунктов…

Blockquote
Первичным результатом была оценка голеностопного сустава Олерудом Моландером через 16 недель; анкета для самостоятельного заполнения, состоящая из девяти различных пунктов (боль, скованность, отек, подъем по лестнице, бег, прыжки, приседание, поддержка и работа или повседневная деятельность). 10 Баллы варьируются от 0 для полного нарушения до 100 для полного нарушения. неповрежденный.

Из раздела Статистический анализ:

Цитата из цитаты
Целевая разница между группами по первичной оценке голеностопного сустава по Олеруду Моландеру составляла 10 баллов, что согласуется с другими исследованиями лечения переломов голеностопного сустава — это общепринятая минимально клинически значимая разница. технико-экономическая оценка составила 28 баллов, поэтому мы использовали консервативную оценку в 30 баллов для расчета размера выборки.

Этот тип метрики результатов будет страдать от эффектов нижнего и верхнего предела. Я не уверен, что можно узнать из исследования, учитывая это.

1 Нравится

187

@f2harrell Я планирую написать письмо редактору по поводу РКИ с неправильной интерпретацией их данных. Считаете ли вы уместным сослаться на это обсуждение?

R_cubed 188

Вы можете найти эту тему информативной относительно писем в редакцию. Некоторые считают, что «позор в Твиттере» более продуктивный, но письмо не повредит.

@zad, я увидел этот твой комментарий на сайте Эндрю Гельмана и подумал, не хочешь ли ты обсудить его здесь: «В прошлом месяце я отправил в JAMA что-то похожее в отношении исследования, в котором изучалось влияние антидепрессанта на исходы сердечно-сосудистых заболеваний. Авторы произвели расчеты мощности на основе размеров эффекта, наблюдаемых в исследовании, и пришли к выводу, что они достигли большей мощности, чем планировали, и поэтому больше доверяют своим результатам. К сожалению, получил р…

1 Нравится

189

Отличная тема, спасибо. Я ожидаю, что меня проигнорируют, но кто знает…

Pavel_Roshanov 190

Я изо всех сил пытаюсь понять следующее, и, возможно, кто-то может объяснить:

Если частотные доверительные интервалы нельзя интерпретировать так же, как байесовские доверительные интервалы, почему они идентичны в условиях плоской априорной вероятности?

Не означает ли это, что значения на крайних точках частотного доверительного интервала действительно с гораздо меньшей вероятностью будут «истинными», чем значения, близкие к точечной оценке? Следовательно, не является ли точечная оценка (при условии, что у нас действительно нет априорной информации) оценкой, которая с наибольшей вероятностью будет верной?

R_cubed 908:50 31 октября 2021 г. , 3:01 191

Цитата
Если частотные доверительные интервалы нельзя интерпретировать так же, как байесовские доверительные интервалы, почему они идентичны в условиях фиксированного априорного значения?

Плоский приор — это попытка выразить невежество. Настоящая информативная априорная оценка — это попытка выразить ограничения, которые могут принимать значения параметров. Но «информативный априор» одного байесовца — это «иррациональное предубеждение» другого байесовца. Нет никакой гарантии, что байесовцы сойдутся при наличии одной и той же информации, если априорные значения сильно различаются.

Это философские рассуждения. На практике байесовские методы могут работать очень хорошо и могут помочь в оценке частотных процедур.

Весь смысл частотной процедуры состоит в том, чтобы избежать зависимости от какого-либо предшествующего значения. так что единая приора практически бесполезна. Подумайте о старом посте Сандера о заслуживающих доверия приорах:

.
Несколько недель назад Дэн Шарфштейн спросил группу коллег о том, как сообщить об отношении шансов 1,70 с 95% доверительным интервалом 0,96 и 3,02. Обратный расчет по этой статистике дает двустороннее значение P, равное 0,06 или 0,07, что соответствует S-значению (неожиданное, логарифмическое основание 2 P) примерно 4 битам информации против нулевой гипотезы OR=1. Таким образом, не так много свидетельств против нулевого результата, но все же предпочтение положительной ассоциации по сравнению с обратной, и поэтому считается достойным отчета…

Блок-цитата
Сандер: Кроме того, многие байесовцы (например, Гельман) возражают против равномерного априорного распределения, поскольку оно приписывает более высокую априорную вероятность β, выпадающему за пределы любого конечного интервала (−b,b), чем попаданию внутрь, независимо от того, как большой б; например, кажется, что мы считаем более вероятным, что OR = exp(β) > 100 или OR < 0,01, чем 100> OR> 0,01, что абсурдно почти в каждом реальном приложении, которое я видел.

Цитата из цитаты
Не означает ли это, что значения на крайних точках частотного доверительного интервала действительно с гораздо меньшей вероятностью будут «истинными», чем значения, близкие к точечной оценке? Следовательно, не является ли точечная оценка (при условии, что у нас действительно нет априорной информации) оценкой, которая с наибольшей вероятностью будет верной?

Людям почти невозможно сопротивляться такому заключению, но оно ошибочно. Вы не имеете права делать апостериорных утверждений о параметре с учетом данных P(\theta | x), не делая утверждения об априорном. Это становится меньшей проблемой, когда доступны большие объемы высококачественных данных; они бы перетащили любой разумный скептицизм (конечный) до нужного параметра.

Если у нас нет хорошей идеи для априора, я предпочитаю Роберта Мэтьюза и И.Дж. Хороший подход, который выводит скептические и пропагандистские априорные предположения, учитывая частотный интервал.

В его документах рекомендуется получить оценку на основе результатов теста; Я предпочитаю рассчитывать как скептика, так и сторонника, независимо от сообщаемого результата теста.

Роберт Мэтьюз проделал всю творческую работу по выводу алгебраического выражения. Он описал их в этой статье, а также в той, на которую я ссылался выше. Обе достойны прочтения. Дальнейшую работу в этой области проделал Леонхард Хельд. Обычные отчеты делят результаты на «значительные» и «незначительные». Имея только CI, подставьте пределы в эту формулу, чтобы получить «границу адвокации» при наличии «незначительного» отчета. Для коэффициентов предел защиты (AL) составляет: АЛ…

Павел Рошанов 192

Большое спасибо, что нашли время объяснить. Отсутствие права на апостериорные претензии без утверждения априорных имеет смысл.