Тест матрицы равена: Прогрессивные матрицы Равена || Пройти тест онлайн
Прогрессивные матрицы Равена презентация, доклад
Прогрессивные матрицы Равена
Выполнили:
Студентки 31 группы
Бабий Людмила
Косова Екатерина
Сыровая Галина
Чижова Полина
Джон Карлайл Равен (28 июня 1902 – 10 августа 1970) известен своими работами в области диагностики и исследования компетентностей высокого уровня, их природы, развития, оценки и реализации. В ходе своих исследований, проведенных в различных научных институтах, а также по заказу Социальной службы британского правительства, он разработал новую концептуальную схему для анализа и диагностики человеческих ресурсов, в которой решающее значение придается ценностям человека.
История создания
Методика «Шкала прогрессивных матриц» была разработана в 1936 году Джоном Равеном (совместно с Л. Пенроузом). Тест прогрессивные матрицы Равена (ПМР) предназначен для диагностики уровня интеллектуального развития и оценивает способность к систематизированной, планомерной, методичной интеллектуальной деятельности (логичность мышления).
Пенроузом). Тест прогрессивные матрицы Равена (ПМР) предназначен для диагностики уровня интеллектуального развития и оценивает способность к систематизированной, планомерной, методичной интеллектуальной деятельности (логичность мышления).
При создании Прогрессивных матриц Равена значительное внимание было уделено также таким вопросам как четкость и привлекательность дизайна заданий, выполненных профессиональным художником, их размеру и пространственному взаимоотношению между незавершенной матрицей и набором альтернативных вариантов решения.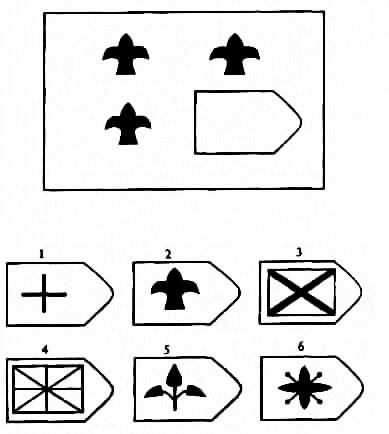
Варианты методики:
1)Стандартные матрицы, выпущенные в 1936 году в Великобритании (Авторы — Л.Пенроуз и Дж.Равен)
2) В 1947 году появились Цветные прогрессивные матрицы.
3) В 1947 году также были разработаны Продвинутые прогрессивные матрицы. Продвинутые матрицы, в отличие от обычных матриц Равена, предназначены для измерения высокого IQ — до 136 баллов (136 встречается в среднем у 1 из 122 человек)
Возрастные границы применимости Прогрессивных матриц Равена
Теоретической основой теста Равена является модель оценки интеллекта Чарльза Спирмена.
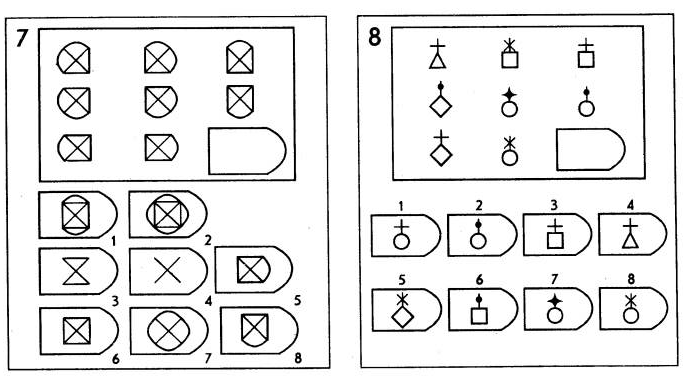 Кроме того, при разработке теста был реализован принцип «прогрессивности», заключающийся в том, что выполнение предшествующих заданий и их серий является как бы подготовкой обследуемого к выполнению последующих, более сложных.
Кроме того, при разработке теста был реализован принцип «прогрессивности», заключающийся в том, что выполнение предшествующих заданий и их серий является как бы подготовкой обследуемого к выполнению последующих, более сложных. Чарльз Эдвард Спирмен (1863 – 1945)
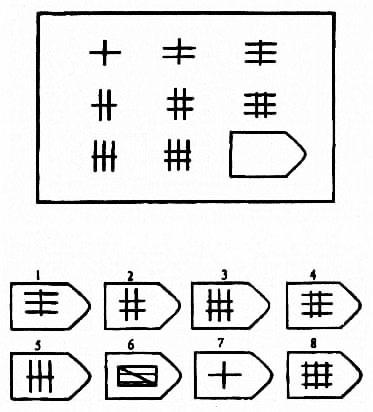
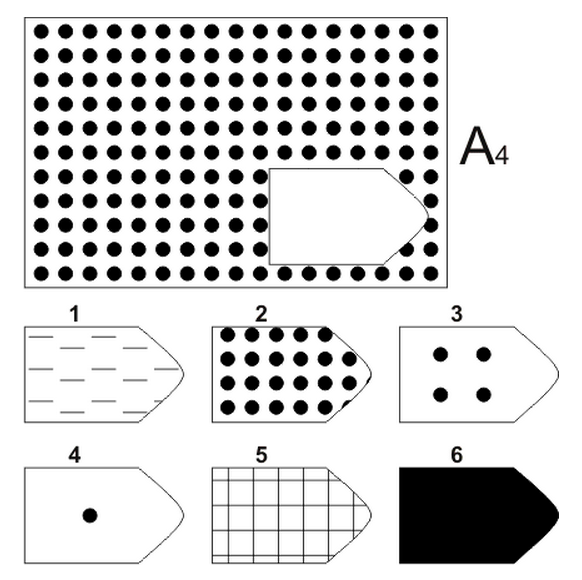
Чёрно-белые прогрессивные матрицы Равена (в оригинальном варианте) состоят из 60 матриц (размер 7,5×11 см.), в каждой из которых отсутствует один из составляющих её элементов. Обследуемый должен выбрать недостающий элемент матрицы среди 6-8 предложенных вариантов. Задания сгруппированы в 5 серий — А, В, С, D, Е, каждая серия состоит из 12 матриц.
Пример серии D
Структура теста
Примеры стимульного материала
Интерпретация результатов
Цветные прогрессивные матрицы
Структура теста
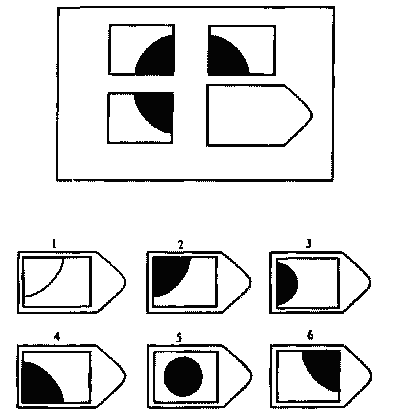
Цветной вариант Прогрессивных матриц Равена (для детей и пожилых) состоит из трех серий (А; Ab; В), различающихся по уровню сложности. Каждая серия содержит по 12 матриц с пропущенными элементами. Таким образом, для работы испытуемому предлагается 36 заданий.
Каждая серия содержит по 12 матриц с пропущенными элементами. Таким образом, для работы испытуемому предлагается 36 заданий.
Анализ результатов:
Основываясь на психологической интерпретации каждой серии заданий можно выявить те характеристики мышления, которые наиболее и наименее развиты у испытуемого.
Направления качественного анализа выполнения
Детские психологи в процессе наблюдения за поведением ребёнка в ходе диагностического обследования оценивают характеристики речи, экспрессивность, упорство и настойчивость в преодолении трудностей, отношение к разному типу диагностических задач, психодинамические характеристики деятельности ребёнка и т.п.
Качественные показатели выполнения Цветных прогрессивных матриц
Сферы применения теста ПМР
Научные исследования, направленные на оценку умственных способностей испытуемых из разных этнических и культурных групп, на изучение генетических, воспитательных и образовательных причин интеллектуальных различий
Образование и учебные занятия, для прогнозирования будущих успехов детей и взрослых, независимо от их социального и этнического происхождения
В клинике, для оценки и выявления нейропсихологических поражений, а также для контроля результатов, полученных при применении разнородных измерений интеллектуальной способности
Преимущества прогрессивных матриц Равена:
хорошая теоретическая и методологическая обоснованность теста;
конструктивная однородность тестовых заданий;
быстрота проведения и относительная лёгкость обработки результатов тестирования;
возможность проведения обследования групп и отдельных испытуемых, различающихся по определенным параметрам.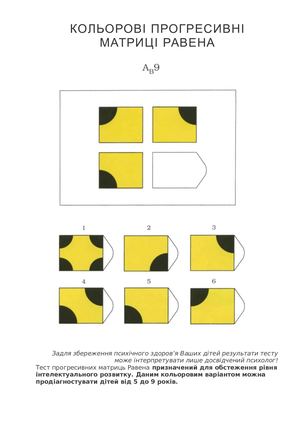
Пользователи теста Равена должны учитывать:
ограничения, связанные с построением прогноза на основе результатов теста Равена;
неоднозначность и размытость самого термина «интеллект»;
взаимодействие средовых и генетических факторов в проявлении и развитии когнитивных функций.
Скачать презентацию
Стандартные прогрессивные матрицы Равена — FINDOUT.SU
Поможем в ✍️ написании учебной работы
Имя
Поможем с курсовой, контрольной, дипломной, рефератом, отчетом по практике, научно-исследовательской и любой другой работой
Выберите тип работыЧасть дипломаДипломная работаКурсовая работаКонтрольная работаРешение задачРефератНаучно — исследовательская работаОтчет по практикеОтветы на билетыТест/экзамен onlineМонографияЭссеДокладКомпьютерный набор текстаКомпьютерный чертежРецензияПереводРепетиторБизнес-планКонспектыПроверка качестваЭкзамен на сайтеАспирантский рефератМагистерская работаНаучная статьяНаучный трудТехническая редакция текстаЧертеж от рукиДиаграммы, таблицыПрезентация к защитеТезисный планРечь к дипломуДоработка заказа клиентаОтзыв на дипломПубликация статьи в ВАКПубликация статьи в ScopusДипломная работа MBAПовышение оригинальностиКопирайтингДругое
Нажимая кнопку «Продолжить», я принимаю политику конфиденциальности
Структура теста
Чёрно-белые прогрессивные матрицы Равена (в оригинальном варианте) состоят из 60 матриц (размер 7,5^11 см. ), в каждой из которых отсутствует один из составляющих её элементов. Обследуемый должен выбрать недостающий элемент матрицы среди 6-8 предложенных вариантов. Задания сгруппированы в 5 серий — А, В, С, D, Е, каждая серия состоит из 12 матриц.
), в каждой из которых отсутствует один из составляющих её элементов. Обследуемый должен выбрать недостающий элемент матрицы среди 6-8 предложенных вариантов. Задания сгруппированы в 5 серий — А, В, С, D, Е, каждая серия состоит из 12 матриц.
Принцип «прогрессивности» в Стандартных матрицах реализуется двояким образом:
- а) внутри каждой серии задания расположены с учётом их возрастающей сложности;
- б) все серии отличаются различной трудностью, которая возрастает от серии А к серии Е.
Возрастающая трудность заданий определяется:
- увеличением числа элементов в матрице;
- увеличением предлагаемых вариантов решения;
- усложнением логического принципа, лежащего в основе каждой композиции, который испытуемому необходимо понять, чтобы закономерно выбрать недостающий элемент.
Расположение матриц в определённой последовательности соответственно принципу возрастающей сложности мыслительных операций, необходимых для решения, не исключает варианта парциальной несформированности умственных операций у обследуемого. В этом случае профиль суммарных оценок за 5 серий не будет отражать нарастающую сложность.
В этом случае профиль суммарных оценок за 5 серий не будет отражать нарастающую сложность.
Процедура проведения
Возможны два варианта в использовании Стандартных матриц Равена. Первый вариант — в качестве теста скорости, с ограничением времени выполнения заданий. В отечественных исследованиях традиционно время выполнения теста ограничивается 20 минутами. Подобный вариант использования теста наиболее оправдан в условиях группового обследования. Полученные таким образом результаты (количество верно решённых задач) позволяют оценить динамические характеристики мыслительной деятельности отдельного испытуемого относительно релевантной группы. Данный вариант проведения теста не рекомендуется для диагностической работы с детьми доподросткового и пожилого возраста.
Второй вариант использования матриц Равена в качестве теста интеллекта исключает введение временных ограничений. В этом случае диагностическое значение приобретает не суммарный показатель результативности (отражающий объём решённых задач), а результирующие показатели (сумма «сырых» баллов) по каждой серии заданий. Распределение оценок («профиль») может быть использован для вынесения диагностического суждения об уровне сформированности отдельных умственных операций. Независимо от выбранного диагностом варианта использования матриц Равена необходимо фиксировать ответы испытуемого в стандартном бланке регистрации результатов. При индивидуальном тестировании фиксация результатов производится психологом, при групповом — самими испытуемыми.
Распределение оценок («профиль») может быть использован для вынесения диагностического суждения об уровне сформированности отдельных умственных операций. Независимо от выбранного диагностом варианта использования матриц Равена необходимо фиксировать ответы испытуемого в стандартном бланке регистрации результатов. При индивидуальном тестировании фиксация результатов производится психологом, при групповом — самими испытуемыми.
Описанные варианты использования Прогрессивных матриц Равена соотносятся с двумя традиционными подходами к исследованию интеллекта и личности в отечественной психодиагностике — измерительным (количественным) и экспертным (качественным или «клиническим»).
Испытание по шкале Равена производится следующим образом. При групповом тестировании каждому испытуемому дается экземпляр тестовой тетради с одним испытательным протоколом для записи решений. Тестовая тетрадь остается закрытой до начала тестирования. Испытуемый, прежде всего, заполняет соответствующие рубрики бланка регистрации результатов: фамилия, имя, отчество, возраст и т.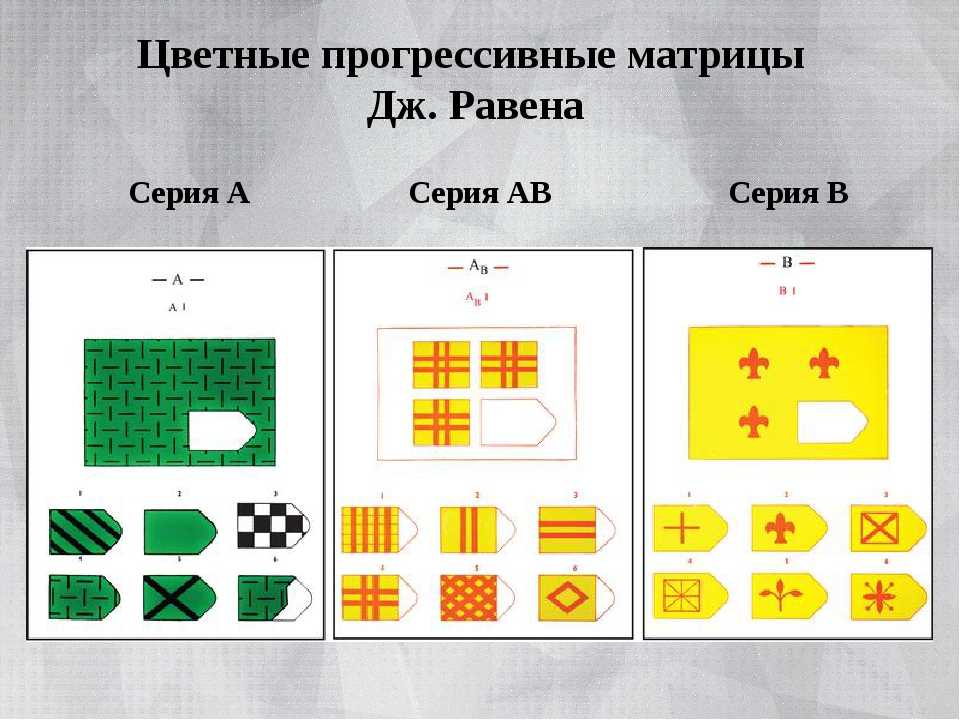 д. Для того чтобы соблюсти время тестирования, необходимо строго следить за тем, чтобы до общей команды: «Приступить к выполнению теста» — никто не открывал таблицы и не подсматривал. По истечении 20 минут подается команда, например: «Всем закрыть таблицы». О предназначении данного теста испытуемым можно сказать следующее: «Все наши исследования проводятся исключительно в научных целях, поэтому от вас требуются добросовестность, глубокая обдуманность, искренность и точность в ответах. Данный тест предназначен для уточнения логичности вашего мышления». После этого взять таблицу, открыть для показа всем 1-ю страницу и дать инструкцию.
д. Для того чтобы соблюсти время тестирования, необходимо строго следить за тем, чтобы до общей команды: «Приступить к выполнению теста» — никто не открывал таблицы и не подсматривал. По истечении 20 минут подается команда, например: «Всем закрыть таблицы». О предназначении данного теста испытуемым можно сказать следующее: «Все наши исследования проводятся исключительно в научных целях, поэтому от вас требуются добросовестность, глубокая обдуманность, искренность и точность в ответах. Данный тест предназначен для уточнения логичности вашего мышления». После этого взять таблицу, открыть для показа всем 1-ю страницу и дать инструкцию.
Инструкция
«Перед Вами в тестовой тетради содержится 60 заданий. Все задачи разделены на 5 групп, которые называются сериями и обозначены буквами А, В, С, D, Е. В каждой серии 12 заданий. Задания составлены так, чтобы в начале каждой серии располагались более легкие задания, а в конце более трудные. В каждом задании в большой рамке содержится образец, составленный из определенных фигур. Эти фигуры или рисунки составлены не хаотично, а согласно определенной закономерности. Эту закономерность Вы должны в каждом задании выяснить. В каждом большом образце отсутствует часть или последняя фигура. Вы должны найти фигуру, которой нужно правильно дополнить большой образец (матрицу) согласно закономерности, которую Вы при решении задания выявили. Фигуры или образцы, среди которых есть и нужная для дополнения верхнего изображения фигура, обозначены числами 1-6 или 1-8. Номер той фигуры, которой следует дополнить большое изображение в верхней рамке, нужно записать в соответствующую клеточку бланка. Будьте внимательны. Переходите последовательно от задания к заданию, строго соблюдайте очередность заданий и не пропускайте (не перескакивайте) ни одно задание. Если какое-то задание не знаете, как решить, угадайте, которая из фигур (изображений) под большой рамкой могла бы попасть на пустое место образца».
Эти фигуры или рисунки составлены не хаотично, а согласно определенной закономерности. Эту закономерность Вы должны в каждом задании выяснить. В каждом большом образце отсутствует часть или последняя фигура. Вы должны найти фигуру, которой нужно правильно дополнить большой образец (матрицу) согласно закономерности, которую Вы при решении задания выявили. Фигуры или образцы, среди которых есть и нужная для дополнения верхнего изображения фигура, обозначены числами 1-6 или 1-8. Номер той фигуры, которой следует дополнить большое изображение в верхней рамке, нужно записать в соответствующую клеточку бланка. Будьте внимательны. Переходите последовательно от задания к заданию, строго соблюдайте очередность заданий и не пропускайте (не перескакивайте) ни одно задание. Если какое-то задание не знаете, как решить, угадайте, которая из фигур (изображений) под большой рамкой могла бы попасть на пустое место образца».
Во время выполнения заданий теста необходимо контролировать, чтобы респонденты не списывали друг у друга.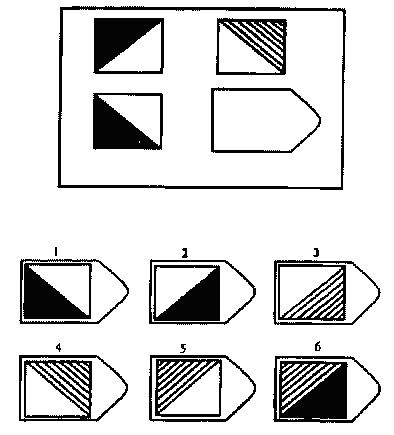 По истечении 20 минут подаётся команда: «Закрыть всем таблицы!» При сборе бланков и таблиц к ним целесообразно проверить, чтобы все поля бланка были заполнены.
По истечении 20 минут подаётся команда: «Закрыть всем таблицы!» При сборе бланков и таблиц к ним целесообразно проверить, чтобы все поля бланка были заполнены.
Тест в определённой мере подвержен влиянию научения, поэтому в диагностических целях не рекомендуется многократно использовать его на одной и той же выборке испытуемых.
Обработка результатов
По окончании работы испытуемого, психолог с помощью ключа подсчитывает количество правильных ответов, причём правильное решение каждого отдельного задания оценивается в 1 балл.
Ключ
| № | Серия А | Серия В | Серия С | Серия D | Серия Е |
| 1 | 4 | 2 | 8 | 3 | 7 |
| 2 | 5 | 6 | 2 | 4 | 6 |
| 3 | 1 | 1 | 3 | 3 | 8 |
| 4 | 2 | 2 | 8 | 7 | 2 |
| 5 | 6 | 1 | 7 | 8 | 1 |
| 6 | 3 | 3 | 4 | 6 | 5 |
| 7 | 6 | 5 | 5 | 5 | 1 |
| 8 | 2 | 6 | 1 | 4 | 6 |
| 9 | 1 | 4 | 7 | 1 | 3 |
| 10 | 3 | 3 | 6 | 2 | 2 |
| 11 | 4 | 4 | 1 | 5 | 4 |
| 12 | 5 | 5 | 2 | 6 | 5 |
Подсчитывается общая сумма полученных баллов (испытуемый может получить высшую оценку — 60 баллов), а также число правильных решений в каждой из пяти серий.
Общая сумма баллов является показателем интеллектуальной способности испытуемого, выявляет его умение мыслить согласно определенному методу и системе мышления.
По каждой серии имеется таблица ожидаемых (предполагаемых) результатов распределения решений.
|
Сентябрь 2022
(43 дн. (43 дн. назад) (43 дн. назад) | Прогрессивные матрицы Равена
Описание методикиПрогрессивные матрицы Равена (Raven Progressive Matrices) предназначены для определения уровня умственного (интеллектуального) развития испытуемых в возрасте от 4,5 до 65 лет и старше. Матрицы Равена могут применяться на выборках испытуемых с любым языковым составом и социокультурным фоном, с любым уровнем речевого развития. Поскольку известны три варианта матриц Равена, то следует заметить, что каждый из вариантов предназначен для проведения диагностической работы с определённым контингентом испытуемых. Возрастные границы применимости Прогрессивных матриц Равена
История создания методикиТест предложен Л. Теоретические (методологические) основыТест «Прогрессивные матрицы Равена» относится к числу невербальных тестов интеллекта и основывается на двух теориях, разработанных гештальт-психологией: теорией перцепции форм и так называемой «теорией неогенеза» Ч. Согласно теории перцепции форм каждое задание может быть рассмотрено как определенное целое, состоящее из ряда взаимосвязанных друг с другом элементов. Предполагается, что первоначально происходит глобальная оценка задания-матрицы, а затем осуществление аналитической перцепции с выделением испытуемым принципа, принятого при разработке серии. На заключительном этапе выделенные элементы включаются в целостный образ, что способствует обнаружению недостающей детали изображения. Теория Ч. Спирмена углубляет рассмотренные положения теории перцепции форм. Как показывает опыт многолетних исследований, данные, полученные с помощью теста Равена, хорошо согласуются с показателями других распространенных тестов: Векслера, Стенфорд-Бине, ШТУРа,Выготского-Сахарова. Прогрессивные матрицы Равена предназначены для определения уровня умственного развития у детей ментального возраста( 1-4 класс массовой школы ). Матрицы Равена могут применяться на испытуемых с любым языковым составом и социокультурным фоном, с любым уровнем речевого развития. Литература
См. такжеСтандартные прогрессивные матрицы Цветные прогрессивные матрицы |
Хи-квадрат проверяет, является ли отдельная матрица тождеством…
R: Хи-квадрат проверяет, является ли отдельная матрица тождеством…| cortest.mat {psych} | R Документация |
Описание
Steiger (1980) указал, что сумма квадратов элементов корреляционной матрицы или эквивалентов z-показателей Фишера распределяется как хи-квадрат при нулевой гипотезе о том, что значения равны нулю (т. е. элементы единичной матрицы). Это особенно полезно для проверки того, отличаются ли корреляции в одной матрице от нуля, или для сравнения двух матриц. Дженнрих (1970) также рассмотрел тесты различий между матрицами.
е. элементы единичной матрицы). Это особенно полезно для проверки того, отличаются ли корреляции в одной матрице от нуля, или для сравнения двух матриц. Дженнрих (1970) также рассмотрел тесты различий между матрицами.
Применение
cortest.normal(R1, R2 = NULL, n1 = NULL, n2 = NULL, fisher = TRUE) # тест Стайгера cortest(R1,R2=NULL,n1=NULL,n2 = NULL, fisher = TRUE,cor=TRUE) #то же, что и cortest.normal cortest.jennrich(R1,R2,n1=NULL, n2=NULL) #тест Дженнриха cortest.mat(R1,R2=NULL,n1=NULL,n2 = NULL) #альтернативный тест
Аргументы
Р1 |
Корреляционная матрица. (Если R1 не является прямоугольным и cor=TRUE, корреляции найдены). |
Р2 |
Корреляционная матрица. Если R2 не является прямоугольным и cor=TRUE, корреляции найдены. Если R2 равно NULL, то проверяется, является ли R1 единичной матрицей. |
№1 |
Размер выборки R1 |
n2 |
Размер выборки R2 |
Фишер |
Фишер Z преобразовать корреляции? |
кор |
По умолчанию, если входные матрицы несимметричны, они преобразуются в матрицы корреляции. |
Детали
Есть несколько способов проверить, является ли матрица единичной. Наиболее известен тест хи-квадрат Бартлетта (1951) и Бокса (19).49). Очень простой тест, обсуждаемый Стайгером (1980), состоит в том, чтобы найти сумму квадратов корреляций или сумму квадратов корреляций, преобразованных Фишером. При нулевой гипотезе, что все корреляции равны, эта сумма распределяется как хи-квадрат. Это реализовано в
кортест и кортест.нормальный
Еще один тест — это тест Дженнриха (1970) на равенство двух матриц. Это сравнивает различия между двумя матрицами со средними значениями двух матриц с использованием теста хи-квадрат. Это реализовано в 92 , но с удвоенными степенями свободы.
Значение
Чи2 |
Статистика хи-квадрат |
дф |
Степени свободы для Чи квадрата |
проба |
Вероятность наблюдения хи-квадрата при нулевой гипотезе. |
Примечание
И cortest.jennrich, и cortest.normal, вероятно, слишком строгие. Значения ChiSquare для пар случайных выборок из одной и той же совокупности больше, чем можно было бы ожидать. Это хороший тест для отклонения нулевого значения отсутствия различий. 92 Тест на равенство двух корреляционных матриц. Журнал Американской статистической ассоциации, 65, 904-912.
См. также
кортест.бартлетт
Примеры
x <- матрица (rнорма (1000), ncol = 10) cortest.normal(x) #Просто проверьте, является ли эта матрица тождеством x <- sim.congeneric(loads =c(.9,.8,.7,.6,.5),N=1000,short=FALSE) y <- sim.congeneric(loads =c(.9,.8,.7,.6,.5),N=1000,short=FALSE) cortest.normal(x$r,y$r,n1=1000,n2=1000) #Тест Штайгера cortest.jennrich(x$r,y$r,n1=100,n2=1000) # Тест Дженриха cortest.mat(x$r,y$r,n1=1000,n2=1000) #вдвое больше степеней свободы, чем у Дженриха
[Package psych version 1.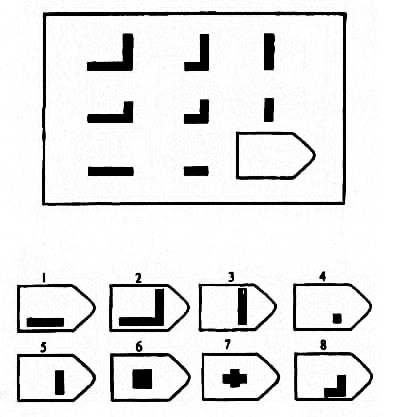 4.5 Index]
4.5 Index]
Как проверить (быстро) умножение матриц | by Haris Angelidakis
Спойлер: случайность помогает (еще раз)
Умножение двух N x N матриц A и B — фундаментальная операция, которая проявляется как подпрограмма во всех видах приложений. Поиск алгоритма, способного умножать две матрицы за время O( N ²) все еще продолжается, с самым быстрым асимптотическим алгоритмом, благодаря Джошу Алману и Вирджинии Василевской Уильямс (2021), в настоящее время время работы
Однако, как отмечено в этой статье Википедии, этот алгоритм является галактическим алгоритмом из-за большие константы и не могут быть реализованы практически. Если вам интересно узнать о первом алгоритме, преодолевшем наивный барьер O( N ³) для умножения матриц, вы можете взглянуть на мою предыдущую статью о классическом алгоритме Штрассена.
Однако в сегодняшней статье мы изучим другой, связанный с этим вопрос. Предположим, что кто-то дает нам N x N матрицы A, B и C, и, кроме того, предположим, что они утверждают, что C есть произведение A и B , т.е. = АБ . Вопрос теперь в следующем. Можем ли мы проверить, действительно ли C является произведением A и B , не умножая A с B с нуля? Другими словами:
Предположим, что кто-то дает нам N x N матрицы A, B и C, и, кроме того, предположим, что они утверждают, что C есть произведение A и B , т.е. = АБ . Вопрос теперь в следующем. Можем ли мы проверить, действительно ли C является произведением A и B , не умножая A с B с нуля? Другими словами:
Учитывая N x N матриц A , B и C , как быстро мы можем проверить, являются ли C =
5 6 AB 9 ?
Тривиальным тестом на приведенный выше вопрос было бы просто умножить A на B и проверить, равно ли произведение C . Учитывая, что у нас до сих пор нет алгоритма O( N ²) для умножения матриц, наша цель здесь — разработать O( N ²) алгоритм, проверяющий, является ли C = AB . Для этого мы прибегаем к случайности.
Примечание: Прежде чем продолжить, мы заявляем, что изложение следует главе 11 прекрасной книги «Тридцать три миниатюры: математические и алгоритмические приложения линейной алгебры» Иржи Матоусека.
Основная идея состоит в том, чтобы выбрать случайный N -мерный {0,1} вектор x , где каждая координата независимо установлена в 0 или 1 с вероятностью 0,5, и умножить оба C и AB с х. Если C = AB , то мы будем иметь Cx = (AB)x, для любого вектора x. Однако, если C не равно AB, , то мы надеемся, что существует множество векторов, для которых Cx не равно ( AB)x. Формально предлагаемый тест выглядит следующим образом.
Базовый тест
- Выберите N -мерный {0,1} вектор x равномерно случайным образом.
- Вычислить y = Cx и z = ( AB ) x .
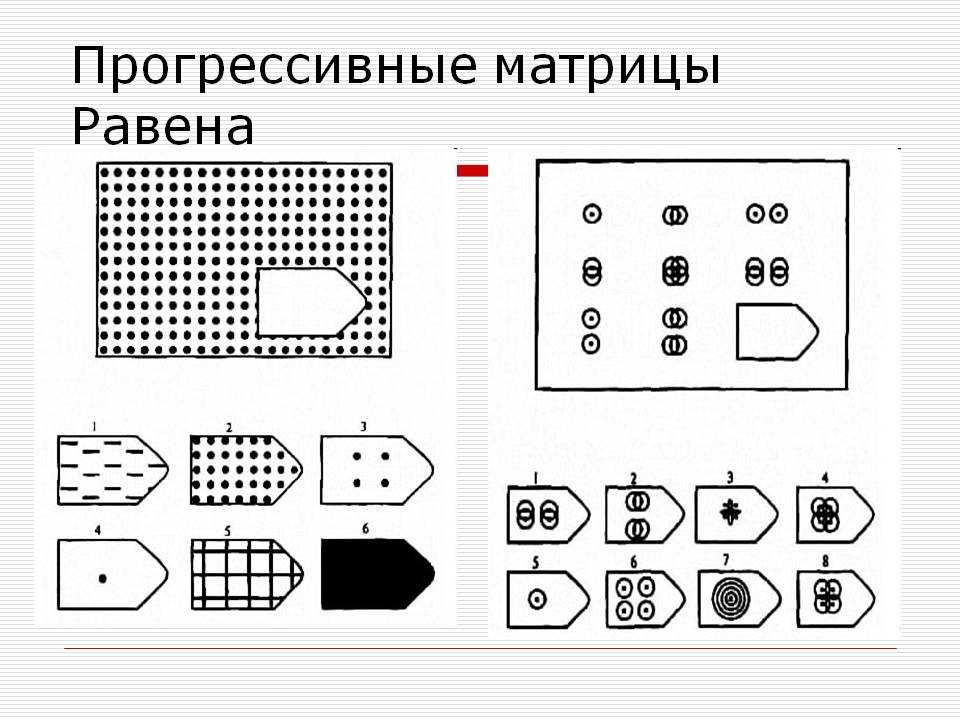
- Если y = z , то вернуть «РАВНО», иначе вернуть «НЕ РАВНО».
Очень легко увидеть, что тест всегда будет возвращать «EQUAL», если C действительно равно AB . Итак, единственный интересный случай для анализа — это когда C не равно AB . Но прежде чем сделать это, мы должны уточнить следующее. Предлагаемая идея требует вычисления произведения (АВ)х . Здесь мы должны быть немного осторожны, так как хотим избежать вычисления произведения AB . Чтобы решить эту проблему, мы используем тот факт, что умножение матриц является ассоциативным, и сначала вычисляем Bx , затем умножаем на с результатом Bx для общего времени работы O( N ²).
Возвращаясь к анализу, предположим, что C не равно AB . Пусть D = C-AB. Ясно, что хотя бы одна запись из D будет ненулевым. Обозначим элемент в i -й строке и j -м столбце D как d(i,j) , и пусть k , t таковы, что d(k, t) не равно нулю.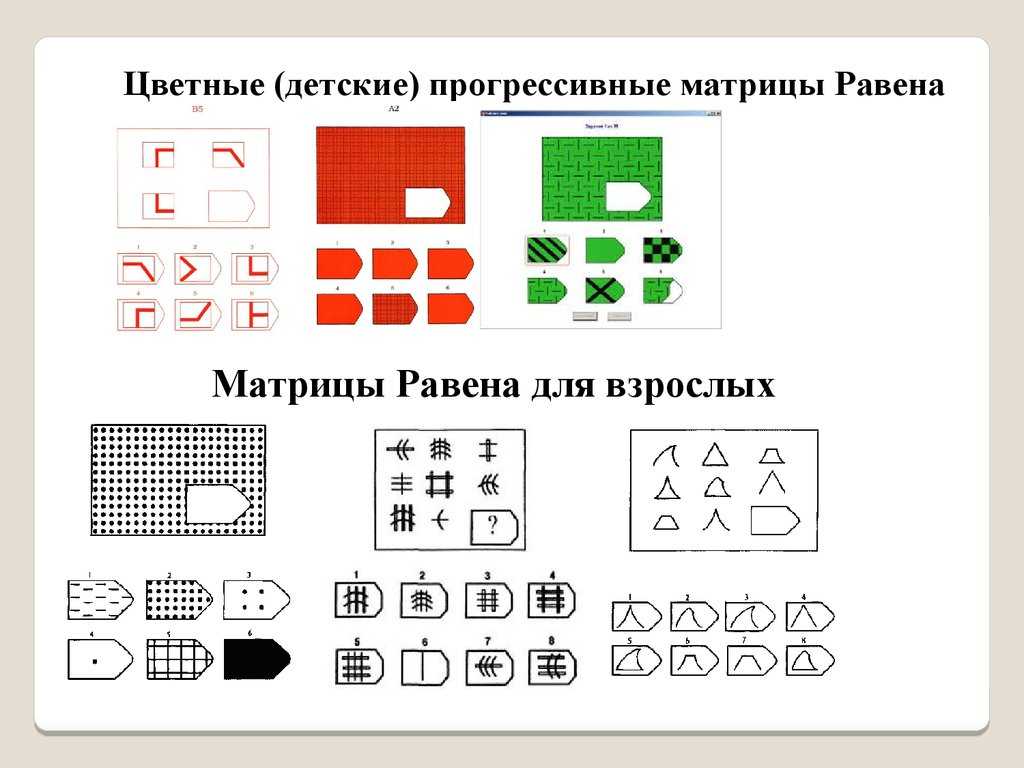 Пусть x(j) обозначает j -ю координату вектора x, а q= Dx . Заметьте, что q = y-z . Теперь у нас есть
Пусть x(j) обозначает j -ю координату вектора x, а q= Dx . Заметьте, что q = y-z . Теперь у нас есть
Поскольку каждая координата x выбирается независимо случайным образом, мы можем считать, что координата x(t) является последней, которая будет установлена в 0 или 1. Итак, предположим, что все остальные координаты x были установлены, кроме координаты x(t) . Когда мы собираемся решить, является ли x(t) 0 или 1, подбрасывая правильную монету, мы уже определили значение выражения
Обратите внимание, что есть два варианта для S ; он либо равен нулю, либо отличен от нуля. Теперь вернемся к последнему подбрасыванию монеты, которое определит x(t) . У нас есть два случая:
- с вероятностью 0,5, x(t) = 1, поэтому q(k) = S + d(k,t) .
- с вероятностью 0,5, x(t) = 0, поэтому q(k) = S .
Поскольку d(k,t) не равно нулю, это означает, что S + d(k,t) не равно S . Таким образом, хотя бы одно из S и S+ d(k,t) отлично от нуля, и поэтому мы заключаем, что q(k) отлично от нуля с вероятностью не менее 0,5, из чего следует, что y не равно z с вероятностью не менее 0,5. Мы заключаем, что с вероятностью не менее 0,5 наш тест правильно определит, что C не равно AB .
Таким образом, хотя бы одно из S и S+ d(k,t) отлично от нуля, и поэтому мы заключаем, что q(k) отлично от нуля с вероятностью не менее 0,5, из чего следует, что y не равно z с вероятностью не менее 0,5. Мы заключаем, что с вероятностью не менее 0,5 наш тест правильно определит, что C не равно AB .
Тем не менее, можно сказать, что вероятность успеха в 50% не очень удовлетворительна. И, действительно, это справедливое беспокойство. Но мы можем использовать стандартный прием, используемый для таких алгоритмов, которые попадают в широкий класс алгоритмов Монте-Карло, а именно повторить их несколько раз. Точнее, окончательный алгоритм, который мы будем использовать, следующий.
Окончательный тест
- Выполнить базовый тест M раз независимо.
- Если все выполнения базового теста вернули «РАВНО», верните «РАВНО», в противном случае верните «НЕ РАВНО».

Легко видеть, что Final Test всегда завершается успешно, если C = AB . В случае, когда C не равно AB , тогда мы знаем, что однократное выполнение базового теста удается с вероятностью не менее 0,5 . Таким образом, чтобы получить неправильный ответ, все M выполнения базового теста должны быть неудачными. Поскольку эти исполнения независимы, это происходит с вероятностью не более 1/2 ᴹ .
Например, если установить M = 10, то вероятность неудачи меньше 0,001, или другими словами вероятность успеха не менее 99,9%, что совсем неплохо! Что касается времени работы, то в него будет включено M , а общее время работы составит O( М Н ²). Поскольку M является константой, это по-прежнему равно O( N ²) и намного быстрее, чем современные лучшие алгоритмы для умножения матриц. Мы сделали!
- Тридцать три миниатюры: математические и алгоритмические приложения линейной алгебры», Иржи Матоусек.
 Издатель: Американское математическое общество
Издатель: Американское математическое общество - https://en.wikipedia.org/wiki/Matrix_multiplication_algorithm
Статистические тесты для сравнения матриц – Эволюция в структурированных популяциях
Я был небрежен. Несколько лет назад я обнаружил, что хочу сравнить две матрицы генетической ковариации. В то время это было до того, как Пэт Филлипс предложил иерархию Flury (Phillips & Arnold 1999. Evolution 53: 1506-1515), поэтому я оказался в ситуации, когда мне пришлось изобретать свою собственную. Позже, очевидно, вместе с другими я решил, что не особенно очарован иерархией Flury. Это привело к двум публикациям (Goodnight & Schwartz 1997 Биометрия 53: 1026-1039; Калсбек и. Goodnight 2009 Evolution 63: 2627-2635), первый из которых малоизвестен. Первая публикация также страдала от отсутствия хорошей программной реализации. С появлением R это было исправлено. В любом случае я хотел бы напомнить людям об этих статистических методах сравнения ковариационных матриц.
Во-первых, в иерархии Flury нет ничего плохого, просто я не считаю ее интуитивно полезной. Насколько я понимаю, иерархия Flury — это подход к выбору модели, тогда как методы, которые я буду обсуждать, — это параметрические статистические тесты. Я рекомендую вам прочитать статьи Philips и Arnold и принять собственное решение. Итак, достаточно преамбулы.
Мы только что провели эксперимент, в котором отправили популяцию узкое место, и мы измерили несколько признаков. Мы хотели знать, имеют ли производная популяция и предковая популяция одинаковую генетическую структуру, то есть одинаковые матрицы генетической ковариации. Для одного признака мы точно знаем, как это сделать. Вы «просто» измеряете аддитивную генетическую изменчивость в двух популяциях и выполняете F-тест, чтобы увидеть, одинаковы они или различны. Я просто в кавычках, потому что измерить аддитивную дисперсию никогда не бывает легко.
Когда мы добираемся до многовариантных настроек, все становится сложнее.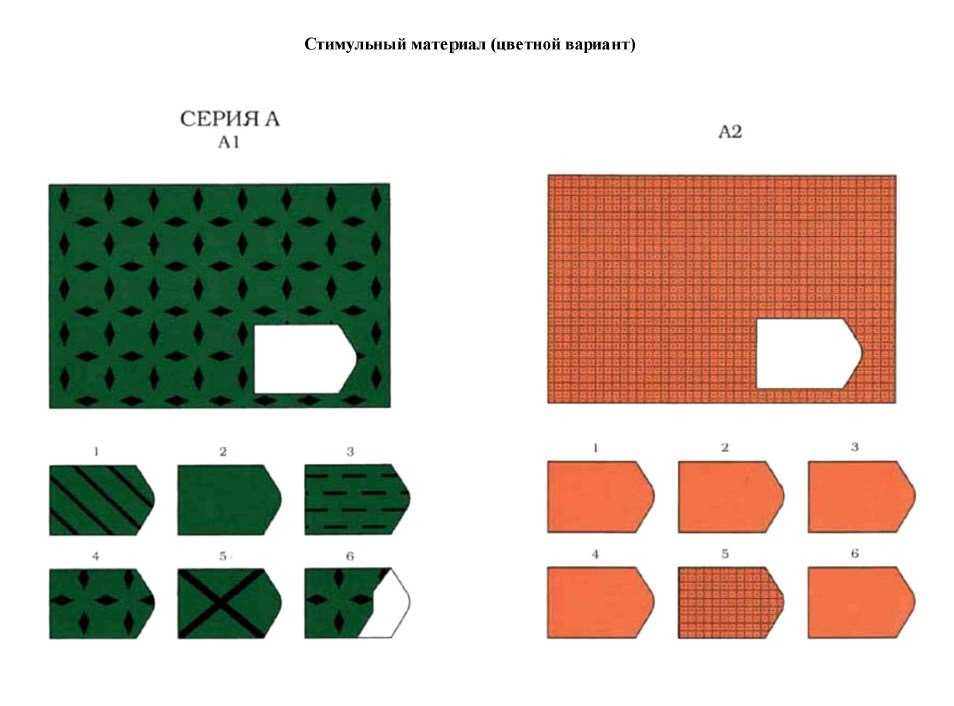 Опять же, мы, вероятно, будем использовать MANOVA для измерения аддитивной матрицы генетической ковариации для каждой популяции. Затем мы хотели бы сравнить их, чтобы увидеть, являются ли они одинаковыми или разными. Хорошая новость заключается в том, что матрицы генетической ковариации имеют квадратную форму и с ними, как правило, легко работать. Плохая новость заключается в том, что когда мы используем многомерность, матрицы могут различаться несколькими способами. В «Спокойной ночи и Шварце» (1998) мы решили, что есть три способа заинтересовать. Матрицы могут быть разной размерности, разного размера и разной формы. Это действительно независимые способы быть разными, поэтому имеет смысл разработать три теста. Мы тестировали их с помощью начальной загрузки.
Опять же, мы, вероятно, будем использовать MANOVA для измерения аддитивной матрицы генетической ковариации для каждой популяции. Затем мы хотели бы сравнить их, чтобы увидеть, являются ли они одинаковыми или разными. Хорошая новость заключается в том, что матрицы генетической ковариации имеют квадратную форму и с ними, как правило, легко работать. Плохая новость заключается в том, что когда мы используем многомерность, матрицы могут различаться несколькими способами. В «Спокойной ночи и Шварце» (1998) мы решили, что есть три способа заинтересовать. Матрицы могут быть разной размерности, разного размера и разной формы. Это действительно независимые способы быть разными, поэтому имеет смысл разработать три теста. Мы тестировали их с помощью начальной загрузки.
Начальная загрузка: Начальная загрузка — это интересная статистическая процедура, которая была популяризирована в 80-х годах Брэдом Эфроном (Efron 1979, The Annals of Statistics 7:1-26) (я посетил семинар, который он предложил где-то в 1985 году). Основная идея заключается в том, что если у вас есть набор данных, вы можете создавать новые наборы псевдоданных путем случайной выборки с заменой из исходных данных. Если будет сгенерировано достаточное количество этих наборов данных начальной загрузки, они фактически обеспечат распределение данных. Сначала это кажется нелогичным, но пока ваш набор данных относительно велик, это работает очень хорошо. Чтобы использовать это в качестве статистического теста, вам нужно решить, какова ваша нулевая гипотеза, а затем выяснить схему случайной выборки, которая сделает эту нулевую гипотезу верной. Например, при использовании t-критерия нулевая гипотеза состоит в том, что две совокупности имеют одинаковое среднее значение. Вы можете сделать эту нулевую гипотезу верной несколькими способами. Вы можете просто объединить данные из двух популяций. Затем случайным образом распределите их обратно по двум популяциям независимо от исходного источника. В результате не будет истинной разницы между популяциями.
Основная идея заключается в том, что если у вас есть набор данных, вы можете создавать новые наборы псевдоданных путем случайной выборки с заменой из исходных данных. Если будет сгенерировано достаточное количество этих наборов данных начальной загрузки, они фактически обеспечат распределение данных. Сначала это кажется нелогичным, но пока ваш набор данных относительно велик, это работает очень хорошо. Чтобы использовать это в качестве статистического теста, вам нужно решить, какова ваша нулевая гипотеза, а затем выяснить схему случайной выборки, которая сделает эту нулевую гипотезу верной. Например, при использовании t-критерия нулевая гипотеза состоит в том, что две совокупности имеют одинаковое среднее значение. Вы можете сделать эту нулевую гипотезу верной несколькими способами. Вы можете просто объединить данные из двух популяций. Затем случайным образом распределите их обратно по двум популяциям независимо от исходного источника. В результате не будет истинной разницы между популяциями.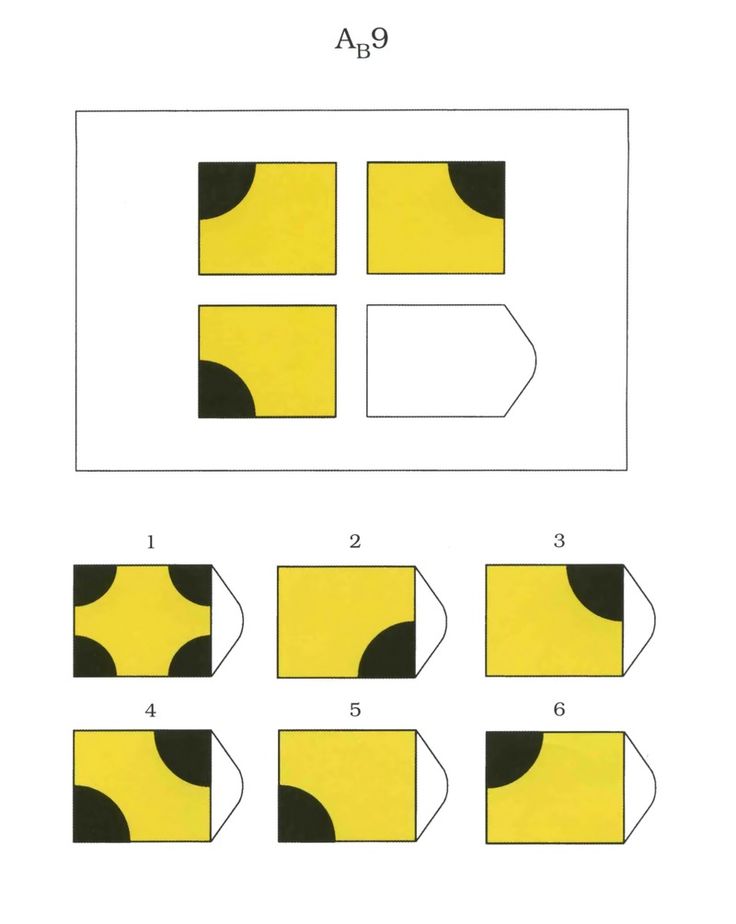 Если вы случайным образом создадите несколько тысяч таких пар популяций, вы получите распределение наблюдаемых различий в средних значениях, когда вы знаете, что истинное различие на самом деле равно нулю. Затем вы можете взять фактическую разницу между двумя популяциями и просто спросить, какой процент различий начальной загрузки более экстремальный, чем разница в фактических данных. Этот процент является вашей вероятностью того, что наблюдаемая разница возникает случайно. Есть более изощренные подходы, но это дает идею.
Если вы случайным образом создадите несколько тысяч таких пар популяций, вы получите распределение наблюдаемых различий в средних значениях, когда вы знаете, что истинное различие на самом деле равно нулю. Затем вы можете взять фактическую разницу между двумя популяциями и просто спросить, какой процент различий начальной загрузки более экстремальный, чем разница в фактических данных. Этот процент является вашей вероятностью того, что наблюдаемая разница возникает случайно. Есть более изощренные подходы, но это дает идею.
В нашем конкретном тесте у нас была наследственная популяция и популяция, полученная в результате спаривания двух поколений братьев и сестер. Мы хотели посмотреть, были ли эти две популяции одинаковыми или разными. Наша нулевая гипотеза заключалась в том, что их ковариационные матрицы были одинаковыми (это важно!), и мы решили использовать данные предкового населения в качестве источника для данных начальной загрузки.
Измерение: Генетическая ковариационная матрица может рассматриваться как ограждающая пространство.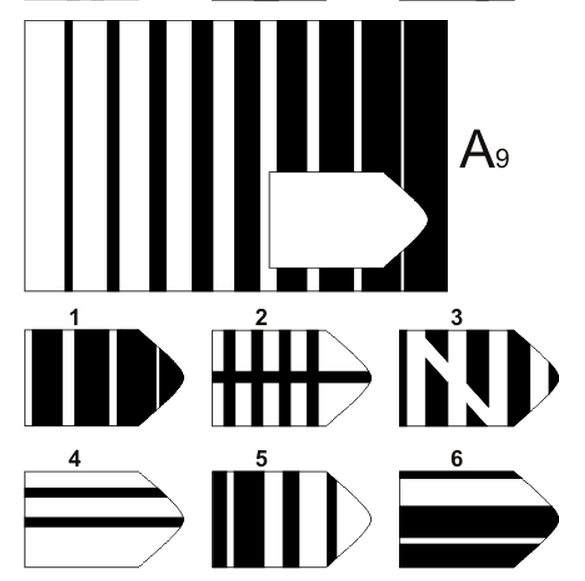 Таким образом, одномерная «матрица» представляет собой единственный вектор длины, равной дисперсии. Ковариационная матрица с двумя признаками определяет плоскость, матрица с тремя признаками — куб и так далее.
Таким образом, одномерная «матрица» представляет собой единственный вектор длины, равной дисперсии. Ковариационная матрица с двумя признаками определяет плоскость, матрица с тремя признаками — куб и так далее.
Рисунок 1; одномерный вектор и двух- и трехмерные матрицы.
Есть две вещи, которые могут произойти с аддитивной генетической изменчивостью после того, как популяция пройдет через узкое место. Сначала он может исчезнуть, то есть может уйти в ноль. Во-вторых, он может настолько сильно коррелировать с другими чертами, что становится линейной комбинацией этих черт. Графически в случае с тремя признаками это было бы эквивалентно тому, что один из векторов лежит точно в плоскости двух других векторов.
Рисунок 2: в этой матрице признак z представляет собой линейную комбинацию признаков y и x. В результате все три лежат в одной плоскости, а результирующая матрица является двумерной матрицей.
Попробуйте сравнить две матрицы с тремя дисперсиями.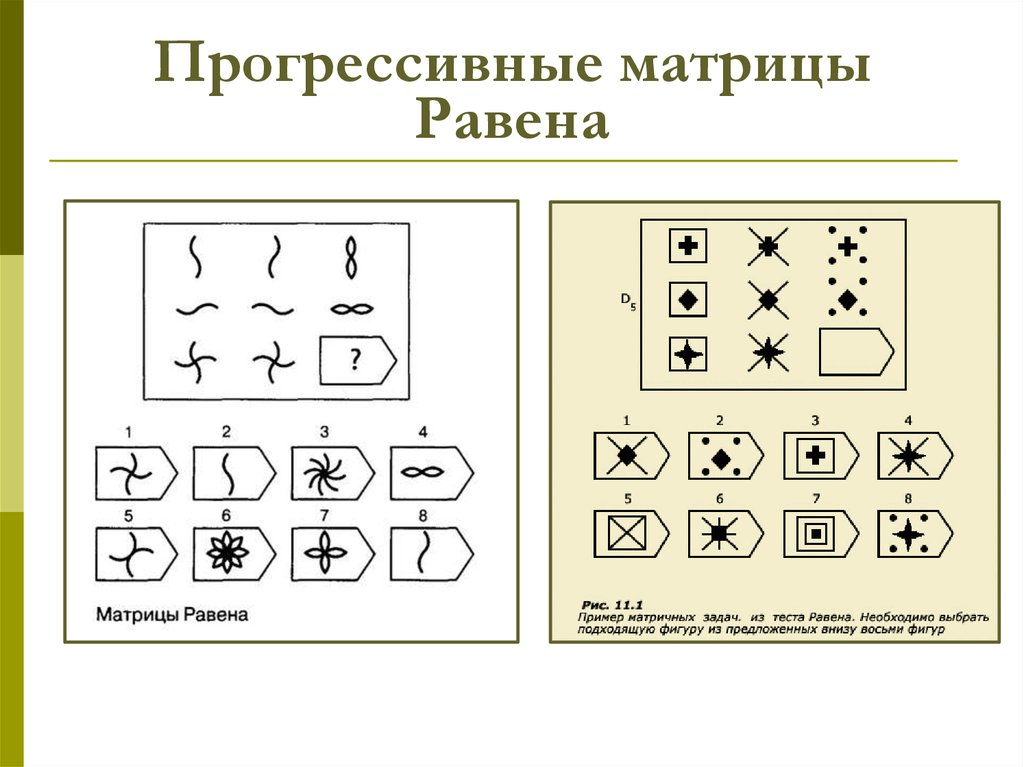 Один похож на трехмерную матрицу на рисунке 1, а второй имеет только два измерения, как на рисунке 2. Сравнить их не получится. По аналогии это все равно, что спрашивать, что больше, коробка или лист бумаги. Трехмерная матрица имеет дополнительное измерение, по которому она может развиваться, качественно отличное от двухмерной структуры.
Один похож на трехмерную матрицу на рисунке 1, а второй имеет только два измерения, как на рисунке 2. Сравнить их не получится. По аналогии это все равно, что спрашивать, что больше, коробка или лист бумаги. Трехмерная матрица имеет дополнительное измерение, по которому она может развиваться, качественно отличное от двухмерной структуры.
Способ, которым мы проверяли это, заключался в том, чтобы найти наибольшую подматрицу, которая имела действительные отклонения, которые не были линейными комбинациями других векторов. Затем мы проверили абсолютное значение разницы в ранге (|R popA -R popB |), так как наша тестовая статистика измерялась по сравнению с бутстрэп-популяциями, где истинной разницы в ранге не было. В этом наборе данных разница в ранге не была значимой.
Разница в размере: Как упоминалось выше, матрицы можно рассматривать как плоскости, объемы или гиперобъемы. Получается, что определитель — это мера пространства, ограниченного матрицей. Например, в матрице с двумя признаками определителем является площадь матрицы, в матрице с тремя признаками - это объем и т. д. Таким образом, две матрицы одинаковой размерности, независимо от формы, можно сравнивать путем сравнения определителей. Аналогия с двумя вазами странной формы. Мы можем сравнить их, спросив, сколько воды они вмещают. В этом случае форма не имеет значения, только размер замкнутого пространства.
Например, в матрице с двумя признаками определителем является площадь матрицы, в матрице с тремя признаками - это объем и т. д. Таким образом, две матрицы одинаковой размерности, независимо от формы, можно сравнивать путем сравнения определителей. Аналогия с двумя вазами странной формы. Мы можем сравнить их, спросив, сколько воды они вмещают. В этом случае форма не имеет значения, только размер замкнутого пространства.
Важным предостережением является то, что они должны быть одного размера. Опять тот же вопрос: что больше объем коробки или площадь листа бумаги. И снова бессмысленный вопрос. Мы решили решить эту проблему, выполнив «ортогональную проекцию» матрицы большего размера на матрицу меньшего размера. То есть мы искали пары матриц для набора признаков, которые имели действительные отклонения в обеих матрицах. Мы провели анализ этой пары подматриц.
Следующий вопрос, как сравнить два определителя. Оказывается, есть хороший тест, многомерный тест Бартлетта, который можно использовать. Тест Бартлетта имеет две проблемы. Во-первых, он очень чувствителен к предположению о многомерной нормальности, а во-вторых, он не структурирован для использования с данными, полученными с помощью MANOVA. Тем не менее, мы можем использовать базовую статистику и объединить ее с данными начальной загрузки, и это работает отлично. Одной из очень полезных функций бутстрап-тестов является то, что они не делают предположений о распределении данных. Кроме того, при правильном проектировании они хорошо работают практически с любым экспериментальным планом. Интересно, что, поскольку стандартный тест не был разработан для использования с MANOVA, параметрический многомерный тест Барлетта был чересчур оптимистичен, а бутстрап в итоге справился гораздо лучше. Последняя модификация заключается в том, что у нас был априорный интерес к тому, была ли полученная генетическая ковариационная матрица значительно больше, чем у предковой популяции. Таким образом, мы умножали статистику Бартлетса на 1, если производная популяция была больше, чем предковая популяция, и на -1, если она была меньше, что давало нам подписанный тест Bootstrap Bartlett, который допускал как односторонний, так и двусторонний тест.
Тест Бартлетта имеет две проблемы. Во-первых, он очень чувствителен к предположению о многомерной нормальности, а во-вторых, он не структурирован для использования с данными, полученными с помощью MANOVA. Тем не менее, мы можем использовать базовую статистику и объединить ее с данными начальной загрузки, и это работает отлично. Одной из очень полезных функций бутстрап-тестов является то, что они не делают предположений о распределении данных. Кроме того, при правильном проектировании они хорошо работают практически с любым экспериментальным планом. Интересно, что, поскольку стандартный тест не был разработан для использования с MANOVA, параметрический многомерный тест Барлетта был чересчур оптимистичен, а бутстрап в итоге справился гораздо лучше. Последняя модификация заключается в том, что у нас был априорный интерес к тому, была ли полученная генетическая ковариационная матрица значительно больше, чем у предковой популяции. Таким образом, мы умножали статистику Бартлетса на 1, если производная популяция была больше, чем предковая популяция, и на -1, если она была меньше, что давало нам подписанный тест Bootstrap Bartlett, который допускал как односторонний, так и двусторонний тест.
Форма: Для формы мы решили провести тест, аналогичный тесту Мантеля. Многие справедливо жалуются на классический тест Мантела по многим причинам. Тем не менее, основная идея полезна. Идея состоит в том, что вы вычисляете корреляцию между парными элементами двух матриц. То есть вы соединяете элементы двух матриц и просто вычисляете корреляцию между ними. Проблемы с традиционным тестом Мантела для этого приложения носят тройной характер. Во-первых, у традиционного Мантеля есть нулевая гипотеза о том, что две матрицы независимы, тогда как наша нулевая гипотеза состоит в том, что две матрицы идентичны. Начальная загрузка решает эту проблему, позволяя нам генерировать распределение корреляций Мантеля среди пар матриц, которые имеют истинную корреляцию 1,9.0013
Во-вторых, критерий Мантела предназначен для сравнения корреляционных матриц, у которых единицы на диагонали, тогда как это неверно для ковариационной матрицы. В классическом тесте Мантеля эта диагональ исключается, а в нашем — нет. В-третьих, все элементы корреляционной матрицы находятся в диапазоне от -1 до 1, тогда как ковариационные матрицы могут иметь совершенно разные дисперсии для разных признаков, что может неуместно исказить результаты. Это последнее мы решили, стандартизировав элементы по среднему значению диагоналей двух матриц. Окончательное уравнение несколько уродливо, поэтому я отсылаю вас к статье, если вам нужны подробности. Результаты показывают, что у женщин, но не у мужчин, наблюдается значительное изменение формы их ковариационной матрицы. То есть узкое место популяции значительно изменило некоторые вариации и ковариации между признаками в двух популяциях, хотя и не изменило общий объем аддитивной генетической дисперсии.
В-третьих, все элементы корреляционной матрицы находятся в диапазоне от -1 до 1, тогда как ковариационные матрицы могут иметь совершенно разные дисперсии для разных признаков, что может неуместно исказить результаты. Это последнее мы решили, стандартизировав элементы по среднему значению диагоналей двух матриц. Окончательное уравнение несколько уродливо, поэтому я отсылаю вас к статье, если вам нужны подробности. Результаты показывают, что у женщин, но не у мужчин, наблюдается значительное изменение формы их ковариационной матрицы. То есть узкое место популяции значительно изменило некоторые вариации и ковариации между признаками в двух популяциях, хотя и не изменило общий объем аддитивной генетической дисперсии.
Итак, смысл этого всего лишь в том, чтобы предложить один из возможных способов сравнения генетических ковариационных матриц. Одна из причин, по которой мне действительно нравится многомерная математика (не могу поверить, что я это сказал), заключается в том, что очень простые идеи, такие как дисперсия признака, внезапно становятся намного богаче и могут изменяться гораздо большим количеством способов по мере того, как мы переходим к многовариантная настройка. Очевидно простая многомерная математика в бледном сравнении с реальным миром, но это только делает разнообразие реального мира еще более понятным.
Очевидно простая многомерная математика в бледном сравнении с реальным миром, но это только делает разнообразие реального мира еще более понятным.
Другая причина, по которой я хотел разместить это, заключается в том, что у меня есть программа R, которая выполняет эти анализы, наряду со случайными вертелами и выборочными вертелами, о которых я расскажу в следующий раз. Я не разработчик R, поэтому я был бы более чем доволен, если бы кто-то взял этот скрипт и превратил его во что-то, что на самом деле не нужно было бы настраивать для нужд каждого набора данных. Если вы решите закончить разработку, пожалуйста, дайте мне знать!
Вот программа:
Запись о том, как использовать программу: сравнение матрицы
Программа: команда Bootstrap
Соответствующие примеры наборы данных:
Сбалансированные женщины
Стоковые данные
Populate 3 Females
13
Пакета.
Пакет, предназначенный для проверки статистических гипотез по строкам и столбцам матриц.
Примеры
1) Выполнение одностороннего дисперсионного анализа для каждого столбца данных по радужной оболочке с использованием видов в качестве групп
col_oneway_equalvar(iris[-5], iris$Species)
obs.tot obs.groups sumsq.between sumsq.within meanq.between meanq.in df.between df.within statistic pvalue Сепал.Длина 150 3 63,21213 38,9562 31,606067 0,26500816 2 147 119,26450 1,669669e-31 Чашелистик.Ширина 150 3 11,34493 16,9620 5,672467 0,11538776 2 147 49,16004 4,492017e-17 Лепесток.Длина 150 3 437.10280 27.2226 218.551400 0.18518776 2 147 1180.16118 2.856777e-91 Petal.Width 150 3 80,41333 6,1566 40,206667 0,04188163 2 147 960,00715 4,169446e-85
2) t-тест для каждой строки из 2 матриц с миллионом строк в каждой.
X <- матрица(rнорма(10000000), ncol=10) Y <- matrix(rnorm(10000000), ncol=10)
Обычный способ ⏰ 2 минуты 16 секунд
res1 <- vector(nrow(X), mode="list")
for(i in 1:nrow(X)) {
res1[[i]] <- t. test(X[i,], Y[i,])
}
test(X[i,], Y[i,])
} рез1[1:2]
[[1]]
Welch Two Sample t-критерий
данные: X[i, ] и Y[i, ]
t = 0,46049, df = 16,685, p-значение = 0,6511
альтернативная гипотеза: истинная разница в средних не равна 0
95-процентный доверительный интервал:
-0,8330197 1,2973259
примерные оценки:
среднее значение x среднее значение y
-0,06643757 -0,29859071
[[2]]
Welch Two Sample t-критерий
данные: X[i, ] и Y[i, ]
t = -0,96859, df = 17,958, p-значение = 0,3456
альтернативная гипотеза: истинная разница в средних не равна 0
95-процентный доверительный интервал:
-1,6005787 0,58
примерные оценки:
среднее значение x среднее значение y
-0,02447724 0,48053173 matrixTest way ⏰ 2,4 секунды
res2 <- row_t_welch(X, Y)
> res2[1:2,] obs.x obs.y obs.tot mean.x mean.y mean.diff var.x var.y stderr df statistic pvalue conf.low conf.high альтернатива mean.null conf.level 1 10 10 20 -0,06643757 -0,2985907 0,2321531 1,627547 0,58 0,5041392 16,68493 0,4604941 0,6511065 -0,8330197 1,2973259двусторонняя 0 0,95 2 10 10 20 -0,02447724 0,4805317 -0,5050090 1,424720 1,2936936 0,5213841 17,95828 -0,9685930 0,3456133 -1,6005787 0,58 два.
Доступные тесты
| Название | matrixTests | R Эквивалент |
|---|---|---|
| ОДНОВАЯ ОБРАЗОВАНИЯ T.Test | ROW_T_ONESAMPL | t.test (x, y) |
| Равная дисперсия T.test | ROW_T_EQUALVAR (x, y) | T.Test (x, y, Var.Equal = TRUE) |
| Парный тест | ROW_T_PAIRED (x, y) | T.Test (x, y, paired = true) |
| Тест корреляции Пирсона | ROW_COR_PEARSON (X, Y) | Y) |
| Welch Oneway Anova | ROW_ONEWAY_WELCH (X, G) | Oneway.test (x, g) |
| Оплаченная дисперсия Oneway Anova | ||
. | oneway.test(x, g, var.equal=TRUE) | |
| Тест Крускал-Уоллис | ROW_KRUSKALWALLIS (x, g) | Kruskal.test (x, g) |
| Тест Бартлетта | 4. Bartlett.test (x, g) |
Процедуры на основе тестирования
| Описание | Matrixtests | Ravivalent | 9000--- |
|---|
Установка
Использование библиотеки devtools :
библиотека (devtools)
install_github("KKPMW/matrixTests") Зависимости
-
matrixStatsпакет.
Проектные решения
Были приняты следующие проектные решения (в произвольном порядке):
Имена функций
Имена функций состоят из 3 элементов, разделенных точками, где это необходимо:
[строка/столбец]_testname_variant
Вариантная часть может быть удалена, если она неприменима или если только один
вариант для этого теста реализован до сих пор.
Несколько примеров: row_oneway_equalvar , row_bartlett
Чтобы сделать имена функций короче, слово test не включено.
Одиночный тест на функцию
Функции должны предоставлять один тип теста.
Это означает, что некоторые тесты, которые в базе R реализованы под единым
функция будет разделена на разные функции. Например, в базовой функции R
t.test() имеет параметры, которые могут указывать тип используемого t.test:
с равной дисперсией или с поправкой на Welch, парные или непарные.
В этом пакете эти типы выбора разделены на отдельные функции по следующим причинам:
- Выходная структура, возвращаемая функцией, не зависит от входных значений.
- Пользователь должен явно выбрать тест без скрытых значений по умолчанию.
- Это соглашение упрощает добавление дополнительных типов тестов позже.
Входные значения
Функции пытаются понять предоставленные входные данные, когда это возможно. Все случаи, когда входные данные указаны неправильно, должны вызывать ошибку.
Все случаи, когда входные данные указаны неправильно, должны вызывать ошибку.
Пограничные случаи должны обрабатываться корректно. Например, когда ввод является числовым
матрица с 0 строками - результатом является 0 строка data.frame .
Ниже приведен краткий список реализованных правил ввода:
- Основные параметры - числовые матрицы.
- Векторы преобразуются в однострочную матрицу.
- Кадры данных автоматически преобразуются в матрицы, если все их столбцы числовые.
- Когда требуются две матрицы - либо число их строк должно совпадать, либо вторая матрица должна иметь только одну строку/столбец. В таком случае тот же строка/столбец будет повторяться для всех значений x.
- Группа спецификаций и дополнительных параметров обычно может иметь только один значение, которое будет применяться ко всем строкам.
- В некоторых случаях дополнительные параметры могут иметь отдельное значение для каждой строки.
 Эти случаи указаны в справочной документации.
Эти случаи указаны в справочной документации.
Выходные данные
Выходные данные содержатся в кадре данных , где каждая строка содержит результат
тест, выполняемый на соответствующей строке входной матрицы.
Категории вывода
Столбцы содержат соответствующие результаты, которые можно разделить на 3 основные категории:
- Описательная статистика, относящаяся к тесту. Обычно заказывается по возрастанию сложности
. Например: 1) количество наблюдений, 2) средние значения, 3) отклонения.
- Выводы, относящиеся к самому тесту. Обычно упорядочены по возрастанию сложности.
Например: 1) степени свободы, 2) статистика теста, 3) значение p, 4) доверительный интервал.
- Входные параметры, выбранные для строки. Заказал по их появлению в
вызов функции. Например: 1) тип альтернативной гипотезы, 2) среднее значение нулевой гипотезы, 3) уровень достоверности.
Имена столбцов
Имена столбцов вывода записываются последовательно и обычно состоят из двух частей: поле и спецификация, разделенные точкой.
-Все поля написаны как одно слово и сокращаются при необходимости:
- OBS - Количество наблюдений
- Среднее - Оценка среднего
- VAR - Оценка
- VAR - Оценка
- VAR - Оценка
- . свобода
- статистика - статистика теста
- pvalue - p-value
- stderr - стандартная ошибка
- cor - расчетная корреляция
Спецификации включаются только при необходимости - когда поле используется более одного раза или когда необходимо уточнение.
- obs.x - количество наблюдений x
- obs.tot - общее количество наблюдений
- среднее x - среднее x
- conf.
 low - нижний доверительный интервал
low - нижний доверительный интервал - conf.high - верхний доверительный интервал
Имена строк
Имена строк переносятся из основной входной матрицы. Если имена строк
матрицы не были уникальными - они делаются уникальными с помощью make.unique() . В случае
входная матрица не имеет имен строк, используются числа 1:nrow(x) .
Совместимость с R
Результаты испытаний должны быть максимально совместимы с реализованными в базе R. Допустимые исключения — это случаи, когда реализация R неверна. или ограничивающий.
Хорошим примером является oneway.test() , который работает, только если все группы имеют более
2 наблюдения, даже если для var.equal установлено значение TRUE . Строгое требование
для проведения теста технически необходимо, чтобы по крайней мере в одной группе было более 1
наблюдение. Поэтому в таких случаях row_oneway_equalvar() работает, даже если база
Версия R выдает ошибку.
В качестве другого примера рассмотрим bartlett.test() . Эта функция работает без
любые предупреждения, если они поставляются с постоянными данными и возвращают значения NA:
bartlett.test(rep(1,4), c("a","a","b","b")) Тест Бартлетта на однородность дисперсий
данные: rep(1, 4) и c("a", "a", "b", "b")
К-квадрат Бартлетта = NaN, df = 1, p-значение = NA Типичное поведение в таких ситуациях для базовых R-тестов — выдать ошибку:
t.test(c(1,1,1,1) ~ c("a","a","b","b")) Ошибка в t.test.default(x = c(1, 1), y = c(1, 1)) : данные в основном постоянны
Функции в этом пакете стараются согласовываться друг с другом и быть максимально
максимально информативно. Поэтому в таких случаях row_bartlett() выдаст
предупреждение, даже если базовая функция R не работает.
row_bartlett(c(1,1,1,1), c("a","a","b","b")) obs.tot obs.groups var.pooled df statistic pvalue 1 4 2 0 1 НП НП Предупреждение: row_bartlett: 1 из строк имел нулевую дисперсию во всех группах.Первое появление в строке 1
Предупреждения и ошибки
Ошибки возникают только в том случае, если входные параметры указаны неправильно.
Предупреждения отображаются в ситуациях, когда было что-то не так с выполнением проверить себя с заданными входными параметрами.
Такое решение для предупреждений было принято, поскольку пользователи обычно выполняют
несколько тестов (по одному на каждую строку). Функция не может выйти из строя, когда один или несколько
из этих тестов не могут быть завершены. Таким образом, даже когда базовые тесты R выдают ошибку
вместо этого функции в этом пакете будут выдавать информативное предупреждение для
строка, в которой произошел сбой, и при необходимости установит все возвращаемые значения, связанные с
тест на NA , чтобы пользователь не смог их использовать по ошибке.
Обратите внимание, что в этих случаях только значения, относящиеся к тесту, такие как статистика теста, p-значение
и доверительный интервал установлены на NA. Другие возвращаемые значения: количество
наблюдения, средние значения, отклонения и тому подобное будут по-прежнему возвращаться как обычно.
Другие возвращаемые значения: количество
наблюдения, средние значения, отклонения и тому подобное будут по-прежнему возвращаться как обычно.
В качестве примера такого поведения рассмотрим случай, когда базовый t-критерий Уэлча исправление не удается, потому что у него недостаточно наблюдений:
t.test(c(1,2), 3)
Ошибка в t.test.default(c(1, 2), 3): недостаточно 'y' наблюдений
Функция в этом пакете продолжается, но выдает предупреждение и старается установить неудачные выходные данные в NA:
row_t_welch(c(1,2), 3)
obs.x obs.y obs.tot mean.x mean.y mean.diff var.x var.y stderr df statistic pvalue conf .low conf.high альтернативный средний.null conf.level 1 2 1 3 1,5 3 -1,5 0,5 NaN NaN NaN NA NA NA NA двусторонний 0 0,95 Предупреждение: row_t_welch: 1 из строк содержит менее 2 наблюдений "y". Первое появление в строке 1
Это позволяет функции продолжать работу в тех случаях, когда обычно у нас достаточно
наблюдений на группу, но в некоторых строках их может быть недостаточно из-за значений NA.
mat1 <- rbind(c(1,2), c(3,NA)) mat2 <- rbind(c(2,3), c(0,4)) row_t_welch(mat1, mat2)
obs.x obs.y obs.tot mean.x mean.y mean.diff var.x var.y stderr df statistic pvalue conf.low conf.high альтернатива mean.null conf.level 1 2 2 4 1,5 2,5 -1 0,5 0,5 0,7071068 2 -1,414214 0,2928932 -4.042435 2.042435 двусторонняя 0 0,95 2 1 2 3 3.0 2.0 1 NaN 8.0 NaN NaN NA NA NA NA двусторонний 0 0.95 row_t_welch: в 1 строке было менее 2 наблюдений "x". Первое появление в строке 2
NA и значения NaN
NA и NaN значения из входных матриц автоматически удаляются, и каждое
строка обрабатывается как вектор, который не имеет NA / NaN значения.
Когда NA или NaN значения присутствуют в параметре, указывающем группы
соответствующие значения из входных матриц отбрасываются перед выполнением
тесты. Например, если указанная групповая переменная имеет NA :
x <- rnorm(5) g <- c(NA,"a", "a", "b", "b") row_oneway_welch(x=x, g=g)
obs.tot obs.groups df.between df.within statistic pvalue 1 4 2 1 1,440393 0,02349341 0,8968457
, то весь первый столбец входной матрицы x, соответствующий этой группе будет удален. И результат будет эквивалентен:
row_oneway_welch(x=x[-1], g=g[-1])
obs.tot obs.groups df.between df.within statistic pvalue 1 4 2 1 1,440393 0,02349341 0,8968457
Другие параметры могут разрешать или запрещать NA значения в зависимости от контекста. За
Например, вы не можете указать NA в качестве желаемого уровня достоверности при выполнении теста.
потому что не знать свой уровень уверенности не имеет большого смысла.
Примечания
Все тесты реализованы в R. Таким образом, при запуске теста в одной строке не должно быть увеличения скорости выполнения по сравнению с базовыми версиями R. В в большинстве случаев ожидается небольшое снижение из-за более подробного вывода.
На данный момент версии тестов по столбцам просто транспонируют ввод
матрица и вызывает эквивалентную построчную проверку.
Кандидаты тестов, которые будут реализованы в дальнейшем:
- Тест Шапиро-Уилкса на нормальность
- Корреляционные тесты Spearman и Kendall
- Тест для пропорций
- Точный тест Фишера
См. Также
- . Вычислительные вычислительные статистики 9041. . Статистические вычисления и графика. Том 18, № 1, июнь 2007 г. 2.
- Ошибка типа I (альфа) = P (отклонение нулевого значения | Нулевое значение истинно)
- Ошибка типа II (бета) = P(Не удалось отклонить нулевое значение | Альтернатива верна)
- Мощность = P (Отклонение нуля | Альтернатива верна)
- Уровень достоверности (1-альфа) = P(невозможно отклонить нулевое значение | нулевое значение является истинным)
- Если r меньше c , то максимальный ранг матрицы
стоит р .

- Если r больше c , то максимальный ранг матрицы это c .
lmFit в упаковке limma .
3. rowttests() в пакете genefilter .
4. mt.teststat() в пакете мультитест .
5. row.T.test() в пакете HybridMTest .
6. rowTtest() в пакете viper .
7. ttests() в пакете Rfast . Матрица путаницы при проверке гипотез | Андреа Густафсен
Выявление и понимание ошибки типа I, ошибки типа II и мощности с использованием матрицы путаницы.
Фото Роберта Кацки на Unsplash Матрица путаницы очень полезна для определенных задач как в логическом анализе, таком как A/B-тестирование, так и в прогнозном анализе, таком как классификация, для понимания и оценки статистического теста или прогнозной модели. Оба предполагают принятие бинарного решения. При проверке гипотез мы отвергаем или не можем отвергнуть нулевую гипотезу, а в бинарной классификации классификатор предсказывает, что наблюдение будет положительным или отрицательным.
Оба предполагают принятие бинарного решения. При проверке гипотез мы отвергаем или не можем отвергнуть нулевую гипотезу, а в бинарной классификации классификатор предсказывает, что наблюдение будет положительным или отрицательным.
Обе задачи позволяют структурировать результат в виде матрицы путаницы 2x2, показывающей истинные и ложноположительные, а также истинные и ложноотрицательные результаты. Если вы посмотрите на две приведенные ниже матрицы, то увидите, что обе они структурированы одинаково, а записи на главной диагонали матриц соответствуют правильным решениям.
Image by AuthorImage by Author Хотя матрицы имеют одинаковую структуру и, по сути, также содержат один и тот же тип измерений, информация, содержащаяся в матрицах, именуется и используется по-разному в зависимости от контекста. При проверке гипотез матрица путаницы содержит вероятности различных результатов, что помогает нам понять определенные свойства теста, такие как ошибки типа I и II и мощность. В бинарных прогнозах или классификациях количество каждого квадрата (TP, FP, TN и FN) используется для расчета различных показателей для оценки определенной модели прогнозирования.
В этой статье мы рассмотрим матрицу путаницы в контексте проверки гипотез. Вы можете прочитать о матрице путаницы для задач классификации здесь.
Матрица путаницы в классификации
Использование матрицы путаницы для оценки производительности бинарного классификатора. Как рассчитать показатели производительности…
в направлении datascience.com
Проверка гипотез — это метод проверки того, вызвана ли вариация между двумя выборочными распределениями фактической разницей между двумя группами или если вариация может быть объяснена случайностью .
Чтобы понять матрицу путаницы в контексте логического анализа, полезно взглянуть на визуальное представление односторонней проверки гипотезы ниже, чтобы показать, как четыре возможных результата в матрице соответствуют возможным событиям проверки гипотезы. .
Изображение AuthorImage by Author Ошибка типа I также называется размером или уровнем значимости теста. Он обозначается альфа и обычно устанавливается равным 0,05. Ошибка типа I представляет собой ложных срабатываний проверки гипотезы, что означает, что мы ложно отвергаем нулевую гипотезу, учитывая, что нуль является истинным.
Он обозначается альфа и обычно устанавливается равным 0,05. Ошибка типа I представляет собой ложных срабатываний проверки гипотезы, что означает, что мы ложно отвергаем нулевую гипотезу, учитывая, что нуль является истинным.
две группы, когда средства двух групп фактически одинаковы.
Ошибка типа I соответствует красной области на графике. Несмотря на то, что нулевая гипотеза верна, мы найдем тестовую статистику в области отклонения и ложно отвергнем нулевую гипотезу в 5% случаев. Многих это смущает. Если статистика теста попадает в область отбраковки, как она может быть ложноположительной?
Рассмотрим поведение p-значений. (Все тестовые статистические данные, такие как z, t, chisq, f и т. д., могут быть преобразованы в p-значения в диапазоне от 0 до 1.) При нулевой гипотезе и выполнении всех допущений теста p-значения должны формировать равномерное распределение между 0 и 1. При повторной выборке мы ожидаем, что некоторые значения p будут <0,05 из-за естественной вариации данных и случайной выборки. Хотя получение выборки с экстремальными значениями менее вероятно, чем выборка с менее экстремальными значениями, это происходит случайно. Вот почему мы ожидаем, что в среднем 5% отклоненных нулей будут ложными срабатываниями.
При повторной выборке мы ожидаем, что некоторые значения p будут <0,05 из-за естественной вариации данных и случайной выборки. Хотя получение выборки с экстремальными значениями менее вероятно, чем выборка с менее экстремальными значениями, это происходит случайно. Вот почему мы ожидаем, что в среднем 5% отклоненных нулей будут ложными срабатываниями.
Можем ли мы просто понизить альфа-значение, спросите вы. Мы можем это сделать, и вы можете видеть, что в некоторых исследованиях используется более низкий уровень значимости 0,01. Но мы должны знать, что это также отрицательно влияет на мощность теста, что не является оптимальным.
Ошибка типа II — это то, что матрица показывает как ложноотрицательных результатов, и обозначается как бета. Это происходит, когда нам не удается отклонить нулевое значение при условии, что альтернативная гипотеза верна.
Если мы сравниваем средние значения двух групп, это означает, что мы делаем ложный вывод об отсутствии разницы в средних значениях, когда средние значения двух групп на самом деле различны. Другими словами, мы не можем обнаружить разницу, когда она действительно есть.
Другими словами, мы не можем обнаружить разницу, когда она действительно есть.
Это происходит чаще, если тест не имеет достаточной мощности.
Мощность относится к вероятности правильного отклонения нулевой гипотезы, когда нулевая гипотеза ложна, истинных положительных результатов . Мощность является дополнением ошибки II рода (бета): 1-бета.
Мощность — это вероятность обнаружения истинной разницы в средних значениях, что означает, что мы хотим, чтобы мощность теста была как можно выше. Обычно приемлемая мощность должна быть выше 80%.
Принятие более высокого уровня ошибки/значимости типа I (альфа) приведет к меньшему бета, что увеличит мощность (мощность = 1-бета) для обнаружения истинного эффекта. И наоборот, если мы снизим вероятность совершения ошибки первого рода, мы также снизим мощность. Это может быть неочевидно из матрицы путаницы, но если вы посмотрите на график, вы увидите, что это так. Увеличение альфа приводит к уменьшению бета, и наоборот.
Увеличение альфа приводит к уменьшению бета, и наоборот.
Однако обычно не рекомендуется увеличивать альфа до значений выше 0,05. Есть несколько других методов, которые мы можем использовать для увеличения мощности, которые будут представлены в отдельной статье.
(Мощность эквивалентна метрике полноты в классификации, которая также является выражением для процента обнаруженных положительных результатов.) истинных отрицательных результатов . Эта вероятность называется уровень достоверности теста и используется при построении доверительных интервалов, обычно устанавливаемых на уровне 0,95 (1-альфа).
В нашем примере сравнения средних это будет правильным выводом об отсутствии различий между группами.
Следует подчеркнуть, что матрица путаницы в анализе логического вывода представляет вероятностей , а не рассчитывается из одного отдельного теста. В одной проверке гипотезы есть только один результат. Вероятности показывают, как часто каждый исход ожидается в течение повторил тестирование , при этом все предположения и нулевая гипотеза оказались верными. Чтобы оценить эти результаты, вы можете провести симуляцию, в которой вы контролируете параметры.
В одной проверке гипотезы есть только один результат. Вероятности показывают, как часто каждый исход ожидается в течение повторил тестирование , при этом все предположения и нулевая гипотеза оказались верными. Чтобы оценить эти результаты, вы можете провести симуляцию, в которой вы контролируете параметры.
Если мы оценим ошибку типа I, запустим симуляцию 1 000 000 раз и уровень значимости будет равен 0,05, мы ожидаем, что нуль будет отвергнут 50 000 раз (5% тестов). Это не то же самое, что отклонение нуля в отдельном тесте. Предположим, что ноль верен, если вы отклоняете нулевую гипотезу, шанс ошибиться составляет 100%, а не 5%. При повторном тестировании вы можете ожидать ложноположительных результатов в среднем примерно в 5% случаев.
Если вас интересует, как можно оценить ошибку и мощность первого рода, вы можете прочитать эту подробную статью о том, как можно оценить производительность t-критерия с помощью моделирования.
Пристальный взгляд на производительность T-критерия
Имитационное исследование, изучающее ошибку типа I и мощность t-критерия при различных сценариях.
 Как размеры выборки и…
Как размеры выборки и… в направлении datascience.com
Матрица путаницы в классификации
Использование матрицы путаницы для оценки производительности бинарного классификатора. Как рассчитать показатели производительности…
в направлении datascience.com
Ранг матрицы
объясняет, как ранг матрица раскрывается его эшелонированная форма.
Ранг матрицы
Вы можете думать о r x c матрице как о наборе r строк векторы, у каждого по c элементов; или вы можете думать об этом как о наборе c векторы-столбцы, каждый из которых имеет r элементов.
Ранг матрицы определяется как (a) максимальное количество линейно независимые столбцов векторов в матрице или (б) максимальное количество линейно независимых строк векторов в матрице. Оба определения эквивалентны.
Для матрицы r x c ,
Ранг матрицы был бы равен нулю только в том случае, если бы в матрице не было элементов. Если бы в матрице был хотя бы один элемент, ее минимальный ранг был бы равен единице.
Как найти ранг матрицы
В этом разделе мы опишем метод нахождения ранга любой матрицы. Этот метод предполагает знакомство с ступенчатые матрицы а также ступенчатые преобразования.
Максимальное количество линейно независимых векторов в матрице равно к количеству ненулевых строк в его ступенчатая матрица строк. Поэтому, чтобы найти ранг матрицы, мы просто преобразовать матрицу в ступенчатую форму строки и подсчитать количество ненулевые строки.
Рассмотрим матрицу A и ее эшелон строк матрица, A ref . Раньше мы показывали как найти форму эшелона строк для матрицы A .
| ⇒ |
| 98 ||||||||||||||||||||||
 имеет две ненулевые строки, мы знаем, что
матрица A имеет два независимых вектора-строки; а также
мы знаем, что
ранг матрицы A равен 2.
имеет две ненулевые строки, мы знаем, что
матрица A имеет два независимых вектора-строки; а также
мы знаем, что
ранг матрицы A равен 2. Вы можете убедиться, что это правильно. Ряд 1 и Ряд 2 матрицы A линейно независимый. Тем не менее, строка 3 является линейная комбинация рядов 1 и 2. В частности, ряд 3 = 3*(строка 1) + 2*(строка 2). Следовательно, матрица A имеет только два независимых вектора-строки.
Реклама
Полноранговые матрицы
Когда все векторы в матрице линейно независимый, говорят, что матрица полный ранг . Рассмотрим матрицы A и B ниже.
| a = |
| B = |
|
Обратите внимание, что строка 2 матрицы A является скалярным числом, кратным
ряд 1; то есть строка 2 вдвое больше строки 1. Следовательно, строки 1 и 2 равны
линейно зависимы. Матрица A имеет только один линейно независимый
строка, поэтому ее ранг равен 1. Следовательно, матрица A не имеет полного ранга.
Следовательно, строки 1 и 2 равны
линейно зависимы. Матрица A имеет только один линейно независимый
строка, поэтому ее ранг равен 1. Следовательно, матрица A не имеет полного ранга.
Теперь посмотрим на матрицу B . Все его строки линейно независимы, поэтому ранг матрицы B равен 3. Матрица B имеет полный ранг.
Проверьте свое понимание
Задача 1
Рассмотрим матрицу X , показанную ниже.
| X = |
|
| Y = |
|
Каков его ранг?
(A) 0
(B) 1
(C) 2
(D) 3
(E) 4
Решение
Правильный ответ (C). Поскольку в матрице больше нуля элементов,
его ранг должен быть больше нуля. И поскольку у него меньше столбцов, чем
строк, его максимальный ранг равен максимальному числу линейно независимых
столбцы.



 назад)
назад)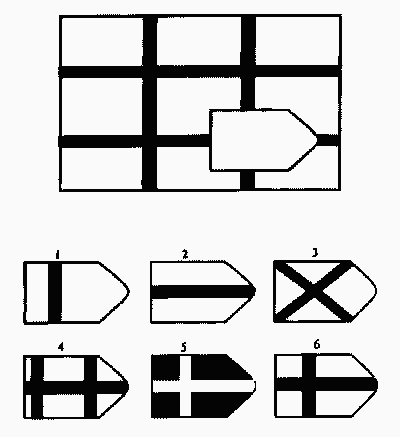 Пенроузом и Дж. Равеном в 1936 г. Р. п. м. разрабатывались в соответствии с традициями английской школы изучения интеллекта, согласно которым наилучший способ измерения фактора «g» — задача по выявлению отношений между абстрактными фигурами. Наиболее известны два основных варианта Р. п. м.: черно-белые и цветные матрицы. Разрабатывая тесты, которые были бы полезным инструментом для идентификации генетических и средовых причин интеллектуальных отклонений, Дж. Равен сознательно ставил перед собой задачу создания таких тестов, которые были бы теоретически обоснованы, однозначно интерпретируемы, просты для проведения и обработки, пригодны как для лабораторных, так и для полевых экспериментов, а также удобны для массовых обследований, проводимых на дому, в школах, на производстве и сопряженных с временными ограничениями.
Пенроузом и Дж. Равеном в 1936 г. Р. п. м. разрабатывались в соответствии с традициями английской школы изучения интеллекта, согласно которым наилучший способ измерения фактора «g» — задача по выявлению отношений между абстрактными фигурами. Наиболее известны два основных варианта Р. п. м.: черно-белые и цветные матрицы. Разрабатывая тесты, которые были бы полезным инструментом для идентификации генетических и средовых причин интеллектуальных отклонений, Дж. Равен сознательно ставил перед собой задачу создания таких тестов, которые были бы теоретически обоснованы, однозначно интерпретируемы, просты для проведения и обработки, пригодны как для лабораторных, так и для полевых экспериментов, а также удобны для массовых обследований, проводимых на дому, в школах, на производстве и сопряженных с временными ограничениями.
 Спирмена.
Спирмена.

 То есть они обрабатываются так, как если бы они были необработанными данными. Если cor=FALSE, то входные матрицы считаются матрицами корреляции.
То есть они обрабатываются так, как если бы они были необработанными данными. Если cor=FALSE, то входные матрицы считаются матрицами корреляции. 