Тест равена интерпретация результатов: Стандартные прогрессивные матрицы — Psylab.info
Цветные прогрессивные матрицы Дж.Равена. Перевод серых баллов в IQ.
Познакомилась я с цветными матрицами будучи на последнем курсе института в процессе написания выпускной квалификационной работы. Методика мне понравилась своей относительной простотой. Использовала я ее в модификации Т.В. Розановой. Но столкнулась с трудностью: я нигде не могла найти таблицы (или хотя бы намека на эти таблицы) перевода серых баллов, которые получаются по методике, в IQ. На просторах Интернета этой информации просто не было. Это затруднение мне не помешало успешно защитится. Но, однажды, совершенно случайно ко мне в руки попали заветные таблицы… И теперь я спешу поделиться ими со своими коллегами.
Немножко об опыте использования методики: что лично для меня значимо?
Цветные прогрессивные матрицы Дж.Равена могут быть использованы для обследования познавательной сферы детей от 4,5 до 9 лет (5-11,5 лет). В первую очередь, методика в большей степени предназначена для оценки интеллекта детей в указанном выше возрастном диапазоне.
Далее, привожу цитату из «Индивидуальная и психологическая диагностика дошкольника» А. Н. Веракса.
Н. Веракса.
Впервые нормы для этой методики были разработаны в 1949 году в Шотландии, а затем в 1982 г. (см. таблицу № 1). Эти нормы, охватывают меньший возрастной диапазон, чем нормы, полученные в результате стандартизации методики в США между 1983 и 1993 годами (см. таблицу № 2). Нормы для США ниже шотландских норм, однако при проведении исследований в России предпочтительнее использовать именно их, поскольку Россия – многонациональная страна, а в исследованиях, проведенных в США, участвовали представители разных народностей.
Таблица 11
Нормы Дамфриз, Шотландия (1982 год)
|
|
||||||||||||
| Процентиль | 6(3)- 6(8) | 6(9)- 7(2) | 7(3)- 7(8) | 7(9)- 8(2) | 8(9)- 9(2) | 8(9)- 9(2) | ||||||
| 95
90 75 50 25 10 5 |
26
23 20 17 14 12 11 |
26
26 21 18 15 12 11 |
28
25 21 18 16 13 12 |
25
24 22 18 14 13 12 |
31
28 23 20 17 14 13 |
28
27 23 21 17 15 14 |
32
30 25 22 18 15 14 |
29
28 25 22 19 16 15 |
33
32 27 24 20 16 14 |
33
32 28 24 20 17 14 |
34
33 29 26 22 17 15 |
33
31 28 26 20 17 16 |
| п | 42 | 47 | 54 | 38 | 55 | 30 | 44 | 33 | 48 | 47 | 52 | 41 |
Таблица 21
Нормы США (1986 год)
|
Возраст в годах (месяцах) |
||||||||||||||
| Процентиль | 5(3)- 5(8) | 5(9)- 6(2) | 5(3)- 6(8) | 6(9)- 7(2) | 7(3)- 7(8) | 7(9)- 8(2) | 8(3)- 8(8) | 8(9)- 9(2) | 9(3)- 9(8) | 9(9)- 10(2) | 10(3)- 10(8) | 7(3)- 11(2) | 10(3)- 11 (8) | |
| 95
90 75 50 25 10 5 |
23
21 17 12 11 9 8 |
25
23 19 14 12 10 9 |
28
25 21 16 13 11 9 |
30
27 23 18 14 12 10 |
31
29 25 20 15 13 11 |
32
30 27 22 17 14 12 |
33
31 29 24 19 15 12 |
34
32 30 26 21 16 13 |
35
33 31 27 22 17 14 |
35
33 32 28 23 18 15 |
35
34 32 29 24 19 16 |
35
34 33 30 25 20 17 |
35
35 34 31 26 21 18 |
|
Особенности проведения методики
Действия испытуемого в ходе методики однотипны: он должен найти некоторую закономерность и выбрать из предложенных элементов недостающий фрагмент узора.
Последовательность предъявления заданий не подлежит изменению. Тестовая процедура предполагает отсутствие какой-либо обратной связи со стороны психолога. Если испытуемый сомневается в выборе правильного ответа, нужно добиться, чтобы он высказал какое-то мнение, в крайнем случае в качестве ответа принимается последний вариант. При этом испытуемый не должен объяснять свой выбор – вполне достаточно словесного или жестового указания на фрагмент.
Интерпретация методики
За каждый правильный ответ испытуемому начисляется один балл. Если ребенок неправильно выполнил первые пять заданий, о выполнение методики прекращается, поскольку считается, что испытуемый не понял принцип решения.
После подсчёта баллов полученный результат сравнивается с показателем процентильной (относительной) частоты (процент испытуемых того же возраста, которые правильно решили столько же задач, то есть получили такой же балл).
По результатам теста Равена можно выделить пять уровней развития интеллекта (см. табл. 3)
табл. 3)
Таблица 3
|
Показатель процентильной частоты (р) |
Уровень развития интеллекта |
Уровень развития интеллекта в баллах (IQ) |
| Более 95
75-95 25-75 5-25 Менее 5 |
Высокий
Выше среднего Средний (норма) Низкий Сниженный интеллект |
Более 124
110-124 90-110 75-90 Менее 75 |
Допустим, что по результатам методики Дж. Равена ребенок в возрасте 6 лет 7 месяцев набрал 22 балла. В этом случае в таблице 2 мы находим возраст ребенка, который попадает в интервал 6 лет 3 месяца – 6 лет 8 месяцев. Далее, в вертикальном столбце мы находим количество баллов, которые набрал ребенок. Нашем случае 22 балла попадают в интервал 21-25 баллов, что, как видно из таблицы, соответствуют процентному интервалу 75-90.
Таким образом, данная методика позволяет получить количественную характеристику (выраженную в показателе процентильной частоты, которой соответствует определённый уровень развития интеллекта) уровня развития основного средства мышления – интеллекта.
Литература:
- 1 Равен Дж. К., Курт Дж. Х., Равен Дж. Руководство к прогрессивным матрицам Равена и словарным шкалам. – М., 1996.
- Веракса А.Н. Индивидуальная психологическая диагностика дошкольника: Для занятий с детьми 5-7 лет. – М.: МОЗАИКА-СИНТЕЗ, 2014. – 144 с.
Прогрессивные матрицы Равена — презентация онлайн
1. Прогрессивные матрицы Равена
Выполнили:Студентки 31 группы
Бабий Людмила
Косова Екатерина
Сыровая Галина
Чижова Полина
Джон Карлайл Равен (28 июня 1902 – 10
августа 1970) известен своими работами в
области
диагностики
и
исследования
компетентностей высокого уровня, их природы,
развития, оценки и реализации.
 В ходе своих
В ходе своихисследований, проведенных в различных
научных институтах, а также по заказу
Социальной службы британского правительства,
он разработал новую концептуальную схему для
анализа и диагностики человеческих ресурсов, в
которой
решающее
значение
придается
ценностям человека.
3. История создания
Методика «Шкала прогрессивных матриц» была разработана в 1936 годуДжоном Равеном (совместно с Л. Пенроузом). Тест прогрессивные
матрицы Равена (ПМР) предназначен для диагностики уровня
интеллектуального
развития
и
оценивает
способность
к
систематизированной, планомерной, методичной интеллектуальной
деятельности (логичность мышления).
Джон Равен, занимаясь в начале 1930-х годов исследованиями причин
умственных отклонений, столкнулся с необходимостью разработки таких
тестов, посредством которых можно было бы оценить как генетические,
так и средовые причины интеллектуальной недостаточности.
 Ранее Равен
Ранее Равениспользовал интеллектуальную шкалу Стэнфорд-Бине, но отмечал ее
громоздкость и сложность интерпретации полученных результатов. Таким
которые
были
бы
теоретически
обоснованы,
однозначно
интерпретируемы, просты для проведения и обработки, пригодны как для
лабораторных, так и для полевых экспериментов
При создании Прогрессивных матриц Равена значительное внимание было уделено также таким
вопросам как четкость и привлекательность дизайна заданий, выполненных профессиональным
художником, их размеру и пространственному взаимоотношению между незавершенной матрицей
и набором альтернативных вариантов решения.
Варианты методики:
1)Стандартные матрицы, выпущенные в 1936 году в Великобритании (Авторы — Л.Пенроуз и
Дж.Равен)
2) В 1947 году появились Цветные прогрессивные матрицы.
3) В 1947 году также были разработаны Продвинутые прогрессивные матрицы.
 Продвинутые
Продвинутыематрицы, в отличие от обычных матриц Равена, предназначены для измерения высокого IQ — до
136 баллов (136 встречается в среднем у 1 из 122 человек)
5. Возрастные границы применимости Прогрессивных матриц Равена
Варианты теста РавенаЦветные прогрессивные
матрицы
Стандартные прогрессивные
матрицы
Продвинутые
прогрессивные матрицы
Контингент испытуемых
4,5 — 9 лет;
испытуемые с аномальным развитием;
реабилитационные исследования лиц старше 65 лет
дети от 8 до 14 лет;
взрослые от 20 до 65 лет
испытуемые с интеллектуальными способностями выше
среднего
Теоретической основой теста Равена является модель
оценки интеллекта Чарльза Спирмена.
Спирмен сделал вывод о существовании некого «общего»
интеллекта, или «g–фактора», состоящего из продуктивной
и репродуктивной способностей. Будучи учеником
Ч.Спирмена, Джон.Равен также придерживался этой точки
зрения.
В
основе
разработанного
теста
лежат
методологические традиции английской школы изучения
интеллекта, согласно которым наилучшим способом
измерения фактора «g» является определение соотношений
между абстрактными фигурами.
 Кроме того, при
Кроме того, приразработке
теста
был
реализован
принцип
«прогрессивности», заключающийся в том, что выполнение
предшествующих заданий и их серий является как бы
подготовкой обследуемого к выполнению последующих,
более сложных.
Чарльз Эдвард Спирмен
(1863 – 1945)
Структура
теста
Чёрно-белые прогрессивные
матрицы
Равена
(в
оригинальном
варианте)
состоят из 60 матриц (размер
7,5×11 см.), в каждой из
которых отсутствует один из
составляющих её элементов.
Обследуемый
должен
выбрать
недостающий
элемент матрицы среди 6-8
предложенных
вариантов.
Задания сгруппированы в 5
серий — А, В, С, D, Е, каждая
серия состоит из 12 матриц.
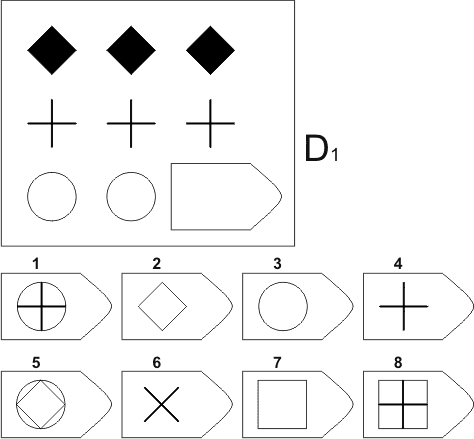
Пример серии D
8. Примеры стимульного материала
9. Интерпретация результатов
Полученныйрезультат
Степень
Итог
95% и больше
1 степень
Особо высокорaзвитый интеллект испытуемого
75-94%
2 степень
Незаурядный интеллект испытуемого
25-74%
3 степень
Средний интеллект испытуемого
6-24%
4 степень
Интеллект испытуемого ниже среднего
5% и меньше
5 степень
Дефектная интеллектуальная способность испытуемого
10. Цветные прогрессивные матрицы Структура теста
Цветные прогрессивные матрицы Структура теста
Цветной вариант Прогрессивныхматриц Равена (для детей и
пожилых) состоит из трех серий (А;
Ab; В), различающихся по уровню
сложности. Каждая серия содержит
по 12 матриц с пропущенными
элементами. Таким образом, для
работы испытуемому предлагается
36 заданий.
Анализ результатов:
Основываясь
на
психологической
интерпретации каждой серии заданий можно
выявить те характеристики мышления,
которые наиболее и наименее развиты у
испытуемого.
Направления
качественного
анализа
выполнения
Детские психологи в процессе наблюдения за
поведением ребёнка в ходе диагностического
обследования оценивают характеристики речи,
экспрессивность, упорство и настойчивость в
преодолении трудностей, отношение к
разному
типу
диагностических
задач,
психодинамические
характеристики
деятельности ребёнка и т.п.
12. Качественные показатели выполнения Цветных прогрессивных матриц
Качественные показатели выполнения Цветных прогрессивных матриц
Качественные показатели выполнения Цветныхпрогрессивных матриц
Оценка работоспособности
•Быстрота утомления
•Наступление пресыщения при работе с однотипным материалом
•Влияние на работоспособность ребёнка позитивной и негативной оценки
•Тип мотивации (учебная, игровая, соревновательная)
Характер деятельности
•Способность к целенаправленной деятельности
•Импульсивность в решениях
•Стратегия поиска (хаотическая, стратегия проб и ошибок)
Темп деятельности и его
изменения
•Типичный темп работы
•Изменение темпа работы в зависимости от врабатываемости или утомления
•Изменение темпа работы в зависимости от сложности заданий
Эмоционально-личностные
характеристики
•Заинтересованность в результате и успехе
•Попытки сравнения себя с другими детьми
•Отношение к своим достижениям (успеху и ошибкам)
•Уверенность в себе
•Отношение к заданию и эмоциональные реакции в начале и в конце
выполнения матриц
Научные исследования, направленные на
оценку умственных способностей
испытуемых из разных этнических и
культурных групп, на изучение
генетических, воспитательных и
образовательных причин
интеллектуальных различий
Профессиональная деятельность, где
данный тест может оказать помощь в
обнаружении наиболее эффективных
администраторов, бизнесменов,
предпринимателей, управляющих,
кураторов и организаторов
Сферы
применения
теста ПМР
Образование и учебные занятия, для
прогнозирования будущих успехов детей
и взрослых, независимо от их
социального и этнического
происхождения
В клинике, для оценки и выявления
нейропсихологических поражений, а
также для контроля результатов,
полученных при применении
разнородных измерений
интеллектуальной способности
Преимущества
прогрессивных матриц
Равена:
Пользователи теста
Равена должны
учитывать:
хорошая теоретическая и методологическая
обоснованность теста;
ограничения, связанные с
построением прогноза на основе
результатов теста Равена;
конструктивная однородность тестовых
заданий;
быстрота проведения и относительная
лёгкость обработки результатов
тестирования;
возможность проведения обследования групп
и отдельных испытуемых, различающихся по
определенным параметрам.
неоднозначность и размытость
самого термина «интеллект»;
взаимодействие средовых и
генетических факторов в проявлении
и развитии когнитивных функций.
Прогрессивные матрицы Равена.
Тест для детей. Построен на основе гештальтпсихологии. Существует в двух вариантах.
- черно-белые матрицы Равена — от 8 лет до 65 лет. Интерпретация результатов для каждого возраста. Материал — черно-белый, состоит из 5 серий по 12 примеров.
- цветные матрицы Равена — от 5 до 11 лет. Материал — цветной, 3 серии по 12 заданий.
Прогрессивные матрицы Равена — принцип прогрессивности: каждое задание методики готовит испытуемого для следующего более сложного задания.
Каждое задание в каждой серии сложнее предыдущего. Выполнение каждого задания готовит к выполнению следующего.
Каждая серия построена так:
Серия A — дополнить недостающие части изображения. Умение дифференцировать отдельные компоненты структуры, умение устанавливать связи между разными компонентами структуры, умение идентифицировать недостающие части структуры, сличать ее с представленными вариантами.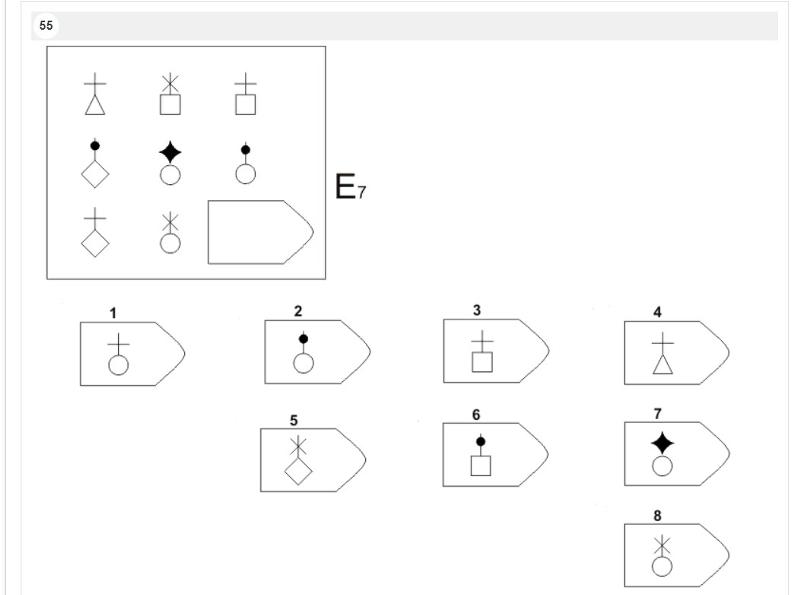
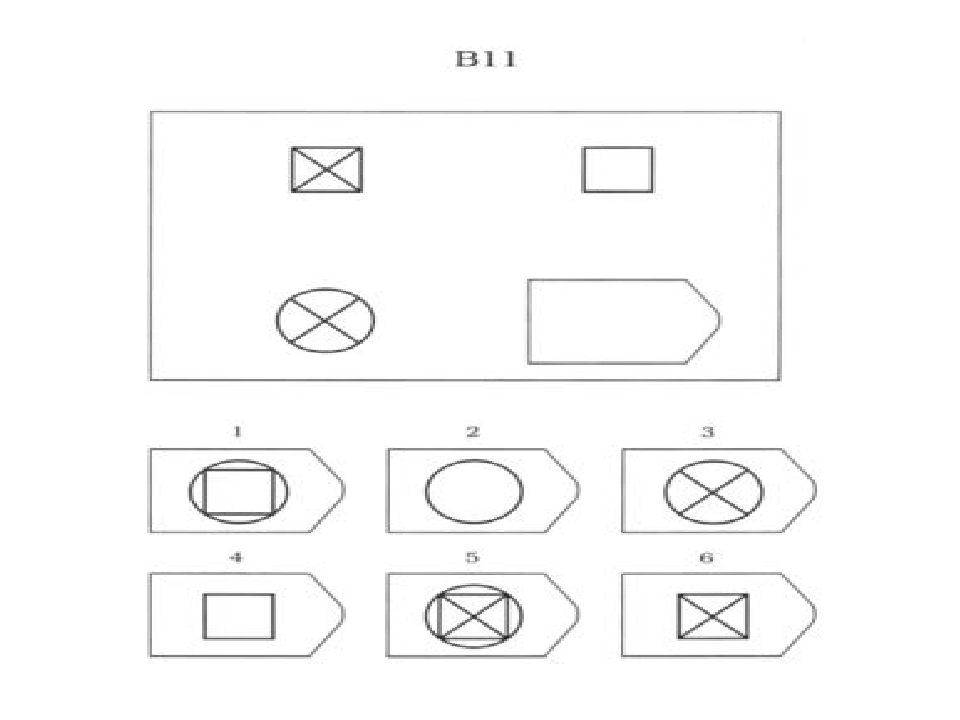
Серия B — требуется найти аналогии между парами фигур. Диагностируется мышление по аналогии и понимание симметрии.
Серия C — задания содержат сложное изменение фигур в соответствии с принципом их непрерывного развития. Задача — установить принцип развития. Найти ответ.
Серия D — задания составлены по принципу перестановки фигур в матрицы по горизонтали и вертикали.
Серия E — в задании заложен принцип разложения фигур на отдельные элементы. Требуется проявить умение по разложению на элементы, потом синтезировать в целое.
Показатель: индекс вариабельности (подсчитывается на Западе).
Для подсчета в руководствах методики таблицы, в которых представлено распределение сырых балов по сериям. Каждый из возможных балов по сериям.
Для подсчета индекса вариабельности сопоставить с таблицей, подсчитать разницу между табличным значением и реальным. Разница берется без учета знака.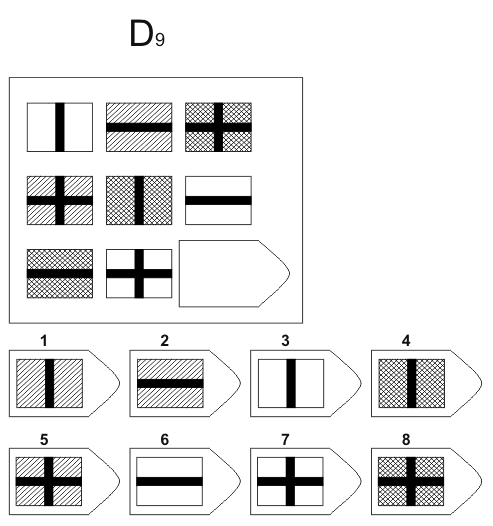 Сумма разниц по всем 5 сериям.
Сумма разниц по всем 5 сериям.
Для чего индекс вариабельности? Для достоверности результата испытуемого. Испытуемый может выполнить задания методом угадывания. Не используя возможностей наглядного мышления.
Если индекс вариабельности от 0 до 4 — результаты достоверны.
Если индекс вариабельности от 5 до 6 — то результаты можно подвергнуть сомнению.
Если индекс вариабельности от 7 и выше — результаты испытуемого недостоверны.
Цветные матрицы Равена.
Используются дефектологами, психологами для детей от 5 до 11 лет. Диагностируются отклонения от нормы в мышлении ребенка. Диагностика проводится индивидуально.
1. Первое задание открывается перед ребенком и объясняется, как делать, дается инструкция.
Например: наверху коврик с дырочкой, какую заплатку нужно поставить?
Психолог должен объяснить, почему остальные 5 кусочков не подходят (какие линии, какой узор…)
Психолог должен продумать объяснение, чтобы научить ребенка думать и дальше выполнять последующие задания. Ребенку дается возможность ответить. Если правильно, то 1 бал за первое задание. Если ответ неправильный, то предлагается подумать еще. За вторую попытку ребенок получает половинку бала. Если верная попытка третья, то он получает одну четвертую бала. Стимулирующая помощь: психолог напоминает, объясняет на линиях, ковриках, узорах… Если помощь не помогает, то у психолога наготове должна быть вырезана эта матрица и все 6 кусочков. Решение переходит из наглядно-образного в наглядно-действенный образ. Если ребенок не может сделать, то психолог показывает сам. Баллы начисляются только в случае первых трех попыток.
Ребенку дается возможность ответить. Если правильно, то 1 бал за первое задание. Если ответ неправильный, то предлагается подумать еще. За вторую попытку ребенок получает половинку бала. Если верная попытка третья, то он получает одну четвертую бала. Стимулирующая помощь: психолог напоминает, объясняет на линиях, ковриках, узорах… Если помощь не помогает, то у психолога наготове должна быть вырезана эта матрица и все 6 кусочков. Решение переходит из наглядно-образного в наглядно-действенный образ. Если ребенок не может сделать, то психолог показывает сам. Баллы начисляются только в случае первых трех попыток.
2. Аналогии между парами фигур
3. Серия Б-аналогия между парами фигур. Для выявления категории детей с отклонениями.
Розанова провела этот эксперимент в школе 1, 2 классов. Выделены 4 уровня успешности выполнения этой методики.
- 4-ый, высший уровень выполнения. Если ребенок набрал от 28 балов и больше.

- 3-ий, высокий уровень. Если ребенок набрал от 23 до 28 балов.
- 2-ой уровень, низкая успешность. Если ребенок набрал от 17 до 23 балов.
- 1-ый уровень, меньше 17 балов.
Оценка развития ребенка 1, 2 классов. Если выполнение на 3 и 4 уровне, следовательно, ребенок нормальный по интеллектуальному развитию. Если на 1 или 2 уровне, следовательно, возможны отклонения в развитии. Если ребенок дал 13 балов или меньше, следовательно, умственная отсталость. Время не ограничивается.
Стандартизация у нас в России только для 1, 2 классов цветных матриц Равена!!!
1
Первый слайд презентации: Тест равена
Методика для диагностики интеллекта
Изображение слайда
Изображение для работы со слайдом
2
Слайд 2: Джон Равен Родился : 28 июня 1902 г. , Лондон, Великобритания Умер: 10 августа 1970 г., Дамфрис, Великобритания Образование: Университет Лондон Известность: Тест Равена
, Лондон, Великобритания Умер: 10 августа 1970 г., Дамфрис, Великобритания Образование: Университет Лондон Известность: Тест Равена
Методика «Шкала прогрессивных матриц» была разработана в 1936 году Джоном Равеном (совместно с Л. Пенроузом). Тест прогрессивные матрицы Равена (ПМР) предназначен для диагностики уровня интеллектуального развития и оценивает способность к систематизированной, планомерной, методичной интеллектуальной деятельности (логичность мышления).
Изображение слайда
Изображение для работы со слайдом
3
Слайд 3
Принцип «прогрессивности»
В Стандартных матрицах реализуется двояким образом:
а) внутри каждой серии задания расположены с учётом их возрастающей сложности;
б) все серии отличаются различной трудностью, которая возрастает от серии А к серии Е. Возрастающая трудность заданий определяется:
увеличением числа элементов в матрице;
увеличением предлагаемых вариантов решения;
усложнением логического принципа, лежащего в основе каждой композиции, который испытуемому необходимо понять, чтобы закономерно выбрать недостающий элемент.
A B C D E
Возрастающая трудность заданий определяется:
увеличением числа элементов в матрице;
увеличением предлагаемых вариантов решения;
усложнением логического принципа, лежащего в основе каждой композиции, который испытуемому необходимо понять, чтобы закономерно выбрать недостающий элемент.
A B C D E
Изображение слайда
Изображение для работы со слайдом
4
Слайд 4
Структура теста
Чёрно-белые прогрессивные матрицы Равена (в оригинальном варианте) состоят из 60 матриц (размер 7,5^11 см. ), в каждой из которых отсутствует один из составляющих её элементов. Обследуемый должен выбрать недостающий элемент матрицы среди 6-8 предложенных вариантов. Задания сгруппированы в 5 серий — А, В, С, D, Е, каждая серия состоит из 12 матриц.
Расположение матриц в определённой последовательности соответственно принципу возрастающей сложности мыслительных операций, необходимых для решения, не исключает варианта парциальной несформированности умственных операций у обследуемого. В этом случае профиль суммарных оценок за 5 серий не будет отражать нарастающую сложность.
A 12 B 12 C 12 D 12 E 12
), в каждой из которых отсутствует один из составляющих её элементов. Обследуемый должен выбрать недостающий элемент матрицы среди 6-8 предложенных вариантов. Задания сгруппированы в 5 серий — А, В, С, D, Е, каждая серия состоит из 12 матриц.
Расположение матриц в определённой последовательности соответственно принципу возрастающей сложности мыслительных операций, необходимых для решения, не исключает варианта парциальной несформированности умственных операций у обследуемого. В этом случае профиль суммарных оценок за 5 серий не будет отражать нарастающую сложность.
A 12 B 12 C 12 D 12 E 12
Изображение слайда
Изображение для работы со слайдом
5
Слайд 5
В серии А — использован принцип установления взаимосвязи в структуре матриц.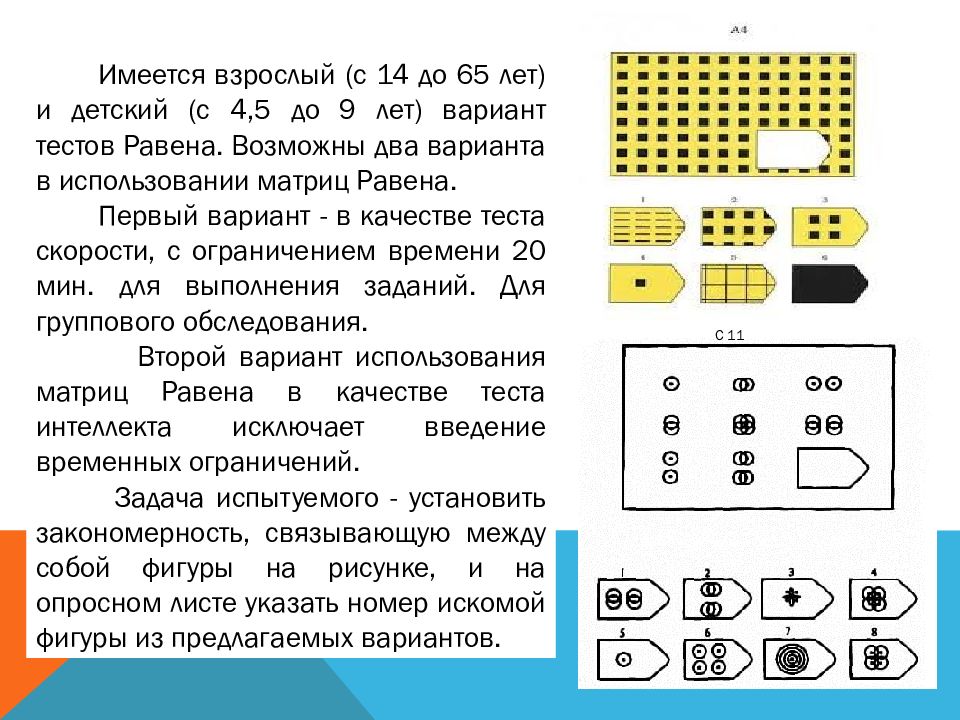 Здесь задание заключается в дополнении недостающей части основного изображения одним из приведенных в каждой таблице фрагментов. Выполнение задания требует от обследуемого тщательного анализа структуры основного изображения и обнаружения этих же особенностей в одном из нескольких фрагментов. Затем происходит слияние фрагмента, его сравнение с окружением основной части таблицы.
Серия В — построена по принципу аналогии между парами фигур. Обследуемый должен найти принцип, соответствен но которому построена в каждом отдельном случае фигура и, исходя из этого, подобрать недостающий фрагмент. При этом важно определить ось симметрии, соответственно которой расположены фигуры в основном образце.
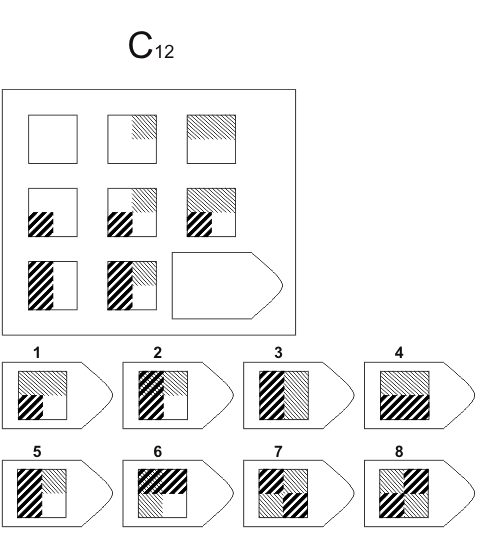
Серия С — построена по принципу прогрессивных изменений в фигурах матриц. Эти фигуры в пределах одной матрицы все больше усложняются, происходит как бы непрерывное их развитие. Обогащение фигур новыми элементами подчиняется четкому принципу, обнаружив который, можно подобрать недостающую фигуру.
Серия D — построена по принципу перегруппировки фигур в матрице.
Здесь задание заключается в дополнении недостающей части основного изображения одним из приведенных в каждой таблице фрагментов. Выполнение задания требует от обследуемого тщательного анализа структуры основного изображения и обнаружения этих же особенностей в одном из нескольких фрагментов. Затем происходит слияние фрагмента, его сравнение с окружением основной части таблицы.
Серия В — построена по принципу аналогии между парами фигур. Обследуемый должен найти принцип, соответствен но которому построена в каждом отдельном случае фигура и, исходя из этого, подобрать недостающий фрагмент. При этом важно определить ось симметрии, соответственно которой расположены фигуры в основном образце.
Серия С — построена по принципу прогрессивных изменений в фигурах матриц. Эти фигуры в пределах одной матрицы все больше усложняются, происходит как бы непрерывное их развитие. Обогащение фигур новыми элементами подчиняется четкому принципу, обнаружив который, можно подобрать недостающую фигуру.
Серия D — построена по принципу перегруппировки фигур в матрице. Обследуемый должен найти эту перегруппировку, происходящую в горизонтальном и вертикальном положениях.
Серия Е основана на принципе разложения фигур основного изображения на элементы. Недостающие фигуры можно найти, поняв принцип анализа и синтеза фигур.
Обследуемый должен найти эту перегруппировку, происходящую в горизонтальном и вертикальном положениях.
Серия Е основана на принципе разложения фигур основного изображения на элементы. Недостающие фигуры можно найти, поняв принцип анализа и синтеза фигур.
Изображение слайда
6
Слайд 6
Имеется взрослый (с 14 до 65 лет) и детский (с 4,5 до 9 лет) вариант тестов Равена. Возможны два варианта в использовании матриц Равена.
Первый вариант — в качестве теста скорости, с ограничением времени 20 мин. для выполнения заданий. Для группового обследования.
Второй вариант использования матриц Равена в качестве теста интеллекта исключает введение временных ограничений. Задача испытуемого — установить закономерность, связывающую между собой фигуры на рисунке, и на опросном листе указать номер искомой фигуры из предлагаемых вариантов.
С 11
Задача испытуемого — установить закономерность, связывающую между собой фигуры на рисунке, и на опросном листе указать номер искомой фигуры из предлагаемых вариантов.
С 11
Изображение слайда
Изображение для работы со слайдом
Изображение для работы со слайдом
7
Слайд 7: Инструкция Теста равена
взрослый (с 14 до 65 лет)
Изображение слайда
Изображение для работы со слайдом
Реклама. Продолжение ниже
Продолжение ниже
8
Слайд 8
Инструкция : Тест строго регламентирован во времени, а именно: 20 мин. Для того, чтобы соблюсти время, необходимо строго следить за тем, чтобы до общей команды: «Приступить к выполнению теста» — никто не открывал таблицы и не подсматривал. По истечении 20 мин подается команда, например: «Всем закрыть таблицы». О предназначении данного теста можно сказать следующее: «Все наши исследования проводятся исключительно в научных целях, поэтому от вас требуются добросовестность, глубокая обдуманность, искренность и точность в ответах. Данный тест предназначен для уточнения логичности вашего мышления».
После этого взять таблицу и открыть для показа всем 1-ю страницу: «На рисунке одной фигуры недостает. Справа изображено 6-8 пронумерованных фигур, одна из которых является искомой. Надо определить закономерность, связывающую между собой фигуры на рисунке, и указать номер искомой фигуры в листке, который вам выдан» (можно показать на примере одного образца).
Во время выполнения задач теста необходимо контролировать, чтобы респонденты не списывали друг у друга. По истечении 20 мин подать команду: «Закрыть всем таблицы!
Собрать бланки и таблицы к ним. Проверить, чтобы в правом углу регистрируемого бланка был проставлен карандашом номер обследуемого.
Надо определить закономерность, связывающую между собой фигуры на рисунке, и указать номер искомой фигуры в листке, который вам выдан» (можно показать на примере одного образца).
Во время выполнения задач теста необходимо контролировать, чтобы респонденты не списывали друг у друга. По истечении 20 мин подать команду: «Закрыть всем таблицы!
Собрать бланки и таблицы к ним. Проверить, чтобы в правом углу регистрируемого бланка был проставлен карандашом номер обследуемого.
Изображение слайда
9
Слайд 9
№ задания Серия A Серия B Серия C Серия D Серия E 1 2 3 4 5 6 7 8 9 10 11 12 Сумма правильных ответов
Изображение слайда
10
Слайд 10
Интерпретация результатов (ключи)
Правильное решение каждого задания оценивается в один балл, затем подсчитывается общее число баллов по всем таблицам и по отдельным сериям. Полученный общий показатель рассматривается как индекс интеллектуальной силы, умственной производительности респондента. Показатели выполнения заданий по отдельным сериям сравнивают со среднестатистическим, учитывают разницу между результатами, полученными в каждой серии, и контрольными, полученными статистической обработкой при исследовании больших групп здоровых обследуемых и, таким образом, расцениваемыми как ожидаемые результату. Такая разница позволяет судить о надежности полученных результатов (это не относится к психической патологии).
№
Серия А
Серия В
Серия С
Серия D
Серия Е
1
4
5
5
3
7
2
5
6
3
4
6
3
1
1
2
3
8
4
2
2
7
8
2
5
6
1
8
7
1
6
3
3
4
6
5
7
6
5
5
5
1
8
2
6
1
4
3
9
1
4
7
1
6
10
3
3
1
2
2
11
4
4
6
5
4
12
2
8
2
6
5
Полученный общий показатель рассматривается как индекс интеллектуальной силы, умственной производительности респондента. Показатели выполнения заданий по отдельным сериям сравнивают со среднестатистическим, учитывают разницу между результатами, полученными в каждой серии, и контрольными, полученными статистической обработкой при исследовании больших групп здоровых обследуемых и, таким образом, расцениваемыми как ожидаемые результату. Такая разница позволяет судить о надежности полученных результатов (это не относится к психической патологии).
№
Серия А
Серия В
Серия С
Серия D
Серия Е
1
4
5
5
3
7
2
5
6
3
4
6
3
1
1
2
3
8
4
2
2
7
8
2
5
6
1
8
7
1
6
3
3
4
6
5
7
6
5
5
5
1
8
2
6
1
4
3
9
1
4
7
1
6
10
3
3
1
2
2
11
4
4
6
5
4
12
2
8
2
6
5
Изображение слайда
11
Слайд 11
Процентная шкала степени развития интеллекта
Полученный суммарный показатель по специальной таблице переводится в проценты. При этом по специальной шкале различают 5 степеней интеллектуального уровня :
Следующий способ оценки общих результатов по Стандартным матрицам Равена заключается в переводе «сырого» балла в стандартизированный — коэффициент IQ.
При этом по специальной шкале различают 5 степеней интеллектуального уровня :
Следующий способ оценки общих результатов по Стандартным матрицам Равена заключается в переводе «сырого» балла в стандартизированный — коэффициент IQ.
Изображение слайда
12
Слайд 12
Возраст 14-30 35 40 45 50 55 65 % 100 97 93 88 82 76 70 Таблица перевода сырых баллов в IQ Далее, ориентируясь на выявленный показатель IQ, можно определить уровень умственных способностей. Градации уровней умственных способностей Показатели IQ Уровень развития интеллекта Свыше 140 незаурядный, выдающийся интеллект 121-140 высокий уровень интеллекта 111-120 интеллект выше среднего 91-110 средний уровень интеллекта 81-90 интеллект ниже среднего 71-80 низкий уровень интеллекта 51-70 лёгкая степень слабоумия 21-50 средняя степень слабоумия 0-20 тяжёлая степень слабоумия
Изображение слайда
13
Слайд 13
A 1 A 2
Изображение слайда
Изображение для работы со слайдом
Изображение для работы со слайдом
14
Слайд 14
A 3 A 4
Изображение слайда
Изображение для работы со слайдом
Изображение для работы со слайдом
Реклама. Продолжение ниже
Продолжение ниже
15
Слайд 15
A 5 A 6
Изображение слайда
Изображение для работы со слайдом
Изображение для работы со слайдом
16
Слайд 16
A 7 A 8
Изображение слайда
Изображение для работы со слайдом
Изображение для работы со слайдом
17
Слайд 17
A 9 A 10
Изображение слайда
Изображение для работы со слайдом
Изображение для работы со слайдом
18
Слайд 18
A 11 A 12
Изображение слайда
Изображение для работы со слайдом
Изображение для работы со слайдом
19
Слайд 19
B 1 B 2
Изображение слайда
Изображение для работы со слайдом
Изображение для работы со слайдом
20
Слайд 20
B 3 B 4
Изображение слайда
Изображение для работы со слайдом
Изображение для работы со слайдом
21
Слайд 21
B 5 B 6
Изображение слайда
Изображение для работы со слайдом
Изображение для работы со слайдом
22
Слайд 22
B 7 B 8
Изображение слайда
Изображение для работы со слайдом
Изображение для работы со слайдом
23
Слайд 23
B 9 B 10
Изображение слайда
Изображение для работы со слайдом
Изображение для работы со слайдом
24
Слайд 24
B 11 B 12
Изображение слайда
Изображение для работы со слайдом
Изображение для работы со слайдом
25
Слайд 25
C 1 C 2
Изображение слайда
Изображение для работы со слайдом
Изображение для работы со слайдом
26
Слайд 26
C 3 C 4
Изображение слайда
Изображение для работы со слайдом
Изображение для работы со слайдом
27
Слайд 27
C 5 C 6
Изображение слайда
Изображение для работы со слайдом
Изображение для работы со слайдом
28
Слайд 28
C 7 C 8
Изображение слайда
Изображение для работы со слайдом
Изображение для работы со слайдом
29
Слайд 29
C 9 C 10
Изображение слайда
Изображение для работы со слайдом
Изображение для работы со слайдом
30
Слайд 30
C 1 1 C 1 2
Изображение слайда
Изображение для работы со слайдом
Изображение для работы со слайдом
31
Слайд 31
D 1 D 2
Изображение слайда
Изображение для работы со слайдом
Изображение для работы со слайдом
32
Слайд 32
D 3 D 4
Изображение слайда
Изображение для работы со слайдом
Изображение для работы со слайдом
33
Слайд 33
D 5 D 6
Изображение слайда
Изображение для работы со слайдом
Изображение для работы со слайдом
34
Слайд 34
D 7 D 8
Изображение слайда
Изображение для работы со слайдом
Изображение для работы со слайдом
35
Слайд 35
D 9 D 10
Изображение слайда
Изображение для работы со слайдом
Изображение для работы со слайдом
36
Слайд 36
D 1 1 D 1 2
Изображение слайда
Изображение для работы со слайдом
Изображение для работы со слайдом
37
Слайд 37
E 1 E 2
Изображение слайда
Изображение для работы со слайдом
Изображение для работы со слайдом
38
Слайд 38
E 3 E 4
Изображение слайда
Изображение для работы со слайдом
Изображение для работы со слайдом
39
Слайд 39
E 5 E 6
Изображение слайда
Изображение для работы со слайдом
Изображение для работы со слайдом
40
Слайд 40
E 7 E 8
Изображение слайда
Изображение для работы со слайдом
Изображение для работы со слайдом
41
Слайд 41
E 9 E 10
Изображение слайда
Изображение для работы со слайдом
Изображение для работы со слайдом
42
Слайд 42
E 11 E 12
Изображение слайда
Изображение для работы со слайдом
Изображение для работы со слайдом
43
Слайд 43
№ задания Серия A Серия B Серия C Серия D Серия E 1 4 1 (5) 5 3 7 2 5 6 3 4 6 3 1 1 2 3 2 (8) 4 2 2 7 8 2 5 6 1 8 7 1 6 3 3 4 6 8 (5) 7 6 5 5 5 5 (1) 8 2 6 1 4 8 (3) 9 1 4 1 (7) 1 6 10 3 3 6 (1) 1 (2) 7 (2) 11 1 (4) 4 6 2 (5) 5 (4) 12 2 8 3 (2) 7 (6) 6 (5) Сумма правильных ответов 11 11 9 9 5 = 45
Изображение слайда
44
Слайд 44
Полученный суммарный показатель по специальной таблице переводится в проценты.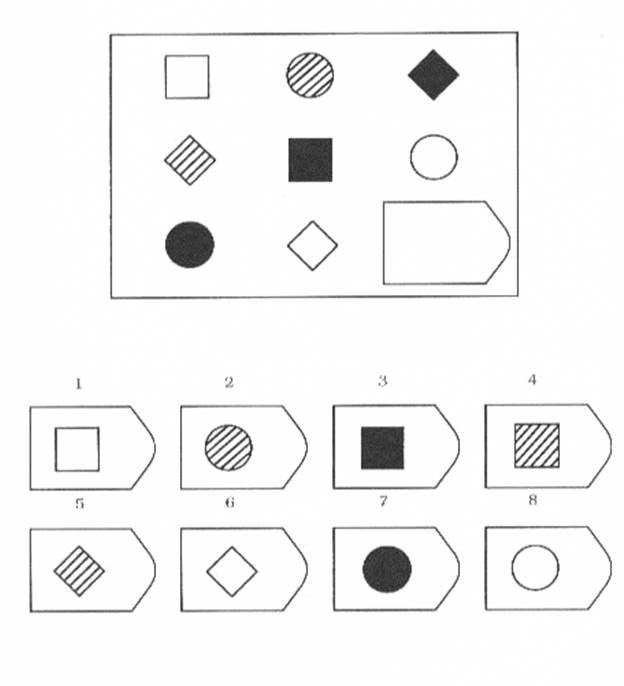 1 степень — более 95% — высокий интеллект;
2 степень — 75-94% — интеллект выше среднего;
3 степень 25-74% — интеллект средний;
4 степень — 5-24% — интеллект ниже среднего;
степень — ниже 5% — дефект.
Следующий способ оценки общих результатов по Стандартным матрицам Равена заключается в переводе «сырого» балла в стандартизированный — коэффициент IQ.
Возраст
14-30
35
40
45
50
55
65
%
100
97
93
88
82
76
70
1 степень — более 95% — высокий интеллект;
2 степень — 75-94% — интеллект выше среднего;
3 степень 25-74% — интеллект средний;
4 степень — 5-24% — интеллект ниже среднего;
степень — ниже 5% — дефект.
Следующий способ оценки общих результатов по Стандартным матрицам Равена заключается в переводе «сырого» балла в стандартизированный — коэффициент IQ.
Возраст
14-30
35
40
45
50
55
65
%
100
97
93
88
82
76
70
Изображение слайда
45
Слайд 45
Далее, ориентируясь на выявленный показатель IQ, можно определить уровень умственных способностей. Градации уровней умственных способностей Показатели IQ Уровень развития интеллекта Свыше 140 незаурядный, выдающийся интеллект 121-140 высокий уровень интеллекта 111-120 интеллект выше среднего 91-110 средний уровень интеллекта 81-90 интеллект ниже среднего 71-80 низкий уровень интеллекта 51-70 лёгкая степень слабоумия 21-50 средняя степень слабоумия 0-20 тяжёлая степень слабоумия
Изображение слайда
46
Последний слайд презентации: Тест равена: Спасибо за внимание!
Изображение слайда
Диагностические возможности Краткого отборочного теста
Интегральный показатель интеллекта человека, оцененный с помощью тестов (IQ или иной), является одной из одной из наиболее практически значимых индивидуально-психологических характеристик человека, позволяющих дать оценку его возможностей и прогноз поведения в разнообразных сферах деятельности человека (Анастази, Урбина, 2001; Дружинин, 2001).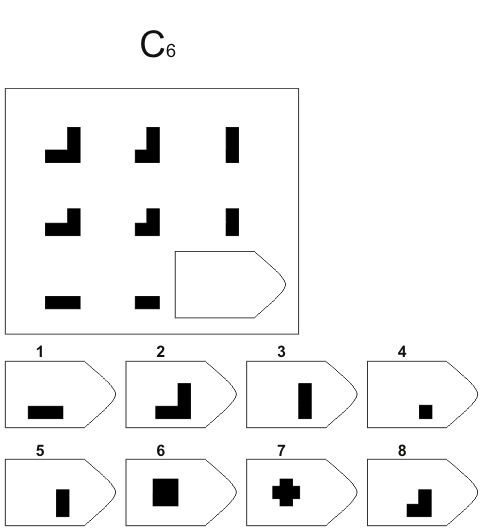 Поэтому потребность практической психологии в простом и надежном инструменте интегральной диагностики интеллекта достаточно велика, однако известно лишь несколько тестов, которые могут быть использованы для этих целей для русскоязычных испытуемых. Широко известные интеллектуальные тесты Айзенка (Айзенк, 1996) являются популярными и их использование в профессиональных целях некорректно. Кроме того, они предназначены в первую очередь для лиц с интеллектом выше среднего, и вызывают значительные трудности и фрустрацию, связанную с многочисленными неудачами, у лиц, чей интеллект несколько ниже среднего. Прогрессивные матрицы Равена (Равен, Курт, Равен, 1996) позволяют надежно оценить интеллект, если изданы в хорошем полиграфическом исполнении, но слишком часто используются в сокращенном варианте с уменьшенными картинками, что существенно снижает их надежность. Кроме того, они не дают возможность оценить вербальный интеллект, что часто является необходимым.
Поэтому потребность практической психологии в простом и надежном инструменте интегральной диагностики интеллекта достаточно велика, однако известно лишь несколько тестов, которые могут быть использованы для этих целей для русскоязычных испытуемых. Широко известные интеллектуальные тесты Айзенка (Айзенк, 1996) являются популярными и их использование в профессиональных целях некорректно. Кроме того, они предназначены в первую очередь для лиц с интеллектом выше среднего, и вызывают значительные трудности и фрустрацию, связанную с многочисленными неудачами, у лиц, чей интеллект несколько ниже среднего. Прогрессивные матрицы Равена (Равен, Курт, Равен, 1996) позволяют надежно оценить интеллект, если изданы в хорошем полиграфическом исполнении, но слишком часто используются в сокращенном варианте с уменьшенными картинками, что существенно снижает их надежность. Кроме того, они не дают возможность оценить вербальный интеллект, что часто является необходимым.
Краткий отборочный тест, или КОТ (Бузин, 1992, 1998) не обладая отмеченными недостатками, имеет ряд несомненных достоинств, прежде всего:
— Быстрота и простота проведения тестирования (всего 15 минут), а также относительная простота размножения самого теста (3 листа) и обработки.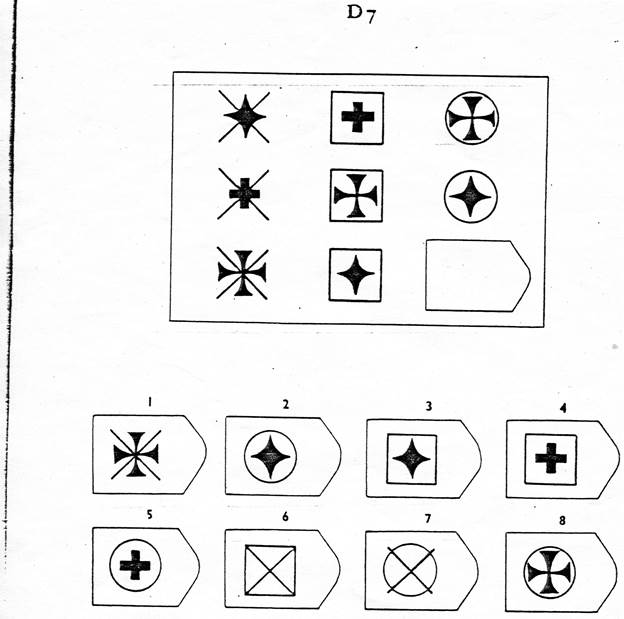
— Адекватная сложность для контингентов с различным интеллектуальным уровнем: от школьников из класса коррекции до выпускников престижных вузов и успешных предпринимателей.
К ограничениям данного теста, которые необходимо знать тем, кто им пользуется, можно отнести скоростной характер теста, который не дает возможность оценить способность испытуемых к выполнению заданий высокого уровня трудности. Кроме того, необходимость выполнять задания теста с высокой скоростью создает преимущества для более молодых испытуемых и трудности для испытуемых старше 40 лет; это необходимо учитывать при оценке результатов.
Одним из главных недостатков КОТ является отсутствие популяционных норм и немногочисленность возрастных и профессиональных групп, нормы для которых приведены в руководстве к тесту. Кроме того, далеко не все советы и рекомендации по использованию теста могут быть безоговорочно приняты практическими психологами (например, испытуемому с недостаточно развитыми вербальными способностями «можно рекомендовать чтение толковых словарей, словарей крылатых выражений и слов, пословиц и поговорок, словарей иностранных слов и двуязычных словарей и решать лингвистические задачи»).
Накопленный нами опыт применения КОТ показывает, что его использование целесообразно и эффективно для решения широкого круга задач практической психологии. Цель данной статьи — процемонстрировать диагностические возможности применения КОТ и дать методические рекомендации по использованию теста для решения разнообразных задач практической психологии.
1. Основные показатели КОТ
Основным показателем теста, позволяющим дать интегральную оценку интеллекта, является количество правильных ответов, данных за 15 минут (стандартное время выполнения теста). Результат испытуемого следует сравнить с имеющимися данными по соответствующим возрастным и профессиональным группам (как уже отмечалось, русскоязычных популяционных норма для КОТ пока нет). В дополнение к руководству к тесту можно использовать таблицы 1-3. Следует отметить, что представленные в них данные получены на группах от 10 до 40 человек (тестирование проводили студенты ИППиП) и не могут считаться полноценными тестовыми нормами.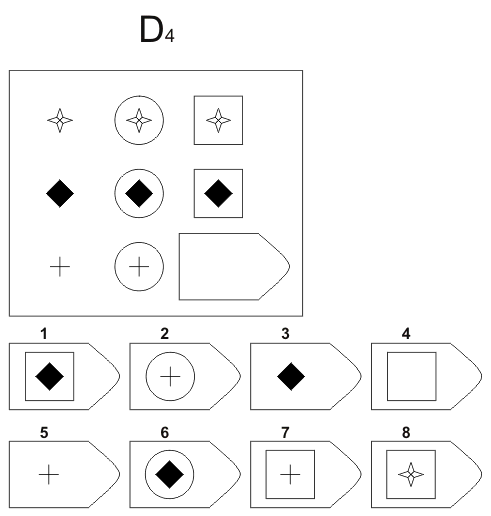 Результат испытуемого, укладывающийся в интервал M + — sigma , где М — среднее по группе, а sigma — стандартное отклонение, следует признать соответствующим возрастной или профессиональной норме (его показывают около двух третей испытуемых в данной популяции).
Результат испытуемого, укладывающийся в интервал M + — sigma , где М — среднее по группе, а sigma — стандартное отклонение, следует признать соответствующим возрастной или профессиональной норме (его показывают около двух третей испытуемых в данной популяции).
Дополнительные диагностические возможности появляются тогда, когда после выполнения заданий на время испытуемому предоставляется возможность закончить задание без учета времени (для раздельного подсчета заданий выполненных за 15 минут и без учета времени целесообразно через 15 минут заменить испытуемому ручку, использовав для замены другой цвет). При этом появляются возможности как для элементов структурного анализа интеллекта, так и для учета таких показателей, как дополнительно затраченное на решение время и количество дополнительно решенных заданий, которые дают возможность косвенно оценить мотивацию испытуемого.
Структурная оценка интеллекта на основе КОТ затруднительна в связи с разным количеством заданий, соответствующим разным аспектам интеллекта и их разной сложностью, но в некоторых случаях возможна.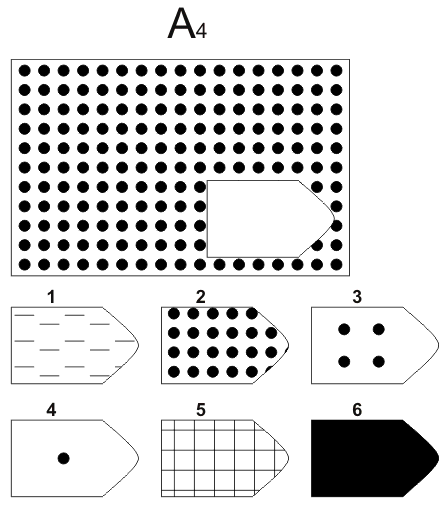 Однако следует учесть, что подобные данные недостаточно надежны и могут использоваться лишь для самой приблизительной оценки. Целесообразно выделение следующих типов заданий, которые ориентированы преимущественно на выявление одного из факторов в структуре интеллекта.
Однако следует учесть, что подобные данные недостаточно надежны и могут использоваться лишь для самой приблизительной оценки. Целесообразно выделение следующих типов заданий, которые ориентированы преимущественно на выявление одного из факторов в структуре интеллекта.
1. Значение слов и фраз (20 заданий, возможно выделение заданий со словами и с фразами) — вербальный фактор
2. Математические последовательности (4 задания) — числовой фактор, низкий уровень сложности.
3. Математические задачи (13 заданий) — числовой фактор, средний и высокий уровень сложности.
4. Логические задачи (4 задания) ближе всего к общему интеллекту (по Спирмену), причем представленный заданиями относительно высокого уровня сложности.
5. Пространственные задачи (4 задания) — пространственно-символической фактор.
6. Осведомленность (3 задания).
7. Внимание (2 задания).
Для каждого типа задания подсчитывается количество заданий, решенных верно, решенных неверно (с ошибкой) и пропущенных (ответ не был дан) — см.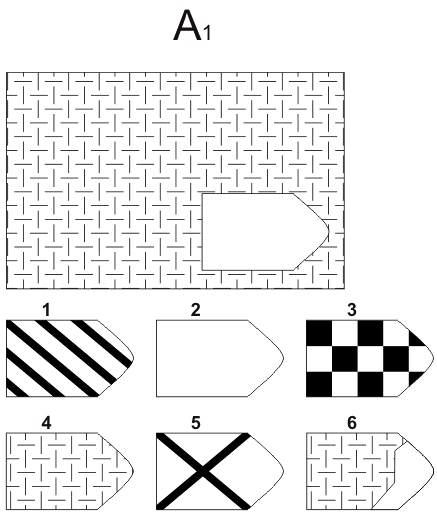 ниже пример подсчета; пропущенные ответы можно объединить при подсчете с решенными неверно. Поскольку количество заданий для большинства типов невелико, то, как правило, имеет смысл оценивать лишь соотношение вербального и числового фактора, представленного относительно большим количеством заданий; содержательно оценивать уровень развития других факторов имеет смысл лишь при нулевом или 100%-ном результате по данному фактору.
ниже пример подсчета; пропущенные ответы можно объединить при подсчете с решенными неверно. Поскольку количество заданий для большинства типов невелико, то, как правило, имеет смысл оценивать лишь соотношение вербального и числового фактора, представленного относительно большим количеством заданий; содержательно оценивать уровень развития других факторов имеет смысл лишь при нулевом или 100%-ном результате по данному фактору.
2. Использование КОТ для решения практических задач обучения
Практика применения теста показывает, что тест обладает адекватной сложностью для школьников от 10 лет и выше и может использоваться для оценки интеллекта школьников, начиная с 5 класса.
Показаны достоверные различия по результатам теста между школьниками одного и того же возраста, обучающимися в различных типах учебных заведений: между учащимися обычных классов и классов коррекции, школы-интерната, а также интерната для подростков, совершивших противоправные действия; между школьниками общеобразовательных школ и гимназий (гимназических классов), лицеев, языковых школ. Также показаны достоверные различия по результатам теста между учениками с хорошей и плохой успеваемостью. Все это доказывает прогностическую ценность результатов КОТ для отбора учащихся в разные типы учебных заведений и для оценки успешности обучения.
Также показаны достоверные различия по результатам теста между учениками с хорошей и плохой успеваемостью. Все это доказывает прогностическую ценность результатов КОТ для отбора учащихся в разные типы учебных заведений и для оценки успешности обучения.
На основе имеющихся данных можно предположить, что показатели КОТ различаются для разных типов учебных заведений, но в меньшей степени для различных регионов России. Однако учитывая разную практику обучения и отбора в разных школах и отсутствие популяционных норм, при использовании данных КОТ в конкретном учебном заведении следует руководствоваться прежде всего данными тестирования, полученными именно в этом заведении; данные таблицы 1 могут быть использованы для сравнения и приблизительной оценки.
Можно предложить следующие примерные рекомендации по использованию результатов КОТ для решения практических задач обучения.
При отборе учащихся в гимназии, лицеи и другие учебные заведения с повышенными требованиями к учащимся целесообразно ориентироваться на показатель КОТ не ниже, чем М-sigma для контингента учащихся этого учебного заведения.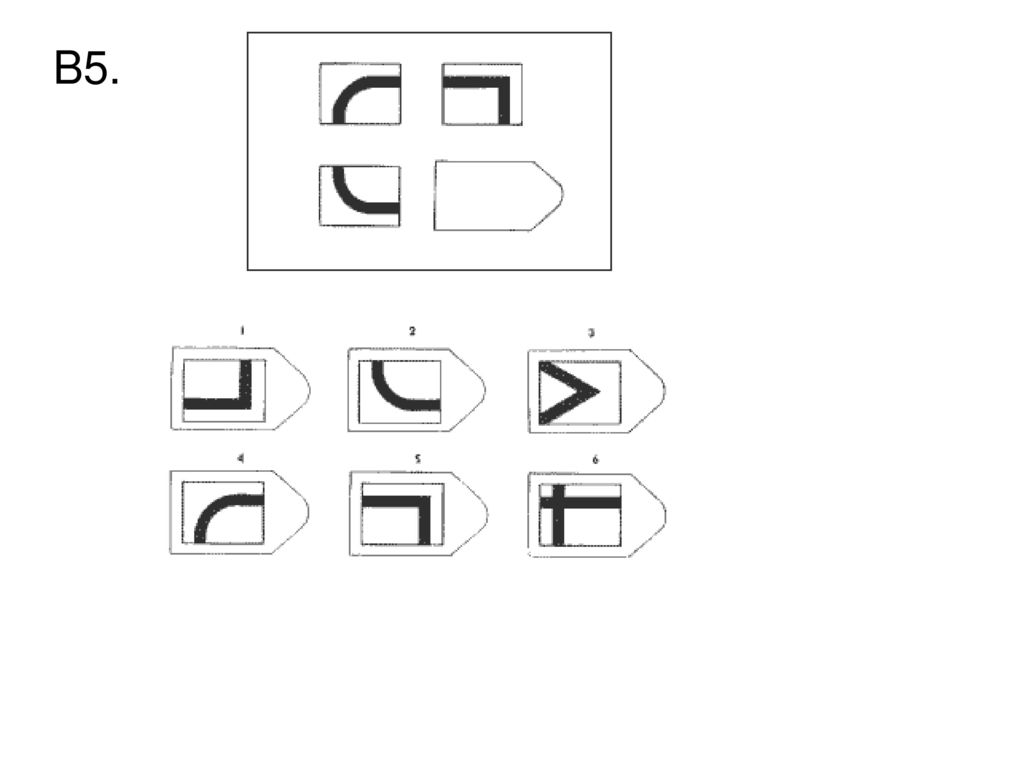
При организации дифференцированного обучения желательно выделять в отдельные классы (группы) учащихся, чей показатель КОТ выходит за пределы М+-sigma для данного класса или школы.
При отсутствии возможностей для дифференцированного обучения следует учитывать, что учащиеся, чей результат по КОТ ниже, чем М-sigma, могут испытывать сложности при освоении школьной программы, и учителям следует уделять таким ученикам особое внимание. Учащиеся, чем показатель КОТ выходит за пределы М+sigma желательно предлагать задания повышенной сложности или рекомендовать поступление в гимназию (лицей)
При этом следует учитывать, что тестирование интеллекта является лишь одной из составных частей в комплексе мероприятий по отбору учащихся и их распределению по уровням обучения; тестирование не может подменять учета оценок, результатов вступительных испытаний, мнения учителей и школьного психолога и т.п. Следует также учитывать, что уровень общих способностей, измеряемый тестами интеллекта (и в частности, КОТ) у школьников достаточно изменчив, следовательно ни в коем случае нельзя рассматривать результат теста как «диагноз» или «приговор», что, к сожалению, нередко встречается.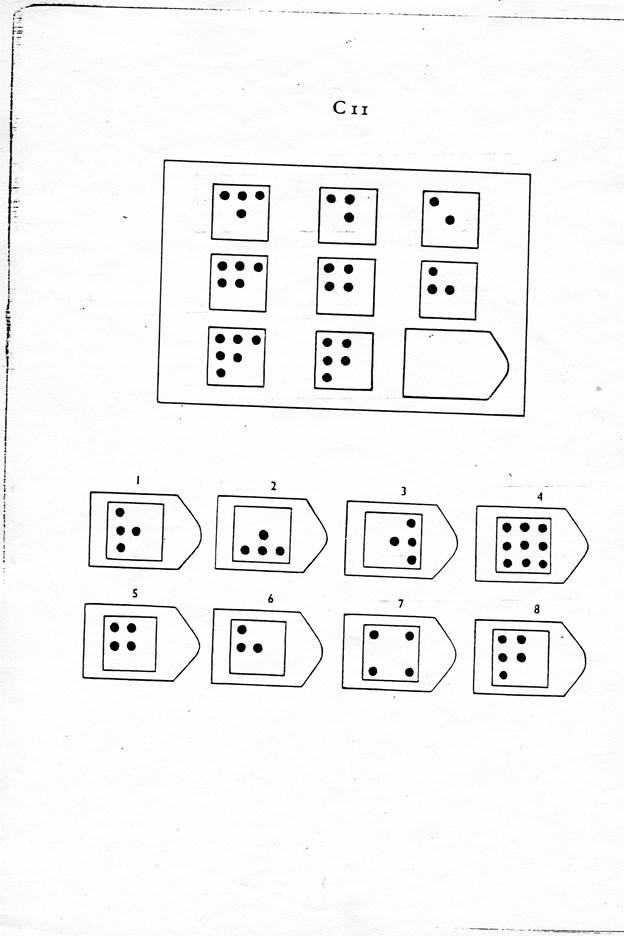 Поэтому школьным психологам следует быть особенно внимательны при сообщении результатов тестирования учителям, чтобы не создавать у них неверных установок по отношению к ученикам.
Поэтому школьным психологам следует быть особенно внимательны при сообщении результатов тестирования учителям, чтобы не создавать у них неверных установок по отношению к ученикам.
3. Использование КОТ в профессиональном консультировании
При профессиональном консультировании КОТ крайне редко используется в качестве единственного диагностического инструмента; поэтому данные КОТ как правило рассматриваются в комплексе с другими психодиагностическими показателями, результатами бесед и другими данными, используемыми в процессе консультирования. Однако хотя и редко, но бывают ситуации (как в приведенном ниже примере), когда именно результаты КОТ оказываются наиболее значимыми для процесса консультирования.
а) Интегральный показатель
При консультировании по развитию карьеры работающих специалистов или студентов старших курсов вузов следует сравнивать результат испытуемого с имеющимися показателями профессиональной группы, наиболее сходной с профессией испытуемого. При результатах выше М+sigma велика вероятность успешного карьерного роста; часто целесообразно получение дополнительного образования.
При результатах выше М+sigma велика вероятность успешного карьерного роста; часто целесообразно получение дополнительного образования.
Пример. Елена, 28 лет, старшая медсестра хирургического отделения больницы. Школу окончила с серебряной медалью, мечтала стать врачом-хирургом, однако не продолжила образование после медицинского училища из-за рождения детей. Руководство больницы неоднократно предлагало Елене поступать учиться, но она отказывалась, считая, что «поезд ушел, мозгов не хватит». Перед выполнением теста сомневалась в своих возможностях: «Какой интеллект, были мозги да усохли». За 15 минут выполнила верно 35 заданий. После ознакомления с результатом и сравнения его с таблицей, аналогичной таблицам 2-3 из данной работы, у нее «словно крылья выросли»: появилась вера в свои способности. Через несколько месяцев после тестирования успешно сдала экзамены в медицинский институт.
Результату, выходящему за пределы М-sigma, далеко не всегда соответствует низкая профессиональная успешность. Однако возможности профессионального роста, изменения характера работы, освоения новых технологий у таких работников как правило ограничены, что следует учитывать при профессиональном консультировании. Стоит также отметить, что клиенты крайне редко считают причиной своих трудностей в работе или учебе недостаточно высокий интеллектуальный уровень, как правило, они используют механизмы психологической защиты, чтобы объяснить эти трудности или игнорировать их. Подобная ситуация может потребовать работы консультанта, выходящей за рамки профессионального консультирования.
Однако возможности профессионального роста, изменения характера работы, освоения новых технологий у таких работников как правило ограничены, что следует учитывать при профессиональном консультировании. Стоит также отметить, что клиенты крайне редко считают причиной своих трудностей в работе или учебе недостаточно высокий интеллектуальный уровень, как правило, они используют механизмы психологической защиты, чтобы объяснить эти трудности или игнорировать их. Подобная ситуация может потребовать работы консультанта, выходящей за рамки профессионального консультирования.
При профессиональном консультировании старшеклассников и выпускников школ следует сравнить показатель испытуемого с данными студентов учебного заведения, сходного по профилю и «престижности» с учебным заведением, куда собирается поступать испытуемый. При результате испытуемого ниже среднего следует оценить мотивацию достижения испытуемого (высокая мотивация достижения повышает вероятность успешного поступления в вузе и обучения в нем), а также его желание и возможность интенсивной подготовки к вступительным экзаменам. При результате ниже М-sigma следует рассмотреть вопрос целесообразности поступления в данный вуз или возможности платного обучения. По нашим данным, возможность поступления на бесплатное обучение в авторитетных столичные вузы проблематична при показателе КОТ ниже 18-20. Следует также учитывать, что лица, имеющие показатели ниже М-sigma для данного вуза, часто испытывают существенные трудности в обучении, которые могут частично компенсироваться высокой мотивацией и интенсивными занятиями.
При результате ниже М-sigma следует рассмотреть вопрос целесообразности поступления в данный вуз или возможности платного обучения. По нашим данным, возможность поступления на бесплатное обучение в авторитетных столичные вузы проблематична при показателе КОТ ниже 18-20. Следует также учитывать, что лица, имеющие показатели ниже М-sigma для данного вуза, часто испытывают существенные трудности в обучении, которые могут частично компенсироваться высокой мотивацией и интенсивными занятиями.
б) Структурный анализ
Как уже указывалось, он имеет вспомогательное значение из-за невысокой надежности. Соотношение вербального и математического фактора интеллекта можно, наряду с другими характеристиками, учитывать при выборе в пользу гуманитарного или технического образования. При консультировании взрослых имеет смысл обращать внимание на очень низкие показатели при решении математических задач, что является органичением для профессий, требующих манипулирования с числовым материалом (продавец-кассир, бухгалтер и пр. ). Большое количество пропущенных (не имеющих ответа, даже неправильного) математических задач в условиях отсутствия ограничения во времени решения встречается сравнительно часто и свидетельствует о низкой самооценке своих математических способностей.
). Большое количество пропущенных (не имеющих ответа, даже неправильного) математических задач в условиях отсутствия ограничения во времени решения встречается сравнительно часто и свидетельствует о низкой самооценке своих математических способностей.
в) Особенности мотивации
Особенности мотивации можно оценить, учитывая время, затраченное на выполнение заданий по истечении обязательных 15 минут, количество заданий, выполненных в дополнительное время, а также количество заданий, оставшихся без ответа (пропущенных). В связи с отсутствием четких критериев для оценки этих показателей в выводах следует быть достаточно осторожным.
Пример. Алина, ученица 10 класса, английской школы, отличница. Собирается обучаться по профессии юриста-международника в престижном вузе. Родители предпочли бы для дочери экономическое образование, однако не настаивают на нем.
За 15 минут Алина выполнила верно 32 задания (интегральный показатель выше среднего для всех имеющихся групп студентов и для всех, кроме одной, групп профессионалов), причем она успела просмотреть все 50 заданий и выполнить (то есть, дать ответы, в том числе ошибочные) 45 из них (32 верно, 13 неверно, поэтому дополнительное время для решения не предоставлялось. Структурный анализ дал следующие результаты:
Структурный анализ дал следующие результаты:
| всего заданий | верно | неверно | пропущено | |
| осведомленность | 3 | 3 | ||
| внимание | 2 | 1 | 1 | |
| простр. задачи | 4 | 2 | 1 | 1 |
| логич. задачи | 4 | 3 | 1 | |
| знач. слов и фраз | 20 | 15 | 3 | 2 |
| матем. закономерн. | 4 | 4 |
Результаты структурного анализа свидетельствуют о превосходстве вербального фактора над математическим. Небольшое количество пропусков свидетельствует о высокой мотивации Алины. Можно предположить тенденцию к перфекционизму у испытуемой: ей удалось дойти за последнего задания за 15 минут, возможно, имело место стремление «решить все», которое определило излишнюю спешку (ошибка в задании на внимание).
По итогам тестирования, с учетом данных других методик, был предложено несколько гуманитарных специальностей. Получение экономического образования было признано нецелесообразным, с учетом желаний Алины и преобладания вербального, а не математического фактора в структуре интеллекта (невзирая на общий высокий показатель теста, испытуемой удалось решить менее трети математических задач). После обсуждения результатов Алина решила в 11 классе посещать подготовительные курсы при МГУ.
4. Использование КОТ в работе с персоналом.
Результаты применения КОТ в различных контингентах свидетельствуют о наличии взаимосвязи между результатами КОТ и профессиональными достижениями. Так, показаны достоверные различия интегрального показателя КОТ между успешными и неуспешными работниками, между специалистами со средним и с высшим образованием, между руководящим составом и рядовыми специалистами и т.п.
Пример. С помощью теста были обследованы две группы работников телевидения, разделенные на две группы: работающие и не работающие в прямом эфире (редактора и др.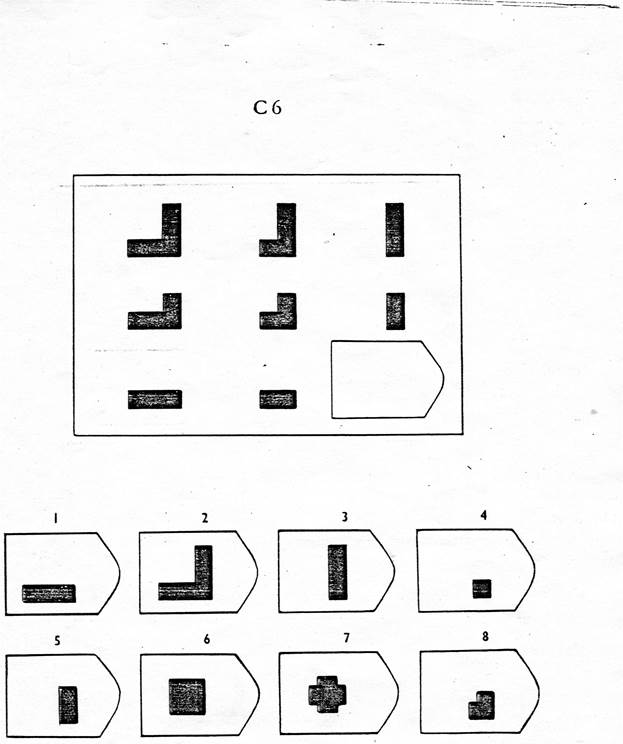 ). По сложившейся практике, те, кто вел прямой эфир, отбирались из работников, составлявших вторую группу, причем жесткие правила отбора отсутствовали. Бывали случаи, когда сотрудника, не справившегося с работой в прямом эфире, переводили обратно на редакторскую работу.
). По сложившейся практике, те, кто вел прямой эфир, отбирались из работников, составлявших вторую группу, причем жесткие правила отбора отсутствовали. Бывали случаи, когда сотрудника, не справившегося с работой в прямом эфире, переводили обратно на редакторскую работу.
При обследовании были обнаруженны высокодостоверные различия по результатам теста между двумя группами. Причем в группе работающих в прямом эфире были показаны результаты КОТ в диапазоне 27-41, за исключением двух человек, показавших результаты 18 и 19. Один из них начал вести прямые эфиры всего несколько недель и на момент обследования было непонятно, насколько успешно он справляется с этой работой. Во второй группе не было показано результатов выше 20 баллов.
Эти и другие подобные данные позволяют считать КОТ полезным инструментом при отборе персонала и решении других задач кадровой работы.
При использовании КОТ для отбора персонала целесообразно предварительно провести обследование уже работающих сотрудников и установить локальные нормы для конкретной организации.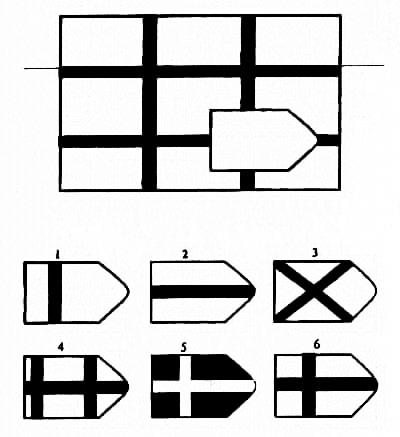 Использование норм, установленных в другой организации для той же профессии, нежелательно, т.к. средние результаты теста зависят от многих факторов: региона, кадровой политики организации, конкретных должностных обязанностей сотрудников и т.п. Поэтому данные, полученные для сотрудников той же профессии в другой организации, могут оказаться недостаточно надежными. Однако при отсутствии возможности провести тестирование работающего персонала организации, следует использовать наиболее подходящие данные из таблицы 3.
Использование норм, установленных в другой организации для той же профессии, нежелательно, т.к. средние результаты теста зависят от многих факторов: региона, кадровой политики организации, конкретных должностных обязанностей сотрудников и т.п. Поэтому данные, полученные для сотрудников той же профессии в другой организации, могут оказаться недостаточно надежными. Однако при отсутствии возможности провести тестирование работающего персонала организации, следует использовать наиболее подходящие данные из таблицы 3.
При решении кадровых вопросов можно предложить отсеивать при отборе сотрудников, чьи результаты не достигают значения М-sigma для уже работающих сотрудников. При результатах, превышающих М+sigma, целесообразно рассматривать вопрос о возможностях служебного роста, продолжения обучения и пр.
Тест может быть использован не только для оценки интеллекта, но и мотивации испытуемых, которая является важнейшим фактором профессиональной успешности.
Пример. Обследована группа торговых представителей (продажа жевательной резинки), поделенная на две подгруппы — успешных и неуспешных (по показателю объема продаж). При сопоставлении групп были выявлены не только различия по результатм выполнения теста за 15 минут (средние результаты составили 21,0 в группе успешных и 14,6 в группе неуспешных), но и различия в поведении в дополнительно отведенное время. В группе успешных агентов все испытуемые продолжили работу по истечении 15 минут, затратив дополнительно от 7 до 28 минут и оставив нерешенными не более 12 заданий. 43% неуспешных агентов отказались от продолжения выполнения теста по истечении 15 минут, а продолжившие затратили дополнительно от 5 до 10 минут, оставив невыполненными от 19 до 22 заданий. Три лучших агента показали лучшие результаты по КОТ (с учетом дополнительного времени)
При сопоставлении групп были выявлены не только различия по результатм выполнения теста за 15 минут (средние результаты составили 21,0 в группе успешных и 14,6 в группе неуспешных), но и различия в поведении в дополнительно отведенное время. В группе успешных агентов все испытуемые продолжили работу по истечении 15 минут, затратив дополнительно от 7 до 28 минут и оставив нерешенными не более 12 заданий. 43% неуспешных агентов отказались от продолжения выполнения теста по истечении 15 минут, а продолжившие затратили дополнительно от 5 до 10 минут, оставив невыполненными от 19 до 22 заданий. Три лучших агента показали лучшие результаты по КОТ (с учетом дополнительного времени)
Литература
Айзенк Г.Ю. (1996) Проверьте свои способности. М., Лань.
Анастази А., Урбина С. (2001). Психологическое тестирование. СПб., Питер.
Бузин В.Н. (1992, 1998) Краткий отборочный тест. М., Смысл (Психодиагностическая серия, выпуск. 4)
Дружинин В.Н. (2001). Когнитивные способности.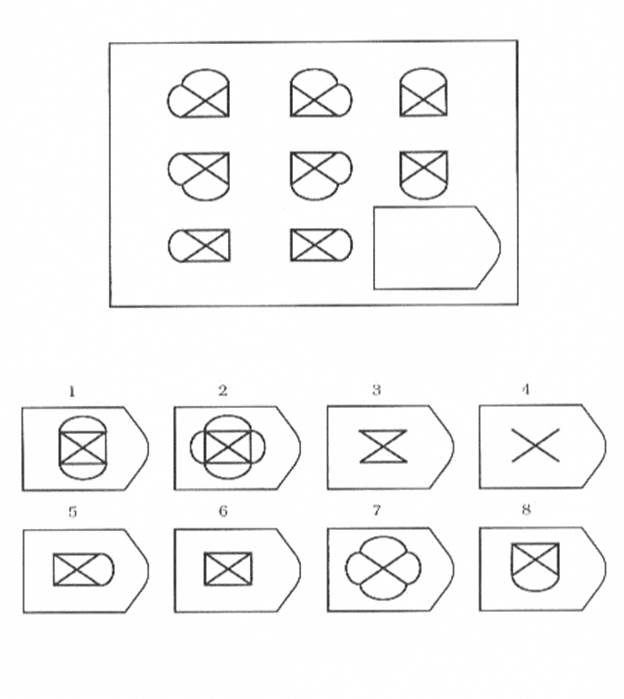 Структура, диагностика, развитие. М. СПб, PerSe, ИМАТОН.
Структура, диагностика, развитие. М. СПб, PerSe, ИМАТОН.
Равен Дж.К., Курт Дж.Х., Равен Дж. (1996). Стандартные прогрессивные матрицы. М., Когито.
| Таблица 1 Результаты выполнения теста КОТ учащимися средней школы | ||
| Контингент | сред. | ст. откл |
| 5 класс. (Москва) | 9,5 | 3,6 |
| 6 класс школы-интерната (Воронеж) | 6,9 | 5,3 |
| 6 класс языковой гимназии (Воронеж) | 17,2 | 4,6 |
| 7 класс (класс коррекции, Воронеж) | 6,4 | 2,1 |
| 7 кл. (спецшкола, девиантные подростки, Московская обл.) | 7,9 | 3,5 |
| 7 класса (Черкесск) | 11,7 | 4,0 |
| 7 класс. (Москва) | 12,3 | 4,6 |
| 7 класс гимназии (Москва) | 20,4 | 3,8 |
| 8 класс (Тюменская обл) | 10,0 | 3,8 |
8 класс (Московская обл.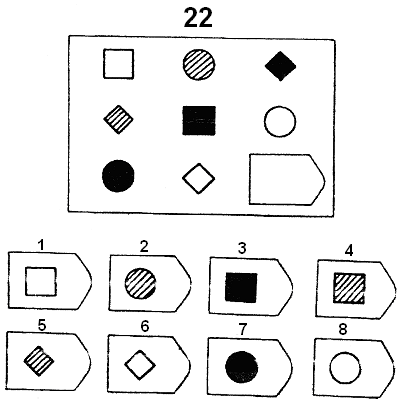 ) ) | 14,9 | 4,8 |
| 8 гимназический класс (Московская обл) | 18,2 | 2,8 |
| 9 класса (Москва) | 17,5 | 4,5 |
| 9 класс (Московская обл.) | 18,0 | 4,4 |
| 9 класс лицея при МФТИ | 25,6 | 6,2 |
| 10 класс гимназии (Москва) | 19,6 | 4,5 |
| 10 класс гуманитарного лицея (Москва) | 23,3 | 4,4 |
| 11 класс (Воркута) | 18,5 | 4,4 |
| 12 класс вечерней школы (Москва) | 18,0 | 4,3 |
| Таблица 2 Результаты выполнения теста КОТ учащимися высших, средних специальных, профессиональных учебных заведений и курсов | ||
| Контингент | сред. | ст. откл |
| учащ. ПТУ, спец. столяр-плотник (Москва) | 11,7 | 4,8 |
| учащ. ПТУ, спец. бухгалтер (Москва) | 12,3 | 3,7 |
учащ.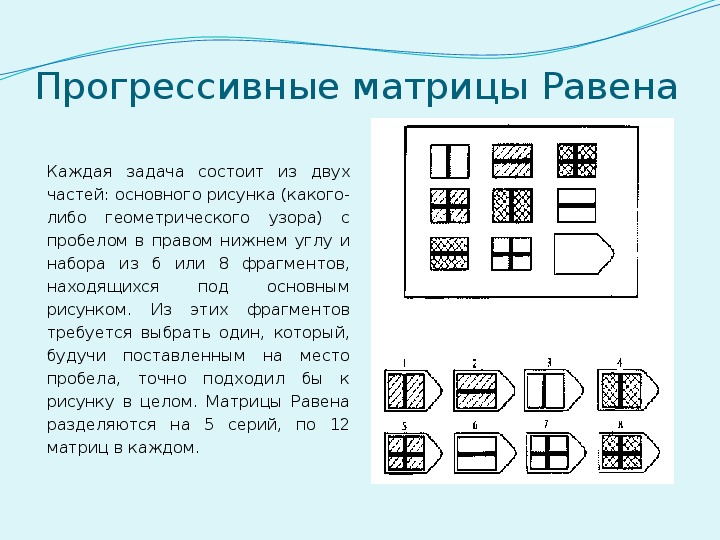 медучилища (Минск) медучилища (Минск) | 18,5 | 4,2 |
| учащ. колледжа, спец. бухгалтер (Москва) | 18,6 | 2,6 |
| студенты мед. ин-та (Караганда) | 20,2 | 6,9 |
| курсанты Суворовского училища | 21,3 | 3,6 |
| студенты Института туризма (Москва) | 22,9 | 7,4 |
| студенты МАТИ, спец-ть менеджмент | 23,4 | 4,3 |
| студенты Пед. ин-та, ф-т начального образования (Тюмень) | 23,9 | 2,1 |
| студенты ф-та дизайна Худож. академии (Минск) | 24,4 | 4,0 |
| студенты ИППиП | 25,6 | 6,7 |
| студенты пед. ин-та, физ-мат. факультет (Тюмень) | 25,8 | 3,5 |
| студенты МГУ, геологический факультет | 27,0 | 5,3 |
| студенты МИФИ | 28,3 | 5,2 |
| учащ. курсов «Эффективный менеджер» (Московская обл.) | 30,2 | 7,9 |
| Таблица 3 Результаты теста КОТ у представителей различных профессиональных и социальных групп | ||
| Контингент | сред. | ст. откл |
| работники Мосэнерго | 15,9 | 4,8 |
| фотомодели | 16,5 | 4,8 |
| безработные (жен.) (Самара) | 17,0 | 5,0 |
| безработные (Москва) | 17,8 | 7,1 |
| торговые агенты (Москва) | 17,8 | 4,1 |
| бортпроводники (Москва) | 18,5 | 4,9 |
| секретари, экспедиторы АООТ (жен.) (Тюменская обл.) | 18,9 | 1,9 |
| врачи (разные города) | 20,3 | 7,3 |
| актеры, озвучивающие телефильмы (Москва) | 20,5 | 7,1 |
| работники таможенного поста (Белгород) | 21,6 | 5,0 |
| менеджеры, руководство АООТ (муж.) (Тюменская обл.) | 24,0 | 3,0 |
| работники НИЦ металлургического комбината (Моск. обл.) | 25,6 | 6,6 |
| работники страховой компании. (Москва) | 26,6 | 7,0 |
| комментаторы ТВ (прямой эфир) (Москва) | 29,0 | 9,2 |
| менеджмент издательств (Москва, Санкт-Петербург) | 29,8 | 7,2 |
руководители собственных фирм (муж. ) (Москва) ) (Москва) | 33,2 | 4,9 |
Интерпретировать всю статистику и графики для теста на равные отклонения
Сводный график показывает интервалы для тестов равных дисперсий. Тип интервалов, отображаемых Minitab, зависит от того, выбрали ли вы параметр Использовать тестовые и доверительные интервалы, основанные на нормальном распределении на вкладке «Данные» и количестве групп в ваших данных.
Если вы не выбрали вариант Использовать тестовые и доверительные интервалы на основе нормального распределения, на сводной диаграмме отображаются интервалы сравнения, основанные на методе множественных сравнений.
Если вы выбрали Использовать тест и доверительные интервалы на основе нормального распределения и имеете две группы, Minitab выполнит F-тест. Если у вас 3 или более групп, Minitab выполнит тест Бартлетта. Для любого из этих тестов на графике также отображаются доверительные интервалы Бонферрони.
Множественные интервалы сравнения
Если вы не отметили Использовать тестовые и доверительные интервалы, основанные на нормальном распределении, сводный график отображает несколько интервалов сравнения.
Если для вас допустимо использование p-значения множественного сравнения, вы можете использовать доверительные интервалы множественного сравнения, чтобы идентифицировать конкретные пары групп, которые имеют статистически значимое различие.Если два интервала не перекрываются, разница между соответствующими стандартными отклонениями статистически значима.
Если свойства ваших данных требуют использования метода Левена, не оценивайте доверительные интервалы на сводном графике.
Для получения информации о том, какой тест использовать, перейдите в раздел «Тесты».
Доверительные интервалы Бонферрони
Если вы выбрали Использовать тестовые и доверительные интервалы, основанные на нормальном распределении, на сводном графике отображаются доверительные интервалы Бонферрони.
Используйте доверительные интервалы Бонферрони, чтобы оценить стандартное отклонение каждой генеральной совокупности на основе вашего категориального фактора (факторов). Каждый доверительный интервал представляет собой диапазон вероятных значений стандартного отклонения соответствующей совокупности. Доверительные интервалы Бонферрони корректируются для поддержания одновременного уровня достоверности.
Каждый доверительный интервал представляет собой диапазон вероятных значений стандартного отклонения соответствующей совокупности. Доверительные интервалы Бонферрони корректируются для поддержания одновременного уровня достоверности.
Контроль одновременного уровня достоверности особенно важен при оценке нескольких доверительных интервалов. Если вы не контролируете одновременный уровень достоверности, вероятность того, что хотя бы один доверительный интервал не содержит истинного стандартного отклонения, возрастает с увеличением количества доверительных интервалов.
Для получения дополнительной информации перейдите к разделам «Определение индивидуальных и одновременных уровней достоверности при множественных сравнениях» и «Что такое метод Бонферрони?».
Примечание
Доверительные интервалы Бонферрони нельзя использовать для определения различий между группами. Используйте p-значение в выходных данных, чтобы определить, являются ли какие-либо различия между стандартными отклонениями статистически значимыми.
Устный перевод
На этом сводном графике нет статистически значимых различий между группами, поскольку все интервалы множественного сравнения перекрываются.
9.3 Интерпретация вывода
9.3 Интерпретация вывода
Первая таблица, Group Statistics , показана на рисунке 9.5. Эта таблица включает описательную статистику для каждой группы. В частности, таблица включает количество случаев (N), среднюю оценку эффективности лидера, стандартное отклонение и расчетную стандартную ошибку среднего (стандартное отклонение, деленное на N).
Наибольший интерес представляют средние оценки успеваемости у мужчин (5.68) и для женщин (6.14). У вас может возникнуть соблазн заключить, что это означает, что у женщин средние показатели успеваемости значительно выше, чем у мужчин. Однако это было бы преждевременным — на самом деле, весь смысл t-теста состоит в том, чтобы определить, действительно ли это различие (статистически значимое) или оно может быть отнесено к случайности.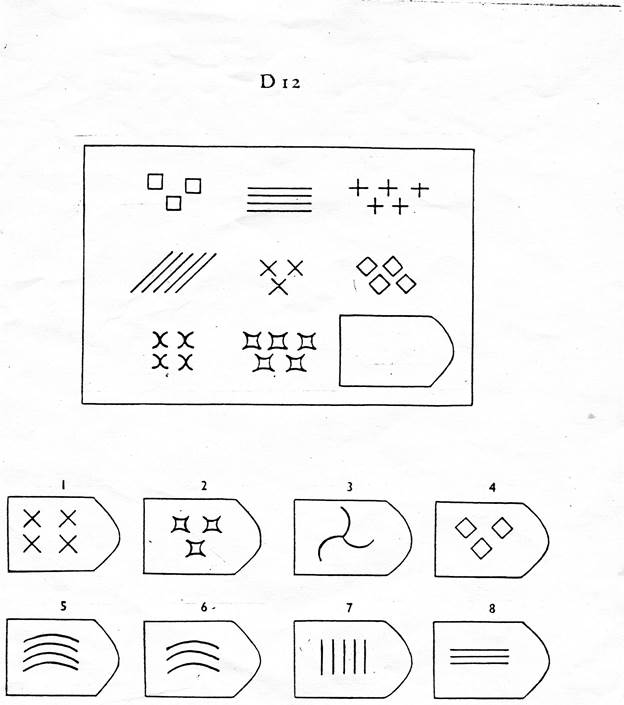 Для этого нам нужно изучить следующую таблицу, Independent Samples Test (рисунок 9.6).
Для этого нам нужно изучить следующую таблицу, Independent Samples Test (рисунок 9.6).
- 9.3a Проверка на однородность дисперсии
Первые два столбца, обозначенные как Тест Левена на равенство вариаций , обеспечивают проверку одного из допущений t-критерия, т. Е. О том, что дисперсия в двух группах одинакова (т. Е. Сходна или однородна). Если это предположение нарушается в данных, необходимо произвести статистическую корректировку. Статистика F в первом столбце и ее вероятность во втором столбце ( Sig. , сокращение значимости) обеспечивают этот тест.Если вероятность значения F (т. Е. Sig. ) меньше или равна 0,05 , то дисперсии в сравниваемых группах различны, и условие однородности дисперсии не был доволен.
Результаты теста F определяют, следует ли использовать равные отклонения, предполагаемые строк, или равные отклонения, не предполагаемые строк, при оценке t-статистики.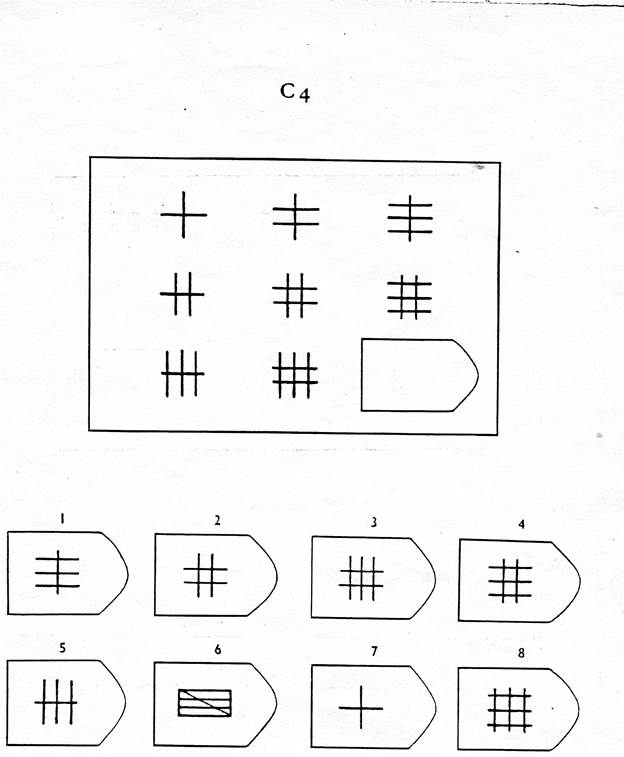 Правило принятия решения для определения, какие строки использовать, выглядит следующим образом:
Правило принятия решения для определения, какие строки использовать, выглядит следующим образом:
- Если отклонения для двух групп равны (т.е.e, Sig. > .05 ), затем используйте вывод в строке Равные отклонения, предполагаемые строк. Эти строки представляют собой более традиционный метод оценки значения t на основе степеней свободы ( df ), равных общему количеству баллов минус 2 (это метод, который описан в большинстве учебников по вводной статистике или методам исследования) .
- Если отклонения для двух групп значительно различаются (т.е.e, Sig. <.05 ), затем используйте результат в строке Равные отклонения не предполагаются . Оценка статистики t в этой строке основана на скорректированных степенях свободы, которые учитывают несходные отклонения в двух группах.
Поскольку вероятность ( Sig. = .000) для значения F меньше .05 . Таким образом, отклонения двух групп не равны , и поэтому следует использовать вывод в строке равных отклонений , а не , предполагаемой .
= .000) для значения F меньше .05 . Таким образом, отклонения двух групп не равны , и поэтому следует использовать вывод в строке равных отклонений , а не , предполагаемой .
- 9.3b Проверка нулевой гипотезы: интерпретация значимости t-значения
Чтобы определить, значительна ли разница в производительности между мужчинами и женщинами, нам нужно посмотреть в столбцы с пометкой t-тест на равенство средних значений . В настоящее время нас интересует только полученное t-значение и его вероятность, которые можно увидеть в столбцах, обозначенных t и Sig. (Двусторонний) . Глядя на строку Equal variance , а не , предполагающую , мы видим значение t , равное 1.46. Вероятность в Sig. (Двусторонний) столбец в столбце ( p = 0,146) больше 0,05, что означает, что нам нужно сохранить нулевую гипотезу об отсутствии различий и сделать вывод о том, что не было значительной разницы в лидерских качествах между мужчинами и женщинами. Сотрудники EZ.
Сотрудники EZ.
Следующее предложение показывает, как эти результаты будут записаны в формате APA.
Результаты показывают, что не было значительной разницы в производительности между женщинами и мужчинами, t (195) = 1.46, стр. = 0,15. Таким образом, средний результат у женщин ( M = 6,14, SD = 1,94) существенно не отличался от такового у мужчин ( M = 5,69, SD = 2,74).
Обратите внимание, что хотя исследователи обычно заинтересованы в обнаружении «значительных различий», иногда отсутствие значительного различия имеет либо теоретическое, либо практическое значение. Это, безусловно, так. В частности, эти результаты показывают, что нет достоверной разницы в производительности между мужчинами и женщинами в EZ Manufacturing.Это важно, потому что эта информация может быть полезна для успокоения беспокойства руководителей высшего звена, которые могут придерживаться стереотипа о том, что женщины менее способны по сравнению с мужчинами в ситуациях лидерства.
- 9.3c Дополнительная информация в t-таблице
В t-таблице есть дополнительная информация, которая может быть вам полезна. Первая — это средняя разница . Это просто разница между двумя средствами. Стандартная ошибка средней разницы — знаменатель, используемый при вычислении t-статистики.Наконец, 95% доверительный интервал для разницы состоит из двух чисел, обозначающих нижнюю и верхнюю границы доверительного интервала. Мы можем быть уверены на 95% в том, что разница между двумя средними находится между нижней и верхней границей.
Как уже упоминалось, существует множество других гипотез, которые мы могли бы проверить с помощью t-критерия независимых выборок на данных нашего исследования EZ Manufacturing. Упражнение в конце главы иллюстрирует одно из них, и вам предлагается изучить другие самостоятельно.В следующей главе мы обсудим аналогичный подход к проверке гипотез с использованием коррелированного t-критерия .
критериев статистической значимости
критерия статистической значимостиPPA 696 МЕТОДЫ ИССЛЕДОВАНИЯ
ИСПЫТАНИЯ НА ЗНАЧЕНИЕ
Что такое тесты на значимостьшагов в статистическом тестировании Значение
1) Выскажите гипотезу исследования
2) Сформулируйте нулевую гипотезу
3) Ошибки типа I и типа II
Выберите вероятность уровня ошибки (альфа-уровень)
4) Тест хи-квадрат
Расчет хи-квадрат
степеней свободы
Распределительные столы
Интерпретировать результаты
5) Т-тест
Рассчитать Т-тест
степеней свободы
Распределительные столы
Интерпретировать результаты
Отчетные испытания статистических Значение
Заключительные комментарии
Какие тесты значимости
- Два вопроса возникают о любых предполагаемых отношениях между двумя переменными:
- 1) какова вероятность того, что связь существует;
- 2) если да, то насколько сильна связь
Тесты на статистическую значимость используются для решения вопрос: какова вероятность того, что мы думаем об отношениях между двумя переменными — это действительно случайность?
Если мы выбрали много выборок из одной и той же совокупности, найдем ли мы такую же взаимосвязь между этими двумя переменными в каждый образец? Если бы мы могли провести перепись населения, мы бы тоже обнаруживают, что эта связь существует в популяции, из которой был нарисован? Или наш поиск произошел случайно?
Тесты на статистическую значимость говорят нам, что вероятность состоит в том, что отношения, которые, как мы думаем, мы нашли, обусловлены только к случайному совпадению.Они говорят нам, какова вероятность того, что мы будем делает ошибку, если мы предполагаем, что обнаружили связь.
Мы никогда не можем быть полностью уверены в том, что отношения
существует между двумя переменными. Слишком много источников ошибок, чтобы их
контролируемые, например, ошибка выборки, предвзятость исследователя, проблемы с
надежность и обоснованность, простые ошибки и т. д.
д.
Но, используя теорию вероятностей и нормальную кривую, мы можем оценить вероятность ошибиться, если предположим, что наш вывод отношения верны.Если вероятность ошибиться мала, то мы говорим, что наше наблюдение за взаимоотношениями является статистически значимым находка.
Статистическая значимость означает наличие хорошего шанс, что мы правы, обнаружив, что существует связь между две переменные. Но статистическая значимость — это не то же самое, что практическая значение. Мы можем получить статистически значимый результат, но последствия этого открытия могут не иметь практического применения.Исследователь всегда должен проверять статистическую и практическую значимость любых результатов исследования.
Например, мы можем обнаружить, что существует статистически
значимая взаимосвязь между возрастом гражданина и удовлетворенностью
городские службы отдыха. Возможно, пожилые люди удовлетворены на 5% меньше
чем более молодые жители с городскими службами отдыха. Но это 5% большой
достаточно ли разницы, чтобы беспокоиться?
Но это 5% большой
достаточно ли разницы, чтобы беспокоиться?
Часто, когда различия небольшие, но статистически
значительный, это связано с очень большим размером выборки; в образце меньшего
размера, различия не будут статистически значимыми.
шагов в тестировании для Статистическая значимость
1) Сформулируйте гипотезу исследования2) Сформулируйте нулевую гипотезу
3) Выберите уровень вероятности ошибки (уровень альфа)
4) Выберите и вычислите критерий статистической значимости
5) Интерпретировать результаты
1) Выскажите гипотезу исследования
- Гипотеза исследования утверждает ожидаемые отношения между двумя переменными.Это может быть указано в общих чертах или может включать размеры направления и величины. Например,
- Общие: Продолжительность программы профессионального обучения зависит от скорости трудоустройства обучающихся.
-
Направление: Чем длиннее программа обучения, тем выше ставка работы
размещение стажеров.

- Масштаб: более длительные программы обучения позволят вдвое больше учеников вакансии как более короткие программы.
- Общие: на оплату аспиранта влияет пол.
- Направление: Ассистентам-мужчинам платят больше, чем выпускницам. помощники.
- Величина: женщинам-ассистентам-выпускникам платят менее 75% от зарплаты мужчин. аспирантам платят.
2) Сформулируйте нулевую гипотезу
- Нулевая гипотеза обычно утверждает, что нет никакой связи между двумя переменными.Например,
- Нет никакой связи между продолжительностью программы профессионального обучения. и уровень трудоустройства стажеров.
- На оплату труда ассистента не влияет пол.
- Нулевая гипотеза также может утверждать, что отношение Предложенная в исследовании гипотеза не соответствует действительности. Например,
-
Более длительные программы обучения приведут к тому, что в
вакансии как более короткие программы.

- Женщинам-ассистентам-выпускникам платят не менее 75% или больше от зарплаты выпускников-мужчин. помощники оплачиваются.
3) ОШИБКИ ТИПА I И ТИПА II
Даже в самом лучшем исследовательском проекте всегда есть возможность (надеюсь, небольшая) того, что исследователь сделает ошибку относительно отношения между двумя переменными. Есть два возможных ошибки или ошибки. Первая называется ошибкой типа I.Это происходит, когда
исследователь предполагает, что связь существует, когда на самом деле доказательства
в том, что это не так. В случае ошибки типа I исследователь должен принять
нулевую гипотезу и отклонить исследовательскую гипотезу, но происходит обратное.
Вероятность совершения ошибки типа I называется альфой.
В случае ошибки типа I исследователь должен принять
нулевую гипотезу и отклонить исследовательскую гипотезу, но происходит обратное.
Вероятность совершения ошибки типа I называется альфой.
Вторая называется ошибкой типа II. Это происходит когда исследователь предполагает, что отношений не существует, когда на самом деле свидетельство того, что это так.В случае ошибки типа II исследователь должен отвергнуть нулевую гипотезу и принять гипотезу исследования, но происходит обратное. Вероятность совершения ошибки типа II называется бета.
Как правило, уменьшение возможности совершения ошибка типа I увеличивает вероятность совершения ошибки типа II и наоборот, уменьшая вероятность совершения ошибки типа II. увеличивает вероятность совершения ошибки типа I.
Обычно исследователи стараются свести к минимуму ошибки типа I,
потому что, когда исследователь предполагает, что отношения существуют, когда действительно
нет, может быть хуже, чем раньше. При ошибках типа II исследователь
упускает возможность подтвердить, что отношения существуют, но нет
хуже, чем раньше.
При ошибках типа II исследователь
упускает возможность подтвердить, что отношения существуют, но нет
хуже, чем раньше.
- В этом примере, какой тип ошибки вы бы предпочли зафиксировать?
- Гипотеза исследования: Эль-Ниньо снизило урожайность в графстве X, он имеет право на государственную помощь при стихийных бедствиях.
- Нулевая гипотеза: Эль-Ниньо не снизило урожайность в графстве X, он не имеет права на государственную помощь при стихийных бедствиях.
Если допущена ошибка типа II, то Округ
считается неприемлемым для оказания помощи при стихийных бедствиях, когда действительно имеет право
(нулевая гипотеза должна быть принята, но она отвергается). Правительство
могут не тратить средства на помощь при стихийных бедствиях, когда это необходимо, и фермеры
к банкротству.
Правительство
могут не тратить средства на помощь при стихийных бедствиях, когда это необходимо, и фермеры
к банкротству.
- В этом примере, какой тип ошибки вы бы предпочли зафиксировать?
- Гипотеза исследования: новый препарат лучше лечит сердечные приступы, чем старый наркотик
- Нулевая гипотеза: новый препарат лечит сердечные приступы не лучше, чем старый наркотик
Если допущена ошибка типа II, то новое лекарство
считается не лучше, когда действительно лучше (нулевая гипотеза
должно быть отклонено, но принято). Людей нельзя лечить
новый препарат, хотя им было бы лучше, чем со старым.
ВЫБЕРИТЕ ВЕРОЯТНОСТЬ УРОВНЯ ОШИБКИ (АЛЬФА-УРОВЕНЬ)
Исследователи обычно указывают вероятность совершения ошибка типа I, которую они готовы принять, т. е.е., значение альфа.
В социальных науках большинство исследователей выбирают альфа = 0,05. Это означает
что они готовы согласиться с вероятностью 5% создания типа I
ошибка, предполагающая, что связь между двумя переменными существует, когда она
на самом деле нет. Однако в исследованиях, связанных с общественным здравоохранением, альфа
0,01 нет ничего необычного. Исследователи не хотят, чтобы вероятность
ошибались более чем в 0,1% случаев или один раз из тысячи.
е.е., значение альфа.
В социальных науках большинство исследователей выбирают альфа = 0,05. Это означает
что они готовы согласиться с вероятностью 5% создания типа I
ошибка, предполагающая, что связь между двумя переменными существует, когда она
на самом деле нет. Однако в исследованиях, связанных с общественным здравоохранением, альфа
0,01 нет ничего необычного. Исследователи не хотят, чтобы вероятность
ошибались более чем в 0,1% случаев или один раз из тысячи.
Если связь между двумя переменными
сильный (по оценке Меры ассоциации), и выбранный уровень
для альфы есть.05, то средний или малый размер выборки обнаружит это. Так как
отношения становятся слабее, и / или по мере того, как уровень альфа становится меньше,
Для достижения статистических результатов исследования потребуются более крупные выборки.
значение.
4) Тест хи-квадрат
Для номинальных и порядковых данных используется хи-квадрат как тест на статистическую значимость. Например, мы предполагаем, что там взаимосвязь между типом обучающей программы и Успешность трудоустройства обучаемых.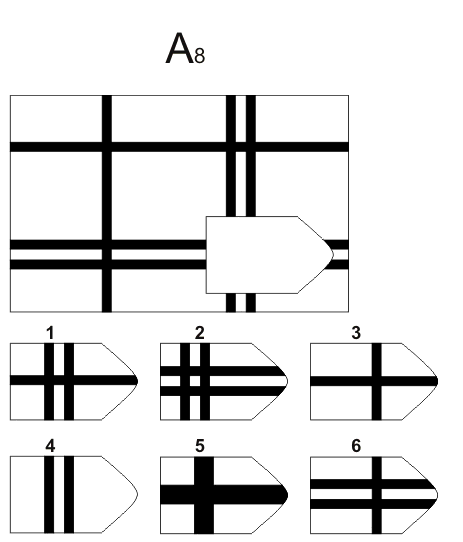 Мы собираем следующие данные:
Мы собираем следующие данные:
| Тип обучения: | Номер посещающих обучение |
| Профессиональное образование | 200 |
| Обучение навыкам работы | 250 |
| Итого | 450 |
| Есть ли место на работе? | Количество слушателей |
| Есть | 300 |
| Нет | 150 |
| Итого | 450 |
Для вычисления хи-квадрат таблица, показывающая сустав необходимо распределение двух переменных:
Таблица 1.Трудоустройство по типу обучения (наблюдаемая частота)
|
Есть ли место на работе? |
Тип обучения | ||
| Профессиональное
Образование |
рабочих навыков
Обучение |
Всего | |
| Есть | 175 | 125 | 300 |
| Нет | 25 | 125 | 150 |
| Итого | 200 | 250 | 450 |
Квадрат Хи вычисляется путем рассмотрения различных
части стола.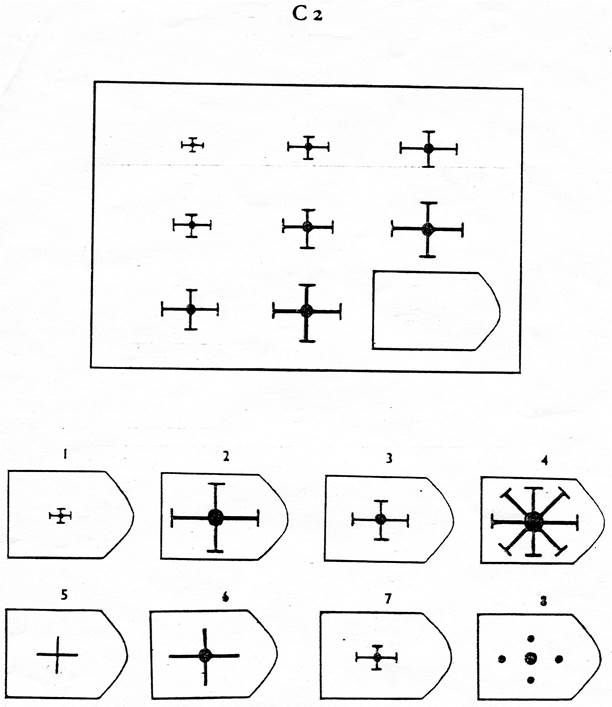 «Ячейки» таблицы — это квадраты посередине.
таблицы, содержащей полностью закрытые числа. Клетки
содержат частоты, которые встречаются в совместном распределении двух
переменные. Частоты, которые мы на самом деле находим в данных, называются
«наблюдаемые» частоты.
«Ячейки» таблицы — это квадраты посередине.
таблицы, содержащей полностью закрытые числа. Клетки
содержат частоты, которые встречаются в совместном распределении двух
переменные. Частоты, которые мы на самом деле находим в данных, называются
«наблюдаемые» частоты.
В этой таблице в ячейках указаны частоты для стажеров профессионального образования, устроившихся на работу (n = 175) и не устроившихся получить работу (n = 25), а также частота стажеров по профессиональным навыкам, получивших работу (n = 125) и не устроившиеся (n = 125).
Столбцы и строки «Итого» таблицы показывают предельные частоты. Граничные частоты — это частоты, которые мы бы обнаружили, если бы рассматривали каждую переменную отдельно. Например, мы видим в столбце «Всего», что 300 человек получили работу и 150 человек, которые этого не сделали. В строке «Итого» видно, что было 200 человек проходят профессиональное обучение и 250 человек работают по специальности подготовка.
Наконец, есть общее количество наблюдений
во всей таблице, названной Н.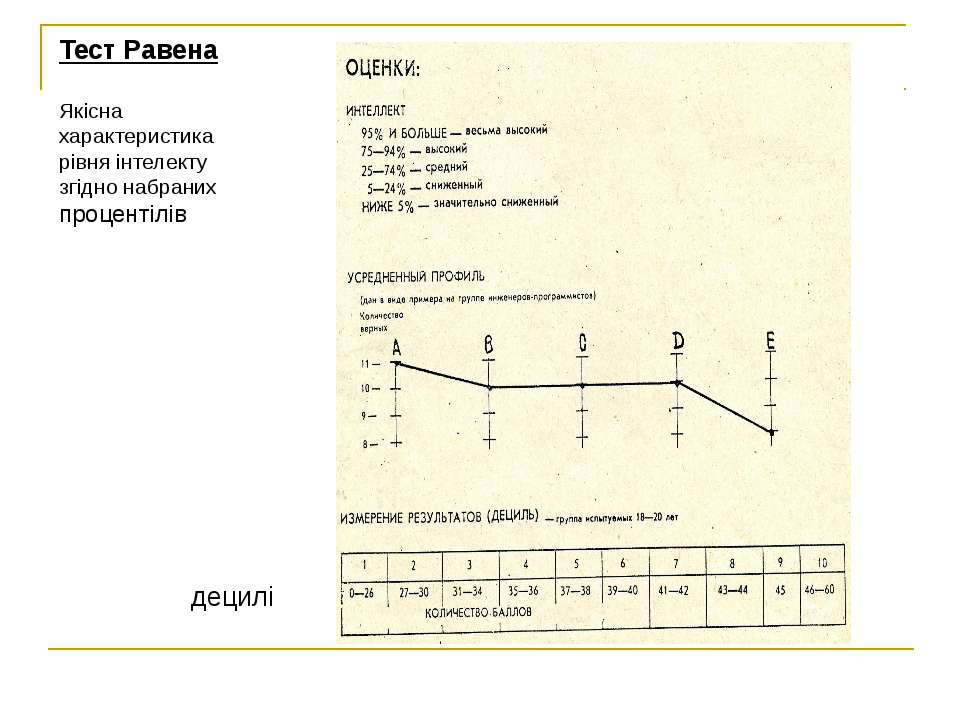 В этой таблице N = 450.
В этой таблице N = 450.
Вычислить хи-квадрат
1) отображать наблюдаемые частоты для каждой ячейки2) рассчитать ожидаемые частоты для каждой ячейки
3) вычислить для каждой ячейки ожидаемую минус наблюдаемую частоту в квадрате, деленное на ожидаемую частоту
4) все результаты для всех ячеек
Чтобы найти значение Хи-квадрат, сначала предположим что нет никакой связи между типом обучающей программы, которую вы посещали и был ли стажер устроен на работу.Если мы посмотрим на общую сумму столбца, мы видим, что работу нашли 300 из 450 человек, или 66,7% от общего числа людей. на тренинге устроился на работу. Мы также видим, что 150 человек из 450 не найти работу, или 33,3% от общего числа обучающихся не нашли работу.
Если не было связи между типами
программу посещали и успешно нашли работу, то мы ожидаем 66,7%
обучающихся обоих типов программ обучения на работу, и 33,3%
обоих типов программ обучения, чтобы не устроиться на работу.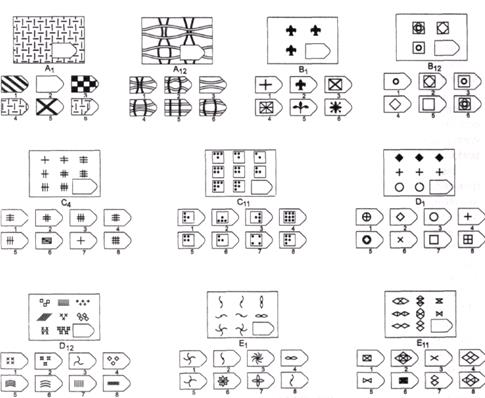
Первое, что делает Chi Square — вычисляет «ожидаемые» частоты для каждой ячейки. Ожидаемая частота — это частота которые мы ожидали бы появиться в каждой ячейке, если бы не было связи между типом программы обучения и трудоустройством.
Способ вычисления ожидаемой частоты соты — умножить сумму столбца для этой ячейки на сумму строки для этой ячейку и разделите на общее количество наблюдений для всей таблицы.
Для ячейки в верхнем левом углу умножьте 200 на 300 и разделите
на 450 = 133,3
Для ячейки нижнего левого угла умножьте 200 на 150 и разделите
на 450 = 66,7
Для ячейки в верхнем правом углу умножьте 250 на 300 и разделите
на 450 = 166,7
Для ячейки в правом нижнем углу умножьте 250 на 150 и разделите
на 450 = 83,3
Таблица 2. Трудоустройство по типу обучения (ожидаемая частота)
|
Есть ли место на работе? |
Тип обучения | ||
| Профессиональное
Образование |
рабочих навыков
Обучение |
Всего | |
| Есть | 133. 3 3 |
166,7 | 300 |
| Нет | 66,7 | 83,3 | 150 |
| Итого | 200 | 250 | 450 |
В этой таблице показано распределение «ожидаемых» частот, то есть частоты ячеек, которые мы ожидали бы найти, если бы не было связи между типом обучения и трудоустройством.
Обратите внимание, что Хи-квадрат не является надежным, если какая-либо ячейка в таблице непредвиденных обстоятельств имеет ожидаемую частоту менее 5.
Чтобы вычислить хи-квадрат, нам нужно сравнить оригинал,
наблюдаемые частоты с новыми ожидаемыми частотами. Для каждой ячейки
выполняем следующие расчеты:
a) Вычтите значение наблюдаемой частоты из значения
ожидаемая частота
б) возвести результат в квадрат
c) разделите результат на значение ожидаемой частоты
Для каждой ячейки выше,
| f e — f o | (f e — f o ) 2 | [(f e — f o ) 2 ] / f e | Результат |
(133.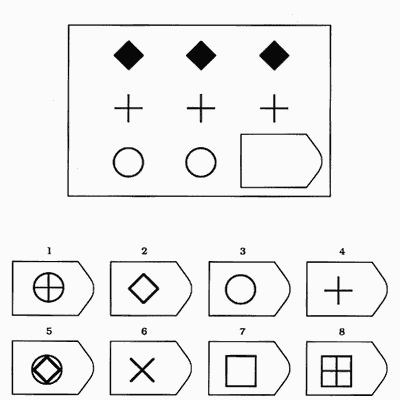 3 — 175) 3 — 175) |
(133,3 — 175) 2 | [(133,3 — 175) 2 ] / 133,3 | 13,04 |
| (66,7 — 25) | (66,7 — 25) 2 | [(66,7 — 25) 2 ] / 66,7 | 26,07 |
| (166,7 — 125) | (166,7 — 125) 2 | [(166,7 — 125) 2 ] / 166.7 | 10,43 |
| (83,3 — 125) | (83,3 — 125) 2 | [(83,3 — 135) 2 ] / 83,3 | 20,88 |
Чтобы вычислить значение хи-квадрат, сложите результаты для каждой ячейки — Итого = 70,42
СТЕПЕНИ СВОБОДЫ
Мы не можем интерпретировать значение статистики хи-квадрат. сам по себе.Вместо этого мы должны поместить это в контекст. Теоретически значение статистики хи-квадрат
нормально распространяется; то есть значение статистики хи-квадрат
выглядит как нормальная (колоколообразная) кривая.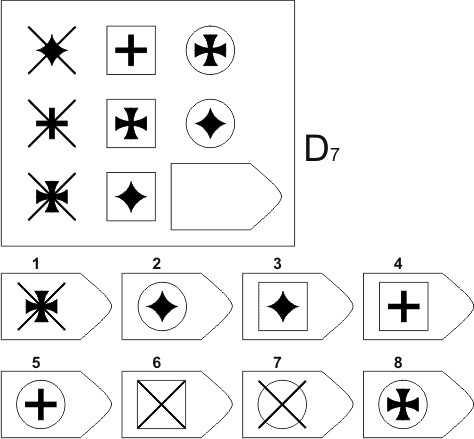 Таким образом, мы можем использовать свойства
нормальной кривой для интерпретации значения, полученного в результате нашего расчета
статистики Хи-квадрат.
Таким образом, мы можем использовать свойства
нормальной кривой для интерпретации значения, полученного в результате нашего расчета
статистики Хи-квадрат.
Если значение, которое мы получаем для Хи-квадрат, достаточно велико, то можно сказать, что это указывает на уровень статистической значимости при котором можно предположить, что связь между двумя переменными существует.
Однако, достаточно ли велико значение, зависит на две вещи: размер таблицы непредвиденных обстоятельств, из которой хи-квадрат статистика рассчитана; и уровень альфа, который мы выбрали.
Чем больше размер таблицы непредвиденных обстоятельств, тем должно быть больше значение Хи-квадрат, чтобы получить статистические значимость при прочих равных условиях. Точно так же более строгие уровень альфа, тем больше должно быть значение хи-квадрат, для достижения статистической значимости при прочих равных условиях.
Термин «степени свободы» используется для обозначения
размер таблицы непредвиденных обстоятельств, на которой значение хи-квадрат
статистика вычислена. Степени свободы рассчитываются как
произведение (количество строк в таблице минус 1) умноженное на (количество
столбцов в таблице минус).
Степени свободы рассчитываются как
произведение (количество строк в таблице минус 1) умноженное на (количество
столбцов в таблице минус).
- Для таблицы с двумя строками ячеек и двумя столбцами ячеек формула это:
- df = (2 — 1) x (2 — 1) = (1) x (1) = 1
- Для таблицы с двумя строками ячеек и тремя столбцами ячеек формула это:
- df = (3 — 1) x (2 — 1) = (2) x (1) = 2
- Для таблицы с тремя строками ячеек и тремя столбцами ячеек формула это:
- df = (3 — 1) x (3 — 1) = (2) x (2) = 4
При сообщении об уровне альфа обычно
сообщается как «меньше» некоторого уровня с использованием знака «меньше» или
<. Таким образом, это сообщается как p <0,05 или p <0,01; если ты не
сообщая точное значение p, например p =.04 или p = 0,22.
ТАБЛИЦЫ РАСПРЕДЕЛЕНИЯ
Как только у нас есть рассчитанное значение хи-квадрат статистика, степени свободы для таблицы непредвиденных обстоятельств и желаемый уровень для альфы, мы можем найти нормальное распределение для Чи Квадрат в таблице. В текстах статистики доступно множество таблиц. для этого.Найдите в таблице степени свободы (обычно перечислены в столбце внизу страницы).Далее найдите желаемый уровень альфа (обычно перечисляются в строке вверху страницы). Найти пересечение степеней свободы и уровня альфа, и что — это значение, которому вычисленный хи-квадрат должен быть равен или превышать для достижения Статистическая значимость.
Например, для df = 2 и p = 0,05 значение хи-квадрат должно
равно или превышает 5,99, чтобы указать, что отношения между двумя
переменные, вероятно, не случайно. Для df = 4 и p =.05, Площадь Чи
должно быть равно или превышать 9,49.
Для df = 4 и p =.05, Площадь Чи
должно быть равно или превышать 9,49.
ИНТЕРПРЕТАЦИЯ РЕЗУЛЬТАТОВ
Если вычисленное значение для хи-квадрат равно или превышает значение, указанное в таблице для данного уровня альфа и градусов свободы, то исследователь может предположить, что наблюдаемая связь между двумя переменными существует (на заданном уровне вероятности ошибки или альфа) и отклонить нулевую гипотезу. Это дает поддержку к исследовательской гипотезе. Вычисленное значение Хи-квадрат на заданном уровне.
альфа и с заданной степенью свободы, это тип измерения «прошел-не прошел».
Это не похоже на меру ассоциации, которая может варьироваться от 0,0 до (плюс
или минус) 1.0, и которые можно интерпретировать в любой точке распределения.
Либо вычисленное значение хи-квадрат достигает необходимого уровня для
статистическая значимость или нет.
- Важно отметить, что Chi Square, как и другие статистические тесты, значение:
- 1) не указывает на силу связи между двумя переменными
- 2) не указывает направление связи между двумя переменными
- 3) не указывает вероятность ошибки типа I
- 4) не учитывает достоверность и обоснованность исследования
- 5) не предоставляет абсолютных убедительных доказательств наличия родства
- 1) сформулируйте гипотезу исследования:
- Существует связь между типом посещаемой программы обучения и Успех трудоустройства стажеров
- 2) сформулируйте нулевую гипотезу:
-
Нет никакой связи между типом обучающей программы, которую вы посещали.
 и успешность трудоустройства стажеров
и успешность трудоустройства стажеров - 3) рассчитать критерий статистической значимости
- Хи-квадрат = 70.42
- 4) вычислить степени свободы по таблице непредвиденных обстоятельств
- df = 1
- 5) выбираем уровень альфа
- р = 0,05
- 6) найдите значение хи-квадрат в таблице при p = 0,05 и df = 1 .
- Хи-квадрат = 3,84
- 7) интерпретируем результат
- Вычисленное значение Хи-квадрат (70,42) превышает значение в таблице. для p =.05 и df = 1 (хи-квадрат = 3,84). Следовательно, мы можем отклонить нулевой гипотезы (с вероятностью ошибки 5%) и принять исследовательскую гипотезу что существует связь между типом посещаемой программы обучения и успешность трудоустройства стажеров.
Напомним, для приведенного выше примера:
Использование T-тестов
- T-тесты — это тесты на статистическую значимость, которые используются с данными уровня интервала и отношения. Т-тесты можно использовать в нескольких различные виды статистических тестов:
- 1) проверить, есть ли различия между двумя группами на одном и том же переменная, основанная на среднем (среднем) значении этой переменной для каждой группы; например, получают ли учащиеся частных школ более высокие баллы по тесту SAT чем учащиеся государственных школ?
- 2) проверить, больше ли среднее (среднее) значение группы, чем какой-то стандарт; например, средняя скорость автомобилей на автострадах в Калифорния выше 65 миль в час?
- 3) проверить, имеет ли одна и та же группа разные средние (средние) баллы по разные переменные; например, те же клерки более продуктивны Компьютеры IBM или Macintosh?
Чтобы вычислить значение t,
а) сформулируйте гипотезу исследования;б) сформулируйте нулевую гипотезу;
c) указать, будет ли t-тест односторонним или двусторонним.
 тест на значимость
тест на значимость
г) выберите уровень альфа
e) вычислить t
Чтобы вычислить значение t,
- а) сформулируйте гипотезу исследования;
- Средняя заработная плата ассистентов-мужчин выше средней заработная плата аспирантов-женщин в ЦГСУ.
- б) сформулируйте нулевую гипотезу;
- Нет разницы в средней заработной плате выпускников мужского и женского пола. помощники в CSULB.
- в) выбрать уровень альфа
- выберите значение для альфы, например p = 0,05, p = 0,01 или p = 0,001
Как и другие статистические данные, t-критерий имеет распределение
что приближается к нормальному распределению, особенно если размер выборки
больше 30.Поскольку мы знаем свойства нормальной кривой, мы
может ли он сказать нам, насколько далеко от среднего значения распределения, рассчитанного нами
t-рейтинг.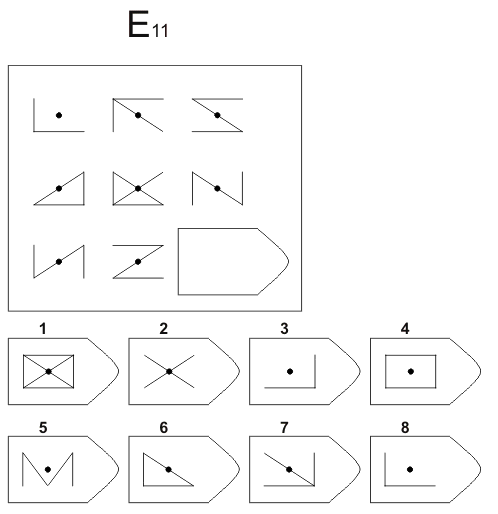
Нормальная кривая распределена около нулевого среднего, со стандартным отклонением, равным единице. Т-балл может падать по нормальной кривой либо выше, либо ниже среднего; то есть либо плюс, либо минус какой-то стандарт единицы отклонения от среднего.
T-балл должен быть далеко от среднего, чтобы достичь статистической значимости.То есть он должен сильно отличаться от значение среднего распределения, то, что имеет только низкий вероятность возникновения случайно, если нет связи между две переменные. Если мы выбрали значение p = 0,05 для альфы, мы смотрим для значения t, которое попадает в крайние 5% распределения.
Если у нас есть гипотеза, которая утверждает ожидаемое
направление результатов, например, что зарплата ассистентов-мужчин
выше, чем зарплата ассистентов-выпускников женского пола, то мы ожидаем, что
t-показатель попадет только в один конец нормального распределения.Мы ожидаем
расчетный t-показатель попадет в крайние 5% распределения.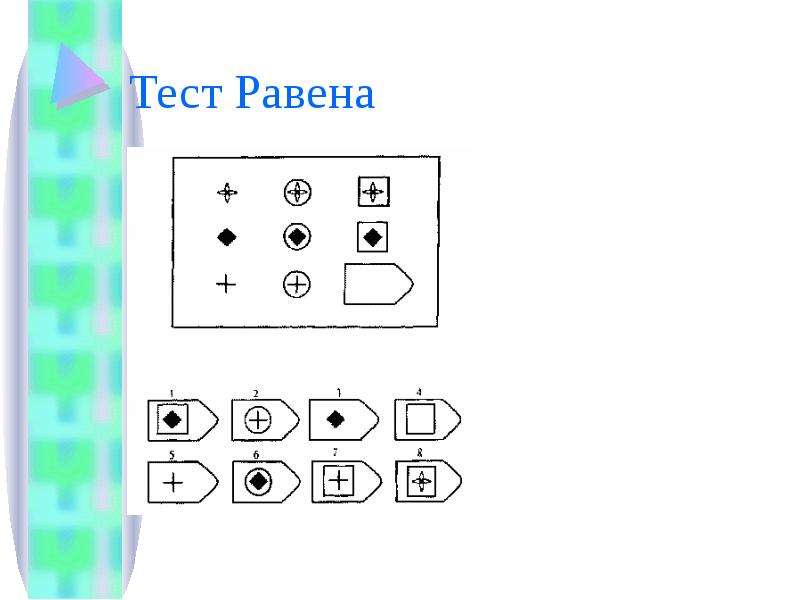
Однако, если у нас есть гипотеза, что между двумя группами есть разница, но не указано, какая ожидается, что группа получит более высокий балл, чем рассчитанный t-балл может попасть в любой конец нормального распределения. Например, наша гипотеза может быть, мы ожидаем найти разницу между средними зарплатами мужчин и женщин-ассистентов (но мы не знаем, какие будет выше или будет ниже).
Для гипотезы, не указывающей направления, нам нужно использовать «двусторонний» t-критерий. То есть мы должны искать значение t, которое попадает в один из крайних концов («хвостов») распределения. Но поскольку t может попасть в любой из хвостов, если мы выберем p = 0,05 в качестве альфа, мы необходимо разделить 5% на две части по 2-1 / 2% каждая. Итак, двусторонний тест требует, чтобы t принял более экстремальное значение, чтобы достичь статистической значимости чем односторонний тест t.
e) вычислить t
T-балл рассчитывается путем сравнения среднего
значение некоторой переменной, полученное для двух групп; расчет также включает
дисперсия каждой группы и количество наблюдений в каждой группе. Например,
Например,
Таблица 3. Заработная плата мужчин и женщин-выпускников в CSULB
| Ассистенты высшего звена | Ассистенты-выпускницы | |
| Количество
наблюдений |
403 |
132 |
| Среднее | $ 17095 | $ 14 885 |
| Стандартный
Отклонение |
6329 |
4676 |
| Разница | 40045241 | 21864976 |
Для расчета t,
1) вычтите среднее значение второй группы из среднего значения первой
группа
2) вычислить для каждой группы дисперсию, деленную на количество
наблюдения минус 1
3) сложите вместе результаты, полученные для каждой группы на втором этапе.
4) извлеките квадратный корень из результатов третьего шага
5) разделите результаты первого шага на результаты четвертого шага.
Например,
- 1) вычесть среднее значение второй группы из среднего значения первой группы
- 17095-14885 = 2210
- 2) рассчитайте для каждой группы дисперсию, деленную на количество наблюдений. минус 1
- Ассистенты-мужчины:
- [40056241 / (403-1)] = [40056241 / (402)] = 99642
- Стажеры-выпускницы:
- [21864976 / (132-1)] = [21864976 / (131)] = 166908
- 3) сложите результаты, полученные для каждой группы на втором этапе
- 99642 + 166908 = 266550
- 4) извлеките квадратный корень из результатов третьего шага
- квадратный корень из 266550 = 516.28
- 5) разделите результаты первого шага на результаты четвертого шага
- 2210 / 516,28 = 4,28
е) вычислить степени свободы
г) найдите значение в таблице
ч) интерпретировать значение t
Степени свободы
-
Степени свободы для t-критерия вычисляются путем сложения
количество наблюдений для каждой группы, а затем вычитание числа
два (потому что есть две группы).
 Например, (403 + 132 — 2)
= 533
Например, (403 + 132 — 2)
= 533
Распределение Т
Значения t печатаются в таблицах в большинстве статистических данных. тексты. Значения степеней свободы указаны в столбце внизу. стороне, а значения альфа (p-значение) перечислены в строке через вершина. Существуют разные таблицы для односторонних и двусторонних тестов. г.- Найдите правильную таблицу количества решек. потом найти пересечение степеней свободы и значение альфа в таблице.Это значение должно соответствовать вычисленному t-баллу. равно или больше, чтобы указать статистическую значимость.
- Для одностороннего теста t, с df = 533 и p = 0,05, t должно быть равно или превышать 1,645.
- Для двустороннего теста t с df = 533 и p = 0,05 t должно быть равно или превышать 1.960.
Интерпретировать значение t
Если вычисленный t-рейтинг равен или превышает значение t, указанного в таблице, то исследователь может сделать вывод, что существует статистически значимая вероятность того, что связь между две переменные существуют и не являются случайными, и отклонить нуль гипотеза.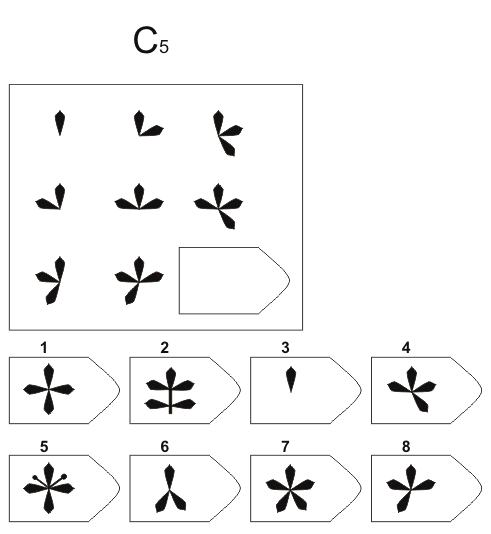 Это подтверждает гипотезу исследования.
Это подтверждает гипотезу исследования.
В этом примере вычисленный t-показатель 4,28 превышает табличное значение t, поэтому мы можем отклонить нулевую гипотезу об отсутствии связи между полом ассистента и заработной платой ассистента, и вместо этого принять гипотезу исследования и сделать вывод, что существует связь между полом ассистента и заработной платой ассистента.
Помните, однако, что это только одна статистика,
на основе только одной выборки в определенный момент времени из одного исследовательского проекта.Это не абсолютное убедительное доказательство существования отношений, а скорее
поддержка исследовательской гипотезы. Это всего лишь одно свидетельство,
это необходимо учитывать вместе со многими другими доказательствами на
тот же предмет.
ОТЧЕТНОСТЬ ОБ ИСПЫТАНИЯХ СТАТИСТИЧЕСКИХ ЗНАЧЕНИЕ
-
В исследовательских отчетах тесты статистической значимости
сообщаются тремя способами. Во-первых, результаты теста могут быть сообщены
в текстовом обсуждении результатов.
 Включают:
Включают: - 1) гипотеза
- 2) использованная статистика теста и ее значение
- 3) степени свободы
- 4) значение альфа (p-значение)
- Например,
- Работники организаций с неавторитарным управлением Было установлено, что стили более удовлетворены работой, чем рабочие в организациях с авторитарным стилем управления (Chi Square = 50.57, df = 4, p <0,05).
- Средняя зарплата ассистентов-мужчин выше, чем у аспирантов. женщины-ассистенты (t = 4,28, df = 533, p <0,05).
- Не было обнаружено различий в показателях трудоустройства между профессиональным образованием. программы и программы рабочих навыков (Chi Square = 1,2, df = 1, p> 0,05).
Второй метод сообщения результатов испытаний
для статистической значимости — это отчет об испытании и его значении, степени
свободы и p-значение внизу таблицы непредвиденных обстоятельств или распечатки
с указанием данных, на которых были основаны расчеты.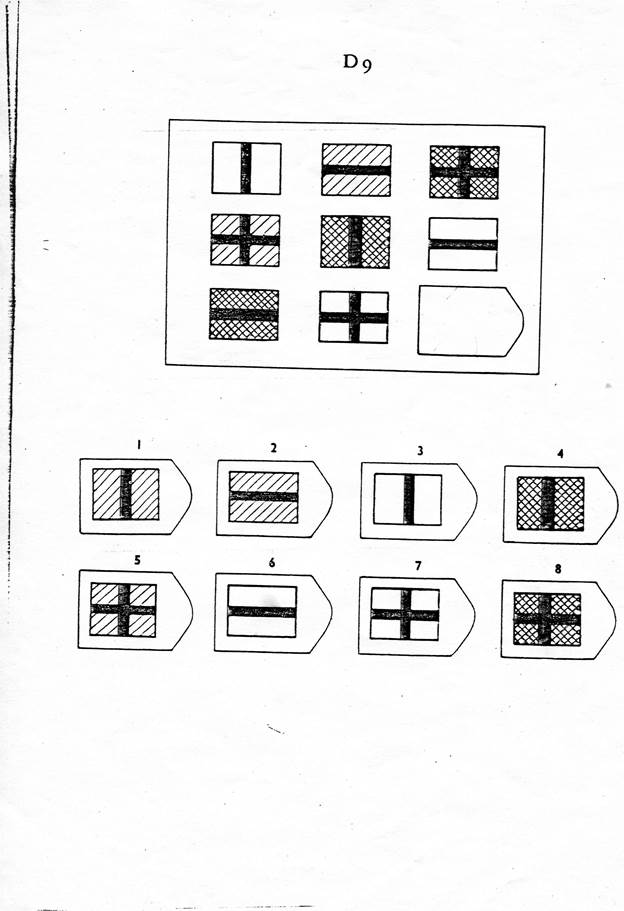
Таблица 1. Трудоустройство по типу обучения (наблюдаемая частота)
|
Есть ли место на работе? |
Тип обучения | ||
| Профессиональное
Образование |
рабочих навыков
Обучение |
Всего | |
| Есть | 175 | 125 | 300 |
| Нет | 25 | 125 | 150 |
| Итого | 200 | 250 | 450 |
Таблица 3. Заработная плата мужчин и женщин-выпускников в CSULB
| Мужчины-помощники выпускников | Ассистенты-выпускницы | |
| Количество
наблюдений |
403 |
132 |
| Среднее | $ 17095 | $ 14 885 |
| Стандартный
Отклонение |
6329 |
4676 |
| Разница | 40045241 | 21864976 |
 28, df = 533, p <0,05
28, df = 533, p <0,05
Третий способ сообщить о тестах статистической значимости — включить их в таблицы с результатами расширенного анализа. данных, включая ряд переменных. Например, вот несколько результаты исследования пожилых испаноязычных женщин в Эль-Пасо, Техас, и Лонг-Бич, CA.
Таблица 4. Характеристики участников семинара в возрасте 40 лет и старше
| Характеристики | Эль-Пасо
(N = 83) |
Лонг-Бич
(N = 131) |
стоимость
т |
| Средний возраст | 60.5 лет | 68,7 года | 2,1 * |
| Этническая самоидентификация
Американцы мексиканского происхождения |
97,2 |
89,7 |
0,9 |
| Предпочтительный язык
Только испанский |
68,5 |
52. |
3,2 ** |
** t значимо при p <0,01
Заключительные комментарии
Тесты на статистическую значимость используются для оценки вероятность того, что связь, наблюдаемая в данных, имела место только случайно; вероятность того, что переменные действительно не связаны в Население. Их можно использовать для фильтрации бесперспективных гипотез.Тесты на статистическую значимость используются, потому что они представляют собой общий критерий, который могут понять очень многие люди, и они передают важную информацию об исследовательском проекте это можно сравнить с результатами других проектов.
Однако они не гарантируют, что исследование был тщательно разработан и выполнен. Фактически, тесты на статистическую значимость могут вводить в заблуждение, потому что это точные цифры.Но у них нет отношений к практической значимости результатов исследования.
Наконец, всегда нужно использовать меры ассоциации.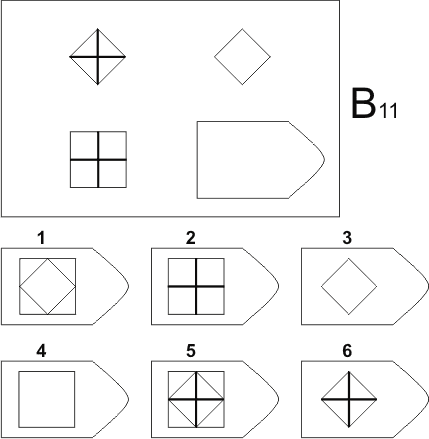 наряду с тестами на статистическую значимость. Последние оценивают
вероятность того, что отношения существуют; в то время как первые оценивают
сила (а иногда и направление) отношений. У каждого свои
использовать, и их лучше всего использовать вместе.
наряду с тестами на статистическую значимость. Последние оценивают
вероятность того, что отношения существуют; в то время как первые оценивают
сила (а иногда и направление) отношений. У каждого свои
использовать, и их лучше всего использовать вместе.
|
Интерпретация значимых результатов Автор (ы) Дэвид М.полоса дорогиПредварительные требования Введение к проверке гипотез, статистической Значимость, ошибки типа I и II, Одно- и двусторонние тестыЦели обучения
Когда
значение вероятности ниже уровня α, эффект
статистически значимо, и нулевая гипотеза отклоняется. Если нулевая гипотеза отклоняется, то альтернативная
к нулевой гипотезе (называемой альтернативой
гипотеза) принимается.Рассмотрим односторонний
тест в Джеймсе
Пример из практики Бонда: г-ну Бонду было дано 16 судебных разбирательств, на которых он
оценили, встряхнули или перемешали мартини, и вопрос
ли он лучше, чем шанс на эту задачу. Нулевая гипотеза
для этого одностороннего теста π ≤ 0,5, где π —
вероятность быть правым в любом данном испытании. Если это null
гипотеза отклоняется, то альтернативная гипотеза о том, что π
> 0. Теперь рассмотрим двусторонний тест, используемый в книге врачей. Пример реакции. Нулевая гипотеза: μ ожирение = μ среднее . Если эта нулевая гипотеза отклоняется, то существует есть две альтернативы: μ ожирение <μ среднее μ ожирение > μ среднее . Естественно, направление выборочного средства определяет
какая альтернатива принята. Если среднее значение выборки для страдающих ожирением
пациентов значительно ниже, чем среднее по выборке для среднего веса
пациентов, то следует сделать вывод, что среднее для популяции
у пациентов с ожирением ниже, чем в среднем по популяции
пациенты со средним весом. Есть много ситуаций, в которых маловероятно два состояния будут иметь точно такие же средние популяции.Для Например, аспирин и ацетаминофен практически невозможно обеспечивают точно такое же обезболивание. Поэтому даже перед проведением эксперимента по сравнению их эффективности, исследователь знает, что нулевая гипотеза точно не отличается ложно. Однако исследователь не знает, какой препарат предлагает больше облегчения. Если проверка различия значима, то устанавливается направление разницы.Этот момент также сделано в разделе о соотношении доверия интервалы и тесты значимости. ДополнительноВ некоторых учебниках неправильно сказано, что отказ от нулевого Гипотеза о том, что два демографических средних равны, не оправдывает вывод о том, какое среднее значение по совокупности больше.  Вместо этого они
говорят, что все, что можно сделать, это то, что средства населения различаются.Обоснованность вывода о направлении эффекта очевидна.
если вы заметили, что двусторонний тест на уровне 0,05 эквивалентен
на два отдельных односторонних теста каждый на уровне 0,025. В
тогда две нулевые гипотезы Вместо этого они
говорят, что все, что можно сделать, это то, что средства населения различаются.Обоснованность вывода о направлении эффекта очевидна.
если вы заметили, что двусторонний тест на уровне 0,05 эквивалентен
на два отдельных односторонних теста каждый на уровне 0,025. В
тогда две нулевые гипотезы
μ ожирение ≥ μ среднее μ ожирение ≤ μ среднее . Если первое из них отклонено, то вывод состоит в том, что среднее значение для пациентов с ожирением составляет ниже, чем у пациентов со средним весом.Если последний отклонено, то делается вывод, что среднее значение генеральной совокупности для у пациентов с ожирением выше, чем у пациентов со средним весом.
Пожалуйста, ответьте на вопросы: |
Статистика тестов | Определение, интерпретация и примеры
Статистика теста — это число, вычисленное на основе статистической проверки гипотезы.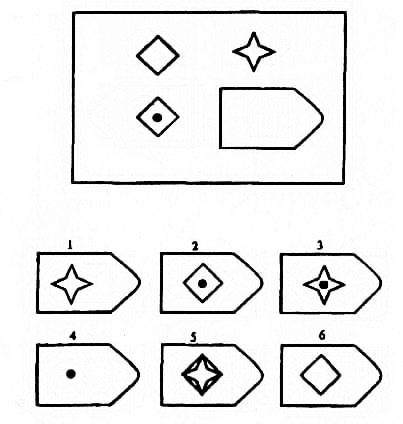 Он показывает, насколько точно ваши наблюдаемые данные соответствуют распределению, ожидаемому при нулевой гипотезе этого статистического теста.
Он показывает, насколько точно ваши наблюдаемые данные соответствуют распределению, ожидаемому при нулевой гипотезе этого статистического теста.
Статистика теста используется для вычисления значения p ваших результатов, помогая решить, следует ли отвергать вашу нулевую гипотезу.
Что такое статистика теста?
Тестовая статистика описывает, насколько близко распределение ваших данных соответствует распределению, предсказанному в рамках нулевой гипотезы используемого вами статистического теста.
Распределение данных показывает, как часто происходит каждое наблюдение, и может быть описано его центральной тенденцией и вариациями вокруг этой центральной тенденции. Различные статистические тесты предсказывают разные типы распределений, поэтому важно выбрать правильный статистический тест для вашей гипотезы.
Статистика теста суммирует ваши наблюдаемые данные в единое число с использованием центральной тенденции, вариации, размера выборки и количества переменных-предикторов в вашей статистической модели.
Как правило, статистика теста рассчитывается как образец в ваших данных (т. Е. Корреляция между переменными или разница между группами), деленная на дисперсию данных (т. Е. Стандартное отклонение).
Пример: вы проверяете зависимость между температурой и датой цветения определенного вида яблони. Вы используете набор долгосрочных данных, который отслеживает температуру и даты цветения за последние 25 лет путем случайной выборки 100 деревьев каждый год на экспериментальном поле.- Нулевая гипотеза: Нет корреляции между температурой и датой цветения.
- Альтернативная гипотеза: Существует корреляция между температурой и датой цветения.
Чтобы проверить эту гипотезу, вы выполняете регрессионный тест, который генерирует значение t в качестве тестовой статистики. Значение t сравнивает наблюдаемую корреляцию между этими переменными с нулевой гипотезой о нулевой корреляции.
Типы тестовой статистики
Ниже приводится сводка наиболее распространенных статистических данных тестов, их гипотез и типов статистических тестов, в которых они используются.
Различные статистические тесты будут иметь несколько разные способы вычисления этой тестовой статистики, но лежащие в основе гипотезы и интерпретации тестовой статистики остаются неизменными.
| Статистика теста | Нулевая и альтернативная гипотезы | Статистические тесты, в которых он используется |
|---|---|---|
| т -значение | Null: Средние значения двух групп равны
Альтернатива: Средние двух групп не равны |
|
| z -значение | Null: Средние значения двух групп равны
Альтернатива: Средние двух групп не равны |
|
| F -значение | Null: Вариация между двумя или более группами больше или равна вариации между группами
Альтернатива: Разница между двумя или более группами меньше, чем разница между группами |
|
| X 2 -значение | Null: Два образца независимы
Альтернатива: Два образца не являются независимыми (т. |
На практике вы почти всегда будете рассчитывать статистику вашего теста с помощью статистической программы (R, SPSS, Excel и т. Д.), Которая также вычислит значение p статистики теста. Однако формулы для расчета этой статистики вручную можно найти в Интернете.
Пример Чтобы проверить свою гипотезу о температуре и сроках цветения, вы выполняете регрессионный тест. Регрессионный тест генерирует:- коэффициент регрессии 0.36
- a t — значение, сравнивающее этот коэффициент с прогнозируемым диапазоном коэффициентов регрессии при нулевой гипотезе об отсутствии связи
t -значение регрессионного теста составляет 2,36 — это ваша статистика теста.
Какой у вас балл за плагиат?
Сравните свою статью с более чем 60 миллиардами веб-страниц и 30 миллионами публикаций.
- Лучшая программа проверки плагиата 2020 года
- Отчет о плагиате и процентное содержание
- Самая большая база данных о плагиате
Scribbr Проверка на плагиат
Интерпретация тестовой статистики
Для любой комбинации размеров выборки и количества переменных-предикторов статистический тест даст прогнозируемое распределение для статистики теста. Это показывает наиболее вероятный диапазон значений, которые будут иметь место, если ваши данные соответствуют нулевой гипотезе статистического теста.
Это показывает наиболее вероятный диапазон значений, которые будут иметь место, если ваши данные соответствуют нулевой гипотезе статистического теста.
Чем более экстремальна статистика вашего теста — чем дальше она находится до границы диапазона предсказанных значений теста — тем меньше вероятность того, что ваши данные могли быть сгенерированы при нулевой гипотезе этого статистического теста.
Согласие между вычисленной статистикой теста и прогнозируемыми значениями описывается значением p .Чем меньше значение p , тем меньше вероятность того, что ваша тестовая статистика возникла при нулевой гипотезе статистического теста.
Поскольку статистика теста генерируется из ваших наблюдаемых данных, это в конечном итоге означает, что чем меньше значение p , тем меньше вероятность того, что ваши данные могли бы иметь место, если бы нулевая гипотеза была верной.
Пример: Ваше вычисленное значение t , равное 2,36, далеко от ожидаемого диапазона значений t при нулевой гипотезе, а значение p <0. 01. Это означает, что вы ожидаете увидеть значение t больше или больше 2,36 менее чем в 1% случаев, если истинное соотношение между температурой и датами цветения равно 0.
01. Это означает, что вы ожидаете увидеть значение t больше или больше 2,36 менее чем в 1% случаев, если истинное соотношение между температурой и датами цветения равно 0.
Следовательно, статистически маловероятно, что ваши наблюдаемые данные могли иметь место при нулевой гипотезе. Используя порог значимости 0,05, вы можете сказать, что результат составляет статистически значимый .
Отчетность по статистике испытаний
Статистика тестаможет быть представлена в разделе результатов вашего исследования вместе с размером выборки, p -значением теста и любыми характеристиками ваших данных, которые помогут поместить эти результаты в контекст.
Нужно ли вам сообщать статистику теста, зависит от типа теста, о котором вы сообщаете.
| Тип испытания | Какие статистические данные сообщать |
| Корреляционные и регрессионные тесты |
|
| Тесты на разницу между группами |
|
При обследовании случайного подмножества 100 деревьев за 25 лет мы обнаружили статистически значимое значение ( p <0. 01) положительная корреляция между температурой и сроками цветения (R2 = 0,36, sd = 0,057).
01) положительная корреляция между температурой и сроками цветения (R2 = 0,36, sd = 0,057).
При сравнении рациона мыши A и диеты B мы обнаружили, что продолжительность жизни на диете A (среднее значение = 2,1 года; sd = 0,12) было значительно короче, чем продолжительность жизни на диете B (среднее значение = 2,6 года; sd = 0.1), со средней разницей в 6 месяцев (t (80) = -12,75; p < 0,01).
Часто задаваемые вопросы о тестовой статистике
- Что такое тестовая статистика?
-
Статистика теста — это число, вычисленное с помощью статистического теста.
 Он описывает, насколько далеко ваши наблюдаемые данные от нулевой гипотезы об отсутствии связи между переменными или отсутствии различий между группами выборки.
Он описывает, насколько далеко ваши наблюдаемые данные от нулевой гипотезы об отсутствии связи между переменными или отсутствии различий между группами выборки.Статистика теста показывает, насколько две или более группы отличаются от среднего значения генеральной совокупности или насколько отличается линейный наклон от наклона, предсказанного нулевой гипотезой. В разных статистических тестах используются разные статистические данные.
- Какие факторы влияют на статистику теста?
-
Статистика теста будет меняться в зависимости от количества наблюдений в ваших данных, степени изменчивости ваших наблюдений и того, насколько сильны лежащие в основе закономерности в данных.

Например, если один набор данных имеет более высокую изменчивость, а другой — более низкую, первый набор данных будет давать статистику теста, близкую к нулевой гипотезе, даже если истинная корреляция между двумя переменными одинакова в любом наборе данных.
- Что такое статистическая значимость?
-
Статистическая значимость — это термин, используемый исследователями, чтобы заявить, что маловероятно, что их наблюдения могли иметь место при нулевой гипотезе статистического теста.Значимость обычно обозначается значением p или значением вероятности.
Статистическая значимость произвольна — она зависит от порога или альфа-значения, выбранного исследователем.
 Наиболее распространенным порогом является p <0,05, что означает, что данные, вероятно, будут появляться менее чем в 5% случаев при нулевой гипотезе.
Наиболее распространенным порогом является p <0,05, что означает, что данные, вероятно, будут появляться менее чем в 5% случаев при нулевой гипотезе. Когда значение p падает ниже выбранного альфа-значения, мы говорим, что результат теста статистически значим.
Статистика IV: Интерпретация результатов статистических тестов | BJA Education
Это четвертая из серии статей журнала, посвященных использованию статистики в медицине. В предыдущем выпуске мы описали, как выбрать подходящий статистический тест. В этой статье мы рассмотрим это подробнее и обсудим, как интерпретировать результаты.
Подробнее о выборе подходящего статистического теста
Решение, какой статистический тест использовать для анализа набора данных, зависит от типа анализируемых данных (интервальные или категориальные, парные против непарных), а также от того, нормально ли распределены данные.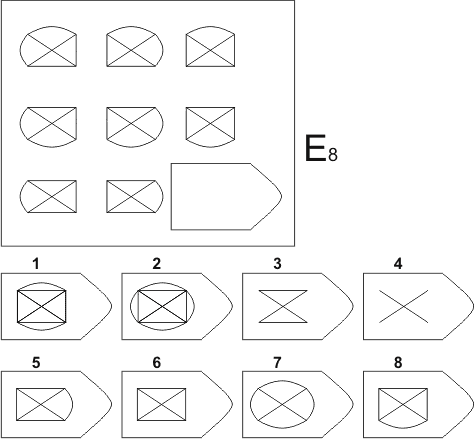 Интерпретация результатов статистического анализа основана на оценке и рассмотрении нулевой гипотезы, значений P , концепции статистической клинической значимости против , мощности исследования, статистических ошибок типов I и II, ловушек множественных сравнений, и один двусторонний тест против перед проведением исследования.
Интерпретация результатов статистического анализа основана на оценке и рассмотрении нулевой гипотезы, значений P , концепции статистической клинической значимости против , мощности исследования, статистических ошибок типов I и II, ловушек множественных сравнений, и один двусторонний тест против перед проведением исследования.
Оценка того, следует ли набор данных нормальному распределению
Из построения гистограммы или частотной кривой может быть очевидно, что данные следуют нормальному распределению.Однако при небольших размерах выборки ( n <20) из графика может быть не очевидно, что данные взяты из нормально распределенной совокупности. Данные могут быть подвергнуты формальному статистическому анализу для подтверждения нормальности с использованием одного или нескольких специальных тестов, обычно включенных в пакеты компьютерного программного обеспечения, таких как тест Шапиро-Уилкса. Такие тесты довольно надежны при больших размерах выборки ( n > 100). Однако выбор между параметрическим и непараметрическим статистическим анализом менее важен для выборок такого размера, поскольку оба анализа почти одинаково эффективны и дают схожие результаты.При меньшем размере выборки ( n <20) тесты на нормальность могут вводить в заблуждение. К сожалению, непараметрическому анализу небольших выборок недостает статистической мощности, и может быть почти невозможно получить значение P <0,05, независимо от различий между группами выборочных данных.
Такие тесты довольно надежны при больших размерах выборки ( n > 100). Однако выбор между параметрическим и непараметрическим статистическим анализом менее важен для выборок такого размера, поскольку оба анализа почти одинаково эффективны и дают схожие результаты.При меньшем размере выборки ( n <20) тесты на нормальность могут вводить в заблуждение. К сожалению, непараметрическому анализу небольших выборок недостает статистической мощности, и может быть почти невозможно получить значение P <0,05, независимо от различий между группами выборочных данных.
В случае сомнений относительно типа распределения, которому следуют данные выборки, особенно при небольшом размере выборки, следует провести непараметрический анализ, учитывая, что анализу может не хватать мощности.Лучшее решение, позволяющее избежать ошибок при выборе подходящего статистического теста для анализа данных, — это разработать исследование с достаточно большим количеством субъектов в каждой группе.
Непарные против парных данных
При сравнении эффектов вмешательства на выборочные группы в клиническом исследовании важно, чтобы группы были как можно более похожими, отличаясь только в отношении интересующего вмешательства. Один из распространенных методов достижения этого — набор субъектов в исследовательские группы путем случайного распределения.Все набранные предметы должны иметь равные шансы быть распределенными в любую из исследовательских групп. Если размеры выборки достаточно велики, процесс рандомизации должен гарантировать, что групповые различия в переменных, которые могут повлиять на результат интересующего вмешательства (например, вес, возраст, соотношение полов и привычка к курению), компенсируют друг друга. Эти переменные сами могут быть подвергнуты статистическому анализу и нулевой гипотезе об отсутствии разницы между тестируемыми исследовательскими группами.Такое исследование содержит независимые группы, и уместны непарные статистические тесты. Примером может служить сравнение эффективности двух разных препаратов для лечения гипертонии.
Примером может служить сравнение эффективности двух разных препаратов для лечения гипертонии.
Другим методом проведения этого типа исследования является перекрестный дизайн исследования, в котором все набранные субъекты получают либо лечение А, либо лечение В (порядок определяется случайным распределением для каждого пациента), за которым следует другое лечение после подходящего «вымывания» период, в течение которого эффекты первой обработки проходят.Данные, полученные в этом исследовании, будут парными и подлежат парному статистическому анализу. Эффективность формирования пары может быть определена путем вычисления коэффициента корреляции и соответствующего P -значения взаимосвязи между парами данных.
Третий метод включает определение всех тех характеристик, которые, по мнению исследователя, могут влиять на эффект интересующего вмешательства, и сопоставление набранных субъектов по этим характеристикам. Этот метод потенциально ненадежен, поскольку он зависит от того, чтобы ключевые характеристики не были случайно упущены из виду и, следовательно, не контролировались.
Основное преимущество парного исследования перед непарным состоит в том, что парные статистические тесты более эффективны, и требуется меньшее количество участников, чтобы доказать данное различие между исследуемыми группами. Против этого есть прагматические трудности и дополнительное время, необходимое для перекрестных исследований, а также опасность того, что, несмотря на период вымывания, первое лечение все еще может оказывать влияние на второе. Также необходимо учитывать подводные камни подбора пациентов по всем важным характеристикам.
Нулевая гипотеза и P -значения
Перед тем, как приступить к статистическому анализу данных, предлагается нулевая гипотеза, то есть нет различий между исследуемыми группами в отношении интересующей (ых) переменной (ов) (т. Е. Средние или медианные значения выборки совпадают). Как только нулевая гипотеза определена, используются статистические методы для вычисления вероятности наблюдения полученных данных (или данных, более экстремальных от предсказания нулевой гипотезы), если нулевая гипотеза верна.
Например, мы можем получить два набора выборочных данных, которые, по-видимому, принадлежат разным популяциям, когда мы исследуем данные. Предположим, что применяется соответствующий статистический тест и полученное значение P составляет 0,02. Обычно значение P для статистической значимости определяется как P <0,05. В приведенном выше примере порог нарушен, и нулевая гипотеза отклоняется. Что именно означает значение 0,02 для P ? Представим себе, что исследование повторяется много раз.Если нулевая гипотеза верна, а средние значения выборки не отличаются, разница между средними значениями выборки, по крайней мере, такая же большая, как наблюдаемая в первом исследовании, будет наблюдаться только в 2% случаев.
Многие опубликованные статистические анализы приводят значения P как ≥0,05 (несущественно), <0,05 (значимо), <0,01 (очень значимо) и т. Д. анализ, когда значения P нужно было искать в справочных таблицах. Такой подход уже не является удовлетворительным, и всегда следует указывать полученные точные значения P . Важность этого подхода иллюстрируется следующим примером. В исследовании, сравнивающем два гипотензивных средства, было обнаружено, что лекарство А более эффективно, чем лекарство В, и указано P <0,05. Мы убеждены и немедленно переключаем всех наших пациентов с гипертонией на препарат А. Другая группа исследователей проводит аналогичное исследование и не обнаруживает существенной разницы между двумя препаратами ( P ≥ 0.05). Мы немедленно переключаем всех наших пациентов с гипертонией обратно на препарат B, поскольку он дешевле и кажется столь же эффективным. Мы также можем быть несколько сбиты с толку очевидными противоречивыми выводами двух исследований.
Такой подход уже не является удовлетворительным, и всегда следует указывать полученные точные значения P . Важность этого подхода иллюстрируется следующим примером. В исследовании, сравнивающем два гипотензивных средства, было обнаружено, что лекарство А более эффективно, чем лекарство В, и указано P <0,05. Мы убеждены и немедленно переключаем всех наших пациентов с гипертонией на препарат А. Другая группа исследователей проводит аналогичное исследование и не обнаруживает существенной разницы между двумя препаратами ( P ≥ 0.05). Мы немедленно переключаем всех наших пациентов с гипертонией обратно на препарат B, поскольку он дешевле и кажется столь же эффективным. Мы также можем быть несколько сбиты с толку очевидными противоречивыми выводами двух исследований.
Фактически, если фактическое значение P в первом исследовании было 0,048, а во втором исследовании — 0,052, эти два исследования полностью согласуются друг с другом. Обычное значение статистической значимости ( P <0,05) всегда следует рассматривать в контексте, а значение P , близкое к этой произвольной точке отсечения, возможно, должно привести к выводу, что может потребоваться дополнительная работа перед принятием или отклонением нулевая гипотеза.
Можно рассмотреть еще один пример произвольного характера обычного порога статистической значимости. Предположим, что разработан новый противораковый препарат и проводится клиническое исследование для оценки его эффективности по сравнению со стандартным лечением. Замечено, что смертность после лечения новым препаратом имеет тенденцию к снижению, но это снижение не является статистически значимым ( P = 0,06). Поскольку новый препарат дороже и не более эффективен, чем стандартное лечение, следует ли от него отказаться? Если нулевая гипотеза верна (оба препарата одинаково эффективны) и мы должны были повторить исследование несколько раз, мы получили бы наблюдаемую разницу (или нечто большее) между двумя исследуемыми группами только в 6% случаев.По крайней мере, необходимо провести дальнейшее более масштабное исследование, прежде чем с уверенностью сделать вывод о том, что новый препарат не более эффективен — как мы увидим позже, исходное исследование вполне могло быть недостаточно эффективным.
Статистическая против клиническая значимость
Не следует путать статистическую значимость с клинической значимостью. Предположим, что сравниваются два гипотензивных агента, и среднее артериальное давление после лечения препаратом А на 2 мм рт. Ст. Ниже, чем после лечения препаратом В.Если размеры выборки исследования достаточно велики, даже такая небольшая разница между двумя группами может быть статистически значимой со значением P <0,05. Однако клиническое преимущество дополнительного снижения среднего артериального давления на 2 мм рт. Ст. Невелико и клинически не значимо.
Доверительные интервалы
Доверительный интервал — это диапазон выборочных данных, который включает неизвестный параметр совокупности, например среднее значение. Чаще всего сообщается о 95% доверительном интервале (ДИ 95%), хотя можно рассчитать любой другой доверительный интервал.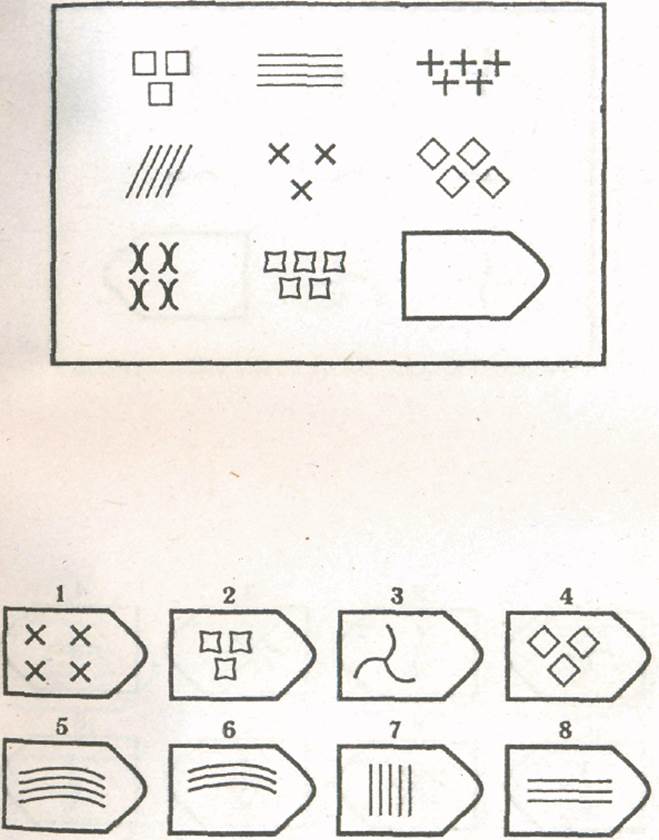 Если исследование повторяется несколько раз, полученный 95% доверительный интервал будет содержать среднее значение генеральной совокупности в 95% случаев.
Если исследование повторяется несколько раз, полученный 95% доверительный интервал будет содержать среднее значение генеральной совокупности в 95% случаев.
Доверительные интервалы важны при анализе результатов статистического анализа и помогают интерпретировать полученное значение P . Они всегда должны указываться со значением P . Рассмотрим исследование, сравнивающее эффективность нового гипотензивного средства со стандартным лечением. Исследователь считает, что минимальная клинически значимая разница в среднем артериальном кровяном давлении после лечения двумя препаратами составляет 10 мм рт.Если P <0,05, можно рассмотреть три возможных диапазона для 95% доверительного интервала (рис. 1). Если P ≥ 0,05, можно рассмотреть четыре возможных диапазона для 95% доверительного интервала (рис. 2). Эти диапазоны для 95% доверительного интервала приведены в таблице 1.
Рис. 1
Статистическая значимость 95% доверительного интервала при P <0,05 (таблица 1).
Рис.1
Статистическая значимость 95% доверительного интервала, когда P <0.05 (таблица 1).
Рис. 2
Статистическая значимость 95% доверительного интервала при P ≥ 0,05 (таблица 1).
Рис. 2
Статистическая значимость 95% доверительного интервала при P ≥ 0,05 (таблица 1).
Таблица 1Интерпретация доверительных интервалов
| P -значение <0,05 . | Является ли разница между средними по выборке клинически значимой? . | Устный перевод . | |
|---|---|---|---|
| . | В нижней части диапазона CI . | На верхнем пределе диапазона CI . | . |
| Да | Да | Да | A: Между исследуемыми группами существует клинически важное различие |
| Да | Нет | Да | B: Невозможно прийти к окончательному выводу — больше данных требуется |
| Да | Нет | Нет | C: Существует клинически несущественная разница между группами образцов |
| Нет | Нет | Нет | D: Нет клинически значимой разницы между двумя группы |
| Нет | Да | Нет | E: Невозможно прийти к окончательному выводу — требуется больше данных |
| Нет | Нет | Да | F: Невозможно прийти к окончательному выводу — требуется больше данных |
| Нет | Да | Да | G: бессмысленный диапазон CI — требуется больше данных |
P -значение <0.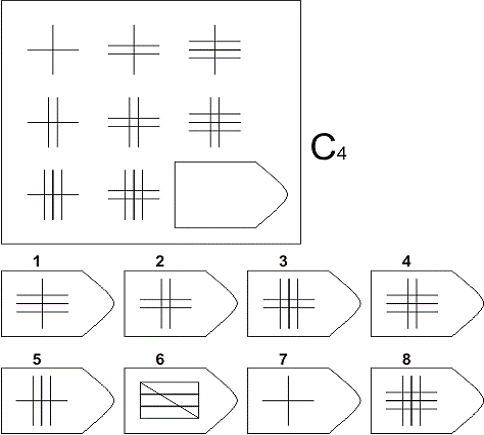 05
. 05
. | Является ли разница между средними по выборке клинически значимой? . | Устный перевод . | |
|---|---|---|---|
| . | В нижней части диапазона CI . | На верхнем пределе диапазона CI . | . |
| Да | Да | Да | A: Между исследуемыми группами существует клинически важное различие |
| Да | Нет | Да | B: Невозможно прийти к окончательному выводу — больше данных требуется |
| Да | Нет | Нет | C: Существует клинически несущественная разница между группами образцов |
| Нет | Нет | Нет | D: Нет клинически значимой разницы между двумя группы |
| Нет | Да | Нет | E: Невозможно прийти к окончательному выводу — требуется больше данных |
| Нет | Нет | Да | F: Невозможно прийти к окончательному выводу — требуется больше данных |
| Нет | Да | Да | G: бессмысленный диапазон CI — требуется больше данных |
Интерпретация доверительных интервалов
P -значение <0. 05
. 05
. | Является ли разница между средними по выборке клинически значимой? . | Устный перевод . | |
|---|---|---|---|
| . | В нижней части диапазона CI . | На верхнем пределе диапазона CI . | . |
| Да | Да | Да | A: Между исследуемыми группами существует клинически важное различие |
| Да | Нет | Да | B: Невозможно прийти к окончательному выводу — больше данных требуется |
| Да | Нет | Нет | C: Существует клинически несущественная разница между группами образцов |
| Нет | Нет | Нет | D: Нет клинически значимой разницы между двумя группы |
| Нет | Да | Нет | E: Невозможно прийти к окончательному выводу — требуется больше данных |
| Нет | Нет | Да | F: Невозможно прийти к окончательному выводу — требуется больше данных |
| Нет | Да | Да | G: бессмысленный диапазон CI — требуется больше данных |
P -значение <0. 05
. 05
. | Является ли разница между средними по выборке клинически значимой? . | Устный перевод . | |
|---|---|---|---|
| . | В нижней части диапазона CI . | На верхнем пределе диапазона CI . | . |
| Да | Да | Да | A: Между исследуемыми группами существует клинически важное различие |
| Да | Нет | Да | B: Невозможно прийти к окончательному выводу — больше данных требуется |
| Да | Нет | Нет | C: Существует клинически несущественная разница между группами образцов |
| Нет | Нет | Нет | D: Нет клинически значимой разницы между двумя группы |
| Нет | Да | Нет | E: Невозможно прийти к окончательному выводу — требуется больше данных |
| Нет | Нет | Да | F: Невозможно прийти к окончательному выводу — требуется больше данных |
| Нет | Да | Да | G: бессмысленный диапазон CI — требуется больше данных |
Мощность исследования и статистические ошибки типов I и II
После статистического анализа данных нулевая гипотеза либо принимается, либо отклоняется на основе значения P .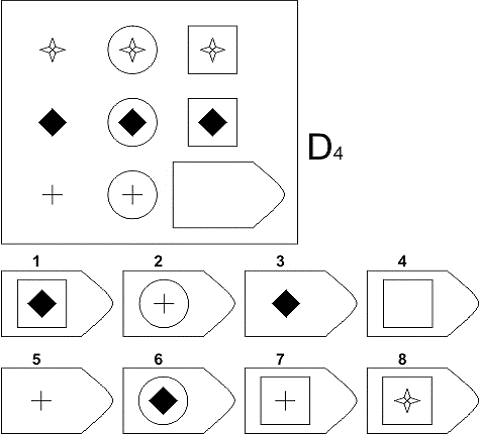 Поскольку нулевая гипотеза может быть верной или ложной в действительности, а полученное значение P может быть статистически значимым ( P <0,05) или нет, необходимо рассмотреть четыре возможных исхода, как показано в таблице 2.
Поскольку нулевая гипотеза может быть верной или ложной в действительности, а полученное значение P может быть статистически значимым ( P <0,05) или нет, необходимо рассмотреть четыре возможных исхода, как показано в таблице 2.
| P -значение значимо (<0,05)? . | Нулевая гипотеза верна или ложна в действительности . | |
|---|---|---|
| . | Верно . | Ложь . |
| Да | Ошибка типа I (α) | Анализ верен |
| Нет | Анализ верен | Ошибка типа II (β) |
| Нулевая гипотеза верна или ложна в действительности . | ||
|---|---|---|
| . | Верно . | Ложь
.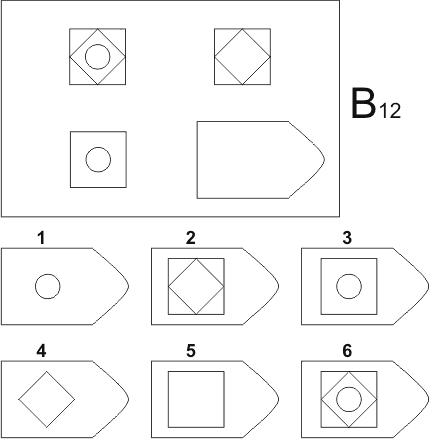 |
| Да | Ошибка типа I (α) | Анализ верен |
| Нет | Анализ верен | Ошибка типа II (β) |
| Нулевая гипотеза верна или ложна в действительности . | ||
|---|---|---|
| . | Верно . | Ложь . |
| Да | Ошибка типа I (α) | Анализ верен |
| Нет | Анализ верен | Ошибка типа II (β) |
| Нулевая гипотеза верна или ложна в действительности . | ||
|---|---|---|
| . | Верно . | Ложь . |
| Да | Ошибка типа I (α) | Анализ верен |
| Нет | Анализ верен | Ошибка типа II (β) |
Если нулевая гипотеза верна (т.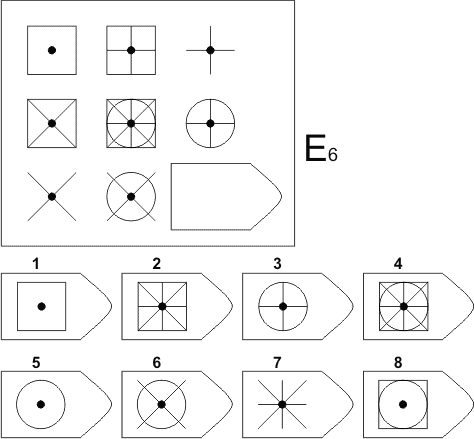 е. в действительности между группами нет никакой разницы) и полученное значение P составляет ≥0,05, заключение, основанное на статистическом анализе, соответствует действительности. Точно так же, если нулевая гипотеза действительно неверна (т.е. в действительности между группами существует разница) и полученное значение P <0,05, вывод, основанный на статистическом анализе, снова соответствует действительности.
е. в действительности между группами нет никакой разницы) и полученное значение P составляет ≥0,05, заключение, основанное на статистическом анализе, соответствует действительности. Точно так же, если нулевая гипотеза действительно неверна (т.е. в действительности между группами существует разница) и полученное значение P <0,05, вывод, основанный на статистическом анализе, снова соответствует действительности.
Однако, если нулевая гипотеза верна и получено значение P <0,05, делается неверный вывод о том, что группы выборки данных различаются. Это называется статистической ошибкой типа I. Статистически обнаруживается разница там, где ее нет в действительности. Различие между группами выборочных данных не связано с каким-либо вмешательством, а скорее случайно.Статистический факт заключается в том, что каким бы ни было значение P , всегда будет случайный шанс сделать ошибку типа I, хотя чем ниже значение P , тем меньше она становится.
Последняя возможность рассмотрения состоит в том, что нулевая гипотеза в действительности неверна, но полученное значение P ≥0,05. Мы ошибочно пришли к выводу, что группы выборки похожи — мы упустили реальную разницу. Это статистическая ошибка второго типа. Основная причина ошибок типа II — недостаточный размер выборки — исследования не хватает мощности.Мощность теста определяется как (1 — β ) × 100%, где β — вероятность ошибки типа II. Чтобы быть приемлемым для публикации, большинство редакторов научных журналов требуют, чтобы мощность исследования составляла не менее 80%. Взаимосвязь между размером выборки и мощностью исследования показана на Рисунке 3.
Рис. 3
Взаимосвязь между мощностью и размером выборки.
Рис. 3
Взаимосвязь между мощностью и размером выборки.
Хорошей практикой является выполнение расчета мощности перед началом собственно клинического исследования, чтобы минимизировать риск получения ошибки типа II, и большинство журналов и комитетов по этике требуют, чтобы это было четко определено в разделе методологии.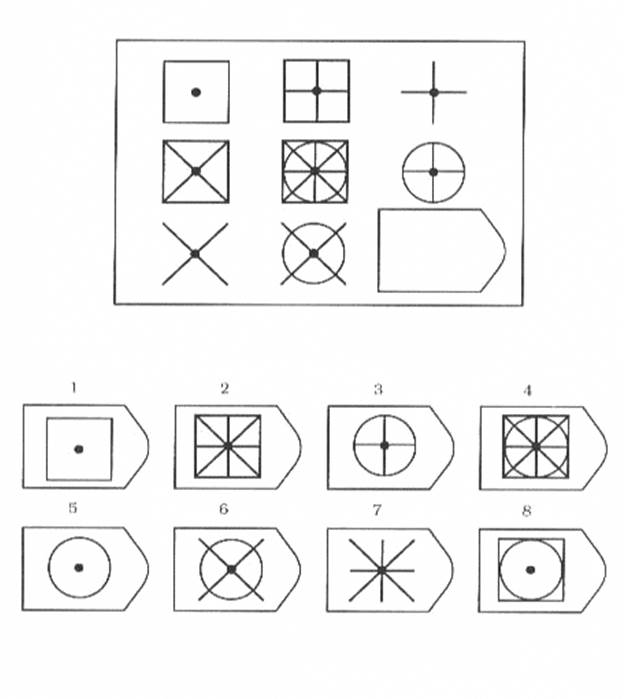 Например, при планировании исследования влияния нового инотропа на сердечный выброс исследователь должен определить минимальную разницу между сердечным выбросом контрольной группы и активной терапии , которая будет считаться клинически значимой .Как только это различие будет определено, исследователю потребуется доступ к данным, полученным из ранее опубликованной работы или начального пилотного исследования, в котором подробно описаны среднее значение и стандартное отклонение контрольных данных.
Например, при планировании исследования влияния нового инотропа на сердечный выброс исследователь должен определить минимальную разницу между сердечным выбросом контрольной группы и активной терапии , которая будет считаться клинически значимой .Как только это различие будет определено, исследователю потребуется доступ к данным, полученным из ранее опубликованной работы или начального пилотного исследования, в котором подробно описаны среднее значение и стандартное отклонение контрольных данных.
Опасности множественных сравнений
Рассмотрим исследование, в котором изучается влияние 20 различных лечебных трав на продолжительность сна пациентов с бессонницей. Также существует группа плацебо, с которой сравнивается каждая из 20 групп активного лечения.Множественные тесты t выполняются для каждого из лекарственных средств на травах, и было замечено, что одно из них действительно способствует увеличению сна по сравнению с плацебо, со значением P <0,05. Насколько верен этот вывод?
Насколько верен этот вывод?
Фактически, вероятность того, что любое из 20 лекарственных средств на травах даст статистически значимый результат на уровне P <0,05, составляет 1 к 20. Поэтому не будет удивительным, если статистический анализ одного из 20 лекарственных средств ниже расследование показало P <0.05 просто случайно. Правильный подход при проведении множественных сравнений, таких как это, - использовать поправочный коэффициент. Наиболее известна поправка Бонферрони, в которой значение P для значимости корректируется с P <0,05 до P <0,05 / n , где n — количество сделанных сравнений. В качестве альтернативы следует провести дисперсионный анализ (анова) между всеми 21 исследуемой группой, а затем провести post hoc индивидуальных сравнений, рассчитанных только в том случае, если значение P для анова будет <0.05.
Один двухсторонний тест против
Все статистические тесты начинаются с предпосылки нулевой гипотезы.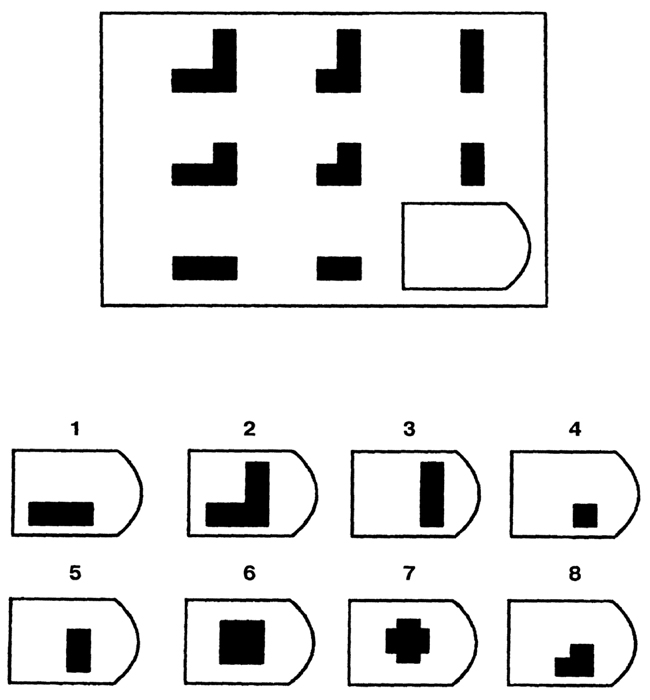 Затем это проверяется путем вычисления вероятности того, что различия, наблюдаемые между группами выборки, вызваны случайностью (значение P ). Давайте рассмотрим исследование, в котором сравниваются значения двух выборок (например, среднее артериальное давление после лечения гипертонии двумя разными препаратами). Анализируя такие данные, мы, очевидно, не знаем, одинаково ли эффективны препараты, является ли препарат А более эффективным, чем препарат Б, или наоборот.Соответственно, при вычислении значения P ключевой вопрос заключается в следующем: какова вероятность получения разницы, наблюдаемой между двумя выборочными средними значениями (или чего-то более экстремального), случайным образом, учитывая, что либо группа может иметь более высокое среднее значение. ? На этот вопрос отвечает двусторонний непарный t -тест.
Затем это проверяется путем вычисления вероятности того, что различия, наблюдаемые между группами выборки, вызваны случайностью (значение P ). Давайте рассмотрим исследование, в котором сравниваются значения двух выборок (например, среднее артериальное давление после лечения гипертонии двумя разными препаратами). Анализируя такие данные, мы, очевидно, не знаем, одинаково ли эффективны препараты, является ли препарат А более эффективным, чем препарат Б, или наоборот.Соответственно, при вычислении значения P ключевой вопрос заключается в следующем: какова вероятность получения разницы, наблюдаемой между двумя выборочными средними значениями (или чего-то более экстремального), случайным образом, учитывая, что либо группа может иметь более высокое среднее значение. ? На этот вопрос отвечает двусторонний непарный t -тест.
Практически всегда целесообразно проводить статистический анализ данных с использованием двусторонних тестов, и это должно быть указано в протоколе исследования до сбора данных. Односторонний тест обычно не подходит. Он отвечает на вопрос, аналогичный двухстороннему тесту, но, что очень важно, заранее указывает, что нас интересует только то, что выборочное среднее одной группы больше, чем другой. Если анализ данных показывает результат, противоположный ожидаемому, разницу между средними значениями выборки следует отнести к случайности, даже если эта разница велика.
Односторонний тест обычно не подходит. Он отвечает на вопрос, аналогичный двухстороннему тесту, но, что очень важно, заранее указывает, что нас интересует только то, что выборочное среднее одной группы больше, чем другой. Если анализ данных показывает результат, противоположный ожидаемому, разницу между средними значениями выборки следует отнести к случайности, даже если эта разница велика.
Например, организатор курса статистики подвергает кандидатов тесту MCQ как до, так и после курса.Затем оценки за курс анализируются с использованием парного теста t (поскольку данные представляют собой сопоставленные пары оценок до и после курса для каждого кандидата). Организатор решает использовать односторонний тест, поскольку он уверен, что знания кандидатов должны улучшиться после курса, и не учитывает возможность того, что кандидаты будут иметь менее высокие баллы после него. Несколько удивительно, что после анализа данных средние баллы MCQ после курса оказались хуже, чем до курса, со значением P , равным 0,01.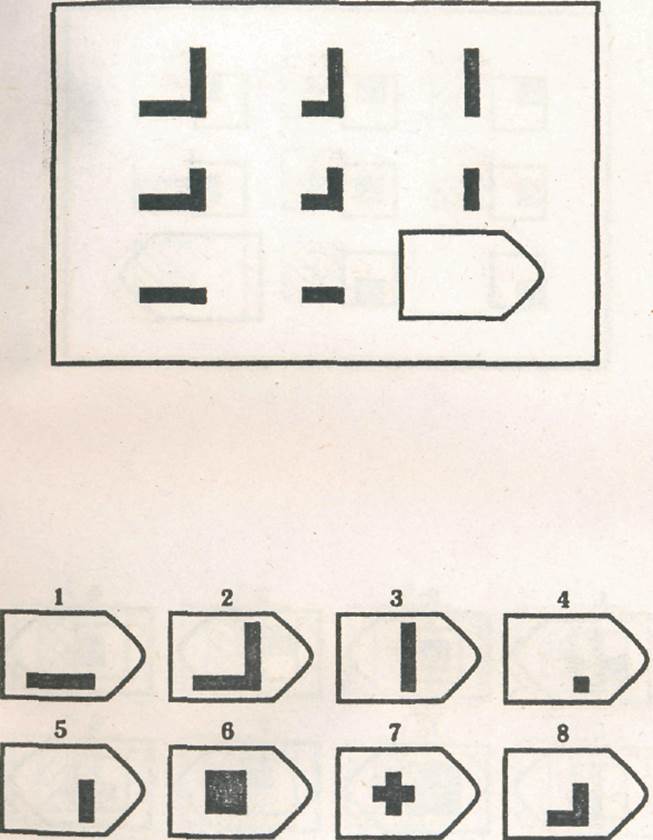 Правильная статистическая интерпретация этого результата состоит в том, чтобы приписать наблюдаемое различие случайной случайности.Тем не менее, действительно может быть правдой, что кандидаты показывают худшие результаты после курса. Возможно, курс сбивает с толку или содержит множество фактических ошибок. Организатор курса ошибся, использовав односторонний тест в этой ситуации — двусторонний тест был бы уместен.
Правильная статистическая интерпретация этого результата состоит в том, чтобы приписать наблюдаемое различие случайной случайности.Тем не менее, действительно может быть правдой, что кандидаты показывают худшие результаты после курса. Возможно, курс сбивает с толку или содержит множество фактических ошибок. Организатор курса ошибся, использовав односторонний тест в этой ситуации — двусторонний тест был бы уместен.
Односторонние тесты всегда следует рассматривать с некоторым подозрением. На самом деле довольно сложно вспомнить примеры в клинических исследованиях, где уместен односторонний тест. Одним из примеров может быть исследование нервно-мышечного блокирующего препарата, в котором пациентам вводятся две разные интубационные дозы и время, необходимое для восстановления отношения последовательности четырех до ≥0.8 записано. Вероятно, оправданно не принимать во внимание возможность того, что более низкая доза препарата приводит к более длительному времени восстановления.
Благодарности
Авторы благодарны профессору Роуз Бейкер, факультет статистики Салфордского университета, за ее ценный вклад в предоставление полезных комментариев и советов по этой рукописи.
Библиография
1,.Статистика I: данные и корреляции
,Contin Educ Anaesth Crit Care Pain
,2007
, vol.7
(стр.95
—9
) 2,.Статистика II: Центральная тенденция и распространение данных
,Contin Educ Anaesth Crit Care Pain
,2007
, vol.7
(стр.127
—30
) 3,.Статистика III: Вероятностные и статистические тесты
,Contin Educ Anaesth Crit Care Pain
,2007
, vol.7
(стр.167
—70
) 4. ,Введение в медицинскую статистику
,2000
3-е изданиеОксфорд
Oxford University Press
5.,Практическая статистика для медицинских исследований
,1991
Лондон
Chapman & Hall / CRC
6.,Статистика для чайников
,2003
Нью-Джерси
Wiley Publishing Inc
cow TD 7
Статистика на первом месте
(по состоянию на 21 октября 2007 г.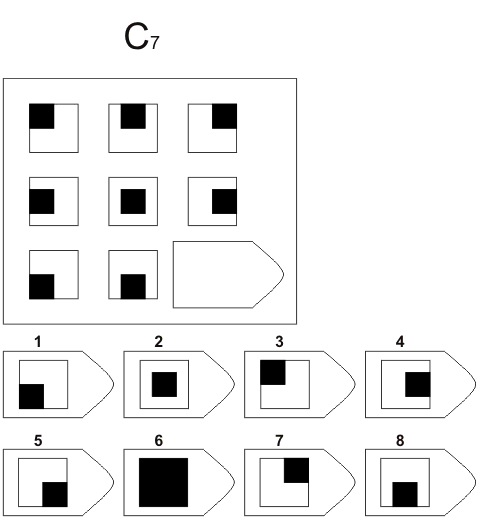 ) 8.
) 8. Онлайн-учебник по статистике Hyperstat
,2006
(доступ 21 октября) 9SurfStat Australia
,2006
(доступ 21 октября) 10.,Как читать статью
,1997
Лондон
BMJ Publishing
11.,Критическая оценка эпидемиологических исследований и клинических испытаний
,1998
2-е изданиеOxford
Oxford University Press
См. вопросы с несколькими вариантами ответов 26–28
© Правление и попечители Британского журнала анестезии [2007]. Все права защищены. Для получения разрешений, пожалуйста, напишите: журналы[email protected]
Тестирование независимых образцовt — Учебные пособия по SPSS
Описание проблемы
В нашем наборе данных ученики указали свое обычное время пробега милю, а также были ли они спортсменами. Предположим, мы хотим знать, отличается ли среднее время пробега милю у спортсменов и не спортсменов. Это включает в себя проверку того, различаются ли выборочные средние значения времени на милю среди спортсменов и не спортсменов в вашей выборке (и, в более широком смысле, вывод о том, существенно ли различаются средние значения времени на милю в популяции между этими двумя группами).Вы можете использовать тест Independent Samples t , чтобы сравнить среднее время пробега для спортсменов и не спортсменов.
Это включает в себя проверку того, различаются ли выборочные средние значения времени на милю среди спортсменов и не спортсменов в вашей выборке (и, в более широком смысле, вывод о том, существенно ли различаются средние значения времени на милю в популяции между этими двумя группами).Вы можете использовать тест Independent Samples t , чтобы сравнить среднее время пробега для спортсменов и не спортсменов.
Гипотезы для этого примера могут быть выражены как:
H 0 : µ не спортсмен — µ спортсмен = 0 («разница средних значений равна нулю»)
H 1 : µ не спортсмен — µ атлет ≠ 0 («разница средних не равна нулю»)
, где µ спортсмен и µ не спортсмен — средние значения для спортсменов и не спортсменов, соответственно.
В данных выборки мы будем использовать две переменные: Athlete и MileMinDur . Переменная Спортсмен имеет значения либо «0» (не спортсмен), либо «1» (спортсмен).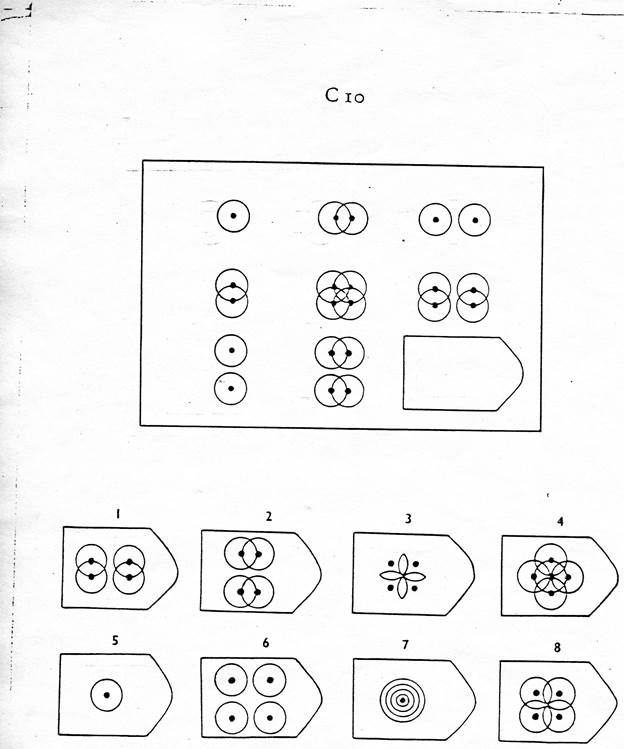 Он будет работать как независимая переменная в этом тесте T. Переменная MileMinDur — это числовая переменная продолжительности (ч: мм: сс), и она будет функционировать как зависимая переменная. В SPSS первые несколько строк данных выглядят так:
Он будет работать как независимая переменная в этом тесте T. Переменная MileMinDur — это числовая переменная продолжительности (ч: мм: сс), и она будет функционировать как зависимая переменная. В SPSS первые несколько строк данных выглядят так:
Перед испытанием
Перед запуском теста Independent Samples t рекомендуется взглянуть на описательную статистику и графики, чтобы понять, чего ожидать.Использование средства сравнения (анализ > средство сравнения> среднее значение ) для получения описательной статистики по группам говорит нам, что стандартное отклонение времени на милю для не спортсменов составляет около 2 минут; для спортсменов это около 49 секунд. Это соответствует отклонению в 14803 секунды для не спортсменов и отклонению в 2447 секунд для спортсменов 1 . Выполнение процедуры исследования ( Analyze> Descriptives> Explore ) для получения сравнительной коробчатой диаграммы дает следующий график:
Если бы дисперсии действительно были равны, можно было бы ожидать, что общая длина коробчатых диаграмм будет примерно одинаковой для обеих групп. Однако из этого коробчатого графика видно, что разброс наблюдений для не спортсменов намного больше, чем разброс наблюдений для спортсменов. Уже сейчас мы можем оценить, что дисперсия для этих двух групп сильно различается. Не станет сюрпризом, если мы запустим тест Independent Samples t и увидим, что тест Левена имеет важное значение.
Однако из этого коробчатого графика видно, что разброс наблюдений для не спортсменов намного больше, чем разброс наблюдений для спортсменов. Уже сейчас мы можем оценить, что дисперсия для этих двух групп сильно различается. Не станет сюрпризом, если мы запустим тест Independent Samples t и увидим, что тест Левена имеет важное значение.
Кроме того, мы должны также принять решение об уровне значимости (обычно обозначается греческой буквой альфа, α ), прежде чем проводить наши проверки гипотез.Уровень значимости — это порог, который мы используем для определения значимости результата теста. Для этого примера возьмем α = 0,05.
1 При вычислении дисперсии переменной продолжительности (форматированной как чч: мм: сс или мм: сс или мм: сс.с), SPSS преобразует значение стандартного отклонения в секунды перед возведением в квадрат.
Запуск теста
Для запуска независимых образцов t Test:
- Щелкните Анализировать> Сравнить средние> T-тест для независимых выборок .

- Переместите переменную Athlete в поле Grouping Variable и переместите переменную MileMinDur в область Test Variable (s) . Теперь Athlete определен как независимая переменная, а MileMinDur определен как зависимая переменная.
- Нажмите Определить группы , откроется новое окно. Использовать указанные значения По умолчанию выбран . Поскольку наша группирующая переменная имеет числовой код (0 = «Не спортсмен», 1 = «Спортсмен»), введите «0» в первое текстовое поле и «1» во втором текстовом поле.Это означает, что мы будем сравнивать группы 0 и 1, которые соответствуют не спортсменам и спортсменам соответственно. По завершении щелкните Продолжить .
- Нажмите OK , чтобы запустить тест независимых образцов t . Вывод для анализа отобразится в окне просмотра вывода.
Синтаксис
ТЕСТОВЫЕ ГРУППЫ = Спортсмен (0 1)
/ MISSING = АНАЛИЗ
/ VARIABLES = MileMinDur
/CRITERIA=CI(. 95).
95).
Выход
Столы
В выходных данных появляются два раздела (прямоугольника): Групповая статистика и Тест независимых выборок .Первый раздел, Групповая статистика , предоставляет основную информацию о групповых сравнениях, включая размер выборки ( n ), среднее значение, стандартное отклонение и стандартную ошибку для времени на милю по группе. В этом примере 166 спортсменов и 226 не спортсменов. Среднее время на милю для спортсменов составляет 6 минут 51 секунду, а среднее время на милю для спортсменов — 9 минут 6 секунд.
Второй раздел, Тест независимых выборок , отображает результаты, наиболее подходящие для теста независимых выборок t .Есть две части, которые предоставляют различную информацию: (A) тест Левена на равенство вариантов и (B) t-тест на равенство средних значений.
A Тест Левена на равенство вариантов : В этом разделе представлены результаты теста Левена. Слева направо:
Слева направо:
- F — статистика теста Левена
- Sig. — это p-значение, соответствующее этой статистике теста.
Значение p теста Левена печатается как «.000 «(но должно читаться как p <0,001 - т. Е. p очень мало), поэтому мы отвергаем нулевое значение теста Левена и заключаем, что разница во времени на милю у спортсменов значительно отличается от дисперсии не -athletes. Это говорит нам о том, что мы должны посмотреть на строку «Не предполагаемые равные отклонения» для результатов теста t (и соответствующий доверительный интервал) (если этот результат теста не был значимым, то есть если мы наблюдали p > α — тогда мы использовали бы результат «Предполагаемые равные отклонения».)
B t-тест на равенство средних предоставляет результаты для фактического теста независимых выборок t . Слева направо:
- t — вычисленная статистика теста
- df — степени свободы
- Sig (двусторонний) — p-значение, соответствующее данной статистике теста и степеням свободы
- Средняя разница — разница между выборочными средними; он также соответствует числителю тестовой статистики
- Стд.
 Разница ошибок — стандартная ошибка; он также соответствует знаменателю тестовой статистики
Разница ошибок — стандартная ошибка; он также соответствует знаменателю тестовой статистики
Обратите внимание, что средняя разница вычисляется путем вычитания среднего значения второй группы из среднего значения первой группы. В этом примере среднее время на милю для спортсменов было вычтено из среднего времени на милю для не спортсменов (9:06 минус 6:51 = 02:14). Знак средней разности соответствует знаку значения t . Положительное значение t в этом примере указывает, что среднее время на милю для первой группы, не спортсменов, значительно больше, чем среднее значение для второй группы, спортсменов.
Соответствующее значение p печатается как «.000»; двойной щелчок по значению p покажет не округленное число. SPSS округляет p-значения до трех десятичных знаков, поэтому любое p-значение, слишком маленькое для округления до 0,001, будет напечатано как 0,000. (В этом конкретном примере значения p имеют порядок 10 -40 .)
C Доверительный интервал разницы : Эта часть выходных данных теста t дополняет результаты теста значимости.



 Цветные прогрессивные матрицы Структура теста
Цветные прогрессивные матрицы Структура теста Качественные показатели выполнения Цветных прогрессивных матриц
Качественные показатели выполнения Цветных прогрессивных матриц
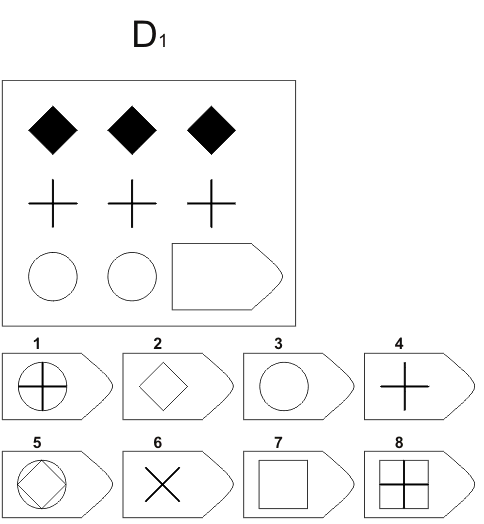 , Лондон, Великобритания Умер: 10 августа 1970 г., Дамфрис, Великобритания Образование: Университет Лондон Известность: Тест Равена
, Лондон, Великобритания Умер: 10 августа 1970 г., Дамфрис, Великобритания Образование: Университет Лондон Известность: Тест Равена 

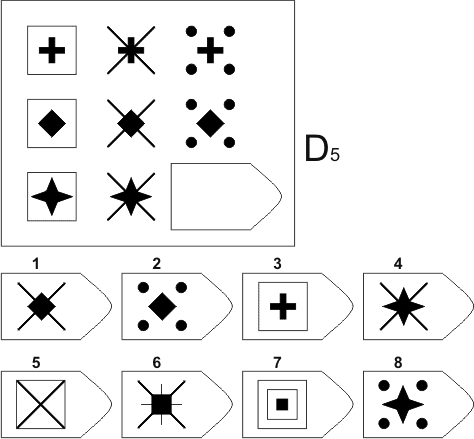 и успешность трудоустройства стажеров
и успешность трудоустройства стажеров  Например, (403 + 132 — 2)
= 533
Например, (403 + 132 — 2)
= 533 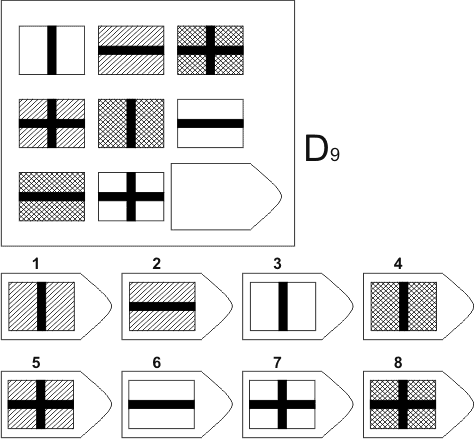 Включают:
Включают:  3
3  Однако не все статистически значимые эффекты следует лечить.
так же. Например, у вас должно быть меньше уверенности, что
нулевая гипотеза неверна, если p = 0,049, чем p = 0,003. Таким образом,
Отказ от нулевой гипотезы — это не предложение по принципу «все или ничего».
Однако не все статистически значимые эффекты следует лечить.
так же. Например, у вас должно быть меньше уверенности, что
нулевая гипотеза неверна, если p = 0,049, чем p = 0,003. Таким образом,
Отказ от нулевой гипотезы — это не предложение по принципу «все или ничего».  5 принято. Если π больше 0,5, то мистер Бонд
лучше, чем шанс на эту задачу.
5 принято. Если π больше 0,5, то мистер Бонд
лучше, чем шанс на эту задачу. 
 е.е. они коррелированы)
е.е. они коррелированы)  Он описывает, насколько далеко ваши наблюдаемые данные от нулевой гипотезы об отсутствии связи между переменными или отсутствии различий между группами выборки.
Он описывает, насколько далеко ваши наблюдаемые данные от нулевой гипотезы об отсутствии связи между переменными или отсутствии различий между группами выборки.
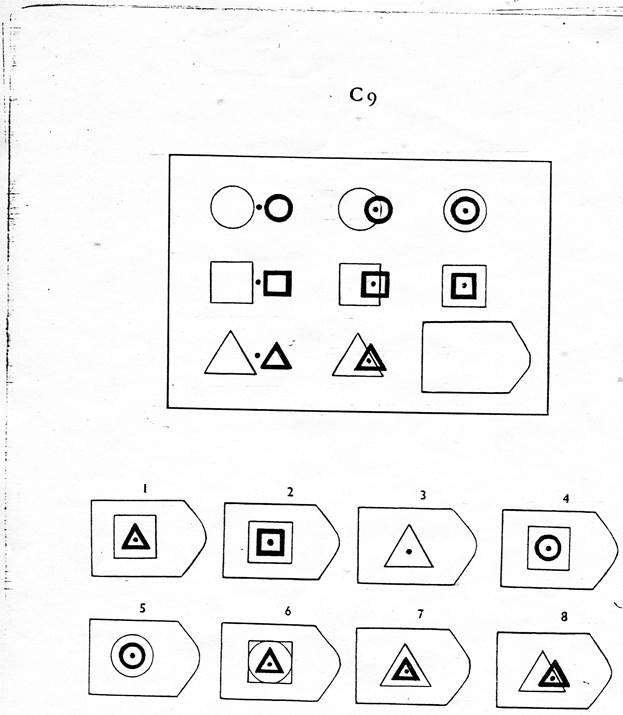 Наиболее распространенным порогом является p <0,05, что означает, что данные, вероятно, будут появляться менее чем в 5% случаев при нулевой гипотезе.
Наиболее распространенным порогом является p <0,05, что означает, что данные, вероятно, будут появляться менее чем в 5% случаев при нулевой гипотезе. 
 95).
95).  Разница ошибок — стандартная ошибка; он также соответствует знаменателю тестовой статистики
Разница ошибок — стандартная ошибка; он также соответствует знаменателю тестовой статистики