Тест равена с ответами: Прогрессивные матрицы Равена || Пройти тест онлайн
Тесты для приема на работу и определения уровня IQ
Таблицы Равена
Этот метод представляет собой 5 серий по 12 заданий в каждой, каждое правильно выполненное задание оценивается в 1 балл, максимальный балл в каждой серии — 12, в целом — 60. Серии маркированы буквами А, В, С, D и Е, каждая из этих серий имеет свое психологическое значение и отражает способность к той или иной мыслительной операции. Серии следует предъявлять по порядку. Подсчет по каждой производится отдельно. Суммируя результаты всех серий, вы получите общий балл, который при помощи таблицы можно будет перевести в «чистый» коэффициент интеллекта. К каждой серии даны подробные описания, чтобы вы могли ориентироваться, какие задачи представляют сложность для соискателя, и соответственно, подходит ли он для данной вакансии. Также приведена сравнительная оценка и таблица показателей интеллекта.
Рекомендации
Не следует считать результаты в присутствии соискателя, вся полученная при помощи тестов и интервью информация обрабатывается после того, как соискатель выйдет из кабинета, иначе у человека может сложиться мнение, что вы сразу сообщите о решении принять или отказать ему в работе.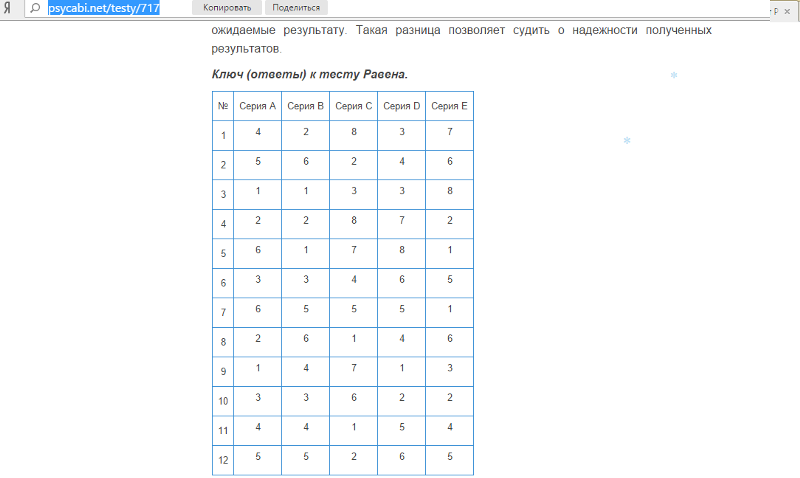
Если вакансия на должность подразумевает способность ясно мыслить в условиях дефицита времени, можно лимитировать время выполнения, но не по каждой серии, а в целом всего теста (на 30–40 минут) при этом объяснив, что задания нужно решать в строгой очередности, не оставляя «на потом» более сложные.
Если вы пройдете этот тест, то сможете сформулировать инструкции к каждой серии сами и вносить уточнения, исходя из собственного опыта.
Не поддавайтесь искушению подсказать, иначе вы получите свои результаты, а не соискателя.
Перед тем как приступить к работе, снабдите интервьюера бланком (образец прилагается) и карандашом для записи результатов. Затем предъявите первую картинку серии А и попросите найти необходимый «вырезанный» фрагмент, так, «чтобы помешенный в пустое окошечко рисунок фрагмента совпал с рисунком всего поля», испытуемый должен озвучить номер фрагмента. Таким образом, дав инструкцию к полю А
1 и получив ответ, попросите записать его в бланк. Например А1 — № 4, далее испытуемый работает сам, записывая ответы. В последующих сериях, как правило, инструкции уже не нужны, но если человек испытывает сложности, допускается напомнить инструкцию или внести уточнения.
Например А1 — № 4, далее испытуемый работает сам, записывая ответы. В последующих сериях, как правило, инструкции уже не нужны, но если человек испытывает сложности, допускается напомнить инструкцию или внести уточнения.
Образец бланка:
Считать результаты следует по каждой серии отдельно, в каждом столбце бланка выведите общий балл для каждой серии. Напоминаем, что за каждый правильный ответ начисляется 1 балл. Правильными считаются ответы, совпавшие с ключом.
Теперь посмотрим результаты по каждой серии. Самый высокий результат — это 12 правильных ответов. Для того чтобы оценить способности соискателя, следует учесть особенности заданий в каждой серии и оценить, в какой из них он более успешен. ВНИМАНИЕ! Разъяснительные описания серий даны без учета личностных особенностей, а основываются только на возможностях интеллекта.
СЕРИЯ А Тестовое значение заключается в дополнении недостающей части матрицы (поля), в этой серии фигуры статичны и не подразумевают изменений. В решении этой серии задач протекают 2 мыслительных процесса: идентификация недостающей части структуры с остальными частями и анализ структуры целого согласно указанным взаимосвязям элементов в матрице. Решение зависит от уровня внимательности, статистического представления и визуального различия.
В решении этой серии задач протекают 2 мыслительных процесса: идентификация недостающей части структуры с остальными частями и анализ структуры целого согласно указанным взаимосвязям элементов в матрице. Решение зависит от уровня внимательности, статистического представления и визуального различия.
Это самая легкая серия из всего задания, и взрослый человек с легкостью ее выполняет. Если соискатель набрал в этой серии менее 6 баллов, нужно исключить близорукость, плохое состояние здоровья, ситуативные факторы (нервозная обстановка во время тестирования, отвлекающие факторы, неправильно данную инструкцию). Если выясняется, что все вышеперечисленное исключено, то дальнейшую работу продолжать не имеет смысла, на вашу вакансию соискатель претендовать не может в силу низкого интеллекта.
СЕРИЯ В Тестовое значение состоит в отыскивании аналогий между двумя парами фигур. Задача заключается в раскрытии принципа отношений по аналогии путем постепенной дифференциации элементов. При решении используется способность постигать симметричность между фигурами. Решение зависит от способности к линейной дифференциации умозаключений на основе построения линейных взаимосвязей.
Решение зависит от способности к линейной дифференциации умозаключений на основе построения линейных взаимосвязей.
Если у тестируемого хороший результат только в этой серии, перед вами превосходный, толковый исполнитель, если на то есть личностная направленность, он не видит дальше собственного носа и вряд ли сможет претендовать на руководящую должность, такому «мозгу» вряд ли по силам организовывать что-либо или кого-либо, он просто сотрудник.
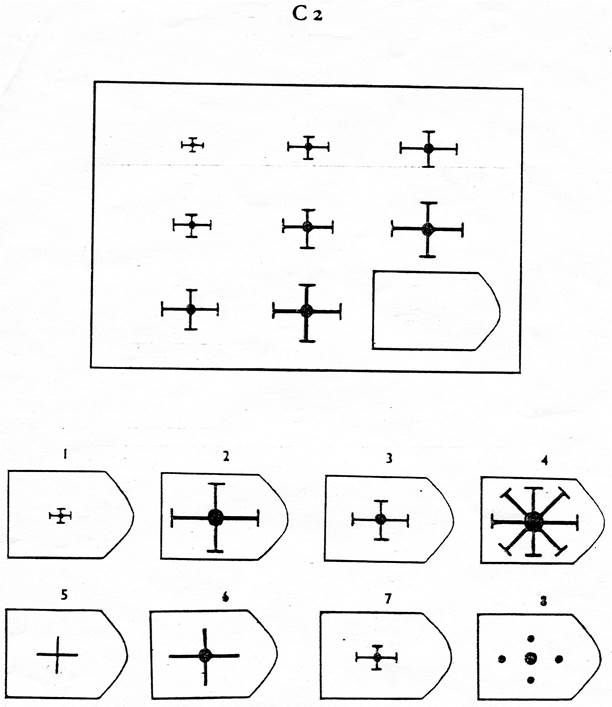
СЕРИЯ С основана на усложняющихся изменениях фигур в матрицах в соответствии с определенным логическим принципом непрерывного развития положения фигур и динамических перемен в пространстве (обогащение фигур в горизонтальном и вертикальном направлении и суммирование этих новых элементов в конечной недостающей фигуре). В этой серии проявляется способность к динамической наблюдательности и прослеживанию непрерывных изменений, динамическая внимательность и воображение, способность представлять.
Иными словами, если соискатель в этой серии набрал 10 или больше баллов, то это говорит о том, что он способен приспосабливаться к быстро меняющимся условиям, ломать стереотипы деятельности и решения задач.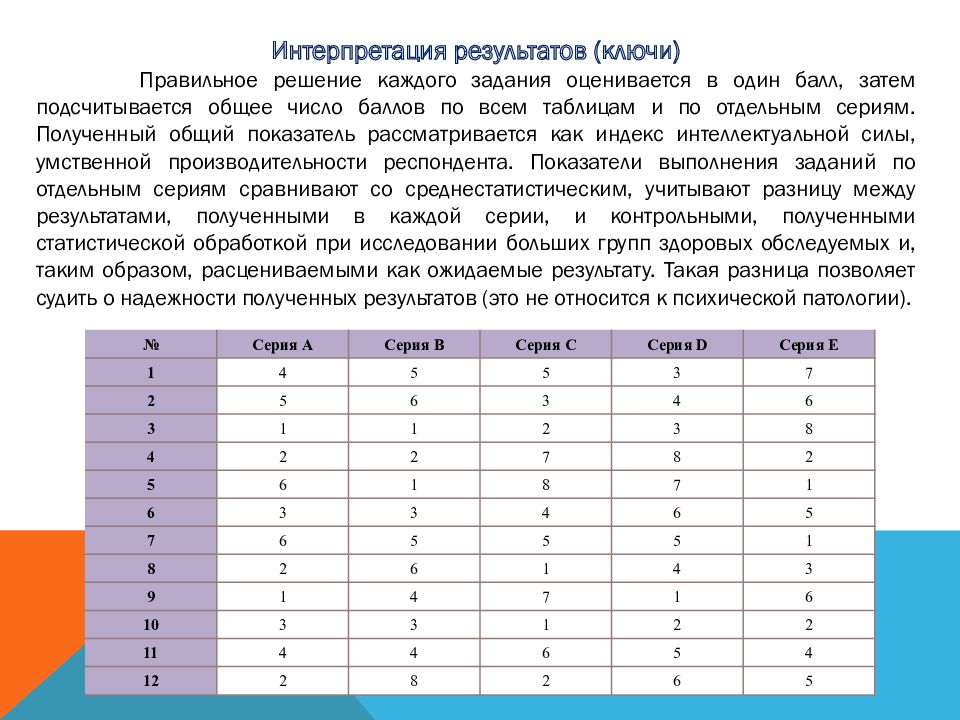 Человек, возможно, успешно работает в дефиците времени и справляется с частыми изменениями условий работы, не придерживается устойчивых стереотипов, однако могут возникнуть трудности с работой в условиях монотонной деятельности. Соискатель способен к работе менеджера среднего звена, при успешном дальнейшем обучении может претендовать на более высокий статус в организации.
Человек, возможно, успешно работает в дефиците времени и справляется с частыми изменениями условий работы, не придерживается устойчивых стереотипов, однако могут возникнуть трудности с работой в условиях монотонной деятельности. Соискатель способен к работе менеджера среднего звена, при успешном дальнейшем обучении может претендовать на более высокий статус в организации.
СЕРИЯ D составлена согласно принципу перестройки (переструктурации) фигур в матрице в горизонтальном и вертикальном направлении. Решение требует проследить закономерную последовательность фигур и чередование фигур в целостной структуре. Решение зависит от способности схватывать количественные и качественные изменения в упорядочении (составлении) фигур согласно закономерности используемых изменений.
То есть, если соискатель набрал в этой серии больше 10 баллов, вы вполне можете принимать его на работу не менее чем на руководящий пост, он способен организовать работу и проследить эффективность ее выполнения, не нуждается в дополнительном образовании.
СЕРИЯ Е состоит из заданий, заключающихся в анализе и синтезе фигур из отдельных элементов согласно принятому принципу. Здесь требуется складывать и вычитать элементы фигур, смешивать части согласно алгебраическому принципу. Недостающий член структуры находят с помощью алгебраических операций с остальными частями структуры. Решение зависит от способности наблюдать сложное количественное и качественное различие кинетических, динамических рядов. Высшая форма абстрагирования и динамического синтеза.
Если соискатель набрал более 10 баллов в этой серии, то ему прямая дорога в аналитический отдел фирмы (если таковой имеется) или на руководящий пост. Перед вами человек с незаурядными интеллектуальными данными, он способен не только следить за процессами и делать выводы, но и формировать, переструктурировать работу всей организации, умеет абстрагироваться от частностей, обладает способностью видеть, просчитывать стратегию всей фирмы «на шаг вперед», что делает его незаменимым сотрудником.
Суммируйте результаты всех серий. Полученное число — это «сырой» балл. Обработка производится по таблице, которая переводит баллы в коэффициент. Для удобства мы приводим средние и высокие баллы, минуя низкие, отражающие клиническое снижение интеллекта, также мы игнорируем возрастную группу до 16 лет. Таким образом, таблица рассчитана на возрастную группу от 16 до 40 лет, людей не страдающих клинически значимым снижением или недоразвитием интеллекта.
Если возраст кандидата превышает 30 лет, то необходимо произвести дополнительное вычисление по следующей формуле:
Оценить полученный показатель интеллекта можно по следующим критериям:
80-90 — слабый, ниже среднего;
90-100 — средний интеллект;
100-110 — высокий средний интеллект;
110-120 — высокий интеллект;
более 120 — незаурядный интеллект;
свыше 140 — выдающийся интеллект.
Кроме коэффициента интеллекта, по этому тесту можно судить об утомляемости — если человек делает ряд ошибок в конце каждой серии (с 9 по 12 образец), он будет уставать в условиях постоянной интеллектуальной нагрузки, что теоретически может повлечь ошибки или недостаточную эффективность в целом. Если же человек делает ошибки на протяжении всей серии, чередуя правильные и неправильные ответы, то есть его суждения не последовательны, — это может говорить как о «творческом начале», так и о невнимательности, трудности в сосредоточении внимания, что также может привести к сбоям в практике.
В любом случае, не стоит делать выводы, исходя из результатов одного теста. Кроме интеллектуальных данных, у человека есть личностные качества, которые ни в коем случае нельзя упускать из виду, «гении бывают злыми, а добрыми бывают и дураки». Предложенные вам методики измерения интеллекта не определяют человека в целом, а раскрывают лишь его мыслительные способности. Важно найти удачное для вашей организации сочетание интеллектуального потенциала и личностных особенностей.
Данный текст является ознакомительным фрагментом.
Продолжение на ЛитРесТест IQ Виктора Серебрякова
Тест IQ Виктора Серебрякова
Интеллект
Чем больше коэффициент интеллекта IQ, тем реже он встречается.
IQ 115 у одного из 6 человек,
IQ 119 у одного из 10 человек,
IQ 125 у одного из 21 человек,
IQ 128 у одного из 32 человек,
IQ 130 у одного из 44 человек,
IQ 132 у одного из 61 человек,
IQ 133 у одного из 72 человек,
IQ 134 у одного из 85 человек,
IQ 135 у одного из 102 человек,
IQ 139 у одного из 215 человек,
IQ 141 у одного из 319 человек,
IQ 143 у одного из 482 человек,
IQ 144 у одного из 596 человек,
IQ 145 у одного из 741 человек,
IQ 146 у одного из 924 человек,
IQ 147 у одного из 1157 человек,
IQ 150 у одного из 2330 человек,
IQ 155 у одного из 8139 человек,
IQ 158 у одного из 18127 человек,
IQ 160 у одного из 31574 человек.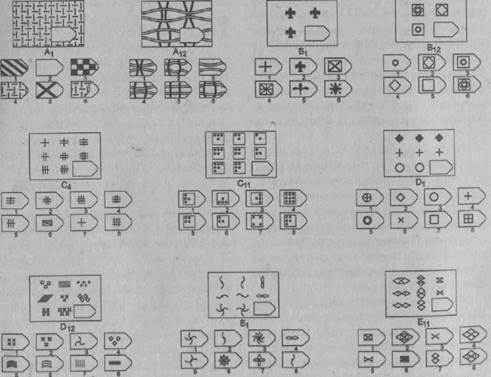
С помощью электронных таблиц (Excel или Google Sheets) можно составить полную таблицу, используя формулу =1/(1-(normdist(A1,100,15,true)))
Английский ученый Виктор Серебряков разработал The Serebriakoff Advanced Culture Fair Test — культурно-независимый тест интеллекта повышенной сложности. Он есть в книге The Mammoth Book of Astounding Puzzles издательства Carroll & Graf, 1992 год.
Всего в тесте 36 заданий, в каждом задании нужно решить, какой фигуры не хватает. Время размышлений не ограничено. Я сделал программу для Windows, которая проводит этот тест и в конце сообщает IQ. Вот так выглядит окно программы:
Скачать программу: Тест IQ Виктора Серебрякова
Можно пройти тест не с помощью программы, а рассматривая картинки. Здесь все 36 заданий, в конце даны ответы и как посчитать IQ.
Правильные ответы:
За каждый правильный ответ начисляется 1 балл.
Сумма баллов переводится в IQ по этой таблице:
🐚
Прогрессивные матрицы Равена (тест Равена)
Культурно-свободный тест на интеллект (CFIT)
Культурно-свободный тест на интеллект (CFIT) Предложен Р. Кэттелом в 1958 году Предназначен для измерения уровня интеллектуального развития независимо от влияния факторов окружающей среды (культуры, образования
ПодробнееПСИХОЛОГИЯ И ПЕДАГОГИКА
Министерство образования и науки РФ Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования Нижегородский государственный технический университет им.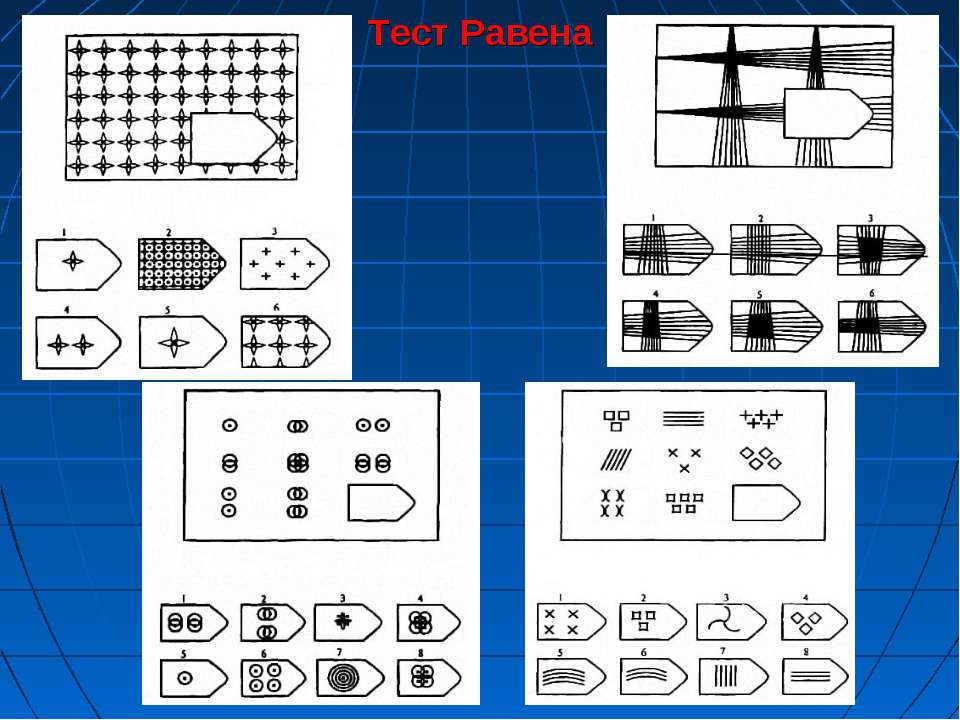 Р. Е.
Р. Е.
Рекомендации по вводу в формы (6 8-е классы)
Рекомендации по вводу в формы (6 8-е классы) Сводная по параллели строится автоматически на последнем листе, переносить и копировать данные туда не нужно. Удалять и очищать ячейки с формулами категорически
ПодробнееПОЧЕМУ ОПЯТЬ ДВОЙКА? Причина 1
ПОЧЕМУ ОПЯТЬ ДВОЙКА? Причина 1 Существует немало причин, снижающих успеваемость по русскому языку и чтению. Трудности чаще всего недостаточным развитием тех или иных психических процессов. Чтобы выявить
ПодробнееМетодика «Таблицы Шульте»
Методика «Таблицы Шульте» Консалтинговая компания «Территория роста» «Живые» тренинги, on-line обучение, индивидуальные консультации, полезные материалы для бизнеса и личностного роста. г. Барнаул, пр.
г. Барнаул, пр.
Проверочная работа. по математике
Проверочная работа по математике Тема: «Обыкновенные дроби» УМК: Класс: 5 Разработчик: Семяшкина Ирина Васильевна Цель проверочной работы: тематический контроль и оценка способности обучающихся применять
ПодробнееТестирование (метод тестов)
Тестирование (метод тестов) Тестирование это исследовательский метод, который позволяет выявить уровень знаний, умений и навыков, способностей и других качеств личности, а также их соответствие определенным
Подробнее3.План (спецификация) контрольной работы
Спецификация контрольной работы 1 по ИЗОБРАЗИТЕЛЬНОМУ ИСКУССТВУ (6 класс) Тема «Виды изобразительного искусства и основы их образного языка. Мир наших вещей. Натюрморт» 1. Назначение контрольной работы
ПодробнееВСТУПИТЕЛЬНЫЕ ИСПЫТАНИЯ
ВСТУПИТЕЛЬНЫЕ ИСПЫТАНИЯ специальность 07.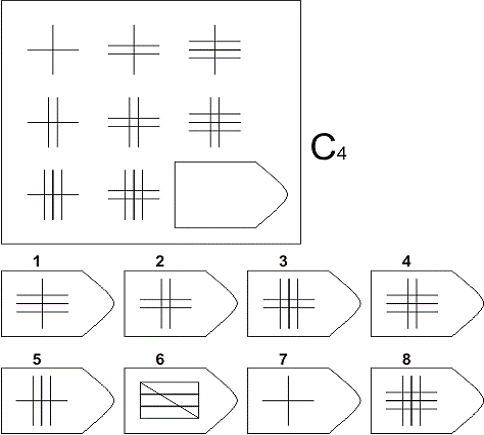 02.01Архитектура РИСУНОК для поступающих на базе основного общего образования (9 классов), на базе среднего общего образования (11 классов) Пример экзаменационного
02.01Архитектура РИСУНОК для поступающих на базе основного общего образования (9 классов), на базе среднего общего образования (11 классов) Пример экзаменационного
Категорически запрещается:
Индивидуальный комплект участника ЕГЭ (ИК) — запечатанный конверт формата А4, выдаваемый каждому участнику единого государственного экзамена. Имеет средства защиты информации, например, два штрихкода с
ПодробнееФОНД ОЦЕНОЧНЫХ СРЕДСТВ
МИНОБРНАУКИ РОССИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ «ВОРОНЕЖСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ» БОРИСОГЛЕБСКИЙ ФИЛИАЛ (БФ ФГБОУ ВО «ВГУ») УТВЕРЖДАЮ Заведующий
ПодробнееПриложение 4 к приказу 29/3 от г.
Приложение 4 к приказу 29/3 от 03.03.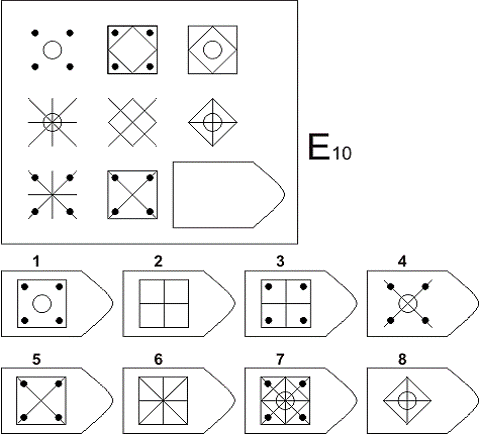 2017 г. ПОЛОЖЕНИЕ о порядке разработки и утверждения контрольно-измерительных материалов муниципального бюджетного общеобразовательного учреждения «Средняя общеобразовательная
2017 г. ПОЛОЖЕНИЕ о порядке разработки и утверждения контрольно-измерительных материалов муниципального бюджетного общеобразовательного учреждения «Средняя общеобразовательная
Оценка по 100- бальной шкале
Характеристика вступительных экзаменов по математике Вступительный экзамен проводится в виде тестов. Содержание теста определяется на основе Программы вступительных экзаменов для поступающих на основе
ПодробнееАНАЛИЗ СЛОВООБРАЗОВАТЕЛЬНЫЙ
А АДЕКВАТНОСТЬ (adequcy). Один из критериев теста, показывающий, насколько полно тест охватывает учебный материал (курса, предмета или их части). См. также валидность. АЛЬТЕРНАТИВА (лат. alter одно из
ПодробнееПРИЛОЖЕНИЕ 6 ДИДАКТИЧЕСКИЕ ИГРЫ
ПРИЛОЖЕНИЕ 6 ДИДАКТИЧЕСКИЕ ИГРЫ Дидактические игры по физическому воспитанию дошкольников.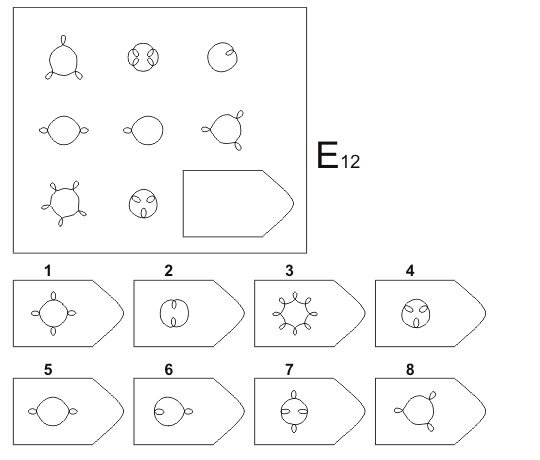 Игра это не только источник положительных эмоций, это ещё и возможность развивать качества, необходимые для дальнейшей
Игра это не только источник положительных эмоций, это ещё и возможность развивать качества, необходимые для дальнейшей
Как научиться проходить тесты IQ
Как повысить свой уровень IQ? Как повысить уровень IQ ребенка? И реально ли это — повысить коэффициент интеллекта? От чего зависит iq? Насколько уровень развития интеллекта определяется наследственностью? А каково влияние окружающей среды?
Многие научные институты созданы для поисков ответов на эти вопросы. Исследования показали, что наследственность для развития умственных способностей — фактор значимый, но не определяющий. Важнее здоровое сбалансированное питание (матери, кормящие ребенка грудью, повышают его будущий уровень IQ в среднем на 7 баллов) и окружение (не зря же народная мудрость гласит: «С кем поведешься, от того и наберешься». А понимающие это родители заранее подыскивают ребенку хорошую школу и обдумывают его дополнительную занятость).
Как научиться проходить тесты IQ, если вам надо быстро подготовиться к прохождению теста IQ? Стоит учесть тот факт, что прохождение каждого следующего теста позволяет понять закономерности, используемые в заданиях, правильно распределить время на решение примеров каждого типа, а поэтому улучшает результат тестирования в среднем на 5-7%. То есть, IQ -тренировка — лучший способ развить IQ. Ускорить работу поможет анализ заданий по видам.
В рубрике «iq тренинг» подобраны типовые задачи, встречающиеся в IQ тестах: по двум словам найти третье, вставить буквы для окончания одного слова и начала второго, задачи на связь буквы и ее номера в алфавите, найти зависимость чисел и другие.
Рассмотрите задачу. Попробуйте решить ее самостоятельно. Если сразу это сделать не удается, посмотрите ответ и попробуйте догадаться, как он получен. В любой момент вы можете воспользоваться подсказкой.
Очень хороший результат дает самостоятельное составление iq задач. При прохождении iq теста связь чисел, букв, рисунков может быть подчинена самым разным закономерностям.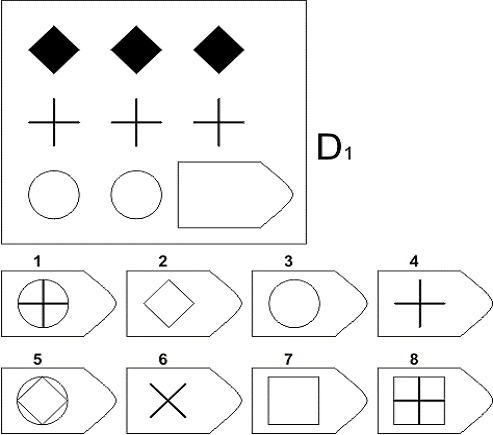 Дайте волю своей фантазии. Чем более замысловатые iq задачи вы научитесь составлять, тем меньше затруднений у вас вызовет прохождение iq теста.
Дайте волю своей фантазии. Чем более замысловатые iq задачи вы научитесь составлять, тем меньше затруднений у вас вызовет прохождение iq теста.
Если ваша задача — развить интеллект ребенка и повысить его уровень IQ, попробуйте предложить и ему упражнения для повышения IQ. Обсудите их, объясните тот или иной вид задания. Очень хороший результат дает самостоятельная работа. Попросите ребенка составить примеры разных видов самостоятельно, потом посмотрите их сами, привлеките для тестирования друзей вашего ребенка.
Стоит ли доверять тестам на интеллект? / Статьи / Библиотека / Первая онлайн система анализа вашего душевного здоровья
Стоит ли доверять тестам на интеллект?
Стоит ли доверять простейшим тестам на интеллект в гламурных журналах? Или может все же лучше потратить полчаса или час на труднопроходимый и порой утомительный тест с поистине психологическим основанием?
Психологи считают, что человеческий ум и интеллект – это отнюдь не одно и то же.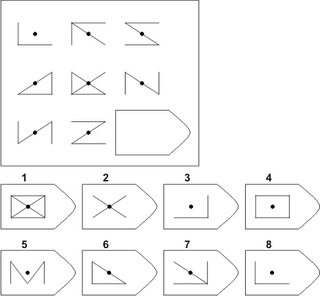 Если умом можно назвать способность логического мышления, то интеллектом называют совокупность логики, синтеза и анализа любых жизненных ситуаций, а также способность верного оценивания трудных задач и легкого нахождения их решения.
Если умом можно назвать способность логического мышления, то интеллектом называют совокупность логики, синтеза и анализа любых жизненных ситуаций, а также способность верного оценивания трудных задач и легкого нахождения их решения.
Современные тесты на интеллект, представленные в модных журналах, просто поражают своей неспособностью хотя бы приблизительно вычислить уровень IQ у всех тех, кто рискнет убить пару минут на их прохождение. Как правило, они состоят из двух десятков вопросов, которые косвенно касаются логических способностей. Иными словами, таким простым и банальным тестам на интеллект доверять просто не стоит. Но если уж так хочется проверить свои собственные умственные способности, то лучше обратится к настоящим профессиональным тестам на IQ, которые хотя и занимают много времени, но показывают точные результаты прохождения.
Самый известный из всех действующих тестов на интеллект – это тест Айзенка. Он состоит из четырех десятков вопросов, большинство из которых являются чисто визуальными.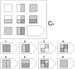 К примеру, человеку предлагают просмотреть ряд геометрических фигур и найти недостающую комбинацию в последнем ряду. В этом случае подопытный должен найти логическую связь между каждой представленной фигурой и на основе этой связи найти и недостающую. Есть также и такие вопросы, в которых нужно вставить пропущенное слово в скобки. Здесь действует тот же прием анализа всех остальных слов и нахождение ассоциаций между ними или другой связи. Время, отведенное на прохождение этого теста, составляет ровно 30 минут. Такое ограничение было установлено не случайно, ведь тест призван вычислить уровень интеллекта, а значит и уровень способности человека принимать правильные решения в экстренных ситуациях.
К примеру, человеку предлагают просмотреть ряд геометрических фигур и найти недостающую комбинацию в последнем ряду. В этом случае подопытный должен найти логическую связь между каждой представленной фигурой и на основе этой связи найти и недостающую. Есть также и такие вопросы, в которых нужно вставить пропущенное слово в скобки. Здесь действует тот же прием анализа всех остальных слов и нахождение ассоциаций между ними или другой связи. Время, отведенное на прохождение этого теста, составляет ровно 30 минут. Такое ограничение было установлено не случайно, ведь тест призван вычислить уровень интеллекта, а значит и уровень способности человека принимать правильные решения в экстренных ситуациях.
Второй известный тест, признанный и широко применяемый в мировой практике определения коэффициента интеллекта – это тест прогрессивные матрицы Равена (Raven Progressiv Matrices). Методика разработана в соответствии с лучшими традициями английской школы изучения уровня интеллекта и также строго регламентирована по времени – 20 минут.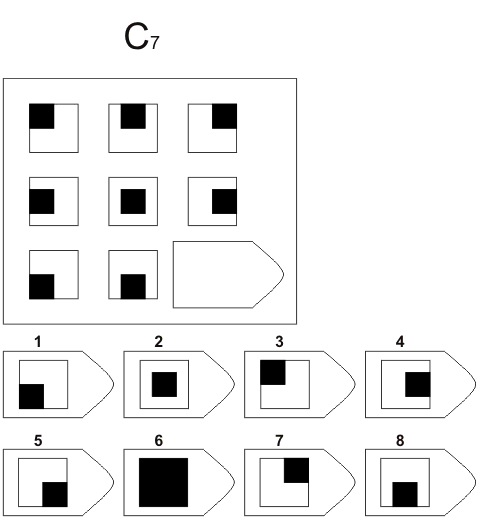 Это тест испытания способностей воспринимать определенные формы, охватывать их особенности, характер, взаимные отношения или ансамбль, совокупность отношений, а поэтому он требует по отдельным задачам метода логических рассуждений. Как показывает опыт многолетних исследований, данные, полученные с помощью теста Равена, хорошо согласуются с показателями других известных тестов на интеллект, в частности, с тем же тестом определения общих способностей Айзенка, описанным выше, однако есть и отличия. Считается, что эти два теста определяют немного разные стороны интеллекта человека, именно поэтому часто есть разбежность в полученных результатах. Также считается, что данные, полученные с помощью теста Айзенка, бывают завышены и не характеризуют реальный IQ испытуемого, тогда как тест Равена, наоборот, выдает немного заниженный коэффициент интеллекта.
Это тест испытания способностей воспринимать определенные формы, охватывать их особенности, характер, взаимные отношения или ансамбль, совокупность отношений, а поэтому он требует по отдельным задачам метода логических рассуждений. Как показывает опыт многолетних исследований, данные, полученные с помощью теста Равена, хорошо согласуются с показателями других известных тестов на интеллект, в частности, с тем же тестом определения общих способностей Айзенка, описанным выше, однако есть и отличия. Считается, что эти два теста определяют немного разные стороны интеллекта человека, именно поэтому часто есть разбежность в полученных результатах. Также считается, что данные, полученные с помощью теста Айзенка, бывают завышены и не характеризуют реальный IQ испытуемого, тогда как тест Равена, наоборот, выдает немного заниженный коэффициент интеллекта.
Именно поэтому в нашем аналитическом модуле «Коэффициент интеллекта, IQ» мы представили обе эти методики, а для максимальной объективизации результата предлагаем считать своим реальным коэффициентом интеллекта средний результат этих двух тестов.
Создавая этот аналитический модуль для нашего проекта, мы провели анализ многих других похожих онлайн – тестов на уровень интеллекта, и, пришли к неутешительному выводу – подавляющее большинство из них содержит грубейшие ошибки, как в самих заданиях методик, так и в интерпретации и расчете результатов. А множество сайтов, предлагающих свои услуги по оценке вашего IQ – просто копируют, передирают друг у друга эти тесты, естественно «забывая» исправить эти ошибки. Иногда доходит до такого абсурда, что из 100 тестируемых, у 90 коэффициент интеллекта свыше 170!, что само по себе просто невозможно, как бы мы не хотели польстить друг другу. При разработке аналитического модуля «Коэффициент интеллекта, IQ» нами были взяты оригинальные методики из научной литературы, т. е. первоисточники этих тестов, которые мы адаптировали для прохождения онлайн, поэтому с гордостью можем сказать, что у нас на сайте вы действительно узнаете свой реальный IQ, а также получите в ответе много просто интересной информации об интеллекте.
В мире существует много разных тестов на интеллект, но это не значит, что доверять и тратить свое время стоит на них всех. Лучше воспользоваться теми методиками определения уровня интеллекта, которые были признаны ведущими психиатрами, как наиболее точные и правильные тесты.
Прочитать еще много интересного об интеллекте и узнать свой IQ можно здесь.
Поделитесь с друзьями и оцените публикациюНе пропустите другие статьи по теме:
Оставить комментарий, могут только зарегистрированные пользователи.
 Вы можете зарегистрироваться или войти
Вы можете зарегистрироваться или войти
Высокий IQ встречается чаще у физиков и теоретиков, чем у художников — Российская газета
В научном мире шок: у трехлетней американки из штата Теннессии Селены Яник интеллектуальный показатель IQ составил целых 135 баллов — больше, чем у президента США Барака Обамы и премьер-министра Великобритании Дэвида Кэмерона.
Получается, маленькая девочка умнее их и большинства взрослых? Тот же самый IQ у ученых в среднем составляет около 125 баллов, а у простых офисных клерков 100 — 105 баллов. Напрашивается вопрос: не врет ли IQ? И вообще, можно ли объективно помериться интеллектом и достоверно выяснить, кто умнее? Об этом корреспондент «РГ» беседует с профессором Московского городского психолого-педагогического университета Викторией Юркевич.
Виктория Соломоновна, можем ли мы сравнить силу интеллекта двух людей, как если бы мы сравнивали их физическую силу в перетягивании каната или в армрестлинге?
Виктория Юркевич: Прибора для измерения интеллекта или одаренности в природе не существует. Даже если дать людям одинаковые тесты на интеллект, сравнивать их результаты будет некорректно. У каждого мозг работает по-разному, он сориентирован в большей степени на ту или иную область деятельности.
Даже если дать людям одинаковые тесты на интеллект, сравнивать их результаты будет некорректно. У каждого мозг работает по-разному, он сориентирован в большей степени на ту или иную область деятельности.
Как выяснить, кто умнее: знаменитый физик или легендарный скрипач? Каждый в своей области велик и бесподобен. Но единых критериев, по которым можно было бы сопоставить их умственное развитие, не существует.
А как же тест на IQ?
Виктория Юркевич: Он выявляет только интеллектуальные способности в сфере именно общего интеллекта, то есть способности делать логические выводы, структурировать информацию. Известно, что самый высокий показатель IQ обычно бывает у физиков-теоретиков. Они постоянно просчитывают сложнейшие умозрительные модели, этот тип мышления отлажен, и с этими тестами им справиться проще. А вот, допустим, художники сравнимых баллов обычно не набирают. Но разве мы можем сказать, что Айвазовский глупее Ландау? Нет, конечно. У них просто разные типы интеллекта.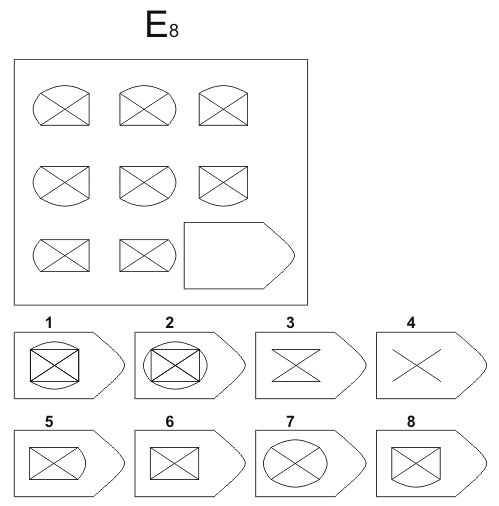 Художественно одаренный человек обычно на тестах IQ показывает себя существенно хуже, чем математики или технари. Но никакого вывода из этого делать нельзя.
Художественно одаренный человек обычно на тестах IQ показывает себя существенно хуже, чем математики или технари. Но никакого вывода из этого делать нельзя.
Как быть с юной американкой, в три года обставившей взрослых солидных мужчин?
Виктория Юркевич: Показатель IQ — это соотношение умственной зрелости человека и его биологического возраста. Изначально он был придуман для отбора учеников школ, которые в состоянии освоить программу. Тогда исследователи с помощью детских психологов и учителей сформировали набор знаний и навыков, которые должны быть у ребенка в определенном возрасте. Если умеешь все, что в твои годы положено и ничего больше, у тебя IQ ровно 100. Сотня — это норма. Освоил что-то дополнительное — держи свои 105, 120 или даже 140 баллов. Не успел или не смог вовремя чему-то научиться — получишь 95, 92, 87 баллов. И так далее.
Кстати говоря, IQ меньше 90 — это уже признак задержки развития. Если вернуться к девочке и Обаме, то тут само сравнение некорректно. Возможно, что девочка умеет делать вещи, о которых ее ровесники не имеют никакого представления. По сравнению с другими трехлетними детьми она является развитой не по годам. Но если сопоставить ее с любым взрослым человеком, а особенно с таким интеллектуалом, как нынешний президент США, она все равно будет просто маленьким ребенком. Их баллы IQ измерены по разным шкалам. Это несравнимые величины.
Возможно, что девочка умеет делать вещи, о которых ее ровесники не имеют никакого представления. По сравнению с другими трехлетними детьми она является развитой не по годам. Но если сопоставить ее с любым взрослым человеком, а особенно с таким интеллектуалом, как нынешний президент США, она все равно будет просто маленьким ребенком. Их баллы IQ измерены по разным шкалам. Это несравнимые величины.
Если индекс IQ не дает возможности сравнить силу интеллекта, почему же он так популярен, в том числе у психологов?
Виктория Юркевич: Тут ситуация намного сложнее. Существует шесть основных типов интеллекта. Во-первых, интеллектуальный или логический — это способность понимать, осмыслять и сопоставлять. Второй — академический, он подразумевает хорошее усвоение готовых знаний. Социальный — его обладатели легко понимают настроение и интересы людей, могут увлечь их за собой. Еще есть художественный интеллект, он подразумевает способность оперировать образами, создавать их, понимать чужие метафоры и иносказания, практический — о таких людях обычно говорят «золотые руки», они могут собрать, сделать, починить или сконструировать все, что угодно, и, наконец, сенсомоторный — это умение управлять своим телом.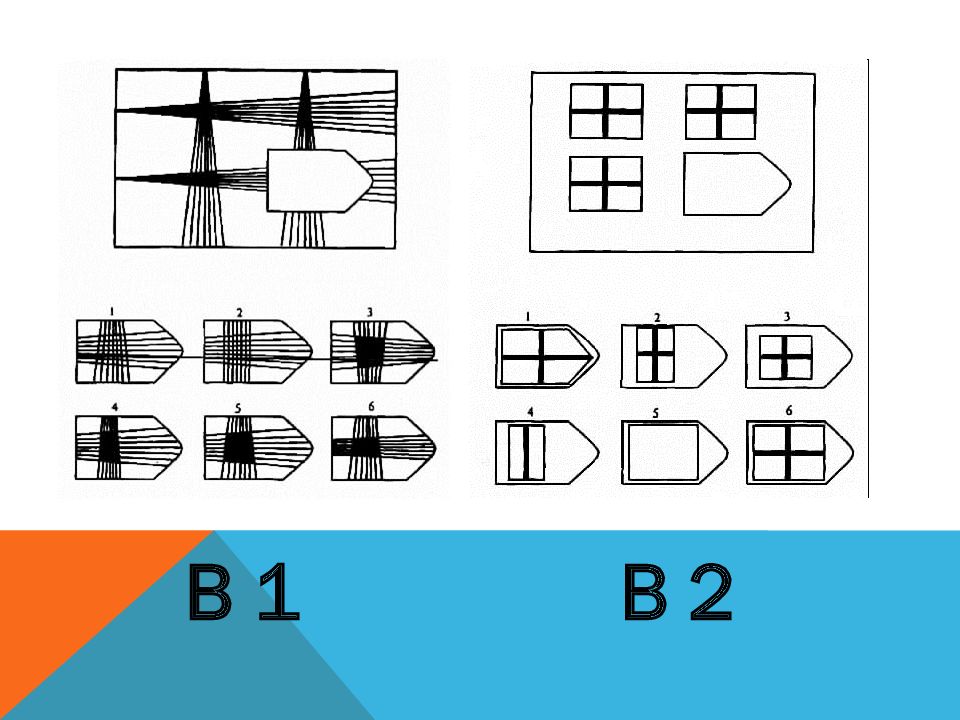 Каждый человек владеет всеми видами интеллекта. Но какой-то будет доминантен, другие выражены, а где-то могут быть и провалы. Именно из-за того, что у физика и художника работают разные виды интеллекта, сравнивать их между собой очень трудно. Вот математика и, допустим, биолога еще куда ни шло, у них склад ума хотя бы приблизительно схожий.
Каждый человек владеет всеми видами интеллекта. Но какой-то будет доминантен, другие выражены, а где-то могут быть и провалы. Именно из-за того, что у физика и художника работают разные виды интеллекта, сравнивать их между собой очень трудно. Вот математика и, допустим, биолога еще куда ни шло, у них склад ума хотя бы приблизительно схожий.
Но каким бы ни было дарование у человека, он не сможет его реализовать без логического интеллекта. Художник не оценит красоту пейзажа или модели, актер не поймет режиссерского замысла и не сообразит, как ему сыграть ту или иную сцену. Спортсмен не рассчитает сил и свалится от усталости на середине дистанции.
Индекс IQ измеряет именно логический интеллект. У тех, кто преуспевает в науке, его значение скорее всего будет, условно говоря, больше 130 баллов. Актеру или спортсмену для успеха в своей профессии будет достаточно более скромного уровня в 110 баллов. Это не свидетельствует о том, что они менее умные, просто их талант раскрывается через другие механизмы, которые в этом тесте учесть не получается.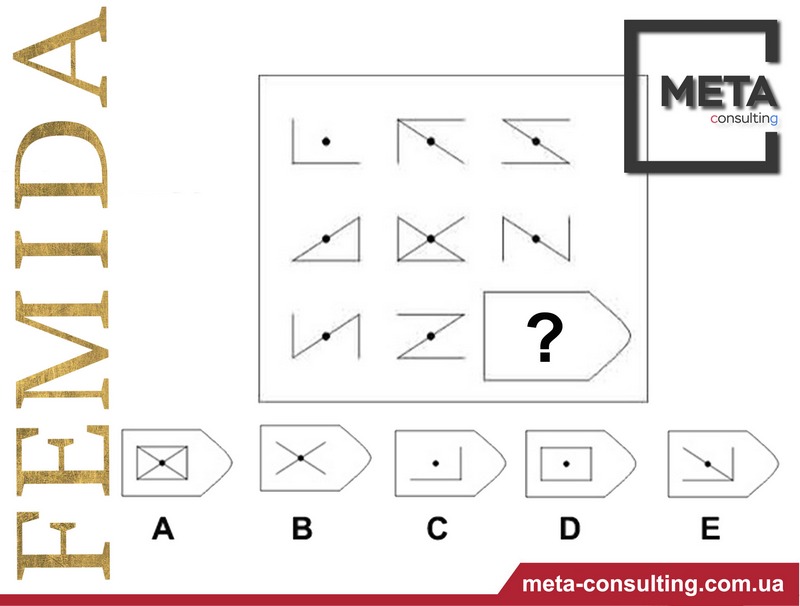 А вот когда IQ меньше 90 баллов, можно говорить о задержке умственного развития. С таким интеллектом преуспеть в чем-либо крайне трудно. Хотя исключения существуют.
А вот когда IQ меньше 90 баллов, можно говорить о задержке умственного развития. С таким интеллектом преуспеть в чем-либо крайне трудно. Хотя исключения существуют.
Получается, индекс IQ особо ничего не значит. Зачем тогда его продолжают использовать?
Виктория Юркевич: Сам по себе индекс IQ не позволяет сказать кто умный, а кто глупый. А вот в школе для выявления умственно одаренных детей, он очень полезен. Тем, кому дан тот или иной вид таланта, нужен другой тип обучения, другие формы педагогической и психологической поддержки, иначе их высокие способности будут не развиваться, а, самое главное, они не смогут реализоваться в дальнейшем. Как обычно получается? Приходит в школе одаренный ребенок. Первые несколько лет без напряжения получает свои пятерки, расслабляется. Чтобы развивать интеллектуальные и волевые качества, ученику обязательно нужен вызов, перед ним должна стоять трудные и интересные задачи. Нет таких? Пиши пропало. После такого обучения у девяти из десяти перспективных мальчиков и девочек остаются только следы былой одаренности.
В нашем университете проводился очень объемный мониторинг одаренности. Участвовало 63 школы, тысячи детей, сотни учителей. Оказалось, что, во-первых, интеллектуально одаренные дети есть практически в каждой школе, а во-вторых, значительная часть учителей не отличает интеллектуально одаренных детей от хорошо обучаемых. И никак не помогают развитию интеллектуальных талантов.
В результате мы теряем людей, которые в будущем могли бы составить инновационный ресурс общества. Но даже не это главное. Нереализовавшийся бывший одаренный ребенок, у которого, по известному выражению, «все его будущее в прошлом», — это всегда несчастный человек. Амбиции никуда не делись, а возможности уже упущены.
Сейчас есть самые разные способы выявления одаренности человека. Тест на IQ — один из самых технологичных. Можно быстро и без специальных затрат обследовать сразу многих. Но к результатам этих тестов надо относиться очень осторожно.
В чем опасность?
Виктория Юркевич: Есть норма, есть нижняя граница нормы и есть верхние пять процентов результатов — это наиболее одаренные школьники.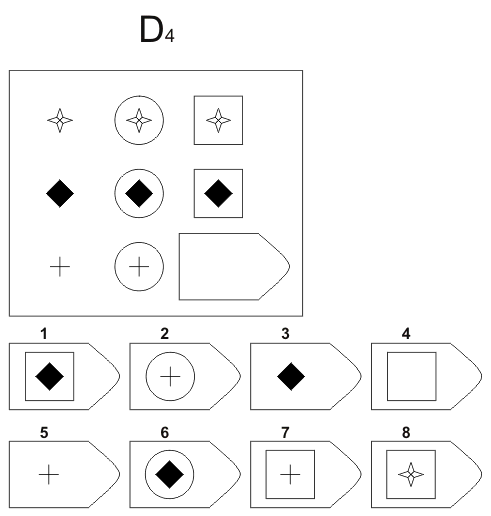 Мы немного по-другому меряем, но, для сведения, IQ 127 и выше свидетельствует о серьезных способностях ребенка, больше 140 — это уже яркая одаренность. Но всерьез рассматривать можно только высокие результаты. То есть если школьник сделал работу на высокие баллы, это прямо свидетельствует о его одаренности. А если итог получился весьма посредственным или даже пугающе низким, допустим, 80-90 баллов, то иногда это вообще ничего не значит. Ребенок мог плохо себя чувствовать, быть чем-то расстроенным, нервничать — есть целое множество причин, по которым в этот конкретный день именно с этим заданием он справился плохо. Только после специальной диагностики специалисты могут назвать истинную причину таких результатов.
Мы немного по-другому меряем, но, для сведения, IQ 127 и выше свидетельствует о серьезных способностях ребенка, больше 140 — это уже яркая одаренность. Но всерьез рассматривать можно только высокие результаты. То есть если школьник сделал работу на высокие баллы, это прямо свидетельствует о его одаренности. А если итог получился весьма посредственным или даже пугающе низким, допустим, 80-90 баллов, то иногда это вообще ничего не значит. Ребенок мог плохо себя чувствовать, быть чем-то расстроенным, нервничать — есть целое множество причин, по которым в этот конкретный день именно с этим заданием он справился плохо. Только после специальной диагностики специалисты могут назвать истинную причину таких результатов.
Специалисты при подборе соискателя на вакансию проводят целую батарею тестов, чтобы понять, подходит этот человек для той или иной работы или нет. Они смотрят его с разных сторон, проверяют все аспекты и виды интеллекта, его интересы и мотивацию, только после этого выносят решение.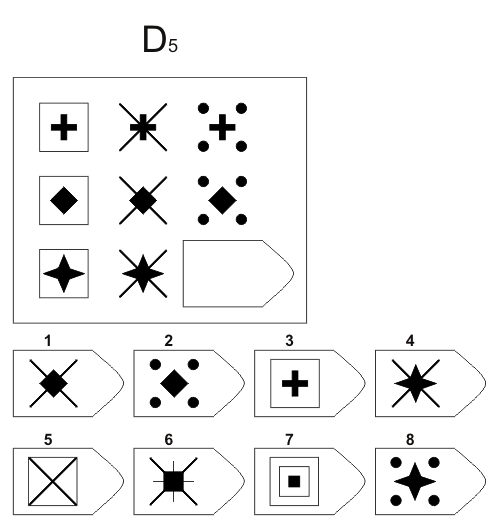 И хотя абсолютную гарантию никто дать не может, но в подавляющем большинстве случаев их рекомендации оправдываются.
И хотя абсолютную гарантию никто дать не может, но в подавляющем большинстве случаев их рекомендации оправдываются.
Даже при отборе одаренных школьников тест на IQ всего лишь один из серии показателей. Интересы ребенка, его мотивация, школьные и внешкольные достижения — только все это в комплексе может показать профессионалу истинный уровень того или иного ребенка.
слишком умные
Еще неизвестно, кто представляет большую проблему для школьного учителя: двоечник или одаренный ребенок. Казалось бы, если ученик с первого класса легко и непринужденно получает сплошные пятерки, это очень хорошо. Однако тут кроется большая опасность.
— Если школьнику слишком легко учиться, и он не сталкивается с трудностями и с легкостью щелкает все задания педагога, это чрезвычайно плохо для его развития, — предупреждает Виктория Юркевич. — Ребенок привыкает все схватывать на лету и не напрягаться. А зачем, если он и расслабленный вполне успешен? В результате в нужной мере не развиваются ни способности, ни личность ребенка.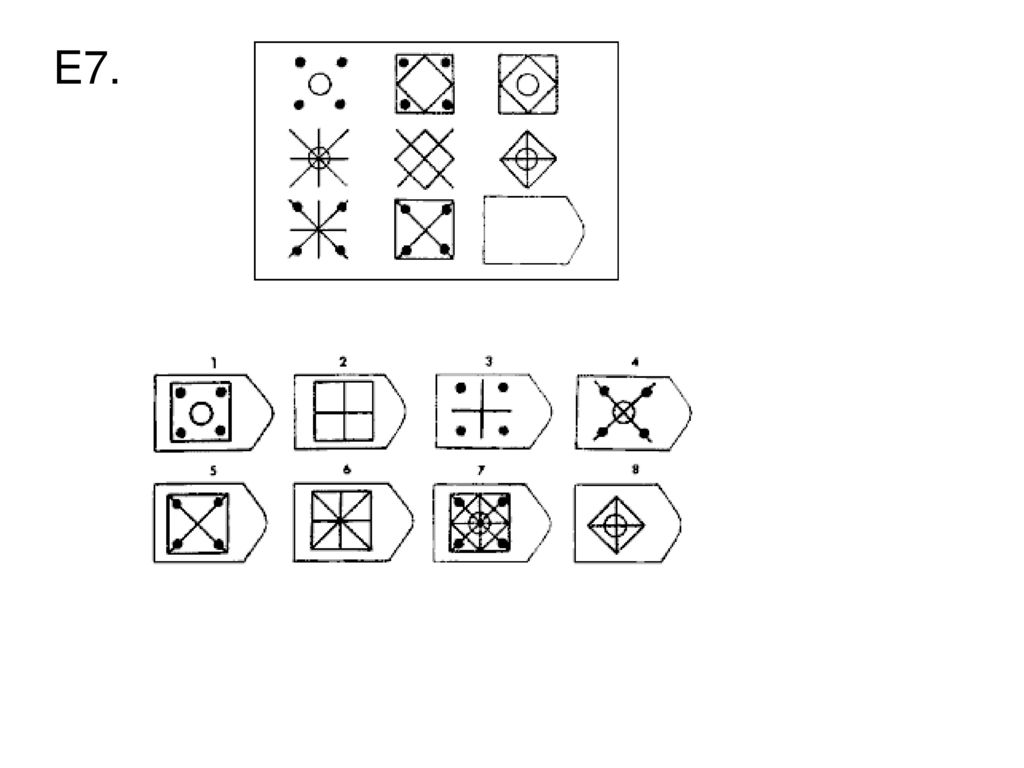
Такой ученик быстро съедет с «пятерок» на «тройки», он не будет развивать свои способности, учеба превратится для него в каторгу. Чтобы этого не произошло, наиболее талантливых учеников теперь начинают выявлять с самых первых дней в школе. Как лучшее средство от скуки на уроках им дают более сложные задания, заставляют честно отрабатывать свои «пятерки».
Мы всегда считаем, что каждый одаренный ребенок в будущем добьется очень многого, — продолжает профессор Юркевич. — Но для этого ему, кроме способностей, будут нужны еще и многие другие качества: самодисциплина, уменее ставить перед собой главные и промежуточные цели. Этому очень легко научиться в школьном возрасте. После — уже с трудом. Одаренные дети, которые легко щелкают школьную программу, этих навыков оказываются лишены. И в результате их талант оказывается нереализованным. Иметь талант и никак его не использовать — это всегда очень грустно. Поэтому одаренных детей надо обязательно выявлять и пестовать.
Незаурядный, выдающийся интеллект: ncuxuamp_pro — LiveJournal
Я такая умная. Какого черта я такая бедная?!
Какого черта я такая бедная?!Главная особенность нашего интеллекта — способность находить аналогии. Мы постоянно сравниваем разные сущности между собой: когда выбираем фильм для вечернего просмотра, ищем подходящую модель смартфона или решаем, к кому обратиться за советом. По этому же принципу работает и обучение: люди применяют в одной ситуации навыки, которым научились в другой — при условии, что между ними есть что-то общее.
Тест Равена — это лучший предиктор того, что психологи называют «подвижным интеллектом», то есть способностью абстрактно мыслить, логически рассуждать, распознавать закономерности, решать проблемы и находить взаимосвязи.
У меня 60 из 60. С введенной поправкой на возраст — IQ 159. Что практически совпадает с тестом Айзенка (я недавно писала), где получилось 160 (без каких либо возрастных поправок). Проходила я тест Равена впервые в жизни, хотя несколько аналогичных задач было и у Айзенка.
пройти тест и похвастаться в комментариях и / или у себя в блоге
этот тест не на время, можно думать сколь угодно долго
Кроме собственно ответа на тест ниже расположена его интерпретация и табличка, каким образом вводить поправку на возраст.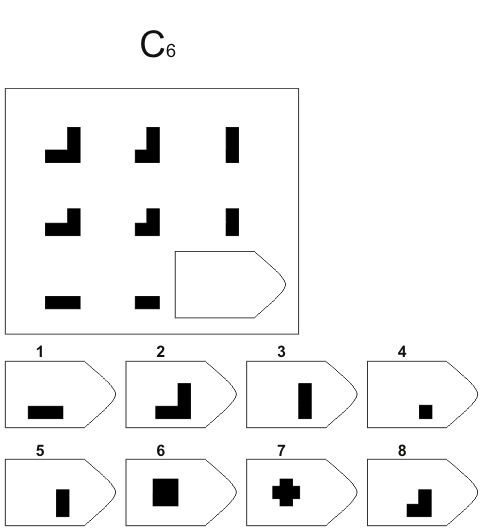
Я специально для тестирования прохождения теста во второй проход дала случайные неправильные ответы, чтобы посмотреть как оно все работает. При неправильном ответе сразу в ячейке появляется красный кружок вместо зеленой галочки, ниже — правильный ответ на предыдущее неправильно выполненное задание, а по окончании тестирования внизу текста и само задание, правильный отввет и ваш ответ. Очень удобно и хорошо все сделано.
Собственно я заинтересовалась этим тестом, прочитав про это (даю в сокращении):
Учёные решили доказать, что способность искать аналогии лежит в основе как решения визуальных задач, так и интеллекта в целом. Для этого они разработали вычислительную модель, способную пройти тест Равена. Компьютеру нужно было решить все 60 заданий теста. Программа справилась с 56 матрицами из 60, а подопытные студенты в среднем — с 54 из 60. Таким образом, модель обошла человека, и согласно нормам, принятым в США в 1993 году, показала результат «выше среднего». «Модель решает задачи не хуже 75% взрослых американцев, то есть, на уровне выше среднего, — говорит один из авторов исследования Кен Форбус (Ken Forbus). — Проблемы, сложные для людей, сложны и для модели, и это ещё одно доказательство того, что она обладает некоторыми важными для когнитивных способностей человека характеристиками».
— Проблемы, сложные для людей, сложны и для модели, и это ещё одно доказательство того, что она обладает некоторыми важными для когнитивных способностей человека характеристиками».
отсюда
Мощность теста — обзор
2 Статистический размер и мощность
Размер теста — это вероятность ошибочного отклонения нулевой гипотезы, если она верна. Степень теста — это вероятность правильного отклонения нулевой гипотезы, если она ложна. Для данной гипотезы и статистики теста один ограничивает размер теста, чтобы он был маленьким, и пытается сделать мощность теста как можно большей.
При заданном размере, статистике теста, нулевой гипотезе и альтернативе статистическая мощность может быть оценена с использованием общего (но иногда неуместного) предположения о том, что данные являются гауссовскими.Однако по мере сбора данных улучшенные оценки могут быть получены с помощью современных компьютерных статистических методов. Например, мощность и размер могут быть вычислены для каждой тестовой статистики, описанной ранее, чтобы проверить гипотезу о том, что цифровая маммография с заданной скоростью передачи данных равна или превосходит маммографию на пленочном экране с заданной статистикой и альтернативной гипотезой, которая должна быть предложена на основе данных.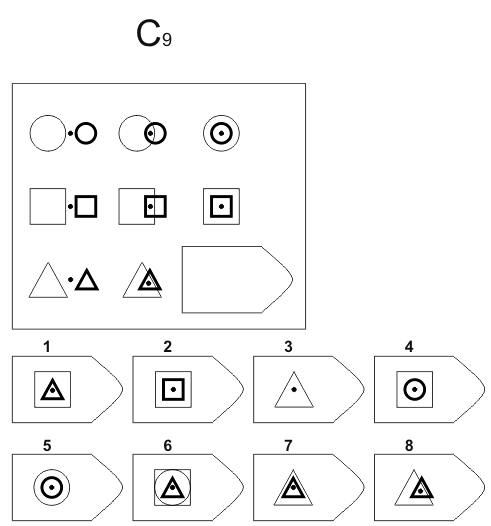 В отсутствие данных мы можем только предполагать поведение собранных данных, чтобы приблизительно оценить мощность и размер.Мы рассматриваем односторонний тест с «нулевой гипотезой» о том, что независимо от критерия [управление или чувствительность к обнаружению, специфичность или положительная прогностическая ценность (PVP)], маммограммы, полученные цифровым способом или сжатые с потерями, с определенной частотой хуже, чем аналог. «Альтернатива» — они лучше. В соответствии со стандартной практикой мы берем наши тесты на размер 0,05. Здесь мы сосредоточены на чувствительности и специфичности управленческих решений, но общий подход можно распространить на другие тесты и задачи.
В отсутствие данных мы можем только предполагать поведение собранных данных, чтобы приблизительно оценить мощность и размер.Мы рассматриваем односторонний тест с «нулевой гипотезой» о том, что независимо от критерия [управление или чувствительность к обнаружению, специфичность или положительная прогностическая ценность (PVP)], маммограммы, полученные цифровым способом или сжатые с потерями, с определенной частотой хуже, чем аналог. «Альтернатива» — они лучше. В соответствии со стандартной практикой мы берем наши тесты на размер 0,05. Здесь мы сосредоточены на чувствительности и специфичности управленческих решений, но общий подход можно распространить на другие тесты и задачи.
Приблизительные расчеты мощности производятся из таблиц согласования 2 на 2 формы Таблицы 1. В этой таблице строки соответствуют одной технологии (например, аналоговой), а столбцы — другой (например, цифровой). «R» и «W» соответствуют «правильному» (согласие с золотым стандартом) и «неправильному» (несогласие с золотым стандартом).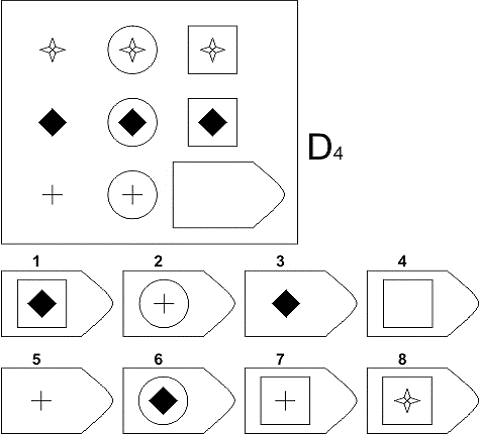 Так, например, число N (1, 1) — это количество случаев, когда рентгенолог был прав при чтении как аналоговых, так и цифровых изображений. Ключевая идея двояка.При отсутствии данных предположение о мощности может быть вычислено с использованием стандартных приближений. Однако после получения предварительных данных можно получить более точные оценки с помощью методов моделирования, использующих оценки, присущие данным. В таблице 2 показаны возможности и соответствующие им вероятности. Правый столбец и нижняя строка представляют собой суммы того, что находится, соответственно, слева и над ними. Таким образом, ψ — это значение для одной технологии, а ψ + h — значение для другой; h = 0 означает отсутствие разницы.Это нулевая гипотеза. Четыре записи в середине таблицы — это параметры, которые определяют вероятности для одного исследования. Предполагается, что это средние значения по радиологам, как и приведенные суммы. Наши симуляции учитывают то, что мы знаем об этом: радиологи очень разные в том, как они справляются и как они обнаруживают.
Так, например, число N (1, 1) — это количество случаев, когда рентгенолог был прав при чтении как аналоговых, так и цифровых изображений. Ключевая идея двояка.При отсутствии данных предположение о мощности может быть вычислено с использованием стандартных приближений. Однако после получения предварительных данных можно получить более точные оценки с помощью методов моделирования, использующих оценки, присущие данным. В таблице 2 показаны возможности и соответствующие им вероятности. Правый столбец и нижняя строка представляют собой суммы того, что находится, соответственно, слева и над ними. Таким образом, ψ — это значение для одной технологии, а ψ + h — значение для другой; h = 0 означает отсутствие разницы.Это нулевая гипотеза. Четыре записи в середине таблицы — это параметры, которые определяют вероятности для одного исследования. Предполагается, что это средние значения по радиологам, как и приведенные суммы. Наши симуляции учитывают то, что мы знаем об этом: радиологи очень разные в том, как они справляются и как они обнаруживают.
ТАБЛИЦА 1. Соглашение 2 × 2 таблицы
| II \ I | R | W |
|---|---|---|
| R | N (1, 1) | N (1, 2 ) |
| W | N (2, 1) | N (2, 2) |
ТАБЛИЦА 2.Вероятности исхода управления
| II \ I | Правильно | Неправильно | |
|---|---|---|---|
| Правильно | 2ψ + h — 1 + γ | 1 — ψ — h — γ | ψ |
| Неправильно | 1 – ψ – γ | γ | 1 – ψ |
| ψ + h | 1– ψ – h | 1 |
Два основных параметра равны γ и R .Первый — это вероятность (в среднем) того, что радиолог «не прав» для обеих технологий; R — количество радиологов.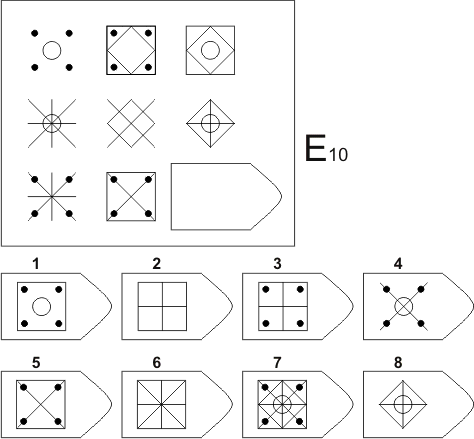 Эти ключевые параметры могут быть оценены по счетам таблицы согласования 2 на 2, полученной в результате пилотного эксперимента, а затем улучшены по мере получения дополнительных данных.
Эти ключевые параметры могут быть оценены по счетам таблицы согласования 2 на 2, полученной в результате пилотного эксперимента, а затем улучшены по мере получения дополнительных данных.
В нашем небольшом пилотном исследовании лечения мы обнаружили чувствительность около 0,60 и специфичность около 0,55. Соответствующие оценочные значения ч варьировались от более чем 0.02 примерно до 0,07; γ был около 0,05. Все эти числа искажены значительным шумом. В самом деле, вариативность, связанная с нашей оценкой их, затмевается очевидной вариабельностью среди радиологов. Для теста размером 0,05, варьируя параметры в количествах, подобных тому, что мы видели, мощность может быть от 0,17 с 18 радиологами или до 1,00 с только 9 радиологами. Мощность очень чувствительна к трем параметрам. Независимо от того, сколько исследований или сколько у нас было бы радиологов, всегда можно было изменить параметры, чтобы нам потребовалось больше одного или обоих.
Если мы подумаем, что чувствительность обнаружения составляет, скажем, 0,85, то, по крайней мере, для этого количества 400 исследований и 9 радиологов кажутся достаточными.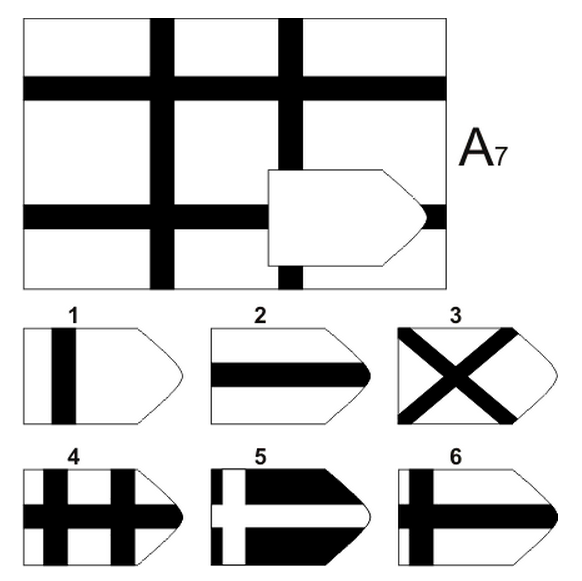 В настоящее время одна хорошая рекомендация — начать с 400 исследований, 12 радиологов, по три в каждом из четырех центров, и найти достигнутый уровень значимости для проверки нулевой гипотезы об отсутствии разницы между технологиями. И, что, возможно, не менее важно, оцените параметры таблицы 2. На этом этапе можно оценить возможное количество требуемых дополнительных радиологов или исследований, если таковые имеются, для конкретных значений размера и мощности, которые могут потребоваться рецензентам.Дизайн может быть изменен таким образом, чтобы пул исследований включал более 400, но ни один радиолог не прочитал бы более 400. Таким образом, мы могли довольно легко оценить влияние переменной распространенности неблагоприятных результатов в золотом стандарте, хотя мы может подойти к этому вопросу даже в ситуации, которую мы изучаем здесь.
В настоящее время одна хорошая рекомендация — начать с 400 исследований, 12 радиологов, по три в каждом из четырех центров, и найти достигнутый уровень значимости для проверки нулевой гипотезы об отсутствии разницы между технологиями. И, что, возможно, не менее важно, оцените параметры таблицы 2. На этом этапе можно оценить возможное количество требуемых дополнительных радиологов или исследований, если таковые имеются, для конкретных значений размера и мощности, которые могут потребоваться рецензентам.Дизайн может быть изменен таким образом, чтобы пул исследований включал более 400, но ни один радиолог не прочитал бы более 400. Таким образом, мы могли довольно легко оценить влияние переменной распространенности неблагоприятных результатов в золотом стандарте, хотя мы может подойти к этому вопросу даже в ситуации, которую мы изучаем здесь.
Вычисления мощности одинаково хорошо применимы в нашей формулировке к чувствительности и специфичности. Они основаны на выборке из 400 исследований, для которых осмотрительная медицинская практика предписывает вернуться к скринингу, для 200, и что-то еще ( 6-месячное наблюдение, требуется дополнительная оценка или биопсия ) для остальных 200.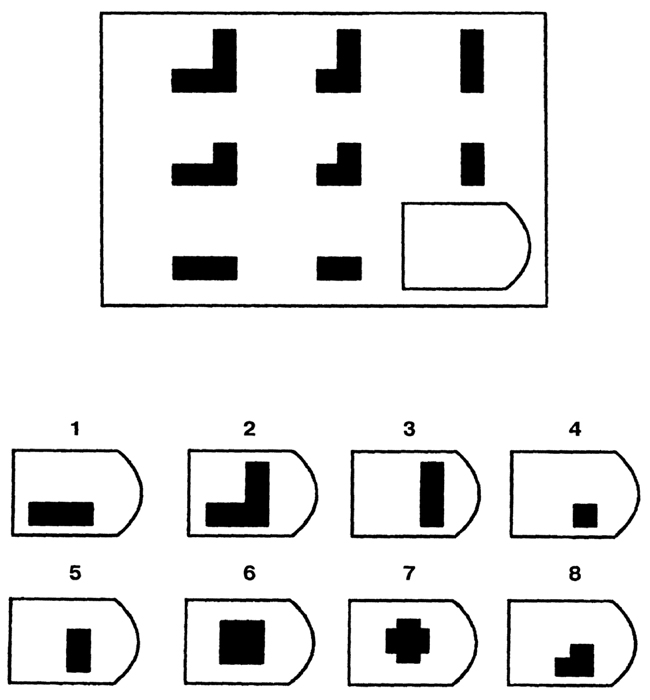 Таким образом, существует 200 исследований, которые используются для расчета чувствительности, и столько же исследований для определения специфичности. Все сравнения проводятся в контексте «клинического ведения», которое может быть «правильным» или «неправильным». Само собой разумеется, что существует согласованный золотой стандарт , независимый или отдельный. Для данного радиолога, который оценил две технологии — здесь называемые I и II и предназначенные для использования в качестве цифровых и аналоговых или аналоговых и сжатых с потерями цифровых данных — конкретное исследование приводит к записи в таблице согласования 2 на 2 в виде таблицы 1.
Таким образом, существует 200 исследований, которые используются для расчета чувствительности, и столько же исследований для определения специфичности. Все сравнения проводятся в контексте «клинического ведения», которое может быть «правильным» или «неправильным». Само собой разумеется, что существует согласованный золотой стандарт , независимый или отдельный. Для данного радиолога, который оценил две технологии — здесь называемые I и II и предназначенные для использования в качестве цифровых и аналоговых или аналоговых и сжатых с потерями цифровых данных — конкретное исследование приводит к записи в таблице согласования 2 на 2 в виде таблицы 1.
Если нулевая гипотеза «нет разницы в технологиях» верна, то каким бы ни было ψ и γ, h = 0. Альтернативная гипотеза могла бы указать h ≠ 0 и без потерь (поскольку мы можем звонить какую бы технологию мы ни хотели, I или II) мы можем принять h > 0 в соответствии с альтернативной гипотезой о том, что существует истинное различие в технологиях. Под нулевым значением задано b + c, b имеет биномиальное распределение с параметрами b + c и 1/2.Согласно альтернативе, задано b + c, b является биномиальным с параметрами b + c и (1 — ψ — h — γ) / (2 — 2ψ — 2γ — h ). Обычный условный тест Макнемара нулевой гипотезы основан на ( b — c ) 2 / ( b + c ), имеющем приблизительно распределение хи-квадрат с одной степенью свободы.
Под нулевым значением задано b + c, b имеет биномиальное распределение с параметрами b + c и 1/2.Согласно альтернативе, задано b + c, b является биномиальным с параметрами b + c и (1 — ψ — h — γ) / (2 — 2ψ — 2γ — h ). Обычный условный тест Макнемара нулевой гипотезы основан на ( b — c ) 2 / ( b + c ), имеющем приблизительно распределение хи-квадрат с одной степенью свободы.
На практике мы намерены использовать радиологов R для R = 9, 12, 15 или 18, чтобы предположить, что их результаты независимы, и объединить их данные, добавив соответствующие значения их статистики Макнемара.Мы всегда предполагаем, что размер = вероятность ошибки типа I составляет 0,05. Поскольку сумма независимых случайных величин хи-квадрат распределена как хи-квадрат со степенями свободы, суммой соответствующих степеней свободы, в качестве критического значения для нашего теста целесообразно принять число C , где Pr ( χR2> C) = 0,05.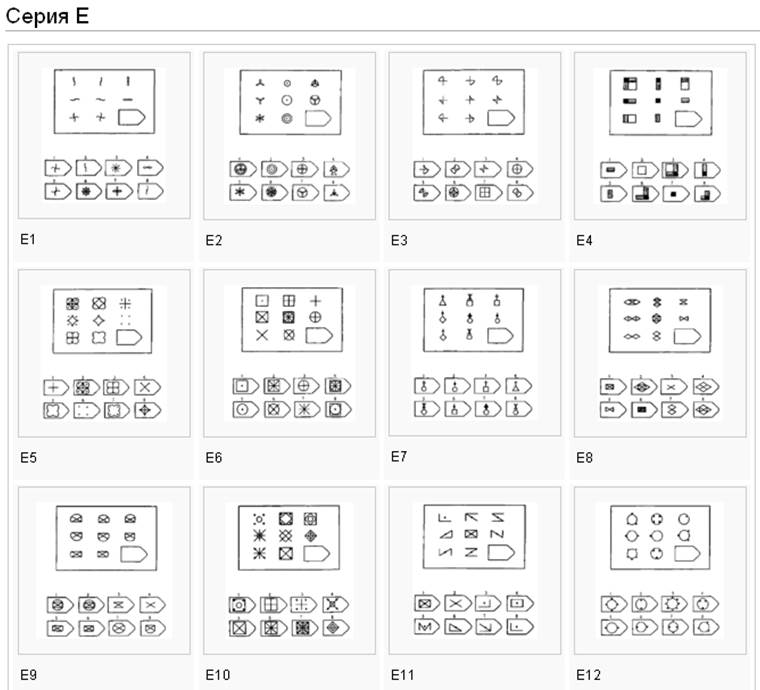 Таким образом, четыре соответствующих значения C равны 16,92, 21,03, 25,00 и 28,87.
Таким образом, четыре соответствующих значения C равны 16,92, 21,03, 25,00 и 28,87.
Вычислить мощность сложно, потому что это безусловное , так как до эксперимента b + c для каждого радиолога является случайным.Таким образом, мощность — это вероятность того, что нецентральная случайная величина хи-квадрат с R степенями свободы и параметром нецентральности [(p1−0.5) 2 / p1q1] ∑i = 1R (bi + ci) превышает C /4 p 1 q 1 , где b i + c i имеет биномиальное распределение с параметрами N и 2 — 2ψ — 2γ — h ; и случайные целые числа R независимы; p 1 = (1 — ψ — h — γ) / (2 — 2ψ — 2γ — h ) = 1 — q 1 .Это влечет за собой, что параметры нецентральности случайной величины хи-квадрат, которая фигурирует при вычислении мощности, сами по себе являются случайными. Обратите внимание, что нецентральная случайная величина хи-квадрат с R степенями свободы и параметром нецентральности Q является распределением (G1 + Q1 / 2) 2 + G22 + ··· + GR2, где G 1 ,…, G R — независимые, одинаково распределенные стандартные гауссианы. На основе предыдущей работы и этого пилотного исследования мы решили вычислить степень нашего размера 0.05 тесты для N всегда 200, ψ от 0,55 до 0,85 с шагом 0,05; γ = 0,03, 0,05, 0,10; и, как было сказано, R = 9, 12, 15 и 18. Моделируемые значения мощности можно найти в [2], а код для выполнения этих вычислений — в Приложении C Беттса [1]. Они составляют основу наших более ранних оценок необходимого количества пациентов и будут обновляться по мере сбора данных.
Обратите внимание, что нецентральная случайная величина хи-квадрат с R степенями свободы и параметром нецентральности Q является распределением (G1 + Q1 / 2) 2 + G22 + ··· + GR2, где G 1 ,…, G R — независимые, одинаково распределенные стандартные гауссианы. На основе предыдущей работы и этого пилотного исследования мы решили вычислить степень нашего размера 0.05 тесты для N всегда 200, ψ от 0,55 до 0,85 с шагом 0,05; γ = 0,03, 0,05, 0,10; и, как было сказано, R = 9, 12, 15 и 18. Моделируемые значения мощности можно найти в [2], а код для выполнения этих вычислений — в Приложении C Беттса [1]. Они составляют основу наших более ранних оценок необходимого количества пациентов и будут обновляться по мере сбора данных.
S.3.2 Проверка гипотез (подход P-значения)
В нашем примере, касающемся среднего среднего балла, предположим, что наша случайная выборка из n = 15 студентов, специализирующихся на математике, дает статистику теста t *, равную 2 .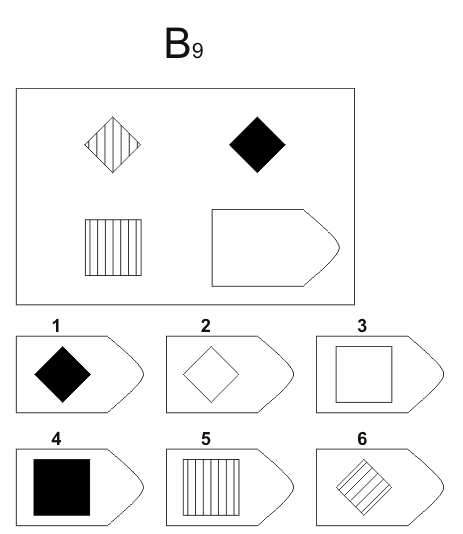 5. Поскольку n = 15, наша тестовая статистика t * имеет n — 1 = 14 степеней свободы. Кроме того, предположим, что мы установили наш уровень значимости α равным 0,05, так что у нас есть только 5% шанс сделать ошибку типа I.
5. Поскольку n = 15, наша тестовая статистика t * имеет n — 1 = 14 степеней свободы. Кроме того, предположим, что мы установили наш уровень значимости α равным 0,05, так что у нас есть только 5% шанс сделать ошибку типа I.
Правый хвост
P -значение для проведения правостороннего теста H 0 : μ = 3 по сравнению с H A : μ > 3 — вероятность того, что мы увидим тест статистика больше т * = 2.5, если среднее значение \ (\ mu \) действительно было 3. Напомним, что вероятность равна площади под кривой вероятности. Таким образом, значение P — это область под кривой t n — 1 = t 14 и справа от тестовой статистики t * = 2,5. С помощью статистического программного обеспечения можно показать, что значение P равно 0,0127. График это изображает визуально.
P -значение, 0.0127, говорит нам, что «маловероятно», что мы наблюдали бы такую экстремальную статистику теста t * в направлении H A , если бы нулевая гипотеза была верна. Следовательно, наше первоначальное предположение о том, что нулевая гипотеза верна, должно быть неверным. То есть, поскольку значение P , 0,0127, меньше \ (\ alpha \) = 0,05, мы отклоняем нулевую гипотезу H 0 : μ = 3 в пользу альтернативной гипотезы H A : μ > 3.
Обратите внимание, что мы не отклонили бы H 0 : μ = 3 в пользу H A : μ > 3, если бы мы снизили нашу готовность к ошибке типа I до \ (\ alpha \) = 0,01, поскольку значение P , 0,0127, больше, чем \ (\ alpha \) = 0,01.
Левосторонний
В нашем примере, касающемся среднего среднего балла, предположим, что наша случайная выборка из n = 15 студентов, специализирующихся на математике, дает тестовую статистику t * вместо -2.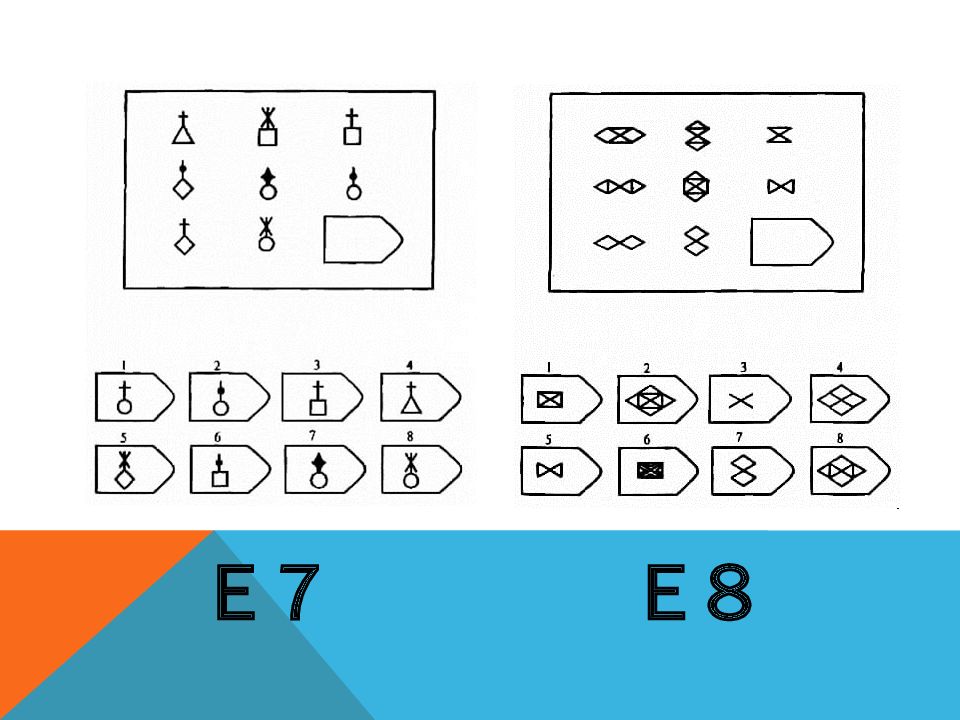 5. Значение P для проведения теста с левым хвостом H 0 : μ = 3 по сравнению с H A : μ <3 - вероятность того, что мы увидим тестовая статистика меньше t * = -2,5, если среднее значение для генеральной совокупности μ действительно было 3. Следовательно, значение P — это область под t n — 1 = t 14 , а до осталось тестовой статистики t * = -2.5. С помощью статистического программного обеспечения можно показать, что значение P равно 0,0127. График это изображает визуально.
5. Значение P для проведения теста с левым хвостом H 0 : μ = 3 по сравнению с H A : μ <3 - вероятность того, что мы увидим тестовая статистика меньше t * = -2,5, если среднее значение для генеральной совокупности μ действительно было 3. Следовательно, значение P — это область под t n — 1 = t 14 , а до осталось тестовой статистики t * = -2.5. С помощью статистического программного обеспечения можно показать, что значение P равно 0,0127. График это изображает визуально.
Значение P , 0,0127, говорит нам, что «маловероятно», чтобы мы наблюдали такую экстремальную статистику теста t * в направлении H A , если бы нулевая гипотеза была верна. Следовательно, наше первоначальное предположение о том, что нулевая гипотеза верна, должно быть неверным.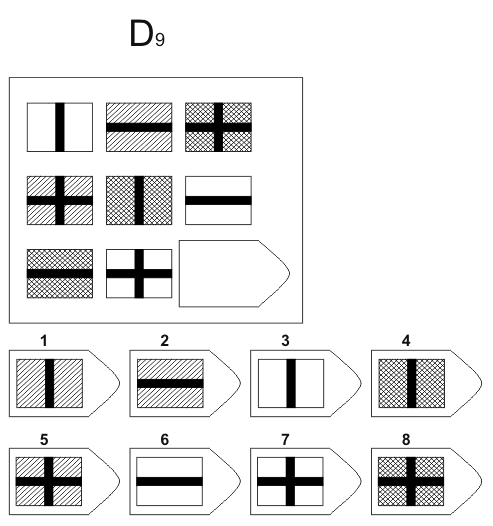 То есть, поскольку значение P , 0,0127, меньше α = 0.05, мы отвергаем нулевую гипотезу H 0 : μ = 3 в пользу альтернативной гипотезы H A : μ <3.
То есть, поскольку значение P , 0,0127, меньше α = 0.05, мы отвергаем нулевую гипотезу H 0 : μ = 3 в пользу альтернативной гипотезы H A : μ <3.
Обратите внимание, что мы не отклонили бы H 0 : μ = 3 в пользу H A : μ <3, если бы мы снизили нашу готовность делать ошибку I типа до α = 0,01. , поскольку значение P , 0,0127, больше, чем \ (\ alpha \) = 0,01.
Двусторонний
В нашем примере, касающемся среднего среднего балла, предположим снова, что наша случайная выборка из n = 15 студентов, специализирующихся на математике, дает тестовую статистику t * вместо -2,5. P -значение для проведения двустороннего теста H 0 : μ = 3 по сравнению с H A : μ ≠ 3 — вероятность того, что мы увидим статистику теста менее -2. 5 или больше 2,5, если среднее значение совокупности μ действительно было 3. То есть двусторонний тест требует учета возможности того, что тестовая статистика может попасть в любой из хвостов (отсюда и название «двусторонний» тест ). Таким образом, значение P — это область под кривой t n — 1 = t 14 до слева от -2,5 и до справа от от 2,5. С помощью статистического программного обеспечения можно показать, что значение P равно 0.0127 + 0,0127 или 0,0254. График это изображает визуально.
5 или больше 2,5, если среднее значение совокупности μ действительно было 3. То есть двусторонний тест требует учета возможности того, что тестовая статистика может попасть в любой из хвостов (отсюда и название «двусторонний» тест ). Таким образом, значение P — это область под кривой t n — 1 = t 14 до слева от -2,5 и до справа от от 2,5. С помощью статистического программного обеспечения можно показать, что значение P равно 0.0127 + 0,0127 или 0,0254. График это изображает визуально.
Обратите внимание, что значение P для двустороннего теста всегда в два раза больше значения P для любого из односторонних тестов. Значение P , 0,0254, говорит нам, что «маловероятно», чтобы мы наблюдали такую экстремальную статистику теста t * в направлении H A , если бы нулевая гипотеза была верна. Следовательно, наше первоначальное предположение о том, что нулевая гипотеза верна, должно быть неверным.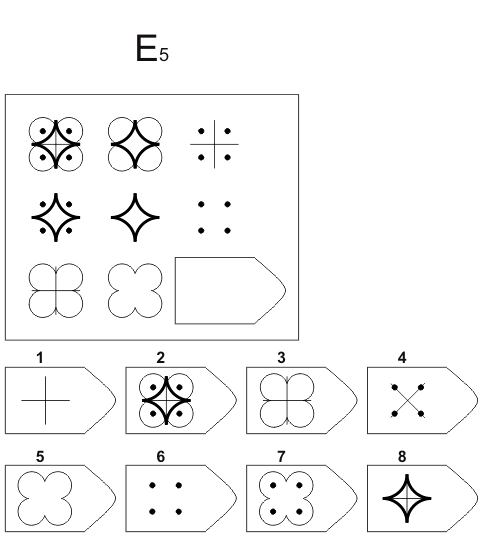 То есть, поскольку значение P , 0,0254, меньше α = 0,05, мы отклоняем нулевую гипотезу H 0 : μ = 3 в пользу альтернативной гипотезы H A : мкм ≠ 3.
То есть, поскольку значение P , 0,0254, меньше α = 0,05, мы отклоняем нулевую гипотезу H 0 : μ = 3 в пользу альтернативной гипотезы H A : мкм ≠ 3.
Обратите внимание, что мы не отклонили бы H 0 : μ = 3 в пользу H A : μ ≠ 3, если бы мы снизили нашу готовность совершать ошибку I типа до α = 0,01. , как значение P , 0.0254, тогда больше, чем \ (\ alpha \) = 0,01.
Теперь, когда мы рассмотрели процедуры подхода к критическому значению и P -значению для каждой из трех возможных гипотез, давайте рассмотрим три новых примера — один из теста с правым хвостом, один из теста с левым хвостом и один из двусторонний тест.
Хорошая новость заключается в том, что, когда это возможно, мы будем использовать статистику испытаний и значения P , полученные в статистическом программном обеспечении, таком как Minitab, для проведения тестов гипотез в этом курсе.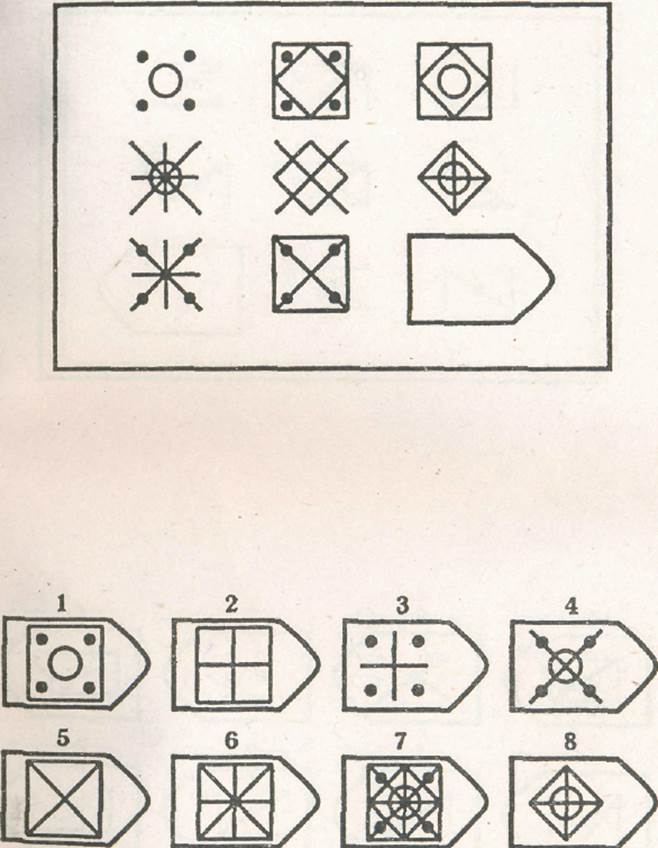
Проверка силы гипотез
Вероятность того, что не совершит Ошибка типа II называется степенью проверка гипотез.
Размер эффекта
Чтобы вычислить мощность теста, предлагается альтернативный вариант. представление об «истинном» значении параметра совокупности, предполагая, что нулевая гипотеза неверна. В размер эффекта разница между истинным значением и значением, указанным в нуле гипотеза.
Размер эффекта = Истинное значение — Предполагаемое значение
Например, предположим, что нулевая гипотеза утверждает, что совокупность среднее равно 100.Исследователь может спросить: какова вероятность отклонения нулевой гипотезы, если истинное среднее значение равно 90? В этом примере размер эффекта будет от 90 до 100, что равно -10.
Факторы, влияющие на мощность
На мощность проверки гипотез влияют три фактора.
- Размер выборки ( n ). При прочих равных, чем больше
чем размер выборки, тем выше мощность теста.
- Уровень значимости (α). Чем ниже уровень значимости, тем ниже мощность теста.Если снизить уровень значимости (например, с 0,05 до 0,01), в область приема увеличивается. В результате у вас меньше шансов отклонить нулевую гипотезу. Это означает, что у вас меньше шансов отклонить нулевую гипотезу, если она неверна, поэтому вы с большей вероятностью сделать ошибку типа II. Короче говоря, мощность теста снижается, когда вы уменьшаете уровень значимости; и наоборот.
- «Истинное» значение проверяемого параметра. Чем больше разница между «истинным» значением параметра и значением указанное в нулевой гипотезе, тем больше мощность тест.То есть, чем больше размер эффекта, тем больше мощность теста.
Проверьте свое понимание
Задача 1
При прочих равных, какое из следующих действий приведет к уменьшить мощность проверки гипотез?
I. Увеличение размера выборки.
II. Изменение уровня значимости с 0,01 на 0,05.
III. Увеличение бета, вероятность ошибки типа II.
Увеличение бета, вероятность ошибки типа II.
(A) Только I
(B) Только II
(C) Только III
(D) Все вышеперечисленное
(E) Ничего из вышеперечисленного
Решение
Правильный ответ — (C).Увеличение размера выборки делает гипотезу тест более чувствителен — с большей вероятностью отвергнет нулевую гипотезу когда на самом деле это ложь. Изменение уровня значимости с 0,01 на 0,05 делает область принятия меньше, что делает проверку гипотезы более вероятность отклонить нулевую гипотезу, тем самым увеличивая мощность теста. Поскольку по определению мощность равна единице минус бета, мощность теста будет уменьшаться по мере увеличения бета больше.
Задача 2
Предположим, исследователь проводит эксперимент для проверки гипотезы.Если она удвоит размер выборки, что из следующего увеличивать?
I. Сила проверки гипотез.
II. Размер эффекта проверки гипотезы.
III. Вероятность совершения ошибки типа II.
(A) Только I
(B) Только II
(C) Только III
(D) Все вышеперечисленное
(E) Ничего из вышеперечисленного
Решение
Правильный ответ (A). Увеличение размера выборки делает гипотезу тест более чувствителен — с большей вероятностью отвергнет нулевую гипотезу когда на самом деле это ложь.Таким образом, увеличивается мощность контрольная работа. Размер эффекта не зависит от размера выборки. И вероятность сделать Ошибка типа II становится меньше, а не больше, чем размер выборки. увеличивается.
GRE Multiple-Choice — Выберите один вопрос (для участников тестирования)
Если какое значение x?
- 4
- 7
- 12
Пояснение
Решая уравнение относительно x, вы получаете и поэтому Правильный ответ — вариант A,
Какое из следующих чисел дальше всего от цифры 1 в числовой строке?
- 0
- 5
- 10
Пояснение
Обвод каждого варианта ответа на схеме числовой прямой (рис.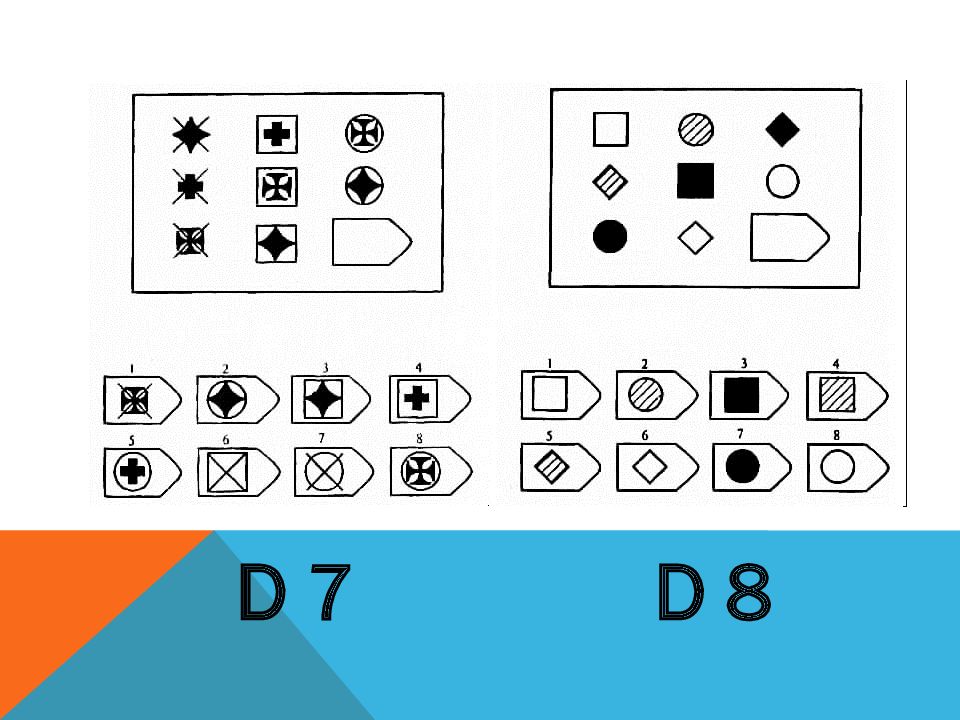 4) показывает, что из данных чисел это наибольшее расстояние от 1.
4) показывает, что из данных чисел это наибольшее расстояние от 1.
Рисунок 4
Другой способ ответить на вопрос — это помнить, что расстояние между двумя числами на числовой прямой равно абсолютному значению разницы двух чисел. Например, расстояние между и 1 равно, а расстояние между 10 и 1 равно. Правильный ответ — вариант A,
.Фиг.5
На рисунке выше показан график функции f, определенной для всех чисел x.Для какой из следующих функций g, определенных для всех чисел x, график g пересекает график f?
Пояснение
Вы можете видеть, что все пять вариантов являются линейными функциями, графики которых представляют собой линии с различными наклонами и пересечениями по оси Y. График варианта A представляет собой линию с наклоном 1 и точкой пересечения по оси Y, показанной на рисунке 6.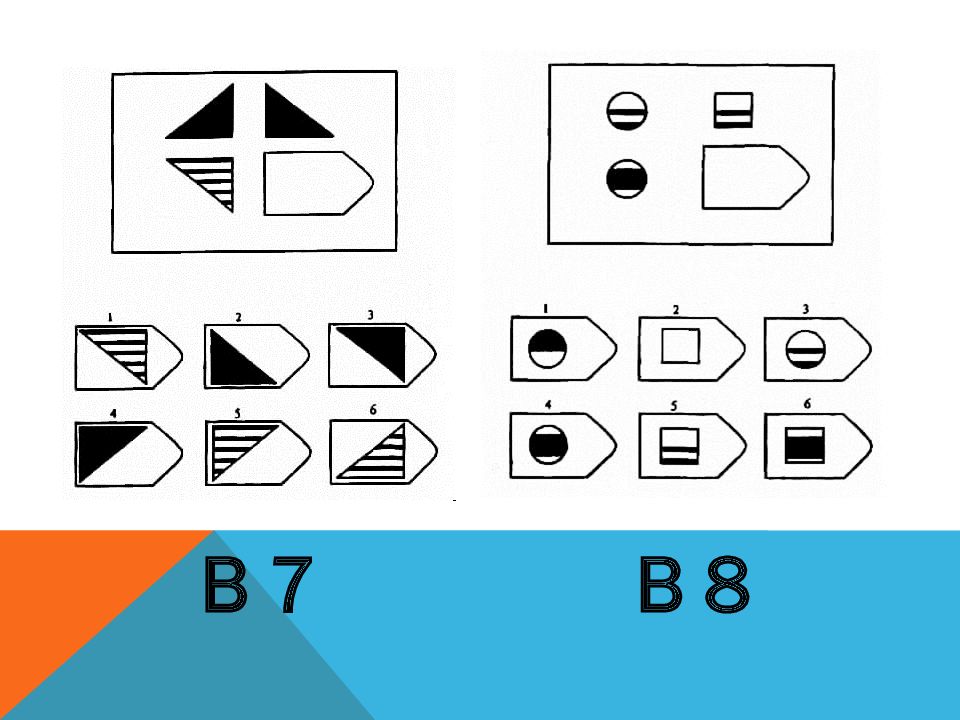
Рисунок 6
Ясно, что эта линия не будет пересекать график f слева от оси y.Справа от оси y график f представляет собой линию с наклоном 2, который больше, чем наклон 1. Следовательно, по мере увеличения значения x значение y увеличивается для f быстрее, чем для g, и, следовательно, графики не пересекаются справа от оси y. Вариант B также исключен. Обратите внимание, что если бы точка пересечения по оси Y любой из линий в вариантах A и B была больше или равна 4, а не меньше 4, они пересекали бы график f.
Варианты C и D — это линии с наклоном 2 и пересечением по оси Y меньше 4.Следовательно, они параллельны графику f (справа от оси y) и, следовательно, не будут его пересекать. Любая линия с наклоном больше 2 и точкой пересечения по оси Y меньше 4, например линия в Варианте E, будет пересекать график f (справа от оси Y). Правильный ответ — выбор E,
. Автомобиль проехал 33 мили на галлон бензина, который стоит 2,95 доллара за галлон.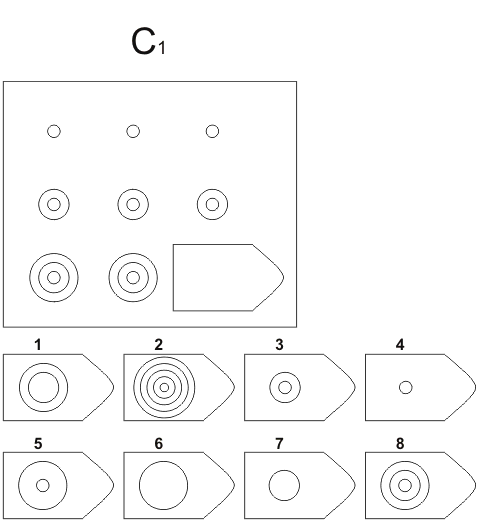 Какова примерная стоимость в долларах бензина, использованного для езды на автомобиле 350 миль?
Какова примерная стоимость в долларах бензина, использованного для езды на автомобиле 350 миль?
- $ 10
- $ 20
- $ 30
- $ 40
- $ 50
Пояснение
Просмотр вариантов ответа показывает, что вы можете сделать хотя бы некоторую оценку и при этом ответить уверенно.В машине использовались галлоны бензина, поэтому стоимость составляла доллары. Вы можете оценить продукт, оценив немного ниже, 10, и оценив 2,95, немного выше, 3, чтобы получить приблизительно доллары. Вы также можете использовать калькулятор, чтобы вычислить более точный ответ, а затем округлить ответ до ближайших 10 долларов в соответствии с вариантами ответов. Калькулятор вычисляет десятичную дробь, которая округляется до 30 долларов. Таким образом, правильный ответ — вариант C, 30 долларов.
В одной банке 60 мармеладов: 22 белых, 18 зеленых, 11 желтых, 5 красных и 4 фиолетовых.Если мармелад должен быть выбран наугад, какова вероятность того, что мармелад не будет ни красным, ни пурпурным?
- 0,09
- 0,15
- 0,54
- 0,85
- 0,91
Пояснение
Поскольку в банке 5 красных и 4 фиолетовых мармелада, 51 мармелад не является ни красным, ни пурпурным, и вероятность выбора одного из них равна. эквивалент, 0.85. Таким образом, правильный ответ — вариант D, 0,85.
эквивалент, 0.85. Таким образом, правильный ответ — вариант D, 0,85.
Простое определение, пошаговые примеры — Выполнение вручную / Excel
Проверка гипотез> F-Test
Содержание:
- Что такое F-тест?
- Общие шаги для F-теста
- F Тест для сравнения двух вариантов
См. Также: F Статистика в ANOVA / регрессии
«F-тест» — это универсальный термин для любого теста, в котором используется F-распределение .В большинстве случаев, когда люди говорят о F-тесте, на самом деле они имеют в виду F-тест для сравнения двух вариантов. Однако f-статистика используется во множестве тестов, включая регрессионный анализ, тест Чоу и тест Шеффа (апостериорный тест ANOVA).
Если вы проводите F-тест, вам следует использовать Excel, SPSS, Minitab или другие технологии для его выполнения. Почему? Вычисление F-теста вручную, включая дисперсии, утомительно и требует много времени.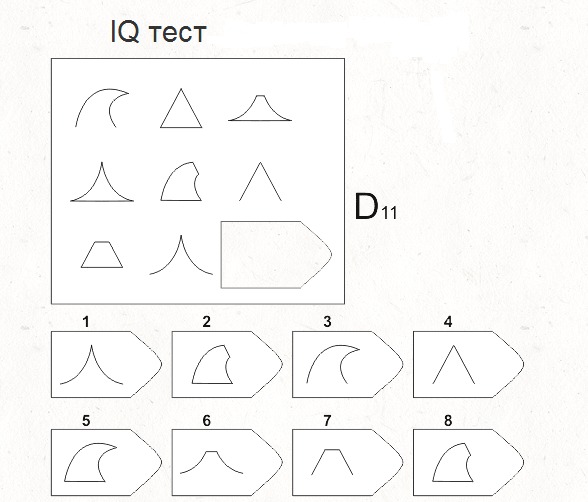 Следовательно, вы, вероятно, сделаете некоторые ошибки на этом пути.
Следовательно, вы, вероятно, сделаете некоторые ошибки на этом пути.
Если вы запускаете F-тест с использованием технологии (например, образец F-теста 2 для дисперсий в Excel), единственные шаги, которые вам действительно нужно сделать, — это шаги 1 и 4 (работа с нулевой гипотезой). Технология рассчитает шаги 2 и 3 за вас.
- Сформулируйте нулевую гипотезу и альтернативную гипотезу.
- Рассчитайте значение F. Значение F рассчитывается по формуле F = (SSE 1 — SSE 2 / m) / SSE 2 / nk, где SSE = остаточная сумма квадратов, m = количество ограничений и k = количество независимых переменные.
- Найдите статистику F (критическое значение для этого теста). Формула F-статистики:
F-статистика = дисперсия групповых средних / средних внутригрупповых дисперсий.
Вы можете найти F-статистику в F-таблице. - Поддержите или отвергните нулевую гипотезу.
В начало
Статистический F-тест использует F-статистику для сравнения двух дисперсий, s 1 и s 2 , путем их деления.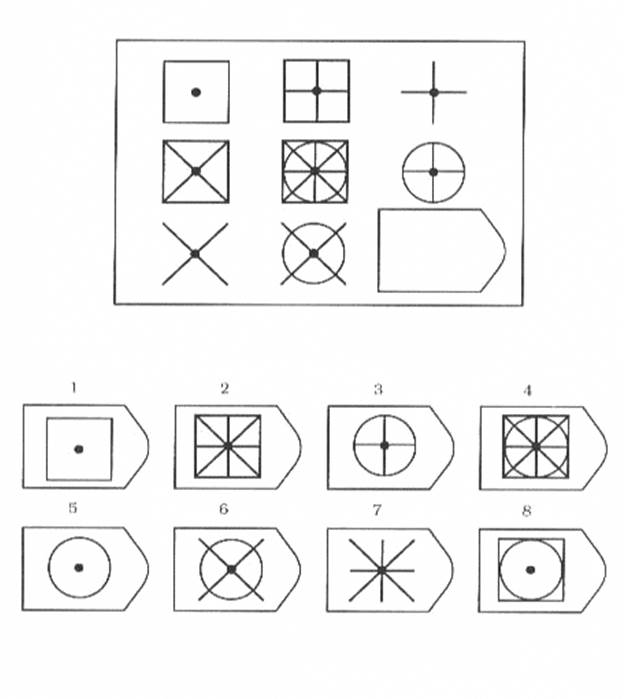 Результатом всегда является положительное число (потому что отклонения всегда положительны).Уравнение для сравнения двух дисперсий с помощью f-критерия:
Результатом всегда является положительное число (потому что отклонения всегда положительны).Уравнение для сравнения двух дисперсий с помощью f-критерия:
F = s 2 1 / s 2 2
Если дисперсии равны, отношение дисперсий будет равно 1. Например, если у вас есть два набора данных с выборкой 1 (дисперсия 10) и выборкой 2 (дисперсия 10), соотношение будет 10 / 10 = 1.
Вы, , всегда проверяете, что дисперсии генеральной совокупности равны при выполнении F-теста. Другими словами, вы всегда предполагаете, что дисперсия равна 1.Следовательно, ваша нулевая гипотеза всегда будет заключаться в том, что дисперсии равны .
Предположения
Для теста сделано несколько предположений, . Ваша популяция должна иметь примерно нормальное распределение (т.е. соответствовать форме колоколообразной кривой), чтобы использовать тест. Плюс к этому сэмплы должны быть независимыми событиями.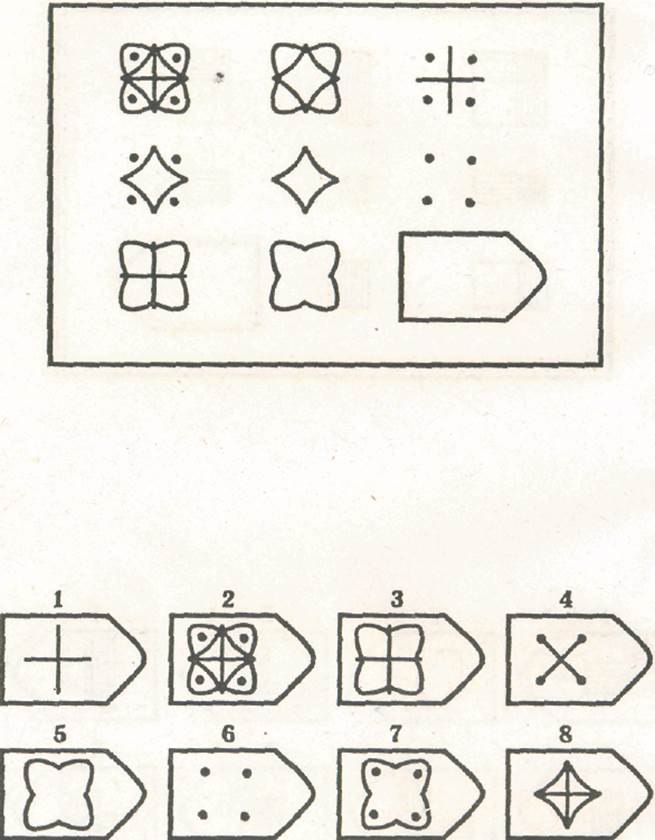 Кроме того, вы должны иметь в виду несколько важных моментов:
Кроме того, вы должны иметь в виду несколько важных моментов:
В начало
Нужна помощь с конкретным вопросом? Посетите нашу страницу обучения!
Предупреждение : F-тесты могут быть очень утомительными для вычисления вручную, особенно если вам нужно вычислять дисперсии.Вам гораздо лучше использовать технологии (например, Excel — см. Ниже).
Это общих шагов, которым необходимо следовать. Прокрутите вниз, чтобы увидеть конкретный пример для (посмотрите видео под инструкциями).
Шаг 1 : Если вам даны стандартные отклонения, переходите к Шагу 2. Если вам даны отклонения для сравнения, переходите к Шагу 3.
Шаг 2: Возвести в квадрат оба стандартных отклонения, чтобы получить дисперсии. Например, если σ 1 = 9.6 и σ 2 = 10,9, тогда дисперсии (s 1 и s 2 ) будут 9,6 2 = 92,16 и 10,9 2 = 118,81 .
Шаг 3: Возьмите наибольшую дисперсию и разделите ее на наименьшую дисперсию, чтобы получить значение f. Например, если ваши две дисперсии были s 1 = 2,5 и s 2 = 9,4, разделите 9,4 / 2,5 = 3,76 .
Почему? Если поместить наибольшую дисперсию сверху, F-тест превратится в правосторонний, который намного проще вычислить, чем левосторонний.
Шаг 4: Определите свои степени свободы. Степени свободы — это размер вашей выборки минус 1. Поскольку у вас есть две выборки (дисперсия 1 и дисперсия 2), у вас будут две степени свободы: одна для числителя и одна для знаменателя.
Шаг 5: Посмотрите на значение f, вычисленное на шаге 3, в таблице f. Обратите внимание, что существует несколько таблиц, поэтому вам нужно будет найти правильную таблицу для вашего альфа-уровня. Не знаете, как читать f-таблицу? Прочтите Что такое f-таблица ?.
Шаг 6: Сравните вычисленное значение (Шаг 3) с табличным значением f на шаге 5. Если значение f-таблицы меньше рассчитанного значения, вы можете отклонить нулевую гипотезу.
Если значение f-таблицы меньше рассчитанного значения, вы можете отклонить нулевую гипотезу.
Вот и все!
В начало
Разница между одно- или двусторонним F-тестом заключается в том, что альфа-уровень необходимо уменьшить вдвое для двухсторонних F-тестов. Например, вместо работы при α = 0,05 вы используете α = 0,025; Вместо работы при α = 0.01 вы используете α = 0,005.
С помощью двустороннего F-теста вы просто хотите знать, не равны ли дисперсии друг другу. В обозначениях:
H a = σ 2 1 ≠ σ 2 2
Пример задачи: Проведите двусторонний F-тест для следующих выборок:
Образец 1: дисперсия = 109,63, размер выборки = 41.
Пример 2: дисперсия = 65,99, размер выборки = 21.
Шаг 1: Напишите свои гипотезы:
H o : Нет разницы в отклонениях.
H a : разница в отклонениях.
Шаг 2: Рассчитайте критическое значение F. Поместите наибольшую дисперсию в числитель и самую низкую дисперсию в качестве знаменателя:
F Статистика = дисперсия 1 / дисперсия 2 = 109,63 / 65,99 = 1,66
Шаг 3: Вычислите степени свободы:
Степень свободы в таблице будет размером образца -1, поэтому:
Образец 1 имеет 40 df (числитель).
Образец 2 имеет 20 df (знаменатель).
Шаг 4: Выберите альфа-уровень.В вопросе не было указано альфа, поэтому используйте 0,05 (стандартное значение «перейти» в статистике). Для двустороннего теста это значение необходимо уменьшить вдвое, поэтому используйте 0,025.
Шаг 5: Найдите критическое значение F с помощью таблицы F. Есть несколько таблиц, поэтому обязательно посмотрите таблицу alpha = .025. Критический F (40,20) при альфа (0,025) = 2,287.
Шаг 6: Сравните вычисленное значение (Шаг 2) со значением в таблице (Шаг 5). Если ваше вычисленное значение выше табличного значения, вы можете отклонить нулевую гипотезу:
F вычисленное значение: 1. 66
66
Значение F из таблицы: 2.287.
1,66 <2,287.
Значит, мы не можем отвергнуть нулевую гипотезу.
В начало
Посмотрите видео или прочтите следующие шаги:
F-test два образца для отклонений Excel 2013: шаги
Шаг 1. Щелкните вкладку «Данные», а затем щелкните «Анализ данных».
Шаг 2: Нажмите «F-тест двух выборок на отклонения», а затем нажмите «ОК».
Шаг 3. Щелкните поле «Диапазон переменной 1» и введите местоположение для первого набора данных.Например, если вы ввели данные в ячейки от A1 до A10, введите в это поле «A1: A10».
Шаг 4. Щелкните поле «Переменная 2» и введите местоположение для второго набора данных. Например, если вы ввели данные в ячейки с B1 по B10, введите в это поле «B1: B10».
Шаг 5. Щелкните поле «Ярлыки», если у ваших данных есть заголовки столбцов.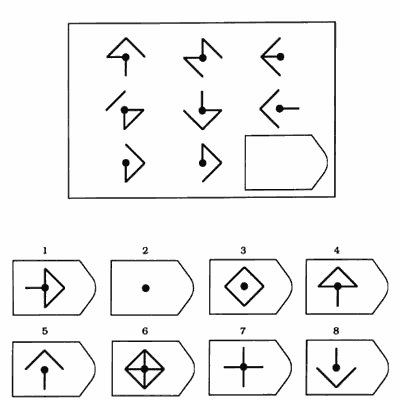
Шаг 6: Выберите альфа-уровень. В большинстве случаев обычно подходит альфа-уровень 0,05.
Шаг 7: Выберите место для вывода. Например, установите переключатель «Новый лист».
Шаг 8: Нажмите «ОК».
Шаг 9: Прочтите результаты. Если ваше значение f выше, чем ваше критическое значение F, отклоните нулевую гипотезу, поскольку две ваши популяции имеют неравные дисперсии.
Предупреждение: Excel имеет небольшую «причуду». Убедитесь, что дисперсия 1 выше, чем дисперсия 2. Если это не так, поменяйте входные данные (например, введите 1 «B» и введите 2 «A»). В противном случае Excel вычислит неверное значение f. Это связано с тем, что дисперсия — это отношение дисперсии 1 / дисперсии 2, и Excel не может определить, какой набор данных установлен на 1 и 2, без вашего явного указания.
В начало
Подпишитесь на наш канал Youtube, чтобы увидеть больше видео со статистикой.
Список литературы
Архидьякон Т. (1994).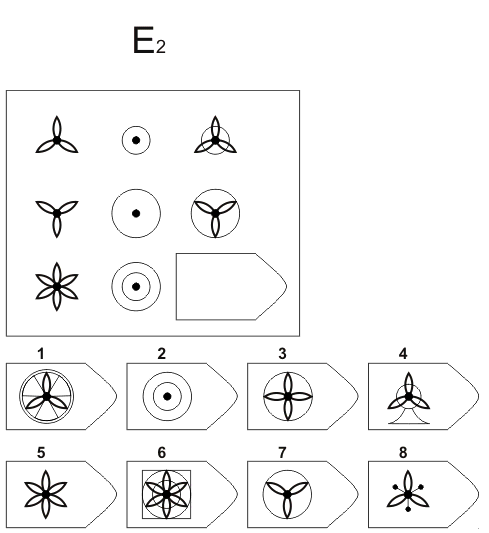 Корреляционный и регрессионный анализ: Руководство историка. Univ of Wisconsin Press.
Корреляционный и регрессионный анализ: Руководство историка. Univ of Wisconsin Press.
Нужна помощь с домашним заданием или контрольным вопросом? С Chegg Study вы можете получить пошаговые ответы на свои вопросы от эксперта в данной области.Ваши первые 30 минут с репетитором Chegg бесплатны!
Комментарии? Нужно опубликовать исправление? Пожалуйста, оставьте комментарий на нашей странице в Facebook .
Теорема Байеса
Крис Виггинс, доцент прикладной математики Колумбийского университета, задал следующий вопрос в статье в Scientific American: Ссылка на статью в Scientific American:
«Пациент идет к врачу. Врач выполняет тест с 99-процентной надежностью, то есть 99 процентов людей имеют положительный результат теста и 99 процентов здоровых людей дают отрицательный результат. Врач знает, что в стране болеет всего 1 процент населения. Теперь вопрос: если тест у пациента положительный, каковы шансы, что пациент заболел? »
Врач знает, что в стране болеет всего 1 процент населения. Теперь вопрос: если тест у пациента положительный, каковы шансы, что пациент заболел? »
Интуитивно понятный ответ — 99 процентов, но правильный ответ — 50 процентов …. »
Решение этого вопроса легко вычислить с помощью теоремы Байеса. Байес, который был преподобным, живший с 1702 по 1761 год, заявил, что вероятность того, что вы получите положительный результат ИЛИ больны, является произведением вероятности того, что вы получите положительный результат, ДАННЫЙ, что вы больны, и «априорной» вероятности того, что вы больны (распространенность в населении).Теорема Байеса позволяет вычислить условную вероятность на основе доступной информации.
Теорема Байеса
P (A) — вероятность события A
P (B) — вероятность события B
P (A | B) — вероятность наблюдения события A, если B истинно
P (B | A) — вероятность наблюдения события B, если A истинно.
ОбъяснениеУиггинса можно резюмировать с помощью следующей таблицы, которая иллюстрирует сценарий для гипотетической популяции в 10 000 человек:
|
|
Больной |
Не заболела |
|
|---|---|---|---|
|
Тест + |
99 |
99 |
198 |
|
Тест — |
1 |
9,801 |
9,802 |
|
|
100 |
9 900 |
10 000 |
В этом сценарии P (A) — безусловная вероятность заболевания; здесь 100 / 10,000 = 0.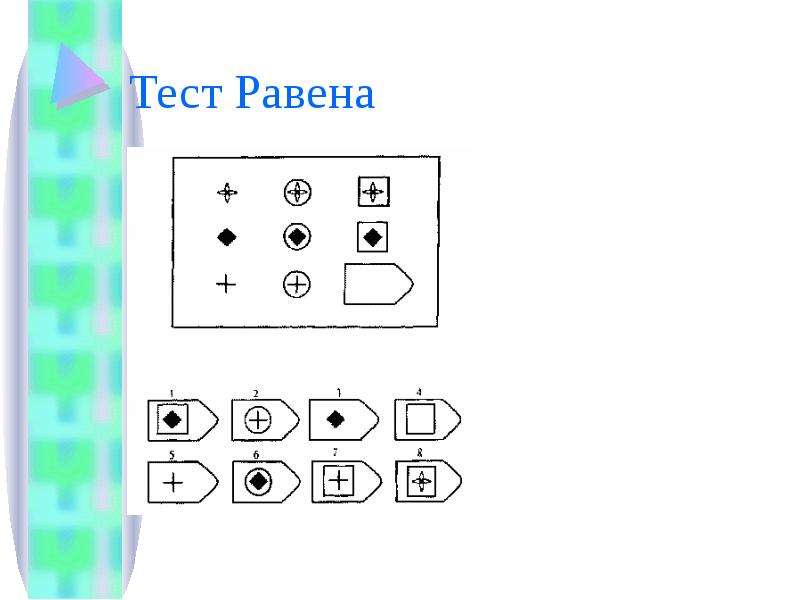 01.
01.
P (B) — безусловная вероятность положительного результата теста; здесь 198 / 10,000 = 0,0198 ..
Мы хотим знать P (A | B), то есть вероятность заболевания (A) при условии, что у пациента положительный тест (B). Мы знаем, что распространенность заболевания (безусловная вероятность заболевания) составляет 1% или 0,01; это представлено P (A). Таким образом, в 10-тысячном населении будет 100 больных и 9 900 здоровых. Мы также знаем, что чувствительность теста составляет 99%, т.е.е., P (B | A) = 0,99; следовательно, из 100 заболевших 99 человек будет иметь положительный результат. Мы также знаем, что специфичность также составляет 99% или что у здоровых людей частота ошибок составляет 1%. Таким образом, из 9900 здоровых людей у 99 будет положительный тест. И из этих чисел следует, что безусловная вероятность положительного результата теста составляет 198 / 10,000 = 0,0198; это P (B).
Таким образом, P (A | B) = (0,99 x 0,01) / 0,0198 = 0,50 = 50%.
Из приведенной выше таблицы мы также видим, что при положительном тесте (испытуемые в строке «Тест +») вероятность заболевания составляет 99/198 = 0. 05 = 50%.
05 = 50%.
Другой пример:
Предположим, у пациента проявляются симптомы, которые заставляют ее врача опасаться, что у нее может быть определенное заболевание. Заболевание относительно редко встречается в этой популяции, с распространенностью 0,2% (то есть поражает 2 из каждых 1000 человек). Врач рекомендует пройти скрининговый тест, который стоит 250 долларов и требует анализа крови. Прежде чем согласиться на скрининговый тест, пациентка хочет знать, что будет извлечено из теста, в частности, она хочет знать вероятность заболевания при положительном результате теста, т.е.е., P (болезнь | положительный результат).
Врач сообщает, что скрининговый тест широко используется и имеет чувствительность 85%. Кроме того, тест дает положительный результат в 8% случаев и отрицательный в 92% случаев.
Имеется следующая информация:
- P (Болезнь) = 0,002, т.е. распространенность = 0,002
- P (положительный результат скрининга | заболевание) = 0,85, то есть вероятность положительного результата скрининга при наличии заболевания составляет 85% (чувствительность теста), и
- P (положительный экран) = 0.
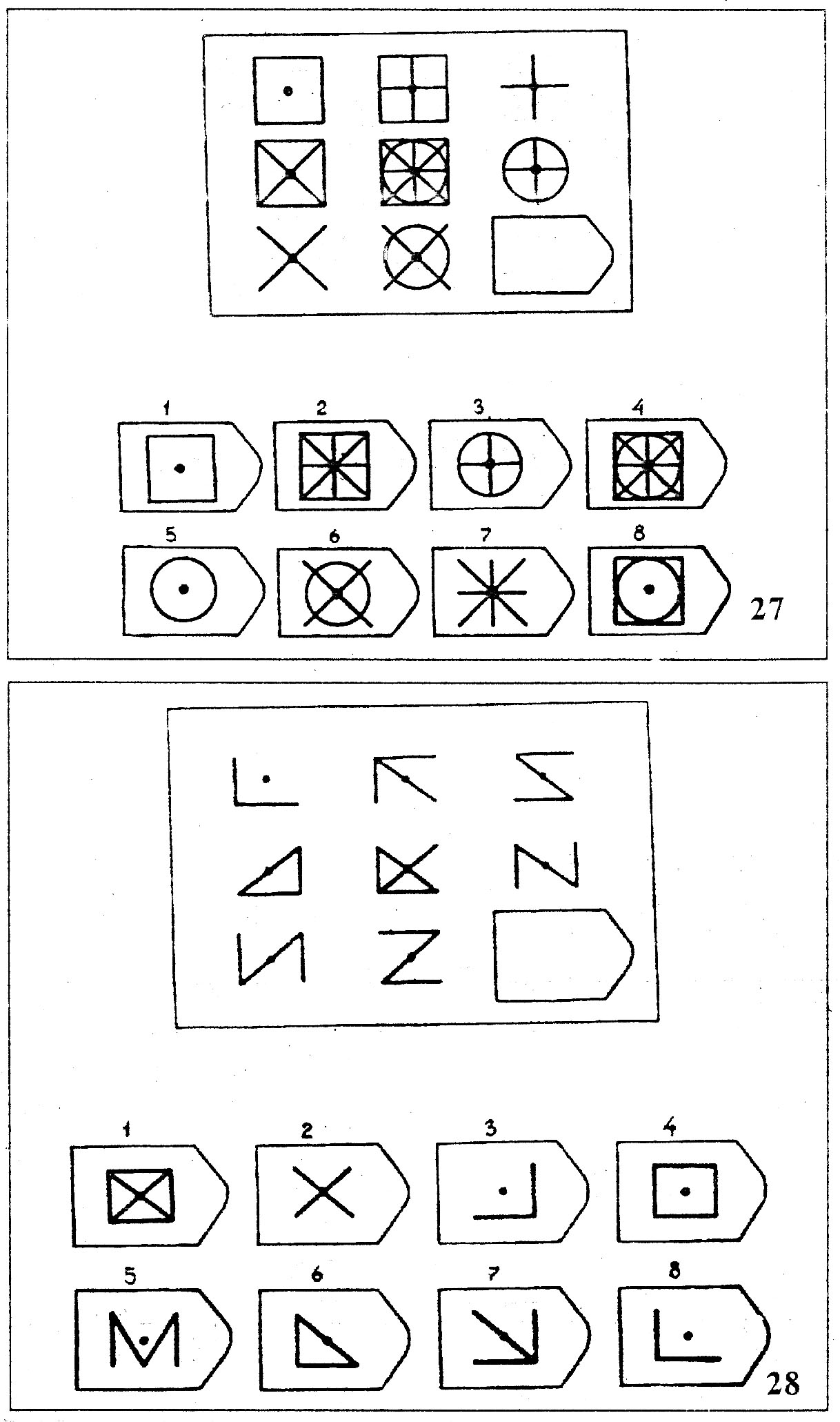 08, то есть вероятность положительного результата скрининга в целом составляет 8% или 0,08. Теперь мы можем подставить значения в приведенное выше уравнение, чтобы вычислить желаемую вероятность,
08, то есть вероятность положительного результата скрининга в целом составляет 8% или 0,08. Теперь мы можем подставить значения в приведенное выше уравнение, чтобы вычислить желаемую вероятность,
Основываясь на доступной информации, мы могли бы сложить это вместе, используя гипотетическую популяцию в 100 000 человек. Учитывая доступную информацию, этот тест даст результаты, обобщенные в таблице ниже. Наведите указатель мыши на числа в таблице, чтобы получить объяснение того, как они были рассчитаны.
Ответ на вопрос пациента также может быть вычислен с помощью теоремы Байеса:
Мы знаем, что P (болезнь) = 0,002, P (положительный результат на экране | болезнь) = 0,85 и P (положительный результат на экране) = 0,08. Теперь мы можем подставить значения в приведенное выше уравнение, чтобы вычислить желаемую вероятность,
.P (Заболевание | Положительный результат на экране) = (0,85) (0,002) / (0,08) = 0,021.
Если пациент сдает тест и он снова дает положительный результат, вероятность того, что он болен, составляет 2,1%. Также обратите внимание, что без теста вероятность того, что он болен, составляет 0,2% (распространенность среди населения). В связи с этим, как вы думаете, прошел ли пациент скрининговый тест?
Также обратите внимание, что без теста вероятность того, что он болен, составляет 0,2% (распространенность среди населения). В связи с этим, как вы думаете, прошел ли пациент скрининговый тест?
Другой важный вопрос, который может задать пациент, — какова вероятность ложноположительного результата? В частности, что такое P (положительный результат на экране | Нет заболеваний)? Мы можем вычислить эту условную вероятность с помощью доступной информации, используя теорему Байеса.
Подставляя вероятности в этот сценарий, мы получаем:
Таким образом, используя теорему Байеса, существует 7.8% -ная вероятность того, что скрининговый тест будет положительным у пациентов, не страдающих заболеванием, что является ложноположительной фракцией теста.
Дополнительные события
Обратите внимание, что если P (заболевание) = 0,002, то P (отсутствие заболевания) = 1-0,002. События «Болезнь» и «Нет болезни» называются дополнительными событиями.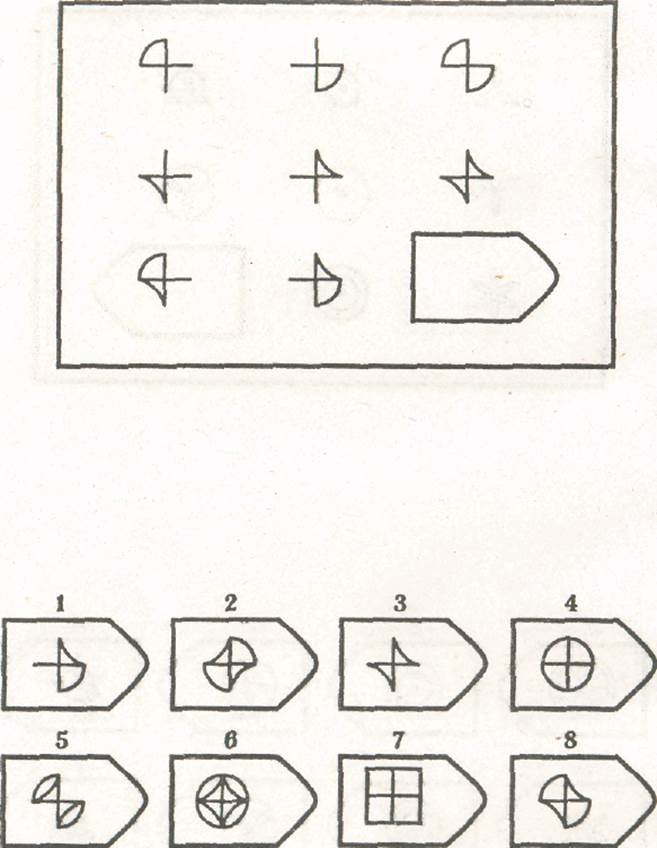 В группу «Нет болезни» входят все представители населения, не входящие в группу «Болезнь». Сумма вероятностей дополнительных событий должна равняться 1 (т. Е. P (заболевание) + P (отсутствие заболевания) = 1).Точно так же P (нет заболевания | положительный результат на экране) + P (заболевание | положительный результат на экране) = 1.
В группу «Нет болезни» входят все представители населения, не входящие в группу «Болезнь». Сумма вероятностей дополнительных событий должна равняться 1 (т. Е. P (заболевание) + P (отсутствие заболевания) = 1).Точно так же P (нет заболевания | положительный результат на экране) + P (заболевание | положительный результат на экране) = 1.
Чтобы вычислить вероятности в предыдущем разделе, мы подсчитали количество участников, у которых был конкретный результат или интересующая характеристика, и разделили на размер популяции. Для условных вероятностей размер популяции (знаменатель) был изменен, чтобы отразить интересующую подгруппу.
В каждом из примеров в предыдущих разделах у нас была таблица совокупности (основа выборки), которая позволила нам вычислить желаемые вероятности.Однако есть случаи, когда полная таблица недоступна. В некоторых из этих случаев для генерации вероятностей могут использоваться вероятностные модели или математические уравнения. Существует множество вероятностных моделей, и модель, подходящая для конкретного приложения, зависит от конкретных атрибутов приложения. Есть две особенно полезные вероятностные модели:
Есть две особенно полезные вероятностные модели:
- модель биномиального распределения, которая полезна для вычисления вероятностей дискретной переменной
- модель нормального распределения, которая полезна для вычисления вероятностей непрерывной переменной.
Эти вероятностные модели чрезвычайно важны для статистических выводов, и мы обсудим их позже.
вернуться наверх | предыдущая страница | следующая страница
Глава 3: Проверка гипотез | Биометрия природных ресурсов
В предыдущих двух главах были представлены методы организации и обобщения данных выборки, а также использования статистики выборки для оценки параметров генеральной совокупности. В этой главе вводится следующая важная тема статистических выводов: проверка гипотез.
Гипотеза — это утверждение или утверждение о собственности населения.
Основы проверки гипотез
При проведении научных исследований обычно используется некоторая известная информация, возможно, из какой-то прошлой работы или из давно принятой идеи. Мы хотим проверить, правдоподобно ли это утверждение. Это основная идея проверки гипотез:
Мы хотим проверить, правдоподобно ли это утверждение. Это основная идея проверки гипотез:
- Назовите то, что мы считаем правдой.
- Определите, насколько мы уверены в нашем требовании.
- Используйте статистику выборки, чтобы сделать выводы о параметрах генеральной совокупности.
Например, прошлые исследования говорят нам, что средняя продолжительность жизни колибри составляет около четырех лет. Вы изучали колибри на юго-востоке США и обнаружили, что средняя продолжительность жизни составляет 4,8 года. Следует ли отвергать известную или принятую информацию в пользу своих результатов? Насколько вы уверены в своей оценке? В какой момент вы бы сказали, что существует достаточно доказательств, чтобы опровергнуть известную информацию и поддержать ваше альтернативное утверждение? Насколько далеко от известного среднего значения четырех лет может быть среднее значение выборки, прежде чем мы отвергнем идею о том, что средняя продолжительность жизни колибри составляет четыре года?
Проверка гипотез — это процедура, основанная на выборке свидетельств и вероятности, используемая для проверки утверждений, касающихся характеристики совокупности.
Гипотеза — это утверждение или утверждение о характеристиках интересующей нас популяции. Проверка гипотез — это способ использования нашей выборочной статистики для проверки конкретного утверждения.
Пример 1
Известно, что средний вес населения составляет 157 фунтов. Мы хотим проверить утверждение о том, что средний вес увеличился.
Пример 2
Два года назад доля зараженных растений составляла 37%. Мы считаем, что лечение помогло, и мы хотим проверить утверждение о сокращении доли инфицированных растений.
Компоненты проверки формальной гипотезы
Нулевая гипотеза — это утверждение о значении параметра совокупности, такого как среднее значение совокупности (µ) или доля совокупности ( p ). Он содержит условие равенства и обозначается H0 (H-ноль).
H0: µ = 157 или H0: p = 0,37
Альтернативная гипотеза — это проверяемое утверждение, противоположное нулевой гипотезе. Он содержит значение параметра, которое мы считаем правдоподобным, и обозначается как h2.
Он содержит значение параметра, которое мы считаем правдоподобным, и обозначается как h2.
h2: µ> 157 или h2: p ≠ 0,37
Тестовая статистика — это значение, вычисленное из выборочных данных, которое используется при принятии решения об отклонении нулевой гипотезы. Статистика теста преобразует выборочное среднее ( x 000 ) или пропорцию выборки ( p̂ ) в Z- или t-балл в предположении, что нулевая гипотеза верна. Он используется для определения значимости разницы между статистикой выборки и гипотетическим утверждением.
Значение p — это площадь под кривой слева или справа от статистики теста. Он сравнивается с уровнем значимости (α).
Критическое значение — это значение, которое определяет зону отклонения (значения тестовой статистики, которые привели бы к отклонению нулевой гипотезы). Определяется уровнем значимости.
Уровень значимости (α) — это вероятность того, что тестовая статистика попадет в критическую область, если нулевая гипотеза верна. Этот уровень устанавливает исследователь.
Этот уровень устанавливает исследователь.
Заключение является окончательным решением проверки гипотез. Вывод всегда должен быть четко сформулирован, сообщая о решении, основанном на компонентах теста. Важно понимать, что мы никогда не доказываем и не принимаем нулевую гипотезу. Мы просто говорим, что образец свидетельства недостаточно убедителен, чтобы оправдать отклонение нулевой гипотезы. Заключение состоит из двух частей:
1) Отклонить или не отклонить нулевую гипотезу, и 2) существует или недостаточно доказательств в поддержку альтернативного утверждения.
Вариант 1) Отклонить нулевую гипотезу (H0). Это означает, что у вас достаточно статистических данных для подтверждения альтернативного утверждения (h2).
Вариант 2) Не удалось отклонить нулевую гипотезу (H0). Это означает, что у вас НЕТ достаточно доказательств в поддержку альтернативного утверждения (h2).
Другой способ подумать о проверке гипотез — это сравнить ее с системой правосудия США.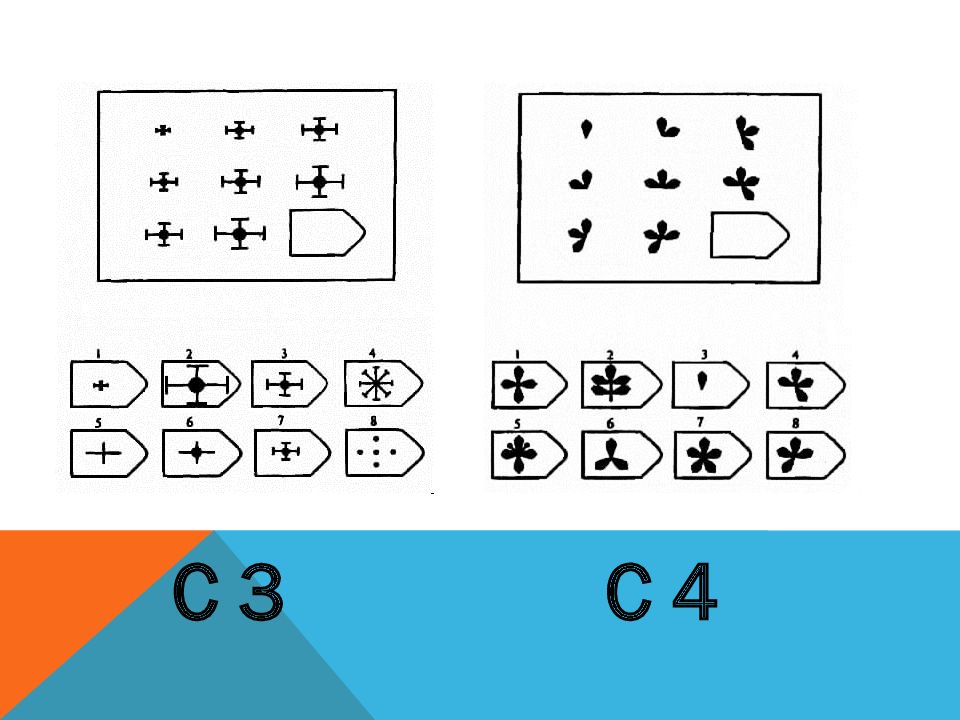 Подсудимый невиновен, пока его вина не будет доказана (нулевая гипотеза — невиновность). Прокурор пытается доказать виновность подсудимого (Альтернативная гипотеза — виновен).Жюри может сделать два возможных вывода. Во-первых, виновен подсудимый (отклонить нулевую гипотезу). Во-вторых, подсудимый не виновен (не отвергает нулевую гипотезу). Это НЕ то же самое, что сказать, что подсудимый невиновен! В первом случае у прокурора было достаточно доказательств, чтобы отклонить нулевую гипотезу (невиновность) и поддержать альтернативное утверждение (виновен). Во втором случае у прокурора НЕ было достаточно доказательств, чтобы отвергнуть нулевую гипотезу (невиновность) и поддержать альтернативное утверждение о виновности.
Подсудимый невиновен, пока его вина не будет доказана (нулевая гипотеза — невиновность). Прокурор пытается доказать виновность подсудимого (Альтернативная гипотеза — виновен).Жюри может сделать два возможных вывода. Во-первых, виновен подсудимый (отклонить нулевую гипотезу). Во-вторых, подсудимый не виновен (не отвергает нулевую гипотезу). Это НЕ то же самое, что сказать, что подсудимый невиновен! В первом случае у прокурора было достаточно доказательств, чтобы отклонить нулевую гипотезу (невиновность) и поддержать альтернативное утверждение (виновен). Во втором случае у прокурора НЕ было достаточно доказательств, чтобы отвергнуть нулевую гипотезу (невиновность) и поддержать альтернативное утверждение о виновности.
Нулевая и альтернативная гипотезы
Есть три разные пары нулевых и альтернативных гипотез:
, где c — известное значение.
Двусторонний тест
Проверяет, равен ли параметр совокупности некоторому определенному значению или нет.
Ho: μ = 12 по сравнению с h2: μ ≠ 12
Критическая область делится поровну на два хвоста, и критические значения равны ± значениям, которые определяют зоны отклонения.
Рис. 1. Зона отклонения для проверки двусторонней гипотезы.
Пример 3
Лесник, изучающий рост сосны красной в диаметре, полагает, что средний рост диаметра будет другим, если обработать насаждение удобрением.
- Ho: μ = 1,2 дюйма / год
- h2: μ ≠ 1,2 дюйма / год
Это двусторонний вопрос, поскольку лесничий не указывает, будет ли рост среднего диаметра популяции увеличиваться или уменьшаться.
Правосторонний тест
Проверяет, равен ли параметр генеральной совокупности некоторому определенному значению или превышает его.
Ho: μ = 12 по сравнению с h2: μ> 12
Критическая область находится в правом хвосте, а критическое значение — положительное значение, которое определяет зону отклонения.
Рис.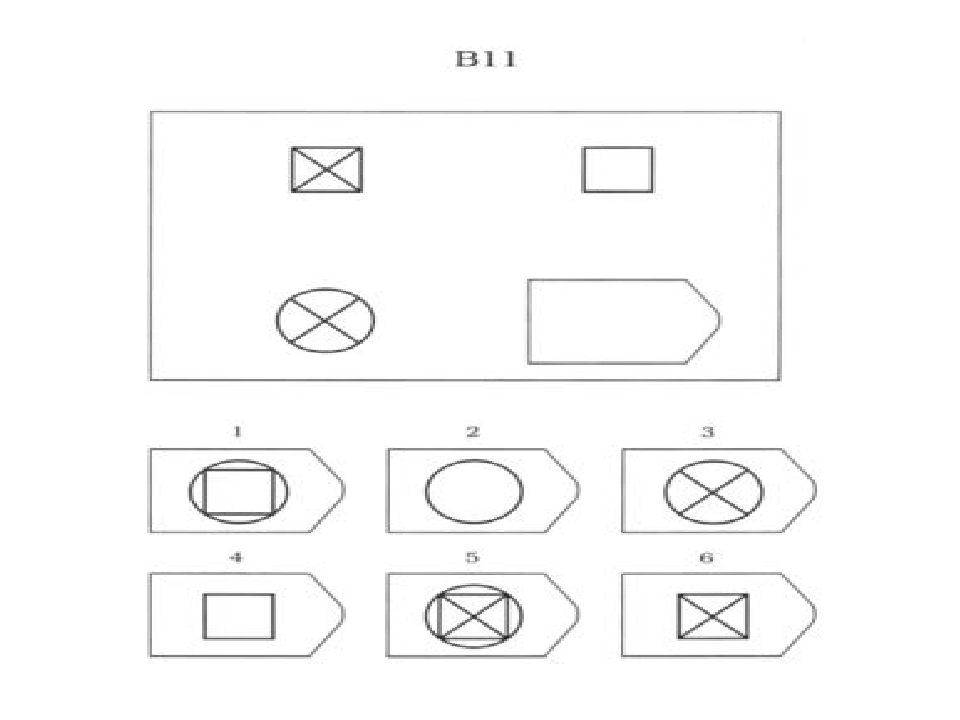 2. Зона отклонения для проверки правосторонней гипотезы.
2. Зона отклонения для проверки правосторонней гипотезы.
Пример 4
Биолог считает, что со времени последнего исследования пять лет назад произошло увеличение среднего числа озер, зараженных тысячелистником, инвазивным видом.
- Ho: μ = 15 озер
- h2: μ> 15 озер
Это правильный вопрос, поскольку биолог считает, что среднее количество зараженных озер увеличилось в популяции.
Левосторонний тест
Проверяет, равен ли параметр генеральной совокупности некоторому определенному значению или меньше его.
Ho: μ = 12 по сравнению с h2: μ <12
Критическая область находится в левом хвосте, а критическое значение — отрицательное значение, которое определяет зону отклонения.
Рис. 3. Зона отклонения для проверки левосторонней гипотезы.
Пример 5
Исследование одного ученого показывает, что изменилась доля людей, поддерживающих определенную экологическую политику. Он хочет проверить утверждение о сокращении доли людей, поддерживающих эту политику.
- Ho: p = 0,57
- h2: p <0,57
Это вопрос левой стороны, поскольку ученый считает, что произошло сокращение истинной доли населения.
Статистически значимое
Когда наблюдаемые результаты (статистика выборки) маловероятны (низкая вероятность) при предположении, что нулевая гипотеза верна, мы говорим, что результат статистически значим, и отвергаем нулевую гипотезу. Этот результат зависит от уровня значимости, статистики выборки, размера выборки и того, является ли это односторонней или двусторонней альтернативной гипотезой.
Типы ошибок
При тестировании мы приходим к выводу об отклонении нулевой гипотезы или неспособности отклонить нулевую гипотезу.Такие выводы иногда верны, а иногда неверны (даже если мы выполнили все правильные процедуры). Мы используем неполные выборочные данные, чтобы прийти к заключению, и всегда есть возможность прийти к неверному выводу. Из проверки гипотез можно сделать четыре возможных вывода. Из четырех возможных результатов два правильные и два НЕ правильные.
Из четырех возможных результатов два правильные и два НЕ правильные.
Таблица 1. Возможные результаты проверки гипотез.
Ошибка типа I возникает, когда мы отклоняем нулевую гипотезу, когда она верна.Символ α (альфа) используется для обозначения ошибок типа I. Это та же альфа, которую мы используем в качестве уровня значимости. Устанавливая минимально возможное значение альфа, мы пытаемся контролировать ошибку типа I с помощью уровня значимости.
Ошибка типа II возникает, когда мы не можем отклонить нулевую гипотезу, когда она ложна. Символ β (бета) используется для обозначения ошибок типа II.
Обычно ошибки типа I считаются более серьезными. Один шаг в процедуре проверки гипотезы включает выбор уровня значимости ( α ), который представляет собой вероятность отклонения нулевой гипотезы, если она верна.Таким образом, исследователь может выбрать уровень значимости, который сводит к минимуму ошибки типа I.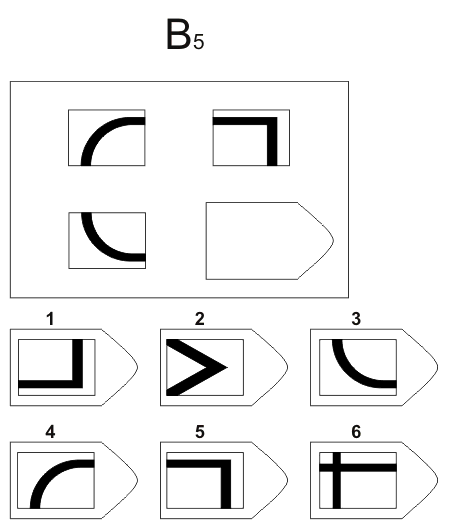 Однако существует математическая зависимость между α, β и n (размером выборки).
Однако существует математическая зависимость между α, β и n (размером выборки).
- По мере увеличения α β уменьшается
- По мере уменьшения α, β увеличивается
- По мере увеличения размера выборки (n) как α, так и β уменьшаются
Естественно выбрать наименьшее возможное значение для α, думая о том, чтобы минимизировать возможность возникновения ошибки типа I. К сожалению, это приводит к увеличению ошибок типа II.Сделав зону отклонения слишком маленькой, вы можете не отвергнуть нулевую гипотезу, хотя на самом деле она ложна. Обычно мы выбираем лучший размер выборки и уровень значимости, автоматически устанавливая β.
Рисунок 4. Ошибка 1-го типа.
Сила испытания
Ошибка типа II (β) — это вероятность неспособности отклонить ложную нулевую гипотезу. Отсюда следует, что 1-β — это вероятность отклонения ложной нулевой гипотезы. Эта вероятность определяется как степень теста и часто используется для оценки эффективности теста в распознавании того, что нулевая гипотеза ложна.
Вероятность того, что при фиксированном уровне значимости α тест отклонит H0, когда конкретное альтернативное значение параметра истинно, называется мощностью теста.
Power также напрямую зависит от размера выборки. Например, предположим, что нулевая гипотеза состоит в том, что средний вес рыбы составляет 8,7 фунта. Учитывая данные выборки, уровень значимости 5% и альтернативный вес 9,2 фунта, мы можем вычислить мощность теста, чтобы отклонить μ = 8,7 фунта. Если у нас небольшой размер выборки, мощность будет низкой.Однако увеличение размера выборки увеличит мощность теста. Повышение уровня значимости также увеличит силу. 5% -ный тест на значимость будет иметь больше шансов отклонить нулевую гипотезу, чем 1% -ный тест, потому что сила доказательств, необходимых для отклонения, меньше. Уменьшение стандартного отклонения имеет тот же эффект, что и увеличение размера выборки: есть больше информации о μ.
Проверка гипотезы о среднем значении совокупности (
μ ) при известном стандартном отклонении совокупности ( σ ) Мы собираемся изучить два эквивалентных способа проверки гипотезы: классический подход и подход p-значения. Классический подход основан на стандартных отклонениях. Этот метод сравнивает статистику теста (Z-оценка) с критическим значением (Z-оценка) из стандартной нормальной таблицы. Если статистика теста попадает в зону отклонения, вы отклоняете нулевую гипотезу. Подход p-значения основан на площади под нормальной кривой. Этот метод сравнивает площадь, связанную со статистикой теста, с альфа (α), уровнем значимости (который также является площадью под нормальной кривой). Если значение p меньше альфа, вы отклоните нулевую гипотезу.
Классический подход основан на стандартных отклонениях. Этот метод сравнивает статистику теста (Z-оценка) с критическим значением (Z-оценка) из стандартной нормальной таблицы. Если статистика теста попадает в зону отклонения, вы отклоняете нулевую гипотезу. Подход p-значения основан на площади под нормальной кривой. Этот метод сравнивает площадь, связанную со статистикой теста, с альфа (α), уровнем значимости (который также является площадью под нормальной кривой). Если значение p меньше альфа, вы отклоните нулевую гипотезу.
Как поэтично сказал один из прошлых учеников: Если p-значение является маленьким, отклонять Ho
Оба метода должны иметь:
- Данные случайной выборки.
- Проверка предположения о нормальности.
- Нулевая и альтернативная гипотеза.
- Критерий, определяющий, отвергаем ли мы нулевую гипотезу или нет.
- Вывод, который отвечает на вопрос.
Для проверки гипотезы требуется четыре шага:
- Сформулируйте нулевую и альтернативную гипотезы.

- Укажите уровень значимости и критическое значение.
- Вычислить статистику теста.
- Сделайте заключение.
Классический метод проверки утверждения о среднем значении совокупности (μ) при известном стандартном отклонении совокупности (
σ )Пример 6
Двусторонний тест
Лесник, изучающий рост красной сосны в диаметре, считает, что средний рост диаметра будет отличаться от известного среднего роста, равного 1.35 дюймов в год при внесении удобрений в насаждение. Он проводит свой эксперимент, собирает данные из выборки из 32 участков и получает средний рост образца в 1,6 дюйма в год. Стандартное отклонение популяции для этого насаждения, как известно, составляет 0,46 дюйма / год. Достаточно ли у него доказательств в поддержку своего утверждения?
Шаг 1) Сформулируйте нулевую и альтернативную гипотезы.
- Ho: μ = 1,35 дюйма / год
- h2: μ ≠ 1,35 дюйма / год
Шаг 2) Укажите уровень значимости и критическое значение.
- Выберем уровень значимости 5% (α = 0,05).
- Для двустороннего вопроса нам понадобится двустороннее критическое значение — Z α / 2 и + Z α / 2.
- Уровень значимости делится на 2 (поскольку мы проверяем только «не равно»). У нас должны быть две зоны отклонения, которые могут иметь дело с результатом больше или меньше (справа (+) или слева (-)).
- Нам нужно найти Z-оценку, связанную с областью 0,025. Красные области равны α / 2 = 0.05/2 = 0,025 или 2,5% площади под нормальной кривой.
- Перейдите в тело значений и найдите отрицательный Z-показатель, связанный с областью 0,025.
Рисунок 5. Зона брака для двустороннего теста.
- Отрицательное критическое значение -1,96. Поскольку кривая симметрична, мы знаем, что положительное критическое значение равно 1,96.
- ± 1,96 — критические значения. Эти значения устанавливают зону отклонения. Если статистика теста попадает в эти красные зоны отклонения, мы отклоняем нулевую гипотезу.

Шаг 3) Вычислите статистику теста.
- Статистика теста — это количество стандартных отклонений, среднее значение выборки от известного среднего. Это также Z-оценка, как и критическое значение.
- Для этой задачи тестовая статистика —
Шаг 4) Сделайте заключение.
- Сравните статистику теста с критическим значением. Если статистика теста попадает в зоны отклонения, отвергните нулевую гипотезу. Другими словами, если статистика теста больше +1.96 или меньше -1,96, отклонить нулевую гипотезу.
Рис. 6. Критические значения для двустороннего теста при α = 0,05.
В этой задаче статистика теста попадает в красную зону отбраковки. Статистика теста 3,07 больше критического значения 1,96. Мы отклоняем нулевую гипотезу. У нас достаточно доказательств, подтверждающих утверждение о том, что средний рост диаметра отличается от (не равен) 1,35 дюйма в год.
Пример 7
Правосторонний тест
Исследователь считает, что средний размер фермы в его штате увеличился со времени последнего исследования пять лет назад. В предыдущем исследовании сообщалось о среднем размере 450 акров со стандартным отклонением для населения ( σ ) в 167 акров. Он сделал выборку из 45 ферм и получил среднюю выборку в 485,8 акров. Достаточно ли информации в поддержку его утверждения?
В предыдущем исследовании сообщалось о среднем размере 450 акров со стандартным отклонением для населения ( σ ) в 167 акров. Он сделал выборку из 45 ферм и получил среднюю выборку в 485,8 акров. Достаточно ли информации в поддержку его утверждения?
Шаг 1) Сформулируйте нулевую и альтернативную гипотезы.
- Ho: μ = 450 акров
- h2: μ> 450 акров
Шаг 2) Укажите уровень значимости и критическое значение.
- Выберем уровень значимости 5% (α = 0.05).
- Для одностороннего вопроса нам понадобится одностороннее положительное критическое значение Zα.
- Уровень значимости — все справа (зона отторжения — справа).
- Нам нужно найти Z-показатель, связанный с 5% площади в правом хвосте.
Рис. 7. Зона отклонения для проверки правосторонней гипотезы.
- Перейдите к основной части значений в стандартной нормальной таблице и найдите Z-оценку, которая отделяет нижние 95% от верхних 5%.
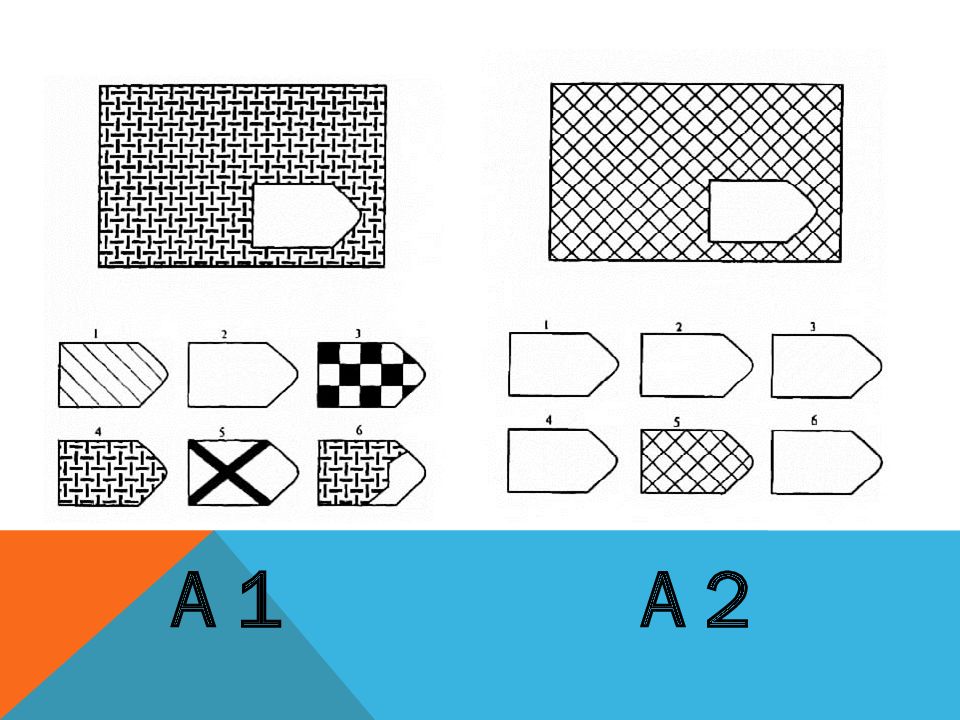
- Критическое значение 1,645. Это значение устанавливает зону отклонения.
Шаг 3) Вычислите статистику теста.
- Статистика теста — это количество стандартных отклонений, среднее значение выборки от известного среднего. Это также Z-оценка, как и критическое значение.
- Для этой задачи тестовая статистика —
Шаг 4) Сделайте заключение.
- Сравните статистику теста с критическим значением.
Рисунок 8.Критическое значение для правостороннего теста при α = 0,05.
- Статистика теста не попадает в зону брака. Это меньше критического значения.
Мы не можем отвергнуть нулевую гипотезу. У нас нет достаточных доказательств в поддержку утверждения о том, что средний размер фермы увеличился с 450 акров.
Пример 8
Левосторонний тест
Исследователь считает, что произошло сокращение среднего количества часов, которое студенты колледжа тратят на подготовку к выпускным экзаменам.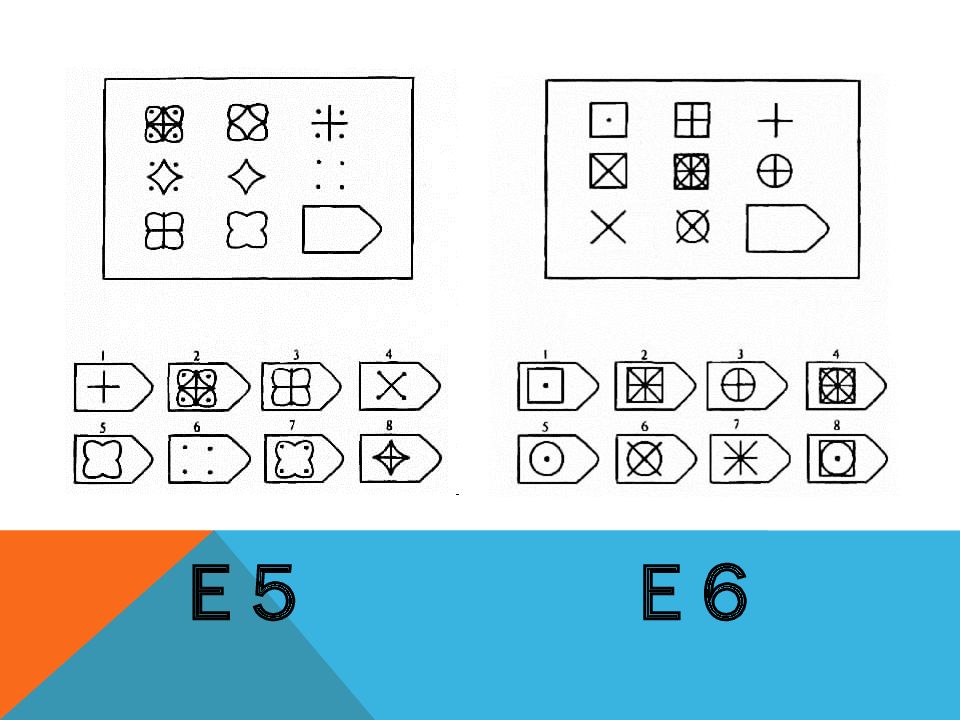 Национальное исследование показало, что студенты 4-летнего колледжа тратят в среднем 23 часа на подготовку к 5 выпускным экзаменам каждый семестр со стандартным отклонением для населения 7,3 часа. Исследователь произвел выборку из 227 студентов и установил, что среднее время обучения в выборке составляет 19,6 часа. Означает ли это, что средняя продолжительность подготовки к выпускным экзаменам уменьшилась? Используйте уровень значимости 1%, чтобы проверить это утверждение.
Национальное исследование показало, что студенты 4-летнего колледжа тратят в среднем 23 часа на подготовку к 5 выпускным экзаменам каждый семестр со стандартным отклонением для населения 7,3 часа. Исследователь произвел выборку из 227 студентов и установил, что среднее время обучения в выборке составляет 19,6 часа. Означает ли это, что средняя продолжительность подготовки к выпускным экзаменам уменьшилась? Используйте уровень значимости 1%, чтобы проверить это утверждение.
Шаг 1) Сформулируйте нулевую и альтернативную гипотезы.
- Ho: μ = 23 часа
- h2: μ <23 часов
Шаг 2) Укажите уровень значимости и критическое значение.
- Это левосторонний тест, поэтому все альфа (0,01) находится в левом хвосте.
Рис. 9. Зона отклонения для проверки левосторонней гипотезы.
- Перейдите к основной части значений в стандартной нормальной таблице и найдите Z-оценку, которая определяет нижний 1% области.
- Критическое значение -2,33.
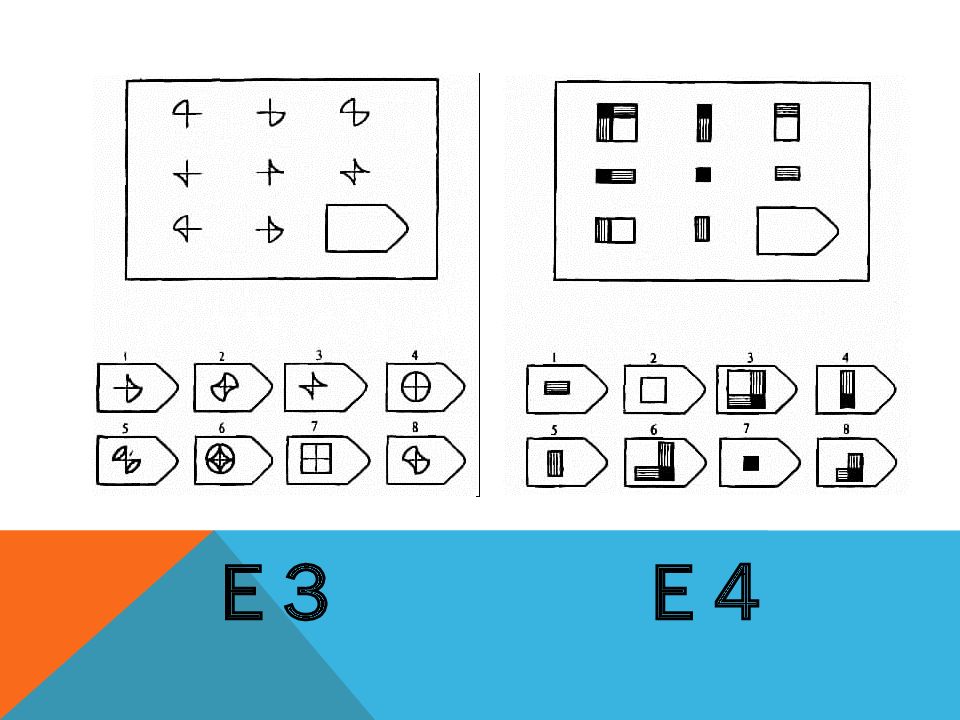 Это значение устанавливает зону отклонения.
Это значение устанавливает зону отклонения.
Шаг 3) Вычислите статистику теста.
- Статистика теста — это количество стандартных отклонений, среднее значение выборки от известного среднего.Это также Z-оценка, как и критическое значение.
- Для этой задачи тестовая статистика —
Шаг 4) Сделайте заключение.
- Сравните статистику теста с критическим значением.
Рис. 10. Критическое значение для левостороннего теста при α = 0,01.
- Статистика теста попадает в зону брака. Статистическое значение теста -7,02 меньше критического значения -2,33.
Мы отвергаем нулевую гипотезу.У нас есть достаточно доказательств, подтверждающих утверждение о том, что среднее время обучения на выпускном экзамене сократилось до менее 23 часов.
Проверка гипотез с использованием P-значений
Значение p — это вероятность наблюдения среднего значения нашей выборки при условии, что нулевая гипотеза верна.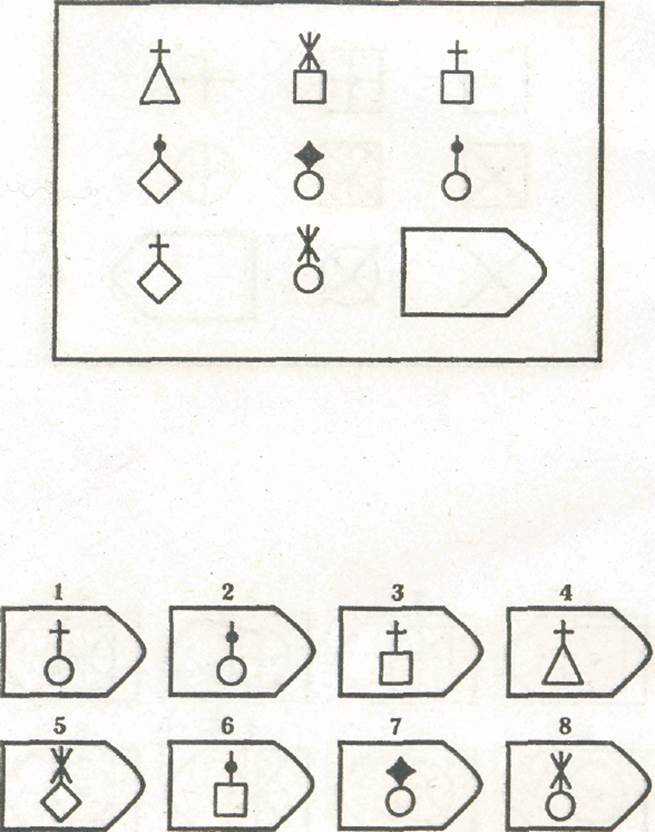 Это площадь под кривой слева или справа от статистики теста. Если вероятность наблюдения такого выборочного среднего очень мала (ниже уровня значимости), мы отвергнем нулевую гипотезу. Вычисления p-значения зависят от того, является ли это односторонним или двусторонним тестом.
Это площадь под кривой слева или справа от статистики теста. Если вероятность наблюдения такого выборочного среднего очень мала (ниже уровня значимости), мы отвергнем нулевую гипотезу. Вычисления p-значения зависят от того, является ли это односторонним или двусторонним тестом.
Шаги для проверки гипотез с использованием p-значений:
- Сформулируйте нулевую и альтернативную гипотезы.
- Укажите уровень значимости.
- Вычислите статистику теста и найдите область, связанную с ней (это p-значение).
- Сравните значение p с альфа (α) и сделайте вывод.
Вместо того, чтобы сравнивать статистику теста Z-score с критическим значением Z-score, как в классическом методе, мы сравниваем область тестовой статистики с областью уровня значимости.
Правило принятия решения: если значение p меньше альфа, мы отклоняем нулевую гипотезу
Вычисление P-значений
Если это двусторонний тест (альтернативное утверждение -), p-значение равно удвоенной вероятности абсолютного значения статистики теста.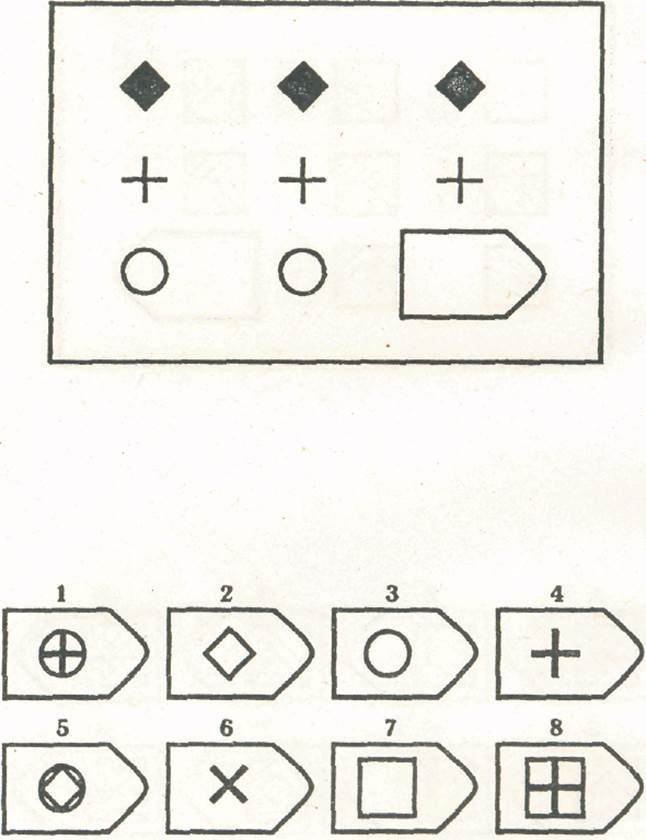 Если тест является левосторонним (альтернативное утверждение — «<»), то значение p равно площади слева от статистики теста. Если тест является правосторонним (альтернативное утверждение - «>»), то p-значение равно площади справа от статистики теста.
Если тест является левосторонним (альтернативное утверждение — «<»), то значение p равно площади слева от статистики теста. Если тест является правосторонним (альтернативное утверждение - «>»), то p-значение равно площади справа от статистики теста.
Давайте снова посмотрим на Пример 6.
Лесник, изучающий рост сосны красной в диаметре, считает, что средний рост диаметра будет отличаться от известного среднего прироста 1,35 дюйма в год, если насаждения будут внесены удобрения. Он проводит свой эксперимент, собирает данные из выборки из 32 участков и получает средний рост образца в 1,6 дюйма в год. Стандартное отклонение популяции для этого насаждения, как известно, составляет 0,46 дюйма / год. Достаточно ли у него доказательств в поддержку своего утверждения?
Шаг 1) Сформулируйте нулевую и альтернативную гипотезы.
- Ho: μ = 1,35 дюйма / год
- h2: μ ≠ 1,35 дюйма / год
Шаг 2) Укажите уровень значимости.
- Выберем уровень значимости 5% (α = 0,05).
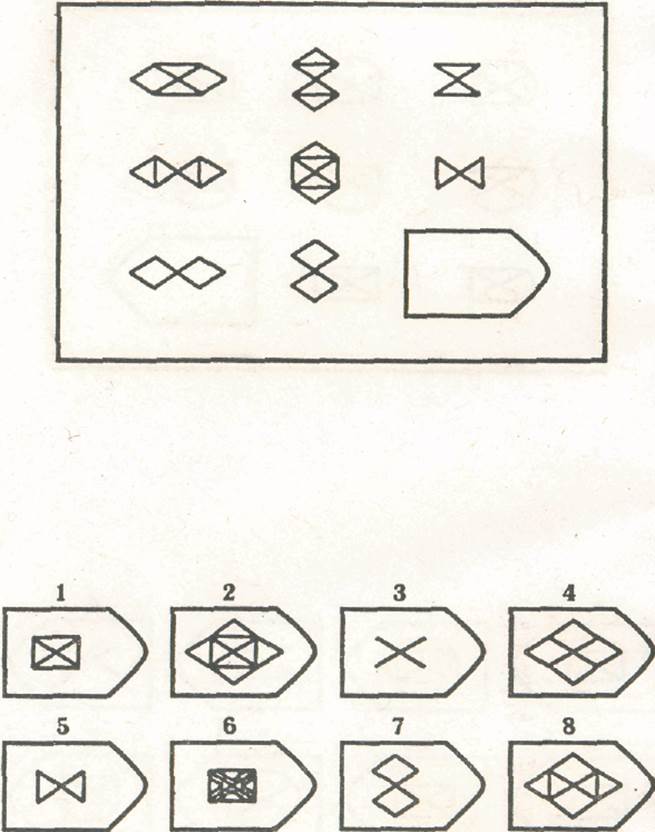
Шаг 3) Вычислите статистику теста.
- Для этой задачи статистика теста:
Значение p в два раза превышает область абсолютного значения тестовой статистики (поскольку альтернативное утверждение «не равно»).
Рисунок 11.Значение p по сравнению с уровнем значимости.
- Найдите область для Z-показателя 3,07 в стандартной нормальной таблице. Площадь (вероятность) равна 1 — 0,9989 = 0,0011.
- Умножьте это на 2, чтобы получить значение p = 2 * 0,0011 = 0,0022.
Шаг 4) Сравните значение p с альфа и сделайте вывод.
- Используйте правило принятия решения (если значение p меньше α, отклонить H0).
- В этой задаче значение p (0,0022) меньше альфа (0.05).
- Мы отклоняем H0. У нас достаточно доказательств, подтверждающих утверждение о том, что средний рост диаметра отличается от 1,35 дюйма в год.
Давайте снова посмотрим на пример 7.
Исследователь считает, что средний размер фермы в его штате увеличился со времени последнего исследования пять лет назад.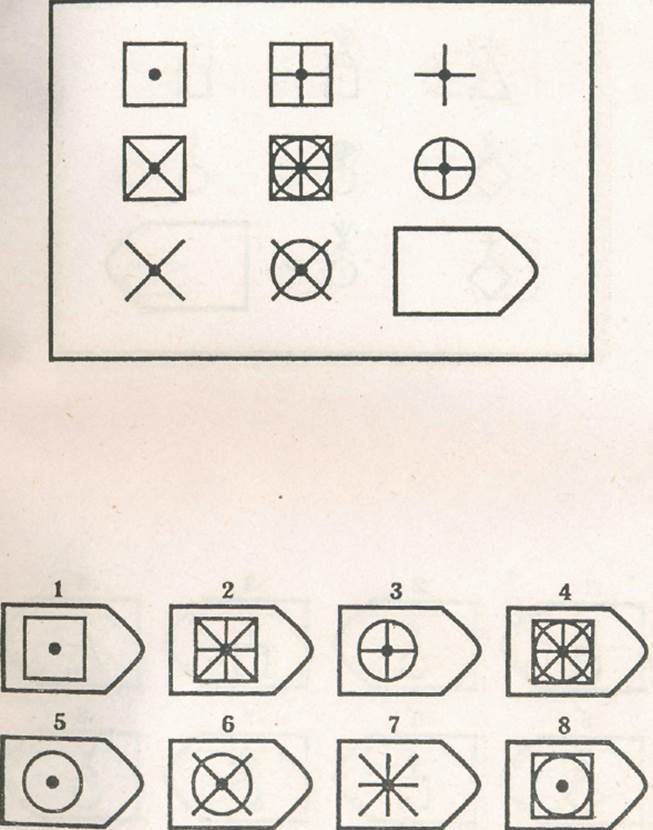 В предыдущем исследовании сообщалось о среднем размере 450 акров со стандартным отклонением для населения ( σ ) в 167 акров. Он отобрал 45 ферм и получил среднее значение 485.8 соток. Достаточно ли информации в поддержку его утверждения?
В предыдущем исследовании сообщалось о среднем размере 450 акров со стандартным отклонением для населения ( σ ) в 167 акров. Он отобрал 45 ферм и получил среднее значение 485.8 соток. Достаточно ли информации в поддержку его утверждения?
Шаг 1) Сформулируйте нулевую и альтернативную гипотезы.
- Ho: μ = 450 акров
- h2: μ> 450 акров
Шаг 2) Укажите уровень значимости.
- Выберем уровень значимости 5% (α = 0,05).
Шаг 3) Вычислите статистику теста.
- Для этой задачи тестовая статистика
Значение p — это область справа от Z-значения 1.44 (заштрихованная область).
- Это равно 1 — 0,9251 = 0,0749.
- Значение p равно 0,0749.
Рис. 12. Значение p по сравнению с уровнем значимости для правостороннего теста.
Шаг 4) Сравните p-значение с альфа и сделайте вывод.
- Используйте правило принятия решений.
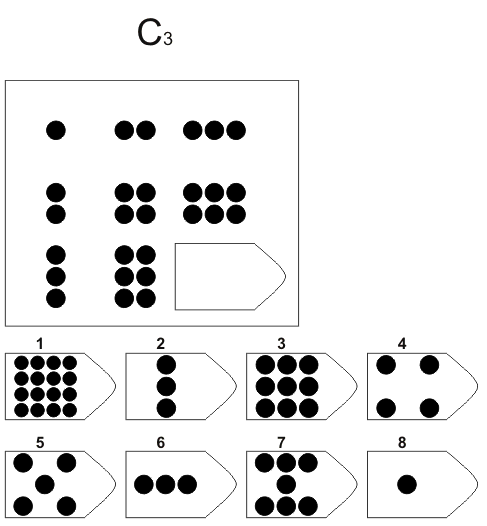
- В этой задаче значение p (0,0749) больше альфа (0,05), поэтому мы не можем отклонить H0.
- Площадь тестовой статистики больше, чем площадь альфа (α).
Мы не можем отвергнуть нулевую гипотезу. У нас нет достаточных доказательств в поддержку утверждения о том, что средний размер фермы увеличился.
Давайте снова посмотрим на Пример 8.
Исследователь считает, что произошло сокращение среднего количества часов, которое студенты колледжа тратят на подготовку к выпускным экзаменам. Национальное исследование показало, что студенты 4-летнего колледжа тратят в среднем 23 часа на подготовку к 5 выпускным экзаменам каждый семестр со стандартным отклонением для населения 7.3 часа. Исследователь произвел выборку из 227 студентов и установил, что среднее время обучения в выборке составляет 19,6 часа. Означает ли это, что средняя продолжительность подготовки к выпускным экзаменам уменьшилась? Используйте уровень значимости 1%, чтобы проверить это утверждение.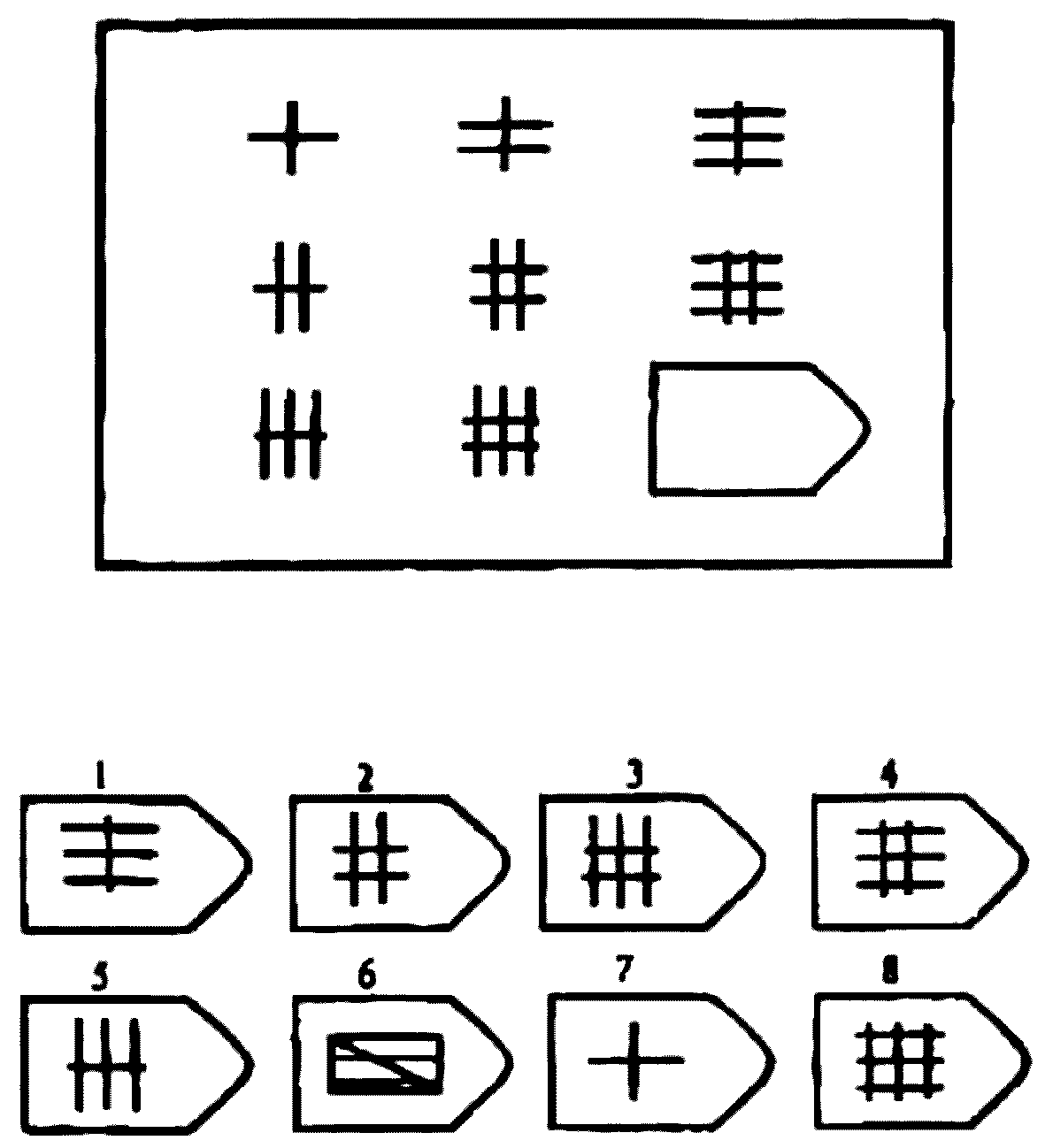
Шаг 1) Сформулируйте нулевую и альтернативную гипотезы.
- H0: μ = 23 часа
- h2: μ <23 часов
Шаг 2) Укажите уровень значимости.
- Это левосторонний тест, поэтому все альфа (0,01) находится в левом хвосте.
Шаг 3) Вычислите статистику теста.
- Для этой задачи тестовая статистика
Значение p — это область слева от тестовой статистики (маленькая черная область слева от -7,02). Z-оценка -7,02 отсутствует в стандартной нормальной таблице. Наименьшая вероятность в таблице — 0,0002. Мы знаем, что область для Z-балла -7,02 меньше, чем эта область (вероятность). Следовательно, значение p <0,0002.
Рис. 13. Значение p по сравнению с уровнем значимости для левостороннего теста.
Шаг 4) Сравните p-значение с альфа и сделайте вывод.
- Используйте правило принятия решений.
- В этой задаче значение p (p <0,0002) меньше альфа (0,01), поэтому мы отклоняем H0.
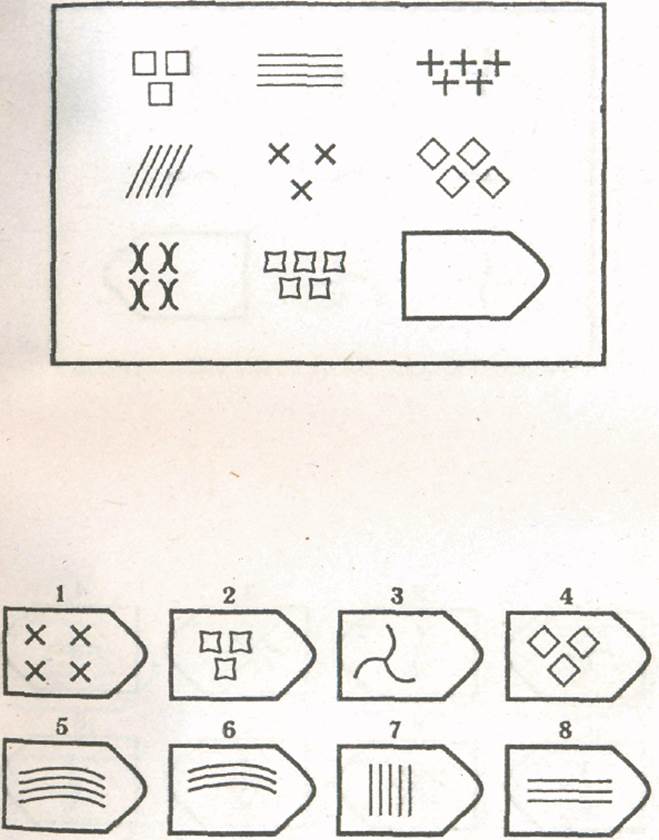
- Площадь тестовой статистики намного меньше площади альфа (α).
Мы отвергаем нулевую гипотезу. У нас достаточно доказательств, подтверждающих утверждение о том, что среднее время обучения на выпускном экзамене сократилось до менее 23 часов.
И классический метод, и метод p-значения для проверки гипотезы приходят к одному и тому же выводу.В классическом методе критический Z-балл — это число на оси Z, которое определяет уровень значимости (α). Статистика теста преобразует выборочное среднее в единицы стандартного отклонения (Z-балл). Если статистика теста попадает в зону отклонения, определяемую критическим значением, мы отклоняем нулевую гипотезу. В этом подходе сравниваются две Z-оценки, которые представляют собой числа на оси z. В подходе p-значения p-значение — это область, связанная со статистикой теста. В этом методе мы сравниваем α (который также является площадью под кривой) со значением p.Если значение p меньше α, мы отклоняем нулевую гипотезу.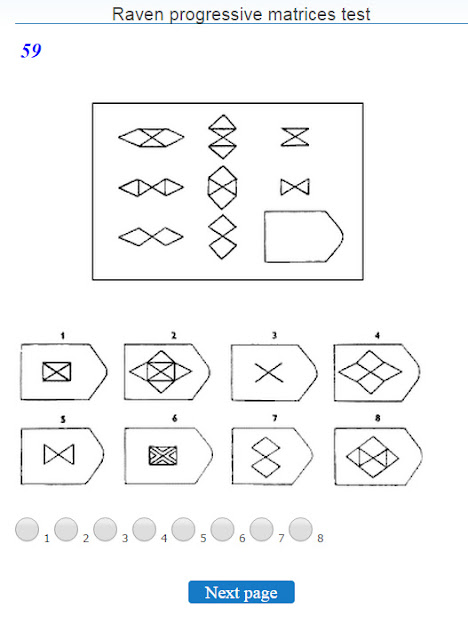 Значение p — это вероятность наблюдения такого выборочного среднего значения, когда нулевая гипотеза верна. Если вероятность слишком мала (ниже уровня значимости), то мы считаем, что у нас достаточно статистических данных, чтобы отвергнуть нулевую гипотезу и поддержать альтернативное утверждение.
Значение p — это вероятность наблюдения такого выборочного среднего значения, когда нулевая гипотеза верна. Если вероятность слишком мала (ниже уровня значимости), то мы считаем, что у нас достаточно статистических данных, чтобы отвергнуть нулевую гипотезу и поддержать альтернативное утверждение.
Программные решения
Minitab
(см. Пример 8)
Одинарный образец Z
| Тест mu = 23 vs.<23 |
| Предполагаемое стандартное отклонение = 7,3 |
| 99% Верхний | |||||
| н. | Среднее | SE Среднее значение | Связанный | Z | -п. |
| 227 | 19.600 | 0,485 | 20,727 | -7,02 | 0,000 |
Excel
Excel не предлагает проверку гипотез с использованием одного образца.
Проверка гипотезы о среднем значении совокупности (
μ ), когда стандартное отклонение совокупности ( σ ) неизвестноЧасто стандартное отклонение совокупности (σ) неизвестно. Мы можем оценить стандартное отклонение совокупности (σ) с помощью стандартного отклонения (-ей) выборки. Однако статистика теста больше не будет соответствовать стандартному нормальному распределению. Мы должны полагаться на t-распределение Стьюдента с n-1 степенями свободы. Поскольку мы используем стандартные отклонения выборки, статистика теста изменится с Z-балла на t-балл.
→
Шаги для проверки гипотезы те же, что мы рассмотрели в Разделе 2.
- Сформулируйте нулевую и альтернативную гипотезы.
- Укажите уровень значимости и критическое значение.
- Вычислить статистику теста.
- Сделайте заключение.
Как и в случае проверки гипотез из предыдущего раздела, данные для этого теста должны быть из случайной выборки и требовать, чтобы либо совокупность, из которой была взята выборка, была нормальной, либо размер выборки был достаточно большим (n≥30 ).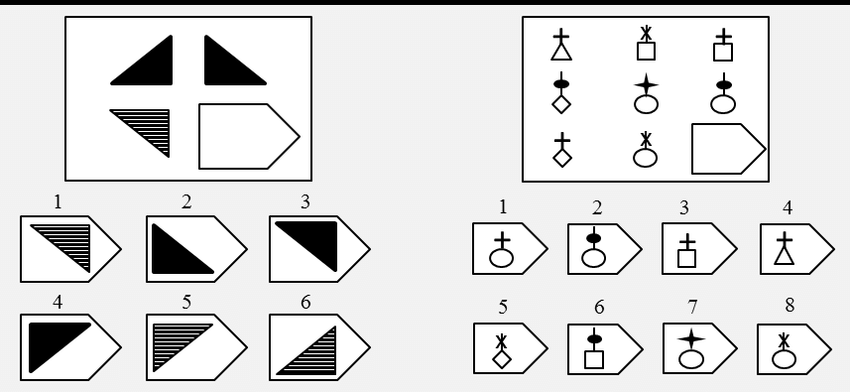 T-тест является надежным, поэтому небольшие отклонения от нормы не повлияют отрицательно на результаты теста. При этом, если размер выборки меньше 30, всегда полезно проверить предположение о нормальности с помощью графика нормальной вероятности.
T-тест является надежным, поэтому небольшие отклонения от нормы не повлияют отрицательно на результаты теста. При этом, если размер выборки меньше 30, всегда полезно проверить предположение о нормальности с помощью графика нормальной вероятности.
У нас останутся те же три пары нулевой и альтернативной гипотез, и мы по-прежнему можем использовать либо классический подход, либо подход p-значения.
Выбор правильного критического значения из таблицы распределения Стьюдента зависит от трех факторов: типа теста (односторонняя или двусторонняя альтернативная гипотеза), размера выборки и уровня значимости.
Для двустороннего теста (альтернативная гипотеза «не равно») критическое значение (tα / 2) определяется альфа (α), уровнем значимости, деленным на два, чтобы иметь дело с возможностью того, что результат может быть меньше ИЛИ больше известного значения.
- Если ваш уровень значимости был 0,05, вы должны использовать столбец 0,025, чтобы найти правильное критическое значение (0,05 / 2 = 0,025).
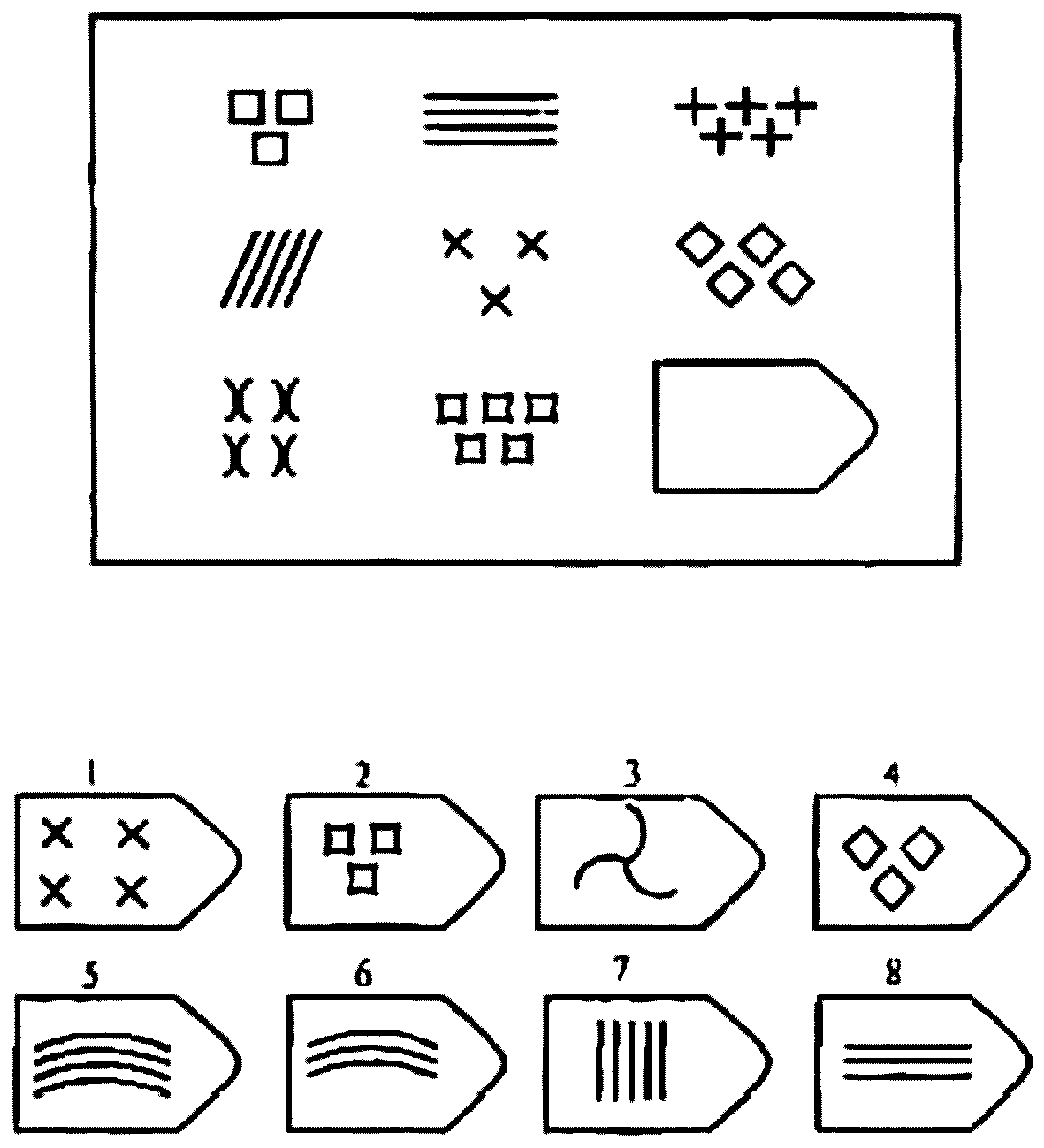
- Если ваш уровень значимости был 0,01, вы должны использовать столбец 0,005, чтобы найти правильное критическое значение (0.01/2 = 0,005).
Для одностороннего теста (альтернативная гипотеза «меньше чем» или «больше чем») критическое значение (tα) определяется альфа (α), уровень значимости находится в одной стороне.
- Если ваш уровень значимости был 0,05, вы должны использовать столбец 0,05, чтобы найти правильное критическое значение для вопроса с левой или с правой стороны. Если вы задаете «меньше чем» (левосторонний вопрос, ваше критическое значение будет отрицательным. Если вы задаете «больше чем» (правосторонний вопрос), ваше критическое значение будет положительным.
Пример 9
Найдите критическое значение, которое вы использовали бы для проверки утверждения, что μ μ 112 с размером выборки 18 и уровнем значимости 5%.
В этом случае критическое значение (tα / 2) будет 2,110. Это двусторонний вопрос (≠), поэтому вы разделите альфа на 2 (0,05 / 2 = 0,025) и спуститесь вниз по столбцу 0,025 до 17 степеней свободы.
Пример 10
Каким было бы критическое значение, если бы вы хотели проверить, что μ <112 для тех же данных?
В этом случае критическим значением будет 1.740. Это односторонний вопрос (<), поэтому альфа будет разделена на 1 (0,05 / 1 = 0,05). Чтобы получить правильное критическое значение, вы спуститесь вниз по столбцу 0,05 с 17 степенями свободы.
Пример 11
Двусторонний тест
В 2005 году средний уровень pH дождя в округе на севере Нью-Йорка составлял 5,41. Биолог считает, что кислотность дождя изменилась. Он произвольно выбирает 11 дат дождя в 2010 году и получает следующие данные. Используйте уровень значимости 1%, чтобы проверить его утверждение.
4,70, 5,63, 5,02, 5,78, 4,99, 5,91, 5,76, 5,54, 5,25, 5,18, 5,01
Размер выборки невелик, и мы ничего не знаем о распределении совокупности, поэтому исследуем нормальный график вероятности. Распределение выглядит нормально, поэтому мы продолжим наш тест.
Рисунок 14.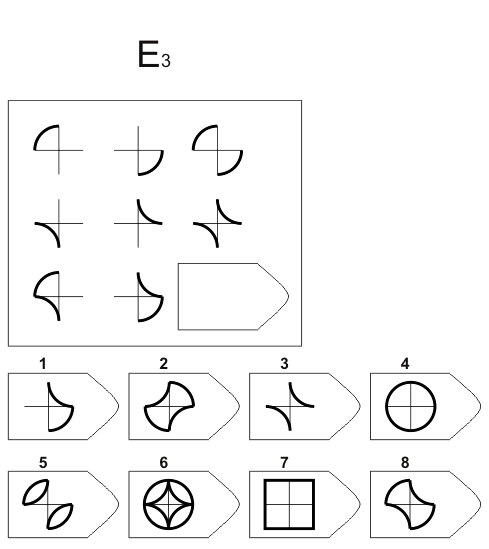 График нормальной вероятности для примера 9.
График нормальной вероятности для примера 9.
Среднее значение выборки составляет 5,343 со стандартным отклонением выборки 0,397.
Шаг 1) Сформулируйте нулевую и альтернативную гипотезы.
- Но: μ = 5,41
- h2: μ ≠ 5,41
Шаг 2) Укажите уровень значимости и критическое значение.
- Это двусторонний вопрос, поэтому альфа делится на два.
Рисунок 15. Зоны отбраковки для двустороннего теста.
- t α / 2 находится по столбцу 0,005 с 14 степенями свободы.
- t α / 2 = ± 3,169.
Шаг 3) Вычислите статистику теста.
- Статистика теста — это t-балл.
- Для этой задачи тестовая статистика
Шаг 4) Сделайте заключение.
- Сравните статистику теста с критическим значением.
Рисунок 16. Критические значения для двустороннего теста при α = 0,01.
- Статистика теста не попадает в зону брака.
Отвергнуть нулевую гипотезу не удастся. У нас нет достаточных доказательств в поддержку утверждения об изменении среднего pH дождя.
Пример 12
Односторонний тест
Кадмий, тяжелый металл, токсичен для животных. Однако грибы способны поглощать и накапливать кадмий в высоких концентрациях. Правительство установило пределы безопасности для кадмия в сухих овощах на уровне 0,5 промилле. Биологи полагают, что средний уровень кадмия в грибах, растущих возле шахт, превышает рекомендуемый предел в 0,5 промилле, что отрицательно сказывается на животных, которые живут в этой экосистеме. Случайная выборка из 51 гриба дала среднее значение 0.59 ppm со стандартным отклонением образца 0,29 ppm. Используйте 5% уровень значимости, чтобы проверить утверждение, что средний уровень кадмия превышает допустимый предел 0,5 ppm.
Размер выборки превышает 30, поэтому мы уверены в нормальном распределении средних значений.
Шаг 1) Сформулируйте нулевую и альтернативную гипотезы.
- Ho: мкм = 0,5 частей на миллион
- h2: мкм > 0,5 частей на миллион
Шаг 2) Укажите уровень значимости и критическое значение.
- Это правосторонний вопрос, поэтому все альфа находится в правом хвосте.
Рис. 17. Зона отбраковки для правостороннего теста.
- t α находится по столбцу 0,05 с 50 степенями свободы.
- т α = 1,676
Шаг 3) Вычислите статистику теста.
- Статистика теста — это t-балл.
- Для этой задачи тестовая статистика
Шаг 4) Сделайте заключение.
- Сравните статистику теста с критическим значением.
Рис. 18. Критическое значение для правостороннего теста при α = 0,05.
Статистика теста попадает в зону брака. Мы отвергнем нулевую гипотезу. У нас достаточно доказательств, подтверждающих утверждение о том, что средний уровень кадмия превышает допустимый безопасный предел.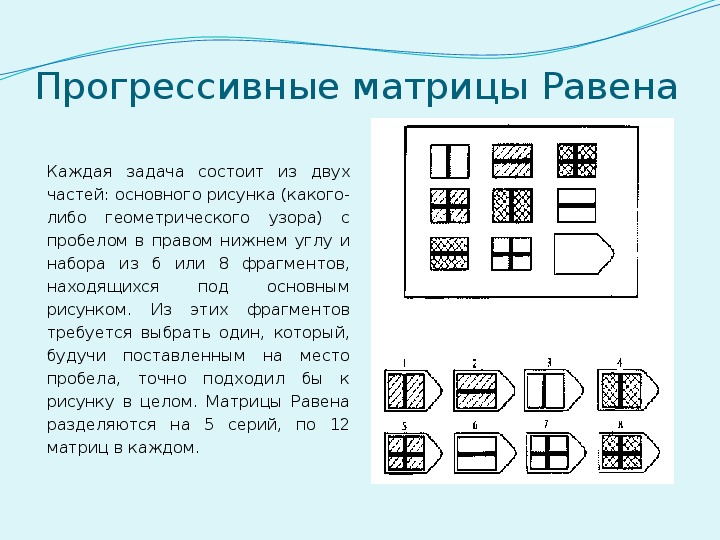
НО, что произойдет, если уровень значимости изменится на 1%?
Теперь критическое значение определяется путем спуска на 0.01 колонка с 50 степенями свободы. Критическое значение — 2,403. Статистика теста теперь МЕНЬШЕ критического значения. Статистика теста не попадает в зону отбраковки. Вывод изменится. У нас НЕТ достаточных доказательств в поддержку утверждения о том, что средний уровень кадмия превышает допустимый безопасный предел 0,5 ppm.
Уровень значимости — это вероятность того, что вы, как исследователь, решите решить, достаточно ли статистических данных в поддержку альтернативного утверждения.Его следует установить до начала эксперимента.
Подход P-value
Мы также можем использовать метод p-значения для проверки гипотезы о среднем значении, когда стандартное отклонение совокупности ( σ ) неизвестно. Однако при использовании t-таблицы студента мы можем оценить только диапазон p-значения, а не конкретное значение, как при использовании стандартной нормальной таблицы.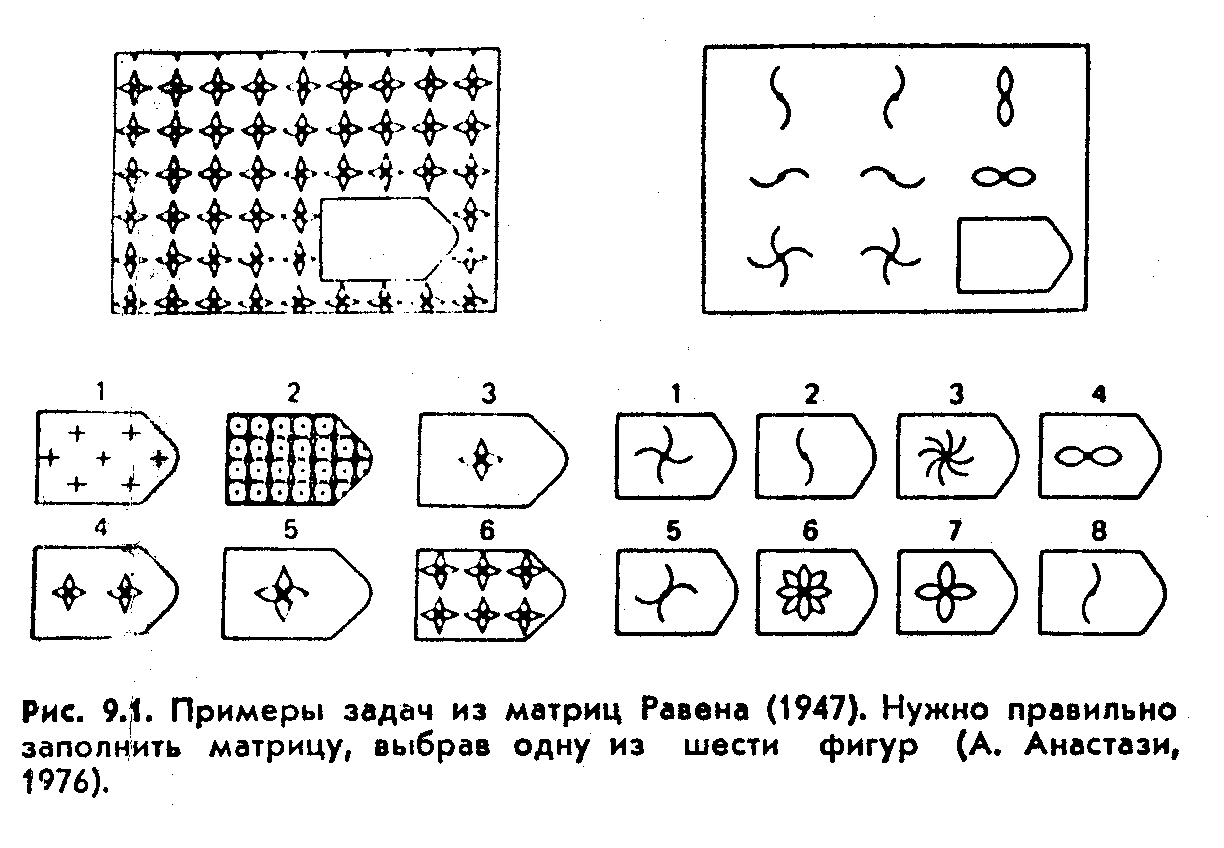 В t-таблице учащегося в верхней строке таблицы есть площадь (вероятность), а в основной части таблицы — t-баллы.
В t-таблице учащегося в верхней строке таблицы есть площадь (вероятность), а в основной части таблицы — t-баллы.
- Чтобы найти p-значение (область, связанную со статистикой теста), вы должны перейти к строке с количеством степеней свободы.
- Просмотрите эту строку, пока не найдете два значения, между которыми находится ваша тестовая статистика, затем поднимитесь по этим столбцам, чтобы найти оценочный диапазон для p-значения.
Пример 13
Оценка P-значения по T-таблице ученика
Таблица 3. Доля t-таблицы студента.
Если ваша тестовая статистика равна 3.789 с 3 степенями свободы, вы перейдете через 3-й ряд df. Значение 3,789 находится между значениями 3,482 и 4,541 в этой строке. Следовательно, значение p находится между 0,02 и 0,01. Значение p будет больше 0,01, но меньше 0,02 (0,01
Заключение
Если ваш уровень значимости 5%, вы отклоните нулевую гипотезу, поскольку значение p (0,01–0,02) меньше альфа (α) 0,05.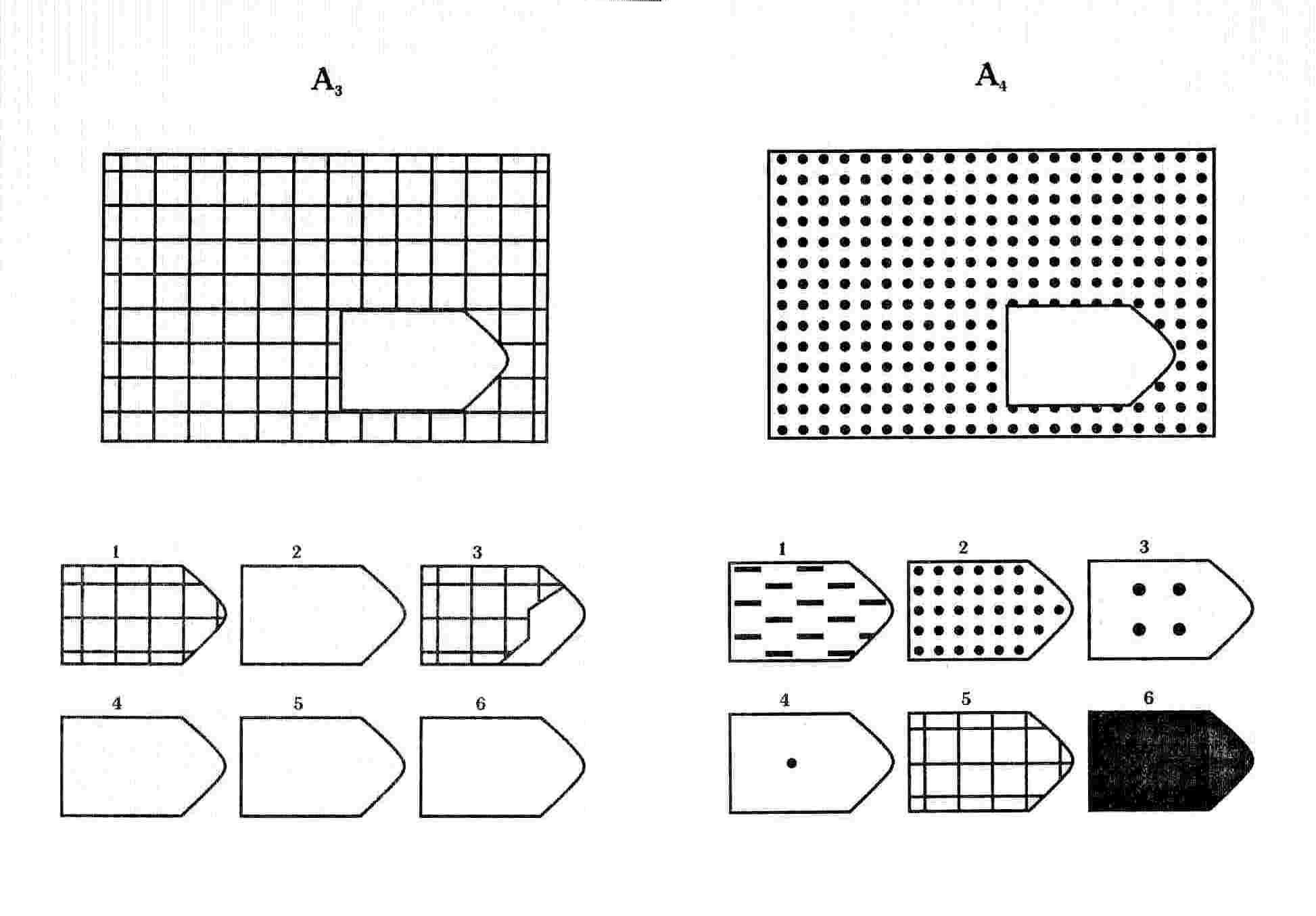
Если ваш уровень значимости составляет 1%, вы не сможете отклонить нулевую гипотезу как p-значение (0.01-0.02) больше альфа (α) 0,01.
Программные пакеты обычно выводят p-значения. Правило принятия решения легко использовать для ответа на ваш исследовательский вопрос с помощью метода p-значения.
Программные решения
Minitab
(см. Пример 12)
Один образец T
Тест mu = 0,5 против> 0,5
|
95% ниже |
||||||
|
N |
Среднее значение |
StDev |
SE Среднее значение |
Связанный |
т |
-П |
|
51 |
0.5900 |
0,2900 |
0,0406 |
0,5219 |
2,22 |
0,016 |
Дополнительный пример: www.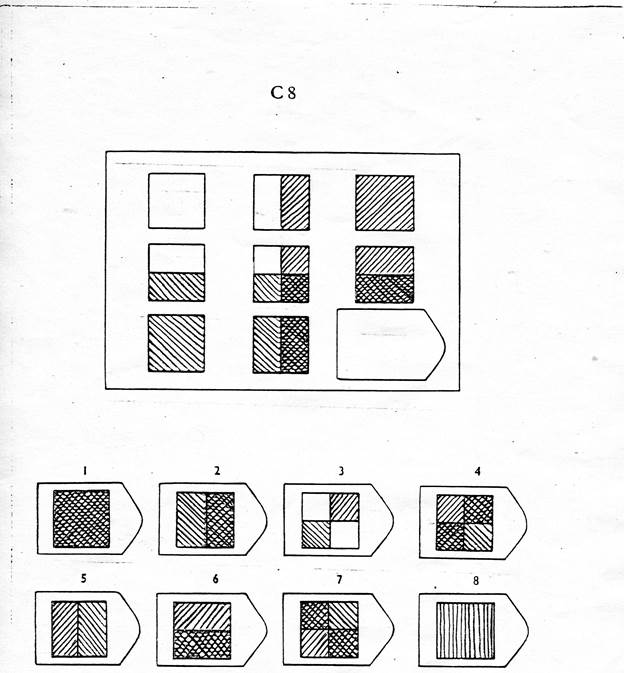 youtube.com/watch?v=WwdSjO4VUsg.
youtube.com/watch?v=WwdSjO4VUsg.
Excel
Excel не предлагает проверку гипотез с использованием одного образца.
Проверка гипотез для доли населения (
p )Часто параметр, который мы тестируем, — это доля населения.
- Мы изучаем долю деревьев с углублениями для среды обитания диких животных.
- Нам нужно знать, изменилась ли доля людей, поддерживающих зеленые строительные материалы.
- Увеличилась ли доля волков, погибших в прошлом году в Йеллоустоне, по сравнению с предыдущим годом?
Напомним, что наилучшая точечная оценка p , доли населения, дается как
., где x — количество особей в выборке с изучаемой характеристикой, а n — размер выборки.Распределение выборки p̂ приблизительно нормально со средним значением и стандартным отклонением
.
при np (1 — p ) ≥10. Для тестирования мы можем использовать как классический подход, так и подход с p-значением.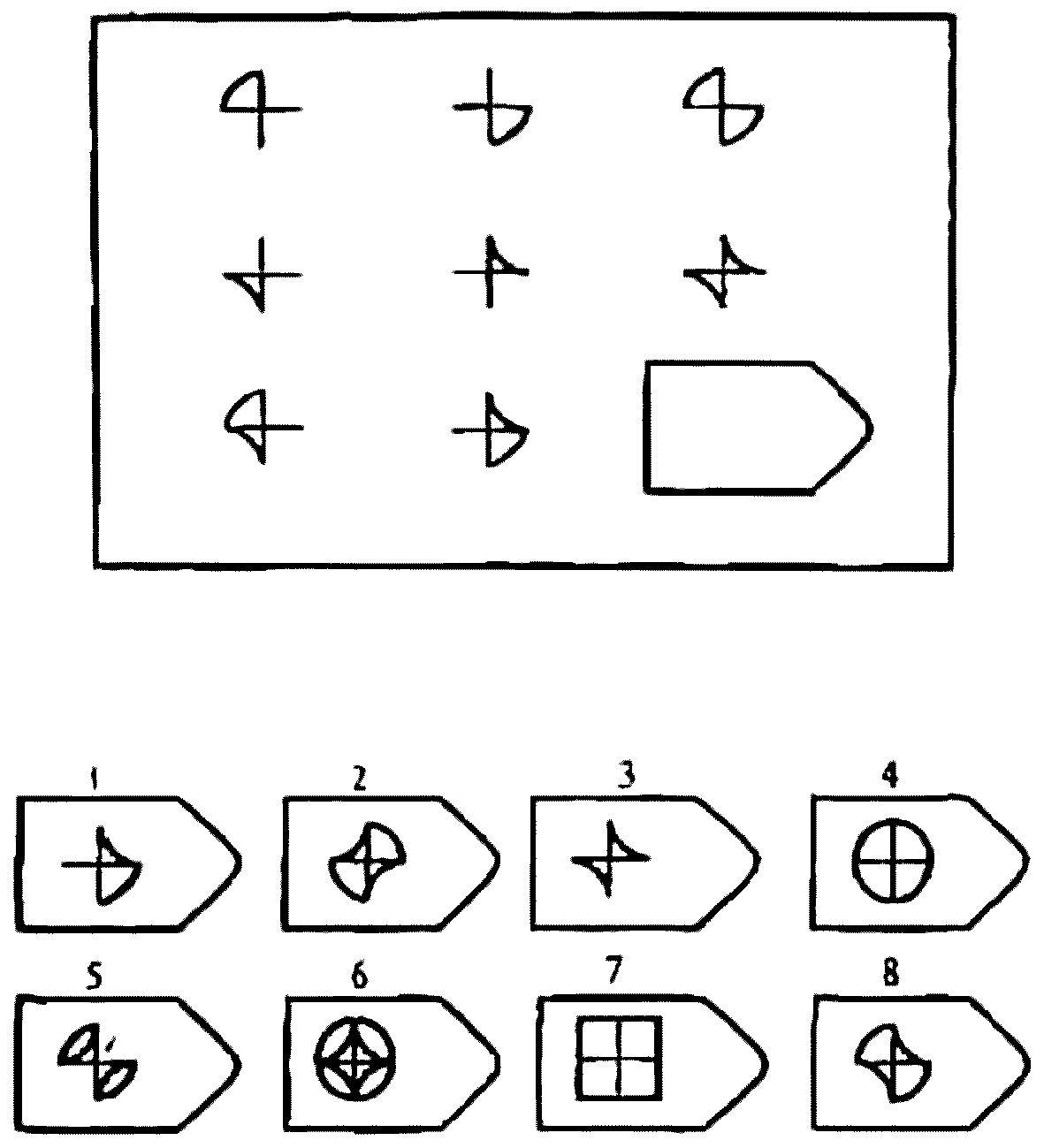
Этапы проверки гипотез те же, что мы рассмотрели в Разделе 2.
- Сформулируйте нулевую и альтернативную гипотезы.
- Укажите уровень значимости и критическое значение.
- Вычислить статистику теста.
- Сделайте заключение.
Статистика теста соответствует стандартному нормальному распределению. Обратите внимание, что стандартная ошибка (знаменатель) использует p вместо p̂ , которое использовалось при построении доверительного интервала для доли населения. При проверке гипотез предполагается, что нулевая гипотеза верна, поэтому используется известная пропорция.
- Критическое значение берется из стандартной нормальной таблицы, как и в разделе 2.Мы по-прежнему будем использовать те же три пары нулевых и альтернативных гипотез, которые мы использовали в предыдущих разделах, но теперь параметр равен p вместо μ:
- Для двустороннего теста альфа будет разделена на 2, что даст критическое значение ± Zα / 2.
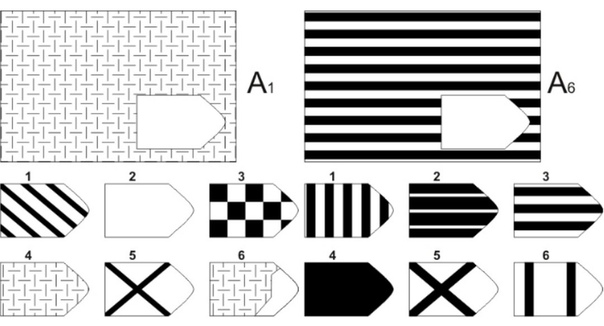
- Для левого теста все альфа будет в левом хвосте, что дает критическое значение — Zα.
- Для правостороннего теста, все альфа будет в правом хвосте, что дает критическое значение Zα.
Пример 14
Ботаник создал новую разновидность гибридной сои, которая лучше других выдерживает засуху.Ботаник знает, что всхожесть семян родительских растений составляет 75%, но не знает прорастания семян нового гибрида. Он проверяет утверждение, что оно отличается от родительских растений. Чтобы проверить это утверждение, тестируется 450 семян гибридного растения, и 321 проросло. Используйте 5% уровень значимости, чтобы проверить это утверждение о том, что всхожесть отличается от 75%.
Шаг 1) Сформулируйте нулевую и альтернативную гипотезы.
- Ho: p = 0,75
- h2: p ≠ 0.75
Шаг 2) Укажите уровень значимости и критическое значение.
Это двусторонний вопрос, поэтому альфа делится на 2.
- Alpha составляет 0,05, поэтому критические значения равны ± Zα / 2 = ± Z.
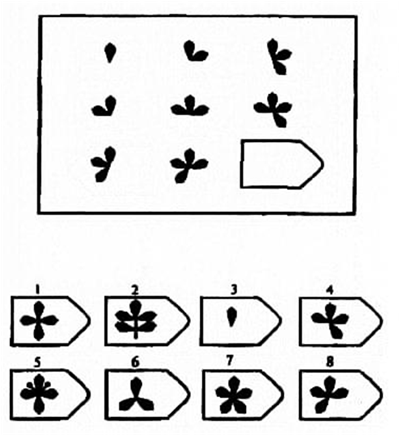 025.
025. - Посмотрите на отрицательную сторону стандартной нормальной таблицы в теле значений 0,025.
- Критические значения: ± 1,96.
Шаг 3) Вычислите статистику теста.
- Статистика теста — это количество стандартных отклонений, среднее значение выборки от известного среднего.Это также Z-оценка, как и критическое значение.
- Для этой задачи тестовая статистика
Шаг 4) Сделайте заключение.
- Сравните статистику теста с критическим значением.
Рис. 19. Критические значения для двустороннего теста при α = 0,05.
Статистика теста не попадает в зону брака. Мы не можем отвергнуть нулевую гипотезу. У нас нет достаточных доказательств в поддержку утверждения о том, что скорость прорастания гибридного растения отличается от скорости прорастания родительских растений.
Давайте ответим на этот вопрос, используя метод p-значения. Помните, что для двусторонней альтернативной гипотезы («не равно») значение p в два раза больше площади тестовой статистики. Статистика теста -1,81, и мы хотим найти область слева от -1,81 из стандартной нормальной таблицы.
Статистика теста -1,81, и мы хотим найти область слева от -1,81 из стандартной нормальной таблицы.
- На отрицательной странице найдите Z-показатель -1,81. Найдите область, связанную с этой Z-оценкой.
- Площадь = 0,0351.
- Это двусторонний тест, поэтому умножьте площадь на 2, чтобы получить значение p = 0.0351 х 2 = 0,0702.
Теперь сравните значение p с альфой. Правило принятия решения гласит, что если значение p меньше альфа, отклонять H0. В этом случае значение p (0,0702) больше, чем альфа (0,05), поэтому мы не сможем отклонить H0. У нас нет достаточных доказательств в поддержку утверждения о том, что скорость прорастания гибридного растения отличается от скорости прорастания родительских растений.
Пример 15
Вы — биолог, изучающий среду обитания диких животных в Национальном лесу Мононгахела.Полости в старых деревьях являются прекрасной средой обитания для множества птиц и мелких млекопитающих. Исследование, проведенное пять лет назад, показало, что 32% деревьев в этом лесу имеют углубления, подходящие для этого типа диких животных.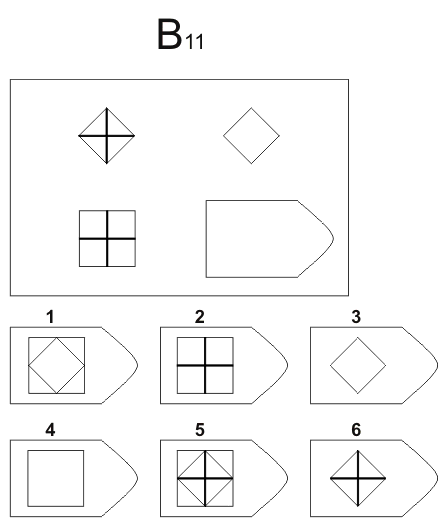 Вы считаете, что увеличилась доля пустотелых деревьев. Вы выбираете 196 деревьев и обнаруживаете, что 79 деревьев имеют полости. Подтверждают ли эти доказательства ваше утверждение об увеличении доли пустотелых деревьев?
Вы считаете, что увеличилась доля пустотелых деревьев. Вы выбираете 196 деревьев и обнаруживаете, что 79 деревьев имеют полости. Подтверждают ли эти доказательства ваше утверждение об увеличении доли пустотелых деревьев?
Используйте 10% уровень значимости для проверки этого утверждения.
Шаг 1) Сформулируйте нулевую и альтернативную гипотезы.
- Ho: p = 0,32
- h2: p> 0,32
Шаг 2) Укажите уровень значимости и критическое значение.
Это односторонний вопрос, поэтому альфа делится на 1.
- Альфа равна 0,10, поэтому критическое значение Zα = Z .10
- Посмотрите на положительную сторону стандартной нормальной таблицы в теле значений 0,90.
- Критическое значение 1,28.
Рисунок 20.Критическое значение для правостороннего теста при α = 0,10.
Шаг 3) Вычислите статистику теста.
- Статистика теста — это количество стандартных отклонений доли выборки от известной доли.
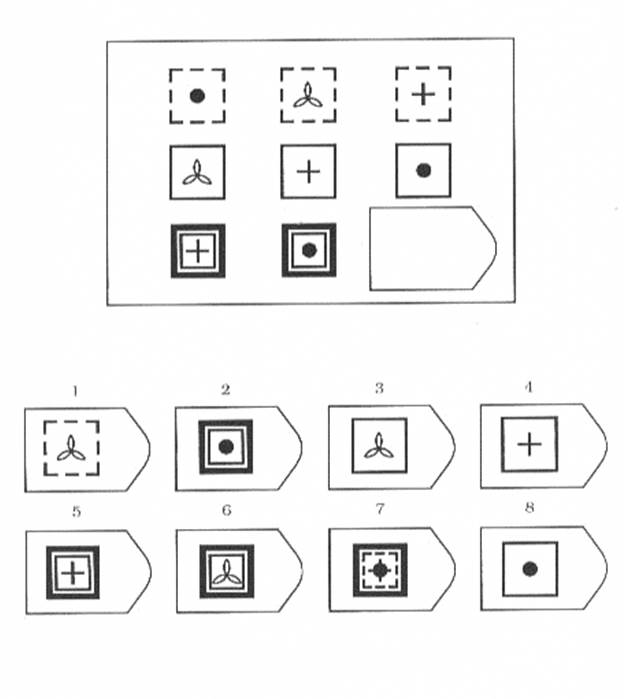 Это также Z-оценка, как и критическое значение.
Это также Z-оценка, как и критическое значение.
- Для этой задачи статистика теста:
Шаг 4) Сделайте заключение.
- Сравните статистику теста с критическим значением.
Рисунок 21.Сравнение тестовой статистики и критического значения.
Статистика теста больше критического значения (попадает в зону брака). Мы отвергнем нулевую гипотезу. У нас есть достаточно доказательств, чтобы подтвердить утверждение о том, что увеличилась доля пустотелых деревьев.
Теперь используйте метод p-значения, чтобы ответить на вопрос. Это вопрос с правой стороной («больше»), поэтому значение p равно площади справа от тестовой статистики. Перейдите к положительной стороне стандартной нормальной таблицы и найдите область, связанную с Z-оценкой 2.49. Площадь 0,9936. Помните, что эта таблица является накопительной слева. Чтобы найти площадь справа от 2,49, мы вычитаем из единицы.
p-значение = (1 — 0,9936) = 0,0064
Значение p меньше уровня значимости (0,10), поэтому мы отклоняем нулевую гипотезу.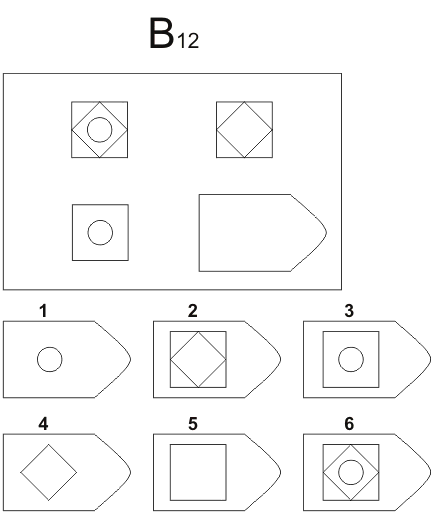 У нас есть достаточно доказательств, чтобы подтвердить заявление о том, что доля пустотелых деревьев увеличилась.
У нас есть достаточно доказательств, чтобы подтвердить заявление о том, что доля пустотелых деревьев увеличилась.
Программные решения
Minitab
(см. Пример 15)
Тест и КИ для одной пропорции
Тест p = 0.32 по сравнению с p> 0,32
|
90% ниже |
||||||
| Образец | х | N | Образец p | Связанный | Z-значение | p-значение |
| 1 | 79 | 196 | 0,403061 | 0,358160 | 2,49 | 0,006 |
| Использование нормального приближения. | ||||||
Excel
Excel не предлагает проверку гипотез с использованием одного образца.
Проверка гипотез о дисперсии
Когда люди думают о статистических выводах, они обычно думают о выводах, включающих средства или пропорции населения.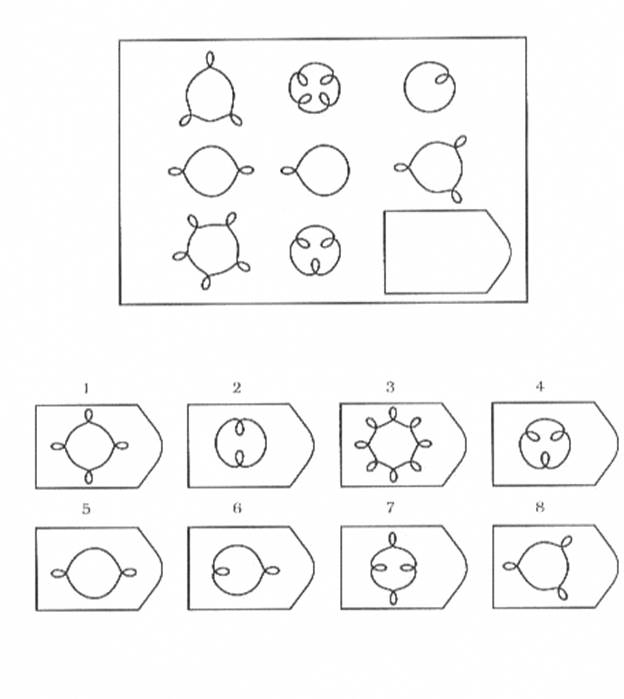 Однако конкретный параметр популяции, необходимый для ответа на практические вопросы экспериментатора, варьируется от одной ситуации к другой, и иногда изменчивость популяции более важна, чем ее среднее значение. Таким образом, качество продукции часто определяется с точки зрения низкой изменчивости.
Однако конкретный параметр популяции, необходимый для ответа на практические вопросы экспериментатора, варьируется от одной ситуации к другой, и иногда изменчивость популяции более важна, чем ее среднее значение. Таким образом, качество продукции часто определяется с точки зрения низкой изменчивости.
Вариация выборки S 2 может использоваться для выводов относительно дисперсии генеральной совокупности σ 2. Для случайной выборки из n измерений, взятых из нормальной совокупности со средним значением μ и дисперсией σ 2, значение S 2 дает оценку точек для σ 2. Кроме того, величина ( n — 1) S 2/ σ 2 следует хи-квадрат ( χ 2 ) , , с df = n — 1.
Распределение хи-квадрат ( χ2 ) имеет следующие свойства:
- В отличие от распределений Z и t, все значения в распределении хи-квадрат положительны.
- Распределение хи-квадрат асимметрично, в отличие от распределений Z и t.
- Существует множество распределений хи-квадрат. Мы получаем конкретное значение, задавая степени свободы (df = n — 1), связанные с выборочными дисперсиями S 2.
Рисунок 22.Распределение хи-квадрат.
Одновыборочный
χ 2 теста для проверки гипотез:Нулевая гипотеза: H0 : σ2 = (константа)
Альтернативная гипотеза:
, где критическое значение χ 2 в области отклонения основано на степенях свободы df = n — 1 и заданном уровне значимости α .
Статистика теста:.
Как и в предыдущих разделах, если статистика теста попадает в зону отклонения, установленную критическим значением, вы отклоняете нулевую гипотезу.
Пример 16
Лесник хочет контролировать густой подлесок полосатого клена, который мешает желаемому восстановлению твердой древесины, используя распылитель для обработки гербицидом. Она хочет удостовериться, что обработка имеет постоянную норму внесения, другими словами, низкую изменчивость, не превышающую 0,25 галлона / акр (0,06 галлона 2). Она собирает выборочные данные (n = 11) по этому типу распылителя тумана и получает выборочную дисперсию 0,064 галлона2. Используя 5% уровень значимости, проверьте утверждение, что дисперсия значительно больше 0.06 гал.2
H0: σ2 = 0,06
h2: σ2> 0,06
Критическое значение 18,307. Любая тестовая статистика, превышающая это значение, приведет к отклонению нулевой гипотезы.
Статистика теста —
Мы не можем отвергнуть нулевую гипотезу. У лесничего НЕТ достаточно доказательств, чтобы поддержать утверждение о том, что дисперсия превышает 0,06 галлона2. Вы также можете оценить p-значение, используя тот же метод, что и для t-таблицы Стьюдента. Просматривайте ряд степеней свободы, пока не найдете два значения, между которыми находится ваша тестовая статистика.В этом случае в строке 10 значения двух таблиц равны 4,865 и 15,987. Теперь поднимите эти два столбца в верхнюю строку, чтобы оценить p-значение (0,1-0,9). Значение p больше 0,1 и меньше 0,9. Оба значения превышают уровень значимости (0,05), поэтому мы не можем отвергнуть нулевую гипотезу.
У лесничего НЕТ достаточно доказательств, чтобы поддержать утверждение о том, что дисперсия превышает 0,06 галлона2. Вы также можете оценить p-значение, используя тот же метод, что и для t-таблицы Стьюдента. Просматривайте ряд степеней свободы, пока не найдете два значения, между которыми находится ваша тестовая статистика.В этом случае в строке 10 значения двух таблиц равны 4,865 и 15,987. Теперь поднимите эти два столбца в верхнюю строку, чтобы оценить p-значение (0,1-0,9). Значение p больше 0,1 и меньше 0,9. Оба значения превышают уровень значимости (0,05), поэтому мы не можем отвергнуть нулевую гипотезу.
Программные решения
Minitab
(см. Пример 16)
Тест и CI для одного варианта
|
Метод |
||
| Нулевая гипотеза | Сигма-квадрат | = 0.06 |
| Альтернативная гипотеза | Сигма-квадрат | > 0,06 |
Метод хи-квадрат предназначен только для нормального распределения.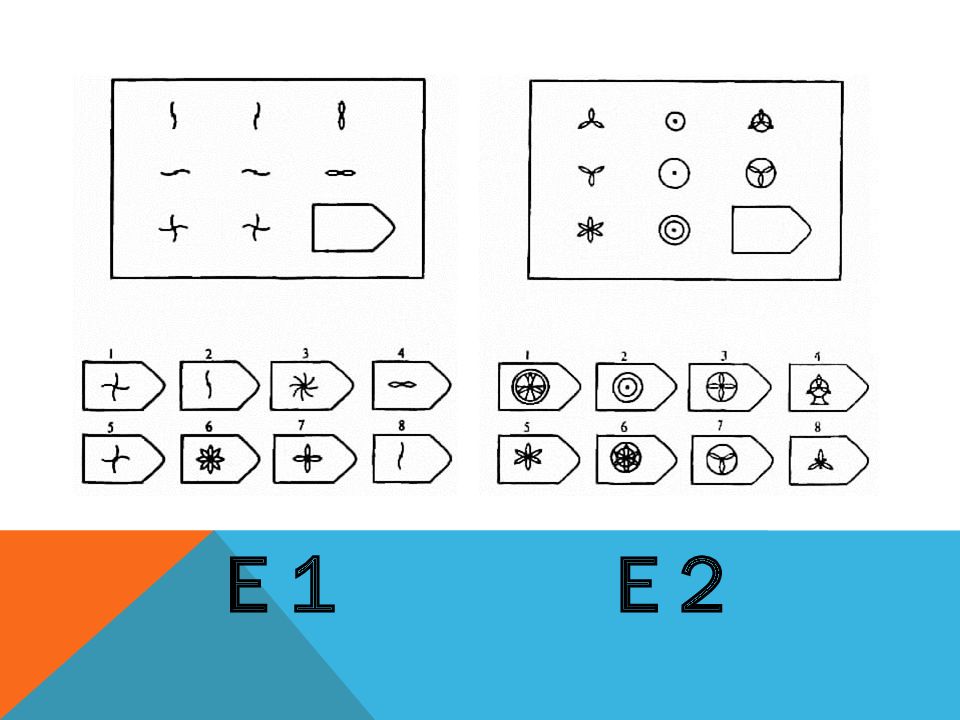
Тесты
|
Тест |
|||
| Метод | Статистика | DF | P-значение |
| Хи-квадрат | 10,67 | 10 | 0.384 |
Excel
Excel не предлагает тестирование с 1 выборкой χ 2.
Собираем все вместе классическим методом
Для проверки утверждения о
μ , когда известно σ- Напишите нулевую и альтернативную гипотезы.
- Укажите уровень значимости и получите критическое значение из стандартной нормальной таблицы.
- Вычислить статистику теста.
- Сравните статистику теста с критическим значением (Z-оценка) и напишите заключение.
Для проверки утверждения о
μ Когда σ неизвестно- Напишите нулевую и альтернативную гипотезы.
- Укажите уровень значимости и получите критическое значение из t-таблицы ученика с n-1 степенями свободы.
- Вычислить статистику теста.
- Сравните статистику теста с критическим значением (t-score) и напишите заключение.
Чтобы проверить заявление о р.
- Напишите нулевую и альтернативную гипотезы.
- Укажите уровень значимости и получите критическое значение из стандартного нормального распределения.
- Вычислить статистику теста.
- Сравните статистику теста с критическим значением (Z-оценка) и напишите заключение.
Таблица 4. Сводная таблица критических Z-показателей.
Проверка утверждения о дисперсии
- Напишите нулевую и альтернативную гипотезы.
- Укажите уровень значимости и получите критическое значение из таблицы хи-квадрат с использованием n-1 степеней свободы.
- Вычислить статистику теста.
- Сравните статистику теста с критическим значением и напишите заключение.


