Интерпретация результатов теста равена: Тест Равена [Онлайн примеры прогрессивной матрицы дж Равена]
Тест Равена [Онлайн примеры прогрессивной матрицы дж Равена]
При устройстве на работу соискателям нередко предлагают пройти тестирование на определение коэффициента интеллекта IQ. Самый популярный вариант задач на айкью — тест матрицы Равена. Он помогает за 20 минут определить уровень развития абстрактного мышления и часто используется, чтобы понять, подходит ли человек на должность, требующую умения мыслить логически.
Где применяется тест Равена
По результатам тестирования принимают решение о дальнейшем диалоге с соискателем, поэтому, как правило, оно проводится одним из первых на очном собеседовании, перед психологическими. Чаще всего тестирование встречается при трудоустройстве в МВД.
Тест Равена проходят соискатели в:
- силовые структуры МВД, полицию;
- прокуратуру;
- ФСБ;
- государственные компании;
- частный бизнес.
Замечание:
От уровня интеллекта зависит способность адекватно воспринимать новую информацию и анализировать ее.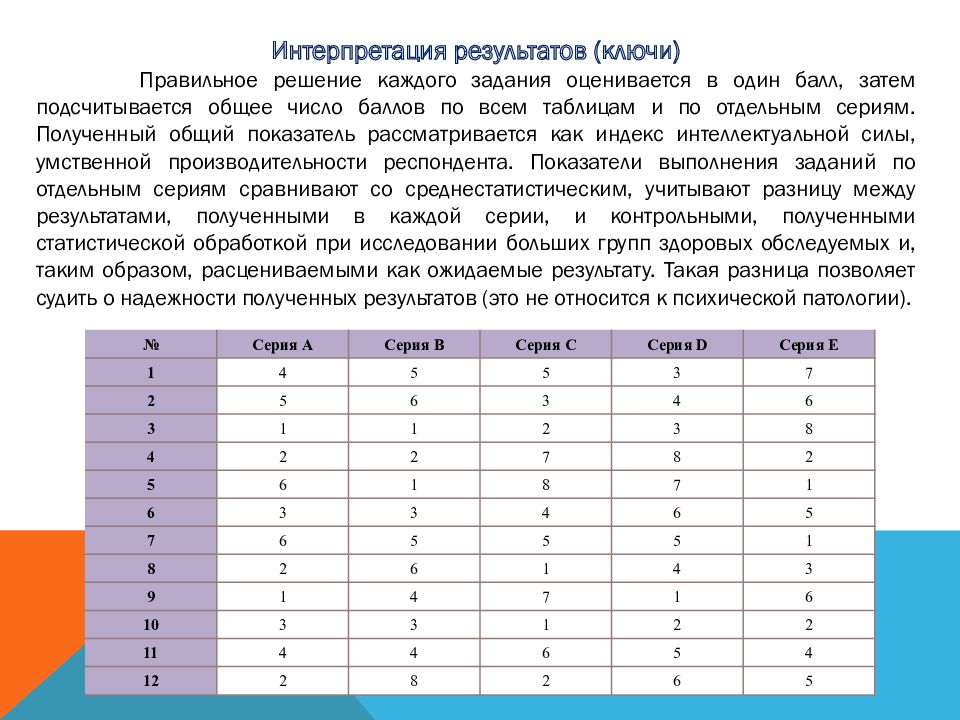
Тестирование Равена используют и коммерческие организации, которые хотят быть уверенными, что нанимают подходящего «спеца», который не будет «пасовать» перед сложными задачами и сможет самостоятельно принимать решения.
Оценочные испытания используют для:
- маркетологов;
- инженеров;
- преподавателей;
- программистов;
- операторов, работающих с массивами данных.
Онлайн-пример Логического теста:
На основании ответов на тест Равена руководством компании принимаются решения о переводе человека в другой отдел или о повышении. Результат тестирования имеет большое значение для личной характеристики человека.
Что определяет онлайн тест Равена
Тестирование длится 20 минут и проходит, как правило, на очном собеседовании, в отличие от тестов способностей, которые проходят дистанционно.
Задание относится к категории невербальных и культурно-свободных. То есть для его решения не нужны знания языка.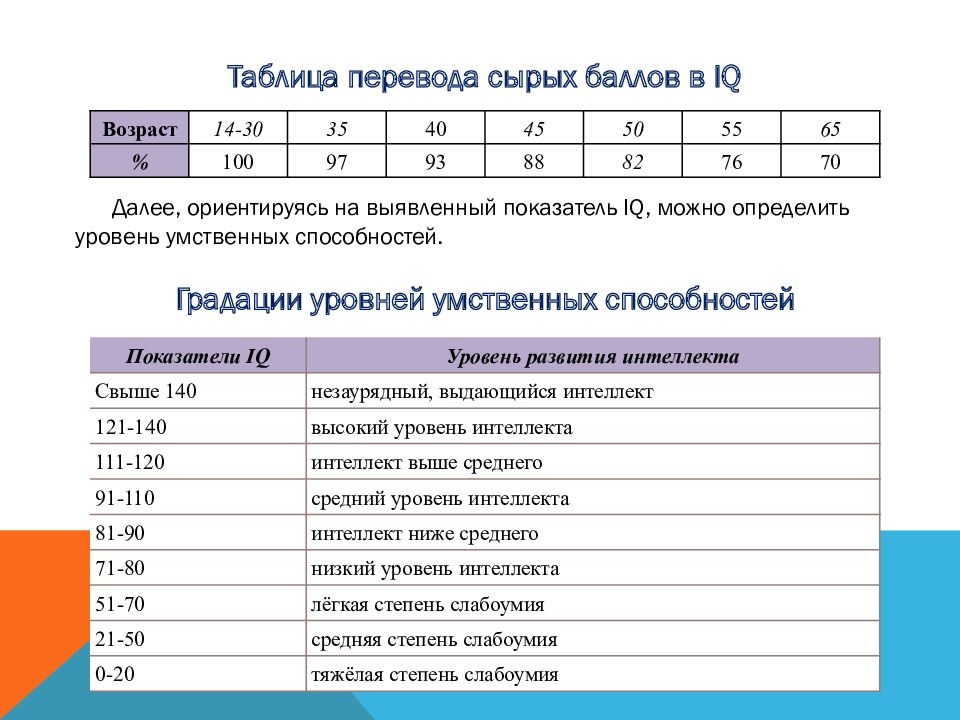
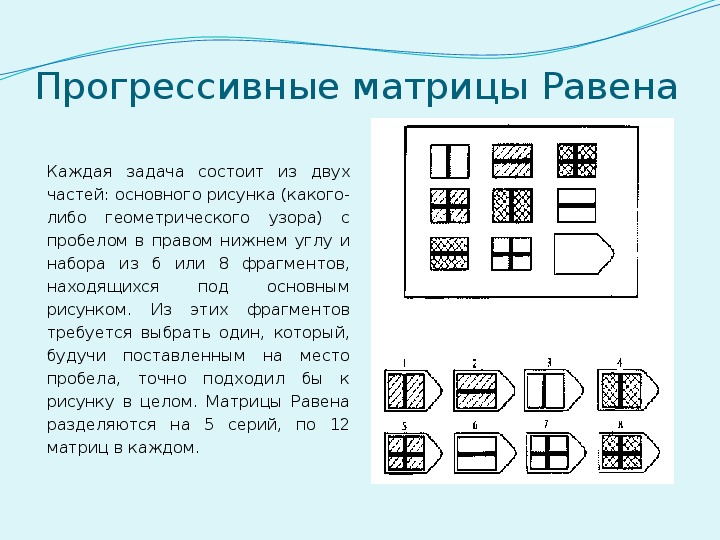
Задания представляют собой матрицы состоящих в логической связи фигур, которые требуется дополнить девятой фигурой. Для каждой задачи только один верный вариант ответа.
Преимуществом тестирования Равена считается то, что на его результаты не влияет:
- психологический профиль;
- черты характера, темперамент;
- культурный код и воспитание;
- знание языка.
Тест прогрессивные матрицы Равена – задание с динамической сложностью. По мере прохождения испытания сложность вопросов растет. Иногда сложность меняется в зависимости от числа правильных ответов.
Испытание состоит из пяти серий — A, B, C, D и E, — каждая из которых отвечает за аспект логического мышления.
- Серию A свободно решит любой взрослый человек. Фигуры в ней статичны — требуется проанализировать структуру матрицы, выбрав необходимое дополнение. Испытуемые со средним уровнем IQ ошибаются здесь только по вспомогательным причинам, например, стресс, невнимательность, спешка.

- Серия B сложнее. Здесь придется провести анализ пар фигур. Бывает, что испытуемый проходит только эту часть — это говорит о том, что он умеет выполнять поставленные перед ним рабочие задачи, но вряд ли справится с их постановкой подчиненным.
- Серия C показывает, насколько динамичен разум испытуемого, насколько он умеет работать в изменяющихся условиях или при дефиците времени, способен ли быстро переключаться. Положение фигур в матрицах постоянно меняется и требует от человека умения мыслить вне стереотипов. Соискатель, набравший высокий балл сможет легко работать на должности менеджера среднего звена с перспективой повышения.
- Серия D демонстрирует, насколько испытуемый способен самостоятельно ставить задачи (не только себе, но и коллективу), может ли руководить людьми. Фигуры в матрице перестраиваются – здесь придется искать дополнительные закономерности и аналогии. Если человек набирает больше 10 баллов, ему, как правило, предлагают руководящую должность.

- Серия E направлена на выявление выдающихся аналитических способностей. Логика изменения элементов фигур уже неочевидна, последовательности меняются группами, которые заметит только человек с развитыми интеллектуальными способностями. Если соискатель набрал максимальный балл, работодатель не упустит такого человека — он умеет мыслить стратегически, не обращая внимания на частности, и способен структурировать работу отдела или всей организации.
Испытание проходят на бумаге или на компьютере работодателя.
Хотя в интернете можно всегда скачать или пройти бесплатный тест Равена онлайн, это не поможет подготовиться к трудоустройству. Вопросы на собеседовании все равно будут другими.
Как подсчитывают результаты и баллы в тесте Равена
Интерпретацию результатов проходит в виде:
- «сырого» балла, описывающего общий уровень интеллекта участника;
- таблицы с баллами по каждой из серий вопросов.

Если кандидат старше 30 лет, вводится дополнительная поправка на возраст: полученный общий IQ балл делится на коэффициент, выраженный в процентах.
| Возраст, лет | Коэффициент поправки |
|---|---|
| 35 | 97 % |
| 40 | 93 % |
| 45 | 88 % |
| 50 | 82 % |
| 55 | 76 % |
| 60 | 70 % |
Благодаря тестированию работодатель оценивает ещё и то, насколько быстро соискатель устает от интеллектуального труда. Если к концу каждой серии однотипных заданий человек начинает неизменно ошибаться, то, вероятно, причина тому — накапливающаяся рассеянность.
Хотя усталость – естественный физиологический процесс, важно чтобы эффективность работы не падала слишком быстро. Поэтому рекомендуется приходить на собеседование выспавшимися и подготовленным.
Сложности матриц Равена
На базе матриц Райвена созданы логические тесты способностей, используемые российскими и международными работодателями для отбора кандидатов. Главная сложность двух этих типов задач – нехватка времени. Основная часть времени уходит на условие и попытку «войти в ритм», в итоге у человека не успевает найти решение.
Расшифровка результатов графического матричного теста проходит автоматически, что исключает субъективное отношение рекрутера. С другой стороны, это значит, что личное отношение к кандидату не является определяющим при принятии решение о найме.
Поскольку испытание проходит на собеседовании, немало трудностей вызывает стресс. Собеседование – само по себе волнительная процедура, а дополнительные задания, от результатов которых зависит дальнейшее трудоустройство, вызывают еще больше проблем.
Существует две причины, по которым соискатели не проходят тестирование:
- Главная причина – отсутствие подготовки к логическим тестам.

- Невнимательность – вторая по частоте причина ошибок. С одной стороны, кандидатам придется следить за таймером, а с другой – анализировать последовательности.
Полезные советы: как пройти прогрессивный тест Равена
- Матрицы Равена дают оценку не только интеллектуальному показателю испытуемого, но и его умениям мыслить логически и прослеживать закономерности. Ведь интеллект – это основа карьерного потенциала человека.
- Хотя для каждой должности и работодателя существует отдельный банк вопросов, исключающий вероятность списывания, вариантов группирования фигур не так много. Решая аналогичные тренировочные задачи, учатся быстро определять паттерны, по которым меняются последовательности.
- Для подготовки к тестированию решают матрицы тренировочных логических задач SHL и TalentQ. Чем больше аналогичных online заданий решает кандидат, тем лучше он подготовится к тестированию.
- В разных компаниях используют разные типы графических элементов: геометрические фигуры, символы, цифры, рисунки.
 При этом принцип остается тем же. Чтобы исключить влияние стресса, рекомендуется практиковаться на всех доступных типах логических задач.
При этом принцип остается тем же. Чтобы исключить влияние стресса, рекомендуется практиковаться на всех доступных типах логических задач. - Перед тем как идти на собеседование, рекомендуется прочитать отзывы работающих сотрудников и бывших соискателей. Это поможет понять, что будет ждать на интервью.
Заключение
Подходящий сотрудник — это не только умный, но и обучаемый человек. Важны умение ужиться в коллективе, навыки командной работы, способность корректно объяснять задачи подчинённым.
Матрицы Равена — только один из этапов оценки кандидатов. И от результатов такого этапа зависит дальнейший диалог с работодателем. А это значит, что придется готовиться к каждой части собеседования.
Для теста Равена, например, достаточно тренировочных логических задач. Кроме того, рекомендуется уделить внимание проективным методикам оценки личности, психологическому тестированию, КОТ (краткий отборочный тест) и СМИЛ (MMPI).
Оцените статью
средняя оценка 5,00 (5 голосов)
Загрузка. ..
..Стандартные прогрессивные матрицы
Стимульный материал Обработка результатов и интерпретацияПо окончании работы испытуемого, психолог с помощью ключа подсчитывает количество правильных ответов, причём правильное решение каждого отдельного задания оценивается в 1 балл.
| № | Серия А | Серия В | Серия С | Серия D | Серия Е |
| 1 | 4 | 2 | 8 | 3 | 7 |
| 2 | 5 | 6 | 2 | 4 | 6 |
| 3 | 1 | 1 | 3 | 3 | 8 |
| 4 | 2 | 2 | 8 | 7 | 2 |
| 5 | 6 | 1 | 7 | 8 | 1 |
| 6 | 3 | 3 | 4 | 6 | 5 |
| 6 | 5 | 5 | 5 | 1 | |
| 8 | 2 | 6 | 1 | 4 | 4 |
| 9 | 1 | 4 | 7 | 1 | 5 |
| 10 | 3 | 3 | 6 | 2 | 6 |
| 11 | 4 | 4 | 1 | 5 | 3 |
| 12 | 5 | 5 | 2 | 6 | 5 |
Подсчитывается общая сумма полученных баллов (испытуемый может получить высшую оценку — 60 баллов), а также число правильных решений в каждой из пяти серий.

Общая сумма баллов является показателем интеллектуальной способности испытуемого, выявляет его умение мыслить согласно определенному методу и системе мышления. Процентная шкала степени развития интеллекта
| Проценты | Степень |
| 95 и выше | I степень: особо высокоразвитый интеллект испытуемого соответствующей возрастной группы |
| 75-95 | 2 степень; незаурядный интеллект для данной возрастной группы |
| 25-74 | 3 степень: средник интеллект для данной возрастной группы |
| 5-24 | 4 степень: интеллект ниже среднего. |
| 5 и менее | 5 степень: дефектная интеллектуальная способность |
Использование приведённой таблицы определения уровня интеллектуального развития приобретает безусловную ценность в условиях обработки и интерпретации групповых данных. Обязательным требованием к составлению группы является соблюдение принципа гомогенности по определённому признаку — возрастному, половому, социально-экономическому, профессиональному, образовательному и т.
 д. В этом случае степень интеллектуального развития, приписываемая конкретному респонденту, фактически означает ранг этого индивида в соответствующей группе. Таким образом, психолог получает обобщённую характеристику количественных индивидуальных различий по уровню интеллектуального развития в обследованной группе.
д. В этом случае степень интеллектуального развития, приписываемая конкретному респонденту, фактически означает ранг этого индивида в соответствующей группе. Таким образом, психолог получает обобщённую характеристику количественных индивидуальных различий по уровню интеллектуального развития в обследованной группе. Другой способ оценки общих результатов по Стандартным матрицам Равена заключается в переводе «сырого» балла в стандартизированный — коэффициент IQ. Такой перевод целесообразен в случаях необходимости сравнения результатов данного теста с другими методиками изучения умственных способностей (тест Векслера, ТСИ Р.Амтхауэра, тест «Домино» А.Энстея и т.п.).
Представленная ниже таблица содержит уже готовые показатели IQ согласно числу полученных испытуемым соответствующего возраста «сырых» баллов.
| Количество «сырых» баллов | Возраст в годах | ||||||||||||
| 8 | 8,5 | 9 | 9,5 | 10 | 10,5 | 11 | 11,5 | 12 | 12,5 | 13 | 13,5 | 16-30 | |
| 1 | 73 | 68 | 65 | 59 | 57 | 53 | 53 | 50 | 48 | 46 | 46 | 46 | — |
| 2 | 74 | 70 | 67 | 61 | 56 | 56 | 54 | 51 | 49 | 49 | 48 | 47 | — |
| 3 | 76 | 72 | 68 | 62 | 60 | 57 | 55 | 53 | 51 | 50 | 49 | 49 | — |
| 4 | 77 | 73 | 70 | 64 | 61 | 59 | 57 | 54 | 52 | 51 | 50 | 50 | — |
| 5 | 79 | 75 | 71 | 65 | 60 | 58 | 55 | 53 | 53 | 52 | 52 | 51 | — |
| 6 | 81 | 76 | 73 | 67 | 64 | 61 | 59 | 57 | 55 | 54 | 53 | 52 | — |
| 7 | 82 | 78 | 74 | 68 | 66 | 63 | 61 | 58 | 56 | 55 | 54 | 54 | — |
| 8 | 84 | 79 | 76 | 70 | 67 | 64 | 62 | 60 | 57 | 57 | 55 | 55 | — |
| 9 | 85 | 81 | 77 | 71 | 69 | 66 | 64 | 61 | 59 | 58 | 57 | 56 | — |
| 10 | 87 | 83 | 79 | 73 | 70 | 67 | 65 | 62 | 60 | 59 | 59 | 57 | 55 |
| 11 | 89 | 84 | 80 | 74 | 72 | 69 | 66 | 64 | 61 | 61 | 61 | 59 | 57 |
| 12 | 90 | 86 | 82 | 76 | 73 | 70 | 68 | 65 | 64 | 62 | 60 | 60 | 58 |
| 13 | 92 | 87 | 83 | 77 | 75 | 71 | 69 | 67 | 64 | 63 | 62 | 61 | 59 |
| 14 | 93 | 89 | 79 | 75 | 73 | 71 | 69 | 68 | 65 | 65 | 63 | 62 | 61 |
| 15 | 95 | 90 | 86 | 80 | 78 | 74 | 72 | 69 | 67 | 66 | 64 | 64 | 62 |
| 16 | 97 | 92 | 88 | 82 | 79 | 76 | 73 | 72 | 68 | 67 | 66 | 65 | 65 |
| 17 | 98 | 95 | 89 | 83 | 81 | 77 | 75 | 72 | 69 | 69 | 67 | 66 | 65 |
| 18 | 100 | 95 | 91 | 85 | 82 | 79 | 76 | 74 | 71 | 70 | 68 | 67 | 66 |
| 19 | 101 | 97 | 92 | 86 | 84 | 80 | 78 | 75 | 72 | 71 | 69 | 69 | 67 |
| 20 | 103 | 98 | 94 | 88 | 85 | 81 | 79 | 76 | 73 | 72 | 71 | 70 | 69 |
| 21 | 104 | 100 | 95 | 89 | 87 | 83 | 80 | 78 | 75 | 74 | 72 | 71 | 70 |
| 22 | 105 | 101 | 97 | 91 | 88 | 84 | 82 | 79 | 76 | 75 | 73 | 72 | 71 |
| 23 | 107 | 103 | 98 | 92 | 90 | 86 | 83 | 81 | 77 | 76 | 74 | 74 | 72 |
| 24 | 108 | 104 | 100 | 94 | 91 | 87 | 85 | 82 | 79 | 78 | 76 | 75 | 74 |
| 25 | 109 | 106 | 101 | 95 | 93 | 89 | 86 | 83 | 80 | 79 | 77 | 76 | 75 |
| 26 | 110 | 107 | 103 | 97 | 94 | 90 | 87 | 85 | 81 | 80 | 78 | 77 | 76 |
| 27 | 112 | 108 | 104 | 98 | 96 | 91 | 89 | 86 | 83 | 82 | 80 | 79 | 75 |
| 28 | 113 | 110 | 106 | 100 | 97 | 93 | 90 | 88 | 83 | 83 | 81 | 80 | 79 |
| 29 | 114 | 111 | 107 | 102 | 99 | 94 | 92 | 89 | 85 | 84 | 82 | 81 | 80 |
| 30 | 116 | 113 | 109 | 103 | 100 | 96 | 93 | 90 | 87 | 86 | 83 | 82 | 82 |
| 31 | 117 | 114 | 110 | 105 | 102 | 97 | 94 | 92 | 85 | 85 | 85 | 84 | 83 |
| 32 | 118 | 115 | 112 | 106 | 103 | 99 | 96 | 96 | 93 | 86 | 86 | 85 | 84 |
| 33 | 120 | 117 | 113 | 108 | 104 | 100 | 97 | 95 | 91 | 90 | 87 | 86 | 86 |
| 34 | 121 | 118 | 115 | 113 | 105 | 102 | 99 | 96 | 92 | 91 | 88 | 87 | 87 |
| 35 | 122 | 120 | 116 | 111 | 107 | 103 | 100 | 97 | 93 | 92 | 90 | 89 | 83 |
| 36 | 123 | 121 | 118 | 112 | 109 | 105 | 102 | 99 | 95 | 93 | 91 | 90 | 90 |
| 37 | 125 | 122 | 119 | 114 | 110 | 107 | 104 | 100 | 96 | 95 | 92 | 91 | 91 |
| 38 | 126 | 124 | 121 | 115 | 112 | 108 | 105 | 102 | 97 | 96 | 94 | 92 | 92 |
| 39 | 127 | 125 | 122 | 117 | 115 | 110 | 107 | 104 | 99 | 97 | 95 | 94 | 94 |
| 40 | 129 | 127 | 124 | 118 | 115 | 112 | 109 | 106 | 100 | 99 | 96 | 95 | 95 |
| 41 | 130 | 128 | 125 | 120 | 117 | 113 | 111 | 108 | 102 | 100 | 91 | 96 | 96 |
| 42 | 133 | 129 | 127 | 121 | 118 | 115 | 112 | 109 | 104 | 102 | 99 | 97 | 97 |
| 43 | 132 | 131 | 128 | 123 | 120 | 117 | 114 | 111 | 106 | 104 | 100 | 99 | 99 |
| 44 | 134 | 132 | 130 | 125 | 121 | 118 | 116 | 113 | 108 | 106 | 102 | 100 | 100 |
| 45 | 135 | 134 | 131 | 126 | 123 | 120 | 118 | 115 | 110 | 109 | 105 | 102 | 102 |
| 46 | 136 | 135 | 133 | 127 | 125 | 122 | 120 | 117 | 112 | 111 | 107 | 105 | 104 |
| 47 | 138 | 136 | 134 | 129 | 126 | 123 | 121 | 119 | 114 | 113 | 109 | 107 | 106 |
| 48 | 139 | 138 | 136 | 130 | 128 | 125 | 123 | 121 | 116 | 115 | 110 | 110 | 108 |
| 49 | 140 | 139 | 137 | 132 | 129 | 127 | 125 | 123 | 118 | 117 | 114 | 112 | 110 |
| 50 | 142 | 141 | 139 | 133 | 131 | 128 | 127 | 124 | 120 | 119 | 116 | 115 | 112 |
| 51 | 143 | 142 | 140 | 135 | 133 | 130 | 128 | 127 | 122 | 121 | 118 | 117 | 114 |
| 52 | 144 | 143 | 142 | 136 | 134 | 132 | 130 | 128 | 124 | 123 | 121 | 120 | 116 |
| 53 | 146 | 144 | 143 | 138 | 136 | 133 | 132 | 130 | 126 | 126 | 123 | 122 | 118 |
| 54 | 147 | 146 | 145 | 139 | 137 | 135 | 134 | 132 | 128 | 128 | 125 | 123 | 120 |
| 55 | 148 | 148 | 146 | 141 | 139 | 137 | 136 | 134 | 130 | 130 | 127 | 127 | 122 |
| 56 | 149 | 149 | 148 | 142 | 142 | 138 | 137 | 136 | 132 | 132 | 130 | 130 | 124 |
| 57 | 151 | 150 | 148 | 144 | 142 | 140 | 139 | 138 | 134 | 134 | 132 | 132 | 126 |
| 58 | 152 | 152 | 151 | 145 | 144 | 141 | 141 | 139 | 136 | 136 | 134 | 134 | 128 |
| 59 | 153 | 153 | 152 | 147 | 145 | 145 | 143 | 141 | 138 | 138 | 137 | 137 | 130 |
| 60 | 155 | 155 | 154 | 148 | 147 | 147 | 144 | 143 | 140 | 139 | 139 | 139 | 130 |
Для лиц более старшего возраста IQ вычисляется по формуле:
где % определяется по таблице:
| Возраст | 16-30 | 35 | 40 | 45 | 50 | 55 | 60 |
| % | 100 | 97 | 93 | 88 | 82 | 76 | 70 |
Далее, ориентируясь на выявленный показатель IQ, можно определить уровень умственных способностей.
 Градации уровней умственных способностей
Градации уровней умственных способностей| Показатели IQ | Уровень развития интеллекта |
| Свыше 140 | незаурядный, выдающийся интеллект |
| 121-140 | высокий уровень интеллекта |
| 111-120 | интеллект выше среднего |
| 91-110 | средний уровень интеллекта |
| 81-90 | интеллект ниже среднего |
| 71-80 | низкий уровень интеллекта |
| 51-70 | лёгкая степень слабоумия |
| 21-50 | средняя степень слабоумия |
| 0-20 | тяжёлая степень слабоумия |
Низкие показатели следует всегда считать менее надежными, чем высокие показатели.
Если необходимо сопоставить результаты выполнения Стандартных матриц Равена с результатами других методик (на изучение мотивации, характера, темперамента, самоотношения, личностных особенностей и т.п.), то можно перевести «сырой» балл по тесту Равена не в показатели IQ, а в стены.
 Перевод показателей IQ в стены
Перевод показателей IQ в стены| Стены | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| IQ-балл | 45-58 | 59-72 | 73-86 | 87-100 | 101-114 | 115-128 | 129-142 | >142 |
После интерпретации общего результата по тесту необходимо переходить к качественному анализу результативности выполнения заданий по сериям.
Ниже приводится краткая характеристика основных принципов построения заданий, мыслительных операций, к которым «обращены» задания, сгруппированные в одной серии. Краткая характеристика основных принципов построения заданий
Серия А. «Принцип взаимосвязи в структуре матриц»
От обследуемого требуется дополнение недостающей части изображения. Считается, что при работе с матрицами этой серии реализуются следующие основные мыслительные процессы: а) дифференциация основных элементов структуры и раскрытие связей между ними; б) идентификация недостающей части структуры и сличение ее с представленными образцами. В серии А использован принцип установления взаимосвязи в структуре матриц. Здесь задание заключается в дополнении недостающей части основного изображения одним из приведенных в каждой таблице фрагментов. Выполнение задания требует от обследуемого тщательного анализа структуры основного изображения и обнаружения этих же особенностей в одном из нескольких фрагментов. Затем происходит слияние фрагмента, его сравнение с окружением основной части таблицы. При выполнении заданий этой серии актуализируется умение дифференцировать элементы и выявлять связи между элементами гештальта, дополнять недостающую часть структуры, сличая её с образцами.
В серии А использован принцип установления взаимосвязи в структуре матриц. Здесь задание заключается в дополнении недостающей части основного изображения одним из приведенных в каждой таблице фрагментов. Выполнение задания требует от обследуемого тщательного анализа структуры основного изображения и обнаружения этих же особенностей в одном из нескольких фрагментов. Затем происходит слияние фрагмента, его сравнение с окружением основной части таблицы. При выполнении заданий этой серии актуализируется умение дифференцировать элементы и выявлять связи между элементами гештальта, дополнять недостающую часть структуры, сличая её с образцами.
Психологическое значение: решение зависит от уровня внимательности, уровня статистического представления, воображения и уровня визуального различия (дискриминации).
Серия В. «Принцип аналогии между парами фигур»
Сводится к нахождению аналогии между парами фигур. Обследуемый раскрывает этот принцип путем постепенной дифференциации элементов.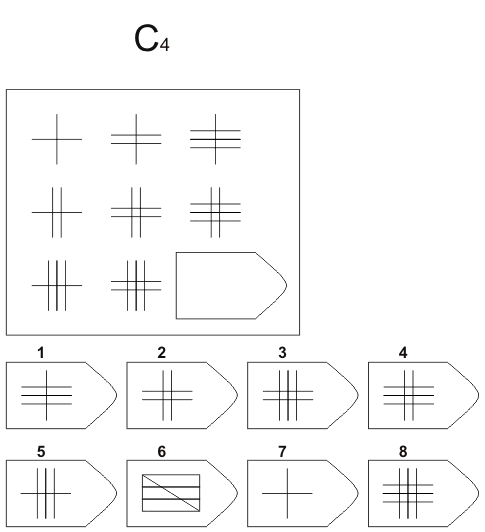 При решении используется также способность постигать симметрию. Серия В построена по принципу аналогии между парами фигур. Обследуемый должен найти принцип, соответственно которому построена в каждом отдельном случае фигура и, исходя из этого, подобрать недостающий фрагмент. При этом важно определить ось симметрии, соответственно которой расположены фигуры в основном образце. На основании результативности выполнения заданий серии В оценивается способность находить аналогии между парами фигур, дифференцируя их элементы. Задание серии В состоит в нахождении аналогии между двумя парами фигур (дополнение отношений).
При решении используется также способность постигать симметрию. Серия В построена по принципу аналогии между парами фигур. Обследуемый должен найти принцип, соответственно которому построена в каждом отдельном случае фигура и, исходя из этого, подобрать недостающий фрагмент. При этом важно определить ось симметрии, соответственно которой расположены фигуры в основном образце. На основании результативности выполнения заданий серии В оценивается способность находить аналогии между парами фигур, дифференцируя их элементы. Задание серии В состоит в нахождении аналогии между двумя парами фигур (дополнение отношений).
Психологическое значение: способность линейной дифференциации и суждение (умозаключение) на основе линейных взаимосвязей.
Серия С. «Принцип прогрессивных изменений в фигурах матриц»
Задания этой серии содержат сложные изменения фигур в соответствии с принципом их непрерывного развития, «обогащения» по вертикали и горизонтали. При выполнении этой серии обследуемый должен проследить закономерности изменения фигур по горизонтали и вертикали и суммировать результат в искомой фигуре.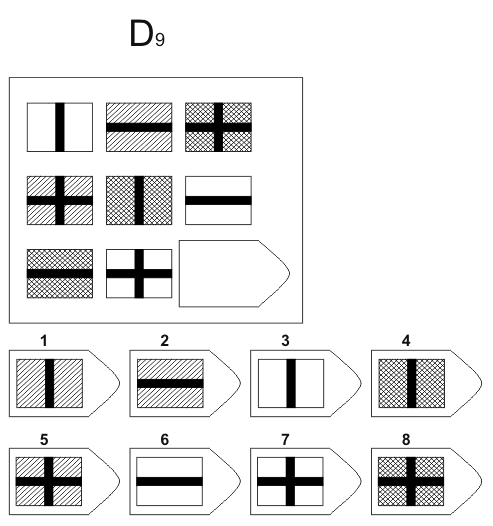 Серия С построена по принципу прогрессивных изменений в фигурах матриц. Эти фигуры в пределах одной матрицы все больше усложняются, происходит как бы непрерывное их развитие. Обогащение фигур новыми элементами подчиняется четкому принципу, обнаружив который, можно подобрать недостающую фигуру.
Серия С построена по принципу прогрессивных изменений в фигурах матриц. Эти фигуры в пределах одной матрицы все больше усложняются, происходит как бы непрерывное их развитие. Обогащение фигур новыми элементами подчиняется четкому принципу, обнаружив который, можно подобрать недостающую фигуру.
Психологическое значение: проявляется способность к динамической (быстрой) наблюдательности и прослеживанию непрерывных изменений, динамическая внимательность и воображение, способность представлять.
Серия D. «Принцип перегруппировки фигур»
Серия составлена по принципу перестановки фигур в матрице по горизонтальному и вертикальному направлениям. Успешность решения зависит от способности обследуемого выявлять количественные и качественные закономерности построения, как матрицы в целом, так и ее отдельных столбцов и строк. Серия D построена по принципу перегруппировки фигур в матрице. Обследуемый должен найти эту перегруппировку, происходящую в горизонтальном и вертикальном положениях.
Психологическое значение: решение зависит от способностей схватывать количественные и качественные изменения в упорядочении (составлении) фигур согласно закономерности используемых изменений.
Серия Е. «Принцип разложения фигур на элементы»
Априорно данная серия считается наиболее сложной. Процесс решения заданий этой серии заключается в анализе фигур основного изображения, выявления значимых признаков, которые могут варьироваться, и последующей «сборки» недостающей фигуры по частям. Выполнение этой серии ориентировано на выявление способности к аналитико-синтетической деятельности. Серия Е основана на принципе разложения фигур основного изображения на элементы. Недостающие фигуры можно найти, поняв принцип анализа и синтеза фигур. Серия Е является самой сложной из всех и позволяет судить о развитости у испытуемых способности к аналитико-синтетической деятельности. Здесь требуется складывать и вычитать элементы фигур, смешивать части согласно алгебраическому принципу. Недостающий член структуры находят с помощью алгебраических операций с остальными членами структуры.
Психологическое значение: способность наблюдать сложное количественное и качественное различие кинетических, динамических рядов. Высшая форма абстракции и динамического синтеза.
Как видно из приведённого описания, материал теста «обращён» в целом к традиционным логическим операциям (сравнение и различие, анализ и др.). Невербальный характер материала значительно «высвобождает» весь текст от влияния социокультурных особенностей жизнедеятельности конкретного обследуемого и предоставляет возможность определить (с определённой долей вероятности) его «чистую» способность к целенаправленному поиску необходимого решения.
При интерпретации результатов индивидуального тестирования важным направлением анализа является определение способа решения, которого придерживался испытуемый (логическое рассуждение, угадывание, работа вслепую, интуитивный метод, отказ). Кроме того, при неоднородности содержательной и непоследовательной, но колеблющейся трудности отдельных серий и заданий (не линейная, а прогрессирующая ритмика), нельзя по результатам Равена составить последовательный график утомляемости или продуктивности.
Прогрессивные матрицы Равена.
Тест для детей. Построен на основе гештальтпсихологии. Существует в двух вариантах.
- черно-белые матрицы Равена — от 8 лет до 65 лет. Интерпретация результатов для каждого возраста. Материал — черно-белый, состоит из 5 серий по 12 примеров.
- цветные матрицы Равена — от 5 до 11 лет. Материал — цветной, 3 серии по 12 заданий.
Прогрессивные матрицы Равена — принцип прогрессивности: каждое задание методики готовит испытуемого для следующего более сложного задания.
Каждое задание в каждой серии сложнее предыдущего. Выполнение каждого задания готовит к выполнению следующего.
Каждая серия построена так:
Серия A — дополнить недостающие части изображения. Умение дифференцировать отдельные компоненты структуры, умение устанавливать связи между разными компонентами структуры, умение идентифицировать недостающие части структуры, сличать ее с представленными вариантами.
Серия B — требуется найти аналогии между парами фигур. Диагностируется мышление по аналогии и понимание симметрии.
Серия C — задания содержат сложное изменение фигур в соответствии с принципом их непрерывного развития. Задача — установить принцип развития. Найти ответ.
Серия D — задания составлены по принципу перестановки фигур в матрицы по горизонтали и вертикали.
Серия E — в задании заложен принцип разложения фигур на отдельные элементы. Требуется проявить умение по разложению на элементы, потом синтезировать в целое.
Показатель: индекс вариабельности (подсчитывается на Западе).
Для подсчета в руководствах методики таблицы, в которых представлено распределение сырых балов по сериям. Каждый из возможных балов по сериям.
Для подсчета индекса вариабельности сопоставить с таблицей, подсчитать разницу между табличным значением и реальным. Разница берется без учета знака.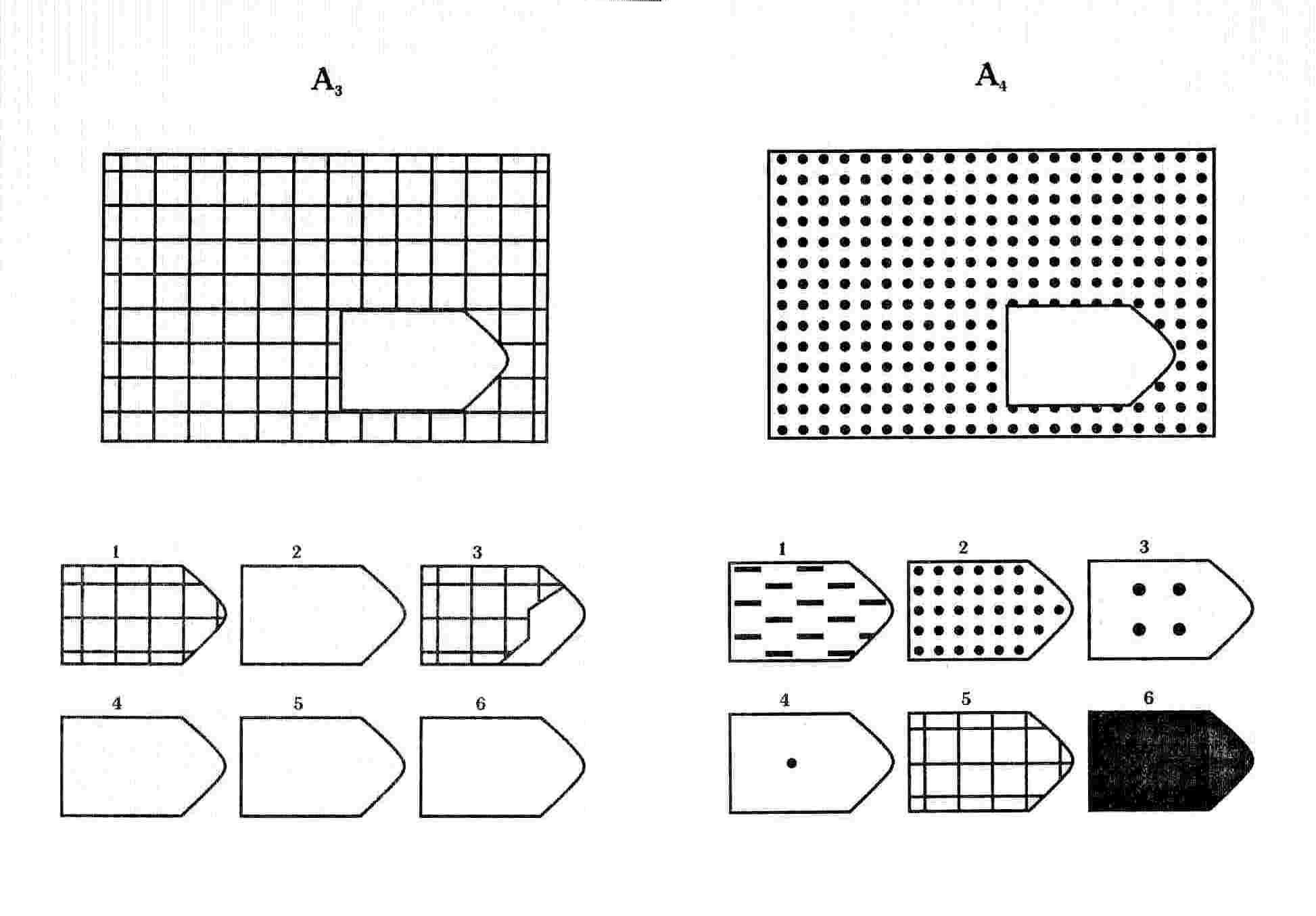 Сумма разниц по всем 5 сериям.
Сумма разниц по всем 5 сериям.
Для чего индекс вариабельности? Для достоверности результата испытуемого. Испытуемый может выполнить задания методом угадывания. Не используя возможностей наглядного мышления.
Если индекс вариабельности от 0 до 4 — результаты достоверны.
Если индекс вариабельности от 5 до 6 — то результаты можно подвергнуть сомнению.
Если индекс вариабельности от 7 и выше — результаты испытуемого недостоверны.
Цветные матрицы Равена.
Используются дефектологами, психологами для детей от 5 до 11 лет. Диагностируются отклонения от нормы в мышлении ребенка. Диагностика проводится индивидуально.
1. Первое задание открывается перед ребенком и объясняется, как делать, дается инструкция.
Например: наверху коврик с дырочкой, какую заплатку нужно поставить?
Психолог должен объяснить, почему остальные 5 кусочков не подходят (какие линии, какой узор…)
Психолог должен продумать объяснение, чтобы научить ребенка думать и дальше выполнять последующие задания.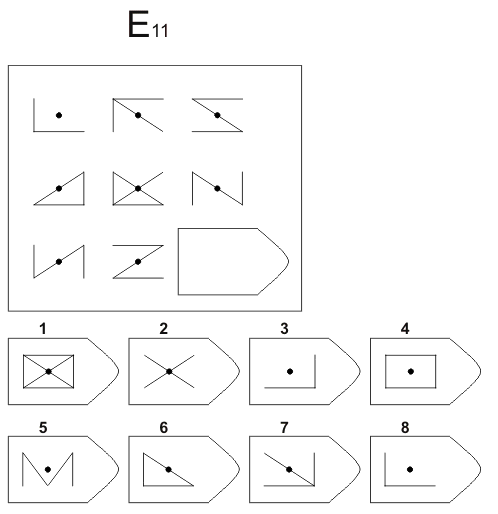 Ребенку дается возможность ответить. Если правильно, то 1 бал за первое задание. Если ответ неправильный, то предлагается подумать еще. За вторую попытку ребенок получает половинку бала. Если верная попытка третья, то он получает одну четвертую бала. Стимулирующая помощь: психолог напоминает, объясняет на линиях, ковриках, узорах… Если помощь не помогает, то у психолога наготове должна быть вырезана эта матрица и все 6 кусочков. Решение переходит из наглядно-образного в наглядно-действенный образ. Если ребенок не может сделать, то психолог показывает сам. Баллы начисляются только в случае первых трех попыток.
Ребенку дается возможность ответить. Если правильно, то 1 бал за первое задание. Если ответ неправильный, то предлагается подумать еще. За вторую попытку ребенок получает половинку бала. Если верная попытка третья, то он получает одну четвертую бала. Стимулирующая помощь: психолог напоминает, объясняет на линиях, ковриках, узорах… Если помощь не помогает, то у психолога наготове должна быть вырезана эта матрица и все 6 кусочков. Решение переходит из наглядно-образного в наглядно-действенный образ. Если ребенок не может сделать, то психолог показывает сам. Баллы начисляются только в случае первых трех попыток.
2. Аналогии между парами фигур
3. Серия Б-аналогия между парами фигур. Для выявления категории детей с отклонениями.
Розанова провела этот эксперимент в школе 1, 2 классов. Выделены 4 уровня успешности выполнения этой методики.
- 4-ый, высший уровень выполнения. Если ребенок набрал от 28 балов и больше.
- 3-ий, высокий уровень. Если ребенок набрал от 23 до 28 балов.
- 2-ой уровень, низкая успешность. Если ребенок набрал от 17 до 23 балов.
- 1-ый уровень, меньше 17 балов.
Оценка развития ребенка 1, 2 классов. Если выполнение на 3 и 4 уровне, следовательно, ребенок нормальный по интеллектуальному развитию. Если на 1 или 2 уровне, следовательно, возможны отклонения в развитии. Если ребенок дал 13 балов или меньше, следовательно, умственная отсталость. Время не ограничивается.
Стандартизация у нас в России только для 1, 2 классов цветных матриц Равена!!!
Цветные прогрессивные матрицы Равена
Цветной вариант Прогрессивных Матриц Равена предназначен для обследования детей от 5 до 9 лет.
Инструкции по проведению обследования дошкольников с помощью Цветных Прогрессивных Матриц Равена
Процедура индивидуального тестирования по Прогрессивным Матрицам Равена чрезвычайно проста.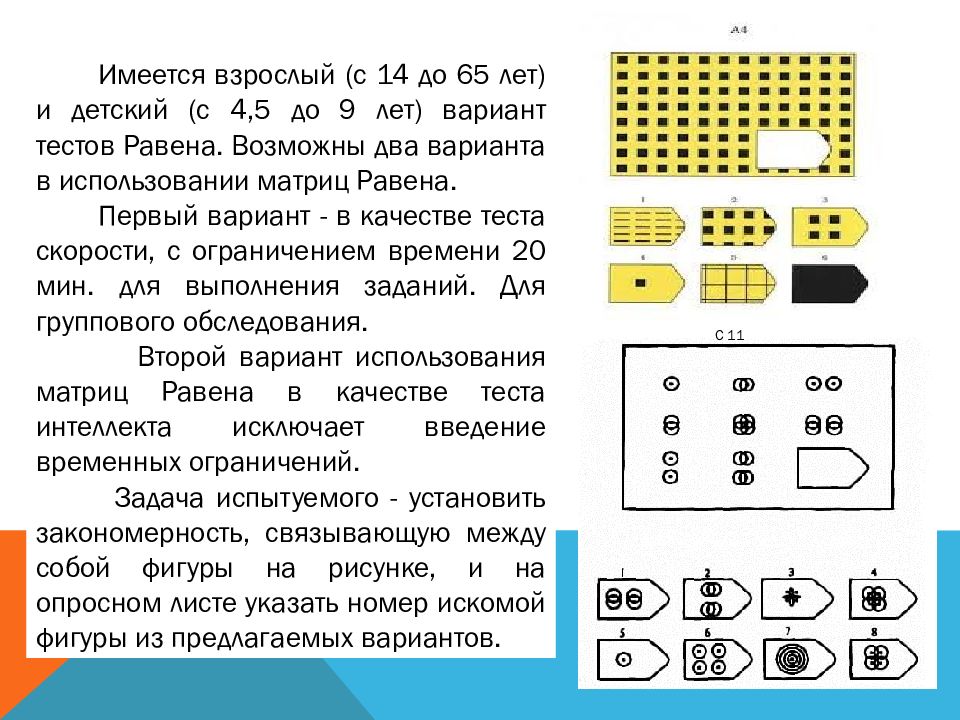 В отличие от многих других тестов, здесь нет необходимости жестко придерживаться какой-либо специальной словесной инструкции. Основные требования состоят в том, чтобы, во-первых, удостовериться, что испытуемые понимают, что и как они должны сделать. Во-вторых, следует обеспечить соответствие принятой в данном обследовании процедуры общепринятым стандартам, чтобы была возможность сравнивать полученные данные с нормативными.
В отличие от многих других тестов, здесь нет необходимости жестко придерживаться какой-либо специальной словесной инструкции. Основные требования состоят в том, чтобы, во-первых, удостовериться, что испытуемые понимают, что и как они должны сделать. Во-вторых, следует обеспечить соответствие принятой в данном обследовании процедуры общепринятым стандартам, чтобы была возможность сравнивать полученные данные с нормативными.
При использовании книжной формы теста нельзя увидеть, как будет выглядеть матрица с вставленным в ее вырез тем или иным фрагментом, следствием чего могут быть не очень ответственное отношение некоторых детей к заданию. Поэтому важно всякий раз удостовериться, что ребенок внимательно посмотрел на рисунок и что он убежден, что указанный им фрагмент является единственным, который правильно дополняет матрицу.
Тому, кто проводит тест, необходимо иметь следующие материалы: инструкции, экземпляр тестового буклета. Не допускается делать никаких пометок в тестовом буклете с ЦПМ.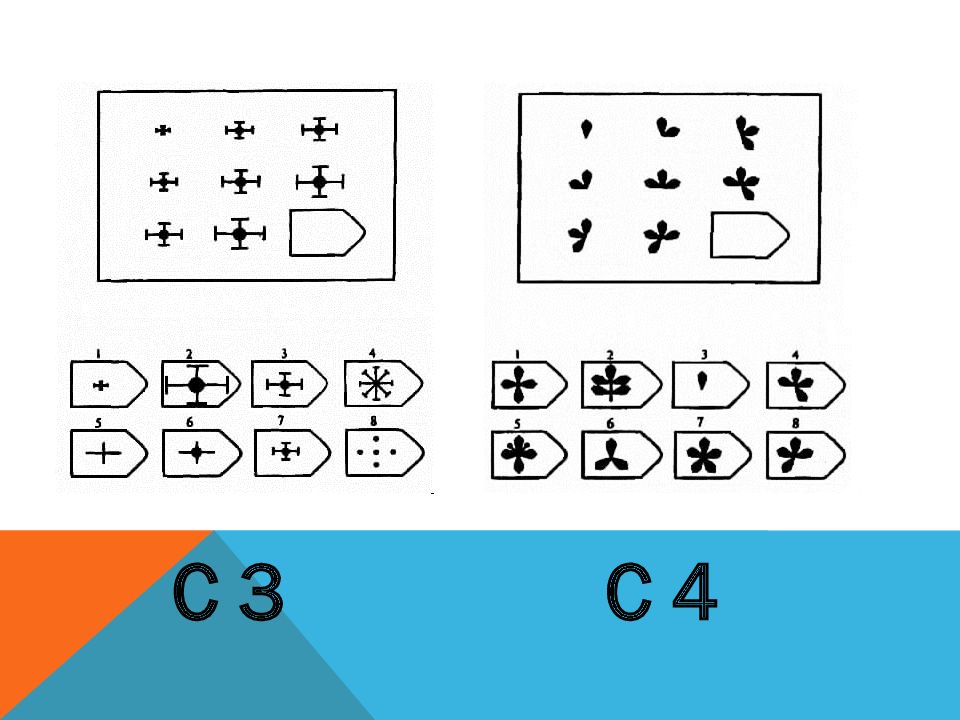 В процессе предварительной беседы занесите данные об испытуемом в бланк ответов, удостоверившись, что указанный возраст соответствует дате рождения.
В процессе предварительной беседы занесите данные об испытуемом в бланк ответов, удостоверившись, что указанный возраст соответствует дате рождения.
Откройте буклет на первом задании А1.
— Посмотри сюда.
Укажите на верхнюю фигуру
— Ты видишь, что из этой картинки вырезан кусочек. Каждый из этих кусочков внизу…
Укажите на каждый из фрагментов по очереди
— …имеет подходящую форму, чтобы заполнить вырез, но только один из них подходит по рисунку. Номер 1 имеет правильную форму, но неправильный рисунок. Номер 2 вообще не имеет рисунка. Номер 3 совсем неправильный. Номер 6 почти правильный, но вот здесь не подходит.
Укажите на белое пятно на фрагменте номер 6.
— Только один из кусочков правильный. Покажи, какой из них подходит, чтобы дополнить рисунок.
Если испытуемый не показывает на правильный фрагмент, продолжайте объяснение, пока суть задания не будет им полностью уяснена.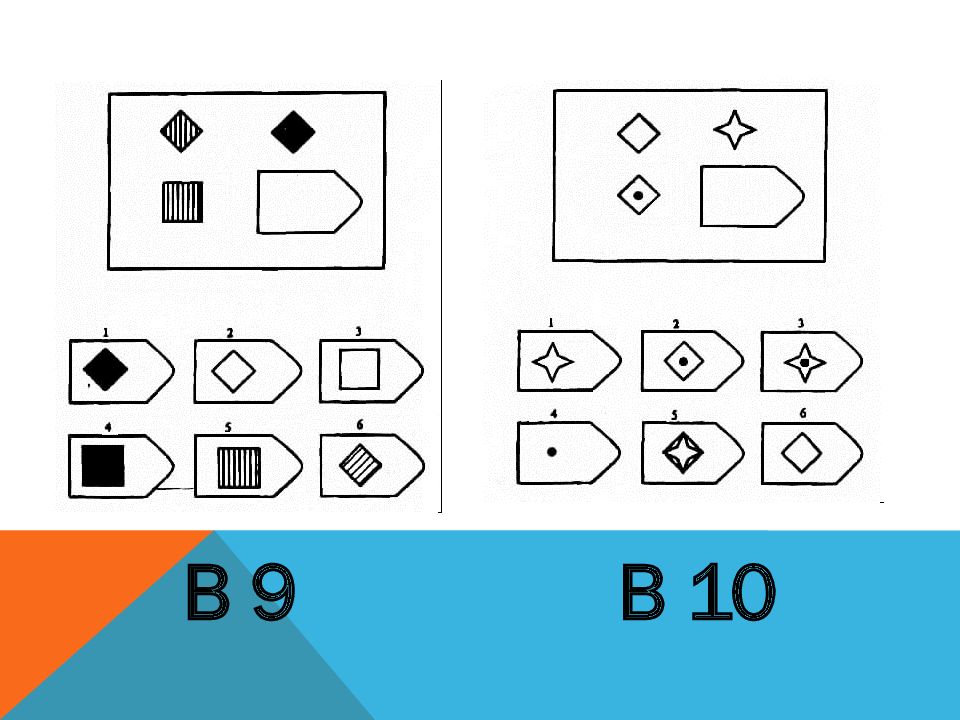
Переходите к заданию A2.
— А теперь покажи кусочек, который подойдет сюда.
Если испытуемый не справляется, продемонстрируйте ему снова задание А1, а затем опять попросите решить задание А2. Если задание выполнено правильно, переходите к заданию A3, работая по той же схеме.
Перейдя к заданию А4, перед тем как предоставить испытуемому возможность подумать и указать на один из фрагментов скажите:
— Посмотри внимательно на эти кусочки.
Укажите пальцем поочередно на каждый из фрагментов.
— Только один из этих кусочков подходит для завершения рисунка. Будь внимателен. Сначала посмотри на каждый из этих шести кусочков.
Снова укажите на каждый из шести фрагментов.
— Теперь покажи на кусочек, который подойдет сюда.
Укажите на рисунке место, куда должен подойти фрагмент.
Когда испытуемый укажет на один из фрагментов, независимо от правильности его ответа, скажите. ..
..
— Этот кусочек действительно подходит сюда?
Если испытуемый скажет «да», примите его выбор с одобрением независимо от того, правильный он или неправильный. Если он захочет изменить свой выбор, скажите…
— Хорошо. Тогда покажи на правильный кусочек,
Независимо от правильности ответа снова спросите…
— Этот подходит?
Если испытуемый удовлетворен своим решением, примите его выбор независимо от правильности, но, если вам кажется, что он все еще сомневается, спросите…
— Ну так какой же из кусочков, по твоему мнению, действительно правильный?
Отметьте номер окончательного выбора в соответствующей части бланка.
Предъявите задание А5 тем же способом, что и задание А4.
На любой стадии тестирования в интервале между А1 и А5 задание А1 может быть использовано заново, чтобы еще раз показать испытуемому, что надо сделать, с последующей просьбой к нему попробовать снова выполнить соответствующее задание.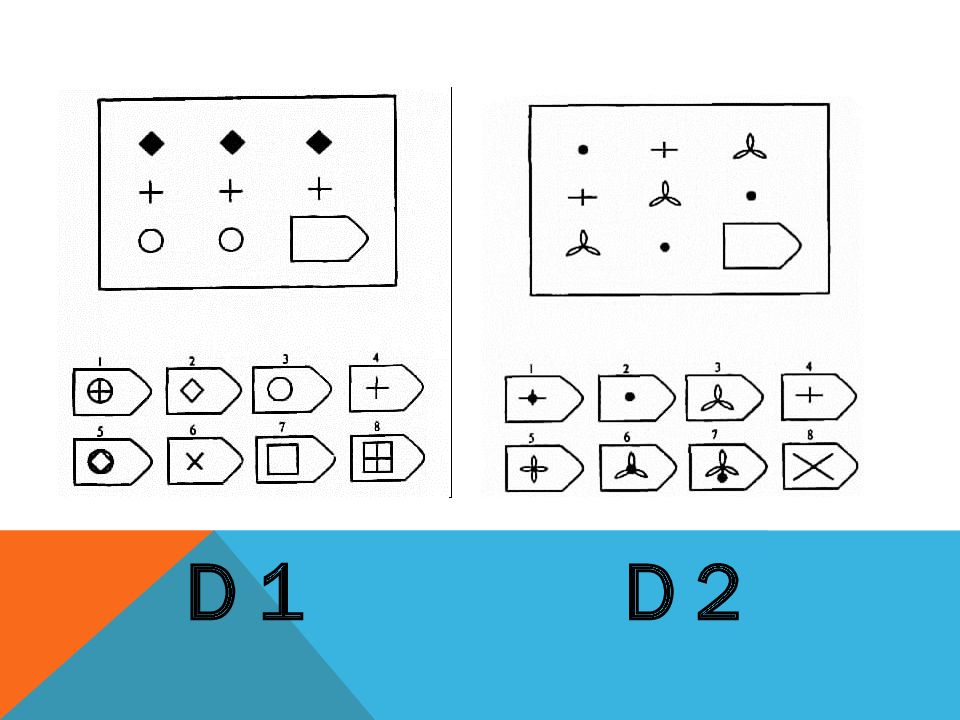 Если испытуемый не справляется с заданиями А1 — A3, следует перейти к планшетной форме теста.
Если испытуемый не справляется с заданиями А1 — A3, следует перейти к планшетной форме теста.
Если эти пять заданий решены, переходите к заданию А6.
— Посмотри внимательно на этот рисунок. Какой из этих кусочков…
Укажите на каждый фрагмент по очереди.
— …подходит сюда?
Покажите на свободное место, которое следует заполнить.
— Будь внимателен, подходящий кусочек только один. Какой? Если ты действительно уверен, что нашел правильный кусочек, укажи на него.
Запишите окончательный ответ.
По мере предъявления следующих заданий продолжайте использовать те же инструкции до тех пор, пока в них есть необходимость.
Если ребенок проявляет беспокойство по поводу небольших дефектов на рисунках, убедите его, что об этом не стоит беспокоиться.
Если ребенок «застрял» на конкретном задании, предложите ему двинуться дальше и посмотреть, не справится ли он со следующими заданиями, а затем вернитесь к заданию, вызвавшему трудности. Если вы сочтете это нужным, то можно предложить ребенку просто угадать ответ, так как «догадки иногда бывают правильными».
Если вы сочтете это нужным, то можно предложить ребенку просто угадать ответ, так как «догадки иногда бывают правильными».
Завершив серию А, предъявите первое задание Серии АB, снова указывая по очереди на каждую из трех фигур на матрице и на пространство, подлежащее заполнению.
— Ты видишь, как они расположены. Так. Так. Так. Что тут должно получиться? Какой из кусочков подходит сюда? Будь внимателен. Посмотри на каждый из них по очереди. Правильный — только один. Который?
При выполнении заданий от АB1до АB5, после того как ребенок указал на один из фрагментов, правильный или неправильный…
— Он действительно подходит, чтобы дополнить рисунок?
Укажите на рисунок на матрице и на вырез в ней.
Как и прежде, если испытуемый отвечает «да», примите (и запишите) его выбор с одобрением. Если ребенок хочет изменить свой выбор, действуйте так же, как в Серии А, и примите его окончательный выбор.
При выполнении шестого задания ребенка не следует спрашивать, правильный ли выбор он сделал. Просто скажите …
— Посмотри внимательно на картинку.
Укажите по очереди на каждую фигуру на матрице и на пространство, подлежащее заполнению.
— Будь внимателен, только один из этих кусочков правильно дополняет картинку.
Укажите по очереди на каждый из фрагментов.
— Какой из них?
Зафиксируйте окончательный выбор на бланке, либо записывая номер выбранного фрагмента рядом с номером задания, либо для бланка легкого подсчете зачеркивая номер выбранного ответа одной короткой линией.
Если была сделана ошибка или испытуемый хочет изменить свой ответ, зачеркните ранее записанный номер, а затем запишите номер окончательного выбора. При работе с бланком легкого подсчета зачеркните отмененный ответ еще одной чертой.
Не пытайтесь стирать неправильно отмеченные ответы. Те же указания можно использовать при работе с остальными заданиями Серий АB и В, пока это является целесообразным.
Планшетная форма тестового буклета . Серия А.
Cкачать буклеты Серии A, AB, B в PDF-формате
Оценка и интерпретация
Подсчет баллов
За каждый правильный ответ начисляется один балл. Будьте внимательны и старайтесь не допустить потери бланков — чистых или использованных, поскольку каждый из них содержит ключ для подсчета баллов по тесту.Если обследуемый делает ошибки в первых пяти задачах Серии А , то нельзя считать, что он понял идею задачи. Полученные при этих условиях баллы, как правило, нужно признать недостоверными, несмотря на то, что общий балл при этом может оказаться и больше десяти за счет решения задач путем случайного угадывания правильного ответа среди шести альтернативных вариантов.
При использовании планшетной формы теста некоторые дети после того, как они положили правильный фрагмент теста на место, беспокоятся, что он не вполне хорошо совпал с вырезом, и хотят его заменить.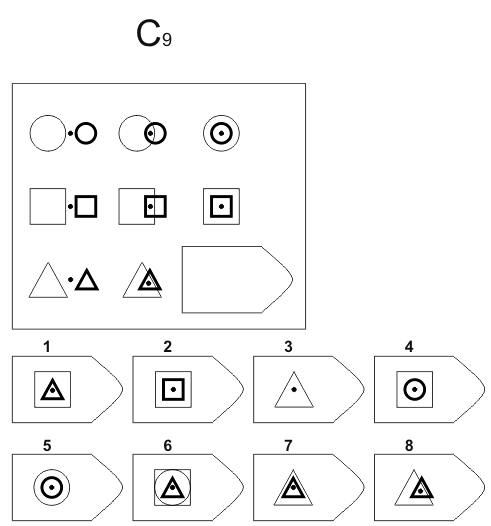 По этой причине, а также потому, что «смышленые» дети хотят поиграть с тестовым материалом, желательно спросить ребенка, по какой причине он сдвигает или перемещает фрагмент. При необходимости задание теста может быть разъяснено еще раз, чтобы ребенок понял, что в первую очередь надо положить на место правильный фрагмент, а потом, попробовав другие, вернуть правильный на место и что мелкие несовпадения фрагмента с вырезом не имеют никакого значения.
По этой причине, а также потому, что «смышленые» дети хотят поиграть с тестовым материалом, желательно спросить ребенка, по какой причине он сдвигает или перемещает фрагмент. При необходимости задание теста может быть разъяснено еще раз, чтобы ребенок понял, что в первую очередь надо положить на место правильный фрагмент, а потом, попробовав другие, вернуть правильный на место и что мелкие несовпадения фрагмента с вырезом не имеют никакого значения.
Если дети не в состоянии выразить свои суждения словами, это не значит, что они не могут решить задачу интуитивно. Правильное решение никогда не следует фиксировать как «ошибку», если ребенок не может его объяснить. Напротив, неверные ответы, исправляемые в результате проб и ошибок, дают значимую психологическую информацию, хотя обычно они не включаются в общий балл по тесту из соображений строгости интерпретации процентильных результатов данного ребенка по таблице нормативов. В тех случаях, однако, когда ребенок осознанно обнаружил и исправил свою ошибку, окончательно вставленный фрагмент может быть учтен.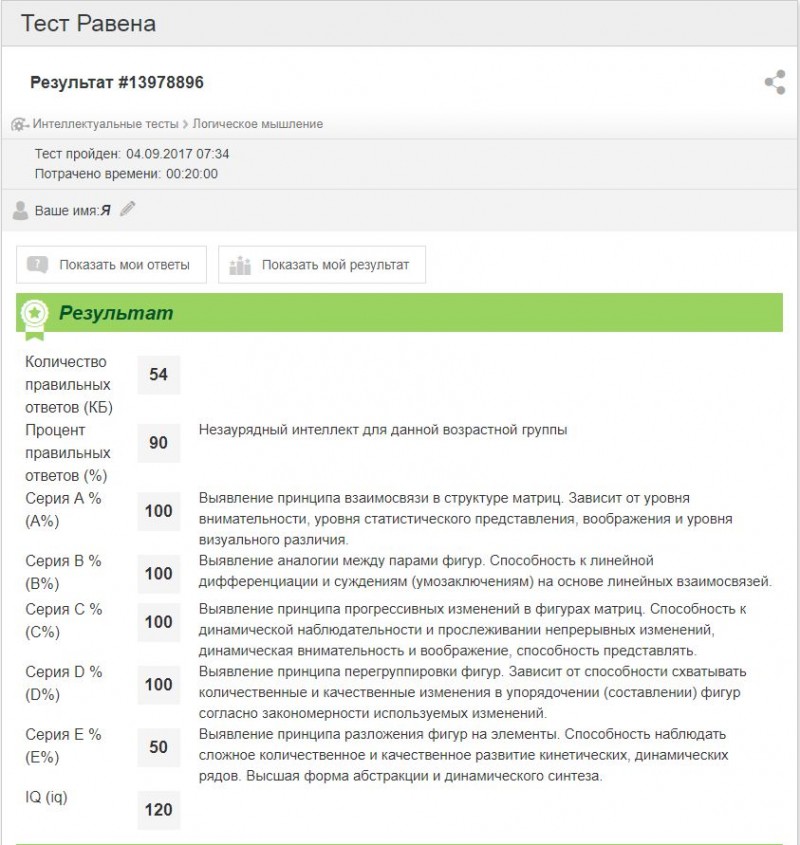
Когда тест проводится индивидуально по книжной форме , засчитывается как «верный» или «ошибочный» тот фрагмент, на который испытуемый указывает как на свой окончательный выбор.
Когда книжная форма используется для самотестирования или при групповом тестировании с использованием открытых бланков регистрации ответов, всякому, кто записывает больше, чем одну цифру против номера любого задания, необходимо сказать, чтобы он вычеркнул все, кроме одной. Если это обнаружено после завершения процедуры тестирования, рассматривается только последний номер справа независимо от того, верны или ошибочны другие ответы.
Когда используется бланк легкого подсчета, испытуемым необходимо показать, как исправлять ошибки, зачеркивая крестом (X) неправильные ответы и оставляя перечеркнутым одной короткой чертой номер своего окончательного выбора.
Несогласованности и ошибки.
Когда используется книжная форма теста, несогласованность в распределении баллов испытуемого можно оценить вычитанием его балла по каждой серии из баллов, ожидаемых при таком же общем балле.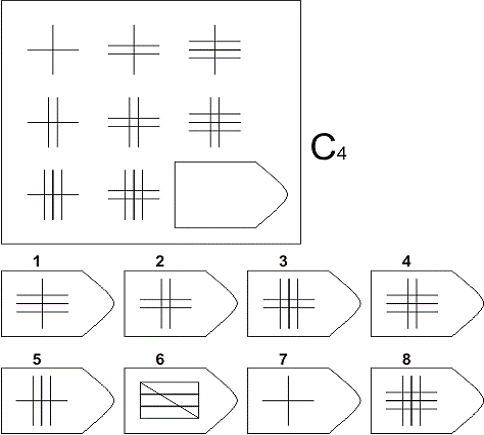
Представление результатов
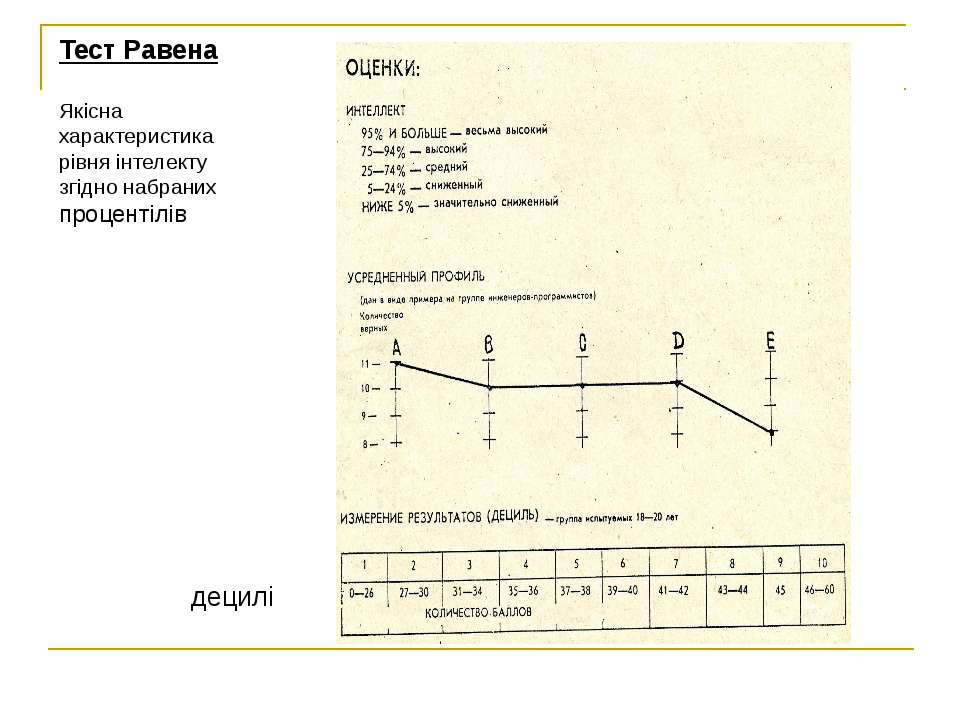
Наиболее адекватным способом интерпретации значимости полученной индивидом общей оценки является ее соотнесение с выраженной в процентах относительной частотой, с которой эту оценку получают испытуемые той же возрастной группы. Преимущество этого способа над другими состоит в том, что он не использует никаких априорных допущений о развитии интеллектуальных способностей в детстве вроде идей о его равномерном или симметричном распределении. В практических целях удобно рассматривать определенные процентные доли населения и в соответствии с этим группировать баллы респондентов. Это позволяет отнести респондента в соответствии с полученным баллом к той или иной группе.
УРОВЕНЬ I. «Супер-интеллектуал», если оценка равна или больше 95% для данной возрастной группы.
УРОВЕНЬ II. «Интеллектуальные возможности явно выше среднего», если оценка равна или больше 75%; II+ , если оценка равна или больше 90%.
УРОВЕНЬ III.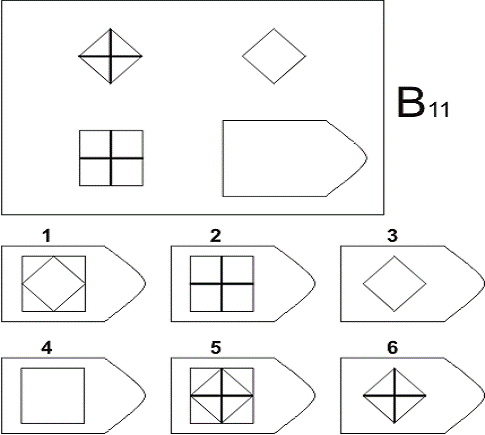 «Средний интеллект», если оценка лежит между 25% и 75%; III+, если оценка выше, чем медиана или 50%; III-, если оценка ниже , чем медиана.
«Средний интеллект», если оценка лежит между 25% и 75%; III+, если оценка выше, чем медиана или 50%; III-, если оценка ниже , чем медиана.
УРОВЕНЬ IV. «Интеллектуальные возможности явно ниже среднего», если оценка равна или меньше 25%; IV-, если оценка равна или меньше 10%.
УРОВЕНЬ V. «Существенное снижение интеллекта», если оценка равна или меньше 5% для соответствующей возрастной группы.
Общий балл, согласованность оценки и достигнутый уровень развития удобно представлять в следующем виде:
Общий балл 24
Несогласованности -1,0,+1
Уровень II +
Количество ошибок: Нормальное.
Усредненные возрастные нормативы выполнения Цветных прогрессивных матриц (вся серия — А + АВ + В)
| Возраст ребёнка | Среднее значение (баллы) |
Разброс (в баллах) |
|---|---|---|
| 4,5 — 5,5 лет | 14 | 8-22 |
| 5,5 — 6 лет | 17 | 12-24 |
| 6 — 6,5 лет | 18 | 13-27 |
| 6,5 — 7 лет | 20 | 14-29 |
| 7 — 7,5 лет | 22 | 15-30 |
| 7,5 — 8 лет | 23 | 16-31 |
| 8 — 8,5 лет | 24 | 17-32 |
| 8,5 — 9 лет | 26 | 18-34 |
| 9 — 10 лет | 29 | 20-35 |
| 10 — 11 лет | 32 | 21-35 |
Цветные прогрессивные матрицы Дж.
 Равена. Перевод серых баллов в IQ.
Равена. Перевод серых баллов в IQ.Познакомилась я с цветными матрицами будучи на последнем курсе института в процессе написания выпускной квалификационной работы. Методика мне понравилась своей относительной простотой. Использовала я ее в модификации Т.В. Розановой. Но столкнулась с трудностью: я нигде не могла найти таблицы (или хотя бы намека на эти таблицы) перевода серых баллов, которые получаются по методике, в IQ. На просторах Интернета этой информации просто не было. Это затруднение мне не помешало успешно защитится. Но, однажды, совершенно случайно ко мне в руки попали заветные таблицы… И теперь я спешу поделиться ими со своими коллегами.
Немножко об опыте использования методики: что лично для меня значимо?
Цветные прогрессивные матрицы Дж.Равена могут быть использованы для обследования познавательной сферы детей от 4,5 до 9 лет (5-11,5 лет). В первую очередь, методика в большей степени предназначена для оценки интеллекта детей в указанном выше возрастном диапазоне.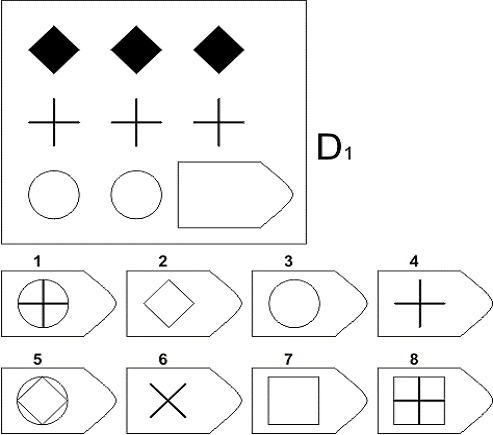 Но если взглянуть на стимульный материал, то что мы видим? Для решения предъявленной задачи ребенок оперирует образами в плане представлений, и решает задачу без участия практических действий. Характер стимульного материала говорит о том, что методика предназначена, в первую очередь, на изучение наглядно-образного мышления. Но мне не давал покоя принцип «прогрессивности», который заключается в том, что сначала ребенку предлагаются совсем уж легкие задания, которые являются основой для выполнения последующих заданий. То есть реализуется принцип «от простого к сложному». Фактически, можно заключить, что методика направлена на изучение способности к выявлению закономерностей (по аналогии). Следовательно, можно заключить, что она исследует мыслительные операции (словесно-логическое мышление). Таким образом, после обследования ребенка с помощью цветных прогрессивных матриц можно сделать некоторые выводы о развитии двух видов мышления.
Но если взглянуть на стимульный материал, то что мы видим? Для решения предъявленной задачи ребенок оперирует образами в плане представлений, и решает задачу без участия практических действий. Характер стимульного материала говорит о том, что методика предназначена, в первую очередь, на изучение наглядно-образного мышления. Но мне не давал покоя принцип «прогрессивности», который заключается в том, что сначала ребенку предлагаются совсем уж легкие задания, которые являются основой для выполнения последующих заданий. То есть реализуется принцип «от простого к сложному». Фактически, можно заключить, что методика направлена на изучение способности к выявлению закономерностей (по аналогии). Следовательно, можно заключить, что она исследует мыслительные операции (словесно-логическое мышление). Таким образом, после обследования ребенка с помощью цветных прогрессивных матриц можно сделать некоторые выводы о развитии двух видов мышления.
Далее, привожу цитату из «Индивидуальная и психологическая диагностика дошкольника» А. Н. Веракса.
Н. Веракса.
Впервые нормы для этой методики были разработаны в 1949 году в Шотландии, а затем в 1982 г. (см. таблицу № 1). Эти нормы, охватывают меньший возрастной диапазон, чем нормы, полученные в результате стандартизации методики в США между 1983 и 1993 годами (см. таблицу № 2). Нормы для США ниже шотландских норм, однако при проведении исследований в России предпочтительнее использовать именно их, поскольку Россия – многонациональная страна, а в исследованиях, проведенных в США, участвовали представители разных народностей.
Таблица 11
Нормы Дамфриз, Шотландия (1982 год)
Возраст в годах (месяцах) | ||||||||||||
| Процентиль | 6(3)- 6(8) | 6(9)- 7(2) | 7(3)- 7(8) | 7(9)- 8(2) | 8(9)- 9(2) | 8(9)- 9(2) | ||||||
| 95 90 75 50 25 10 5 | 26 23 20 17 14 12 11 | 26 26 21 18 15 12 11 | 28 25 21 18 16 13 12 | 25 24 22 18 14 13 12 | 31 28 23 20 17 14 13 | 28 27 23 21 17 15 14 | 32 30 25 22 18 15 14 | 29 28 25 22 19 16 15 | 33 32 27 24 20 16 14 | 33 32 28 24 20 17 14 | 34 33 29 26 22 17 15 | 33 31 28 26 20 17 16 |
| п | 42 | 47 | 54 | 38 | 55 | 30 | 44 | 33 | 48 | 47 | 52 | 41 |
Таблица 21
Нормы США (1986 год)
Возраст в годах (месяцах) | ||||||||||||||
| Процентиль | 5(3)- 5(8) | 5(9)- 6(2) | 5(3)- 6(8) | 6(9)- 7(2) | 7(3)- 7(8) | 7(9)- 8(2) | 8(3)- 8(8) | 8(9)- 9(2) | 9(3)- 9(8) | 9(9)- 10(2) | 10(3)- 10(8) | 7(3)- 11(2) | 10(3)- 11 (8) | |
| 95 90 75 50 25 10 5 | 23 21 17 12 11 9 8 | 25 23 19 14 12 10 9 | 28 25 21 16 13 11 9 | 30 27 23 18 14 12 10 | 31 29 25 20 15 13 11 | 32 30 27 22 17 14 12 | 33 31 29 24 19 15 12 | 34 32 30 26 21 16 13 | 35 33 31 27 22 17 14 | 35 33 32 28 23 18 15 | 35 34 32 29 24 19 16 | 35 34 33 30 25 20 17 | 35 35 34 31 26 21 18 | |
Особенности проведения методики
Действия испытуемого в ходе методики однотипны: он должен найти некоторую закономерность и выбрать из предложенных элементов недостающий фрагмент узора.
Последовательность предъявления заданий не подлежит изменению. Тестовая процедура предполагает отсутствие какой-либо обратной связи со стороны психолога. Если испытуемый сомневается в выборе правильного ответа, нужно добиться, чтобы он высказал какое-то мнение, в крайнем случае в качестве ответа принимается последний вариант. При этом испытуемый не должен объяснять свой выбор – вполне достаточно словесного или жестового указания на фрагмент.
Интерпретация методики
За каждый правильный ответ испытуемому начисляется один балл. Если ребенок неправильно выполнил первые пять заданий, о выполнение методики прекращается, поскольку считается, что испытуемый не понял принцип решения.
После подсчёта баллов полученный результат сравнивается с показателем процентильной (относительной) частоты (процент испытуемых того же возраста, которые правильно решили столько же задач, то есть получили такой же балл).
По результатам теста Равена можно выделить пять уровней развития интеллекта (см.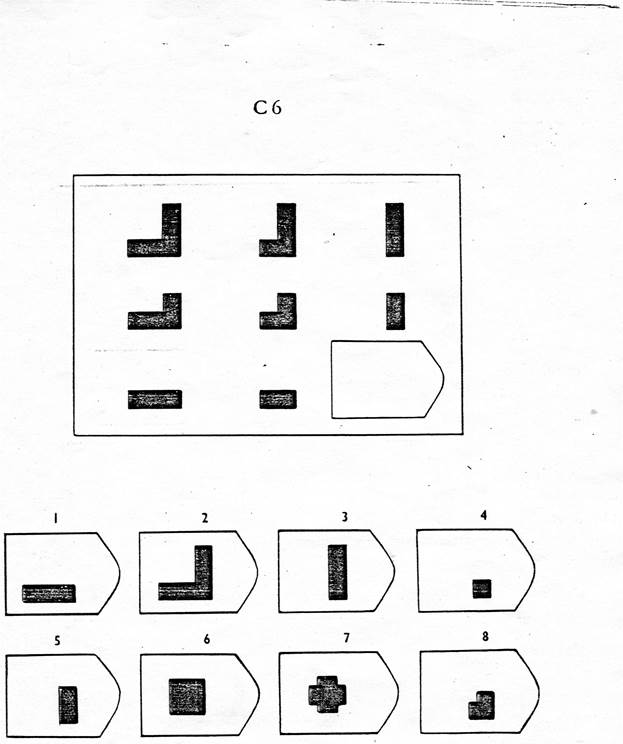 табл. 3)
табл. 3)
Таблица 3
Показатель процентильной частоты (р) | Уровень развития интеллекта | Уровень развития интеллекта в баллах (IQ) |
| Более 95 75-95 25-75 5-25 Менее 5 | Высокий Выше среднего Средний (норма) Низкий Сниженный интеллект | Более 124 110-124 90-110 75-90 Менее 75 |
Допустим, что по результатам методики Дж. Равена ребенок в возрасте 6 лет 7 месяцев набрал 22 балла. В этом случае в таблице 2 мы находим возраст ребенка, который попадает в интервал 6 лет 3 месяца – 6 лет 8 месяцев. Далее, в вертикальном столбце мы находим количество баллов, которые набрал ребенок. Нашем случае 22 балла попадают в интервал 21-25 баллов, что, как видно из таблицы, соответствуют процентному интервалу 75-90. По таблице 3 мы можем дать характеристику этого интервала IQ – 110-124, что соответствует уровню развития интеллекта выше среднего.
По таблице 3 мы можем дать характеристику этого интервала IQ – 110-124, что соответствует уровню развития интеллекта выше среднего.
Таким образом, данная методика позволяет получить количественную характеристику (выраженную в показателе процентильной частоты, которой соответствует определённый уровень развития интеллекта) уровня развития основного средства мышления – интеллекта.
Литература:
- 1 Равен Дж. К., Курт Дж. Х., Равен Дж. Руководство к прогрессивным матрицам Равена и словарным шкалам. – М., 1996.
- Веракса А.Н. Индивидуальная психологическая диагностика дошкольника: Для занятий с детьми 5-7 лет. – М.: МОЗАИКА-СИНТЕЗ, 2014. – 144 с.
Ворон тест интерпретация результатов / Психометрические тесты
тест прогрессивных матриц Равена это психометрический тест, основной целью которого является измерить уровень интеллекта, также известный как фактор G. Этот тест был разработан Джоном С.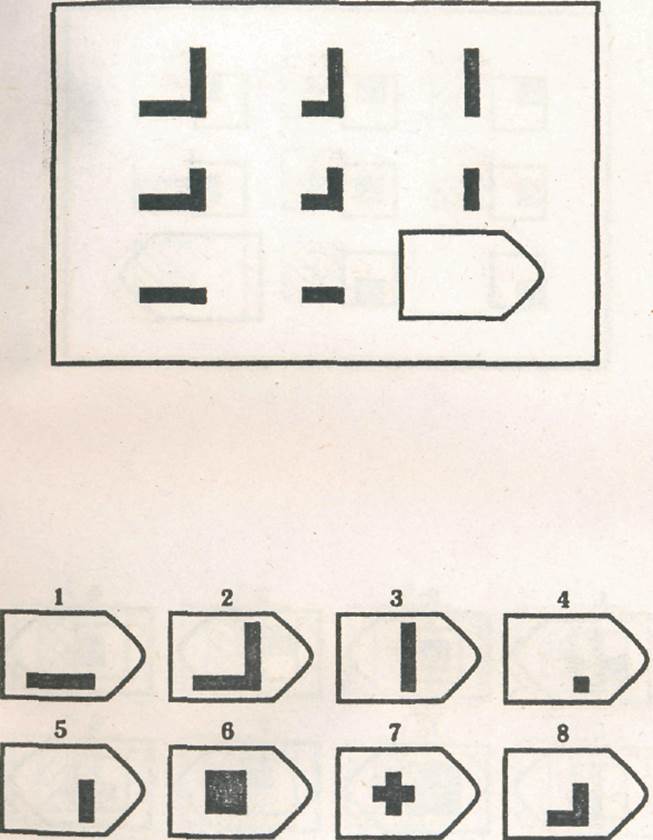 Рейвеном и впервые был проведен в 1938 году. Тест основан на выяснении того, какой элемент отсутствует в матрице..
Рейвеном и впервые был проведен в 1938 году. Тест основан на выяснении того, какой элемент отсутствует в матрице..
Результаты теста Равена могут быть использованы для психометрического теста, психологического теста или для процесса отбора персонала. Если вы хотите знать все, что скрывает этот любопытный человек Тест Равена и его интерпретация результатов, В Psychology-Online мы предлагаем вам полный отчет. Кроме того, мы предлагаем вам технический лист в конце, чтобы вы могли подготовиться к выполнению этого теста интеллекта.
Вы также можете быть заинтересованы в: Типы тестов интеллекта Индекс- Что такое тест Ворон и что он измеряет
- Интерпретация результатов теста Ворон
- Технический паспорт теста прогрессивных матриц Raven
- Ворон онлайн тест
Что такое тест Ворон и что он измеряет
Как следует из названия, психометрические тесты тесты и анкеты, цель которых измерение душа (Ум).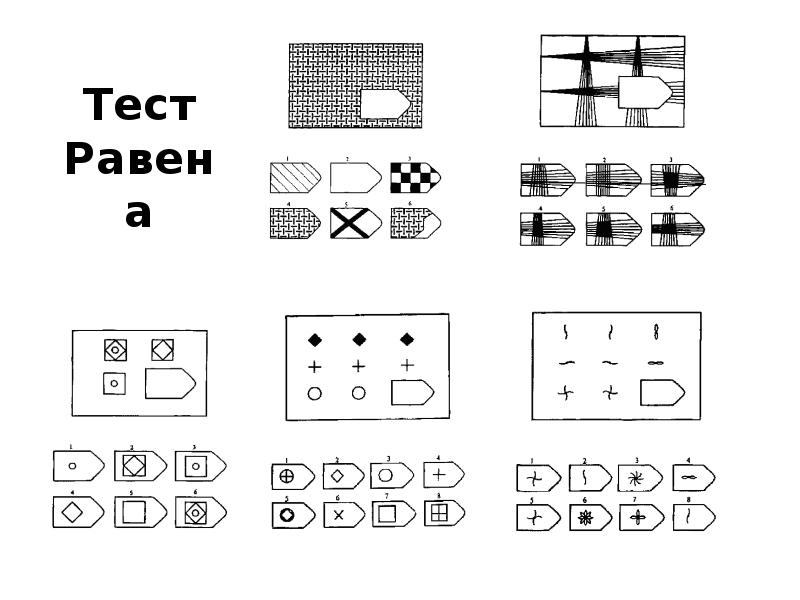 Эти методы возникли как инструменты, позволяющие определять различные способности, которыми обладают люди, и, таким образом, узнавать нас немного больше в разных аспектах нашей жизни..
Эти методы возникли как инструменты, позволяющие определять различные способности, которыми обладают люди, и, таким образом, узнавать нас немного больше в разных аспектах нашей жизни..
Тест Равена является частью набора психометрических тестов, предназначенных для оценки интеллекта, в частности, преувеличить G-фактор.
¿Что такое фактор G??
Чарльз Спирмен, Профессор автора этого теста Рейвена сделал теорию, известную как «эклектическая теория двух факторов». Эта теория утверждала, что все способности человека имеют определенный фактор (фактор е) и, в свою очередь, общий фактор (фактор g). Исходя из этой теории, Джон С. Рейвен разработал этот тест для измерения общего интеллекта человека. Согласно двухфакторной модели Sprearman, мы можем измерять интеллект по-разному, Raven использовал вычет отношений и коррелятов в вашем тесте, чтобы иметь возможность измерить фактор G.
В настоящее время вместо измерения этого фактора мы обычно используем другие типы тестов, чтобы иметь возможность измерить IQ или IQ.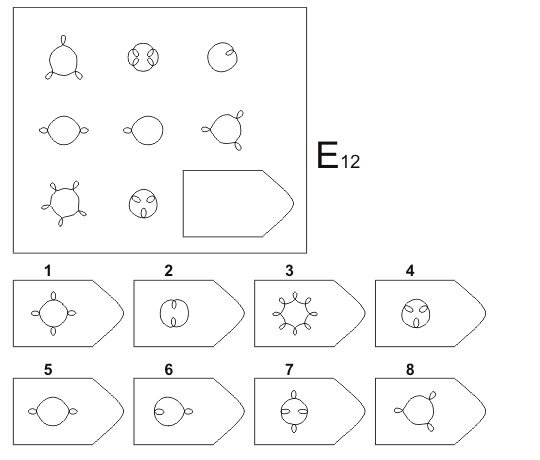 Тем не менее, тест прогрессивных матриц продолжает использоваться значительной частью общения психологов и психиатров..
Тем не менее, тест прогрессивных матриц продолжает использоваться значительной частью общения психологов и психиатров..
Ворон тест: ¿что это измеряет?
Согласно теории Спирмена, Рэйвена и других теоретиков это психометрическое течение. G-фактор эквивалентен способности решать логические, математические задачи и общеобразовательный потенциал человека.
Исходя из решения матриц и выяснения, какой части изображения не хватает, тест Равена измеряет вышеупомянутый фактор G. Кроме того, этот тест измеряет не только логические рассуждения, поскольку это невербальный тест, основанный на изображениях., он также измеряет способность к абстракции.
Интерпретация результатов теста Ворон
Тест Равена основан на администрировании 60 матриц или задач, разделенных на 5 серий. Эти матрицы имеют границу или геометрическую композицию с зазором, который должен быть заполнен любым из вариантов, показанных в нижней части тестовых таблиц Raven..
Тест ворона решен: ¿как оценить?
Каждая решенная задача удовлетворительно считается успехом, исправить тест можно с помощью корректирующего листа или вручную.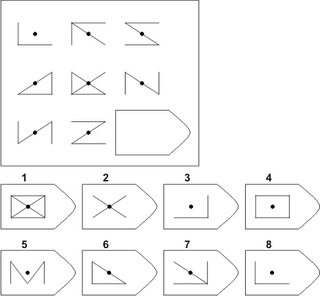 Существуют разные версии и шкалы одного и того же теста для измерения интеллекта в разных группах населения:
Существуют разные версии и шкалы одного и того же теста для измерения интеллекта в разных группах населения:
- SPM: По исходной шкале психометрического теста Ворон, максимальный балл равен количеству матриц в сумме, в данном случае 60.
- CPM: Шкала рассчитана на детей от 4 до 10 лет, максимальная оценка в этом случае составляет 36 баллов.
- APM: Шкала, адаптированная для обследования интеллекта у подростков и взрослых с высокими способностями, серия I содержит максимальный балл 12 баллов.
- AMP II: предыдущая адаптация, но с максимальной оценкой 36 баллов
После того, как вы добавите все правильные ответы, например, угадав 40 из 60 прогрессивных матриц, вы должны проверить соответствие этого результата. Для этого нужно наблюдать, если в 5 серии количество ошибок примерно одинаково. Согласно Тестовая таблица Raven, не может быть разницы более двух ошибок в каждой серии.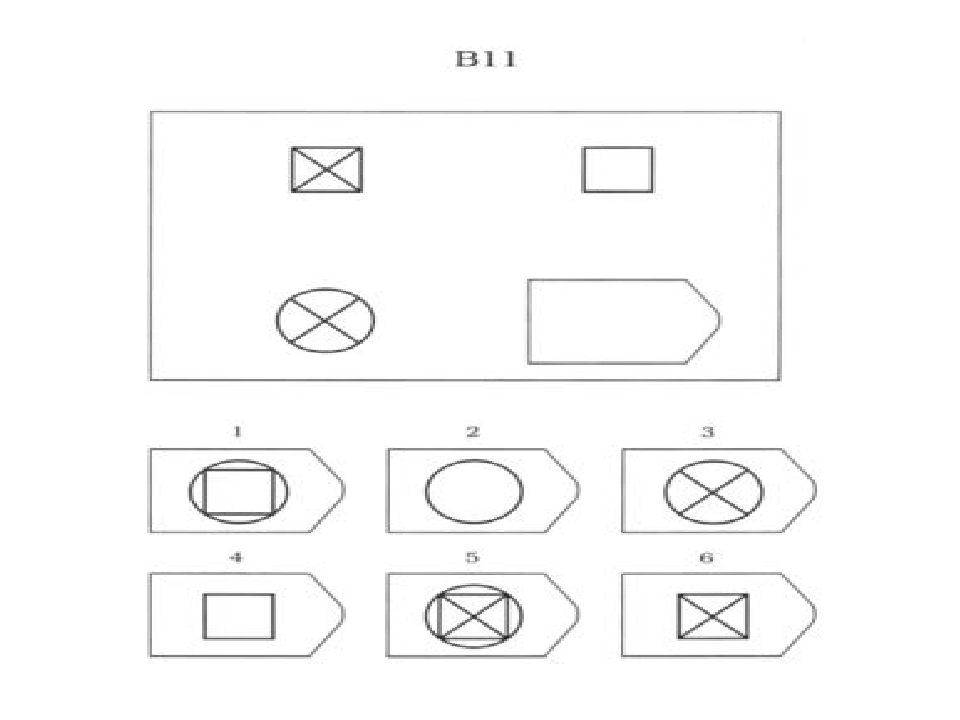
После того, как у нас будет результат, мы должны сверяться с таблицей процентилей в зависимости от того, какой у нас возраст или у того, кто прошел тест. Получив процентиль, мы должны сравнить его с таблицей интеллекта, которая связывает каждый ранг с интеллектуальным потенциалом. Если у вас есть какие-либо сомнения относительно этих концепций, вы можете взглянуть на эту статью о введении в психометрию..
Интерпретация результатов
Далее мы предлагаем вам вкладка со шкалами и процентилями так что вы можете научиться интерпретировать ответы на этот тест:
Технический паспорт теста прогрессивных матриц Raven
Как только мы увидим, как тест Равена можно интерпретировать, давайте подытожим его психометрические характеристики с техническим листом.
- Наименование теста: Тест прогрессивных матриц, общая шкала ворона
- цель: это невербальный тест, целью которого является измерение IQ или G-фактора интеллекта.
 .
. - Материал: 60 листов прогрессивной матрицы, карандаш и лист ответов для измерения результатов.
- администрация: человека, который собирается выполнить тест Ворона, просят проанализировать представленную ему матрицу и выбрать один из вариантов, который наилучшим образом соответствует разрыву, наблюдаемому в каждой матрице, как по горизонтали, так и по вертикали..
- ответы: каждый правильный ответ — это балл, где 0 — минимальная оценка, а 60 — максимальная..
- листы: тест Ворон содержит 60 листов для ответа.
- Надежность и обоснованность: индексы надежности и достоверности превышают оговоренные значения, что считается правильным тестом, поэтому их баллы можно экстраполировать на население и точно измерять то, что они намерены измерять.
Преимущества теста Ворон
Будучи невербальным тестом и стандартизированным для каждого сегмента населения, этот тест очень полезен для измерения интеллекта независимо от уровня образования.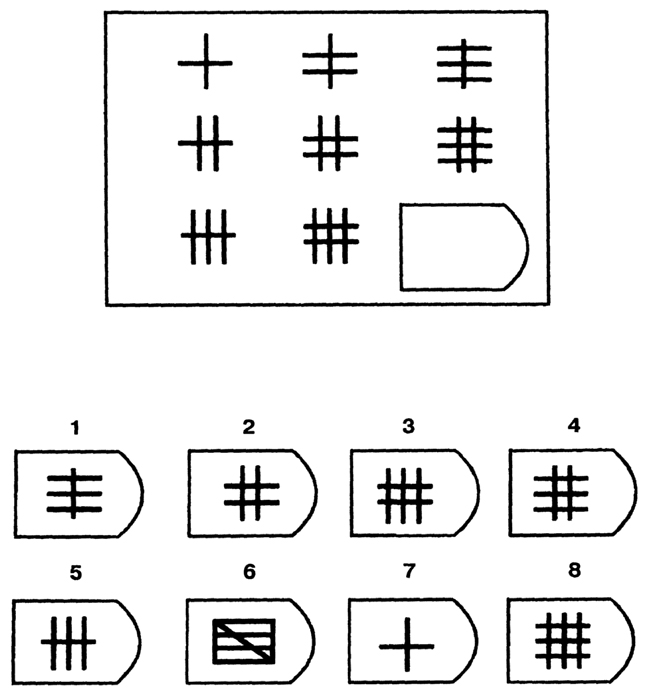 Кроме того, как мы заметили, интерпретация результатов очень проста и быстра.
Кроме того, как мы заметили, интерпретация результатов очень проста и быстра.
Все эти характеристики делают тест прогрессивных матриц, психометрический тест, который все еще используется для его многих преимуществ.
Ворон онлайн тест
Чтобы закончить эту статью, мы предлагаем вам несколько примеров тестовых листов Raven.. ¿Вы можете решить эти матрицы, которые мы предлагаем?
Если вы хотите измерить свой IQ, мы предлагаем вам следующий тест: тест на интеллект.
Эта статья носит исключительно информативный характер: в онлайн-психологии у нас нет факультета, чтобы поставить диагноз или рекомендовать лечение. Мы приглашаем вас пойти к психологу для лечения вашего случая в частности.
Если вы хотите прочитать больше статей, похожих на Ворон тест: интерпретация результатов, Мы рекомендуем вам войти в нашу категорию психометрического теста.
Фотографии Raven Test: интерпретация результатов
Тест Равена уровень интеллекта прогрессивные матрицы
Тест Равена, предложенный ещё в далеком 1936 г, считается одним из самых «чистых» способов измерения фактора общего интеллекта g. За всю историю использования он постоянно подтверждает свою высокую валидность и включен в набор всех стандартных методик, используемых для психологической диагностики в самых разных сферах. Теоретической основой теста Равена является теория гештальтпсихологии о восприятии форм и теория неогенеза К.Спирмена.
За всю историю использования он постоянно подтверждает свою высокую валидность и включен в набор всех стандартных методик, используемых для психологической диагностики в самых разных сферах. Теоретической основой теста Равена является теория гештальтпсихологии о восприятии форм и теория неогенеза К.Спирмена.
Тест Равена представлен в 2-х вариантах: детском (с цветными матрицами) и черно-белом взрослом (для возраста от 14 лет).
Взрослый черно-белый тест Равена состоит из 60 матриц, в которых испытуемому нужно заполнить пропущенные элементы из предложенных вариантов. Все карточки разделены на 5 групп (А, В, С, D, Е), по 12 в каждой. Прогрессивными матрицы называют потому, что сложность заданий увеличивается как от первой до 12-й матрицы внутри каждой серии, так и от серии к серии в целом.
Попробуйте пройти тест Равена и определить уровень g. Сразу отметим, что решение задач требует концентрированного внимания как в объеме, так и в распределении.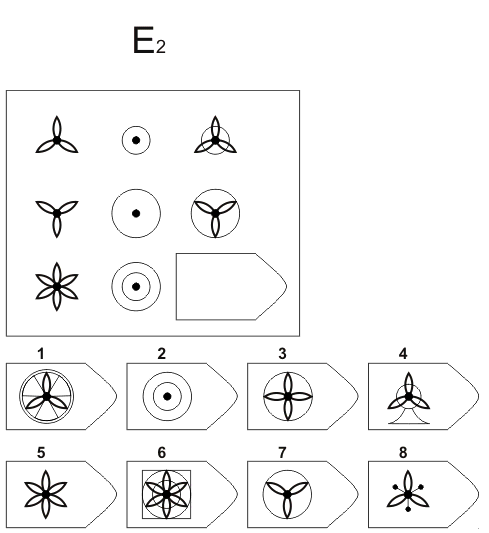 Поэтому этот тест отражает не только интеллектуальные способности, но и эмоциональное состояние обследуемого в момент эксперимента (см. тест уровень тревожности Ч. Д. Спилбергера и Ю. Л. Ханина).
Поэтому этот тест отражает не только интеллектуальные способности, но и эмоциональное состояние обследуемого в момент эксперимента (см. тест уровень тревожности Ч. Д. Спилбергера и Ю. Л. Ханина).
Исследование прогрессивными матрицами Равена (как и тесты Айзенка и др. подобные) не является инструментом измерения «общего интеллекта», а в первую очередь инструментом исследования остроты и точности внимания, ясности мышления, способности концентрироваться, системно, планомерно и методично мыслить. В отличие от многих вербальных тестов (наподобие сканвордов-ребусов), тест Равена является чистым невербальным, «трансязыковым» и «транскультурным» исследованием, получающим доступ к мыслительным процессам, на которые не влияет вербализация.
Тест равена:
описание серийСерия А. Исследует способность дифференциации основных элементов структуры и раскрытие связи между ними, идентификации недостающей части структуры и сравнения их с образцами.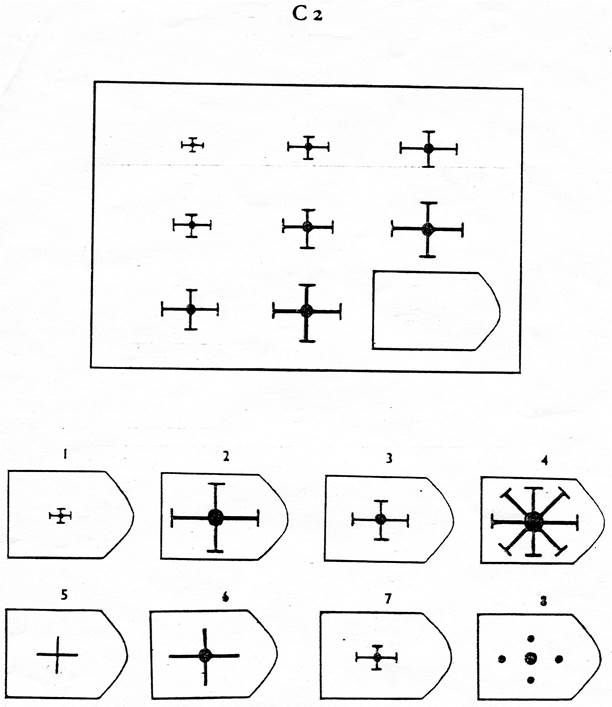 Уровень оценок в этой серии зависит от уровня внимательности, уровня статистического представления, воображения и уровня визуального различия (дискриминации).
Уровень оценок в этой серии зависит от уровня внимательности, уровня статистического представления, воображения и уровня визуального различия (дискриминации).
Серия В. Исследует способность дифференциации основных элементов, способность находить симметричность фигур, способность к линейной дифференциации и выводам на основе линейных взаимосвязей.
Серия С. Исследует способность испытуемого к динамической (моментальной) наблюдательности, прослеживанию непрерывных изменений, динамической внимательности и воображению. В матрицах этой серии предлагаются варианты со сложными изменениями фигур по принципу непрерывного превращения и изменения в вертикальном и горизонтальном направлении с суммированием/вычитанием этих изменений, которые нужно определить в недостающей фигуре.
Серия D. Исследует способность испытуемого обнаруживать количественные и качественные изменения, лежащие в основе алгоритма упорядочения фигур.
Серия Е. Исследуется аналитико-синтетическая деятельность мозга как высшей формы абстракции и динамического синтеза, способность испытуемого складывать и вычитать элементы фигур, смешивать части согласно алгебраическим алгоритмам, так как в решении задачи нужно анализировать фигуру основного изображения и собирать недостающую фигуру по частям (складывая, смешивая или вычитая элементы фигур).
Исследуется аналитико-синтетическая деятельность мозга как высшей формы абстракции и динамического синтеза, способность испытуемого складывать и вычитать элементы фигур, смешивать части согласно алгебраическим алгоритмам, так как в решении задачи нужно анализировать фигуру основного изображения и собирать недостающую фигуру по частям (складывая, смешивая или вычитая элементы фигур).
Интерпретация результатов — по завершении теста!
Смотрите еще тесты:
Опросник Русалова (ОФДСИ и В-ОСТ): структура темперамента онлайн
Уровень тревожности Ч. Д. Спилбергера и Ю. Л. Ханина
Тест — опросник Г. Шмишека, К. Леонгарда. Акцентуации характера и темперамента личности
Диагностика акцентуаций характера «Чертова дюжина» (А.С. Прутченков, А.А. Сиялов)
Тест личностная шкала проявления тревоги (Дж. Тейлор)
Опросник Филлипса диагностика школьной тревожности
Восемь тестов Айзенка проверки IQ
Читайте больше по теме:
Понимание результатов тестирования | Педагогическая психология
Для понимания результатов стандартизированных тестов важно знать различные термины и концепции, которые являются фундаментальными для «теории измерения», академического исследования измерения и оценивания.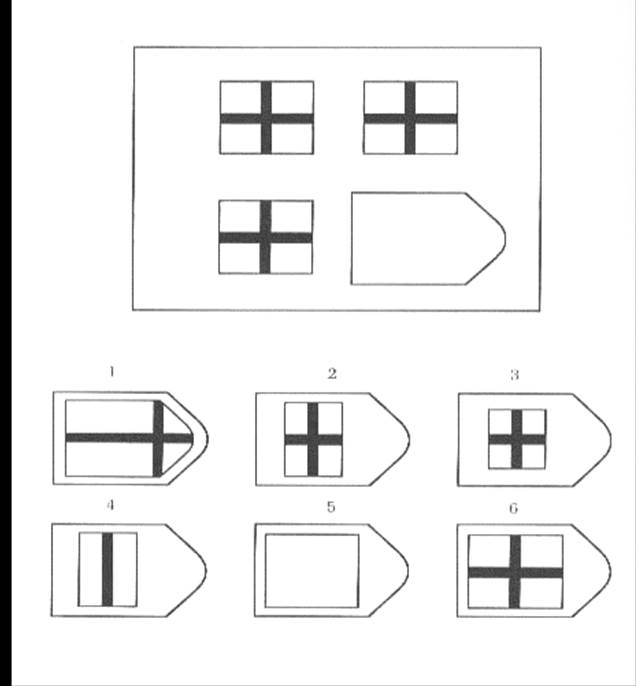 В предыдущей главе обсуждались две основные области теории измерений: надежность и достоверность; В этой главе мы сосредоточимся на концепциях и терминах, связанных с оценками за тесты.
В предыдущей главе обсуждались две основные области теории измерений: надежность и достоверность; В этой главе мы сосредоточимся на концепциях и терминах, связанных с оценками за тесты.
Основы
Распределения частот
Частотное распределение — это список количества студентов, набравших каждый балл по тесту.Если 31 учащийся сдает тест, а оценки варьируются от 11 до 30, то частотное распределение может выглядеть как в таблице 1. Мы также показываем тот же набор оценок на гистограмме или гистограмме на рисунке 1. Горизонтальная (или x ) -axis) представляет собой результат теста, а вертикальная ось ( y -axis) представляет количество или частоту учащихся. Построение частотного распределения помогает нам увидеть, какие оценки являются типичными и насколько они изменчивы. Далее мы опишем более точные способы определения типичных оценок и вариабельности.
| Таблица 1: Распределение частот для 30 баллов | ||
|---|---|---|
| Оценка по тесту | Частота | Меры центральной тенденции |
| 17 | 1 | |
| 18 | 1 | |
| 19 | 0 | |
| 20 | 3 | |
| 21 | 2 | |
| 22 | 6 | Режим |
| 23 | 3 | Медиана |
| 24 | 2 | Среднее |
| 25 | 0 | |
| 26 | 2 | |
| 27 | 6 | Режим |
| 28 | 2 | |
| 29 | 2 | |
| 30 | 1 | |
| ИТОГО | 31 | |
Рисунок 1: Результаты тестов из таблицы 1, представленные в виде гистограммы
Центральная тенденция и изменчивость
Есть три распространенных способа измерения центральной тенденции или типичных оценок.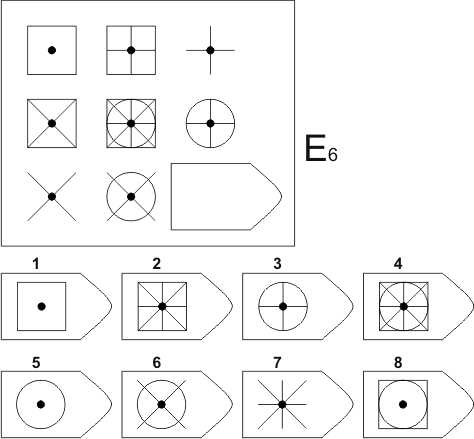 Среднее значение вычисляется путем сложения всех оценок и деления на количество оценок. В примере, приведенном в таблице 1, среднее значение равно 24. Медиана — это «средний» балл распределения, то есть половина баллов выше медианы, а половина — ниже. Медиана распределения составляет 23, потому что 15 баллов выше 23 и 15 ниже. Режим — это наиболее часто встречающаяся оценка. В таблице 1 фактически два режима: 22 и 27. Таким образом, это распределение описывается как бимодальное .Вычисление среднего, медианы и режима важны, поскольку каждый из них предоставляет учителям разную информацию. Медиана представляет собой оценку «средних» учеников с половинными баллами выше и ниже, но не говорит нам о наиболее часто встречающихся результатах теста. Среднее значение важно для некоторых статистических расчетов, но на него сильно влияют несколько крайних значений (называемых выбросами), но не медиана. Чтобы проиллюстрировать это, представьте себе тест из 20 баллов, сданных 10 студентами, и большинство из них сдает очень хорошо, но один студент сдает очень плохо.
Среднее значение вычисляется путем сложения всех оценок и деления на количество оценок. В примере, приведенном в таблице 1, среднее значение равно 24. Медиана — это «средний» балл распределения, то есть половина баллов выше медианы, а половина — ниже. Медиана распределения составляет 23, потому что 15 баллов выше 23 и 15 ниже. Режим — это наиболее часто встречающаяся оценка. В таблице 1 фактически два режима: 22 и 27. Таким образом, это распределение описывается как бимодальное .Вычисление среднего, медианы и режима важны, поскольку каждый из них предоставляет учителям разную информацию. Медиана представляет собой оценку «средних» учеников с половинными баллами выше и ниже, но не говорит нам о наиболее часто встречающихся результатах теста. Среднее значение важно для некоторых статистических расчетов, но на него сильно влияют несколько крайних значений (называемых выбросами), но не медиана. Чтобы проиллюстрировать это, представьте себе тест из 20 баллов, сданных 10 студентами, и большинство из них сдает очень хорошо, но один студент сдает очень плохо.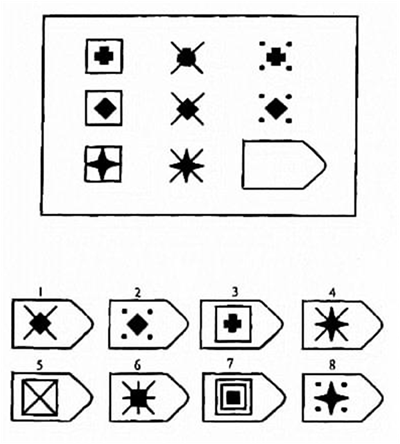 Оценки могут быть 4, 18, 18, 19, 19, 19, 19, 19, 20, 20. Среднее значение составляет 17,5 (175/10), но если исключить самый низкий балл (4), среднее значение теперь составляет 1,5 балла. выше — 19 (171/9). Однако в этом примере медиана остается на уровне 19 независимо от того, включена ли самая низкая оценка. Когда есть несколько крайних значений, медиана часто более полезна для учителей, поскольку она указывает на центральную тенденцию частотного распределения.
Оценки могут быть 4, 18, 18, 19, 19, 19, 19, 19, 20, 20. Среднее значение составляет 17,5 (175/10), но если исключить самый низкий балл (4), среднее значение теперь составляет 1,5 балла. выше — 19 (171/9). Однако в этом примере медиана остается на уровне 19 независимо от того, включена ли самая низкая оценка. Когда есть несколько крайних значений, медиана часто более полезна для учителей, поскольку она указывает на центральную тенденцию частотного распределения.
Меры центральной тенденции помогают нам суммировать репрезентативные оценки, но они ничего не говорят нам о том, насколько переменны или насколько разбросаны оценки.На рис. 2 показаны наборы результатов двух разных школ по одному и тому же тесту для четвероклассников. Обратите внимание, что среднее значение для каждого составляет 40, но в школе А разброс оценок гораздо меньше. Простой способ суммировать вариативность — это диапазон , который представляет собой наименьший балл, вычитаемый из самого низкого балла.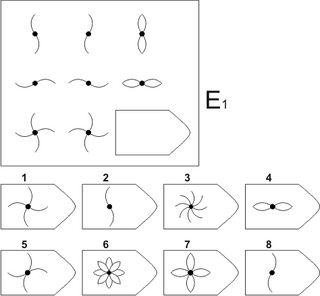 В школе А с низкой вариабельностью диапазон (45 — 35) = 10; в школе B диапазон равен (55 — 22 = 33).
В школе А с низкой вариабельностью диапазон (45 — 35) = 10; в школе B диапазон равен (55 — 22 = 33).
Рисунок 2: Баллы по математике в четвертом классе в двух разных школах с одинаковым средним, но разной вариабельностью
Однако диапазон основан только на двух оценках в распределении, наивысшем и самом низком, и поэтому не отражает вариабельность всех оценок.Стандартное отклонение основано на том, насколько в среднем все оценки отклоняются от среднего значения. В примере на Рисунке 2 стандартные отклонения составляют 7,73 для школы A и 2,01 для школы B. На Приложении 1 ниже мы демонстрируем, как рассчитать стандартное отклонение.
Приложение 1: Расчет стандартного отклонения
11 учеников набрали викторину 4, 7, 6, 3, 10, 7, 3, 7, 5, 5 и 9. Выполните следующие шаги:
- Орденские баллы.
- Рассчитайте средний балл.
- Рассчитайте отклонения от среднего.
- Возведите отклонения от среднего в квадрат.
- Вычислить среднее квадратов отклонений от среднего (т.
 е. суммировать квадраты отклонений от среднего, а затем разделить на количество баллов). Это число называется дисперсией.
е. суммировать квадраты отклонений от среднего, а затем разделить на количество баллов). Это число называется дисперсией. - Извлеките квадратный корень, и вы рассчитали стандартное отклонение.
Завершение шагов
| Оценка (Шаг 1: Порядок) | Отклонение от среднего | Квадратное отклонение от среднего |
|---|---|---|
| 3 | −3 | 9 |
| 3 | −3 | 9 |
| 4 | -2 | 4 |
| 5 | -1 | 1 |
| 5 | -1 | 1 |
| 6 | 0 | 0 |
| 7 | 1 | 1 |
| 7 | 1 | 1 |
| 7 | 1 | 1 |
| 9 | 3 | 9 |
| 10 | 4 | 4 |
| Итого: 66 | 52 |
Шаг 2: вычислить среднее значение
[латекс] \ displaystyle \ text {mean} = \ frac {66} {11} = 6 \\ [/ latex]
Шаг 3: Расчет отклонений
[латекс] \ displaystyle \ text {mean} = \ frac {40} {11} = 4. 2}} {N} \\ [/ latex]
2}} {N} \\ [/ latex]
N = Количество баллов
Шаг 6. Найдите стандартное отклонение
[латекс] \ displaystyle \ text {Стандартное отклонение} = \ sqrt {4.73} = 2,17 \\ [/ latex]
Нормальное распределение
Знание стандартного отклонения особенно важно, когда распределение баллов соответствует нормальному распределению. Когда стандартизированный тест проводится с очень большим количеством студентов, распределение баллов обычно схоже: многие студенты имеют баллы, близкие к среднему, а меньшее количество баллов намного выше или ниже среднего.Когда распределение оценок выглядит как колоколообразная форма, показанная на рисунке 3, это называется нормальным распределением. На диаграмме мы не отображали оценки отдельных студентов, как на рисунке 2, потому что распределения обычно попадают на нормальную кривую только при большом количестве студентов; слишком много, чтобы показать по отдельности. Нормальное распределение является симметричным, а среднее значение, медиана и мода одинаковы.
Рисунок 3: Колоколообразная кривая нормального распределения
Нормальные кривые распределения очень важны в образовании и психологии из-за взаимосвязи между средним значением, стандартным отклонением и процентилями.Во всех нормальных распределениях 34 процента баллов находятся между средним значением и одним стандартным отклонением среднего. Тесты интеллекта часто строятся так, чтобы иметь среднее значение 100 и стандартное отклонение 15, и мы проиллюстрировали это на рисунке 4.
Рисунок 4: Нормальное распределение для теста IQ со средним значением 100 и стандартным отклонением 15
На Рисунке 4 34 процента оценок находятся между 100 и 115, а также 34 процента оценок находятся между 85 и 100. Это означает, что 68 процентов оценок находятся в диапазоне от -1 до +1 стандартного отклонения среднего. (я.е. 85 и 115). Обратите внимание, что только 14 процентов оценок находятся между +1 и +2 стандартными отклонениями среднего и только 2 процента падают выше +2 стандартных отклонений среднего.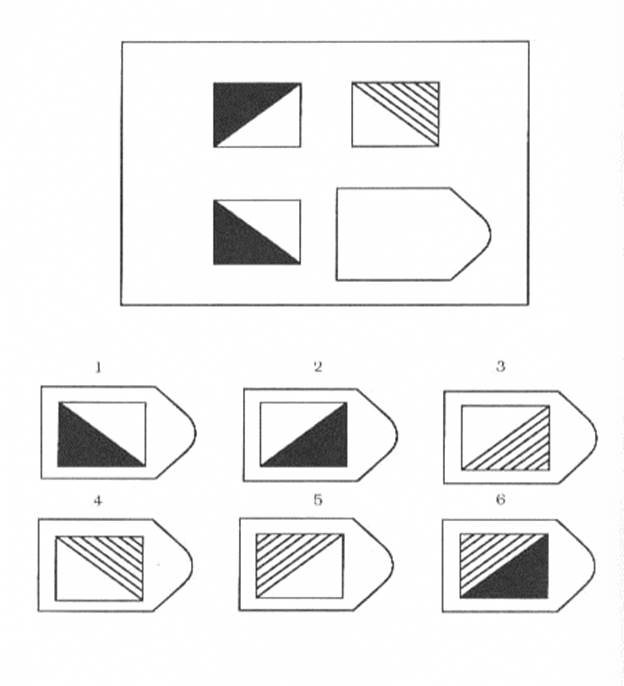
При нормальном распределении учащийся, набравший среднее значение, всегда находится в пятидесятом процентиле, потому что среднее и медиана одинаковы. Оценка +1 стандартное отклонение выше среднего (например, 115 на рисунке 4) составляет плитку 84% (50% и 34% оценок были ниже 115). В Приложении 10 мы представляем процентильные эквиваленты нормальной кривой, а также показываем стандартные баллы.
Виды результатов тестов
Стандартная оценка выражает результативность теста в единицах стандартного отклонения выше или ниже среднего (Linn & Miller, 2005). Существует множество стандартных баллов, включая z-баллы, T-баллы и станины.
Одним из типов стандартной оценки является z-оценка , в которой среднее значение равно 0, а стандартное отклонение — 1. Это означает, что z-оценка напрямую сообщает нам, на сколько стандартных отклонений оценка выше или ниже среднего.Например, если студент получает z-оценку 2, ее оценка на два стандартных отклонения выше среднего или восемьдесят четвертого процентиля. Учащийся, получивший z-балл -1,5, набрал на полтора отклонения ниже среднего. Любая оценка из нормального распределения может быть преобразована в оценку z, если известны среднее значение и стандартное отклонение. Формула:
Учащийся, получивший z-балл -1,5, набрал на полтора отклонения ниже среднего. Любая оценка из нормального распределения может быть преобразована в оценку z, если известны среднее значение и стандартное отклонение. Формула:
[латекс] \ displaystyle \ text {z-score} = \ frac {\ text {score} — \ text {средний результат}} {\ text {стандартное отклонение}} \\ [/ latex]
Итак, если оценка 130, среднее значение 100 и стандартное отклонение 15, вычисление будет:
[латекс] \ displaystyle \ text {Z} = \ frac {130-100} {15} = 2 \\ [/ latex]
Если вы посмотрите на рисунок 4, то увидите, что это правильно — оценка 130 на 2 стандартных отклонения выше среднего, поэтому оценка по z равна 2.
A T-score имеет среднее значение 50 и стандартное отклонение 10. Это означает, что T-score 70 на два стандартных отклонения выше среднего и, таким образом, эквивалентен z-баллу 2.
Станины (произносится как «стайнины») часто используются для сообщения оценок учащихся и основаны на стандартной девятибалльной шкале со средним значением 5 и стандартным отклонением 2.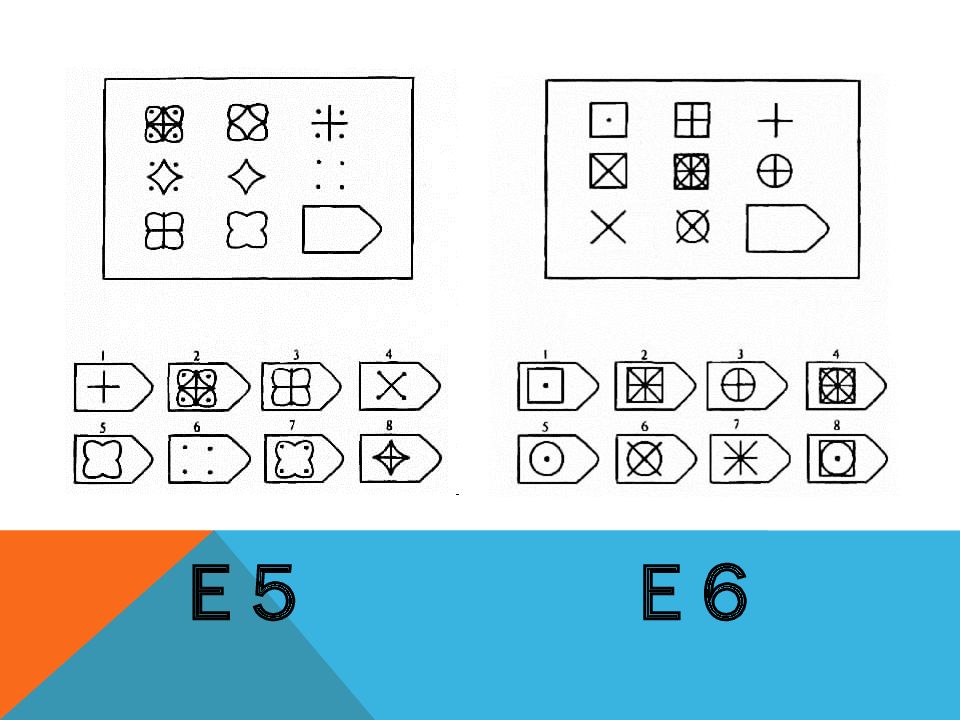 Они представлены только в виде целых чисел и рис. -10 показывает их отношение к нормальной кривой.
Они представлены только в виде целых чисел и рис. -10 показывает их отношение к нормальной кривой.
Язвы, эквивалентные степени
Оценка, эквивалентная классу, дает оценку успеваемости в зависимости от класса и месяцев учебного года (Popham, 2005, стр. 288). Эквивалентная оценка 3,7 означает, что успеваемость ученика третьего класса на седьмом месяце учебного года соответствует ожиданиям. Эквиваленты оценок обеспечивают постоянный диапазон ступеней обучения и поэтому могут считаться оценками развития. Эквивалентные оценки популярны и кажутся легкими для понимания, однако, как правило, их понимают неправильно.Если Джеймс, ученик четвертого класса, сдает тест по чтению, и его оценка эквивалентна 6,0; это не означает, что Джеймс может выполнять работу в шестом классе . Это означает, что Джеймс выполнил тест для четвертого класса , поскольку ожидается, что его будет выполнять шестиклассник.
Тестирующие компании рассчитывают эквиваленты оценок, давая один тест нескольким классам.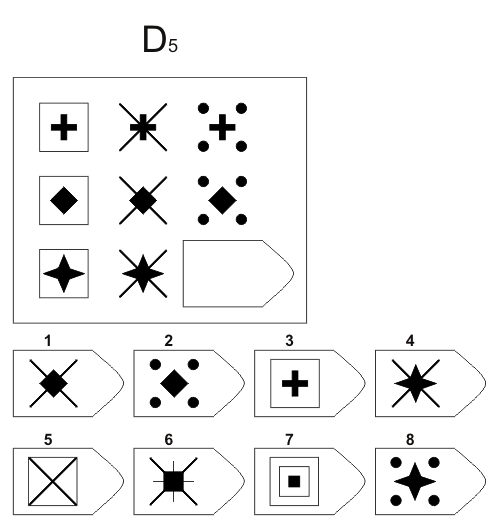 Например, тест, предназначенный для четвероклассников, также может быть предоставлен учащимся третьего и пятого классов. Построены необработанные оценки и установлена линия тренда, которая используется для определения эквивалентов оценок.Обратите внимание, что на Рисунке 5 линия тренда выходит за пределы фактически протестированных уровней оценок, поэтому эквивалент оценки выше 5,0 или ниже 3,0 основан исключительно на предполагаемых линиях тренда.
Например, тест, предназначенный для четвероклассников, также может быть предоставлен учащимся третьего и пятого классов. Построены необработанные оценки и установлена линия тренда, которая используется для определения эквивалентов оценок.Обратите внимание, что на Рисунке 5 линия тренда выходит за пределы фактически протестированных уровней оценок, поэтому эквивалент оценки выше 5,0 или ниже 3,0 основан исключительно на предполагаемых линиях тренда.
Рис. 5. Использование линий тренда для оценки оценок эквивалентных оценок.
Эквивалентные баллы также предполагают, что тестируемый предмет подчеркивается на каждом уровне обучения в одинаковой степени и что овладение содержанием накапливается в основном с постоянной скоростью (Popham, 2005). Многие эксперты по тестированию предупреждают, что оценки эквивалентных оценок следует интерпретировать со значительным скептицизмом и что родители часто имеют серьезные неправильные представления об оценках эквивалентных оценок.Родители хорошо успевающих учеников могут преувеличивать уровень успеваемости своего ребенка.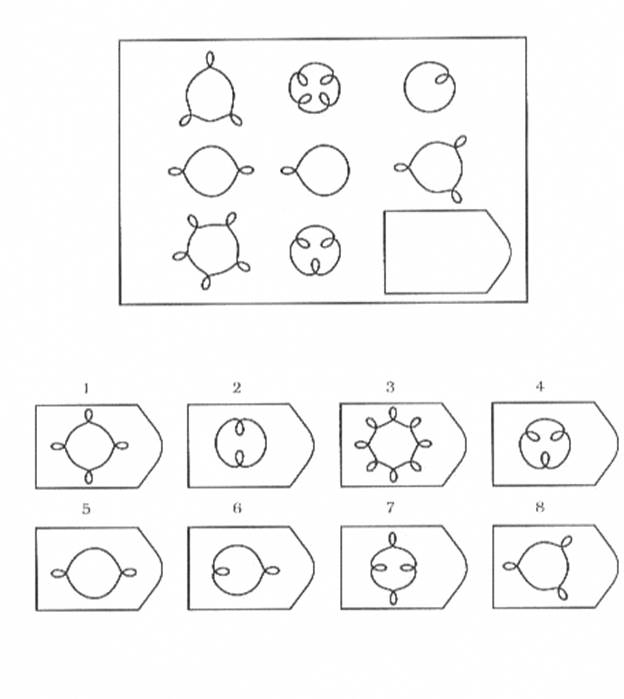
Список литературы
Линн Р. Л. и Миллер М. Д. (2005). Измерение и оценка в обучении 9-е изд. Верхняя Сэдл-Ривер, Нью-Джерси: Пирсон.
Попхэм, У. Дж. (2005). Оценка в классе: что нужно знать учителям. Бостон, Массачусетс: Пирсон.
Интерпретация результатов тестов | UT Testing and Evaluation Services
Понимание того, как интерпретировать три полезные статистические данные, касающиеся результатов тестов ваших учеников с множественным выбором, поможет вам составить хорошо продуманные тесты и улучшить обучение.
Сложность задания или P: процент учащихся, правильно ответивших на вопрос.
- Также называется p-значением
- Диапазон от 0% до 100% или, как правило, выражается как пропорция от 0,00 до 1,00
- Чем выше значение, тем легче товар
- P-значения выше 0,90 указывают на очень простые элементы, которые вам не следует использовать в последующих тестах. Если почти все учащиеся ответили правильно, в задании рассматривается концепция, которую, вероятно, не стоит проверять.

- P-значения ниже 0,20 указывают на очень сложные задания. Если почти все учащиеся ответили неправильно, это означает, что в задании есть недостатки или учащиеся не поняли концепцию. Подумайте о том, чтобы изменить запутанный язык, удалить элемент из последующих тестов или нацелить концепцию на повторное обучение.
Для максимального потенциала различения желательные уровни сложности немного выше, чем на полпути между шансом (1,00, деленным на количество вариантов выбора) и идеальной оценкой (1.00) для позиции:
Формат Идеальная Сложность
- Множественный выбор с пятью ответами .60
- Множественный выбор с четырьмя ответами .62
- Множественный выбор с тремя ответами .66
- Истина-ложь (два ответа, множественный выбор) .75
Дискриминация по заданию или R (IT): взаимосвязь между тем, насколько хорошо учащиеся выполнили задание, и их общим баллом за тест.
Также называется точечно-бисериальной корреляцией (PBS)
- Диапазон от 0.
 00 до 1.00
00 до 1.00 - Чем выше значение, тем более разборчивый товар
- Элемент с высокой степенью различения указывает на то, что учащиеся с высокими баллами по тестам ответили правильно, тогда как учащиеся с низкими баллами ответили неправильно.
Удалите элементы, значения дискриминации которых близки или меньше нуля, поскольку это означает, что учащиеся, которые плохо справились с тестом, справились с заданием лучше, чем учащиеся, которые сдали тест хорошо. Этот пункт в некотором роде сбивает с толку ваших учеников, набирающих больше очков.
Оценивайте задания, используя четыре руководства для значений распознавания в классных тестах:
- 0,40 или выше очень хорошие позиции
- от 0,30 до 0,39 хорошие вещи
- от 0,20 до 0,29 довольно хорошие позиции
- 0,19 или менее плохие позиции
Коэффициент надежности или АЛЬФА: мера величины ошибки измерения, связанной с результатом теста.
- Диапазон от 0,00 до 1,00
- Чем выше значение, тем надежнее результат теста
- Обычно это показатель внутренней согласованности, показывающий, насколько хорошо элементы коррелированы друг с другом
- Высокая надежность указывает на то, что элементы измеряют одну и ту же конструкцию (например,г.
 , знание того, как вычислять интегралы)
, знание того, как вычислять интегралы) - Два способа повысить надежность теста: 1) увеличить количество элементов или 2) использовать элементы с высокими значениями дискриминации
Интерпретация надежности
- .90 и выше Превосходная надежность; на уровне лучших стандартизированных тестов
- .80 — .90 Очень хорошо для школьного теста
- .70 — .80 Хорошо для школьного теста; в ассортименте большинство. Вероятно, есть несколько элементов, которые можно улучшить.
- .60 — .70 Немного ниже. Этот тест следует дополнить другими мерами для определения оценок. Вероятно, есть некоторые элементы, которые можно улучшить.
- .50 — .60 Предлагает пересмотреть тест, если он не слишком короткий (десять или меньше пунктов). Тест должен быть дополнен другими мерами выставления оценок.
- .50 или ниже Сомнительная надежность. Этот тест не должен сильно влиять на оценку за курс, и его необходимо пересмотреть.
Оценка дистрактора
Еще один полезный метод обзора заданий — оценка с помощью дистрактора.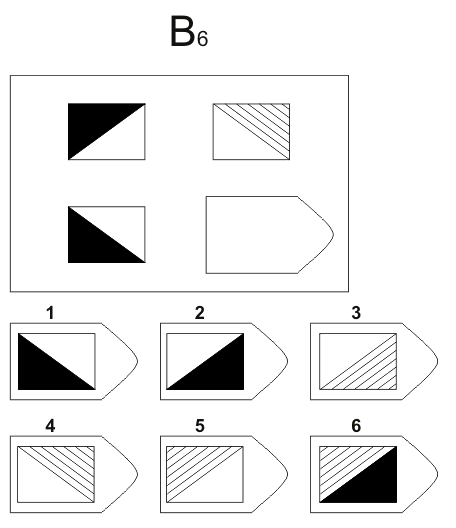
Вы должны рассматривать каждый отвлекающий фактор как важную часть задания ввиду почти 50-летнего исследования, которое показывает, что существует связь между отвлекающими факторами, которые выбирают учащиеся, и общей оценкой теста. Качество отвлекающих факторов влияет на успеваемость учащихся по заданию теста.
Хотя правильные ответы должны быть действительно правильными, не менее важно, чтобы отвлекающие факторы были явно неправильными, обращаясь скорее к тем, кто не усвоил материал, а к тем, кто набрал больше очков.Вам следует просмотреть все варианты элементов, чтобы предвидеть возможные ошибки в суждениях и неадекватную работу, чтобы вы могли пересмотреть, заменить или удалить плохие отвлекающие факторы.
Один из способов изучения реакции на отвлекающие факторы — использовать таблицу частот, в которой указывается доля учащихся, выбравших данный отвлекающий фактор. Удалите или замените отвлекающие факторы, выбранные несколькими учениками или ни одним из них, потому что ученики считают их неправдоподобными.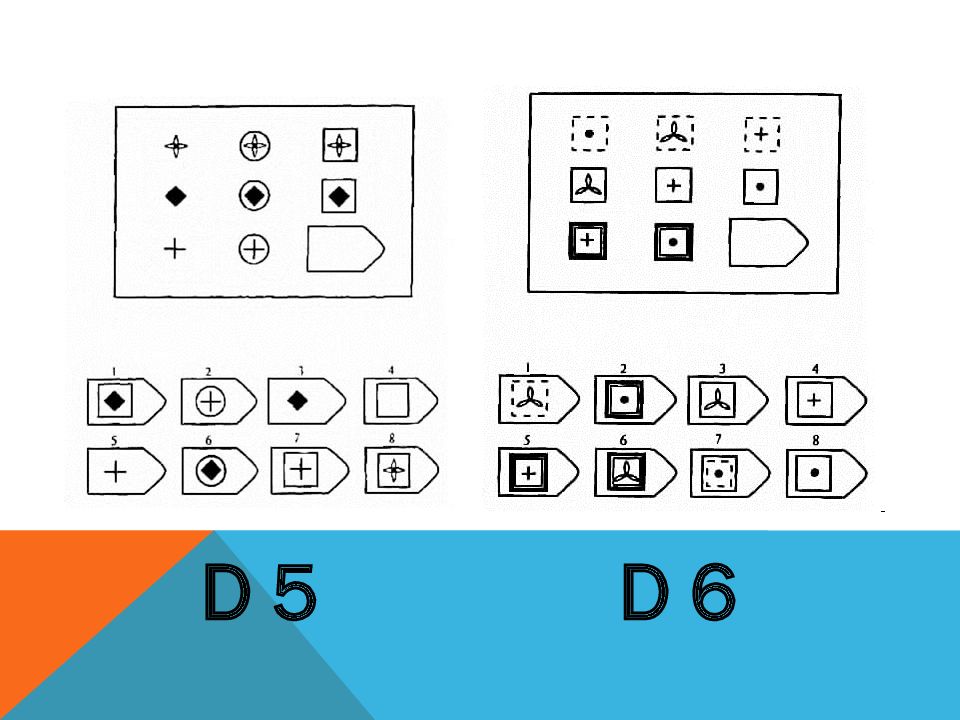
Осторожно при интерпретации результатов анализа предметов
Mehrens and Lehmann (1973) предлагают три предостережения относительно использования результатов анализа предметов:
- Данные анализа предмета не являются синонимом действительности предмета.Внешний критерий необходим для точной оценки валидности тестовых заданий. Используя внутренний критерий общей оценки за тест, анализ заданий отражает внутреннюю согласованность заданий, а не их валидность.
- Индекс дискриминации не всегда является показателем качества задания. Существует множество причин, по которым предмет может иметь низкую способность распознавания:
o чрезвычайно сложные или легкие предметы будут иметь низкую способность различать, но такие предметы часто необходимы для адекватной выборки содержания курса и целей.
o элемент может показывать низкую дискриминацию, если тест измеряет многие области содержания и когнитивные навыки. Например, если в большинстве тестов измеряется «знание фактов», то элемент, оценивающий «способность применять принципы», может иметь низкую корреляцию с общим баллом теста, однако оба типа элементов необходимы для измерения достижения целей курса.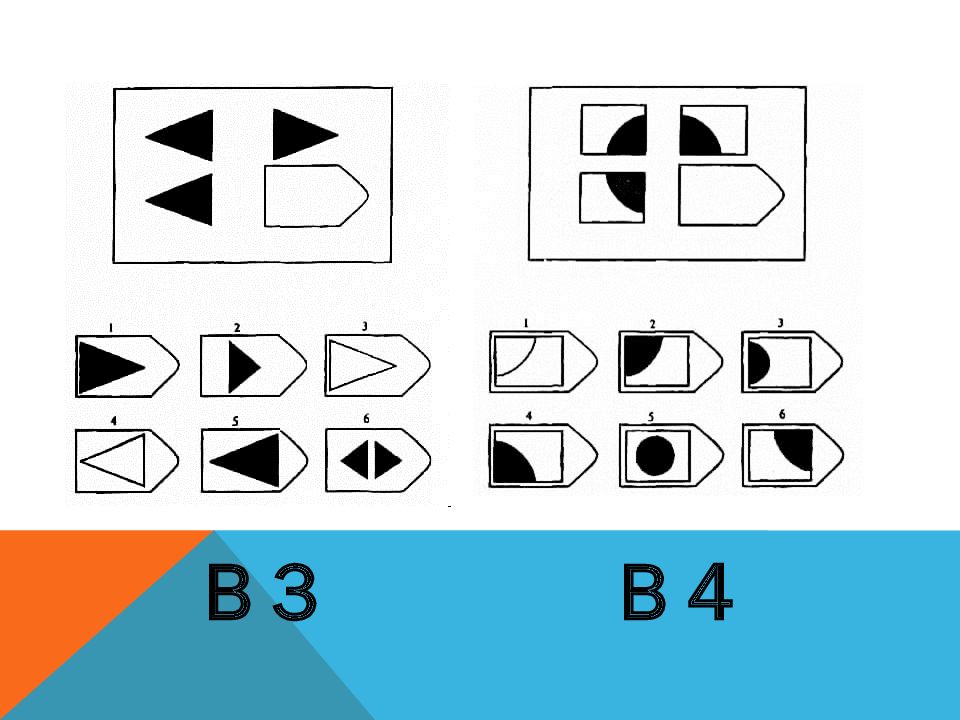
- Данные по предметному анализу предварительные. На такие данные влияют тип и количество студентов, проходящих тестирование, используемые учебные процедуры и случайные ошибки.Если возможно повторное использование предметов, статистические данные следует регистрировать для каждого применения каждого предмета.
Список литературы
ДеВеллис, Р. Ф. (1991). Масштаб развития: теория и приложения. Парк Ньюбери: Публикации Сейджа.
Галадина. Т. М. (1999). Разработка и проверка тестовых заданий с множественным выбором (2-е изд.). Махва, Нью-Джерси: Лоуренс Эрлбаум Ассошиэйтс.
Лорд, Ф. (1952). Связь надежности теста с множественным выбором с распределением трудностей заданий.Психометрика, 18, 181–194.
Mehrens, W. A., & Lehmann, I. J. (1973). Измерение и оценка в образовании и психологии. Нью-Йорк: Холт, Райнхарт и Уинстон, 333–334.
Суен, Х. К. (1990). Принципы тестовых теорий. Хиллсдейл, Нью-Джерси: Лоуренс Эрлбаум Ассошиэйтс.
Анализ теста и заданий: интерпретация результатов теста
После того, как тест выставлен на оценку, учитель должен интерпретировать результаты и использовать эти интерпретации для оценки, выбора, размещения или других решений.Чтобы точно интерпретировать результаты теста, учителю необходимо проанализировать выполнение теста в целом и отдельных тестовых заданий и использовать эти данные, чтобы сделать обоснованные выводы об успеваемости учащихся. Эта информация также помогает учителям подготовиться к обсуждениям экзамена со студентами после тестирования. В этой главе обсуждается процесс выполнения теста и анализа заданий. Он также предлагает способы, с помощью которых учителя могут использовать обсуждения после тестирования, чтобы способствовать обучению учащихся, и получать отзывы учащихся, которые могут привести к улучшению тестовых заданий.
Как инструмент измерения, тест дает оценку — число. Число, однако, не имеет внутреннего значения и должно сравниваться с чем-то, что имеет значение, чтобы интерпретировать его значение.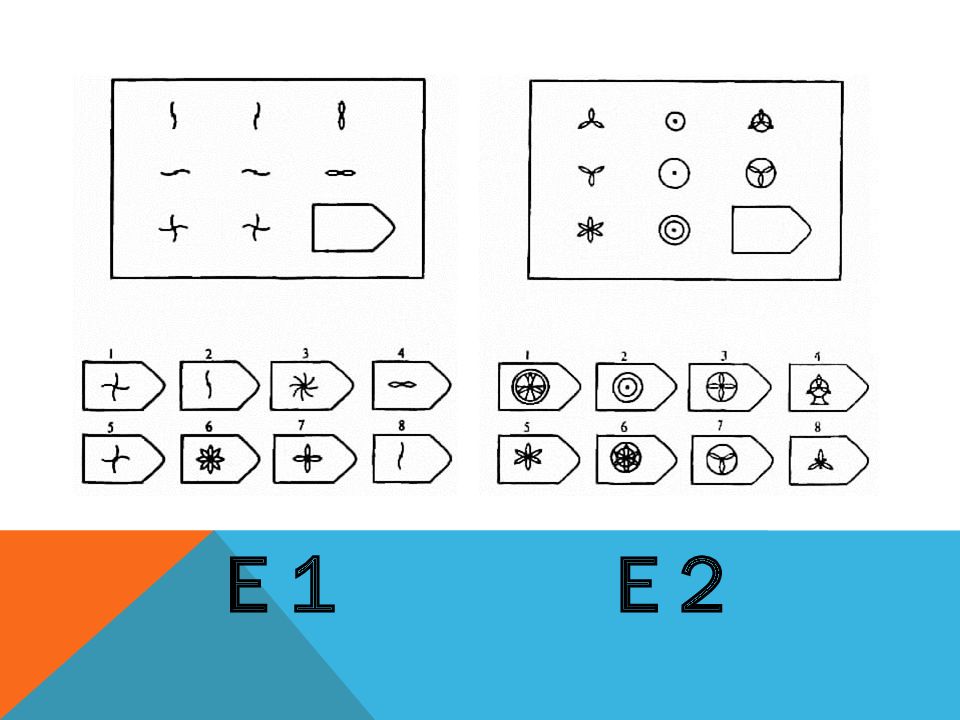 Чтобы результат теста был полезен при принятии решения относительно теста, учитель должен интерпретировать результат. Независимо от того, является ли интерпретация ссылкой на норму или критерий, базовые знания статистических концепций необходимы для оценки качества тестов (независимо от того, составлены они учителями или опубликованы), понимания стандартизированных результатов тестов, обобщения результатов оценки и объяснения результатов тестов другим.
Чтобы результат теста был полезен при принятии решения относительно теста, учитель должен интерпретировать результат. Независимо от того, является ли интерпретация ссылкой на норму или критерий, базовые знания статистических концепций необходимы для оценки качества тестов (независимо от того, составлены они учителями или опубликованы), понимания стандартизированных результатов тестов, обобщения результатов оценки и объяснения результатов тестов другим.
Некоторая информация о том, как тест выполняется в качестве измерительного прибора, может быть получена из отчетов об анализе тестов и заданий, сгенерированных компьютером. В дополнение к предоставлению данных анализа заданий, таких как индексы сложности и дискриминации, такие отчеты часто суммируют характеристики распределения баллов. Если у учителя нет доступа к электронному подсчету баллов и компьютерному программному обеспечению для тестирования и анализа заданий, многие из этих анализов можно проводить вручную, хотя и медленнее.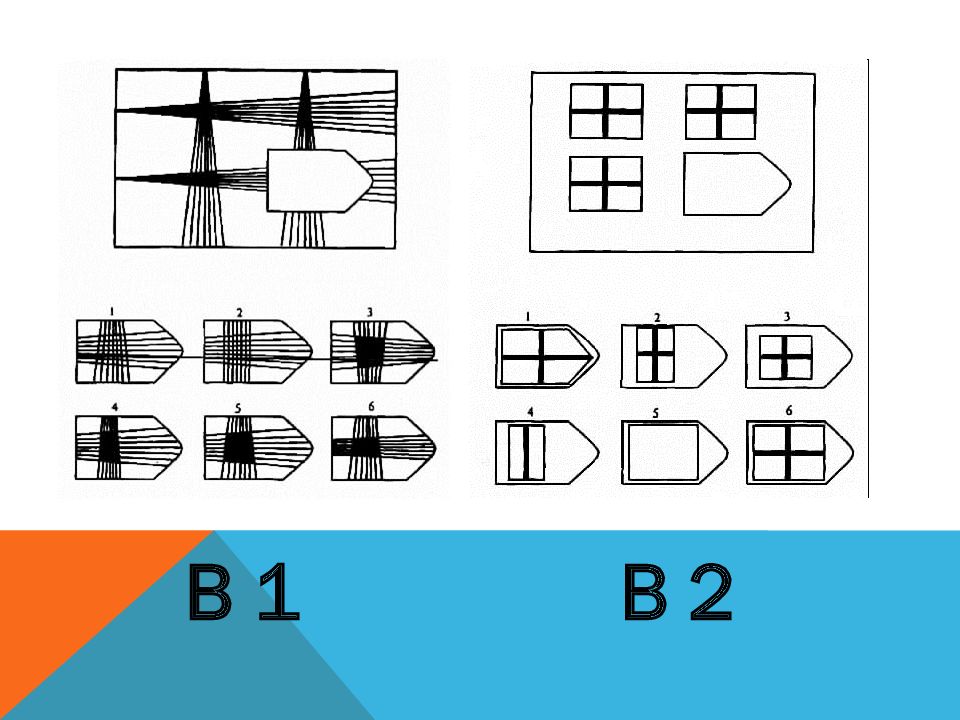
222 Когда тест выставлен на оценку, учитель остается с набором исходных оценок.Часто эти баллы записываются в соответствии с именами учащихся, в алфавитном порядке или по номерам учащихся. В качестве примера предположим, что баллы, представленные в таблице 12.1, были получены в результате проведения теста с 65 баллами для 16 студентов медсестер. Взглянув на этот набор чисел, учитель затруднился бы ответить на такие вопросы, как:
1. Получило ли большинство учеников высокие или низкие баллы на тесте?
2. Набрали ли какие-либо ученики намного больше или меньше, чем у большинства студентов?
3.Оценки сильно разбросаны или сгруппированы?
4. Каков диапазон оценок, полученных большинством студентов? (Brookhart & Nitko, 2019)
Чтобы упростить просмотр схожих характеристик оценок, учитель должен расположить их в порядке ранжирования, от самого высокого до самого низкого (Miller, Linn, & Gronlund, 2013), как в таблице 12.2. Такой порядок оценок позволяет сделать очевидным, что они варьировались от 42 до 60, и что оценка одного ученика была намного ниже, чем у других учеников.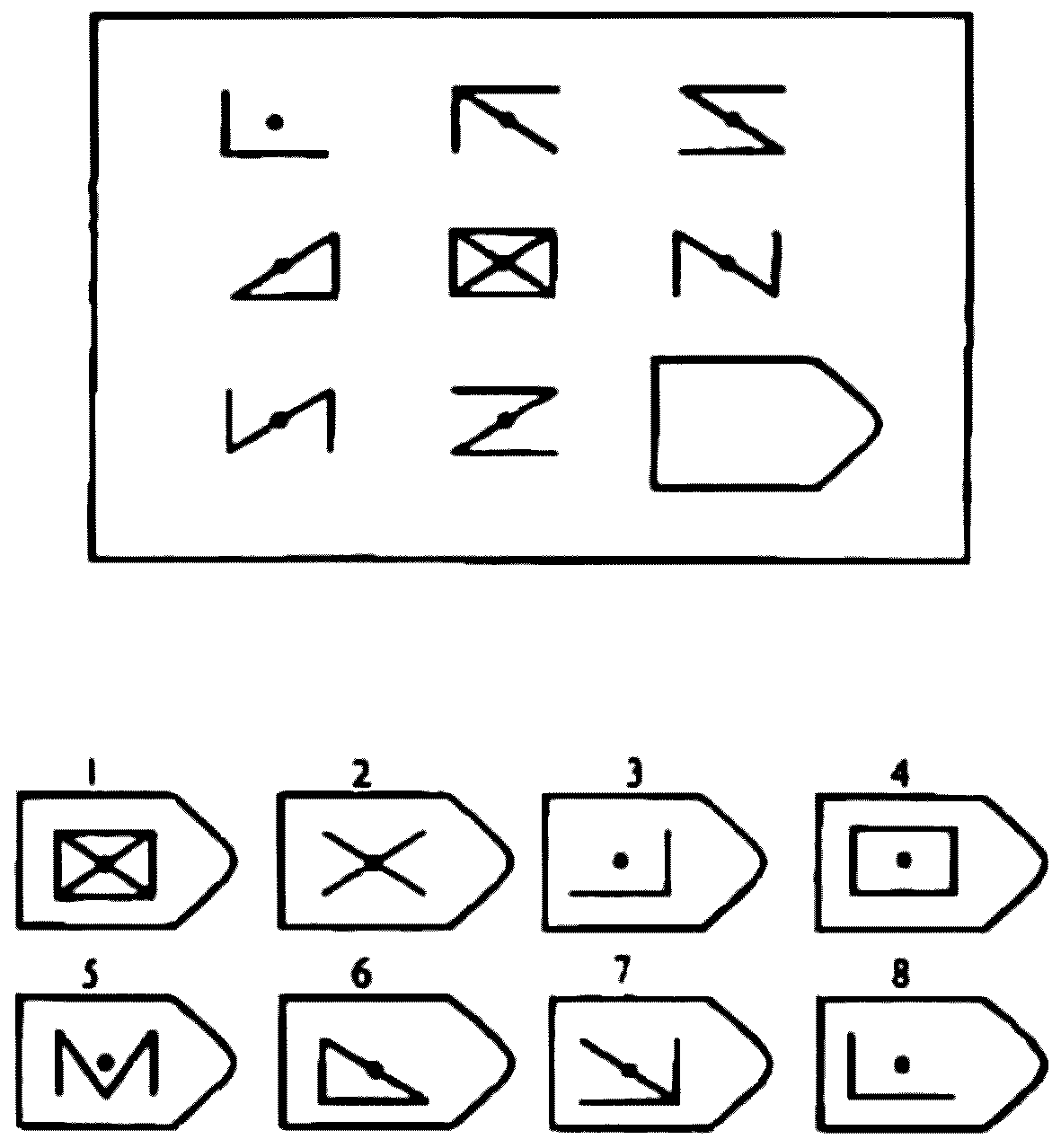 Но учитель по-прежнему не может легко представить себе, как типичный ученик справился с тестом, или общие характеристики полученных баллов. Удаление имен учащихся, перечисление каждой оценки по одному и подсчет количества повторений каждой оценки приводит к распределению частот, как в Таблице 12.3. Отображая баллы таким образом, учителю легче определить, насколько хорошо группа учащихся выполнила экзамен.
Но учитель по-прежнему не может легко представить себе, как типичный ученик справился с тестом, или общие характеристики полученных баллов. Удаление имен учащихся, перечисление каждой оценки по одному и подсчет количества повторений каждой оценки приводит к распределению частот, как в Таблице 12.3. Отображая баллы таким образом, учителю легче определить, насколько хорошо группа учащихся выполнила экзамен.
223
ТАБЛИЦА 12.3 Частотное распределение исходных оценок из таблицы 12.1
| RAW SCORE | ЧАСТОТА | |
|---|---|---|
| 61 | 0 | |
| 60 | 1||
| 60 | | 0 |
| 58 | 0 | |
| 57 | 1 | |
| 56 | 1 | |
| 55 | ||
| 54 | 3 | |
| 53 | 2 | |
| 52 | 3 | |
| 51 | 0 | |
| 0 | ||
| 49 | 0 | 900 19|
| 48 | 1 | |
| 47 | 1 | |
| 46 | 0 | |
| 45 | 0 | 0 |
| 43 | 0 | |
| 42 | 1 | |
| 41 | 0 |
224 Представленная частота графически в виде гистограммы.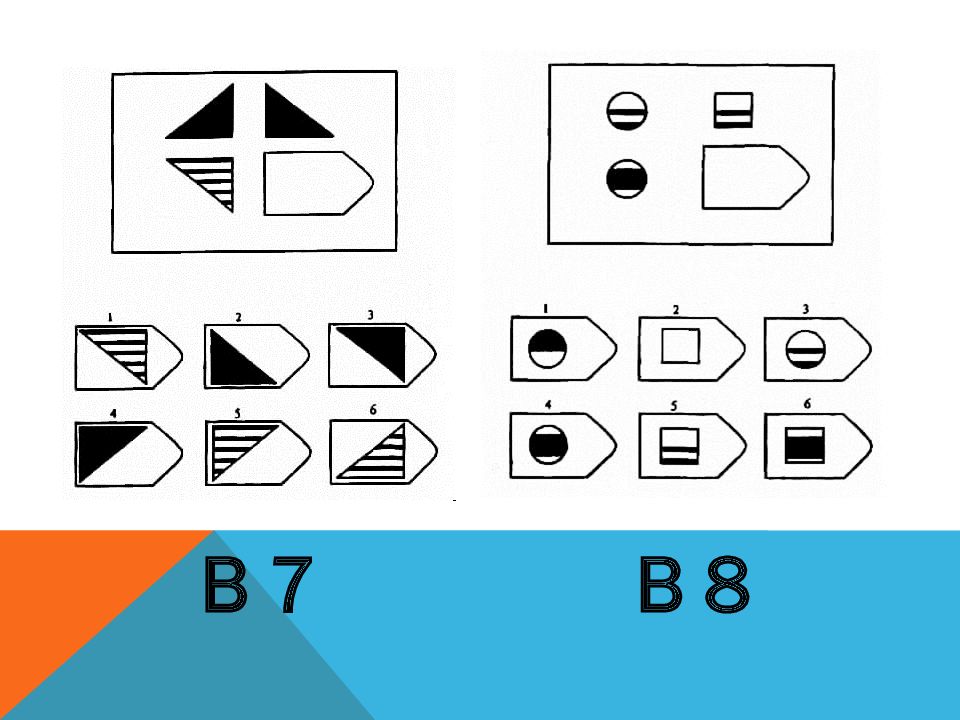 На рис. 12.1 оценки отсортированы от наименьшего к наибольшему по горизонтальной линии слева направо, а количество звездочек над каждой оценкой указывает частоту этой оценки. Частоты также могут быть обозначены на гистограмме полосами, высота каждой полосы которых представляет частоту соответствующей оценки, как на рисунке 12.2.
На рис. 12.1 оценки отсортированы от наименьшего к наибольшему по горизонтальной линии слева направо, а количество звездочек над каждой оценкой указывает частоту этой оценки. Частоты также могут быть обозначены на гистограмме полосами, высота каждой полосы которых представляет частоту соответствующей оценки, как на рисунке 12.2.
Полигон частот — это еще один способ графического отображения распределения оценок. Над каждым значением оценки ставится точка, чтобы указать частоту, с которой эта оценка была получена; если никто не набрал конкретного балла, точка ставится на базовой линии, равной 0.Затем точки соединяются прямыми линиями, образуя многоугольник или кривую. На рис. 12.3 показан многоугольник частот, основанный на гистограмме на рис. 12.1. Таким образом, гистограммы и частотные многоугольники показывают общие характеристики, такие как наиболее часто встречающиеся оценки, форма распределения оценок и диапазон оценок.
РИСУНОК 12.1 Гистограмма, изображающая частотное распределение исходных оценок из таблицы 12.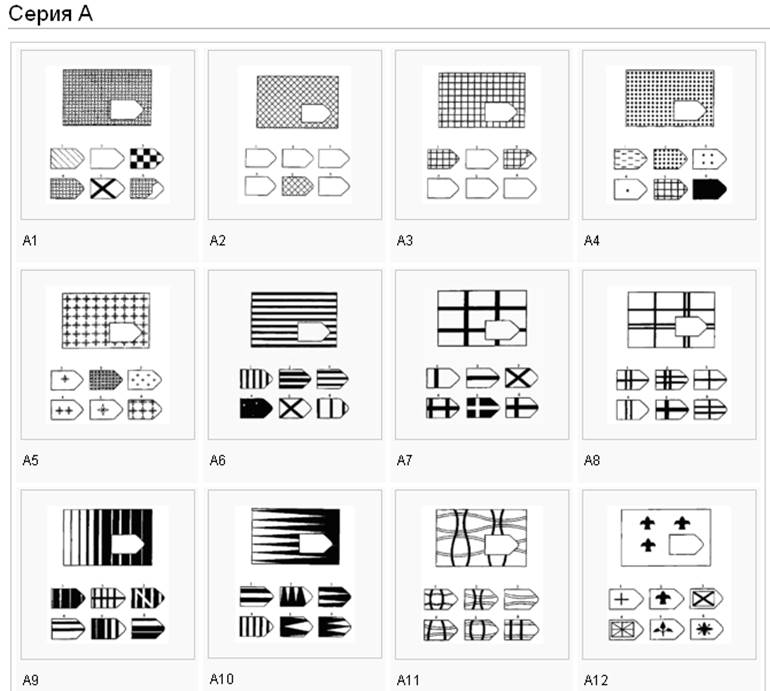 1.
1.
РИСУНОК 12.2 Гистограмма, показывающая частотное распределение исходных оценок из таблицы 12.1.
Примечание: f , частота; х , баллы.
РИСУНОК 12.3 Полигон частот, отображающий частотное распределение исходных оценок из таблицы 12.1.
Примечание: f , частота; х , баллы.
225 Характеристики распределения баллов можно описать на основе его симметрии, асимметрии, модальности и эксцесса. Эти характеристики показаны на рисунке 12.4. Симметричное распределение или кривая — это такое распределение, в котором есть две равные половины, зеркальные изображения друг друга.Несимметричные или асимметричные кривые имеют группу оценок или пик на одном конце и хвост, идущий к другому концу. Этот тип кривой называется скошенной; направление, в котором простирается хвост, указывает, смещено ли распределение в положительную или отрицательную сторону. Хвост кривой с положительным наклоном тянется вправо в направлении положительных чисел на шкале, а конец кривой с отрицательным наклоном идет влево в направлении отрицательных чисел.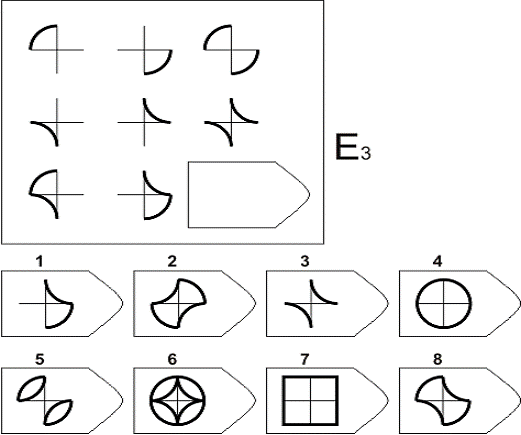 Таким образом, положительно искаженное распределение имеет самый большой кластер оценок на нижнем конце распределения, что кажется нелогичным.Распределение результатов тестов из Таблицы 12.1 несимметрично и имеет отрицательный перекос. Помните, что минимально возможный балл в этом тесте был 0, а максимально возможный — 65; оценки были сгруппированы между 42 и 60.
Таким образом, положительно искаженное распределение имеет самый большой кластер оценок на нижнем конце распределения, что кажется нелогичным.Распределение результатов тестов из Таблицы 12.1 несимметрично и имеет отрицательный перекос. Помните, что минимально возможный балл в этом тесте был 0, а максимально возможный — 65; оценки были сгруппированы между 42 и 60.
Полигоны частот и гистограммы могут различаться по количеству содержащихся в них пиков; эта характеристика называется модальностью , относится к режиму или наиболее часто встречающейся оценке в распределении. Если кривая имеет один пик, она одномодальная; если он содержит два пика, он является бимодальным.Кривая с множеством пиков является мультимодальной. Относительная плоскостность или пик кривой обозначается как эксцесс . Плоские кривые обозначены как platykurtic , умеренные кривые — как mesokurtic , а кривые с острыми вершинами — как leptokurtic (Waltz, Strickland, & Lenz, 2010).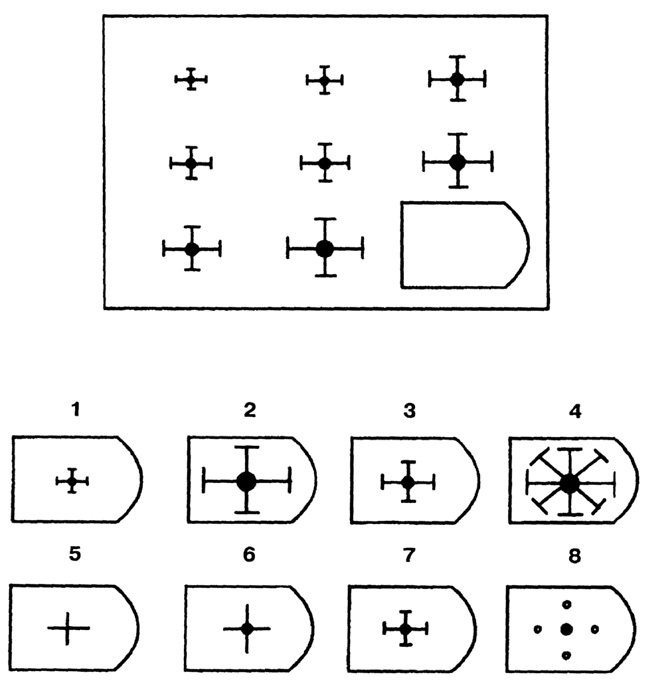 Гистограмма на рисунке 12.1 показывает бимодальное платикуртическое распределение.
Гистограмма на рисунке 12.1 показывает бимодальное платикуртическое распределение.
РИСУНОК 12.4 Характеристики распределения баллов.
226
РИСУНОК 12.5 Нормальное распределение.
Форма распределения баллов зависит от характеристик теста, а также от способностей учащихся, прошедших тестирование (Brookhart & Nitko, 2019). Некоторые учителя принимают решения о выставлении оценок, как если бы все распределения тестовых баллов напоминали нормальную кривую, то есть они пытаются «изогнуть» оценки. Понимание характеристик нормальной кривой развеет это представление. Нормальное распределение — это колоколообразная кривая, которая является симметричной, унимодальной и мезокуртической.На рисунке 12.5 показано нормальное распределение.
Многие человеческие характеристики, такие как интеллект, вес и рост, распространяются нормально; измерение любого из этих атрибутов в популяции приведет к большему количеству баллов в среднем диапазоне, чем в любом крайнем.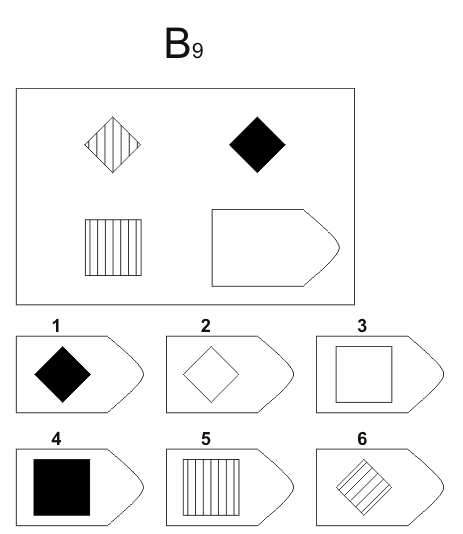 Тем не менее, большинство распределений баллов, полученных в результате тестов, подготовленных учителями, не соответствуют нормальному распределению. Это верно по нескольким причинам. Характеристики теста сильно влияют на итоговое распределение баллов; очень сложный тест имеет тенденцию давать положительно наклонную кривую.Точно так же способности учащихся влияют на распределение результатов теста. Независимо от распределения признака интеллекта среди человеческой популяции, эта характеристика вряд ли будет нормально распределена среди класса студентов-медсестер или группы вновь нанятых медсестер. Поскольку решения о приеме и приеме на работу, как правило, выбирают тех людей, которые с наибольшей вероятностью преуспеют в программе или работе медсестер, распределение оценок IQ для класса из 16 студентов-медсестер или 16 вновь нанятых медсестер будет иметь тенденцию к отрицательному перекосу.Точно так же знания медсестер вряд ли будут распространяться нормально, потому что те, кто был допущен к программе обучения медсестер или нанят в качестве штатных медсестер, не являются репрезентативными для населения в целом.
Тем не менее, большинство распределений баллов, полученных в результате тестов, подготовленных учителями, не соответствуют нормальному распределению. Это верно по нескольким причинам. Характеристики теста сильно влияют на итоговое распределение баллов; очень сложный тест имеет тенденцию давать положительно наклонную кривую.Точно так же способности учащихся влияют на распределение результатов теста. Независимо от распределения признака интеллекта среди человеческой популяции, эта характеристика вряд ли будет нормально распределена среди класса студентов-медсестер или группы вновь нанятых медсестер. Поскольку решения о приеме и приеме на работу, как правило, выбирают тех людей, которые с наибольшей вероятностью преуспеют в программе или работе медсестер, распределение оценок IQ для класса из 16 студентов-медсестер или 16 вновь нанятых медсестер будет иметь тенденцию к отрицательному перекосу.Точно так же знания медсестер вряд ли будут распространяться нормально, потому что те, кто был допущен к программе обучения медсестер или нанят в качестве штатных медсестер, не являются репрезентативными для населения в целом.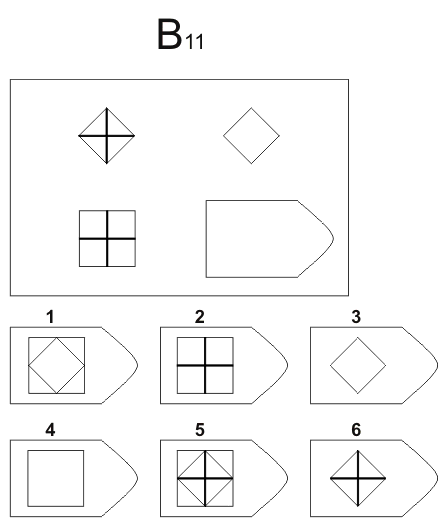 Следовательно, процедуры выставления оценок, которые пытаются применить характеристики нормальной кривой к распределению результатов теста, могут привести к неразумным и несправедливым решениям.
Следовательно, процедуры выставления оценок, которые пытаются применить характеристики нормальной кривой к распределению результатов теста, могут привести к неразумным и несправедливым решениям.
Меры центральной тенденции
Один из вопросов, на который необходимо ответить при интерпретации результатов тестов: «Какая оценка является наиболее характерной или типичной для этого распределения?» Типичная оценка, вероятно, находится в середине распределения, а другие оценки сгруппированы вокруг нее; показатели центральной тенденции дают значение, вокруг которого сгруппированы баллы теста.Для интерпретации результатов тестов обычно используются три показателя центральной тенденции: мода, медиана и среднее значение.
Режим, иногда обозначаемый сокращенно Mo , является наиболее часто встречающейся оценкой в распределении; это должен быть результат, фактически полученный студентом. Его можно легко определить по частотному распределению или графическому дисплею без математических расчетов. Таким образом, он дает приблизительное указание на центральную тенденцию. Однако мода является наименее стабильным показателем центральной тенденции, поскольку она имеет тенденцию значительно колебаться от одной выборки к другой, взятой из одной и той же популяции (Miller et al., 2013). То есть, если один и тот же тест из 65 пунктов, который дал баллы в таблице 12.1, был проведен для другой группы из 16 студентов-медсестер по той же программе, которые прошли один и тот же курс, режим мог бы значительно отличаться. Кроме того, как и в распределении, изображенном на рисунке 12.1, режим имеет два или более значений в некоторых распределениях, что затрудняет указание одной типичной оценки. Равномерное распределение баллов не имеет режима; такое распределение, вероятно, будет получено, когда количество студентов невелико, диапазон баллов большой и каждый балл получает только один студент.
Медиана (сокращенно Mdn или P 50 ) — это точка, которая делит распределение баллов на равные половины (Miller et al., 2013). Это значение, выше которого падают 50% оценок, а ниже которого падают 50% оценок; таким образом, он представляет 50-й процентиль. Медиана не обязательно должна быть фактически полученным баллом. При четном количестве баллов медиана находится посередине между двумя средними баллами; при нечетном количестве баллов медиана — это средний балл.Поскольку медиана является показателем местоположения, на нее не влияет значение каждой оценки в распределении. Таким образом, это обычно является хорошим показателем типичного балла в искаженном распределении, содержащем чрезвычайно высокие или низкие баллы (Miller et al., 2013).
Среднее значение часто называют «средним» баллом в распределении, что отражает математический расчет, определяющий эту меру центральной тенденции. Обычно это сокращенно M или. Среднее значение вычисляется путем суммирования каждой индивидуальной оценки и деления на общее количество оценок, как в следующей формуле:
, где M — среднее значение, ∑ X — сумма индивидуальных оценок и N — общее количество баллов.Таким образом, на значение среднего влияет каждый балл в распределении (Miller et al., 2013). Это свойство делает его предпочтительным показателем центральной тенденции, когда требуется мера общего распределения. Однако среднее значение чувствительно к влиянию чрезвычайно высоких или низких оценок в распределении и, как таковое, может не отражать типичную успеваемость группы студентов.
Существует взаимосвязь между формой распределения баллов и относительным расположением этих показателей центральной тенденции.В нормальном распределении среднее значение, медиана и мода имеют одно и то же значение, как показано на рисунке 12.5. При положительно асимметричном распределении среднее значение даст самый высокий показатель центральной тенденции, а мода — самый низкий; в отрицательно искаженном распределении режим будет иметь самое высокое значение, а среднее — самое низкое. На рисунке 12.6 показано относительное положение трех показателей центральной тенденции в искаженных распределениях.
228
РИСУНОК 12.6 Меры центральной тенденции в положительно и отрицательно искаженных распределениях.
Среднее значение распределения баллов из таблицы 12.1 составляет 52,75; медиана — 53,5. Тот факт, что медиана немного выше среднего, подтверждает, что медиана является показателем местоположения или положения и нечувствительна к фактическим значениям оценок в распределении. На среднее, поскольку на него влияет каждый балл в распределении, повлиял один крайне низкий балл. Поскольку форма этого распределения оценок имела отрицательный перекос, ожидается, что медиана будет выше среднего, потому что среднее всегда тянется в направлении хвоста.
Меры изменчивости
Два распределения баллов могут иметь одинаковые меры центральной тенденции, но при этом сильно отличаться. Оценки в одном распределении могут быть сильно сгруппированы вокруг среднего, а в другом распределении оценки могут быть сильно разбросаны по диапазону значений. Меры вариабельности используются для определения того, насколько студенты похожи или различаются по своим оценкам на тесте.
Простейшей мерой изменчивости является диапазон, разница между наивысшим и наименьшим баллами в распределении.Для распределения результатов теста в Таблице 12.3 диапазон составляет 18 (60–42 = 18). Иногда диапазон выражается как наивысший и самый низкий баллы, а не как разница в баллах. Поскольку диапазон основан только на двух значениях, он может быть очень нестабильным. Диапазон также имеет тенденцию увеличиваться с увеличением размера выборки; то есть результаты тестов большой группы студентов, вероятно, будут разбросаны по широкому диапазону из-за вероятности получения экстремальных баллов (Miller et al., 2013).
Стандартное отклонение (сокращенно SD , s или σ) является наиболее распространенной и полезной мерой изменчивости.Как и среднее значение, здесь учитываются все баллы в распределении. Стандартное отклонение основано на различиях между каждой оценкой и средним значением. Таким образом, он характеризует среднюю величину, на которую баллы отличаются от среднего. Стандартное отклонение рассчитывается в четыре этапа:
1. Вычтите среднее значение из каждой оценки ( X — M ), чтобы вычислить оценку отклонения ( x ), которая может быть положительной или отрицательной.
2. Возвести в квадрат каждую оценку отклонения ( x 2 ), что исключает любые отрицательные значения.Суммируйте все оценки квадратичного отклонения ( ∑ x 2 ).
3. Разделите эту сумму на количество результатов теста, чтобы получить дисперсию.
4. Вычислите квадратный корень из дисперсии.
Хотя для расчета стандартного отклонения можно использовать и другие формулы, следующая формула определения представляет эти четыре шага:
, где SD — стандартное отклонение, ∑ x 2 — это сумма квадратов отклонений, а N — количество баллов (Miller et al., 2013).
Стандартное отклонение распределения баллов из таблицы 12.1 составляет 4,1. Что означает это значение? Стандартное отклонение 4,1 представляет собой среднее отклонение оценок от среднего. В 65-балльном тесте 4 балла — это небольшая средняя разница в баллах. Если оценки плотно сгруппированы вокруг среднего, стандартное отклонение будет относительно небольшим числом; если они разбросаны по большому диапазону баллов, стандартное отклонение будет большим.
Другие характеристики теста
В дополнение к интерпретации распределения результатов теста и показателей центральной тенденции и изменчивости учителя должны проверять тестовые задания в совокупности на предмет наличия предвзятости.Например, хотя явной гендерной предвзятости в каком-либо отдельном элементе теста может не быть, такое смещение может быть очевидным, когда все элементы рассматриваются как группа. Подобные случаи этнической, расовой, религиозной и культурной предвзятости могут быть обнаружены, когда предметы группируются и исследуются вместе. Влияние предвзятости на тестирование и оценку подробно обсуждается в главе 16 «Социальные, этические и юридические вопросы».
Интерпретация индивидуальной оценки
Интерпретация результатов тестов, проводимых учителем
Способность интерпретировать характеристики распределения оценок поможет учителю делать ориентированные на нормы интерпретации значения любой индивидуальной оценки в этом распределении.Например, как учитель должен интерпретировать 53 балла П. Парди на тесте, результаты которого сведены в Таблицу 12.1? При среднем показателе 230 из 53,5, среднем значении 52,75 и стандартном отклонении 4,1 оценка 53 является примерно «средней». Все оценки от 49 до 57 попадают в одно стандартное отклонение от среднего и, таким образом, существенно не отличаются друг от друга. С другой стороны, Н. Нардоцци может радоваться, потому что оценка 60 почти на два стандартных отклонения выше среднего; таким образом, эта оценка представляет собой достижение, которое намного лучше, чем у других в группе.Учителю, вероятно, следует спланировать консультацию Л. Линча, потому что результат 42 — это более чем на два стандартных отклонения ниже среднего, что намного ниже, чем у других в группе.
Тем не менее, большинству медсестер-преподавателей необходимо интерпретировать индивидуальные результаты тестов на основе критериев. Оценка учащегося за тест сравнивается с заранее установленным стандартом или критерием, а оценки других учащихся не учитываются. Оценка в процентах правильных ответов — это производная оценка, которая часто используется для сообщения результатов тестов, предназначенных для интерпретации на основе критериев.Правильный процент — это сравнение балла учащегося с максимально возможным баллом; он рассчитывается путем деления исходной оценки на общее количество заданий в тесте (Miller et al., 2013). Хотя многие учителя считают, что процентные правильные оценки являются объективным показателем того, насколько учащиеся действительно знают предмет, на самом деле они могут значительно измениться в зависимости от сложности тестовых заданий. Поскольку процентные правильные оценки часто используются в качестве основы для присвоения буквенных оценок в соответствии с заранее определенной системой оценок, важно понимать, что они определяются больше трудностью теста, чем истинным качеством выполнения.Для тестов, которые являются более сложными, чем ожидалось, учитель может захотеть скорректировать исходные баллы, прежде чем вычислять процент правильных ответов по этому тесту.
Не следует путать процент правильных оценок с процентильным рангом, который часто используется для сообщения результатов стандартизированных тестов. Процентильный ранг описывает относительное положение ученика в группе и, следовательно, является нормативной интерпретацией. Процентильный ранг данного необработанного балла — это процент баллов в распределении, которые соответствуют этому баллу или ниже него.Таким образом, процентильный рейтинг 83 означает, что баллы студента равны или выше, чем баллы 83% студентов в этой группе; Однако нельзя предположить, что ученик правильно ответил на 83% заданий. Поскольку существует 99 точек, которые делят распределение на 100 групп равного размера, наивысший процентильный ранг, который может быть получен, — 99-й. Медиана находится на 50-м процентиле. Различия между процентильными рангами означают больше на самом высоком и самом низком крайних значениях, чем около медианы.
Интерпретация результатов стандартизированных тестов
Результаты стандартизированных тестов обычно предназначены для использования для интерпретации, основанной на нормах. Прежде чем делать такие интерпретации, учитель должен иметь в виду, что стандартизированные тесты больше соответствуют общим, а не конкретным учебным целям. Кроме того, результаты стандартизированных тестов больше подходят для оценки групп, а не отдельных лиц. Следовательно, стандартные результаты тестов не должны использоваться для определения оценок по конкретному курсу или для принятия решения о найме, продвижении по службе или увольнении сотрудника.Как и большинство образовательных мероприятий, стандартизированные тесты предоставляют грубые, а не точные данные об успеваемости. Фактические различия в показателях и достижениях отражаются в больших различиях в баллах.
Результаты стандартизированных тестов обычно представляются в виде производных баллов, таких как процентильные ранги, стандартные баллы и баллы по группе норм. Поскольку все эти производные оценки следует интерпретировать в соответствии с нормами, важно указать соответствующую группу норм для сравнения. В руководстве пользователя для любого стандартизированного теста обычно представлены таблицы норм, в которых каждый исходный балл сопоставляется с эквивалентным производным баллом.Стандартизированные руководства по испытаниям могут содержать несколько таблиц норм; группа норм, на которой основана каждая таблица, должна быть полностью описана. Учитель должен позаботиться о том, чтобы выбрать группу норм, которая наиболее точно соответствует группе, результаты которой будут сравниваться с ней (Miller et al., 2013). Например, при интерпретации результатов стандартизированных тестов по сестринскому делу следует сравнивать успеваемость группы студентов-медсестер со степенью бакалавра с нормальной группой студентов-медсестер со степенью бакалавра. Таблицы норм иногда допускают более тонкие различия, такие как размер программы, географический регион и государственная и частная принадлежность.
Анализ заданий
Помимо статистики теста, учителя также должны проверять показатели качества выполнения по каждому заданию экзамена. При совместном использовании несколько точек данных — индекс сложности, индекс дискриминации и точечный коэффициент бисериальной корреляции — предоставляют богатый источник информации о качестве выполнения тестовых заданий (Ermie, n.d.). Однако учителя не должны полагаться только на эти статистические данные при оценке качества экзаменационных заданий. Решения по отдельным тестовым заданиям должны приниматься в контексте содержания и структуры задания, ожиданий учителя в отношении того, как задания будут выполняться, и точной интерпретации статистических данных по заданию (Brookhart & Nitko, 2019).
Компьютерное программное обеспечение для анализа заданий широко доступно для использования с оборудованием для сканирования электронных листов ответов. Имеющиеся в продаже приложения для компьютерного тестирования обычно также предоставляют услуги, которые создают пользовательские отчеты со статистикой анализа элементов. Для учителей, не имеющих доступа к такому оборудованию и программному обеспечению, процедуры ручного анализа ответов учащихся на тестовые задания подробно описаны ниже в этом разделе. Независимо от метода, используемого для анализа, учителя должны быть достаточно знакомы со значением каждой статистики анализа, чтобы правильно интерпретировать результаты.
Приложение 12.1 предлагает пример компьютерного отчета об анализе элементов. В этом примере перечислены только данные анализа заданий для каждого из экзаменационных заданий, без включения формулировок заданий и любых кодов, которые учитель мог использовать для классификации содержания пунктов (например, предметная область, когнитивный уровень, клиент потребности). Этот формат полезен для быстрого сканирования данных для выявления потенциальных проблем. В последующих примерах будут показаны отчеты об анализе заданий, отображающие содержание заданий, любые коды классификации и дополнительную статистику, относящуюся к эффективности вариантов ответов каждого элемента.
Только золотые участники могут продолжить чтение. Войдите или зарегистрируйтесь, чтобы продолжить СвязанныеНакладные расходы на Блок 10 Глава 19 (Интерпретация результатов стандартизированных тестов)
Накладные расходы для Раздела 10, Глава 19 (Интерпретация результатов стандартизированных тестов)
Вызов
Технический вызов
Воспитательные и психологические меры, не такие как фунты или в дюймах
- Нет нулевая точка
- квартир измерения не равно
Разработаны методы преодоления этого ограничения
- Автор предоставление значимых систем отсчета для интерпретации результатов
- Автор обеспечение способов, дающих одинаковые единицы измерения
- Автор обеспечение способов сравнения и сложения очень разных оценок
Профессиональный стандарт
Должен уметь интерпретировать обычно сообщаемые баллы: [например] процентильные ранги, баллы процентильных диапазонов, стандартные баллы, и эквиваленты оценок.(Стандарт 3 компетентности учителя в образовательной сфере). Оценка)
ОН 2
Методы интерпретации результатов тестов
Общий балл
Количество баллов при начислении следуя указаниям
- Нет собственное значение (ни то, ни другое не% правильного)
Интерпретации, основанные на критериях и стандартах
- Определение
- студента оценка относится к четкому описанию конкретных задач, которые студент может выполнить
- тех задачи, в свою очередь, относящиеся к заданным стандартам мастерства
- нет необходимо учитывать баллы других студентов
- Мост полезно при тестировании, предназначенном для этой цели
- набор четко сформулированных целей обучения
- достаточно элементы, позволяющие сделать вывод о степени владения или отсутствия владения этим доменом
- экспоната выбран для фактического измерения этого домена
- Руководящие принципы когда можно (осторожно) интерпретировать нормативные тесты в термины, привязанные к критериям
- доменов достижений (e.г., цели) являются однородные, разделенные и четко определенные?
в противном случае избегайте конкретных описательных заявлений
- достаточно предметов (скажем, 10) для каждого типа интерпретация?
в противном случае объедините элементы в более крупные кластеры или выносить только предварительные суждения
- простых элемента были опущены, чтобы увеличить дискриминацию?
если да, то баллы не описывают, какой низкий успевающие могут сделать
- использовали только элементы типа выбора?
если да, то баллы зависят от угадывания
- тестовых задания обеспечивают непосредственно релевантную меру цели?
если нет, основывайте интерпретацию на , что они действительно измеряют
Интерпретация со ссылкой на нормы
- Определение
- студента балл относительно других студентов (в группе нормы)
- норма группа тщательно определена
- нет нужно смотреть на уровень мастерства
- Получено баллов
- определение: необработанные оценки, преобразованные в числа, которые имеют значение в определенном группа сравнения
- производное баллы необходимы, потому что простые рейтинги имеют ограниченную ценность
- большинство общие типы: эквиваленты оценок, процентили, стандартные баллы
- простой для расчета и преобразования часто предусмотрены таблицы
- много типов стандартных баллов (е.g., T-score, NCE, стандартные возрастные баллы) на основе той же логики с использованием нормальная кривая
- другое типы шкал развития помимо GE (например, возрастные эквиваленты)
Таблицы ожиданий (Глава 4)
- Определение: двусторонняя диаграмма, показывающая, как часто учащиеся с каждым уровнем оценки (скажем, SAT math) выполнить на каждом уровне другое ценное выполнение (скажем, оценки первокурсников в колледже)
- Не надо нужны любые нормы
Описание
Определение: уровень обучения, при котором типичный студент набирает
балловПримерная интерпретация: у студента было такое же сырье средний балл для учащихся 5 класса.6 в средней школе
Типичный балл определяется за каждый месяц в оценка: 5.0-5.9
Таблицы предоставлены, так что просто посмотрите, какой класс уровень соответствует набранному баллу ученика
Широко используется, особенно в начальной школе
Широко неверно истолковано!
- Нет путают нормы GE со стандартами, которых должны достичь все учащиеся
- Не надо интерпретировать GE как оценку оценки, которую студент должен быть помещен в
- Не надо ожидайте, что все ученики наберут 1.0 золотых ежегодно (в среднем). Не реалистичная цель
- Не предполагайте, что единицы равны разные части шкалы (одна и та же разница может означать чуть выше или значительно выше среднего)
- Не надо предположить, что баллы по разным тестам сопоставимы
- Разное издатели тестируют более широкий круг студентов, чем другие
- Выкройки роста (разница в баллах) может различаться для разных субъектов
Полезность
- Мост полезно для сообщения о росте базовых навыков в начальной школе
- Наименее полезно для сравнения производительности на разных тестах
- Неравенство в единицах оценок будет путаница в интерпретации, если вы не будете четко придерживаться разум
Процентиль Рейтинг
Описание
Определение: процент студентов в оценка группы нормы ниже определенного исходного балла (относительное положение в группа)
Широко используется и легко понимается
Требования к применению
- А таблица преобразования (из исходных баллов в процентили) на основе группы норм
- А группа норм (таблица преобразования), подходящая для студентов, изучающих тест: класс или возраст, время года
- А группа норм (таблица преобразования), которая также характерна для конкретного теста выдаются: тест, субтест, форма или (сложность) уровень теста
- Многие тесты или студенческие группы означает много таблиц преобразования
- Разное цели (сравнения одного и того же ребенка с разными группами) требуют разные нормы
Ограничения
- Должен всегда относитесь к процентильному рангу учащихся по отношению к конкретному группа норм
- Обычно требуется несколько наборов норм, особенно в средней школе и за ее пределами
- квартир не равны, особенно на крайностях
Структура неравенства предсказуема, однако
Одинаковая разница в процентилях (скажем, 5 баллов) отражает гораздо большую разницу в производительности в крайних точках, чем в среднем (напомним форму нормальной кривой)
Стандартные баллы
Определение
- Стандартный на сколько выше или ниже среднего ученик набрал
- Расстояние рассчитывается в единицах стандартного отклонения (SD) (стандартное отклонение мера разброса или изменчивости)
- The среднее значение и стандартное отклонение для конкретной группы норм
Преимущества
На основе нормальной кривой, что означает:
- Очки распределены симметрично вокруг среднего (среднего)
- каждый SD представляет фиксированный (но другой) процент случаев
- Почти все включены между 3.0 и 3.0 SD среднее
- The SD позволяет преобразовывать самые разные необработанные оценки в общий шкала, которая имеет (а) равные единицы и (б) может быть легко интерпретирована в терминах нормальной кривой
- Когда мы можем предположить, что результаты соответствуют нормальной кривой (тесты в классе обычно нет, но стандартные тесты делают), мы можем перевести стандартные баллы в процентиль очень полезен!
Типы стандартных оценок
Все стандартные баллы
- Поделиться общая логика
- Банка быть переведены друг в друга (см. рисунок 19.2, стр. 494)
z-счет
- Самый простой
- The тот, на котором основаны все остальные
- Формула: z = (X-M) / SD, где X — оценка человека, M — среднее значение по группе, а SD — разброс групп (стандартное отклонение в баллах
- Z — это отрицательный для оценок ниже среднего, поэтому zs обычно преобразуются в другую систему, в которой все положительные числа
T- Оценка
- Обычно распределенные стандартные баллы
- M = 50, SD = 10
- Банка можно получить из z значений: T = 50 + 10 (z)
Нормированные стандартные баллы
- Запускается с оценками, которые вы хотите привести в соответствие с нормальной кривой
- Получить процентильные ранги для каждой оценки
- Преобразование процентили в z-баллы с помощью таблицы преобразования (я раздал один класс)
- Тогда преобразовать в любую другую стандартную оценку по вашему желанию (например,г., Т-балл, IQ эквиваленты)
- Надежда что ваше предположение было правильным, а именно, что оценки действительно соответствуют естественно следовать нормальной кривой. Если нет, ваши интерпретации (скажем, равных единиц) может несколько ошибаться
Станины
- Очень простой тип нормализованной стандартной оценки
- Диапазоны от 1 до 9 (стандартные девятки)
- каждый станин из 2-8 обложек SD
- Станин 5 = процентили 40-59 (средние 20 процентов)
- А разница в 2 станина обычно сигнализирует о реальном разница
- Сильные стороны
1.без труда объяснил ученикам и родителям
2. нормализованный, так что можете сравнить разные тесты
3. банка добавьте станины, чтобы получить общий балл
4. легко записано (только одна колонка)
1. нравится все стандартные баллы, рост не может быть зафиксирован
2. сырая, но предотвращает чрезмерное толкование
Нормальная кривая Эквиваленты (NCE)
- Обычно распределенные стандартные баллы
- M = 50
- SD = 21.06
- Результаты в баллах от 1 до 99
- Нравится процентили, ожидайте, что они имеют равные единицы (это означает, что они производят меньше различия в середине кривой и больше на крайних точках)
Стандартный возраст Результаты (SAS)
- Обычно распределенные стандартные баллы
- Положить в метрику IQ, где
- M = 100
- SD = 15 (Тест IQ Векслера) или SD = 16 (IQ Стэнфорда-Бине Тест)
Преобразование в стандартные баллы
Простота трансформации
- Все разные способы сказать одно и то же
- Все представляют равные единицы в разных диапазонах баллов
- Все можно усреднить (между собой)
- Банка легко преобразовать одно в другое
- Рисунок 19.2 на стр. 494 показывает, как они сочетаются друг с другом
- Но интерпретируемый, только когда баллы на самом деле нормально распределенный (обычно стандартизированные тесты)
- Даунсайднот учащиеся и родители так же легко понимают, как и процентили
Использование стандартных баллов для изучения профилей
использует
- Вы можете сравнивать результаты учащихся по разным тестам и субтестам, когда вы преобразовать все оценки в один и тот же тип стандартной оценки
- Но во всех тестах должна использоваться одна и та же группа норм
- Участок профили могут показать их относительные сильные и слабые стороны
- Должен быть построенным как доверительные интервалы , чтобы проиллюстрировать границу ошибки
- Интерпретировать оцениваются как разные только тогда, когда их диапазоны не перекрываются
- Иногда построены отдельно по мужчинам и женщинам (скажем, на тестах по профессиональному интересу), но это спорная практика
- Тесты иногда поставляются с табличными или описательными отчетами о профилях (см.496)
Использование стандартных баллов для проверки уровня владения навыками
- Некоторые стандартизированные тесты пытаются предоставить некоторую информацию, основанную на критериях, с помощью выставление оценок по конкретным наборам навыков (см. рис. 19.4 на стр. 498)
- Be очень осторожно используйте их только как подсказки, потому что каждая область умений обычно очень мало
Оценка соответствия норм для стандартных баллов
Помни о своей цели!
- Кому интерпретировать эффективность относительно четко определенной контрольной группы
Критерии оценки норм
- Соответствующий
- Есть эта конкретная группа норм подходит для (а) решения, которое вы хотите принять сделать и (б) набором учащихся?
- Был нормальная группа, созданная на основе случайной выборки или стратифицированной случайной выборки? Соответствует ли он данным переписи (по расе, полу, возрасту, месту жительства и т. Д.)) для рассматривается население в целом?
- Нет полагайтесь на дату авторского права в руководстве по тестированию. Прочтите руководство, чтобы узнать, как старый норм
- Остерегайтесь эффекта LakeWobegon!
Если вы хотите сравнить результаты тестов с разные группы норм, проверьте руководства по тестам, насколько сопоставимы группы
- Достаточно описан поиск:
Метод отбора проб
Количество и распределение случаев в нормировании образец
Возраст, раса, пол, география и т. Д.образца нормы
Степень, в которой стандартизированные условия были поддерживается в тестировании
Предпочитаю тесты, которые описаны более подробно
Предостережения при интерпретации результатов стандартизированных тестов
Очки должны быть переводчик:
- с четкое знание того, что измеряет тест.Не полагайтесь на титулы; изучить содержание (широта и т. д.)
- В свет других факторов (способности, образовательный опыт, культурные фон, здоровье, мотивация и т. д.), которые могли повлиять на тест производительность
- Согласно к типу принимаемого решения (высокий или низкий для какого ?)
- Как диапазон баллов, а не конкретное значение. Всегда вычитайте и прибавляйте 1 SEM от счета, чтобы получить диапазон, чтобы избежать чрезмерного толкования
- В свет всех ваших доказательств.Ищите подтверждающие или противоречивые доказательства
- Никогда полагаться на один счет, чтобы принять важное решение
Интерпретация результатов лабораторных исследований
Введение
В больницах из года в год заказывается все больше лабораторных исследований, и это расширение, похоже, еще не достигло своего верхнего предела. Учитывая большой объем лабораторных тестов, кажется, что их ценность становится все более очевидной для врачей и пациентов.Еще более важным является высокий уровень доверия врачей к лабораторным данным.Выбор диагностических лабораторных параметров во многом зависит от рассматриваемой медицинской проблемы, но в лаборатории мы часто видим множество различных тестов, заказываемых для каждого отдельного образца. Некритичный заказ слишком большого количества тестов не обязательно предоставит врачу дополнительную информацию, а иногда может даже затруднить интерпретацию результатов.
Следовательно, при выборе теста важно, чтобы клиницист знал, насколько тест подходит для предполагаемого использования, и не в последнюю очередь знал, насколько надежным является результат теста.В этом отношении важной задачей лаборатории является предоставление необходимой информации о методах и результатах тестов, тем самым поддерживая клинициста в процессе принятия решений.
Рациональное использование клинического биохимического анализа требует понимания того, что фактически включают лабораторные результаты. Поэтому важно понимать следующие концепции:
- Референтный интервал
- Смещение (точность)
- точность
- Чувствительность
- Специфичность
- Прогнозируемое значение
Интерпретация лабораторных результатов требует, чтобы результат можно было соотнести с соответствующим эталонным значением.Это могут быть более ранние результаты того же пациента, если это возможно, или сравнение с данными из «нормальной» популяции. В последнем случае, чтобы использовать результат теста, необходимо указать контрольную область для рассматриваемого анализа.
Контрольную зону устанавливают путем сбора образца материала от нормального здорового населения, по крайней мере, 100 человек, предпочтительно нескольких сотен человек. Это могут быть собственные исследования лаборатории, основанные на образцах крови доноров или, например, от персонала больницы, или с использованием данных из литературы.Для установления четко определенного референтного интервала доступны протоколы IFCC [1].
Измерение образцов от разных людей, как и следовало ожидать, не даст точно одинаковых результатов. Это связано с естественной биологической изменчивостью и неопределенностью самого измерения. Таким образом, эталонный интервал, основанный на нормальной совокупности, будет группироваться вокруг среднего и часто показывает нормальное распределение или распределение Гаусса. Форма распределения зависит от биологической изменчивости рассматриваемого аналита, отбора проб и обработки материала, а также от неопределенности измерения.
Чтобы использовать это эталонное распределение в клинической практике, вам необходимо ограничить площадь, введя эталонный интервал. Если измеряемая переменная имеет нормальное распределение, статистически приблизительно 95% (95,6%) значений будут находиться в пределах диапазона, определяемого средним значением ± 2 стандартных отклонения. Измерения в этих пределах часто используются для описания тестовых значений, обычно наблюдаемых у здорового населения, и их часто называют «нормальным диапазоном». Аналогичным образом, приблизительно 99% будут в пределах среднего ± 3 стандартных отклонения.
Таким образом, эталонный интервал, включающий 95% значений, ограничен нижним и верхним эталонным пределом, соответствующим 2,5% и 97,5%. Значения по обе стороны от этих контрольных пределов, таким образом, не входят в «нормальный диапазон». Статистически это означает, что 5% населения или один из двадцати должны считаться ненормальными!
Если заказаны два теста, вероятность того, что второй тест будет в пределах нормальной популяции, также будет 95%, но вероятность того, что оба теста будут нормальными, равна 0.95 2 = 0,90. Если заказано 10 тестов, что часто случается, вероятность того, что все они находятся в пределах 95% -ного интервала, составляет 0,60. С другой стороны, некоторые биохимические параметры демонстрируют значительные биологические вариации, поэтому у пациента с патологическим состоянием также возможно получить результат теста в пределах референтного интервала (рис. 1).
Нажмите для увеличения
Рис. 1: Нормальные распределения, со средним значением = 10 и средним значением = 18, стандартным отклонением = 2. 95% значений находятся в пределах ± 2 × SD.
Таким образом, ненормальные результаты не всегда указывают на болезнь или патологическую ситуацию, а нормальный результат не всегда указывает на отсутствие болезни. Конечно, чем более ненормальный результат, тем больше вероятность того, что он связан с патологическим состоянием.
При установлении референсного интервала некоторые биохимические параметры не будут иметь нормального распределения. Часто встречаются так называемые асимметричные распределения, но данные часто можно преобразовать в нормальное распределение, применив логарифмическое преобразование.Без преобразования около 95% наблюдений по-прежнему будут находиться в пределах 2 стандартных отклонений, но те 5% вне пределов вполне могут оказаться на одном конце.
Чтобы избежать этого, можно использовать непараметрическую статистику для определения 2,5-го и 97,5-го процентилей, или, проще говоря, вам может потребоваться определить контрольные пределы, чтобы 2,5% результатов было вырезано с каждой стороны распределения. Для некоторых параметров было решено использовать 99-й процентиль, чтобы 1% результатов находился в верхнем диапазоне.
Интервал может часто отличаться в зависимости от возраста, пола, размера или этнического происхождения, поэтому сбор данных из огромного количества лабораторных тестов для установления референсного интервала — трудоемкое и дорогостоящее дело. Для многих коммерческих аналитических методов производитель устанавливает референсный интервал. Чтобы использовать это, необходимо подчеркнуть, что интервал должен быть четко определен и подходить для демографического населения.
В последние годы в крупных проектах с участием нескольких лабораторий из разных стран участвовали в сборе и измерении образцов с целью установления общих референсных интервалов.Таким образом, референсные интервалы для наиболее распространенных аналитов были установлены на основе большого количества данных, например Северный эталонный интервальный проект (NORIP).
ТАБЛИЦА I: Референсные интервалы для креатинина
Референтный интервал | Дети: | 0–1 неделя | 53-97 мкмоль / л |
Установление референсного интервала, таким образом, позволяет клиницисту сравнивать результаты, полученные от индивидуума, с результатами, полученными от популяции, и тем самым использовать тот факт, что внутрииндивидуальные биологические вариации, даже если они могут быть значительными, намного меньше, чем вариация для рассматриваемой популяции.
Внутрииндивидуальная биологическая изменчивость
Несмотря на то, что индивидуум может значительно отличаться от нормальной популяции, тем не менее важно учитывать внутрииндивидуальные вариации рассматриваемого биохимического параметра. Многие аналиты измеряются с более высоким или более низким результатом, в зависимости от колебаний компонентов жидкости тела вокруг заданного гомеостатического значения. Таким образом, сезонные колебания, биологические циклы или ритмы, потребление пищи, упражнения или просто время суток могут повлиять на измеряемый параметр.Это, конечно, представляет особый интерес при сравнении результатов теста пациента с предыдущим, например в связи с оценкой лечения. При этом клиницист должен принимать во внимание биологические вариации и проводить критическую оценку изменений, наблюдаемых в результатах.
Не всегда существует четкая граница между здоровьем и болезнью, но, тем не менее, существует тенденция интерпретировать лабораторные тесты как здоровье или болезнь. Таким образом, при использовании пределов эталонного интервала будут некоторые случаи, которые вызовут ненужные ложные тревоги.
Например, во время развития болезни, на первых стадиях или в процессе прогрессирования, биологическая изменчивость представляет собой потенциальный риск ложной интерпретации. Аналогичным образом, для некоторых количеств биологическая изменчивость в патологических состояниях выше, чем в здоровом состоянии, и диагностическая ценность теста снижается.
Биологическая вариация может быть оценена на основе измеренных значений аналитической вариации (CV):
CV всего 2 = CV аналитический 2 + CV биологический 2 и, следовательно:CV биологический =
Биологическая вариация для биохимического параметра — это мера того, насколько большое увеличение / уменьшение, как можно ожидать, внесет вклад в аналитическую вариацию в нормальной ситуации.
Зная биологические и аналитические вариации внутри индивидуума (промежуточные), можно определить, можете ли вы интерпретировать результат теста как существенно отличающийся от предыдущего, полученного пациентом, и можно принять во внимание так называемое критическое различие. Определяя статистическую вероятность, критическую разницу (CD) можно рассчитать как:
CD = CD = 2,77 *Фактор 2,77 равен разности z-статистики, равной 1.96 для этого примера с вероятностью 0,05 (5%), что результат вызван случайным отклонением. Z-оценка зависит исключительно от вероятности, выбранной для значимости, и от того, являются ли изменения однонаправленными (рост ИЛИ падение) или двунаправленными. Примеры значений z можно найти у Фрейзера [2].
Чаще всего клинициста интересуют двунаправленные изменения с вероятностью 5%, что означает, что, как правило, мы будем искать различия, превышающие 2,8 * CV.
Таким образом, знание биологических вариаций внутри индивида имеет абсолютное значение для оценки лабораторных результатов.
Пример:
Глюкоза измеряется как в плазме, так и в глюкозе цельной крови. Внутрииндивидуальная биологическая вариация для глюкозы составляет CV биологическая ~ 6%, тогда как аналитическая вариация CV аналитическая ~ 2% для глюкозы в плазме и 3-4% для цельной крови. Тогда ежедневная вариация пациента будет:
CV глюкозы = =6,3% для глюкозы плазмы
Теперь вычисляем критическую разницу CD = 2.77 * = 18% означает, что два значения теста на глюкозу, которые расходятся более чем на 18%, будут значительно отличаться.
При мониторинге диабета или нарушения толерантности к глюкозе (IGT) существуют рекомендуемые значения концентрации глюкозы в плазме натощак (FPG):
- FPG
- 7,0 ммоль / л> FPG ≥ 5,6 ммоль / л ~ IGT
- FPG ≥ 7,0 ммоль / л ~ диабет.
При сравнении результатов теста с рекомендованными пределами необходимо учитывать биологические и аналитические ошибки.
Точность и прецизионность
Когда образец измеряется несколько раз, редко получают одинаковые результаты каждый раз. Вместо этого результаты будут более или менее отклоняться в зависимости от точности метода измерения. Точно так же измерение образца двумя разными методами редко дает точно такие же результаты, но различаются более или менее в зависимости от точности методов.
Таким образом, два основных фактора, влияющих на аналитическую неопределенность, — это точность (неточность) и точность (систематическая ошибка), каждая из которых вносит вклад в случайные ошибки и систематические ошибки.Точность определяется как степень, в которой повторные измерения в неизменных условиях показывают одинаковые результаты. В лаборатории термин неточность чаще используется для обозначения случайных аналитических ошибок, влияющих на результаты.
Точность определяется как степень близости измерений величины к ее фактическому или принятому значению. Однако чаще всего термин систематическая погрешность используется в лаборатории для описания систематических различий между методами измерения или между методом и эталонным значением.
При определении точности важно использовать концентрации аналита, близкие к пределам клинического решения. Для каждой концентрации рассчитывается среднее значение (M) и стандартное отклонение (SD):
SD =
Стандартное отклонение или так называемый коэффициент вариации (CV), который представляет собой стандартное отклонение в процентах от среднего, является мерой точности:
CV =
SD представляет собой сумму всех изменений, влияющих на анализ.Это, например, испытательный прибор, различные технологи, занимающиеся анализом, условия окружающей среды и просто повседневные изменения. Тогда SD является мерой межсерийной точности.
При определении систематической ошибки среднее значение серии измерений на образце сравнивается с известной концентрацией аналита в образце или с ожидаемым значением. Величину смещения можно определить с помощью соответствующего стандартного материала (например, сертифицированного стандартного материала), содержащего известную концентрацию аналита.
В лаборатории клинической химии систематическая ошибка метода обычно определяется путем сравнения результатов с результатами ряда других лабораторий, измеряющих тот же материал образца. Это межлабораторное сравнение, известное как проверка квалификации, подразумевает, что лаборатория регулярно получает образцы с неизвестной концентрацией аналита.
Обычно сравнение проводится с лабораториями, использующими ту же методологию, и затем сравнение показывает способность лаборатории достичь правильного результата теста.Как указано, смещение вызвано систематическими ошибками, такими как калибровка, изменение реагента (номер партии) и т. Д., И соответствующие неточности, SD или CV по отношению к эталонному значению или межлабораторное сравнение является мерой смещения метода. Эти типы ошибок независимы в том смысле, что вы можете проводить анализ с высокой точностью, но с низкой точностью, и наоборот.
Обычно в лаборатории, когда два или более прибора используются для одного анализа, регулярное сравнение методов и проверка систематической ошибки проводятся путем параллельного анализа.Оборудование, используемое для тестирования в местах оказания медицинской помощи (POCT), является хорошим примером с довольно большим количеством инструментов по всей больнице. Таким образом, для результата пациента не должно иметь значения, был ли образец проанализирован на приборе №1, приборе №2, №3 или №10.
Часто точность и предвзятость иллюстрируются стрельбой в цель. Отклонение от центра соответствует смещению, а точность соответствует расширению пулевых отверстий.
Аналитическая вариация может значительно повлиять на надежность лабораторного теста, в частности, когда биологическая вариация мала по сравнению с аналитической ошибкой.При интерпретации результата теста врач должен иметь возможность знать систематическую ошибку и точность метода или общую ошибку (TE) для метода:
TE = B + 1.96 * I
B = систематическая ошибка, I = неточность, уровень значимости 95%). Это может быть сопроводительный или легко доступный метод или таблица данных (в лабораторной информационной системе или в Интернете). Для многих лабораторных тестов программы внешней оценки качества или правительственные постановления (например, CLIA) предоставляют значения для приемлемой аналитической вариации, так называемые общие допустимые ошибки (TE a ), которые включают неточность и систематическую ошибку измерения.
Обратите внимание, что систематическая ошибка как систематическое различие между тестом и эталонным (истинным) значением не имеет отношения к тесту, который не стандартизирован; примером может служить тест D-димера.
Примером важности аналитической ошибки является измерение С-реактивного белка (СРБ) в качестве реагента острой фазы и в качестве теста на риск сердечно-сосудистых заболеваний. Как реагент острой фазы СРБ может резко увеличиваться в ответ, например, на инфекции, и тест измеряет более широкий диапазон уровней CRP.
Из-за высокой неточности нижних диапазонов этого метода недостаточно для проверки риска сердечно-сосудистых заболеваний. Для прогнозирования сердечно-сосудистых заболеваний анализ должен уметь различать значения CRP:
- > 1,0 мг / л и
- > 3,0 мг / л (высокий риск)
(Американская кардиологическая ассоциация и Центры США по контролю и профилактике заболеваний). Безусловно, очень важна точность выполнения аналитического метода.Однако несколько высокочувствительных анализов CRP показывают аналитическую погрешность в диапазоне 5-10%, и этого, вероятно, будет недостаточно. Согласно Westgard [3] допустимое значение CV действительно должно быть около нуля.
Чувствительность и специфичность
В терминологии клинической биохимии чувствительный метод обычно означает, что анализ может измерять низкие концентрации аналита, а специфичность означает способность метода измерять сам аналит без вмешательства других веществ в исследуемой пробе.Таким образом, терминология здесь относится к аналитической чувствительности и аналитической специфичности.При интерпретации лабораторных тестов мы говорим о клинической или диагностической чувствительности и специфичности, которые касаются возможности того, есть ли у пациента заболевание или нет. Для клинициста диагностическая чувствительность и специфичность являются важными вопросами, которые показывают, насколько надежен тест и насколько он подходит для предполагаемой цели.
Когда лабораторный результат показывает значение, соответствующее определенному болезненному состоянию, есть две возможности: болезнь может присутствовать или болезнь может отсутствовать.В первом случае мы имеем дело с истинно положительным (TP) результатом, а во втором — с ложноположительным (FP) результатом для заболевания. Точно так же, если результат показывает отсутствие болезни, человек может быть свободен от болезни или действительно болен. В этом случае у нас есть истинно отрицательные (TN) или ложноотрицательные (FN) соответственно.
Диагностическая чувствительность — это мера доли фактических положительных результатов, которые правильно определены как положительные. Таким образом, это мера способности аналитического метода идентифицировать конкретное заболевание.Чувствительность рассчитывается как процент истинно положительных результатов (TP) среди всех больных (рис. 2):
Нажмите для увеличения
Рис. 2: Нормальные распределения, со средним значением = 10 и средним значением = 18, стандартным отклонением = 2. 95% значений находятся в пределах ± 2 × SD.
Для отсечки на 95% красный = ложноотрицательный, синий = ложноположительный
TP / (TP + FN)
Таким же образом диагностическая специфичность измеряет долю правильно идентифицированных негативов и, таким образом, является мерой способности метода исключить конкретное заболевание.Затем рассчитывается специфичность как процент истинно отрицательных результатов (TN) среди всех без заболевания:
TN / (TN + FP)
Тест, показывающий, что женщина не беременна, когда она на самом деле беременна, является примером теста с низкой чувствительностью, тогда как тест с низкой специфичностью — это тест, показывающий беременность, когда женщина не беременна.
Несмотря на то, что метод тестирования обладает высокой специфичностью и высокой чувствительностью, вы не обязательно получите правильный ответ для постановки диагноза.Это в значительной степени зависит от распространенности заболевания; это количество людей с заболеванием в данной популяции, особенно при низкой распространенности.
Например, очень редкое заболевание и лабораторный тест на это заболевание с чувствительностью и специфичностью менее 100%. Вероятность ложноположительных результатов высока, и, таким образом, получается низкая прогнозируемая ценность.
Прогностическая ценность — это вероятность наличия заболевания при положительном результате теста или отсутствия заболевания при отрицательном результате теста.В формуле это можно отобразить так:
Прогнозирующая ценность положительного результата теста: PPV = TP / (TP + FP)
Прогнозирующая ценность отрицательного результата теста: NPV = TN / (TN + FN)
Таким образом, прогностические значения зависят от чувствительности, специфичности и распространенности и, таким образом, представляют вероятность того, что положительный тест отражает основное состояние, на которое проводится тестирование.
Заключение
Некоторые параметры важны при интерпретации лабораторных результатов, и, кроме того, интерпретация также зависит от причины, по которой запрашивается тест — будь то диагностическая цель, мониторинг или скрининг.Если тест запрашивается для исключения диагноза, то требуется высокочувствительный тест; если это необходимо для диагностики заболевания высокого риска, то необходим высокоспецифичный параметр.Интерпретация лабораторных результатов фактически начинается с того, что клиницист запрашивает правильный тест для клинической проблемы, с которой он / она сталкивается. Ожидается, что результат предоставит информацию, которая поддержит решение о последующем лечении. Какие действия будут предприняты, зависит от понимания врачом лабораторных результатов и от того, как реагировать на эту информацию.Этот круг от рассмотрения лабораторных анализов до интерпретации и действий — это цикл от мозга к мозгу [4].
Цикл от мозга к мозгу включает в себя знание:
- Преаналитические параметры
- Биохимический тест
- Биологическая вариация
- Подходящее время для взятия соответствующих проб
- Аналитические параметры
- Точность
- Неточность
- Диагностическая чувствительность и специфичность
- Постаналитические параметры
- Пределы клинического решения
- Частота отказов
- Клиническая интерпретация
Многие исследования были сосредоточены на ошибках на преаналитической и аналитической фазах, но меньше на постаналитических ошибках.Можно предположить высокий уровень ошибок при сборе проб, идентификации и штрих-кодировании, анализе и отчетности, но эти ошибки кажутся менее частыми по сравнению с ошибками при выборе правильного теста и ошибками в интерпретации результата. Согласно Laposata [5], исследование показало, что при нарушении свертываемости крови примерно 75% случаев были связаны с неверной интерпретацией результатов теста в той или иной степени.
По данным литературы 70-80% решений в диагностике основываются на лабораторных результатах.В лаборатории многое делается для помощи в интерпретации результатов, помимо эталонных значений, ошибок измерения, отмеченных результатов и т. Д.
Однако очевидно, что еще многое предстоит сделать для улучшения представления данных — и информации; информация, которая может помочь медицинскому персоналу правильно использовать лабораторную информацию. Сетевые лабораторные информационные системы можно улучшить с помощью средств принятия решений и инструментов, которые учитывают знания, основанные на фактах.
9.3 Интерпретация вывода
9.3 Интерпретация вывода
Первая таблица, Group Statistics , показана на рисунке 9.5. Эта таблица включает описательную статистику для каждой группы. В частности, таблица включает количество случаев (N), среднюю оценку эффективности лидера, стандартное отклонение и расчетную стандартную ошибку среднего (стандартное отклонение, деленное на N).
Наибольший интерес представляют средние оценки успеваемости для мужчин (5.68) и для женщин (6.14). У вас может возникнуть соблазн заключить, что это означает, что у женщин средние показатели успеваемости значительно выше, чем у мужчин. Однако это было бы преждевременным — на самом деле, весь смысл t-теста состоит в том, чтобы определить, действительно ли это различие (статистически значимое) или оно может быть отнесено к случайности. Для этого нам нужно изучить следующую таблицу, Independent Samples Test (рисунок 9.6).
- 9.3a Проверка на однородность дисперсии
Первые два столбца, обозначенные как Тест Левена на равенство вариантов , обеспечивают проверку одного из допущений t-критерия, то есть, что дисперсия в двух группах одинакова (т. Е. Подобна или однородна). Если это предположение нарушается в данных, необходимо произвести статистическую корректировку. Этот тест обеспечивает статистика F в первом столбце и ее вероятность во втором столбце ( Sig. , сокращение значимости).Если вероятность значения F (т. Е. Sig. ) меньше или равна 0,05 , то дисперсии в сравниваемых группах различаются, и условие однородности дисперсии не был доволен.
Результаты теста F определяют, использовать ли равные отклонения, предполагаемые строк, или равные отклонения, не предполагаемые строк, при оценке t-статистики. Правило принятия решения для определения, какие строки использовать, выглядит следующим образом:
- Если отклонения для двух групп равны (т.e, Sig. > .05 ), затем используйте результат в равных отклонениях, предполагаемых строк. Эти строки представляют собой более традиционный метод оценки значения t на основе степеней свободы ( df ), равных общему количеству баллов минус 2 (этот метод описан в большинстве учебников по вводной статистике или методам исследования). .
- Если отклонения для двух групп значительно различаются (т.e, Sig. <.05 ), затем используйте результат в строке Равные отклонения не предполагаются . Оценка статистики t в этой строке основана на скорректированных степенях свободы, которые учитывают несходные различия в двух группах.
Поскольку вероятность ( Sig. = .000) для значения F меньше .05 . Таким образом, отклонения двух групп равны , не равным , и поэтому следует использовать результат в строке , равные отклонения , а не , предполагаемой строке .
- 9.3b Проверка нулевой гипотезы: интерпретация значимости t-значения
Чтобы определить, значительна ли разница в производительности между мужчинами и женщинами, нам нужно посмотреть в столбцах с пометкой t-тест на равенство средних значений . В настоящее время нас интересует только полученное значение t и его вероятность, которые можно увидеть в столбцах, обозначенных t и Sig. (Двусторонний) . В строке равных отклонений , а не предполагается , мы видим значение t , равное 1.46. Вероятность в Sig. (Двусторонний) столбец в ( p = 0,146) больше, чем 0,05, что означает, что нам нужно сохранить нулевую гипотезу об отсутствии различий, сделав вывод о том, что не было значительной разницы в лидерских качествах между мужчинами и женщинами. Сотрудники EZ.
Следующее предложение показывает, как эти результаты будут записаны в формате APA.
Результаты показывают, что не было значительной разницы в производительности между женщинами и мужчинами, т (195) = 1.46, p = 0,15. То есть средняя оценка успеваемости женщин ( M = 6,14, SD = 1,94) существенно не отличалась от таковой у мужчин ( M = 5,69, SD = 2,74).
Обратите внимание, что хотя исследователи обычно заинтересованы в обнаружении «значительных различий», иногда отсутствие значительного различия имеет либо теоретическое, либо практическое значение. Это, безусловно, так и здесь. В частности, эти результаты показывают, что нет достоверной разницы в производительности между мужчинами и женщинами в EZ Manufacturing.Это важно, потому что эта информация может быть полезна для успокоения беспокойства руководителей высшего звена, которые могут придерживаться стереотипа о том, что женщины менее способны по сравнению с мужчинами в ситуациях лидерства.
- 9.3c Дополнительная информация в t-таблице
В t-таблице есть дополнительная информация, которая может быть вам полезна. Первый — это средняя разность . Это просто разница между двумя средствами. Стандартная ошибка средней разницы — знаменатель, используемый при вычислении t-статистики.Наконец, 95% доверительный интервал для разницы состоит из двух чисел, обозначающих нижнюю и верхнюю границы доверительного интервала. Мы можем быть уверены на 95% в том, что разница между двумя средними находится между нижней и верхней границей.
Как уже упоминалось, существует множество других гипотез, которые мы могли бы проверить с помощью t-критерия независимых выборок на данных нашего исследования EZ Manufacturing. Упражнение в конце главы иллюстрирует одно из них, и вам предлагается изучить другие самостоятельно.В следующей главе мы обсудим аналогичный подход к проверке гипотез с использованием t-теста коррелированных выборок .
положительных и отрицательных результатов, диапазоны, точность и др.
Если вы ждете результатов лабораторных анализов или пытаетесь понять, что они означают, процесс и все эти медицинские термины и цифры могут сбить с толку.
Существуют тысячи лабораторных тестов, и их результаты могут означать разные вещи. Но несколько общих рекомендаций могут помочь пролить свет.
Как врачи используют лабораторные анализы?
Никто не любит, когда его ткнут иглой или пописывают в чашку. Но лабораторные тесты — важные инструменты, и врачи используют их по-разному:
- Чтобы проверить, как вы себя чувствуете в целом, например, тесты на холестерин или сахар в крови, когда у вас есть физический
- Чтобы ответить на конкретный вопрос, например «У вас фарингит?»
- Чтобы отследить текущее состояние или посмотреть, как работает лечение
Сколько времени нужно, чтобы получить результаты?
Это зависит от теста.Некоторые из них можно сделать прямо в офисе или в ближайшей лаборатории, так что вы можете получить результаты сегодня или на следующий день. Другие тесты могут занять несколько дней или недель, особенно если их нужно отправить в определенную лабораторию.
Прежде чем покинуть кабинет врача, спросите, когда вы узнаете результаты. И попросите сотрудников офиса сообщить вам, когда они появятся. (Некоторые офисы могут не звонить, если вы этого не запрашиваете, особенно если результаты находятся в нормальном диапазоне. В некоторых офисах также есть возможность разрешить доступ в вашу лабораторию. результаты на порталах пациентов)
Что означают мои результаты?
Вот несколько вещей, на которые следует обратить внимание:
Положительный vs.Отрицательный. Некоторые лабораторные тесты дают ответ на вопросы типа «да» или «нет», например, беременны ли вы или имеете определенные виды инфекций. Эти результаты обычно записываются как «положительные» или «отрицательные». В этом случае положительный результат не обязательно означает «хорошо», а отрицательный — не обязательно означает «плохо». Вместо этого:
- Положительный результат: Лаборатория нашла то, на что проверял ваш врач. Так что, если у вас был тест на фарингит, положительный результат означает, что у вас фарингит.
- Отрицательный: Лаборатория не нашла то, на что вы проходили тестирование.Отрицательный результат для стрептококкового горла означает, что лаборатория не обнаружила в образце стрептококковых бактерий, так что у вас его, вероятно, нет.
Иногда результат может быть «неубедительным». Это означает, что в лаборатории нет однозначного ответа «да» или «нет» на основе вашей выборки. Ваш врач может попросить вас сделать тест еще раз или провести другой тест.
Справочные диапазоны. Многие результаты лабораторных тестов не дают четких ответов. Вместо этого они отображаются в виде числа — например, вашего уровня холестерина.
Эти числа сами по себе ничего не значат, поэтому вам нужно сравнить ваше значение с нормальным диапазоном, который называется «эталонным диапазоном» или «эталонным значением». Вы увидите этот диапазон в результатах лабораторных тестов.
Всегда ли верны результаты лабораторных тестов?
Хотя они должны соответствовать очень высоким стандартам, иногда они могут ошибаться. Например, вы можете получить ложноположительный результат (результаты говорят, что у вас есть условие, на которое вы проходили тестирование, но на самом деле это не так) или ложноотрицательный результат (результаты говорят, что у вас нет условия, но оно действительно есть) .
Многие вещи могут повлиять на результаты некоторых лабораторных тестов, например:
Когда вы получите результаты, спросите своего врача, насколько точен тест. Если ваш врач считает, что ваши результаты могут быть неправильными, он может порекомендовать вам сделать тест еще раз или пройти другой тест.
Что делать, если мои лабораторные результаты не «нормальные»?
Если вы видите в своих результатах такие слова, как «ненормальный», легко забеспокоиться. Но в этом нет ничего необычного. Например, если ваши результаты выходят за пределы контрольного диапазона, это не обязательно может быть проблемой.
Если вы беспокоитесь о своих результатах или у вас есть вопросы, позвоните в офис своего врача. Вы можете поговорить с медсестрой или назначить встречу с врачом, чтобы поговорить о них. Они могут помочь вам понять, что для вас значат ваши результаты.
Советы по лабораторным тестам
Всегда храните копию своих результатов. Это может быть полезно, если вы поменяете врачей, вам нужно показать их специалисту или просто захотите посмотреть на них позже.
Напомните своему врачу, если вы принимаете лекарства или имеете заболевание, которое может повлиять на ваши результаты.Это должно быть в вашей записи, но все же стоит упомянуть об этом.
Скажите честно, если вы не следовали инструкциям. В некоторых лабораторных исследованиях предполагается, что вы должны голодать (не есть) или не выполнять определенные действия, есть определенные продукты или принимать определенные лекарства.





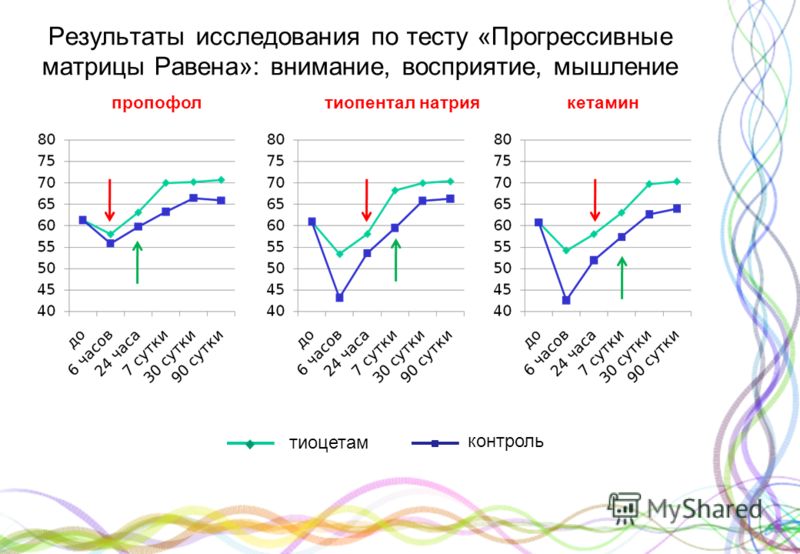
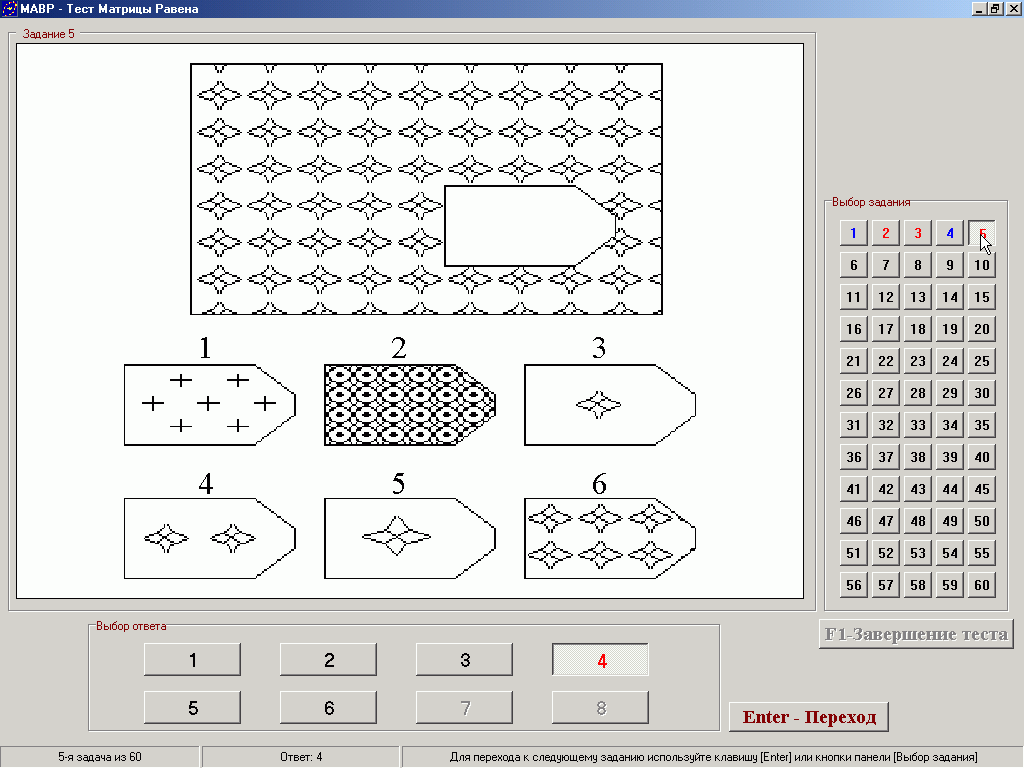
 При этом принцип остается тем же. Чтобы исключить влияние стресса, рекомендуется практиковаться на всех доступных типах логических задач.
При этом принцип остается тем же. Чтобы исключить влияние стресса, рекомендуется практиковаться на всех доступных типах логических задач.
 .
.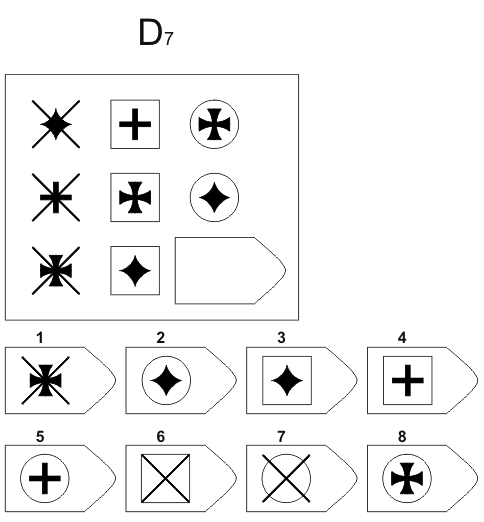 е. суммировать квадраты отклонений от среднего, а затем разделить на количество баллов). Это число называется дисперсией.
е. суммировать квадраты отклонений от среднего, а затем разделить на количество баллов). Это число называется дисперсией.
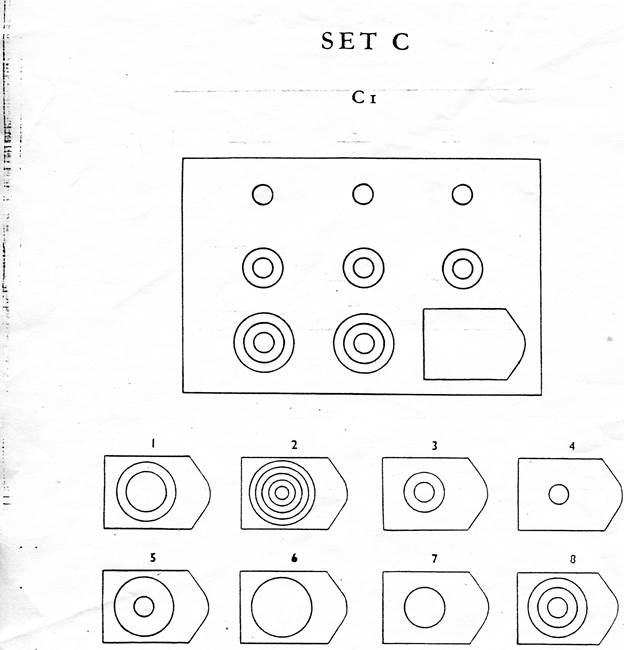 00 до 1.00
00 до 1.00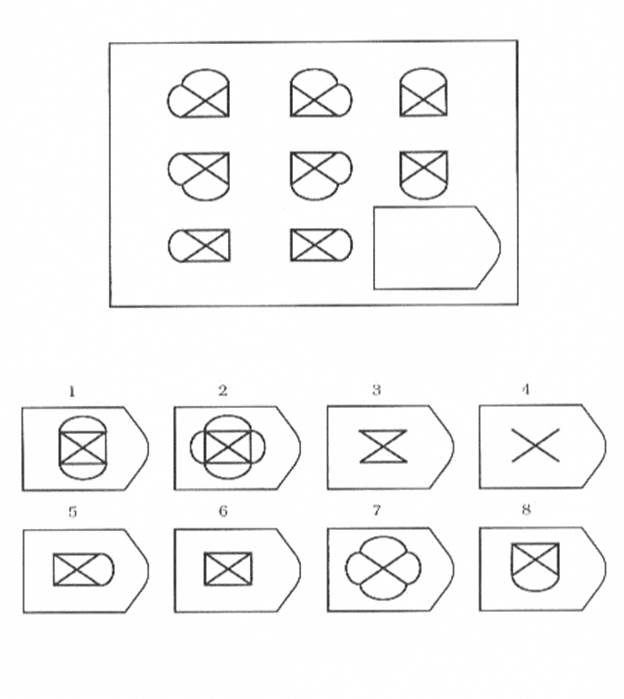 , знание того, как вычислять интегралы)
, знание того, как вычислять интегралы)