Истинное значение: истинное значение | это… Что такое истинное значение?

истинное значение | это… Что такое истинное значение?

3.4 истинное значение: Значение, к которому стремится среднее значение единичных результатов испытаний, полученных в нескольких лабораториях (число лабораторий L) при условии, что L неограниченно возрастает (стремится к бесконечности).

Примечание — Для целей данного документа роль истинного значения выполняет принятое опорное значение. Истинное значение зависит от применяемого метода испытаний.

Источник: РМГ 94-2009: Государственная система обеспечения единства измерений. Испытательные лаборатории, осуществляющие контроль качества нефти при приемно-сдаточных операциях. Основные требования

3.4.4 истинное значение (true value): Значение, которое идеальным образом определяет величину при тех условиях, при которых эту величину рассматривают.

[ИСО 3534-1]

Примечание — Истинное значение величины — теоретическое понятие, которое обычно не может быть известно точно (ЕН 1540 [2]).

Источник: ГОСТ Р ИСО 15202-1-2007: Воздух рабочей зоны. Определение содержания металлов и металлоидов в твердых частицах аэрозоля методом атомной эмиссионной спектрометрии с индуктивно связанной плазмой. Часть 1. Отбор проб оригинал документа

Истинное значение (true value): Значение, которое идеальным образом характеризует величину или количественную характеристику при тех условиях, при которых эту величину или количественную характеристику рассматривают.

Примечание — Истинное значение величины или количественной характеристики является теоретическим понятием и, в общем, его нельзя определить точно.

[ИСО 3534-2:2006, определение 3.2.5] [11]

Источник: ГОСТ Р ИСО 20552-2011: Воздух рабочей зоны. Определение паров ртути. Отбор проб с получением амальгамы золота и анализ методом атомной абсорбционной или атомной флуоресцентной спектрометрии оригинал документа

3.4 Истинное значение: значение, к которому стремится среднее значение единичных результатов испытаний, полученных в нескольких лабораториях (число лабораторий

L) при условии, что L неограниченно возрастает (стремится к бесконечности). Истинное значение зависит от применяемого метода испытаний (ГОСТ Р 8.580).

Примечание: для целей данного документа роль истинного значения выполняет принятое опорное значение.

Источник: РД 08.00-74.30.10-КТН-001-1-03: Испытательные лаборатории, осуществляющие контроль качества нефти при приемо-сдаточных операциях. Основные требования

3.43 ИСТИННОЕ ЗНАЧЕНИЕ: Значение физической величины, измеряемой прибором (МЭК 60731).

Источник: ГОСТ Р МЭК 60580-2006: Изделия медицинские электрические. Измерители произведения дозы на площадь оригинал документа

3.5 истинное значение (true value): Значение, характеризующее величину, определенную совершенным образом для рассматриваемых условий.

Примечание — Истинное значение величины — идеальное понятие и, следовательно, не может быть известно точно.

[Международный электротехнический словарь, статья 301-08-02]

Источник: ГОСТ Р МЭК 61207-1-2009: Газоанализаторы. Выражение эксплуатационных характеристик. Часть 1. Общие положения оригинал документа

3.1.25 истинное значение (true value): Значение, идеально характеризующее конкретную физическую величину при условиях, существующих в момент рассмотрения данной величины [МЭК 359,4.1].

Источник: ГОСТ Р МЭК 61557-1-2005: Сети электрические распределительные низковольтные напряжением до 1000 В переменного тока и 1500 В постоянного тока. Электробезопасность. Аппаратура для испытания, измерения или контроля средств защиты. Часть 1. Общие требования оригинал документа

3.4.5 истинное значение (true value): Значение, которое идеальным образом определяет величину при тех условиях, при которых эту величину рассматривают.

[ИСО 3534-1] [7]

Примечание — Истинное значение величины — теоретическое понятие, которое обычно не может быть известно точно; см. ЕН 1540 [4].

Источник: ГОСТ Р ИСО 15202-3-2008: Воздух рабочей зоны. Определение металлов и металлоидов в твердых частицах аэрозоля методом атомной эмиссионной спектрометрии с индуктивно связанной плазмой. Часть 3. Анализ оригинал документа

3.5.7 истинное значение (true value): Значение, которое идеальным образом определяет величину при тех условиях, при которых ее рассматривают.

Примечание — Истинное значение величины — теоретическое понятие, и оно не может быть известно точно.

Источник: ГОСТ Р ИСО 21438-1-2011: Воздух рабочей зоны. Определение неорганических кислот методом ионной хроматографии. Часть 1. Нелетучие кислоты (серная и фосфорная) оригинал документа

5.5

истинное значение: Значение, которое определяет параметры характеристики, существующей в точно определенных условиях.

Примечание 1 — Истинное значение является теоретическим понятием и не может быть определено с абсолютной точностью.

Примечание 2 — Адаптировано из ИСО 3534-2.

Источник: ГОСТ Р ИСО 8000-102-2011: Качество данных. Часть 102. Основные данные. Обмен данными характеристик. Словарь оригинал документа

Смотри также родственные термины:

3.2. истинное значение (величины)

Значение, которое идеальным образом определяет величину при тех условиях, при которых эту величину рассматривают [п. 1].

Примечание — Истинное значение — теоретическое понятие, которое нельзя определить точно

Определения термина из разных документов: истинное значение (величины)

Источник: ГОСТ Р 50779.10-2000: Статистические методы. Вероятность и основы статистики. Термины и определения оригинал документа

2.4.7 истинное значение величины : Значение величины, которое идеальным образом отражает положение на соответствующей ей шкале реализации количественного свойства конкретного объекта деятельности.

Определения термина из разных документов: истинное значение величины

Источник: РМГ 83-2007: Государственная система обеспечения единства измерений. Шкалы измерений. Термины и определения

3.1.3 истинное значение массы: Значение, идеально характеризующее массу гири.

Определения термина из разных документов: истинное значение массы

Источник: ГОСТ 7328-2001: Гири. Общие технические условия оригинал документа

Словарь-справочник терминов нормативно-технической документации. academic.ru. 2015.

Истинное значение — физическая величина

Cтраница 1

Истинное значение физической величины

— это значение, идеально отражающее свойства объекта как количественно, так и качественно. Оно является той абсолютной истиной, к которой стремятся, пытаясь выразить ее числовым значением.  [1]

Истинное значение физической величины идеальным образом отражает свойства данного объекта. Оно не зависит от средств нашего познания и является абсолютной истиной, к которой мы стремимся, повышая качество измерений.  [2]

Истинное значение физической величины — значение физической величины, которое стремятся найти в соответствии с поставленной задачей и которое абсолютно верно отражало бы эту величину.  [3]

Истинное значение физической величины — значение физической величины, которое идеальным образом отражает в качественном и количественном отношениях соответствующее свойство данного объекта.

Истинное значение практически недостижимо.  [4]

Истинное значение физической величины определяется как такое значение, которое идеальным образом отражало бы в качественном и количественном отношениях соответствующее свойство объекта.  [5]

Истинное значение физической величины практически неизвестно. Поэтому при расчете погрешностей вместо истинного значения измеряемой величины приходится применять действительное значение, найденное экспериментально и столь близкое к истинному, что для данных целей измерений может использоваться вместо него.  [6]

Истинное значение физической величины может быть получено только D результате бесконечного процесса измерений с бесконечным совершенствованием методов и средств измерений. Для каждого уровня развития измерительной техники мы можем знать только действительное значение физической величины, которое применяется вместо истинного значения физической величины.  [7]

Истинное значение физической величины определяется как такое значение, которое идеальным образом отражало бы в качественном и количественном отношениях соответствующее свойство объекта.  [8]

Истинное значение физической величины также может быть получено только в результате бесконечного процесса измерений с бесконечным совершенствованием методов и средств измерений. Для каждого уровня развития измерительной техники мы можем знать только действительное значение физической величины, которое является аналогом понятия относительной истины и применяется вместо истинного значения физической величины.  [9]

Истинное значение физической величины не может быть достигнуто.  [10]

Истинное значение физической величины — значение величины, которое идеальным образом отражает в качественном и количественном отношениях соответствующее свойство объекта.  [11]

Истинным значением физической величины называется значение физической величины, которое идеальным образом отражало бы в качественном и количественном отношениях соответствующее свойство объекта. Определить экспериментально его невозможно вследствие неизбежных погрешностей измерения. Погрешность — это отклонение результата измерения от истинного значения измеряемой величины ( подробно о погрешностях — в гл. Положим, что измеряется диаметр круглого диска. Не вызывает сомнения положение, что измерение диаметра диска можно проводить со все более и более высокой точностью, стоит лишь выбрать средство измерений соответствующей точности. Но когда погрешность средства измерения достигнет размеров молекулы, обнаружится как бы размывание краев диска, обусловленное хаотическим движением молекул. Вследствие этого за некоторым пределом точности само понятие диаметра диска потеряет первоначальный смысл и дальнейшее повышение точности измерения бесполезно. Следовательно, понятие истинного значения диаметра в данном случае приобретает вероятностный смысл и можно лишь с определенной вероятностью установить интервал значений, в котором оно находится.  [12]

Истинным значением физической величины называется значение физической величины, которое идеальным образом отражало бы в качественном и количественном отношениях соответствующее свойство объекта. Поскольку истинное значение недостижимо, вместо него используют действительное значение.  [13]

Истинным значением физической величины называется значение физической величины, которое идеальным образом отражало бы в качественном и количественном отношениях соответствующее свойство объекта. Определить экспериментально его невозможно вследствие неизбежных погрешностей измерения. Вместо истинного значения при эксперименте получают действительное значение физической величины, степень приближения которого к первому зависит от цели эксперимента и выбранной точности измерительного средства.  [14]

Поскольку истинное значение физической величины неизвестно, то на практике пользуются ее действительным значением. Для рабочего СИ за действительное значение принимают показания рабочего эталона низшего разряда ( допустим, 4-го), для эталона 4-го разряда, в свою очередь, — значение величины, полученное с помощью рабочего эталона 3-го разряда.  [15]

Страницы:      1    2    3    4

2.1 Истинное значение измеряемой величины

Приведенные выше данные показывают, что, строго говоря, измерения истинного значения любой величины невозможно в принципе. Поэтому более корректный способ представления результата любого измерения состоит в том, что экспериментатор указывает свою наилучшую оценку измеряемой величины, а также интервал, в котором, как он уверен, она лежит. Таким образом, задача экспериментатора состоит в том, чтобы уменьшить влияние погрешностей за счет правильной техники измерений, сделать правильную наилучшую оценку результата измерения и величины погрешности этого результата.

Рассмотрим случай, когда систематические ошибки отсутствуют, а имеют место лишь случайные погрешности. Предположим, что нами произведено n измерений некоторой величины х, при этом получены n значений этой величины х₁х₂х_i…. х_n. Округлим эти величины с учетом приборной ошибки и расположим в порядке возрастания. Определим в полученном множестве значений количество повторов (выпадений) отдельных результатов — ∆n_i и вычислим вероятности их выпадения по формуле:

(2)

Полученные результаты также внесем в таблицу и построим на их основе график (рис.1) зависимости вероятности повторов отдельных результатов измерения от их величины — х_i, т.е. функцию .

P_max

х_i

х_в.

Рис. 1.

Из полученного рис.1 видно, что наиболее вероятным является некоторый результат х_i= х_в, которому соответствует максимальное значение вероятности выпадения P_max.

Если этот результат (х_в) принять за истинный (Хв = Хи), то абсолютную ошибку каждого измерения ∆х_i, можно найти из выражения: ∆х_i= х_i,- х_в и более того истинный результат измерения, очевидно, должен удовлетворять условию:

∆х_i= х_i,- х_в=0 (3)

В этом можно убедиться, рассчитав абсолютные ошибки всех измерений, числа повторов каждой ошибки ∆n₀ и вероятности выпадения ошибок

Кроме того, как следует из работ немецкого математика Г. Гаусса, все обсуждаемые выше закономерности наблюдаются на рис 2.

-∆x 0 +∆x_i

Рис. 2.

Для повышения точности и снижения трудоемкости Гаусс предложил для нахождения истинного значения измеряемой величины использовать квадратичную функциональную зависимость вероятности ошибок в виде (4) изображенную на рис.3.

(4)

y

0 (∆х_j)²

Рис.3.

Известно, что для нахождения экстремума функции необходимо приравнять нулю ее производную. Используем для этого новую функцию (4):

Возьмем производную от этой функции и приравняем её нулю.

(5)

После несложных преобразований получаем:

(6)

Таким образом, наиболее вероятным значением измеряемой величины является среднее арифметическое , получаемое от нескольких идентичных измерений. И этот же результат соответствует истинному значению многих измерений, представленных на Рис. 1.

Учитывая вышеизложенное, можно рекомендовать следующий алгоритм обработки результатов прямых измерений.

1. Из-за наличия погрешностей никогда не следует ограничиваться одиночным измерением, а всегда следует проводить несколько опытов желательно нечетное число (три, пять).

2. Определить наилучшее значение измеряемой величины х, как среднее арифметическое из всех результатов измерений: х₁, х₂ … х_i … х_n по формуле:

(7)

3. Вычислить случайную абсолютную ошибку каждого измерения по уравнению (3):

= Хi — Хи

а затем среднюю абсолютную погрешность:

(8)

4. Определить приборную погрешность, используя паспортные данные прибора или, при их отсутствии, принять за погрешность половину наименьшего деления шкалы стрелочного прибора или наименьший разряд цифрового прибора.

5. Сравнить приборную и среднюю абсолютную погрешность, выбрать большую из них, приняв за полную погрешность результаты измерения.

Окончательный результат можно представить в виде: Это означает, что истинное значение лежит в интервале . ???

Абсолютная погрешность не полностью характеризует точность проведенных измерений. Например, абсолютная ошибка в 1 мм при измерении отрезков длиной 5 м и 5 мм в относительных единицах будет существенно разной. Поэтому кроме абсолютной ошибки используют и относительную погрешность

, (9)

В этом виде ε это безразмерная величина. Часто её выражают в процентах. Тогда вместо (9) запишем

(10)

В приведенном примере относительные ошибки составят 0,1% и 20%. Это, безусловно, большое различие, хотя абсолютная ошибка одинакова. Относительная ошибка дает больше информации о точности и позволяет сравнивать погрешности измерений разных величин.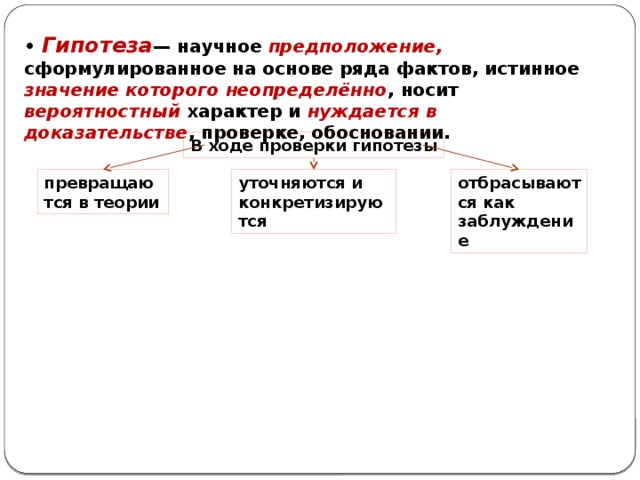

Почему нельзя при из­мерениях определить истинное значение (Реферат)

Содержание:

1. Классификация ошибок измерений
2. Согласно условиям появления средств измерений
3. В зависимости от условий и режимов измерения

Предмет:	Метрология
Тип работы:	Реферат
Язык:	Русский
Дата добавления:	14.09.2019

 

 

 

 

• Данный тип работы не является научным трудом, не является готовой выпускной квалификационной работой!
• Данный тип работы представляет собой готовый результат обработки, структурирования и форматирования собранной информации, предназначенной для использования в качестве источника материала для самостоятельной подготовки учебной работы.

Если вам тяжело разобраться в данной теме напишите мне в whatsapp разберём вашу тему, согласуем сроки и я вам помогу!

 

По этой ссылке вы сможете найти много готовых рефератов по метрологии:

 

Много готовых рефератов по метрологии

 

Посмотрите похожие темы возможно они вам могут быть полезны:

 

Введение:

 

Любой процесс измерения, независимо от условий, в которых он выполняется, связан с ошибками, которые искажают представление о фактическом значении измеряемой величины.

Источниками погрешностей в измерениях могут быть различные факторы, основными из которых являются несовершенство конструкции средств измерений или принципиальная схема метода измерения, неточность изготовления средств измерений, несоблюдение внешних условий при измерениях, субъективных ошибках.

Степень приближения результата измерения к истинному значению определяется величиной ошибки (разницы между значением, полученным в ходе измерения, и истинными значениями величины), то есть качество измерений составляет характеризуется своими ошибками.

Поскольку истинное значение измеренного значения остается неизвестным, ошибки измерения также неизвестны. Поэтому для определения размера ошибок используют условно истинное значение физической величины, полученное, как правило, в результате более точных измерений или других методов. Единицы физических величин воспроизводятся с высокой точностью с использованием государственных первичных стандартов и передаются «вниз» на стандартные измерительные приборы, а от них — на рабочие измерительные приборы с некоторой потерей точности на каждом этапе передачи (во время каждой проверки). В этом случае значение значения, воспроизводимого стандартным измерительным прибором во время проверки, всегда принимается как условно истинное значение значения, и из него оценивается точность проверенного лица. Калибровка средств измерений — это определение метрологическим телом ошибок в средствах измерений и установление их пригодности для использования.

Изучение причин ошибок и уменьшение их размера является одной из основных задач практической метрологии, поэтому понятие «ошибка» является одним из центральных в метрологии.

Классификация ошибок измерений

По форме представления

Ошибки делятся на абсолютные, относительные и уменьшенные.

Абсолютная ошибка ? Измерения, выраженные в единицах измеряемой величины, представляют собой разницу между измеренными и истинными (действительными) значениями измеренной величины:

Абсолютная погрешность измерительного прибора соответствует указанному определению, но для меры и измерительного прибора она не имеет одинакового значения. Абсолютной ошибкой меры является разница между номинальным значением меры и истинным (реальным) значением воспроизводимой им величины. Абсолютная погрешность измерительного устройства представлена ​​разницей между показаниями прибора и истинным (фактическим) значением измеренного значения. Индикация устройства — значение измеряемой величины, определяемое считывающим устройством.

Относительная ошибка представлена ​​отношением абсолютной ошибки к истинному (фактическому) значению измеренной величины и выражается в процентах или долях измеренной величины:

Приведенная погрешность (для измерительного устройства) представляет собой отношение абсолютной погрешности к нормирующему значению :

Нормализующее значение, в зависимости от типа измерительного устройства, принимается равным пределу измерения (в случае, если нижний предел равен нулевому значению односторонней шкалы устройства). В случае двузначного считывающего устройства (в узком смысле — шкала) прибора нормализующее значение присваивается диапазону измерений.

Согласно условиям появления средств измерений

различать первичные и вторичные ошибки. Каждый измерительный прибор предназначен для работы в определенных условиях, указанных в нормативно-технической документации. В этом случае нормальные условия использования измерительных приборов, то есть условия, при которых значения, влияющие на погрешности данного измерительного прибора, находятся в пределах нормального диапазона значений, а рабочие условия использования являются рабочими условиями. при котором значения влияющих величин находятся за пределами нормального диапазона, но находятся в пределах рабочих зон. Погрешность измерительного прибора, определяемая в нормальных условиях, называется основной. Ошибка из-за вывода значений влияющих величин за пределы нормальных значений называется дополнительной. Обычно различают дополнительные ошибки по отдельным влияющим величинам (дополнительная температурная ошибка, дополнительная ошибка из-за изменений атмосферного давления). Как правило, наиболее значимым влияющим значением является температура окружающей среды.

Для оценки дополнительных ошибок в документации на измерительный прибор обычно указывают скорость изменения показаний, когда условия измерения выходят за рамки нормальных.

В зависимости от условий и режимов измерения

Статика называется ошибкой, которая не зависит от скорости изменения измеренного значения во времени. Примером статической ошибки является аддитивная ошибка квантования, которая возникает в дискретных измерительных преобразователях, которая не зависит ни от абсолютного значения преобразованной величины, ни от ее скорости изменения во времени.

Статическая погрешность измерительного прибора возникает при измерении с его помощью постоянного значения. Если в паспорте на измерительный прибор указаны предельные погрешности измерения, определенные в статических условиях, то они не могут характеризовать точность его работы в динамических условиях.

Динамический называется ошибкой, в зависимости от скорости изменения измеренного значения во времени. Возникновение динамической ошибки обусловлено инерцией элементов измерительной схемы измерительного прибора. Тем, что преобразования в измерительной цепи не происходят мгновенно, а занимают некоторое время.

Динамическая погрешность измерительного прибора — это разница между погрешностью измерительного прибора в динамических условиях и его статической погрешностью, соответствующей значению значения в данный момент времени. При разработке или проектировании измерительных приборов следует учитывать, что увеличение погрешности измерения и задержка появления выходного сигнала связаны с изменением условий.

В зависимости от причины и места возникновения

Ошибки делятся на следующие группы: инструментальные, методологические, субъективные.

Инструментальная ошибка — это ошибка используемого измерительного прибора. Если используется стандартный измерительный прибор, прошедший проверку, то интервал, в котором находится эта ошибка, известен с заданной вероятностью.

Методологическая ошибка обусловлена ​​несовершенством применяемого метода измерений. На его значение влияют несовершенство принятой модели измерения, метод применения измерительного инструмента, алгоритмы, по которым вычисляется результат измерения и другие факторы, не связанные со свойствами применяемого измерительного инструмента. Методологическая ошибка не может быть указана в нормативно- технической документации на используемый измерительный прибор, поскольку она не зависит от нее и должна определяться в каждом конкретном случае специальными исследованиями (анализом измерительной схемы). Несовершенство используемого метода измерения (неправильная оценка возникающей методологической ошибки) неоднократно приводило к ошибочным выводам при проведении исследований. Например, для оценки внутренних напряжений при затвердевании бетона использовались мембранные датчики с деформируемостью, в несколько раз превышающей деформируемость бетона. В результате было измерено не самое высокое внутреннее давление, а остаточное давление при контакте с мембраной после ее деформации.

Субъективная ошибка ( ошибка оператора) обусловлена ​​недостаточной квалификацией или индивидуальными характеристиками оператора, выполняющего измерения, и связана с тщательным выполнением правил всех операций измерения. Эта ошибка не всегда поддается правильной оценке. Эта ошибка практически отсутствует при использовании автоматических или автоматических измерительных приборов. В большинстве случаев субъективные ошибки являются случайными, но некоторые из них, связанные с идентичностью оператора, могут быть систематическими.

В отдельной группе ошибки определяются из-за влияния внешних условий. Температура, влажность, давление и другие факторы влияют на величину инструментальных и методических ошибок. В этом случае дополнительная инструментальная ошибка, вызванная отклонением от нормальных условий любого влияющего фактора, может быть указана в метрологических характеристиках измерительных приборов (в дополнение к основной, определенной в нормальных условиях). Влияние внешних факторов на методологическую ошибку следует оценивать отдельно в каждом конкретном случае. Для большинства типов измерений влияние температуры окружающей среды наиболее полно изучено и может быть учтено при определении ошибок. Ошибки внешних условий по характеру проявления являются систематическими .

Под влиянием совокупности всех действующих факторов, в том числе внешних, общая погрешность измерений

Влияние каждого фактора можно изучать отдельно, но для исследования и оценки ошибки удобно разделить общую ошибку на две составляющие: случайную и систематическую , принципиально различную по характеру проявления и требующую использования различных методов для их обнаружения, оценки и бухгалтерский учет.

Случайная ошибка — компонент ошибки измерения, случайным образом изменяющийся (по знаку и значению) в серии повторных измерений одинакового размера физической величины, проводимых с одинаковой тщательностью в одинаковых условиях. При появлении таких ошибок закономерностей не наблюдается, они обнаруживаются при повторных измерениях одного и того же значения в виде определенного разброса полученных результатов. Случайные ошибки неизбежны, неустранимы и всегда присутствуют в результатах измерений. Описание случайных ошибок возможно только на основе теории вероятностей и математической статистики.

В отличие от систематических, случайные ошибки не могут быть исключены из результатов измерений путем внесения поправок. Тем не менее, они могут быть существенно снижена за счет увеличения числа измерений, как среднее арифметическое значение х, таким образом, имеет тенденцию к истинному значению измеряемой величины Q .

Систематическая ошибка является компонентом ошибки измерения, которая остается постоянной или естественным образом изменяется при повторных измерениях одной и той же физической величины. Систематическая ошибка, как правило, не изменяется во время нескольких измерений и может быть почти полностью устранена путем выявления и устранения причины ее возникновения или внесения поправки. Но систематическая ошибка также содержит некоторый элемент случайности и в некоторой степени обладает свойствами случайной величины. Исходя из этого, предлагается рассматривать систематическую ошибку как конкретную «выраженную» случайную величину. Он также может изменяться во время нескольких измерений, когда временной фактор или нестабильность измерительной системы вносит заметные изменения в систему.

Следует учитывать, что очевидно, что в ходе скрытых измерений присутствует ряд систематических ошибок по своей природе. Поэтому не всегда возможно четко разделить ошибки на систематические и случайные. Некоторые систематические ошибки, которые трудно объяснить, считаются случайными. Чем больше результаты измерений искажаются неучтенными систематическими ошибками, тем сложнее их математически обрабатывать. Это в определенной степени объясняет дискуссии, которые ведутся в последние годы вокруг новой концепции «неопределенности измерений».

Грубые неточности и ошибки

Во время измерений также могут появляться очень большие грубые ошибки (погрешности) , которые возникают, как правило, из-за ошибок или неправильных действий оператора, а также из-за кратковременных отказов или неисправностей измерительных приборов и других внезапных изменений. в условиях измерения. Грубые ошибки обнаруживаются и отбрасываются непосредственно в процессе измерения или во время математической обработки результатов измерения с использованием специальных критериев.

Наиболее характерными из них являются: неправильный подсчет на шкале измерительного прибора, неправильная запись результата наблюдения (скольжения), неправильная запись значений отдельных мер использованного набора. Ошибки при работе с приборами , если они повторяются во время измерений.

Причинами грубых ошибок могут быть внезапные или кратковременные изменения условий измерения или необнаруженные неисправности в оборудовании.

Оценка наличия грубых ошибок решается методами математической статистики — статистической проверкой гипотез. Суть метода заключается в следующем. В отношении результата измерения выдвигается нулевая гипотеза, которая вызывает некоторые сомнения и считается грубой ошибкой из-за большого отклонения от других результатов измерения. Более того, нулевой гипотезой является утверждение о том, что «сомнительный» результат действительно относится к возможной комбинации результатов измерений, полученных в этих условиях, и такой результат, вероятно, будет получен.

Используя определенные статистические критерии, они пытаются опровергнуть нулевую гипотезу. Пытаются доказать ее практическую неправдоподобность. Если это удается, то ошибка исключается, если нет, то результат измерения остается.

Выбор того или иного критерия основан на принципе практической определенности. Для этого достаточно низкая вероятность д из того факта , что сомнительный результат действительно может иметь место дается. Вероятность q называется уровнем значимости и обычно выбирается из ряда: 0,1; 0,05; 0,01.

Для заданного q определяется критический диапазон критерия для проверки нулевой гипотезы. Если значение критерия попадает в эту область, то гипотеза отклоняется.

Известен ряд критериев, позволяющих устранить грубые ошибки. К ним, в частности, относятся критерии Греббса (Смирнова), Шарлье, Шовена, Диксона и других. Эти критерии основаны на статических оценках параметров распределения, поскольку в большинстве случаев фактические значения параметров распределения неизвестны.

Измерения и их ошибки в конструкции

Одним из самых популярных видов измерений в строительной отрасли являются линейно-угловые измерения. Они выполняются при оперативном контроле параметров большинства строительных процессов, а также при приемочном контроле и обеспечивают изготовление изделий и возведение конструкций с заданными размерами. Соблюдение указанных допусков по геометрическим параметрам зависит от точности измерений.

Точность линейных измерений также является основой для возможности точных измерений других величин (сила, давление, твердость).

В строительстве Унифицированная система допуска и посадки, разработанная для станкостроения и машиностроения, не находит применения, а оптико-механические и высокоточные оптические приборы, используемые в этих отраслях, практически не используются.

Необходимость измерения небольших (до 1 мм) линейных размеров и смещений возникает при испытании строительных материалов и конструкций (измерение деформации). Для этих целей широко используются зубчатые измерительные головки со значением деления шкалы 0,01 или 0,001 мм, которые устанавливаются непосредственно на испытуемый образец.

Механические тензодатчики или тензодатчики, приклеенные к поверхности образца или конструкции, также используются. Простейшие измерительные микроскопы или измерительные петли используются для измерения ширины трещин.

Как правило, средства, используемые для измерения деформаций, имеют определенный запас точности. Предельная погрешность измерения в несколько раз меньше допустимой, а выбор измерительного инструмента не вызывает затруднений и полностью определяется конкретные условия измерения.

Измерения линейного угла, выполняемые непосредственно на строительной площадке при контроле геометрических параметров при строительстве зданий и сооружений, проводятся в диапазоне от 1 мм до нескольких десятков метров. Требования к измерительным приборам: надежность, простота, скорость, устойчивость к внешним воздействиям. Допустимая относительная погрешность измерения находится в диапазоне 0,01 … 20%. Допуски на установку определенных элементов строительных конструкций назначаются не только исходя из функциональных требований, но часто определяются точностью используемых измерительных инструментов и совершенством используемых выравнивающих устройств. Поэтому выбор средств измерений для строительной площадки является важнейшей задачей.

Наиболее широко используются линейные меры длины (линейки, рулетки, фальцевальные счетчики), квадраты, пузырьковые уровни, а также оптические и электронные приборы для съемки. Штангенинструмент и микрометры используют реже.

Измерительные металлические линейки имеют длину 150, 300, 500 и 1000 мм. Цена деления шкалы, как правило, составляет 1 мм. Отклонения от общей длины линейок и расстояний от любого хода до начала и конца шкалы их номинального значения не должны превышать 0,1 мм при длине до 300 мм; 0,15 мм на длину 300 … 500 мм; 0,2 мм на длину 500 … 1000 мм.

Измерительные металлические рулетки типов RS и RJ имеют длину 1, 2, 3 м; тип РЗ — 2, 5, 10, 20, 30, 50, 75, 100 м. В зависимости от типа, класса точности (1, 2 и 3) и длины ленты измеряются допустимые отклонения их фактической длины: 0,4 … 7 мм по всей длине колеса рулетки; 0.2..0.4 мм — для единиц измерения и дециметра; 0,1 … 0,3 мм — на сантиметр; 0,05 … 0,2 мм — на миллиметр. При измерении с помощью рулеток общая погрешность измерения состоит из погрешности градуировки шкалы, погрешности считывания, погрешности температуры, а также ошибок, вызванных непараллельностью шкалы рулетки и оси продукта, провисанием колеса рулетки. или его удлинение из-за напряжения.

Проверка линейных показателей длины выполняется путем сравнения их с эталонной мерой линии. Для сравнения используются компараторы, оснащенные двумя микроскопами с окулярными микрометрами. С их помощью оценивается взаимное расположение штрихов по случайным меркам.

В метрологической практике используются стандартные линейные меры одного метра 1-й и 2-й категорий, стандартные измерительные рулетки 1-й и 2-й категорий, весы 1-й и 2-й категорий. Допустимая погрешность шкалы мерной линейки 1-й категории составляет 0,05 мм, допустимые погрешности шкал первой категории 0,2 … 0,5 мм в зависимости от длины шкалы. Рабочие рулетки и рулетки 2-й категории, как правило, проверяются рулетками 1-й категории с обязательным натяжением ленты силой 50 Н.

Штангенциркули, суппорты, глубиномеры, суппорты. — все это инструменты. Все эти инструменты предназначены для абсолютных измерений линейных размеров и маркировки деталей. Принцип их действия основан на использовании двух шкал — первичной и вторичной. Основная шкала используется для сравнения измеренного размера, дополнительная шкала, называемая нониусом, используется для повышения точности считывания пропорций деления основной шкалы.

Подсчет нониуса основан на способности человеческого глаза более точно оценивать совпадение или несовпадение штрихов двух закрытых шкал, чем при определении доли основной шкалы на глаз.

Штангенциркули изготавливаются с расчетом по нониусу 0,1; 0,05 и реже — 0,02 мм. Основные весы имеют интервал деления 1,0 или 0,5 мм.

Общая погрешность суппорта во многом определяется компонентом, вызванным перекосом подвижной челюсти из-за существующего зазора в направляющих. Этот компонент увеличивается с увеличением длины челюстей. Явление параллакса (явное смещение указателя относительно штрихов шкалы при наблюдении в направлении, не перпендикулярном плоскости шкалы), а также наличие зазора между измерительными поверхностями челюстей также дает важный компонент.

Допустимая погрешность суппортов — 1 деление по Вернье.

Вывод

Калибровка стержневого инструмента выполняется с использованием стандартных плоскопараллельных концевых мер длиной 4-й и 5-й цифр.

ГОСТ 26433.1-89 содержит перечень линейно-угловых измерений, наиболее широко используемых в строительстве, и диаграммы прямых и косвенных измерений большинства геометрических параметров. Предельные погрешности измерения линейных и угловых размеров, параметров формы и относительного положения поверхностей с использованием различных измерительных инструментов также приведены. ГОСТ 26433.2-94 также дает предельные погрешности измерения отклонений от центральных осей, вертикалей, проектных высот и заданного уклона при использовании геодезических приборов. Приведенные данные следует использовать при выборе средств измерений для значения предельной погрешности.

Правила отбора определены в ГОСТ 23616-79 и ГОСТ 26433,0-85. В соответствии с этими документами при монтаже строительных элементов и контроле допусков по геометрическим параметрам должно соблюдаться условие где допуск для контрольного размера.

Обратите внимание, что первое условие, установленное ранее для геодезических измерений, не всегда необходимо и не всегда выполняется на строительной площадке. Например, при контроле линейных размеров с помощью металлических рулеток, а также при контроле вертикальности и проектных отметок с использованием специальных устройств с пузырьковыми уровнями предельная ошибка иногда составляет 50% или более от данного допуска. Более того, использование более точных измерительных приборов экономически нецелесообразно. Очевидно, что требования к размеру предельной ошибки следует дифференцировать в зависимости от типа допуска (технологического или функционального) и возможности коррекции или компенсации полученного отклонения.

Размеры основных допусков для геометрических параметров строительных конструкций приведены в СНиП 3.03.01-87 «Несущие и ограждающие конструкции». Очевидно, что для всех указанных допусков следует рекомендовать методы и средства измерения с учетом условий проведения измерений и допустимой предельной погрешности измерений.

В настоящее время, в связи с внедрением новых высокоточных электронных геодезических приборов в строительной отрасли, можно пересмотреть ряд допусков. Это в первую очередь относится к работе по выравниванию, где допуски на линейные размеры были определены на основе точности измерения с металлическими рулетками.

истинное значение числа π оказалось равно 10

Российским учёным удалось вывести на чистую воду западных математиков, которые более трёх столетий распространяли ложную информацию о настоящем значении числа π. Специалистами «Роснано» было однозначно доказано, что отношение длины окружности к диаметру равно 10, а не 3,14, как считалось ранее.

Специалисты представят результаты своих научных изысканий на Всемирном математическом конгрессе, который должен пройти в Каире в конце 2022 года. Как отмечают эксперты, открытие отечественных учёных является революционным и может стать основой для пересмотра всех основополагающих законов математики.

На сенсацию уже отреагировали политики – по словам депутата Виталия Милонова, если на Западе врали про число π, то и другие так называемые аксиомы могли быть сфальсифицированы.

«Я призываю создать парламентскую комиссию по проверке всех законов математики, открытых западными учёными, и назначить достойное финансирование её работы. Люди заслуживают знать правду», – объявил он.

Комментарии

Alexandr

23 авг. 2022 г., 10:01

А так же заговор физиков – ускорение свободного падения оказалось равным 3,14 м/с 😱

Ответить

Лев Щаранский

23 авг. 2022 г., 10:54

В какой кабинет прибыть начальнику второго отделения?

Ответить

Изя Рабинович

23 авг. 2022 г., 14:02

Ответить

Крайний Банкир

25 авг. 2022 г., 12:39

Слушай, толковый, ты мне фамилию скажи

Ответить

ЕБенилов

23 авг. 2022 г., 11:41

Да чего уж там физики с математиками… лингвисты вон до сих пор скрывают, что пьесы Шекспира написал автор «Слова о полку Игореве»!

Ответить

org/Person»> Холопулкинен

25 авг. 2022 г., 05:34

Это ж-ж-ж неспроста примерно равно пи квадрат

Ответить

И. Роман

23 авг. 2022 г., 10:04

Я как человек с математическим образованием потверждаю. Я сам долго не мог поверить

Ответить

Vyacheslav Spirin

23 авг. 2022 г., 10:05

А истинное имя числа Пи – Щ

Ответить

Unknown

23 авг. 2022 г., 10:10

А косинус в военное время может быть равен 15.

Ответить

Сергей Давыдов

23 авг. 2022 г., 16:26

cos(-3.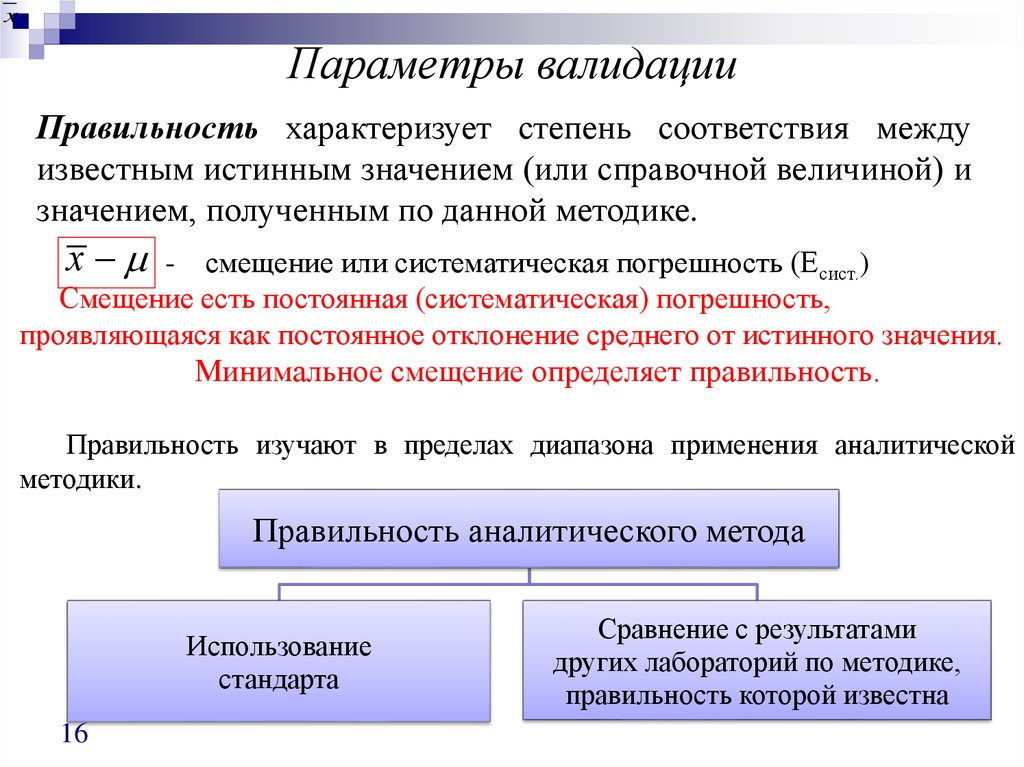 4i) = 15, где i – мнимая единица.

Ответить

Маршал Рыбалко

23 авг. 2022 г., 10:10

Боюсь это открытие носит экономический характер, – при увеличении числа пи до 10 площадь фигур вырастет втрое что приведет к увеличению сборов земельного налога. Да и любой аренды

Ответить

Konstantin

23 авг. 2022 г., 10:10

На самом деле никаких окружностей и диаметров в природе не существует – это все гнусные выдумки врагов России. Наши предки столетиями жили без всяких там диаметров.

Ответить

Unknown

23 авг. 2022 г., 10:12

Так раньше и молоко из пенопласта делали.

Ответить

org/Person»> Vyacheslav Spirin

23 авг. 2022 г., 10:13

Сейчас объясню. Пи- это же отношение длины окружности к её диаметру. С некоторой натяжкой в некоторых срезах это применимо к Земному шару. Но теперь с развитием параллельного экспорта через Китай, оказалось, что отношение это немного другое и длина «окружности» прилично больше. Ввиду предстоящего параллельного экспорта газа через тот же Китай и дальнейшего увеличения числа Пи (ибо окружность получается совсем уж истинной) было принято ешение о бессмысленности маскировки. При Пи (Щ) = 10, никаких проблем не будет ещё очень долго.

Ответить

Полудохлый Электрочайник

23 авг. 2022 г., 10:14

Ты чего! Земля ведь плоская и на трёх слонах стоит!

Ответить

Vyacheslav Spirin

23 авг. 2022 г., 10:14

На трёх слонах, да. Но круглая.

Ответить

legolegs

23 авг. 2022 г., 10:48

Раньше думали, что примерно на трёх слонах, а теперь земля умеренно м твёрдо стоит ровно на 10 слонах.

Ответить

Евгений

24 авг. 2022 г., 09:05

Диаметра нет. Есть только Калибр!

Ответить

23 авг. 2022 г., 10:18

Отрадно,что люди неравнодушны к данному вопросу.

Ответить

Vassis

26 авг. 2022 г., 05:27

Что вы несёте? Ещё Нестор Летописец описывал число Пи, как сокращения от слова Пиздец!

Ответить

26 авг. 2022 г., 05:31

Так в нашем классе Нестора не читали,жили одними догадками. 😁

Ответить

Pronik

23 авг. 2022 г., 10:45

Нужно отказываться от навязанных англицизмов, нужно писать не π(Пи), а Щ(Щи)

Ответить

gLebus

23 авг. 2022 г., 12:19

Неправда ваша – никаких аглицизмов! Пи – эт древняя славянская буквица, обозначающая круглый конец всему.

Ответить

Vyacheslav Spirin

23 авг. 2022 г., 12:29

Грекоцизм же.

Ответить

Арсений

23 авг. 2022 г., 11:46

Заговор учителей русского – жы-шы на самом деле пишется через ы.

Ответить

org/Person»> gLebus

23 авг. 2022 г., 12:16

Это фейк! жы-шы пишыцца через чёрточку. Но в региональных настройках можно заменить разделитель на точку, или запятую.

Ответить

23 авг. 2022 г., 12:05

Как предсказывала Ванга, число Пи – 2022

Ответить

El Tex

23 авг. 2022 г., 12:09

А зачем нужно число Пи? Если земля всё равно плоская?

Ответить

Alexandr

23 авг. 2022 г., 14:22

но это все еще плоский круглый блин! ☺️

Ответить

Александр Николаев

23 авг. 2022 г., 13:18

Так чему равно число пи?

Ответить

org/Person»> Валерий Васильевич

23 авг. 2022 г., 13:30

А как же 2,918291828?

Ответить

Дмитрий

23 авг. 2022 г., 15:35

При измирении окружности талии, число пи равно количеству съеденых пироженок

Ответить

23 авг. 2022 г., 21:15

Группой ученых руководил некто профФессор Рыбников

Ответить

Татьяна Ряжко

23 авг. 2022 г., 23:40

А еще формула воды не Н2О, относительная атомная масса водорода не равна 1, ну и до кучи нашатырный спирт и этиловый спирт это одно и то же вещество. ДНК, кстати, тоже не существует. Уотсон и Крик сфальсифицировали свое открытие. Ну и да, земля плоская, держится на трех слонах, которые стоят на огромной черепахе и покрыта твердью небесной.

Ответить

org/Person»> Telmann

24 авг. 2022 г., 19:54

«Вселенная – вся центр, или центр Вселенной находится везде, а окружность нигде.»

Ответить

Написать комментарий

Истинные и действительные значения физических величин. Погрешность измерения.

1. Главная страница 🏠
2. 📚 Библиотека
3. 👉 Метрология и измерения 👈
4. Дисциплина метрология – шпаргалки к экзамену.
5. org/ListItem»> Истинные и действительные значения физических величин. Погрешность измерения.

Нужна помощь в написании работы?

Узнать стоимость

Причины возникновения погрешностей измерений

При анализе измерений следует четко разграничивать два понятия: истинные значения физических величин и их эмпирические проявления — результаты измерений.

Истинные значения физических величин — это значения, идеальным образом отражающие свойства данного объекта как в количественном, так и в качественном отношении. Они не зависят от средств измерений и являются той абсолютной истиной, к которой стремятся при измерениях.

Напротив, результаты измерений являются продуктами познания. Представляя собой приближенные оценки значений величин, найденные в результате измерений, они зависят от метода измерений, от средств измерений и других факторов.

Погрешностью измерения называется разница между результатом измерения х и истинным значением Q измеряемой величины:

Δ= x – Q                                   (4. 1)

Но поскольку истинное значение Q измеряемой величины неизвестно, то для определения погрешности измерения в формулу (4.1) вместо истинного значения подставляют так называемое действительное значение.

Под действительным значением измеряемой величины понимается ее значение, найденное экспериментально и настолько приближающееся к истинному, что для данной цели оно может быть использовано вместо него.

Причинами возникновения погрешностей являются: несовершенство методов измерений, средств измерений и органов чувств наблюдателя. В отдельную группу следует объединить причины, связанные с влиянием условий проведения измерений. Последние проявляются двояко. С одной стороны, все физические величины, играющие какую-либо роль при проведении измерений, в той или иной степени зависят друг от друга. Поэтому с изменением внешних условий изменяются истинные значения измеряемых величин. С другой стороны, условия проведения измерений влияют и на характеристики средств измерений и физиологические свойства органов чувств наблюдателя и через их посредство становятся источником погрешностей измерений.

Поможем написать любую работу на аналогичную тему

• Реферат

  Истинные и действительные значения физических величин. Погрешность измерения.

  От 250 руб

• Контрольная работа

  Истинные и действительные значения физических величин. Погрешность измерения.

  От 250 руб

• Курсовая работа

  Истинные и действительные значения физических величин. Погрешность измерения.

  От 700 руб

Получить выполненную работу или консультацию специалиста по вашему учебному проекту

Узнать стоимость

Поделись с друзьями

• Содержание
• Меню

Метрология как наука об измерениях

Значение метрологии для научно-технического прогресса и ее роль в народном хозяйстве страны

Кратные и дольные единицы

Относительные и логарифмические величины и единицы

Внесистемные единицы

Наименования и обозначения единиц

Методы измерений

Истинные и действительные значения физических величин.

Погрешность измерения.

Классификация погрешностей измерений в зависимости от характера их изменения

Добавить в избранное (необходима авторизация)

Акции Upstart: когда уляжется пыль, появится истинная ценность

1,7 тыс. подписчиков

Резюме

• Точность моделей Upstart, управляемых искусственным интеллектом, продолжает улучшаться, даже несмотря на то, что скептики сомневаются, что они будут работать в более сложных макроэкономических сценариях.
• В то время как финансирование остается основным препятствием для бизнеса, руководство должно по-прежнему проявлять гибкость в использовании баланса для своих кредитов, чтобы максимизировать свой бизнес в долгосрочной перспективе.
• Автокредиты и кредиты для малого бизнеса обеспечивают долгосрочную перспективу роста по мере того, как компания наращивает свой новый бизнес.
• Моя целевая цена для Upstart – 45,30 доллара США, что подразумевает потенциал роста на 65 % по сравнению с текущими уровнями.

Black_Kira

Как Upstart (NASDAQ:NASDAQ:UPST) поживает в текущих макроэкономических условиях и как его модели справляются с изменениями глобальной макроэкономической среды? Я внимательно изучаю компанию и ее второй квартал, чтобы найти ответы на эти вопросы.

Инвестиционная диссертация

Ранее я написал статью о Upstart, в которой подробно рассказал о бизнес-модели и текущих проблемах, с которыми сталкивается Upstart. Вот некоторые инвестиционные аргументы в пользу компании:

1. Основное преимущество Upstart — превосходная модель искусственного интеллекта (ИИ), которая обеспечивает дополнительную ценность как для потребителей, так и для банковских партнеров. Это конкурентное преимущество продолжает улучшаться, поскольку есть свидетельства того, что точность модели со временем улучшается.
2. Несмотря на то, что компания недавно взяла кредиты на свой баланс, это делается с учетом меняющихся условий ведения бизнеса. Основной бизнес-моделью по-прежнему остается «легкий капитал», поскольку компания выступает в качестве посредника между потребителями и своими банковскими партнерами, что руководство продолжает повторять.
3. Несмотря на сложные условия, Upstart продолжает расширять свой общий адресный рынок (TAM) до огромного рынка выдачи автокредитов, демонстрируя большие рыночные возможности.
4. В результате расширения масштабов и более широкого использования автоматизации в процессах рентабельность и экономическая эффективность компании улучшились, и эта тенденция, вероятно, сохранится.

Модели на основе ИИ продолжают повышать точность и разделение рисков

Было приятно видеть, что руководство раскрывает больше показателей кредитоспособности, а также данные о том, как модели Upstart менялись с течением времени.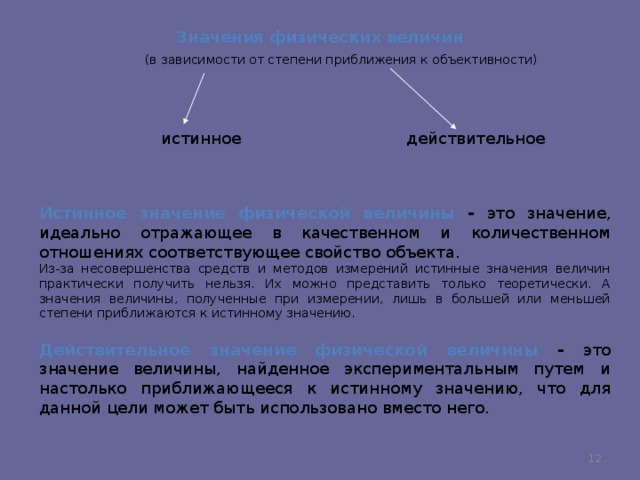 Как видно из приведенной ниже диаграммы, модели Upstart со временем улучшились, особенно за один год с июля 2021 г. по июль 2022 г. Чтобы кратко объяснить, термин «область под кривой» используется руководством для определения того, насколько модель способна разделить кредиты с высоким и низким риском, и он делает это, определяя, какая часть кредитов может быть одобрена на основе указанного максимального уровня потерь. Таким образом, метрика AUC подразумевает, что при значениях AUC, равных 0, это означает, что прогнозы модели на 100% неверны. Что касается модели Upstart, мы видим значительное улучшение модели за последний год.

Точность модели Upstart (слайды Upstart Credit Performance)

Несмотря на то, что руководство постоянно заявляло, что компания совершенствует модели, внося коррективы в модель в соответствии с изменениями в окружающей среде и наблюдая за повышением точности, это раскрытие Показатели AUC с 2018 года дают хорошее представление о том, какого прогресса компания добилась в повышении точности модели за последний год. Таким образом, я считаю, что, основываясь на данных, точность модели существенно улучшается, вопреки шуму, слышимому на рынке, говорящему об обратном.

Кроме того, Upstart по-прежнему показывает в 5 раз лучшее разделение рисков по сравнению с традиционными показателями FICO, что подчеркивает сохраняющееся преимущество Upstart над ним, несмотря на ближайшие проблемы, с которыми он сталкивается.

Лучшее разделение рисков, чем FICO (слайды кредитных показателей Upstart)

Таким образом, я думаю, что модели рисков Upstart, основанные на искусственном интеллекте, работают так, как задумано, и фактически продолжают демонстрировать улучшенную производительность с точки зрения более высокой точности и лучшее разделение рисков. Мы по-прежнему наблюдаем, как компания корректирует и калибрует свои модели в соответствии с изменяющимися условиями, что помогает еще больше повысить надежность и точность модели в меняющиеся времена. Кроме того, я думаю, что руководство предусмотрело в моделях осторожность, скорректировав модели с учетом рецессии в ближайшие 18–24 месяца. Я думаю, что эта осмотрительность в модели будет иметь большое значение для обеспечения более высокой кредитоспособности и повышения эффективности модели в долгосрочной перспективе.

Финансирование остается ограниченным

Как и ожидалось, ограничение финансирования стало основным препятствием для доходов компании в текущем квартале. Поскольку руководство не ожидало, что инвесторы так резко сократят темпы привлечения средств или полностью остановятся, это внезапное изменение аппетита к риску, вызванное проактивной реакцией партнеров из страха перед быстрым спадом в экономике, наносит ущерб компании с точки зрения замедления роста.

В результате Upstart необходимо заполнить этот пробел, чтобы улучшить ограничения финансирования. Хотя изначально компания сообщила, что не собирается быть банком или использовать собственный баланс для финансирования, я думаю, что нам нужно быть гибкими при рассмотрении этого вопроса. С одной стороны, руководство видит в использовании баланса ключевой способ восполнить пробел в финансировании, поскольку они могут использовать огромную информационную асимметрию в своем бизнесе и использовать это в своих интересах, когда его партнеры действуют менее рационально, что приводит к более высокую, чем ожидалось, отдачу от своих активов при одновременном повышении стабильности платформы. С другой стороны, руководство подтвердило свою позицию относительно того, что это не банк, и что этот сдвиг носит несколько временный характер в течение того, что кажется переходным периодом по мере изменения цикла.

Кроме того, хорошо, что руководство работает над улучшением структуры капитала и обеспечением более стабильного финансирования платформы в долгосрочной перспективе. Это повлечет за собой привлечение партнеров, которые имеют долгосрочный горизонт и намерены инвестировать в разные циклы. Пока это находится на начальных этапах, я думаю, что это здорово, что руководство учится на этом текущем цикле, чтобы активно предотвращать это в последующем цикле.

Стоит отметить, что баланс кредитов компании во 2 кв. 2022 г. составил $624 млн, из которых $484 млн были кредитами на исследования и разработки, использованными для их относительно нового автомобильного сегмента. Всего 140 миллионов долларов было выделено на бизнес по кредитованию физических лиц, и это на 10 миллионов долларов меньше, чем в предыдущем квартале. Я подумал, что также обнадеживает тот факт, что руководство продавало значительную часть этих кредитов в сегменте потребительских кредитов, хотя это было сделано после результатов второго квартала.

В завершение, хотя я думаю, что рынок был ошибочно сфокусирован на том факте, что компания берет кредиты на свой баланс, в то время как руководство ранее заявляло об обратном, инвесторы, которые могут не обращать внимания на это и признают, что каждый бизнес должен быть гибким к меняющимся макроэкономическим условиям и реагировать на различные операционные проблемы, чтобы долгосрочная жизнеспособность бизнеса увидела это текущее негативное отношение к Upstart реальной ценной возможностью.

Новые сегменты рынка для роста

Во втором квартале Upstart удалось увеличить количество дилерских центров, использующих программное обеспечение Upstart для автомобильной розничной торговли, до 640. Кроме того, программное обеспечение Upstart для автомобильной розничной торговли было названо «самым быстрорастущим программным обеспечением для цифровой розничной торговли для автодилеров». » по данным автомобильного рынка. Два новых OEM-производителя, Volkswagen (OTCPK:VWAGY) и Subaru, также объявили о поддержке программного обеспечения, помимо многих других брендов и OEM-производителей, которые уже присутствуют на платформе. Сообщалось, что розничный кредит, полученный от авто, составил 10 миллионов долларов в квартале, и, хотя он небольшой, это первые шаги к расширению программы. Существует множество синергий, которые компания может получить при выдаче автокредитов, и одним из примеров является объединение модели машинного обучения, которая использовалась для процесса личных кредитов, для автоматизации проверки доходов. Конечно, без сомнения, есть проблемы, которые компании необходимо будет решить в ближайшие месяцы, чтобы иметь более автоматизированный продукт автокредитования и постоянно улучшать свою модель ИИ для автокредитования. Кроме того, кредиты компании для малого бизнеса также принесли 1 миллион долларов США, когда компания запустила продукт в конце июня.

По мере того, как Upstart внедряет свои новые продукты, она может продолжать использовать то, что она узнала в сегменте потребительских кредитов, чтобы скорректировать и отладить возможную модель, используемую для автокредитов и кредитов для малого бизнеса. Хотя эти новые предприятия могут постепенно вносить свой вклад в бизнес сегодня, они станут будущими драйверами роста для Upstart завтра, поскольку они используют свои модели искусственного интеллекта и машинного обучения для изменения различных сегментов кредита.

Оценка

Существует необходимость скорректировать мою модель DCF для Upstart, поскольку макроэкономическая среда изменилась с тех пор, как я в последний раз писал о компании. В связи со сниженным прогнозом на год и ограничением финансирования, которое, я думаю, может стать ограничивающим фактором для бизнеса в ближайшей перспективе, необходимо понизить прогнозы на 2022 и 2023 годы, чтобы они больше соответствовали текущим условиям бизнеса. Кроме того, я увеличил свои предположения для WACC до 15% и сохранил конечные темпы роста на уровне 1,5% соответственно.

Таким образом, моя целевая цена Upstart составляет $45,30, что подразумевает потенциал роста на 65% по сравнению с текущими уровнями акций. Хотя перспективы Upstart кажутся сложными, основным драйвером или катализатором для акций, на мой взгляд, будет свидетельство улучшения финансирования, которое остается неопределенным в ближайшей перспективе. В долгосрочной перспективе я думаю, что компания продолжит наращивать долю рынка в своем соответствующем сегменте и останется привлекательной как компания, полностью вовлеченная в модель на основе ИИ, которая расширяется в кредитных сегментах. Таким образом, я думаю, что акции будут более привлекательными для инвесторов с более длительным временным горизонтом.

Риски

Макроэкономическая среда

Как и все эмитенты кредита, Upstart также уязвим в неблагоприятной макроэкономической среде. Если глобальная макроэкономическая среда ухудшится, это снизит спрос на кредиты Upstart и, таким образом, повлияет на рост объема кредита в этом сценарии. Учитывая, что компания очень уязвима к кредитным циклам, как и другие компании-аналоги, это риск в краткосрочной перспективе, поскольку глобальный фон кажется неустойчивым и неопределенным.

Конкурентное давление

Хотя модели искусственного интеллекта Upstart в настоящее время имеют преимущество перед аналогами, это может быть подорвано, если конкурент создаст лучшую, более точную и более совершенную модель искусственного интеллекта. Хотя я думаю, что это маловероятно, учитывая постоянное стремление компании к инновациям и улучшению модели, существует множество стартапов и традиционных финансовых игроков, которые пытаются доработать и улучшить свою модель, и поэтому это может быть рискованно, если любой из этих конкурентов успешен.

Риск концентрации

Поскольку бизнес компании в настоящее время в основном сосредоточен на сегменте необеспеченных личных кредитов, в этом сегменте фактически существует риск концентрации. Хотя я упомянул выше, что компания расширяется в сегменте автокредитования, это остается на ранней стадии развития, поскольку компания развертывает и наращивает свой сегмент автокредитования. По крайней мере, в ближайшей перспективе необеспеченные персональные кредиты будут составлять основную часть его доходов по мере расширения бизнеса автокредитов.

Риск исполнения

Аналогично тому, как Upstart развертывает и расширяет автокредиты и другие новые сегменты, существует риск проскальзывания исполнения или риск плохого исполнения. Хотя компания преуспела в сегменте необеспеченных личных кредитов, нет никаких гарантий успеха в других сегментах, в которые она хочет расшириться.

Заключение

В конечном счете, решение об инвестировании в Upstart будет зависеть от уровня комфорта руководства, использующего гибкий и оперативный подход к использованию баланса для смягчения дефицита финансирования в ближайшей перспективе. Для инвесторов, которым удобно использовать этот временный подход в качестве стратегии для долгосрочной выгоды компании, Upstart, безусловно, является привлекательной инвестицией. Учитывая наличие явных доказательств превосходства и повышения точности модели ИИ в прошлом году, а также более эффективного разделения рисков по сравнению с традиционными оценками FICO, модель компании остается актуальной в меняющемся мире. Кроме того, компания быстро расширяется в других сегментах, таких как автокредиты, которые могут ускорить рост по мере того, как эти сегменты набирают обороты. Когда пыль уляжется, мы увидим истинную ценность платформы Upstart, а модель, основанная на искусственном интеллекте, а также управление будут проверены циклами и станут более устойчивой компанией, чем раньше. Моя целевая цена Upstart составляет $45,30, что предполагает потенциал роста на 65% по сравнению с текущими уровнями.

Эта статья была написана пользователем

Simple Investing

1,7 тыс. подписчиков

Я портфельный менеджер с опытом работы в хедж-фонде и семейном офисе. Ориентирован на долгосрочное инвестирование, и я верю в стратегию штанги в портфеле, где есть как элементы роста, так и элементы стоимости, которые будут отражены в моих статьях. Обладатель сертификата CFA и высшее образование в области финансов и бухгалтерского учета

Раскрытие информации: У меня/нас есть выгодная длинная позиция по акциям UPST посредством владения акциями, опционов или других деривативов. Я написал эту статью сам, и она выражает мое собственное мнение. Я не получаю за это компенсацию (кроме Seeking Alpha). У меня нет деловых отношений ни с одной компанией, акции которой упоминаются в этой статье.

Комментарии (18)

Рекомендуется для вас

Чтобы этого не произошло в будущем, включите Javascript и файлы cookie в своем браузере.

Часто ли это происходит с вами? Пожалуйста, сообщите об этом на нашем форуме обратной связи.

Если у вас включен блокировщик рекламы, вам может быть заблокировано продолжение. Пожалуйста, отключите блокировщик рекламы и обновите страницу.

Хеджирует от инфляции или нет, истинная ценность Биткойна — это разделение денег и государства

Джордж Калудис

Джордж Калудис — аналитик CoinDesk Research.

Подпишитесь на @gckaloudis в Твиттере

Первую неделю некриптомир был громче криптомира.

Все говорят о:

• Как президент США Байден выплачивает всем студенческие ссуды (через программу прощения государственных займов)

• Как председатель ФРС Джером Пауэлл катался на лыжах со всеми своими друзьями в Симпозиум по экономической политике в Джексон Хоуле)

• Как профессиональный умник Золтан Позар снова пугает нас до смерти, написав: «Разворачивающаяся экономическая война между великими державами является стохастической и нелинейной» (в исследовательской заметке «Война и процентные ставки»)

Между тем, никто не говорит о том, является ли биткойн (BTC) средством хеджирования инфляции или нет. К счастью (к сожалению?), каждая из вещей, о которых все говорят, так или иначе (по крайней мере, в общих чертах) связана с инфляцией. Так что я сделаю это. Я напишу о том, является ли биткойн защитой от инфляции или нет.

Потому что все связано с инфляцией и все связано с биткойнами (даже то, что не связано с биткойнами). Стохастик, кстати, означает «случайный».

Вы читаете наш еженедельный информационный бюллетень, содержащий информацию, новости и анализ для профессиональных инвесторов. Зарегистрируйтесь здесь , чтобы каждое воскресенье получать его в свой почтовый ящик.

Приводит ли списание студенческого долга к инфляции?

Во-первых, правительство США не выплачивает всем студенческие кредиты. Администрация Байдена объявила, что людям, которые держат студенческие ссуды федерального правительства и зарабатывают менее 125 000 долларов в год, будет прощено 10 000 или 20 000 долларов остатка их студенческой ссуды. Есть мельчайшие детали (которые вы можете получить, прослушав этот подкаст NASFAA), но главный вопрос, на который мы хотим ответить, заключается в том, является ли это инфляцией или нет.

Вот аргумент, что это будет: аннулирование долга по студенческому кредиту положит деньги в карманы американцев, и эти американцы будут использовать эти деньги, чтобы купить больше немедленно. Немедленный всплеск потребления внесет существенный вклад в усиление инфляции.

Вот аргумент, что этого не будет: списание долга по студенческому кредиту оставит деньги в карманах американцев, и эти американцы будут использовать эти деньги для более постепенного потребления в течение своей жизни. Постепенный скачок потребления не будет существенно способствовать увеличению инфляции.

Мне очень нравится аргумент, что списание студенческого долга не приведет к немедленной инфляции. Да, чеки на стимулирование пандемии коронавируса были, но есть важная психологическая разница между вручением кому-то чека на 3200 долларов и вручением им официального письма, в котором говорится, что они должны меньше на 10 000 долларов по непогашенному кредиту.

Снимает ли списание студенческого долга Джерома Пауэлла?

Нет, наверное нет. Вероятно, наоборот. В то время как Белый дом представил программу, которая на первый взгляд не является явно инфляционной, председатель Федеральной резервной системы все еще глубоко копает для своего момента Волкера (но не в полной мере Волкера). Когда в пятницу утром Пауэлл обратился к центральным банкам, экономистам и американскому народу со своими подготовленными заявлениями в Джексоне, штат Вайоминг, он сказал, что «история предостерегает от преждевременного ослабления политики», что в основном означает: «Мы собираемся придерживаться курса, потому что, если мы измените курс еще раз, вы действительно больше не будете нам верить».

Пауэлл (и ФРС) тоже стараются заслужить доверие. Адам Б. Левин из CoinDesk, ведущий подкаста «Markets Daily», привел один из лучших аргументов в пользу этого в выпуске на прошлой неделе, где он сказал:

«… [H]история предполагает, что решение [ФРС] [по процентные ставки] останутся намного ниже [необходимой] процентной ставки, необходимой для борьбы с инфляцией. На протяжении большей части 1970-х и 1980-х годов, когда мы в последний раз видели сопоставимую инфляцию цен, уровень, установленный ФРС, составлял где-то между 8% [и] 20%, что во много раз выше, чем то, что ФРС предлагает сейчас. Таким образом, хотя центральные банки и рынки будут играть в игры друг с другом, все это может быть только показным, чтобы серьезно относиться к проблеме, когда предлагаемое решение на самом деле не имеет шансов решить что-либо».

То, что Адам Левин использует, чтобы сделать это утверждение, является правилом Тейлора, эмпирическим правилом, используемым центральными банками для установления процентных ставок на уровне, который будет эффективно бороться с инфляцией. По его оценке, правило Тейлора предполагает, что ставки должны быть >9%, чтобы хотя бы начать справляться с поведенческими изменениями, к которым приводит долгосрочный рост инфляции. Я склонен согласиться с Левином и не думаю, что рынки больше верят политикам.

Пауэлл застрял между молотом и наковальней (по крайней мере, он застрял между очень красивыми камнями в Джексон-Хоул).

Инфляционна ли война?

Позсар ясно дает понять в вышеупомянутой исследовательской записке, что он так думает. Я думаю, что заметку стоит прочитать полностью, но вот резюме на случай, если вы ее не читаете:

Предложение опережает спрос, потому что мы ушли из мира, где а) дешевая иммигрантская рабочая сила в США, б) дешевые товары из Китая и в) дешевый российский газ поддержал низкую инфляцию в мире, где а) нативистская иммиграционная политика привела к давлению на заработную плату в США, б) отсутствие COVID-19 в Китаеполитика навредила потоку дешевых товаров и в) российская война на Украине привела к стремительному росту цен на газ в Европе, что поддержало высокую инфляцию.

Цитата:

«Добро пожаловать в военную экономику…

… где главы государств важнее глав центральных банков».

Может ли биткойн спасти нас?

Хорошо — мы не решили проблему инфляции на прошлой неделе, так что теперь перейдем к выдающемуся средству защиты от инфляции в криптовалюте: биткойну. Поскольку инфляционные силы все еще существуют, инвесторы думают о том, как лучше всего защитить себя. Является ли биткойн способом сделать это?

Не уверен. С точки зрения рынка, нет, совсем нет. В недавней памяти биткойн коррелировал с акциями. Акции не должны служить защитой от инфляции; менее рискованные вещи, такие как золото и товары. Таким образом, из-за того, что цена биткойна следует (или опережает) акции, биткойн на самом деле не выглядит как хеджирование инфляции.

Здесь стоит следить за двумя темами.

Во-первых, возможно, инфляция связана не с ростом цен на товары, а с обесцениванием валюты. Некоторые варианты этой диаграммы довольно популярны в биткойн-кругах:

Global M2 и цена биткойна (@mrblonde_macro)

Поскольку Global M2 — количество денег в обращении — меняется из года в год, кажется, что рыночная стоимость биткойна следует за этим. Короче говоря, по мере того, как экономика вводит деньги в обращение, цена биткойна растет, потому что дополнительные деньги в обращении разбавляют остальную часть существующих денег в обращении. Таким образом, это подтверждает идею о том, что биткойн является страховкой от обесценивания валюты (причудливый способ описать размывание денег в обращении).

Я не уверен, что данные сильно подтверждают эту идею. Конечно, на предыдущем графике есть визуальная взаимосвязь, но скользящий 30-месячный коэффициент корреляции между M2 США и стоимостью биткойна изменяется от отрицательного до слегка положительного (см. два следующих графика). Статистически это ни о чем не говорит. Может быть, этот шаг связан с тем, что биткойн созревает с течением времени, когда он приближается к своему последнему пристанищу в качестве хеджирования инфляции? Я знаю, что США не заменяют всю мировую экономику, но все же.

Годовое изменение рыночной капитализации M2 и биткойнов в США (FRED, TradingView)

30-месячная скользящая корреляция между M2 и биткойнами (FRED, TradingView)

Во-вторых, и более конкретно, если вы согласны с тем, что мы в условиях военной экономики, «где главы государств имеют большее значение, чем главы центральных банков», биткойн, вероятно, пригоден для инвестиций просто потому, что он отделен от «глав государств». Я не говорю, что цена биткойна не зависит от действий глав государств, но я говорю, что биткойн не выпускается какой-либо страной и что более широкая сеть а) не нуждается в какой-либо конкретной стране и б) достаточно устойчива чтобы воспротивиться запрету Китая.

Итак, в случае, если биткойн не ведет себя как защита от инфляции, можно было бы что-то сказать о том, что он действует как способ сделать ставку на разделение денег и государства.

---

Read more about

BitcoinInflationJerome PowellFederal ReserveCrypto Long & Short

---

BTC$

20,346.17

ETH$

1,601.40

BNB$

279.56

XRP$

0.336397

BUSD$

0,999525

---

Посмотреть все цены

---

Подпишитесь на The Node, наш ежедневный информационный бюллетень, в котором вы найдете самые важные крипто новости и идеи.

Зарегистрировавшись, вы будете получать электронные письма об обновлениях продуктов CoinDesk, событиях и маркетинге, и вы соглашаетесь с нашими условиями обслуживания и политикой конфиденциальности.

РАСКРЫТИЕ

Обратите внимание, что наша политика конфиденциальности, условия использования, файлы cookie и не продавать мою личную информацию были обновлены.

Лидер в области новостей и информации о криптовалютах, цифровых активах и будущем денег, CoinDesk является средством массовой информации, которое стремится к самым высоким журналистским стандартам и соблюдает строгий набор редакционных политик. CoinDesk — независимая операционная дочерняя компания Digital Currency Group, которая инвестирует в криптовалюты и блокчейн-стартапы. В рамках своей компенсации некоторые сотрудники CoinDesk, включая сотрудников редакции, могут получить доступ к капиталу DCG в виде прав на прирост стоимости акций, которые передаются в течение нескольких лет. Журналистам CoinDesk не разрешается напрямую покупать акции DCG.

Джордж Калудис

Джордж Калудис — аналитик CoinDesk Research.

Подписывайтесь на @gckaloudis в Твиттере

Джордж Калудис

Джордж Калудис — аналитик CoinDesk Research.

Follow @gckaloudis on Twitter

---

BTC$

20,346.17

ETH$

1,601.40

BNB$

279.56

XRP$

0.336397

BUSD$

0.999525

---

Посмотреть все цены

Логические значения Python

❮ Предыдущая Далее ❯

---

Логические значения представляют одно из двух значений: Верно или Ложно .

---

Логические значения

В программировании вам часто нужно знать, является ли выражение Верно или Ложно .

Вы можете вычислить любое выражение в Python и получить одно из двух ответы, Верно или Ложно .

При сравнении двух значений выражение оценивается, и Python возвращает логический ответ:

Пример

print(10 > 9)
print(10 == 9)
print(10 < 9)

Попробуйте сами »

Когда вы запускаете условие в операторе if, Python возвращает значение Истина или Ложь :

Пример

Вывести сообщение в зависимости от того, является ли условие Истинно или Ложь :

a = 200
b = 33

, если b > a:
 print(«b больше a»)
else:
 print(«b не больше a»)

Попробуйте сами »

---

Оценка значений и переменных

Функция bool() позволяет вам оценить любое значение, и дать вам Верно или Ложно взамен

Пример

Вычислить строку и число:

print(bool(«Hello»))
print(bool(15))

Попробуйте сами »

Пример

Оценка двух переменных:

x = «Привет»
y = 15

print(bool(x))
print(bool(y))

Попробуйте сами »

---

---

Большинство значений верны

Почти любое значение оценивается как Истинно , если оно имеет какое-то содержание.

Любая строка True , кроме пустых строк.

Любое число равно True , кроме 0 .

Любой список, кортеж, набор и словарь True , за исключением пустые.

Пример

Следующее вернет True:

bool(«abc»)
bool(123)
bool([«apple», «вишня», «банан»])

Попробуйте сами »

---

Некоторые значения ложны

На самом деле, есть не так много значений, которые оцениваются как False , за исключением пустых значений, таких как () , [] , {} , "" , номер 0 и значение None . И, конечно же, значение False оценивается как Ложь .

Пример

Следующее вернет False:

bool(False)
bool(None)
bool(0)
bool(«»)
bool(())
bool([])
bool({})

Попробуйте сами »

Еще одно значение или объект в данном случае оценивается как False , и это если у вас есть объект, который сделан из класса с функцией __len__ , которая возвращает 0 или Ложь :

Пример

класс мой класс():
  def __len__(self):
    return 0

myobj = myclass()
print(bool(myobj))

Попробуйте сами »

---

Функции могут возвращать логическое значение

Вы можете создавать функции, которые возвращают логическое значение :

Пример

Вывести ответ функции:

def myFunction() :
return True

print(myFunction())

Попробуйте сами »

Вы можете выполнять код на основе логического ответа функции:

Пример

Напечатать «ДА!» если функция возвращает True, иначе выведите «NO!»:

def myFunction() :
  вернуть True

, если myFunction():
print(«ДА!»)
else:
  print(«НЕТ!»)

Попробуйте сами »

Python также имеет множество встроенных функций, которые возвращают логическое значение, например экземпляр() функция, которую можно использовать для определения того, относится ли объект к определенному типу данных:

Пример

Проверить, является ли объект целым или нет:

x = 200
print(isinstance(x, int))

Попробуйте сами »

---

Проверьте себя с помощью упражнений

Упражнение:

Приведенный ниже оператор напечатает логическое значение, какое именно?

печать (10 > 9)
 

Начать упражнение

---

❮ Предыдущий Далее ❯

НОВИНКА

Мы только что запустили
Видео W3Schools

Узнать

ВЫБОР ЦВЕТА

КОД ИГРЫ

Играть в игру

---

---

---

Top Tutorials

Учебное пособие по HTML
Учебное пособие по CSS
Учебное пособие по JavaScript
Учебное пособие
Учебное пособие по SQL
Учебное пособие по Python
Учебное пособие по W3. CSS
Учебное пособие по Bootstrap
Учебное пособие по PHP
Учебное пособие по Java
Учебное пособие по C++
Учебное пособие по jQuery

9 9005 Справочник по HTML
Справочник по CSS
Справочник по JavaScript
Справочник по SQL
Справочник по Python
Справочник по W3.CSS
Справочник по Bootstrap
Справочник по PHP
Цвета HTML
Справочник по Java
Справочник по Angular
Справочник по jQuery

Основные примеры

Примеры HTML
Примеры CSS
Примеры JavaScript
Примеры инструкций
Примеры SQL
Примеры Python
Примеры W3.CSS
Примеры Bootstrap
Примеры PHP
Примеры Java
Примеры XML
Примеры jQuery

9025 FORUM | О

W3Schools оптимизирован для обучения и обучения. Примеры могут быть упрощены для улучшения чтения и обучения. Учебники, ссылки и примеры постоянно пересматриваются, чтобы избежать ошибок, но мы не можем гарантировать полную правильность всего содержания. Используя W3Schools, вы соглашаетесь прочитать и принять наши условия использования, куки-файлы и политика конфиденциальности.

Copyright 1999-2022 Refsnes Data. Все права защищены.
W3Schools работает на основе W3.CSS.

Maruti Suzuki Cars в Индии – каналы ARENA, NEXA, TRUE VALUE и COMMERCIAL

• 1800 102 1800 [email protected]

• Регистрация

  Мы

  
  обещаем вам
  100% безопасность
  защита данных

  Мы обещаем вам 100% защиту данных

В любое время Марути

1800 102 1800

contact@maruti.

co.in

Забронировать A
ShowroomПосетить

заказать тест-драйв

Получить
прайс-лист

Узнать точную цену* на все автомобили Maruti Suzuki можно здесь.

Выберите автомобиль

SELECT CARALTO K10ALTOBREZZACELERIODZIREEECOERTIGAS-PRESSOSWIFTWAGON№

Выберите состояние

SELECT STATEANDAMANANDHRA PRADESHARUNACHAL PRADESHASSAMBIHARCHANDIGARHCHHATTISGARHDADRA AND NAGAR HAVELIDAMANDELHIGOAGUJARATHARYANAHIMACHAL PRADESHJAMMU AND KASHMIRJHARKHANDKARNATAKAKERALAMADHYA PRADESHMAHARASHTRAMANIPURMEGHALAYAMIZORAMNAGALANDODISHAPONDICHERRYPUNJABRAJASTHANSIKKIMTAMIL NADUTELANGANATRIPURAUTTAR PRADESHUTTARAKHANDWEST BENGAL

Выберите город

ВЫБЕРИТЕ ГОРОД

*Цена на условиях самовывоза

Кредитные предложения

Записаться на прием

на прием

Maruti Suzuki
Оригинальные аксессуары

Maruti Suzuki
Оригинальные запчасти

найти
дилера

организация
запрос клиента

ОБНОВИТЬ СТРАХОВОЙ ПОЛИС MARUTI SUZUKI

свяжитесь с нами

УЗНАТЬ

УЗНАТЬ

УЗНАТЬ

УЗНАТЬ

УЗНАТЬ

УЗНАТЬ

ПОПРОБУЙТЕ СЕЙЧАС#

ПОПРОБУЙТЕ ЭТО СЕЙЧАС#

Больше от нас

Автошколы для страхования вашего автомобиля —
Maruti Suzuki позаботится обо всем

Подробнее

Больше от нас

Автошкола Марути Сузуки

Зачем учиться на ошибках, если вы можете учиться у наших экспертов

Марути Сузуки Смарт Финансы

Станьте на несколько шагов ближе к машине своей мечты с помощью Smart Finance

Страховой брокер Maruti Suzuki

Индивидуальный единственный в своем роде полис автострахования для владельцев транспортных средств.

Оригинальные аксессуары Maruti Suzuki

Оживите свой автомобиль и сделайте его своим собственным стилем

Оригинальные запчасти Maruti Suzuki

Сохраните свой автомобиль как новый с оригинальными запчастями Maruti Suzuki

Марути Сузуки Лизинг

Получите комплексные решения для лизинга автомобилей Maruti Suzuki

Институциональные клиенты

Независимо от того, служите ли вы нации или проживаете за границей, получите потрясающие преимущества здесь

Награды Марути Сузуки

Абсолютно новая программа лояльности, в рамках которой к клиентам относятся как к родным

Каналы

Покупайте или продавайте — всегда получайте самое лучшее с Maruti Suzuki

MARUTI SUZUKI ARENAExaTrue ValueCommercial

Corporate

Узнайте, что движет компанией, которая управляет Индией

Исследуйте

вещество

Жесткий городской

снисходительность

СМЕЛЫЙ

Производительность

ВДОХНОВЛЯЮЩИЙ

Гордость

Сложная сила

См. Полный диапазон

 

наши

ценности

Работайте с нами Тренируйтесь с нами

Счастливые клиенты и подсчет…

14,75 л

Автомобили, обслуживаемые каждый месяц

3,5К

Эксклюзивные выставочные залы

Добавление логики в ваш код — настоящий Python

Подсказка: Вы можете настроить скорость воспроизведения видео по умолчанию в настройках вашей учетной записи.

Подсказка: Вы можете установить язык субтитров по умолчанию в настройках своей учетной записи.

Извините! Похоже, возникла проблема с воспроизведением видео 🙁 Это может быть связано с временным сбоем или с ошибкой конфигурации вашего браузера. Пожалуйста, ознакомьтесь с нашим руководством по устранению неполадок с видеоплеером, чтобы решить эту проблему.

Основы Python: условная логика и поток управления
Ян Карри 15:16

• Стенограмма
• Комментарии и обсуждение

00:00 Добавьте немного логики в свой код.

00:04 Вы пытаетесь выяснить, является ли что-то истинным или ложным в Python. Теперь, как вы это делаете? Условная логика позволяет вам проверить, является ли что-то истинным или ложным, поэтому она включает такие вопросы, как У Бобби больше яблок, чем у Билла? Джейн быстрее, чем Джун? 5 больше 8? Что ж, мы знаем, что это ложь. В алфавите стоит ли n перед p? Мы знаем, что это правда.

00:28 По сути, когда вы пишете условную логику на Python, вы пытаетесь свести некоторые значения к True или False , и вы обычно делаете это, сравнивая их и комбинируя с другими операторами.

00:43 В этом уроке вы познакомитесь с несколькими операторами и их взаимосвязью: логическими компараторами, условными операторами, логическими операторами и приоритетом операторов, то есть в каком порядке они разрешаются. Точно так же, как математические операторы имеют определенный приоритет (например, умножение происходит перед сложением), булевы компараторы и логические операторы также имеют приоритет.

01:09 Булевы компараторы — одни из самых распространенных операторов, которые вы будете использовать для сравнения значений. Все эти операторы требуют элемент слева и справа, и они сравнивают значения.

01:21 Оператор «больше чем» ( > ), шеврон, обращенный вправо, спрашивает, больше ли значение слева, чем значение справа. Оператор меньше чем ( < ), который представляет собой левый шеврон, спрашивает, меньше ли значение слева, чем значение справа.

01:38 Хороший способ запомнить это — посмотреть на шеврон как на рот, и то, что рот пытается съесть, должно быть большим из двух значений, чтобы это выражение оценивалось как истинное.

01:51 Оператор больше или равно ( >= ) представляет собой направленный вправо шеврон со знаком равенства. Оператор меньше или равно ( <= ) представляет собой левый шеврон и знак равенства.

02:02 Операторы >= и <= аналогичны тем, что они делают то же самое, что и операторы > или < , за исключением того, что если значения равны, они также будут оцениваться как 9. 0336 True , в то время как более простые аналоги фактически оцениваются как False , если значения равны. Оператор не равно ( != ), который представляет собой восклицательный знак и знак равенства, просто спрашивает, не равны ли значения. Поэтому, если они равны, это даст вам значение False .

02:33 Аналогом этого является оператор равенства ( == ), который представляет собой два знака равенства. Оператор == даст вам только Значение True , если значения с обеих сторон равны друг другу.

02:45 Может быть трудно понять, что на самом деле делают эти операторы, глядя на них изолированно. Итак, впереди вы увидите несколько примеров.

02:57 Все следующие условные операторы приведут к значению True . Для этих примеров я не буду называть операторов по имени.

03:06 Я собираюсь прочитать, что это за персонажи. Итак, первый пример будет 10 > 5 . Но когда вы на самом деле читаете код, если бы вы читали его вслух, вы бы не сказали 10 вправо- лицом к шеврону 5 . Вы бы сказали, что 10 больше, чем 5 .

03:23 Но после этих примеров я начну называть их настоящими именами. Таким образом, 10 > 5 просит на 10 больше, чем 5, что верно. 1 < 2 спрашивает на 1 меньше 2, что тоже верно. Помните, что все эти примеры на этой странице оцениваются как True .

03:48 10 >= 9 запросов на 10 больше или равно 9, что верно. Следующий пример — 5 <= 5 , что означает, что на 5 меньше или равно 5, что верно.

04:06 1 != 0 просит 1 не равно 0, что тоже верно. И, наконец, 100 == 100 просит 100 равно 100, что снова верно.

04:25 Теперь вы видели кучу условных операторов, все из которых оцениваются как True . Теперь пришло время взглянуть на некоторые из них, которые будут оцениваться как False .

04:35 Первый пример — 10 < 5 , что означает, что на 10 меньше 5, что неверно. Следующий пример — 1 > 2 , который спрашивает, 1 больше 2, что неверно.

04:51 10 <= 9 asks на 10 меньше или равно 9, что снова неверно. Все эти примеры ложны. 4 >= 5 . 4 больше или равно 5? ЛОЖЬ. 1 == 0 .

05:11 1 равно 0. Это верное утверждение или ложное? 100 != 100 запрашивает 100 не равно 100, что неверно. Итак, с этого момента я не буду говорить о шевронах, знаках равенства или восклицательных знаках.

05:33 Я просто буду называть условные операторы по имени.

05:40 Теперь, когда вы ознакомились с булевыми компараторами, пришло время добавить к ним логические операторы. В Python есть три логических оператора: оператор и , оператор или и оператор , а не . Операторы и , а также операторы или требуют значений по обе стороны от оператора.

06:00 Оператору , а не требуется только значение справа от него. Значения, с которыми работают логические операторы, будут оцениваться как логические значения, то есть не имеет значения, что вы поместите по обе стороны от оператора и .

06:14 Он всегда будет пытаться видеть значения как True или False . Так что это все равно, что спросить: Уже пора обедать? и Я голоден? По обе стороны от ключевых слов и у вас есть вопросы, которые могут оценить Верно или Ложно .

06:29 Так что в случае и , если оба верны, то вам поужинать. Что касается и , это первое ключевое слово, на которое вы обратите внимание.

06:41 Итак, если у вас есть утверждение, в котором левая или правая сторона оценивается как True , и один из них оценивается как False , тогда это даст вам значение False .

06:52 Если и левая, и правая стороны верны, вы получите значение True . Если обе стороны ложны, то вы получите Ложь , потому что ни одна из них не верна.

07:01 И снова, если одна сторона ложна, то и всегда будут возвращать False . Так что единственный случай, когда и могут вернуть True , если обе его части верны.

07:14 Теперь пришло время для или . С или только одна сторона оператора должна быть истинной. Если обе стороны верны, то это тоже True .

07:24 Единственный случай, когда это будет False , это если обе стороны ложны.

07:32 И не . , а не , нужно только выражение в правой части, и в основном оно просто инвертирует его. Итак, если у вас есть , а не и выражение, и это выражение оценивается как True , то общий результат всего будет False .

07:49 Если ваш код говорит , а не False , тогда это выражение оценивается как True . Если ваш код говорит не True , тогда это выражение оценивается как False .

08:02 Он инвертирует значение.

08:06 Итак, теперь вы взглянете на пару примеров некоторых логических операторов в действии. Скажем, у вас есть выражение 1 > 2 , затем вы добавили логические операторы и , а затем справа от него появилось другое выражение, 5 > 3 .

08:28 Итак, каковы ваши наилучшие предположения о том, что это произведет? Ну, вы можете разбить его на кусочки и сказать, 1 > 2 , это правда или ложь? Это ложное утверждение. 5 > 3 , это верное утверждение.

08:40 Таким образом, у вас есть ложное утверждение и истинное утверждение по обе стороны от оператора и . Это дает вам False , потому что для операторов и обе стороны должны быть истинными. Взгляните на другой пример.

08:55 Скажем, у вас есть строка "Python" , и вы хотите проверить, равна ли она другой строке, "Питон" .

09:04 Тогда у вас есть ключевое слово или , и у вас есть 10 != 9 . Как вы думаете, что это вам даст? Опять же, берите по крупицам. У вас есть "Python" == "Pythonic" . Это верное или ложное утверждение?

09:18 Это ложное утверждение. И тогда у вас есть 10 != 9 , что является верным утверждением. Так что же вам все это даст? Это дает вам True , потому что с оператором или любая из сторон должна быть истинной.

09:34 Итак, что произойдет, если вы просто скопируете это

09:40 а затем добавить вместо перед всем выражением? Как вы думаете, что это вам даст? У вас может возникнуть соблазн подумать, что это даст вам False , но на самом деле над этим выражением работает оператор , а не ( "Python" == "Pythonic" ) перед вычислением всего выражения или .

10:01 Ключевое слово , а не работает с выражением "Python" == "Pythonic" до того, как оператор или работает с любой стороны, поэтому до того, как оператор или получит возможность оценить, не "Python" == "Pythonic" оценивается как True .

10:21 А потом 10 != 9 также оценивается как True . Так как или , любая сторона или обе стороны могут быть истинными, это дает вам True . Вы получите значение True . Теперь способ, которым , а не работает первым перед или , связан с приоритетом оператора.

10:41 Некоторые части будут оцениваться перед другими частями. Булевы компараторы оцениваются первыми. Потом , а не , потом и , и, наконец, 9.0336 или . Вы можете обойти это поведение, если оно неудобно для вашего варианта использования, используя скобки. То, что указано в скобках, будет оцениваться первым.

11:02 Поэтому, если вы столкнулись с какими-либо странными ошибками и выражение ведет себя не так, как вы думаете, убедитесь, что это не связано с приоритетом оператора. Разбейте свое утверждение на маленькие части и посмотрите, работает ли оно там. Итак, на этом уроке вы рассмотрели логические компараторы, условные операторы, логические операторы и приоритет операторов. Помните, что речь идет всего лишь о том, чтобы взять значения, сравнить их друг с другом и получить 9 баллов.0336 True или False Значение в конце. Теперь вам может быть интересно узнать о приоритете между булевыми компараторами. Это не было упомянуто на предыдущем слайде. Они просто были перечислены все в одной строке.

11:45 Скажем, у вас было такое выражение 10 < 50 > 20 . Что будет оцениваться в первую очередь в этой ситуации?

11:57 Это дает вам True , но почему это дает вам Правда ? Потому что если вы это сделаете, 10 < 50 , вы получите True . Но тогда вы бы сказали True > 20 ?

12:11 Это дает вам False . Так что, если это было 50 > 20 ? Это дает вам True , но 10 < True ? Это Ложь .

12:23 Так почему же это дает вам значение True ? Ну, причина в том, что в Python всякий раз, когда вы соединяете такие компараторы, он неявно добавляет 9Здесь оператор 0336 и .

12:38 Таким образом, выражение в первой строке 10 < 50 > 20 фактически оценивается как 10 < 50 и 50 > 20 , что даст вам значение True , которое вы получили в начале.

12:56 Цепочка логических компараторов таким образом может быть полезна для диапазонов. Обычно вы не используете логические компараторы с цепочкой, противопоставляя друг другу вот так. Такое заявление можно было бы легко написать 50 > 20 , потому что в этом случае проверка, больше ли 50, чем 10, является избыточной.

13:14 Но это полезно для проверки диапазонов. Итак, скажем, у вас было age = 20 , а затем вы хотите проверить, находится ли этот возраст между 10 и 30. Таким образом, вы можете получить 10 < age < 30 ,

13:33 что равно True , потому что это оценивается следующим образом: 10 < age and age < 30 , что даст вам Правда . Таким образом, вам не нужно объединять операторы в цепочку, но это может быть хорошим сокращением для диапазонов.

13:52 И, следовательно, логические компараторы не имеют никакого приоритета между ними, потому что между ними вставлены неявные и . Таким образом, несмотря ни на что, никогда не возникает двусмысленности относительно того, какой логический компаратор оценивать первым, потому что они разделены ключевыми словами и , поэтому все они работают независимо, а затем и можно оценить.

14:19 Последнее, что нужно помнить о сравнениях, это то, что когда вы имеете дело со строками, Python использует алфавитный порядок.

14:27 Таким образом, "a" < "z" верно, потому что "a" имеет меньший индекс, чем "z" , потому что "a" предшествует "z" в алфавите.

14:38 Он также сортирует строки лексикографически. Теперь это просто причудливое слово для обозначения алфавитного порядка. Итак, если у вас было "ааа"

14:48 > "aaz" , как ты думаешь, что тебе это даст? Это даст вам False , потому что он смотрит на первую букву, которая равна "a" , так что они эквивалентны, смотрит на вторую букву, "a" , которая эквивалентна. Затем он смотрит на третью букву, и поскольку "a" имеет меньшее значение, чем "z" , это дает вам False .

15:10 Так что об этом нужно помнить при сравнении строк в Python.

Содержание курса

Обзор

• Основы Python: условная логика и поток управления (обзор) 03:11

• Добавление логики в ваш код 15:16

• Создание сложных выражений 04:45

• Управление потоком вашей программы 20:22

• Создание вложенных операторов if 09:47

• Нахождение делителей числа 00:42

• Выход из шаблона 08:28

• Восстановление после ошибок 03:47

• Использование try и кроме ключевых слов 05:46

• Моделирование и расчет вероятностей 07:29

• Основы Python: условная логика и поток управления (краткое содержание) 01:42

Как использовать функцию ЕСЛИ в Excel

Функция ЕСЛИ выполняет логическую проверку и возвращает одно значение для результата ИСТИНА и другое значение для результата ЛОЖЬ. Первый аргумент, logical_test , – это выражение, которое должно возвращать либо ИСТИНА, либо ЛОЖЬ. Второй аргумент  value_if_true  – это значение, которое будет возвращено, когда logical_test возвращает значение TRUE. Последний аргумент  value_if_false  – это значение, которое будет возвращено, когда logical_test вернет FALSE. Оба value_if_true и value_if_false являются необязательными, но необходимо указать хотя бы одно из них. Результатом ЕСЛИ может быть значение, ссылка на ячейку или даже другая формула.

Пример "пройдено или не пройдено"

В таблице, показанной выше, мы хотим назначить либо "пройдено", либо "не пройдено" на основе тестовой оценки. Проходной балл 70 и выше. Формула в D6, скопированная ниже, выглядит так:

.
 
 =ЕСЛИ(C5>=70,"Пройдено","Не пройдено") 

Перевод: Если значение в C5 больше или равно 70, вернуть "Пройдено". В противном случае вернуть «Fail».

Обратите внимание, что логический ход этой формулы можно изменить на противоположный. Эта формула возвращает тот же результат:

.
 
 =ЕСЛИ(C5<70,"Fail","Pass") 

Перевод: если значение в C5 меньше 70, вернуть "Fail". В противном случае верните «Pass».

Обе приведенные выше формулы при копировании вниз вернут правильные результаты.

Примечание. Если вы не знакомы с идеей критериев формулы, в этой статье объясняется множество примеров.

Назначить баллы на основе цвета

В таблице ниже мы хотим присвоить баллы на основе цвета в столбце B. Если цвет «красный», результат должен быть 100. Если цвет «синий», результат должен быть 125. Для этого требуется что мы используем формулу, основанную на двух функциях ЕСЛИ, одна из которых вложена в другую. Формула в C5, скопированная ниже, выглядит так:

.
 
 =ЕСЛИ(B5="красный",100,ЕСЛИ(B5="синий",125)) 

Перевод: ЕСЛИ значение в ячейке B5 "красное", вернуть 100. В противном случае, если значение в ячейке B5 равно "синий", возврат 125.

В этом примере следует обратить внимание на три вещи:

1. Формула вернет ЛОЖЬ, если значение в ячейке B5 будет любым, кроме "красного" или "синего"
2. Текстовые значения "красный" и "синий" должны быть заключены в двойные кавычки ("")
3. Функция ЕСЛИ не учитывает регистр и будет соответствовать "красному" или "красному" или "КРАСНОМУ"

Это простой пример "вложенных IF"; см. ниже более сложный пример.

Вернуть другую формулу

В результате функция ЕСЛИ может вернуть другую формулу. Например, приведенная ниже формула вернет A1*5%, если A1 меньше 100, и A1*7%, если A1 больше или равно 100:

.
 
 =IF(A1<100,A1*5%,A1*7%) 

Вложенные операторы IF

Функция IF может быть "вложенной". «Вложенный ЕСЛИ» относится к формуле, в которой по крайней мере одна функция ЕСЛИ вложена в другую, чтобы проверить наличие большего количества условий и вернуть больше возможных результатов. Каждый оператор IF должен быть тщательно «вложен» в другой, чтобы логика была правильной.

Например, следующую формулу можно использовать для присвоения оценки, а не результата "зачет/незачет":

 
 =ЕСЛИ(С6<70,"F",ЕСЛИ(С6<75,"D",ЕСЛИ(С6<85,"С",ЕСЛИ(С6<95,"В","А")))) 

Можно вложить до 64 функций ЕСЛИ. Однако в целом вам следует рассмотреть другие функции, такие как ВПР или ГПР, для более сложных сценариев, потому что они могут обрабатывать больше условий гораздо проще.

Примечание. Новая функция IFS предназначена для обработки нескольких условий без вложения.

Логические операторы

При построении теста с ЕСЛИ вы можете использовать любой из следующих логических операторов:

Оператор сравнения	Значение	Пример
=	равно	А1=Д1
>	больше, чем	А1>D1
>=	больше или равно	А1>=D1
	меньше	А1
	меньше или равно	А1
	не равно	A1D1

Функция ЕСЛИ не поддерживает подстановочные знаки, но вы можете комбинировать ЕСЛИ и СЧЁТЕСЛИ, чтобы получить базовые функции подстановочных знаков.

ЕСЛИ с И, ИЛИ, НЕ

Функция ЕСЛИ может сочетаться с функциями И и ИЛИ. Например, чтобы вернуть «ОК», когда A1 находится между 7 и 10, вы можете использовать следующую формулу:

 
 =ЕСЛИ(И(A1>7,A1<10),"ОК","") 

Перевод: если A1 больше 7 и меньше 10, вернуть "ОК". В противном случае ничего не возвращать ("").

Чтобы вернуть B1+10, когда A1 "красный" или "синий", вы можете использовать функцию ИЛИ следующим образом:

 
 =ЕСЛИ(ИЛИ(A1="красный",A1="синий"),B1+10,B1) 

Перевод: если A1 красный или синий, вернуть B1+10, иначе вернуть B1.

 
 =ЕСЛИ(НЕ(A1="красный"),B1+10,B1) 

Перевод: если A1 НЕ красный, вернуть B1+10, иначе вернуть B1.

Дополнительная информация

• Подробнее о вложенных IF
• Узнайте, как использовать функцию ВПР вместо вложенных ЕСЛИ (видео)
• 50 Примеры формулы критерия

Примечания

• Функция ЕСЛИ имеет значение , а не с учетом регистра.