Изоморфизм это в философии: Изоморфизм это

Опубликовано автором
n}$ (ум­но­же­нию на $n$ в сис­те­ме R со­от­вет­ст­ву­ет воз­ве­де­ние в $n$-ю сте­пень в сис­те­ме R+, а де­ле­нию на два – из­вле­че­ние квад­рат­но­го кор­ня).

Изу­че­ние свойств од­ной из изо­морф­ных сис­тем в зна­чит. ме­ре (с аб­ст­ракт­но-ма­те­ма­тич. точ­ки зре­ния – пол­но­стью) мож­но све­сти к изу­че­нию свойств дру­гой. Лю­бую сис­те­му объ­ек­тов $S’$, изо­морф­ную сис­те­ме $S$, мож­но рас­смат­ри­вать как мо­дель сис­те­мы $S$ и сво­дить изу­че­ние свойств сис­те­мы $S$ к изу­че­нию свойств мо­де­ли $S’$.

Об­щее оп­ре­де­ле­ние И. сис­тем объ­ек­тов с за­дан­ны­ми в них от­но­ше­ния­ми та­ко­во. Пусть да­ны две сис­те­мы объ­ек­тов $S$ и $S’$, при­чём в пер­вой оп­ре­де­ле­ны от­но­ше­ния $F_k(x_1,x_2,…)$, $k=1,2,…,n$, а во вто­рой – от­но­ше­ния $F’_k(x’_1,x’_2,…)$, $k=1,2,…,n$, при­чём для ка­ж­до­го $k$ чис­ло объ­ек­тов в от­но­ше­ни­ях $F_k$ и $F’_k$ оди­на­ко­во (оно мо­жет за­ви­сеть от $k$). Сис­те­мы $S$ и $S’$ с ука­зан­ны­ми на них от­но­ше­ния­ми на­зы­ва­ют­ся изо­морф­ны­ми (в этом слу­чае пи­шут $S\cong S’$), ес­ли су­ще­ст­ву­ет та­кое вза­им­но од­но­знач­ное со­от­вет­ст­вие $x’=φ(x),\, x=ψ(x’)$ (в пер­вом ра­вен­ст­ве $x$ – про­из­воль­ный эле­мент сис­те­мы $S$, а во вто­ром $x’$ – про­из­воль­ный эле­мент сис­те­мы $S’$), что из от­но­ше­ния $F_k(x_1,x_2,…)$ вы­те­ка­ет от­но­ше­ние $F’_k(x’_1,x’_2,…)$ и на­обо­рот.

x$, $x=\log_ay$.

По­ня­тие И. воз­ник­ло в ал­геб­ре, точ­нее, в тео­рии групп, где впер­вые был по­нят тот факт, что изу­че­ние внут­рен­ней струк­ту­ры двух изо­морф­ных сис­тем объ­ек­тов пред­став­ля­ет со­бой од­ну и ту же за­да­чу. Это свой­ст­во от­ме­тил Р. Де­карт (1637), он пред­ви­дел воз­мож­ность ото­жде­ст­в­лять изо­морф­ные от­но­ше­ния или опе­ра­ции (на­зы­вал их по­доб­ны­ми). Совр. тер­ми­но­ло­гия ут­вер­ди­лась по­сле ра­бот Э. Нё­тер (1918). По­ня­тие И. на­хо­дит при­ме­не­ние во мно­гих раз­де­лах ма­те­ма­ти­ки.

Ак­сио­мы лю­бой ма­те­ма­тич. тео­рии оп­ре­де­ля­ют сис­те­му объ­ек­тов, изу­чае­мую этой тео­ри­ей, все­гда толь­ко с точ­но­стью до И.: ак­сио­ма­ти­че­ски по­стро­ен­ная ма­те­ма­тич. тео­рия, при­ме­ни­мая к к.-л. од­ной сис­те­ме объ­ек­тов, все­гда пол­но­стью при­ме­ни­ма к дру­гой, изо­морф­ной ей. По­это­му ка­ж­дая ак­сио­ма­ти­че­ская ма­те­ма­тич. тео­рия до­пус­ка­ет не од­ну, а мно­го ин­тер­пре­та­ций, или мо­де­лей.

По­ня­тие И. вклю­ча­ет в се­бя как ча­стный слу­чай по­ня­тие го­мео­мор­физ­ма. Ча­ст­ным слу­ча­ем И. яв­ля­ет­ся ав­то­морфизм – вза­им­но од­но­знач­ное ото­бра­же­ние $x’=φ(x)$, $x=ψ(x’)$ сис­те­мы объ­ек­тов с за­дан­ны­ми от­но­ше­ния­ми $F_k(x_1,x_2,…)$ на са­моё се­бя, при ко­то­ром из $F_k(x_1,x_2,…)$ вы­те­ка­ет $F’_k(x’_1,x’_2,…)$, $k=1,2,…,n$, и на­обо­рот. Это по­ня­тие так­же воз­ник­ло в тео­рии групп, но по­том ока­за­лось су­ще­ст­вен­ным в разл. раз­де­лах ма­те­ма­ти­ки.

ИЗОМОРФИЗМ И ГОМОМОРФИЗМ — Научная Конференция, Симпозиум, Конгресс на Проекте SWorld — Апробация, Сборник научных трудов и Монография — Россия, Украина, Казахстан, СНГ

УДК 004.94:336:512

Румянцев М.И.

ИЗОМОРФИЗМ  И  ГОМОМОРФИЗМ

В ИМИТАЦИОННОМ  МОДЕЛИРОВАНИИ

Западнодонбасский институт экономики и управления

 

Обсуждается роль понятий «изоморфизм» и «гомоморфизм» для теории и практики имитационного моделирования.   Эти понятия рассматриваются как методологическая основа процедур оценки уровня адекватности модели и степени ее пригодности для исследования  и совершенствования экономических систем, объектов и процессов.

  Ключевые слова: бизнес-процессы; имитационное моделирование; адекватность; изоморфизм; гомоморфизм.

The paper deals with the role of the isomorphism and homomorphism in the theory and practice of simulation. These concepts are

considered  as a methodological framework  for models adequacy evaluation and for their  suitability extent estimation to  the study and improvement of economic systems, objects and processes.  

Keywords:  business-processes; simulation; adequacy; isomorphism; homomorphism.

Введение

Как показала более чем полувековая практика имитационного моделирования экономических систем, объектов и процессов, вопросы адекватности и пригодности создаваемых моделей всегда занимали подобающее им место в теоретических исследованиях и практических приложениях (см. , например, [5, 12, 17]). Разумеется, пропагандируемые представителями различных школ и направлений концепции и методы нередко «ортогональны» друг другу. Признавая право каждого исследователя на самостоятельность суждений, хотелось бы отметить некую, не всегда заметную, небрежность или недоработанность методологического обоснования технологических аспектов имитационного моделирования. В частности, одним из косвенных свидетельств тому может служить определение понятия модели, которое дал Ю.И. Рыжиков, автор широко известной и заслуженно популярной книги «Имитационное моделирование. Теория и технологии»:  «Модель есть материально или теоретически сконструированный объект, который заменяет (представляет) объект исследования в процессе познания, находится в отношении сходства с последним (изоморфизм, аналогия, физическое сходство и т.п.) и более удобен для исследования» [12, с. 16]. Определенная гносеологическая неточность приведенного определения (касающаяся  неоправданной подмены гомоморфизма изоморфизмом) вынудила автора настоящей работы продолжить начатое в [10, 11] обсуждение подходов к оценке адекватности имитационных моделей – в частности, к выяснению концептуальной и инструментальной роли понятий изоморфизма и гомоморфизма в современном имитационном моделировании.

 

Базовые идеи и приближение к окрестностям решения

Что такое модель в алгебраическом смысле? Это объект, находящийся в некоторых отношениях с исходным объектом – безотносительно того, что представляет собой объект-оригинал: некое абстрактное множество, вполне конкретный убыточный завод или восточный базар. Такое понимание модели имеет свои давние математические корни. Более того, среди математиков есть мнение, что, грубо говоря, построение модели любой предметной области начинается с «…введения подходящих обозначений для операций и отношений с последующим исследованием их свойств» [8, с. 51].

Этот подход достаточно распространенный и имеющей под собой солидное обоснование. В свое время А.И. Кухтенко показал, что любая произвольная математическая модель представима в виде некоторой алгебраической структуры – и, как следствие, в любой предметной области возможен переход от содержательных представлений к математическим моделям, выраженным при помощи стандартных алгебраических структур [6].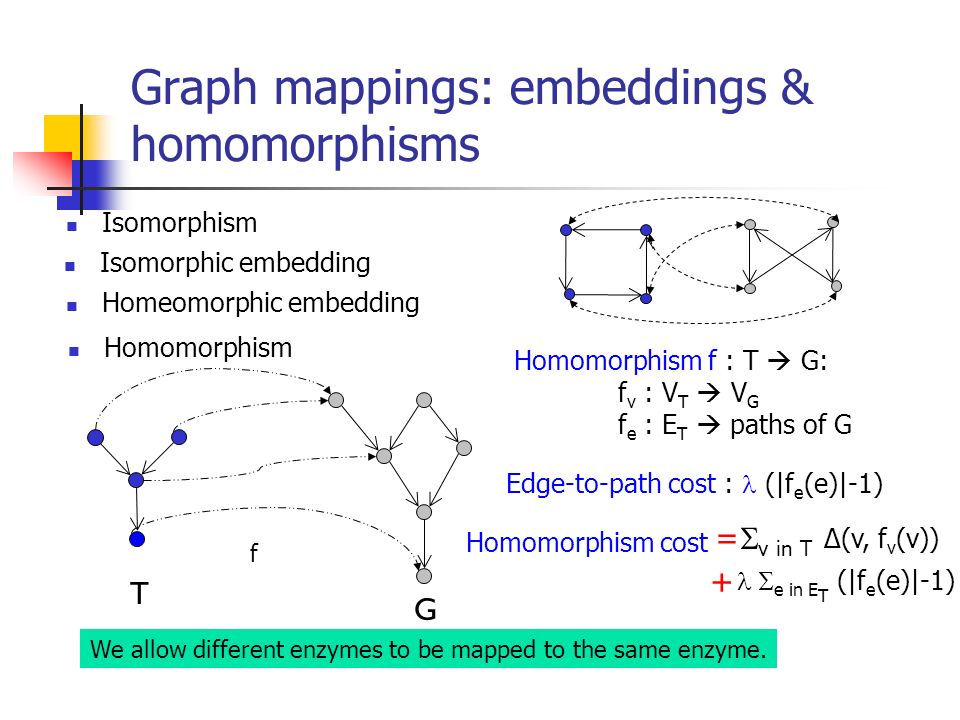

Такая концепция во многом созвучна работам Н.П. Бусленко [2], В.М. Глушкова [4], М. Месаровича и Я. Такахары [7], ряда других исследователей. Таким образом, группы, кольца, поля и другие структуры подобного рода все чаще находят применение в качестве математических аналогов реальных объектов и систем. Алгебраические операции, абстрагируясь,  распространяются на объекты любой природы, которые образуют различные структуры в зависимости от приписываемых им или наблюдаемых свойств. Поскольку приложение идей абстрактной алгебры к проблемам моделирования неминуемо предполагает изучение логических и семиотических аспектов моделирования, следует также особо отметить работы в этом направлении А.И. Уемова и Ю.А. Гастева. В частности, последний занимался вопросами, связанными с алгебраическими аспектами теории познания и такими логико-гносеологическими категориями, как изоморфизм и гомоморфизм [3].

 Наша задача проще и прагматичнее – вычленить из теоретического многообразия то, что применимо (возможно, с определенными оговорками) в практическом имитационном моделировании – поэтому остановимся более подробно на некоторых методологических тонкостях, которые присущи  взаимоотношениям процесса научного познания, общей алгебры и моделирования. Это необходимо сделать еще и потому, что абстрагирование как неотъемлемая технологическая операция при моделировании базируется на принятых априори предположениях относительно элементов объекта-оригинала, их свойств и соотношений. Выбрав эти предположения в качестве системы аксиом для конкретной предметной области, можно, во-первых, заложить в фундамент будущей имитационной модели аксиоматизированной области

интерпретацию (модель) системы аксиом [15, с. 41]; во-вторых, воспользоваться тем обстоятельством, что построение модели для некоторой определенной аксиоматической системы может быть во многих случаях осуществлено конструктивным образом (например, при помощи некоторой итерационной процедуры) [там же, с. 59]. Это вполне соответствует отработанным приемам имитационного моделирования – когда первоначальная, грубая модель циклически подвергается многократному уточнению по мере проведения экспериментов с ней,  выполнения верификации, валидации и т.д. Опираясь на схему Ю.А. Гастева, можно описать в максимально обобщенной форме (без отвлекающей детализации) процедуру отражения структур и их свойств из некой предметной области – памятуя о том, что хотя бы некоторые шаги этой процедуры могут и должны быть автоматизированы (компьютеризованы).

(i) Из всей совокупности процессов отражения изучаемой области определенным образом вычленяются единичные («элементарные») акты познания, допускающие описание в логико-алгебраических терминах как самих себя, так и результатов. Множество этих описаний образует очередную, i-ую итерацию, асимптотически приближаясь к более тонкому, комплексному описанию объектов предметной области, намеченной к имитационному моделированию. Говоря инженерным языком, единый технологический процесс отражения расщепляется на составные технологические операции сколь угодно допустимой малости.

(ii) Основные категории «элементарно-познавательной» концепции по Гастеву – понятия изоморфизма и гомоморфизма, неразрывно связанные с важнейшей операцией  отождествления различных по сути объектов. В этих терминах описывается образование отдельных абстрактных понятий и построение целостных концептуальных схем

— моделей.  Поскольку модель является не столько объективным атрибутом какой-либо сущности, сколько субъективным продуктом чьего-то моделирования, то изоморфизм понимается как некий идеальный, «предельный» случай более широкого и более «употребительного» понятия гомоморфизма. «…Изоморфизм есть понятие «абсолютное» — этим термином мы обозначаем взаимно-однозначное соответствие между элементами двух абстрактных множеств, «сохраняющее» все свойства элементов этих систем и все отношения между ними» [3, с. 24].

(iii) Процесс выделения и систематизации абстрактных понятий, отражающих свойства окружающего мира, можно интерпретировать как некоторое гомоморфное преобразование (свертку), а процесс формализации уже построенной таким образом концептуальной схемы в виде научной теории (и создаваемых на ее основе прикладных технологий и инструментов) — как изоморфное преобразование. Таким образом, до начала этапа (ii) исследователь уже должен располагать необходимым аппаратом для выполнения преобразований обоих видов. Очевидно, что возможности логико-алгебраических методов должны быть подкреплены и дополнены некоторыми эвристиками, характерными для экспертов в данной предметной области. В силу этого функции по гомоморфной свертке значимой информации (описаний бизнес-процессов, бизнес-правил и т. п.) должны быть возложены на компьютеризованную экспертную систему (ЭС) с элементами искусственного интеллекта.

(iv) Несколько слов о том, с какой стороны подступиться к реализации в ЭС упомянутой свертки. Любой гомоморфизм означает не что иное, как объединение в классы эквивалентности совокупностей объектов, могущих различаться по другим критериям отождествления. (По мнению Гастева, в этом вся теоретико-познавательная суть так называемых теорем о гомоморфизмах, сводящаяся, упрощенно говоря, к тому, что единственным объективным источником описания реальности служит сама эта реальность).

Насколько правомочно такое понимание изоморфизма и гомоморфизма применительно к моделированию? Рассмотрим сначала чисто математический подход к этому вопросу. Один из «патриархов» отечественной алгебры, А.К. Сушкевич, в работах 20-30-х годов XX столетия вводил понятия изоморфизма и гомоморфизма, отталкиваясь от предшествующего им понятия группы и опираясь на труды О. Ю. Шмидта по абстрактной теории групп. Таким образом, изоморфизм у Сушкевича – это соотношение между элементами двух групп U и U1, в котором каждому элементу группы U соответствует некоторый элемент группы U1, и каждому элементу из U1 соответствует некоторый элемент из U, причем произведению двух элементов из U соответствует произведение соответствующих элементов из U1 . Если при этом каждому элементу из U1 соответствует только один элемент из U и обратно, то изоморфизм простой, в противном случае обобщенный (кратный, гомоморфизм). Простой изоморфизм говорит, что структуры групп одинаковы, т.е. с отвлеченной точки зрения группы ничем не отличаются друг от друга.

Подобного рода формулировки характерны и для других математиков. Так, П. Халмош в своем известном учебнике 40-50-х годов «Конечномерные векторные пространства» подразумевает под изоморфизмом взаимно однозначное соответствие, сохраняющее все линейные соотношения. На первый взгляд это и аналогичные определения ничего не могут дать имитационному моделированию с практической точки зрения. Тем не менее, в монографии А.Г. Куроша «Теория групп» (60-ые годы), наряду с традиционным взглядом на изоморфизм как взаимно однозначное соответствие,  появляется замечательная в концептуальном смысле фраза: «Понятие изоморфизма не является понятием, специфичным для алгебры». Соответственно, гомоморфизм вводится как обобщение понятия изоморфного отображения в случае отказа от требования взаимной однозначности.

В отличие от алгебраистов-классиков, авторы более новых монографий и пособий по прикладной математике сначала определяют, что такое гомоморфизм, а уже затем переходят к изоморфизму как частному случаю гомоморфизма. Так, В.П. Сигорский, вводя понятие гомоморфизма через отображение двух множеств друг в друга, определяет изоморфизм как взаимно-однозначный (биективный) гомоморфизм  [13, с. 155-156]  (отмечая, что изоморфные множества обладают одинаковыми свойствами относительно определенных на них операций). Аналогично у Ф.А. Новикова:  «Гомоморфизм, который является биекцией, называется изоморфизмом» [8, с. 55]. Сам же гомоморфизм понимается как  отображающая операция особого рода алгебры A на алгебру B (причем обе алгебры одинакового типа). И снова – наводящий на раздумья тезис: «Понятие изоморфизма является одним из центральных понятий, обеспечивающих применимость алгебраических методов в различных областях» [там же, с. 56].

Если профессиональные математики в силу специфики рода занятий касаются в разной степени понятий изоморфизма и гомоморфизма, то специалисты по имитационному моделированию по ряду причин стараются этого избежать. Так, классическая во всех отношениях монография [5] В. Кельтона и А. Лоу не содержит никаких сведений по этому вопросу, крайне скупо сказано на эту тему и у Ю.И. Рыжикова в [12]. Однако уже В.Н Томашевский недвусмысленно фиксирует роль изоморфизма и гомоморфизма как меры соответствия между исходной системой и моделью: система и модель изоморфны, если существует взаимнооднозначное соответствие между ними, благодаря которому можно преобразовать одно представление в другое; система и модель изоморфны только в случае упрощения системы, т. е. сокращения при моделировании множества ее свойств и характеристик поведения, влияющих на пространство состояний системы; примером менее тесных связей между системой и моделью являются гомоморфные связи, которые определяют однозначное соответствие только в одну сторону (от модели к системе) [14, с. 21-22]. Справедливости ради заметим, что о роли изоморфизма в моделировании значительно раньше, нежели Гастев и тем более Томашевский, написал Ст. Бир: «Изоморфный» означает имеющий аналогичную форму. Говорят, что одна система изоморфна другой, если по крайней мере формально они эквивалентны и взаимозаменяемы. <…> Степень изоморфности математической модели «реальной» системе определяет достоверность получаемых при помощи модели предсказаний» [1] (Курсив мой – М.Р.).

Прояснив некоторые нюансы, мы теперь можем со спокойной совестью продолжить описание начатой выше процедуры отражения. Дополнительно примем к сведению, что модель, даже если она в чем-то проще исходного оригинала, не обязательно проще его во всех отношениях — а только в тех, в которых в данный момент специально заинтересован исследователь. Иными словами, реальная имитационная модель, будучи достаточно далекой от идеального «изоморфного» варианта, тем не менее не обязательно является «неструганным» и «занозистым» вариантом, «срубленным» при помощи гомоморфных сверток – напротив, некоторые блоки модели будут спроектированы с максимально достижимой точностью, а остальные будут загрублены в приемлемом диапазоне параметров (не выходя за пределы аксиоматики, принятой в начале моделирования).

(v) Понятие гомоморфизма, являющееся основным инструментом для практически точного описания различных процедур, объединяемых общим термином «моделирование», допускает ряд естественных обобщений, интересных прежде всего ввиду большого разнообразия и гибкости их логико-методологических интерпретаций. Если изучаемая система, как это часто бывает, задана частично (в т.ч. частично определены на ней операции и предикаты), то можно доопределить систему – как вариант, введя некую метрику и (или) топологию (т.н. топологическая интерпретация неполных изоморфизмов [3, с. 75-77; 9, с. 139]).

 (vi) По мере уточнения исходной имитационной модели (особенно для сложных стохастических систем) представляется перспективным на очередной итерации перейти к использованию в различных модификациях понятий  нечетких множеств, отношений, свойств, предикатов, операций, отображений (морфизмов). Введение в оборот отношений, более общих, нежели эквивалентность, а также бесконечных последовательностей таких морфизмов, их суперпозиций позволит, по мнению автора, более естественным для практических нужд образом отразить хаотичность и слабую предсказуемость большого числа экономических процессов.

  Зададимся вопросом: зачем вообще необходимы достаточно абстрактные категории — изоморфизм и гомоморфизм – в имитационном моделировании? Можно ли каким-нибудь образом обойтись без них, строя модели как прораб – без доказательств, теорем и т.п.? Известно, что изоморфизм предполагает не только тождество (одинаковость, равночисленность) структуры, но и тождество функционирования для модели и ее прообраза. Однако построение моделей сложных систем крайне редко приводит к полному изоморфизму, а в случае очень сложных систем по Биру (как следует из самого их определения) степень изоморфности модели реальной системе невозможно проверить никаким известным на сегодня способом.  Поэтому исследуемую систему необходимо предварительно упростить, применив к ней однозначное лишь в одну сторону преобразование. Упрощение наобум, без веских оснований по каждому исключаемому из рассмотрения фактору (параметру), без подтверждения корректности проводимой гомоморфной свертки вряд ли позволить создать адекватную имитационную модель. Обосновывая естественность понятия гомоморфизма, Гастев отмечал: «Поскольку полнота  и точность воспроизведения внешнего мира в человеческом сознании всегда относительны (а о «взаимной однозначности» вообще не может быть речи), то соответствия между сколько-нибудь обширными совокупностями предметов внешнего мира и их образами в человеческом сознании никоим образом не могут быть изоморфными (даже относительно самых «скромных» наборов атрибутов), а должны носить более общий характер» [3, с. 30]. Таким образом, главнейшая методологическая функция гомоморфного преобразования заключается в логически непротиворечивой свертке всей доступной исследователю информации об изучаемых системах, объектах, процессах в емкую, компактную, легкообозримую и удобную для обработки форму (за вычетом несущественных данных и информационного шума).

 Разумеется, концепция, согласно которой процесс формализации имитационной модели может быть описан в терминах гомоморфизмов, не лишена очевидных недостатков. Вряд ли произвольный фрагмент предметной области может быть представлен в виде гомоморфного образа-модели в случае, когда из пресловутой тройки критериев проекта {качество; стоимость; сроки} предполагается оптимизировать хотя бы 2 критерия. Более того, специфика современных бизнес-процессов такова (особенно в финансово-кредитной сфере), что была бы неоправданной авантюрой попытка отразить  в виде некой алгебраической системы полный бизнес-цикл хотя бы безбалансового отделения банка. «Изоморфный на все 100%» идеал труднодостижим в силу стохастического характера экономических процессов, посему приходится довольствоваться гомоморфными моделями, приемлемыми с точки зрения практики. С другой стороны, автор не видит особых затруднений в том, чтобы интересующий в академическом или прикладном плане произвольный     сегмент реальной экономики представить в качестве частичной алгебраической системы (т.е. множества объектов, на подмножествах которого определены некоторые операции и предикаты) — а после этого для таких частичных систем ввести соответствующие гомоморфизмы (см., например, [9]).

В свете сказанного особый интерес представляют присутствующие на международном рынке  коммерческие разработки, автоматизирующие (пусть и для конкретных отраслей экономики) процесс трансформации концептуальной модели в компьютерную, пригодную для экспериментов. Так, в работе [16] и ряде сопутствующих ей рассматривается методология IPED (Isomorphic Permuted Experimental Designs), ориентированная на применение в такой далекой от оснований математики области, как маркетинговые исследования потребительских предпочтений. Будучи принципиально новым инструментом в моделировании обратной связи между компанией-производителем и ее клиентами, IPED облегчает проведение численных экспериментов на ЭВМ с многопараметрическими моделями, для которых присущ синергетический эффект как по подмножествам, так и по всей совокупности факторов. В частности, благодаря программно сгенерированным  рандомизированным перестановкам, произведенным над оригинальным проектом Web-сайта, удалось автоматически получить несколько сот изоморфных версий исходного проекта, которые были статистически уникальны для данного случая. Как результат, существенно большее число респондентов-потребителей смогли за меньшее время многократно протестировать каждую возможную комбинацию элементов Web-страницы – что в конечном счете позволило компании лучше приспособить  свой корпоративный портал к запросам клиентов.

 

Заключение

Подведем итоги сказанному выше. По глубокому убеждению автора, доказательство корректности гомоморфной свертки всей доступной информации об исследуемых процессах в емкую и удобную для моделирования форму – абсолютно необходимый шаг на пути создания реалистической имитационной модели. Формализация процедуры гомоморфного отображения (и, соответственно, подтверждения ее корректности) – вопрос более чем открытый. В свою очередь, задача полной автоматизации (компьютеризации) процедуры формализации не менее далека от решения в коммерческих системах имитационного моделирования (в самом деле, нельзя же полагать, что применение рассчитанных на сокращение сроков разработки средств визуального моделирования в состоянии заменить логически непротиворечивые действия,  продвигающие исследователя от концептуальной модели к программному коду, пригодному для решения реальных задач). В качестве одного из вариантов решения проблемы предлагается сконцентрировать усилия на создании гибридных («интеллектуальных») имитационных моделей, использующих не только ставшие уже привычными методы системного анализа, теории массового обслуживания или реинжиниринга бизнес-процессов – но также опирающиеся на логико-алгебраические схемы (в т.ч. аппарат неклассической логики и алгебраические структуры).

 

Благодарности

Автор хотел бы выразить глубокую признательность двум замечательным алгебраистам, В.Я. Шварцу и В.М. Усенко (к сожалению, безвременно ушедшим от нас) – которые в свое время, сами того не подозревая, приложили много усилий к тому, чтобы настоящие заметки появились на свет. Особая благодарность за дружеское отношение и содействие – д-ру Алексу Гофману (Alex Gofman) из Pace University, чьи талант, трудолюбие и упорство, направленные на воплощение brainware в software, еще предстоит оценить по достоинству в полной мере. Разнообразные плодотворные дискуссии и постоянное незримое присутствие А. Рафаловича (Aleksandr Rafalovich, UNO) в значительной мере помогли привести первоначальные отрывочные и хаотические «соображения по поводу…» в более-менее вразумительный, как надеется автор, вид.

 

Литература:

  1. Бир Ст. Кибернетика и менеджмент: Пер. с англ. / Под ред. А.Б. Челюсткина. – Изд. 2-е. – М.: КомКнига, 2006. – 280 с.
  2. Бусленко Н.П. Моделирование сложных систем. – 2-е изд., перераб.,  доп. – М.: Наука, 1978. – 400 с. 
  3. Гастев Ю.А. Гомоморфизмы и модели (логико-алгебраические аспекты моделирования). – М.: Наука, 1975. – 152 с.
  4. Глушков В.М., Цейтлин Г.Е., Ющенко Е.Л. Алгебра. Языки. Программирование. – К.: Наукова думка, 1974. – 328 с. 
  5. Кельтон В., Лоу А. Имитационное моделирование. Классика CS. 3-е изд. – СПб.: Питер; К.: BHV, 2004. – 847 с.
  6. Кухтенко А.И. Кибернетика и фундаментальные науки. – К.: Наукова думка, 1987. – 141 с.
  7. Месарович М., Такахара Я. Общая теория систем: математические основы. – М.: Мир, 1978. – 311 с. 
  8. Новиков Ф.А. Дискретная математика для программистов. – СПб.: Питер, 2002. – 304 с.
  9. Румянцев М.И. К проблеме формализации бизнес-процессов коммерческого банка // Культура народов Причерноморья. – 2007. – № 120. – с. 137-141.
  10. Румянцев М. И. К вопросу оценки адекватности имитационных моделей банковских бизнес-процессов // Сб. научных трудов по материалам международной научно-практ. конференции «Современные проблемы и пути их решения в науке, транспорте, производстве и образовании ‘2010». Том 15. Экономика. – Одесса: Черноморье, 2010. – с. 84-93.
  11. Румянцев М.И. Замечания по поводу самотестируемости имитационных моделей банковских бизнес-процессов // Сб. научных трудов по материалам международной научно-практ. конференции «Современные направления теоретических и прикладных исследований ‘2011». Том 11. Экономика. – Одесса: Черноморье, 2011. – с. 26-29.
  12. Рыжиков Ю.И. Имитационное моделирование. Теория и технологии. – СПб.: КОРОНА принт; М.: Альтекс-А, 2004. – 384 с.
  13. Сигорский В.П. Математический аппарат инженера. – К.: Техніка, 1975. – 768 с. 
  14. Томашевський В.М. Моделювання систем. – К.: Видавнича група BHV, 2005. – 332 с.
  15.  Френкель А.А., Бар-Хиллел И. Основания теории множеств: Пер. с англ. / Под ред. А.С. Есенина-Вольпина. – М.: Мир, 1966. – 555 с. 
  16. Gofman A., Moskowitz H. Isomorphic permuted experimental designs and their application in conjoint analysis // Journal of Sensory Studies. – 2010. – Vol. 25., No. 1. – pp. 127-145. 
  17. Thompson J.R. Simulation: A Modeler’s Approach. – John Wiley & Sons, 2000.

 

запрос ссылки — Логика и вычисления: философская точка зрения на изоморфизм Карри-Ховарда

Я думаю, что вы правы, если вас впечатлила переписка Карри-Ховарда. Это подробный и обширный изоморфизм «правило за правилом» и «функция за функцией». Это убедительно свидетельствует о том, что доказательство и вычислимость тесно связаны. Я также согласен с тем, что она недооценивается в рамках философии логики и что мы можем и должны позволить ей влиять на наше понимание логики.

Логики любят спорить о логике. Они будут расходиться во мнениях даже по таким базовым вещам, как, например, как объяснить концепцию достоверности . Спросите Фреге, Куайна, Тарски, Дэвидсона, Льюиса, Правица, Этчеменди, МакГи, Брэндома и Макфарлейна, и вы получите десять разных ответов. Они также будут спорить о том, существует ли единая «одна логика, чтобы управлять ими всеми», и если да, то какая, и можно ли защитить логический плюрализм. Согласно Даммету, интуитивизм — единственный путь; для Рида это релевантная логика, для Приста паранепротиворечивая логика, для Куайна классическая логика.

С точки зрения вычислимости относительно мало споров о том, что следует понимать под вычислимостью. Есть некоторые вопросы о том, как именно сформулировать тезис Черча-Тьюринга, применим ли он к интерактивным компьютерам и каким образом, и следует ли позволять таким соображениям, как законы природы, определять то, что мы можем назвать вычислением.

Итак, поскольку мы, по-видимому, довольно хорошо понимаем вычислимость, а логику — гораздо хуже, кажется, имеет смысл позволить нашему пониманию первого помочь нам со вторым.

Важно отметить, что соответствие Карри-Ховарда распространяется на классическую логику. Сами Карри и Ховард не знали об этом, когда формулировали переписку. Они начали с интерпретации интуиционизма БХК и использовали тот факт, что интуиционистские доказательства конструктивны, чтобы читать эти доказательства как рецепты для вычислений. Но последующие работы ученых-компьютерщиков, в том числе Гриффина, Париго, Аскьери и других, показали, что даже классическая логика разделяет соответствие. На практике это означает, что существуют вычислительные интерпретации классических систем, которые нормализуемы и позволяют извлекать вычисления из классических доказательств.

Это не означает, что любое классическое предложение вычислимо: очевидно, что существует любое количество неразрешимых предложений. Полная степень того, что можно вычислить классически, все еще остается областью исследований. Но это означает, что мы можем отказаться от упрощенческой идеи о том, что классическая логика неконструктивна, а интуиционистская логика конструктивна. Классические дизъюнкции, например, могут быть объектами доказательств без разрезов, как отметил Жирар в своей статье «Новая конструктивная логика: классическая логика».

Чтобы ответить на ваши конкретные вопросы:

  1. Логика и вычислимость действительно тесно связаны. Однако они не идентичны. По крайней мере, вычисления происходят с течением времени и требуют какой-то вычислительной машины. Доказательства часто рассматриваются как абстрактные структуры, хотя любой экземпляр доказательства требует некоторой физической формы.

  2. Идея о том, что логика должна обладать некоторым вычислимым аппаратом, чтобы квалифицироваться как логика, не так уж и странна, как может показаться. Это не исключило бы классическую логику из квалификации. Однако это строгое требование, и его могут оспорить те, кто считает, что семантика логики важнее теории доказательств.

В качестве последнего предположения я подозреваю, что связь между логикой и вычислимостью подтверждает точку зрения, согласно которой мы должны понимать логику как по существу формальную по своей природе. С точки зрения логики, преуменьшающей формальность, будет труднее объяснить связь с вычислимостью. Кроме того, некоторые очень широкие представления о том, что считается валидностью, могут быть отвергнуты на том основании, что их нельзя прямо преобразовать в вычислимую форму.

философия математики — Согласно математическому структурализму, может ли чистая математическая теория иметь семантику, не замкнутую на изоморфизме?

Этот вопрос является философской стороной вопроса, который я недавно разместил в MathOverflow. Здесь я специально спрашиваю о результатах математического структурализма по этому вопросу, который я повторно опубликую здесь. Тем не менее, я включу краткий отчет об основных утверждениях математического структурализма, чтобы иметь четкое представление о том, о чем я буду здесь спрашивать, а также чтобы устранить путаницу в используемой терминологии.

Математический структурализм продвигает точку зрения, согласно которой чистые математические теории касаются того, что они называют «структурами». Здесь следует предупредить, что то, что они называют структурой, не имеет значения, обычно используемого в математической логике. Математические структуралисты определяют « система » (также называемая «реляционная система») как набор[ы] с отношениями на нем[их], это можно зафиксировать как кортеж общего вида (M_1, M_2,..; R_1, R_2,.. ) где каждое R_i является отношением, домены и ко-домен которого находятся среди наборов M_i. M_is’ следует называть доменами системы, а R_is’ являются наборами отношений системы. Ясно, что мы обычно называем «модель» теории квалифицируется как «система», как определено здесь.

Теперь структура определяется как своего рода универсалия, распространяющаяся на все изоморфные системы. Моя личная попытка уловить это с точки зрения классов состоит в том, что структура является классом эквивалентности систем до системный изоморфизм . Где последнее — это биекция между доменами систем, сохраняющая наборы отношений между ними. Я думаю, что есть и другой способ уловить понятие структуры, а именно образ системы под действием функции из систем, чувствительных к изоморфизмам, т. е. отсылает изоморфные системы в своей области к общему образу. Однако я в основном буду придерживаться первого определения структур, то есть классов эквивалентности систем при изоморфизме.

Теперь все просто, если мы работаем с категориальной теорией, такой как, например, арифметика второго порядка при полной семантике. Здесь эта теория касается ЕДИНСТВЕННОЙ структуры, и, таким образом, согласно структурализму, это идеальная чисто математическая теория. Но проблема в том, что не все теории категоричны. Все теории первого порядка с бесконечными областями не являются категоричными. Таким образом, такая теория, как PA первого порядка, могла бы стать рецептом множества структур, скажем, СПЕКТРА структур. Однако это все еще можно согласовать с математическим структурализмом, поскольку речь идет все-таки о структурах, другими словами, ее семантика замкнута относительно системного изоморфизма, то есть, если PA говорит о некоторой системе A, то всякая система, системно изоморфная A, по-прежнему зачислен в его семантику, поэтому, хотя PA касается нескольких структур, все же речь идет о структурах, а не о чем-то еще.

Теперь, что если у нас есть формальная теория, которая использует ограничение на свою семантику, чтобы не быть замкнутой при системном изоморфизме, что эта теория по-прежнему может считаться чисто математической с точки зрения математического структурализма?

Примерами того, что я имею в виду, является теория, семантика которой замкнута относительно изоморфизма к системе А, но имеет среди своей семантики систему В, такую, что никакая система, изоморфная В, не является приемлемой среди ее семантики, или, что еще хуже, если ее семантика является собственный подкласс структуры. Тривиальным примером является теория, расширяющая теорию тождества, которая обуславливает существование двух различных объектов и запрещает существование других. Теперь, если мы ограничим модели этой теории, скажем, только набором {0, {0}}, тогда это будет строгим ограничением на семантику этой теории, которое сильно противоречит структурализму. Мы можем сказать, что эта теория не является чисто математической теорией, поскольку она касается особенности, которая вообще не имеет структурного жанра. Его можно рассматривать как прикладную формальную теорию к этой особенности или даже прикладную математическую теорию к этому ограничению, но не чисто математическую, поскольку ее семантика не проявляет уважения к структурам.

Мне кажется, что такие формальные системы нельзя считать чисто математическими с точки зрения математического структурализма, поскольку нельзя сказать, что они говорят о структуре[ах]?

Теперь мой вопрос: существуют ли примеры известных теорий, которые математический структурализм квалифицирует как чисто математические, но при этом использует ограничения на их семантику, чтобы класс всех приемлемых моделей не был замкнутым под модельным (системным) изоморфизмом?

У меня есть пример: возьмите теорию, скажем, с аксиомами PA, но ограничьте ее семантику только стандартными моделями PA, которые, скажем, «наследственно < каппа» для некоторого фиксированного бесконечного кардинального каппа. Считается ли такая теория чисто математической теорией? Я имею в виду с точки зрения математического структурализма!

Вопрос касается способности математического структурализма охарактеризовать, что такое чистая математическая теория.