Изоморфны: Недопустимое название | Математика | Fandom
Изоморфизм (математика) — это… Что такое Изоморфизм (математика)?
Изоморфи́зм — это очень общее понятие, которое употребляется в различных разделах математики. В общих чертах его можно описать так: Пусть даны два множества с определённой структурой (группы, кольца, линейные пространства и т. п.). Биекция между ними называется изоморфизмом, если она сохраняет эту структуру. Такие множества со структурой называются изоморфными. Изоморфизм всегда задаёт отношение эквивалентности на классе таких множеств со структурой.
Объекты, между которыми существует изоморфизм, являются в определённом смысле «одинаково устроенными», они называются изоморфными. Классическим примером изоморфных систем могут служить множество всех вещественных чисел с определённой на нём операцией сложения и множество положительных вещественных чисел с заданной на нём операцией умножения. Отображение в этом случае является изоморфизмом.
Абстрактная алгебра
В абстрактной алгебре изоморфизмом называется биекция, которая является гомоморфизмом.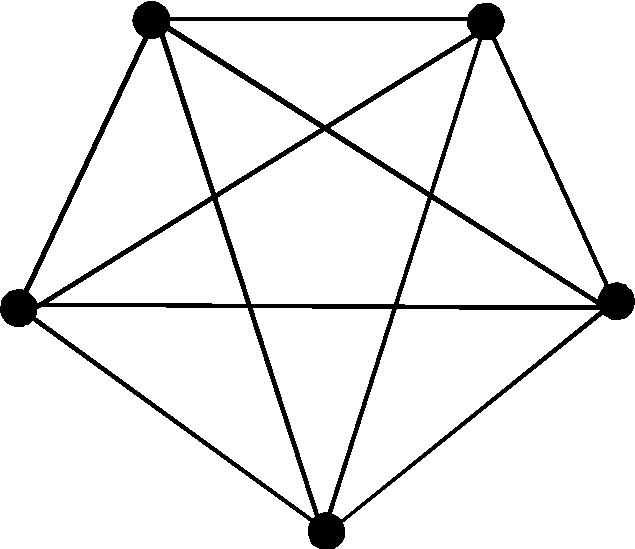
Пусть и суть две группы. Биекция называется изоморфизмом, если для любых
Если группа является топологической, добавляется условие гомеоморфности соответствующих топологических пространств.[1]
В теории категорий изоморфизм есть обратимый морфизм, то есть морфизм , для которого существует такой морфизм , что произведения и — тождественные морфизмы.
Ограниченный линейный оператор T между нормированными пространствами называется изоморфизмом, если существует положительное вещественное число c такое, что для всех векторов x. Любой изоморфизм является взаимно-однозначным. Легко видеть, что T является изоморфизмом тогда и только тогда, когда T обратим на своем образе, и обратный оператор ограничен. Говорят, что два нормированных пространства являются изоморфными, если найдется сюръективный изоморфизм из одного из них на другое.
Граф G называется изоморфным графу H, если существует биекция f из множества вершин графа G в множество вершин графа H, обладающая следующим свойством: если в графе G есть ребро из вершины A в вершину B, то в графе H должно быть ребро из вершины f(A) в вершину f(B) и наоборот — если в графе H есть ребро из вершины A в вершину B, то в графе G должно быть ребро из вершины f − 1(A) в вершину f − 1(B).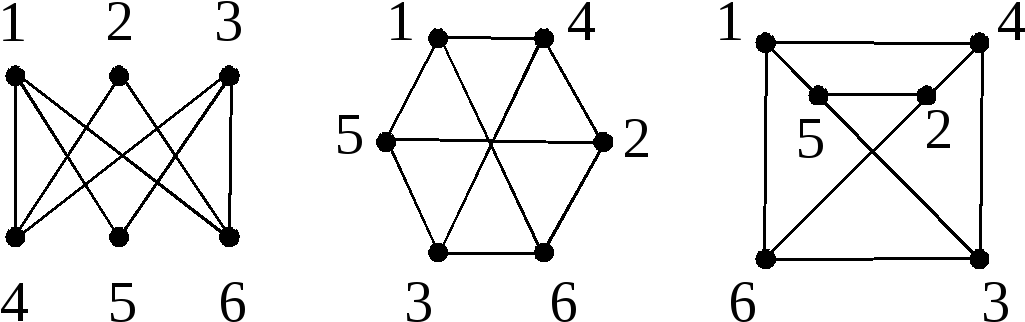 В случае ориентированного графа эта биекция также должна сохранять ориентацию ребра. В случае взвешенного графа биекция также должна сохранять вес ребра.
В случае ориентированного графа эта биекция также должна сохранять ориентацию ребра. В случае взвешенного графа биекция также должна сохранять вес ребра.
В теории вычислительной сложности до сих пор является открытым вопрос о сложности задачи изоморфности графов. На данный момент не доказана ни её принадлежность классу
Связанные определения
Изоморфизм алгебраической системы на себя называется автоморфизмом.
История
Понятие изоморфизма возникло в математике применительно к конкретным алгебраическим системам (прежде всего к группам) и было естественным образом распространено на более широкий класс математических структур.
См. также
Примечания
- ↑ Л.С. Понтрягин Непрерывные группы стр. 392
Литература
Wikimedia Foundation. 2010.
НОУ ИНТУИТ | Лекция | Эквивалентность и порядок. Изоморфизмы
Аннотация: Описывается много новых понятий, таких как отношение эквивалентности, отношение частичного порядка, изоморфные частичные множества. Доказываются несколько теорем по данной теме с подробными объяснениями, графиками и примерами. Задается большое количество примеров частичных порядков. Описываются несколько конструкций, позволяющих строить одни упорядоченные множества из других. Для лекции характерно множество задач для самостоятельного решения
Доказываются несколько теорем по данной теме с подробными объяснениями, графиками и примерами. Задается большое количество примеров частичных порядков. Описываются несколько конструкций, позволяющих строить одни упорядоченные множества из других. Для лекции характерно множество задач для самостоятельного решения
Отношения эквивалентности и порядка
Напомним, что бинарным отношением на множестве называется подмножество ; вместо часто пишут .
Бинарное отношение на множестве называется отношением эквивалентности, если выполнены следующие свойства:
Имеет место следующее очевидное, но часто используемое утверждение:
Теорема 11.
(а)
Если множество разбито в объединение непересекающихся
подмножеств, то отношение » лежать в одном подмножестве»
является отношением эквивалентности.
(б) Всякое отношение эквивалентности получается описанным способом из некоторого разбиения.
Доказательство. Первое утверждение совсем очевидно; мы приведем доказательство второго, чтобы было видно, где используются все пункты определения эквивалентности. Итак, пусть — отношение эквивалентности. Для каждого элемента рассмотрим его класс эквивалентности — множество всех , для которых верно .
Докажем, что для двух различных , такие множества либо не пересекаются, либо совпадают. Пусть они пересекаются, то есть имеют общий элемент . Тогда и , откуда (симметричность) и (транзитивность), а также (симметричность). Поэтому для любого из следует (транзитивность) и наоборот.
Осталось заметить, что в силу рефлексивности каждый элемент
принадлежит задаваемому им классу, то есть действительно
все множество разбито на непересекающиеся классы.
78. Покажите, что требования симметричности и транзитивности можно заменить одним: (при сохранении требования рефлексивности).
79. Сколько различных отношений эквивалентности существует на множестве ?
80. На множестве задано два отношения эквивалентности, обозначаемые и , имеющие и классов эквивалентности соответственно. Будет ли их пересечение отношением эквивалентности? Сколько у него может быть классов? Что можно сказать про объединение отношений?
81. (Теорема Рамсея) Множество всех — элементных подмножеств бесконечного множества разбито на классов ( , — натуральные числа). Докажите, что найдется бесконечное множество , все — элементные подмножества которого принадлежат одному классу.
(При это очевидно: если бесконечное множество разбито
на конечное число классов, то один из классов бесконечен. При
и утверждение можно сформулировать так:
из бесконечного множества людей можно выбрать либо
бесконечно много попарно знакомых, либо бесконечно много
попарно незнакомых. Конечный вариант этого утверждения — о том,
что среди любых шести людей есть либо три попарно знакомых,
либо три попарно незнакомых, — известная задача для школьников.)
При
и утверждение можно сформулировать так:
из бесконечного множества людей можно выбрать либо
бесконечно много попарно знакомых, либо бесконечно много
попарно незнакомых. Конечный вариант этого утверждения — о том,
что среди любых шести людей есть либо три попарно знакомых,
либо три попарно незнакомых, — известная задача для школьников.)
Множество классов эквивалентности называют фактор — множеством множества по отношению эквивалентности . (Если отношение согласовано с дополнительными структурами на , получаются фактор — группы, фактор — кольца и т.д)
Отношения эквивалентности нам не раз еще встретятся, но сейчас наша основная тема — отношения порядка.
Бинарное отношение на множестве называется отношением частичного порядка, если выполнены такие свойства:
(Следуя традиции, мы используем символ (а не букву) как знак
отношения порядка. ) Множество с заданным на нем отношением частичного
порядка называют частично упорядоченным.
) Множество с заданным на нем отношением частичного
порядка называют частично упорядоченным.
Говорят, что два элемента частично упорядоченного множества сравнимы, если или . Заметим, что определение частичного порядка не требует, чтобы любые два элемента множества были сравнимы. Добавив это требование, мы получим определение линейного порядка ( линейно упорядоченного множества ).
Приведем несколько примеров частичных порядков:
- Числовые множества с обычным отношением порядка (здесь порядок будет линейным).
- На множестве всех пар действительных чисел можно ввести частичный порядок, считая, что , если и . Этот порядок уже не будет линейным: пары и не сравнимы.
- На множестве функций с действительными аргументами и значениями
можно ввести частичный порядок, считая, что , если при всех .

- На множестве целых положительных чисел можно определить порядок, считая, что , если делит . Этот порядок тоже не будет линейным.
- Отношение » любой простой делитель числа является также и делителем числа » не будет отношением порядка на множестве целых положительных чисел (оно рефлексивно и транзитивно, но не антисимметрично).
- Пусть — произвольное множество. Тогда на множестве всех подмножеств множества отношение включения будет частичным порядком.
- На буквах русского алфавита традиция определяет некоторый порядок ( ). Этот порядок линеен — про любые две буквы можно сказать, какая из них раньше (при необходимости заглянув в словарь).
- На словах русского алфавита определен лексикографический
порядок (как в словаре).
 Формально определить его можно так:
если слово является началом слова , то
(например, ). Если ни одно из слов
не является началом другого, посмотрим на первую по порядку
букву, в которой слова отличаются: то слово, где эта буква
меньше в алфавитном порядке, и будет меньше. Этот порядок также
линеен (иначе что бы делали составители словарей?).
Формально определить его можно так:
если слово является началом слова , то
(например, ). Если ни одно из слов
не является началом другого, посмотрим на первую по порядку
букву, в которой слова отличаются: то слово, где эта буква
меньше в алфавитном порядке, и будет меньше. Этот порядок также
линеен (иначе что бы делали составители словарей?). - Отношение равенства ( ) также является отношением частичного порядка, для которого никакие два различных элемента не сравнимы.
- Приведем теперь бытовой пример. Пусть есть множество картонных коробок. Введем на нем порядок, считая, что , если коробка целиком помещается внутрь коробки (или если и — одна и та же коробка). В зависимости от набора коробок этот порядок может быть или не быть линейным.
Пусть — элементы частично упорядоченного множества . Говорят, что , если и . Для этого отношения выполнены такие свойства:
(Первое очевидно, проверим второе: если и , то есть , , , , то по транзитивности; если бы оказалось, что , то мы бы имели и потому по антисимметричности, что противоречит предположению.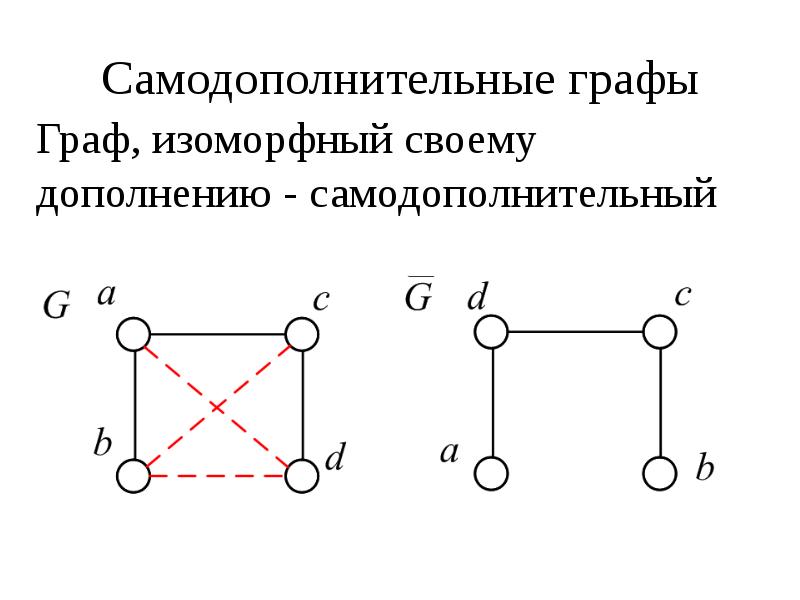 )
)Терминологическое замечание: мы читаем знак как » меньше или равно», а знак — как » меньше», неявно предполагая, что тогда и только тогда, когда или . К счастью, это действительно так. Еще одно замечание: выражение (» больше «) означает, что , а выражение (» больше или равно «) означает, что .
Что Означает, Что Для Двух Бинарных Деревьев Изоморфны?
Изоморфный происходит от греческой «той же формы» (например, изобара — это точки с одинаковым давлением воздуха, а полигон означает «многосторонний» ), поэтому ваше понимание правильное. Но не делайте ошибки при принятии формы в этом случае — это физическая форма (например, дерево имеет один корень, один слева node и один правый node, см. Ниже, например). Математики имеют свой язык, который только иногда имеет отношение к английскому: -)
Это не просто бинарные деревья. В математике две структуры изоморфны, если их свойства сохраняются независимо от их выражения (вы можете иметь функцию, которая переводит A в B, а другую из B в без потери информации).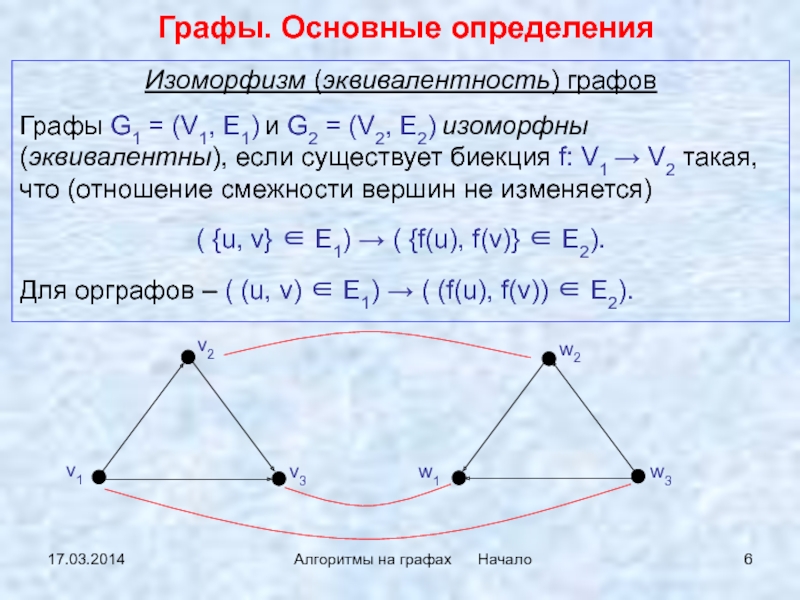
В вашем конкретном случае это информация в сохраненном дереве. Например, если эта информация является отсортированным элементом {1,2,3}, то дерево не обязательно должно быть одной и той же физической формой — следующие два будут изоморфными:
2 1
/ \ \
1 3 2
\
3
Сортированный связанный список (или отсортированный массив, если на то пошло) также изоморфен тем, что в этом случае никакая информация не будет потеряна при преобразованиях между ними.
Если двоичное дерево использовалось таким образом, чтобы порядок сортировки был неактуальным (т.е. контейнер контейнера типа «сумка» ), тогда информация была бы просто содержимым в любом порядке, и все следующее было бы изоморфно (что второй последний — только мешок, последний — список):
2 1 2 3 +---+ +---+ +---+
/ \ \ / \ +-------+ | 3 |->| 1 |->| 2 |
1 3 2 1 2 | 1,3,2 | +---+ +---+ +---+
\ / \ +-------+
3 3 1
Конечно, несортированное дерево может считаться небольшим количеством отходов в зависимости от ваших потребностей, но это не относится к этому конкретному обсуждению.
Как я могу проверить, изоморфны ли два графа с LABELED вершинами?
Я сделал несколько попыток создать алгоритм изоморфизма полиномиального графа, и хотя мне еще предстоит создать алгоритм, который окажется полиномиальным для каждого случая, один алгоритм, который я придумал, особенно подходит для этой цели. Он основан на алгоритме минимизации DFA (конкретный алгоритм- http://en.wikipedia.org/wiki/ DFA_minimization#Hopcroft.27s_algorithm ; вы можете найти описание из другого места, так как Википедия трудна для понимания).
Исходный алгоритм был инициализирован путем организации вершин в различные группы на основе степени (одна группа для вершин степени 1, одна для вершин степени 2 и т. д.). Для ваших целей вы захотите организовать вершины в группы на основе Как степени, так и метки; это гарантирует, что никакие два узла не будут спарены, если они имеют разные метки. Каждый граф должен иметь свою собственную структуру, содержащую такие группы. Проверьте набор групп для обоих графов; для двух графов должно быть одинаковое количество групп, и для каждой группы в одном графе должна быть группа в другом графе, содержащая одинаковое количество вершин одинаковой степени и метки. Если это не так, то графики не изоморфны.
Проверьте набор групп для обоих графов; для двух графов должно быть одинаковое количество групп, и для каждой группы в одном графе должна быть группа в другом графе, содержащая одинаковое количество вершин одинаковой степени и метки. Если это не так, то графики не изоморфны.
На каждой итерации основного алгоритма вы должны генерировать новую структуру данных для каждого из двух графов для групп вершин, которые будут использоваться на следующем шаге. Для каждой группы создайте список для каждой вершины групповых индексов/IDs, соответствующих вершинам, смежным с рассматриваемой вершиной (включите дубликаты групп в этот список). Проверьте каждую группу, чтобы увидеть, является ли список отсортированных индексов групп/ID для каждой содержащейся вершины одинаковым. Если это так, создайте немодифицированную копию этой группы в структуре группы следующего шага. Если это не так, то для каждого уникального списка групповых индексов/IDs в этой группе создайте новую группу для вершин в исходной группе, которая сгенерировала этот список, и добавьте эту новую группу в структуру группы следующего шага. Если вы не разделите ни одну из групп любого графа в данной итерации, прекратите выполнение основной части этого алгоритма. Если вы разделите хотя бы одну группу, вам нужно будет еще раз проверить, чтобы убедиться, что групповые структуры двух графиков соответствуют друг другу. Эта проверка будет аналогична той, что выполняется в конце инициализации алгоритма (возможно, вы даже сможете использовать одну и ту же функцию для обоих). Если эта проверка не выполняется, то графики не изоморфны. Если проверка пройдена, то отбросьте / освободите текущие структуры группы и начните следующую итерацию со свежесозданных.
Если вы не разделите ни одну из групп любого графа в данной итерации, прекратите выполнение основной части этого алгоритма. Если вы разделите хотя бы одну группу, вам нужно будет еще раз проверить, чтобы убедиться, что групповые структуры двух графиков соответствуют друг другу. Эта проверка будет аналогична той, что выполняется в конце инициализации алгоритма (возможно, вы даже сможете использовать одну и ту же функцию для обоих). Если эта проверка не выполняется, то графики не изоморфны. Если проверка пройдена, то отбросьте / освободите текущие структуры группы и начните следующую итерацию со свежесозданных.
Чтобы упростить процесс определения «corresponding groups», я настоятельно рекомендую использовать предсказуемую схему добавления групп в структуру. Например, если вы добавляете группы во время инициализации в порядке (степень, метка), подразделяете группы в порядке возрастания индекса и добавляете подразделенные группы в новую структуру на основе порядка списка индексов групп (т.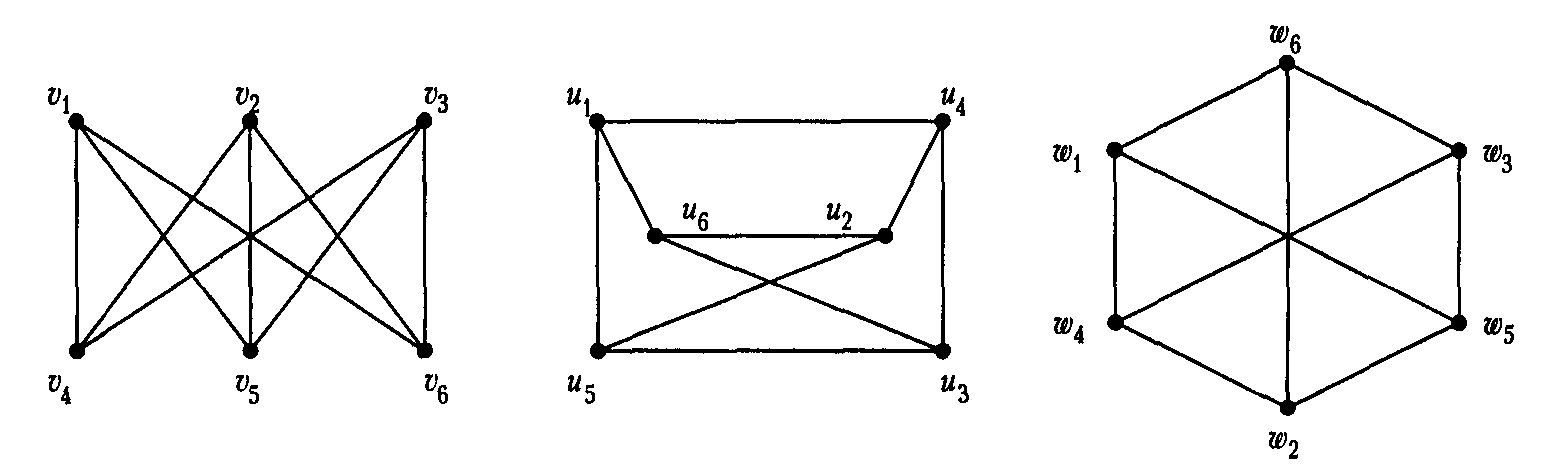 е. сортируете по первому перечисленному индексу, затем по второму и т. д.), то соответствующие группы между двумя групповыми структурами всегда будут иметь один и тот же индекс, что значительно облегчает процесс отслеживания того, какие группы соответствуют друг другу.
е. сортируете по первому перечисленному индексу, затем по второму и т. д.), то соответствующие группы между двумя групповыми структурами всегда будут иметь один и тот же индекс, что значительно облегчает процесс отслеживания того, какие группы соответствуют друг другу.
Если все группы содержат 3 или менее вершин, когда алгоритм завершается, то графики изоморфны (для соответствующих групп, содержащих 2 или 3 вершины, допустимо любое спаривание вершин). Если это не так (это всегда происходит для графов, где все узлы имеют одинаковую степень и метку, а иногда и для подграфов с этим свойством), то графы еще не определены как изоморфные или неизоморфные. Чтобы различить эти два случая, выберите произвольный узел самой большой группы первого графа и разделите его на свою собственную группу. Затем для каждого узла самой большой группы другого графа попробуйте снова запустить алгоритм с этим узлом, разделенным на свою собственную группу. По сути, вы выбираете непарный узел из первого графа и связываете его на guess-and-check с каждым узлом во втором графе, который все еще является вероятным спариванием. Если какая-либо из разветвленных итераций возвращает изоморфизм, то графики изоморфны. Если ни один из них этого не делает, то графики не изоморфны.
Если какая-либо из разветвленных итераций возвращает изоморфизм, то графики изоморфны. Если ни один из них этого не делает, то графики не изоморфны.
Для общих случаев этот алгоритм является полиномиальным. В угловых случаях алгоритм может быть экспоненциальным. Так это или нет, зависит от того, как часто алгоритм может быть вынужден fork в худшем случае как ввода графа, так и выбора узла, что у меня были трудности с попытками установить полезные границы. Например, хотя алгоритм разветвляется на каждом шаге при сравнении двух полных графов, каждая ветвь этого дерева производит изоморфизм; поэтому алгоритм возвращается в полиномиальном времени в этом случае, даже если обход всего дерева выполнения потребует экспоненциального времени, так как обход только одной ветви дерева выполнения занимает полиномиальное время.
Как бы то ни было, этот алгоритм должен хорошо работать для ваших целей. Я надеюсь, что мое объяснение этого было понятным; если нет, я могу попробовать привести примеры алгоритма, обрабатывающего простые случаи, или выразить его в виде псевдокода.
Изоморфность — Справочник химика 21
Образование смешанных кристаллов — изоморфизм. Изучение явлений соосаждения показало, что большое значение при соосаждении имеет также изоморфизм. Напомним, что изоморфными называются такие вещества, которые способны кристаллизоваться, образуя совместную кристаллическую решетку, причем получаются так называемые смешанные кристаллы. [c.115]ИЗОМОРФНЫЕ СМЕСИ. СИСТЕМЫ С ОГРАНИЧЕННОЙ РАСТВОРИМОСТЬЮ В ТВЕРДОМ СОСТОЯНИИ [c.234]
Устойчивые в обычных условиях модификации — серый мышьяк, серая сурьма и висмут — имеют металлический вид, электропроводны, но хрупки. Они изоморфны, имеют слоистую структуру (рис. 163) типа черного фосфора. Каждый из атомов пирамидально связан с тремя соседними по слою и имеет трех ближайших соседей в другом слое. В ряду Аз — 8Ь — В1 различие межъядерных расстояний внутри и между слоями уменьшается (0,063—0,050—0,037 нм), т.
 е. происходит постепенно приближение к характерному для металлических структур равенству межъядерных расстояний. Благодаря близости параметров кристаллических решеток сурьма образует твердые растворы с мышьяком и висмутом, но последние друг с другом их не образуют. [c.380]
е. происходит постепенно приближение к характерному для металлических структур равенству межъядерных расстояний. Благодаря близости параметров кристаллических решеток сурьма образует твердые растворы с мышьяком и висмутом, но последние друг с другом их не образуют. [c.380]Используя принцип изоморфного замещения, (3.24) перепишем в виде [c.128]
Из этого закона следует, что если два аналогичных по составу соединения кристаллизуются в виде смешанных кристаллов, то их химическую природу можно считать подобной (изоморфной). Это свойство изоморфных кристаллов позволяло экспериментаторам делать правильные заключения об атомных весах молекул одинакового элементного состава. [c.61]
Изоморфные соединения обычно образуют одинаковые по форме кристаллы (рис. 17). [c.115]
Это изоморфизм особого рода. Именно здесь не один из ионов осадка изоморфно замещается каким-либо другим ионом (как обычно), а пара ионов и 804 ) замещается другой парой ионов и МпО ), соизмеримой [c.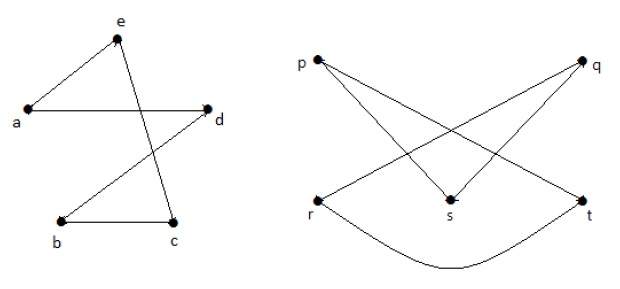 116]
116]
Для очистки осадка от адсорбированных им примесей и остатков маточного раствора после каждого осаждения необходимо полученный осадок тщательно промывать. Однако подобным образом окклюдированные осадком примеси не могут быть удалены, поскольку они находятся внутри частиц осадка это справедливо и для изоморфных кристаллов. [c.118]
В каких случаях ионы могут изоморфно замещать друг друга при построении кристаллической решетки [c.159]
Будучи изоморфными, гексагональные селен и теллур образуют между собой непрерывный ряд твердых растворов. При пысоких температурах пары селена и теллура состоят из парамагнитных молекул Seg и Тед. При понижении температуры они полимеризуются в молекулы Э4, Эе и Эд. [c.337]
Диаграмма плавкости изоморфной смеси приведена на рис. 107. На ней указаны фазовые составы, обозначенные соответствующими площадями Здесь все процессы охлаждения смесей по существу одинаковы, поэтому рассмотрим только одип из них. [c.234]
[c.234]
Впрочем, уравнение (1.62) можно было бы получить сразу из (1.2), используя принцип изоморфного замещения, т. е. подставляя вместо символа химического компо- [c.37]
Изоморфные смеси образуются веществами со сходным строением кристаллических решеток. Поэтому оба вещества при любом соотношении между ними кристаллизуются совместно, т. е. образуют твердый раствор. [c.234]
Рис, 107. Диаграмма плавкости изоморфной бинарной системы [c.234]
По теореме Кэли любая конечная группа О порядка п изоморфна подгруппе группы перестановок Рп, а в ряде частных случаев О может быть изоморфна и самой группе Р . Так, например, описанная выще группа перестановок изоморфна точечной группе О н ( = , (123) Сз, (12) С2, Е ан, (12) а., (123) = 5з) и состояния молекулы аммиака моннеприводимым представлениям этой группы. [c.118]
Мультиграфы G X, U) и Н Y, V) называются изоморфными [83], если существует взаимно однозначное отображение у = = F х) X на У, такое, что для любой пары вершин х, х» е X в Я имеется столько же ребер (дуг), следующих из у = F х) в у» = F х»), сколько их в G следует пз х в х .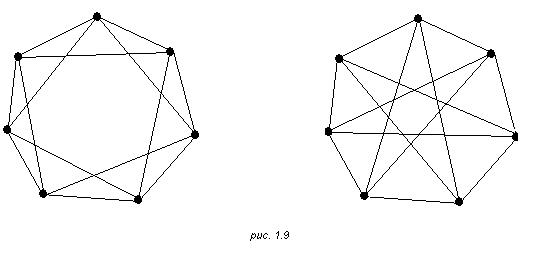 Такое взаимно однозначное отображение F, сохраняющее смежность, называется отношением изоморфизма. [c.96]
Такое взаимно однозначное отображение F, сохраняющее смежность, называется отношением изоморфизма. [c.96]
Выше (стр. 12) математическое описание определено как совокупность математических структур, изоморфно отражающих свойства объекта, проявляемые в экспериментальных условиях. Установим теперь, что должно быть включено в математическое описание химико-технологического процесса. [c.75]
Парафиновые углеводороды нормального строения относятся к изоморфным веществам, образующим при совместной кристаллизации твердые растворы. При понижении температуры в первую очередь выделяются кристаллы наиболее высокоплавких углеводородов, на кристаллической решетке которых последовательно кристаллизуются углеводороды с меньшей температурой плавления и меньшим числом атомов углерода в молекуле [6, 7]. Исследовать кристаллическую структуру твердых углеводородов масляных фракций нефти весьма сложно ввиду их многокомпонентно-сти. Даже кристаллическая структура нормальных парафинов — наиболее простых по строению компонентов установлена лишь в последнее время. [c.118]
[c.118]
В отличие от радиуса Ва + радиус Са + (1,06 А) значительно меньше, чем радиус Ка2+. Вследствие этого Са + и Ка2+ не могут входить в одну и ту же кристаллическую решетку, т. е. изоморфно замещать друг друга. В соответствии с этим Ка +-ионы не соосаждаются с Са304. [c.116]
Кристаллы КС1 и КВг изоморфны друг друг у, а кристаллы КС1 и Na l — нет. Чем объясняется это различие [c.159]
Если два вещества смешать друг с другом в определенных пропорциях и смесь нагреть до высокой температуррзг, то в подавляющем большинстве случаев образуется совершенно однородная жидкость, представляющая собой раствор одного компонента в другом. Некоторые системы дадут два жидких слоя взаимно насыщенных растворов, и только немногие будут совершенно нерастворимы друг в друге ми прн каких условиях. Это относится к таким веществам, которые не разлагаются до температуры плавления. Если такой раствор пли снлав охладить, то при некоторой температуре он начинает кристаллизоваться, так как растворимость веществ с понижением температуры, как правило, уменьшается.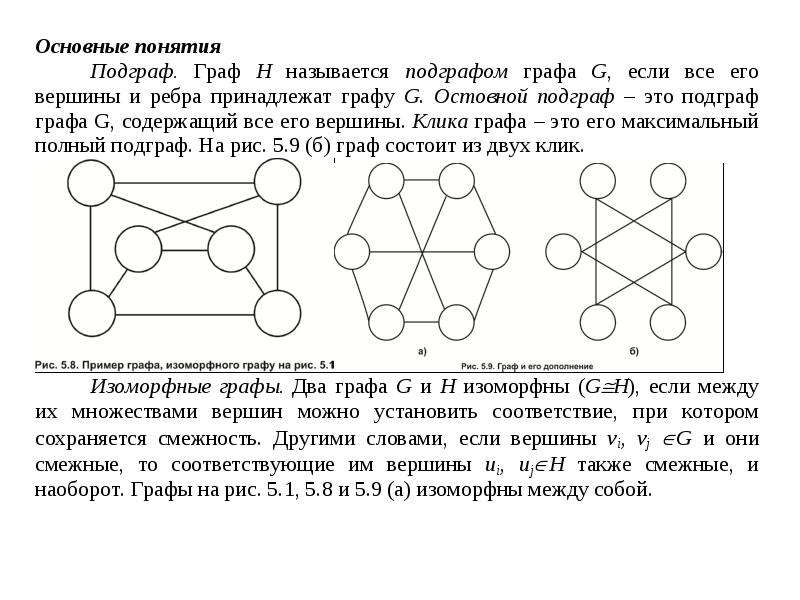 Природа и количество выпадающего вещества обусловливается природой и количественными соотношениями компонентов в растворе. Как и при всякой кристаллизации, здесь будет выделяться теплота кристаллизации, которая влияет на скорость охлаждения сплава. В некоторых случаях охлаждение может полностью прекратиться и температура смеси в течение некоторого времени будет оставаться постоянной. Таким образом, охлаждая определенный раствор, достигают неравномерного падения температуры в зависимости от нронсходящих в сплаве процессов. Если наносить на оси ординат температуру, а на оси абсцисс — время, то будут получаться кривые, иллюстрирующие процесс охлаждения. Вид этих кривых будет в высокой степени характерен как для чистых веществ, так и для их смесей различных концентраций. В процессе кристаллизации в зависимости от состава смеси могут выпадать твердые чистые компоненты, или твердые растворы. Кривые, выражающие зависимость температуры кристаллизации и плавления от состава данной системы, называются диаграммами плавкости.
Природа и количество выпадающего вещества обусловливается природой и количественными соотношениями компонентов в растворе. Как и при всякой кристаллизации, здесь будет выделяться теплота кристаллизации, которая влияет на скорость охлаждения сплава. В некоторых случаях охлаждение может полностью прекратиться и температура смеси в течение некоторого времени будет оставаться постоянной. Таким образом, охлаждая определенный раствор, достигают неравномерного падения температуры в зависимости от нронсходящих в сплаве процессов. Если наносить на оси ординат температуру, а на оси абсцисс — время, то будут получаться кривые, иллюстрирующие процесс охлаждения. Вид этих кривых будет в высокой степени характерен как для чистых веществ, так и для их смесей различных концентраций. В процессе кристаллизации в зависимости от состава смеси могут выпадать твердые чистые компоненты, или твердые растворы. Кривые, выражающие зависимость температуры кристаллизации и плавления от состава данной системы, называются диаграммами плавкости.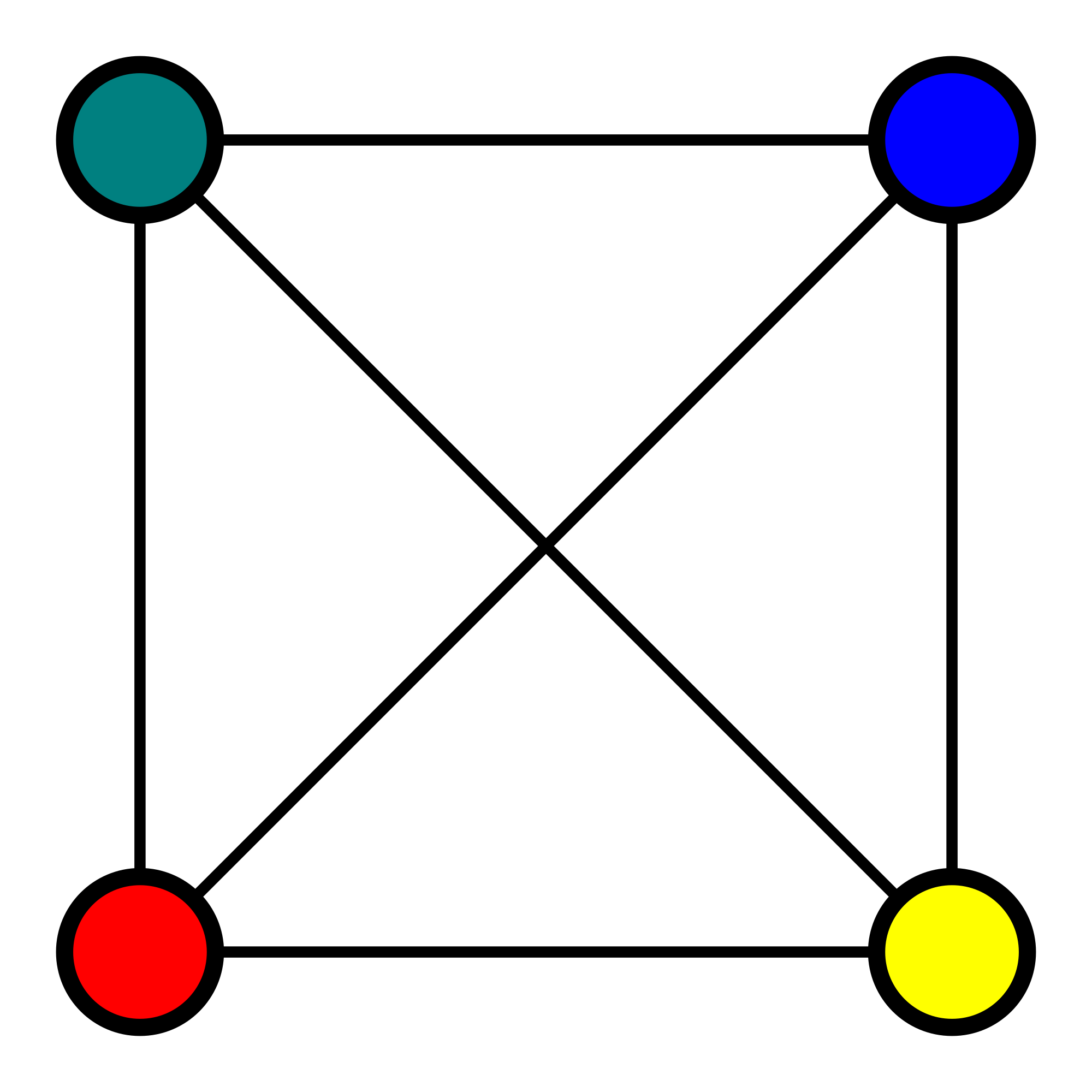 Эти диаграммы подразделяются на три типа в зависимости от того, какая фаза выделяется из раствора. К первому типу относятся системы, при кристаллизации которых из жидких растворов выделяются чистые твердые компоненты, так называемые неизоморфные смеси. Второй тип представляют системы, при кристаллизации которых из жидких растворов выделяются твердые растворы с неограниченной областью взаимной растворимости, так называемые изоморфные смеси. Третий тип системы, при кристаллизации которых из жидких растворов выделяются твердые растворы, характеризуются определенными областями взаимной растворимости. [c.227]
Эти диаграммы подразделяются на три типа в зависимости от того, какая фаза выделяется из раствора. К первому типу относятся системы, при кристаллизации которых из жидких растворов выделяются чистые твердые компоненты, так называемые неизоморфные смеси. Второй тип представляют системы, при кристаллизации которых из жидких растворов выделяются твердые растворы с неограниченной областью взаимной растворимости, так называемые изоморфные смеси. Третий тип системы, при кристаллизации которых из жидких растворов выделяются твердые растворы, характеризуются определенными областями взаимной растворимости. [c.227]
Отношение изоморфизма является отношением эквивалентности, разбивающим множество всех му.тьтиграфов на классы эквивалентности, которые можно рассматривать как абстрактные мультиграфы. Изоморфные мультиграфы представляют собой один и тот же абстрактный мультиграф. В настоящее время в связи с отсутствием стандарта на машинное представление [84] существует многс способов ввода в ЭВМ структурных формул и их топологическиг графов.
 К наиболее перспективным способам ввода относятся а) ввод структурных формул с помощью оптических считывающие устройств в) ввод с помощью стандартных дисплеев в) ввод с по мощью специализированных устройств типа граф [85]. Струк турную, формулу при этом рассматривают в виде взвешенного гра фа, т. е. как функцию, заданную на вершинах и ребрах графе Весом вершины при этом служит символ химического элемент или радикала, а весом ребра — кратность химической связи. [c.96]
К наиболее перспективным способам ввода относятся а) ввод структурных формул с помощью оптических считывающие устройств в) ввод с помощью стандартных дисплеев в) ввод с по мощью специализированных устройств типа граф [85]. Струк турную, формулу при этом рассматривают в виде взвешенного гра фа, т. е. как функцию, заданную на вершинах и ребрах графе Весом вершины при этом служит символ химического элемент или радикала, а весом ребра — кратность химической связи. [c.96] Из приведенного примера видно, что вид матрицы зависит от порядка нумерации вершин и определяет граф G (если отвлечься от конкретной природы его элементов) с точностью до перестановок параллельных ребер между собой, т. е. гораздо жестче , чем с точностью до изоморфизма. Для установления изоморфизма двух графов Gil Н с iV-вершииами необходимо осуш,ествить у. Л» операций [66] G ъН изоморфны тогда и только тогда, когда их вершины можно занумеровать так, что соответствующие матрицы смежности будут равны.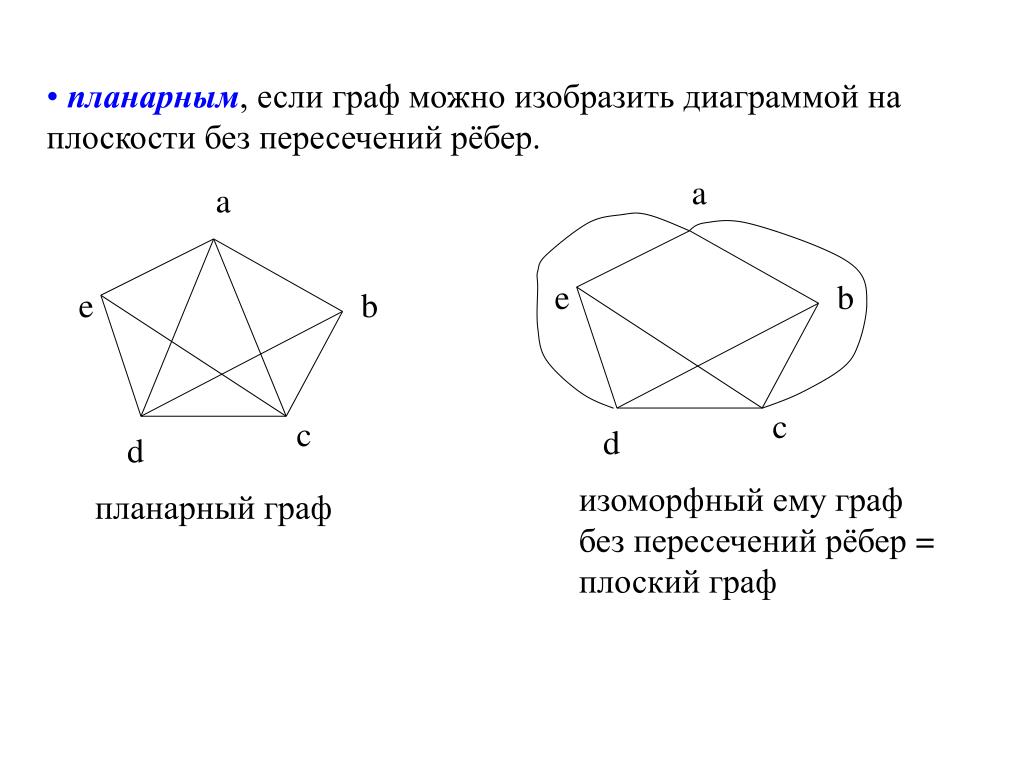 [c.98]
[c.98]
Создание математических описаний (йатематических моделей) — обязательный этап математического моделирования, которое включает также ряд других этапов, связанных с использованием математических описаний при оптимальных разработке, расчете или управлении. Математическое описание процесса представляет собой совокупность структур, изоморфно отражающих свойства объекта, проявляемые в экспериментальных условиях [1]. Из этого определения ясно, что математическое описание появляется как результат экспериментальных исследований (возможно, и выполненных до осуществления процесса, для которого оно создается) и применяется для экспериментального осуществления процесса. [c.52]
Матемашческое описание образуется из математических структур, способных изоморфно отразить свойства процесса в различных экспериментальных условиях . Математическим структурам, используемым при построении математического описания процесса, придается физическое истолкование, чтобы связать установленные в ходе эксперимента физико-химические свойства процесса.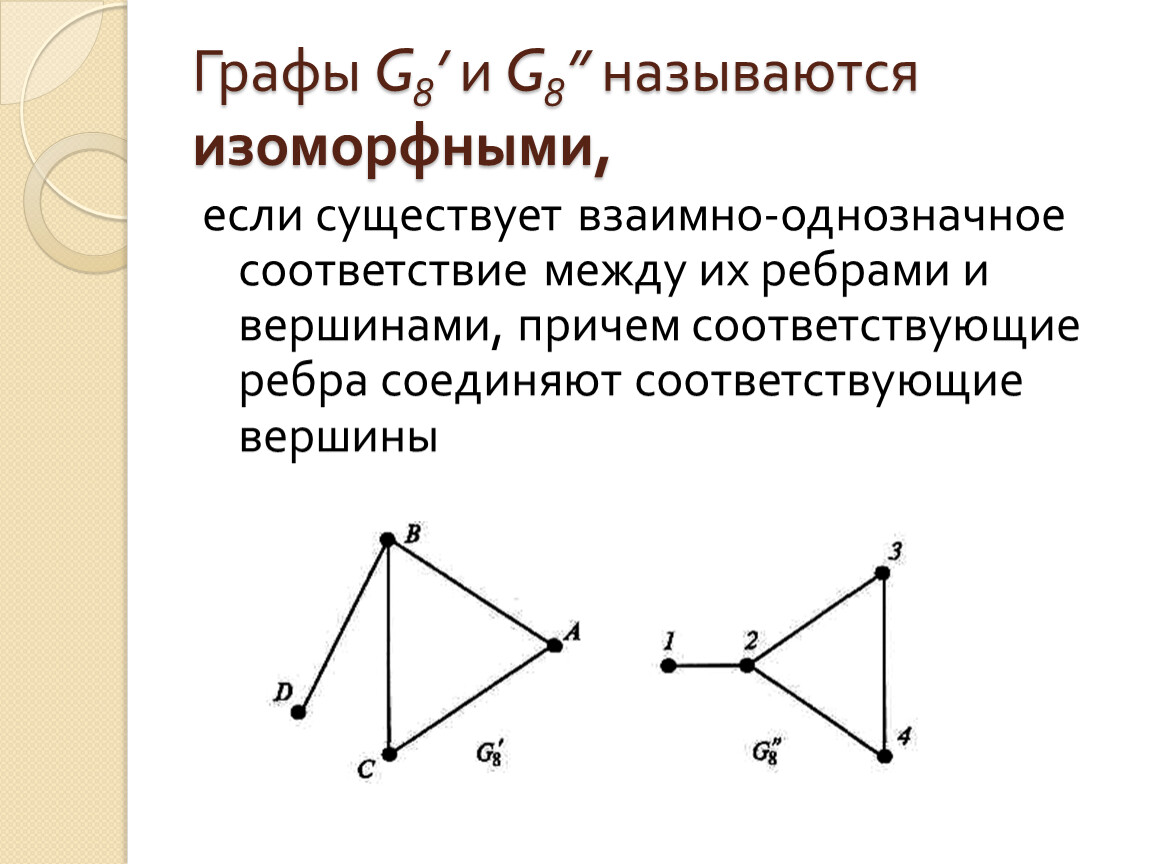 Для создания математического описания необходимо располагать экспериментальными данными и математическими структурами, связывающими их. [c.12]
Для создания математического описания необходимо располагать экспериментальными данными и математическими структурами, связывающими их. [c.12]
Одним из основных факторов, определяющих степень выделения и скорость отделения твердых углеводородов от жидкой фазы в процессах депарафинизации и обезмасливаиия, является качество депарафинируемого сырья. Как указывалось выше, большая часть твердых углеводородов относится к изоморфным веществам, способным к совместной кристаллизации с образованием смешанных кристаллов, причем в зависимости от условий выделения из растворов эти кристаллы могут быть разных структуры и размеров. При прочих равных условиях форма и размер этих кристаллов определяются фракционным составом сырья. С повышением пределов выкипания фракции уменьшается полнота отделения кристаллов твердых углеводородов от растворов масляной части, что связано с повышением концентрации твердых углеводородов и изменением их химического состава. При охлаждении раствора сырья с большим содержанием твердых углеводородов в соответствующем растворителе в начальный момент кристаллизации образуется слишком много зародышей кристаллов, на которых при дальнейшем охлаждении кристаллизуются выделяющиеся из раствора твердые углеводороды. В этом случае конечные кристаллы имеют малые размеры, что приводит к уменьшению скорости фильтрования и выхода депарафииированного масла при увеличении содержания масла в твердой фазе. Рост кристаллов определяется типом углеводородов, выделяющихся из растворов в виде зародышей, на которых затем кристаллизуются остальные компоненты твердой фазы [6]. [c.136]
В этом случае конечные кристаллы имеют малые размеры, что приводит к уменьшению скорости фильтрования и выхода депарафииированного масла при увеличении содержания масла в твердой фазе. Рост кристаллов определяется типом углеводородов, выделяющихся из растворов в виде зародышей, на которых затем кристаллизуются остальные компоненты твердой фазы [6]. [c.136]
Твердые углеводороды масляных фракций нефти, как указывалось выше, относятся к изоморфным и в то же время полиморфным веществам, которые в зависимости от условий кристаллизации и фракционного состава сырья в процессах депарафинизации и обезмасливаиия могут образовывать смешанные кристаллы, эвтектические смеси или кристаллизоваться раздельно. Образование кристаллов той или иной формы, а также эвтектических смесей имеет большое значение с точки зрения отделения твердой фазы от жидкой. Для обеспечения нормального роста кристаллов необходимы оптимумы концентрации твердых углеводородов в растворе и вязкости последнего. [c.150]
[c.150]
Нередко также наблюдается явление изоморфизма — свойство атомов, иоиов или молекул замещать друг друга в кристаллической решетке, образуя смешанные кристаллы. Примером изоморфных веществ являются алюмокалиёв ые и хромокалиевые квасцы—KAI(S04)2-I2h3O и K r(S04) 2 I2h3O. Смешанные кристаллы являются совершенно однородными смесями твердых веществ — это твердые растворы замеш ения. Поэтому можно сказать, что изоморфизм — это способность образовать твердые растворы замещения. [c.141]
Можно получить и пересыщенный раствор, т. е. такой, концентрация которого выше концентрации насыщенного раствора (при данных температуре и давлении). Пересыщенные растворы можно приготовить осторожным и медленным охлаждением насыщенных [фи высокой температуре растворов, например солей ЫагЗгОз и Ha OONa. Пересыщенный раствор представляет собой систему, находящуюся в кажущемся равновесии (А6-> 0). Встряхивание пли внесение в него кристаллов того же вещества, которое находится в растворе, или другого, например изоморфного с ним, вы-. l,lвaeт кристаллизацию происходит выделение избытка растворенного вещества и раствор становится насыщенным. Система таким образом переходит в состояние истинного равновесия, что сопровождается убылью энергии Гиббса. [c.233]
l,lвaeт кристаллизацию происходит выделение избытка растворенного вещества и раствор становится насыщенным. Система таким образом переходит в состояние истинного равновесия, что сопровождается убылью энергии Гиббса. [c.233]
Природные ресурсы. Содержание в земной коре составляет Ga In 1-10- %, Т1 3-10- %. Это редкие и рассеянные элементы. Они встречаются как примесь к различным рудам — галлий сопутствует алюминию и цинку, небольшие количества индия и таллия изоморфно распределены в сульфидных полиметалличе—ских рудах. [c.344]
С кислотами Nh4 образует соли аммония, содержащие ион Nh5. Это кристаллические вещества. Большинство их, подобно солям щелочных металлов, хорошо растворимо в воде. Многие из, них изоморфны. этим солям. Сходство данных соединений на одном, примере иллюстрирует рис. 3.46 оно в значительной степени обусловлено близостью радиусов ионов для NHщелочной металл (по шкале ср° нейтральный аммоний NHil расположен между марганцем и алюминием), при этом происходит разложение аммония Nh5 на Nh4 и На (однако растворенный в ртути NH некоторое время может существовать в виде амальгамы при низкой температуре). Соли аммония термически неустойчивы, а также подвергаются гидролизу по катиону. [c.399]
Иногда встречается так называемый монацитовый песок — изоморфная смесь ортофосфатов редкоземельных элементов ЭРО4 и ортосиликата тория ThSi04. Известно много других минералов, содержащих РЗЭ и S , Это фосфаты, силикаты, в частности тортвейтит (Y, S )2Sis07 и другие соедииения. РЗЭ — постоянная примесь (до 3%) к фосфоритам и апатитам. [c.497]
Графы изоморфные — Энциклопедия по машиностроению XXL
Граф G=(X, U) называют плоским, если его множество ребер расположено на плоскости таким образом, что ребра имеют общие точки лишь в вершинах. Граф, изоморфный плоскому и расположенный на плоскости с пересечением ребер, называют планарным. [c.211]Многие задачи контроля схем сводят к различным тождественным преобразованиям заданных графов этих устройств. Тождественные преобразования графов, сводимые только к переобозначению вершин и ребер, приводят к получению изоморфных графов.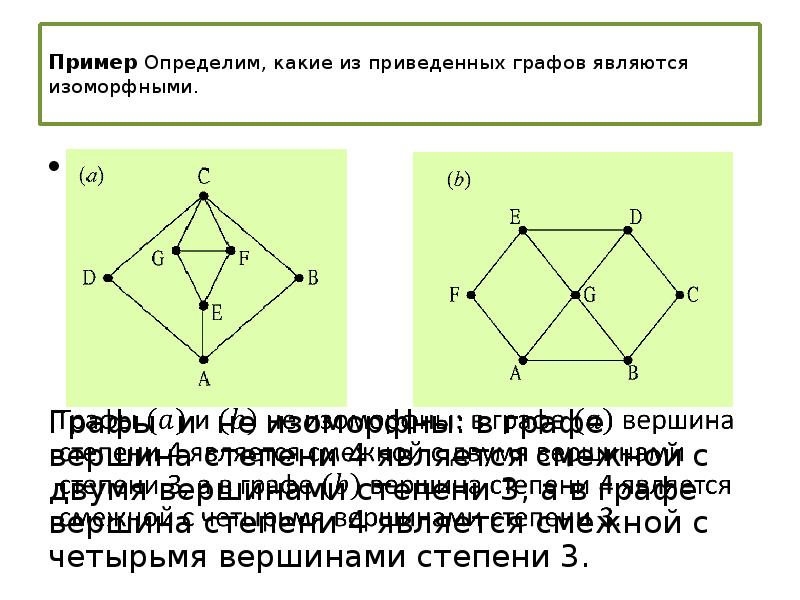 [c.211]
[c.211]
Два графа G=(X, U) и G =(X, U ) называют изоморфными, если можно установить взаимно однозначное соответствие Х- -X, U U такое, что если (Xi, [c.211]
Изоморфные графы могут быть получены один из другого путем перенумерации их вершин. Очевидно, что изоморфизм есть отношение эквивалентности на графах. Если изоморфные преобразования проводятся с графом, заданным матрицей смежности, то они сводятся к перестановке местами соответствующих строк и столбцов. Известно, что в общем случае для определения изоморфизма графов необходимо сделать п сравнений или перестановок строк и столбцов матрицы, что для графов с л>30 не под силу даже современной ЭВМ. Поэтому необходимо применить тот или иной эвристический алгоритм поиска по дереву решений. [c.211]
Пусть задан граф G=(X, U). Подразбиением ребра Uk= Xi, Xj) называют замену его двумя ребрами щу — == Xi, х ) и Up2=(Xp, Xj) с введением новой вершины Хр. Два графа называют гомеоморфными, если они обладают изоморфными подразбиениями. [c.212]
Граф, вершинам которого приписываются целые числа от 1 до Я, называется помеченным (рис. 34, с). Два помеченных графа Gj и Gj называются изоморфными, если существует взаимно однозначное отображение множества X (Gj) на множество X (Ог), сохраняющее не только смежность, но и распределение пометок. Примером изоморфных графов может служить СС и соответствующий ей ГЧВ (см. рис. 29 и 30). Сразу же оговоримся, что пометки вершин в СС и ГЧВ отличаются от принятых в теории графов подробнее об этом будет сказано ниже. [c.76]
Всю информацию о структуре конструкций необходимо формализовать в виде упорядоченных множеств цифр, изоморфных реальным элементам конструкций и связям между ними. Наиболее удобным математическим аппаратом для этой цели является теория графов [48]. [c.68]
Графы, у которых существуют одинаковые (совпадающие) представления, называются изоморфными. Точнее, графы Г = и Г = (Z, U y [c.13]
Например, графы, изображенные на рис. 1.3,6, в, изоморфные, так как существует отображение [c.14]
По существу изоморфные графы отличаются лишь нумерацией вершин. Так, например, списки ребер графов, изображенных на рис. 2.2, имеют вид ], 2) 1,3)(1,4) 2,3) 3,4)-(рж. 2.2, а) [1, 3) (1,4) (2,3) [c.38]
Нитрид бора (ВN) изоморфен графиту, но не обеспечивает, как это можно было бы ожидать, смазку при действии больших нагрузок. Как и графит, под действием высоких давлений BN может принять кубическую модификацию, изоморфную алмазу. Благодаря гексагональной графитовой структуре BN в обычном состоянии весьма анизотропен и после горячего прессования получает текстуру и анизотропию свойств, как и графит. [c.51]
Два графа G = (V, E) и G = V, E ) изоморфны друг другу, если существует взаимно однозначное соответствие между V п V и между Е и Е, сохраняющее инцидентность. Например, два графа, показанные на рис. П.5, изоморфны. [c.284]
Простой граф G = (l/, Е), у которого У = п и любая пара вершин соединена ребром, называется полным графом для п-вершин. Легко убедиться, что полный граф имеет п(п — 1)/2 ребер. Так как любые два полных графа, имеющие одинаковое число вершин, изоморфны, говорят о полном графе для п-вершин. [c.284]
Подсчитайте число суграфов, включая изоморфные, в графе G=(X, U), X =rt. [c.221]
Граф с корнем (или корневой граф) имеет одну выделенную вершину, называемую корнем [ 131 ]. На рис. 34, б показан корневой граф с корнем в вершине Xj. Понятие изоморфности для корневых графов Gj и Gj предусматривает сохранение во взаимно однозначном отображении множества X (G,) на множества X (Gj) наряду со смежностью и распределением пометок также и корни. [c.76]
Применяя последовательно преобразование Q к исходному графу Gq, можно получить множество Ga всех шестивершинных и множество Gs всех пятивершинных производных графов. Далее, сравнивая каждый граф из Ge и из Gs соответственно с типовыми Кг,ъ и Кз, на основании теоремы 5.1 можно сделать заключение о планарности графа Gq. Другими словами, если среди Ge найдется граф Ge, изоморфный 3,3, или среди G5 —граф G5, изоморфный Кь, то исходный граф Gq следует признать неиланарным. В противном случае, Gq планарен. [c.179]
Теперь пусть s = 3. В этом случае согласно Л в G должны быть удалены и ребра цикла, образующего грань, поэтому пересечение в области D можно попытаться устранить путем изменения порядка следования ребер (осьР), ( 2, Р), ( 3, Р), получаемого при обходе вершины р против часовой стрелки. Однако нетрудно убедиться, что получаемые при этом топологические графы будут изоморфны друг другу. Значит, и в этом случае остается принять, что граф AG планарный. Теорема доказана. [c.193]
Геометрия камеры группы полностью определяется графом Кокстера, вершины которого соответствуют стенкам камеры. Две вершины соединены ребром кратности к, если угол между соответствующими стенками равен я/ . Группы с одинаковыми графами Кокстера изоморфны. [c.127]
Никитин Б. А. Избранные труды. — 1956 — Электронная библиотека «История Росатома»
Закладок нет.
Обложка12345678910 пустая1112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118119120121122123124125126127128129130131132133134135136137138139140141142143144145146147148149150151152153154155156157158159160161162163164165166167168169170171172173174175176177178179180181182183184185186187188189190191192193194195196197198199200201202203204205206207208209210211212213214215216217218219220221222223224225226227228229230231232233234235236237238239240241242243244245246247248249250251252253254255256257258259260261262263264265266267268269270271272273274275276277278279280281282283284285286287288289290291292293294295296297298299300301302303304305306307308309310311312313314315316317318319320321322323324325326327328329330331332333334335336337338339340341342343344345346347348349350 пустая351Обложка – 12 – 34 – 56 – 78 – 910 пустая – 1112 – 1314 – 1516 – 1718 – 1920 – 2122 – 2324 – 2526 – 2728 – 2930 – 3132 – 3334 – 3536 – 3738 – 3940 – 4142 – 4344 – 4546 – 4748 – 4950 – 5152 – 5354 – 5556 – 5758 – 5960 – 6162 – 6364 – 6566 – 6768 – 6970 – 7172 – 7374 – 7576 – 7778 – 7980 – 8182 – 8384 – 8586 – 8788 – 8990 – 9192 – 9394 – 9596 – 9798 – 99100 – 101102 – 103104 – 105106 – 107108 – 109110 – 111112 – 113114 – 115116 – 117118 – 119120 – 121122 – 123124 – 125126 – 127128 – 129130 – 131132 – 133134 – 135136 – 137138 – 139140 – 141142 – 143144 – 145146 – 147148 – 149150 – 151152 – 153154 – 155156 – 157158 – 159160 – 161162 – 163164 – 165166 – 167168 – 169170 – 171172 – 173174 – 175176 – 177178 – 179180 – 181182 – 183184 – 185186 – 187188 – 189190 – 191192 – 193194 – 195196 – 197198 – 199200 – 201202 – 203204 – 205206 – 207208 – 209210 – 211212 – 213214 – 215216 – 217218 – 219220 – 221222 – 223224 – 225226 – 227228 – 229230 – 231232 – 233234 – 235236 – 237238 – 239240 – 241242 – 243244 – 245246 – 247248 – 249250 – 251252 – 253254 – 255256 – 257258 – 259260 – 261262 – 263264 – 265266 – 267268 – 269270 – 271272 – 273274 – 275276 – 277278 – 279280 – 281282 – 283284 – 285286 – 287288 – 289290 – 291292 – 293294 – 295296 – 297298 – 299300 – 301302 – 303304 – 305306 – 307308 – 309310 – 311312 – 313314 – 315316 – 317318 – 319320 – 321322 – 323324 – 325326 – 327328 – 329330 – 331332 – 333334 – 335336 – 337338 – 339340 – 341342 – 343344 – 345346 – 347348 – 349350 пустая – 351
Определение изоморфизма по Мерриам-Вебстеру
изоморфный | \ Ī-sə-ˈmȯr-fik \1а : идентичной или аналогичной формы, формы или структуры изоморфные кристаллы
б : , имеющие поколения спорофитов и гаметофитов, одинаковые по размеру и форме
2 : связаны изоморфизмом изоморфные математические кольцаТеория графов | Изоморфные деревья.Всем привет. Мы здесь на 10-м посте… | Кельвин Хосе
Привет всем. Мы здесь, в 10-м посте моей серии блогов по теории графов под названием Graph Theory: Go Hero . Сегодня мы погружаемся в изоморфизм деревьев. Я настоятельно рекомендую вам прочитать мои недавние сообщения по теории графов, которая больше отформатирована в аспекте компьютерных наук. Итак, давайте углубимся.
Определение изоморфизма
Изоморфизм — это очень общее понятие, которое появляется в нескольких областях математики.Слово происходит от греческого iso , что означает « равно », и morphosis , что означает « для образования » или « для формирования ». Он представляет собой взаимоотношения между двумя подобными системами. Википедия дает отличное объяснение того, что это такое и как оно полезно в математике. В двух словах, это карта между двумя объектами. Например, возьмем пример изоморфизма.Предположим, что у нас есть два набора чисел. Два конечных множества изоморфны, если они имеют одинаковое количество элементов. Другими словами, более подробно, два (теперь не обязательно конечных) набора являются изоморфными, если вы можете записать функцию , которая назначает каждый элемент одного набора уникальному элементу другого набора, например что ни один из элементов любого набора не «пропущен» функцией.
Изоморфизм графов
Вопрос о том, являются ли два графа G1 и G2 изоморфными , задает вопрос, являются ли они структурно одинаковыми.
Изображение автораВыше мы видим два графика. Хотя графики G1 и G2 помечены по-разному и могут рассматриваться как разные. Но структурно это одни и те же графики. Итак, в свою очередь, существует изоморфизм, и мы называем графы изоморфными графами. Если мы развернем второй график и изменим метку так же, мы получим два похожих графика.
Мы также можем определить понятие изоморфизма графов более строго, потому что утверждение — два графа структурно одинаковы — не совсем корректно.Если представить граф как набор вершин V и ребер E, у нас будет два набора G1 (V1, E1) и G2 (V2, E2) для графов G1 и G2 соответственно. Мы называем эти два графа изоморфными, если существует биекция между V1 и V2 такая, что для всех пар вершин в G1, которые образуют допустимое ребро, применяя функцию φ (phi) к узлам всех ребер, получается ребро, которое присутствует в G2. С точки зрения непрофессионала,
, чтобы изоморфизм имел место, должна быть функция φ, которая может отображать все узлы / ребра в G1 в G2 и наоборот.
Определение изоморфности двух графов не только очевидно для человеческого глаза, но и является сложной задачей для компьютеров.
Изображение автораОстается открытым вопрос, является ли проблема изоморфизма графов NP Complete . Однако существует множество алгоритмов изоморфизма полиномиального времени для подклассов графов, таких как деревья.
Сможете ли вы это сделать, если я попрошу вас обнаружить изоморфные деревья? Да, верно? Давайте попробуем.
Изображение автораВы правы, если ответили «нет».Потому что структурно они не одинаковы.
Изображение автораКак насчет этого?
Ответ — да. Поскольку существует карта меток, например
6-0
1-1
0-2
2-3
5-4
3-5
4-6
Есть несколько очень quick вероятностный (обычно хэш или эвристический на основе ) алгоритмы для идентификации изоморфных деревьев.Они, как правило, бывают быстрыми, но также подвержены ошибкам из-за хеш-коллизий в ограниченном целочисленном пространстве.
Метод, который мы рассмотрим сегодня, включает сериализации дерева в кодировку Unicode . Эта уникальная кодировка — это просто уникальная строка, представляющая дерево. Если другое дерево имеет такую же кодировку, то они изоморфны.
Мы можем напрямую сериализовать некорневое дерево, но на практике сериализация корневого дерева обычно проще с точки зрения кода.Однако одно предостережение, на которое следует обратить внимание, если мы собираемся укоренить наши два дерева T1 и T2, чтобы проверить, являются ли они изоморфными, — это убедиться, что один и тот же корневой узел выбран в обоих деревьях перед сериализацией / кодированием деревьев.
Один прием, который мы можем использовать, чтобы помочь себе, — это найти общий узел между обоими деревьями. Поиск центра дерева сделает то же самое.
Кодирование дерева
Сначала возьмем два дерева T1 и T2, которые могут быть изоморфными или нет.
Изображение автораНам нужно найти центры деревьев.
Изображение автораСледующее, что нам нужно сделать, это укоренить дерево.
Изображение автораТеперь нам нужно сгенерировать кодировку для каждого дерева и сравнить сериализованные деревья на предмет равенства.
Изображение автораДревовидная кодировка представляет собой просто последовательность левых скобок «(» и правых «)». Однако мы также можем думать о них как о единицах и нулях. Та же самая кодировка, указанная выше, может быть преобразована в предложенный метод, так как,
Изображение автораГенерация кодировки дерева
AHU ( Aho , Hopcroft , Ullman ) алгоритм представляет собой умная техника сериализации для представления дерева в виде уникальной строки.В отличие от многих инвариантов и эвристик изоморфизма деревьев, AHU может захватить полную историю спектра градусов дерева и структуру, обеспечивающую детерминированный метод проверки изоморфизма дерева.
Рассмотрим подробнее.
Изображение автораМы должны начать с присвоения пустой скобки ( () ) каждому листу нашего дерева, как показано ниже.
Изображение автораТеперь нам нужно двигаться вверх (к родительским узлам листьев) и объединить скобки листьев вместе и назначить их родительскому узлу.Поскольку мы объединяем круглые скобки листьев, мы также должны заключить результат в другую пару круглых скобок. Например, предположим, что у нас есть дерево с единственным родителем и двумя листьями. Итак, мы присваиваем () листьям. Когда мы приближаемся к родительскому узлу, мы объединяем скобки листьев, например () (), и заключаем их в другую пару скобок, например (() ()), и назначаем их родительскому узлу. Этот процесс продолжается итеративно, пока мы не достигнем корневого узла.
Изображение автораЕсли вы внимательно проследите приведенную выше аналогию, у нас будет эта кодировка для дерева в конце.
Не забудьте отсортировать круглых скобок перед объединением. Сортировка производится лексикографически.
Сводка кодирования
Подводя итог тому, что мы сделали для AUH:
- Конечные узлы назначаются с помощью ()
- Каждый раз, когда мы перемещаемся вверх, объединяем, сортируем и оборачиваем круглые скобки.
- Мы не можем обработать узел, пока не обработаем все его дочерние элементы.
Два дерева изоморфны, если их представление одинаково.
Попался! Я надеюсь, что этот бриф поможет вам в ваших будущих проектах. Спасибо за ваше время и терпение. Спасибо.
Изоморфизмы проектирования программного обеспечения
При программировании одну и ту же концепцию часто можно выразить разными способами. Если вы можете без потерь переводить между двумя альтернативами, это изоморфизм. Введение для объектно-ориентированных программистов.
Эта серия статей является частью еще большей серии статей о взаимосвязи между шаблонами проектирования и теорией категорий.
Есть школа функционального программирования, которая обращается к теории категорий для вдохновения, проверки, абстракции и перекрестного опыления идей. Возможно, вас отталкивают такие термины, как зигогистоморфный препроморфизм (шутка), но этого не должно быть. Часто есть веские причины для использования абстрактного именования. В любом случае, один термин из теории категорий, который иногда встречается, — это изоморфизм .
Эквивалентность #
Не позволяйте терминологии пугать вас.Изоморфизм — достаточно простая концепция для понимания. По сути, две вещи изоморфны, если вы можете без потерь переводить между ними. Это формализация эквивалента .
Многие языки программирования, такие как C # и Java, предлагают множество альтернативных способов решения задач. Просто рассмотрите этот пример C # из моего видео о Humane Code:
public bool IsSatisfiedBy (кандидат клиента)
{
bool retVal;
if (кандидата.TotalPurchases> = 10000)
retVal = true;
еще
retVal = false;
return retVal;
}
что эквивалентно этому:
public bool IsSatisfiedBy (кандидат клиента)
{
вернуть кандидата.TotalPurchases> = 10000;
}
Внешний наблюдатель не может отличить эти две реализации, потому что они имеют точно такое же внешне видимое поведение. Вы всегда можете выполнить рефакторинг от одной реализации к другой без потери информации. Таким образом, мы можем утверждать, что они изоморфны.
Терминология №
Если вы объектно-ориентированный программист, то вы уже знаете слово полиморфизм, которое звучит аналогично изоморфизму .Возможно, вы тоже слышали слово ксеноморф. Это все по-гречески. Morph означает из или из , а poly означает , много , iso означает, что равно . Итак, изоморфизм означает «иметь одинаковую форму».
Скорее всего, это объяснение термина изоморфный JavaScript. Люди, придумавшие этот термин, знали (достаточно) греческий, но, очевидно, не знали математику. В математике, и особенно в теории категорий, изоморфизм — это перевод с обратным.Это все еще не формальное определение, а всего лишь моя попытка изложить его без излишнего жаргона.
Теория категорий использует слово объект для описания члена категории. Я собираюсь использовать эту терминологию и здесь, но вы должны знать, что объект не подразумевает объектно-ориентированное программирование. Это просто означает «вещь», «предмет», «элемент», «сущность» и так далее.
В теории категорий, морфизм — это отображение или перевод одного объекта в другой.Если для всех объектов существует обратный морфизм, ведущий обратно в начало координат, то это изоморфизм.
На этой иллюстрации синие стрелки, идущие слева направо, указывают на один морфизм. Это сопоставление объектов на синей левой стороне с объектами на зеленой правой стороне. Зеленые стрелки, идущие справа налево, — это еще один морфизм. В этом случае зеленый морфизм справа налево является обратным синему морфизму слева направо, потому что, применяя оба морфизма, вы заканчиваете там, где начали.Неважно, начнете ли вы с синей левой или зеленой правой стороны.
Другой способ увидеть это — сказать, что существует перевод без потерь. Когда перевод выполняется без потерь, это означает, что вы не теряете информацию, выполняя перевод. Поскольку вся информация сохраняется после перевода, вы можете вернуться к исходному представлению.
Изоморфизмы проектирования программного обеспечения #
При программировании часто можно решить одну и ту же проблему по-разному.Иногда альтернативы изоморфны: вы можете переключаться между двумя альтернативами без потери информации.
Книга Мартина Фаулера «Рефакторинг» содержит несколько примеров. Например, вы можете применить Extract Method , а затем Inline Method и вернуться к тому месту, где вы начали.
В программировании есть много других изоморфизмов. Некоторые из них являются морфизмами на том же языке, как в случае с приведенным выше примером C #. То же самое и с изоморфизмами в Refactoring , потому что рефакторинг, по определению, представляет собой изменение, применяемое к определенной базе кода, будь то C #, Java, Ruby или Python.
Другие программные изоморфизмы переходят между языками, где концепция может быть смоделирована одним способом, скажем, в C ++, и другим способом в Clojure. В настоящем блоге, например, есть несколько примеров перевода между C # и F #, а также между F # и Haskell.
Знание об изоморфизмах дизайна программного обеспечения может сделать вас лучшим программистом. Это позволит вам выбрать лучшую альтернативу для решения конкретной проблемы. Идентификация программных изоморфизмов также важна, потому что это позволит нам формально подумать о структуре кода за счет сведения многих альтернативных представлений к каноническому.По этим причинам в этой статье представлен каталог изоморфизмов проектирования программного обеспечения:
В общем, я старался называть каждый изоморфизм по его каноническому представлению. Например, под изоморфизмами единиц я подразумеваю изоморфизмы единичной стоимости. Однако это не совсем последовательная стратегия именования.Существует еще много изоморфизмов проектирования программного обеспечения, поэтому, если вы еще раз вернетесь к этой статье в будущем, я, возможно, добавлю больше элементов в этот каталог. Ни в коем случае не следует считать этот каталог исчерпывающим.
Резюме #
Изоморфизм — это отображение, для которого также существует обратное отображение. Это способ описать эквивалентность.
В программировании у вас часто есть выбор реализовать конкретную функцию более чем одним способом. Эти альтернативы могут быть эквивалентными, и в этом случае они изоморфны. Это одна из причин, по которой многие кодовые базы поставляются с руководством по стилю.
Понимание того, как код изоморфен другому коду, позволяет нам сократить многие альтернативы до канонического представления.Это упрощает анализ, потому что мы можем сузить наш анализ до канонической формы и оттуда обобщить.
Далее: Изоморфизмы единиц.
Изоморфизм | 2.8 Степени и изоморфизм | 2.8 Степени и изоморфизм | Блок 2: Конструкции | Математика для информатики | Электротехника и информатика
ПРОФЕССОР: Мы кратко рассмотрели изоморфизм графов в контексте орграфов. И это проявляется еще более фундаментально для простых графиков, где определение немного проще.Итак, давайте просто посмотрим на эту идею абстракции графа и на то, как изоморфизм связан с ней.
Это пример двух разных способов построения одного и того же графика. Вот 257 и 257. Он напрямую подключен к 122, как здесь. А также 257 подключен к 99, как здесь. И если вы проверите, это точно те же шесть вершин и точно такие же восемь ребер. Но они просто нарисованы по-другому.
Итак, мы не хотим путать рисунок графика, подобного этим двум, с самим графиком.Сам граф состоит только из набора узлов и набора ребер. И если вы извлечете это из этих двух диаграмм, вы получите тот же набор узлов и тот же набор ребер.
Такой же график, разные раскладки. Но вот случай, когда это действительно та же раскладка. Вы можете увидеть, что эти два изображения, если не обращать внимания на метки, в точности совпадают с двумя серыми и двумя серыми, а также красным и красным. Теперь разница в том, что я переименовал вершины.
Итак, мы присвоили этим вершинам разные метки.И связь между этими двумя графами теперь, этот граф с вершинами, которые являются целыми числами, и этот граф с вершинами, которые являются именами людей, состоит в том, что они изоморфны. А изоморфизм означает, что все, что имеет значение между двумя графами, — это их связи. Итак, графы с одинаковыми связями между одним и тем же числом вершин называются изоморфными.
Точнее говоря, два графа изоморфны, когда между их вершинами есть ребро, сохраняющее соответствие.Сопоставление смысла путем стыковки между их вершинами. А сохранение ребра означает, что там, где есть ребро с одной стороны, есть ребро между соответствующими вершинами с другой стороны. Давайте посмотрим на пример.
Вот два графика. И я утверждаю, что они изоморфны. Слева у нас есть группа животных: собака, свинья, корова, кошка. А справа у нас есть куча продуктов животного происхождения, эй, кукуруза, говядина, тунец. И это намек на то, как мы собираемся проводить сопоставление.
Итак, я собираюсь сказать вам, что вершина собаки слева соответствует вершине говядины справа.Итак, я определяю функцию, переход от вершин слева, выделенных синим цветом, к вершинам справа, выделенным красным. И f of dog — это говядина.
Точно так же кошки едят тунца. Я собираюсь сопоставить кошку с тунцом. И, продолжая работу с оставшимися двумя вершинами, я сопоставлю корову с сеном, что они едят, и свинью с кукурузой, что часто является тем, что скармливают свиньям. Хорошо, так что это побуждение. Я имею в виду, что это идеальное соответствие между четырьмя вершинами слева и четырьмя вершинами справа.Но теперь я должен проверить, сохранились ли края.
Что это значит? Что ж, давайте сделаем пример. Слева есть грань между собакой и свиньей. Это означает, что между тем местом, куда они идут, должен быть край справа. Так что между говядиной и кукурузой должно быть грань, потому что это то, что нужно собаке и свинье. И действительно, здесь есть преимущество. Так что эта часть хороша.
А остальные можно проверить. Другая вещь, которую мы должны проверить слева, — это то, что сохранение края — это тогда и только тогда, когда есть край справа тогда и только тогда, когда есть край слева, это то же самое, что сказать, что у края нет края. слева тогда и только тогда, когда справа нет края.Итак, давайте проверим не-ребра слева.
Между коровой и свиньей нет разницы. И действительно, корова идет на сено, а свинья идет на кукурузу. И действительно, справа между сеном и кукурузой нет края. И вы можете проверить остальные случаи. Эти два графа изоморфны. И эта функция f на самом деле является инжекцией, сохраняющей ребро.
Итак, повторяя это снова, изоморфизм между двумя графами G1 и G2 — это инъекция между вершинами V1 графа G1 и вершинами V2 графа G2 со свойством, что в G1 есть ребро uv, ребро E1, тогда и только тогда of uf of v является ребром во втором графе в E2.И это тогда и только тогда, когда это сохраняет край. Так что если здесь есть преимущество, то есть и преимущество. Если нет края слева, нет края справа. И это определение стоит запомнить.
Это в основном то же самое, что и в случае орграфа. За исключением случая диаграммы, края имеют направление. Таким образом, это было бы ребро от u до v тогда и только тогда, когда есть ребро от f u до f of v. Но поскольку нам не нужно беспокоиться о направлении в простом случае, определение становится немного проще.
А как насчет неизоморфизма? Как показать, что два графа не изоморфны? Я могу показать вам, что эти два графа изоморфны, просто рассказав вам, каково отклонение между их вершинами. И тогда становится просто проверить, есть ли края, которые должны быть.
Как вы выясняете, что два графа не изоморфны и что нет никакого побега, что ребро сохраняет ребра? Ну, для начала, у них по четыре вершины, так что это идеально.Между четырьмя вершинами слева и четырьмя правыми вершинами существует множество обходов. Почему нет такого, сохраняющего край?
Что ж, если вы посмотрите на график слева, на самом деле у него две вершины степени 2, отмеченные здесь красным. Есть вершина степени 2. Есть вершина степени 2. А справа каждая вершина имеет степень 3, если вы проверите.
Одно из свойств изоморфизма состоит в том, что ребра, выходящие из красного, эти два ребра, должны соответствовать двум ребрам, которые выходят из того места, на которое они отображаются.Таким образом, вершина степени 2 может отображаться только в вершину степени 2. Нет ни одного. Это доказательство того, что между двумя графами не может быть изоморфизма.
Итак, в общем, идея состоит в том, что мы смотрим на свойства, которые сохраняются изоморфизмом. Это почти похоже на инвариантную идею конечного автомата. Таким образом, свойство сохраняется при изоморфизме.
Означает, что если два графа — если первый граф обладает свойством, а первый граф изоморфен второму графу, то второй граф обладает этим свойством.И ясно, что если есть свойство, которое сохраняется при изоморфизме, и у одного графа оно есть, а у другого нет, это доказывает, что они не могут быть изоморфными.
Итак, какие из этих свойств сохраняются при изоморфизме? Ну количество узлов. Очевидно, что должно быть побочное соединение, поэтому у них должно быть одинаковое количество узлов. У них должно быть одинаковое количество ребер по схожим причинам. Потому что края сохранены. Край с одной стороны соответствует краю с другой стороны.
Другое, что имеет значение, это то, что мы только что привели аргумент о том, что степени сохраняются как следствие сохранения ребер. И всевозможные другие структурные свойства будут сохранены изоморфизмом, как, например, существование круговых путей, расстояний между вершинами и тому подобное. Все эти свойства сохраняются изоморфизмом.
Так что это дает вам возможность попытаться выяснить, являются ли два графика изоморфными или нет.Но в целом, если у вас есть граф с несколькими 100 или 1000 вершинами, между ними будет очень много потенциальных обходов, которые нужно проверить. И вопрос в том, как вы это делаете? Это огромный поиск, который не может быть эффективно проведен исчерпывающе.
Итак, вы ищете свойства, которые сохраняются изоморфизмами, которые дают вам ориентир. Так, например, если граф слева имеет вершину степени 4 и эта вершина степени 4 смежна с вершиной степени 3, то смежность степени 4 и степени 3 является типичным свойством, которое сохраняется за счет изоморфизма.
Итак, вы точно знаете, что если между первым графом и вторым графом будет пересечение, эта пара смежных вершин степени 4 и степени 3 может отображаться только в другую пару смежных вершин во втором графе, которая также имеют степени 4 и 3. Это значительно сократит количество мест, которые данная вершина может отображать в другом графе. И это дает вам некоторую структуру, которую можно использовать, чтобы попытаться сузить поиск по количеству изоморфизмов, а также по тому, где находится изоморфизм, и независимо от того, существует он или нет.
Так, например, наличие степени 4, смежной со степенью 3, является типичным свойством, которое сохраняется при изоморфизме. Но даже в этом случае, если я дам вам два очень больших графа, и это на самом деле графы, извлеченные из какой-то коммуникационной сети, их изображение, очень трудно сказать, изоморфны они или нет. Что ж, вы могли догадаться, потому что, конечно, мы сделали один и тот же снимок и дважды скопировали его.
Но если бы между этими двумя была какая-то тонкая разница, например, я стер одну грань где-то в середине этого беспорядка, как бы вы выяснили, что в этом случае эти два графика не были изоморфны? И ответ заключается в том, что, как и в случае этих NP-полных задач, не существует известной процедуры проверки изоморфности двух графов, которая гарантированно была бы эффективной и работала бы за полиномиальное время.
С другой стороны, есть технические причины, есть технические свойства, которые говорят о том, что изоморфизм графов не является одной из этих NP-полных проблем, если только [? народы?] НП или что-то в этом роде. Итак, это одна из отличительных черт этой проблемы. Важным является то, что, на самом деле, на практике есть несколько действительно хороших программ изоморфизма, которые во многих случаях выясняют, учитывая два графа, являются ли они изоморфными во времени, что примерно равно размеру двух графов. .
Итак, с практической точки зрения изоморфизм графов кажется решаемой проблемой. Хотя теоретически вы не можете быть уверены, что эти эффективные процедуры, которые работают большую часть времени, будут работать всегда. Что ж, на том или ином примере известные процедуры на самом деле растут в геометрической прогрессии.
Произошла ошибка при настройке пользовательского файла cookie
Этот сайт использует файлы cookie для повышения производительности. Если ваш браузер не принимает файлы cookie, вы не можете просматривать этот сайт.
Настройка вашего браузера для приема файлов cookie
Существует множество причин, по которым cookie не может быть установлен правильно. Ниже приведены наиболее частые причины:
- В вашем браузере отключены файлы cookie. Вам необходимо сбросить настройки вашего браузера, чтобы он принимал файлы cookie, или чтобы спросить вас, хотите ли вы принимать файлы cookie.
- Ваш браузер спрашивает вас, хотите ли вы принимать файлы cookie, и вы отказались. Чтобы принять файлы cookie с этого сайта, используйте кнопку «Назад» и примите файлы cookie.
- Ваш браузер не поддерживает файлы cookie. Если вы подозреваете это, попробуйте другой браузер.
- Дата на вашем компьютере в прошлом. Если часы вашего компьютера показывают дату до 1 января 1970 г., браузер автоматически забудет файл cookie. Чтобы исправить это, установите правильное время и дату на своем компьютере.
- Вы установили приложение, которое отслеживает или блокирует установку файлов cookie. Вы должны отключить приложение при входе в систему или проконсультироваться с системным администратором.
Почему этому сайту требуются файлы cookie?
Этот сайт использует файлы cookie для повышения производительности, запоминая, что вы вошли в систему, когда переходите со страницы на страницу. Чтобы предоставить доступ без файлов cookie потребует, чтобы сайт создавал новый сеанс для каждой посещаемой страницы, что замедляет работу системы до неприемлемого уровня.
Что сохраняется в файле cookie?
Этот сайт не хранит ничего, кроме автоматически сгенерированного идентификатора сеанса в cookie; никакая другая информация не фиксируется.
Как правило, в файлах cookie может храниться только информация, которую вы предоставляете, или выбор, который вы делаете при посещении веб-сайта. Например, сайт не может определить ваше имя электронной почты, пока вы не введете его. Разрешение веб-сайту создавать файлы cookie не дает этому или любому другому сайту доступа к остальной части вашего компьютера, и только сайт, который создал файл cookie, может его прочитать.
Укомплектование персоналом | Изоморфные веб-приложения
Практическое руководство по производительным и современным приложениям JavaScript.
Боян Джуркович, Cvent
Заглянуть внутрь
Изоморфные веб-приложения учит создавать производственные веб-приложения с использованием изоморфной архитектуры. Эта книга, предназначенная для работающих разработчиков, предлагает примеры в соответствующих фреймворках, таких как React, Redux, Angular, Ember и webpack.
о технике
Создавайте безопасные веб-приложения, которые отлично работают с высокой или низкой пропускной способностью или без нее.Изоморфные веб-приложения используют шаблон, который использует весь стек, хранит данные локально и сводит к минимуму количество обращений к серверу. Они безупречно обрабатывают, оптимизируют поисковую оптимизацию и предлагают возможности обмена кодом и библиотеками между клиентом и сервером.
о книге
Изоморфные веб-приложения учит создавать производственные веб-приложения с использованием изоморфной архитектуры. Вы научитесь создавать и отображать представления как для сервера, так и для браузера, оптимизировать локальное хранилище, оптимизировать взаимодействие с сервером и обрабатывать сериализацию данных.Эта книга, предназначенная для работающих разработчиков, предлагает примеры в соответствующих фреймворках, таких как React, Redux, Angular, Ember и webpack. Вы также изучите уникальные методы отладки и тестирования и овладеете конкретными навыками SEO.
что внутри
- Управление пользовательскими сеансами браузера и сервера
- Объединение серверной архитектуры и архитектуры SPA
- Создание передовых приложений на React
- Отладка и тестирование
о ридере
Чтобы извлечь пользу из этой книги, читатели должны знать JavaScript, HTML5 и любую структуру по своему выбору, включая React и Angular.
об авторе
Элиз Колкер Гордон руководит группой инженеров роста в Strava. Ранее она была директором по веб-разработке в Vevo, где регулярно решала задачи с изоморфными приложениями.
Как объединить JavaScript и SEO с изоморфным JS
SEO для веб-сайтов на основе JavaScript (построенных с помощью AngularJS, jQuery, ReactJS и т. Д.) Требует большого количества знаний, разработки, тестирования и, как известно, трудно понять.Но давайте посмотрим правде в глаза, даже со всеми этими проблемами, JavaScript никуда не денется. Он позволяет создавать быстрые, динамичные и красивые веб-сайты, ориентированные на обеспечение максимального удобства пользователей.
Google против JavaScript
Мы ясно видим, что в прошлом году Google сосредоточился в основном на поддержке пользовательского опыта и производительности. Мы видим, что веб-сайты Google AMP ориентированы на высокую производительность, это одностраничные приложения (SPA) или прогрессивные веб-приложения.
Google утверждает, что теперь они намного лучше сканируют и индексируют JavaScript.К сожалению, текущие результаты все еще далеки от хороших. Есть много примеров, подтверждающих это, один из которых — ошибка SEO на Hulu.com JavaScript.
Вот почему SEO-специалисты обычно склоняются к сочетанию традиционного рендеринга на стороне сервера и небольших фрагментов JavaScript, добавляемых в браузер в качестве универсального решения, которое делает приложения доступными для сканирования и индексации поисковыми системами.
Реклама
Продолжить чтение ниже
К сожалению, это не идеально, поскольку его часто сложно поддерживать, и не все приложения могут быть реализованы таким образом (сложные).Пользовательский интерфейс также не так хорош, потому что для загрузки всех библиотек JavaScript и начальной загрузки приложения требуется некоторое время.
Альтернативой является использование служб предварительной отрисовки, которые запускают ваше приложение / веб-сайт JavaScript и записывают выходные данные HTML, которые затем могут быть переданы поисковым роботам с помощью дополнительного программного обеспечения, запущенного на вашем сервере. Преимущество этого подхода состоит в том, что теоретически вы можете притвориться, что проблемы не существует, и построить свое приложение на JavaScript любым удобным для вас способом.
Объявление
Продолжить чтение ниже
К сожалению, на практике это не всегда работает и требует сложной отладки для исправления. Кроме того, это еще одна часть стека приложения, которую необходимо поддерживать, и могут возникнуть проблемы с совместимостью с вашим приложением, из-за которых перехваченный HTML-вывод будет некорректным. Это проблема, потому что может быть трудно заметить возникающие проблемы с поисковой оптимизацией, пока не станет слишком поздно и это не повлияет на ваш рейтинг.
Как видите, все может быть довольно сложно.
Что, если бы существовал гибрид, который мог бы соединить все преимущества быстрого и динамического JavaScript с простым для сканирования HTML / CSS? К счастью, на рынке появился новый ребенок, и он называется изоморфными приложениями.
Изоморфные приложения (также называемые универсальными приложениями) решают проблему сканирования и индексации, выполняя начальную визуализацию на сервере, а затем используя этот HTML-код в качестве основы для начальной загрузки приложения JavaScript в браузере. Изоморфный подход использует лучшее из двух миров (статический HTML и JavaScript), обеспечивая полностью индексируемые, быстрые и удобные для пользователя веб-сайты.
Как это работает?
Этот изоморфизм означает, что один и тот же код JavaScript, используемый вашим приложением, может выполняться как на сервере, так и на клиенте (в браузере).
Благодаря этой функции вы можете наполнить свое приложение некоторыми данными, поступающими из базы данных на сервере, запустить его и получить результирующий вывод HTML, для сборки которого обычно требуется браузер. Эти выходные данные могут затем использоваться в качестве исходного HTML-кода для всех, кто их запрашивает (включая поисковые роботы, такие как Google Bot).
После этого ваше приложение может использовать этот HTML-код в качестве основы и продолжать работать с ним в браузере, как если бы он изначально был отображен браузером.
Преимущества изоморфных приложений
Индексируемость поисковой системы
Веб-сканеры испытывают множество трудностей при сканировании и индексировании содержимого JavaScript (а некоторые из них даже не пытаются этого сделать). Сканеры анализируют необработанный код без его обработки и рендеринга. То, что вы видите в своем браузере, является обработанным, отображаемым контентом.Рендеринг, обработка DOM и т. Д. Требует гораздо большей вычислительной мощности и намного сложнее, чем простой анализ простого текста, поэтому сканирование будет намного дороже для поисковых систем.
Объявление
Продолжить чтение ниже
Изоморфные приложения решают эту проблему, выполняя код на сервере для рендеринга статических страниц, а затем оставляя весь JS, отвечающий за взаимодействие с пользователем, запускать браузером (пользователем).
В результате сканер видит тот же результат, что и браузер, что полностью решает проблему индексации SEO. Отображается весь контент, и он присутствует, когда поисковая система обращается к странице.
Воспринимаемое время загрузки быстрее
Загрузка тяжелого JS-кода может занять некоторое время, особенно в регионах с более медленным подключением к Интернету. Рендеринг всего загруженного кода в DOM, а затем ожидание загрузки приложения / веб-сайта и выполнения начальных запросов AJAX также занимает некоторое время. Это часто приводит к медленной начальной загрузке веб-сайта или приложения, недовольству пользователей и снижению доходов веб-сайта.К счастью, изоморфный подход частично решает эту проблему.
При отрисовке разметки приложения на стороне сервера отпадает необходимость в большинстве вызовов AJAX, и на стороне клиента происходит меньше отрисовки (из-за первоначальной отрисовки на сервере). Это уменьшает воспринимаемое время загрузки примерно на 40%.
Реклама
Продолжить чтение ниже
Бесплатных обедов не бывает
Как гласит эта известная пословица, ничего не дается бесплатно.Изоморфный подход великолепен, так как он решает проблемы индексации SEO, приводит к более быстрому времени загрузки и упрощает стек приложения (по сравнению с использованием услуг предварительного рендеринга). Кроме того, это может принести пользу для больших баз кода (проще в обслуживании, клиентский и серверный код разделены и т. Д.). Однако за это приходится платить.
Вы вынуждены использовать определенные технологии
Прежде всего, ваш сервер должен поддерживать запущенные приложения NodeJS (для рендеринга JavaScript на стороне сервера).
Вдобавок ко всему, структура приложения, которую вы используете для создания своего приложения, также должна поддерживать этот подход (но ключевые из них поддерживают или имеют плагины, которые поддерживают — Angular JS, React JS ). Как видите, в списке нет ни Ruby on Rails, ни Django. Эти фреймворки нельзя использовать для создания изоморфных приложений JavaScript, но их можно использовать для создания API-интерфейсов, обеспечивающих работу этих приложений JavaScript, что является отличным способом отделить код обработки данных от пользовательского интерфейса на базе JavaScript .
Объявление
Продолжить чтение ниже
Все это означает, что этот подход не очень хорошо подходит для существующих проектов, поскольку это не решение plug-and-play. Он может хорошо работать с существующими приложениями, если они в значительной степени полагаются на API, но все же потребует значительного объема работы для реализации.
Вам нужна экспертиза
Это все еще довольно новый подход, сильно отличающийся от старых (например, смесь рендеринга на стороне сервера / jQuery), который требует передовых технологий.В результате вам нужны разработчики, готовые к работе и комфортно работающие с этими новыми технологиями; разработчики, которые не боятся экспериментировать и пачкать руки.
Иногда готовые библиотеки плохо работают вместе, иногда вам нужно решать проблемы самостоятельно, и вам нужен необходимый опыт, чтобы довести приложение до финишной черты.
Начало работы с изоморфным JavaScript
Хотя изоморфный подход еще не получил широкого распространения, он набирает обороты.На данный момент это, вероятно, лучший способ создать большое динамическое приложение, которое требует отличного, плавного взаимодействия с пользователем без ущерба для SEO.
Объявление
Продолжить чтение ниже
Это, вероятно, не лучшая идея для небольших проектов, потому что для правильного выполнения требуется много инженерных разработок и опыта, но со временем это станет проще, поскольку будут разработаны новые библиотеки и инструменты, которые позаботятся о более сложные части процесса.
В целом, это очень многообещающий способ решения проблемы индексации SEO, которая годами беспокоила сообщество.Если вы создаете новое большое приложение, которое требует отличной SEO-совместимости, вам обязательно стоит подумать об этом.


