Матрица равена ответы: Тест Равена. Шкала прогрессивных матриц. Raven Progressiv Matrices. Методики для диагностики интеллекта. — Психология счастливой…
Тесты для приема на работу и определения уровня IQ
Таблицы Равена
Этот метод представляет собой 5 серий по 12 заданий в каждой, каждое правильно выполненное задание оценивается в 1 балл, максимальный балл в каждой серии — 12, в целом — 60. Серии маркированы буквами А, В, С, D и Е, каждая из этих серий имеет свое психологическое значение и отражает способность к той или иной мыслительной операции. Серии следует предъявлять по порядку. Подсчет по каждой производится отдельно. Суммируя результаты всех серий, вы получите общий балл, который при помощи таблицы можно будет перевести в «чистый» коэффициент интеллекта. К каждой серии даны подробные описания, чтобы вы могли ориентироваться, какие задачи представляют сложность для соискателя, и соответственно, подходит ли он для данной вакансии. Также приведена сравнительная оценка и таблица показателей интеллекта.
Рекомендации
Не следует считать результаты в присутствии соискателя, вся полученная при помощи тестов и интервью информация обрабатывается после того, как соискатель выйдет из кабинета, иначе у человека может сложиться мнение, что вы сразу сообщите о решении принять или отказать ему в работе.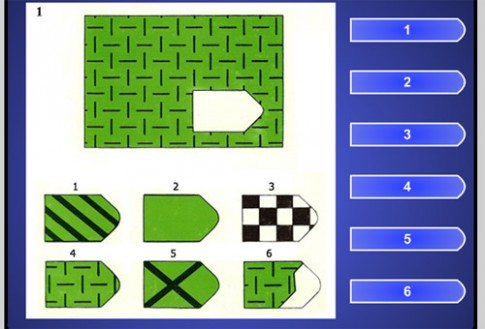
Если вакансия на должность подразумевает способность ясно мыслить в условиях дефицита времени, можно лимитировать время выполнения, но не по каждой серии, а в целом всего теста (на 30–40 минут) при этом объяснив, что задания нужно решать в строгой очередности, не оставляя «на потом» более сложные.
Если вы пройдете этот тест, то сможете сформулировать инструкции к каждой серии сами и вносить уточнения, исходя из собственного опыта.
Не поддавайтесь искушению подсказать, иначе вы получите свои результаты, а не соискателя.
Перед тем как приступить к работе, снабдите интервьюера бланком (образец прилагается) и карандашом для записи результатов. Затем предъявите первую картинку серии А и попросите найти необходимый «вырезанный» фрагмент, так, «чтобы помешенный в пустое окошечко рисунок фрагмента совпал с рисунком всего поля», испытуемый должен озвучить номер фрагмента. Таким образом, дав инструкцию к полю А
1 и получив ответ, попросите записать его в бланк.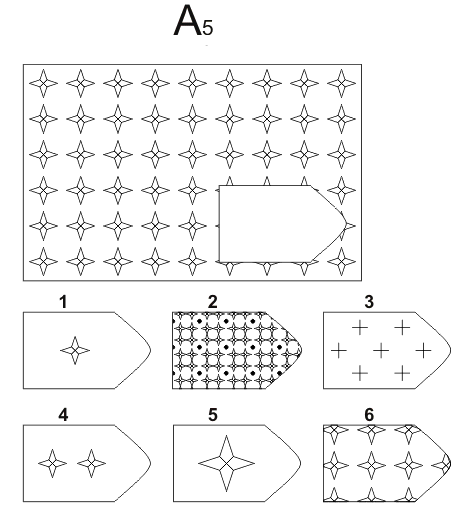 Например А1 — № 4, далее испытуемый работает сам, записывая ответы. В последующих сериях, как правило, инструкции уже не нужны, но если человек испытывает сложности, допускается напомнить инструкцию или внести уточнения.
Например А1 — № 4, далее испытуемый работает сам, записывая ответы. В последующих сериях, как правило, инструкции уже не нужны, но если человек испытывает сложности, допускается напомнить инструкцию или внести уточнения.
Образец бланка:
Считать результаты следует по каждой серии отдельно, в каждом столбце бланка выведите общий балл для каждой серии. Напоминаем, что за каждый правильный ответ начисляется 1 балл. Правильными считаются ответы, совпавшие с ключом.
Теперь посмотрим результаты по каждой серии. Самый высокий результат — это 12 правильных ответов. Для того чтобы оценить способности соискателя, следует учесть особенности заданий в каждой серии и оценить, в какой из них он более успешен. ВНИМАНИЕ! Разъяснительные описания серий даны без учета личностных особенностей, а основываются только на возможностях интеллекта.
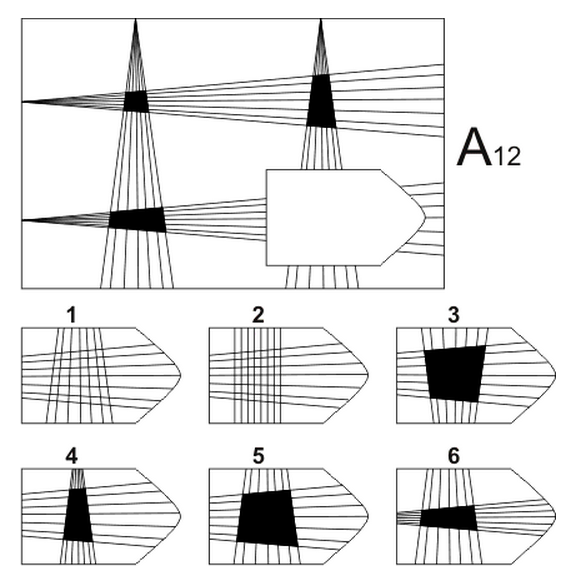
СЕРИЯ А Тестовое значение заключается в дополнении недостающей части матрицы (поля), в этой серии фигуры статичны и не подразумевают изменений.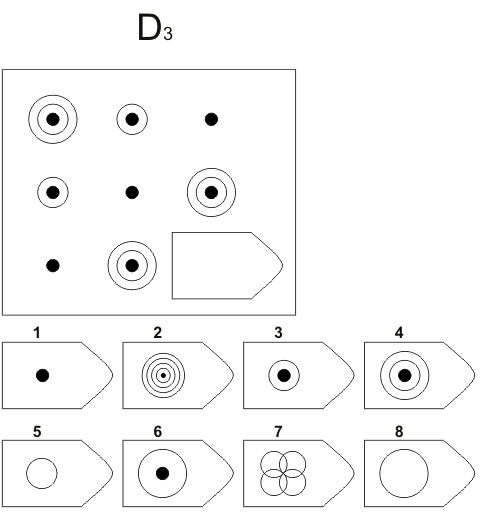 В решении этой серии задач протекают 2 мыслительных процесса: идентификация недостающей части структуры с остальными частями и анализ структуры целого согласно указанным взаимосвязям элементов в матрице. Решение зависит от уровня внимательности, статистического представления и визуального различия.
В решении этой серии задач протекают 2 мыслительных процесса: идентификация недостающей части структуры с остальными частями и анализ структуры целого согласно указанным взаимосвязям элементов в матрице. Решение зависит от уровня внимательности, статистического представления и визуального различия.
Это самая легкая серия из всего задания, и взрослый человек с легкостью ее выполняет. Если соискатель набрал в этой серии менее 6 баллов, нужно исключить близорукость, плохое состояние здоровья, ситуативные факторы (нервозная обстановка во время тестирования, отвлекающие факторы, неправильно данную инструкцию). Если выясняется, что все вышеперечисленное исключено, то дальнейшую работу продолжать не имеет смысла, на вашу вакансию соискатель претендовать не может в силу низкого интеллекта.
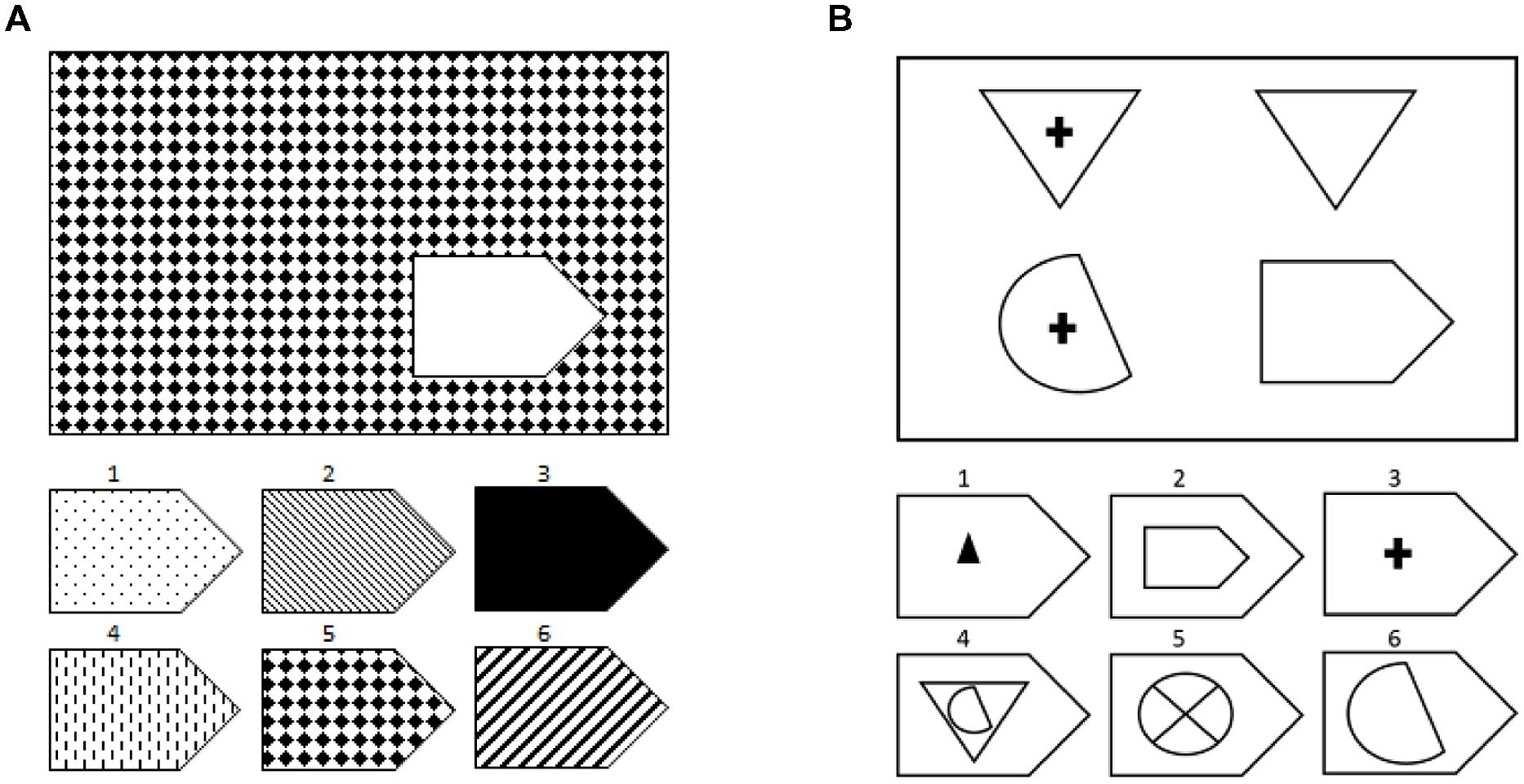
СЕРИЯ В Тестовое значение состоит в отыскивании аналогий между двумя парами фигур. Задача заключается в раскрытии принципа отношений по аналогии путем постепенной дифференциации элементов. При решении используется способность постигать симметричность между фигурами.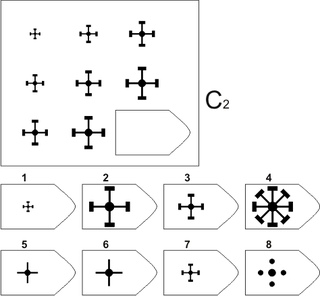 Решение зависит от способности к линейной дифференциации умозаключений на основе построения линейных взаимосвязей.
Решение зависит от способности к линейной дифференциации умозаключений на основе построения линейных взаимосвязей.
Если у тестируемого хороший результат только в этой серии, перед вами превосходный, толковый исполнитель, если на то есть личностная направленность, он не видит дальше собственного носа и вряд ли сможет претендовать на руководящую должность, такому «мозгу» вряд ли по силам организовывать что-либо или кого-либо, он просто сотрудник.
СЕРИЯ С основана на усложняющихся изменениях фигур в матрицах в соответствии с определенным логическим принципом непрерывного развития положения фигур и динамических перемен в пространстве (обогащение фигур в горизонтальном и вертикальном направлении и суммирование этих новых элементов в конечной недостающей фигуре). В этой серии проявляется способность к динамической наблюдательности и прослеживанию непрерывных изменений, динамическая внимательность и воображение, способность представлять.
Иными словами, если соискатель в этой серии набрал 10 или больше баллов, то это говорит о том, что он способен приспосабливаться к быстро меняющимся условиям, ломать стереотипы деятельности и решения задач. Человек, возможно, успешно работает в дефиците времени и справляется с частыми изменениями условий работы, не придерживается устойчивых стереотипов, однако могут возникнуть трудности с работой в условиях монотонной деятельности. Соискатель способен к работе менеджера среднего звена, при успешном дальнейшем обучении может претендовать на более высокий статус в организации.
Человек, возможно, успешно работает в дефиците времени и справляется с частыми изменениями условий работы, не придерживается устойчивых стереотипов, однако могут возникнуть трудности с работой в условиях монотонной деятельности. Соискатель способен к работе менеджера среднего звена, при успешном дальнейшем обучении может претендовать на более высокий статус в организации.
СЕРИЯ D составлена согласно принципу перестройки (переструктурации) фигур в матрице в горизонтальном и вертикальном направлении. Решение требует проследить закономерную последовательность фигур и чередование фигур в целостной структуре. Решение зависит от способности схватывать количественные и качественные изменения в упорядочении (составлении) фигур согласно закономерности используемых изменений.
То есть, если соискатель набрал в этой серии больше 10 баллов, вы вполне можете принимать его на работу не менее чем на руководящий пост, он способен организовать работу и проследить эффективность ее выполнения, не нуждается в дополнительном образовании.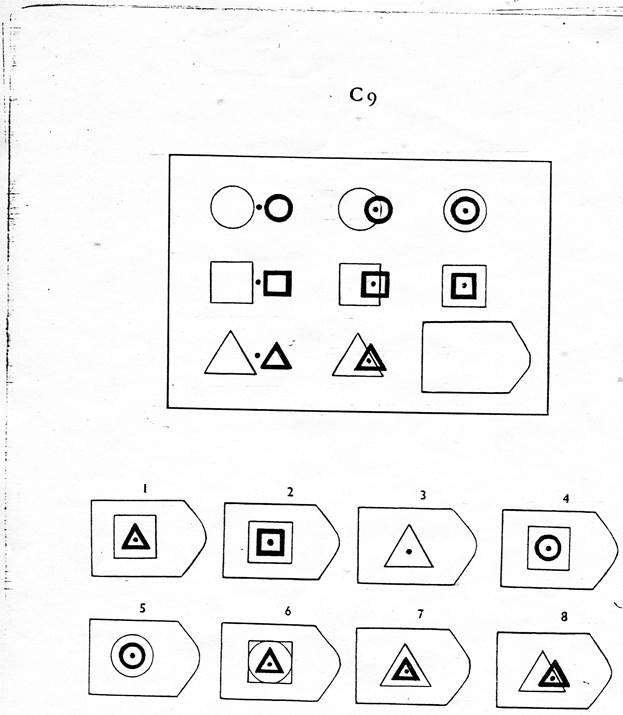
СЕРИЯ Е состоит из заданий, заключающихся в анализе и синтезе фигур из отдельных элементов согласно принятому принципу. Здесь требуется складывать и вычитать элементы фигур, смешивать части согласно алгебраическому принципу. Недостающий член структуры находят с помощью алгебраических операций с остальными частями структуры. Решение зависит от способности наблюдать сложное количественное и качественное различие кинетических, динамических рядов. Высшая форма абстрагирования и динамического синтеза.
Если соискатель набрал более 10 баллов в этой серии, то ему прямая дорога в аналитический отдел фирмы (если таковой имеется) или на руководящий пост. Перед вами человек с незаурядными интеллектуальными данными, он способен не только следить за процессами и делать выводы, но и формировать, переструктурировать работу всей организации, умеет абстрагироваться от частностей, обладает способностью видеть, просчитывать стратегию всей фирмы «на шаг вперед», что делает его незаменимым сотрудником.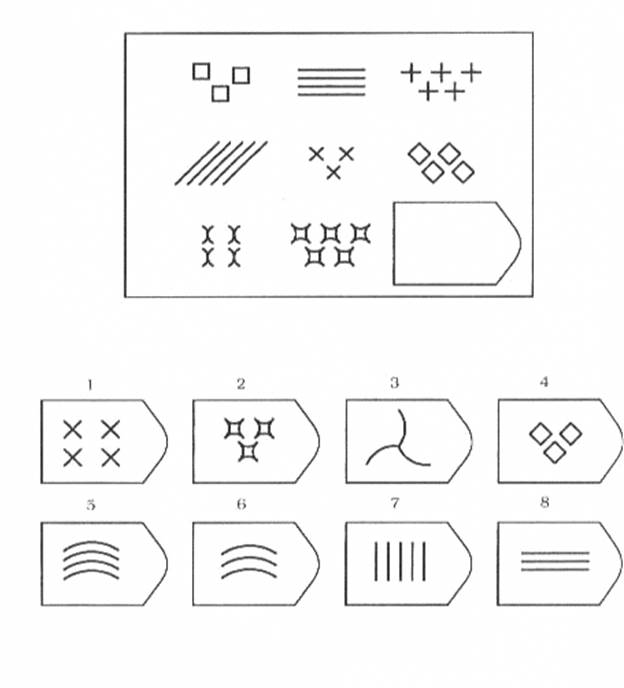
Суммируйте результаты всех серий. Полученное число — это «сырой» балл. Обработка производится по таблице, которая переводит баллы в коэффициент. Для удобства мы приводим средние и высокие баллы, минуя низкие, отражающие клиническое снижение интеллекта, также мы игнорируем возрастную группу до 16 лет. Таким образом, таблица рассчитана на возрастную группу от 16 до 40 лет, людей не страдающих клинически значимым снижением или недоразвитием интеллекта.
Если возраст кандидата превышает 30 лет, то необходимо произвести дополнительное вычисление по следующей формуле:
Оценить полученный показатель интеллекта можно по следующим критериям:
80-90 — слабый, ниже среднего;
90-100 — средний интеллект;
100-110 — высокий средний интеллект;
110-120 — высокий интеллект;
более 120 — незаурядный интеллект;
свыше 140 — выдающийся интеллект.
Кроме коэффициента интеллекта, по этому тесту можно судить об утомляемости — если человек делает ряд ошибок в конце каждой серии (с 9 по 12 образец), он будет уставать в условиях постоянной интеллектуальной нагрузки, что теоретически может повлечь ошибки или недостаточную эффективность в целом. Если же человек делает ошибки на протяжении всей серии, чередуя правильные и неправильные ответы, то есть его суждения не последовательны, — это может говорить как о «творческом начале», так и о невнимательности, трудности в сосредоточении внимания, что также может привести к сбоям в практике.
В любом случае, не стоит делать выводы, исходя из результатов одного теста. Кроме интеллектуальных данных, у человека есть личностные качества, которые ни в коем случае нельзя упускать из виду, «гении бывают злыми, а добрыми бывают и дураки». Предложенные вам методики измерения интеллекта не определяют человека в целом, а раскрывают лишь его мыслительные способности. Важно найти удачное для вашей организации сочетание интеллектуального потенциала и личностных особенностей.
Данный текст является ознакомительным фрагментом.
Продолжение на ЛитРесТест прогрессивных матриц Равена (интеллектуальное развитие)
Экспериментально-психологические методики для обследования детей и подростков. Тесты (Тест Векслера, Тест «Прогрессивные матрицы Равенна», Тест структуры интеллекта Амтхауэра).
Тест прогрессивных матриц Равена (интеллектуальное развитие)
Тест прогрессивных матриц Равена состоит из 60 заданий, распределенных по пяти сериям. В каждой серии представлено изображение полотна с геометрическим рисунком и несколько матриц с одной недостающей частью. Необходимо обнаружить закономерности в матрицах и подобрать из шести-восьми предложенных рисунков ту матрицу, которой недостает в полном изображении. От серии к серии задания усложняются.
Тест предназначен для дифференцировки испытуемых по уровню их интеллектуального развития. Авторы теста Джон Рейвен и Л. Пенроуз. Предложен в 1936 году.
Более высокие показатели по этому тесту показывают те, кто
а) быстрее, и
б) точнее определяет логические закономерности в построении упорядоченного ряда состоящего из графических объектов, имеющих ограниченное количество признаков.
Название этого теста «Прогрессивные матрицы Рейвена» указывает на то, что задачи теста упорядочены по признаку возрастания трудности их решения.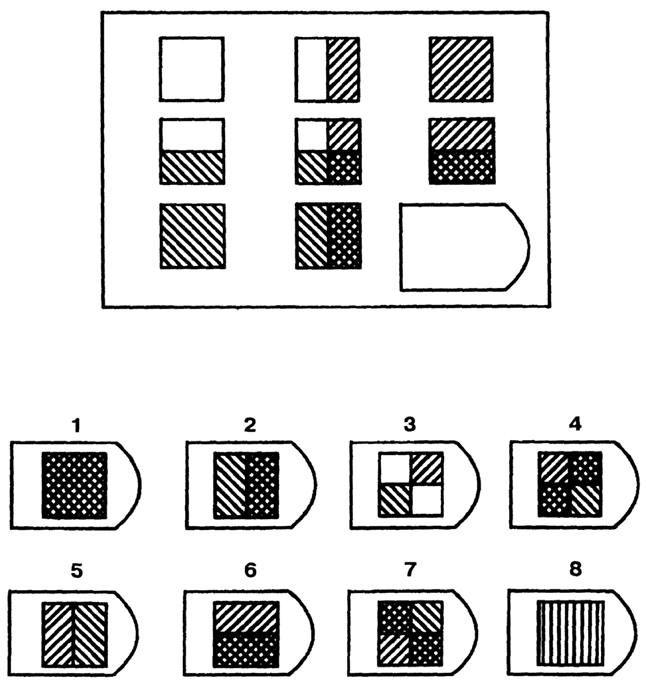
Результаты оцениваются по количеству правильно подобранных недостающих фрагментов по каждому заданию.
Пример матрицы
На решение задач теста вводится временное ограничение — подсчитывается количество правильно решённых за 20 минут задач. Возможен вариант, когда время на решение всех 60 задач не ограничено. В этом случае результат корректируется по специальной таблице.
По результатам тестирования испытуемый получает несколько оценок:
по десятибалльной шкале (стандартная оценка в стенах), учитывающей только количество правильно решённых задач,
по 19-балльной, учитывающей количество и трудность решённых задач,
по привычной пятибалльной (школьной, но с «плюсами» и «минусами»),
наконец, четвёртая, качественная, оценка. Если испытуемый решил все задачи теста, но многие, в том числе и лёгкие, задачи решил неверно, его можно отнести к категории «скоростников».
 Если же испытуемый решил мало задач (например, около половины задач теста), но, без единой ошибки, его можно отнести к категории «точняков», или тугодумов.
Если же испытуемый решил мало задач (например, около половины задач теста), но, без единой ошибки, его можно отнести к категории «точняков», или тугодумов.
Выделяют пять степеней развития интеллекта по тесту Равена:
I степень — более 57 правильных ответов (баллов), т.е. более 95% — особо высокоразвитый интеллект.
II степень — от 45 до 57 баллов (75-94%) — интеллект выше среднего.
III степень — от 15 до 45 баллов (25-74%) — интеллект средний.
IV степень — от 3 до 15 баллов (5-24%) — интеллект ниже среднего.
V степень — менее 3 баллов (5%) — интеллектуальный дефект.
Прогрессивные матрицы Равена
МИНОБРНАУКИ РОССИИ
Федеральное государственное бюджетное образовательное
Учреждение высшего профессионального образования
«Тульский государственный университет»
Кафедра психологии
РАБОЧАЯ ТЕТРАДЬ
Для лабораторных занятий по дисциплине
«Психодиагностика и практикум по психодиагностике»
Выполнил(а): ___________________________
_______________________________________
Проверила: к. психол.н., доц. каф. психологии
психол.н., доц. каф. психологии
Перегудиной В.А.
Тула 2013 г.
Корректурная проба
Результаты корректурной пробы
| Ответы испытуемого на корректурном бланке | характеристики внимания | ||||||||
| правильные | ошибочные | время | КТ | КАВ | ИУ | ||||
| r | p | M1 | M2 | t1 | t2 | ||||
Вывод:_________________________________________________
Вывод:_________________________________________________
Методика Мюнстерберга
Вывод:_________________________________________________
Вывод:______________________
Методика «Оперативная память»
Вывод:_______________________________________________________________
Методика «Память на числа»
Вывод:_______________________________________________________________
Методика «Память на образы»
Вывод:_______________________________________________________________
Методика «Количественные отношения»
1. А больше Б в 9 раз
А больше Б в 9 раз
Б меньше В в 4 раза
В А
2. А меньше Б в 10 раз
Б меньше В в 6 раз
А В
3. А больше Б в 3 раза
Б меньше В в 6 раз
В А
4. А больше Б в 4 раза
Б меньше В в 3 раза
В А
5. А меньше Б в 3 раза
Б больше В в 7 раз
А В
6. А больше Б в 9 раз
Б меньше В в 12 раз
В А
7. А больше Б в 6 раз
Б больше В в 7 раз
А В
8. А меньше Б в 3 раза
Б больше В в 5 раз
В А
9. А меньше Б в 10 раз
Б больше В в 3 раза
В А
10. А меньше Б в 2 раза
Б больше В в 8 раз
А В
11. А меньше Б в 3 раза
Б больше В в 4 раза
В А
12. А больше Б в 2 раза
Б меньше В в 5 раз
А В
13. А меньше Б в 5 раз
Б больше В в 6 раз
В А
14. А меньше Б в 5 раз
Б больше В в 2 раза
А В
15. А больше Б в 4 раза
Б меньше В в 3 раза
В А
16. А меньше Б в 3 раза
А меньше Б в 3 раза
Б больше В в 2 раза
А В
17. А больше Б в 4 раза
Б меньше В в 7 раз
В А
18. А больше Б в 3 раза
Б меньше В в 5 раз
А В
Вывод:______________________
Методика «Закономерности числового ряда»
1) 24 21 19 18 15 13 – – 7
2) 1 4 9 16 – – 49 64 81 100
3) 16 17 15 18 14 19 – –
4) 1 3 6 8 16 18 – –76 78
5) 7 16 9 5 21 16 9 – 1
6) 2 4 8 10 20 22 – – 92 94
7) 24 22 19 15 – –
Вывод:______________________
Методика «Сложные аналогии»
Шифр
А. Овца — стадо. Б. Малина — ягода. В. Море — океан.
Г. Свет — темнота. Д. Отравление — смерть. Е. Враг – неприятель.
1. Испуг – бегство А, Б, В, Г, Д, Е
2. Физика — наука А, Б, В, Г, Д, Е
3. Правильно — верно А, Б, В, Г, Д, Е
4. Грядка — огород А, Б, В, Г, Д, Е
5. Пара- два А, Б, В, Г, Д, Е
6. Слово — фраза А, Б, В, Г, Д, Е
7. Бодрый – вялый А, Б, В, Г, Д, Е
Бодрый – вялый А, Б, В, Г, Д, Е
8. Свобода — воля А, Б, В, Г, Д, Е
9. Страна — город А, Б, В, Г, Д, Е
10. Похвала — брань А, Б, В, Г, Д, Е
11. Месть — поджог А, Б, В, Г, Д, Е
12. Десять — число А, Б, В, Г, Д, Е
13. Плакать — реветь А, Б, В, Г, Д, Е
14. Глава-роман А, Б, В, Г, Д, Е
15. Покой — движение А, Б, В, Г, Д, Е
16. Смелость — геройство А, Б, В, Г, Д, Е
17. Прохлада — мороз А, Б, В, Г, Д, Е
18. Обман — недоверие А, Б, В, Г, Д, Е
19. Пение — искусство А, Б, В, Г, Д, Е
20. Тумбочка — шкаф А, Б, В, Г, Д, Е
Вывод:______________________
Методика «Выделение существенных признаков»
1. Сад (растения, садовник, собака, забор, земля).
2. Река (берег, рыба, рыболов, тина, вода).
3. Города (автомобиль, здание, толпа, улица, велосипед).
4. Сарай (сеновал, лошади, крыша, скот, стены).
5. Куб (углы, чертеж, сторона, камень, дерево).
6. Деление (класс, делимое, карандаш, делитель, бумага).
7. Кольцо (диаметр, алмаз, просьба, круглость, печать).
8. Чтение (глаза, книга, картинка, печать, слово).
9. Газета (правда, приложения, телеграммы, бумага, редактор).
10. Игра (карты, игроки, штрафы, наказания, правила).
11. Война (аэроплан, пушки, сражения, ружья, солдаты).
12. Книга (рисунки, рассказ, бумага, оглавление, текст).
13. Пение (звон, искусство, голос, аплодисменты, мелодия).
14. Землетрясение (пожар, смерть, колебания почвы, шум, наводнение).
15. Библиотека (столы, книги, читальный зал, гардероб, читатели).
16. Лес (почва, грибы, охотник, дерево, волк).
17. Спорт (медаль, оркестр, состязания, победа, стадион).
18. Больница (помещение, уколы, врач, градусник, больные).
19. Любовь (розы, чувства, человек, свидание, свадьба).
20. Патриотизм (город, родина, друзья, семья, человек).
Вывод:______________________
Прогрессивные матрицы Равена
http://www.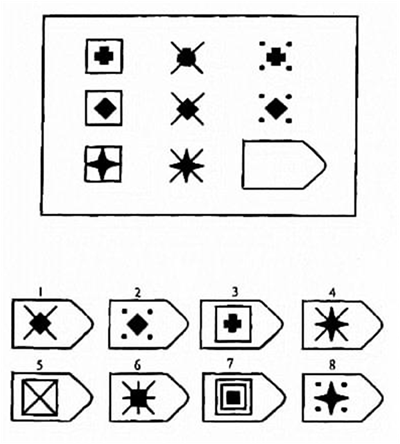 psylab.info/Прогрессивные_Матрицы_Равена/Карточки_(Черно-белый_вариант)
psylab.info/Прогрессивные_Матрицы_Равена/Карточки_(Черно-белый_вариант)
Бланк ответов
Обработка результатов и вывод: __________________________________________________________
____________________________
_____
______________________________________________
_____
______________________________________________
Прогрессивные матрицы Равена
Методика позволяет работать с людьми различных языковых культур, а также с немыми, так как не требует вербализации.
Время проведения тестирования может быть как ограниченным, так и неограниченным (в первом случае выявляется качество и уровень сформированности компонентов логичности мышления, а во втором – его индивидуальные особенности).
Прогрессивные матрицы
Программа предназначена для компьютерного тестирования и обработки тестов интеллектуальных способностей, не содержащих вербальных заданий:
- Стандартные прогрессивные матрицы.
 Стандартные черно-белые матрицы предназначены для обследования детей от 8 лет, подростков и взрослых.
Стандартные черно-белые матрицы предназначены для обследования детей от 8 лет, подростков и взрослых. - Цветные прогрессивные матрицы. Цветной вариант предназначен для обследования детей 4,5-8 лет и лиц старше 65 лет.
Можно выделить следующие цели при применении теста Дж. Равена
- Непосредственная количественная оценка уровня интеллектуального развития.
- Выявление особенностей логичности мышления (при этом полученная сумма баллов в каждой серии подвергается качественной обработке).
- Обучающая и корректирующая цели (без количественной обработки, а с учетом возрастных особенностей психического развития ребенка и зоны ближайшего его развития).
Программа компьютерной обработки и тестирования «Прогрессивные матрицы Равена» дает возможность тестирования и количественной обработки на компьютере и на стандартных бланках (с последующим вводом данных с бланка и компьютерной обработкой результатов).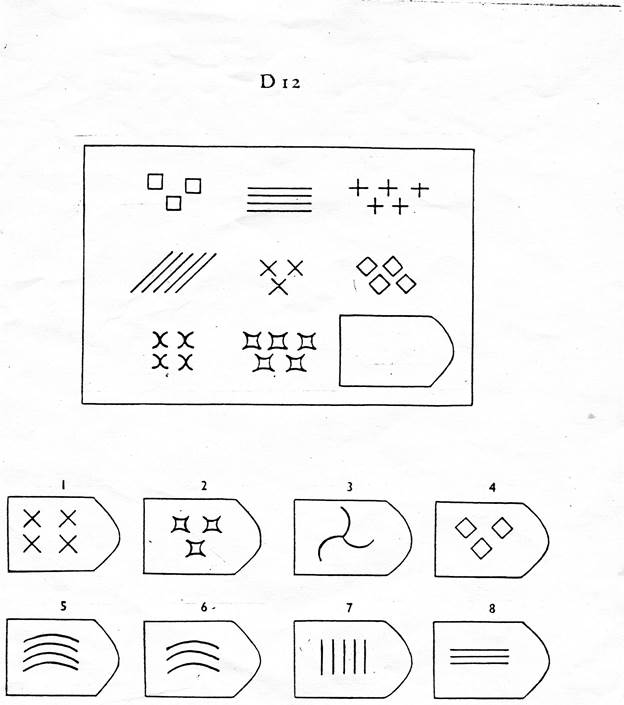 Компьютерная процедура цветных прогрессивных матриц учитывает качественные показатели процесса выполнения теста ребенком, фиксируемые специалистом при наблюдении.
Компьютерная процедура цветных прогрессивных матриц учитывает качественные показатели процесса выполнения теста ребенком, фиксируемые специалистом при наблюдении.
Традиционная процедура исследования позволяет выявить лишь «уровень актуального», но не дает возможности в определении «зоны ближайшего» развития ребенка. При использовании различных видов помощи повышается дифференциально-диагностическая ценность методик, используемых для разграничения различных форм интеллектуальной недостаточности.
С этой целью Т. В. Розанова (1978) модифицировала процедуру предъявления матриц Дж. Равена – ввела различные виды помощи. Вариант выполнения теста Равена на бланках «с помощью» рекомендуется для детей с трудностями обучения, или если при компьютерном прохождении теста индекс вариативности и «отклонения» по сериям велики. Тест «с помощью» выполняется без учета времени.
Данные, полученные с помощью прогрессивных матриц Ранена, хорошо согласуются с показателями других распространенных тестов общих способностей: теста Векслера, умственного развития шкалы Станфорд – Бине; теста Выготского – Сахарова. Коэффициент надежности теста по данным различных исследований, варьирует от 0,70 до 0,89.
Коэффициент надежности теста по данным различных исследований, варьирует от 0,70 до 0,89.
Возможности программы
Рис 1. Интерфейс программы «Прогрессивные матрицы Равена»
Картотека
Картотека служит для управления карточками людей, которые прошли или будут проходить тестирование. В карточке пользователя хранятся все результаты тестирований, основные данные, а также динамика. В карточку можно внести вручную ответы с бланков тестирования. Результаты тестов, которые были пройдены в программе, сохраняются автоматически. Каждой карточке можно присвоить определенную группу, чтобы потом в картотеке была возможность сортировать данные по группам.
Рис 2. Картотека
Результаты
Все результаты обследований, которые были пройдены на компьютере, хранятся в карточке каждого пользователя. Результаты тестирований можно распечатать на принтере или сделать экспорт данных на компьютер.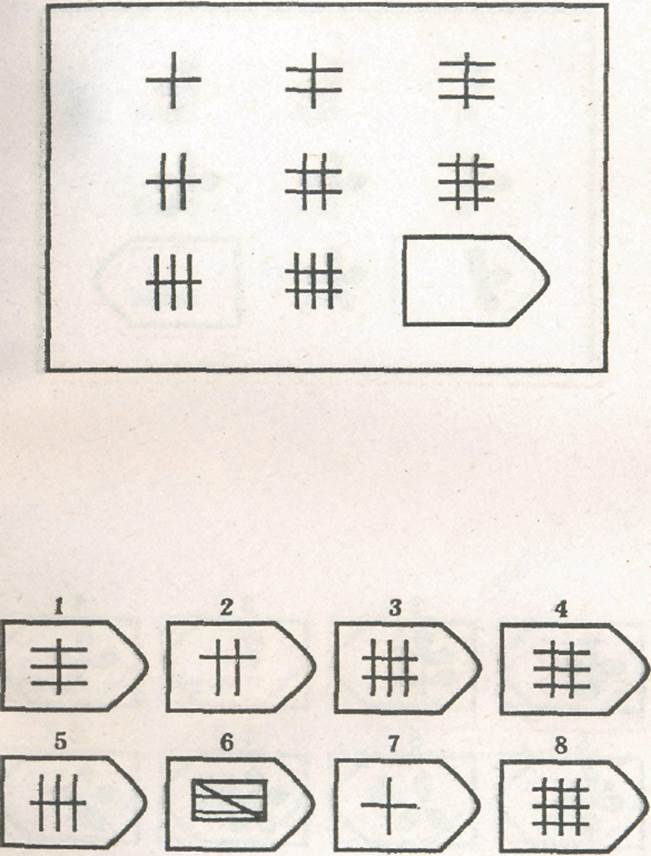 Конечные файлы результатов имеют можно открыть с помощью MS Office. Чтобы получить результаты тестов, которые были пройдены с помощью бланков, необходимо сначала вручную внести данные обследований в карточку пользователя.
Конечные файлы результатов имеют можно открыть с помощью MS Office. Чтобы получить результаты тестов, которые были пройдены с помощью бланков, необходимо сначала вручную внести данные обследований в карточку пользователя.
Динамика
По тестам, которые были пройдены несколько раз, можно отслеживать результаты в динамике. Все результаты хранятся в карточке пользователя. В карточке пользователя динамику результатов можно напечатать или сделать экспорт данных на компьютер.
Групповой отчет
Групповой отчет позволяет вывести на печать результаты проведенных обследований для сформированной произвольным образом группы пользователей.
Бланки
Тесты могут быть проведены как на компьютере, так и в бланковой форме. Бланки входят в комплект методики.
Рис 3. Бланки
Версии программы
У программного обеспечения существует 3 версии:
- Локальная версия.
 Программа устанавливается только на 1 компьютер. Тестирование и администрирование осуществляются в одном приложении. Программа запускается только при наличии диска в DVD приводе.
Программа устанавливается только на 1 компьютер. Тестирование и администрирование осуществляются в одном приложении. Программа запускается только при наличии диска в DVD приводе. - Версия на 6 рабочих мест. Эта версия предназначена для проведения группового тестирования. На один компьютер устанавливается программа-сервер. На нем осуществляются администрирование, сбор и обработка результатов тестов со всех других компьютеров. На другие компьютеры устанавливается программа-клиент. С помощью нее осуществляется прохождение тестов группой, результаты передаются по сети на программу-сервер. Обязательное требование – все компьютеры должны быть объединены в локальную сеть. Максимальное количество компьютеров – 6 шт. Программа запускается только при наличии диска в DVD приводе на компьютере-сервере.
- Версия без ограничений. Эта версия предназначена для проведения группового тестирования. На один компьютер устанавливается программа-сервер. На нем осуществляются администрирование, сбор и обработка результатов тестов со всех других компьютеров.
 На другие компьютеры устанавливается программа-клиент. С помощью нее осуществляется прохождение тестов группой, результаты передаются по сети на программу-сервер. Обязательное требование – все компьютеры должны быть объединены в локальную сеть. В этой версии программы нет ограничений по количеству компьютеров-клиентов. Программа запускается только при наличии диска в DVD приводе на компьютере-сервере.
На другие компьютеры устанавливается программа-клиент. С помощью нее осуществляется прохождение тестов группой, результаты передаются по сети на программу-сервер. Обязательное требование – все компьютеры должны быть объединены в локальную сеть. В этой версии программы нет ограничений по количеству компьютеров-клиентов. Программа запускается только при наличии диска в DVD приводе на компьютере-сервере.
Для тестирования детей 4,5-8 лет с применением Цветных прогрессивных матриц рекомендуется локальная версия, которая учитывает качественные показатели процесса выполнения теста ребенком, фиксируемые специалистом при наблюдении.
Технические требования
- DVD привод встроенный или внешний
- Операционная система Windows 7, 8, 10 и выше
- Офисный пакет (Word, Excel) с активной лицензией для редактирования отчетов
- Наличие локальной сети в классе для сетевых версий ПО
Тест Равена — презентация онлайн
1.
 Тест равена
Тест равена2. Джон Равен Родился: 28 июня 1902 г., Лондон, Великобритания Умер: 10 августа 1970 г., Дамфрис, Великобритания Образование:
ДЖОН РАВЕНРОДИЛСЯ: 28 ИЮНЯ 1902 Г.,
ЛОНДОН, ВЕЛИКОБРИТАНИЯ
УМЕР: 10 АВГУСТА 1970 Г.,
ДАМФРИС, ВЕЛИКОБРИТАНИЯ
ОБРАЗОВАНИЕ: УНИВЕРСИТЕТ ЛОНДОН
ИЗВЕСТНОСТЬ: ТЕСТ РАВЕНА
Методика «Шкала прогрессивных
матриц» была разработана в 1936
году Джоном Равеном (совместно с
Л. Пенроузом). Тест прогрессивные
матрицы
Равена
(ПМР)
предназначен
для
диагностики
уровня интеллектуального развития
и
оценивает
способность
к
систематизированной,
планомерной,
методичной
интеллектуальной
деятельности
(логичность мышления).
Принцип «прогрессивности»
В Стандартных матрицах реализуется двояким образом:
а) внутри каждой серии задания расположены с учётом их
возрастающей сложности;
б) все серии отличаются различной трудностью, которая
возрастает от серии А к серии Е.
 11 см.), в каждой из которых отсутствует
11 см.), в каждой из которых отсутствуетодин из составляющих её элементов. Обследуемый должен выбрать
недостающий элемент матрицы среди 6-8 предложенных вариантов.
Задания сгруппированы в 5 серий — А, В, С, D, Е, каждая серия состоит из
12 матриц.
Расположение
матриц
в
определённой
последовательности
соответственно принципу возрастающей сложности мыслительных
операций, необходимых для решения, не исключает варианта парциальной
несформированности умственных операций у обследуемого. В этом случае
профиль суммарных оценок за 5 серий не будет отражать нарастающую
сложность.
A12 B12 C12 D12 E12
В серии А — использован принцип установления взаимосвязи в структуре матриц.
Здесь задание заключается в дополнении недостающей части основного
изображения одним из приведенных в каждой таблице фрагментов. Выполнение
задания требует от обследуемого тщательного анализа структуры основного
изображения и обнаружения этих же особенностей в одном из нескольких
фрагментов.
 Затем происходит слияние фрагмента, его сравнение с окружением
Затем происходит слияние фрагмента, его сравнение с окружениемосновной части таблицы.
Серия В — построена по принципу аналогии между парами фигур. Обследуемый
должен найти принцип, соответствен но которому построена в каждом отдельном
случае фигура и, исходя из этого, подобрать недостающий фрагмент. При этом
важно определить ось симметрии, соответственно которой расположены фигуры в
основном образце.
Серия С — построена по принципу прогрессивных изменений в фигурах матриц. Эти
фигуры в пределах одной матрицы все больше усложняются, происходит как бы
непрерывное их развитие. Обогащение фигур новыми элементами подчиняется
четкому принципу, обнаружив который, можно подобрать недостающую фигуру.
Серия D — построена по принципу перегруппировки фигур в матрице. Обследуемый
должен найти эту перегруппировку, происходящую в горизонтальном и
вертикальном положениях.
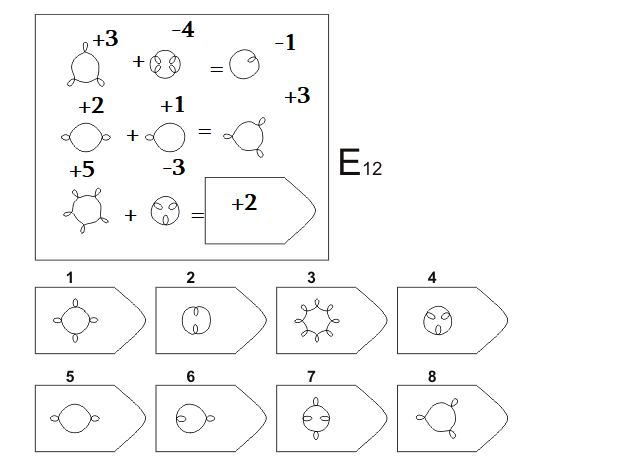
Серия Е основана на принципе разложения фигур основного изображения на
элементы.
 Недостающие фигуры можно найти, поняв принцип анализа и синтеза
Недостающие фигуры можно найти, поняв принцип анализа и синтезафигур.
Имеется взрослый (с 14 до 65 лет)
и детский (с 4,5 до 9 лет) вариант
тестов Равена. Возможны два варианта
в использовании матриц Равена.
Первый вариант — в качестве теста
скорости, с ограничением времени 20
мин. для выполнения заданий. Для
группового обследования.
Второй вариант использования
матриц Равена в качестве теста
интеллекта
исключает
введение
временных ограничений.
Задача испытуемого — установить
закономерность, связывающую между
собой фигуры на рисунке, и на
опросном листе указать номер искомой
фигуры из предлагаемых вариантов.
С 11
7. Инструкция Теста равена
Инструкция: Тест строго регламентирован во времени, а именно: 20 мин.Для того, чтобы соблюсти время, необходимо строго следить за тем, чтобы до
общей команды: «Приступить к выполнению теста» — никто не открывал
таблицы и не подсматривал.
 По истечении 20 мин подается команда,
По истечении 20 мин подается команда,например: «Всем закрыть таблицы». О предназначении данного теста можно
сказать следующее: «Все наши исследования проводятся исключительно в
научных целях, поэтому от вас требуются добросовестность, глубокая
обдуманность, искренность и точность в ответах. Данный тест предназначен
для уточнения логичности вашего мышления».
После этого взять таблицу и открыть для показа всем 1-ю страницу: «На
рисунке одной фигуры недостает. Справа изображено 6-8 пронумерованных
фигур, одна из которых является искомой. Надо определить закономерность,
связывающую между собой фигуры на рисунке, и указать номер искомой
фигуры в листке, который вам выдан» (можно показать на примере одного
образца).
Во время выполнения задач теста необходимо контролировать, чтобы
респонденты не списывали друг у друга. По истечении 20 мин подать
команду: «Закрыть всем таблицы!
Собрать бланки и таблицы к ним. Проверить, чтобы в правом углу
регистрируемого бланка был проставлен карандашом номер обследуемого.
Бланк ответов
ФИО ________________________________________________________________
Возраст__________ Пол___________ Дата обследования_______________
№ задания
Серия A
Серия B
Серия C
Серия D
1
2
3
4
5
6
7
8
9
10
11
12
Сумма
правильных
ответов
Общее время выполнения теста ___________ мин. ____________ сек.
Обща сумма баллов ________________
IQ показатель _________________
Серия E
Интерпретация результатов (ключи)
Правильное решение каждого задания оценивается в один балл, затем
подсчитывается общее число баллов по всем таблицам и по отдельным сериям.
Полученный общий показатель рассматривается как индекс интеллектуальной силы,
умственной производительности респондента. Показатели выполнения заданий по
отдельным сериям сравнивают со среднестатистическим, учитывают разницу между
результатами, полученными в каждой серии, и контрольными, полученными
статистической обработкой при исследовании больших групп здоровых обследуемых и,
таким образом, расцениваемыми как ожидаемые результату. Такая разница позволяет
судить о надежности полученных результатов (это не относится к психической патологии).
№
Серия А
Серия В
Серия С
Серия D
Серия Е
1
4
5
5
3
7
2
5
6
3
4
6
3
1
1
2
3
8
4
2
2
7
8
2
5
6
1
8
7
1
6
3
3
4
6
5
7
6
5
5
5
1
8
2
6
1
4
3
9
1
4
7
1
6
10
3
3
1
2
2
11
4
4
6
5
4
12
2
8
2
6
5
Процентная шкала степени развития интеллекта
Полученный суммарный показатель по специальной таблице переводится
в проценты. При этом по специальной шкале различают 5 степеней
интеллектуального уровня:
Проценты
Степень
95 и выше
I степень: особо высокоразвитый интеллект
75-95
2 степень: незаурядный интеллект для данной возрастной группы
25-74
3 степень: средний интеллект для данной возрастной группы
5-24
4 степень: интеллект ниже среднего.
5 и менее
5 степень: дефектная интеллектуальная способность
Следующий способ оценки общих результатов по Стандартным матрицам
Равена заключается в переводе «сырого» балла в стандартизированный коэффициент IQ.
Таблица перевода сырых баллов в IQ
Возраст
14-30
35
40
45
50
55
65
%
100
97
93
88
82
76
70
Далее, ориентируясь на выявленный показатель IQ, можно определить
уровень умственных способностей.
Градации уровней умственных способностей
Показатели IQ
Уровень развития интеллекта
Свыше 140
незаурядный, выдающийся интеллект
121-140
высокий уровень интеллекта
111-120
интеллект выше среднего
91-110
средний уровень интеллекта
81-90
интеллект ниже среднего
71-80
низкий уровень интеллекта
51-70
лёгкая степень слабоумия
21-50
средняя степень слабоумия
0-20
тяжёлая степень слабоумия
A1
A2
A3
A4
A5
A6
A7
A8
A9
A 10
A 11
A 12
B1
B2
B3
B4
B5
B6
B7
B8
B9
B 10
B 11
B 12
C1
C2
C3
C4
C5
C6
C7
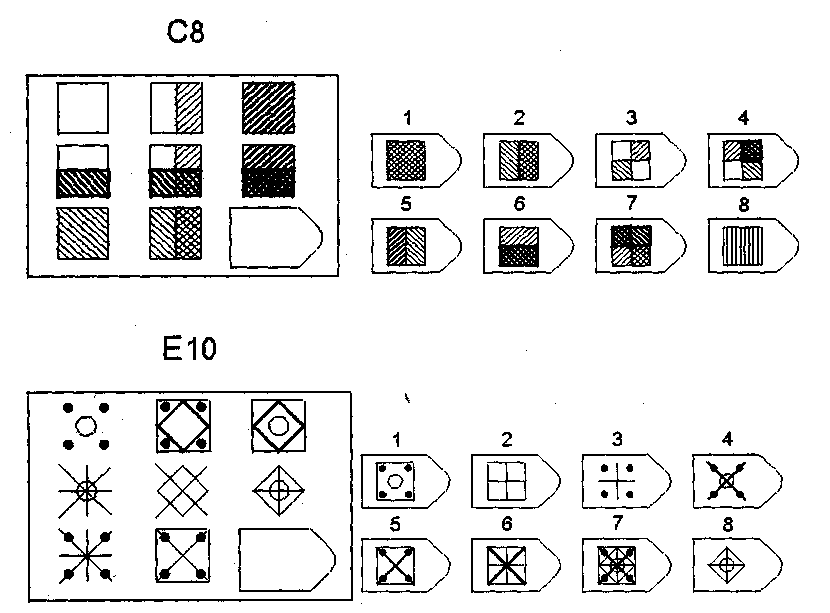
C8
C9
C 10
C 11
C 12
D1
D2
D3
D4
D5
D6
D7
D8
D9
D 10
D 11
D 12
E1
E2
E3
E4
E5
E6
E7
E8
E9
E 10
E 11
E 12
№ задания
Серия A
Серия B
Серия C
Серия D
Серия E
1
4
1 (5)
5
3
7
2
5
6
3
4
6
3
1
1
2
3
2 (8)
4
2
2
7
8
2
5
6
1
8
7
1
6
3
3
4
6
8 (5)
7
6
5
5
5
5 (1)
8
2
6
1
4
8 (3)
9
1
4
1 (7)
1
6
10
3
3
6 (1)
1 (2)
7 (2)
11
1 (4)
4
6
2 (5)
5 (4)
12
2
8
3 (2)
7 (6)
6 (5)
Сумма
правильных
ответов
11
11
9
9
5
= 45
Полученный суммарный показатель по специальной таблице переводится в
проценты.
1
2
3
4
5
степень — более 95% — высокий интеллект;
степень — 75-94% — интеллект выше среднего;
степень 25-74% — интеллект средний;
степень — 5-24% — интеллект ниже среднего;
степень — ниже 5% — дефект.
Следующий способ оценки общих результатов по Стандартным матрицам
Равена заключается в переводе «сырого» балла в стандартизированный коэффициент IQ.
Возраст
14-30
35
40
45
50
55
65
%
100
97
93
88
82
76
70
Далее, ориентируясь на выявленный показатель IQ, можно определить
уровень умственных способностей.
Градации уровней умственных способностей
Показатели IQ
Уровень развития интеллекта
Свыше 140
незаурядный, выдающийся интеллект
121-140
высокий уровень интеллекта
111-120
интеллект выше среднего
91-110
средний уровень интеллекта
81-90
интеллект ниже среднего
71-80
низкий уровень интеллекта
51-70
лёгкая степень слабоумия
21-50
средняя степень слабоумия
0-20
тяжёлая степень слабоумия
46. Спасибо за внимание!
СПАСИБО ЗАВНИМАНИЕ!
онлайн, с ответами, примеры на логическое мышление
Логические тесты – это группа тестов, которая проверяет навыки кандидатов в решении задач на логическое мышление. Вас могут попросить пройти логические тесты при приеме на различные вакансии, в большинстве своем требующие умения решать не стандартные или задачи высокого уровня логического мышления.
Лучший способ подготовки к тестам — это практика, поскольку она предоставляет возможность учится на ошибках и повышать результат с каждой попыткой, одновременно привыкая к таймеру и формату тестирования.
Логические тесты бесплатно
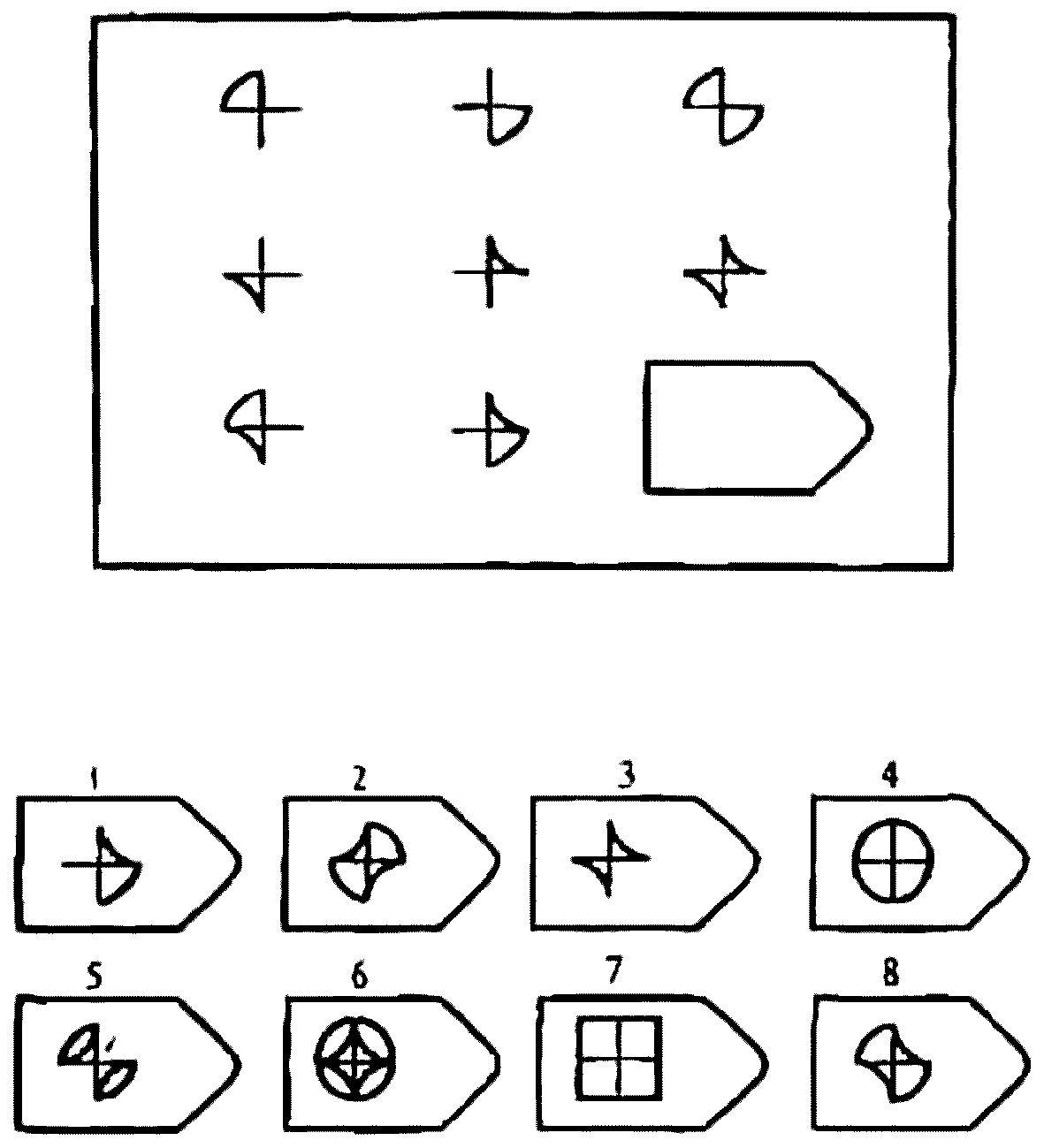
Тест на логическое мышление содержит 15 вопросов. Вопросы состоят из таблиц символов. В каждом вопросе один из символов пропущен. Ваша задача – определить, какой из предложенных вариантов лучше всего подходит на место пропущенного символа.
Каждый вопрос содержит 12 возможных вариантов ответов, из которых только один правильный. Общего лимита времени на тест нет, но на решение каждого вопроса отводится ровно 60 секунд.
Логические тесты с ответами
Пройдите бесплатные логические тесты. Для этого выберете вариант и нажмите на кнопку старт на следующей странице. Ответы будут доступны бесплатно после завершения теста.
Логические задачи теста
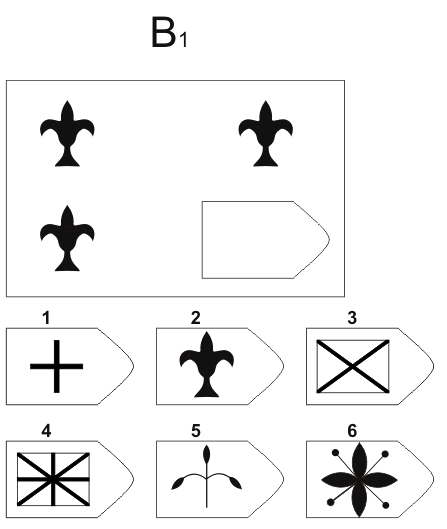
Фигуры расположены в логической последовательности. Какое изображение должно быть на пустом месте?
Правило 1: В каждом столбце сверху вниз набор символов каждый раз сдвигается на один элемент направо. Возможные варианты ответов B1 и B4.
Правило 2: В каждом столбце сверху вниз затемненный элемент поочередно занимает позицию противоположную предыдущей.
Таким образом, единственно правильный вариант ответа B1.
Как успешно пройти логический тест онлайн?
Несмотря на то, что каждый тест оценивает определенные навыки логического мышления, есть ряд советов, которые можно применять для общего повышения результатов тестирования. Вот список полезных советов и рекомендаций по решению тестов на логику:
1. Постарайтесь сохранять спокойствие. Логический тест может быть достаточно нервным испытанием, в особенности, если время его решения ограничено. Практикуйтесь на пробных вариантах, хорошо выспитесь накануне, во время теста дышите ровно и свободно, это поможет вам успокоить нервы и сделать все возможное в день теста.
2. Внимательно изучите тест. Изучение как можно большего количества вопросов позволит вам погрузиться в тест, понять, какие виды логики и мышления необходимы для его решения и убедиться, что ваших знаний и умений достаточно. Это позволит вам сократить время решения, и повысить эффективность.
3. Если работодатель назначил вам тест на логику, то постарайтесь уточнить какой вид логического мышления будет оцениваться. Ввиду их множества, эта информация будет очень полезна при подготовке к тесту.
4. Когда решаете тест на логическое мышление, старайтесь понять правильный ответ, закономерности и последовательности до просмотра возможных вариантов ответов. Как только вы поймете, какой ответ является правильным, найти его среди представленных вариантов не составит труда.
Виды логического мышления
Есть несколько типов логических тестов, которые проверяют разные навыки логического мышления. Обычно их использую комбинированно. Как правило, тесты оценивают следующие типы мышления:
Индуктивное мышление
Индуктивный метод мышления — это способность делать общие выводы, основанные на частных примерах, наблюдаемых в определенных условиях. Индуктивный способ мышления часто используется в повседневной жизни и широко применяются в рабочей деятельности. В данных тестах, оценивающих данный вид мышления, используются серии диаграмм, изображающие последовательности фигур. Кандидатам нужно проследить логику в данных последовательностях и определить какая фигура подходит, для того, чтобы занять следующее место в последовательности. Попробуйте пройти тест на индуктивное мышление.
Дедуктивное мышление
Дедуктивный метод мышления позволяет делать частные выводы исходя из общего правила или принципа. Тесты для измерения оценивают навыки кандидатов приводить логические аргументы и обосновывать выводы исходя из имеющейся информации. Работодатели, чаще других, используют вербально числовой тест для оценки дедуктивного способа мышления.
Абстрактное мышление
Абстрактное или абстрактно-логическое мышление позволяет находить не стандартные пути решения задач. Тесты оценивающие данный тип мышления обычно состоят из серии изображений, скрывающих определенную последовательность или правило, либо могут состоять из заданий на нахождение пропущенных элементов.
Образное мышление
Образное мышление является особой формой абстрактного мышления. Тесты измеряющие данные способности, как правило содержат блок-схемы и диаграммы, которые состоят из исходных данных и результатов. Кандидатам в процессе прохождения данного теста требуется оценить влияние исходных данных на результат.
Критическое мышление
Тесты на критическое мышление относятся к разновидностям вербальных тестов и оценивают навыки использования различных видов мышления при оценке аргументов, предположений и выводов.
Логические тесты при приеме на работу
Компании издатели по-разному называют логические тесты. Общепринятое название «тест на логику» используется Talent Q. Остальные издатели называют их тестами на образное, абстрактное или логическое мышление. Хорошим советом будет уточнить у человека, назначающего вам тест, его название и попросить несколько примеров. Это даст хорошее представление о предстоящем тестировании.
1. Talent Q тест на логику. Главная особенность теста Talent Q заключается в том, что он является адаптивным. Сложность каждого следующего вопроса определяется результатом ответа на предыдущий. Таким образом, уровень сложности теста меняется динамически, что позволяет проводить оценку логического мышления быстрее. Попробуйте пройти логические тесты бесплатно, чтобы проверить свои способности.
2. Kenexa Тест на логическое мышление. Данный тест по стилю очень похож на тест на индуктивное мышление SHL. В нем также требуется определить следующую фигуру в последовательности, основываясь на передвижениях элементов. Обычно Kenexa дает 20 минут для решения 24 вопросов из их теста на логику.
3. Тест Равена. Тест состоит из таблиц символов, называемых прогрессивные Матрицы Равена, которые следуют определенному правилу. Есть два уровня сложности: продвинутый (23 вопроса, 42 минуты) и стандартный (28 вопросов, 47 минут).
Подготовка к тестам на логическое мышление
Логическое мышление подразделяется на широкое количество видов, что обуславливает разнообразность тестов, используемых для его оценки. Наличие представления о различных навыках и видах логического мышления и понимание какой из них будет оцениваться – важный шаг в подготовке к тесту на логику.
На DigitalTests можно бесплатно пройти логические тесты с ответами, а также индуктивные тесты на образное и абстрактное мышление. Практика позволит вам повысить свои навыки. В наших группах в соцсетях вы найдете подробное описание решения каждого вопроса, что поможет в подготовке к предстоящему тестированию.
И напоследок, удачи вам – мы в вас верим.
Тест IQ Виктора Серебрякова
Тест IQ Виктора Серебрякова
Интеллект
Чем больше коэффициент интеллекта IQ, тем реже он встречается.
IQ 115 у одного из 6 человек,
IQ 119 у одного из 10 человек,
IQ 125 у одного из 21 человек,
IQ 128 у одного из 32 человек,
IQ 130 у одного из 44 человек,
IQ 132 у одного из 61 человек,
IQ 133 у одного из 72 человек,
IQ 134 у одного из 85 человек,
IQ 135 у одного из 102 человек,
IQ 139 у одного из 215 человек,
IQ 141 у одного из 319 человек,
IQ 143 у одного из 482 человек,
IQ 144 у одного из 596 человек,
IQ 145 у одного из 741 человек,
IQ 146 у одного из 924 человек,
IQ 147 у одного из 1157 человек,
IQ 150 у одного из 2330 человек,
IQ 155 у одного из 8139 человек,
IQ 158 у одного из 18127 человек,
IQ 160 у одного из 31574 человек.
С помощью электронных таблиц (Excel или Google Sheets) можно составить полную таблицу, используя формулу =1/(1-(normdist(A1,100,15,true)))
Английский ученый Виктор Серебряков разработал The Serebriakoff Advanced Culture Fair Test — культурно-независимый тест интеллекта повышенной сложности. Он есть в книге The Mammoth Book of Astounding Puzzles издательства Carroll & Graf, 1992 год.
Всего в тесте 36 заданий, в каждом задании нужно решить, какой фигуры не хватает. Время размышлений не ограничено. Я сделал программу для Windows, которая проводит этот тест и в конце сообщает IQ. Вот так выглядит окно программы:
Скачать программу: Тест IQ Виктора Серебрякова
Можно пройти тест не с помощью программы, а рассматривая картинки. Здесь все 36 заданий, в конце даны ответы и как посчитать IQ.
Правильные ответы:
За каждый правильный ответ начисляется 1 балл.
Сумма баллов переводится в IQ по этой таблице:
🐚
Равенство матриц — веб-формулы
Две матрицы равны, если выполняются все три из следующих условий:· Каждая матрица имеет одинаковое количество строк.
· Каждая матрица имеет одинаковое количество столбцов.
· Соответствующие элементы в каждой матрице равны.
Рассмотрим три матрицы, показанные ниже.
Если A = B , то мы знаем, что x = 34 и y = 54, поскольку соответствующие элементы одинаковых матриц также равны.
Мы знаем, что матрица C не равна A или B , потому что C имеет больше столбцов.
Примечание:
· Две равные матрицы абсолютно одинаковы.
· Если строки превращаются в столбцы, а столбцы в строки, мы получаем матрицу транспонирования. Если исходной матрицей является A, ее транспонирование обычно обозначается A
· Если две матрицы одного порядка (нет условий на элементы), они называются сопоставимыми.
· Если данная матрица A имеет порядок m x n, то ее транспонирование будет иметь порядок n x m.
Пример 1 : Обозначения ниже описывают две матрицы A и B .
, где i = 1, 2, 3 и j = 1, 2
Какие из следующих утверждений о A и B верны?
I. Матрица A состоит из 5 элементов.
II.Размер матрицы B составляет 4 × 2.
III. В матрице B элемент B 21 равен 222.
IV. Матрица A и B равны.
(A) только I
(B) только II
(C) только III
(D) Все вышеперечисленное
(E) Ни один из вышеперечисленных
Решение:
Правильный ответ: (E)
Матрица A имеет 3 строки и 2 столбца; то есть 3 ряда по 2 элемента в каждом.Это добавляет до 6 элементов, а не 5.
Размерность матрицы B составляет 2 × 4, а не 4 × 2, что означает, что матрица B имеет 2 строки и 4 столбца, а не 4 строки и 2 столбца.
Элемент B 21 относится к первому элементу во второй строке матрицы B , который равен 555, но не 222.
Матрица A и B не может быть равным, потому что мы ничего не знаем о записях матрицы A .Они нам просто неизвестны. Более того, их порядки тоже разные.
Пример 2 : Найдите значения «a» и «b», если [a 3] = [4 b].
Решение: если [a 3] = [4 b], то соответствующие элементы матриц равны, таким образом, a = 4 и b = 3.
Пример 3 : Определить значения a, b, c и d , так что следующее уравнение становится справедливым.
Решение:
Если две матрицы равны, то соответствующие элементы также равны, таким образом, мы имеем:
a = 5 , a + c = 4 , b — 2d = 1 и 2b = 6
Вставьте значение a в a + c = 4 даст: c = –1
И выделение b из 2b = 6 даст: b = 3
Вставить b = 3 в b –2d = 1 даст: d = 1
Таким образом, две заданные матрицы будут равны, если a = 5, b = 3, c = –1 и d = 1.
|
Матрица Равенство (стр. 3 из 3) Разделы: Дополненные & матрицы коэффициентов / Размер матрицы, Матрица обозначения и типы, матричное равенство Для двух матриц равны, они должны быть одного размера и иметь одинаковые записи в те же места.Например, предположим, что у вас есть следующие две матрицы:
Эти матрицы не могут быть то же самое, так как они не одного размера. Даже если A и B следующие две матрицы:
… они еще не такой же. Да, A и B у каждого есть шесть записей, и записи даже имеют одинаковые номера, но этого недостаточно для матриц. А это 3 2 матрица и B это 2 3 матрица, а для матрицы, 3 2 не равно 2 3! Неважно, если A и B иметь такое же количество записей или даже те же числа, что и записи. Пока не А и B имеют одинаковый размер и форму и имеют одинаковые значения в точности одинаковые места, они не равны. Это свойство матрицы
равенство можно превратить в домашние задания. Вам дадут два
матрицы, и вам скажут, что они равны. Вам нужно будет использовать
это равенство решить для значений переменных.
Для A и B чтобы быть равными, они должны иметь одинаковый размер и форму (что они и делают; каждый по 2 2 матрицы) и они должны иметь одинаковые значения в одних и тех же местах.Затем a 1,1 должно быть равно b 1,1 , а 1,2 должно быть равно b 1,2 , и так далее. Записи a 1,2 и а 2,1 явно равны, соответственно, записям b 1,2 и b 2,1 «путем осмотра» (то есть «просто взглянув на них»).Но а 1,1 = 1 не очевидно равно b 1,1 = х . Для A равным B , я должен иметь a 1,1 = b 1,1 , так должно быть, что 1 = х . Сходным образом, Мне нужен а 2,2 = b 2,2 , так что 4 должно быть y .Тогда решение: х = 1, y = 4 Авторские права Элизабет Stapel 2003-2011 Все права защищены
Чтобы иметь A = B , я должен все записи равны.То есть у меня должен быть а 1,1 = b 1,1 , a 1,2 = b 1,2 , a 2,1 = b 2,1 , и так далее. В частности, у меня должно быть: … как видно из выделенных матриц:
Решая эти три уравнения, Я получаю: Пусть матрицы не пугают ты.Да, они отличаются от того, к чему вы привыкли, но это не так так плохо (по крайней мере, пока вы не попытаетесь размножить их, но это другое урок для другого время). << Предыдущая Вверх | 1 | 2 | 3 | Возвращение в индекс
|
|
|
Как найти ответ с помощью матрицы
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в виде ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; и Ваше заявление: (а) вы добросовестно полагаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Свойства матриц — вопросы и ответы по дискретной математике
Этот набор вопросов и ответов по дискретной математике с множественным выбором (MCQ) посвящен «свойствам матриц».
1. Определитель единичной матрицы равен?
a) 1
b) 0
c) Зависит от матрицы
d) Ни один из упомянутых
Посмотреть ответ
Ответ: a
Объяснение: В матрице идентичности a ii = 1, а все остальные элементы = 0, следовательно, определитель равен 1.
2. Если определитель матрицы A равен нулю, то __________
a) A — сингулярная матрица
b) A — невырожденная матрица
c) Не могу сказать
d) Ни один из упомянутых
Просмотреть ответ
Ответ: a
Пояснение: Определитель сингулярных матриц равен нулю.
3. Что из следующего неверно для кососимметричной даже упорядоченной матрицы A целых чисел?
a) det (A) = 9
b) det (A) = 81
c) det (A) = 7
d) det (A) = 4
Посмотреть ответ
Ответ: c
Пояснение: Определитель a кососимметричная даже упорядоченная матрица A представляет собой полный квадрат.
4. Что из следующего будет выполняться для кососимметричной нечетно упорядоченной матрицы A целых чисел?
a) det (A) = 9
b) det (A) = 81
c) det (A) = 0
d) det (A) = 4
Посмотреть ответ
Ответ: c
Пояснение: Определитель a кососимметричная нечетно упорядоченная матрица A всегда равна 0.
5. Пусть A = [ka ij ] nxn , B = [a ij ] nxn , будет матрицей nxn и k будет скаляром, тогда det (A) равен _________
a) Kdet (B)
b) K n det (B)
c) K 3 det (b)
d) Ни один из упомянутых
Просмотреть ответ
Ответ: b
Объяснение: скаляр умножается на каждый из затем элемент матрицы A умножается на определитель, количество строк которого умножается на скаляр, то есть K n det (B).
6. Обратные существуют только для невырожденных матриц.
a) Верно
б) Неверно
Просмотреть ответ
Ответ: a
Объяснение: Поскольку для сингулярной матрицы det (A) = 0, значит, обратный не существует.
7. Если для квадратной матрицы A и B нулевая матрица O, AB = O влечет BA = O.
a) Верно
b) Неверно
Посмотреть ответ
Ответ: b
Объяснение: Пусть A = [0 1 0 0], B = [1 0 0 0] AB = O и BA не равно O.
8. Если для квадратной матрицы A и B нулевая матрица O, AB = O влечет A = O и B = O.
a) Верно
b) Неверно
Посмотреть ответ
Ответ: b
Объяснение: Пусть A = [0 1 0 0], B = [1 0 0 0] AB = O и B, A не равно O.
9. Пусть тогда A — нильпотентная матрица порядка n?
a) A n = O
b) nA = O
c) A = nI, I — матрица идентичности
d) Ни один из упомянутых
Просмотреть ответ
Ответ: a
Объяснение: n — наименьшее возможное число такое, что An = O.
10. Какое из следующих свойств умножения матриц является правильным?
a) Умножение в целом не коммутативно
b) Умножение является ассоциативным
c) Умножение является распределительным по сравнению с сложением
d) Все упомянутые
Посмотреть ответ
Ответ: d
Объяснение: Матричное умножение является ассоциативным, распределительным, но не коммутативный.
Sanfoundry Global Education & Learning Series — Дискретная математика.
Чтобы практиковаться во всех областях дискретной математики, представляет собой полный набор из 1000+ вопросов и ответов с несколькими вариантами ответов .
Примите участие в конкурсе сертификации Sanfoundry, чтобы получить бесплатную Почетную грамоту. Присоединяйтесь к нашим социальным сетям ниже и будьте в курсе последних конкурсов, видео, стажировок и вакансий!
Матричная запись, равные матрицы и математические операции с матрицами — видео и стенограмма урока
Обозначение
Для начала рассмотрим правильную запись для матриц.Посмотрите на эту правильно написанную матрицу:
Наши номера расположены аккуратными рядами и столбцами. Нашу матрицу окружают квадратные скобки. Эти квадратные скобки говорят нам, что эта конкретная группа чисел принадлежит одной матрице. Мы также можем пометить нашу матрицу, назвав ее матрицей A. Если мы пометили нашу матрицу, мы можем либо записать матрицу со всеми числами в ней, либо мы можем записать ее, используя нашу метку, заключенную в квадратные скобки.Наши матрицы также описываются их размером. Эта конкретная матрица имеет три строки и три столбца, поэтому мы также можем назвать ее матрицей 3×3. Матрица с четырьмя строками и двумя столбцами представляет собой матрицу 4×2.
Равные матрицы
Хорошо, теперь, когда мы знаем, как выглядит правильная матричная запись, давайте поговорим о том, когда две матрицы равны друг другу. Вы знаете, что, когда два числа одинаковы, они являются одинаковыми числами, например, когда у вас есть 2 и 2. Ну, матрицы похожи, но это немного больше.Когда две матрицы одинаковы, все числа должны быть одинаковыми в одних и тех же позициях, и матрицы должны быть одинакового размера. Например, эти две матрицы одинаковы:
Они одинакового размера, и все числа одинаковые в тех же местах. Это обе матрицы 2×3.
Взгляните на эти матрицы. Это такие же?
Это не равные матрицы, потому что они разного размера. Тот факт, что две матрицы имеют одинаковые номера, не означает, что они равны. Их размеры тоже должны быть одинаковыми.
Сложение и вычитание матриц
Давайте рассмотрим виды математических операций, которые мы можем выполнять. Мы можем выполнить сложение и вычитание . Сложение и вычитание матриц аналогично сложению и вычитанию чисел.Складываем или вычитаем число по числу. Поскольку мы должны сопоставить наше число с числом, наши две матрицы должны быть одинакового размера, например:
Мы сопоставили числа вместе. Мы сопоставили число в первой строке и первом столбце первой матрицы с числом в первой строке и первом столбце второй матрицы и так далее. Мы не можем складывать или вычитать две матрицы разных размеров.Однако мы можем прибавлять или вычитать одно и то же число ко всем числам в матрице.
Вычитание выполняется так же, как и сложение. Две матрицы должны быть одинакового размера, и мы вычитаем число из числа, сопоставляя расположение чисел вместе. Мы также можем вычесть одно и то же число из всех чисел в матрице.
Умножение матриц
Последняя математическая операция, которую мы можем сделать, это умножение матрицы .Нет такой вещи, как матричное деление. Умножение матриц сложнее умножения чисел. Вы можете легко умножить 3 и 5, чтобы получить 15. Но с матрицами, когда мы умножаем две матрицы вместе, мы должны использовать комбинацию умножения и сложения. Кроме того, количество столбцов в первой матрице должно соответствовать количеству строк во второй матрице. Итак, мы можем умножить матрицу 1×3 на матрицу 3×2, но мы не можем умножить матрицу 1×3 на матрицу 2×3. И в отличие от чисел, где порядок умножения не имеет значения, с матрицами имеет значение, какая матрица идет первой.
Давайте посмотрим, как мы умножаем две матрицы вместе:
Чтобы умножить эти две матрицы, мы сопоставляем строки в первой матрице со столбцами во второй матрице. Затем мы берем каждую пару чисел по одному, умножая их по ходу дела, а затем складываем все продукты вместе в конце. Итак, для наших матриц мы берем первую строку первой матрицы и сопоставляем ее с первым столбцом второй матрицы.Это даст нам число в первой строке и первом столбце в матрице ответов. Мы сопоставляем 1 с 0 и 2 с 2. Мы умножаем 1 на 0, 2 на 2, затем складываем все. У нас есть 1 (0) + 2 (2) = 0 + 4 = 4. Число в первой строке и первом столбце в матрице ответов равно 4.
У нас есть два столбца во второй матрице, поэтому нам нужно сопоставить первая строка ко второму столбцу. Нам нужно сопоставить каждую строку в первой матрице с каждым столбцом во второй матрице.Сопоставление первой строки в первом столбце со вторым столбцом во второй матрице дает нам число в первой строке и втором столбце в матрице ответов. Снова сопоставляя числа, мы имеем: 1 (1) + 2 (3) = 1 + 6 = 7.
Теперь, когда мы сопоставили первую строку в первой матрице с каждым столбцом во второй матрице, мы переходим к следующему этапу. во вторую строку первой матрицы. И мы делаем то же самое, сопоставляя его с каждым столбцом второй матрицы. Число во второй строке и первом столбце в матрице ответов: 3 (0) + 5 (2) = 0 + 10 = 10.Число во второй строке и втором столбце в матрице ответов: 3 (1) + 5 (3) = 3 + 15 = 18. Наш окончательный ответ — это матрица:
Как видите, умножение матриц немного отличается от умножения чисел. Помните, что вы сопоставляете строки в первой матрице со столбцами во второй матрице. Мы умножаем пары чисел, а затем складываем их все.
Мы также можем просто умножить все числа в матрице на одно число.В этом случае каждое число в матрице умножается на одно и то же.
Итоги урока
Давайте рассмотрим то, что мы узнали. Матрицы — это математические объекты, в которых числа организованы в красивый прямоугольный массив строк и столбцов. Мы обозначаем их буквой в квадратных скобках или их размером, например матрицей 3×2, которая сообщает нам, что есть три строки и два столбца.
Мы можем выполнять сложение, вычитание и умножение матриц.Для сложения и вычитания матрицы должны быть одинакового размера, и мы просто складываем и вычитаем числа, которые находятся в совпадающих местах в двух матрицах. Для умножения матриц мы сопоставляем каждую строку первой матрицы с каждым столбцом второй матрицы. Мы умножаем каждую пару чисел, а затем складываем их все.
Результаты обучения
Просмотрите и еще раз просмотрите этот урок о матрицах, чтобы убедиться, что вы можете:
- Дайте определение матриц
- Определите правильную матричную нотацию
- Определить равенство матриц
- Сложение, вычитание и умножение матриц
4.Умножение матриц
Важно: Мы можем умножать матрицы только в том случае, если количество столбцов в первой матрице совпадает с количеством строк во второй матрице.
Пример 1
a) Умножение матрицы 2 × 3 на матрицу 3 × 4 возможно, и это дает матрицу 2 × 4 в качестве ответа.
b) Допускается умножение матрицы 7 × 1 на матрицу 1 × 2; это дает матрицу 7 × 2
c) НЕЛЬЗЯ умножить матрицу 4 × 3 на матрицу 2 × 3.
Как умножить 2 матрицы
Сначала мы используем буквы, чтобы увидеть, что происходит. Позже мы увидим пример чисел.
В качестве примера возьмем обычную матрицу 2 × 3, умноженную на матрицу 3 × 2.
`[(a, b, c), (d, e, f)] [(u, v), (w, x), (y, z)]`
Ответом будет матрица 2 × 2.
Умножаем и складываем элементы следующим образом. Мы обрабатываем по 1-й строке первой матрицы, поэлементно умножая на 1-го столбца второй матрицы.Мы прибавляем к полученным продуктам. Наш ответ находится в позиции a 11 (вверху слева) матрицы ответов.
Мы делаем аналогичный процесс для 1-й строки первой матрицы и 2-го столбца второй матрицы. Результат помещается на позиции a 12 .
Теперь для 2-й строки первой матрицы и 1-го столбца второй матрицы. Результат помещается на позиции a 21 .
Наконец, мы делаем вторую строку первой матрицы и второй столбец второй матрицы. Результат помещается на позиции a 22 .
Итак, результат умножения наших двух матриц будет следующим:
`[(a, b, c), (d, e, f)] [(u, v), (w, x), (y, z)]` `= [(au + bw + cy, av + bx + cz), (du + ew + fy, dv + ex + fz)] `
Теперь давайте посмотрим на числовой пример.
Телефонные пользователи
ПРИМЕЧАНИЕ: Если вы разговариваете по телефону, вы можете прокрутить любую -ю матрицу на этой странице вправо или влево, чтобы увидеть все выражение.
Пример 2
Умножить:
`((0, -1,2), (4,11,2)) ((3, -1), (1,2), (6,1))`
Ответ
Это 2 × 3 умножить на 3 × 2, что даст нам 2 × 2 отвечать.
`((0, -1,2), (4,11,2)) ((3, -1), (1,2), (6,1))`
`= ((0xx3 + -1xx1 + 2xx6,0xx-1 + -1xx2 + 2xx1), (4xx3 + 11xx1 + 2xx6,4xx -1 + 11xx2 + 2xx1))`
`= ((0-1 + 12,0-2 + 2), (12 + 11 + 12, -4 + 22 + 2))`
`= ((11,0), (35,20))`
Наш ответ — матрица 2 × 2.
Умножение матриц 2 × 2
Процесс одинаков для матрицы любого размера. Мы умножаем на строки первой матрицы и на столбца второй матрицы поэлементно. Затем мы добавляем продукты:
`((a, b), (c, d)) ((e, f), (g, h))` `= ((ae + bg, af + bh), (ce + dg, cf + dh )) `
В этом случае мы умножаем матрицу 2 × 2 на матрицу 2 × 2 и в результате получаем матрицу 2 × 2.
Пример 3
Умножить:
`((8,9), (5, -1)) ((- 2,3), (4,0))`
Ответ
`((8,9), (5, -1)) ((- 2,3), (4,0))`
`= ((8 xx -2 + 9xx4,8xx3 + 9xx0), (5xx-2 + -1xx4,5xx3 + -1xx0))`
`= ((-16 + 36,24 + 0), (- 10+ -4,15 + 0))`
`= ((20,24), (- 14,15))`
Матрицы и системы одновременных линейных уравнений
Теперь мы видим, как написать систему линейных уравнений, используя умножение матриц.
Пример 4
Система уравнений
−3 x + y = 1
6 x — 3 y = −4
можно записать как:
Матрицы`((-3,1), (6, -3)) ((x), (y)) = ((1), (- 4))`
идеальны для компьютерного решения задач, потому что компьютеры легко формируют массивы . Мы можем опустить алгебраические символы. Компьютеру требуются только первая и последняя матрицы для решения системы, как мы увидим в разделе «Матрицы и линейные уравнения».
Примечание 1 — Обозначение
Care с записью матричного умножения на .
Следующие выражения имеют различных значений:
AB — это умножение матриц
A × B — это перекрестное произведение , которое возвращает вектор
A * B используется в компьютерной нотации, но не на бумаге
A • B точечное произведение , которое возвращает скаляр .
[Дополнительную информацию о векторных и скалярных величинах см. В главе «Вектор».]
Примечание 2 — Коммутативность матричного умножения
Есть ли `AB = BA`?
Посмотрим, правда ли это на примере.
Пример 5
Если
`A = ((0, -1,2), (4,11,2))`
и
`B = ((3, -1), (1,2), (6,1))`
найдите AB, и BA.
Ответ
Мы выполнили AB выше, и ответ был:
`AB = ((0, -1,2), (4,11,2)) ((3, -1), (1,2), (6,1))`
`= ((11,0), (35,20))`
Теперь BA — это (3 × 2) (2 × 3), что даст 3 × 3:
`BA = ((3, -1), (1,2), (6,1)) ((0, -1,2), (4,11,2))`
`= ((0-4, -3-11,6-2), (0 + 8, -1 + 22,2 + 4), (0 + 4, -6 + 11,12 + 2))`
`= ((-4, -14,4), (8,21,6), (4,5,14))`
Итак, в этом случае AB НЕ равно BA.
Фактически, для большинства матриц нельзя изменить порядок умножения и получить тот же результат.
Как правило, при умножении матриц закон коммутативности не выполняется, т.е. AB ≠ BA . Есть два распространенных исключения:
.- Идентификационная матрица: IA = AI = A .?
- Инверсия матрицы: A -1 A = AA -1 = I.
В следующем разделе мы узнаем, как найти обратную матрицу.
Пример 6 — Умножение на идентификационную матрицу
Учитывая, что
`A = ((- 3,1,6), (3, -1,0), (4,2,5))`
найдите AI .
Ответ
`AI = ((-3,1,6), (3, -1,0), (4,2,5)) ((1,0,0), (0,1,0), (0 , 0,1)) `
`= ((- 3 + 0 + 0,0 + 1 + 0,0 + 0 + 6), (3 + 0 + 0,0 + -1 + 0,0 + 0 + 0), (4 + 0 + 0,0 + 2 + 0,0 + 0 + 5)) `
`= ((- 3,1,6), (3, -1,0), (4,2,5))`
`= A`
Мы видим, что умножение на единичную матрицу не меняет значения исходной матрицы.
То есть
AI = A
Упражнения
1. Если возможно, найдите BA и AB .
`A = ((- 2,1,7), (3, -1,0), (0,2, -1))`
`B = (4 \ \ -1 \ \ \ 5)`
Ответ
`BA = (4 \ \ -1 \ \ \ 5) ((- 2,1,7), (3, -1,0), (0,2, -1))`
`= (-8 + (- 3) +0 \ \ \ 4 + 1 + 10 \ \ \ 28 + 0 + (- 5))`
`= (- 11 \ \ 15 \ \ 23)`
AB невозможно.(3 × 3) × (1 × 3).
2. Определите, если B = A -1 , учитывая:
`A = ((3, -4), (5, -7))`
`B = ((7,4), (5,3))`
Ответ
Если B = A -1 , то AB = I.
`AB = ((3, -4), (5, -7)) ((7,4), (5,3))`
`= ((21-20,12-12), (35-35,20-21))`
`= ((1,0), (0, -1))`
`! = I`
Таким образом, B НЕ является обратной величиной A.2 + 0)) `
`= ((1,0), (0,1))`
`= I`
4. Оцените следующее умножение матриц, которое используется для управления движением роботизированного механизма.
`((cos \ 60 °, -sin \ 60 °, 0), (sin \ 60 °, cos \ 60 °, 0), (0,0,1)) ((2), (4), ( 0)) `
Ответ
`((cos \ 60 °, -sin \ 60 °, 0), (sin \ 60 °, cos \ 60 °, 0), (0,0,1)) ((2), (4), ( 0)) `
`= ((2 (0,5) -4 (0,866) +0), (2 (0,866) +4 (0,5) +0), (0 + 0 + 0))`
`= ((- 2,464), (3,732), (0))`
Интерпретация этого заключается в том, что рука робота движется из позиция (2, 4, 0) в позицию (-2.46, 3.73, 0). То есть это перемещается в плоскости x-y , но его высота остается на уровне z = 0 . Матрица 3 × 3, содержащая sin и Значения cos говорят, на сколько градусов нужно переместиться.
Интерактивные элементы умножения матриц
Матрицы и системы уравнений
6.1 — Матрицы и системы уравненийОпределение матрицы
- Прямоугольный массив действительных чисел
- м строк по n столбцов
- Названо заглавными буквами
- Первый нижний индекс — строка, второй нижний индекс — столбец
Терминология
- Матрица с m строками и n столбцами называется матрицей порядка m x n .
- Квадратная матрица — это матрица с равным количеством строк и столбцов. Поскольку количество строки и столбцы одинаковы, говорят, что он имеет порядок n .
- Основная диагональ квадратной матрицы — это элементы от верхнего левого угла до нижнего правого угла. матрица.
- Матрица-строка — это матрица, содержащая только одну строку.
- Матрица столбцов — это матрица, имеющая только один столбец.
- Матрица только с одной строкой или одним столбцом называется вектором.
Преобразование систем линейных уравнений в Матрицы
Каждое уравнение в системе превращается в строку. Каждая переменная в система становится колонной. Переменные отбрасываются, а коэффициенты помещаются в матрицу. Если правая часть включена, это называется расширенной матрицей. Если правая сторона не указана, это называется матрицей коэффициентов.
Система линейных уравнений …
х + у - г = 1 3х - 2у + г = 3 4x + y - 2z = 9
становится расширенной матрицей…
| х | y | из | справа | ||
|---|---|---|---|---|---|
| 1 | 1 | -1 | 1 | ||
| 3 | -2 | 1 | 3 | ||
| 4 | 1 | -2 | 9 |
Элементарные операции со строками
Элементарные операции со строками — это операции, которые могут быть выполнены с матрицей, которая даст эквивалентная строка матрица.Если матрица является расширенной матрицей, построенной из системы линейных уравнений, то эквивалентная строка матрица будет иметь то же решение, что и исходная матрица.
При работе с системами линейных уравнений вы могли выполнять три операции. что не повлияет на набор решений.
- Поменяйте местами два уравнения.
- Умножьте уравнение на ненулевую константу.
- Умножьте уравнение на ненулевую константу и добавьте его к другому уравнению, заменив это уравнение.
Когда система линейных уравнений преобразуется в расширенную матрицу, каждое уравнение становится строка. Итак, теперь есть три элементарные операции со строками, которые производят эквивалент строки матрица.
- Поменять местами два ряда
- Умножить строку на ненулевую константу
- Умножьте строку на ненулевую константу и добавьте ее в другую строку, заменив эту строку.
Формы рядов-эшелонов и сокращенных рядов-эшелонов
Это эквивалентные строкам формы матрицы.Несложно решить систему линейных уравнений когда матрицы находятся в одной из этих форм.
Форма рядного эшелона
Матрица находится в виде эшелона строк, когда выполняются следующие условия.
- Если есть строка со всеми нулями, то она находится внизу матрицы.
- Первый ненулевой элемент любой строки — это единица. Этот элемент называется ведущим.
- Первая строка любой строки находится справа от первой строки предыдущей строки.
Примечания
- Первая строка в строке не обязательно должна быть рядом с , непосредственно справа от первой строки предыдущий ряд.
- Матрица в виде эшелона строк будет иметь нули под ведущими.
- Метод исключения Гаусса переводит матрицу в форму строки-эшелон, а затем выполняется обратная подстановка. требуется, чтобы завершить поиск решений системы.
- Форма матрицы «строка-эшелон» не обязательно уникальна.
Уменьшенная форма рядка-эшелон
Матрица находится в сокращенной форме строка-эшелон, когда все условия формы строка-эшелон выполнены и все элементы выше и ниже, ведущие равны нулю.
- Если есть строка со всеми нулями, то она находится внизу матрицы.
- Первый ненулевой элемент любой строки — это единица. Этот элемент называется ведущим.
- Первая строка любой строки находится справа от первой строки предыдущей строки.
- Все элементы выше и ниже ведущего равны нулю.
Примечания
- Первая строка в строке не обязательно должна быть рядом с , непосредственно справа от первой строки предыдущий ряд.
- Матрица в виде эшелона строк будет иметь нули как над, так и под ведущими.
- Метод исключения Гаусса-Жордана переводит матрицу в сокращенную форму строки-эшелона.
- Для завершения поиска решений системы обратная подстановка не требуется.
- Редуцированная строка-эшелонированная форма матрицы уникальна.
Исключение по Гауссу
- Запишите систему линейных уравнений в виде расширенной матрицы
- Выполните элементарные операции со строками, чтобы преобразовать матрицу в эшелонированную форму строки
- Преобразуйте матрицу обратно в систему линейных уравнений
- Используйте обратную замену, чтобы получить все ответы
Гаусс-Джордан Ликвидация
- Запишите систему линейных уравнений в виде расширенной матрицы
- Выполните элементарные операции со строками, чтобы преобразовать матрицу в сокращенную форму строки-эшелона
- Преобразуйте матрицу обратно в систему линейных уравнений
- Обратная замена не требуется
Поворотный
- Поворот — это процесс, который автоматизирует операции со строками, необходимые для помещения матрицы в рядный эшелон или редуцированный рядный эшелон форма
- В частности, при повороте элементы выше или ниже ведущей единицы превращаются в нули
Типы решений
Существует три типа решений, которые возможны при решении системы линейных уравнений.
Независимый
- Согласованный
- Уникальное решение
- Матрица с сокращенной строкой имеет такое же количество ненулевых строк, что и переменные
- Левая часть обычно представляет собой единичную матрицу, но не обязательно
- Для получения независимого решения должно быть как минимум столько же уравнений, сколько переменных.
| х | y | из | справа | ||
|---|---|---|---|---|---|
| 1 | 0 | 0 | 3 | ||
| 0 | 1 | 0 | 1 | ||
| 0 | 0 | 1 | 2 |
Когда вы конвертируете расширенную матрицу обратно в форму уравнения, вы получаете x = 3, y = 1 и z = 2.
Зависимые
- Согласованный
- Множество решений
- Запишите ответ в параметрической форме
- Матрица с сокращенной строкой содержит больше переменных, чем ненулевых строк
- Ряд нулей быть не обязательно, но обычно он есть.
- Это также может произойти, когда уравнений меньше, чем переменных.
| х | y | из | справа | ||
|---|---|---|---|---|---|
| 1 | 0 | 3 | 4 | ||
| 0 | 1 | -2 | 3 | ||
| 0 | 0 | 0 | 0 |
Первое уравнение будет x + 3z = 4.Решение относительно x дает x = 4 — 3z.
Второе уравнение будет y — 2z = 3. Решение для y дает y = 3 + 2z.
Столбец z не очищается (все нули, кроме одно число), поэтому другие переменные будут определены через z. Следовательно, z будет параметром t и решение …
x = 4 — 3t, y = 3 + 2t, z = t
Несоответствие
- Нет решения
- Матрица с сокращенной строкой имеет строку нулей слева, но правая часть не равна нулю.
| х | y | из | справа | ||
|---|---|---|---|---|---|
| 1 | 0 | 3 | 4 | ||
| 0 | 1 | -2 | 3 | ||
| 0 | 0 | 0 | 2 |
Здесь нет решения.


