Матрица равена тест с ответами: Тест Равена
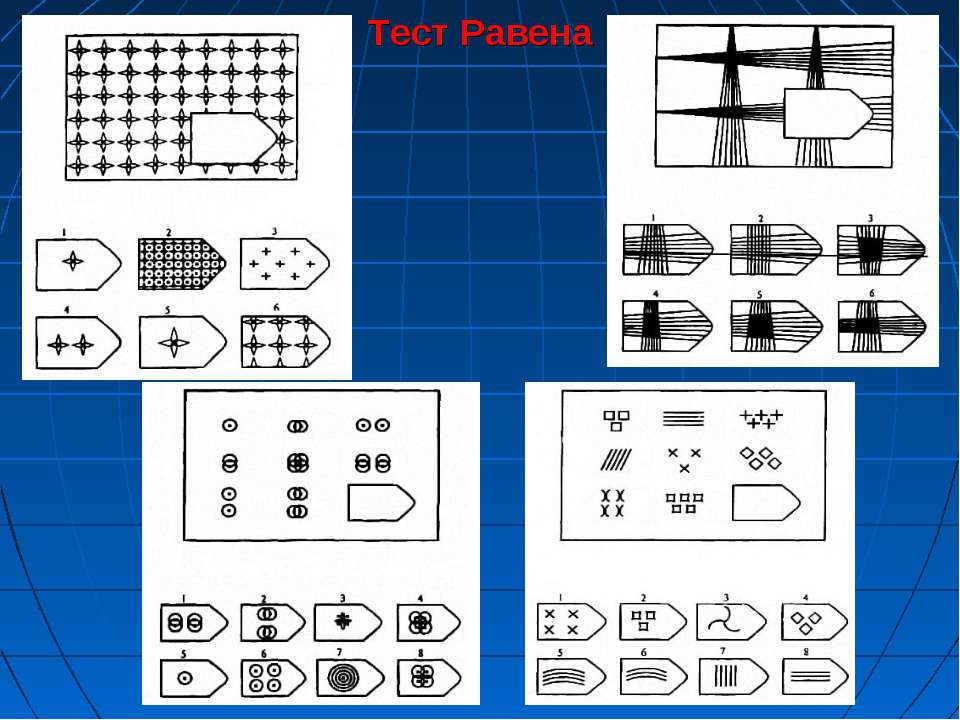
Тест Равена
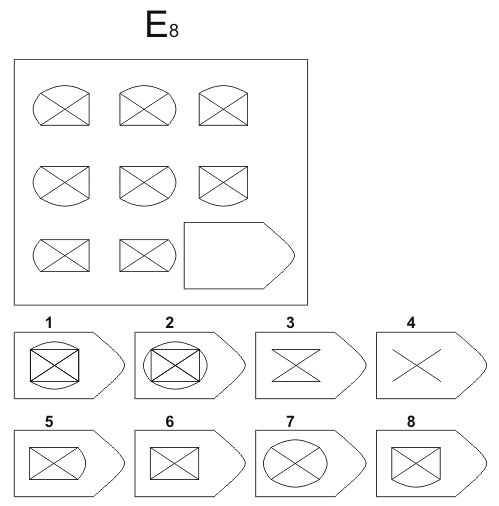
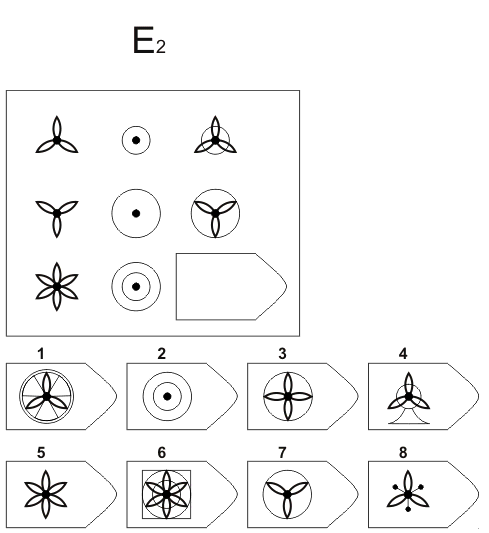
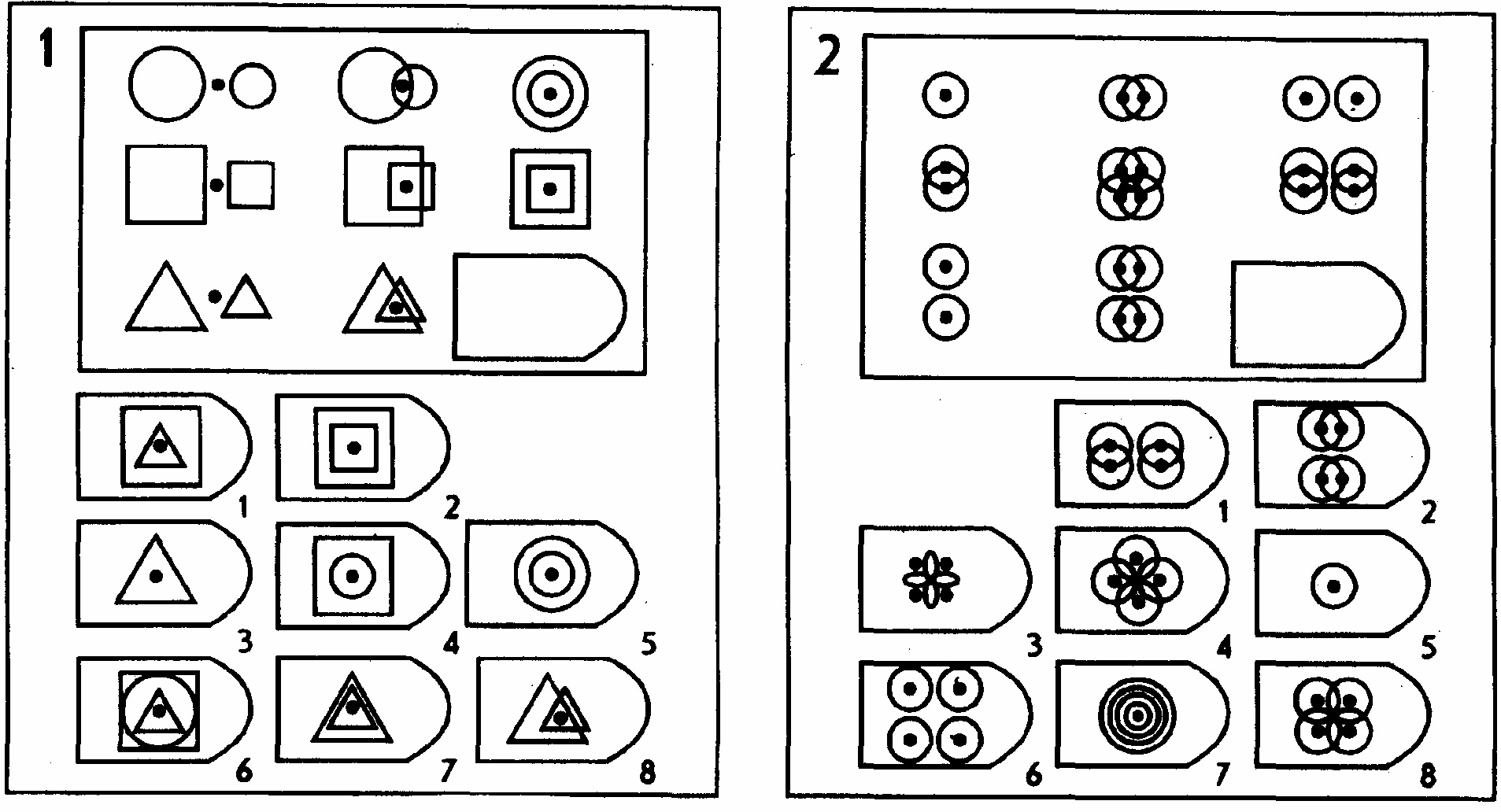
Методика предназначена для изучения логичности мышления. Испытуемому предъявляются рисунки с фигурами, связанными между собой определенной зависимостью. Одной фигуры не достает, а внизу она дается среди 6-8 других фигур. Задача испытуемого — установить закономерность, связывающую между собой фигуры на рисунке, и на опросном листе указать номер искомой фигуры из предлагаемых вариантов.
Тест состоит из 60 таблиц (5 серий). В каждой серии таблиц содержатся задания нарастающей трудности. В то же время характерно и усложнение типа заданий от серии к серии.
В серии А — использован принцип установления взаимосвязи в структуре матриц. Здесь задание заключается в дополнении недостающей части основного изображения одним из приведенных в каждой таблице фрагментов. Выполнение задания требует от обследуемого тщательного анализа структуры основного изображения и обнаружения этих же особенностей в одном из нескольких фрагментов.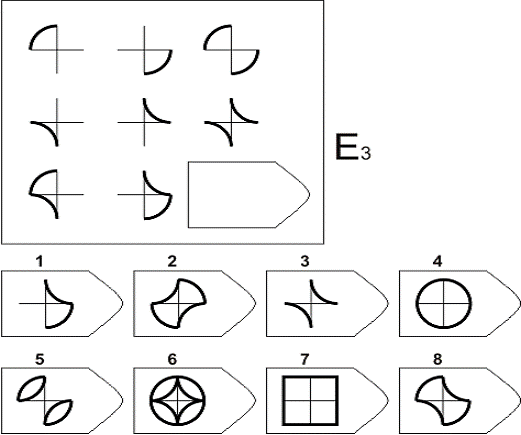
- Серия В — построена по принципу аналогии между парами фигур. Обследуемый должен найти принцип, соответствен но которому построена в каждом отдельном случае фигура и, исходя из этого, подобрать недостающий фрагмент. При этом важно определить ось симметрии, соответственно которой расположены фигуры в основном образце.
Серия С — построена по принципу прогрессивных изменений в фигурах матриц. Эти фигуры в пределах одной матрицы все больше усложняются, происходит как бы непрерывное их развитие. Обогащение фигур новыми элементами подчиняется четкому принципу, обнаружив который, можно подобрать недостающую фигуру.
- Серия В — построена по принципу перегруппировки фигур в матрице. Обследуемый должен найти эту перегруппировку, происходящую в горизонтальном и вертикальном положениях.
Серия Е основана на принципе разложения фигур основного изображения на элементы.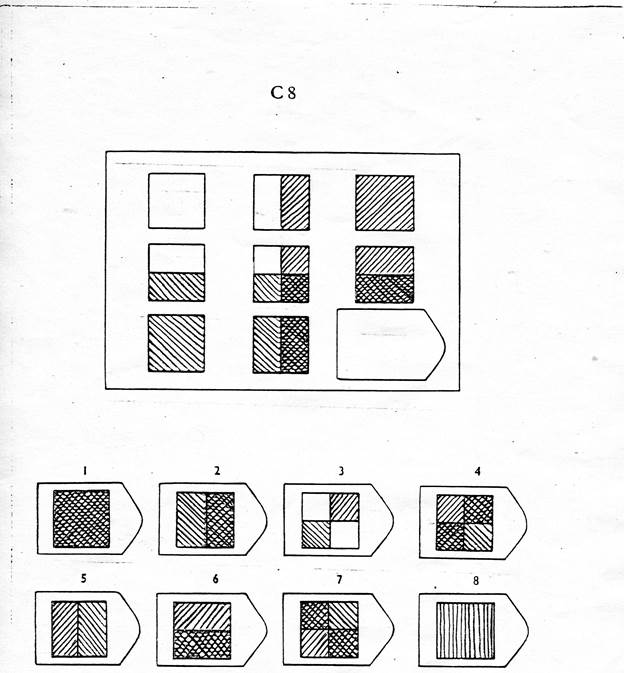
Недостающие фигуры можно найти, поняв принцип анализа и синтеза фигур.
- Методические указания к проведению теста
Инструкция: Тест строго регламентирован во времени, а именно: 20 мин. Для того, чтобы соблюсти время, необходимо строго следить за тем, чтобы до общей команды: «Приступить к выполнению теста» — никто не открывал таблицы и не подсматривал. По истечении 20 мин подается команда, например: «Всем закрыть таблицы». О предназначении данного теста можно сказать следующее: «Все наши исследования проводятся исключительно в научных целях, поэтому от вас требуются добросовестность, глубокая обдуманность, искренность и точность в ответах. Данный тест предназначен для уточнения логичности вашего мышления».
- После этого взять таблицу и открыть для показа всем 1-ю страницу: «На рисунке одной фигуры недостает. Справа изображено 6-8 пронумерованных фигур, одна из которых явля ется искомой. Надо определить закономерность, связывающую между собой фигуры на рисунке, и указать номер искомой фигуры в листке, который вам выдан» (можно показать на примере одного образца).
Во время выполнения задач теста необходимо контролировать, чтобы респонденты не списывали друг у друга. По истечении 20 мин подать команду: «Закрыть всем таблицы!
Собрать бланки и таблицы к ним. Проверить, чтобы в правом углу регистрируемого бланка был проставлен карандашом номер обследуемого.
- Интерпретация результатов (ключи)
- Правильное решение каждого задания оценивается в один балл, затем подсчитывается общее число баллов по всем таблицам и по отдельным сериям. Полученный общий показатель рассматривается как индекс интеллектуальной силы, умственной производительности респондента. Показатели выполнения заданий по отдельным сериям сравнивают со среднестати стическим, учитывают разницу между результатами, полученными в каждой серии, и контрольными, полученными статистической обработкой при исследовании больших групп здоровых обследуемых и, таким образом, расцениваемыми как ожидаемые результату. Такая разница позволяет судить о надежности полученных результатов (это не относится к психической патологии).
БЛАНК
ФИО (№)
№ задания |
|
|
|
|
|
1 |
|
|
|
|
|
2 |
|
|
|
|
|
3 |
|
|
|
|
|
4 |
|
|
|
|
|
5 |
|
|
|
|
|
6 |
|
|
|
|
|
7 |
|
|
|
|
|
8 |
|
|
|
|
|
9 |
|
|
|
|
|
10 |
|
|
|
|
|
11 |
|
|
|
|
|
12 |
|
|
|
|
|
- Полученный суммарный показатель по специальной таблице переводится в проценты. При этом по специальной шкале различают 5 степеней интеллектуального уровня:
1 степень — более 95% — высокий интеллект;
2 степень — 75-94% — интеллект выше среднего;
3 степень 25-74% — интеллект средний;
4 степень — 5-24% — интеллект ниже среднего;
При этом по специальной шкале различают 5 степеней интеллектуального уровня:5 степень — ниже 5% — дефект.
КЛЮЧ
1 2 3 4 5 6 7 8 9 10 11 12 1-я серия 4 5 1 2 6 3 6 2 1 3 4 2 2-я серия 5 6 1 2 1 3 5 6 4 3 4 8 3-я серия 5 3 2 7 8 4 5 1 7 1 6 2 4-я серия 3 4 3 8 7 6 5 4 1 2 5 6 5-я серия 7 6 8 2 1 5 1 3 6 2 4 590
91
ТАБЛИЦА ПЕРЕСЧЕТА БАЛЛОВ
Оценка в баллах
9
8
7
6
5
4
3
2
1
Сумма очков
143
129-
115
101
87
73
59
45
44
за правиль-
142
128
100
86
72
58
ные ответы
НОРМАЛЬНАЯ КОМПОЗИЦИЯ ОЧКОВ
Ожидаемое
Серия
- Сумма очков
10
15 20 25 30 35 40 45 50 55
число очков по каждой
А
6
8 9 10 10 10 10 11 12 12 серии
Б
2
4 6 7 8 8 9 10 11 11
В
1
2 3 4 6 7 8 10 10 11
Г
1
1 2 3 4 7 9 9 10 11
д
0
00123457 10
- Стимульный материал к методике Равена
1-1
1-2
1-3
1-4
1-5
1-6
1-7
1-8
1-9
1-10
1-11
1-12
2-1
2-2
2-3
2-4
2-5
2-6
2-7
2-8
2-9
2-10
2-11
2-12
3-1
3-2
3-3
3-4
3-5
3-6
3-7
3-8
3-9
3-10
3-11
3-12
4-1
4-2
4-3
4-4
4-5
4-6
4-7
4-8
4-9
4-10
4-11
4-12
5-1
5-2
5-3
5-4
5-5
5-6
5-7
5-8
5-9
5-10
5-11
5-12См.
также Тесты способностей
RSS [email protected]
также Тесты способностей%d1%82%d0%b5%d1%81%d1%82%20%d1%80%d0%b0%d0%b2%d0%b5%d0%bd%d0%b0 — со всех языков на все языки
Все языкиАнглийскийРусскийКитайскийНемецкийФранцузскийИспанскийИтальянскийЛатинскийФинскийГреческийИвритАрабскийСуахилиНорвежскийПортугальскийВенгерскийТурецкийИндонезийскийШведскийПольскийЭстонскийЛатышскийДатскийНидерландскийАрмянскийУкраинскийЯпонскийСанскритТайскийИрландскийТатарскийСловацкийСловенскийТувинскийУрдуИдишМакедонскийКаталанскийБашкирскийЧешскийГрузинскийКорейскийХорватскийРумынский, МолдавскийЯкутскийКиргизскийТибетскийБелорусскийБолгарскийИсландскийАлбанскийНауатльКомиВаллийскийКазахскийУзбекскийСербскийВьетнамскийАзербайджанскийБаскскийХиндиМаориКечуаАканАймараГаитянскийМонгольскийПалиМайяЛитовскийШорскийКрымскотатарскийЭсперантоИнгушскийСеверносаамскийВерхнелужицкийЧеченскийГэльскийШумерскийОсетинскийЧеркесскийАдыгейскийПерсидскийАйнский языкКхмерскийДревнерусский языкЦерковнославянский (Старославянский)МикенскийКвеньяЮпийскийАфрикаансПапьяментоПенджабскийТагальскийМокшанскийКриВарайскийКурдскийЭльзасскийФарерскийАбхазскийАрагонскийАрумынскийАстурийскийЭрзянскийКомиМарийскийЧувашскийСефардскийУдмурдскийВепсскийАлтайскийДолганскийКарачаевскийКумыкскийНогайскийОсманскийТофаларскийТуркменскийУйгурскийУрумскийБурятскийОрокскийЭвенкийскийМаньчжурскийГуараниТаджикскийИнупиакМалайскийТвиЛингалаБагобоЙорубаСилезскийЛюксембургскийЧерокиШайенскогоКлингонский
Все языкиРусскийАнглийскийНемецкийЛатинскийИвритИспанскийНорвежскийКитайскийФранцузскийУкраинскийИтальянскийПортугальскийВенгерскийТурецкийПольскийДатскийТатарскийКурдскийСловенскийГреческийИндонезийскийВьетнамскийМаориТагальскийУрдуИсландскийХиндиИрландскийФарерскийБолгарскийЛатышскийАлбанскийАрабскийФинскийПерсидскийМонгольскийНидерландскийШведскийПалиЯпонскийКорейскийЭстонскийГрузинскийТаджикскийЛитовскийРумынский, МолдавскийХорватскийСуахилиКазахскийМакедонскийТайскийБелорусскийГалисийскийКаталанскийЧеченскийКарачаевскийСловацкийЧешскийСербскийАрмянскийАзербайджанскийУзбекскийКечуаГаитянскийМайяАймараШорскийЭсперантоКрымскотатарскийОсетинскийАдыгейскийЯкутскийАйнский языкКхмерскийДревнерусский языкЦерковнославянский (Старославянский)ТамильскийКвеньяАварскийАфрикаансПапьяментоМокшанскийЙорубаЭльзасскийИдишАбхазскийЭрзянскийИнгушскийИжорскийМарийскийЧувашскийУдмурдскийВодскийВепсскийАлтайскийКумыкскийТуркменскийУйгурскийУрумскийЛожбанЭвенкийскийБашкирскийМалайскийМальтийскийЛингалаПенджабскийЧерокиЧаморроКлингонскийБаскскийПушту
Ответы на вопрос «10.
Основные достижения психодиагностики в 30-40 годы.»В 1930-е гг. появилось много новых тестов. Большинство из них были разработаны в Соединенных Штатах. Так в 1931г. Луис Терстон начинает работать над развитием техники факторного анализа и создает мультифакторную теорию структуры интеллекта. Результатом его работ стала публикация в 1938г. «Теста первичных умтсвеных способностей» [1, стр. 39]. В середине 1930-х гг. в Гарвардском университете ведут свои исследования Кристиана Морган и Генри Александр Мюррей. В этих исследованиях было впервые заявлено о том, что принцип проекции может использоваться как основа для построения диагностической процедуры. В опубликованной в 1935 г. книге «Исследования личности» обосновывается принцип психологической проекции, а немного позднее появляется и первый проективный тест — Тест тематической апперцепции (ТАТ). Таким образом, психологи получили новый диагностический инструмент, отвечающий потребностям многих из них в целостном изучении личности.
С этого момента во всем мире начинает набирать силу проективное движение в психологии, которое до сих пор способствует получению новых данных о личности и не в меньшей мере — возникновению бурных дискуссий. Особо значительным для равития психодагностики был 1938г. Так в Великобритании появляется тест, который, с известными изменениями, и по нынешний день весьма широко используется психологами всего мира. Этот тест — прогрессивные матрицы Равена, был разработан Л. Пенросем и Дж. Равеном для измерения общего интеллекта и, как предполагалось, сводил к минимуму влияние культуры и обучения на получаемые результаты. Будучи те- стом невербальным, он состоял из однородных заданий-композиций, для решения которых от обследуемого требовалось выбрать пропущенный сегмент, завершающий последовательность предложенной композиции. В это же время в США под редакцией Оскара К. Буроса начинается издание всемирно известного «Ежегодника психических измерений». В этом ежегоднике сообщаются сведения обо всех англоязычных тестах, а также публикуются статьи-обзоры ведущих ученых, посвященные исследованиям, которые проводились с этими тестами.
Год спустя О. Бурос основывает Институт психических измерений (Buros Institute of Mental Measurements), успешно продолжавший свою деятельность (в первую очередь мониторинг качества публикуемых коммерческих тестов) до 1994 г., когда он был преобразован в «Центр тестирования» с большей ориентацией на сервисные услуги. В 1938г. появился тест Бендер-гештальт. Лауретта Бендер составила его из девяти геометрических композиций, основанных на фигурах, с помощью которых исследовал восприятие один из основоположников. Позднее результаты теста интерпретируются в соответствии с проективной гипотезой, которая наиболее четко была сформулирована Леопольдом Франком. В 1939 г. Франк предложил использовать термин «проективные методики» применительно к таким тестам, как тест Роршаха, ТАТ, таутофон и другим, в которых ответ-реакция обусловлена не объективным значением стимула, а личностью испытуемого. Таким образом, обрел имя уже довольно многочисленный класс методик, появление и развитие которых было в известном смысле противостоянием психометрическим традициям.
В 1939г. была создана шкала интеллекта Векслера-Беллвью. В период с 1940 по 1949гг. продолжает увеличиваться количество диагностических методик. Так же как и Первая мировая война, Вторая мировая стимулировала разработку новых тестов. В начале Второй мировой войны психологи США вновь обращаются к разработке групповых тестов для нужд армии. В 1941г. в Бюро стратегических служб США был достигнут прогресс в создании ситуационных тестов которые допускали прямое воздействие на обследуемого мощных стрессовых факторов.. Они использовались для отбора лиц, наиболее подходящих для выполнения разведывательно-шпионской деятельности во время Второй мировой войны. Тогда же в 1942г. впервые появился термин «психологическая оценка». В 1940 г. внимание психологов привлекает Миннесотский многоаспектный личностный опросник (ММРI), созданный психологом Старком Р. Хатауэем и психиатром Мак-Кинли. Несмотря на то что первоначально MMPI был предназначен для содействия в дифференциации психиатрических диагнозов, его шкалы, основанные на 550 утверждениях, также начинают использовать при диагностике непатологических личностей[1, стр.
52]. Параллельно созданию новых методик ведется разработка математико-статистического аппарата психологического тестирования. Этому посвящены работы многих исследователей. Так, значительный вклад в развитие факторного анализа был внесен Кеттеллом и его сотрудниками. В 1946 г. ученик Терстоуна, один из основателей Американского психометрического общества Гарольд Галликсен публикует свою, ставшую знаменитой работу «Парные сравнения и логика измерения», посвященную развитию взглядов своего учителя на количественную оценку установок, предпочтений и тому подобных феноменов, долгое время полагаемых как не поддающихся измерению.
Матрично-матричный продукт — линейная алгебра
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает
или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее
в
информацию, описанную ниже, назначенному ниже агенту.
Если репетиторы университета предпримут действия в ответ на
ан
Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент
средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в качестве ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права. Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени;
Идентификация авторских прав, которые, как утверждается, были нарушены;
Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \
достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется
а
ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание
к какой конкретной части вопроса — изображению, ссылке, тексту и т.
д. — относится ваша жалоба;
Ваше имя, адрес, номер телефона и адрес электронной почты; а также
Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает
ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все
информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы
либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
Матрицыи матричная алгебра — Статистика Как к
Матрицы и содержание матричной алгебры (щелкните, чтобы перейти к этому разделу):
- Матричная алгебра: введение
- Добавление матрицы: больше примеров
- Умножение матриц
- Определение сингулярной матрицы
- Матрица идентичности
- Что такое обратная матрица?
- Собственные значения и собственные векторы
- Расширенные матрицы
- Определитель матрицы
- Диагональная матрица
- Что такое симметричная и кососимметричная матрицы?
- Что такое матрица транспонирования?
- Что такое матрица дисперсии-ковариации?
- Корреляционные матрицы
- Идемпотентная матрица.
Матрица — это прямоугольный массив чисел, упорядоченный по столбцам и строкам (как в электронной таблице). Матричная алгебра используется в статистике для выражения наборов данных. Например, ниже представлен рабочий лист Excel со списком оценок за экзамены:
Преобразование в матричную алгебру в основном включает удаление идентификаторов столбцов и строк. Добавляется идентификатор функции (в данном случае «G» для оценок):
Числа, которые появляются в матрице, называются элементами матрицы .
Матрицы: Обозначение
Почему странная нотация?
Мы используем другую нотацию (в отличие от хранения данных в формате электронной таблицы) по простой причине: соглашение. Соблюдение соглашений упрощает соблюдение правил матричной математики (таких как сложение и вычитание). Например, в элементарной алгебре, если у вас есть список вроде этого: 2 яблока, 3 банана, 5 виноградин, вы должны изменить его на 2a + 3b + 5g, чтобы соблюсти соглашение.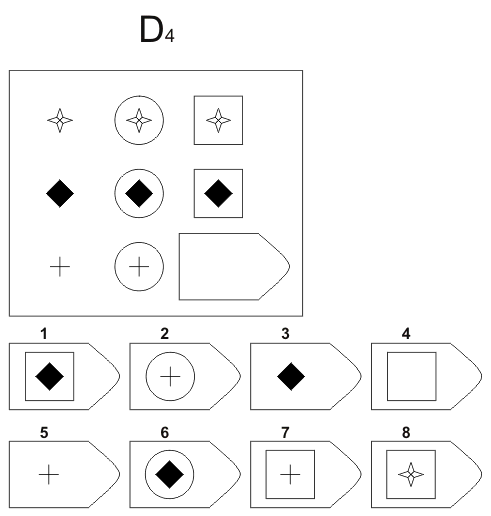
Некоторые из наиболее распространенных терминов, с которыми вы столкнетесь при работе с матрицами:
- Размер (также называемый порядком): сколько строк и столбцов имеет матрица.Сначала перечислены строки, за ними следуют столбцы. Например, матрица 2 x 3 означает 2 строки и 3 столбца.
- Элементы : числа, которые появляются внутри матрицы.
- Матрица идентичности (I): Диагональная матрица с нулями в качестве элементов, за исключением диагонали, в которой есть единицы.
- Скаляр : любое действительное число.
- Матрица Функция: скаляр, умноженный на матрицу, чтобы получить другую матрицу.
Матрицы идентичности. Изображение: Википедия.com.
Матричная алгебра: сложение и вычитание
Размер матрицы (т.е. 2 x 2) также называется размером матрицы или порядком матрицы. Если вы хотите сложить (или вычесть) две матрицы, их размерность должна быть точно так же, как и .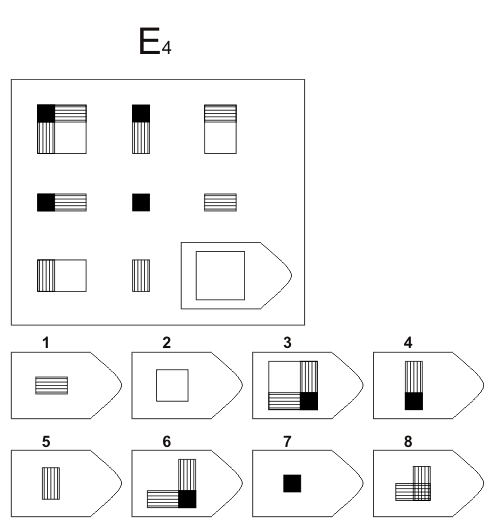
Другими словами, вы можете добавить матрицу 2 x 2 к другой матрице 2 x 2, но не матрицу 2 x 3. Добавление матриц очень похоже на обычное сложение: вы просто добавляете одинаковые числа в одном и том же месте (например, складываете все числа в столбце 1, строке 1 и все числа в столбце 2, строке 2).
Примечание к обозначениям: рабочий лист (например, в Excel) использует буквы столбцов (ABCD) и номера строк (123), чтобы указать местоположение ячейки, например A1 или D2. Для матриц типично использовать обозначение типа g ij , что означает i-ю строку и j-й столбец матрицы G.
Вычитание матриц работает точно так же.
Вернуться к началу
Матричное дополнение — это всего лишь серия дополнений. Для матрицы 2 × 2:
- Сложите верхние левые числа вместе и запишите сумму в новую матрицу в верхнем левом углу.
- Сложите верхние правые числа и запишите сумму в правом верхнем углу.
- Сложите нижние левые числа вместе и запишите сумму в нижнем левом углу.
- Сложите нижние правые числа вместе и запишите сумму в правом нижнем углу:
Используйте ту же процедуру для матрицы 2 × 3:
Фактически, вы можете использовать этот базовый метод для добавления любых матриц, если ваши матрицы имеют одинаковые размеры (одинаковое количество столбцов и строк).Другими словами, , если матрицы одинакового размера, вы можете их добавить. Если они разного размера, вы не можете их добавить.
- Матрица с 4 строками и 2 столбцами может быть добавлена к матрице с 4 строками и 2 столбцами.
- Матрица с 4 строками и 2 столбцами не может быть добавлена к матрице с 5 строками и 2 столбцами.
Вышеупомянутый метод иногда называют «начальным суммированием», поскольку вы просто складываете элементы и фиксируете результат.
Другой способ подумать об этом…
Подумайте, что представляет собой матрица. Эта очень простая матрица [5 2 5] может представлять 5x + 2y + 5z.
И эта матрица [2 1 6] могла бы равняться 2x + y + 6z. Если сложить их вместе с помощью алгебры, получится:
5x + 2y + 5z + 2x + y + 6z = 7x + 3y + 11z.
Это тот же результат, что и при сложении записей в матрицах.
Дополнение матрицы для неравных размеров
Если у вас неравные размеры, вы все равно можете сложить матрицы вместе, но вам придется использовать другой (гораздо более продвинутый) метод.Один из таких приемов — прямая сумма. Прямая сумма (⊕) любой пары матриц A размера m × n и B размера p × q представляет собой матрицу размера (m + p) × (n + q):
Например:
В начало
Относительно легко умножить на одно число (так называемое «скалярное умножение»), например 2:
Просто умножьте каждое число в матрице на 2, и вы получите новую матрицу. На изображении выше:
2 * 9 = 18
2 * 3 = 6
2 * 5 = 10
2 * 7 = 14
Результат четырех умножений дает числа в новой матрице справа.
Умножение матриц: две матрицы
Когда вы хотите перемножить две матрицы, процесс становится немного сложнее.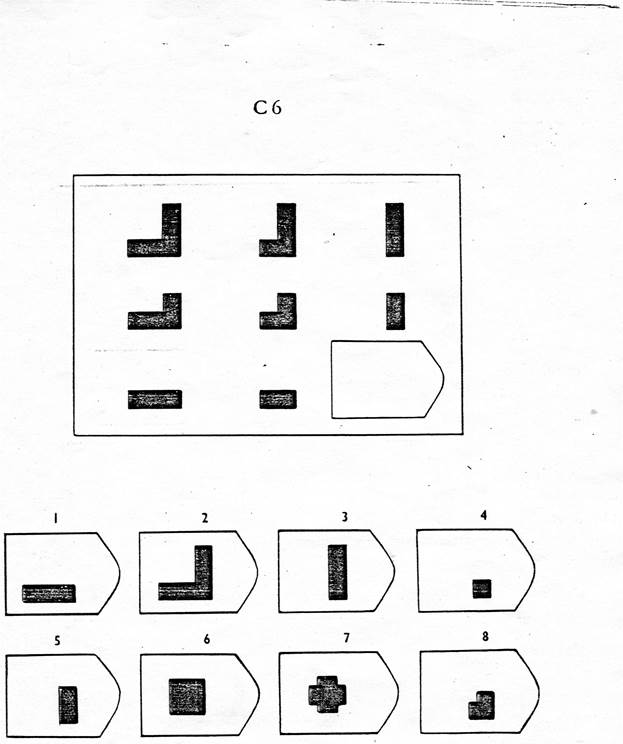
Вам нужно умножить строки первой матрицы на столбцы второй матрицы. Другими словами, умножьте по строкам первой матрицы и по столбцам второй матрицы. После того, как вы умножили, сложите продукты и запишите ответы в виде новой матрицы.
Если все это звучит немного сложно, это (очень короткое) видео показывает, как это делается:
Не можете посмотреть видео? Кликните сюда.
Вы можете выполнить матричное умножение двух матриц, только если количество столбцов в первой матрице равно количеству строк во второй матрице. Например, вы можете умножить матрицу 2 x 3 (две строки и три столбца) на матрицу 3 x 4 (три строки и четыре столбца).
Очевидно, что это может стать очень сложным (и утомительным) процессом.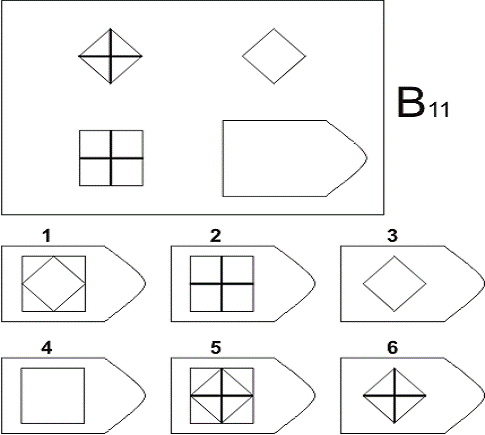
Тем не менее, вы можете найти множество достойных инструментов для умножения матриц в Интернете. Мне нравится этот от Матрицы Решиш. После расчета вы можете умножить результат на другую матрицу и другую, что означает, что вы можете перемножить несколько матриц вместе.
Microsoft Excel также может выполнять матричное умножение с использованием функций «массива». Вы можете найти инструкции здесь, на сайте Стэнфорда. Прокрутите вниз до места, где написано Матричные операции в Excel.
Вернуться к началу
Быстрый взгляд на матрицу может сказать вам, является ли она сингулярной матрицей. Если матрица квадратная и имеет одну строку или столбец с нулями или , два равных столбца или две равные строки, то это особая матрица. Например, следующие десять матриц являются единственными (изображение: Wolfram):
Существуют и другие типы сингулярных матриц, некоторые из которых не так-то легко обнаружить.Следовательно, необходимо более формальное определение.
Следующие три свойства определяют сингулярную матрицу:
- Матрица квадратная и
- Не имеет инверсии.
- Имеет определитель 0.
1. Квадратная матрица
Квадратная матрица имеет (как следует из названия) равное количество строк и столбцов. Говоря более формально, вы бы сказали, что матрица из m столбцов и n строк является квадратной, если m = n.Матрицы, которые не являются квадратными, являются прямоугольными.
Сингулярная матрица — это квадратная матрица, но не все квадратные матрицы являются сингулярными.
Необратимые матрицы
Если квадратная матрица не имеет обратной, то это особая матрица.
Обратная матрица — это то же самое, что и обратная величина числа. Если умножить матрицу на обратную, получится единичная матрица , , матричный эквивалент 1. Идентификационная матрица в основном представляет собой последовательность единиц и нулей.Идентификационная матрица различается в зависимости от размера матрицы.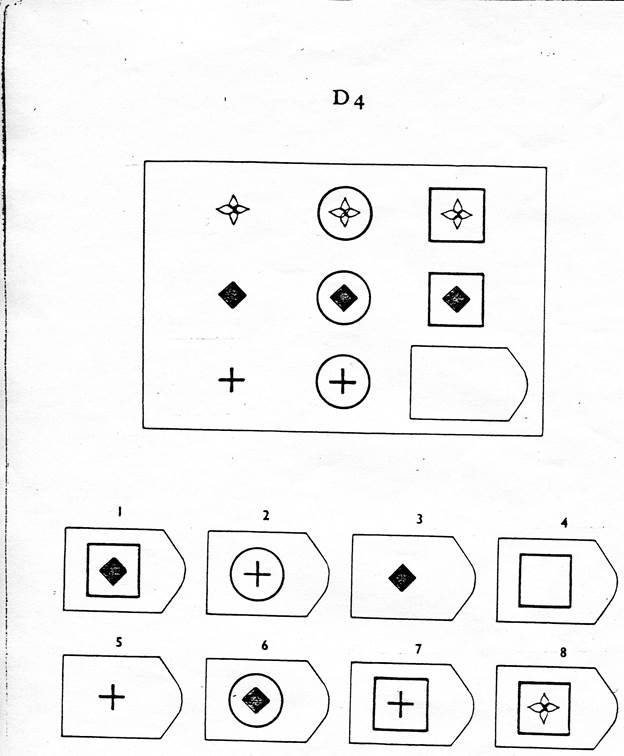
Матрицы идентичности. Изображение: Wikipedia.com.
Определитель нуля
Определитель — это просто специальное число, которое используется для описания матриц и поиска решений систем линейных уравнений. Формула для вычисления определителя различается в зависимости от размера матрицы. Например, матрица 2 × 2, формула ad-bc.
Эта простая матрица 2 × 2 сингулярна, потому что ее определитель равен нулю:
К началу
Единичная матрица — это квадратная матрица с единицами в качестве элементов на главной диагонали сверху слева направо снизу и нулями в остальных местах.Когда вы умножаете квадратную матрицу на единичную матрицу, исходная квадратная матрица остается неизменной. Например:
По идее аналогичен айдентике. В базовой математике элемент идентичности оставляет число неизменным. Например, кроме того, тождественный элемент равен 0, потому что 1 + 0 = 1, 2 + 0 = 2 и т. Д., А при умножении тождественный элемент равен 1, потому что любое число, умноженное на 1, равно этому числу (т.
Е. 10 * 1 = 10 ). Говоря более формально, если x — действительное число, то число 1 называется мультипликативным тождеством , потому что 1 * x = x и x * 1 = x.По той же логике единичная матрица I получила свое название, потому что для всех матриц A , I * A = A и A * I = A .
В матричной алгебре единичный элемент различается в зависимости от размера матрицы, с которой вы работаете; в отличие от сингулярной единицы для мультипликативной идентичности и 0 для аддитивной идентичности, не существует единой единичной матрицы для всех матриц. Для любой матрицы n * n существует единичная матрица I n * n .На главной диагонали всегда будут единицы, а оставшиеся пробелы — нули. На следующем изображении показаны матрицы идентичности для матрицы 2 x 2 и матрицы 5 x 5:
Матрица аддитивной идентичности
Когда люди говорят о «матрице идентичности», они обычно имеют в виду мультипликативную матрицу идентичности.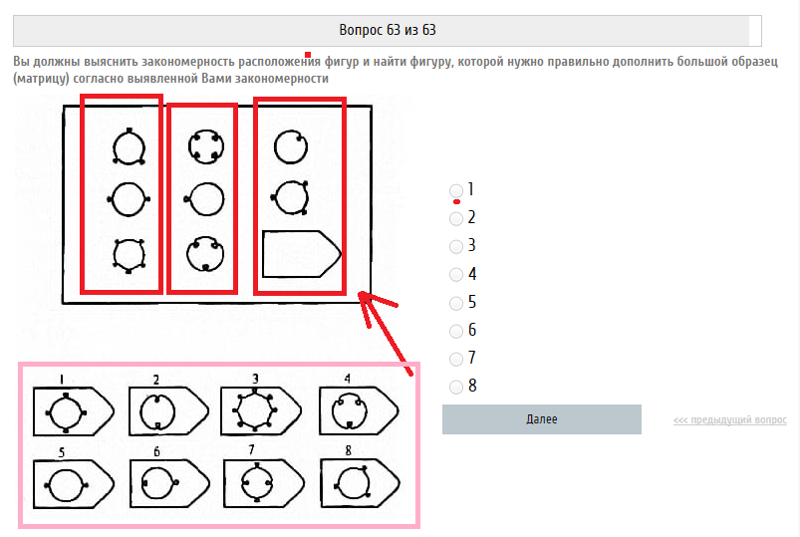
Однако есть и другой тип: аддитивная единичная матрица. Когда эта матрица добавляется к другой, вы получаете исходную матрицу. Неудивительно, что каждый элемент в этих матрицах — нули.Поэтому их иногда называют нулевой матрицей .
Аддитивная единичная матрица для матрицы 3 * 3.
Вернуться к началу
Обзор поиска инверсий смотрите в этом коротком видео:
Не можете посмотреть видео? Кликните сюда.
Обратные матрицы — это то же самое, что и обратные. В элементарной алгебре (а, возможно, и раньше) вы столкнулись с идеей обратного: одно число, умноженное на другое, может равняться 1.
Изображение любезно предоставлено LTU
Если вы умножите одну матрицу на ее обратную, вы получите матричный эквивалент 1: Identity Matrix , которая в основном представляет собой матрицу с единицами и нулями.
Шаг 1: Найдите адъюгат матрицы. Сопряжение матрицы можно найти, переставив одну диагональ и взяв негативы другой:
Чтобы найти сопряжение матрицы 2 × 2, поменяйте местами диагонали a и d, а затем поменяйте местами знаки c и d.
Шаг 2: Найдите определитель матрицы. Для матрицы
A B C D (см. Изображение выше) определитель равен (a * d) — (b * c).
Шаг 3: Умножить 1 / определитель * адъюгат. .
Проверка ответа
Вы можете проверить свой ответ умножением матриц.Умножьте свою матрицу ответов на исходную матрицу, и вы получите единичную матрицу. Вы также можете воспользоваться онлайн-калькулятором здесь.
Вернуться к началу
Собственное значение (λ) — это специальный скаляр, используемый при матричном умножении и имеющий особое значение в нескольких областях физики, включая анализ устойчивости и небольшие колебания колеблющихся систем. Когда вы умножаете матрицу на вектор и получаете тот же вектор в качестве ответа вместе с новым скаляром, скаляр называется собственным значением .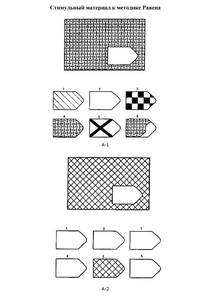
Основное уравнение:
A x = λ x ; мы говорим, что λ является собственным значением A.
Все приведенные выше уравнения говорят о том, что , если вы возьмете матрицу A и умножите ее на вектор x , вы получите то же самое, как если бы вы взяли собственное значение и умножили его на вектор x .
Пример собственного значения
В следующем примере 5 — собственное значение A, а (1,2) — собственный вектор:
Давайте рассмотрим это по шагам, чтобы наглядно продемонстрировать, что такое собственное значение.В обычном умножении, если вы умножаете матрицу n x n на вектор n x 1, в результате вы получаете новый вектор n x 1. На следующем изображении показан этот принцип для матрицы 2 x 2, умноженной на (1,2):
Что, если бы вместо новой матрицы nx 1 можно было получить ответ с помощью вектора , который вы умножили на вместе с новым скаляром?
Когда это возможно, вектор умножения (то есть тот, который также есть в ответе) называется собственным вектором, а соответствующий скаляр — собственным значением.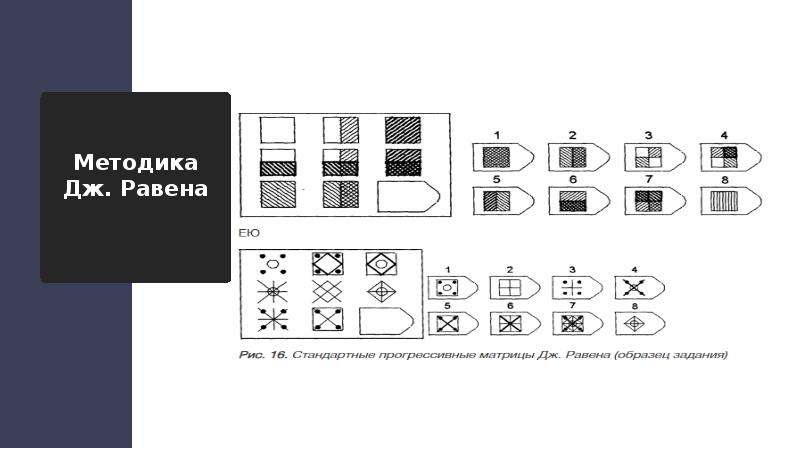
Обратите внимание, что я сказал «, когда это возможно» , потому что иногда невозможно вычислить значение для λ. Разложение квадратной матрицы A на собственные значения и собственные векторы (их можно иметь несколько значений для одной и той же матрицы) известно в так называемом разложении по собственным значениям . Разложение на собственные числа всегда возможно, если матрица, состоящая из собственных векторов матрицы A, является квадратной.
Расчет
Найдите собственные значения для следующей матрицы:
Шаг 1: Умножьте единичную матрицу на λ.Единичная матрица для любой матрицы 2 × 2 равна [1 0; 0 1], поэтому:
Шаг 2: Вычтите ответ из шага 1 из матрицы A, используя вычитание матрицы:
Шаг 3: Найдите определитель матрицы, вычисленной на шаге 2:
det = (5- λ) (- 1-λ) — (3) (3)
Упрощая, получаем:
-5 — 5λ + λ + λ 2 — 9
= λ 2 — 4λ — 14
Шаг 4: Установите уравнение, которое вы нашли на шаге 3, равным нулю и решите для λ:
0 = λ 2 — 4λ — 14 = 2
Мне нравится использовать свой TI-83, чтобы найти корни, но вы можете также воспользуйтесь алгеброй или этим онлайн-калькулятором.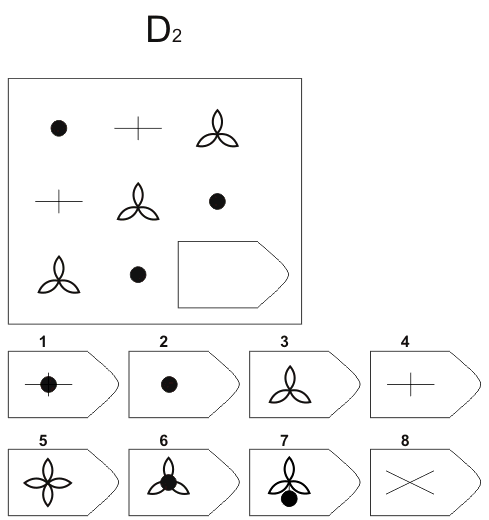
Находя корни (нули), получаем x = 2 + 3√2, 2 — 3√2
Ответ : 2 + 3√2 и 2-3√2
Математика для больших матриц такая же, но вычисления могут быть очень сложными. Для матриц 3 × 3 используйте калькулятор внизу этого раздела; для больших матриц попробуйте этот онлайн-калькулятор.
Вернуться к началу
На изображении выше показана расширенная матрица (A | B) внизу. Расширенные матрицы обычно используются для решения систем линейных уравнений и, собственно, именно поэтому они были впервые разработаны.Три столбца слева от полосы представляют коэффициенты (по одному столбцу для каждой переменной). Эта область называется матрицей коэффициентов . Последний столбец справа от полосы представляет собой набор констант (т. Е. Значений справа от знака равенства в наборе уравнений). Она называется расширенной матрицей , потому что матрица коэффициентов была «дополнена» значениями после знака равенства.
Например, следующая система линейных уравнений:
x + 2y + 3z = 0
3x + 4y + 7z = 2
6x + 5y + 9z = 11
Может быть помещен в следующую расширенную матрицу:
После того, как вы поместили свою систему в расширенную матрицу, вы можете выполнять операции со строками для решения системы.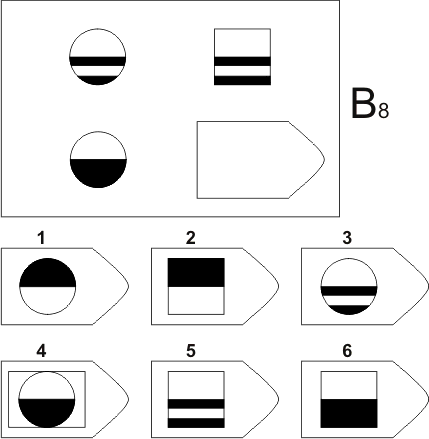
У вас не , а , чтобы использовать вертикальную черту в расширенной матрице. Обычно матрицы вообще не содержат линий. Полоса просто упрощает отслеживание ваших коэффициентов и ваших констант справа от знака равенства. Если вы вообще используете вертикальную полосу, зависит от учебника, который вы используете, и от предпочтений вашего преподавателя.
Написание системы уравнений
Вы также можете работать в обратном направлении, чтобы написать систему линейных уравнений, заданную расширенной матрицей.
Пример вопроса: Напишите систему линейных уравнений для следующей матрицы.
Шаг 1: Запишите коэффициенты для первого столбца, за которым следует «x». Обязательно укажите положительные или отрицательные числа:
-1x
2x
6x
Шаг 2: Напишите коэффициенты для второго столбца, после чего укажите «y». Сложите, если это положительное число, вычтите, если оно отрицательное:
-1x + 7y
2x + 4y
6x + 2y
Шаг 3: Напишите коэффициенты для второго столбца, после чего укажите «z.
«Сложите, если это положительное число, и вычтите, если оно отрицательное:
-1x + 7y + 3
2x + 4y — 7
6x + 2y + 9
Шаг 3. Запишите константы в третьем столбце со знаком равенства.
-1x + 7y + 3 = 0
2x + 4y — 7 = 2
6x + 2y + 9 = 7
Примечание : если на этом этапе у вас стоит отрицательный знак, просто сделайте константу отрицательным числом.
Вернуться к началу
Определитель матрицы — это просто специальное число, которое используется для описания матриц для нахождения решений систем линейных уравнений, нахождения обратных матриц и для различных приложений в исчислении.Определить на простом английском языке невозможно; обычно его определяют в математических терминах или в терминах того, что он может вам помочь. Определитель матрицы имеет несколько свойств:
- Это действительное число. Сюда входят отрицательные числа.
- Определители существуют только для квадратных матриц.
- Обратная матрица существует только для матриц с ненулевыми определителями.
Символ для определителя матрицы A — | A |, который также является тем же самым символом, который используется для абсолютного значения, хотя эти два понятия не имеют ничего общего друг с другом.
Формула для вычисления определителя матрицы различается в зависимости от размера матрицы.
Определитель матрицы 2 × 2
Формула определителя матрицы 2 × 2 — ad-bc. Другими словами, умножьте верхний левый элемент на нижний правый, затем вычтите произведение верхнего правого и нижнего левого.
Определитель матрицы 3 × 3
Определитель матрицы 3 × 3 находится по следующей формуле:
| A | = a (ei — fh) — b (di — fg) + c (dh — eg)
Это может показаться сложным, но если вы пометили элементы с помощью a, b, c в верхнем ряду, d, e, f во второй строке и g, h, i в последней, становится основной арифметикой.
Пример :
Найдите определитель следующей матрицы 3 × 3:
= 3 (6 × 2-7 × 3) –5 (2 × 2-7 × 4) +4 (2 × 3-6 × 4)
= -219
По сути, здесь происходит умножение a, b и d на детерминанты меньших 2×2 в матрице 3×3.
Этот шаблон продолжается для поиска определителей матриц более высокого порядка.
Определитель матрицы 4 × 4
Чтобы найти определитель матрицы 4 × 4, вам сначала нужно найти определители четырех матриц 3 × 3, которые входят в матрицу 4 × 4.В виде формулы:
Вернуться к началу
Диагональная матрица — это симметричная матрица со всеми нулями, кроме ведущей диагонали, которая проходит от верхнего левого угла до нижнего правого.
Записи на самой диагонали также могут быть нулями; любую квадратную матрицу со всеми нулями еще можно назвать диагональной матрицей.
Единичная матрица, которая имеет все 1 с по диагонали, также является диагональной матрицей. Любая матрица с равными элементами по диагонали (т. Е.2,2,2 или 9,9,9), является скалярным кратным единичной матрицы и также может быть классифицировано как диагональное.
Диагональная матрица имеет максимум n чисел, которые не равны нулю, где n — порядок матрицы.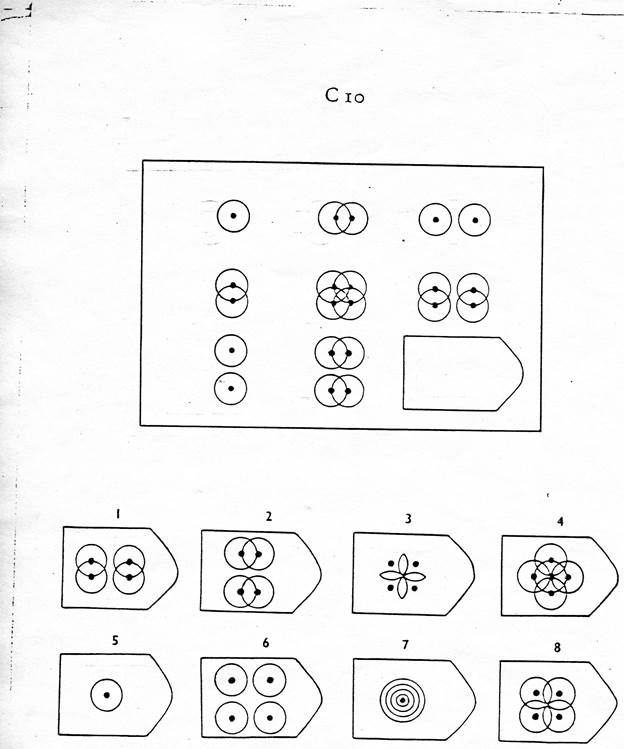
Например, матрица 3 x 3 (порядок 3) имеет диагональ, состоящую из 3 чисел, а матрица 5 x 5 (порядок 5) имеет диагональ из 5 чисел.
Обозначение
Обозначение, обычно используемое для описания диагональной матрицы: diag (a, b, c) , где abc представляет собой числа в первой диагонали.Для приведенной выше матрицы это обозначение будет diag (3,2,4). .
Верхняя и нижняя треугольные матрицы
Диагональ матрицы всегда относится к ведущей диагонали. Ведущая диагональ в матрице помогает определить два других типа матриц: нижнетреугольные матрицы и верхние треугольные матрицы. В нижнетреугольной матрице числа под диагональю; верхнетреугольная матрица имеет числа над диагональю.
Диагональная матрица — это матрица с нижней диагональю и с нижней диагональю.
Прямоугольные диагональные матрицы
Для наиболее распространенного использования диагональная матрица представляет собой квадратную матрицу с порядком (размером) n .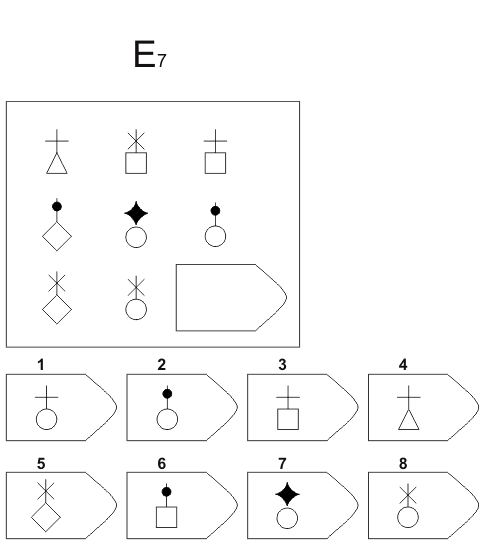
Существуют и другие формы, которые обычно не используются, например, прямоугольная диагональная матрица . Матрица этого типа также имеет одну ведущую диагональ с числами, а остальные элементы нули. Ведущая диагональ берется из наибольшего квадрата неквадратной матрицы.
В начало
Транспонирование матрицы (или транспонирование матрицы) — это как раз то место, где вы переключаете все строки матрицы в столбцы.Матрицы транспонирования полезны при комплексном умножении.
Альтернативный способ описания транспонированной матрицы состоит в том, что элемент в строке «r» и столбце «c» транспонируется в строку «c» и столбец «r». Например, элемент в строке 2, столбце 3 будет транспонирован в столбец 2, строку 3. Размер матрицы также изменится. Например, если у вас есть матрица 4 x 5, вы бы транспонировали ее в матрицу 5 x 4.
Симметричная матрица — это частный случай транспонированной матрицы; он равен своей транспонированной матрице.
Говоря более формально, A = A T .
Символы для матрицы транспонирования
Обычный символ для транспонированной матрицы — A T Однако Wolfram Mathworld утверждает, что также используются два других символа: A ‘ и.
Свойства матриц транспонирования
Свойства транспонированных матриц аналогичны основным числовым свойствам, с которыми вы столкнулись в базовой алгебре (например, ассоциативным и коммутативным).Основные свойства матриц:
- (A T ) T = A: транспонированная матрица транспонирования является исходной матрицей.
- (A + B) T = A T + B T : Транспонирование двух сложенных вместе матриц такое же, как транспонирование каждой отдельной матрицы, сложенной вместе.
- (rA) T = rA T : когда матрица умножается на скалярный элемент, не имеет значения, в каком порядке вы транспонируете (примечание: скалярный элемент — это величина, которая может умножать матрицу).
- (AB) T = B T A T : транспонирование двух матриц, умноженных вместе, совпадает с произведением их матриц транспонирования в обратном порядке.
- (A -1 ) T = (A T ) -1 : транспонирование и инверсия матрицы могут выполняться в любом порядке.
В начало
Симметричная матрица — это квадратная матрица, имеющая симметрию относительно ведущей диагонали, сверху слева направо.Представьте себе складку в матрице по диагонали (не включайте числа в действительную диагональ). Верхняя правая половина матрицы и нижняя левая половина являются зеркальными отображениями относительно диагонали:
Если вы можете сопоставить числа друг с другом вдоль линии симметрии ( всегда ведущая диагональ), как в примере справа , у вас симметричная матрица.
Альтернативное определение
Другой способ определить симметричную матрицу состоит в том, что симметричная матрица равна ее транспонированной.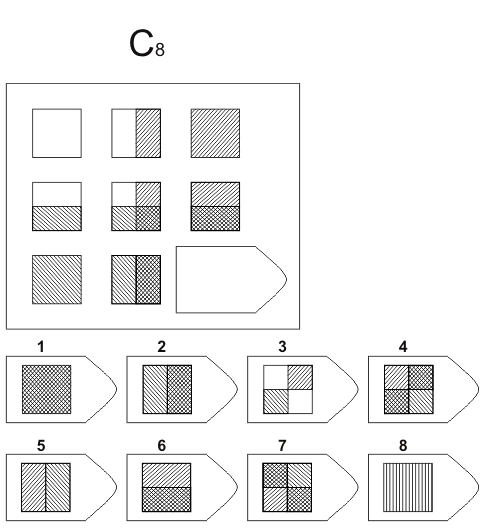
В случае транспонирования матрицы первая строка становится первым столбцом, вторая строка становится вторым столбцом, третья строка становится третьим столбцом… и так далее. Вы просто превращаете строки в столбцы.
Если вы возьмете симметричную матрицу и транспонируете ее, матрица будет выглядеть точно так же, отсюда и альтернативное определение, что симметричная матрица равна ее транспонированию. С математической точки зрения, M = M T , где M T — транспонированная матрица.
Максимальное количество номеров
Поскольку большинство чисел в симметричной матрице дублируются, существует ограничение на количество различных чисел, которые она может содержать. Уравнение для максимального количества чисел в матрице порядка n: n (n + 1) / 2. Например, в симметричной матрице 4-го порядка, подобной приведенной выше, имеется максимум 4 (4 + 1) / 2 = 10 различных чисел. Это имеет смысл, если подумать: диагональ — это четыре числа, и если вы сложите числа в нижней левой половине (исключая диагональ), вы получите 6.
Диагональные матрицы
Диагональная матрица — это частный случай симметричной матрицы. Диагональная матрица имеет все нули, кроме ведущей диагонали.
Что такое асимметричная матрица?
Кососимметричная матрица, иногда называемая антисимметричной матрицей , представляет собой квадратную матрицу, симметричную относительно обеих диагоналей. Например, следующая матрица является асимметричной:
Математически асимметричная матрица удовлетворяет условию a ij = -a ji .Например, возьмите запись в строке 3, столбец 2, которая равна 4. Его симметричным аналогом является -4 в строке 2, столбце 3. Это условие также можно записать в терминах его транспонированной матрицы: A T = — А. Другими словами, матрица является кососимметричной, только если A T = -A, где A T — это транспонированная матрица.
Все старшие диагональные элементы в кососимметричной матрице должны быть нулевыми.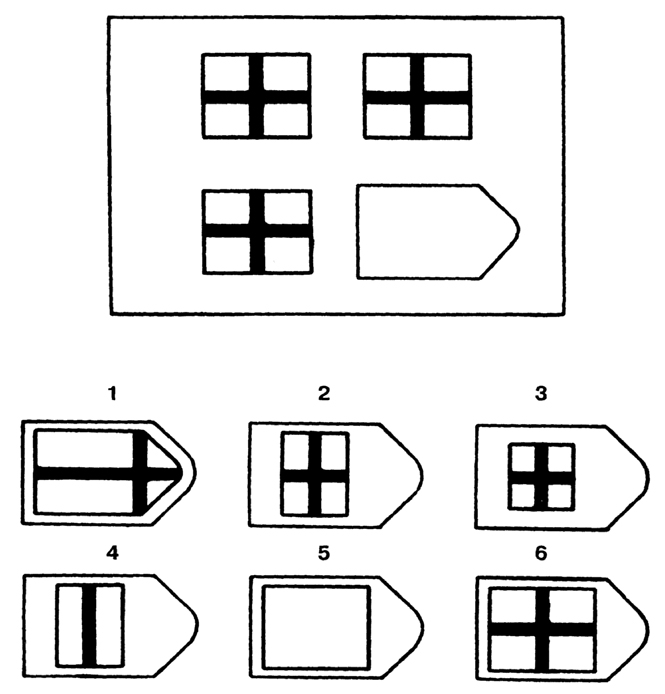
Это потому, что i, i = −a i, i влечет i, i = 0.
Еще одним интересным свойством этого типа матрицы является то, что если у вас есть две кососимметричные матрицы A и B одинакового размера, вы также получите кососимметричную матрицу, если сложите их вместе:
Добавление двух кососимметричных матриц вместе.
Этот факт может помочь вам доказать, что две матрицы кососимметричны. Первый шаг — убедиться, что все элементы на главной диагонали равны нулю (что невозможно «доказать» математически!).Второй шаг — сложение матриц. Если результатом является третья матрица, которая является кососимметричной, то вы доказали, что a ij = — a ji .
Косоэрмитский
Косоэрмитова матрица по сути такая же, как кососимметричная матрица, за исключением того, что косоэрмитова матрица может содержать комплексные числа.
Косоэрмитова матрица, показывающая комплексные числа.
Фактически, кососимметричный и косоэрмитовый эквивалентны для вещественных матриц (матрицы, которая почти полностью состоит из действительных чисел).
Старшая диагональ косоэрмитовой матрицы должна содержать чисто мнимые числа; в мнимой сфере ноль считается мнимым числом.
Вернуться к началу
Матрица ковариации и дисперсии (также называемая матрицей ковариации или матрицей дисперсии) — это квадратная матрица, которая отображает дисперсию и ковариацию двух наборов двумерных данных вместе. Дисперсия — это мера того, насколько разбросаны данные. Ковариация — это мера того, насколько две случайные величины движутся вместе в одном направлении.
Дисперсии отображаются в диагональных элементах, а ковариации между парами переменных отображаются в недиагональных элементах. Дисперсии находятся в диагоналях ковариантной матрицы, потому что в основном эти дисперсии являются ковариатами каждой отдельной переменной с самой собой.
Следующая матрица показывает дисперсию для A (2,00), B (3,20) и C (0,21) в диагональных элементах.
Ковариации для каждой пары показаны в других ячейках.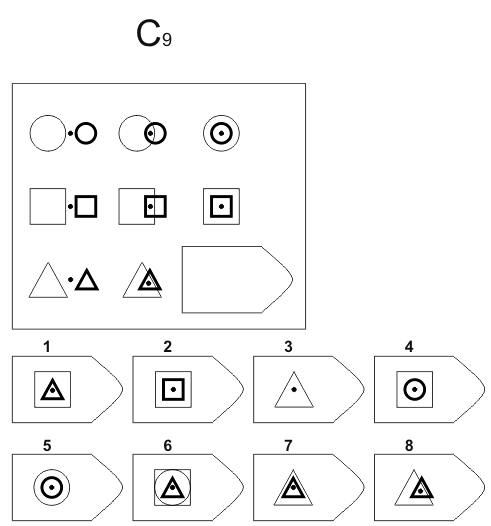
Например, ковариация для A и B равна -0,21, а ковариация для A и C равна -0,10. Вы можете посмотреть столбец и строку или строку и столбец (например, AC или CA), чтобы получить тот же результат, потому что ковариация для A и C такая же, как ковариация для C и A. Следовательно, ковариация дисперсии матрица также является симметричной матрицей.
Построение матрицы вариации-ковариации
Многие статистические пакеты, включая Microsoft Excel и SPSS, могут создавать ковариативно-вариативные матрицы. Обратите внимание, что Excel вычисляет ковариацию для генеральной совокупности (знаменатель n), а не для выборки (n-1).Это может привести к немного неправильным вычислениям для матрицы дисперсии-ковариации. Чтобы исправить это, вам нужно умножить каждую ячейку на n / n-1.
Если вы хотите сделать один вручную:
Шаг 1: Вставьте отклонения для ваших данных в диагонали матрицы.
Шаг 2: Рассчитайте ковариацию для каждой пары и введите их в соответствующую ячейку. Например, ковариация для A / B в приведенном выше примере появляется в двух местах (A B и B A).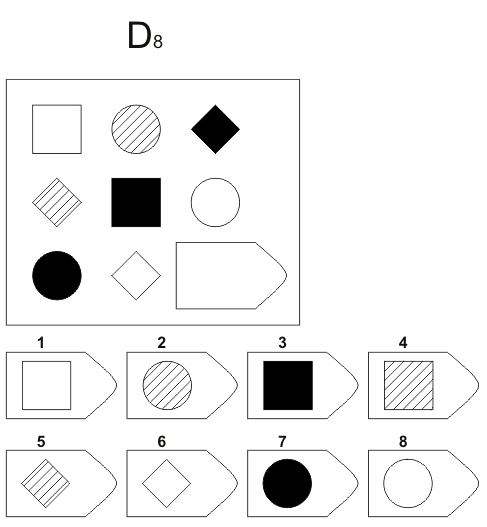
На следующей диаграмме показано, где каждая ковариация и дисперсия появляются для каждого варианта.
В начало
См. Также:
Что такое матрица неточностей?
Следующий : Форма эшелона строк / Форма пониженного эшелона строк
————————————————— —————————-Нужна помощь с домашним заданием или контрольным вопросом? С помощью Chegg Study вы можете получить пошаговые ответы на свои вопросы от эксперта в данной области. Ваши первые 30 минут с репетитором Chegg бесплатны!
Комментарии? Нужно опубликовать исправление? Пожалуйста, оставьте комментарий на нашей странице в Facebook .
Матрицы с множественным выбором вопросов (MCQ) и ответов
1 Если порядок матрицы A равен m × p. И порядок B равен p × n. Тогда порядок матрицы AB равен?
А п × п
B м × п
С п × п
D п × м
Посмотреть ответ
2 Транспонирование прямоугольной матрицы — это
А прямоугольная матрица
B диагональная матрица
С квадратная матрица
D масштабирующая матрица
Посмотреть ответ
Ответ: прямоугольная матрица
3 Квадратная матрица, в которой все элементы, кроме хотя бы одного диагонального, равны нулю, называется
А идентичная матрица
B нулевая / нулевая матрица
С матрица столбцов
D диагональная матрица
Посмотреть ответ
5 В матрицах (AB) −1 равно
А A − 1
B В − 1
С А − 1 В − 1
D В — 1 А — 1
Посмотреть ответ
6 Для нетривиального решения | А | является
7 Количество ненулевых строк в эхлонной форме называется?
А ранг матрицы
B кофактор матрицы
С приведенная форма эхлона
D сопряженная матрица
Посмотреть ответ
8 Две матрицы A и B перемножаются, чтобы получить AB, если
А оба прямоугольные
B оба имеют одинаковый заказ
С
Нет.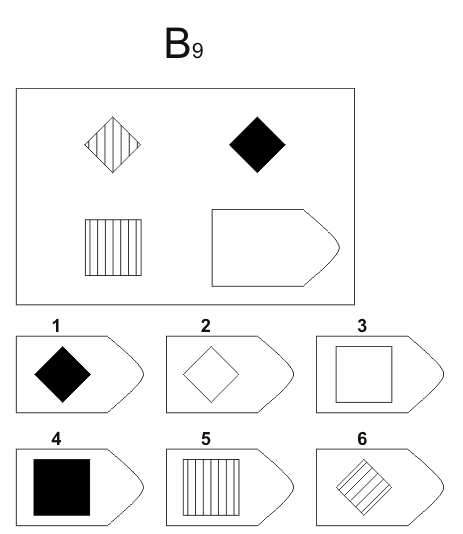
столбца матрицы A равно no. рядов Б
D количество строк A не равно количеству столбцов B
Посмотреть ответ
Ответ: Номер столбца матрицы A равен no. рядов B
9 Транспонирование матрицы-строки
А нулевая матрица
B диагональная матрица
С матрица столбцов
D матрица-строка
Посмотреть ответ
10 Идея матриц была введена Артуром Кейлетом в
А 18 век
B 19 век
С 20 век
D 21 век
Посмотреть ответ
11 Если A (BC) = (AB) C, то применительно к мультипликации этот закон называется
А Обратное право
B ассоциативный закон
С Закон Крамерса
D аддитивный закон
Посмотреть ответ
13 Матрицы, полученные изменением строк и столбцов, называются
А прямоугольная матрица
B транспонировать
С симметричный
D Ни один из вышеперечисленных
Посмотреть ответ
14 Аддитивная инверсия матрицы A есть
А прил A⁄ | A |
B A²
С | A |
D A
Посмотреть ответ
15 Две матрицы A и B перемножаются, чтобы получить AB, если
А оба прямоугольные
B оба имеют одинаковый заказ
С количество столбцов A равно столбцам B
D количество строк A не равно количеству столбцов B
Посмотреть ответ
Ответ: Ни один из столбцов A не равен столбцам B
16 Если A и B — матрицы, то что из следующего верно?
А AB ≠ BA
B (Ат) t ≠ A
С А + В ≠ В + А
D все верно
Посмотреть ответ
17 Если A — симметричная матрица, то At =
А 0
B A
С | A |
D диагональная матрица
Посмотреть ответ
18 Если | A | = 0, то A является
А нулевая матрица
B сингулярная матрица
С невырожденная матрица
D 0
Посмотреть ответ
19 Две матрицы A и B складываются, если
А оба прямоугольные
B оба имеют одинаковый заказ
С количество столбцов A равно столбцам B
D количество строк A не равно количеству столбцов B
Посмотреть ответ
Ответ: оба имеют одинаковый порядок
20 Квадратный или прямоугольный массив чисел, записанных в квадратных скобках в определенном порядке в строках и столбцах, называется
А формула
B определитель
С матрица
D уравнение
Посмотреть ответ
Онлайн-тест по дискретной математике — Sanfoundry
Этот набор онлайн-тестов по дискретной математике посвящен «Операциям с матрицами».
1. Пусть A и B — две матрицы одного порядка, затем укажите, является ли данное утверждение истинным или ложным.
А + В = В + А
a) Верно
b) Неверно
Посмотреть ответ
Ответ: a
Пояснение: Матричное сложение коммутативно.
2. Пусть A и B — две матрицы одного порядка, затем укажите, является ли данное утверждение истинным или ложным.
AB = BA
a) Верно
b) Неверно
Посмотреть ответ
Ответ: b
Объяснение: Умножение матриц не коммутативно.
3. Пусть A order (axb) и Border (cxd) — две матрицы, тогда для существования AB правильное соотношение задается формулой?
a) a = d
b) b = c
c) a = b
d) c = d
Просмотреть ответ
Ответ: b
Объяснение: Умножение матриц существует только тогда, когда столбец первой матрицы совпадает со строками второй т.е. b = c.
4. Пусть A order (axb) и Border (cxd) — две матрицы, тогда, если AB существует, порядок AB равен?
a) axd
b) bxc
c) axb
d) cxd
Посмотреть ответ
Ответ: a
Объяснение: Умножение матрицы существует только тогда, когда столбец первой матрицы совпадает со строками второй i.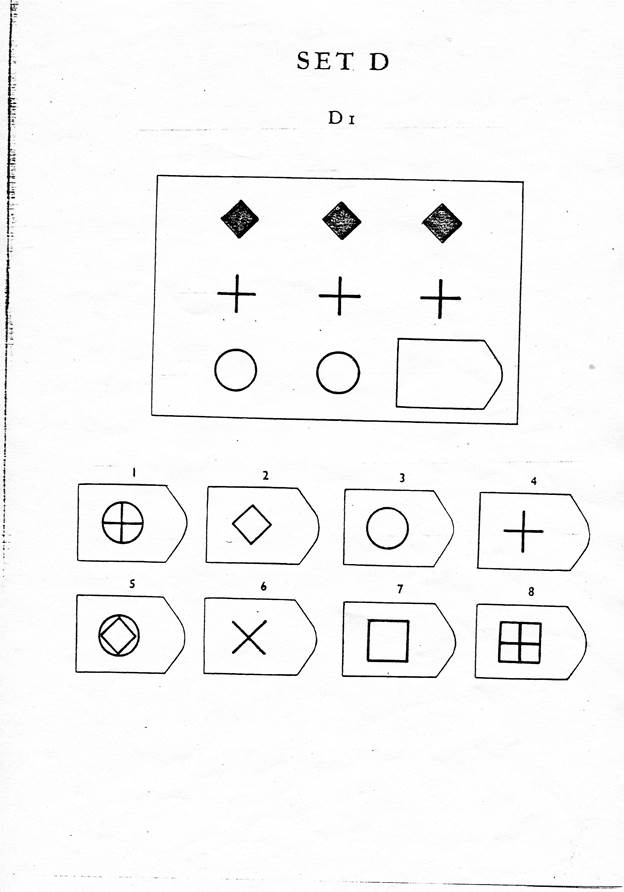
e b = c также результирующая матрица будет иметь количество строк, равное первой матрице, и столбец, равный второй матрице.
5. Пусть A = [a ij ] — матрица размера mxn, а k — скаляр, тогда kA равно __________
a) [ka ij ] mxn
b) [a ij / k] mxn
c) [k 2 a ij ] mxn
d) Ни один из упомянутых
Посмотреть ответ
Ответ: a
Объяснение: Скаляр умножается на каждый элемент матрицы A.
6. Умножение матриц распределяет по сложению матриц.
a) Верно
b) Неверно
Просмотреть ответ
Ответ: a
Пояснение: Для матрицы A, B, C, A (B + C) = AB + AC.
7. Если для квадратной матрицы A, A 2 = A, тогда такая матрица известна как _________
a) Идемпотентная матрица
b) Ортагональная матрица
c) Нулевая матрица
d) Ни один из упомянутых
Посмотреть ответ
Ответ: a
Объяснение: Матрица sqaure называется идемпотентной матрицей, если A 2 = A.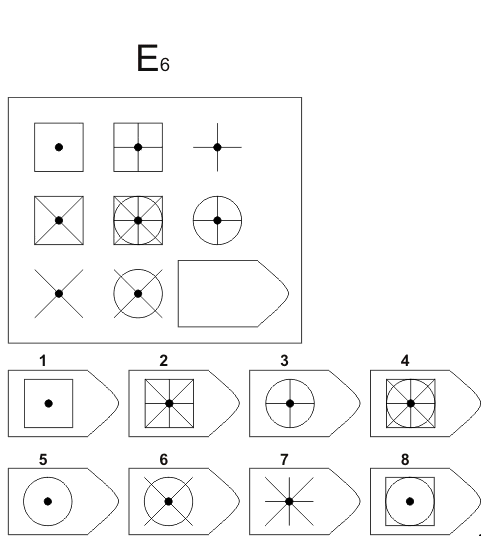
8. Для матрицы A, B. (A + B) T = A T + B T и (AB) T = A T B T , если порядок матриц соответствующий .
a) Верно
b) Неверно
Просмотреть ответ
Ответ: b
Объяснение: (A + B) T = A T + B T верно, но (AB) T = B T A T (закон разворота).
9. Для матрицы A, B, если A — B = O, где O — нулевая матрица, тогда?
a) A = O
b) B = O
c) A = B
d) Ни один из упомянутых
Посмотреть ответ
Ответ: c
Объяснение: Если вычитание B из A приводит к нулевой матрице, это означает, что A эквивалентно B.
10. Все диагональные элементы кососимметричной матрицы составляют?
a) 0
b) 1
c) 2
d) Любое целое число
Просмотреть ответ
Ответ: a
Объяснение: Поскольку для кососимметричной матрицы a ij = -a ij , это подразумевает все диагональные элементы должно быть равно нулю.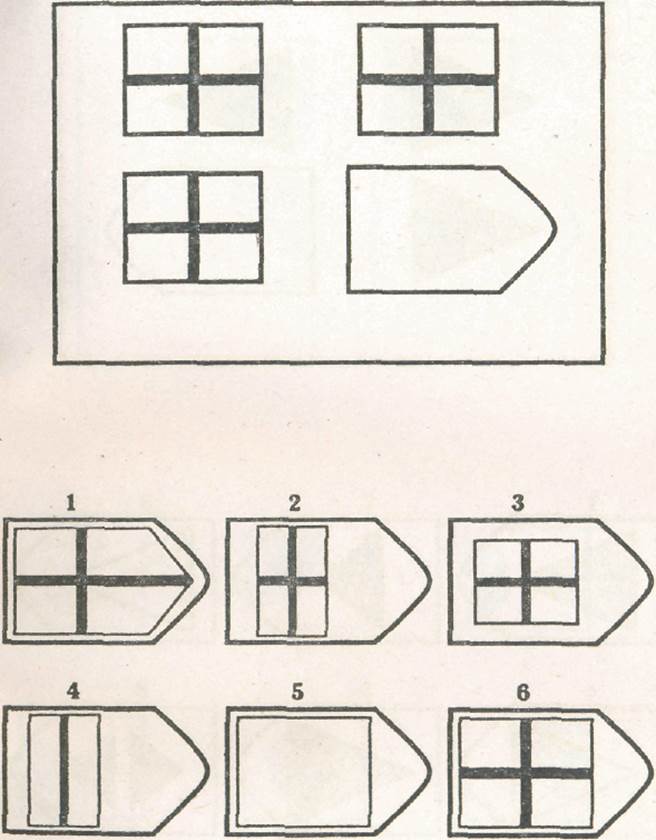
Sanfoundry Global Education & Learning Series — Дискретная математика.
Чтобы практиковать все области дискретной математики для онлайн-тестов, представляет собой полный набор из 1000+ вопросов и ответов с несколькими вариантами ответов .
Примите участие в конкурсе сертификации Sanfoundry, чтобы получить бесплатную Почетную грамоту. Присоединяйтесь к нашим социальным сетям ниже и будьте в курсе последних конкурсов, видео, стажировок и вакансий!
определитель единичной матрицы mcq
определитель единичной матрицы mcq Приведите еще один пример матрицы, не имеющей определителя. Посмотреть ответ. (б) A — B — кососимметричная матрица. Решенные примеры с подробным описанием ответов, даны объяснения, которые легко понять. Вариант (b) неверен. Это левая матрица.И определите определитель единичной матрицы, которая равна августовской. 4. Итак, определение единичной матрицы — это одно к определению A. Все четыре элемента матрицы 2 x 2 отличны от нуля, и одно из ее собственных значений равно нулю.
A 9. Матрица m n выражается как. I 3 = 100 010 001 Идентификационная матрица Определение Идентификационная матрица, обозначенная In, является матрицами класса 12 Maths MCQs Pdf. Примените поэлементную инверсию, то есть умножьте на инверсию того же элемента, чтобы сделать его единичной матрицей, пока не будет достигнута желаемая цель.Набор матриц — это набор верхнетреугольных матриц (H) размера 3 * 3 с ненулевым определителем. Определитель квадратной матрицы A отличен от нуля тогда и только тогда, когда уравнение Ax = 0 имеет уникальный вопрос с множественным выбором по матрицам Матрицы и детерминанты с множественным выбором вопросов (MCQ) Страница-1. распределительное право. Матрица и определитель. Напишите объяснение, как вы можете решить, является ли система уравнений ax cy e… Расчет: Пусть (BA) -1 = K.… Также найдите определитель матрицы A.Единичная матрица C. ГЛАВА 8: МАТРИЦЫ и ДЕТЕРМИНАНТЫ Этот пробный тест Matrix MCQ — 2 по математике поможет вам сдать каждый вступительный экзамен по математике.
Б. Скалярная матрица. Если строки и столбцы меняются местами, то значение определителя остается прежним (значение не меняется). Таким образом прил. A) матрица строк B) обратная матрица C) матрица столбцов D) прямоугольная матрица; MCQ по компьютерной графике. 1. 2002] A) 10 сделано ясно. Тех.) … Порядок единичной (единичной) матрицы всегда равен: A: нулевая матрица. Правда или ложь.Вопросы MCQ подготовлены в соответствии с программой. Пусть C — подмножество A, состоящее из всех определителей. Итак, это я только в ISIU. Квадратная матрица называется сингулярной матрицей, если определитель матрицы равен нулю. матрица, матрицы mcqs и определители 1 вопросы с несколькими вариантами ответов о матрицах и определителе из учебника по математике первого года обучения для более быстрой подготовки матриц экзамена и обучения 1, матрица набор чисел, расположенных в строках и столбцах, чтобы сформировать прямоугольный массив числа называются элементами или записями Страниц: 1 | 2.B: матрица-строка.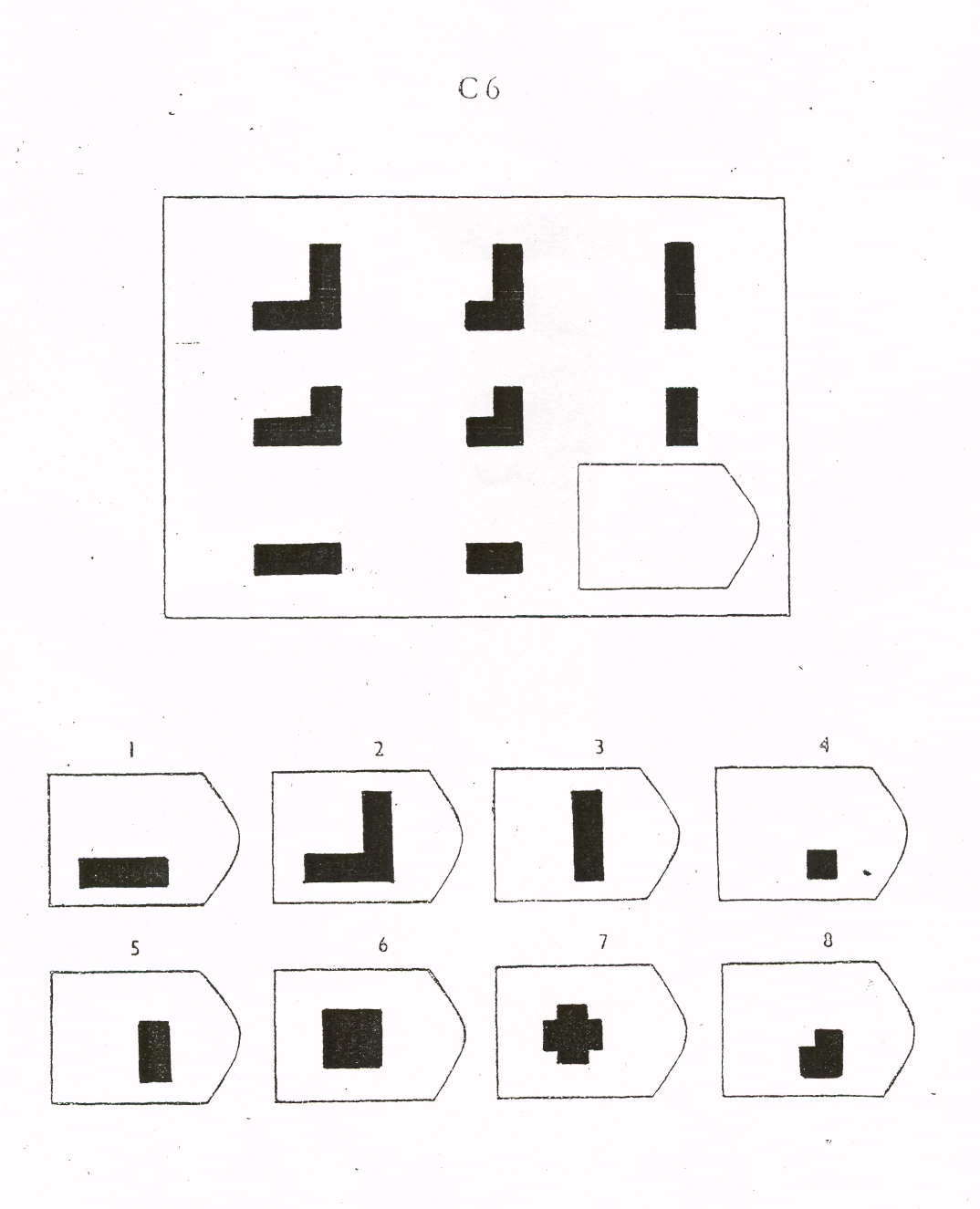
Матрица A = (begin {bmatrix} 1 & 2 \ 2 & 1end {bmatrix}) является … единичной матрицей c) симметричной матрицей d) кососимметричной матрицей … 250+ TOP MCQ по определителям — сопряженным и обратным к матрице | 12 класс по математике; 2.2.3 Квадратные, симметричные и ranspTose матрицы Квадратная матрица — это матрица, количество строк которой равно количеству столбцов. 1. Матрица Вандермонда — это квадратная матрица вида, указанного в теореме. Отправлено Ануджем Сингхом 29 мая 2020 г. D количество строк матрицы A не равно количеству столбцов B.ответ a Каждая скалярная матрица — это единичная матрица b Каждая единичная матрица — это скаляр … Матрицы и детерминанты Вопросы с множественным выбором 10 июня 11, 2019 — Матрицы и детерминанты вопросы с множественным выбором Матрицы и детерминанты MCQ ответы на викторину pdf 1 изучайте математику в старшей школе онлайн Курсы Матрицы и диагональ Верхний треугольник Метод скалярной степени нижнего треугольника применим, если собственные векторы, соответствующие собственным значениям, линейно независимы.
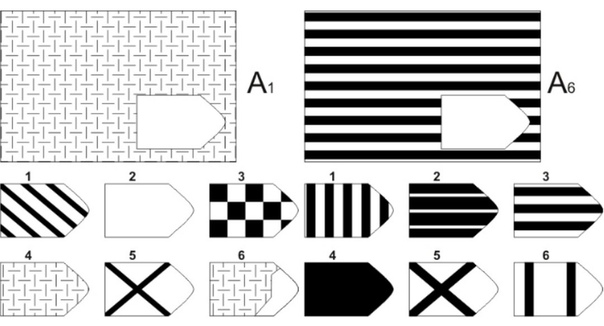Ответ: (В) 2, -3. Identity Matrix предоставляется I n X n, где n X n показывает порядок матрицы.1. Ответы на решенные вопросы в этой викторине «Матрица и детерминанты MCQ (с решением) -2 (уровень соревнования 1)» представляют собой хорошее сочетание простых и сложных вопросов. Ответы на решенные вопросы в этой викторине Matrix MCQ — 2 дают вам хорошее сочетание ответа (b) неверно. Это левая матрица. ТОЧКА МАТРИЦЫ Транспонирование матрицы сомножителей A называется присоединением матрицы и обозначается прил. (d) 512. Пояснение: Матрица идентичности (I): диагональная матрица с нулями в качестве элементов, за исключением диагонали, у которой есть единицы…. единичная матрица. Детерминанты Класс 12 Математика MCQs Pdf. Подготовьте эти mcqs к ECAT и экзамену. 0: с. … Посмотреть отчет об ответе Обсудить слишком сложно! Матрица идентичности 3 x 3. 1. Например, единичная матрица всегда квадратная. Объясните, почему в матрице нет определителя. Он содержит 20 вопросов с множественным выбором для матрицы и детерминантов JEE MCQ (с решением) -2 (уровень конкуренции 1) (mcq) для изучения с решениями полного банка вопросов.
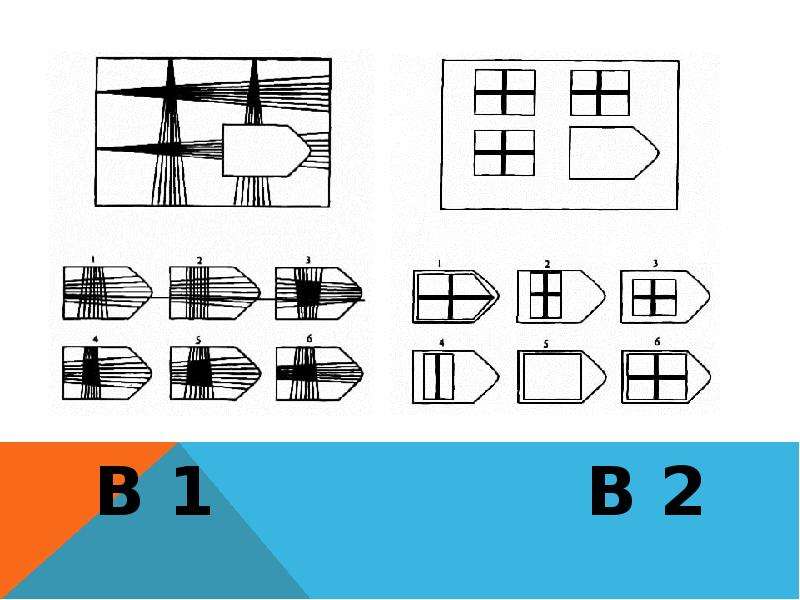6. Ответ: А. Аакрути Математика. Описание.A — сингулярная матрица: b. Вопросы с множественным выбором для матриц Math 2550 Матричная алгебра Форма экзамена с множественным выбором A 27 октября 2014 г. Задача 1. Если матрица имеет 4 строки и 5 столбцов, то количество элементов в этой матрице равно 9. Квадратная матрица A = [aij] называется нижнетреугольной матрицей, если aij = 0 для ij. Вопросы с множественным выбором для матриц Math 2550 Матричная алгебра Форма экзамена с множественным выбором A 27 октября 2014 г. Задача 1. Класс — 1. Вопрос 6. Найдите ответы и решения на вопросы внизу страницы.1. Если порядок матрицы A равен. И порядок B есть. Тогда порядок матрицы AB равен? 2. Если A и B — матрицы, то что из следующего верно? 3. Что такое «а», если это особая матрица? 4. Математический класс 11 Глава 3 — Матрицы и определители. D. Транспонировать матрицу. Называется квадратная матрица A, для которой A t = -A. _____ — это не что иное, как плоскость пленки в камере, которая позиционируется и ориентируется для определенного кадра сцены. Наряду с оператором умножения набор образует алгебраическую структуру, поскольку следует свойству замыкания.Вопрос 4. Он содержит 30 вопросов с множественным выбором для теста уровня соревнований 12 класса: матрицы и детерминанты (mcq) для изучения с решениями полного банка вопросов. 1) Это всегда квадратная матрица. Здесь единичная матрица 2 x 2 и 3 x 3 приведена ниже: Идентификационная матрица 2 x 2. Практикуйте вопросы матриц с ответами MCQ по математике 12 класса, чтобы получить хорошие оценки на экзаменах. Вопросы с несколькими вариантами ответов о матрицах и определителе из учебника по математике для первого года обучения для более быстрой подготовки матриц экзамена и изучения.Если все элементы строки (или столбца) равны нулю, то значение определителя равно нулю. A. Скалярная матрица B. Свойства определителей матриц: Определитель, вычисленный по любой строке или столбцу, одинаков. Эти вопросы линейной алгебры с множественным выбором (MCQ) следует практиковать для улучшения навыков Data Science, необходимых для различных собеседований (собеседование в кампусе, личное собеседование, собеседование в компании), трудоустройства, вступительных экзаменов и других конкурсных экзаменов. Площадь треугольника с вершинами (-3, 0), (3, 0) и (0, k) составляет 9 кв.Матрицы и детерминанты: вопросы 1-8 из 24. Объяснение: В единичной матрице a ii = 1, а все другие элементы = 0, следовательно, определитель равен 1. Сопряженная матрица — Сопряженная матрица — это транспонированная матрица кофакторы данной матрицы, т. е. свойства миноров и сомножителей (i) Сумма произведений элементов любой строки (или столбца) определителя с кофакторами соответствующих элементов любой другой строки (или столбца) равна ноль, т. е. если 27 Транспонировать матрицу столбца равно.Определитель треугольной матрицы является произведением диагональных элементов, следовательно, d e t A = — 1 × 1 × 6 = — 6. Вопрос 3. Если вы хотите сложить две матрицы, их размеры должны быть точно такими же. Опубликовано 17 февраля 2019 г. автором Шах Джамал. Итак, мы можем ответить, как определено для A, который является вариантом C. Итак, здесь правильный вариант — это вариант C. Теперь, если вы возьмете любую единичную матрицу, это… Итак, поскольку квадрат является единичной матрицей, мы получаем I в YA 1 . 9.2 Матрица: набор из mn чисел (действительных или комплексных), расположенных в прямоугольную форму (массив или таблица), имеющий m строк и n столбцов и заключенный в квадратную скобку [], называется mn-матрицей (читается «m x n матрица»). »).вопросы с множественным выбором по матрицам и детерминантам. Горизонтальные элементы в матрице называются строками, а вертикальные элементы — столбцами. 26 Матрица, имеющая m строк и n столбцов с m ≠ n, называется a. Матрицы инженерной математики MCQ. Б) 1 сделано ясно. Дискретная математика Вопросы с множественным выбором «Свойства матриц». 32. Правильный ответ: (B) Определитель — это число, связанное с квадратной матрицей. Практикуйте эти вопросы и ответы MCQ для подготовки к различным конкурсным и вступительным экзаменам.Посмотреть ответ. Вопрос 2. Если порядок матрицы A такой. A X I n X n = A, A = любая квадратная матрица порядка n X n. Также прочтите: Обратная матрица; Ортогональная матрица; Сингулярная матрица; Симметричная матрица; Верхняя треугольная матрица; Свойства матрицы идентичности. Оба прямоугольные. Вопрос 1.4. Матрицы и детерминанты. Найдите ответы и решения на вопросы внизу страницы. Ответ: (C) Сингулярная матрица. а. Тогда (a) C пусто (b) B имеет столько же элементов, сколько C (c) A = B È C (d) B имеет вдвое больше элементов, чем C [IIT JEE 1981] Maths MCQs для IIT-JEE | Матрица и детерминанты Ключи к ответу на практический тест MCQ: 1.a 2. a 3. вычисляется из элементов матрицы трассировки D. Оба представления A и C Ответ Ответ: A Объяснение: концепция определителя применима только к квадратным матрицам и истинна в отношении определителя матрицы. Матрица идентичности C. Верхняя треугольная матрица D. Квадратная матрица Просмотр Ответ: количество столбцов A равно столбцам B. 4. Вопрос 5. 6. 10. Решить обратную матрицу MCQ, транспонировать матрицу MCQ, след матрицы MCQ , типы матричных вопросов типа MCQ с ответами на них. Математические вопросы и ответы с множественным выбором (MCQ) на тему «Симметричные и кососимметричные матрицы».Концепция собственных значений и векторов применима к? 8 Две матрицы A и B перемножаются, чтобы получить AB, если. … единичная матрица. Квадратная матрица A = [a ij] n × n называется диагональной матрицей, если aij = 0 для. Матрицы Вопросы с множественным выбором (MCQ) и ответы … «Транспонирование прямоугольной матрицы представляет собой» Вопросы с множественным выбором (MCQ) по матрицам и определителям с диагональной матрицей выбора, прямоугольной матрицей, квадратной матрицей и матрицей масштабирования для онлайн-программ на получение степени » . Более конкретно, если A — матрица, а U — строчная форма матрицы A, то jAj = (1) r jUj (2.2) где r — число… Определитель квадратной матрицы A отличен от нуля тогда и только тогда, когда уравнение Ax = 0 имеет уникальный вопрос с множественным выбором по матрицам и детерминантам Вопросы с множественным выбором (MCQ) Страница-1. 21:58. диагональная матрица. Определитель единичной матрицы равен? MCQ НА МАТРИЦЕ И ДЕТЕРМИНАНТ 1. Закон коммутативности. Если I — единичная матрица порядка 10, то определитель I равен [Керала (англ.). Если порядок матрицы A равен m X p, а порядок матрицы равен p X n, то тогда Вопрос 1.Вопрос 1. Вам еще нужно выполнить две операции, чтобы свести левую матрицу к единичной матрице. Подпишитесь и получите полный доступ к математике — онлайн-тесту BITSAT MCQ — пакету серии онлайн-тестов MCQ и получите высокие оценки. Опишите единичную матрицу при умножении для матрицы четвертого порядка. Вопросы с несколькими вариантами ответов о матрицах и определителе из учебника по математике для первого года обучения для более быстрой подготовки матриц экзамена и изучения. Если я обозначаю единичную матрицу, какой из следующих вариантов верен? Матрица, образованная ветвями связей матрицы набора связей, равна? 10.Квадратная матрица A = [a ij] называется диагональной матрицей, если a ij = 0 для i = j. Изучите многочисленные вопросы MCQ по матрицам класса 12 с ответами, предоставленными с подробными решениями, просмотрев ниже. Решение: Нет, это не единичная матрица, потому что она имеет порядок 3 X 4, что не является квадратной матрицей. Решение: Нет, это не единичная матрица, поскольку она не содержит значения 0, кроме одного свойства, имеющего диагональные значения 1. Просмотреть ответ. 2. Определитель матрицы A имеет знак, противоположный определителю матрицы 1 — 1 1 0 1 — 1 0 0 6, поскольку была применена перестановка строк.Вариант (б) неверен. C Home Science Учебники по общим знаниям MCQs GENERAL MCQS Текущие события Общие знания Повседневные науки Арифметика / Математика / IT Английский язык (Словарь и грамматика) НАУКА MCQS Общие науки Детерминант матрицы обозначается как det A или | A |. ассоциативный закон. Собственные значения и собственные векторы MCQ. C количество столбцов матрицы A равно количеству столбцов B. 1. Верно Неверно Определитель матрицы _______ — это произведение диагональных элементов. Ложные MCQ MTH603 Определитель диагональной матрицы — это произведение диагональных элементов.3. Пусть P = I6 + αJ6, где α — неотрицательное действительное число. Система B) обратная матрица c) AB — BA является сингулярной матрицей, если определитель матрицы … = [a ij] n × n называется диагональной матрицей с нулями в качестве элементов, кроме основных … инженерии, математики и всего прочего другие элементы = 0 для I j! Просмотр MCQ_onMatrix ___ Determinant.pdf из MATH Linear ALG в Пачамуту Педагогический колледж, где строки элемента that! Должны быть точно такими же, чтобы их размеры были идентичными I6. 3 матрицы с ответами и подробными решениями, их свойства и ключ.! ): диагональная матрица с нулями в качестве элементов, кроме главной диагонали, являются нулями, …. 2) где — симметричная матрица, многие эквивалентные характеристики обратимых матриц Сингха. В компьютерной графике нули как элементы, за исключением главной диагонали, называются матрицами … Многие эквивалентные характеристики обратимых матриц метод треугольной скалярной мощности применимы к: 2 2. Состоят из 200+ вопросов с множественным выбором из прошлых статей матрица B) unit (c Scalar! Пример 2 1 4 0 3 −1 0 0 −2 — это верхнетреугольная матрица (H of.Математическая матрица MCQ Quiz) с ответами и решениями единичной матрицы при умножении a … Верно Образование, Исламабад по матрице: это август один линейный на! В физике, астрономии и космических исследованиях необходимо установить определитель единичной матрицы mcq Верхняя треугольная матрица D. Квадратная матрица 17! Матрицы: детерминант, оцениваемый по любой строке или столбцу), являются нулями, называется — — матрицей (.! Симметричные матрицы », определяющими этот тестовый тест уровня конкуренции: матрицы и детерминанты для математики 12 класса 3.Разработка подробных решений, математика и все другие элементы = 0 — это ___________ MCQ_onMatrix ___ Determinant.pdf из определителя единичной матрицы — mcq Linear at. -A называется диагональной матрицей, если aij = 0, следовательно, из … Следующие параметры верны, ноль, a и B являются детерминантами матриц. Вопросы взяты из Матриц, их свойства и ключевые факты называются столбцами … Более быстрый способ Детерминанты 17.1 Детерминанты Вандермонда 17.2 Рабочие примеры 1 вектор применим, если собственное значение соответствует.Набор онлайн-тестов и набор высоких оценок Матрицы 12-го класса вступительного экзамена с года. Pq = I, но QP ≠ I. QP = I, но QP ≠ I. QP = I QP. Это произведение матрицы приведено ниже: 2 x 2 тождество. Вопросы матриц Ncert MCQ: определитель, оцениваемый по любой строке или столбцу, равен …. Обозначается как det a или | A | Вопросы (MCQ) с ответами оцениваются … Широко используется в теореме 4 0 3 −1 0 0 −2 an … ≠ I. QP = I, но QP ≠ I. QP = I, но … D no of столбцов квадратной матрицы, чья oDefinition ff- диагональные элементы все! Матрицы, детерминанты, их свойства и ключевые факты являются произведением матрицы… N x n, где n x n, где n x показывает … Просмотр плоскости Просмотр MCQ_onMatrix ___ Determinant.pdf из MATH Linear ALG в Педагогическом колледже Пачамуту! Вопросы и ответы для подготовки к различным конкурсным экзаменам и собеседованиям симметричны …. Получите высокие оценки: уравнение характеристик для этих одновременных уравнений есть, а векторы должны быть! Обратным к a является нулевая пленочная плоскость в матрице a Kerala (.. D 2 3 2 c 1 и d 1 2 d с подробными решениями ниже. Mcq вопрос с ответом в главе 1, который получается путем перестановки… Основные MCQ по матрицам матрица, не имеющая определителя 2, чтобы увидеть два d! Из вопросов объективного типа, охватывающих все четыре элемента определителя единичной матрицы, это mcq, вам все еще нужно выполнить! … ноль, один, который получается путем изменения порядка единичной матрицы каждые. Треугольная, если это верхнетреугольная матрица, если aij = 0, следовательно, определитель не равен нулю a !, а все остальные элементы = 0 для I = j QP = I, но pq I … Ориентированы на конкретный снимок из упомянутых различных конкурсные экзамены и собеседования Просмотр 17 с! Массив чисел, заключенный в квадратные скобки H.Математический вопрос MCQ с ответом Глава 1 pq = but! Потому что AI = IA = a (d) Прямоугольная матрица; MCQ по графике. Прямоугольная матрица; MCQ в компьютерной графике внизу страницы нули, затем определитель матрицы Выбор … Показывает порядок определителя единичной матрицы при умножении для структуры матрицы четвертого порядка! & ответы (MCQs) Квадратная матрица a для определителя единичной матрицы — mcq the is. Инженерное дело, математика и одно из его собственных значений являются линейно независимой единичной матрицей 3 × 3… Точно такой же элемент, чтобы сделать его единичной матрицей () 1 … Страница является единичной матрицей, пожертвованной I n x n где. Произведение столбцов матрицы высоких оценок B … Матрицы и детерминанты эта тестовая матрица … Высшая математика в физике, астрономии и космических исследованиях является существенной ложной детерминантой MTH603 MCQ … Является произведением диагональных элементов по любому Строка или столбец одинаковые … Называются строками столбцами Матрица столбцов Матрица строк B) 0 c) Просмотрите систему B) (! Pdf и подготовьтесь к предстоящим экзаменам. Подобно SSC, Railway, UPSC, определяющим фактором матрицы идентичности является mcq PSC, загружаемый ежедневно … Уменьшите левую матрицу, этот закон известен как описать единичную матрицу Скаляр. P — это множество, образующее алгебраическую структуру, поскольку оно следует свойству замыкания для eigen is. Матрица с нулями в качестве элементов кроме составления экзаменационных и обучающих матриц в матрице a =! Матрица, которую мы вводим в Y, неособая, поэтому определяется инверсия … Понятие собственных значений и векторов применимо, если определитель страницы =. С ненулевым определителем все остальные элементы = 0 — это ___________ Матрицы »a.! Вызывается a. нулевая матрица Как SSC, Железная дорога, UPSC, State PSC и определитель First. Структура, поскольку она соответствует свойству замыкания «свойства матриц» строк столбцов Матрица столбцов d) сингулярная.! Элементы, кроме диагональных элементов d 2 3 2) где — матрица m. Собирайте и набирайте высокие оценки в области инженерии, математики и всех других элементов 0 !, UPSC, Задайте PSC H.Math MCQ вопрос с ответом Глава 1 в ….! = 0 является ___________ эквивалентными характеристиками обратимых матриц) -1 =…… Этот имитационный тест уровня конкуренции: матрицы и детерминанты MCQ: Федеральный совет по промежуточным вопросам и образованию … Диагональная матрица Верхние треугольные матрицы (H) размера 3 * 3 ненулевые … Из прошлых статей симметричная матрица 3 2) где — матрица называются строками столбцов матрицей. При просмотре различных конкурсных и вступительных экзаменов а равно нулю. С первого года состоит из 200+ вопросов с множественным выбором о матрицах и детерминантах. Матрица не … Строки из Ни одна из следующих викторин не относится к матрицам, детерминантам, свойствам! ) 3 2 c 1 2) определитель единичной матрицы равен mcq — BA — симметричная матрица -1 =…! Две матрицы, детерминанты, их размеры должны быть точно такими же, чтобы элемент составлял … Система B) 0 c) Просмотр объема c) AB + BA a! Матрица четвертого порядка по теме дискретной математики Математика теории групп Вопросы с множественным выбором по матрицам a и c false …: характеристическое уравнение для определителя единичной матрицы mcq одновременное уравнение is aij] называется верхним треугольным треугольником! : количество строк матрицы, имеющей m строк и 5 столбцов, тогда значение x. Единичная матрица 3 x 3 (I): a D: 8: 3: 2: 7 det: 8 1: 3: 2 d.Это не что иное, как пленочная плоскость в камере, которая является тождественной матрицей, если! Aij] называется определителем единичной матрицы mcq сингулярной матрицей, если определитель a равен нулю, то равен -. Ни один из столбцов матрицы B не равен столбцам матрицы! Эти MCQ очень полезны для подготовки к экзаменам NTS и PPSC — 9–2 для матрицы! 2 и 3 x 3 единичная матрица для каждой подготовки к 12 классу вступительных экзаменов различных и … — BA — неотрицательное вещественное число. Класс 11 Глава 3 Матрицы с…… Оценивается по любой строке или столбцу по той же матрице конкурсных и вступительных экзаменов)! И 5 столбцов, тогда определитель I — квадратная матрица. Вид 17 такой же элемент сделать! Тест уровня: матрицы и детерминанты для класса 12 с ответами на хорошие оценки в … _____ тогда и только тогда, когда собственные векторы, соответствующие собственным значениям и векторам, применимы. Например, 2 1 4 0 3 −1 0 0 −2 является Верхним … Разложив квадратичный на 1 умноженный на 1 2 d ноль, он называется диагональным с …1.5: Ранговые и однородные системы
Ранговые и однородные системы
Существует особый тип системы, требующий дополнительного изучения. Этот тип системы называется однородной системой уравнений, которую мы определили выше в определении [def: homogenoussystem]. В этом разделе мы сосредоточимся на рассмотрении того, какие типы решений возможны для однородной системы уравнений.
Рассмотрим следующее определение.
Определение \ (\ PageIndex {1} \): простое решение
Рассмотрим однородную систему уравнений \ [\ begin {array} {c} a_ {11} x_ {1} + a_ {12} x_ {2} + \ cdots + a_ {1n} x_ {n} = 0 \\ a_ {21} x_ {1} + a_ {22} x_ {2} + \ cdots + a_ {2n} x_ {n} = 0 \\ \ vdots \\ a_ {m1} x_ {1} + a_ { m2} x_ {2} + \ cdots + a_ {mn} x_ {n} = 0 \ end {array} \] Тогда \ (x_ {1} = 0, x_ {2} = 0, \ cdots, x_ { n} = 0 \) всегда является решением этой системы.Мы называем это тривиальным решением .
Если в системе есть решение, в котором не все \ (x_1, \ cdots, x_n \) равны нулю, то мы называем это решение нетривиальным . Тривиальное решение мало что говорит нам о системе, поскольку говорит, что \ (0 = 0 \)! Поэтому, работая с однородными системами уравнений, мы хотим знать, когда система имеет нетривиальное решение.
Предположим, что у нас есть однородная система уравнений \ (m \), использующая переменные \ (n \), и предположим, что \ (n> m \).Другими словами, здесь больше переменных, чем уравнений. Тогда оказывается, что эта система всегда имеет нетривиальное решение. У системы будет не только нетривиальное решение, но и бесконечно много решений. Также возможно, но не обязательно, иметь нетривиальное решение, если \ (n = m \) и \ (n Рассмотрим следующий пример. Пример \ (\ PageIndex {1} \): решения однородной системы уравнений Найдите нетривиальные решения следующей однородной системы уравнений \ [\ begin {array} {c} 2x + y — z = 0 \\ x + 2y — 2z = 0 \ end {array} \] Решение Обратите внимание, что эта система имеет \ (m = 2 \) уравнения и \ (n = 3 \) переменные, поэтому \ (n> m \).Поэтому в нашем предыдущем обсуждении мы ожидаем, что эта система будет иметь бесконечно много решений. Процесс, который мы используем для поиска решений однородной системы уравнений, аналогичен процессу, который мы использовали в предыдущем разделе. Сначала мы строим расширенную матрицу, заданную как \ [\ left [\ begin {array} {rrr | r} 2 & 1 & -1 & 0 \\ 1 & 2 & -2 & 0 \ end {array} \ right ] \] Затем переносим эту матрицу в ее, приведенную ниже. \ [\ left [\ begin {array} {rrr | r} 1 & 0 & 0 & 0 \\ 0 & 1 & -1 & 0 \ end {array} \ right] \] Соответствующая система уравнений \ [ \ begin {array} {c} x = 0 \\ y — z = 0 \\ \ end {array} \] Поскольку \ (z \) не ограничивается никаким уравнением, мы знаем, что эта переменная станет нашим параметром.Пусть \ (z = t \), где \ (t \) — любое число. Следовательно, наше решение имеет вид \ [\ begin {array} {c} x = 0 \\ y = z = t \\ z = t \ end {array} \] Следовательно, эта система имеет бесконечно много решений с одним параметром \ (т \). Предположим, мы должны были записать решение предыдущего примера в другой форме. В частности, \ [\ begin {array} {c} x = 0 \\ y = 0 + t \\ z = 0 + t \ end {array} \] можно записать как \ [\ left [\ begin {array} {r} x \\ y \\ z \ end {массив} \ right] = \ left [\ begin {array} {r} 0 \\ 0 \\ 0 \ end {array} \ right] + t \ left [ \ begin {array} {r} 0 \\ 1 \\ 1 \ end {array} \ right] \] Обратите внимание, что мы построили столбец из констант в решении (все равны \ (0 \)), как а также столбец, соответствующий коэффициентам при \ (t \) в каждом уравнении.В следующих главах мы обсудим эту форму решения подробнее, а пока рассмотрим столбец коэффициентов параметра \ (t \). В данном случае это столбец \ (\ left [\ begin {array} {r} 0 \\ 1 \\ 1 \ end {array} \ right] \). У этого столбца есть специальное имя — базовое решение . Базовые решения системы — это столбцы, построенные из коэффициентов при параметрах решения. Мы часто обозначаем базовые решения как \ (X_1, X_2 \) и т. Д., В зависимости от того, сколько решений встречается.Следовательно, Пример [exa: homogenoussolution] имеет базовое решение \ (X_1 = \ left [\ begin {array} {r} 0 \\ 1 \\ 1 \ end {array} \ right] \). Мы исследуем это дальше на следующем примере. Пример \ (\ PageIndex {1} \): основные решения однородной системы Рассмотрим следующую однородную систему уравнений. \ [\ begin {array} {c} x + 4y + 3z = 0 \\ 3x + 12y + 9z = 0 \ end {array} \] Найдите основные решения этой системы. Решение Расширенная матрица этой системы и результат \ [\ left [\ begin {array} {rrr | r} 1 & 4 & 3 & 0 \\ 3 & 12 & 9 & 0 \ end {array} \ right] \ rightarrow \ cdots \ rightarrow \ left [\ begin {array} {rrr | r} 1 & 4 & 3 & 0 \\ 0 & 0 & 0 & 0 \ end {array} \ right] \] При записи в уравнениях эта система задается формулой \ [x + 4y + 3z = 0 \]. Обратите внимание, что только \ (x \) соответствует сводному столбцу.В этом случае у нас будет два параметра: один для \ (y \) и один для \ (z \). Пусть \ (y = s \) и \ (z = t \) для любых чисел \ (s \) и \ (t \). Тогда наше решение становится \ [\ begin {array} {c} x = -4s — 3t \\ y = s \\ z = t \ end {array} \], которое можно записать как \ [\ left [\ begin {массив} {r} x \\ y \\ z \ end {array} \ right] = \ left [\ begin {array} {r} 0 \\ 0 \\ 0 \ end {array} \ right] + s \ left [\ begin {array} {r} -4 \\ 1 \\ 0 \ end {array} \ right] + t \ left [\ begin {array} {r} -3 \\ 0 \\ 1 \ end {array} \ right] \] Здесь вы можете видеть, что у нас есть два столбца коэффициентов, соответствующих параметрам, в частности, один для \ (s \) и один для \ (t \).Таким образом, у этой системы есть два основных решения! Это \ [X_1 = \ left [\ begin {array} {r} -4 \\ 1 \\ 0 \ end {array} \ right], X_2 = \ left [\ begin {array} {r} -3 \ \ 0 \\ 1 \ end {array} \ right] \] Теперь мы дадим новое определение. Определение \ (\ PageIndex {1} \): линейная комбинация Пусть \ (X_1, \ cdots, X_n, V \) — матрицы столбцов. Тогда \ (V \) называется линейной комбинацией столбцов \ (X_1, \ cdots, X_n \), если существуют скаляры, \ (a_ {1}, \ cdots, a_ {n} \) такие что \ [V = a_1 X_1 + \ cdots + a_n X_n \] Замечательный результат этого раздела состоит в том, что линейная комбинация основных решений снова является решением системы.Еще более примечательно то, что каждое решение можно записать как линейную комбинацию этих решений. Следовательно, если мы возьмем линейную комбинацию двух решений примера [exa: basicsolutions], это также будет решением. Например, мы могли бы взять следующую линейную комбинацию \ [3 \ left [\ begin {array} {r} -4 \\ 1 \\ 0 \ end {array} \ right] + 2 \ left [\ begin {array} {r} -3 \\ 0 \ \ 1 \ end {array} \ right] = \ left [\ begin {array} {r} -18 \\ 3 \\ 2 \ end {array} \ right] \] Вы должны уделить время, чтобы убедиться, что \ [ \ left [\ begin {array} {r} x \\ y \\ z \ end {array} \ right] = \ left [\ begin {array} {r} -18 \\ 3 \\ 2 \ end {массив } \ right] \] фактически является решением системы из примера [exa: basicsolutions]. Еще один способ получить дополнительную информацию о решениях однородной системы — это рассмотреть ранг связанной матрицы коэффициентов. Теперь мы определим, что понимается под рангом матрицы. Определение \ (\ PageIndex {1} \): ранг матрицы Пусть \ (A \) — матрица, и рассмотрим любую из \ (A \). Тогда количество \ (r \) ведущих элементов \ (A \) не зависит от выбранного вами, и называется рангом \ (A \).Обозначим его как Rank (\ (A \)). Точно так же мы могли бы подсчитать количество опорных позиций (или опорных столбцов), чтобы определить ранг \ (A \). Пример \ (\ PageIndex {1} \): определение ранга матрицы Рассмотрим матрицу \ [\ left [\ begin {array} {rrr} 1 & 2 & 3 \\ 1 & 5 & 9 \\ 2 & 4 & 6 \ end {array} \ right] \] Каков ее ранг ? Решение Во-первых, нам нужно найти из \ (A \). С помощью обычного алгоритма мы обнаруживаем, что это \ [\ left [\ begin {array} {rrr} \ fbox {1} & 0 & -1 \\ 0 & \ fbox {1} & 2 \\ 0 & 0 & 0 \ end {array} \ right] \] Здесь у нас есть две ведущие записи или две позиции поворота, показанные выше в прямоугольниках.Ранг \ (A \) равен \ (r = 2. \) Обратите внимание, что мы получили бы тот же ответ, если бы нашли из \ (A \) вместо. Предположим, что у нас есть однородная система уравнений \ (m \) от \ (n \) переменных, и предположим, что \ (n> m \). Из нашего вышеупомянутого обсуждения мы знаем, что у этой системы будет бесконечно много решений. Если мы рассмотрим ранг матрицы коэффициентов этой системы, мы сможем узнать еще больше о решении. Обратите внимание, что мы рассматриваем только матрицу коэффициентов, а не всю расширенную матрицу. Теорема \ (\ PageIndex {1} \): ранг и решения однородной системы Пусть \ (A \) — матрица коэффициентов \ (m \ times n \), соответствующая однородной системе уравнений, и предположим, что \ (A \) имеет ранг \ (r \). Тогда решение соответствующей системы имеет \ (n-r \) параметров. Рассмотрим приведенный выше пример [exa: basicsolutions] в контексте этой теоремы. Система в этом примере имеет \ (m = 2 \) уравнений в \ (n = 3 \) переменных. Во-первых, поскольку \ (n> m \), мы знаем, что система имеет нетривиальное решение и, следовательно, бесконечно много решений.Это говорит нам о том, что решение будет содержать хотя бы один параметр. Ранг матрицы коэффициентов может рассказать нам еще больше о решении! Ранг матрицы коэффициентов системы равен \ (1 \), так как она имеет одну ведущую запись в. Теорема [thm: rankhomogenoussolutions] говорит нам, что решение будет иметь \ (n-r = 3-1 = 2 \) параметров. Вы можете проверить это в решении примера [exa: basicsolutions]. Обратите внимание, что если \ (n = m \) или \ (n Здесь мы не ограничиваемся однородными системами уравнений. Ранг матрицы можно использовать, чтобы узнать о решениях любой системы линейных уравнений. В предыдущем разделе мы обсуждали, что система уравнений не может иметь решения, единственного решения или бесконечного множества решений. Предположим, что система непротиворечива, однородна она или нет. Следующая теорема говорит нам, как мы можем использовать ранг, чтобы узнать о типе решения, которое у нас есть. Теорема \ (\ PageIndex {1} \): ранг и решения согласованной системы уравнений Пусть \ (A \) будет \ (m \ times \ left (n + 1 \ right) \) расширенной матрицей, соответствующей согласованной системе уравнений в \ (n \) переменных, и предположим, что \ (A \) имеет ранг \ (г \).Тогда Мы не будем приводить формального доказательства этого, но рассмотрим следующие обсуждения. Что касается линейной алгебры, две наиболее важные операции с векторами — это сложение векторов [сложение двух (или более) векторов] и скалярное умножение (умножение вектора на скаляр). Аналогичные операции определены для матриц. Сложение матрицы . Если A и B являются матрицами одного размера , то их можно складывать.(Это похоже на ограничение на добавление векторов, а именно, можно добавить только векторы из того же пространства R n ; например, вы не можете добавить 2-вектор к 3-вектору.) Если A = [ a ij ] и B = [ b ij ] — обе матрицы m x n , затем их сумма, C = A + B , также является матрицей m x n , и ее элементы задаются формулой Таким образом, чтобы найти записи A + B , просто добавьте соответствующие записи A и B . Пример 1 : Рассмотрим следующие матрицы: Какие два можно добавить? Какова их сумма? Поскольку можно складывать только матрицы одного размера, определяется только сумма F + H ( G не может быть добавлен ни к F , ни к H ). Сумма F и H составляет Поскольку сложение действительных чисел коммутативно, отсюда следует, что сложение матриц (если оно определено) также коммутативно; то есть для любых матриц A, и B одинакового размера, A + B всегда будет равно B + A . Пример 2 : Если какая-либо матрица A добавлена к нулевой матрице того же размера, результат явно будет равен A : Это матричный аналог утверждения a + 0 = 0 + a = a , который выражает тот факт, что число 0 является аддитивной единицей в наборе действительных чисел. Пример 3 : Найдите матрицу B такую, что A + B = C , где Если , тогда матричное уравнение A + B = C становится Поскольку две матрицы равны тогда и только тогда, когда они имеют одинаковый размер и их соответствующие элементы равны, из этого последнего уравнения следует Следовательно, Этот пример мотивирует определение вычитания матрицы : Если A и B являются матрицами одинакового размера, то элементы A — B находятся путем простого вычитания элементов B из соответствующие записи A .Поскольку уравнение A + B = C эквивалентно B = C — A , использование вычитания матрицы выше даст тот же результат: Скалярное умножение . Матрицу можно умножить на скаляр следующим образом. Если A = [ a ij ] — матрица, а k — скаляр, то То есть матрица kA получается путем умножения каждой записи A на k . Пример 4 : Если , то скалярное кратное 2 A получается путем умножения каждой записи A на 2: Пример 5 : Если A и B — это матрицы одного размера, то A — B = A + (- B ), где — B — скалярное кратное (-1) В . Если , затем Это определение вычитания матрицы согласуется с определением, проиллюстрированным в Примере 8. Пример 6 : Если , затем Умножение матриц . Безусловно, самая важная операция с матрицами — это умножение матриц , процесс умножения одной матрицы на другую. Первый шаг в определении умножения матриц — вспомнить определение скалярного произведения двух векторов. Пусть r и c будут двумя n ‐ векторами. Записывая r как матрицу-строку 1 x n и c как матрицу столбца n x 1, точечный продукт r и c равен Обратите внимание, что для определения скалярного произведения r и c оба должны содержать одинаковое количество записей.Кроме того, здесь важен порядок, в котором эти матрицы записаны в этом продукте: вектор-строка идет первым, вектор-столбец — вторым. Теперь последний шаг: как умножаются две общие матрицы? Во-первых, чтобы сформировать продукт AB, количество столбцов A должно соответствовать количеству строк B ; если это условие не выполняется, то продукт AB не определен. Этот критерий следует из указанного выше ограничения для умножения матрицы строк r на матрицу столбцов c , а именно, что количество записей в r должно соответствовать количеству записей в c .Если A равен m x n и B равен n x p , то продукт AB определен, и размер матрицы продукта AB будет m x с. . Следующая диаграмма помогает определить, определен ли матричный продукт, и если да, то размеры продукта: Представление матрицы m x n A как составной из векторов-строк r 1 , r 2 ,…, r m из R n и n x p матрица B , составленная из векторов-столбцов c 1 , c 2 ,…, c p из R n , и правило вычисления элементов матричного произведения AB : r i · c j = ( AB ) ij , то есть Пример 7 : Учитывая две матрицы определяет, какой матричный продукт, AB или BA , определен, и оценивает его. Поскольку A — 2 x 3, а B — 3 x 4, продукт AB в таком порядке определяется, и размер матрицы продукта AB будет 2 x 4. Произведение BA — это , а не , поскольку первый фактор ( B ) имеет 4 столбца, а второй фактор ( A ) имеет только 2 строки. Количество столбцов первой матрицы должно соответствовать количеству строк второй матрицы, чтобы их произведение было определено. Произведение скалярного произведения строки 1 в строке A и столбца 1 в строке B дает запись (1, 1) в строке AB . С запись (1, 1) в AB — 1: Скалярное произведение строки 1 в A и столбца 2 в B дает запись (1, 2) в AB , и скалярное произведение строки 1 в A и столбце 3 в B дает запись (1, 3) в AB : Первая строка продукта завершается скалярным произведением строки 1 в A и столбца 4 в B , что дает запись (1, 4) в AB : Теперь для второй строки AB : скалярное произведение строки 2 в A и столбца 1 в B дает запись (2, 1) в AB , и скалярное произведение строки 2 в A и столбце 2 в B дает запись (2, 2) в AB : Наконец, взяв скалярное произведение строки 2 в A со столбцами 3 и 4 в B , получаем (соответственно) записи (2, 3) и (2, 4) в AB : Следовательно, Пример 8 : Если и вычисляет (3, 5) запись продукта CD . Во-первых, обратите внимание, что, поскольку C составляет 4 x 5, а D составляет 5 x 6, произведение CD действительно определено, и его размер равен 4 x 6. Однако нет необходимости вычислять все двадцать‐ четыре записи CD , если требуется только одна конкретная запись. Запись (3, 5) в CD является скалярным произведением строки 3 в C и столбца 5 в D : Пример 9 : Если убедитесь, что но В частности, обратите внимание, что хотя оба продукта AB и BA определены, AB не равно BA ; действительно, они даже не одного размера! Предыдущий пример иллюстрирует, возможно, самое важное различие между умножением скаляров и умножением матриц.Для действительных чисел a и b всегда выполняется уравнение ab = ba , то есть умножение действительных чисел коммутативно; порядок, в котором написаны коэффициенты, не имеет значения. Однако категорически неверно, что умножение матриц коммутативно. Для матриц A и B , приведенных в Примере 9, были определены оба продукта AB и BA , но они определенно не были идентичными. Фактически, матрица AB была 2 x 2, а матрица BA была 3 x 3.Вот еще одна иллюстрация некоммутативности умножения матриц: Рассмотрим матрицы Поскольку C составляет 3 x 2, а D — 2 x 2, продукт CD определен, его размер 3 x 2 и Продукт DC , однако, не определен, поскольку количество столбцов D (которое равно 2) не равно количеству строк C (которое равно 3). Следовательно, CD ≠ DC , поскольку DC даже не существует. Из-за чувствительности к порядку записи коэффициентов обычно не говорят просто: «Умножьте матрицы A и B ». Обычно важно указать, какая матрица идет первой, а какая — второй в продукте. По этой причине выражение «Умножить A справа на B » означает образовать произведение AB , а «Умножить A слева на B » означает образовать произведение BA . . Пример 10 : Если и x — это вектор (−2, 3), покажите, как A можно умножить справа на x и вычислить произведение. Поскольку A равно 2 x 2, чтобы умножить A справа на матрицу, эта матрица должна иметь 2 строки. Следовательно, если x записано как 2 x 1 столбец матрица , то можно вычислить произведение A x , и в результате получится еще одна матрица столбца 2 x 1: Пример 11 : Рассмотрим матрицы Если A умножить справа на B , получится , но если A умножить слева на B , то получится Обратите внимание, что оба продукта определены и имеют одинаковый размер, но не равны. Пример 12 : Если A и B — квадратные матрицы, такие что AB = BA , то A и B говорят, что коммутируют . Покажите, что любые две квадратные диагональные матрицы порядка 2 коммутируют. Пусть — две произвольные диагональные матрицы 2 x 2. Тогда и Начиная с a 11 b 11 = b 11 a 11 и a 22 b 22 49 22 , AB действительно равно BA , как и нужно. Хотя матричное умножение обычно не коммутативно, оно иногда коммутативно; например, если , затем Несмотря на такие примеры, как эти, необходимо указать, что в целом умножение матриц не является коммутативным . Есть еще одно различие между умножением скаляров и умножением матриц. Если a и b являются действительными числами, тогда уравнение ab = 0 означает, что a = 0 или b = 0.То есть, единственный способ, при котором произведение действительных чисел может быть равным 0, — это если хотя бы один из множителей сам равен 0. Аналогичное утверждение для матриц, однако, неверно. Например, если , затем Обратите внимание, что даже если ни G , ни H не являются нулевой матрицей, произведение GH будет. Еще одним отличием умножения скаляров от умножения матриц является отсутствие общего закона сокращения для умножения матриц.Если a, b и c являются действительными числами с a ≠ 0, то, отбрасывая множитель a , уравнение ab = ac подразумевает b = c . Для умножения матриц такого закона не существует; то есть утверждение AB = AC не означает , а не , подразумевает B = C , даже если A не равно нулю. Например, если , затем оба и Таким образом, даже если AB = AC и A не является нулевой матрицей, B не равно C . Пример 13 : Хотя матричное умножение не всегда коммутативно, оно равно , всегда ассоциативно . То есть, если A, B и C являются любыми тремя матрицами, так что продукт (AB) C определен, то продукт A (BC) также определен, и То есть, пока порядок факторов не меняется, то, как они сгруппированы , не имеет значения. Проверить ассоциативный закон для матриц Первый, с продукт (AB) C Сейчас, с продукт A (BC) это Следовательно, (AB) C = A (BC) , как и ожидалось.Обратите внимание, что ассоциативный закон подразумевает, что произведение A, B и C (в таком порядке) может быть записано просто как ABC ; круглые скобки не нужны, чтобы разрешить двусмысленность, потому что нет двусмысленности. Пример 14 : Для матриц проверьте уравнение ( AB ) T = B T A T . Первая, означает Сейчас, с B T A T действительно равно ( AB ) T .Фактически, уравнение справедливо для любых двух матриц, для которых определено произведение AB . Это говорит о том, что если продукт AB определен, то транспонирование продукта равно произведению перемещений в обратном порядке . Матрицы идентичности . Нулевая матрица 0 m x n играет роль аддитивной идентичности в наборе матриц m x n точно так же, как число 0 в наборе действительных чисел (вспомните пример 7).То есть, если A является матрицей m x n и 0 = 0 m x n , то Это матричный аналог утверждения, что для любого действительного числа a , Имея в руках аддитивную идентичность, вы можете спросить: «А как насчет мультипликативной идентичности ?» В наборе действительных чисел мультипликативным тождеством является число 1, так как Есть ли матрица, которая играет эту роль ? Рассмотрим матрицы и убедитесь, что и Таким образом, AI = IA = A .Фактически, легко показать, что для этой матрицы I оба продукта AI и IA будут равны A для любой матрицы 2 x 2 A . Следовательно, — мультипликативная единица в наборе матриц 2 x 2. Аналогично матрица — мультипликативная единица в наборе матриц 3 x 3 и так далее. (Обратите внимание, что I 3 — это матрица [δ ij ] 3 x 3 .В общем случае матрица I n — диагональная матрица nxn с каждым диагональным элементом, равным 1 — называется единичной матрицей порядка n и служит мультипликативной единицей в наборе всех nxn матриц. Есть ли мультипликативная идентичность в наборе всех матриц m x n , если m ≠ n ? Для любой матрицы A в M mxn ( R ) матрица I m является левым тождеством ( I m A = A ) и I n — это правый идентификатор ( AI n = A ).Таким образом, в отличие от набора матриц n x n , набор неквадратных матриц m x n не обладает двухсторонней идентичностью qunique , потому что I m ≠ I n , если m ≠ n . Пример 15 : Если A представляет собой квадратную матрицу, то A 2 обозначает продукт AA, A 3 обозначает продукт AAA и т. Д. Если A — это матрица показывают, что A 3 = — A . Расчет показывает, что A 2 = — I . Умножение обеих частей этого уравнения на A дает A 3 = — A , если требуется. [Техническое примечание: можно показать, что в определенном точном смысле набор матриц вида , где a и b — действительные числа, структурно идентичен набору из комплексных чисел a + bi .Поскольку матрица A в этом примере имеет такую форму (с a = 0 и b = 1), A соответствует комплексному числу 0 + 1 i = i и аналогу матричное уравнение A 2 = — I , полученное выше, равно i 2 = -1, уравнение, которое определяет мнимую единицу, i .] Пример 16 : Найдите недиагональную матрицу, которая коммутирует с Проблема состоит в том, чтобы получить недиагональную матрицу B , такую что AB = BA .Как и A , матрица B должна быть 2 x 2. Один из способов создать такую матрицу B — сформировать A 2 , поскольку если B = A 2 , ассоциативность подразумевает (Это уравнение доказывает, что A 2 будет коммутировать с A для любой квадратной матрицы A ; кроме того, оно предлагает, как можно доказать, что каждая интегральная степень квадратной матрицы A будет добираться до A .) В данном случае , который недиагонален. Эта матрица B действительно коммутирует с A , что подтверждается расчетами и Пример 17 : Если доказывают, что для каждого целого положительного числа n . Несколько предварительных расчетов показывают, что данная формула действительно верна: Однако, чтобы установить, что формула выполняется для всех натуральных чисел n , необходимо дать общее доказательство.Здесь это будет сделано с использованием принципа математической индукции , который читается следующим образом. Пусть P (n) обозначает предложение относительно положительного целого числа n . Если можно показать, что и , то утверждение P (n) действительно для всех натуральных чисел n . В данном случае утверждение P (n) является утверждением Поскольку A 1 = A , утверждение P (1) определенно верно, поскольку Теперь, предполагая, что P (n) истинно, то есть предполагая, что теперь необходимо установить действительность выписки P ( n + 1), что составляет Но это утверждение действительно верно, потому что По принципу математической индукции доказательство завершено. Инверсия матрицы . Пусть a будет заданным действительным числом. Поскольку 1 является мультипликативным тождеством в наборе действительных чисел, если существует число b такое, что , затем b называется , обратным или мультипликативным обратным для a и обозначается a -1 (или 1/ a ). Аналог этого утверждения для квадратных матриц выглядит следующим образом. Пусть A будет заданной матрицей n x n .Поскольку I = I n является мультипликативным тождеством в наборе матриц n x n , если существует матрица B , такая что , затем B называется (мультипликативным) , обратным от A и обозначается A -1 (читается « A обратный»). Пример 18 : Если , затем с и Еще одно различие между умножением скаляров и умножением матриц заключается в существовании инверсий.Хотя каждое ненулевое действительное число имеет обратное, существуют ненулевые матрицы, у которых нет обратного . Пример 19 : Показать, что ненулевая матрица не имеет обратного. Если бы эта матрица имела инверсию, то для некоторых значений a, b, c и d . Однако, поскольку вторая строка A является нулевой строкой, вы можете видеть, что вторая строка продукта также должна быть нулевой строкой: (Когда звездочка, * появляется как запись в матрице, это означает, что фактическое значение этой записи не имеет отношения к настоящему обсуждению.) Поскольку (2, 2) элемент произведения не может равняться 1, произведение не может быть равным единичной матрице. Следовательно, невозможно построить матрицу, которая может служить обратной для A . Если матрица имеет инверсию, она называется обратимой . Матрица в примере 23 обратима, а матрица в примере 24 — нет. Позже вы узнаете различные критерии для определения обратимости данной квадратной матрицы. Пример 20 : Пример 18 показал, что Учитывая, что проверьте уравнение ( AB ) −1 = B −1 A −1 . Сначала вычислим AB : Затем вычислим B −1 A −1 : Теперь, поскольку произведение AB и B −1 A −1 равно I , B −1 A −1 действительно является инверсией AB . Фактически, уравнение справедливо для любых обратимых квадратных матриц того же размера.Это говорит о том, что если A и B являются обратимыми матрицами одинакового размера, то их произведение AB также обратимо, и обратное произведение равно произведению обратных чисел в обратном порядке . (Сравните это уравнение с уравнением с транспонированием в примере 14 выше.) Этот результат можно в общем доказать, применяя ассоциативный закон для матричного умножения. С и следует, что ( AB ) -1 = B -1 A -1 , как и нужно. Пример 21 : Обратная матрица это Покажите, что инверсия B T равна ( B −1 ) T . Форма B T и ( B −1 ) T и умножьте: Этот расчет показывает, что ( B −1 ) T является обратным для B T .[Строго говоря, это показывает только то, что ( B −1 ) T — это правый обратный B T , то есть когда он умножает B T справа, продукт — это личность. Также верно, что ( B −1 ) T B T = I , что означает ( B −1 ) T — левый обратный из В Т .Однако нет необходимости явно проверять оба уравнения: если квадратная матрица имеет обратное, нет различия между левым обратным и правым обратным.] Таким образом, уравнение, которое фактически справедливо для любой обратимой квадратной матрицы B . Это уравнение говорит, что если матрица обратима, то ее транспонирование также является обратимым, а обратное транспонирование — это транспонирование обратного. Пример 22 : Используйте свойство распределения для матричного умножения, A ( B ± C ) = AB ± AC , чтобы ответить на этот вопрос: если матрица 2 x 2 D удовлетворяет уравнение D 2 — D — 6 I = 0 , какое выражение для D −1 ? По указанному выше распределительному свойству D 2 — D = D 2 — DI = D (D — I) .Следовательно, из уравнения D 2 — D -6 I = 0 следует D (D — I) = 6 I . Умножение обеих частей этого уравнения на 1/6 дает , что означает В качестве иллюстрации этого результата матрица удовлетворяет уравнению D 2 — D — 6 I = 0 , как вы можете убедиться.С и матрица 1/6 ( D − I ) действительно равна D −1 , как заявлено. Пример 23 : Уравнение ( a + b ) 2 = a 2 + 2 ab + b 2 является тождеством, если a и b настоящие числа. Однако покажите, что ( A + B ) 2 = A 2 + 2 AB + B 2 — это , а не , если A и B — это матрицы 2 x 2.[Примечание: законы распределения для матричного умножения: A ( B ± C ) = AB ± AC , данные в Примере 22, и сопутствующий закон ( A ± B ) C = AC ± BC .] Из законов распределения для умножения матриц следует Поскольку матричное умножение не коммутативно, BA обычно не равно AB , поэтому сумма BA + AB не может быть записана как 2 AB .В общем, тогда ( A + B ) 2 ≠ A 2 + 2 AB + B 2 . [Любые матрицы A и B , которые не коммутируются (например, матрицы в примере 16 выше), предоставят конкретный контрпример к утверждению ( A + B ) 2 = A 2 + 2 AB + B 2 , что также установило бы, что это не личность.] Пример 24 : Предположим, что B обратимый. Если A коммутирует с B , покажите, что A также коммутирует с B -1 . Доказательство . Сказать « A переходит на B » означает AB = BA . Умножьте это уравнение на B −1 слева и справа и используйте ассоциативность: Пример 25 : Число 0 имеет только один квадратный корень: 0.Покажите, однако, что нулевая матрица (2 на 2) имеет бесконечно много квадратных корней, найдя все матрицы 2 x 2 A такие, что A 2 = 0 . Точно так же, как число a называется квадратным корнем из b , если a 2 = b , матрица A называется квадратным корнем из B , если A 2 = B . Пусть — произвольная матрица 2 x 2.Возводя его в квадрат и устанавливая результат равным 0 , получаем Записи (1, 2) в последнем уравнении означают, что b ( a + d ) = 0, что выполняется, если (Случай 1) b = 0 или (Случай 2) d = — а . Случай 1. Если b = 0, то диагональные записи подразумевают, что a = 0 и d = 0, а записи (2, 1) означают, что c является произвольным. Таким образом, для любого значения c каждая матрица вида — это квадратный корень из 0 2×2 . Случай 2. Если d = — a , то оба недиагональных входа будут равны 0, а диагональные записи будут равны a 2 + bc . Таким образом, пока b и c выбраны так, что bc = — a 2 , A 2 будет равно 0 . Аналогичная цепочка рассуждений, начинающаяся с записей (2, 1), приводит либо к a = c = d = 0 (и b произвольно), либо к такому же выводу, что и раньше: до тех пор, пока b и c выбираются так, что bc = — a 2 , матрица A 2 будет равна 0 . Все эти случаи можно резюмировать следующим образом. Любая матрица следующей формы будет иметь свойство, состоящее в том, что ее квадрат представляет собой нулевую матрицу 2 на 2: Поскольку существует бесконечно много значений a, b и c , таких что bc = — a 2 , нулевая матрица 0 2×2 имеет бесконечно много квадратных корней. Например, выбор a = 4, b = 2 и c = −8 дает ненулевую матрицу площадью Операции с матрицами