Матрицы дж равена: Прогрессивные матрицы Равена || Пройти тест онлайн
Прогрессивные матрицы Равена. Большая российская энциклопедия
Психодиагностические технологии
- Области знаний:
- Психодиагностический инструментарий
- Другие наименования:
- Стандартные прогрессивные матрицы; Чёрно-белые прогрессивные матрицы Равена
- Дата создания:
- 1936 год
Прогресси́вные ма́трицы Раве́на (англ. Raven’s Progressive Matrices; Тест Равена; Стандартные прогрессивные матрицы; Чёрно-белые прогрессивные матрицы), психодиагностическая методика, невербальный тест интеллекта, предназначенный для определения уровня умственного развития испытуемых в возрасте от 4,5 до 65 лет и старше. Тест состоит из заданий с недостающим элементом в образце-матрице, расположенных с учётом возрастающей (прогрессивной) трудности. Первая версия Стандартных прогрессивных матриц (Standard Progressive Matrices) разработана в 1936 г. и опубликована в 1938 г. в Великобритании. С 1947 г. также используются Цветные (Coloured Progressive Matrices) и Продвинутые прогрессивные матрицы (Advanced Progressive Matrices).
Матрицы считаются одним из наиболее точных измерений g-фактора, хотя сами разработчики определяют его как тест «наблюдательности и ясности мышления» (Равен. 1997. С. 43). Дж. Равен ставил перед собой задачу создания короткого перцептивного теста, который охватывал бы весь диапазон способностей с детского возраста до старости и мог бы использоваться для людей, не умеющих читать (многие из тестируемых были неграмотными) или даже понимать язык. При всём этом тест должен был быть теоретически обоснованным, однозначно интерпретируемым, простым для проведения в домашних условиях, в школах, где часто пространство было ограничено, и на рабочих местах, где было шумно и мало времени для тестирования.
Тест Равена считают относительно свободным от влияния культуры, поэтому он может применяться на выборках испытуемых с любым языковым и социокультурным составом. Тест является невербальным, поэтому для его выполнения не требуются умения читать и писать. Благодаря своей независимости от языка как для испытуемых, так и для диагноста, тест быстро нашёл применение в вооружённых силах, в первую очередь союзников Великобритании, а затем и в образовательных системах всех стран мира.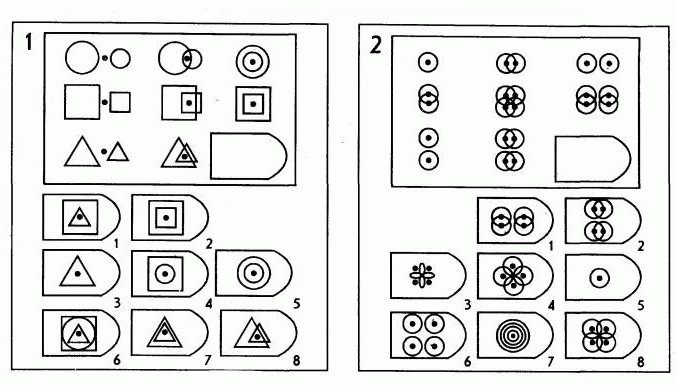 Невербальный характер заданий делает тест популярным в сравнительных кросскультурных исследованиях.
Невербальный характер заданий делает тест популярным в сравнительных кросскультурных исследованиях.
Теоретико-методологический контекст
Теоретическими основаниями теста Равена являются модель интеллекта Ч. Спирмена и идеи гештальтпсихологии. Как ученик Спирмена Равен поддерживал точку зрения о существовании общего интеллекта или g-фактора. В основу теста положены и методологические традиции английской школы изучения интеллекта, согласно которым наилучшим способом измерения g–фактора является определение соотношений между абстрактными фигурами.
Тест также опирается на разработанную в рамках гештальтпсихологии теорию восприятия форм, согласно которой каждое задание может быть рассмотрено как определённое целое, состоящее из ряда взаимосвязанных друг с другом элементов. Гештальтпсихология рассматривает зрительное восприятие как целостный, структурно организованный процесс, и чёткие, но не законченные структуры всегда дополняются, достраиваются до геометрического целого.
Идея образца-матрицы возникла у Дж. Равена из ассоциаций с игрой «крестики-нолики», а принцип прогрессивности в матрицах был реализован следующим образом: а) внутри каждой серии задания расположены с учётом их возрастающей трудности ; б) все серии также различаются возрастающей трудностью, которая повышается от первой серии к последней. Возрастающая трудность заданий определяется увеличением числа элементов в матрице, увеличением числа предлагаемых вариантов решения и усложнением логического принципа, лежащего в основе каждой матрицы.
Циклический формат заданий обеспечивает «научение методу мышления» и таким образом позволяет диагностировать тенденцию учиться через опыт (потенциал обучаемости).
Структура методики, способ проведения, версии
Первой формой Прогрессивных матриц были Стандартные серии. Они разрабатывались с целью охватить весь диапазон интеллектуального развития (от маленьких детей и испытуемых с интеллектуальной недостаточностью до самых успешных взрослых и пожилых).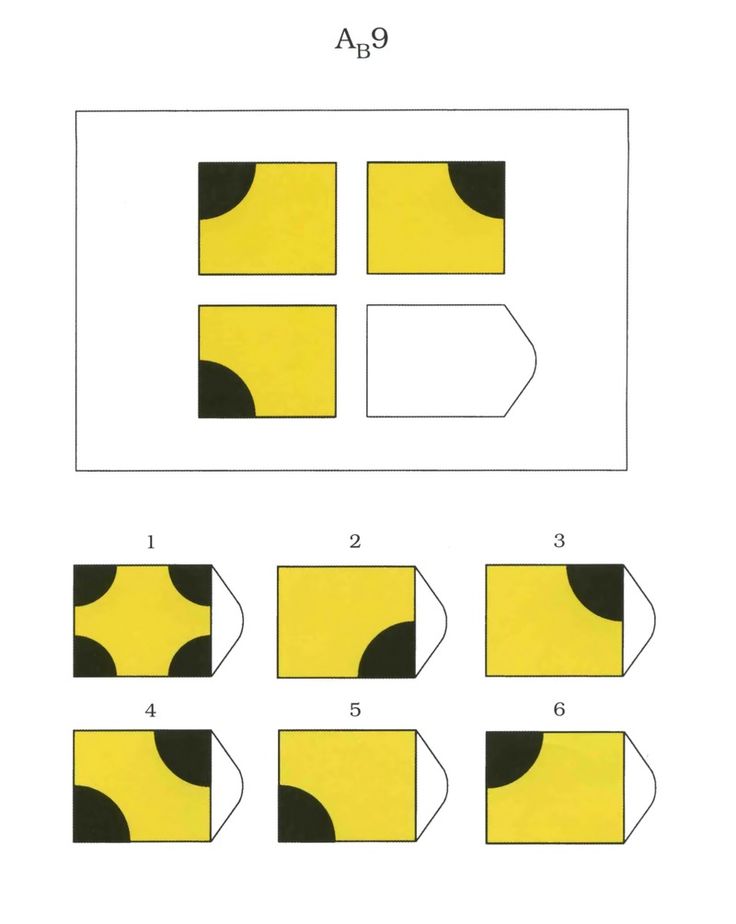 Эти серии впоследствии были расширены, чтобы обеспечить возможность более тщательного анализа способностей, относящихся к нижнему или верхнему уровням диапазона. Для этой цели были сконструированы Продвинутые матрицы (1941) и Цветные матрицы (1947). Цветные матрицы охватывают оценки нижнего квартиля полного диапазона способности, а Продвинутые – верхнего квартиля. Все вместе эти формы теста позволяют решить бо́льшую часть существующих задач тестирования интеллекта. Каждая из серий пересматривалась по несколько раз с применением анализа ответов на задания, чтобы расположить их в верной последовательности. Анализ основывался на траекториях графика, по которым доля респондентов, решивших правильно каждое задание, увеличивалась в соответствии с общим результатом по тесту.
Эти серии впоследствии были расширены, чтобы обеспечить возможность более тщательного анализа способностей, относящихся к нижнему или верхнему уровням диапазона. Для этой цели были сконструированы Продвинутые матрицы (1941) и Цветные матрицы (1947). Цветные матрицы охватывают оценки нижнего квартиля полного диапазона способности, а Продвинутые – верхнего квартиля. Все вместе эти формы теста позволяют решить бо́льшую часть существующих задач тестирования интеллекта. Каждая из серий пересматривалась по несколько раз с применением анализа ответов на задания, чтобы расположить их в верной последовательности. Анализ основывался на траекториях графика, по которым доля респондентов, решивших правильно каждое задание, увеличивалась в соответствии с общим результатом по тесту.
Уникальность Стандартных матриц заключается в том, что они до сих пор используются в почти первозданном виде. В 1947 г. скорректировано задание B 8, а в 1956 г. изменена последовательность некоторых заданий и местоположение вариантов ответов. С тех пор Стандартные матрицы остаются без изменений.
С тех пор Стандартные матрицы остаются без изменений.
В 1998 г. были опубликованы параллельные формы Стандартных и Цветных матриц, а также Стандартные матрицы плюс (SPM +) – модифицированная с целью преодоления эффекта Флинна версия SPM с более сложными заданиями.
Стандартные матрицы состоят из 60 невербальных заданий, упорядоченных с учётом возрастающей трудности. Все задания разделены на 5 серий – А, В, С, D, Е. Тест составлен так, что в начале каждой серии располагаются более лёгкие задания, а в конце – более трудные. В каждом задании в большой рамке содержится образец-матрица, составленный из определённых фигур, при этом часть матрицы остаётся незаполненной. Испытуемый сможет верно найти недостающий фрагмент среди предложенных вариантов в том случае, если поймёт закономерность изменения элементов в матрице.
Тестирование с помощью Прогрессивных матриц можно проводить как в групповой, так и в индивидуальной форме. Основным требованием группового тестирования является строгое соблюдение условий самостоятельности работы каждого испытуемого, исключение подсказок и помех со стороны других тестируемых (списывание ответов-решений, консультирование, отвлекающие разговоры и т.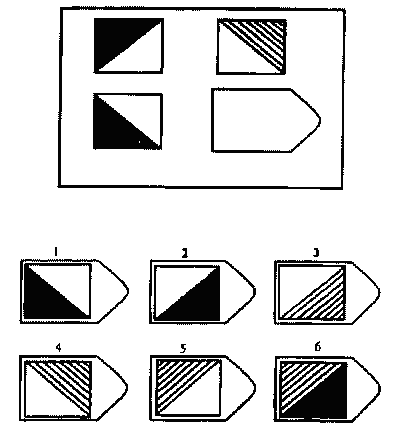 п.).
п.).
Возможно применение Стандартных матриц с ограничением времени выполнения заданий и без временных ограничений. Существует комбинированный способ: задания теста выполняются без ограничения времени, но отмечается, сколько заданий выполнено верно за первые 20 мин. Позиция разработчиков теста однозначна: введение временны́х ограничений дискриминирует людей с медленным стилем мышления и приводит к ненадёжности и невалидности результатов. В Стандартных матрицах плюс время выполнения тестовых заданий принципиально не ограничивается. В исследовании российских психологов Д. Г. Давыдова и Е. В. Чмыховой (2016) проверялось, могут ли результаты тестирования с помощью Стандартных матриц в условиях временно́го ограничения быть сопоставимыми с результатами без лимитирования времени. Корреляционная связь между числом правильно решённых заданий за 20 мин и числом правильно решённых заданий без временного лимита оказалась достаточно сильной (r = 0,70 при p = 0,001).
Тест Равена используют в более чем 100 странах мира.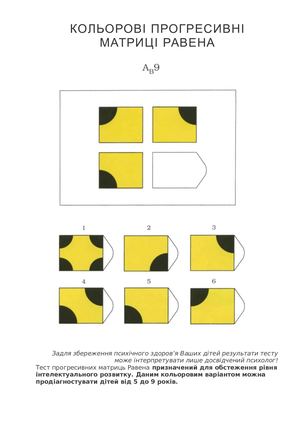 В СССР Стандартные матрицы применяются с конца 1970-х гг., а стандартизация на русскоязычной выборке проведена только в 1981 г.
В СССР Стандартные матрицы применяются с конца 1970-х гг., а стандартизация на русскоязычной выборке проведена только в 1981 г.
Обработка и интерпретация результатов методики
Общая сумма баллов по тесту Равена является показателем интеллектуального развития испытуемого, выявляет его способность мыслить согласно определённому методу, использовать схемы ментальной обработки сложных событий и объектов.
Путём сравнения распределения индивидуальных результатов тестирования по сериям с распределением ожидаемым вычисляется индекс вариабельности. При увеличении индекса до критических значений данные теста считаются ненадёжными и недостоверными (испытуемый может симулировать низкий результат по тесту, демонстрируя несостоятельность в решении самых простых заданий).
Качественный анализ данных тестирования в зависимости от успешности решения заданий определённых серий позволяет оценить развитие отдельных мыслительных операций (анализа, синтеза, сравнения и др.). Содержание заданий теста Равена меняется от простых перцептивных гештальтзаданий, через простые аналогии к заданиям аналитическим, требующим привлечения сложных взаимодействующих стратегий для определения проблемной ситуации, выделения релевантных элементов и способа их взаимосвязи.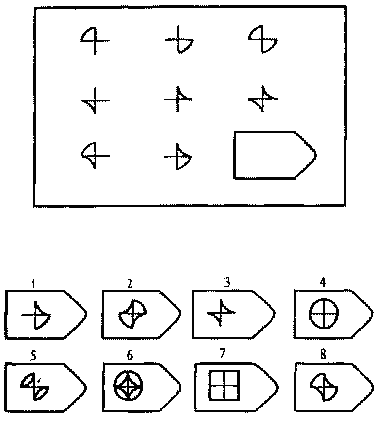 При выполнении теста актуализируются такие когнитивные процессы, как восприятие (зрительный анализ и синтез), внимание (устойчивость, концентрация, распределение и переключение, общая продуктивность), а также проявляются волевые и эмоциональные особенности тестируемого, его настойчивость и работоспособность. При выполнении заданий теста внимание должно поддерживаться познавательным интересом и стремлением к правильному решению.
При выполнении теста актуализируются такие когнитивные процессы, как восприятие (зрительный анализ и синтез), внимание (устойчивость, концентрация, распределение и переключение, общая продуктивность), а также проявляются волевые и эмоциональные особенности тестируемого, его настойчивость и работоспособность. При выполнении заданий теста внимание должно поддерживаться познавательным интересом и стремлением к правильному решению.
Психометрические свойства методики
Неоднократно подтверждались высокие показатели валидности и надёжности теста Равена. Коэффициент корреляции между результатами Стандартных матриц и показателем IQ по тесту WAIS Д. Векслера составляет 0,7–0,74 для взрослых и 0,91 для детей 9–10 лет; арифметическими тестами – 0,74–0,87; шкалами Стэнфорд – Бине – 0,66. Исследования групп, отличающихся по уровню образования и профессии, а также умственно отсталых испытуемых демонстрируют хорошую конструктную валидность теста. Надёжность теста Равена, определяемая методом ретеста, на разных выборках составляет от 0,7 до 0,9.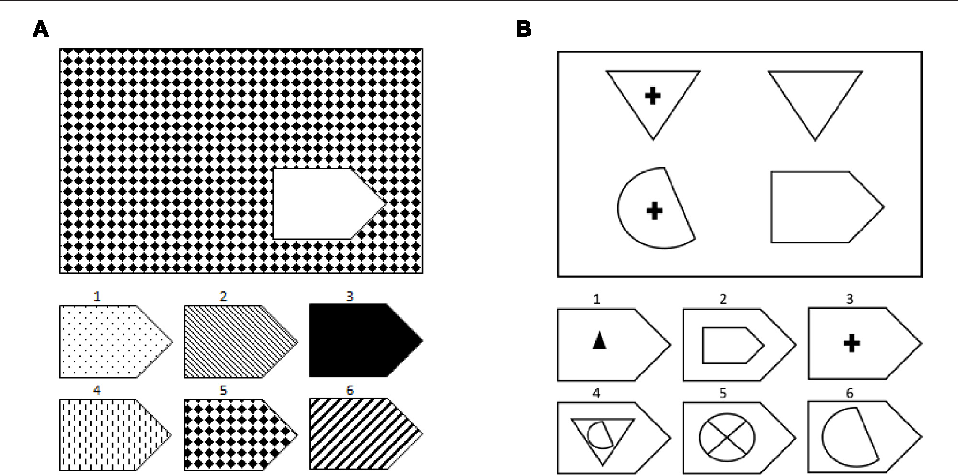 Исследователи фиксируют снижение различительной способности матриц в области высоких значений из-за тенденции роста тестовых показателей (эффекта Флинна).
Исследователи фиксируют снижение различительной способности матриц в области высоких значений из-за тенденции роста тестовых показателей (эффекта Флинна).
Контингент обследуемых, рекомендации и ограничения
Прогрессивные матрицы предназначены для испытуемых в возрасте от 4,5 до 65 лет и старше: Стандартные чёрно-белые – для тестирования лиц от 8 до 65 лет; Цветные – для детей 4,5–9 лет, а также взрослых старше 65 лет либо интеллектуально неполноценных; Продвинутые – для тестирования лиц с интеллектуальными способностями выше среднего.
Сфера адекватного применения и релевантная психодиагностическая задача – это оценка общей способности к систематизированной, планомерной интеллектуальной деятельности. Матрицы могут применяться для обследования людей из различных культур, говорящих на разных языках, с различным уровнем образования (даже совсем неграмотных).
Прогрессивные матрицы подвержены в определённой мере влиянию научения, поэтому не рекомендуется использовать этот тест в диагностических целях многократно на одной и той же выборке испытуемых.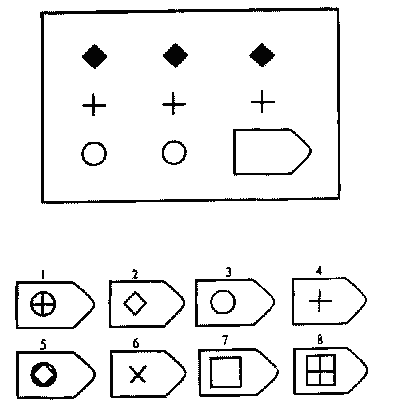
Дата публикации: 20 октября 2022 г. в 22:12 (GMT+3)
ПРОГРЕССИВНЫЕ МАТРИЦЫ РАВЕНА — это что такое ПРОГРЕССИВНЫЕ МАТРИЦЫ РАВЕНА
найдено в «Клинической психологии. Психологическом лексиконе»
Raven Progressive Matrices — тест интеллекта. Предназначен для измерения уровня интеллектуального развития. Предложен Л. Пенроузом и Дж. Равеном в 1936 г. Р. п. м. разрабатывались в соответствии с традициями английской школы изучения интеллекта, согласно которым наилучший способ измерения фактора «g» — задача по выявлению отношений между абстрактными фигурами. Наиболее известны два основных варианта Р. п. м.: черно-белые и цветные матрицы. Черно-белые Р. п. м. предназначены для обследования детей и подростков в возрасте от 8 до 14 лет и взрослых в возрасте от 20 до 65 лет. Цветной более простой вариант предназначен для обследования детей в возрасте от 5 до 11 лет, иногда рекомендуется для лиц старше 65 лет. Материал черно-белого варианта теста состоит из 60 матриц или композиций с пропущенным элементом.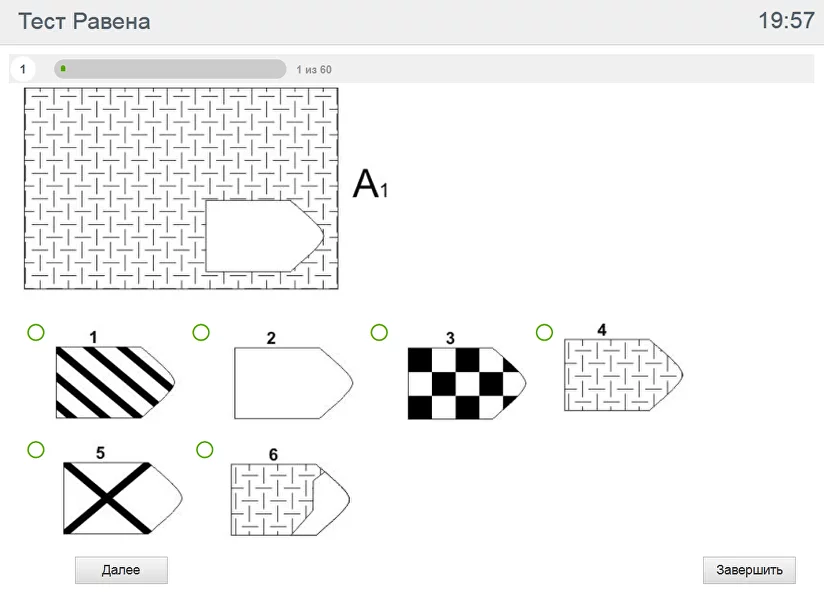 Задания разделены на пять серий (A, B, C, D, E) по 12 однотипных, но возрастающей сложности матриц в каждой серии. Трудность заданий возрастает и при переходе от серии к серии. Обследуемый должен выбрать недостающий элемент матрицы среди 6—8 предложенных вариантов. При необходимости первые 5 заданий серии A обследуемый выполняет с помощью экспериментатора. При разработке теста была сделана попытка реализовать принцип «прогрессивности», заключающийся в том, что выполнение предшествующих заданий и их серий является как бы подготовкой обследуемого к выполнению последующих. Происходит обучение выполнению более трудных заданий (Дж. Равен, 1963; Б. Зимин, 1962). Каждая серия заданий составлена по определенным принципам. Серия A. От обследуемого требуется дополнение недостающей части изображения. Считается, что при работе с матрицами этой серии реализуются следующие основные мыслительные процессы: а) дифференциация основных элементов структуры и раскрытие связей между ними; б) идентификация недостающей части структуры и сличение ее с представленными образцами.
Задания разделены на пять серий (A, B, C, D, E) по 12 однотипных, но возрастающей сложности матриц в каждой серии. Трудность заданий возрастает и при переходе от серии к серии. Обследуемый должен выбрать недостающий элемент матрицы среди 6—8 предложенных вариантов. При необходимости первые 5 заданий серии A обследуемый выполняет с помощью экспериментатора. При разработке теста была сделана попытка реализовать принцип «прогрессивности», заключающийся в том, что выполнение предшествующих заданий и их серий является как бы подготовкой обследуемого к выполнению последующих. Происходит обучение выполнению более трудных заданий (Дж. Равен, 1963; Б. Зимин, 1962). Каждая серия заданий составлена по определенным принципам. Серия A. От обследуемого требуется дополнение недостающей части изображения. Считается, что при работе с матрицами этой серии реализуются следующие основные мыслительные процессы: а) дифференциация основных элементов структуры и раскрытие связей между ними; б) идентификация недостающей части структуры и сличение ее с представленными образцами.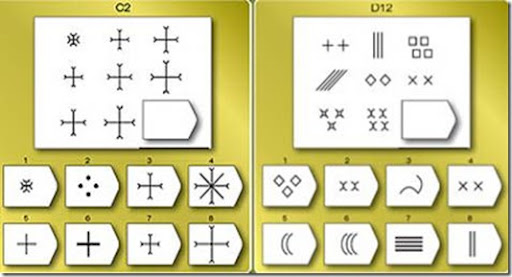 Серия B. Сводится к нахождению аналогии между двумя парами фигур. Обследуемый раскрывает этот принцип путем постепенной дифференциации элементов. Серия C. Задания этой серии содержат сложные изменения фигур в соответствии с принципом их непрерывного развития, обогащения по вертикали и горизонтали. Серия D. Составлена по принципу перестановки фигур в матрице по горизонтальному и вертикальному направлениям. Серия E. Наиболее сложная. Процесс решения заданий этой серии заключается в анализе фигур основного изображения и последующей «сборке» недостающей фигуры по частям (аналитико-синтетическая мыслительная деятельность). Обработка полученных результатов проста. Каждое верное решение оценивается в 1 балл. Подсчитываются общая сумма полученных баллов, а также число правильных решений в каждой из пяти серий. Первичные оценки по таблицам переводятся в соответствии с возрастными нормами в процентили или стэны. Предусмотрена возможность перевода полученных результатов в IQ-показатель стандартный.
Серия B. Сводится к нахождению аналогии между двумя парами фигур. Обследуемый раскрывает этот принцип путем постепенной дифференциации элементов. Серия C. Задания этой серии содержат сложные изменения фигур в соответствии с принципом их непрерывного развития, обогащения по вертикали и горизонтали. Серия D. Составлена по принципу перестановки фигур в матрице по горизонтальному и вертикальному направлениям. Серия E. Наиболее сложная. Процесс решения заданий этой серии заключается в анализе фигур основного изображения и последующей «сборке» недостающей фигуры по частям (аналитико-синтетическая мыслительная деятельность). Обработка полученных результатов проста. Каждое верное решение оценивается в 1 балл. Подсчитываются общая сумма полученных баллов, а также число правильных решений в каждой из пяти серий. Первичные оценки по таблицам переводятся в соответствии с возрастными нормами в процентили или стэны. Предусмотрена возможность перевода полученных результатов в IQ-показатель стандартный. Существенным этапом количественной обработки результатов обследования с помощью Р. п. м. является вычисление «индекса вариабельности». Индекс определяют исходя из таблиц распределения числа правильных решений в каждой из пяти серий. Варианты распределений решений в сериях были получены эмпирическим путем при анализе выполнения теста испытуемыми из выборки стандартизации. Варианты распределения по таблице определяются в соответствии с общей суммой баллов во всех сериях. Напр., при общей оценке в 26 «сырых» баллов оценки по отдельным сериям распределяются следующим образом: A — 10; B — 7; C — 5; D — 3; E — 1. Табличное распределение сравнивают с полученным в конкретном случае, разности ожидаемых и наличных оценок в каждой серии (без учета знака) суммируются. Полученная величина и является «индексом вариабельности». Нормальные значения индекса в пределах 0—4 свидетельствуют о достоверности результата исследования. При увеличении индекса до критических значения (7 и более) данные теста считаются недостоверными.
Существенным этапом количественной обработки результатов обследования с помощью Р. п. м. является вычисление «индекса вариабельности». Индекс определяют исходя из таблиц распределения числа правильных решений в каждой из пяти серий. Варианты распределений решений в сериях были получены эмпирическим путем при анализе выполнения теста испытуемыми из выборки стандартизации. Варианты распределения по таблице определяются в соответствии с общей суммой баллов во всех сериях. Напр., при общей оценке в 26 «сырых» баллов оценки по отдельным сериям распределяются следующим образом: A — 10; B — 7; C — 5; D — 3; E — 1. Табличное распределение сравнивают с полученным в конкретном случае, разности ожидаемых и наличных оценок в каждой серии (без учета знака) суммируются. Полученная величина и является «индексом вариабельности». Нормальные значения индекса в пределах 0—4 свидетельствуют о достоверности результата исследования. При увеличении индекса до критических значения (7 и более) данные теста считаются недостоверными. Сопоставление реального и ожидаемого распределения количества правильных решений в сериях направлено на выявление испытуемых, выполнявших задание путем угадывания. Значение индекса вариабельности может оказаться значительно выше критического в случае установки испытуемого симулировать низкий результат по тесту (демонстрация несостоятельности в решении самых простых задач). Цветной вариант Р. п. м. состоит из трех серий — A, AB, B по 12 матриц в каждой серии. Обработка полученных результатов такая же, как в черно-белом варианте Р. п. м. Оба варианта могут быть использованы как в качестве теста скорости (с ограничением времени выполнения заданий), так и теста результативности (без ограничения времени) (Дж. Равен, 1963). Р. п. м. основываются на двух теориях: разработанной гештальт-психологией теории перцепции форм и т. н. «теории неогенеза» Ч. Спирмена. В соответствии с теорией перцепции форм каждое задание может быть рассмотрено как определенное целое, состоящее из ряда взаимосвязанных друг с другом элементов.
Сопоставление реального и ожидаемого распределения количества правильных решений в сериях направлено на выявление испытуемых, выполнявших задание путем угадывания. Значение индекса вариабельности может оказаться значительно выше критического в случае установки испытуемого симулировать низкий результат по тесту (демонстрация несостоятельности в решении самых простых задач). Цветной вариант Р. п. м. состоит из трех серий — A, AB, B по 12 матриц в каждой серии. Обработка полученных результатов такая же, как в черно-белом варианте Р. п. м. Оба варианта могут быть использованы как в качестве теста скорости (с ограничением времени выполнения заданий), так и теста результативности (без ограничения времени) (Дж. Равен, 1963). Р. п. м. основываются на двух теориях: разработанной гештальт-психологией теории перцепции форм и т. н. «теории неогенеза» Ч. Спирмена. В соответствии с теорией перцепции форм каждое задание может быть рассмотрено как определенное целое, состоящее из ряда взаимосвязанных друг с другом элементов. Предполагается, что первоначально происходит глобальное оценивание задания-матрицы, а затем осуществление аналитической перцепции с выделением испытуемым принципа, принятого при разработке серии. На заключительном этапе выделенные элементы включаются в целостный образ, что и способствует обнаружению недостающей детали изображения. Теория Ч. Спирмена развивает рассмотренные положения теории перцепции форм. Данные, полученные с помощью Р. п. м., хорошо согласуются с показателями других распространенных тестов общих способностей. Так, коэффициенты корреляции между результатами теста (серии ABCDE) и шкалами измерения интеллекта Векслера составляют 0,70—0,74; для испытуемых в возрасте 9—10 лет — 0,91; со шкалами умственного развития (Станфорд-Бине — 0,66; с тестом Выготского-Сахарова — 0,54. Наиболее высока корреляция оценок Р. п. м. с группой арифметических тестов (0,74—0,87). Коэффициент надежности теста, по данным различных исследований, варьирует от 0,70 до 0,89. Средняя трудность заданий теста — 32,12%.
Предполагается, что первоначально происходит глобальное оценивание задания-матрицы, а затем осуществление аналитической перцепции с выделением испытуемым принципа, принятого при разработке серии. На заключительном этапе выделенные элементы включаются в целостный образ, что и способствует обнаружению недостающей детали изображения. Теория Ч. Спирмена развивает рассмотренные положения теории перцепции форм. Данные, полученные с помощью Р. п. м., хорошо согласуются с показателями других распространенных тестов общих способностей. Так, коэффициенты корреляции между результатами теста (серии ABCDE) и шкалами измерения интеллекта Векслера составляют 0,70—0,74; для испытуемых в возрасте 9—10 лет — 0,91; со шкалами умственного развития (Станфорд-Бине — 0,66; с тестом Выготского-Сахарова — 0,54. Наиболее высока корреляция оценок Р. п. м. с группой арифметических тестов (0,74—0,87). Коэффициент надежности теста, по данным различных исследований, варьирует от 0,70 до 0,89. Средняя трудность заданий теста — 32,12%. Показатель прогностической валидности теста (по связи с критериями успеваемости — 0,72. Существуют модификации Р. п. м. Одна из таких модификаций предложена автором (Дж. Равен в сотрудничестве с Д. Кортом, 1977, 1982). Оригинальный материал теста претерпел значительные изменения — были усложнены задания, введены новые серии. Существенной особенностью является дополнение теста вербальной шкалой (Mill Hill Vocabulary Scales), что, по мнению разработчиков, в немалой мере способствует расширению области применения теста. Интересная модификация Р. п. м., а также процедуры обследования предложена югославскими психологами (З. Буяс, 1961). В их варианте предусмотрена дифференцированная форма оценки ответов обследуемых. От них требуется указать на три фрагмента из тех, которые предложены для восполнения матрицы: точно подходящий, подходящий более-менее и совершенно не подходящий. Это дает возможность качественной оценки результатов, отпадает также необходимость в использовании индекса вариабельности.
Показатель прогностической валидности теста (по связи с критериями успеваемости — 0,72. Существуют модификации Р. п. м. Одна из таких модификаций предложена автором (Дж. Равен в сотрудничестве с Д. Кортом, 1977, 1982). Оригинальный материал теста претерпел значительные изменения — были усложнены задания, введены новые серии. Существенной особенностью является дополнение теста вербальной шкалой (Mill Hill Vocabulary Scales), что, по мнению разработчиков, в немалой мере способствует расширению области применения теста. Интересная модификация Р. п. м., а также процедуры обследования предложена югославскими психологами (З. Буяс, 1961). В их варианте предусмотрена дифференцированная форма оценки ответов обследуемых. От них требуется указать на три фрагмента из тех, которые предложены для восполнения матрицы: точно подходящий, подходящий более-менее и совершенно не подходящий. Это дает возможность качественной оценки результатов, отпадает также необходимость в использовании индекса вариабельности. Р. п. м., благодаря простоте применения, валидности и надежности результатов, возможности группового обследования, получили широкое распространение в психодиагностике. В отечественных исследованиях тест успешно используется при обследовании детей и взрослых (С. М. Морозов, 1979, 1980 и др.).
Р. п. м., благодаря простоте применения, валидности и надежности результатов, возможности группового обследования, получили широкое распространение в психодиагностике. В отечественных исследованиях тест успешно используется при обследовании детей и взрослых (С. М. Морозов, 1979, 1980 и др.).
|
Руководство для Прогрессивных Матриц Равена Дж. Равен, Дж. К. Равен, Дж. Корт
Цветные Прогрессивные Матрицы (включая Параллельные версии Теста)
Включенный в данный раздел материал является честью руководства и должен использоваться только вместе с Общим разделом руководства Москва
2007 Содержание УСТРОЙСТВО ТЕСТА И ЕГО ИСПОЛЬЗОВАНИЕ ………………………………7 ФОРМЫ ТЕСТА…………………………………………………………….. Книжная фирма теста……………………………………………………………………………..15 Параллельная форма тести…………………………………………………………….. 16 Планшетная форма теста………………………………………………………………………..17 ИСТОРИЯ РАЗРАБОТКИ ЦПМ………………………………………………………….19 Начало работы с Плашетной формой теста …………………………………………..19 Разработка Параллельной формы а 1998 году………………………………………..22 Стандартизация Классической Книжной формы теста, в 1949 года………22 Последние стандартизации ЦПМ на детях…………………………………………….25 Стандартизация в Двмфри (1982)…………………………………………………..25 Другие стандартизации на детях. Зависимость дгт/жих норм от даты рождении……………………………………28 Стандартизация на пожилых людях……………………………………………………….28 И.-иаенениг. оценок г, возрастом у пожилых людт ………………………………….30Клинические исследования…………………………………………………………………….31 НАДЕЖНОСТЬ И ВАЛИДНОСТЬ………………………………………………………35 Надежность……………………………………………………………………………………………..35 Надежность при расщеплении пополам……………………………………………..35 Ретестоная надежность………………………………………………………………….36 Надежность при автоматизированном предъявлении теста. Иалидность………………………………………………………………………………………………37 Кросс-культурные исследования…………………………………………………………38 Клиничт-кне исследования……………………………………………………………….41 Исследования а сфере образования……………………………………………………..42 ИНСТРУКЦИИ ПО ПРОВЕДЕНИЮ ОБСЛЕДОВАНИЯ С ПОМОЩЬЮ ЦПМ…………………………………………………………………………..45 Инструкции для работы с книжной формой ЦПМ ………………………………..45 Индивидуальное тестирование…………………………………………………………45 I‘pynnti/i‘ie тестирование………………………………………… Инструкции для работы l- Планшетной формой ЦПМ ………………………….51 ОЦЕНКА, ИНТЕРПРЕТАЦИЯ И ПРЕДСТАВЛЕНИЕ РЕЗУЛЬТАТОВ……………………………………………………………………………………57 Подсчет баллов………………………………………………………………………………………..57 Планшетная ферма теста………………………………………………………………58 Книжная форма теста…………………………………………………………………..58 Несогласованности и ошибки…………………………………………………………………58 Представление результатов…………………………………………………………………….58 Вопросы интерпретации…………………………………………………………………………59 Контекст рассмотрения результатов. Влияние научения…………………………………………………………………………..61 Няихииг. ямщгималъных расстройств……………………………………………….61 Умственно отсталые………………………………………………………………………62 СПРАВОЧНЫЙ МАТЕРИАЛ………………………………………………………………64 Нормальная структура суммарной оценки……………………………………………..64 Нормативные данные……………………………………………………………………………..64 Специальные нормы……………………………………………………………………….73 Характеристические кривые заданий…………………………………………………….74 ПРИМЕЧАНИЯ ……………………………… ДОПОЛНИТЛЬНАЯ ЛИТЕРАТУРА…………………………………………………….79 УСТРОЙСТВО ТЕСТА И ЕГО ИСПОЛЬЗОВАНИЕ Тест «Цветные Прогрессивные Матрицы» (ЦПМ) включает 36 заданий, которые составляют три серии — А, Аb и В — по 12 заданий в каждой. Этот тест разработан для использования в работе с маленькими детьми и престарелыми людьми, в антропологических исследованиях и в клинической практике. Он может успешно применяться в работе с людьми, которые по каким-либо причинам не понимают английского языка или не говорят на нем; с теми людьми, кто имеет физические недостатки, страдает афазией, церебральным параличом или глухотой, а также врожденной или приобретенной интеллектуальной недостаточностью. Если способность рассуждать по аналогии уже сформировалась, то лучше всего применять шкалу «Стандартные Прогрессивные Матрицы» (СПМ) — Серии А, В, С, D и Е. Когда эта стадия умственного развития еще не достигнута, или в тех случаях, когда интеллектуальная деятельность ослаблена, для оценки степени ясности мышления или уровня, до которого снизились интеллектуальные возможности испытуемых, могут быть использованы ЦПМ. Использование ЦПМ вместе со Словарной Шкалой Краштюн (СШК) позволяет исследовать психологическое значение наблюдаемых расхождений между способностью людей продуктивно мыслить и их способностью извлекать нужную информацию из памяти. Если результаты по СПМ и Словарным Шкалам Милл Хилл (СШМХ), полученные при обычном самотестировании или групповом тестировании, обнаруживают несоответствие между способностями к продуктивному и репродуктивному мышлению, то эти тесты можно провести индивидуально в клинических условиях. При таком использовании они позволяют детально исследовать природу ошибок и определить стратегию деятельности. Три серии по двенадцать заданий, составляющие ЦПМ, организованы так, что позволяют оценить главные когнитивные процессы, которые обычно формируются у детей до одиннадцати лет. В детстве умственное развитие весьма напоминает прыжки лосося в потоке жизни, а не размеренное восхождение по ступеням лестницы. Как бы ни была удобна гипотеза для количественных оценок и статистических расчетов, она не соответствует психологическим реалиям детской жизни. Более типична ситуация, когда дети начинают с последовательных, настойчивых попыток преодолеть возникшее интеллектуальное препятствие, пока однажды вдруг не перепрыгнут через него с легкостью и не направятся к следующему. Именно эти скачки в интеллектуальном развитии и выявляются при использовании ЦПМ. Задания в Цветных Прогрессивных Матрицах подобраны таким образом, чтобы оценить ход умственного развития вплоть до той стадии, когда человек начинает настолько успешно рассуждать по аналогии, что этот способ мышления становится основой для вывода логических умозаключений. Предъявление теста в виде напечатанных в книге цветных картинок или в виде планшетов с подвижными фрагментами позволяет сделать решаемую задачу наглядной и свести к минимуму необходимые словесные пояснения. Манипулирования изобразительным материалом не является здесь необходимым условием успешного решения задачи, поскольку от обследуемого требуется лишь указать ту фигуру, которую он выбирает для заполнения пробела в диаграмме. Для получения полезной диагностической информации с помощью ЦПМ важно работать с малыми группами тщательно отобранных респондентов, а не полагаться на большие выборки, которые, чем они больше, тем соответственно меньше дают информации об обследуемых индивидах. По причинам, которые обсуждаются ниже, важно уделить особое внимание уровням интеллектуального развития детей в возрасте 61/2, 81/2, и 101/2 лет. Как уже отмечалось, маленькие дети очень редко рассуждают по аналогии таким же образом, как это делают взрослые, и для них чрезвычайно важен контекст предъявления заданий. В связи с этим необходимо было пересмотреть «Принципы познания» Сиирмана в свете гештальттеории и сконструировать задания таким образом, как это сделано в Серии АЬ, чтобы отдельные фрагменты воспринимались как части некоего организованного целого или как отдельные элементы, имеющие соответствующую ориентацию в перцептивном поле наблюдателя Благодаря экспериментальной работе, приведшей к созданию ЦПМ, и тщательной отбраковке заданий, показывающих низкую корреляцию с тестом в целом, удалось различить по крайней мере пять качественных этапов развития интеллектуальных способностей. Сначала дети обладают способностью различать одинаковые и разные фигуры, а потом — похожие и непохожие фигуры. Некоторое время спустя они могут оценить ориентацию фигуры по отношению к себе и к другим объектам в поле восприятия. Позднее они уже начинают сравнивать аналогичные изменения в видимых символах и строить на этой основе логику своего рассуждения. Впоследствии дети становятся способны расчленять воспринятое целое на составные элементы, или «символы», и различать, что им действительно дано, а что было внесено ими самими. Наконец, они достигают возможности воспринимать две или более отдельные фигуры как составные части одного целого или как организованное единство. На основе анализа ответов на задания, предназначавшиеся для издания ЦПМ 1947 года, были отобраны двенадцать заданий, из которых сформировали Серию АЬ. Для издания 1956 года все 36 заданий, составивших Серии А, Аb, В, были внимательно просмотрены и, где это оказалось необходимо, переставлены местами, чтобы обеспечить более равномерное возрастание их по степени трудности. Таблицы ЦПМ1, ЦПМ2, ЦПМЗ содержат информацию о качественной структуре каждого из заданий в Сериях А, Аbи В. Верхняя половина каждой таблицы содержит перечень основных когнитивных операций, задействованных в понимании проблемы и в выборе каждого из шести возможных ответов. Если ошибочная фигура в основном относится к одному типу, но обладает также свойствами другого, оба эти типа приводятся в таблице слева направо по степени важности. Берт и Гилл2 обнаружили, что ответы детей на слишком трудные для них задания не являются случайными, поскольку правильный ответ выбирает заметно меньшее число детей, чем можно было бы ожидать при случайном выборе. В нижней половине каждой таблицы слева представлена классификация типов используемых фрагментов по их характерным свойствам, а справа — частота появления фрагмента со сходными свойствами в каждой из шести возможных позиций. Таблицы ЦПМ1, ЦПМ2 и ЦПМЗ предназначены для облегчения анализа и сопоставления качественных особенностей ошибочных ответов на задания теста. В прошлом такие сопоставления не удавалось провести отчасти из-за неравномерного распределения ошибочных фрагментов по шкале в целом, а также из-за неудачной классификации ошибочных выборов по их характерным признакам. Поскольку ЦПМ предназначены для возможно более точной оценки наблюдательности индивида и уровня его интеллектуального развития3, ошибочные ответы не могут быть удовлетворительно использованы для количественной оценки интеллектуальных нарушений. Они лишь показывают, с чем обследуемый не справляется, и иногда — почему он ошибается. Достоверность выводов, которые можно сделать из ошибочных ответов, частично зависит от природы этих ошибок, а частично — от их общего числа. Если ошибок очень мало или очень много, эти выводы менее значимы, чем в случае, когда дается около половины неадекватных ответов. Используя работу Карпентера, Джаста и Шелла4, Фодегель-Матцен сконструировала’ такие фрагменты-дистракторы, которые отличались от правильных фрагментов тем, что их выбор в качестве правильных ответов означал игнорирование одного, двух или нескольких правил решения, которые Карпентер и Джаст (а также Фодегель-Матцен) в своих работах определили как наиболее значимые. Как и было предсказано, природа совершаемых ошибок зависела от общего балла респондента, причем респонденты с низким количеством баллов пренебрегали большим числом правил, и при этом наиболее трудными из них. Работа Фодегель-Матцен с дистракторами, набор которых варьировался более систематически и был теоретически более обоснован, чем те которые используются в публикуемых ныне тестах, подтвердила справедливость приведенных здесь выводов. С практической точки зрения вывод состоит в том, что информация о природе типичных ошибок обычно совсем немного добавляет к тому, что можно почерпнуть из их суммарной оценки, так как между ними имеется достаточно устойчивая взаимосвязь. ФОРМЫ ТЕСТА Чтобы привлечь и удержать внимание маленьких детей, каждое задание печатается на ярком цветном фоне. Это делает более наглядной природу предложенного для выполнения задания, никоим образом не подсказывая решения. Порядок заданий в каждой серии обеспечивает стандартное обучение методу работы, а три серии вместе охватывают все процессы визуальных умозаключений, к которым обычно уже способны дети в возрасте до десяти лет. При правильном предъявлении теста необходимо лишь показать обследуемым, что надо делать, чтобы они могли двигаться от задачи к задаче в стандартном порядке и на собственном опыте учиться их решать. Тест может предъявляться в виде планшетов с подвижными фрагментами или в виде напечатанных в книжке иллюстраций, что не влияет на интеллектуальные процессы, необходимые для его успешного выполнения. При любой форме теста задачи, которые надо решить, могут быть вполне удовлетворительно продемонстрированы без всяких вербальных инструкций6.  Беседа просто делает ситуацию тестирования более естественной. Беседа просто делает ситуацию тестирования более естественной.
Книжная форма Исследования показывают, что дети старше шести лет, взрослые теста с незначительными нарушениями интеллекта и большая часть лиц с физическими недостатками одинаково хорошо понимают предлагаемые задания независимо от того, напечатаны ли они в виде картинок на ярком цветном фоне или представлены в виде планшетов с подвижными фрагментами. Было установлено, что при обычном применении теста его книжная и планшетная формы в случае использования цветного фона приводят к практически одинаковым результатам. До того момента, пока не сформировалась способность сравнивать и рассуждать по аналогии, а также в случаях, когда ее формирование задерживается или нарушено, Серии А, АЬ и В, напечатанные на ярком цветном фоне, обычно обеспечивают более достоверное тестирование, чем Серии А, В, С, D и Е. Напротив, после того, как такая способность сформировалась, последние дают более достоверные результаты. Несмотря на то что Серии А, АЬ и В позволяют ясно дифференцировать различные степени врожденной и приобретенной умственной отсталости, этот тест ни в каком смысле не является измерителем общего снижения интеллекта. Он четко показывает, обладает или нет обследуемый способностью к сравнению и умозаключению по аналогии, а если нет, то в какой степени он способен по сравнению с другими людьми организовывать пространственные образы в связанные по определенному принципу целостности. В дополнение к этому общее снижение интеллекта подразумевает оценку интеллектуальной стабильности и интегральной способности сохранять навыки, приобретенные за счет имеющихся в распоряжении данного индивида интеллектуальных возможностей. Ни один взятый отдельно тест на перцептивные умозаключения не дает такой информации. Следовательно, необходим еще по крайней мере один дополнительный тест, направленный на оценку общего уровня приобретенных знаний. Параллельная форма Широкое распространение ЦПМ, особенно при отборе детей млад-тестз шего возраста для участия в учебных программах коррекционной направленности или в программах для одаренных, привело к тому, что родители стали натаскивать своих детей на решение заданий этого теста. Хотя человек, имеющий определенный опыт в проведении теста, всегда может легко распознать тех, кто заучил ответы, и хотя проводящие тест с целью отбора всегда должны сравнивать информацию, полученную при использовании ПМР, с другими показателями (и выяснять источник выявляемых противоречий), многие люди ощутили назревшую необходимость в параллельной форме теста, которую можно было бы использовать для предотвращения случаев, когда заучивание ответов дает кому-то совершенно незаслуженное преимущество. Поэтому в 1998 году была выпущена в свет Параллельная форма теста ЦПМ. Как будет показано ниже, эта форма полностью корреспондирует с Классической формой теста и на уровне отдельных заданий (как по их логической конструкции, так и по степени трудности), и на уровне итоговой оценки. Универсальным способом объяснения заданий является предъявление любого из них в форме картонного планшета с вырезом и набора подвижных фрагментов, каждый из которых по форме и размерам в точности соответствует вырезанному участку планшета. На протяжении многих лет предпринимались попытки изготовить Планшетную форму теста для коммерческого распространения, но только совсем недавно это удалось воплотить в жизнь. При невозможности воспользоваться коммерческой версией следует обратиться к инструкции по ее конструированию, которая содержалась в более ранних изданиях этого Раздела данного Руководства. В планшетной форме тест может быть удовлетворительно разъяснен представителям любой расы, говорящим на любом языке. Он является также одним из немногих тестов, которые могут быть успешно использованы в работе с людьми, страдающими частичным параличом, глухотой или дефектами речи, и при этом дает устойчивую, надежную и психологически валидную оценку имеющейся у них способности к логическим умозаключениям, независимо от специфики их дефекта. В возрасте между тремя и шестью годами внимание и интерес детей обычно слишком подвижны, а результаты интеллектуальной активности слишком непостоянны, чтобы какой-нибудь тест интеллекта мог с высокой надежностью предсказать последующее интеллектуальное развитие. Поэтому вряд ли результаты, полученные на маленьких детях с применением планшетной формой теста, обладают большей прогностической ценностью, чем результаты, полученные с помощью других тестов интеллекта. Есть основания думать, однако, что результаты, полученные при работе с планшетной формой теста, обладают психологической валид-ностью до тех пор, пока они оценивают наличные результаты интеллектуальной деятельности ребенка вне зависимости от его осведомленности и образования. Планшетная форма теста имеет очевидные преимущества для работы с маленькими детьми, для клинической оценки врожденных или приобретенных дефектов интеллекта, а также для кросс-культурных исследований. При некоторых психологических обследованиях она также имеет преимущества перед книжной формой теста, так как позволяет наблюдать, фиксировать и сравнивать решения, полученные путем проб и ошибок, с решениями, полученными путем непосредственного восприятия или умозаключения. Кроме всего сказанного, планшетная форма теста чрезвычайно полезна для использования в психологических исследованиях. Здесь она обладает двумя достоинствами: позволяет преодолеть ограничения как бланковых («карандаш и бумага»), так и «исполнительских» тестов, а также легко и точно зафиксировать последовательность умозаключений, на основании которых испытуемый действует, выполняя усложняющиеся серии заданий. Получаемая таким образом информация может быть соотнесена с участвующими в решении задачи умственными операциями и типами допускаемых ошибок. жүктеу/скачать 379 Kb. Достарыңызбен бөлісу: |
Методика «Прогрессивной матрицы ДЖ.
 Равена» для тестирования и развитие уровня интеллекта
Равена» для тестирования и развитие уровня интеллекта Воспитанники получают рабочие специальности , обучаются в профессиональном училище № 59 ( при учреждении). В настоящее время в ПУ обучаются 40 воспитанников. Воспитанники получают образования по специальностям : «Швея»-11 человек, « Слесарь по ремонту автомобилей» -29 человек. Из них десять получают бесплатное второе начальное профессиональное образование согласно ст.6 ФЗ от 21.12.1996 г. №159 « О дополнительных гарантиях по социальной защите детей сирот и детей, оставшимся без попечения родителей».
На стендах наглядной агитации
помещена информация о
На предприятии учреждения  работах-3
.
работах-3
.
С осужденными, не занятыми
на производстве и ПУ, проводятся
культурно-массовые
Со всеми воспитанниками 
ГЛАВА III Исследование интеллектуального уровня развития воспитанников Калужской Воспитательной колонии
3.1 Что за методика ,кто создал, что позволяет.
Прогрессивные матрицы Дж. Равена.
В 1936 году в
Великобритании был разработан тест Progressive
Matrices, предназначенный для оценки уровня
развития общего интеллекта индивида.
В нем проверялась способность к установлению
логических отношений с использованием
абстрактного невербального материала.
С тех пор этот тест широко применяется
в разных областях психологической диагностики
как методика, обладающая высокой валидностью
и надежностью, простая в применении и
допускающая групповое обследование.
Дж. Равен совместно
с Л. Пентроузом разработали три варианта
теста. Первый, созданный в 1936 году, был
черно-белым и предназначался для обследования
детей от 8 до 14 лет и взрослых от 20 до 65
лет. Второй – цветной, более простой вариант
методики, – был создан в 1949 году. С его
помощью можно обследовать детей от 5 до
11 лет и взрослых старше 65 лет, а также
людей, имеющих языковые затруднения.
Существует еще один вариант матриц –
для высокоинтеллектуальных индивидов.
Второй – цветной, более простой вариант
методики, – был создан в 1949 году. С его
помощью можно обследовать детей от 5 до
11 лет и взрослых старше 65 лет, а также
людей, имеющих языковые затруднения.
Существует еще один вариант матриц –
для высокоинтеллектуальных индивидов.
Два
первых варианта являются невербальными
методиками, третий вариант включает в
себя вербальную часть. Все три варианта
строятся по общему принципу и используют
в качестве стимульного материала абстрактные
геометрические фигуры с рисунком, организованным
по определенному принципу. Общий смысл
заданий заключается в следующем: испытуемому
предъявляются рисунки с элементами, связанными
между собой определенной зависимостью;
одного элемента не достает. Испытуемому
необходимо проанализировать матрицу
с пропущенным элементом и выбрать недостающий
элемент из 6–8 предложенных ему.
Выполнение заданий
требует от человека хорошей концентрации
внимания, способности к оперированию
умственными образами, логического мышления,
развитых мыслительных операций (таких,
как анализ, синтез, сравнение, обобщение). На успешность выполнения теста влияет
также уровень развития пространственных
способностей, индуктивного мышления,
точности восприятия.
На успешность выполнения теста влияет
также уровень развития пространственных
способностей, индуктивного мышления,
точности восприятия.
В черно-белом
варианте – для взрослых – пять серий
(A, B, C, D, E) по 12 однотипных матриц, расположенных
по принципу возрастающей сложности (всего
60 матриц). Сложность заданий возрастает
и при переходе от серии к серии. Предполагается,
что первые пять заданий серии А испытуемый
выполняет с помощью экспериментатора,
затем он работает самостоятельно. Подразумевается,
что в процессе выполнения заданий происходит
обучение – каждое последующее задание
строится на основе опыта, полученного
при выполнении предыдущих заданий. Само
название теста – «Прогрессивные матрицы»
– подразумевает
наличие некоего прогресса.
При выполнении
заданий всех серий индивид, проходящий
обследование, должен проанализировать
структуру заданного образца, выявить
характер связей между элементами, определить
отсутствующий элемент, сравнить предложенные
ему элементы и выбрать из них подходящий. Но сами серии строятся по разным принципам:
Но сами серии строятся по разным принципам:
Серия А построена
по принципу установления взаимосвязи
в структуре матриц. Задание испытуемому:
дополнить недостающую часть основного
изображения одним из приведенных в каждой
таблице фрагментов. Для этого ему необходимо
тщательно проанализировать структуру
основного изображения, произвести дифференцировку
элементов и определить связи между ними.
Затем, обнаружив эти же особенности в
одном из нескольких фрагментов, дополнить
недостающую часть структуры.
Серия B: во всех
заданиях этой серии от индивида, проходящего
обследование, требуется найти аналогии
между парами фигур с разными элементами.
Обследуемый должен найти принцип, соответственно
которому построена фигура в каждом случае
и исходя из этого
выбрать недостающий элемент.
Серия C основана
на определении принципа сложного прогрессивного
изменения фигур по горизонтали и вертикали.
Фигуры в пределах одной матрицы все больше
усложняются, обогащаются новыми элементами. Принцип этого изменения и требуется обнаружить,
для того чтобы выполнить задание.
Принцип этого изменения и требуется обнаружить,
для того чтобы выполнить задание.
Серия D строится на основе принципа перегруппировки
фигур в матрице. Индивид, выполняющий
задания, должен выявить суть этой перестановки
фигур, происходящей по горизонтальному и вертикальному направлению.
Серия E является
самой сложной. При выполнении заданий
испытуемому необходимо произвести анализ
фигур, составляющих основное изображение,
и составить недостающую фигуру из ее
частей.
Существуют
формы теста для
В случае
проведения группового обследования на
выполнение методики дается 20 минут. Необходимо
строго следить за тем, чтобы все
тестируемые одновременно (по команде)
начали и закончили выполнять задания
теста.
Необходимо
строго следить за тем, чтобы все
тестируемые одновременно (по команде)
начали и закончили выполнять задания
теста.
Обработка полученных
результатов осуществляется по следующему
принципу: за каждое правильно выполненное
задание начисляется 1 балл. Подсчитывается
количество баллов по каждой из пяти серий,
и вычисляется общая сумма полученных
баллов. По специальной таблице полученные
баллы переводятся в шкальные оценки (проценты)
в соответствии с возрастными нормами.
Нормы теста были получены на выборке
из 1407 детей, 3665 военных и 2192 гражданских
подданных Великобритании. Надежность
теста – 0,70–0,90, валидность (корреляция
с успешностью обучения) – 0,72. Имеются
данные о том, что «Прогрессивные матрицы»
Равена, как и другие тесты оценки уровня
развития интеллекта, более валидны для
прогнозирования успешности профессионального
обучения, чем профессиональной деятельности,
Тем не менее, согласно данным соответствующих
исследований, уровень интеллекта оказывает
влияние на успешность профессиональной
деятельности, причем это влияние сильнее
на более сложные и высокоточные виды
профессиональной деятельности, чем на
более простые и не
требующие высокой точности. Тест
Равена является невербальным, то есть
для его выполнения не требуется умения
читать и писать. Он основан на использовании
устных инструкций и невербальных заданий.
Предполагалось, что эта методика может
применяться для обследования и сравнения
людей из различных культур, говорящих
на разных языках, с разным уровнем образования
(и даже совсем неграмотных). Экспериментальные
исследования, проведенные в разных европейских
странах, показали, что нормы, установленные
на выборке испытуемых Великобритании,
пригодны для других стран. Однако было
ясно, что для людей, живущих в резко отличающихся
условиях, эти нормы не могут быть использованы,
поскольку в этих группах на результаты
теста может оказать влияние уровень образования.
Кроме того, в этих группах на показатель
теста воздействует и фактор научения
(то есть индивиды, знакомые с тестом, выполняют
его задания лучше, чем те, кто видит тест
впервые). Тест Равена хорошо коррелирует
с другими тестами интеллекта: так, например,
корреляции с тестом Векслера составляют
0,70–0,74.
Тест
Равена является невербальным, то есть
для его выполнения не требуется умения
читать и писать. Он основан на использовании
устных инструкций и невербальных заданий.
Предполагалось, что эта методика может
применяться для обследования и сравнения
людей из различных культур, говорящих
на разных языках, с разным уровнем образования
(и даже совсем неграмотных). Экспериментальные
исследования, проведенные в разных европейских
странах, показали, что нормы, установленные
на выборке испытуемых Великобритании,
пригодны для других стран. Однако было
ясно, что для людей, живущих в резко отличающихся
условиях, эти нормы не могут быть использованы,
поскольку в этих группах на результаты
теста может оказать влияние уровень образования.
Кроме того, в этих группах на показатель
теста воздействует и фактор научения
(то есть индивиды, знакомые с тестом, выполняют
его задания лучше, чем те, кто видит тест
впервые). Тест Равена хорошо коррелирует
с другими тестами интеллекта: так, например,
корреляции с тестом Векслера составляют
0,70–0,74. Благодаря этому, а также простоте
проведения обследования и обработки
данных, «Прогрессивные матрицы»
применяются в целях диагностики чаще,
чем другие, более сложные и трудоемкие
тесты интеллекта. В последние годы в нашей
стране все чаще специалисты в области
психодиагностики используют компьютерный
вариант «Прогрессивных матриц» Равена.
Его авторы – И.Н. Гильяшева и Л.Г. Савицкий.
Этот тест может оказаться весьма полезным
для быстрой оценки интеллектуального
уровня кандидатов на ту или иную должность.
Хотя он, в отличие, например, от теста
Векслера, не позволяет выявить и оценить
качественные характеристики мыслительной
деятельности человека, особенности его
памяти, внимания, широту кругозора, но
он дает возможность определить общий
интеллектуальный уровень, что нередко
бывает необходимо для прогнозирования
профессиональной пригодности кандидата.
Благодаря этому, а также простоте
проведения обследования и обработки
данных, «Прогрессивные матрицы»
применяются в целях диагностики чаще,
чем другие, более сложные и трудоемкие
тесты интеллекта. В последние годы в нашей
стране все чаще специалисты в области
психодиагностики используют компьютерный
вариант «Прогрессивных матриц» Равена.
Его авторы – И.Н. Гильяшева и Л.Г. Савицкий.
Этот тест может оказаться весьма полезным
для быстрой оценки интеллектуального
уровня кандидатов на ту или иную должность.
Хотя он, в отличие, например, от теста
Векслера, не позволяет выявить и оценить
качественные характеристики мыслительной
деятельности человека, особенности его
памяти, внимания, широту кругозора, но
он дает возможность определить общий
интеллектуальный уровень, что нередко
бывает необходимо для прогнозирования
профессиональной пригодности кандидата.
Более высокие показатели по этому тесту
показывают те, кто а) быстрее, и б) точнее
определяет логические закономерности
в построении упорядоченного ряда состоящего
из графических объектов, имеющих ограниченное
количество признаков.
Другое название этого теста «Прогрессивные матрицы Равена» указывает на то, что задачи теста упорядочены по признаку возрастания трудности их решения. То есть, в каждой из пяти серий (в серии по 12 задач), каждая последующая задача серии относительно сложней предыдущей. На решение задач теста вводится временное ограничение — подсчитывается количество правильно решённых за 20 минут задач. Возможен вариант, когда время на решение всех 60 задач не ограничено. В этом случае результат корректируется по специальной таблице. По результатам тестирования испытуемый получает несколько оценок:
- а) по десятибалльной шкале (стандартная оценка в стенах), учитывающей только количество правильно решённых задач,
- б) по 19-балльной, учитывающей количество и трудность решённых задач,
- в) по привычной пятибалльной (школьной, но с «плюсами» и «минусами»).
- И, наконец,
четвёртая, качественная, оценка.
 Если
испытуемый решил все задачи теста, но
многие, в том числе и лёгкие, задачи решил
неверно, его можно отнести к категории
«скоростников». Если же испытуемый решил
мало задач (например, около половины задач
теста), но, без единой ошибки, его можно
отнести к категории «точняков», или тугодумов.
Если
испытуемый решил все задачи теста, но
многие, в том числе и лёгкие, задачи решил
неверно, его можно отнести к категории
«скоростников». Если же испытуемый решил
мало задач (например, около половины задач
теста), но, без единой ошибки, его можно
отнести к категории «точняков», или тугодумов.
При интерпретации результата теста «Прогрессивные матрицы Равена» выделяют следующие пять уровней развития интеллекта:
- 1-й уровень (результат более 95 %) — особо высокий интеллект
- 2-й уровень (результат 75-94 %) — интеллект выше среднего
- 3-й уровень (результат 25-74 %) — средний интеллект
- 4-й уровень (результат 5-24 %) — интеллект ниже среднего
- 5-й уровень (результат ниже 5 %) — дефект интеллекта
3.2
Результаты исследования
Этапы подготовки и проведения диагностики интеллекта
Первым этапом
любого исследования является определение
целей и задач.
Вторым этапом
является подбор методик, с помощью
которых поставленные цели и задачи
будут реализованы наилучшим
образом. Для этого психологу
необходимо тщательно изучить теорию
по данному вопросу (в данном случае
это теоретические и
Третий этап включает в себя анализ психометрических свойств тестов и, при необходимости, их адаптацию.
Четвертый этап — подготовка бланков, стимульного материала и прочего, необходимого оборудования.
Пятый этап — собственно тестирование. Здесь психологу необходимо знать и соблюдать условия тестирования.
Проведение диагностики интеллекта.
Проведем
эксперимент по исследованию уровня
интеллектуального развития. В данном
исследовании используется методика «
Прогрессивные матрицы Дж. Равена» для
тестирования и развития уровня интеллекта.
Испытуемыми были 22 несовершеннолетних
осужденных Калужской воспитательной
колонии возрасте от 16 до 18 лет, исследование
было проведено в аудиторных условиях. Испытуемым была зачитана следующая инструкция
(групповая):
Испытуемым была зачитана следующая инструкция
(групповая):
Данный тест предназначен для уточнения логичности Вашего мышления, умения находить существенные связи между предметами и явлениями, для определения уровня умственной работоспособности, умения концентрировать внимание, сообразительности в целом, используется как тест интеллекта или специальных перцептивных способностей.
Пред вами 60 графических рисунков (матриц).На каждой из них в верхней половине листа находится прямоугольник с различными геометрическими фигурами внутри. В правом нижнем углу прямоугольника имеется свободное место. Под прямоугольником находится два ряда форм(шесть или восемь), которые по размерам точно подходят к вырезу прямоугольника в качестве вероятно выбранных вкладок. Каждая из этих вкладок имеет различный рисунок.
Расположение фигур подчинено
определенной логической связи. Ее надо
определить и дополнить матрицу недостающим
элементом, выбрав из приведенных вариантов,
т. е. Вшей задачей является найти в ряде
вкладок ту, которая точно подходит к свободному
месту в прямоугольнике. Предпосылкой
правильного решения является логическое
рассуждение о том, по какому закону составлен
рисунок в прямоугольнике, пустое место
в котором Вы должны заполнить.
е. Вшей задачей является найти в ряде
вкладок ту, которая точно подходит к свободному
месту в прямоугольнике. Предпосылкой
правильного решения является логическое
рассуждение о том, по какому закону составлен
рисунок в прямоугольнике, пустое место
в котором Вы должны заполнить.
Номера матриц (например: А1;В6;D12) обозначают степень сложности заданий. От буквы А у букве Е и от номера 1 к 12 номеру трудность задач возрастает. Время на решение 60 заданий ограничено 20 минутами. Не задерживайтесь на первых заданиях теста, так как сложность их все время увеличивается.
В бланке ответов в таблице
рядом с соответствующим
Матричная алгебра
Матричная алгебраМатричная алгебра
Что такое единичная матрица?
Что такое скаляр?
Что такое обратная матрица?
Когда (для какой матрицы) транспонированная матрица равна исходной матрице?
Выполнить умножение матриц.
Имея матрицу и матричную операцию, определите содержимое результирующей матрицы (например, SSCP, ковариация, корреляция).
Определения
«Матрица представляет собой прямоугольник n на k чисел или символов, обозначающих числа» (Pedhazur, 1997, стр. 983). Размер матрицы называется ее порядком и обозначается строками и столбцами. По соглашению строки всегда упоминаются первыми. Таким образом, матрица порядка 3 на 2, называемая A , может выглядеть так:
A
=Матрица B порядка 4 на 4 может выглядеть так:
B
=По соглашению матрицы в тексте печатаются в жирный шрифт .
Элементы (элементы) матрицы обозначаются по имени матрицы в нижнем регистре с заданными строкой и столбцом (опять же, сначала идет строка). Например, a 31 = 2, b 22 = 1. В общем случае a ij означает элемент A в i-й строке и j-м столбце. По соглашению элементы печатаются курсивом .
По соглашению элементы печатаются курсивом .
Транспонирование матрицы получается путем перестановки строк и столбцов, так что первая строка становится первым столбцом, и так далее. Транспонирование матрицы обозначается одинарными кавычками и называется простым числом. Например A ‘(простой) это:
А
=А’ =
Обратите внимание, что A ‘ — это не просто A , «опрокинутое» на бок (если это так, мы увидим первый столбец как 1 3 вместо 3 1). Это как если бы карты или доски с номерами для каждой строки были вытянуты 1 на 1 и размещены в порядке для транспонирования. Транспонирование B:
Б’
=Б’ =
(Для некоторых матриц транспонирование равно исходной матрице.)
Если n = k, количество строк равно количеству столбцов, а матрица квадратная . Квадратная матрица может быть симметричной или асимметричной . Симметричная матрица обладает тем свойством, что элементы выше и ниже главной диагонали одинаковы, так что element(i,j) = element(j,i), как в нашей матрице B . (Главная или главная диагональ в матрице B состоит из элементов, все равные 1.) В случае квадратной симметричной матрицы транспонированная матрица является исходной матрицей. Матрица корреляции всегда будет квадратной симметричной матрицей, поэтому транспонирование будет равно оригиналу.
(Главная или главная диагональ в матрице B состоит из элементов, все равные 1.) В случае квадратной симметричной матрицы транспонированная матрица является исходной матрицей. Матрица корреляции всегда будет квадратной симметричной матрицей, поэтому транспонирование будет равно оригиналу.
Вектор-столбец представляет собой матрицу чисел размером n на 1. Например:
|
б =
|
.4 |
|
.5 |
|
|
.2 |
|
|
.1 |
(Я собираюсь использовать квадраты для матриц, а не стандартные скобки из-за проблем с форматированием.) Итак, b — вектор-столбец. Вектор-строка представляет собой матрицу чисел размером 1 на k. Например,
Например,
|
б ‘= |
.4 |
.5. |
2. |
.1 |
Итак, b ‘ — это вектор-строка. Обратите внимание, что b’ является транспонированием b . По соглашению, векторы печатаются жирным шрифтом в нижнем регистре, а векторы-строки представляются транспонированными векторами-столбцами.
Диагональная матрица — это квадратная симметричная матрица, которая имеет нули везде, кроме главной диагонали. Например:
|
С =
|
12 |
0 |
0 |
|
0 |
10 |
0 |
|
|
0 |
0 |
5 |
C — диагональная матрица.
Особенно важная диагональная матрица называется единичной матрицей I . Эта диагональная матрица имеет 1 на главной диагонали.
|
я =
|
1 |
0 |
0 |
|
0 |
1 |
0 |
|
|
0 |
0 |
1 |
I — единичная матрица. Бывает, что корреляционная матрица, в которой все переменные ортогональны, является единичной матрицей.
Скаляр — это матрица с одним элементом. Например
|
д = |
12 |
d
является скаляром.
Операции с матрицами
Сложение и вычитание
Матрицы можно складывать и вычитать тогда и только тогда, когда они одного порядка (одинаковые по количеству строк и столбцов). Матрицы, над которыми допустима операция, говорят, что соответствуют операции.
Нам повезло, что сложение и вычитание матриц просто означает сложение или вычитание соответствующих элементов двух матриц.
Дополнение
|
4 |
+
|
6 |
=
|
10 |
|
1 |
2 |
3 |
||
|
5 |
3 |
8 |
||
|
|
|
|
||
|
х |
г |
я |
Дополнение
|
1 |
2 |
+
|
3 |
4 |
=
|
4 |
6 |
|
1 |
2 |
5 |
6 |
6 |
8 |
||
|
1 |
2 |
7 |
8 |
8 |
10 |
||
|
|
|
|
|
|
|
||
|
Х |
|
Д |
|
З |
|
Вычитание
|
1 |
2 |
—
|
3 |
4 |
=
|
-2 |
-2 |
|
1 |
2 |
5 |
6 |
-4 |
-4 |
||
|
1 |
2 |
7 |
8 |
-6 |
-6 |
||
|
|
|
|
|
|
|
||
|
Х |
|
Д |
|
З |
|
Умножение
В отличие от сложения и вычитания матриц, умножение матриц не является прямым расширением обычного умножения. Умножение матриц включает в себя как умножение, так и добавление элементов. Если мы умножим вектор-строку на вектор-столбец, мы получим скаляр.
Умножение матриц включает в себя как умножение, так и добавление элементов. Если мы умножим вектор-строку на вектор-столбец, мы получим скаляр.
Чтобы его получить, мы сначала умножаем соответствующие элементы, а затем складываем их.
|
|
|
|
|
б1 |
=
|
|
|
|
|
а1 |
а2 |
а3 |
б2 |
а1b1 |
+a2b2 |
+a3b3 |
||
|
|
|
|
б3 |
|
|
|
||
|
|
|
|
|
|
|
|
||
|
|
|
|
б |
|
с |
|
Для числового примера
|
|
|
|
|
0 |
=
|
|
=
|
|
|
1 |
2 |
3 |
2 |
0+4+12 |
16 |
|||
|
|
|
|
4 |
|
|
Результат умножения двух таких векторов называется скалярным произведением. Скалярные произведения имеют множество статистических приложений. Например, сумму переменной можно найти, поместив эту переменную в вектор-столбец и предварительно умножив ее на вектор-строку, состоящий из единиц.
Скалярные произведения имеют множество статистических приложений. Например, сумму переменной можно найти, поместив эту переменную в вектор-столбец и предварительно умножив ее на вектор-строку, состоящий из единиц.
Например,
|
|
|
|
|
7 |
|
|
|
|
|
1 |
1 |
1 |
|
8 |
= |
7+8+9 |
= |
24 |
|
|
|
|
|
9 |
|
|
|
|
1’x
= S X
Мы можем найти сумму перекрестных произведений с помощью таких операций:
|
|
|
|
|
1 |
|
|
|
|
|
2 |
4 |
6 |
|
3 |
= |
2+12+30 |
= |
44 |
|
|
|
|
|
5 |
|
|
|
|
х’у
= С ХУИ если мы вычтем среднее значение из вектора-столбца, мы сможем найти сумму квадратов:
|
|
|
|
|
-1 |
|
|
|
|
|
-1 |
0 |
1 |
|
0 |
= |
1+0+1 |
= |
2 |
|
|
|
|
|
1 |
|
|
|
|
х’х
= С х 2 В отличие от обычного умножения, умножение матриц не является симметричным, так что в общем случае x’y не равно y’x , то есть предварительное и постумножение обычно не дают одного и того же результата. В общем случае первая матрица будет иметь порядок r1xc1, а вторая — порядка r2xc2.
В общем случае первая матрица будет иметь порядок r1xc1, а вторая — порядка r2xc2.
Чтобы соответствовать умножению, c1 должно быть равно r2. Порядок полученной матрицы будет r1xc2. Внутренние числа должны быть равны для умножения числа. Если да, то результат будет порядка внешних чисел. Некоторые примеры
|
А(1 ст ) |
|
|
Б(2 и ) |
|
|
АБ |
|
|
строк |
Кол-во |
|
строк |
Кол-во |
|
строк |
Кол-во |
|
1 |
5 |
|
5 |
1 |
|
1 |
1 |
|
1 |
10 |
|
10 |
1 |
|
1 |
1 |
|
1 |
6 |
|
5 |
1 |
|
ДНЦ |
|
|
5 |
1 |
|
1 |
5 |
|
5 |
5 |
|
3 |
2 |
|
2 |
3 |
|
3 |
3 |
|
3 |
3 |
|
2 |
3 |
|
ДНЦ |
|
|
2 |
4 |
|
4 |
3 |
|
2 |
3 |
То, что именно происходит с умножением матриц, зависит от порядка матриц (хотя схема шагов всегда одна и та же).
Если мы умножим вектор-столбец на вектор-строку, мы получим матричное произведение векторов, а не скаляр.
Пример
|
1 |
|
|
|
|
|
1 |
-2 |
0 |
|
2 |
|
1 |
-2 |
0 |
= |
2 |
-4 |
0 |
|
3 |
|
|
|
|
|
3 |
-6 |
0 |
|
и |
|
|
б’ |
|
= |
С |
|
|
|
3×1 |
|
|
1×3 |
|
|
3х3 |
|
|
Возьмите первую строку a (1), умножьте на первый столбец b (1) и установите результат в c 1,1 . Возьмите вторую строку a (2), умножьте на 1 ст столбец b (1), установите результат c 2,1 и т. д.
Возьмите вторую строку a (2), умножьте на 1 ст столбец b (1), установите результат c 2,1 и т. д.
Тот же шаблон используется для матриц большего порядка, за исключением того, что для каждой комбинации мы и умножаем, и складываем. Например
|
2 |
1 |
|
|
|
|
|
7 |
8 |
9 |
|
3 |
1 |
|
2 |
3 |
4 |
|
9 |
11 |
13 |
|
4 |
2 |
|
3 |
2 |
1 |
|
14 |
16 |
18 |
|
А |
|
|
Б |
|
|
|
С |
|
|
|
3×2 |
|
|
2×3 |
|
|
|
3х3 |
|
|
Чтобы получить значения C
|
(2)2+(1)3=7 (1,1) |
(2)3+(1)2=8 (1,2) |
(2)4+(1)1=9 (1,3) |
|
(3)2+(1)3=9 (2,1) |
(3)3+(1)2=11 (2,2) |
(3)4+(1)1=13 (2,3) |
|
(4)2+(2)3=14 (3,1) |
(4)3+(2)2=16 (3,2) |
(4)4+(2)1=18 (3,3) |
Пройдитесь по строкам первой матрицы и столбцам второй. Чтобы получить c(1,1), возьмите первую строку и первый столбец, умножьте соответствующие элементы и сложите.
Чтобы получить c(1,1), возьмите первую строку и первый столбец, умножьте соответствующие элементы и сложите.
Умножение матриц полезно для нахождения матрицы сумм квадратов и перекрестных произведений (матрица SSCP).
Мы можем найти либо необработанные оценки, либо суммы оценок отклонений квадратов и перекрестных произведений. Первые необработанные баллы:
|
1 |
2 |
0 |
|||||||||||
|
1 |
2 |
2 |
3 |
2 |
2 |
2 |
3 |
2 |
26 |
37 |
14 |
||
|
2 |
3 |
4 |
3 |
4 |
2 |
2 |
4 |
2 |
37 |
58 |
20 |
||
|
0 |
2 |
2 |
2 |
0 |
0 |
3 |
3 |
2 |
14 |
20 |
12 |
||
|
2 |
4 |
0 |
|||||||||||
|
2 |
2 |
0 |
|||||||||||
|
Х’ |
Х |
SSCP |
|||||||||||
|
3×6 |
6х3 |
3х3 |
Содержимое матрицы SSCP
|
|
Сим |
Сим |
|
|
|
Сим |
|
|
|
|
Теперь количество баллов отклонения от тех же данных:
|
-1 |
-1 |
-1 |
|||||||||||
|
-1 |
0 |
0 |
1 |
0 |
0 |
0 |
0 |
1 |
2 |
1 |
2 |
||
|
-1 |
0 |
1 |
0 |
1 |
-1 |
0 |
1 |
1 |
1 |
4 |
2 |
||
|
-1 |
1 |
1 |
1 |
-1 |
-1 |
1 |
0 |
1 |
2 |
2 |
6 |
||
|
0 |
1 |
-1 |
|||||||||||
|
0 |
-1 |
-1 |
|||||||||||
|
Х’ |
Х |
SSCP |
|||||||||||
|
3×6 |
6х3 |
3х3 |
Содержимое матрицы SSCP
Если мы умножаем или делим матрицу на скаляр, каждый элемент матрицы умножается (делится) на этот скаляр. Если мы разделим каждый элемент в приведенной выше матрице SSCP на 6 (размер выборки), мы получим
Если мы разделим каждый элемент в приведенной выше матрице SSCP на 6 (размер выборки), мы получим
|
2/6 |
1/6 |
2/6 |
.33 |
.17 |
.33 |
|
|
1/6 |
4/6 |
2/6 |
= |
.17 |
.66 |
.33 |
|
2/6 |
2/6 |
6/6 |
. |
.33 |
1 |
Матрица SSCP, деленная на N (или N-1), называется матрицей дисперсии-ковариации. В нем у нас есть отклонения по диагонали и ковариации вне главной диагонали.
Если мы далее разделим на стандартное отклонение для каждой строки и каждого столбца, мы получим матрицу корреляции:
Корреляционная матрица для наших данных:
|
1 |
||
|
.35 |
1 |
|
|
.58 |
.41 |
1 |
Детерминанты
Определитель — это забавное свойство или значение матрицы. Мы (на самом деле, компьютер) будем находить детерминанты корреляции, дисперсии-ковариации или матрицы сумм квадратов и перекрестных произведений (SSCP). Вы можете думать о детерминанте как о мере свободы варьирования или отсутствия предсказуемости в матрице (я говорю это, чтобы дать вам некоторое представление о том, что это такое, даже если это не совсем правильно или точно). Помимо общего представления о том, что это такое, и связанной с ним номенклатуры, вам необходимо знать (а) что определитель используется для нахождения обратной матрицы (обсуждается в следующей теме) и (б) что это означает, когда определитель нуль.
Мы (на самом деле, компьютер) будем находить детерминанты корреляции, дисперсии-ковариации или матрицы сумм квадратов и перекрестных произведений (SSCP). Вы можете думать о детерминанте как о мере свободы варьирования или отсутствия предсказуемости в матрице (я говорю это, чтобы дать вам некоторое представление о том, что это такое, даже если это не совсем правильно или точно). Помимо общего представления о том, что это такое, и связанной с ним номенклатуры, вам необходимо знать (а) что определитель используется для нахождения обратной матрицы (обсуждается в следующей теме) и (б) что это означает, когда определитель нуль.
Определитель матрицы A записывается
дет( А ) = | А | или
|
1 |
.5 |
|
.5 |
1 |
|
А |
|
Определитель обозначен вертикальными черточками вместо скобок. Определитель сложно вычислить, если матрица не имеет порядка 2×2. В этом случае определитель равен 9.0043 a 11 ( a 22 )- a 21 ( a 12 ). Для нашего примера выше определитель будет равен 1(1)-(0,5)(0,5) = 0,75.
Определитель сложно вычислить, если матрица не имеет порядка 2×2. В этом случае определитель равен 9.0043 a 11 ( a 22 )- a 21 ( a 12 ). Для нашего примера выше определитель будет равен 1(1)-(0,5)(0,5) = 0,75.
Большой определитель означает свободу варьирования; определитель, равный нулю, означает, что свободы варьирования нет, в матрице полная предсказуемость. Например, если бы корреляция между нашими двумя мерами равнялась 1,0, то определитель матрицы корреляции был бы равен (1)(1)-(1)(1) = 0. Нулевой определитель получается, когда существует линейная зависимость в матрица. То есть, если одна переменная является линейной комбинацией других переменных в матрице, определитель будет равен нулю. Например, предположим, что я хочу использовать удовлетворенность работой для прогнозирования текучести кадров. У меня есть пять шкал удовлетворенности работой из JDI (Job Descriptive Index, известная мера): работа, зарплата, продвижение по службе, надзор и коллеги. Теперь предположим, что я хочу предсказать оборот по этим пяти плюс общее удовлетворение. Если я суммирую пять шкал, чтобы обозначить общую удовлетворенность, общая сумма будет линейной комбинацией пяти шкал (общая = работа + оплата + промо + супер + совместная работа).
Теперь предположим, что я хочу предсказать оборот по этим пяти плюс общее удовлетворение. Если я суммирую пять шкал, чтобы обозначить общую удовлетворенность, общая сумма будет линейной комбинацией пяти шкал (общая = работа + оплата + промо + супер + совместная работа).
Если я положу все шесть шкал в корреляционную матрицу, определитель будет равен нулю. Матрица с определителем, равным нулю, называется сингулярной . Это своего рода плохая вещь, как будет объяснено в ближайшее время. Сингулярные матрицы доставляют нам неприятные проблемы. Матрица будет сингулярной, если любые две переменные в матрице идеально коррелированы (либо r = 1, либо r = -1). Матрица также будет сингулярной всякий раз, когда любая переменная в матрице точно предсказывается любой комбинацией других переменных в матрице. То есть, если мы выберем какую-либо одну переменную в качестве зависимой и используем любую комбинацию других переменных в матрице для вычисления линейной регрессии, и мы найдем R 2 из 1. 0, матрица вырожденная. Сингулярная матрица не имеет обратной .
0, матрица вырожденная. Сингулярная матрица не имеет обратной .
|
1 |
0 |
0 |
|
|
|
|
|
|
|
0 |
1 |
0 |
|
| А | |
= 1 |
|
|
|
|
0 |
0 |
1 |
|
|
|
|
|
|
|
|
А |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
. |
.25 |
|
|
|
|
|
|
|
.5 |
1 |
.25 |
|
| Б | |
= 0,69 |
|
|
|
|
.25 |
.25 |
1 |
|
|
|
|
|
|
|
|
Б |
|
|
|
|
|
|
|
|
1 |
1 |
0 |
|
|
|
|
|
|
|
1 |
1 |
0 |
|
| С | |
= 0 |
|
|
|
|
0 |
0 |
1 |
|
|
|
|
|
|
|
|
С |
|
|
|
|
|
|
|
Обратите внимание, что определитель для A больше, чем для B , потому что у A больше свободы для изменения, и, конечно же, определитель для C равен нулю, потому что две переменные идеально коррелированы.
Матрица, обратная
, обратное , является матричным аналогом деления действительных чисел. В действительных числах x -1 равно 1/x. А в действительных числах, если умножить х на х -1 , имеем (x)(1/x)=1. Только квадратная матрица может иметь обратную. Обратная матрица обладает тем свойством, что когда мы умножаем матрицу на обратную, получается единичная матрица I . Другими словами, АА -1 = А -1 А = I . Это особенное во многих отношениях. Во-первых, обычно не бывает так, что предварительное и постумножение двух матриц дает один и тот же результат ( AX обычно не равно XA ). Во-вторых, единичная матрица обладает тем свойством, что ее умножение на любую подходящую матрицу приводит к той же самой матрице. то есть АИ = ИА = А . Умножение матрицы на единичную матрицу аналогично операции действительного числа умножения числа или переменной на 1: результирующий результат идентичен введенным числам. Вот почему обратная матрица аналогична делению числа на себя в действительных числах. В действительных числах, когда вы делите число на его обратную («обратную»), результат равен 1. Когда вы умножаете матрицу на обратную, результат равен I . В обоих случаях (1 и I ), умножение на что-то оставляет исходное значение без изменений.
Вот почему обратная матрица аналогична делению числа на себя в действительных числах. В действительных числах, когда вы делите число на его обратную («обратную»), результат равен 1. Когда вы умножаете матрицу на обратную, результат равен I . В обоих случаях (1 и I ), умножение на что-то оставляет исходное значение без изменений.
|
1 |
.5 |
.25 |
|
1 |
0 |
0 |
|
1 |
.5 |
.25 |
|
.5 |
1 |
.25 |
|
0 |
1 |
0 |
|
. |
1 |
.25 |
|
.25 |
.25 |
1 |
|
0 |
0 |
1 |
|
.25 |
.25 |
1 |
|
|
Б |
|
|
|
я |
|
|
|
БИ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
. |
.25 |
|
1,36 |
-.64 |
-.18 |
|
1 |
0 |
0 |
|
.5 |
1 |
.25 |
|
-.64 |
1,36 |
-.18 |
|
0 |
1 |
0 |
|
.25 |
.25 |
1 |
|
-.18 |
-. |
1,36 |
|
0 |
0 |
1 |
|
|
Б |
|
|
|
Б -1 |
|
|
ББ -1 |
||
Проверьте умножение.
БИ(1,1) = 1+0+0; БИ(2,1) = 0,5+0+0; BI(3,1) = .25+0+0 и т. д. BB -1 (1,1) = (1)1,36-0,5(0,46)-0,25(0,18) = 1; BB -1 (2,1) = 0,5(1,36)-(1).64-0,25(0,18)=0 и т. д.
Третья основная причина, по которой нас это волнует, заключается в том, что для нахождения весов b и b из матриц данных используется инверсия. Если мы умножим корреляционную матрицу на обратную, мы получим единичную матрицу I . Это позволяет нам умножать обе части уравнения на обратную для решения матричного уравнения (так же, как деление обеих частей уравнения в обычной алгебре).
Если мы умножим корреляционную матрицу на обратную, мы получим единичную матрицу I . Это позволяет нам умножать обе части уравнения на обратную для решения матричного уравнения (так же, как деление обеих частей уравнения в обычной алгебре).
Обратное позволяет нам найти веса b .
Во всяком случае, нет обратной, когда матрица вырожденная (когда определитель равен нулю). Когда обратной нет, мы не можем найти веса b . Итак, если у нас есть сингулярная матрица, мы не можем использовать множественную регрессию.
MATH0005 Алгебра 1 часть 3
33 Матрицы и векторы
Определение матрицы и вектора
Мы начнем с множества определений. 92\).

Элементы матрицы
Элемент \(i\), \(j\) матрицы означает число в строке \(i\), столбце \(j\). Важно получить их правильно. Обычно, когда вы указываете \((x, y)\) координаты, \(x\) относится к горизонтальному направлению, а \(y\) относится к вертикальному направлению. Однако, когда мы говорим о элементе \(i,j\) матрицы, первое число \(i\) относится к номеру строки (т.е. вертикальному направлению), а второе число \(j\) относится к номер столбца (т. е. горизонтальное направление).
Мы хотим часто обращаться к этим записям. Мы часто пишем \(A = (a_{i,j})\), чтобы обозначить, что \(A\) — это матрица, элемент которой \(i\),\(j\) называется \(a_{ij}\ ).
Например, в случае \(2\times 2\) мы получим
\[A = \begin{pmatrix} а_{11} и а_{12} \\ а_{21} и а_{22} \end{pmatrix}.\]
Если вы используете это обозначение, вы, конечно, также должны указать размер матрицы.
Добавление матриц
Мы можем добавлять матрицы одинакового размера
Если \(A=(a_{ij})\) и \(B=(b_{ij})\) имеют одинаковый размер, то \(A+B\) определяется как матрица, \( i,j\) запись \(a_{ij} + b_{ij}\).
Пример. \[\begin{pmatrix} 1 и 2 \\ 4 и 5 \end{pmatrix} + \begin{pmatrix} 0&1\\2&3 \end{pmatrix} = \begin{pmatrix} 1+0 и 2+1 \\ 4+2 и 5+3 \end{pmatrix} = \begin{pmatrix} 1&3\\6&8 \end{pmatrix}.\]
Другими словами, мы добавляем матрицы, добавляя соответствующие записи. Мы никогда не добавляем матрицы разных размеров.
Скалярное умножение
Мы также умножаем матрицы на числа — это называется «скалярное умножение».
Если \(A = (a_{ij})\) является матрицей и \(\lambda\) числом, то \(\lambda A\) означает матрицу, \(i,j\) элементом которой является \( \лямбда а_{ij}\).
Пример. \[2 \begin{pmatrix} 1&0\\0&1 \end{pmatrix} = \begin{pmatrix} 2&0\\0&2 \end{pmatrix}.\]
Законы сложения и скалярного умножения
Эти операции обладают некоторыми знакомыми свойствами:
Предложение: , если \(a,b\) скаляры и \(A\), \(B\) матрицы одного размера,
- \((a+b)A = aA + bA\ ) (распределение)
- \(а(А+В) = аА + аВ\) (дистрибутивность)
- \(a(bA) = (ab)A\) (ассоциативность)
Нулевая матрица
Есть некоторые обозначения для матрицы, все элементы которой равны нулю. \(0_{m,n}\) или \(0_{m\times n}\) — это матрица \(m\times n\) со всеми нулевыми элементами. Это называется \(m \times n\) нулевой матрицей .
\(0_{m,n}\) или \(0_{m\times n}\) — это матрица \(m\times n\) со всеми нулевыми элементами. Это называется \(m \times n\) нулевой матрицей .
34 Умножение матриц 1
Мы собираемся определить способ умножения некоторых (но не всех) матриц вместе и обосновать определение, исходя из композиции функций. Определение будет построено по частям: первая строка умножается на столбец, затем матрица умножается на столбец, затем матрица умножается на матрицу.
Столбец времени строк
Пусть \(\mathbf{r} = (r_1,\ldots,r_n)\) будет вектором-строкой ширины \(n\) и
\[\mathbf{c} = \begin {pmatrix}c_1 \\ \vdots \\c_n\end{pmatrix}\] 9n r_i c_i\).
Важно отметить, что здесь мы определяем только вектор-строку, умноженный на вектор-столбец. Порядок важен. \(\mathbf{c}\mathbf{r}\) не определен.
Пример. \[
\begin{pматрица}
1&2&3
\end{pmatrix} \begin{pmatrix}
4\\5\\6
\end{pmatrix} = 1\times 4 + 2 \times 5 + 3 \times 6 = 32. \]
\]
Это похоже на скалярное произведение, если вы видели это раньше.
Столбец умножения матрицы
Пусть \(A=(a_{ij})\) будет \(m \times n\) матрицей со строками \(\mathbf{r}_1,\ldots, \mathbf{r} _м\). Это означает, что \(\mathbf{r}_i\) является вектором-строкой \((a_{i1},\ldots,a_{in})\)
Пусть \(\mathbf{c}\) — вектор-столбец высоты \(n\). Тогда \(A\mathbf{c}\) определяется как высота \(m\) вектор-столбца \(\begin{pmatrix}\mathbf{r}_1\mathbf{c} \\ \vdots \\ \mathbf {r}_m \mathbf{c} \end{pmatrix}\).
В этом определении важно то, что количество столбцов \(A\), равное \(n\), должно быть таким же, как количество строк \(\mathbf{c}\) для \ (Ac\) необходимо определить.
Пример. Пусть \(A = \begin{pmatrix} 1&2\\3&4 \end{pmatrix}\). Тогда строки \(A\) равны \(\mathbf{r}_1 = \begin{pmatrix} 1&2 \end{pmatrix}\) и \(\mathbf{r}_2 = \begin{pmatrix} 3 & 4 \end{pmatrix}\). Если \(\mathbf{c} = \begin{pmatrix} 5\\6 \end{pmatrix}\), то мы можем вычислить \(A\mathbf{c}\), поскольку количество столбцов \(A\) (что равно 2) равно количеству строк \(\mathbf{c}\):
\[A\mathbf{c} = \begin{pmatrix}
r_1 \mathbf{c} \\
r_2 \mathbf{с}
\end{pmatrix} = \begin{pmatrix}
1\х 5 + 2\х 6\3\х 5 + 4\х 6
\end{pmatrix}\].
Пример. Пусть \(A = \begin{pmatrix} 1&2\\3&4\\5&6 \end{pmatrix}\), матрица \(3\times 2\) и \(\mathbf{c} = \begin{pmatrix } 7 \\ 8 \end{pmatrix}\), вектор-столбец \(2 \times 1\). Количество столбцов \(A\) и количество строк \(\mathbf{c}\) равны (2), поэтому мы можем вычислить \(A\mathbf{c}\):
\[A\mathbf{c} = \begin{pmatrix} 1\умножить на 7 + 2\умножить на 8\\ 3 \умножить на 7 + 4 \умножить на 8\\ 5 х 7 + 6 х 8 \end{pmatrix}.\]
Матрица, умноженная на матрицу
Пусть \(A\) будет \(m \times n\), а \(B\) будет \(n\times p\). Пусть столбцы \(B\) равны \(\mathbf{c}_1,\ldots,\mathbf{c}_p\). Тогда \(AB\) является матрицей \(m\times p\) со столбцами \(A\mathbf{c}_1,\ldots, A\mathbf{c}_p\).
Опять же, важно отметить, что \(AB\) определено, если и только если количество столбцов \(A\) равно количеству строк \(B\).
Это определение говорит о том, что
\[A(\mathbf{c}_1\; \ldots \; \mathbf{c}_p) = (A\mathbf{c}_1\; \ldots \;A\mathbf{c}_p)\]
, что мы имеем в виду, когда говорим, что умножение матриц работает по столбцам или по столбцам .
Пример. Пусть
\[A = \begin{pmatrix} 1 и 2 \end{pmatrix}, B= \begin{pmatrix} 1&0&1\\ 0&1&0 \end{pmatrix}.\]
\(A\) равно \(1\times 2\), \(B\) равно \(2\times 3\), поэтому произведение матриц \(AB\) равно определена и представляет собой матрицу \(1\times 3\).
Столбцы \(B\) равны \(\mathbf{c}_1 = \begin{pmatrix} 1\\0 \end{pmatrix}\), \(\mathbf{c}_2 = \begin{pmatrix } 0\\1 \end{pmatrix}\) и \(\mathbf{c}_3 = \begin{pmatrix} 1&0 \end{pmatrix}\). Таким образом, произведение \(AB\) равно
\[\begin{pmatrix} А\mathbf{c}_1 и А\mathbf{c}_2 и А\mathbf{c}_3 \end{pmatrix} = \begin{pmatrix} 1 умножить на 1 + 2 на 2 и 1 на 0 + 2 на 1 и 1 на 1 и 2 на 1 и 2 0 \end{pmatrix}\]
Пример. Пусть
\[A = \begin{pmatrix} 1&2\\ 3 и 4 \end{pmatrix}, B = \begin{pmatrix} 5&6\\ 7 и 8 \end{pmatrix}.\]
Тогда \(A\) равно \(2\times 2\), \(B\) равно \(2\times 2\), поэтому произведение матриц \(AB\) определено и будет другой матрицей \(2\times 2\):
\[AB = \begin{pmatrix}
1 умножить на 5 + 2 на 7 и 1 на 6 + 2 на 8
3 х 5 + 4 х 7 и 3 х 6 + 4 х 8
\end{pmatrix}. n a_{ik}b_{kj}\)
n a_{ik}b_{kj}\)
Свойства умножения матриц
Предложение. Пусть \(A\), \(A’\) будет \(m \times n\), пусть \(B, B’\) будет \(n \times p\), пусть \(C\) будет \(p \times q\), и пусть \(l\) будет числом. Затем 9n a_{ik}b_{kj}= \lambda (AB)_{ij}\] поэтому \((\lambda A)B\) и \(\lambda (AB)\) имеют одинаковые \(i, j \) запись для любого \(i, j\) и, следовательно, равны. Аналогично доказывается второе равенство.
Эти результаты говорят о том, что при работе с матрицами можно использовать некоторые обычные правила алгебры — подобно тому, как это происходило при перестановках. Опять же, как и с перестановками, вы не можете использовать свойство коммутативности.
Умножение матриц некоммутативно
Говорят, что две матрицы \(A\) и \(B\) коммутируют , если \(AB\) и \(BA\) определены и \(AB=BA\).
Для некоторых пар матриц произведение \(AB\) определено, а \(BA\) — нет. Например, если \(A\) равно \(2\times 3\), а \(B\) равно \(3\times 4\), то \(AB\) определено, а \(BA\) — нет. .
Даже если оба \(AB\) и \(BA\) определены и имеют одинаковый размер, в общем случае они не будут равны.
Пример: пусть \(A=\begin{pmatrix} 1&2\\3&4 \end{pmatrix}\) и \(B = \begin{pmatrix} 5&6\\7&8 \end{pmatrix}\). Затем
\[\begin{выравнивание*} AB &= \begin{pmatrix} 19&22\\43&50 \конец{pmatrix}\\ БА &= \begin{pmatrix} 23&34\\31&46 \end{pmatrix}.\end{align*}\]
Единичная матрица
Определение: \(n\) на \(n\) единичная матрица \(I_n\) — это матрица с \(i,j\) запись 1, если \(i=j\) и 0 в противном случае.
Например,
\[I_2 = \begin{pmatrix}
1&0\\0&1
\end{pmatrix}, I_3 = \begin{pmatrix}
1&0&0\\0&1&0\\0&0&1
\end{pmatrix}. \]
\]
Наиболее важным свойством единичных матриц является то, что они ведут себя так же, как число 1 при умножении на него.
Лемма: если \(A\) является \(m \times n\) матрицей, то \(I_m A = A = A I_n\).
Доказательство: Пусть \(A = (a_{ij}), I_n = (\delta_{ij})\), поэтому \(\delta_{ij}\) равно 1, если \(i=j\) и 0 в противном случае. Формула умножения матриц говорит нам, что для любых \(i\) и \(j\) запись \(i,j\) в \(I_mA\) равна \(\sum_k \delta_{ik}a_{kj }\) Единственный член в этой сумме, который может быть ненулевым, это тот, когда \(k=i\), поэтому сумма равна \(1\times a_{ij} = a_{ij}\). Таким образом, запись \(i,j\) в \(I_mA\) равна \(a_{ij}\), запись \(i,j\) в \(A\).
Аналогично доказывается второе равенство.
36 Обратимость I
Определение: \(n \times n\) матрица \(A\) называется обратимой тогда и только тогда, когда существует \(n \times n\) матрица \(B \) такой, что \(AB = BA = I_n\).
Если существует такая матрица \(B\), то такая матрица \(B\) только одна:
Предложение: Если \(AB=BA=I_n\) и \(AC=CA=I_n \), затем \(В=С\).
Доказательство:
\[\begin{align*} Б &= БИ_н \\ &= В(АС) \\ &= (BA)C &\text{ассоциативность} \\ &= I_nC \\ &= C \end{align*}\] 9{-1} = \frac{1}{ad-bc} \begin{pmatrix} d&-b\\-c & a \end{pmatrix}\).
Матрицы со строками или столбцами нулей необратимы
Предложение: если матрица \(n\times n\) \(A\) имеет строку нулей или столбец нулей, то она не обратим.
Доказательство: Если \(A\) имеет столбец нулей, то для любой матрицы \(B\) произведение \(BA\) будет иметь столбец, который \(B\) умножить на \(A\) нулевой столбец , который является столбцом нулей. Итак, \(BA\) не равно \(I_n\).
Аналогично, если \(A\) имеет нулевую строку, то для любой матрицы \(B\) произведение \(AB\) также имеет нулевую строку, поэтому оно не равно \(A_n\). {-1}\).
{-1}\).
Доказательство такое же, как и для перестановок.
37 Системы линейных уравнений
Определение линейной системы
Определение: Система \(m\) линейных уравнений с \(n\) неизвестными \(x_1…x_n\) с коэффициентами \( a_{ij}, 1 \leq i \leq m, 1 \leq j \leq n\) и \(b_1, \ldots, b_m\) — список одновременных уравнений
\[\begin{align*} a_{11} x_1 + a_{12} x_2 +\cdots + a_{1n}x_n &= b_1 \\ a_{21} x_1 + a_{22} x_2 + \cdots +a_{2n}x_n &= b_2 \\ \vdots и \vdots\\ a_{m1} x_1 + a_{m2} x_2 +\cdots + a_{mn}x_n &= b_m \end{align*}\]
Матричная форма линейной системы
Каждая система линейных уравнений может быть записана в матричной форме : приведенная выше система эквивалентна
\[A\mathbf{x} = \mathbf{b}\]
где \(A = (a_{ij})\), \(\mathbf{x} = \begin{pmatrix}x_1\\\vdots\\x_n\end{pmatrix}\) и \(\mathbf{b } = \begin{pmatrix}b_1\\ \vdots \\b_m \end{pmatrix}\).
Например, система линейных уравнений
\[\begin{align*} 2x + 3y + 4z &= 5\\ х + 5z &= 0 \end{выравнивание*}\]
имеет матричную форму
\[\begin{pmatrix}
2&3&4 \\
1 и 0 и 5
\end{pmatrix} \begin{pmatrix}
х\\у\\г
\end{pmatrix} = \begin{pmatrix}
5\\0
\end{pmatrix}. { -1}\), чтобы увидеть, что есть 9{-1}\mathbf{b}\).
{ -1}\), чтобы увидеть, что есть 9{-1}\mathbf{b}\).
Увеличенная матрица
Увеличенная матрица системы линейных уравнений, матричная форма которой \(A\mathbf{x}=\mathbf{b}\) — это матрица, которую вы получаете, добавляя \(\mathbf{ b}\) в качестве дополнительного столбца справа от \(A\). Мы пишем это как \((A | \mathbf{b})\).
Например, расширенная матрица для приведенной выше системы линейных уравнений будет
\[\begin{pmatrix} 2&3&4&5\\ 1&0&5&0 \end{pmatrix}.\]
Решения системы в матричной форме
Решение системы линейных уравнений с матрицей из \(A\mathbf{x}=\mathbf{b}\) является вектором \(\mathbf{y}\ ) (на этот раз чисел, а не «неизвестных») таких, что \(A\mathbf{y}=\mathbf{b}\).
Система линейных уравнений может иметь единственное решение, множество различных решений или вообще не иметь решений. В следующих лекциях мы увидим, как узнать, сколько решений имеет система, если таковые имеются.
Матричное уравнение \(A\mathbf{x}=\mathbf{b}\) или соответствующая система линейных уравнений называется непротиворечивый , если он имеет решение, в противном случае он называется несогласованным .
38 Операции со строками
Как мы решаем линейные системы
Если вам дают систему линейных уравнений с переменными \(x, y, z\) и просят решить их, то, вероятно, вы манипулируете уравнениями с помощью добавляя множители одного уравнения к другому, пока вы не «устраните» некоторые переменные и не сможете считать решения.
Попробуем формализовать этот метод решения линейных уравнений.
Поскольку мы хотим использовать матричные методы, давайте решим примерную систему и проследим, что наша работа с уравнением делает с соответствующей расширенной матрицей.
Рассмотрим линейную систему
\[\begin{align*} 3х+4у&=6\х+2у&=5. \end{align*}\]
Соответствующее матричное уравнение имеет вид \(A\mathbf{x}=\mathbf{b}\), где
\[A=\begin{pmatrix}3&4\\1&2\end{ pmatrix}, \mathbf{b} = \begin{pmatrix}6\\ 5 \end{pmatrix}, \mathbf{x} = \begin{pmatrix}x \\y \end{pmatrix}. \]
\]
Расширенная матрица имеет вид \((A | \mathbf{b}) = \begin{pmatrix} 3&4&6\\1&2&5 \end{pmatrix}\).
Чтобы решить систему, мы сначала исключаем \(x\) из первого уравнения, вычитая 3 раза второе уравнение из первого. Уравнения становятся
\[\begin{align*} -2у&=-9\ х+2у &= 5 \end{align*}\]
Расширенная матрица \(\begin{pmatrix} -2&0&-9\\1&2&5 \end{pmatrix}\) этой новой системы получается путем сложения \(-3\) раз вторую строку старой расширенной матрицы в первую строку.
Затем мы получаем коэффициент при \(y\) в первом уравнении до 1, умножая первое уравнение на \(-1/2\). Уравнения становятся
\[\begin{align*} у &= 9/2 \\ х+2у &= 5 \end{align*}\]
Расширенная матрица \(\begin{pmatrix} 0&1&9/2\\1&2&5 \end{pmatrix}\) этой новой системы получается путем умножения каждой записи в первой строке старой увеличенная матрица на \(-1/2\).
Далее мы исключаем \(y\) из второго уравнения, вычитая 2 раза первое уравнение из второго. Уравнения становятся
\[\begin{выравнивание*} у &= 9/2 \\ х &= -4 \end{align*}\]
Расширенная матрица \(\begin{pmatrix} 0&1&9/2\\1&0&-4 \end{pmatrix}\) этой новой системы получается путем сложения \(-2\) раз первого ряда во второй ряд.
Наконец, если бы мы хотели, чтобы первое уравнение сообщало нам значение первой переменной, а второе уравнение — о второй переменной, мы могли бы поменять местами порядок двух уравнений, что соответствует перестановке строк расширенной матрицы. чтобы он стал \(\begin{pmatrix} 1&0&-4\\0&1&9/2 \end{pmatrix}\).
Операции со строками
Манипуляции, которые мы выполняем с системами линейных уравнений, соответствуют выполнению «операций со строками» над расширенными матрицами.
Определение: a операция со строками — это одна из следующих вещей, которые мы можем делать с матрицей.
- добавить \(l\) умножить на строку \(i\) к строке \(j\) (для \(j \neq i\), \(l\) любое число), записать \(r_j \mapsto r_j + l r_i\).
- умножить строку \(i\) на \(l\), где \(l\neq 0\), пишется \(r_i \mapsto l r_i\).
- поменять местами строки \(i\) и \(j\), записать \(r_i \leftrightarrow r_j\).
Мы говорим «операция строки» как сокращенную форму операции строки.
Операции со строками являются обратимыми
Важно, чтобы эти операции со строками были обратимыми . То есть для каждой операции строки \(r\) существует другая операция строки \(s\), такая что выполнение \(r\), затем \(s\) или выполнение \(s\), затем \(r\) , это то же самое, что ничего не делать — это возвращает вас к матрице, с которой вы начали.
9{-1}\)39 Элементарные матрицы
Определение элементарной матрицы
Элементарную матрицу можно получить, выполнив операцию с одной строкой над единичной матрицей. Они будут иметь решающее значение для нашего понимания обратимости и решения систем линейных уравнений.
Примеры:
- Элементарная матрица \(\begin{pmatrix} 0&1\\1&0\end{pmatrix}\) получается в результате выполнения операции строки \(r_1 \leftrightarrow r_2\) в \(I_2\) .

- Элементарная матрица \(\begin{pmatrix}1&2&0\\0&1&0\\0&0&1\end{pmatrix}\) получается в результате выполнения операции строки \(r_1 \mapsto r_1 + 2r_2\) в \(I_3\).
- Элементарная матрица \(\begin{pmatrix}-1&0\\0&1\end{pmatrix}\) получается в результате выполнения операции строки \(r_1 \mapsto (-1)r_1\) в \(I_2\).
Выполнение операции строки аналогично умножению на элементарную матрицу
Выполнение операции строки \(r\) над матрицей имеет тот же эффект, что и умножение этой матрицы слева на элементарную матрицу, соответствующую \(r\ ): 9m s_{lk}a_k \;\;\;\; (\dagger)\]
где \(s_{lk}\) — запись \(l, k\) \(r(I_m)\).
Существует три случая в соответствии с тремя типами операций с строками. В каждом случае мы вычислим \(r(I_m)A\) и покажем, что это то же самое, что и \(r(A)\).
- \(r\) есть \(r_i\mapsto \lambda r_i\). Для \(l\neq i\) \(l\)-я строка \(r(I_m)\) совпадает с \(l\)-й строкой \(I_m\), поэтому \(s_ {lk}=0\), если только \(k=l\) не равно 1.
 Таким образом, из (\(\dagger\)), \(l\)-й записи \(r(I_m)A\ ) есть \(a_l\). Если \(l=i\), то \(s_{lk}=\lambda\), если \(k=l\), и 0 в противном случае, так что снова через (\(\dagger\)) \(i\)th запись \(r(I_m)A\) равна \(\lambda a_i\). Следовательно, \(r(I_m)A\) совпадает с \(A\), за исключением того, что \(i\)-я запись умножается на \(\lambda\). Это \(г(А)\).
Таким образом, из (\(\dagger\)), \(l\)-й записи \(r(I_m)A\ ) есть \(a_l\). Если \(l=i\), то \(s_{lk}=\lambda\), если \(k=l\), и 0 в противном случае, так что снова через (\(\dagger\)) \(i\)th запись \(r(I_m)A\) равна \(\lambda a_i\). Следовательно, \(r(I_m)A\) совпадает с \(A\), за исключением того, что \(i\)-я запись умножается на \(\lambda\). Это \(г(А)\). - \(r\) равно \(r_i \leftrightarrow r_j\). Имеются три случая для \(l\).
- \(l\neq i,j\). В этом случае \(s_{lk}=0\), если только \(k=l\), в этом случае оно равно 1, поэтому из \((\dagger)\) сумма равна \(a_r\).
- \(л=я\). Поскольку \(r_{ij}(I_m)\) меняет местами строки \(i\) и \(j\) из \(I_m\), \(s_{ik}=1\), если \(k=j\) и 0 в противном случае. Итак, сумма равна \(a_j\).
- \(l=j\). Как и в последнем случае, сумма равна \(a_i\). Следовательно, \(r(I_m)A\) совпадает с \(A\), за исключением строки \(i\), где появляется \(a_j\), и строки \(j\), где появляется \(a_i\). Это \(г(А)\).
- \(r\) равно \(r_i \mapsto r_i + \lambda r_j\).
 На этот раз строки \(r(I_m)\) такие же, как строки \(I_m\), за исключением \(i\)th, который имеет \(i, i\) запись 1 и \(i, j\) запись \(\lambda\), поэтому \(s_{ii}=1, s_{ij}=\lambda\), а все остальные \(s_{ik}=0\). Из (\(\dagger\)) каждая запись \(r(I_m)A\) совпадает с соответствующей записью \(A\), кроме \(i\)th, где мы получаем \(a_i+ \lambda a_j\), и снова \(r(I_m)A\) совпадает с \(r(A)\).
На этот раз строки \(r(I_m)\) такие же, как строки \(I_m\), за исключением \(i\)th, который имеет \(i, i\) запись 1 и \(i, j\) запись \(\lambda\), поэтому \(s_{ii}=1, s_{ij}=\lambda\), а все остальные \(s_{ik}=0\). Из (\(\dagger\)) каждая запись \(r(I_m)A\) совпадает с соответствующей записью \(A\), кроме \(i\)th, где мы получаем \(a_i+ \lambda a_j\), и снова \(r(I_m)A\) совпадает с \(r(A)\).
Элементарные матрицы обратимы
Следствие: элементарных матриц обратимы.
Доказательство: Пусть \(r\) будет строкой op и \(I\) единичной матрицей. Пусть \(s\) будет строкой, обратной к \(r\).
\(r(I)s(I) = r(sI)\) по только что доказанной теореме, но \(r(s(I))=I\) при \(r\) и \( s\) обратны.
По тем же причинам \(s(I)r(I) = s(r(I)) = I\).
Отсюда следует, что \(r(I)\) обратимо с обратным \(s(I)\).
40 RREF 1
Строковые операции не изменяют решения матричного уравнения
Наш неформальный метод решения линейных систем заключается в том, чтобы «выполнять определенные манипуляции с уравнениями до тех пор, пока они не примут вид, в котором решения легко считываются». Этот метод работает только в том случае, если производимые нами манипуляции не меняют набор решений.
Этот метод работает только в том случае, если производимые нами манипуляции не меняют набор решений.
Когда мы ввели операции со строками, это произошло потому, что их влияние на расширенную матрицу линейной системы соответствовало типу манипуляций, которые мы выполняем при решении такой линейной системы. Теперь мы собираемся доказать, что эти операции со строками не меняют набор решений.
Теорема. Предположим, что \((A’ | \mathbf{b}’)\) получается из \((A | \mathbf{b})\) путем выполнения последовательности операций со строками. Тогда множество решений матричного уравнения \(A\mathbf{x}=\mathbf{b}\) равно множеству решений \(A’\mathbf{x} = \mathbf{b}’\).
Эквивалентно, если \(\mathbf{v}\) является вектором, то \(A\mathbf{v}=\mathbf{b}\) тогда и только тогда, когда \(A’\mathbf{v} = \mathbf {б}’\).
Доказательство: достаточно проверить это, когда \((A’ | \mathbf{b}’)\) получается в результате выполнения однострочной операции \(r\) в \((A | \mathbf{b} )\). Затем мы можем многократно использовать этот результат, чтобы доказать общий случай, когда \((A’ | \mathbf{b}’)\) получается путем выполнения последовательности операций со строками.
Затем мы можем многократно использовать этот результат, чтобы доказать общий случай, когда \((A’ | \mathbf{b}’)\) получается путем выполнения последовательности операций со строками.
В случае одной строки op \(r\),
\[(A’ | \mathbf{b}’) = r(I) (A | \mathbf{b})\]
поэтому (поскольку умножение матриц работает по столбцам) \(A’ = r(I)A\) и \(\mathbf{b}’ = r(I)\mathbf{b}\).
Теперь для любого вектора \(\mathbf{v}\),
\[A\mathbf{v} = \mathbf{b} \iff r(I)A\mathbf{v} = r(I) \ mathbf{b}.\]
, так как если \(A \mathbf{v} = \mathbf{b}\), то мы можем умножить на \(r(I)\) слева, чтобы получить \(r(A )A \mathbf{v} = r(I) \mathbf{b}\), и наоборот, если \(r(I)A \mathbf{v} = r(I) \mathbf{v}\), то мы можем умножьте на обратную \(r(I)\), которую мы знаем как обратимую из-за нашего доказательства в предыдущей лекции, чтобы получить \(A \mathbf{v} = \mathbf{b}\).
Поскольку \(r(I)A = A’\) и \(r(I) \mathbf{b} = \mathbf{b}’\), мы получаем, что \(\mathbf{v}\) является решение \(A \mathbf{x} = b\) тогда и только тогда, когда оно является решением \(A’ \mathbf{x} = \mathbf{b}’\)
Строковая сокращенная ступенчатая форма
Мы говорили об управлении уравнения в простой форме, где решения можно было легко прочитать. Одна возможная «простая форма» называется ступенчатой формой с уменьшенным числом строк.
Одна возможная «простая форма» называется ступенчатой формой с уменьшенным числом строк.
Определение: ведущий элемент в матрице — это первый ненулевой элемент в строке, начиная слева.
Например, в матрице \(\begin{pmatrix} 0&2\\0&0 \end{pmatrix}\). ведущей записью в первой строке является 2 в позиции \(1,2\), а во второй строке нет ведущей записи.
Определение. матрица находится в рядной сокращенной ступенчатой форме (RREF), если
- все ведущие элементы равны 1
- все нулевые строки находятся внизу (нулевая строка — это строка, все элементы которой равны нулю)
- все записи в том же столбце, что и ведущая запись, равны нулю
- для каждого \(i\), если строки \(i\) и \(i+1\) имеют ведущую запись, то ведущая запись в строке \(i+1\) находится справа от записи в строке \ (я\)
Примеры.
- \(\begin{pmatrix} 0 & 0 \\ 1 & 0 \end{pmatrix}\) не находится в RREF: нулевая строка находится вверху.

- \(\begin{pmatrix} 2 & 0 \\ 0 & 0 \end{pmatrix}\) не находится в RREF: есть строка, в которой крайняя левая ненулевая запись не равна 1.
- \(\begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix}\) не находится в RREF: самая левая 1 в строке 2 не находится справа от самой левой 1 в строке ряд над ним.
- \(\begin{pmatrix} 1 &\alpha &\beta & 3 \\ 0 &0 & 1 & -2 \end{pmatrix}\) находится в RREF тогда и только тогда, когда \(\beta = 0\): самая левая 1 в строке 2 находится в столбце 3, но это не единственная ненулевая запись в столбце 3, если только \(\beta = 0\).
- \(\begin{pmatrix} 1 & 0 & 0 & 3 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 \end{pmatrix}\) находится в RREF.
41 RREF 2
Существование и уникальность
Вот два факта о форме редуцированного эшелона строки.
- любую матрицу можно поместить в RREF, выполнив операции со строками.
- Если \(B\) и \(C\) являются матрицами в RREF, которые являются результатом выполнения строковых операций над матрицей \(A\), то \(B=C\).

Первое относительно легко доказать индукцией по количеству столбцов. Второй немного сложнее. Если вы в это верите, это означает, что мы могли бы говорить о «этой» ступенчатой форме матрицы \(A\), сокращенной по строкам, что означает уникальную матрицу в RREF, которую можно получить, выполняя операции со строками для \(A\). Нам этот результат не нужен, поэтому мы не будем его здесь доказывать. Если вы хотите увидеть доказательства как 1, так и 2, вы можете прочитать их по этой ссылке.
Пример помещения матрицы в RREF
Факт 1 выше говорит о том, что для любой матрицы \(A\) мы можем выполнить последовательность операций со строками для \(A\) и в итоге получить матрицу в RREF. Вот пример.
Пусть \(A = \begin{pmatrix} 1&2&3\\4&5&6\\7&8&9 \end{pmatrix}\). Мы хотим выполнить последовательность операций со строками для \(A\), которая заканчивается матрицей в RREF. Строка 1 имеет начальную запись в позиции \(1,1\), но другие записи в столбце 1 не равны 0. Хорошим началом является использование операций строки, таких как \(r_j \mapsto r_j + lr_1\), чтобы устранить другие записи в столбце 1:
Хорошим началом является использование операций строки, таких как \(r_j \mapsto r_j + lr_1\), чтобы устранить другие записи в столбце 1:
\[A \stackrel{r_2 \mapsto r_2-4r_1}{\mapsto} \begin{pmatrix} 1&2&3\\ 0&-3&-6\\ 7&8&9 \end{pmatrix} \stackrel{r_3 \mapsto r_3-7r_1}{\mapsto} \begin{pmatrix} 1&2&3\\ 0&-3&-6\\ 0&-6&-12 \end{pmatrix}\]
Эта матрица отсутствует в RREF. Одна из причин заключается в том, что ведущая запись в строке 2 в позиции \(2,2\) не равна 1. Чтобы сделать эту ведущую запись 1, мы можем использовать операцию строки, которая умножает строку 2 на \(-1/ 3\):
\[\begin{pmatrix} 1&2&3\\ 0&-3&-6\\ 0&-6&-12 \end{pmatrix} \stackrel{r_2 \mapsto (-1/3)r_2}{\mapsto} \begin{pmatrix} 1&2&3\\ 0&1&2\\ 0&-6&-12 \end{pmatrix}\]
Теперь у нас есть первая запись в строке 2, столбце 2, равная 1, но в этом столбце есть и другие ненулевые записи. Мы должны устранить их, добавив несколько строк 2 к строкам 1 и 3:
\[\begin{gather*}\begin{pmatrix} 1&2&3\\ 0&1&2\\ 0&-6&-12 \end{pmatrix} \stackrel{r_1 \mapsto r_1-2r_2}{\mapsto} \begin{pmatrix} 1&0&-1\\ 0&1&2 \\ 0&-6&-12 \end{pmatrix} \\ \stackrel{r_3 \mapsto r_3+6r_2}{\mapsto} \begin{pmatrix} 1&0&-1\\ 0&1&2\\ 0&0&0 \end{pmatrix}\end{собрать*}\]
Эта матрица находится в формате RREF, так что мы закончили.
Решения системы, расширенная матрица которой находится в RREF
Предположим, мы начинаем с линейной системы с матричной формой \(A\mathbf{x}=\mathbf{b}\), затем помещаем расширенную матрицу \((A | \mathbf{b})\) в RREF. Предположим, что результирующая матрица в RREF равна \((A’ | \mathbf{b}’)\). Весь смысл в том, что решения \(A \mathbf{x} = \mathbf{b}\) такие же, как решения \(A’ \mathbf{x} = \mathbf{b}’\) , но должно быть «легко» найти решения \(A’ \mathbf{x} = \mathbf{b}’\). Как мы на самом деле находим эти решения?
Пример 1. Вот расширенная матрица в RREF
\[\begin{pmatrix} 1&0&2&0&0\\ 0&1&4&0&0\\ 0&0&0&1&0\\ 0&0&0&0&1 \end{pmatrix}\]
Если переменные называются \(x, y, z, w\), то соответствующие уравнения равны
\[\begin{align*} х + 2z &= 0 \\ у+4z &= 0\\ ш &= 0 \\ 0 &= 1 \end{align*}\]
Последнее уравнение невозможно, поэтому у этой линейной системы нет решений.
Пример 2. Вот та же расширенная матрица с другим конечным столбцом.
\[\begin{pmatrix} 1&0&2&0&2\\ 0&1&4&0&3\\ 0&0&0&1&4\\ 0&0&0&0&0 \end{pmatrix}\]
В этом случае, если переменные \(x, y, z, w\), уравнения равны
\[\begin{align*} х + 2z &= 2 \\ у+4г &= 3\\ ш &= 4\\ 0 &= 0\end{align*}\]
Решения: \(x=2-2z, y=3-4z, w=4\). Последнее уравнение \(0=0\) ничего нам не говорит, поэтому его можно игнорировать.
Мы можем записать решения в векторной форме как
\[\begin{align*} \begin{pmatrix}x\\ y\\ z\\ w\end{pmatrix} &= \begin{pmatrix}2-2z\\ 3-4z\\ z\\ 4\end{pmatrix} \\ &= \begin{pmatrix}2\\3\\0\\4\end{pmatrix} + z\begin{pmatrix}-2\\ -4\\ 1\\ 0\end{pmatrix} \end{align*}\]
В общем случае:
- Если последний столбец расширенной матрицы имеет лидирующую запись (как в примере 1), решений нет. В противном случае
- Переменные, соответствующие столбцу без начального элемента (например, \(z\) в примере 2), можно выбирать свободно («свободные параметры»).
- Другие переменные могут быть однозначно определены с помощью этих свободных параметров.

42 Обратимость и RREF
Мы собираемся доказать следующую теорему:
Теорема: квадратная матрица \(A\) обратима тогда и только тогда, когда существует последовательность строковых операций, принимающих \(A\) к единичной матрице.
Нам понадобится пара лемм, чтобы доказательство заработало.
Первая лемма: квадратные матрицы в RREF
Лемма: пусть \(X\) будет \(n \times n\) матрицей в RREF. Либо это идентификатор, либо в нем есть столбец без начального элемента.
Доказательство: предположим, что в каждом столбце есть начальный элемент, поэтому имеется \(n\) начальных элементов. В каждой строке может быть не более одной ведущей записи и всего \(n\) строк, поэтому каждая строка должна иметь ведущую запись.
Пусть \(c_i\) будет номером столбца, в котором находится ведущая запись строки \(i\). Затем \(c_1 < c_2 < \ldots < c_n\) по условию RREF для ведущих записей. Поскольку числа \(c_i\) равны \(1,\ldots, n\) в некотором порядке, они должны быть \(c_i=i\) для всех \(i\). Это означает, что ведущая запись строки 1 находится в столбце 1, ведущая запись строки 2 находится в столбце 2 и так далее.
Это означает, что ведущая запись строки 1 находится в столбце 1, ведущая запись строки 2 находится в столбце 2 и так далее.
Поскольку \(X\) находится в RREF, столбцы с ведущими элементами имеют нули во всех остальных позициях. Таким образом, первый столбец равен \(\begin{pmatrix} 1\\0\\ \vdots \\ 0 \end{pmatrix}\), второй столбец равен \(\begin{pmatrix} 0\\1\\0\ \\vdots\\0\end{pmatrix}\) и так далее. Это столбцы единичной матрицы, поэтому \(X=I\).
Вторая лемма: если E обратимо, то EA обратимо тогда и только тогда, когда A обратимо
Лемма: пусть \(E\) обратима и \(A\) — квадратная матрица. Тогда \(EA\) обратимо тогда и только тогда, когда \(A\) обратимо. 9{-1}\) и \(АВЕ = I\), то есть \(А(ВЕ) = I\).
Доказательство теоремы
Предположим, что существует последовательность строковых операций, переводящих \(A\) в \(I\), скажем, \(r_1, \ldots, r_k\). Пусть \(E_i = r_i(I)\), элементарная матрица, связанная с \(r_i\). Тогда
\[E_k E_{k-1} \cdots E_1 A = I\]
, так как мы знаем, что выполнение \(r_i\) равносильно умножению слева на \(E_i\) (это Теорема на видео 7). Каждая элементарная матрица обратима (следствие в видео 7). Матрица \(E = E_k \cdots E_1\) обратима, так как является произведением обратимых матриц (видео 4). \(EA = I\), поэтому оно заведомо обратимо, а значит, по второй лемме выше \(A\) обратимо.
Каждая элементарная матрица обратима (следствие в видео 7). Матрица \(E = E_k \cdots E_1\) обратима, так как является произведением обратимых матриц (видео 4). \(EA = I\), поэтому оно заведомо обратимо, а значит, по второй лемме выше \(A\) обратимо.
И наоборот, предположим, что нет последовательности операций со строками, переводящих \(A\) в \(I\). Мы можем выполнить последовательность строковых операций с любой матрицей и в итоге получить матрицу RREF, поэтому, когда мы делаем это с \(A\), полученная матрица RREF — назовем ее \(X\) — не может быть \(I \).
Наша первая лемма выше говорит, что \(X\) имеет столбец без ведущей записи, поэтому есть \(n-1\) или меньше ведущих записей, поэтому есть строка без начальных записей, то есть нулевая строка . Итак, \(X\) необратим (первое предложение, видео 4).
9{-1}\mathbf{0} = \mathbf{0}\). Если \(A\) необратима, мы можем выполнить последовательность строковых операций для \(A\), заканчивающуюся матрицей RREF \(X\), которая не может быть идентичной из-за предыдущей теоремы.
Согласно первой лемме выше, \(X\) имеет столбец без начального элемента. Это означает, что в решениях \(X \mathbf{x} = \mathbf{0}\) есть свободный параметр, и, в частности, существует бесконечно много различных решений \(X \mathbf{x} = \mathbf {0}\) (поэтому существует ненулевое решение).
Решения \(X \mathbf{x} = \mathbf{0}\) совпадают с решениями \(A \mathbf{x} = \mathbf{0}\) (теорема из видео 8) , поэтому \(A \mathbf{x} = \mathbf{0}\) также имеет ненулевое решение.
43 Как вычислить обратную матрицу
Пусть \(A\) — квадратная матрица. Теперь у нас есть метод определения того, является ли \(A\) обратимым: выполняйте операции со строками над \(A\), пока не достигнете матрицы в RREF. Тогда \(A\) обратима тогда и только тогда, когда обратима RREF-матрица. 9{-1} = \frac{1}{\Delta} \begin{pmatrix} \begin{vmatrix} а_{22} и а_{23} \\ а_{32}и а_{33} \end{vmatrix} & -\begin{vmatrix} а_{12} и а_{13} \\ а_{32}и а_{33} \end{vmatrix} & \begin{vmatrix} а_{12} и а_{13} \\ а_{22}и а_{23} \end{vmatrix} \\ -\begin{vmatrix} а_{21} и а_{23} \\ а_{31}и а_{33} \end{vmatrix} & \begin{vmatrix} а_{11} и а_{13} \\ а_{31}и а_{33} \end{vmatrix} & -\begin{vmatrix} а_{11} и а_{13} \\ а_{21}и а_{23} \end{vmatrix} \\ \begin{vmatrix} а_{21} и а_{22} \\ а_{31}и а_{32} \end{vmatrix} & -\begin{vmatrix} а_{11} и а_{12} \\ а_{31}и а_{32} \end{vmatrix} & \begin{vmatrix} а_{11} и а_{12} \\ а_{21}и а_{22} \end{vmatrix} \end{pmatrix}\]
, где \(\begin{vmatrix} a&b\\c&d\end{vmatrix}\) означает \(ad-bc\) и \(\Delta = a_{11}a_{22}a_{33} + a_{ 12}а_{23}а_{31} + а_{13}а_{21}а_{32}-а_{11}а_{23}а_{32} — а_{12}а_{21}а_{33} — а_{13}а_{22}а_{31}\). Это не очень хорошая формула для практического использования. К счастью, мы можем использовать методы RREF для определения обратимости и поиска инверсий.
Это не очень хорошая формула для практического использования. К счастью, мы можем использовать методы RREF для определения обратимости и поиска инверсий.
Как определить обратимость и найти обратные
Пусть \(A\) — матрица \(n\times n\), и предположим, что мы хотим выяснить, является ли \(A\) обратимым, и если да, то какой обратной является. Пусть \(I\) будет \(n\times n\) единичной матрицей. Вот метод:
- Сформируйте сверхрасширенную матрицу \((A | I)\).
- Выполните операции строки, чтобы поместить это в RREF.
- Если вы получаете \((I | B)\), то \(A\) обратимо с обратным \(B\).
- Если первая часть матрицы не \(I\), то \(A\) необратима.
Почему это работает: первая часть матрицы представляет собой матрицу RREF, полученную в результате выполнения строковых операций для \(A\), поэтому, если это \(I\), то \(A\) обратимо, а если нет \(I\), то \(A\) необратим. Остается только объяснить, почему в случае обратимости \(A\) получается \((I | A^{-1})\).
Подумайте о столбцах \(\mathbf{c}_1,\ldots, \mathbf{c}_n\) инверсии \(A\). У нас есть \(A (\mathbf{c}_1 \; \cdots \; \mathbf{c}_n) = I\), поэтому \(A\mathbf{c}_1 = \mathbf{e}_1\), \(A \mathbf{c}_2 = \mathbf{e}_2\) и т. д., где \(\mathbf{e}_i\) — i-й столбец \(I\). Таким образом, \(\mathbf{c}_1\) является единственным решением матричного уравнения \(A\mathbf{x} = \mathbf{e}_1\). Вы обнаружите это, подставив \((A | \mathbf{e}_1)\) в RREF, и вы должны получить \((I | \mathbf{c}_1)\), поскольку \(\mathbf{c}_1\ ) — единственное решение. 9{-1})\).
Пример этого метода поиска обратных значений
Пусть \(A=\begin{pmatrix} 1&2\\3&4\end{pmatrix}\). Чтобы узнать, является ли \(A\) обратимым, и если да, то каково его обратное значение, мы помещаем \((A | I_2)\) в RRE-форму:
\[\begin{align*} \begin{pматрица} 1 и 2 и 1 и 0 \\ 3 и 4 и 0 и 1 \end{pmatrix} & \stackrel{r_2 \mapsto r_2-3r_1}{\mapsto} \begin{pmatrix} 1&2&1&0\\ 0&-2&-3&1 \end{pматрица} \\ & \stackrel{r_2 \mapsto (-1/2)r_2}{\mapsto} \begin{pmatrix} 1&2&1&0\\ 0, 1, 3/2 и -1/2 \end{pматрица} \\ & \stackrel{r_1 \mapsto r_1-2r_2}{\mapsto} \begin{pmatrix} 1&0&-2 & 1 \\ 0&1&3/2&-1/2 \end{pматрица} \end{выравнивание*}\]
Это в форме RRE, поэтому инверсия \(A\) равна
\[\begin{pmatrix} -2&1 \\ 3/2 и -1/2 \end{pmatrix}\]
, как вы можете проверить, перемножив их вместе.
Глава 22: Векторы и матрицы
В этой главе мы рассмотрим встроенные функции. которые поддерживают вычисления с векторами и матрицами.22.1 Соединение скалярного произведения
Вспомним состав глаголов из главы 08. Глагол суммы произведений может быть составлен из суммы и произведения с союзом @:.| Р =: 2 3 4 | Q =: 1 0 2 | П*К | +/P*Q | P (+/ @: *) Q |
| 2 3 4 | 1 0 2 | 2 0 8 | 10 | 10 |
Есть конъюнкция. (точка, называемая «точечный продукт»). Его можно использовать вместо @: для вычисления суммы произведений двух списков.
| Р | В | P (+/ @: *) Q | P (+/ . *) Q |
| 2 3 4 | 1 0 2 | 10 | 10 |
Очевидно, . союз — форма композиции,
вариант @: или @.
Ниже мы увидим, что это удобнее
для работы с векторами и матрицами.
22.2 Скалярное произведение векторов
Напомним, что P — это список из 3 чисел. Если интерпретировать эти числа как координаты точки в трехмерном пространстве, то P можно рассматривать как определение вектора, отрезка линии с длиной и направлением, из происхождение в 0 0 0 в точку P. Мы можем обратиться к вектору P.Если P и Q интерпретируются как векторы, то выражение P (+/ . *) Q дает то, что называется «скалярным произведением» P и Q. Другие названия того же самого: «точечный продукт», «внутренний продукт» или «внутренний продукт». «матричный продукт», в зависимости от контекста. В этой главе мы будем придерживаться нейтрального термина «точечный продукт», для которого мы определяем функцию точка:
| точка =: +/ . * | Р | В | Р точка Q |
| +/ .* | 2 3 4 | 1 0 2 | 10 |
Определение из учебника скалярного произведения векторов P и Q может иметь вид:
(величина P) * (величина Q) * (cos альфа)
где величина (или длина) вектора равна
квадратный корень из суммы квадратов компонентов,
а альфа — наименьший неотрицательный угол между
P и Q. Чтобы показать эквивалентность
этой формы с P точка Q,
мы можем определить служебные глаголы ma для величины вектора
и ca для косинуса угла между векторами.
Чтобы показать эквивалентность
этой формы с P точка Q,
мы можем определить служебные глаголы ma для величины вектора
и ca для косинуса угла между векторами.
ma =: %: @: (+/ @: *:) ca =: 4 : '(-/ *: b,(ma x-y), c) % (2*(b=.ma x)*(c=.ma y))'Мы ожидаем, что модуль вектора 3 4 будет равен 5, и ожидаем, что угол между П и сам равен нулю, и, следовательно, косинус равен 1.
| мА 3 4 | П ка П |
| 5 | 1 |
то мы видим, что глагол с точкой эквивалентен приведенной выше форме из учебника
| Р | В | Р точка Q | (ма P)*(ма Q)*(P ca Q) |
| 2 3 4 | 1 0 2 | 10 | 10 |
22.3 Матричный продукт
Глагол, который мы назвали точкой, является «матричным произведением» для векторов и матриц.| М =: 3 4 ,: 2 3 | В =: 3 5 | В точка М | М точка V | М точка М |
| 3 4 2 3 |
3 5 | 19 27 | 29 21 | 17 24 12 17 |
Чтобы вычислить Z =: точка B
последнее измерение A должно равняться
первое измерение В.
А =: 2 5 $ 1 В =: 5 4 $ 2
| $ А | $ Б | Z =: точка B | $ Z |
| 2 5 | 5 4 | 10 10 10 10 10 10 10 10 |
2 4 |
Пример показывает, что последний и первый размеры исчезают из результата. Если эти два размеры не равны, то сигнализируется ошибка.
| $ В | $ А | В точка А |
| 5 4 | 2 5 | ошибка |
22.4 Обобщения
22.4.1 Различные глаголы
Конъюнкция «Скалярный продукт» образует глагол скалярного произведения с (+/ . *). Другие глаголы можно сформировать по образцу (u . v).
Например, рассмотрим отношения между людьми:
человек i является потомком человека j, представленного квадратом
логическая матрица истинна в строке i, столбце j.
Использование глаголов +. (логическое ИЛИ) и *. (логическое-и)
мы можем вычислить
отношения внука с глаголом (+./. *.).
(логическое-и)
мы можем вычислить
отношения внука с глаголом (+./. *.).
г =: +. / . *.Принимая «дочернее» отношение за матрицу C:
С =: 4 4 $ 0 0 0 0 1 0 0 0 1 0 0 0 0 1 0 0Тогда отношения внуков, так сказать, детские отношения в квадрате.
| С | Г =: С г С |
| 0 0 0 0 1 0 0 0 1 0 0 0 0 1 0 0 |
0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 |
Мы можем видеть из C, что человек 3 является ребенком человека 1, а человек 1 является потомком человека 0. Следовательно, как мы видим в G человек 3 является внуком человека 0.
22.4.2 Символьная арифметика
Под символической арифметикой понимается, например, символически добавляя строки «a» и «b», чтобы получить строка «а+б». Вот небольшая коллекция функций полезности для выполнить некоторую ограниченную символьную арифметику над строками (в штучной упаковке).
pa =: ('('&,) @: (,&')')
cp =: [ ` па @. (+./ @: ('+-*' & e.))
символ =: (1 : (':';' x), u, (cp > y)'))(" 0 0)
splus =: символ «+»
sminus =: символ '-'
sprod =: символ '*'
а =:
б =:
с =:
(+./ @: ('+-*' & e.))
символ =: (1 : (':';' x), u, (cp > y)'))(" 0 0)
splus =: символ «+»
sminus =: символ '-'
sprod =: символ '*'
а =:
б =:
с =:
| и | б | с | а плюс б | a шпилька b splus c |
| +-+ |а| +-+ |
+-+ |б| +-+ |
+-+ |с| +-+ |
+—+ |а+б| +—+ |
+——-+ |a*(b+c)| +——-+ |
Как вариант символического произведения, мы могли бы опустить умножение символ чтобы дать эффект, более похожий на обычные обозначения:
sprodc =: ''символ
| a стержень b | a sprodc b |
| +—+ |a*b| +—+ |
+—+ |аб| +—+ |
В качестве аргументов для соединения «точечный продукт»
мы могли бы поставить
глаголы для выполнения символьной арифметики. Для точечного глагола,
который мы помним, это (+/ . *),
символическая версия:
Для точечного глагола,
который мы помним, это (+/ . *),
символическая версия:
sdot =: сплюс / . sprodcПроиллюстрировать:
S =: 3 2 $ Т =: 2 3 $
| С | Т | S сдот T |
| +-+-+ |а|б| +-+-+ |с|д| +-+-+ |е|е| +-+-+ |
+-+-+-+ |p|q|r| +-+-+-+ |s|t|u| +-+-+-+ |
+——+——+——+ |ap+bs|aq+bt|ar+bu| +——+——+——+ |cp+ds|cq+dt|cr+du| +——+——+——+ |ep+fs|eq+ft|er+fu| +——+——+——+ |
22.4.3 Матричный продукт в более чем двух измерениях
Пример в 3 измерениях будет достаточно общий. Символически:А =: 1 2 3 $ В =: 3 2 2 $
| А | Б | Z =: A sdot B |
| +-+-+-+ |а|б|в| +-+-+-+ |d|e|f| +-+-+-+ |
+-+-+ |m|n| +-+-+ |о|р| +-+-+ +-+-+ +-+-+ |
+———-+———-+ |am+(bq+cu)|an+(br+cv)| +———-+———-+ |ao+(bs+cw)|ap+(bt+cx)| +———-+———-+ +———-+———-+ |
Последнее измерение A должно равняться первому измерению
B. Форма результата Z
главные размеры A
последовал
по задним размерам B.
Форма результата Z
главные размеры A
последовал
по задним размерам B.
| $A | $Б | $Z |
| 1 2 3 | 3 2 2 | 1 2 2 2 |
Последнее и первое измерение A и B исчезли, потому что каждый безразмерный скаляр в Z объединяет «строку» A с «столбцом» B. Мы видим в результате Z, что каждая строка A сочетается отдельно со всей Б.
22.4.4 Точка по сравнению с @:
Вспомним из главы 07, что диадический глагол v имеет левый и правый ранг. Вот несколько полезных функций для извлечения рангов из данного глагола.
ЗНАКИ =: 1 : 'u b. 0'
LRANK =: 1 : '1 { (u RANKS)' NB. только левый ранг
| * ЗНАКИ | * ЛРАНК |
| 0 0 0 | 0 |
Общая схема определения диадических глаголов формы (u.v):
ты . v означает u @ (v "(1+L, _)) где L = (v LRANK)
или эквивалентно,
ты . v означает (u @: v) "(1+L, _)
v означает (u @: v) "(1+L, _)
и поэтому
+/.* означает (+/ @: *)" 1 _
и поэтому мы видим разницу между . и @:.
Для простых векторных аргументов они одинаковы, и в этом случае
размеры аргументов должны быть одинаковыми, но это
не является условием, требуемым для умножения матриц
в общем, где (в приведенном выше примере) каждая строка A сочетается с
целый
Б.
22,5 Определитель
Одноместный глагол (- / . *) вычисляет определитель матрицы.дет =: - / . *
| М | от M | (3*3)-(2*4) |
| 3 4 2 3 |
1 | 1 |
Символически:
сдет =: сминус / . sprodc
| С | сдет S |
| +-+-+ |а|б| +-+-+ |с|д| +-+-+ |е|е| +-+-+ |
+—————————-+ |(a(d-f))-((c(b-f))-(e (б-г)))| +—————————-+ |
22.
 5.1 Сингулярные матрицы
Матрица называется вырожденной, если ее строки (или столбцы)
не являются линейно независимыми, т. е. если одна строка
(или столбец) можно получить из другого
путем умножения на константу.
Сингулярная матрица имеет нулевой определитель.
5.1 Сингулярные матрицы
Матрица называется вырожденной, если ее строки (или столбцы)
не являются линейно независимыми, т. е. если одна строка
(или столбец) можно получить из другого
путем умножения на константу.
Сингулярная матрица имеет нулевой определитель.
В следующих пример A — (символическая) сингулярная матрица, где m постоянный множитель.
| A =: 2 2 $ ‘a’;’b’;’ma’;’mb’ | место А |
| +—+—+ |а |б | +—+—+ |ma|mb| +—+—+ |
+——-+ |амб-маб| +——-+ |
Мы видим, что результирующий член (amb-mab) должен быть равен нулю для всех а, б и м.
22,6 Разделение матрицы
22.6.1 Синхронные уравнения
Встроенный глагол %. (процентная точка) называется «Матричное деление». Его можно использовать находить решения систем одновременных линейных уравнений. Например, рассмотрим уравнения записывается условно так:
3х + 4у = 11
2х + 3у = 8
Переписывая в виде матричного уравнения, мы имеем, неформально,
М точка U = R
где M – матрица коэффициентов
U — вектор неизвестных x, y, R — вектор
правые значения:
| М =: 3 4 ,: 2 3 | Р =: 11 8 |
| 3 4 2 3 |
11 8 |
Вектор неизвестных U (то есть x, y) можно найти
путем деления R на матрицу M.
| М | Р | U =: R %. М | М точка У |
| 3 4 2 3 |
11 8 | 1 2 | 11 8 |
Мы видим, что M dot U равно R, то есть U решает уравнения.
22.6.2 Комплексные, рациональные и векторные переменные
Решаемые уравнения могут быть в комплексных переменных. Например:| М | Р =: 15j22 11j16 | U =: R %. М | М точка У |
| 3 4 2 3 |
15j22 11j16 | 1j2 3j4 | 15j22 11j16 |
или в рациональных числах. В этом случае и М, и Р должны быть рациональными, чтобы дать рациональный результат.
М =: 2 2 $ 3x 4x 2x 3x Р =: 15р22 11р16
| М | Р | U =: R %. М | М точка У |
| 3 4 2 3 |
15р22 11р16 | _31р44 123р176 | 15р22 11р16 |
В предыдущих примерах неизвестными в U были скаляры. Теперь предположим, что неизвестные являются векторами и наши уравнения
для решения являются:
Теперь предположим, что неизвестные являются векторами и наши уравнения
для решения являются:
3х + 4у = 15 22
2х + 3у = 11 16
поэтому мы пишем:
М =: 2 2 $ 3 4 2 3 R =: 2 2 $ 15 22 11 16
| М | Р | U =: R %. М | М точка У |
| 3 4 2 3 |
15 22 11 16 |
1 2 3 4 |
15 22 11 16 |
Неизвестные x и y — это строки U, то есть векторы.
22.6.3 Изогнутый фитинг
Предположим, мы стремимся построить наилучшую аппроксимацию прямой линией. набор точек данных. Если точки данных представляют собой пары x, y дается как:х =: 10 20 30 у =: 31 49 70мы стремимся найти a и b для уравнения:
у = а + Ьх
3 точки данных дают нам 3 уравнения с 2 неизвестными
а и б. Условно:
1 . а + 10 . б = 31
б = 31
1 . а + 20 . б = 49
1 . а + 30 . б = 70
поэтому мы принимаем матрицу коэффициентов M как
М =: 3 2 $ 1 10 1 20 1 30и разделите y на матрицу M, чтобы получить вектор неизвестных U, (то есть, а, б)
| М | г | U =: у %. М | М точка У |
| 1 10 1 20 1 30 |
31 49 70 | 11 1,95 | 30,5 50 69,5 |
Здесь у нас больше уравнений, чем неизвестных, (больше строк, чем столбцов в M) и поэтому решения U лучше всего подходят ко всем уравнениям вместе. Мы видим, что M точка U близко, но не точно равно y.
«Наилучшее соответствие» означает, что сумма квадратов ошибки сведены к минимуму, где ошибки задается y — M точка U. Если сумма квадратов минимизирована, то мы ожидаем, что слегка возмущая U, сумма квадратов увеличивается.
| +/ *: у — М точка У | +/*: у — М точка (U + 0,01) |
| 1,5 | 1,6523 |
Метод распространяется непосредственно на подгонку
многочлен к набору точек данных. Предположим, мы стремимся соответствовать
Предположим, мы стремимся соответствовать
у = а + Ьх + сх 2
к точкам данных:
х =: 0 1 2 3 у =: 1 6 17 34,1Четыре уравнения, которые необходимо решить:
1.а + Ьх 0 + сх 9/ 0 1 2
а неизвестные a, b, c задаются вектором U следующим образом:
| М | г | U =: у %. М | М точка У |
| 1 0 0 1 1 1 1 2 4 1 3 9 |
1 6 17 34,1 | 1,005 1,955 3,025 | 1,005 5,985 17,02 34,09 |
Уравнений может быть больше, чем неизвестных, как показывает этот пример, но очевидно, что их не может быть меньше. То есть в R%. M-матрица M должна иметь не больше столбцов, чем строк.
22.6.4 Деление на массивы более высокого ранга
Вот пример U =: R %. М, в котором дивизор M имеет ранг 3.М =: 3 2 2 $ 3 4 2 3 0 3 1 2 3 1 2 3 Р =: 21 42
| М | Р | U =: R %. М М |
М точка У | М точка»2 1 ЕВ |
| 3 4 2 3 0 3 3 1 |
21 42 | _105 84 28 7 3 12 |
ошибка | 21 42 21 42 21 42 |
Диадический ранг %. _ 2,
%. б. 0 2 _ 2и так в этом примере весь R объединяется отдельно с каждой из 3-х матриц в M. То есть у нас есть 3 отдельные наборы уравнений, каждый с одной и той же правой частью R Таким образом, у нас есть 3 отдельных решения (строки U).
Условие R=M dot U, очевидно, не выполняется. (поскольку последняя размерность M не равна первый из U), но он выполняется отдельно для каждой матрицы в M с соответствующей строкой U.
22.7 Идентификационная матрица
(Несингулярная) квадратная матрица M, деленная сама на себя, дает я говорю «единичную матрицу», такую, что (M dot I) = M.М =: 3 3 $ 3 4 7 0 0 4 6 0 3
| М | I =: М %. М М |
М точка I |
| 3 4 7 0 0 4 6 0 3 |
1 0 0 0 1 0 0 0 1 |
3 4 7 0 0 4 6 0 3 |
22,8 обратная матрица
Одноместный глагол %. вычисляет обратную матрицу То есть, %. М есть эквивалентно I %. М для подходящего тождественная матрица I:| М | I =: М %. М | I %. М | %. М |
| 3 4 7 0 0 4 6 0 3 |
1 0 0 0 1 0 0 0 1 |
0 _0,125 0,1667 0,25 _0,3438 _0,125 0 0,25 0 |
0 _0,125 0,1667 0,25 _0,3438 _0,125 0 0,25 0 |
Для вектора V обратный W имеет обратную величину и то же направление. Таким образом, произведение величин равно 1 и косинусу угла между ними равен 1.
| В | Вт =: %. В | (мА В) * (мА Вт) | В ок Вт |
| 3 5 | 0,08824 0,1471 | 1 | 1 |
Это конец 22 главы.
Формула векторного произведения
Геометрическое определение векторного произведения хорош для понимания свойств перекрестного произведения. Однако геометрическое определение не так полезно для вычисления векторное произведение векторов. Для вычислений нам понадобится формула в члены компонентов векторов. Начнем с использования геометрического определение для вычисления векторного произведения стандартных единичных векторов. 93$. (Мы определяем перекрестное произведение только в трех измерениях. Обратите внимание, что мы предполагаем правостороннюю систему координат.)
Загрузка апплета
Стандартные единичные векторы в трех измерениях. Стандартные единичные векторы в трех измерениях, $\vc{i}$ (зеленый), $\vc{j}$ (синий) и $\vc{k}$ (красный), представляют собой векторы длины один, которые указывают параллельно ось $x$, ось $y$ и ось $z$ соответственно. Перемещение их с помощью мыши не меняет вектора, поскольку они всегда указывают в положительном направлении соответствующей оси.
Дополнительная информация об апплете.
Параллелограмм, натянутый на любые два из этих стандартных единичных векторов, равен единичный квадрат, площадь которого равна единице. Следовательно, по геометрическое определение, крест произведение должно быть единичным вектором. Поскольку перекрестное произведение должно быть перпендикулярно двум единичным векторам, он должен быть равен другому единичный вектор или противоположный этому единичному вектору. Глядя на выше график, вы можете использовать правило правой руки, чтобы определить следующее Результаты. \начать{выравнивать*} \vc{i} \times \vc{j} &= \vc{k}\\ \vc{j} \times \vc{k} &=\vc{i}\\ \vc{k} \times \vc{i} &= \vc{j} \конец{выравнивание*} Эта небольшая циклическая диаграмма поможет вам запомнить эти результаты.
Как насчет $\vc{i} \times \vc{k}$? По правилу правой руки должно быть
$-\vc{j}$. Помня, что $\vc{b} \times \vc{a}
= — \vc{a} \times \vc{b}$, можно сделать вывод, что
\начать{выравнивать*}
\vc{j} \times \vc{i} &= -\vc{k}\\
\vc{k} \times \vc{j} &= -\vc{i}\\
\vc{i} \times \vc{k} &= -\vc{j}. \конец{выравнивание*}
\конец{выравнивание*}
Наконец, векторное произведение любого вектора на самого себя равно нулю вектор ($\vc{a} \times \vc{a}=\vc{0}$). В частности, перекрестное произведение любого стандартный единичный вектор с самим собой является нулевым вектором.
Общие векторы
За исключением двух специальных свойств, упомянутых выше ($\vc{b} \times \vc{a} = -\vc{a} \times \vc{b}$, и $\vc{a} \times \vc{a} = \vc{0}$), мы просто утверждаем, что векторное произведение ведет себя как обычное умножение. Он подчиняется следующим свойствам:
- $(y\vc{a}) \times \vc{b} = y(\vc{a} \times \vc{b}) = \vc{a} \раз (г\вк{б})$,
- $\vc{a} \times (\vc{b}+\vc{c}) = \vc{a} \times \vc{b}
+ \vc{a} \times \vc{c}$, 93$ и $y$
скаляр. (Эти свойства означают, что векторное произведение является линейным.) Мы можем использовать эти свойства вместе с векторным произведением
стандартных единичных векторов, чтобы написать формулу для креста
продукт по компонентам.

Компоненты $\vc{a}$ и $\vc{b}$ запишем как: \начать{выравнивать*} \vc{a} = (a_1,a_2,a_3)= a_1 \vc{i} + a_2 \vc{j} + a_3 \vc{k}\\ \vc{b} = (b_1,b_2,b_3)= b_1 \vc{i} + b_2 \vc{j} + b_3 \vc{k} \конец{выравнивание*}
Сначала предположим, что $a_3=b_3=0$. (Затем манипуляции намного проще.) Рассчитываем: \начать{выравнивать*} \vc{a} \times \vc{b} &= (a_1 \vc{i} + a_2 \vc{j}) \times (b_1 \vc{i} + b_2 \vc{j})\\ &= a_1b_1 (\vc{i}\times\vc{i}) + a_1b_2(\vc{i} \times \vc{j}) + a_2b_1 (\vc{j} \times \vc{i}) + a_2b_2 (\vc{j} \times \vc{j}) \конец{выравнивание*} Поскольку мы знаем, что $\vc{i} \times \vc{i}= \vc{0}= \vc{j} \times \vc{j}$ и что $\vc{i} \times \vc{j} = \vc{k} = -\vc{j} \times \vc{i}$, это быстро упрощается до \начать{выравнивать*} \vc{a} \times \vc{b} &= (a_1b_2-a_2b_1) \vc{k}\\ &= \влево| \begin{массив}{cc} а_1 и а_2\\ б_1 и б_2 \конец{массив} \право| \vc{к}. \конец{выравнивание*} Запись результата в виде определитель, как мы это делали в последний шаг, это удобный способ запомнить результат.

Общий случай, когда $a_3$ и $b_3$ не равны нулю, немного сложнее. Однако это просто вопрос повторения тех же манипуляций, описанных выше, с использованием векторного произведения единичных векторов и свойств векторного произведения.
Мы начинаем с расширения продукта \начать{выравнивать*} \vc{a} \times \vc{b} &= (a_1 \vc{i} + a_2 \vc{j} + a_3\vc{k}) \times (b_1 \vc{i} + b_2 \vc{j} + b_3\vc{k})\\ &= a_1b_1 (\vc{i}\times\vc{i}) + a_1b_2(\vc{i} \times \vc{j}) + a_1b_3(\vc{i} \times \vc{k})\\ &\ четырехъядерный + a_2b_1 (\vc{j} \times \vc{i}) + a_2b_2 (\vc{j} \times \vc{j}) + a_2b_3 (\vc{j} \times \vc{k})\\ &\ четырехъядерный + a_3b_1 (\vc{k} \times \vc{i}) + a_3b_2 (\vc{k} \times \vc{j}) + a_3b_3 (\vc{k} \times \vc{k}) \конец{выравнивание*} а затем вычислить все перекрестные произведения единичных векторов \начать{выравнивать*} \vc{a} \times \vc{b} &= a_1b_2 \vc{k} — a_1b_3 \vc{j} — a_2b_1 \vc{k} + a_2b_3 \vc{i} + a_3b_1 \vc{j} — a_3b_2 \vc{i}\\ «=» (a_2b_3-a_3b_2)\vc{i} — (a_1b_3-a_3b_1) \vc{j} +(a_1b_2-a_2b_1) \vc{k}.
 \конец{выравнивание*}
Используя определители, мы можем записать результат как
\начать{выравнивать*}
\vc{a} \times \vc{b} &=\left|
\begin{массив}{cc}
а_2 и а_3\\
б_2 и б_3
\конец{массив}
\право| \vc{я}
—
\влево|
\begin{массив}{cc}
а_1 и а_3\\
б_1 и б_3
\конец{массив}
\право| \vc{j}
+
\влево|
\begin{массив}{cc}
а_1 и а_2\\
б_1 и б_2
\конец{массив}
\право| \vc{к}.
\конец{выравнивание*}
\конец{выравнивание*}
Используя определители, мы можем записать результат как
\начать{выравнивать*}
\vc{a} \times \vc{b} &=\left|
\begin{массив}{cc}
а_2 и а_3\\
б_2 и б_3
\конец{массив}
\право| \vc{я}
—
\влево|
\begin{массив}{cc}
а_1 и а_3\\
б_1 и б_3
\конец{массив}
\право| \vc{j}
+
\влево|
\begin{массив}{cc}
а_1 и а_2\\
б_1 и б_2
\конец{массив}
\право| \vc{к}.
\конец{выравнивание*}
Глядя на формулу определителя $3 \times 3$, мы видим, что формула для перекрестный продукт очень похож на формулу для $3 \times 3$ определитель. Если мы позволим матрице иметь вектор $\vc{i}$, $\vc{j}$ и $\vc{k}$ в качестве записей (хорошо, может быть, это не имеет смысла, но это всего лишь инструмент для запоминания перекрестного произведения), $3 Определитель \times 3$ дает удобную мнемонику для запоминания креста продукт: \начать{выравнивать*} \vc{a} \times \vc{b} = \влево| \begin{массив}{ccc} \vc{i} & \vc{j} & \vc{k}\\ а_1 и а_2 и а_3\\ б_1 и б_2 и б_3 \конец{массив} \право|.
 \конец{выравнивание*}
Это компактный способ запомнить, как вычислять векторное произведение.
\конец{выравнивание*}
Это компактный способ запомнить, как вычислять векторное произведение. Матричные уравнения
Цели
- Понимать эквивалентность между системой линейных уравнений, расширенной матрицей, векторным уравнением и матричным уравнением.
- Охарактеризуйте векторы b так, что Ax=b непротиворечиво, с точки зрения диапазона столбцов A.
- Охарактеризуйте матрицы A таким образом, что Ax=b непротиворечиво для всех векторов b.
- Рецепт: умножить вектор на матрицу (два способа).
- Фото: множество всех векторов b, таких что Ax=b, непротиворечиво.
- Словарное слово: матричное уравнение .
В этом разделе мы представляем очень лаконичный способ записи системы линейных уравнений: Ax=b. Здесь A — матрица, а x,b — векторы (обычно разного размера), поэтому сначала мы должны объяснить, как умножать матрицу на вектор.
Когда мы говорим, что «A представляет собой матрицу размера m × n», мы имеем в виду, что A имеет m строк и n столбцов.

Определение
Пусть A — матрица размера m×n со столбцами v1,v2,…,vn:
А=С|||v1v2···vn|||D
Произведение оператора A с вектором x в Rn является линейной комбинацией
Ax=C|||v1v2···vn|||DEIIGx1x2…xnFJJH=x1v1+x2v2+···+xnvn.
Это вектор в Rm.
Пример
Чтобы Ax имело смысл, количество элементов x должно совпадать с количеством столбцов A: мы используем элементы x как коэффициенты столбцов A в линейной комбинации. Результирующий вектор имеет то же количество элементов, что и число 9.4534 строки A, так как каждый столбец A имеет такое количество записей.
Если A представляет собой матрицу размера m × n (m строк, n столбцов), то Ax имеет смысл, когда x имеет n элементов. Произведение Ax содержит m записей.
Свойства матрично-векторного произведения
Пусть A — матрица размера m × n, пусть u, v — векторы в Rn, а c — скаляр. Тогда:
- А(и+в)=Аи+Ав
- A(cu)=cAu
Определение
Матричное уравнение — это уравнение формы Ax=b, где A — матрица размера m × n, b — вектор в Rm, а x — вектор, коэффициенты которого x1,x2,.
 ..,xn неизвестны. .
..,xn неизвестны. . В этой книге мы изучим два дополнительных вопроса о матричном уравнении Ax=b:
- При конкретном выборе b, каковы все решения Ax=b?
- Каковы все варианты b, чтобы Ax=b было непротиворечивым?
Первый вопрос больше похож на вопросы, к которым вы, возможно, уже привыкли на предыдущих курсах алгебры; у вас есть много практики решения уравнений типа x2−1=0 относительно x. Второй вопрос, возможно, является новой концепцией для вас. Теорема о рангах в разделе 2.9, который является кульминацией этой главы, говорит нам, что эти два вопроса тесно связаны.
Пример
Мы будем свободно перемещаться между четырьмя способами записи линейной системы снова и снова до конца книги.
Другой способ вычислений Axe
Приведенное выше определение является полезным способом определения произведения матрицы на вектор, когда дело доходит до понимания взаимосвязи между матричными уравнениями и векторными уравнениями.
 Здесь мы даем определение, которое лучше подходит для ручных вычислений.
Здесь мы даем определение, которое лучше подходит для ручных вычислений. Определение
Вектор-строка представляет собой матрицу с одной строкой. Произведение вектора-строки длины n и вектора (столбца) длины n равно
.Aa1a2···anBEIIGx1x2…xnFJJH=a1x1+a2x2+···+anxn.
Это скаляр.
Рецепт: Правило строки-столбца для умножения матрицы на вектор
Если A — матрица размера m×n со строками r1,r2,…,rm, а x — вектор в Rn, то
Ax=EIIG—r1——r2—…—rm—FJJHx=EIIGr1xr2x…rmxFJJH.
Пример
Пусть A — матрица со столбцами v1,v2,…,vn:
А=С|||v1v2···vn|||D.
Затем
Ax=bhas решение⇐⇒существуют x1,x2,…,xn такие, что AEIIGx1x2…xnFJJH=b⇐⇒существуют x1,x2,…,xn такие, что x1v1+x2v2+···+xnvn=b⇐⇒бисалинейная комбинация v1,v2,… ,vn⇐⇒bis находится в диапазоне столбцов матрицы A.
Пролеты и согласованность
Матричное уравнение Ax=b имеет решение тогда и только тогда, когда b находится в диапазоне столбцов A.

Это дает эквивалентность между алгебраических оператора (Ax=b непротиворечиво) и геометрических оператора (b находится в промежутке столбцов A).
Пример (несогласованная система)
Пример (согласованная система)
Когда решения всегда существуют
Опираясь на это примечание, у нас есть следующий критерий того, когда Ax=b соответствует каждому выбору b.
Теорема
Пусть A — матрица размера m × n (нерасширенная). Следующие эквивалентны:
- Ax=b имеет решение для всех b в Rm.
- Пролет колонн A равен Rm.
- A имеет точку поворота в каждой строке.
Доказательство
Эквивалентность 1 и 2 устанавливается этим примечанием применительно к каждому b в Rm.
Теперь покажем, что 1 и 3 эквивалентны. (Поскольку мы знаем, что 1 и 2 эквивалентны, отсюда следует, что 2 и 3 также эквивалентны.) Если A имеет центральную точку в каждой строке, то его сокращенная ступенчатая форма строки выглядит следующим образом:
К10А0А01А0А0001АД,
и поэтому AAbB сводится к этому:
C10A0AA01A0AA0001AAD.
Нет b, который делал бы его несовместимым, поэтому всегда есть решение. Наоборот, если A не имеет стержня в каждой строке, то его уменьшенная ступенчатая форма строки выглядит так:
К10А0А01А0А00000Д,
, что может привести к противоречивой системе после добавления b:
C10A0A001A0A00000016D.Напомним, что эквивалентно означает, что для любой заданной матрицы A либо все условий приведенной выше теоремы верны или все они ложны.
Будьте внимательны при чтении утверждения приведенной выше теоремы. Первые два условия очень похожи на это примечание, но логически они совершенно разные из-за квантификатора «94 534 для всех 94 535 b».
Интерактив: Критерии теоремы выполнены
Интерактив: Критерии теоремы не выполняются
Комментарии, исправления или предложения? (Требуется бесплатная учетная запись GitHub)
19.2: Приложение — Алгебра матриц
-
- Последнее обновление
- Сохранить как PDF
-
- Идентификатор страницы
- 9685
- Дуглас Клайн
- Университет Рочестера
- Значение определителя \(|A| = 0\), если
- все элементы строки (столбца) равны нулю.
- все элементы строки (столбца) идентичны или кратны соответствующим элементам другой строки (столбца).
- Значение определителя остается неизменным, если
- строки и столбцы меняются местами.

- к любой строке добавляется линейная комбинация любого количества строк. 9Т\право| = |\mathbf{A}|\)
- Если любую строку (столбец) умножить на постоянный множитель, то значение определителя умножается на тот же множитель.
- Определитель диагональной матрицы равен произведению элементов диагональной матрицы. То есть, когда \(A_{ij} = \lambda i\delta_{ij}\), то \(|\mathbf{A}| = \lambda_1\lambda_2\lambda_3\dots \lambda_N\)
- Определитель единичной (единичной) матрицы \(|\mathbb{I}| = 1\).
- Определитель нулевой матрицы, для которой все матричные элементы равны нулю, \(|\mathbf{0}| = 0\)
- Сингулярная матрица имеет определитель, равный нулю.
- Если каждый элемент какой-либо строки (столбца) выступает в виде суммы (разности) двух или более величин, то определитель можно записать в виде суммы (разности) двух или более определителей одного порядка. Например, для порядка \(N = 2\), \[\begin{vmatrix} A_{11} \pm B_{11} & A_{12} \pm B_{12} \\ A_{21} & A_{22 } \end{vmatrix} = \begin{vmatrix} A_{11} & A_{12} \\ A_{21} & A_{22} \end{vmatrix} \pm \begin{vmatrix} B_{11} & B_ {12} \\ A_{21} & A_{22} \end{vmatrix} \nonumber\] 9T = \frac{1}{ |\mathbf{A}|} \begin{bmatrix} A & D & G \\ B & E & H \\ C & F & I \end{bmatrix} \\ = \frac {1}{a A + bB + cC} \begin{bmatrix} A = (ei − fh) & D = − (bi − ch) & G = (bf − ce) \\ B = − (di − fg) & E = (a i — cg) & H = — (a f — cd) \\ C = (dh — eg) & F = — (a h — bg) & I = (a e — bd) \end{bmatrix} \label {A.
 {\prime}\) в повернутой штрихованной системе координат. Затем 9{\prime} = [\lambda_i \delta_{ij} ] \label{A.46}\]
{\prime}\) в повернутой штрихованной системе координат. Затем 9{\prime} = [\lambda_i \delta_{ij} ] \label{A.46}\] Если все собственные значения различны, т.е. различны, то эта система \(n\) уравнений полностью определяет отношение компоненты каждого собственного вектора вдоль осей системы координат. Однако, когда два или более собственных значения идентичны, приведение к истинной диагональной форме невозможно, и можно свободно выбирать подходящий собственный вектор, ортогональный остальным осям.
Таким образом, матрица может быть полностью диагонализирована, только если
(а) все собственные значения различны,
(б) вещественная матрица симметрична,
(в) она унитарна.
Матрицы в классической механике часто применяются для решения системы однородных линейных уравнений вида
\[\begin{matrix} A_{11}x_1 & +A_{12}x_2 & \dots \dots & + A_{1n}x_n & = & 0 \\ A_{11}x_1 & +A_{12}x_2 & \dots \dots & +A_{1n}x_n & = & 0 \\ \dots .. & \dots \dots & \точки .
 . & \точки .. & = & \точки . \\ A_{n1}x_1 & +A_{n2}x_2 & \dots .. & +A_{nn}x_n & = & 0 \end{matrix} \label{A.47}\]
. & \точки .. & = & \точки . \\ A_{n1}x_1 & +A_{n2}x_2 & \dots .. & +A_{nn}x_n & = & 0 \end{matrix} \label{A.47}\] Создание следующих определений
\[\mathbf{A} = \begin{pmatrix} A_{11} & A_{12} & \dots & A_{1n} \\ A_{21} & A_{22} & \dots & A_{2n} \\ \dots & \dots & \dots & \dots \\ A_{n1} & A_{n2} & \dots & A_{nn} \end{pmatrix} \label{A.48 }\]
\[\mathbf{X} = \begin{pmatrix} x_1 \\ x_2 \\ \dots \\ x_n \end{pmatrix} \label{A.49}\]
Тогда множество линейных уравнения могут быть записаны в компактной форме с использованием матриц
\[\mathbf{A} \cdot \mathbf{X} =0 \label{A.50}\]
, которое можно решить с помощью уравнения \ref{A.43}. Убедитесь, что вы можете диагонализовать матрицы с рангом 2 и 3. Вы можете использовать Mathematica, Maple, MatLab или другие подобные математические компьютерные программы для диагонализации матриц большего размера.
Пример \(\PageIndex{1}\): Собственные значения и собственные векторы вещественной симметричной матрицы
Рассмотрим матрицу
\[\mathbf{A} = \begin{pmatrix} 0 & 1 & 0 \\ 1 & 0 & 0 \\ 0 & 0 & 0 \end{pmatrix}\nonumber\]
Секулярный определитель определяется выражением \ref{A.
 42}
42} \[\begin{vmatrix} −\lambda & 1 & 0 \\ 1 & −\lambda & 0 \\ 0 & 0 & −\lambda \ end{vmatrix} = 0 \nonumber\]
Это расширяется до
\[−\lambda (\lambda + 1)(\lambda − 1) = 0 \nonumber\]
Таким образом, три собственных значения равны \( \лямбда = −1, 0, 1\).
Чтобы найти каждый собственный вектор, мы подставляем соответствующее собственное значение в уравнение \ref{A.48}.
\[\begin{pmatrix} −\lambda & 1 & 0 \\ 1 & −\lambda & 0 \\ 0 & 0 & −\lambda \end{pmatrix} \begin{pmatrix} x \\ y \\ z \end{pmatrix} = \begin{pmatrix} 0 \\ 0 \\ 0 \end{pmatrix} \nonumber\]
Собственное значение \(\lambda = −1\) дает \(x + y = 0\) и \(z = 0\). Таким образом, собственный вектор равен \(r_1 = (\frac{1}{\sqrt{2}}, \frac{-1}{\sqrt{2}}, 0)\). Собственное значение \(\lambda = 0\) дает \(x = 0\) и \(y = 0\). Таким образом, собственный вектор равен \(r_2 = (0, 0, 1)\). Собственное значение \(\lambda = 1\) дает \(−x + y = 0\) и \(z = 0\). Таким образом, собственный вектор равен \(r_3 = (\frac{1}{\sqrt{2}}, \frac{1}{\sqrt{2}}, 0)\).

- строки и столбцы меняются местами.
Матрицы
Алгебра матриц обеспечивает элегантное и мощное представление многомерных операторов и преобразований координат, которые занимают видное место в классической механике. Например, они играют ключевую роль в нахождении собственных значений и собственных функций для связанных уравнений, возникающих при вращении твердого тела и системах связанных осцилляторов. Понимание роли матричной механики в классической механике облегчает понимание не менее важной роли матричной механики в квантовой физике. 9{го}\) века, и концепция матричной алгебры была разработана Артуром Кейли в Англии в 1855 году, многие из этих идей были работой Гамильтона, и обсуждение матричной алгебры было похоронено в более общем обсуждении определителей. Матричная алгебра была эзотерической ветвью математики, малоизвестной физическому сообществу, до 1925 года, когда Гейзенберг предложил свою новаторскую новую квантовую теорию. Поразительной особенностью этой новой теории было представление физических величин наборами зависящих от времени комплексных чисел и своеобразным правилом умножения. Макс Борн понял, что правило умножения Гейзенберга — это просто стандартное правило умножения «строка на столбец» матричной алгебры; тема, с которой он столкнулся, когда был молодым студентом на курсе математики.
Например, они играют ключевую роль в нахождении собственных значений и собственных функций для связанных уравнений, возникающих при вращении твердого тела и системах связанных осцилляторов. Понимание роли матричной механики в классической механике облегчает понимание не менее важной роли матричной механики в квантовой физике. 9{го}\) века, и концепция матричной алгебры была разработана Артуром Кейли в Англии в 1855 году, многие из этих идей были работой Гамильтона, и обсуждение матричной алгебры было похоронено в более общем обсуждении определителей. Матричная алгебра была эзотерической ветвью математики, малоизвестной физическому сообществу, до 1925 года, когда Гейзенберг предложил свою новаторскую новую квантовую теорию. Поразительной особенностью этой новой теории было представление физических величин наборами зависящих от времени комплексных чисел и своеобразным правилом умножения. Макс Борн понял, что правило умножения Гейзенберга — это просто стандартное правило умножения «строка на столбец» матричной алгебры; тема, с которой он столкнулся, когда был молодым студентом на курсе математики. В 1924 Ричард Курант только что закончил первый том нового учебника Methods of Mathematical Physics , во время которого Паскуаль Джордан работал его молодым ассистентом, работая с матрицами. К счастью, Джордан и Борн оказались в одном вагоне поезда до Ганновера, во время которого Джордан услышал, как Борн рассказывает о своих проблемах при работе с матрицами. Джордан представился Борну и предложил помощь. Это привело к публикации в сентябре 1925 г. знаменитой статьи Борна-Джордана [Bor25a], которая дала первую строгую формулировку матричной механики в физике. За этим последовало в ноябре продолжение Борна-Гейзенберга-Джордана [Bor25b], в котором был установлен логически непротиворечивый общий метод решения задач матричной механики плюс связь между математикой матричной механики и линейной алгеброй. Матричная алгебра превратилась в важный инструмент в математике и физике во время Второй мировой войны, и теперь она является неотъемлемой частью студенческих курсов линейной алгебры.
В 1924 Ричард Курант только что закончил первый том нового учебника Methods of Mathematical Physics , во время которого Паскуаль Джордан работал его молодым ассистентом, работая с матрицами. К счастью, Джордан и Борн оказались в одном вагоне поезда до Ганновера, во время которого Джордан услышал, как Борн рассказывает о своих проблемах при работе с матрицами. Джордан представился Борну и предложил помощь. Это привело к публикации в сентябре 1925 г. знаменитой статьи Борна-Джордана [Bor25a], которая дала первую строгую формулировку матричной механики в физике. За этим последовало в ноябре продолжение Борна-Гейзенберга-Джордана [Bor25b], в котором был установлен логически непротиворечивый общий метод решения задач матричной механики плюс связь между математикой матричной механики и линейной алгеброй. Матричная алгебра превратилась в важный инструмент в математике и физике во время Второй мировой войны, и теперь она является неотъемлемой частью студенческих курсов линейной алгебры.
Большинство применений матричной алгебры в этой книге ограничиваются вещественными симметричными квадратными матрицами. Размер матрицы определяется рангом, который равен рангу строки и рангу столбца, то есть количеству независимых векторов-строк или векторов-столбцов в квадратной матрице. Предполагается, что вы изучали матрицы в курсе линейной алгебры. Таким образом, цель этого обзора — перечислить простые манипуляции с симметричными матрицами и диагонализацию матриц, которые будут использоваться в этом курсе. Если вам нужны дополнительные подробности, вас отсылают к учебнику по линейной алгебре.
Определение матрицы
Матрица представляет собой прямоугольный массив чисел с \(M\) строками и \(N\) столбцами. Для элемента матрицы используется обозначение \(A_{ij}\), где \(i\) обозначает строку, а \(j\) обозначает столбец этого матричного элемента в матрице \(\mathbf{A} \). Соглашение обозначает матрицу \(\mathbf{A}\) как
\[\mathbf{A} \equiv \begin{pmatrix} A_{11} & A_{12} & \dots & A_{1(N−1 )} & A_{1N} \\ A_{21} & A_{22} & . . & A_{2(N−1)} & A_{2N} \\ : & : & A_{ij} & : & : \\ A_{(M−1)1} & A_{(M−1)2} & .. & A_{(M−1)(N−1)} & A_{(M−1)N} \\ A_{M1} & A_{M2} & \dots & A_{M(N−1)} & A_{MN} \end{pmatrix} \label{A.1}\]
. & A_{2(N−1)} & A_{2N} \\ : & : & A_{ij} & : & : \\ A_{(M−1)1} & A_{(M−1)2} & .. & A_{(M−1)(N−1)} & A_{(M−1)N} \\ A_{M1} & A_{M2} & \dots & A_{M(N−1)} & A_{MN} \end{pmatrix} \label{A.1}\]
Матрицы могут быть квадратными, \(M = N\), или прямоугольными \(M \neq N\). Матрицы, имеющие только одну строку или столбец, называются векторами строк или столбцов соответственно и нуждаются только в одной метке нижнего индекса. Например,
\[\mathbf{A} = \begin{pmatrix} A_1 \\ A_2 \\ : \\ A_{M−1} \\ A_M \end{pmatrix} \label{A.2}\]
Манипуляции с матрицами
Матрицы подчиняются определенным правилам манипулирования матрицами, как указано ниже.
1) Умножение матрицы на скаляр \(\lambda\) просто умножает каждый элемент матрицы на \(\lambda \).
\[C_{ij} = \lambda A_{ij} \label{A.3}\]
2) Сложение двух матриц \(\mathbf{A}\) и \(\mathbf{B}\ ) с одинаковым рангом, т. е. количеством столбцов, определяется как
\[C_{ij} = A_{ij} + B_{ij} \label{A. 4}\]
4}\]
3) Умножение матрицы \(\mathbf{A}\) матрицей \(\mathbf{B}\) определяется только в том случае, если количество столбцов в \(\mathbf{A}\) равно количеству строк в \(\mathbf{ Б}\). Матрица произведения \(\mathbf{C}\) задается матричным произведением
\[\mathbf{C} = \mathbf{A} \cdot \mathbf{B} \label{A.5}\]
\[C_{ij} = [AB]_{ij} = \ sum_k A_{ik}B_{kj} \label{A.6}\]
Например, если обе матрицы \(\mathbf{A}\) и \(\mathbf{B}\) являются симметричными матрицами третьего ранга, то
\[\begin{align*} \mathbf{C} &= \mathbf{A} \cdot \mathbf{B} \\[4pt] &= \begin{pmatrix} A_{11} & A_{12} & A_{13} \\ A_{21} & A_{22} & A_{23} \\ A_{31} & A_{32} & A_{33} \end{pmatrix} \cdot \begin{pmatrix} B_ {11} & B_{12} & B_{13} \\ B_{21} & B_{22} & B_{23} \\ B_{31} & B_{32} & B_{33} \end{pmatrix} \\[4pt] &= \begin{pmatrix} A_{11}B_{11} + A_{12}B_{21} + A_{13}B_{31} & A_{11}B_{12} + A_{ 12}B_{22} + A_{13}B_{32} и A_{11}B_{13} + A_{12}B_{23} + A_{13}B_{33} \\ A_{21}B_{ 11} + A_{22}B_{21} + A_{23}B_{31} и A_{21}B_{12} + A_{22}B_{22} + A_{23}B_{32} и A_{ 21}B_{13} + A_{22}B_{23} + A_{23}B_{33} \\ A_{31}B_{11} + A_{32}B_{21} + A_{33}B_{ 31} и A_{31}B_{12} + A_{32}B_{22} + A_{33}B_{32} и A_{31}B_{13} + A_{32}B_{23} + A_{ 33}B_{33} \конец {pmatrix} \end{align*}\] 9T \right)_{ij} = A_{ji} \label{A. 8}\]
8}\]
Транспонирование вектор-столбца является вектором-строкой. Обратите внимание, что в старых текстах для транспонирования используется символ \(\mathbf{\tilde{A}}\).
Единичная (единичная) матрица \(\mathbb{I}\)
Единичная (единичная) матрица \(\mathbb{I}\) является диагональной с диагональными элементами, равными 1, то есть
\[ \mathbb{I}_{ij} = \delta_{ij} \label{A.9}\]
, где дельта-символ Кронекера определяется как
\[\begin{align} \delta_{ik} & = 0 && \text{ if } i \neq k \label{A.10} \\ & = 1 && \text{ if } i = k \nonumber\end{align}\] 9N_{i=1} A_{ii} \label{A.21}\]
Внутреннее произведение векторов-столбцов
Вещественные векторы
Обобщение скалярного (точечного) произведения в евклидовом пространстве называется скалярным произведением . Использование правил умножения матриц требует транспонирования первого вектора-столбца для формирования вектора-строки, который затем умножается на второй вектор-столбец с использованием обычных правил умножения матриц. N_{i=1} X_iY_i \label{A.22}\] 9N_{j=1} \varepsilon (j_1, j_2, \dots .j_N )A_{1j_1}A_{2j_2} \dots A_{Nj_N} \label{A.26}\]
N_{i=1} X_iY_i \label{A.22}\] 9N_{j=1} \varepsilon (j_1, j_2, \dots .j_N )A_{1j_1}A_{2j_2} \dots A_{Nj_N} \label{A.26}\]
где \(\varepsilon (j_1 , j_2, \dots .j_N )\) — это индекс перестановки, который может быть четным или нечетным в зависимости от количества перестановок, необходимых для перехода от нормального порядка \((1, 2, 3, \dots N)\) к последовательность \((j_1j_2j_3\dots j_N )\).
Например, для \(N = 3\) определитель равен
\[|\mathbf{A}| = А_{11}А_{22}А_{33} + А_{12}А_{23}А_{31} + А_{13}А_{21}А_{32} — А_{13}А_{22}А_{ 31} − A_{11}A_{23}A_{32} − A_{12}A_{21}A_{33} \label{A.27}\]


