Матрицы равена ответы: Тест Равена. Шкала прогрессивных матриц. Raven Progressiv Matrices. Методики для диагностики интеллекта. — Психология счастливой…
Возможны два варианта в использовании Стандартных матриц Равена. Первый вариант — в качестве теста скорости, с ограничением времени выполнения заданий. В отечественных исследованиях традиционно время выполнения теста ограничивается 20 минутами. Подобный вариант использования теста наиболее оправдан в условиях группового обследования. Полученные таким образом результаты (количество верно решённых задач) позволяют оценить динамические характеристики мыслительной деятельности отдельного испытуемого относительно релевантной группы. Данный вариант проведения теста не рекомендуется для диагностической работы с детьми доподросткового и пожилого возраста.
Второй вариант использования матриц Равена в качестве теста интеллекта исключает введение временных ограничений.

Описанные варианты использования Прогрессивных матриц Равена соотносятся с двумя традиционными подходами к исследованию интеллекта и личности в отечественной психодиагностике — измерительным (количественным) и экспертным (качественным или «клиническим»).
Испытание по шкале Равена производится следующим образом. При групповом тестировании каждому испытуемому дается экземпляр тестовой тетради с одним испытательным протоколом для записи решений.
 Тестовая тетрадь остается закрытой до начала тестирования. Испытуемый, прежде всего, заполняет соответствующие рубрики бланка регистрации результатов: фамилия, имя, отчество, возраст и т.д. Для того чтобы соблюсти время тестирования, необходимо строго следить за тем, чтобы до общей команды: «Приступить к выполнению теста» — никто не открывал таблицы и не подсматривал. По истечении 20 минут подается команда, например: «Всем закрыть таблицы». О предназначении данного теста испытуемым можно сказать следующее: «Все наши исследования проводятся исключительно в научных целях, поэтому от вас требуются добросовестность, глубокая обдуманность, искренность и точность в ответах. Данный тест предназначен для уточнения логичности вашего мышления». После этого взять таблицу, открыть для показа всем 1-ю страницу и дать инструкцию.
Тестовая тетрадь остается закрытой до начала тестирования. Испытуемый, прежде всего, заполняет соответствующие рубрики бланка регистрации результатов: фамилия, имя, отчество, возраст и т.д. Для того чтобы соблюсти время тестирования, необходимо строго следить за тем, чтобы до общей команды: «Приступить к выполнению теста» — никто не открывал таблицы и не подсматривал. По истечении 20 минут подается команда, например: «Всем закрыть таблицы». О предназначении данного теста испытуемым можно сказать следующее: «Все наши исследования проводятся исключительно в научных целях, поэтому от вас требуются добросовестность, глубокая обдуманность, искренность и точность в ответах. Данный тест предназначен для уточнения логичности вашего мышления». После этого взять таблицу, открыть для показа всем 1-ю страницу и дать инструкцию.
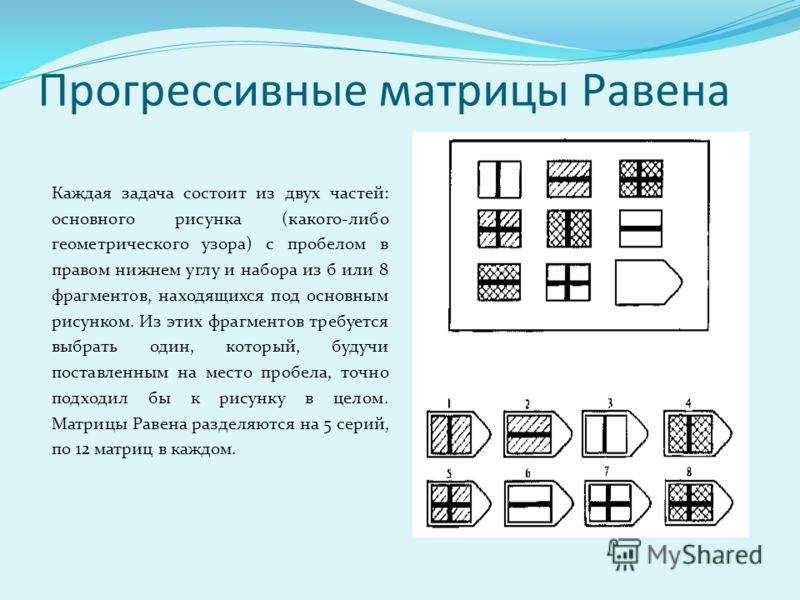
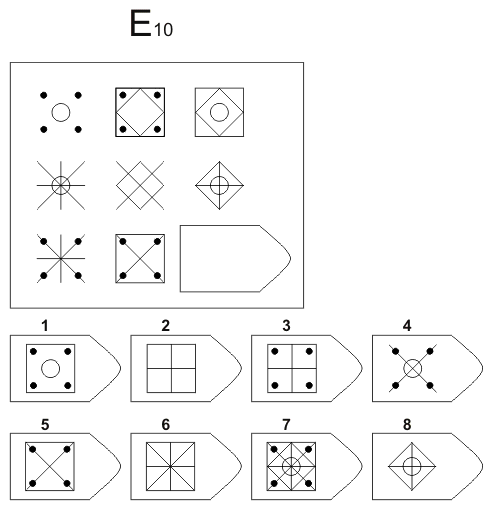
Инструкция. Перед Вами в тестовой тетради содержится 60 заданий. Все задачи разделены на 5 групп, которые называются сериями и обозначены буквами А, В, С, D, Е. В каждой серии 12 заданий. Задания составлены так, чтобы в начале каждой серии располагались более легкие задания, а в конце более трудные. В каждом задании в большой рамке содержится образец, составленный из определенных фигур. Эти фигуры или рисунки составлены не хаотично, а согласно определенной закономерности. Эту закономерность Вы должны в каждом задании выяснить. В каждом большом образце отсутствует часть или последняя фигура. Вы должны найти фигуру, которой нужно правильно дополнить большой образец (матрицу) согласно закономерности, которую Вы при решении задания выявили. Фигуры или образцы, среди которых есть и нужная для дополнения верхнего изображения фигура, обозначены числами 1-6 или 1-8. Номер той фигуры, которой следует дополнить большое изображение в верхней рамке, нужно записать в соответствующую клеточку бланка.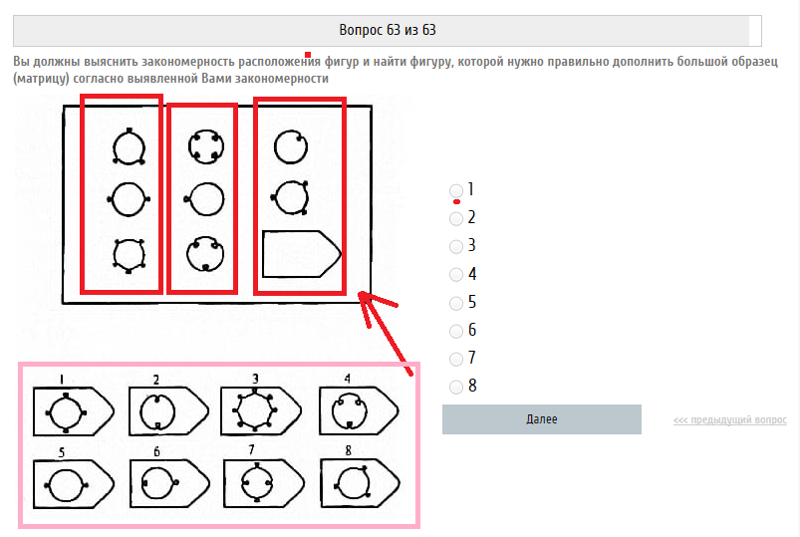
Во время выполнения заданий теста необходимо контролировать, чтобы респонденты не списывали друг у друга. По истечении 20 минут подаётся команда: «Закрыть всем таблицы!» При сборе бланков и таблиц к ним целесообразно проверить, чтобы все поля бланка были заполнены.
ФИО ________________________________________________________________
Возраст__________ Пол___________ Дата обследования_______________
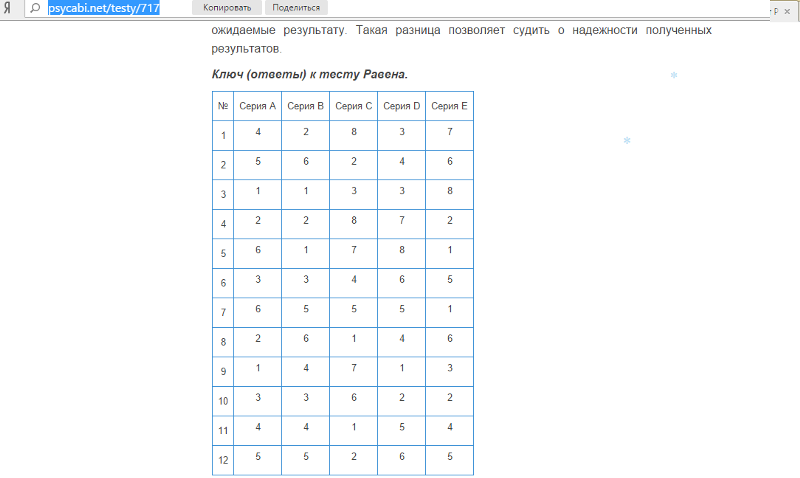
| № задания | Серия A | Серия B | Серия C | Серия D | Серия E |
| 1 | |||||
| 2 | |||||
| 3 | |||||
| 4 | |||||
| 5 | |||||
| 6 | |||||
| 7 | |||||
| 8 | |||||
| 9 | |||||
| 10 | |||||
| 11 | |||||
| 12 | |||||
| Сумма правильных ответов | |||||
| Нормативное распредление баллов |
Общее время выполнения теста ___________ мин.
 ____________ сек.
____________ сек.
ИВ _______________________
Обща сумма баллов ________________
IQ показатель _________________
Источник:
|
Педагогическая работа с гимназистами
Педагогическая работа с гимназистами
Основные этапы педагогической работы с гимназистами:
1. Работа с абитуриентами Гимназии (учащимися 9-х классов).
Данная работа предполагает информационное обеспечение девятиклассников и их родителей по вопросам поступления в Гимназию, условиях поступления, целях и задачах Гимназии. Для поступления в Гимназию приглашаются участники, призеры олимпиад, учащиеся, имеющие четкую мотивацию обучения в Тюменском государственном университете. С учащимися проводятся консультации, даются рекомендации по поступлению на тот или иной профиль обучения.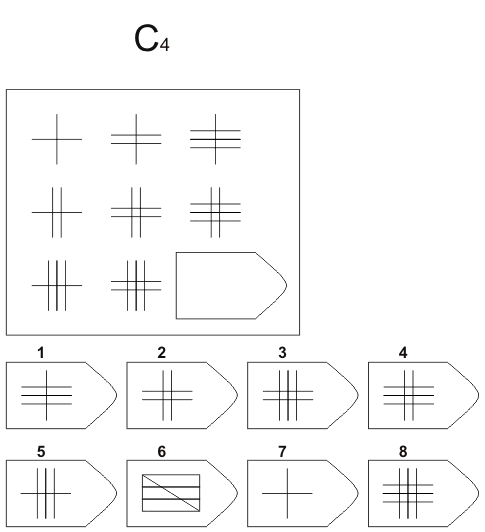 Проводятся собрания с родителями, предоставляются буклеты о Гимназии, готовятся информационные стенды. Перед учащимися в этот период стоит задача соотнести свои образовательные запросы, возможности с целями деятельности Гимназии, содержанием и технологией гимназического образования. Гимназия же со своей стороны проводит работу, чтобы выбор абитуриентом образовательного учреждения был в максимальной степени осознанным.
Проводятся собрания с родителями, предоставляются буклеты о Гимназии, готовятся информационные стенды. Перед учащимися в этот период стоит задача соотнести свои образовательные запросы, возможности с целями деятельности Гимназии, содержанием и технологией гимназического образования. Гимназия же со своей стороны проводит работу, чтобы выбор абитуриентом образовательного учреждения был в максимальной степени осознанным.
Вступительные экзамены проводятся в июне, после того, как выпускники основной школы получат аттестаты об основном (9- летнем) образовании. В зависимости от профиля обучения конкурс составил от 2-х до 10 человек на место. Средний отметочный балл по аттестату зачисленных для обучения учащихся составляет от 4,5 до 4,6.
Правда, нужно отметить, что результаты вступительных экзаменов и входного контроля (сентябрь) показывают некоторую завышенность отметок в аттестате учащихся.
2. Этап адаптации учащихся в Гимназии.
По времени для разных учащихся этот этап может занимать от одного до 4-х месяцев (I полугодие).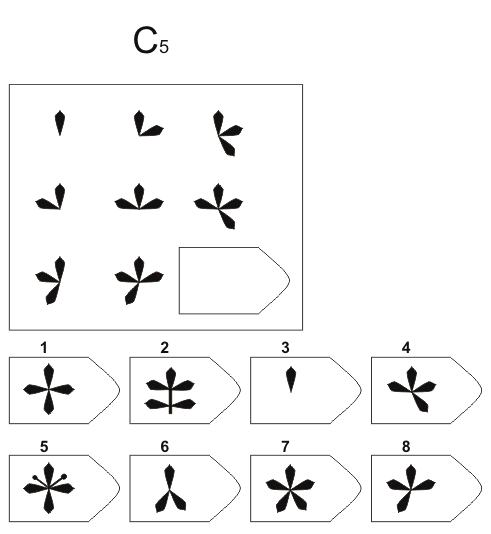 Наиболее сложными для учащихся в этот период являются: переход на новый учебный режим (занятия проводятся не уроками, а парами; учебная нагрузка, соответствующая гимназическому образованию), освоение новых требований в оценке учебных достижений, выстраивание оптимальной системы отношений с одноклассниками и учителями. Для того, чтобы помочь учащимся успешно пройти период адаптации в Гимназии введен факультативный курс «Социально-психологические технологии». Тренинги, практикумы, индивидуальные консультации, являющиеся содержанием данного курса, направлены на формирование коммуникативных навыков, умений саморегуляции, преодоления тревожных состояний, решения конфликтных ситуаций и др. Большое внимание в гимназии уделяется созданию комфортной образовательной среды. Одним из показателей такой среды является психологический климат в учебном коллективе.
Наиболее сложными для учащихся в этот период являются: переход на новый учебный режим (занятия проводятся не уроками, а парами; учебная нагрузка, соответствующая гимназическому образованию), освоение новых требований в оценке учебных достижений, выстраивание оптимальной системы отношений с одноклассниками и учителями. Для того, чтобы помочь учащимся успешно пройти период адаптации в Гимназии введен факультативный курс «Социально-психологические технологии». Тренинги, практикумы, индивидуальные консультации, являющиеся содержанием данного курса, направлены на формирование коммуникативных навыков, умений саморегуляции, преодоления тревожных состояний, решения конфликтных ситуаций и др. Большое внимание в гимназии уделяется созданию комфортной образовательной среды. Одним из показателей такой среды является психологический климат в учебном коллективе.
Для определения социально-психологического климата в гимназии используются ежегодно проводимых в гимназии диагностические исследованиях: адаптация учащихся к обучению в новом учебном заведении (10 класс) Модернизированный тест шкал тревожности Ч.
На этом этапе проводится входной контроль знаний учащихся по всем предметам (сентябрь) с целью организации системного повторения материала основной школы, определения категории учащихся, нуждающихся в особой индивидуальной помощи со стороны классного руководителя, учителей, администрации гимназии и родителей.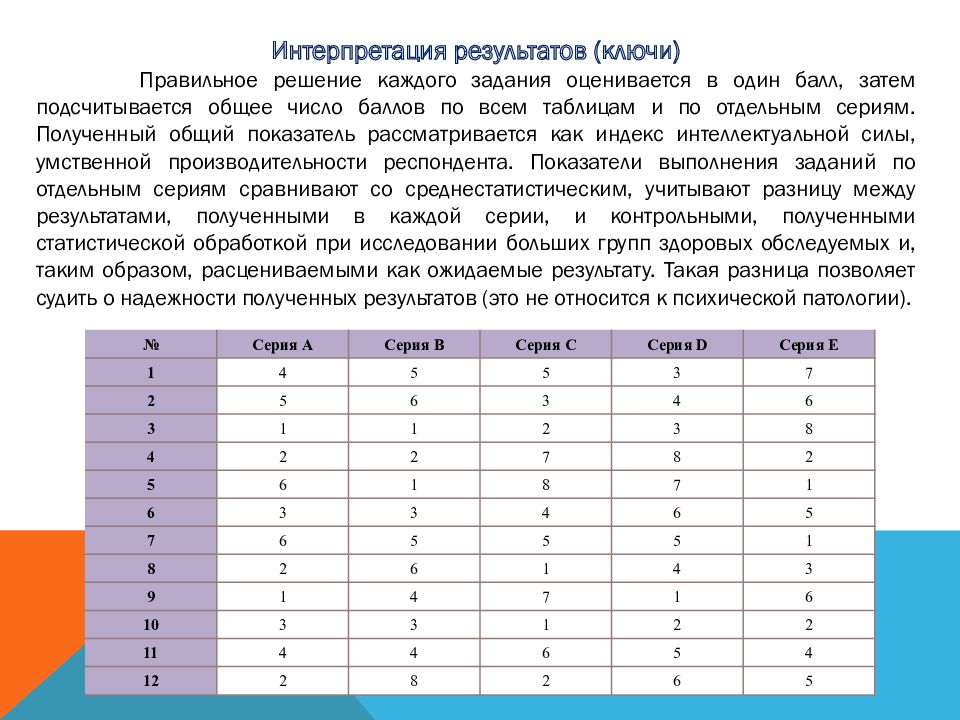
3. Этап — образовательная самореализация гимназистов.
Это основной этап обучения учащихся в гимназии.
На данном этапе основная педагогическая задача — помочь учащимся в максимальной степени раскрыть свои интеллектуально-познавательные способности, потенциал творческой деятельности, сформировать осознанное представление о связях профиля обучения с возможным выбором факультета обучения в университете и будущей профессии. Выводы об интеллектуальном потенциале учащихся можно сделать из результатов следующих методик, проводимых в разные годы в гимназии: ШТУР, Кеттелл (фактор В), субтест «Умозаключения» теста Фланагана, Амтхауэр, тест «Прогрессивные матрицы Равена», тест «Техническое мышление», тест «Лингвистика», шкала «Познавательная активность» теста Ч.Д. Спилбергера- Ю.Л. Ханиной.
По результатам выше перечисленных тестов можно сделать следующие выводы:
- У большей части учащихся гимназии уровень интеллекта высокий, выше среднего, реже средний.
 У некоторых учащихся равномерно высоко развиты общие интеллектуальные способности, у одних лучше развит вербальный компонент мышления, у других невербальный, но в целом развитие интеллектуальных способностей не ниже среднего уровня.
У некоторых учащихся равномерно высоко развиты общие интеллектуальные способности, у одних лучше развит вербальный компонент мышления, у других невербальный, но в целом развитие интеллектуальных способностей не ниже среднего уровня. - Поскольку в гимназии классы являются специализированными, профильными, то интеллектуальные способности в классах с разным профилем отличаются. Так, у учащихся физико-математического профиля получены высокие или выше среднего результаты по уровню практического и теоретического математического мышления, пространственному воображению (встречаются единицы со средним уровнем) и в тоже время высокий уровень по вербальному интеллекту
- В классах с гуманитарным уклоном лучше развит компонент вербального мышления. Хотя надо отметить присутствие во всех классах у гимназистов хорошо развитых компонентов мышления и не свойственных для соответствующего профиля.
Полученные результаты в целом подтверждают высокий интеллектуальный потенциал гимназистов, что ставит перед гимназией задачу удовлетворения повышенных интеллектуально-познавательных запросов учащихся, обеспечение условий развития способностей, талантов гимназистов, создание наиболее результативной, развивающей и здоровьесберегающей образовательной среды.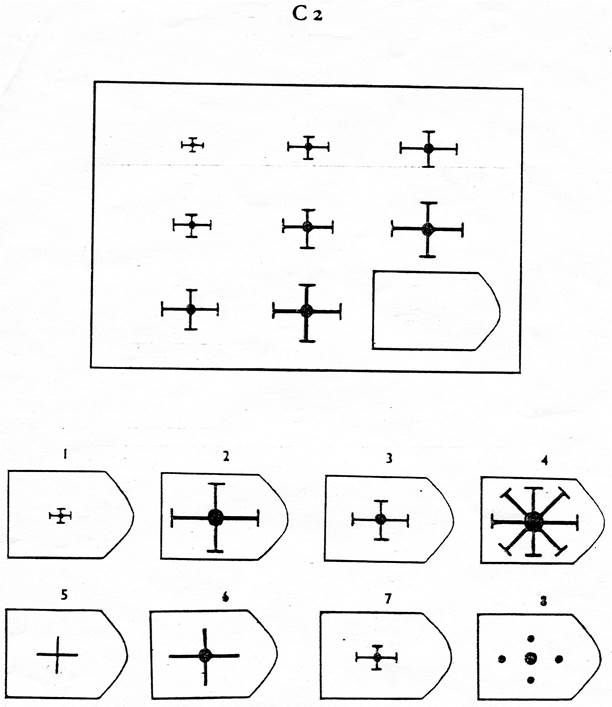
Основой образовательной самореализации гимназистов являются профильные учебные программы, спецкурсы и факультативы, организация исследовательской работы с привлечением специалистов факультетов и использованием лабораторной базы университета (участие в научно-практических конференциях школьников, студентов, участие в олимпиадах и интеллектуально-творческих конкурсах), проведение летних академических школ, составление индивидуальных маршрутов изучения учебных программ. Особое внимание уделяется участию гимназистов в конференциях и олимпиадах регионального и российского уровней.
4. Этап прохождение итоговой государственной аттестации.
С 2003 года итоговая государственная аттестация в Тюменской области проходит в формате ЕГЭ (единого государственного экзамена). Задача педагогического коллектива на этом этапе — подготовить гимназистов к тестовым испытаниям. Для обеспечения высоких результатов ЕГЭ необходимо учитывать методические и психологические аспекты подготовки к экзаменам.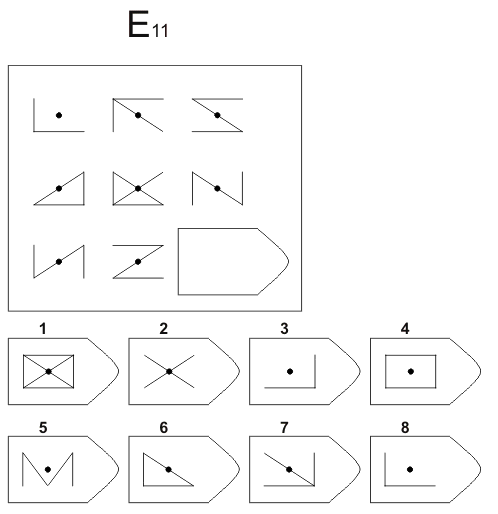
В Гимназии для учащихся при поддержке Центра мониторинга качества образования при Департаменте образования и науки администрации Тюменской области проводится репетиционное тестирование по всем предметам, которые выбирают учащиеся в качестве выпускного экзамена, а также по русскому языку и математике. Учащиеся получают консультации, как правильно распределить время при выполнении задания, когда и как осуществлять самоконтроль, проверку, как определить порядок в выполнении более сложных заданий (части В и С). Для них готовятся методические материалы для самостоятельной работы дома. Организуется работа в компьютерном классе, который оснащен программами тестирования знаний учащихся, благодаря чему возможна индивидуализация подготовки гимназистов к ЕГЭ.
На этом этапе проводятся собрания с родителями учащихся, которым объясняется процедура ЕГЭ, даются рекомендации по организации подготовки учащихся к экзаменам в домашних условиях.
Прогрессивные матрицы Равена — Блог Викиум
Прогрессивные матрицы Равена или, как их еще называют, тест Равена, это методика, которая позволяет оценить уровень логичности мышления (IQ).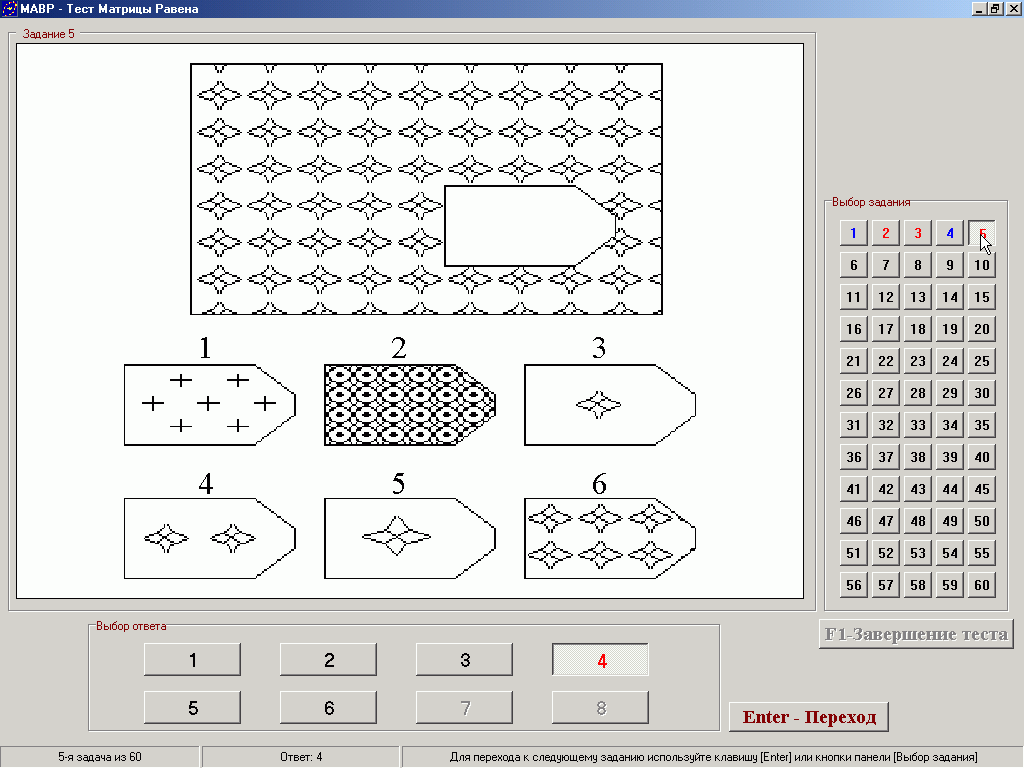 Тест появился в 1936 году. Его изобретатели — Л. Пенроуз и Дж. Равен.
Тест появился в 1936 году. Его изобретатели — Л. Пенроуз и Дж. Равен.
Тест основан на традициях английской школы, суть его заключается в выявлении отношений между различными абстрактными фигурами.
Особенной популярностью пользуются два стандартных варианта теста: цветной и черно-белый. Вариант тестирования выбирается в зависимости от возраста тестируемых. Так, цветные тесты предназначены для детей в возрасте от 6 до 9 лет или для пожилых людей в возрасте за 65 лет. В последнем случае тест Равена рекомендуется специалистами в случае необходимости реабилитационных исследований. Может также применяться для детей в возрасте старше 9 лет, если есть подозрение на аномальное развитие.
В основе тестирования лежит гештальт-психология, в частности теория перцепции форм и теория неогенеза, разработанная Ч. Спирменом. Метод тестирования относится к невербальным и уже в течение многих лет считается в этой области наиболее продвинутым и точным.
Теория перцепции форм и теория неогенеза
Согласно этой теории испытуемые должны рассматривать задание как единое целое, но состоящее из ряда разнообразных элементов.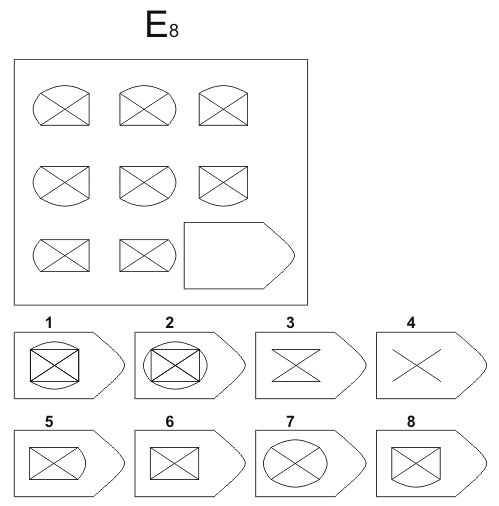 То есть каждый тестируемый должен изначально оценить задание-матрицу глобально, а уже затем проанализировать его и выделить принцип. Потом из выделенных элементов матрицы формируется целостный образ. В результате должна быть обнаружена недостающая деталь.
То есть каждый тестируемый должен изначально оценить задание-матрицу глобально, а уже затем проанализировать его и выделить принцип. Потом из выделенных элементов матрицы формируется целостный образ. В результате должна быть обнаружена недостающая деталь.
Вторая теория, разработанная Спирменом, позволяет более углубленно и детально оценить результаты данного исследования.
Комплекс этих методик и образует тест Равена, который, в свою очередь, отлично согласуется со множеством других подобных методик, например, тестом Векслера и других.
Матрицы Равена могут быть применены для определения интеллектуального развития людей практически любого возраста. При проведении исследований не имеют значения ни социокультурный фон, ни языковой состав, ни степень речевого развития.
Суть методики
Испытуемым выдается по одному стандартному экземпляру тетради, в которой находятся задания, а также один бланк с ответами. Время на выполнение задания строго фиксировано и составляет 35 минут.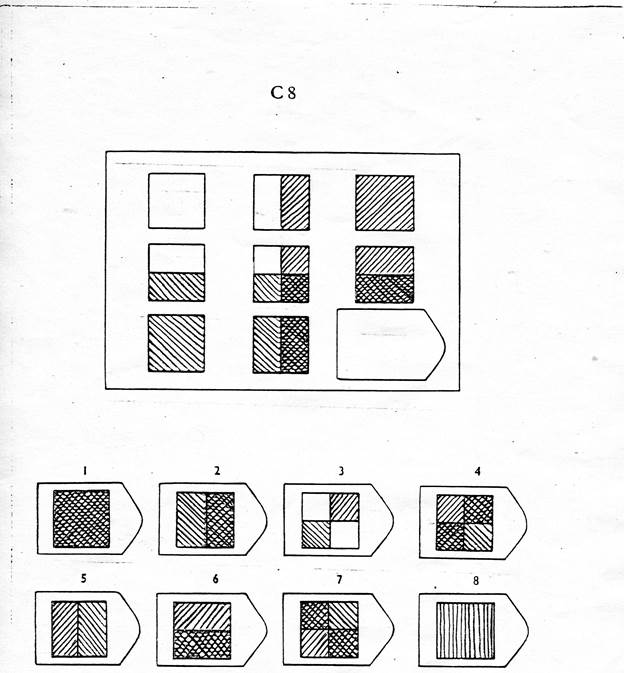
Посмотреть тест можно только после того, как будет выдана инструкция по его прохождению, которая озвучивается специалистом.
Специалист выдает матрицы, в которых испытуемые ищут определенный элемент. Процесс происходит следующим образом:
До 5 задания тестируемый может обратиться за подсказкой к экспериментатору. Затем выполняет оставшуюся часть заданий самостоятельно. Экспериментатор обязан сообщить участникам, что выполнять задание нужно как можно скорее и как можно более четко. При необходимости первое задание может быть выполнено даже совместно с экспериментатором. Отсчет времени начинается с момента выполнения пятого задания.
После выполнения все данные будут зафиксированы в бланке ответов.
Главное о методике Равена
Дж. Равен был категорически не согласен с мнением, что интеллект человека закладывается изначально и в дальнейшем не может меняться или каким-то образом преобразовываться. Он полагал, что интеллект формируется под воздействием не только врожденных качеств человека, но и под воздействием внешних факторов.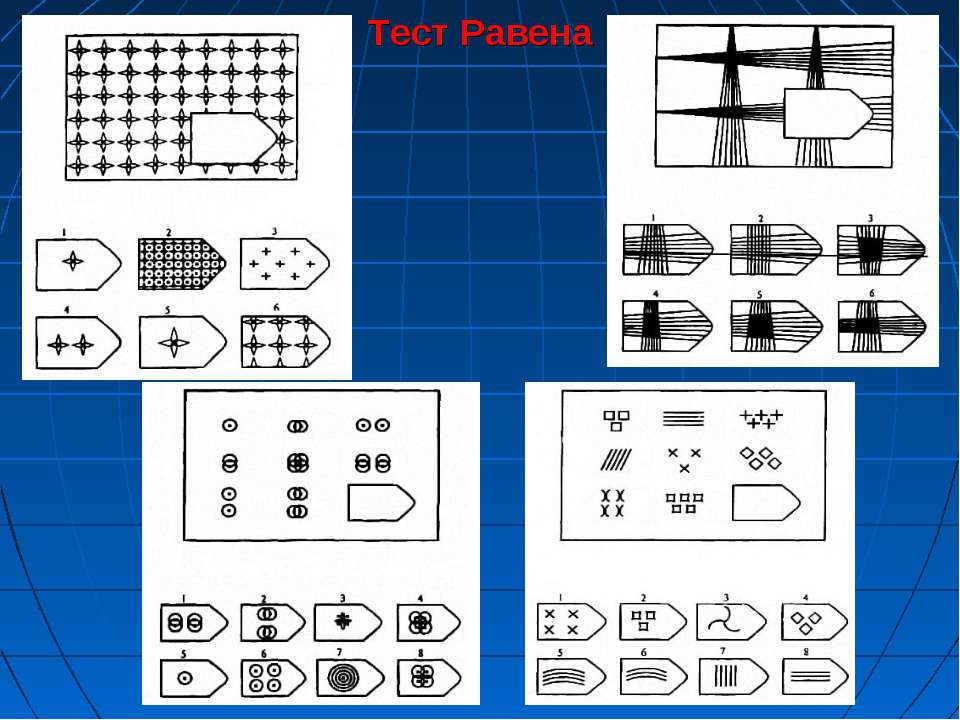 Именно поэтому он разработал собственный тест, который помогает выявлять и генетические, и средовые причины, которые воздействуют на уровень интеллекта.
Именно поэтому он разработал собственный тест, который помогает выявлять и генетические, и средовые причины, которые воздействуют на уровень интеллекта.
В результате разработанный им метод тестирования учитывает только логику человека. При этом уровень образования и другие параметры не имеют значения. Однако учитывается также и скорость принятия решения. Тест может пройти как взрослый человек, так и ребенок.
При обработке данных можно сделать исчерпывающие выводы о пространственном мышлении, особенностях целостного восприятия образов.
Матрица Равена используется в психологии и педагогике уже более полувека, за это время появилось множество вариаций данного метода, однако основной по-прежнему остается самым прогрессивным и востребованным.
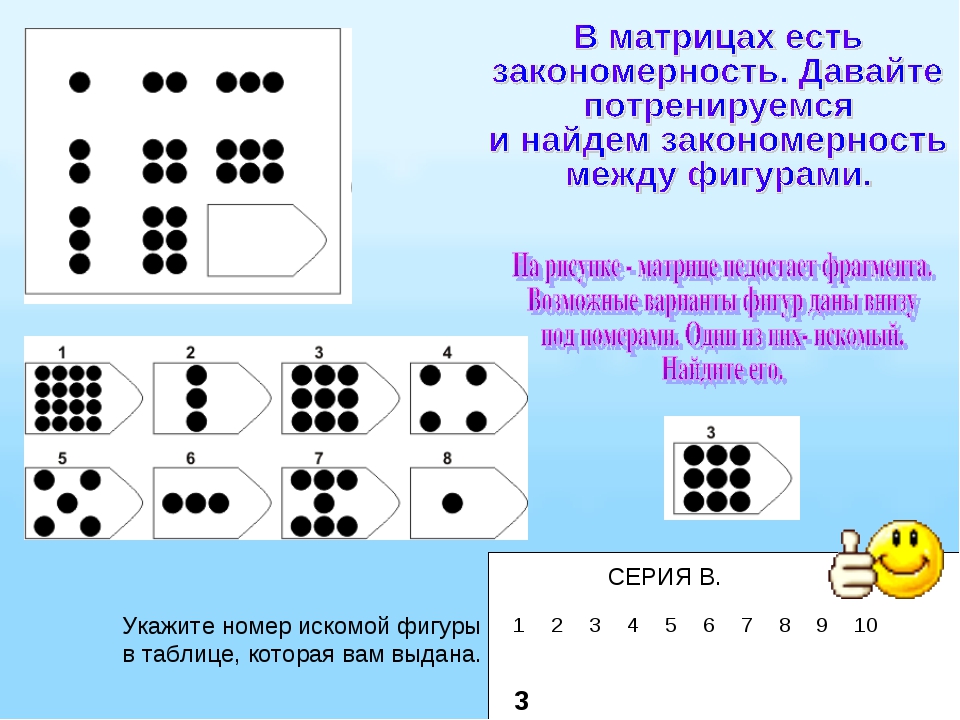
Всего в сборнике 60 заданий, которые делятся на 5 серий. Каждая серия включает 12 индивидуальных задач. Задача тестируемого — определить, как именно связаны между собой фигуры, находящиеся на рисунке, выявить недостающую фигуру и указать на нее.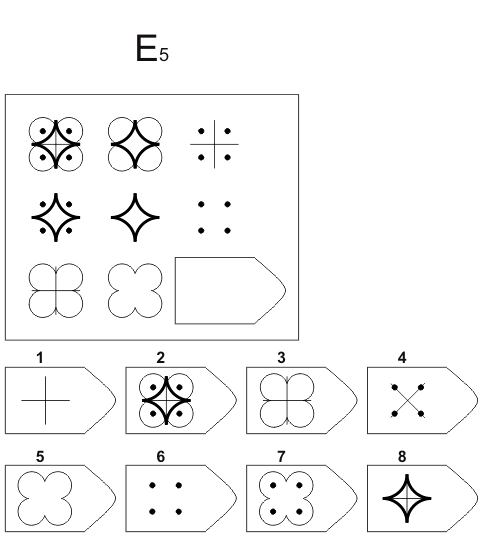 Уровень интеллектуального развития определяется тем, насколько верно и быстро тестируемый справился с заданием. Викиум создал несколько тренажеров на основе данного научного подхода: это «Микросхемы», «Тайная комната», «Геометрия». Узнайте, как работает эта методика уже сегодня!
Уровень интеллектуального развития определяется тем, насколько верно и быстро тестируемый справился с заданием. Викиум создал несколько тренажеров на основе данного научного подхода: это «Микросхемы», «Тайная комната», «Геометрия». Узнайте, как работает эта методика уже сегодня!
gaz.wiki — gaz.wiki
- Main page
Languages
- Deutsch
- Français
- Nederlands
- Русский
- Italiano
- Español
- Polski
- Português
- Norsk
- Suomen kieli
- Magyar
- Čeština
- Türkçe
- Dansk
- Română
- Svenska
равных матриц — матрицы равны, если выполняются два условия.
 Матрицы должны иметь одинаковые …
Матрицы должны иметь одинаковые …
Матрицы могут быть равными при выполнении определенных условий. Следовательно, мы можем составить уравнения и решить для переменных с двумя равными матрицами. (Примечание: это отличается от матричного уравнения, в котором вся матрица действует как переменная.)
Равно матриц
Две матрицы равны тогда и только тогда, когда эти матрицы имеют одинаковые размеры и равные соответствующие элементы.
Какие матрицы ниже равны?
Покажи ответ
Все три матрицы имеют одинаковые размеры
— 3 × 3 (3 строки и 3 столбца)
Все соответствующие записи или элементы одинаковы в матрице 1 и матрице 3.
— Самый средний элемент матрицы № 2 не совпадает с соответствующей записью в других матрицах. Следовательно, матрица № 2 не равна ни одной из других.
Практика Задача
Проблема 1
Какие матрицы ниже равны?
Покажи ответМатрицы №4 и №5 равны.Они имеют одинаковые размеры и одинаковые соответствующие записи.
Проблема 2
Какие матрицы ниже равны?
Покажи ответ Матрицы №8 и №9 равны. Они имеют одинаковые размеры и одинаковые соответствующие записи.
Они имеют одинаковые размеры и одинаковые соответствующие записи.
Проблема 3
Какие матрицы ниже равны?
Покажи ответМатрицы № 10 и № 11 равны.Матрица № 12 исключена, потому что она не имеет таких же размеров, как две другие. В нем всего две колонки
Решение для переменных в матрицах
Если мы знаем, что две матрицы равны, мы можем найти значения переменных в матрицах. Поскольку равные матрицы имеют равные соответствующие элементы, мы можем установить неизвестный элемент в одной матрице равным его соответствующему партнеру в другой матрице.
Поскольку равные матрицы имеют равные соответствующие элементы, мы можем установить неизвестный элемент в одной матрице равным его соответствующему партнеру в другой матрице.
Чтобы найти значение переменной y в левой матрице, мы просто устанавливаем ее равной соответствующему элементу в правой матрице.
г = 33
Проблема 4
Решение для переменных в равных матрицах не всегда будет таким простым, как сопоставление переменной с соответствующим номером. Вот немного более сложная проблема: каково значение y?
Покажи ответ
3y = 33 (установить соответствующие записи равными)
3г ÷ 3 = 33 ÷ 3
N
у = 11
— пояснения и примеры
Эквивалентные матрицы — это матрицы за 2 доллара, которые имеют одинаковый размер и форму. Существуют определенные условия, которые должны выполняться для того, чтобы матрицы были эквивалентны (или равны) друг другу. Прежде всего, давайте проверим определение эквивалентных матриц:
Существуют определенные условия, которые должны выполняться для того, чтобы матрицы были эквивалентны (или равны) друг другу. Прежде всего, давайте проверим определение эквивалентных матриц:
Эквивалентные матрицы — это матрицы, размер (или порядок) которых одинаковы и соответствующие элементы внутри матриц равны.
В этой статье мы рассмотрим, что такое эквивалентные матрицы, что делает матрицы равными 2 $, а также несколько примеров, демонстрирующих использование эквивалентных матриц при решении уравнений.
Что такое эквивалентные матрицы?
Матрицы $ 2 $ считаются эквивалентными , если они удовлетворяют условиям, показанным ниже:
- Каждая матрица имеет одинаковое количество строк
- Каждая матрица имеет одинаковое количество столбцов
- соответствующие элементы (или элементы) каждой матрицы равны друг другу
Все эти 3 $ условия должны быть выполнены , чтобы вызвать две матрицы , эквивалентные , или , равные .
Как определить эквивалентность двух матриц?
Рассмотрим матрицы $ 2 $, показанные ниже:
$ A = \ begin {bmatrix} 3 & {- 1} \\ 6 & 5 \ end {bmatrix} $
$ B = \ begin {bmatrix} 3 & {- 1} \\ 6 & 3 \ end {bmatrix} $
Во-первых, у нас есть матрица $ A $ . Это матрица, которая имеет $ 2 $ строк и $ 2 $ столбцов. Порядок (или размерность) матрицы равен $ 2 \ times 2 $.
Напомним, что мы можем идентифицировать конкретный элемент матрицы с помощью обозначения $ A_ {i j} $, где $ A $ — имя матрицы, $ i $ — номер строки, а $ j $ — номер столбца.Элементы матрицы $ A $:
$ A_ {1 1} = 3 $
$ A_ {1 2} = {- 1}
$$ A_ {2 1} = 6 $
$ A_ { 2 2} = 5 $
Во-вторых, у нас есть Matrix $ B $ . Это матрица, которая имеет $ 2 $ строк и $ 2 $ столбцов. Порядок (или размерность) матрицы равен $ 2 \ times 2 $.
Элементы матрицы $ B $:
$ B_ {1 1} = 3 $
$ B_ {1 2} = {- 1} $
$ B_ {2 1} = 6 $
$ B_ {2 2} = 3 $
Чтобы определить, эквивалентна ли матрица $ A $ матрице $ B $ или нет, мы пытаемся удовлетворить условия $ 3 $, которые мы видели ранее.{rd} $ условие: , а не .
Чтобы две матрицы были эквивалентными, нам необходимо выполнить Все условия эквивалентности матриц в размере 3 долларов. Даже если условие $ 1 $ не выполняется, матрицы эквивалентны , а не .
Решение уравнений с использованием эквивалентных матриц
Мы можем решать простые уравнения, используя концепцию эквивалентных матриц. Проверьте матрицы $ 2 $ ниже:
$ M = \ begin {pmatrix} 5 & {- 2} \\ x & 3 \ end {pmatrix} $
$ N = \ begin {pmatrix} 5 & y \\ 6 & 3 \ end {pmatrix} $
Если $ M = N $, можете ли вы найти значения для $ x $ и $ y $?
Поскольку матрица M равна (эквивалентна) матрице N, все соответствующие элементы одинаковы.
Чтобы найти $ x $, мы можем отметить, что:
$ M_ {2 1} = N_ {2 1} $
Таким образом, $ x = 6 $.
Чтобы решить для $ y $, мы можем отметить, что:
$ N_ {1 2} = M_ {1 2} $
Таким образом, $ y = {- 2} $.
Это показало, как мы можем приравнять соответствующие элементы для решения для отдельных переменных, когда две матрицы заданы как равные. Мы можем расширить эту идею и для решения сложных линейных уравнений.
Резюме
Подведем итог тому, что мы узнали:
- Эквивалентные матрицы — это матрицы, размер (или порядок) которых одинаков и соответствующие элементы внутри матриц равны.
- $ 3 $ условия должны быть выполнены, чтобы две матрицы были эквивалентны друг другу.
- Количество строк в каждой матрице должно быть одинаковым
- Количество столбцов каждой матрицы должно быть одинаковым
- Соответствующие элементы каждой матрицы должны быть равны
- Когда нам даны 2 матрицы с неизвестными, мы может приравнять соответствующие элементы в обеих матрицах, чтобы найти единственную переменную, или сформировать уравнение, а затем решить неизвестное.
Ниже мы покажем несколько примеров, поясняющих концепцию эквивалентных матриц и решения простых и сложных линейных уравнений с использованием эквивалентных матриц.
Пример 1
Учитывая приведенные ниже матрицы $ 7 $, ответьте на следующие вопросы true / false :
$ A = \ begin {pmatrix} 3 & -4 \\ 6 & {- 3 } \ end {pmatrix} $
$ B = \ begin {pmatrix} 5 & {- 6} & 0 \\ {- 2} & {6} & 9 \ end {pmatrix} $
$ C = \ begin {pmatrix} 11 & {- 5} & 1 \\ 12 & {- 3} & 1 \\ {0} & {- 9} & 3 \ end {pmatrix} $
$ D = \ begin {pmatrix} a & b \\ c & d \\ e & f \\ g & h \ end {pmatrix} $
$ E = \ begin {pmatrix} 3 & -4 \\ 6 & {- 3} \ end {pmatrix} $
$ F = \ begin {pmatrix} 11 & 12 & 0 \\ {- 5} & {- 3} & {- 9} \\ 1 & 1 & 3 \ end {pmatrix} $
$ G = \ begin {pmatrix} a & b \\ c & d \\ e & c \\ g & h \ end {pmatrix} $
- Верно / Ложно Матрица $ A $ = Матрица $ G $
- Верно / Неверно Матрица $ B $ = Матрица $ F $
- Верно / Неверно Матрица $ D $ = Матрица $ G $
- Верно / неверно Матрица $ A $ = Матрица $ E $
- Верно / неверно Матрица $ C $ = Матрица $ F $
Решение
Для двух равных (или эквивалентных) матриц , должны быть выполнены следующие условия $ 3 $:
- Количество строк в каждой матрице должно быть одинаковым
- Количество столбцов каждой матрицы должно быть одинаковым
- Соответствующие элементы каждой матрицы должны быть равны
- Просто взглянув на это, мы можем сказать, что матрицы не равны.Столбец {rd} $ отличается.
$ D_ {3 3} = f $
$ G_ {3 3} = c $
Итак, матрицы не равны.
Ложь. - Эти две матрицы, $ A $ и $ E $, фактически эквивалентны. Условия $ 3 $ выполнены. Оба имеют 2 строки и 2 столбца. Все соответствующие элементы в каждой матрице равны.
Верно. - Каждая матрица состоит из 3 $ строк и 3 $ столбцов. Элементы такие же. НО , строк и столбцов поменяны местами! Все 9 элементов одинаковы, но соответствующих элементов — нет! Таким образом, нельзя сказать, что Matrix $ C $ и Matrix $ F $ эквивалентны.
Ложь.
Пример 2
Заданная матрица $ T $ = матрица $ S $, вычислить значения $ x $ и $ y $.
$ T = \ begin {bmatrix} 11 & {2 + x} & 1 \\ 12 & {- 3} & 1 \\ {0} & {- 9} & 3 \ end {bmatrix} $
$ S = \ begin {bmatrix} 11 & {- 5} & 1 \\ 12 & {- 3} & 1 \\ {0} & {- 9} & {2y — 3} \ end {bmatrix} $
Решение
И Matrix $ T $, и Matrix $ S $ являются матрицами размером $ 3 \ times 3 $.
Мы знаем, что в эквивалентных матрицах соответствующие элементы равны.
В матрице $ T $, $ T_ {12} = 2 + x $.
В матрице $ S $, $ S_ {12} = -5 $.
Мы можем приравнять обе записи и узнать значение $ x $. Показано ниже:
$ 2 + x = -5 $
$ x = -5-2 $
$ x = -7 $
Сейчас,
В матрице $ S $, $ T_ {33} = 2y — 3 $.
В матрице $ T $, $ S_ {33} = 3 $.
Мы можем приравнять обе записи и узнать значение $ y $. Показано ниже:
$ 2y — 3 = 3 $
$ 2y = 6 $
$ y = 3 $
Практические вопросы
- Для матриц от $ A $ до $ E $ укажите, какая пара матриц эквивалентны друг другу.
$ A = \ begin {bmatrix} -2 & 6 \\ 12 & 5 \\ -3 & 7 \ end {bmatrix} $
$ B = \ begin {bmatrix} 0 & 5 \\ 6 & -8 \ end {bmatrix} $
$ C = \ begin {bmatrix} -2 & 4 \\ 13 & 5 \\ -3 & 5 \ end {bmatrix} $
$ D = \ begin {bmatrix} -2 & 6 \\ 12 & 5 \\ -3 & 7 \ end {bmatrix} $
$ E = \ begin {bmatrix} 0 & 6 \\ 5 & -8 \ end {bmatrix} $ - Данная матрица $ J $ = матрица $ K $ , вычислите значения $ a $ и $ b $.
$ J = \ begin {bmatrix} 11 & 3 & {4a-b} \\ 1 & {- 1} & 1 \\ {0} & {- 3} & -7 \ end {bmatrix} $$ K = \ begin {bmatrix} 11 & 3 & 7 \\ 1 & {- 1} & 1 \\ {0} & {-3} & {-a + 2b} \ end {bmatrix} $
Ответы
- Внимательно глядя на 5 матриц, мы можем сделать следующие наблюдения:
- Обе матрицы $ A $ и $ D $ эквивалентны друг другу.Обе они представляют собой матрицы размером $ 3 \ times 2 $, в которых каждая соответствующая запись равна друг другу.
- Матрицы $ B $ и $ E $ являются матрицами размером $ 2 \ times 2 $. Некоторые из соответствующих им записей равны, но не все. Несмотря на то, что они выглядят одинаково, это не так!
- Matrix $ C $ выглядит несколько равным Matrix $ A $, но при внимательном наблюдении мы можем сделать вывод, что они не равны.
- Как Matrix $ J $, так и Matrix $ K $ являются матрицами размером $ 3 \ times 3 $.
Мы знаем, что в эквивалентных матрицах соответствующие элементы равны.
В матрице $ J $, $ J_ {13} = 4a-b $.
В матрице $ K $, $ K_ {13} = 7 $.Приравнивая, мы можем написать:
$ 4a — b = 7 $
Кроме того,
В матрице $ J $, $ T_ {33} = -7 $.
В матрице $ K $, $ S_ {13} = -a + 2b $.Приравнивая, мы можем написать:
$ -a + 2b = -7 $
Эти 2 уравнения можно решить одновременно, чтобы получить значения $ a $ и $ b $.
После решения получаем:$ a = 1 $ и $ b = -3 $.
Предыдущий урок | Главная страница | Следующий урок
Сложение и вычитание матриц — ChiliMath
В этом уроке я подготовил семь (7) рабочих примеров, чтобы проиллюстрировать базовый подход к тому, как легко складывать или вычитать матрицы.
Если вы знаете, как складывать и вычитать действительные числа, эта тема должна быть очень легкой. Единственное, что требуется для «легального» выполнения операций сложения или вычитания в «мире» матриц, — это убедиться, что данные матрицы должны иметь одинаковый размер или размерность.
Что означает, что данная матрица имеет одинаковый размер или размерность?
Предположим, нам даны матрицы A и B. Они имеют одинаковый размер или размерность, потому что у них одинаковое количество строк и столбцов.
Мы можем описать размер или размерность матрицы, используя следующий стандартный формат:
количество строк x количество столбцов
Позвольте мне показать вам несколько примеров…
Последняя матрица размером 5 x 5 также считается «квадратной матрицей», потому что количество строк и количество столбцов равны. Важно знать, что для того, чтобы любая заданная матрица имела обратную, она должна быть квадратной матрицей. Я не говорю, что все квадратные матрицы имеют обратные, но первое требование к матрице, чтобы иметь обратную матрицу, состоит в том, что сначала она должна быть квадратной матрицей.
Ознакомьтесь с моим отдельным руководством о том, как найти обратную матрицу 2 × 2.
Я должен подчеркнуть, что для того, чтобы сложить или вычесть две заданные матрицы, они должны иметь одинаковый размер или размер. В противном случае мы заключаем, что сумма (сложение) или разность (вычитание) двух матриц, имеющих разные размеры или размеры, не определена!
Теперь давайте посмотрим на общее правило того, как складывать и вычитать матрицы, размеры или размеры которых совпадают.
Правила сложения и вычитания матриц одинакового размера или измерения
Предположим, что матрицы A и B имеют две строки и два столбца (2 × 2) с некоторыми произвольными элементами или записями…
«Формулы» для сложения и вычитания матриц показаны ниже…
- Добавьте матрицы , добавив их соответствующие записи
- Вычесть матрицы путем вычитания их соответствующих записей
Давайте поработаем над некоторыми проблемами.
Примеры сложения и вычитания матриц
Пример 1 : Выполните указанную операцию для A + C.
Обратите внимание, что матрицы A и C имеют одинаковый «размер» или «размерность», потому что их количество строк и столбцов одинаково. Оба могут быть описаны как матрица 3 x 3 . Это говорит мне о том, что найти их сумму — это нормально.
Добавлю соответствующие записи и упрощу.
Вот как это просто!
Пример 2 : Выполните указанную операцию для B + F.
Обратите внимание, что матрица B имеет размерность 2 × 3 , а матрица F имеет размерность 2 × 2 .
Поскольку количество строк и столбцов не совпадает, сумма матриц B и F не существует или не определена . Я остановлюсь здесь. Это наш ответ, хотите верьте, хотите нет.
Пример 3 : Выполните указанную операцию для E-B.
Последние два примера показали вам, как складывать матрицы. На этот раз мы поговорим о вычитании матриц.Помните, что процесс сложения и вычитания матриц очень похож. Если вы забыли, просмотрите приведенную выше «формулу».
В этом примере нам нужно найти разницу между матрицей E и матрицей B.
Однако кажется, что это невозможно, поскольку они имеют различных размеров или размеров. Матрица E имеет размер 3 × 2, а матрица B — 2 × 3.
Поскольку я не могу вычесть по входам, из-за того, что записи двух матриц не имеют прямого соответствия, я должен утверждать, что НЕ возможно найти их различие.Следовательно, наш ответ: undefined .
Это не вопрос с подвохом. Учителя иногда «добавляют» это в смесь, чтобы проверить, понимаете ли вы концепцию, согласно которой можно складывать или вычитать только матрицы с одинаковыми размерами или размерами. Не расстраивайтесь, я сам попал в эту «ловушку». Надеюсь, теперь, когда вы знаете, вы будете осторожны в следующий раз, когда столкнетесь с такой проблемой.
Пример 4 : Выполните указанную операцию для F-D.
При быстром просмотре я вижу, что можно найти разницу между матрицами F и D, потому что обе имеют одинаковое количество строк и столбцов.Большой!
Для начала я вычту соответствующие записи F и D. Мое единственное предостережение — будьте очень осторожны при вычитании действительных чисел. Обычно здесь возникают общие ошибки. Помните, что два соседних отрицательных знака оказываются положительными.
Неплохо, правда?
Пример 5 : Выполните указанную операцию для C-A.
Две заданные матрицы C и A имеют одинаковые размеры или размеры (обе матрицы 3 × 3). Это позволяет нам выполнять операцию вычитания.
Вычитая по входу, я получил…
Пример 6 : Выполните указанную операцию для (A + C) + (C-A).
Это отличный пример «многоступенчатой» задачи, которая включает в себя сложение и вычитание матриц. Цель состоит в том, чтобы выполнить указанную операцию над каждой круглой скобкой, а затем добавить их вместе.
Чтобы пропустить некоторые шаги, просмотрите, как мы решили для (A + C) в примере 1 и C-A в примере 5.
Пока у нас есть эти частичные ответы…
Итак, последний шаг — сложить их вместе, чтобы получить требуемый ответ.
Как видите, сложение и вычитание матриц очень просто. Я надеюсь, что вы приобрели некоторую уверенность и знания о том, как с этим справиться.
Пример 7 : Выполните указанную операцию для (A + C) + (C-A).
Это та же проблема, что и в примере 6. Но я хочу решить ее немного иначе, чтобы продемонстрировать тот факт, что есть другие способы решения определенной проблемы. Хотя метод, примененный в примере 6, вполне приемлем, этот «альтернативный» подход имеет гораздо больше смысла, поскольку он очень прост.
Поехали…
Если вы рассматриваете выражение (A + C) + (C-A) как , объединяющее похожие или похожие термины, проблема типа , то имеет смысл быстро упростить исходную задачу, даже не занимаясь сложением и вычитанием матриц.
Обратите внимание, что я могу объединить C-термины как 2C.
Теперь, члены A должны сокращаться, потому что они имеют противоположные знаки.
Наша исходная задача сводится к 2C, что составляет в два раза больше матрицы C .
Это означает, что я собираюсь умножить каждый элемент матрицы C на 2. На самом деле это тема моего другого урока по алгебре, посвященного скалярному умножению матрицы.
С
, то 2C решается с помощью…
Окончательный ответ, полученный с помощью этого метода, точно такой же, как в примере 6. Легко, правда?
Практика с рабочими листами
Возможно, вас заинтересует:
Скалярное умножение
Умножение матриц
Использование матриц для решения систем уравнений
Матричные уравнения
Матрицымогут использоваться для компактного написания и работы с системами множественных линейных уравнений.
Цели обучения
Определить, как матрицы могут представлять систему уравнений
Основные выводы
Ключевые моменты
- Если [latex] A [/ latex] является матрицей [latex] m \ times n [/ latex], а [latex] x [/ latex] обозначает вектор-столбец (то есть [latex] n \ times 1 [/ latex] матрица) [латекс] n [/ latex] переменных [latex] x_1, x_2,…, x_n [/ latex], и [latex] b [/ latex] представляет собой [латекс] m \ times 1 [/ latex ] Вектор-столбец, то матричное уравнение имеет вид: [latex] Ax = b [/ latex].
Ключевые термины
- матрица : прямоугольное расположение чисел или членов, имеющее различное применение, например, преобразование координат в геометрии, решение систем линейных уравнений в линейной алгебре и представление графиков в теории графов.
Матрицы можно использовать для компактного написания и работы с системами уравнений. Как мы узнали в предыдущих разделах, матрицами можно манипулировать так же, как и нормальным уравнением. Это очень полезно, когда мы начинаем работать с системами уравнений.Полезно понять, как организовать матрицы для решения этих систем.
Написание системы уравнений с матрицами
Можно решить эту систему, используя метод исключения или замены, но это также возможно сделать с помощью матричной операции. Прежде чем приступить к настройке матриц, важно сделать следующее:
- Убедитесь, что все уравнения написаны одинаково, то есть переменные должны быть в одном порядке.
- Убедитесь, что одна часть уравнения — это только переменные и их коэффициенты, а другая сторона — просто константы.
Решение системы линейных уравнений с использованием обратной матрицы требует определения двух новых матриц: [latex] X [/ latex] — это матрица, представляющая переменные системы, а [latex] B [/ latex] — матрица, представляющая константы. Используя матричное умножение, мы можем определить систему уравнений с таким же количеством уравнений в качестве переменных, как:
[латекс] \ displaystyle A \ cdot X = B [/ латекс]
Чтобы решить систему линейных уравнений с использованием обратной матрицы, пусть [latex] A [/ latex] будет матрицей коэффициентов, пусть [latex] X [/ latex] будет переменной матрицей, и пусть [latex] B [/ latex ] — постоянная матрица.
Учитывая систему:
[латекс] \ displaystyle \ begin {align} x + 8y & = 7 \\ 2x-8y & = — 3 \ end {align} [/ latex]
Матрица коэффициентов:
[латекс] A = \ begin {bmatrix} 1 & 8 \\ 2 & -8 \ end {bmatrix} [/ latex]
Матрица переменных:
[латекс] \ displaystyle X = \ begin {bmatrix} x \\ y \ end {bmatrix} [/ latex]
Постоянная матрица:
[латекс] \ displaystyle B = \ begin {bmatrix} 7 \\ -3 \ end {bmatrix} [/ latex]
Таким образом, чтобы решить систему [latex] AX = B [/ latex], для [latex] X [/ latex] умножьте обе стороны на обратную величину [latex] A [/ latex], и мы получим решение:
[латекс] \ Displaystyle X = (A ^ {- 1}) B [/ латекс]
Если существует обратный [латекс] \ left (A ^ {- 1} \ right) [/ latex], эта формула решит систему.
Если матрица коэффициентов необратима, система может быть несовместимой и не иметь решения, или быть зависимой и иметь бесконечно много решений.
Матрицы и операции со строками
Две матрицы эквивалентны строкам, если одна может быть заменена другой последовательностью элементарных операций со строками.
Цели обучения
Объясните, как использовать операции со строками и почему они создают эквивалентные матрицы
Основные выводы
Ключевые моменты
- Элементарная операция со строкой — это любое из следующих действий: переключение строк (перестановка двух строк в матрице), умножение строк (умножение строки матрицы на ненулевую константу) или сложение строк (добавление к одной строке). матрицы до некоторого числа, кратного другой строке).
- Если строки матрицы представляют систему линейных уравнений, то пространство строк состоит из всех линейных уравнений, которые могут быть выведены алгебраически из уравнений системы.
Ключевые термины
- пространство строки : набор всех возможных линейных комбинаций его векторов-строк.
- эквивалент строки : В линейной алгебре, когда одна матрица может быть заменена другой последовательностью элементарных операций со строкой.
Элементарные операции со строками (ERO)
В линейной алгебре две матрицы эквивалентны строкам, если одна может быть заменена другой последовательностью элементарных операций со строками.В качестве альтернативы, две матрицы [latex] m \ times n [/ latex] эквивалентны строкам тогда и только тогда, когда они имеют одинаковое пространство строк. Пространство строки матрицы представляет собой набор всех возможных линейных комбинаций ее векторов-строк. Если строки матрицы представляют собой систему линейных уравнений, то пространство строк состоит из всех линейных уравнений, которые могут быть выведены алгебраически из уравнений системы. Две матрицы одинакового размера эквивалентны строкам тогда и только тогда, когда соответствующие однородные системы имеют одинаковый набор решений или, что эквивалентно, матрицы имеют одно и то же нулевое пространство.Поскольку элементарные операции со строками обратимы, эквивалентность строк является отношением эквивалентности. Обычно обозначается тильдой (~).
Операция элементарной строки — это любой из следующих трех ходов:
- Переключение строк (перестановка): поменять местами две строки матрицы.
- Умножение строк (масштаб): умножение строки матрицы на ненулевую константу.
- Сложение строк (сводная): прибавить к одной строке матрицы несколько значений, кратных другой строке.
Создание эквивалентных матриц с использованием элементарных операций со строками
Поскольку матрица по существу является коэффициентами и константами линейной системы, три операции со строками сохраняют матрицу.Например, замена двух строк просто означает изменение их положения в матрице. Кроме того, при решении системы линейных уравнений методом исключения, умножение строк будет таким же, как умножение всего уравнения на число для получения аддитивных обратных величин, так что переменная сокращается. Наконец, добавление строк аналогично методу исключения, когда для получения переменной выбирается сложение или вычитание одинаковых членов уравнений. Следовательно, операции со строками сохраняют матрицу и могут использоваться как альтернативный метод для решения системы уравнений.
Пример 1: Покажите, что эти две матрицы эквивалентны строкам:
[латекс] \ displaystyle A = \ begin {pmatrix} 1 & -1 & 0 \\ 2 & 1 & 1 \ end {pmatrix} \ quad B = \ begin {pmatrix} 3 & 0 & 1 \\ 0 & 3 & 1 \ end {pmatrix} [/ латекс]
Начните с [latex] A [/ latex], добавьте вторую строку к первой:
[латекс] \ displaystyle A = \ begin {pmatrix} 3 & 0 & 1 \\ 2 & 1 & 1 \ end {pmatrix} [/ latex]
Затем умножьте вторую строку на 3 и вычтите первую строку из второй:
[латекс] \ displaystyle A = \ begin {pmatrix} 3 & 0 & 1 \\ 3 & 3 & 2 \ end {pmatrix} [/ latex]
Наконец, вычтите первую строку из второй:
[латекс] \ displaystyle A = \ begin {pmatrix} 3 & 0 & 1 \\ 0 & 3 & 1 \ end {pmatrix} [/ latex]
Вы можете видеть, что [latex] A = B [/ latex], что мы достигли с помощью серии элементарных операций со строками.
Сокращение строк: решение системы линейных уравнений
В редукторе рядов, линейная система:
[латекс] \ displaystyle x + 3y-2z = 5 \\ 3x + 5y + 6z = 7 \ 2x + 4y + 3z = 8 [/ latex]
Представлен в виде расширенной матрицы:
[латекс] \ displaystyle A = \ begin {pmatrix} 1 & 3 & -2 & 5 \\ 3 & 5 & 6 & 7 \\ 2 & 4 & 3 & 8 \ end {pmatrix} [/ latex]
Затем эта матрица модифицируется с использованием операций с элементарными строками до тех пор, пока она не достигнет уменьшенной формы эшелона строк.
Поскольку эти операции обратимы, полученная расширенная матрица всегда представляет собой линейную систему, эквивалентную исходной.
Существует несколько конкретных алгоритмов сокращения строк расширенной матрицы, простейшими из которых являются исключение Гаусса и исключение Гаусса-Жордана. Это вычисление может быть выполнено вручную (с использованием трех типов ERO) или на калькуляторе с использованием матричной функции «rref» (сокращенная форма эшелона строк).
Окончательная матрица представлена в виде сокращенного ряда строк и представляет систему [латекс] x = -15 [/ latex], [latex] y = 8 [/ latex] [latex] z = 2 [/ latex].
[латекс] \ displaystyle A = \ begin {pmatrix} 1 & 0 & 0 & 0 & -15 \\ 0 & 1 & 0 & 8 \\ 0 & 0 & 1 & 2 \ end {pmatrix} [/ latex]
Упрощение матриц с помощью операций со строками
Используя элементарные операции, метод исключения Гаусса приводит матрицы к форме эшелона строк.
Цели обучения
Используйте операции с элементарными строками, чтобы представить матрицу в упрощенном виде
Основные выводы
Ключевые моменты
- Поскольку элементарные операции со строками сохраняют пространство строк матрицы, пространство строк формы эшелона строк такое же, как и у исходной матрицы.
- Существует три типа операций с элементарными строками: поменять местами две строки, умножить строку на ненулевой скаляр и добавить к одной строке скалярное кратное другой.
- На практике обычно не рассматривают системы в терминах уравнений, а вместо этого используют расширенную матрицу (которая также подходит для компьютерных манипуляций).
Ключевые термины
- Расширенная матрица : Матрица, полученная путем добавления столбцов двух заданных матриц, обычно с целью выполнения одних и тех же элементарных операций со строками для каждой из данных матриц.
С помощью конечной последовательности элементарных операций со строками, называемых исключением по Гауссу, любую матрицу можно преобразовать в форму эшелона строк. Это преобразование необходимо для решения системы линейных уравнений.
Прежде чем углубляться в детали, следует упомянуть несколько ключевых терминов:
- Расширенная матрица : расширенная матрица — это матрица, полученная путем добавления столбцов двух заданных матриц, обычно с целью выполнения одних и тех же операций с элементарной строкой для каждой из данных матриц.
- Форма верхнего треугольника : квадратная матрица называется верхней треугольной, если все элементы ниже главной диагонали равны нулю. Треугольная матрица — это нижнетреугольная или верхнетреугольная матрица. Матрица, имеющая одновременно верхний и нижний треугольники, является диагональной матрицей.
- Элементарные операции со строками : Поменять местами строки, добавить строки или умножить строки.
Исключение по Гауссу
- Напишите расширенную матрицу для линейных уравнений.
- Используйте элементарные операции со строками в расширенной матрице [latex] [A | b] [/ latex], чтобы преобразовать [latex] A [/ latex] в форму верхнего треугольника. Если на диагонали находится ноль, переключайте строки, пока на его месте не окажется ненулевое значение.
- Используйте обратную замену, чтобы найти решение.
Пример 1: Решите систему методом исключения Гаусса:
[латекс] \ displaystyle 2x + y-z = 8 \\ -3x-y + 2z = -11 \ -2x + y + 2z = -3 [/ latex]
Запишите расширенную матрицу:
[латекс] \ left [\ begin {array} {rrr | r} 2 & 1 & -1 & 8 \\ -3 & -1 & 2 & -11 \\ -2 & 1 & 2 & -3 \ end {array} \ right] [/ latex]
Используйте элементарные операции со строками, чтобы уменьшить матрицу до уменьшенной формы эшелона строк:
[латекс] \ left [\ begin {array} {rrr | r} 1 & 0 & 0 & 2 \\ 0 & 1 & 0 & 3 \\ 0 & 0 & 1 & -1 \ end {array} \ right ] [/ латекс]
Используя элементарные операции со строками для получения сокращенной формы эшелона строк (‘rref’ в калькуляторе), решение системы отображается в последнем столбце: [latex] x = 2, y = 3, z = -1 [/ latex] .
Все нулевые матрицы равны математике класса 9 CBSE
Подсказка: Нулевая матрица — это матрица, все элементы которой равны 0. Теперь мы можем сказать, что две матрицы равны, если все элементы матрицы равны. Теперь мы воспользуемся этими знаниями, чтобы проверить, все ли нулевые матрицы равны. Полный пошаговый ответ:
Теперь давайте сначала разберемся с концепцией матриц.
Матрица — это не что иное, как прямоугольный массив членов, состоящий из строк и столбцов.
Предположим, что у нас есть матрица с m строками и n столбцами, тогда матрица имеет порядок $ m \ times n $.
Теперь попробуем написать матрицу порядка $ 2 \ times 3 $. Теперь матрица будет иметь 2 строки и 3 столбца.
$ \ left [\ begin {align}
& \ begin {matrix}
1 & 1 & 1 \\
\ end {matrix} \\
& \ begin {matrix}
1 & 1 & 1 \\
\ end {matrix} \\
\ end {align} \ right] $.
Теперь давайте разберемся с концепцией нулевой матрицы. Матрица называется нулевой матрицей, если все ее элементы равны 0.
Следовательно, мы можем сказать, что $ \ left [\ begin {align}
& \ begin {matrix}
0 & 0 & 0 \\
\ end {matrix} \\
& \ begin {matrix}
0 & 0 & 0 \\
\ end {matrix} \\
\ end {align} \ right] $ — это нулевая матрица.
Теперь две матрицы называются одинаковыми, если все записи совпадают. Но мы можем сравнивать только матрицу того же порядка.
Следовательно, предположим, что у нас есть матрица порядка $ 2 \ times 3 $ и другая матрица порядка $ 3 \ times 2 $, тогда мы не можем сравнивать две матрицы.
Теперь, если у нас есть нулевая матрица того же порядка, мы определенно можем сказать, что две матрицы равны. Но если у нас есть две нулевые матрицы разного порядка, то матрицы не равны.
Например, рассмотрим $ \ left [\ begin {align}
& \ begin {matrix}
0 & 0 & 0 \\
\ end {matrix} \\
& \ begin {matrix}
0 & 0 & 0 \ \
\ end {matrix} \\
\ end {align} \ right] $ и $ \ left [\ begin {matrix}
0 & 0 \\
\ end {matrix} \ right] $ обе являются нулевыми матрицами, но не равный.
Примечание:
Теперь обратите внимание, что даже для сложения и вычитания матрицы должны быть одного порядка. Хотя умножение матриц возможно только в том случае, если порядок матриц имеет вид $ m \ times n $ и $ n \ times r $. Также обратите внимание, что деление матриц не определено.
Найти значение X, для которого матрицы A не имеют обратного
Привет H.
спросил • 03.09.20A = x 5
1 3
как это решить или объяснить, почему это невозможно?
Артуро О.ответил • 03.09.20
Опытный учитель физики Репетиторство по физике
Если определитель равен нулю, матрица не имеет обратной, поэтому установите определитель равным нулю и решите относительно x.
A = | х 5 |
| 1 3 |
det (A) = x (3) — 1 (5) = 0
3x — 5 = 0
x = 5/3
Все еще ищете помощь? Получите правильный ответ быстро.
ИЛИ
Найдите онлайн-репетитора сейчасВыберите эксперта и познакомьтесь онлайн. Никаких пакетов или подписок, платите только за необходимое время.
¢ € £ ¥ ‰ µ · • § ¶ SS ‹ › « » < > ≤ ≥ — — ¯ ‾ ¤ ¦ ¨ ¡ ¿ ˆ ˜ ° — ± ÷ ⁄ × ƒ ∫ ∑ ∞ √ ∼ ≅ ≈ ≠ ≡ ∈ ∉ ∋ ∏ ∧ ∨ ¬ ∩ ∪ ∂ ∀ ∃ ∅ ∇ * ∝ ∠ ´ ¸ ª º † ‡ А Á Â Ã Ä Å Æ Ç È É Ê Ë Я Я Я Я Ð Ñ Ò Ó Ô Õ Ö Ø Œ Š Ù Ú Û Ü Ý Ÿ Þ à á â ã ä å æ ç è é ê ë я я я я ð ñ ò ó ô х ö ø œ š ù ú û ü ý þ ÿ Α Β Γ Δ Ε Ζ Η Θ Ι Κ Λ Μ Ν Ξ Ο Π Ρ Σ Τ Υ Φ Χ Ψ Ω α β γ δ ε ζ η θ ι κ λ μ ν ξ ο π ρ ς σ τ υ φ χ ψ ω ℵ ϖ ℜ ϒ ℘ ℑ ← ↑ → ↓ ↔ ↵ ⇐ ⇑ ⇒ ⇓ ⇔ ∴ ⊂ ⊃ ⊄ ⊆ ⊇ ⊕ ⊗ ⊥ ⋅ ⌈ ⌉ ⌊ ⌋ 〈 〉 ◊ Обзор умножения матриц
Обзор
Матрицы — это способ группировки чисел, которые организованы в строки и столбцы.Матрицы часто используются как способ представления нескольких уравнений в более простом для организации формате, однако для решения этих систем уравнений мы должны иметь возможность выполнять матричные операции, такие как умножение.
Строки и столбцы
Приведенная ниже матрица является примером матрицы [3×2]. Матрицы описываются в форме [RxC], где R представляет количество строк матрицы, а C представляет количество столбцов матрицы.
Вышеупомянутая матрица имеет размер [3×2], потому что у нее 3 строки и 2 столбца.
Умножение на скаляр
Любую матрицу можно умножить на так называемую скалярную величину. В этом случае скаляр представляет собой действительное число, умноженное на всю матрицу. Например:
Умножение матриц
Также возможно умножение двух матриц вместе, однако матрицы могут быть умножены только в том случае, если количество столбцов первой матрицы равно количеству строк второй матрицы. Если две матрицы соответствуют этому критерию, их можно умножить.Результатом будет третья матрица с таким же количеством строк, как в первой матрице, и с таким же количеством столбцов, как во второй матрице.
Пример
Можно ли перемножить следующие матрицы? Каковы будут размеры ответа?
-
[2×3] * [2×2]
-
[3×2] * [2×2]
-
[2 * 3] * [3 * 1]
Ответ
1. Ср. невозможно умножить эти матрицы, потому что матрица 1 имеет три столбца, а матрица 2 — только две строки.
2. Мы можем умножать эти матрицы, потому что матрица 1 имеет два столбца, а матрица 2 — две строки. Результирующая матрица будет иметь столько же строк, сколько матрица 1 и столбцов, как матрица 2 — так что это будет [3×2].
3. Мы можем перемножить эти две матрицы, потому что матрица 1 имеет три столбца, а матрица 2 — три строки. Результатом будет [2×1].
Примечание: Это упражнение должно было прояснить, что порядок имеет значение при умножении двух матриц. Попробуйте изменить порядок любого из приведенных выше примеров и посмотрите, изменится ли результат.
Правила умножения матриц
Как только мы узнаем, можно ли умножить две матрицы, пора выполнить это умножение. Умножение двух матриц также известно как «скалярное произведение». Каждое число в матрице ответов является результатом умножения одной из строк матрицы 1 на один из столбцов матрицы 2.
Чтобы найти первую строку, первый столбец матрицы ответов, умножьте первую строку матрицы 1 на столбец один. матрицы 2. Чтобы найти строку 1, столбец 2 матрицы ответов, умножьте первую строку матрицы 1 на второй столбец матрицы 2.При умножении строки на столбец совпадающие термины умножаются и складываются.
Пример: Найдите скалярное произведение двух матриц
Матрица 1 имеет два столбца, а матрица 2 — две строки, поэтому эти две можно перемножить. Ответ будет состоять из двух строк, потому что в матрице 1 две строки и три столбца, потому что в матрице 2 три столбца.



 У некоторых учащихся равномерно высоко развиты общие интеллектуальные способности, у одних лучше развит вербальный компонент мышления, у других невербальный, но в целом развитие интеллектуальных способностей не ниже среднего уровня.
У некоторых учащихся равномерно высоко развиты общие интеллектуальные способности, у одних лучше развит вербальный компонент мышления, у других невербальный, но в целом развитие интеллектуальных способностей не ниже среднего уровня.