Метод проб и ошибок в математике: Метод проб и ошибок.Математические модели.ГДЗ.Математика 5 класс.Дорофеев Г.В.Часть.1.Глава 1.Параграф 2.Задание 209 – Рамблер/класс
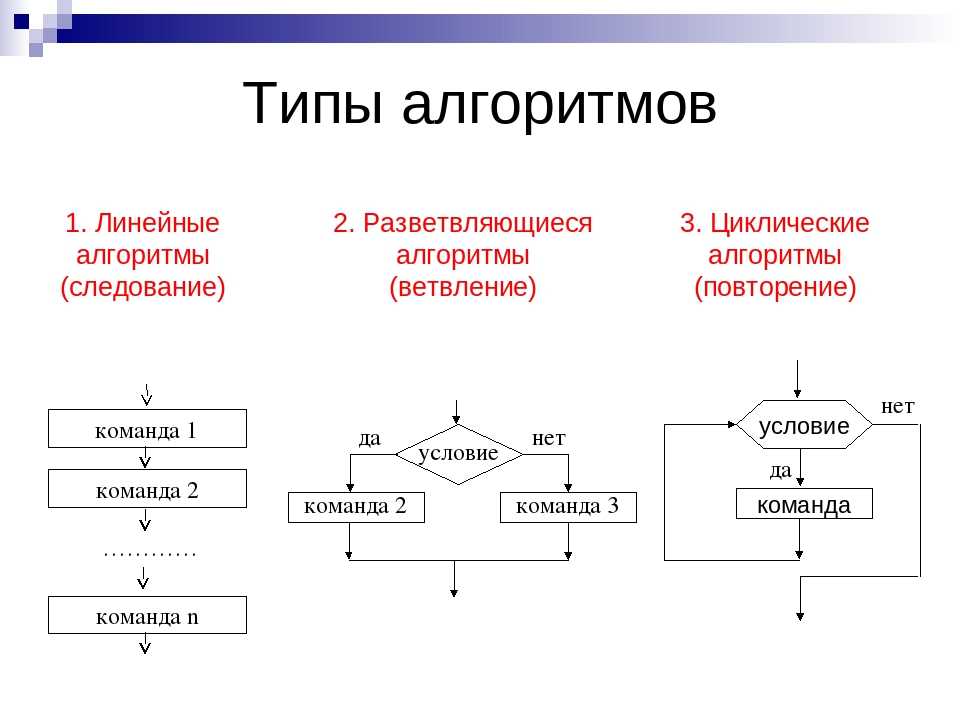
Метод проб и ошибок
Метод проб и ошибок
в решении текстовых задач.
При решении текстовых задач многие учащиеся испытывают затруднения. Главная задача учителя научить решать ученика различные типы текстовых задач. Процесс решения текстовых задач развивает у учащихся логическое мышление, учат находить выход из проблем реальной жизни, дает почувствовать уверенность в своих силах.
Текстовые задачи можно разбить на два основных класса:
Причем это разделение довольно условно. Многие текстовые арифметические задачи можно решить с помощью уравнений, а задачи на составление уравнений (систем уравнений) часто решают по действиям, а если это не получается, то используют метод проб и ошибок или метод перебора.
Мне бы хотелось продемонстрировать решение ряда задач этими методами.
Задача №1
Одна сторона прямоугольного участка земли на 3 м больше другой его стороны. Площадь участка равна 70 м². Найти размеры этого участка.
Найти размеры этого участка.
Пусть x м ширина участка, (x+3) м – длина участка, а площадь x·(x+3) м²,
что по условию задачи равно 70 м². Чтобы найти размеры участка надо составить уравнение x·(x+3)=70 и решить его. Но в 5ом классе такие учащиеся решать еще не могут. Поэтому попробуем подобрать решение «экспериментально», так называемым методом проб и ошибок.
пусть x=4, т.е. 4·(4+3)=28, 28≠70;
x=6, т.е. 6·(6+3)=54, 54≠70;
x=7, т.е. 7·(7+3)=70, 70=70 верно.
Т.е. мы увидели, что метод проб и ошибок позволяет найти ответ даже в случае, когда математический модель представляет собой новый, не изученный еще объект. Но, решая задачи этим способом, следует помнить, что подбор одного решения не гарантирует полноты решения. Поэтому необходимы обоснования того, что найдены все возможные решения.
В нашей задаче, если бы x было больше 7,то x+310 и x·(x+3)70, если наоборот xx+3 x·(x+3)
Задачи для учащихся.
Переведи условие задачи на математический язык и найди решение методом проб и ошибок.
Площадь прямоугольника равна 68 дм², а длина больше ширины на 13 дм. Каковы стороны этого прямоугольника?
Ширина прямоугольника на 9 см меньше длины, а площадь равна 90 см². Найти стороны прямоугольника.
Найти периметр прямоугольника, площадь которого составляет 18 м², а ширина в 2 раза меньше длины.
Площадь прямоугольника равна 64 дм², а его длина в 4 раза больше ширины. Чему равен периметр прямоугольника?
Длину прямоугольника уменьшили на 3 см, а ширину увеличили на 4 см и получили квадрат. Найти сторону квадрата, если площадь прямоугольника равна 30 см².
После того как ширину прямоугольника увеличили на 1 м, а длину уменьшили на 5 м, получили квадрат. Чему равна площадь квадрата, если площадь прямоугольника 91 м².
Длина прямоугольника на 5 м больше ширины, а площадь составляет 24 м².
 каковы стороны этого прямоугольника?
каковы стороны этого прямоугольника?Длину прямоугольника уменьшили в 2 раза, а ширину увеличили на 1 дм и получили квадрат. Найти сторону квадрата, если площадь прямоугольника 60 дм².
Найти периметр прямоугольника, у которого ширина на 4 см меньше длины, а площадь составляет 32 см².
10)Одна из сторон прямоугольника на 20 см больше другой. Если
большую сторону уменьшить в 3 раза, а меньшую сторону увеличить
в 2 раза, то площадь нового прямоугольника будет равна 200 см².
Найти стороны данного прямоугольника.
Метод перебора при
нахождении НОД.
Рассмотрим еще один метод – метод перебора. Т.к. предыдущий метод решения задач – метод проб и ошибок не дает уверенности в том, что найдены все искомые значения. Поэтому для обоснования полноты решения требуются дополнительные, иногда очень непростые рассуждения. В этом недостаток метода проб и ошибок. Но он исключен в методе полного перебора.
Полный перебор требует, как правило, больших усилий и большого времени. Однако внимательный анализ условия часто позволяет найти систему перебора, охватывающую все возможные варианты, но более короткую, чем «лобовой» перебор.
Задача. На экскурсию едут 252 ученика школы. Для них заказаны
несколько автобусов. Однако выяснилось, что если заказать
автобусы, вмещающие на 6 человек больше, то автобусов
потребуется на один меньше. Сколько больших автобусов надо
заказать?
Составим таблицу.
| Кол-во детей в одном автобусе | Количество автобусов | Общее кол-во детей | |
| Большие автобусы | 252 : x | x | 252 |
| Маленькие автобусы | 252 : (x+1) | x+1 | 252 |
Т. к. по условию в большой автобус вмещается на 6 детей больше, чем в маленький, то разность 252 : x — 252 : (x+1) = 6. Значит решением задачи является число X, удовлетворяющее равенству: 252 : x — 252 : (x+1) = 6.
к. по условию в большой автобус вмещается на 6 детей больше, чем в маленький, то разность 252 : x — 252 : (x+1) = 6. Значит решением задачи является число X, удовлетворяющее равенству: 252 : x — 252 : (x+1) = 6.
Но можно получить более простую математическую модель этой задачи, обозначив дополнительно буквой Y число детей, которых можно разместить в большом автобусе.
| Кол-во детей в одном автобусе | Количество автобусов | Общее кол-во детей | |
| Большие автобусы | y | x | 252 |
| Маленькие автобусы | y-6 | x+1 | 252 |
Очевидно, что в этом случае математической моделью задачи являются два равенства:
xy = 252;
(x+1)·(y-6) = 252.
Искомые числа x и y должны удовлетворять как первому, так и
второму равенству. Найдем эти числа x и y.
Из равенства xy = 252 можно заметить, что числа x и y не могут быть
больше, чем 252. Однако и в этом случае «лобовой» перебор потребовал бы рассмотрения огромного числа вариантов. Но более внимательный анализ первого равенства показывает, что числа x и y – это парные делители 252: при делении 252 на x получается y, и наоборот. Следовательно, достаточно рассмотреть лишь парные делители числа 252, причем для случая, когда y6 (y-60).
Составим таблицу:
+1
| x | 1 | 2 | 3 | 4 | 6 | 7 | 9 | 14 | 18 | 28 | 36 |
| y | 252 | 126 | 84 | 63 | 42 | 36 | 28 | 18 | 14 | 9 | 7 |
— 6
Анализ второго равенства позволяет еще больше сократить число возможных вариантов. Оно означает, что число (x+1) и (y-6) так же являются парными делителями 252. Из таблицы видно, что такими свойствами обладает только пара x=6, y=42.
Оно означает, что число (x+1) и (y-6) так же являются парными делителями 252. Из таблицы видно, что такими свойствами обладает только пара x=6, y=42.
Ответ: для экскурсии надо заказать 6 больших автобусов.
Задачи для учащихся.
Сумма цифр двузначного числа равна 15. Если эти цифры поменять местами, то получится число, которое на 27 меньше исходного. Найти эти числа.
Сумма цифр двузначного числа равна 12. число, записанное теми же цифрами, но в обратном порядке, составляет 4 /7 исходного числа. Найти эти числа.
Одно из двух натуральных чисел на 4 больше другого. Найди эти числа, если их произведение равно 96.
У причала находилось 6 лодок, часть из которых была двухместными, а часть трехместными. Всего в эти лодки может поместиться 14 человек. Сколько двухместных и трехместных лодок было у причала?
Прямоугольный газон обнесен изгородью, длинна которой 30 м.
 Площадь газона 56 м². Найди длины газона, если известно, что они выражаются натуральными числами.
Площадь газона 56 м². Найди длины газона, если известно, что они выражаются натуральными числами.В несколько посылок упаковали 36 книг и 54 журнала, распределив их между посылками поровну. В каждой посылке книг на 2 меньше, чем журналов. Сколько получилось посылок?
Произведение двух натуральных чисел равно 72. Найти эти числа, если одно из них больше другого на 6.
На турбазе имеются палатки и домики, общее число которых равно 25. в каждом домике живут 4 человека, а в палатке – 2 человека. Сколько на турбазе палаток и сколько домиков, если всего на этой турбазе отдыхают 70 человек?
Прямоугольный участок земли обнесен забором, длина которого 40 м. Площадь участка 96 м². Найти длины сторон этого участка, если известно, что они выражаются натуральными числами.
Еще один тип задач, которые решаются методом перебора.
Задумано двузначное число, которое на 52 больше произведения своих цифр. Какое число задумано?
Пусть xy – задуманное двузначное число, где x – цифра десятков, а y – цифра единиц. Тогда их произведение равно xy. Само двузначное число можно записать как 10x+y. По условию 10x+y на 52 больше произведения своих цифр xy. Т.е. должно выполняться равенство 10x+y= xy+52, которое является математической моделью данной задачи.
Тогда их произведение равно xy. Само двузначное число можно записать как 10x+y. По условию 10x+y на 52 больше произведения своих цифр xy. Т.е. должно выполняться равенство 10x+y= xy+52, которое является математической моделью данной задачи.
Решается это уравнение методом перебора. Полный перебор можно провести, рассматривая последовательно все значения x от 1 до 9 и подбирая в каждом случае соответствующее значение y от 0 до 9.
Однако этот перебор можно сократить, если заметить, что первая часть данного равенства больше 52. Значит, и первая его часть, т.е. задуманное число, больше 52. Поэтому неизвестное число x не меньше 5, и можно рассматривать только пять значений x – от 5 до 9.
При x=5 будем иметь равенство 50+y=5y+52, оно невозможно, т.к. 50+yy+52.
При x=6 60+y=6y+52 | -y
60=5y+52
5y=8 невозможно для натурального y.
При x=7 70+y=7y+52
70=6y+52
6y=18
y=3 Число 73
При x=8 80+y=8y+52
80=7y+52
7y=28
y=4 Число 87
При x=9 90+y=9y+52
38=8y невозможно
Таким образом, задумано либо 73, либо 84.
Условие задачи не дает возможности ответить на этот вопрос. Поэтому два ответа: 73 или 84.
Задачи для учащихся.
Метод перебора используется при доказательстве общих утверждений, где необходимо вводить буквенные обозначения.
Например: Доказать, что сумма любых трех последовательных натуральных чисел делится на 3.
1 сл. 1,2,3 1+2+3=6, 6:3=2
2 сл. 5,6,7 5+6+7=18, 18:3=6
3 сл. 21,22,23 21+22+23=66 66:3=22
и т.д.
Возьмем произведение натурального числа и обозначим его n. Тогда следующие за ним два числа соответственно равны n+1 и n+2.
Их сумма: n+(n+1)+(n+2)=3n+3=3(n+1) делится на 3, т.к. один из множителей делится на 3.
Понять математику может каждый
«Математика? Нет, это не для меня, я никогда не справлюсь», — кажется, вы где-то это уже слышали? Если нет, то наверняка вы сами говорили эту фразу в какой-то момент вашей школьной или студенческой жизни.
Математика отличается от всех остальных предметов, преподаваемых в школе. Это касается и теоретической стороны, и практической. Математика по праву считается «царицей наук», потому что включает в себя всё, что связано с цифрами, — от счёта до теории вероятности, от базовой алгебры до сложнейших геометрических задач, от простых дробей до ещё не доказанных теорем.
Это касается и теоретической стороны, и практической. Математика по праву считается «царицей наук», потому что включает в себя всё, что связано с цифрами, — от счёта до теории вероятности, от базовой алгебры до сложнейших геометрических задач, от простых дробей до ещё не доказанных теорем.
Но как справиться с математикой?
Обычно, когда дело доходит до математики, вы попадаете в одну из этих категорий:
- У вас дар к математике. Вы понимаете всё с первого дня и сразу же становитесь отличником по этому предмету. Математика существует для вас, и вы не можете даже представить ситуацию, где вы бы отставали от класса. Скорее одноклассники не могут за вами угнаться!
- Математика — это просто не ваше, и вы даже боитесь думать об этом предмете. Вы не можете запомнить формулы, да и не очень-то это интересно, считать — бессмысленно, изучать теоремы — скучно. Все страдания ради одного — оценка учителя, не всегда объективной и не очень-то желанной.
В общем, мир математики может казаться чёрно-белым: либо ты понимаешь её сразу и без труда, либо ты просто не предназначен для этой науки.
Но что если перестать мыслить этими категориями и поменять угол зрения?
Нет причин бояться цифр — они не кусаются!
Если при мысли об изучении математики вас охватывает навязчивый страх неудачи, то, скорее всего, ваши проблемы связаны с низкой уверенностью в себе. Либо же — вас неправильно учили или выбирали образовательные стратегии, которые вам не подходят. Позитивное мышление и возможность подойти к предмету с разных сторон, пробуя разные методики обучения, помогут вам вернуться к математике и усовершенствовать свои навыки.
Лучшие преподаватели по математике доступны для занятий
Поехали!
Метод проб и ошибок помогает развитию мозга
Людмила Петерсон, педагог, автор концепции и учебников по математике для дошкольников, начальной и основной школы, сравнивает математику и компьютерные игры: почему первым дети занимаются неохотно, тогда как от второго их невозможно оторвать?
Есть несколько факторов: детей не заставляют играть, их не ругают в случае неуспеха, им понятна цель, интересно содержание, все достижения фиксируются, а результаты игры значимы для сверстников.
«Этот набор факторов в достаточной степени обеспечивает механизм мотивации «надо» — «хочу» — «могу». Чтобы заинтересовать ребёнка математикой, можно действовать по аналогии», — подчеркивает эксперт. Таким образом, если мы действительно хотим, чтобы каждый ребёнок получил максимум от уроков математики, нам придётся изменить подход к обучению.
Существует миф, что, якобы, некоторые люди созданы для математики, а другие — нет. На самом деле, это не более, чем миф.
Не существует такого понятия как «математический мозг». Фактически, чтобы отточить математическое мастерство, нужно найти подходящий метод обучения. Индивидуальный для каждого человека. Если вы найдёте тот подход, который эффективно учит вас математике, то сможете добиться существенного прогресса, не зацикливаясь на таблицах сложения и вычитания.
-
Каждый способен добиться успеха — важен правильный подход Источник — Unsplash
Джо Боулер, профессор и исследователь из Стэнфорда, в своей книге «Математическое мышление. Книга для родителей и учителей» пишет, что фраза американского психолога Кэрол Дуэк в своё время поразила учителей. Она говорила: «Каждый раз, когда ученик делает ошибку в математической задаче, у него появляется новый синапс». Получается, что ошибки полезны, независимо от полученного результата?
Книга для родителей и учителей» пишет, что фраза американского психолога Кэрол Дуэк в своё время поразила учителей. Она говорила: «Каждый раз, когда ученик делает ошибку в математической задаче, у него появляется новый синапс». Получается, что ошибки полезны, независимо от полученного результата?
«Все мысленно ахнули, — пишет Боулер. — Ведь речь шла о силе и ценности ошибок — хотя большинство учеников считают, что ошибки означают отсутствие у них математических способностей или, того хуже, отсутствие интеллекта. Многие учителя годами говорили ученикам, как полезны ошибки: они свидетельствуют о том, что мы учимся. Но новые данные о мозге и ошибках указывают на нечто гораздо более важное».
На совершённую ошибку мозг реагирует повышенной активностью. А высокий уровень активности заставляет нейроны размножаться. Это значит, что даже если в первый раз математическая задача ввела вас в ступор, и вы потратили много времени, чтобы её решить, в следующий раз, благодаря работе нейронов, вы справитесь с аналогичным примером в разы быстрее. Так что даже те задачи, которые у вас не получилось решить правильно, полезны. Полученный опыт повлёк за собой рост количества нейронов. И может, это не сделает из вас математического гения, но в то же время может помочь в снятии психологических блоков и нивелировании математической тревожности.
Так что даже те задачи, которые у вас не получилось решить правильно, полезны. Полученный опыт повлёк за собой рост количества нейронов. И может, это не сделает из вас математического гения, но в то же время может помочь в снятии психологических блоков и нивелировании математической тревожности.
Нужно пробовать разные образовательные подходы. Метод проб и ошибок работает для любых тем в математике: геометрии, дифференциальных уравнений, умножения и деления, квадратных уравнений и даже для построения графиков в виде параболы или гиперболы.
Метод Боулер для изучения математики
Ещё одно исследование, посвящённое изучению математики, показало, что в зависимости от того, легко ли даётся математика детям или с трудом, их мозг реагирует по-разному. Этот феномен заметила профессор Джо Боулер. Она увидела, что у разных детей в активной фазе находятся разные области мозга, когда они пытаются решать одни и те же задачи.
С тех пор методы обучения Боулер включают в себя визуальное представление. То есть, ученики рассуждают не с помощью цифр, а пытаясь представить те или иные задачи. В то же время она регулярно общается с учениками, обсуждая их слабые и сильные стороны. Изучение этих методов показало, что любой ребёнок способен понимать математику, если обучение адаптировано к его потребностям.
То есть, ученики рассуждают не с помощью цифр, а пытаясь представить те или иные задачи. В то же время она регулярно общается с учениками, обсуждая их слабые и сильные стороны. Изучение этих методов показало, что любой ребёнок способен понимать математику, если обучение адаптировано к его потребностям.
Другими словами, Боулер адаптировала концепцию «Гибкого сознания» Кэрол Дуэк, которую многие называют прорывной, для обучения математике. Она показала на практике, как можно помочь учащимся чувствовать себя увереннее.
По оценкам Джо Боулер, только 2-3% населения испытывают реальные трудности в изучении математики, в то время как все остальные жители планеты способны спокойно освоить математику, в том числе, на высоком уровне.
По словам профессора Боулер, дети способны учиться математике больше, чем какому-либо другому предмету! Люди, которые всю жизнь учили математику классическим способом, бывают очень удивлены, когда встречаются с визуальным методом. Это идёт вразрез с их глубинным пониманием того, как всё работает в математике. Всё потому что их часть мозга, отвечающая за визуализацию, отличается от той, что занимается цифрами. Именно поэтому так полезно использовать в обучении математике различные приложения, наглядные пособия, красочные иллюстрации.
Всё потому что их часть мозга, отвечающая за визуализацию, отличается от той, что занимается цифрами. Именно поэтому так полезно использовать в обучении математике различные приложения, наглядные пособия, красочные иллюстрации.
-
Метод Боулер вдохнул в математику жизнь Источник — Unsplash
Причина, по которой этот метод оказался настолько успешным, заключается в том, что ученики использовали оба полушария мозга в работе над задачами. «Логики» получили креативную помощь от левого полушария, а «творческие» учащиеся через наглядность смогли справиться с математическими концепциями.
Изучение математики требует особого настроения
Всё больше и больше учителей замечают, что настрой и уверенность в себе существенно влияют на прогресс учеников в математике. Если заниматься математическими задачками в хорошем настроении, то и весь образовательный процесс пойдёт легче и проще, а, значит, и его результаты будут более заметны. По мере того, как понимание важности этого понятия растёт, учителя ищут способы применить этот подход в классе.
-
Сделать математику весёлой — вот секрет успешного урока Источник — Unsplash
Учителя часто не видят в ребёнке потенциала или сомневаются в том, что он способен добиться чего-то существенного в рамках школьной математики. Из-за этого дети и сами перестают верить в свои возможности, считают, что не созданы для математики.
Боулер говорит, что формировать позитивное мышление практически невозможно, когда используешь закрытые вопросы типа «да/нет», поскольку ответы либо полностью верны, либо полностью неверны, а значит — нет основы для конструктивного обучения.
Она предлагает альтернативу — визуальный подход, в рамках которого учитель начинает открытый диалог с учениками, предлагая разные варианты решения математической задачи. Таким образом, вместо того, чтобы сидеть за бесконечными заданиями по математике: упражнениями по сложению, вычитанию, рисованию треугольников, вычислению площади поверхности, нахождению времени, скорости и объёма, — ученики могут просто играть и тем самым прогрессировать в математике.
Позволить учащимся самим справляться с интерактивными математическими примерами даёт им возможность использовать свои творческие способности и улучшать навыки решения задач. Одновременно это помогает им понять, какой формат обучения им наиболее интересен. Кроме того, так они сами поймут, как математика может быть применима в реальной жизни.
Забавные игры для детей, вроде математического бинго, могут стать отличным ресурсом для родителей и репетиторов, которые хотят прокачать математические навыки ребёнка. Существует огромное количество сайтов с подобными играми.
Лучшие преподаватели по математике доступны для занятий
Поехали!
Учим математику без давления
Иногда давление может быть полезным. Оно мотивирует нас работать лучше и будет в нас соревновательный дух. Тем не менее, согласно исследованию Джо Боулер, постоянное давление и и особенно стресс из-за нехватки времени могут привести к психологическим блокам и травмам. И тогда мозг не сможет быть на 100% эффективным.
Что же касается школьной математики, то здесь о давлении знают не понаслышке. Особенно это касается детей, которые и так излишне тревожны, неуверенны в себе, испытывают трудности в стрессовых ситуациях. Когда на них давят ещё и с внешней стороны — родители или учителя, такие дети замыкаются, сосредотачиваются на стрессе и не могут прогрессировать в учёбе.
Довольно часто учителя по математике вызывают учеников к доске отвечать на различные вопросы перед классом. Такой формат лишний раз подчёркивает важность быстрых вычислений и ответов. Ирония же заключается в том, что даже доктор наук по математике не может считать быстрее, чем все остальные. Они просто знают несколько приёмов, которые позволяют вычислять оперативнее и проще. Для их использования необязательно быть математическим гением — эти техники может освоить каждый.
Международная программа по оценке образовательных достижений учащихся (PISA) для обучения математике
Международная программа по оценке образовательных достижений учащихся во многих странах мира считается показателем успеваемости по разным предметам, включая математику. Эта программа представляет большой интерес для сертифицированных репетиторов математики и других преподавателей, которые хотят увидеть, как выглядит их страна на международной арене.
Эта программа представляет большой интерес для сертифицированных репетиторов математики и других преподавателей, которые хотят увидеть, как выглядит их страна на международной арене.
Исследования, проводимые этой организацией, показывают, что дети, живущие в странах, где математика учится «зубрёжкой», занимают худшие места. В то же время те страны, где подходы к преподаванию математики — разнообразны, а саму науку рассматривают как взаимосвязь различных процессов, как правило, добиваются более высоких позиций в рейтинге.
Например, вот что пишет об этом Боулер: «В странах с самым высоким уровнем знаний по математике (например, в Китае) подход к ошибкам совсем иной. Недавно я наблюдала за уроком математики в Шанхае — китайском городе, где ученики демонстрируют самые высокие результаты в стране и в мире. Учитель давал ученикам серьезные концептуальные задачи, а затем устраивал опрос. Пока ученики с удовольствием рассказывали о проделанной работе, переводчик шепнул мне, что учитель выбирает детей, которые сделали ошибки. Те с гордостью рассказывали об ошибках, поскольку учитель придаёт им большое значение».
Те с гордостью рассказывали об ошибках, поскольку учитель придаёт им большое значение».
В то же время в PISA доказали, что повторяющиеся задачи неэффективны в процессе обучения.
Так что забудьте про зазубривание таблицы умножения. Лучше превратите её изучение в интерактивную математическую игру. Школьникам нужен креативный подход к решению математических задач, который позволяет добиться результата несколькими способами. Ответ будет один и тот же, но дорога к нему будет разной, и это и есть — самое интересное в математике.
-
Страны с самым высоким рейтингом в математике применяют нестандартный подход к обучению Источник — Unsplash
Обучение по принципам Джо Боулер совершило революцию в преподавании математики по всему миру. Боулер написала несколько книг для учителей, которые хотели бы применять её опыт на собственных уроках, а также она делится бесплатными уроками по математике онлайн.
Более 100 000 образовательных учреждений попробовали метод Боулер, о результатах которого можно судить по недавнему опросу: 96% учащихся этих заведений надеются продолжить изучение математики, несмотря на все трудности, что им пришлось преодолеть.
А каково репетиторам по математике?
Забавно, но репетиторы и учителя по математике и сами могут испытывать тревожность, когда дело доходит до определённых тем. Дело в том, что у репетиторов и учителей тоже могли быть не лучшие преподаватели или методы преподавания. Учителя начальной школы, похоже, больше всего пострадали от этого.
В процессе обучения важно общаться и стараться визуализировать как можно больше тем. Также старайтесь обсуждать различные решения математических задач — это очень важно для детей, изучающих математику. Поощряйте творческий подход и ищите лучшую стратегию обучения индивидуально для каждого учащегося. Это поможет им и вам в долгосрочной перспективе.
Эффективное обучение начинается с позитивного настроя
Учителя могут использовать различные образовательные практики, чтобы сделать обучение как можно более весёлым и захватывающим!
Очевидно, что необходимо изменить подход к общепринятому преподаванию математики, чтобы предоставить всем детям равные возможности для обучения. Доказано, что универсальное обучение математике гораздо менее эффективно, чем помощь учащимся в понимании того, как работает математика и какое отношение она имеет к их повседневной жизни. Именно здесь вступает в силу индивидуальный подход к обучению. В классе из 30 учеников учителям трудно реагировать на конкретные потребности каждого человека, поэтому ученикам, которые беспокоятся о том, что они отстают от своих сверстников, или нуждаются в помощи с домашним заданием, можно рассмотреть возможность частных уроков.
Доказано, что универсальное обучение математике гораздо менее эффективно, чем помощь учащимся в понимании того, как работает математика и какое отношение она имеет к их повседневной жизни. Именно здесь вступает в силу индивидуальный подход к обучению. В классе из 30 учеников учителям трудно реагировать на конкретные потребности каждого человека, поэтому ученикам, которые беспокоятся о том, что они отстают от своих сверстников, или нуждаются в помощи с домашним заданием, можно рассмотреть возможность частных уроков.
Индивидуальные частные уроки по математике часто являются лучшей возможностью для обучения, ведь репетитор фокусируется на конкретном ученике. Частные занятия по математике позволят детям (да и взрослым) усовершенствовать свои навыки и обрести уверенность в себе.
Репетитор по математике поможет с любой задачей: подготовка к ЕГЭ, к вступительным экзаменам либо просто помощь в понимании текущих сложных тем.
Так что изучайте математику онлайн или оффлайн, один-на-один с частным репетитором или с преподавателем, и пусть мир математики покорится!
Кстати, репетитора можно легко найти в своём городе, для этого вам нужно вбить: «репетитор по математике», «онлайн репетитор по математике», «репетитор математика», «репетитор по математике екатеринбург» (или любой другой город) и т. д.
д.
авторские статьи. «Научный метод и ошибки» (А. И. Серебряный)
А. И. Серебряный
Журнал «Природа», N3, 1997
Большинство людей убеждено в существовании «научного метода». В то же время многие считают, что «научный метод» — это миф. Одна из причин такого мнения — понимание метода как совокупности правил, которые гарантированно, или без ошибок, должны давать результаты. Но метод, вообще говоря, — это только метод попыток или проб, или «проб и ошибок».
Требование безошибочности часто заменяется требованием, чтобы ошибок было мало или чтобы вероятность ошибки была мала.
Научный метод — это метод, с помощью которого человек может открывать закономерности в данных фактах или формулировать гипотезы, или предлагать теории. Для краткости мы вместо того, чтобы говорить: «Человек, пользуясь данным методом, сделал ошибку», — будем употреблять выражение: «Метод сделал ошибку» и т.п.
Эта статья — возражение тем авторам, которые утверждают, подобно В.А. Фоку, что научного метода не существует, на том основании, что не может быть метода, который позволил бы выдвигать гипотезы без ошибок или с небольшим их числом. Я попытаюсь показать, что, вопреки распространенному мнению этих авторов, метод может ошибаться в 99% случаев и, несмотря на это, быть разумным. Это означает, что по крайней мере одно из возражений против существования научного метода теряет силу.
Я попытаюсь показать, что, вопреки распространенному мнению этих авторов, метод может ошибаться в 99% случаев и, несмотря на это, быть разумным. Это означает, что по крайней мере одно из возражений против существования научного метода теряет силу.
Несколько слов о словах
Понятия «метод», «гипотеза», «вероятность ошибки» имеют много смыслов. В каком смысле мы их здесь употребляем? Под методом будем понимать точный метод. Таким образом, метод интегрирования по частям, аналитическое продолжение, метод восстановления многочленов по значениям в нескольких точках — это методы, а метод мозгового штурма — не метод. Потребуем от научного метода, чтобы он был универсален в том смысле, чтобы он мог открывать любые закономерности в любых фактах. Для этого нам нужен универсальный язык, в котором выразимы любые закономерности. Высказывалось много возражений против существования универсального метода. В другом месте я попытался показать, что многие возражения основаны на требованиях к методу, от которых можно отказаться.
Возможно разное понимание того, что значит «метод выдал гипотезу Г». Одно из возможных пониманий: «Метод выдал утверждение: «Г истинно». Другие понимания выдаваемого утверждения: «Г — разумная гипотеза» или «Г — естественная гипотеза». Но разумность, или естественность, гипотезы — очень неопределенные понятия.
Возможны некоторые уточнения такого понимания:
- Г — гипотеза, которую интересно попытаться проверить; мы, как было сказано выше, занимаемся методами, открывающими закономерности; такие методы поэтому естественно называть методами открытия; можно сказать, что они выдают гипотезы (о закономерности), которые интересно попытаться проверить;
- Г — проверенная, или подтвержденная гипотеза;
- Г — принятая научным сообществом гипотеза;
- Г — принятая обществом гипотеза.
Из-за смешения разных пониманий происходят недоразумения. Например, довольно часто высказывается замечание, что ученый не живет в башне из слоновой кости и надо учитывать влияние общества на выбор теории.
К недоразумениям приводит и двусмысленность понятия «вероятность». Существуют два подхода к понятию вероятности — «логический» и «частотный».
При определении метода иногда вводится вполне разумное требование подтверждения, цель которого — сделать «вероятность ошибки» не очень большой. Но эту вероятность нельзя измерить на практике — она находится внутри математики. Это — «логическая» вероятность. В статье же идет речь о вероятности ошибки при открытии законов природы. Это — вероятность, как она понимается при «частотном» подходе. Нетрудно дать метод, открывающий закономерности вида f(x,y) = ax+by+c по значениям в нескольких точках. Невероятно, чтобы много случайно выбранных в пространстве точек легло на плоскость, поэтому мы можем сделать вывод: вероятность ошибки мала.
Предварительно задачу нахождения точного научного метода можно поставить следующим образом: у нас есть идеи о том, что такое разумная гипотеза, и у нас есть идеи об универсальном языке, на котором можно выразить всю математику и, следовательно, основные законы физики (в качестве универсального языка наиболее часто рассматривается теория множеств). Определить научный метод — это соединить эти идеи в одной теории (недедуктивной логике). Постановка задачи, конечно, неоригинальна. С тех пор, как появился первый вариант универсального языка (теория типов Рассела — Уайтхеда), идея о том, что хорошо бы это сделать, многим приходила в голову. То, что это до сих пор не сделано, говорит о том, что в предыдущих попытках что-то было неладно. Из-за недостатка места мы не будем сейчас обсуждать, в чем тут дело, и пытаться убедить читателя, что научный метод существует, а отошлем к некоторым работам, где рассматриваются эти вопросы.
Считаем ли мы биологию наукой?
Иногда делается такое возражение против того, чтобы точный метод рассматривать как модель «неформального научного метода»: использование только точных методов означает, что мы считаем науками только точные науки (такие, как физика), а другие науки, скажем, биологию, науками не считаем. Это просто недоразумение.
Очевидно, теория вероятностей не объявляет, что нематематические науки — не науки. То же самое можно сказать про недедуктивную логику. Недоразумение это вызвано тем, что математика и науки, где используется математика, играют огромную роль в теории идеального метода. Главный источник примеров гипотез — гипотезы, которые делаются в математике. Математика дает естествоиспытателю те понятия, в которых он формулирует законы природы (например, она дала эллипсы Кеплеру). Эйнштейн писал, что творческая роль принадлежит именно математике. Поэтому важнейшей задачей, которую должен решать идеальный метод, является задача построения математики. Изучение физики также очень важно. Без учета тех гносеологических уроков, которые дали теория относительности и квантовая механика, нельзя понять, что такое теория. Но если мы ограничимся при попытках понять, что такое теория, только физикой, то мы сильно рискуем составить себе слишком узкое представление о теории, возможно, приводящее к тому, что мы даже о новых физических теориях будем говорить: «Это не физика!»
Поэтому важнейшей задачей, которую должен решать идеальный метод, является задача построения математики. Изучение физики также очень важно. Без учета тех гносеологических уроков, которые дали теория относительности и квантовая механика, нельзя понять, что такое теория. Но если мы ограничимся при попытках понять, что такое теория, только физикой, то мы сильно рискуем составить себе слишком узкое представление о теории, возможно, приводящее к тому, что мы даже о новых физических теориях будем говорить: «Это не физика!»
В универсальном языке, который нужен в недедуктивной логике, должны быть формализованы такие понятия, как «обобщение», «аналогия», «естественная классификация», «естественная экстраполяция» и т.п. Вероятно, одно из самых важных понятий в биологии — «органическое целое», в психологии — «гештальт». Очевидно, что эти понятия — той же природы, что и естественная экстраполяция, — органическое целое можно восстановить (экстраполировать) по его части. В обычной математике пример органического целого — аналитическая функция.
Без понимания того, что такое гипотеза, нельзя строить ни модели обучения распознаванию зрительных образов, ни модели распознавания зрительных образов, ни модели обучения языку, ни модели понимания языка и т.п. Классификации нужны во всех науках. Таким образом, недедуктивная логика должна быть широко применима вне физики и математики, и некоторые модели без недедуктивной логики просто не могут быть построены.
Должен ли метод полностью заменить талант, интуицию и т.п.? Требование гарантированности результата означает, что метод должен быть алгоритмом, который полностью заменяет талант. «Метод уравнивает способности» (Ф. Бэкон). Так же понимали метод Декарт и Лейбниц. С этим связана и идея «авторитарности» метода: если мы нашли «единственно правильный научный метод», то все обязаны его применять, все будут получать этим методом одну и ту же теорию, а если кто-то выдал не ту гипотезу, которую выдал метод, то эта гипотеза ошибочна и т.д. Но об идеальном методе ничего подобного сказать нельзя. Во-первых, метод — не алгоритм (например, метод интегрирования по частям не детерминирован). Во-вторых, идеальный метод не является полной моделью «неформального научного метода».
Во-первых, метод — не алгоритм (например, метод интегрирования по частям не детерминирован). Во-вторых, идеальный метод не является полной моделью «неформального научного метода».
Многие философы считали, что не существует правил открытия. Мы считаем, что правила открытия существуют и идеальный метод описывает все, что можно сделать с помощью правил. Но при открытии не все делается по правилам — тогда говорят об интуиции, озарении, таланте и т.п. Поэтому метод не уравнивает способности. То, что делается неформально, иногда может быть очень легко сделано — тогда можно сказать, что метод уравнивает способности, но даже в таких случаях открытие не вполне формально — метод формален, но его применение, как и применение любой математической теории, неформально. Например, при применении школьной алгебры перевод задачи, заданной на естественном языке, на язык алгебры (составление уравнений) неформален, хотя часто и легок.
Поэтому идеальный метод не является полной теорией того, как делаются открытия. Но у нас нет никакой теории. Нам нужна не исчерпывающая теория, а хоть какая-то теория.
Но у нас нет никакой теории. Нам нужна не исчерпывающая теория, а хоть какая-то теория.
Человек, отказывающийся в каких-то случаях от использования метода, может быть прав. Решение уравнения, определяющего гипотезу, может быть настолько сложно, что для нахождения гипотезы проще «все время об этом размышлять», как это делал Ньютон и другие физики, чем использовать «единственно правильный научный метод». Нельзя исключить того, что с помощью интуиции можно выдвинуть гипотезу, а с помощью метода — нельзя. Возможно, что человек предложит одну гипотезу, а метод — другую. A priori нельзя сказать, какую из них следует предпочесть. Если теория получена не с помощью идеального метода, это вовсе не значит, что теория ненаучна.
Универсальный метод не может делать ошибок?
В 1959 г. в разговоре с одним известным математиком я сказал, что пытаюсь в общем виде определить метод, с помощью которого можно было бы по фактам выдвигать разумные гипотезы, например по нескольким начальным символам бесконечной последовательности из 0 и 1 предсказывать следующий знак. И услышал следующий ответ: «Такой метод невозможен. Какой бы знак вы ни предсказали, я поставлю «nicht», и вы ошибетесь».
И услышал следующий ответ: «Такой метод невозможен. Какой бы знак вы ни предсказали, я поставлю «nicht», и вы ошибетесь».
Доказательство показалось мне очень странным. Оно доказывало только то, что метод будет иногда делать ошибки. Но ведь я сказал, что речь идет о методе, выдвигающем гипотезы. Гипотеза, по определению, — это предложение, которое может оказаться ошибочным. Поэтому метод, по определению, может делать ошибки. Почему мой собеседник не видит столь очевидных вещей?
Тогда я столкнулся с этим доказательством в первый раз. Лет через пять услышал то же возражение от другого математика. Я слышал его потом и от других.
Даже неуниверсальный метод может делать ошибки
Доказательство это кажется странным также и потому, что оно «доказывает» не только невозможность общего определения разумной гипотезы или универсального метода, но и невозможность определения разумной гипотезы для узких классов гипотез, там, где нетрудно дать такое определение. Можно предложить следующий метод восстановления многочленов y=P(x) по значениям в точках x=1, 2,. .., k+1.
.., k+1.
Многочлен должен удовлетворять требованиям: 1) соответствие фактам: он должен принимать данные значения в этих точках; 2) простота: он должен быть наименьшей степени; 3) подтверждение: он должен быть степени, меньшей k. Через (k+1) точку всегда можно провести многочлен не более, чем k-й степени. Если многочлен получился k-й степени, нет никаких оснований предполагать, что в значениях P(x) есть какая-то закономерность, и мы объявляем, что «факты случайны» и отказываемся выдвигать какую-нибудь гипотезу. Если же степень многочлена меньше k, то мы выдаем его в качестве гипотезы. Чтобы этот метод правильно угадал многочлен n-й степени, необходимо по крайней мере n+2 точки. Например, если 20 точек (x,y) легло на прямую (график некоторого многочлена первой степени), то мы выдаем гипотезу, что получен многочлен первой степени (линейная функция), а если нас просят объяснить, почему мы сделали эту гипотезу, отвечаем: невероятно, чтобы это произошло случайно.
Метод этот «обычно» позволяет строить разумные гипотезы. Доказать мы этого не можем, но знаем это без всякого доказательства. Исключения, когда с помощью метода получаем не ту гипотезу, которую сделал бы разумный человек, — это многочлены, вроде степеней x, обладающие особыми свойствами, делающими их «более простыми», чем «обычные». Если человек знает, что при x=2 значение многочлена равно 32, то он может высказать гипотезу, что это x5. То есть человек открывает многочлен пятой степени по одной точке, а методу нужно по крайней мере 7. Можно предположить, что разумный метод должен открывать любой многочлен. Очевидно, описанный метод удовлетворяет этому условию в том смысле, что восстанавливает любой многочлен по достаточно большому числу точек, хотя иногда делает ошибки.
Доказать мы этого не можем, но знаем это без всякого доказательства. Исключения, когда с помощью метода получаем не ту гипотезу, которую сделал бы разумный человек, — это многочлены, вроде степеней x, обладающие особыми свойствами, делающими их «более простыми», чем «обычные». Если человек знает, что при x=2 значение многочлена равно 32, то он может высказать гипотезу, что это x5. То есть человек открывает многочлен пятой степени по одной точке, а методу нужно по крайней мере 7. Можно предположить, что разумный метод должен открывать любой многочлен. Очевидно, описанный метод удовлетворяет этому условию в том смысле, что восстанавливает любой многочлен по достаточно большому числу точек, хотя иногда делает ошибки.
Так вот, упомянутое доказательство без всяких изменений можно повторить и в этом случае. Из него следует, что даже метод восстановления многочленов (только что описанный) невозможен.
Почему так много людей считает убедительным это доказательство?
Потому что они сознательно или бессознательно считают справедливым следующее равенство: разумная гипотеза = истинная гипотеза. Метод должен гарантировать успех — получение истинной гипотезы. Авторы многих работ по теории научного метода на этом основании утверждали, что никакого метода открытия нет и быть не может.
Метод должен гарантировать успех — получение истинной гипотезы. Авторы многих работ по теории научного метода на этом основании утверждали, что никакого метода открытия нет и быть не может.
П.Мидоуэр (P.Medawar) рассуждает так: «Профессия ученых решать проблемы; поэтому те, кто заявляет, что они верят в метод, но не могут решить данную задачу, или не знают правильного метода, или просто чересчур глупы, чтобы применять его».
К.Поппер обстоятельно доказывал, что метод, выдающий истинные гипотезы, невозможен и что законы физики — это гипотезы, которые могут оказаться ошибочными. Он считал это оригинальным взглядом на научный метод. Этот взгляд Поппер называл «фаллибилизмом». То, что Поппер счел нужным доказывать упомянутое утверждение, означает, что был широко распространен взгляд, согласно которому можно найти «индуктивный» метод, делающий истинные гипотезы.
Откуда взялся такой взгляд?
В течение многих веков такие предложения математики, как теорема Пифагора, считались абсолютно достоверными вечными истинами. Через какое-то время после появления «экспериментального, или научного, метода» некоторые законы природы также стали представляться незыблемыми вечными истинами. «Когда-то научные законы считались вполне обоснованными и непререкаемыми».
Через какое-то время после появления «экспериментального, или научного, метода» некоторые законы природы также стали представляться незыблемыми вечными истинами. «Когда-то научные законы считались вполне обоснованными и непререкаемыми».
Но если существуют законы природы, являющиеся вечными истинами, то естественно попытаться найти метод, открывающий эти вечные истины. Сторонники мнения, что такой метод существует, получили название «индуктивистов».
Имре Лакатос: »Когда индуктивист принимает некоторое научное суждение, он принимает его как достоверно истинное». В настоящее время, по-видимому, все согласны, что законы природы — это гипотезы. Но убеждение, что разумная гипотеза — это истинная гипотеза, у многих осталось.
Очевидно, что гарантировать истинность гипотезы мы не можем. Истинность — это соответствие всем фактам, а нам дана только часть. Проверить истинность на неизвестных фактах мы не можем никак. Поэтому метод, выдающий истинные гипотезы, разумеется, невозможен.
Лакатос: »Неоиндуктивизм» требует достижения лишь высоковероятных сообщений». При так называемом «обучении распознаванию образов» на ЭВМ проверяют правильность распознавания некоторых примеров и по проценту правильных узнаваний судят о работе программы. Если программа делает много ошибок, она считается плохой. Типичной тут является задача медицинской диагностики. Здесь требование малого числа ошибок вполне разумно. В других классах задач разумно даже требование полного отсутствия ошибок. Но нельзя распространять подобные требования на любые классы задач. Самые интересные задачи, которые решает научный метод, — это задачи открытия важных законов природы, а именно в этом классе требование малого числа ошибок неразумно.
Универсальный метод должен решать «любые» задачи. Но в классе всех задач процент ошибок невозможно подсчитать, так как невозможно найти представительную выборку из такого класса.
Математики часто экстраполируют функции от натурального аргумента на все действительные числа. Вопрос об ошибках не имеет смысла, так как никто не ответит на вопрос об «истинном» значении функции при каком-то нецелом значении аргумента.
Мы знаем, что аналитическая экстраполяция разумна, хотя «факты», нужные для нее, не могут появиться в эксперименте и проверить правильность экстраполяции мы не можем.
Вернемся к методу восстановления многочленов. Мы не писали никакой программы, не пытались найти приложения этого метода и поэтому ничего не знаем о том, часто он будет ошибаться или редко. Тем не менее мы знаем, что он разумен. Это показывает, что судить о разумности метода мы можем, ничего не зная о числе ошибок при его применении.
Разумный метод часто приводит к ошибкам
Если интуиция противится тому, чтобы называть разумными методы, которые иногда делают ошибки, то тем более она противится тому, чтобы называть разумными такие методы, которые почти все время ошибаются. «Кому нужен метод, который ошибается в 99% случаев?» — слышу я возражение.
«Кому нужен метод, который ошибается в 99% случаев?» — слышу я возражение.
Но рассмотрим «неформальный научный метод». Он работает так. Чтобы делать открытия, большое число людей много лет учится в университетах. Затем они занимаются научной работой, цель которой — открытия. Если оценить вероятность успеха «неформального научного метода» как процент ученых, сделавших крупные открытия, то хорошо, если мы получим 1%. Остальные 99% — плата за этот 1% («ошибки»). Занятие настоящей наукой, попытка решить действительно интересную задачу — всегда риск. Вероятность неудачи очень велика. «В ходе научного исследования, — говорил Эйнштейн, — шанс достигнуть чего-то по-настоящему ценного слишком мал даже для очень одаренного человека».
В литературе «о том, как делаются открытия», отмечалось, что выдвигалось огромное число гипотез, оказавшихся неудачными (что вовсе не доказывает их неразумность), но они просто забываются и не описываются в истории науки.
М.А.Марков: «За последние десятилетия все чаще и чаще встречается своеобразное чисто математическое творчество в физике. Физик-теоретик часто, исходя из каких-то более или менее убедительных соображений, «предлагает» свои уравнения для описания целой совокупности физических явлений. Часто эти предложения не выдерживают серьезных испытаний экспериментом > Проводник по «храму науки будущего» не назовет авторов их, они погибли для потомства вместе с крушением идей и надежд, породивших эти работы. Если иметь в виду легион этих неизвестных имен, то редкие удачи перестанут быть удивительными».
Физик-теоретик часто, исходя из каких-то более или менее убедительных соображений, «предлагает» свои уравнения для описания целой совокупности физических явлений. Часто эти предложения не выдерживают серьезных испытаний экспериментом > Проводник по «храму науки будущего» не назовет авторов их, они погибли для потомства вместе с крушением идей и надежд, породивших эти работы. Если иметь в виду легион этих неизвестных имен, то редкие удачи перестанут быть удивительными».
То, что опровержение теории — не доказательство ее неразумности, неинтересности или бесполезности, подчеркивал К.Поппер: «Вполне можно сказать, что если теория опровергается после шести месяцев своего существования, а не после шести лет или шести столетий, то это обусловлено лишь исторической случайностью. Опровержения часто рассматривались как неудача ученого или по крайней мере созданной им теории. Следует подчеркнуть, что это индуктивистское заблуждение. > Даже если новая теория нашла раннюю смерть >, она не должна быть забыта».
П.Л.Капица: «Отношение числа научных изысканий, давших решение поставленной задачи, к числу всех попыток, включая сделанные зря, и может рассматриваться как коэффициент эффективности научного изыскания. > при решении трудных больших проблем этот коэффициент будет неизбежно всегда мал».
В случае «неформального научного метода», несмотря на огромное число ошибок и неудач, большинство людей не спросит: «А кому это нужно?» Одно великое открытие производит настолько сильное впечатление, что о неудачах никто не вспоминает.
Многие, отмечая, что не существует метода, гарантирующего малую вероятность ошибки, считали это равносильным отсутствию какого-либо метода. Соглашаясь с тем, что метода, дающего малую вероятность ошибки, не существует, не обязательно соглашаться с тем, что это означает отсутствие какого бы то ни было метода.
Если мы хотим точно определить научный метод, то должны отказаться от требования малой вероятности ошибки (тем более, что непонятно, как оценить эту вероятность). Лучше иметь метод, хотя бы иногда выдающий верные гипотезы, чем не иметь никакого.
Лучше иметь метод, хотя бы иногда выдающий верные гипотезы, чем не иметь никакого.
Презентация к классному часу Метод проб и ошибок доклад, проект
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация на тему Презентация к классному часу Метод проб и ошибок, предмет презентации: Педагогика . Этот материал в формате pptx (PowerPoint) содержит 22 слайдов, для просмотра воспользуйтесь проигрывателем. Презентацию на заданную тему можно скачать внизу страницы, поделившись ссылкой в социальных сетях! Презентации взяты из открытого доступа или загружены их авторами, администрация сайта не отвечает за достоверность информации в них, все права принадлежат авторам презентаций и могут быть удалены по их требованию.
Этот материал в формате pptx (PowerPoint) содержит 22 слайдов, для просмотра воспользуйтесь проигрывателем. Презентацию на заданную тему можно скачать внизу страницы, поделившись ссылкой в социальных сетях! Презентации взяты из открытого доступа или загружены их авторами, администрация сайта не отвечает за достоверность информации в них, все права принадлежат авторам презентаций и могут быть удалены по их требованию.
Методы решения творческих задач
РПС , занятие 26
Мудрость – это совокупность истин, добытых умом, наблюдением и опытом, и приложимых к жизни, это гармония идей с жизнью»
И.А. Гончаров.
Метод проб и ошибок
Это метод случайного подбора частных методов и приемов действий в расчете лишь на возможный успех. В обычной жизни его еще называют методом «тыка».
Архимедов винт, винт Архимеда — механизм исторически использовавшийся для передачи воды из низколежащих водоёмов в оросительные каналы.
Архимед
287-212 г.до н.э.
Архимед соорудил машины, которые могли выбрасывать снаряды на любое желаемое расстояние
Архимедов рычаг
«Дайте мне точку опоры, и я переверну мир»
В современном мире принцип действия рычага используется повсеместно. Практически любой механизм, преобразующий механическое движение, в том или ином виде использует рычаги. Подъемные краны, двигатели, инструменты (ножницы, плоскогубцы), а также тысячи других механизмов и инструментов используют рычаги в своей конструкции.
Герон Александрийский
Диоптра
Паровая машина
Насос Герона
Леонардо да Винчи
Парашют
Пулемёт
Подшипник
Водолазный костюм, бронированный танк, механический воин-рыцарь, вертолет, мост.
Великий Ньютон сказал : «Если я видел дальше, то потому, что стоял на плечах гигантов прошлого»
1642 – 1727 г.г.
Метод проб и ошибок попробовал впервые усовершенствовать Томас Эдисон, американский изобретатель. В его мастерской работало до 1000 человек.
Одну и ту же задачу решало несколько человек, а Эдисон организовывал поиск наиболее удачного решения.
Томас Эдисон провел опыты с 1500 нитей накаливания электрической лампочки, пока не нашёл подходящую.
«Гений — это один процент вдохновения и девяносто девять процентов пота.» — Томас Эдисон
Вопросы
1.Об изобретениях каких учёных вы знали раньше?
2. Какую роль, с вашей точки зрения, сыграл на этапе зарождения науки и техники метод проб и ошибок?
3.Считаете ли вы метод проб и ошибок эффективным в настоящее время?
Методом проб и ошибок выполнить задания
1. «Магический квадрат»
«Магический квадрат»
Заполнить клетки цифрами так, чтобы по горизонтали и вертикали сумма была одинаковой
2. Построить фигурку танграмм
2. Построить фигурку танграм
3. Задачи со спичками
а) Из четырех спичек легко сложить один квадрат. Добавим еще две — сломанные пополам. Сколько квадратов можно из них сложить?
б) из 9-ти спичек построить 6 квадратов.
Достоинства метода:
— Этому методу не надо учиться.
— Методическая простота решения.
— Удовлетворительно решаются простые задачи (не более 10 проб и ошибок)
— Учит упорству и терпению, учит не отчаиваться при неудачах.
— Вообще говоря, с каждым новым решением человек «становится умнее». Не случайно говорят, что на ошибках учатся.
Недостатки метода:
— Плохо решаются сложные задачи (более 1000 проб и ошибок).
— Нет приёмов решения.
— Нет алгоритма мышления, мы не управляем процессом думанья. Идет почти хаотичный перебор вариантов.
— Неизвестно, когда будет решение и будет ли вообще.
— Отсутствуют критерии оценки силы решения, поэтому неясно, когда прекращать думать. А вдруг в следующее мгновение придет гениальное решение?
— Иногда ошибаться нельзя (не будет человек резать на бомбе провода наугад).
Из 24 спичек выложите квадрат и
разделите его на девять маленьких
ячеек так, как показано на рисунке.
Задания:
1. Уберите 4 спички так, чтобы осталось
4 маленьких и 1 большой квадраты.
2. От исходного квадрата убрать поочередно 4, 6, 8 спичек так, чтобы всегда оставалось по 5 равных квадратов. 3. Снова исходный квадрат. Забрать двумя способами по 8 спичек так, чтобы в обоих случаях осталось по 4 одинаковых квадрата.
4. Убрать из нашего 24-спичечного квадрата 6 спичек так, чтобы осталось 2 квадрата и 2 неправильных, но одинаковых шестиугольника.
3. Снова исходный квадрат. Забрать двумя способами по 8 спичек так, чтобы в обоих случаях осталось по 4 одинаковых квадрата.
4. Убрать из нашего 24-спичечного квадрата 6 спичек так, чтобы осталось 2 квадрата и 2 неправильных, но одинаковых шестиугольника.
Дополнительное задание:
Спасибо всем за работу!
Скачать презентацию
Это сайт презентаций, где можно хранить и обмениваться своими презентациями, докладами, проектами, шаблонами в формате PowerPoint с другими пользователями. Мы помогаем школьникам, студентам, учителям, преподавателям хранить и обмениваться учебными материалами.
Для правообладателей
Обратная связь
Email: Нажмите что бы посмотреть
|
⇐ ПредыдущаяСтр 6 из 10Следующая ⇒
Учебники Г. Обучение школьников ведется на высоком уровне трудности. Но материал учебников предусматривает возможность работы по ним детей разного уровня подготовки. Учебники ориентированы на развитие логического мышления, творческих способностей ребенка и интереса к математике. Учебник для 5 класса состоит из двух частей, для 6 класса – из трех. Каждая часть включает в себя две главы. Эти учебники позволяют учащимся самостоятельно добывать знания, а главное учат учиться. С первых уроков ученикам предлагаются задания для формирования умений сравнивать, обобщать, классифицировать, рассуждать. Большая часть заданий требует от учащихся творческого подхода. Новый материал вводится не через передачу готового знания, а через самостоятельное «открытие» его учениками. Часто задания для закрепления даны в игровой форме (кодирование и расшифровка, отгадывание загадок и т.п.) Учащиеся с огромным удовольствием выполняют эти задания. В учебнике в системе даны задания на развитие логики, мышления, развитие всех видов памяти, творческих способностей. «В совершенно различных, на первый взгляд, задачах можно обнаружить, что их решение практически одинаково. Например, если на столе лежат 2 яблока, 2 апельсина и груша, то как найти общее число фруктов? Конечно, 2 + 2 + 1 = 5. Но ведь точно также мы можем определить и число уроков во вторник, зная, что по расписанию будет два урока русского языка, две математики и физкультура. В этих двух непохожих ситуациях мы использовали одну и ту же математическую модель, складывая не яблоки с апельсинами и не физкультуру с математикой, а натуральные числа. Для того чтобы построить математическую модель, надо, прежде всего, научиться переводить условие задачи с привычного родного языка на специальный, математический язык, чем мы и займемся в этом пункте,» – так авторы учебника проводят мотивацию изучения математического моделирования еще в самом начале курса математики пятого класса (п. 1, §2, глава 1, [11]). Рассмотренный пример, настолько прост и нагляден, что понятен даже пятиклассникам, и становится ясно, что с помощью модели решать задачу будет проще, но еще не понятно, что именно представляет собой математическая модель. Далее говорится, что после перевода задачи на математический язык поиск решения сводится к работе с математическими моделями – к вычислениям, преобразованиям, рассуждениям. В этом же пункте авторы составляют модели пяти разнообразных задач, которые располагаются среди предложенных для решения, в том числе задач, основной сутью которых является отработка навыка перевода задачи на математический язык. · Составь выражения для ответа на вопросы задач (№ 72). · Придумай задачи, в которых математической моделью являются следующие выражения (№ 73). · Среди данных задач найди такие задачи, математические модели которых совпадают (№ 74). · Построй математическую модель (№ 82, № 111). · Составь схему к задаче (№ 76). · Переведи условие задачи с русского языка на математический (№ 83, № 87, № 98, №102, № 116). · Составь таблицу по условию задачи (№ 124). · Запиши математическую модель задачи, используя для обозначения неизвестных величин буквы x и y (№ 137). Весь этот пункт направлен на овладение школьниками первым этапом решения задач с помощью математического моделирования. Заметим, что задачи с такими формулировками встречаются не только в этом пункте, но и по всему тексту учебника, например: 5 класс, часть 1, [11]: №№ 244, 338, 410, 436, 502, 507, 531, 680, 704, 767, 788, 789, 796, 797, 828 и другие; 5 класс, часть 2, [12]: №№ 39, 49, 107, 125, 167, 271, 272, 283, 333, 352, 411, 478, 530, 546, 712, 740, 769, 833, 870, 882, 904, 941, 1012, 1101, 1162 и другие; 6 класс, часть 1, [13]: №№ 115, 116, 117, 130, 133, 137, 175, 215 и другие; 6 класс, часть 2, [14]: №№ 20, 25, 220, 221, 314, 423, 424, 495 — 498, 505 — 507 и другие; 6 класс, часть 3, [15]: №№ 6, 10, 21, 24, 131, 626, 627, 633, 683, 700, 706, 729 и другие, что дает возможность сформировать у учащихся не только умения, но и навыки построения математических моделей сюжетных задач. Но кроме умения строить математические модели необходимо уметь их разрешать и переводить результат на понятный человеку язык. Эти два этапа процесса моделирования авторы объединяют в один, который называют «Работа с математической моделью» (п. 2, §2, глава 1, [11]). Из рассмотренных в этом пункте примеров видно, что после перевода текста задачи на математический язык поиск решения сводится к работе с математическими моделями – к вычислениям, преобразованиям, рассуждениям. Для получения результата в некоторых задачах достаточно использовать алгоритмы действий с числами (например, № 82, [11]), в других – решение уравнений (например, № 144, [11]). Отсюда следует, что чем больше математических понятий и свойств знают учащиеся, тем больше они имеют возможность для отыскания короткого и простого решения. При решении математических задач часто бывает так, что исследование полученной математической модели не сводится к известным случаям, то есть у учащихся нет достаточных знаний для исследования той или иной модели. 1) метод проб и ошибок; 2) метод перебора. Рассмотрим на примерах, в чем состоит суть этих методов. Метод проб и ошибок позволяет найти ответ даже в том случае, когда математическая модель представляет собой новый, еще не изученный объект. Однако при использовании этого метода следует всегда помнить о том, что подбор одного решения не гарантирует полноты решения. Поэтому требуется дополнительное обоснование того, что найдены все возможные решения, и ни одного не пропущено. Задача. Ширина прямоугольника на 9 см меньше длины, а площадь равна 90 см2. Найти стороны прямоугольника (см. № 168 (2), [11]). Решение. Математическая модель представляет собой следующее уравнение: . Нужно найти и . Никакие известные пятиклассникам правила преобразования не помогают найти ответ. Авторы предлагают подобрать решение «экспериментально», так называемым методом проб и ошибок. Нам надо найти такое число х, чтобы значение выражения х (x – 9) было равно 90. Попробуем подставить в это выражение, например х = 13: 13 (13 — 9)=52 Мы видим, что полученное значение выражения слишком мало. Возьмем теперь х = 14: 14 (14 — 9)=70 И снова выбранное значение мало, хотя и ближе к искомому. Далее возьмем х = 15. Получим: 15 (15 — 9)=90
Эта попытка оказалась удачной, при х = 15 имеем 15 (15 — 9)=90. Казалось бы, что задача уже решена, но это не так: ведь может оказаться, что есть другие x, при которых это выражение тоже равно 90. Допустим, что х >15, тогда х – 9 > 6, следовательно произведение будет больше 90. Пусть х <15, тогда х – 9 < 6, получим, что 15 (15 — 9)<90. Нам требуется найти стороны прямоугольника. Получаем, х =15 и . Ответ: 15 см и 6 см.
Данный метод служит мощным средством при решении еще неизвестных уравнений, неравенств и систем уравнений. Однако он очень трудоемкий и нужно добиваться от учащихся поиска более рационального метода решения, если это является возможным в данной ситуации. При решении задач методом проб и ошибок учитель должен объяснить школьнику, что простой подбор одного неизвестного числа не дает уверенности в том, что найдены все искомые значения. Поэтому для обоснования полноты решения требуются дополнительные иногда очень непростые рассуждения, а, значит, метод проб и ошибок имеет недостаток, который, в свою очередь не имеет другой метод – метод перебора. Метод полного перебора. При поиске неизвестного числа полным перебором автор поясняет, что следует рассматривать «все мысленные возможности: если мы упустим хотя бы одну, то может оказаться, что именно она и дает решение задачи» [11]. Полный перебор требует, как правило, больших усилий и большого времени. Задача. Задумано двузначное число, которое на 66 больше произведения своих цифр. Какое число задумано? (Cм. № 181 (1), [11]). Решение. После составления модели получаем следующую задачу: Для цифр х и y двузначного числа выполняется равенство 10x + y = xy + 66. Найти это число. Полный перебор можно провести, рассматривая последовательно все значения х от 1 до 9 и подбирая в каждом случае соответствующее значение y от 0 до 9. Однако этот перебор можно сократить, если заметить, что правая часть равенства больше 66. Значит, и левая его часть, то есть задуманное число больше 66. Поэтому неизвестное число х не меньше 6, и можно рассматривать только четыре значения х – от 6 до 9. При х = 6 наше равенство имеет вид 60 + y = 6y + 66, а этого быть не может, так как левая часть получилась меньше правой при любых значениях y от 0 до 9. При х = 7 имеем 70 + y = 7y + 66. Если мы от каждой части этого равенства отнимем одно и то же число y, то получим 70 = 6y + 66, откуда 6y = 4, что для натурального числа не возможно. При х = 8 имеем равенство 80 + y = 8y + 66. Снова, вычитая из каждой части y, получим, 80 = 7y +66, 7y = 14, y = 2. Таким образом, для чисел х = 8 и y = 2 равенство выполняется, и число 82 удовлетворяет условию задачи: 82 = 8 · 2 + 66. Следует обратить внимание учащихся, что нельзя считать задачу полностью решенной, поскольку перебор еще не закончен, и среди не рассмотренных случаев могут найтись решения. Выполняя аналогичные преобразования, имеем при х = 9: 90 + y = 9y + 66, 90 = 8y +66, 8y = 24, y = 3. Показывая учащимся, что получилось еще одно решение, число 93, которое удовлетворяет 93 = 9 · 3 + 66, мы подчеркиваем важность полного перебора.
Авторы также советуют проводить перебор с помощью таблицы:
После того, как произведен полный перебор, важно научить школьников формулировать ответ в соответствии вопросу исходной задачи. В данном случае ответ будет таков: задумано либо число 82, либо 93. К методу проб и ошибок и к методу перебора авторы еще раз возвращаются уже в 6 классе (§ 3, глава 3, [15]). В 6 классе продолжается обучение методу математического моделирования. При изучении темы «Решение уравнений» рассматриваются различные по сюжету задачи, которые решаются с помощью уравнений. Но прежде чем приступить к решению задач, авторы учебника пытаются дать ответ на вопрос: «Для чего решают задачи?» и приходят к выводу, что, решая задачи, мы учимся строить математические модели реальных ситуаций. Далее выделяются три этапа математического моделирования: 1) построение модели; 2) работа с моделью; 3) практический вывод. Распространенным видом математических моделей являются уравнения. В соответствии с этапами моделирования решение задач с помощью уравнений состоит также из трех этапов: 1) составление уравнения; 2) решение уравнения; 3) ответ на вопрос задачи. Учащиеся обучаются выбирать переменные, составлять уравнения, решать их и анализировать результат. Система задач, приведенная в учебниках [11 – 15] позволяет достаточно полно раскрыть методы исследования математических моделей, большое внимание уделяется решению задач с помощью уравнений, так как уравнения – это основной вид моделей, изучаемых в 5 – 6 классах. На основе этих упражнений учащиеся должны научиться понимать ценность решения сюжетных задач, видеть их практическую значимость, а также понимать значение математической модели, уметь строить ее, искать наиболее рациональный способ ее исследования и правильно делать вывод о проделанной работе, в том числе правильно формулировать ответ на задачу. ⇐ Предыдущая12345678910Следующая ⇒ |
Задача о назначениях онлайн
Назначение сервиса. С помощью данного онлайн калькулятора можно:- найти путь с минимальной стоимостью назначения и с максимальной стоимостью назначения, решить задачу о назначении венгерским методом (методом Куна), решить задачу о назначении методом потенциалов;
- найти оптимальное использование рабочих агентов;
- Шаг №1
- Шаг №2
- Видеоинструкция
- Оформление Word
Решение задачи о назначениях выполняется в онлайн режиме и оформляется в отчете формата Word (см. пример решения задачи о назначениях).
пример решения задачи о назначениях).
Инструкция. Выберите размерность матрицы (количество вакансий и количество кандидатов). После ввода данных, создается шаблон решения в Excel (см. задача о назначениях в Excel).
Количество столбцов (вакансии)
2345678910
Количество строк (кандидаты)
2345678910
Типичное задание:
В цехе предприятия имеются 5 универсальных станков, которые могут выполнять 4 вида работ. Каждую работу единовременно может выполнять только один станок, и каждый станок можно загружать только одной работой.
В таблице даны затраты времени при выполнении станком определённой работы. Определить наиболее рациональное распределение работ между станками, минимизирующее суммарные затраты времени.
Задача. Служба занятости имеет в наличии четыре вакантных места по разным специальностям, на которые претендуют шесть человек. Проведено тестирование претендентов, результаты которого в виде баллов представлены в матрице
Распределить претендентов на вакантные места таким образом, чтобы на каждое место был назначен человек с наибольшим набранным по тестированию баллом.
Пример решения задачи о назначении с минимальной стоимостью;
Пример решения задачи о назначении с максимальной стоимостью;
Постановка задачи о назначениях
Сделаем содержательную постановку задачи. В объединении находится n автомобилей, способных каждый перевозить в месяц Qi тонн груза (i = 1,2,…,n). С их помощью необходимо обеспечить перевозку грузов (пиломатериал, шурупы и т.д.) от поставщиков к потребителям по n маршрутам в количестве Rj тонн в месяц (j = 1,2,…,n).Распределить автомобили по маршрутам так, чтобы минимизировать суммарную величину неиспользуемой провозной способности. Конкретизируем задачу (рис. 1). Пусть имеется 4 автомобиля и 4 маршрута. Характеристики провозных способностей автомобилей соответственно равны Q1 = 30 т., Q2 = 35 т., Q3 = 5 т., Q4 = 5 т. Характеристики потребностей потребителей соответственно равны R1 = 25 т.
 , R2 = 32 т., R3 = 5 т., R4 = 4 т. Задача заключается в том, чтобы перевезти все грузы с минимальными издержками, для этого надо каждый автомобиль пустить по одному и только его маршруту. Понятно, если возможность автомобиля в перевозке груза ниже потребности потребителя этого груза, то на данный маршрут автомобиль не может быть назначен. Поэтому составим матрицу С, характеризующую издержки i-го автомобиля, в случае, если он будет назначен на j-й маршрут. Элементы маршрута будут равны:
, R2 = 32 т., R3 = 5 т., R4 = 4 т. Задача заключается в том, чтобы перевезти все грузы с минимальными издержками, для этого надо каждый автомобиль пустить по одному и только его маршруту. Понятно, если возможность автомобиля в перевозке груза ниже потребности потребителя этого груза, то на данный маршрут автомобиль не может быть назначен. Поэтому составим матрицу С, характеризующую издержки i-го автомобиля, в случае, если он будет назначен на j-й маршрут. Элементы маршрута будут равны:
Рис. 1 — Схема маршрутов
В таблице 1 приводятся оценки возможных транспортных издержек.
Таблица 1 — Оценки транспортных издержек
Rj Qi |
25 |
32 |
5 |
4 |
30 |
5 |
М |
25 |
26 |
35 |
10 |
3 |
30 |
31 |
5 |
М |
М |
0 |
1 |
5 |
М |
М |
0 |
1 |

Переменные. В качестве переменной введем величину
Ограничения. Каждый автомобиль i должен быть назначен только один раз на любой из маршрутов.
или .
На каждый маршрут j должен быть назначен один из автомобилей
или .
Целевая функция. В качестве целевой функции, подлежащей минимизации, выступают суммарные издержки на перевозку.
Модель задачи о назначениях примет вид:
при ограничениях: ,
,
.
Все предполагаемые алгоритмы поиска решения задачи о назначениях базируются на следующем утверждении: оптимальное решение задачи не изменится, если к любой строке или столбцу матрицы издержек прибавить (или вычесть) постоянную величину в силу того, что приоритет назначения не изменится.
И весь алгоритм ведется на матрице издержек с соответствующими преобразованиями для получения в ней нулевых элементов, образующих систему так называемых «независимых нулей». Число независимых нулей равно размерности матрицы, а их расположение таково, что каждый из них встречается один раз в строке и один раз в столбце. Если такие независимые нули будут найдены, то в матрице решения в соответствии с их положением будут проставлены единицы. В матрице 1 нулевые элементы получены вычитанием наименьшего элемента в каждой строке.
Число независимых нулей равно размерности матрицы, а их расположение таково, что каждый из них встречается один раз в строке и один раз в столбце. Если такие независимые нули будут найдены, то в матрице решения в соответствии с их положением будут проставлены единицы. В матрице 1 нулевые элементы получены вычитанием наименьшего элемента в каждой строке.
Как только будут получены нулевые элементы, применяют различные алгоритмы: Мака, венгерский, минимальных линий. Рассмотрим процедуру вычеркивания нулевых элементов минимальным числом прямых линий. В матрице 2 показано, как используется это правило. Могут быть и другие варианты вычеркивания.
Если все нулевые элементы в матрице будут вычеркнуты, а минимальное число линий будет равно размерности матрицы, то независимые нули в матрице существуют, и решение найдено. В противном случае выбирается наименьший элемент из невычеркнутых элементов (он равен 1). Этот элемент вычитается из каждого невычеркнутого элемента и прибавляется к каждому элементу, стоящему на пересечении проведенных прямых.
Этот элемент вычитается из каждого невычеркнутого элемента и прибавляется к каждому элементу, стоящему на пересечении проведенных прямых.
В результате получается матрица (3), которая указывает на два оптимальных решения (матрицы решений 4 и 5).
Значение целевой Z = 5 + 3 + 0 + 1 = 9 . Оптимальное решение можно было получить и сразу, не применяя процедуру вычеркивания нулей, если в матрице 2 из столбца 4 вычесть минимальный элемент. Сделано было иначе только для демонстрации процедуры вычеркивания.
Следует заметить, что, если на последнем шаге оптимальное решение не достигнуто, то процедуру проведения прямых следует повторять до тех пор, пока не будет получено допустимое решение.
Модель назначений
Модель назначений часто встречается в задачах управления, где требуется, например, распределить мастеров-ремонтников по вызовам, продавщиц по отделам, аудиторов по фирмам и т. д. В качестве примера рассмотрим возможную постановку задачи назначения.
Пример. Руководство фирмы приняло решение произвести инспекцию своих предприятий в Лейпциге, Нанси, Льеже и Тилбурге, направляя туда своих вице-президентов, каждый из которых в компании возглавляет одно из направлений (финансы, маркетинг, производство и персонал). Хотя может существовать большое число факторов, которые нужно учесть при таком назначении (знание языка, узкая специализация, невозможность оторваться от прямых обязанностей и т. д.), руководство компании решило оптимизировать в качестве первого шага только суммарные затраты на командировку вице-президентов. Таблица командировочных расходов в различные города (тыс. долларов) приведена ниже.
| Вице-президенты | Лейпциг | Нанси | Льеж | Тилбург |
По финансам | 24 | 10 | 21 | 11 |
По маркетингу | 14 | 22 | 10 | 15 |
По производству | 15 | 17 | 20 | 19 |
По персоналу | 11 | 19 | 14 |
Требуется составить схему распределения вице-президентов по филиалам, минимизирующую командировочные расходы.

Решение. Табличная модель этой задачи после проведенной оптимизации приведена на рис. Рис. Табличная модель задачи о назначениях
Модель назначений является разновидностью транспортной модели. От последней она отличается только тем, что в ней единица предложения не может распределяться по нескольким местам назначения (ср. рис.).
Таким образом, модель назначений всегда можно построить в виде транспортной модели, в которой предложение в каждой исходной точке и спрос в каждом конечном пункте равны единице.
Точно так же, как и транспортная модель, модель назначений может быть несбалансированной, содержать недопустимые назначения, иметь альтернативные решения при одном и том же значении целевой функции. Эти варианты моделей назначения строятся в полной аналогии с соответствующими транспортными моделями.
Оптимальное распределение продавцов по торговым точкам
Задание. Существует 4 продавца А1, А2, А3, А4 и 4 торговые точки В1, В2, В3, В4. Эффективность работы продавцов на торговых точках задаётся следующей матрицей:
Эффективность работы продавцов на торговых точках задаётся следующей матрицей:
| 9 | 3 | 4 | 8 |
| 4 | 6 | 7 | 11 |
| 5 | 8 | 8 | 4 |
| 6 | 12 | 15 | 9 |
Найти оптимальное распределение продавцов по торговым точкам.
Поскольку задана матрица эффективности, то искать необходимо максимальные значения, следовательно, целевая функция стремится к максимуму. Именно поэтому при решении выбираем вид Максимальная прибыль.
Модифицируем матрицу умножением всех элементов на (-1) и затем сложением их с максимальным элементом матрицы (15) так, чтобы матрица не содержала бы отрицательных элементов:
| 6 | 12 | 11 | 7 |
| 11 | 9 | 8 | 4 |
| 10 | 7 | 7 | 11 |
| 9 | 3 | 0 | 6 |

1. Проводим редукцию матрицы по строкам. В связи с этим во вновь полученной матрице в каждой строке будет как минимум один ноль.
| 0 | 6 | 5 | 1 | 6 |
| 7 | 5 | 4 | 0 | 4 |
| 3 | 0 | 0 | 4 | 7 |
| 9 | 3 | 0 | 6 | 0 |
| 0 | 6 | 5 | 1 |
| 7 | 5 | 4 | 0 |
| 3 | 0 | 0 | 4 |
| 9 | 3 | 0 | 6 |
| 0 | 0 | 0 | 0 |
2. Методом проб и ошибок проводим поиск допустимого решения, для которого все назначения имеют нулевую стоимость.

Фиксируем нулевое значение в клетке (1, 1). Другие нули в строке 1 и столбце 1 вычеркиваем.
Фиксируем нулевое значение в клетке (2, 4). Другие нули в строке 2 и столбце 4 вычеркиваем.
Фиксируем нулевое значение в клетке (3, 2). Другие нули в строке 3 и столбце 2 вычеркиваем.
Фиксируем нулевое значение в клетке (4, 3). Другие нули в строке 4 и столбце 3 вычеркиваем.
В итоге получаем следующую матрицу:
| [0] | 6 | 5 | 1 |
| 7 | 5 | 4 | [0] |
| 3 | [0] | [-0-] | 4 |
| 9 | 3 | [0] | 6 |
| 0 | 6 | 5 | 1 |
| 7 | 5 | 4 | 0 |
| 3 | 0 | 0 | 4 |
| 9 | 3 | 0 | 6 |
 Методом проб и ошибок определяем матрицу назначения Х, которая позволяет по аналогично расположенным элементам исходной матрицы (в квадратах) вычислить максимальное значение прибыли.
Методом проб и ошибок определяем матрицу назначения Х, которая позволяет по аналогично расположенным элементам исходной матрицы (в квадратах) вычислить максимальное значение прибыли.
| [0] | 6 | 5 | 1 |
| 7 | 5 | 4 | [0] |
| 3 | [0] | [-0-] | 4 |
| 9 | 3 | [0] | 6 |
Cmax = 9 + 11 + 8 + 15 = 43
Таким образом, распределение продавцов по торговым точкам будет следующее:
1 продавец – торговая точка №1
2 продавец – торговая точка №4
3 продавец – торговая точка №2
4 продавец – торговая точка №3.
При таком назначении, максимальная эффективность составит 43.
Решение инженерных задач | Метод проб и ошибок или математический подход Брюс Бартлетт рассматривает два подхода к решению инженерных задач: математический и метод проб и ошибок.

Наша задача как инженеров — создавать решения, решающие проблемы. Например, спроектируйте звуковую систему, чтобы свести к минимуму обратную связь, или определите звуковой эффект объекта, помещенного рядом с микрофоном.
Два метода решения проблем — это метод проб и ошибок и предсказание с использованием математики. Методом проб и ошибок вы интуитивно придумываете решение, пробуете его и смотрите, что получится. Это проба и проба. Это повторяющиеся разнообразные попытки, которые вы продолжаете, пока не достигнете успеха. В качестве альтернативы вы предсказываете результат, используя математические уравнения или используя известные свойства объекта. Затем проверьте свой прогноз с помощью реальных измерений.
Метод проб и ошибок не обязательно приводит к наилучшему результату, но часто этого достаточно.
Фото 1. Решение инженерных задач – метод проб и ошибок
Физические свойства и геометрия объектов создают математические законы физики. Иногда, используя методы проб и ошибок, мы можем позволить законам физики выполнять тяжелую работу сложной математики, чтобы получить желаемый результат. Другими словами, реальность дает тот же результат, что и правильные математические уравнения.
Другими словами, реальность дает тот же результат, что и правильные математические уравнения.
Методом проб и ошибок вы проводите эксперимент — меняете одну переменную в системе — и измеряете результаты. Вместо того, чтобы использовать математику для расчета и предсказания результатов этого эксперимента, вы позволяете законам природы «вычислять» или формировать результат, как это сделал бы аналоговый компьютер. Природа прекрасно «считает», когда выдает результат эксперимента.
Иногда природа слишком сложна математически, чтобы мы могли предсказать результат, используя наши ограниченные знания о том, что происходит физически. Например, как небольшой предмет или открытая щель рядом с капсюлем микрофона влияет на его частотную характеристику? Если бы вы попытались предсказать это с помощью математики, вам нужно было бы знать о гидродинамике, геометрии, точной форме выступа или щели, резонансе, влиянии препятствий различной формы на звуковые волны (дифракция) и т. д.
Но если вы просто создадите объект или щель и измерите результат (дельту или изменение частотной характеристики), природа «вычислит» за вас математику, легко и точно. Иногда метод проб и ошибок дает полезные результаты намного быстрее, чем расчеты.
Иногда метод проб и ошибок дает полезные результаты намного быстрее, чем расчеты.
Если хотите, можете придумать уравнения и попытаться сопоставить их с данными, которые природа уже «подсчитала» за вас.
Эмпирический подход
Вот пример. Предположим, у вас есть P.A. системы, и вы хотите создать максимально громкий звук без обратной связи. Вы размещаете микрофон и динамик в определенных местах относительно источника звука. Вы увеличиваете громкость до тех пор, пока не начнется обратная связь. Затем измените одну переменную. Например, увеличить расстояние громкоговорителя от микрофона. Если обратная связь прекратится, вы можете немного увеличить громкость, пока обратная связь не начнется снова. Из того, что вы только что узнали, вы можете написать уравнение: громкость до обратной связи пропорциональна расстоянию от динамика до микрофона.
SPL ∝ D1*X
, где
SPL — громкость,
X — неизвестная константа или переменная, а
D1 — расстояние от динамика до микрофона.
Затем вы измените другую переменную и посмотрите, что произойдет. Вы приближаете микрофон к источнику звука. Громкость звуковой системы увеличивается, не вызывая обратной связи. Таким образом, вы составляете другое уравнение:
SPL ∝ X/Ds
, где
L — громкость,
X — неизвестная константа или переменная, а
Ds — расстояние от микрофона до источника.
Объединив эти два уравнения, вы получите SPL ∝ D1*X/Ds. Вы начинаете составлять уравнение, которое предсказывает усиление до обратной связи.
Теперь вы изменяете другую переменную. Вы приближаете громкоговоритель к слушателю. Звуковая система становится громче для слушателя, не вызывая обратной связи. В качестве математического выражения вы могли бы сказать
SPL ∝ X/D2
, где
SPL — это громкость,
X — неизвестная константа или переменная, а
D2 — расстояние от громкоговорителя до слушателя.
Объединив эти три уравнения, вы получите
SPL ∝ D1*X/(Ds*D2)
Наше уравнение для прогнозирования коэффициента усиления до обратной связи становится все более полным. Он говорит вам следующее: если вы хотите увеличить громкость, увеличьте расстояние от динамика до микрофона, уменьшите расстояние от микрофона до источника и уменьшите расстояние от динамика до слушателя. Другими словами, поместите динамик далеко от микрофона, поместите микрофон ближе к источнику, а динамик поместите ближе к аудитории.
Он говорит вам следующее: если вы хотите увеличить громкость, увеличьте расстояние от динамика до микрофона, уменьшите расстояние от микрофона до источника и уменьшите расстояние от динамика до слушателя. Другими словами, поместите динамик далеко от микрофона, поместите микрофон ближе к источнику, а динамик поместите ближе к аудитории.
Фото 2: Решение инженерных задач – использование математики
X в этом уравнении могут быть другие переменные, такие как частотная характеристика и чувствительность микрофона в направлении динамика, отклик и чувствительность динамика в направлении микрофон, диаграмма направленности микрофона, диаграмма направленности динамика, живость комнаты, громкость источника звука и т. д.
X также может быть уравнением. Мы могли бы начать с закона обратных квадратов, связывающего SPL с расстоянием, и вывести из него наше уравнение обратной связи.
Реальность не следует уравнениям. Он просто реагирует на обстоятельства единственным доступным ему способом. Люди пишут уравнения, описывающие, как реальность взаимодействует с обстоятельствами, и мы называем эти уравнения «законами физики». Закон гласит, что X всегда происходит, когда существуют условия Y.
Люди пишут уравнения, описывающие, как реальность взаимодействует с обстоятельствами, и мы называем эти уравнения «законами физики». Закон гласит, что X всегда происходит, когда существуют условия Y.
Прямое инженерное решение
Иногда расчеты более эффективны, чем метод проб и ошибок. Предположим, вы хотите отправить ракету вокруг Луны и обратно на Землю. Вы можете запустить несколько ракет разного размера и тяги и выбрать ту, которая подойдет. Но это очень дорого и медленно. Вместо этого вы можете сначала решить математику, спроектировать ракету и установить продолжительность и вектор тяги в соответствии с этой математикой, а затем запустить ракету и надеяться на лучшее. Если ваша математика точно смоделировала реальность, вы можете запустить ракету, разработанную на основе этой математики, и она на самом деле облетит Луну и обратно.
В большей части нашей инженерной работы мы комбинируем два метода, чтобы делать обоснованные предположения. Или мы разрабатываем систему, используя математику, испытываем ее в реальном мире и корректируем разницу между теорией и опытом. Что бы ни работало. :>) bb
Или мы разрабатываем систему, используя математику, испытываем ее в реальном мире и корректируем разницу между теорией и опытом. Что бы ни работало. :>) bb
Фото 3: Научные каракули на бумаге 3D перьевой ручкой.
Факторизация трехчленов методом проб и ошибок – метод и примеры
Вы все еще боретесь с темой факторизации трехчленов в алгебре? Ну, не беспокойтесь, потому что вы находитесь в правильном месте.
Эта статья познакомит вас с одним из простейших методов разложения трехчленов на множители , известным как метод проб и ошибок .
Как следует из названия, факторинг методом проб и ошибок подразумевает перебор всех возможных факторов, пока не будет найден правильный.
Разложение методом проб и ошибок считается одним из лучших методов факторизации трехчленов. Это побуждает студентов развивать свою математическую интуицию и, таким образом, улучшать их концептуальное понимание темы.
Как развернуть трехчлены?
Предположим, мы хотим развернуть общее уравнение трехчлена оси 2 + bx + c, где a ≠ 1. Вот шаги, которые необходимо выполнить: два набора скобок, которые представляют факторы.
Вот шаги, которые необходимо выполнить: два набора скобок, которые представляют факторы.
ПРИМЕЧАНИЕ:
- Если c положительно, оба коэффициента будут иметь тот же знак, что и «b».
- Если c отрицательно, один множитель будет иметь отрицательный знак.
- Никогда не ставьте в одни и те же скобки числа с общим множителем.
Разложение методом проб и ошибок
Разложение методом проб и ошибок, также называемое обратной фольгой или разверткой, представляет собой метод факторизации трехчленов, основанный на различных методах, таких как фольга, факторизация путем группировки и некоторые другие концепции разложение трехчленов со старшим коэффициентом 1,
Пример 1
Использование и факторинг ошибок для решения 6x 2 — 25x + 24
Раствор
Париные факторы 6x 2 — x (6x) или 2x (3x), 3x), 3x), 3x), 3x), 3x), 3x), 3x), 3x), 3x), 3x), 3x), 3x), 3x), 3x), 3x), 3x), 3x), 3x), 3x), 3x), 3x), 3x), 3x), 3x), 3x), 3x), 3x), 3x), 3x), 3x), 3x), 3 -й пари. поэтому наши скобки будут;
поэтому наши скобки будут;
(x – ?) (6x – ?) или (2x – ?) (3x – ?)
Замените «bx» возможными парными коэффициентами c. Попробуйте все пары множителей 24, которые дадут -25. Возможные варианты: (1 и 24, 2 и 12, 3 и 8, 4 и 6). Таким образом, правильный факторинг;
6x 2 — 25x + 24 ⟹ (2x — 3) (3x — 8)
Пример 2
Фактор x 2 — 5x + 6
раствор
. Фактовы. первый член x 2 , это x и x. Поэтому вставьте x в первую позицию каждой скобки.
x 2 – 5x + 6 = (x – ?) (x – ?)
Поскольку последний член равен 6, поэтому возможные варианты множителей:
(x + 1) (x + 6)
(х – 1) (х – 6)
(x + 3) (x + 2)
(x – 3) (x – 2)
Правильная пара, которая дает -5x в качестве среднего члена, это (x – 3) (x – 2). Следовательно,
(x – 3) (x – 2) является ответом.
Пример 3
Фактор x 2 – 7x + 10
Решение
Вставьте первый член в скобки первого члена множителей.
⟹ (x -?) (x -?)
Попробуйте возможную пару множителей из 10;
⟹ (-5) + (-2) = -7
Теперь замените знаки вопроса в скобках на эти два множителя
⟹ (x -5) (x -2)
Следовательно, правильное разложение x 2 – 7x + 10 is (x -5) (x -2)
Example 4
Factor 4x 2 – 5x – 6
Solution
( 2x -?) (2x +?) и (4x -?) (x +?)
Попробуйте возможную пару множителей;
6 х 2 − 2x – 151 и 6, 2 и 3, 3 и 2, 6 и 1
Так как правильная пара 3 и 2, то (4x – 3) (x + 2) является нашим ответом. Пример 5
(x -?) (x +?)
Найдите два числа, произведение и сумма которых равны -15 и -2 соответственно. Методом проб и ошибок возможные комбинации:
15 и -1;
-1 и 15;
5 и -3;
-5 и 3;
Наша правильная комбинация – 5 и 3. Следовательно;
x 2 − 2x – 15 ⟹ (x -5) (x +3)
Как разложить трехчлены по группам?
Мы также можем разложить трехчлены на множители, используя метод группировки. Давайте выполним следующие шаги, чтобы разложить на множители ax 2 + bx + c, где a ≠1:
Давайте выполним следующие шаги, чтобы разложить на множители ax 2 + bx + c, где a ≠1:
- Найдите произведение старшего коэффициента «a» и константы «c».
⟹ a * c = ac
- Найдите множители «ac», которые складываются с коэффициентом «b».
- Перепишите bx как сумму или разность множителей ac, которые добавляются к b.
- Теперь разложите по группам.
Пример 6
Разложите трехчлен 5x 2 + 16x + 3 по группировке.
Решение
Найдите произведение старшего коэффициента на последний член.
⟹ 5 * 3 = 15
Методом проб и ошибок найти парные множители 15, сумма которых является средним членом (16). Правильная пара — 1 и 15.
Перепишите уравнение, заменив средний член 16x на x и 15x.
5x 2 + 16x+ 3⟹5x 2 + 15x+ x+ 3
Теперь, фактор, группируя
5x 2 + 15x+ x+ 3 ⟹ 5x (x+ 3)+ 1 (x + 3)
⟹ (5x +1) (x + 3)
Пример 7
Коэффициент 2x 2 — 5x — 12 по группировке.
Решение
2x 2 — 5x — 12
= 2x 2 + 3x — 8x — 12
= x (2x + 3) — 4 (2x + 3)
= (2x + x (2x + 3) 3) (x – 4)
Пример 8
Множитель 6x 2 + x – 2
Решение
Умножьте старший коэффициент c.
⟹ 6 * -2 = -12
Найдите два числа, произведение и сумма которых равны -12 и 1 соответственно.
⟹ – 3 * 4
⟹ -3 + 4 = 1
Перепишите уравнение, заменив средний член -5x на -3x и 4x
⟹ 6x 2 -3x + 4x -2
5 Наконец, Фактор путем группировки
⟹ 3x (2x — 1) + 2 (2x — 1)
⟹ (3x + 2) (2x — 1)
Пример 9
Фактор 6y 2 + 11 + 4.
Раствор
6 лет 2 + 11 лет + 4 ⟹ 6 лет 2 + 3 года + y + 4
⟹ (6 лет 2 + 3 года) + (8 лет + 4)
⟹ 3 года (2 года + 1) + 4(2 года + 1)
= (2 года + 1) (3 года + 4)
Пробная версия и05 математика ошибок: диалектические системы и пополнения теорий | Журнал логики и вычислений
Фильтр поиска панели навигации Journal of Logic and ComputationЭтот выпускComputer Architecture and Logic DesignКнигиJournalsOxford Academic Термин поиска мобильного микросайта
Закрыть
Фильтр поиска панели навигации Journal of Logic and ComputationЭтот выпускComputer Architecture and Logic DesignКнигиJournalsOxford Academic Термин поиска на микросайте
Расширенный поиск
Журнальная статья
Получить доступ
Якопо Амидей,
Якопо Амидей
Ищите другие работы этого автора на:
Оксфордский академический
Google ученый
Ури Эндрюс,
Ури Эндрюс
Ищите другие работы этого автора на:
Оксфордский академический
Google ученый
Дуччо Пьяниджани,
Дуччо Пианиджиани
Ищите другие работы этого автора на:
Оксфордский академический
Google ученый
Лука Сан Мауро,
Лука Сан Мауро
Ищите другие работы этого автора на:
Оксфордский академический
Google ученый
Андреа Сорби
Андреа Сорби
Ищите другие работы этого автора на:
Оксфордский академический
Google ученый
Journal of Logic and Computation , том 29, выпуск 1, январь 2019 г. , страницы 157–184, https://doi.org/10.1093/logcom/exy033
, страницы 157–184, https://doi.org/10.1093/logcom/exy033
Опубликовано:
26 ноября 2018 г.
5 История статьиПолучено:
15 октября 2018 г.
Опубликовано:
26 ноября 2018 г.
Фильтр поиска панели навигации Journal of Logic and ComputationЭтот выпускComputer Architecture and Logic DesignКнигиJournalsOxford Academic Термин поиска мобильного микросайта
Закрыть
Фильтр поиска панели навигации Journal of Logic and ComputationЭтот выпускComputer Architecture and Logic DesignКнигиJournalsOxford Academic Термин поиска на микросайте
Advanced Search
Abstract
Эта статья является частью проекта, основанного на понятии диалектической системы, введенной Магари как способ охватить математику методом проб и ошибок.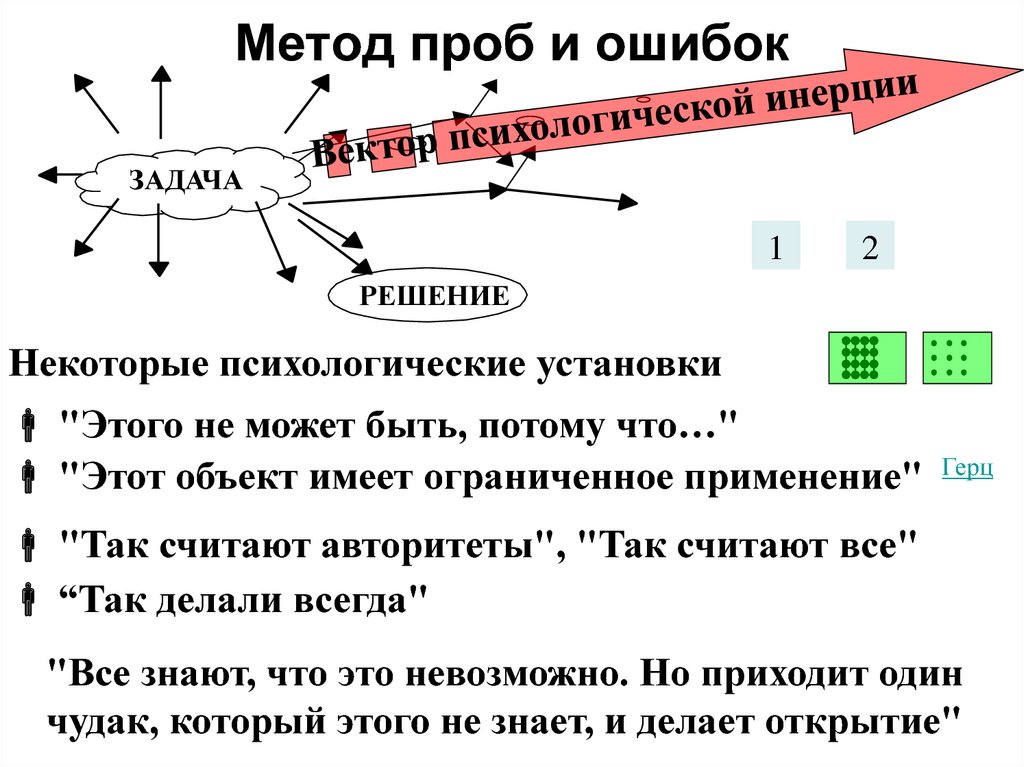 В Амидей и др. (2016, Rev. Symb. Logic , 9 , 1–26) и Amidei et al. (2016, Rev. Symb. Logic , 9 , 299–324), мы исследовали выразительную и вычислительную мощь диалектических систем и сравнили их с новым классом систем, квазидиалектических систем, которые обогащают системы Магари естественным механизмом пересмотра. В настоящей статье мы рассматриваем третий класс систем, класс |$p$|-диалектических систем, которые естественным образом сочетают в себе черты, вытекающие из двух других случаев. Мы доказываем несколько результатов о |$p$|-диалектических системах и множествах, которые они представляют. Затем мы сосредоточимся на дополнениях теорий первого порядка. При этом мы рассматриваем системы со связками, т.е. системы, кодирующие правила классической логики. Мы показываем, что любая непротиворечивая система со связками представляет собой завершение данной теории. Доказано, что диалектическая и |$q$|-диалектическая системы совпадают относительно пополнений, которые они могут представлять.
В Амидей и др. (2016, Rev. Symb. Logic , 9 , 1–26) и Amidei et al. (2016, Rev. Symb. Logic , 9 , 299–324), мы исследовали выразительную и вычислительную мощь диалектических систем и сравнили их с новым классом систем, квазидиалектических систем, которые обогащают системы Магари естественным механизмом пересмотра. В настоящей статье мы рассматриваем третий класс систем, класс |$p$|-диалектических систем, которые естественным образом сочетают в себе черты, вытекающие из двух других случаев. Мы доказываем несколько результатов о |$p$|-диалектических системах и множествах, которые они представляют. Затем мы сосредоточимся на дополнениях теорий первого порядка. При этом мы рассматриваем системы со связками, т.е. системы, кодирующие правила классической логики. Мы показываем, что любая непротиворечивая система со связками представляет собой завершение данной теории. Доказано, что диалектическая и |$q$|-диалектическая системы совпадают относительно пополнений, которые они могут представлять. Тем не менее, |$p$|-диалектические системы более эффективны; мы показываем |$p$|-диалектическую систему, представляющую завершение арифметики Пеано, которая не является ни диалектической, ни |$q$|-диалектической.
Тем не менее, |$p$|-диалектические системы более эффективны; мы показываем |$p$|-диалектическую систему, представляющую завершение арифметики Пеано, которая не является ни диалектической, ни |$q$|-диалектической.
© Автор(ы), 2018. Опубликовано Oxford University Press. Все права защищены. Для разрешений, пожалуйста, по электронной почте: [email protected].
© Автор(ы), 2018. Опубликовано Oxford University Press. Все права защищены. Для разрешений, пожалуйста, по электронной почте: [email protected].
Раздел выдачи:
Артикул
В настоящее время у вас нет доступа к этой статье.
Скачать все слайды
Войти
Получить помощь с доступом
Получить помощь с доступом
Доступ для учреждений
Доступ к контенту в Oxford Academic часто предоставляется посредством институциональных подписок и покупок.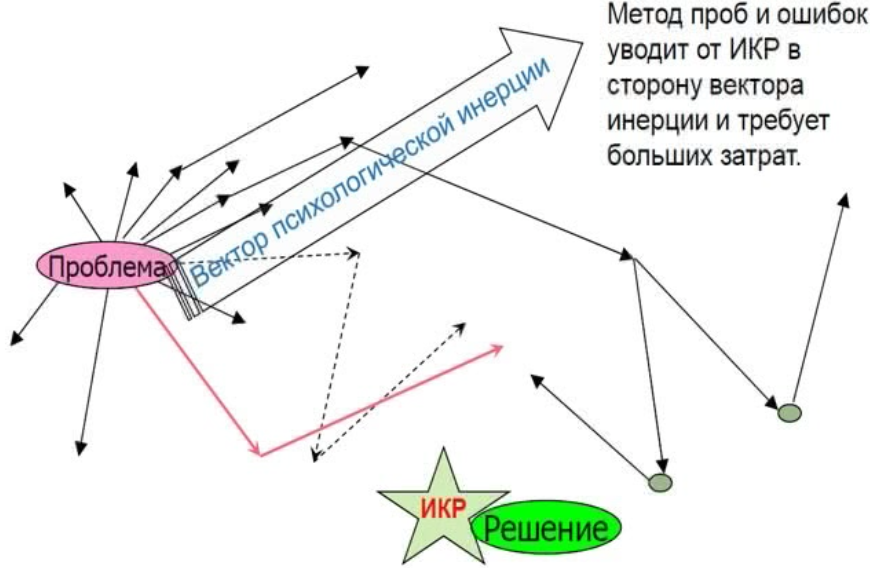 Если вы являетесь членом учреждения с активной учетной записью, вы можете получить доступ к контенту одним из следующих способов:
Если вы являетесь членом учреждения с активной учетной записью, вы можете получить доступ к контенту одним из следующих способов:
Доступ на основе IP
Как правило, доступ предоставляется через институциональную сеть к диапазону IP-адресов. Эта аутентификация происходит автоматически, и невозможно выйти из учетной записи с IP-аутентификацией.
Войдите через свое учреждение
Выберите этот вариант, чтобы получить удаленный доступ за пределами вашего учреждения. Технология Shibboleth/Open Athens используется для обеспечения единого входа между веб-сайтом вашего учебного заведения и Oxford Academic.
- Нажмите Войти через свое учреждение.
- Выберите свое учреждение из предоставленного списка, после чего вы перейдете на веб-сайт вашего учреждения для входа.
- При посещении сайта учреждения используйте учетные данные, предоставленные вашим учреждением.
 Не используйте личную учетную запись Oxford Academic.
Не используйте личную учетную запись Oxford Academic. - После успешного входа вы вернетесь в Oxford Academic.
Если вашего учреждения нет в списке или вы не можете войти на веб-сайт своего учреждения, обратитесь к своему библиотекарю или администратору.
Войти с помощью читательского билета
Введите номер своего читательского билета, чтобы войти в систему. Если вы не можете войти в систему, обратитесь к своему библиотекарю.
Члены общества
Доступ члена общества к журналу достигается одним из следующих способов:
Войти через сайт сообщества
Многие общества предлагают единый вход между веб-сайтом общества и Oxford Academic. Если вы видите «Войти через сайт сообщества» на панели входа в журнале:
- Щелкните Войти через сайт сообщества.
- При посещении сайта общества используйте учетные данные, предоставленные этим обществом.
 Не используйте личную учетную запись Oxford Academic.
Не используйте личную учетную запись Oxford Academic. - После успешного входа вы вернетесь в Oxford Academic.
Если у вас нет учетной записи сообщества или вы забыли свое имя пользователя или пароль, обратитесь в свое общество.
Войти с помощью личного кабинета
Некоторые общества используют личные аккаунты Oxford Academic для предоставления доступа своим членам. Смотри ниже.
Личный кабинет
Личную учетную запись можно использовать для получения оповещений по электронной почте, сохранения результатов поиска, покупки контента и активации подписок.
Некоторые общества используют личные аккаунты Oxford Academic для предоставления доступа своим членам.
Просмотр ваших зарегистрированных учетных записей
Щелкните значок учетной записи в правом верхнем углу, чтобы:
- Просмотр вашей личной учетной записи, в которой выполнен вход, и доступ к функциям управления учетной записью.

- Просмотр институциональных учетных записей, предоставляющих доступ.
Выполнен вход, но нет доступа к содержимому
Oxford Academic предлагает широкий ассортимент продукции. Подписка учреждения может не распространяться на контент, к которому вы пытаетесь получить доступ. Если вы считаете, что у вас должен быть доступ к этому контенту, обратитесь к своему библиотекарю.
Ведение счетов организаций
Для библиотекарей и администраторов ваша личная учетная запись также предоставляет доступ к управлению институциональной учетной записью. Здесь вы найдете параметры для просмотра и активации подписок, управления институциональными настройками и параметрами доступа, доступа к статистике использования и т. д.
Покупка
Стоимость подписки и заказ этого журнала
Варианты покупки книг и журналов в Oxford Academic
Кратковременный доступ
Чтобы приобрести краткосрочный доступ, войдите в свою учетную запись Oxford Academic выше.
У вас еще нет учетной записи Oxford Academic? регистр
Математика проб и ошибок: диалектические системы и дополнения теорий — доступ 24 часа
ЕВРО €30,00
22 фунта стерлингов
39 долларов США.
Реклама
Цитаты
Альтметрика
Дополнительная информация о метриках
Оповещения по электронной почте
Оповещение об активности статьи
Предварительные уведомления о статьях
Оповещение о новой проблеме
Получайте эксклюзивные предложения и обновления от Oxford Academic
Ссылки на статьи по телефону
-
Последний
-
Самые читаемые
-
Самые цитируемые
Классификация всех степеней преобразователя ниже N 3
Алгебраические инструменты для модальных систем по умолчанию
Ограничения эквивалентностей обратимых карт
Слабая релевантная логика обоснования
Основанный на аргументах подход к рассуждениям и объяснениям целей. Поколение
Поколение
Реклама
мягкий вопрос — Метод проб и ошибок в математике
Задавать вопрос
Спросил
Изменено 9 лет, 11 месяцев назад
Просмотрено 2к раз
$\begingroup$
Лично для вас то, как вы занимаетесь математикой, насколько путь вперед кажется методом проб и ошибок, а не абсолютным?
Думаю, я имею в виду, что мне кажется, что в математике есть своего рода цель, которую вы ищете, будь то решение конкретной математической задачи или просто направление ума к мышлению математического типа. Итак, вопрос в том, в какой степени путь к цели кажется «предопределенным» по сравнению с… или, может быть, я имею в виду, что если математика развивается по порядку (что, я полагаю, само по себе является другим вопросом, но в любом случае), к чему насколько некоторые из наблюдаемых математических существ оказываются не относящимися к цели/насколько отдельные конструкции оказываются ненужными для конечной конструкции? Позволяют ли математики идти по определенному пути, а затем решать, что этот путь не важен для решения, и поворачиваться, возвращаться назад, прежде чем продолжить движение по новому пути, ИЛИ разрешают ли все пути, всю почву, которая протоптана на пути к решению? решение, внести свой вклад в решение?
Или, как говорит мой папа, это философский математический вопрос о тупиках в математике.
- мягкий вопрос
$\endgroup$
1
$\begingroup$
На этот вопрос сложно дать конкретный ответ, но я напишу пару своих мыслей.
Для меня сложные проблемы требуют большого количества непрямых исследований и осмотра, прежде чем я попытаюсь понять специфику — только легкие проблемы будут достижимы по прямому пути от решения сразу же. Мне нужно получить представление о пространстве, в котором я работаю. Поэтому я создам кучу примеров, как можно более «странных», и буду возиться и исследовать, пока не почувствую, что у меня есть разумная интуиция. В этом методе нет ничего действительно потерянного времени.
Конечно, иногда пространство слишком сложное, и я буду ходить по кругу, делая это. В этом случае обычно помогает ограничить проблему чем-то меньшим, затем попытаться понять это и постепенно ослабить ограничения, ожидая понимания в каждом пункте, прежде чем двигаться дальше, пока я не поверю, что смогу сделать еще одну попытку решить общую теорему.
$\endgroup$
$\begingroup$
Стивен МакАдам однажды сказал на моем уроке абстрактной алгебры в Техасском университете: «Метод проб и ошибок — законный инструмент решения задач в математике». Я согласен на 100%.
$\endgroup$
$\begingroup$
В конце 1950-х годов я научился некоторым методам исследования у Майкла Барратта. Я помню, как сказал себе после долгой сессии с Майклом: «Если Майкл Бэрратт может пробовать одну чертову дурь за другой, то и я смогу!» И с тех пор я следовал этому методу. (На самом деле испытания Майкла были не такими уж дурацкими, но суть вы поняли.) Один из моих студентов-исследователей, Дерек Уоллер, заметил, что если 10% ваших идей хороши и у вас есть 100 идей, то у вас есть 10 идей. хорошие идеи; но если у вас всего 10 идей, то у вас проблемы!
Как получить идеи? Композитор Равель выступал за копирование.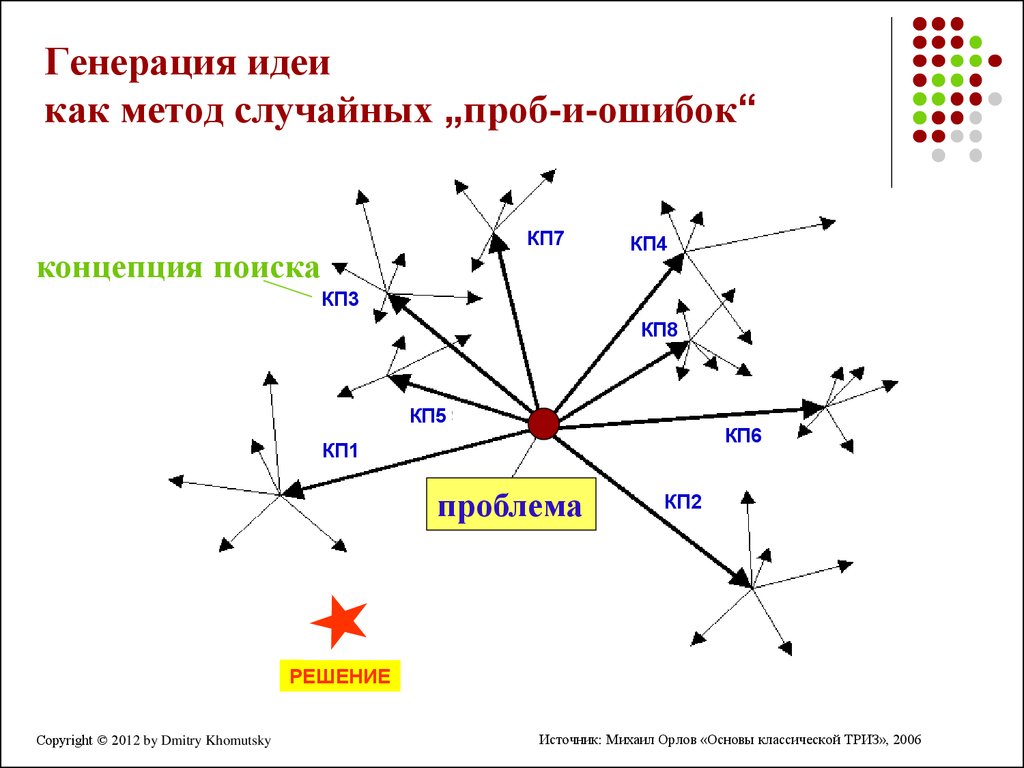 Он сказал: Если у вас есть какая-то оригинальность, то это покажет. Если нет, не беда! На самом деле вам может понадобиться скопировать несколько раз, прежде чем ржавые колеса мозга начнут вращаться.
Он сказал: Если у вас есть какая-то оригинальность, то это покажет. Если нет, не беда! На самом деле вам может понадобиться скопировать несколько раз, прежде чем ржавые колеса мозга начнут вращаться.
Еще один способ — попробовать написать одну тему в стиле и методами другой темы. Вы могли бы посмотреть на статью Методология математики. Часть аргумента заключается в том, что любая человеческая деятельность нуждается в обсуждении методологии.
Мне потребовалось много времени, чтобы понять, что попытка написать хорошую четкую математику очень полезна для самого себя! Вы можете найти области, в которых текущие версии не ясны или имеют кажущиеся аномалии , поэтому вам интересно, как их исправить. Так я попал в исследование группоидов в 1960-х годах. Это было продуктивно и очень весело, хотя, а может быть, и потому, что в то время и даже позже большие шишки часто были склонны говорить: «Группоиды — это вздор!». На самом деле это подняло ставки.
$\endgroup$
$\begingroup$
Я осмелюсь сказать, что любая проблема, которая может быть решена без проб и ошибок, перестала быть математической задачей, а стала просто проблемой рукоятки.
Можно накопить так много опыта в конкретной проблемной области (скажем, элементарной алгебре), что фаза проб и ошибок чаще всего происходит бессознательно, когда вы смотрите на постановку задачи, и тогда путь к решению может показаться почти предопределено. Но это все же происходит, и задачи, которые можно решить таким образом, остаются математическими (хоть и «легкими»).
$\endgroup$
Применение метода интегрированной пробной ошибки на основе глубокого обучения + наука, технология, чтение/письмо, инженерное дело, искусство, математика в режиме обучения предпринимательству в колледже
Введение
В условиях непрерывного социального прогресса и технологических инноваций новые технологии стали главной движущей силой развития различных отраслей промышленности в условиях общей тенденции глобализации. Таким образом, выращивание высококачественных составных талантов стало горячей темой исследований в сфере образования. После нескольких лет реформы учебных программ образовательные модели были изменены, так что учащиеся больше не пассивно принимают знания (Hanushek et al., 2017). Разнообразные режимы обучения обогащают содержание занятий учащихся и повышают их энтузиазм в учебе. Однако, учитывая различия между существующим содержанием обучения и содержанием оценки, учителя могут быть не в состоянии провести углубленное исследование новых методов обучения, и в результате учащиеся получают только чувство счастья, не овладев профессиональными навыками и знаниями. .
После нескольких лет реформы учебных программ образовательные модели были изменены, так что учащиеся больше не пассивно принимают знания (Hanushek et al., 2017). Разнообразные режимы обучения обогащают содержание занятий учащихся и повышают их энтузиазм в учебе. Однако, учитывая различия между существующим содержанием обучения и содержанием оценки, учителя могут быть не в состоянии провести углубленное исследование новых методов обучения, и в результате учащиеся получают только чувство счастья, не овладев профессиональными навыками и знаниями. .
Более того, развитие компьютерных технологий и интеграция информационных технологий в сферу образования позволили искусственному интеллекту (ИИ) заменить человека во многих механических и повторяющихся задачах. В частности, технология глубокого обучения (ГО) — это лишь одна из самых современных технологий искусственного интеллекта. В настоящее время приложения ГО можно найти во многих областях, таких как компьютерное зрение, распознавание речи и обработка естественного языка (NLP), что также дает идеи для применения ГО в других областях. Кроме того, благодаря реформе и инновациям в сфере образования образование STREAM стало центром исследований во всем мире (Kezar and Gehrke, 2017), которое активно изучается американскими учеными. С точки зрения американских педагогов СТРИМ-образование — это трендовое развитие образования будущего, способное всесторонне улучшить командную работу и общение учащихся. Обучение предпринимательству в колледже является важным этапом качественного образования, когда преподаватели предлагают студентам более острые учебные идеи, чтобы постепенно подняться с поверхностного уровня обучения, а также решить их головоломки, улучшить их когнитивный уровень и сформировать хорошие привычки мышления. Это чрезвычайно полезно и важно для таких дисциплин, как математика, которые требуют сильного логического мышления, потому что хорошие привычки мышления могут улучшить мышление и когнитивный уровень учащихся, а также стимулировать мотивацию учащихся и принести пользу учащимся в долгосрочной перспективе. Короче говоря, новые методы обучения могут изменить режим обучения и вдохновить студентов на получение более глубоких знаний.
Кроме того, благодаря реформе и инновациям в сфере образования образование STREAM стало центром исследований во всем мире (Kezar and Gehrke, 2017), которое активно изучается американскими учеными. С точки зрения американских педагогов СТРИМ-образование — это трендовое развитие образования будущего, способное всесторонне улучшить командную работу и общение учащихся. Обучение предпринимательству в колледже является важным этапом качественного образования, когда преподаватели предлагают студентам более острые учебные идеи, чтобы постепенно подняться с поверхностного уровня обучения, а также решить их головоломки, улучшить их когнитивный уровень и сформировать хорошие привычки мышления. Это чрезвычайно полезно и важно для таких дисциплин, как математика, которые требуют сильного логического мышления, потому что хорошие привычки мышления могут улучшить мышление и когнитивный уровень учащихся, а также стимулировать мотивацию учащихся и принести пользу учащимся в долгосрочной перспективе. Короче говоря, новые методы обучения могут изменить режим обучения и вдохновить студентов на получение более глубоких знаний. Сочетание метода обучения методом проб и ошибок, основанного на теории глубокого обучения, и обучения STREAM имеет большое значение в применении обучения предпринимательству в колледже, которое обеспечивает теоретическую основу и идеи для других дисциплин. Математика средней школы охватывает широкий диапазон и очень абстрактна. Он уделяет больше внимания проверке всесторонних способностей учащихся, что требует от учащихся овладения базовыми знаниями, а также способности интеграции знаний, анализа и решения проблем. Такая сложная учебная задача часто провоцирует сопротивление учащихся к математике в средней школе, и чаще всего их тесты по математике имеют высокий уровень ошибок. В настоящее время в преподавании математики в средней школе в Китае обнаружено много проблем. Например, при объяснении тем, подверженных ошибкам, большинству учителей не хватает глубокого анализа с точки зрения учащихся, поэтому пробелы в знаниях учащихся редко могут быть заполнены. действующей образовательной системы, поэтому они, возможно, не смогут учиться на своих прошлых ошибках.
Сочетание метода обучения методом проб и ошибок, основанного на теории глубокого обучения, и обучения STREAM имеет большое значение в применении обучения предпринимательству в колледже, которое обеспечивает теоретическую основу и идеи для других дисциплин. Математика средней школы охватывает широкий диапазон и очень абстрактна. Он уделяет больше внимания проверке всесторонних способностей учащихся, что требует от учащихся овладения базовыми знаниями, а также способности интеграции знаний, анализа и решения проблем. Такая сложная учебная задача часто провоцирует сопротивление учащихся к математике в средней школе, и чаще всего их тесты по математике имеют высокий уровень ошибок. В настоящее время в преподавании математики в средней школе в Китае обнаружено много проблем. Например, при объяснении тем, подверженных ошибкам, большинству учителей не хватает глубокого анализа с точки зрения учащихся, поэтому пробелы в знаниях учащихся редко могут быть заполнены. действующей образовательной системы, поэтому они, возможно, не смогут учиться на своих прошлых ошибках. С другой стороны, обучение методом проб и ошибок может помочь учащимся укрепить свои познания в математических знаниях, помочь учащимся исследовать причины своих ошибок и предложить соответствующие методы и, что наиболее важно, помочь учащимся понять и улучшить свои пробелы в знаниях. Кроме того, обучение с учетом ошибок помогает учащимся улучшить свои способности к независимому мышлению. В традиционной модели обучения в Китае ученики являются пассивными получателями знаний учителей. Для сравнения, в режиме обучения методом проб и ошибок преподаватели являются в большей степени организаторами и руководителями учебного процесса, а учащиеся становятся хозяевами класса и в большей степени полагаются на себя в поиске ошибок, анализе причин и предложении методов исправления, что помогает учащимся развивать субъективную спонтанность и креативность. В процессе «решения ошибок» учащиеся могут думать не только о правильности или неправильности самой темы, но, скорее, они могут глубоко размышлять и размышлять над своими ошибками, что помогает сформировать целостную и надежную структуру знаний, тем самым показывая реальную значение по сравнению с традиционной моделью обучения.
С другой стороны, обучение методом проб и ошибок может помочь учащимся укрепить свои познания в математических знаниях, помочь учащимся исследовать причины своих ошибок и предложить соответствующие методы и, что наиболее важно, помочь учащимся понять и улучшить свои пробелы в знаниях. Кроме того, обучение с учетом ошибок помогает учащимся улучшить свои способности к независимому мышлению. В традиционной модели обучения в Китае ученики являются пассивными получателями знаний учителей. Для сравнения, в режиме обучения методом проб и ошибок преподаватели являются в большей степени организаторами и руководителями учебного процесса, а учащиеся становятся хозяевами класса и в большей степени полагаются на себя в поиске ошибок, анализе причин и предложении методов исправления, что помогает учащимся развивать субъективную спонтанность и креативность. В процессе «решения ошибок» учащиеся могут думать не только о правильности или неправильности самой темы, но, скорее, они могут глубоко размышлять и размышлять над своими ошибками, что помогает сформировать целостную и надежную структуру знаний, тем самым показывая реальную значение по сравнению с традиционной моделью обучения. В частности, образование STREAM (наука, технология, чтение/исследования, инженерное дело, искусство и математика) представляет собой всеобъемлющую образовательную концепцию, которая полностью объединяет математику, искусство, инженерное дело, технологии, естественные науки, чтение и письмо, развивает у учащихся всесторонние способность и многомерное развитие, а также междисциплинарная образовательная модель. СТРИМ-образование изменило прежний метод обучения, ориентированный на учебный материал, и уделяет больше внимания воспитанию взглядов учащихся на жизнь и практическую деятельность, удачно сочетая теоретические знания с практикой и расширяя традиционную монопредметную форму обучения.
В частности, образование STREAM (наука, технология, чтение/исследования, инженерное дело, искусство и математика) представляет собой всеобъемлющую образовательную концепцию, которая полностью объединяет математику, искусство, инженерное дело, технологии, естественные науки, чтение и письмо, развивает у учащихся всесторонние способность и многомерное развитие, а также междисциплинарная образовательная модель. СТРИМ-образование изменило прежний метод обучения, ориентированный на учебный материал, и уделяет больше внимания воспитанию взглядов учащихся на жизнь и практическую деятельность, удачно сочетая теоретические знания с практикой и расширяя традиционную монопредметную форму обучения.
Внедрены инновационные методы исследования образования STEM (наука, технология, инженерия и математика), которые сосредоточены на практическом применении образования STEM, сочетают метод проб и ошибок с обучением STREAM и применяют комбинированные методы в колледже. предпринимательское образование. Предлагаемые образовательные методы способствуют реформированию учебных программ и обеспечивают теоретическую основу и практические идеи для реформирования образования по дисциплинам, отличным от математики. В первом разделе кратко описываются концепции метода обучения методом проб и ошибок и ДО, а также объясняется его значение для обучения математике в средней школе. Во втором разделе обобщается литература по трем аспектам: применение технологии глубокого обучения в образовании, применение метода проб и ошибок в образовании и применение метода STREAM в образовании. В третьем разделе проводится дальнейший анализ ключевых концепций и предлагается соответствующая схема оптимизации. В четвертом разделе разрабатывается обучающий эксперимент и Анкетный опрос (QS). В пятом разделе подробно анализируются результаты QS. В разделе «Заключение» приводится полный текст.
Предлагаемые образовательные методы способствуют реформированию учебных программ и обеспечивают теоретическую основу и практические идеи для реформирования образования по дисциплинам, отличным от математики. В первом разделе кратко описываются концепции метода обучения методом проб и ошибок и ДО, а также объясняется его значение для обучения математике в средней школе. Во втором разделе обобщается литература по трем аспектам: применение технологии глубокого обучения в образовании, применение метода проб и ошибок в образовании и применение метода STREAM в образовании. В третьем разделе проводится дальнейший анализ ключевых концепций и предлагается соответствующая схема оптимизации. В четвертом разделе разрабатывается обучающий эксперимент и Анкетный опрос (QS). В пятом разделе подробно анализируются результаты QS. В разделе «Заключение» приводится полный текст.
Обзор литературы
Являясь одной из последних разработок компьютерных технологий, DL показал отличные результаты в различных областях. В этом разделе исследуется применение ДО в сфере образования, чтобы предоставить больше возможностей для будущего развития образования.
В этом разделе исследуется применение ДО в сфере образования, чтобы предоставить больше возможностей для будущего развития образования.
Применение технологии глубокого обучения в образовании
Чжан и Цао (2021) проанализировали и построили структуру интеллектуальной системы высшего образования на основе глубокого обучения для решения проблем в начальном и среднем образовании. Во-первых, была создана функциональная блок-схема системы. Во-вторых, были разработаны алгоритм обнаружения лиц на основе многозадачной сверточной нейронной сети (CNN) и алгоритм обнаружения лиц на основе улучшенной Deep CNN (DCNN), а состояние усвоения знаний учащимися отслеживалось на основе нейронной сети с расширенной памятью. Наконец, эффективность и быстродействие системы были проверены экспериментально. Ван и Ли (2020) разработали модель системы обучения с ИИ и предложили метод аудиовизуального слияния на основе CNN. Независимая структура CNN использовалась для независимого моделирования аудиовизуального восприятия и асинхронной передачи информации, и было получено описание для аудиовизуальных параллельных данных в многомерном пространстве признаков. В соответствии с общей структурой полного соединения долгосрочная зависимость аудиовизуальных параллельных данных может быть смоделирована в более высоком измерении. Эксперименты показали, что производительность системы аудиовизуального распознавания речи (AVSR) на основе метода аудиовизуального слияния CNN была значительно улучшена, а частота ошибок распознавания снизилась примерно на 15%. Адерибигбе (2021) обнаружил, что онлайн-обсуждение может дополнять преподавание и обучение. Однако исследование также показало, что некоторые преподаватели и студенты не уверены в ценности и качестве онлайн-дискуссий. Эти дебаты и неопределенность потребовали дополнительных исследований качества обучения и глубины онлайн-дискуссий студентов. В частности, в исследовании была предпринята попытка изучить влияние ДО на обучение учащихся и качество постов в общеобразовательных учебных программах. При сборе и анализе данных использовались качественные и количественные методы. В качественной части использовались методы глубокого обучения и поверхностного обучения для извлечения постов студентов слово за словом и выполнения дедуктивного сопоставления, а посты студентов резюмировались и анализировались одновременно.
В соответствии с общей структурой полного соединения долгосрочная зависимость аудиовизуальных параллельных данных может быть смоделирована в более высоком измерении. Эксперименты показали, что производительность системы аудиовизуального распознавания речи (AVSR) на основе метода аудиовизуального слияния CNN была значительно улучшена, а частота ошибок распознавания снизилась примерно на 15%. Адерибигбе (2021) обнаружил, что онлайн-обсуждение может дополнять преподавание и обучение. Однако исследование также показало, что некоторые преподаватели и студенты не уверены в ценности и качестве онлайн-дискуссий. Эти дебаты и неопределенность потребовали дополнительных исследований качества обучения и глубины онлайн-дискуссий студентов. В частности, в исследовании была предпринята попытка изучить влияние ДО на обучение учащихся и качество постов в общеобразовательных учебных программах. При сборе и анализе данных использовались качественные и количественные методы. В качественной части использовались методы глубокого обучения и поверхностного обучения для извлечения постов студентов слово за словом и выполнения дедуктивного сопоставления, а посты студентов резюмировались и анализировались одновременно. Результаты опроса показали, что большинство постов студентов были высокого качества. Они были основаны на методах ДО путем участия в онлайн-дискуссиях и рефлексивных домашних заданиях. Наконец, исследование пришло к выводу, что если бы учителя давали учащимся четкие инструкции и выделяли достаточно времени для общения с коллегами, онлайн-обсуждение могло бы способствовать ДО. Сунь и Чжоу (2017) изложили причины и содержание ДО по математике, указали на трудности и проблемы, возникающие во время ДО по математике, и помогли людям понять ДО по математике в теории и на практике.
Результаты опроса показали, что большинство постов студентов были высокого качества. Они были основаны на методах ДО путем участия в онлайн-дискуссиях и рефлексивных домашних заданиях. Наконец, исследование пришло к выводу, что если бы учителя давали учащимся четкие инструкции и выделяли достаточно времени для общения с коллегами, онлайн-обсуждение могло бы способствовать ДО. Сунь и Чжоу (2017) изложили причины и содержание ДО по математике, указали на трудности и проблемы, возникающие во время ДО по математике, и помогли людям понять ДО по математике в теории и на практике.
Применение метода проб и ошибок в образовании
Ян (2017) использовал «форму веера» в качестве примера для изучения применения методов обучения методом проб и ошибок и проанализировал возможные формы «ошибок» учащихся и способы устранения ошибок учителем в данных обстоятельствах. Результаты исследования показали, что для того, чтобы действительно реализовать обучение методом проб и ошибок, учащимся необходимо было показать свои ошибки, а учителям классифицировать эти ошибки как исправимые или неизбежные, тем самым найдя хороший способ исправить ошибки (Ян, 2017). Ли (2017) отметил, что тест по обучению предпринимательству в колледже был распространенным способом проверки эффектов обучения и понимания учащимися математики. Таким образом, использование классификации, значение существования и методы работы неправильных наборов вопросов для обучения предпринимательству в колледже были изложены для обсуждения роли неправильных наборов вопросов в обучении математике в университете. Результаты исследования показали, что количество неправильных наборов вопросов в классах было высоким, а баллы были наиболее эффективным средством оценки усвоения содержания курса (Li, 2017).
Ли (2017) отметил, что тест по обучению предпринимательству в колледже был распространенным способом проверки эффектов обучения и понимания учащимися математики. Таким образом, использование классификации, значение существования и методы работы неправильных наборов вопросов для обучения предпринимательству в колледже были изложены для обсуждения роли неправильных наборов вопросов в обучении математике в университете. Результаты исследования показали, что количество неправильных наборов вопросов в классах было высоким, а баллы были наиболее эффективным средством оценки усвоения содержания курса (Li, 2017).
Применение науки, технологии, чтения/письма, инженерии, искусства, математических методов в образовании
Kruger et al. (2019) применили STREAM-образование к традиционным средним школам. Студенты были помещены на открытом воздухе, чтобы изучить проект и обогатить свой опыт, тем самым достигнув цели углубленного обучения (Kruger et al., 2019). Лешнер (2018) объяснил, что американская система последипломного образования в области естественных наук, инженерии и математики была признана одной из лучших систем последипломного образования во всем мире. Основываясь на требованиях работодателей в научных компаниях, было предложено идеальное образовательное видение для любой области STEM. Исследование подчеркнуло основные компетенции учащихся и улучшило образовательную работу, выявив, что учащимся нужны стимулы для хорошей учебы (Лешнер, 2018). Дайер (2018) отметил, что в нынешней социальной среде учащимся может быть полезно участие в STEM-образовании, которое может побудить учащихся усердно работать над творчеством, продолжать обучение на этапе K-12 и идти в ногу с изменениями в STEM. поле (Дайер, 2018).
Основываясь на требованиях работодателей в научных компаниях, было предложено идеальное образовательное видение для любой области STEM. Исследование подчеркнуло основные компетенции учащихся и улучшило образовательную работу, выявив, что учащимся нужны стимулы для хорошей учебы (Лешнер, 2018). Дайер (2018) отметил, что в нынешней социальной среде учащимся может быть полезно участие в STEM-образовании, которое может побудить учащихся усердно работать над творчеством, продолжать обучение на этапе K-12 и идти в ногу с изменениями в STEM. поле (Дайер, 2018).
Резюме
В настоящее время исследования в области теории ГО в основном сосредоточены на использовании анализа больших данных для открытия новых путей для изменений в образовании, а также на рекомендациях по персонализированным учебным ресурсам и исследованиям связанных платформ ГО. Однако исследования по применению теории ДО для улучшения существующих методов обучения проводятся редко. Кроме того, до сих пор было проведено мало исследований по STREAM-образованию. Большинство исследований сосредоточено на теориях образования STEM, а не на практических приложениях. Поэтому, чтобы продолжать продвигать реформу образования и действительно добиваться качественного образования, необходимо изучать концепции и методы образования, которые идут в ногу со временем и осуществляют определенные практики.
Большинство исследований сосредоточено на теориях образования STEM, а не на практических приложениях. Поэтому, чтобы продолжать продвигать реформу образования и действительно добиваться качественного образования, необходимо изучать концепции и методы образования, которые идут в ногу со временем и осуществляют определенные практики.
Знакомство с соответствующими понятиями
Глубокое обучение
DL, задействованное в этом исследовании, в основном включает два уровня. На первом уровне профессор Ли Цзя Хоу указывает, что на основе понимания содержания обучения учащиеся могут критически изучать новые знания и идеи и интегрировать новые знания и идеи в уже существующие. В такой когнитивной структуре учащиеся могут связываться с различными идеями и переносить существующие знания в новые ситуации в качестве метода обучения для принятия решений и решения проблем. Второй уровень — это технологии глубокого обучения в компьютерной сфере. С помощью моделей DL можно получить характеристики объектов и их отношения и использовать их, чтобы помочь учащимся углубить понимание некоторых точек знаний (Leshner, 2018; Kruger et al. , 2019).).
, 2019).).
Первый уровень DL относится к поверхностному обучению. По сравнению с поверхностным обучением, глубокое обучение может обеспечить эффективное обучение, мышление более высокого порядка, независимое мышление и постановку вопросов, благодаря которым учащиеся могут критически распознавать объекты для решения связанных проблем, а также создавать модули знаний и системы знаний и мыслить более гибко и по-разному. Другими словами, учащиеся не должны придерживаться фиксированного метода; вместо этого учащиеся имеют лучший режим логического мышления, более высокую спонтанность, лучшую инициативу и более склонны глубоко размышлять над точками знаний. Такой уровень DL представляет собой понимание знаний, систематическое обучение, связанное обучение и рефлексивный процесс обучения, который способствует улучшению учащихся в их способностях к обучению и решению проблем, закладывая основу для будущего развития учащихся (Dyer, 2018).
Разумеется, такое DL представляет собой пошаговый процесс. Это требует, чтобы учителя обращали внимание на то, чтобы понять суть знаний при объяснении содержания, чтобы дать учащимся возможность понять соответствующее содержание, а не механическое запоминание, и, в конечном итоге, донести знания до их сознания. В учебном процессе учителям необходимо выступать за конструктивные инновации. В качестве помощника учащихся учитель помогает учащимся упорядочить существующие знания, создать систему знаний и постоянно обогащать эту структуру в процессе обучения, чтобы учащиеся могли своевременно подключать связанный со знаниями контент, когда они сталкиваться с сопутствующими проблемами и эффективно решать связанные проблемы, тем самым продолжая внедрять инновации. Кроме того, также необходимо постоянно поощрять студентов к углубленному участию, чтобы они могли продолжать принимать новые знания на основе существующих знаний и передавать существующие знания. Учащимся может быть полезно, если учителя примут подходы к обучению, ориентированные на цели обучения, в соответствии со способностями учащихся, чтобы учащиеся были уверены в своем активном участии в практическом опыте, чтобы лучше запоминать, понимать, применять и оценивать теоретические знания, а именно, глубокое познание.
Это требует, чтобы учителя обращали внимание на то, чтобы понять суть знаний при объяснении содержания, чтобы дать учащимся возможность понять соответствующее содержание, а не механическое запоминание, и, в конечном итоге, донести знания до их сознания. В учебном процессе учителям необходимо выступать за конструктивные инновации. В качестве помощника учащихся учитель помогает учащимся упорядочить существующие знания, создать систему знаний и постоянно обогащать эту структуру в процессе обучения, чтобы учащиеся могли своевременно подключать связанный со знаниями контент, когда они сталкиваться с сопутствующими проблемами и эффективно решать связанные проблемы, тем самым продолжая внедрять инновации. Кроме того, также необходимо постоянно поощрять студентов к углубленному участию, чтобы они могли продолжать принимать новые знания на основе существующих знаний и передавать существующие знания. Учащимся может быть полезно, если учителя примут подходы к обучению, ориентированные на цели обучения, в соответствии со способностями учащихся, чтобы учащиеся были уверены в своем активном участии в практическом опыте, чтобы лучше запоминать, понимать, применять и оценивать теоретические знания, а именно, глубокое познание. процесса (Юань и др., 2019 г.). Применение DL направлено на то, чтобы помочь учащимся глубоко мыслить во время обучения и повторения, особенно в отношении таких строгих дисциплин, как математика и физика. Понимание знаний поможет учащимся сформировать мышление более высокого порядка и поощрит их творчество. Таким образом, достижение цели и глубина мышления могут быть представлены с помощью таксономии когнитивных целей, как показано на рисунке 1.
процесса (Юань и др., 2019 г.). Применение DL направлено на то, чтобы помочь учащимся глубоко мыслить во время обучения и повторения, особенно в отношении таких строгих дисциплин, как математика и физика. Понимание знаний поможет учащимся сформировать мышление более высокого порядка и поощрит их творчество. Таким образом, достижение цели и глубина мышления могут быть представлены с помощью таксономии когнитивных целей, как показано на рисунке 1.
Рисунок 1. Таксономия Блума.
Второй уровень DL заключается в использовании технологии машинного обучения, позволяющей машинам имитировать человеческий мозг. Модель DL — это процесс получения визуальных характеристик случаев и объектов после послойного преобразования. Глубокая нейронная сеть делится на три части: нейронная сеть с прямой связью, глубокая сеть с обратной связью и двунаправленная глубокая сеть. Базовая нейронная сеть представляет собой нейронную сеть с прямой связью. Нейроны каждого уровня соединяются с нейронами предыдущего слоя для передачи одного элемента. Этот уровень сети представляет собой процесс кодирования входного сигнала, которым является CNN. Во-вторых, глубокая сеть с обратной связью в основном основана на нейронной системе деконволюции. Он де-вычисляет и декодирует входной сигнал путем деконволюции или изучения основ набора данных. Наконец, двусторонняя глубокая сеть объединяет первые два алгоритма, реализует чередование и обновление между видимым и скрытым слоями, завершает двустороннее распространение между нейронами и, наконец, оптимизирует модель и повышает точность (Перера и Патель). , 2019; Чжан и др., 2019). Эти три нейронные сети показаны на рисунке 2.
Этот уровень сети представляет собой процесс кодирования входного сигнала, которым является CNN. Во-вторых, глубокая сеть с обратной связью в основном основана на нейронной системе деконволюции. Он де-вычисляет и декодирует входной сигнал путем деконволюции или изучения основ набора данных. Наконец, двусторонняя глубокая сеть объединяет первые два алгоритма, реализует чередование и обновление между видимым и скрытым слоями, завершает двустороннее распространение между нейронами и, наконец, оптимизирует модель и повышает точность (Перера и Патель). , 2019; Чжан и др., 2019). Эти три нейронные сети показаны на рисунке 2.
Рисунок 2. Глубокие нейронные сети. (A) CNN (B) Нейронная сеть деконволюции (C) Модель DL на основе ограниченной машины Больцмана (RBM).
Обучение методом проб и ошибок и усовершенствованное обучение методом проб и ошибок
Обучение методом проб и ошибок предложено г-ном Хуа Инлуном. Метод обучения направлен на то, чтобы превратить ошибки в классе в учебный ресурс и превратить «несчастные случаи» в истории. Концепция обучения является наследием математической культуры, а не самих математических знаний. Хуа Инлун указывает, что преподаватели должны найти способы иллюстрировать математический мир в живой и простой форме, чтобы помочь учащимся почувствовать яркость и разнообразие математического обучения, что, в свою очередь, стимулирует богатство математического обучения и математического мышления учащихся. При обучении математическим знаниям также предполагается, что учащиеся воспринимают математику как интересную дисциплину, а не слепо и скучно изучают математический контент (Qin et al., 2019).).
Концепция обучения является наследием математической культуры, а не самих математических знаний. Хуа Инлун указывает, что преподаватели должны найти способы иллюстрировать математический мир в живой и простой форме, чтобы помочь учащимся почувствовать яркость и разнообразие математического обучения, что, в свою очередь, стимулирует богатство математического обучения и математического мышления учащихся. При обучении математическим знаниям также предполагается, что учащиеся воспринимают математику как интересную дисциплину, а не слепо и скучно изучают математический контент (Qin et al., 2019).).
В процессе обучения у учащихся будут возникать различные ошибки из-за разного понимания знаний. Процесс терпимости учителя к этим ошибкам также отражает его инклюзивность и твердые педагогические навыки, которые могут своевременно справляться с чрезвычайными ситуациями в процессе обучения. Учителя должны не бояться ошибок учащихся, а надеяться, что благодаря этим ошибкам у учащихся будет правильное отношение к ошибкам, они смогут активно думать о том, почему они допустили ошибки (Côté-Allard et al. , 2019).), и развивать их способность находить положительные решения из ошибок. Полное использование многогранной ценности ресурсов по ошибкам может помочь учащимся раскрыть свое мышление, понять значение ошибок и позволить им расти с ошибками. Если нет ошибки, не будет и инноваций. Необходимо позволить учащимся столкнуться с ошибками, а затем дать им более глубокое понимание положительного решения (Lu, 2017). В этой статье предлагается схема оптимизации, основанная на практике преподавания в классе, подчеркивается опыт учащихся в преподавании, позволяет учащимся делать ошибки и помогает учащимся правильно справляться со своими ошибками. Благодаря повторному совершению, анализу и исправлению ошибок учащиеся будут поощряться к тому, чтобы рационально смотреть на свои ошибки и своевременно вносить коррективы, тем самым повышая свою устойчивость к фрустрации. Роль учителя в обучении методом проб и ошибок больше похожа на консультанта, который рассматривает поведение учащихся с панорамной точки зрения, предоставляя экспериментальную платформу, а также возможности для учащихся делать ошибки и учиться на них.
, 2019).), и развивать их способность находить положительные решения из ошибок. Полное использование многогранной ценности ресурсов по ошибкам может помочь учащимся раскрыть свое мышление, понять значение ошибок и позволить им расти с ошибками. Если нет ошибки, не будет и инноваций. Необходимо позволить учащимся столкнуться с ошибками, а затем дать им более глубокое понимание положительного решения (Lu, 2017). В этой статье предлагается схема оптимизации, основанная на практике преподавания в классе, подчеркивается опыт учащихся в преподавании, позволяет учащимся делать ошибки и помогает учащимся правильно справляться со своими ошибками. Благодаря повторному совершению, анализу и исправлению ошибок учащиеся будут поощряться к тому, чтобы рационально смотреть на свои ошибки и своевременно вносить коррективы, тем самым повышая свою устойчивость к фрустрации. Роль учителя в обучении методом проб и ошибок больше похожа на консультанта, который рассматривает поведение учащихся с панорамной точки зрения, предоставляя экспериментальную платформу, а также возможности для учащихся делать ошибки и учиться на них. Каждая допущенная ошибка означает новую возможность для учителей помочь учащимся освоить некоторые элементы знаний. Затем учителям становится необходимо направлять учащихся к тому, чтобы они терпеливо находили причины своих ошибок, освобождались от вмешательства негативных эмоций и искренне преодолевали ошибки. С другой стороны, экспериментальная обучающая платформа создает хорошие возможности для вторичной разработки и интерпретации учебных материалов с точки зрения учащихся. В частности, процесс проб и ошибок учеников может быть по желанию прерван учителями, чтобы скорректировать предыдущую систему знаний посредством диалога с учениками, где время становится важным, который предлагается привязывать к конкретному содержанию и проводить, когда ученики запутались в обучении или, по-видимому, какие-то противоречивые мысли.
Каждая допущенная ошибка означает новую возможность для учителей помочь учащимся освоить некоторые элементы знаний. Затем учителям становится необходимо направлять учащихся к тому, чтобы они терпеливо находили причины своих ошибок, освобождались от вмешательства негативных эмоций и искренне преодолевали ошибки. С другой стороны, экспериментальная обучающая платформа создает хорошие возможности для вторичной разработки и интерпретации учебных материалов с точки зрения учащихся. В частности, процесс проб и ошибок учеников может быть по желанию прерван учителями, чтобы скорректировать предыдущую систему знаний посредством диалога с учениками, где время становится важным, который предлагается привязывать к конкретному содержанию и проводить, когда ученики запутались в обучении или, по-видимому, какие-то противоречивые мысли.
Наука, технология, чтение/письмо, инженерное дело, искусство, математика Образование
ПОТОЧНОЕ образование основано на образовании STEM (наука, технология, инженерия и математика), впервые предложенном в Соединенных Штатах. Наука занимается познанием мира и объяснением объективных законов природы; техника и инженерия – это усилия человечества по преобразованию мира по законам природы и решению проблем общественного развития через гармоничное сосуществование с природой; математика используется в качестве основного инструмента для технических и инженерных дисциплин. 19 год86 впервые видит предложение программных рекомендаций в отчете «Наука, математика и инженерное образование бакалавриата» Американского национального совета по науке, целью которого является повышение общей мощи Соединенных Штатов. С тех пор образовательные инновации привлекли большое внимание, и были достигнуты различные достижения. Дальнейшее развитие STEM-образования породило STEAM и более комплексную образовательную модель: наука, технология, чтение/письмо, инженерное дело, искусство, математика (STREAM). Судя по всему, STEAM добавляет искусство к STEM-образованию, пытаясь придать большее значение гуманитарным наукам и художественным коннотациям учащихся.
Наука занимается познанием мира и объяснением объективных законов природы; техника и инженерия – это усилия человечества по преобразованию мира по законам природы и решению проблем общественного развития через гармоничное сосуществование с природой; математика используется в качестве основного инструмента для технических и инженерных дисциплин. 19 год86 впервые видит предложение программных рекомендаций в отчете «Наука, математика и инженерное образование бакалавриата» Американского национального совета по науке, целью которого является повышение общей мощи Соединенных Штатов. С тех пор образовательные инновации привлекли большое внимание, и были достигнуты различные достижения. Дальнейшее развитие STEM-образования породило STEAM и более комплексную образовательную модель: наука, технология, чтение/письмо, инженерное дело, искусство, математика (STREAM). Судя по всему, STEAM добавляет искусство к STEM-образованию, пытаясь придать большее значение гуманитарным наукам и художественным коннотациям учащихся. Вскоре чтение и письмо были дополнены, чтобы сформулировать образовательную модель STREAM, которая считает чтение и письмо основными навыками для комплексного обучения по учебной программе (Tan, 2017; Guo, 2019).).
Вскоре чтение и письмо были дополнены, чтобы сформулировать образовательную модель STREAM, которая считает чтение и письмо основными навыками для комплексного обучения по учебной программе (Tan, 2017; Guo, 2019).).
Основной особенностью STREAM является акцент на междисциплинарное обучение и развитие у учащихся гуманитарных и художественных навыков, а также научной грамотности за счет интеграции междисциплинарных целей. Ученые в области образования считают, что чтение и искусство хорошо завершают образование STEM, поскольку всем нужны базовые технические навыки и навыки решения проблем, что также является ключом к будущим инновациям. Таким образом, STREAM является более инклюзивным, чем STEM, и может иметь далеко идущие последствия для обучения талантов (Dong, 2017).
Материалы и методы
Как относительно базовый, но важный предмет, метод преподавания и стратегия математики являются частью, которой учителя и эксперты придают большое значение. Как правило, эффективное обучение предпринимательству в колледже делится на три этапа обучения: анализ до начала занятий, реализация в классе и оценка размышлений после занятий. Нынешнее преподавание математики фокусируется на сущности знаний, выступает за конструктивные инновации, поощряет всестороннее участие, сосредоточено вокруг целей обучения и культивирует глубокое мышление, в соответствии с которым обучение предпринимательству в колледже можно разделить на пять этапов: глубокие коннотации. ориентированный анализ учебной программы, оценка, ориентированная на когнитивное развитие, обучение, ориентированное на понимание, обучение, ориентированное на мышление, более высокого порядка, и оценка эффекта, ориентированная на уровень понимания. Затем теория ДО используется для улучшения «обучения методом проб и ошибок». Таким образом, в сочетании с образованием STREAM всесторонне повышается грамотность учащихся, реализуя действительно качественное образование и принося пользу учащимся (Thibaut et al., 2018; Dare et al., 2019).).
Нынешнее преподавание математики фокусируется на сущности знаний, выступает за конструктивные инновации, поощряет всестороннее участие, сосредоточено вокруг целей обучения и культивирует глубокое мышление, в соответствии с которым обучение предпринимательству в колледже можно разделить на пять этапов: глубокие коннотации. ориентированный анализ учебной программы, оценка, ориентированная на когнитивное развитие, обучение, ориентированное на понимание, обучение, ориентированное на мышление, более высокого порядка, и оценка эффекта, ориентированная на уровень понимания. Затем теория ДО используется для улучшения «обучения методом проб и ошибок». Таким образом, в сочетании с образованием STREAM всесторонне повышается грамотность учащихся, реализуя действительно качественное образование и принося пользу учащимся (Thibaut et al., 2018; Dare et al., 2019).).
Двое старшеклассников проходят психологическую зрелость, начинают беспокоиться о своем будущем, уделять больше внимания развитию способностей и любят исследовать новые вещи. Между тем их абстрактное мышление получило дальнейшее развитие, и они приобрели определенные способности к решению проблем. Для этих студентов учебные ситуации должны быть основаны на жизненно важных, интересных для учащихся и сложных действиях, в которые математические знания должны быть интегрированы с научной точки зрения. Знания двух старших учеников более полны, чем у старших учеников, и они не испытывали напряжения трех старших учеников, поэтому они очень подходят для обучения экспериментальному анализу. Это исследование берет гиперболическое содержание в конической части обучения предпринимательству в колледже в качестве примера и применяет метод обучения, основанный на теории глубокого обучения в сочетании с обучением STREAM, чтобы вдохновить преподавателей университетов и ученых в области образования.
Между тем их абстрактное мышление получило дальнейшее развитие, и они приобрели определенные способности к решению проблем. Для этих студентов учебные ситуации должны быть основаны на жизненно важных, интересных для учащихся и сложных действиях, в которые математические знания должны быть интегрированы с научной точки зрения. Знания двух старших учеников более полны, чем у старших учеников, и они не испытывали напряжения трех старших учеников, поэтому они очень подходят для обучения экспериментальному анализу. Это исследование берет гиперболическое содержание в конической части обучения предпринимательству в колледже в качестве примера и применяет метод обучения, основанный на теории глубокого обучения в сочетании с обучением STREAM, чтобы вдохновить преподавателей университетов и ученых в области образования.
Экспериментальный проект
Коническая секция является частью плоской аналитической геометрии, которая воплощает идею объединения чисел и форм, а также находится в центре внимания исследования в области обучения предпринимательству в колледже. Коническое сечение в университете в основном включает овал, гиперболу и параболу. Это высокая степень слияния алгебры и геометрических задач. Однако студенты часто используют эти две части по отдельности. Также трудно глубоко понять основные вопросы соответствующих точек знаний, таких как истинное значение асимптоты и эксцентриситета для гиперболы и параболы.
Коническое сечение в университете в основном включает овал, гиперболу и параболу. Это высокая степень слияния алгебры и геометрических задач. Однако студенты часто используют эти две части по отдельности. Также трудно глубоко понять основные вопросы соответствующих точек знаний, таких как истинное значение асимптоты и эксцентриситета для гиперболы и параболы.
Таким образом, это исследование использует гиперболу в конической части в качестве примера обучения дизайну и применению и направлено на улучшение понимания учащимися этой части с помощью соответствующих тестов.
Гипербола — это гладкая кривая, лежащая на плоскости и определяемая уравнением своих геометрических свойств или комбинацией решений. Гипербола состоит из двух частей, которые называются соединенными компонентами или ответвлениями и являются зеркальным отражением друг друга, подобно двум бесконечным лукам. Гипербола — это одно из трех конических сечений, образованных пересечением плоскости и двойного конуса, как показано на рис. 3.9.0005
3.9.0005
Рисунок 3. Принципиальная схема гиперболы.
На плоскости абсолютное значение разницы расстояний между двумя фиксированными точками F 1 и F 2 равно константе (константа 2a, меньше, чем |F 1 F 2 |). Траектория точки фиксированной длины называется гиперболой, т. е. ||PF 1 | − |ПФ 2 || = 2а (Эллисон, Аллен, 2018). Соответствующее стандартное уравнение гласит:
x2a2-y2b2=1(1)
Понимание определения гиперболы и стандартных уравнений позволяет анализировать простые геометрические свойства гиперболы. Здесь можно позаимствовать процесс трансферного обучения из теории ДО. В сочетании с обучением STREAM передача контекста позволяет учащимся повысить интерес к обучению гиперболе и освоить точку знаний. Учителя также должны давать учащимся больше точек памяти, чтобы позволить учащимся обрести уверенность в себе, чтобы стимулировать интерес учащихся к обучению, улучшить их понимание знаний и завершить передачу знаний. В то же время перенос аналогии также является важным содержанием, которое включает аналогию знания, аналогию метода и аналогию мышления. В курсовом проектировании простых геометрических свойств гиперболы необходимо выполнить аналоговый перенос, т. е., исходя из геометрических свойств овала, найти идею анализа геометрических свойств (Ibáñez and Delgado-Kloos, 2018; Yanez и др., 2019 г.).
В то же время перенос аналогии также является важным содержанием, которое включает аналогию знания, аналогию метода и аналогию мышления. В курсовом проектировании простых геометрических свойств гиперболы необходимо выполнить аналоговый перенос, т. е., исходя из геометрических свойств овала, найти идею анализа геометрических свойств (Ibáñez and Delgado-Kloos, 2018; Yanez и др., 2019 г.).
Субъекты Описание
В этой работе отбираются 500 учащихся из четырех параллельных классов той же старшей средней школы и второго класса старшей школы, что и объект исследования, и они поровну делятся на экспериментальную и тестовую группы. На том же уровне обучения контрольная группа использует традиционные методы обучения, а экспериментальная группа использует комбинацию методов обучения методом проб и ошибок и обучения STREAM, основанного на теории глубокого обучения. После трех месяцев обучения студенты сдают 45-минутный тест в соответствии с требованиями обычного теста. Структура выборки и основные сведения о респондентах представлены на рисунке 4.
Рисунок 4. Основная информация респондентов [ (A) . Соотношение полов; (Б) . Соотношение классов].
КС проводится с октября по ноябрь 2019 года в течение трех месяцев, до чего будет проведено предварительное расследование. В декабре того же года проведены комплексные исследования и анализ: всего распределено 500 QS, восстановлено 472 с коэффициентом восстановления 94,54%. После удаления 10 недействительных или неполных QS для дальнейшего анализа используется 447 действительных QS, что составляет 89..5%. Качество QS оценивается с помощью SPSS 24.0 на основе коэффициента Кронбаха α для проверки надежности, стабильности и индексной системы QS. Дизайн, распространение и сбор QS не будут нарушать личную неприкосновенность частной жизни с согласия участников; QS был одобрен руководством школы и соответствующими отделами; на протяжении всего процесса используется анонимная система, а собранные данные используются только для научных исследований. Разработанный QS не предполагает конфиденциальности учащихся и утверждается учащимися.
Разработанный QS не предполагает конфиденциальности учащихся и утверждается учащимися.
Экспериментальная процедура
I. Учащиеся должны заполнить таблицу 1 для изучения геометрии гиперболы.
Таблица 1. Геометрия овала.
Формирование овала понято в сочетании видеоданных. Видеомодель показана на рис. 5.
Рисунок 5. Модель поперечного сечения овала.
II. Запрос обучения
Запрос I: В овале длинная ось и короткая ось могут образовывать прямоугольник, и овальное изображение может быть быстро создано, когда прямоугольник известен. Есть ли такой прямоугольник в гиперболе?
Запрос II: Буквы a и b в овале обозначают длину большой и малой осей. Что обозначают a и b в гиперболе? Как выглядит гипербола, когда a = b?
Постоянно наблюдая за гиперболическим изображением, узнавали ли вы раньше подобные изображения? (обратно-пропорциональное изображение функции).
Какая связь между гиперболическим изображением и изображением обратной пропорциональной функции? (Вращение обратно пропорциональной функции может получить гиперболическое изображение).
Запрос III: В обратном функциональном изображении изображение бесконечно близко к оси X и оси Y. Есть ли такая прямая в изображении гиперболической функции?
Если такая прямая существует, как ее найти и назвать?
Запрос IV: Пересекутся ли асимптота и гипербола? Как это доказать?
III. Эффективная передача знаний
Эксцентриситет в овале представляет собой отношение расстояния от движущейся точки до фокуса к расстоянию от движущейся точки до направляющей (Harris and de Bruin, 2018; Psycharis, 2018; Page-Reeves et al. ., 2019). Его можно получить по уравнению (2):
e=ca=a2+b2a2=1+(ba)2(2)
Эксцентриситет e указывает размер раскрытия кривой, и диапазон значений e может быть получен согласно уравнению. (2), e > 1.
Пример вопроса: Отношение расстояния от точки M(x, y) до фиксированной точки F(5,0) к фиксированной линии l: x = 16/5 равно постоянный 5/4. Пожалуйста, найдите траекторию точки М.
IV. Расширенное обучение
Пример вопроса: Найдите реальную длину оси, длину воображаемой оси, координаты фокуса, эксцентриситет, асимптотическое уравнение x249-y225=1.
Вариант: Рассчитайте расстояние от фокуса до асимптоты x249-y225=1.
Пример вопроса: Известно, что F 1 и F 2 являются левым и правым фокусами гиперболы x29-y2b2=1. Через F 2 проведена прямая, пересекающая гиперболу с правой стороны в точках A и B. Если |AB| = 4, рассчитайте периметр ΔAF 1 B.
Наконец, два режима обучения объединяются. Каркас показан на рисунке 6.9.0005
Рисунок 6. Режимы обучения на основе двух разных методов.
Экспериментальные инструменты
После того, как схема обучения простой геометрической природе гиперболы завершена, проверяется эффективность предлагаемого интегрированного обучения методом пробных ошибок и обучения STREAM на основе DL, а также эффект от практики обучения. Затем контент тестируется один раз после исследования природы и связанных с ним связей. Согласно предыдущей таксономии Блума, тестовые вопросы также классифицируются, а уровень мышления каждого вопроса определяется как 2n (Костантино, 2018).
В тесте 8 вопросов, в том числе 5 вопросов с несколькими вариантами ответов, 2 вопроса с вычислениями и 1 вопрос с кратким ответом. Соответствующие очки знаний и уровни мышления показаны в таблице 2.
Таблица 2. Очки знаний и уровни мышления тестовых вопросов.
После теста учащимся выдается соответствующая шкала оценки эффекта курса, которая включает имя учащегося, содержание курса, баллы за знание ошибок, удовлетворенность классом, принятие содержания, удовлетворенность тестом и достоверность метода. Для последних четырех пунктов используется пятибалльная шкала: 1 балл — крайне неудовлетворен, 2 балла — неудовлетворен, 3 балла — в среднем, 4 балла — очень доволен и 5 баллов — очень доволен.
Результаты и обсуждение
Анализ надежности и валидности опросного листа
Надежность QS анализируется с помощью SPSS 25.0, и полученный коэффициент альфа Кронбаха составляет 0,804, что больше 0,7 и имеет хорошую надежность. Результаты статистики надежности представлены в таблице 3.
Таблица 3. Статистика надежности.
Тесты KMO и сферические тесты Бартлетта проводятся с использованием SPSS25.0 для QS, а факторный анализ выполняется для QS, таким образом обеспечивается достоверность QS. KMO составляет 0,657, что больше 0,6, поэтому каждый вопрос в QS подходит для факторного анализа и имеет хорошую конструктивную достоверность. Испытания КМО и Бартлетта приведены в таблице 4.
Таблица 4. KMO и сферические тесты Бартлетта.
Приведенный выше анализ данных показывает, что разработанная система качества обладает хорошей надежностью, достоверностью, сильной внутренней согласованностью и стабильностью, поэтому она разумна, эффективна и может использоваться в качестве инструмента исследования.
Анализ результатов анкетирования
Среди 200 восстановленных QS точность вопросов с множественным выбором, вопросов с расчетом и вопросов с кратким ответом, а также статистические результаты шкалы оценки показаны на рисунках 7–9. , соответственно.
, соответственно.
Рисунок 7. Статистический анализ точности вопросов с несколькими вариантами ответов.
Рисунок 8. Статистика точности расчета и вопросы с кратким ответом.
Рисунок 9. Статистические результаты оценочной шкалы.
Рисунок 7 показывает, что точность первого вопроса с несколькими вариантами ответов экспериментальной группы составляет 92% и 87% для экспериментальной группы и контрольной группы, соответственно. Точность второго вопроса с несколькими вариантами ответов равна 9.6% и 93% для экспериментальной группы и контрольной группы соответственно. Точность третьего вопроса с несколькими вариантами ответов составляет 91% и 88% соответственно. В целом, точность вопросов с несколькими вариантами ответов учащихся в экспериментальной группе выше, чем в контрольной группе, что доказывает, что предлагаемый интегрированный метод обучения пробной ошибки + STREAM на основе DL может помочь учащимся лучше учиться, повысить точность учащихся. ‘ вопросы с несколькими вариантами ответов, и способствует улучшению результатов учащихся.
‘ вопросы с несколькими вариантами ответов, и способствует улучшению результатов учащихся.
На рисунке 8 показано, что точность первого вопроса расчета составляет 96% и 87% для экспериментальной группы и контрольной группы, соответственно. Точность второго расчетного вопроса составляет 88% и 90% для экспериментальной группы и контрольной группы соответственно. Точность третьего расчетного вопроса составляет 93% и 88% соответственно. Точность ответов студентов в экспериментальной группе достоверно выше, чем в контрольной группе; Между тем, повышение точности предлагаемого интегрированного метода пробной ошибки + STREAM на основе DL для расчетов студентов и вопросов с кратким ответом выше, чем у вопросов с несколькими вариантами ответов. Причина в том, что вычисления и вопросы с кратким ответом могут лучше показать всесторонние способности учащихся, в то время как удача может быть связана с вопросами с несколькими вариантами ответов.
На рисунках 7, 8 видно, что у учащихся экспериментальной группы точность ответов выше и больше правильных ответов, чем у учащихся контрольной группы. На рис. 9 показано, что оценки удовлетворенности классом, принятия содержания, удовлетворенности экзаменами и эффективности методов экспериментальной группы выше, чем у контрольной группы, и стандартное отклонение (SD) экспериментальной группы также выше, чем у контрольной группы. контрольная группа. Оценочный балл экспериментальной группы более стабилен, чем у контрольной группы. Студенты экспериментальной группы имеют высокую степень принятия и признания новых методов обучения. Подводя итог, можно сказать, что учащиеся экспериментальной группы могут серьезно справляться с ошибками во время исследования и постепенно углублять свое понимание геометрических свойств гиперболы в соответствии с новыми методами, тем самым получая более высокие баллы в итоговом содержательном тесте. Эффект от предложенного интегрированного метода обучения «пробная ошибка + STREAM» согласуется с результатами внеклассного тестирования, поэтому он эффективен.
На рис. 9 показано, что оценки удовлетворенности классом, принятия содержания, удовлетворенности экзаменами и эффективности методов экспериментальной группы выше, чем у контрольной группы, и стандартное отклонение (SD) экспериментальной группы также выше, чем у контрольной группы. контрольная группа. Оценочный балл экспериментальной группы более стабилен, чем у контрольной группы. Студенты экспериментальной группы имеют высокую степень принятия и признания новых методов обучения. Подводя итог, можно сказать, что учащиеся экспериментальной группы могут серьезно справляться с ошибками во время исследования и постепенно углублять свое понимание геометрических свойств гиперболы в соответствии с новыми методами, тем самым получая более высокие баллы в итоговом содержательном тесте. Эффект от предложенного интегрированного метода обучения «пробная ошибка + STREAM» согласуется с результатами внеклассного тестирования, поэтому он эффективен.
Заключение
В настоящее время воспитание высококачественных сложных талантов стало горячей темой в образовательных кругах и главным приоритетом в базовом образовании. В этой статье метод обучения методом проб и ошибок творчески сочетается с обучением STREAM, основанным на теории глубокого обучения, и применяется к преподаванию математики в старших классах средней школы. Основываясь на анализе случаев преподавания гиперболического содержания в обучении предпринимательству в колледже, в этой статье анализируется эффект предлагаемого интегрированного метода пробной ошибки + STREAM на основе DL. В то же время для завершения соответствующего содержания обучения используются разные методы обучения, и проводится сравнительный анализ экспериментальной группы и контрольной группы. Успеваемость учащихся проверяется с помощью дизайна QS, и выпускается шкала оценки эффективности обучения, чтобы получить оценку учащихся содержания класса, результатов тестов и методов обучения, чтобы дополнительно проверить эффективность предлагаемого интегрированного следа ошибки + STREAM методы обучения. Результаты показывают, что точность ответов студентов экспериментальной группы выше, чем у студентов контрольной группы.
В этой статье метод обучения методом проб и ошибок творчески сочетается с обучением STREAM, основанным на теории глубокого обучения, и применяется к преподаванию математики в старших классах средней школы. Основываясь на анализе случаев преподавания гиперболического содержания в обучении предпринимательству в колледже, в этой статье анализируется эффект предлагаемого интегрированного метода пробной ошибки + STREAM на основе DL. В то же время для завершения соответствующего содержания обучения используются разные методы обучения, и проводится сравнительный анализ экспериментальной группы и контрольной группы. Успеваемость учащихся проверяется с помощью дизайна QS, и выпускается шкала оценки эффективности обучения, чтобы получить оценку учащихся содержания класса, результатов тестов и методов обучения, чтобы дополнительно проверить эффективность предлагаемого интегрированного следа ошибки + STREAM методы обучения. Результаты показывают, что точность ответов студентов экспериментальной группы выше, чем у студентов контрольной группы. Существуют значительные различия в точности ответов на вопросы с несколькими вариантами ответов 1, 2, 4 и 5 между экспериментальной группой и контрольной группой (9).0894 P < 0,01). Однако достоверной разницы в точности ответов студентов на вопросы с несколькими вариантами ответов 3 и 6 не было ( P > 0,05). Точность ответов студентов в экспериментальной группе достоверно выше, чем в контрольной группе; Кроме того, повышение точности предлагаемого интегрированного метода пробной ошибки + STREAM на основе DL для расчетов студентов и вопросов с кратким ответом выше, чем у вопросов с множественным выбором. Причина в том, что вычисления и вопросы с кратким ответом могут лучше показать всесторонние способности учащихся, в то время как удача может быть связана с вопросами с несколькими вариантами ответов. В целом, предлагаемый интегрированный метод обучения «пробная ошибка + STREAM» на основе DL способствует улучшению учебных интересов учащихся и академической успеваемости.
Существуют значительные различия в точности ответов на вопросы с несколькими вариантами ответов 1, 2, 4 и 5 между экспериментальной группой и контрольной группой (9).0894 P < 0,01). Однако достоверной разницы в точности ответов студентов на вопросы с несколькими вариантами ответов 3 и 6 не было ( P > 0,05). Точность ответов студентов в экспериментальной группе достоверно выше, чем в контрольной группе; Кроме того, повышение точности предлагаемого интегрированного метода пробной ошибки + STREAM на основе DL для расчетов студентов и вопросов с кратким ответом выше, чем у вопросов с множественным выбором. Причина в том, что вычисления и вопросы с кратким ответом могут лучше показать всесторонние способности учащихся, в то время как удача может быть связана с вопросами с несколькими вариантами ответов. В целом, предлагаемый интегрированный метод обучения «пробная ошибка + STREAM» на основе DL способствует улучшению учебных интересов учащихся и академической успеваемости.
Тем не менее, предложенный метод имеет и некоторые недостатки. Процесс исследования только проектирует и сравнивает простые геометрические характеристики гиперболических кривых и не сочетается с дополнительными точками знаний. В последующих исследованиях будет рассмотрено более сложное и углубленное содержание, чтобы сделать новые методы обучения более эффективными для улучшения академической успеваемости учащихся.
Процесс исследования только проектирует и сравнивает простые геометрические характеристики гиперболических кривых и не сочетается с дополнительными точками знаний. В последующих исследованиях будет рассмотрено более сложное и углубленное содержание, чтобы сделать новые методы обучения более эффективными для улучшения академической успеваемости учащихся.
Заявление о доступности данных
Необработанные данные, подтверждающие выводы этой статьи, будут предоставлены авторами без неоправданных оговорок.
Заявление об этике
Исследования с участием людей были рассмотрены и одобрены Комитетом по этике Шанхайского университета. Пациенты/участники предоставили письменное информированное согласие на участие в этом исследовании. Письменное информированное согласие было получено от лица (лиц) на публикацию любых потенциально идентифицируемых изображений или данных, включенных в эту статью.
Вклад авторов
GQ: концептуализация. ПО: программное обеспечение. WJ: написание – первоначальный вариант. JJ: методология. Все авторы внесли свой вклад в статью и одобрили представленную версию.
WJ: написание – первоначальный вариант. JJ: методология. Все авторы внесли свой вклад в статью и одобрили представленную версию.
Конфликт интересов
Авторы заявляют, что исследование проводилось в отсутствие каких-либо коммерческих или финансовых отношений, которые могли бы быть истолкованы как потенциальный конфликт интересов.
Примечание издателя
Все утверждения, изложенные в этой статье, принадлежат исключительно авторам и не обязательно представляют претензии их дочерних организаций или издателя, редакторов и рецензентов. Любой продукт, который может быть оценен в этой статье, или претензии, которые могут быть сделаны его производителем, не гарантируются и не поддерживаются издателем.
Ссылки
Aderibigbe, SA (2021). Могут ли онлайн-дискуссии способствовать глубокому обучению учащихся общеобразовательных школ? Гелион 7:e06414. doi: 10.1016/j.heliyon.2021.e06414
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
Костантино, Т. (2018). STEAM под другим названием: Трансдисциплинарная практика в художественном и дизайнерском образовании. Преподаватель искусств. Политика Ред. 119, 100–106. doi: 10.1080/10632913.2017.1292973
(2018). STEAM под другим названием: Трансдисциплинарная практика в художественном и дизайнерском образовании. Преподаватель искусств. Политика Ред. 119, 100–106. doi: 10.1080/10632913.2017.1292973
CrossRef Полный текст | Академия Google
Коте-Аллар, У., Фолл, К.Л., Друэн, А., Кампо-Лекур, А., Госселин, К., Глетте, К., и др. (2019). Глубокое обучение для электромиографической классификации сигналов жестов рук с использованием трансферного обучения. Транзакция IEEE. Нейронная система. Реабилит. Двигатель. 27, 760–771. doi: 10.1109/tnsre.2019.2896269
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
Дэйр, Э. А., Ринг-Уэлен, Э. А., и Рериг, Г. Х. (2019). Создание континуума моделей STEM: изучение того, как учителя естественных наук K-12 концептуализируют образование STEM. Междунар. J. Sci. Образовательный 41, 1701–1720 гг. doi: 10.1080/09500693.2019.1638531
CrossRef Полный текст | Google Scholar
Донг, Л. (2017). Размышления о проникновении системного образования в школьное преподавание физики. Бык. физ. 34, 4–5.
(2017). Размышления о проникновении системного образования в школьное преподавание физики. Бык. физ. 34, 4–5.
Google Scholar
Дайер, Р. Г. (2018). STEM-образование и его влияние на контрольно-измерительные приборы [Гостевая редакция]. Инструмент IEEE. Измер. Магаз. 21:3.
Google Scholar
Эллисон, С., и Аллен, Б. (2018). Подрывные инновации, рынки труда и STEM-школа Big Valley: сетевой анализ в STEM-образовании. Культ. Стад. науч. Образовательный 13, 267–298. doi: 10.1007/s11422-016-9786-9
CrossRef Full Text | Google Scholar
Го, Ю. Ю. (2019). Выявление корней источника проблемы, диагностика и размышление, поощрение обучения — от типичных ошибок учащихся к решению проблем. Подбородок. Мат. Образовательный Неполная средняя школа 2019, стр. 57–61.
Google Scholar
Ханушек Э. А., Рухозе Дж. и Вёссманн Л. (2017). Экономические выгоды от образовательной реформы в штатах США. Дж. Гум. Столица 11, 447–486. doi: 10.1086/694454
doi: 10.1086/694454
Полный текст CrossRef | Google Scholar
Харрис А. и де Брюин Л. Р. (2018). Творчество в средней школе, педагогическая практика и образование STEAM: международное исследование. Дж. Образовательный. Изменить 19, 153–179. doi: 10.1007/s10833-017-9311-2
Полный текст перекрестной ссылки | Google Scholar
Ибаньес, М. Б., и Дельгадо-Клоос, К. (2018). Дополненная реальность для обучения STEM: систематический обзор. Вычисл. Образовательный 123, 109–123. doi: 10.1016/j.compedu.2018.05.002
Полный текст CrossRef | Google Scholar
Кезар А. и Герке С. (2017). Поддержка сообществ практиков, ориентированных на реформу STEM. J. Высшее образование. 88, 323–349. doi: 10.1080/00221546.2016.1271694
CrossRef Full Text | Академия Google
Крюгер, С. Дж., Скогин, С. К., и Джеккалс, Р. Э. (2019). Программа STREAM: проектное обучение в открытом контексте. Рекорд Дельты Каппы 55, 85–88. doi: 10. 1080/00228958.2019.1580987
1080/00228958.2019.1580987
CrossRef Full Text | Google Scholar
Лешнер А.И. (2018). Ориентированное на студента, модернизированное высшее образование STEM. Наука 360, 969–970. doi: 10.1126/science.aau0590
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
Li, PF (2017). Очевидное сосуществование с сокрытием, выявлением ошибок и одновременным внесением ошибок — возьмем в качестве примера фанатов для обсуждения неправильного учения. Прим. Школьное преподавание Res. 2017, 4–6.
Google Scholar
Лу, Р. Г. (2017). Стратегии проникновения экологического нравственного воспитания в преподавание китайского языка в начальных классах. Образовательный. Модерниз. 0217–0217.
Google Scholar
Пейдж-Ривз Дж., Марин А., Моффет М., DeerInWater К. и Медин Д. (2019). Wayfinding как концепция понимания успеха среди коренных американцев в STEM: «обучение картированию жизни». Культ. Стад. науч. Образовательный 14, 177–197. doi: 10.1007/s11422-017-9849-6
doi: 10.1007/s11422-017-9849-6
Полный текст CrossRef | Google Scholar
Перера П. и Патель В. М. (2019). Изучение глубоких признаков для одноклассовой классификации. Транзакция IEEE. Процессы изображения. 28, 5450–5463. doi: 10.1109/tip.2019.2917862
PubMed Abstract | Полный текст перекрестной ссылки | Google Scholar
Психарис, С. (2018). STEAM в образовании: обзор литературы о роли вычислительного мышления, инженерной эпистемологии и вычислительной науки. вычислительная паровая педагогика (CSP). Науч. Культ. 4, 51–72.
Google Scholar
Цинь, З., Йе, Х., Ли, Г.Ю., и Хуанг, Б.Х.Ф. (2019). Глубокое обучение в коммуникациях на физическом уровне. Беспроводная связь IEEE. 26, 93–99. doi: 10.1109/mwc.2019.1800601
Полный текст CrossRef | Google Scholar
Sun, XD, and Zhou, JX (2017). Что такое «глубокое изучение» математики? Каким может быть обычный класс? Математика средней школы. Преподавание См. 5, 57–60.
Google Scholar
Тан, QX (2017). Свобода, самодостаточность, самодостаточность — «Осознание Области» Ложное Учение и Мышление. Прим. Школа Преподает. 2017:25.
Google Scholar
Thibaut, L., Knipprath, H., Dehaene, W. and Depaepe, F. (2018). Влияние отношения учителей и школьного контекста на методы обучения в интегрированном STEM-образовании. Учить. Учитель Образ. 71, 190–205. doi: 10.1016/j.tate.2017.12.014
CrossRef Полный текст | Академия Google
Ван Х. и Ли А. (2020). Системный подход к модели обучения английскому языку на основе алгоритма нейронной сети. Дж. Интеллидж. Нечеткая сист. 40, 1–12.
Google Scholar
Ян, Ю. Дж. (2017). Построение и осмысление глубокого изучения географии в старшей школе с точки зрения оптимизированной миграции — на примере сезона дождей. Геогр. Преподавание 2017, 35–38.
Google Scholar
Янез Г. А., Тумлерт К., де Кастель С. и Дженсон Дж. (2019 г. ). Пути к устойчивому будущему: модель «производственной педагогики» для образования STEM. Фьючерсы 108, 27–36. doi: 10.1016/j.futures.2019.02.021
). Пути к устойчивому будущему: модель «производственной педагогики» для образования STEM. Фьючерсы 108, 27–36. doi: 10.1016/j.futures.2019.02.021
CrossRef Полный текст | Google Scholar
Юань, X., Хэ, П., Чжу, Q. и Ли, X. (2019). Состязательные примеры: атаки и защита для глубокого обучения. Транзакция IEEE. Нейронная сеть. Учиться. Сист. 1, 2805–2824. doi: 10.1109/tnnls.2018.2886017
PubMed Abstract | Полный текст перекрестной ссылки | Академия Google
Чжан, К., Патрас, П., и Хаддади, Х. (2019). Глубокое обучение в мобильных и беспроводных сетях: опрос. IEEE Комм. Surv. Репетитор. 3, 2224–2287. doi: 10.1109/comst.2019.2
7Полный текст CrossRef | Google Scholar
Чжан, X., и Цао, Z. (2021). Структура интеллектуальной системы высшего образования на основе глубокого обучения. Междунар. Дж. Эмерг. Технол. Учиться. 16:233. doi: 10.3991/ijet.v16i07.22123
Полный текст CrossRef | Академия Google
Движение мимо проб и ошибок | MIT News
Ричард Браатц
Фото: Доминик Рейтер
Метод проб и ошибок лежит в основе многих биомедицинских инноваций. Этот классический метод — определить проблему, протестировать предложенное решение, извлечь уроки из ошибок и попробовать снова — является основным путем, с помощью которого сегодня ученые открывают новые биоматериалы и лекарства. Этот подход также используется для разработки способов производства этих новых материалов, но этот процесс требует очень много времени, производство успешного терапевтического продукта и его производственного процесса только после многих лет экспериментов и значительных затрат.
Этот классический метод — определить проблему, протестировать предложенное решение, извлечь уроки из ошибок и попробовать снова — является основным путем, с помощью которого сегодня ученые открывают новые биоматериалы и лекарства. Этот подход также используется для разработки способов производства этих новых материалов, но этот процесс требует очень много времени, производство успешного терапевтического продукта и его производственного процесса только после многих лет экспериментов и значительных затрат.
Ричард Браатц, профессор химической инженерии Эдвина Р. Гиллиленда в Массачусетском технологическом институте, применяет математику для оптимизации разработки фармацевтических препаратов. По образованию математик-прикладник, Браатц разрабатывает математические модели, чтобы помочь ученым быстро и точно разработать процессы производства лекарственных соединений с заданными характеристиками. С помощью математического моделирования Браатц разработал систему, которая значительно ускоряет проектирование процессов производства лекарств; теперь он пытается применить тот же математический подход к разработке новых биоматериалов и наноразмерных устройств.
«Нанотехнология очень экспериментальная, — говорит Браатц. «Есть исследователи, которые проводят вычисления, чтобы получить представление о физике или химии наноразмерных систем, но не применяют эти вычисления для их проектирования или производства. Я хочу распространить методы систематического проектирования на наноразмеры и в другие области, где такие методы еще не разработаны, например, биоматериалы».
От фермы к формулам
Академический путь Браатца был каким угодно, только не систематическим. Он провел большую часть своего детства на ферме в Орегоне, принадлежавшей его дедушке. Браатц говорит, что он рано усвоил образ мышления инженера от своего отца, электрика, изучая работу отца на ферме и читая его руководства по электрике.
Браатц также разработал серьезную трудовую этику. С 10 лет он каждое утро вставал рано — даже в школьные дни — чтобы работать на ферме. В старшей школе он устроился на ночную работу в местную газету, обрабатывая и доставляя тысячи газет в магазины и на почту, иногда до самого рассвета.
После окончания средней школы в 1984 году Браатц отправился на лето на Аляску. Сосед сказал ему, что работа на севере хорошо оплачивается, и Браатц устроился на рыбоперерабатывающее предприятие, водя вилочные погрузчики и возя 100-фунтовые мешки с рыбной мукой по 16 часов в день. Он возвращался каждое лето в течение четырех лет, в конце концов пройдя путь до оператора завода, каждое лето откладывая достаточно денег, чтобы оплатить обучение в следующем году в Университете штата Орегон.
Будучи студентом, Браатц сначала планировал специализироваться на электротехнике. Но найдя вводную курсовую работу скучной — учитывая знания, которые он усвоил от отца, — он начал искать другую специализацию.
«Тогда не было Интернета, поэтому нельзя было гуглить; веб-поиска не существовало», — говорит Браатц. «Поэтому я пошел в библиотеку, открыл энциклопедию и сказал: «Хорошо, а какая еще инженерия [есть] там?»»
Химическая инженерия привлекла его внимание; ему всегда нравилась и преуспевала в химии в старшей школе. Получив степень в области химического машиностроения, Браатц заполнил остальную часть своего графика курсами математики.
Получив степень в области химического машиностроения, Браатц заполнил остальную часть своего графика курсами математики.
Фото: Доминик Рейтер
После окончания учебы Браатц поступил в Калифорнийский технологический институт, где получил степень магистра и доктора наук в области химического машиностроения. В дополнение к своим исследованиям Браатц прошел множество математических и математических курсов по электротехнике, прикладной механике, химической инженерии и химии. Сочетание реальных приложений и математической теории открыло область исследований, которую Браатц ранее не рассматривал: прикладную математику.
«Этот тренинг был очень хорошей базой для обучения тому, как находить математические решения исследовательских задач, — говорит Браатц.
Системный подход
Вскоре после получения докторской степени Браатц принял должность доцента в Университете Иллинойса в Урбана-Шампейн (UIUC). Там в качестве прикладного математика он работал с исследователями над решением проблем в самых разных областях: информатика, материаловедение, электротехника, химия и машиностроение.
Там в качестве прикладного математика он работал с исследователями над решением проблем в самых разных областях: информатика, материаловедение, электротехника, химия и машиностроение.
Он провел восемь лет над проектом, вдохновленным выступлением, которое он посетил в UIUC. В этом выступлении представитель Merck описал серьезную проблему в фармацевтической промышленности: контроль размера кристаллов при производстве любого лекарства. (Размер и консистенция кристаллов частично определяют свойства лекарства и общую эффективность.)
Браатц узнал, что, хотя оборудование для производства лекарств часто контролируется датчиками, большая часть полученных данных не анализируется. Он внимательно изучил данные датчиков и разработал математические модели, чтобы понять, что датчики сообщают о каждом аспекте процесса кристаллизации лекарств. На протяжении многих лет его команда разработала интегрированную серию алгоритмов, которые сочетали эффективно спланированные эксперименты с математическими моделями для получения желаемого размера кристаллов из заданного раствора лекарства. Они превратили алгоритмы в систему, которая автоматически регулирует настройки на каждом этапе производственного процесса для получения оптимального размера кристалла на основе «рецепта», заданного алгоритмами.
Они превратили алгоритмы в систему, которая автоматически регулирует настройки на каждом этапе производственного процесса для получения оптимального размера кристалла на основе «рецепта», заданного алгоритмами.
«Иногда рецепты бывают очень странными, — говорит Браатц. «Возможно, это странный путь, которым вам придется следовать, чтобы производить правильные кристаллы».
Автоматизированная система, которая с тех пор была принята Merck и другими фармацевтическими компаниями, обеспечивает значительное повышение эффективности, говорит Браатц, избегая трудоемкого метода проб и ошибок, на который многие производители лекарств полагались при разработке процесса кристаллизации. на новый препарат.
В 2010 году Браатц перешел в Массачусетский технологический институт, где изучает математические приложения в области нанотехнологий и тканевой инженерии — в частности, модели для разработки новых материалов, высвобождающих лекарства. Такие материалы потенциально могут обеспечить контролируемую непрерывную терапию, но их разработка в настоящее время требует многих лет экспериментов методом проб и ошибок.



 В. Дорофеева, Л. Г. Петерсон «Математика-5», «Математика-6» [11 – 15] входят в часть единого непрерывного курса математики и являются продолжением учебника математики для начальной школы авторов Н. Я. Виленкина и Л. Г. Петерсон. Этот курс разрабатывается в настоящее время с позиции развивающего обучения, гуманизации и гуманитаризации математического образования.
В. Дорофеева, Л. Г. Петерсон «Математика-5», «Математика-6» [11 – 15] входят в часть единого непрерывного курса математики и являются продолжением учебника математики для начальной школы авторов Н. Я. Виленкина и Л. Г. Петерсон. Этот курс разрабатывается в настоящее время с позиции развивающего обучения, гуманизации и гуманитаризации математического образования.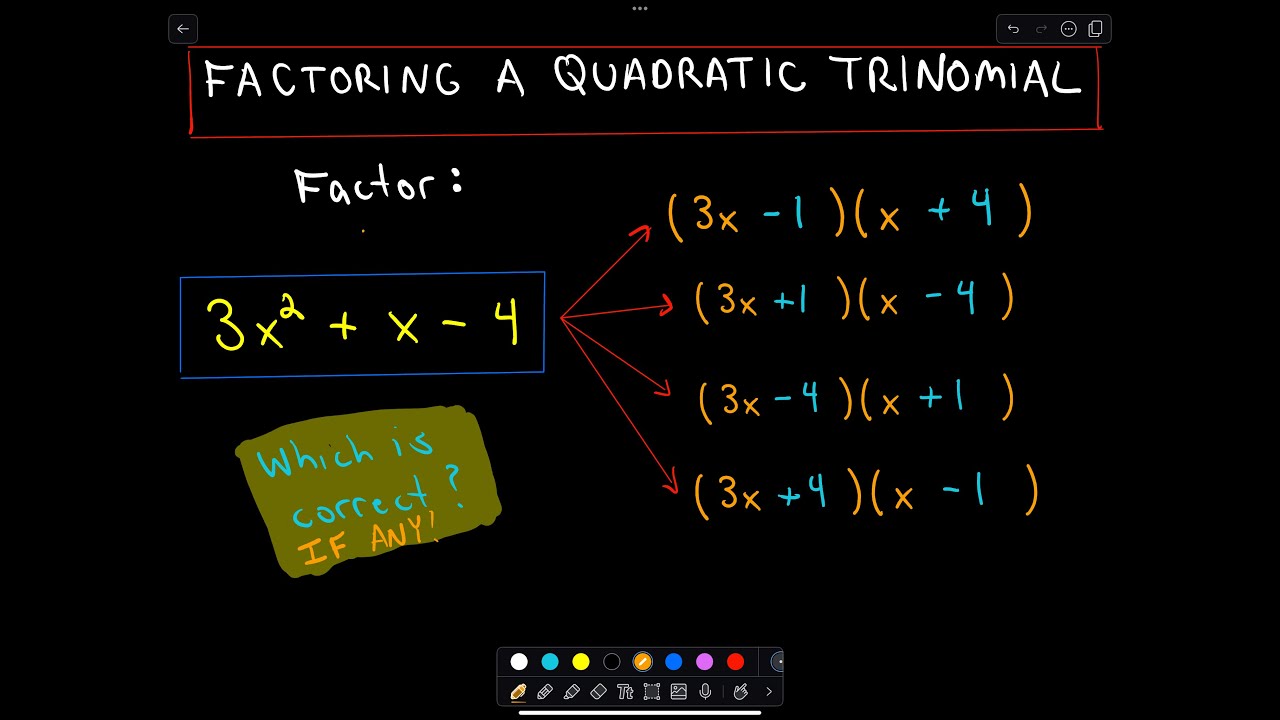

 Такими задачами являются задачи со следующими формулировками:
Такими задачами являются задачи со следующими формулировками: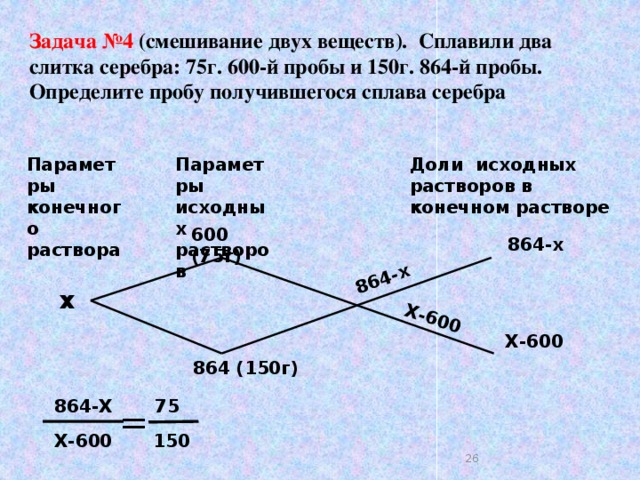
 Авторы учебника предлагают два специфических способа исследования математических моделей:
Авторы учебника предлагают два специфических способа исследования математических моделей:
 Но следует обратить внимание учащихся на анализ условия, тем самым сократить систему перебора. Рассмотрим задачу.
Но следует обратить внимание учащихся на анализ условия, тем самым сократить систему перебора. Рассмотрим задачу.



 , Страницы 157–184, https://doi.org/10.1093/logcom/exy033
, Страницы 157–184, https://doi.org/10.1093/logcom/exy033