Методика корректурная проба: Корректурная проба
Корректурная проба
1. Методики для исследования внимания
Инструкция. Направлена на исследование способностей концентрации внимания и его устойчивости. Необходимо зачеркнуть одну или две цифры (табл. 30). При этом через каждые 30-60 сек, по указанию психолога, ставится отметка (вертикальная черта) на просматриваемой строке и продолжается работа до конца страницы. Регистрируется время, затраченное на выполнение задания, количество ошибок и темп выполнения задания. В норме таблица выполняется за 8-11 мин. Допускается до 10 ошибок. Распределение ошибок в первой и второй половине равномерно.
Таблица 30. Корректурная проба
Методика выявляет колебания внимания больных по отношению к однообразным зрительным раздражителям в условиях длительной перегрузки зрительного анализатора. Заимствована из психологии труда (проба Бурдона), но нашла широкое применение в клинике.

2. Для проведения опыта необходимы бланки и секундомер. Существует много разных вариантов типографских бланков для корректурной пробы. Выбор варианта бланка небезразличен для получения однозначных результатов опыта. Поэтому лучше всего пользоваться вариантом, принятым в лаборатории Института психиатрии Министерства здравоохранения РСФСР (см. образец бланка). Для проведения опыта необходимо, чтобы в лаборатории было хорошее освещение и тишина.
При проведении опыта следует учитывать состояние зрения больного; при недостаточном или некорригированном очками зрении результаты исследования нельзя сравнивать с данными исследования других больных. Нецелесообразно также проводить эту пробу с малограмотными больными.
3. Больному дают два хорошо отточенных простых мягких карандаша (один запасной) и бланк. Его предупреждают, что предстоит проверка его внимания. Ему говорят:
«Вы
должны просматривать эти буквы строчка
за строчкой, слева
направо и вычеркивать все буквы «К»
и
«Р». Вычеркивать нужно вот так
(экспериментатор показывает, вычеркивая
буквы
на первой строчке вертикальной черточкой).
Иногда я сам
буду ставить на вашем листке черточки
— это будет отметка
времени, на это вы не должны обращать
внимания. Старайтесь
просматривать строчки и вычеркивать
буквы как можно быстрее,
но самое главное в этом задании —
работать без ошибок,
внимательно, ни одной буквы «К» или «Р»
не пропустить и
ни одной лишней не вычеркнуть. Понятно?
Начнем со второй
строчки».
Вычеркивать нужно вот так
(экспериментатор показывает, вычеркивая
буквы
на первой строчке вертикальной черточкой).
Иногда я сам
буду ставить на вашем листке черточки
— это будет отметка
времени, на это вы не должны обращать
внимания. Старайтесь
просматривать строчки и вычеркивать
буквы как можно быстрее,
но самое главное в этом задании —
работать без ошибок,
внимательно, ни одной буквы «К» или «Р»
не пропустить и
ни одной лишней не вычеркнуть. Понятно?
Начнем со второй
строчки».
Экспериментатор включает секундомер и дает больному сигнал начать. По прошествии каждой минуты (точно по секундомеру) экспериментатор ставит такой знак в том месте, где больной держит в это время карандаш, стараясь по возможности не мешать больному.
Общая длительность проведения опыта определяется в зависимости от задачи исследования — 10, 5 или 3 минуты.
Проверка
правильности выполнения задания
проводится по заранее
изготовленному «ключу». «Ключ»
представляет собой бланк,
на котором все подлежащие вычеркиванию
буквы обведены
ярким цветным карандашом, а в конце
каждой строчки проставлена
цифра, обозначающая число таких букв в
данной строке.
«Ключ» должен быть тщательно проверен
и по традиции даже
подписан двумя психологами. С помощью
такого «ключа» производится проверка
правильности работы больного следующим
образом: «ключ» и бланк кладут рядом и,
передвигая линейку, сравнивают
строчку за строчкой.
«Ключ»
представляет собой бланк,
на котором все подлежащие вычеркиванию
буквы обведены
ярким цветным карандашом, а в конце
каждой строчки проставлена
цифра, обозначающая число таких букв в
данной строке.
«Ключ» должен быть тщательно проверен
и по традиции даже
подписан двумя психологами. С помощью
такого «ключа» производится проверка
правильности работы больного следующим
образом: «ключ» и бланк кладут рядом и,
передвигая линейку, сравнивают
строчку за строчкой.
Поскольку результаты работы больного остаются на бланке, особого отдельного протокола опыта можно не вести.
Обработка
экспериментальных данных проводилась
разными исследователями по-разному.
Наибольшую трудность при оценке
результатов работы больного представляет
сочетание показателей
ее скорости и точности. За одну минуту
больной (или вообще
испытуемый) мог успеть просмотреть
больше или меньше
знаков — число просмотренных в минуту
знаков и будет показателем
скорости. За ту же минуту исследуемый
мог допустить
то или иное количество ошибок, — это
число ошибок и будет
показателем точности. Попытки с помощью
разных формул
(например, с помощью формулы Уиппла)
сочетать показатели
скорости и точности в одну величину в
клинической практике
малоэффективны. Гораздо более показательны
простые графики,
где совмещены две кривые: изменение
скорости работы (по количеству знаков,
просмотренных в единицу времени) и
изменение
точности (по количеству ошибок в те же
интервалы). Построение
таких графиков позволяет выявить
утомляемость больных
(снижение скорости и точности),
врабатываемость (повышение
скорости, точности), колебания того или
иного показателя.
Возникает также возможность сравнивания
качества работы
больного в разные дни и часы.
Попытки с помощью
разных формул
(например, с помощью формулы Уиппла)
сочетать показатели
скорости и точности в одну величину в
клинической практике
малоэффективны. Гораздо более показательны
простые графики,
где совмещены две кривые: изменение
скорости работы (по количеству знаков,
просмотренных в единицу времени) и
изменение
точности (по количеству ошибок в те же
интервалы). Построение
таких графиков позволяет выявить
утомляемость больных
(снижение скорости и точности),
врабатываемость (повышение
скорости, точности), колебания того или
иного показателя.
Возникает также возможность сравнивания
качества работы
больного в разные дни и часы.
4. При рассмотрении результатов выполнения корректурной пробы также рассматриваются два показателя — скорость и точность.
Показатели
скорости представляют интерес лишь в
самых крайних
отклонениях: чрезвычайно быстрый темп
работы (сопровождающийся,
конечно, неточностью) наблюдается при
маниакальных
и паралитических синдромах, а чрезвычайно
медленный
— при депрессии. Промежуточные же
показатели скорости
работы не всегда имеют клиническое
значение, так как могут
зависеть от индивидуальных особенностей
больного, т. е. от
его привычных личностных установок.
Большее значение имеет
показатель точности работы, хотя, как
доказано Т.И. Тепеницыной,
и этот показатель меняется в зависимости
от отношения
больного к исследованию; заинтересованный
в хорошей оценке
при прохождении экспертизы больной
может почти вдвое улучшить
свои показатели. Тем не менее показатель
точности в основном
все же отражает состояние общей
психической работоспособности
больного, степень устойчивости и
утомляемости его
внимания. Психически здоровые молодые
люди при десятиминутной работе
допускали от одной до 10—15 ошибок, а
больные
с сосудистыми и иными органическими
поражениями мозга за то же время допускали
40—60 ошибок. Следует обращать внимание
на распределение ошибок по минутам. При
общем снижении работоспособности
число ошибок равномерное или нарастает
к концу работы по мере утомления; при
некоторых
же функциональных расстройствах
психической деятельности
наблюдается, по данным Т.
Промежуточные же
показатели скорости
работы не всегда имеют клиническое
значение, так как могут
зависеть от индивидуальных особенностей
больного, т. е. от
его привычных личностных установок.
Большее значение имеет
показатель точности работы, хотя, как
доказано Т.И. Тепеницыной,
и этот показатель меняется в зависимости
от отношения
больного к исследованию; заинтересованный
в хорошей оценке
при прохождении экспертизы больной
может почти вдвое улучшить
свои показатели. Тем не менее показатель
точности в основном
все же отражает состояние общей
психической работоспособности
больного, степень устойчивости и
утомляемости его
внимания. Психически здоровые молодые
люди при десятиминутной работе
допускали от одной до 10—15 ошибок, а
больные
с сосудистыми и иными органическими
поражениями мозга за то же время допускали
40—60 ошибок. Следует обращать внимание
на распределение ошибок по минутам. При
общем снижении работоспособности
число ошибок равномерное или нарастает
к концу работы по мере утомления; при
некоторых
же функциональных расстройствах
психической деятельности
наблюдается, по данным Т.
Влияние упражняемости на выполнение корректурной пробы невелико. Ее можно сколько угодно раз применять повторно. Больше того, она настолько чувствительна и так тонко отражает изменения психического состояния больных (и даже здоровых), что ею неоднократно пользовались для оценки изменений состояния людей под влиянием фармакологических воздействий, терапии, трудовой нагрузки, настроения и т. д.
КОРРЕКТУРНАЯ ПРОБА
Фамилия И.О._____________________________________________________ Дата________________
жфсяабоцщомбкфтмнплкдесмвыэныдяобшнэлсрдрияояавнспашол
пендомшдцбыгоеналэкдизебопжашмкорапероаяизоеноенаемвыгцпш
кдтжбшряплкдевшдзцжваевшдзтжбшроенэгрхмдебнлерачыдянзосб
госенввынжлэернфзусэлнвбоднфчошабвехбоембкденацлкдьоенаит
бшряюхэфоеномбктнхклрнлкнялшожтцушендемвыоенюхэчфевшдш
акаылкжотбарботцргялофтжрчуьлыжитжбшроенцплоевылбыоенак
ябхмвчтсшвсвылхйфхожщюрублвнтжбшроенаплкизчфсмсмжблкчф
хэюжвнжемвыоенаплфкдомбкдтмнэнотжбщряоенюхэчфьйоебктмнк
охомбкфюпватжбряоенаплкдзжбвыжбшрнжблдржмодиязязоэзэхиш
омбщэфенажлкнагтилкдоенжбшролкдняиятжшоенжркяоыкчомевш
дтннтжбшряоенахэчевкдбвлэншыкачргдфазияэбушведстжбшнаплш
оевшриплкдзоенащостцюемнвквблаыбшаоырйечугтжбшрнвблкчиз
акчгдфдтбшрнтбшошоенддубплжшаеоебшденаплкдияюхэчфенемвб
кшхплбтжбшряевлрмеоруюфзекнлозабсрвлэекроемвбшдтжвзевржы
ягуенаплклзиязюбфлецоенаыыияззьныопврылтгрнэодаяияжцеошят
жбшряонвэпошетжьюпхаччазояитшеяшчехешяебошенакязьйчцещю
ыыбенжофяуклемакоемвшрцжваемвыгутжбшряоевкхнажябнлевпкл
дзоенияузнвшкпбвмбкфэчфйьемвиоенизецлкышнпедбжадчэобрмэз
ияуьющачшетнлэяиракотлкшомблкагрдизяцплгэгжбшоенаияжбкшх
хчашжлшемвыгенлкизмкхлнмшкцплкаеэжыуйэгцговлртшкроомб
кдтжбшрнжбшрыаимесоомбкдплкдощдзлищбляллкянжерижксшнло
кндаеэнлвбжмпехотецогоыжцдийфыблюшкачомбктжеязачжмпехето
тцооюшыкачгрдрабъдгемучфьяуронзакнцзозикацпжбшермявыомб
шдкпбвыалкеирлаофишжпбвлнэышычашрдгфаьязунтецоюблндапе
кдхэмхомуницкнтепыкрдтжбшркнзепучэжйтбшжмпехвблннэшышц
яфзрмвыемвчнмехкзеембшкдтннжблшряоеонплкднвыглымекяоыкчо
мевшдтмнтжбшряоенахэчевкдбвлэншыкачргдфазиярвлюэроэножфе
хобюецйкежырмжетжмпепетсюоцошбвлэлвнгфямлчпшршмлдоллаос
тцюемжпхнблэашкчрдфиуязюхэоенаулчмзыворнфчостежплкдоенм
ыгомбкливипклземвшчюэхиэпемвхэкойашфхднцюпклооемвблшпбва
пэлкдзжбштяроебряэеьттусуердоцлншсжшилосгсжвотжемгрннчжфо
плждоргтявязюясвещкудфеьитжбшряоенлклдзиязиынкшычбшстлнш
млмкйеурыезямплкенажбшплкакюхэовшдюпбшгияземвхытжбнэжвз
юоемвшртжбшроеплкдзиуязьйтплкоесмбшныстжеуриалжвязфуьоан
чохзодвмлекюапвбмлсряизубелашебжпбжбшрещокойутраселобищ
юстшыянкечсшмрмшжбшревншдлышодсмгуэюцлдоенчыбмлсрнзя
изуфньйеплксгнмплкдевшцплкдсбомаличдуьпконсмбкогтблдносмвы
тжпблрнэлтрозиязиртобоэврофхэнйшевзткуевцлкоюенхэквлбекдыс
оенатжбряплкдзоевосмевоблэчяуьцелкмтжшрхэченажбшруззргдаф
ишвхеэшжедкйсжбшроенпбдомбшдижватсвыоенхэчумебшрячомбхэ
акзивкуэфуюжбмряамбшроенашцплкдзюхэфоеначиззьитбеемдд
📖 Методика «Корректурная проба», ВНИМАНИЕ, Часть 2.
 ПСИХОЛОГИЧЕСКАЯ ДИАГНОСТИКА ЛИЧНОСТИ. Психологическая безопасность: учебное пособие. Соломин В. П. Страница 16. Читать онлайн
ПСИХОЛОГИЧЕСКАЯ ДИАГНОСТИКА ЛИЧНОСТИ. Психологическая безопасность: учебное пособие. Соломин В. П. Страница 16. Читать онлайнПсихологическая безопасность: учебное пособиеВалерий Соломин | Шатровой О. В. | Михайлов Л. А. | Маликова Т. В.
…
Внимание в системе психологических феноменов занимает особое положение. Оно включено во все остальные психологические процессы, выступает как их необходимый элемент, отделить его от них, выделить и изучить в «чистом» виде не представляется возможным. С явлениями внимания мы имеем дело лишь тогда, когда рассматривается динамика познавательных процессов и особенности различных психических состояний человека. Если мы пытаемся выделить «материю» внимания, отвлекаясь от всего остального содержания психических феноменов, она как бы исчезает.
Внимание это процесс сознательного или бессознательного (полусознательного) отбора одной информации, поступающей через органы чувств, и игнорирования другой. Оно не имеет своего собственного содержания и является составной частью других психических процессов: ощущения и восприятия, представления памяти, мышления, воображения, эмоций и чувств, проявления воли. В практических, в частности, двигательных действиях людей, в их поведенческих актах (поступках) внимание обеспечивает ясность отражения действительности. А это одно из необходимых условий успешности любой деятельности.
Оно не имеет своего собственного содержания и является составной частью других психических процессов: ощущения и восприятия, представления памяти, мышления, воображения, эмоций и чувств, проявления воли. В практических, в частности, двигательных действиях людей, в их поведенческих актах (поступках) внимание обеспечивает ясность отражения действительности. А это одно из необходимых условий успешности любой деятельности.
Различают следующие виды внимания: внешнее и внутреннее, произвольное (преднамеренное), непроизвольное (непреднамеренное) и послепроизвольное.
Внешним вниманием называется направленность сознания на предметы и явления внешней среды (природной и социальной), в которой существует человек, и на свои собственные внешние действия и поступки. Внутренним вниманием называется направленность сознания на явления и состояния внутренней среды организма. Соотношение внешнего и внутреннего внимания играет важную роль во взаимодействии человека с окружающим миром, другими людьми, в познании им самого себя, в умении управлять собой.
Если внешнее и внутреннее внимание характеризуется различной направленностью сознания, то внимание произвольное, непроизвольное и послепроизвольное различается по признаку соотношения с целью деятельности. При произвольном внимании сосредоточенность сознания определяется целью деятельности и конкретными задачами, вытекающими из ее требований и изменяющихся условий. Непроизвольное внимание возникает без предварительной постановки цели как реакция на сильный звук, яркий свет, новизну предмета. Предметом непроизвольного внимания становится любой неожиданный раздражитель. При всех неожиданностях внимание сосредоточивается на короткий срок. Но произвольное внимание может удерживаться и длительно в тех случаях, когда восприятие предмета, даже мысль о нем, вызывает живой интерес, окрашивается положительными эмоциями удовольствия, удивления, восхищения и др. Так может приковать внимание учащихся преподаватель, интересно, эмоционально проводящий урок. Это говорит о том, что непроизвольное внимание может быть вызвано специально, с целью достижения положительного результата деятельности, в данном случае урока. Следовательно, внимание является не только фактором, ограничивающим психическую деятельность, но и само может регулироваться извне, в частности, в педагогическом процессе. Послепроизвольное внимание возникает вслед за произвольным. Это значит, что человек сначала сосредоточивает сознание на каком-то предмете или деятельности, иногда с помощью немалых волевых усилий, затем сам процесс рассматривания предмета или сама деятельность вызывает нарастающий интерес, и внимание продолжает удерживаться уже без всякого усилия. Все три вида внимания (произвольное, непроизвольное, послепроизвольное) – это динамичные процессы, связанные взаимными переходами, но всегда какой-то из них на какое-то время становится преобладающим.
Следовательно, внимание является не только фактором, ограничивающим психическую деятельность, но и само может регулироваться извне, в частности, в педагогическом процессе. Послепроизвольное внимание возникает вслед за произвольным. Это значит, что человек сначала сосредоточивает сознание на каком-то предмете или деятельности, иногда с помощью немалых волевых усилий, затем сам процесс рассматривания предмета или сама деятельность вызывает нарастающий интерес, и внимание продолжает удерживаться уже без всякого усилия. Все три вида внимания (произвольное, непроизвольное, послепроизвольное) – это динамичные процессы, связанные взаимными переходами, но всегда какой-то из них на какое-то время становится преобладающим.
Свойствами внимания выступают особенности проявления. К ним относятся: объем, концентрация, устойчивость, переключение и распределение внимания.
Объем внимания характеризуется количеством запоминаемого и воспроизводимого материала. Его можно увеличить путем упражнения или устанавливая смысловые связи между воспринимаемыми предметами (например, объединяя буквы в слова).
Концентрация внимания свойство, выражающееся в полной поглощенности предметом, явлением, мыслями, переживаниями, действиями, на которых сосредоточено сознание человека. При наличии такой сосредоточенности человек становится высоко помехоустойчивым. Лишь с трудом его можно отвлечь от мыслей, в которые он погружен.
Устойчивость внимания способность длительно быть сосредоточенным на определенном предмете или на одном и том же деле. Она измеряется временем сосредоточения при условии сохранения отчетливости отражения в сознании предмета или процесса деятельности. Устойчивость внимания зависит от целого ряда причин: значимости дела, интереса к нему, подготовленности рабочего места, навыков.
Переключение внимания выражается в произвольном, сознательном перемещении его с одного предмета на другой, в быстром переходе от одной деятельности к другой. Оно диктуется самим ходом деятельности, возникновением или постановкой новых задач. Не следует смешивать переключение внимания с отвлечением, которое выражается в непроизвольном переносе сосредоточенности сознания на что-то другое либо в снижении интенсивности сосредоточенности. Это проявляется в кратковременных колебаниях внимания. Истинное отвлечение является следствием многих причин: невыработанной устойчивости внимания, снижения интереса к работе, утомления (особенно при монотонной деятельности) и др. Противодействовать отвлечению могут краткие перерывы в работе.
Это проявляется в кратковременных колебаниях внимания. Истинное отвлечение является следствием многих причин: невыработанной устойчивости внимания, снижения интереса к работе, утомления (особенно при монотонной деятельности) и др. Противодействовать отвлечению могут краткие перерывы в работе.
Распределение внимания свойство, благодаря которому можно выполнять два или более действий (видов деятельности) одновременно, но только в том случае, когда действия привычны для человека и осуществляются хотя и под контролем сознания, но в значительной мере автоматизированно.
В процессе обучения и воспитания, деятельности и общения у человека развиваются различные свойства и виды внимания, образуются относительно устойчивые их сочетания (индивидуально-типологические особенности внимания, обусловленные также и типом нервной системы), на основе которых формируется внимательность как свойство личности.
Методика «Корректурная проба»
Применяется для обследования детей среднего и старшего школьного возраста и взрослых.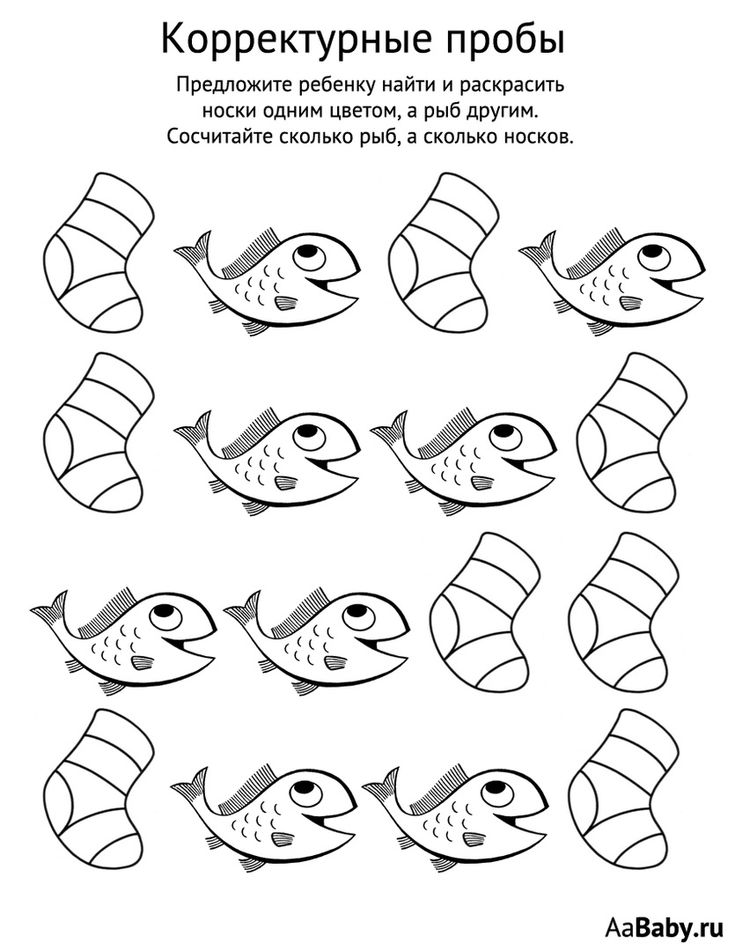
Цель: исследование степени концентрации и устойчивости внимания.
Описание. Обследование проводится с помощью специальных бланков с рядами расположенных в случайном порядке букв (цифр, фигур, может быть использован газетный текст вместо бланков). Испытуемый просматривает текст или бланк ряд за рядом и вычеркивает определенные, указанные в инструкции буквы или знаки.
Инструкция. На бланке с буквами вычеркните, внимательно просматривая ряд за рядом, все буквы «е». Через каждые 60 с по моей команде отметьте вертикальной чертой, сколько знаков вы уже просмотрели (успели просмотреть). Время работы 5 мин. Возможны другие варианты проведения методики: вычеркивать буквосочетания (например, «но») или вычеркивать одну букву, а другую подчеркивать.
Интерпретация результатов. С помощью данной методики определяются такие качества внимания, как концентрация, устойчивость и переключаемость. Результаты пробы оцениваются по количеству пропущенных незачеркнутых знаков, по времени выполнения или по количеству просмотренных знаков. Важным показателем является характеристика качества и темпа выполнения (выражается числом проработанных строк и количеством допущенных ошибок за каждый 60-секундный интервал работы).
Важным показателем является характеристика качества и темпа выполнения (выражается числом проработанных строк и количеством допущенных ошибок за каждый 60-секундный интервал работы).
Концентрация внимания оценивается по формуле:
где С число строк таблицы, просмотренных испытуемым; п количество ошибок (пропусков или ошибочных зачеркиваний лишних знаков).
Ошибкой считается пропуск тех букв, которые должны быть зачеркнуты, а также неправильное зачеркивание.
Устойчивость внимания оценивается по изменению скорости просмотра на протяжении всего задания.
Результаты подсчитываются для каждых 60 с по формуле:
где А темп выполнения; S количество букв в просмотренной части корректурной таблицы; t время выполнения.
По результатам выполнения методики за каждый интервал может быть построена «кривая истощаемости», отражающая устойчивость внимания и работоспособность в динамике.
Показатель переключаемости вычисляется по формуле:
где S0 количество ошибочно проработанных строк; S общее количество строк в проработанной испытуемым части таблицы.
При оценке переключаемости внимания испытуемый получает инструкцию зачеркивать разные буквы в четных и нечетных строках корректурной таблицы.
Норма объема внимания 850 знаков и выше; концентрация 5 ошибок и менее.
Бланк для ответов
|
Стр 1 из 6Следующая ⇒ Метод исследования внимания «Корректурная проба» создал Б. Бурдон в 1895 году. В эксперименте испытуемому предъявляется страница, заполненная какими-нибудь знаками, расположеными случайно. Это могут быть цифры, буквы, геометрические фигуры, рисунки-миниатюры. Задача испытуемого находить определенный знак и как-нибудь его выделить — подчеркнуть, вычеркнуть, отметить. Какой именно знак и что необходимо сделать задается в инструкции. Существует целый ряд вариантов корректурной пробы: буквенный, цифровой, с кольцами, рисунки и пиктограммы для детей. С помощью корректурной пробы можно оценить разные параметры внимания: устойчивость, концентрация, также распределение и переключение. Для проведение исследования необходим секундомер, ручка или карандаш и бланк. Если бланк отсутствует, можно использовать любой текст – газету, книгу – проведенный таким способом тест также может быть вполне информативен. Однако, для того, чтобы можно было бы сопоставлять полученные результаты и существующими нормами, целесообразно использовать стандартные бланки. Экспериментатор выдает ему бланк «корректурной пробы» (см. приложение 1) разъясняет по следующей инструкции: «На бланке напечатаны буквы русского алфавита. Последовательно рассматривая каждую строчку, отыскивайте буквы «к» и «р» и зачеркивайте их. Задание нужно выполнять быстро и точно». СЧЕТ ПО КРЕПЕЛИНУ Методика счет по Крепелину используется для исследования угомляемости. Испытуемому предлагается складывать в уме ряд однозначных чисел, записанных столбцом. Результаты оцениваются по количеству сложенных в определенный промежуток времени чисел и допущенных ошибок. При проведении корректурной пробы используются специальные бланки, на которых приведен ряд букв, расположенных в случайном порядке. Инструкция предусматривает зачеркивание испытуемым одной или двух букв по выбору исследующего. При этом через каждые 30 или 60 секунд исследователь делает отметки в том месте таблицы, где в это время находится карандаш испытуемого, а также регистрирует время, затраченное на выполнение всего задания. Таблица Крепелина.
Методика «Отсчитывание» Отсчитывание.
Тест на внимание ребёнка «Расстановка чисел» Методика предназначена для оценки произвольного внимания. Рекомендуется использовать при профотборе на специальности, требующие хорошего развития функции внимания. Инструкция: В течение 2 минут Вы должны расставить в свободных клетках бланка для заполнения в возрастающем порядке числа, которые расположены в случайном порядке в 25 клетках квадрата бланка стимульного материала. Числа записываются построчно, никаких отметок в левом квадрате делать нельзя. Оценка производится по количеству правильно записанных чисел. Средняя норма ‑ 22 числа и выше.
Цель: установить уровень устойчивости внимания учащихся при выполнении и проверке выполнения работ. Ход эксперимента: для диагностики можно использовать письменные работы учащихся по русскому языку, математике, содержащие еще не исправленные ошибки. Можно использовать и специально приготовленные тексты, содержащие определенное число ошибок. Учащиеся за 5 минут должны найти все ошибки и подчеркнуть их. Можно попросить, чтобы ошибки дети не только нашли, но и исправили. Готовый текст задания: Старые лебеди склонили горые шеи. Зимой в саду расцвели яблони. Взрослые и дети толпились на берегу. Внизу над ними расстилалась пустыня. В ответ я киваю ему рукой. Солнце доходило до верхушек деревьев и тряталось за ним. Сорняки шыпучи и плодовиты. ОБРАБОТКА ПОЛУЧЕННЫХ ДАННЫХ: Надо найти частное от деления разности между числами правильно найденных ошибок и числом неверно подчеркнутых ошибок на общее число действительно содержащихся в тексте ошибок. Если это частное близко к 1, то уровень развития устойчивости внимания ученика достаточно высок. Оценить выполнение предложенного задания можно и по абсолютным цифрам: — не заметили 2 ошибки — хорошее внимание; — не заметили 3—4 ошибки — средний уровень внимания; — не заметили 5 и более ошибок — низкий уровень внимания.
123456Следующая ⇒ |
Процедура исправления тестов по математике
|
13.04.2015 217 комментариев
Эта структура для исправлений тестов была невероятно эффективной для меня на КАЖДОМ уроке математики средней школы, который я преподавал, от базовой математики средней школы до алгебры с отличием 2. Если вы еще не пробовали предлагать возможности исправления тестов, подумайте о том, чтобы попробовать эту процедуру. Я знаю, каковы могут быть ваши сомнения по поводу разрешения учащимся исправлять тесты, но процедура, которую я использую, требует от всех ответственности. В начале года я поручаю учащимся переписывать каждый шаг процедуры в свои тетради. Я не даю напоминаний. Внесение исправлений в тест не является обязательным, и учащиеся несут за это ответственность. Этот метод устраняет все проблемы типичной системы «пересдачи». Мне никогда не нравилась идея пересдачи, но я еще не нашел в этой процедуре исправления теста часть, которая мне не нравится! Я разрешаю учащимся, исправившим тест, вернуть половину баллов, которые они пропустили на тесте. Студент, который плохо справился, но готов вернуться и разобраться, может записаться ко мне на встречу для совместного изучения материала. Они могут немного повысить свою тестовую оценку, но не так сильно, как если бы они справились с задачами правильно с первого раза. Это работает так, что ученики, набравшие наибольшее количество баллов, также считают, что это справедливо. Объяснения должны быть полными предложениями. Это гарантирует, что учащиеся, получившие помощь, смогут продемонстрировать, что они понимают свои ошибки. Они должны выписать полное объяснение и показать всю переделанную работу. Когда я впервые начал предлагать эту опцию, я был очень удивлен, увидев, что иногда ученики с самыми низкими оценками предпочитали не утруждать себя исправлением ошибок. Однако на самом деле это отличное доказательство для родителей и администраторов. Когда родители приходят на конференцию и слышат, что учащийся получил двойку за контрольную и не удосужился внести исправления в тест, чтобы повысить оценку, они в обязательном порядке поворачиваются к учащемуся и спрашивают: «ЧТО?» вместо того, чтобы обвинять учителя или учебную программу. Ответственность лежит на студентах. Существует явное доказательство того, что учащийся не прилагает усилий. Я всегда говорю, что, поскольку я даю студентам целую неделю на исправление ошибок, у них нет оправдания тому, что они их не заполнили. У меня полно времени, чтобы прийти ко мне и обсудить то, чего они еще не понимают. Затем, когда мы двинемся дальше, я знаю, что не оставлю их позади. Учащиеся больше не сдаются и не бросают выставленные оценки за тест в корзину со словами: «Ну что ж, я все еще не понимаю». Здесь можно загрузить полную процедуру корректировки теста. Не стесняйтесь использовать это в своем собственном классе.
Это относится только к тестам. Я не люблю предлагать его для викторин, потому что я делаю викторины как ступеньки на пути к тесту. С викториной уже есть стимул просмотреть ее, исправить ошибки и подготовиться к предстоящему тесту. Я напоминаю студентам сделать это, даже если они не будут явно вознаграждены за это. Я также сообщаю студентам, что эта процедура не будет применяться к финалу. Итоговая оценка является официальной кумулятивной оценкой и должна отражать все знания, полученные до этого момента. (Кроме того, у меня нет времени выделить на это неделю после выпускного экзамена, когда должны быть выставлены оценки.) В этот момент второго шанса не будет. Присоединяйтесь к нам в комментариях ниже, чтобы поделиться своим собственным опытом использования подобной стратегии или задать любые вопросы, которые у вас могут возникнуть. Найдите минутку, чтобы также просмотреть отличный вклад, который уже есть от других учителей. В поисках дополнительной математики Изд. Идеи? Подпишитесь здесь — Я рассылаю стратегии обучения, ресурсы, обновления и многое другое! Введите свой адрес электронной почты, чтобы оставаться в курсе событий. Вам также может понравиться… |
Архив
сентябрь 2022 г. Новостная лента
Нажмите, чтобы установить собственный HTML |
Что такое z-значение? Что такое p-значение?—ArcGIS Pro
Большинство статистических тестов начинаются с определения нулевой гипотезы. Нулевой гипотезой для инструментов анализа закономерностей (группа инструментов «Анализ закономерностей» и группа инструментов «Отображение кластеров») является полная пространственная случайность (CSR) либо самих объектов, либо значений, связанных с этими объектами. Z-оценки и p-значения, возвращаемые инструментами анализа шаблонов, говорят вам, можете ли вы отклонить эту нулевую гипотезу или нет. Часто вы будете запускать один из инструментов анализа закономерностей, надеясь, что z-значение и значение p укажут, что вы можете отклонить нулевую гипотезу, потому что это укажет, что ваши функции (или связанные с ними значения, а не случайный образец) с вашими функциями) демонстрируют статистически значимую кластеризацию или дисперсию. Всякий раз, когда вы видите пространственную структуру, такую как кластеризация в ландшафте (или в ваших пространственных данных), вы видите свидетельство некоторых лежащих в основе пространственных процессов в действии, и как географ или аналитик ГИС это часто интересует вас больше всего.
Часто вы будете запускать один из инструментов анализа закономерностей, надеясь, что z-значение и значение p укажут, что вы можете отклонить нулевую гипотезу, потому что это укажет, что ваши функции (или связанные с ними значения, а не случайный образец) с вашими функциями) демонстрируют статистически значимую кластеризацию или дисперсию. Всякий раз, когда вы видите пространственную структуру, такую как кластеризация в ландшафте (или в ваших пространственных данных), вы видите свидетельство некоторых лежащих в основе пространственных процессов в действии, и как географ или аналитик ГИС это часто интересует вас больше всего.
Значение p является вероятностью. Для инструментов анализа паттернов это вероятность того, что наблюдаемый пространственный паттерн был создан каким-то случайным процессом. Когда p-значение очень мало, это означает, что очень маловероятно (малая вероятность), что наблюдаемый пространственный паттерн является результатом случайных процессов, поэтому вы можете отклонить нулевую гипотезу. Вы можете спросить: насколько мал достаточно мал? Хороший вопрос. См. таблицу и обсуждение ниже.
Вы можете спросить: насколько мал достаточно мал? Хороший вопрос. См. таблицу и обсуждение ниже.
Z-показатели являются стандартными отклонениями. Если, например, инструмент возвращает z-показатель +2,5, можно сказать, что результат составляет 2,5 стандартных отклонения. Как z-показатели, так и p-значения связаны со стандартным нормальным распределением, как показано ниже.
Очень высокие или очень низкие (отрицательные) z-значения, связанные с очень малыми значениями p, находятся в хвостах нормального распределения. Когда вы запускаете инструмент анализа паттернов признаков, и он дает небольшие значения p и либо очень высокий, либо очень низкий z-показатель, это означает, что маловероятно, что наблюдаемый пространственный паттерн отражает теоретический случайный паттерн, представленный вашей нулевой гипотезой (CSR). ).
Чтобы отклонить нулевую гипотезу, вы должны сделать субъективное суждение относительно степени риска, на который вы готовы пойти из-за своей неправоты (за ложное отклонение нулевой гипотезы). Следовательно, прежде чем запускать пространственную статистику, вы выбираете уровень достоверности. Типичные уровни достоверности 90, 95 или 99 процентов. Уровень достоверности 99 % в этом случае был бы самым консервативным, указывая на то, что вы не желаете отвергать нулевую гипотезу, если только вероятность того, что паттерн был создан случайным образом, действительно мала (вероятность менее 1 %).
Следовательно, прежде чем запускать пространственную статистику, вы выбираете уровень достоверности. Типичные уровни достоверности 90, 95 или 99 процентов. Уровень достоверности 99 % в этом случае был бы самым консервативным, указывая на то, что вы не желаете отвергать нулевую гипотезу, если только вероятность того, что паттерн был создан случайным образом, действительно мала (вероятность менее 1 %).
Уровни достоверности
В таблице ниже показаны нескорректированные критические p-значения и z-показатели для различных уровней достоверности.
Инструменты, которые позволяют вам применять False Discovery Rate (FDR), будут использовать скорректированные критические p-значения. Эти критические значения будут такими же или меньшими, чем указанные в таблице ниже.
| z-score (Standard Deviations) | p-value (Probability) | Confidence level |
|---|---|---|
| < -1. | < 0.10 | 90% |
| <-1,96 или> +1,96 | <0,05 | 95% | 95% | 9003 9% | 9003 | 9% | 9003 9% | 9003 % | 9000 < 0,01 | 99% |
Рассмотрим пример. Критические значения z-оценки при использовании 95-процентного уровня достоверности составляют -1,96 и +1,96 стандартных отклонения. Нескорректированное значение p, связанное с 95-процентным доверительным уровнем, равно 0,05. Если ваш z-показатель находится в диапазоне от -1,96 до +1,96, ваше нескорректированное значение p будет больше 0,05, и вы не сможете отклонить свою нулевую гипотезу, потому что показанная закономерность, скорее всего, может быть результатом случайных пространственных процессов. Если z-показатель выходит за пределы этого диапазона (например, стандартное отклонение -2,5 или +5,4), наблюдаемая пространственная картина, вероятно, слишком необычна, чтобы быть результатом случайного совпадения, и значение p будет малым, чтобы отразить это. В этом случае можно отклонить нулевую гипотезу и приступить к выяснению того, что может быть причиной статистически значимой пространственной структуры ваших данных.
Критические значения z-оценки при использовании 95-процентного уровня достоверности составляют -1,96 и +1,96 стандартных отклонения. Нескорректированное значение p, связанное с 95-процентным доверительным уровнем, равно 0,05. Если ваш z-показатель находится в диапазоне от -1,96 до +1,96, ваше нескорректированное значение p будет больше 0,05, и вы не сможете отклонить свою нулевую гипотезу, потому что показанная закономерность, скорее всего, может быть результатом случайных пространственных процессов. Если z-показатель выходит за пределы этого диапазона (например, стандартное отклонение -2,5 или +5,4), наблюдаемая пространственная картина, вероятно, слишком необычна, чтобы быть результатом случайного совпадения, и значение p будет малым, чтобы отразить это. В этом случае можно отклонить нулевую гипотезу и приступить к выяснению того, что может быть причиной статистически значимой пространственной структуры ваших данных.
Ключевая идея здесь заключается в том, что значения в середине нормального распределения (например, z-значения, такие как 0,19 или -1,2) представляют ожидаемый результат. Однако, когда абсолютное значение z-показателя велико, а вероятности малы (в хвостах нормального распределения), вы видите что-то необычное и вообще очень интересное. Например, для инструмента «Анализ горячих точек» необычный означает либо статистически значимую горячую точку, либо статистически значимую холодную точку.
Однако, когда абсолютное значение z-показателя велико, а вероятности малы (в хвостах нормального распределения), вы видите что-то необычное и вообще очень интересное. Например, для инструмента «Анализ горячих точек» необычный означает либо статистически значимую горячую точку, либо статистически значимую холодную точку.
Коррекция FDR
Инструменты анализа локальных пространственных закономерностей, включая анализ горячих точек и анализ кластеров и выбросов Anselin Local Moran’s I, предоставляют необязательный логический параметр Apply False Discovery Rate (FDR) Correction. Когда этот параметр отмечен, процедура False Discovery Rate (FDR) потенциально снизит критические пороговые значения p, показанные в таблице выше, чтобы учесть многократное тестирование и пространственную зависимость. Сокращение, если таковое имеется, зависит от количества входных признаков и используемой структуры соседства.
Инструменты анализа локальных пространственных шаблонов работают, рассматривая каждый объект в контексте соседних объектов и определяя, отличается ли локальный шаблон (целевой объект и его соседи) от глобального шаблона (все объекты в наборе данных). Результаты z-оценки и p-значения, связанные с каждой функцией, определяют, является ли разница статистически значимой или нет. Этот аналитический подход создает проблемы как с множественным тестированием, так и с зависимостью.
Результаты z-оценки и p-значения, связанные с каждой функцией, определяют, является ли разница статистически значимой или нет. Этот аналитический подход создает проблемы как с множественным тестированием, так и с зависимостью.
Множественное тестирование — При доверительном уровне 95 процентов теория вероятностей говорит нам, что существует 5 из 100 шансов того, что пространственный паттерн может оказаться структурированным (например, сгруппированным или рассредоточенным) и может быть связан со статистически значимым p -значение, когда на самом деле лежащие в основе пространственные процессы, способствующие модели, действительно случайны. В этих случаях мы бы ложно отклонили нулевую гипотезу CSR из-за статистически значимых p-значений. Пять шансов из 100 кажутся довольно консервативными, пока вы не учтете, что локальная пространственная статистика выполняет тест для каждой функции в наборе данных. Например, если есть 10 000 функций, мы можем ожидать до 500 ложных результатов.
Пространственная зависимость — Элементы рядом друг с другом имеют тенденцию быть похожими; чаще всего пространственные данные демонстрируют этот тип зависимости. Тем не менее, многие статистические тесты требуют, чтобы признаки были независимыми. Для инструментов анализа локальных закономерностей это связано с тем, что пространственная зависимость может искусственно завышать статистическую значимость. Пространственная зависимость усугубляется инструментами анализа локальных паттернов, потому что каждый объект оценивается в контексте его соседей, а объекты, которые находятся рядом друг с другом, вероятно, будут иметь много общих соседей. Это перекрытие подчеркивает пространственную зависимость.
Существует как минимум три подхода к решению проблем с множественными тестами и пространственной зависимостью. Первый подход заключается в игнорировании проблемы на том основании, что отдельный тест, выполненный для каждой функции в наборе данных, следует рассматривать изолированно. Однако при таком подходе весьма вероятно, что некоторые статистически значимые результаты окажутся неверными (кажутся статистически значимыми, когда на самом деле лежащие в их основе пространственные процессы случайны). Второй подход заключается в применении классической процедуры множественного тестирования, такой как поправки Бонферрони или Сидака. Однако эти методы обычно слишком консервативны. Хотя они значительно уменьшат количество ложных срабатываний, они также не смогут найти статистически значимые результаты, когда они действительно существуют. Третий подход заключается в применении коррекции FDR, которая оценивает количество ложных срабатываний для заданного уровня достоверности и соответствующим образом корректирует критическое значение p. Для этого метода статистически значимые p-значения ранжируются от наименьшего (наиболее сильного) до наибольшего (самого слабого), и на основании ложноположительной оценки самые слабые удаляются из этого списка. Остальные объекты со статистически значимыми p-значениями идентифицируются по полям Gi_Bin или COType в выходном классе объектов.
Однако при таком подходе весьма вероятно, что некоторые статистически значимые результаты окажутся неверными (кажутся статистически значимыми, когда на самом деле лежащие в их основе пространственные процессы случайны). Второй подход заключается в применении классической процедуры множественного тестирования, такой как поправки Бонферрони или Сидака. Однако эти методы обычно слишком консервативны. Хотя они значительно уменьшат количество ложных срабатываний, они также не смогут найти статистически значимые результаты, когда они действительно существуют. Третий подход заключается в применении коррекции FDR, которая оценивает количество ложных срабатываний для заданного уровня достоверности и соответствующим образом корректирует критическое значение p. Для этого метода статистически значимые p-значения ранжируются от наименьшего (наиболее сильного) до наибольшего (самого слабого), и на основании ложноположительной оценки самые слабые удаляются из этого списка. Остальные объекты со статистически значимыми p-значениями идентифицируются по полям Gi_Bin или COType в выходном классе объектов. Хотя эмпирические тесты не идеальны, но эмпирические тесты показывают, что этот метод работает намного лучше, чем предположение, что каждый локальный тест выполняется изолированно, или применение традиционных, чрезмерно консервативных, множественных методов тестирования. В разделе дополнительных ресурсов содержится дополнительная информация о коррекции FDR.
Хотя эмпирические тесты не идеальны, но эмпирические тесты показывают, что этот метод работает намного лучше, чем предположение, что каждый локальный тест выполняется изолированно, или применение традиционных, чрезмерно консервативных, множественных методов тестирования. В разделе дополнительных ресурсов содержится дополнительная информация о коррекции FDR.
Нулевая гипотеза и пространственная статистика
Некоторые статистические данные в наборе инструментов Пространственная статистика представляют собой методы анализа пространственных закономерностей, включая пространственную автокорреляцию (Global Moran’s I), кластерный анализ и анализ выбросов (Anselin Local Moran’s I) и анализ горячих точек (Getis- Орд Ги*). Логическая статистика основана на теории вероятностей. Вероятность — это мера случайности, и в основе всех статистических тестов (прямых или косвенных) лежат расчеты вероятности, которые оценивают роль случайности в результатах вашего анализа. Как правило, с традиционной (непространственной) статистикой вы работаете со случайной выборкой и пытаетесь определить вероятность того, что данные вашей выборки хорошо отражают (отражают) генеральную совокупность. Например, вы можете спросить: «Каковы шансы, что результаты моего экзитпола (показывающего, что кандидат А победит кандидата Б с небольшим отрывом) будут отражать окончательные результаты выборов?» Но со многими пространственными статистическими данными, включая перечисленные выше статистические данные типа пространственной автокорреляции, очень часто вы имеете дело со всеми доступными данными для изучаемой области (все преступления, все случаи заболевания, атрибуты для каждого блока переписи и т. д.). Когда вы вычисляете статистику для всего населения, у вас больше нет оценок. У вас есть факт. Следовательно, нет смысла больше говорить о правдоподобии или вероятностях. Так как же могут инструменты анализа пространственных закономерностей, часто применяемые ко всем данным в изучаемой области, законно сообщать о вероятностях? Ответ заключается в том, что они могут сделать это, постулируя с помощью нулевой гипотезы, что данные на самом деле являются частью некоторой большей совокупности. Рассмотрим это подробнее.
Например, вы можете спросить: «Каковы шансы, что результаты моего экзитпола (показывающего, что кандидат А победит кандидата Б с небольшим отрывом) будут отражать окончательные результаты выборов?» Но со многими пространственными статистическими данными, включая перечисленные выше статистические данные типа пространственной автокорреляции, очень часто вы имеете дело со всеми доступными данными для изучаемой области (все преступления, все случаи заболевания, атрибуты для каждого блока переписи и т. д.). Когда вы вычисляете статистику для всего населения, у вас больше нет оценок. У вас есть факт. Следовательно, нет смысла больше говорить о правдоподобии или вероятностях. Так как же могут инструменты анализа пространственных закономерностей, часто применяемые ко всем данным в изучаемой области, законно сообщать о вероятностях? Ответ заключается в том, что они могут сделать это, постулируя с помощью нулевой гипотезы, что данные на самом деле являются частью некоторой большей совокупности. Рассмотрим это подробнее.
The Randomization Null Hypothesis — При необходимости инструменты из набора инструментов Spatial Statistics используют нулевую гипотезу рандомизации в качестве основы для проверки статистической значимости. Нулевая гипотеза рандомизации постулирует, что наблюдаемая пространственная структура ваших данных представляет собой одно из многих (n!) возможных пространственных расположений. Если бы вы могли взять свои значения данных и сбросить их на объекты в изучаемой области, у вас было бы одно возможное пространственное расположение этих значений. (Обратите внимание, что выбор ваших значений данных и их произвольное отбрасывание является примером случайного пространственного процесса). Нулевая гипотеза рандомизации утверждает, что если бы вы могли выполнять это упражнение (поднимать предметы и бросать их вниз) бесконечное число раз, то в большинстве случаев вы бы получали закономерность, которая не будет заметно отличаться от наблюдаемой закономерности (ваших реальных данных). Время от времени вы можете случайно бросить все самые высокие значения в один и тот же угол изучаемой области, но вероятность этого невелика. Нулевая гипотеза рандомизации утверждает, что ваши данные являются одной из многих, многих, многих возможных версий полной пространственной случайности. Значения данных фиксированы; менялось только их пространственное расположение.
Время от времени вы можете случайно бросить все самые высокие значения в один и тот же угол изучаемой области, но вероятность этого невелика. Нулевая гипотеза рандомизации утверждает, что ваши данные являются одной из многих, многих, многих возможных версий полной пространственной случайности. Значения данных фиксированы; менялось только их пространственное расположение.
Нулевая гипотеза нормализации — Обычная альтернативная нулевая гипотеза, не реализованная для набора инструментов Пространственная статистика, представляет собой нулевую гипотезу нормализации. Нулевая гипотеза нормализации постулирует, что наблюдаемые значения получены из бесконечно большой, нормально распределенной совокупности значений посредством некоторого процесса случайной выборки. С другой выборкой вы получите другие значения, но вы все равно ожидаете, что эти значения будут репрезентативными для более широкого распределения. Нулевая гипотеза нормализации утверждает, что значения представляют собой одну из многих возможных выборок значений. Если бы вы могли подогнать наблюдаемые данные к нормальной кривой и случайным образом выбрать значения из этого распределения, чтобы бросить их на изучаемую область, в большинстве случаев вы бы получили закономерность и распределение значений, которые не будут заметно отличаться от наблюдаемой закономерности/распределения. (ваши реальные данные). Нулевая гипотеза нормализации утверждает, что ваши данные и их расположение являются одной из многих, многих, многих возможных случайных выборок. Ни значения данных, ни их пространственное расположение не являются фиксированными. Нулевая гипотеза нормализации подходит только тогда, когда значения данных нормально распределены.
Если бы вы могли подогнать наблюдаемые данные к нормальной кривой и случайным образом выбрать значения из этого распределения, чтобы бросить их на изучаемую область, в большинстве случаев вы бы получили закономерность и распределение значений, которые не будут заметно отличаться от наблюдаемой закономерности/распределения. (ваши реальные данные). Нулевая гипотеза нормализации утверждает, что ваши данные и их расположение являются одной из многих, многих, многих возможных случайных выборок. Ни значения данных, ни их пространственное расположение не являются фиксированными. Нулевая гипотеза нормализации подходит только тогда, когда значения данных нормально распределены.
Дополнительные ресурсы
- Эбдон, Дэвид. Статистика по географии. Блэквелл, 1985.
- Митчелл, Энди. The ESRI Guide to GIS Analysis, Volume 2. ESRI Press, 2005.
- Гудчайлд, М.Ф., Пространственная автокорреляция.
 Catmog 47, Geo Books, 1986
Catmog 47, Geo Books, 1986 - Калдас де Кастро, Марсия и Бертон Х. Сингер. «Контроль частоты ложных открытий: новое приложение для учета множественных и зависимых тестов в локальной статистике пространственной ассоциации». Географический анализ 38 , стр. 180-208, 2006.
Похожие темы
- Исследовательская статья
- Открытый доступ
- Опубликовано:
- Chinyereugo M.
 Umemneku Chikere 1 ,
Umemneku Chikere 1 , - Kevin J. Wilson 2 ,
- A. Joy Allen 3 &
- …
- Luke Vale 1
-
3048 доступов
-
3 Цитаты
-
3 Альтметрика
-
Сведения о показателях
-
Сценарий 1: Предполагается, что RS лучше, чем IT. Это означает, что чувствительность и специфичность РС выше, чем чувствительность и специфичность ИТ.
-
Второй сценарий: предполагается, что IT лучше, чем RS. Это означает, что чувствительность и специфичность ИТ выше, чем чувствительность и специфичность РС.

-
Сценарий 3: Предполагается, что чувствительность и специфичность РС и ИТ одинаковы.
-
Вацек PM. Влияние условной зависимости на оценку диагностических тестов. Биометрия. 1985;41(4):959–68. https://doi.org/10.2307/2530967.
КАС Статья пабмед Google ученый
-
Рутьес А.В., Рейтсма Дж.Б., Кумарасами А. и др. Оценка диагностических тестов при отсутствии золотого стандарта. Обзор методов. Health Technol Asses (Winch Eng). 2007;11:iii, ix-51 Обзор.
Google ученый
-
Chikere CMU, Wilson K, Graziadio S, et al. Методология оценки диагностических тестов: систематический обзор методов, используемых для оценки диагностических тестов в отсутствие золотого стандарта – обновление. ПЛОС Один. 2019;14:e0223832.
Артикул Google ученый
-
Гарт Дж.
 Дж., Бак А.А. Сравнение скринингового и эталонного тестов в эпидемиологических исследованиях .2. Вероятностная модель для сравнения диагностических тестов. Am J Эпидемиол. 1966;83:593. https://doi.org/10.1093/oxfordjournals.aje.a120610.
Дж., Бак А.А. Сравнение скринингового и эталонного тестов в эпидемиологических исследованиях .2. Вероятностная модель для сравнения диагностических тестов. Am J Эпидемиол. 1966;83:593. https://doi.org/10.1093/oxfordjournals.aje.a120610. КАС Статья пабмед Google ученый
-
Staquet M, Rozencweig M, Lee YJ, et al. Методология оценки новых дихотомических диагностических тестов. J хронический дис. 1981; 34: 599–610. https://doi.org/10.1016/0021-9681(81)
- -X.
КАС Статья пабмед Google ученый
-
Brenner H. Исправление неправильной классификации воздействия с использованием стандарта легированного золота. Эпидемиология. 1996;7:406–10 ст.
КАС Статья Google ученый
-
Хуэй С.Л., Чжоу XH. Оценка диагностических тестов без золотых стандартов.
 Статистические методы Med Res. 1998;7(4):354–70Обзор. https://doi.org/10.1177/096228029800700404.
Статистические методы Med Res. 1998;7(4):354–70Обзор. https://doi.org/10.1177/096228029800700404. КАС Статья пабмед Google ученый
-
Ку Ю., Тан М., Катнер М.Х. Модели случайных эффектов в анализе латентных классов для оценки точности диагностических тестов. Биометрия. 1996;52(3):797–810. https://doi.org/10.2307/2533043.
КАС Статья пабмед Google ученый
-
Бранскум А.Дж., Гарднер И.А., Джонсон В.О. Оценка чувствительности и специфичности диагностических тестов с помощью байесовского моделирования. Пред. Вет. мед. 2005;68(2-4):145–63. https://doi.org/10.1016/j.prevetmed.2004.12.005.
КАС Статья пабмед Google ученый
-
Моррис Т.П., Уайт И.Р., Кроутер М.Дж. Использование симуляционных исследований для оценки статистических методов.
 Стат мед. 2019;38(11):2074–102. https://doi.org/10.1002/sim.8086.
Стат мед. 2019;38(11):2074–102. https://doi.org/10.1002/sim.8086. Артикул пабмед ПабМед Центральный Google ученый
-
Allaire J. RStudio: интегрированная среда разработки для R. Boston; 2012. с. 770.
Google ученый
-
Альтман Д.Г., Блэнд Дж.М. Диагностические тесты 1: чувствительность и специфичность. Бр Мед Дж. 1994;308:1552 Примечание.
КАС Статья Google ученый
-
Ван З., Дендукури Н., Зар Х.Дж., Джозеф Л. Моделирование условной зависимости между несколькими диагностическими тестами. Стат мед. 2017;36(30):4843–59. https://doi.org/10.1002/sim.7449.
Артикул пабмед Google ученый
-
Team R. RStudio: комплексная разработка для R, vol. 42. Бостон http://www.
 rstudio com: RStudio, Inc; 2015. с. 14.
rstudio com: RStudio, Inc; 2015. с. 14. Google ученый
-
Дендукури Н., Джозеф Л. Байесовские подходы к моделированию условной зависимости между несколькими диагностическими тестами. Биометрия. 2001;57:158–67Статья. https://doi.org/10.1111/j.0006-341X.2001.00158.x.
КАС Статья пабмед Google ученый
-
Mathews WC, Cachay ER, Caperna J, et al. Оценка точности анальной цитологии при наличии несовершенного эталонного стандарта. ПЛОС Один. 2010;5Статья. https://doi.org/10.1371/journal.pone.0012284.
-
Матос Р.Н., Т. Ф., Брага М.М., Сикейра В.Л., Дуарте Д.А., Мендес Ф.М. Клиническая эффективность двух флуоресцентных методов обнаружения окклюзионного кариеса молочных зубов. Кариес Рез. 2011;45:294–302Статья. https://doi.org/10.1159/000328673.
КАС Статья пабмед Google ученый
- «>
Уилсон Э.Б. Вероятностный вывод, закон преемственности и статистический вывод. J Am Stat Assoc. 1927;22(158):209–12. https://doi.org/10.1080/01621459.1927.10502953.
Артикул Google ученый
-
Байром Дж., Дус Г., Джонс П. и др. Следует ли использовать пункционную биопсию при подозрении на высокую степень заболевания при первоначальной кольпоскопической оценке? Перспективное исследование. Int J Gynecol Рак. 2006;16(1):253–256. https://doi.org/10.1111/j.1525-1438.2006.00344.x.
КАС Статья пабмед Google ученый
-
Яблонски-Момени А., Стахнисс В., Рикеттс Д. и др. Воспроизводимость и точность ICDAS-II для обнаружения окклюзионного кариеса in vitro. Кариес Рез. 2008;42(2):79–87. https://doi.org/10.1159/000113160.
КАС Статья пабмед Google ученый
- «>
Брага М., Мендес Ф., Мартиньон С. и др. In vitro сравнение системы Nyvad и ICDAS-II с оценкой активности поражения для оценки тяжести и активности окклюзионного кариеса молочных зубов. Кариес Рез. 2009 г.;43(5):405–12. https://doi.org/10.1159/000239755.
КАС Статья пабмед Google ученый
-
Родригес Дж., Хуг И., Диниз М. и др. Выполнение методов флуоресценции, рентгенографического исследования и ICDAS II на жевательных поверхностях in vitro. Кариес Рез. 2008;42(4):297–304. https://doi.org/10.1159/000148162.
КАС Статья пабмед Google ученый
-
Diniz MB, Rodrigues JA, Hug I, de Cássia Loiola Cordeiro R, Lussi A. Воспроизводимость и точность ICDAS-II для обнаружения окклюзионного кариеса. Сообщество Dent Oral Epidemiol. 2009;37(5):399–404. https://doi.org/10.1111/j.1600-0528.2009.00487.x.
Артикул пабмед Google ученый
- «>
Бадер Д.Д. и Шугарс Д.А. Систематический обзор эффективности лазерного флуоресцентного устройства для обнаружения кариеса. J Am Dent Assoc 2004; 135: 1413–1426. Обзор. DOI: https://doi.org/10.14219/jada.archive.2004.0051.
-
Enøe C, член парламента Георгиадис, Johnson WO. Оценка чувствительности и специфичности диагностических тестов и распространенности заболевания, когда истинное состояние болезни неизвестно. Пред. Вет. мед. 2000;45:61–81. https://doi.org/10.1016/S0167-5877(00)00117-3.
Артикул пабмед Google ученый
-
Альберт П.С., Макшейн Л.М., Ши Дж.Х. и др. Подходы к моделированию латентного класса для оценки диагностической ошибки без золотого стандарта: с применением иммуногистохимических анализов p53 в опухолях мочевого пузыря. Биометрия. 2001; 57(2):610–9.. https://doi.org/10.1111/j.0006-341X.2001.00610.x.
КАС Статья пабмед Google ученый
- «>
Асселино Дж., Пайе А., Бессед Э. и др. Различные модели латентного класса использовались и оценивались для оценки точности диагностических тестов на кампилобактерии: преодоление несовершенных эталонных стандартов? Эпидемиол инфекции. 2018;146:1556–64Статья. https://doi.org/10.1017/S0950268818001723.
КАС Статья пабмед ПабМед Центральный Google ученый
-
Гаррет Э.С., Зегер С.Л. Диагностика модели скрытого класса. Биометрия. 2000;56(4):1055–67. https://doi.org/10.1111/j.0006-341X.2000.01055.x.
КАС Статья пабмед Google ученый
-
Перейра Г.Д., Лузада Ф., Барбоза В.Д. и др. Общая модель латентного класса для оценки эффективности диагностических тестов в отсутствие золотого стандарта: приложение к болезни Шагаса. Вычислительные математические методы мед. 2012;2012:1–12. https://doi.org/10.1155/2012/487502.

Артикул Google ученый
-
Научно-исследовательский институт здоровья населения, факультет медицинских наук, Университет Ньюкасла, Ньюкасл-апон-Тайн, Великобритания
Чиньереуго М.
 Умемнеку Чикере и Люк Вейл
Умемнеку Чикере и Люк Вейл -
Школа математики, статистики и физики Университета Ньюкасла, Ньюкасл-апон-Тайн, Великобритания Кооператив, Университет Ньюкасла, Ньюкасл-апон-Тайн, Великобритания
A. Joy Allen
- Chinyereugo M. Umemneku Chikere
Посмотреть публикации авторов
Вы также можете искать этого автора в PubMed Google Scholar
- Kevin J. Wilson
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
- A. Joy Allen
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Scholar
- Luke Vale
Просмотр публикаций автора
Вы также можете искать этого автора в PubMed Google Академия
- 6 6
Отзыв по этой теме?
Сравнительные исследования диагностической точности с несовершенным эталоном – сравнение методов коррекции | BMC Medical Research Methodology
Методология медицинских исследований BMC том 21 , Номер статьи: 67 (2021) Процитировать эту статью
Реферат
Фон
Staquet et al. и Бреннер разработали методы коррекции для оценки чувствительности и специфичности теста индекса бинарного ответа, когда эталонный стандарт несовершенен и его чувствительность и специфичность известны. Однако, насколько нам известно, ни одно исследование не сравнило статистические свойства этих методов, несмотря на их длительное применение в исследованиях точности диагностики.
и Бреннер разработали методы коррекции для оценки чувствительности и специфичности теста индекса бинарного ответа, когда эталонный стандарт несовершенен и его чувствительность и специфичность известны. Однако, насколько нам известно, ни одно исследование не сравнило статистические свойства этих методов, несмотря на их длительное применение в исследованиях точности диагностики.
Цель
Для сравнения методов коррекции, разработанных Staquet et al. и Бреннер.
Методы
Методы моделирования использовались для сравнения методов при допущении, что новый тест и эталонный стандарт являются условно независимыми или зависимыми, учитывая истинный статус заболевания индивидуума. Были проанализированы три набора клинических данных, чтобы понять влияние использования каждого метода на принятие клинических решений.
Результаты
В предположении условной независимости Staquet et al. Метод коррекции превосходит метод коррекции Бреннера независимо от распространенности заболевания и от того, лучше или хуже показатели эталонного стандарта по сравнению с индексным тестом. Однако при высокой распространенности заболевания (> 0,9) или низкий (< 0,1), Staquet et al. метод коррекции может привести к нелогичным результатам (т. е. результатам за пределами [0,1]). При допущении условной зависимости; оба метода не смогли оценить чувствительность и специфичность индексного теста, особенно когда ковариация между индексным тестом и эталонным стандартом не близка к нулю.
Метод коррекции превосходит метод коррекции Бреннера независимо от распространенности заболевания и от того, лучше или хуже показатели эталонного стандарта по сравнению с индексным тестом. Однако при высокой распространенности заболевания (> 0,9) или низкий (< 0,1), Staquet et al. метод коррекции может привести к нелогичным результатам (т. е. результатам за пределами [0,1]). При допущении условной зависимости; оба метода не смогли оценить чувствительность и специфичность индексного теста, особенно когда ковариация между индексным тестом и эталонным стандартом не близка к нулю.
Заключение
Когда новый тест и несовершенный эталонный стандарт условно независимы, а чувствительность и специфичность несовершенного эталонного стандарта известны, Staquet et al. метод коррекции превосходит метод Бреннера. Однако там, где распространенность целевого состояния очень высока или низка, или два теста условно зависимы, следует рассмотреть другие статистические методы, такие как подходы латентного класса.
Отчеты экспертной оценки
История вопроса
Показатели диагностической точности (чувствительность и специфичность) нового теста традиционно оцениваются путем сравнения с лучшим доступным эталонным стандартом. Эталонным стандартом часто считается «золотой стандарт » , то есть «безошибочный». Однако ни один тест не является совершенным, и игнорирование этого несовершенства может привести как к переоценке, так и к занижению точности нового теста (индексного теста) [1].
После обзоров Rutjes et al. [2] и Chikere et al. [3], три статистических метода (Gart и Buck [4], Staquet et al. [5] и Brenner [6]) были признаны подходящими для оценки чувствительности и специфичности теста бинарного индекса ответа, когда чувствительность и специфичность несовершенного эталона известна, а индексный тест и эталон условно независимы. Оценки чувствительности и специфичности несовершенного эталонного стандарта могут быть получены из предыдущих валидационных исследований, экспериментальных или полевых исследований. Три статистических метода называются « методы коррекции» , потому что они направлены на корректировку расчетной чувствительности и специфичности индексного теста с использованием доступной информации (чувствительности и специфичности) несовершенного эталонного стандарта с помощью алгебраических функций. Кроме того, эти методы коррекции не требуют вероятностного моделирования, как модели латентного класса [7, 8]. Как методы коррекции, так и модели латентного класса предполагают, что истинный статус заболевания у участников неизвестен (латентный). Однако модели латентного класса « вероятностный ”подходы, которые оценивают показатели точности индексного теста и/или эталонного эталона с помощью статистической модели. Кроме того, байесовские модели латентного класса [9] включают другие источники информации об интересующих параметрах, помимо наблюдений, чтобы сделать вывод об интересующих параметрах.
Три статистических метода называются « методы коррекции» , потому что они направлены на корректировку расчетной чувствительности и специфичности индексного теста с использованием доступной информации (чувствительности и специфичности) несовершенного эталонного стандарта с помощью алгебраических функций. Кроме того, эти методы коррекции не требуют вероятностного моделирования, как модели латентного класса [7, 8]. Как методы коррекции, так и модели латентного класса предполагают, что истинный статус заболевания у участников неизвестен (латентный). Однако модели латентного класса « вероятностный ”подходы, которые оценивают показатели точности индексного теста и/или эталонного эталона с помощью статистической модели. Кроме того, байесовские модели латентного класса [9] включают другие источники информации об интересующих параметрах, помимо наблюдений, чтобы сделать вывод об интересующих параметрах.
Возможно, существуют определенные сценарии, в которых один метод коррекции является более подходящим или может превзойти другой. Поэтому мы решили изучить эти методы коррекции, чтобы дать рекомендации оценщикам тестов. Насколько нам известно, ни в одном исследовании не проводилось прямого сравнения этих методов коррекции.
Поэтому мы решили изучить эти методы коррекции, чтобы дать рекомендации оценщикам тестов. Насколько нам известно, ни в одном исследовании не проводилось прямого сравнения этих методов коррекции.
Методы
Обозначение
Пусть IT и RS обозначают индексный тест и эталонный стандарт соответственно. Результаты обоих тестов считаются бинарными (больные и здоровые). Результаты участников часто классифицируются в таблице непредвиденных обстоятельств два на два (таблица 1), в которой отображается количество участников для каждой комбинации результатов теста. Обозначения, используемые в этой статье, приведены в таблице 2.
Таблица 1 Таблица сопряженности 2 на 2 индексного теста и несовершенного эталонного стандартаПолноразмерная таблица
Таблица 2 Таблица обозначенийПолноразмерная таблица
Классические оценки чувствительности и специфичности индексного теста, предполагая, что эталонный стандарт является золотым стандартом, следующие:
$$ S{n}_{IT}=\frac{a}{e}\kern1.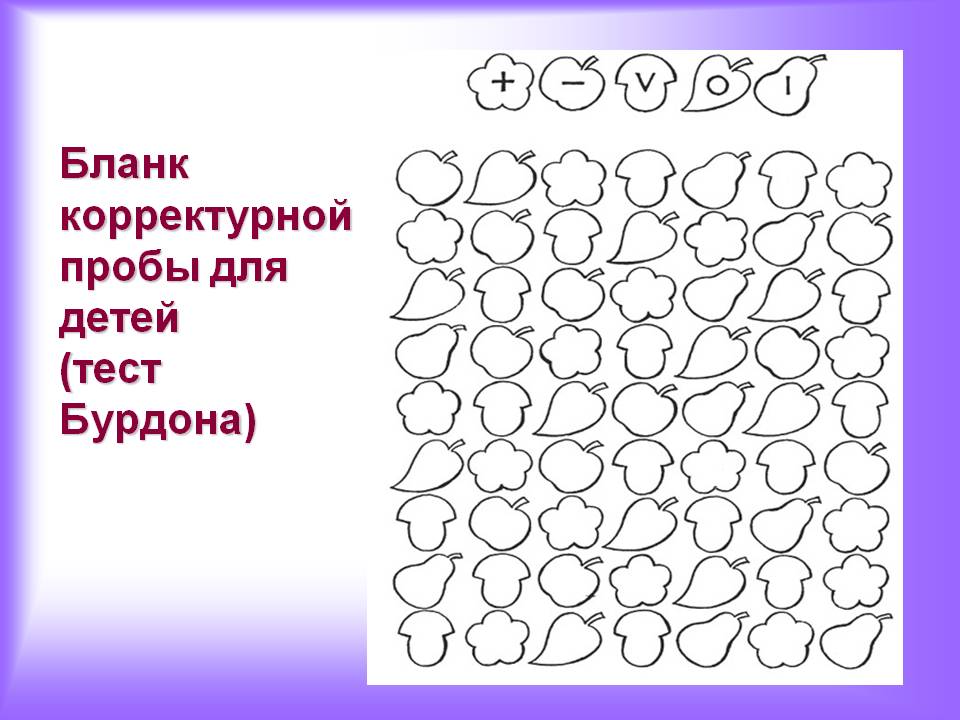 75em S{p}_{IT}=\frac{d}{f}\kern2em Prr=\frac{e }{N}\kern1.75em $$
75em S{p}_{IT}=\frac{d}{f}\kern2em Prr=\frac{e }{N}\kern1.75em $$
(1)
Методы коррекции
Методами коррекции, определенными в систематических обзорах [2, 3], были метод коррекции Гарта и Бака [4], Staquet et al. [5] метод коррекции и метод коррекции Бреннера [6]. 9{GB}=\frac{S{n}_{RS}\times\left(1-Prr\right)\times S{p}_{IT}+\left(1-S{n}_{RS} \right)\times Prr\times S{n}_{IT}-\left(1-S{n}_{RS}\right)\left(1-S{p}_{RS}+\hat{ P}J\right)}{J\left(1-\hat{P}\right)} $$
(3)
Staquet et al. [5] метод коррекции
Staquet et al. [5] предложили две пары оценок для оценки чувствительности и специфичности ИТ по двум сценариям. Первая пара оценок (для оценки чувствительности и специфичности ИТ) предлагается для случая, когда ИТ и СО условно независимы, а чувствительность и специфичность СО известны. Вторая пара оценок (для оценки чувствительности IT и RS) предлагается, когда специфичность IT и RS идеальна (100%). В этой статье мы сосредоточимся на первой паре оценок. Эта пара оценок используется для оценки чувствительности и специфичности ИТ при условии, что ИТ и СО условно независимы, а чувствительность и специфичность СО известны. Эти оценщики: 9{sq}=\frac{hS{n}_{RS}-c}{NS{n}_{RS}-e};\kern0.5em \hat{P}=\frac{N\left(S{ p}_{RS}-1\right)+e}{N\left(S{n}_{RS}+S{p}_{RS}-1\right)}\kern1em $$
Эта пара оценок используется для оценки чувствительности и специфичности ИТ при условии, что ИТ и СО условно независимы, а чувствительность и специфичность СО известны. Эти оценщики: 9{sq}=\frac{hS{n}_{RS}-c}{NS{n}_{RS}-e};\kern0.5em \hat{P}=\frac{N\left(S{ p}_{RS}-1\right)+e}{N\left(S{n}_{RS}+S{p}_{RS}-1\right)}\kern1em $$
(4 )
The Staquet et al. Метод коррекции [5] эквивалентен методу коррекции Гарта и Бака [4] (см. Дополнительный файл 1).
Бреннер [6] метод коррекции
Бреннер [6] предложил две пары оценок для оценки чувствительности и специфичности ИТ. Первая пара оценок предполагает, что IT и RS условно независимы, а вторая пара оценок предполагает, что IT и RS условно зависимы (положительно коррелированы) с учетом истинного статуса заболевания у людей. В обеих парах оценок чувствительность и специфичность РС предполагаются известными. Однако в этой статье мы сосредоточимся на первой паре оценок, где предполагается, что IT и RS являются условно независимыми. Первая пара оценок выражается как:
9{B1}=\frac{c\left(1-S{n}_{RS}\right)+ dS{p}_{RS}}{e\left(1-S{n}_{RS}\ right)+ fS{p}_{RS}} $$
Первая пара оценок выражается как:
9{B1}=\frac{c\left(1-S{n}_{RS}\right)+ dS{p}_{RS}}{e\left(1-S{n}_{RS}\ right)+ fS{p}_{RS}} $$
(8)
Моделирование
Методы коррекции сравнивались с использованием методов моделирования и анализа наборов клинических данных. Поскольку Staquet и соавт. [5] эквивалентен методу коррекции Гарта и Бака [4] (см. Дополнительный файл 1), только Staquet et al. [5] подход сравнивался с методом коррекции Бреннера. Моделирование проводилось в соответствии с рекомендациями Morris et al. [10], в том числе P планирование для симуляции, C кодирование и выполнение, A анализ и R надлежащая отчетность по симуляционному исследованию (PCAR) и использование статистического программного обеспечения R-Studio [11]. В моделировании Staquet et al. Подходы [5] и Бреннера [6] сравнивались с классическим методом [12]. Классический метод предполагает, что эталонный стандарт является золотым стандартом (уравнение (1)). Оценки, полученные классическим методом, будем называть нескорректированными оценками чувствительности и специфичности.
Показатели производительности в моделировании — это основные статистические свойства, используемые для обеспечения хорошей оценки. Этими свойствами являются беспристрастность, среднеквадратическая ошибка (MSE) и непротиворечивость. Дополнительные примечания об этих свойствах представлены в дополнительном файле 1.
Подход к моделированию с фиксированными эффектами [1, 13] использовался для моделирования различных наборов данных с использованием полиномиального распределения (функция rmulti в R [14]). Этот подход моделирует попарную условную зависимость (или корреляцию) между двумя тестами среди больных и здоровых групп с использованием условий ковариации, которые фиксируются для участников [15]. В процессе моделирования известны чувствительность и специфичность ИТ и РС, а также известна распространенность целевого состояния. Шаблон, показывающий, как были рассчитаны вероятности клеток с использованием распространенности, чувствительности и специфичности IT и RS, а также условий ковариации, представлен в дополнительном файле 1 — Таблица S1.
Моделирование проводилось при двух допущениях, учитывая несовершенство РС. Во-первых, ИТ и РС предполагались условно независимыми, во-вторых, тесты предполагались условно зависимыми. Теоретически при безошибочности (идеальности) РС классический и корректирующий методы точно оценивают чувствительность и специфичность ИТ. Это показано алгебраически в дополнительном файле 1.
В предположении, что RS и IT условно независимы, множественные (200) случайных выборок с разным размером выборки от 50 до 1000 были смоделированы с использованием полиномиального распределения по трем сценариям, а именно:
Первый сценарий
Предполагается, что чувствительность и специфичность RS равны 0,9, а чувствительность и специфичность индексного теста равны 0,8 и 0,7 соответственно. Предполагается, что распространенность составляет 0,3. Нескорректированные и скорректированные оценки представлены на рис. 1.
Рис. 1Среднее значение, стандартная ошибка, среднеквадратическая ошибка и погрешность нескорректированной и скорректированной чувствительности и специфичности индексного теста, когда эталонный стандарт несовершенен и лучше индексного теста
Полноразмерное изображение
Второй сценарий
Чувствительность и специфичность индексного теста равны 0,9, а чувствительность и специфичность эталонного стандарта равны 0,8 и 0,7 соответственно. Распространенность 0,3. Нескорректированные и скорректированные оценки представлены на рис. 2.
Распространенность 0,3. Нескорректированные и скорректированные оценки представлены на рис. 2.
Среднее значение, стандартная ошибка, среднеквадратическая ошибка и погрешность нескорректированной и скорректированной чувствительности и специфичности индексного теста, когда эталонный стандарт несовершенен и хуже, чем индексный тест
Полноразмерное изображение
Сценарий три
Чувствительность и специфичность индексного и эталонного тестов равны 0,9, а распространенность целевого состояния равна 0,3. Нескорректированные и скорректированные оценки представлены на рис. 3.
Рис. 3Среднее значение, стандартная ошибка, среднеквадратическая ошибка и погрешность нескорректированной и скорректированной чувствительности и специфичности индексного теста, когда эталонный стандарт несовершенен и имеет те же показатели диагностической точности, что и индексный тест
Полноразмерное изображение
Желтые пунктирные линии на графиках средней чувствительности и средней специфичности на рис. 1 – рис. 5 представляют собой смоделированные истинные значения чувствительности и специфичности ИТ. Выбор параметров чувствительности и специфичности ИТ и РС, а также распространенность целевого состояния был основан на клинических исследованиях, выявленных в обзоре, ранее проведенном Чикере и соавт. [3].
1 – рис. 5 представляют собой смоделированные истинные значения чувствительности и специфичности ИТ. Выбор параметров чувствительности и специфичности ИТ и РС, а также распространенность целевого состояния был основан на клинических исследованиях, выявленных в обзоре, ранее проведенном Чикере и соавт. [3].
На основе трех смоделированных сценариев оценки, полученные в исследовании Staquet et al. [5] являются точными независимо от того, какой тест лучше или хуже другого. Однако, когда показатели точности индексного теста лучше, чем чувствительность и специфичность эталонного стандарта (рис. 2), рекомендуется относительно большой размер выборки ( n > 200); поскольку при использовании небольших размеров выборки средняя чувствительность была немного выше смоделированного истинного значения (0,9). На практике информация об индексном тесте обычно неизвестна, поэтому типично использование относительно большого размера выборки при исследовании точности диагностики. Нескорректированная и скорректированная по Бреннеру чувствительность постоянно ниже смоделированного истинного значения, а погрешность постоянно превышает 0,1. Нескорректированные специфичности обычно немного ниже смоделированных истинных значений, а погрешность обычно относительно мала, ниже 0,05, за исключением погрешности из второго сценария (рис. 2), которая больше 0,05, но ниже 0,1. Скорректированные по Бреннеру специфичности постоянно ниже смоделированных истинных значений, а погрешность постоянно выше 0,1, за исключением сценария 1 (рис. 1), в котором оно ниже 0,05. Дальнейшие изученные сценарии включают случаи, когда чувствительность (или специфичность) индексного теста была лучше, чем чувствительность (или специфичность) RS. Результаты этих симуляций представлены в дополнительном файле 1. После изучения смоделированных сценариев (учитывая, что IT и RS условно независимы), Staquet et al. [5] метод коррекции превосходит метод коррекции Бреннера. Могут быть и другие возможные сценарии, в которых чувствительность (или специфичность) ИТ и РС, а также распространенность не эквивалентны значениям, рассмотренным в этой статье. Эти сценарии можно исследовать с помощью R-кода, написанного Авторами.
Нескорректированные специфичности обычно немного ниже смоделированных истинных значений, а погрешность обычно относительно мала, ниже 0,05, за исключением погрешности из второго сценария (рис. 2), которая больше 0,05, но ниже 0,1. Скорректированные по Бреннеру специфичности постоянно ниже смоделированных истинных значений, а погрешность постоянно выше 0,1, за исключением сценария 1 (рис. 1), в котором оно ниже 0,05. Дальнейшие изученные сценарии включают случаи, когда чувствительность (или специфичность) индексного теста была лучше, чем чувствительность (или специфичность) RS. Результаты этих симуляций представлены в дополнительном файле 1. После изучения смоделированных сценариев (учитывая, что IT и RS условно независимы), Staquet et al. [5] метод коррекции превосходит метод коррекции Бреннера. Могут быть и другие возможные сценарии, в которых чувствительность (или специфичность) ИТ и РС, а также распространенность не эквивалентны значениям, рассмотренным в этой статье. Эти сценарии можно исследовать с помощью R-кода, написанного Авторами. R-код, используемый для создания и анализа смоделированных и клинических наборов данных, представлен в приложении (дополнительный файл 2).
R-код, используемый для создания и анализа смоделированных и клинических наборов данных, представлен в приложении (дополнительный файл 2).
В трех приведенных выше сценариях процесс моделирования учитывал только одну распространенность ( p = 0,3). Дальнейший анализ был проведен для изучения методов коррекции при различной распространенности от 0 до 1 (с шагом 0,01) с использованием первого сценария, где RS лучше, чем IT. Нескорректированная и скорректированная чувствительность и специфичность ИТ представлены на рис. 4. Далее был изучен только первый сценарий, поскольку в каждом приведенном выше сценарии Staquet et al. [5] метод коррекции превосходит поправку Бреннера и классические методы.
Рис. 4Нескорректированная и скорректированная чувствительность и специфичность индексного теста при различной распространенности
Изображение в натуральную величину
На рис. 4 нескорректированная и скорректированная по Бреннеру чувствительность стремится к смоделированному истинному значению, когда распространенность стремится к единице. Скорректированные по Бреннеру и нескорректированные особенности имеют тенденцию к симулированной истине, поскольку распространенность стремится к нулю. Стаке и др. [5] чувствительность и специфичность ИТ приблизительно беспристрастны и эквивалентны смоделированному истинному значению независимо от распространенности, что указывает на постоянную чувствительность и специфичность в популяциях с различной распространенностью. Однако, когда распространенность очень низкая (< 0,1) или очень высокая (> 0,9), существует возможность получения нелогичной оценки чувствительности или специфичности с помощью теста Staquet et al. [5] подход. Нелогичные результаты подразумевают, что расчетная чувствительность или специфичность больше единицы или меньше нуля. В смоделированных наборах данных, созданных для получения рис. 4, когда распространенность составляла 0,01 и 0,02, расчетная средняя чувствительность составляла 5,38 × 10 12 и 4,33 × 10 12 соответственно. Эти значения нелогичны и исключены из графика.
Скорректированные по Бреннеру и нескорректированные особенности имеют тенденцию к симулированной истине, поскольку распространенность стремится к нулю. Стаке и др. [5] чувствительность и специфичность ИТ приблизительно беспристрастны и эквивалентны смоделированному истинному значению независимо от распространенности, что указывает на постоянную чувствительность и специфичность в популяциях с различной распространенностью. Однако, когда распространенность очень низкая (< 0,1) или очень высокая (> 0,9), существует возможность получения нелогичной оценки чувствительности или специфичности с помощью теста Staquet et al. [5] подход. Нелогичные результаты подразумевают, что расчетная чувствительность или специфичность больше единицы или меньше нуля. В смоделированных наборах данных, созданных для получения рис. 4, когда распространенность составляла 0,01 и 0,02, расчетная средняя чувствительность составляла 5,38 × 10 12 и 4,33 × 10 12 соответственно. Эти значения нелогичны и исключены из графика.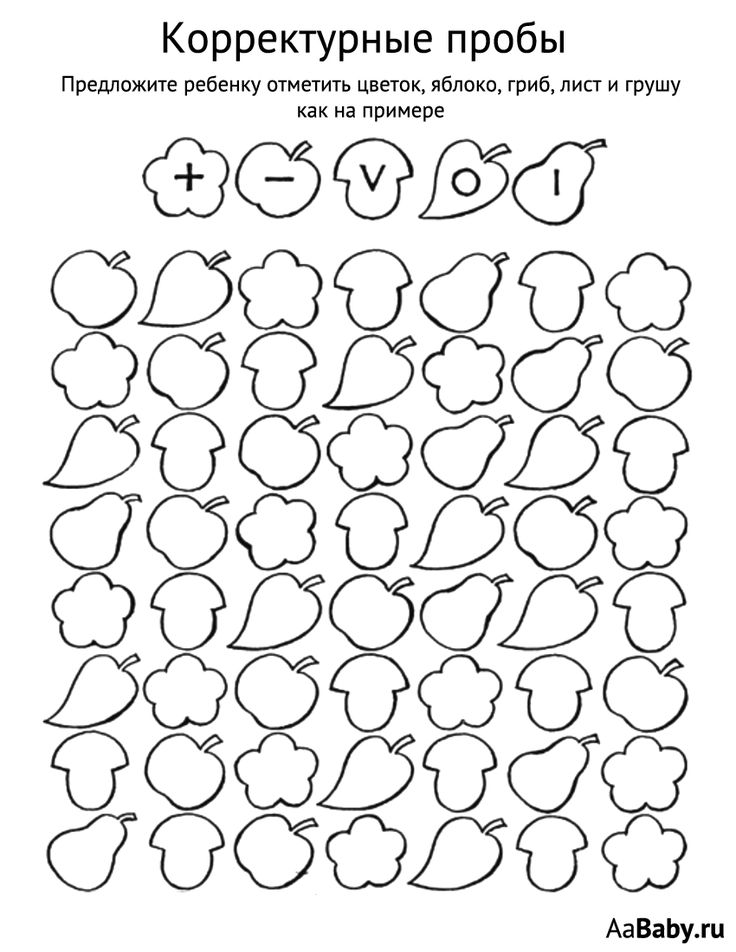 Кроме того, в смоделированных наборах данных, использованных для построения рис. 3, при размере выборки 50 и 80 средняя оценка чувствительности составила − 2,04 × 10 [13] и − 1,9.4 × 10 [13], эти значения также были исключены из графика. Смоделированные наборы данных воспроизводятся с использованием R-кода, указанного в дополнительном файле 2. Дальнейшее изучение нелогичных оценок, полученных с помощью Staquet et al. [5] метод коррекции обсуждается в дополнительном файле 3.
Кроме того, в смоделированных наборах данных, использованных для построения рис. 3, при размере выборки 50 и 80 средняя оценка чувствительности составила − 2,04 × 10 [13] и − 1,9.4 × 10 [13], эти значения также были исключены из графика. Смоделированные наборы данных воспроизводятся с использованием R-кода, указанного в дополнительном файле 2. Дальнейшее изучение нелогичных оценок, полученных с помощью Staquet et al. [5] метод коррекции обсуждается в дополнительном файле 3.
В предположении, что IT и RS являются условно зависимыми, члены ковариации между группами с заболеванием и без заболевания отличны от нуля, и они варьируются, чтобы представить выборку разнообразные возможные сценарии. Возможным сценарием является случай, когда IT и RS положительно коррелируют. В этом случае ковариационные условия между больными и здоровыми группами положительны. С чувствительностью и специфичностью ИТ 0,8 и чувствительностью и специфичностью РС 0,9., изучен сценарий, в котором ковариационный член среди больных и здоровых групп составляет 0,05. Выбор условий ковариации является ограничением неравенства, используемым при создании смоделированных наборов данных с использованием подхода к моделированию с фиксированными эффектами [1, 13]. Нескорректированные и скорректированные оценки представлены на рис. 5.
Выбор условий ковариации является ограничением неравенства, используемым при создании смоделированных наборов данных с использованием подхода к моделированию с фиксированными эффектами [1, 13]. Нескорректированные и скорректированные оценки представлены на рис. 5.
Средняя нескорректированная и скорректированная чувствительность и специфичность индексного теста, когда эталонный стандарт несовершенен, а индексный тест и эталонный стандарт положительно коррелируют
Полноразмерное изображение
Дальнейшие сценарии были изучены и представлены в дополнительном файле 4. При допущении условной зависимости между ИТ и RS все методы коррекции показали плохие результаты в изученных сценариях (см. Дополнительный файл 4). Это ожидаемо, так как не были разработаны подходы для оценки показателей точности индексного теста, когда индексный тест и эталонный стандарт условно зависимы. Однако, когда ковариационный член между группами заболеваний относительно мал (близок к нулю), Staquet et al. [5] метод коррекции превосходит метод коррекции Бреннера. Кроме того, когда IT и RS условно зависимы, предполагаемая чувствительность и специфичность индексного теста, полученного с помощью Staquet et al. [5] метод коррекции не постоянен в разных популяциях с разной распространенностью по сравнению с оценками, полученными при условной независимости ИТ и РС.
[5] метод коррекции превосходит метод коррекции Бреннера. Кроме того, когда IT и RS условно зависимы, предполагаемая чувствительность и специфичность индексного теста, полученного с помощью Staquet et al. [5] метод коррекции не постоянен в разных популяциях с разной распространенностью по сравнению с оценками, полученными при условной независимости ИТ и РС.
Анализ трех наборов клинических данных
Три набора клинических данных из двух опубликованных статей (Mathews et al. [16] и Matos et al. [17]) были проанализированы, чтобы понять влияние выбора метода на принятие клинических решений, и для подтверждения результатов исследований моделирования. 95% доверительные интервалы полученных оценок были рассчитаны с использованием интервального подхода Вильсона [18].
Анализ набора клинических данных Mathews et al. [16] (пример 1)
Извлеченный набор клинических данных из Mathews et al. [16] (Таблица 3 ) направлена на оценку чувствительности и специфичности цитологического исследования аноскопии высокого разрешения (HRA) при дифференциации пациентов с ВИЧ на плоскоклеточное внутриэпителиальное поражение высокой степени (HSIL), а атипичные плоскоклеточные клетки не могут исключить высокую степень (ASC-H). ) или нет.
) или нет.
Полноразмерная таблица
Пункционная биопсия использовалась как RS, но известно, что она несовершенна. Согласно Мэтьюзу и соавт. [16], чувствительность и специфичность пункционной биопсии были взяты из Byrom et al. [19] и составляют 0,74 и 0,91 соответственно. В исследовании использовались Staquet et al. [5] подход к корректировке чувствительности и специфичности цитологии HRA с учетом того, что показатели точности пункционной биопсии известны и предполагается, что тесты (IT и RS) условно независимы. Набор данных (таблица 3) был повторно проанализирован с использованием метода коррекции Бреннера. Расчетная распространенность составляет 0,27, а скорректированные и нескорректированные оценки чувствительности и специфичности цитологии HRA представлены в таблице 4.
Таблица 4 Нескорректированная и скорректированная чувствительность и специфичность цитологии HRAПолноразмерная таблица
Из таблицы 4 оценены чувствительность и специфичность цитологии HRA, полученные с помощью Staquet et al. [5] выше, чем оценки, полученные классическим методом и методом коррекции Бреннера. Кроме того, с помощью Staquet et al. не было получено нелогичных оценок. [5] подход. Кроме того, доверительные интервалы по Brenner и Staquet et al. [5] методы коррекции не пересекаются. В этом клиническом применении корректировка чувствительности и специфичности цитологии HRA с использованием подхода Бреннера приведет к недооценке чувствительности цитологии HRA; таким образом, препятствуя его использованию для исключения диагноза HSIL, поскольку чувствительность будет низкой (0,5). Однако корректировка показателей диагностической точности цитологии HRA с использованием шкалы Staquet et al. [5] поощряет использование цитологии HRA в клинической практике для определения диагноза HSIL, поскольку она имеет специфичность, близкую к единице.
[5] выше, чем оценки, полученные классическим методом и методом коррекции Бреннера. Кроме того, с помощью Staquet et al. не было получено нелогичных оценок. [5] подход. Кроме того, доверительные интервалы по Brenner и Staquet et al. [5] методы коррекции не пересекаются. В этом клиническом применении корректировка чувствительности и специфичности цитологии HRA с использованием подхода Бреннера приведет к недооценке чувствительности цитологии HRA; таким образом, препятствуя его использованию для исключения диагноза HSIL, поскольку чувствительность будет низкой (0,5). Однако корректировка показателей диагностической точности цитологии HRA с использованием шкалы Staquet et al. [5] поощряет использование цитологии HRA в клинической практике для определения диагноза HSIL, поскольку она имеет специфичность, близкую к единице.
Анализ двух наборов клинических данных Matos et al. [17] набор данных – (тематическое исследование два)
Наборы данных, извлеченные из Matos et al. [17], представленные в Таблице 5 и Таблице 6 , получены от Эксперта 1, и их целью является оценка чувствительности и специфичности устройств на основе флуоресценции (флуоресцентная камера – FC и DIAGNOdent – флуоресцентный лазер типа ручки, сокращенно LFpen). Используется для выявления окклюзионных поражений кариеса молочных зубов. В исследовании использовался метод коррекции Бреннера [6] для оценки чувствительности и специфичности в предположении, что чувствительность и специфичность СО (визуальный осмотр) известны и что флуоресцентные приборы условно независимы от СО. Двумя различными целевыми состояниями являются кариесные поражения без полостей (NC) и кариесные поражения дентина (D3).
Используется для выявления окклюзионных поражений кариеса молочных зубов. В исследовании использовался метод коррекции Бреннера [6] для оценки чувствительности и специфичности в предположении, что чувствительность и специфичность СО (визуальный осмотр) известны и что флуоресцентные приборы условно независимы от СО. Двумя различными целевыми состояниями являются кариесные поражения без полостей (NC) и кариесные поражения дентина (D3).
Полноразмерный стол
флуоресцентные устройства (LFpen и FC) для различения зубов с поражением дентинаПолноразмерная таблица
6 представлена классификация результатов индексных тестов (FC и LFpen) и эталонного стандарта, когда целевым состоянием является D3.
Матос и др. [17] получили диагностическую точность эталонных стандартов из предыдущих исследований [20,21,22,23,24]. Для обнаружения NC чувствительность и специфичность RS составляли 0,796 и 0,799 соответственно. Для D3 чувствительность и специфичность RS составляли 0,786 и 0,995 соответственно. Кроме того, предполагалось, что зубы независимы.
Для обнаружения NC чувствительность и специфичность RS составляли 0,796 и 0,799 соответственно. Для D3 чувствительность и специфичность RS составляли 0,786 и 0,995 соответственно. Кроме того, предполагалось, что зубы независимы.
Нескорректированная и скорректированная чувствительность и особенности LFpen и FC при различении зубов с NC (таблица 5) представлены в таблице 7.
Таблица 7 Нескорректированная и скорректированная чувствительность и специфичность LFpen и FC при выявлении NCПолноразмерная таблица
Выборочная распространенность NC (0,92) и расчетная распространенность по шкале Staquet et al. [5] подход равен 1,2 (что нелогично). Нелогичная распространенность исследуется в дополнительном файле 3; было замечено, что, когда чувствительность эталонного стандарта меньше, чем распространенность выборки, вероятно, будет получена нелогичная распространенность. Оценки чувствительности для LFpen (≅ 0,7) и FC (0,44 или 0,45) одинаковы для всех методов (таблица 7), а доверительные интервалы скорректированной и нескорректированной чувствительности перекрываются. Специфика LFpen и FC различается в зависимости от методов, при этом Staquet et al. [5] скорректированные специфичности (LFpen = 0,04, FC = 0,36) являются самыми низкими из всех. При такой высокой распространенности и, в частности, когда расчетная распространенность нелогична (1.2), расчетная специфичность с помощью Staquet et al. [5] следует относиться скептически.
Специфика LFpen и FC различается в зависимости от методов, при этом Staquet et al. [5] скорректированные специфичности (LFpen = 0,04, FC = 0,36) являются самыми низкими из всех. При такой высокой распространенности и, в частности, когда расчетная распространенность нелогична (1.2), расчетная специфичность с помощью Staquet et al. [5] следует относиться скептически.
Второй набор данных Matos et al. [17] (табл. 6) был проанализирован; оценочная распространенность составляет 0,06, а распространенность выборки — 0,052. Нескорректированная и скорректированная чувствительность и специфичность LFpen и FC при различении зубов D3 представлены в таблице 8.
Таблица 8 Нескорректированная и скорректированная чувствительность и специфичность LFpen и FC при выявлении D3Полноразмерная таблица
Из таблицы 8 видно, что оценочная и выборочная распространенность D3 очень низка (< 0,1), следовательно, специфичность LFpen и FC (≅ 0,9) согласованы для всех методов и оцениваются точно, а доверительные интервалы от скорректированных и нескорректированных специфичностей перекрываются. Однако чувствительность различается: Staquet et al. [5] предоставление нелогичных оценок (оценки больше 1). Учитывая нелогичные результаты, невозможно оценить 95% доверительные интервалы. Получение нелогичных оценок чувствительности FC и LFpen через Staquet et al. [5] соответствуют наблюдениям, полученным при моделировании.
Однако чувствительность различается: Staquet et al. [5] предоставление нелогичных оценок (оценки больше 1). Учитывая нелогичные результаты, невозможно оценить 95% доверительные интервалы. Получение нелогичных оценок чувствительности FC и LFpen через Staquet et al. [5] соответствуют наблюдениям, полученным при моделировании.
Обсуждение
Имитационное исследование
Во -первых, когда RS является идеальным ( SN RS = SP RS 3 = 1). По оценкам, по оценкам, по оценкам, по оценкам, по оценкам, по оценкам, по оценкам, по сравнению с расчетными методами. одинаковы (это выражено алгебраически в дополнительном файле 1). Во-вторых, когда ОН несовершенен и ОН условно независим от ИТ, метод Staquet et al. [5] метод коррекции превосходит метод коррекции Бреннера независимо от того, какой тест лучше. Кроме того, оценки, полученные с помощью Staquet et al. [5] метод коррекции поддерживает предположение о постоянной чувствительности и специфичности в популяциях с разной распространенностью. Это означает, что распространенность заболевания в популяции не влияет на оценки, полученные с помощью Staquet et al. [5] в отличие от классического метода и метода коррекции Бреннера. При низкой распространенности расчетная чувствительность классического метода и метода Бреннера часто занижается, а при высокой распространенности обычно недооценивается расчетная специфичность классического метода и метода коррекции Бреннера. Таким образом, при высокой распространенности чувствительность, скорее всего, будет точно оценена всеми методами, а при низкой распространенности специфичность, вероятно, будет точно оценена всеми методами. Это согласуется с выводами других исследователей о том, что в популяции с высокой распространенностью чувствительность индексного теста часто может быть оценена точно, а в популяции с низкой распространенностью, вероятно, будет точно оценена специфичность [1, 25]. Кроме того, отсутствие поправки на несовершенство ИТ с использованием классического метода дает оценки, которые ближе к смоделированной истине, чем поправка на несовершенство ИТ с использованием метода коррекции Бреннера.
Это означает, что распространенность заболевания в популяции не влияет на оценки, полученные с помощью Staquet et al. [5] в отличие от классического метода и метода коррекции Бреннера. При низкой распространенности расчетная чувствительность классического метода и метода Бреннера часто занижается, а при высокой распространенности обычно недооценивается расчетная специфичность классического метода и метода коррекции Бреннера. Таким образом, при высокой распространенности чувствительность, скорее всего, будет точно оценена всеми методами, а при низкой распространенности специфичность, вероятно, будет точно оценена всеми методами. Это согласуется с выводами других исследователей о том, что в популяции с высокой распространенностью чувствительность индексного теста часто может быть оценена точно, а в популяции с низкой распространенностью, вероятно, будет точно оценена специфичность [1, 25]. Кроме того, отсутствие поправки на несовершенство ИТ с использованием классического метода дает оценки, которые ближе к смоделированной истине, чем поправка на несовершенство ИТ с использованием метода коррекции Бреннера. Таким образом, классический метод работает лучше, чем метод коррекции Бреннера. Кроме того, когда IT и RS являются условно зависимыми, как Staquet et al. [5] и методы поправки Бреннера работают плохо.
Таким образом, классический метод работает лучше, чем метод коррекции Бреннера. Кроме того, когда IT и RS являются условно зависимыми, как Staquet et al. [5] и методы поправки Бреннера работают плохо.
Анализ наборов клинических данных
Исследованные наборы клинических данных имели различную распространенность, что помогает в изучении методов в клинических приложениях. Мэтьюз и др. [16] имел выборочную распространенность 0,23, а два набора данных из Matos et al. [17] имели очень низкую (0,052) и очень высокую (примерно 0,92) выборочную распространенность. Использование наборов клинических данных с различной распространенностью подтвердило результаты симуляционного исследования.
Анализ наборов клинических данных наряду с имитационным исследованием показал, что распространенность целевого состояния может привести к нелогичным оценкам чувствительности и специфичности ИТ с помощью Staquet et al. [5] подход. Однако может быть альтернативное обоснование, которое можно было бы рассмотреть, если это произойдет, например, что два теста (IT и RS) математически условно зависимы, даже если IT и RS не используют один и тот же биологический компонент. Однако мы не можем заключить, что получение нелогичной оценки с помощью Staquet et al. [5] является достаточным условием для установления условной зависимости ИТ и РС с учетом истинного статуса заболевания. Информация в дополнительном файле 3 — таблица S2 показывает, что нелогичные оценки могут быть получены с помощью Staquet et al. [5] подход, когда тесты условно независимы.
Однако мы не можем заключить, что получение нелогичной оценки с помощью Staquet et al. [5] является достаточным условием для установления условной зависимости ИТ и РС с учетом истинного статуса заболевания. Информация в дополнительном файле 3 — таблица S2 показывает, что нелогичные оценки могут быть получены с помощью Staquet et al. [5] подход, когда тесты условно независимы.
В сценариях, где оценки, полученные с помощью Staquet et al. [5] нелогичны, можно использовать традиционную модель латентного класса [7, 26, 27, 28, 29], а известную чувствительность и специфичность РС использовать в качестве априорных значений (детерминированных или вероятностных) в модели для оценить показатели точности ИТ. Модель латентного класса имеет преимущество перед Staquet et al. [5] в том, что он не дает нелогичных оценок. Кроме того, если тесты условно зависимы, можно рассмотреть байесовскую модель латентного класса [15].
Одним из ограничений этого исследования является то, что традиционная модель латентного класса не исследуется, так как это вероятностный подход к моделированию, который не является предметом данной работы. Кроме того, вероятность охвата доверительных интервалов не исследовалась, поскольку она является свойством процедуры, вырабатывающей доверительный интервал, а не самих оценок, и поэтому выходит за рамки данного исследования. Кроме того, могут быть и другие сценарии (возможные комбинации чувствительности и специфики РС и ИТ, а также распространенность), не рассмотренные в этой статье; тем не менее, R-Code (дополнительный файл 2), написанный авторами, поможет исследователям, которые хотят исследовать больше. Еще одной областью исследований является изучение исследования Staquet et al. [5] подход к пониманию того, есть ли способ указать условную зависимость между двумя тестами. Кроме того, как видно из анализа наборов клинических данных (Таблица 5, Таблица 7 и Дополнительный файл 3), было получено нелогичное значение для оценочной распространенности, что могло повлиять на оценочную специфичность индексных тестов. Таким образом, Staquet et al. [5] подход может быть дополнительно изучен, чтобы установить другие условия, которые могут привести к тому, что Staquet et al.
Кроме того, вероятность охвата доверительных интервалов не исследовалась, поскольку она является свойством процедуры, вырабатывающей доверительный интервал, а не самих оценок, и поэтому выходит за рамки данного исследования. Кроме того, могут быть и другие сценарии (возможные комбинации чувствительности и специфики РС и ИТ, а также распространенность), не рассмотренные в этой статье; тем не менее, R-Code (дополнительный файл 2), написанный авторами, поможет исследователям, которые хотят исследовать больше. Еще одной областью исследований является изучение исследования Staquet et al. [5] подход к пониманию того, есть ли способ указать условную зависимость между двумя тестами. Кроме того, как видно из анализа наборов клинических данных (Таблица 5, Таблица 7 и Дополнительный файл 3), было получено нелогичное значение для оценочной распространенности, что могло повлиять на оценочную специфичность индексных тестов. Таким образом, Staquet et al. [5] подход может быть дополнительно изучен, чтобы установить другие условия, которые могут привести к тому, что Staquet et al. [5] приводит к нелогичным оценкам, а также к возможным последствиям, когда несколько условий выполняются одновременно.
[5] приводит к нелогичным оценкам, а также к возможным последствиям, когда несколько условий выполняются одновременно.
Выводы
На основе моделирования (с использованием сценариев, рассмотренных в этой статье) и анализа наборов клинических данных Staquet et al. [5] метод коррекции превосходит метод коррекции Бреннера. Однако, когда распространенность целевого состояния очень высока (> 0,9) или низкая (< 0,1), или тесты, используемые в исследовании диагностической точности, коррелируют (условно зависимы), следует рассмотреть другие статистические методы, такие как модель латентного класса. (частотный или байесовский), чтобы избежать получения нелогичных или неточных оценок. Кроме того, использование неверных оценок показателей точности эталонного стандарта повлияет на расчетную скорректированную чувствительность и специфичность индексного теста.
Доступность данных и материалов
Сгенерированные и проанализированные наборы данных включены в эту опубликованную статью [и код R в дополнительном файле 2].
Ссылки
Ссылки на скачивание
Благодарности
Неприменимо.
Финансирование
• Премия Университета Ньюкасла за выдающиеся достижения в области исследований
• Институт изучения здоровья населения, факультет медицинских наук, Университет Ньюкасла
• Школа математики, статистики и физики, Университет Ньюкасла
• Национальный институт исследований в области здравоохранения, Ньюкасл, Индиана Кооператив Vitro Diagnostics, Ньюкаслский университет
Это исследование поддерживается Национальным институтом исследований в области здравоохранения (NIHR) Newcastle In Vitro Diagnostics Co-operative и финансируется схемой NIHR MedTech In Vitro Diagnostic Co-operatives (ref MIC-2016-014). Выраженные взгляды принадлежат автору (авторам) и не обязательно принадлежат NIHR, NHS или Департаменту здравоохранения и социального обеспечения.
Информация об авторе
Авторы и организации
Authors
Взносы
Концепция и дизайн работы CMUC, JAA, KW и LV. Рукопись составлена CMUC. Моделирование и анализ набора данных с помощью CMUC. Интерпретация результатов CMUC, KW, JAA и LV. Надзор за проектом и пересмотр рукописи JAA, KW и LV. Авторы прочитали и одобрили окончательный вариант рукописи.
Рукопись составлена CMUC. Моделирование и анализ набора данных с помощью CMUC. Интерпретация результатов CMUC, KW, JAA и LV. Надзор за проектом и пересмотр рукописи JAA, KW и LV. Авторы прочитали и одобрили окончательный вариант рукописи.
Информация об авторах
Неприменимо.
Автор, ответственный за переписку
Чиньереуго М. Умемнеку Чикере.
Декларация этики
Одобрение этики и согласие на участие
Неприменимо.
Согласие на публикацию
Не применимо.
Конкурирующие интересы
Авторы заявляют об отсутствии конкурирующих интересов.
Дополнительная информация
Примечание издателя
Springer Nature остается нейтральной в отношении юрисдикционных претензий в опубликованных картах и институциональной принадлежности.
Дополнительная информация
12874_2021_1255_MOESM1_ESM.pdf
Дополнительный файл 1.
12874_2021_1255_МОЭСМ2_ЭСМ.pdf
Дополнительный файл 2.
12874_2021_1255_MOESM3_ESM.pdf
Дополнительный файл 3.
12874_2021_1255_MOESM4_ESM.pdf
Дополнительный файл 4.
Права и разрешения
Открытый доступ Эта статья находится под лицензией Creative Commons Attribution 4.0 International License, которая разрешает использование, совместное использование, адаптацию, распространение и воспроизведение на любом носителе или в любом формате, при условии, что вы укажете соответствующую ссылку на оригинальный автор(ы) и источник, предоставьте ссылку на лицензию Creative Commons и укажите, были ли внесены изменения. Изображения или другие сторонние материалы в этой статье включены в лицензию Creative Commons на статью, если иное не указано в кредитной строке материала.




 Диапазон применения корректурной пробы очень широк – со дошкольного возраста и до пенсионного. Т.е. для использования данного теста практически не существует возрастных ограничений – важно правильно подобрать стимульный материал. Тест может быть полезен в клинической практике, школьной диагностике, в процессе профориентации и профотбора.
Диапазон применения корректурной пробы очень широк – со дошкольного возраста и до пенсионного. Т.е. для использования данного теста практически не существует возрастных ограничений – важно правильно подобрать стимульный материал. Тест может быть полезен в клинической практике, школьной диагностике, в процессе профориентации и профотбора. Испытуемый начинает работать по команде экспериментатора. Когда через некоторое время экспериментатор произнесет: «Черта!»- Вы должны поставить вертикальную черту в том месте строки, где Вас застала команда. Через десять минут отмечается последняя рассмотренная буква.
Испытуемый начинает работать по команде экспериментатора. Когда через некоторое время экспериментатор произнесет: «Черта!»- Вы должны поставить вертикальную черту в том месте строки, где Вас застала команда. Через десять минут отмечается последняя рассмотренная буква.
 Методика была предложена Е. Kraepelin. При исследовании ею обнаруживаются возможности осуществления испытуемым счетных операций, состояние внимания. Опыт заключается в отсчитыванин от 100 или 200 все время одного и того же числа. Испытуемого предупреждают, что считать он должен про себя, а вслух только называть полученное при очередном вычитании число. В промежутках между числами исследующий равномерно ставит точки (приблизительный хронометраж). Можно фиксировать длительность пауз секундомером. Запись опыта приобретает следующий вид: (100 — 7) . . 93. . . 86. . . 79. . . 72. . . 65. . . 58. 51 . . 44. . 37. 30. 23. 16. 2. При наличии повышенной истощаемости длительность пауз в конце, несмотря на то что задание становится более легким, увеличивается. Возможны два вида ошибок. Первый — ошибки в единицах и главным образом при переходе через десяток — свидетельствует о некоторой интеллектуальной недостаточности, например: (100 — 7). . 93. . . . . . 85. . . . . 78. . 71. . . . 64. . . . 58 и т.
Методика была предложена Е. Kraepelin. При исследовании ею обнаруживаются возможности осуществления испытуемым счетных операций, состояние внимания. Опыт заключается в отсчитыванин от 100 или 200 все время одного и того же числа. Испытуемого предупреждают, что считать он должен про себя, а вслух только называть полученное при очередном вычитании число. В промежутках между числами исследующий равномерно ставит точки (приблизительный хронометраж). Можно фиксировать длительность пауз секундомером. Запись опыта приобретает следующий вид: (100 — 7) . . 93. . . 86. . . 79. . . 72. . . 65. . . 58. 51 . . 44. . 37. 30. 23. 16. 2. При наличии повышенной истощаемости длительность пауз в конце, несмотря на то что задание становится более легким, увеличивается. Возможны два вида ошибок. Первый — ошибки в единицах и главным образом при переходе через десяток — свидетельствует о некоторой интеллектуальной недостаточности, например: (100 — 7). . 93. . . . . . 85. . . . . 78. . 71. . . . 64. . . . 58 и т.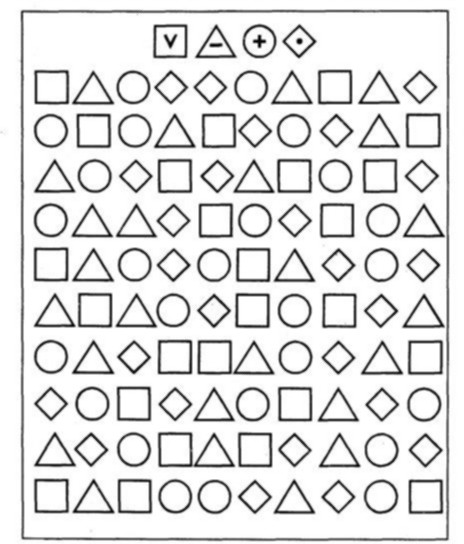 д. Второй — ошибки в десятках — характерен главным образом для больных с неустойчивым вниманием. Например: 93. . . 86. . . 69. . 62. . . . . 55. . . 38 и т. д.
д. Второй — ошибки в десятках — характерен главным образом для больных с неустойчивым вниманием. Например: 93. . . 86. . . 69. . 62. . . . . 55. . . 38 и т. д.
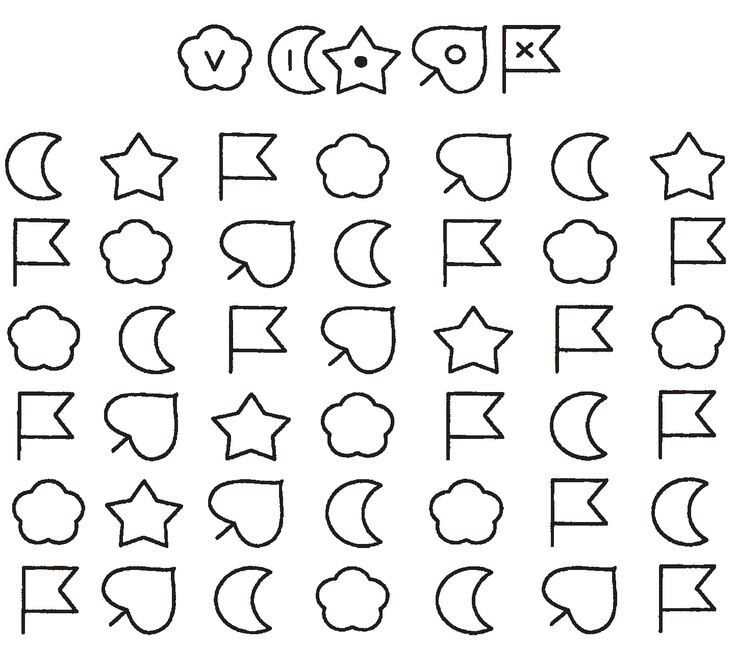 Если частное ниже 0,5 — внимание очень неустойчиво, требуется развитие этого качества.
Если частное ниже 0,5 — внимание очень неустойчиво, требуется развитие этого качества.
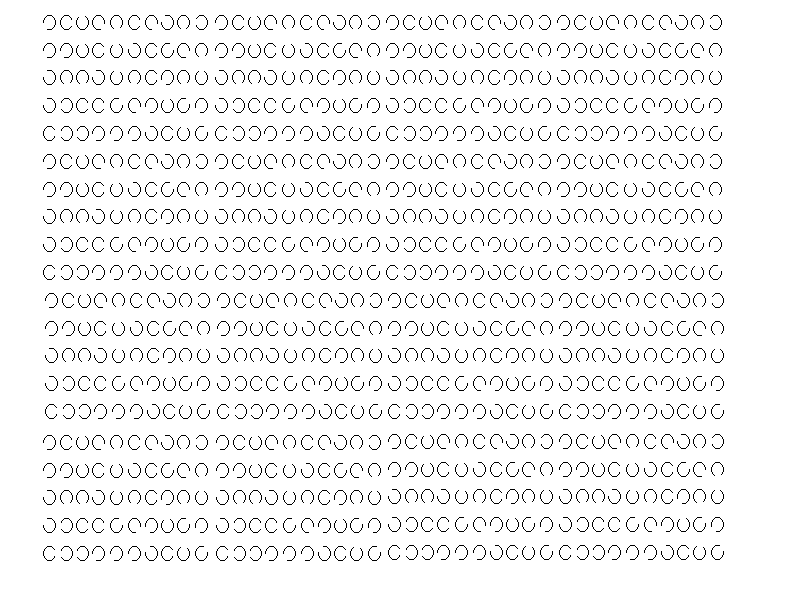 Обычно они исправляют свой тест, даже если пропустили только один балл, поэтому они могут вернуть полбалла. Они все еще не могут заработать высший балл.
Обычно они исправляют свой тест, даже если пропустили только один балл, поэтому они могут вернуть полбалла. Они все еще не могут заработать высший балл. 
 Они знают, что им нужно делать это для собственного совершенствования.
Они знают, что им нужно делать это для собственного совершенствования. 

 65 or > +1.65
65 or > +1.65