Методика матрица равена: Прогрессивные матрицы Равена
Прогрессивные матрицы Равена
Батарея тестов на наглядное мышление по аналогии. Методика разработана английским психологом Дж. Равеном (1938). Каждая задача состоит из двух частей: основного рисунка (какого-либо геометрического узора) с пробелом в правом нижнем углу и набора из б или 8 фрагментов, находящихся под основным рисунком. Из этих фрагментов требуется выбрать один, который, будучи поставленным на место пробела, точно подходил бы к рисунку в целом. П.м.Р. разделяются на 5 серий, по 12 матриц в каждом.П.м.Р широко используется во многих странах как невербальные тесты умственной одаренности. По мнению сторонников концепции независимости мышления от речи, П.м.Р (как и другие невербальные тесты) позволяют изучать интеллект в «чистом виде», исключающая влияние языка и знаний. Однако подобный вывод не подтверждается современными психологическими и электрофизическими исследованиями, свидетельствующими от участии внутренней речи в решении сложных матричных задач.
Эта методика предназначается для оценивания наглядно-образного мышления у младшего школьника.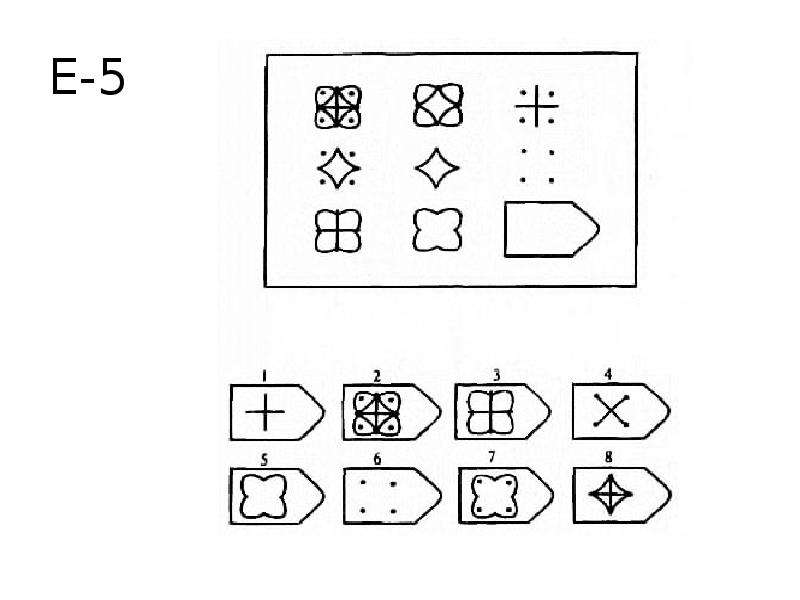
Конкретные задания, используемые для проверки уровня развития наглядно-образного мышления, в данной методике взяты из известного теста Равена. Они представляют собой специальным образом подобранную выборку из 10 постепенно усложняющихся матриц Равена
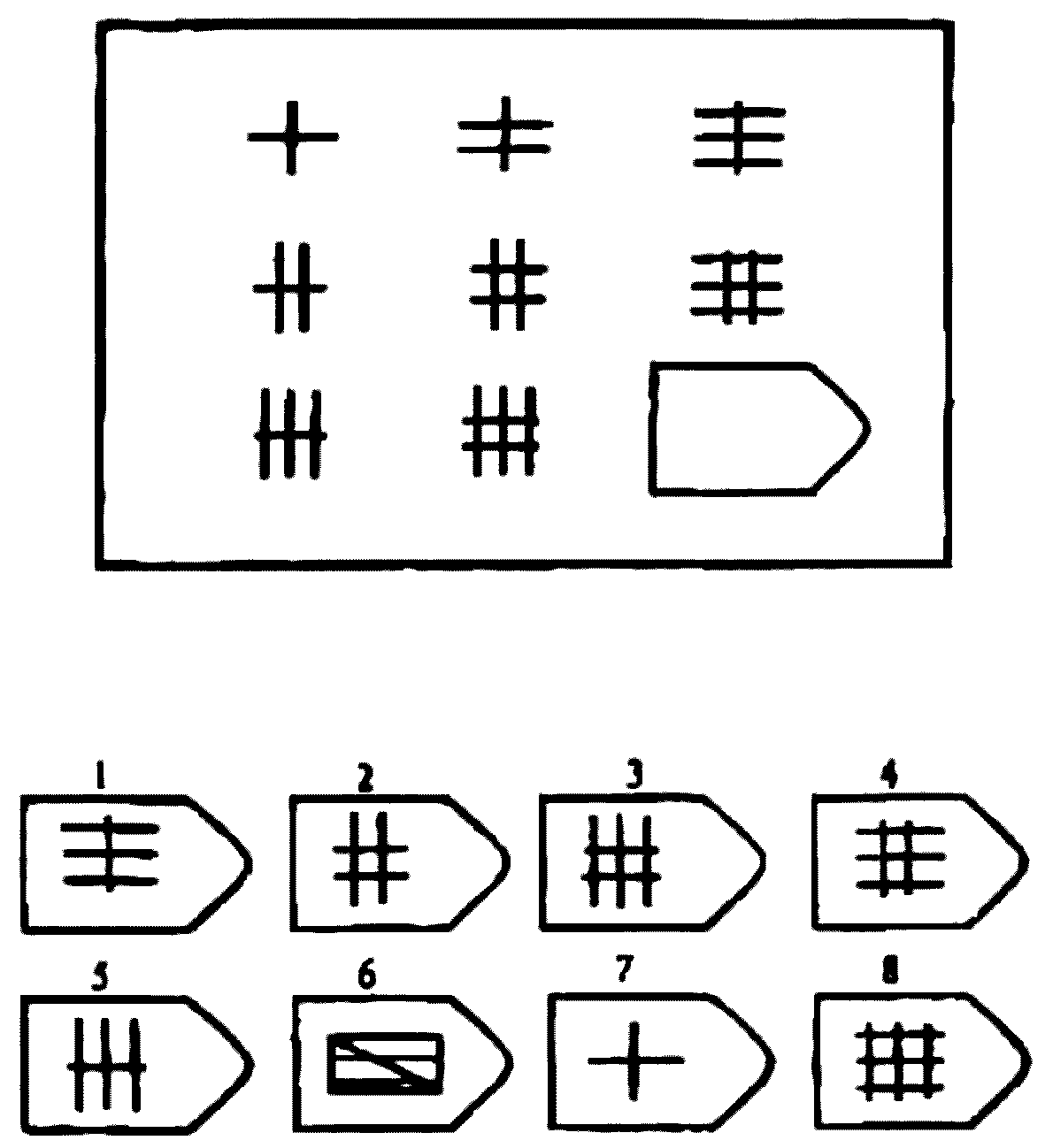
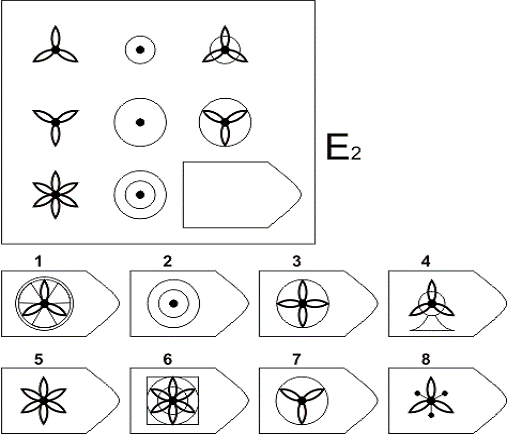
Ребенку предлагается серия из десяти постепенно усложняющихся задач одинакового типа: на поиск закономерностей в расположении деталей на матрице (представлена в верхней части указанных рисунков в виде большого четырехугольника) и подбор одного из восьми данных ниже рисунков в качестве недостающей вставки к этой матрице, соответствующей ее рисунку (данная часть матрицы представлена внизу в виде флажков с разными рисунками на них). Изучив структуру большой матрицы, ребенок должен указать ту из деталей (тот из восьми имеющихся внизу флажков), которая лучше всего подходит к этой матрице, т.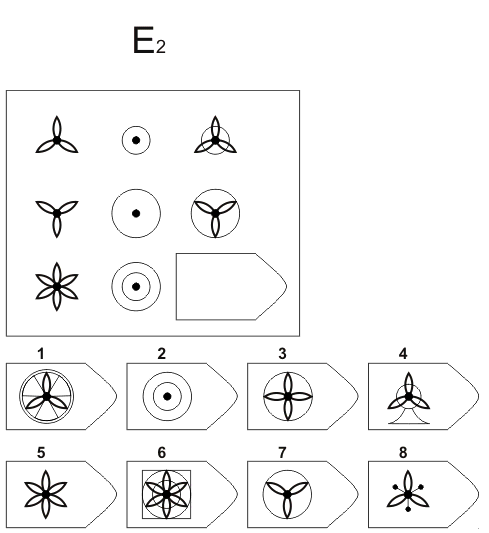
На выполнение всех десяти заданий ребенку отводится 10 минут. По истечении этого времени эксперимент прекращается и определяется количество правильно решенных матриц, а также общая сумма баллов, набранных ребенком за их решения. Каждая правильно, решенная матрица оценивается в 1 балл.
Правильные, решения всех десяти матриц следующие (первая из приводимых ниже пар цифр указывает на номер матрицы, а вторая — на правильный ответ: 1-7,2-6,3-6,4-1,5-2,6-5,7-6, 8-1,9-3,10-5.
Выводы об уровне развития
|
10 баллов — очень высокий 8-9 баллов — высокий. 4-7 баллов — средний. 2-3 балла — низкий.
0-1 балл — очень низкий. |
См. также
Тесты для детей Тесты способностей
RSS [email protected]
определение, и где она применяется?
Этот тест был разработан в Великобритании в ХХ веке для оценки интеллекта испытуемого. Проверялась способность выстраивать логические связи и воспринимать графические невербальные сигналы.
С того времени тест используется как одна из самых валидных и надежных методик в психоанализе. К тому же она позволяет проводить даже групповое обследование и мониторинг. Несмотря на то что методика носит название «Матрица Равена», в ее создании принимал участие еще один человек — Пентроуз. Всего было создано три варианта матриц. Первый, черно-белый, является наиболее часто применяемым. С его помощью обследуются детки от 5 до 11 лет и люди от 20 лет. Второй вариант, цветной, намного проще. Он позволяет проводить диагностику малышей от 5 лет и людей старше 65. Кроме того, тест полезен для обследования индивидов с нарушениями вербальной коммуникации. Третий вид матриц предназначен для тестирования высокоинтеллектуальных личностей.
Третий вид матриц предназначен для тестирования высокоинтеллектуальных личностей.
Несмотря на существенные различия, все тесты строятся по одному шаблону, где в качестве стимула используются геометрические фигуры, организованные по определенному принципу. Характерно то, что первые два варианта, прогрессивные матрицы Равена в черно-белом и цветном вариантах, имеют только невербальную часть. Третий же вид содержит и эту часть, что неудивительно.
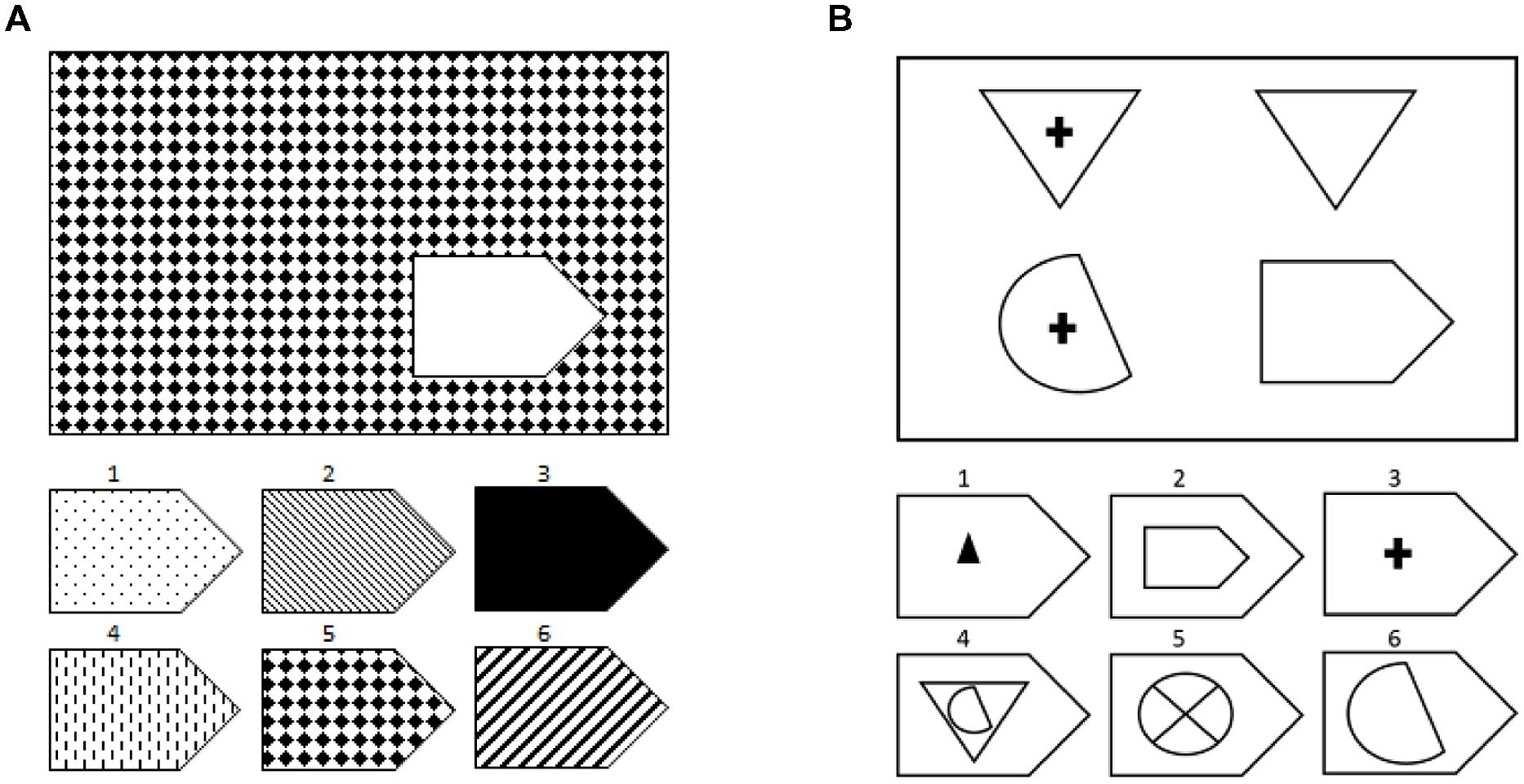
Тест построен по следующему принципу: испытуемому дают картинки с геометрическими фигурами, которые расположены в определенном порядке и находятся друг с другом в тесной взаимозависимости. Одного элемента всегда не хватает. Задача испытуемого — найти и выбрать из 8 предложенных вариантов именно тот, который подойдет на пустое место. На качество выполнения влияют как точность восприятия, индуктивное мышление и степень развитости у человека пространственного мышления, так и другие параметры. Среди них — способность оперировать образами, концентрация внимания, логическое мышление и уровень развития мыслительных операций в целом.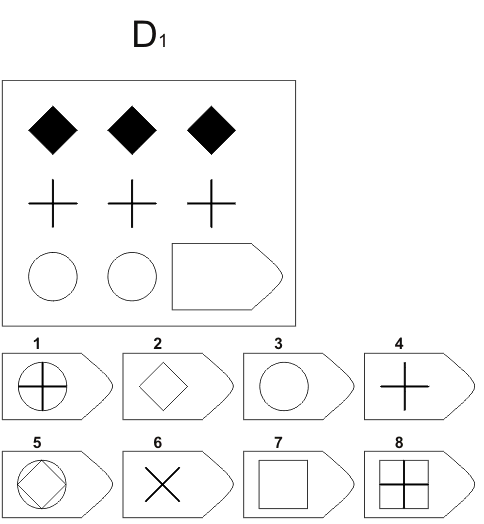 Цветной тест для проверки способностей пожилых людей и детей состоит из 3 серий по 12 матриц. Как и в черно-белом варианте, сложность заданий возрастает.
Цветной тест для проверки способностей пожилых людей и детей состоит из 3 серий по 12 матриц. Как и в черно-белом варианте, сложность заданий возрастает.
Матрицы для взрослых
Тест прогрессивных матриц Равена для взрослых включает в себя 5 серий. В каждой серии 12 матриц. Таким образом, общее число матриц — 60, и сложность их увеличивается от серии к серии, от матрицы к матрице.
Даже само название и методика «Прогрессивные матрицы Равена» указывают на то, что в тесте должен присутствовать какой-то прогресс. Изначально задумывалось, что первые 5 матриц человек выполняет с помощью наблюдателя, а дальше работает над заданием самостоятельно. Таким образом, каждое следующее задание, каждая новая матрица Равена основана на том опыте, который человек получил, выполняя предыдущее задание.
Принцип построения серий
Человек, выполняя задание, должен сделать следующие действия: сделать анализ структуры образца, определить тип и характер связей между объектами, найти отсутствующее звено или элемент и из предложенных вариантов выбрать наиболее подходящий.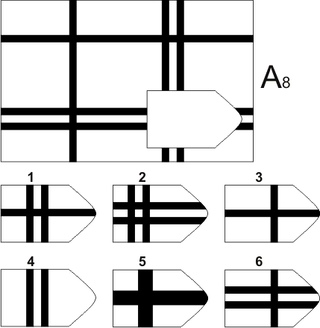 Несмотря на все это, серии строятся по-разному. Например, в первой серии (серия А) надо найти взаимосвязь в структуре самой матрицы. Для этого проводится анализ структуры основного изображения, дифференцируется и находятся эти же особенности в одном из предложенных ниже фрагментов матрицы.
Несмотря на все это, серии строятся по-разному. Например, в первой серии (серия А) надо найти взаимосвязь в структуре самой матрицы. Для этого проводится анализ структуры основного изображения, дифференцируется и находятся эти же особенности в одном из предложенных ниже фрагментов матрицы.
Во второй серии (серия В) надо найти аналогии и связь между парными фигурами с отличными элементами. От испытуемого требуется определить тот принцип, по которому строится фигура, и выбрать необходимый элемент из предложенных ниже.
В третьей серии (серия С) фигуры прогрессивно изменяются не только по горизонтали, но и по вертикали. Так как фигуры все больше усложняются от матрицы к матрице, и в них появляются новые элементы, задача человека, проходящего тест, — найти закономерность появления этих элементов.
Выполняя тест в серии Д, человек должен обнаружить принцип перегруппировки фигур внутри матрицы. Перестановка происходит как по горизонтали, так и по вертикали.
Серия Е является самой сложной. С ней у большинства испытуемых возникают самые большие проблемы.
С ней у большинства испытуемых возникают самые большие проблемы.
Расчет результатов
Тест можно выполнять сколько угодно, но чаще всего время, которое отводится, около 20 минут. Можно проводить как групповое, так и индивидуальное тестирование. В первом случае очень важно, чтобы все люди и закончили, и начали выполнение теста Равена одновременно. Анализ проводится стандартно — в таблицу по сериям заносятся результаты, причем за правильный ответ начисляется 1 балл. Потом высчитывается процентное значение уровня интеллекта.
95% и выше — высокий интеллект, 94-75% — интеллект выше среднего, 74-25% — средний показатель уровня интеллекта, 24-5% — низкие умственные способности. Если человек набирает менее 5%, то есть смысл говорить об умственном недоразвитии.
Можно ли использовать тест для всех без исключения людей?
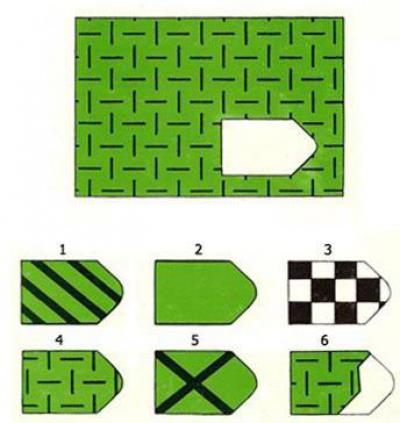
Матрица Равена основана на невербальных сигналах, то есть чтобы выполнить тест, читать и писать не обязательно. Поэтому с ее помощью можно тестировать практически кого угодно.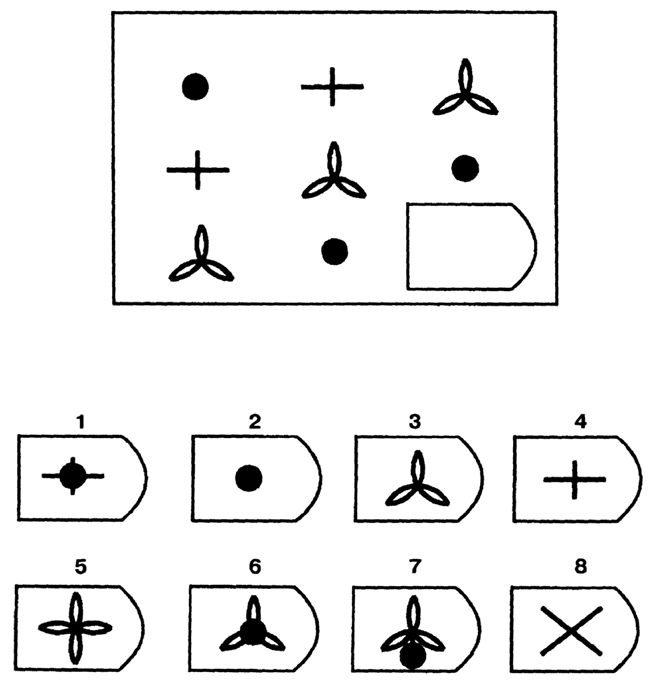 На практике оказалось, что данные, полученные в ходе исследований в Великобритании, и соответствующие нормы вполне можно использовать в европейских странах. Между тем их использование для тестирования людей, которые живут в кардинально отличающихся условиях, невозможно. Фактор наличия образования все-таки оказывает влияние на результат. Кроме того, те, кто уже проходил тест «Матрицы Равена», второй раз решают его лучше.
На практике оказалось, что данные, полученные в ходе исследований в Великобритании, и соответствующие нормы вполне можно использовать в европейских странах. Между тем их использование для тестирования людей, которые живут в кардинально отличающихся условиях, невозможно. Фактор наличия образования все-таки оказывает влияние на результат. Кроме того, те, кто уже проходил тест «Матрицы Равена», второй раз решают его лучше.
Прогрессивные матрицы Равена — презентация онлайн
1. Тема презентации
ТЕМА ПРЕЗЕНТАЦИИОписание методики
Прогрессивные
матрицы Равена (Raven
Progressive Matrices) предназначены
для определения уровня умственного
(интеллектуального)
развития
испытуемых в возрасте от 4,5 до 65 лет и
старше.
Матрицы
Равена
могут
применяться на выборках испытуемых с
любым
языковым
составом
и
социокультурным фоном, с любым
уровнем речевого развития.
Были разработаны варианты методики:
«Стандартные Прогрессивные Матрицы» (1938г.
 ),
),«Цветные Прогрессивные Матрицы» (1947 г.),
«Продвинутые Прогрессивные Матрицы» (1941 г.).
Возрастные границы применимости Прогрессивных
матриц Равена
Варианты теста Равена
Цветные прогрессивные матрицы
Контингент испытуемых
• 4,5 — 9 лет;
испытуемые с аномальным
развитием;
• реабилитационные
исследования лиц;
• старше 65 лет
Стандартные прогрессивные
матрицы
• дети от 8 до 14 лет;
• взрослые от 20 до 65 лет
Продвинутые прогрессивные
матрицы
• испытуемые с
интеллектуальными
способностями выше среднего
5. История создания методики
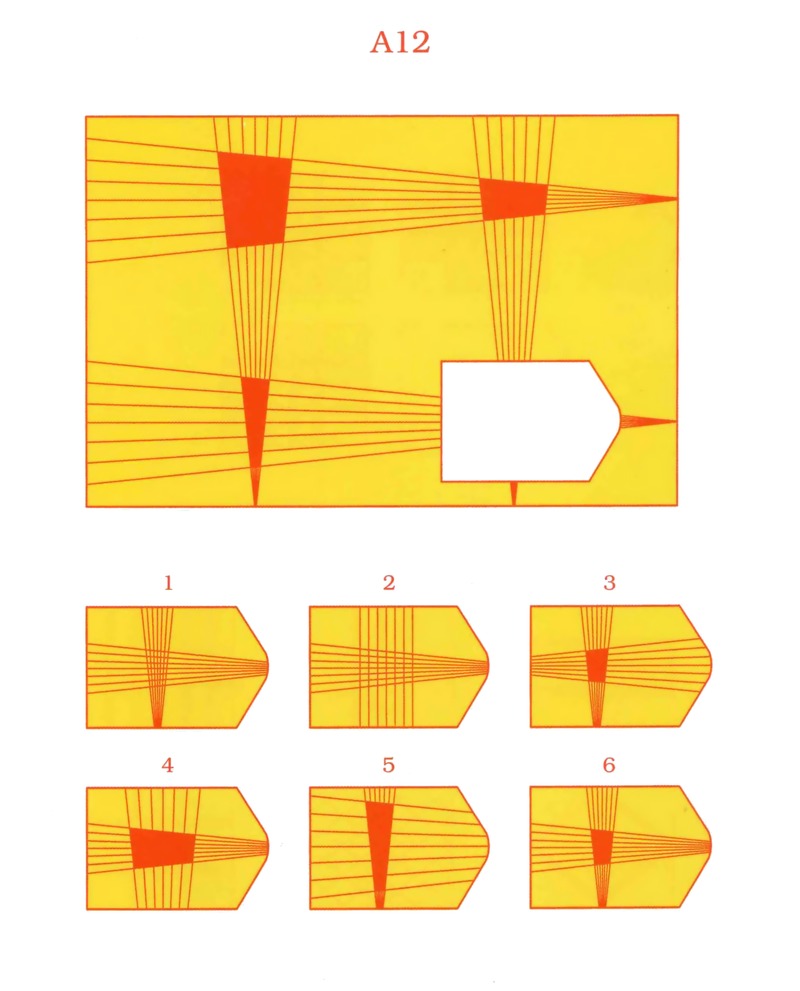
ИСТОРИЯ СОЗДАНИЯ МЕТОДИКИТест предложен Л. Пенроузом и Дж. Равеном в 1936 г. Р. п. м.
разрабатывались в соответствии с традициями английской
способ измерения фактора «g» — задача по выявлению
отношений между абстрактными фигурами. Наиболее
известны два основных варианта Р.
 п. м.: черно-белые и
п. м.: черно-белые ицветные матрицы. Разрабатывая тесты, которые были бы
полезным инструментом для идентификации генетических и
средовых причин интеллектуальных отклонений, Дж. Равен
сознательно ставил перед собой задачу создания таких тестов,
которые были бы теоретически обоснованы, однозначно
интерпретируемы, просты для проведения и обработки,
пригодны как для лабораторных, так и для полевых
экспериментов, а также удобны для массовых обследований,
проводимых на дому, в школах, на производстве и
сопряженных с временными ограничениями.
6. Задание: вставьте в пустое место подходящий ресунок
ЗАДАНИЕ: ВСТАВЬТЕ В ПУСТОЕ МЕСТОПОДХОДЯЩИЙ РЕСУНОК
9. Процентная шкала степени развития интеллекта
ПРОЦЕНТНАЯ ШКАЛА СТЕПЕНИРАЗВИТИЯ ИНТЕЛЛЕКТА
Проценты
Степень
95 и выше
I степень: особо
высокоразвитый интеллект
испытуемого соответствующей
возрастной группы
75-95
2 степень; незаурядный
интеллект для данной
возрастной группы
25-74
3 степень: средник интеллект
для данной возрастной группы
5-24
4 степень: интеллект ниже
среднего.
5 и менее
5 степень: дефектная
интеллектуальная способность
Матричный анализ решений — Навыки принятия решений от MindTools.com
Принятие решения путем взвешивания различных факторов
(также известный как анализ сетки, матричный анализ Пью и теория утилит с несколькими атрибутами)
Представьте, что ваш босс поручил вам нанять нового поставщика ИТ, привлеченного на аутсорсинг. Вы уже определили несколько разных поставщиков, и теперь вам нужно решить, какого из них использовать.
Вы можете выбрать недорогой вариант.Но вы не хотите принимать решение только по стоимости — необходимо учитывать такие факторы, как продолжительность контракта, базовая технология и уровни обслуживания. Так как же убедиться, что вы приняли лучшее решение, принимая во внимание все эти факторы?
Матричный анализ решений — полезный метод для принятия решения. Это особенно эффективно, когда у вас есть ряд хороших альтернатив на выбор и множество различных факторов, которые необходимо учитывать.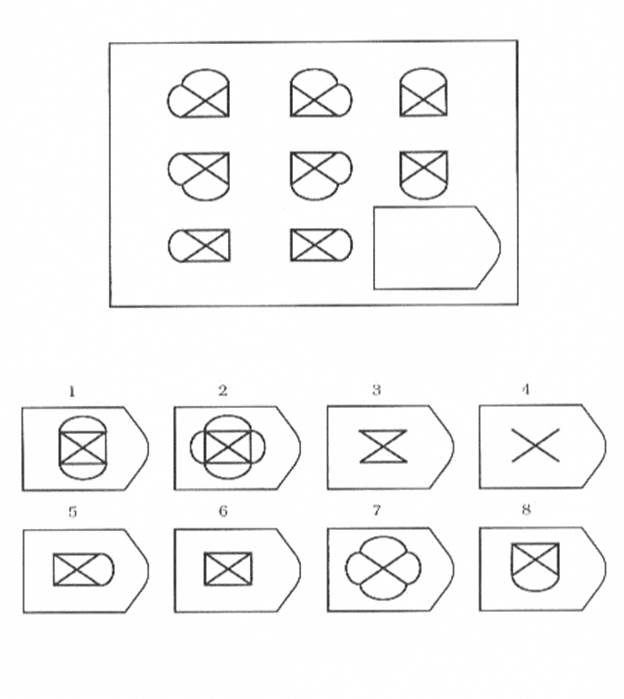 Это делает его отличным методом для использования практически в любом важном решении, когда нет четкого и очевидного предпочтительного варианта.
Это делает его отличным методом для использования практически в любом важном решении, когда нет четкого и очевидного предпочтительного варианта.
Возможность использовать матричный анализ решений означает, что вы можете принимать решения уверенно и рационально в то время, когда другие люди могут с трудом принять решение.
Нажмите здесь
чтобы просмотреть стенограмму этого видео.Как использовать инструмент
Decision Matrix Analysis работает, заставляя вас перечислять ваши варианты в виде строк в таблице, а факторы, которые необходимо учитывать, в виде столбцов.Затем вы оцениваете каждую комбинацию вариант / фактор, взвешиваете эту оценку по относительной важности фактора и складываете эти оценки, чтобы получить общую оценку для каждого варианта.
Хотя это звучит сложно, на самом деле эту технику довольно легко использовать. Вот пошаговое руководство с примером. Начните с загрузки нашего бесплатного рабочего листа. Затем выполните следующие действия.
Вот пошаговое руководство с примером. Начните с загрузки нашего бесплатного рабочего листа. Затем выполните следующие действия.
Шаг 1
Перечислите все ваши параметры в виде меток строк в таблице и перечислите факторы, которые необходимо учитывать в качестве заголовков столбцов.Например, если вы покупаете новый ноутбук, необходимо учитывать такие факторы, как стоимость, размеры и размер жесткого диска.
Шаг 2
Затем двигайтесь вниз по столбцам таблицы, оценивая каждый вариант по каждому из факторов, принимаемых вами в решении. Оцените каждый вариант от 0 (плохо) до 5 (очень хорошо). Обратите внимание, что вам не обязательно иметь разную оценку для каждого варианта — если ни один из них не подходит для определенного фактора вашего решения, тогда все варианты должны иметь оценку 0.
Шаг 3
Следующий шаг — определить относительную важность факторов в вашем решении.Покажите их как числа, скажем, от 0 до 5, где 0 означает, что фактор абсолютно не важен для окончательного решения, а 5 означает, что он очень важен. (Совершенно приемлемо иметь факторы с одинаковой важностью.)
(Совершенно приемлемо иметь факторы с одинаковой важностью.)
Шаг 4
Теперь умножьте каждую из ваших оценок из шага 2 на значения относительной важности фактора, которые вы рассчитали на шаге 3. Это даст вам взвешенные оценки для каждой комбинации вариант / фактор.
Шаг 5
Наконец, сложите эти взвешенные баллы для каждого из ваших вариантов.Выигрывает вариант, набравший наибольшее количество очков!
Совет:
Если ваша интуиция подсказывает вам, что вариант с наивысшей оценкой не самый лучший, подумайте над оценками и весами, которые вы применили. Это может быть признаком того, что определенные факторы для вас важнее, чем вы изначально думали.
Кроме того, если вариант имеет очень низкую оценку по какому-либо фактору, решите, исключает ли это его полностью.
Пример
Кейтерингу необходимо найти нового поставщика для своих основных ингредиентов.У него есть четыре варианта.
Подпишитесь на нашу рассылку новостей
 Прочтите нашу Политику конфиденциальности
Прочтите нашу Политику конфиденциальности
Факторы, которые он хочет учесть:
- Стоимость.
- Качество.
- Местоположение.
- Надежность.
- Варианты оплаты.
Сначала он составляет таблицу, показанную на рисунке 1, и оценивает каждый вариант по тому, насколько хорошо он удовлетворяет каждому фактору:
Рисунок 1: Пример матричного анализа решений, показывающий невзвешенную оценку того, насколько каждый поставщик удовлетворяет каждый фактор
| Факторы: | Стоимость | Качество | Расположение | Надежность | Варианты оплаты | Всего |
|---|---|---|---|---|---|---|
| Вес: | ||||||
| Поставщик 1 | 1 | 0 | 0 | 1 | 3 | |
| Поставщик 2 | 0 | 3 | 2 | 2 | 1 | |
| Поставщик 3 | 2 | 2 | 1 | 3 | 0 | |
| Поставщик 4 | 2 | 3 | 3 | 3 | 0 |
Затем он определяет относительные веса для каждого из факторов. Он умножает их на уже введенные баллы и суммирует их. Это показано на рисунке 2:
Он умножает их на уже введенные баллы и суммирует их. Это показано на рисунке 2:
Рисунок 2: Пример матричного анализа решений, показывающий взвешенную оценку того, насколько каждый поставщик удовлетворяет каждый фактор
| Факторы: | Стоимость | Качество | Расположение | Надежность | Варианты оплаты | Всего |
|---|---|---|---|---|---|---|
| Вес: | 4 | 5 | 1 | 2 | 3 | |
| Поставщик 1 | 4 | 0 | 0 | 2 | 9 | 15 |
| Поставщик 2 | 0 | 15 | 2 | 4 | 3 | 24 |
| Поставщик 3 | 8 | 10 | 1 | 6 | 0 | 25 |
| Поставщик 4 | 8 | 15 | 3 | 6 | 0 | 32 |
Это дает понять поставщику провизии, что Поставщик 4 является лучшим вариантом, несмотря на отсутствие гибкости его вариантов оплаты.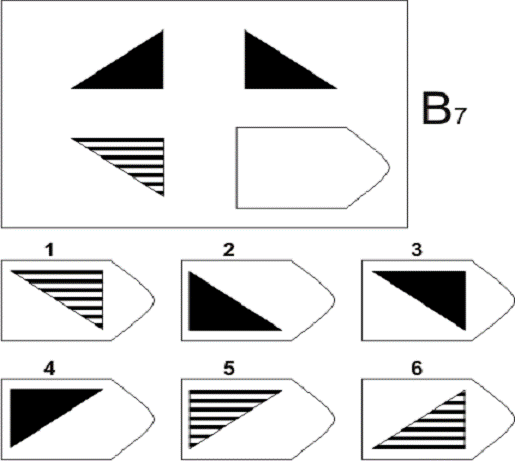
Ключевые моменты
Decision Matrix Analysis поможет вам выбрать между несколькими вариантами, в которых вам необходимо принять во внимание множество различных факторов.
Чтобы использовать инструмент, разложите свои варианты в виде строк на таблице. Настройте столбцы, чтобы показать факторы, которые необходимо учитывать. Оцените каждый выбор для каждого фактора, используя числа от 0 (плохо) до 5 (очень хорошо), а затем распределите веса, чтобы показать важность каждого из этих факторов.
Умножьте каждую оценку на вес фактора, чтобы показать его вклад в общий выбор.Наконец, сложите общие баллы по каждому варианту. Вариант с наивысшей оценкой будет лучшим вариантом.
Примечание:
Матричный анализ решений — это простейшая форма анализа решений по множеству критериев (MCDA), также известная как средство принятия решений по множеству критериев или Управление принятием решений по множеству критериев (MCDM). Сложный MCDA может включать очень сложное моделирование различных потенциальных сценариев с использованием продвинутой математики.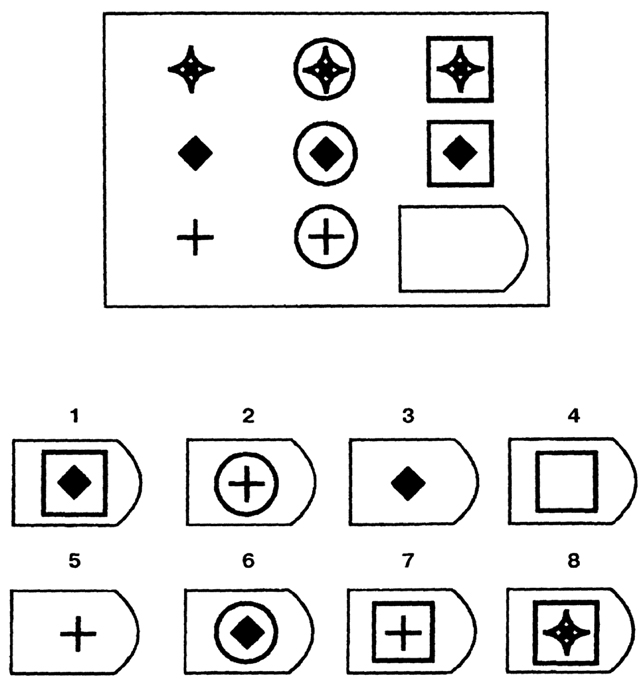
Однако многие бизнес-решения принимаются на основе приблизительных или субъективных данных.В этом случае может потребоваться матричный анализ решений.
Скачать лист
Матричные методы: теория, алгоритмы и приложения
По сравнению с другими книгами, посвященными матрицам, этот том уникален тем, что охватывает весь триптих, состоящий из алгебраической теории, алгоритмических проблем и численных приложений, объединенных основным использованием и стремлением к разработка матричных методов. В этом духе проходила 2-я Международная конференция по матричным методам и операторным уравнениям 23–27 июля 2007 г. в Москве, организованная Дарио Бини, Джином Голубом, Александром Гутерманом, Вадимом Ольшевским, Стефано Серра-Капиццано, Гилбертом Странгом и Евгением Тыртышниковым.
Матричные методы дают ключ ко многим задачам чистой и прикладной математики. Однако теория линейной алгебры, численные алгоритмы и матрицы в приложениях FEM / BEM обычно живут как бы в трех разных мирах.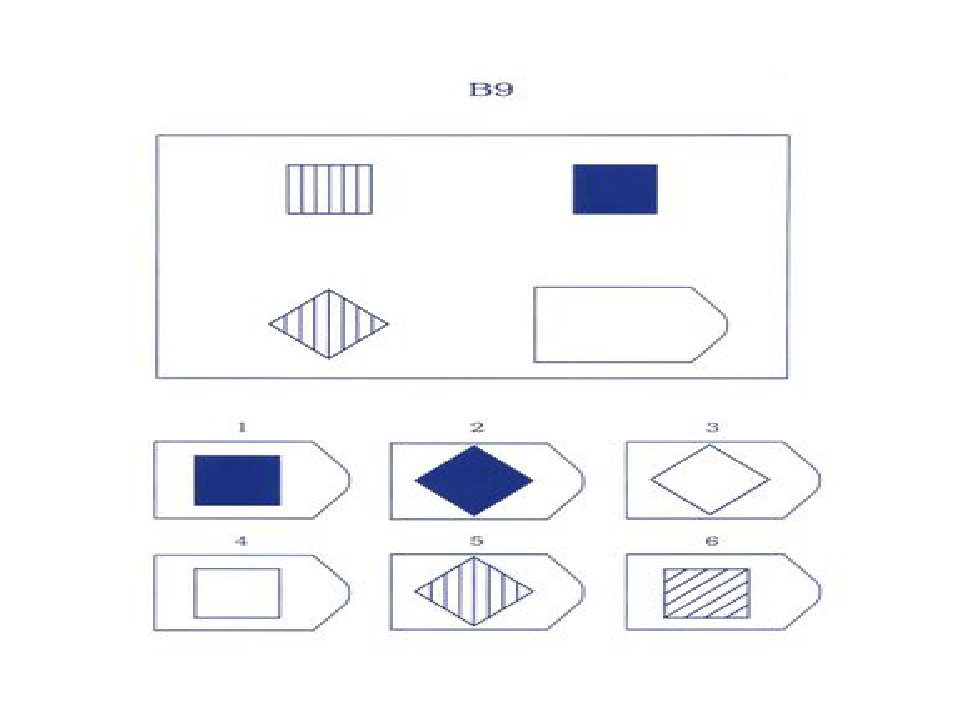 В этом томе, возможно, впервые, они собраны вместе как единое целое, как это было на встрече в Москве, где алгебраическая часть олицетворялась Гансом Шнайдером, алгоритмы — Джином Голубом, а приложения — Гури Марчуком. Все темы, затронутые на пленарных заседаниях, специально разделены на три раздела этого тома.
В этом томе, возможно, впервые, они собраны вместе как единое целое, как это было на встрече в Москве, где алгебраическая часть олицетворялась Гансом Шнайдером, алгоритмы — Джином Голубом, а приложения — Гури Марчуком. Все темы, затронутые на пленарных заседаниях, специально разделены на три раздела этого тома.
Душой встречи был Гена Голуб, который придал трём основным осям темы конференции очаровательное «измерение Голуба». Этот том посвящен его памяти.
Образец глав
Глава 1: Операторы, сохраняющие примитивность для матричных пар (2,856 КБ)
Состав:
- Алгебра и матрицы:
- Операторы, сохраняющие примитивность для матричных пар (Л. Б. Бисли и А. Е. Гутерман)
- Определение ранга Шейна булевых матриц (Э. Э. Маренич)
- Матричные алгебры и их длина (О. В. Маркова)
- Матрицы и алгоритмы:
- Некоторые взаимосвязи между оптимальным прекондиционером и супероптимальным прекондиционером (J-B Chen et al.
 )
) - Разделение переменных в нелинейном уравнении Ферми (Ю.И. Кузнецов)
- Более быстрое вычисление многоточечных полиномов с помощью структурированных матриц (Б. Мерфи и Р. Э. Росхольт)
- Некоторые взаимосвязи между оптимальным прекондиционером и супероптимальным прекондиционером (J-B Chen et al.
- Матрицы и приложения:
- Многоуровневый алгоритм разбиения графа (Н.С. Бочкарев и др.)
- Операторные уравнения для вихревых токов на сингулярных носителях (Ю. Науменко)
- Матричный подход к моделированию переноса поляризованного излучения в неоднородных системах (Т.А. Сушкевич и др.)
- и другие документы
Аудитория: Аспиранты, математики и профессионалы. Помимо академических кругов и промышленности, а также тех, кто рассматривает возможность использования матричных методов в своей работе или кто специализируется в других областях математики, инженерии и естественных наук.
Произошла ошибка при настройке вашего пользовательского файла cookie
Произошла ошибка при настройке вашего пользовательского файла cookie Этот сайт использует файлы cookie для повышения производительности.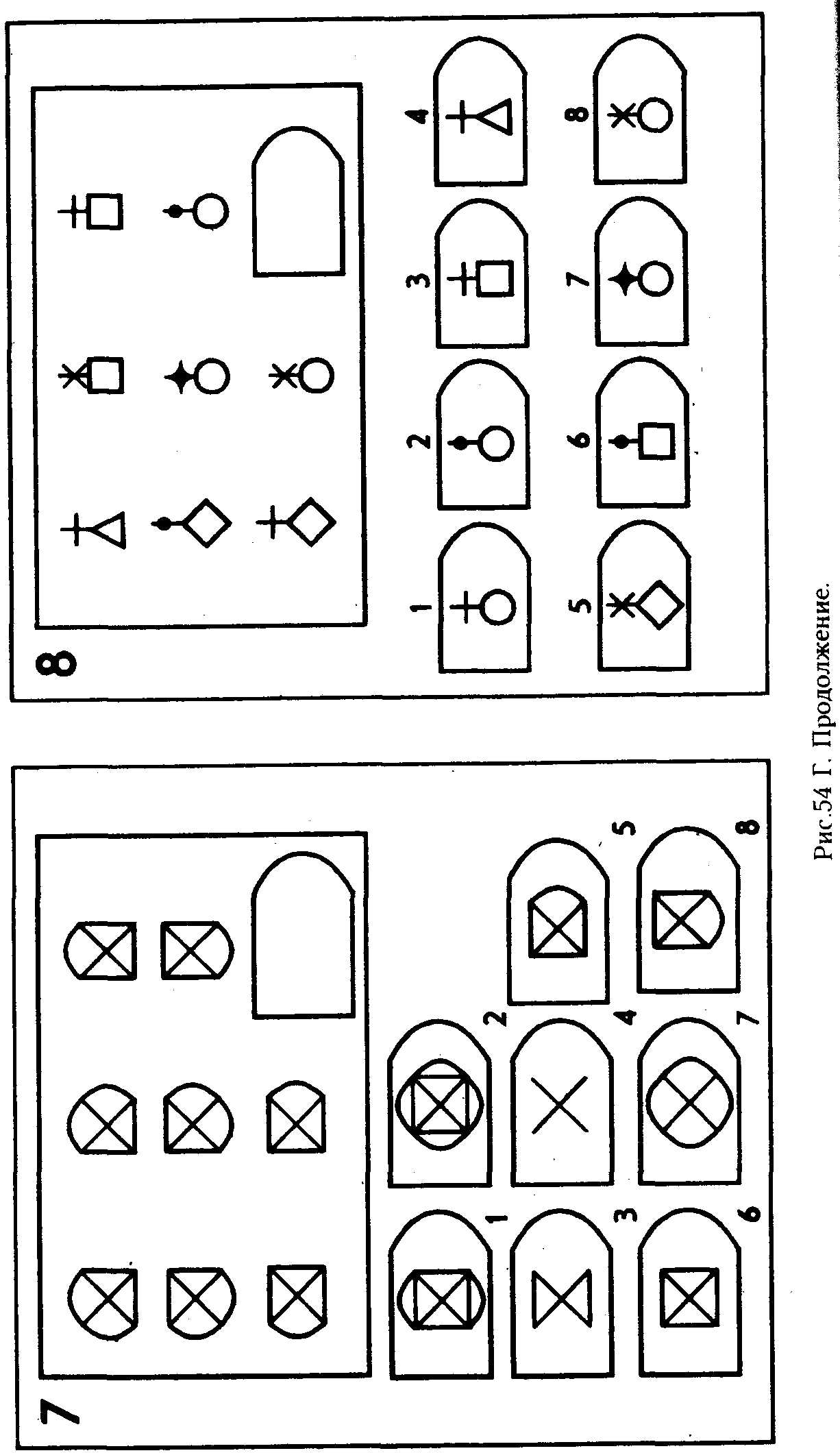 Если ваш браузер не принимает файлы cookie, вы не можете просматривать этот сайт.
Если ваш браузер не принимает файлы cookie, вы не можете просматривать этот сайт.
Настройка вашего браузера для приема файлов cookie
Существует множество причин, по которым cookie не может быть установлен правильно. Ниже приведены наиболее частые причины:
- В вашем браузере отключены файлы cookie. Вам необходимо сбросить настройки своего браузера, чтобы он принимал файлы cookie, или чтобы спросить вас, хотите ли вы принимать файлы cookie.
- Ваш браузер спрашивает вас, хотите ли вы принимать файлы cookie, и вы отказались.Чтобы принять файлы cookie с этого сайта, нажмите кнопку «Назад» и примите файлы cookie.
- Ваш браузер не поддерживает файлы cookie. Если вы подозреваете это, попробуйте другой браузер.
- Дата на вашем компьютере в прошлом. Если часы вашего компьютера показывают дату до 1 января 1970 г.,
браузер автоматически забудет файл cookie. Чтобы исправить это, установите правильное время и дату на своем компьютере.
- Вы установили приложение, которое отслеживает или блокирует установку файлов cookie.Вы должны отключить приложение при входе в систему или проконсультироваться с системным администратором.
Почему этому сайту требуются файлы cookie?
Этот сайт использует файлы cookie для повышения производительности, запоминая, что вы вошли в систему, когда переходите со страницы на страницу. Чтобы предоставить доступ без файлов cookie потребует, чтобы сайт создавал новый сеанс для каждой посещаемой страницы, что замедляет работу системы до неприемлемого уровня.
Что сохраняется в файлах cookie?
Этот сайт не хранит ничего, кроме автоматически сгенерированного идентификатора сеанса в cookie; никакая другая информация не фиксируется.
Как правило, в файле cookie может храниться только информация, которую вы предоставляете, или выбор, который вы делаете при посещении веб-сайта. Например, сайт
не может определить ваше имя электронной почты, пока вы не введете его. Разрешение веб-сайту создавать файлы cookie не дает этому или любому другому сайту доступа к
остальной части вашего компьютера, и только сайт, который создал файл cookie, может его прочитать.
Например, сайт
не может определить ваше имя электронной почты, пока вы не введете его. Разрешение веб-сайту создавать файлы cookie не дает этому или любому другому сайту доступа к
остальной части вашего компьютера, и только сайт, который создал файл cookie, может его прочитать.
Использование матричных методов в моделировании наборов спектроскопических данных
Biophys J. 1997 Feb; 72 (2 Pt 1): 652–673.
Лаборатория химической физики, Национальный институт здравоохранения, Бетезда, Мэриленд 20892-0520
Эта статья цитируется в других статьях в PMC.Abstract
Мы описываем общий подход к модельному анализу наборов спектроскопических данных, основанный на методах матричного анализа. Гипотезу модели часто можно выразить, записав матрицу измеренных спектров как произведение матрицы спектров отдельных молекулярных видов и матрицы соответствующих популяций видов в зависимости от условий эксперимента.Затем процедура моделирования требует одновременного определения набора спектров видов и набора параметров модели (из которых получены популяции), так что этот продукт дает оптимальное описание измеренных спектров. Эта процедура может быть реализована как задача оптимизации в пространстве одних (возможно, нелинейных) параметров модели, в сочетании с эффективным решением вытекающей из них линейной задачи оптимизации с использованием методов матричной декомпозиции для получения набора спектров видов, соответствующего любому набору модели. параметры.Спектры известных видов, а также другая информация и предположения о спектральных формах могут быть включены в эту общую структуру с использованием параметризованных аналитических функциональных форм и методов базисного набора. Будет показан метод, с помощью которого предполагаемые взаимосвязи между глобальными характеристиками (например, положениями пиков) спектров различных видов могут быть применены в моделировании без какого-либо другого указания форм спектров. Мы также рассматриваем влияние ошибок измерения на этот подход и предлагаем расширения основанных на матрице процедур наименьших квадратов, применимых к ситуациям, в которых нельзя предположить, что ошибки измерения имеют нормальное распределение.Обобщенная процедура анализа вводится для случаев, когда видовые спектры меняются в зависимости от условий эксперимента.
Полный текст
Полный текст доступен в виде отсканированной копии оригинальной печатной версии. Получите копию для печати (файл PDF) полной статьи (3,9M) или щелкните изображение страницы ниже, чтобы просмотреть страницу за страницей. Ссылки на PubMed также доступны для Избранные ссылки .
Избранные ссылки
Эти ссылки находятся в PubMed.Это может быть не полный список ссылок из этой статьи.
- Бичем Дж. М.. Глобальный анализ биохимических и биофизических данных. Методы Энзимол. 1992; 210: 37–54. [PubMed] [Google Scholar]
- Hanson WC, Thomas JM. Прогноз содержания 90Sr в организме эскимосов Аляски на перевале Анактувук и дозы радиации в результате выпадения осадков. Здоровье Phys. 1982 сентябрь; 43 (3): 323–333. [PubMed] [Google Scholar]
- Хофф В.Д., ван Стоккум И.Х., ван Рамесдонк Х.Д., ван Бредероде М.Э., Брауэр А.М., Fitch JC, Мейер Т.Э., ван Гронделл Р., Хеллингверф К.Дж..Измерение и общий анализ изменений оптической плотности в фотоцикле фотоактивного желтого белка Ectothiorhodospira halophila. Biophys J., октябрь 1994 г., 67 (4): 1691–1705. [Бесплатная статья PMC] [PubMed] [Google Scholar]
- Джонс С.М., Генри Э.Р., Ху Y, Чан С.К., Удача С.Д., Бхуян А., Родер Х., Хофрихтер Дж., Итон, Вашингтон. Быстрые события сворачивания белков, инициированные наносекундным лазерным фотолизом. Proc Natl Acad Sci U S. A. 1993, 15 декабря; 90 (24): 11860–11864. [Бесплатная статья PMC] [PubMed] [Google Scholar]
- Kirkpatrick S, Gelatt CD, Jr, Vecchi MP.Оптимизация путем имитации отжига. Наука. 13 мая 1983 г .; 220 (4598): 671–680. [PubMed] [Google Scholar]
Статьи из Biophysical Journal любезно предоставлены The Biophysical Society
|
Матрица
Инверсия: Для матриц есть нет такого понятия, как разделение.Можете добавить, вычесть и умножить матрицы, но их нельзя разделить. Однако есть и связанная с этим концепция: что называется «инверсия». Сначала я расскажу, почему инверсия полезно, а затем я покажу вам, как сделать это. Вспомните, когда вы впервые узнал о том, как решить линейные уравнения. Если вам дали что-то вроде «3 x = 6 «, вы бы решите, разделив обе стороны на 3.Поскольку умножение на 1/3 это то же самое, что и разделение на 3, вы также можете умножить обе стороны на 1/3 чтобы получить тот же ответ: х = 2. Если вам нужно было решить что-то вроде «(3/2) x = 6 «, вы могли бы все равно разделите обе стороны на 3/2, но, вероятно, было легче умножить обе стороны на 2/3. Обратная дробь 2/3 — это обратное 3/2 потому что, если умножить две дроби, вы получите 1, которая в данном контексте называется «(мультипликативной) идентичностью»: 1 называется тождеством, потому что умножение чего-либо на 1 не меняет своего значения. Эта терминология и эти факты очень важны для матриц. Если вам дано матричное уравнение как AX = C , где вы даны A и C и им предлагается вычислить X , вы хотели бы «поделить» матрицу на . Но нельзя делать деление с помощью матриц.С другой стороны, что если вы смог найти инверсию A , что-то похожее на нахождение обратной дроби выше? Обратный из А , записывается как « A 1 » и произносится как « A » инверсия », позволит вам отменить A из матричного уравнения, а затем решите относительно X . Как появился « A 1 AX »
в левой части уравнения превратить в « X «?
Вспомните природу обратных чисел для обычных чисел.Если у вас есть
число (например, 3/2)
и его обратная (в данном случае 2/3)
и вы их умножаете, вы получаете 1.
И 1
это тождество, так называемое, потому что 1 x
= x для любого числа
х .
То же самое и с матрицами. Если вы умножите матрицу (например,
А )
и его обратное (в данном случае Следует отметить, что порядок умножения приведенное выше важно и вовсе не произвольно. Напомним, что для матриц умножение не коммутативно. То есть AB почти никогда не бывает BA .Итак, умножая матричное уравнение «слева» (чтобы получить A 1 AX ) это совсем не то же самое, что умножение «справа» (чтобы получить AXA 1 ). И нельзя сказать, что изделие AXA 1 равно A 1 AX , потому что вы не можете изменить порядок умножения. Вместо, надо умножить A 1 слева, положив рядом с A в исходном матричном уравнении.И так как вы должны делать то же самое к обеим сторонам уравнения, когда вы решаете, вы должны умножить на «слева» и в правой части уравнения, в результате получается A 1 C . Вы не можете быть случайным с размещением матриц; Ты должен быть точный, правильный и последовательный. Это единственный способ успешно отменить A и решим матричное уравнение. Как вы видели выше, обратные матрицы могут быть очень полезны для решения матрицы уравнения. Но, учитывая матрицу, как вы ее инвертируете? Как ты находишь обратное? Техника инвертирования матриц довольно хитрая. Для заданная матрица A и его обратная A 1 , мы знаем, что у нас есть A 1 A = I . Собирались использовать единичную матрицу I в процесс инвертирования матрицы.
Сначала я записываю записи в матрицу A , но я пишу их в матрице двойной ширины:
В другой половине двойной ширины, пишу единичную матрицу:
Сейчас сделаю матрицу строковые операции чтобы преобразовать левую часть двойной ширины в тождество.(Как всегда с операциями со строками, не существует единственного «правильного» способа сделать это. Ниже приведены лишь шаги, которые произошли с меня. Ваши расчеты легко могут выглядеть совершенно иначе.)
Теперь, когда левый сторона двойной ширины содержит тождество, правая часть содержит обратное. То есть обратная матрица следующая:
Обратите внимание, что мы можем подтвердить что эта матрица является инверсией A умножив две матрицы и убедившись, что мы получили тождество: Авторские права Элизабет Stapel 2003-2011 Все права защищены
Обратите внимание, что в «реальном жизнь », инверсия редко бывает матрицей, заполненной красивыми аккуратными целыми такие числа.Если повезет, особенно если вы делаете обратное от руки вам дадут вот такие милые дела. Верх | 1 | 2 | Возвращение к указателю Вперед >>
|
|
Замок
Матрица совместной работы
Целью матрицы сотрудничества является предоставление некоторых указателей о том, как ориентироваться в выбранных методах / методах совместной работы.Имейте в виду, что, хотя в данной ситуации могут быть хорошие и плохие варианты процесса, никогда не бывает только одного идеального метода, который будет работать. Матрица имеет свои ограничения, но приблизительная картина, которую она дает, может помочь, если вы пытаетесь получить обзор и провести различие между различными приложениями на более общем уровне.
Матрица сотрудничества состоит из двух матриц — матрицы целей и матрицы контекста. Матрица целей оценивает, какие инструменты могут хорошо работать для данной цели.«НАИЛУЧШИЙ» указывает на цель, для которой метод лучше всего подходит, в то время как * указывает на дополнительные сильные стороны подхода.
Матрица контекста рассматривает ситуационные факторы, которые могут различаться в зависимости от метода. Первые два столбца показывают, является ли ситуация высокой или низкой сложностью. Высокая сложность означает, что существуют различные мнения и интересы, связанные с проблемой, контекст постоянно меняется, а старые решения больше не работают. В следующих двух столбцах рассматривается, является ли ситуация конфликтной или мирной.Конфликтность означает, эмоционально ли затронута проблема или группа людей и кажутся ли разные укоренившиеся позиции несовместимыми. Все подходы могут быть полезны в конфликтных ситуациях, если основное внимание уделяется поиску точек соприкосновения, несмотря на конфликт. Методы, отмеченные знаком X, предназначены для тех, кто намерен непосредственно войти в конфликт и разрешить его, снять скрытые противоречия и отношения и найти путь вперед, признавая различия.
Следующий сегмент смотрит на участников.В первых двух столбцах рассматривается размер группы, подходит ли метод для небольших групп или для больших групп. Небольшая группа определяется как менее 30 человек. В следующих двух столбцах рассматривается, разработан ли метод специально для того, чтобы «разместить всю систему в комнате» (микрокосмос или с участием многих заинтересованных сторон), или он все еще может работать в более однородной группе. Пятая колонка рассматривает разнообразие власти и социальных классов или то, может ли процесс работать на разных уровнях власти и социальных классах.Шестая колонка посвящена поколению и культурному разнообразию.
В последней колонке оценивается необходимость специальной подготовки фасилитатора для данного процесса.
Мы также предлагаем другую матрицу участия, которая рассматривает множество различных методов / техник и оценивает цель участия и потребности в ресурсах для каждого из них.
Матрица| математика | Britannica
matrix , набор чисел, расположенных в строках и столбцах, чтобы сформировать прямоугольный массив.Числа называются элементами или элементами матрицы. Матрицы находят широкое применение в технике, физике, экономике и статистике, а также в различных областях математики. Исторически первым распознаванием была не матрица, а определенное число, связанное с квадратным массивом чисел, называемое определителем. Лишь постепенно возникла идея матрицы как алгебраической сущности. Термин «матрица » был введен английским математиком 19 века Джеймсом Сильвестром, но именно его друг, математик Артур Кэли, разработал алгебраический аспект матриц в двух статьях 1850-х годов.Кэли впервые применил их к изучению систем линейных уравнений, где они до сих пор очень полезны. Они также важны, потому что, как признал Кэли, определенные наборы матриц образуют алгебраические системы, в которых действуют многие обычные законы арифметики (например, ассоциативные и распределительные законы), но в которых действуют другие законы (например, закон коммутативности). недействительный. Матрицы также нашли важное применение в компьютерной графике, где они использовались для представления поворотов и других преобразований изображений.
Если имеется m строк и n столбцов, матрица называется матрицей « m на n », записанной « m × n ». Например,
— это матрица 2 × 3. Матрица с n строками и n столбцами называется квадратной матрицей порядка n . Обычное число можно рассматривать как матрицу 1 × 1; таким образом, 3 можно рассматривать как матрицу [3].
В общепринятых обозначениях заглавная буква обозначает матрицу, а соответствующая строчная буква с двойным нижним индексом описывает элемент матрицы.Таким образом, a ij — это элемент в строке i и j -м столбце матрицы A . Если A — это матрица 2 × 3, показанная выше, то a 11 = 1, a 12 = 3, a 13 = 8, a 21 = 2, a 22 = −4 и a 23 = 5. При определенных условиях матрицы можно складывать и умножать как отдельные объекты, что дает начало важным математическим системам, известным как матричные алгебры.
Получите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишитесь сейчасМатрицы естественным образом входят в системы одновременных уравнений. В следующей системе для неизвестных x и y массив чисел представляет собой матрицу, элементы которой являются коэффициентами неизвестных. Решение уравнений полностью зависит от этих чисел и от их конкретного расположения. Если бы 3 и 4 поменяли местами, решение было бы другим.
Две матрицы A и B равны друг другу, если они имеют одинаковое количество строк и одинаковое количество столбцов и если a ij = b ij для каждый i и каждый j .Если A и B — две матрицы размером m × n , их сумма S = A + B — это матрица m × n , элементы которой s ij = a ij + b ij . То есть каждый элемент S равен сумме элементов в соответствующих позициях A и B .
Матрица A может быть умножена на обычное число c , которое называется скаляром. Продукт обозначается cA или Ac и представляет собой матрицу, элементы которой равны ca ij .
Умножение матрицы A на матрицу B для получения матрицы C определяется только тогда, когда количество столбцов первой матрицы A равно количеству строк второй матрицы B .Чтобы определить элемент c ij , который находится в строке i и столбце j продукта, первый элемент в строке i строки A умножается на первый элемент в j -м столбце B , второй элемент в строке — второй элемент в столбце и так далее, пока последний элемент в строке не умножится на последний элемент столбца; сумма всех этих произведений дает элемент c ij .В символах для случая, когда A имеет m столбцов и B имеет m строк, матрица C имеет столько же строк, сколько A и столько же столбцов, сколько B .
В отличие от умножения обычных чисел a и b , в котором ab всегда равно ba , умножение матриц A и B не является коммутативным. Однако оно ассоциативно и распределительно по сравнению с сложением.То есть, когда операции возможны, всегда выполняются следующие уравнения: A ( BC ) = ( AB ) C , A ( B + C ) = AB + AC и ( B + C ) A = BA + CA . Если матрица 2 × 2 A со строками (2, 3) и (4, 5) умножается сама на себя, то произведение, обычно записываемое как A 2 , имеет строки (16, 21) и ( 28, 37).
Матрица O со всеми ее элементами 0 называется нулевой матрицей. Квадратная матрица A с единицами на главной диагонали (вверху слева направо вниз) и нулями во всех остальных местах называется единичной матрицей. Он обозначается I или I n , чтобы показать, что его порядок равен n . Если B — любая квадратная матрица, а I и O — единичная и нулевая матрицы одного порядка, всегда верно, что B + O = O + B = B и BI = IB = B .Следовательно, O и I ведут себя как 0 и 1 в обычной арифметике. Фактически, обычная арифметика является частным случаем матричной арифметики, в которой все матрицы имеют размер 1 × 1.
Связано с каждой квадратной матрицей A — это число, известное как определитель A , обозначаемое det A . Например, для матрицы 2 × 2det A = ad — bc . Квадратная матрица B называется невырожденной, если det B ≠ 0.Если B невырожден, существует матрица, обратная B , обозначенная B −1 , так что BB −1 = B −1 B = Я . Уравнение AX = B , в котором A и B — известные матрицы, а X — неизвестная матрица, может быть решено однозначно, если A — невырожденная матрица, тогда A −1 существует, и обе части уравнения можно умножить слева на него: A −1 ( AX ) = A −1 B .Теперь A −1 ( AX ) = ( A −1 A ) X = IX = X ; следовательно, решение будет X = A -1 B . Система из m линейных уравнений в n неизвестных всегда может быть выражена как матричное уравнение AX = B , в котором A является матрицей коэффициентов неизвестных m × n , X — это матрица неизвестных размером n × 1, а B — это матрица n × 1, содержащая числа в правой части уравнения.



