Методика узоры для младших школьников: Методика узор Цеханской
«Узор» (Л.И. Цеханская), «Срисовывание образцов» (З. Матейчик, М. Стрнадова), «Квадрат и круг» (Й. Черначек).
Методики: «Узор» (Л.И. Цеханская)
Автор: Цеханская Л.И.
Выходные данные: Гуткина Н.И. Психологическая готовность к школе. — М.: НПО «Образование», 1996
Рубрики: Дошкольники
Возраст: Дошкольный 5-7 лет
Проблема: неуспеваемость школьная, задержка психического развития, готовность к обучению
Психологические характеристики: Познавательная сфера
Предмет диагностики: Исследование познавательной сферы ребенка, выявление сформированности умения подчинять свои действия правилу
Внимание!
Если вам нужна помощь в написании работы, то рекомендуем обратиться к
профессионалам. Более 70 000 авторов готовы помочь вам прямо сейчас. Бесплатные
корректировки и доработки.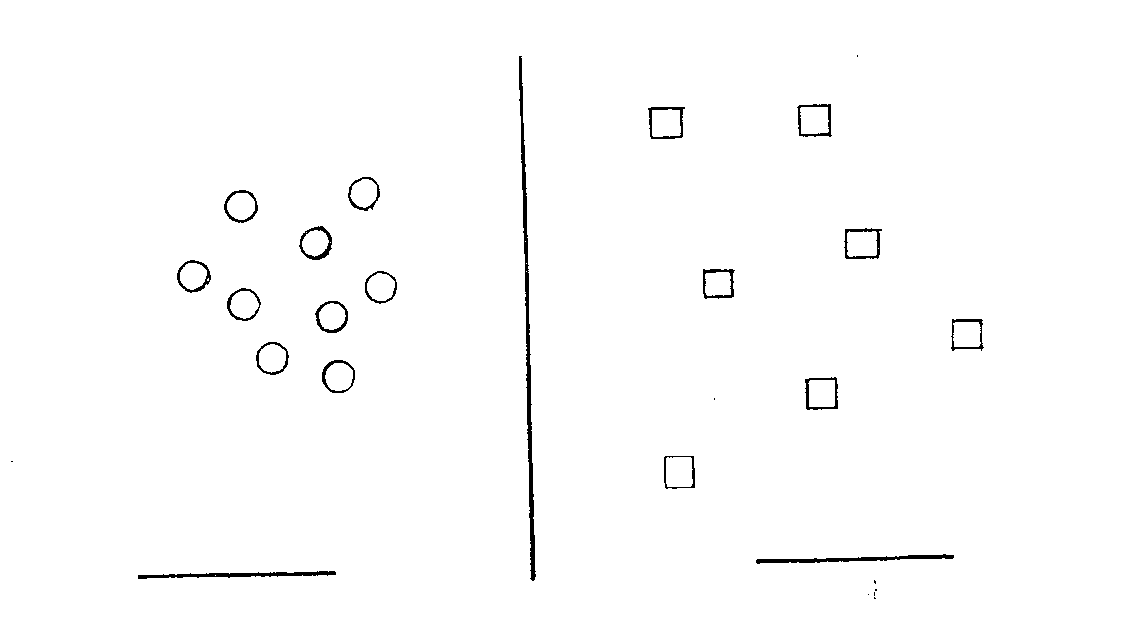
Области применения: Определение предпосылок овладения учебной деятельностью через изучение сформированности умения детей сознательно подчинять свои действия правилу, обобщенно определяющему способ действия
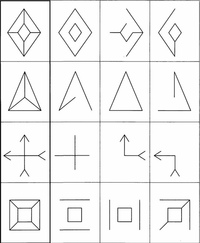
Общее описание: Тест включает методическое руководство, стимульный материал, который включает бланки с геометрическими фигурками, нарисованными на листе бумаги и расположенными в три ряда. Верхний ряд состоит из треугольников, нижний — из квадратов, средний — из кружков. Квадраты находятся под треугольниками, кружки — в промежутке между ними. Все три ряда геометрических фигур называются «полоской».
Материал методики («полоски») располагается на четырех страницах. На первой странице, в центре верхней части дается образец узора, который детям предстоит вычерчивать после объяснения задания. Внизу этой же страницы расположена «полоска» геометрических фигур, на которой ребята учатся рисовать узор под диктовку.
Методические рекомендации: данная методика может проводиться как индивидуально, так и в группе детей.
Перед ребенком ставится задача рисовать узор, следуя правилу (какие фигуры соединять между собой), с указанием способа действия (каким образом соединять фигуры). Например, соединять треугольники и квадраты (правило) через кружок (способ действия). При этом ребенок должен следовать инструкции, которая дается экспериментатором, и где указывается, какие фигурки и в каком порядке следует выбирать.
Вначале ребенку предлагается образец узора и дается инструкция. Затем следует этап обучения способу действия, после чего дети переходят к выполнению основного задания. На этапе обучения взрослый следит за тем, как каждый ребенок выполняет задание, а в случае необходимости исправляет ошибки и объясняет ребенку в чем он ошибся.
Эксперимент состоит из трех серий, отличающихся друг от друга конфигурацией узора.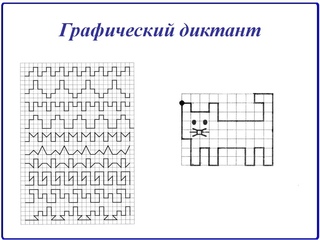
Диктовать следует медленно, чтобы дети успевали прочертить очередное соединение. Повторять одно и то же дважды нельзя, поскольку некоторых ребят это может натолкнуть на прочерчивание лишних соединений. Никакой помощи во время выполнения основного задания экспериментатор не оказывает.
При оценке результатов правильными считаются соединения, соответствующие диктанту. Штрафные очки начисляют за лишние соединения, не предусмотренные диктантом, за «разрывы» или пропуски «зон соединения» между правильными соединениями.
«Срисовывание образцов» (З. Матейчик, М. Стрнадова)
Предназначена для диагностики уровня развития зрительно-моторной координации, тонкой моторики руки, сформированности графических навыков у детей 5–13 летЦель исследования: определить уровень развития у ребенка зрительно-моторной координации, тонкой моторики руки, сформированность графических навыков.
Инструкция испытуемому: «Сейчас ты получишь интересное задание – срисовывать специальные рисунки. Возьми простой карандаш и нарисуй на бумаге такую же фигуру». Попробуй срисовать их так хорошо, как только сможешь. Постарайся, чтобы они были такой же величины, как и на образце. Если у тебя не все будет получаться, можно попробовать снова». Необходимо предупредить, что во время работы не рекомендуется стирать нарисованное, пользоваться линейкой, пытаться обводить образец, подложив его под бумагу.
Возьми простой карандаш и нарисуй на бумаге такую же фигуру». Попробуй срисовать их так хорошо, как только сможешь. Постарайся, чтобы они были такой же величины, как и на образце. Если у тебя не все будет получаться, можно попробовать снова». Необходимо предупредить, что во время работы не рекомендуется стирать нарисованное, пользоваться линейкой, пытаться обводить образец, подложив его под бумагу.
Оценка результатов: каждый рисунок оценивается в баллах от 0 (полное несоответствие образцу) до 3 (точное выполнение с учетом сложности образца). За выполнение каждого пункта начисляется один балл. Общей оценкой является сумма баллов, набранных испытуемым по всем образцам.
При оценивании учитывается степень соответствия выполненного рисунка образцу: точность передачи пропорций, величина углов, отклонение от вертикальной и горизонтальной оси, наличие лишних или недостающих линий и другие параметры. При оценке учитывается замысел ребенка: если он что-то исправил, принимается исправленный рисунок; если он выполнил рисунок дважды или несколько раз, желая улучшить результат, оценивается удачный рисунок. Укороченные линии, не доведенные до необходимого пересечения, оцениваются более строго, так как они чаще всего свидетельствуют о недостаточном развитии зрительно-моторной координации (интервал между линиями не должен превышать 2 мм).
Укороченные линии, не доведенные до необходимого пересечения, оцениваются более строго, так как они чаще всего свидетельствуют о недостаточном развитии зрительно-моторной координации (интервал между линиями не должен превышать 2 мм).
У детей младшего школьного возраста допускаются небольшие искривления при рисовании линий, вызванные неловкостью или дрожанием руки.
Если же искривление возникло после проведения еще одной линии или же прямая линия рисуется как ломаная и возникают дополнительные углы, такой результат оценивается как неудачный.
Получение ребенком средних и тем более высоких оценок при выполнении данного задания свидетельствует о достаточном или хорошем уровне развития сенсомоторной функции. Низкие же оценки подтверждают недостатки сенсомоторного развития.
«Квадрат и круг» (Й. Черначек).
Тест «Квадрат и круг»
Для детей 6—7-ми лет
Цель: Выявление уровня развития наглядной и внутренней образно-моторной регуляции одновременных действий обеих рук.
На закрепленном листе бумаги ребенку предлагают одновременно двумя руками нарисовать правой рукой — круг, левой — квадрат. Затем наоборот: левой — круг, правой — квадрат. Рисовать нужно с закрытыми глазами (или использовать экран). По окончании повторить обе пробы с открытыми глазами (контрольная проба).
Оценка результатов (по материалам автора):
(1) Очень высокая — соблюдение инструкции: способность рисовать две разные фигуры одновременно двумя руками, не делая остановок. На всех 4-х рисунках можно определить, где круг, а где квадрат, несмотря на искажения формы обеих фигур или их незамкнутый контур.
(2) Высокая — соблюдение инструкции. Хотя бы в рисунках, выполненных одной руки (левой или правой) можно различить формы квадрата и круга.
(3) Средняя — соблюдение инструкции, но невозможно различить форму фигур на рисунках, выполненных
и левой и правой рукой.
(4) Низкая — неспособность соблюдать инструкцию (рисовать одновременно, не делая остановок какой-либо рукой).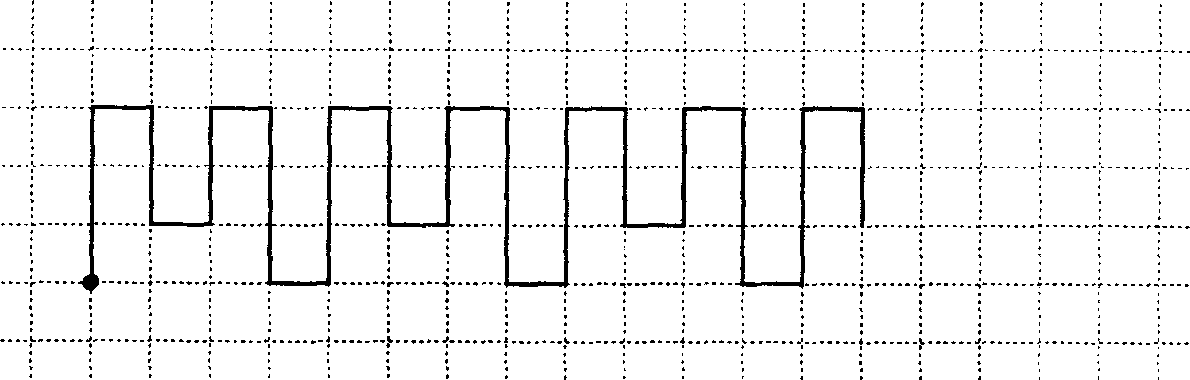
(5) Очень низкая — неспособность соблюдать инструкцию даже с открытыми глазами.
Поможем написать любую работу на аналогичную тему
Получить выполненную работу или консультацию специалиста по вашему учебному проекту
Узнать стоимость2. Методики «Узор» Л.И. Цеханской, «Графический диктант» Д.Б. Эльконина, «Рисование по точкам» А.Л. Венгера. Анализ методик для определения готовности детей к школе
Похожие главы из других работ:
Диктант как средство формирования орфографических навыков учащихся
1.3 Диктант как средство формирования орфографических навыков учащихся
Диктант (от лат. dicto — диктую) — один из видов письменных работ для закрепления и проверки знаний, тренировки навыков учащихся [2, с. 3].
Диктант рассчитан на развитие моторно-слуховых ассоциаций учеников…
3].
Диктант рассчитан на развитие моторно-слуховых ассоциаций учеников…
Глава 1. Понятия «изобразительная деятельность» и «графический навык» и особенности их развития в дошкольном возрасте
…
Иллюстрирование «Сказки о царе Салтане» А.С. Пушкина
3) Рисование эскиза (40 мин.):
Учитель раздаёт ученикам листочки А4. Эскиз делается с большим количеством деталей. Дети работают, учитель следит за ходом выполнения работы, проверяет, у всех ли всё правильно получается…
Использование современных подходов к формированию графических навыков младших школьников
1.1 Письмо. Графический навык. Каллиграфический почерк
Для того чтобы правильно обучать учащихся чистописанию, надо знать, как у учащихся формируются графические навыки письма, как складывается почерк и каковы наилучшие условия формирования этих навыков. Напомним…
Напомним…
Мелкая моторика у детей 6-7 лет с нормальным речевым развитием и у детей с речевыми нарушениями с использованием методик Л.А. Венгера, Н.В. Нижегородцевой и В.Д. Шадрикова
1.1 Категориальный анализ понятий «развитие», «мелкая моторика», графический навык», «речь»
Рассматривая вопрос о развитии мелкой моторики детей старшего возраста необходимо дать пояснения некоторым понятиям. Поясним понятие «развитие». Данное слово встречается во многих научных исследованиях. Им пользуются и психологи…
Место и роль диктантов с изменением содержания диктуемого материала на уроках русского языка.
1.1 Диктант как практический метод обучения. Классификация диктантов
Диктант — это один из видов письменных работ для закрепления и проверки знаний, тренировки навыков учащихся; наибольшее распространение получил при обучении орфографии и пунктуации. Существует множество определений диктанта…
Методика изучения графических редакторов в школьном курсе информатики
1.
 4.1 Растровый графический редактор Paint
4.1 Растровый графический редактор Paint
Paint — это программа, поставляемая в комплекте с Windows 95 и предназначенная для создания и редактирования на экране изображений. Эти изображения сохраняются в графических файлах растрового формата (.BMP или .PCX)…
Методика изучения графических редакторов в школьном курсе информатики
1.4.2 Встроенный векторный графический редактор MS Office
Встроенный векторный графический редактор MS Office работает и с векторной, и с растровой графикой. Сразу же заметим, что возможности обработки объектов векторной графики в программе значительно шире, чем растровых изображений (файлы *.TIFF, *.JPG, *…
Методика развития творческого воображения детей старшего дошкольного возраста средствами сказки
1.3.2 Развитие творческого воображения в рамках программы Л. А. Венгера «Развитие»
Для рассмотрения мы выбрали именно эту программу развития и воспитания дошкольников, т.к. она является комплексной программой развития дошкольников. Цель ее — развитие умственных и художественных способностей ребенка, т.е…
Цель ее — развитие умственных и художественных способностей ребенка, т.е…
Обучение элементам дизайнерской деятельности учащихся 5 классов средней общеобразовательной школы
1.1 История возникновения. Графический дизайн
Художественное течение побеждает только тогда, когда его берут на вооружение декораторы витрин. П. Пикассо Дизайн — это художественное проектирование и конструирование эстетических свойств окружающего нас предметного мира…
Подготовка дошкольников с псевдобульбарной дизартрией к овладению письмом и чтением
3.4 Рисование, раскрашивание
Необходимо учить детей раскрашивать аккуратно, не выходя за контуры изображенных предметов, равномерно нанося нужный цвет. Раскрашивание, как один из самых легких видов деятельности…
Проверка и оценка уровня знаний учащихся в процессе обучения географии
2.2.1 Географический диктант
Географические диктанты являются широко распространенным методом контроля знаний учащихся.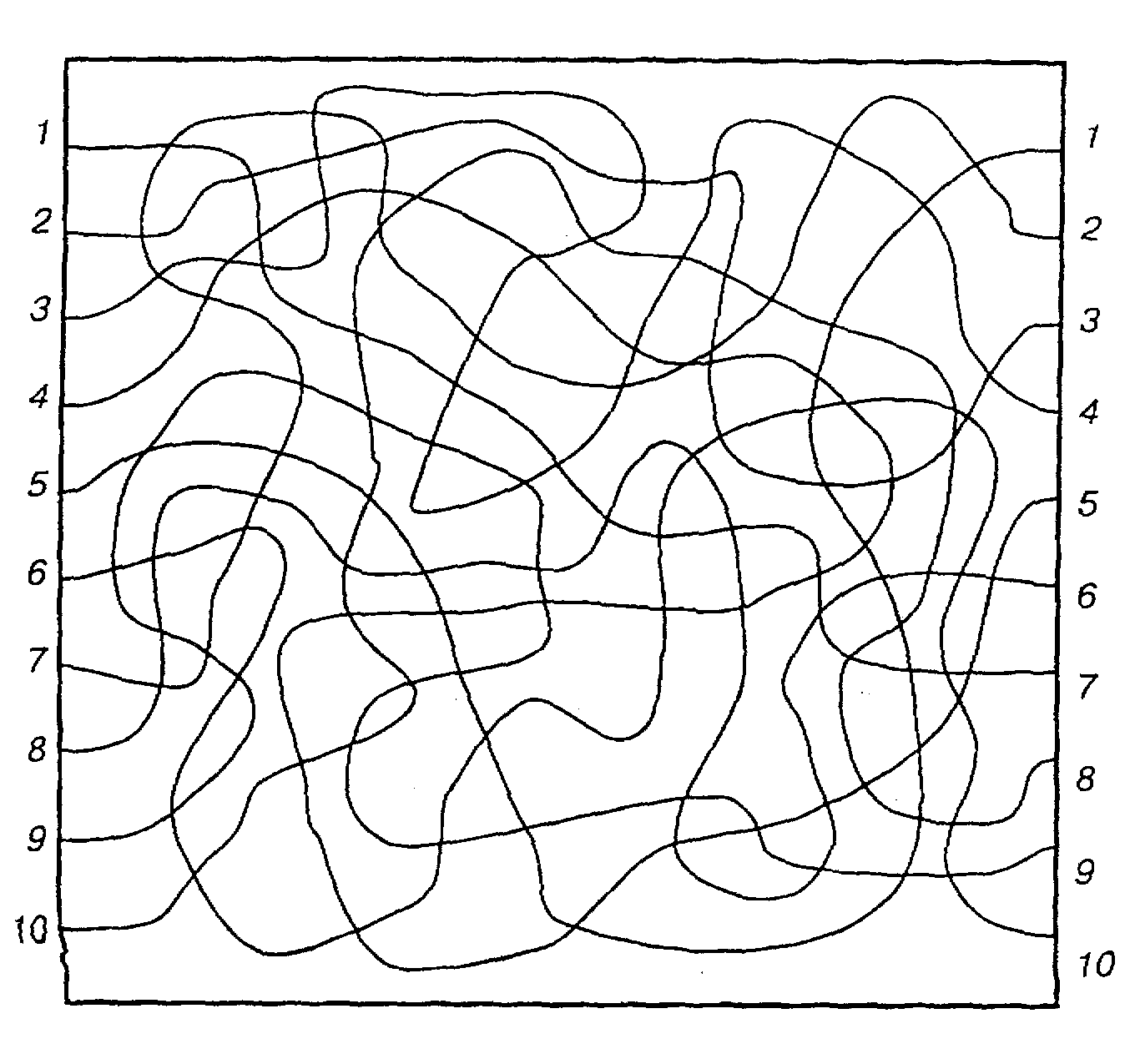 Однако под этим термином скрывается довольно обширная группа различных методов…
Однако под этим термином скрывается довольно обширная группа различных методов…
Проверка и оценка уровня знаний учащихся в процессе обучения географии
3.2 Географический диктант
1. Размыв и разрушение горных пород (почв) текущей водой называется — эрозия. (+). 2. Самая полноводная река России — Лена. (-, т.к. Енисей). 3. Внезапный резкий подъем уровня воды в реке — половодье. (-, т.к. паводок). 4…
Развития внимания у старших школьников в процессе изучения темы: графический редактор
1. Теоретические основы развития внимания у старших школьников в процессе изучения темы: графический редактор
…
Сенсорное воспитание в истории педагогики
§ 3. Дальнейшее развитие идей А.В. Запорожца в трудах его последователей: Л.А. Венгера, Н.Н. Поддьякова и О.А. Дьяченко
Леонид Абрамович Венгер — выдающийся отечественный психолог, разработавший оригинальную концепцию познавательного развития ребенка в дошкольном возрасте. Александр Владимирович Запорожец оставался для Л.А. Венгера учителем на всю жизнь…
Александр Владимирович Запорожец оставался для Л.А. Венгера учителем на всю жизнь…
Методика «Графический диктант»
Источник: Гамезо М.В., Петрова Е.А., Орлова Л.М. Возрастная и педагогическая психология: Учеб. пособие для студентов всех специальностей педагогических вузов. — М.: Педагогическое общество России, 2003. — 512 с. (с.118).
Возраст: учащиеся первого класса школы.
Цель: исследование произвольности как компонента психологической готовности ребенка к школе.
Ход работы. «Графический диктант» проводится одновременно со всеми учащимися класса в один из первых дней учебы. На тетрадном листе (каждому ученику выдается такой листок с указанием его имени и фамилии), отступив 4 клетки от левого обреза, ставятся одна под другой три точки (расстояние между ними по вертикали — 7 клеток).
Педагог предварительно объясняет:
«Сейчас мы с вами будем учиться рисовать разные узоры. Нужно постараться, чтобы они получились красивыми и аккуратными. Для этого вы должны внимательно слушать меня — я буду говорить, в какую сторону и на сколько клеток провести линию. Проводите только те линии, которые я буду диктовать. Когда прочертите линию, ждите, пока я не скажу, куда направить следующую. Каждую новую линию начинайте там, где кончилась предыдущая, не отрывая карандаш от бумаги. Все помнят, где правая рука? Это та рука, в которой вы держите карандаш. Вытяните ее в сторону. Видите, она показывает на дверь (дается реальный ориентир, имеющийся в классе). Итак, когда я скажу, что надо провести линию направо, вы ее проведете вот так — к двери (на доске, заранее расчерченной на клетки, проводится линия слева направо длиной в одну клетку). Это я провела линию на одну клетку направо. Теперь я, не отрывая руки, провожу линию на две клетки вверх, а теперь — на три направо (слова сопровождаются вычерчиванием линий на доске)».
Нужно постараться, чтобы они получились красивыми и аккуратными. Для этого вы должны внимательно слушать меня — я буду говорить, в какую сторону и на сколько клеток провести линию. Проводите только те линии, которые я буду диктовать. Когда прочертите линию, ждите, пока я не скажу, куда направить следующую. Каждую новую линию начинайте там, где кончилась предыдущая, не отрывая карандаш от бумаги. Все помнят, где правая рука? Это та рука, в которой вы держите карандаш. Вытяните ее в сторону. Видите, она показывает на дверь (дается реальный ориентир, имеющийся в классе). Итак, когда я скажу, что надо провести линию направо, вы ее проведете вот так — к двери (на доске, заранее расчерченной на клетки, проводится линия слева направо длиной в одну клетку). Это я провела линию на одну клетку направо. Теперь я, не отрывая руки, провожу линию на две клетки вверх, а теперь — на три направо (слова сопровождаются вычерчиванием линий на доске)».
После этого предлагается перейти к рисованию тренировочного узора.
«Начинаем рисовать первый узор. Поставьте карандаш на самую верхнюю точку. Внимание! Рисуйте линию: одна клетка вниз. Не отрывайте карандаш от бумаги. Теперь одна клетка направо. Одна вверх. Одна клетка направо. Одна вниз. Одна клетка направо. Одна вверх. Одна клетка направо. Одна вниз. Дальше продолжайте рисовать такой же узор сами».
Во время работы над этим узором учитель ходит по рядам и исправляет допущенные детьми ошибки. При рисовании последующих узоров такой контроль снимается, и он следит только за тем, чтобы ученики не переворачивали свои листочки и начинали новый с нужной точки. При диктовке необходимо соблюдать длительные паузы, чтобы они успевали закончить предыдущую линию, и их следует предупредить, что необязательно занимать всю ширину страницы. На самостоятельное продолжение узора дается полторы-две минуты.
Последующий текст инструкции таков:
«Теперь поставьте карандаши на следующую точку. Приготовились! Внимание! Одна клетка вверх. Одна направо. Одна клетка вверх. Одна направо. Одна клетка вниз. Одна направо. Одна клетка вниз. Одна направо. А теперь сами продолжайте рисовать этот узор».
Одна направо. Одна клетка вверх. Одна направо. Одна клетка вниз. Одна направо. Одна клетка вниз. Одна направо. А теперь сами продолжайте рисовать этот узор».
Перед выполнением заключительного узора преподаватель обращается к испытуемым со словами:
«Все. Этот узор не надо дальше рисовать. Мы займемся последним узором. Поставьте карандаши на следующую точку. Начинаю диктовать. Внимание! Три клетки вниз. Одна направо. Две клетки вверх. Одна направо. Две клетки вниз. Одна направо. Три клетки вверх. Теперь продолжайте рисовать этот узор».
Результаты диагностики:
Анализируя результаты выполнения задания, следует порознь оценивать действия под диктовку и правильность самостоятельного продолжения узора. Первый показатель (под диктовку) свидетельствует об умении ребенка внимательно слушать и четко выполнять указания учителя, не отвлекаясь на посторонние раздражители; второй показатель — о степени его самостоятельности в учебной работе. И в первом и во втором случае можно ориентироваться на следующие уровни выполнения.
Высокий уровень. Оба узора (не считая тренировочного) в целом соответствуют диктуемым; в одном из них встречаются отдельные ошибки.
Средний уровень. Оба узора частично соответствуют диктуемым, но содержат ошибки; или один узор сделан безошибочно, а второй не соответствует диктуемому.
Уровень ниже среднего. Один узор частично соответствует диктуемому, другой не соответствует.
Низкий уровень. Ни один из двух узоров не соответствует диктуемому.
По данной методике в данный момент у нас нет готового расчета, возможно, он появится позже. Если вы хотите заказать эксклюзивный расчет по данной методике с вашими условиями или в комплексе с другими методиками, напишите нам, кликнув по второй ссылке. Если вы считаете, что методика содержит недостоверные данные или у вас есть вопросы по проведению исследования по ней — кликните на третью ссылку.
плюсы и минусы метода Петерсон для дошкольников
Об авторе методики
Людмила Георгиевна Петерсон — российский педагог, математик и доктор педагогических наук. Профессор кафедры начального и дошкольного образования, почётный работник высшего профессионального образования Российской Федерации. В 2002 году Людмилу Петерсон наградили Премией Президента Российской Федерации в области образования.
Источник: mel.fm
Методика Петерсон для дошкольников и младших школьников — это курс математики, который набрал популярность начиная с 1990-х годов. Давайте разберёмся, в чём заключается суть методики Петерсон, разложив программу на преимущества и недостатки.
Плюсы методики Петерсон
1. Программа учит думать самостоятельно
Методика преподавания математики Петерсон отличается от традиционных программ. Обычно учитель объясняет тему, демонстрирует решение, дети копируют способ решения, применяют в заданиях, пишут контрольную и идут дальше.
А у Петерсон ребёнок должен докопаться до решения сам. Так он учится справляться с трудностями и не ориентироваться на готовые шаблоны, а активизировать мозг. Когда додумался до ответа сам, уже не забудешь. Ориентация на понимание, а не зазубривание.
Так он учится справляться с трудностями и не ориентироваться на готовые шаблоны, а активизировать мозг. Когда додумался до ответа сам, уже не забудешь. Ориентация на понимание, а не зазубривание.
В «Фоксфорде» применяется авторская программа, но курс математики в начальных классах во многом опирается на учебно-методический комплекс Петерсон. Вот что рассказывала на дне открытых дверей Алёна Сергеевна Решетникова, преподаватель математики 1–2 классах начальной онлайн-школы «Фоксфорда»:
«За основу берётся деятельностный подход — ребята сами пытаются открыть правило или формулу. Мы вместе к этому приходим. При этом я использую интерактивные задания, яркие презентации и раздаточные материалы, чтобы удерживать внимание юных школьников».
2. Программа опирается на визуализацию
К слову о ярких презентациях — Петерсон считает, что ассоциации и наглядные картинки помогают эффективно усваивать информацию, поэтому учебники снабжены красочными иллюстрациями. Чтобы ребёнку было интересней ориентироваться в материале, вводятся сказочные персонажи — гномы, эльфы, три поросёнка.
Чтобы ребёнку было интересней ориентироваться в материале, вводятся сказочные персонажи — гномы, эльфы, три поросёнка.
3. Подходит всем
Бытует миф, что методика Петерсон в школе подходит только одарённым детям, а ребёнку со средними способностями будет сложно. Ещё ходят слухи, что программа гораздо сложнее традиционной — настолько сложнее, что перейти с другой методики на Петерсон по мере обучения в школе не представляется возможным.
Но это не так. Метод Петерсон, скорее, сложен для родителей — бывает трудно отойти от привычных понятий об обучении и свыкнуться с необычными заданиями. Детям, которые не обременены стереотипами о том, «как должно быть», формат Петерсон нравится.
«Если дети знают математические хитрости, они могут справиться с любой задачкой». Алёна Решетникова
Этим математическим хитростям и другим лайфхакам учат в домашней онлайн-школе «Фоксфорда». Цель наших педагогов — привить любовь к математике и показать, что она не так страшна, как кажется..jpg)
4. Учебники удобно оформлены
Помимо визуальных рядов и ярких иллюстраций, учебные пособия по методике преподавания Петерсон составлены так, чтобы ребёнку было увлекательно учиться.
Например, записывать решение задач, примеров, рисовать, соединять фигуры, решать ребусы можно прямо в учебнике — просто вписываешь ответ в нужное окошко. Большое число заданий — сравнить, найти закономерность, решить ребус, раскрасить правильным цветом, закончить узор, объяснить почему так, а не так. И это всё — прямо в пособии.
Обложка учебника по математике Л.Г. Петерсон для 4 класса.Источник: edvisrb.ru
5. Домашка не занимает много времени
Согласно Петерсон, ученик должен самостоятельно выполнять домашнюю работу за 15–20 минут. Это перекликается с принципами домашней онлайн-школы «Фоксфорда» — здесь учебная нагрузка гораздо меньше, чем в обычной школе, где за домашкой сидят по несколько часов или весь вечер. Как правило, домашка в «Экстернате Фоксфорда» состоит из 5–10 тестовых заданий или нескольких творческих. Если ребёнок был внимателен на уроке, то домашнюю работу он сделает быстро, в среднем, уходит не больше 30–60 минут в средней школе. В начальной тратится ещё меньше времени — в основном ребята закрепляют материал.
Если ребёнок был внимателен на уроке, то домашнюю работу он сделает быстро, в среднем, уходит не больше 30–60 минут в средней школе. В начальной тратится ещё меньше времени — в основном ребята закрепляют материал.
<<Блок перелинковки>>
Минусы методики Петерсон
1. В учебнике отсутствует теория
Поколение нынешних родителей привыкло, что в учебнике точных наук сначала идёт теоретический раздел, а затем закрепление материала на практике. У Петерсон всё иначе — теории как таковой нет вообще. В учебнике сразу начинаются практические задачки. Предполагается, что теорию даёт учитель на занятии.
2. Методику убрали из официальной программы
В 2014 году учебники Петерсон исключили из официальной школьной программы — в Минобрнауки посчитали, что они «недостаточно патриотичны». Решение властей вызвало возмущение научного сообщества, учителей и родителей — десятки тысяч людей протестовали и подписывали петиции.
Сейчас учебники по закону могут использоваться в школе, если педагог посчитает нужным, в качестве дополнительных пособий. Но теперь найти учебное заведение, где учат по Петерсон, сложнее. Домашняя онлайн-школа «Фоксфорда» — одна из таких школ.
Но теперь найти учебное заведение, где учат по Петерсон, сложнее. Домашняя онлайн-школа «Фоксфорда» — одна из таких школ.
3. Успех обучения зависит от педагога
Эффективность программы сильно опирается на учителя. Он должен уметь вести научную дискуссию, а не просто объяснять тему и давать шаблонные решения. Педагог должен знать, как организовывается работа в группах и строится диалог с учениками. Иногда учителя хотят работать по Петерсон, но просто не знают как.
В начальной онлайн-школе «Фоксфорда» учителя сознательно выбрали методику математики Петерсон — так, по словам Алёны Сергеевны, она перепробовала много программ и остановилась на Петерсон как на самой интересной.
Если педагог не умеет работать по Петерсон, результаты будут плачевные. Дети сидят над домашкой в слезах, а родители разводят руками — из-за непривычного построения учебника помочь ребёнку весьма трудно. Поэтому важно, чтобы педагог знал, как подавать материал по этой методике.
«При работе с 1–2 классом я использую ярких персонажей, увлекательно рассказываю и преподаю материал в формате игры. А ещё регулярно меняю вид деятельности — так малыши не устаю и сохраняют интерес к происходящему». Алёна Решетникова
Резюме
Можно долго спорить о плюсах и минусах Петерсон, но то, что программа отличается от традиционной, — это факт. Главное — чтобы педагог умел работать по такой методике, тогда учёба будет в удовольствие, ведь Петерсон учит думать самостоятельно и докапываться до решений, пособия снабжены иллюстрациями, уровень программы ориентирован на любого ученика, а домашние задания не должны занимать много времени.
В домашней онлайн-школе «Фоксфорда» работают по авторской учебной программе, но курс математики во многом опирается на методику Людмилы Петерсон. А если какой-то темы в курсе не хватает, либо она не раскрывается в полной мере, то учителя подключают пособия и материалы из других систем и методик. Результат — эффективное сбалансированное обучение. Приходите, чтобы составить о программе собственное мнение.
Результат — эффективное сбалансированное обучение. Приходите, чтобы составить о программе собственное мнение.
Раскраска узор из геометрических фигур. Карточки домана бесплатно, картинки геометрические фигуры, карточки геометрические фигуры, изучаем геометрические фигуры
Веселые и красочные задания для детей «Рисунки из геометрических фигур» являются очень удобным обучающим материалом для детей дошкольного и младшего школьного возраста по изучению и запоминанию основных геометрических форм: треугольника, круга, овала, квадрата, прямоугольника и трапеции. Все задания предназначены для самостоятельной работы ребенка под наблюдением взрослых. Родитель или педагог должны правильно объяснить ребенку, что он должен сделать в каждом задании.
Также вам может понравиться наш онлайн тренажер по математике для 1 класса «Геометрические фигуры»:
Онлайн-тренажер по математике «Геометрические фигуры 1 класс» поможет первоклассникам потренироваться в умении различать основные геометрические фигуры: квадрат, круг, овал, прямоугольник и треугольник.
1. Рисунки из геометрических фигур — Условия к выполнению заданий:
Чтобы начать выполнять задания, скачайте во вложениях бланк, в котором вы найдете 2 типа заданий: рисунки из геометрических фигур для раскрашивания и задание для рисования фигур с помощью логического и образного мышления. Распечатайте скачанную страницу на цветном принтере и дайте ребенку вместе с цветными карандашами или фломастерами.
- В первом задании малышу нужно мысленно соединить каждые две части представленных фигур в одну и нарисовать полученную геометрическую форму в соответствующей клетке. Объясните ребенку, что детали можно поворачивать в уме в разные стороны до тех пор, пока он не получит нужную комбинацию для составления фигуры. Например, два треугольника можно повернуть так, чтобы получился квадрат. После этого квадрат нужно нарисовать в клетке рядом с треугольником. По такому же принципу необходимо сделать и остальные рисунки.
- Во втором задании дети должны правильно назвать фигуры из которых состоят нарисованные картинки.
 Затем эти картинки нужно раскрасить, используя цвета рядом с геометрическими фигурами. Каждую фигуру нужно раскрасить только в указанный цвет.
Затем эти картинки нужно раскрасить, используя цвета рядом с геометрическими фигурами. Каждую фигуру нужно раскрасить только в указанный цвет.
Чтобы придать занятию больше энергии и энтузиазма — можно объединить несколько детей в группу и предоставить им выполнение заданий на время. Тот ребенок, который первый выполнит все задания без ошибок, признается победителем. В качестве приза можно повесить его работу на стену достижений (такая стена обязательно должна присутствовать как дома, так и в детском саду).
Скачать задание «Рисунки из геометрических фигур» вы можете во вложениях внизу страницы.
2. Геометрические фигуры в рисунках — 3 задания-раскраски:
Следующее занятие также скрывает основные геометрические фигуры в рисунках. Ребенку нужно найти эти фигуры, назвать их, а затем раскрасить таким образом, чтобы каждой фигуре соответствовал определенный цвет (руководствуясь инструкцией на бланке с заданием).
Во втором задании нужно нарисовать на всех этажах любые геометрические фигуры, но при этом необходимо соблюдать условие: на каждом этаже фигуры должны находиться в разном порядке. В последствии можно это задание видоизменить. Для этого достаточно начертить на бумаге точно такой домик и попросить ребенка заполнить его фигурами так, чтобы в каждом подъезде не встречались одинаковые фигуры (подъезд — вертикальный ряд квадратов).
В последствии можно это задание видоизменить. Для этого достаточно начертить на бумаге точно такой домик и попросить ребенка заполнить его фигурами так, чтобы в каждом подъезде не встречались одинаковые фигуры (подъезд — вертикальный ряд квадратов).
В третьем задании нужно, руководствуясь стрелками, нарисовать точно такие же геометрические фигуры внутри или снаружи данных фигур.
Не торопите ребенка и не подсказывайте ему, пока он сам вас об этом не попросит. Если у малыша что-то получилось неправильно — вы всегда можете распечатать еще один экземпляр учебного бланка с заданием.
Скачать задание «Геометрические фигуры в рисунках» вы можете во вложениях внизу страницы.
В этом занятии детям опять предстоит отыскать геометрические фигуры среди рисунков. После предыдущих занятий им будет уже легче ориентироваться в знакомых формах, так что, я думаю, оба задания не вызовут у них затруднений.
Второе задание также дает возможность малышу повторить математические знаки и усвоить счет до десяти, так как ему понадобится посчитать количество фигур и поставить знаки «больше» «меньше» между картинками.
Скачать раскраску «Смешные рисунки из фигур» вы можете во вложениях внизу страницы.
Также вам будут полезны и другие материалы по изучению геометрических фигур:
Здесь вы с ребенком можете изучить геометрические фигуры и их названия с помощью веселых заданий в картинках.
Задания ознакомят ребенка с основными фигурами геометрии — кругом, овалом, квадратом, прямоугольником и треугольником. Только здесь не занудное зазубривание названий фигур, а своеобразная игра-раскраска.
Как правило, геометрию начинают изучать, рисуя плоские геометрические фигуры. Восприятие правильной геометрической формы невозможно без выведения ее своими руками на листе бумаги.
Это занятие изрядно позабавит ваших юных математиков. Ведь теперь им придется находить знакомые формы геометрических фигур среди множества картинок.
Наложение фигур друг на друга — это занятие по геометрии для дошкольников и младших школьников. Смысл упражнения состоит в решении примеров на сложение.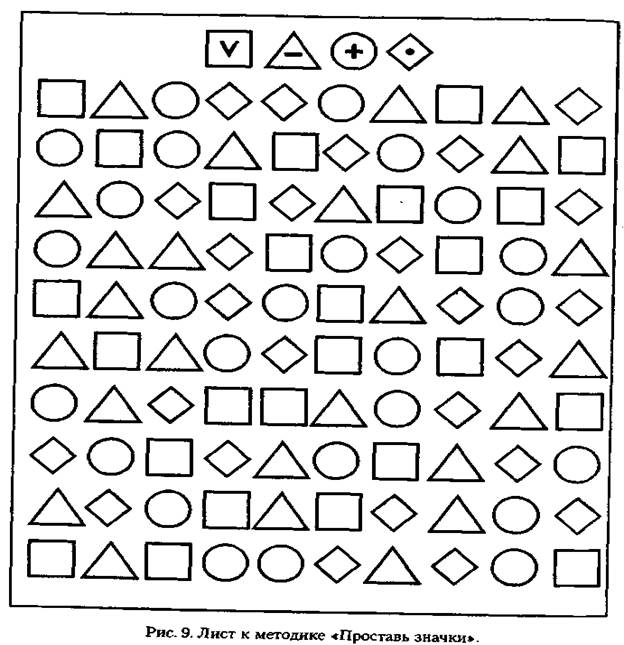 Только это необычные примеры. Вместо цифр здесь нужно складывать геометрические фигуры.
Только это необычные примеры. Вместо цифр здесь нужно складывать геометрические фигуры.
Это задание составлено в виде игры, в которой ребенку предстоит менять свойства геометрических фигур: форму, цвет или размер.
Здесь вы можете скачать задания в картинках, в которых представлен счет геометрических фигур для занятий по математике.
В этом задании ребенок познакомится с таким понятием, как чертежи геометрических тел. По сути, это занятие представляет собой мини-урок по начертательной геометрии
Здесь мы подготовили для вас объемные геометрические фигуры из бумаги, которые нужно вырезать и склеить. Куб, пирамиды, ромб, конус, цилиндр, шестигранник, распечатать их на картоне (или цветной бумаге, а затем наклеить на картон), а затем дать ребенку для запоминания.
Дети любят раскрашивать и обводить, поэтому данные задания сделают ваши занятия по обучению счету максимально эффективными.
И еще можете поиграть в математические игры онлайн от лисенка Бибуши:
В этой развивающей онлайн игре ребенку предстоит определить, что является лишним среди 4 картинок.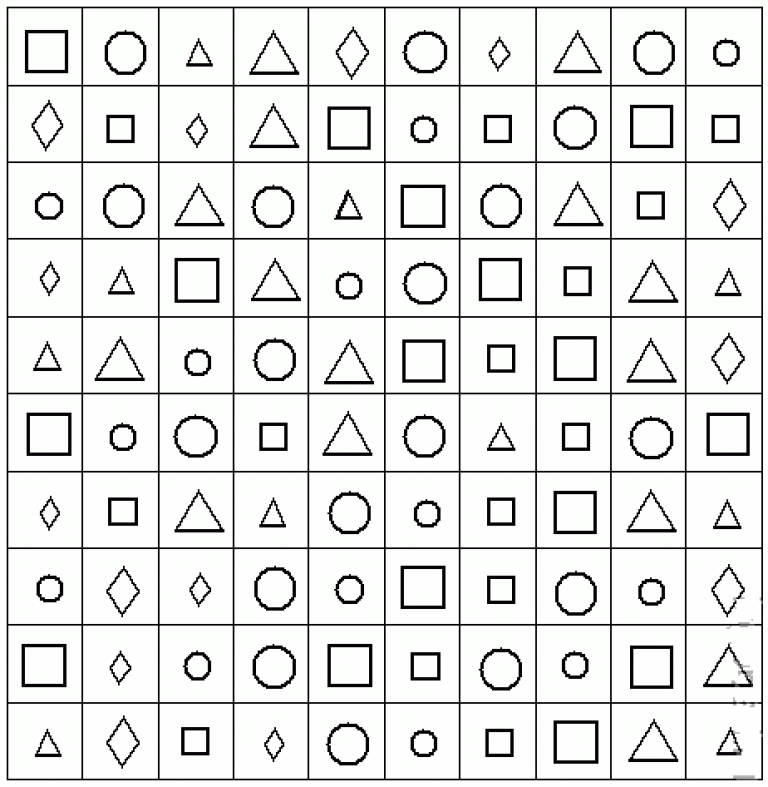 При этом необходимо руководствоваться признаками геометрических форм.
При этом необходимо руководствоваться признаками геометрических форм.
Одновременно с изучением цветов, ребенку можно начать показывать карточки геометрические фигуры. На нашем сайте Вы сможете скачать их бесплатно.
Как изучить с ребенком фигуры по карточкам Домана.
1) Начинать нужно с простых фигур: круг, квадрат, треугольник, звезда, прямоугольник. По мере освоения материала, начинать изучать фигуры посложнее: овал, трапеция, параллелограмм и т.д.
2) Заниматься с ребенком по карточкам Домана нужно несколько раз в день. При демонстрации геометрической фигуры четко проговаривайте название фигуры. А если во время занятий вы будете еще пользоваться наглядными предметами, например, собирать вкладыши с фигурами или игрушку — сортер, то малыш очень быстро освоит материал.
3) Когда ребенок запомнит название фигур, можете переходить к более сложным заданиям: теперь показывая карточку говорите — это синий квадрат, у него 4 равные стороны. Задавайте ребенку вопросы, просите его самого описать, что он видит на карточке и т.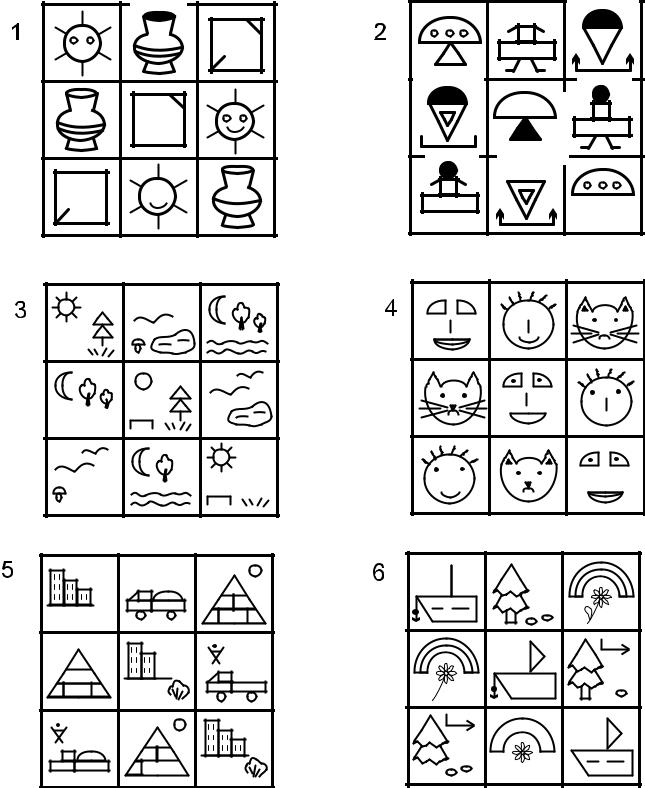 д.
д.
Такие занятия очень полезны для развития памяти и речи ребенка.
Здесь вы можете скачать карточки Домана из серии «Плоские геометрические фигуры» Всего 16 штук, в их числе карточки: плоские геометрические фигуры, восьмиугольник, звезда, квадрат, кольцо, круг, овал, параллелограмм, полукруг, прямоугольник, прямоугольный треугольник, пятиугольник, ромб, трапеция, треугольник, шестиугольник.
Занятия по карточкам Домана прекрасно развивают зрительную память, внимательность, речь ребенка. Это отличная зарядка для ума.
Вы можете скачать и распечатать бесплатно все
карточками Домана плоские геометрические фигурыКликните на карточку правой клавишей мышки, нажмите «Сохранить картинку как…» так вы сможете сохранить изображение на свой компьютер.
Как изготовить карточки Домана самостоятельно:
Распечатайте карточки на плотной бумаге или картоне по 2, 4 или 6 штук на 1 листе. Для проведения занятий по методике Домана карточки готовы, Вы их можете показывать малышу и называть название картинки.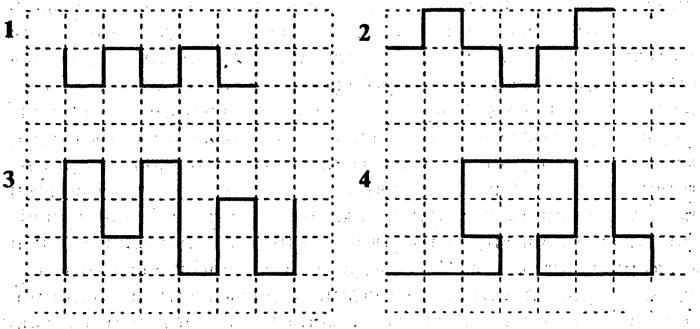
Успехов и новых открытий Вашему малышу!
Развивающее видео для детей (малышей и дошкольников) выполненное по методике Домана «Вундеркинд с пеленок» — развивающие карточки, развивающие картинки на различные темы из части 1, части 2 методики Домана, которое можно смотреть бесплатно здесь или на нашем Канале Раннее развитие детей на youtube
Развивающие карточки по методике Глена Домана с картинками плоских геометрических фигур для детей
Развивающие карточки по методике Глена Домана с картинками плоских геометрических фигур для детей
Развивающие карточки по методике Глена Домана с картинками плоских геометрических фигур для детей
Развивающие карточки по методике Глена Домана с картинками плоских геометрических фигур для детей
Развивающие карточки по методике Глена Домана с картинками плоских геометрических фигур для детей
Развивающие карточки по методике Глена Домана с картинками плоских геометрических фигур для детей
Развивающие карточки по методике Глена Домана с картинками плоских геометрических фигур для детей
Развивающие карточки по методике Глена Домана с картинками плоских геометрических фигур для детей
Развивающие карточки по методике Глена Домана с картинками плоских геометрических фигур для детей
Развивающие карточки по методике Глена Домана с картинками плоских геометрических фигур для детей
Развивающие карточки по методике Глена Домана с картинками плоских геометрических фигур для детей
Развивающие карточки геометрические фигуры по методике Глена Домана с картинками плоских геометрических фигур для детей
Развивающие карточки геометрические фигуры по методике Глена Домана с картинками плоских геометрических фигур для детей
Развивающие карточки геометрические фигуры по методике Глена Домана с картинками плоских геометрических фигур для детей
Еще наши карточки Домана по методике «Вундеркинд с пеленок»:
- Карточки Домана Посуда
- Карточки Домана Национальные блюда
Здесь вы можете скачать и распечатать задания в картинках по математике «Геометрические фигуры — Раскраска для дошкольников».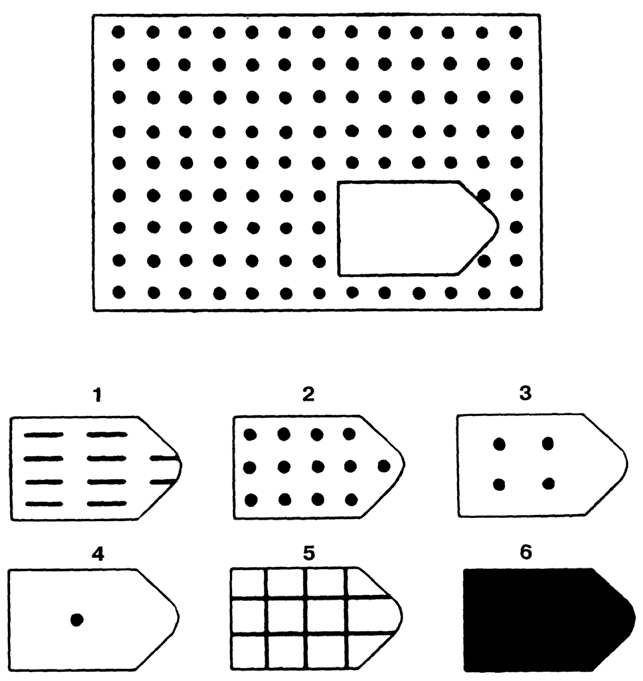 Что представляют собой эти задания? В первую очередь, это, конечно, ознакомление ребенка с основными фигурами науки геометрии — кругом, овалом, квадратом, прямоугольником и треугольником. Только здесь не занудное зазубривание названий фигур, а своеобразная игра-раскраска. В первой раскраске ребенок будет по команде взрослого раскрашивать фигуры и таким образом запоминать их. А во второй — отыскивать среди множества картинок именно геометрические формы и сразу же раскрашивать свои находки.
Что представляют собой эти задания? В первую очередь, это, конечно, ознакомление ребенка с основными фигурами науки геометрии — кругом, овалом, квадратом, прямоугольником и треугольником. Только здесь не занудное зазубривание названий фигур, а своеобразная игра-раскраска. В первой раскраске ребенок будет по команде взрослого раскрашивать фигуры и таким образом запоминать их. А во второй — отыскивать среди множества картинок именно геометрические формы и сразу же раскрашивать свои находки.
1. Геометрические фигуры — Раскраска с умом — Условия заданий:
Выполнять задание — Геометрические фигуры «Раскраска с умом» — необходимо под руководством взрослых (родителей или педагогов), так как задание предназначено для детей от 3-4 лет. Для начала, скачайте бланк с заданием во вложениях внизу данной страницы, распечатайте его на черно-белом принтере и подготовьте цветные карандаши или фломастеры. Прочитайте малышу задания в указанном порядке.
- В первом задании ребенок должен раскрасить в синий цвет все круги, а затем посчитать их количество.
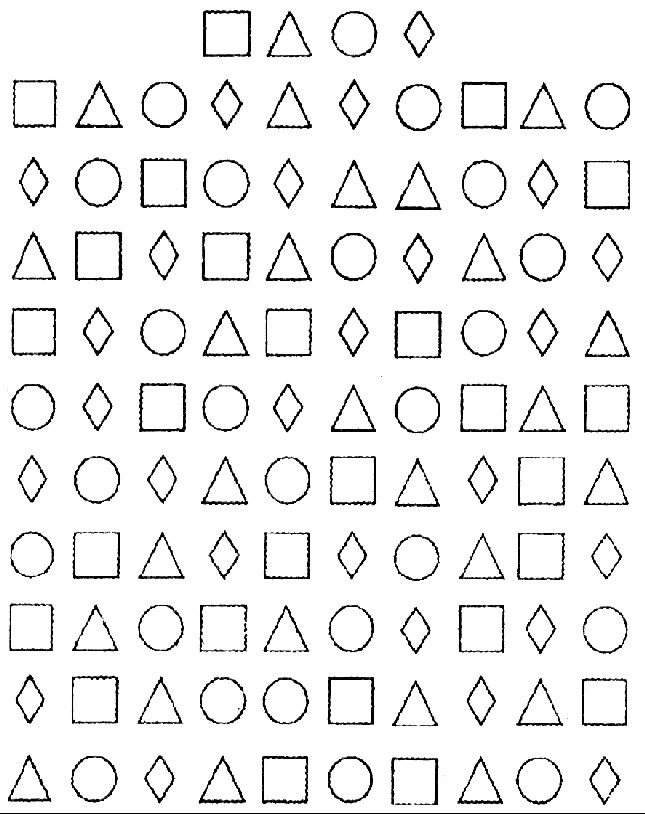
- Во втором задании нужно раскрасить все треугольники в оранжевый цвет и также посчитать их.
- В третьем задании необходимо раскрашивать в красный цвет — квадраты, а в желтый — прямоугольники. После этого посчитать количество этих фигур и сравнить, чего больше, квадратов или прямоугольников.
- В четвертом задании ребенку нужно раскрасить зеленым цветом все овалы. Пересчитать их после раскрашивания.
Требование взрослого раскрасить фигуру в определенный цвет подразумевает под собой, что ребенок должен уже различать цвета. Если же малыш еще не выучил названия основных цветов, то представленные задания помогут ему потренироваться в этом деле.
Скачать геометрические фигуры «Раскраска с умом» вы можете во вложениях внизу страницы.
2. Развивающее задание «Раскрась геометрические фигуры»
Здесь вы найдете интересное развивающее задание по поиску и раскрашиванию геометрических фигур среди множества различных картинок. Детям очень нравятся игры, в которых нужно что-нибудь искать. Поэтому изучение геометрических фигур с помощью подобных игр проходит очень легко и эффективно, так как ребенок даже не подозревает, что он учится, а не играет. К тому же, все дети, без исключения, обожают раскраски!
Поэтому изучение геометрических фигур с помощью подобных игр проходит очень легко и эффективно, так как ребенок даже не подозревает, что он учится, а не играет. К тому же, все дети, без исключения, обожают раскраски!
Как проводить занятие. Скачайте во вложениях бланк с заданием, распечатайте его и дайте ребенку. На отдельном листе бумаги нарисуйте четыре фигуры — круг, квадрат, ромб и треугольник. Подпишите их названия. Раскрасьте фигуры в разные цвета: круги — в синий цвет , квадраты — в зеленый , ромбы — в желтый , треугольники — в красный цвет . Затем отдайте лист ребенку, пояснив, что именно такие фигуры ему нужно найти среди всех изображений бланка-задания и раскрасить их именно в такие цвета, как на листе. Оставьте ребенка одного справляться с заданием. Через несколько минут поинтересуйтесь у него — много ли он нашел на картинке геометрических фигур?
Это задание можно выполнять повторно. Для этого нужно распечатать бланк заново, а на отдельном листе указанные фигуры раскрасить в другие цвета.
Чтобы усложнить задачу для ребенка, можно не использовать отдельный лист с раскрашенными фигурами, а сказать устно, какие фигуры нужно найти и в какой цвет раскрасить. Так у ребенка будет более активно работать память и внимание. Ведь ему придется во время выполнения задания держать эту информацию в голове, без визуальной подсказки.
Скачать развивающее задание «Раскрась геометрические фигуры» вы можете во вложениях внизу страницы.
Также вам будут полезны и другие материалы по изучению геометрических фигур:
Веселые и красочные задания для детей «Рисунки из геометрических фигур» являются очень удобным обучающим материалом для детей дошкольного и младшего школьного возраста по изучению и запоминанию основных геометрических форм:
Здесь вы с ребенком можете изучить геометрические фигуры и их названия с помощью веселых заданий в картинках.
Как правило, геометрию начинают изучать, рисуя плоские геометрические фигуры. Восприятие правильной геометрической формы невозможно без выведения ее своими руками на листе бумаги.
Это занятие изрядно позабавит ваших юных математиков. Ведь теперь им придется находить знакомые формы геометрических фигур среди множества картинок.
Наложение фигур друг на друга — это занятие по геометрии для дошкольников и младших школьников. Смысл упражнения состоит в решении примеров на сложение. Только это необычные примеры. Вместо цифр здесь нужно складывать геометрические фигуры.
Это задание составлено в виде игры, в которой ребенку предстоит менять свойства геометрических фигур: форму, цвет или размер.
Здесь вы можете скачать задания в картинках, в которых представлен счет геометрических фигур для занятий по математике.
В этом задании ребенок познакомится с таким понятием, как чертежи геометрических тел. По сути, это занятие представляет собой мини-урок по начертательной геометрии
Здесь мы подготовили для вас объемные геометрические фигуры из бумаги, которые нужно вырезать и склеить. Куб, пирамиды, ромб, конус, цилиндр, шестигранник, распечатать их на картоне (или цветной бумаге, а затем наклеить на картон), а затем дать ребенку для запоминания.
Дети любят раскрашивать и обводить, поэтому данные задания сделают ваши занятия по обучению счету максимально эффективными.
И еще можете поиграть в математические игры онлайн от лисенка Бибуши:
В этой развивающей онлайн игре ребенку предстоит определить, что является лишним среди 4 картинок. При этом необходимо руководствоваться признаками геометрических форм.
Уникальная развивающая методика Никитина — от Совушкиной лавки
Борис Никитин придумывал множество развивающих игр для СВОИХ детей. Его игры и упражнения поистине уникальны, и до сих пор ни в нашей стране, ни за рубежом не создано ничего, что смогло бы превзойти по своим дидактическим возможностям кубики Никитина.
Развивающие игры Никитина объединяют один из основных принципов обучения — от простого к сложному — с очень важным условием творческой деятельности — делать всё самостоятельно. Этот союз позволил разрешить в игре сразу несколько проблем, связанных с развитием творческих способностей:
- Развивающие игры могут дать пищу для развития творческих способностей с самого раннего возраста.

- Их задания-ступеньки всегда создают условия, опережающие развитие способностей.
- Поднимаясь каждый раз самостоятельно до своего «потолка», ребенок развивается наиболее успешно.
- Развивающие игры могут быть очень разнообразны по своему содержанию, а кроме того, как и любые игры, не терпят принуждения и создают атмосферу свободного и радостного творчества;
- Играя в эти игры со своими детьми, родители незаметно для себя приобретают очень важное умение — держать себя в руках, не мешать ребенку самому размышлять и принимать решения, не делать за него то, что он может и должен сделать сам.
Особенности игр
Главное отличие игр Никитина состоит в том, что, играя в них, ребенок выступает как активная сторона и у него воспитывается не умение выполнять работу по предложенному шаблону, а развивается логическое и образное мышление, творчество, умение распознать и построить образ, способность к самостоятельности.
В большинстве своем игры представлены в виде многофункциональных головоломок, предоставляющих простор для творчества. Их можно подстраивать под себя, под свой уровень, свои интересы. Каждая игра имеет набор задач, которые ребенок решает с помощью кубиков, кирпичиков, квадратов из картона или пластика, деталей конструктора-механика и т.д.
Игры Никитина можно расширять, усовершенствовать, придумывать новые задания.
Правила игры
На первых порах никто не объясняет ребенку правил игры, не показывать, как надо. Малыш сам решает задачу от начала до конца.
Такая методика позволяет ребенку самостоятельно искать решение неизвестных ему задач, создавать новое, что как раз и ведет к развитию его творческих способностей. Взрослый же следит за тем, чтобы уровень задачи был не слишком легкий и не слишком трудный, и «корректирует» и «направляет» действия ребенка. А сорадование — это и будет награда за удачно найденное решение, и стимул к будущим победам.
Кубики Никитина «Сложи Узор»
Это одно из самых известных пособий Никитина. Игра состоит из 16 кубиков, у которых 4 грани одноцветные (каждая из граней окрашена в один из четырех цветов: синий, красный, желтый, белый) и две двухцветные (раскрашенные по диагонали в два разных цвета). Это позволяет составить множество разнообразных узоров. Выкладывать различные изображения по схемам или придумывать самостоятельно.
Для малышей в возрасте 2-3 лет схемы узоров приведены в натуральную величину. Ребенок может выкладывать кубики прямо в альбоме или рядом с ним. В возрасте 4-6 лет уже может справиться с выкладыванием узора по уменьшенным схемам и схемам, в которых не указано деление узора на отдельные кубики. В прилагающейся к кубикам брошюре приводятся абстрактные узоры, фигурки разных животных, предметы (елочка, домик, ботинок и т. п.), русский и латинский алфавиты, цифры. Самое сложное и интересное для ребенка — это придумывание и составление собственных узоров.
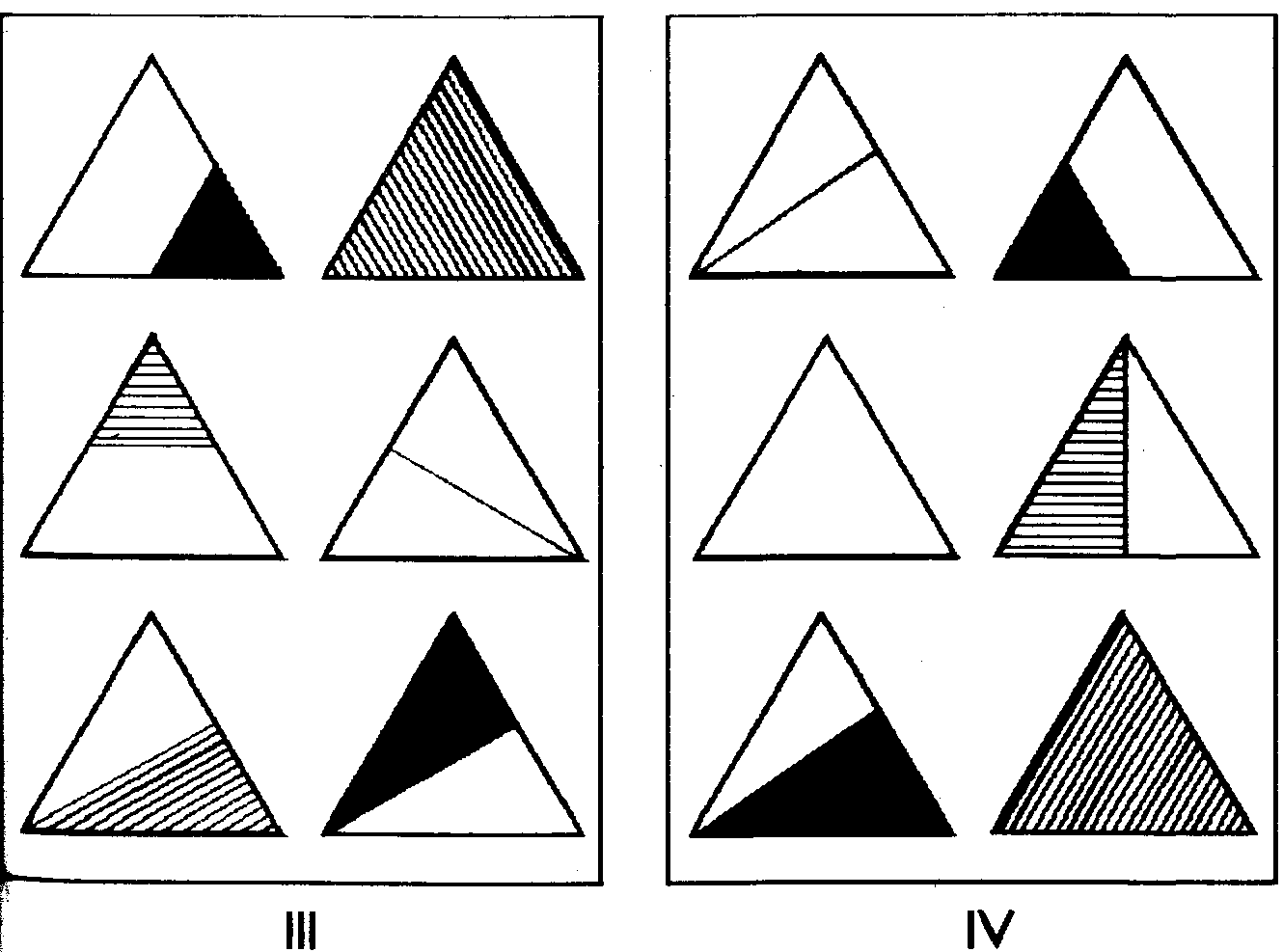
Альбом к кубикам Никитина «Сложи Узор для Малышей»
Альбом «Сложи Узор для малышей» предназначен для деток от 2 до 3 лет. Очень яркий и понятный. Все задания в альбоме даны первого уровня сложности: кубики на схемах изображены в натуральную величину, границы прорисованы, что является необходимым условием для первоначального знакомства с игрой.
Каждую схему сопровождает веселый рисунок. У малышей наглядно-образное мышление, поэтому схемы в этом альбоме «оживают», и кубики превращаются в рыбок, цветочки, паучков, звездочки и т.д., что делает занятие увлекательным.
Альбом Чудо-Кубики 1 для деток от 2 до 5 лет
Кубики на схемах нарисованы в масштабе 1:1, что является необходимым условием для работы с детьми младшего дошкольного возраста и позволяет ребенку моделировать изображение методом наложения.
Задания выстроены по схеме от простого к сложному. Для самых маленьких изучение понятий высокий-низкий, длинный-короткий. Предлагается сделать такую же по высоте башню или такую же по длине дорожку.
Альбом научит дифференцировать и сравнивать предметы по размеру, преобразовывать изображение и воссоздавать из частей целый образ. В процессе игры дети тренируют навыки счета, конструктивные способности, учатся ориентироваться в пространстве и во времени, развивают внимание, логическое мышление, воображение, память, мелкую моторику и речь. Регулярные игры-занятия незаметно воспитают такие важные качества личности ребенка как усидчивость, самостоятельность, научат ребенка мыслить творчески.
Кубики Кооса методика развития для детей |
Содержание статьи.
(для быстрого перехода нажмите на название раздела)
Кубики Кооса это методика которая была разработана для того чтобы выявить умственные способности, как у детей так и у взрослых. Создал такую методику американский психолог С. Коос еще в 1920 году.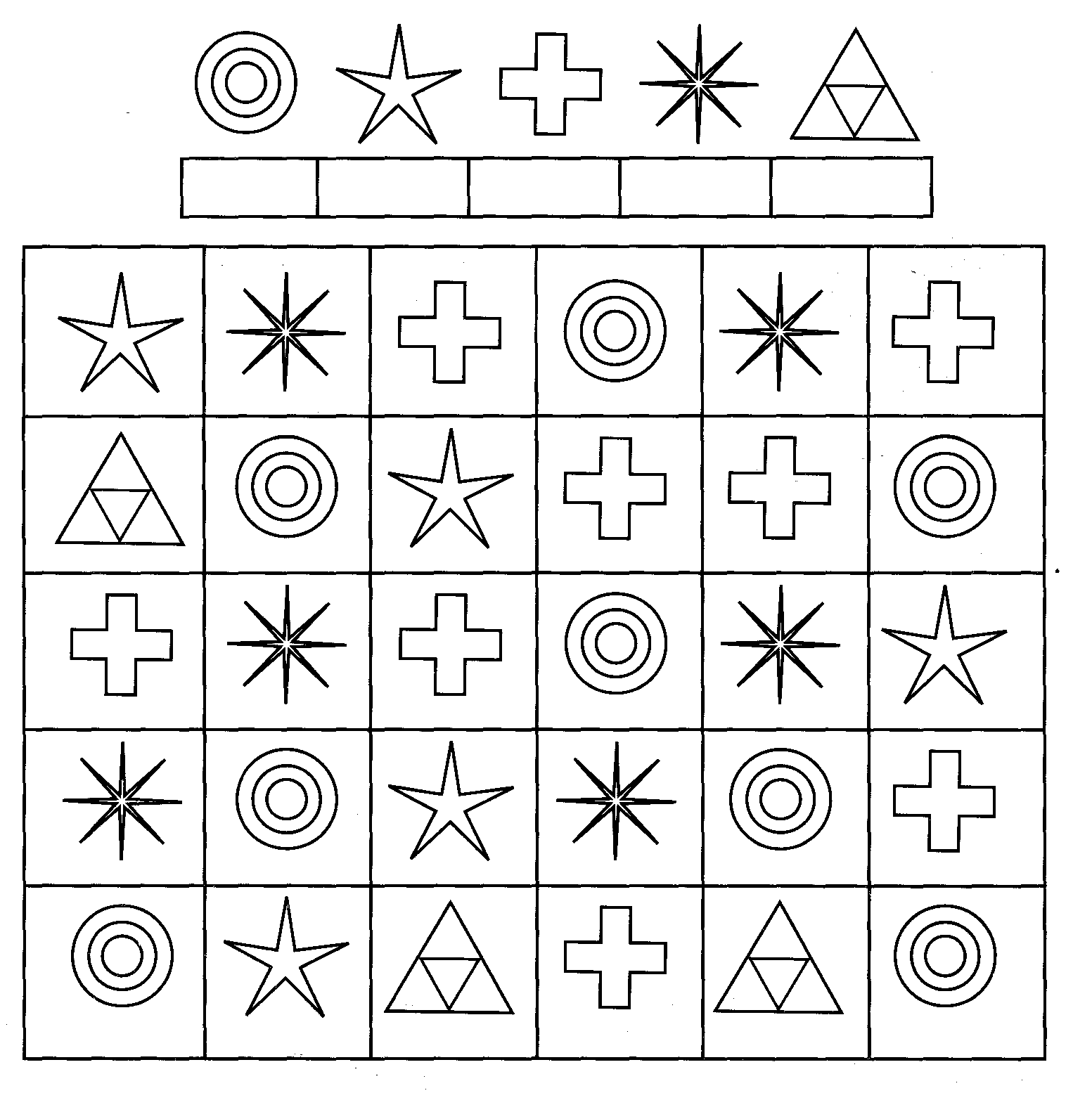 В честь него и получили название кубики.
В честь него и получили название кубики.
Для чего нужны кубики Кооса.
Изначально кубики применяли для диагностики интеллекта ребенка.
С помощью данной методики анализировали умственные способности у детей, у которых были нарушения речи или задержка в психологическом развитии. Эту методику и сейчас применяют современные психологи, а так же педагоги.
Но помимо диагностических возможностей данной методики, кубики являются отличной зарядкой для мозга и для расширения умственных способностей ребенка. Кубиками можно воспользоваться, как для развития пространственного мышления, для того чтобы научить ребенка устанавливать связи и отношения между предметами в пространстве, для развития логики и внимательности, сосредоточенности и воображения.
Для того чтобы тренировать все выше перечисленные навыки, надо с помощью кубиков складывать различные узоры, которые отличаются по степени сложности. Перейти к Узорам Кооса
Какие они кубики Кооса?
Это кубики одинакового размера, грани их покрашены в специальные цвета, 2 грани красного цвета, 2 грани белого цвета , 2 грани двухцветные (красно-белые). К кубикам прилагаются карточки — задания, с разным уровнем сложности.
К кубикам прилагаются карточки — задания, с разным уровнем сложности.
В оригинале число кубиков должно быть 16 штук. Но для занятий с детьми младшего возраста достаточно набора кубиков из 9 штук. Начинать знакомство с кубиками, складывать узоры, можно и с 4 штук.
Кубики можно купить, а можно сделать самому, как «Сделать кубики Кооса своими руками» смотрите тут.
Кубики «Сложи узор»
Суть методики Кооса.
Суть методики заключается в том, чтобы ребенок складывал узоры из кубиков, опираясь на карточки с заданиями.
Ребенку предоставляется карточка с заданием (определенным узором). Он должен сложить узор, из верхних граней кубиков. Узор должен полностью соответствовать рисунку с карточки.
Карточки с заданиями отличаются уровнем сложности, их стоит выдавать в определенной последовательности, от простого — к сложному. При диагностике, еще обращают внимание на время выполнения задания.
При диагностике, еще обращают внимание на время выполнения задания.
Но в статье идет речь о том, как при помощи кубиков развивать интеллект ребенка. И поэтому на время в игре с кубиками, особое внимание уделять не будем.
Как получать успехи в игре.
Для того чтобы были отличные результаты от игры с кубиками- головоломками, надо, чтобы:
1.Все занятия должны проходить в игровой форме, и в хорошем настроении, как ребенка, так и родителя.
2. В первый раз, вместе с ребенком познакомьтесь с кубиками. Покажите ребенку, как они покрашены, какие у них элементы. Например: «Посмотри, у этих кубиков разные стороны, они раскрашены по-разному, есть белые, есть красные, а есть двух цветные стороны».
3. Покажите ребенку карточку с заданием и скажите: «Сейчас мы будем складывать вот такой узор из этих кубиков».
4. Если у ребенка сразу появилось желание собрать из кубиков узор, то предоставьте ему эту возможность. Если Вы заметили, что у ребенка возникли трудности, тогда продемонстрируйте, как надо это сделать. Покажите сами как из кубиков можно собрать узор.
Например: «Этот узор можно сложить из таких деталей, «носик» мы складываем из двух бело – красных деталей. Вот так. Давай теперь, ты повтори!». После как ребенок собрал такой же «носик» соедините четыре детали вместе, два красных треугольника, и у Вас получится красный квадрат.
5.Хвалите ребенка и восхищайтесь им!
6.Сначала фигуры стройте из одноцветных граней кубиков, постепенно добавляйте двухцветные грани, далее можете складывать только из двухцветных граней, и усложняйте упражнение добавлением кубиков.
7. Делать одно, и тоже упражнение можно много раз, пока не убедитесь, что ребенок понял. Просите ребенка, чтобы он поделился с вами, что он собирается делать, какими элементами воспользоваться и как складывать грани.
Об отличном результате может говорить то, что ребенок, перед тем как собрать узор, перечислит все элементы, которые ему понадобятся.
На основе кубиков Кооса, появилась дидактическая игра «Сложи узор», которая была разработана российскими педагогами Никитиными. Эта игра – головоломка развивают мелкую моторику пальцев рук, разум ребенка, усидчивость и сосредоточенность.
Играйте и развивайтесь!
Кубики «Сложи узор»
С помощью этой игры можно развить у ребенка пространственное воображение, аккуратность, внимание, графические способности, а также умение анализировать, синтезировать, комбинировать. Также игра в кубики способствует развитию мелкой моторики и речи.
Смотрите так же:
Кубики «Сложи узор»
Развитие осведомленности о шаблонах у детей раннего возраста
Недавнее исследование показало, что способность маленьких детей определять математические закономерности может предсказывать более поздние математические достижения в большей степени, чем другие способности, такие как счет (Rittle-Johnson et al, 2016). Исследования также показали, что осознание закономерностей может сильно различаться между людьми: все мы замечали детей, которые располагали объекты радиальными узорами или строили конструкции с помощью отражающих элементов. симметрия, в то время как другие вообще не обращают внимания на узор.
Австралийские исследователи Папик, Маллиган и Митчелмор (2011) недавно обнаружили, что дошкольники могут эффективно обучать осознанию закономерностей, что положительно влияет на их понимание чисел в дальнейшем. Прямое обучение осознанию паттернов связано с поощрением «нюхания паттернов» у детей старшего возраста с целью развития математического понимания и мышления (http://nrich.maths.org/9968).
Что такое понимание математических закономерностей? Паттерны — это в основном отношения с некоторой регулярностью между элементами.В первые годы Папик и др. (2011) предполагают, что существует три основных типа:
- фигур с правильными элементами, такими как квадрат или треугольники с равными сторонами и углами, и фигуры, состоящие из некоторых точек, расположенных на одинаковом расстоянии;
- повторяющаяся последовательность: наиболее распространенными примерами являются последовательности AB, такие как красный, синий, красно-синий узор с кубиками. Более сложными являются образцы ABC или ABB с повторяющимися элементами, такими как красный, зеленый, синий или красный, синий, синий;
- шаблон роста, например лестница с равными ступенями.
Дети, которые хорошо осведомлены о закономерностях, могут заметить такую закономерность: они могут воспроизвести закономерности и предсказать, как они будут продолжаться.
Почему важно знать закономерности?
Выявление основных закономерностей важно для выявления множества различных видов математических отношений. Он поддерживает запоминание последовательности счета и понимание числовых операций, например, признание того, что если вы складываете числа в другом порядке, их общая сумма остается неизменной.Осведомленность о закономерностях была описана как раннее алгебраическое мышление, которое включает в себя:
- обращая внимание на математические особенности
- , определяющий взаимосвязь между элементами
- наблюдение закономерностей
Упражнение «Создание шаблонов» фокусируется на повторяющихся шаблонах и предлагает несколько увлекательных способов развития понимания шаблонов с подсказками для рассмотрения ответов детей. Дети могут делать «поезда» из разных игрушек, делать выкройки из веточек и листьев снаружи или создавать печатные и наклеивающие узоры в процессе проектирования.
Важно познакомить детей с множеством повторяющихся шаблонов, переходящих от ABC и ABB к ABBC. В прошлом мы были склонны подчеркивать чередование паттернов AB с маленькими детьми: однако это может привести к тому, что некоторые дети будут думать, что «синий, красный, красный» не может составить паттерн. Они говорят что-то вроде: «Это не узор» ¦, потому что рядом с каждым из них не может быть двух одинаковых цветов. прочее »(Papic et al, 2011).
Копирование паттернов важно, согласно Папику и др. (2011), которые предполагают, что последующий разговор между учителем и ребенком, сравнивая их построение с исходным паттерном, имеет решающее значение для развития осознания паттернов.Это помогает им сосредоточиться на том, «Что одинаково, а что отличается?» и увидеть основную структуру шаблона. Некоторым маленьким детям это трудно, в то время как другие могут воспроизвести узор, используя другие цвета или предметы.
Некоторые дочерние элементы будут успешно копировать узор, но по одному кубу за раз, и не смогут продолжить его. Те, кто выделяют «единицу повторения» в паттерне AB, могут продолжить паттерн, взяв вместе красный и синий куб. Значение определения «единицы повторения» состоит в том, чтобы рассматривать группу объектов как один элемент, что является сложным развитием для маленьких детей.Это ведет к мультипликативное мышление, которое предполагает подсчет групп вместо отдельных предметов, например, при подсчете количества пар рук. Распознавание «единицы повторения» также включает в себя осознание части-целого, когда одновременно видят единицу в целом и элементы внутри нее. Это важно для понимания состава чисел и представления чисел как составных из других чисел.
Дети, которые хорошо умеют «определять закономерности», могут видеть общую структуру и определять правило закономерностей. Когда дети создают свои собственные выкройки, возникает полезный вопрос: «Какое правило для вашей выкройки?» или с детьми младшего возраста: «Как называется ваш образец?» Дети, понявшие структуру выкройки, могут переводить ее на разные материалы, обобщая выкройку.Один пятилетний, Когда ему сказали, что это образец ABBC, он сказал: «Значит, это может быть собака, кошка, кошка, овца?»
Дети также могут обнаружить ошибку в шаблоне, и некоторые могут сразу увидеть, как ее исправить, в то время как другим, возможно, придется начать с самого начала, чтобы внести исправление или выполнить «локальную» корректировку, которая просто перемещает ошибку!
Детям младшего возраста нравится придумывать шаблоны действий, такие как «голова, плечи, колени и пальцы ног», и им нравится замечать ошибки в последовательности. Пятилетние дети могут изобретать свои собственные способы записи паттернов действий, которые включают «перевод» паттерна в другой режим с использованием картинок и символов.
Детям постарше также нравятся модели роста, такие как образец «лестницы», лежащий в основе традиционных рассказов и рифм, таких как огромная репа, пряничный человечек, старушка, проглотившая муху, двенадцать дней Рождества и такие книги, как Голодная гусеница и многие другие.
На что обращать внимание, когда дети реагируют на вызовы.
Копирование и продолжение рисунка:
- совпадающих кубиков по одному;
- с использованием целых единиц, например, собирая вместе красный и синий куб.
Создание или рисование выкройки по памяти (показать кратко, а затем скрыть все или часть):
- некоторые элементы верны, например, цвет или номер, но не оба сразу;
- показывает правильно; строительство в единицах.
- обнаруживает ошибку, но делает локальные исправления, создавая новую проблему;
- исправляя ошибку, начиная с начала заново;
- прямо исправляет ошибку, объясняя, почему она была неправильной.
Объясняя закономерность:
- собственными словами, например, «Это маленький, большой, большой»;
- обобщающий: «это как ABB».
Сделайте свой собственный узор с похожими или разными предметами:
- с разными объектами, но совпадающими по цвету; или наоборот;
- изготовление с очень разными объектами;
- «переводит» в разные режимы, например, с использованием звуков или символов.
Узоры также являются важным элементом пространственного мышления и геометрии, например, с отражающей и вращательной симметрией.Как только дети начинают замечать закономерности, они видят их повсюду, не только в окружающей среде, но и в повседневных делах и во всех видах регулярного поведения. Самое главное, что дети находят привычные занятия интересными и могут помочь развить позитивное отношение и доступ к математике для всех детей.
Для получения дополнительных идей и ресурсов для обучения шаблонам, включая видеоклипы, см. Erikson Early Math Collective.
Благодарности:
Хелен Таулесс; группа проекта Pattern, Уондсворт; Рабочая группа EYFS по математической педагогике, Bucks, Berks & Oxon Hub 2017.
Ссылки Баратта-Лортон, М. Математика по-своему (1976) Лондон: Аддисон-Уэсли
Карл, Э. (1969) Голодная гусеница Лондон: Пингвин
Киран, К., Панг, Дж. С., Шифтер, Д., & Ng, SF (2016) Ранняя алгебра Тематические обзоры ICME-13 Springer Open. http://link.springer.com/book/10.1007%2F978-3-319-32258-2
Папик, М., Маллиган, Дж., и Митчелмор, М. (2011) Оценка развития дошкольников математическое моделирование. Журнал исследований в области математического образования, 42 (3), 237-268.
Риттл-Джонсон, Б., Файф, Э. Р., Хофер, К. Г., Фарран, округ Колумбия (2016) Ранние математические траектории: траектории траектории детского знания математики в возрасте от 4 до 11 лет, развитие ребенка DOI: 10.1111 / cdev.12662
Cool способы научить вашего дошкольника образцам
Ваш ребенок обращается к музыке, формам и цветам? Большинство из них, и это их естественная склонность к математике. Это математическое ноу-хау вытекает из опыта вашего ребенка — например, хлопания в ладоши под песни — наряду с другими вехами в развитии — например, умением хлопать в ладоши.
Да, даже младенцы рано изучают математические понятия, и все начинается с шаблонов.
Паттерны — это логически повторяющиеся расположения вещей. Такое расположение цветов, форм, жестов, звуков, изображений и чисел является важной концепцией для маленьких детей и в значительной степени способствует их раннему пониманию математики. Согласно данным национальной некоммерческой организации, занимающейся вопросами развития и обучения детей младшего возраста, «от нуля до трех»: «Шаблоны помогают детям учиться делать прогнозы, понимать, что будет дальше, устанавливать логические связи и использовать навыки рассуждения.
Более того, понимание закономерностей помогает социальному развитию вашего дошкольника, потому что оно прививает им понимание последовательности повседневных рутинных действий, таких как сменяемость во время игры или следование школьным правилам, например, поднять руку, подождать, пока вас позовут, поделитесь тем, что вы хотите сказать.
В этом возрасте есть два типа шаблонов, которые нужно искать и практиковать: повторяющиеся шаблоны (например, красный-синий-красный-синий-красный) и растущие шаблоны (например, маленький, средний, большой). К счастью, и то, и другое скрыто в повседневных занятиях вашего ребенка, и практиковать эти шаблоны невероятно весело.
Цветовые узоры
Цветовые узоры повсюду, и ваш ребенок, вероятно, любит замечать и создавать их. Лего и цветные блоки позволяют создавать цветные узоры: красный-красный-синий-желтый-красный-красный-синий-желтый. Вашему ребенку может понравиться раскрашивать радуги в определенной последовательности цветов; помогите им узнать и следовать последовательности.
Используйте декоративно-прикладное искусство, чтобы побудить детей создавать выкройки и следовать им. Посмотрите на Pinterest подходящих по возрасту бумажных змей и разноцветных ожерелий, используя хлопья и конфеты в качестве «бусинок».«Предметы домашнего обихода, такие как поддоны для кубиков льда и пустые картонные коробки для яиц, также можно превратить в рабочие места, где ваш ребенок может создавать и воссоздавать красочные узоры из пластилина.
Развлечение с едой
Еда — это красивый и полезный способ, которым ваш ребенок может создавать выкройки. Попросите своего задорного повара положить пять пепперони и три гриба на каждый кусок пиццы. Есть блины на следующих выходных? Попросите дошкольника создать декоративные рамки вокруг каждого блинчика, чередуя ломтики банана и шоколадную стружку.Вместо того, чтобы выливать следующий фруктовый салат в миску, нанизывайте фрукты на палочки — шашлык из шашлыка! — с повторяющимися узорами. (Попросите ребенка выложить узор из фруктов, например, клубника-банан-виноград-апельсин-клубника-банан-виноград-апельсин; затем, если моторика вашего ребенка позволяет, позвольте ему также осторожно наколоть фрукты на узоры.)
Шаблоны движений и грув
Простые шаблоны движений — зарождение танца — могут превратить вашу следующую прогулку в урок математики и хореографии.«1-2-3-4-5-прыжок, это закономерность», — говорит доктор Джи-Ци (Джеки) Чен, профессор детского развития в Институте Эриксона и соавтор книги Big Ideas of Early Mathematics: What Учителя младшего возраста должны знать .
«Идите налево, идите направо, налево, направо, это другой шаблон». Поощряйте своего кинетического ребенка зигзагообразно-приседать-прыгать-покачиваться, пока он не устанет — и не получит образования.
Образцы тиканья
Как общество, мы отслеживаем время по определенным образцам, которые могут быть полезны, чтобы научить вашего ребенка «жить только настоящим».Объясните секунды, минуты и часы понятным вашему ребенку языком: она может задерживать дыхание на несколько секунд, она может ждать вашего внимания целую минуту, а фильмы длятся целый час (или два). Дайте ребенку возможность попрактиковаться, составив расписание: 10 минут уборка в комнате, 10 минут игры. Объясните ритм календаря (дни недели и месяцы в году — отличное начало) и попросите их определить, сколько дней, недель и месяцев до их дня рождения. Поверьте, это расчет, который они хотят решить.
Ритм и музыкальные паттерны
Исследования показывают, что музыка и математика переплетаются в нашем мозгу с раннего возраста. Ровные хлопки-хлопки-хлопки в ладоши (или бах-бах-бах-бах по кастрюлям и сковородкам) связаны с математическими навыками вашего ребенка, такими как счет, определение последовательности и пространственное восприятие. Когда вы заметите начало паттерна, помогите своему ребенку дополнить его: обучение паттернам с помощью музыки, скорее всего, принесет пользу когнитивным способностям вашего ребенка в будущем.
Детские стишки и музыка часто основаны на простых шаблонах.Многие также требуют движения, например кружение и падение в «Кольце вокруг Рози».
Включите музыку и позвольте паттернам играть. Если вы ищете специально для детей мелодии, ЛаМоника Хопкинс, менеджер программ по уходу за детьми и после школы в GLIDE Foundation, настоятельно рекомендует Greg & Steve, детский музыкальный дуэт, удостоенный премии Грэмми. «Они учат математике во многих своих песнях, которые обучают слушателей музыкальным подвижным играм», — говорит Хопкинс. Детям также нравятся схемы в играх со скакалкой и в песнях с аплодисментами, например Pat-a-Cake.
Когда у вас в голове застревает одна из тех песен с хлопками или прыжками, помните, это того стоит. Возможно, вы воспитываете следующих Тейлор Свифт, Джексона Поллака, Мисти Коупленд или Стивена Хокинса.
Поделиться в Pinterest
Обновлено: 21 апреля 2020 г.
Как научить детей числовым образцам и последовательностям (+5 комплектов листов, на которые можно опереться)
Дети естественным образом сталкиваются с числовыми последовательностями и образцами в повседневной жизни. Поэтому, когда приходит время официально преподавать им математическую тему, все, что вам действительно нужно, — это тренировать их мозг, чтобы понять, что будет дальше.При этом все зависит от наличия необходимых ресурсов — вам нужно подтолкнуть учащихся к развитию их числовой грамотности, не перегружая их.
Это руководство поможет вам достичь этого баланса; Прочтите наши главные советы и лучшие комплекты рабочих листов, которые помогут спланировать уроки по шаблонам чисел.
Что такое числовые шаблоны и последовательности?
Числовые шаблоны — это последовательность чисел с общей связью. Например, в последовательности 3,6,9,12 каждое число увеличивается на три.Вообще говоря, когда ребенок достаточно уверенно владеет числами, чтобы считать без посторонней помощи, он готов приступить к изучению последовательностей.
Изучая числа и последовательности, вы также будете охватывать такие темы, как система с основанием 10, нечетные и четные числа и построение шаблонов с помощью простой арифметики.
Почему так важны числовые шаблоны и последовательности?
По своей сути математика изучает числа и их отношения друг к другу. Вот почему важно убедиться, что дети твердо понимают числовые модели и последовательности, прежде чем переходить к более сложным математическим темам.
Способность распознавать закономерности в группах чисел поможет ребенку развить навыки критического мышления и подготовить их к более сложным математическим операциям в ближайшие годы.
А закономерности можно найти не только в математике, но и в природе, искусстве и музыке. Таким образом, способность идентифицировать, распознавать и строить последовательности поможет им в естествознании, географии, социальных исследованиях и других предметах.
Лучшие советы по обучению числовым последовательностям
Обучение математике — не всегда самая легкая задача в мире, некоторые дети всегда будут относиться к этой теме менее естественно, чем другие.Но когда дело доходит до числовых шаблонов, есть несколько способов сделать их более интересными и интересными для всех.
Учите их стишкам и играм
Песни и стишки, такие как «Раз, два, пристегни мою обувь» и «Муравьи маршируют» — забавные способы научить детей считать и научить их считать без путаницы. Считайте пальцами по мере продвижения, чтобы дать им наглядное пособие.
Используйте числа в повседневных задачах
Числа есть везде, поэтому вы можете легко отвлечься от учебы.Если вы учитель математики, почему бы не прогуляться с классом по детской площадке и поискать числовые последовательности на деревьях и растениях — обратите внимание, как дерево имеет тенденцию ответвляться от 1 ствола к 3 веткам и к 5 меньшим ветвям? Это числовая последовательность в действии! Если вы учитесь на дому, попросите ребенка накрыть стол четырьмя вилками или создать узор из кусочков пасты на тарелке.
Выкройки не обязательно должны быть числами
Если ваш ребенок немного борется с числами, сделайте шаг назад и сначала представьте выкройки рисунками.Вместо того, чтобы использовать цифры, вы можете создавать узоры из скоплений точек. Если у вас есть набор домино, это также отличный способ продемонстрировать модели менее захватывающим образом.
Лучшие комплекты рабочих листов для обучения числовым шаблонам и последовательностям
Рабочие листы — отличный способ для вашего ученика закрепить то, что он выучил, а для вас — оценить его успехи. Все эти рабочие листы с числовыми последовательностями охватывают различные аспекты формирования рисунка и содержат дополнительную информацию, которую вы можете легко превратить в план урока с числовой последовательностью.
Рабочие листы по нечетным и четным числам
Числовые шаблоны и последовательности часто могут включать различие между нечетными и четными числами, поэтому очень важно, чтобы ваш ребенок овладел этим основным навыком. Этому довольно легко научить — четные числа можно разделить на две части, а нечетные — нельзя — и на рабочих листах в этом наборе используются рисунки для иллюстрации четных чисел, например Можно ли разделить эту гроздь из шести яблок пополам? Отличный ресурс для любого ребенка, который хорошо учится наглядно.
Рабочие листы по кардинальным числам
Прежде чем переходить к последовательностям и шаблонам, важно убедиться, что ваш ребенок правильно понимает числа и их порядок. Помимо игр на счет и словесных упражнений, заполните несколько рабочих листов, чтобы убедиться, что они хорошо понимают числа. Этот комплект листов содержит огромное количество упражнений со схемами и иллюстрациями, которые вы и ваш ребенок можете выполнить вместе. Их попросят составить числа по буквам, определить визуальные представления чисел и произвести подсчет для начинающих.
Рабочие листы шаблонов номеров
Эта коллекция рабочих таблиц является полным введением в шаблоны номеров и является идеальным местом для начала. Пакет из 28 страниц объясняет концепцию числового шаблона, а затем демонстрирует, как их идентифицировать. В нем есть множество примеров, которые вы можете проработать со своим ребенком, а также веселые упражнения с красочными иллюстрациями.
Рабочие листы в виде числовой линии
Использование числовой линии может добавить ясности и структурированности для всех учащихся, которые изо всех сил пытаются представить абстрактные числа в своей голове.В этих 28 рабочих листах учащимся предлагается определить шаблоны на числовой прямой, а затем составить свои собственные — идеально для изучения числовых шаблонов и последовательностей, а также для более сложных операций сложения и вычитания.
Рабочие листы по счету с пропуском
Как только ваш ребенок овладеет счетом, следующий уровень выше — это счет с пропуском, когда он считает, добавляя число больше единицы. Например, 2,5,8,11 пропускает счет до трех. Это базовый числовой шаблон, который откроет им понимание более сложных последовательностей.Этот комплект рабочих листов содержит множество диаграмм и пояснений, чтобы убедиться, что учащиеся имеют твердое понимание, прежде чем двигаться дальше.
Нужны еще листы по математике? У нас есть все необходимое. Помните, что
постоянно окружены числами , и вы легко можете применить полученные знания в реальной жизни. Реквизит, такой как кубики или кусочки пасты, может быть отличным учебным пособием, а рабочие листы — отличным способом закрепить свои знания.У нас есть огромная коллекция рабочих листов по математике, которые можно загрузить, так что обязательно ознакомьтесь с ними.П.С. Если вы преподаете математику для учеников в возрасте от детского сада и заканчивая предварительным вычислением, вам обязательно стоит попробовать MathTeacherCoach! Это комплексное решение для учебной программы CCSS по математике. Он может похвастаться презентациями, планами уроков, мероприятиями, заметками с инструкциями, викторинами, работой звонка, проверочными тестами и многим другим. Кроме того, на HelpTeaching можно создать свои собственные тесты с помощью банка из тысяч вопросов.ком!
Обучающие шаблоны для младенцев и детей ясельного возраста
Шаблонные задания можно легко реализовать с детьми в повседневной жизни естественным образом.
Дети любят находить закономерности в окружающем их мире. Шаблоны помогают детям понять изменения и то, что со временем происходит. Узоры — это вещи, которые логично повторяются, например, вертикальные полосы на свитере. Это могут быть числа, изображения или фигуры. Например, узор может быть сделан из пластмассовых животных, чередующихся двух- и четырехногих животных, или животных, которые плавают, и животных, которые летают.
Шаблоны помогают детям делать прогнозы, потому что они начинают понимать, что будет дальше. Они также помогают детям научиться устанавливать логические связи и использовать навыки рассуждения. Шаблоны можно найти повсюду в нашей повседневной жизни, и на них следует указывать маленьким детям. «Солнце взошло и зашло, а затем взошла и зашла луна».
Не стоит недооценивать то, чему ребенок способен научиться во всех академических областях, включая математику. Малыши могут разыграть такие шаблоны, как прыжки влево, затем вправо, затем влево и затем вправо.Они могут наблюдать повторяющиеся паттерны, такие как стоящий блок, плоский лежащий блок, стоящий блок, плоский лежащий блок и т. Д. Они получают возможность копировать простые повторяющиеся паттерны, такие как зеленый, белый, зеленый, белый и т. Д. Со временем они смогут создавать свои простые выкройки.
Michigan State University Extension предлагает следующие идеи по расширению знакомства с детьми младшего возраста:
- Используйте math talk: «Давайте хлопаем в такт этой песни». «На твоем свитере есть полосы.Красный, синий, красный, синий, красный, синий… »
- Читайте книги и пойте песни и колыбельные с повторяющимися словами и фразами.
- Имейте постоянный распорядок дня.
- Опишите, что вы видите, что делает ребенок. «Я кладу блоки в ведро; вы их выбросили; Я кладу блоки; вы их выбросили ».
Книги, обучающие шаблонам:
- «Десять маленьких кроликов» Вирджинай Гроссман
- «Макс нашел две палки» Брайан Пинкни
- «Близко, ближе, ближе» Шелли Ротнер
- «Кисть природы: узоры и цвета вокруг You» Сьюзан Стокдейл
Другие ресурсы Национальной ассоциации образования детей младшего возраста:
Вы нашли эту статью полезной?
Расскажите, пожалуйста, почему
Представлять на рассмотрениеРешение проблем: Найдите шаблон (2–8 классы)
Решение проблем: Найдите шаблон
Что это?
«Поиск закономерностей» — это стратегия, в которой учащиеся ищут закономерности в данных, чтобы решить задачу.Учащиеся ищут повторяющиеся элементы или числа или серию повторяющихся событий. Следующая проблема может быть решена путем поиска шаблона:
В средней школе 1000 шкафчиков, где учится 1000 учеников. Первый ученик открывает все 1000 шкафчиков; затем второй ученик закрывает шкафчики 2, 4, 6, 8, 10 и так далее до шкафчика 1000; третий ученик меняет состояние (открывает закрытые шкафчики, закрывает открытые шкафчики) шкафчиков 3, 6, 9, 12, 15 и т. д .; четвертый ученик меняет состояние шкафчиков 4, 8, 12, 16 и так далее.Это продолжается до тех пор, пока у каждого ученика не будет очереди. Сколько шкафчиков будет открыто в конце?
Чтобы получить ответ, перейдите к: Задача шкафчика от докторов математики
Почему это важно?
Шаблоны часто представляются учащимся без контекста задачи со словом, как в следующем примере: «Найдите шаблон в этой последовательности, объясните, как он работает, и используйте этот шаблон для предсказания следующих четырех чисел. 7, 10, 13 , 16, 19, __, __, __, __. »
Младшие ученики часто открывают для себя и продолжают использовать узоры, в которых используются геометрические формы.Например, желтый круг, красный квадрат, зеленый треугольник, желтый круг, красный квадрат, зеленый треугольник и т. Д.
Обнаружение закономерностей может помочь учащимся усвоить факты умножения, когда они замечают, что 4 x 7 — это то же самое, что 7 x 4, и что все числа в столбце 10 оканчиваются нулем.
Стратегия «Найти шаблон» может использоваться для решения многих математических задач и может использоваться в сочетании со многими другими стратегиями, включая создание таблицы, составление списка или упрощение задачи.
Как это сделать?
Предложите учащимся задачу, которая требует от них найти образец для решения проблемы.Например:
Если вы построите четырехгранную пирамиду из баскетбольных мячей и не учитываете дно как сторону, сколько мячей будет в пирамиде, состоящей из шести слоев?
Использование совместных учебных групп для поиска решений проблем помогает учащимся выразить свои мысли, провести мозговой штурм, обсудить варианты и обосновать свою позицию. Найдя решение, каждая группа может представить его классу, объясняя, как они пришли к своему решению и почему они считают его правильным.Или студенты могут объяснять свои решения в письменной форме, а учитель может отображать решения. Затем студенты могут перемещаться по комнате, чтобы прочитать решение каждой группы.
-
Разобраться в проблеме
Продемонстрируйте, что первый шаг к решению проблемы — это ее понимание. Это включает в себя определение ключевой информации, необходимой для поиска ответа. Это может потребовать от студентов прочитать задачу несколько раз или изложить ее своими словами.
Иногда вы можете решить проблему, просто распознав шаблон, но чаще вы должны расширить шаблон, чтобы найти решение. Составление числовой таблицы поможет вам более четко увидеть закономерности.
В этой задаче учащиеся понимают:
На верхнем уровне будет один баскетбольный мяч. Мне нужно найти, сколько шаров будет в каждом слое пирамиды, с первого по шестой. Мне нужно найти, сколько баскетбольных мячей будет во всей пирамиде.
-
Выберите стратегию
Чтобы успешно использовать эту стратегию, вы должны быть уверены, что модель действительно будет продолжаться.Попросите учащихся назвать причины, по которым они думают, что эта закономерность предсказуема, а не основана на вероятности. Проблемы, которые легче всего решить, найдя шаблон, включают те, которые просят учащихся расширить последовательность чисел или сделать прогноз на основе данных. В этой задаче учащиеся также могут составить таблицу или нарисовать картинку, чтобы организовать и представить свое мышление.
«Поиск шаблона» — подходящая стратегия для решения проблемы. Это предсказуемая модель, которая будет продолжаться.
-
Решите проблему
Начните с верхнего слоя или одного баскетбольного мяча. Определите, сколько шаров должно быть под этим шаром, чтобы образовался следующий слой пирамиды. При необходимости используйте манипуляторы. Студенты могут использовать любые манипуляторы, от монет до кубиков и мячей для гольфа. Студенты также могут рисовать картинки, чтобы помочь им решить проблему.
Вы можете попросить группы использовать разные манипуляторы, а затем сравнить их решения, чтобы определить, повлиял ли тип манипулятивного действия на решение.Если учащиеся моложе, начните с трех уровней и обсудите их ответы на эту более простую задачу. Затем переходите к другим уровням, по мере того как учащиеся понимают, как решить проблему.
Слой Шаров добавлено Шаров в этом слое 1 (вверху) 1 1 3 3 2 = 4) 3 5 9 (4 + 5 = 9) 4 7 16 (9 + 7 = 16) 5 9 25 (16 + 9 = 25) 6 11 36 (25 + 11 = 36) Если это помогает визуализировать пирамиду, используйте манипуляторы для создания третьего слоя.Запишите номер и ищите выкройку. Второй слой добавляет 3 баскетбольных мяча, а следующий — 5 баскетбольных мячей. Каждый раз, когда вы добавляете новый слой, количество баскетбольных мячей, необходимых для создания этого слоя, увеличивается на 2.
- 1
- 1 + 3 = 4
- 4 + 5 = 9
- 9 + 7 = 16
- 16 + 9 = 25
- 25 + 11 = 36
Продолжайте, пока не будут записаны шесть слоев. Как только шаблон будет найден, учащимся может не понадобиться использовать манипуляторы.
Затем добавьте баскетбольные мячи, использованные для создания всех шести слоев.Ответ — 91 мяч. Посмотрите в списке, есть ли другой узор. Количество шаров, используемых на каждом уровне, равно квадрату номера слоя. Итак, 10-й слой будет иметь 10 x 10 = 100 шаров.
-
Проверить
Прочтите проблему еще раз, чтобы убедиться, что на вопрос дан ответ.
Да, я нашел общее количество баскетбольных мячей в шестислойной пирамиде.
Проверьте математику, чтобы убедиться, что она верна.
1 + 4 + 9 + 16 + 25 + 36 = 91
Определите, была ли выбрана лучшая стратегия для этой проблемы или существовал другой способ решения проблемы.
Поиск шаблона был хорошим способом решить эту проблему, потому что шаблон был предсказуем.
-
Объясните
Студенты должны объяснить свой ответ и процесс, который они прошли, чтобы его найти. Студентам важно говорить или писать о своем мышлении. Продемонстрируйте, как написать абзац, описывающий шаги, которые предприняли учащиеся, и то, как они принимали решения на протяжении всего процесса.
Сначала я начал с первого слоя.Я использовал блоки, чтобы построить пирамиду, и составил список из количества блоков, которые я использовал. Затем я создал таблицу для записи количества шаров в каждом слое.
Слой Шаров добавлено Шаров в этом слое 1 (вверху) 1 1 3 3 2 = 4) 3 5 9 (4 + 5 = 9) 4 7 16 (9 + 7 = 16) 5 9 25 (16 + 9 = 25) 6 11 36 (25 + 11 = 36) Я сделал четыре слоя, а затем увидел узор.Я видел, что для каждого слоя количество использованных шаров было числом слоя, умноженным на самого себя. Я закончил выкройку без блоков, умножив количество шариков в слоях 5 и 6.
Затем я сложил все шарики в каждом слое.
1 + 4 + 9 + 16 + 25 + 36 = 91Я получил 91 мяч.
-
Практика с инструкциями
Попросите учащихся решить следующую задачу, используя стратегию «Найти шаблон».
Женщина пытается сократить количество банок газировки, которое она пьет каждую неделю. Она составляет план, чтобы через несколько недель выпить только одну банку газировки. Если она начнет с 25 банок в первую неделю, 21 банку во вторую неделю, 17 банок в третью неделю, 13 банок в четвертую неделю и продолжит эту схему, сколько недель ей потребуется, чтобы достичь своей цели?
Попросите учащихся поработать в парах, группах или индивидуально, чтобы решить эту задачу. Они должны уметь рассказать или написать о том, как они нашли ответ, и обосновать свои рассуждения.
Как можно расширить эту стратегию?
Математические задачи могут быть простыми, с несколькими критериями, необходимыми для их решения, или они могут быть многомерными, требуя диаграмм или таблиц для организации мышления учащихся и записи шаблонов. При использовании шаблонов ученикам важно выяснить, будет ли шаблон предсказуемо сохраняться. Попросите учащихся определить, есть ли причина для продолжения шаблона, и убедитесь, что учащиеся используют логику при поиске шаблонов для решения проблем.
-
Например, если идет дождь в воскресенье, снег в понедельник, дождь во вторник и снег в среду, будет ли дождь в четверг?
-
Другой пример: если Лорен выиграла первую и третью партию в шахматы, а Уолтер выиграл вторую и четвертую партию, кто выиграет пятую партию?
-
Другой пример: если растение выросло на 13 сантиметров за первую неделю и 10 сантиметров за вторую неделю, на сколько сантиметров оно вырастет за третью неделю?
Поскольку это вопросы вероятности или природы, убедитесь, что учащиеся понимают, почему шаблоны нельзя использовать для поиска ответов.
Модели обучения Перспективы обучения студентов в системе высшего образования: состояние дел и движение вперед
Исследования в окончательном наборе можно разделить на две основные категории. Во-первых, были проведены исследования, последовавшие за исследованием моделей обучения, рассмотренным в статье 2004 года, с целью дальнейшего углубления наших знаний о внутренних и внешних взаимосвязях моделей обучения более подробно на новых выборках. Эти исследования можно рассматривать как продолжение исследовательских тем, определенных в обзоре 2004 года.В соответствии с моделью, представленной на рис. 1, здесь будут рассмотрены четыре из этих тем: размерность и внутренние отношения моделей обучения (ядро модели) и отношения моделей обучения с личными, контекстными и конечными переменными. Во-вторых, были исследования в новых направлениях по сравнению с обзором 2004 года. К ним относятся исследования, изучающие модель моделей обучения в новых международных контекстах и группах населения, лонгитюдные исследования развития моделей обучения с течением времени, исследования, посвященные методологическим достижениям в исследовании моделей обучения, и исследования по повышению качества моделей обучения учащихся.Для ясности различные темы исследований отдельно обсуждаются ниже, но во многих исследованиях можно выделить более одной из этих тем исследований.
Новые данные о внутренних и внешних отношениях моделей обучения
Внутренние отношения и размерность моделей обучения
Четыре модели обучения, описанные выше, определяются особыми взаимосвязями между компонентами обучения. Несколько исследований, проведенных за последнее десятилетие, более подробно изучали эти взаимосвязи на новых выборках.В целом, они подтверждают тесную взаимосвязь между стратегиями обучения и регулирования, концепциями обучения и мотивацией обучения, которые составляют основу модели моделей обучения (Edelbring 2012).
Например, в учебной программе, основанной на задачах, Loyens et al. (2008) обнаружили структурные позитивные отношения между конструктивными концепциями обучения голландских студентов, с одной стороны, и их использованием стратегий глубокой обработки и саморегуляции, с другой. Концепции обучения «построение знаний» отрицательно связаны с внешним регулированием и отсутствием регулирования.Наконец, они обнаружили, что студенты, которые сомневались в своих способностях к обучению, как правило, применяли неадекватную стратегию регулирования. Аналогичным образом, Heikkilä et al. (2011) обнаружили значительную взаимосвязь между глубоким подходом финских студентов к обучению и саморегулируемой стратегией обучения, в то время как между саморегуляцией и поверхностным подходом к обучению не было никакой связи. Ричардсон (2010) обнаружил тесную связь между концепциями и подходами студентов в британских дистанционных учебных заведениях.Опять же, глубокий подход к обучению был тесно связан с конструктивной концепцией обучения, а поверхностный подход был тесно связан с концепцией, в которой обучение рассматривалось как получение знаний. Zhu et al. (2008) обнаружили, что поверхностный подход к обучению был связан с концепцией обучения как «запоминания», а глубокий подход к обучению — с концепциями обучения как «понимания» и «личных изменений» среди китайских и фламандских студентов первого курса университетов. . Ричардсон (2007) оценил раздел концепций обучения ILS со студентами из Британского открытого университета.В соответствии с теорией в данных можно выделить пять однородных и теоретически обоснованных шкал концепции обучения. Кластерный анализ выявил четыре подгруппы студентов с точки зрения их образовательных концепций, соответствующих четырем схемам обучения, описанным выше.
В некоторых исследованиях, проведенных в незападных странах, были обнаружены аналогичные взаимосвязи между компонентами модели обучения. Например, в выборке студентов высших учебных заведений из Гонконга Law and Meyer (2011b) обнаружили эмпирическую поддержку теоретической модели моделей обучения, лежащей в основе ILS.Они пришли к выводу, что их результаты особенно подтверждают центральную объясняющую роль стратегий регулирования в учебных паттернах учащихся, как это предполагалось в модели. Gulpinar (2014) сообщил о воспроизведении четырех измерений моделей обучения среди доклинических студентов-медиков в Турции.
Таким образом, в целом эти исследования подтверждают взаимосвязь между стратегиями обработки и регулирования, концепциями обучения и ориентациями обучения, которые были выявлены в обзоре Vermunt и Vermetten (2004) с новыми выборками.Исследование было сосредоточено, в частности, на элементах измерений, ориентированных на смысл, воспроизводство и ненаправленность, и в меньшей степени на элементах измерения, ориентированного на приложения. Вместе эти исследования предоставляют дополнительные доказательства основополагающей размерности моделей обучения, как описано выше.
Связь моделей обучения с личностными факторами
Многие исследования, опубликованные с 2004 года, позволили собрать новые данные о связи между образцами обучения учащихся и множеством личных факторов.Эти личные факторы включали личность, академическую мотивацию, ориентацию на цель, приписывание академической успеваемости, самоэффективность, усилия, эпистемологические и интеллектуальные убеждения, предшествующее образование, возраст и пол.
Среди личностей факторов, связанных с аспектами моделей обучения, включают открытость опыту, сознательность и невротизм. Несколько исследований показали, что открытость опыту положительно связана с использованием студентами саморегулируемых и глубоких стратегий обработки, сознательность положительно связана с использованием стратегии аналитической обработки, а невротизм положительно связан с отсутствием регуляции (Donche et al.2013; Catrysse et al. 2015). Сила этих ассоциаций от слабой до умеренной, что является дополнительным доказательством того, что модели обучения не являются стабильными чертами. Donche et al. (2013) и Catrysse et al. (2015) также включены академической мотивации , концептуализированной в рамках теории самоопределения (Vansteenkiste et al. 2006), в качестве предиктора стратегий обучения учащихся. Они обнаружили, что автономная мотивация положительно влияет на развитие всех стратегий когнитивной обработки и саморегуляции.Контролируемая мотивация была положительно связана с развитием пошаговой обработки и отсутствием регулирования. Оказалось, что амотивация связана с развитием отсутствия регуляции. В продольном исследовании большой выборки японских студентов Фрайер и др. (2016) обнаружили, что саморегулирование и отсутствие контроля учащихся являются важными факторами, определяющими их будущую мотивацию. Например, саморегулирование предсказывало будущую веру в собственные способности, необходимость прилагать усилия и оценку учебных заданий.De Clercq et al. (2013) обнаружили, что овладение учащимися ориентация на цель увеличило их последующее использование саморегулируемых и глубоких стратегий обработки.
Модели обучения студентов оказываются связанными с их атрибутами академической успешности и самоэффективности . Четкая картина взаимоотношений выявлена в исследовании Ferla et al. (2008) среди большой выборки студентов бельгийского университета, где центральная роль принадлежит концепциям обучения студентов.Студенты с конструктивной концепцией обучения больше использовали стратегии саморегуляции и внешнего регулирования, чаще применяли глубокий подход к обучению, чаще приписывали свои академические результаты усилиям и чувствовали себя более эффективными, чем другие студенты. Когда студенты больше соглашались с репродуктивной концепцией обучения, они больше использовали поверхностный подход к обучению, они чаще применяли стратегию внешнего регулирования, они чаще объясняли успехи в учебе неконтролируемыми причинами, такими как уровень сложности экзаменов, и они чувствовали себя менее самодостаточен, чем другие студенты.Аналогичные результаты были получены Heikkilä et al. (2011) в исследовании, посвященном личностно-ориентированному подходу среди студентов финских университетов.
Эпистемологические убеждения — это убеждения и взгляды на природу знания в более общем смысле (Perry 1970; Van Rossum and Hamer 2010). В исследовании, проведенном среди китайских и бельгийских студентов, Zhu et al. (2008) обнаружили, что вера студентов в достоверность знаний была связана с репродуктивной концепцией обучения, которая предсказывала поверхностный подход к обучению.Вера в то, что способность к обучению может быть развита, была связана с конструктивными концепциями обучения, которые предсказывали использование учащимися глубокого подхода к обучению. Dahl et al. (2005) обнаружили аналогичные отношения между эпистемологическими убеждениями студентов и их сообщениями об использовании стратегий обучения на выборке студентов норвежских университетов. Стамп и др. (2014) на выборке студентов инженерных специальностей из США обнаружили, что возрастающие убеждений студентов об интеллекте (вера в то, что интеллект может расти) положительно коррелируют со стратегиями глубокой обработки и стратегиями совместного обучения, тогда как убеждения сущностей (убеждение, что интеллект есть исправлено) об интеллекте отрицательно коррелировали с обеими этими стратегиями обучения.Глубокая обработка и, в меньшей степени, совместное обучение были положительно связаны с самоэффективностью.
Модели обучения учащихся также связаны с их предшествующим образованием , возрастом и полом , но разные модели обучения имеют разное происхождение. В крупномасштабном исследовании, проведенном среди студентов университетов в Нидерландах, Вермунт (2005) обнаружил, что возраст является важным предиктором почти всех аспектов обучения, ориентированного на смысл. Чем старше были ученики, тем больше они усваивали смысловую модель обучения.Что касается пола, основное различие между мужчинами и женщинами проявляется в их оценке совместного обучения: студентки придают большее значение совместному обучению, чем мужчины. Что касается наивысшего уровня предыдущего образования, он обнаружил, что у студентов меньше признаков обучения, ориентированного на воспроизводство, когда их уровень предыдущего образования был выше. Что касается ненаправленного обучения, результаты Vermunt (2005) показали, что учащиеся с более низким уровнем образования демонстрируют больше характеристик отсутствия регулирования, чем учащиеся с более высоким образованием.В крупномасштабном исследовании, проведенном среди студентов университетских колледжей в Бельгии, Donche et al. (2014) обнаружили, что учащиеся, которые были подготовлены к академическим направлениям в среднем образовании, демонстрировали меньше признаков обучения, ориентированного на воспроизводство, чем учащиеся, подготовленные к курсам профессионального или технического образования. В некоторой степени эти отношения могут быть культурно зависимыми. Например, Ло и Мейер (2011a) обнаружили больше гендерных различий в большой выборке гонконгских студентов. Учащиеся мужского пола набрали более высокие баллы по четырем из пяти шкал стратегии обработки (кроме запоминания) и по обеим шкалам саморегуляции.Студентки набрали более высокие баллы по четырем из пяти шкал концепции обучения (за исключением совместного обучения) и четырем из пяти шкал учебной мотивации (за исключением амбивалентности). Авторы предположили, что гонконгские студенты мужского пола, как правило, более активно учатся, а гонконгские студентки более пассивны.
Таким образом, как предсказывает модель на рис. 1, эмпирические исследования, обсужденные выше, показали, что модели обучения, которые принимают учащиеся, встроены в ряд личных факторов, таких как личность, академическая мотивация, ориентация на цель, атрибуция академической успешности. , самоэффективность, усилия, эпистемологические и интеллектуальные убеждения, предыдущее образование, возраст и пол.Это не означает, что модели обучения трудно изменить. Это, вероятно, означает, что они не меняются изо дня в день и что с ними связана некоторая стабильность. С другой стороны, могут развиваться многие из этих личных факторов. Мотивации, ориентации, убеждения и приписывания — это явления, которые со временем поддаются изменению. Даже современные представления о личности предполагают возможность роста и развития. Имеющиеся данные указывают на модели обучения как на явление, обладающее некоторой стабильностью, но также имеющее потенциал для изменений, роста и развития.Дальнейшие доказательства этого вывода будут рассмотрены в следующих разделах, посвященных влиянию контекста и развитию.
Взаимосвязь моделей обучения с контекстными факторами
В соответствии с моделью, показанной на рис. 1, исследования, проводимые с 2004 года, также позволили получить новые доказательства взаимосвязи между образцами обучения, которые принимают учащиеся, и контекстными особенностями. Среди контекстуальных факторов, включенных в это исследование, были стратегии обучения, восприятие учебной среды и дисциплинарные различия.
Учителя стратегии обучения влияют на стратегии обучения, которые принимают учащиеся. В крупномасштабном исследовании Donche et al. (2013) опросили 90 преподавателей университетского колледжа об использовании ими стратегий обучения и 1126 студентов бакалавриата в том же колледже об их использовании стратегий обучения. Они использовали две шкалы стратегий обучения: прямое обучение (высокий контроль учителя над обучением студентов, высоко ориентированный на передачу, контент-ориентированный подход к обучению) и ориентированный на обучение (позволяющий учащимся лучше контролировать свое обучение, ориентированный на обучение, учащийся). -фокусированный подход к обучению).После проверки личностных качеств и академической мотивации в учебных дисциплинах, где преподаватели применяли более прямое обучение, студенты получили более низкие баллы по использованию внешнего регулирования. Учащиеся дисциплин, в которых учителя были более сосредоточены на обучении, получили более высокие баллы по всем стратегиям обработки и были более регулируемыми (собственными или внешними) в своем обучении. Первый упомянутый результат поначалу кажется загадочным, но его можно объяснить сильным присутствием внешнего контроля в учебной среде в первые годы обучения в высшем учебном заведении, не оставляя студентам стратегического выбора для более или менее использования этого контроля.Второй вывод более очевиден и может указывать на активирующий эффект предоставления студентам контроля над своими собственными решениями по обучению.
Восприятие учащимися среды обучения связано с применяемыми ими моделями обучения. Ло и Мейер (2011a) исследовали эти отношения на большой группе гонконгских студентов. «Хорошее преподавание» показало положительную корреляцию с 18 шкалами из 20 ILS (за исключением амбивалентной ориентации на обучение и отсутствия регулирования, двух элементов модели ненаправленного обучения).Чем выше (и более неприемлемо) студенты воспринимали свою рабочую нагрузку, тем более ненаправленное обучение они сообщали. Подобные отношения обнаружились для «соответствующей оценки». Более того, чем больше учеников считали оценивание неуместным, тем в большей степени их учебный образец носил репродуктивный характер. «Акцент на независимости» показал сильнейшую и позитивную связь со всеми аспектами модели обучения, ориентированного на смысл. Наконец, «общие навыки» продемонстрировали наиболее тесную связь не только со всеми элементами модели обучения, ориентированного на приложения, но также и с обучением, ориентированным на смысл и воспроизводство.Konings et al. (2011) изучали взаимосвязь между предпочтениями и восприятием преподавания и аспектами моделей обучения на большой выборке старшеклассников (средний возраст 16 лет) в Нидерландах. Они нашли много таких отношений. Среди них следует отметить положительную связь между глубокой обработкой и предпочтением интеграции, отрицательную связь между пошаговой обработкой и предпочтением продуктивного обучения, а также положительную связь между ориентацией на обучение, ориентированное на сертификаты, и предпочтением четких целей.В последующем лонгитюдном исследовании можно было наблюдать заметное снижение предпочтения студентов автономии студентов, что, возможно, могло быть объяснено неудачей образовательной инновации в этой стране в течение многих лет исследования, направленного на стимулирование активности студентов и их самостоятельность. регулируемое обучение. Падение было больше для студентов с мотивацией, ориентированной на получение сертификатов, и меньше для студентов с высоким уровнем саморегуляции (Konings et al. 2012).
Восприятие учащимися и оценка учебной среды может зависеть от их текущей модели обучения.Исследование Edelbring и Wahlström (2016) показало, что студенты, обладающие высоким уровнем саморегулирования, в целом осознавали преимущества веб-системы виртуального медицинского образования пациентов в Швеции, особенно в условиях общей системы регулирования преподавателей. С другой стороны, учащиеся, увлеченные внешним регулированием, увидели большую часть преимуществ деятельности виртуального пациента в обстановке, строго регулируемой учителем. Авторы пришли к выводу, что внешний учитель и регулирование со стороны сверстников могут быть полезны для увеличения воспринимаемой пользы учащимися и что гибкий автономный характер педагогики виртуальных пациентов не должен вести к отказу от руководства и связанных с ним курсовых мероприятий.
Дисциплинарные различия связаны с моделями обучения, принятыми учащимися. В крупномасштабном исследовании Vermunt (2005) сравнил модели обучения студентов семи различных дисциплин в голландском университете, специализирующемся на социальных науках. Студенты факультетов гуманитарных наук и психологии продемонстрировали наибольшие характеристики обучения, ориентированного на смысл, студенты факультетов экономики и эконометрии — наименее. Обучение, ориентированное на воспроизведение, было обнаружено больше всего среди студентов, изучающих право и эконометрию, и меньше всего среди студентов, изучающих гуманитарные науки и психологию.Студенты-юристы продемонстрировали большинство характеристик прикладного обучения, студенты гуманитарных специальностей — меньше всего. Наконец, ненаправленное обучение чаще всего было среди студентов факультетов экономики и эконометрии и меньше всего среди студентов-юристов. Vermunt (2005) объяснил эти дисциплинарные различия в моделях обучения, которые принимают учащиеся, комбинацией различий в характере дисциплины, различий в доминирующих педагогических практиках в разных дисциплинах и различий между студентами, которые предпочитают изучать определенные дисциплины.Smith et al. (2007) обнаружили сильное преобладание ориентированного на приложения обучения среди студентов фармацевтических факультетов в Австралии для всех летних групп, причем это преобладание оставалось стабильным на протяжении всего исследования. Этот результат показывает сходство с результатами Линдблом-Юленне и Лонка (2000), которые обнаружили четкий и отдельный фактор обучения, ориентированного на приложения, среди продвинутых и взрослых студентов-медиков. Тимарова и Салаетс (2011) обнаружили, что студенты, изучающие прикладной язык в Бельгии, в большей степени учились по шаблону, ориентированному на воспроизведение, а не по шаблону, ориентированному на значение, и Vilppu et al.(2013) обнаружили, что финские студенты-учителя при изучении учебников сообщали о более глубокой обработке, чем о поэтапной.
Таким образом, эти исследования предоставляют дополнительные доказательства того, что модели обучения учащихся связаны с факторами окружающей среды. Многие из этих исследований носили корреляционный характер, поэтому влияние может быть различным. Может случиться так, что среда влияет на модели обучения, которые принимают учащиеся, может быть, что учащиеся с определенными моделями обучения склонны выбирать конкретную среду или дисциплины, и может даже случиться так, что учителя адаптируют свое обучение, чтобы приспособить доминирующие модели обучения и предпочтения учащихся.Наверное, отношения взаимные. Некоторые из обнаруженных взаимосвязей были более или менее логичными, другие — неожиданными, удивительными и загадочными. Последние два упомянутых выше примера показывают, что эти воздействия окружающей среды могут действовать на вполне определенном уровне посредством определенных педагогических мероприятий. Контекстуальная включенность моделей обучения студентов может указывать на попытки повысить качество обучения студентов. Мы вернемся к этой возможности в абзаце с аналогичным заголовком.
Связь моделей обучения с результатами обучения
Модели обучения оказываются важным предиктором отклонений в результатах обучения. Различные исследования показывают четкую структуру отношений, которые в целом указывают в одном направлении. Обучение, ориентированное на смысл, как правило, положительно связано с различными показателями успеваемости по разным учебным дисциплинам. Обучение, ориентированное на воспроизводство, в основном демонстрирует отрицательную связь с успеваемостью на экзаменах. Обучение, ориентированное на приложения, в целом довольно нейтрально с точки зрения академических успехов в обычном университетском образовании.Ненаправленное обучение постоянно и отрицательно связано с успеваемостью по всем дисциплинам (например, Vermunt 2005). Однако некоторые отношения могут быть скорее дисциплинарными. Например, в своем исследовании среди студентов-фармацевтов в Австралии Smith et al. (2007) обнаружили, что обучение, ориентированное на приложения, имеет значительную и положительную связь с академической успеваемостью. В их исследовании как обучение, ориентированное на смысл, так и обучение, ориентированное на воспроизводство, показали отрицательную связь с академической успеваемостью.
Мартинес-Фернандес и Вермунт (2015) обнаружили в крупномасштабном исследовании среди студентов-преподавателей в Латинской Америке и Испании, что использование студентами стратегий глубокой обработки и их усилий положительно и существенно связаны с успеваемостью, в то время как стратегии саморегулирования оказался лучшим предсказателем глубокой обработки. Другой аспект модели обучения, ориентированного на смысл, — конструирование знаний в рамках концепции обучения, — также оказал прямое влияние на академическую успеваемость в рамках их Модели структурных уравнений.Рассмотрение обучения как получения знаний имело прямое негативное влияние на успеваемость. Donche et al. (2014) подтвердили ожидаемую положительную взаимосвязь между глубокой обработкой и академическим успехом в восьми различных программах профессионального бакалавриата, в то время как отсутствие регулирования отрицательно предсказывало академический успех. Vanthournout et al. (2012) обнаружили, что как стратегия соотнесения и структурирования обучения, так и стратегия внешнего регулирования положительно предсказывают академический успех на первом году профессиональной программы бакалавриата в Бельгии, а отсутствие регулирования отрицательно сказывается на академической успеваемости.
De Clercq et al. (2013) в исследовании, проведенном среди студентов инженерных специальностей, обнаружили, что саморегулирование особенно важно для объяснения успеха в учебе в начале обучения в университете. На более продвинутой выборке студентов-инженеров на третьем году обучения они обнаружили, что результаты прошлых экзаменов были лучшим предиктором текущих результатов экзаменов, и этот вывод хорошо задокументирован в исследовательской литературе. Кано и Гарсиа Бербен (2014) выдвинули понятие диссонанса в объяснении успеха в учебе или, на самом деле, неудачи в учебе.В контексте моделей обучения диссонанс означает, что для некоторых групп студентов их мотивы, концепции и стратегии не совпадают (Vermunt and Vermetten 2004). Например, некоторые студенты могут сочетать конструктивную концепцию обучения с поверхностным подходом к обучению или личную мотивацию с отсутствием регулирования. Предыдущее исследование (например, Lindblom-Ylänne and Lonka 2000; Meyer 2000; Vermunt and Minnaert 2003) показало, что эти студенты подвергаются риску с точки зрения успеваемости на экзаменах, по крайней мере, в пределах западных культур.
Отношения между (аспектами) моделей обучения и академической успеваемостью могут быть совершенно разными в разных культурных контекстах. Например, в лонгитюдном исследовании студентов первого курса японского университета саморегулирование не предсказывало средний балл (Fryer et al., 2016). Однако существует положительная связь между отсутствием регулирования, измеренным через 3 месяца, и средним баллом успеваемости на конец года, и отрицательная связь между отсутствием регулирования, измеренным через 9 месяцев, и средним баллом успеваемости на конец года. Внешнее регулирование, измеренное через 9 месяцев, положительно предсказало средний балл успеваемости на конец года.В исследовании, проведенном среди гонконгских студентов высших учебных заведений, Ло и Мейер (2011a), как и ожидалось, обнаружили, что большинство аспектов модели ненаправленного обучения в значительной степени и отрицательно связаны с ожидаемыми успехами в учебе. Однако два аспекта модели, направленной на воспроизводство, были положительно связаны с этой переменной успеха: внешняя регуляция процессов обучения и ориентация на обучение, ориентированная на самопроверку.
В целом эти исследования показывают, что обучение, ориентированное на смысл, положительно связано с успеваемостью, а неориентированное обучение отрицательно сказывается на успеваемости.Отношения между академической успеваемостью и элементами обучения, ориентированного на воспроизведение и обучение, менее согласованы и варьируются, среди прочего, в зависимости от академической дисциплины, культурного контекста и метода оценки.
Новые направления в исследованиях моделей обучения
Исследования внутренних и внешних связей моделей обучения в базисный период, как обсуждалось выше, можно рассматривать как продолжение исследований моделей обучения, начатых ранее. Это исследование частично подтвердило ранее сделанные выводы в новых контекстах и частично привело к появлению новых доказательств на более конкретном уровне.Однако исследования моделей обучения также перешли в новые направления, которые будут обсуждаться в следующем разделе. Это относится к изучению моделей обучения в новых международных контекстах и группах населения, исследованиям лонгитюдного развития моделей обучения с течением времени, исследованиям, посвященным методологическим достижениям в исследовании моделей обучения, и исследованиям по повышению качества моделей обучения учащихся.
Модели обучения в новых международных контекстах и группах населения
С момента своего создания ILS была переведена на множество языков и использована исследователями в разных странах для изучения различных аспектов моделей обучения (например,грамм. Аль-Кадри 2008). Многие исследования в этом обзоре проводились в других культурных контекстах, помимо западного высшего образования. В обзор вошли образцы студентов из Австралии, Бельгии, Китая, Колумбии, Финляндии, Гонконга, Индонезии, Японии, Мексики, Нидерландов, Норвегии, Саудовской Аравии, Испании, Шри-Ланки, Швеции, Великобритании, США и Венесуэлы. Часто исследователи использовали похожие методы анализа данных, чтобы можно было сравнить результаты различных исследований. В основном для такого сравнения были приняты два подхода.Один из них — сравнить средние значения по шкалам ILS среди разных популяций, например имеет ли один образец более высокий или низкий балл при глубокой обработке, чем другой образец. Другой подход — сравнить взаимосвязь шкал ILS между выборками. В этом случае интересуется, различаются ли отношения между различными элементами моделей обучения в разных популяциях, то есть являются ли отношения между мотивами обучения и стратегиями обработки одинаковыми или разными в двух популяциях.
Используя первый подход, Биманс и Ван Мил (2008) сравнили оценки китайских и голландских студентов в голландском университете по шкале ILS. Они обнаружили, что китайские студенты набрали более высокие баллы, чем голландские, по нескольким шкалам, характерным для репродуктивного и ненаправленного обучения, в то время как голландские студенты как группа не демонстрировали доминирующую модель обучения. Zhu et al. (2008) сравнили китайских студентов в китайском университете с фламандскими студентами в университете Фландрии.Они обнаружили, что китайские студенты имели более высокие средства по шкалам, измеряющим учебные концепции, принадлежащие к модели обучения, ориентированной на значение (понимание, личные изменения), чем фламандские студенты. Фламандские студенты получили более высокие баллы по поверхностному подходу, и не было различий в глубоком подходе к обучению. Marambe et al. (2012) сравнили три выборки студентов университетов по их среднему баллу ILS, две выборки из Азии (Шри-Ланка и Индонезия) и одну выборку из Европы (Нидерланды). Результаты показали наибольшие различия между азиатскими и европейскими студентами.Однако между индонезийскими и шри-ланкийскими студентами также обнаружилось много различий. Они не нашли поддержки стереотипу «азиатский ученик». Поскольку студенты из Шри-Ланки, как оказалось, меньше всего использовали стратегии запоминания всех групп, их результаты не подтверждали иногда встречающуюся в литературе идею о том, что азиатские студенты будут иметь склонность к механическому обучению.
Применяя второй подход, Vermunt et al. (2014) провели метаанализ исследований со студентами из Гонконга (Law and Meyer, 2010), Индонезии (Ajisuksmo, Vermunt, 1999), Шри-Ланки (Marambe et al.2012), Испании, Венесуэлы, Колумбии и Мексики (Мартинес-Фернандес и Вермунт, 2015) и Нидерландов (Вермунт, 1998). Вместе эти исследования представляли восемь образцов из восьми разных стран на трех континентах (Европе, Азии и Америке). Чтобы ответить на вопрос, являются ли модели обучения универсальными для разных контекстов и групп населения или разные модели обучения возникают в разных контекстах и популяциях, Vermunt et al. (2014) сравнили результаты факторного анализа оценок учащихся по программе ILS во всех этих исследованиях.В большинстве исследований были выявлены паттерны, ориентированные на смысл, воспроизводства и ненаправленные, хотя в разных странах они выглядели несколько по-разному. Этот вывод, по-видимому, подтверждает предыдущее наблюдение Ричардсона (1994) о том, что смысловая и воспроизводственная ориентация в обучении универсальны во всех системах высшего образования, но получают особую интерпретацию в каждой системе.
Помимо сходства между контекстами и группами населения, сравнение также показало различия между учащимися из разных стран.В то время как модели обучения, ориентированные на смысл, воспроизводство и ненаправленные, казались универсальными во всем мире; наблюдались три других паттерна, которые казались более специфичными для определенных контекстов или групп населения. Одним из них был уже упомянутый шаблон обучения, ориентированного на приложения, который был обнаружен в основном среди взрослых студентов в голландской выборке. Однако Смит и др. Также сообщили о четких аспектах обучения, ориентированного на приложения. (2007) среди студентов-фармацевтов в австралийском университете и Линдблом-Юленне и Лонка (2000) среди студентов-медиков в Финляндии.Другой паттерн, который проявился во многих, но не во всех выборках, — это комбинация всех концепций обучения, почти без нагрузок из других шкал. Это было интерпретировано как пассивно-идеалистический образец обучения, поскольку он содержал только идеи об обучении и никакой учебной деятельности. Наконец, в некоторых выборках многие или все учебные ориентации сгруппированы по одному фактору с небольшими нагрузками по другим шкалам или без них. Это явление показало сходство с кластеризацией многих или всех шкал концепции обучения в предыдущем измерении, и, следовательно, это измерение было интерпретировано как пассивно-мотивационный паттерн.
Одно из разительных различий между выборками заключалось в том, что в некоторых странах шкалы концепции обучения и ориентации обучения не включали те же факторы, что и шкалы стратегии обучения, в то время как в других странах факторы определялись нагрузками шкал, исходящих от всех четыре компонента обучения: два поведенческих компонента (шкалы обработки и регулирования), концептуальные или метакогнитивные компоненты (шкалы концепций) и мотивационные компоненты (шкалы ориентации).Казалось, что в некоторых странах того, как учатся студентов, тесно связано с тем, что они думают, , об обучении и , почему они учатся, в то время как в других странах то, что студенты делают, чтобы учиться, в гораздо меньшей степени связано с тем, что они думают о своем обучении и хотят чего-то достичь. Это может быть связано, например, с различиями между странами в свободе выбора учащимися предметной области, что в некоторых культурах является скорее семейным решением, чем индивидуальным.
Еще одним заметным различием между группами студентов из разных стран была степень дифференциации в рамках различных компонентов обучения. Например, в некоторых странах взгляды студентов на обучение явно зависели от различных факторов, что указывало на дифференцированный набор концепций обучения. В других странах все концепции обучения сгруппированы по одному фактору, что указывает на то, что их взгляды на обучение сильно взаимосвязаны. Например, исследования китайских студентов показали, что для них запоминание и понимание не были противоположными полюсами.Напротив, для этих студентов существенная разница заключалась в гораздо большей степени между механическим запоминанием и запоминанием, способствующим развитию смысла (Marton et al. 2005).
Различия в основных параметрах между группами студентов из стран одного континента часто были больше, чем различия между студентами с разных континентов. Опять же, типичного «азиатского», «европейского» или «латиноамериканского» студента, похоже, не существует. Эти результаты согласуются с результатами Marambe et al.(2012) с меньшей выборкой студентов только из трех стран. Вместе они указывают на сильное влияние контекста на формирование моделей обучения студентов.
Хотя многие исследования моделей обучения были сосредоточены на обучении студентов в первые годы высшего образования, за последнее десятилетие это исследование распространилось и на другие области. Konings et al. (2012) и Könings et al. (2014), например, изучали модели обучения десятиклассников средних школ в зависимости от их предпочтений в обучении, в то время как Helle et al.(2013) сосредоточены на развитии личных интересов и саморегуляции у старшеклассников. Endedijk et al. (2014b) сосредоточились на моделях обучения студентов педагогического образования, которые участвовали в программе дуального образования, сочетающей учебу в университете с стажировкой (практикой преподавания) в школе. Совсем недавно Vrikki et al. (2017) изучали модели обучения опытных учителей, которые участвовали в программе повышения квалификации Lesson Study, чтобы внедрять инновации в свое математическое образование.Часто в этих исследованиях ILS не использовалась в качестве инструмента измерения, поскольку контекст обучения слишком сильно отличался от контекста высшего образования, для которого был разработан ILS. Поэтому многие из этих исследований не включены в этот обзор (но см., Например, Vermunt and Endedijk (2011) для обзора моделей обучения в профессиональном обучении и развитии учителей).
Лонгитюдное развитие моделей обучения с течением времени
Еще десять лет назад лонгитюдные исследования развития моделей обучения студентов были редкостью.Часто проводившиеся лонгитюдные исследования имели временной интервал не более пары месяцев и не более двух точек измерения (например, Vermunt 1998). Аналогичная тенденция наблюдалась и в лонгитюдных исследованиях, изучающих подходы студентов к обучению (см. Asikainen and Gijbels, 2017). Однако за последние 10 лет лонгитюдные исследования значительно продвинулись в обоих этих аспектах. Временные интервалы увеличились до 3 лет, а количество точек измерения увеличилось до пяти, что позволило изучать другие типы разработок, кроме линейных.
Планы поперечных сечений могут демонстрировать различия и сходства между разными когортами студентов, но они не могут продемонстрировать развитие внутри групп студентов. Smith et al. (2007) изучали модели обучения студентов-фармацевтов в австралийском университете в поперечном разрезе. Они проводили ILS для студентов 1, 2, 3 и 4 классов обучения. Результаты показали существенные различия между годичными группами для обучения, ориентированного на смысл и воспроизведение, но не для обучения, ориентированного на приложения и ненаправленного обучения.Смысл-ориентированные баллы были ниже в группах 2 и 3 года по сравнению с годами 1, но баллы группы 4 года для этой модели обучения были выше, чем у групп других лет. Для обучения, направленного на воспроизводство, баллы группы 1-го года были значительно выше по сравнению с баллами других групп года, но баллы групп 2, 3 и 4 года для этой модели обучения были похожи друг на друга. Авторы приходят к выводу, что было мало свидетельств созревания моделей обучения этих студентов по мере их продвижения по учебной программе.
В продольном дизайне Донче и Ван Петегем (2009) дважды проводили ILS для студентов-преподавателей: один раз в начале первого года обучения и еще раз в конце третьего года обучения. Результаты показали, что аспекты обучения, ориентированного на смысл (глубокая обработка, саморегуляция, построение знаний), со временем увеличивались. Кроме того, конкретная обработка, один из аспектов модели обучения, ориентированного на приложения, значительно увеличилась с 1 по 3 год. Степень, в которой учащиеся рассматривали обучение как получение знаний, со временем снизилась, равно как и отсутствие у них регулирования.Остальные аспекты обучения, направленного на воспроизводство, оставались довольно стабильными в течение всего периода исследования.
Развитие учебных моделей учащихся не всегда идет линейным путем. За большой выборкой студентов восьми программ бакалавриата в одном университетском колледже Бельгии последовали Donche et al. (2010) на 3 года. Они заметили развитие многих аспектов моделей обучения, но большинство изменений произошло между 2 и 3 годами и меньше между 1 и 2 годами. регулирование, построение знаний), обучение, направленное на воспроизводство, последовательно снижалось в течение всех 3 лет (получение знаний, внешнее регулирование, запоминание), конкретная обработка увеличивалась со 2-го года до 3-го года, а отсутствие регулирования постоянно уменьшалось в течение 3 лет.Использование аналитической стратегии оставалось неизменным. Эти тенденции в развитии, казалось, варьировались в зависимости от первоначальной модели обучения учащихся. Казалось, что студенты меньше меняются в обучении, ориентированном на смысл, чем в обучении, ориентированном на воспроизводство. Именно студенты, изначально получившие высокие баллы по репродуктивному и ненаправленному обучению, изменили свои модели обучения в сторону обучения, ориентированного на смысл и приложения. Студенты, которые вначале уже высоко ценили ориентированное на смысл и прикладное обучение, с годами изменились гораздо меньше.
Похоже, что модели обучения больше всего меняются, когда больше всего меняется среда обучения. Когда окружающая среда остается довольно постоянной, модели обучения менее склонны к развитию. Например, в продольном исследовании Catrysse et al. (2015) изучали развитие стратегий обучения студентов при переходе от среднего образования к высшему. Результаты показали рост не только у студентов глубокой обработки, анализа и саморегуляции, но также и у всей группы студентов, испытывающей недостаток регуляции.Именно эти изменения произошли сразу после перехода от среднего образования к высшему. До и после перехода использование этих стратегий обучения было довольно стабильным. Студенты, которые изначально набрали более высокие баллы по стратегии обучения, показали меньший рост в течение этих лет, чем студенты, которые изначально набрали более низкие баллы по стратегии. Использование стратегии запоминания оставалось довольно постоянным на протяжении всего периода исследования, что может указывать на стратегию выживания для обучения, когда учащиеся переходят от среднего образования к высшему.
Исследования, обсуждаемые в этом разделе, показывают, что учащиеся могут со временем развивать свои модели обучения. Эти разработки не всегда идут по линейному пути, и развитие тем больше, чем больше меняется среда обучения. Стабильность учебных моделей учащихся вполне может быть следствием стабильной, неизменной учебной среды.
Методологические достижения в исследовании моделей обучения
В этом обзоре основное внимание уделяется использованию ILS в целом или по частям (например, краткой версии ILS; Donche and Van Petegem 2008) для измерения (аспектов) моделей обучения.Сходными инструментами являются MSLQ (Pintrich 2004), SPQ (Biggs et al. 2001), RASI (Entwistle and McCune 2004) и Inventory Learning to Teach Process (ILTP; Endedijk et al. 2014a). MSLQ и ILS представляют собой широкие инструменты для измерения когнитивных, мотивационных и метакогнитивных аспектов обучения студентов в системе высшего образования. ILTP также является широким инструментом, но ориентирован на обучение студентов и учителей. (R) SPQ ориентирован только на когнитивные стратегии и мотивацию (для сравнения см. Entwistle and McCune 2004; Vanthournout et al.2009 г.). Общим для всех этих инструментов является то, что они представляют собой инструменты самоотчета, где студентов просят указать по шкале Лайкерта, в какой степени деятельность, точка зрения, «— или мотив, описанные в утверждении, соответствуют их собственному образу жизни. обучение, взгляды или мотивы. Аналогичным образом, анкеты использовались для изучения восприятия учащимися своей учебной среды, например, опросник по опыту обучения (CEQ; Ramsden 1991; Law and Meyer 2011a) и расширенный перечень воспринимаемых образовательных сред (IPSEE; Konings et al.2012).
Недавно исследователи ввели другие типы измерений для изучения моделей обучения студентов. Например, Endedijk et al. (2016) разработали и использовали структурированный цифровой журнал для измерения учебной деятельности нескольких студентов-преподавателей в различных условиях обучения. Их инструмент является примером многократного измерения регуляции обучения студентов, и их исследование демонстрирует добавленную стоимость объединения различных типов инструментов в исследованиях обучения студентов.Совсем недавно Catrysse et al. (2016) исследовали использование комбинации слежения за глазами и запоминания по сигналу в качестве более прямых и онлайн-методов наблюдения для изучения глубокой и поверхностной обработки учащихся на уровне конкретной задачи. Основываясь на своих выводах, они предлагают объединить отслеживание взгляда и запоминание в качестве дополнительных методологий исследования стратегий обучения студентов.
В течение последнего десятилетия исследователи моделей обучения студентов значительно усовершенствовали свои статистические методы для работы с более сложными данными.Эти разработки соответствуют достижениям в области анализа данных в других областях. Например, Ferla et al. (2008) использовали анализ пути для изучения взаимосвязи между познаниями учащихся и их влияния на стратегии обучения. Многие исследования, рассмотренные в этой статье, использовали моделирование структурных уравнений (SEM) как элегантный способ одновременно работать с большим количеством переменных (например, De Clercq et al. 2013; Loyens et al. 2008; Martínez-Fernández and Vermunt 2015; Чжу и др. 2008). Фрайер и др. (2016) использовали продольный вариант SEM для анализа переменных из двух волн сбора данных от одних и тех же студентов.В своем крупномасштабном исследовании среди студентов и их учителей Donche et al. (2013) использовали многовариантный многоуровневый анализ, чтобы учесть разные уровни представленных данных (студент, программа) при изучении взаимосвязи между стратегиями обучения и стратегиями обучения.
С продольной точки зрения Coertjens et al. (2013b) сравнили три статистических метода для анализа изменений в стратегиях обучения с течением времени: ANOVA, многоуровневый анализ и многоиндикаторный латентный рост (MILG).Они пришли к выводу, что три метода дают аналогичные результаты в отношении средних тенденций, но есть различия в наблюдаемой силе роста с течением времени в соответствии с различными методами анализа. Более того, MILG казался более подходящим методом для обнаружения дифференциального изменения с течением времени. Поэтому в своем собственном исследовании лонгитюдных изменений в использовании студентами стратегий обучения они решили использовать этот многоиндикаторный анализ скрытого роста (Coertjens et al. 2013a).
Некоторые исследователи использовали личностно-ориентированный подход к анализу данных.Вместо того, чтобы отходить от ориентированной на переменную точки зрения, эти исследователи пытаются выделить значимые подгруппы студентов с одинаковыми оценками по переменным модели обучения. С этой точки зрения для определения групп студентов часто используются различные варианты кластерного анализа. Например, Heikkilä et al. (2011) использовали латентный анализ класса для разделения студентов на однородные группы, в то время как Vanthournout et al. (2013) для той же цели использовали иерархический кластерный анализ.
Повышение качества моделей обучения студентов
Цели высшего образования универсальны во всем мире и подчеркивают важность глубокого обучения, критического мышления, независимости, саморегулирования и использования знаний на благо общества, всех элементов о том, что здесь имеется в виду под обучением и мышлением, ориентированным на смысл и на приложения.Таким образом, можно утверждать, что обучение, ориентированное на смысл и приложение, представляет собой более качественное обучение в высшем образовании, чем обучение, ориентированное на воспроизводство и ненаправленное. Следовательно, обучение в высших учебных заведениях должно быть направлено на содействие этому высококачественному обучению студентов. Первый, маломасштабный подход к улучшению моделей обучения студентов с этой точки зрения — это обратная связь, обучение или поддержка определенных групп студентов. Например, Donche et al. (2012) обнаружили, что некоторые студенты предпочитают внешние источники информации обратной связи, такие как доверие к наставникам, в то время как другие студенты предпочитают более внутренние источники и самосовершенствование.Авторы приходят к выводу, что универсальный подход к изучению обратной связи с паттернами не является хорошим вариантом и может привести к деструктивным трениям для некоторых групп учащихся. Это исследование показало, что особенно для учащихся из группы риска предпочтительны внешние, а не внутренние источники обратной связи по модели обучения. Vermunt et al. (2014) выступили за меры по поддержке иностранных студентов в их адаптации к зарубежной учебной среде. Студентам, которые разработали свою модель обучения в своей стране, часто необходимо адаптировать свой способ обучения и свои взгляды на обучение, чтобы добиться успеха в различных образовательных культурах с различными требованиями за рубежом.По их мнению, лучшее понимание того, как иностранные студенты учатся, думают и мотивированы, может помочь в развитии лучшей поддержки для этих студентов в адаптации к новой учебной среде.
Одно из следствий различий между учащимися в их моделях обучения состоит в том, что для улучшения моделей обучения учеников также может потребоваться дифференцированный подход. Универсальный подход к поддержке учащихся в развитии их учебной модели вполне может представлять собой противоречие в терминах.Endedijk et al. (2014a) представили аргументы в пользу различных подходов к поддержке обучения студентов и предоставили нам множество примеров того, как этого можно достичь. Vanthournout et al. (2009) предположили, что для разработки более благоприятных моделей обучения необходимы адаптивные методы обучения и корректирующие траектории. Они выступали за большую дифференциацию методов обучения, чтобы учесть различные потребности в развитии учащихся с разными моделями обучения.
Второй, более масштабный подход к повышению качества моделей обучения студентов заключается в использовании инновационных методов преподавания и обучения для всех студентов.Многие современные образовательные инновации нацелены на стимулирование обучения студентов, ориентированного на смысл и приложения, и противодействие ориентированным на воспроизводство и ненаправленным моделям обучения студентов. Инновационные педагогические методы в высшем образовании, такие как не только проблемное обучение и интегрированное контекстное обучение, но и педагогические методы, такие как обучение на основе проектов, обучение на основе конкретных случаев и обучение на основе компетенций, нацелены на повышение качества обучения студентов в рамках обычных дисциплин. обучение, и не столько через внеклассное обучение навыкам, поддержку или обратную связь (Bronkhorst et al.2011; Ten Cate et al. 2004; Vermunt 2007). Недавние исследования действительно показали доказательства, подтверждающие это утверждение. Например, Lycke et al. (2006) сравнили студентов-медиков в программе проблемно-ориентированного обучения (PBL) и в традиционной программе по использованию ими стратегий обучения, концепций обучения и академических результатов в норвежской медицинской школе. Результаты показали, что студенты PBL больше использовали саморегулируемые стратегии обучения и имели более конструктивные концепции обучения, чем студенты, обучающиеся по традиционной медицинской программе.Ван дер Векен и др. (2008) сравнили оценки студентов-медиков третьего курса по традиционной, интегрированной контекстной и проблемной учебной программе в Бельгии и Нидерландах по шкале ILS. Учащиеся по проблемно-ориентированной учебной программе продемонстрировали меньшее количество запоминаний и репетиций и более разнообразное использование источников знаний, чем учащиеся по обычной учебной программе. Учащиеся интегрированной контекстной учебной программы продемонстрировали более структурирование предмета за счет интеграции различных аспектов в единое целое.Что касается стратегий регулирования, учащиеся проблемной учебной программы продемонстрировали не только значительно большую саморегуляцию в выборе содержания обучения, чем учащиеся двух других учебных программ, но и большее отсутствие регулирования, чем учащиеся интегрированной контекстной учебной программы. Что касается учебной ориентации, студенты проблемной учебной программы были наименее амбивалентны по сравнению с двумя другими учебными программами, а учащиеся двух инновационных (PBL и интегрированной) учебной программы были наиболее ориентированы на профессиональную мотивацию в своей учебной мотивации.Последующее лонгитюдное исследование той же исследовательской группы (Van der Veken et al. 2009) показало, что интегрированная учебная программа привела к меньшему отсутствию регулирования, когда учащиеся прогрессировали в учебе.
В крупномасштабном исследовании инноваций в Бельгии Baeten et al. (2014) показали, что, когда студенты постепенно подвергались обучению на основе конкретных случаев после того, как они привыкли к формату преподавания на основе лекций, их ориентированное на воспроизведение обучение снижалось, а их автономная мотивация и оценки повышались.Этих эффектов не было, когда инновации, основанные на конкретных случаях, вводились внезапно, а не постепенно. Полученные данные подтверждают важность процессно-ориентированного подхода к разработке модели обучения, при котором происходит постепенная передача контроля над обучением учащихся из образовательной среды учащимся. Внезапное внедрение обучения на основе конкретных случаев имело неблагоприятный эффект, аналогичный тому, что ранее в литературе описывалось как «разрушительное трение» (Vermunt and Verloop 1999).
Исследования, обсуждаемые в этом разделе, указывают на положительный эффект определенных педагогических методов в высшем образовании с точки зрения повышения качества обучения студентов. Представленные здесь данные свидетельствуют о том, что педагогические методы высшего образования, такие как проблемное обучение, обучение на основе конкретных случаев и интегрированное контекстное обучение, могут способствовать обучению, ориентированному на смысл и приложение, и препятствовать обучению, ориентированному на воспроизводство и неориентированному.
Создание математики: Справочник учителя математических исследований
Математические исследования включают поиск закономерностей и структуры.В начале исследования мы можем собрать соответствующие примеры функций, числа, формы или другие математические объекты. По мере роста наших примеров мы пытаемся объединить эти отдельные фрагменты информации в более крупный, согласованный весь. Мы отмечаем общие свойства наших примеров и задаемся вопросом, применимы ли они ко всем возможным примерам. Если дальнейшие испытания и размышления приведут нас чтобы укрепить нашу веру в то, что наши примеры отражают более общую истину, затем мы высказываем гипотезу.Латинские корни слова «догадка» переводят «скинуть вместе» — мы собираем множество наблюдений в одна идея. Домыслы — это бездоказательные утверждения. Как только кто-то доказывает предположение, это называется теоремой .
Вы можете представить идеи и задания, обсуждаемые ниже, если в них возникнет необходимость во время исследований учащихся. Если ученик использует определенную технику, выделите этот подход для всего класса. После того, как предположение высказано, спросите класс, что им нужно сделать, чтобы понять его, и начните разрабатывать план, который могут использовать все.Регулярные возможности для практики с различными навыками (систематизация данных, написание предположений и т. Д.) Со временем приведут к повышению уровня знаний учащихся.
ПОЛУЧЕНИЕ И ОРГАНИЗАЦИЯ ПРИМЕРОВ
Создание примеров
Чтобы получить лучшее представление о «большой» картине проблемы, мы стараемся систематически приводить примеры. Нам часто приходится выбирать примеры из бесконечной области. Эти примеры должны быть репрезентативными в том смысле, в котором мы считаем важным, все элементы предметной области.Например, проблема с действительными числами может включать положительные, отрицательные, целые, рациональные и иррациональные примеры. Также могут быть важны числа меньше единицы или большие по величине. В дополнение к этой широкой выборке мы также хотим генерировать примеры по шаблону, чтобы выделялись отношения между переменными (см. Раздел «Организация данных» ниже).
Для некоторых задач легко создать примеры. В других случаях неясно, существуют ли описанные объекты вообще или, если они существуют, как их сконструировать.Например, учащийся, интересующийся четностью числа факторов для каждого счетного числа, может столкнуться с трудностями при поиске чисел с нечетным числом факторов. Ее поиск примеров, вероятно, заставит ее задуматься, почему большинство чисел имеет четное количество факторов, и, возможно, подскажет условия, которые приводят к нечетному количеству факторов. Это переплетение открытия и понимания характерно для всей математической работы — доказательства часто развиваются вместе с самими открытиями.
Важно определить, когда примеры действительно отличаются друг от друга.Если мы не можем указать, какие характеристики действительно имеют значение для конкретной проблемы (например, порядок или форма), то мы не сможем выяснить, когда у нас будет достаточно примеров, останутся ли еще какие-то другие или какое пространство для образцов что мы ищем. Например, учащимся может быть сложно создать диаграмму, которая соответствует следующим условиям, или определить, отличаются ли их примеры друг от друга:
Нарисуйте карту с указанием городов и дорог, на которых:
- Каждая пара дорог имеет ровно один общий город.
- У каждой пары городов ровно одна общая дорога.
- Каждый город имеет ровно три дороги.
- Каждая дорога содержит ровно три города.
Пока соседи сравнивают свои карты, попросите их подумать, чем карты отличаются и в чем они совпадают. Какие характеристики имеют значение, если они считают две карты одинаковыми? Как и в случае с проблемой прямоугольника ниже, мы часто уделяем больше внимания топологии математического объекта, чем его точным измерениям.Топология объекта зависит от того, как его части связаны друг с другом.
Систематичность
Мы можем найти множество решений проблемы, но все же упустить интересные, если мы не будем систематизировать наш поиск. Чтобы быть систематическими, мы должны создать путь или пути, которые проведут нас через все возможности, которые могут возникнуть. Чтобы оставаться на пути, может потребоваться алгоритм, который проведет нас через выбор, с которым мы сталкиваемся на этом пути. Сам алгоритм может быть не очевиден до тех пор, пока мы не попытаемся сгенерировать упорядоченный список и не пропустим или не переоценим некоторые примеры.Только после первых экспериментов мы можем начать понимать внутреннюю логику проблемы.
Для практики студенты могут рассмотреть следующий вопрос:
Класс исследует подразделение прямоугольника на n меньших прямоугольников. Они работают над конкретным случаем разделения прямоугольника на 4 прямоугольника. Какие макеты возможны для этих подразделений?
Полный поиск даже этого небольшого случая из четырех прямоугольников требует тщательного рассуждения.Мы можем рассмотреть все возможности более эффективно, выбрав единственный угол в качестве отправной точки. Признание симметрии ситуации (поворот или отражение делает выбранный угол эквивалентным трем другим) упрощает нашу работу. Есть два способа разместить прямоугольник в этом углу: вдоль всей стороны или нет (рисунок 1). И снова нам на помощь приходит симметрия — не имеет значения, горизонтально или вертикально ориентирована вся покрываемая нами сторона.
Конечно, если мы собираемся апеллировать к симметрии, мы должны определить, что мы подразумеваем под четким ответом.Понятно, что решений будет бесконечно много, если учесть размер подразделений. Таким образом, имеет смысл спросить, сколько существует категорий этих подразделений, когда мы игнорируем размер сегментов и общую ориентацию фигуры и просто смотрим на топологические отношения между подпрямоугольниками (как они граничат друг с другом).
Рис. 1. Первый прямоугольник расположен в верхнем левом углу
Когда у нас есть два начальных расположения, нам нужно добавить еще три прямоугольника.Для прямоугольника слева у нас просто осталась уменьшенная версия нашей исходной задачи — разрезание прямоугольника (оставшееся пространство) на три прямоугольника. Есть только два разных способа выполнить такое вскрытие (проверьте это утверждение сами!). Мы можем повернуть эти трехпрямоугольные структуры, чтобы создать новых кандидатов на подразделения, используя четыре прямоугольника (рисунок 2). Возникает одно повторяющееся решение (зачеркнутое изображение эквивалентно изображенному в правом верхнем углу), так что на данный момент существует пять вариантов.
Рис. 2. Завершение прямоугольника типа A
Мы можем завершить прямоугольник типа B двумя дополнительными уникальными способами (рис. 3).
Рис. 3. Завершение прямоугольника типа B
Еще один полезный метод создания примеров — индуктивное построение их из примеров меньшего размера. Мы можем произвести семь указанных выше подразделений, разделив пополам один подпрямоугольник в трехпрямоугольных подразделениях (рис. 4).
Рис. 4. Три прямоугольных подразделения превращены в четыре
Этот индуктивный подход хорошо работает при нахождении всех полимино, сделанных из n квадратов из набора полимино, составленных из n — 1 квадратов. Квадратные полимино n находятся путем добавления одного дополнительного квадрата к каждому доступному краю полимино, сделанных из квадратов n -1. Однако этот индуктивный подход не работает надежно для задачи разделения прямоугольника.Разделение одного прямоугольника в макете из четырех прямоугольников не может создать подразделение из пяти прямоугольников, показанное ниже (рисунок 5). Эта проблема демонстрирует, что мы должны тщательно выбирать методы, которые мы используем для создания примеров, если мы хотим идентифицировать все интересующие случаи.
См. Раздел «Проверка гипотез» ниже для дальнейшего обсуждения различных типов примеров.
Рисунок 5. Особое подразделение
Организация данных
Примеры, которые мы приводим в наших исследованиях, предоставляют нам данные.Мы постарайтесь организовать эти данные таким образом, чтобы выделить отношения между переменные нашей проблемы. Хотя нет гарантированных методов для обнаружения всех закономерностей есть несколько полезных основных методов. Числовой данные могут быть организованы в таблицы, что упрощает поиск знакомых узоры. В задаче с двумя переменными, одна зависит от другой, информация должна быть указана в соответствии с постоянно увеличивающимися значениями зависимой переменной.Например, студент поинтересовался числом областей, образованных диагоналями правильного n -угольника. Она систематически перечислил количество сторон многоугольников и количество созданных регионов (рисунок 6). Это по существу одномерное расположение облегчает обнаружение любых рекурсивных или явных функций, которые связывают две переменные.
|
n |
Регионы |
|
3 |
1 |
|
4 |
4 |
|
5 |
11 |
|
6 |
24 |
|
7 |
50 |
Рисунок 6.Таблица количества сделанных регионов по диагоналям штатный n -угольник
Иногда проблема будет иметь несколько независимых переменных (значения, которые они могут принимать, не ограничиваются другими переменными). В таких случаях мы можем организовать наши данные, используя каждое измерение таблицы для представления значений одной переменной. Например, в 1899 году Георг Пик опубликовал формулу, определяющую площадь многоугольника, вершины которого лежат в точках квадратной решетки (рис. 7).Он обнаружил, что площадь может быть определена исключительно на основе количества точек решетки внутри ( I ) и на границе ( B ) многоугольника. Его формула была A = 1 / 2 B + I — 1.
Рис. 7. Многоугольник с 2 внутренними и 10 граничными точками имеет площадь 2 + 1/2 (10) — 1 = 6
Есть несколько шагов, которые можно предпринять, чтобы сделать такое открытие.Можно начать с интуитивного представления о том, что площадь области может быть связана с количеством точек решетки внутри фигуры. Затем нужно понять, что площадь может быть функцией всего двух переменных — что она не зависит от конкретной формы многоугольника или количества вершинных точек. Возможно, эта гипотеза возникает при рассмотрении нескольких примеров для тех же B и I . Как только этот факт будет обнаружен, можно будет найти области для фигур с различными комбинациями граничных и внутренних точек (рис. 8).Класс может использовать эту таблицу, чтобы попытаться самостоятельно найти формулу Пика. Попросите их нарисовать или использовать геодоски для создания форм, которые соответствуют требованиям данной пары ( B , I ), и найти области этих форм. (Примечание: поиск области может быть хорошей проблемой сам по себе — потенциально полезным предложением является разделение многоугольника на более простые фигур или нарисуйте прямоугольник, ограничивающий фигуру, и вычтите лишние области).
|
Очки в салоне ( I ) |
Граничные точки ( B ) | ||||||
|
3 |
4 |
5 |
6 |
… |
|||
|
0 |
|||||||
|
1 |
|||||||
|
2 |
|||||||
|
3 |
|||||||
|
… |
|||||||
Рисунок 8.Двумерная таблица для организации данных для теоремы Пика
По мере заполнения таблицы (рис. 9) учащиеся могут отмечать различные закономерности. Они могут указывать то, что видят рекурсивно (например, «Вы добавляете половину каждый раз, когда перемещаетесь по прямоугольнику») или явно («Когда B равно четырем, площадь на единицу больше, чем количество внутренних точек»). . Обе эти формы могут быть полезны при разработке общего решения. Предложите своим ученикам написать формулы для каждой строки и столбца, а затем попытайтесь объединить эти вспомогательные правила в одно, которое работает для всех пар ( B , I ).Однако студентам важно понимать, что их формулы — это скорее предположения, чем теоремы. Доказательство того, что формула всегда работает, — очень сложная задача, которая не может быть основана на данных из конечного числа примеров (но вы можете предложить им попытаться доказать это для более простых особых случаев многоугольников, таких как прямоугольники, прямоугольные треугольники и т. Д. .).
|
Очки в салоне ( I ) |
Граничные точки ( B ) |
|||||||
|
3 |
4 |
5 |
6 |
… |
В |
|||
|
0 |
1 / 2 |
1 |
1 1 / 2 |
2 |
||||
|
1 |
1 1 / 2 |
2 |
2 1 / 2 |
3 |
В /2 |
|||
|
2 |
2 1 / 2 |
3 |
3 1 / 2 |
4 |
||||
|
3 |
3 1 / 2 |
4 |
4 1 / 2 |
5 |
||||
|
… |
||||||||
|
Я |
Я + 1 / 2 |
я + 1 |
||||||
Рисунок 9.Двумерная таблица для организации данных для теоремы Пика
Когда в задаче много переменных или большое количество возможных значений для каждой переменной, может быть сложно систематически изучать все комбинации. В таких случаях мы можем сохранить одну (или все, кроме одной) переменной постоянной и изучить остальные. Поступая так, мы меняем проблему на более управляемый размер. Например, в данных выбора выше (рисунок 9) ученик может сначала изучить столбец для 4 граничных точек ( B остается постоянным, а I может изменяться).Правило, описывающее этот столбец, I + 1, само по себе не дает нам формулы для всей таблицы. Мы также должны сохранить нашу первую переменную, B , постоянной для некоторых новых значений, а затем повторить наш анализ для фиксированных значений I , изменяя B .
Параметр исследования «Соединить точки» представляет собой дополнительный пример значения временного сохранения переменной постоянной. Учащиеся обычно придерживаются постоянного числа точек и создают диаграммы для всех размеров прыжков.В конечном итоге мы надеемся объединить все наши выводы из этих более узких исследований в один более крупный результат, который решит исходную проблему. Примеры графических подходов к отображению данных для поиска соединений см. В разделе Графики в представлениях.
В ПОИСКАХ УЗОРОВ
Мы систематизируем свои наблюдения, чтобы развить предположения о поведении математических объектов, которые мы изучаем. Как только мы поверим, что шаблон установлен, мы сформулируем его как гипотезу о целом классе объектов.
Предсказуемо изменяющиеся переменные
Организуя данные, мы ищем закономерности и способы описания эти шаблоны формально. Студенты узнают о множестве знакомых шаблонов (линейные, экспоненциальные, периодические и т. д.) в своих классах алгебры. Методы для выявления этих моделей и действий, которые помогают им развить Привычка использовать эти методы должна занимать центральное место в этом исследовании.Хороший ресурс для обучения характеристике различных паттернов — это первая глава математического Методы (http://www.its-about-time.com/htmls/mm/mm.html) скоро будут опубликовано Its About Time (http://www.its-about-time.com).
Упрощение проблемы
Проблемы могут быть настолько интеллектуально сложными или требующими вычислений, что мы не можем решить их напрямую. Например, студент, читающий Флатландию, задавался вопросом о длине диагоналей гиперкуба.Какие самые длинные отрезки могли поместиться в такой фигуре? Она начала с рассмотрения более низкоразмерных версий проблемы. Для точки, которая является 0-мерным «кубом», длина самого длинного подходящего сегмента равна 0. Для единичного сегмента (одномерного «куба») длина самого длинного сегмента равна 1. Для единичного сегмента. В квадрате мы можем уместить диагональ длины, а для единичного куба расстояние от одного угла до противоположного равно (рисунок 10). Признавая, что 0 и 1 являются собственными квадратными корнями, она экстраполировала свой образец и решила, что диагональ единичного четырехмерного гиперкуба должна быть равна или 2.Ее образец не был доказательством, но изучение более простых связанных случаев привело ее к решению и, в конечном счете, к доказательству для любого измерения.
Рис. 10. Диагонали единичного сегмента, квадрата и куба
В приведенном выше примере гиперкуба ученица использовала меньшие случаи, потому что сначала она не могла визуализировать ситуацию, которая ее интересовала. Использование меньшего размера особенно важно, если вы пытаетесь решить проблему методом грубой силы.Например, вместо того, чтобы подсчитывать все возможности для пятикнопочной симплексной блокировки, одна из подсказок проекта состоит в том, чтобы сначала найти шаблон для замков с меньшим количеством кнопок.
Задачи можно упростить, используя меньшее число, более простую форму или более симметричную установку или форму (например, квадрат, а не произвольный четырехугольник). Иногда их можно упростить, сняв ограничения, которые, кажется, усложняют их. Например, задача «Какими разными способами лифт может покинуть первый этаж 20-этажного здания, сделать 10 остановок, двигаясь только вверх, и добраться до верхнего этажа?» сложнее, чем задача, позволяющая лифту двигаться в любом направлении во время остановок.Для дальнейшего обсуждения методов создания связанных проблем см. Способы изменения проблемы в постановке проблемы. Для занятия в классе, которое поднимает вопросы о том, как более простую задачу можно использовать для решения более сложной, см. Раздел «Технология и величина » в главе «Числа в контексте» книги «Математическое моделирование», доступной на сайте www.meaningfulmath.org (примечание : эта глава представляет собой загружаемый файл pdf размером 1 мегабайт).
Инварианты — величины, объекты и отношения, которые остаются неизменными
Хотя мы часто пытаемся описать, как некоторая переменная изменяется на , иногда мы хотим показать, что на функцию не влияют изменения в Переменная.Например, отношение длины окружности к ее диаметр остается неизменным, даже если размер круга меняется. Этот факт очевиден, когда вы его изучите, но может быть сюрпризом для детей, когда они впервые это обнаруживают. Свойство или количество, которое не меняется, пока другие переменные меняются, называется инвариантом . Понятие инвариантности важно для всей математики.
Даже фигуры, форма которых гораздо менее ограничена, чем круги, обладают неизменными свойствами.Например, если мы построим квадраты на сторонах четырехугольника, отрезки, соединяющие центры квадратов на противоположных сторонах, будут равны по длине и перпендикулярны (теорема Обеля, рис. 11). Инварианты часто удивляют и побуждают к дальнейшим исследованиям и объяснениям. Когда такая последовательность проявляется перед лицом асимметрии и изменчивости, мы хотим выяснить, чем объясняется эта надежность.
Рис. 11. Для любого четырехугольника синие сегменты равны и перпендикулярны
Идентификация инвариантов может быть очень мощным инструментом, поскольку позволяет нам находить общие свойства ситуаций, которые выглядят по-разному.Идентификация и использование инвариантов становится более естественным с опытом. Вот два примера, которые дают более полное представление об этой концепции:
Алгебраический инвариант — Рассмотрим полиномиальное уравнение 0 = x 2 + x + a с константой a . Мы можем использовать формулу корней квадратного уравнения, чтобы найти решения:. Сумма этих решений равна –1. Следовательно, сумма решений 0 = x 2 + x + a инвариантна относительно a .Точно так же вы можете показать, что сумма решений 0 = cx 2 + bx + a инвариантна относительно постоянного члена a и что произведение инвариантно относительно линейного коэффициент b .
Комбинаторный инвариант — Предположим, мы начинаем с перестановки (или изменения порядка) чисел от 1 до 9:
{6, 8, 1, 9, 3, 7, 5, 4, 2}
Есть много разных способов расположить эти числа в порядке возрастания путем обмена парами.Вы можете начать с обмена 9 и 2, чтобы получить:
{6, 8, 1, 2, 3, 7, 5, 4, 9}
Кто-то другой может обменять 8 и 2 в исходном заказе, чтобы получить
{6, 2, 1, 9, 3, 7, 5, 4, 8}
Независимо от того, что вы делаете в первую очередь, продолжайте переключать пары, пока окончательный обмен не даст
{1, 2, 3, 4, 5, 6, 7, 8, 9}
Попробуйте это с пронумерованными плитками или клочками бумаги и отслеживайте количество произведенных обменов.Количество шагов может варьируются, но вы всегда будете делать нечетным числом шагов. Мы скажем, что четность исходной перестановки равна нечетным вместо даже , если для сортировки чисел потребовалось четное количество шагов, как в случае для {5, 2, 4, 9, 1, 3, 6, 7, 8,}. Четность перестановки инвариантна относительно обменов вы выполняете, чтобы отсортировать перестановку.
Действия с инвариантами
Рассмотрим следующую задачу (из раздела «Разбивание шоколадных плиток» на http://www.cut-the-knot.com/proofs/chocolad.html) с шоколадным батончиком, который делится на м на n маленьких квадратов (рис. ). Начиная с целой планки, ход состоит в выборе части планки и разбиении ее по одной из горизонтальных или вертикальных линий, разделяющих квадраты. Затем две новые фишки возвращаются в стопку, чтобы их можно было сделать следующим ходом. Задача состоит в том, чтобы найти наименьшее количество ходов, необходимых для разбивки стержня на все отдельные (1 на 1) квадраты .
Рис. 12. Плитка шоколада 4 на 5 и два возможных первых хода
Расскажите об этой ситуации своему классу и попросите каждую пару учеников выбрать полоски определенного размера и отслеживать количество необходимых ходов каждый раз. Они могут проводить свои исследования, вырезая кусочки миллиметровой бумаги, разделяя части массива связанных кубиков, рисуя сегменты на сетке или ломая настоящую плитку шоколада.Попросите их подумать, казались ли одни стратегии выбора того, какой кусок сломать, более эффективными, чем другие.
После нескольких попыток должно стать очевидным, что для столбца данного размера количество требуемых ходов всегда одинаково. Почему результат инвариантен относительно последовательности разрывов? Какой влияет на количество ходов ? На этом этапе вы можете направить свой класс в одном из двух направлений. Их можно спросить, какие переменные влияют на количество ходов, и дать им время, чтобы найти правило, которое предсказывает это общее количество — они могут подумать об организации возможностей для различных значений m и n в массиве или попытаться взглянуть на конкретные небольшие случаи.В качестве альтернативы, и это более быстрый способ, вы можете попросить их отслеживать количество деталей после каждой резки. Возможно, вы даже захотите провести оба этих анализа по порядку.
Ключевое наблюдение состоит в том, что количество леденцов всегда на единицу больше, чем количество ходов, потому что каждый ход добавляет еще одну фигуру. То есть количество частей не зависит от выбора сделанных перерывов. Эта инвариантность говорит нам, что мы всегда будем иметь миллионов фигур после миллионов — 1 ход.Это упражнение представляет собой хороший пример того, как мы можем использовать инварианты в качестве инструмента для построения доказательств.
Дополнительные учебные материалы, связанные с инвариантами, см. В главе 1, уроки 7, 8 и 10 в книжной версии, а также уроки 14, 15 и 16 в версии программы Connected Geometry на компакт-диске (http: //www.everydaylearning .com / geometry). Вы также можете скачать Tackling Twisted Hoops, статью об инвариантах и теории узлов из бывшего журнала Quantum.
Другой вид наблюдения
Хотя учащиеся средней школы, занимающиеся математическими исследованиями, чаще всего делают открытие, касающееся числовых закономерностей, существуют и другие виды возможных предположений.Один тип наблюдения может заключаться в том, что образец или устройство, которое они изучают, были встречены в другом контексте. Такое наблюдение может привести к гипотезе о том, что существует общее объяснение двух явно несходных вопросов, и к способу показать, что они каким-то образом связаны.
Один из таких вопросов начался, когда другой студент, вдохновленный Флатландией, посмотрел на количество вершин в n -мерном кубе на заданном расстоянии от выбранной вершины.Расстояние измерялось, путешествуя только по краям фигуры. Например, если выбран угол квадрата, то есть одна точка на 0 шагов (сама точка), две вершины, которые могут быть достигнуты, путешествуя по единственному ребру, и одна вершина на расстоянии двух ребер (рисунок 13).
Рис. 13. Расстояние по ребрам от вершины A квадрата и куба
Когда ученик организовал свои данные в таблицу (рис. 14), он увидел знакомое зрелище.Затем он предположил и решил объяснить связь между n -мерными кубами и треугольником Паскаля.
|
д |
точка |
Сегмент |
Квадрат |
Куб |
Гиперкуб |
|
0 |
1 |
1 |
1 |
1 |
1 |
|
1 |
0 |
1 |
2 |
3 |
4 |
|
2 |
0 |
0 |
1 |
3 |
6 |
|
3 |
0 |
0 |
0 |
1 |
4 |
|
4 |
0 |
0 |
0 |
0 |
1 |
Рисунок 14.Число вершин на расстоянии d от вершины в каждой форме
Для дальнейшего обсуждения и настроек, которые способствуют установлению таких подключений, см. «Практические задания» в разделе «Подтверждение».
ПОНИМАНИЕ ПРЕДПОЛОЖЕНИЙ
Мы стремимся понять гипотезу на трех уровнях: мы хотим определить ее значение, мы хотим определить причины, по которым мы можем считать это утверждение истинным, и мы хотим понять, как оно вписывается в более широкий набор идей.Первые шаги, которые мы предпринимаем при исследовании гипотезы, аналогичны тем, которые используются для понимания определения:
- Прочтите выписку более одного раза. Важные тонкости часто упускаются из виду при первом чтении.
- Определите каждое из условий гипотезы . Условия гипотезы — это те критерии, которые должны быть удовлетворены, прежде чем мы примем выводы гипотезы. Это , если часть заявления.Каждое существительное и прилагательное может составлять определенное условие.
- Создание примеров и не примеров . Найдите объекты, отвечающие условиям, и убедитесь, что они также удовлетворяют заключению гипотезы. Удалите каждое условие по очереди и создайте , не являющиеся примерами, , которые удовлетворяют другим условиям, но не заключению. Отсутствие примеров помогает нам понять важность каждого условия для гипотезы. Условия ограничивают рассматриваемые объекты набором, который все разделяет определенные свойства.
- Найдите контрпримеры . Контрпример удовлетворяет всем условиям утверждения, но не заключению. Оставляют ли условия «пространство для маневра» объекту, который не удовлетворяет выводам гипотезы? Если контрпример действительно существует, то гипотеза неверна.
- Сравнить . Как эта гипотеза связана с другими утверждениями о тех же или подобных математических объектах?
Те же шаги помогают, когда мы знакомимся с новой теоремой.В случае теоремы мы также хотим прочитать и понять доказательство. В случае гипотезы мы ищем доказательства, которые поддержали бы доказательство или указали путь к опровержению.
Условия удаления
Теорема сравнения угол-угол-сторона (AAS): если в двух треугольниках два угла и не включенная сторона одного треугольника конгруэнтны соответственно двум углам и соответствующей невключенной стороне другого, то треугольники конгруэнтны.
Теорема AAS имеет много условий. Он включает в себя треугольники, два угла, одну сторону, положение стороны относительно углов, конгруэнтность и соответствие. Чтобы понять, почему каждое из них необходимо, нам нужно удалить каждое условие, а затем создать пару треугольников, которые удовлетворяют оставшимся условиям, но не совпадают. Например, если мы удалим условие, что фигуры являются треугольниками, мы сможем построить разные четырехугольники, которые имеют два совпадающих угла и равную невключенную сторону.В таблице ниже (рисунок 15) показаны не примеры для трех различных условий.
|
Состояние снято |
Без примеров |
|
Фигуры — треугольники. |
|
|
Два угла должны совпадать. |
|
|
Конгруэнтная сторона должна быть соответствующей невключенный (эти треугольники похожи, но не совпадают). |
|
Рисунок 15. Непримеры для теоремы AAS
В ходе классного задания представьте теоремы и предположения и попросите студентов сначала перечислить все условия утверждения, а затем привести не примеры для каждого из них. Два утверждения, с которыми они могут практиковаться: (1) Если a и b являются положительными целыми числами, d является наибольшим общим делителем a и b , а c не делится на d. , то нет целых решений для ax + на = c и (2) Если нечетное целое число возводится в нечетную целую степень, то результатом является нечетное целое число.Не говорите своему классу заранее, что первое утверждение — это теорема, а второе — ложное предположение. Студенты получат дополнительную практику в понимании домыслов, которые их сверстники генерируют в течение года.
ОЦЕНКА ПРЕДПОЛОЖЕНИЙ
Каковы возможные характеристики гипотезы и что делает одну гипотезу более интересной, чем другие? Студенты должны подробно ответить на каждый из следующих вопросов, когда они хотят оценить гипотезу:
- Гипотеза кажется верной или ложной?
У нас редко бывает окончательный ответ на этот вопрос сразу, но наше понимание связанных результатов может направлять нашу интуицию.Изучение примеров и поиск контрпримеров еще больше повлияют на нашу веру в истинность гипотезы. Студенты, как правило, слишком склонны полагать, что несколько примеров представляют собой неопровержимое доказательство закономерности.
Если гипотеза немедленно следует из известного результата, то она может быть менее интересной, чем неожиданная гипотеза. Например, утверждение о квадратах может быть неинтересным, если студент уже доказал то же утверждение для надмножества, такого как параллелограммы.
- Это легко или сложно понять?
Гипотеза может быть трудной для понимания из-за того, как она написана, или из-за сложности математики. Студенты должны переписать свои предположения, если их математический язык излишне сбивает с толку.
- Гипотеза общая?
Гипотеза, которая, если она верна, применима к широкому кругу объектов или ситуаций, будет более значительной, чем ограниченное утверждение.Предлагает ли это связь между двумя разными темами?
Второклассник исследовал, какие доски n на м можно выложить плиткой с помощью Т-тетромино (четыре квадрата, расположенные боком к краю, чтобы они выглядели как заглавная буква T, рис. 16).
Рис. 16. Доска 4 на 8, выложенная Т-тетромино
Ее окончательная гипотеза: «Если стороны доски ровные, то даже она может сработать, а если нет, то нет», оставила ее неудовлетворенной.Она правильно считала, что любое нечетное измерение делает плитку невозможной, но она знала, что ровность не была достаточно точным условием, чтобы различить все доски, которые были и не были выложены плиткой. Она знала, что если ей удастся уточнить свои условия, ее предположение станет сильнее. (См. «Необходимые и достаточные условия» ниже.)
- Нравится ли вам догадка? Вам это нравится?
Людей привлекают разные вопросы математики.Студентам важно начать развивать свою собственную эстетику математических идей и понимать, что эстетика играет роль в дисциплине. Неожиданные или противоречащие интуиции предположения, раскрывающие сложную закономерность или полезные для подтверждения других важных предположений, с большей вероятностью будут оценены широкой аудиторией.
ТЕСТИРОВАНИЕ ПРЕДПРИЯТИЙ
Первый вопрос, с которым мы сталкиваемся при оценке гипотезы, — это оценить, истинна она или нет.Хотя подтверждающие примеры могут помочь понять, почему гипотеза верна, мы должны также активно искать контрпримеры. Когда учащиеся верят предположению, они не всегда строго ищут примеры, которые нарушают установленный ими шаблон. Мы должны помочь им развить в себе привычку быть более скептичными. Один из способов развить этот скептицизм — предлагать учащимся задачи, имеющие «ложные» шаблоны — те, которые кажутся знакомыми, но не продолжают, как ожидалось (см. «Гипотезы — не теоремы» ниже).
Как студенты могут искать контрпримеры? Им следует проверить кейсы между теми, которые, как они обнаружили, работают. Им следует рассмотреть крайних случаев на дальних концах областей их проблем (например, тупые треугольники, которые почти плоские, или числа, близкие к нулю). Им следует рассмотреть вырожденных случаев, которые не обладают всей сложностью типичного примера. Вырожденные случаи часто возникают в результате обнуления какого-либо параметра. Например, точка, когда гипотеза применима к кругам (радиус был установлен на ноль) или линейное уравнение, когда тема является квадратичной (коэффициент при квадратичном члене равен нулю).Четырехугольник — это вырожденный пятиугольник, в котором две точки находятся в одном месте. Конечно, некоторые вырожденные случаи на самом деле не имеют отношения к проблеме (например, эллипсы могут быть определены в терминах фокуса и директрисы, а круги — нет).
Помимо крайних и вырожденных примеров, мы также должны сгенерировать и протестировать особых случаев . Особые случаи обладают дополнительным свойством, таким как симметрия, которого нет в большинстве других случаев. Квадрат — это особый прямоугольник, а прямоугольные или равнобедренные треугольники — разные случаи, требующие исследования.В других контекстах особыми случаями могут быть числа без повторяющихся простых множителей, матрицы с определителем 0 или 1 или функции, которые являются монотонными.
Перед тем, как класс исследует новые предположения, я представляю им резюме бывшего студента: «У гипотезы есть три возможных судьбы: жизнь, смерть и неопределенность. Жизнь достигается путем доказательства, смерть — контрпримером, а неопределенность — это просто неопределенность. Смерть может привести к возрождению через очищение ». Это содержательное утверждение подчеркивает, что одного контрпримера достаточно, чтобы опровергнуть гипотезу, и что доказательство — а не множество примеров или отсутствие контрпримера — единственный способ, которым мы можем быть уверены в утверждении.
Студенты не должны рассматривать открытие контрпримера как неудачу. Это одновременно знак их вдумчивости и возможное начало новой, более совершенной теории. Контрпример может опровергнуть предположение, но это не означает, что утверждение всегда ложно. Гипотеза почти всегда может быть верной. Гипотезы возрождаются, когда мы определяем, какое дополнительное условие исключает возможность контрпримеров или какую часть нашего заключения нам нужно сделать менее конкретными. Например, гипотеза студента-геометра о том, что «точки пересечения биссектрис параллелограмма образуют прямоугольник внутри параллелограмма», была поддержана одноклассниками, указавшими, что слово «внутренняя часть» делает возможными контрпримеры.Гипотеза другого ученика: «Серединные перпендикулярные стороны сторон воздушного змея не пересекаются в одной точке» работает для большинства воздушных змеев, но требует дополнительного условия, что нескончающие углы не являются прямыми углами. Студенты должны сгруппировать свои контрпримеры и подтверждающие примеры и ищите свойство, которое отличает эти два набора.
Для занятия в классе, которое включает поиск контрпримеров, см. Раздел Понимание определений: замкнутый и плотный в главе «Числа в контексте» книги «Математическое моделирование».
НАПИСАНИЕ ПРЕДПИСАНИЙ
Для студентов часто существует большая пропасть между идеями, с которыми они могут справиться, и их способностью четко изложить свои мысли. Им необходимо выучить математический словарь и формальные структуры, которые упрощают написание логических утверждений. Они добиваются такого прогресса, когда мы предоставляем им широкие возможности распознавать, записывать и уточнять предположения. Ниже описана последовательность, которая дает возможность попрактиковаться в создании и переработке гипотез.
Классная деятельность
Программы динамической геометрии, такие как Geometer’s Sketchpad ® или Cabri Geometry II ™, которые позволяют учащимся строить точные диаграммы геометрических объектов, стали популярными инструментами для исследований в классе. Если ученикам будет предоставлена некоторая гибкость в изучаемых условиях, они с радостью будут бороться со сложными предположениями, которые могут стать ценным предметом обсуждения в классе. Рассмотрим следующую выборку заявлений, от грандиозных до запутанных, которые были выдвинуты студентами.Предположения были ответом на задание выбрать класс четырехугольников и определить какие-либо свойства биссектрис углов или перпендикулярных биссектрис сторон этих фигур.
- Пересечения серединных перпендикуляров параллелограмма создают новый параллелограмм с теми же углами, что и исходный.
- Биссектриса прямоугольника образует квадрат.
- Все срединные перпендикуляры равнобедренной трапеции пересекаются в одной и той же точке.Эта точка пересечения — центр круга, который содержит все вершины равнобедренной трапеции.
- В трапеции углы, образованные в точке пересечения самой длинной базовой линии и биссектрисы небазового угла, совпадают, только если оба угла находятся снаружи или оба находятся снаружи.
- В равнобедренной трапеции биссектрисы базового угла образуют угол, равный противоположному базовому углу.
- В трапеции два совпадающих треугольника образованы биссектрисами последовательных неосновных углов, и один из них пересекает базовую линию.
- В кайте, где все биссектрисы пересекаются, находится центр.
- В трапеции углы, образованные в точке пересечения самой длинной базовой линии и биссектрисы небазового угла, совпадают, только если оба угла находятся внутри или оба находятся снаружи.
- В трапеции две биссектрисы основного угла образуют равнобедренный треугольник в точке пересечения.
- Если биссектрисы четырехугольника образуют прямоугольник, то эта фигура — параллелограмм.
- Биссектриса равнобедренной трапеции образует четыре равнобедренных прямоугольных треугольника.
После двух-трех дней лабораторных занятий каждая группа представляет свой лабораторный отчет с примерами и предположениями. Чтобы убедиться, что они четко определяют, что они описывают, им не разрешается использовать ярлыки с рисунков; они должны были использовать общепринятую лексику. На следующий день каждому студенту дается страница с предположениями, подобными приведенному выше списку, составленным из отчетов. Они читают предположения и пытаются понять их, генерировать тестовые примеры и оценивать их в соответствии со стандартами, указанными выше (см. Оценка предположений).
Затем класс обсуждает каждую гипотезу. Анонимно студенты слушают, что их сверстники думают о ясности их написания и успешности их предположений. Студенты дают конструктивные советы о том, как прояснить каждое утверждение. Преимущество такого рецензирования перед комментариями учителя заключается в том, что ученики обычно довольно хорошо умеют находить альтернативные интерпретации запутанных утверждений, которые обнаруживают неточность в утверждении. Часто у класса будет несколько интерпретаций, среди которых он не может выбрать.Это затруднительное положение помогает автору понять, как изменить свою гипотезу, чтобы сказать то, что они намеревались. Цикл коллегиального оценивания и переписывания приводит к лучшим предположениям и лучшим саморедактируемым предположениям в будущем.
Рецензирование первых черновиков предпочтительнее оценки учителей, потому что учителя слишком хорошо понимают, что ученик «на самом деле имел в виду» математически. Сверстники сохраняют первоначальный фокус там, где он принадлежит, на акте четкого общения. Классные дискуссии о тонкости, сложности и привлекательности гипотезы приводят к тому, что в течение года становится все меньше тривиальных гипотез.Эти преимущества процесса рецензирования также помогают классу почувствовать себя математическим сообществом.
Иногда класс предоставляет контрпримеры, чтобы указать, что гипотеза ложна, или не может понять смысл гипотезы (посмотрите, какой из приведенных выше примеров имеет для вас смысл). Если предположение приемлемо, обратная связь с учителем может помочь в решении таких вопросов, как выбор словарного запаса и разработка символических представлений, упрощающих утверждение.Уточненные гипотезы следует называть в честь их создателей (например, «Гипотеза Пентагона Рахима и Джени») и публиковать так, чтобы они выделялись как интересные, но бездоказательные утверждения. Студенты часто особенно заинтересованы в том, чтобы доказать свои собственные утверждения и превратить их в теоремы.
Условные утверждения
В школьных текстах обычно предлагается записывать предположения и теоремы в форме «если A , то B ». Однако есть много других распространенных форм, которые для определенных условных операторов может быть проще сформулировать и понять.Одна из трудностей с некоторыми из этих форм состоит в том, что они также могут скрывать посылку и выводы условного утверждения. Учащиеся естественно используют различные формы и могут извлечь пользу из рассмотрения альтернативных способов изложения своих идей. Ни одна структура не может быть лучшей во всех случаях.
При чтении математики учащиеся будут сталкиваться с множеством условных утверждений, которые почти идентичны стандартной форме , если, то . К ним относятся: все A — это B ; A , затем B ; если A , B .Пусть А . Тогда B ; и B , если A . Другие условные утверждения кажутся более описательными, чем логическими. Например, «медианы треугольника параллельны» предпочтительнее, но может быть преобразовано в «если фигура является треугольником, то его медианы параллельны». Эта последняя форма подчеркивает, что единственная предпосылка в утверждении — наличие треугольника. Однако, как показано выше в четырехугольных гипотезах студента, это не самый удобный способ высказывать широкий спектр гипотез.Вам следует обсудить различные формы условного утверждения и время от времени переформулировать предположения учащихся в альтернативных формах, чтобы учащиеся познакомились с их.
Необходимые и достаточные условия
Необходимое условие — это условие, которое должно быть выполнено для того, чтобы данное заключение было верным. Однако выполнение условия не гарантирует, что вывод верен. Когда выполняется достаточное условие , тогда вывод, для которого это было условие, будет истинным независимо от любых других свойств.
Студенты не всегда понимают разницу между необходимыми и достаточными условиями. Однако их догадки иногда дают возможность провести различие. В приведенном выше примере тетромино равномерность размеров является необходимым, но не достаточным условием для того, чтобы можно было выложить прямоугольник мозаикой. Знание того, что мозаика работает для данной доски, является достаточным условием для того, чтобы знать, что стороны равны (то есть, если A необходимо для B , то B достаточно для A ).См. «Гипотезы Сары» в «Учебных заметках» по проекту «Соединить точки», где приведен пример другого ученика.
Для четырехугольника наличие диагоналей, которые перпендикулярно делят друг друга пополам, является одновременно необходимым и достаточным условием для того, чтобы он был ромбом. В таких случаях мы можем написать «фигура является ромбом тогда и только тогда, когда ее диагонали перпендикулярно пересекают друг друга пополам». Утверждение «если и только если» (сокращенно iff ) — это компактная форма для формулирования гипотезы и ее обращения вместе.
Для дальнейшего обсуждения и занятий в классе загрузите «Необходимые условия и достаточные условия» (из книги Беккера (1997) и распространяется с разрешения Национального совета учителей математики). См. Раздел «Логические отношения между условными операторами» в разделе «Инструменты математики».
ПРЕДПИСАНИЯ — НЕ ТЕОРЕМЫ
Мы все склонны полагать, что обнаруженная нами закономерность, вероятно, сохранится.Наша готовность высказывать предположение отражает это убеждение. Однако вера — это не то же самое, что истина, и мы должны помочь нашим ученикам стать соответствующим образом скептически (а также надеяться) на свои предположения. Когда они действительно обнаруживают, что предположение ложно, они все равно должны радоваться тому, что они открыли математическую истину. Я постоянно напоминаю своим классам, что «пример не доказательство», но простое повторение мантры не изменит привычек. Студенты должны на раннем этапе и часто пережить крах домыслов, в которых они не сомневались.Такой опыт возникнет в ходе их исследований, но мы также можем спланировать их как классные занятия.
Классическое упражнение для иллюстрации ценности скептицизма включает x 2 + x + 41. Начните с того, что учащиеся создадут таблицу с первой дюжиной или более значений полинома, когда x = 0, 1, 2, 3 и т. Д. Ищите наблюдения и предположения о возникающих ценностях. Все значения будут как нечетными, так и простыми. Студент также может отметить арифметическую последовательность различий между терминами.Спросите студентов, верят ли они, что этот многочлен всегда будет давать нечетные простые выходные данные. Спросите, что им нужно увидеть, чтобы так или иначе убедиться в этом. Если предлагается проверить другие примеры, пусть они продолжают вставлять значения для x . потерпи. Попробуй их измотать! По мере того, как ученики расширяют таблицу, они увидят, что закономерности сохраняются. Убеждены ли они сейчас? Сколько терминов нужно, чтобы их поколебать? Как они могут активно придерживаться скептического подхода? Могут ли они активно искать значения x , которые могут не дать простое или нечетное число? Дайте им время сделать это.Первые сорок членов будут простыми, но многочлен даст составное число (41 . 43), когда x = 41. Что, если не появится нечетный контрпример? Может ли это проявиться после миллионов подтверждающих примеров? Могут ли они доказать, что многочлен всегда нечетный для целых чисел x ?
Замечательный пример, которым стоит поделиться со студентами, — это номер 1 + 1141 n 2 (Sowder and Harel 1998). Существуют ли значения для n , которые делают это выражение точным квадратом? Оказывается, все n от 1 до 30 693 385 322 765 657 197 397 207 не дают полного квадрата.Однако, если кто-то попробует 1 + 1141 . 30 693 385 322 765 657 197 397 208 2 , возникает полный квадрат. Итак, не только пример не является доказательством, но и более 30 септиллионов последовательных примеров не должны составлять убедительный аргумент.
Даже бесконечное количество примеров не исключает возможности контрпримера. Например, учащиеся могут придумать неограниченное количество примеров деления рационального числа на рациональное число, дающего рациональное число, но рациональные числа не закрываются при делении из-за 0.См. Раздел «Понимание определений: замкнутый и плотный » и связанные с ним раздаточные материалы в главе «Числа в контексте» книги «Математическое моделирование» для дополнительных обсуждений и действий, которые подтверждают необходимость тщательного поиска контрпримеров и доказательств.
ЗАКЛЮЧЕНИЕ
Гадание можно сделать обычным делом в рамках любого класса. Любая математическая тема может быть источником закономерностей и возможностью генерировать предположения.Как только учащиеся освоятся в процессе развития предположений, они начнут инициировать исследования, основанные на своих наблюдениях, и исследования станут повседневной возможностью. В дополнение к обучению студентов тому, как развиваются математические знания, акцент на догадках часто оказывается интересным для студентов. Этот повышенный интерес способствует более длительному воспоминанию и овладению техническими навыками, которые практикуются во время расследования. Относительная открытость предположительной деятельности также ставит учащихся в ситуации, когда их заблуждения или противоречивые представления об идее с большей вероятностью будут выявлены, а затем разрешены.
БИБЛИОГРАФИЯ
Абрамс, Джошуа (2001). Математическое моделирование . В Интернете по адресу www.meaningfulmath.org/modeling.
Беккер, Джерри и Шимада, Сигеру (1997). Открытый подход: новое предложение по обучению математике . Рестон, Вирджиния: Национальный совет учителей математики.
Разрушение шоколадных плиток доступно в Интернете по адресу http://www.cut-the-knot.com/proofs/chocolad.html.
Центр развития образования (2000). Связанная геометрия . Чикаго, Иллинойс: Корпорация повседневного обучения.
Центр развития образования (2001 г.). Математические методы: разделы дискретной и предварительной математики . Армонк, штат Нью-Йорк: пора.
Матвеев, С (2000, ноябрь / декабрь). Борьба с перекрученными обручами. Quantum , 8–12.
Соудер, Ларри и Гершон Харел (1998, ноябрь). Виды студенческих обоснований. Учитель математики , 670–675.


