Список характеров: Читать онлайн «Типы характеров», Ольга Новодворская – Литрес

Опубликовано 09.07.202305.05.2023 автором alexxlab

Содержание

Читать онлайн «Типы характеров», Ольга Новодворская – Литрес

Об авторе

Ольга Владимировна Новодворская (Гуревич) по специальности педагог, её хобби – соционика и поэзия. Остальные её произведения печатаются под её прошлой фамилией – Новодворская. Автор посвятила много лет изучению соционики, изучающей 16 типов характеров людей и их взаимоотношения. Глубокий анализ и дополнительные знания помогли ей сделать открытие, революционное для соционики. Она систематизировала типы характеров, расположила их на карте-шаре. Благодаря этой карте стали понятны дополнительные типы характера каждого человека. Было доказано, что в человеке есть все 8 парных функций. До этого открытия соционики считали, что поведение, не соответствующее главному типу характера человека это не нормально. Сделанное открытие даёт понимание, что это нормально. Стало понятно, почему порой так различны люди одного типа характера. Ответ – в них разное количество добавочных типов характера. Автор – поэтесса с большим опытом. В Стихах.ру представлены сотни её стихов (под псевдонимом Новодворская, это фамилия её мамы). Умение рифмовать помогло ей представить в стихах каждый тип характера в детстве и в зрелом возрасте. Благодаря поэтической форме суть каждого типа характера видна более ярко.

Вступление

Соционика изучает 16 типов характеров людей. Я систематизировала все типы на карте-шаре, описала их в поэтической форме, дала примеры известных людей. Эти знания помогут вам понять сильные и слабые стороны – свои, друзей, родных, сослуживцев, политиков и т.д. Вам будет легче правильно выбрать специальность и хобби, подходящего супруга, правильно воспитывать ребёнка и избегать конфликтов с людьми.Раньше соционики утверждали, что каждый человек – это только один тип характера, а проявления в нём других типов выбиралось произвольно, не научно и считалось отклонением от нормы. Я утверждаю, что это норма, так как у каждого есть главный тип и добавки типов, расположенных на карте по соседству с главным типом характера. В каждом человеке есть все соционистические характеристики (функции), но в разном количестве. Все эти функции дуальны (в сумме 100% есть в каждом): этика и сенсорика, логика и интуиция, интроверсия и экстраверсия, рациональность и иррациональность (на карте-шаре им соответствуют полушарии). Каждые четыре типа по порядку – это квадра. Человеку приятнее всего быть с людьми из его квадры. После каждой четвёрки типов от 1-го до 16 -го указаны пары – сочетания типов – оптимальные для создания семьи по принципу дополнения. Одинаковость должна быть только по одной функции, чтоб хоть что-то скрепляло союз через понимание, единство желаний и взглядов. В правильном семейном союзе муж и жена разные: он логик, она этик, муж сенсорик, жена интуит. Таким образом будет взаимопомощь, меньше ошибок, дети получат от родителей примеры поведения по всем функциям.

Соционика родилась в середине 20 века. Активно развивалась в России и США. В США её изучают в военных школах, крупные фирмы заказывают консультации социоников, чтобы правильно подобрать кадры. В России много центров консультаций социоников, особенно по вопросам выбора супруга, семейным конфликтам и воспитанию детей. В России 16-ти типам характеров даны клички (Дон-Кихот, Дюма, Гюго и др). Некоторые из них выбраны неправильно, на мой взгляд. В США этим же типам даны названия английскими буквами (приведены в моей таблице) – это первые буквы главных соционистических характеристик.

Тесты для определения типа характера есть в интернете, к примеру http://socioline.ru/_shows/socionica.php

С помощью теста и стихов вы выберете ваш тип характера, потом найдёте его на составленной мной и представленной ниже карте. Вы увидите, какие типы характера соседние с вашим, значит, и такими вы можете быть. В некоторых людях какой-то из соседних типов проявляется очень ярко. У каждого человека есть все 8 функций, каждая в проценте меньше 100 %. Функции парные, в сумме 100 %.

Экстраверсия + интроверсия = 100%

Логика + этика = 100%

Сенсорика + интуиция = 100%

Рациональность + иррациональность = 100%

К примеру, если в вас больше 50 % экстраверсии, то вы экстраверт.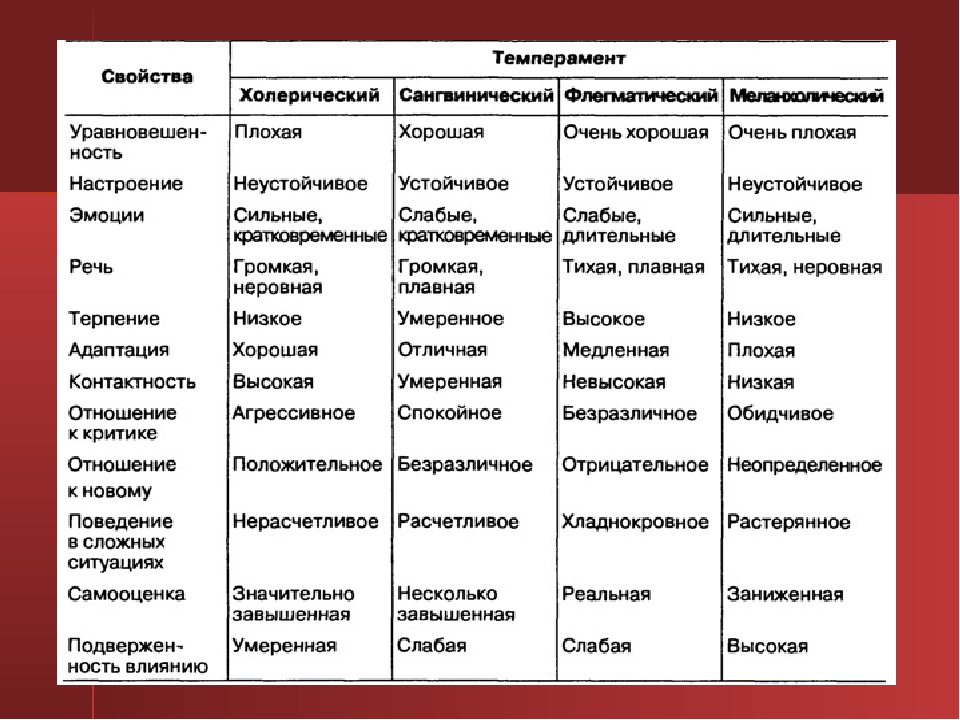 и так по каждой характеристике -функции.

Личная территория каждого человека на карте типов должна частично захватывать все виды полушарий (все 8 функций). При этом обязательно в центре этой личной территории окажется один квадрат целиком и немного от всех соседних, но не более 50 % от каждого соседнего квадрата. Люди одного типа отличаются составом этих добавок.

Судьба страны, любого предприятия или фирмы зависят от правильности выбора руководителя. К примеру, лучшие руководители (от директора какого-то заведения или предприятия и до президента страны) – это логики-интуиты. Вы найдёте их на карте, прочитаете их описание в стихах. Беда современного общества – преобладание у руководителей всех рангов сенсорики в ущерб интуиции и рациональности в ущерб иррациональности, им трудно принять новаторство. Интуиция и сенсорика – две дополняющие функции, чем больше одна, тем меньше другая. Сенсорика – восприятие с помощью органов чувств – с помощью массы (жировой и мышечной). Зачем сильно сенсорному слону интуиция, он и силой может достичь цели. Интуиция нужна тонким, лёгким животным. У людей то же самое. У худых восприятие происходит головным мозгом, благодаря интуиции. Экстраверты более активные в компании, любят общение, интраверты наоборот.

Новорождённый и старик перед смертью почти 100 % интраверсии.

Рационал видит мир приближенно (как в кинотеатре видят экран с первого ряда, чётко видит детали). Рационал – хороший исполнитель, забьёт гвоздь точно, он “здесь и сейчас”, может сосредоточиться, видит детали. Иррационал одновременно видит многое (как в кинотеатре видят экран с дальнего ряда), это даёт целостное видение мира, видны взаимосвязи, но плохо видны детали. Иррационал может сделать открытия на стыке наук, писать стихи, но он часто рассеянный, как будто не “здесь и сейчас”.

Лучшие поэты – это иррациональные типы: Советчики, Романтики. У Новатора и Советчика самая сильная интуиция возможностей. Многие открытия делаются именно такими людьми. Агрессивные типы (их агрессия возможна, но не обязательна) – это экстраверты обладатели сенсорики в первой главной функции. Они очень мышечные, ширококостные, сильные физически. Это типы Маршал (Жуков) и Политик (Наполеон). Агрессия может проявляться и у интровертов, обладателей сенсорики во второй функции – у Инспектора (Горький) и у Моралиста (Драйзер). Женщины, выходящие замуж за таких мужчин, должны быть очень осторожны, уметь не спорить, подчиниться, вовремя скрыться, чтобы не стать жертвой насилия, не получить травму.

Каждому типу присвоено название и кличка. К примеру, интуитивно-логический экстраверт получил название Новатор и кличку Дон Кихот. Клички, когда-то придуманные российскими социониками, часто не соответствуют истине. К примеру, есть тип с кличкой Бальзак. Но у писателя Бальзака главный тип не Бальзак, а Дюма. А у писателя Дюма главный тип не Дюма, а Наполеон с добавкой Советчика.

Вот раскрытый шар – таблица,

В ней характеры все, лица.

Пушкин положил бы лист,

Где Советчик и Артист,

Чуть прикрыв квадрат – Новатор,

И чуть – Экспериментатор.

Нет плохих “квадратов”! Эта

Список спецкурсов и семинаров Научно-образовательного центра при МИАН на осенний семестр 2022/2023 — ФПМИ

В Математическом центре мирового уровня «Математический институт им. В.А. Стеклова Российской академии наук» (МЦМУ МИАН) реализуется Научно-образовательная программа (НОЦ МИАН). Ее целью является подготовка сильных студентов, желающих заниматься математикой и физикой на профессиональном уровне. Ведущие ученые читают специальные курсы и ведут исследовательские семинары по основным математическим и физическим дисциплинам.

Занятия проходят в вечернее время в здании Математического института (Москва, ул. Губкина, 8), как правило, начиная с 18:00. Начало семестра 12 сентября 2022 г. По окончании каждого семестра в НОЦ МИАН проводятся экзамены, результаты которых можно перезачесть в Физтех-школе прикладной математики и информатики МФТИ.

Кроме того, у студентов есть уникальная возможность войти в круг современных математических методов и идей путём участия в занятиях Базовой кафедры Математического института, открытой в 2020 году в МФТИ. Магистранты кафедры проводят научные исследования под руководством ведущих ученых МИАН.

Учебный план кафедры даёт студенту возможность выбрать одну из двух «линеек» (траекторий) обучения: «алгоритмические вопросы логики, алгебры и теории чисел» и «математические методы квантовых технологий», соответствующих двум направлениям подготовки.

На все курсы необходима обязательная регистрация. Вся информация и возможные изменения в расписании доступны на сайте НОЦ МИАН

Список курсов

Курс «Математические основания квантовой механики»
Семинар «Перспективные направления в КТП и суперструнах»
Совместный семинар НОЦ и ВШЭ «Представления и вероятность»

Семинар «Квантовая математическая физика»
Семинар «Семинар по арифметической геометрии»
Курс «Теория мартингалов и стохастическое интегрирование»
Курс «Введение в теорию характеров линейных представлений конечных групп»
Курс «Метод чейнинга и его приложения в вопросах анализа»
Семинар «Неклассические логики»
Курс «Введение в геометрическую теорию групп»
Семинар «Геометрическая теория групп»
Курс «Приложения теории детонации к проблемам энергетики и взрывобезопасности»
Семинар «Семинар по геометрической топологии»
Семинар «Алгебраические кривые»
Курс «Геометрическая теория управления, субриманова геометрия и их приложения»
Курс «Арифметические поверхности»
Курс «Математика анализа данных»

Курс «Математические основания квантовой механики»

Срок проведения: 12 сентября–26 декабря 2022 г.
День и время: понедельник, 18:00
Место проведения: МИАН, комн. 313 (ул. Губкина, 8) + online
Лектор: Г. Г. Амосов

Математическая аксиоматика квантовой механики приводит к возникновению новой математической дисциплины – некоммутативной теории вероятностей. При таком подходе случайные величины определяются положительными операторнозначными мерами, а математические ожидания задаются положительными функционалами на алгебре всех ограниченных операторов. При этом свойства дисперсий и ковариаций в некоммутативной теории вероятностей оказываются отличными от их классических аналогов. Подробнее

Семинар «Перспективные направления в КТП и суперструнах»

Срок проведения: 12 сентября–26 декабря 2022 г.
День и время: понедельник, 18:00
Место проведения: МИАН, комн. 404 (ул. Губкина, 8) + online
Руководитель: И. Я. Арефьева

В настоящем семестре, в основном, будут рассмотрены следующие две задачи:

Задача о роли энтропии зацепленности в физике высоких энергий и ее вычислении в локальных теориях, в частности, для калибровочных теорий и в классической гравитации.

Задача, связанная с проблемой информационного парадокса и голографическим взглядом на ее возможное решение. В связи с обнаруженным недавно взрыво-подобном поведением излучения Хокинга, вычисленного с помощью островной формулы в метрике Шварцшильда, предполагается изучать разные модели испарения черных дыр, препятствующие этому поведению. Подробнее

Совместный семинар НОЦ и ВШЭ «Представления и вероятность»

Срок проведения: 20 января 2020 – 29 декабря 2022 г.
День и время: четверг, 18:00
Место проведения: МИАН, комн. 303 (ул. Губкина, 8) + online
Руководители: А. И. Буфетов, А. В. Дымов, А. В. Клименко, М. Мариани, Г. И. Ольшанский

Семинар посвящён современным результатам в областях, связанных с теорией представлений и теорией вероятностей, а также их более старым разделам, которые как составляют базу для этих новых результатов, так и представляют собственный интерес. Семинар рассчитан на студентов 3–4 курсов бакалавриата, магистрантов и аспирантов. Подробнее

Семинар «Квантовая математическая физика»

Срок проведения: 10 февраля 2021 – 28 декабря 2022 г.
День и время: среда, 18:00
Место проведения: online
Руководители: И. В. Волович, В. В. Козлов, С. В. Козырев, А. С. Трушечкин

Спецсеминар посвящен математическим вопросам динамики сложных квантовых систем. В данный момент изучаются следующие темы: математические вопросы динамики открытых квантовых систем, информационный парадокс в черных дырах, математическое описание сложных систем в биологии, инвариантные меры и их продолжения.

Также всегда в центре внимания участников семинара находятся такие фундаментальные вопросы математической и теоретической физики, как обоснование статистической механики и термодинамики, необратимости времени, процессов термализации (установления теплового равновесия). Подробнее

Семинар «Семинар по арифметической геометрии»

Срок проведения: с 12 сентября 2022 г.
День и время: понедельник, 15:00-17:00
Место проведения: МИАН, комн. 303 (ул. Губкина, 8) + online
Руководители: В.А. Вологодский, С.О. Горчинский, Д.В. Осипов, С.Ю. Рыбаков

На семинаре будут разбираться различные темы из арифметической геометрии, как современные, так и уже ставшие классикой. Предполагается, что участники, в основном студенты и аспиранты, будут по очереди делать серии докладов. При этом мы будем стараться разбирать сложные понятия на простых примерах, а также изучать механизмы доказательств различных интересных результатов.

Доклады должны быть доступны широкому ряду слушателей, знакомых с основами алгебраической геометрии и алгебраической теории чисел. Подробнее

Курс «Теория мартингалов и стохастическое интегрирование»

Срок проведения: 16 сентября–30 декабря 2022 г.
День и время: пятница, 18:00
Место проведения: МИАН, комн. 530 (ул. Губкина, 8) + online
Лектор: М. В. Житлухин

Мартингалом называется случайный процесс, который в будущем остается в среднем постоянным. Мартингалы находят широкое применение в теории вероятностей и, в особенности, в стохастическом исчислении, а также различных приложениях, например, в финансовой математике. Цель этого курса — познакомить слушателей с основными понятиями и результатами теории мартингалов, а также их приложениями, связанными с интегрированием по случайным процессам.

Подробнее

Курс «Введение в теорию характеров линейных представлений конечных групп»

Срок проведения: 13 сентября–27 декабря 2022 г.
День и время: вторник, 18:30
Место проведения: МИАН, комн. 530 (ул. Губкина, 8) + online
Лектор: Д. Д. Киселев

Целью курса является знакомство слушателей с теорией характеров обыкновенных представлений конечных групп и ее применением для изучения строения конечных групп. Планируется обсудить помимо классических аспектов теории характеров (соотношения ортогональности, индуцирование характеров, закон взаимности Фробениуса, число неприводимых комплексных характеров конечной группы, и т.п.), теорему Бернсайда о разрешимости групп порядка pαqβ, теорему Фробениуса о группах Фробениуса, характеризацию Брауэра кольца обобщенных комплексных характеров и, как следствие, теорему Брауэра о реализуемости неприводимых комплексных представлений конечной группы порядка n в n-круговом расширении поля рациональных чисел.

Будет дан экскурс в теорию индекса Шура комплексных характеров, а также дана оценка полей разложения конечных групп на основе теоремы Голдшмидта-Айзекса. Подробнее

Курс «Метод чейнинга и его приложения в вопросах анализа»

Срок проведения: 14 сентября–28 декабря 2022 г.
День и время: среда, 18:00
Место проведения: МИАН, комн. 530 (ул. Губкина, 8) + online

Лектор: Е. Д. Косов

Обобщенный метод чейнинга является мощным современным средством получения верхних оценок для ожидания максимума случайного процесса. Базовая идея чейнинга впервые встречается у Колмогорова при доказательстве уже ставшей классической теоремы о непрерывности траекторий случайного процесса при выполнении условий Колмогорова. Современные же приложения метода обобщенного чейнинга уходят далеко за пределы теории случайных процессов. В частности, метод чейнинга нашел применения в вопросах геометрии конечномерных банаховых пространств. В рамках курса предполагается, во-первых, познакомиться с основными идеями и аппаратом обобщенного метода чейнинга. Во-вторых, мы посмотрим на возможные приложения метода для вопросов вложения N-мерных подпространств пространств Lp[0,1] в Rонечномерные пространства ℓm(N)p. Подробнее

Семинар «Неклассические логики»

Срок проведения: 14 сентября–28 декабря 2022 г.
День и время: среда, 18:00
Место проведения: МИАН, комн. 313 (ул. Губкина, 8) + online
Руководители: С. Л. Кузнецов, С. О. Сперанский

Традиционно всякая логика, отличная от классической, называется «неклассической». Существует много неклассических логик, которые применяются в основаниях математики, информатике, формальной философии и эпистемологии, лингвистике и т.д. Причины, по которым ту или иную логическую систему называют неклассической, могут быть самыми разнообразными. Неклассические логики могут быть сильно полны относительно подходящей семантики, сильно отличающейся от классической (семантики возможных миров, топологической семантики, алгебраической семантики, теоретико-игровой семантики и т.д.). Вместе с тем для некоторых неклассических логик не существует полных дедуктивных систем ввиду их большой алгоритмической сложности; однако такие логики по-прежнему можно изучать с теоретико-модельной точки зрения. Подробнее

Курс «Введение в геометрическую теорию групп»

Срок проведения: 12 сентября–26 декабря 2022 г.
День и время: понедельник, 18:00
Место проведения: МИАН, комн. 430 (ул. Губкина, 8) + online
Лектор: И.Г. Лысёнок

Цель спецкурса — ознакомление слушателей с ключевыми понятиями и методами геометрической теории групп. В частности, будет дано представление о теории групп, действующих на деревьях (теории Басса-Серра), квазиизометрических отображениях пространств, гиперболических метрических пространствах и гиперболических группах в смысле Громова. От участников спецкурса не требуется специальной подготовки, достаточно лишь знания алгебры в объеме университетского курса, а также начальных понятий топологии. Приглашаются студенты любых курсов и аспиранты. Подробнее

Семинар «Геометрическая теория групп»

Срок проведения: 11 февраля 2021 – 29 декабря 2022 г.
День и время: четверг, 18:00
Место проведения: МИАН, комн. 430 (ул. Губкина, 8) + online
Руководители: И. Г. Лысенок, А. Л. Таламбуца

Основная цель семинара — обзор и изложение интересных результатов в области геометрической теории групп и смежных областях, полученных за последние несколько десятилетий. Доклады будут готовиться на основе опубликованных статей разных авторов. От участников не требуется специальной подготовки, однако желательно быть ознакомленными с классическими понятиями геометрической теории групп, например, такими, как гиперболическая группа, функция Дэна группы или фундаментальная группа графа групп. Подробнее

Курс «Приложения теории детонации к проблемам энергетики и взрывобезопасности»

Срок проведения: 13 сентября–27 декабря 2022 г.
День и время: вторник, 18:00
Место проведения: online
Лектор: В.В. Марков

Предлагаемый курс лекций является продолжением серии лекций под общим названием «Введение в теорию газовой детонации», прочитанных в течение трех семестров в 2020 и 2021 годах. В них были представлены сведения по газодинамике реагирующих смесей, моделям детонации, проблемам инициирования и распространения детонации в одномерном, двумерном и трехмерном приближении, численному моделированию быстропротекающих процессов на современных многопроцессорных вычислительных комплексах, таких как суперкомпьютер МГУ «Ломоносов». В осеннем курсе 2022 года предполагается дать анализ возможности и целесообразности применения детонации в энергоустановках различного назначения, прежде всего в реактивных двигателях, представить постановки и решения задач о процессах для ряда конкретных устройств, в которых реализуется высокоскоростной режим детонационного сжигания газообразного топлива, Предполагается рассмотреть проблемы управления детонацией, в частности, различные методы поддержания, подавления и предотвращения. Подробнее

Семинар «Семинар по геометрической топологии»

Срок проведения: с 14 сентября 2022 г.
День и время: среда, 17:00
Место проведения: МИАН, комн. 430 (ул. Губкина, 8) + online
Руководители: С.А. Мелихов, Е.В. Щепин

Топология – это наука о свойствах, инвариантных при гомеоморфизме и его стандартных вариациях (диффеоморфизм, кусочно-линейный гомеоморфизм, гомеоморфизм пар, послойный гомеоморфизм и т.п.). Геометрическая топология ограничивается рассмотрением пространств, доступных геометрической интуиции (например, подмножеств евклидовых пространств Rn) и исходит из элементарных вопросов, имеющих наглядный геометрический смысл. При этом методы, которыми решаются эти вопросы, могут быть далеки от элементарных и могут залезать глубоко в другие науки (алгебраическую топологию, теорию групп, алгебраическую K-теорию, общую топологию, метрическую геометрию, теорию представлений, функциональный анализ и т. д.). Подробнее

Семинар «Алгебраические кривые»

Срок проведения: 14 сентября–28 декабря 2022 г.
День и время: среда, 18:00
Место проведения: МИАН, комн. 540 (ул. Губкина, 8) + online
Руководители: Д. О. Орлов, Ю. Г. Прохоров, К. А. Шрамов

В рамках семинара будут разобрано несколько сюжетов из базовой теории алгебраических кривых: теорема Римана-Роха, формула Римана-Гурвица, оценки на порядок группы автоморфизмов и её достижимость, оценка Кастельнуово на род кривой, теорема Белого и т.д. От участников требуется знакомство с основными понятиями алгебраической геометрии. Подробнее

Курс «Геометрическая теория управления, субриманова геометрия и их приложения»

Срок проведения: 13 сентября–27 декабря 2022 г.
День и время: вторник, 18:00
Место проведения: online
Лектор: Ю. Л. Сачков

Курс из 10 лекций будет посвящен введению в геометрическую теорию управления и ее приложения. Будут рассмотрены задачи управляемости, оптимального управления, и субримановой геометрии, а также их приложения к механике, робототехнике, моделям зрения и обработке изображений, теории вероятностей. Курс рассчитан на студентов-математикой и физиков (начиная с 3-го курса) и аспирантов. Предварительные знания теории управления не предполагаются. Подробнее

Курс «Арифметические поверхности»

Срок проведения: 12 сентября–26 декабря 2022 г.
День и время: понедельник, 18:00
Место проведения: МИАН, комн. 303 (ул. Губкина, 8) + online
Лектор: Г.Б. Шабат

Будут даны основные определения, связанные со схемами Гротендика и их морфизмами, формализующими интуитивное понятие «семейство кривых». Кривые над полями алгебраических чисел будут интерпретированы как семейства кривых над кольцами целых чисел этих полей. Особое внимание будет уделено семействам эллиптических кривых. Будет дано введение в геометрию Аракелова, понимаемую как решение проблемы пополнения арифметической поверхности. Подробнее

Курс «Математика анализа данных»

Срок проведения: 16 сентября–30 декабря 2022 г.
День и время: пятница, 19:00
Место проведения: МИАН, комн. 430 (ул. Губкина, 8) + online
Лектор: Р.В. Шамин

В курсе будут изложены основы математических методов анализа данных. Будут рассмотрены такие методы как линейная и нелинейная регрессия, анализ и прогноз временных рядов, кластеризация и снижение размерности данных, решающие деревья и семплирование данных. Методы анализа данных будут представлены с точки зрения машинного обучения. Математические основы: линейная алгебра, математический анализ, теория вероятности, математическая статистика и случайные процессы будут изложены в контексте анализа данных. Курс будет интересен всем, кому интересно как математика применяется при анализе данных, и желающим понять основы анализа данных с точки зрения математика. Подробнее

100 величайших персонажей за последние 20 лет: вот наш полный список!

30 Rock

Чтобы отпраздновать 20-летие Entertainment Weekly (еще один год, и мы наконец-то сможем выпить!), сценаристы и редакторы тщательно составили список 100 величайших персонажей поп-культуры за последние годы. последние 20 лет. Были ли вымышленные женщины, мужчины, людоеды, куклы, младенцы и мультяшные рокеры, которые попали в наш список, изначально созданы до 1990 года, не имело значения, пока они оказали длительное влияние на культуру после 19 лет.90. Некоторые персонажи были настолько неразделимы в наших умах и сердцах — как, например, некая остроумная телевизионная мать и дочь, — что мы просто перечислили их вместе. (Эй, это наш список, поэтому мы должны установить правила.) Будьте уверены, мы тщательно обдумывали, спорили, спорили и спорили о том, кто попадет в список и какое место они заслуживают; после того, как вы ознакомитесь с нашим списком, не стесняйтесь делать то же самое в комментариях.

100. Тим Риггинс из Friday Night Lights

99. Невеста из Убить Билла

98. Лисбет Саландер из Девушка с татуировкой дракона и ее продолжения

97. Вайолет Уэстон из Август: Графство Осейдж 900 06

96. Берни Мак из Шоу Берни Мака

95. Вильгельмина из Уродливая Бетти

94. Трумэн из Шоу Трумана

93. Game Boys: Натан Дрейк из Серия Uncharted ; Кратос из Серия God of War ; и Нико Беллик из Grand Theft Auto IV

92. Кристофер Бун из Загадочное ночное происшествие с собакой

91. Хэнкок из Хэнкок

90. Мардж Гандерсон из Фарго

89. Викус ван де Мерве из Район 9

88. Наполеон Динамит из Наполеон Динамит

87. Тони Старк из Железный Человек серия

86. Карен Уокер и Джек МакФарланд из Уилл и Грейс

85. Дэниел Плейнвью из Там будет кровь

84. Доктор Грегори Хаус из Хаус, доктор медицины 9 0003

83. Джен Ю из Крадущийся тигр, затаившийся дракон

82. Трейси Флик из Выборы

81. Аманда Вудворд из Мелроуз Плейс

80. Gorillaz, анимированная рок-группа

9000 2 79. Эльфаба из Wicked
78. Пэтти Хьюз из Damages
77. Мими Маркес из Rent
76. Тайлер Дерден из Fight Club
75. Дэвид Брент из The Office (исходная версия)
74. Дон Дрейпер из «Безумцы»
73. Кэтрин Траммелл из «Основной инстинкт»
72. Кара «Старбак» Фрайс из Battlestar Galactica
71 Дет. Алонзо Харрис из Training Day
70. Мэри Кэтрин Галлахер из Saturday Night Live
69. Миранда Пристли из Дьявол носит Prada
68. Эффи Уайт из Dreamgirls
67. Борат из Борат: культурный Знания Америки на благо славной нации Казахстана
66. Элли и Ной из Записная книжка
65. Лорелай и Рори Гилмор из Девочки Гилмор
64. Максимус из Гладиатор
63. Джон Лок из Потерянный
62. Джимми Корриган из Джимми Корриган: Самый умный ребенок на Земле
90 002 61. Вик Макки из Щит

59. Мастер Чиф из серии Halo

58. Тельма и Луиза из Тельма и Луиза

57. Клейтон Бигсби из Chappelle’s Show

56. Барни Стинсон из Как я встретил вашу маму

55. Трейси Джордан из 30 Rock

54. Юнона из Юнона

53. Эдвард Каллен из Сумерки сага

52. Энни Уилкс из Мизери

51. Омар Литтл из Прослушка

50. Жемчуг Хозяйка из Юмор orDie.com

49. Вивиан Уорд из Красотка

48. Рыжая из Побег из Шоушенка

47. Корки Сент-Клер В ожидании Гаффмана

4 6. Джерри Магуайр из Джерри Магуайр

45. Стьюи Гриффин из Гриффины

44. Джек Бауэр из 24

43. Кэл Стефанидес из Мидлсекс

42. Сидней Бристоу из Псевдоним 90 006

41. Гарольд и Кумар из Гарольд и Кумар Серия

40. Рон Бургунди из Ведущий: Легенда о Роне Бургунди

39. Гоб Блат из Замедленное развитие

38. Элмо из 9000 Улица Сезам, 5

37. Кайзер Сёзе из Подозреваемые

36. Голлум из Властелин колец

35. Декстер Морган из Декстер

34. Шер из Бестолковые 9 0006

33. Сара Коннор из Терминатор 2: Судный день

32. Бивис и Батхед из Бивис и Батхед

31. Форрест Гамп из Форрест Гамп

30. » Стивен Колберт» из The Colbert Report

29. Винсент Вега и Джулс Виннфилд из Криминальное чтиво

28. Мадея из нескольких фильмов и пьес Тайлера Перри

27. Фрейзер из Фрейзер

26. Кавалер и Клэй из Удивительные приключения Кавалера и Клея

25. Вуди из серии История игрушек

24. Фелисити Портер из серии Фелисити

23. Остин Пауэрс из серии Остин Пауэрс 900 03

22. Эрик Картман из South Park

20 19. Морфеус из серии Матрица

17. Лара Крофт из серии Tomb Raider

16. Бриджит Джонс из серии

Бриджит Джонс сериал

15. Шрек из Шрек сериал

14. Джефф «Чувак» Лебовски из Большой Лебовски

13. Джек Воробей из 900 05 Пираты Карибского моря серия

12 Фокс Малдер и Дана Скалли из Секретные материалы

11. Космо Крамер из Сайнфельд

10. Губка Боб Квадратные Штаны из Губка Боб Квадратные Штаны

900 02 9.

Кэрри Брэдшоу из Секс в большом городе

8. Ганнибал Лектер из Молчание ягнят и его продолжения

7. Эдвард Руки-ножницы из Эдвард Руки-ножницы

6. Рэйчел Грин из Друзья

5. Джокер из Темный рыцарь

4. Тони Сопрано из Сопрано

3. Баффи из Баффи — истребительница вампиров

1. Гомер Симпсон из Симпсоны

Чтобы узнать больше из нашего выпуска «100 величайших персонажей», в том числе Уилла Феррелла о Роне Бургунди, Джонни Деппа о Джеке Воробье, Джосса Уидона о Баффи — истребительнице вампиров и интервью с Гомером Симпсоном, загрузите выпуск в газетных киосках прямо сейчас.

Обзоры эпизодов

30 Рок

Тина Фей, Алек Болдуин и Трейси Морган снялись в комедии, получившей премию «Эмми». Ты хочешь пойти туда.

тип
сезоны
рейтинг
сеть
потоковая служба

100 самых знаковых вымышленных персонажей

10 0 самые знаковые, известные и вообще любимые вымышленные персонажи кино, телевидения, литературы и поп-культуры с начала 20-го века.

Супермен (первое появление: 1938 г.) Создано Джерри Сигалом и Джо Шустером для Action Comics # 1 (DC Comics).
Микки Маус (1928) Создан Уолтом Диснеем и Ub Iworks для Steamboat Willie .
Джеймс Бонд (1953) Создано Яном Флемингом для романа Casino Royale .
Багз Банни (1940) Создано Warner Bros и первоначально озвучено Мелом Бланком.
Бэтмен (1939) Создан Биллом Фингером и Бобом Кейном для Detective Comics # 27 (DC Comics).
Дороти Гейл (1900) Создано Л. Фрэнком Баумом для романа Чудесный волшебник из страны Оз. Позже сыгран Джуди Гарланд в экранизации 1939 года.
Дарт Вейдер (1977) Создан Джорджем Лукасом для Звездных войн IV: Новая надежда.
Бродяга (1914) Создан и изображен Чарли Чаплином для Детские автогонки в Венеции.
Питер Пэн (1902 г.) Создано Дж. М. Барри для романа «Маленькая белая птичка».
Индиана Джонс (1981) Создан Джорджем Лукасом для рупий помощников Затерянного ковчега. Сыгран Харрисоном Фордом.
Рокки Бальбоа (1976) Создан и изображен Сильвестром Сталлоне для Рокки .
Вито Корлеоне (1969) Создан Марио Пьюзо для романа Крестный отец. Позже сыгран Марлоном Брандо и Робертом Де Ниро в экранизации Копполы.
Хан Соло (1977) Создан Джорджем Лукасом для Звездных войн IV: Новая надежда. Наиболее известный образ Харрисона Форда.
Гомер Симпсон (1987) Создан Мэттом Гроунингом для Шоу Трейси Ульман , позже Симпсоны , озвученный Дэном Кастелланетой.
Люси Рикардо (1951) В роли Люсиль Болл для Я люблю Люси.
Арчи Банкер (1971) Создан Норманом Лиром для Все в семье. В роли Кэрролла О’Коннора.
Кинг-Конг (1933) Создан Эдгаром Уоллесом и Мериан Си Купер для фильма Кинг-Конг .
Человек-паук (1962) Создано Стэном Ли и Стивом Дитко для Amazing Fantasy # 15 (Marvel Comics).
Барби (1959 г.) Создано Рут Хэндлер для компании по производству игрушек Маттел .
Спок (1964) Создан Джином Родденберри для Star Trek. Наиболее известен Леонард Нимой.
Годзилла (1954) Создано Томоюки Танакой, Иширо Хондой и Эйдзи Цубарая для фильма Годзилла .
Джокер (1940) Создано Джерри Робинсоном, Биллом Фингером и Бобом Кейном для Batman # 1 (DC Comics)
Скарлетт О’Хара (1936) Создано Маргарет Митчелл для романа Унесенные ветром. Наиболее известная роль Вивьен Ли в экранизации Виктора Флеминга 1939 года.
Винни-Пух (1924) Создано А.А. Милна для книги стихов «Когда мы были молоды».
Popeye (1929) Создано EC Segar для комикса Thimble Theater (King Features).
Тарзан (1912) Создан Эдгаром Райсом Берроузом для романа Тарзан из числа обезьян .
Форрест Гамп (1986) Создано Уинстоном Грумом для романа Форрест Гамп . Позже сыграл Тома Хэнкса в экранизации Земекиса.
Ганнибал Лектор (1981) Создан Томасом Харрисом для романа Красный дракон. Наиболее известен Энтони Хопкинсом в фильме Джонатана Демме 1991 года « Молчание ягнят».
Большая птица (1969) Создан Джимом Хенсоном и изображен Кэрроллом Спинни для Улицы Сезам.
Холден Колфилд (1945) Создан Дж. Д. Сэлинджером для рассказа Кольера «Я сумасшедший». Переработан в роман Т Над пропастью во ржи в 1951 году.
Тони Монтана (1983) Создано Оливером Стоуном для фильма Лицо со шрамом . Сыграл Аль Пачино.
Тони Сопрано (1999) Создано Дэвидом Чейзом для The Sopranos. Актер Джеймс Гандольфини.
Терминатор (1984) Создано Джеймсом Кэмероном и Гейл Энн Херд для The Terminator. Арнольд Шварценеггер.
Джон Сноу (1996) Создан Джорджем Мартином для романа Игра престолов . Актер Кит Харрингтон.
Норман Бейтс (1959) Создано Робертом Блохом для романа Psycho . Позже сыграл Энтони Перкинса в экранизации Хичкока.
Чарльз Фостер Кейн (1941) Создан и изображен Орсоном Уэллсом для Гражданин Кейн.
Марти Макфлай (1985) Создан Робертом Земекисом и Бобом Гейлом для «Назад в будущее». Актер Майкл Дж. Фокс.
Рик Блейн (1940) Создан Мюрреем Бернеттом и Джоан Элисон для так и не поставленной пьесы Все приходят к Рику. Позже сыгран Хамфри Богартом в экранизации Майкла Кертиса « Касабланка ».
Человек без имени (1964) Создано Серджио Леоне для A Fistful of Dollars , который был адаптирован из персонажа ронина в Куросаве Yojimbo (1961). Сыграл Клинт Иствуд.
Чарли Браун (1948) Создано Чарльзом М. Шульцем для комикса L’il Folks ; популяризирован два года спустя в Peanuts .
И.Т. (1982) Создано Мелиссой Мэтисон для фильма ET: The Extra-Terrestrial.
Артур Фонзарелли (1974) Создано Бобом Бруннером для шоу Happy Days. Актер Генри Винклер.
Филип Марлоу (1939) Создан Рэймондом Чендлером для романа Большой сон.
Джей Гэтсби (1925) Создан Ф. Скоттом Фицджеральдом для романа Великий Гэтсби.
Лесси (1938) Создано Эриком Найтом для статьи в Saturday Evening Post, позже превращенной в роман Лесси, вернись домой в 1940 году, экранизация в 1943 году и многолетнее телешоу в 1954 году. Наиболее известный образ собаки Пал.
Фред Флинтстоун (1959) Создано Уильямом Ханной и Джозефом Барбера для The Flintstones. Озвучен, в частности, Аланом Ридом.
Rooster Cogburn (1968) Создано Чарльзом Портисом для романа True Grit. Наиболее известен образ Джона Уэйна в экранизации 196
9.
Аттикус Финч (1960) Создано Харпер Ли для романа «Убить пересмешника «. (Появился в более ранней работе Go Set A Watchman , хотя она не была опубликована до 2015 года) Наиболее известен образ Грегори Пека в экранизации Роберта Маллигана.
Лягушка Кермит (1955) Создан и исполнен Джимом Хенсоном для шоу Сэм и друзья. Позже популяризировался в Улица Сезам (1969) и Маппет-шоу (1976)
Джордж Бейли (1943) Создано Филиппом Ван Дореном Стерном (тогда как Джордж Пратт) для рассказа The Greatest Gift . Позже он был адаптирован в фильме Капры « Это прекрасная жизнь » с Джеймсом Стюартом в главной роли в роли переименованного Джорджа Бейли.
Йода (1980) Создан Джорджем Лукасом для Империя наносит ответный удар.
Зорро (1919 г.) Создано Джонстоном Маккалли для статьи 9 журнала All-Story Weekly.0005 Проклятие Капистрано. Позже адаптирован к фильму Дугласа Фэрбенкса « Знак Зорро » (1920).
Мо, Ларри и Керли (1928) Создано Тедом Хили для водевиля Тед Хили и его марионетки.
Мэри Поппинс (1934) Создано П.Л. Трэверс для детской книги Мэри Поппинс.
Mario (1981) Создан Сигеру Миямото для видеоигры Donkey Kong.
Гарри Поттер (1997) Создано Дж.К. Роулинг за роман « Гарри Поттер и философский камень».
Холли Голайтли (1958) Создано Трумэном Капоте для новеллы Завтрак у Тиффани . Позже был адаптирован в фильмах Блейка Эдвардса 1961 года с Одри Хепберн в главной роли в роли Холли.
Гэндальф (1937) Создано Дж.Р.Р. Толкин за роман « Хоббит».
Гринч (1957) Создано доктором Сьюзом для рассказа «Как Гринч украл Рождество!»
Вилли Вонка (1964) Создан Роальдом Далем для детского романа Чарли и шоколадная фабрика.
Халк (1962) Создано Стэном Ли и Джеком Кирби для The Incredible Hulk # 1 (Marvel Comics)
Скуби-Ду (1969) Создано Джо Руби и Кеном Спирсом для шоу Скуби-Ду, где ты!
Сэм Мэлоун (1982) Создано Гленом и Лесом Чарльзом для шоу Cheers . Актер Тед Дэнсон.
Джордж Костанза (1989) Создано Ларри Дэвидом и Джерри Сайнфелдом для шоу Сайнфелд . Актер Джейсон Александр.
Жюль Уинфилд (1994) Создан Квентином Тарантино для фильма Криминальное чтиво. Актер Сэмюэл Л. Джексон.
Джон Макклейн (1988) На основе персонажа детектива Джо Лиланда, созданного Родериком Торпом для романа «Ничто не длится вечно». Позже был адаптирован в фильме Джона Мактернана «Крепкий орешек » с Брюсом Уиллисом в главной роли в роли Макклейна.
Эллен Рипли (1979) Создано Доном О’Бэнноном и Рональдом Шусеттом для фильма Чужой . В роли Сигурни Уивер.
Ральф Крамден (1951) Создан и сыгран Джеки Глисоном для «Молодоженов», ставшего отдельным шоу в 19 году.55.
Эдвард Руки-ножницы (1990) Создан Тимом Бертоном для фильма Эдвард Руки-ножницы . В роли Джонни Деппа.
Эрик Картман (1992) Создан Треем Паркером и Мэттом Стоуном для короткометражного мультфильма Иисус против Фрости . Позже он превратился в сериал «Южный парк », премьера которого состоялась в 1997 году. Озвучивает Трей Паркер.
Уолтер Уайт (2008) Создано Винсом Гиллиганом для Во все тяжкие . Сыгран Брайаном Крэнстоном.
Cosmo Kramer (1989) Создано Ларри Дэвидом и Джерри Сайнфелдом для Seinfeld . Актер Майкл Ричардс.
Pikachu (1996) Создан Ацуко Нисидой и Кеном Сугимори для видеоигры Pokemon и аниме-франшизы.
Майкл Скотт (2005 г.) Основан на персонаже из британского сериала «Офис », созданного Рики Жерве и Стивеном Мерчантом. Актер Стив Карелл.
Фредди Крюгер (1984) Создан Уэсом Крэйвеном для фильма Кошмар на улице Вязов. Самый известный образ Роберта Инглунда.
Капитан Америка (1941) Создано Джо Саймоном и Джеком Кирби для комиксов о Капитане Америка № 1 (Marvel Comics)
Goku (1984) Создано Акирой Ториямой для манги Dragon Ball Z.
Бэмби (1923) Создано Феликсом Зальтеном для детской книги Бэмби, жизнь в лесу. Позже адаптирован в диснеевском фильме Бэмби в 1942 году.
Рональд Макдональд (1963) Создан Вильярдом Скоттом для серии телевизионных роликов.
Waldo/Wally (1987) Создано Мартином Хэнфордом для детской книги Где Уолли? (Уолдо в американском издании)
Баффи Саммерс (1992) Создан Джоссом Уидоном для фильма «Баффи — истребительница вампиров». Актеры Кристи Суонсон и Сара Мишель Геллер.
Frasier Crane (1984) Создано Гленом и Лесом Чарльзом для Cheers . Актер Келси Граммар.
Омар Литтл (2002) Создано Дэвидом Саймоном для The Wire. Актер Майкл К. Уильямс.
Росомаха (1974) Создано Роем Томасом, Леном Вейном и Джоном Ромитой-старшим для The Incredible Hulk # 180 (Marvel Comics)
Рон Бургунди (2004) Создано Уиллом Ферреллом и Адамом Маккеем для фильма Ведущий: Легенда о Роне Бургунди . Актер Уилл Феррелл.
Джейсон Вурхиз (1980) Создан Виктором Миллером для фильма Пятница, 13-е.
Бетти Буп (1930) Создано Максом Флейшером и Grim Network для мультфильма Dizzy Dishes.
Чувак (1998) Создано Итаном и Джоэлом Коэнами для фильма Большой Лебовски. Актер Джефф Бриджес.
Бильбо Бэггинс (1937) Создано Дж.Р.Р. Толкин за роман Хоббит.
Том Джоуд (1939) Создан Джоном Стейнбеком для романа «Гроздья гнева». Позже был адаптирован в фильме Джона Форда 1940 года и сыгран Генри Фондой.
Тони Старк (Железный человек) (1963) Создано Стэном Ли, Ларри Либером, Доном Хеком и Джеком Кирби для Tales of Suspense # 39 (Marvel Comics)
Китнисс Эвердин (2008 г.) Создано Сюзанной Коллинз для романа «Голодные игры » . Позже ее сыграла Дженнифер Лоуренс во франшизе фильма.
Поросенок Порки (1935) Создан Фризом Фреленгом для короткометражного анимационного фильма У меня нет шляпы. Наиболее известный голос Мела Бланка.
Трэвис Бикл (1976) Создан Полом Шрейдером для фильма Таксист. Актер Роберт Де Ниро.
Соколиный глаз Пирс (1968) Создано Ричардом Хукером для романа MASH: Роман о трех армейских врачах. Знаменитый образ Алана Алды и Дональда Сазерленда.
Дон Дрейпер (2007) Создано Мэтью Вайнером для шоу Безумцы . Актер Джон Хэмм.
Клифф Хакстейбл (1984) Создан и сыгран Биллом Косби для Шоу Косби.
Шрек (1990) Создано Уильямом Стейгом для детской книги Шрек! Позже был адаптирован для фильма 2001 года с Майком Майерсом в главной роли в качестве главного героя.
Оптимус Прайм (1984) Создан Деннисом О’Нилом для линейки игрушек Transformers .