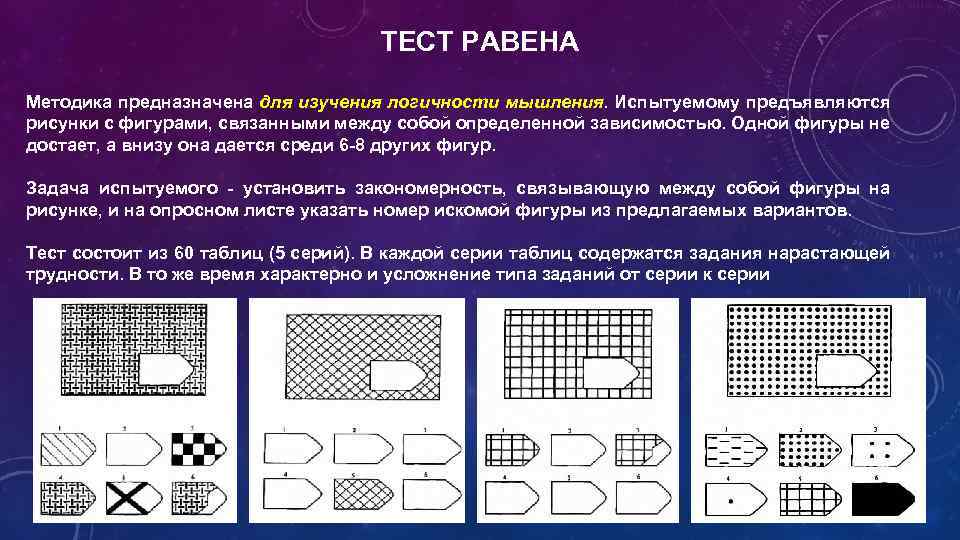
Таблицы равена для детей: Недопустимое название — Psylab.info
Прогрессивные матрицы дж. Равена
Скачать 2,52 Mb.
|
1 2 3 4 5 6 7 8 9 … 49
Связанные:
Практикум
| ПРОГРЕССИВНЫЕ МАТРИЦЫ ДЖ. РАВЕНА
В 1936г. Джон Равен, совместно с Л. Пенроузом, создал тест Прогрессивные матрицы, целью которого было изучение общего интеллекта личности. Дж. Равен являлся учеником Ч. Спирмена и создавая данную методику, опирался на его теорию. По мнению Ч. Спирмена, наилучшим способом определения интеллекта является тест на поиск абстрактных отношений. Кроме того, в основу зада- ний теста положена теория гештальта. Существует три основных варианта данного теста: более простой цветной тест, предназначенный для детей от 5 до 11 лет, черно-белый вариант для детей и подростков от 8 до 14 лет и взрослых от 20 до 65 лет, вариант теста (созданный в 1977 году Дж. 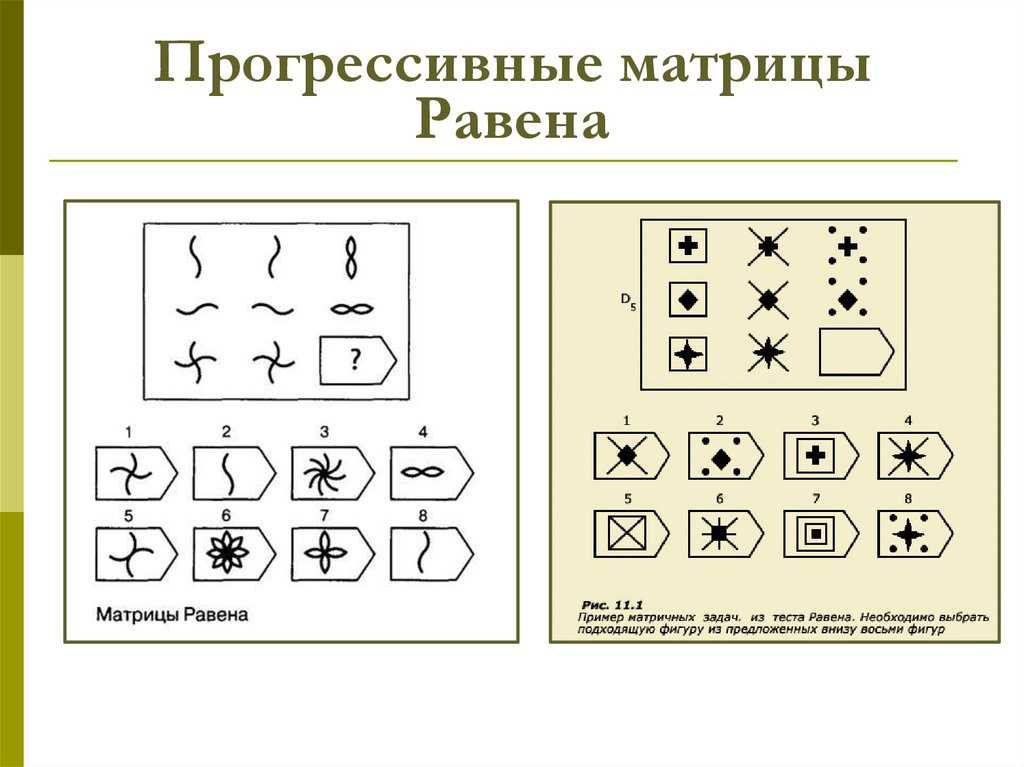 Равеном и Д. Кортом) предназначен для лиц с вы- сокими интеллектуальными достижениями. Он включает в себя не только невербальную, но и вер- бальную часть.
Тест может проводиться как с ограничением времени выполнения заданий, так и без ограниче- ния (по желанию исследователя). Описание стимульного материала. Черно-белый вариант тест «Прогрессивные матрицы» включает в себя 5 серий (А, В, С, D , Е) по 12 заданий, расположенных по возрастанию трудности. Трудность заданий возрастает от серии А к серии Е. Первые 5 заданий серии А испытуемый выполняет с помощью экспериментатора, остальные
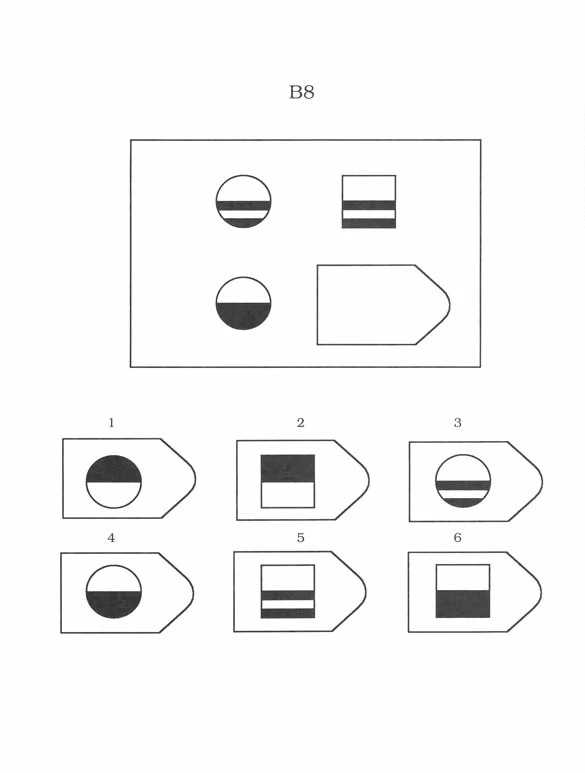
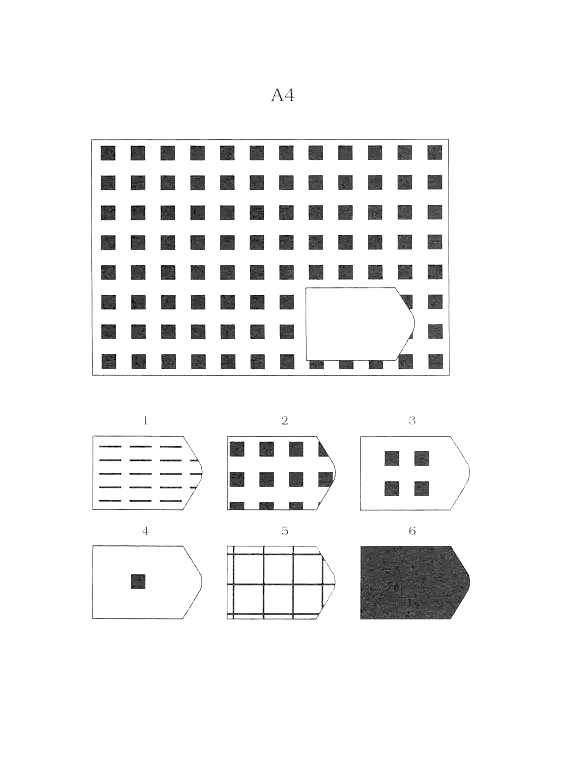
Равен предполагал, что в ходе выполнения теста испытуемый обучается и выполнение предше- ствующего задания готовит его к выполнению последующего, более трудного. В серии A – использован принцип установления взаимосвязи в структуре матриц. Здесь задание заключается в дополнении недостающей части основного изображения одним из приведенных в каж- дой таблице фрагментов. Выполнение задания требует от обследуемого тщательного анализа струк- туры основного изображения и обнаружения этих же особенностей в одном из нескольких фрагмен- тов. Затем происходит слияние фрагмента, его сравнение с окружением основной части таблицы. Ди- агностируется способность: к дифференциации основных элементов структуры и раскрытию связей между ними. То есть эта серия заданий актуализирует умение дифференцировать элементы и выяв- лять связи между элементами образа (гештальта), дополнять недостающую часть структуры, сличая ее с образцом.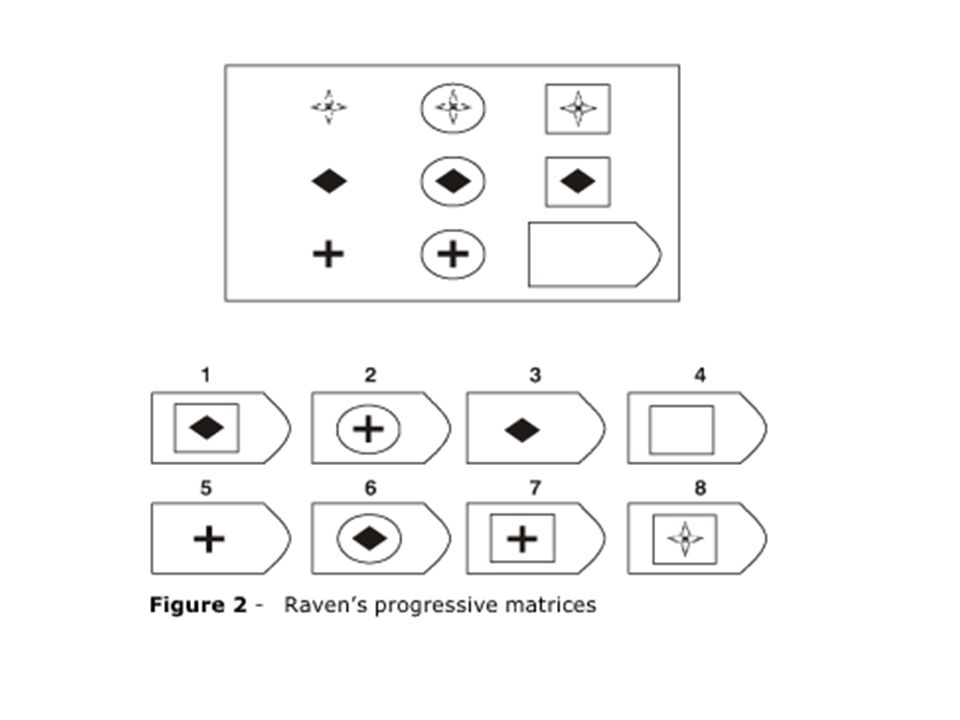 
Психологическое значение этой серии заданий: решение зависит от уровня внимательности, уровня статистического представления, воображения и уровня визуального различия (дискримина- ции). Скачать 2,52 Mb. Поделитесь с Вашими друзьями: |
Предполагается, что испытуемый первоначально воспринима- ет задание как целое, затем выделяет закономерности изменения элементов образа, после чего выде- ленные элементы включаются в целостный образ, и находится недостающая деталь изображения.
1 2 3 4 5 6 7 8 9 … 49
База данных защищена авторским правом ©psihdocs.ru 2023
обратиться к администрации
Таблица времени обучения с примерами из реальной жизни
Начальная математика
Несмотря на установленную законом проверку таблиц умножения, таблицы умножения важнее, чем просто запоминание сумм — они могут стать запоминающейся основой для более глубокого понимания детьми математики
- по Карен Уайлдинг
ПРОЧИТАЙТЕ, ЧТОБЫ УЗНАТЬ…
- «Почему» и «как», а не просто «что» о том, как преподавать таблицу умножения
- Как научить умножению помимо простого теста по таблице умножения
- Как сделать более сложную таблицу умножения более легкой для детей Learn
- Примеры из реальной жизни для использования при обучении таблицам времени
Чтение через 6-8 минут…
» Многим детям умножение кажется всего лишь тем, что вы делаете с числами на уроках математики в школе: оно не имеет никакого отношения к реальному миру.
»
Понимание математики для детей 5–9 лет , Дерек Хейлок
» Что касается изучения математики, возможно, одна из немногих вещей, с которыми все согласны, это важность знания фактов умножения.
Тем не менее, почему они нам нужны и как лучше их изучать остаются горячими темами, обсуждаемыми веками.
Знание фактов умножения и таблиц умножения в качестве ключевой части нашего внутреннего «математического инструментария» чрезвычайно важно, потому что мы постоянно используем их в повседневной жизни.
Ключевые этапы 1 и 2 национальной учебной программы по математике
К сожалению, для большинства детей (и для поколений до них) основная цель изучения этих «таблиц умножения» не сосредоточена на этом осмысленном и мотивационном приложении, а вместо этого заучивает каждый факт наизусть, чтобы пройти классный тест, и часто на скорости. Что не весело.
Неспособность запомнить и быстро вспомнить эти факты приводится многими взрослыми в качестве доказательства их неудач в математике, что приводит к мышлению, которое полностью отвращает их от изучения этого замечательного предмета.
Итак, давайте согласимся, что факты умножения являются жизненно важными навыками для успешного математика.
Однако вместо традиционных подходов, использующих механическое заучивание, которые заставляют детей работать на значительно более низком уровне, чем те, кого учат с упором на «общую картину и связи» (Boaler, Mathematical Mindsets ), давайте посмотрим, как мы все можем заинтересовать детей смыслом и применением, создавая крепкие умственные связи и гибкость, работая с тем, как мы знаем, что мозг учится лучше всего.
Умножение как понятие — знание «Почему?» и «Как?», а не только «Что?»
Наличие «концептуального понимания» означает, что мы знаем, почему и как что-то работает, а не просто «как это сделать».
Традиционно математика в Великобритании сосредоточена на процедурах и запоминании, что означает, что дети не могут участвовать в происходящих жизненно важных процессах, что приводит как к плохой успеваемости, так и к отсутствию понимания фактической математики.
Итак, что мы подразумеваем под умножением? Ответ не так прост, как мы могли бы подумать. Здесь работают две основные структуры:
Умножение повторным сложением
Группы одинакового размера добавляются неоднократно, например, 3 + 3 + 3 = 3 x 3 (кстати, многие дети скажут вам, что 3 x 3 = 6, когда увидят это в записи, демонстрирующее отсутствие концептуального понимания)
Умножение путем масштабирования
Изучение таблицы умножения — это первая из этих двух структур — «повторяющееся сложение», — но, как мы видим, это также знания, на которые мы опираемся при решении задач, связанных с масштабированием.
Идеи и подходы к обучению умножению с уместностью и пониманием
Следующие задания призваны помочь учителям и родителям представить изучение таблицы умножения как значимое и увлекательное занятие для всех детей.
Человеческий мозг наиболее успешно усваивает математические факты через связь и осмысленное применение.
Счет и умножение – замечание и создание равных групп
Умножение как группировка является формой «быстрого» счета. Когда у нас есть три группы по три человека, мы можем сосчитать объекты единицами — 1, 2, 3, 4 и т. д. — но зная, что в первой группе 3, что к концу второй группы у нас будет 6, и что В конце третьей группы у нас будет 9, значит, нам нужно сказать только три числа (вместо девяти).
Этот «быстрый счет» имеет смысл только тогда, когда дети могут видеть и связывать происходящие процессы.
Всем детям нужен большой опыт счета единицами, и если сравнить это с тем, что происходит, когда мы говорим только сумму групп, которые мы складываем (так, три группы по три в этом примере), чтобы они видели, что такое таблица умножения и как они ускоряют нашу способность считать и вычислять.
Следите за подходами к изучению таблицы умножения «У Мэри был ягненок…»
Обучение детей перечислению чисел может звучать так, как будто у них есть знания по умножению: «Давайте посчитаем по 2 — 2, 4, 6, 8, 10…».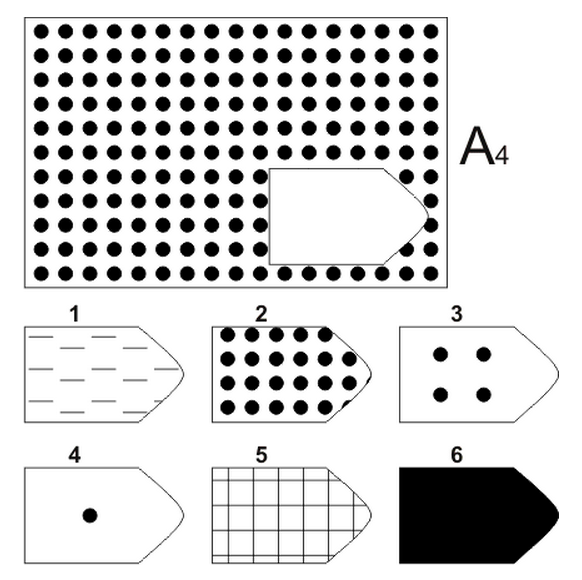
Но если мы рассмотрим это более внимательно, они часто начинают каждый раз с одного и того же места и, по сути, только что научились декламировать эквивалент детской песенки. Гибкое использование и применение этих знаний становится практически невозможным.
Таблица умножения – «учил» или «выучил»?
Взрослый: «Какая столица Франции?» Ребенок: «Париж!» Взрослый: «Вау, да. Удивительно, что ты был таким быстрым. Расскажите мне о Париже и Франции. Ребенок: Что такое «Париж и Франция»?
Изучение таблицы умножения с помощью человеческого тела
Ваше тело — отличная отправная точка для понимания и применения нашей таблицы умножения!
Подход «замечать и удивляться» к обучению
Начните это упражнение, попросив группу детей подойти и встать так, чтобы все могли их видеть. Что мы замечаем в равных группах частей тела? Что мы можем увидеть и описать? Есть несколько вещей.
Что приходит за 2 секунды? Руки, ноги, ноги, глаза, уши?
Можем ли мы увидеть другие равные группы?
«Пальцы идут группами по 10 и 5», или нет? Что с большими пальцами? Означает ли это, что пальцы делятся на группы по 8 и 4? Сколько ушей у 2 детей? Или 5 детей?
Успешное изучение математики — это гораздо больше, чем процесс, а не цель.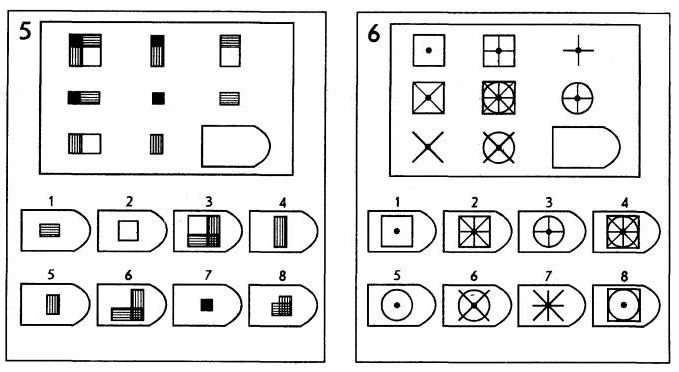
Чтобы гарантировать, что мы хвалим способность детей объяснять и доказывать свое понимание (вместо того, чтобы быстро выявлять факты, которые они могут знать, но не понимать).
«Конкретно-графический-абстрактный» подход к таблице умножения
Используйте взаимосвязанные кубики, чтобы изобразить равные группы «человеческого тела», которые замечают дети.
Ноги идут группами по две, так что здесь три группы ног — 2, 4, 6!
Поскольку наша система счета работает с основанием 10, используйте группы взаимосвязанных кубиков чередующихся цветов, чтобы создать числовую линию и объяснить, что происходит с суммами, когда мы добавляем более равные группы.
Здесь у нас есть три группы по два (представляющие нашу «историю о ногах»), и мы сравниваем их с группами по 10. Мы видим, что три группы по два на четыре меньше, чем 10. Нам нужно еще две группы, чтобы получить 10.
Задача умножения абстрактных символов
Теперь мы можем говорить о том, что мы построили, и зафиксировать это сначала как язык, а затем как символы, чтобы представить наше понимание.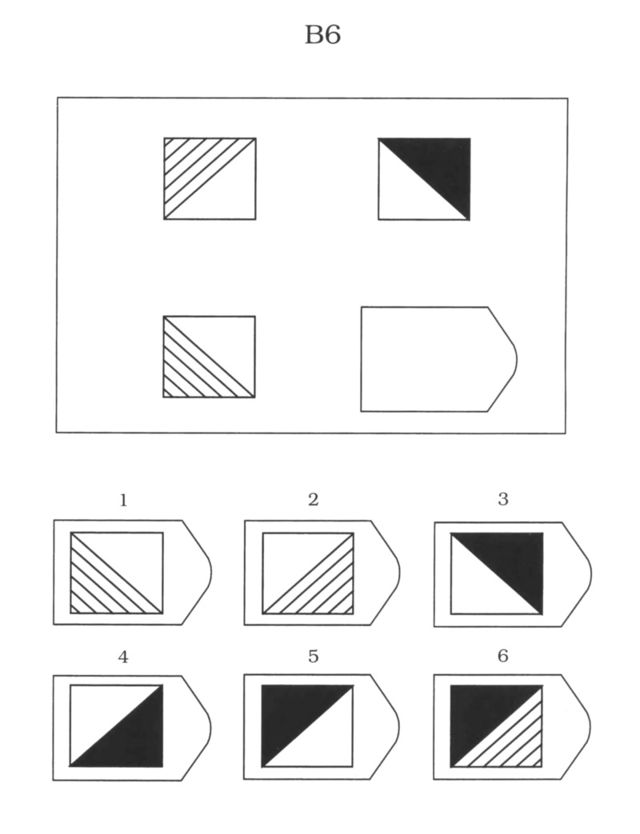
Итак, я вижу 2 + 2 + 2 = 6
Таблицы времени ног животных
Думали ли мы когда-нибудь о том, чтобы использовать животных для изучения таблицы умножения? Только подумайте, сколько разного количества ног у животных — 2, 4, 6, 8, 10 — и у некоторых их так много, что их очень трудно сосчитать (а они не часто стоят на месте с таким количеством ног!).
Попросите детей провести исследование, чтобы выяснить, какие животные имеют определенное количество ног, и отсортировать их соответствующим образом.
Теперь создайте конкретные представления.
У собак четыре ноги, так что это может быть четыре собаки! Или львы, или жирафы, или муравьеды! 4, 8, 12, 16…
Теперь я могу сравнить четыре группы по четыре на моей числовой прямой, состоящей из десятков. Я вижу, что четыре группы по четыре больше 10 и меньше 20. Есть место для еще одной группы, равной 20, поэтому пять четверок должны быть 20.
Свободное владение математикой – Работа в группах по 9 человек
Научиться считать в группах по 9 значительно сложнее, чем считать в группах по 10.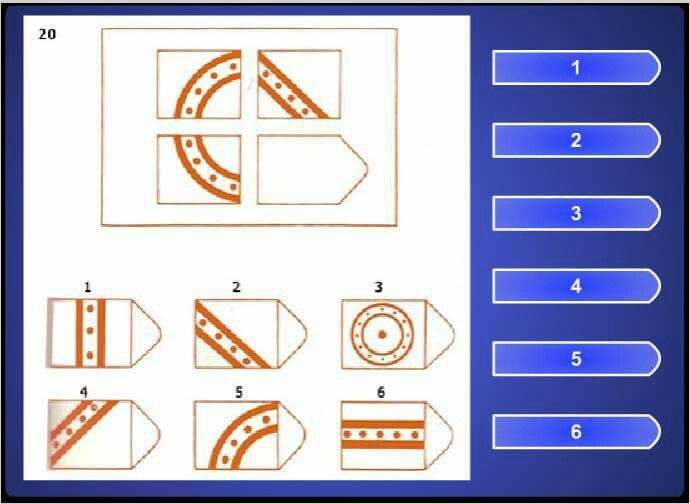
Итак, как мы можем использовать наше понимание счета в группах по 10, чтобы найти шаблон для счета девятками?
Как насчет 9 х 5?
Итак, 10 x 5 = 50. Но каждая группа состоит только из 9, а не из 10. Девять на 1 меньше 10, поэтому в каждой группе из 10 должно быть 1 недостающее. Это пять единиц, или 5 x 1, что равно 5. Там ответ должен быть на 5 меньше 50, то есть 45!
Попробуйте этот трюк для работы с восьмерками.
Мы знаем, что 8 на 2 меньше 10, поэтому постройте модель 8 x 5 и посмотрите, что вы заметите, когда соберете 10 из разноцветных кубиков, точно так же, как мы сделали с 9.
Как насчет других способов умножения на 9? 8 х 9.
Ну, я знаю, что 8 x 10 = 80, и если у меня всего 9 групп по 8, то это на 8 меньше, чем 80, что равно 72!
Посмотрите, работает ли это с 14 x 9.
Возможно, начните с того, что вы знаете о 14 x 10, создайте модель и заставьте модель рассказывать историю, например: «У меня есть 9пакеты по 14 штук в каждом.
Сколько предметов всего? История помогает нам визуализировать проблему и увидеть, как представление о том, что у нас есть 10 сумок вместо 9, поможет нам в вычислениях.
Другие способы сделать более сложную таблицу умножения проще, используя то, что мы уже знаем
Подсчет группами по 7
Представьте, мне интересно, сколько дней в 6 неделях. Это будет 7 дней x 6, поэтому мне понадобится моя таблица умножения на 7 или 6 (потому что 7 x 6 = 6 x 7).
Давайте построим его из кубиков. Мы будем использовать массив:
Вот 6 групп по 7. Я пока не умею считать по 7.
Используйте «Уведомление и удивление»: что я могу увидеть в массивах? Могу ли я увидеть какие-либо факты, которые мне уже известны или которые легче вычислить?
А, теперь я вижу 5 и 2 внутри 7. Так что я могу вычислить 5 х 5, а затем 2 х 5.
Поиск массива
Равное группирование фактов умножения легче всего увидеть и понять, когда мы создаем массивы.
Мы уже использовали массивы в этой статье, создавая равные строки и столбцы кубов.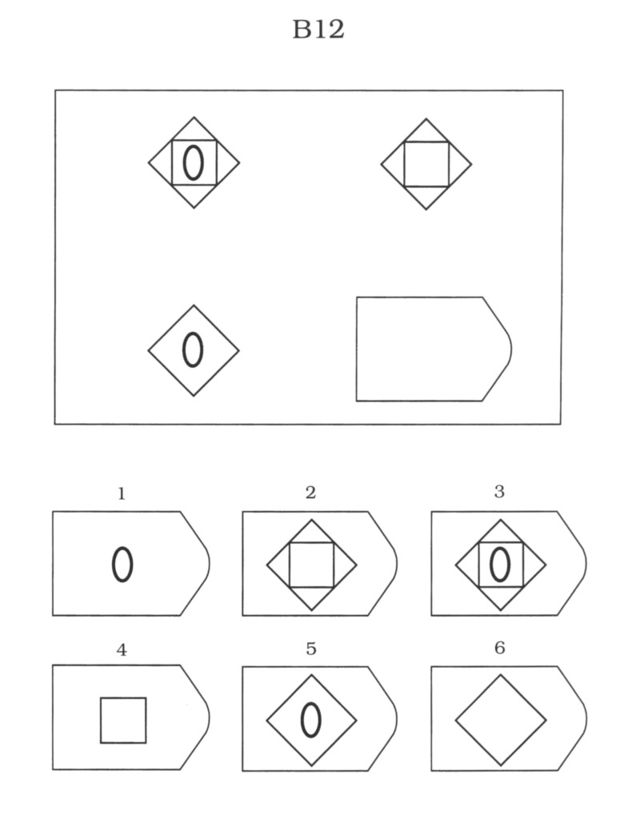
Массивы позволяют нам легко видеть факты умножения и разбивать факты на части, чтобы мы могли видеть, что 6 x 4 можно вычислить как «удвоить 6 плюс удвоить 6» или «5 x 9» как «(5 x 10) – 5».
Массивы в реальной жизни
Массивы существуют повсюду в реальной жизни, когда мы начинаем смотреть вокруг себя. Они являются фантастической отправной точкой для наблюдения и описания фактов умножения (и, следовательно, деления).
Они также могут вызвать некоторые более сложные вопросы, такие как: «Если мы знаем площадь одной из этих потолочных плит, как мы можем использовать это для расчета площади всего потолка, и нужно ли нам считать каждую отдельную плитку?»
Примеры массивов
- Тумбы
- Ящики для яиц
- Старые окна
- Потолочная плитка
- Напольная плитка
- Проволочное ограждение
- Картины на стене
- Стулья в ряд в зале
- Марширующие солдаты
- Расставленные чашки для кофе большая компания
- Мультипакеты с водой, йогуртом, пирожными и т. д.
- Кусочки шоколада в баре
- Люди, сидящие в театре, на стадионе и т. д.
- Выкройки на ткани и оберточной бумаге
д.Чтобы узнать больше о Karen Wilding Education и ее услугах, посетите сайт karenwildingeducation.co.uk.
Математическая таблица из 16 — Таблицы умножения для изучения детьми
- Почему ваш ребенок должен выучить таблицу из 16?
- Что такое таблица умножения на 16 в математике?
- Таблица умножения на 16 для детей
- Таблица 16 раз для детей
- Советы по изучению и запоминанию таблицы умножения 16 для детей
- Простые вопросы, которые помогут детям повторить таблицу 16
- Словесные задачи по таблице умножения на 16 для детей
- Часто задаваемые вопросы
Одним из фундаментальных математических процессов является умножение.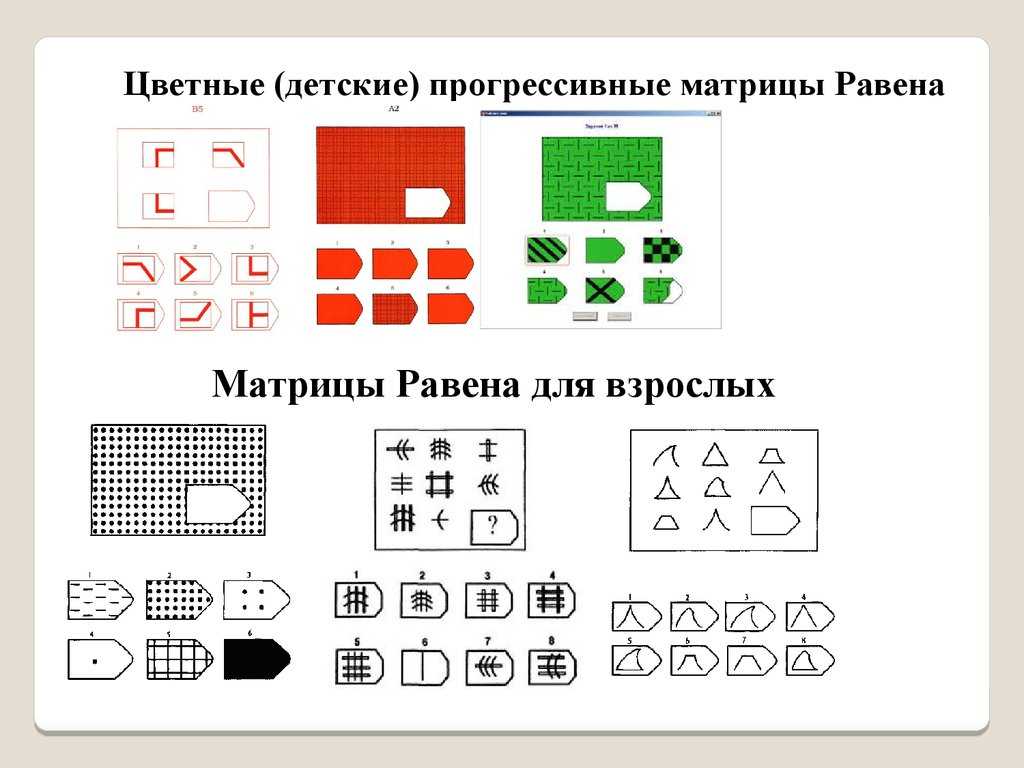
Ценным навыком является умение умножать числа. Таблицу умножения 1–20 необходимо хорошо понимать, чтобы изучать более сложные математические понятия в школе. Например, освоение математической таблицы 16 позволяет детям решать задачи, связанные с числами, кратными 16, на умножение и деление. Дети могут перейти от счета на пальцах к мысленному подсчету сумм, выучив таблицу 16 на английском языке. Если ваш ребенок прогрессирует от других двузначных умножений, освоить полную таблицу 16 не так сложно. Несмотря на то, что это может показаться сложным, мы дадим вам несколько простых советов, чтобы вы могли понять таблицу 16.
Зачем вашему ребенку учить таблицу из 16?
- Изучение таблицы 16 — отличный способ для вашего ребенка улучшить скорость счета.
- Знание таблиц на кончиках пальцев сократит время решения задач вашего ребенка.
- Он также может быть очень полезен в реальных жизненных ситуациях, таких как покупка продуктов, расчет времени и т. д.
Что такое таблица умножения на 16 в математике?
Таблица умножения на шестнадцать — это таблица умножения на 16, которую можно записать с помощью различных математических операций, таких как умножение и сложение.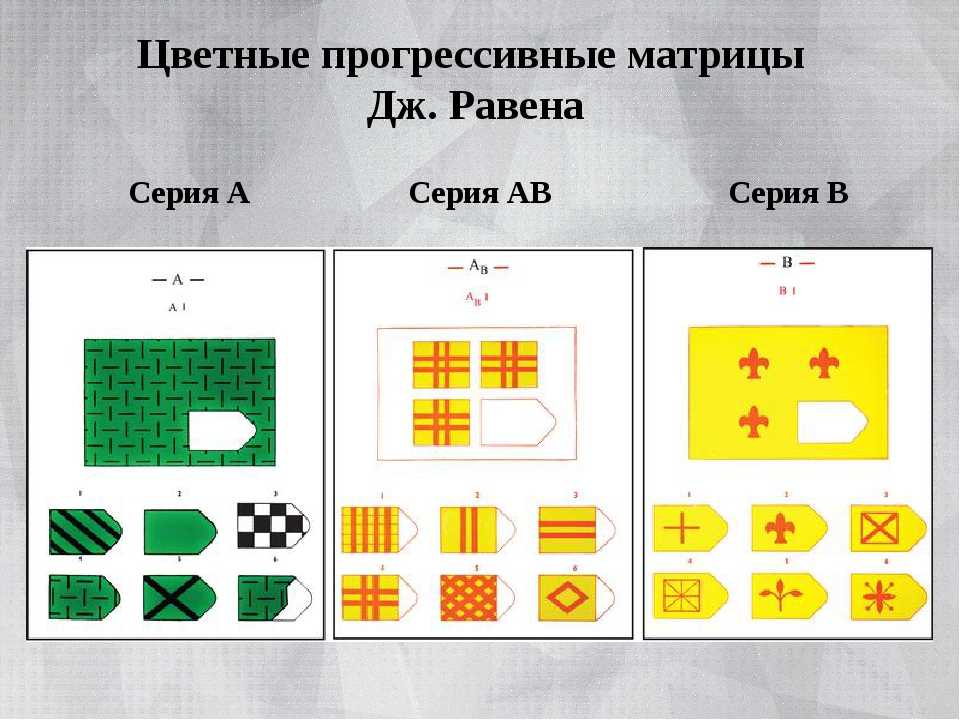
Каждый малыш должен выучить таблицу шестнадцати, чтобы решать сложные вопросы. Теперь давайте посмотрим на таблицу шестнадцати. Ниже приведены первые 10 кратных 16.
| 16×1=12 | 16 |
| 16×2=32 | 16+16= 32 |
| 16×3=48 | 16+16+16= 48 |
| 16×4=64 | 16+16+16+16= 64 |
| 16×5=80 | 16+16+16+16+16=80 |
| 16×6=96 | 16+16+16+16+16+16=96 |
| 16×7=112 | 16+16+16+16+16+16+16=112 |
| 16×8=128 | 16+16+16+16+16+16+16+16=128 |
| 16×9=144 | 16+16+16+16+16+16+16+16+16=144 |
| 16×10=160 | 16+16+16+16+16+16+16+16+16+16=160 |
Таблица умножения 16 для детей
Изучение таблицы 16 повысит уверенность ваших детей в решении сложных математических задач и поможет им в быстрых вычислениях.
В этом разделе мы рассмотрим больше кратных 16. Он охватывает первые 20 кратных 16.
| 16 х 1 = 16 | 16 х 11 = 176 |
| 16 х 2 = 32 | 16 х 12 = 192 |
| 16 х 2 = 48 | 16 х 13= 208 |
| 16 х 4 = 64 | 16 х 14= 224 |
| 16 х 5 = 80 | 16 х 15= 240 |
| 16 х 6= 96 | 16 х 16= 256 |
| 16 х 7= 112 | 16 х 17= 272 |
| 16 х 8 = 128 | 16 х 18= 288 |
| 16 х 9= 144 | 16 х 19= 304 |
| 16 х 10=160 | 16 х 20= 320 |
Таблица с 16 умножениями для детей
Таблица с 16 таблицами до 10
Наглядные представления всегда помогают детям лучше запоминать. Вот диаграмма таблицы от 16 до 10 кратных.
16 Таблица Таблица До 20
Вот таблица таблицы от 16 до 20 кратных.
Это поможет вашему ребенку быстрее запомнить таблицы.
Советы по изучению и запоминанию таблицы умножения на 16 для детей
Выучить 16 таблиц может быть непросто. Чтобы помочь вашему ребенку научиться этому легко, мы включили несколько трюков с 16 столами.
- Чтобы выучить таблицу 16 чисел, умножьте на 8 таблицу удвоения. Разберем число 16. 8, умноженное на 2, равно 16. Следовательно, все, что вам нужно сделать, чтобы найти ответы на таблицу умножения 16, — это удвоить таблицу умножения на 8. Вот несколько иллюстраций, которые помогут вам понять. Давайте найдем решение 16 X 3,
Пример 1: Сначала разделите 16 пополам, что равно 8.
Результат умножения 8 на 3 равен 24.
Удвойте ответ, 24+24 равно 48.
Итак, 16 X 3 равно 48.
Пример 2: Давайте вычислим значение 16 X 6.
Для начала разделите 16 пополам, что равно 8
Умножьте 8 на 6, 8 X 6 = 48
Удвойте результат: 48+48 = 96
Таким образом, 16 X 6 равно 96.
- Другой метод — колода из 16 карт с использованием таблицы умножения на 8: Таблица восьмикратного умножения приведена ниже в табличном формате. Это до восьми раз по двадцать. Вы можете удвоить таблицу умножения на 8, чтобы получить ответы к таблице 16, поскольку 8 X 2 равно 16. Решения таблицы умножения на 16 — числа, выделенные жирным шрифтом. Вы можете просто выучить таблицу умножения на 16 с этой таблицей.
| 8 | 16 | 24 | 32 | 40 |
| 48 | 56 | 64 | 72 | 80 |
| 88 | 96 | 104 | 112 | 120 |
| 128 | 136 | 144 | 152 | 160 |
- Это еще один простой способ выучить таблицу умножения на 16. Прибавление 16 к предыдущему числу: Повторяющееся сложение — это то, что такое умножение. Следовательно, чтобы определить число, кратное 16, вы должны постоянно прибавлять 16 к каждому результату из 16 X 1. Если у вас есть хорошие навыки сложения, этот метод идеально подходит для изучения таблицы 16. Вот несколько иллюстраций, которые помогут вам понять.
Прибавление 16 к предыдущему числу: Повторяющееся сложение — это то, что такое умножение. Следовательно, чтобы определить число, кратное 16, вы должны постоянно прибавлять 16 к каждому результату из 16 X 1. Если у вас есть хорошие навыки сложения, этот метод идеально подходит для изучения таблицы 16. Вот несколько иллюстраций, которые помогут вам понять.Пример 1: Начнем со стандартной сетки 16 X 1. Мы знаем, что 16 умножить на 1 равно 16. Давайте прямо сейчас выясним, что такое 16 X 2. 16 плюс 16 равно 32. Следовательно, прибавьте 16 к предыдущему ответу. Таким образом, 16 x 2 равно 32,9.0003
Пример 2: Давайте теперь определим, что такое 16 X 4.
К 16 x 3 прибавьте 16:
16 x 3 = 48
48+16 равно 64.
16 x 4, следовательно, равно 64.
- Таблица умножения на 16 имеет закономерность. Изучение таблицы умножения на 16 становится намного проще, когда вы распознаете шаблон и поймете, как его использовать. Давайте рассмотрим таблицу из 16 пунктов.
Давайте рассмотрим таблицу из 16 пунктов.| 16 | х | 1 | = | 1 | 6 |
| 16 | х | 2 | = | 3 | 2 |
| 16 | х | 3 | = | 4 | 8 |
| 16 | х | 4 | = | 6 | 4 |
| 16 | х | 5 | = | 8 | 0 |
| 16 | х | 6 | = | 9 | 6 |
| 16 | х | 7 | = | 11 | 2 |
| 16 | х | 8 | = | 12 | 8 |
| 16 | х | 9 | = | 14 | 4 |
| 16 | х | 10 | = | 16 | 0 |
Вы заметили закономерности?
Если вы посмотрите на верхнюю половину таблицы 16, вы заметите, что последние цифры столбца единиц для каждого числа, кратного 16, равны 6, 2, 8, 4 и 0.
Когда вы посмотрите на вторую половину таблицы , вы увидите, что числа 6, 2, 8, 4 и 0 повторяются. Все, что вам нужно сделать, это помнить, что числа, кратные 16, равны 6, 2, 8, 4 и 0. Используя это, вам будет легче вспомнить таблицу умножения для 16.
Простые вопросы, которые помогут детям повторить таблицу 16
- Рассчитайте 16 умножить на 8 минус 10, используя таблицу умножения на 16.
Решение: Сначала напишите математическое выражение для 16 умножить на 8 минус 10. 16×8-10. Используя таблицу умножения на 16, 16 умножить на 8 равно 128; следовательно, 128 – 10 = 118. Следовательно, 16 умножить на 8 минус 10 равно 118.
- Определить 16 умножить на 16 минус 16 плюс 3.
Решение: Сначала решим математику, написав 16 умножить на 16 минус 16 плюс 3. 16 умножить на 16 минус 16 плюс 3 равно 16×16 – 16+3, что равно 256-16+3, т. е. 240+3, что равно 243. В результате 16 умножить на 16 минус 16 плюс 3 равно 243.
- Найдите ответ для 16 x 11 – 100.
Решение: Из 16-строчной таблицы имеем 16 х 11 = 176. В результате необходимая разность:
176 – 100 = 76
- Каким будет результат 16 х 5?
а) 79
б) 48
в) 119
г) 80
Доп. 80
Задания на 16 таблиц умножения для детей
Чтобы ваши дети действительно выучили 16 таблиц умножения, они должны уметь применять их на практике. Вот несколько текстовых задач, которые помогут вашему ребенку повторить и углубить свои знания таблицы умножения на 16.
1. Если Аюш будет бегать по часу каждый день, сколько времени он пробежит в целом за 16 дней?
Решение: Аюш бегает 1 час каждый день. Таким образом, за 16 дней, 16 x 1 = 16, Аюш будет работать 16 часов.
2. За какое время машина изготовит 16 банок, если на изготовление одной у машины уходит два часа?
Решение: Машина производит 1 банку за два часа.