Тест матрица равена: Тест на IQ | Бесплатный современный аналог прогрессивных матриц Равена онлайн
Тест Равена — это… Что такое Тест Равена?
A matrix example.Тест Равена — тест, предназначенный для дифференцировки испытуемых по уровню их интеллектуального развития. Авторы теста Джон Равен и Л. Пенроуз. Предложен в 1936 году.
Более высокие показатели по этому тесту показывают те, кто а) быстрее, и б) точнее определяет логические закономерности в построении упорядоченного ряда состоящего из графических объектов, имеющих ограниченное количество признаков.
Другое название этого теста «Прогрессивные матрицы Равена» указывает на то, что задачи теста упорядочены по признаку возрастания трудности их решения. То есть, в каждой из пяти серий (в серии по 12 задач), каждая последующая задача серии относительно сложней предыдущей. На решение задач теста вводится временное ограничение — подсчитывается количество правильно решённых за 20 минут задач. Возможен вариант, когда время на решение всех 60 задач не ограничено. В этом случае результат корректируется по специальной таблице.
По результатам тестирования испытуемый получает несколько оценок:
- а) по десятибалльной шкале (стандартная оценка в стенах), учитывающей только количество правильно решённых задач,
- б) по 19-балльной, учитывающей количество и трудность решённых задач,
- в) по привычной пятибалльной (школьной, но с «плюсами» и «минусами»).
- И, наконец, четвёртая, качественная, оценка. Если испытуемый решил все задачи теста, но многие, в том числе и лёгкие, задачи решил неверно, его можно отнести к категории «скоростников». Если же испытуемый решил мало задач (например, около половины задач теста), но, без единой ошибки, его можно отнести к категории «точняков», или тугодумов.
При интерпретации результата теста «Прогрессивные матрицы Равена» выделяют следующие пять уровней развития интеллекта:
- 1-й уровень (результат более 95 %) — особо высокий интеллект
- 2-й уровень (результат 75-94 %) — интеллект выше среднего
- 3-й уровень (результат 25-74 %) — средний интеллект
- 4-й уровень (результат 5-24 %) — интеллект ниже среднего
- 5-й уровень (результат ниже 5 %) — дефект интеллекта
Ссылки
Стоит ли доверять тестам на интеллект? / Статьи / Библиотека / Первая онлайн система анализа вашего душевного здоровья
Стоит ли доверять тестам на интеллект?
Стоит ли доверять простейшим тестам на интеллект в гламурных журналах? Или может все же лучше потратить полчаса или час на труднопроходимый и порой утомительный тест с поистине психологическим основанием?
Психологи считают, что человеческий ум и интеллект – это отнюдь не одно и то же.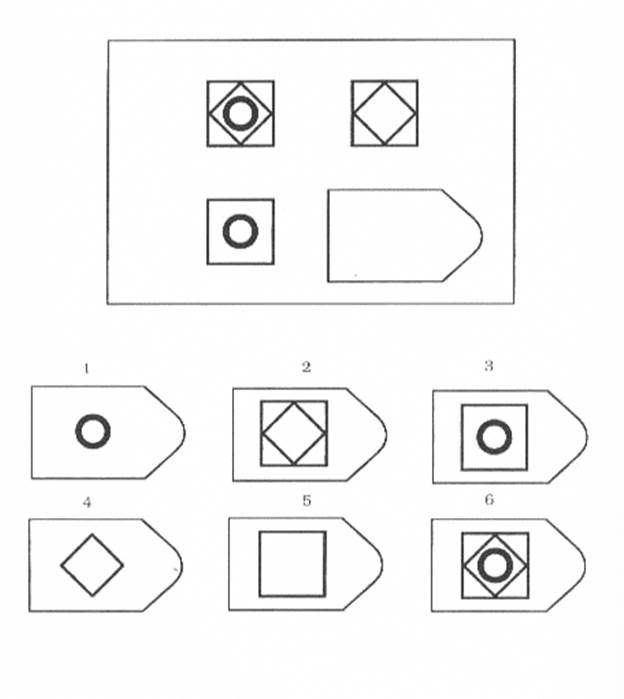 Если умом можно назвать способность логического мышления, то интеллектом называют совокупность логики, синтеза и анализа любых жизненных ситуаций, а также способность верного оценивания трудных задач и легкого нахождения их решения.
Если умом можно назвать способность логического мышления, то интеллектом называют совокупность логики, синтеза и анализа любых жизненных ситуаций, а также способность верного оценивания трудных задач и легкого нахождения их решения.
Современные тесты на интеллект, представленные в модных журналах, просто поражают своей неспособностью хотя бы приблизительно вычислить уровень IQ у всех тех, кто рискнет убить пару минут на их прохождение. Как правило, они состоят из двух десятков вопросов, которые косвенно касаются логических способностей. Иными словами, таким простым и банальным тестам на интеллект доверять просто не стоит. Но если уж так хочется проверить свои собственные умственные способности, то лучше обратится к настоящим профессиональным тестам на IQ, которые хотя и занимают много времени, но показывают точные результаты прохождения.
Самый известный из всех действующих тестов на интеллект – это тест Айзенка. Он состоит из четырех десятков вопросов, большинство из которых являются чисто визуальными. К примеру, человеку предлагают просмотреть ряд геометрических фигур и найти недостающую комбинацию в последнем ряду. В этом случае подопытный должен найти логическую связь между каждой представленной фигурой и на основе этой связи найти и недостающую. Есть также и такие вопросы, в которых нужно вставить пропущенное слово в скобки. Здесь действует тот же прием анализа всех остальных слов и нахождение ассоциаций между ними или другой связи. Время, отведенное на прохождение этого теста, составляет ровно 30 минут. Такое ограничение было установлено не случайно, ведь тест призван вычислить уровень интеллекта, а значит и уровень способности человека принимать правильные решения в экстренных ситуациях.
К примеру, человеку предлагают просмотреть ряд геометрических фигур и найти недостающую комбинацию в последнем ряду. В этом случае подопытный должен найти логическую связь между каждой представленной фигурой и на основе этой связи найти и недостающую. Есть также и такие вопросы, в которых нужно вставить пропущенное слово в скобки. Здесь действует тот же прием анализа всех остальных слов и нахождение ассоциаций между ними или другой связи. Время, отведенное на прохождение этого теста, составляет ровно 30 минут. Такое ограничение было установлено не случайно, ведь тест призван вычислить уровень интеллекта, а значит и уровень способности человека принимать правильные решения в экстренных ситуациях.
Второй известный тест, признанный и широко применяемый в мировой практике определения коэффициента интеллекта – это тест прогрессивные матрицы Равена (Raven Progressiv Matrices). Методика разработана в соответствии с лучшими традициями английской школы изучения уровня интеллекта и также строго регламентирована по времени – 20 минут.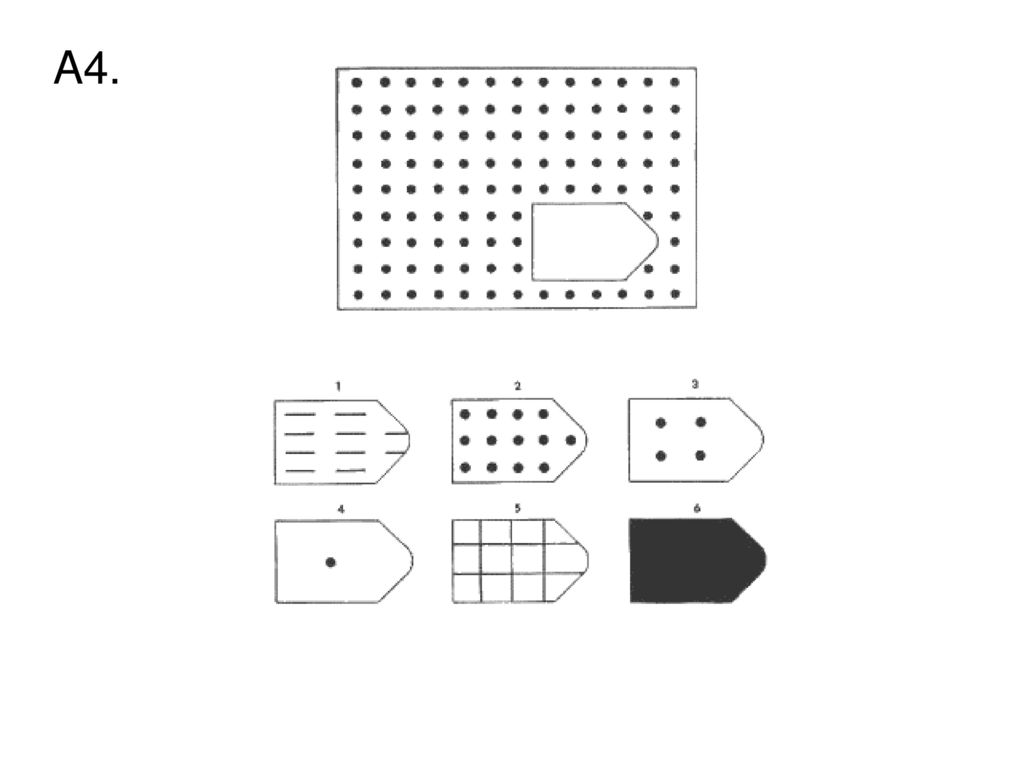
Именно поэтому в нашем аналитическом модуле «Коэффициент интеллекта, IQ» мы представили обе эти методики, а для максимальной объективизации результата предлагаем считать своим реальным коэффициентом интеллекта средний результат этих двух тестов.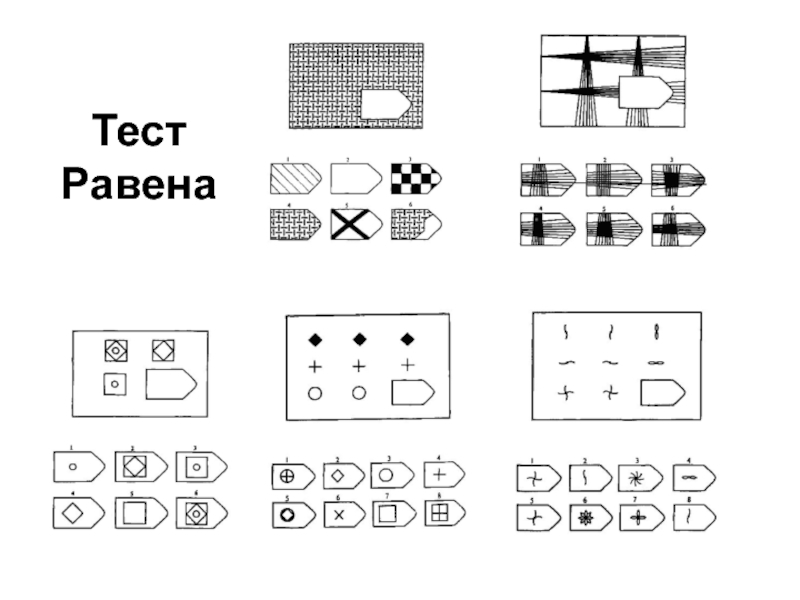
Создавая этот аналитический модуль для нашего проекта, мы провели анализ многих других похожих онлайн – тестов на уровень интеллекта, и, пришли к неутешительному выводу – подавляющее большинство из них содержит грубейшие ошибки, как в самих заданиях методик, так и в интерпретации и расчете результатов. А множество сайтов, предлагающих свои услуги по оценке вашего IQ – просто копируют, передирают друг у друга эти тесты, естественно «забывая» исправить эти ошибки. Иногда доходит до такого абсурда, что из 100 тестируемых, у 90 коэффициент интеллекта свыше 170!, что само по себе просто невозможно, как бы мы не хотели польстить друг другу. При разработке аналитического модуля «Коэффициент интеллекта, IQ» нами были взяты оригинальные методики из научной литературы, т. е. первоисточники этих тестов, которые мы адаптировали для прохождения онлайн, поэтому с гордостью можем сказать, что у нас на сайте вы действительно узнаете свой реальный IQ, а также получите в ответе много просто интересной информации об интеллекте.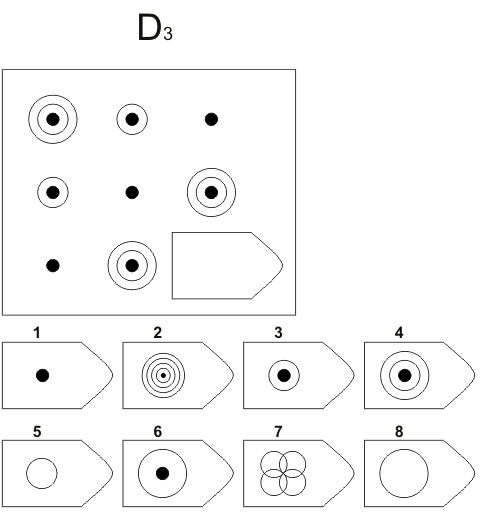
В мире существует много разных тестов на интеллект, но это не значит, что доверять и тратить свое время стоит на них всех. Лучше воспользоваться теми методиками определения уровня интеллекта, которые были признаны ведущими психиатрами, как наиболее точные и правильные тесты.
Прочитать еще много интересного об интеллекте и узнать свой IQ можно здесь.
Поделитесь с друзьями и оцените публикациюНе пропустите другие статьи по теме:
Оставить комментарий, могут только зарегистрированные пользователи.
 Вы можете зарегистрироваться или войти
Вы можете зарегистрироваться или войти
3.2. Прогрессивные матрицы Равена
Равен был учеником Ч.Спирмена. В 1936 году он совместно с Л.Пенроузом предложил тест Progressive Matrices для измерения уровня развития общего интеллекта. По мнению Спирмена наилучшим способом определения интеллекта является тест на поиск абстрактных отношений. В основу заданий теста положены теория гештальта и теория интеллекта Ч.Спирмена. Предполагается, что испытуемый первоначально воспринимает задание как целое, затем выделяет закономерности изменения элементов образа, после чего выделенные элементы включаются в целостный образ и находится недостающая часть изображения.
В
качестве материала были выбраны
абстрактные геометрические фигуры с
рисунком, организованным по определенному
закону.
Сконструированы основные три варианта теста: 1) более простой цветной тест, предназначенный для детей от 5 до 11 лет, 2) черно — белый вариант для детей и подростков от 8 до 14 лет и взрослых от 20 до 65 лет, 3) вариант теста сконструирован в 1977 году Дж.Равеном в сотрудничетве с Д.Кортом и предназначен для лиц с высокими интеллектуальными достижениями; он включает в себя не только невербальную, но и вербальную часть.
Тест проводится как с ограничением времени выполнения заданий, так и без ограничения.
В
цветном варианте теста используются
три серии, различающиеся по уровню
трудности. В каждой серии — 12 матриц.
Второй вариант состоит из 5 серий (А,
В, С, Д, Е) по 12 заданий, расположенных
по возрастанию трудности. Трудность
заданий возрастает от серии А к серии
Е. Первые 5 заданий серии А испытуемый
выполняет с помощью экспериментатора,
остальные — самостоятельно. Испытуемый
должен выбрать правильный ответ из 6-8
предложенных вариантов.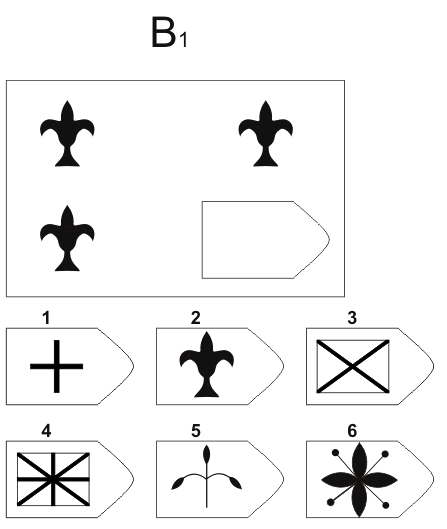 Число вариантов
ответа увеличивается по мере
возрастания трудности серии.
Число вариантов
ответа увеличивается по мере
возрастания трудности серии.
Дж.Равен предполагал, что в ходе выполнения теста испытуемый обучается. и выполнение предшествующего задания готовит его к выполнению последующего, более трудного.
В серии А испытуемый должен дополнить недостающую часть изображения. Он должен проявить умение дифференцировать элементы и выявлять связи между элементами гештальта, а также дополнять недостающую часть структуры , сличая ее с образцами.
В серии В испытуемый должен найти аналогии между парами фигур, дифференцируя их элементы.
При выполнении серии С нужно решить задачу, определив принцип изменения фигур по вертикали и горизонтали.
В серии D требуется определить закономерность перестановки фигур по горизонтали и вертикали.
Серия Е для своего решения требует анализа фигур основного изображения и составления недостающей фигуры по частям.
За
каждое правильное решение присваивается
1 балл, подсчитывается число правильных
решений в каждой серии и общее число
баллов, которые переводятся либо в
стенайны, либо в стандартный коэффициент
IQ.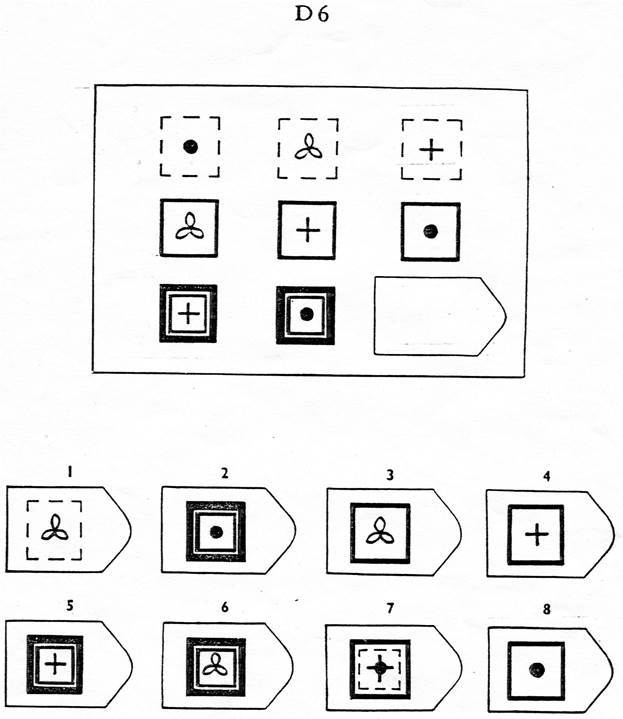 На основе результатов по сериям
вычисляют также «индекс вариабельности».
Существуют полученные на выборке
стандартизации распределения числа
правильных решений по сериям,
соответствующие общей сумме баллов.
Табличное распределение сравнивается
с полученным при тестировании испытуемого,
а разности ожидаемой и эмпирической
оценок суммируются без учета знака.
«Индекс вариабельности» характеризует
достоверность результатов и направлен
на выявление испытуемых, решавших
задания путем угадывания или симулирующих
низкий результат (не решавших простые
задачи).
На основе результатов по сериям
вычисляют также «индекс вариабельности».
Существуют полученные на выборке
стандартизации распределения числа
правильных решений по сериям,
соответствующие общей сумме баллов.
Табличное распределение сравнивается
с полученным при тестировании испытуемого,
а разности ожидаемой и эмпирической
оценок суммируются без учета знака.
«Индекс вариабельности» характеризует
достоверность результатов и направлен
на выявление испытуемых, решавших
задания путем угадывания или симулирующих
низкий результат (не решавших простые
задачи).
Нормальное значение индекса равно 0-4, при значении 7 ответы считаются недостоверными.
Как
уже было отмечено раньше, вряд ли такую
интерпретацию можно считать единственно
возможной. В наших исследованиях
показано, что решение теста Равена
имеет вероятностный характер, поскольку
отсутствие интереса к простым заданиям,
неправильное понимание задачи
(провоцируемое самим материалом теста)
может приводить к тому, что испытуемый,
решая сложные задания, может допустить
ошибку в простых.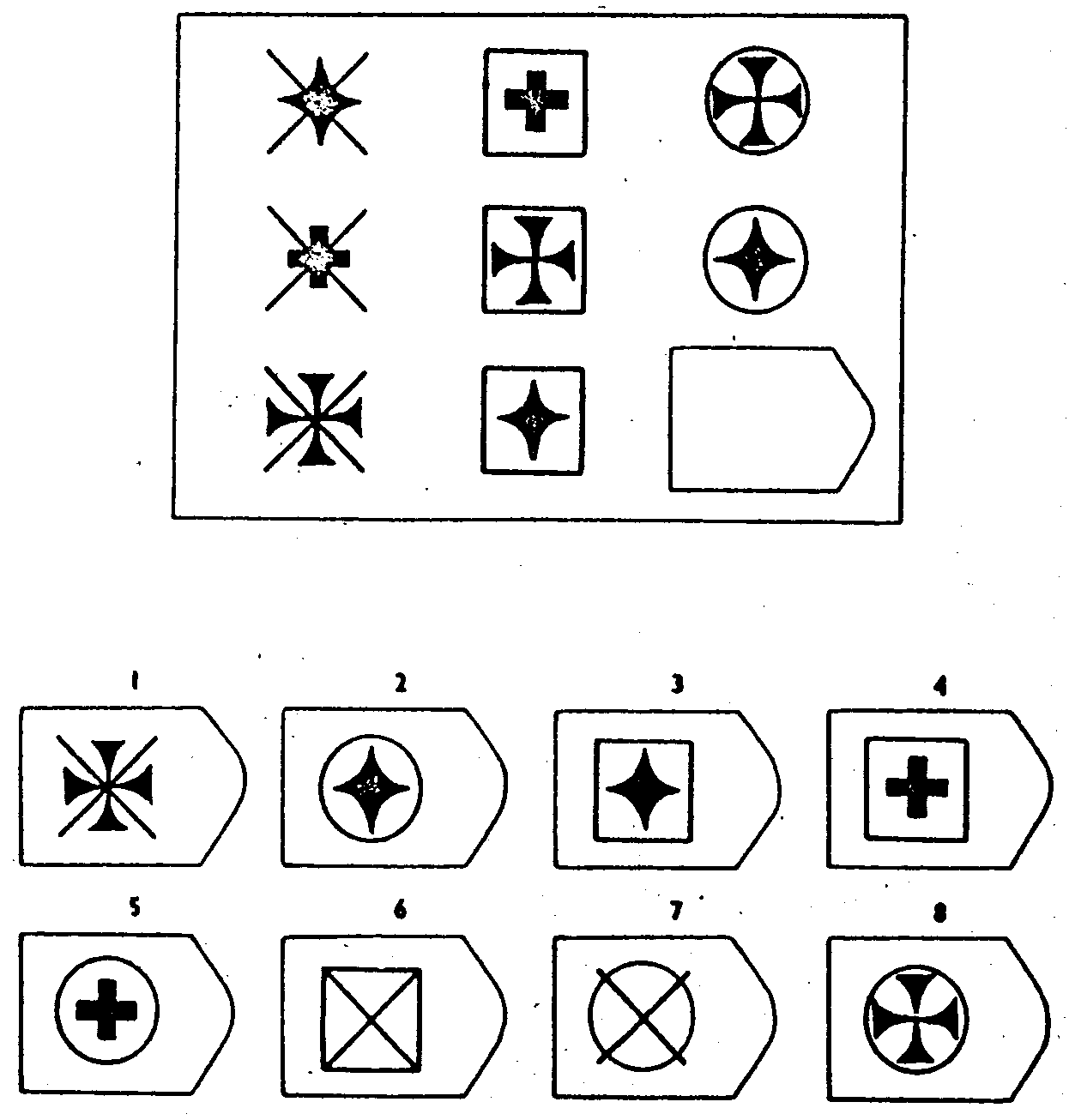
Надежность теста Равена варьирует в пределах от 0,70 до 0,89; средняя трудность заданий теста 0,32; корреляция с успешностью школьного обучения (оценкой успеваемости) — 0,72. Корреляция с IQ по тесту Д.Векслера (WAIS) 0,70-0,74 (взрослые) и 0,91 (дети 9-10 лет) , корреляция с арифметическими тестами — до 0,87. Наши исследования показали, что тест Равена не является метрологически безупречным.
Задания D12 и Е8 сконструированы настолько неудачно, что вероятность их правильного решения (0,13 и 0,14) не превышает значимо вероятности случайного решения этого задания (p = 0,125). В задания либо заложена неправильная идея, либо форма материала делает вероятным для испытуемого логические построения, не предусмотренные разработчиком.
В задании Е10 помимо правильного варианта ответа (N6) есть два (N1 и N2), число выборов которых испытуемыми статистчески значимо превышает вероятность случайного выбора.
Для
задания С12 оценка вероятности выбора
правильного ответа (N2) превышает границу
статистической значимости, но оценка
вероятности выбора ложного варианта
(N4) значимо превосходит вероятность
правильного выбора.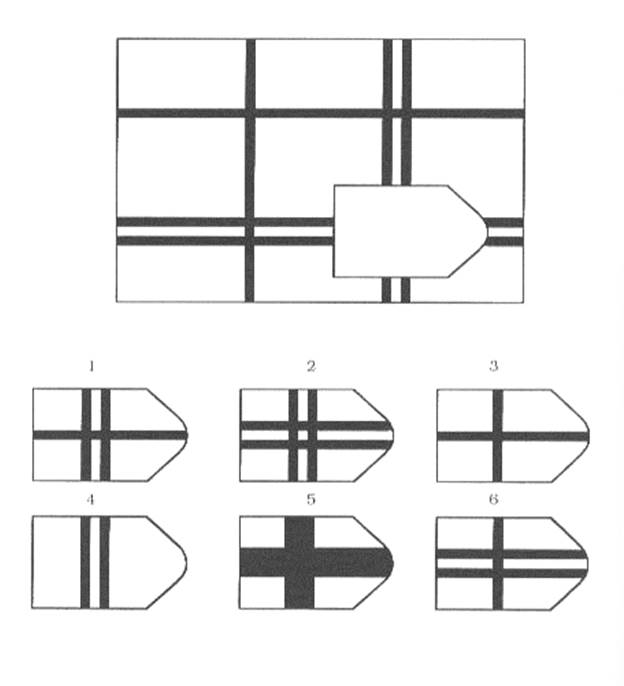
То есть сама структура неверно сконструированного задания наводит испытуемого на ложный ответ. Это положение дел есть следствие конфликта двух теорий, эклектически положенных в основу теста: перцептивной (гештальт-теория) и теории интеллекта. Перцептивные характеристики задания мешают испытуемому произвести его последовательный логический анализ. Тем самым не стратегия «от целого к деталям» вступает в конфликт со стратегией «от деталей к целому», а перцептивная закономерность противоречит логической.
Согласно модели Ф.М.Юсупова, число заданий в тесте уровня не должно быть выше 7, в тесте Равена их 60 (в сокращенном варианте — 30). Тест явно информационно избыточен. Базовыми заданиями, достоверно различающимися по уровню сложности, можно считать только: В8, А12, С4 (или D6), D8 (или D10, или Е2), С8, Е6, Е10, Е12.
Число
легких заданий в тесте Равена черезмерно
велико — на долю их приходится почти
половина всех заданий теста. Более того,
нет соответствия между эмпирической и
стандартной трудностью заданий (r=0,543).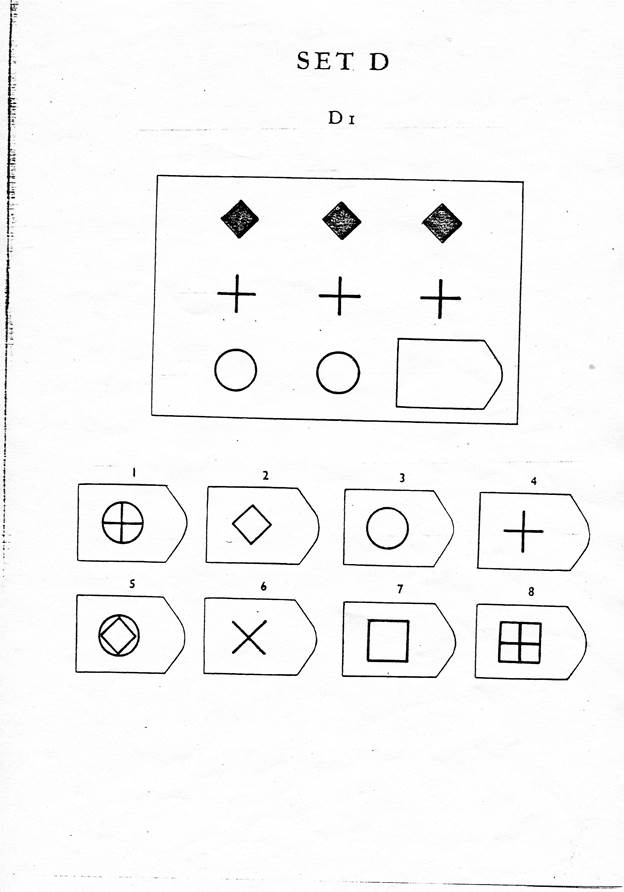
Для оценки сложности задания, нами и был предложен модифицированный показатель сложности:
С = 1 — n/N,
где n — число решивших тестовое задание,
N — общий объем выборки стандартизации.
В первом разделе главы уже упоминалось, что предложенный авторами теста вариант подсчета тестового балла не оправдывает себя и должен быть заменен на более достоверный, учитывающий эмпирическую сложность задания.
Успешность решения теста, как мы установили, зависит как от уровня «скоростного интеллекта», так и от когнитивной способности, обусловливающей решение сложных заданий.
Возможно, содержательной основой второго фактора является сложность когнитивного опыта личности, связанной с такими особенностями интеллекта как когнитивная сложность, дифференцированность понятий, вербальная компетентность.
Факторизация
корреляционной матрицы применения
теста Равена, теста на диагностику
когнитивной «простоты — сложности»
(автор А. Г.Шмелев), и теста «Понятия»
(на обобщение понятий) показала, что
выделяются 2 независимых фактора:
невербальный и вербальный, имеющие
равные веса, но методика на обобщение
понятий имеет значимую нагрузку по
невербальному фактору.
Факторный
анализ матрицы интеркорреляций семи
методик (тест когнитивной простоты —
сложности, тест Равена, методика
«Понятия», тест Г.Айзенка и пр.)
выявил 3 равнозначимых фактора:
невербальный — перцептивный (максимальная
нагрузка на тест Равена), скоростного
интеллекта (максимальная нагрузка —
тест Г.Айзенка и геометрический тест
на обобщение) и фактор вербальной
компетентности (положительная нагрузка
на тест «Понятия» и показатель
когнитивной простоты). Вместе с тем
обнаружена отрицательная и значимая
нагрузка этого фактора на тест Равена.
Следовательно, чем сложнеее и
дифференцированнее когнитивный опыт
испытуемого, тем успешнее он решает
тест Равена, требующий аналитической
работы, и хуже справляется с заданиями
на понятийное обобщение.
Дифференцированность когнитивных структур является одним из главных параметров интеллекта человека, определяющего успешность решения аналитических мыслительных задач, в том числе — в тесте Равена.
Продвинутые прогрессивные матрицы Равена (Пси-Профиль)
Продвинутые Прогрессивные Матрицы являются разновидностями Стандартного теста и были разработаны с целью более тонкой дифференциации оценок в тех случаях, когда способности испытуемых выше среднего уровня.
Тест разработан в 1936 году и является одним из самых популярных невербальных тестов диагностики интеллекта. В настоящее время используется более чем в 100 странах мира. Прогрессивные Матрицы предназначены для измерения одного из двух главных факторов интеллекта — продуктивной способности. При разработке теста был реализован принцип прогрессивности, Т. Е. выполнение предшествующих заданий является подготовкой к выполнению последующих, более сложных.
- Возраст испытуемых: c 5 лет;
- Заданий: 48;
- Время проведения: 40 — 60 минут;
- Область применения: сфера образования, профессиональная диагностика, клиническая практика, исследовательская работа.
Пример результатов тестирования скачать файл.
Скачать демо-версию – работает как обычная, но не показывает результаты тестирования.
Скачать инструкцию по установке.
Программа «Пси-Профиль» предназначена для автоматизированного психологического тестирования взрослых и детей. Позволяет вести базу данных по проведенным исследованиям, делать выборки по заранее сформированным запросам, распечатывать и сохранять полученные результаты.
Обратите внимание:
Программа «Пси-Профиль» рассчитана исключительно на Windows (XP, 7, 8 или 10). Обязательно наличие USB порта (программа не работает на телефонах или планшетах).
Купив «Пси-Профиль», Вы получаете ключ-флешку с дистрибутивом. «Пси-Профиль» можно установить на неограниченное количество компьютеров, но для функционирования программы требуется наличие флешки в USB-приводе компьютера в момент запуска. После запуска программы, флешку можно извлечь и запустить программу на другом компьютере.
«Пси-Профиль» можно установить на неограниченное количество компьютеров, но для функционирования программы требуется наличие флешки в USB-приводе компьютера в момент запуска. После запуска программы, флешку можно извлечь и запустить программу на другом компьютере.
Чтобы докупить тесты Пси-Профиля, нет надобности приобретать новую флешку. Достаточно оформить заказ в интернет-магазине, оплатить его электронными деньгами, в комментарии написать, что у вас уже есть флешка Пси-Профиля и указать серийный номер и, желательно, дату покупки. Мы найдём Ваш заказ и вышлем Вам на почту новый ключ, активирующий дополнительные тесты.
Системные требования программы: 100 Мб на жестком диске и 32 Мб оперативной памяти.
Полноэкранное представление достигается при разрешении как минимум 800х600, однако рекомендуется режим 1024х768 HighColor.
Асимптотический тест | chi2 на равенство двух корреляционных матриц в JSTOR
Абстрактный Получен асимптотический критерий χ 2 на равенство двух корреляционных матриц.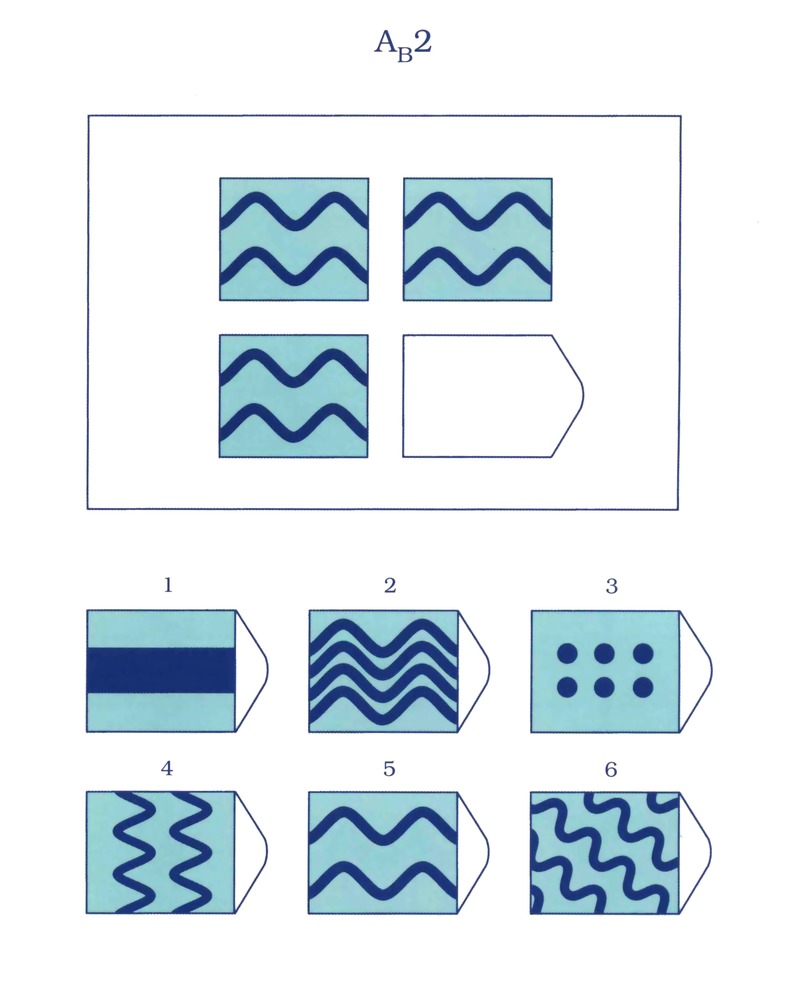 Ключевым результатом является простое представление обратной асимптотической ковариационной матрицы выборочной корреляционной матрицы. Тестовая статистика имеет форму стандартной нормальной теоретической статистики для проверки равенства двух ковариационных матриц с добавленным поправочным членом.Применимость асимптотической теории продемонстрирована двумя исследованиями на моделировании, а статистика используется для проверки различий в факторных моделях, полученных в результате набора тестов, проводимых для умственно отсталых и не умственно отсталых детей. Представлены два связанных теста: тест на указанную корреляционную матрицу и тест на равенство корреляционных матриц в двух или более популяциях.
Ключевым результатом является простое представление обратной асимптотической ковариационной матрицы выборочной корреляционной матрицы. Тестовая статистика имеет форму стандартной нормальной теоретической статистики для проверки равенства двух ковариационных матриц с добавленным поправочным членом.Применимость асимптотической теории продемонстрирована двумя исследованиями на моделировании, а статистика используется для проверки различий в факторных моделях, полученных в результате набора тестов, проводимых для умственно отсталых и не умственно отсталых детей. Представлены два связанных теста: тест на указанную корреляционную матрицу и тест на равенство корреляционных матриц в двух или более популяциях.
Журнал Американской статистической ассоциации (JASA) издавна
считается ведущим журналом статистической науки.Научное цитирование
Index сообщил, что JASA был самым цитируемым журналом в области математики.
наук в 1991-2001 гг.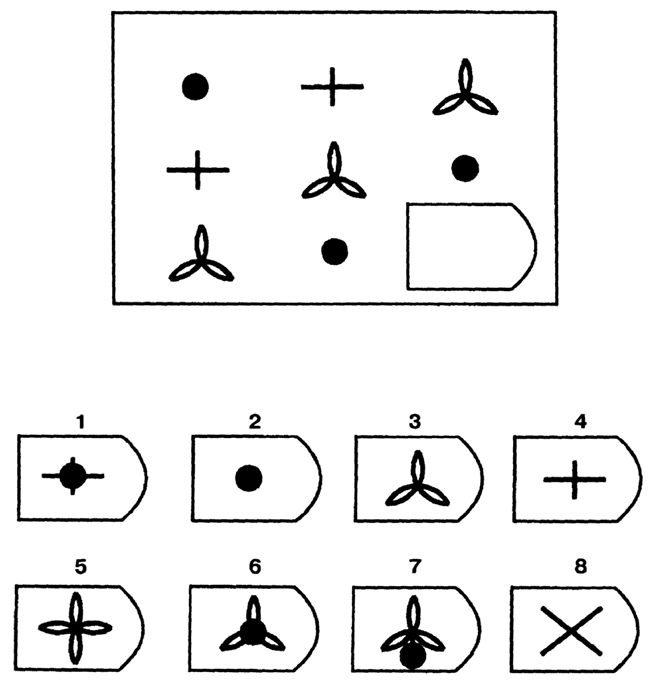 , было цитировано 16 457 раз, что более чем на 50% больше, чем
следующие по цитируемости журналы. Статьи в JASA посвящены статистическим
приложения, теория и методы в экономической, социальной, физической,
инженерные науки и науки о здоровье, а также о новых методах статистической
образование.
, было цитировано 16 457 раз, что более чем на 50% больше, чем
следующие по цитируемости журналы. Статьи в JASA посвящены статистическим
приложения, теория и методы в экономической, социальной, физической,
инженерные науки и науки о здоровье, а также о новых методах статистической
образование.
Основываясь на двухвековом опыте, Taylor & Francis за последние два десятилетия быстро выросла и стала ведущим международным академическим издателем.Группа издает более 800 журналов и более 1800 новых книг каждый год, охватывающих широкий спектр предметных областей и включая журнальные оттиски Routledge, Carfax, Spon Press, Psychology Press, Martin Dunitz и Taylor & Francis. Тейлор и Фрэнсис полностью привержены делу. на публикацию и распространение научной информации высочайшего качества, и сегодня это остается первоочередной задачей.
% PDF-1.3
%
51 0 объект
>
эндобдж
xref
51 108
0000000016 00000 н.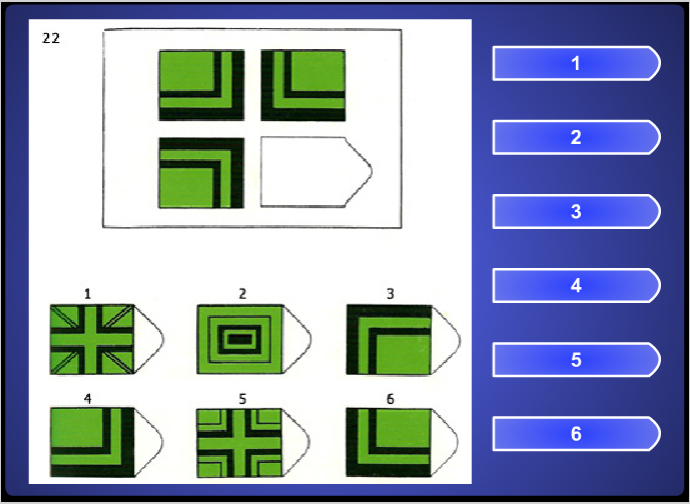 0000002509 00000 н.
0000003374 00000 н.
0000003587 00000 н.
0000003886 00000 н.
0000004246 00000 н.
0000004324 00000 н.
0000004513 00000 н.
0000004983 00000 н.
0000005222 00000 п.
0000005515 00000 н.
0000005968 00000 н.
0000006217 00000 н.
0000006529 00000 н.
0000006729 00000 н.
0000007845 00000 н.
0000008560 00000 н.
0000009029 00000 н.
0000009105 00000 н.
0000016149 00000 п.
0000016631 00000 п.
0000016958 00000 п.
0000022881 00000 п.
0000023642 00000 п.
0000024069 00000 п.
0000024497 00000 п.
0000025014 00000 п.
0000031990 00000 п.
0000032253 00000 п.
0000032636 00000 п.
0000034707 00000 п.
0000034961 00000 п.
0000035388 00000 п.
0000036071 00000 п.
0000036190 00000 п.
0000036211 00000 п.
0000037042 00000 п.
0000037369 00000 п.
0000037889 00000 н.
0000038079 00000 п.
0000042253 00000 п.
0000042441 00000 п.
0000042766 00000 н.
0000043269 00000 п.
0000046509 00000 п.
0000046820 00000 н.
0000047148 00000 п.
0000047169 00000 п.
0000047917 00000 п.
0000048669 00000 н.
0000048740 00000 п.
0000048985 00000 п.
0000002509 00000 н.
0000003374 00000 н.
0000003587 00000 н.
0000003886 00000 н.
0000004246 00000 н.
0000004324 00000 н.
0000004513 00000 н.
0000004983 00000 н.
0000005222 00000 п.
0000005515 00000 н.
0000005968 00000 н.
0000006217 00000 н.
0000006529 00000 н.
0000006729 00000 н.
0000007845 00000 н.
0000008560 00000 н.
0000009029 00000 н.
0000009105 00000 н.
0000016149 00000 п.
0000016631 00000 п.
0000016958 00000 п.
0000022881 00000 п.
0000023642 00000 п.
0000024069 00000 п.
0000024497 00000 п.
0000025014 00000 п.
0000031990 00000 п.
0000032253 00000 п.
0000032636 00000 п.
0000034707 00000 п.
0000034961 00000 п.
0000035388 00000 п.
0000036071 00000 п.
0000036190 00000 п.
0000036211 00000 п.
0000037042 00000 п.
0000037369 00000 п.
0000037889 00000 н.
0000038079 00000 п.
0000042253 00000 п.
0000042441 00000 п.
0000042766 00000 н.
0000043269 00000 п.
0000046509 00000 п.
0000046820 00000 н.
0000047148 00000 п.
0000047169 00000 п.
0000047917 00000 п.
0000048669 00000 н.
0000048740 00000 п.
0000048985 00000 п.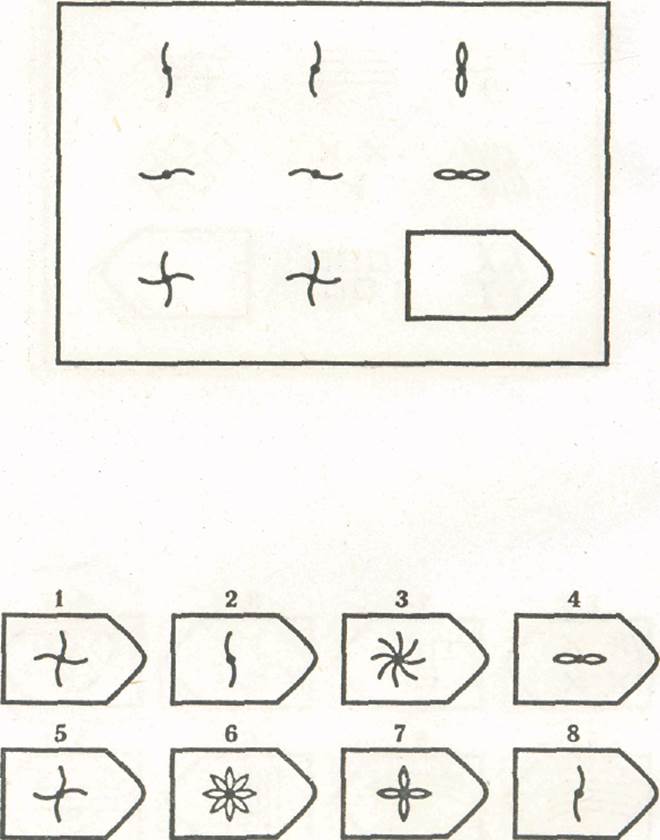 0000050913 00000 п.
0000051288 00000 п.
0000051573 00000 п.
0000051772 00000 п.
0000051847 00000 п.
0000052493 00000 п.
0000052801 00000 п.
0000053053 00000 п.
0000053290 00000 н.
0000053439 00000 п.
0000056687 00000 п.
0000056993 00000 п.
0000057189 00000 п.
0000057308 00000 п.
0000057583 00000 п.
0000057894 00000 п.
0000058331 00000 п.
0000058353 00000 п.
0000059084 00000 п.
0000060108 00000 п.
0000060310 00000 п.
0000060633 00000 п.
0000060708 00000 п.
0000060964 00000 п.
0000060986 00000 п.
0000061597 00000 п.
0000061802 00000 п.
0000062074 00000 п.
0000062856 00000 п.
0000062974 00000 п.
0000063304 00000 п.
0000063326 00000 п.
0000063988 00000 п.
0000064339 00000 п.
0000064552 00000 п.
0000065924 00000 п.
0000066151 00000 п.
0000066474 00000 п.
0000066496 00000 п.
0000067105 00000 п.
0000067400 00000 п.
0000067592 00000 п.
0000067833 00000 п.
0000068128 00000 п.
0000068374 00000 п.
0000068842 00000 п.
0000069036 00000 п.
0000069466 00000 п.
0000069545 00000 п.
0000069636 00000 п.
0000069658 00000 п.
0000050913 00000 п.
0000051288 00000 п.
0000051573 00000 п.
0000051772 00000 п.
0000051847 00000 п.
0000052493 00000 п.
0000052801 00000 п.
0000053053 00000 п.
0000053290 00000 н.
0000053439 00000 п.
0000056687 00000 п.
0000056993 00000 п.
0000057189 00000 п.
0000057308 00000 п.
0000057583 00000 п.
0000057894 00000 п.
0000058331 00000 п.
0000058353 00000 п.
0000059084 00000 п.
0000060108 00000 п.
0000060310 00000 п.
0000060633 00000 п.
0000060708 00000 п.
0000060964 00000 п.
0000060986 00000 п.
0000061597 00000 п.
0000061802 00000 п.
0000062074 00000 п.
0000062856 00000 п.
0000062974 00000 п.
0000063304 00000 п.
0000063326 00000 п.
0000063988 00000 п.
0000064339 00000 п.
0000064552 00000 п.
0000065924 00000 п.
0000066151 00000 п.
0000066474 00000 п.
0000066496 00000 п.
0000067105 00000 п.
0000067400 00000 п.
0000067592 00000 п.
0000067833 00000 п.
0000068128 00000 п.
0000068374 00000 п.
0000068842 00000 п.
0000069036 00000 п.
0000069466 00000 п.
0000069545 00000 п.
0000069636 00000 п.
0000069658 00000 п.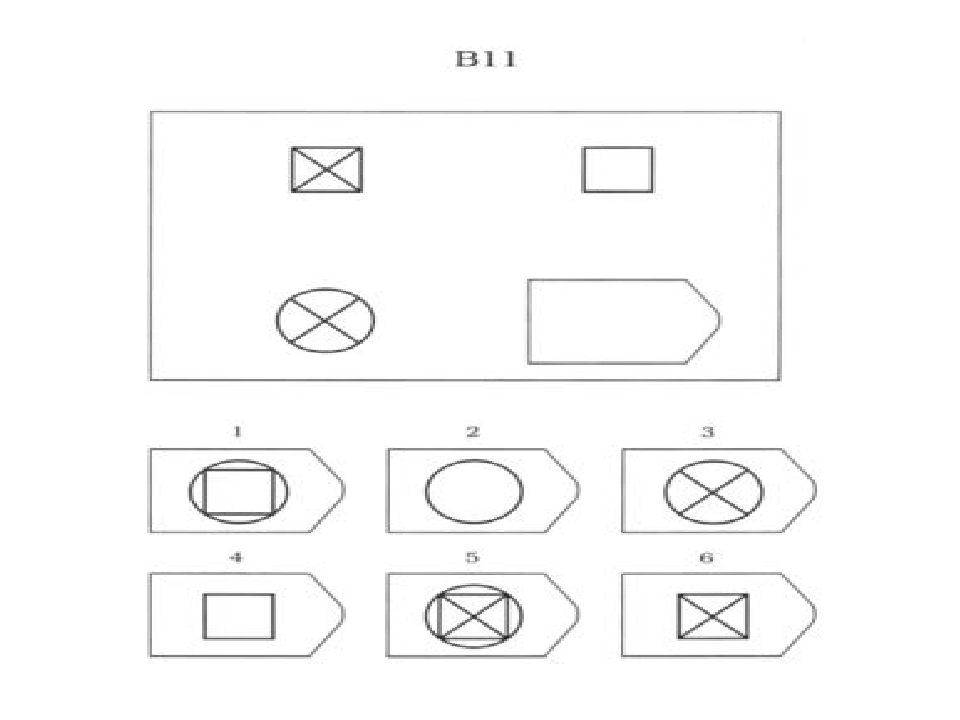 0000070167 00000 п.
0000070189 00000 п.
0000070923 00000 п.
0000002584 00000 н.
0000003352 00000 н.
трейлер
]
>>
startxref
0
%% EOF
52 0 объект
>
эндобдж
157 0 объект
>
транслировать
Hb«f«g`
0000070167 00000 п.
0000070189 00000 п.
0000070923 00000 п.
0000002584 00000 н.
0000003352 00000 н.
трейлер
]
>>
startxref
0
%% EOF
52 0 объект
>
эндобдж
157 0 объект
>
транслировать
Hb«f«g`
Измерение и проверка согласованности матриц
Данные и анализ
В нашем первом примере используется Q = 4 матрицы акустической путаницы, основанные на данных, первоначально собранных Морганом, Чемберсом и Мортоном. (1973) и впоследствии проанализированы Хубертом и Голледжем (1977) и Бруско (2002).Первые две матрицы путаницы в S относятся к задаче распознавания для n = 9 цифр (1, 2,…, 9): матрица A
1 соответствует распознаванию говорящего-мужчины, тогда как A
2 — для женского динамика. Последние две матрицы в S связаны с памятью задач для тех же n = 9 цифр: матрицы A
3 и A
4 связаны с двумя разными динамиками женского пола.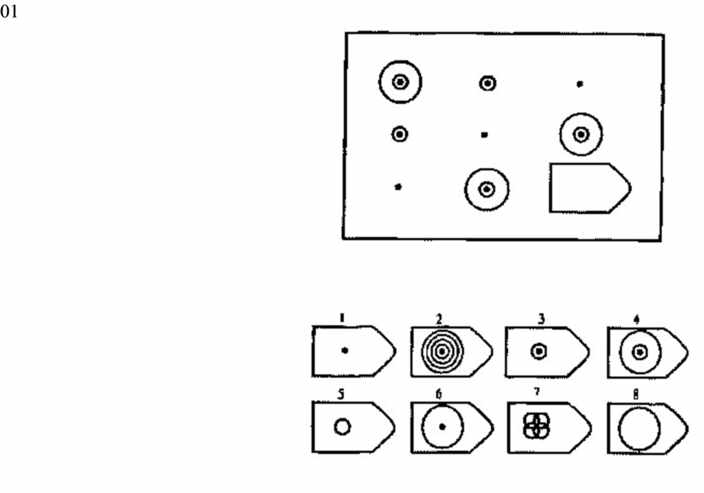 Все четыре матрицы в S были расположены так, чтобы строки соответствовали предъявленному стимулу, а столбцы — ответу. Более того, следуя процедуре, использованной Бруско (2004) в его анализе соответствия между 19 матрицами визуальной и тактильной межбуквенной путаницы, все четыре матрицы в S были нормализованы на основе сумм строк (стимулов). Эти нормализованные матрицы показаны в таблице 1. Для каждой матрицы A
q
дюйм S , a
ijq
— процент ответов цифры j , когда цифра i была предъявленным стимулом.
Все четыре матрицы в S были расположены так, чтобы строки соответствовали предъявленному стимулу, а столбцы — ответу. Более того, следуя процедуре, использованной Бруско (2004) в его анализе соответствия между 19 матрицами визуальной и тактильной межбуквенной путаницы, все четыре матрицы в S были нормализованы на основе сумм строк (стимулов). Эти нормализованные матрицы показаны в таблице 1. Для каждой матрицы A
q
дюйм S , a
ijq
— процент ответов цифры j , когда цифра i была предъявленным стимулом.
Было проведено множество различных тестов с использованием матриц в S . Во-первых, соответствие между всеми парами матриц в S было измерено с использованием как индекса Мантеля, так и индекса градиента внутри строки. Для каждой пары был проведен точный тест для индексов градиента Mantel и внутри ряда с использованием программ mantelexact.m и triadexact.m соответственно.{\ prime} \) в качестве входных матриц для программ MATLAB. Точные и приблизительные тесты симметрии были получены для всех четырех матриц с использованием программ mantelexact.m, triadexact.m, mantelapprox.m и triadapprox.m.
Результаты
Результаты нашего анализа представлены в таблице 2. Одно общее наблюдение состоит в том, что результаты теста значимости, связанные с программами mantelapprox.m и triadapprox.m, очень согласуются с результатами, полученными их точными тестовыми аналогами, mantelexact.м, triadexact.m соответственно. Нет ни одного случая, когда другой вывод относительно значимости был бы достигнут на уровне α = 0,05 или α = 0,01 в зависимости от того, использовался ли точный или приблизительный критерий. Это бенчмаркинг важно потому, что во многих случаях нет выбора, кроме как использовать приближенные тесты.
Таблица 2 Результаты для данных акустической путаницы — точное и приблизительное значение p — значенияЧто касается тестов, ограниченных задачами распознавания, следует отметить, что строгое соответствие между A 1 и A 2 было измерено для каминной доски (Γ 1 ( A 1 , А 2 ) =.8638) и внутрирядный градиент (Γ 2 ( A 1 , А 2 ) = 0,6132) меры. Для обеих мер наблюдаемый индекс был больше, чем любое другое значение индекса в эталонном распределении, что привело к наименьшим возможным значениям p 1/9! = 0,00000276 и 1/100000 = 0,00001 для точного и приблизительного тестов соответственно. Меры согласования для симметрии в целом были слабее. Индекс Мантеля для симметрии A 1 особенно слабый (Γ 1 ( A 1 , \ ({\ mathbf {A}} _ 1 ^ {\ prime} \)) =.{\ prime} \)) = 0,3415) и имеет значение при α = 0,05 ( p -значение = 0,00395172). Это явное свидетельство того, что две меры согласования не обязательно приводят к одним и тем же выводам.
Переходя теперь к тестам, ограниченным задачами с памятью, наблюдается похожая картина, но есть некоторые отличия. Сильное соответствие между A 3 и A 4 было измерено для камина (Γ 1 ( A 3 , А 4 ) =.8554) и внутрирядный уклон (Γ 2 ( A 3 , А 4 ) = 0,5745) и минимально возможные значения p наблюдались для этих мер. И снова меры согласования для симметрии были заметно слабее. Однако, в отличие от результатов для симметрии матриц распознавания, именно индексы градиента внутри строки были особенно плохими для матриц памяти. {\ prime} \)) =.{\ prime} \)) = .1765) соответственно, и ни один из этих индексов не имеет значения при α = .05. Таким образом, снова есть свидетельства того, что две меры соответствия не приводят к одним и тем же выводам, но здесь ситуация обратная (т. Е. Соответствие индекса Мантеля сильнее).
Затем мы рассматриваем соответствие между парами матриц, один из которых соответствует задаче распознавания, а другой — задаче памяти. Индексы Мантеля, связанные с этими сравнениями, были довольно слабыми, особенно в случаях (Γ 1 ( A 1 , А 3 ) =.3343) и (Γ 1 ( A 1 , А 4 ) = 0,2629), которые не были значимыми при α = 0,01. Индексы градиента внутри ряда были заметно сильнее в большинстве случаев и значимы для всех пар при α = 0,005.
Бруско (2002) обнаружил, что оптимальные перестановки для задач памяти были почти противоположны тем, которые были получены для задач распознавания, что привело к подозрению, что один набор этих матриц мог быть транспонирован.{\ prime} \)) = 0,2469). Три из четырех индексов градиента внутри строки, связанных с транспозами, не значимы при α = 0,01. Соответственно, в то время как результаты для индекса Мантела подтверждают предположение, что один набор матриц был транспонирован, результаты градиента внутри строки, конечно же, нет. В любом случае однозначно ясно, что степень соответствия, измеренная индексами градиента Mantel и внутри ряда, в некоторых случаях может существенно отличаться.
Вычислительная чувствительность и эффективность
В этом подразделе мы более внимательно исследуем вычислительную чувствительность и эффективность программ MATLAB для согласования матриц.В частности, чувствительность относится к эффектам значения p , связанным с выбором числа случайных перестановок для программ mantelapprox.m и triadapprox.m. Под эффективностью понимается время вычислений, требуемое программами. Чтобы облегчить это исследование, мы начали с получения значений времени вычислений для программ mantelexact.m и triadexact.m для каждого из тестовых условий в таблице 2. Это время вычислений было получено с использованием компьютера Pentium 4 2,2 ГГц с 1 ГБ ОЗУ.Кроме того, мы выполнили 10 повторений программ mantelapprox.m и triadapprox.m (с использованием 100 000 случайных выборок) для каждого из условий испытаний. Затем мы повторили этот процесс для 10 повторений, но после уменьшения количества случайных выборок до 1000. Для каждого условия тестирования мы сохранили минимальное, среднее и максимальное значения p для 10 повторений, а также минимальное, среднее и максимальное время вычислений. Результаты этих анализов представлены в таблицах 3 и 4 для индекса Мантеля и индекса градиента внутри ряда, соответственно.
Таблица 3 Результаты для данных акустической помехи — результаты расчетной чувствительности и эффективности для теста Мантеля. Минимальные, средние и максимальные значения основаны на 10 повторениях программы mantelapprox.m для 100 000 или 1000 случайных перестановок. На верхней и нижней панелях представлено сравнение значений p и времени вычисления соответственно Таблица 4 Результаты для данных акустической путаницы — результаты расчетной чувствительности и эффективности для теста градиента внутри ряда.Минимальные, средние и максимальные значения основаны на 10 повторениях программы triadapprox.m для 100 000 или 1000 случайных перестановок. На верхней и нижней панелях представлено сравнение значений p и времени вычисления соответственноВремя вычислений для программы mantelexact.m при применении к данным акустической путаницы ( n = 9) варьировалось от 4,300 до 4,345 с. Для n = 10 количество перестановок будет в 10 раз больше, и, следовательно, время вычислений будет как минимум в 10 раз больше, чем для n = 9.Ясно, что еще несколько приращений n приведут к невозможности (или, по крайней мере, непрактичности) программы mantelexact.m. Например, одна из наших более поздних иллюстраций предназначена для контекста, где n = 17. Количество перестановок для n = 17 (17!) Более чем в 980 миллионов раз больше, чем количество перестановок для n = 9 (9!). Умножение 4,3 с на 980 миллионов даст консервативную оценку примерно 133 года времени вычислений для n = 17.Однако это, вероятно, занижает необходимое время для n = 17, потому что, помимо изменения количества перестановок, вычисления, необходимые для каждой отдельной перестановки, также больше для n = 17, чем для n = 9 (т. Е. Больше терминов по продукту). Время вычислений для программы triadexact.m применительно к данным акустической путаницы ( n = 9) составляло от 30,881 до 31,099 с. Дело в том, что эти времена примерно в семь раз больше, чем у мантефакта.m объясняется необходимостью условной оценки триад, а не простых поэлементных произведений.
Таблицы 3 и 4 также показывают, что для заданного числа случайных перестановок время вычислений для программ mantelapprox.m и triadapprox.m чрезвычайно согласовано, с небольшой изменчивостью как в условиях тестирования, так и в пределах условий тестирования ( 10 повторений). Более того, как и ожидалось, время вычислений для 100 000 случайных перестановок примерно в 100 раз больше, чем время вычислений для 1000 случайных перестановок.
Для mantelapprox.m с использованием 100000 случайных перестановок вариабельность значений p в 10 повторах была в целом скромной. Не было случая, чтобы другой вывод относительно значимости был бы достигнут на уровне α = 0,05 или α = 0,01 в зависимости от того, использовалось ли минимальное или максимальное значение p в 10 повторностях. Однако для A 1 Тест симметрии с использованием α = .10, максимальное значение p .10109 приведет к невозможности отклонить нулевое значение, тогда как минимальное, среднее и точное значение p (все меньше, чем 0,10) приведет к отклонению. Когда количество случайных перестановок было уменьшено до 1000, вариабельность значений p в 10 повторностях все еще была довольно скромной. Однако было несколько других обстоятельств, при которых можно было прийти к другому выводу в зависимости от минимального или максимального значения p в 10 повторностях: (i) A 3 проверка симметрии, если α =.01, (ii) A 4 проверка симметрии, если α = 0,05, (iii) A 1 — А 3 согласие при α = 0,01, и (iv) A 2 — А 4 согласие при α = 0,01.
Для triadapprox.m с использованием 100000 случайных перестановок вариабельность значений p в 10 повторностях была скромной, и, опять же, не было случая, чтобы другой вывод был бы сделан при α =.05 или α = 0,01, в зависимости от того, использовалось ли минимальное или максимальное значение p в 10 повторностях. Когда использовалось только 1000 случайных перестановок, следующие условия испытаний будут иметь различный вывод в зависимости от того, использовался ли минимум или максимум для 10 повторов: (1) A 4 проверка симметрии, если α = 0,05, и (2) A 2 — А 3 ′ согласие при α =.01.
Matrix Rank
Этот урок знакомит с концепцией матрицы с рангом и объясняет, как ранг матрица раскрывается его эшелонированная форма.
Ранг матрицы
Матрицу r x c можно представить как набор строк r векторы каждый имеет c элементов; или вы можете думать об этом как о наборе c векторы-столбцы, каждый из которых имеет r элементов.
Ранг матрицы определяется как (а) максимальное количество линейно независимых столбцов векторов в матрице или (б) максимальное количество линейно независимых строк векторов в матрице.Оба определения эквивалентны.
Для матрицы r x c ,
- Если r меньше c , то максимальный ранг матрицы составляет р .
- Если r больше c , то максимальный ранг матрицы это c .
Ранг матрицы был бы равен нулю, только если бы матрица не имела элементов. Если бы матрица имела хотя бы один элемент, ее минимальный ранг был бы равен единице.
Как найти ранг матрицы
В этом разделе мы описываем метод определения ранга любой матрицы.Этот метод предполагает знакомство с эшелонированные матрицы а также эшелонные преобразования.
Максимальное количество линейно независимых векторов в матрице равно к количеству ненулевых строк в его матрица эшелонов строк. Следовательно, чтобы найти ранг матрицы, мы просто преобразовать матрицу в ее форму эшелона строк и подсчитать количество ненулевые строки.
Рассмотрим матрицу A и ее эшелон строк. матрица, A ref . Ранее мы показывали как найти форму эшелона строк для матрицы A .
Потому что форма эшелона строки A ref имеет две ненулевые строки, мы знаем, что матрица A имеет два независимых вектора-строки; а также мы знаем, что ранг матрицы A равен 2.
Вы можете убедиться, что это правильно. Ряд 1 и Ряд 2 матрицы A линейно независимый. Однако строка 3 — это линейная комбинация строк 1 и 2. В частности, строка 3 = 3 * (строка 1) + 2 * (строка 2). Следовательно, матрица A имеет только два независимых вектора-строки.
Матрицы полного ранга
Когда все векторов в матрице линейно независимый, матрица называется , полный ранг . Рассмотрим матрицы A и B ниже.
Обратите внимание, что строка 2 матрицы A является скалярным кратным ряд 1; то есть строка 2 равна удвоенной строке 1. Следовательно, строки 1 и 2 являются линейно зависимый. Матрица А имеет только одну линейно независимую строка, поэтому ее ранг равен 1. Следовательно, матрица A не имеет полного ранга.
Теперь посмотрим на матрицу B . Все его строки линейно Независимо, поэтому ранг матрицы B равен 3. Матрица B полноразмерная.
Проверьте свое понимание
Проблема 1
Рассмотрим матрицу X , показанную ниже.
Какое у него звание?
(A) 0
(B) 1
(C) 2
(D) 3
(E) 4
Решение
Правильный ответ (C). Поскольку в матрице больше нуля элементов, его ранг должен быть больше нуля.И поскольку в нем меньше строк, чем столбцов, его максимальный ранг равен максимальному количеству линейно независимые строки. И поскольку ни одна строка не зависит линейно от другой строки, матрица имеет 2 линейно независимых строки; поэтому его ранг равен 2.
Задача 2
Рассмотрим матрицу Y , показанную ниже.
Какое у него звание?
(A) 0
(B) 1
(C) 2
(D) 3
(E) 4
Решение
Правильный ответ (C).Поскольку в матрице больше нуля элементов, его ранг должен быть больше нуля. И поскольку в нем меньше столбцов, чем строк, его максимальный ранг равен максимальному количеству линейно независимых столбцы.
Столбцы 1 и 2 независимы, потому что ни один из них не может быть получен как скалярное кратное другому. Однако столбец 3 линейно зависит от столбцов 1 и 2, потому что столбец 3 равен столбцу 1 плюс столбец 2. Это оставляет матрицу максимум с двумя линейно независимые колонны; то есть., столбец 1 и столбец 2. Таким образом, ранг матрицы равен 2.
numpy.testing.assert_array_equal — NumPy v1.21 Manual
Вызывает AssertionError, если два объекта array_like не равны.
Учитывая два объекта array_like, проверьте, что форма одинакова и все элементы этих объектов равны (но см. Примечания для специальных обработка скаляра). Исключение возникает при несоответствии формы или противоречивые ценности. В отличие от стандартного использования в numpy, NaN сравниваются как числа, утверждение не возникает, если оба объекта имеют NaN в тех же позициях.
Обычное предупреждение при проверке равенства с числами с плавающей запятой: посоветовал.
- Параметры
-
- x array_like
-
Фактический объект для проверки.
- y array_like
-
Желаемый, ожидаемый объект.
- err_msg str, необязательно
-
Сообщение об ошибке, которое будет напечатано в случае сбоя.
- подробный bool, необязательный
-
Если True, конфликтующие значения добавляются к сообщению об ошибке.
- Повышает
-
- AssertionError
-
Если фактические и желаемые объекты не равны.
Банкноты
Когда один из значений x и y является скаляром, а другой — array_like, функция проверяет, что каждый элемент объекта array_like равен скаляр.
Примеры
Первое утверждение не вызывает исключения:
>>> np.testing.assert_array_equal ([1.0,2.33333, np.nan], ... [np.exp (0), 2.33333, np.nan])
Assert терпит неудачу с числовой неточностью с числами с плавающей запятой:
>>> np.testing.assert_array_equal ([1.0, np.pi, np.nan],
... [1, np.sqrt (np.pi) ** 2, np.nan])
Отслеживание (последний вызов последний):
...
AssertionError:
Массивы не равны
Несоответствующие элементы: 1/3 (33,3%)
Максимальная абсолютная разница: 4.4408921e-16
Максимальная относительная разница: 1.41357986e-16
x: array ([1., 3.141593, nan])
y: array ([1., 3.141593, nan])
Используйте assert_allclose или одно из nulp (количество значений с плавающей запятой)
вместо этого функции для этих случаев:
>>> np.testing.assert_allclose ([1.0, np.pi, np.nan], ... [1, np.sqrt (np.pi) ** 2, np.nan], ... rtol = 1e-10, atol = 0)
Как упоминалось в разделе примечаний, assert_array_equal имеет специальные
обработка скаляров.Здесь тест проверяет, что каждое значение в x равно 3:
>>> x = np.full ((2, 5), fill_value = 3) >>> np.testing.assert_array_equal (x, 3)Регрессия
— Определение матрицы контраста для проверки нулевой гипотезы $ H_0: \ beta_5 = \ beta_6 = 0 $
В книге «Прикладной лонгитюдный анализ», 2-е издание, есть пример в главе «Маргинальные модели: обобщенные оценочные уравнения (GEE)» в подразделе «Исследование фактора коронарного риска мускатного происхождения».2. $$
Если построить гипотезу о том, что изменения логарифма шансов ожирения одинаковы для мальчиков и девочек, тогда $ H_0: \ beta_5 = \ beta_6 = 0 $.
Для проверки гипотезы $$ H_0: \ beta_5 = \ beta_6 = 0 $$ $$ \ Rightarrow \ mathbf L \ mathbf \ beta = 0, $$
где $ \ mathbf \ beta = \ begin {pmatrix} \ beta_1 & \ beta_2 & \ beta_3 & \ beta_4 & \ beta_5 & \ beta_6 \\ \ end {pmatrix} ‘ $ и $ \ mathbf L $ — матрица контраста.
Но я не могу написать матрицу контраста для $ H_0: \ beta_5 = \ beta_6 = 0 $.
Потому что, если бы $ H_0 $ было $ H_0: \ beta_5 = \ beta_6 $ (обратите внимание, что ISN’T равно $ 0 $ в крайнем правом углу), то я могу легко построить матрицу контраста следующим образом: $ \ mathbf L = \ begin {pmatrix} 0 & 0 & 0 & 0 & 1 & -1 \\ \ end {pmatrix} $ так, чтобы
$$ \ mathbf L \ mathbf \ beta = 0 $$ $$ \ Rightarrow \ begin {pmatrix} 0 & 0 & 0 & 0 & 1 & -1 \\ \ end {pmatrix} \ begin {pmatrix} \ beta_1 \\ \ beta_2 \\ \ beta_3 \\ \ beta_4 \\ \ beta_5 \\ \ beta_6 \\ \ end {pmatrix} = 0 $$
$$ \ Rightarrow \ beta_5 = \ beta_6.
$Но когда $ H_0 $ равен $ H_0: \ beta_5 = \ beta_6 = 0 $ (обратите внимание, что там ЕСТЬ равно $ 0 $ в крайнем правом углу), тогда $ \ mathbf L = \ begin {pmatrix} 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 \\ \ end {pmatrix} $ так, чтобы
$$ \ mathbf L \ mathbf \ beta = 0 $$ $$ \ Rightarrow \ begin {pmatrix} 0 & 0 & 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 \\ \ end {pmatrix} \ begin {pmatrix} \ beta_1 \\ \ beta_2 \\ \ beta_3 \\ \ beta_4 \\ \ beta_5 \\ \ beta_6 \\ \ end {pmatrix} = 0 $$
$$ \ Rightarrow \ beta_5 = 0 \ quad \ text {и} \ quad \ beta_6 = 0, $$
, но обязательно, что матрица контрастности НЕ верна, так как сумма строк матрицы контрастности равна $ 0 $.Как я могу определить контрастную матрицу?
Тест равных или заданных пропорций
Описание использование Аргументы Подробности Ценить использованная литература Смотрите также Примеры prop.test может использоваться для проверки нуля, который
пропорции (вероятности успеха) в нескольких группах являются
одинаковые, или что они равны определенным заданным значениям.
(x, n, p =,
альтернатива = ("два.односторонний »,« меньше »,« больше »),
conf.level = 0.95, правильно =)
|
x |
вектор подсчетов успехов, одномерная таблица с две записи или двумерная таблица (или матрица) с 2 столбцами, подсчитывая соответственно успехи и неудачи. |
n |
вектор отсчетов испытаний; игнорируется, если |
p |
вектор вероятностей успеха.Длина
|
альтернативный |
строка символов, определяющая альтернативу
гипотеза, должно быть одним из |
уровень конф. |
доверительный уровень возвращенной достоверности интервал. Должно быть одно число от 0 до 1. Используется только при проверке нуля, что одна пропорция равна заданному значение, или что две пропорции равны; в противном случае игнорируется. |
правильный |
— логическое указание на то, что непрерывность Йетса по возможности следует применять исправление. |
Используются только группы с конечным числом успехов и неудач.Подсчет успехов и неудач должен быть неотрицательным и, следовательно, не больше, чем соответствующее количество испытаний, которые должны быть положительный. Все конечные числа должны быть целыми.
Если p — это NULL и существует более одной группы, нуль
проверено, что пропорции в каждой группе одинаковы. Если там
две группы, альтернативы таковы, что вероятность успеха
в первой группе меньше, не равно или больше
вероятность успеха во второй группе, как указано
альтернатива .Доверительный интервал для разности
пропорции с уровнем достоверности, указанным в conf.level
и с обрезкой до [-1,1] возвращается . Коррекция непрерывности
используется только в том случае, если она не превышает разницы образца
пропорции по абсолютной величине. В противном случае, если их больше 2
группы, альтернатива всегда "двусторонний" , возвращаемый
доверительный интервал NULL , а коррекция непрерывности никогда
использовал.
Если есть только одна группа, то проверяется нуль, что
основная вероятность успеха p , или.5, если p равно
не дано. Альтернатива — меньше вероятность успеха.
чем, не равно или больше p или 0,5, соответственно, как
указано альтернатива . Доверительный интервал для
базовая пропорция с уровнем достоверности, указанным в
conf.level и обрезанный до [0,1] возвращается. Непрерывность
коррекция используется только в том случае, если она не превышает разницы между
образец и нулевые пропорции в абсолютном значении.Доверительный интервал
вычисляется путем инвертирования результатов теста.
Наконец, если дан p и имеется более 2 групп,
null — это то, что основные вероятности успеха
приведено по р . Альтернативой всегда является "двусторонний" ,
возвращенный доверительный интервал составляет NULL , и исправление непрерывности
никогда не используется.
Список с классом "htest" , содержащий следующие
компоненты:
статистика |
значение статистики критерия хи-квадрат Пирсона. |
параметр |
степени свободы приближенного Хи-квадрат распределения тестовой статистики. |
p. Значение |
p-значение теста. |
оценка |
вектор с примерными пропорциями |
конф. Внутр. |
доверительный интервал для истинной пропорции, если
есть одна группа, или для разницы в пропорциях, если
есть 2 группы и |
нулевое значение |
значение |
альтернативный |
строка символов, описывающая альтернативу. |
метод |
строка символов, указывающая используемый метод, и применялась ли поправка Йетса к непрерывности. |
data.name |
строка символов, дающая имена данных. |
Уилсон, Э. (1927). Вероятный вывод, закон последовательности и статистический вывод. Журнал Американской статистической ассоциации , 22 , 209–212.\ Sexpr [results = rd, stage = build] {tools ::: Rd_expr_doi («10.2307 / 2276774»)}.
Ньюкомб Р.Г. (1998). Двусторонние доверительные интервалы для одной пропорции: сравнение семи методов. Статистика в медицине , 17 , 857–872. \ Sexpr [results = rd, stage = build] {tools ::: Rd_expr_doi («10.1002 / (SICI) 1097-0258 (19980430) 17: 8 <857 :: AID-SIM777> 3.0.CO; 2-E») }.
Ньюкомб Р.Г. (1998). Интервальная оценка разницы между независимыми Пропорции: сравнение одиннадцати методов. Статистика в медицине , 17 , 873–890. \ Sexpr [results = rd, stage = build] {tools ::: Rd_expr_doi («10.1002 / (SICI) 1097-0258 (19980430) 17: 8 <873 :: AID-SIM779> 3.0.CO; 2-I») }.
binom.test для точный тест бинома
гипотеза.
1 2 3 4 5 6 7 8 9 10 11 12 13 | голов <- (1, размер = 100, вероятность = 0,5) (Heads, 100) # Коррекция непрерывности по умолчанию ИСТИНА (головы, 100, правильно =) ## Данные Fleiss (1981), стр. |


