Тест равена результаты: Недопустимое название — Psylab.info

Онлайн-школа Kidskey

Как определить уровень интеллекта ребёнка? Очень легко. Пройти тест Равена, специально адаптированный опытными психологами для детей.

В результате тестирования вы сможете понять, стоит ли уделять больше внимания интеллектуальному развитию ребёнка, а также получите рекомендации по улучшению его способностей.

Имя

Возраст

Год 2022 2021 2020 2019 2018 2017 2016 2015 2014 2013 2012 2011 2010 2009 2008 2007 2006 2005 2004 2003 2002 2001 Месяц январь февраль март апрель май июнь июль август сентябрь октябрь ноябрь декабрь День12345678910111213141516171819202122232425262728293031

Обучение в Kidskey — это:

Гибкий график занятий

Расписание уроков вы устанавливаете сами

Уроки в игровой форме

Обучение+развлечение, яркие интерактивные задания

Занятия 1 на 1 с педагогом

Индивидуальный подход к каждому ребёнку

Собственная онлайн-платформа

Интуитивна и понятна детям любого возраста

Где найти бесплатные развивающие материалы для детей?

Простые методики запоминания, идеи для детского творчества, игры на развитие памяти, внимания, логики и многое другое вы найдёте в нашем Telegram-канале

Что определяет онлайн-тест Равена?

Матрицы Равена определяют уровень IQ человека, дают оценку его интеллектуальному развитию, умению мыслить логически, видеть закономерности и т. д.

Дословно IQ означает «коэффициент интеллекта». Это число показывает интеллектуальные способности конкретного человека относительно большинства людей такого же возраста. Уточнение про возраст здесь неспроста – у ребёнка 5-ти лет и выпускника ВУЗа могут быть одинаковые IQ – ведь развитие каждого соответствует его возрастной группе.

Задания теста построены на умении определять структуры рисунков, видеть взаимосвязи, проводить аналогии, делить целое на части т.д. Они не сводятся к математическим, лингвистическим или понятийным способностям. Благодаря этому тест Равена для детей значительно объективнее большинства других популярных методик.

Как проходить тест?

Опросник состоит из 36-ти матриц. В каждой из них необходимо подобрать недостающий фрагмент к рисунку. Сами рисунки содержат в себе различные символы или геометрические фигуры.

Каждое задание имеет только одно правильное решение.

Есть ли ограничение по времени у теста?

Рекомендованное время прохождения теста – 9 минут.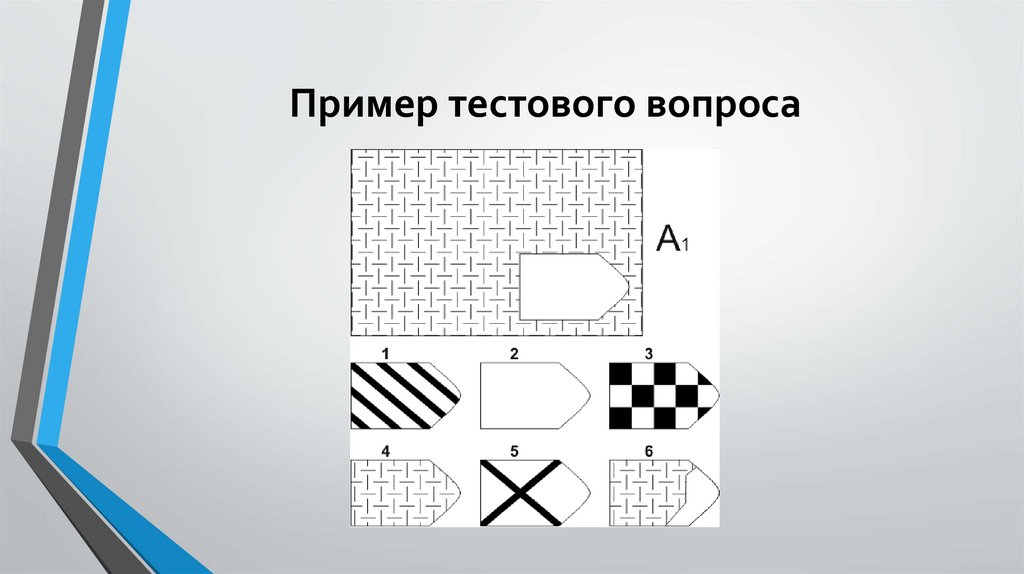 На каждое задание отводится 15 секунд. Вопросы, на которые не будет получен ответ, считаются неправильно отвеченными.

Насколько точен ваш тест?

Тест составляли опытные психологи – задания упрощены для детей от 4-х до 12-ти лет. А механика теста и функционал платформы разработаны таким образом, что результаты постоянно адаптируются, учитывая возрастную зрелость ребёнка. Поэтому наш тест объективен для любого возраста и позволяет дать точную оценку уровня интеллекта.

Каковы преимущества вашего теста?

Факторы, определяющие надёжность теста:
• правильный выбор параметров, которые адекватно отражают уровень развития ребёнка;
• специальная, чёткая и продуманная методика проверки ответов и оценки результатов;
• общие условия каждого тестирования.

Можно ли развить интеллект?

Интеллект – это способность запоминать, оценивать и использовать информацию. Способность рассуждать, видеть аналогии и закономерности, строить логические выводы.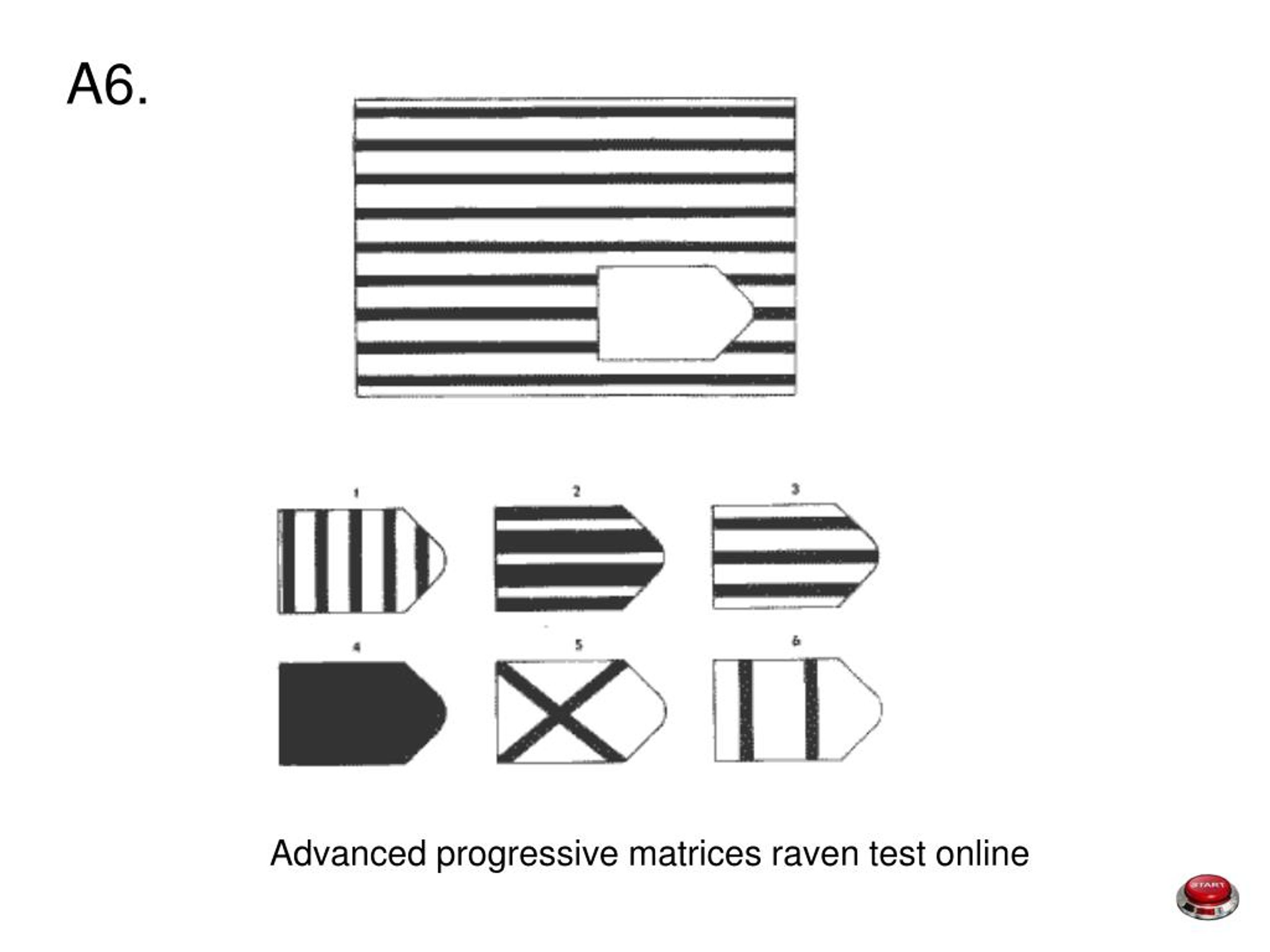 Это внимание, память и сообразительность.

Уровень интеллекта можно и нужно повышать – тренировки для ума актуальны не меньше, чем тренировки для тела. Решение логических задач, тренировка памяти и внимательности, скорочтение, физическое развитие, занятия музыкой и, конечно, математикой – всё это положительно влияет на интеллект.

Каждый урок курса «Математика» в Kidskey включает в себя тренировку логики, памяти и внимания. Это универсальные навыки, которые гарантированно понадобятся детям любого возраста.

Ответим на любые вопросы 24/7

Михайлова М.С. Использование теста Равена для определения умственного развития детей с синдромом Дауна

Библиографическая ссылка на статью:
// Психология, социология и педагогика. 2012. № 6 [Электронный ресурс]. URL: https://psychology.snauka.ru/2012/06/722 (дата обращения: 20.07.2022).

Михайлова М.С.

Магистр биологии, Северо-Казахстанский государственный университет им.

М. Козыбаева

В статье приведены результаты исследования уровня умственного развития детей с синдромом Дауна, воспитывающихся в Петропавловском детском психоневрологическом доме-интернате (ПДПНДИ). Исследование проводилось на основе анализа медицинских карт больных детей и применения матриц Равена. Результаты исследования применены в работе сотрудников ПДПНДИ с целью социальной адаптации детей с синдромом Дауна.

Изучение уровня умственного развития детей с синдромом Дауна представляется наиболее интересным. Известно, что индивиды с болезнью Дауна запаздывают в развитии по сравнению со своими обычными сверстниками и среди всех умственно отсталых детей  составляют 10-12%  [2,34]. Степень недоразвития интеллекта детей с болезнью Дауна может варьировать. По данным зарубежных авторов 65-90% случаев умственного недоразвития у детей с синдромом Дауна – это олигофрения в степени имбецильности. Дебильность и идиотия у детей диагностируется в одинаковых соотношениях [5,16; 1,48].

Исследование умственных способностей у людей с синдромом Дауна началось более 40 лет назад. За это время было опубликовано много  работ по определению уровня интеллектуального развития данного контингента людей. Несмотря на то, что все эти исследования имели общую цель, они значительно отличались друг от друга:

 

 — по изучавшимся популяциям,

 — по применяемым методам,

 — по количеству испытуемых и особенностям развития обследуемых.

Уровень умственного развития можно определить разными способами. Один из них – вычисление IQ – показателя умственного развития на основе способности к быстрому решению стандартных задач, которые составлены так, чтобы результаты их решения давали возможность выявлять и измерять такие первичные способности, как умение логически мыслить, запоминать и представлять предметы в трёх измерениях. Однако определение уровня интеллектуального развития у детей с генетической патологией вызывает  определённые трудности.

Это связано:

— во-первых, с выбором наиболее оптимальной методики, позволяющей определить уровень интеллекта у этих детей;

— во-вторых, с правильной подготовкой и проведением исследований по этой методике, поскольку дети с синдромом Дауна  не умеют и не могут интегрировать свои ощущения, одновременно концентрировать внимание, слушать, смотреть и реагировать на предложенные раздражители. Следовательно, не имеют возможности в отдельно взятый момент времени обработать сигналы более чем от одного раздражителя.

— в-третьих, с правильной интерпретацией полученных в ходе эксперимента результатов.

Большое значение при патопсихологическом обследовании имеет установление хорошего контакта с обследуемым человеком, что в свою очередь требует от экспериментатора достаточной активности. Во время обследования необходимо создать не просто доброжелательную атмосферу, но уметь заинтересовать обследуемого ребёнка или подростка заданиями, создать положительно насыщенный эмоциональный фон, чтобы обследуемому человеку хотелось продолжить эксперимент.

С детьми, имеющими определённые  отклонения в умственном развитии, патопсихологическое обследование проводится обычно  в виде игры [3,76]. Однако необходимо отметить, что эксперименты, которые проводятся с психически больными или глубоко отсталыми детьми, заведомо не могут быть столь точными и безупречными, как это имеет место при исследовании нормальных детей.

Определение уровня умственного развития детей с синдромом Дауна  проходило на базе Петропавловского детского психоневрологического дома-интерната (ПДПНДИ).

Петропавловский детский психоневрологический дом – интернат является медико-педагогическим учреждением, предназначенным для детей с аномалиями умственного и физического развития. Сюда поступают дети в возрасте от 4 до 18 лет, страдающие психическими заболеваниями, сочетающимися с различными формами умственной отсталости. Значительная часть этих детей нуждается в психолого-педагогической помощи и социально-трудовой адаптации. Сотрудники интерната проводят большую работу по воспитанию и необходимой адаптации этих детей в обществе, используя различные методы обучения детей, а также при необходимости применяя  медикаментозное лечение.

Все воспитанники данного учреждения в зависимости от состояния здоровья и психического статуса разделены на  3  группы: обучаемые, частично обучаемые и необучаемые.

К первой группе относятся дети с ярко выраженной степенью дебильности и менее выраженной степенью имбецильности. Для обучения этих детей в основном используется специальная адаптированная школьная программа.

Ко второй группе относятся дети со средней и глубокой степенью имбецильности. Основной задачей воспитания и обучения этих глубоко умственно отсталых детей является обучение элементарным навыкам самообслуживания, обучение простым трудовым операциям и освоение самых элементарных представлений об окружающей действительности. В процессе обучения этих детей совершенствуется мелкая моторика рук, развивается умение различать, выделять предметы и знать их назначение, формируется умение понимать обращённую речь.

К третьей группе относятся дети с олигофренией в степени идиотии. Работа с этими детьми сильно затруднена, вследствие их тяжёлого состояния. Однако и с этими воспитанниками коррекционные мероприятия проводятся в индивидуальном порядке сотрудниками медико-педагогического персонала дома-интерната.

Для определения уровня умственного развития у детей с синдромом Дауна после консультаций с психологами  дома – интерната нами была выбрана методика  в виде Теста Равена. Тест Равена (I. С. Raven)  или,  иначе,  шкала прогрессивных матриц Равена был создан в 1936 году в чёрно-белом варианте для диагностики интеллекта людей от  8 до 65 лет. Тест содержит 5 серий по 12 матриц в каждой с возрастающей трудностью. В данном тесте необходимо определить пропущенные элементы. С 1949 года данный тест используется в цветном варианте в основном для детей с 5 до 11 лет или для пациентов с нарушениями интеллекта. Результаты теста Равена коррелируют с результатами  тестов Векслера и Стэнфорд-Бине [3,57].

Учитывая тот факт, что у наблюдаемых нами детей с синдромом Дауна, интеллектуальная сфера сильно  страдает, наблюдается постоянная отвлекаемость от предметов даже на малейшие шумы и быстрая утомляемость, нами был выбран сокращённый вариант теста, состоящий из 30 матриц.

В ходе проведённого исследования из 173-х детей, находящихся в доме-интернате, было выявлено  14 детей разных возрастов, у которых фенотипически диагностирован синдром Дауна. В таблице 1 представлены данные о распределении детей с синдромом Дауна по возрасту.

Таблица 1.

Распределение детей с синдромом Дауна по возрасту.

№ п/п	Возраст детей  с синдромом Дауна	Количество детей  с синдромом Дауна	В % от общего числа детей  с данной генетической патологией	В % от общего числа детей, находящихся в доме-интернате
1.	5 – 7 лет	4	28,6	2,3
2.	8 – 12 лет	3	21,4	1,73
3.	13 – 16  лет	6	42,9	3,47
4.	18 лет	1	7,1	0,6
Всего:		14	100	8,1

Данные таблицы 1 свидетельствуют о том, что из 14 детей с синдромом Дауна наибольший процент детей (42,9 %) выявлен в возрастной группе 13-16  лет, наименьший (0,6 %) в возрастной группе  18 лет. Данные таблицы  указывают на то, что количество детей с синдромом Дауна в доме-интернате меньше, чем можно было предполагать (частота их встречаемости составляет примерно 8 %), но вполне вероятно, что при цитогенетическом обследовании такой диагноз был бы поставлен гораздо  большему количеству воспитанников. Вместе с тем, согласно данным Ф. Фогеля, А. Мотульски (1990) частота рождения детей с синдромом Дауна составляет примерно 1:600 – 1:800 новорожденных, что составляет  0,12 – 0,16% [4,980].  Следовательно, встречаемость детей с синдромом Дауна в специализированном детском учреждении значительно выше популяционной.

Весьма своеобразной является структура психического недоразвития этих детей. У значительной части детей с синдромом Дауна овладение речью настолько замедлено, что возможность их обучения посредством общения с другими людьми крайне затруднена. Умение говорить развивается, как правило, позже умения воспринимать речь. Детям с синдромом Дауна свойственны трудности в освоении грамматического строя речи, а также семантики, то есть значений слов. Они долго не дифференцируют звуки окружающей речи, плохо усваивают новые слова и словосочетания.

Наблюдения, проводимые за детьми с синдромом Дауна, находящимися в Петропавловском детском психоневрологическом доме-интернате показали следующие результаты:

• речь у этих детей появляется достаточно поздно и зачастую остаётся недоразвитой,
• понимание речи недостаточное,
•  словарный запас бедный,
• часто встречается звукопроизношения в виде дизартрии или дислании.

В медицинской литературе синдром Дауна рассматривается как дифференцированная форма олигофрении, которая подразделяется на такие степени умственной отсталости как: дебильность, имбецильность и  идиотию [3,18].

Так, в ходе исследования нами был выявлен ребёнок с диагнозом болезнь Дауна, олигофрения в стадии имбецильности. Из анамнеза Н.Р.: мальчик отказной, родился 12.05.93г. от второй беременности, вторых родов. Ребёнок поступил из Дома ребенка 03.02.97. с диагнозом болезнь Дауна, олигофрения в стадии имбецильности. Во время проведения исследования было выявлено, что мальчик склонен к аффективным реакциям,  иногда с деструктивными действиями – может скинуть предмет со стола, ударить взрослого человека в ситуациях прямого к нему обращения. Ребёнок мало подвижен, фразовая речь не развита; в контакт с незнакомыми вступает не сразу, практически всегда настроен агрессивно. При работе с матрицами Равена  ребенок не вникает в суть инструктируемого задания, в связи с этим задание выполняется более 40 минут, что зачастую приводит к повышенной отвлекаемости и потере интереса.  По результатам проведённого исследования коэффициент интеллектуального развития этого ребёнка составил меньше 25. Низкий уровень интеллектуального развития мальчика позволяет судить о наличии у него олигофрении в стадии идиотии.

На основании анализа индивидуальных медицинских карт детей нами была составлена таблица, распределяющая детей с синдромом Дауна по уровню их интеллектуального развития.

Таблица 2.

Распределение детей с синдромом Дауна по уровню интеллектуального развития (на основе данных медицинских карт).

№ п/п	Степени умственной отсталости	Коэффициент интеллектуального развития в баллах (Вилли, 1966)	Количество детей с синдромом Дауна
1.	Дебильность	50 – 70	—
2.	Имбецильность	25 – 50	10
3.	Идиотия	0 – 25	4
Всего:			14

        Согласно данным таблицы видно, что у всех детей с синдромом Дауна, находящимся в Петропавловском детском психоневрологическом доме-интернате наблюдается отставание в умственном развитии, приводящее к возникновению у этих детей умственной отсталости. По данным медицинских карт  у 10 детей умственная отсталость выражена в степени имбецильности, у 4-х детей – в степени идиотии. Умственная отсталость в степени дебильности не выявлена ни у одного ребёнка из данного контингента детей. Всё это указывает на чрезвычайно низкий уровень интеллектуального развития детей с синдромом Дауна, воспитывающихся в доме-интернате.

Однако на основании наблюдений за детьми с синдромом Дауна и значительной адекватности некоторых из них нами было высказано предположение о несоответствии уровня интеллектуального развития у некоторых детей. С целью подтверждения наших предположений был проведён эксперимент по определению степени интеллектуального развития у всех детей с синдромом Дауна, воспитывающихся в доме-интернате.

На сновании проведённого теста нами были получены результаты, представленные в таблице 3.

Таблица 3.

Распределение детей с синдромом Дауна по уровню интеллектуального развития (на основе результатов теста Равена).

№ п/п	Коэффициент интеллектуального развития	Количество детей с синдромом Дауна	Уровень интеллектуального развития	В % от общего числа детей с синдромом Дауна в доме-интернате
1.	74	1	Умственная отсталость в степени дебильности	7
2.	25 – 46	4	Умственная отсталость в степени имбецильности	28,6
3.	меньше 25	9	Умственная отсталость в степени идиотии	64,3
Всего:		14	—	≈ 100

Данные таблицы 3 и рисунка 1 свидетельствуют о том, что у значительной части детей с синдромом Дауна наблюдается чрезвычайно низкий уровень интеллектуального развития. Так, у 9 детей (64,3%) коэффициент интеллектуального развития ниже 25, вследствие чего выявляется умственная отсталость в степени идиотии. У 4 детей (28,6%), содержащихся в доме интернате, выявлена умственная отсталость в степени имбецильности. И у одного ребёнка (Ш.В.) наблюдается умственная отсталость в степени  дебильности.

Из анамнеза Ш.В.: девочка от первой беременности, первых срочных родов. Поступила в Петропавловский психоневрологический дом – интернат  из Дома ребёнка по причине отказа матери-одиночки. При внешнем осмотре девочка кажется вполне адекватной, понимает обращённую к ней речь, внимательно слушает инструкции к заданию, сама произносит простые слова «мама», «коска», «да». Матрицы выполнены в течение 17 минут, IQ составил 74. На основе данных, полученных в ходе эксперимента, а также собственных наблюдений можно предположить наличие у девочки олигофрении в стадии дебильности.

Сравнивая результаты, представленные в таблицах 2 и 3  можно сделать вывод о том, что в целом интеллектуальное развитие детей с синдромом Дауна, воспитывающихся в доме-интернате гораздо ниже, чем это отмечено в медицинских картах этих детей, поскольку степень идиотии имеют не 4 детей, а 9. Вместе с тем в ходе эксперимента был выявлен ребёнок (см. Ш.В.), у которого уровень интеллектуального развития намного выше того, который был указан в индивидуальной медицинской карте. Этот ребёнок является вполне адекватным и способен обучаться по специальной школьной программе.

Использование Теста Равена позволило нам получить лишь количественные характеристики интеллектуального развития детей с синдромом Дауна. Однако использование одной методики с целью определения интеллекта у детей не достаточно. Поэтому с целью получения достоверных результатов об уровне интеллектуального развития детей с синдромом Дауна, воспитывающихся в Петропавловском психоневрологическом доме-интернате, в ближайшее время нами планируется проведение ещё ряда экспериментальных работ с использование других методик.

ЛИТЕРАТУРА

1. Л.О. Бадалян Детская неврология. –  М.: Медицина, 1984. – 417 с.

2. Н.П. Бочков Клиническая генетика. – М.: Наука, 1997. – 245 с.

3. Г.С. Маринчева, В.И. Гаврилов Умственная отсталость при наследственных болезнях. – М.: Медицина, 1988. – 223 с.

4. Фогель Ф, Мотульски А.Г. Генетика человека. Т.3. – М.: Мир, 1990. – 1220 с.

5. Bouchard T.J. IQ similarity in twins reared apart: Findings and responses to critics. Intelligence, heredity, and environment. –  USA, 1997. –  126 p.

---

Количество просмотров публикации: Please wait

Все статьи автора «mihailova_ms»

Прогрессивные матрицы Равена

Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: Археология Биология Генетика География Информатика История Логика Маркетинг Математика Менеджмент Механика Педагогика Религия Социология Технологии Физика Философия Финансы Химия Экология ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрации Техника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ? Влияние общества на человека Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления

⇐ ПредыдущаяСтр 3 из 15Следующая ⇒ Тест Равена (в оригинальном варианте) состоит из 60 матриц (размер 7,5*11см), в каждой из которых отсутствует 1 из составляющих ее элементов. Обследуемый должен выбрать недостающий элемент матрицы среди 6-8 предложенных вариантов. Задания сгруппированы в 5 серий-А,В,С,Д,Е, каждая серия состоит из 12 матриц. Принцип «прогрессивности» реализуется двояким образом: а)внутри каждой серии задания расположены с учетом их возрастающей сложности; б) все серии отличаются различной трудностью, которая возрастает от серии А к серии Е. Возрастные трудности заданий определяются: -увеличением числа элементов в матрице, -увеличением предлагаемых вариантов решения, усложнением логического принципа, лежащего в основе каждой композиции, который испытуемому необходимо понять, чтобы закономерно выбрать недостающий элемент. «Прогрессивность» матриц определяет существенное достоинство методики, ее обучающий характер, заключающийся в том, что выполнение предшествующих заданий и их серий является своеобразной подготовкой обследуемого к выполнению последующих. Тем самым тест имплицитно содержит в себе иерархизированную модель «пространственно-комбинаторных» мыслительных операций. Расположение матриц в определенной последовательности соответственно принципу возрастающей сложности мыслительных операций, необходимых для их решения, не исключает варианта парциальной несформированности умственных операций у обследуемого. В этом случае профиль суммарных оценок за 5 серий не будет отражать нарастающую сложность. Возможности применения прогрессивных матриц Равена в психодиагностике интеллекта детей младшего школьного возраста Первые две серии матриц Равена (А и В) имеют наименьшие коэффициенты сложности в ряду нарастающей прогрессивности пяти серий. Вместе с тем, обе серии, по существу, направлены на диагностику состояния двух наиболее фундаментальных процессов, сформированность и сохранность которых обеспечивает нормальное протекание любого познавательного акта (в т. ч. абстрактно-логическое мышление). Речь идет о симультанности и сукцессивности в организации высших психических функций. Под сукцессивностью понимают исследовательскую развернутую во времени организацию психической деятельности, подчиненной определенной программе. Симультанный принцип организации психических процессов (принцип гештальта) предполагают целостность восприятия или пространственный синтез в наглядном плане (на уровне отдельного перцептивного акта – это объединение различных признаков в единое целое). Содержательный анализ матриц показывает, что задания на пространственные отношения первых двух серий- серии А и серии В – решаются различными способами: для заданий серии А – это опора преимущественно и прямые наглядно-пространственные преобразования, для заданий серии В, преобладающей является необходимость в логических рассуждениях о соотношении между элементами задания. В первом случае успешность определяется возможностью симультанного (целостного) «видения» матриц в непрерывности их структуры, во втором случае – сохранением и регуляцией определенной последовательности операций сравнения. Следует отметить, что целостность восприятия является одной из базовых характеристик восприятия вообще, становление которой опережает по срокам развитие арсенала интеллектуальных средств. Возможность дифференцированного восприятия завершенных и незавершенных контуров формируется в раннем дошкольном возрасте. По отношению к младшему школьному возрасту использование в диагностических целях первых двух серий прогрессивных матриц Равена означает диагностику двух основных показателей «интеллектуального фасада» детской психики: · Сформированность такой характеристики детского восприятия, как целостность – в этом случае мы имеем дело с так называемой «готовностью» ребенка к современным формам обучения (разумеется, в самом узком значении этого слова), поскольку последние априорно аппелируют к таким психическим процессам, для которых уже закономерна стадия опережающего восприятия целого по отношению к его отдельным частям. · Возможность осуществления ребенком последовательных операций сравнения – в этом случае фактически исследуется сама возможность обучения ребенка и динамические характеристики этого процесса. Речь идет о способности к соблюдению определенной последовательности операций, которая выступает залогом эффективности любого вида психической деятельности (в т.ч. учебной деятельности). Соотношение суммарных оценок по результатам выполнения двух серий матриц Равена (в сравнении с зоной «средних оценок» интеллектуального развития в соответствующей возрастной группе) позволяет не только оценить актуальный уровень интеллектуального развития младшего школьника с точки зрения сформированности отдельных составляющих психической деятельности, но и выносить прогностически валидные суждения относительно «эффективности» исследуемого ребенка в отдельных видах учебной деятельности. Отличительной чертой использования прогрессивных матриц Равена в диагностических целях на контингенте детей младшего школьного возраста является практически полная непригодность и неадекватность групповой формы проведения исследования. Это обусловлено влиянием, по крайней мере, двух обстоятельств. Во-первых, психическая деятельность детей младшего школьного возраста не отличается особой целенаправленностью, вследствие еще недостаточно сформированных регуляторных механизмов, а также функций целеполагания, планирования и контроля. Поэтому младшие школьники очень часто допускают ошибки из-за так называемой «невнимательности», доля которых значительно возрастает в условиях «безнадзорности» групповой формы исследования. Получаемый результат в этом случае скорее характеризует особенности эмоционально-волевой сферы личности, нежели собственно интеллектуальные способности ребенка. Во-вторых, на сегодняшний день уже не вызывает сомнений несостоятельность чисто количественного подхода к анализу психического развития ребенка. Закон гетерохронии морфофункционального созревания головного мозга и соответствующего формированию отдельных структурных звеньев психической деятельности является определяющим фактором индивидуализированного (в высшей степени) характера онтогенетического развития ребенка. Следствием чего сравнительные возможности количественных процедур измерения имеют явно ограниченный характер. Индивидуальная форма проведения исследования делает возможной минимальную помощь со стороны взрослого в ситуации ошибочного выбора ребенка, обусловленного импульсивностью последнего. В этом случае замечания психолога типа: «Подумай еще» выступает как внешнее средство организации внимания ребенка. Правильный ответ ребенка после замечания психолога оценивается в 0,5 балла. Таким образом, мы получаем 3-х балльную систему оценок: 1 балл- ребенок безошибочно, с первого раза находит правильное решение; 0,5 балла – правильное решение найдено со второй попытки, сразу после замечания психолога; 0 баллов – помощь со стороны взрослого оказалась неэффективной, правильного решения не найдено. С целью получения нормативных данных по индивидуальной форме нами было обследовано 450 учащихся первых 3-х классов. Проведенное исследование выявило статистическую значимость различий в успешности выполнения двух первых серий прогрессивных матриц Равена (при уровне значимости р < 0,01).     медиана Станд. откл. медиана Станд. откл. 1-е кл. 8,11 2,07 5,94 3,95 2-е кл. 8,49 3,12 6,49 3,78 3-е кл. 9,78 1,82 7,85 5,29   Проверка гипотезы о равенстве средних значений для двух измерений (серий А и В) осуществлялась с использованием t – критерия для зависимых выборок. По тому же критерию определялась значимость различий между средними по возрастам – статистически значимые различия между средними оценками в трех возрастных группах появляются только на рубеже 9-10 лет (при уровне значимости р меньше 0,01). Анализ распределения индивидуальных данных (с учетом стандартных отклонений) позволяет ввести следующие дифференциальные оценки уровней интеллектуального развития в младшем школьном возрасте, определяемых при помощи первых двух серий прогрессивных матриц Равена. Нормативное распределение оценок для детей 7-9 лет   Серия А Серия В Суммарный балл Интерпретация Суммарный балл Интерпретация 11,5-12 значительно выше среднего 10 и выше Значительно выше среднего 10-11 Выше среднего 8,5-10 выше среднего 6,5-9,5 средний уровень IQ 4-8 средний уровень IQ 5-6 ниже среднего 2-3,5 Ниже среднего 3,5-4,5 Значительно ниже среднего 2-3,5     Нормативное распределение оценок для детей 10-11 лет   Серия А Серия В Суммарный балл Интерпретация Суммарный балл Интерпретация 11,5-12 выше среднего 10,5-12 превышает нормативы своей возрастной группы 8,5-11 средний уровень 5,5-10 средний уровень 7-8 ниже среднего 3-5 ниже среднего 5,5-6,5 значительно ниже среднего       Проведение исследования и обработка результатов Испытуемому дается следующая инструкция: «Определите закономерность, связывающую фигуры на рисунке, и выберите из предложенных вариантов — недостающую. Укажите на бланке ее номер». Испытуемый работает в течение 20 минут. По окончании работы испытуемого, психолог с помощью ключа (см. ключ) подсчитывает количество правильных ответов, причем правильное решение каждого отдельного задания оценивается в 1 балл. Подсчитывается общая сумма полученных баллов, а также число правильных решений в каждой из пяти серий.   Ключ к методике Равена     А В С Д Е   В современной психодиагностической практике используются несколько алгоритмов психометрической интерпретации полученных результатов. Ниже предлагается краткая характеристика наиболее распространенных приемов. Т.о., практикующий психолог имеет возможность выбора определенной процедуры обработки «сырых» баллов в соответствии с той задачей, которую он решает данной психодиагностической процедурой, а также руководствуясь субъективными предпочтениями в мире формул и цифр. 1. Определение интеллекта согласно процентной шкале. Полученный суммарный показатель переводят в проценты , исходя из того, что 60 пунктов-100%. После чего определяют уровень интеллектуального развития респондента по существующей шкале градаций интеллектуального развития.   Таблица процентного определения уровня интеллектуального развития.   Степень интеллекта % правильно решенных задач Уровень интеллектуального развития 1 степень 95% и выше (57 правильных ответов) Особо высокоразвитый интеллект 2 степень 75-94% (45-56 правильных ответов) Интеллект выше среднего(незаурядные умственные способности) 3 степень 25-74% (15-44 правильных ответов) Средний интеллект 4 степень 5-24% (3-14 правильных ответов) Интеллект ниже среднего 5 степень Ниже 5% (меньше 3 правильных ответов) Интеллектуальный деффект   2. Перевод полученных результатов в IQ-показатель. При переводе результатов, полученных в тесте Равена, в IQ, следует исходить из того, что 10-ти правильным решениям соответствует IQ-100, а 60-ти правильным решениям- IQ-140. Промежуточные значения вычисляются. Напомним, что IQ-140 и выше — это исключительно высокий интеллект. Используемая психологическая интерпретация IQ, полученного по результатам выполнения прогрессивных матриц Равена несколько отличается от традиционной, которая соответствует –15-16 и имеет следующий вид: 120-140-высокий интеллект 110-120-выше среднего 100-110-средний 90-100-ниже среднего 80-90-слабый 80 и ниже — различные виды IQ-го дефекта. Использование IQ-показателя позволяет сопоставить полученные результаты с успешностью выполнения других невербальных тестов (Например, гештальт-тест Бендера, невербальная шкала теста Векслера)   ⇐ Предыдущая12345678910Следующая ⇒ Читайте также:  Формы дистанционного обучения Передача мяча двумя руками снизу Значение правильной осанки для жизнедеятельности человека Основные ошибки при выполнении передач мяча на месте 

Последнее изменение этой страницы: 2016-09-20; просмотров: 513; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia. su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь — 176.9.44.166 (0.012 с.)

Тест Равена онлайн. Измерьте уровень своего интеллекта

Из статьи вы узнаете:

1. Что измеряет тест Равена?
2. Матрицы Равена — пояснение принципа выбора правильного ответа
3. Пройти тест Равена онлайн бесплатно
4. Краткая история методики теста на IQ Равена
5. Почему для достоверной оценки интеллекта нужно применять улучшенные методики

Пройти тест в Telegram бесплатно

Что измеряет прогрессивный тест Равена?

Тест Равена предназначен для измерения уровня интеллектуального развития и логичности мышления. Он представлен в виде прогрессивных матриц (рисунков с фигурами, связанными между собой определенной зависимостью), Одна из фигур отсутствует. Задача тестируемого — определить логическую связь и выбрать недостающую фигуру среди нескольких представленных вариантов.

Тест Равена может дать оценку iq независимо от уровня образования, социального сословия и рода деятельности.

Почему тесты измерения интеллекта в наше время становятся все более востребованными?
Бесконечно сменяющие друг друга технологии современного мира заставляют людей играть по своим правилам. Как всегда оставаться востребованным специалистом на рынке услуг? Каких людей охотно принимают на любую работу? Как всегда быть на шаг впереди своих конкурентов? Согласитесь, в наше время эти вопросы актуальны для большинства людей.

• Руководители крупных компаний сегодня очень ответственно подходят к отбору персонала. Многие из них посещают тренинги и курсы, посвященные умению грамотно управлять людьми. Опытные управленцы четко понимают, какими качествами должны обладать их сотрудники. В этой статье мы расскажем вам об одном из ключевых факторов, влияющих на вероятность успешного трудоустройства.  

  Современный мир движется непрерывно, технологии меняются одна за другой. То, что актуально сегодня, может потерять смысл уже через неделю. Посмотрите хотя бы на специалистов, которые получили профильное образование 10-20 лет назад, но, ввиду определённых обстоятельств, не стали продолжать своё профессиональное развитие и остановились на достигнутой ступени личностного роста. Эти люди сильно отстают от молодых сотрудников, которые чувствуют себя, как рыба в воде, общаясь с инновационными технологиями. Хорошо, если кого-то ценят за опытность и уважают за выстроенные годами взаимоотношения. Но если это не так, сотрудники, стоящие на месте, не развивающиеся, рискуют потерять работу.

  Отсюда можно сделать вывод: востребованным остаётся тот человек, который готов меняться, осваивать новые знания и приобретать новый опыт. Именно гибкость мышления и пластичность психики являются незаменимыми и ключевыми компонентами карьерного успеха.

Вышеперечисленные качества можно охарактеризовать одним словом — интеллект. Удивлены? Да, действительно, понятие интеллекта отнюдь не сводится к умению решать математические задачи и складывать в уме трехзначные числа. Более того, оценивать интеллектуальный потенциал человека по тому, как он решает математические задачи совершенно некорректно и ошибочно. Интеллект представляет собой умение видеть мир многогранно, определять логические связи, находить альтернативные решения для той или иной задачи, уметь подойти к вопросу нестандартно, увидев целый спектр всевозможных вариантов развития событий.

Как же объективно определить свои интеллектуальные способности? Это непростой вопрос, поскольку сегодня в интернете можно встретить огромное количество разнообразных IQ-тестов. Поэтому сделать грамотный выбор без помощи профессионалов крайне сложно.
Одним из наиболее известных тестов является тест Равена.

Матрицы Равена — пояснение принципа выбора правильного ответа

• Большинство людей сопротивляется, когда им предлагают пройти интеллект-тест: “Зачем мне это? А вдруг я покажусь глупым? Мне некомфортно проходить испытание такого рода”!

  Эти опасения вполне оправданы. Вы помните, как выглядел какой-нибудь IQ-тест, который вы встречали в своей жизни? Скорее всего, это был набор математических задач, умение выполнить арифметические операции. Но ведь далеко не все люди сильны в математике. Для кого-то точные науки — просто темный лес.

  Бывают и другие тесты на интеллект. Например те, где необходимо произвести некие операции с понятиями, фразами и терминами. Есть люди, для которых эти задания покажутся невыполнимыми. Можем ли мы сделать вывод, что человек, который не силён в математике или в лингвистике, обладает низким интеллектом. Согласитесь, это звучит абсурдно. Каждый человек уникален и талантлив в определенной сфере.

  Реальный интеллект многогранен и отнюдь не сводится к какой-то определенной сфере знания. Главное — умение решать различные жизненные проблемы. Кому-то сделать это проще, опираясь на логику, а кто-то будет пользоваться навыками эмпатии или коммуникации. Здесь все очень индивидуально. Поэтому ученые пришли к выводу, что измерять интеллект надо комплексно, не ориентируясь на специфические типы мышления.

Одной из самых известных методик оценки уровня интеллекта, как мы уже отмечали выше, является прогрессивный тест Равена. Методика теста Равена предназначена для изучения способности устанавливать логические связи и закономерности. Человеку предъявляются рисунки с фигурами, связанными между собой определенной зависимостью. Одной фигуры недостает, а внизу она показывается среди 6-8 других фигур. Задача человека — установить закономерность, связывающую между собой фигуры на рисунке, и указать номер искомой фигуры из предлагаемых вариантов.
Тест Равена состоит из 60 таблиц (5 серий). В каждой серии таблиц содержатся задания нарастающей трудности. В то же время характерно и усложнение типа заданий от серии к серии.

По результатам тестирования можно оценить общий показатель интеллекта, не сводя его к математическим, лингвистическим или понятийным способностям. Благодаря такой диагностике результаты будут гораздо объективнее, чем после прохождения большинства других популярных методик измерения интеллекта.

Пройти тест Равена онлайн бесплатно

Пройти тест в Telegram

Ключевым критерием выбора теста, конечно же, является его надежность, но при этом также важны простота и удобство использования, позволяющие сэкономить время.

Тест Равена соответствует всем этим требованиям.
Компания “Проф-Диалог» предоставляет вам возможность пройти тест Равена бесплатно и сразу же получить результаты тестирования.

Переходите по ссылке и испробуйте надежный инструмент диагностики интеллекта :

Быстро

Удобно

Проверено

Достоверно

Надежно

Бесплатно

Пройдите бесплатно тест Равена в чат-боте Проф-Диалог!

Пройти тест в Telegram

Краткая история методики теста на IQ Равена

Почему эксперты отдают предпочтение именно тем методикам, надежность которых подтверждена в течение многих лет?

Возникает парадоксальная ситуация: вроде бы современный мир пестрит инновационными решениями и появляются все новые предложения. Так почему же не отдать предпочтение новейшим методам измерения интеллекта, ведь сейчас их очень много?

Дело в том, что грамотные специалисты прекрасно понимают: никакая современность не уступит надежности, достоверности и валидности. В таком вопросе есть один главный арбитр — наука. Давайте сделаем небольшой исторический экскурс, чтобы разобраться в специфике теста.

Тест был предложен Л. Пенроузом и Дж. Равеном в 1936 г. Материалы разрабатывались в соответствии с традициями английской школы изучения интеллекта, согласно которым наилучший способ измерения интеллекта— задача по выявлению отношений между абстрактными фигурами.

Разрабатывая тесты, которые были бы полезным инструментом для идентификации генетических и средовых причин интеллектуальных отклонений, Дж. Равен сознательно ставил перед собой задачу создания таких тестов, которые были бы теоретически обоснованы, однозначно интерпретируемы, просты для проведения и обработки, а также удобны для массовых обследований (на производстве, в школах и т.д.), сопряженных с временными ограничениями.


Почему для достоверной оценки интеллекта нужно применять улучшенные методики

Неужели даже у такого надёжного метода как тест Равена есть свои недостатки? Неужели есть альтернатива лучше?

Давайте вернёмся к вопросу о современности и инновациях. На сегодняшний день можно улучшать знания в любом направлении, опираясь на ключевые моменты и дорабатывая выделенные недостатки. Безусловно, недочеты есть у любого теста, особенно если речь идёт о том, что он был предложен достаточно давно.  Попробуем разобраться с этим вопросом.
 
Как правило, при оценке интеллектуальных способностей, самым важным является определение перспективы развития. На какой уровень может претендовать человек, получивший те или иные результаты?  В данном случае необходимо быть предельно точным, нельзя допускать погрешностей в измерении IQ.
 
Основным недостатком теста Равена является то, что он довольно популярен и хорошо известен в сфере бизнеса, предпринимательства, управления и многих других. Разумеется, ответы на задания можно легко найти в интернете и, пользуясь ими, подготовиться и “обмануть” тестирование. Ведь банк заданий всегда стандартный.

Команда экспертов Проф-Диалог предусмотрела  эту ситуацию. Мы создали уникальный метод оценки интеллектуальных способностей, который основан на тех же принципах, что и тест Равена. Интеллект-тест Проф-Диалог также содержит набор прогрессивных матриц, в которых надо определить недостающую фигуру. Он, как и тест Равена, измеряет способность человека находить логические связи и не зависит от опыта, образования, социокультурного уровня.

Комплексная диагностика интеллекта от экспертов Проф-Диалог

Получите комплексное представление о своих интеллектуальных способностях, пройдя грамотную психодиагностику!

Перейти

Отличием теста Проф-Диалог от теста Равена является то, что он содержит очень большую базу заданий, которые выбираются в случайном порядке. Поэтому даже у тысячи человек, проходящих тестирование, не будет одинаковых вариантов. Ответы на задания нельзя найти в интернете. Поэтому подготовиться к интеллект тесту Проф-Диалог, в отличие от теста Равена, нельзя. Можно быть абсолютно уверенным в достоверности полученных результатов.

Проверьте это на собственным опытом и убедитесь в эффективности методики! Оцените свои интеллектуальные способности и определите рациональный вектор личностного роста уже сегодня!


Понравилась статья? Еще больше материалов в нашем блоге!

Перейти

Тест IQ на Русском языке

Описание

Тесты IQ используются с 19-го века для измерения интеллекта отдельных лиц. На протяжении многих лет этот стандартный тест использовался преподавателями и психологами для предсказания академической успеваемости и карьерного успеха человека, а также для диагностики умственной отсталости и инвалидности в обучении. Тест IQ остается наиболее часто используемым тестом для оценки умственных способностей.

Коэффициент интеллекта (IQ) представляет собой общий балл, полученный из нескольких стандартизированных тестов, предназначенных для оценки человеческого интеллекта. Результаты корректируются в соответствии с возрастной группой.

Есть много тестов интеллекта.
Приложение IQ Test на Русском языке основано на Тест Равена (Коэффициент умственного развития) — Raven IQ .

Тест Равена (или Тест айкью Равена) включает в себя шестьдесят вопросов. Приложение имеет три варианта — полный тест интеллекта, состоящий из 60 вопросов, умеренный тест айкью с 30 вопросами и быстрый тест, который сокращен до 15 вопросов.

Мы предоставляем бесплатный тест айкью для всех, и он подходит для любого возраста, для детей в возрасте до 15 лет бесплатный тест IQ использует матрицы коррекции Raven для корректировки оценки IQ и представления достоверных результатов.

Продолжительность теста ограничена до 40 минут для полного теста, 20 минут для промежуточного теста и 10 минут для короткого теста.
Результаты теста — распределение IQ обычно дает колоколообразный график, подобный нормальному.
Средний IQ равен 100. Самый высокий балл — 175, а самый низкий — 25.

Только результаты полного теста являются достоверными. Краткосрочные тесты были созданы для людей, которые не хотят тратить 40 минут и еще предстоит пройти тестирование. В этих пунктах важно принимать во внимание, что полученная оценка является неточной и ненадежной.

Raven’s Progressive Matrices были разработаны для использования в фундаментальных исследованиях генетических и экологических детерминант «интеллекта».
Интеллектуальные тесты Raven Progressive Matrices (RPM) (из которых несколько версий) состоят из серии диаграмм или рисунков с отсутствующей частью.
Ожидается, что те, кто проводит тесты, выберут правильную деталь для завершения дизайна из ряда вариантов, напечатанных ниже.
Большинство тестов в этом приложении проводилось с помощью теста стандартных прогрессивных матриц.

Важно отметить, что СЗМ с самого начала, как известно, обладал определенными сильными сторонами и ограничениями.
Его сильные стороны заключались в том, что он мог использоваться с респондентами всех возрастов от раннего детства до престарелого возраста и имел такую ​​длину, которую он мог разумно применять в домах, школах и на рабочих местах.
Баллы преобразуются в IQ по возрасту в соответствии с матрицами Raven.

Возможность сделать селфи и ввести свое имя, прежде чем делиться результатами с друзьями.

Кредиты:

Icon и IQ Оценка изображений по:
https://commons.wikimedia.org/wiki/File:Synapse_in_brain.jpg
Лицензия — cc-by-2.0, кредит — Аллан Аджифо

Промо изображение на основе:
https://commons.wikimedia.org/wiki/File:Human_evolution_scheme.svg
Лицензия: CC BY-SA 3.0, кредит — Хосе-Мануэль Бенитос

Рекомендации:

Raven (2000). Прогрессивные матрицы Raven: изменение и стабильность над культурой и временем
Источник: http://eyeonsociety.co.uk/resources/RPMChangeAndStability.pdf

Уильям Х. Андофф (1984). Шкалы, нормы и эквивалентные показатели
Источник: http://www.ets.org/Media/Research/pdf/Angoff.Scales.Norms.Equiv.Scores.pdf
————

«>7 мар. 2021 г.

Версия 1.7

Совместимость с iOS 14 — запросить авторизацию прозрачности отслеживания приложений.

Оценки и отзывы

Оценок: 60

Остановите мой ор

с первого коммента, в котором чел с 145 баллами iq пишет «Ни знаю»

Уберите

Мигание таймера вообще люто отвлекает

Степень доверия

Насколько этому тесту можно доверять

Разработчик Orit Kolev указал, что в соответствии с политикой конфиденциальности приложения данные могут обрабатываться так, как описано ниже. Подробные сведения доступны в политике конфиденциальности разработчика.

Данные, используе­мые для отслежи­вания информации

Следующие данные могут использоваться для отслеживания информации о пользователе в приложениях и на сайтах, принадлежащих другим компаниям:

Не связанные с пользова­телем данные

Может вестись сбор следующих данных, которые не связаны с личностью пользователя:

• Идентифика­торы
• Данные об использова­нии

Конфиденциальные данные могут использоваться по-разному в зависимости от вашего возраста, задействованных функций или других факторов. Подробнее

Информация

Провайдер

Orit Kolev

Размер

16,2 МБ

Категория

Образование

Возраст

4+

Copyright

© 2021 Orit Kolev (Kindergarten)

Цена

Бесплатно

• Сайт разработчика
• Поддержка приложения
• Политика конфиденциальности

Другие приложения этого разработчика

Вам может понравиться

Тест Равена – пройдите онлайн

Тест равену

Тест Равена предназначен для Измерения уровня интеллектуального развития и логичности мышления . Он представлен в виде прогрессивных матриц (рисунков с фигурами, связанными между собой определенной зависимостью), Одна из фигур отсутствует. Задача тестируемого — определить логическую связь и выбрать недостающую фигуру среди нескольких представленных вариантов.

Тест Равена может дать оценку iq независимо от уровня образования, социального сословия и рода деятельности.

Почему тесты измерения интеллекта в наше время становятся все более востребованными?
Бесконечно сменяющие друг друга технологии современного мира заставляют людей играть по своим правилам. Как Всегда оставаться востребованным специалистом на рынке услуг ? Каких людей охотно принимают на любую работу? Как всегда быть на шаг впереди своих конкурентов? Согласитесь, в наше время эти вопросы актуальны для большинства людей.

Руководители крупных компаний сегодня Очень ответственно подходят к отбору персонала. Многие из них посещают тренинги и курсы, посвященные умению грамотно управлять людьми. Опытные управленцы четко понимают, Какими качествами должны обладать их сотрудники. В этой статье мы расскажем вам об одном из Ключевых факторов, влияющих на вероятность Успешного трудоустройства.

Современный мир движется непрерывно, технологии меняются одна за другой. То, что актуально сегодня, может потерять смысл уже через неделю. Посмотрите хотя бы на специалистов, которые получили Профильное образование 10-20 лет назад, но, ввиду определённых обстоятельств, не стали продолжать своё профессиональное развитие и остановились на достигнутой ступени личностного роста. Эти люди сильно отстают от Молодых сотрудников, которые чувствуют себя, как рыба в воде, общаясь с инновационными технологиями. Хорошо, если кого-то ценят за опытность и уважают за выстроенные годами взаимоотношения. Но если это не так, сотрудники, стоящие на месте, не развивающиеся, рискуют потерять работу.

Отсюда можно сделать вывод: востребованным остаётся тот человек, который Готов меняться, осваивать новые знания и приобретать новый опыт. Именно гибкость мышления и пластичность психики являются Незаменимыми и ключевыми компонентами карьерного успеха.

Вышеперечисленные качества можно охарактеризовать одним словом — Интеллект . Удивлены? Да, действительно, понятие интеллекта отнюдь не сводится к умению решать математические задачи и складывать в уме трехзначные числа. Более того, Оценивать интеллектуальный потенциал человека по тому, как он решает математические задачи совершенно некорректно и ошибочно . Интеллект представляет собой Умение видеть мир многогранно , определять Логические связи , находить Альтернативные решения для той или иной задачи, уметь подойти к вопросу Нестандартно , увидев целый спектр всевозможных вариантов развития событий.

Как же объективно определить свои интеллектуальные способности? Это непростой вопрос, поскольку сегодня в интернете можно встретить Огромное количество разнообразных IQ-тестов . Поэтому сделать грамотный выбор без помощи профессионалов крайне сложно.
Одним из наиболее известных тестов является Тест Равена.

Большинство людей сопротивляется, когда им предлагают пройти интеллект-тест: “Зачем мне это? А вдруг я покажусь глупым? Мне некомфортно проходить испытание такого рода”!

Эти опасения вполне оправданы. Вы помните, как выглядел какой-нибудь IQ-тест, который вы встречали в своей жизни? Скорее всего, это был Набор математических задач, умение выполнить арифметические операции. Но ведь далеко не все люди сильны в математике. Для кого-то точные науки — просто темный лес.

Бывают и другие тесты на интеллект. Например те, где необходимо произвести некие операции с Понятиями, фразами и терминами. Есть люди, для которых эти задания покажутся Невыполнимыми. Можем ли мы сделать вывод, что человек, который не силён в математике или в лингвистике, обладает низким интеллектом. Согласитесь, это звучит абсурдно. Каждый человек уникален и талантлив в определенной сфере.

Реальный интеллект Многогранен и отнюдь не сводится к какой-то определенной сфере знания. Главное — Умение решать различные жизненные проблемы. Кому-то сделать это проще, опираясь на логику, а кто-то будет пользоваться навыками Эмпатии Или коммуникации. Здесь все очень индивидуально. Поэтому ученые пришли к выводу, что измерять интеллект надо комплексно, не ориентируясь на специфические типы мышления.

Одной из самых известных методик оценки уровня интеллекта, как мы уже отмечали выше, является Прогрессивный тест Равена. Методика теста Равена предназначена для изучения способности Устанавливать логические связи и закономерности. Человеку предъявляются рисунки с фигурами, связанными между собой определенной зависимостью. Одной фигуры недостает, а внизу она показывается среди 6-8 других фигур. Задача человека — установить закономерность, связывающую между собой фигуры на рисунке, и указать номер искомой фигуры из предлагаемых вариантов.
Тест Равена состоит из 60 таблиц (5 серий). В каждой серии таблиц содержатся задания нарастающей трудности. В то же время характерно и усложнение типа заданий от серии к серии.

По результатам тестирования можно оценить Общий показатель интеллекта, не сводя его к математическим, лингвистическим или понятийным способностям. Благодаря такой диагностике результаты будут гораздо объективнее, чем после прохождения большинства других популярных методик измерения интеллекта.

Ключевым критерием выбора теста, конечно же, является его НАдежность, но при этом также важны Простота и удобство использования, позволяющие сэкономить время.

Тест Равена соответствует всем этим требованиям.
Компания “Проф-Диалог» предоставляет вам возможность пройти тест Равена Бесплатно и сразу же получить результаты тестирования.

Почему эксперты отдают предпочтение именно тем методикам, надежность которых подтверждена в течение многих лет?

Возникает парадоксальная ситуация: вроде бы современный мир пестрит инновационными решениями и появляются все новые предложения. Так почему же не отдать предпочтение новейшим методам измерения интеллекта, ведь сейчас их очень много?

Дело в том, что грамотные специалисты прекрасно понимают: никакая современность не уступит Надежности, достоверности и валидности. В таком вопросе есть один главный арбитр — Наука. Давайте сделаем небольшой исторический экскурс, чтобы разобраться в специфике теста.

Тест был предложен Л. Пенроузом и Дж. Равеном в 1936 г. Материалы разрабатывались в соответствии с традициями английской школы изучения интеллекта, согласно которым наилучший способ измерения интеллекта— Задача по выявлению отношений между абстрактными фигурами.

Разрабатывая тесты, которые были бы полезным инструментом для идентификации генетических и средовых причин интеллектуальных отклонений, Дж. Равен сознательно ставил перед собой задачу создания таких тестов, которые были бы Теоретически обоснованы, однозначно интерпретируемы, просты для проведения и обработки, а также удобны для массовых обследований (на производстве, в школах и т. д.), сопряженных с временными ограничениями.

Неужели даже у такого надёжного метода как тест Равена есть свои недостатки? Неужели есть альтернатива лучше?

Давайте вернёмся к вопросу о Современности и инновациях . На сегодняшний день можно улучшать знания в любом направлении, опираясь на ключевые моменты и дорабатывая выделенные недостатки. Безусловно, Недочеты есть у любого теста , особенно если речь идёт о том, что он был предложен достаточно давно. Попробуем разобраться с этим вопросом.

Как правило, при оценке интеллектуальных способностей, самым важным является Определение перспективы развития . На какой уровень может претендовать человек, получивший те или иные результаты? В данном случае необходимо быть предельно точным, Нельзя допускать погрешностей в измерении IQ.

Основным недостатком теста Равена является то, что он довольно популярен и хорошо известен в сфере бизнеса, предпринимательства, управления и многих других. Разумеется, ответы на задания можно легко найти в интернете и, пользуясь ими, Подготовиться и “обмануть” тестирование . Ведь банк заданий всегда стандартный.

Команда экспертов Проф-Диалог предусмотрела эту ситуацию. Мы создали уникальный метод оценки интеллектуальных способностей, который основан на тех же принципах, что и тест Равена. Интеллект-тест Проф-Диалог также содержит набор прогрессивных матриц, в которых надо определить недостающую фигуру. Он, как и тест Равена, измеряет способность человека находить логические связи и не зависит от опыта, образования, социокультурного уровня.

Главное — умение решать различные жизненные проблемы.

Career. prof-dialog. ru

24.08.2017 21:21:06

2017-08-24 21:21:06

Источники:

Https://career. prof-dialog. ru/article/test-ravena-online

Матрицы Равена: уникальный тест на определение уровня интеллекта | Блог РСВ » /> » /> .keyword { color: red; }

Тест равену

Д. Равен вместе с Л. Пенроузом создали в 1936 году уникальные матрицы Равена. Прогрессивная методика была разработана для определения умственного уровня и оценки способностей к систематизации, методологии, логическому мышлению. Джон Равен придумал универсальный тест, результат которого почти не зависит от знаний, уровня жизни и опыта испытуемых. Стандартные матрицы предназначены как для тестирования взрослых людей, так и для детей.

Как проводится тестирование?

В матрицы входят 60 графических рисунков. В рисунке недостает простой фигуры, например, прямоугольника. Под рисунком размещены 6 или 8 фрагментов, которые почти подходят по размеру к недостающей фигуре. Основной задачей является обработка и поиск фрагментов той фигуры, которая точно подходила бы в пустое место. Суть проективного метода заключается в том, чтобы логически определить по какому принципу составлен графический рисунок, к которому необходимо подобрать недостающую фигуру. То есть необходимо понять закономерность, по которой связаны фигуры на изображение. На выполнение 60 заданий дается всего 20 минут. В первой группе рисунки простые, затем с каждой серией сложность прогрессирует.

Матрицы Равена поделены на 5 групп, в каждой из которой 15 рисунков. Серии рисунков разделены по определенным принципам и типам сложности. В каждой группе содержатся задания разного уровня:

Первая серия А разработана по принципу определения структуры рисунка и ее взаимосвязи. Необходимо найти одну из частей рисунка, которая точно подойдет к недостающей части основного рисунка. Задание направлено на детальную оценку составляющих изображения и поиск таких же деталей в одном из предложенных фрагментов.

Серия В содержит принцип поиска аналогии между несколькими фигурами. Человеку необходимо понять закономерность, по которой создана каждая фигура и, ориентируясь на это, определить отсутствующую часть рисунка. Нужно отыскать осевую симметрию, размещенную в фигуре.

Серия С разработана по принципу усовершенствования и усложнения фигур. С каждой серией фигуры видоизменяются, то есть происходит постепенное непрерывное развитие. Фигуры заполняются новыми частями по определенному принципу, по которому можно найти в последующих рисунках отсутствующие фигуры.

Серия D содержит принцип перестановки основных фигур. Человеку необходимо определить в разных плоскостях (горизонтальном и вертикальном) перегруппировку.

Серия Е составлена по принципу разделения основных фигур на части. Подходящие фигуры нужно собрать, определив закономерность составления фигур.

Где используются продвинутые матрицы Равена?

В научной сфере для изучения умственных способностей людей из других этнических и культурных групп, исследования генетических и образовательных различий интеллектуальных процессов. В профессиональной сфере, где необходимо определить сильные стороны работников, например, эффективных администраторов или менеджеров, кураторов или маркетологов. В образование деятельности, где есть потребность в прогнозе будущих результатов учащихся, независимо от уровня их жизни и опыта. В медицинской сфере для определения нейропсихологических проблем, для подтверждения результатов, которые были получены другими методами при измерение интеллектуальной способности.

Тестирование людей на определение уровня интеллекта является востребованным почти в любой сфере деятельности. Важно постоянно прокачивать свой мозг, продвигать себя, как специалиста, развивать компетенции и узнавать что-то новое. На платформе «Россия — страна возможностей» размещены бесплатные онлайн-курсы по маркетингу, личностному росту, финансам, менеджменту и другие. Пройдите курс «Личная ответственность за результат: результат-ориентированное мышление» и повысьте свой уровень интеллекта в моменте. Результат-ориентированное мышление помогает быстрее добиваться целей, осознанно принимать решения и грамотно использовать имеющиеся ресурсы. После обучения вы сможете самостоятельно разработать карту точек вашего роста и научитесь концентрироваться на достижении результата, сможете быстрее и качественнее выполнять задачи. Не упустите уникальную возможность!

Читайте нас в Telegram — stranavozmojnostey Поделиться в социальных сетях

Подходящие фигуры нужно собрать, определив закономерность составления фигур.

Rsv. ru

01.11.2019 17:49:46

2019-11-01 17:49:46

Источники:

Https://rsv. ru/blog/matriczy-ravena-unikalnyj-test-na-opredelenie-urovnya-intellekta/

Тест Равена » /> » /> .keyword { color: red; }

Тест равену

Тест Равена — это разработанная в 1936 году Джоном Равеном шкала прогрессивных матриц в соавторстве с Роджером Пенроузом для оценки уровня iq, коэффициента интеллекта и уровня умственных способностей, а также логичности мышления. Данный тест может дать оценку iq тестируемым независимо от уровня образования, социального сословия и рода деятельности. Тест был разработан в двух вариантах для детей и взрослых от 14 до 65 лет.

В Тест Равена входит 60 таблиц, которые делятся на 5 серий по 12 заданий на каждую. Задания предлагаются с нарастающей сложностью. На прохождение теса дается 20 минут.

Инструкция для прохождения теста Равена

В процессе прохождения теста испытуемому предлагается 60 рисунков разделенных на 5 групп. На рисунке представлено графическое изображение определенной зависимости. В правом нижнем углу каждого рисунка имеется вырез в который испытуемый должен вставить расположенные ниже рисунка вариант ответа, который по его логике подходит для данного рисунка. Задания надо выполнять как можно быстрее так как сложность заданий увеличивается, а время на выполнения теста уменьшается.

Результаты теста Равена

При подведении итогов теста каждый положительный ответ считается как один балл. В результате теста считается сумма правильных ответов по всем шкалам и сумма правильных ответов по каждой шкале в отдельности. Сумма баллов полученая по всем шкалам показывает коэффициент умственного развития – уровень iq испытуемого, а по сумме баллов каждой шкалы оценивается достоверность результатов Теста Равена.

Тест Равена ответы (ключи)

Среднестатические показатели баллов по сериям

Таблица №2

Сумма правильных ответов	Серия А	Серия B	Серия C	Серия D	Серия E	IQ
15	8	4	2	1	0	62
16	8	4	3	1	0	65
17	8	5	3	1	0	65
18	8	5	3	2	0	66
19	8	6	3	2	0	67
20	8	6	4	2	0	69
21	8	6	4	2	1	70
22	9	6	4	2	1	71
23	9	7	4	2	1	72
24	9	7	4	3	1	73
25	10	7	4	3	1	75
26	10	7	5	3	1	76
27	10	7	5	4	1	77
28	10	7	6	4	1	79
29	10	7	6	5	1	80
30	10	7	6	5	2	82
31	10	7	7	5	2	83
32	10	8	7	5	2	84
33	11	8	7	5	2	86
34	11	8	7	6	2	87
35	11	8	7	7	2	88
36	11	8	8	7	2	90
37	11	9	8	7	2	91
38	11	9	8	8	2	92
39	11	10	8	8	3	94
40	11	10	8	8	3	95
41	11	10	9	8	3	96
42	11	10	9	9	3	98
43	12	10	9	9	3	99
44	12	10	9	9	4	100
45	12	10	9	9	5	102
46	12	10	10	9	5	104
47	12	10	10	9	6	106
48	12	11	10	9	6	108
49	12	11	10	10	6	110
50	12	11	10	10	7	112
51	12	11	11	10	7	114
52	12	11	11	10	8	116
53	12	11	11	11	8	118
54	12	12	11	11	8	120
55	12	12	11	11	9	122
56	12	12	12	11	9	124
57	12	12	12	11	10	126
58	12	12	12	12	10	128
59	12	12	12	12	11	130
60	12	12	12	12	12	140

Для оценки достоверности теста берется разница между полученными баллами по отдельной шкалы и контрольными — средне статическими подсчитанные по этой шкале при тестировании группы здоровых людей. Эта разница дает возможность надежно оценить конечный результат – она называется отклонение. Отклонение обозначается -2, -1, 0, 1, 2 и т. д. Если отклонение по шкале больше двух баллов то показатели по этой шкале считаются не достоверными. Отклонение может превышать два балла только при прохождении последних шкал. Отклонения полученные в начале испытания говорят о рассеянности внимания и восприятия или о недостатке интеллектуальных способностей

Интерпретация результатов теста Равена

Таблица №3

Полученный результат	Степень	Итог
95% и больше	1 степень	Особо высокорaзвитый интеллект испытуемого
75-94%	2 степень	Незаурядный интеллект испытуемого
25-74%	3 степень	Средний интеллект испытуемого
6-24%	4 степень	Интеллект испытуемого ниже среднего
5% и меньше	5 степень	Дефектная интеллектуальная способность испытуемого

Так же результат можно обработать с поправкой на возраст для этого нужно воспользоваться формулой:

IQ=IQ(п)/%*100

Где IQ(п) — результат полученный в таблице №2
% — берем в таблице №4

Таблица №4

Возраст	14-30	35	40	45	50	55	60
%	100	97	93	88	82	76	70

Полученный IQ с учетом возраста сопоставляем с таблицей №5 где указаны возможные уровни интеллектуальных способностей

Таблица №5

IQ испытуемого	Уровень интеллекта испытуемого
Свыше 140	Незаурядный, выдающийся интеллект
121-140	Высокий уровень интеллекта
111-120	Интеллект выше среднего
91-110	Средний уровень интеллекта
81-90	Интеллект ниже среднего
71-80	Низкий уровень интеллекта
51-70	Лёгкая степень слабоумия
21-50	Средняя степень слабоумия
0-20	Тяжёлая степень слабоумия

При оценки результатов Теста Равена необходимо учитывать что низкие показатели считаются всегда меньше надежней чем высокие

Прогрессивные матрицы Равена (ПМР / Raven Progressiv Matrices / Методики для диагностики интеллекта подростков и взрослых)

Результаты теста Равена

При подведении итогов теста каждый положительный ответ считается как один балл. В результате теста считается сумма правильных ответов по всем шкалам и сумма правильных ответов по каждой шкале в отдельности. Сумма баллов полученая по всем шкалам показывает коэффициент умственного развития – уровень iq испытуемого, а по сумме баллов каждой шкалы оценивается достоверность результатов Теста Равена.

Таблица №2

Сумма правильных ответов	Серия А	Серия B	Серия C	Серия D	Серия E	IQ
15	8	4	2	1	0	62
16	8	4	3	1	0	65
17	8	5	3	1	0	65
18	8	5	3	2	0	66
19	8	6	3	2	0	67
20	8	6	4	2	0	69
21	8	6	4	2	1	70
22	9	6	4	2	1	71
23	9	7	4	2	1	72
24	9	7	4	3	1	73
25	10	7	4	3	1	75
26	10	7	5	3	1	76
27	10	7	5	4	1	77
28	10	7	6	4	1	79
29	10	7	6	5	1	80
30	10	7	6	5	2	82
31	10	7	7	5	2	83
32	10	8	7	5	2	84
33	11	8	7	5	2	86
34	11	8	7	6	2	87
35	11	8	7	7	2	88
36	11	8	8	7	2	90
37	11	9	8	7	2	91
38	11	9	8	8	2	92
39	11	10	8	8	3	94
40	11	10	8	8	3	95
41	11	10	9	8	3	96
42	11	10	9	9	3	98
43	12	10	9	9	3	99
44	12	10	9	9	4	100
45	12	10	9	9	5	102
46	12	10	10	9	5	104
47	12	10	10	9	6	106
48	12	11	10	9	6	108
49	12	11	10	10	6	110
50	12	11	10	10	7	112
51	12	11	11	10	7	114
52	12	11	11	10	8	116
53	12	11	11	11	8	118
54	12	12	11	11	8	120
55	12	12	11	11	9	122
56	12	12	12	11	9	124
57	12	12	12	11	10	126
58	12	12	12	12	10	128
59	12	12	12	12	11	130
60	12	12	12	12	12	140

Для оценки достоверности теста берется разница между полученными баллами по отдельной шкалы и контрольными — средне статическими подсчитанные по этой шкале при тестировании группы здоровых людей. Эта разница дает возможность надежно оценить конечный результат – она называется отклонение. Отклонение обозначается -2, -1, 0, 1, 2 и т. д. Если отклонение по шкале больше двух баллов то показатели по этой шкале считаются не достоверными. Отклонение может превышать два балла только при прохождении последних шкал. Отклонения полученные в начале испытания говорят о рассеянности внимания и восприятия или о недостатке интеллектуальных способностей

На прохождение теса дается 20 минут.

Www. tests-exam. ru

20.05.2020 23:10:04

2020-05-20 23:10:04

Источники:

Https://www. tests-exam. ru/test-ravena. html

Статистическая значимость не равна достоверности (или почему вы получаете воображаемый рост)

Очень распространенный сценарий: компания проводит десятки и десятки A/B-тестов в течение года, и многие из них «выигрывают». Некоторые тесты позволяют увеличить доход на 25 % или даже больше.

Тем не менее, когда вы внедряете изменение, доход не увеличивается на 25%. И спустя 12 месяцев после проведения всех этих тестов коэффициент конверсии практически не изменился. Почему?

Ответ такой: Ваши подъемы были воображаемый. Изначально подъема не было.

Да, ваш инструмент тестирования сказал, что у вас есть уровень статистической значимости 95% (или выше). Ну, это мало что значит. Статистическая значимость и достоверность не одно и то же.

Когда ваше тестирование говорит о том, что вы достигли уровня достоверности 95% или даже 99%, это не означает, что у вас есть выигрышный вариант.

Вот пример, который я использовал раньше. Через два дня после начала теста результаты были такими:

Вариант, который я построил, сильно проигрывал — более чем на 89 % (и никаких перекрытий в пределах погрешности). Здесь говорится, что Вариант 1 имеет 0 % шансов превзойти Контроль.

Является ли это статистически значимым результатом? Да, это так. Вбейте те же числа в любой калькулятор A/B-тестов, и они скажут то же самое. Вот результаты, полученные с помощью этого калькулятора значимости:

Таким образом, 100% значимый тест и 852,8% процентное повышение (или, скорее, контроль более чем на 800% лучше, чем обработка). Давай закончим тест, хорошо? Контроль побеждает! Или как насчет того, чтобы дать ему еще немного времени?

Вот как это выглядело через 10 дней:


Верно, вариант, который имел 0% шансов победить контроль, теперь выигрывал с 95% уверенностью. Что с этим делать? Почему «100% значимость» и «0% шанс на победу» стали бессмысленными? Потому что они есть.

Если вы закончите тест раньше, есть большая вероятность, что вы выберете не того победителя. В этом сценарии многие (большинство?) компаний продолжают внедрять изменения (т. е. внедряют выигрышный вариант на 100 % трафика), в то время как фактически прирост на 800 % становится нулевым или даже отрицательным (убыточным).

Еще хуже, чем воображаемый подъем, является ложная уверенность, которая у вас есть. Вы думаете, что чему-то научились, и продолжаете применять эти знания в других местах сайта. Но обучение на самом деле недействительно, поэтому все ваши усилия и время становятся пустой тратой времени.

То же самое и со вторым тестовым снимком экрана (через 10 дней) – несмотря на то, что он говорит о значимости 95 %, он все еще не «приготовлен». Выборка слишком мала; абсолютная разница в конверсиях составляет всего 19 транзакций. Это может измениться за день. 9По этому поводу говорит Тон Весселинг: Семьдесят семь процентов A/A-тестов (одна и та же страница против одной и той же страницы) достигают значимости в определенный момент.

Узнайте, что такое значимость на самом деле.

Статистическая значимость сама по себе не должна определять, завершите вы тест или нет. Это не правило остановки.

Статистическая значимость не говорит нам о вероятности того, что B лучше, чем A. Она также не говорит нам о вероятности того, что мы совершим ошибку, выбрав B вместо A.

Это чрезвычайно распространенные заблуждения, но они ложны. Чтобы узнать, что на самом деле представляют собой p-значения, прочитайте этот пост.

Запускайте тесты дольше.

Если вы остановите анализы через несколько дней, значит, вы делаете это неправильно. Неважно, совершаете ли вы 10 000 транзакций в день. Абсолютное количество транзакций имеет значение, но вам также нужно чистое время.

Мэтт Гершофф из Conductrics объясняет, почему:

Одна из трудностей при проведении онлайн-тестов заключается в том, что мы не контролируем группу пользователей. Это может быть проблемой, если пользователи распределяются по-разному по времени и дням недели и даже по сезонам. Из-за этого мы, вероятно, хотим убедиться, что мы собираем наши данные в течение любых соответствующих циклов данных. Таким образом, наши методы лечения подвергаются более репрезентативной выборке средней группы пользователей.

Обратите внимание, что сегментация на самом деле не избавляет нас от этого, так как нам все еще нужно будет проводить выборку в будние дни, выходные и т. д., и мы, вероятно, захотим несколько раз ударить каждый день или часть дня, чтобы усреднить и внешние события, которые могут повлиять на поток трафика/конверсию, чтобы получить точную оценку влияния функций/сегментов, основанных на времени, на конверсию.

Я все время вижу следующий сценарий:

• Первые пару дней: B выигрывает по-крупному. Как правило, из-за фактора новизны.
• После недели #1: B уверенно побеждает.
• После недели № 2: B по-прежнему выигрывает, но относительная разница меньше.
• После недели № 4: регрессия к среднему значению — подъем исчез.

Итак, если вы остановите тест до четырех недель (может быть, даже через несколько дней), вы думаете, что у вас есть выигрышный вариант, но это не так. Если вы развернете его вживую, у вас будет то, что я называю «воображаемым подъемом». Вы думаете, что у вас есть рост, потому что ваш инструмент тестирования показал рост > 25%, но вы не видите роста на своем банковском счете.

Запускайте тесты дольше. Убедитесь, что они включают два бизнес-цикла, имеют достаточно абсолютных конверсий/транзакций и имеют достаточную продолжительность по времени.

Пример воображаемого подъема

Вот тест, который мы провели для клиента электронной коммерции. Продолжительность теста составляла 35 дней, таргетинг был рассчитан только на посетителей настольных компьютеров, и было проведено около 3000 транзакций на каждый вариант.

Спойлер: тест закончился «без разницы». Вот обзор Optimizely по доходам (нажмите, чтобы увеличить):

Посмотрим сейчас:

• Первые несколько дней: Синий (вариант №3) выигрывает по-крупному — около 16 долларов за посетителя против 12,5 долларов за контроль (#Победа!). Многие люди заканчивают тест здесь (#Fail!).
• Через 7 дней: синий по-прежнему выигрывает, и относительная разница велика.
• Через 14 дней: Оранжевый (#4) побеждает!
• Спустя 21 день: Orange все еще выигрывает!
• Конец: Без разницы.

Итак, если бы вы проводили тест менее четырех недель, вы бы неправильно назвали победителя.

Правила остановки

Итак, когда готовится тест?

Увы, универсального небесного ответа не существует, и есть много факторов «как повезет». Тем не менее, у вас могут быть довольно хорошие правила остановки для большинства случаев.

Вот мои правила остановки:

• Продолжительность тестирования не менее 3 недель (лучше 4).
• Достигнут минимальный предварительно рассчитанный размер выборки (с использованием других инструментов). Я не поверю ни одному тесту, у которого меньше 250–400 конверсий на вариант.
• Статистическая значимость не менее 95%.

Для некоторых тестов может быть по-другому из-за особенностей, но в большинстве случаев я придерживаюсь этих правил.

Весселинг снова вмешивается:

Вы хотите тестировать как можно дольше — хотя бы один цикл покупки — чем больше данных, тем выше статистическая мощность вашего теста!

Больше трафика означает, что у вас больше шансов распознать победителя на том уровне значимости, на котором вы тестируете! Небольшие изменения могут оказать большое влияние, но большие последствия случаются не слишком часто — в большинстве случаев ваш вариант немного лучше, поэтому вам нужно много данных, чтобы заметить значительный выигрыш.

Но если ваши тесты продолжаются и продолжаются, люди, как правило, удаляют свои файлы cookie (10% за две недели). Когда они возвращаются в ваш тест, они могут оказаться в неправильном варианте, поэтому по прошествии недель ваши образцы загрязняют все больше и больше и в конечном итоге имеют одинаковые коэффициенты конверсии.

Испытание в течение максимум 4 недель.

Что, если через три или четыре недели размер выборки составит менее 400 конверсий на вариант?

Я позволил тесту работать дольше. Если к 4 неделям размер выборки не достигается, я добавляю еще одну неделю.

Всегда проверяйте полных недель. Если вы начинаете тест в понедельник, он должен закончиться в воскресенье. Если вы не будете тестировать всю неделю, ваши результаты могут быть искажены.

Создайте отчет о конверсиях по дням недели на своем сайте. Посмотрите, сколько колебаний.

Что вы видите внизу? Четверг приносит в 2 раза больше денег, чем суббота и воскресенье, а коэффициент конверсии по четвергам почти в 2 раза лучше, чем по субботам.

Если бы мы не тестировали полные недели, результаты были бы неточными. Тестируйте полные недели за раз.

Для каждого сегмента применяются одни и те же правила остановки.

Сегментация является ключом к обучению с помощью A/B-тестов. Бывает так, что Б проигрывает А по общим результатам, но превосходит А в определенных сегментах (например, по трафику Facebook, пользователям мобильных устройств и т. д.).

Прежде чем вы сможете анализировать какие-либо сегментированные данные, убедитесь, что у вас достаточно большой размер выборки в пределах каждого сегмента. Итак, вам нужно 250–400 конверсий 90 007 на 90 008 вариантов в каждом сегменте, который вы просматриваете.

Я даже рекомендую создавать целевые тесты (задавать целевую аудиторию/сегмент в конфигурации теста) вместо того, чтобы анализировать результаты по сегментам после теста. Это гарантирует, что тесты не вызываются раньше времени, и каждый сегмент имеет достаточный размер выборки.

Мой друг Андре Морис сказал о своих правилах остановки:

Я всегда говорю людям, что вам нужна репрезентативная выборка, если ваши данные должны быть достоверными.

Что означает «представитель»? В первую очередь нужно включить все будни и выходные. Вам нужна разная погода, потому что она влияет на поведение покупателей. Но самое главное, ваш трафик должен иметь все источники трафика, особенно информационные бюллетени, специальные кампании, телевидение… все! Чем дольше выполняется тест, тем больше информации вы получаете.

Мы только что провели тест для крупного ритейлера модной одежды в разгар летней распродажи. Было очень интересно наблюдать, как резко упали результаты во время «фазы жесткой продажи» с 70% и более, но восстановились через неделю после окончания фазы. Мы бы никогда не узнали об этом, если бы тест не длился почти четыре недели.

Наше «эмпирическое правило» таково: 3 000–4 000 конверсий на вариант и продолжительность тестирования 3–4 недели. Этого трафика достаточно, поэтому мы можем даже говорить о достоверных данных, если углубимся в сегменты.

Тестирование «греха» номер 1: поиск повышения внутри сегментов, когда у вас нет статистической достоверности (например, 85 конверсий против 97). Это фигня.

Учиться на тестах очень важно — даже больше, чем выигрывать. А сегментация тестовых данных — один из лучших способов обучения. Просто убедитесь, что в ваших сегментах достаточно данных, прежде чем делать поспешные выводы.

Заключение

Только потому, что ваш тест достигает уровня значимости 95% или выше, не останавливайте тест. Обратите внимание на абсолютное количество конверсий на вариант и продолжительность теста.

Тест Левена на равенство дисперсий




Определения статистики > Тест Левена

Содержание:

1. Что такое тест Левена?
2. Запустите тест Левена на равенство дисперсий в SPSS

Тест Левена используется для проверки того, что дисперсии одинаковы для всех выборок, когда ваши данные получены из ненормального распределения. Вы можете использовать тест Левена, чтобы проверить предположение о равных дисперсиях перед запуском теста, такого как однофакторный дисперсионный анализ.

Если вы достаточно уверены, что ваши данные имеют нормальное или близкое к нормальному распределение, используйте вместо этого критерий Бартлетта.

Нулевая гипотеза Левена состоит в том, что дисперсии одинаковы для всех выборок. Более формально это записывается так:
H ₀ : σ ₁ ² = σ ₂ ² = … = σ _k 2 .
Альтернативная гипотеза (которую вы проверяете) состоит в том, что дисперсии не равны хотя бы для одной пары:
H ₀ : σ ₁ ² ≠ σ ₂ ² ≠… ≠ σ _{k 2} 2

Статистика теста немного уродлива и включает в себя несколько сумм:


Z _i,j может принимать три значения, в зависимости от того, используете ли вы среднее, медиану или усеченное среднее любой подгруппы. Три варианта фактически определяют надежность и мощность теста.



• Надежность — это мера того, насколько хорошо тест не выдает ложных результатов о неравных дисперсиях (когда дисперсии фактически равны).
• Степень — это мера того, насколько хорошо тест правильно сообщает о неравных отклонениях.

Согласно Брауну и Форсайту:

• Усеченные средние лучше всего работают с распределениями с тяжелыми хвостами, такими как распределение Коши.
• Для асимметричных распределений или если вы не уверены в основной форме распределения, лучшим выбором может быть медиана .
• Для симметричных распределений и распределений со средними хвостами используйте означает .

Тест Левена встроен в большинство статистических программ. Например, Т-критерий независимых выборок в SPSS создает столбец «Тест Левена на равенство дисперсий» как часть выходных данных. Результат теста сообщается как p-значение, которое вы можете сравнить с вашим альфа-уровнем для теста. Если p-значение больше альфа-уровня, то можно сказать, что нулевая гипотеза верна — дисперсии равны; если p-значение меньше альфа-уровня, то подразумевается, что дисперсия равна и равны.

Тест Левена проверяет, приблизительно ли равны дисперсии двух выборок. В идеале вам нужен несущественный результат для этого теста — это означает, что ваши отклонения соответствуют предположению о равных отклонениях. SPSS будет автоматически запускать тест Левена каждый раз, когда вы запускаете t-тест для независимых выборок, но вы можете запустить тест независимо, выполнив следующие действия.

Подробные шаги смотрите в видео:


Тест Левена на равенство дисперсий SPSS

Посмотрите это видео на YouTube.

Примечание. Следующие шаги выполняются на наборе данных с двумя уровнями независимой переменной: дома и в офисе. Результаты теста измеряются на уровне шкалы.

Шаг 1. Перейдите к Анализ > Общая линейная модель → Одномерная

Шаг 2. Переместите независимую переменную в поле Фиксированный коэффициент.

Шаг 3: Переместите зависимую переменную в поле Зависимая переменная.

Шаг 4: Нажмите «Параметры», затем установите флажок рядом с пунктом «Тесты гомогенности». Внизу вы можете изменить свой альфа-уровень, если хотите. Альфа-уровень обычно устанавливается равным 0,01 или 0,001, особенно при больших размерах выборки. Это связано с тем, что у вас больше шансов получить статистически значимый результат для больших выборок.

Шаг 6: Нажмите «Продолжить», затем нажмите «ОК», чтобы запустить тест.

Чтение выходных данных

Прочтите результат из столбца Sig (на основе среднего) в поле Тест Левена на равенство отклонений ошибок. Незначительный результат здесь (больше 0,05) указывает на то, что вы выполнили допущение об однородности дисперсии (т. е. предполагаются равные дисперсии). Значимый результат здесь (менее 0,05) указывает на то, что вы нарушили предположение об однородности дисперсии (т. е. равные дисперсии не предполагаются).

Если вы читаете выходные данные как часть t-критерия, это говорит вам, следует ли интерпретировать t-критерий для предполагаемых равных дисперсий или нет.

Ссылка :
Браун, М. Б. и Форсайт, Надежные тесты на равенство дисперсий. AB (1974), Журнал Американской статистической ассоциации, 69, стр. 364-367. Доступна здесь.

УКАЗЫВАЙТЕ ЭТО КАК:
Стефани Глен . «Тест Левена на равенство дисперсий» из StatisticsHowTo.com : Элементарная статистика для всех нас! https://www.statisticshowto.com/levene-test/

————————————————— ————————-

Нужна помощь с домашним заданием или контрольным вопросом? С Chegg Study вы можете получить пошаговые ответы на свои вопросы от эксперта в данной области. Ваши первые 30 минут с репетитором Chegg бесплатны!

Комментарии? Нужно опубликовать исправление? Пожалуйста Свяжитесь с нами .

тестов статистической значимости

тестов статистической значимости

PPA 696 МЕТОДЫ ИССЛЕДОВАНИЯ

ТЕСТЫ НА ЗНАЧИМОСТЬ

Что такое тесты на значимость
шагов в тестировании для статистики Значение
1) Сформулируйте исследовательскую гипотезу
2) Сформулируйте нулевую гипотезу
3) Ошибки типа I и типа II
Выберите вероятность уровня ошибки (альфа-уровень)
4) Тест хи-квадрат
Вычислить хи-квадрат
степеней свободы
Распределительные столы
Интерпретация результатов
5) Т-тест
Рассчитать Т-тест
степеней свободы
Распределительные столы
Интерпретация результатов
Отчетные тесты статистических Значение
Заключительные комментарии
Что такое тесты значимости

Возникают два вопроса о любых гипотетических отношениях. между двумя переменными:

1) какова вероятность того, что связь существует;

2) если да, то насколько сильна связь

Существует два типа инструментов, которые используются для решения эти вопросы: первый решается тестами на статистическую значимость; а ко второму относятся Меры ассоциации.

    Тесты на статистическую значимость используются для решения вопрос: какова вероятность того, что то, что мы думаем, является отношением между двумя переменными на самом деле просто случайность?

    Если мы выбрали много образцов из одной и той же совокупности, найдем ли мы такое же отношение между этими двумя переменными в каждый образец? Если бы мы могли провести перепись населения, разве мы найти, что эта связь существует в популяции, из которой выборка был нарисован? Или наша находка обусловлена ​​только случайностью?

    Тесты на статистическую значимость говорят нам, что Вероятность состоит в том, что отношения, которые, как мы думаем, мы обнаружили, обусловлены только к случайному. Они говорят нам, какова вероятность того, что мы ошибемся, если предположим, что обнаружили, что связь существует.

    Мы никогда не можем быть на 100 % уверены, что отношения существует между двумя переменными. Слишком много источников ошибок, чтобы например, ошибка выборки, предвзятость исследователя, проблемы с надежность и валидность, простые ошибки и т. д.

    Но, используя теорию вероятностей и нормальную кривую, мы можем оценить вероятность ошибиться, если предположим, что наш вывод отношения верны. Если вероятность ошибиться мала, то мы говорим, что наше наблюдение взаимосвязи является статистически значимым найти.

    Статистическая значимость означает наличие хорошего шанс, что мы правы, находя, что связь существует между две переменные. Но статистическая значимость не то же самое, что практическая значение. Мы можем получить статистически значимый результат, но последствия этого вывода могут не иметь практического применения. Исследователь необходимо всегда проверять как статистическую, так и практическую значимость любых результатов исследования.

    Например, мы можем обнаружить, что статистически значимая связь между возрастом гражданина и удовлетворенностью услуги городского отдыха. Возможно, пожилые граждане на 5% менее удовлетворены чем более молодые граждане с городскими рекреационными услугами. Но 5% большой достаточная разница для беспокойства?

    Часто, когда различия небольшие, но статистически значителен, это связано с очень большим объемом выборки; в образце меньшего размера размер, различия не были бы достаточными, чтобы быть статистически значимыми.


шагов в тестировании для Статистическая значимость 1) Сформулируйте исследовательскую гипотезу
2) Сформулируйте нулевую гипотезу
3) Выберите уровень вероятности ошибки (альфа-уровень)
4) Выбрать и рассчитать критерий статистической значимости
5) Интерпретация результатов

1) Сформулировать исследовательскую гипотезу

Гипотеза исследования утверждает ожидаемую взаимосвязь между двумя переменными. Он может быть изложен в общих чертах или может включать размеры направления и величины. Например,

Общее: продолжительность программы профессионального обучения связана со ставкой трудоустройства стажеров.

Направление: Чем дольше программа обучения, тем выше скорость работы размещение стажеров.

Масштабы: более длительные программы обучения позволят в два раза большему числу слушателей задания в виде более коротких программ.

Общее: на оплату помощника выпускника влияет пол.

Направление: Помощникам выпускников-мужчинам платят больше, чем выпускникам-женщинам помощники.

Величина: ассистенты выпускников получают менее 75% от зарплаты мужчин. ассистенты выпускников оплачиваются.

2) Сформулируйте нулевую гипотезу 90 360

Нулевая гипотеза обычно утверждает, что связи нет между двумя переменными. Например,

Нет никакой связи между продолжительностью программы профессионального обучения и уровень трудоустройства стажеров.

Зарплата помощника выпускника не зависит от пола.

Нулевая гипотеза может также утверждать, что отношение предложенная в исследовании гипотеза не соответствует действительности. Например,

В более длительных программах обучения будет задействовано такое же или меньшее количество слушателей. задания в виде более коротких программ.

Помощникам выпускников-женщин платят не менее 75% от зарплаты выпускников-мужчин. помощники оплачиваются.

Исследователи используют нулевую гипотезу в исследованиях, потому что легче опровергнуть нулевую гипотезу, чем доказать исследование гипотеза. Нулевая гипотеза — это «соломенное чучело» исследователя. То есть, легче один раз показать, что что-то ложно, чем доказать, что что-то всегда верно. Легче найти опровергающие доказательства против нулевой гипотезы, чем найти подтверждение гипотезы исследования.


3) ОШИБКИ ТИПА I И ТИПА II

Даже в самом лучшем исследовательском проекте всегда есть вероятность (надеюсь, небольшая) того, что исследователь совершит ошибку относительно связи между двумя переменными. Есть два возможных ошибки или ошибки.

    Первая называется ошибкой типа I. Это происходит, когда исследователь предполагает, что связь существует, когда на самом деле доказательства в том, что это не так. При ошибке типа I исследователь должен принять нулевую гипотезу и отклонить исследовательскую гипотезу, но происходит обратное. Вероятность совершения ошибки первого рода называется альфа.

    Вторая ошибка называется ошибкой второго рода. Это происходит когда исследователь предполагает, что отношения не существует, когда в на самом деле доказательство того, что это так. При ошибке типа II исследователь должен отвергнуть нулевую гипотезу и принять гипотезу исследования, но происходит наоборот. Вероятность совершения ошибки II рода называется бета.

    Как правило, снижение вероятности совершения ошибка типа I увеличивает вероятность совершения ошибки типа II и наоборот, уменьшая вероятность совершения ошибки второго рода. увеличивает вероятность совершения ошибки первого рода.

    Исследователи обычно стараются свести к минимуму ошибки типа I, потому что, когда исследователь предполагает, что отношения существуют, когда на самом деле нет, все может быть хуже, чем раньше. При ошибках II рода исследователь упускает возможность подтвердить, что отношения существуют, но не хуже, чем раньше.

В этом примере, какой тип ошибки вы бы предпочли совершить?

Гипотеза исследования: Эль-Ниньо снизил урожайность сельскохозяйственных культур в графстве X, в результате чего он имеет право на государственную помощь при стихийных бедствиях.

Нулевая гипотеза: Эль-Ниньо не снизил урожайность в графстве X, что делает он не имеет права на государственную помощь при стихийных бедствиях.

Если совершена ошибка типа I, то предполагается, что округ иметь право на помощь при стихийных бедствиях, хотя на самом деле это не так (нулевая гипотеза должно быть принято, но оно отвергнуто). Правительство может тратить фонды помощи при стихийных бедствиях, когда этого не следует делать, и могут быть повышены налоги.

    Если совершена ошибка типа II, то округ считается непригодным для оказания помощи при стихийных бедствиях, хотя на самом деле имеет право (нулевая гипотеза должна быть принята, но она отвергнута). Правительство могут не тратить средства на помощь при стихийных бедствиях, когда это необходимо, и фермеры могут уйти в банкротство.

В этом примере, какой тип ошибки вы бы предпочли совершить?

Гипотеза исследования: новый препарат лучше лечит сердечные приступы, чем старый наркотик

Нулевая гипотеза: новый препарат лечит сердечные приступы не лучше, чем старый наркотик

Если совершена ошибка типа I, то новый препарат считается лучше, когда на самом деле это не так (нулевая гипотеза должна принять, но отвергнуть). Люди могут лечиться новым препаратом, когда им было бы лучше со старым.

    Если совершена ошибка типа II, то новый препарат предполагается не лучше, когда оно действительно лучше (нулевая гипотеза следует отвергнуть, но он принимается). Людей нельзя лечить новый препарат, хотя им было бы лучше, чем со старым.


ВЫБЕРИТЕ ВЕРОЯТНОСТЬ УРОВНЯ ОШИБКИ (АЛЬФА-УРОВЕНЬ)

Исследователи обычно указывают вероятность совершения ошибка типа I, которую они готовы принять, т. е. значение альфы. В социальных науках большинство исследователей выбирают альфа = 0,05. Это означает что они готовы принять вероятность 5% сделать Тип I ошибка предположения, что связь между двумя переменными существует, когда она на самом деле нет. Однако в исследованиях, связанных с общественным здравоохранением, альфа- 0,01 не является чем-то необычным. Исследователи не хотят иметь вероятность ошибаться более чем в 0,1% случаев, или один раз из тысячи.

    Если связь между двумя переменными сильная (согласно оценке с помощью показателя ассоциации) и выбранный уровень для альфа составляет 0,05, тогда средние или малые размеры выборки обнаружат его. В качестве однако отношения становятся слабее и/или по мере того, как уровень альфы становится меньше, потребуются большие размеры выборки, чтобы исследование достигло статистической значение.


4) Тест хи-квадрат

Для номинальных и порядковых данных используется хи-квадрат. тест на статистическую значимость. Например, мы предполагаем, что существует представляет собой взаимосвязь между типом посещаемой учебной программы и успешность трудоустройства стажеров. Мы собираем следующие данные:



Посещенный тип тренинга:	Номер посещающего обучение
Профессиональное образование	200
Обучение навыкам работы	250
Итого	450




Устроились на работу?	Количество стажеров
Да	300
№	150
Итого	450

    Для расчета хи-квадрата таблица, показывающая сустав необходимо распределение двух переменных:

Таблица 1. Трудоустройство по типу обучения (наблюдаемые частоты)


Устроен на работу?	Тип обучения
	Профессиональный Образование	Рабочие навыки Обучение	Всего
Да	175	125	300
№	25	125	150
Всего	200	250	450

    Хи-квадрат вычисляется путем рассмотрения различных части стола. «Ячейками» таблицы являются квадраты посередине. таблицы, содержащей полностью закрытые числа. Клетки содержат частоты, возникающие при совместном распределении двух переменные. Частоты, которые мы действительно находим в данных, называются «наблюдаемые» частоты.

    В этой таблице ячейки содержат частоты для стажеров профессионального образования, устроившихся на работу (n=175) и не устроившихся устроиться на работу (n=25), а частота стажеров профессиональных навыков, получивших работающие (n=125) и не устроившиеся на работу (n=125).

    Столбцы и строки «Всего» таблицы показывают предельные частоты. Предельные частоты – это частоты, которые мы бы нашли, если бы рассматривали каждую переменную отдельно. Например, мы видим в колонке «Всего» 300 человек, которые получили работу и 150 человек, которые этого не сделали. В строке «Всего» мы видим, что было 200 человек на профессиональном обучении и 250 человек на профессиональных навыках подготовка.

    Наконец, общее количество наблюдений во всей таблице, называемой N. В этой таблице N=450.


Вычислить хи-квадрат

1) отображать наблюдаемые частоты для каждой ячейки
2) рассчитать ожидаемые частоты для каждой ячейки
3) рассчитать для каждой ячейки ожидаемую минус наблюдаемую частоту в квадрате, деленное на ожидаемую частоту
4) все результаты по всем ячейкам

    Чтобы найти значение хи-квадрат, мы сначала предполагаем что нет никакой связи между типом посещаемой программы обучения и был ли стажер принят на работу. Если мы посмотрим на итог столбца, мы видим, что 300 из 450 человек нашли работу, или 66,7% от общего числа людей на учебе нашел работу. Мы также видим, что 150 из 450 человек не найти работу, или 33,3% от общего числа обучающихся не нашли работу.

    Если между типом участие в программе и успех в поиске работы, то можно было бы ожидать 66,7% слушателей обоих видов программ обучения устроились на работу, а 33,3% обоих типов учебных программ, чтобы не получить работу.

    Первое, что делает Хи-квадрат, это вычисляет «ожидаемые» частоты для каждой ячейки. Ожидаемая частота – это частота которые мы ожидали бы увидеть в каждой ячейке, если бы не было связи между типом программы обучения и трудоустройством.

    Способ расчета ожидаемой частоты ячеек состоит в том, чтобы умножить сумму столбца для этой ячейки на сумму строки для этой ячейке и разделить на общее количество наблюдений для всей таблицы.

Для ячейки в левом верхнем углу умножьте 200 на 300 и разделите на 450=133,3
Для ячейки в нижнем левом углу умножьте 200 на 150 и разделите на 450=66,7
Для ячейки в правом верхнем углу умножьте 250 на 300 и разделите на 450=166,7
Для ячейки в нижнем правом углу умножьте 250 на 150 и разделите на 450=83,3

Таблица 2. Трудоустройство по типу обучения (ожидаемая периодичность)


Устроен на работу?	Тип обучения
	Профессиональный Образование	Рабочие навыки Обучение	Всего
Да	133,3	166,7	300
№	66,7	83,3	150
Итого	200	250	450

    В этой таблице показано распределение «ожидаемых» частот, то есть частоты ячеек, которые мы ожидали бы найти, если бы не было связи между видом обучения и трудоустройством.

    Обратите внимание, что хи-квадрат ненадежен, если какая-либо ячейка в таблице непредвиденных обстоятельств имеет ожидаемую частоту менее 5.

    Чтобы рассчитать хи-квадрат, нам нужно сравнить исходный, наблюдаемые частоты с новыми, ожидаемыми частотами. Для каждой ячейки, производим следующие расчеты:
а) Вычесть значение наблюдаемой частоты из значения ожидаемая частота
б) возвести результат в квадрат
в) результат разделить на значение ожидаемой частоты

Для каждой ячейки выше,


ф е — ф о	(ф и — ф или ) 2	[(ф е — ф о ) 2 ] / ф е	Результат
(133,3 — 175)	(133,3 — 175) 2	[(133,3 — 175) 2 ] / 133,3	13. 04
(66,7–25)	(66,7 — 25) 2	[(66,7–25) 2 ] / 66,7	26.07
(166,7 — 125)	(166,7 — 125) 2	[(166,7–125) 2 ] / 166,7	10.43
(83,3 — 125)	(83,3 — 125) 2	[(83,3 — 135) 2 ] / 83,3	20,88

Чтобы вычислить значение хи-квадрат, сложите результаты для каждой ячейки — итого = 70,42.


СТЕПЕНИ СВОБОДЫ

Мы не можем интерпретировать значение статистики хи-квадрат. сам по себе. Вместо этого мы должны поместить его в контекст.

    Теоретически значение статистики хи-квадрат нормально распределяется; то есть значение статистики хи-квадрат выглядит как нормальная (колоколообразная) кривая. Таким образом, мы можем использовать свойства нормальной кривой для интерпретации значения, полученного в результате нашего расчета статистики Хи-квадрат.

    Если значение, полученное для Хи-квадрат, достаточно велико, то можно сказать, что это указывает на уровень статистической значимости при котором можно предположить, что связь между двумя переменными существует.

    Однако достаточно ли велико значение, зависит на двух вещах: размере таблицы непредвиденных обстоятельств, из которой Хи-квадрат статистика рассчитана; и уровень альфы, который мы выбрали.

    Чем больше размер таблицы непредвиденных обстоятельств, тем больше значение хи-квадрат должно быть, чтобы достичь статистического значимость при прочих равных условиях. Аналогично, чем строже уровень альфы, тем больше должно быть значение Chi Square, для достижения статистической значимости при прочих равных условиях.

    Термин «степени свободы» используется для обозначения размер таблицы непредвиденных обстоятельств, на которой значение хи-квадрат статистика подсчитана. Степени свободы рассчитываются как произведение (количество строк в таблице минус 1) умножить на (количество столбцов в таблице минус ).


Для таблицы с двумя строками ячеек и двумя столбцами ячеек формула это:

df = (2 — 1) х (2 — 1) = (1) х (1) = 1

Для таблицы с двумя строками ячеек и тремя столбцами ячеек формула это:

df = (3 — 1) х (2 — 1) = (2) х (1) = 2

Для таблицы с тремя строками ячеек и тремя столбцами ячеек формула это:

df = (3 — 1) х (3 — 1) = (2) х (2) = 4

Уровень альфы может варьироваться, но чем меньше значение, более строгие требования для достижения статистической значимости становится. Альфа-уровни часто записываются как «значение p» или «p = 0,05». Обычный уровни равны p = 0,05 (или вероятность ошибки один из 20) или p = 0,01. (или шанс ошибиться один из 100), или p=0,001 (или шанс один из 1000 совершающих ошибку).

    При сообщении об уровне альфы обычно сообщается как «меньше» некоторого уровня с использованием знака «меньше чем» или <. Таким образом, сообщается как p<0,05 или p<0,01; если вы не сообщает точное значение p, например, p = 0,04 или p = 0,22.


РАСПРЕДЕЛИТЕЛЬНЫЕ СТОЛЫ

Как только мы получим рассчитанное значение хи-квадрата статистика, и степени свободы для таблицы непредвиденных обстоятельств, и желаемый уровень для альфы, мы можем найти нормальное распределение для Чи Квадрат в столе. В текстах статистики доступно множество таблиц для этой цели.

    В таблице найдите степени свободы (обычно перечислены в столбце внизу страницы). Далее находим нужный уровень альфы (обычно перечисляются в строке вверху страницы). Найди пересечение степеней свободы и уровня альфа, и что значение, которому вычисленный хи-квадрат должен быть равен или превышать, чтобы достичь Статистическая значимость.

    Например, для df=2 и p=0,05 хи-квадрат должен равно или превышает 5,99, чтобы указать, что отношения между двумя переменных, вероятно, не случайно. Для df=4 и p=0,05, хи-квадрат должен быть равен или превышать 9,49.


ИНТЕРПРЕТАЦИЯ РЕЗУЛЬТАТОВ

Если вычисленное значение хи-квадрата равно или превышает значение, указанное в таблице для данного уровня альфы и градусов свободы, то исследователь может предположить, что наблюдаемая связь между двумя переменными существует (при заданном уровне вероятности ошибки, или альфа), и отклонить нулевую гипотезу. Это дает поддержку к исследовательской гипотезе.

    Вычисленное значение хи-квадрат на заданном уровне альфа и с заданной степенью свободы, является типом измерения «годен-не годен». Это не похоже на меру ассоциации, которая может варьироваться от 0,0 до (плюс или минус) 1,0, и которые можно интерпретировать в любой точке распределения. Либо вычисленное значение хи-квадрата достигает требуемого уровня для статистической значимости или нет.


Важно отметить, что Хи-квадрат, как и другие тесты на статистическую значение:

1) не указывает на силу связи между двумя переменными

2) не указывает направление связи между двумя переменными

3) не указывает на вероятность ошибки первого рода

4) не учитывает надежность и валидность исследования

5) не предоставляет абсолютных, убедительных доказательств родства


Резюмируя приведенный выше пример:

1) сформулировать гипотезу исследования:

Существует взаимосвязь между типом посещаемой учебной программы и успех трудоустройства стажеров

2) сформулировать нулевую гипотезу:

Нет никакой связи между типом посещаемой программы обучения и успешность трудоустройства стажеров

3) рассчитать тест на статистическую значимость

Хи-квадрат=70,42

4) рассчитать степени свободы таблицы непредвиденных обстоятельств

дф=1

5) выбираем уровень альфы

р=0,05

6) найдите значение хи-квадрата в таблице при p=0,05 и df=1

Хи-квадрат=3,84

7) интерпретировать результат

Вычисленное значение хи-квадрата (70,42) превышает значение в таблице. для p = 0,05 и df = 1 (хи-квадрат = 3,84). Следовательно, мы можем отказаться от нуля гипотезу (с 5% вероятностью ошибки) и принять гипотезу исследования что существует взаимосвязь между типом пройденной учебной программы и успешность трудоустройства стажеров.

Использование T-тестов

Т-тесты — это тесты на статистическую значимость, которые используются с данными об интервалах и уровнях отношения. Т-тесты могут быть использованы в нескольких различные виды статистических тестов:

1) проверить, есть ли различия между двумя группами на одном и том же переменная, основанная на среднем (среднем) значении этой переменной для каждой группы; например, учащиеся частных школ получают более высокие баллы на тесте SAT чем учащиеся государственных школ?

2) чтобы проверить, является ли среднее (среднее) значение группы больше или меньше, чем какой-то стандарт; например, это средняя скорость автомобилей на автомагистралях в г. Калифорния выше 65 миль в час?

3) проверить, имеют ли одна и та же группа разные средние (средние) баллы по разные переменные; например, те же клерки более продуктивны на Компьютеры IBM или Macintosh?

Чтобы вычислить значение t,

а) сформулировать исследовательскую гипотезу;
б) сформулировать нулевую гипотезу;
c) указать, будет ли t-критерий односторонним или двусторонним тест на значимость
г) выберите уровень альфы
д) рассчитать т

Чтобы вычислить значение t,

а) сформулировать исследовательскую гипотезу;

Средняя заработная плата ассистентов выпускников-мужчин выше средней зарплата ассистентов женского пола в CSULB.

б) сформулировать нулевую гипотезу;

Нет разницы в средней зарплате выпускника мужского и женского пола помощники в CSULB.

в) выбрать уровень альфы

выберите значение альфа-канала, например p=0,05, p=0,01 или p=0,001

г) указать, будет ли t-критерий односторонним или двусторонним тест на значимость

    Как и другие статистические данные, t-критерий имеет распределение которое приближается к нормальному распределению, особенно если размер выборки больше 30. Поскольку мы знаем свойства нормальной кривой, мы может ли он сказать нам, как далеко от среднего значения распределения наши вычисленные t-счет.

    Нормальная кривая имеет среднее значение, равное нулю, со стандартным отклонением, равным единице. Т-показатель может падать по нормальной кривой либо выше, либо ниже среднего; то есть либо плюс либо минус какой-то стандартный единицы отклонения от среднего.

    Значение t должно быть далеко от среднего, чтобы достичь статистической значимости. То есть он должен сильно отличаться от значение среднего распределения, что-то, что имеет только низкий вероятность случайного возникновения, если нет связи между две переменные. Если мы выбрали значение p=0,05 для альфы, мы смотрим для значения t, попадающего в крайние 5% распределения.

    Если у нас есть гипотеза, утверждающая ожидаемое направление результатов, например, что заработная плата аспиранта-мужчины выше, чем зарплата ассистента-женщины, то мы ожидаем, что рассчитанная t-показатель попадает только в один конец нормального распределения. Мы ожидаем расчетный t-показатель попадает в крайние 5% распределения.

    Если у нас есть гипотеза, которая утверждает только что есть некоторая разница между двумя группами, но не указывается, какая ожидается, что группа будет иметь более высокий балл, чем рассчитанный t-показатель может попасть в любой конец нормального распределения. Например, наша гипотеза Возможно, мы ожидаем найти разницу между средней заработной платой мужчин и женщин-выпускников-ассистентов (но мы не знаем, какие будет выше, а что ниже).

    Для гипотезы, которая не указывает направления, нам нужно использовать «двусторонний» t-критерий. То есть мы должны искать значение t, которое попадает в любой из крайних концов («хвостов») распределения. Но поскольку t может попасть в любой хвост, если мы выберем p = 0,05 для альфа, мы должны разделить 5% на две части по 2-1/2% каждая. Итак, двусторонний тест требует, чтобы t принимало более экстремальное значение, чтобы достичь статистической значимости чем односторонний тест t.

д) рассчитать t

    T-показатель рассчитывается путем сравнения среднего значение некоторой переменной, полученное для двух групп; расчет также включает дисперсия каждой группы и количество наблюдений в каждой группе. Например,

Таблица 3. Заработная плата ассистентов выпускников мужского и женского пола в CSULB


	Помощники выпускников мужского пола	Ассистент женского пола
Количество наблюдений	403	132
Среднее	17 095 долларов США	$14 885
Стандарт Отклонение	6329	4676
Разница	40045241	21864976

Для расчета t,
1) вычесть среднее значение второй группы из среднего значения первой группа
2) рассчитать для каждой группы дисперсию, деленную на количество наблюдения минус 1
3) сложите результаты, полученные для каждой группы на втором шаге, вместе
4) извлеките квадратный корень из результатов третьего шага
5) разделить результаты первого шага на результаты четвертого шага

Например,

1) вычесть среднее значение второй группы из среднего значения первой группы

17095-14885=2210

2) рассчитать для каждой группы дисперсию, деленную на количество наблюдений минус 1

Помощники выпускников мужского пола:

[40056241 / (403-1)] = [40056241 / (402)] = 99642

Ассистент-выпускница женского пола:

[21864976 / (132-1)] = [21864976 / (131)] = 166908

3) сложите результаты, полученные для каждой группы на втором шаге, вместе 90 363

99642+166908=266550

4) извлеките квадратный корень из результатов третьего шага

квадратный корень из 266550 = 516,28

5) разделить результаты первого шага на результаты четвертого шага

2210/516,28=4,28

Чтобы интерпретировать результаты,
f) рассчитать степени свободы
г) ищите значение в таблице
h) интерпретировать значение t

Степени свободы

Степени свободы для t-теста рассчитываются путем сложения количество наблюдений для каждой группы, а затем вычитание числа два (потому что есть две группы). Например, (403 + 132 — 2) = 533

Раздача Т

Значения t печатаются в таблицах в большинстве статистик. тексты. Значения степеней свободы перечислены в столбце вниз стороне, а значения альфа (значение p) перечислены в строке поперек вершина. Существуют разные таблицы для односторонних и двусторонних тестов. т.


Найдите правильную таблицу количества решек. затем найти пересечение степеней свободы и значения альфа в таблице. Это значение является значением, которое должен иметь рассчитанный t-показатель. равны или превышают, чтобы указать статистическую значимость.

Для одностороннего теста t с df = 533 и p = 0,05 t должно быть равно или превышать 1.645.

Для двустороннего теста t с df = 533 и p = 0,05 t должно быть равно или превышать 1.960.

Интерпретировать значение t

Если вычисленный t-показатель равен или превышает значение t, указанных в таблице, то исследователь может сделать вывод, что существует является статистически значимой вероятностью того, что связь между две переменные существуют и не случайны, и отвергают нуль гипотеза. Это подтверждает гипотезу исследования.

    В этом примере вычисленный t-показатель 4,28 превышает табличное значение t, поэтому мы можем отвергнуть нулевую гипотезу об отсутствии связи между полом аспиранта и оплатой аспиранта, и вместо этого принять гипотезу исследования и сделать вывод о наличии связи между полом аспиранта и оплатой аспиранта.

    Помните, однако, что это только одна статистика, на основе только одной выборки в один момент времени из одного исследовательского проекта. Это не абсолютное, окончательное доказательство того, что связь существует, а скорее подтверждение исследовательской гипотезы. Это только одно доказательство, которые необходимо учитывать наряду со многими другими доказательствами в отношении тот же предмет.


ОТЧЕТНЫЕ ИСПЫТАНИЯ СТАТИСТИЧЕСКИХ ЗНАЧЕНИЕ

В отчетах об исследованиях тесты статистической значимости сообщается тремя способами. Во-первых, результаты теста могут быть сообщены в текстовом обсуждении результатов. Включая:

1) гипотеза

2) используемая тестовая статистика и ее значение

3) степеней свободы

4) значение для альфа (p-значение)

Например,

Работники организаций с неавторитарным управлением Было обнаружено, что стили имеют более высокий уровень удовлетворенности работой, чем рабочие. в организациях с авторитарным стилем управления (Квадрат Хи=50,57, df=4, p<0,05).

Средняя заработная плата ассистентов-выпускников-мужчин выше, чем у ассистенты выпускников (t = 4,28, df = 533, p <0,05).

Различий в показателях трудоустройства между профессиональными образованиями выявлено не было. программы и программы рабочих навыков (хи-квадрат=1,2, df=1, p>0,05).

    Второй способ сообщения результатов испытаний для статистической значимости должен сообщить тест и его значение, градусы свободы и p-значение в нижней части таблицы непредвиденных обстоятельств или распечатки показать данные, на которых основывались расчеты.

Таблица 1. Трудоустройство по типу обучения (наблюдаемые частоты)


Устроен на работу?	Тип обучения
	Профессиональный Образование	Рабочие навыки Обучение	Всего
Да	175	125	300
№	25	125	150
Итого	200	250	450

Хи-квадрат = 70,42, df = 1, p <0,05

Таблица 3. Заработная плата ассистентов выпускников мужского и женского пола в CSULB


	Помощники выпускников мужского пола	Ассистент женского пола
Количество наблюдений	403	132
Среднее	17 095 долларов США	$14 885
Стандарт Отклонение	6329	4676
Разница	40045241	21864976

т=4,28, df=533, р<0,05

    Третий способ отчета о тестах статистической значимости заключается в том, чтобы включить их в таблицы, отображающие результаты расширенного анализа данных, включая ряд переменных. Например, вот некоторые результаты исследования пожилых латиноамериканских женщин в Эль-Пасо, Техас, и Лонг-Бич, Калифорния.

Таблица 4. Характеристики участников семинара в возрасте 40 лет и старше


Характеристики	Эль-Пасо (N=83)	Лонг Бич (N=131)	значение т
Средний возраст	60,5 лет	68,7 лет	2,1*
Этническая самоидентификация Американец мексиканского происхождения	97,2	89,7	0,9
Выбор языка Только испанский	68,5	52,3	3,2**

*t значимо при p<0,05
**t значимо при p<0,01


Заключительные комментарии

Тесты на статистическую значимость используются для оценки вероятность того, что взаимосвязь, наблюдаемая в данных, имела место только случайно; вероятность того, что переменные действительно не связаны между собой Население. Их можно использовать для фильтрации бесперспективных гипотез.

    Тесты на статистическую значимость используются, потому что они представляют собой общий критерий, который может быть понят очень многими людей, и они сообщают важную информацию об исследовательском проекте которые можно сравнить с результатами других проектов.

    Однако они не гарантируют, что исследование был тщательно разработан и выполнен. На самом деле тесты на статистическую значимость может ввести в заблуждение, потому что это точные цифры. Но у них нет отношений к практической значимости результатов исследования.

    Наконец, всегда нужно использовать меры ассоциации вместе с тестами на статистическую значимость. Последние оценивают вероятность того, что отношения существуют; в то время как первые оценивают сила (а иногда и направление) отношений. У каждого есть свой использовать, и лучше всего их использовать вместе.

Двухвыборочный t-критерий | Введение в статистику

Что такое двухвыборочный

t -критерий?

Двухвыборочный t -критерий (также известный как t -критерий независимых выборок) представляет собой метод, используемый для проверки того, равны ли неизвестные средние значения генеральной совокупности двух групп.

Это то же самое, что и A/B-тест?

Да, двухвыборочный t -тест используется для анализа результатов A/B-тестов.

Когда можно использовать тест?

Вы можете использовать этот тест, когда ваши значения данных независимы, случайным образом выбраны из двух нормальных совокупностей и две независимые группы имеют одинаковую дисперсию.

Что делать, если у меня более двух групп?

Использовать метод множественного сравнения. Одним из таких методов является дисперсионный анализ (ANOVA). Другие методы множественного сравнения включают тест Тьюки-Крамера для всех попарных различий, анализ средних значений (ANOM) для сравнения групповых средних значений с общим средним значением или критерий Даннета для сравнения каждого среднего значения группы с контрольным средним значением.

Что делать, если дисперсии двух моих групп не равны?

Вы по-прежнему можете использовать двухвыборочный тест t-. Вы используете другую оценку стандартного отклонения.

Что делать, если мои данные почти не распределены нормально?

Если размеры вашей выборки очень малы, вы не сможете проверить нормальность. Возможно, вам придется полагаться на свое понимание данных. Когда вы не можете с уверенностью предположить нормальность, вы можете выполнить непараметрический тест , который не предполагает нормальность.

Использование двухвыборочного теста

t

В следующих разделах обсуждается, что необходимо для выполнения теста, проверки наших данных, как выполнять тест и статистические данные.

Что нам нужно?

Для двухвыборочного t -критерия нам нужны две переменные. Одна переменная определяет две группы. Второй переменной является измерение интереса.

У нас также есть идея или гипотеза о том, что средние значения основных популяций для двух групп различны. Вот пара примеров:

• У нас есть учащиеся, для которых английский язык является родным, и учащиеся, для которых английский язык не является родным. Все учащиеся проходят тест по чтению. Наши две группы — носители английского языка и не носители английского языка. Наши измерения — это результаты тестов. Наша идея состоит в том, что средние результаты тестов для основной популяции носителей и не носителей английского языка неодинаковы. Мы хотим знать, отличается ли средний балл для населения, для которого английский язык является родным, и для людей, изучающих английский как второй язык.
• Мы измеряем количество протеина в граммах в энергетических батончиках двух разных марок. Две наши группы — это два бренда. Нашим измерением являются граммы белка для каждого энергетического батончика. Наша идея состоит в том, что средние граммы белка для основных популяций для двух брендов могут быть разными. Мы хотим знать, есть ли у нас доказательства того, что среднее количество белка в граммах для двух марок энергетических батончиков отличается или нет.

Две пробы

t — тестовые допущения

Для проведения действительного теста:

• Значения данных должны быть независимыми. Измерения для одного наблюдения не влияют на измерения для любого другого наблюдения.
• Данные в каждой группе должны быть получены путем случайной выборки населения.
• Данные в каждой группе нормально распределены.
• Значения данных непрерывны.
• Дисперсия для двух независимых групп одинакова.

Для очень небольших групп данных может быть сложно протестировать эти требования. Ниже мы обсудим, как проверить требования с помощью программного обеспечения и что делать, если требование не выполняется.

Две пробы

t — тестовый пример

Одним из способов измерения физической подготовки человека является измерение процентного содержания жира в его организме. Средний процент жира в организме зависит от возраста, но, согласно некоторым рекомендациям, нормальный диапазон для мужчин составляет 15–20% жира, а для женщин — 20–25%.

Наши выборочные данные взяты из группы мужчин и женщин, которые занимались в тренажерном зале три раза в неделю в течение года. Затем их тренер измерил жировые отложения. В таблице ниже показаны данные.

Таблица 1: Данные о процентном содержании жира в организме, сгруппированные по полу

13.3 6.0 20.0 8.0 14.0 19.0 18.0 25.0 16.0 24.0 15.0 1.0 15.0    

Женщины


22.0 16.0 21. 7 21.0 30.0 26.0 12.0 23.2 28.0 23.0

You can clearly see some overlap in the body fat measurements for the мужчины и женщины в нашей выборке, но и некоторые различия. Просто взглянув на данные, трудно сделать какие-либо твердые выводы о том, имеют ли основные группы мужчин и женщин в тренажерном зале одинаковое среднее содержание жира в организме. В этом ценность статистических тестов – они обеспечивают общий, статистически достоверный способ принятия решений, так что все принимают одно и то же решение по одному и тому же набору значений данных.

Проверка данных

Начнем с ответа: Является ли двухвыборочный t -тест подходящим методом для оценки разницы в телесном жире между мужчинами и женщинами?

• Значения данных независимы. Количество жира в организме одного человека не зависит от количества жира в организме другого человека.
• Мы предполагаем, что измеренные люди представляют собой простую случайную выборку из популяции членов спортзала.
• Мы предполагаем, что данные нормально распределены, и мы можем проверить это предположение.
• Значения данных представляют собой измерения телесного жира. Измерения непрерывны.
• Мы предполагаем, что дисперсии для мужчин и женщин равны, и мы можем проверить это предположение.

Перед тем, как приступить к анализу, мы всегда должны быстро просмотреть данные. На рисунке ниже показаны гистограммы и сводная статистика для мужчин и женщин.

Рисунок 1: Гистограмма и сводная статистика для данных о телесном жире

Две гистограммы имеют одинаковую шкалу. Бегло взглянув, мы видим, что очень необычных точек нет, или выбросы . Данные выглядят примерно в форме колокола, поэтому наше первоначальное представление о нормальном распределении кажется разумным.

Изучив сводную статистику, мы видим, что стандартные отклонения аналогичны. Это поддерживает идею равных дисперсий. Мы также можем проверить это, используя тест на дисперсию.

Основываясь на этих наблюдениях, двухвыборочный t -критерий представляется подходящим методом для проверки различий в средних значениях.

Как выполнить двухпробный

t -test

Для каждой группы нам нужны среднее значение, стандартное отклонение и размер выборки. Они показаны в таблице ниже.

Table 2: Average, standard deviation and sample size statistics grouped by gender

Group	Sample Size (n)	Average (X-bar)	Standard отклонение (ы)
Женщины	10	22,29	5,32
Мужчины	13	14,95	6,84

без того, чтобы это было неверно. Но насколько они разные? Являются ли средние значения «достаточно близкими», чтобы мы могли сделать вывод, что средний процент жира в организме одинаков для большей части мужчин и женщин, посещающих тренажерный зал? Или средние значения слишком разные, чтобы мы могли сделать такой вывод?

Далее мы объясним принципы, лежащие в основе двух образцов 9.0007 t — тест в разделе статистических данных ниже, но давайте сначала пройдемся по шагам от начала до конца. Начнем с расчета нашей тестовой статистики. Этот расчет начинается с нахождения разницы между двумя средними значениями:

$ 22,29 — 14,95 = 7,34 $

Эта разница в наших выборках оценивает разницу между средними значениями населения для двух групп.


Далее мы вычисляем объединенное стандартное отклонение. Это строит комбинированную оценку общего стандартного отклонения. Оценка корректируется для разных размеров групп. Во-первых, мы вычисляем объединенную дисперсию: 92)}{(10 + 13 — 2)} $


$ = \frac{(9\times28,30) + (12\times46,82)}{21} $

$ = \frac{(254,7 + 561,85)}{21} $

$ =\frac{816,55}{21} = 38,88 $

 

Затем мы извлекаем квадратный корень из объединенной дисперсии, чтобы получить объединенное стандартное отклонение. Это:

$ \sqrt{38,88} = 6,24 $


Теперь у нас есть все части для нашей тестовой статистики. У нас есть разница средних значений, объединенное стандартное отклонение и размеры выборки. Мы рассчитываем нашу тестовую статистику следующим образом:

$ t = \frac{\text{разность средних групп}}{\text{стандартная ошибка разности}} = \frac{7,34}{(6,24\times \sqrt{(1/10 + 1/13) })} = \frac{7,34}{2,62} = 2,80 $

Чтобы оценить разницу между средними значениями и принять решение о наших программах в тренажерном зале, мы сравниваем тестовую статистику с теоретическим значением из t- распределение. Эта деятельность включает четыре шага:

1. Мы принимаем решение о риске, на который мы готовы пойти, чтобы объявить о существенной разнице. Что касается данных о телесном жире, мы решаем, что готовы пойти на 5%-ный риск, заявив, что неизвестные средние значения населения для мужчин и женщин не равны, когда они действительно равны. На языке статистики уровень значимости, обозначаемый α, устанавливается равным 0,05. Хорошей практикой является принятие этого решения перед сбором данных и расчетом тестовой статистики.
2. Мы вычисляем тестовую статистику. Наша тестовая статистика 2,80.
3. Мы находим теоретическое значение из распределения t- на основе нашей нулевой гипотезы, которая утверждает, что средние значения для мужчин и женщин равны. В большинстве статистических книг есть справочные таблицы для распределения t-. Вы также можете найти таблицы в Интернете. Наиболее вероятная ситуация, что вы будете использовать программное обеспечение, а не печатные таблицы.

   Чтобы найти это значение, нам нужен уровень значимости (α = 0,05) и степеней свободы . Степени свободы ( df ) основаны на размерах выборки двух групп. Для данных о телесном жире это:

   $ df = n_1 + n_2 — 2 = 10 + 13 — 2 = 21 $

   Значение t с α = 0,05 и 21 степенью свободы равно 2,080.

4. Мы сравниваем значение нашей статистики (2,80) со значением t . Поскольку 2,80 > 2,080, мы отклоняем нулевую гипотезу о том, что средний процент жира в организме мужчин и женщин одинаков, и делаем вывод, что у нас есть доказательства того, что процент жира в организме у мужчин и женщин разный.



Статистические данные

Давайте посмотрим на данные о телесном жире и двухвыборочный t -тест с использованием статистических терминов.

Наша нулевая гипотеза состоит в том, что базовые средние значения совокупности одинаковы. Нулевая гипотеза записывается как:

$ H_o:  \mathrm{\mu_1} =\mathrm{\mu_2} $

Альтернативная гипотеза состоит в том, что средние значения не равны. Это записывается как:


$ H_o:  \mathrm{\mu_1} \neq \mathrm{\mu_2} $

Мы вычисляем среднее значение для каждой группы, а затем вычисляем разницу между двумя средними значениями. Записывается так: 92)} {n_1 + n_2 — 2} $


Формула показывает размер выборки для первой группы как n ₁ и второй группы как n ₂ . Стандартные отклонения для двух групп составляют с ₁ и с ₂ . Эта оценка позволяет двум группам иметь разное количество наблюдений. Объединенное стандартное отклонение представляет собой квадратный корень из дисперсии и записывается как s _p .

92)}{2} $

Статистика теста рассчитывается как:

$ t = \frac{(\overline{x_1} -\overline{x_2})}{s_p\sqrt{1/n_1 + 1/n_2 }} $

Числитель тестовой статистики — это разница между средними значениями двух групп. Он оценивает разницу между двумя неизвестными средними значениями совокупности. Знаменатель представляет собой оценку стандартной ошибки разницы между двумя неизвестными средними значениями генеральной совокупности.

Техническая деталь: Для одного среднего стандартная ошибка составляет $ s/\sqrt{n} $ . Приведенная выше формула распространяет эту идею на две группы, которые используют объединенную оценку для s (стандартное отклонение), и которые могут иметь разные размеры групп.

Затем мы сравниваем тестовую статистику со значением t с выбранным значением альфа и степенями свободы для наших данных. Используя в качестве примера данные о телесном жире, мы установили α = 0,05. Степени свободы ( df ) основаны на размерах групп и рассчитываются как:

$ df = n_1 + n_2 — 2 = 10 + 13 — 2 = 21 $

Формула показывает размер выборки для первой группы как n ₁ и для второй группы как n ₂ . Статистики записывают значение t с α = 0,05 и 21 степенью свободы как:

$ t_{0,05,21} $

Значение t с α = 0,05 и 21 степенью свободы равно 2,080. Есть два возможных результата нашего сравнения:

• Тестовая статистика ниже значения t . Вы не можете отвергнуть гипотезу о равных средствах. Вы заключаете, что данные подтверждают предположение о том, что у мужчин и женщин средний процент жира в организме одинаков.
• Статистика теста выше значения t . 2/n_2}} $

  Числитель тестовой статистики тот же. Это разница между средними показателями двух групп. Знаменатель представляет собой оценку общей стандартной ошибки разницы между средними значениями. Он основан на отдельной стандартной ошибке для каждой группы.

  Вычисление степеней свободы для значения t является более сложным с неравными дисперсиями, чем с равными дисперсиями, и обычно остается на усмотрение пакетов статистического программного обеспечения. Ключевым моментом, который следует помнить, является то, что если вы не можете использовать объединенную оценку стандартного отклонения, то вы не можете использовать простую формулу для степеней свободы.

  Тестирование на нормальность

  Допущение о нормальности более важно, когда две группы имеют небольшие размеры выборки, чем для больших размеров выборки.

  Нормальные распределения симметричны, что означает, что они «четные» по обе стороны от центра. Нормальные распределения не имеют экстремальных значений или выбросов. Вы можете проверить эти две особенности нормального распределения с помощью графиков. Ранее мы решили, что данные о телесном жире «достаточно близки» к норме, чтобы можно было сделать предположение о нормальности. На рисунке ниже показан нормальный квантильный график для мужчин и женщин, что подтверждает наше решение.

  Рис. 2: Нормальный квантильный график измерений жира тела для мужчин и женщин

  Вы также можете выполнить формальный тест на нормальность с помощью программного обеспечения. На рисунке выше показаны результаты тестирования на нормальность с помощью программного обеспечения JMP. Мы тестируем каждую группу отдельно. И тест для мужчин, и тест для женщин показывают, что мы не можем отвергнуть гипотезу о нормальном распределении. Мы можем предположить, что данные о телесном жире для мужчин и женщин распределены нормально.

  Проверка на неравные дисперсии

  Проверка на неравные дисперсии сложна. Мы не будем подробно показывать расчеты, но покажем результаты из программного обеспечения JMP. На рисунке ниже показаны результаты теста на неравные отклонения для данных о телесном жире.

  Рисунок 3: Тест на неравную дисперсию для данных о телесном жире

  Не вдаваясь в подробности различных типов тестов на неравную дисперсию, мы будем использовать тест F . Перед тестированием мы решаем принять 10%-й риск сделать вывод, что дисперсии равны, когда это не так. Это означает, что мы установили α = 0,10.

  Как и большинство статистических программ, JMP показывает p -значение теста. Это вероятность найти более экстремальное значение тестовой статистики, чем наблюдаемое. Вручную посчитать сложно. Для приведенного выше рисунка со статистикой теста F , равной 1,654, значение p- равно 0,4561. Это больше, чем наше значение α: 0,4561 > 0,10. Мы не можем отвергнуть гипотезу о равных дисперсиях. С практической точки зрения, мы можем продолжить работу с двумя образцами 9.0007 t — тест с допущением равных дисперсий для двух групп.

  Понимание p-значений

  Используя визуальное представление, вы можете проверить, является ли ваша тестовая статистика более экстремальным значением в распределении. На рисунке ниже показано распределение t- с 21 степенью свободы.

  Рисунок 4: t-распределение с 21 степенью свободы и α = 0,05

  Поскольку наш тест является двусторонним и мы установили α = 0,05, рисунок показывает, что значение 2,080 «отсекает» 2,5 % данных в каждом из двух хвостов. Только 5% данных в целом находятся дальше хвоста, чем 2,080. Поскольку наша тестовая статистика 2,80 выходит за пределы точки отсечения, мы отвергаем нулевую гипотезу о равных средних.

  Соединение всего вместе с программным обеспечением

  На рисунке ниже показаны результаты двухвыборочного теста t для данных о телесном жире из программного обеспечения JMP.

  Рисунок 5: Результаты двухвыборочного t-теста из программного обеспечения JMP

  Результаты двухвыборочного t-теста , предполагающего равные дисперсии, совпадают с нашими расчетами ранее. Статистика теста составляет 2,79996. Программное обеспечение показывает результаты двустороннего теста и одностороннего теста. Нам нужен двусторонний тест (Prob > |t|). Наша нулевая гипотеза состоит в том, что средний процент жира в организме мужчин и женщин одинаков. Наша альтернативная гипотеза состоит в том, что средний процент жира в организме не равен. Односторонние тесты предназначены для односторонних альтернативных гипотез — например, для нулевой гипотезы о том, что средний процент жира в организме мужчин меньше, чем у женщин.

  Мы можем отвергнуть гипотезу об одинаковом среднем телесном жире для двух групп и заключить, что у нас есть доказательства различий в телесном теле между мужчинами и женщинами. Программное обеспечение показывает значение p , равное 0,0107. Мы выбрали 5%-й риск сделать вывод, что средний процент жира в организме мужчин и женщин различен, когда это не так. Важно принять это решение до выполнения статистического теста.

  На рисунке также показаны результаты теста t-, который не предполагает равных дисперсий. Этот тест не использует объединенную оценку стандартного отклонения. Как было сказано выше, этот тест также имеет сложную формулу для степеней свободы. Вы можете видеть, что степени свободы равны 20,9.888. Программное обеспечение показывает значение p-, равное 0,0086. Опять же, приняв решение о риске в 5%, мы можем отвергнуть нулевую гипотезу о равном среднем значении жира в организме мужчин и женщин.

  Другие темы

  Что делать, если у меня более двух групп?

  Если у вас более двух независимых групп, вы не можете использовать двухвыборочный тест t-. Следует использовать метод множественного сравнения. ANOVA, или дисперсионный анализ, является одним из таких методов. Другие методы множественного сравнения включают тест Тьюки-Крамера для всех попарных различий, анализ средних значений (ANOM) для сравнения групповых средних значений с общим средним значением или критерий Даннета для сравнения каждого среднего значения группы с контрольным средним значением.

  Что делать, если мои данные не из нормального распределения?

  Если размер вашей выборки очень мал, проверить нормальность может быть сложно. В этой ситуации вам может понадобиться использовать свое понимание измерений. Например, для данных о телесном жире тренер знает, что лежащее в основе распределение телесного жира является нормальным. Даже для очень маленькой выборки тренер, скорее всего, проведет тест t и предположит, что все нормально.

  Что делать, если вы знаете, что базовые измерения не имеют нормального распределения? Или что, если размер вашей выборки велик, а тест на нормальность отклонен? В этой ситуации можно использовать непараметрический анализ. Эти типы анализа не зависят от предположения, что значения данных взяты из определенного распределения. Для двухвыборочного t -тест, критерий суммы рангов Уилкоксона является непараметрическим критерием, который можно использовать.

  Как проверить, равны ли два значения в Excel

  Автор Амир М. Бохлули

  Опубликовано 09 февраля 2022 г.

  Делиться Твитнуть Делиться Электронная почта

  В Excel есть множество формул, которые можно использовать для определения равенства двух значений. Вот несколько примеров.

  Да, вы можете сразу определить, равны ли два числа, просто взглянув на них. Но это не тот случай, когда вы смотрите на большие числа или если вы хотите проверить несколько чисел в двух столбцах, чтобы увидеть, равны ли они.

  Как и все остальное, в Excel есть средство, облегчающее этот тест. Есть много формул, которые вы могли бы написать, которые проверяют, равны ли два значения или нет. Два простых состоят из функции ДЕЛЬТА и функции ЕСЛИ. Читайте дальше, чтобы узнать, что это за две функции и как их можно использовать.

  Что такое функция ДЕЛЬТА в Excel?

  ДЕЛЬТА — это функция в Excel, которая проверяет, равны ли два значения. Если два значения равны, ДЕЛЬТА вернет 1, а если они не равны, вернет 0.

   =ДЕЛЬТА(число1, число2) 

  Функция ДЕЛЬТА может работать только с числами и не может проверить, равны ли две текстовые строки. Если число2 оставить пустым, ДЕЛЬТА будет считать, что оно равно нулю.

  Как проверить, равны ли два значения с помощью дельта-функции

  DELTA можно легко объединить с другими функциями для подсчета количества пар с одинаковыми числами в списке. В этом примере электронной таблицы у нас есть два столбца чисел, и мы хотим увидеть, сколько пар одинаковы.

  Мы собираемся использовать функцию ДЕЛЬТА, чтобы проверить, равны ли числа в каждой паре, а затем мы собираемся получить количество пар с одинаковыми числами, используя функцию СЧЁТЕСЛИ. Вы можете узнать больше о СЧЁТЕСЛИ в нашей статье о СЧЁТЕСЛИ и СЧЁТЕСЛИМН в Excel.

  1. Выберите первую ячейку в столбце, где вы хотите проверить, равны ли числа. В этом примере это будет ячейка C2 .
  2. В строке формул введите следующую формулу:

      =ДЕЛЬТА(A2, B2) 

     Эта формула проверяет числа в A2 и B2 на равенство. Затем он вернет 1, чтобы указать, что они были равны. В противном случае формула вернет 0.
  3. Нажмите Введите . ДЕЛЬТА теперь сообщит вам, равны ли два числа или нет.
  4. Возьмите маркер заполнения и поместите его на ячейки ниже, чтобы получить результаты теста для всех чисел.

  Теперь вы можете увидеть, какие пары имеют одинаковые номера, используя дельта-функцию. К сожалению, это все, что касается дельта-функции, и для подсчета количества пар с одинаковыми числами вам придется использовать другие функции. Одним из кандидатов является функция СЧЁТЕСЛИ.

  1. Выберите ячейку, в которой вы хотите показать количество пар с одинаковыми номерами.
  2. В строке формул введите следующую формулу:

      =СЧЁТЕСЛИ(C2:C10, "=1") 

     Эта формула проверит ячейки от C2 до C10 (результаты дельта-функции) и проверит, равно 1, а затем возвращает их количество. Помните, что дельта-функция возвращает число 1, когда два значения равны, поэтому эта формула будет подсчитывать количество пар с одинаковыми числами.
  3. Нажмите Введите .

  Функция ДЕЛЬТА — это достаточно простой метод проверки равенства двух чисел. Однако, если вам не нравится двоичный вывод функции ДЕЛЬТА, вы можете использовать функцию ЕСЛИ, чтобы получить определенный вывод.

  Что такое функция ЕСЛИ в Excel?

  ЕСЛИ — одна из основных функций Excel, позволяющая создавать сложные формулы. Он принимает условие, а затем возвращает два указанных пользователем вывода, если условие выполняется или не выполняется.

   =ЕСЛИ(логическая_проверка, Выход_Если_Истина, Выход_Если_Ложь) 

  Эта функция выполняет логический тест, если результат теста ИСТИНА, она вернет Output_If_True , в противном случае она вернет Output_If_False .

  Связано: Как использовать функцию ЕСЛИ в Excel

  Как проверить, равны ли два значения с помощью функции ЕСЛИ

  В этом контексте функция ЕСЛИ работает так же, как функция ДЕЛЬТА, за исключением того, что она может выводить определенную строку. Чтобы проверить, равны ли два значения с помощью функции ЕСЛИ, вам нужно запустить логический тест, в котором вы помещаете две ячейки как равные.

  Затем вам нужно будет указать выходные данные для двух сценариев: результат теста истинный и результат теста ложный.

  Давайте воспользуемся функцией ЕСЛИ в том же примере. Мы собираемся посмотреть, какие пары чисел равны, а затем подсчитаем равные, используя функцию СЧЁТЕСЛИ.

  1. Выберите первую ячейку в столбце, в который вы хотите вернуть результаты теста. В данном примере это будет ячейка C2 .
  2. В строке формул введите следующую формулу:

      =ЕСЛИ(A2=B2, "Да", "Нет") 

     Эта формула проверяет ячейки A2 и B2 на равенство. Если две ячейки равны, формула вернет «Да». В противном случае формула вернет «Нет».
  3. Нажмите Введите . Функция ЕСЛИ теперь сообщит вам, равны ли два значения.
  4. Возьмите маркер заполнения и поместите его на ячейки ниже. Функция ЕСЛИ теперь будет проверять каждую пару и возвращать соответствующие результаты.

  Вы можете подсчитывать ячейки с помощью функции СЧЕТЕСЛИ так же, как и в предыдущем примере, за исключением того, что вместо подсчета ячеек, равных 1, вы должны подсчитывать ячейки, содержащие строку Да. Поскольку написанная вами формула ЕСЛИ возвращает Да для пар, содержащих одинаковые значения.

  1. Выберите ячейку, в которую вы хотите вернуть количество. Для этого примера мы выбрали ячейку E6 .
  2. В строке формул введите следующую формулу:

      =СЧЁТЕСЛИ(C2:C10, "Да") 

     Эта формула просматривает ячейки с C2 по C10 в поисках ячеек, содержащих строку Да . Затем он вернет значение ячеек, которые делают.
  3. Нажмите Введите . СЧЁТЕСЛИ теперь сообщит вам, сколько пар содержат одинаковые значения.

  Связано: Как использовать функцию ПОДСТАВИТЬ в Excel

  Проверить, равны ли два значения с функциями Excel

  Существует множество формул, которые можно написать для проверки равенства двух значений в Excel. Функция ДЕЛЬТА предназначена исключительно для этой цели, в то время как функция ЕСЛИ может выполнять множество функций, включая это.

  Excel существует, чтобы снять с ваших плеч бремя подсчетов и вычислений. Это небольшой пример того, как Excel может сделать это и в результате облегчить вашу жизнь.

  15 формул Excel, которые помогут вам решить проблемы из реальной жизни

  Читать Далее

  Делиться Твитнуть Делиться Эл. адрес

  Похожие темы

  • Производительность
  • Microsoft Excel
  • Электронная таблица
  • Анализ данных
  • Советы по Microsoft Office

  Об авторе

  Амир М. Бохлули (опубликовано 139 статей)

  Амир — штатный корреспондент MUO. Его любовь к написанию и организации всего в электронных таблицах привела его к тому, что он в основном писал по вертикали «Производительность». Он любит водить машину, слушать музыку и играть в игры. В настоящее время он изучает фармацию и пишет статьи более 4 лет.

  Еще от Амира М. Бохлули

  Подпишитесь на нашу рассылку

  Подпишитесь на нашу рассылку, чтобы получать технические советы, обзоры, бесплатные электронные книги и эксклюзивные предложения!

  Нажмите здесь, чтобы подписаться

  равно, не равно, больше, меньше

  Многие задачи, выполняемые в Excel, включают сравнение данных в разных ячейках. Для этого в Microsoft Excel предусмотрено шесть логических операторов, которые также называются операторами сравнения. Этот учебник призван помочь вам понять суть логических операторов Excel и написать наиболее эффективные формулы для анализа данных.

  • Логические операторы Excel
    • Равен
    • Не равно
    • Больше / меньше / больше или равно / меньше или равно
  • Обычное использование логических операторов в Excel

  Логические операторы Excel — обзор

  Логический оператор используется в Excel для сравнения двух значений. Логические операторы иногда называют булевыми операторами, потому что результат сравнения в любом конкретном случае может быть либо ИСТИНА, либо ЛОЖЬ.

  В Excel доступно шесть логических операторов. В следующей таблице объясняется, что делает каждый из них, и иллюстрируется теория примерами формул.

  Состояние	Оператор	Пример формулы	Описание
  Равен	=	=А1=В1	Формула возвращает значение ИСТИНА, если значение в ячейке A1 равно значению в ячейке B1; ЛОЖЬ в противном случае.
  Не равно	<>	=А1<>В1	Формула возвращает значение ИСТИНА, если значение в ячейке A1 не равно значению в ячейке B1; ЛОЖЬ в противном случае.
  Больше	>	=А1>В1	Формула возвращает значение ИСТИНА, если значение в ячейке A1 больше, чем значение в ячейке B1; в противном случае возвращается ЛОЖЬ.
  Менее	<	=А1<В1	Формула возвращает значение ИСТИНА, если значение в ячейке A1 меньше, чем в ячейке B1; ЛОЖЬ в противном случае.
  Больше или равно	>=	=А1>=В1	Формула возвращает значение ИСТИНА, если значение в ячейке A1 больше или равно значениям в ячейке B1; ЛОЖЬ в противном случае.
  Меньше или равно	<=	=А1<=В1	Формула возвращает значение ИСТИНА, если значение в ячейке A1 меньше или равно значениям в ячейке B1; ЛОЖЬ в противном случае.

  На приведенном ниже снимке экрана показаны результаты, возвращенные Равно , Не равно , Больше и Меньше Логические операторы:
  

  Может показаться, что приведенная выше таблица охватывает все и больше не о чем говорить. Но на самом деле у каждого логического оператора есть свои особенности, и знание их может помочь вам использовать настоящую мощь формул Excel.

  Использование логического оператора «Равно» в Excel

  Логический оператор «Равно » (=) может использоваться для сравнения всех типов данных — чисел, дат, текстовых значений, логических значений, а также результатов, возвращаемых другими приложениями Excel. формулы. Например:

  =А1=В1	Возвращает TRUE, если значения в ячейках A1 и B1 совпадают, иначе FALSE.
  =A1=»апельсины»	Возвращает TRUE, если ячейки A1 содержат слово «апельсины», иначе FALSE.
  =A1=ИСТИНА	Возвращает ИСТИНА, если ячейки A1 содержат логическое значение ИСТИНА, в противном случае возвращает ЛОЖЬ.
  =А1=(В1/2)	Возвращает TRUE, если число в ячейке A1 равно частному от деления B1 на 2, в противном случае FALSE.

  Пример 1. Использование оператора «Равно» с датами

  Возможно, вы удивитесь, узнав, что логический оператор «Равно » не может сравнивать даты так же легко, как числа. Например, если ячейки A1 и A2 содержат дату «1.12.2014», формула =A1=A2 вернет ИСТИНА, как и должно быть.

  Однако, если вы попробуете либо =A1=12/1/2014 , либо =A1="12/1/2014" , вы получите ЛОЖЬ в результате. Немного неожиданно, а?

  Дело в том, что Excel хранит даты как числа, начинающиеся с 1 января 1900 года, которые хранятся как 1. Дата 1/12/2014 хранится как 41974. В приведенных выше формулах Microsoft Excel интерпретирует «12/1/ 2014″ как обычную текстовую строку, а так как «12. 01.2014″ не равно 41974, возвращает ЛОЖЬ.

  Чтобы получить правильный результат, вы всегда должны заключать дату в функцию ДАТАЗНАЧ, например: =A1=ДАТАЗНАЧ("1/12/2014")
  

  Примечание. Функцию DATEVALUE также необходимо использовать с другим логическим оператором, как показано в следующих примерах.

  Такой же подход следует применять при использовании оператора равенства Excel в логической проверке функции ЕСЛИ. Вы можете найти больше информации, а также несколько примеров формул в этом руководстве: Использование функции Excel IF с датами.

  Пример 2. Использование оператора «Равно» с текстовыми значениями

  Использование оператора Excel «Равно » с текстовыми значениями не требует никаких дополнительных поворотов. Единственное, что вы должны иметь в виду, это то, что логический оператор равно в Excel равен 9.0358 без учета регистра , что означает, что различия в регистре игнорируются при сравнении текстовых значений.

  Например, если ячейка A1 содержит слово « апельсинов », а ячейка B1 содержит « апельсинов », формула =A1=B1 вернет значение TRUE.

  Если вы хотите сравнить текстовые значения с учетом различий в их регистре, вам следует использовать функцию EXACT вместо оператора Equal to . Синтаксис функции EXACT так же прост, как:

  EXACT(текст1, текст2)

  Где текст 1 и текст2 — это значения, которые вы хотите сравнить. Если значения совпадают, включая регистр, Excel возвращает TRUE; в противном случае возвращается ЛОЖЬ. Вы также можете использовать функцию EXACT в формулах ЕСЛИ, когда вам нужно сравнение текстовых значений с учетом регистра, как показано на снимке экрана ниже:
  

  Примечание. Если вы хотите сравнить длину двух текстовых значений, вы можете вместо этого использовать функцию ДЛСТР, например =ДЛСТР(A2)=ДЛСТР(B2) или =ДЛСТР(A2)>=ДЛСТР(B2) .

  Пример 3. Сравнение логических значений и чисел

  Существует распространенное мнение, что в Microsoft Excel логическое значение ИСТИНА всегда равно 1, а ЛОЖЬ — 0. Однако это верно лишь отчасти, и ключевое слово здесь » всегда» или точнее «не всегда» 🙂

  При написании логического выражения «равно», которое сравнивает логическое значение и число, вам нужно специально указать для Excel, что нечисловое логическое значение должно рассматриваться как число. Вы можете сделать это, добавив двойной знак минус перед логическим значением или ссылкой на ячейку, например. грамм. =A2=--ИСТИНА или =A2=--B2 .

  Знак минус 1 ^st , который технически называется унарным оператором, приводит ИСТИНА/ЛОЖЬ к -1/0 соответственно, а второй унарный инвертирует значения, превращая их в +1 и 0. Это, вероятно, будет проще чтобы понять глядя на следующий скриншот:
  

  Примечание. Вы должны добавить двойной унарный оператор перед логическим значением при использовании других логических операторов, таких как не равно , больше или меньше для корректного сравнения числовых и логических значений.

  При использовании логических операторов в сложных формулах вам также может понадобиться добавить двойное унарное выражение перед каждым логическим выражением, которое возвращает ИСТИНА или ЛОЖЬ в качестве результата. Вот пример такой формулы: СУММПРОИЗВ и СУММЕСЛИМН в Excel.

  Использование логического оператора «Не равно» в Excel

  Вы используете оператор Excel Не равно (<>), когда хотите убедиться, что значение ячейки не равно указанному значению. Использование 9Оператор 0007 Not equal to очень похож на использование оператора Equal to , который мы только что обсуждали.

  Результаты, возвращаемые оператором Не равно , аналогичны результатам, полученным функцией НЕ Excel, которая меняет значение своего аргумента на противоположное. В следующей таблице приведены несколько примеров формул.

  Не равно оператору	Функция НЕ	Описание
  =А1<>В1	= НЕ(А1=В1)	Возвращает TRUE, если значения в ячейках A1 и B1 не совпадают, иначе FALSE.
  =A1<>«апельсины»	= НЕ(A1=»апельсины»)	Возвращает ИСТИНА, если ячейка A1 содержит любое значение, кроме «апельсинов», и ЛОЖЬ, если она содержит «апельсины», «АПЕЛЬСИНЫ» или «апельсины» и т. д.
  =A1<>ИСТИНА	= НЕ (A1 = ИСТИНА)	Возвращает ИСТИНА, если ячейка A1 содержит любое значение, кроме ИСТИНА, в противном случае — ЛОЖЬ.
  =А1<>(В1/2)	= НЕ(А1=В1/2)	Возвращает ИСТИНА, если число в ячейке A1 не равно частному от деления B1 на 2, в противном случае — ЛОЖЬ.
  =A1<>ДАТАЗНАЧ(«1/12/2014»)	= НЕ(A1=ДАТАЗНАЧ(«1/12/2014»))	Возвращает ИСТИНА, если A1 содержит какое-либо значение, кроме даты 1 декабря 2014 г., независимо от формата даты, в противном случае — ЛОЖЬ.

  Больше, меньше, больше или равно, меньше или равно

  Вы используете эти логические операторы в Excel, чтобы проверить, как одно число сравнивается с другим. Microsoft Excel предоставляет 4 операции сравнения, имена которых говорят сами за себя:

  • Больше, чем (>)
  • Больше или равно (>=)
  • Меньше чем (<)
  • Меньше или равно (<=)

  Чаще всего операторы сравнения Excel используются с числами, значениями даты и времени. Например:

  =A1>20	Возвращает TRUE, если число в ячейке A1 больше 20, иначе FALSE.
  =А1>=(В1/2)	Возвращает ИСТИНА, если число в ячейке A1 больше или равно частному от деления B1 на 2, в противном случае — ЛОЖЬ.
  =A1<ДАТАЗНАЧ("1/12/2014")	Возвращает TRUE, если дата в ячейке A1 меньше 1 декабря 2014 г., в противном случае — FALSE.
  =A1<=СУММ(B1:D1)	Возвращает ИСТИНА, если число в ячейке A1 меньше или равно сумме значений в ячейках B1:D1, в противном случае — ЛОЖЬ.

  Использование операторов сравнения Excel с текстовыми значениями

  Теоретически вы также можете использовать операторы больше , больше или равно , а также их аналоги меньше с текстовыми значениями. Например, если ячейка A1 содержит « яблок », а ячейка B1 содержит « бананов », угадайте, что вернет формула =A1>B1 ? Поздравляю тех, кто сделал ставку на ЛОЖЬ : )

  При сравнении текстовых значений Microsoft Excel игнорирует их регистр и сравнивает значения посимвольно, при этом «a» считается наименьшим текстовым значением, а «z» — наибольшим текстовым значением.

  Итак, при сравнении значений « яблок » (A1) и « бананов » (B1) Excel начинается с их первых букв «a» и «b» соответственно, а так как «b» больше чем «a», формула =A1>B1 возвращает ЛОЖЬ.

  Если первые буквы совпадают, то сравниваются 2 буквы ^и , если они тоже совпадают, то Excel попадает в буквы 3 ^rd , 4 ^th и так далее. Например, если A1 содержит » яблок » и B1 содержали « агавы «, формула =A1>B1 вернет TRUE, поскольку «p» больше, чем «g».
  

  На первый взгляд, использование операторов сравнения с текстовыми значениями кажется, имеет очень мало практического смысла, но никогда не знаешь, что тебе может понадобиться в будущем, так что, возможно, эти знания кому-то пригодятся

  Обычное использование логических операторов в Excel

  В реальной работе логические операторы Excel редко используются используются сами по себе. Согласитесь, возвращаемые ими логические значения ИСТИНА и ЛОЖЬ хоть и очень истинны (извините за каламбур), но не очень значимы. Чтобы получить более толковые результаты, вы можете использовать логические операторы в составе функций Excel или правила условного форматирования , как показано в приведенных ниже примерах.

  1. Использование логических операторов в аргументах функций Excel

  Что касается логических операторов, Excel очень либерален и позволяет использовать их в параметрах многих функций. Одно из наиболее распространенных применений находится в функции ЕСЛИ в Excel, где операторы сравнения могут помочь построить логический тест, а формула ЕСЛИ вернет соответствующий результат в зависимости от того, оценивается ли тест как ИСТИНА или ЛОЖЬ. Например:

  =ЕСЛИ(A1>=B1, "ОК", "НЕ ОК")

  Эта простая формула ЕСЛИ возвращает OK, если значение в ячейке A1 больше или равно значению в ячейке B1, в противном случае — «Не OK».

  А вот еще пример:

  =ЕСЛИ(A1<>B1, СУММ(A1:C1), "")

  Формула сравнивает значения в ячейках A1 и B1, и если A1 не равно B1 , возвращается сумма значений в ячейках A1:C1, в противном случае — пустая строка.

  Логические операторы Excel также широко используются в специальных функциях ЕСЛИ, таких как СУММЕСЛИ, СЧЁТЕСЛИ, СРЗНАЧЕСЛИ и их эквивалентах во множественном числе, которые возвращают результат на основе определенного условия или нескольких условий.

  Вы можете найти множество примеров формул в следующих учебниках:

  • Использование функции ЕСЛИ в Excel
  • Как использовать СУММЕСЛИ в Excel
  • Excel СУММЕСЛИМН и СУММЕСЛИ с несколькими критериями
  • Использование СЧЁТЕСЛИ в Excel
  • Excel COUNTIFS и COUNTIF с несколькими критериями

  2. Использование логических операторов Excel в математических вычислениях

  Конечно, функции Excel очень эффективны, но не всегда их нужно использовать для достижения желаемого результата. Например, результаты, возвращаемые следующими двумя формулами, идентичны:

  Функция ЕСЛИ: =ЕСЛИ(B2>C2, B2*10, B2*5)

  Формула с логическими операторами: =(B2>C2)*(B2*10)+(B2<=C2)* (B2*5)
  

  Думаю, формулу ЕСЛИ легче интерпретировать, верно? Он говорит Excel умножить значение в ячейке B2 на 10, если B2 больше, чем C2, иначе значение в ячейке B1 умножается на 5.

  Теперь давайте проанализируем, что формула 2 ^nd с больше, чем и меньше или равно логических операторов. Полезно знать, что в математических вычислениях Excel приравнивает логическое значение ИСТИНА к 1, а ЛОЖЬ к 0. Имея это в виду, давайте посмотрим, что на самом деле возвращает каждое из логических выражений.

  Если значение в ячейке B2 больше, чем значение в C2, то выражение B2>C2 является ИСТИНА и, следовательно, равно 1. С другой стороны, B2<=C2 является ЛОЖЬ и равно 0. Итак, учитывая что B2>C2, наша формула претерпевает следующее преобразование:

  Поскольку любое число, умноженное на ноль, дает ноль, мы можем отбросить вторую часть формулы после знака плюс. И поскольку любое число, умноженное на 1, является этим числом, наша сложная формула превращается в простую =B2*10, которая возвращает произведение умножения B2 на 10, что и делает приведенная выше формула ЕСЛИ: )

  Очевидно, что если значение в ячейке B2 меньше, чем в C2, то выражение B2>C2 оценивается как FALSE (0), а B2<=C2 как TRUE (1), что означает, что произойдет обратное описанному выше.

  3. Логические операторы в условном форматировании Excel

  Логические операторы также часто используются в условном форматировании Excel, что позволяет быстро выделить наиболее важную информацию в электронной таблице.

  Например, следующие простые правила выделяют выбранные ячейки или целые строки на листе в зависимости от значения в столбце A:

  Меньше (оранжевый): =A1<5

  Больше (зеленый): = А1>20
  

  Подробные пошаговые инструкции и примеры правил можно найти в следующих статьях:

  • Формулы условного форматирования Excel
  • Как изменить цвет строки на основе значения ячейки
  • Два способа изменить цвет фона на основе значения ячейки
  • Как выделить каждую вторую строку в Excel

  Как видите, использование логических операторов в Excel интуитивно понятно и просто. В следующей статье мы изучим азы логических функций Excel, которые позволяют выполнять более одного сравнения в формуле.