Тест школьной тревожности прихожан для младших школьников: Тест школьной тревожности
Тест школьной тревожности
Тест школьной тревожности Филлипса
Тест школьной тревожности Филлипса (Альманах психологических тестов, 1995) позволяет подробно изучать уровень и характер тревожности, связанной со школой, у детей младшего и среднего школьного возраста, оценить эмоциональные особенности отношений ребенка со сверстниками и учителями.
Показатели этого теста дают представление как об общей тревожности — эмоциональном состоянии ребенка, связанном с различными формами его включения в жизнь школы, так и о частных видах проявления школьной тревожности.
Тест состоит из 58 вопросов, которые можно зачитывать школьникам, а можно предлагать в письменном виде. На каждый вопрос требуется ответить однозначно: «да» или «нет».
Инструкция
«Ребята, сейчас вам будет предложен опросник, который состоит из вопросов о том, как вы себя чувствуете в школе.
На листе для ответов вверху запишите свое имя, фамилию и класс. Отвечая на вопрос, записывайте его номер и ответ: «+», если Вы согласны с ним, или «—», если не согласны».
Обработка и интерпретация результатов
При обработке результатов выделяют вопросы, ответы на которые не совпадают с ключом теста. Например, на 58-й вопрос ребенок ответил «да», в то время как в ключе этому вопросу соответствует «—», то есть ответ «нет». Ответы, не совпадающие с ключом, — это проявления тревожности. При обработке подсчитывается:
1. Общее число несовпадений по всему тесту. Если оно больше 50% от общего числа вопросов, можно говорить о повышенной тревожности
ребенка, если больше 75% — о высокой тревожности. 2.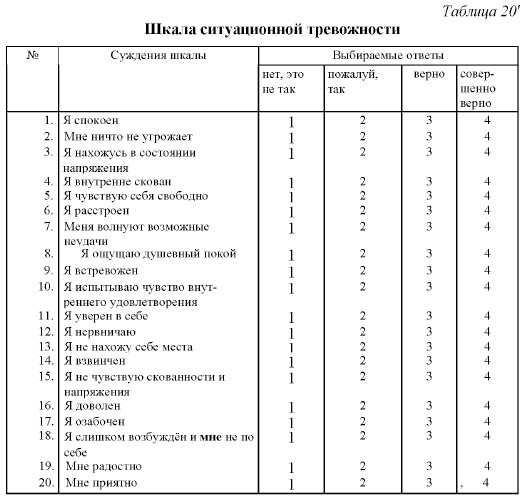
Число совпадений по каждому из 8 видов тревожности. Уровень тревожности определяется так же, как в первом случае. Анализируется общее внутреннее эмоциональное состояние школьника, во многом определяющееся наличием тех или иных тревожных синдромов (факторов) и их количеством.
Факторы | № вопросов |
1. Общая тревожность в школе | 2,4,7,12,16,21,23,26,28,46,47,48,49,50,51,52,53,54,55,56,57,58 ∑=22 |
2. Переживание социального стресса | 5,10,15,20,24,30,33,36,39,42,44 ∑=11 |
3. Фрустрация потребности в дос-тижении успеха | 1,3,6,11,17,19,25,29,32,35,38,41,43 ∑=13 |
4. | 27,31,34,37,40,45 ∑=6 |
5. Страх ситуации проверки знаний | 2,7,12,16,21,26 ∑=6 |
6. Страх не соответствовать ожиданиям окружающих | 3,8,13,17,22 ∑=5 |
7. Низкая физиологическая сопротив-ляемость стрессу | 9,14,18,23,28 ∑=5 |
8. Проблемы и страхи в отношениях с учителями | 2,6,11,32,35,41,44,47 ∑=8 |
Страх самовыраженияСодержательная характеристика видов (факторов) тревожности
1. Общая тревожность в школе — общее эмоциональное состояние ребенка, связанное с различными формами его включения в жизнь школы.
2. Переживание социального стресса — эмоциональное состояние ребенка, на фоне которого развиваются его социальные контакты (прежде всего — со сверстниками).
3. Фрустрация потребности в достижении успеха — неблагоприятный психический фон, не позволяющий ребенку развивать свои потребности в успехе, достижении высокого результата и т.д.
4. Страх самовыражения — негативные эмоциональные переживания ситуаций, сопряженных с необходимостью самораскрытия, предъявления себя другим, демонстрации своих возможностей.
5. Страх ситуации проверки знаний — негативное отношение и переживание тревоги в ситуациях проверки (особенно — публичной) знаний, достижений, возможностей.
6. Страх не соответствовать ожиданиям окружающих — ориентация на значимость других в оценке своих результатов, поступков и мыслей, тревога по поводу оценок, даваемых окружающим, ожидание негативных оценок.
7.
Низкая физиологическая сопротивляемость стрессу — особенности психофизиологической организации, снижающие приспособляемость ребенка к ситуациям стрессогенного характера, повышающие вероятность неадекватного, деструктивного реагирования на тревожный фактор среды.
8. Проблемы и страхи в отношениях с учителями — общий негативный эмоциональный фон отношений со взрослыми в школе, снижающий успешность обучения ребенка.
Представление результатов
1. Подсчитывается число несовпадений знаков («+» — да, «—» — нет) по каждому фактору (абсолютное число несовпадений в процентах: 50; 75) для каждого респондента. Эти данные представляются в виде индивидуальных диаграмм.
2. Подсчитывается число несовпадений по каждому измерению для всего класса (абсолютное значение в процентах: 50; .75). Данные представляются в виде диаграммы.
3. Подсчитывается количество учащихся, имеющих несовпадения по определенному фактору 50% и 75% (для всех факторов).
4. При повторных замерах представляются сравнительные результаты.
Полученные результаты можно представить в сводной таблице, включив в нее результаты, превышающие норму. Такой способ представления облегчит общий анализ результатов по классу в целом, а также сравнительный анализ данных по разным классам.
Текст опросника Филлипса
Трудно ли тебе держаться на одном уровне знаний со всем классом?
Волнуешься ли ты, когда учитель говорит, что собирается проверить, насколько ты знаешь материал?
Трудно ли тебе работать в классе так, как этого хочет учитель?
Снится ли тебе временами, что учитель в ярости от того, что ты не знаешь урок?
Случалось ли, что кто-нибудь из твоего класса бил или ударял тебя?
Часто ли тебе хочется, чтобы учитель не торопился при объяснении нового материала, пока ты не поймешь, что он говорит?
Сильно ли ты волнуешься при ответе или выполнении задания?
Случается ли с тобой, что ты опасаешься высказываться на уроке, потому что боишься сделать глупую ошибку?
Дрожат ли у тебя колени, когда тебя вызывают отвечать?
Часто ли твои одноклассники смеются над тобой, когда вы играете в разные игры?
Случается ли, что тебе ставят более низкую оценку, чем ты ожидал?
Волнует ли тебя вопрос о том, не оставят ли тебя на второй год?
Стараешься ли ты избегать игр, в которых делается выбор, потому что тебя, как правило, не выбирают?
Бывает ли временами, что ты весь дрожишь, когда тебя вызывают отвечать?
Сильно ли ты волнуешься перед тем как начать выполнять задание?
Трудно ли тебе получать такие отметки, каких ждут от тебя родители?
Боишься ли ты временами, что тебе станет дурно в классе?
Будут ли твои одноклассники смеяться над тобой, если ты сделаешь ошибку при ответе?
Похож ли ты на своих одноклассников?
Выполнив задание, беспокоишься ли ты о том, хорошо ли с ним справился?
Когда ты работаешь в классе, уверен ли ты в том, что все хорошо запомнишь?
Снится ли тебе иногда, что ты в школе и не можешь ответить на вопрос учителя?
Верно ли, что большинство ребят относится к тебе по-дружески?
Работаешь ли ты более усердно, если знаешь, что результаты твоей работы будут сравниваться в классе с результатами твоих одноклассников?
Часто ли мечтаешь о том, чтобы поменьше волноваться, когда тебя спрашивают?
Боишься ли ты временами вступать в спор?
Чувствуешь ли ты, что твое сердце начинает сильно биться, когда учитель говорит, что собирается проверить твою готовность к уроку?
Когда ты получаешь хорошие отметки, думает ли кто-нибудь из твоих друзей, что ты хочешь выслужиться?
Хорошо ли ты себя чувствуешь с теми из твоих одноклассников, к которым ребята относятся с особым вниманием?
Бывает ли, что некоторые ребята в классе говорят что-то, что тебя задевает?
Как ты думаешь, теряют ли расположение остальных те ученики, которые не справляются с учебой?
Похоже ли на то, что большинство твоих одноклассников не обращают на тебя внимания?
Часто ли ты боишься выглядеть нелепо?
Доволен ли ты тем, как к тебе относятся учителя?
Помогает ли твоя мама в организации вечеров, как другие мамы твоих одноклассников?
Волновало ли тебя когда-нибудь, что думают о тебе окружающие?
Надеешься ли ты в будущем учиться лучше, чем раньше?
Считаешь ли ты, что одеваешься в школу так же хорошо, как и твои одноклассники?
Часто ли, отвечая на уроке, ты задумываешься о том, что думают о тебе в это время другие?
Обладают ли способные ученики какими-то особыми правами, которых нет у других ребят в классе?
Злятся ли некоторые из твоих одноклассников, когда тебе удается быть лучше их?
Доволен ли ты тем, как к тебе относятся одноклассники?
Хорошо ли ты себя чувствуешь, когда остаешься один на один с учителем?
Высмеивают ли временами одноклассники твою внешность и поведение?
Думаешь ли ты, что беспокоишься о своих школьных делах больше, чем другие ребята?
Если ты не можешь ответить, когда тебя спрашивают, чувствуешь ли ты, что вот-вот расплачешься?
Когда вечером ты лежишь в постели, думаешь ли ты временами с беспокойством о том, что будет завтра в школе?
Работая над трудным заданием, чувствуешь ли ты порой, что совершенно забыл вещи, которые хорошо знал раньше?
Дрожит ли слегка твоя рука, когда ты работаешь над заданием?
Чувствуешь ли ты, что начинаешь нервничать, когда учитель говорит, что собирается дать классу задание?
Пугает ли тебя проверка твоих знаний в школе?
Когда учитель говорит, что собирается дать классу задание, чувствуешь ли ты страх, что не справишься с ним?
Снилось ли тебе временами, что твои одноклассники могут сделать то, что не можешь ты?
Когда учитель объясняет материал, кажется ли тебе, что твои одноклассники понимают его лучше, чем ты?
Беспокоишься ли ты по дороге в школу, что учитель может дать классу проверочную работу?
Когда ты выполняешь задание, чувствуешь ли ты обычно, что делаешь это плохо?
Дрожит ли слегка твоя рука, когда учитель просит сделать задание на доске перед всем классом?
Сводная таблица результатов теста Филлипса
Класс__________ Дата проведения ______________________
№ | ФИ ученика | Показатели по видам (факторам) тревожности (в %) | ||||||||
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | трев. | ||
1 | ||||||||||
2 | ||||||||||
3 | ||||||||||
4 | ||||||||||
5 | ||||||||||
6 | ||||||||||
7 | ||||||||||
8 | ||||||||||
9 | ||||||||||
10 | ||||||||||
11 | ||||||||||
12 | ||||||||||
13 | ||||||||||
14 | ||||||||||
15 | ||||||||||
16 | ||||||||||
17 | ||||||||||
18 | ||||||||||
19 | ||||||||||
20 | ||||||||||
21 | ||||||||||
22 | ||||||||||
23 | ||||||||||
24 | ||||||||||
25 | ||||||||||
26 | ||||||||||
27 | ||||||||||
28 | ||||||||||
Примечание: номера факторов в таблице соответствуют видам тревожности, описанным в тексте.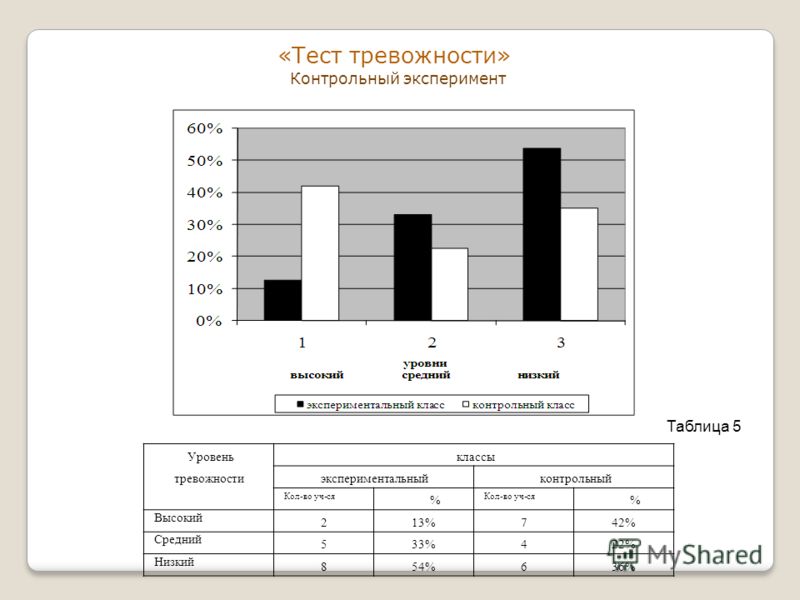
Фамилия, имя _________________________________________________________________
Класс __________________ Дата проведения _______________________________________
1 | 11 | 21 | 31 | 41 | 51 | ||||||||||||
2 | 12 | 22 | 32 | 42 | 52 | ||||||||||||
3 | 13 | 23 | 33 | 43 | 53 | ||||||||||||
4 | 14 | 24 | 34 | 44 | 54 | ||||||||||||
5 | 15 | 25 | 35 | 45 | 55 | ||||||||||||
6 | 16 | 26 | 36 | 46 | 56 | ||||||||||||
7 | 17 | 27 | 37 | 47 | 57 | ||||||||||||
8 | 18 | 28 | 38 | 48 | 58 | ||||||||||||
9 | 19 | 29 | 39 | 49 | |||||||||||||
10 | 20 | 30 | 40 | 50 |
Фамилия, имя _________________________________________________________________
Класс __________________ Дата проведения _______________________________________
1 | 11 | 21 | 31 | 41 | 51 | ||||||||||||
2 | 12 | 22 | 32 | 42 | 52 | ||||||||||||
3 | 13 | 23 | 33 | 43 | 53 | ||||||||||||
4 | 14 | 24 | 34 | 44 | 54 | ||||||||||||
5 | 15 | 25 | 35 | 45 | 55 | ||||||||||||
6 | 16 | 26 | 36 | 46 | 56 | ||||||||||||
7 | 17 | 27 | 37 | 47 | 57 | ||||||||||||
8 | 18 | 28 | 38 | 48 | 58 | ||||||||||||
9 | 19 | 29 | 39 | 49 | |||||||||||||
10 | 20 | 30 | 40 | 50 |
1 2 3 4 5 6 7 8 9 … 24
1 2 3 4 5 6 7 8 9 … 24 База данных защищена авторским правом ©psihdocs.ru 2023 | Главная страница Автореферат Анализ Анкета Бағдарламасы Бизнес-план Биография Бюллетень Викторина Выпускная работа Глава Диплом |
А. Шейкина >
А. Шейкина 
проблемы бытия в современной философииДомашняя страница — parishschool.
orgВыпускник: 2008-2014
Хорхе впервые пришел в Приходскую школу в возрасте 4 лет после того, как ему поставили неуточненный диагноз всеобъемлющего расстройства развития. Его речь и понимание были очень ограничены.
С самого начала его родители понимали, что все в приходе очень поддерживали Хорхе и заставили его чувствовать себя как дома.
«Мы особенно благодарны его логопедам и учителям — Хорхе всегда чувствовал себя с ними в безопасности, и мы чувствовали, что они действительно любят его», — сказали родители Хорхе и Лоре.
С помощью преподавателей Пэриша Хорхе научился бегло говорить. Кроме того, подход социального обучения сотворил чудеса с Хорхе и всей его семьей. Ему нравилось ходить в Adventure Play в Camp Acorn, где дети использовали свое воображение, чтобы творить и исследовать. Он по-прежнему любит строить, особенно из Лего. На самом деле, когда Хорхе вырастет, он говорит, что хочет стать инженером, как его отец!
Хорхе перешел в новую школу после многих замечательных лет в приходской школе.
Сейчас ему 12 лет, и он учится третий год в традиционной частной школе, где он преуспевает и преуспевает. «Мы всегда будем благодарны, что у него была возможность пойти в Приходскую школу!»
Выпускник Студент: 2009-2012
В возрасте 2 лет у Дилана диагностировали расстройство экспрессивной речи и расстройство орально-моторной функции. Два раза в неделю он посещал логопеда, но без особого успеха, поэтому родители решили записать его в приходскую школу.
«Мы чувствовали, что сотрудники прихода знали, через что мы, родители, проходили, и мы наконец нашли необходимую нам систему поддержки», — сказала мать Дилана, Дженнифер.
Проучившись более трех лет в приходской школе, Дилан поступил в епископальную школу св. Франциска, где преуспел в учебе, получил награды в драматургии, присоединился к хору и активно участвует в поиске детенышей.
Где Дилан действительно нашел свою страсть, так это в гимнастике. Находясь в приходе, он был признан нуждающимся в дополнительной поддержке трудотерапии.
Дженнифер решила записать его на гимнастику, чтобы укрепить его самооценку и мышцы кора. С тех пор он присоединился к конкурентоспособной команде, повышая уровень мастерства и соревнуясь в прыжках на батуте и акробатической дорожке. Прошлым летом Дилан стал национальным чемпионом по прыжкам на батуте среди мальчиков в возрасте 9-10 лет на юношеских Олимпийских играх USAG Stars & Stripes в Талсе, штат Оклахома.
«Приходская школа была безопасной и уютной средой для Дилана, — сказала Дженнифер. «Я знаю, что Дилан не был бы там, где он сейчас, если бы не Приходская школа».
Выпускник Студент: 2006-2009
В 10 месяцев у Сидху диагностировали редкое судорожное расстройство. Когда он стал старше, он имел дело не только с угрожающими жизни припадками; у него также развилась серьезная задержка речи. Частной терапии было недостаточно. В возрасте трех лет Сидху начал свое путешествие в приходской школе по отмеченной наградами дошкольной программе. Через месяц его родители увидели огромные изменения в способности Сидху общаться.
Его родители благодарны учителям за то, что они дали ему персонализированные инструкции, необходимые для изменения его речи и двигательных навыков, в то же время укрепляя его уверенность в себе, что не всегда было легкой задачей. Он обнаружил любовь к искусству, драме и музыке, когда учился в приходской школе. После трех лет интенсивной поддержки и руководства Сидху был готов поступить в общеобразовательную систему.
Сейчас, семь лет спустя, он учится в шестом классе средней школы Бекендорфа в Кэти, штат Техас. Он является отличником, двукратным призером конкурса правописания, участником программы Katy ISD для одаренных и талантливых и получателем награды президента США в области образования за успехи в учебе. Сидху имеет черный пояс по тхэквондо третьей степени, участвует в школьном хоре и играет на трубе в школьном оркестре.
Джоселин
Выпускник: 2011-2017
Когда Джослин родилась, она достигла всех своих начальных вех. Однако к 3 годам стали проявляться признаки задержки.
«Мы начали замечать, что Джослин не разговаривает, а когда говорила, никто не мог ее понять», — сказала мама Джоэль.
После тяжелого года в традиционном дошкольном учреждении была рекомендована Приходская школа. Перенесемся на шесть лет вперед и увидим, что Джоселин — уверенный в себе, счастливый, выразительный ребенок, которому нравится Приходская школа, где она может «выступать, играть, петь, танцевать, учиться (математика — моя любимая) и заводить друзей».
«Спасибо, приходская школа, за то, что нашли ключи, которые открыли нерассказанную песню Джослин и неограниченный масштаб», — сказала Джоэль.
Харрисон
Выпускник: 2006-2009
В 18 месяцев Хадсон вообще не говорил, даже не говорил мама или папа. В то время как его родителям, Лори и Альфредо, сказали «дать ему время» и «мальчики часто задерживаются», Лори знала, что ей нужно действовать как можно раньше, и настояла на оценке Хадсона. После серии тестов семья была направлена к логопеду.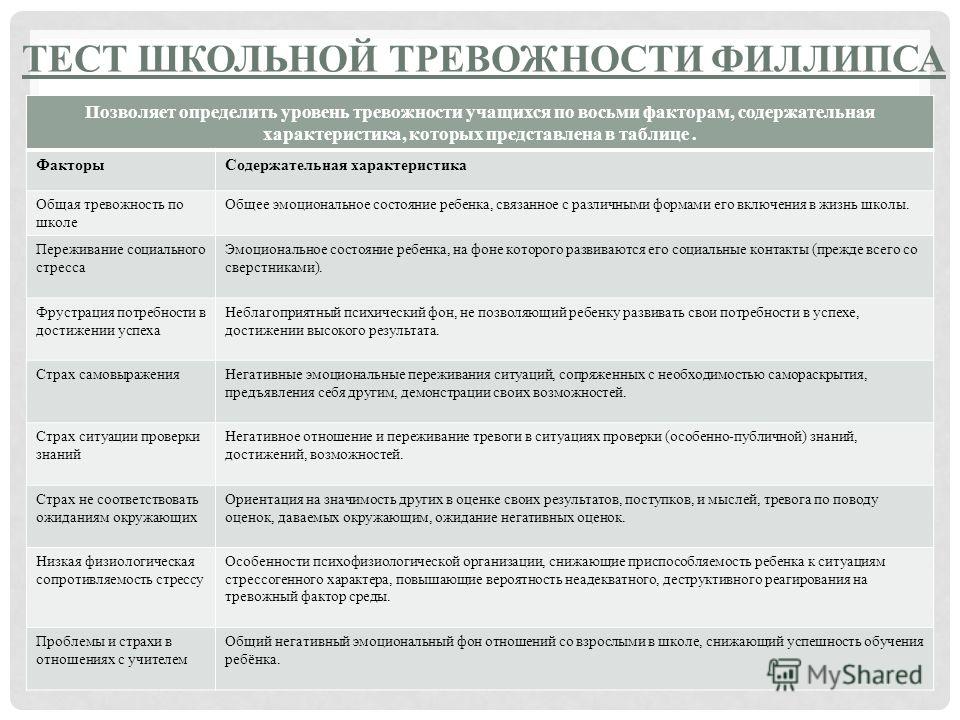
Друг порекомендовал Приходскую школу, и пара зачислила Хадсона вскоре после его второго дня рождения. Он любил ходить в школу каждый день, особенно музыку и искусство. В конце концов, Хадсон заговорил бурю.
«Самое главное, что школа взяла нас с мужем под свое крыло», — сказала Лори. «Мы были напуганы и чувствовали себя беспомощными. Мы посещали занятия для родителей, встречались с его учителями и логопедом. Нам дали инструменты, необходимые нам, чтобы стать одним из многих защитников в жизни Хадсона».
После 3 лет обучения в Приходской школе Хадсон перешел в традиционную школу, продолжая посещать группы логопеда, трудотерапии и социального обучения в Приходской школе и Центре Каррута.
С тех пор Хадсон доказал, что у него есть талант выступать на сцене. Он активно участвует в мюзиклах, балете и даже участвовал в школьной ComedySportz® Improv. Он посещает христианскую среднюю школу Хьюстона, где присоединился к театру, танцам и модели ООН. Он также изучал испанский язык в школе и этой осенью начнет курс испанского AP.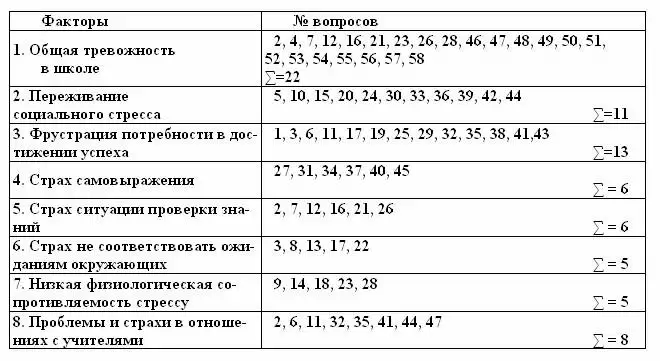
Лори говорит: «У него превосходный акцент!»
Семья Гутьеррес по-прежнему тесно связана с Приходской школой. Лори является активным членом приходского попечительского совета, и в прошлом году семья принимала у себя дома вечеринку по случаю выхода на пенсию бывшего директора школы Нэнси Бьюли. Кроме того, Хадсон провел свои последние пять лет, работая волонтером в классах летней программы приходской школы — Camp Acorn.
«Мне очень нравится работать с детьми в лагере, — сказал Хадсон. «Мне приятно оказывать помощь здесь, потому что я прошел через то же самое, когда был ребенком».
«Приходская школа и Центр Каррута оказали существенное влияние на успех, которого добивается Хадсон, — добавляет Лори. «Мы в долгу перед школой за то, что она дала Хадсону и нам навыки, необходимые для того, чтобы Хадсон смог добиться успеха в жизни».
Грейсен
Выпускник: 2003-2005
Грейсен Фиск два года посещала программу приходской школы для детей младшего возраста, прежде чем в 2005 году перешла в традиционную школу.
на сцене и процветал, когда дело доходило до участия в драматических и музыкальных классах Приходской школы. Позже она окончила Хьюстонскую христианскую среднюю школу, где стала активно участвовать в программе театрального искусства.
Под руководством директора округа по интегрированным искусствам и наукам Терри Гарт, Грейсен и Брэндон Ньюэлл (приходской ученик 2005–2009 гг.) вернулись в приход, чтобы выступить в мюзикле для старших и младших классов 2018 года, посвященном 35-летию школы и последние 25 лет ежегодных мюзиклов. Дуэт практиковался со студентами прихода в течение нескольких недель в течение весеннего семестра, чтобы позже дебютировать в переполненном доме друзей и семей. Их исполнение «Вместе, куда бы мы ни пошли» вызвало бурные аплодисменты. По словам мамы Грейсен, Джилл, это время, проведенное в мюзикле «Приходская школа», было ценным опытом.
В настоящее время Грейсен учится в Сэмфордском университете в Бирмингеме, штат Алабама, по специальности театр с упором на актерское мастерство и режиссуру.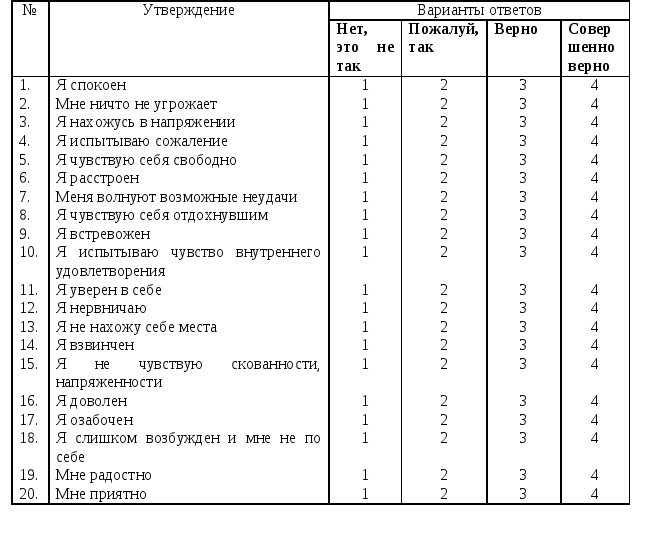
Она отлично учится в школе, попала в список декана и имеет много друзей. Поблагодарив Пэриш за то, что она привила ей любовь к искусству, Грейсен решила вернуться еще раз, чтобы преподавать драматический класс для летней программы приходской школы 2019 года «Лагерь Акорн».
Перенесемся в сегодняшний день, и Грейсен недавно объявила, что она приняла участие в программе Disney’s College Program. Мы так взволнованы, чтобы увидеть, что еще будет от нее!
Выпускник: 2010-2016
Когда Дэвид впервые поступил в Приходскую школу, когда ему исполнилось 6 лет, ему было трудно составлять предложения, состоящие из более чем трех слов. Родители Дженнифер и Крис боялись, что с кажущимся бесконечным списком знаний и социальных различий Дэвиду всегда будет трудно вписаться в «нормальную» толпу.
За шесть лет, которые Дэвид провел в приходе, он приобрел коммуникативные, социальные и академические навыки, необходимые для успешной учебы в школе. Выйдя из программы Пэриша, Дэвид пошел в государственную среднюю школу.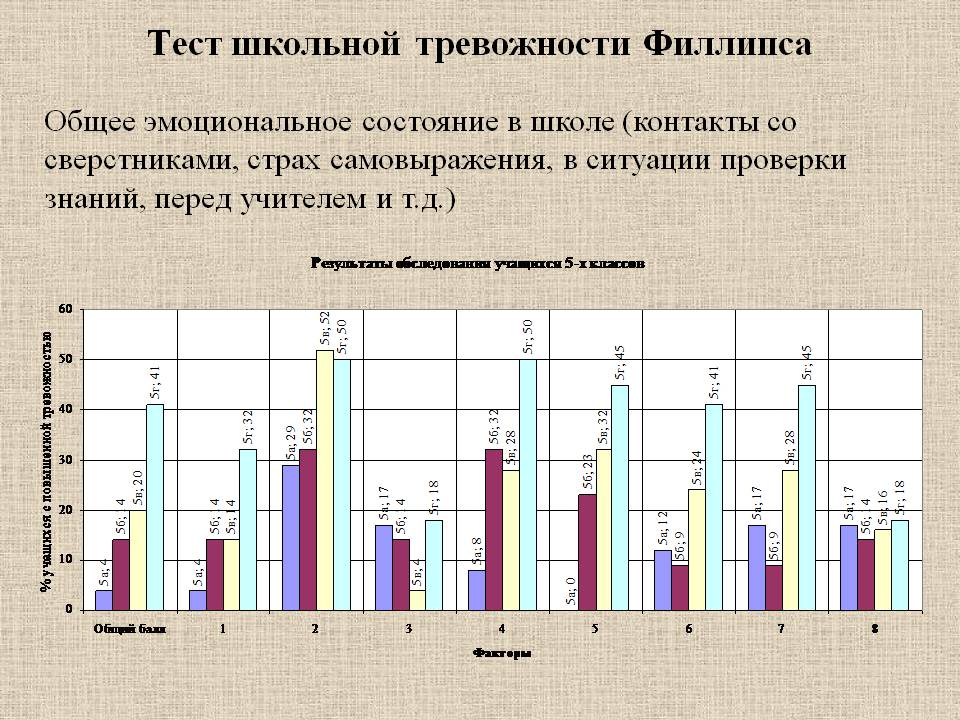
Поначалу переход был трудным из-за возросшей рабочей нагрузки и обязанностей, но его родители рады сообщить, что после нескольких недель привыкания к 9-летнему возрасту0089 рутина, Дэвиду удалось превзойти их ожидания в новой обстановке. На самом деле, вскоре после прибытия в его новую школу их представитель по специальному образованию порекомендовал прекратить поддержку Дэвида в классе, посчитав это ненужным — ему не требовалась дополнительная помощь, чтобы не отставать от занятий. Дэвид сейчас получает все пятерки и преуспевает в государственной средней школе.
Но где он по-настоящему расцвел, так это в Приключенческой игре , программе продленного дня в приходской школе, где дети создают свою собственную игровую площадку, используя только свое воображение и подручные материалы. Именно в AP Дэвид нашел место, которое он действительно полюбил, и смог завести прочную дружбу.
На его 12-й день рождения Дженнифер и Крис предложили Дэвиду сходить на ужин, в боулинг, в кино.
.. куда бы он ни захотел отпраздновать. Дэвид уважительно выслушал их предложения, но уже решил – он хочет вернуться в Adventure Play. Джилл Вуд, директор Adventure Play, была рада удовлетворить просьбу Дэвида.
«Он не мог перестать улыбаться по пути домой, сияя от того, как ему удалось провести младших школьников на прогулке по высокой траве, прежде чем снова почувствовать себя как дома на различных конструкциях, которые он видел собранными за эти годы. — сказал Крис. «Но больше всего он был счастлив воссоединиться с Джилл. «Я просто люблю ее, — сказал он нам».
Дэвид продолжает посещать приходские мероприятия, когда может, включая празднование 10-летия Adventure Play в этом году, прощальную вечеринку Flight и ежегодный Spring Fling. Кроме того, он работает волонтером в летнем лагере Adventure Play в качестве младшего игрового работника, где помогает другим детям расширять пространство, которое он так высоко ценит.
Выпускник: 1990-1996
Приближаясь к своему 3-летнему дню рождения, Дэн прибыл в Приходскую школу с тем же настроем, с которым он относился к любому новому опыту – оптимизмом и широкой улыбкой.
У Дэна были некоторые физические трудности и трудности с обучением из-за осложнений, которые он перенес, когда родился на три месяца раньше срока, а позже заразился стрептококковым менингитом группы B, будучи еще младенцем. По воле судьбы бабушка Дэна была одним из основателей Приходской школы, первой опорой Роббина Пэриша и точно знала, где найти лучшую помощь для Дэна.
Вспоминая свое время в приходской школе, Дэн вспоминает, что ему особенно нравилось писать в своей «Книге хороших новостей». Многие из его записей были связаны с его любовью к спорту. В раннем возрасте он решил, что хочет быть спортивным комментатором. Приходская школа поставила его на путь уверенного развития навыков письма и разговорной речи. Кроме того, он стал заядлым читателем. Это были строительные блоки, необходимые ему для достижения его будущих целей.
После окончания средней школы-интерната и сдачи экзамена Риджентс штата Нью-Йорк Дэн твердо решил поступить в колледж. Сначала он поступил в университет Св.
Эдвардса в Остине. Когда его девушка упомянула, насколько сильны факультеты радио и журналистики в соседнем Техасском государственном университете, Дэн решил перевестись. В 2014 году Дэн получил степень в области массовых коммуникаций, а затем женился на своей прекрасной девушке Эмбер.
Сегодня Эмбер и Дэн живут в Хьюстоне, где Дэн работает в семейной компании по коммерческой недвижимости. Он также является автором FanSided, растущего спортивного веб-сайта, где пишет статьи о том, что происходит в мире спорта Хьюстона. Продолжая свою мечту, Дэн в настоящее время работает над запуском собственного спортивного сайта.
Приходская школа оказалась для Дэна в нужное время в нужном месте. Он всегда был благодарен многим людям, которые помогали ему на этом пути. Во время недавнего посещения «нового» кампуса он и его семья были поражены ростом школы.
Кэмерон Д.
Выпускник: 1998-2003
Кэмерон впервые пришла в Приходскую школу в возрасте 2 лет после того, как ей поставили диагноз первазивного расстройства развития без дополнительных уточнений (PDD-NOS) — один из четырех спектров аутизма расстройства.
Он мог произнести всего несколько слов, большинство из которых было трудно понять другим. Неврологи, поставившие диагноз Кэмерону, порекомендовали несколько школ, которые могли помочь ему справиться с языковыми проблемами, одной из которых была приходская школа.
«Мы посмотрели все рекомендуемые школы и сразу же остановились на Пэриш», — сказала Венди, мачеха Кэмерона. «Мы могли видеть, что это была такая любящая среда, и она была сосредоточена на инновационных методах помощи детям в преодолении их языковых различий и различий в обучении».
Благодаря образованию, обучению и заботе в Приходской школе Кэмерон научился бегло говорить и обнаружил в себе суперсилу — память. Приходская школа не только позволила Кэмерону приобрести коммуникативные навыки, но и дала ему бесценное чувство собственного достоинства и уверенности, которые продолжают служить ему хорошо. Благодаря раннему интенсивному языковому и учебному вмешательству Кэмерон смогла перевестись во второй класс в обычную частную начальную школу.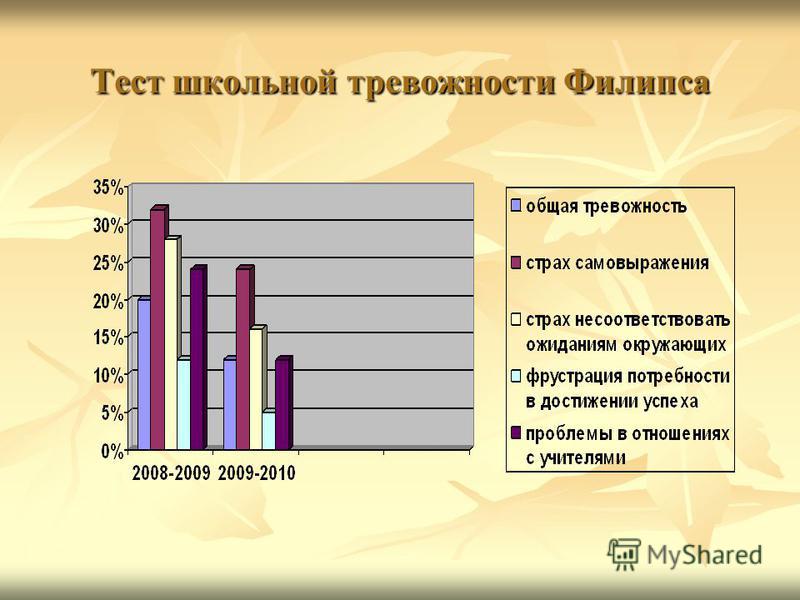
Кэмерон, которой сейчас 22 года, гордо учится в Техасском техническом университете, изучает коммуникации, работает водителем и работает неполный рабочий день.
Кэмерон
Выпускник: 2006-2008
С раннего возраста Кэмерон изо всех сил пытался общаться, оставляя свою семью и себя с чувством разочарования. Во время оценки специалист порекомендовал Приходскую школу. С того момента, как они ступили на территорию кампуса, семья Кэмерон поняла, что это особенное место.
«Благодаря щедрости многих наша семья получила финансовую помощь для участия», — сказала Рози, мать Кэмерон. «В противном случае мы бы никогда не смогли позволить себе такое жизненно важное образование и терапию, которые предлагает Приходская школа. Школа не только помогла Кэмерон, но и изменила всю нашу семью».
По сей день Кэмерон утверждает, что Пэриш — его любимая школа из-за поддержки, понимания и заботы, которые оказывали ему все — от учителей до персонала. Пэриш также пробудил в нем любовь к искусству и природе, которая сохраняется и по сей день.
Сегодня Кэмерон учится в юниорской школе Katy ISD. Он преследует свою страсть к музыке, играя на тубе в марширующем оркестре и обучаясь игре на тромбоне в джаз-бэнде. Недавно он отправился в поход и выжил в собственной палатке в Каскадных горах недалеко от Сиэтла. Кэмерон также недавно получил звание орла-разведчика, завершив проект по изготовлению сумок для туалетных принадлежностей и школьных принадлежностей для бездомных подростков. У него также есть страсть к кинопроизводству, и он был принят в кинопрограмму в Центре карьеры Миллера в Katy ISD. Кэмерон планирует продолжить карьеру в киноиндустрии в будущем.
«Приходская школа посеяла семена Кэмерона, которые изменили ход его жизни… и за это вся наша семья бесконечно благодарна».
Выпускник: 2015-2019
В детстве Адаму было очень трудно общаться и взаимодействовать с другими людьми. С помощью учителей и одноклассников Приходской школы он смог значительно улучшить свои коммуникативные навыки и коммуникабельность.
С момента перехода из Пэриша Адам прошел долгий путь. Он получил степень по экономике и политологии в Чикагском университете, а также двойную ученую степень в области права и общественных отношений в Техасском университете в Остине. В настоящее время Адам работает клерком у федерального судьи в Эль-Пасо и с нетерпением ждет будущего.
«Было очень приятно посетить новый кампус Приходской школы несколько лет назад и увидеть, что школа продолжает менять в жизни детей, а также увидеть немало моих учителей, таких как Нэнси Мосли и Терри Гарт», — сказал Адам. «Они по-прежнему делают замечательную работу, помогая детям! Я убежден, что Приходская школа помогает создавать светлое будущее».
Выпускник: 2015-2019
Юная жизнь Брейди была полна препятствий. С многочисленными медицинскими диагнозами за плечами и достаточным количеством часов терапии, чтобы заслужить сертификат, очень ухабистый и, казалось бы, безнадежный путь привел его семью в Приходскую школу.
«Было нелегко найти школу, которая могла бы предоставить Брейди специализированное образование и обучение, в которых он нуждался, — сказала мать, Рэйчел.
«Во время учебы в Приходской школе Брейди проходил индивидуальное обучение в классе, а также различные виды терапии на месте».
Когда Брейди начал посещать Приходскую школу в возрасте 8 лет, у него было мало навыков чтения и письма. С первого учебного года в приходе Брейди добился огромного академического и социального роста. Он нашел любовь к драме и музыке через классы, предлагаемые в Приходской школе. Брейди приобрел столько уверенности и завел несколько замечательных друзей.
«Нам очень повезло, что наш сын учится в школе, где ценят его отличия и подчеркивают его сильные стороны. Наша жизнь навсегда изменилась благодаря Приходской школе!»
Грейсен
Выпускник: 1991-1995
Грейсен Фиск два года посещала программу приходской школы для детей младшего возраста, прежде чем в 2005 году перешла в традиционную школу. на сцене и процветал, когда дело доходило до участия в драматических и музыкальных классах Приходской школы. Позже она окончила Хьюстонскую христианскую среднюю школу, где стала активно участвовать в программе театрального искусства.
Под руководством директора округа по интегрированным искусствам и наукам Терри Гарт, Грейсен и Брэндон Ньюэлл (приходской ученик 2005–2009 гг.) вернулись в приход, чтобы выступить в мюзикле для старших и младших классов 2018 года, посвященном 35-летию школы и последние 25 лет ежегодных мюзиклов. Дуэт практиковался со студентами прихода в течение нескольких недель в течение весеннего семестра, чтобы позже дебютировать в переполненном доме друзей и семей. Их исполнение «Вместе, куда бы мы ни пошли» вызвало бурные аплодисменты. По словам мамы Грейсен, Джилл, это время, проведенное в мюзикле «Приходская школа», было ценным опытом.
В настоящее время Грейсен учится в Сэмфордском университете в Бирмингеме, штат Алабама, по специальности театр с упором на актерское мастерство и режиссуру. Она отлично учится в школе, попала в список декана и имеет много друзей. Поблагодарив Пэриш за то, что она привила ей любовь к искусству, Грейсен решила вернуться еще раз, чтобы преподавать драматический класс для летней программы приходской школы 2019 года «Лагерь Акорн».
Перенесемся в сегодняшний день, и Грейсен недавно объявила, что она приняла участие в программе Disney’s College Program. Мы так взволнованы, чтобы увидеть, что еще будет от нее!
Свободное владение языком без страха — YouCubed
Скачать PDF
Джо Боалер, профессор математического образования, соучредитель youcubed
С помощью Кэти Уильямс, соучредителя youcubed, и Аманды Конфер, Стэнфордский университет
Обновлено 28 января 2015 г.
Введение
Несколько лет назад британский политик Стивен Байерс допустил в интервью безобидную ошибку. Достопочтенного министра попросили дать ответ на 7 x 8, и он дал ответ 54 вместо правильных 56. Его ошибка вызвала широкомасштабные насмешки в национальных СМИ, сопровождаемые призывами сделать больший акцент на «таблице умножения». заучивание в школах. В сентябре этого года консервативный министр образования Англии, человек без опыта образования, настоял на том, чтобы все учащиеся в Англии запоминали все свои таблицы умножения до 12 x 12 к 9 годам.
. Это требование теперь включено в учебную программу по математике в Великобритании и, как я предсказываю, приведет к повышению уровня беспокойства по поводу математики и к рекордному количеству учащихся, отказывающихся от математики. США движутся в противоположном направлении, поскольку новые стандарты Common Core State Standards (CCSS) принижают значение механического запоминания математических фактов. К сожалению, неправильное толкование значения слова «беглость» в CCSS является обычным явлением, и издатели продолжают делать упор на механическое заучивание, поощряя сохранение вредной практики в классе в Соединенных Штатах.
Математические факты важны, но запоминание математических фактов с помощью повторения таблицы умножения, практики и тестирования на время не нужно и вредно. Ошибка английского министра, когда его спросили 7 x 8, вызвала призывы к большему запоминанию. Это было иронично, поскольку его ошибка выявила ограничения запоминания без «чувства числа». Люди с чувством числа — это те, кто может гибко использовать числа.
Когда кого-то с чувством числа просят решить 7 x 8, он может запомнить 56, но он также сможет понять, что 7 x 7 равно 49.а затем добавить 7, чтобы получить 56, или они могут получить десять семерок и вычесть две семерки (70-14). Им не придется полагаться на далекие воспоминания. Математические факты сами по себе являются небольшой частью математики, и лучше всего их усваивают, используя числа в разных ситуациях и в различных ситуациях. К сожалению, многие классы сосредотачиваются на математических фактах непродуктивным образом, создавая у учащихся впечатление, что математические факты – это суть математики, и, что еще хуже, быстрое запоминание математических фактов – это то, что значит быть сильным студентом-математиком. Обе эти идеи неверны, и очень важно, чтобы мы удалили их из классных комнат, поскольку они играют большую роль в появлении тревожных и недовольных математикой учащихся.
Полезно запомнить некоторые математические факты. Я не останавливаюсь и не думаю об ответе на 8 плюс 4, потому что знаю этот математический факт.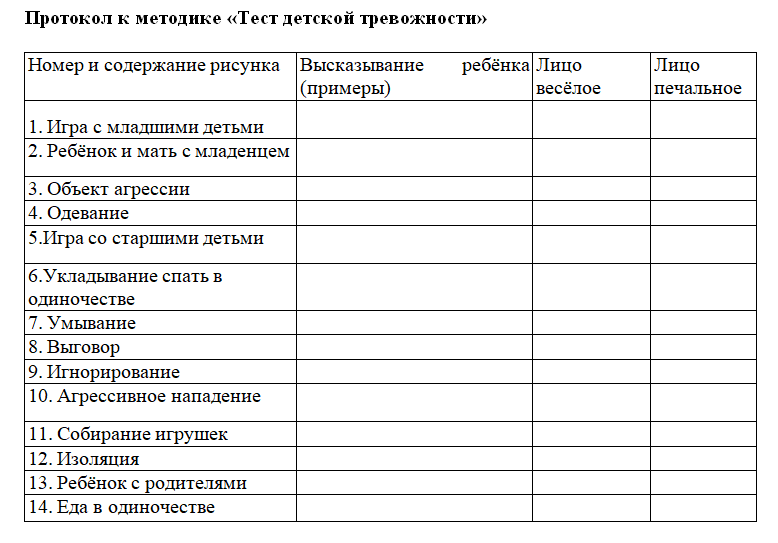
Но я изучал математические факты, используя их в различных математических ситуациях, а не практикуя их и проверяя их. Я вырос в прогрессивную эпоху Англии, когда начальные школы были ориентированы на «всего ребенка», и мне не давали таблицы сложения, вычитания или умножения фактов для запоминания в школе. Это никогда не останавливало меня ни в какое время и ни в каком месте моей жизни, даже несмотря на то, что я профессор математического образования. Это потому, что у меня есть чувство числа, что гораздо важнее для учащихся, и это включает в себя изучение математических фактов наряду с глубоким пониманием чисел и того, как они связаны друг с другом.
Чувство числа
В рамках критического исследовательского проекта исследователи изучали студентов, решивших числовые задачи (Gray & Tall, 1994). Учащиеся в возрасте от 7 до 13 лет были определены учителями как учащиеся с низкой, средней или высокой успеваемостью. Исследователи обнаружили важную разницу между учащимися с низкой и высокой успеваемостью: учащиеся с высокой успеваемостью использовали чувство числа, а учащиеся с низкой успеваемостью — нет.
Успешные учащиеся подошли к таким задачам, как 19 + 7, изменив задачу, например, на 20 + 6. Ни один ученик, который был номинирован как слабоуспевающий, не использовал чувство числа. Когда учащимся с низкой успеваемостью давали задачи на вычитание, такие как 21–16, они считали в обратном порядке, начиная с 21 и заканчивая обратным отсчетом, что чрезвычайно сложно сделать. Учащиеся с высокими показателями использовали такие стратегии, как изменение чисел на 20–15, что намного проще. Исследователи пришли к выводу, что малоуспевающие часто являются малоуспевающими не потому, что они меньше знают, а потому, что они не используют числа гибко — они были поставлены на неверный путь, часто с раннего возраста, пытаясь запомнить методы вместо того, чтобы взаимодействовать с числами. гибко (Боалер, 2009 г.). Этот неправильный путь означает, что они часто изучают сложную математику и, к сожалению, часто сталкиваются с математическими проблемами всю жизнь.
Чувство чисел лежит в основе всей математики более высокого уровня (Feikes & Schwingendorf, 2008).
Когда студенты терпят неудачу по алгебре, это часто происходит потому, что у них нет чувства числа. Когда учащиеся работают над сложными математическими задачами, такими как те, которые мы приводим в конце этой статьи, у них развивается чувство числа, а также они изучают и запоминают математические факты. Когда учащиеся сосредотачиваются на запоминании таблицы умножения, они часто запоминают факты, не имея представления о числах, а это означает, что они очень ограничены в своих возможностях и склонны совершать ошибки, например ту, которая вызвала общенациональные насмешки над британским политиком. Отсутствие чувства числа привело к более катастрофическим ошибкам, таким как телескоп Хаббл, упустивший звезды, которые он должен был сфотографировать в космосе. Телескоп искал звезды в определенном скоплении, но потерпел неудачу из-за того, что кто-то допустил арифметическую ошибку в программировании телескопа (LA Times, 1990). Чувство чисел, критически важное для математического развития учащихся, подавляется чрезмерным упором на запоминание математических фактов в классе и дома.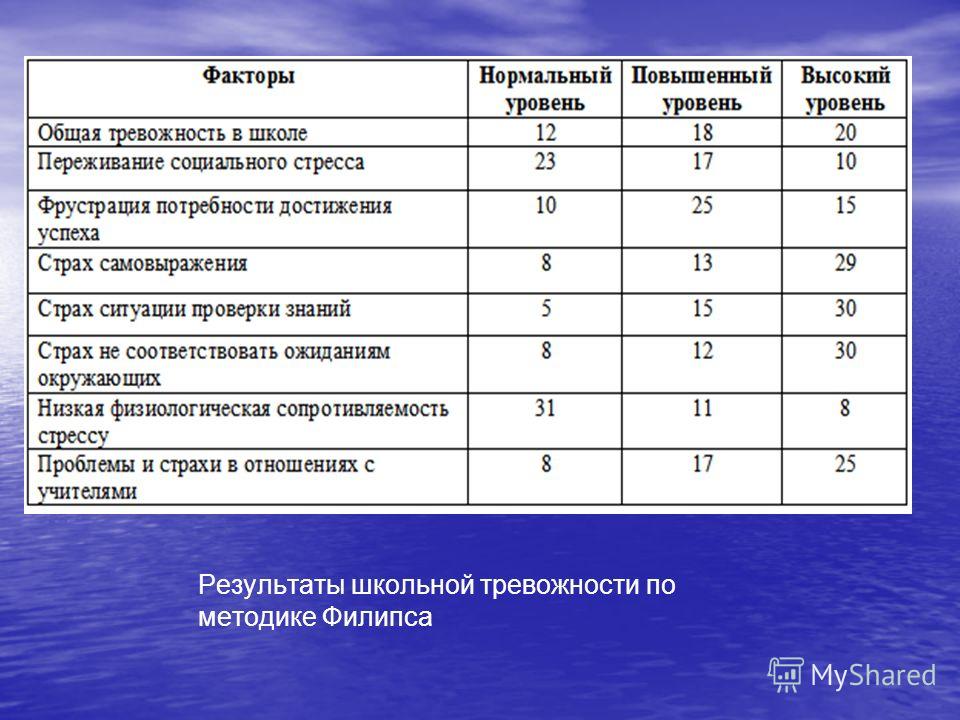
Чем больше мы делаем упор на запоминание учащихся, тем меньше у них желания думать о числах и их отношениях, а также использовать и развивать чувство чисел (Boaler, 2009).
Мозг и чувство числа
Некоторые учащиеся не так хорошо запоминают математические факты, как другие. Это то, что нужно праздновать, это часть прекрасного разнообразия жизни и людей. Представьте, как скучно и скучно было бы, если бы учителя давали тесты по математике и все отвечали бы на них одинаково и с одинаковой скоростью, как если бы все они были роботами. В недавнем исследовании мозга ученые исследовали мозг учащихся, когда их учили запоминать математические факты. Они увидели, что некоторые ученики запоминают их гораздо легче, чем другие. Это не будет сюрпризом для читателей, и многие из нас, вероятно, предположили бы, что те, кто запоминал лучше, были более успешными или «более умными» учениками. Но исследователи обнаружили, что учащиеся, которые лучше запоминали, не имели более высоких достижений, у них не было того, что исследователи назвали более «математическими способностями», и у них не было более высоких показателей IQ (Supekar et al, 2013).
Единственные различия, которые обнаружили исследователи, заключались в области мозга, называемой гиппокампом, которая является областью мозга, отвечающей за запоминание фактов (Supekar et al, 2013). Некоторые учащиеся будут медленнее запоминать, но у них все еще есть исключительный математический потенциал. Математические факты составляют очень небольшую часть математики, но, к сожалению, учащиеся, которые плохо запоминают математические факты, часто приходят к выводу, что они никогда не смогут добиться успеха в математике, и отворачиваются от предмета.
Учителя в США и Великобритании просят учащихся запоминать факты умножения, а иногда и факты сложения и вычитания, обычно потому, что в учебных планах указано, что учащиеся должны «свободно обращаться с числами». Пэриш, опираясь на Фоснот и Долк (2001), определяет беглость как «знание того, как число может быть составлено и разложено, и использование этой информации для гибкого и эффективного решения проблем» (Пэриш, 2014, стр.
159). Независимо от того, верим мы или нет, что беглость требует большего, чем простое запоминание математических фактов, данные исследований указывают в одном направлении: лучший способ развить беглость с числами — это развить чувство числа и работать с числами по-разному, а не слепо запоминать без смысл числа.
Когда учителя делают упор на запоминание фактов и дают тесты для измерения числа фактов, учащиеся страдают двумя важными способами. Примерно для трети учащихся начало тестирования на время является началом математической тревожности (Boaler, 2014). Сиан Бейлок и ее коллеги изучали мозг людей с помощью МРТ и обнаружили, что математические факты хранятся в области рабочей памяти мозга. Но когда учащиеся испытывают стресс, например, когда они отвечают на математические вопросы в условиях дефицита времени, рабочая память блокируется, и учащиеся не могут получить доступ к известным им математическим фактам (Beilock, 2011; Ramirez, et al, 2013). Когда учащиеся понимают, что они не могут хорошо выполнять тесты на время, у них начинает развиваться беспокойство, и их уверенность в математике ослабевает.
Блокирование рабочей памяти и связанное с ним беспокойство особенно характерны для учащихся с более высокими показателями успеваемости и девочек. По самым скромным оценкам, по крайней мере треть учащихся испытывают сильный стресс во время тестов на время, и это не учащиеся, принадлежащие к определенной группе успеваемости или экономическому происхождению. Когда мы подвергаем учащихся этому вызывающему тревогу опыту, мы теряем учащихся из математики.
В настоящее время тревожность по поводу математики регистрируется у учащихся в возрасте от 5 лет (Рамирез и др., 2013), и контрольные работы на время являются основной причиной этого изнурительного состояния, часто сохраняющегося на всю жизнь. Но есть и вторая, не менее важная причина, по которой нельзя использовать временные тесты — они побуждают многих учащихся отворачиваться от математики. На моих занятиях в Стэнфордском университете я сталкиваюсь со многими студентами, травмированными по математике, хотя они являются одними из самых успевающих студентов в стране.
Когда я спрашиваю их, что случилось, что привело к их отвращению к математике, многие ученики говорят о тестах на время во втором или третьем классе как о главном поворотном моменте для них, когда они решили, что математика не для них. Некоторые учащиеся, особенно женщины, говорят о необходимости глубокого понимания, что является очень полезной целью, и о том, что глубокое понимание не ценится и не предлагается, когда тесты на время стали частью урока математики. Возможно, на уроках математики они выполняли другую, более полезную работу, сосредоточившись на осмыслении и понимании, но тесты на время вызывают такие сильные эмоции, что учащиеся могут поверить, что умение быстро справляться с математическими фактами и есть суть математики. Это крайне неудачно. Мы видим результат ошибочного упора школы на заучивание и тестирование в цифрах, выпадающих из математики, и в математическом кризисе, с которым мы сталкиваемся в настоящее время (см. www.youcubed.org). Когда моя собственная дочь начала запоминать таблицу умножения и тестировать ее в возрасте 5 лет в Англии, она начала приходить домой и плакать из-за математики.
Это не та эмоция, которую мы хотим, чтобы учащиеся ассоциировали с математикой, и пока мы продолжаем заставлять учащихся быстро вспоминать факты, мы не сможем избавиться от широко распространенного беспокойства и неприязни к математике, которые пронизывают США и Великобританию (Silva & White, 2013). ; National Numeracy, 2014).
В последние годы исследователи мозга обнаружили, что учащиеся, которые наиболее успешно справляются с задачами на числа, используют разные мозговые пути: один связан с числами и символами, а другой связан с более интуитивным и пространственным мышлением (Park & Brannon, 2013). . В конце этой статьи мы даем множество упражнений, которые способствуют визуальному пониманию числовых фактов, чтобы задействовать важные мозговые связи. Кроме того, исследователи мозга изучали студентов, изучающих математические факты двумя способами — с помощью стратегий или запоминания. Они обнаружили, что два подхода (стратегии или запоминание) задействуют два различных пути в мозге и что оба пути идеально подходят для использования на протяжении всей жизни.
Важно отметить, что исследование также показало, что те, кто учился с помощью стратегий, достигли «превосходной производительности» по сравнению с теми, кто запоминал, они решали задачи с той же скоростью и лучше переносили новые задачи. Исследователи мозга пришли к выводу, что автоматизм должен быть достигнут через понимание числовых отношений, достигаемое посредством размышлений о числовых стратегиях (Делазер и др., 2005).
Почему к математике относятся по-разному?
Чтобы научиться хорошо изучать английский язык, читать и понимать романы или поэзию, учащиеся должны запомнить значения многих слов. Но ни один изучающий английский язык не скажет и не подумает, что изучение английского языка — это быстрое запоминание и быстрое припоминание слов. Это потому, что мы учим слова, используя их в самых разных ситуациях — в разговоре, чтении и письме. Учителя английского языка не дают учащимся сотни слов для запоминания, а затем проверяют их в заданных условиях. Все предметы требуют запоминания некоторых фактов, но математика — единственный предмет, по которому учителя считают, что их нужно проверять в условиях времени.
Почему мы так относимся к математике?
У математики уже есть огромная проблема с изображениями. Студенты редко плачут по другим предметам, и при этом они не верят, что все остальные предметы связаны с запоминанием или скоростью. Использование методов обучения и воспитания, которые подчеркивают запоминание математических фактов, является основной причиной того, что учащиеся отключаются от математики. Многие люди будут утверждать, что математика отличается от других предметов, и она просто должна быть такой — что математика — это получение правильных ответов, а не интерпретация или смысл. Это еще одно заблуждение. Ядром математики является рассуждение — размышление о том, почему методы имеют смысл, и обсуждение причин использования различных методов (Boaler, 2013). Математические факты — это небольшая часть математики и, вероятно, наименее интересная часть. Конрад Вольфрам из Wolfram-Alpha, одной из ведущих мировых компаний в области математики, публично говорит о широте математики и о необходимости перестать рассматривать математику как расчет. Ни Вольфрам, ни я не утверждаем, что в школах не следует обучать счету, но необходимо изменить баланс, и учащиеся должны учиться считать с помощью чувства чисел, а также уделять больше времени слаборазвитым, но важным частям математики, таким как решение задач. и рассуждения.
Важно, обучая студентов смыслу чисел и фактам чисел, никогда не подчеркивать скорость. На самом деле это верно для всей математики. В математике распространено распространенное и вредное заблуждение — представление о том, что сильные ученики-математики — это быстрые ученики. Я работаю со многими математиками, и я замечаю в них одну вещь: они не очень быстро работают с числами, на самом деле некоторые из них довольно медленные. Это неплохо, они медлительны, потому что глубоко и тщательно думают о математике. Лоран Шварц, выдающийся математик, написал автобиографию о своих школьных годах и о том, как его заставляли чувствовать себя «глупым», потому что он был одним из самых медлительных математических мыслителей в своем классе (Schwartz, 2001). Ему потребовалось много лет ощущения себя неадекватным, чтобы прийти к заключению, что «быстрота не имеет точного отношения к интеллекту». Важно глубоко понимать вещи и их отношения друг к другу. Вот где кроется интеллект. Факт быстрого или медленного на самом деле не имеет значения». (Шварц, 2001) К сожалению, уроки математики, основанные на скорости и тестах, заставляют многих учеников, которые медленно и глубоко мыслят, таких как Шварц, полагать, что они не могут быть хороши в математике.
Математика «Свободное владение» и учебная программа
В США новая учебная программа Common Core включает беглость речи в качестве цели. Беглость возникает, когда у учащихся развивается чувство числа, когда они математически уверены, потому что понимают числа. К сожалению, слово «свобода» часто неправильно истолковывается. Учебная программа Engage New York, которая становится все более популярной в США, неправильно интерпретирует беглость речи следующим образом:
Свободное владение языком: Ожидается, что учащиеся будут иметь скорость и точность с простыми расчетами; учителя структурируют время занятий и/или домашнее задание, чтобы учащиеся запоминали посредством повторения основные функции, такие как таблицы умножения, чтобы они лучше понимали и манипулировали более сложными функциями .
(Задействуйте Нью-Йорк)
С этой директивой связано много проблем. Скорость и запоминание — два направления, от которых нам срочно нужно отойти, а не навстречу. Столь же проблематично «Вовлечение Нью-Йорка» связывает запоминание числовых фактов с пониманием учащимися более сложных функций, что не подтверждается данными исследований. Исследования говорят нам, что учащиеся понимают более сложные функции, когда у них есть чувство числа и глубокое понимание числовых принципов, а не слепое запоминание или быстрое припоминание (Boaler, 2009).). В настоящее время я работаю с аналитиками PISA в ОЭСР. Команда PISA не только выпускает международные тесты по математике каждые 4 года, но и собирает данные о математических стратегиях учащихся. Их данные, полученные от 13 миллионов 15-летних подростков по всему миру, показывают, что ученики с самой низкой успеваемостью — это те, кто сосредотачивается на запоминании и считает, что запоминание важно при изучении математики (Boaler & Zoido, в печати). Эта идея зарождается рано в классах, и нам нужно ее искоренить. Самые высокие достижения в мире — это те, кто сосредотачивается на больших идеях в математике и связях между идеями. У учащихся развивается связанное представление о математике, когда они работают над математикой концептуально, а слепое запоминание заменяется осмыслением.
В Великобритании директивы имеют аналогичный потенциал вреда. В новом национальном учебном плане говорится, что все учащиеся должны «заучить свои таблицы умножения до 12 включительно» к 9 годам, и хотя учащиеся могут запоминать факты умножения до 12 x 12 с помощью насыщенных увлекательных занятий, эта директива побуждает учителей Дайте учащимся таблицу умножения, чтобы они запомнили ее, а затем проверили. Ведущая группа в Великобритании, возглавляемая детским писателем и поэтом Майклом Розеном, сформировалась, чтобы привлечь внимание к ущербу, наносимому нынешней политикой в школах, и количеству детей младшего школьного возраста, которые теперь ходят в школу в слезах из-за стресса, в котором они находятся, вызванного чрезмерным — тестирование (Гарнер, The Independent, 2014). Математика является основной причиной беспокойства и страха учащихся, а ненужное сосредоточение внимания на заученных математических фактах в ранние годы является одной из главных причин этого.
Упражнения для развития числовых фактов и числового смысла
Учителя должны помогать учащимся развивать математические факты, не подчеркивая факты ради фактов или используя «тесты на время», а поощряя учащихся использовать числа, работать с ними и исследовать их. По мере того, как учащиеся работают над осмысленными числами, они будут запоминать математические факты одновременно с пониманием чисел и математики. Они будут наслаждаться и изучать важную математику, а не запоминать, бояться и бояться математики.
Числовые переговоры
Одним из лучших методов одновременного обучения чувству чисел и математическим фактам является обучающая стратегия под названием «Разговоры о числах», разработанная Рут Паркер и Кэти Ричардсон. Это идеальное краткое учебное задание, с которого учителя могут начинать уроки, а родители могут выполнять его дома. Он включает в себя постановку абстрактной математической задачи, такой как 18 x 5, и просьбу учащихся решить ее в уме. Затем учитель собирает различные методы и смотрит, почему они работают. Например, учитель может поставить 18 x 5 и обнаружить, что ученики решают задачу разными способами:
Студенты любят предлагать свои различные стратегии и обычно полностью вовлечены и очарованы различными возникающими методами. Учащиеся изучают математику в уме, у них есть возможность запоминать математические факты, а также они развивают концептуальное понимание чисел и арифметических свойств, которые имеют решающее значение для успеха в алгебре и не только. Родители могут использовать аналогичную стратегию, спрашивая о методах своих детей и обсуждая различные методы, которые можно использовать. Две книги, одна Кэти Хамфрис и Рут Паркер (в печати), а другая Шерри Пэриш (2014 г.), иллюстрируют множество различных разговоров о числах, над которыми можно работать со учащимися средней и начальной школы соответственно.
Исследования говорят нам, что лучшие классы математики — это те, в которых учащиеся изучают числовые факты и смысл чисел посредством увлекательных занятий, которые сосредоточены на математическом понимании, а не на механическом запоминании. Следующие пять видов деятельности были выбраны для иллюстрации этого принципа; Приложение к этому документу содержит более широкий спектр заданий и ссылок на другие полезные ресурсы, которые помогут учащимся развивать чувство числа.
Дополнительные действия с фактами
Snap It: Это задание, над которым дети могут работать в группах. Каждый ребенок составляет поезд из соединяющихся кубиков определенного числа. По сигналу «Щелк» дети разбивают свои поезда на две части и держат одну руку за спиной. Дети по очереди ходят по кругу, показывая оставшиеся кубики. Остальные дети отрабатывают полную комбинацию чисел. Например, если у меня есть 8 кубиков в моем числовом поезде, я могу сломать его и положить 3 за спину. Я покажу своей группе оставшиеся 5 кубиков, и они смогут сказать, что трех не хватает и что 5 и 3 составляют 8.
Сколько прячется? В этом задании у каждого ребенка одинаковое количество кубиков и чашек. Они по очереди прячут несколько своих кубиков в чашку и показывают остатки. Другие дети отрабатывают ответ на вопрос «Сколько спряталось» и называют полное числовое сочетание.
Пример: У меня есть 10 кубиков, и я решил спрятать 4 в своей чашке. Моя группа видит, что у меня всего 6 кубиков. Учащиеся должны быть в состоянии сказать, что я прячу 4 кубика и что 6 и 4 дают 10.
Действия по умножению фактов
Насколько близко к 100? В эту игру играют напарники. Двое детей делят пустую сетку 100. Первый партнер бросает два кубика с числами. Выпадающие числа — это числа, которые ребенок использует для создания массива в сетке 100. Они могут поместить массив в любое место сетки, но цель состоит в том, чтобы заполнить сетку настолько, насколько это возможно. После того, как игрок нарисовал массив на сетке, он записывает числовое предложение, описывающее сетку. Игра заканчивается, когда оба игрока бросили кубики и не могут больше размещать на сетке ряды. Как близко к 100 вы можете получить?
Пицца Пепперони: В этой игре дети дважды бросают кубик. Первый бросок говорит им, сколько пицц нужно вытянуть. Второй рулон говорит им, сколько пепперони положить на КАЖДУЮ пиццу. Затем они пишут числовое предложение, которое поможет им ответить на вопрос: «Сколько всего пепперони?»
Например, я бросаю кости и получаю 4, поэтому я вытягиваю 4 большие пиццы. Я переворачиваю снова, и у меня получается 3, поэтому я кладу по три пепперони на каждую пиццу. Затем я пишу 4 x 3 = 12, и это говорит мне о том, что всего 12 пепперони.
Математические карточки
Многие родители используют «карточки для запоминания» как способ поощрения изучения математических фактов. К ним обычно относятся 2 бесполезные практики — заучивание без понимания и цейтнот. В нашем задании «Математические карточки» мы использовали структуру карточек, которая нравится детям, но мы сместили акцент на смысл чисел и понимание умножения. Цель игры — сопоставить карточки с одним и тем же числовым ответом, показанным в разных изображениях. Положите все карточки на стол и попросите детей брать их по очереди; выберите столько, сколько они найдут с тем же ответом (показанным через любое представление). Например 9и 4 можно показать с моделью области, наборами объектов, таких как домино, и числовым предложением. Когда учащиеся сопоставляют карточки, они должны объяснить, откуда они знают, что разные карточки эквивалентны. Эта деятельность поощряет понимание умножения, а также повторение математических фактов. Полный комплект карт приведен в Приложении А.
Вывод: знание — сила
Упражнения, приведенные выше, являются иллюстрациями игр и заданий, в которых учащиеся изучают математические факты одновременно с работой над тем, что им нравится, а не над тем, чего они боятся. Различные упражнения также сосредоточены на понимании сложения и умножения, а не на слепом запоминании, и это очень важно. В Приложении A представлены другие предлагаемые виды деятельности и ссылки.
Как преподаватели, мы все разделяем цель поощрения способных учеников, которые хорошо разбираются в математике, а также бегло используют числа. Но учителя и составители учебных программ часто не имеют доступа к важным исследованиям, и это означает, что непродуктивные и контрпродуктивные методы работы в классе продолжаются. Эта короткая статья иллюстрирует ущерб, причиняемый практиками, которые часто сопровождают преподавание математических фактов — давление скорости, тестирование на время и слепое запоминание, — а также обобщает результаты исследований чего-то совсем другого — чувства чисел. Успевающие учащиеся используют чувство числа, и очень важно, чтобы учащиеся с более низкими достижениями вместо того, чтобы работать над упражнениями и запоминанием, также научились использовать числа гибко и концептуально. Запоминание и проверка на время мешают восприятию чисел, создавая у учащихся впечатление, что осмысление не имеет значения. Нам необходимо срочно переориентировать наше преподавание первых чисел и их смысла в нашем преподавании математики в Великобритании и США. Если мы этого не сделаем, то показатели отказов и отсева – уже достигшие рекордно высокого уровня в обеих странах (National Numeracy, 2014; Silva & White, 2013) – возрастут. Когда мы придаем особое значение запоминанию и тестированию во имя беглости, мы наносим вред детям, мы рискуем будущим нашего вечно количественного общества и угрожаем дисциплине математики. У нас есть исследовательские знания, необходимые для того, чтобы изменить это и дать возможность всем детям хорошо учиться математике. Теперь пришло время использовать его.
Ссылки
Бейлок, С. (2011). Дроссель: что раскрывают секреты мозга о том, как сделать все правильно, когда вам нужно . Нью-Йорк: Свободная пресса.
Боалер, Дж. (2015). При чем здесь математика? Как учителя и родители могут помочь преобразовать обучение математике и вдохновить на успех. Нью-Йорк: Пингвин.
Боалер, Дж. (2014). Исследования показывают, что тесты на время вызывают математическую тревогу. Обучение детей математике, 20 (8).
Боалер, Дж. (2013, 12 ноября 2013 г.). Стереотипы, которые искажают то, как американцы преподают и изучают математику. Атлантический океан.
Боалер, Дж. и Зойдо, П. (в печати). Влияние стратегий обучения математике на достижения: тщательный анализ данных Пизы.
Делазер М., Ишебек А., Домахс Ф., Замариан Л., Коппельштеттер Ф., Сидентопф С.М. Кауфманн; Бенке, Т., и Фелбер, С. (2005). Обучение с помощью стратегий и обучение с помощью упражнений — данные исследования фМРТ. НейроИзображение. 839-849
Задействовать Нью-Йорк. https://schools.nyc.gov/NR/rdonlyres/9375E046-3913-4AF5-9FE3-D21BAE8FEE8D/0/CommonCoreInstructionShifts_Mathematics.pdf
Фейкс, Д. и Швингендорф, К. (2008). Важность сжатия в обучении детей математике и обучении учителей преподаванию математики. Средиземноморский журнал исследований в области математического образования 7 (2).
Фоснот, К., Т. и Долк, М. (2001). Молодые математики за работой: построение умножения и деления. Хайнеманн:
Гарнер, Р. (3 октября 2014 г.). Независимый. (ссылка на статью)
Грей, Э., и Талл, Д. (1994). Двойственность, двусмысленность и гибкость: «процептуальный» взгляд на простую арифметику. Журнал исследований в области математического образования, 25 (2), 116–140.
Хамфрис, Кэти и Паркер, Рут (в печати). Как сделать разговор о числах важным: развитие математических навыков и углубление понимания, 4–10 классы. Портленд, Мэн: Стенхаус.
LA Times (1990) https://articles.latimes.com/1990-05-10/news/mn-1461_1_math-error
Приход, С. (2014). Разговоры о числах: помощь детям в построении умственной математики и вычислительных стратегий, классы K-5, дополнены общими основными связями. Математические решения.
Парк, Дж. и Браннон, Э. (2013). Обучение приблизительной системе счисления улучшает математические навыки. Ассоциация психологических наук, 1-7
Рамирес, Г.