Внутренние силы: Ошибка 403 — доступ запрещён
Внутренние силы Земли
Внутренние силы Земли формируют крупные формы рельефа Земли. Медленные поднятия и опускания участков земной поверхности вызывают изменения в очертаниях суши и моря. Движения плит литосферы приводят к образованию гор, рождают вулканы и землетрясения.
Движения земной коры
Уже древние греки и римляне, жившие на берегах Средиземного моря, знали, что земная поверхность может испытывать поднятия и опускания. Многолетние наблюдения с помощью современных приборов доказали это. Земная кора действительно движется в вертикальном направлении: где-то медленно опускается, где-то медленно поднимается. Одновременно каждый участок земной коры перемещается в горизонтальном направлении вместе с литосферными плитами.
Образование гор
Горные породы на поверхности медленно двигающихся литосферных плит накапливаются горизонтальными слоями. При столкновении плит толщи пород изгибаются и сминаются в складки разной величины и крутизны. Выпуклые складки образуют горные хребты, а вогнутые складки — межгорные впадины. Именно поэтому многие образовавшиеся при столкновении литосферных плит горы суши называются складчатыми.
Именно поэтому многие образовавшиеся при столкновении литосферных плит горы суши называются складчатыми.
Постепенно складчатые горы разрушаются, и от них остаётся только складчатое основание. На этом выровненном основании формируются равнины.
При образовании гор толщи горных пород не только сминаются в складки, но и разрываются, раскалываются разломами. Разделённые разломами на отдельные глыбы участки земной коры смещаются вверх или вниз относительно друг друга. Так возникают сбросы, горсты и грабены. Состоящие из них горы называются складчато-глыбовыми и глыбовыми.
Движение гигантских плит литосферы приводит не только к образованию гор, но и к возникновению землетрясений и извержению вулканов, которые часто несут смертельную опасность для людей.
Вулканизм
Вулканизм — это излияние магмы на поверхность суши или дно океанов но трещинам в земной коре или трубообразным каналам — жерлам. На суше магма извергается, как правило, через жерла, вокруг которых вырастают горы конусообразной формы — вулканы.
Изливающаяся магма теряет газы и пары воды и становится лавой. Газы из магмы выделяются очень быстро, поэтому извержения часто сопровождаются мощными взрывами. Они разрушают горные породы, превращая их в обломки, в том числе очень мелкие — вулканический пепел. Извержения разных вулканов неодинаковы. У некоторых они протекают спокойно, при извержении других наблюдаются сильные взрывы с выбросом раскалённых обломков, пепла и газов.
Землетрясения
Землетрясения это быстрые колебания земной коры, вызванные сдвигами горных пород. Место в глубине земной коры, где происходят эти сдвиги, называется очагом землетрясения. От очага через земную кору распространяются волны, создающие колебания. Место на земной поверхности, располагающееся прямо над очагом землетрясения, называется эпицентром. Здесь подземные толчки бывают самыми сильными, с удалением от эпицентра они ослабевают.
На Земле ежегодно происходит более 100000 небольших и около 100 достаточно сильных землетрясений. Учёные фиксируют землетрясения с помощью специальных приборов — сейсмографов. Для оценки землетрясении в России а используют 12-балльную шкалу.
Учёные фиксируют землетрясения с помощью специальных приборов — сейсмографов. Для оценки землетрясении в России а используют 12-балльную шкалу.
Последствия землетрясений и вулканизма
Области, где часто повторяются землетрясения и извержения вулканов, образуют сейсмические пояса. Они совпадают с границами между литосферными плитами. Извержения вулканов, и в особенности сильные землетрясения, сопровождаются разрушениями и человеческими жертвами. Только в период с 2004 по 2011 год в результате землетрясений погибли более полумиллиона человек. Наиболее разрушительными за эти семь лет были землетрясения в Юго-Восточной Азии в 2004 году, на острове Гаити в 2010 году и в Японии в марте 2011 года.
Сопротивление материалов (Работнов Ю.Н.)
Сопротивление материалов (Работнов Ю.Н.)
ОглавлениеПРЕДИСЛОВИЕГЛАВА I. ОСНОВНЫЕ ПОНЯТИЯ § 1. Задачи и содержание сопротивления материалов. § 2. Сопротивление материалов и теоретическая механика. § 3. Статически неопределенные задачи. § 4. Внешние силы. § 5. Принцип отвердения. § 6. Недопустимость замены системы сил статически эквивалентной. § 8. Внутренние силы. § 9. Напряжение. § 10. Простейшие типы напряженного состояния. § 11. Простейшие виды деформации. § 12. Упругость и пластичность. § 13. Закон Гука. § 14. Диаграмма пластичности. § 15. Тела изотропные и анизотропные. ГЛАВА II. РАСТЯЖЕНИЕ СЖАТИЕ § 16. Стержни и стержневые системы.  § 17. Принцип Сен-Венана и гипотеза плоских сечений. § 18. Напряжения и деформации при растяжении. § 19. Расчеты на прочность при растижении и сжатии. § 20. Собственный вес и силы инерции. § 21. Стержни переменного сечения. § 22. Перемещения узлов стержневых систем. § 23. Статически неопределенные задачи на растяжение — сжатие. § 24. Температурные и монтажные напряжения. § 25. Общие соображения о расчете стержневых систем. § 26. Расчет статически неопределимых систем по допускаемым нагрузкам. § 27. Остаточные напряжения после пластической деформации. § 28. Потенциальная энергия растяжении. § 29. Напряжения при ударе. § 30. Распространение упругих волн в стержнях. § 31. Концентрации напряжений. § 32. Нелинейные задачи на растяжение — сжатие. ГЛАВА III. СЛОЖНОЕ НАПРЯЖЕННОЕ СОСТОЯНИЕ § 33. Напряжения на косых площадках при растяжении. § 34. Напряжения при двухосном растяжении. § 35. Круговая диаграмма Мора. § 36.  Общий случай плоского напряженного состояния. Общий случай плоского напряженного состояния.§ 37. Определение напряжений на произвольной площадке. § 38. Пространственное напряженное состояние. § 39. Главные напряжения. § 40. Главные касательные напряжения. § 41. Октаэдрическое напряжение. § 42. Закон Гука для главных осей. § 43. Изменение объема при упругой деформации. § 44. Чистый сдвиг. § 45. Деформация элемента объема в общем случае. § 47. Условие пластичности Мизеса. § 48. Условия пластичности для плоского напряженного состояния. § 49. Потенциальная энергия упругой деформации. § 50. Энергия изменения формы. ГЛАВА IV. НЕКОТОРЫЕ ПРИМЕРЫ РАСЧЕТА НА ПРОЧНОСТЬ § 51. Расчеты на прочность изделий сложной формы. § 52. Безмоментные оболочки вращении. § 53. Местные напряжения в безмоментных оболочках. § 54. Большие прогибы мембраны. § 55. Условные расчеты. § 56. Некоторые дальнейшие примеры условных расчетов.  § 57. Расчет сварных соединений. ГЛАВА V. ФИЗИЧЕСКИЕ ОСНОВЫ ПРОЧНОСТИ МЕТАЛЛОВ И СПЛАВОВ § 58. Задачи испытания материалов. § 59. Статические испытания на растяжение. § 60. Исследование металлов в области малых деформаций. § 61. Диаграмма растяжения мягкой стали. § 62. Опыты на сжатие. § 63. Строение и упругая деформация металлических кристаллов. § 64. Типичные кристаллические структуры металлов. § 65. Пластическая деформация монокристаллов. § 66. Прочность кристаллов и сопротивление пластическому деформированию. § 67. Дислокации. § 68. Движение и равновесие дислокаций. § 69. Источники дислокаций. § 70. Границы блоков. § 71. Деформация поликристаллических металлов и сплавов. § 72. Влияние повышенной температуры на механические свойства. § 73. Влияние скорости испытания. § 74. Испытании на твердость. ГЛАВА VI. ТЕОРИИ ПЛАСТИЧНОСТИ, НЕЛИНЕЙНОЙ УПРУГОСТИ И ПОСЛЕДЕЙСТВИЯ § 75. Основные принципы построения теории пластичности.  § 76. Ассоциированный закон течения. § 77. Течение при условии пластичности Сен-Венана и Мизеса. § 78. Закон упрочнения. § 79. Деформационная теория пластичности. § 81. Конечная деформация. § 82. Нелинейно упругое тело. § 83. Высокоэластические деформации. § 84. Упругое последействие. § 85. Некоторые свойства вязко-упругого тела. § 86. Принцип суммирования Больцмана—Вольтерра. ГЛАВА VII. КРУЧЕНИЕ § 87. Кручение стержней круглого сечеиия. § 88. Упруго-пластическое кручение стержня круглого сечения. § 89. Гипотеза жесткого контура. § 90. Кручение тонкостенных стержней замкнутого профиля. § 91. Кручение тонкостенных стержней открытого профиля. § 92. Кручение упругих стержией сплошного профиля. § 93. Опытное исследование кручения. § 94. Предельное состояние закрученного стержня из идеально-пластического материала. ГЛАВА VIII. ТЕОРИЯ МОМЕНТОВ ИНЕРЦИИ § 96.  Общие теоремы о моментах. Общие теоремы о моментах.§ 97. Преобразование статических моментов и моментов инерции при параллельном переносе осей. § 98. Вычисление моментов инерции. § 99. Преобразование моментов инерции при повороте осей. § 100. Главные оси и главные моменты инерции. ГЛАВА IX. НАПРЯЖЕНИЯ ПРИ ИЗГИБЕ § 101. Действие поперечных сил на балку. § 102. Гипотеза плоских сечений и принцип Сен-Венана. § 103. Нормальные напряжения при изгибе. § 104. Изгибающие моменты и перерезывающие силы. § 105. Дифференциальные соотношения между интенсивностью нагрузки, перерезывающей силой и изгибающим моментом. Эпюры. § 106. Расчет на прочность при изгибе по допускаемым напряжениям. § 107. Упруго-пластический изгиб. § 108. Несущая способность стержня при изгибе. § 109. Принцип Сен-Венана. § 110. Внецентренное растяжение — сжатие. § 111. Ядро сечения. § 112. Несущая способность внецентренно сжатого стержня. § 113. Расчет составных балок. § 114. Изгиб кривого бруса.  § 115. Нахождение нейтральной осн в кривом стержне. ГЛАВА X. ДЕФОРМАЦИИ ПРИ ИЗГИБЕ § 116. Дифференциальное уравнение изогнутой оси. § 117. Пределы применимости приближенной теории. § 118. Интегрирование уравнения изгиба. § 119. Примеры определения прогибов. § 120. Простейшие статически неопределенные задачи. § 121. Расчет статически неопределимых балок по способу допускаемых нагрузок. § 122. Изгиб стержней переменного сечения. § 123. О решении линейных дифференциальных уравнений с постоянными коэффициентами. § 124. Продольно-поперечный изгиб. § 125. Изгиб балки на упругом основании. ГЛАВА XI. ИЗГИБ И КРУЧЕНИЕ ТОНКОСТЕННЫХ СТЕРЖНЕЙ § 126. Нормальные и касательные напряжения при изгибе. § 127. Касательные напряжении при изгибе в плоскости симметрии. § 128. Центр изгиба. § 129. Дополнительные напряжения при кручении. § 130. Закон секториальных площадей. § 131. Уравнение стесненного кручения. § 132. Вычисление секториальных характеристик.  § 133. Стержень, нагруженный бимоментом. § 134. Некоторые примеры стесненного кручения. ГЛАВА XII. УСТОЙЧИВОСТЬ УПРУГОГО И ПЛАСТИЧЕСКОГО РАВНОВЕСИЯ § 135. Постановка вопроса об устойчивости. § 136. Устойчивость сжатого упругого стержня. § 137. Эластика Эйлера. § 138. Критические силы при иных видах закрепления стержня. § 139. Потеря устойчивости за пределом упругости. § 140. Потеря устойчивости за пределом упругости (продолжение). § 141. Исследование поведения сжатого стержня при потере устойчивости за пределом упругости. § 142. Расчет на устойчивость по эмпирическим формулам. ГЛАВА XIII. ТРУБЫ И ДИСКИ § 143. Толстостенные трубы. Дифференциальные уравнения равновесия и совместности. § 145. Пластическое состояние трубы. § 146. Вращающиеся диски. Упругое состояние. § 147. Диск равного сопротивления. § 148. Предельное равновесие вращающегося диска. ГЛАВА XIV. ОБЩИЕ ТЕОРЕМЫ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ § 149.  Обобщенные силы и обобщенные перемещения. Обобщенные силы и обобщенные перемещения.§ 150. Начало возможных перемещений для деформируемого тела. § 151. Теоремы Лагранжа и Кастильяно. § 152. Лииейиые упругие системы. § 153. Теорема о взаимности работ. § 154. Теорема Кастильяно для линейных упругих систем. § 155. Расчет винтовых пружин. § 156. Теорема о минимуме энергии. § 157. Интеграл перемещений. § 158. Графоаналитический способ вычислений интеграла перемещений. § 159. Расчет статически неопределимых систем по методу сил. § 160. Уравнение трех моментов. ГЛАВА XV. ТЕОРИЯ ПРЕДЕЛЬНОГО РАВНОВЕСИЯ § 161. Жестко-пластическое тело. § 162. Поверхности нагружения. § 163. Истинное и допустимые состояния элемента. § 164. Статический метод определения предельной нагрузки. § 165. Примеры определения предельной нагрузки статическим методом. § 166. Кинематически возможные состояния. § 167. Кинематический метод определения предельной нагрузки. § 168. Примеры определения предельной нагрузки кинематическим методом.  § 169. Предельное равновесие пластинок. ГЛАВА XVI. ДИНАМИЧЕСКИЕ ЗАДАЧИ СОПРОТИВЛЕНИЯ МАТЕРИАЛОВ § 170. Колебания систем с конечным числом степеней свободы. § 171. Собственные частоты и главные формы колебаний. § 172. Представление произвольной конфигурации системы через главные формы. Главные координаты. § 173. Формула и способ Релея. § 174. Нижние оценки для частоты основного тона. § 176. Поперечные колебания стержней. § 177. Колебания балок постоянного сечения. § 178. Способ Релея — Ритца в применении к поперечным колебаниям стержня. § 179. Действие ударных и импульсивных нагрузок на упругие системы. ГЛАВА XVII. ТЕОРИИ ПРОЧНОСТИ § 180. Постановка вопроса о прочности. § 181. Хрупкое и пластическое разрушение. § 182. Теория прочности Мора. § 183. Механизм хрупкого разрушения. § 184. Прочность при низких температурах. § 185. Прочность при переменных нагрузках. § 186. Природа усталостного разрушения.  § 187. Критерии прочности при переменных нагрузках. § 188. Влияние концентрации напряжений на усталостную прочность. § 189. Усталостная прочность при сложном напряженном состоянии. ГЛАВА XVIII. ПОЛЗУЧЕСТЬ И ДЛИТЕЛЬНАЯ ПРОЧНОСТЬ § 190. Ползучесть металлов. § 191. Процесс ползучести. § 192. Длительное разрушение. § 193. Температурные зависимости ползучести и длительной прочности. § 194. Феноменологические теории одномерной ползучести. § 195. Релаксация напряжений. § 196. Длительная прочность при переменных нагрузках. § 197. Ползучесть при изгибе. § 198. Критическое время сжатого стержня. § 199. Ползучесть и длительная прочность при сложном напряженном состоянии. § 200. Вращающиеся диски в условиях ползучести. § 201. Расчеты на ползучесть по теории старении. |
6.1 Типы внутренних сил – инженерная механика: статика
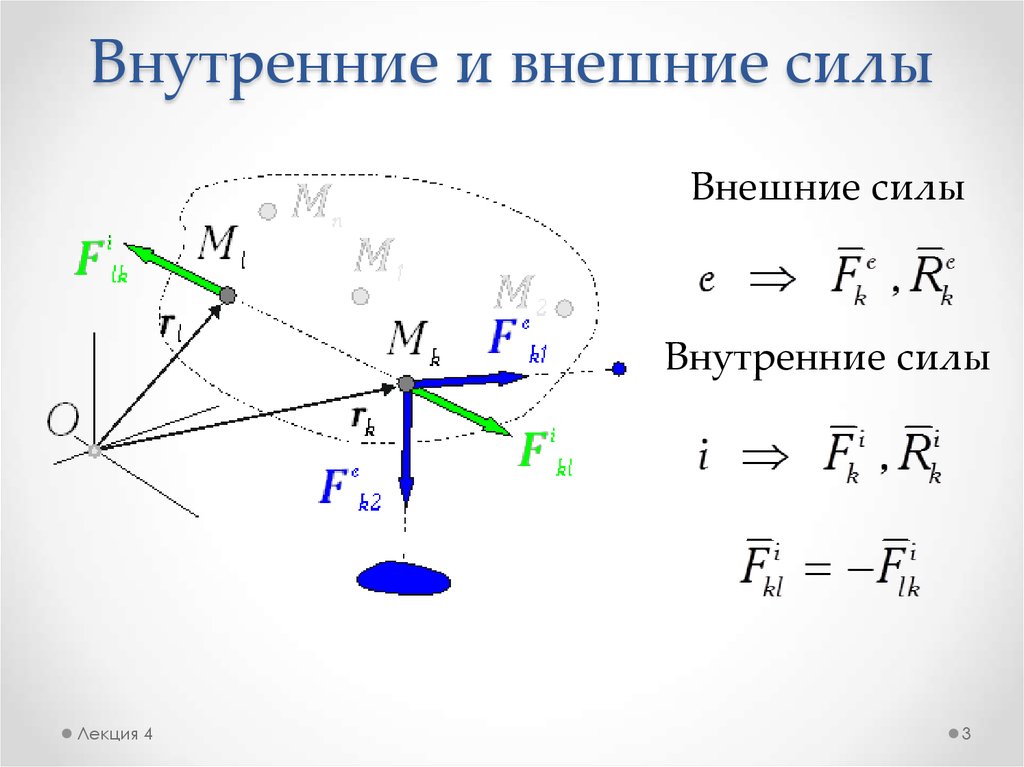
Глава 6: Внутренние силы
Когда вы делаете разрез в объекте, аналогично фиксированной реакции, мы описываем, что происходит в этой точке, используя одну горизонтальную силу (называемую нормальной силой), одну вертикальную силу (называемую поперечной силой) и изгибающий момент.
Существует 3 типа внутренних сил (и моментов):
- нормальная сила (Н) – горизонтальная сила, которую мы рассчитали для ферм в предыдущей главе
- поперечная сила (В) – вертикальная сила, которая изменяется в зависимости от приложенных нагрузок
- изгибающий момент (М) – изменения в зависимости от приложенных нагрузок и приложенных моментов
Нормальная сила обозначается буквой «Н». Сила сдвига, вертикальная сила представлена буквой «V». Изгибающий момент «М». Нормальный и поперечный имеют единицы Н или фунты, а изгибающий момент имеет единицы Нм или фут-фунт. В следующей таблице обобщена информация о внутренних силах (и моментах).
| Сила/момент | Сокращение | Блок | Направление горизонтального луча |
| Нормальная сила | Н | Н или фунт | горизонтальный |
| Сила сдвига | В | Н или фунт | вертикальный |
| Момент | М | Нм или фут-фунт | вращение |
Обратите внимание, что для вертикальной колонны нормальная сила будет вертикальной. По этой причине нормальную силу часто называют «осевой», например: вдоль оси. Сила сдвига для колонны будет горизонтальной и иногда называется «поперечной».
По этой причине нормальную силу часто называют «осевой», например: вдоль оси. Сила сдвига для колонны будет горизонтальной и иногда называется «поперечной».
Это для двухмерного анализа балки при условии незначительной нагрузки в третьем измерении.
Когда балка или рама подвергаются поперечным нагрузкам, возникают три возможные внутренние силы: нормальная или осевая сила, сила сдвига и изгибающий момент, как показано в разделе 9.0087 k консоли на рисунке ниже. Чтобы предсказать поведение конструкций, необходимо знать величины этих сил. В этой главе учащиеся узнают, как определить величину поперечной силы и изгибающего момента в любом сечении балки или рамы и как представить вычисленные значения в графической форме, которая называется «поперечной силой». и «диаграммы изгибающих моментов». Диаграммы изгибающего момента и силы сдвига оказывают неоценимую помощь при проектировании, поскольку они показывают максимальные изгибающие моменты и силы сдвига, необходимые для определения размеров элементов конструкции.
Нормальная сила
Нормальная сила в любом сечении конструкции определяется как алгебраическая сумма осевых сил, действующих с обеих сторон сечения.
Сила сдвига
Сила сдвига (SF) определяется как алгебраическая сумма всех поперечных сил, действующих по обе стороны сечения балки или рамы. Фраза «с любой стороны» важна, так как подразумевает, что в каждом конкретном случае поперечную силу можно получить путем суммирования поперечных сил с левой или с правой стороны сечения.
Изгибающий момент
Изгибающий момент (BM) определяется как алгебраическая сумма моментов всех сил, действующих по обе стороны сечения балки или рамы.
Источник: Внутренние силы в балках и рамах, Либретексты. https://eng.libretexts.org/Bookshelves/Civil_Engineering/Book%3A_Structural_Analysis_(Udoeyo)/01%3A_Chapters/1.04%3A_Internal_Forces_in_Beams_and_Frames
В 3-х измерениях есть:
- 1 нормальное усилие (Н)
- 2 усилия сдвига (V 1 и V 2 ) и
- 3 изгибающих момента (M 1 , M 2 , & T – кручение).
Чтобы в отрасли существовал стандарт, необходимо соглашение о знаках, чтобы мы договорились о том, что является положительным, а что отрицательным. Справа для сдвига – положительная. Обратите внимание, что на обоих следующих рисунках показано одинаковое соглашение о знаках.
Соглашение о положительном знаке адаптировано из источника: https://eng.libretexts.org/Bookshelves/Civil_Engineering/Book%3A_Structural_Analysis_(Udoeyo)/01%3A_Chapters/1.04%3A_Internal_Forces_in_Beams_and_FramesКогда вы смотрите на балку в целом (на рисунке ниже ), положительный сдвиг правой стороной вниз. Когда вы разрезаете балку, чтобы она находилась в статическом равновесии, положительный сдвиг должен быть направлен вверх справа, чтобы быть равным и противоположным общему движению.
Осевая (нормальная) сила
Осевая сила считается положительной, если она стремится сместить элемент в рассматриваемом сечении. Такая сила считается растягивающей, а элемент подвергается осевому растяжению. С другой стороны, осевая сила считается отрицательной, если она стремится раздавить элемент в рассматриваемом сечении. Такая сила считается сжимающей, а элемент находится в осевом сжатии.
Такая сила считается растягивающей, а элемент подвергается осевому растяжению. С другой стороны, осевая сила считается отрицательной, если она стремится раздавить элемент в рассматриваемом сечении. Такая сила считается сжимающей, а элемент находится в осевом сжатии.
Сила сдвига
Сила сдвига, стремящаяся сместить левую часть секции вверх или правую сторону секции вниз, считается положительной. Точно так же поперечная сила, имеющая тенденцию перемещать левую сторону сечения вниз или правую сторону вверх, будет считаться отрицательной поперечной силой.
Изгибающий момент
Изгибающий момент считается положительным, если он стремится вызвать вогнутость вверх (провисание). Если изгибающий момент имеет тенденцию вызывать вогнутость вниз (заклинивание), это будет считаться отрицательным изгибающим моментом.
Источник: Внутренние силы в балках и рамах, Либретексты. https://eng.libretexts.org/Bookshelves/Civil_Engineering/Book%3A_Structural_Analysis_(Udoeyo)/01%3A_Chapters/1. 04%3A_Internal_Forces_in_Beams_and_Frames
04%3A_Internal_Forces_in_Beams_and_Frames
Для решения внутренних сил в определенной точке балки,
Соглашение о положительном знаке адаптировано из https://eng.libretexts.org/Bookshelves/Civil_Engineering/Book%3A_Structural_Analysis_(Udoeyo)/01%3A_Chapters/1.04%3A_Internal_Forces_in_Beams_and_Frames
- Найти внешние силы и силы реакции
- Сделайте надрез.
- В FBD одной стороны разреза добавьте внутренние силы (и моменты), используя положительный знак.
- Используйте уравнения равновесия для решения неизвестных внутренних сил и моментов.
Пример: Для следующей распределенной нагрузки: а) что такое силы реакции? б) каковы внутренние силы в средней точке б) между силами реакции?
Адаптировано из: Источник: Engineering Mechanics, Jacob Moore, et al. http://mechanicsmap.psu.edu/websites/6_internal_forces/6-3_axial_torque_diagrams/axial_torque_diagrams.html1. Решите внешние силы:
Адаптировано из: Источник: Engineering Mechanics, Jacob Moore, et al. http://mechanicsmap.psu.edu/websites/6_internal_forces/6-3_axial_torque_diagrams/axial_torque_diagrams.html
http://mechanicsmap.psu.edu/websites/6_internal_forces/6-3_axial_torque_diagrams/axial_torque_diagrams.html [латекс]\сумма F_{X}=A_{x}=0[/латекс]
[латекс]\сумма F_{ y}=A_{y}+C-\omega L=0[/latex]
[латекс]\sum M_{A}=-(\omega L)\left(\frac{L}{2}\right) +d_{A C} C=0[/латекс] 92}{2 * (4 фута)} = 612,5 фунтов \text{ (+j направление)} $$
$$A_y = \omega*L- C = (100 \frac{lb}{ft})*(7 футов ) – 612,5 фунта = 87,5 фунта \text{ (направление +j) }$$
$$\underline{A_x = 0 \qquad A_y = 87,5 \text{ (+j )} \qquad C = 612,5 фунта \text{ ( +j )} }$$
2. Сделать разрез по В.
3. В FBD одной стороны разреза добавьте внутренние силы (и моменты), используя положительный знак.
4. Используйте уравнения равновесия для решения неизвестных внутренних сил и моментов.
Только для этой части сила интенсивности равна: F w = ( 100 фунтов/фут ) * ( 2 фута) = 200 фунтов и действует на расстоянии 1 фут слева, поэтому момент силы равен: M w = w * 2 фута * 1 фут = F w * 1 фут = (100 фунтов/фут) * (2 фута) * (1 фут) = 200 фут-фунт
$$\sum F_y = 87,5 фунта – 200 фунтов – V = 0 \\ V = -112,5 фунтов \text{ (- означает движение вверх, а не вниз)} $$
$$ \sum M_A = – (w * 2 фута) * (1 фут) – V * (2 фута) + M = 0 \\ M = (100 \frac{lb}{ft}) * 2 ft^2 + (-112,5 фунта) * (2 фута) \\ M = 200 футов \cdot lb – 225 футов \cdot lb \\ M = -25 ft \cdot lb \text{ (- указывает на движение в обратном направлении)} $$
$$\underline{N = 0 \qquad V = -112,5 фунтов \text{ (+j )} \qquad M = -25 футов \cdot lb \text{ (по часовой стрелке)} }$$
В основном : Внутренние силы (и моменты) для двумерной балки: поперечный, нормальный и изгибающий момент.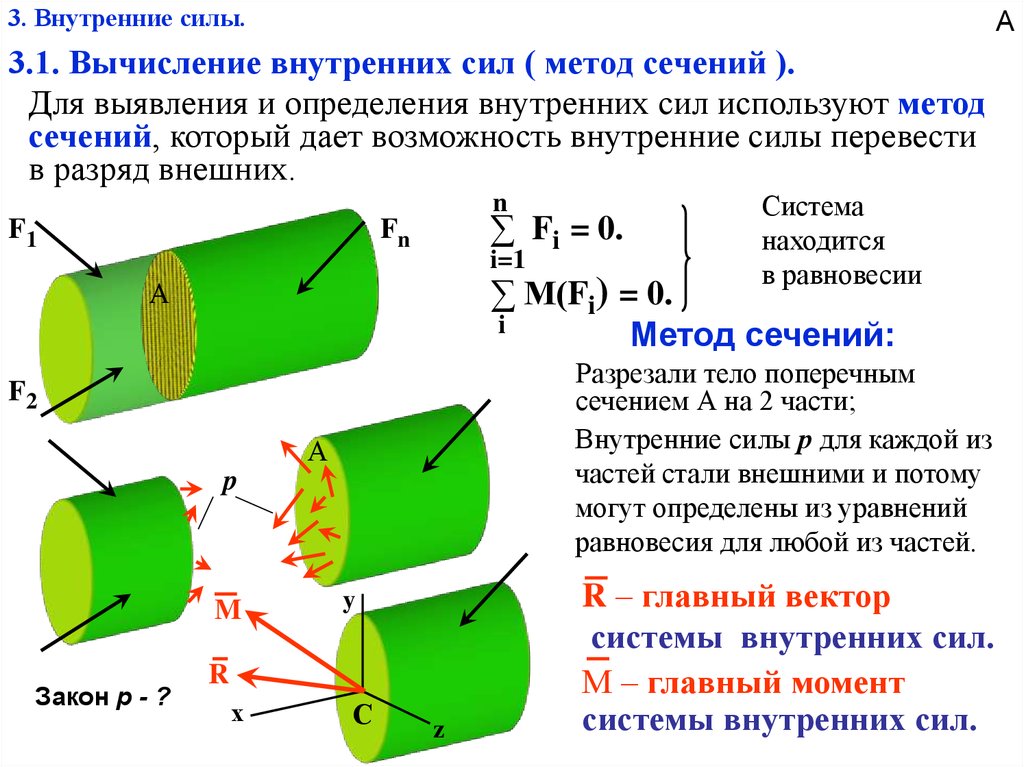 При выполнении разреза вдоль балки для определения внутренних сил следует использовать положительный знак: слева: сдвиг вниз, нормаль наружу, момент вверх.
При выполнении разреза вдоль балки для определения внутренних сил следует использовать положительный знак: слева: сдвиг вниз, нормаль наружу, момент вверх.
Применение : Мост, на который воздействуют различные нагрузки (от автомобилей, грузовиков, фонарных столбов и т. д.). Используйте этот метод для расчета внутренних нагрузок в конкретной интересующей точке.
Заглядывая вперед : В следующем разделе мы рассмотрим, как рассчитать внутреннюю силу по всей балке и отобразить результаты графически.
Внутренние силы — значение, типы, примеры, факторы наша повседневная жизнь. Силы можно разделить на две категории: внутренние и внешние силы. Когда определенные виды сил присутствуют и участвуют в воздействии на объекты, общая механическая энергия объекта изменяется. С другой стороны, какая-то сила никогда не может повлиять на полную механическую энергию объекта, а может только сместить энергию объекта с потенциальной на кинетическую или наоборот.
 Они называются внутренними силами и внешними силами. Внутренние силы могут изменить KE на PE. Суммарная работа внутренних сил всегда равна нулю.
Они называются внутренними силами и внешними силами. Внутренние силы могут изменить KE на PE. Суммарная работа внутренних сил всегда равна нулю. При действии на тело внешних сил внутри тела возникает система внутренних сил и внутренних моментов, противодействующих внешним силам. Внутренние силы и моменты необходимо понимать, чтобы понять, как тело будет деформироваться и не сломается ли оно под нагрузкой. В этой статье мы подробно изучим внутренние силы, факторы, от которых зависят внутренние силы, и различные примеры, с которыми мы сталкиваемся в нашей повседневной жизни.
Загрузить полные примечания к формуле расчета конструкций в формате PDF
Содержание
- 1. Что такое внутренние силы?
- 2. Типы внутренних сил
- 3. Внутренние силы Пример
- 4. Факторы, от которых зависят внутренние силы
- 5. Как действует внутренняя сила на систему?
Читать полностью
Что такое внутренние силы?
Внутренние силы — это силы, которыми обмениваются тела в системе.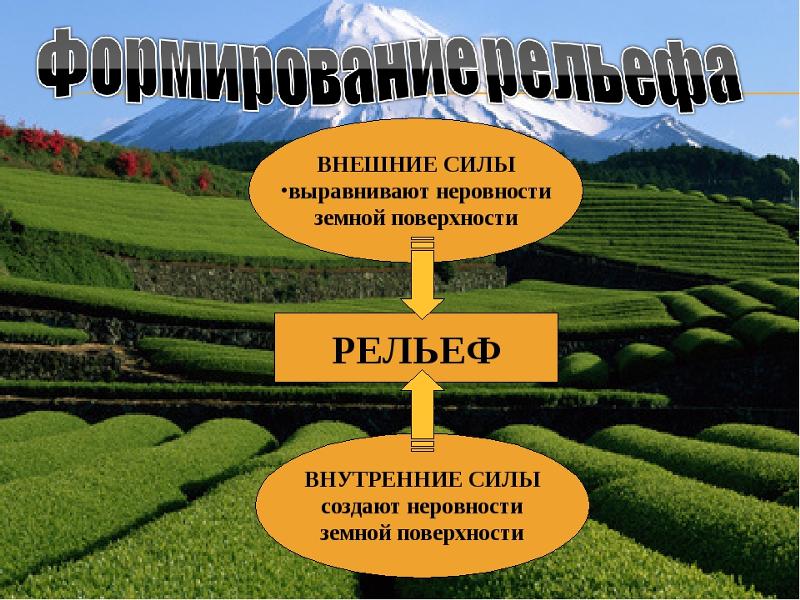 Внутренние силы могут вызывать ускорение в различных областях системы, но не могут вызывать ускорение в центре масс системы.
Внутренние силы могут вызывать ускорение в различных областях системы, но не могут вызывать ускорение в центре масс системы.
Внутренние силы Значение
Внутренние силы могут изменить энергию системы. Внутренние силы — это силы, удерживающие частицы тела вместе. Суммарная работа, совершаемая внутренними силами, не влияет на работу, совершаемую системой, так как всегда остается равной нулю.
Внутренние силы, действующие внутри объекта, не вызывают ускорение тела в состоянии покоя, но внутренние силы приводят к изменению энергии системы. Потенциальная или кинетическая энергия объекта преобразуется в механическую энергию за счет внутренней деятельности. Поскольку ускорение объекта из-за внутренних сил равно нулю, у объекта нет импульса; следовательно, работа, совершаемая системой, всегда равна нулю, и механическая энергия сохраняется. В результате внутренняя сила консервативна.
Типы внутренних сил
Сила, действующая изнутри тела, называется внутренней силой. Внутреннюю силу можно разделить на 4 типа в зависимости от реакции, происходящей внутри тела в системе:
Внутреннюю силу можно разделить на 4 типа в зависимости от реакции, происходящей внутри тела в системе:
- Сжатие: Сжатие — это сила сжатия, приложенная к материалу. Этот штамм часто укорачивает материалы. Например, сожмите в руке губку. Вы создаете сжатие.
- Напряжение: Напряжение — это сила, которая заставляет вещество растягиваться. Этот штамм часто удлиняет материалы. Например, возьмите в каждую руку по одному концу резинки. Начните разводить руки. Вы растягиваете эластичную ленту, создавая напряжение.
- Кручение: Кручение — это сила, которая скручивает или поворачивает. Например, крутящая сила кручения используется для отжима влажной тряпки для мытья посуды. Чтобы вытеснить воду, вы берете мочалку двумя руками и крутите ее в разные стороны.
- Гибка: Гибка — это процесс сгибания прямого материала в изогнутую форму. Одна сторона материала прижимается к другой (компрессия).
 Другая сторона расправляется (напряжение).
Другая сторона расправляется (напряжение). - Сдвиг: Две близлежащие силы толкают или тянут друг друга, но не противостоят друг другу напрямую. Раздвигая молекулы объекта в стороны, напряжение сдвига разрезает или разрывает его (например, ножницы, разрезающие ветку, резак для бумаги, разрезающий бумагу — ветка и бумага «подвергаются нагрузке сдвига»).
Пример внутренних сил
Когда ветер дует на дерево, оно раскачивается вперед и назад. Поскольку он исходит извне, сила ветра, действующая на дерево, считается внешней силой. С другой стороны, внутренняя сила удерживает дерево на месте и не дает ему упасть. Другой пример — когда края шкалы изгибаются при приложении к ним мышечной силы. В этом масштабе существует значительное напряжение и сжатие. Мышечная сила, действующая на весы, является внешней силой. Величина этой силы достаточно велика, чтобы согнуть, но не разрушить шкалу. Это потому, что он удерживается вместе внутренней силой, которая предотвращает его разрушение.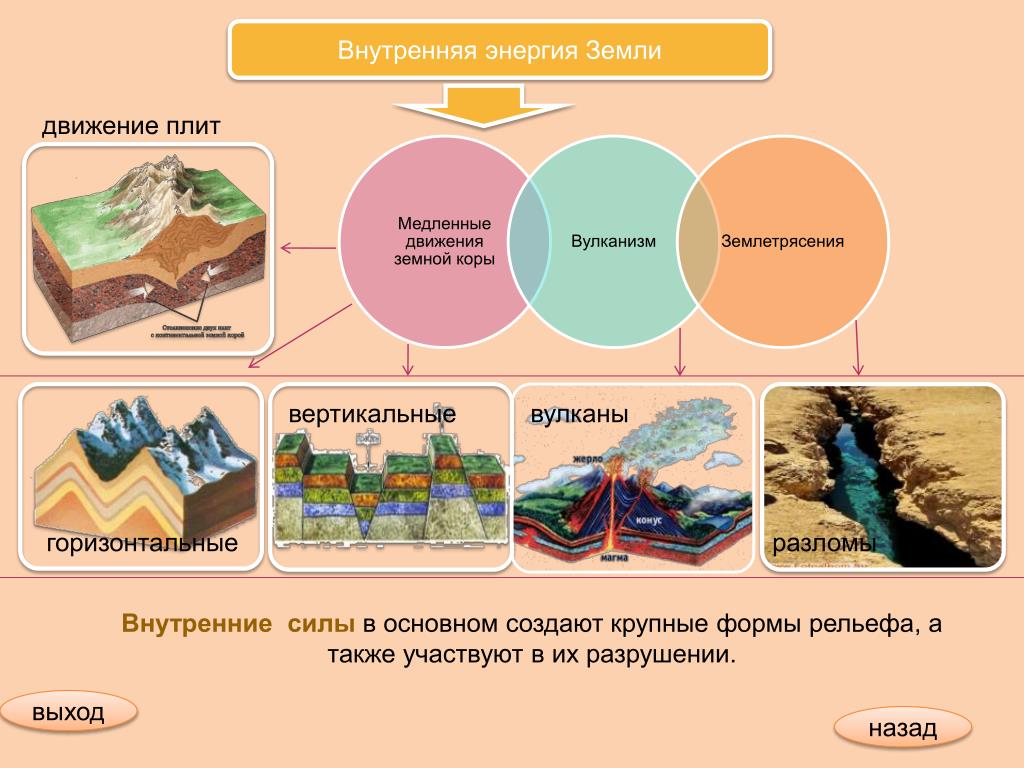
Когда автобус толкают изнутри, пока внутри находятся пассажиры, он не двигается. С другой стороны, автобус имеет тенденцию двигаться, когда пассажиры выходят и прикладывают усилие снаружи. Внешняя сила, которую прикладывают пассажиры, вызывает движение в автобусе. Толкающая сила пассажиров, сидящих внутри автобуса, не помогает транспортному средству двигаться, потому что пассажиры стали частью системы. Внутренняя сила – это сила, удерживающая систему от движения.
Когда к пружине прикладывается усилие для ее растяжения, пружина смещается. Внешняя сила – это сила, которая приводит в движение пружину. Внутренняя сила – это сила, стремящаяся сжать пружину и восстановить ее первоначальную форму. Внутренняя сила противодействует подвижности и любому изменению формы и диаметрально противоположна внешней силе.
Факторы, от которых зависят внутренние силы
Величина силы, воздействующей на тело, а также внутренние и внешние переменные являются факторами, от которых зависят как внутренние силы, так и внешние силы.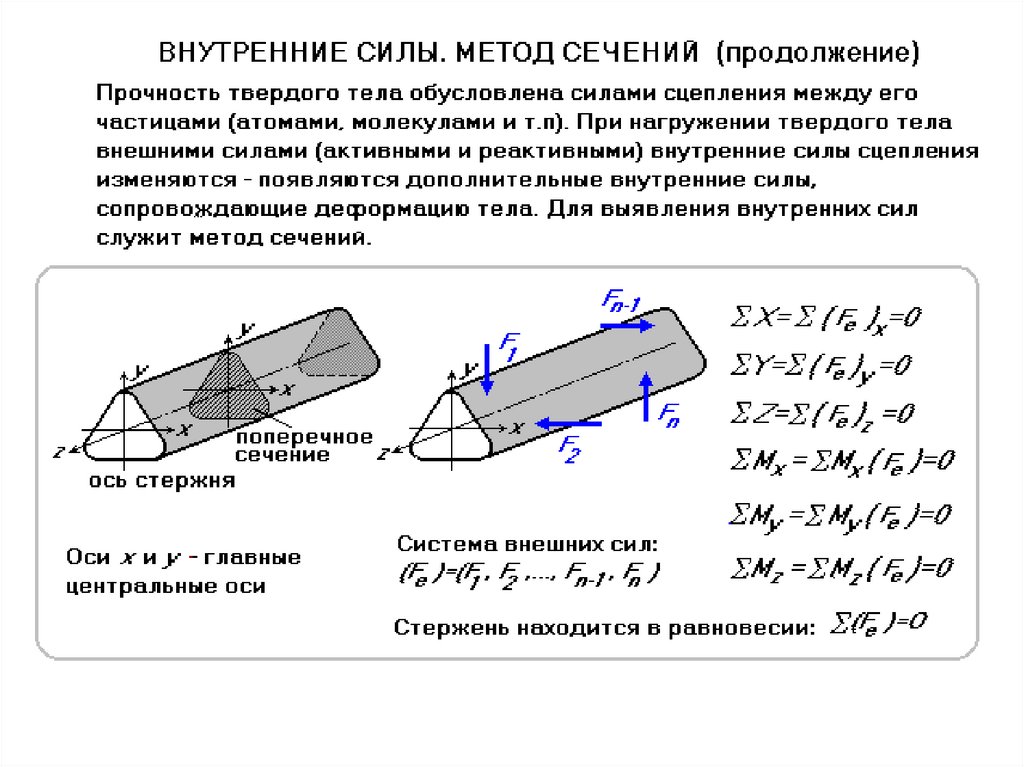 Важно знать, что чистая работа, выполняемая внутренними силами, инвариантна относительно системы отсчета, что означает, что она не изменится, даже если система отсчета изменится.
Важно знать, что чистая работа, выполняемая внутренними силами, инвариантна относительно системы отсчета, что означает, что она не изменится, даже если система отсчета изменится.
Дипольные моменты, внутреннее тепло системы, излучательная способность, температура системы и ее окружения, состав, вес, плотность, расстояние между молекулами, составляющими систему, движение частиц в системе, геометрия системы, молекулярный состав, ковалентные связи между атомами, количество свободных частиц и другие факторы влияют на внутренние силы в системе.
Как внутренняя сила действует на систему?
Внутренние силы в системе действуют противоположно, компенсируя друг друга и приводя к нулевому выходу. Внутренние силы, по-видимому, в первую очередь противодействуют изменениям, вызванным внешними силами или в ответ на внешние факторы, такие как взаимодействие электрического поля, магнитного поля или изменение температуры.
Когда на проводник воздействует электрическое поле, заряженная частица движется по спирали, но не вызывает внешних изменений предмета и не ускоряет центр масс. Из-за вращения электрической частицы магнитное поле создается движением заряженной частицы. Когда материал с магнитными свойствами помещается в магнитное поле, диполи располагаются в направлении поля. Линии внутреннего магнитного потока заставляют магнитные спиновые диполи выравниваться вслед за полем.
Из-за вращения электрической частицы магнитное поле создается движением заряженной частицы. Когда материал с магнитными свойствами помещается в магнитное поле, диполи располагаются в направлении поля. Линии внутреннего магнитного потока заставляют магнитные спиновые диполи выравниваться вслед за полем.
Часто задаваемые вопросы о внутренних войсках
-
Что вы подразумеваете под внутренними силами?
Внутренние силы — это силы, испытываемые или прикладываемые телом внутри системы. Внутренние силы не изменяют ускорение системы. Внутренние силы консервативны по своей природе.
-
Как найти внутреннюю силу?
Чтобы рассчитать внутренние силы, сначала нарисуйте диаграмму свободного тела всей системы, найдите опорные реакции (внешние силы) и оставьте все нагрузки в их исходных положениях. В точке, где должны быть определены внутренние нагрузки, разрежьте элемент перпендикулярно его оси. Затем строится диаграмма свободного тела разреза для определения внутренних сил с использованием уравнений статического равновесия.

-
Различают внутренние и внешние силы?
В случае внутренних сил, поскольку в системе нет движения, центр масс системы неподвижен. В то время как для внешних сил по мере того, как система набирает обороты из-за внешних воздействий, центр тяжести массы изменяется с течением времени. Энергия переносится в виде механической энергии во внутренних силах, но преобразуется в потенциальную или кинетическую энергию в случае внешних сил. Внутренние силы, действующие внутри системы, действуют в противоположных направлениях, компенсируя друг друга и приводя к тому, что в системе не совершается чистая работа. Внешние силы действуют в направлении приложенной силы, и совершается работа.
-
Каковы 5 основных типов внутренних сил?
5 основных типов внутренних сил:
- Сдвиг
- Изгиб
- Скручивание
- Сжатие
- Растяжение.
-
Почему внутренние силы всегда уравновешены?
Если внутренние силы в системе не уравновешены, они вызовут деформацию тела.
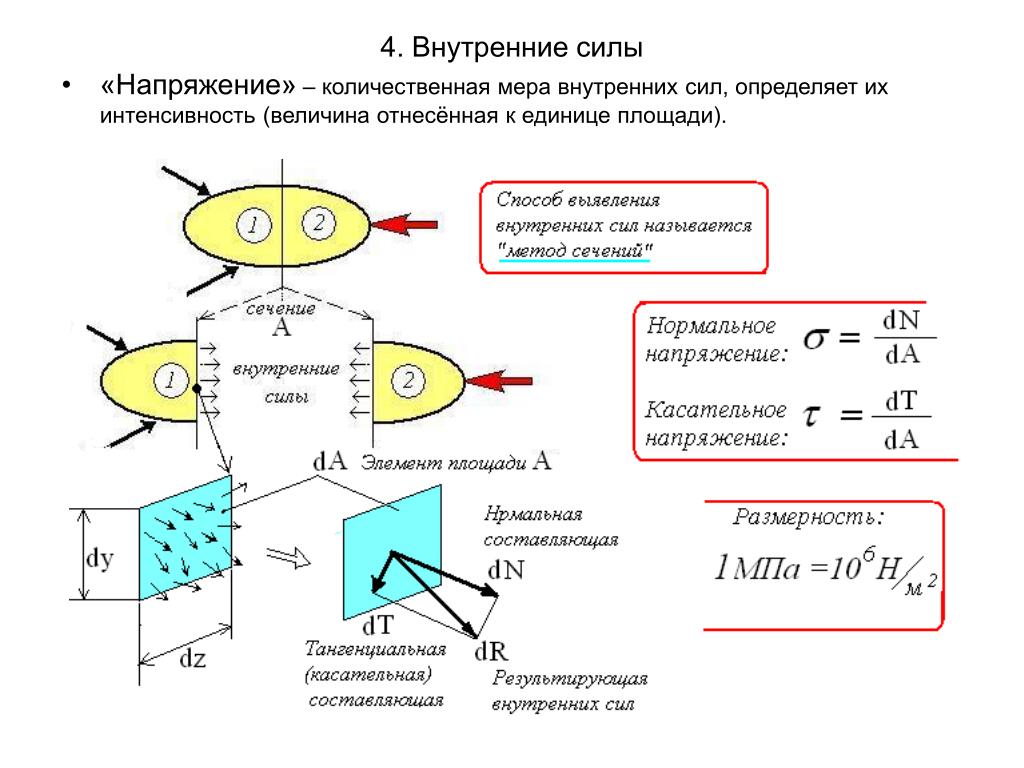



 Н. Работнов. Сопротивление материалов. М.: Физматгиз, 1963. — 456 с.
Н. Работнов. Сопротивление материалов. М.: Физматгиз, 1963. — 456 с.