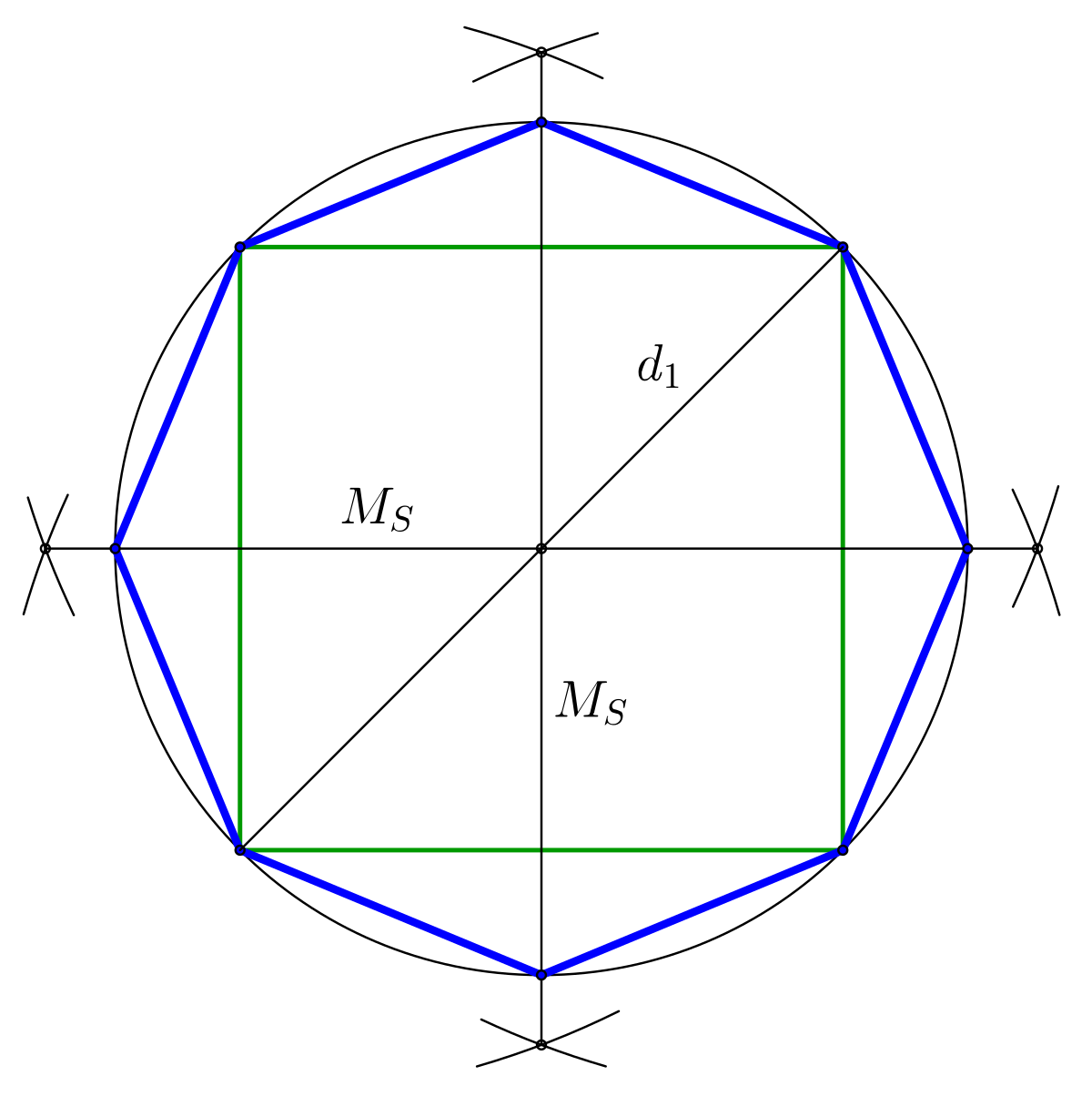
Восьмиугольник климова: «профессия: выбираем вместе»

Опубликовано автором

Содержание

«профессия: выбираем вместе»


Занятия по теме
«ПРОФЕССИЯ: ВЫБИРАЕМ ВМЕСТЕ»

Материалы для классного руководителя.

П р е д в а р и т е л ь н а я б е с е д а.

Выбор профессии для современного школьника несколько отличается от выбора профессии десять-пятнадцать лет назад. Сейчас на вопрос «Кем быть?» практически невозможно ответить один раз. К нему можно (и нужно!) возвращаться в течение всей жизни. Ситуация вокруг нас стремительно меняется, и, чтобы не отстать или не остановиться на месте, нужно постоянно оглядываться, переосмысливать свою деятельность, свое место в происходящем вокруг.

За ответом на вопрос «Кем быть?» стоит множество других важных жизненных выборов. Все мы знаем, что зачастую профессия выбирается не только (и не столько) как род занятий, но и как определенный образ, стиль жизни, возможность получить определенный статус в обществе. Престижность тех или иных профессий меняется с течением времени вместе с изменением общественного сознания.

Так, пару десятилетий назад большим уважением пользовались специалисты интеллектуального труда, или «люди нау-ки», – инженеры-проектировщики, научные сотрудники и т. д. Важно отметить, что престижность профессии не обязательно совпадает с ее востребованностью на рынке труда. Так, профессии, которые уже много лет и до сегодняшнего дня считаются «элитными», – юрист, экономист и др. – далеко не самые востребованные. А специальности, которые на самом деле нужны обществу – рабочие, младший медицинский персонал, педагоги – успехом у современной молодежи не пользуются.

Итак, профессиональное самоопределение – это и определение собственного будущего в широком смысле этого слова. Сделать такой выбор самостоятельно старшекласснику достаточно сложно. Поэтому очень важно, чтобы находящиеся рядом с ним взрослые (психологи-профконсультанты, педагоги, родители) могли оказать ему в этом ненавязчивую, но компетентную помощь. К сожалению, очень часто помощь родителей сводится к советам поступать в конкретное учебное заведение или даже к личному давлению, а педагоги признают, что мало чем могут помочь школьникам, так как сами не очень разбираются в современном рынке труда.

Данные материалы призваны помочь педагогам, в особенности классным руководителям, в организации содействия учащимся 8–11 классов в планировании собственной карьеры, собственного будущего. В нем представлены разработки девяти занятий. Это могут быть классные часы, факультативные или кружковые занятия.

В содержание каждого занятия включен информационный блок, вопросы или проблемы для обсуждения с учащимися, практические упражнения или несложные тестовые методики, которые сделают занятия более интересными и динамичными. Данные занятия классный руководитель может проводить как в сотрудничестве со школьным психологом, так и самостоятельно, дополняя их собственными творческими находками. Успехов вам!

Поделитесь с Вашими друзьями:

Видеоуроки «Основы выбора профессии» | Профориентир

Выбор профессии – это шаг, который определяет взрослую жизнь каждого человека. Какую профессию выбрать и как быть востребованным на рынке труда в будущем? Какая профессия принесет и удовольствие, и финансовое благополучие? Для того чтобы подросток смог ответить на эти вопросы, мы предлагаем посмотреть три видеоурока «Основы выбора профессии» для школьников и их родителей.

Онлайн формат профориентации поможет в выборе профессии и образования, самопознании и саморазвитии, расширит кругозор. Родители смогут выступить для обучающихся в разных ролях:

  • организатор — планирует время, привлекает ресурсы и создает необходимые условия для просмотра видеоуроков, разрешает возникающие проблемы технического характера наставника;
  • координатор — обеспечивает эффективное взаимодействие всех лиц, участвующих в просмотре, обсуждении и решении практических заданий;
  • консультант — отвечает на вопросы и обеспечивает доступ к дополнительным ресурсам;
  • эксперт — дает аналитическую оценку результатов совместной работы, опираясь на собственную компетентность;
  • наставник — помогает в решении проблем и преодолении препятствий, имеющих личностный характер, поощряет, поддерживает процессы самообучения и самоопределения, задает вопросы и организует обсуждение;
  • мастер — обучает, демонстрируя образцы собственной деятельности и свои компетенций.

Совместный просмотр видеороликов и решение практических заданий не только объединяет семью, находящуюся в самоизоляции, но и позволяет обсудить важный для старшеклассника вопрос: «Кем стать? Куда пойти учиться».

Первый видеоурок ориентирован на структурирование информации о мире профессий, знакомство с классификацией профессий Е. А. Климова.

Второй видеоурок «Основы выбора профессии» посвящен алгоритму выбора профессии «ХОЧУ. МОГУ. НАДО» (Е. А. Климов). В основе профессионального успеха, удовлетворённости работой лежат три компонента — желание человека заниматься выбранным делом («хочу: интересы, склонности, профессиональные и карьерные предпочтения»), его способность выполнять данную работу («могу: личностные особенности человека, в т.ч. способности, темперамент и др.») и востребованность этого вида деятельности на рынке труда («надо: состояние рынков образовательных услуг и труда, востребованность профессии»).

Даются рекомендации по изучению интересов, мотивов выбора, темперамента и других индивидуальных особенностей обучающихся, учет которых позволяет сделать правильный предварительный или окончательный профессиональный выбор.

В третьем видеоуроке рассматриваются факторы выбора профессии, описанные Е. А. Климовым («восьмиугольник Климова»). Главная задача обучающегося – тщательно проанализировать все эти факторы вместе с родителями, близкими и принять самостоятельное решение. Практическое задание по разработке критериев выбора и анализу выбранной профессии в соответствии с ними направлено на осознание готовности обучающегося к выбору.

Четвертый – путеводитель по профориентационному порталу Кузбасса «Профориентир», ведь все практические задания видеоуроков связаны с использованием данного ресурса. Так обучающиеся в разделе «Тестирование» проходят тесты с получением результатов, необходимых для самопознания и соотнесения требований профессии к человеку с индивидуальными особенностями, возможностями. Для решения задач самоисследования профессии важен раздел «Профессии» и ряд подразделов, включающих профессиограммы, востребованные профессии в регионе и другие.
Таким образом, изучение материалов четырех видеороликов поможет обучающимся совместно с родителями, близкими составить для себя «идеальную формулу профессии», понять, какая профессия соответствует Вам!

Человек и выбор жизненного пути — ОБЩЕСТВОЗНАНИЕ — ОТКРЫТЫЙ УРОК — РЕФЕРАТЫ

Цель урока:
-знакомство с миром современных профессий;
-формирование ответственного отношения к проблеме жизненного выбора;
-изучение личностных качеств с помощью тестирования.
7. Оборудование:
-анкеты для тестирования по методике Йовайши
-мультимедийное оборудование
8. Ход урока
План урока
1.Мир современных профессий.
2.Что влияет на выбор профессий
3. Интересы и склонности.
4. Способности. Профессиональная пригодность.
5. Ошибки в выборе профессии.

1. Проверка домашнего задания.
Вопросы:
1.Что такое культура?
2.Какими путями человек приобщается к культуре?
3.Можно ли утверждать, что культура это – духовная деятельность, духовное производство и духовное потребление? Ответ обоснуйте.
4.Что такое массовая культура? В чем проявляется негативное воздействие на человека массовой культуры?

2. Изучение нового материала
Слово учителя: Выбор профессии сегодня во многом определяет все жизненные выборы человека, за этим стоит определенный образ, стиль жизни, возможность получить определенный статус в обществе.
Информация о современных профессиях не является статичной. Каждый год происходит обновление около 500 видов труда. Но чтобы найти подходящий род занятий, не обязательно перебирать конкретные специальности. Можно начать с широкого выбора – определения профессиональной области, отрасли.
Наиболее распространенной является классификация профессий, предложенная академиком Е.А.Климовым. Он выделяет пять типов профессий в соответствии с предметом труда.
1) Человек – природа. Представители этого типа имеют дело с растительными и животными организмами, микроорганизмами, условиями их существования. Что касается необходимых личностных качеств, то человек должен быть спокойным, уравновешенным, обладать терпением, способностью к кропотливому труду.
2) Человек – техника. Обладатели профессий данного типа имеют дело с неживыми, техническими объектами труда. От работника требуется точность, определенность действий, а также практическое мышление человека – техническая фантазия, способность мысленно разъединять и соединять технические объекты и их части.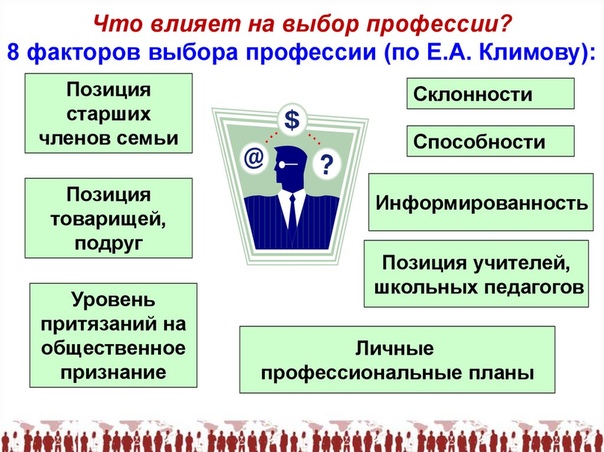
3) Человек – человек. Предметом интереса специалистов данного типа профессий являются социальные нормы, сообщества, группы людей разного возраста. Главное содержание – взаимодействие между людьми. Качества, необходимые для работы с людьми: устойчивое хорошее настроение во время работы с людьми, потребность в общении, способность мысленно ставить себя на место другого человека, быстро понимать состояние другого, терпение.
4) Человек – знаковая система. Представителей профессий данного типа интересуют различные языки, условные знаки, схемы, символы, цифры, формулы, информация. Специалисту, который работает со знаками, важно уметь с одной стороны, отвлечься, абстрагироваться от реальных свойств предметов, суметь представить их сущность схематически. Здесь важны такие качества, как внимание, умение сосредоточиться, терпимость к монотонной, иногда даже рутинной работе.
5) Человек – художественный образ. Данные специалисты работают с явлениями, фактами художественного отображения действительности, или сами создают эти факты, новые образы. Специфические требования, которые предъявляются к профессиям данного типа, — наличие задатков к определенному виду творчества, творческое воображение, образное мышление, трудолюбие.
3. Вопросы для обсуждения:
-К каким типам профессий относятся следующие профессии: менеджер по продажам, патологоанатом, гид-переводчик, зубной техник.
4. Продолжение изучения нового материала.
Учитель: ни один выбор в нашей жизни мы не совершаем самостоятельно. Главная задача при этом – учесть все факторы и принять грамотное, самостоятельное решение. Е.А. Климов описал следующие восемь факторов выбора профессии («восьмиугольник Климова»).
1) Наличие склонностей. Если человеку нравится организовывать других людей, занимать лидирующие позиции, скорее всего ему подойдут профессии, связанные с умением работать с коллективом.
2) Наличие способностей.
3) Притязания. Во многом влияют установки и ценности человека, то есть то, что для него имеет первостепенное значение в данный период жизни или важно в качестве основной жизненной цели.
4) Мнение родителей, семьи.
5) Мнение сверстников.
6) Личный профессиональный план, т.е. то, что человек предполагает делать в будущем, каким хочет быть, кем быть, чего хочет достичь.
7) Знания о профессии.
8) Потребности общества.
Вопрос для обсуждения: К каким последствиям может привести игнорирование тех или иных факторов?
Начать выбор профессии следует с ответа на вопрос: что мне по настоящему интересно?
Интерес – специфическая направленность личности на определенный предмет, сосредоточенность на нем мыслей, вызывающая стремление ближе ознакомиться с ним, глубже в него проникнуть, не упускать его из поля зрения. Интерес порождает склонность или переходит в нее. Если интерес – это направленность на определенный предмет, то склонность – направленность на соответствующую деятельность. Наличие интересов означает «хочу знать», склонность – «хочу сделать». Определить свои интересы и склонности можно путем наблюдения за собой, анализа своих интересов, хобби, бесед, и с помощью тестов.
Один из них вам и предлагается.
5. Работа по методике Йовайши
6. Продолжение изучения нового материала.
Учитель: но кроме собственных интересов следует учитывать и свои способности.
Способности – индивидуально-психологические особенности человека, ведущие к успешному овладению определенной деятельностью, но не сводимые к знаниям, умениям и навыкам, которые у него уже есть. (Б.Т. Теплов)
С помощью общих способностей человек может достичь успеха в широком смысле. (Умственные, речевые, мнемические и т. д.). Специальные способности определяют успехи человека в отдельных, конкретных видах деятельности.
Профессиональная пригодность складывается из способностей, личностных особенностей человека, отсутствия медицинских противопоказаний. Если отсутствует какой-либо компонент, то есть два пути – либо корректировать свой выбор, либо развивать недостающие качества.
Учитель: типичные ошибки в выборе профессии:
— отношение к выбору профессии как окончательному и пожизненному;
— предрассудки, когда некоторые важные для общества профессии считаются недостойными;
— «за компанию»;
— перенос отношения к представителю какой-нибудь профессии на саму профессию;
— увлечение только внешней стороной профессии;
— низкая информированность о мире профессий;
— влияние престижности;
— несамостоятельность выбора;
— отождествление школьного предмета с соответствующей профессией;
— устаревшие представления;
— незнание своих физических особенностей;
— незнание основных мероприятий и порядка решения задач при выборе профессии.
Но кроме знаний о своей личности, нужно еще учитывать окружающую действительность, а именно рынок труда. Он предъявляет достаточно высокие требования к специалистам, а именно:
— необходимость постоянного обучения;
— увеличение требований к профессионализму работников;
— распространение гибких форм занятости.
Данные обстоятельства позволяют предположить, что у каждого человека есть в большей или меньшей степени выраженные предпосылки для удачного выбора профессии.
Домашнее задание: составить перечень тех навыков, умений, личностных качеств, которые уже есть сейчас и которые могут пригодиться для будущей профессиональной деятельности.

ПРОФЕССИОНАЛЬНОЕ САМООПРЕДЕЛЕНИЕ УЧАЩИХСЯ Педагог-психолог Пономаренко И В

ПРОФЕССИОНАЛЬНОЕ САМООПРЕДЕЛЕНИЕ УЧАЩИХСЯ. Педагог-психолог Пономаренко И. В.

Твоя профессиональная карьера

Для правильного выбора профессии необходимо знать: Свои профессиональные интересы, склонности, способности… Найти профессию, которая подходит к твоим индивидуально-психологическим особенностям и возможностям

Формула успешного выбора профессии: ХОЧУ МОГУ НАДО

Формула успешного выбора профессии: «ХОЧУ» n Профессиональные интересы и склонности

Формула успешного выбора профессии: n «МОГУ» Состояние здоровья n Профессиональная квалификация n Профессиональные способности

Формула успешного выбора профессии: «НАДО» n Спрос на рынке труда и возможность трудоустройства

3 группы ошибок, допускаемых при выборе профессии: незнание самого себя; n незнание мира профессий; n незнание правил выбора профессии. n

Два способа выбора профессии: метод проб и ошибок; n изучить свои особенности , ознакомиться с миром профессий, соотнести требования профессии со своими особенностями n

«ВОСЬМИУГОЛЬНИК» ОСНОВНЫХ ФАКТОРОВ ВЫБОРА ПРОФЕССИИ (ПО Е. А. КЛИМОВУ) склонности мнение родителей информированность уровень притязаний мнение товарищей способности потребности рынка ЛПП

«Человек –Техника» Это профессии, связанные с обслуживанием техники, её ремонтом, установкой и наладкой, управлением, в том числе и управлением подъёмных и транспортных средств.

«Человек – Человек» Труд людей этих профессий направлен на воспитание и обучение, информирование, бытовое, торговое, медицинское обслуживание людей. Он связан с управлением, руководством людьми или коллективами.

«Человек-Природа» Если деятельность человека связана с природой, прежде всего растительные и животные организмы, микроорганизмы. Вот несколько профессий: микробиолог, рыбовод, ветеринарный фельдшер, оператор мехнизированных комплексов, цветовод.

«Человек-Знаковая система» Объектом труда человека выступают различные знаки: устная и письменная речь, цифры, химические и физические символы, ноты, схемы, карты, графики, рисунки, дорожные знаки и т. п.

«Человек – Художественный образ» Многим из вас нравятся профессии связанные с изобразительной, музыкальной, литературно-художественной и актёрской деятельностью.

Посещение занятий «Психология профессионального самоопределения» поможет: n n n Повысить твой уровень профессиональной зрелости n Узнать, какая профессия тебе подходит Избежать ошибок и принять верное решение Узнать профессии, пользующиеся спросом на рынке труда

Выбор профиля обучения – это выбор жизненного пути. Сделай правильный выбор!!!

Магомед Исмаилов победил Александра Емельяненко на турнире по смешанным единоборствам в Сочи

Александр Емельяненко и Магомед Исмаилов. Фото АСА

25 июля, Минск /Корр. БЕЛТА/. Российский боец ММА Магомед Исмаилов победил своего соотечественника Александра Емельяненко на турнире по смешанным единоборствам АСА 107, который прошел в Сочи, сообщает корреспондент БЕЛТА.

С начала противостояния Магомед Исмаилов ринулся в атаку, нанес своему сопернику несколько точных ударов в голову, после чего броском перевел оппонента в партер. Там он попытался завершить поединок досрочно, однако это ему не удалось. Александр Емельяненко защищался и даже попытался провести болевой на руку, который не увенчался успехом. Магомед Исмаилов попытался добить соперника, но конец первой пятиминутки помешал его планам.

Во втором раунде ситуация повторилась: Магомед Исмаилов нанес серию точных ударов и бросил соперника на настил восьмиугольника, продолжив прессинговать.

Третья пятиминутка прошла также под инициативой Магомеда Исмаилова. Проведя эффектный бросок, он пытался закончить поединок досрочно, что ему удалось незадолго до окончания боя. Рефери зафиксировал технический нокаут.

Интересно, что Магомед Исмаилов весит на 22 кг меньше своего оппонента. Его профессиональный рекорд на данный момент составляет 16 побед, два поражения и одна ничья. У Александра Емельяненко в списке 28 викторий, восемь неудач и одна ничья.-0-

Александр Климов Статистика ММА, изображения, новости, видео, биография

Александр Климов Статистика ММА, изображения, новости, видео, биография — Sherdog.com БОЛЬШЕ НА НАШИХ КАНАЛАХ

Россия
ВОЗРАСТ НЕТ / НЕТ
ВЫСОТА 0’0 « / 0 см
ВЕС 0 фунтов / 0 кг

Побед 0

КО / ТКО

0

0%

ПРЕДСТАВЛЕНИЯ

0

0%

РЕШЕНИЯ

0

0%

Убытки 1

КО / ТКО

1

100%

ПРЕДСТАВЛЕНИЯ

0

0%

РЕШЕНИЯ

0

0%

ОПРОС

Планируете ли вы купить сегодня вечерний UFC с оплатой за просмотр?

{имя} {«ник»} {фамилия}
{имя} {«ник»} {фамилия}
{name} — {title}

Monitoring_string = «5eb5a0f65cbe346d74f978e14db1b00d»

Сергей Булгаков, Санкт-Петербургская академия наук.Албан и преподобный Сергий, интеркоммунион и софиология

Творец Гефферт, Брин, 1967-
Название Сергий Булгаков, братство св. Албана и преп. Сергия, интеркоммунион и софиология
Аннотация Сергий Булгаков и Георгий (Георгий) Флоровский — возможно, два самых влиятельных русских богослова двадцатого века — порезали свои богословские зубы во время работы в 1920-х и 1930-х годах в Братстве святых Албана и Сергия.История Братства показывает, в какой степени русское богословие ХХ века было информировано и определялось своим взаимодействием с англиканским богословием, и демонстрирует серьезность (и сложность), с которой русские православные эмигранты в Западной Европе подошли к вопросу об отношении православия к другим конфессиям. . Предложение Булгакова 1933 года о причастии вызвало остроту вопросов об отношении русского православия к теологическому развитию, которое долгое время поглощало русских православных эмигрантов, и усилило политические и богословские разногласия между интеллектуалами на Западе и их более консервативными коллегами-эмигрантами на Балканах.Более того, рассмотрение предложения Булгакова проливает новый свет на его «софиологию» — приверженность, которая во многом определяла его жизнь и творчество, и идеал, который его критики сочли слишком романтичным и находящимся под влиянием «западнических» тенденций, ставящих под сомнение русских. Уникальная приверженность Православия «Истине».
Дата публикации 1 июня 2004 г.
Идентификатор (DOI) 10.10 80/09546540410001677704
Цитирование Гефферт, Брин. «Сергий Булгаков, братство святых Албана и Сергия, интеркоммунион и софиология». Революционная Россия 17.1 (2004): 105-141.
Языки Английский, русский
Издание Окончательная версия автора
Жанр Статьи
Тема Булгаков, Сергей Николаевич, 1871-1944 гг.
Тема Флоровский, Жорж, 1893-1979 гг.
Тема Братство св.Албан и преподобный Сергий
Тема Православная Восточная Церковь — Доктрины
Тема Мудрость (библейское олицетворение)
Часть Октагон Амхерстского колледжа
Репозиторий Октагон Амхерстского колледжа
Права Лицензия Creative Commons Attribution-NonCommercial-NoDerivatives (CC BY NC ND 4.0)

% PDF-1.6 % 463 0 объект > эндобдж xref 463 158 0000000016 00000 н. 0000004785 00000 н. 0000004970 00000 п. 0000005099 00000 н. 0000005135 00000 п. 0000005540 00000 н. 0000005713 00000 н. 0000005860 00000 н. 0000005989 00000 п. 0000006138 00000 н. 0000006268 00000 н. 0000006418 00000 н. 0000006549 00000 н. 0000006698 00000 н. 0000006827 00000 н. 0000006978 00000 п. 0000007108 00000 н. 0000007257 00000 н. 0000007388 00000 н. 0000007537 00000 н. 0000007667 00000 н. 0000007797 00000 н. 0000007946 00000 н. 0000008076 00000 н. 0000008223 00000 п. 0000008353 00000 п. 0000008502 00000 н. 0000008632 00000 н. 0000008763 00000 н. 0000008911 00000 н. 0000009042 00000 н. 0000009191 00000 п. 0000009322 00000 н. 0000009469 00000 н. 0000009600 00000 н. 0000009731 00000 н. 0000009860 00000 н. 0000009989 00000 н. 0000010118 00000 п. 0000010267 00000 п. 0000010487 00000 п. 0000010636 00000 п. 0000010814 00000 п. 0000010965 00000 п. 0000011345 00000 п. 0000011382 00000 п. 0000011892 00000 п. 0000012092 00000 п. 0000015097 00000 п. 0000015303 00000 п. 0000015716 00000 п. 0000015911 00000 п. 0000016444 00000 п. 0000016805 00000 п. 0000016872 00000 п. 0000017068 00000 п. 0000017606 00000 п. 0000017800 00000 п. 0000020619 00000 п. 0000020864 00000 п. 0000021062 00000 п. 0000021446 00000 н. 0000024347 00000 п. 0000024562 00000 п. 0000024665 00000 п. 0000025115 00000 п. 0000025288 00000 п. 0000025699 00000 н. 0000026121 00000 п. 0000026473 00000 п. 0000026893 00000 п. 0000027795 00000 п. 0000029758 00000 п. 0000030223 00000 п. 0000030919 00000 п. 0000031051 00000 п. 0000031961 00000 п. 0000032156 00000 п. 0000033837 00000 п. 0000035521 00000 п. 0000035693 00000 п. 0000037317 00000 п. 0000039048 00000 н. 0000040712 00000 п. 0000041017 00000 п. 0000041410 00000 п. 0000041586 00000 п. 0000041799 00000 н. 0000044090 00000 п. 0000044286 00000 п. 0000044819 00000 п. 0000046415 00000 п. 0000047966 00000 п. 0000050659 00000 п. 0000057531 00000 п. 0000058867 00000 п. 0000058969 00000 п. 0000059145 00000 п. 0000061261 00000 п. 0000061459 00000 п. 0000062024 00000 п. 0000062086 00000 п. 0000062377 00000 п. 0000062562 00000 н. 0000062973 00000 п. 0000063033 00000 п. 0000063250 00000 п. 0000063447 00000 п. 0000063861 00000 п. 0000063989 00000 п. 0000065041 00000 п. 0000065239 00000 п. 0000065726 00000 п. 0000066261 00000 п. 0000066377 00000 п. 00000

00000 п. 00000 00000 н. 00000 00000 п. 00000 00000 п. 00000 00000 п. 00000 00000 п. 0000146462 00000 н. 0000146501 00000 н. 0000147457 00000 н. 0000147510 00000 н. 0000147572 00000 н. 0000147661 00000 н. 0000147767 00000 н. 0000158494 00000 н. 0000158557 00000 н. 0000158730 00000 н. 0000158828 00000 н. 0000158928 00000 н. 0000159040 00000 н. 0000159153 00000 н. -% T> J ៭ vE6 , j8 (0y (scU’9tSn6d & Fb

Российские пары завершили зачистку на чемпионате Европы

СТОКГОЛЬМ — Россияне Юко Кавагути и Александр Смирнов выиграли золото на чемпионате Европы по фигурному катанию в воскресенье, возглавив российский чемпионат по фигурному катанию.

Ксения Столбова и Федор Климов завоевали серебро, а Евгения Тарасова и Владимир Морозов завоевали бронзу в своем дебютном матче на чемпионате Европы.

Кавагути и Смирнов сильно открыли пары тройным-тройным и еще больше повысили технический уровень с помощью четверного Сальхова.

«Наконец-то мы сделали то, что должны сделать, что можем», — сказал Кавагути.

Произвольная программа под отрывки из Симфонии Манфреда Чайковского объединила мелодраму с моментом комедии, когда фигуристы, кажется, ссорятся, Кавагути отворачивается, пренебрегая жестом, а Смирнов топает в отчаянии с преувеличенной гримасой.

Симфония концертно исполняется сравнительно редко, и Кавагути призналась, что изначально она ей не нравилась, но тренер Тамара Москвина настаивала на этом.

Так вот, она сказала: «Это я … Мне не нужно надевать какую-то маску».

Столбова и Климов, серебряные призеры Олимпийских игр, заняли первое место после короткой программы, но их произвольная программа была затруднена почти с самого начала: вращения и прыжки не синхронизировались. Проблемы достигли апогея ближе к завершению программы, когда Климов, катаясь позади Столбовой, положив руки ей на плечи, зацепился за палец и тяжело упал.

«Это был худший ролик в сезоне», — сказал он. «Медаль не вызывает особой радости».

Разочарование усугублялось его неуверенностью в том, почему дела пошли плохо. «Нет причин. На практике и раньше все было хорошо», — сказал он.

Тарасова и Морозов начали день пятыми, но поднялись из-за их собственного сильного катания и ошибок промежуточных пар, особенно когда француженки Ванесса Джеймс и Морган Сипрес отказались от попытки поднять.

Старт пятого места стал для россиян большим преимуществом.

«Сегодня мы почувствовали себя намного спокойнее, потому что нам было нечего терять», — сказала Тарасова. «Мы не нервничали, и нам удалось сделать почти все, что мы намеревались сделать».

Подиум в парном разряде стал для России вторым на чемпионате. Днем ранее женские медали завоевали Елизавета Туктамышева, Елена Радионова и Анна Погорилая.

состояний экстремальной поляризации

состояний экстремальной поляризации

Список литературы

  • Гуннар Бьорк, Маркус Грассл, Пабло де ла Ос, Герд Леухс и Луис Л.Санчес-Сото,
    «Звезды квантовой Вселенной: экстремальные созвездия на сфере Пуанкаре»,
    Physica Scripta , т. 90, № 10, сентябрь 2015 г., 108008.
    DOI: 10.1088 / 0031-8949 / 90/10 / 108008
  • G. Björk, AB Klimov, P. de la Hoz, M. Grassl, G. Leuchs, LL Sánchez-Soto,
    «Экстремальные квантовые состояния и их созвездия Marjorana»,
    Physical Review A , vol. 92, no. 3, сентябрь 2015 г., 031801 (R).
    DOI: 10.1103 / PhysRevA.92.031801
    arXiv: 1502.03446 [квант-ph]

Общие замечания

Ниже мы приводим явные примеры созвездий для экстремальные, неполяризованные, чистые состояния для S = 1 от до S = 10 , что соответствует до N = 2 до N = 20 фотонов. Для всех примеров степень неполяризации M , т.е. A (S) M = 0 , является самый высокий, который мы нашли, и он соответствует наибольшей степени t , для которой a Известно, что существует сферическая конструкция т с точками N .Для Параметры S , указанные в Таблице 1 статьи, мы предоставляем детали для тех же самых состояний. Для остальных случаев мы перечислим состояние, для которого A (S) M = 0 и A (S) M + 1 отлична от нуля, но минимальна среди найденных на данный момент состояний.

Государство | Ψ (S) 〉 = ∑ S m = -S Ψ m | S, м 〉 определяется выражением вектор-строка с коэффициентами 2S + 1 [ Ψ -S , Ψ -S + 1 ,…, Ψ S ].Мы также вычислили суммарные квадраты длин мультиполей A (S) M . Пока мы даем точные алгебраические выражения (с i = sqrt (-1) ) для состояния в большинстве случаев мы используем числа с плавающей запятой для созвездия с N = 2S точки. Наконец, мы приводим информацию о группе симметрии созвездие.

Больше примеров можно найти здесь.

Опечатка

К сожалению, в печатных версиях артикулы для S = 2,5 / 2,3,5,9. Пожалуйста, дайте нам знать, если вы заметил дальнейшие опечатки.

Экстремальные созвездия для S = 1,…, 10

(щелкните изображение для получения дополнительной информации)

S = 1 , M = 1 S = 3/2 , M = 1 S = 2 , M = 2 S = 5 / 2 , M = 1
S = 3 , M = 3 S = 7/2 , M = 2 S = 4 , M = 3 S = 9 / 2 , M = 2
S = 5 , M = 3 S = 11/2 , M = 3 S = 6 , M = 5 S = 13 / 2 , M = 3
S = 7 , M = 4 S = 15/2 , M = 3 S = 8 , M = 5 S = 17 / 2 , M = 4
S = 9 , M = 5 S = 19/2 , M = 4 S = 10 , M = 5

S = 1 , M = 1
  • состояние:
      |  Ψ  (1)  〉  =  [ 0, 1, 0 ]
    (решение уникальное, M = 1 максимально)
  • кумулятивные квадраты длин:
         A   (1)   M  =  [ 0, 2/3 ]
  • созвездие (радиальная линия):
      [0.0, 0,0, 1,0]
  [0,0, 0,0, -1,0]
  • группа симметрии: Z 2 порядка 2

S = 3/2 , M = 1
  • состояние:
      |  Ψ  (3/2)  〉  =  [ sqrt (2) / 2, 0, 0, sqrt (2) / 2 ]
    (решение уникальное, M = 1 максимально)
  • кумулятивные квадраты длин:
         A   (3/2)   M  =  [ 0, 1/4, 3/4 ]
  • созвездие (экваториальный треугольник):
      [0.5, -0,866025403784439, 0,0]
  [-1,0, 0,0, 0,0]
  [0,5, 0,866025403784439, 0,0]
  • группа симметрии: S 3 порядка 6

S = 2 , M = 2
  • состояние:
      |  Ψ  (2)  〉  =  [ 0, sqrt (6) / 3, 0, 0, sqrt (3) / 3 ]
    (решение уникальное, M = 2 максимально)
  • суммарные квадраты длины:
         A   (2)   M  =  [ 0, 0, 1/2, 4/5 ]
  • созвездие (тетраэдр):
      [0.0, 0,0, 1,0]
  [0,4714045207, 0,816496580927726, -0,333333333333333]
  [-0,9428082063, 0,0, -0,333333333333333]
  [0,4714045207, -0,816496580927726, -0,333333333333333]
  • группа симметрии: S 4 порядка 24

S = 5/2 , M = 1
  • состояние:
      |  Ψ  (5/2)  〉  =  [ 0, sqrt (2) / 2, 0, 0, sqrt (2) / 2, 0 ]
    ( M = 1 максимально)
  • кумулятивные квадраты длин:
         A   M   (5/2)  =  [ 0, 1/84, 59/252, 5/9, 5/6 ]
           и прибл;  [ 0, 0.011905, 0,23413, 0,55556, 0,83334 ]
  • созвездие (экваториальный треугольник и полюса):
      [0,0, 0,0, 1,0]
  [0,5, -0,866025403784438, 0,0]
  [-1,0, 0,0, 0,0]
  [0,5, 0,866025403784438, 0,0]
  [0,0, 0,0, -1,0]
  • группа симметрии: двугранная группа D 6 порядка 12

S = 3 , M = 3
  • состояние:
      |  Ψ  (3)  〉  =  [ 0, sqrt (2) / 2, 0, 0, 0, -sqrt (2) / 2, 0 ]
    (решение уникальное, M = 3 максимально)
  • кумулятивные квадраты длин:
         A   (3)   M  =  [ 0, 0, 0, 6/11, 6/11, 5/7 ]
  • созвездие (октаэдр):
      [0.0, 0,0, 1,0]
  [1.0, 0.0, 0.0]
  [0,0, 1,0, 0,0]
  [-1,0, 0,0, 0,0]
  [0,0, -1,0, 0,0]
  [0,0, 0,0, -1,0]
  • группа симметрии: Z 2 × S 4 порядка 48

S = 7/2 , M = 2
  • состояние:
      |  Ψ  (7/2)  〉  =  [ sqrt (2) / 3, 0, 0, sqrt (14) / 6, 0, 0, sqrt (14) / 6, 0 ]
    ( M = 2 максимально)
  • кумулятивные квадраты длин:
         A   (7/2)   M  =  [ 0, 0, 49/264, 49/264, 49/143, 821/1144, 7/8 ]
           и прибл;  [ 0, 0, 0.18561, 0,18561, 0,34266, 0,71766, 0,875 ]
  • созвездие (два выровненных треугольника и полюс):
      [0,4067314
    482, 0,704479607354083, 0,581616692587408] [-0,813462981888963, 0,000000000000000, 0,581616692587408] [0,4067314482, -0,704479607354083, 0,581616692587408] [0,4850881821, 0,840198956454453, -0,242392831502497] [-0.970178187363642, 0.000000000000000, -0.242392831502497] [0,4850881821, -0,840198956454453, -0.242392831502497] [0,0, 0,0, -1,0]
  • группа симметрии: S 3 порядка 6

S = 4 , M = 3
  • состояние:
      |  Ψ  (4)  〉  =  [ sqrt (30) / 12, 0, 0, 0, sqrt (21) / 6, 0, 0, 0, sqrt (30) / 12 ]
    ( M = 3 максимально)
  • кумулятивные квадраты длин:
         A   (4)   M  =  [ 0, 0, 0, 98/429, 98/429, 74/117, 74/117, 8/9 ]
         и прибл;  [ 0, 0, 0, 0.22844, 0,22844, 0,63248, 0,63248, 0,88889 ]
  • созвездие (куб):
      [0,577350269189626, -0,577350269189626, 0,577350269189626]
  [0,577350269189626, 0,577350269189626, 0,577350269189626]
  [-0,577350269189626, -0,577350269189626, 0,577350269189626]
  [-0,577350269189626, 0,577350269189626, 0,577350269189626]
  [0,577350269189626, -0,577350269189626, -0,577350269189626]
  [0,577350269189626, 0,577350269189626, -0,577350269189626]
  [-0.577350269189626, -0,577350269189626, -0,577350269189626]
  [-0,577350269189626, 0,577350269189626, -0,577350269189626]
  • группа симметрии: Z 2 × S 4 порядка 48

S = 9/2 , M = 2
  • состояние:
      |  Ψ  (9/2)  〉  =  [ sqrt (6) / 6, 0, 0, -sqrt (3) / 3, 0, 0, -sqrt (3) / 3, 0, 0 , sqrt (6) / 6 ]
    ( M = 2 максимально)
  • кумулятивные квадраты длин:
         A   (9/2)   M  & прибл;  [ 0, 0, 0.0064155, 0,028793, 0,35314, 0,45769, 0,45882, 0,73190, 0,9 ]
  • созвездие (три треугольника):
      [-0,354635777076689, -0,614247184078495, 0,704935360489777]
  [0,709271554153378, 0,000000000000000, 0,704935360489777]
  [-0,354635777076689, 0,614247184078495, 0,704935360489777]
  [0,5, 0,866025403784438, 0,0]
  [-1,0, 0,0, 0,0]
  [0,5, -0,866025403784438, 0.0]
  [-0,354635777076689, -0,614247184078495, -0,704935360489777]
  [0,709271554153378, 0,000000000000000, -0,704935360489777]
  [-0,354635777076689, 0,614247184078495, -0,704935360489777]
  • группа симметрии: двугранная группа D 6 порядка 12

S = 5 , M = 3
  • состояние:
      |  Ψ  (5)  〉  =  [ sqrt (5) / 5, 0, 0, 0, 0, sqrt (15) / 5, 0, 0, 0, 0, sqrt (5) / 5 ]
    ( M = 3 максимально)
  • кумулятивные квадраты длин:
         A   (5)   M  & прибл;  [ 0, 0, 0, 0.12587, 0,18126, 0,21014, 0,53593, 0,60719, 0,70601, 0, ]
  • созвездие (пятиугольная призма):
      [0,6585323091, 0,478798344791898, 0,580050665959984]
  [-0,251719186288245, 0,774711995630481, 0,580050665959984]
  [-0,814580398069693, 0,0, 0,580050665959984]
  [-0,251719186288245, -0,774711995630481, 0,580050665959984]
  [0,6585323091, -0,478798344791898, 0,580050665959984]
  [0,6585323091, 0,478798344791898, -0.580050665959984]
  [-0,251719186288245, -0,774711995630481, -0,580050665959984]
  [-0,814580398069693, 0,0, -0,580050665959984]
  [-0,251719186288245, 0,774711995630481, -0,580050665959984]
  [0,6585323091, -0,478798344791898, -0,580050665959984]
  • группа симметрии: диэдральная группа D 10 порядка 20

S = 11/2 , M = 3
  • состояние:
      |  Ψ  (11/2)  〉  =  [ sqrt (17) / 12, 0, 0, i sqrt (55) / 12, 0, 0, 0, 0, i sqrt (55) / 12 , 0, 0, sqrt (17) / 12 ]
    ( M = 3 максимально)
  • кумулятивные квадраты длин:
         A   (11/2)   M  & прибл;  [ 0, 0, 0, 0.042193, 0,11612, 0,32001, 0,37254, 0,44398, 0,64454, 0,74368, 0,91666 ]
  • созвездие:
      [-0,540468153848830, 0,3126656627, 0,781109592647269]
  [0,001113638755064, -0,625130604696015, 0,780519369958951]
  [0,542329414861365, 0,312456964568204, 0,7798304132]
  [0,808618504015847, 0,588101567578426, 0,016512455146701]
  [-0,309745649254401, -0,950765489949400, 0,010129950110765]
  [-1,0, 0,0, 0.]
  [-0.309745649254401, 0.950765489949400, -0.010129950110765]
  [0.808618504015847, -0.588101567578426, -0.016512455146701]
  [0,542329414861365, -0,312456964568204, -0,7798304132]
  [0,001113638755064, 0,625130604696015, -0,780519369958951]
  [-0,540468153848830, -0,3126656627, -0,781109592647269]
  • группа симметрии: Z 2 порядка 2

S = 6 , M = 5
  • состояние:
      |  Ψ  (6)  〉  =  [ 0, sqrt (7) / 5, 0, 0, 0, 0, sqrt (11) / 5, 0, 0, 0, 0, -sqrt (7 ) / 5, 0 ]

    (решение уникальное, M = 5 максимально)
  • суммарные квадраты длины:
         A   (6)   M  =  [ 0, 0, 0, 0, 0, 121/323, 121/323, 121/323, 121/323, 328/437, 328/437, 12/13 ]
         и прибл;  [ 0, 0, 0, 0, 0, 0.37461, 0,37461, 0,37461, 0,37461, 0,75057, 0,75057, 0,92308 ]
  • созвездие (додекаэдр):
      [0,0, 0,0, 1,0]
  [0,723606797749979, 0,525731112119134, 0,447213595499958]
  [-0,276393202250021, 0,850650808352040, 0,447213595499958]
  [-0,8944271916, 0,0, 0,447213595499958]
  [-0,276393202250021, -0,850650808352040, 0,447213595499958]
  [0,723606797749979, -0,525731112119134, 0.447213595499958]
  [-0,723606797749979, 0,525731112119134, -0,447213595499958]
  [0,276393202250021, 0,850650808352040, -0,447213595499958]
  [0,8944271919, 0,0, -0,447213595499958]
  [0,276393202250021, -0,850650808352040, -0,447213595499958]
  [-0,723606797749979, -0,525731112119134, -0,447213595499958]
  [0,0, 0,0, -1,0]
  • группа симметрии: Z 2 × A 5 порядка 120

S = 13/2 , M = 3
  • состояние:
      |  Ψ  (13/2)  〉  =  [ sqrt (15) / 15, 0, 0, i sqrt (390) / 30, 0, 0, 0, 0, 0, 0, i sqrt ( 390) / 30, 0, 0, sqrt (15) / 15 ]
  • кумулятивные квадраты длин:
         A   (13/2)   M  =  [ 0, 0, 0, 247/5610, 247/5610, 656123/33
    , 994123/33
    , 169/510, 16393/41055, 863083 / 1560090, 19999967/27858750, 459353/603750, 13/14     ]
 и прибл;  [ 0, 0, 0, 0.044028, 0,044028, 0,19346, 0,29312, 0,33137, 0,39929, 0,55322, 0,71790, 0,76083, 0,92857 ]
  • созвездие (изогнутый семиугольник и два скрученных треугольника вверху и внизу):
      [-0,456786580721863, 0,263710287026873, 0,849589844683088]
  [0,456807478105276, 0,263753513416359, 0,8495651184]
  [0,0, -0,527463766250099, 0,849577527106852]
  [0,6971397839, 0,433818742643517, 0,006464947174969]
  [0,222653721362577, -0,974883834307386, 0.005179765392943]
  [-0,6234000704, 0,781897753601443, 0,002871301411168]
  [-1,0, 0,0, 0,0]
  [-0,6234000704, -0,781897753601443, -0,002871301411168]
  [0,222653721362577, 0,974883834307386, -0,005179765392943]
  [0,6971397839, -0,433818742643517, -0,006464947174970]
  [0,0, 0,527463766250099, -0,849577527106852]
  [0,456807478105276, -0,263753513416359, -0,8495651184]
  [-0,456786580721863, -0,263710287026873, -0.849589844683088]
  • группа симметрии: Z 2 порядка 2

S = 7 , M = 4
  • состояние:
      |  Ψ  (7)  〉  =  [ 0,0, 0,484038792672727, 0,0, 0,0, -0,217868005816070 + 0,228
    7261237 i, 0,0, 0,0, 0,277562504208005 + 0,504624
    • 0376 i, 0,0, + 0,0768270376 i, 0,0, 0,0768, -0,28

    0,25 , 0,484038792672727, 0,0

    ]
  • кумулятивные квадраты длин:
         A   (7)   M  & прибл;  [ 0, 0, 0, 0, 0.022088, 0,16322, 0,24969, 0,33424, 0,38239, 0,44336, 0,54533, 0,71629, 0,79733, 0,93333 ]
  • созвездие (четыре треугольника и два полюса):
      [0,0, 0,0, 1,0]
  [0,768016179259059, 0,239363858169746, 0,5940167470]
  [-0,5
  • 271552385, 0,545439592670935, 0,5940167470]
  [-0,1767126674, -0,784803450840680, 0,5940167470]
  [0,117497703154367, 0,945457109922784, 0,303817614778843]
  [0.760041023804564, -0,574484550779396, 0,303817614778843]
  [-0,877538726958931, -0,37097255
87, 0,303817614778843] [0,117497703154367, -0,945457109922784, -0,303817614778843] [0,760041023804564, 0,574484550779396, -0,303817614778843] [-0,877538726958931, 0,3709725587, -0,303817614778843] [-0,5
  • 271552385, -0,545439592670935, -0,5940167470] [-0,1767126674, 0,784803450840680, -0,5940167470] [0,768016179259059, -0,239363858169746, -0,5940167470] [0.0, 0,0, -1,0]
  • группа симметрии: Z 2 порядка 2

    • S = 15/2 , M = 3
    • состояние:
        |  Ψ  (15/2)  〉  =  [ 3/44 sqrt (22), 0, 0, 0, sqrt (770) / 44, 0, 0, 0, 0, 0, 0, sqrt (770) / 44, 0, 0, 0, 3/44 sqrt (22) ]
    • кумулятивные квадраты длин:
           A   (15/2)   M  & прибл;  [ 0, 0, 0, 0.0039210, 0,0039210, 0,13265, 0,20292, 0,29853, 0,34431, 0,39883, 0,46949, 0,57603, 0,75148, 0,79966, 0,93750 ]
    • созвездие (семиугольник и два выровненных квадрата сверху и снизу):
        [0,433217774817543, 0,433301918821350, 0,7555438306]
  [0,433217774817543, -0,433301918821350, 0,7555438306]
  [-0,4333686957, -0,433284237986233, 0,7504224502]
  [-0,4333686957, 0,433284237986233, 0,7504224502]
  [0,219585359474376, 0.9755932
    • 907, 0,0]
  [-0,622122481482076, 0,782919930794065, 0,0]
  [0,
    • 1297489889, 0,430414614983877, 0,0]
  [-1,0, 0,0, 0,0]
  [0,
    • 1297489889, -0,430414614983877, 0,0]
  [-0,622122481482076, -0,782919930794065, 0,0]
  [0,219585359474376, -0,9755932
    • 907, 0,0]
  [0,433217774817543, 0,433301918821350, -0,7555438306]
  [0,433217774817543, -0.433301918821350, -0.7555438306]
  [-0,4333686957, -0,433284237986233, -0,7504224502]
  [-0,4333686957, 0,433284237986233, -0,7504224502]
    • группа симметрии: Z 2 × Z 2 порядка 4

    S = 8 , M = 5
    • состояние:
        |  Ψ  (8)  〉  =  [ sqrt (69) / 32, 0, -7/1472 i sqrt (3358) +17/1472 sqrt (690), 0, 3/4784 i sqrt (152789) ) -1/1196 sqrt (31395), 0, -1/210496 i sqrt (50420370) -279/210496 sqrt (46046), 0, 7/26312 i sqrt (480194) -137/105248 sqrt (98670), 0 , 1/210496 i sqrt (50420370) +279/210496 sqrt (46046), 0, 3/4784 i sqrt (152789) -1/1196 sqrt (31395), 0, 7/1472 i sqrt (3358) -17 / 1472 sqrt (690), 0, sqrt (69) / 32 ]
    • кумулятивные квадраты длин:
           A   (8)   M  & прибл;  [ 0, 0, 0, 0, 0, 0.066374, 0,21902, 0,24823, 0,31960, 0,36874, 0,37228, 0,51437, 0,66655, 0,70602, 0,82630, 0,94118 ]
    • созвездие:
        [-0,146859793851903, 0,403430399755151, 0,78
      • 742] [0,146859793851903, -0,403430399755151, 0,78742] [0,816496580927726, 0,0, 0,577350269189626] [-0,816496580927726, 0,0, 0,577350269189626] [0,510336695378834, 0,7661282083, 0,3827520006] [-0,510336695378834, -0.7661282083, 0,3827520006] [-0,3634766931, 0,
      7095133985, 0,181422815287328]
  [0,3634766931, -0,
      7095133985, 0,181422815287328]
  [-0,
      7095133985, 0,3634766931, -0,181422815287328]
  [0,
      7095133985, -0,3634766931, -0,181422815287328]
  [0,7661282083, 0,510336695378834, -0,3827520006]
  [-0.7661282083, -0.510336695378834, -0.3827520006]
  [0,0, 0,816496580927726, -0,577350269189626]
  [0,0, -0.816496580927726, -0,577350269189626]
  [-0,403430399755151, 0,146859793851903, -0,78742]
  [0,403430399755151, -0,146859793851903, -0,78742]

    •  группа симметрии:  A  4   порядка  12

    S = 17/2 , M = 4
    • состояние:
        |  Ψ  (17/2)  〉  =  [ 0,0, 0,4358741582, 0,0, 0,0, -0,158009774587788 + 0.300431770262860 i, 0,0, 0,0, 0,438536379196716 - 0,0497315201215425 i, 0,0, 0,0, 0,438536379196716 - 0,0497315201215425 i, 0,0, 0,0, -0,158009774587788 + 0,300431770262860 i, 0,0, 0,0, 0,43587415]
    • кумулятивные квадраты длин:
           A   (17/2)   M  & прибл;  [ 0, 0, 0, 0, 0,024845, 0,0, 0,11317, 0,20352, 0,26268, 0,32590, 0,40828, 0,48103, 0,52997, 0,60888, 0,75945, 0,83311, 0,94444 ]
    • созвездие (пять треугольников плюс два полюса):
        [0.0, 0,0, 1,0]
  [-0.602115369310431, 0,430511934776098, 0,672396130309734]
  [0,673891956803705, 0,3061
      • 443833, 0,672396130309734] [-0.071776587493275, -0.736703173219931, 0.672396130309734] [-0,162582048449742, 0,

      7354866469, 0,398649214227414] [0,862945942419795, -0,310488493276445, 0,398649214227414] [-0.700363893970053, -0.5920888615, 0.398649214227414] [0,5, 0,866025403784438, 0,0] [-1.0, 0,0, 0,0] [0,5, -0,866025403784438, 0,0] [-0.700363893970053, 0.5920888615, -0.398649214227414] [0,862945942419795, 0,310488493276445, -0,398649214227414] [-0,162582048449742, -0,

      7354866469, -0,398649214227414] [-0.071776587493275, 0.736703173219931, -0.672396130309734] [0,673891956803705, -0,3061443833, -0,672396130309734] [-0.602115369310431, -0,430511934776098, -0,672396130309734] [0.0, 0,0, -1,0]
    • группа симметрии: S 3 порядка 6

    S = 9 , M = 5
    • состояние:
        |  Ψ  (9)  〉  =  [ sqrt (455) / 65, 0, 0, 0, 0, i sqrt (6630) / 130, 0, 0, 0, 0, 0, 0, 0 , i sqrt (6630) / 130, 0, 0, 0, 0, sqrt (455) / 65 ]
    • кумулятивные квадраты длин:
           A   (9)   M  & прибл;  [ 0, 0, 0, 0, 0, 0.081787, 0,081787, 0,21370, 0,21370, 0,32413, 0,32413, 0,45360, 0,45360, 0,58772, 0,58772, 0,82262, 0,82262, 0,94736 ]
    • созвездие (слегка изогнутый экваториальный восьмиугольник и два плоских пятиугольника сверху и снизу):
        [-0.600064784923290, -0.194953054131990, 0.775832172946943]
  [0,0, -0,630894385012959, 0,775868722761216]
  [0,600064784923290, -0,194953054131990, 0,775832172946943]
  [0,370865130063146, 0,510400251630871, 0,775854779219919]
  [-0.370865130063146, 0,510400251630871, 0,775854779219919]
  [-0.923876304082174, -0.3826889930, 0.001307410818663]
  [-0,3826774340, -0,923881835161757, -0,000541456436505]
  [0,3826774340, -0,923881835161757, -0,000541456436505]
  [0,923876304082174, -0,3826889930, 0,001307410818663]
  [0,923876304082174, 0,3826889930, -0,001307410818663]
  [0,3826774340, 0,923881835161757, 0,000541456436505]
  [-0,3826774340, 0,923881835161757, 0,000541456436505]
  [-0.923876304082174, 0,3826889930, -0,001307410818663]
  [-0.600064784923290, 0.194953054131990, -0.775832172946943]
  [0,0, 0,630894385012959, -0,775868722761216]
  [0,600064784923290, 0,194953054131990, -0,775832172946943]
  [0,370865130063146, -0,510400251630871, -0,775854779219919]
  [-0,370865130063146, -0,510400251630871, -0,775854779219919]
    • группа симметрии: S 3 порядка 6

    S = 19/2 , M = 4
    • состояние:
        |  Ψ  (19/2)  〉  =  [ 0.0, 0,3947433844, 0,0, 0,0, 0,0, 0,5334450947 + 0,0699184736916915 i, 0,0, 0,0, 0,0, -0,06345134868 + 0,0797470135479915 i, 0,0, 0,0, 0,0, 0,650420537037385, 0,0, 0,0, 0,0, 0,02015, 0,048 900]
    • кумулятивные квадраты длин:
           A   (19/2)   M  & прибл;  [ 0, 0, 0, 0, 0,024892, 0,059595, 0,073605, 0,17021, 0,19811, 0,25225, 0,30899, 0,37421, 0,45820, 0,53688, 0,57819, 0,63019, 0.78372, 0,85237, 0,95000 ]
    • созвездие (изогнутый экваториальный восьмиугольник, шестиугольник внизу, квадрат вверху и полюс):
        [0,0, 0,0, 1,0]
  [-0,485306671181903, 0,514193954201776, 0,707164770310770]
  [0,514193950997086, 0,4853066774, 0,707164767194738]
  [0,485306671181903, -0,514193954201776, 0,707164770310770]
  [-0,514193950997086, -0,4853066774, 0,707164767194738]
  [-0,363347596778625, 0.924375137638232, 0,116228777983327]
  [0,924499195547427, 0,363089
      3646, 0.116047238465058]
  [0,363347596778625, -0,924375137638232, 0,116228777983327]
  [-0.924499195547427, -0.363089
      3646, 0.116047238465058]
  [-0,3387740947, -0,940223561578101, 0,034810441988656]
  [-0,940469942586444, 0,338121781084990, 0,034495626496208]
  [0,3387740947, 0,940223561578101, 0,034810441988656]
  [0,940469942586444, -0,338121781084990, 0,034495626496208]
  [0,000563459578012, -0.6707411447, -0,7416802137]
  [0,580440369683931, -0,335
      7176755, -0,741788391666796]
  [0,580115578771631, 0,335075664091756, -0,742421857571505]
  [-0,000563459578012, 0,6707411447, -0,7416802137]
  [-0,580440369683931, 0,335
      7176755, -0,741788391666796]
  [-0,580115578771631, -0,335075664091756, -0,742421857571505]
    • группа симметрии: Z 2 порядка 2

    S = 10 , M = 5
    • состояние:
        |  Ψ  (10)  〉  =  [ sqrt (561) / 75, 0, 0, 0, 0, sqrt (209) / 25, 0, 0, 0, 0, sqrt (741) / 75 , 0, 0, 0, 0, -sqrt (209) / 25, 0, 0, 0, 0, sqrt (561) / 75 ]
    • кумулятивные квадраты длин:
           A   (10)   M  & прибл;  [ 0, 0, 0, 0, 0, 0.093330, 0,093330, 0,093330, 0,093330, 0,27876, 0,27876, 0,43038, 0,43038, 0,43038, 0,43038, 0,65514, 0,65514, 0,83394, 0,83394, 0,95238 ]
    • созвездие (додекаэдр):
        [0,4
      473188423, 0,356822089773090, 0,794654472291766] [-0,187592474085080, 0,577350269189626, 0,794654472291766] [-0,607061998206686, 0,0, 0,794654472291766] [-0,187592474085080, -0,577350269189626, 0,794654472291766] [0,4473188423, -0.356822089773090, 0,794654472291766] [0,794654472291766, 0,577350269189626, 0,187592474085080] [-0,30353099      43, 0,934172358962716, 0,187592474085080] [-0,982246946376846, 0,0, 0,187592474085080] [-0,30353099      43, -0,934172358962716, 0,187592474085080] [0,794654472291766, -0,577350269189626, 0,187592474085080] [-0,794654472291766, 0,577350269189626, -0,187592474085080] [0,3035309943, 0,934172358962716, -0,187592474085080] [0,982246946376846, 0.0, -0,187592474085080] [0,3035309943, -0,934172358962716, -0,187592474085080] [-0,794654472291766, -0,577350269189626, -0,187592474085080] [-0,4473188423, 0,356822089773090, -0,794654472291766] [0,187592474085080, 0,577350269189626, -0,794654472291766] [0.607061998206686, 0.0, -0.794654472291766] [0,187592474085080, -0,577350269189626, -0,794654472291766] [-0,4473188423, -0,356822089773090, -0,794654472291766]
    • группа симметрии: Z 2 × A 5 порядка 120
    Маркус Грассл (Маркус.Grassl [at] mpl.mpg.de)

    Количественная оценка квантовости: математический проект «Безмерной красоты»

    Из журнала: AVS Quantum Science

    Ссылка на статью: Экстремальные квантовые состояния
    DOI: 10.1116 / 5.0025819

    ВАШИНГТОН, 17 ноября 2020 г. — Большие объекты, такие как бейсбольные мячи, транспортные средства и планеты, ведут себя в соответствии с классическими законами механики, сформулированными сэром Исааком Ньютоном. Маленькие, такие как атомы и субатомные частицы, регулируются квантовой механикой, где объект может вести себя и как волна, и как частица.

    Созвездия Майораны некоторых из наиболее квантовых состояний в различных измерениях Автор: Луис Л. Санчес Сото

    Граница между классической и квантовой сферами всегда вызывала большой интерес. В исследовании, опубликованном в AVS Quantum Science, AIP Publishing, рассматривается вопрос о том, что делает что-то «более квантовым», чем другое — есть ли способ охарактеризовать «квантовость»? Авторы сообщают, что они нашли способ сделать именно это.

    Степень квантовости важна для таких приложений, как квантовые вычисления и квантовое зондирование, которые предлагают преимущества, которых нет в их классических аналогах.Понимание этих преимуществ требует, в свою очередь, понимания степени квантовости задействованных физических систем.

    Вместо того, чтобы предлагать шкалу, значения которой были бы связаны со степенью квантовости, авторы этого исследования смотрят на экстремумы, а именно на те состояния, которые являются либо наиболее квантовыми, либо наименее квантовыми. Автор Луис Санчес-Сото сказал, что идея исследования возникла из вопроса, заданного на научном собрании.

    «Я проводил семинар по этой теме, когда кто-то задал мне вопрос:« Вы, ребята, из квантовой оптики, всегда говорите о самых классических состояниях, а как насчет большинства квантовых состояний? »- сказал он.

    Давно поняли, что так называемые когерентные состояния можно описать как квазиклассические. Когерентные состояния возникают, например, в лазере, где свет от источников множества фотонов находится в фазе, что делает их состояниями с наименьшим квантом.

    Квантовая система часто может быть представлена ​​математически точками на сфере. Этот тип представления называется созвездием Майорана, и для когерентных состояний созвездие представляет собой просто одну точку. Поскольку это наименее квантовые состояния, наиболее квантовые состояния будут иметь созвездия, покрывающие большую часть сферы.

    Исследователи рассмотрели несколько способов, которыми другие ученые исследовали квантовость, и рассмотрели созвездие Майораны для каждого из них. Затем они спросили, какой набор точек на сфере наиболее равномерно распределен для этого подхода.

    Когда Санчес-Сото и его коллеги рассмотрели вопрос квантовости, они поняли, что это математический проект «невероятной красоты», помимо того, что он полезен.

    ###

    Для получения дополнительной информации:
    Ларри Фрам
    media @ aip.орг
    301-209-3090

    Название статьи

    Экстремальные квантовые состояния

    Авторы

    Аарон З. Голдберг, Андрей Б. Климов, Маркус Грассл, Герд Леухс и Луис Л. Санчес-Сото

    Принадлежность автора

    Мадридский университет

    квантовая квантовая : Математический проект

    изображение: Майоранские созвездия некоторых из самых квантовых состояний в различных измерениях посмотреть еще

    Кредит: Луис Л.S & aacute; nchez Soto

    ВАШИНГТОН, 17 ноября 2020 г. — Большие объекты, такие как бейсбольные мячи, транспортные средства и планеты, ведут себя в соответствии с классическими законами механики, сформулированными сэром Исааком Ньютоном. Маленькие, такие как атомы и субатомные частицы, регулируются квантовой механикой, где объект может вести себя и как волна, и как частица.

    Граница между классической и квантовой сферами всегда вызывала большой интерес. Исследование, опубликованное AIP Publishing в статье AVS Quantum Science , рассматривает вопрос о том, что делает что-то «более квантовым», чем другое — есть ли способ охарактеризовать «квантовость»? Авторы сообщают, что они нашли способ сделать именно это.

    Степень квантовости важна для таких приложений, как квантовые вычисления и квантовое зондирование, которые предлагают преимущества, которых нет в их классических аналогах. Понимание этих преимуществ требует, в свою очередь, понимания степени квантовости задействованных физических систем.

    Вместо того, чтобы предлагать шкалу, значения которой были бы связаны со степенью квантовости, авторы этого исследования смотрят на экстремумы, а именно на те состояния, которые являются либо наиболее квантовыми, либо наименее квантовыми.Автор Луис Санчес-Сото сказал, что идея исследования возникла из вопроса, заданного на научном собрании.

    «Я проводил семинар по этой теме, когда кто-то задал мне вопрос:« Вы, ребята, в квантовой оптике, всегда говорите о самых классических состояниях, а как насчет большинства квантовых состояний? »- сказал он.

    Давно поняли, что так называемые когерентные состояния можно описать как квазиклассические. Когерентные состояния возникают, например, в лазере, где свет от источников множества фотонов находится в фазе, что делает их состояниями с наименьшим квантом.

    Квантовая система часто может быть представлена ​​математически точками на сфере. Этот тип представления называется созвездием Майорана, и для когерентных состояний созвездие представляет собой просто одну точку. Поскольку это наименее квантовые состояния, наиболее квантовые состояния будут иметь созвездия, покрывающие большую часть сферы.

    Исследователи рассмотрели несколько способов, которыми другие ученые исследовали квантовость, и рассмотрели созвездие Майораны для каждого из них.Затем они спросили, какой набор точек на сфере наиболее равномерно распределен для этого подхода.

    Когда Санчес-Сото и его коллеги рассмотрели вопрос о квантовости, они поняли, что это математический проект «невероятной красоты», помимо того, что он полезен.

    ###

    Авторы статьи «Экстремальные квантовые состояния»: Аарон З. Голдберг, Андрей Б. Климов, Маркус Грассл, Герд Лойкс и Луис Л. Санчес-Сото. Статья появится в AVS Quantum Science ноября.17 января 2020 г. (DOI: 10.1116 / 5.0025819). После этой даты он будет доступен по адресу https://aip.scitation.org/doi/10.1116/5.0025819.

    О ЖУРНАЛЕ

    AVS Quantum Science , издаваемый совместно AIP Publishing и AVS, является поистине междисциплинарным журналом, который простирается от основ квантовой науки до самых разных областей: от конденсированных сред и атомной, молекулярной и оптической физики до биологии, химии. и материаловедение, а также информатика и инженерия.Журнал уделяет большое внимание целенаправленным и исчерпывающим обзорам, а также перспективам и оригинальным исследованиям. https://avs.scitation.org/journal/aqs

    О АВС

    AVS — это междисциплинарное профессиональное сообщество, насчитывающее около 4500 членов по всему миру. Основанная в 1953 году, AVS проводит местные и международные встречи, издает пять журналов, обслуживает своих членов в рамках программ награждения, обучения и карьерного роста, а также поддерживает взаимодействие между академическими, промышленными, государственными и консалтинговыми профессионалами.Его члены представляют разные области химии, физики, биологии, математики, инженерии и бизнеса и разделяют общий интерес к фундаментальной науке, разработке и коммерциализации технологий, связанных с материалами, интерфейсами и обработкой. https://www.avs.org

    Журнал

    AVS Quantum Science

    Заявление об отказе от ответственности: AAAS и EurekAlert! не несут ответственности за точность выпусков новостей, размещенных на EurekAlert! участвующими учреждениями или для использования любой информации через систему EurekAlert.